方程思想在初中几何中的应用
浅谈方程思想在初中数学中的应用

浅谈方程思想在初中数学中的应用方程思想在初中数学中的应用方程是初中数学中重要的思想之一。
它是通过符号和运算符来表示变量之间关系的数学语言。
方程思想在初中数学中应用广泛,为学生提供了解决实际问题的重要工具,本文将从方程的定义、形式及应用等方面展开讨论。
一、方程的定义方程是指将变量与常数之间用符号连接成式子,通过等号将式子分为左右两边的数学表达式。
方程中的变量通常用字母表示,可以是未知数或变化的数。
例如,x+y=5就是一个方程,其中x和y为变量,5为常数,"+"和"="为运算符号。
方程的基本特征是等式关系,即左右两边的值相等。
方程中存在未知数或变量,我们需要通过运算和变换来求解未知数的值,以满足等式关系。
因此,方程思想可以帮助我们解决各种数学问题。
二、方程的形式1. 一元一次方程一元一次方程是指方程中只有一个未知数,且未知数的最高次幂为1的方程。
一元一次方程的一般形式为ax+b=c,其中a、b、c为已知数,x为未知数。
解一元一次方程的方法是消元法,通过加减乘除等运算将未知数移至等式左边并将已知数移到等式右边,直到未知数的系数为1。
例如,在方程2x+3=7中,我们可以通过将3移到等式右边再将2除以得到x=2,从而求出未知数x的值。
2. 一元二次方程一元二次方程是指方程中只有一个未知数,且未知数的最高次幂为2的方程。
一元二次方程的一般形式为ax^2+bx+c=0,其中a、b、c为已知数,x为未知数。
解一元二次方程的方法有因式分解法、配方法、公式法、解关于二次项系数的方程等方法,具体方法可以根据题目情况选择。
例如,在方程x^2-3x+2=0中,我们可以通过因式分解得到(x-1)(x-2)=0,从而求出未知数x的值为1或2。
三、方程思想的应用1. 解代数方程代数方程是指根据实际问题所建立的含有未知数和已知数关系的方程。
代数方程可以帮助我们解决各种实际问题,例如长方形、三角形、平面和立体图形的边和面积等问题。
方程思想在解决几何问题中的运用

龙源期刊网
方程思想在解决几何问题中的运用
作者:郭永兰
来源:《甘肃教育》2018年第15期
【关键词】数学教学;几何问题;方程思想
【中图分类号】 G633.6 【文献标识码】 A
【文章编号】 1004—0463(2018)15—0125—01
方程思想是初中数学中的基本思想。
方程思想是从分析问题的数量关系入手,适当设定未知数,把所研究的数学问题中已知量和未知量之间的数量关系,转化为方程或方程组的数学模型,从而使问题得到解决的思维方法。
这种思想在代数、几何及生活实际中有着广泛的应用。
一般人们把代数称为“数”,把几何图形称为“形”,往往认为方程属于“数”的范畴,只有在解代数问题时才会想到运用方程,而解几何问题时会把方程抛之脑后,其实“数”与“形”在一定条件下是可以相互转化的。
有些几何问题表面上看起来与代数问题无关,只要找到几何图形中隐含的等量关系,就可以利用代数方法“列方程”来解决。
下面举例谈谈方程思想在解决几何问题中的经典运用。
一、运用直角三角形的边与角的关系
在运用三角函数(直角三角形的边与角的关系)解决问题的过程中,往往把所求的量看作未知量,其余有关的量用含有未知量的式子表示出来并集中在一个直角三角形中,再通过直角三角形的边与角的关系列出关于未知量的方程以达到求解的目的。
总之,方程思想应用非常广泛,而熟练地利用方程思想解决问题,要做到以下两点:第一要具备用方程思想解题的意识。
第二要根据已知条件,寻找等量关系列方程。
数学思想是数学的精髓和灵魂,是对数学内容的一种本质认识。
作为数学教师,更应该以培养学生数学思想为目标,让孩子们拥有终身受益的数学思想方法。
编辑:张昀。
方程思想在初中几何中的运用

方程思想在初中几何中的运用作者:吴春红来源:《天津教育·中》2020年第12期【摘要】初中阶段所涉及的各种知识点中都有方程思想的影子,方程思想从本质上说是一种同代数相关的思想,因此部分几何问题似乎同方程思想没有联系,不过在解决这类问题的过程中人们往往发现没有方程思想的参与是行不通的。
所以,教师应培养学生掌握问题中“隐形”条件并借助此类条件对数学问题加以解决的能力,也就是要培养学生将方程思想运用于各类数学问题解决的能力。
本文就方程思想在初中几何中的运用做了一点探索。
【关键词】方程思想;几何;运用中图分类号:G633.63 文献标识码:A 文章编号:0493-2099(2020)35-0141-02The Application of Equation Thought in Junior Middle School Geometry(Xiting Junior High School, Tongzhou District, Nantong City, Jiangsu Province,China)WU Chunhong【Abstract】The various knowledge points involved in the junior high school stage have the shadow of equation thinking. Equation thinking is essentially a kind of algebra-related thinking.Therefore, some geometric problems seem to have no connection with equation thinking, but they are solving such problems. In the process, people often find that the participation without equation thought is not feasible. Therefore, teachers should cultivate students' ability to master the "invisible" conditions in problems and use such conditions to solve mathematical problems, that is, to cultivate students' ability to apply equation thinking to solving various mathematical problems. This article does a little exploration on the application of equation thinking in junior high school geometry.【Keywords】Thoughts of equation;Geometry; Application一、初中几何知识概况在初中数学学科中,方程思想是始终涉及其中的,初中阶段几何教学中的知识点主要涉及针对三角形、圆形以及四边形的求解。
例谈方程思想在解题中的应用

数学篇学思导引方程思想就是以方程的观点去分析和研究问题,通过挖掘问题的数量关系,把繁难、陌生的问题转化为简单、熟悉的方程或方程组问题,然后运用所学的方程知识达到顺利解题的目的.用方程思想解题的关键是利用已知条件或公式、定理构造方程(组).这种思想在代数及几何问题中有着广泛的应用.一、方程思想在解代数题中的应用在解答某些代数式化简、求值、证明问题时,若按照常规思路难以下手时,同学们不妨转变思维视角,从方程思想入手,把已知等式看作是有关某些字母的方程,或将已知、结论中的代数式设为辅助元,构造适当的方程或方程组,将问题转化为方程或方程组问题,从而实现轻松解题.例1设m +2n -8p =0,2m -3n +5p =0,则5m 2+4n 2+3p 210m 2-9n 2+8p 2的值为.分析:此题直接求值难度较大,若能把已知条件中的两个等式看作是关于m ,n 的方程组,通过解方程组得出m ,n ,p 三者的关系,则可以使问题快速得解.解:由题意可得{m +2n -8p =0,2m -3n +5p =0,解方程组可得{m =2p ,n =3p .当p =0时,5m 2+4n 2+3p 210m 2-9n 2+8p 2的值不存在;当p ≠0时,5m 2+4n 2+3p 210m 2-9n 2+8p 2=20p 2+36p 2+3p 240p 2-81p 2+8p 2=59p 233p 2=5933.例2证明不论a 为何实数,代数式a 2-4a +4a 2+1的可能值中,最多有三个偶数.分析:本题不易直接证明.若能利用方程思想,设a 2-4a +4a 2+1=t ,把代数式转化为关于a 的方程,再运用根的判别式,得出代数式的取值范围,即可使问题得证.证明:设a 2-4a +4a 2+1=t ,则a 2-4a +4=ta 2+t (a 2+1≠0),即(t -1)a 2+4a +(t -4)=0.当t =1时,即a =34时,代数式a 2-4a +4a 2+1的值不是整数.所以上述方程可以看作是关于a 的二次方程.因为a 为实数,所以△=16-4(t -4)(t -1)≥0,化简可得t 2-5t ≥0,解得0≤t ≤5,即0≤a 2-4a +4a 2+1≤5,显然,代数式a 2-4a +4a 2+1的可能值中,最多有0,2,4这三个偶数.评注:方程思想是转化思想的具体体现.许多代数问题借助方程思想均可以实现转化,从而快速找到解题突破口.同学们在平时的解题过程中,不要形成思维定势,局限于常规解法,要及时转变思路,结合题目的结构特点,灵活运用方程知识去思考、分析并解答问题.二、方程思想在解几何题中的应用几何问题中有许多的几何计算题,这些计算题所涉及的几何量之间蕴含着一定的数量关系.在解题时,同学们要仔细审题,结合已知条件、图形特点、几何定理、公式等,挖掘几何量之间的数量关系,合理设出未知数,列27数学篇出方程或方程组,将几何问题转化为代数问题,然后利用方程思想巧妙解题.例3如图,已知正方形EFGH的边长为12,M是GH的中点,EM的垂直平分线NO交EF的延长线于N,MN交FG于Q,求FQ与GQ的长.分析:本题涉及几何量之间的数量关系,对此可以采用方程思想求解.很多同学在设未知数时,直接设所求的目标线段FQ=x,GQ=12-x,再通过Rt△FQN∽Rt△GQM,用x的代数式表示出FN的长.显然,该求解过程较为复杂.若能设FN=x,则EN=12+x,MP=6+x,这样易求出MN、FN的长,再利用Rt△FQN∽Rt△GQM,得出FQ与GQ的比值,即可求出FQ与GQ的长度.所以,结合题中特殊的线段位置关系,本题宜采用间接设元来求解.解:如图所示,过N作NP⊥EN与HG的延长线交于P.设FN=x,那么EN=12+x,MP=6+x.由题意可知,在Rt△MNP中,MN2=MP2+NP2.因为MN=EN,NP=FG=EH,所以(12+x)2=(6+x)2+122,解得x=3,即FN=3.因为Rt△FQN∽Rt△GQM,所以FQGQ=FN GM=36=12,即GQ=2FQ,又FQ+GQ=FG=12,所以FQ=4,GQ=8.评注:在利用方程思想求解几何计算题时,关键是要找出几何量之间的等量关系,选取恰当的几何量作为未知数,建立方程或方程组.有的几何量之间的等量关系从已知中不易获得,这就需要结合图形,挖掘潜在的隐含条件,考虑以某个几何量为桥梁,间接设元,以降低求解的难度.一般地,当题目涉及线段长度或角度比、三角形周长与面积、特殊的图形位置关系时,常常采取间接设元法.总之,方程思想不仅是数学中的基本思想,更是破解数学问题的重要工具.同学们在解题的过程中,要注意根据题意,建立合适的方程或者方程组,灵活运用方程思想,将问题转换为方程问题来解答.上期《〈一次函数〉巩固练习》参考答案1.B;2.C;3.D;4.C;5.D;6.k>0;7.225;8.增大;9.-2;10.y=1.2x+10(0<x≤10)11.(1)y=2x-5;(2)点(-1,-5)不在该函数的图象上.12.解:(1)轿车出发时,两车相距60×1.4=84(km),(2)若轿车比货车提前0.6小时到达乙地,则C(4.4,300),设线段BC对应的函数表达式为y=kx+b,将C(4.4,300),B(1.4,0)代入得:ìíî4.4k+b=300,1.4k+b=0,,解得ìíîk=100,b=-140,∴线段BC对应的函数表达式为y=100x-140;由图象可知,a小时轿车追上货车,∴100a-140=60a,解得a=3.5,∴a的值为3.5;(3)∵轿车出发1.6h,与货车的距离小于12km,∴ìíî1.6v-(1.4+1.6)×60<12,(1.4+1.6)×60-1.6v<12,解得:105<v<120,∴轿车速度v的取值范围是105<v<120.学思导引28。
应用“方程思想”解决角度计算问题
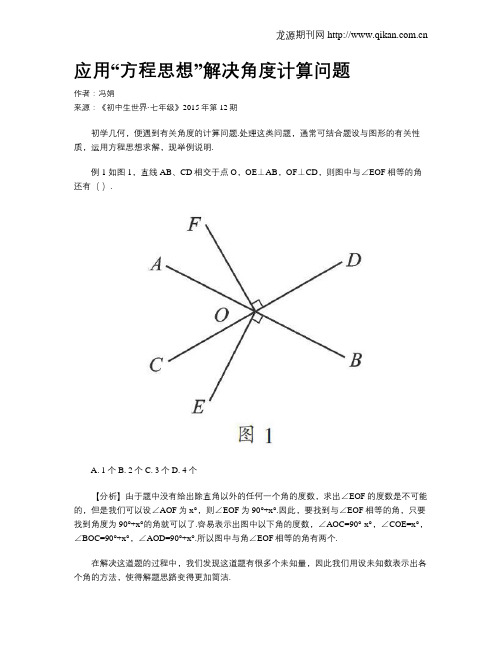
应用“方程思想”解决角度计算问题作者:冯娟来源:《初中生世界·七年级》2015年第12期初学几何,便遇到有关角度的计算问题.处理这类问题,通常可结合题设与图形的有关性质,运用方程思想求解,现举例说明.例1 如图1,直线AB、CD相交于点O,OE⊥AB,OF⊥CD,则图中与∠EOF相等的角还有().A. 1个B. 2个C. 3个D. 4个【分析】由于题中没有给出除直角以外的任何一个角的度数,求出∠EOF的度数是不可能的,但是我们可以设∠AOF为x°,则∠EOF为90°+x°.因此,要找到与∠EOF相等的角,只要找到角度为90°+x°的角就可以了.容易表示出图中以下角的度数,∠AOC=90°-x°,∠COE=x°,∠BOC=90°+x°,∠AOD=90°+x°.所以图中与角∠EOF相等的角有两个.在解决这道题的过程中,我们发现这道题有很多个未知量,因此我们用设未知数表示出各个角的方法,使得解题思路变得更加简洁.方程是数学中的天平,结合题中的已知量和未知量,我们可以将各个实际问题中的等量关系“翻译”成方程.例2 如图2,直线BC、DE相交于点O,OA、OF为射线,AO⊥OB,OF平分∠COE,∠COF+∠BOD=51°,求∠AOD的度数.【分析】首先理解题目条件可以得知,∠BOD=∠COE,∠BOE=∠COD,∠AOB=∠AOC=90°,∠EOF=∠COF.设∠COF=x°,则∠BOD=∠EOC=2x°,根据∠COF+∠BOD=51°列出方程x+2x=51,求解.当然也可以通过算式计算,两种描述方法的比较,我们可以发现方程是比算式更有力的数学工具. 列算式时,只能使用已知数,列方程时,未知数可以像已知数一样参与运算,比列算式更直接、更自然、更宽松,从而给解决问题提供便利,体现了从算术方法到代数方法的进步.在有些数学问题中,设定一些未知数,不需要求出未知数,而根据题目本身的特点,将未知数消去或代换,使问题的解决变得简捷、明快,在这里不妨称之为“设而不求”.例3 如图3,在△ABC中,∠ACB=90°,AD=AC,BE=BC,D、E两点在AB边上,求∠DCE的度数.显然这道题利用设未知数的方法,将复杂的角的关系变得一目了然,但参与其中的未知数并没有计算出具体数值.有时题目需要,我们甚至可以设几个未知数求解.方程是刻画现实世界数量关系的有效模型,是分析、解决问题的有效工具.这类几何角度的计算问题是较为隐性的“方程模型”问题,同学们在解题中很难想到设未知数、构造方程解决问题.我们要以数学的眼光观察问题,恰当地设定未知数,用好方程这个工具,能拓宽解题视野,积累更多的解题经验.(作者单位:江苏省如皋市实验初级中学)。
方程思想在几何中的有关应用

由于相 似 三 角形 的对 应边 成 比例 ,所 以 ,在 解 决有 关 问题 时 , 常 常要用 到这 一性 质搭桥 建立 联 系 ,达 到我们 解决 问题 的 目的.
例2 如 图 1 ,在 AA 中 ,A = ,A = ,B = . 线 段 B BC B 7 C 6 C8 C所
在 直 线 以每秒 2 单位 的速度 沿B 个 A方 向运动 ,并 始 终保 持 与原 位 置
数.
解 析 :设这 个多边 形 的边数州 瓤 _ 爨 《 — ㈨ 麓 0 蠢 为 ,根 据多边 形 内角 和公式 ,得 蚓 期“
( ) 10 = 6 .8 o 3
■ 赫 赫
;
维普资讯
Байду номын сангаас
解 之 .得x 9 =.
答 :这 个 多 边 形 是 9 形 . 边 二 、 用 相 似 三 角 形 的 性 质 构 建 方 程
, 来 寻 找答 案 .就 十分 便 捷 . 因此 ,在 同学 们 平 时 的学 习
中 .应学 会用 方程 思想来 处 理几何 中的有 关 问题 .不断 提 高 自己 的综 合能 力.
舔 ,} 。 l l l
维普资讯
方 程 是初 中数 学 的重要 内容 ,方 程思 想 是数 学 中的一 种重 要 思 想方 法. 数学 教材 指 出 : “ 方程 是反 映现实 世界 数量关 系 的一个 有 效 的数学模 型. ”方程 思想 不仅在 代数 中应 用广泛 ,而且在 处理 几 何 中的某 些 问题 时 ,常常 也需要 利 用 图形 的有关 性质 ,建立 方程 来 寻求 答案. 举 例说 明如 下 :
yzO0= , 解之 , { 2 , += 23 6 得 y . =5
利用微分方程思想解决物理问题的应用举例

利用微分方程思想解决物理问题的应用举例微分方程是数学中的一个重要分支,不仅在数学中有着广泛的应用,还可以被用于解决物理中的问题。
物理学家们在对物理现象进行建模和分析时经常会遇到微分方程,例如引力、波动、热力学等方面的问题。
利用微分方程的思想,可以对这些问题进行深入研究和分析。
本文将以几个例子来说明微分方程如何被用于解决物理问题。
首先我们将考虑一个经典的物理问题 - 自由落体。
当一个物体在没有任何阻力的情况下自由落下时,它的运动可以由微分方程描述。
假设在运动的过程中,物体在高度为h的位置上以初速度v0开始自由落体。
我们可以通过分析重力的作用和牛顿第二定律来获得微分方程。
该微分方程可以写成如下形式:$$\frac{d^2s}{dt^2}=-g$$其中s是物体的下落距离,t是时间,g是重力加速度。
这个微分方程可以被解析求解,例如,可以通过积分获得物体在任意时间点的速度和位置。
通过这种方式,我们可以对自由落体的运动进行深入分析,并获得许多关于它的性质的重要信息。
下一个例子是关于弯曲的钢铁梁的问题。
当一条长的钢梁弯曲时,它的形状会发生变化,且弯曲的部位会承受压力。
因此,理解弯曲过程的数学模型对于诊断问题和设计解决方案非常重要。
我们可以通过微分方程的方法来解决这个问题。
假设一条长,圆柱形的钢梁沿其长度方向均匀受力,在其任意截面处的弯曲量可以用y(x)表示,其中x是其长度的距离。
通过平衡方程和几何关系,可以得到如下微分方程:$$\frac{d^2y}{dx^2}=\frac{M}{EI}$$其中M是弯矩,E是钢的弹性模量,I是截面结构的惯性矩。
这个微分方程可以用于预测钢梁弯曲的形状,并确定承受弯曲的部位。
最后一个例子是关于热传导方程的问题。
当一个材料被加热或冷却时,它的温度分布会发生变化。
我们可以通过微分方程的方法来预测材料温度随时间和空间的变化。
假设我们要研究一个均匀的材料,其平均温度可以用u(y,t)表示,其中y是其在空间中的位置,t是时间。
函数与方程思想在三角问题中的应用

函数与方程思想在三角问题中的应用在三角形几何学中,函数和方程是用来表示三角形各部分参数关系的有用工具。
函数和方程的应用使我们能够在研究三角形的特性时,更加有效地对三角形进行分析和推断。
具体来说,函数与方程在三角形问题中的应用包括:一、直角三角形函数:1. hypotenuse函数:定义两条直角边的长度之和等于直角边的平方,即勾股定理公式c^2 = a^2 + b^2。
2. Angle bisector函数:定义一条通过三角形共边腰而成的垂直线,其长度等于两个斜边的长度之和,即 a/c + b/c = c。
3. Law of Cosines函数:定义两个角的夹角的余弦值等于两个斜边的乘积除以直角边的平方,即cosA= a^2 + b^2 - c^2 / 2ab。
二、任意三角形函数:1. Law of Sines函数:定义两个角的夹角的正弦值等于两个斜边的比值,即a/sinA=b/sinB=c/sinC。
2. Triangle Inequality函数:定义三角形内角之和为180度,以及两个边之和大于第三条边,即a + b ≥ c。
3. altitude函数:定义三角形内高线(垂线)与直角边的比值等于对边和斜边的比值,即ah/c=b/a。
4. Circumscribed Circles函数:定义三角形内的外接圆的半径为夹角的边等于三角形的斜边的长度的比值的平方,即rho = a/c x b/c。
三、三角形方程:1、倾斜角三角形方程:定义三角形的斜边长度与斜边与两个直角边长度之间的比值,即 c^2 = a^2 + b^2 -2ab cosA。
2、Circumcenter三角形方程:定义三角形外接圆的半径等于三角形内角与边的积之和的二次方之和,即r = sqrt(Aa + Bb + Cc)。
3、Heron’s formula三角形方程:定义三角形内角的面积等于三角形的周长的半径的一半,即s = (a+b+c) / 2。
数学与应用数学毕业论文--函数与方程思想在中学数学中的应用

毕业论文(设计)文献综述毕业论文(设计)翻译文章函数与方程思想在中学数学中的应用目录中文摘要、关键词 (Ⅰ)1引言 (1)2 方程中的函数思想 (1)3 函数中的方程观点 (3)4函数与方程思想在中学数学中的应用 (5)4.1函数与方程思想在数列中的应用 (6)4.2函数与方程思想在三角中的应用 (7)4.3函数与方程思想在不等式中的应用 (8)4.4函数与方程思想在解析几何中的应用 (8)4.5函数与方程思想在二项式定理中的应用 (12)4.6函数与方程思想在概率中的应用 (12)4.7函数与方程思想在多元问题中的应用 (13)4.8讨论方程f(x)=0在某个区间上根的个数 (13)4.9函数与方程思想在复数问题中的应用 (14)参考文献 (15)英文摘要、关键词 (Ⅱ)函数与方程思想在中学数学中的应用摘要:函数的思想,就是用运动变化的观点,分析和研究具体问题中的数量关系,建立函数关系,运用函数的知识,使问题得到解决。
这种思想方法在于揭示问题的数量关系的本质特征,重在对问题的变量的动态研究,从变量的运动变化,联系和发展角度拓宽解题思路。
和函数有必然联系的是方程,方程f (x)=0的解就是函数y=f (x)的图像与x 轴的交点的横坐标,函数y=f (x)也可以看作二元方程f (x)-y=0通过方程进行研究,要确定变化过程的某些量,往往要转化为求出这些量满足的方程,希望通过方程(组)来求得这些量。
这就是方程的思想,方程思想是动中求静,研究运动中的等量关系。
在中学数学中,函数与方程是相互联系不可分割的,涉及这两个方面的问题可以相互转化。
许多方程问题常常可以运用函数思想去解决,而不少函数问题又往往须转化为方程来求解。
因此,在解决一些函数和方程问题时,既要善于运用函数思想解决方程问题,又要学会灵活运用方程的观点去观察、处理函数问题。
关键词函数思想,方程思想,应用1引言函数思想就是要用运动变化的观点,分析和研究具体问题中的数量关系,通过函数的形式把这种数量关系表示出来,并加以研究,从而使问题获得解决。
求角度的方程思想总结初二

求角度的方程思想总结初二角度的方程是解决与角度有关的问题的一种方法。
在几何学和三角学中,我们经常需要计算角度的大小,以及找到满足一定角度条件的未知量。
为此,我们可以使用角度的方程来解决这些问题。
角度的方程思想主要包括以下几个方面:1. 角度的定义:首先,我们需要明确角度的定义。
在几何学中,角度是由两条直线或线段之间的旋转所形成的。
角度可以用度或弧度来表示。
在三角学中,角度是两条射线之间的夹角,通常用弧度来表示。
2. 角度的单位换算:在使用角度的方程时,我们需要注意不同单位之间的换算关系。
例如,度和弧度的换算关系是π/180,即一个完整的圆周有360度或2π弧度。
3. 角度的加法和减法:当我们需要计算两个角度之和或差时,可以使用角度的加法和减法公式。
根据这些公式,我们可以将两个角度转化为同一个单位后相加或相减。
例如,两个角度的和等于它们对应弧度之和,两个角度的差等于它们对应弧度之差。
4. 角度的关系与比较:在解决角度的方程时,我们常常需要比较不同角度的大小或关系。
对于已知角度的大小,我们可以使用角度的比较符号(例如<、>、=)来表示它们之间的大小关系;对于未知角度的问题,则可以表示为方程,通过求解方程来确定未知角度的大小。
5. 角度的性质和公式:在解决角度的方程时,我们还可以利用角度的性质和公式来简化计算过程。
例如,通过使用余角、补角、同位角等概念,我们可以将复杂的角度问题转化为简单的计算题。
6. 角度的应用:角度的方程不仅在几何学和三角学中有应用,在物理学、工程学、地理学等学科中也有广泛的应用。
例如,在力学中,我们可以利用角度的方程来求解物体在斜面上的运动问题;在建筑设计中,我们可以使用角度的方程来计算房屋的倾斜角度等。
总之,角度的方程是解决与角度有关的问题的一种有效方法。
通过明确角度的定义,实现单位换算,利用角度的加减法和角度的关系进行比较,应用角度的性质和公式,我们可以解决各种与角度相关的数学问题。
初中几何题方程思想总结

初中几何题方程思想总结几何题方程思想是指在解决几何问题时,将问题所涉及到的几何图形的特性和关系转化成数学方程,并通过求解方程得到问题的解的思想和方法。
这种思想是数学与几何的有机结合,能够帮助我们更好地理解和解决几何问题。
在初中阶段,几何题方程思想主要应用于解决一些与线段、角、三角形、四边形和圆相关的问题。
首先,我们来看一下解决线段问题时的方程思想。
对于给定的线段问题,我们常常需要根据已知条件来求解未知的线段长度。
例如,给定一个线段AB,已知线段的中点是C,我们需要求解线段AB的长度。
通过将问题转化成方程,我们可以根据已知条件写出线段的数学方程,比如AC=CB,然后通过解方程得到未知线段的长度。
类似地,我们在解决角问题时也可以应用方程思想。
对于一些已知条件下的角问题,我们可以将角的关系转化成方程,从而求解未知角的大小。
例如,已知角A和角B是互补角,我们需要求解角A的度数。
通过将已知条件转化成方程,比如A+B=90°,然后通过解方程可以得到未知角的度数。
当涉及到三角形问题时,几何题方程思想也扮演着重要的角色。
例如,给定一个三角形ABC,我们需要求解三角形的边长或者角度。
通过将三角形的特性和关系转化成方程,我们可以得到解题的进一步线索。
比如,根据正弦、余弦和正切的定义,我们可以得到一些与三角形相关的方程,通过解这些方程可以求解出三角形的未知量。
在解决四边形问题时,几何题方程思想同样也是十分有效的。
对于给定的四边形ABCD,我们可能需要求解四边形的边长、角度或者对角线的长度。
通过将给定条件转化成方程,我们可以得到解题的线索。
例如,已知四边形ABCD是矩形,我们需要求解矩形的对角线的长度。
通过将矩形对角线的特性转化成方程,我们可以得到解开题目的方程,比如AC^2=BC^2+BD^2,然后通过解方程得到对角线的长度。
最后,在解决圆问题时,几何题方程思想同样也是十分重要的。
对于给定的圆的问题,我们常常需要求解圆的半径、直径或者与圆相关的角度和长度。
89[1].方程思想在几何题中的应用(朱跃)
![89[1].方程思想在几何题中的应用(朱跃)](https://img.taocdn.com/s3/m/a7daf5de33d4b14e8524685b.png)
子提单, 需要的也是统一性, 因此, 国际性的统一规 定会使电子数据交换及电子提单更加简单易行。在 国际上尚无统一公约的情况下,我国法律应对此作 出相关的规定, 对海商法进行增补和修改, 订立单行
的电子提单规则也是必要的。
注释 :
《 ①傅廷中. 关于电子提单的应用和法 律问 题》 . 《 世界海 运》 , 1 9 9 8 年第6 期。 ②《 我国 < 海商法>下提单运输法律之完善》 《 世界海运》 , 第2 6 卷第4 期。 ③傅廷中. 《 关于电子提单的应用和法 律问 题》 . 《 世界海运》 , 1 9 9 8 年第6 期。 ④林春雨. 《 电 子提单法 律问 题研究》. 《 世界海 运》 , 第2 6 卷第2 期。 ⑤杨敏. 《 电子提单法律问 题浅析》. 《 科技导 报》 , 1 9 9 8 年第2 期, 第3 4 一 3 5 页。
1 2 8
上 y(Y
即 C o s 乙 C O A 二 乎, … 乙 C O A 二 3 0 0
如图( a ) , L C A B = 冬( 1 8 0 0 一 3 0 0 ) 二 7 5 0 乙
x - 1 1)2
① ②
+ 二
十
十
S R
”BC
, . y 二 一 h  ̄ a 二 _ A E D , 即 : 着 二 h h - x.
h一x . , 今a h = n x ’ 一 h ’ a
L
h一a
解: 设S H A D 。 二 S A B E . 二 X 7 0
… S A A B C 二 n S m i B P Q R S ,
则R 2 = A C・ B C , R ' 二 A C ' ・ B C ' 作C D 一 A B 于D , 则A C ' = A D・ 2 R , B C 2 二 B D・ 2 R
函数与方程的思想方法在立体几何中的应用

函数与方程的思想方法在立体几何中的应
用
立体几何是一门关于物体三维空间结构与表示的学科,它的学习要求我们能够准确地把握和描述物体的位置、形状和大小等特征,以及物体之间的关系。
函数和方程是我们研究物体的结构和大小的一种有力的方法,它们能够有效地表达和描述物体间的关系,而在立体几何中函数和方程的应用可以说是无处不在。
首先,函数和方程可以用来描述立体物体的形状和大小。
比如,我们可以使用椭圆方程来描述圆柱体的形状,这样,我们就可以准确地表示圆柱体的近似形状,知道它的形状和大小。
同时,函数和方程还可以用来描述立体物体的位置。
比如,我们可以定义一个平面上三维物体的三个方向,从而可以确定物体在某一点处的绝对坐标,从而可以使用几何函数和方程来表示它们的位置。
此外,函数和方程还可以用来描述立体物体之间的关系。
比如,要描述球和圆柱体之间的关系,我们可以使用双曲线方程和三次曲线
方程来表示球面大小和圆柱体的表面的曲率,从而计算出球和圆柱体之间的关系,可以确定它们的相对位置。
最后,函数和方程可以用来建模立体物体的空间结构,这是立体几何学科中最重要的内容之一。
使用函数和方程,我们可以把立体物体抽象为点、线、面等几何元素,从而可以绘制完整的立体结构,而结构的精度和准确度又取决于函数和方程本身的精度和准确度。
总而言之,函数和方程是立体几何学科中一种最为重要的计算工具,它们可以有效地描述物体的形状、大小、位置以及物体之间的关系,并可以用来建模立体物体的空间结构,因此在立体几何学科中,函数和方程的应用无处不在。
关于方程的数学小论文400字

随着教育事业的不断发展,在初中数学教学中,学生的培养不仅仅是成绩的高低,也越来越重视对学生在数学思想方面的渗透,教师在教学中充分发挥教师“授业解惑者”的作用,教会学生解决棘手的数学题,举一反三,学生高效率、高质量的学习,从而提高学生对数学的自信,使得原本苍白、枯燥的数学题变得更加直观、生动。
一、方程思想在初中数学学习中的意义所谓方程思想,便是在题目给出的已知量中与所求量或未知量之间寻求等量关系,将问题转化为代数问题,进而利用数学负号将等量关系化归为方程(组)解决,通过解方程(组),从而解决问题,尤其当面对题目中给出的已知量较少,或有含参函数等问题时,利用方程思想化未知为已知,巧妙的运用使得题目的难度有所降低,有利于提高学生的解题思想和综合实践能力,拓展学生面对数学问题的思路,提高学生的解题能力和应用能力,养成学生良好的严谨思考问题的习惯,可见,方程思想的渗透学习在初中教学中的重要性。
二、方程思想在初中数学学习中的应用在初中的教学中,方程思想应用在方方面面。
在学生具备一定的解方程(组)能力的基础上,针对具体问题的数量关系列出方程,化难为简,使学生对数学的理解有质的提升。
三、总结在以上简单的论述之后,可见方程思想在数学解题过程中的重要性,利用方程解决实际生活问题时,需要结合相应的生活经验,寻求等量关系列方程视为重点;在面对复杂的代数问题时,仔细观察所求式子的特征,类比所学过的公式、定理,巧借方程的等量关系,问题便能迎刃而解;学生面对几何题,尤其动点问题时,应注重方法的归纳,氟妨将未知转化为已知,以便求证。
而在函数问题上,函数总是离不开解方程,将坐标转化为线段长度问题,化归为几何问题,最终成为代数问题。
因此,教师在课堂上应该注重学生的解题思路,争取快、精、准的教与学,营造良好的数学学习氛围。
方程思想在初中几何题中的应用

教法研究离是20,求AB、CD的长解:设BD=x,则AB=3x,CD=4x2解:设∠AOE=x,∠BOF=y,则∠DOE=3x,∠COF=3yAED.求∠EDC的度数.解:设∠EDC=xDBF相等的角?请说明理由.解:(1)∵BE平分∠ABC交,BD平分∠EBC2019年21期┆99教法研究代数式表示出来,可以简化计算过程。
例5:如图,⊙O为△ABC的内切圆,切点分别为D,解:连结OE,OD,OF.四、落实“八项规定精神”,持续推进廉政建设。
中央“八项规定”的出台,公司党委一直严格执行其精神,以整治形式主义、官僚主义为基础,坚定推进公司党风廉政建设。
每到重大节日,公司党委书记都要集中对各级党员干部集体谈话,各分管领导、部门负责人都要对所属人员进行集中谈话,公司纪委也将对每个关键岗位人员发送廉洁提醒短信进行警示,并要求开展专项监督检查节日后,将对发现的问题进行查处。
同时,在每个季度,对主管及中层管理人员,每月都要进行自查自评,看有没有违纪违规情况发生。
即使自己自评没有,但一旦发现,就将从重处罚。
在涉及收受红包礼金、公款吃喝、违规接待、红白喜事上都予以了重点监管,确保这些环节中不出现违规不守纪律事件。
五、努力提升监督执纪能力,强化纪检队伍建设作为反腐倡廉的首要部门,纪委、纪检人员担子不轻,压力巨大。
随着企业的发展,腐败可能会出新的变化,或许更加隐秘,更加难于查到。
这就需要我们的纪检队伍中专、兼职人员,不仅要有极高的政治素养,还要有更多的专业知专门拟定了具体的措施。
首先,必须强化纪检监察人员的政治思想建设,对执纪违纪的情况坚决查处,失职失责的坚决问责,严防、严控“灯下黑”现象发生;其次对纪检监察工作不断提出新要求,通过各种学习、培训、轮训、考试,以案例教学,努力提升他们的政治素养和办案能力,努力打造一支忠诚、干净、担当的纪检监察队伍,为企业发展作出重要贡献。
参考文献:[1]刘征文.强化反腐倡廉建设培育廉洁企业文化[J].现代国企研究,2018(20):237.[2]谢鑫建.反腐风暴契机下大学生廉洁教育体系的构建与强化[J].高教学刊,2015(23):247-248.[3]宋婷.传承核电企业廉洁文化强化反腐倡廉思想教育机制[J].东方企业文化,2015(06):23-24.(作者单位:中国五冶集团有限公司第四工程分公司)100┆好日子。
数学的方程思想

数学的方程思想一、方程思想的特点:初中阶段的方程和方程组,有一元一次方程、一元二次方程、二元(三元)一次方程组和分式方程,方程和方程组是解决应用题、实际问题和许多方面的数学问题的重要基础知识,应用范围非常广泛。
很多数学问题,包括一些实际应用问题,特别是几何题的计算问题,就需要用方程或方程组的知识来解决。
近几年中考题以考察学生解决问题的能力为主,这种方程思想就显得尤其重要了。
在解决问题时,把某一个未知量或几个未知量用字母来表示,根据已知的条件或有关的性质、定理或公式,建立起未知量和已知量之间的等量关系,列出方程或方程组,通过解方程或方程组,来达到解决问题的目的,这种方法就是方程思想。
初中数学学习期间,不但要掌握所有的知识点,更要多多地了解常用的数学思想,这不但对我们解决问题有帮助,更有利于培养我们的思维能力,提高我们解决问题的能力。
具有了方程思想,我们就能够很好地求得问题中的未知元素或未知量,这对解决和计算有关的数学问题,特别是综合题,是非常需要的。
二、方程思想的方法:纵观初中阶段的所有列方程或方程组解应用题,所用方法和步骤都一样,通过“①审题,②用字母表示未知数,③根据等量关系布列方程或方程组,④解方程或方程组,求未知数的值,⑤检验、答题”这五个步骤来完成。
审题是关键,在审题过程中,要带着问题去分析题意,找出题目中的已知量、未知量以及它们之间的等量关系尤其重要。
而设未知数也不可小视,应选择那些具有代表性的未知量,权且称之为“牛鼻子”,以达到“牵一发而动全身”的目的。
未知数选择的准,其它有关的代数式并可用这个字母表示,对列方程或方程组起着简便的作用。
再补充一句:“未知数设的多,相对来说方程好列但难解;未知数设的少,相对来讲方程难列但列出的方程好解。
”在应用方程思想解决问题时,还要注意和不等式、函数相联系,这对于解决综合性问题很有帮助。
三、例题精讲:P30米l1、(08江西中考题)甲、乙两同学玩“托球赛跑”游戏,商定:用球拍托着乒乓球从起跑线起跑,绕过P点跑回到起跑线(如图所示);途中乒乓球掉下时须捡起并回到掉球处继续赛跑,用时少者胜.结果:甲同学由于心急,掉了球,浪费了6秒钟,乙同学则顺利跑完.事后,乙同学说:“我俩所用的全部时间的和为50秒,捡球过程不算在内时,甲的速度是我的1.2倍”.根据图文信息,请问哪位同学获胜?解法一:设乙同学的速度为米/秒,则甲同学的速度为米/秒,根据题意,得,解得.经检验,是方程的解,且符合题意.甲同学所用的时间为:(秒),乙同学所用的时间为:(秒).∵26>24,乙同学获胜.解法二:设甲同学所用的时间为秒,乙同学所用的时间为秒,根据题意,得解得经检验,是方程组的解,且符合题意.∵x>y,乙同学获胜.2、(08湖北中考题)某车间要生产220件产品,做完100件后改进了操作方法,每天多加工10件,最后总共用4天完成了任务.求改进操作方法后,每天生产多少件产品?解:设改进操作方法后每天生产件产品,则改进前每天生产件产品.依题意有.整理得.解得或.当=5时,,舍去..答:改进操作方法后每天生产60件产品.他不知道他家乡离北京有多远,问列车员得知单程铁道部门共设计了28种不同的车票,你知道这次列车中间共停几站吗?解:设单程共有x个车站,由题意得:x(x-1)=28,解一元二次方程得:x=-7或8,经检验,x=-7不符合题意,应舍去,∴x=8。
方程思想在解几何题中的应用

方程思想在解几何题中的应用
数学方程思想在几何题解中的应用
几何描述认为,物体的运动受到多种因素的影响,这些因素可以用方程来表示。
根据几何问题的具体要求,可以选择不同的方程来描述物体的运动。
因此,方程思想在几何题解中有重要的作用。
首先,由于几何中有各种图形,所以方程可以帮助我们描述几何图形中的特征。
比如说,有三角形ABC,三角形ABC的边长可以用如下方程来描述:
AB = a;BC = b;AC = c。
其次,用方程表示几何图形可以得出重要的关系。
比如说,有一个等腰三角形ABC,三个边长都是a,则可以得到a的平方加上2a的平方等于3a的平方,从而推出等腰三角形的定理:等腰三角形的两个直角边的平方之和等于斜边的平方。
最后,方程还可以用来计算某个几何图形的特征参数。
比如说,我们可以根据面积方程、体积方程等来计算三角形、四边形、圆柱体的面积、体积等,从而得出它们的特征参数。
这样,就不需要我们重复地测量几何图形,只需要用相应的方程计算就可以了。
综上所述,方程思想在几何题解中有着重要的作用,它可以帮助我们描述几何图形、推出几何定理以及计算几何图形的特征参数。
因此,运用方程思想来解决几何题,只要掌握方程知识,就可以非常有效地解决几何问题。
方程思想总结知识点归纳

方程思想总结知识点归纳一、方程的基本概念1.方程的定义方程是数学中一个常见的概念,它描述了一个等式关系。
一般地,方程可以表示为一个未知数和常数之间的等式,如:ax + b = c。
其中,a、b、c为已知的常数,x为未知数。
2.方程的分类根据方程中未知数的个数和幂数,方程可以分为一元方程、二元方程、多元方程;一次方程、二次方程、高次方程等。
3.方程的解方程的解是能够使得等式成立的未知数的值。
对于一元一次方程ax + b = c,它的解为x = (c - b) / a。
4.方程的解的性质方程的解可能有一个、多个或无解。
在一元一次方程中,当a不等于0时,方程有唯一解;当a等于0且b等于c时,方程有无穷多解;当a等于0但b不等于c时,方程无解。
二、方程的解法1.一元一次方程的解法对于一元一次方程ax + b = c,解法有化简、解方程等方法。
通过移项、通分、消去等操作,可以求得方程的解。
2.一元二次方程的解法对于一元二次方程ax^2 + bx + c = 0,解法有因式分解、配方法、求根公式等方法。
通过因式分解得到方程的解。
3.多元方程的解法对于多元方程,解法一般需要用到代数的方法。
通过消元、替换、化简等操作,可以求得多元方程的解。
三、方程的应用1.方程在几何中的应用方程在几何中有着广泛的应用。
例如,直线的方程、圆的方程、抛物线的方程等,都是几何中重要的概念。
2.方程在物理中的应用方程在物理中也有着重要的应用。
例如,牛顿第二定律F=ma、万有引力定律F=G(m1m2/r^2)等,都可以用方程进行描述和求解。
3.方程在经济学中的应用方程在经济学中有着重要的应用。
例如,投资收益模型、供求关系模型等,都可以用方程进行描述和求解。
四、方程的拓展1.方程的应用拓展方程的应用不仅局限于数学、物理、经济学等领域,还可以拓展到其他领域。
例如,生物学中的种群增长模型、化学中的化学反应速率等,都可以用方程进行描述和求解。
2.方程的研究拓展除了一般的方程,人们还研究了一些特殊的方程。
初中数学几个重要的数学思想介绍

初中数学几个重要的数学思想介绍1、“方程”的思想数学是研究事物的空间形式和数量关系的,初中最重要的数量关系是等量关系,其次是不等量关系。
最常见的等量关系确实是“方程”。
比如等速运动中,路程、速度和时刻三者之间就有一种等量关系,能够建立一个相关等式:速度*时刻=路程,在如此的等式中,一样会有已知量,也有未知量,像如此含有未知量的等式确实是“方程”,而通过方程里的已知量求出未知量的过程确实是解方程。
我们在小学就差不多接触过简易方程,而初一则比较系统地学习解一元一次方程,并总结出解一元一次方程的五个步骤。
假如学会并把握了这五个步骤,任何一个一元一次方程都能顺利地解出来。
初二、初三我们还将学习解一元二次方程、二元二次方程组、简单的三角方程;到了高中我们还将学习指数方程、对数方程、线性方程组、、参数方程、极坐标方程等。
解这些方程的思维几乎一致,差不多上通过一定的方法将它们转化成一元一次方程或一元二次方程的形式,然后用大伙儿熟悉的解一元一次方程的五个步骤或者解一元二次方程的求根公式加以解决。
物理中的能量守恒,化学中的化学平稳式,现实中的大量实际应用,都需要建立方程,通过解方程来求出结果。
因此,同学们一定要将解一元一次方程和解一元二次方程学好,进而学好其它形式的方程。
所谓的“方程”思想确实是关于数学问题,专门是现实当中碰到的未知量和已知量的错综复杂的关系,善于用“方程”的观点去构建有关的方程,进而用解方程的方法去解决它。
2、“数形结合”的思想大千世界,“数”与“形”无处不在。
任何事物,剥去它的质的方面,只剩下形状和大小这两个属性,就交给数学去研究了。
初中数学的两个分支棗-代数和几何,代数是研究“数”的,几何是研究“形”的。
然而,研究代数要借助“形”,研究几何要借助“数”,“数形结合”是一种趋势,越学下去,“数”与“形”越密不可分,到了高中,就显现了专门用代数方法去研究几何问题的一门课,叫做“解析几何”。
在初三,建立平面直角坐标系后,研究函数的问题就离不开图象了。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
方程思想在初中几何中的应用
作者:林锐利
来源:《新课程·中学》2018年第10期
摘要:方程思想是初中数学中一种最重要的数学思想,它在解决某些几何问题时具有很强的优越性,可以帮助我们从代数角度去分析几何问题,使几何问题简单化。
通过一些具体实例来探讨方程思想在几何中的应用。
关键词:方程;方程思想;方程模型
方程思想是初中代数中一种非常重要的解题方法,它是从分析问题的数量关系入手,将问题中的已知量和未知量之间的数量关系通过设未知数来建立方程或方程组,再通过解方程或方程组来解决问题的一种思维方式。
利用方程思想来解决问题的关键是建立方程模型。
而在初中几何部分知识所涉及的一些线段与角的求解中,基本都具备方程的特性,若能根据题意及图形之间的关系找出其中蕴含的等量关系,建立方程(组),把几何问题转化为代数问题,则会使思路更加清晰,解决过程更加简便,达到把几何问题简单化的目的。
一、用方程思想求解线段长
在某些几何题目中,已知条件有的较为复杂,让很多学生理不清要求解的线段与已知之间的关系而无从下手。
如若能根据线段之间的等量关系建立方程模型,把几何问题转化成方程来求解,往往会达到意想不到的解决效果。
利用相似三角形对应边相等来求解线段长,是相似三角形知识的一个常见应用,也是中考23题一个常考的考点,利用相似的比例,把几何问题转化为方程求解线段长,这种题目对考生来说,有一定的难度,但是学生如果能够掌握解题方法,能从图形中抽取出相似三角形的模型,根据比例关系转化为方程模型,问题就会迎刃而解。
二、用方程思想求解角度
利用三角形内角和、多边形内外角和及余补角性质等求角度,也是一个常考的考点,关键之处还在于根据题意,将几何问题转化为方程问题进行求解。
三、用方程思想求解有关动点问题
动点问题是中考的热点、难点问题,一般的解决思路是动中求静,先假设运动到某时刻结论成立,从结论出发逆向推理,得到符合条件的数量关系,建立方程,即可求出变量的值,再对所求的值进行检验和取舍。
在这种解决问题的过程中,应用方程思想仍是突破难点的关键。
由以上几个简单例子我们可以看出,在解决几何相关问题的过程中,方程能够帮助我们清晰地反映题目中的数量关系,使问题得到简化。
因此,我们在日常的教学中,一定要对学生强化方程思想的认识,通过典型例题引导学生掌握方程思想的精髓,从而提高学生分析问题及解决问题的能力。
参考文献:
[1]项彬.方程思想在几何解题中的应用[J].中学生数学,2011(4):18-19.
[2]程志南.利用方程思想求解几何计算题[J].初中数学教与学,2013(1):19-21.。
