2011年高考数学试题分类汇编6——算法初步
2011年高三数学一模试题(15):算法初步分类解析
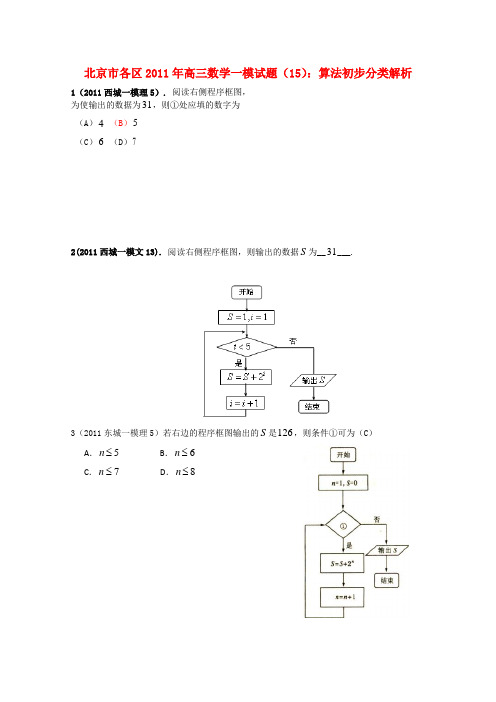
北京市各区2011年高三数学一模试题(15):算法初步分类解析1(2011西城一模理5). 阅读右侧程序框图, 为使输出的数据为31,则①处应填的数字为 (A )4 (B )5 (C )6 (D )72(2011西城一模文13). 阅读右侧程序框图,则输出的数据S 为__31___.3(2011东城一模理5)若右边的程序框图输出的S 是126,则条件①可为(C ) A .5n ≤ B .6n ≤ C .7n ≤ D .8n ≤4(2011东城一模文6)若右边的程序框图输出的S 是126,则条件①可为(A )5n ≤ (B )6n ≤ (C )7n ≤ (D )8n ≤6(2011朝阳一模理12).执行右图所示的程序框图,若输入 5.2x =-,则输出y 的值为 0.8 .开始输入x是 ?i ≥5输出y结束 x y =|2|y x =-否0, 0y i ==1i i =+7(2011海淀一模理4).执行如图所示的程序框图,若输出x的值为23,则输入的x值为 CA.0B.1 C.2D.118(2011石景山一模理10). 阅读如图所示的程序框图,运行该程序后输出的k的值是______4_________.9(2011朝阳一模文13).执行右图所示的程序框图,若输入 5.2x=,则输出y的值为0.8.21x x=+是否3n≤1n n=+x输入开始1n=x输出结束10(2011海淀一模文4). 执行如图所示的程序框图,若输入x 的值为2,则输出的x 值为 CA. 25 B .24 C. 23 D .2211(2011门头沟一模文11).右上图所示为一个判断直线0=++C By Ax 与圆222)()(r b y a x =-+-的位置关系的程序框图的一部分,在?处应该填上C Bb Aa ++ .11题图)12(2011石景山一模文10).阅读如图所示的程序框图,运行该程序后输出的k的值是________4_______.。
2011年高考数学试题分类解析(七)--算法初步与框图

② 基本算 法语 句 :理 解几 种基 本算 法语 句——输 入语 句 、
输出语句 、赋值语句 、条件语句 、循① 流 程图 :了解 程序框 图 ;了解工序流程 图 ( 即统 筹图) ;
能绘制 简单实 际问题 的流程 图 ,了解流程 图在解 决实际 问题 中
( C)4 ( D)5 ( A)2 ( B)3
例 1 ( 苏卷 4 江 )根 据 如 图 1 示 的 所
●
伪 代码 ,当输入 n 、b分 别为 2 ,3时 ,最
后输 出的 i n的值 为
解 析 :本题 程序 涉及 输入 语 句 、输 出
语句 、赋值语句 和条 件语句 .
的和.
本题答 案为 3 .
图
2
图4
59
解析 :与 理科试题 一样 ,本试 题也是一个 关于满 足 S =l ,
S =S + — 。的递推数 列 { 的问题 ,要求 写 出满 足 S ≤ 2 S}
n + 1
解析 :本题 同样是一个递推数 列的问题
依次写出循 环体被执行后各变量 的值得到下表
1
1
l 3
2
2
1 2
3
3 -3
4
4 2
简单 . 但在今后 的高考复 习中应提醒学生注意基本算法语句在算
法 表示 中的应 用 ,用程序表 示的算法试 题也许 会是今 后算法考
查 的一 种新 方式.
由上表得答 案为 D . ( 北京卷 ・ 6 文 )执行 如 图 4所 示 的程 序框 图 ,若输 入 A 的 值为 2 ,则输 出的 P值 为 ( ) .
从上表我们可 以得 出 2 1 年高考数 学算法试题有如下特点 . 0 1 () 1 出现的算法试题均是选择题或填 空题 ,难度 均为 “ 中等 或容易” ,比较而言 ,理科试题 整体要难 于文科试题. 。 福建卷理科试题外 ,其他试题均考查 了三种基本逻辑结构. () 3 试题均是要求考生根据给定的算法得出答案的类型. 示算法 的试题 ,此类试题较简单 ,不涉及循环语句. () 5 文科试题没有涉及框 图中结构 图的 内容.
2011年高考数学(文科)分类汇编----算法框图

2011年高考文科数学分类汇编---算法初步一、选择题:1.(2011年高考江西卷文科13)下图是某算法的程序框图,则程序运行后输出的结果是____.【答案】27【解析】由框图的顺序,s=0,n=1,s=(s+n)n=(0+1)*1=1,n=n+1=2,依次循环S=(1+2)*2=6,n=3,注意此刻3>3仍然是否,所以还要循环一次s=(6+3)*3=27,n=4,此刻输出,s=27.2. (2011年高考陕西卷文科7)如右框图,当126,9,x x ==8.5p =时,3x 等于(A) 7 (B) 8 (C)10 (D )11【答案】B【解析】:12697.522x x ++==而8.5p =则1223||||x x x x ->- 所以23398.522x x x p ++===即38x =故选B 二、填空题:3.(2011年高考安徽卷文科12)如图所示,程序框图(算法流程图)的输出结果是 .【答案】15【命题意图】本题考查算法框图的识别,考查等差数列前n 项和. 【解析】由算法框图可知(1)1232k k T k +=++++= ,若T =105,则K =14,继续执行循环体,这时k =15,T >105,所以输出的k 值为15.(2011年高考福建卷文科5)阅读右图所示的程序框图,运行相应的程序,输出的结果是A.3B.11C.38D.123【答案】B【解析】221,10,123;310,3211;1110a a a a a a =<=+==<=+==>,所以输出11a =,选B.5.(2011年高考湖南卷文科11)若执行如图2所示的框图,输入12341,2,4,8,x x x x ====则输出的数等于 . 答案:154解析:由框图功能可知,输出的数等于12341544x x x x x +++==。
图2。
2011年全国各地高考数学试题及解答分类汇编大全(15概率、随机变量及其分布)
2011年全国各地高考数学试题及解答分类汇编大全(15概率、随机变量及其分布)一、选择题:1.(2011安徽文)从正六边形的6个顶点中随机选择4个顶点,则以它们作为顶点的四边形是矩形的概率等于( )(A )110(B) 18 (C) 16 (D) 151.答.D 【解析】本题主要考查了计数和等可能时间求概率,培养学生审慎思维的习惯.假设正六边形的六个定点分别为A 、B 、C 、D 、E 、F ,则从6个顶点中任取4个共有15种基本结果,所取四个点构成矩形四个顶点的结果数为3,所以概率为15。
【易错提示】重复计数是解决本题最易犯的错误,特别是四个点构成矩形有几种情况,学生容易主观臆断。
2. (2011福建文、理)如图,矩形ABCD 中,点E 为边CD 的重点,若在矩形ABCD 内部随机取一个点Q ,则点Q 取自△ABE 内部的概率等于( )A .14 B. 13 C. 12 D. 232. 解析:12ABE ABCD S P S ∆==,答案应选C 。
3.(2011广东理)甲、乙两队进行排球决赛,现在的情形是甲队只要再赢一局就获冠军,乙队需要再赢两局才能得冠军.若两队胜每局的概率相同,则甲队获得冠军的概率为( ) A .12 B .35 C .23 D .34解析:(D ).乙获得冠军的概率为111224⨯=,则甲队获得冠军的概率为13144-=4. (2011湖北理)已知随机变量ξ服从正态分布()2,2σN ,且()8.04=<ξP ,则()=<<20ξP ( )A. 6.0 B . 4.0 C. 3.0 D. 2.0【答案】C 解析: 如图,正态分布的密度函数示意图所示,函数关于 直线2=x 对称,所以()5.02=<ξP ,并且()()4220<<=<<ξξP P则()()()2420<-<=<<ξξξP P P 3.05.08.0=-=所以选C.5. (2011湖北理)如图,用21A A K 、、三类不同的元件连接成一个系统,K 正常工作且21A A 、至少有一个正常工作时,系统正常工作.已知21A A K 、、正常工作的概率依次为9.0、8.0、8.0,则系统正常工作的概率为( )A. 960.0 B . 864.0 C. 720.0 D. 576.05.【答案】B解析:21A A 、至少有一个正常工作的概率为()()211A P A P -()()94.004.018.018.011=-=-⨯--=,系统正常工作概率为()()()()864.096.09.0121=⨯=-A P A P K P ,所以选B .6.(2011辽宁理)从1,2,3,4,5中任取2个不同的数,事件A =“取到的2个数之和 为偶数”,事件B =“取到的2个数均为偶数”,则P (B ︱A )=( ) A .18 B .14 C .25 D .127.(2011全国新课标卷文、理)有3个兴趣小组,甲、乙两位同学各自参加其中一个小组,每位同学参加各个小组的可能性相同,则这两位同学参加同一个兴趣小组的概率为( )(A )13 (B) 12 (C) 23 (D) 347. 解析:本题考查古典概型,属于容易题。
2011届高考数学模拟题 算法初步与复数分类汇编 文 新人教版
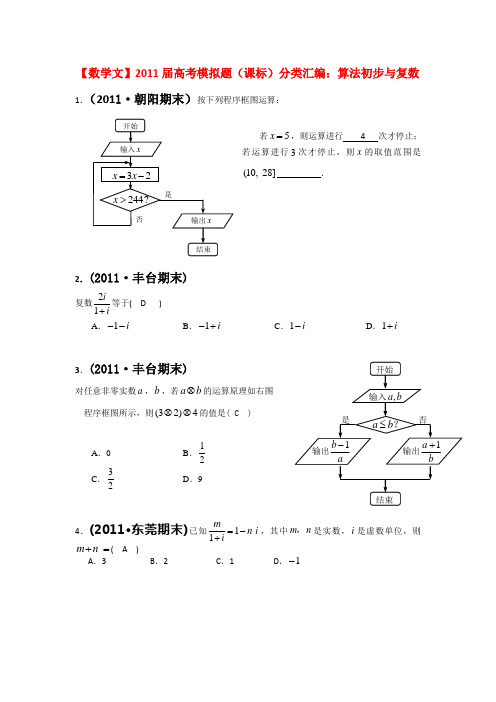
【数学文】2011届高考模拟题(课标)分类汇编:算法初步与复数1.(2011·朝阳期末)按下列程序框图运算:若5x =,则运算进行 4 次才停止;若运算进行3次才停止,则x 的取值范围是(10, 28] .2.(2011·丰台期末) 复数21ii+等于( D ) A .1i -- B .1i -+C .1i -D .1i +3.(2011·丰台期末)对任意非零实数a ,b ,若a b ⊗的运算原理如右图 程序框图所示,则(32)4⊗⊗的值是( C )A .0B .12C .32D .94.(2011·东莞期末)已知1 1mn i i=-+,其中m n ,是实数,i 是虚数单位,则 m n +=( A )A .3B .2C .1D .1-第7题图5. (2011·东莞期末)如右图所示的流程图,现输入以下函数,则可以输出的函数是( D )A .x x f sin )(=B . x x f =)(C .)22(21)(x x x f -+=D .xxx f +-=22ln)(6.(2011·佛山一检)已知i 为虚数单位,a 为实数,复数(12i)(i)z a =-+在复平面内对应的点为M ,则“12a >”是“点M 在第四象限”的( C ) A .充分而不必要条件 B .必要而不充分条件 C .充要条件 D .既不充分也不必要条件7.(2011·佛山一检)某程序框图如图所示,该程序运行后输出的S 的值是( B ) A .3- B .12-C .13D .28.(2011·广东四校一月联考)在复平面内,复数1iiz -=(i 是虚数单位)的共轭复数z 对应的点位于 ( B )A .第一象限B .第二象限C .第三象限D .第四象限是输入函数)(x f)()(x f x f -=-?函数)(x f 在]1,1[-上是减函数?输出函数)(x f开始 结束否是否9.(2011·广东四校一月联考)下图是把二进制数(2)11111化成十进制数的一个程序框图,则判断框内应填入的条件是( A )4i ≤5i ≤4i >5i >10.(2011·广州期末)已知i 为虚数单位, 则复数z =i (1+i )在复平面内对应的点位于( B )A .第一象限B .第二象限C .第三象限D .第四象限 11.(2011·广州期末)如果执行图1的程序框图,若输入6,4n m ==,那么输出的p等于 ( B )A .720B .360C .240D .12012.(2011·哈九中高三期末)若bi a i+=-12(i R b a ,,∈为虚数单位),则=+b a 【答案】2 【分析】求出21i-,然后根据复数相等的充要条件即可。
2011-2012年算法初步高考题整理
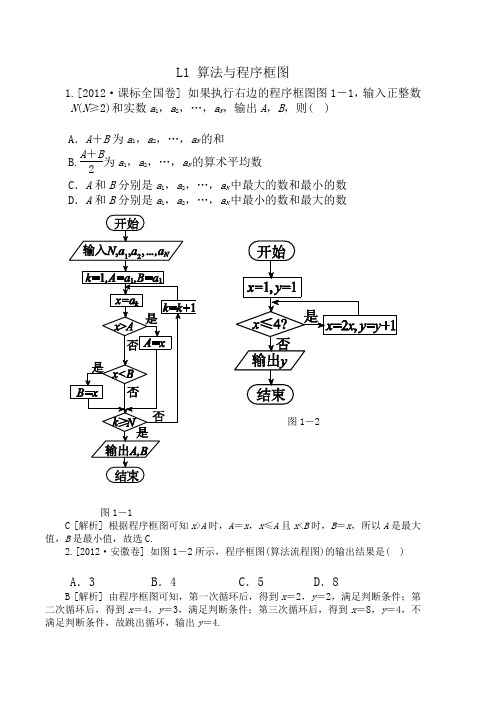
L1 算法与程序框图1.[2012·课标全国卷] 如果执行右边的程序框图图1-1,输入正整数N (N ≥2)和实数a 1,a 2,…,a N ,输出A ,B ,则( )A .A +B 为a 1,a 2,…,a N 的和B.A +B 2为a 1,a 2,…,a N 的算术平均数 C .A 和B 分别是a 1,a 2,…,a N 中最大的数和最小的数D .A 和B 分别是a 1,a 2,…,a N 中最小的数和最大的数图1-2图1-1C [解析] 根据程序框图可知x >A 时,A =x ,x ≤A 且x <B 时,B =x ,所以A 是最大值,B 是最小值,故选C.2.[2012·安徽卷] 如图1-2所示,程序框图(算法流程图)的输出结果是( )A .3B .4C .5D .8B [解析] 由程序框图可知,第一次循环后,得到x =2,y =2,满足判断条件;第二次循环后,得到x =4,y =3,满足判断条件;第三次循环后,得到x =8,y =4,不满足判断条件,故跳出循环,输出y =4.3.[2012·北京卷] 执行如图1-3所示的程序框图,输出的S值为( )A.2 B.4 C.8 D.16图1-3图1-4C [解析] 本题考查了循环结构的流程图,简单的整数指数幂计算等基础知识.根据循环k=0,S=1;k=1,S=2;k=2,S=8,当k=3,时,输出S=8.4.[2012·福建卷] 阅读如图1-4所示的程序框图,运行相对应的程序,输出的s 值等于( )A.-3 B.-10 C.0 D.-2A [解析] 第一次循环因为k=1<4,所以s=2-1=1,k=2;第二次循环k=2<4,所以s=2-2=0,k=3;第三次循环k=3<4,所以s=0-3=-3,k=4,结束循环,所以输出s=-3.5.[2012·广东卷] 执行如图1-5所示的程序框图,若输入n的值为6,则输出s 的值为( )A.105 B.16 C.15 D.1C [解析] 第一次循环结果是:s=1,i=3;第二次循环结果是:s=3,i=5;第三次循环结果是:s=15,i=7,此时i>n,结束循环,输出s=15.所以选择C.6.[2012·湖南卷] 如果执行如图1-6所示的程序框图,输入x=4.5,则输出的数i =________.4 [解析] 本题考查程序框图和循环结构,意在考查考生的逻辑推理水平和对循环结构的理解水平;具体的解题思路和过程:依次循环,达到条件退出.当i=1时x=3.5,当i=2时x=2.5,当i=3时x=1.5,当i=4时x=0.5,此时退出循环,故i=4.图1-5 图1-67.[2012·江苏卷] 图1-7是一个算法流程图,则输出的k的值是________.图1-7 图1-85 [解析] 本题为对循环结构的流程图的含义的考查.解题突破口为从循环终止条件入手,再一一代入即可.将k =1,2,3,…,分别代入可得k =5.8.[2012·辽宁卷] 执行如图1-8所示的程序框图,则输出的S 值是( )A .4 B.32 C.23D .-1 D [解析] 本小题主要考查程序框图的应用.解题的突破口为分析i 与6的关系.当i =1时,S =22-4=-1;当i =2时,S =22--1=23;当i =3时,S =22-23=32;当i =4时,S =22-32=4;当i =5时,S =22-4=-1;当i =6时程序终止,故而输出的结果为-1.9. [2012·山东卷] 执行如图1-9所示的程序框图,如果输入a =4,那么输出的n 的值为( )图1-9 图1-10A .2B .3C .4D .5B [解析] 本题考查算法与程序框图,考查数据处理水平,容易题.当n =0时,P =1,Q =3,P <Q 成立,执行循环;当n =1时,P =5,Q =7,P <Q 成立,执行循环;当n =2时,P =21,Q =15,P <Q 不成立,但是n =2+1=3后,再输出.10.[2012·陕西卷] 图1-10是计算某年级500名学生期末考试(满分为100分)及格率q 的程序框图,则图中空白框内应填入( )A .q =N MB .q =M NC .q =N M +ND .q =M M +ND [解析] 从框图中能够看出M 代表及格的人数,N 代表不及格的人数,M +N 代表总人数,故填入的应为及格率q =MM +N .11.[2012·天津卷] 阅读如图1-11所示的程序框图,运行相对应的程序,则输出S 的值为( )A .8B .18C .26D .80C [解析] 当n =1时,S =2;当n =2时,S =2+32-3=8;当n =3时,S =8+33-32=26;当n =4时输出S =26.图1-11 图1-1212.[2012·浙江卷] 若某程序框图如图1-12所示,则该程序运行后输出的值是________.1 120 [解析] 当i=1时,T=11=1,而i=1+1=2,不满足条件i>5;接下来,当i=2时,T=12,而i=2+1=3,不满足条件i>5;接下来,当i=3时,T=123=16,而i=3+1=4,不满足条件i>5;接下来,当i=4时,T=164=124,而i=4+1=5,不满足条件i>5;接下来,当i=5时,T=1245=1120,而i=5+1=6,满足条件i>5;此时输出T=1120,故应填1120.13.[2012·银川一中检测] 运行下面的程序,如果输入的n是6,那么输出的p 是( )INPUT “n=”;nk=1p=1WHILE k<=np=p*kk=k+1WENDPRINT pEND图1-13 图1-14A.120 B.720 C.1440 D.5040B [解析] 如果输入的n是6,k=1,p=1;k=2,p=2;k=3,p=6;k=4,p=24;k=5,p=120;k=6,p=720;输出720.14.[2012·南阳质量评估] 执行下面的程序框图,若p=4,则输出的S等于________. 1516 [解析] 因p =4,n =0,S =0;n =1,S =12;n =2,S =12+122;n =3,S =12+122+123;n =4,S =12+122+123+124=1516;不满足n <p ,输出S =1516.15.[2011·安徽卷] 如图1-15所示,程序框图(算法流程图)的输出结果是________.15【解析】 第一次进入循环体有T =0+0,第二次有:T =0+1,第三次有T =0+1+2,…第k +1次有T =0+1+2+…+k =k (k +1)2,若T =105,解得k =14,继续执行循环,这时k =15,T >105,所以输出的k 的值是15.图1-15 图1-1616.[2011·安徽卷] 如图1-16所示,程序框图(算法流程图)的输出结果是________.17.[2011·课标全国卷] 执行下面的程序框图,如果输入的N 是6,那么输出的p 是( )A .120B .720C .1440D .5040B【解析】 k =1时,p =1;k =2时,p =1×2=2;k=3时,p=2×3=6;k=4时,p=6×4=24;k=5时,p=24×5=120;k=6时,p=120×6=720.图1-17 图1-1818. [2011·山东卷] 执行图1-18所示的程序框图,输入l=2,m=3,n =5,则输出的y的值是________.68 【解析】把l=2,m=3,n=5代入y=70l+21m+15n得y=278,此时y=278>105,第一次循环y=278-105=173,此时y=173>105,再循环,y=173-105=68,输出68,结束循环.19.[2011·江苏卷] 根据如图所示的伪代码,当输入a,b分别为2,3时,最后输出的m的值为________.3 【解析】因为a=2<b=3,所以m=3.Read a,bIf a>b Thenm←aElsem←bEnd IfPrint m图1-1920.[2011·天津卷] 阅读图1-20所示的程序框图,运行相对应的程序,若输入x的值为-4,则输出y的值为( )A.0.5 B.1 C.2 D.4图1-20图1-21B 【解析】i=1时,a=1×1+1=2;[来源:学|科|网]i=2时,a=2×2+1=5;i=3时,a=3×5+1=16;i=4时,a=4×16+1=65>50,∴输出i=4,故选B.21.[2011·浙江卷] 某程序框图如图1-18所示,则该程序运行后输出的k的值是________.5【解析】k=3时,a=43=64,b=34=84,a<b;k=4时,a=44=256,b=44=256,a=b;k=5时,a=45=256×4,b=54=625,a>b.。
2011年高考数学试题分类汇编-数列、极限和数学归纳法

2011年高考数学试题分类汇编-数列、极限和数学归纳法数列、极限和数学归纳法安徽理(11)如图所示,程序框图(算法流程图)的输出结果是____________(11)15【命题意图】本题考查算法框图的识别,考查等差数列前n 项和. 【解析】由算法框图可知(1)1232k k T k +=++++=,若T =105,则K =14,继续执行循环体,这时k =15,T >105,所以输出的k 值为15.(18)(本小题满分12分)在数1和100之间插入n 个实数,使得这2n +个数构成递增的等比数列,将这2n +个数的乘积记作nT ,再令,lg nn aT =1n ≥.(Ⅰ)求数列{}na 的通项公式; (Ⅱ)设1tan tan ,nn n ba a +=求数列{}nb 的前n 项和nS .(本小题满分13分)本题考查等比和等差数列,指数和对数的运算,两角差的正切公式等基本知识,考查灵活运用知识解决问题的能力,综合运算能力和创新思维能力. 解:(I )设221,,,+n l l l 构成等比数列,其中,100,121==+n t t则,2121++⋅⋅⋅⋅=n n n t t t t T ①, ,1221t t t t Tn n n⋅⋅⋅⋅=++ ②q =________;12||||||n a aa +++=________.【解析】112a =,442a q =-⇒=-,{||}na 是以12为首项,以2为公比的等比数列,1121||||||22n n a aa -+++=-。
20.若数列nA :1a ,2a ,…,(2)na n ≥满足1||1k k aa +-=(k =1,2,…,1n -),则称nA 为E 数列。
记12()nnS A a aa =+++.(1)写出一个满足150a a ==,且5()0S A >的E 数列5A ;(2)若112a=,2000n =,证明:E 数列nA 是递增数列的充要条件是2011na=;(3)对任意给定的整数(2)n n ≥,是否存在首项为0的E 数列nA ,使得()0nS A =?如果存在,写出一个满足条件的E 数列nA ;如果不存在,说明理由。
2011年高考数学试题分类汇编大全

一、集合与常用逻辑用语一、选择题1.(重庆理2)“x <-1”是“x 2-1>0”的 A .充分而不必要条件 B .必要而不充分条件 C .充要条件 D .既不充分也不必要【答案】A2.(天津理2)设,,x y R ∈则“2x ≥且2y ≥”是“224x y +≥”的 A .充分而不必要条件 B .必要而不充分条件 C .充分必要条件 D .即不充分也不必要条件 【答案】A3.(浙江理7)若,a b 为实数,则“01m ab <<”是11a b b a <或>的 A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件【答案】A4.(四川理5)函数,()f x 在点0x x =处有定义是()f x 在点0x x =处连续的 A .充分而不必要的条件 B .必要而不充分的条件 C .充要条件 D .既不充分也不必要的条件 【答案】B【解析】连续必定有定义,有定义不一定连续。
5.(陕西理1)设,a b 是向量,命题“若a b =-,则∣a ∣= ∣b ∣”的逆命题是A .若a b ≠-,则∣a ∣≠∣b ∣B .若a b =-,则∣a ∣≠∣b ∣C .若∣a ∣≠∣b ∣,则a b ≠-D .若∣a ∣=∣b ∣,则a = -b【答案】D6.(陕西理7)设集合M={y|y=2cos x —2sin x|,x ∈R},N={x||x —1i为虚数单位,x ∈R},则M ∩N 为 A .(0,1) B .(0,1]C .[0,1)D .[0,1]【答案】C7.(山东理1)设集合 M ={x|260x x +-<},N ={x|1≤x ≤3},则M ∩N =A .[1,2)B .[1,2]C .( 2,3]D .[2,3] 【答案】A8.(山东理5)对于函数(),y f x x R =∈,“|()|y f x =的图象关于y 轴对称”是“y =()f x 是奇函数”的 A .充分而不必要条件 B .必要而不充分条件C .充要条件D .既不充分也不必要【答案】B9.(全国新课标理10)已知a ,b 均为单位向量,其夹角为θ,有下列四个命题12:||1[0,)3p a b πθ+>⇔∈ 22:||1(,]3p a b πθπ+>⇔∈13:||1[0,)3p a b πθ->⇔∈ 4:||1(,]3p a b πθπ->⇔∈其中真命题是(A ) 14,p p (B ) 13,p p (C ) 23,p p (D ) 24,p p 【答案】A10.(辽宁理2)已知M ,N 为集合I 的非空真子集,且M ,N 不相等,若 N ð=M I ∅,则=N M(A )M (B )N (C )I(D )∅【答案】A11.(江西理8)已知1a ,2a ,3a 是三个相互平行的平面.平面1a ,2a 之间的距离为1d ,平面2a ,3a 之间的距离为2d .直线l 与1a ,2a ,3a 分别相交于1p ,2p ,3p ,那么“12PP=23P P ”是“12d d =”的 A .充分不必要条件 B .必要不充分条件C .充分必要条件D .既不充分也不必要条件 【答案】C12.(湖南理2)设集合{}{}21,2,,M N a ==则 “1a =”是“N M ⊆”的A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分又不必要条件 【答案】A13.(湖北理9)若实数a,b 满足0,0,a b ≥≥且0ab =,则称a 与b互补,记(,),a b a b ϕ=-,那么(),0a b ϕ=是a 与b 互补的A .必要而不充分的条件B .充分而不必要的条件C .充要条件D .即不充分也不必要的条件【答案】C14.(湖北理2)已知{}21|log ,1,|,2U y y x x P y y x x ⎧⎫==>==>⎨⎬⎩⎭,则U C P = A .1[,)2+∞ B .10,2⎛⎫ ⎪⎝⎭ C .()0,+∞ D .1(,0][,)2-∞+∞【答案】A15.(广东理2)已知集合(){,A x y = ∣,x y 为实数,且}221x y +=,(){,B x y =,x y 为实数,且}y x =,则A B ⋂的元素个数为A .0B .1C .2D .3【答案】C16.(福建理1)i 是虚数单位,若集合S=}{1.0.1-,则A .i S ∈B .2i S ∈ C .3i S ∈D .2S i ∈【答案】B 17.(福建理2)若a ∈R ,则a=2是(a-1)(a-2)=0的 A .充分而不必要条件 B .必要而不充分条件C .充要条件 C .既不充分又不必要条件 【答案】A 18.(北京理1)已知集合P={x ︱x 2≤1},M={a }.若P ∪M=P,则a 的取值范围是 A .(-∞, -1] B .[1, +∞) C .[-1,1]D .(-∞,-1] ∪[1,+∞) 【答案】C 19.(安徽理7)命题“所有能被2整聊的整数都是偶数”的否定是 (A )所有不能被2整除的数都是偶数 (B )所有能被2整除的整数都不是偶数 (C )存在一个不能被2整除的数都是偶数 (D )存在一个能被2整除的数都不是偶数 【答案】D20.(广东理8)设S 是整数集Z 的非空子集,如果,,a b S ∀∈有ab S ∈,则称S 关于数的乘法是封闭的.若T,V 是Z 的两个不相交的非空子集,,T U Z ⋃=且,,,a b c T ∀∈有;,,,abc T x y z V ∈∀∈有xyz V ∈,则下列结论恒成立的是A .,T V 中至少有一个关于乘法是封闭的B .,T V 中至多有一个关于乘法是封闭的C .,T V 中有且只有一个关于乘法是封闭的D .,T V 中每一个关于乘法都是封闭的 【答案】A 二、填空题21.(陕西理12)设n N +∈,一元二次方程240x x n -+=有正数根的充要条件是n = 【答案】3或422.(安徽理8)设集合{}1,2,3,4,5,6,A =}8,7,6,5,4{=B 则满足S A ⊆且S B φ≠ 的集合S 为 (A )57 (B )56(C )49(D )8【答案】B 23.(上海理2)若全集U R =,集合{|1}{|0}A x x x x =≥≤ ,则U C A = 。
2011年高考数学试题分类汇编 数列

十、数列 一、选择题 1.(天津理4)已知{}n a 为等差数列,其公差为-2,且7a 是3a 与9a 的等比中项,n S 为{}n a 的前n 项和,*n N ∈,则10S 的值为A .-110B .-90C .90D .110 【答案】D 2.(四川理8)数列{}n a 的首项为3,{}n b 为等差数列且1(*)n n n b a a n N +=-∈.若则32b =-,1012b =,则8a =A .0B .3C .8D .11【答案】B 【解析】由已知知128,28,n n n b n a a n +=--=-由叠加法3.(上海理18)设{}n a 是各项为正数的无穷数列,iA 是边长为1,i i a a +的矩形面积(1,2,i =),则{}n A 为等比数列的充要条件为 A .{}n a 是等比数列。
B .1321,,,,n a a a -或242,,,,n a a a 是等比数列。
C .1321,,,,n a a a -和242,,,,n a a a 均是等比数列。
D .1321,,,,n a a a -和242,,,,n a a a 均是等比数列,且公比相同。
【答案】D4.(全国大纲理4)设nS 为等差数列{}n a 的前n 项和,若11a =,公差2d =,224k k S S +-=,则k =A .8B .7C .6D .5【答案】D5(江西理5) 已知数列{na }的前n 项和nS 满足:n m n mS S S ++=,且1a =1.那么10a =A .1B .9C .10D .55【答案】A 二、填空题8.(湖南理12)设nS 是等差数列{}n a ()n N *∈,的前n 项和,且141,7a a ==,则9S = .【答案】259.(重庆理11)在等差数列{}n a 中,3737a a +=,则2468a a a a +++=__________【答案】7410.(北京理11)在等比数列{an}中,a1=12,a4=-4,则公比q=______________;12...n a a a +++=____________。
2011年高考数学试题分类解析(七)——算法初步与框图

2011年高考数学试题分类解析(七)——算法初步与框图欧阳才;郭慧清
【期刊名称】《中国数学教育(高中版)》
【年(卷),期】2011(000)008
【摘要】分析2011年全国各地高考数学试卷中出现的关于“算法初步与框图”的试题,归纳试题的特点与类型,并指出试题的现状和需要改进的地方,力求为将来的数学教学与高考备考提供帮助.
【总页数】7页(P58-64)
【作者】欧阳才;郭慧清
【作者单位】湖南省宁乡县第一高级中学;广东省深圳市深圳中学
【正文语种】中文
【相关文献】
1.2011年高考数学试题分类解析(六)--不等式 [J], 王连笑
2.2011年高考数学试题分类解析(八)——立体几何 [J], 张健
3.2011年高考数学试题分类解析(七)--算法初步与框图 [J], 欧阳才;郭慧清
4.2010年高考数学试题(新课程卷)分类解析(七)——算法初步与框图 [J], 郭慧清
5.2010年高考数学试题(新课程卷)分类解析(七)--算法初步与框图 [J], 郭慧清
因版权原因,仅展示原文概要,查看原文内容请购买。
2011年高考数学试题分类汇编6——算法初步
六、算法初步1.(天津理3)阅读右侧的程序框图,运转相应的程序,则输出i 的值为A. 3B.4C. 5D. 6【答案】B2.(全国新课标理( A) 1203)履行右边的程序框图,假如输入的( B) 720(C)1440(D)N 是 6,那么输出的5040p 是【答案】 B3.(辽宁理6)履行右边的程序框图,假如输入的n 是 4,则输出的P 是(A) 8(B)5(C) 3(D)2【答案】 C4.(北京理 4)履行如下图的程序框图,输出的s 值为A. -31B.- 21C.3D. 2【答案】 D5.(陕西理8)右图中,x1,x2,x3为某次考试三个评阅人对同一道题的独立评分,P为该题的最后得分。
当x16, x29.p=8.5时,x3等于A. 11B.10C. 8D. 7【答案】 C6.(浙江理12)若某程序框图如下图,则该程序运转后输出的k 的值是。
【答案】 57.(江苏 4)依据如下图的伪代码,当输入a, b 分别为 2, 3 时,最后输出的m 的值是Read a,bIf a>b Thenm aElsem bEnd IfPrint m【答案】 38.(福建理11)运转如下图的程序,输出的结果是_______。
【答案】 39.(安徽理11)如下图,程序框图(算法流程图)的输出结果是.【答案】 1510.(湖南理 13)若履行如图 3 所示的框图,输入x11,x2 2, x33, x 2,则输出的数等于。
2【答案】 311.(江西理 13)下列图是某算法的程序框图,则程序运转后输出的结果是【答案】 1012.(山东理13)履行右图所示的程序框图,输入l=2 , m=3, n=5,则输出的y 的值是【答案】68。
湖南省2011届高考数学一轮复习:《系统集成_算法初步》(课件)

月总收入S和月净盈利V, 那么在图中空白的判断
框和处理框中, 应分别填入下列选项中的( )
A.A>0, V=S-T
B.A<0, V=S-T
C.A>0, V=S+T
D.A<0, V=S+T
第五页,编辑于星期日:十六点 十五分。
第六页,编辑于星期日:十六点 十五分。
【例2】 一个算法的程序框图如下图 所示, 若该程序输 出的结果为 4,则判
第三页,编辑于星期日:十六点 十五分。
考题3 (2009年上海卷)
某算法的程 序框图如右图所 示, 则输出量y
与输入量x满足 的关系式是___.
第四页,编辑于星期日:十六点 十五分。
热点突破
【例1】某店一个月的收入与支出总共
记录了N个数据a1, a2, ……, aN, 其中收入记为正
数, 支出记为负数, 该店用右边的程序框图计算
i=1 s=1 n=0 Do s<=560 s=s+i i=i+1 n=n+1 WEND PRRRT n+1 END
第九页,编辑于星期日:十六点 十五分。
【例4】根据如图所示
的程序框图, 将输出的x、y
值依次分别记为x1, x2, ……,
xn, ……, x2006;y1, y2, ……,
yn,……, y2008.
专题六
第一讲 算法初步
第一页,编辑于星期日:十六点 十五分。
领悟高考
考题1(2009年浙江卷) 某程序框图如图1 所示,该程序运行后 输出的k的值是( ) A.4 B.5 C .6 D.7
第二页,编辑于星期日:十六点 十五分。
考题2(2009年山东卷)
数学高考题(理)分类精选-算法

25.(2016 年新课标 3)执行右面的程序框图,如果输入的 a=4,b=6, 那么输出的 n=
(A)3(B)4(C)5(D)6
数学高考题(理)分类精选-算法
数学高考题(理)分类精选-算法
1.【2011 年北京理】执行如图
所示的程序框图,输出的 s 值
为( ) A.-3
B.- 1 C. 1 D.2
23
2. 【2011 年辽宁理】执行右面的程序框图,
如果输入的 n 是 4,则输出的 P 是( )
A.8 B.5
C.3 D.2
则输出的 S= ( )
A. 4
B. 5
C. 6
D. 7
18. 【2014 年全国课标 1 理】执行下图的程序框图,若输入的 a,b,k 分别为 1,2,3,则输出的 M =
A . 20 B . 16
3
5
C . 7 D .15
2
8
19. 【2015 年陕西理】根据右边的图,
当输入 x 为 2005时,输出的 y ( ).
A.28
B.10
C.4
D.2
20. 【2015 年全国课标 1 理】执行右 面的程序框图,如果输入的 t 0.01,则 输出的 n (A)5(B)6(C)7(D)8
输入t 1
S=1,n=0,m= 2
S=S-m
m m= ,m=n+1
2
是
S>t
否
输出n
结束
21. 【2015 年全国课标 2 理】右边程
1000
1000
7.【2012 年辽宁理】执行如图所示的程序框图,则输出的 S 值是
A. -1 B. 2 C. 3 D.4
2011届高三数学一轮复习试题 算法 新人教A版
2011届高三数学一轮复习试题:算法
一、选择题
1.如果执行右面的程序框图,那么输出的s 是(
A .2550
B .-2550
C .2548
D .-2552
2.如右图所示的程序框图的输出结果是()
A .2
B .4
C .8
D .16
3.已知数列{}n a 满足
*111
33,(2,)
n n n a a a n n N a --==-
≥∈,记M 为下列程序框图的输出结果,则行列式
1 1 M -1 1 M 1 1 1
中元素
1-的代数余子式的值是( )
A .2
B .2-
C .132
D .132
-
二、填空题
1.如果执行下面的程序框图,那么输出的S =_________ .
2.运行如图所示的程序流程图,则输出I 的值为_________________.
3.执行右面的程序框图,如果输入的50k =,那么输出的S =________________. 4.根据右面的框图,打印的最后一个数据是.
2011届高三数学一轮复习试题:算法
参考答案
一、选择题 1-3CCA 二、填空题
1.10000 2.7 3.2548 4.63
(第1题图)。
2011年~2015年全国1、2卷高考数学真题分类汇编(理科)

2011年~2015年全国1、2卷高考数学真题分类汇编(理科)第一章 集合与常用逻辑用语第一节 集合题型1 集合的基本概念1. (2012全国理1)已知集合{}1,2,3,4,5A =,(){},,,B x y x A y A x y A =∈∈-∈,则B中所含元素的个数为( ).A. 3B. 6C. 8D.10题型2 集合间的基本关系2.(2013课标全国Ⅰ,理1)已知集合A ={x |x 2-2x >0},B ={x |-5<x <5},则( ).A .A ∩B = B .A ∪B =RC .B ⊆AD .A ⊆B 3.(2013全国Ⅱ理1)已知集合(){}{}21<410123M x x x N =-∈=-R ,,,,,,,则M N =I ( ).A. {}012,,B. {}1012-,,,C. {}1023-,,,D. {}0123,,, 4.(2014全国Ⅰ理1).已知集合A={x |2230x x --≥},B={}22x x -≤<,则A B ⋂=A .[-2,-1]B .[-1,2)C .[-1,1]D .[1,2)5.(2014全国Ⅱ理1)设集合{}0,1,2M =,{}2=320N x x x -+≤,则M N =I(A) {}1 (B) {}2 (C) {}0,1 (D) {}1,26. (2015全国Ⅱ理1).已知集合{}2,1,0,2A =--,()(){}120B x x x =-+<,则A B =I ( ).A.{}1,0-B.{}0,1C.{}1,0,1-D.{}0,1,2题型3 集合的运算第二节 命题及其关系、充分条件与必要条件题型4 四种命题及关系题型5 充分条件、必要条件、充要条件的判断与证明 题型6 充分条件、必要条件中的含参数问题第三节 简单的逻辑联结词、全称量词与存在量词题型7 判断含逻辑联结词的命题的真假 题型8 全(特)称命题的否定7. (2015全国I 理3)设命题:p n ∃∈N ,22n n >,则p ⌝为( ). A .n ∀∈N ,22n n > B .n ∃∈N ,22n n „ C .n ∀∈N ,22n n „ D .n ∃∈N ,22n n =题型9 根据命题真假求参数的范围第一章 试题详解1.分析 利用集合的概念及其表示求解. 解析 因为(){},,,B x y x A y A x y A =∈∈-∈,{}1,2,3,4,5A =,所以2,1x y ==;3,1,2x y ==;4,1,2,3x y ==;5,1,2,3,4x y ==.所以()(){()()()()()2,1,3,1,3,2,4,1,4,2,4,3,5,1,B =()()()}5,2,5,3,5,4,所以B 中所含元素的个数为10.故选D. 2.答案:B解析:∵x (x -2)>0,∴x <0或x >2. ∴集合A 与B 可用图象表示为:由图象可以看出A ∪B =R ,故选B.3.分析 先求出集合M ,然后运用集合的运算求解.解析:集合{}13,M x x x =-∈R <<,所以{}0,1,2M N =I ,故选A. 4.【答案】:A【解析】:∵A={x |2230x x --≥}={}13x x x ≤-≥或,B={}22x x -≤<, ∴A B ⋂={}21x x -≤≤,选A..5.解析:∵{}{}2=32012N x x x x x -+≤=≤≤,∴M N =I {}1,2 答案:D6. 解析对于B 集合,由已知得,{}21B x x =-<<,由数轴可得{}1,0A B =-I . 故选A.评注常规考题,比较容易.考查不等式解集和集合的交运算,注意A 集合中的元素是数,B 集t1501401301201101000.0300.0250.0200.0150.010频率/组距合是数的范围,用数轴较直观.7.解析 否命题是对原命题的条件与结论同时否定,因为存在的否定是任意,大于的否定是小于等于,所以:p n ⌝∀∈N ,22nn ….故选C .第二章 函数第一节 函数的概念及其表示题型10 映射与函数的概念 题型11 同一函数的判断 题型12 函数解析式的求法1.(2013全国II 理 19)经销商经销某种农产品,在一个销售季度内,每售出1t 该产品获利润500元,未售出的产品,每1t 亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了130t 该农产品.以X (单位:t ,100150x ≤≤)表示市场需求量,T 表示下一个销售季度内经销该农产品的利润.(1)将T 表示为X 的函数;题型13 函数定义域的求解 题型14 函数值域的求解第二节 函数的基本性质—奇偶性、单调性、周期性题型15 函数的奇偶性2.(2011全国理2).下列函数中,既是偶函数又在(0,)+∞单调递增的函数是( ). A.3y x = B.||1y x =+ C.21y x =-+ D.||2x y -=3.(2013课标全国Ⅰ,理16)若函数f (x )=(1-x 2)(x 2+ax +b )的图像关于直线x =-2对称,则f (x )的最大值为__________.4.(2014全国Ⅰ理3)设函数()f x ,()g x 的定义域都为R ,且()f x 是奇函数,()g x 是偶函数,则下列结论正确的是A .()f x ()g x 是偶函数B .|()f x |()g x 是奇函数C .()f x |()g x |是奇函数D .|()f x ()g x |是奇函数5.(2015全国Ⅰ理13).若函数()()2ln f x x x a x =++为偶函数,则a = .题型16 函数的单调性(区间)6.(2011全国卷理2)下列函数中,既是偶函数又在(0,)+∞单调递增的函数是( ). A.3y x = B.||1y x =+ C.21y x =-+ D.||2x y -=7.(2013课标全国Ⅰ,理12)设△A n B n C n 的三边长分别为a n ,b n ,c n ,△A n B n C n 的面积为S n ,n =1,2,3,….若b 1>c 1,b 1+c 1=2a 1,a n +1=a n ,b n +1=2n n c a +,c n +1=2n nb a +,则( ).A .{S n }为递减数列B .{S n }为递增数列C .{S 2n -1}为递增数列,{S 2n }为递减数列D .{S 2n -1}为递减数列,{S 2n }为递增数列题型17 函数的周期性 题型18 函数性质的综合8.(2014全国Ⅱ理科15)已知偶函数()f x 在[0,)+∞单调递减,(2)0f =.若(1)0f x ->,则x 的取值范围是 .第三节 二次函数与幂函数题型19 二次函数图像的应用题型20 二次函数、一元二次方程、二次不等式的关系 题型21 二次方程()200ax bx c a ++=≠的实根分布及条件 题型22 二次函数“动轴定区间”、“定轴动区间”问题 题型23 二次函数恒成立问题 题型24 幂函数的定义及其图像 题型25 幂函数性质的综合应用第四节 指数函数与对数函数题型26 指(对)运算及指(对)方程、不等式9.(2015全国Ⅱ理5) 设函数()()2111log 2,12,x x x f x x -⎧+-<⎪=⎨⎪⎩…,则()()22log 12f f -+=( )A.3B. 6C. 9D. 12题型27 指数函数、对数函数的图像及性质10.(2012全国理12)设点P在曲线1e2xy=上,点Q在曲线()ln2y x=上,则PQ的最小值为().A. 1ln2- B. ()21ln2- C. 1ln2+ D.()21ln2+11.(2013全国Ⅱ理8)设357log6log10log14a b c===,,则().A. >>c b a B. >>b c a C. >>a cb D. >>a b c题型28 指数函数与对数函数中的恒成立问题第五节函数的图像及应用题型29 知式选图(识图)题型30 函数图像的应用12.(2011全国理12)函数11yx=-的图像与函数2sinπy x=(24x-剟)的图像所有交点的横坐标之和等于().A.2B.4C.6D.813(2012全国理10)已知函数()1()ln1f xx x=+-,则()y f x=的图像大致为().A. B. C. D.14(2015全国Ⅱ理10) 如图,长方形ABCD的边2AB=,1BC=,O是AB的中点,点P 沿着边,BC CD与DA运动,记BOP x∠=.将动点P到,A B两点距离之和表示为x的函数()f x,则()y f x=的图像大致为().xPOD CBA2π3π4π2π4y O x2xO y π4π23π4π2xO y π4π23π4π2π3π4π2π4y O xA. B. C. D.第六节 函数的综合题型31 函数与数列的综合 题型32 函数与不等式的综合 题型33 函数中的创新题第二章 试题详解 第三章 导数与定积分第一节 导数的概念与运算题型34 导数的定义 题型35 求函数的导数 题型36 导数的几何意义15(2011全国理21)已知函数ln ()1a x bf x x x=++,曲线()y f x =在点(1,(1))f 处的切线方程为230x y +-=. (1)求a ,b 的值;16(2014全国Ⅱ理8)设曲线ln(1)y ax x =-+在点(0,0)处的切线方程为2y x =,则a = (A) 0(B) 1(C) 2(D) 317(2015全国Ⅰ理20)在直角坐标系xOy 中,曲线2:4x C y =与直线():0l y kx a a =+>交于M ,N 两点.(1)当0k =时,分别求C 在点M 和N 处的切线方程;18(2015全国Ⅰ理21)已知函数()314f x x ax =++,()ln g x x =-.(1) 当a 为何值时,x 轴为曲线()y f x =的切线;第二节 导数的应用题型37 利用导函数研究函数的图像19.(2013课标全国Ⅰ,理21)(本小题满分12分)设函数f (x )=x 2+ax +b ,g (x )=e x (cx +d ).若曲线y =f (x )和曲线y =g (x )都过点P (0,2),且在点P 处有相同的切线y =4x +2.(1)求a ,b ,c ,d 的值; 20(2013全国Ⅱ理10) 已知函数()32f x x ax bx c =+++,下列结论中错误的是( ).A. ()000x f x ∃∈=R ,B. 函数()y f x =的图象是中心对称图形C. 若0x 是()f x 的极小值点,则()f x 在区间()0x -∞,单调递减D. 若0x 是()f x 的极值点,则()00f x '=题型38 利用导数研究函数的单调性21. (2012全国理21)已知函数()f x 满足121()'(1)e (0)2x f x f f x x -=-+.(1)求()f x 的解析式及单调区间;(2)若21()2f x x ax b ++…,求(1)a b +的最大值22(2013全国Ⅱ理10) 已知函数()32f x x ax bx c =+++,下列结论中错误的是( ).A. ()000x f x ∃∈=R ,B. 函数()y f x =的图象是中心对称图形C. 若0x 是()f x 的极小值点,则()f x 在区间()0x -∞,单调递减D. 若0x 是()f x 的极值点,则()00f x '=23(2013全国Ⅱ理16)等差数列{}n a 的前n 项和为n S ,已知1015025S S ==,,则n nS 的最小值为 . 24. (本小题共12分)已知函数()()e ln xf x x m =-+.(1)设0x =是()f x 的极值点,求m ,并讨论()f x 的单调性; (2)当2m ≤时,证明()>0f x .25设函数()'f x 是奇函数()()f x x ∈R 的导函数,()10f -=,当0x >时, ()()'0xf x f x -<,则使得()0f x >成立的x 的取值范围是( ). A. ()(),10,1-∞-U B. ()()1,01,-+∞U C. ()(),11,0-∞--U D. ()()0,11,+∞U26设函数()2emxf x x mx =+-.(1)证明:()f x 在(),0-∞单调递减,在()0,+∞单调递增; (1)证明:因为()2e mxf x x mx =+-,题型39 函数的极值与最值 (27)27.(2013课标全国Ⅰ,理21)(本小题满分12分)设函数f (x )=x 2+ax +b ,g (x )=e x (cx +d ).若曲线y =f (x )和曲线y =g (x )都过点P (0,2),且在点P 处有相同的切线y =4x +2.(1)求a ,b ,c ,d 的值;(2)若x ≥-2时,f (x )≤kg (x ),求k 的取值范围. 28.已知函数()()e ln x f x x m =-+.(1)设0x =是()f x 的极值点,求m ,并讨论()f x 的单调性;29.设函数()'f x 是奇函数()()f x x ∈R 的导函数,()10f -=,当0x >时, ()()'0xf x f x -<,则使得()0f x >成立的x 的取值范围是( ). A. ()(),10,1-∞-U B. ()()1,01,-+∞U C. ()(),11,0-∞--U D. ()()0,11,+∞U30.设函数()2emxf x x mx =+-.(1)证明:()f x 在(),0-∞单调递减,在()0,+∞单调递增;题型40 方程解(函数零点)的个数问题31. (2014全国Ⅰ理11)已知函数()f x =3231ax x -+,若()f x 存在唯一的零点0x ,且0x>0,则a 的取值范围为A .(2,+∞)B .(-∞,-2)C .(1,+∞)D .(-∞,-1)32(2015全国Ⅱ理21)已知函数()314f x x ax =++,()ln g x x =-.(1)当a 为何值时,x 轴为曲线()y f x =的切线;(2)用{}min ,m n 表示m ,n 中的最小值,设函数()()(){}min ,h x f x g x =()0x >,讨论()h x 零点的个数.题型41 利用导数证明不等式33.设函数1(0ln x xbe f x ae x x-=+,曲线()y f x =在点(1,(1)f 处的切线为(1)2y e x =-+. (Ⅰ)求,a b ; (Ⅱ)证明:()1f x >.题型42 不等式恒成立与存在性问题 (30)34(2015全国Ⅰ理12)设函数()()e21xf x x ax a =--+,其中1a <,若存在唯一的整数0x 使得()00f x <,则a 的取值范围是( ). A .3,12e ⎡⎫-⎪⎢⎣⎭ B .33,2e 4⎡⎫-⎪⎢⎣⎭C .33,2e 4⎡⎫⎪⎢⎣⎭D .3,12e ⎡⎫⎪⎢⎣⎭35(2015全国Ⅱ理21)设函数()2emxf x x mx =+-.(1)证明:()f x 在(),0-∞单调递减,在()0,+∞单调递增;(2)若对于任意[]12,1,1x x ∈-,都有()()121e f x f x --…,求m 的取值范围.题型43 导数在实际问题中的应用第三节 定积分和微积分基本定理题型44 定积分的计算36(2011全国理9)由曲线y x =,直线2y x =-及y 轴所围成的图形的面积为( ).A.103B.4C.163D.6题型45 求曲边梯形的面积第三章 试题详解1.分析 (1)根据题意购进了130t ,应分两段进行求解;解析:解:(1)当[)100,130X ∈时,()50030013080039000T X X X =--=-. 当[]130,150X ∈时,50013065000T =⨯=.所以80039000,100130,65000,130150.X X T X -⎧=⎨⎩≤≤≤<2.【解析】四个选项中的偶函数只有B ,C ,D ,故排除A ,当x ∈(0,)+∞时,三个函数分别为1y x =+单调递增,21y x =-+单调递减,122xxy -⎛⎫== ⎪⎝⎭单调递减.故选择B .3.答案:16解析:∵函数f (x )的图像关于直线x =-2对称, ∴f (x )满足f (0)=f (-4),f (-1)=f (-3),即15164,0893,b a b a b =-(-+)⎧⎨=-(-+)⎩解得8,15.a b =⎧⎨=⎩∴f (x )=-x 4-8x 3-14x 2+8x +15. 由f ′(x )=-4x 3-24x 2-28x +8=0, 得x 1=-2-5,x 2=-2,x 3=-2+5.易知,f (x )在(-∞,-2-5)上为增函数,在(-2-5,-2)上为减函数,在(-2,-2+5)上为增函数,在(-2+5,+∞)上为减函数.∴f (-2-5)=[1-(-2-5)2][(-2-5)2+8(-2-5)+15] =(-8-45)(8-45) =80-64=16.f (-2)=[1-(-2)2][(-2)2+8×(-2)+15] =-3(4-16+15) =-9.f (-2+5)=[1-(-2+5)2][(-2+5)2+8(-2+5)+15] =(-8+45)(8+45) =80-64=16. 故f (x )的最大值为16. 4.【答案】:C【解析】:设()()()F x f x g x =,则()()()F x f x g x -=--,∵()f x 是奇函数,()g x 是偶函数,∴()()()()F x f x g x F x -=-=-,()F x 为奇函数,选C. 5.解析 由题意可知函数()2ln y x a x =++是奇函数,所以()2ln x a x +++()2ln 0x a x -++=,即 ()22ln ln 0a x x a +-==,解得1a =.6.【解析】四个选项中的偶函数只有B ,C ,D ,故排除A ,当x ∈(0,)+∞时,三个函数分别为1y x =+单调递增,21y x =-+单调递减,122xxy -⎛⎫== ⎪⎝⎭单调递减.故选择B .综上可知:a ∈[-2,0]. 7.答案:B8.解析:∵()f x 是偶函数,∴(1)0(1)0(2)f x f x f ->⇔->=,又∵()f x 在[0,)+∞单调递减,∴12x -<,解之:13x -<< 答案:(1,3)-9. 解析 由题意可得,2(2)1log 4123f -=+=+=.又由22log 12log 21>=, 故有2222212log log 121log 12log 2log 622(log 12)22226f --=====,所以有2(2)(log 12)369f f -+=+=.故选C.评注 本题是一个涉及指数、对数和分段函数的综合题,考察面很广,但运算难度不大, 需要考生熟知基本的概念、性质和运算.10.分析 利用互为反函数的函数的图像性质结合导数求解. 解析 由题意知函数1e 2xy =与ln(2)y x =互为反函数,其图像关于直线y x =对称,两曲线上点之间的最小距离是y x =与1e 2x y =上点的最小距离的2倍,设1e 2x y =上点()00,x y 处的切线与y x =平行,有01e 12x =,0ln 2x =,01y =,所以y x =与1e 2xy =上点的最小距离是()21ln 22-,所求距离为()()21ln 2221ln 22-⨯=-.故选B. 11.分析 结合对数的运算性质进整理,利用对数函数的性质求解.解析:3333log 6log 3log 21log 2,a ==+=+5555log 10log 5log 21log 2,b ==+=+7777log 14log 7log 21log 2,c ==+=+因为357log 2log 2log 2,>>所以a b c >>,故选D.12.【解析】本题考查利用数形结合思想求解函数交点个数问题.在同一直角坐标系中画出两个函数的图像(注意利用函数图像变换观点求作函数图像!111(1)y x x ==---可看作由函数1y x=-向右平移一个单位得到)利用两个函数有共同的对称中心(1,0),设8个交点的横坐标分别为1x ,2x ,…,8x ,结合函数图像,由对称性得18272,2,x x x x +=+=⋅⋅⋅,故所有交点的横坐标之和等于8.13分析 结合函数的图像,利用特殊函数值结合排除法求解. 解析 当1x =时,10ln 21y =<-,排除A ;当0x =时,y 不存在,排除D ;当x 从负方向无限趋近0时,y 趋向于-∞,排除C.故选B. 14. 解析 由已知可得,当P 点在BC 边上运动时,即π04x 剟时,2tan 4tan PA PB x x +=++; 当P 点在CD 边上运动时,即π3π44x 剎?,π2x ≠时, 22111111tan tan PA PB x x ⎛⎫⎛⎫+=-++++ ⎪ ⎪⎝⎭⎝⎭;当π2x =时,22PA PB +=;当P 点在AD 边上运动时,即3ππ4x 剎?时,2tan 4tan PA PB x x +=+-.从点P 的运动过程可以看出,轨迹关于直线π2x =对称,ππ42f f ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭, 且轨迹非直线型,故由此知选B.评注 本题以几何图形为背景考查了函数图像的识别与作法,特别是体现了分类讨论和数形结合的思想.15.解析(1)()()221ln 1x a x xb f x xx ⎛⎫⎪⎝⎭+-=-'+,由于直线230x y +-=的斜率为12-,且过点()1,1,故()()11112f f ⎧⎪⎨⎪⎩==-',即1122b a b ⎧⎪⎨⎪⎩=-=-,解得1a =,1b = 16解析:∵1'1y a x =-+,且在点(0,0)处的切线的斜率为2,∴01'|201x y a ==-=+,即3a = 答案:D17.解析 (1)由题意知,0k =时,联立24y a x y =⎧⎪⎨=⎪⎩,解得()2,M a a ,()2,N a a -.又2xy '=,在点M 处,M k a =,切线方程为()2y a a x a -=-,即0ax y a --=,在点N 处,N k a =-,切线方程为()2y a a x a -=-+,即0ax y a ++=.故所求切线方程为0ax y a --=和0ax y a ++=.18解析 (1)由题意知,0k =时,联立24y a x y =⎧⎪⎨=⎪⎩,解得()2,M a a ,()2,N a a -.又2xy '=,在点M 处,M k a =,切线方程为()2y a a x a-=-,即0ax y a --=,在点N 处,N k a =-,切线方程为()2y a a x a -=-+,即0ax y a ++=.故所求切线方程为0ax y a --=和0ax y a ++=.19.分析 (1)利用所给的点及切线方程列出方程组求解字母的取值;(2)构造函数,利用导数求解函数的最大值,求解时需要注意分类讨论. 解:(1)由已知得f (0)=2,g (0)=2,f ′(0)=4,g ′(0)=4. 而f ′(x )=2x +a ,g ′(x )=e x (cx +d +c ), 故b =2,d =2,a =4,d +c =4. 从而a =4,b =2,c =2,d =2.20.分析 结合函数与导数的基础知识进行逐个推导.解析:A 项,因为函数()f x 的值域为R ,所以一定存在0x ∈R ,使()00f x =.A 正确.B 项,假设函数()32f x x ax bx c =+++的对称中心为(),m n ,按向量(),m n =--a 将函数的图象平移,则所得函数()y f x m n =+-是奇函数.所以()()20f x m f x m n ++-+-=,化简得()23230m a x m am bm c n +++++-=.上式对x ∈R 恒成立,故30m a +=,得3a m =-,323a n m am bm c f ⎛⎫=+++=- ⎪⎝⎭,所以函数()32f x x ax bx c =+++的对称中心为,33a a f ⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭,故()y f x =的图象是中心对称图形.B 正确.C 项,由于()232f x x ax b '=++是二次函数,()f x 有极小值点0x ,必定有一个极大值点1x ,若10x x <,则()f x 在区间()0,x -∞上不单调递减.C 错误.D 项,若0x 是极值点,则一定有()00f x '=.故选C. 21解析 (1)由已知得1'()'(1)e(0)x f x f f x -=-+,所以'(1)'(1)(0)1f f f =-+,即(0)1f =.又1(0)'(1)e f f -=,所以'(1)e f =.从而21()e 2xf x x x =-+.由于'()e 1x f x x =-+,故当 (),0x ∈-∞时,'()0f x <;当()0,x ∈+∞时,'()0f x >.从而,()f x 单调递减区间为(),0-∞,单调递增区间为()0,+∞.(2)由已知条件得()e 1xa xb -+… ()*①若10a +<,则对任意实数b ,当0x <,且11b x a -<+时,可得()e 1xa xb -+<,因此()*式不成立.②若10a +=,则()10a b +=.③若10a +>,设()()g =e 1xx a x -+,则()()g'=e 1xx a -+.当(),ln(1)x a ∈-∞+时, '()0g x <;当()ln(1),x a ∈++∞时,'()0g x >.从而()g x 在(),ln(1)a -∞+上单调递减,在()ln(1),a ++∞上单调递增.故()g x 有最小值()ln(1)1(1)ln(1)g a a a a +=+-++.所以21()2f x x ax b ++…等价于1(1)ln(1)b a a a +-++„ ()**.因此22(1)(1)(1)ln(1)a b a a a ++-++„.设22()(1)(1)ln(1)h a a a a =+-++,则 ()'()(1)12ln(1)h a a a =+-+.所以()h a 在121,e 1⎛⎫-- ⎪⎝⎭上单调递增,在12e 1,⎛⎫-+∞ ⎪⎝⎭上单调递减,故()h a 在12e 1a =-处取得最大值.从而 ()h a e 2„,即()e 12a b +b?.当12e 1a =-,12e2=b 时,()**式成立,故21()2f x x ax b ++….综上得,(1)a b +的最大值为e 2. 22.分析 结合函数与导数的基础知识进行逐个推导.解析:A 项,因为函数()f x 的值域为R ,所以一定存在0x ∈R ,使()00f x =.A 正确.B 项,假设函数()32f x x ax bx c =+++的对称中心为(),m n ,按向量(),m n =--a 将函数的图象平移,则所得函数()y f x m n =+-是奇函数.所以()()20f x m f x m n ++-+-=,化简得()23230m a x m am bm c n +++++-=.上式对x ∈R 恒成立,故30m a +=,得3a m =-,323a n m am bm c f ⎛⎫=+++=- ⎪⎝⎭,所以函数()32f x x ax bx c =+++的对称中心为,33a a f ⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭,故()y f x =的图象是中心对称图形.B 正确.C 项,由于()232f x x ax b '=++是二次函数,()f x 有极小值点0x ,必定有一个极大值点1x ,若10x x <,则()f x 在区间()0,x -∞上不单调递减.C 错误.D 项,若0x 是极值点,则一定有()00f x '=.故选C. 23.分析 先根据已知条件求出首项和公差,代入n nS 再运用导数知识进行求解.解析:设等差数列{}n a 的首项为1a ,公差为d ,由等差数列前n 项和可得11109100,215141525,2a d a d ⨯⎧+=⎪⎪⎨⨯⎪+=⎪⎩ 解得13,2.3a d =-⎧⎪⎨=⎪⎩所以()()222232311111032333n n n n nS n a d n n n n -=+=-+-=-, 所以()2203n n nS n '=-,令()0n nS '=,解得0n =(舍去)或203n =.当203n >时,n nS 是单调递增的;当2003n <<时,n nS 是单调递减的,故当7n =时, n nS 取最小值,所以()23min11077=4933n nS ⨯=⨯--.24.分析 (1)先根据极值点确定出m 的值,然后运用导数求出函数的单调区间,要注意定义域; 解析:(1)解:()1e xf x x m'=-+.由0x =是()f x 的极值点得()00f '=,所以1m =. 于是()()e ln 1x f x x =-+,定义域为()1,-+∞,()1e 1xf x x '=-+.函数()1e 1x f x x '=-+在()1,-+∞上单调递增,且()00f '=,因此当()1,0x ∈-时,()0f x '<;当()0,x ∈+∞时,()0f x '>.所以,()f x 在()1,0-上单调递减,在()0,+∞上单调递增.25 解析 由题意,设函数()()f x g x x =,则''2()()()xf x f x g x x -=,因为当0x >时,'()()0xf x f x -<,故当0x >时,'()0g x <,所以()g x 在(0,)+∞单调递减;又因为函数()()f x x ∈R 是奇函数,故函数()g x 是偶函数,所以()g x 在(,0)-∞上单调递增,且有(1)(1)0g g -==.当01x <<时,()0g x >,则()0f x >;当1x <-时,()0g x <,则()0f x >. 综上所述,使得()0f x >成立的x 的取值范围是(,1)(0,1)-∞-U ,故选A . 评注 本题用导数来研究函数的性质,注意构造函数()g x ,然后用其对称性和奇偶性对单调性的影响,必要时可以用图像来辅助说明. 26解析:求导得,()'e2mxf x m x m =+-()e 12mx m x =-+.若0m …,则当(),0x ∈-∞时,e 10mx-„,()'0f x <;当()0,x ∈+∞时,e10mx-…,()'0f x >.若0m <,则当(),0x ∈-∞时,e 10mx ->>,()'0f x <; 当()0,x ∈+∞时,e 10mx -<<,()'0f x >. 所以()f x 在(),0-∞上单调递减,在()0,+∞上单调递增.27.分析 (1)利用所给的点及切线方程列出方程组求解字母的取值;(2)构造函数,利用导数求解函数的最大值,求解时需要注意分类讨论.解:(1)由已知得f (0)=2,g (0)=2,f ′(0)=4,g ′(0)=4. 而f ′(x )=2x +a ,g ′(x )=e x (cx +d +c ), 故b =2,d =2,a =4,d +c =4. 从而a =4,b =2,c =2,d =2.(2)由(1)知,f (x )=x 2+4x +2,g (x )=2e x (x +1). 设函数F (x )=kg (x )-f (x )=2k e x (x +1)-x 2-4x -2, 则F ′(x )=2k e x (x +2)-2x -4=2(x +2)(k e x -1). 由题设可得F (0)≥0,即k ≥1. 令F ′(x )=0得x 1=-ln k ,x 2=-2.①若1≤k <e 2,则-2<x 1≤0.从而当x ∈(-2,x 1)时,F ′(x )<0;当x ∈(x 1,+∞)时,F ′(x )>0.即F (x )在(-2,x 1)单调递减,在(x 1,+∞)单调递增.故F (x )在[-2,+∞)的最小值为F (x 1).而F (x 1)=2x 1+2-21x -4x 1-2=-x 1(x 1+2)≥0. 故当x ≥-2时,F (x )≥0,即f (x )≤kg (x )恒成立. ②若k =e 2,则F ′(x )=2e 2(x +2)(e x -e -2).从而当x >-2时,F ′(x )>0,即F (x )在(-2,+∞)单调递增. 而F (-2)=0,故当x ≥-2时,F (x )≥0,即f (x )≤kg (x )恒成立. ③若k >e 2,则F (-2)=-2k e -2+2=-2e -2(k -e 2)<0. 从而当x ≥-2时,f (x )≤kg (x )不可能恒成立. 综上,k 的取值范围是[1,e 2].28解析:先根据极值点确定出m 的值,然后运用导数求出函数的单调区间,要注意定义域; (1)解:()1e xf x x m'=-+.由0x =是()f x 的极值点得()00f '=,所以1m =. 于是()()e ln 1x f x x =-+,定义域为()1,-+∞,()1e 1xf x x '=-+.函数()1e 1x f x x '=-+在()1,-+∞上单调递增,且()00f '=,因此当()1,0x ∈-时,()0f x '<;当()0,x ∈+∞时,()0f x '>.所以,()f x 在()1,0-上单调递减,在()0,+∞上单调递增.29解析 由题意,设函数()()f x g x x=,则''2()()()xf x f x g x x -=,因为当0x >时,'()()0xf x f x -<,故当0x >时,'()0g x <,所以()g x 在(0,)+∞单调递减;又因为函数()()f x x ∈R 是奇函数,故函数()g x 是偶函数,所以()g x 在(,0)-∞上单调递增,且有(1)(1)0g g -==.当01x <<时,()0g x >,则()0f x >;当1x <-时,()0g x <,则()0f x >. 综上所述,使得()0f x >成立的x 的取值范围是(,1)(0,1)-∞-U ,故选A . 评注 本题用导数来研究函数的性质,注意构造函数()g x ,然后用其对称性和奇偶性对单调性的影响,必要时可以用图像来辅助说明.【答案】:B31【解析1】:由已知0a ≠,2()36f x ax x '=-,令()0f x '=,得0x =或2x a =,当0a >时,()22,0,()0;0,,()0;,,()0x f x x f x x f x a a ⎛⎫⎛⎫'''∈-∞>∈<∈+∞> ⎪ ⎪⎝⎭⎝⎭;且(0)10f =>,()f x 有小于零的零点,不符合题意。
2011高考真题数学

2011高考真题数学
2011年高考数学试题难度适中,考察了考生对数学知识的掌握和运用能力。
下面我们来逐题进行分析。
第一题,给出了一个边长为6cm的正方形,要求计算其面积。
这是一个基础的几何面积计算题,只需要将正方形的边长进行平方即可求得答案。
第二题,考查了函数的基本性质。
通过函数的图像,要求求出一定范围内的函数值。
考生需要了解函数的图像在不同区间内的性质,掌握函数的变化规律,从而计算出相应的函数值。
第三题,涉及到平面向量的知识。
要求计算两个向量的点积,并判断其正交性。
考生需要了解向量的运算规则,掌握点积的计算方法,以及正交向量的判断条件。
第四题,考查了三角函数的性质。
通过给定的三角函数值,要求计算相关的三角函数值,并判断其大小关系。
考生需要熟练掌握三角函数的计算方法,了解各个三角函数在不同象限内的正负关系,从而解答题目。
第五题,涉及到概率统计知识。
通过给定的条件,要求计算事件发生的概率。
考生需要掌握基本的概率计算方法,理解事件的互斥和独立性,从而计算出相应的概率。
总的来说,2011年高考数学试题考察了考生对数学基础知识的掌握程度和运用能力。
通过认真学习,掌握基本方法,考生可以顺利应对
高考数学考试,取得优异的成绩。
希望考生们在备考过程中不断努力,取得理想的成绩。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
六、算法初步
1.(天津理3)阅读右边的程序框图,运行相应的程序,则输出i的值为
A.3 B.4
C.5 D.6
【答案】B
2.(全国新课标理3)执行右面的程序框图,如果输入的N是6,那么输出的p是
(A)120 (B)720 (C)1440 (D)5040
【答案】B
3.(辽宁理6)执行右面的程序框图,如果输入的n是4,则输出的P是
(A)8
(B)5
(C)3
(D)2
【答案】C
4.(北京理4)执行如图所示的程序框图,输出的s值为
A .-3
B .-12
C .13
D .2
【答案】D
5.(陕西理8)右图中,
1x ,2x ,3x 为某次考试三个评阅人对同一道题的独立评分,P
为该题的最终得分。
当126,9.x x ==p=8.5时,3x 等于
A .11
B .10
C .8
D .7
【答案】C
6.(浙江理12)若某程序框图如图所示,则该程序运行后输出的k 的值是 。
【答案】5
7.(江苏4)根据如图所示的伪代码,当输入a ,b 分别为2,3时,最后输出的m 的值是
【答案】3
8.(福建理11)运行如图所示的程序,输出的结果是_______。
【答案】3
9.(安徽理11)如图所示,程序框图(算法流程图)的输出结果是 .
【答案】15
10.(湖南理13)若执行如图3所示的框图,输入11x =,232,3,2x x x ==-=,
则输出的数等于 。
【答案】2
3
11.(江西理13)下图是某算法的程序框图,则程序运行后输出的结果是
【答案】10
12.(山东理13)执行右图所示的程序框图,输入l=2,m=3,n=5,则输出的y的值是【答案】68。
