浙教版初一数学代数式
浙教版初中数学初一数学上册《代数式的值》说课稿

浙教版初中数学初一数学上册《代数式的值》说课稿一、说教材本节课我们将学习《代数式的值》,这是浙教版初中数学初一数学上册的内容。
通过本节课的学习,我们将了解代数式的含义、代数式的基本运算规律,以及如何求代数式的值。
这对于我们理解数学中的代数概念,掌握基本运算规律,培养我们的逻辑思维能力都非常重要。
二、说教学目标本节课的教学目标主要有以下几点:1.了解代数式的定义及其基本概念。
2.掌握代数式的基本运算规律,包括合并同类项、提取公因数、分配率等。
3.能够根据给定代数式的值求解其未知数的值。
4.培养学生的逻辑思维能力,能够运用所学知识解决实际问题。
三、说教学重难点本节课的教学重点和难点有以下几点:1.理解代数式的含义及其基本概念,能够正确地使用代数式的定义进行分析和判断。
2.掌握代数式的基本运算规律,包括合并同类项、提取公因数、分配率等,能够灵活运用这些规律进行计算。
3.能够根据给定代数式的值求解其未知数的值,培养学生的逻辑思维和推理能力。
四、说教学过程1. 导入通过一个简单的问题导入,引发学生思考:小明去菜市场买水果,苹果每斤3元,橘子每斤2元,根据他买了3斤苹果和4斤橘子,我们如何计算他买水果的总价呢?引导学生从解决这个问题的思路中,理解代数式的基本概念和运算规律。
2. 学习代数式的定义和基本概念给学生呈现代数式的定义和基本概念,让学生进行思考和讨论。
代数式是由数及代数符号通过运算符号相连而成的式子。
代数式由数字常量、字母常量、运算符号和算符号相连所形成的合法的表达式。
3. 学习代数式的基本运算规律讲解合并同类项、提取公因数、分配率等代数式的基本运算规律,并通过具体的例子让学生理解和掌握这些运算规律。
合并同类项:将代数式中相同字母的项相加或相减合并为一个项。
提取公因数:将代数式中各项的公因数提取出来,合并为一个因子。
分配率:将一个因子与另一个因子相乘,然后再与第三个因子相乘,等于将第一个因子与第三个因子相乘后再与第二个因子相乘。
七级数学上册(浙教版)课件:4.2 代数式 (共22张PPT)

A.3x
B.13x
C.x+3 D.x+13
初中数学
3.如果两个数的和为10,其中一个数为x,那么表示这两个数的积的
代数式是( C ) A.10x
B.x(10+x)
C.x(10-x)
D.x(x-10)
4.(2016•大连)某文具店三月份销售铅笔100支,四、五两个月销售量
连续增长.若月平均增长率为x,则该文具店五月份销售铅笔的支数是
(1)a与b的平方差可表示为___a_2_-__b_2__; (2)x是两位数,y是一位数,如果把y放在x的左边,则组成的三位数表示为 __1_0_0__y_+__x_;
初中数学
(3)学生校服每套成本为x元,售价为y元,则每套的利润是 __(_y_-__x_)_元___;
(4)一圆形跑道长 s(m),甲、乙两人在跑道上练习跑步,甲 的速度为 x(m/s),乙的速度为 y(m/s),且 x>y.若两人同时同地
初中数学
15.某种书每本定价8元,若购书不超过10本,按原 价付款;若一次购书10本以上,超过10本部分按八 折付款.设一次购书数量为x本(x>10),则付款金 额为__(6_._4_x_+__1_6_)_元.
初中数学
16.方方和圆圆的房间窗帘的装饰物如图,它们分别由两个四分之一 圆和四个半圆组成(半径都分别相同).她们的窗户能射进阳光的面积 分别是多少(窗框面积不计)?
s 反向而行,则__(x_+__y_)__s 后两人第一次相遇;若两人同时同地同 向而行,则__(_x_-s_y__) _s 后两人第一次相遇.
初中数学
9.农民张大伯因病住院,手术费用为a元,其他费用为b元,由于参加 农村合作医疗,手术费用报销85%,其他费用报销60%.则张大伯此次住 院可报销__(_8_5_%__a_+__6_0_%__b_) _元. 10.代数式8x+5y可以表示很多意义,例如:若x表示苹果每千克的钱 数,y表示香蕉每千克的钱数,则8x+5y表示买8 kg苹果和5 kg香蕉共 花的钱数.请你给8x+5y赋予另一种实际意义.
浙教版数学七年级上册第四章《代数式》复习教学设计

浙教版数学七年级上册第四章《代数式》复习教学设计一. 教材分析浙教版数学七年级上册第四章《代数式》是学生在初中阶段首次系统接触代数式的学习,本章内容主要包括代数式的概念、代数式的运算、列代数式等。
通过本章的学习,使学生理解和掌握代数式的基本概念和基本运算,培养学生运用代数式解决实际问题的能力。
二. 学情分析七年级的学生已经具备了一定的数学基础,对数学符号和运算有一定的认识,但部分学生可能对代数式的抽象概念理解起来较为困难。
因此,在教学过程中,需要关注学生的个体差异,针对不同层次的学生进行教学,使他们在原有基础上得到提高。
三. 教学目标1.理解代数式的概念,掌握代数式的基本运算方法。
2.能够运用代数式解决实际问题,提高学生的应用能力。
3.培养学生的逻辑思维能力和团队合作能力。
四. 教学重难点1.代数式的概念及其运用。
2.代数式的运算方法,如合并同类项、去括号等。
五. 教学方法1.情境教学法:通过生活实例引入代数式,使学生能够直观地理解代数式的实际意义。
2.小组合作学习:分组讨论,培养学生团队合作精神和沟通能力。
3.引导发现法:教师引导学生发现代数式的规律,激发学生的探究欲望。
4.实践操作法:让学生在实际操作中掌握代数式的运算方法。
六. 教学准备1.教学课件:制作精美的课件,辅助教学。
2.练习题:准备适量的练习题,巩固所学知识。
3.教学道具:如卡片、小黑板等,用于展示和讲解。
七. 教学过程1.导入(5分钟)利用生活实例引入代数式,如“某商店进行打折活动,原价100元的商品打8折,求打折后的价格。
”让学生感受代数式在实际生活中的应用。
2.呈现(10分钟)讲解代数式的概念,如“代数式是由数字、字母和运算符号组成的表达式。
”并通过PPT展示一些代数式的例子,让学生加深理解。
3.操练(10分钟)让学生进行代数式的书写练习,如根据给出的情境,写出相应的代数式。
教师巡回指导,解答学生的疑问。
4.巩固(10分钟)讲解代数式的运算方法,如合并同类项、去括号等。
七年级数学上册第4章代数式4.3代数式的值说课稿(新版浙教版)

七年级数学上册第4章代数式4.3代数式的值说课稿(新版浙教版)一. 教材分析《浙教版七年级数学上册》第4章介绍了代数式,而4.3节着重讲解了代数式的值。
这部分内容是学生在掌握了代数式的基本概念和运算法则后,进一步深化对代数式理解的重要环节。
通过本节课的学习,学生将能够求解各种代数式的值,从而为后续的方程和不等式学习打下基础。
二. 学情分析七年级的学生已经具备了一定的数学基础,对代数式有一定的认识。
但是,他们在处理复杂的代数式求值问题时,可能会感到困惑,特别是对于含有多个未知数的代数式。
因此,在教学过程中,我需要关注学生的认知水平,针对性地进行教学。
三. 说教学目标1.知识与技能目标:学生会求解简单代数式的值,并能运用所学知识解决实际问题。
2.过程与方法目标:学生通过自主学习、合作交流,培养观察、分析和解决问题的能力。
3.情感态度与价值观目标:学生体会数学与生活的联系,增强学习数学的兴趣和自信心。
四. 说教学重难点1.教学重点:求解代数式的值,熟练运用代数式的运算法则。
2.教学难点:对于含有多个未知数的代数式,如何正确求解其值。
五. 说教学方法与手段1.教学方法:采用问题驱动法、案例教学法和合作学习法。
2.教学手段:利用多媒体课件、黑板和教学卡片等辅助教学。
六. 说教学过程1.导入新课:通过一个实际问题,引入代数式的值的概念。
2.自主学习:学生根据导学案,独立探索代数式的值求解方法。
3.合作交流:学生分组讨论,分享解题心得,互相答疑。
4.课堂讲解:教师针对学生遇到的问题,进行讲解和示范。
5.练习巩固:学生完成课后练习,巩固所学知识。
6.课堂小结:教师引导学生总结本节课的主要内容和收获。
7.课后作业:布置适量的课后作业,巩固所学知识。
七. 说板书设计板书设计要清晰、简洁,能够突出本节课的重点内容。
主要包括以下几个部分:1.代数式的值的概念;2.代数式的运算法则;3.求解代数式的值的步骤;4.实例分析。
第4章 代数式(单元小结)-2023-2024学年七年级数学上册同步精品课堂(浙教版)
单元小结
知识点二 同类项、合并同类项
1.同类项:所含字母__相__同____,并且相同字母的次数也__相__同__的项叫做同类 项.常数项与常数项也是同类项.
2.合并同类项:把多项式中的同类项合并成一项,叫做合并同类项. 3.合并同类项法则:同类项系数相加,所得结果作为系数,字母和字母的次 数不变. [注意] (1)同类项不考虑字母的排列顺序,如-7xy与yx是同类项; (2)只有同类项才能合并,如x2+x3不能合并.
单元小结
2.化简: (1)(x+2y)-(-2x-y).
(2)6a-3(-a+2b).
解:(1)原式=x+2y+2x+y =3x+3y;
(2)原式=6a+3a-6b =9a-6b;
(3)3(a2-ab)-5(ab+2a2-1). (3)原式=3a2-3ab-5ab-10a2+5
=-7a2-8ab+5.
数学(浙教版)
七年级 上册
第4章 代数式
单元小结
单元小结
知识点一 整式的有关概念
1.代数式:用加、乘、除及乘方等运算符号将数或表示数的字母连接而成 的式子,叫做代数式.单个的数或字母也是代数式.
2.单项式:都是数或字母的__积__,这样的式子叫做单项式,单独的一个数 或一个字母也是单项式.
3.单项式的系数:单项式中的数字因数叫做这个单项式的系数. 4.单项式的次数:一个单项式中,所有字母的指数的和叫做这个单项式的 次数.
4,
其中x=-2.
解:原式=3x2 x2 6x 3 4 2x2 6x 1.
当x=-2时,原式=2×(-2)2+6×(-2)+1=-3.
(2)3x2+(2x2-3x)-(-x+5x2),其中x=314.
七年级数学上册第4章代数式4.4整式教学设计新版浙教版

七年级数学上册第4章代数式4.4整式教学设计新版浙教版一. 教材分析本节课的内容是浙教版七年级数学上册第4章代数式4.4整式。
这部分内容是学生在学习了有理数、分数、方程等基础知识后的进一步拓展,是学生初步接触代数的重要阶段。
本节课主要介绍整式的概念、性质和运算,为学生今后学习更高级的代数知识打下基础。
二. 学情分析七年级的学生已经具备了一定的数学基础,对于概念的理解和运算的掌握都有一定的能力。
但是,由于整式是代数的基础,学生对于整式的理解和应用可能还存在一定的困难。
因此,在教学过程中,需要注重引导学生从实际问题中抽象出整式,培养学生的抽象思维能力。
三. 教学目标1.了解整式的概念,掌握整式的性质。
2.学会整式的运算,能够进行简单的整式运算。
3.能够运用整式解决实际问题,提高学生的应用能力。
四. 教学重难点1.整式的概念和性质。
2.整式的运算方法。
五. 教学方法采用问题驱动法、案例教学法和小组合作学习法。
通过设置问题,引导学生主动探索,培养学生的抽象思维能力。
通过案例分析,让学生了解整式在实际问题中的应用,提高学生的应用能力。
通过小组合作学习,培养学生的团队协作能力。
六. 教学准备1.教学PPT。
2.相关案例资料。
3.练习题。
七. 教学过程1.导入(5分钟)通过一个实际问题引入整式的概念,如:某商店进行打折活动,原价为100元,打8折后的价格是多少?引导学生从实际问题中抽象出整式,激发学生的学习兴趣。
2.呈现(10分钟)介绍整式的概念、性质和运算方法。
通过PPT展示相关知识点,让学生初步了解整式的基本概念和性质,掌握整式的运算方法。
3.操练(10分钟)让学生进行一些整式的运算练习,巩固所学知识。
可以设置一些具有代表性的题目,让学生独立完成,然后进行讲解和分析。
4.巩固(10分钟)通过一些具体的案例,让学生了解整式在实际问题中的应用。
可以让学生分组讨论,每组选取一个案例进行分析,最后进行分享和交流。
七年级数学上册第4章代数式4.2代数式说课稿(新版浙教版)

七年级数学上册第4章代数式4.2代数式说课稿(新版浙教版)一. 教材分析《七年级数学上册》第4章代数式4.2代数式,是学生继学习算术运算后,进一步认识和理解数学符号和表达式的重要章节。
本节内容主要包括代数式的概念、代数式的分类和代数式的运算。
通过本节的学习,学生将能够理解代数式的含义,掌握代数式的基本运算方法,为后续的方程和不等式学习打下基础。
二. 学情分析七年级的学生已经具备了一定的算术基础,对于数学符号和运算规则有一定的认识。
但代数式作为一种抽象的表达方式,对于学生来说还是一个新的概念,需要通过实例和练习来逐步理解和掌握。
三. 说教学目标1.知识与技能:理解代数式的概念,掌握代数式的分类和基本运算方法。
2.过程与方法:通过观察、思考、交流、归纳等活动,培养学生的逻辑思维能力和解决问题的能力。
3.情感态度与价值观:激发学生对数学的兴趣,培养学生的团队合作意识和积极向上的学习态度。
四. 说教学重难点1.重点:代数式的概念、分类和基本运算方法。
2.难点:理解代数式的抽象意义,熟练进行代数式的运算。
五. 说教学方法与手段1.教学方法:采用问题驱动法、实例教学法、合作学习法等,引导学生主动探究和发现。
2.教学手段:利用多媒体课件、黑板、粉笔等传统教学工具,结合学习任务单、练习册等辅助材料。
六. 说教学过程1.导入:通过一个实际问题,引入代数式的概念,激发学生的兴趣。
2.自主学习:学生通过阅读教材,了解代数式的定义和分类。
3.合作交流:学生分组讨论,总结代数式的基本运算方法。
4.教师讲解:针对学生的讨论结果,进行讲解和总结,强调重点和难点。
5.练习巩固:学生进行课堂练习,巩固所学知识。
6.拓展提高:学生通过解决实际问题,运用代数式进行分析和解答。
七. 说板书设计板书设计要清晰、简洁,能够突出代数式的概念和基本运算方法。
主要包括以下内容:1.代数式的概念2.代数式的分类3.代数式的基本运算方法八. 说教学评价通过课堂表现、课堂练习和课后作业等多种方式进行评价。
专题4 代数式(考点串讲,7大考点 12大题型 易错串讲)七年级数学上学期期中考点(浙教版2024)

数。在判别单项式的系数时,要注意数字前面的符号,形如a或﹣a的系数是1或﹣1,不能误
以为没有系数,一个单项式的次数是几,通常称这个单项式为几次单项式。
考点透视
考点四:多项式
(1)定义:几个单项式的和叫做多项式,每个单项式叫做多项式的项,其中不含字母的项叫
做常数项。多项式中次数最高项的次数叫做多项式的次数。
A. − + = − +
B. − + =
− − −
C. − + =
D. − + =
+ −
− −
题型剖析
题型十一:整式的加减
【例 11】一个多项式加上 3
A.
C.
3
+3
3
−6
2
+2
2
−3
得
3
2
2
−311-1】已知 =
2
2
2
D.
2
−
+
2
, =
2
+
,则这个多项式是( C )
.
A. × 5B.4 ×
C.1
2
3
D.−
1
2
【变式 2-1】下列各式中是代数式的是( )
A.
2
− 2 = 0
C.4 > 3
B.6
D.5 − 2 ≠ 0
【变式 2-2】下列代数式符合通常书写规范的是( )
.
A. × 4
B.1
1
3
C. ÷
D.
+1 元
题型剖析
题型三:代数式的值
【例 3】若代数式
−9 5 ,则第 n 个单项式是什么?”
新浙教版七年级上册数学第四章《代数式》知识点及典型例题
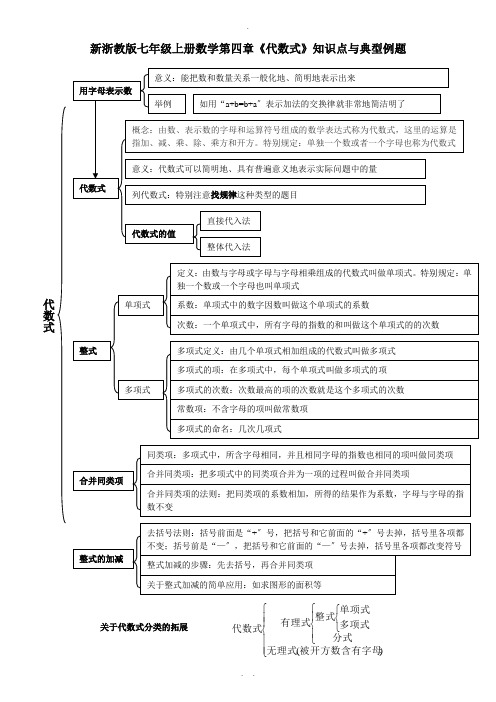
新浙教版七年级上册数学第四章《代数式》知识点与典型例题关于代数式分类的拓展⎪⎪⎪⎨⎧⎪⎩⎪⎨⎧⎩⎨⎧分式多项式单项式整式有理式代数式考点一、关于代数式的书写是否正确的问题 考点二、关于去括号的问题考点三、关于代数式中考概念的题目考点四、关于代数式求值的问题,主要有先化简再直接代入、整体代入、稍作变形后再代入〔把整式的加减也归入这一类〕考点五、用代数式表示实际生活中的问题 考点六、用代数式表示图形的长度与面积问题 考点七、用代数式求关于规律性的题目将考点与相应习题联系起来考点一、关于代数式的书写是否正确的问题 1、下列代数式书写规X 的是〔 〕 A .512ab 2 B .a b ÷c C .a-cbD .m ·3 2、下列代数式书写规X 的是〔 〕 A .a ÷3 B .8×a C .5a D .212a 考点二、关于去括号的问题 1、下列运算正确的是〔 〕A .-3(x-1)=-3x-1B .-3(x-1)=-3x+1C .-3(x-1)=-3x-3D .-3(x-1)=-3x+3 2、下列去括号中错误的是〔 〕 A .2x 2-(x-3y)=2x 2-x+3y B .13x 2+(3y 2-2xy)=13x 2-2xy +3y 2 C .a 2-4(-a+1)=a 2-4a-4 D .- (b-2a)-(-a 2+b 2)=- b+2a+a 2-b 23、下列去括号,错误的有〔 〕个① x 2+(2x-1)= x 2+2x-1,② a 2-(2a-1)=a 2-2a-1,③ m-2(n-1)=m-2n-2,④ a-2(b-c)=a-2b+c A. 0 B. 1 C. 2 D. 3 4、去括号:-[-(1-a)-〔1-b 〕]=考点三、关于代数式中与概念有直接关系的题目1、单项式中-27πa 2b 的系数和次数分别是〔 〕 A .-27,4 B .27,4 C .-27π,3 D .27π,32.下列代数式中,不是整式的是〔 〕 A.13a 2+12a+1 B. a 2+1b C. m+12 D. 2006x +y 3.下列说法正确的是〔 〕 A. x 2-3x 的项是x 2,3x B.3a b 是单项式 C. 12,πa ,a 2+1都是整式 D. 3a 2bc-2是二次二项式 4、若m ,n 为自然数,则多项式x m-y n-2m+n的次数是〔 〕A. mB. nC. m+nD. m ,n 中较大的数 5、下列各项式子中,是同类项的有〔 〕组 ① -2xy 3与5y 3x ,② -2abc 与5xyz ,③ 0与136,④ x 2y 与xy 2,⑤ -2mn 2与mn 2,⑥ 3x 与-3x 2A. 2B. 3C. 4D. 56、若A和B都是三次多项式,则A+B一定是〔〕A. 六次多项式B. 次数不高于三次的多项式或单项式C. 三次多项式D. 次数不低于三次的多项式或单项式0或27、已知-6a9b4和5a4m b n是同类项,则代数式12m+n-10的值为8、多项式2b-14ab2-5ab-1中次数最高的项是,这个多项式是次项式9、若2a2m-5b与mab3n-2的和是单项式,则m2n2=考点四、关于代数式求值的问题,主要有先化简再直接代入、整体代入、稍作变形后再代入〔把整式的加减也归入这一类〕1、若代数式x2+3x-3的值为9,则代数式3x2+9x-2的值为〔〕A、0B、24C、34D、442、已知a-b=2,a-c=12,则代数式(b-c)2+3(b-c)+94的值为〔〕A、-32B、32C、0D、973、若a+b=3,ab=-2,则〔4a-5b-3ab〕-(3a-6b+ab)=4、已知a2-ab=15,b2-ab=10,则代数式3a2-3b2的值为5、先化简,再求值-12a-3(2a-23a2)-6(32a+13a2)-1,其中a=-26、先化简,再求值〔1〕3a2-5b2+12ab-5a2-b2-12ab+4a2,其中a=112,b= -12〔2〕5(x-y)3-3(x-y)2+7(x-y)-5(x-y)3+(x-7)2-5(x-y),其中x-y=1 37、有这样一道题:计算〔2x3-3x2y-2xy2〕-〔x3-2xy2+y3〕+〔-x3+3x2y-y3〕的值,其中x=12,y=-1,小明把x=12错抄成x= -12,但他的计算结果也是正确的,请你帮他找出原因。
4.2 代数式 浙教版七年级数学上册课件

kg;另一片有n hm2 ,平均每公顷产棉花b kg,用式子表示两片棉田上棉花的总产
量.
(am bn )kg
(4)在一个大正方形铁片中挖去一个小正方形铁片,大正方形的边长是a mm,
小正方形的边长是b mm,用式子表示剩余部分的面积.
(a2-b2 )mm2
2.说出下列代数式的意义: (1)圆珠笔每支售价a元,练习簿每本售价b元,那么,3a+4b表示什么?
2
方等运算符号把数或表示数的字母连接而成的式子,叫做代数式.
注意: 1.单个的数或字母也是代数式;
2.代数式中除了含有数,字母和运算符号外,还可以含有括 号;
3.代数式不含____“__=_”_____“__>_”_____“__<_”___.“≧” “≦”
在代数式中,应注意:
① 出现称号,相乘时省略乘号,数与字母相乘时数字在前;
(2)某产品前年的产量是n件,去年的产量是前年产量的3倍少20件,去年 的产量是_(_3_n____2_0__)件 _ ;
(3)某一正方形菜地的边长为a m,它的面积是另一菜地面积的2倍,另一 菜地的面积为___a2_2_m__2__.
知识总结:
a2
在上述例子中,出现了a+b,3n-20,
等,像这样用加、减、乘、除及乘
4.2 代数式
教学目标
1.了解代数式的发生发展过程,揭示代数式概念与一次式 的联系与区别,初步掌握与运用代数式的概念解决问题; 2.了解式的扩充是从特殊到一般,再由一般到特殊的认识 过程; 3.用代数式概念作为载体,设计探究过程,发展学生的数 学探究能力.
教学难点
难点:代数式概念的形式和使用.
情境导入
示船在这条河中ห้องสมุดไป่ตู้水行驶和逆水行驶时的速度;
第4章 代数式 知识梳理-浙教版七年级数学上册章节复习(word版)

代数式知识梳理一、代数式基础1.用字母表示数用字母表示数,可以简明地表达一些一般的数量和数量关系,即把问题中与数量有关的语句,用含数、字母和运算符号的式子表示出来.2.代数式用运算符号(加、减、乘、除、乘方、开方)把数或表示数的字母连接所成的式子,叫做代数式,单独的一个数或一个字母也是代数式.【注】代数式中不含“=”、“>”、“<”、“≠”等符号,如33x =,33x >,33x ≠等都不是代数式.3.列代数式在解决实际问题时,常常先把问题中与数量有关的词语用代数式表示出来,即列出代数式,使问题变得简洁,更具一般性.【注1】代数式的书写规范:(1)字母与数字或字母与字母相乘时,通常把乘号写成“· ”或省略不写;(2)除法运算一般写成分数的形式;(3)字母与数字相乘时,通常把数字写在字母的前面;(4)字母前面的数字是分数的,如果既能写成带分数又能写成假分数,一般写成假分数的形式;(5)如果字母前面的数字是1或-1,“1”通常省略不写,如1×ab 写作ab ,-1×ab 写作-ab ;(6)相同字母的积用乘方表示;(7)在实际问题需要用单位时,如果代数式中含加、减运算,则要把整个式子用括号括起来再写单位,否则可直接写单位.【注2】列代数式的步骤(1)读懂题意,弄清其中的数量关系,抓住题目中表示运算关系的关键词,如和、差、积、商、比、倍、分、大、小、增加了、增加到、减少、几分之几等.(2)分清运算顺序,注意关键性的断句及括号的恰当使用.4.代数式的值一般地,用数值代替代数式里的字母,按照代数式中的运算关系计算得出的结果,叫做代数式的值.【注】求代数式的值的方法和一般步骤方法:一是直接代入法,二是整体代入法.步骤:(1)代入;用数值代替代数式里的字母;(2)计算:按照代数式指明的运算,计算结果.二、整式1.单项式(1)单项式的概念:表示数与字母或字母与字母的积式子叫单项式,特别地,单独的一个数或一个字母也是单项式.巧记:单项式中“只含乘或乘方,不含加减”.(2)单项式的系数:单项式中的数字因数叫做这个单项式的系数.【注】①单项式的系数包括符号;②当单项式的系数是1或-1时,“1”通常省略不写;当单项式的系数是带分数时,通常化成假分数;③圆周率π是常数,单项式中出现π时应看作系数.(3)单项式的次数:一个单项式中,所有字母的指数的和叫做这个单项式的次数.【注】单项式的次数是指单项式中所有字母的指数和,不包括系数的指数,单独一个非零的数是零次单项式.2.多项式(1)多项式的概念:几个单项式的和叫做多项式.(2)多项式的项:多项式中的每个单项式叫做多项式的项,不含字母的项叫做常数项.【注】①一个多项式含有几项,就叫几项式,如:2627x x --是一个三项式.②多项式的每一项都包括它前面的符号.(3)多项式的次数:多项式中次数最高项的次数,叫做这个多项式的次数.(4)升幂排列与降幂排列:为便于多项式的运算,可以用加法交换律将多项式中各项按照某个字母的指数的大小顺序重新排列;降幂排列:把一个多项式按某一个字母的指数从大到小的顺序排列起来;升幂排列:按某一个字母的指数从小到大的顺序排列起来.如:多项式2x 3y 2-xy 3+21x 2y 4-5x 4-6是六次五项式,按x 的降幂排列为-5x 4+2x 3y 2+21x 2y 4-xy 3-6,在这里只考虑x 的指数,而不考虑其它字母;按y 的升幂排列为-6-5x 4+2x 3y 2-xy 3+21x 2y 4. 【注】①将多项式各项重新排列后还是多项式的形式,各项的位置发生变化,其他都不变; ②各项移动时要连同它前面的符号一起移动;③某项前的符号是“+”,它在第一项位置时,“+”可省略,在其他位置时不能省略.3.整式:单项式与多项式统称为整式.【注】所有的整式的分母中不含字母.三、整式的加减运算1.同类项:所含字母相同,并且相同字母的指数也分别相等的项叫做同类项.几个常数项也是同类项.【注】①判断几个项是否是同类项有两个条件:①所含字母相同;②相同字母的指数分别相等.同时具备这两个条件的项是同类项,二者缺一不可.②同类项与系数无关,与字母的排列顺序无关.2.合并同类项(1)概念:把多项式中的同类项合并成一项,叫做合并同类项.(2)法则:合并同类项后,所得项的系数是合并前各同类项的系数的和,且字母连同它的指数不变.(3)步骤:合并同类项的依据是乘法的分配律逆用,一般步骤如下:①准确找出同类项;②利用法则,系数跟系数相加,字母和字母的指数不变;③写出结果,不要漏项.【注】如果两个同类项的系数互为相反数,合并同类项后,结果为0;3.去括号(1)去括号法则括号前面是“+”,把括号和它前面的“+”去掉,括号内各项都不改变符号;括号前面是“-”,把括号和它前面的“-”去掉,括号内各项都改变符号.(2)添括号法则所添括号前面是“+”,括到括号里的各项都不改变符号;所添括号前面是“-”,括到括号里的各项都改变符号.4.整式的加减(1)步骤:一般地,几个整式相加减,如果有括号就先去括号,然后再合并同类项.(2)结果要求:①不能含有同类项,即要合并到不能再合并为止;②一般按照某一字母的降幂或升幂排列;③不能出现带分数,带分数要化成假分数.。
第17课代数式(学生版)七年级数学上册讲义(浙教版)

第17课代数式目标导航学习目标1.通过实例经历代数式概念的产生过程.2.了解代数式的概念.3.会用代数式表示简单的数量关系.知识精讲知识点01 代数式的概念由数、表示数的字母和运算符号组成的数学表达式称为代数式. 单独一个数或者一个字母也称代数式.能力拓展考点01 代数式的概念【典例1】在式子5,x=2,a ,,m+n>0,中,属于代数式的有()个.A.3 B.4 C.5 D.6【即学即练1】下列式子不是代数式的为()A .B.5a+8=7 C.2020 D .考点02 列代数式【典例2】“a,b两数的平方差减去它们的差的平方”用代数式表示为()A.(a﹣b)2﹣(a2﹣b2)B.a2﹣b2﹣(a﹣b)2C.b2﹣a2﹣(b﹣a)2D.(b﹣a)2﹣b2﹣a2【即学即练2】下列代数式表示正确的是()A.a,b两数的平方和:(a+b)2B.a,b两数的差的平方:a2﹣b2 C.y与2的差的两倍:2(y﹣2)D.m,n 两数的倒数和:分层提分题组A 基础过关练1.下列式子a+b,S =ab,5,m,8+y,m+3=2,中,代数式有()A.6个B.5个C.4个D.3个2.用代数式表示“a、b的和除以m所得的商”()A .B .C .D .3.列出“m的2倍与n的差的平方”的代数式,正确的是()A.2m﹣n2B.(2m﹣n)2C.2(m﹣n2)D.m﹣2n24.某品牌电脑原价n元,降价20%后又降低m元,该电脑现价(单位:元)为()元A .(n﹣m)B .(n﹣m)C .(n﹣m)D .(m﹣n)5.用代数式表示:a与b的平方的和.6.用代数式表示“a与b的和的平方”为.题组B 能力提升练7.某商品原价为a元,以(5)元出售,则下列说法中,能正确表达该商品出售价格的是()A.先打3折,再降5元B.先打7折,再降5元C.先降5元,再打3折D.先降5元,再打7折8.代数式的意义是()A.a除以b加1 B.b加1除aC.a除以b与1的和所得的商D.b与1的和除以a9.用6米长的铝合金做成一个长方形的窗框,设长方形窗框的横条长度为x米,则长方形窗框的面积为()A.x(6﹣x)平方米B.x(6﹣3x)平方米C.平方米D.平方米10.一个三位数,百位数字是a,十位数字是b,个位数字是c,则这个三位数是()A.abc B.100a+10b+c C.a+b+c D.100c+10b+a11.如图所示,在一块长为a米,宽为b米的长方形草地上,有两条宽都为1米的纵、横相交的小路,这块草地的绿地面积为平方米.12.某企业有A、B两类经营收入.今年A类年收入为a元,B类年收入是A类年收入的2倍,预计明年A类年收入将增加10%,B类年收入将减少10%.则明年该企业的年总收入为元.(用含a的代数式表示)13.如图1,将一个边长为a的正方形纸片剪去两个小矩形,得到一个“”的图案,如图2所示,再将剪下的两个小矩形拼成一个新的矩形,如图3所示,则新矩形的周长可表示为.题组C 培优拔尖练14.边长分别为a和b(其中a>b)的两个正方形按如图摆放,则图中阴影部分的面积为()A.B.2ab C.a2+ab D.15.把四张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为m,宽为n)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示.则图②中两块阴影部分的周长和是()A.4n B.4m C.2(m+n)D.4(m﹣n)16.“a,b两数的平方和与a,b乘积的差”可用代数式表示为.17.用一生活情景描述1.5a+2b的实际意义:.18.为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段达到节水的目的,该市自来水收费的价目表如表(注:水费按一个月结算一次):请根据价目表的内容解答下列问题:每月用水量(m3)单价(元/m3)不超出26m3的部分3超出26m3不超出34m3的部分4超出34m3的部分7(1)填空:若该户居民1月份用水20立方米,则应收水费元;若该户2月份用水30立方米,则应收水费元;(2)若该户居民3月份用水x立方米(其中26<x≤34),则应收水费多少元?(结果用含x的代数式表示)(3)若该户居民3月份用水a立方米(其中a>34),则应收水费多少元?(结果用含a的代数式表示)。
代数式教案浙教版

2y = 12
y = 6
例题四:代数式的乘法公式
题目:利用完全平方公式计算 (x + 3)²。
解答:
(x + 3)² = x² + 2 * x * 3 + 3²
= x² + 6x + 9
例题五:代数式的因式分解
题目:对代数式 4x² - 9 进行因式分解。
解答:
4x² - 9 = (2x)² - 3²
2. 一个长方形的长是XX厘米,宽是XX厘米,求长方形的面积。
- 化简以下代数式:
1. 3x + 5x - 2x
2. 4y(3y - 2) + 2y(2y + 1)
(2)能力提升题:
- 完成教材第XX页的习题XX、XX、XX。
- 利用代数式解决以下实际问题:
1. 某商店举行打折活动,原价为XX元的商品打八折后,再减去XX元,请列出代数式并计算打折后的价格。
- 对学生的回答进行评价,激发学生的创新意识和探索精神。
- 引导学生关注学科与生活的联系,培养学生的社会责任感。
典型例题讲解
例题一:代数式的化简
题目:化简代数式 3x + 5x - 2x。
解答:合并同类项,得到 6x。
例题二:一元一次方程的解法
题目:解方程 2(x - 3) = 4x + 6。
解答:
7. 代数式的乘法公式
- 完全平方公式:a² = (a+b)² = a² + 2ab + b²。
- 平方差公式:a² - b² = (a+b)(a-b)。
8. 代数式的因式分解
- 提公因式法:找出代数式的公因数,提取公因数。
4.1.2 代数式 浙教版数学七年级上册课件

举例
方法及注意点
对层次较多的题目,可以 采取“浓缩原题,分段处理, 最后组装”的方式来处理.
正确运用括号,先括号内, 后括号外;先小括号,再 中括号,最后大括号.
举例
续表
典例2 用代数式表示:
知识点3 代数式表示的实际意义 难点
实际问题中的数量关系可以用代数式表示出来,反过来,我们可以列举出一个代数 式所表示的实际意义. 敲黑板 代数式的实际意义主要从两个方面考虑:①联系实际生活,对代数式的字母赋予实 际意义;②结合几何背景,如从图形的周长、面积、体积等方面考虑.
所以(1)(3)(5)(7)(8)是代数式,(2)(4)(6)不是代数式.
知识点2 用代数式表示数量关系 重点
1.列代数式的意义:代数式可以简明地、具有普遍意义地表示实际问题中的量,给 数量关系的研究带来方便.
2.列代数式的方法: 方法及注意点
抓住关键性词语,如 “大”“小”“多”“少”“和”“差”“积”“商”“倍”等, 说出一个可以用下列代数式表示结果的实际问题.
本节知识归纳
中考常考考点 考点:列代数式,主要考查根据语言叙述列代数式和 在实际问题中列代数式.
考点 列代数式
难度
常考题型
选择题、填空题
B
D
链接教材 典例7,典例8分别取材于教材第92页作业题第1题,第93页作业题第4题. 典例7考查了直接根据几何语言列代数式,典例8考查了根据实际问题列代数式.中考 真题来源于教材习题,列代数式的关键是把握各个量之间的数量关系.
第4章 代数式
4.2 代数式
学习目标 1.了解代数式的概念,会用代数式表示简单的数量关系. 2.能解释一些简单代数式的实际意义或几何背景.
浙教版七年级数学上册第4章《代数式》课件1

A= (x2 + 3x – 1) + ( - 3x )= x2 – 1
4、一列数 1 ,
3 4
,
5 9
,7 16
,9 25
,
2n 1
按此规律写下去,第n个数是
n2
,
。
5、若 a 是一个有理数,则下列式子中一定
正确的是 ( D )
用数代替代数式里的字母,计算后所得的 结果叫做 代数式的值 。
用代数式表示:
(1)比 a 的5倍小 3 的数是 5a - 3 。
(2)某产品的价格是 p 元,其中成本比 其价格少10%,则此产品的成本是
Z.x.x. K
0.9p 。
(3)一本书有 m 页,第一天读了全书页数 的 四分之一,第二天读了剩下的三分
当 b=360时 c = 40 ,所以 46c = 1840 (人)
3、多项式中,所含 字母 相同,并且 相同字母的指数 也相同的项,叫做 同类项。
下列各题两项,哪些是同类项?
10与1 25x2y与5x2y
33a2b与 2ab2 Zx.xk
423a3b2c与 32b2ca3
请思考:
若 5an1b2与 3a3bm是同,则 类 m_ 项 _____ n___ . __
2、由数与字母或字母与字母相乘组成的代 式叫做单项式 ;单项式中数字因数叫 做这个单项式的系数 ;所有字母的 指数的和叫做这个单项式的 次数 。
由几个 单项式 相加组成的代数式叫做 多项式。在Zx.xk 多项式中,每个单项式叫做多项 式的 项 ;不含字母的项叫做 常数项; 次数最高的项的次数 就是这个多项式的次 数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
wpf04xsz
了撇嘴。不行,他们两个在那里不停地唧唧歪歪,鬼知道什么时候会说完。我必须想办法让那个撩妹的家伙赶快离开,不然我 迟早是饿死的料。“据我所知,会试历来是由礼部主持。”慕容凌娢生硬的插嘴道,“所以……不管你怎么说,都是改变不了 这个事实的。”“这位是……”那人在此时才注意到了慕容凌娢。原来你刚才根本就没有正眼看我啊?现在才发现我的存在, 也太不尊重人了吧……慕容凌娢平复了一下自己的情绪,仔细想想,这也不能怪他啊,毕竟自己在这里如坐针毡的等了半天, 都没有敢发表一下自己的意建,他没注意也是可以理解的。“这是我的远房表妹,初次来京城。没见过世面,也不懂礼数,还 请公子恕罪。”百蝶一边介绍一边用眼神示意慕容凌娢别在多说,“白绫,还不快给韩公子赔罪!”为什么要我给他赔罪?我 说的明明就是实话啊。慕容凌娢看了他一眼,并没有要道歉的意思。那人没有等到慕容凌娢的道歉,倒是产生了一丝惊奇。 “原来如此,我说怎么没见过,原来不是醉影楼的人啊。”他饶有兴趣的看了一眼慕容凌娢,继续说到,“这醉影楼里,还从 未有人敢反驳我。”“没有人反驳不代表你是正确的,而且大多数客观存在的事情即是不用反驳,也是事实。”“你的大道理 还真有意思。”他起身便准备离去,“别被你所相信的真理给骗了。”“韩公子……莺凝,去送送韩公子。”百蝶对站在走廊 上的一个女子说道。可算是走了,慕容凌娢心里高兴的不能行,可偏偏还要装出什么都不知道的样子。可是……为什么感觉现 在的气氛那么奇怪呢……沉闷的气氛持续了好一会儿,百蝶才幽幽的开口。“凌娢,你是不是故意的啊……”她危险的眯起了 眼睛,“我可是在帮你套科举考试的信息啊,现在可好,我刚刚的努力都白费了!”“啊?不是,百蝶姐姐我……”慕容凌娢 的大脑仿佛进行了一次弯道超越,差点因为没刹住车而飞出悬崖,“你跟那个人好像很久之前就认识吧?他是谁啊?”“他 啊……晴国的六皇子,韩皓泽。”“那我现在狗带还来得及吗?”(古风一言)那时,谁渡江湖雨漂泊。而今,征战沙场千里外。 (注:筱玦的这部小说属于架空穿越,但大多数情况下都是仿照明朝的制度来写的。也包括科举制度。会试:通过乡试以后, 第二年春天在京城礼部,由礼部侍郎主持的考试,或由皇帝特派正、副总裁主考官主持。辰、戌、丑、未年会试,为正科;也 有恩科,叫会试因科。因为在春天考试,所以又称「春试」、「春闱」。考中的当「贡士」,第一名叫「会元」。)第021章 少女的名字叫茉莉“凌娢,你是不是故意的?”百蝶危险的眯起了眼睛,“我可是在帮你套科举考试的信息啊,现在可好,我 刚刚的努力都白费了!”“啊?不是,百蝶姐
(3)一个五彩的花圃的形状如 2a² 右图,花圃的面积为______ (4)一个正方形的面积为y,
则它的边长为___________
我们一起来看一下我们刚才得到的式子:
(10a+2b) ,__________ , ,2a² ,
大家通过观察可以考虑一下:这些式子和我们以前学过 的式子有什么区别吗?
我们把像这些式子,含有字母的数学表达式称为 (algebraic expression) 我们强调:
(1)3x - 2 (4) v=s/t
答:(1),(5)是代数式,其他都不是代数式
注:因为等号、不等号都不是运算符号, 所以等式、不等式都不是代数式
例题练习: 例1:用代数式表示
(1) x的3倍与3的差 (2) x的2倍与y的 的和
(3) a与b的和的平方
(4)a与b的平方的和
(5)a、b两数的平方和 (7) 2a的立方
1、代数式:含有字母的数学表达式; 2、代数式是由数、表示数的字母和运算符号组成;
(运算符号:加、减、乘、除、乘方和开方)
3、单独的一个数或一个字母也是代数式
(比如:1,0,- 4,π都是代数式,a , s ,x 也是代数式)
练习:
1、指出下列各式哪些是代数式?哪些不是代数式 (2) x+y = 1 (5) π (3) a>b (6) m千克
(6)2a的立方根
实习:
完成课本P92页课内练习
第 1 题
议一,互相交流
例 2、
解:
一辆汽车以80千米/时的速度行使,从A城到 B城需t时,如果该车的行使速度增加v千米/时,那么 从A城到B城需多少时间? 80t A城至B城之间的路程为______千米 如果该车的速度增加v千米/时,那么 ( 80+v ) 千米/时 汽车的速度为_________
4.2
代 数 式
主讲人:横港中学
干於平
一、创设情景问题,引入新课题
一隧道长l米,一列火车长180米,如果该列火车穿 过隧道所花的时间为t分,则列车的速度怎么表示?
速度为:
米/分
我们再来看下面的问题:
(1)大米的单价为a元/千克,食油的单价为b元/千克, (10a+2b) 元; 买10千克大米、2千克食油共需___________ (2)日平均气温是指一天中 2:00 ,8:00 ,14:00, 20:00四个时刻气温的平均值,若上述四个时刻气温的 摄氏度数分别是a,b,c,d,则日平均气温的摄氏度数 是 __________
_______ 此时从A城到B城需________时
考虑: _______ ) 此时所用的时间比原来快了( t - 时
实习:
完成课本P92页课内练习
第
2
题
课堂小结
亲爱的同学们,你在今天这节课上学到了什么呢?
代数式的概念 1、
2、 列代数式
软文发布 软文发布
