概率统计(江浦11~12-2A)课程考试试题
概率统计试题及答案

概率统计试题及答案在概率统计学中,试题和答案的准确性和清晰度非常重要。
下面将给出一系列关于概率统计的试题和详细的解答,以帮助读者更好地理解和应用概率统计的基本概念和技巧。
试题一:基础概率计算某餐厅有3个主菜,每个主菜又有4种不同的配菜。
如果顾客在选择主菜和配菜时是随机的,那么一个顾客会选择哪种搭配的概率是多少?解答一:根据概率统计的基本原理,计算顾客选择搭配的概率可以使用“事件数除以样本空间”的方法。
在这个问题中,总共有3个主菜和4种配菜,所以样本空间的大小为3 × 4 = 12。
而一个顾客选择一种特定的搭配可以有1种选择,因此事件数为1。
因此,顾客选择某种搭配的概率为1/12。
试题二:概率的加法规则某班级有25名男生和15名女生。
从中随机选择一名学生,那么选择一名男生或选择一名女生的概率分别是多少?解答二:根据概率统计的加法规则,选择一名男生或选择一名女生的概率可以通过计算每个事件的概率然后相加来得到。
在这个问题中,男生和女生分别属于两个互斥事件,因此可以直接相加。
男生的概率为25/40,女生的概率为15/40。
因此,选择一名男生或选择一名女生的概率为25/40 + 15/40 = 40/40 = 1。
试题三:条件概率计算某电子产品的退货率是0.05,而该产品是有瑕疵的情况下才会退货。
对于一台已经退货的产品,有0.02的概率是有瑕疵的。
那么一台被退货且有瑕疵的电子产品占所有退货产品的比例是多少?解答三:根据条件概率的定义,求一台被退货且有瑕疵的电子产品占所有退货产品比例的问题,可以用有瑕疵且被退货的产品数除以所有被退货的产品数来得到。
假设有1000台电子产品被退货,根据退货率的定义,有5%的产品会被退货,即退货的产品数为0.05 * 1000 = 50台。
而在这50台退货产品中,有2%有瑕疵,即有瑕疵且被退货的产品数为0.02 * 50 = 1台。
因此,一台被退货且有瑕疵的电子产品占所有退货产品的比例为1/50,即0.02。
南京工业大学概率统计(江浦12~13-2B)t

南京工业大学 概率统计 课程考试试题(B 、闭)2012-2013学年第二学期(公办)所在学院 班 级 学号 姓名一、填空题(每题3分,计18分)1、袋中有5个黑球,3个白球,大小相同,一次随机摸出4球,其中恰有3个白球的概率为 。
2、设A 、B 为随机事件,且11(),(|)43P A P B A ==,1(|)2P A B =,则()P B = 。
3、已知随机变量X ,Y 的方差为DX =49,DY =64,相关系数0.5XY ρ=,则()D X Y -= 。
4、设随机变量X 的概率密度为23, 01,()0, x x f x ⎧<<=⎨⎩其他,以Y 表示对X 的三次独立重复观察中事件{0.5}X ≤出现的次数,则P {Y =2}= 。
5、设随机变量X 服从(1,2)-上的均匀分布,则随机变量1, 0,0, 0,1, 0X Y X X >⎧⎪==⎨⎪-<⎩的数学期望EY = 。
6、设(X 1,…,X 5)为来自正态总体N (0,1)的样本,若统计量服从t 分布,则c = 。
二、选择题(每题3分,计12分)1、假设事件A 和B 满足P (B |A )=1,则( )。
(A )A 是必然事件 (B )0)|(=A B P (C )A ⊃B (D )A ⊂B2、设随机变量X 服从参数为n ,p 二项分布,且已知EX =2.4,DX =1.44,则此二项分布中的参数(n ,p )=( )。
(A ) (3,0.8) (B ) (4,0.6) (C ) (6,0.4) (D ) (8,0.3)3、设二维随机变量(X ,Y )的联合概率密度是(),0,0(,)0,x y e x y f x y -+⎧>>=⎨⎩其它,则X 与Y 为( )的随机变量。
(A )独立同分布 (B ) 独立不同分布 (C )不独立同分布 (D ) 不独立也不同分布 4、在假设检验中,H 0为原假设,则称( )为犯第二类错误。
2022概率统计考试题及答案

2022概率统计考试题及答案一、选择题(每题3分,共30分)1. 以下哪个事件是随机事件?A. 抛硬币出现正面B. 太阳从东方升起C. 明年今天下雨D. 一个数除以自身等于1答案:A2. 某工厂生产的零件,合格率为95%,则一个零件不合格的概率为:A. 0.05B. 0.95C. 0.5D. 1.0答案:A3. 设随机变量X服从二项分布B(n, p),其中n=10,p=0.3,那么P(X=3)的值为:A. 0.2668B. 0.3927C. 0.2411D. 0.5答案:B4. 对于连续型随机变量,其概率密度函数f(x)在区间(a, b)上的概率为:A. ∫_a^b f(x) dxB. f(a) + f(b)C. f(a) * f(b)D. 1/(a - b)答案:A5. 以下哪个是大数定律的表述?A. 样本均值收敛于总体均值B. 样本方差收敛于总体方差C. 样本中极值出现的概率趋于0D. 样本容量增大,样本均值的分布趋于正态答案:A6. 在一次抽奖活动中,有3个奖品,分别是A、B、C,抽到A的概率为1/4,抽到B的概率为1/3,抽到C的概率为1/2。
那么抽到A或B 的概率为:A. 5/12B. 1/3C. 7/12D. 5/6答案:C7. 以下哪个统计量是度量数据集中趋势的?A. 方差B. 标准差C. 中位数D. 极差答案:C8. 总体均值为μ,方差为σ²,样本容量为n,样本均值为x̄,那么样本均值的期望值为:A. σ²B. nC. μD. x̄答案:C9. 在一次考试中,成绩服从正态分布N(80, 100),那么成绩在70到90之间的概率为:A. 0.6827B. 0.9545C. 0.3827D. 0.8413答案:C10. 以下哪个选项是中心极限定理的内容?A. 样本均值的分布随着样本容量的增大而趋于正态B. 样本方差的分布随着样本容量的增大而趋于正态C. 样本中位数的分布随着样本容量的增大而趋于正态D. 总体均值的分布随着样本容量的增大而趋于正态答案:A二、填空题(每题4分,共20分)11. 设随机变量X服从泊松分布,λ=2,则P(X=1)=_________。
概率统计考试试卷及答案

概率统计考试试卷及答案一、填空题(每小题4分,共20分)1.设,且,则。
2.设随机变量X的分布函数,则3.已知则4.已知随机变量则随机变量的密度函数5.设随机变量X与Y相互独立,且则二、计算下列各题(每小题8分,共40分)1.设随机变量X的概率密度为已知Y=2X,求E(Y),D(Y).2.两封信随机地投入标号为I,II,III,IV的四个邮筒,求第二个邮筒恰好投入1封信的概率。
3.设X,Y是两个相互独立的随机变量,X在(0,1)上服从均匀分布,Y的概率密度为求含有a的二次方程有实根的概率。
4.假设是来自总体的简单随机样本,求系数a,b,c使服从分布,并求其自由度。
5.某车间生产滚珠,从长期实践知道,滚珠直径X服从正态分布。
从某天产品里随机抽取6个,测得直径为(单位:毫米)14。
6,15.1,14。
9,14。
8,15。
2, 15.1 若总体方差, 求总体均值的置信区间()三、(14分)设X,Y相互独立,其概率密度函数分别为,求X+Y的概率密度四、(14分)设,且是总体X的简单随机样本,求(1)的矩估计量,(2)五、(12分)据以往经验,某种电器元件的寿命服从均值为100小时的指数分布,现随机地取16只,设它们的寿命是相互独立的,求这16只元件的寿命的总和大于1920小时的概率。
()普通本科概率统计期末考试试卷答案:一、填空题(每小题4分,共20分)1、;2、1;3、;4、;5、二、计算下列各题(每小题8分,共40分)1、解:。
...。
.。
.。
..。
2分。
..。
.。
.4分。
.。
...。
.。
6分。
...。
..。
8分2、解:。
.。
.。
.。
.。
.。
4分。
...。
.。
8分3、解:有题意知,的概率密度为。
.。
.。
.。
.。
2分于是的联合概率密度为。
.4分于是原方程有实根的概率即为。
..。
.。
....。
6分。
.。
.。
..。
..8分4、解:因为为来自于总体~(0,22)的简单样本,故有,,...。
..。
2分于是有,,。
概率统计试题库及答案

7、设事件A、B、C,将下列事件用A、B、C间的运算关系表示:(1)三个事件都发生表示为:_____________;(2)三个事件不都发生表示为:_____________;(3)三个事件中至少有一个事件发生表示为:___________。( , , )
54、5人排成一排照相,其中a.,b两人不能相邻照相的概率为_________。( )
55、4.3个人选等可能地选择五条不同的道路,则至少有两人选择同一条道路的概率为:_________。( )
56、两人在1到10个号码中允许重复地各选取一个,则最大号码为5的概率为_________。( )
57、甲乙两人赌博约定五局三胜,设两人每局的胜率相等.在甲已胜二场,乙已胜一场的情况下,乙最终获胜的概率为_________。( )
63、已知P(A)=0﹒6,P(B)=0﹒4,P(A︱B)=0﹒45,则P(A B)=。(0.82)
64、某车间有5台相互独立运行的设备,开工率均为p,若至少有3台设备同时开工生产才能正常进行,则生产能正常进行的概率为_________。(只写算式)( )
65、设试验 的样本空间为 , 为 的事件, 为 的一个划分,且 ,则 ____________。( )
28、已知 , , ,则 ____________。(0.60)
29、计算下列算式:(1) =_________;(2) =_________;(3)若A,B独立,P(A)=0.3, P(B)=0.2,则P(B-A)=_________。( , ,0.14)
30、设A、B是两个事件,若 ,则有 _______________。( )
南京工业大学概率论与数理统计试卷(全-吐血整理-必做) (1)

南京工业大学 概率统计 课程考试试卷(A闭)(2011/2012学年第1学期-2012年1月)所在系(院) 班 级 学号 姓名一、填空题(每空3分,共18分)1.假设()14P A =,()13P B A =,()12P A B =,则=)(B P ,()P A B = .1/6, 1/32. 设连续随机变量的密度函数为)(x f ,则随机变量X e Y 3=的概率密度函数为=)(y f Y.⎩⎨⎧≤>=000)])3/[ln()(1y y y f y f yY 3. 随机变量);4,0;1,0(~),(ρN Y X =221122(,;,;)N μσμσρ,已知(2)1D X Y -=,则ρ=答: 7 / 8 (或0.875) ;4. 在0H 为原假设,1H 为备择假设的假设检验中,若显著性水平为α,则表示概率:P ( )=α10(|);P H H α=接受成立5. 设某种清漆干燥时间),(~2σμN X (单位:小时),取9=n 的样本,得样本均值和方差分别为33.0,62==S X ,则μ的置信度为95%的单侧置信区间上限为 答:上限为 6.356 .二、 选择题(每题3分,共12分)1. 掷一颗骰子600次,则“1”点出现次数的均值为 . (A) 50; (B) 100; (C) 120; (D)150.2. 随机变量,X Y 相互独立且服从同一分布,3/)1()()(+====k k Y P k X P ,1,0=k ,则()P X Y ==.(A )1/9; (B )4/9;(C )5/9; (D )1.3. 离散型随机变量X 的概率分布为k A k X P λ==)(( ,2,1=k )的充要条件是 . (A )1)1(-+=A λ且0>A ; (B )λ-=1A 且10<<λ; (C )11-=-λA 且1<λ; (D )0>A 且10<<λ.4. 设10个电子管的寿命i X (10~1=i )独立同分布,且A X D i =)((10~1=i ),则10个电子管的平均寿命Y 的方差=)(Y D .(A )A ; (B )A 1.0; (C )A 2.0; (D )A 10.答:(C )(B )(A )(B )三.(8分) 某厂卡车运送防“非典”用品下乡,顶层装10个纸箱,其中5箱民用口罩、2箱医用口罩、3箱消毒棉花. 到目的地时发现丢失1箱,不知丢失哪一箱. 现从剩下9箱中任意打开2箱,结果都是民用口罩,求丢失的一箱也是民用口罩的概率. 解: A —任取2箱都是民用口罩,k B —丢失的一箱为k , 3,2,1=k 分别表示民用口罩,医用口罩,消毒棉花. 2分3685110321)()()(29252925292431=⋅+⋅+⋅==∑=C C C C C C B A P B P A P k k k3分 .83368363)(/21)(/)()()(2924111=÷=⋅==A P C C A P B A P B P A B P3分四.(8分)设连续型随机变量X 的分布函数为⎪⎩⎪⎨⎧≥-<≤<=--1,110,0,)()1(x Ae x B x Ae x F x x 求:(1)A ,B 的值;(2)X 的概率密度函数()f x ;(3){}1/3P X >。
概率统计试题及答案

概率统计试题及答案一、选择题(每题2分,共20分)1. 某随机事件的概率为0.3,那么它的对立事件的概率是多少?A. 0.7B. 0.4C. 0.6D. 0.52. 以下哪个选项不是概率的属性?A. 非负性B. 有限性C. 规范性D. 可加性3. 抛一枚均匀硬币两次,出现正面向上的概率是多少?A. 0.25B. 0.5C. 0.75D. 14. 随机变量X服从二项分布B(n, p),当n=10,p=0.2时,求P(X=2)。
A. 0.33B. 0.38C. 0.41D. 0.455. 正态分布N(μ, σ^2)中,μ和σ^2分别代表什么?A. 均值和方差B. 方差和均值C. 方差和标准差D. 标准差和均值二、填空题(每题2分,共10分)6. 概率论中,事件的______是指在一定条件下,该事件发生的可能性大小。
7. 随机变量X的数学期望E(X),也称为X的______。
8. 随机变量X和Y的协方差Cov(X, Y)表示的是X和Y之间的______。
9. 样本均值的方差公式为S^2/n,其中S^2表示样本的______。
10. 假设检验中的P值是指在零假设为真的情况下,观察到的样本结果或更极端结果出现的概率,通常用______表示。
三、简答题(每题10分,共20分)11. 简述大数定律和中心极限定理的区别和联系。
12. 描述什么是条件概率,并给出一个实际应用的例子。
四、计算题(每题15分,共30分)13. 某工厂生产的产品中,次品率为0.05,求以下概率:(1) 从100件产品中随机抽取10件,至少有1件次品的概率;(2) 从100件产品中随机抽取10件,全部是次品的概率。
14. 某地区连续两天下雨的概率为0.6,求以下概率:(1) 连续三天都下雨的概率;(2) 至少有一天下雨的概率。
五、论述题(每题20分,共20分)15. 论述统计推断在数据分析中的重要性,并举例说明。
答案:1. A2. B3. B4. B5. A6. 概率7. 期望值8. 线性相关程度9. 方差10. P值11. 大数定律描述了随机变量的算术平均数收敛到期望值的趋势,而中心极限定理说明了在一定条件下,大量独立随机变量之和的分布趋于正态分布。
南京工业大学《概率统计》课程试题A及参考答案

南京工业大学概率统计课程考试试题(A 、闭)(江浦)(第二学期)1.假设P (A )=0.4, P (A ∪B )=0.7,那么(1)若A 与B 互不相容,则P (B )= ______ ;(2)若A 与B 相互独立,则P (B )= ____ 。
2.将英文字母C,C,E,E,I,N,S 随机地排成一行,那么恰好排成英文单词SCIENCE 的概率为____________。
3.设随机变量X 的概率密度为442e 1)(-+-=x xx f π,则=2EX 。
4.设随机变量X 与Y 相互独立,且均服从参数为0.6的0-1分布,则{}Y X p ==______。
5.某人有外观几乎相同的n 把钥匙,只有一把能打开门,随机地取出一把开门,记X 为直到把门打开时的开门次数,则平均开门次数为__________。
6.设随机变量X 服从)21,8(B (二项分布), Y 服从参数为3的泊松分布,且X 与Y 相互独立,则)32(--Y X E =__________;)32(--Y X D =__________。
7.设总体X ~),(2σμN , (X 1,X 2,…X n )是来自总体X 的样本,已知2111)(∑-=+-⋅n i i i X Xc 是2σ的无偏估计量,则=c 。
二、选择题(每题3分,计9分)1.当事件A 和B 同时发生时,必然导致事件C 发生,则下列结论正确的是( )。
(A )P (C )≥ P (A )+ P (B )1- (B )P (C )≤P (A )+ P (B )1- (C )P (C )=P (A ⋃B ) (D )P (C )= P (AB )2.设X 是一随机变量,C 为任意实数,E X 是X 的数学期望,则( )。
(A )E (X -C )2=E (X -E X )2 (B ) E (X -C )2≥E (X -E X )2 (C ) E (X -C )2 <E (X -E X )2 (D ) E (X -C ) 2 = 03.设总体X ~),(2σμN , (X 1,X 2, X 3)是来自总体X 的样本,则下列估计总体X 的均值μ的估计量中最好的是( )。
概率统计期末考试试题附答案
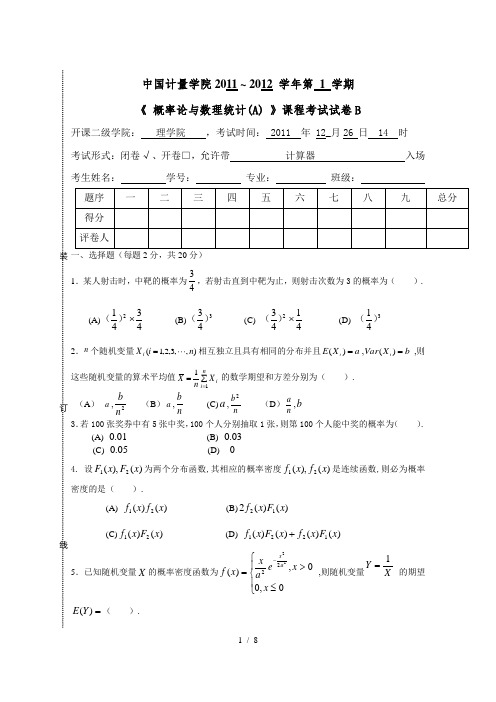
中国计量学院2011 ~ 2012 学年第 1 学期 《 概率论与数理统计(A) 》课程考试试卷B开课二级学院: 理学院 ,考试时间: 2011 年 12_月26 日 14 时 考试形式:闭卷√、开卷□,允许带 计算器 入场 考生姓名: 学号: 专业: 班级:1.某人射击时,中靶的概率为43,若射击直到中靶为止,则射击次数为3的概率为( ). (A) 43412⨯)( (B) 343)( (C) 41432⨯)( (D) 341)( 2.n 个随机变量),,3,2,1(n i X i =相互独立且具有相同的分布并且a X E i =)(,b X Var i =)(,则这些随机变量的算术平均值∑==ni i X n X 11的数学期望和方差分别为( ). (A ) a ,2n b (B )a ,n b (C)a ,n b 2 (D )n a,b3.若100张奖券中有5张中奖,100个人分别抽取1张,则第100个人能中奖的概率为( ). (A) 01.0 (B) 03.0 (C) 05.0 (D) 0 4. 设)(),(21x F x F 为两个分布函数,其相应的概率密度)(),(21x f x f 是连续函数,则必为概率密度的是( ). (A) )()(21x f x f (B))()(212x F x f (C))()(21x F x f (D) )()()()(1221x F x f x F x f +5.已知随机变量X 的概率密度函数为⎪⎩⎪⎨⎧≤>=-0,00,)(2222x x e a x x f a x ,则随机变量X Y 1= 的期望=)(Y E ( ).(A)a 22π (B) π (C) a 21(D) aπ2 6.设)(),(x f x F 分别为某随机变量的分布函数和密度函数,则必有( ).(A) )(x f 单调不减 (B) 0)(=-∞F (C)⎰+∞∞=-1)(F dx x (D) ⎰+∞∞=-)(f )(dx x x F7.设二维离散型随机变量),(Y X 的联合分布律为则==}{Y X P ( ).(A) 0.8 (B) 0.7 (C) 0.3 (D) 0.58.设两个独立的随机变量Y X ,分别服从正态分布)1,0(N 和)1,1(N ,则( ).(A) 21}0{=≤-Y X P (B) 21}0{=≤+Y X P (C) 21}1{=≤-Y X P (D) 21}1{=≤+Y X P9.设二维连续型随机变量),(Y X 的联合概率密度函数为⎪⎩⎪⎨⎧≤+=其它,,01,1)(22y x y x f π, 则X 和Y 为( )的随机变量.(A) 独立同分布 (B) 独立不同分布 (C) 不独立同分布 (D) 不独立不同分布10.设总体X 服从正态分布),(2σμN ,其中2σ已知,μ为未知参数,则μ的等尾双侧置信区间长度L 与置信度α-1的关系是( ).(A) 当α-1减少时,L 变小 (B) 当α-1减少时,L 增大 (C) 当α-1减少时,L 不变 (D) 当α-1减少时,L 增减不定二、填空题(每空2分,共20分)1. 已知5.0)(=A P , 3.0)(=AB P ,则=-)(B A P .2. 设123,,X X X 是来自正态总体X ~(),1N μ的样本,则当=k 时,3213141ˆkX X X ++=μ是总体均值μ的无偏估计. 3. 设]6,1[~X U ,则方程012=++Xt t 有实根的概率为 .4. 袋内有3个白球与2个黑球,从其中任取两个球,求取出的两个球都是白球的概率 . 5. 设,4.0,36)(,25)(===XY Y Var X Var ρ则.)(=-Y X Var6. 设总体X 的概率密度为:⎪⎩⎪⎨⎧≤≤=-其它,010,)(1x xx f θθ, 是未知参数,0>θX X X X n 为,,,21 的一个样本,则θ的矩估计量=θˆ7. 设XeY N X -=),1,0(~,则Y 的密度函数=)(y f Y .8.设Y X ,为两个随机变量,且74}0{}0{,73}0,0{=≥=≥=≥≥Y P X P Y X P ,则=≥}0),{max(Y X P .9. 设Y X ,相互独立,且概率密度分别为: ⎩⎨⎧≤≤=其它,010,1)(x x f X ,⎩⎨⎧≤>=-0,00,)(y y e y f y Y ,则Y X Z +=的概率密度=)(z f Z .10.将n 只球(1~n 号)随机地放进n 只盒子(1~n 号)中去,一只盒子装一只球,若一只球装入与球同号的盒子中,称为一个配对,记X 为总的配对数,则=)(X E . 三、(本小题10分)设A 和B 是两个事件,8.0)(,6.0)(==B P A P ,试问:(1)在什么条件下)(AB P 取到最大值,最大值是多少; (2) 在什么条件下)(AB P 取到最小值,最小值是多少.装 订 线四、(本小题10分)已知随机变量X 的概率分布如右表, 求随机变量:(1)X 的分布函数)(x F . (2)X Y 2-=的概率分布.五、(本小题10分)设连续型随机变量X 的分布函数为 ⎪⎩⎪⎨⎧≥<≤<=e x e x x x x F ,11,ln 1,0)(求:(1) 随机变量的概率密度函数)(x f ; (2) )5.20(≤<X P ;(3) 期望)(X E .六、(本小题10分)某产品主要由三个厂家供货,甲、乙、丙三个厂家的产品分别占总数的15%,80%和5%,其次品率分别为0.02,0.01和0.03.试计算: (1) 从这批产品中任取一件,是不合格品的概率为多大?(2) 已知从这批产品中随机地抽取一件是不合格品,问这件产品是甲厂生产的概率?装七、(本小题6分)设总体X 密度函数为⎩⎨⎧≤≤=-其它,010,),(1x x x f θθθ,其中0>θ为未知参数,如果取得样本观测值为n x x x ,,,21 ,求参数θ的极大似然估计值.八、(本小题4分)设随机变量X 的分布函数)(x F 连续且严格单调增加,求)(X F Y =的概率密度.九、(本小题10分)设随机变量),(Y X 的概率密度为⎩⎨⎧>>=+-,其它,,00,0),()43(y x ke y x f y x (1)求常数k ; (2)}20,10{≤<≤<Y X P ;(3)求),(Y X 的联合分布函数),(y x F ;(4)判断Y X ,的独立性.中国计量学院2011 ~ 2012 学年第 1 学期《 概率论与数理统计(A ) 》课程 试卷 B 参考答案及评分标准开课二级学院:理学院,学生班级:10 测控1,2,3,4,5等 教师: 邹海雷等一、选择题(20分)1 A2 B3 C4 D5 A6 B 7C 8 D 9 C 10 A 二、填空题(20分)1 0.2,2 5/12 ,3 0.8 ,4 0.3,5. 37 6 2-1X )(X , 7 ⎪⎩⎪⎨⎧≤>=-,00,21)(2)(ln 2y y e yy f y π , 8 5/7 , 9 ⎪⎪⎩⎪⎪⎨⎧<<-≤≥-=--10,10,01),1()(z e z z e e z f z z , 10, 1三、(10分)1)B A ⊂ 时,取得最大值6.0)(=AB P ………………………5分 2)Ω=⋃B A 时,取得最小值4.0)(=AB P ………………………10分 四、(10分)⎪⎪⎪⎩⎪⎪⎪⎨⎧≥<≤<≤<≤-<=4 1429.020 5.0 012.0-1x 0 )(x x x x x F ………………………5分………………………10分五、(10分) 解:(1)⎩⎨⎧<≤=elseex x x f ,01,1)( …………………4分 (2)5.2ln )0()5.2()5.20(=-=≤<F F X P …………………7分 (3)11)()(1-===⎰⎰+∞∞-e dx xx dx x xf X E e…………………10分六、(10分)设 B 表示取得不合格品事件,)3,2,1(=i A i 表示取得的产品是甲、乙、丙次厂家的1)0125.003.005.001.080.002.015.0)/()()(31=⨯+⨯+⨯==∑=ii iA B P A P B P………………………5分 2)24.0)/()()/()()/(31111==∑=i iiA B P A P A B P A P B A P (10)分七、(6分)1-11-1)(θθθθθi ni n i ni x xL ==∏=∏= ……2分∑=+=ni ix n L 1ln 1-ln )(ln )(θθθ ……3分令:0ln )(ln 1=+=∑=ni i x n d L d θθθ ……5分解得极大似然估计值为:∑=∧-=ni ixn1ln θ ……………… 6分八、(本小题4分)当,10时<<yy y F X P y X F P y Y P y F Y =≤=≤=≤=-)}({})({}{)(1 ……………2分,0)(0=≤y F y 时,,1)(1=≥y F y 时, …………………3分综上,,1,110,0,0)(⎪⎩⎪⎨⎧≥<<≤=y y y y y F故:⎩⎨⎧<<=others y y f ,010,1)(……………4分九、(10分)1)由1),(0403==⎰⎰⎰⎰∞+-∞+-+∞∞-+∞∞-dy e dx e k dxdy y x f y x k=12 (3)分2))1)(1(12),(}20,10{83201)43(--+---===≤<≤<⎰⎰⎰⎰e e dxdy e dxdyy x f Y X P y x ……………5分3)⎩⎨⎧>>--=--其它00,0)1)(1(),(43y x e e y x F y x ………………………7 分4)由),(y x f 可分离变量,故X 与Y 独立。
概率论与数理统计考试题及答案

概率论与数理统计考试题及答案1. 选择题1. 某城市的天气预报表明明天有80%的可能性会下雨,20%的可能性会晴天。
如果明天下雨,那么有70%的可能性会有雷电。
如果明天晴天,那么有10%的可能性会有雷电。
请问明天下雨并且有雷电的概率是多少?A) 0.56B) 0.14C) 0.08D) 0.02答案: B) 0.142. 某班级有30名男生和20名女生。
如果从班级中随机选择两名学生做代表,那么两名学生都是男生的概率是多少?A) 0.42B) 0.50C) 0.17D) 0.33答案: A) 0.423. 某电子产品的生产线上,6%的产品存在缺陷。
从该生产线上随机抽取8个产品,至少有一个产品存在缺陷的概率是多少?A) 0.06B) 0.47C) 0.40D) 0.26答案: B) 0.472. 计算题1. 有一批100个零件,其中10个存在缺陷。
从中随机抽取5个进行检测,求出恰好有两个存在缺陷的概率。
解答:总共有 C(100, 5) 种抽取方式,其中选择2个缺陷零件的方式为C(10, 2)。
因此恰好有两个存在缺陷的概率为 C(10, 2) / C(100, 5)。
计算结果:恰好有两个存在缺陷的概率为12495 / 77175 ≈ 0.16152. 某门考试的成绩服从正态分布,均值为75,标准差为8。
求出高于90分的概率。
解答:将题目所给的分数转化为标准正态分布的 Z 值。
Z = (90 - 75) / 8 ≈ 1.875。
然后查找标准正态分布表,可以得知 Z 值为1.875时,对应的累积概率为 0.969。
因此高于90分的概率为 1 - 0.969 = 0.031。
3. 应用题某城市的每日客流量服从泊松分布,平均每天有10,000人次进入公交车站。
请回答下列问题:1) 在任意一天,有6,000人次进入公交车站的概率是多少?解答:根据泊松分布的概率公式 P(X = k) = (e^-λ * λ^k) / k!,其中λ 为平均每日客流量。
南京工业大学《概率统计》课程试题B及答案

南京工业大学《概率统计》课程试题(B 、闭)(江浦)(第二学期) 院(系) ____班 级 ___ 学号 __ 姓名 ___ 得分 一、填空题(每空2分,共20分)1.假设4.0)(=A P ,7.0)|(=A B P ,那么(1)=)(AB P ______ ;(2)=-)(B A P ______。
2.设随机变量)1,0(~N X ,)1,0(~N Y 且Y X ,独立,则~Y X - ,~2X 。
3.设随机变量),(~2σμN X ,则=EX ,=DX 。
4.设随机变量X 与Y 相互独立,且均服从同一分布,则{}Y X P ≤=______。
5.设随机变量)1.0,10(~B X (二项分布), )1(~E Y (指数分布1=λ),且X 与Y 相互独立,则)3(++Y X E =__________;)3(++Y X D =__________。
6.设总体),(~2σμN X , ),,,(21n X X X 是来自总体X 的样本,∑=--=ni i X X n S 12)(11,则=)(2S E 。
二、单项选择题(每题2分,共10分)1. 设B A ,为两个随机事件,若0)(=AB P ,则( )(A )A 和B 两事件互不相容(互斥) (B )AB 是不可能事件(C )AB 未必是不可能事件 (D )0)(=A P 或0)(=B P2. 设 ,3,2,1,)41(~==k C p X kk ,则常数=C ( ) (A )3 (B )31 (C ) 2 (D )21 3. 设相互独立的随机变量X 与Y 分别服从正态分布)1,1()1,0(N N 和,则( ) (A ){}210=≤+Y X P (B ){}211=≤+Y X P (C ){}210=≤-Y X P (D ){}211=≤-Y X P 4. 设X 是一随机变量,C 为任意实数,则( )。
(A ) 22)()(EX X E C X E -=- (B ) 22)()(EX X E C X E -≥-(C ) 22)()(EX X E C X E -≤- (D ) 0)(2=-C X E 5.在假设检验中,0H 为原假设,备择假设1H ,则称( )为犯第一类错误。
概率统计考试试题

证明题
总结词
此类题目要求考生对给定命题进行证明,主要考察考生的逻 辑推理能力。
详细描述
证明题通常涉及概率统计中的定理、性质的证明,如证明大 数定律、中心极限定理等。
03
试题解析
单项选择题解析
总结词
单项选择题是概率统计考试中的基本题型 之一,主要考察对基本概念和公式的理解 和应用。
详细描述
单项选择题通常由一个题干和四个选项组 成,其中只有一个选项是正确的。这类题 目主要考察学生的判断和理解能力,需要 考生对相关概念和公式有深入的理解和扎 实的数学基础。
详细描述
计算题通常由一个题干和若干个小问题组 成,需要考生根据题目要求进行计算并得 出答案。这类题目需要考生掌握各种概率 统计相关的计算方法和公式,同时也需要 考生具备良好的计算能力和细心程度。
证明题解析
总结词
证明题是概率统计考试中考察推理能力的一种题型,主要考察考生的逻辑推理和证明能力。
详细描述
连续型随机变量的概率 分布,通常用来描述大 多数自然现象和社会现 象的分布情况。
当样本数量较小时,使 用t分布来描述数据的概 率分布。
当n个相互独立的随机变 量服从标准正态分布时 ,它们的平方和服从卡 方分布。
05
考试技巧和注意事项
答题方法和技巧
仔细阅读题意
在开始答题前,一定要仔细阅读题目,确保理解了题目的要求和含义。
详细描述
填空题通常由一个题干和一个空格组成,需 要考生根据题目要求填写正确的答案。这类 题目需要考生对相关概念和公式有较为扎实 的应用能力和掌握程度,同时也需要考生具
备良好的语言表达能力。
计算题解析
总结词
计算题是概率统计考试中考察计算能力的 一种题型,主要考察考生的计算能力和对 公式的应用能力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
南京工业大学 概率统计 课程考试试题(A 、闭)
2011-2012学年第二学期
所在学院 班 级 学号 姓名
一、填空题(每题3分,计15分)
1、将数字1,2,3,4,5写在5张卡片上,任意取出3张排列成一个三位数,这个数是奇数的概率
p = 。
2、若事件A 、B 相互独立,且2.0)(=A P ,6.0)(=B P ,则()P AB = 。
3、已知随机变量X ~N (-3,1),Y ~N (2,1),且X ,Y 相互独立,设随机变量27Z X Y =-+,则
~Z 。
4、设二维随机变量(X ,Y )的联合概率密度为,0(,)0,
y axe x y f x y -⎧<<<+∞
=⎨⎩其它 ,则a = 。
5、设总体X ~N (0,1),12,,,n X X X 为来自总体的一个样本,则统计量2
1234X X X X ⎛⎫
- ⎪+⎝⎭
服从
分布。
二、选择题(每题3分,计12分)
1、以A 表示事件“甲种产品畅销,乙种产品滞销”,则其对立事件为( )。
(A )“甲种产品滞销,乙种产品畅销” (B )“甲乙两种产品均畅销”
(C )“甲种产品滞销” (D )“甲种产品滞销,或乙种产品畅销” 2、某电子元件使用寿命在1000小时以上的概率为0.2,则3个电子元件使用1000小时后,最多只有一个坏了的概率为( )。
(A ) 0.008 (B ) 0.096 (C ) 0.104
(D )
0.016
3、设X ,Y 是相互独立的随机变量,其分布函数分别为)(x F X ,)(y F Y ,则),min(Y X Z =的分布函数是( )。
(A ))()(z F z F X Z =
(B ))()(z F z F Y Z =
(C ))](1)][
(1[1)(z F z F z F Y X Z ---= (D )()()()Z X Y F z F z F z =⋅ 4、设总体),(~2
σμN X ,其中2
σ已知,则总体均值μ的置信区间长度l 与置信度1α-的关系是( )。
(A )当1α-缩小时,l 缩短 (B )当1α-缩小时,l 增大
(C )当1α-缩小时,l 不变
(D )以上说法均不准确
三(10分)、有朋友自远方来访,他乘火车、轮船、汽车、飞机来的概率分别是0.3、0.2、0.1、0.4.如果他乘火车、轮船、汽车、飞机来的话,迟到的概率分别是
14,13,1
12
,而乘飞机不会迟到。
(1)他迟到的概率是多少?(2)如果他迟到了,试问他是乘火车来的概率为多少?
四(12分)、连续型随机变量X 的分布函数为 20 , 0() , 0(1)x F x b
a x cx <⎧⎪
=⎨+≥⎪+⎩
,又知EX =2。
试求:(1)待定系数a ,b ,c ;(2) X 落在区间⎪⎭
⎫
⎝⎛1,21内的概率。
五(8分)、袋装奶粉规定每袋净重1000克,标准差30克,每箱装有100袋,计算一箱奶粉净重不足99400克的概率 ((1)0.8413,(2)0.9772Φ=Φ=,其中)(x Φ是标准正态分布函数)。
六(13分)、设随机变量(X ,Y )在矩形区域{(,)|02,01}G x y x y =≤≤≤≤上服从均匀分布,即联
合概率密度为0.5, 02,01, (,)0, . x y f x y ≤≤≤≤⎧=⎨⎩其它,记0,,0,2,
1,.1,2.
X Y X Y X Y X Y ξη≤≤⎧⎧==⎨⎨
>>⎩⎩ (1)求(,)ξη的联合分布;(2)ξ与η的相关系数ξηρ。
七(12分)、设总体X 的概率密度函数为
||
1(),2x f x e x θ
θ
-=-∞<<+∞
其中θ>0为待估参数,12,,,n X X X 来自总体X 的简单随机样本。
(1)求θ的矩估计量1ˆθ;(2)求θ的极大似然估计量2ˆθ;(3)证明2
ˆθ是θ的无偏估计。
八(10分)、假设0.50,1.25,0.80,2.00是来自总体X 的简单随机样本值,已知ln Y X =服从正态分布(,1)N μ。
求:(1)X 的数学期望EX (记EX 为a );(2)μ的置信度为0.95的置信区间;(3)利用上述结果a 的置信度为0.95的置信区间。
(已知(1.65)0.95Φ=,(1.96)0.975Φ=)
九(8分)、某厂生产的电子元件的寿命(单位:h )X ~N (2,σμ),其中2,σμ未知。
但据以往的经验,电子元件的寿命一直稳定在μ0=200小时,现该厂对生产工艺作了某些改进,为了了解技术革新的效果,从刚生产的电子元件中任意抽取16只,具体计算后得到375.223=x ,707.40=s 。
试问:工艺改进后,在检验水平α=0.05下是否可以认为元件的平均寿命有了显著的提高(7351.1)15(05.0=t ,1315.2)15(025.0=t )?。
