怎样用几何画板制作成中心对称的旋转动画?
玲珑画板三角函数图像旋转动画.docx

用玲珑画板制作sin x 图像关于y 轴对称的旋转动画 第一步:点左侧栏黑色三角,选三角坐标系。
:S :S: 凶>L 四銀限坐标浆 2JSS6 >2■简易坐标系>4-三角形 >4.2^标浆1 5-四奶 >标票2 6■立体图形 >6-三角坐标系 7-球内接夕厢孩閒体>8■前组件 >第二步:点参数一 >y=f(x)函数第三步:输入函数色数衰达式 Xy=sin(x), 0<x<3*pi确定 取消■ (V091S] • asme 9 9 ■ > o第四步:全选整个图,右键一>合成组件■ •【耒■穴创 Ml(t» MX) feBM) MA) MX «BG) 6S<$) ・D(W) H«XH )V=sin(x). 0<x<3*piLikA^/ld ■ • sas ■ > o第五步:用左侧栏线段工具画一段线段,在线段上取一个点(线段本 来是蓝色的,取线段上的点吋候会变成绿色)■注!■ gg [M<1»■ Mkt) M*a MM) MCA) M «BG) »D(W) MW)第六步:点上面菜单栏:动画一>旋转动画把角度值改成180y^sin(x), 0<x<3 ^pi 亠亠亠LkAfiVld ■■ 000"a >£ 0 O S ■ > aM G 然后选中线段上的那个点一>设定变量,再选中y轴上半段一>设为旋转轴:接着选中右侧图像和X轴止半轴一>添加到动画:然后拖动线段上的点就可以旋转了。
因为旋转过去之后右侧就没有图像了,可以再画一个sim x的图像放在右侧,这样旋转完了就是完整的sin |x|To最后还可以点上面菜单栏:创建一>控制类按钮一>自动动画按钮■■ d x■MW) MM, «Ut(C) MtM) MkA) KT KXW) WDM ■ • x□ ■®s s ■ > o然后选中线段上的点一>添加对象一>确定,就可以了,点动画按钮它就会自己动,(双击动画按钮左侧蓝色的区域可以打开这个控制板)■giflB • KE■5T7)MbM) MkA) WO) «BS) gW) .CJM。
几何画板中,制作旋转图形的几条路径

几何画板中,制作旋转图形的几条路径赵化中学 郑宗平路径一:标记中心→选定要制作的旋转图形→变换→旋转→固定角度→输入旋转角度→旋转即可完成.路径二:数据→新建参数→角度→输好名称和角度→确定→在工作区得到“角度参数”标签→标记中心→选定要制作的旋转图形→变换→旋转→点选工作区的新建的“角度参数”标签→标记角度→旋转即可完成.路径三:画一个角→依次点选边上的点、顶点、边上的点(或依次点选边、顶点、边)→度量→角度→在工作区得到度量的“角度标签” →标记中心→选定要制作的旋转图形→变换→旋转→点选工作区的度量的“角度标签”→标记角度→旋转即可完成.路径四:画一条弧→构造弧上的点→依次点选弧的一个端点、构造点、弧的另一个端点→度量→角度→在工作区得到度量的“角度标签”→标记中心→选定要制作的旋转图形→变换→旋转→点选工作区的度量的“角度标签”→标记角度→旋转即可完成.路径五:画三个点→依次点选三个点→度量→角度→在工作区得到度量的“角度标签” →标记中心→选定要制作的旋转图形→变换→旋转→点选工作区的“角度标签”→标记角度→旋转即可完成.路径六:画一条线段(或弧)→构造线段(或弧)上的点→选定点→度量→点的值(或选定端点和构造点来度量比)→在工作区得到度量的“点的值”的标签→数据→计算→点选工作区的“点的值”的标签→点计算器键盘上“*” →从计算器键盘上输入所需要设置的数据(注意:单位选“度”)→ 在工作区得到“点的值*度数的值”的标签→标记中心→选定要制作的旋转图形→变换→旋转→点选工作区的“点的比*度数的值”的标签→标记角度→旋转即可完成.补充说明:其中路径二点选新建的“角度参数”标签后,通过键盘上的“-”键和按住Shift 后通过键盘上的“+”键可以减少、增加角度来改变旋转;路径三至路径六可以设置角度变化范围,并且均手动旋转;路径二中可以把“角度参数”标签设置成动画,来达到对图形动画的控制;路径四、路径六还可以把构造的点设置成动画,来达到对图形动画的控制. 路径六是最为实用设置旋转动画的方式.下面是根据路径六把△D EF 设置成旋转360°动画后工作区示意图:2014年4月27日星期日 原创 C 在AB 上 360° = 91.43°C 在AB 上= 0.25F'A B C。
几何画板变换功能操作方法

几何画板变换功能操作方法几何画板变换功能是一种非常有用的几何学工具,可以帮助我们实现图形的平移、旋转、缩放和镜像等操作。
今天,我将向您介绍一下几何画板变换功能的操作方法。
首先,我将要讲解的是平移操作。
平移是指保持图形大小和形状不变,仅仅改变它在平面上的位置。
要在几何画板中进行平移操作,首先需要选择你想要进行平移的图形。
然后,在几何画板上选择平移工具,这通常是一个箭头图标。
接下来,点击你想要平移的图形上的一个顶点或中心点,并拖动它到新的位置。
一旦你找到适合的位置,释放鼠标按钮即可完成平移操作。
旋转是几何画板中另一个常用的操作。
旋转是指围绕某一点将图形以一定的角度旋转。
在几何画板中进行旋转操作时,首先选择你想要旋转的图形。
然后,在几何画板中找到旋转工具,通常是一个圆的图标。
点击旋转工具后,你将看到图形上出现一个点,这个点被称为旋转中心。
你可以通过拖动这个旋转中心来改变旋转的中心位置。
接下来,将鼠标移动到一个顶点或中心点上,并拖动它。
你会注意到图形正在旋转。
将其旋转到你想要的角度后,释放鼠标按钮即可完成旋转操作。
缩放是几何画板中另一个重要的变换。
缩放是指改变图形的大小而不改变其形状。
在几何画板中进行缩放操作时,首先选择你想要缩放的图形。
然后,在几何画板中找到缩放工具,通常是一个放大镜和缩小镜的图标。
点击缩放工具后,你会看到图形上出现一个点,这个点被称为缩放中心。
你可以通过拖动这个缩放中心来改变缩放的中心位置。
接下来,将鼠标移动到一个顶点或中心点上,并拖动它。
你会注意到图形正在缩放。
将其缩放到你想要的大小后,释放鼠标按钮即可完成缩放操作。
最后,我们将介绍镜像操作。
镜像是指将图形沿着某一直线对称翻转。
在几何画板中进行镜像操作时,首先选择你想要镜像的图形。
然后,在几何画板中找到镜像工具,通常是一个左右对称的图标。
点击镜像工具后,你会看到图形上出现一条直线,这条直线被称为镜像轴。
你可以通过拖动这个镜像轴来改变镜像的位置。
几何画板中函数图像的旋转和对称

几何画板中函数图像的旋转和对称利用变换菜单作图对象的平移、旋转、缩放、反射等各种作图,但我们如何让函数图像也能够进行平移、旋转、缩放、反射呢?如果还是按照老方法操作,显然是不成功的,那么该怎么操作呢?下面我们通过一个小实例来看一看做法。
定义域是(a,b)的函数y=x2 的图像绕某一点P旋转和关于某直线l的对称操作步骤:1、图表菜单——定义坐标系,然后用点工具在x轴上做任意两点,并同时选中这两点,点击度量菜单——横坐标,出现两个度量值,在度量结果右键——属性——标签中,设置两个度量值标签分别为a、b(a<b)2、同时选中第一步中的两点,构造——线段,然后继续构造——线段上的点X,然后继续度量——横坐标,设置度量结果的标签为x,然后度量——计算,出现一个计算器窗口,点击刚才的估量结果x,然后点击计算器中的^符号,继续点击2键,然后确定,得到一个计算结果,设置标签为y。
3、按顺序选中度量结果x和y,点击图表——绘制点(x,y),此时新绘制出来的点处于被选中状态,继续选中X点,构造——轨迹。
至此,定义域为(a,b)的函数y=x2 的图像已经绘制完成,下面看看该如何绕某一点旋转(呵呵,其实非常简单)4、用直尺工具绘制一条线段M N,并在线段上构造一个点K,度量MN两点的距离,再度量MK两点距离,度量——计算,打开计算器,计算(MK/MN)* 360度的结果,注意360度中的单位度的选择方式,选中计算结果,变换菜单——标记角度。
5、用点工具在平面内任意画一个点P,并用选择工具双击点P将其标记为旋转中心,选中在第3步中那个绘制点(x,y)得到的点,变换——旋转,墨认为按标记角度旋转,点击旋转按钮即可。
6、上一步点击了旋转按钮之后,得到一个新的点,这个点处于被选中状态,继续选中X点,构造——轨迹,好了,出现了新的轨迹了感觉怎么样,用鼠标拖动K点,可以改变旋转的角度,当然你也可以改变P点的位置,调整旋转中心的位置。
几何画板之图像旋转、平移、对称

几何画板之图像旋转、平移、对称西乡四中王荣刚我是一位农村初中数学教师,写这篇文章,一方面是我在做关于几何画板的课题,另一方面,我发现周围的数学老师对几何画板知道的十之一二,更不用说用它了,所以想通过这些豆腐块文章让更多的数学老师(特别是农村的数学老师)知道并了解几何画板,让他们明白,几何画板很简单,比powerpoint,excel,word简单多了,而且几何画板就是为数学而生,它会让你的课堂变得简单、活泼、有趣。
之前在县上的教育刊物上发表了“几何画板之函数”,前几天同行问我找关于“平移”的课件,于是就想总结下关于这方面的技巧。
语言简单,无华丽辞藻,不妥之处望同行们批评指正。
一、首先简单介绍《几何画板》的功能。
For personal use only in study and research; not for commercial use1、《几何画板》有超强的作图功能,而且做出的图形不会像word 那样容易“散架”。
作图时最大的特点是遵循了“尺规作图”法则,使做出的图形有了一定内涵。
2、能根据函数表达式作函数图像,这样在研究函数图像和性质时就容易多了。
3、度量和计算功能。
《画板》可以将你作出的图形根据要求进行度量,包括线段长度,角的度数,面积,点的坐标等等。
当然也可以进行函数计算。
For personal use only in study and research; not for commercial use4、动态演示功能。
《画板》可以用简单的几步达到flash样的动画效果,在平移、旋转、轴对称和中心对称,圆的相关性质等教学中效果明显。
本文将重点阐述在图形的旋转,平移,轴对称和中心对称教学中使用几何画板,使教学过程不再变得生硬,让学生理解起来更加容易些。
二、作图形的旋转。
要旋转一个图形,必须有旋转中心和旋转角度,所以在作图之前,这两个因素必须首先考虑。
实例1,旋转三角形。
操作步骤:1,画三角形ABC;2,选中点A,点击菜单“变换”——“标记中心”,将点A标记为旋转中心(也可用选择工具双击点A,标记为中心)。
利用几何画板制作几何图形的平移及动画的途径和方法
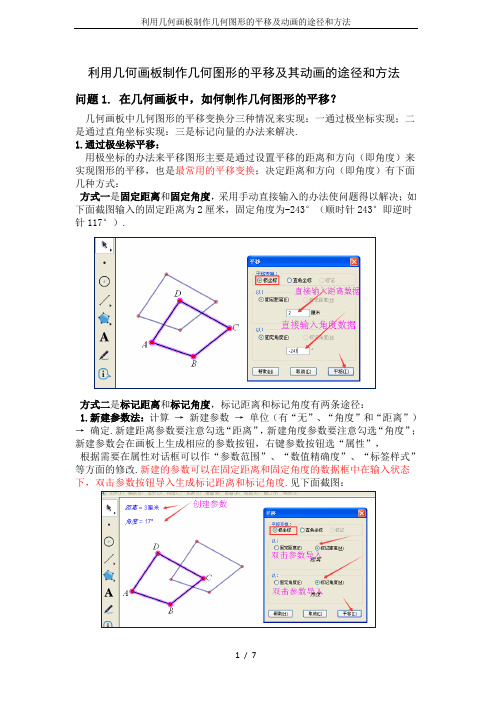
利用几何画板制作几何图形的平移及其动画的途径和方法问题1. 在几何画板中,如何制作几何图形的平移?几何画板中几何图形的平移变换分三种情况来实现:一通过极坐标实现;二是通过直角坐标实现:三是标记向量的办法来解决.1.通过极坐标平移:用极坐标的办法来平移图形主要是通过设置平移的距离和方向(即角度)来实现图形的平移,也是最常用的平移变换;决定距离和方向(即角度)有下面几种方式:方式一是固定距离和固定角度,采用手动直接输入的办法使问题得以解决;如下面截图输入的固定距离为2厘米,固定角度为-243°(顺时针243°即逆时针117°).方式二是标记距离和标记角度,标记距离和标记角度有两条途径:1.新建参数法:计算→新建参数→单位(有“无”、“角度”和“距离”)→确定.新建距离参数要注意勾选“距离”,新建角度参数要注意勾选“角度”;新建参数会在画板上生成相应的参数按钮,右键参数按钮选“属性”,根据需要在属性对话框可以作“参数范围”、“数值精确度”、“标签样式”等方面的修改.新建的参数可以在固定距离和固定角度的数据框中在输入状态下,双击参数按钮导入生成标记距离和标记角度.见下面截图:2.度量法:直接度量两点之间的距离和角的度数,会在画板上生成相应的按钮,右键按钮选“属性”,根据需要通过属性对话框可以作“数值精确度”、“标签样式”等修改.度量参数也可以在固定距离和固定角度中在输入状态下,双击参数按钮导入或勾选“标记距离”以及“标记角度”生成标记距离和标记角度.方式三是标记与固定相结合.比如距离采用参数导入的办法,角度采用固定角度的办法设置.以此类推!注:1.标记的新建参数法和度量均可以“手动”方式改变数据,从而改变图形的平移距离和方式;2.平移变换前要注意事先选定图形,否则不能调出对话框进行后续操作.2.通过直角坐标平移:直角坐标中的平移主要是通过平移的水平距离和垂直距离来实现图形的平移,水平距离和垂直距离的设置通过两个方面进行 . 决定垂直距离和水平距离也是有三种方式:方式一是水平距离和垂直距离,采用直接手动输入的办法使问题得以解决;这里不再举例.方式二是标记距离,标记距离有两条途径:一是新建参数法:二是度量法.其操作方式与在“极坐标”中的操作是一样的.所以在这里不再赘述.下面这个截图的⊿DEF的平移“水平距离”是创建的参数导入的,而垂直距离、两点间的距离参数导入的. “水平距离”可以利用键盘的“+”和度量A B“-”调节大小,(用“+”键需Shift配合)“垂直距离”可以拉动线段的端点来改变距离的大小.方式三是标记与固定相结合.比如水平距离采用参数导入的办法,垂直距离采用度量参数导入的办法.这里不再举例.3.通过标记向量的办法平移:向量即为“矢量”,是带有方向和长度的一条线段.“标记向量”和“平移”是不可分的,一般情况下“标记向量”的后一步即为“平移”.“标记向量”的基本操作是:选中线段两个端点(选点的顺序决定方向的正反)→变换→标记向量即可.拉伸线段可以调整图形平移的方向角度和距离.问题2. 在几何画板中,如何制作几何图形的平移并转换成动画?虽然上面我们总结了几何画板中图形的平移的方式,但不是每一种方式都可以制成易操作的平移动画.下面我以举例的方式介绍几种简单的较基础的平移动画,其它图形的平移可以类推!方法1.标记向量来平移图形,并制成动画例.将四边形ABCD沿线段MN或NM方向进行平移,并制作成动画。
最新在几何画板中,如何制作几何图形的平移及其动画?
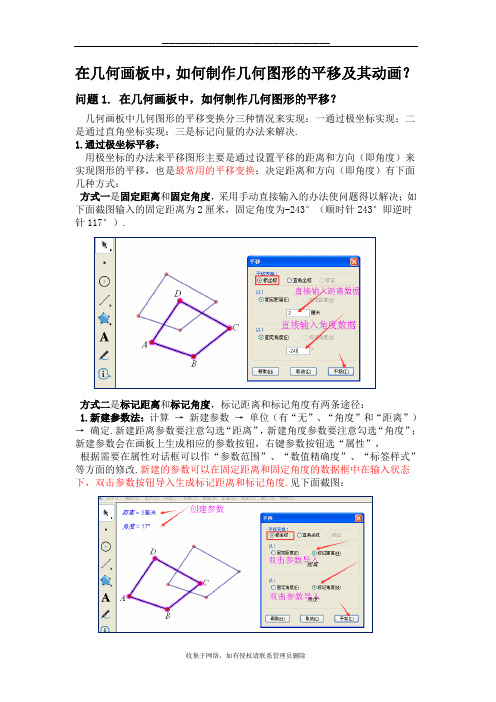
在几何画板中,如何制作几何图形的平移及其动画?问题1. 在几何画板中,如何制作几何图形的平移?几何画板中几何图形的平移变换分三种情况来实现:一通过极坐标实现;二是通过直角坐标实现:三是标记向量的办法来解决.1.通过极坐标平移:用极坐标的办法来平移图形主要是通过设置平移的距离和方向(即角度)来实现图形的平移,也是最常用的平移变换;决定距离和方向(即角度)有下面几种方式:方式一是固定距离和固定角度,采用手动直接输入的办法使问题得以解决;如下面截图输入的固定距离为2厘米,固定角度为-243°(顺时针243°即逆时针117°).方式二是标记距离和标记角度,标记距离和标记角度有两条途径:1.新建参数法:计算→新建参数→单位(有“无”、“角度”和“距离”)→确定.新建距离参数要注意勾选“距离”,新建角度参数要注意勾选“角度”;新建参数会在画板上生成相应的参数按钮,右键参数按钮选“属性”,根据需要在属性对话框可以作“参数范围”、“数值精确度”、“标签样式”等方面的修改.新建的参数可以在固定距离和固定角度的数据框中在输入状态下,双击参数按钮导入生成标记距离和标记角度.见下面截图:2.度量法:直接度量两点之间的距离和角的度数,会在画板上生成相应的按钮,右键按钮选“属性”,根据需要通过属性对话框可以作“数值精确度”、“标签样式”等修改.度量参数也可以在固定距离和固定角度中在输入状态下,双击参数按钮导入或勾选“标记距离”以及“标记角度”生成标记距离和标记角度.方式三是标记与固定相结合.比如距离采用参数导入的办法,角度采用固定角度的办法设置.以此类推!注:1.标记的新建参数法和度量均可以“手动”方式改变数据,从而改变图形的平移距离和方式;2.平移变换前要注意事先选定图形,否则不能调出对话框进行后续操作.2.通过直角坐标平移:直角坐标中的平移主要是通过平移的水平距离和垂直距离来实现图形的平移,水平距离和垂直距离的设置通过两个方面进行 . 决定垂直距离和水平距离也是有三种方式:方式一是水平距离和垂直距离,采用直接手动输入的办法使问题得以解决;这里不再举例.方式二是标记距离,标记距离有两条途径:一是新建参数法:二是度量法.其操作方式与在“极坐标”中的操作是一样的.所以在这里不再赘述.下面这个截图的⊿DEF的平移“水平距离”是创建的参数导入的,而垂直距离、两点间的距离参数导入的. “水平距离”可以利用键盘的“+”和度量A B“-”调节大小,“垂直距离”可以拉动线段的端点来改变距离的大小.方式三是标记与固定相结合.比如水平距离采用参数导入的办法,垂直距离采用度量参数导入的办法.这里不再举例.3.通过标记向量的办法平移:向量即为“矢量”,是带有方向和长度的一条线段.“标记向量”和“平移”是不可分的,一般情况下“标记向量”的后一步即为“平移”.“标记向量”的基本操作是:选中线段两个端点(选点的顺序决定方向的正反)→变换→标记向量即可.拉伸选段可以调整图形平移的方向角度和距离.问题2. 在几何画板中,如何制作几何图形的平移并转换成动画?虽然上面我们总结了几何画板中图形的平移的方式,但不是每一种方式都可以制成易操作的平移动画.下面我易举例的方式介绍几种简单的较基础的平移动画,其它图形的平移可以类推!方法1.标记向量来平移图形,并制成动画例.将四边形ABCD沿线段MN或NM方向进行平移,并制作成动画。
利用几何画板制作几何图形的平移及其动画的途径和方法
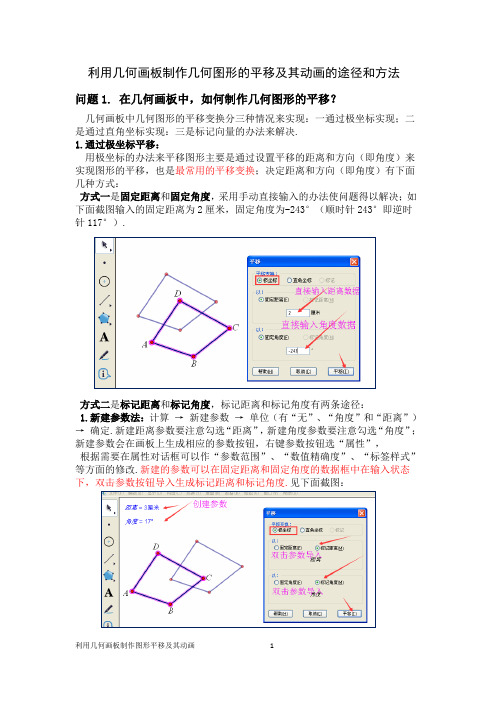
利用几何画板制作几何图形的平移及其动画的途径和方法问题1. 在几何画板中,如何制作几何图形的平移?几何画板中几何图形的平移变换分三种情况来实现:一通过极坐标实现;二是通过直角坐标实现:三是标记向量的办法来解决.1.通过极坐标平移:用极坐标的办法来平移图形主要是通过设置平移的距离和方向(即角度)来实现图形的平移,也是最常用的平移变换;决定距离和方向(即角度)有下面几种方式:方式一是固定距离和固定角度,采用手动直接输入的办法使问题得以解决;如下面截图输入的固定距离为2厘米,固定角度为-243°(顺时针243°即逆时针117°).方式二是标记距离和标记角度,标记距离和标记角度有两条途径:1.新建参数法:计算→新建参数→单位(有“无”、“角度”和“距离”)→确定.新建距离参数要注意勾选“距离”,新建角度参数要注意勾选“角度”;新建参数会在画板上生成相应的参数按钮,右键参数按钮选“属性”,根据需要在属性对话框可以作“参数范围”、“数值精确度”、“标签样式”等方面的修改.新建的参数可以在固定距离和固定角度的数据框中在输入状态下,双击参数按钮导入生成标记距离和标记角度.见下面截图:2.度量法:直接度量两点之间的距离和角的度数,会在画板上生成相应的按钮,右键按钮选“属性”,根据需要通过属性对话框可以作“数值精确度”、“标签样式”等修改.度量参数也可以在固定距离和固定角度中在输入状态下,双击参数按钮导入或勾选“标记距离”以及“标记角度”生成标记距离和标记角度.方式三是标记与固定相结合.比如距离采用参数导入的办法,角度采用固定角度的办法设置.以此类推!注:1.标记的新建参数法和度量均可以“手动”方式改变数据,从而改变图形的平移距离和方式;2.平移变换前要注意事先选定图形,否则不能调出对话框进行后续操作.2.通过直角坐标平移:直角坐标中的平移主要是通过平移的水平距离和垂直距离来实现图形的平移,水平距离和垂直距离的设置通过两个方面进行 . 决定垂直距离和水平距离也是有三种方式:方式一是水平距离和垂直距离,采用直接手动输入的办法使问题得以解决;这里不再举例.方式二是标记距离,标记距离有两条途径:一是新建参数法:二是度量法.其操作方式与在“极坐标”中的操作是一样的.所以在这里不再赘述.下面这个截图的⊿DEF的平移“水平距离”是创建的参数导入的,而垂直距离、两点间的距离参数导入的. “水平距离”可以利用键盘的“+”和度量A B“-”调节大小,(用“+”键需Shift配合)“垂直距离”可以拉动线段的端点来改变距离的大小.方式三是标记与固定相结合.比如水平距离采用参数导入的办法,垂直距离采用度量参数导入的办法.这里不再举例.3.通过标记向量的办法平移:向量即为“矢量”,是带有方向和长度的一条线段.“标记向量”和“平移”是不可分的,一般情况下“标记向量”的后一步即为“平移”.“标记向量”的基本操作是:选中线段两个端点(选点的顺序决定方向的正反)→变换→标记向量即可.拉伸线段可以调整图形平移的方向角度和距离.问题2. 在几何画板中,如何制作几何图形的平移并转换成动画?虽然上面我们总结了几何画板中图形的平移的方式,但不是每一种方式都可以制成易操作的平移动画.下面我以举例的方式介绍几种简单的较基础的平移动画,其它图形的平移可以类推!方法1.标记向量来平移图形,并制成动画例.将四边形ABCD沿线段MN或NM方向进行平移,并制作成动画。
如何使用玲珑画板创建动态图形7. 位移动画及整个几何体旋转动画

如何使用玲珑画板创建动态图形(之七)位移动画及整个几何体旋转动画一、练习目标:长方体的切割开。
二、作图步骤。
2.1 制作思路:本例是分割的典型,原理是:两个几何体。
分别对它们的顶点做位移动画。
开合:分别对两个几何体的所有顶点做反向的位移动画。
偏移:分别对两个几何体的相邻顶点做同向的位移动画。
旋转:对整个几何体进行旋转,做法简单。
2.2 画一个三维坐标系及两个正方体。
2.2.1说明:由于几何体的顶点在移动,所以平移动画的平移轴需另外画,因为后面还有旋转动画,所以我们画一个三维轴。
做为平移动画的平移轴及旋转动画的旋转轴。
用菜单生成生正六面体长度为4,所以画的三维坐标系,我们也画长为4,这样平移动画的长度就不用再计算了。
2.2.2画一个三维坐标系右键菜单:3D网格模式,画左图。
切换到2D网格模式,画右图。
然后,合成组件,合成前取消设置/合成时自动创建面的勾选。
2.2.3创建两正方体。
单击菜单:创建/正多面体/正六面体。
创建两次。
框选中所有,右键菜单:删除标签。
2.3 画三条线及线上点作为变量点(开合,偏移,旋转)使用。
单击菜单:动画/位移动画。
只选中线上的点,单击按钮[设定变量]。
只选中先前画的坐标系水平那根线,单击按钮[设定平移轴]。
2.4.1起值终值改为0,1,位移值-1.0。
(负值)只选中如图的点,单击按钮[添加到动画]。
2.4.2起值终值改为0,1,位移值1.0。
(正值)只选中如图的点,单击按钮[添加到动画]。
2.5 进行对齐。
(必须)特别注意:先将开合变量点拖动到0处位置。
单击菜单:编辑/精确定位/点到点对齐。
选中如上左图,按钮[设置定点],选中如上右图,按钮[对齐]结果如右图。
只选中第二个线上的点,单击按钮[设定变量]。
只选中先前画的坐标系水平那根线,单击按钮[设定平移轴]。
起值终值改为0,1,位移值2.0。
(2倍边长,)只选中如图的点,单击按钮[添加到动画]。
注意:因为在后面这八个点对齐到左边统一处理,所以实际位移长度是两个正方体左右边长的和。
利用几何画板制作函数图象生成动画的方法途径

利用几何画板制作函数图象生成动画的方法途径 赵化中学 郑宗平 建立平面直角坐标系的路径: 打开几何画板5.06(也可选择其它版本) → 自定义工具 → 经典坐标系 → 选择蚂蚁坐标系(无参版)(注:也可选择其他类型的坐标系) → 系统初始化 → 建立直角坐标平面 → 根据函数图象的需要利用操作控制台调整xy 的单位长、字体等等.制作函数图象生成动画的的方法途径:方法一.自定义变换法(下面以二次例函数2y x 为例)1.通过绘图 → 绘制新函数 → 在直角坐标平面内绘制出二次函数的图象:并把抛物线的粗细改成中等;选定图象通过属性x 的取值范围改为-3.3到3.3之间,同时把抛物线两端的箭头去掉.2.对应二次函数图象的取值范围在x 轴上对应构造点A (-3.3,0)和B (3.3,0)的两个点,连接AB 两点构造一条线段,在这条线段上构造一点P ,作过这一点并垂直于该线段的垂线,选中抛物线和垂线构造出抛物线和垂线的交点为E (也可以在交点处直接点击出来).3.⑴.依次选取点P(初始点)和点E(变换点)(注意选点的顺序)→单击变换菜单下的创建自定义变换→调出对话框“创建P到E的变换”→确定;生成后在变换下拉菜单中的最后会显示该项目.⑵.依次单击点A和P →构造线段AP →选定线段AP →变换→从P到E 的变换; 选定原抛物线隐藏,余下的抛物线暂时显示为一部分,选定设置动画部分的抛物线的颜色.注:两点创建自定义变换和线段添加此变换很重要,要注意操作顺序.4.制作点P到点B的移动按钮作为抛物线的生成按钮:依次选定点P和点B →编辑→操作性按钮→移动(选好速度,这里我选“中速”);再制作一个点P 到点A的移动按钮作为抛物线的重置按钮.其制作路径是一样的,速度这里我选“高速”.注:前面一个按钮是显示动画生成的按钮,后面一个按钮是回归原位的按钮.5.隐藏不需要在展示过程中线点等,这里我把“移动P→B”的名称修改为“图象生成”,把“移动P→A”的名称修改为“回归复位”;隐藏不需要显示点、线等(可以把线段AB上的点P保留,便于手动操作).点击动画按钮观看动画生成的过程的效果.1.自定义变换都需要都要有两个点,一个“初始点”(上面例子中线段AB 构造的P 点),还有一个 “变换点”(上面垂线和函数图象的交点E .),通过这样一对点就形成“自定义变换”;移动初始点时,变换的曲线会跟踪变化,这样课件用于教学,可以提升学生学习数学的兴趣.2.非特殊的二次函数的以及反比例、一次函数的图象的生成动画制作步骤方法是一样的.自定义变换与迭代过程类似,并且平移放缩等均可以照此方法进行“自定义变换”的创建.方法二 .轨迹法(下面以二次例函数.2y 05x x 6=-++为例)1.绘制函数的图象:绘图 → 绘制新函数 → 输入.205x x 6-++ → 在“方程”选好函数字母的符号表达形式(这里我选“符号y =”)→ 确定即可得到二次函数的图象并显示.2y 05x x 6=-++表达式.2.确定显示图象的自变量x 的取值范围,并利用参数的办法在x 轴上对应的描出起点和终点 :①. 这里取自变量我取-4~6,注意最好显示图象要具有轴对称性(因为本例对称轴为直线x 1=,则起点与终点的横坐标之和为12x x 2+=).②..在x 轴绘制起点:新建参数1x 4=-,把此参数导入绘制点的对话框描出起点()M 4,0-;在x 轴绘制终点:新建参数n 10=,计算1x n 6+=(作为2x ),把点1x n 6+=参数导入绘制点的对话框描出终点()N 6,0.注意:由于本例显示的是二次函数自变量在-4~6范围内的图象,所以要保证1x n 6+=的值在-4~6范围内,所以参数n 的取值范围有讲究,这里的n 取的范围为0~10,根据需要而取.3.构造轨迹:连接MN →选中线段并通过“构造”构造出线段的点A ;过点A 作x 轴的垂线,构造垂线和二次函数的交点B , 依次选定A B 、→ 构造 → 轨迹.4.隐藏不需要演示的点、线、标签等(包括二次函数的原图象)、5.选定迭代次数的按钮n 10=,制作动画按钮(设置好范围、速度、方向以及播放的次数等).1.“轨迹法”和前面的“自定义变换法”不同的是重新播放时需要把参数回归到起点的参数,所以若课件不需要显示某些点的坐标和标注线,最好用前面的“变换法”;2.反比例函数和一次函数图象照此方法可以类推!方法三 .迭代法迭代法(一)(下面以二次例函数2y 2x x 3=-++为例)1.新建六个参数:x (自变量),t (迭代初象),n (迭代深度)2.计算函数的值(注意全部采用导入计算),把标签修改为=y ”的形式,计 算迭代的初象+x t 的值;3.在平面直角坐标系中描出参数点()x,y ;4.深度迭代:选中参数x 和n ,并按住Shift → 变换 → 深度迭代导入 “+x t "→ 迭代;5. 修改迭代深度n 的的最高值可以得到迭代点数(最好是x 的范围除以t 的值,比如本例的=÷=n 4.50.0590);6.把迭代深度n 设置动画按钮(这里我命为“增加迭代点”,播放一次,速度30单位/秒.),制作函数图象两个隐藏/显示按钮(把函数图象和所描起点都选进去),一个属性设置为“总是显示”,一个属性设置为“总是隐藏”.依次选定“隐藏”、“动画”、“显示”制作系列按钮(这里我命为“动画按钮”,依序执行,设置好间隔时间.)7. 把n 的值设置为0,并隐藏函数图象;点击动画按钮观察效果.迭代法(二)1. 新建六个参数:a,b,c (系数常数),x (自变量),t (迭代初象),n (迭代深度);2. 计算()++a x ^2bx c 的值(即++2ax bx c 的值,注意全部采用导入计算),把标签修改为“=y ”的形式,计算迭代的初象+x t 的值;3.在平面直角坐标系中描出参数点()x,y;4.深度迭代:选中参数x和n,并按住Shift→变换→深度迭代导入“+x t" →迭代;5.修改迭代深度n的值可以得到迭代点数(最好是x的范围除以t的值,比如本例的=÷=n60.02300);修改n为起点的值(范围根据对称关系设置),修改t 的值可以达到迭代点的稀密程度,越小越密;也可以修改a,b,c值来调整抛物线的位置和开口方向等;6.把自变量x根据需要设置成动画参数,设置动画参数的范围.(最好把每秒单位取道谢)7.点击动画按钮可以观察点汇集成线并的过程,可以事先把x的取值设置到起始数据,这样动画放完后就会回归到一个完整图象.注:1.以上方法可以类推到其它形式的函数图象生成的动画制作,总体上讲“自定义变换法”更实用,更容易操作;2.方法途径的归纳是个人实践的总结,是个人所见,仅供参考!2020.1.4。
超级画板旋转功能的应用

超级画板旋转功能的应用几何画板软件以它强大的功能被数学教师赞美。
旋转功能更被数学教师用来作各种图形的旋转动画。
但遗憾的是,几何画板使用起来很不方便。
数学教师为制作一个能体现图形动态变化过程的动画,往往投入很多时间,花费很大精力,增加了数学教师的备课难度。
随着我国基础教育改革的深入,信息技术逐步走进普通中学数学课堂。
为了减轻数学教师的工作压力,让他们从繁忙的劳动中解脱出来,在教育部的支持下,一款由我国计算机技术人员研制的数学教育软件——超级画板应运而生。
超级画板使用方便、简单快捷、省时省力。
本文仅对旋转功能用具体实例说明超级画板的这些优点。
1 用超级画板制作平面图形的旋转动画1.1 函数图像的旋转例1 将函数2x y =的图像旋转得到x y =2的图像。
用几何画板不能直接完成函数的图像旋转,只能用技巧方法间接做到,并且步骤多[1],数学老师很是辛苦。
下面我们用超级画板完成旋转,其简单的过程会让你惊叹。
(1)打开超级画板→作图→函数或参数方程曲线,在弹出的对话框中函数栏目输入“2^x ”。
则绘出函数2x y =的图像;(2)选中原点→变换→指定旋转或放缩中心;(3)选中抛物线→变换→旋转角或放缩参数,在弹出的对话框中设旋转角为-t ;(4)作图→动画,在弹出的对话框中选择运动类型为“一次运动”,最小值为“0”,最大值为“pi/2”(pi 代表π)。
完成按钮制作如图1所示。
点击动画按钮,抛物线按顺时针方向旋转90°后自动停止。
分析这是图像绕顶点旋转的例子。
由此例可以看出,与文献[1]比较,同样是旋转,达到的效果相同,几何画板操作步骤多,而且画面杂乱,需要隐藏的对象很多;相比之下,超级画板操作步骤非常少,而且画面简单,不需要隐藏任何对象。
1.2 平面几何图形的旋转图1 旋转抛物线图2 旋转平行四边形例2 演示平行四边形中心对称。
(1)打开超级画板,隐藏坐标系,用智能画笔作三个点A、B、C;(2)选中点A、B、C→作图→常见多边形→平行四边形,则平行四边形ABCD作出;(3)选中点A、C→作图→点→线段的中点,则线段AC和中点E同时作出;(4)选中点E指定E为旋转中心,指定旋转参数为t;(5)选择所有对象→变换→旋转几何对象,则作出与平行四边形MNKL;(6)击右键→动画→运动参数设为t,运动类型选择“一次运动”,运动范围设为0到pi;(7)选择点A、B、C、D→作图→多边形→填充颜色→增加颜色透明度,如图2所示。
玲珑画板三角函数图像旋转动画

用玲珑画板制作sinx图像关于y轴对称的旋转动画第一步:点左侧栏黑色三角,选三角坐标系。
第二步:点参数—>y=f(x)函数
第三步:输入函数
第四步:全选整个图,右键—>合成组件
第五步:用左侧栏线段工具画一段线段,在线段上取一个点(线段本来是蓝色的,取线段上的点时候会变成绿色)
第六步:点上面菜单栏:动画—>旋转动画
把角度值改成180
然后选中线段上的那个点—>设定变量,再选中y轴上半段—>设为旋转轴:
接着选中右侧图像和x轴正半轴—>添加到动画:
然后拖动线段上的点就可以旋转了。
因为旋转过去之后右侧就没有图像了,可以再画一个sinx的图像放在右侧,这样旋转完了就是完整的sin|x|了。
最后还可以点上面菜单栏:创建—>控制类按钮—>自动动画按钮
然后选中线段上的点—>添加对象—>确定,就可以了,点动画按钮它就会自己动,(双击动画按钮左侧蓝色的区域可以打开这个控制板)。
也谈用_几何画板_制作图形的旋转动画

函数的奇偶性是高中数学的一项重要内容,为了说明奇函数图像关于原点对称的性质,需要将图像绕原点旋转180度。
《几何画板》变换菜单中有“旋转”变换,可以将图像绕某点旋转需要的角度。
但其中的变换过程——图像的旋转不能展现出来。
用Flash软件制作的课件,画面固然好看,但总有编造之感,其中的函数性质也不能很好地阐述。
有人曾撰文介绍了利用《几何画板》制作轨迹旋转动画的方法,因以函数y=x2为例的,其本身图像关于y轴对称,不具有一般性。
应先做出y轴的对称图像,再应用“反射”菜单即可。
现以函数y=x3为例,制作图像的旋转动画。
1.绘制函数y=x3的图像;2.在图像上任取一点D,标记y轴为镜面,反射点D得到对称点E;3.任作一圆A,在圆上任取一点B,作直线AB;4.过原点O作AB的平行线L,并“标记镜面”,再作E关于镜面L的反射点F;5.单击F、D,作轨迹,并隐藏直线L;6.使点B在圆A上运动,即可看到旋转的图像。
若利用坐标轴旋转公式x′=xcosθ-ysinθ,y′=xsinθ+ycosθ,又可得以下作法(同样以函数y=x3为例):(1)绘制函数y=x3的图像;(2)在图像上任取一点C,度量出C点横坐标XC、纵坐标YC; / 陶慧萍 柏永红(3)作圆D→作平行于x轴的直径FG→取半圆弧FG→在其上任取一点H,定义∠FDH=θ,→设置H在半圆弧FG上运动的动画.使θ从0°变到180°;(4)用度量中的计算器功能求出① XCcosθ-YCsinθ,定义为X′;② XCsinθ+YCcosθ,定义为Y′;(5)以(X′,Y′)为坐标绘制点I,同时取点I、C在构造(作图)菜单里作轨迹;(6)双击动画按钮即可看到绕原点旋转的曲线。
(作者单位:安徽铜陵市第三中学)刘金国等.运用《几何画板》制作轨迹的旋转动画[J].中学数学月刊.2005,(11).也谈用《几何画板》 制作图形的旋转动画。
利用几何画板制作图形的旋转动画的几条途径

利用几何画板制作图形的旋转动画的几条途径赵化中学郑宗平在几何画板中,制作一个几何图形的固定或者标记角度的旋转并不难,但要把旋转图形制作成可控的旋转动画其程序要多些,稍显繁琐!下面我根据自己平时的操作,简单介绍其中几种可控的旋转动画的途径(后面还附有两个与教材相衔接的实例的动画制作介绍).途径一.创建参数控制1.创建“旋转参数”:打开几何画板→数据→新建参数(名称可以自己定,比如:旋转角度.)→单位注意勾“角度”→右键“参数按钮”→属性→根据需要进行“标签”、“数值”、“参数(数值主要是反映精确度,参数包括角度范围、动画速度预设以及键盘调节等)”等的修改→确定→标记中心→选定要制作的旋转图形→变换→旋转→点选工作区的新建的“参数”标签→标记角度→旋转即可完成.可以根据设置利用键盘的“+”,“-”手动调节图形的旋转(利用“+”调节需要先按住Shift键).2.制作旋转动画;右键“参数按钮”(这里为“旋转角度”)→编辑→操作性按钮→“标签”设置好名称,“数值”设置好方向、改变数值的速度、范围等→确定即可以生成一个旋转的动画按钮→点击按钮观看动画的效果.注:把参数按钮制作成动画的方向有“增加”、“减少”、“双向”和“随机”. 选“增加”是逆时针旋转,选“减少”是顺时针旋转.一个参数可以同时制作“增加”、“减少”等多个动画按钮;分别制作不同方向按钮的好处是使旋转动画的方向具有可控性,制成系列按钮后使旋转形态具有之间的间隔时间可以随意“自定义”.注:根据课件的需要有碍画面美观的部分标签可以设置为隐藏(下同).路径二.线段或弧线上的点值控制1.度量“点的值”并计算所需参数:画一条线段(或弧)→构造线段(或弧)上的点→选定点→度量→点的值(或选定端点和构造点来度量比)→在工作区得到度量的“点的值”的标签→数据→计算→点选工作区的“点的值”的标签导入“计算”的编辑框→点计算器键盘上“*”→从计算器键盘上输入所需要设置的旋转最大角度数据(注意:单位选“度”)→在工作区得到“点的值*度数的值”的标签(这里设置为150°,标签重新名为“旋转角度”,见下面截图的左图.) →修改角度的精确度(注意:选“单位”表示精确到个位.)→标记旋转中心→选定要制作的旋转图形→变换→旋转→点选工作区的“点的比*度数的值”的标签→标记角度→旋转即可完成.(见下面截图右图)2.制作旋转动画;方式一.构造线段(或弧)上的点动画来制作旋转图形选定“构造线段(或弧)上的点”→编辑→操作性按钮→“标签”设置好名称,“动画”的方向、速度围等→确定即可以生成一个动画按钮→点击按钮观看动画的效果. 线段(或弧)上的点可以制作“向前”、“向后”动画按钮,便于分别制作不同方向按钮的好处是使旋转动画的方向具有可控性,制成系列按钮后使旋转形态具有之间的间隔时间可以随意“自定义”.(见下面截图)线段或弧线上的点值控制的好处在于其一.鼠标点定线段或弧线构造的弧线的点可以手动调节图形的旋转;其二.在播放图形的旋转时,可以拉动点来控制图形的旋转的起始位置.方式二. 构造线段(或弧)上的点移动来制作可控停的旋转图形1. 先度量“点的值”(这里的点命为“郑”)并计算所需的旋转角度参数(值得注意的是若计算旋转角度时前面填上“-”号,则旋转方向和默认的相反),然后先仿照方式一制作四边形ABCD关于点O为旋转中心的一个旋转图形;(见截图)2.依序点击选构造的点“郑、N”→编辑→操作类按扭→移动→速度(勾选一个)→勾选好“指定点或值开始的移动”→确定后可以生成移动按钮(郑→N);照此方法制作一个移动按钮(郑→M).把两个移动按钮制成一个系列按钮,这里命为“顺逆旋转”,可以展现旋转离开和回归的动画过程. “复位”按钮是动点和起点的平移动画的重合状态,这里和隐藏/显示(注意勾“总是隐藏”或“总是显示”)按钮做成一个系列按钮,这里命为“复位显示”,点击此按钮,图形回到原初状态,其它动画可以照此法制作.(见下面截图.)3.点击动画按钮,观看动画效果.有碍画面效果的标签可以隐藏.注:利用这种方式制作旋转动画,动画完成后图形不会自动弹回原来的出发处,“叫停即停”,是一种可控的旋转动画,比较有实用价值.路径三.构造角来控制1.构造控制角构造一个符合需要的角→以此角为圆心角构造一段弧→构造弧上的点依次点选弧的一个端点、构造点、弧的其中一个端点→度量→角度(可以隐藏弧)→在工作区得到度量的“角度标签”→以一个点标记中心→选定要制作的旋转图形→变换→旋转→点选工作区的度量的“角度标签”→标记角度→旋转即可完成.2.制作旋转动画;选定“构造的弧上的点”→编辑→操作性按钮→“标签”设置好名称,“动画”的方向、速度等→确定即可以生成一个动画按钮→点击按钮观看动画的效果.制作这个点“向前”、“向后”两个动画按钮;分别制作不同方向按钮的好处是使旋转动画的方向具有可控性,制成系列按钮后使旋转形态具有之间的间隔时间可以随意“自定义”.路径四.把弧的半径为基础构造一个图形来制作旋转动画.1.画一个圆⊙O→构造⊙O上的一段弧AB→构造AB上的一点C;;2.连接半径半径OC→作OC的一条垂线(见截图右图);3.在半径OC所在的直线和垂线上分别取点构成⊿DEF,并构造⊿DEF的内部颜色;4.选中点C→选择“构造”→“操作类按钮”→“动画”,运动方向设置为向前→速度为中速→确定→点击“动画点”按钮即可看到三角形绕点旋转的动画,制作两个不同方向的动画点,分别命为“向前”、“向后”(见截图)5.隐藏不需要的部分(见截图右图).点击动画按钮观看效果.从上面制作旋转动画四个途径来看,途径三、四这个动画和途径二似乎有些相同,但是控制的方式是不同的:途径二是通过弧上的“点的值”(点在弧长中的比列)为基础来计算角度参数来作为旋转依据的(不受弧度数控制,),而途径三、四受角度控制(实际上是受弧度控制),这四种途径方法各有优缺点,总体上讲途径二更适用于课件的制作所使用,特别是途径二的方式二比较适用于制作课件!附1:怎样用几何画板制作成中心对称的旋转重合的动画?新人教版九年级数学上册23.2节讲述了中心对称是指在平面内把一个图形绕着某一点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或称为成中心对称;中心对称图形是指在平面内把一个图形绕着某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形.在多媒体演示中,若能通过动画演示其重合过程,可以让学生加深领会;那么在几何画板中如何制作成中心对称的旋转动画呢?下面我以三角形为例简单谈谈其操作过程:1.在几何画板中画一个⊿ABC,并在适当的地方取一点O(根据课件需要而定);2.双击点O标记为中心(或选定点O→变换→标记中心)→选中⊿ABC →变换→旋转→固定角度输入180°→确定.得到⊿ABC关于点O成中心对称的⊿'''A B C.(主要是为观察⊿ABC旋转180°与之重合的动画所用.)3.画一条线段MN,构造线段MN上的一点D(直接取一点也可);180”(见下面的截图)这里前面我加了一个“-标记为中心(或选定点O → 变换 → 标记中心) →180” → 变换 → 标记角度 → 选中⊿ABC 及其构造的内部颜色 旋转→ 确定.得到⊿ABC 关于点O 旋转并按“-D 在MN 180”旋转的图形,看后面的截图.(也可以不先标记角度的方式,在固定角度的对话框呈 单击“-D 在*MN 180”标签即可导入并会转换为标记角度)绕点O 旋转出来的形态,根据可以课件需要可8.制作动画按钮:依次点选D N 、 → 编辑 → 操作性按钮 → 移动 → 设置→ “速度”等(这里选“中速”) → 确定即可得到“移动D N ”的动画按钮. 可以同法再做 “移动D M ”,速度选“高速”,可以把标签名称改为“回归原位”;点击此按钮图形瞬间回归到起始位置,可以重新从开始操作顺时针旋转180°.9.点击动画按钮“移动D N ”,观看旋转180°动画效果;可以把有碍画面美观的动画展示不需要的点、线以及标签作隐藏,比如本动画只留“移动D N ”和“回归原位”按钮.注:1.制作中心对称旋转180°动画也可以用新建角度参数然后制成动画的办法,但这种办法每次动画播送完后会总是自动弹回原位,不像利用线段上“点的值”的办法制作的动画具有可控性,不能留给学生观察停留重合的时间;2.制作中心对称图形旋转180°后的图形能与原来的图形重合的动画制作方法是一样的.附2:怎样利用几何画板制作一个图形旋转“任意”角度与另一个图形重合的动画?在初中几何图形变换中,旋转变换是基本的图形变换之一;通过旋转重合来认识和领会旋转的“保角、保距、保形”的性质是教学中常见的一种途径;那么在几何画板中,怎样制作两个图形旋转非特殊角重合的动画呢?下面我以三角形旋转非特殊角(这里我举旋转100°)为例简单谈谈其操作的一些基本步骤:1.先制作△ABC 绕着点O 顺时针旋转固定角度100°得到△'''A B C ;2.构造线段MN → 构造线段MN 的一个点P →度量 → 点的值 → 计算 →在计算器输入框点击“点在MN 的值”导入 → 依次输入“*”、100 → 右侧“单位”的下拉中选“度”→ 确定;(见下面截图的右面的箭头标示)注:若制作顺时针旋转,角度参数需要通过计算器面板在前面添加一个“-”号,3.双击点O 标记为旋转中心 → 选中△ABC → 变换 → 旋转 → 标记 → 确定 → 得到一个三角形(根据需要看是否制作顶点的字母标签,为了增强旋转重合的视觉效果,这里我构造这个三角形的内部填充色);4.同时制作两个三角形填充色的隐藏/显示按钮:一个属性设置为“总是显示”,另一个属性设置为“总是隐藏”;5.制作平移动画的按钮:依次选中P N、→编辑→操作性按钮→移动→选好移动的速度和移动的位置选项→确定,即可得到一个“移动P→N”动画按钮,此时点击这个按钮已经可以显示旋转重合的动画过程.5.制作两个系列按钮:⑴.制作显示内部填充色和旋转重合按钮:依次选中“显示三角形”和“移动P→N”动画按钮编辑→操作性按钮→系列→依序执行→这里间隔时间我设置为0.6秒→确定→标签命名为“旋转重合”;⑵.制作一个回归原始状态的按钮:①.依次选中P M、→编辑→操作性按钮→移动→选好移动的速度(这里的速度最好选“高速”)和移动的位置选项→确定,即可得到一个“移动P→M”动画按钮;②.依次选中“隐藏三角形”和“移动P→M”动画按钮编辑→操作性按钮→系列→同时执行→确定→标签命名为“回归复位”.点击“回归复位”就回归到原始状态,点击“旋转重合”就展示从旋转到重合的动画过程.注:手动点P可以通过拉动展示其旋转重合,且可以手动改变三角形的形态.6.根据课件需要可以制作动态显示旋转角度相等的标签(这里我制作3个标签,见下面截图.)和显示顶点旋转路径的虚线和对应点到旋转中心虚线,若需要也可制作成距离标签;这样在动态展示过程中会展示其角度数据变化相同的特征,让学生感知和领会旋转的“三保”;可以隐藏一部分按妞和标签.其它的旋转重合动画的制作可以类推!以上个人所见,仅供参考!2019年7月27日编创。
创建动态图形 旋转动画(中心旋转)
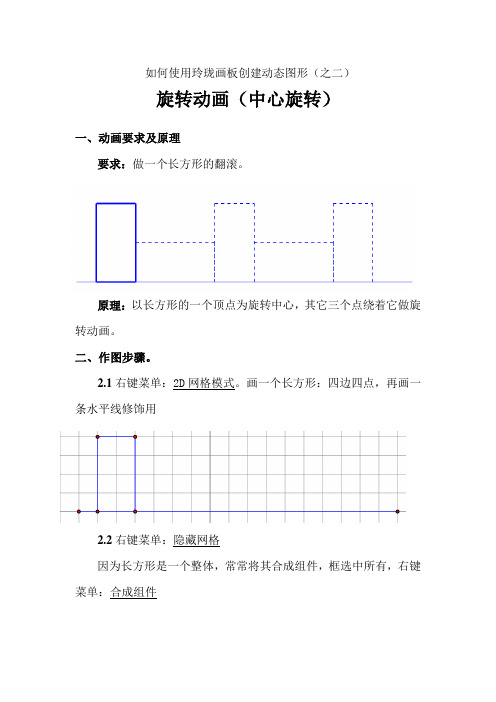
如何使用玲珑画板创建动态图形(之二)
旋转动画(中心旋转)
一、动画要求及原理
要求:做一个长方形的翻滚。
原理:以长方形的一个顶点为旋转中心,其它三个点绕着它做旋转动画。
二、作图步骤。
2.1右键菜单:2D网格模式。
画一个长方形:四边四点,再画一条水平线修饰用
2.2右键菜单:隐藏网格
因为长方形是一个整体,常常将其合成组件,框选中所有,右键菜单:合成组件
2.3在画面上画一条线及一个点,做为
动画控制条和控制点
2.4长方形的翻滚实际上是一个旋
转动画,上图我们设计翻滚四次,每
次90度,开始我们的动画之旅了。
单
击菜单:动画/旋转动画
2.5起值终值是表示动画控制点在线上的那一段时执行动画,最小是0,最大是1,在这里我们做四次翻滚,每次都是90度,所以起值终值就分别为,0——0.25,0.25——0.5,0.5——0.75,0.75——1。
这里不涉及三维,所以用中心旋转。
第一步:选中这个点,点按钮[设为旋转中心],如左图。
然后选中这个控制点,点按钮[设定变量],如右图。
2.6然后选中其它三个点,点按钮[添加到对象],然后拖动动画
点,可以看出长方形进行了一次翻滚
2.7然后再做第二次翻滚的动画,类似,起值,终值是0.25——0.5
2.8然后拖动控制点试试。
再做第三次动画,第四次动画类似,起值终值做相应改变。
三、注意事项。
1、绕中心旋转的旋转动画一般用于平面图形处理。
立体的一般都是旋转轴旋转动画。
2、做好动画后,一般会添加些线及面修饰一下,效果会更好。
利用几何画板制作旋转体的侧面拉动展开动画

利用几何画板制作旋转体的侧面拉动展开动画几何画板是一种能够帮助我们进行几何学习和教学的工具。
通过它,我们可以更直观地了解各种几何图形的性质和特点。
今天,我们就来利用几何画板制作一个旋转体的侧面拉动展开动画,让我们一起来探索一下吧!我们需要准备一些材料:一个几何画板、一根铅笔和一根细绳。
接下来,我们就来具体操作一下。
第一步,我们先要在几何画板上绘制一个旋转体。
我们可以选择一个简单的旋转体,比如圆柱体或圆锥体。
在画板上画一个圆,然后在圆的一侧画一条直线,这就是圆柱体的侧面。
如果要画圆锥体,可以画一个圆,然后从圆心向圆的边缘画一条直线,这就是圆锥体的侧面了。
第二步,我们需要在几何画板上固定一根细绳,这样我们就可以利用绳子来模拟旋转体的侧面展开。
把绳子绑在画板的一端,然后穿过绘制的圆柱体或圆锥体的侧面,再绑在画板的另一端。
这样,绳子就可以在画板上来回拉动,模拟出旋转体的侧面展开动画了。
第三步,我们可以开始拉动绳子,观察圆柱体或圆锥体的侧面是如何展开的。
当我们拉动绳子时,圆柱体或圆锥体的侧面会随着绳子的移动而展开,这样就可以形成一个动画效果了。
我们可以多次尝试,调整拉动的速度和力度,来观察不同展开效果。
第四步,我们还可以在画板上标注一些坐标或角度的信息,以帮助我们更直观地理解旋转体的展开过程。
比如可以在画板上标注不同位置的坐标,或者在侧面展开的不同阶段标注出展开的角度。
这样,我们就可以更清晰地了解旋转体的侧面展开过程了。
通过这样的操作,我们可以更直观地了解旋转体的侧面展开过程,从而更好地理解旋转体的性质和特点。
利用几何画板制作旋转体的侧面拉动展开动画也可以帮助我们培养一些动手能力和观察能力,是一种非常有益的几何学习方式。
在日常教学中,老师们也可以利用这种方法来教授学生们关于旋转体的知识。
通过让学生们自己动手操作,他们可以更深入地了解旋转体的性质和特点,从而更好地掌握相关知识。
利用几何画板制作旋转体的侧面拉动展开动画是一种很有趣、很有教育意义的活动。
利用几何画板制作旋转体的侧面拉动展开动画

利用几何画板制作旋转体的侧面拉动展开动画
旋转体是由一个平面图形绕着一个轴旋转而形成的立体图形。
要制作旋转体的侧面拉动展开动画,我们可以利用几何画板来实现。
我们需要准备一个几何画板,或者在纸上绘制一个正方形的图形,这个图形将作为旋转体的侧面展开动画的基础。
接下来,我们选择一个旋转点,这个点将作为旋转体的旋转轴。
在几何画板上,我们可以选择一个合适的点作为旋转点。
然后,我们可以在旋转点的附近画一个小圆来表示旋转点。
接下来,我们开始制作旋转体的侧面拉动展开动画。
我们可以选择一个角度作为旋转角度,然后将整个图形按照这个角度绕着旋转点旋转。
为了制作动画效果,我们可以使用步骤式的旋转,即每次旋转一个小角度,然后依次累加起来,直到旋转到一个完整的旋转角度。
在旋转的过程中,我们可以将每一次旋转的结果绘制在几何画板上,形成一个连续的旋转动画。
为了使旋转的过程更加流畅,我们可以根据需要选择一个合适的旋转速度和旋转步长。
在绘制旋转动画的我们还可以通过绘制相关的标记线和角度信息,帮助观众更好地理解旋转体的形状和结构。
当完成旋转动画的绘制时,我们可以回顾整个过程,并进行必要的修改和调整,以达到完美的效果。
通过利用几何画板制作旋转体的侧面拉动展开动画,我们可以更直观地理解旋转体的形状和结构,同时也可以增加观赏性和趣味性。
通过这种方式,我们可以更好地学习和理解几何学的相关知识。
怎样用几何画板制作成中心对称的旋转动画?

怎样用几何画板制作成中心对称的旋转动画? 中心对称是指在平面内把一个图形绕着某一点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称; 中心对称图形是指在平面内把一个图形绕着某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形.那么在几何画板中如何制作成中心对称的旋转动画呢?下面我以三角形为例简单谈谈其操作过程:1.在几何画板中画一个⊿ABC ,并在适当的地方取一点O (根据课件需要而定);2.双击点O 标记为中心 (或选定点O → 变换 → 标记中心)→ 选中⊿ABC → 变换 → 旋转 → 固定角度输入180°→ 确定.得到⊿ABC 关于点O 成中心对称的⊿'''A B C .(主要是为观察⊿ABC 旋转180°与之重合的动画所用.)3.画一条线段MN ,构造线段MN 上的一点D (直接取一点也可);4.选中点D → 度量 → 点的值;5.数据 → 计算 → 选中单击点的值的标签(D 在MN 上)→ * → 180 → “单位”的下拉菜单中选“度”(这一点要注意) → 确定即可得到关于角度的标签“-D 在*MN 180o ”(见下面的截图).注:这里前面我加了一个“-”号,图形旋转变换将按顺时针旋转,如果不加“-”号几何画板默认的是逆时针旋转.6.双击点O 标记为中心(或选定点O → 变换 → 标记中心) → 然后选中“-D 在*MN 180o ” → 变换 → 标记角度 → 选中⊿ABC 及其构造的内部颜色 → 变换 → 旋转→ 确定.得到⊿ABC 关于点O 旋转并按“-D 在*MN 180o ”旋转的图形,看后面的截图.(也可以不先标记角度的方式,在固定角度的对话框呈B'A'C 'OB A C8.制作动画按钮:依次点选D N 、 → 编辑 → 操作性按钮 → 移动 → 设置→ “速度”等(这里选“中速”) → 确定即可得到“移动D N ”的动画按钮. 可以同法再做 “移动D M ”,速度选“高速”,可以把标签名称改为“回归原位”;点击此按钮图形瞬间回归到起始位置,可以重新从开始操作顺时针旋转180°.9.点击动画按钮“移动D N ”,观看旋转180°动画效果;可以把有碍画面美观的动画展示不需要的点、线以及标签作隐藏,比如本动画只留“移动D N ”和“回归原位”按钮.注:1.制作中心对称旋转180°动画也可以用新建角度参数然后制成动画的办法,但这种办法每次动画播送完后会总是自动弹回原位,不像利用线段上“点的值”的办法制作的动画具有可控性,不能留给学生观察停留重合的时间;2.制作中心对称图形旋转180°后的图形能与原来的图形重合的动画制作方法是一样的.郑宗平2018.5.19。
几何画板在初中数学教学中的应用案例——几何画板中怎样围绕一点做旋转动画

几何画板在初中数学教学中的应用案例——几何画板中怎样围绕一点做旋转动画发布时间:2021-12-07T06:40:15.608Z 来源:《教育研究》2021年12月中35期作者:许薇[导读] 随着素质教育改革的全面展开,信息技术的迅速发展和计算机的普及,多媒体作为一种先进的教学手段,给课堂教学改革注入了无限的生机和活力。
几何画板在初中数学教学中体现它的直观性和动态性以及把抽象的数学问题变得具体、形象,使复杂的“数”通过直观的“形”来表示,能为数学活动提供探索的平台,为数学知识的建构提供技术支持。
昌吉市第七中学许薇新疆昌吉市 831100随着素质教育改革的全面展开,信息技术的迅速发展和计算机的普及,多媒体作为一种先进的教学手段,给课堂教学改革注入了无限的生机和活力。
几何画板在初中数学教学中体现它的直观性和动态性以及把抽象的数学问题变得具体、形象,使复杂的“数”通过直观的“形”来表示,能为数学活动提供探索的平台,为数学知识的建构提供技术支持。
在数学教学中,常常涉及到图形的旋转变换,教课书上呈现给学生们的,都是呆板的变换之后的图形,无法展现其变换过程。
而几何画板被称为“动态几何”,该软件能把较为抽象的几何图形形象化,并保持其“动态”的特点。
比如怎样实现某平面图形围绕一个点做旋转动画呢?黑板上是无法实现的,利用几何画板,就可以轻松实现了,我们以《义务教育教科书·人教版·九年级数学上册》第二十三章第1节的内容《图形的旋转》为例,以制作“三角形绕平面上任意一点旋转的动画”为例,具体的操作步骤如下:步骤一打开几何画板,使用左侧“线段工具”绘制任意三角形ABC,然后使用“点工具”在三角形外绘制任意一点O,双击点O,标记为旋转中心步骤二点击上方的“数据”菜单,在下拉菜单选择“新建参数”命令,在弹出的新建参数对话框将单位改为角度,然后点击“确定”;步骤三选中上步新建的角度参数,然后点击上方的“变换”菜单,在下拉菜单选择“标记角度”命令。
用几何画板如何制作一个正方形绕另一个正方形对角线交点旋转动画并展示重叠的阴影部分

用几何画板如何制作一个正方形绕着另一个正方形对角线交点旋转的动画并展示重叠的阴影部分一个正方形绕着另一个正方形对角线交点旋转是指一个正方形的顶点放在另一个正方形对角线交点上旋转的意思,制作这样的动画并不难,关键是旋转到不同位置还要同时展示重叠的阴影部分,这样步骤就多了一些.下面我根据自己的操作分两种情况谈谈其简要步骤:一.旋转的最大角度为90°.1.制作一个正方形ABCD,对角线AC BD、交于点O;2.构造正方形ABCD的边DA上的一点F:选中线段→构造→线段上的点(在线段取一点也可);3.作射线OF,并在射线OF上以点O为端点截取一条线段来等于正方形ABCD 的一边长;在射线OF上来截取这点很重要!4.以3点中截取的线段为边长作一个与正方形ABCD全等的的正方形;(见下面左图中蓝色正方形)5.依次选中部分重叠部分的四边形的四个顶点→构造→四边形内部→取好颜色;(见下面右图中绿色部分)A”的动画按钮F D”的动画按钮;可以把刚才的两个按钮做成一个系列按钮,其操作是:按需要顺序选中“A”和“移动F D”按钮性按钮→系列依序执行→设置好间隔时间等→动画按钮(这里我命为“顺逆旋转”);B7.点击动画按钮观看效果.旋转角度的最大角度为90°的制作比较简单.二.旋转的最大角度不小于90°.旋转的最大角度不小于90°的制作起来步骤要多些,有点繁琐!下面我以顺5.依次选中部分重叠部分的四边形的四个顶点→构造→四边形内部→取好颜色(见下面左图中红色部分);分别拉动边界点F到正方形不同的边上可把蓝色正方形旋转至下面中图和右图的位置,同法构造重叠部分的四边形内部颜色(见下面左图中绿色部分和右图中黄色部分);6.制作5点中的重叠阴影部分的三种情况下总是显示的按钮:分别选中重叠四边形内部→编辑→操作性按钮→隐藏/显示→即可得到一个隐藏/显示的按钮→右键按钮→属性勾选“总是显示对象”.→命好标签名称(这里的这里三个显示按钮我分别命为显示1、显示2、显示3,见下面的截图左.)7.同法作三种情况下重叠部分的总是隐藏按钮分别命为隐藏1、隐藏2、隐藏3(见下面的截图左);注意勾选“总是隐藏对象”.8.分别按前面的操作方法制作点F在每一边上的移动动画按钮:“移动F D”、“移动F C”、“移动F B”、“移动F A”(见下面的截图左,这里“移动F A”是为制作图形高速回归原位起始位置所用);9.点击在8点的动画按钮虽然可以看到相应的旋转动画,但在不同的位置其重叠部分的阴影不能正常展示出来.解决的的办法是把动画按钮与隐藏、显示按钮相的做成系列按钮,比如:“移动F D”要与“显示1”、“隐藏2”和“隐藏3”结合按前面制作系列办法做成组合按钮.这里命为“动态展示1”(注:点F 移动在AD边上时只显示红色阴影,而绿色和和黄色阴影会隐藏,).照此法“移动F C”要与“隐藏1”、“显示2”和“隐藏3”结合制作“动态展示2”,“移动F B”要与“隐藏1”、“隐藏2”和“显示3”结合制作“动态展示2”.以此类推!10.依序选中“动态展示1”、“动态展示2”、“动态展示3”做一个系列按钮命为“依次动态展示”,可以连续展现旋转重叠部分的情况(见截图右);注意按钮选定的顺序!11.把“移动F A”要与“显示1”、“隐藏2”和“隐藏3”结合制作一个“回归原位”的移动动画按钮,以备重新从起始位置观看旋转以及展示重叠阴影部分的动画,注意速度选“高速”.12.点击动画按钮,观看动画展示的效果.可以把有碍画面美观的其它标签、点、线作隐藏.郑宗平 2018.5.13原创。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
怎样用几何画板制作成中心对称的旋转动画? 中心对称是指在平面内把一个图形绕着某一点旋转
180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称; 中心对称图形是指在平面内把一个图形绕着某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形.那么在几何画板中如何制作成中心对称的旋转动画呢?下面我以三角形为例简单谈谈其操作过程:
1.在几何画板中画一个⊿ABC ,并在适当的地方取一点O (根据课件需要而定);
2.双击点O 标记为中心 (或选定点O → 变换 → 标记中心)→ 选中⊿ABC → 变换 → 旋转 → 固定角度输入180°→ 确定.得到⊿ABC 关于点O 成中心对称的⊿'''A B C .(主要是为观察⊿ABC 旋转180°与之重合的动画所用.)
3.画一条线段MN ,构造线段MN 上的一点D (直接取一点也可);
4.选中点D → 度量 → 点的值;
5.数据 → 计算 → 选中单击点的值的标签(D 在MN 上)→ * → 180 → “单位”的下拉菜单中选“度”(这一点要注意) → 确定即可得到关于角度的标签“-D 在*MN 180o ”(见下面的截图).
注:这里前面我加了一个“-”号,图形旋转变换将按顺时针旋转,如果不加“-”号几何画板默认的是逆时针旋转.
6.双击点O 标记为中心(或选定点O → 变换 → 标记中心) → 然后选中“-D 在*MN 180o ” → 变换 → 标记角度 → 选中⊿ABC 及其构造的内部颜色 → 变换 → 旋转→ 确定.得到⊿ABC 关于点O 旋转并按“-D 在*MN 180o ”旋转的图形,看后面的截图.(也可以不先标记角度的方式,在固定角度的对话框呈B'A'
C 'O
B A C
8.制作动画按钮:依次点选D N 、 → 编辑 → 操作性按钮 → 移动 → 设置→ “速度”等(这里选“中速”) → 确定即可得到“移动D N ”的动画按钮. 可以同法再做 “移动D M ”,速度选“高速”,可以把标签名称改为“回归原位”;点击此按钮图形瞬间回归到起始位置,可以重新从开始操作顺时针旋转180°.
9.点击动画按钮“移动D N ”,观看旋转180°动画效果;可以把有碍画面美观的动画展示不需要的点、线以及标签作隐藏,比如本动画只留“移动D N ”和“回归原位”按钮.
注:
1.制作中心对称旋转180°动画也可以用新建角度参数然后制成动画的办法,但这种办法每次动画播送完后会总是自动弹回原位,不像利用线段上“点的值”的办法制作的动画具有可控性,不能留给学生观察停留重合的时间;
2.制作中心对称图形旋转180°后的图形能与原来的图形重合的动画制作方法是一样的.
郑宗平
2018.5.19。
