第5章 张角定理及应用
张角定理在证明调和数列中的应用

由张角定理得 曼B 十 A : 。P 卫 P :
m m
.
’
② 一
为视 点 ,对 D, , CE 用张角定理 , 得
一
把①代入②并整理得
图5
+ : , 证毕.
r m
s 0 = 一 i + — i—— 9— —— ) i9 。 s n n 。—n(— o——— s— — 0— . — — ——
,
由题设易证 A , E DA 分别 为 AB C的 内 A 角与外 角的平 分线.
设 A = ,B = , D dA 6 AC cA e 则 以 A = , E= ,
G
在 R AA D和 R AP E中, t P t B 分别得
P = R if, B 2s . A 2 s l P = rn n i ④
求证 :B,, C成调和数列. A dA 证 明 如图 2 曰 ,
以 A为视点 , 则对线 段 B , C 的 张 角 OO a1 4。 = = 5 ,由张角定 3 理及 =
一
F及 , , C G用 张 角
定理 , 得
K8 = KL + 。
F L
G
// E
图6
P = 求证 : ,, C m, 尺 rm
成 调和数 列.
D
c 使 : , A , 连 G交 加 于 c 求证 :E , B ,
D ,E成调和数列. EC
证 明 如 图 5 ,
F
证明 作两圆的直径 A , B 2, 0D和 OE 连 结P P P P. A,B, D,E 容易证 明 A,, PE和 B P ,, D分别共线. / P =_ = , B C LD 设 _ C /E a / P = = A _
[张角定理在平面几何中的应用]什么是张角定理
![[张角定理在平面几何中的应用]什么是张角定理](https://img.taocdn.com/s3/m/0513e8c22e3f5727a5e962b1.png)
[张角定理在平面几何中的应用]什么是张角定理江苏泰州实验学校 225300 摘要:由面积原理推导出的张角定理在平面几何中有着极其广泛的应用. 本文现分类举例说明,以供初中数学教师阅读时参考.关键词:张角定理;应用[?]张角定理已知由点P发出的三条射线PA,PB,PC,且∠APC=α,∠CPB=β,∠APB=α+β<180°,那么A,B,C三点在一直线上的充分必要条件是=+.证明如图1,如果A,B,C三点共线,那么△PAB=△PAC+△PCB. 所以PA?PB?sin(α+β)=PA?PC?sinα+PB?PC?sinβ. 两边同时除以PA?PB?PC,即得所要证的等式.[α][β][P][A][C][B]图1反之,如果命题中等式成立,那么反推可得△PAB=△PAC+△PCB,这说明△ABC=△PAB-△PAC-△PCB=0,故A,B,C三点共线.[?]定理的应用1. 证线段相等例1如图2,以⊙O的直径AB为一边作等边三角形ABC,同时将另一侧的半圆三等分,其分点为M,N,连结CM,分别交AB于点D,E. 求证:AD=DE=EB.证明如图2,连结AM,OM,则以A为视点,对C,D,M用张角定理,得=+.所以AD=.[C][A][D][O][E][B][M][N]图2设⊙O的半径为R,则AD==R.由图形的对称性知BE=R.所以DE=2R-R-R=R.故AD=DE=EB.2. 证线段的和差关系例2在正五边形ABCDE中,AC交BE于点F,求证:AC=AB+BF.证明如图3,以B为视点,对A,F,C用张角定理,得=+. 设AB=BC=k(k>0),则BF=k.所以AB+BF=k+k=k=k=2kcosα.而在△ABC中,由正弦定理,得AC==k=k=2kcosα. 故AC=AB+BF.3. 证复杂比例式例3在△ABC中,∠A的平分线为AD,求证:AD2=AB?AC-BD?DC.证明如图4,以A为视点,对B,D,C用张角定理,得=+,所以AD=.在△BDA和△ADC中,由余弦定理,得BD2=c21-cos2α,DC2=b21-cos2α.所以BD?DC=bc1-cos2α. 故AB?AC-BD?DC=cos2α=AD2.4. 证线段倒数的和差关系例4已知四边形ABCD两对对边的延长线分别交于点K,L,过点K,L作直线,对角线AC,DB的延长线分别交直线KL于点G,F. 求证:+=.[D][A][K][F][L][G][C][B][α][β]图5证明如图5,设KA=a,KB=b,KC=c,KD=d,KF=f,KG=g,KL=l,则以K为视点,分别对A,B,L;D,C,L;D,B,F及A,C,G用张角定理,得=+,①=+,②=+,③=+. ④所以①+②-③-④,得--=0.所以+=,即+=.5. 证三点共线例5如图6,在⊙O内,直径AB⊥半径OC,⊙O′与OB,OC相切于点D,E,并与⊙O内切于点F,求证:A,E,F三点共线.[A][O][O′][D][B][F][E][C]图6证明设OD=O′D=O′E=r,则OO′=r,且∠O′OD=45°,O,O′,F三点共线. 再设OA=OF=R.因为OO′=R-r=r,所以r==(-1)R.所以==.所以=+.由张角定理知A,E,F三点共线.6. 证三线共点例6在△ABC中,自B,C分别向∠A的外角平分线作垂线,得垂足M,N,求证:BN,CM与∠A的内角平分线共点.证明如图7,设CM与∠A的内角平分线交于K点,则以A为视点,对C,K,M用张角定理得=+,即=+.①同理,设BN与∠A的内角平分线交于K′点,则以A为视点,对B,K′,N用张角定理,得=+.②因为AM=ABsinα,AN=ACsinα,故将其分别代入①②得=+=.所以AK=AK′,故K与K′点重合. 因此BN,CM与∠A的内角平分线共点.综上所述可知:应用张角定理证明几何题时,关键在于根据题设,寻找与结论有关的线段所在的三角形,找准视点,利用张角定理写出关系式:=+,再结合正弦、余弦定理,三角函数的定义和三角形的面积公式S=bcsinA,……通过变形化简,消去无用的参数即可.该方法简捷明快,富有规律,而且不添或少添辅助线,符合新课程改革关于“拓宽视野、注重科研、探究应用”的理念要求,故笔者认为,在今后的教学过程中,对这类专题有必要引起重视.教学实践表明,研究几何定理,对于帮助学生理解课本内容,提高分析问题和解决问题的能力,启迪思维、勤于探究、掌握“双基”、感悟数学思想均有益处. 另外,这样的专题研究,对于培养学生的探索精神和创新意识将会起到积极的推动作用. 因而,随着教育的不断现代化,引导学生探究几何定理的应用,体现数学研究的潜能是十分重要的.本文为全文原貌未安装PDF浏览器用户请先下载安装原版全文内容仅供参考。
米勒圆最大张角定理

米勒圆最大张角定理
米勒圆最大张角定理,又称米勒外切定理,是一种引人注目的几何定理。
它说明如果一个点在一个圆的外切线上,那么它和另一个圆心之间的角度是最大的,而不管它在外切线上的具体位置。
这种定理最早由德国几何家和历史学家威廉·米勒提出。
米勒圆最大张角定理解释如下:若在一个圆内有一个点,与它的切点相连接形成一条射线,从另一个圆的圆心穿过该射线,那么该点到另一个圆心之间的夹角是最大的。
可以用一个直观的例子来证明米勒圆最大张角定理。
假设我们有三个圆,分别是A,B和C的圆。
我们有一个点P,它位于圆A 的外切线上。
根据米勒圆最大张角定理,我们能够确定点P和圆B 的圆心士P B之间的夹角最大。
同样,当点P位于圆A外切线上时,它和圆C的圆心之间夹角也是最大的,因此,米勒圆最大张角定理有证。
米勒圆最大张角定理具有重要的实际应用,有助于改善产品工艺中所用到的圆滑曲线。
例如,在航空航天工程中,米勒圆最
大张角定理可以帮助设计出更好的飞行空域,以充分利用飞行器的机动性。
此外,米勒圆最大张角定理还可以用来帮助改进飞行器的性能和高度,使其更安全。
米勒圆最大张角定理是一个非常有趣的几何定理,从它可以看到,一个点在一个圆的外切线上时,它和另一个圆心之间的夹角最大。
它不仅有着重要的实际应用,而且也在代数几何学中有着深远的意义。
张角定理

张角定理在△ABC中,D是BC上的一点,连结AD。
那么sin∠BAD/AC+sin∠CAD/AB=sin∠BAC/AD。
分角定理在△ABC中,D是边BC上异于B,C或其延长线上的一点,连结AD,则有BD/CD=(sin∠BAD/sin∠CAD)*(AB/AC)。
斯坦纳—莱默斯定理如图,已知△ABC中,两内角的平分线BD=CE。
求证:AB=AC。
证法①:(斯坦纳原证) 如图1,假设AB>AC.则∠BEC>∠BDC (1)在△BCE与△CBD中,斯坦纳原证∵BD=CE,BC公共,∠BCE>∠CBD,∴BE>CD.作平行四边形BDCF,连接EF.∵BE>CD=BF.∴∠1<∠2.∵CE=BD=CF .∴∠3=∠4.∴∠BEC<∠BFC=∠BDC (2)(1)与(2)矛盾.∴AB≯AC.同理AC≯AB.故AB=AC.证法②:(海塞证法,德国数学家(L.O.Hesse,1811-1874))作∠BDF=∠BCE;并使DF=BC∵BD=EC,∴△BDF≌△ECB,BF=BE,∠BEC=∠DBF.示意图设∠ABD=∠DBC=α,∠ACE=∠ECB=β,∠FBC=∠BEC+α=180°-2α-β+α=180°-(α+β);∠CDF=∠FDB+∠CDB=β+180°-2β-α=180°-(α+β);∴∠FBC=∠CDF,∵2α+2β<180°,∴α+β<90°,∴∠FBC=∠CDF>90°∴过C点作FB的垂线和过F点作CD的垂线必都在FB和CD的延长线上.设垂足分别为G、H;∠HDF=∠CBG;∵BC=DF,∴Rt△CGB≌Rt△FHD,∴CG=FH,BC=FD连接CF,∵CF=FC,FH=CG,∴Rt△CGF≌△FHC(HL),∴FG=CH, 又∵BG=DH,∴BF=CD, 又∵BF=BE,∴CD=BE,∵BE=CD,BC=CB,EC=DB,∴△BEC≌△CDB,∴∠ABC=∠ACB∴AB=AC.证法③设二角的一半分别为α、βsin(2α+β)/ sin2α= BC/CE = BC/BD = sin(α+2β)/ sin2β,∴2sinαcosαsin(α+2β) - 2sinβcosβsin(2α+β) =0→sinα[sin2(α+β)+sin 2β]- sinβ[sin2(α+β)+ sin2α]=0→sin2(α+β)[sinα-sinβ]+2 sinαsinβ[cosβ- cosα]=0→sin [(α-β)/2][sin2(α+β) cos[(α+β)/2] + 2 sinαsinβsin [(α+β)/2]=0,∴sin[(α-β)/2]=0∴α=β,∴AB=AC.证法④用张角定理:2cosα/BE=1/BC+1/AB2cosβ/CD=1/BC+1/AC若α>β 可推出AB>AC矛盾!若α<β 可推出AB <AC矛盾!所以AB=AC梅涅劳斯定理证明一过点A作AG∥DF交BC的延长线于点G.则证毕证明二过点C作CP∥DF交AB于P,则两式相乘得西木松定理证明一:△ABC外接圆上有点P,且PE⊥AC于E,PF⊥BC于F,PD⊥AB于D,分别连FE、FD、BP、CP.易证P、B、D、F和P、F、C、E分别共圆,(四点共圆)在PBDF圆内,∠DBP+∠DFP=180度,在ABPC圆内∠ABP+∠ACP =180度,∴∠DFP=∠ACP ①,在PFCE圆内∠PFE=∠PCE②而∠ACP+∠PCE=180°③∴∠DFP+∠PFE=180°④即D、F、E共线. 反之,当D、F、E共线时,由④→②→③→①可见A、B、P、C共圆.证明一证明二:如图,若L、M、N三点共线,连结BP,CP,则因PL垂直于BC,PM垂直于AC,PN垂直于AB,有B、L、P、N和P、M、C、L分别四点共圆,有∠NBP = ∠NLP= ∠MLP= ∠MCP.故A、B、P、C四点共圆。
张角定理(2013)S

张角定理张角定理:设A,C,B顺次分别是平面内一点P所引三条射线PA,PC,PB上的点,线段AC,CB对点P的张角分别为α,β,α+β< 180°,则A,C,B三点共线的充要条件是例题选讲:例1、如图,已知ABCD为四边形,两组对边延长后得交点E,F,对角线BD// EF,AC的延长线交EF于G.求证:EG=GF.例6例7 已知△ABC的重心,过G作直线分别交△ABC的两边AB,AC于E,F. 求证:EG 2GF例8 如图,“筝形”ABCD中,AB = AD,BC=DC.经过AC与BD的交点O任作两条直线,分别交AD于E,交BC于F,交AB于G,交CD于H,GF,EH 分别交BD于I,J.求证:OI=OJ .例9如图,在线段AB上取内分点M,使AM≤BM,分别以MA,MB为边,在AB的同侧作正方形AMCD和MBEF,⊙O和⊙Q分别是这两个正方形的外接圆,两圆交于M,N.求证:B,C,N三点共线.练习题1.在矩形ABCD中,AB= a,BC= b,M为BC中点,DE⊥射线AM于E,求DE之长.(用a,b表示)2. △ABC中,AB=AC,AD为BC边上的高,AD的中点为M,CM的延长线交AB于K.求证:AB=3AK.3.已知AC⊥AB,BD⊥AB,AD和BC相交于点E,EF⊥AB于F.又AC=P,BD=Q,EF=r,ΑF=m,FB=n.求证:111p q r+=.4.梯形ABCD (AB // DC)的对角线AC,BD相交于P,过P作梯形下底的平行线交两腰AD于M,BC于N.求证:PM=PN.5.设∠XOY的平分线上任一点为P,过P作两条任意直线AB,CD,分别交OX,OY于A,C,B,D.求证:OC ·OA·BD=OB·OD·AC.参考答案:。
张角定理及应用

张角定理及应用张角定理是指:在三角形ABC中,如果点D是边AB上的一点,且AE是边AC 的平分线(E为BC的中点),则有AD^2 = AE·AB。
这个定理是根据相似三角形来推导的。
我们知道,如果一条直线与另外一条平行直线交截其中一条直线的部分,则交截部分上的两个线段的比例等于这两条直线在另一条直线上对应线段的比例。
在三角形ABC中,如果点D在边AB上,且点E是边AC的中点,则根据张角定理可知,AD^2与AE·AB之间存在某种比例关系。
具体来说,AD^2和AE·AB 之间的比例关系是乘法关系,即AD^2 = AE·AB。
这个定理的应用非常广泛。
以下是几个与张角定理相关的应用:1. 求解三角形内部的线段比例:根据张角定理,我们可以通过已知线段的长度,来推导出未知线段的长度。
例如,如果已知一条边长和此边上的一个点到顶点的距离,我们可以通过张角定理来求解此点到另一顶点的距离。
2. 证明三角形内部的线段相等:如果我们已知两个线段在三角形的一条边上等长,并且这两个线段与此边上的一个顶点分别相交于两个不同的点,那么根据张角定理我们就可以推导出这两个点到另一顶点的距离相等。
3. 探讨几何图形的对称性:通过应用张角定理,我们可以证明某些几何图形具有对称性。
例如,在一个等腰三角形中,如果我们在等腰边上选择两个互为中点的点,然后根据张角定理可以推导出这两个点到另一顶点的距离相等,从而证明此等腰三角形具有轴对称性。
4. 解决面积相关问题:通过张角定理,我们可以推导出两个三角形面积之间的比例关系。
例如,如果我们已知一个三角形和一条平行于其中一边的直线,根据张角定理可以推导出两个三角形的底边相等,进而可以得出两个三角形的面积之间的比例。
综上所述,张角定理是一个基于相似三角形的几何定理,它可以应用于求解三角形内部的线段比例、证明线段相等、探讨几何图形的对称性以及解决面积相关问题。
这个定理对于理解和分析各种几何问题都非常有用。
米勒定理求最大张角

米勒定理求最大张角
摘要:
1.米勒定理简介
2.张角的概念及求最大张角的意义
3.应用米勒定理求最大张角的方法
4.结论
正文:
1.米勒定理简介
米勒定理,又称为米勒引理,是数论中的一个重要定理。
它由美国数学家乔治·米勒(George ler)于1901 年提出。
该定理主要描述了整数n 和m 的最大公约数以及它们的乘积与最小公倍数之间的关系。
具体来说,米勒定理表明:对于任意整数n 和m,它们的最大公约数d 与最小公倍数l 的比值等于两数的乘积,即d/l = n*m。
2.张角的概念及求最大张角的意义
张角,又称张开角,是指两条射线共同围成的角度,它的大小可以用度数或弧度表示。
在几何学中,求最大张角通常意味着寻找两条射线之间能够形成的最大角度。
在许多实际问题中,求最大张角具有重要意义,例如在光学、力学等领域。
3.应用米勒定理求最大张角的方法
在求解最大张角的问题时,我们可以将问题转化为求解两个整数的最大公约数和最小公倍数的问题。
具体操作步骤如下:
(1)将两条射线分别表示为整数a 和b,其中a 和b 的取值范围可以
是任意整数;
(2)根据米勒定理,求解a 和b 的最大公约数d;
(3)根据米勒定理,求解a 和b 的最小公倍数l;
(4)最大张角θ可表示为θ= arccos(d/l),其中arccos 表示反余弦函数。
4.结论
通过应用米勒定理,我们可以方便地求解最大张角问题。
这种方法将复杂的角度计算问题转化为简单的数论问题,为解决实际问题提供了一种有效途径。
天体运动中的几何张角问题

天体运动中的几何张角问题
天体运动中的几何张角问题是一个复杂的问题,涉及到天体之间的相对运动和引力相互作用。
几何张角是指两个天体之间的角度,通常用于描述它们的相对位置和运动轨迹。
在解决天体运动中的几何张角问题时,需要考虑以下几个因素:
1. 天体的位置和速度:天体的位置和速度是描述其运动状态的基本参数。
我们需要知道每个天体在某个时刻的位置和速度,以便计算它们之间的相对运动轨迹和几何张角。
2. 引力相互作用:天体之间的引力相互作用是影响它们运动轨迹的重要因素。
我们需要考虑不同天体之间的引力作用,以便更准确地描述它们的相对运动轨迹。
3. 时间演化:天体的运动轨迹是一个时间依赖的过程。
我们需要考虑时间演化对天体运动轨迹的影响,以便更准确地预测它们之间的几何张角。
解决天体运动中的几何张角问题通常需要使用数值方法,例如数值积分和数值逼近等。
这些方法可以帮助我们精确地计算天体的运动轨迹和几何张角,从而更好地理解天体之间的相对运动和引力相互作用。
张角相等四点共圆证明

张角相等四点共圆证明你知道吗,咱们这道题可不是随随便便的那种几何题。
它可牵扯到圆,四个点,以及一个大家不太熟悉但又特别有趣的概念——张角。
看你现在可能有点懵,啥是张角?别急,咱慢慢来讲。
张角,顾名思义,就是两条射线从一个点出发,所形成的角度。
如果这两条射线和圆的切线有所关联,那就不单单是普通的角了。
哈哈,没错,数学的世界里,有时候你想不到的事,它就悄悄发生了。
想象一下,一块饼,咱这四个点就像是饼上的四个樱桃,而张角的关系呢,就是饼上四颗樱桃的位置和饼皮的切割方式。
也就是说,这四个点不仅仅是随便在哪儿的,它们得满足某些条件——啥条件呢?这些点得能在同一个圆上,嘿!这就是所谓的四点共圆。
你要知道,如果四个点在同一个圆上,那它们就有个奇特的联系——什么联系?就是它们之间的角度。
哎,不信你试试,画个圆,随便撒上几个点,但这四个点,哦不,得要特别的,那可不随便哪四个点能做得到了。
这时,数学的魔法开始悄悄显现,张角的神奇之处就出来了。
说到这,你可能会想,“哎,四个点怎么能共圆?我随便找几个点,能不能共圆呢?”这问题问得好!让我们来推理一下。
如果你随便找四个点,它们不一定能共圆。
为啥呢?因为四个点之间的关系得满足一定的条件。
就比如说,假如说这四个点的张角相等,那你就有可能把这四个点放到同一个圆上。
是的,张角相等,四点共圆的定理就是这样诞生的。
这个问题在古代几何学里可是个大问题,很多数学家都费了好大力气才证明了它。
你看,张角相等这条件,可不是随便谁都能满足的。
但一旦满足了,哎,这四个点就成了圆的点,像是圆的朋友,永远挂在圆上不离开。
再举个简单的例子,假设你有四个点,A、B、C、D,它们的张角相等。
你可以通过圆的几何特性推算出,这四个点一定可以被圆圈住——它们在一个圆上。
这不是说随便给几个点画个圆,而是它们的角度关系让它们天生就有了在同一个圆上的“磁场”,好像是圆本身把它们吸引过去一样。
你想啊,圆这个东西,它有种神奇的力量,能够“容纳”很多点,所有的这些点,彼此之间的关系都会变得和谐。
张角的几何原理

张角的几何原理张角是中国古代数学家、天文学家、医学家以及典籍编辑家,他是中国古代数学的重要代表之一。
他对数学的贡献主要体现在《九章算术》中。
在《九章算术》中,张角提出了几何原理的一些基本概念和方法,这些基本概念和方法对后世数学的发展起到了重要的推动作用。
首先,张角提出了三韦弧的概念。
三韦弧可以看作是圆的一种特殊情况,在几何上起到了重要的作用。
张角通过三韦弧的研究,进一步深化了对圆的认识。
他发现,只要确定了两条边和它们之间的角,就可以确定三韦弧的弧长。
这个发现在几何计算中应用广泛,对于解决实际问题具有重要意义。
其次,张角提出了三角形的面积公式。
在《九章算术》中,张角给出了通过计算三角形的三边长度来求解三角形面积的公式。
这个公式被后世广泛应用,成为几何学的基础知识之一。
张角的面积公式提供了计算三角形面积的一种简单有效的方法,为后世数学家的研究提供了基础。
此外,张角还提出了类似勾股定理的定理。
勾股定理在中国古代已有所发现,但是张角在《九章算术》中独立推导出了类似的定理。
他指出,在一个直角三角形中,直角边的平方等于两条直角边在一直角边上所作的正弦、余弦的乘积之和。
这个定理在几何计算中具有重要意义,为后来勾股定理的发展提供了重要的推动力。
此外,张角还提出了计算圆的面积和体积的方法。
他发现,圆的面积可以通过计算圆的半径和圆周长的乘积来得到。
他还提出了用立方单位计算体积的方法,为后世几何计算提供了重要的思路。
综上所述,张角是中国古代数学的杰出代表之一,他提出了许多重要的几何原理和方法。
这些几何原理和方法不仅在当时对数学的发展起到了重要的推动作用,而且在后世的数学研究中也具有重要的意义。
张角的几何原理对中国古代的数学造诣以及文化传统的发展起到了积极的促进作用,对中国古代数学的研究有着重要的价值。
平面几何4--张角定理及西姆松定理
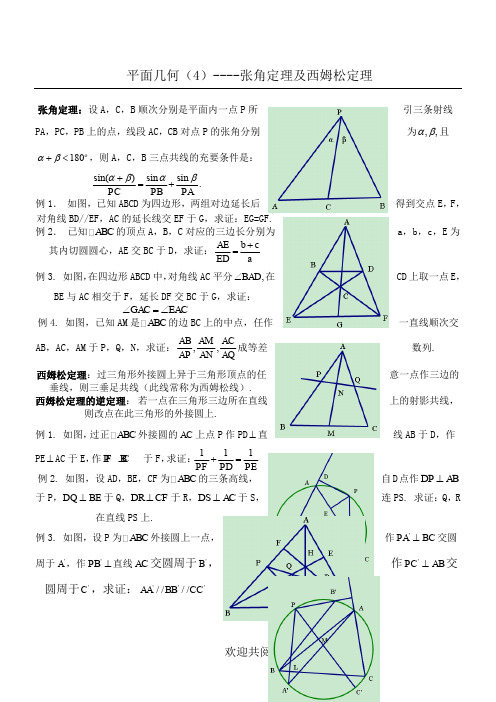
例2.已知 的顶点A,B,C对应的三边长分别为a,b,c,E为其内切圆圆心,AБайду номын сангаас交BC于D,求证:
例3.如图,在四边形ABCD中,对角线AC平分 在CD上取一点E,BE与AC相交于F,延长DF交BC于G,求证:
例4.如图,已知AM是 的边BC上的中点,任作一直线顺次交AB,AC,AM于P,Q,N,求证: 成等差数列.
平面几何(4)----张角定理及西姆松定理
张角定理:设A,C,B顺次分别是平面内一点P所引三条射线PA,PC,PB上的点,线段AC,CB对点P的张角分别为 且 ,则A,C,B三点共线的充要条件是: .
例1.如图,已知ABCD为四边形,两组对边延长后得到交点E,F,对角线BD//EF,AC的延长线交EF于G,求证:EG=GF.
西姆松定理:过三角形外接圆上异于三角形顶点的任意一点作三边的垂线,则三垂足共线(此线常称为西姆松线).
西姆松定理的逆定理:若一点在三角形三边所在直线上的射影共线,则改点在此三角形的外接圆上.
例1.如图,过正 外接圆的 上点P作PD 直线AB于D,作PE AC于E,作 于F,求证:
例2.如图,设AD,BE,CF为 的三条高线,自D点作 于P, 于Q, 于R, 于S,连PS.求证:Q,R在直线PS上.
最大张角定理证明过程

最大张角定理是几何中的重要定理,它的本质是将四边形的三个角划分成两部分,使得其中两个角的和最大。
下面我们来讨论最大张角定理及其证明过程。
一、最大张角定理的描述最大张角定理是指:在任意四边形ABCD中,若两个对顶角A、C,两个对角线AB和CD都存在,则有:∠A + ∠C ≤ 180°这里右边的180°就是最大张角的角度。
二、最大张角定理的证明接下来,我们就来证明最大张角定理:(1)先假设最大张角的角度是n,即∠A + ∠C = n 。
(2)由于四边形ABCD的四个角的和为360°,所以有:∠A + ∠B + ∠C + ∠D = 360°(3)由于∠A + ∠C = n,则有:∠A + ∠B + n + ∠D = 360°(4)联立(2)和(3)得:∠B + ∠D = 360° - n(5)由于∠B + ∠D为两条相邻的边所形成的夹角,所以有:∠B + ∠D ≤ 180°(6)由(5)得:360° - n ≤ 180°(7)联立(1)和(6)得:n ≤ 180°(8)由(7)结论得:∠A + ∠C ≤ 180°以上就是最大张角定理的证明过程。
三、最大张角定理的几个例子下面我们来看几个最大张角定理的具体例子:例1:在四边形ABCD中,连接AC,若∠A=60°,∠B=50°,则∠C的最大可能值是多少?解:由最大张角定理,∠A+∠C ≤ 180°,所以∠C的最大可能值为:∠C ≤ 180°-∠A = 180°-60° = 120°例2:在四边形ABCD中,连接AD,若∠A=60°,∠B=70°,则∠D的最大可能值是多少?解:由最大张角定理,∠A+∠D ≤ 180°,所以∠D的最大可能值为:∠D ≤ 180°-∠A = 180°-60° = 120°例3:在四边形ABCD中,连接BC,若∠A=50°,∠B=50°,则∠C的最大可能值是多少?解:由最大张角定理,∠B+∠C ≤ 180°,所以∠C的最大可能值为:∠C ≤ 180°-∠B = 180°-50° = 130°四、总结以上就是最大张角定理及其证明过程的介绍,它是几何中重要的定理,用于分析四边形的角度。
米勒张角定理

米勒张角定理米勒-拉宾定理,又称米勒张角定理,是数论中的一个重要定理,它可以用来判断一个整数是否是素数。
该定理由加利福尼亚大学伯克利分校的计算机科学家Gary L. Miller于1976年提出。
米勒-拉宾定理的核心思想是利用随机性来判断一个整数是否是素数。
在传统的试除法中,需要对待判断的数进行一一试除,判断其能否被其他数整除。
这种方法在大数的情况下非常耗时,因此需要一种高效的方法来判断大数是否是素数。
米勒-拉宾定理的判断过程如下:首先,选择一个较小的整数a,使得1 < a < n-1,其中n是待判断的数。
然后,将n-1表示为2^s * d的形式,其中d是一个奇数。
接下来,计算a^d mod n的值,如果结果为1或者n-1,则n可能是一个素数;如果结果不是1且不是n-1,则继续计算a^(2^r * d) mod n的值,其中0 ≤ r < s-1。
如果存在一个r使得a^(2^r * d) mod n的值等于n-1,则n可能是一个素数;如果所有的计算结果都不等于1和n-1,则n一定不是一个素数。
米勒-拉宾定理的判断过程可以通过重复进行多次来提高准确性。
当经过多次判断后,如果n始终满足定理中的条件,则可以十分确信n是一个素数。
米勒-拉宾定理的时间复杂度为O(k * log^3(n)),其中k是判断的次数。
相比传统的试除法,该定理在判断大数是否是素数时具有明显的优势。
然而,米勒-拉宾定理并不是绝对可靠的。
存在一些特殊的合数,它们也可能通过米勒-拉宾定理的判断。
这些合数被称为“米勒-拉宾伪素数”。
为了提高判断的准确性,可以选择更大的k值,但这会增加计算的时间。
米勒-拉宾定理的应用非常广泛。
在密码学中,素数的选择是非常重要的。
通过利用米勒-拉宾定理,可以快速地生成一个大素数,从而保证密码的安全性。
此外,该定理还在计算机科学的其他领域得到广泛应用。
米勒-拉宾定理是一个重要的数论定理,它通过利用随机性来判断一个整数是否是素数。
第5章 张角定理及应用

第5章 张角定理及应用【基础知识】张角定理 设A ,C ,B 顺次分别是平面内一点P 所引三条射线PA ,PC ,PB 上的点,线段AC ,CB 对点P 的张角分别为α,β,且180αβ+<︒,则A ,C ,B 三点共线的充要条件是:sin()PCαβ+=sin sin PB PAαβ+. 证明 如图5-1,A ,C ,B 三点共线ABP ACP CBP S S S ⇔=+△△△βαCBAP图5-1111sin()sin sin 222PA PB PA PC PC PB αβαβ⇔⋅⋅+=⋅⋅+⋅⋅ sin()sin sin PC PB PAαβαβ+⇔=+. 推论 在定理的条件下,且αβ=,即PC 平分APB ∠,则A ,C ,B 三点共线的充要条件是:2cos PCα=11PB PA+. 注 若规定角的绕向,逆时针方向为正,否则为负,则上述定理、推论中的点C 可表示在AB 的延长线上的情形.上述定理把平面几何和三角函数紧密相联,它给出了用三角法处理平面几何问题的一个颇为有用的公式.用它去解几何题,适当地配合三角形面积公式、正弦定理、三角公式、几何知识,可以大大简化解题步骤,众多的几何问题可以简捷地解决. 【典型例题与基本方法】1.恰当地选择共一端点的两线段对同一视点的两张角,是应用张角定理的关键例1 如图5-2,已知ABCD 为四边形,两组对边延长后得交点E ,F ,对角线BD EF ∥,AC 的延长线交EF 于G .求证:EG GF =. (1978年全国竞赛题)ββαGFEDCB A图5-2证明 以E 为视点,令BEC α=∠,CEG β=∠,分别对B ,C ,F ;A ,D ,F 及A ,C ,G 应用张角定理,得sin()sin sin EC EF EB αβαβ+=+, ① sin()sin sin ED EF EA αβαβ+=+, ② sin()sin sin EC EG EAαβαβ+=+.③又由BD EF ∥,有BDE β=∠,在△BED 中应用正弦定理,有sin()sin ED EBαββ+=. 由①+②-③-④,得2sin sin EF EGαα=, ∴ 2EF EG =,即EG GF =.例2 已知ABC △的顶点A ,B ,C 对应的三边长分别为a ,b ,c ,E 为其内切圆圆心,AE 交BC 于D .求证:AE b cED a+=. (1979年广东省竞赛题) 证明 如图5-3,连BE 并延长交AC 于F ,令BAE α=∠,由于E 为内心,则EAF α=∠.以A 为视点,分别对B ,E ,F 及B ,D ,C 应用张角定理的推论,得FEDCBA图5-32cos 11AE AB AF α=+,2cos 11AD AB AC α=+. 上述两式相除,得()()AC AB AF AD AE AF AC AB +=+, 而1AD AE ED EDAE AE AE+==+, 从而 ()()AB AC AF ED AB CFAE AF AC AB AF AB AC-==⋅++. ①又BF 平分B ∠,则AB AF BC CF =,即AB BCAF CF=. 于是,由上式代入①式,得ED BC AE AB AC =+,故AE b cED a+=. 例3 如图5-4,在四边形ABCD 中,对角线AC 平分BAD ∠.在CD 上取一点E ,BE 与AC 相交于F ,延长DF 交BC 于G .求证:GAC EAC =∠∠. (1999年全国高中联赛题) (G ')GFEDCBA图5-4证明 作CAG CAE '=∠∠,交BC 于G '.只须证G ',F ,D 三点共线,设BAC CAD θ==∠∠,CAG CAE α'==∠∠.以A 为视点,分别对B ,F ,E ;B ,G ',C ;C ,E ,D 应用张角定理,有 ()sin sin sin AF AB AE θααθ+=+, ① sin sin sin()AG AB ACθαθα-=+', ② sin sin sin()AE AD AC θαθα-=+,③由①-②+③式,得sin()sin sin AF AD AG θααθ+=+'. 又以A 为视点,对G ',F ,D 应用张角定理,知G ',F ,D 三点共线. 由此,知G '与G 重合,故GAC EAC =∠∠.例4 如图5-5,已知AM 是ABC △的边BC 上的中线,任作一直线顺次交AB ,AC ,AM 于P ,Q ,N .求证:AB AP ,AMAN,AC AQ 成等差数列.(1979年辽宁省竞赛题)θβαCBA MN PQ图5-5证明 令BAM α=∠,MAC β=∠,AMB θ=∠.以A 为视点,分别对P ,N ,Q 及B ,M ,C 应用张角定理,有sin()sin sin AN AP AQαββα+=+, ①sin()sin sin AM AB ACαββα+=+. ② 又在△ABM 和△AMC 中,由正弦定理,有 sin sin AB MB θα=,sin sin AC MC θβ=. 注意到MB MC =,上述两式相除得sin sin AC ABαβ=. 于是②式变为sin()2sin 2sin AM AB ACαββα+==. 由①式除以上式,得12AM AB AC AN AP AQ ⎛⎫=+ ⎪⎝⎭. 故AB AP ,AMAN,AC AQ 成等差数列.2.找准视点,寻找到与题设条件或结论有关的线段所在的三角形,是灵活应用张角定理的前提.例5 如图5-6,圆的割线PAB 通过圆心O ,自P 作圆的任一割线PCD 交圆于C ,D .又在圆上取一点E ,使BE BD =,连CE 交AB 于F .求证:211AB BP BF=+.BP图5-6证明 连AC ,BC ,令1ECB =∠∠,2BCD =∠∠,3ACE =∠∠,4ACP =∠∠,AC a =,BC b =. 由BE BD =,有12=∠∠.连BD ,由AE AD =,有34ABD ==∠∠∠.以C 为视点,考察线段AB ,BP ,BF 所在的三角形ABC △和△PBC ,分别应用张角定理,有sin90sin 1sin 3CF a b ︒=+∠∠, sin(904)sin 4sin90a b CP ︒+︒=+∠∠. 即 sin 1sin 3cos 3sin 3ab abCF b a b a ==++∠∠∠∠, cos 4sin 4cos 3sin 3ab abCP b a b a ==--∠∠∠∠. 由此,知cos 3sin 30b a ->∠∠. 在△CPB 中,由余弦定理,得 122222cos(903)cos 3sin 3cos 3sin 3ab ab BP b b a b a ⎡⎤⎛⎫=+-⋅⋅︒+⎢⎥ ⎪--⎝⎭⎢⎥⎣⎦∠∠∠∠∠. 因034180<+<︒∠∠,则03490<=<︒∠∠,即cos 30>∠. 于是,()122222cos 3(cos 3sin 3)b a b BP b a 2⎡⎤⋅+⎢⎥==-⎢⎥⎣⎦∠∠∠同理,在CFP △中,有BF .又在Rt ABC △中,AB , 故211AB BP BF ==+. 注 此例结论表示AB 是BP 与BF 的调和平均,亦表示1PF 调和分割弦AB . 例6 (第一章例12)任意四边形ABCD 的一组对边BA 与CD 交于M ,过M 作割线交另一组对边所在直线于H 、L ,交对角线所在直线于H '、L '.求证:1111MH ML MH ML +=+''. 证明 如图5-7,MBL α=∠,CML β=∠,BMC αβ=+∠, L'H 'DCA MH图5-7由张角定理得:sin()sin sin MH MD MAαβαβ+=+, ① sin()sin sin MH MC MA αβαβ+=+', ② sin()sin sin ML MD MA αβαβ+=+', ③ sin()sin sin ML MC MB αβαβ+=+.④由①+④-②-③得sin()sin()sin()sin()0MH ML MH ML αβαβαβαβ+++++--='',故1111MH ML MH HL +=+''. 注 此例也可运用线段的调和分割来证明,可参见第十一章例9.对于第十一章的例10,也可运用张角定理来证.请看下例:例7 圆内接四边形ABCD 一组对边DA 、CB 延长线交P 点,过P 点任作直线PF 分别交圆于E 、F ,交AB 、CD 所在直线于N 、M ,求证:1111PE PF PN PM+=+. 证明 设APM α=∠,BPM β=∠,并分别取AD 、EF 、BC 中点R 、G 、H ,如图5-8,显然P 、R 、G 、H 和圆心O 五点共圆,由托勒密定理可知:PG RH RG PH PR GH ⋅=⋅+⋅.对△RGH 三边用正弦定理代入得:()sin sin sin PG PH PR αβαβ⋅+=⋅+⋅,两边乘2,即()sin()PE PF αβ++=()()sin sin PB PC PA PD αβ+++.又PE PF PB PC PA PD ⋅=⋅=⋅,则11sin()PE PF αβ⎛⎫++= ⎪⎝⎭1111sin sin PB PC PA PD αβ⎛⎫⎛⎫+++ ⎪ ⎪⎝⎭⎝⎭.由张角定理:sin()sin sin PN PB PA αβαβ+=+,sin()sin sin PM PC PD αβαβ+=+,因此1111PE PF PN PM+=+. PD图5-8当PF 与AB 、DC 的延长线相交同时与圆相交(或相切),如图5-9,例7仍然成立,证法相同.OPR MN K H GFE DCBA 图5-9当PF 与CA ,BD 相交或与它们的延长线相交,同时也与圆相交(或相切),例题7也成立,证法也相同.如图5-10,相切时11PE PF=.P图5-10例8 圆内接ABC △,切线C 点交BA 的延长线于P ,过P 任作直线交圆于E 、F ,交AC 、BC 分别于N 、M ,求证:1111PE PF PN PM+=+. 证明 设APM α=∠,MPC β=∠,并分别取AB 、EF 中点G 、H ,如图5-11,显然P 、G 、H 、C 和圆心O 五点共圆,由托勒密定理可知PH GC GH PC PG HC ⋅=⋅+⋅,对△GHC 三边用正弦定理代入得()sin sin sin PH PC PG αβαβ⋅+=⋅+⋅,两边乘2,即()sin()2sin PE PF PC αβα++=⋅⋅+()sin PA PB β+.因为2PE PF PC PA PB ⋅==⋅,从而11211sin()sin PE PF PC PA PB αβα⎛⎫⎛⎫++=++ ⎪ ⎪⎝⎭⎝⎭sin β.图5-11由张角定理,sin()sin sin PN PC PA αβαβ+=+,sin()sin sin PM PC PBαβαβ+=+. 因此1111PE PF PN PM +=+. 【解题思维策略分析】1.给出著名问题的一种新证法 例9(斯坦纳定理) 在ABC △中,BD ,CE 分别是ABC ∠,ACB ∠的平分线.若BD CE =,则AB AC =. 证明 如图5-12,令ABD DBC α==∠∠,BCE ACE β==∠∠,分别以B ,C 为视点,对ABC △应用张角定理的推论,有2cos 11BD AB BC α=+,2cos 11CE AC BCβ=+. βαβαED CBA图5-12亦有2cos 2cos AB BC AC BC BD CE AB BC AC BC αβ⋅⋅⋅⋅===++, 亦即()()cos cos AB AC BC AC AB BC βα+=+. 对上式应用分比定理,把cos cos βα-化为积,并变形可得 ()2sinsincos 22AC AB BC AB AC BC βαβαα++--=-⋅⋅⋅. ①显然,α,β,αβ±均只能为锐角. 若AB AC >,则①式左端为正,而右端为负,若AB AC <,则①式左端为负,而右端为正. 所以AB AC =.例10(蝴蝶定理) 已知M 是O 的弦AB 的中点,过M 任作两弦CD ,EF ,连CF ,DE 分别交AB 于G ,H ,则MH MG =. 证明 如图5-13,令AMF BME α==∠∠,BMD AMC β==∠∠.以M 为视点,对△MDE 和△MCF 分别应用张角定理,有G H 'C图5-13sin()sin sin MH ME MDαββα+=+, sin()sin sin MG MF MC αββα+=+. 上述两式相减,得()()11sin sin sin()MF ME MD MC MH MG ME MFMC MD βααβ⎛⎫+-=--- ⎪⋅⋅⎝⎭. 设P ,Q 分别是CD ,EF 的中点,由OM AB ⊥,有 22cos(90)2sin ,22cos(90)2sin .MD MC MP OM OM MF ME MQ OM OM ββαα-==⋅︒-=⋅⎧⎨-==⋅︒-=⋅⎩于是,()11sin 0MH MG αβ⎛⎫+-= ⎪⎝⎭.而180αβ+≠︒,知sin()0αβ+≠.故MH MG =.注 类似地应用张角定理,可证明如图5-8中的AG BH ''=. 2.获得线段倍分关系的一种途径例11 已知G 是ABC △的重心,过G 作直线分别交ABC △的两边AB ,AC 于E ,F .求证:2EG GF ≤.证明 如图5-14,作中线BGM ,CGN ,令MGF BGE α==∠∠,CGF NGE β==∠∠.βαGFECBAM N 图5-14以G 为视点,分别对△GCM ,△BGN 应用张角定理,有sin()sin sin GF MG GC αββα+=+,sin()EGαβ+=sin sin BG NGβα+. 注意到,2BG GM =,2GC NG =,则 sin()sin sin 2GF GM GN αββα+=+, ① sin()sin sin 2EG GM GN αββα+=+.②①12⋅-②,得 ()113sin sin 024GF EG GN ααβ⎛⎫-⋅+=-⋅ ⎪⎝⎭≤. 而 ()()sin 0090αβαβ+><+<︒,故1102EG GF-≥,即2EG GF ≤.例12 如图5-15,平行四边形ABCD 中,在AB 边上取一点P ,使3AB AP =,在边AD 上取点Q ,使4AD AQ =,且PQ 交AC 于M .求证:7AC AM =. βαDCBAM OPQ 图5-15证明 连BD 交AC 于O ,则12AO AC =.令DAM α=∠,BAM β=∠,3AB a =,4AD b =.以A 为视点,分别对△APQ 和△ABD 应用张角定理,有 sin()sin sin sin sin b a AM a b abαβαβαβ+⋅+⋅=+=,sin()sin sin 4sin 3sin 3412b a AO a b ab αβαβαβ+⋅+⋅=+=. 因ADO ABO S S =△△,则4sin 3sin b a αβ⋅=⋅. 于是,4sin 3sin 6sin 212sin 12sin 9sin 12sin 7AM b a a AO b a a a αββαβββ⋅+⋅⋅===⋅+⋅⋅+⋅. 故7AC AM =.例13 如图5-16,筝形ABCD 中,AB AD =,BC DC =.经过AC 与BD 的交点O 任作两条直线,分别交AD 于E ,交BC 于F ,交AB 于G ,交CD 于H ,GF ,EH 分别交BD 于I ,J .求证:OI OJ =. (CMO -5试题)δγβαOIJ HGFE D CBA图5-16证明 令AOE α=∠,EOD β=∠,DOH γ=∠,COH δ=∠.由题设,知AC 垂直平分BD 于O ,以O 为视点,考虑分别在OJ ,OI 所在的三角形△FOH 及△GOF 中应用张角定理.但在△EOH 中,涉及OE ,OH ,于是,又在△AOD ,△COD 及△EOH 中分别应用张角定理,有sin90sin sin OE OD OA αβ︒=+,sin90sin sin OH OC OD γδ︒=+,sin()sin sin OJ OH OE βγβγ+=+. 由上述三式,有sin()sin sin sin sin sin sin sin sin OJ OC OD OD OAβγβγβδγαγβ+⋅⋅⋅⋅=+++. 同理,在△AOB ,△COB 及△GOE 中分别应用张角定理,有 sin()sin sin sin sin sin sin sin sin OI OC OB OB OAγβγβγαβδβγ+⋅⋅⋅⋅=+++. 注意到OD OB =,则有11OJ OI=,故OI OJ =. 例14 如图5-17,已知G 是ABC △的重心,过点G 任作一条直线l ,分别交边AB 、AC 于点D 、E ,若AD xAB =,AE y AC =,求证:11x y +为定值.l βαGFEDCBA图5-17证明 当点D 与点B 重合,即1x =时,E 为AC 之中点,即12y =,此时113x y +=,因此只需证明113x y+=即可. 如图,延长AG 交BC 于F ,则F 为BC 的中点,设BAF α=∠,FAC β=∠,由D ,G ,E 三点共线,可得sin()sin sin AG AE AD αβαβ+=+,因为23AG AF =,AD xAB =.AE yAC =,所以()3sin 2AF αβ+= sin sin yAC xAB αβ+,即sin()2sin 2sin 33AF yAC xAB αβαβ+=+①,由B ,F ,C 三点共线可得()sin sin sin AF AC ABαβαβ+=+②,①式减②式可得sin 2sin 211033AC y AB x αβ⎛⎫⎛⎫-+-= ⎪ ⎪⎝⎭⎝⎭,因为F 为BC 的中点,所以ABF AFC S S =△△,即11sin sin 22AF AB AF AC αβ⋅=⋅,即sin sin 0AC AB αβ=≠,所以2211033y x ⎛⎫⎛⎫-+-= ⎪ ⎪⎝⎭⎝⎭,即113x y +=.3.证明线段比例关系式的一种方法例15 如图5-18,已知AD ,AE 分别是ABC △的内外角平分线,点D 在BC 边上,点E 在BC 边的延长线上.求证:112BE CE DE+=. ααbaED CBA图5-18证明 设AD a =,AE b =,BAD DAC α==∠∠.以A 为视点,分别对△ADE 和△ABE 应用张角定理,得sin90sin sin(90)AC b a αα︒︒-=+,sin(90)sin90sin a AB bαα︒+︒=+.于是 cos sin ab AC b a αα=+,cos sin abAB b a αα=-.在△ABE 中,由余弦定理,并注意cos 0α>,cos sin 0b a αα->(0AB >), 有BE ===.同理,在△ACE 中,求得CE =.而在Rt △ADE 中,DE =故112BE CE DE +==. 注 112BE CE DE+=表示DE 是CE 与BE 的调和平均,亦表示DE 被B 、C 或BC 被D 、E 调和分割(即DB BEDC CE=). 用张角定理也可以证明如下调和分割问题:凸四边形ABDF 的两组对边延长相交于点C ,E ,直线AD 交BF 于M ,交CE 于点N ,则112AM AN AD +=或AM MDAN ND=. 事实上,如图5-19,令CAN α=∠,NAE β=∠,以A 为视点,分别对△ABF ,△ABE ,△ACF ,△ACE 应用张角定理,有FEDCBAM N图5-19sin()sin sin AM AF AB αβαβ+=+,sin()sin sin AD AE AB αβαβ+=+, sin()sin sin AD AF AC αβαβ+=+,sin()sin sin AN AE AC αβαβ+=+. 上述第一式与第四式相减后减去其余两式,得112sin()sin()AM AN ADαβαβ⎛⎫++=⋅+ ⎪⎝⎭.而sin()0αβ+≠,故112AM AN AD+=. 或由2AD AD AM AN AM AN AM AN +==+得AM MDAN ND =. 这个调和分割问题可以参见第九章中的性质2.例16 如图5-20设I ,H 分别为锐角ABC △的内心和垂心,点1B ,1C 分别为边AC ,AB 的中点.已知射线1B I 交边AB 于点2B (2B B ≠),射线1C I 交AC 的延长线于点2C ,22B C 与BC 相交于K ,1A 为△BHC 的外心.试证:A ,I ,1A 三点共线的充分必要条件是△2BKB 和△2CKK 的面积相等.(CMO -18试题)A 1B 2B 1C 1C 2C BAHK 图5-20证明 首先证明:2260BKB CKK S S BAC =⇔=︒△△∠.设ABC △的外接圆半径为R ,连IC ,在△ACI 与ABC △中运用正弦定理,有1sin sin 2AI ACAIC C =∠∠ 14sin 12cos 2AC R B B ==⋅∠∠,即114sin sin 22AI R B C =⋅⋅∠∠. 又 11sin 2AB AC R B ==⋅∠. 在△12AB B 中,注意AI 平分A ∠,以A 为视点,在此三角形中应用张角定理的推论,有12cos 2AAI=∠ 1211AB AB +, 即有 21112cos sin 12211112cos cos cos sin 12222R B CAB A A B CAI AB ⋅⋅==⋅--∠∠∠∠∠∠112cos sin 221sin 2R B CA ⋅⋅=∠∠∠. 同理,2112cos sin 221sin 2R C BAC A ⋅⋅=∠∠∠. 从而 222222BKB CKC ABC AB C S S S S AB AC AB AC =⇔=⇔⋅=⋅△△△△ 1111sin cos sin cos 2222sin sin 11sin sin 22C B B C C B A A ⋅⋅⇔⋅=⋅∠∠∠∠∠∠∠∠ 24sin 12A⇔=∠,注意到A ∠为三角形内角60BAC ⇔=︒∠. 其次,再证60BAC A =︒⇔∠,I ,1A 三点共线.连1BA ,1CA ,在△1ABA 和△1ACA 中分别应用正弦定理,有 1111sin sin A A A B ABA A AB =∠∠,1111sin sin A A AC ACA A AC=∠∠. 因I 为ABC △的内心,A ,I ,1A 共线111A AB A AC ABA ⇔=⇔∠∠∠与1ACA ∠均为锐角,1111sin sin ABA ACA ABA ACA =⇔≠∠∠∠∠(因AB AC ≠)时,111180,,,ABA ACA A B A C+=︒⇔∠∠四点共圆. 注意到1A 中圆周角与圆心角的关系,有()1360236021802BAC BHC A A =︒-=︒-︒-=∠∠∠∠,且118060BAC A BAC +=︒⇔=︒∠∠∠. 例17 如图5-21,设O ,I 分别是ABC △的外心和内心,AD 是BC 边上的高,I 在线段OD 上,求证:ABC △的外接圆半径R 等于BC 边上的旁切圆的半径a r .(1998年全国高中联赛题)证明 因BC 边上的旁切圆的半径4sincos cos 222a A B C r R =,故只需证明4sin cos cos 1222A B C⋅=即可.由图,易得90OAC BAD B ==︒-∠∠,因为2A BAI CAI ==∠∠,所以()902ADAI OAI B ==-︒-∠∠ 902A B α=+-︒=,由于点D ,I ,O 共线,由张角定理可得sin 2sin sin AI AO AD ααα=+,即2cos 1AI AOα=+1AD ,即2sin 112A B AI AO AD ⎛⎫+ ⎪⎝⎭=+,其中AO R =,sin 2sin sin AD AB B R C B ==. 设ABC △的内切圆半径为r ,则csc2A AI r =,因为4sin sin sin 222A B C r R =,则4sin sin 22B CAI R =⋅,所以有2sin 1122sin sin 4sin sin 22A B B C R R B C R ⎛⎫+ ⎪⎝⎭=+,即4sin cos cos 2sin sin 1222A B C B B C ⎛⎫+=+ ⎪⎝⎭,即2sin 2A B ⎛⎫+ ⎪⎝⎭cos cos 2sin sin 122B C B C B C +-⎛⎫+=+ ⎪⎝⎭,即sin sin 2sin cos 2sin sin 2222A A A B C B B B C -⎛⎫⎛⎫+⋅++= ⎪ ⎪⎝⎭⎝⎭1+,即()3cos cos sin sin 2sin sin 12222B A C A B C B B A B C ++⎛⎫-+++-+=+ ⎪⎝⎭,cos cos cos()B C B C ++-= cos()cos()B C B C --+,即cos cos cos 0B C A +-=,即22coscos 2sin 10222B C B C A+-+-=,即2sincos 2sin cos 12222A B C A B C -+⋅+=,即4sin cos cos 1222A B C=. 14.证明三点共线的又一个工具例18 如图5-22,已知AB 是圆的直径,PA ,PC 是圆的切线,A ,C 为切点.作CD AB ⊥于D ,Q 为CD 的中点.求证:P ,Q ,B 三点共线.BAP图5-22证明 以C 为视点,考察线段PQ ,QB 所张的角的情形. 连AC ,BC ,则90ACB =︒∠,令PCA α=∠,则CBA ACD α==∠∠,令PC a =,易知2cos AC a α=⋅,cot 2cos cot BC AC a ααα=⋅=⋅⋅,2sin 2cos CD BC a αα=⋅=⋅,2cos CQ αα=⋅.所以2sin sin(90)cos 1cos cos PCB CQ CQ a a αααα︒+===⋅⋅∠,2sin sin sin 2cos sin cos 2cos cot cos PCQ QCB CB CP a a a a ααααααα+=+=+⋅⋅∠∠22sin cos 1cos cos a a αααα+==⋅⋅.故sin sin sin PCB PCQ QCBCQ CB CP=+∠∠∠. 由张角定理,知P ,Q ,B 三点共线.例19 如图5-23,在线段AB 上取内分点M ,使AM BM ≤,分别以MA ,MB 为边,在AB 的同侧作正方形AMCD 和MBEF ,P 和Q 分别是这两个正方形的外接圆,两圆交于M ,N .求证:B ,C ,N 三点共线.(IMO -1试题)图5-23证明 连MD ,ME ,NE ,ND ,NM ,则90DNM ENM ==︒∠∠,则D ,N ,E 三点共线,注意454590DME =︒+︒=︒∠.设DMN NEM α==∠∠,P ,Q 的半径分别为1r ,2r ,则MC =,MB ,12cos MN r α=⋅= 22sin r α⋅.对视点M,考察点B ,C ,N 所在的三角形△MBN .由 22sin sin sin 902sin CMB CMN MN MB r α︒+=+=∠∠()2111sin cos sin cos sin cos 2cos 2cos r r αααααααα+⋅-+⋅==⋅11cos sin 2r αα+===sin 9045sin NMBMCα︒+︒-==∠.应用张角定理,即知B ,C ,N 三点共线.例20 如图5-24,在ABC △中,令A α=∠,B β=∠,C γ=∠,且αβ>,AD ,BE ,CF 是它的三条垂线;AP ,BQ 是两条角平分线;I ,O 分别是它的内心和外心.证明:点D ,I ,E 共线当且仅当P ,O ,Q 共线,当且仅当O ,I ,F 共线.(IMO -38预选题或由1998年全国高中联赛题改编)IOFE DCBAP Q图5-24证明 由于外心O 有在ABC △内、外、边上三种情形,故须对α分三种情况讨论. (Ⅰ)当α为锐角时.设ABC △的外接圆半径为R ,内切圆半径为r ,令BC a =,CA b =,AB c =,连CO ,CI ,则abCP b c=+,ab CQ a c =+,π2OCQ β=-∠,π2OCP α=-∠,cos CD b γ=⋅,cos CE a γ=⋅,sin 2r CI γ=,OCI ICF =∠∠ π22γβ=--(或π22γα+-),π2OCF βγ=--∠(或2πγα+-). 以C 为视点,分别考察△PCQ ,△DCE ,△OCF ,并应用张角定理. P ,O ,Q 共线sin sin sin OCP OCQOC CQ CPγ⇔=+∠∠ []sin ()cos ()cos ab R a c b c γαβ⇔⋅=+⋅++⋅[]224sin sin sin sin 2sin 22sin (cos cos )R R αβγαβγαβ⇔⋅⋅⋅=+++22(sin 2sin 2sin 2)[sin 2sin 22sin (cos cos )]R R αβγαβγαβ⇔++=+++sin 22sin (cos cos )cos cos cos γγαβγαβ⇔=+⇔=+.D ,I ,E 共线()sinsinsin 22sin cos ab r a b CI CD CEγγγγγ⇔=+⇔⋅=+ ()cos ()()(1cos )cos r a b c r a b a b c γγγ⇔++⋅=+⇔+-=⋅(sin sin )(1cos )sin cos αβγγγ⇔+-=⋅22cos cos2sin sin cos 222γαβγγγ-⇔⋅⋅=⋅2sin coscos cos cos cos 22γαβγγαβ-⇔⋅=⇔=+. O ,I ,F 共线sin sin sin OCF OCI ICFCI CF CO⇔=+∠∠∠ ()cos cos sin 2222sin sin 22sin sin CI CI a R R γγβββγγββαβ⎛⎫⎛⎫++ ⎪ ⎪+⎛⎫⎝⎭⎝⎭⇔=+⇔+=+ ⎪⋅⋅⎝⎭2sinsin sin sin22rr R R γγαβ+⋅⋅⋅⋅(注意π22γβ+≠,4sin sin sin 222r R αβγ=⋅⋅) 12sin 4sin sin 2222cos cos 22γαββαβ⎛⎫⇔+=+⋅ ⎪⎝⎭⋅4sin cos cos 12sin sin 222γαββαβ⎛⎫⇔+⋅⋅=+⋅ ⎪⎝⎭sin sin sin sin 22222222222αβγβγααβγαβββ⎛⎫⎛⎫⎛⎫⎛⎫⇔+++++-++++-+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭1cos()cos()αβαβ=+--+cos cos 1cos()1cos()cos cos cos cos βααβαβγγαβ⇔+++-=+-+⇔=+. 因此,D ,I ,E 共线⇔P ,O ,Q 共线⇔O ,I ,F 共线.(Ⅱ)当α为钝角时,注意π2OCP α=-∠,依照(Ⅰ)类似证明. (Ⅲ)当α为直角时,易证点D ,I ,E 共线当且仅当ABC △是等腰直角三角形;点P ,O ,Q 共线当且仅当ABC △是等腰直角三角形;点O ,I ,F 共线当且仅当ABC △是等腰直角三角形.综合即证. 注 在ABC △中,可证得:cos cos cos C A B =+∠∠∠,当且仅当ABC △的外接圆半径等于AB 边上的旁切圆半径.因此本例题还等价于ABC △的外接圆半径等于AB 边上的旁切圆半径,此为例17即1998年全国高中联赛平面几何题结论.5.注意张角定理与斯特瓦尔特定理的等价性例21 如图5-25,设B ,P ,C 依次分别为从A 点引出的三条射线AB ,AP ,AC 上的点.线段BP ,PC 对点A 的张角分别为α,β,且180αβ+<︒,则B ,P ,C 三点共线的下述两个充要条件等价:βαCBA EF P 图5-25(Ⅰ)sin()sin sin AP AC ABαβαβ+=+(张角定理); (Ⅱ)222AB PC AC BP AP BC BP PC BC ⋅+⋅=⋅+⋅⋅(斯特瓦尔特定理). 证明sin()sin sin sin()sin sin AB AC AP AB AP AC AP AC ABαβαβαβαβ+=+⇔⋅⋅+=⋅⋅+⋅⋅ sin cos cos sin sin sin AB AC AB AC AP AB AP AC αβαβαβ⇔⋅⋅⋅+⋅⋅⋅=⋅⋅+⋅⋅.作BE ⊥射线AP 于E ,作CF ⊥射线AP 于F ,则 sin sin AB BE BP k BPAC CF PC k PCαβ⋅⋅===⋅⋅cos cos AC k BP AB k PC AP k BP AP k PC AP k BC βα⇔⋅⋅⋅+⋅⋅⋅=⋅⋅+⋅⋅=⋅⋅222222222AC AP PC AB AP BP AP AC BP AP AB PC AP BC AC AP AB AP +-+-⇔⋅⋅⋅+⋅⋅⋅=⋅⋅⋅222AB PC AC BP AP BC BP PC BC ⇔⋅+⋅=⋅+⋅⋅.【模拟实战】习题A1.在矩形ABCD 中,AB a =,BC b =,M 为BC 中点,DE ⊥射线AM 于E ,求DE 之长.(用a ,b 表示)2.ABC △中,AB AC =,AD 为BC 边上的高,AD 的中点为M ,CM 的延长线交AB 于K .求证:3AB AK =.3.已知AC AB ⊥,BD AB ⊥,AD 和BC 相交于点E ,EF AB ⊥于F .又AC p =,BD q =,EF r =,AF m =,FB n =.求证:111p q r+=. 4.梯形ABCD (AB DC ∥)的对角线AC ,BD 相交于P ,过P 作梯形下底的平行线交两腰AD 于M ,BC 于N .求证:PM PN =.5.设XOY ∠的平分线上任一点为P ,过P 作两条任意直线AB ,CD ,分别交OX ,OY 于A ,C ,B ,D .求证:OC OA BD OB OD AC ⋅⋅=⋅⋅.6.直线l 的同侧有三个相邻的等边三角形△ADE ,△AFG ,ABC △,且G ,A ,B 都在直线l 上.设这三个三角形的边长依次为b ,c ,a ,连GD 交AE 于N ,连BN 交AC 于L .求证:abcAl ab bc ac =++.7.在O 中,过弦GH 的中点M 作弦AB ,CD ,令AMG α=∠,CMG β=∠.求证:sin sin MB MAMC MDαβ-=-. 8.在平行四边形ABCD 的CD 边上取一点P ,使12CP PD =∶∶,在对角线上取一点Q ,使13CQ QA =∶∶.求证:B ,Q ,P 三点共线. 习题B1.已知四边形ABCD 两组对边的延长线分别交于K ,L .过K ,L 作直线,对角线AC ,BD 之延长线分别交KL 于G ,F .求证:1KF ,1KL ,1KG成等差数列. 2.在锐角三角形ABC 中,AC AB >.求证:B ∠的平分线BD 小于C ∠的平分线CE .3.在O 内,直径AOB ⊥半径OC ,O '与OB ,OC 相切于D ,E ,并与O 内切于F .求证:A ,E ,F 三点共线.4.在Rt ABC △中,90ACB =︒∠,CD AB ⊥于D ,△ADC 和△CDB 的内心分别为1O ,2O ,12O O 与CD 交于K .求证:111BC AC CK+=. 5.设P 为ABC △内任一点,顶点A ,B ,C 与P 的连线分别与BC ,CA ,AB 交于点D ,E ,F .P '为△DEF 周界上任一点,过P '作PD ,PE ,PF 的平行线分别与BC ,CA ,AB 交于D ',E ',F '.证明:在比值P D PD '',P E PE '',P F PF''中必有一个等于另两个的和.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第5章 张角定理及应用【基础知识】张角定理 设A ,C ,B 顺次分别是平面内一点P 所引三条射线PA ,PC ,PB 上的点,线段AC ,CB对点P 的张角分别为α,β,且180αβ+<︒,则A ,C ,B 三点共线的充要条件是:sin()PCαβ+=sin sin PB PAαβ+. 证明 如图5-1,A ,C ,B 三点共线ABP ACP CBP S S S ⇔=+△△△βαCBAP图5-1111sin()sin sin 222PA PB PA PC PC PB αβαβ⇔⋅⋅+=⋅⋅+⋅⋅ sin()sin sin PC PB PAαβαβ+⇔=+. 推论 在定理的条件下,且αβ=,即PC 平分APB ∠,则A ,C ,B 三点共线的充要条件是:2cos PCα= 11PB PA+. 注 若规定角的绕向,逆时针方向为正,否则为负,则上述定理、推论中的点C 可表示在AB 的延长线上的情形.上述定理把平面几何和三角函数紧密相联,它给出了用三角法处理平面几何问题的一个颇为有用的公式.用它去解几何题,适当地配合三角形面积公式、正弦定理、三角公式、几何知识,可以大大简化解题步骤,众多的几何问题可以简捷地解决. 【典型例题与基本方法】1.恰当地选择共一端点的两线段对同一视点的两张角,是应用张角定理的关键例1 如图5-2,已知ABCD 为四边形,两组对边延长后得交点E ,F ,对角线BD EF ∥,AC 的延长线交EF 于G .求证:EG GF =. (1978年全国竞赛题)ββαGFEDCB A图5-2证明 以E 为视点,令BEC α=∠,CEG β=∠,分别对B ,C ,F ;A ,D ,F 及A ,C ,G 应用张角定理,得sin()sin sin EC EF EBαβαβ+=+, ① sin()sin sin ED EF EA αβαβ+=+, ② sin()sin sin EC EG EAαβαβ+=+.③又由BD EF ∥,有BDE β=∠,在△BED 中应用正弦定理,有sin()sin ED EBαββ+=. 由①+②-③-④,得2sin sin EF EGαα=, ∴ 2EF EG =,即EG GF =.例2 已知ABC △的顶点A ,B ,C 对应的三边长分别为a ,b ,c ,E 为其内切圆圆心,AE 交BC于D .求证:AE b cED a +=. (1979年广东省竞赛题)证明 如图5-3,连BE 并延长交AC 于F ,令BAE α=∠,由于E 为内心,则EAF α=∠.以A 为视点,分别对B ,E ,F 及B ,D ,C 应用张角定理的推论,得FEDCBA图5-32cos 11AE AB AF α=+,2cos 11AD AB AC α=+. 上述两式相除,得()()AC AB AF AD AE AF AC AB +=+, 而1AD AE ED EDAE AE AE+==+, 从而 ()()AB AC AF ED AB CFAE AF AC AB AF AB AC-==⋅++. ①又BF 平分B ∠,则AB AF BC CF =,即AB BCAF CF=. 于是,由上式代入①式,得ED BC AE AB AC =+,故AE b cED a+=. 例3 如图5-4,在四边形ABCD 中,对角线AC 平分BAD ∠.在CD 上取一点E ,BE 与AC 相交于F ,延长DF 交BC 于G .求证:GAC EAC =∠∠. (1999年全国高中联赛题)(G ')GFEDCBA图5-4证明 作CAG CAE '=∠∠,交BC 于G '.只须证G ',F ,D 三点共线,设BAC CAD θ==∠∠,CAG CAE α'==∠∠.以A 为视点,分别对B ,F ,E ;B ,G ',C ;C ,E ,D 应用张角定理,有 ()sin sin sin AF AB AE θααθ+=+, ① sin sin sin()AG AB ACθαθα-=+', ② sin sin sin()AE AD AC θαθα-=+, ③由①-②+③式,得sin()sin sin AF AD AG θααθ+=+'. 又以A 为视点,对G ',F ,D 应用张角定理,知G ',F ,D 三点共线.由此,知G '与G 重合,故GAC EAC =∠∠.例4 如图5-5,已知AM 是ABC △的边BC 上的中线,任作一直线顺次交AB ,AC ,AM 于P ,Q ,N .求证:AB AP ,AMAN,AC AQ 成等差数列.(1979年辽宁省竞赛题)θβαCBA MN PQ图5-5证明 令BAM α=∠,MAC β=∠,AMB θ=∠.以A 为视点,分别对P ,N ,Q 及B ,M ,C 应用张角定理,有sin()sin sin AN AP AQαββα+=+, ① sin()sin sin AM AB ACαββα+=+.②又在△ABM 和△AMC 中,由正弦定理,有 sin sin AB MB θα=,sin sin AC MC θβ=. 注意到MB MC =,上述两式相除得sin sin AC ABαβ=. 于是②式变为sin()2sin 2sin AM AB ACαββα+==. 由①式除以上式,得12AM AB AC AN AP AQ ⎛⎫=+ ⎪⎝⎭. 故AB AP ,AMAN,AC AQ 成等差数列.2.找准视点,寻找到与题设条件或结论有关的线段所在的三角形,是灵活应用张角定理的前提.例5 如图5-6,圆的割线PAB 通过圆心O ,自P 作圆的任一割线PCD 交圆于C ,D .又在圆上取一点E ,使BE BD =,连CE 交AB 于F .求证:211AB BP BF=+.BP图5-6证明 连AC ,BC ,令1ECB =∠∠,2BCD =∠∠,3ACE =∠∠,4ACP =∠∠,AC a =,BC b =. 由BE BD =,有12=∠∠.连BD ,由AE AD =,有34ABD ==∠∠∠.以C 为视点,考察线段AB ,BP ,BF 所在的三角形ABC △和△PBC ,分别应用张角定理,有 sin90sin 1sin 3CF a b︒=+∠∠, sin(904)sin 4sin90a b CP ︒+︒=+∠∠. 即 sin 1sin 3cos 3sin 3ab abCF b a b a ==++∠∠∠∠, cos 4sin 4cos 3sin 3ab abCP b a b a ==--∠∠∠∠. 由此,知cos 3sin 30b a ->∠∠. 在△CPB 中,由余弦定理,得122222cos(903)cos 3sin 3cos 3sin 3ab ab BP b b a b a ⎡⎤⎛⎫=+-⋅⋅︒+⎢⎥ ⎪--⎝⎭⎢⎥⎣⎦∠∠∠∠∠. 因034180<+<︒∠∠,则03490<=<︒∠∠,即cos 30>∠. 于是,()122222cos 3(cos 3sin 3)b a b BP b a 2⎡⎤⋅+⎢⎥==-⎢⎥⎣⎦∠∠∠ 同理,在CFP △中,有BF .又在Rt ABC △中,AB , 故211AB BP BF ==+. 注 此例结论表示AB 是BP 与BF 的调和平均,亦表示1PF 调和分割弦AB . 例6 (第一章例12)任意四边形ABCD 的一组对边BA 与CD 交于M ,过M 作割线交另一组对边所在直线于H 、L ,交对角线所在直线于H '、L '.求证:1111MH ML MH ML +=+''. 证明 如图5-7,MBL α=∠,CML β=∠,BMC αβ=+∠,L'H 'DCBA MH图5-7由张角定理得:sin()sin sin MH MD MAαβαβ+=+, ① sin()sin sin MH MC MA αβαβ+=+', ② sin()sin sin ML MD MA αβαβ+=+', ③ sin()sin sin ML MC MBαβαβ+=+.④由①+④-②-③得sin()sin()sin()sin()0MH ML MH ML αβαβαβαβ+++++--='',故1111MH ML MH HL +=+''. 注 此例也可运用线段的调和分割来证明,可参见第十一章例9.对于第十一章的例10,也可运用张角定理来证.请看下例:例7 圆内接四边形ABCD 一组对边DA 、CB 延长线交P 点,过P 点任作直线PF 分别交圆于E 、F ,交AB 、CD 所在直线于N 、M ,求证:1111PE PF PN PM+=+. 证明 设APM α=∠,BPM β=∠,并分别取AD 、EF 、BC 中点R 、G 、H ,如图5-8,显然P 、R 、G 、H 和圆心O 五点共圆,由托勒密定理可知:PG RH RG PH PR GH ⋅=⋅+⋅.对△RGH 三边用正弦定理代入得:()sin sin sin PG PH PR αβαβ⋅+=⋅+⋅,两边乘2,即()sin()PE PF αβ++= ()()sin sin PB PC PA PD αβ+++.又PE PF PB PC PA PD ⋅=⋅=⋅,则11sin()PE PF αβ⎛⎫++= ⎪⎝⎭1111sin sin PB PC PA PD αβ⎛⎫⎛⎫+++ ⎪ ⎪⎝⎭⎝⎭.由张角定理:sin()sin sin PN PB PA αβαβ+=+,sin()sin sin PM PC PD αβαβ+=+,因此1111PE PF PN PM+=+. PFD图5-8当PF 与AB 、DC 的延长线相交同时与圆相交(或相切),如图5-9,例7仍然成立,证法相同.OPR MN K H GFE DCBA 图5-9当PF 与CA ,BD 相交或与它们的延长线相交,同时也与圆相交(或相切),例题7也成立,证法也相同.如图5-10,相切时11PE PF=.P图5-10例8 圆内接ABC △,切线C 点交BA 的延长线于P ,过P 任作直线交圆于E 、F ,交AC 、BC 分别于N 、M ,求证:1111PE PF PN PM+=+. 证明 设APM α=∠,MPC β=∠,并分别取AB 、EF 中点G 、H ,如图5-11,显然P 、G 、H 、C 和圆心O 五点共圆,由托勒密定理可知PH GC GH PC PG HC ⋅=⋅+⋅,对△GHC 三边用正弦定理代入得()sin sin sin PH PC PG αβαβ⋅+=⋅+⋅,两边乘2,即()sin()2sin PE PF PC αβα++=⋅⋅+()sin PA PB β+.因为2PE PF PC PA PB ⋅==⋅,从而11211sin()sin PE PF PC PA PB αβα⎛⎫⎛⎫++=++ ⎪ ⎪⎝⎭⎝⎭sin β.图5-11由张角定理,sin()sin sin PN PC PA αβαβ+=+,sin()sin sin PM PC PBαβαβ+=+. 因此1111PE PF PN PM+=+. 【解题思维策略分析】1.给出著名问题的一种新证法 例9(斯坦纳定理) 在ABC △中,BD ,CE 分别是ABC ∠,ACB ∠的平分线.若BD CE =,则AB AC =. 证明 如图5-12,令ABD DBC α==∠∠,BCE ACE β==∠∠,分别以B ,C 为视点,对ABC △应用张角定理的推论,有2cos 11BD AB BC α=+,2cos 11CE AC BCβ=+. βαβαED CBA图5-12亦有2cos 2cos AB BC AC BC BD CE AB BC AC BC αβ⋅⋅⋅⋅===++, 亦即()()cos cos AB AC BC AC AB BC βα+=+. 对上式应用分比定理,把cos cos βα-化为积,并变形可得 ()2sinsincos 22AC AB BC AB AC BC βαβαα++--=-⋅⋅⋅. ①显然,α,β,αβ±均只能为锐角. 若AB AC >,则①式左端为正,而右端为负,若AB AC <,则①式左端为负,而右端为正. 所以AB AC =.例10(蝴蝶定理) 已知M 是O 的弦AB 的中点,过M 任作两弦CD ,EF ,连CF ,DE 分别交AB 于G ,H ,则MH MG =. 证明 如图5-13,令AMF BME α==∠∠,BMD AMC β==∠∠.以M 为视点,对△M DE 和△MCF 分别应用张角定理,有G H 'C图5-13sin()sin sin MH ME MD αββα+=+, sin()sin sin MG MF MCαββα+=+. 上述两式相减,得()()11sin sin sin()MF ME MD MC MH MG ME MF MC MD βααβ⎛⎫+-=--- ⎪⋅⋅⎝⎭. 设P ,Q 分别是CD ,EF 的中点,由OM AB ⊥,有 22cos(90)2sin ,22cos(90)2sin .MD MC MP OM OM MF ME MQ OM OM ββαα-==⋅︒-=⋅⎧⎨-==⋅︒-=⋅⎩ 于是,()11sin 0MH MG αβ⎛⎫+-= ⎪⎝⎭.而180αβ+≠︒,知sin()0αβ+≠.故MH MG =.注 类似地应用张角定理,可证明如图5-8中的AG BH ''=. 2.获得线段倍分关系的一种途径例11 已知G 是ABC △的重心,过G 作直线分别交ABC △的两边AB ,AC 于E ,F .求证:2EG GF ≤.证明 如图5-14,作中线BGM ,CGN ,令MGF BGE α==∠∠,CGF NGE β==∠∠.βαGFECBAM N 图5-14以G 为视点,分别对△GCM ,△BGN 应用张角定理,有sin()sin sin GF MG GC αββα+=+,sin()EGαβ+=sin sin BG NGβα+. 注意到,2BG GM =,2GC NG =,则 sin()sin sin 2GF GM GNαββα+=+, ① sin()sin sin 2EG GM GN αββα+=+. ②①12⋅-②,得 ()113sin sin 024GF EG GN ααβ⎛⎫-⋅+=-⋅⎪⎝⎭≤. 而 ()()sin 0090αβαβ+><+<︒,故1102EG GF-≥,即2EG GF ≤.例12 如图5-15,平行四边形ABCD 中,在AB 边上取一点P ,使3AB AP =,在边AD 上取点Q ,使4AD AQ =,且PQ 交AC 于M .求证:7AC AM =. βαDCBAM OPQ 图5-15证明 连BD 交AC 于O ,则12AO AC =.令DAM α=∠,BAM β=∠,3AB a =,4AD b =.以A 为视点,分别对△APQ 和△ABD 应用张角定理,有 sin()sin sin sin sin b a AM a b abαβαβαβ+⋅+⋅=+=,sin()sin sin 4sin 3sin 3412b a AO a b ab αβαβαβ+⋅+⋅=+=. 因ADO ABO S S =△△,则4sin 3sin b a αβ⋅=⋅. 于是,4sin 3sin 6sin 212sin 12sin 9sin 12sin 7AM b a a AO b a a a αββαβββ⋅+⋅⋅===⋅+⋅⋅+⋅. 故7AC AM =.例13 如图5-16,筝形ABCD 中,AB AD =,BC DC =.经过AC 与BD 的交点O 任作两条直线,分别交AD 于E ,交BC 于F ,交AB 于G ,交CD 于H ,GF ,EH 分别交BD 于I ,J .求证:OI OJ =. (CMO -5试题)δγβαOIJ HGFE D CBA图5-16证明 令AOE α=∠,EOD β=∠,DOH γ=∠,COH δ=∠.由题设,知AC 垂直平分BD 于O ,以O 为视点,考虑分别在OJ ,OI 所在的三角形△FOH 及△GOF 中应用张角定理.但在△EOH 中,涉及OE ,OH ,于是,又在△AOD ,△COD 及△EOH 中分别应用张角定理,有sin90sin sin OE OD OA αβ︒=+,sin90sin sin OH OC OD γδ︒=+,sin()sin sin OJ OH OEβγβγ+=+. 由上述三式,有sin()sin sin sin sin sin sin sin sin OJ OC OD OD OA βγβγβδγαγβ+⋅⋅⋅⋅=+++. 同理,在△AOB ,△COB 及△GOE 中分别应用张角定理,有 sin()sin sin sin sin sin sin sin sin OI OC OB OB OA γβγβγαβδβγ+⋅⋅⋅⋅=+++. 注意到OD OB =,则有11OJ OI=,故OI OJ =. 例14 如图5-17,已知G 是ABC △的重心,过点G 任作一条直线l ,分别交边AB 、AC 于点D 、E ,若AD xAB =,AE y AC =,求证:11x y+为定值.l βαGFEDCBA图5-17证明 当点D 与点B 重合,即1x =时,E 为AC 之中点,即12y =,此时113x y +=,因此只需证明113x y+=即可. 如图,延长AG 交BC 于F ,则F 为BC 的中点,设BAF α=∠,FAC β=∠,由D ,G ,E 三点共线,可得sin()sin sin AG AE AD αβαβ+=+,因为23AG AF =,AD xAB =.AE yAC =,所以()3sin 2AF αβ+= sin sin yAC xAB αβ+,即sin()2sin 2sin 33AF yAC xAB αβαβ+=+①,由B ,F ,C 三点共线可得()sin sin sin AF AC ABαβαβ+=+②,①式减②式可得sin 2sin 211033AC y AB x αβ⎛⎫⎛⎫-+-= ⎪ ⎪⎝⎭⎝⎭,因为F 为BC 的中点,所以ABF AFC S S =△△,即11sin sin 22AF AB AF AC αβ⋅=⋅,即sin sin 0AC AB αβ=≠,所以2211033y x ⎛⎫⎛⎫-+-= ⎪ ⎪⎝⎭⎝⎭,即113x y +=.3.证明线段比例关系式的一种方法例15 如图5-18,已知AD ,AE 分别是ABC △的内外角平分线,点D 在BC 边上,点E 在BC 边的延长线上.求证:112BE CE DE+=. ααbaED CBA图5-18证明 设AD a =,AE b =,BAD DAC α==∠∠.以A 为视点,分别对△ADE 和△ABE 应用张角定理,得sin90sin sin(90)AC b a αα︒︒-=+,sin(90)sin90sin a AB b αα︒+︒=+. 于是 cos sin ab AC b a αα=+,cos sin abAB b a αα=-.在△ABE 中,由余弦定理,并注意cos 0α>,cos sin 0b a αα->(0AB >), 有BE ===.同理,在△ACE 中,求得CE =.而在Rt △ADE 中,DE = 故112BE CE DE +==. 注 112BE CE DE +=表示DE 是CE 与BE 的调和平均,亦表示DE 被B 、C 或BC 被D 、E 调和分割(即DB BEDC CE=). 用张角定理也可以证明如下调和分割问题:凸四边形ABDF 的两组对边延长相交于点C ,E ,直线AD 交BF 于M ,交CE 于点N ,则112AM AN AD +=或AM MDAN ND=. 事实上,如图5-19,令CAN α=∠,NAE β=∠,以A 为视点,分别对△ABF ,△ABE ,△ACF ,△ACE 应用张角定理,有FEDCBAM N图5-19sin()sin sin AM AF AB αβαβ+=+,sin()sin sin AD AE AB αβαβ+=+, sin()sin sin AD AF AC αβαβ+=+,sin()sin sin AN AE AC αβαβ+=+. 上述第一式与第四式相减后减去其余两式,得112sin()sin()AM AN AD αβαβ⎛⎫++=⋅+ ⎪⎝⎭. 而sin()0αβ+≠,故112AM AN AD+=. 或由2AD AD AM AN AM AN AM AN +==+得AM MDAN ND=.这个调和分割问题可以参见第九章中的性质2.例16 如图5-20设I ,H 分别为锐角ABC △的内心和垂心,点1B ,1C 分别为边AC ,AB 的中点.已知射线1B I 交边AB 于点2B (2B B ≠),射线1C I 交AC 的延长线于点2C ,22B C 与BC 相交于K ,1A 为△BHC 的外心.试证:A ,I ,1A 三点共线的充分必要条件是△2BKB 和△2CKK 的面积相等.(CMO -18试题)1B 2B 1C 1C 2C BAHK 图5-20证明 首先证明:2260BKB CKK S S BAC =⇔=︒△△∠.设ABC △的外接圆半径为R ,连IC ,在△ACI 与ABC △中运用正弦定理,有1sin sin 2AI ACAIC C =∠∠ 14sin 12cos 2AC R B B ==⋅∠∠,即114sin sin 22AI R B C =⋅⋅∠∠. 又 11sin 2AB AC R B ==⋅∠. 在△12AB B 中,注意AI 平分A ∠,以A 为视点,在此三角形中应用张角定理的推论,有12cos 2AAI=∠ 1211AB AB +, 即有 21112cos sin 12211112cos cos cos sin 12222R B CAB A A B CAI AB ⋅⋅==⋅--∠∠∠∠∠∠ 112cos sin 221sin 2R B CA ⋅⋅=∠∠∠.同理,2112cos sin 221sin 2R C BAC A ⋅⋅=∠∠∠. 从而 222222BKB CKC ABC AB C S S S S AB AC AB AC =⇔=⇔⋅=⋅△△△△ 1111sin cos sin cos 2222sin sin 11sin sin 22C B B C C B A A ⋅⋅⇔⋅=⋅∠∠∠∠∠∠∠∠ 24sin 12A⇔=∠,注意到A ∠为三角形内角60BAC ⇔=︒∠. 其次,再证60BAC A =︒⇔∠,I ,1A 三点共线.连1BA ,1CA ,在△1ABA 和△1ACA 中分别应用正弦定理,有 1111sin sin A A A B ABA A AB =∠∠,1111sin sin A A AC ACA A AC=∠∠. 因I 为ABC △的内心,A ,I ,1A 共线111A AB A AC ABA ⇔=⇔∠∠∠与1ACA ∠均为锐角,1111sin sin ABA ACA ABA ACA =⇔≠∠∠∠∠(因AB AC ≠)时,111180,,,ABA ACA A B A C+=︒⇔∠∠四点共圆. 注意到1A 中圆周角与圆心角的关系,有()1360236021802BAC BHC A A =︒-=︒-︒-=∠∠∠∠,且118060BAC A BAC +=︒⇔=︒∠∠∠. 例17 如图5-21,设O ,I 分别是ABC △的外心和内心,AD 是BC 边上的高,I 在线段OD 上,求证:ABC △的外接圆半径R 等于BC 边上的旁切圆的半径a r .(1998年全国高中联赛题)证明 因BC 边上的旁切圆的半径4sincos cos 222a A B C r R =,故只需证明4sin cos cos 1222A B C⋅=即可. 由图,易得90OAC BAD B ==︒-∠∠,因为2A BAI CAI ==∠∠,所以()902ADAI OAI B ==-︒-∠∠ 902A B α=+-︒=,由于点D ,I ,O 共线,由张角定理可得sin 2sin sin AI AO AD ααα=+,即2cos 1AI AOα=+1AD ,即2sin 112A B AI AO AD ⎛⎫+ ⎪⎝⎭=+,其中AO R =,sin 2sin sin AD AB B R C B ==. 设ABC △的内切圆半径为,则csc2A AI r =,因为4sin sin sin 222A B C r R =,则4sin sin 22B CAI R =⋅,所以有2sin 1122sin sin 4sin sin 22A B B C R R B C R ⎛⎫+ ⎪⎝⎭=+,即4sin cos cos 2sin sin 1222A B C B B C ⎛⎫+=+ ⎪⎝⎭,即2sin 2A B ⎛⎫+ ⎪⎝⎭cos cos 2sin sin 122B C B C B C +-⎛⎫+=+ ⎪⎝⎭,即sin sin 2sin cos 2sin sin 2222A A A B C B B B C -⎛⎫⎛⎫+⋅++= ⎪ ⎪⎝⎭⎝⎭1+,即()3cos cos sin sin 2sin sin 12222B A C A B C B B A B C ++⎛⎫-+++-+=+ ⎪⎝⎭,cos cos cos()B C B C ++-= cos()cos()B C B C --+,即cos cos cos 0B C A +-=,即22coscos 2sin 10222B C B C A+-+-=,即2sincos 2sin cos 12222A B C A B C -+⋅+=,即4sin cos cos 1222A B C=. 14.证明三点共线的又一个工具例18 如图5-22,已知AB 是圆的直径,PA ,PC 是圆的切线,A ,C 为切点.作CD AB ⊥于D ,Q 为CD 的中点.求证:P ,Q ,B 三点共线.BAP图5-22证明 以C 为视点,考察线段PQ ,QB 所张的角的情形. 连AC ,BC ,则90ACB =︒∠,令PCA α=∠,则CBA ACD α==∠∠,令PC a =,易知2cos AC a α=⋅,cot 2cos cot BC AC a ααα=⋅=⋅⋅,2sin 2cos CD BC a αα=⋅=⋅,2cos CQ αα=⋅.所以2sin sin(90)cos 1cos cos PCB CQ CQ a a αααα︒+===⋅⋅∠, 2sin sin sin 2cos sin cos 2cos cot cos PCQ QCB CB CP a a a a ααααααα+=+=+⋅⋅∠∠22sin cos 1cos cos a a αααα+==⋅⋅.故sin sin sin PCB PCQ QCBCQ CB CP=+∠∠∠. 由张角定理,知P ,Q ,B 三点共线.例19 如图5-23,在线段AB 上取内分点M ,使AM BM ≤,分别以MA ,MB 为边,在AB 的同侧作正方形AMCD 和MBEF ,P 和Q 分别是这两个正方形的外接圆,两圆交于M ,N .求证:B ,C ,N 三点共线.(IMO -1试题)图5-23证明 连MD ,ME ,NE ,ND ,NM ,则90DNM ENM ==︒∠∠,则D ,N ,E 三点共线,注意454590DME =︒+︒=︒∠.设DMN NEM α==∠∠,P ,Q 的半径分别为1r ,2r ,则MC =,2MB =,12cos MN r α=⋅= 22sin r α⋅.对视点M,考察点B ,C ,N所在的三角形△MBN .由 22sin sin sin 902sin CMB CMN MN MB r α︒+=+=∠∠()2111sin cos sin cos sin cos 2cos 2cos r r αααααααα+⋅-+⋅==⋅11cos sin cos(45)22r r ααα+︒-===sin 9045sin NMBMCα︒+︒-==∠.应用张角定理,即知B ,C ,N 三点共线.例20 如图5-24,在ABC △中,令A α=∠,B β=∠,C γ=∠,且αβ>,AD ,BE ,CF 是它的三条垂线;AP ,BQ 是两条角平分线;I ,O 分别是它的内心和外心.证明:点D ,I ,E 共线当且仅当P ,O ,Q 共线,当且仅当O ,I ,F 共线.(IMO -38预选题或由1998年全国高中联赛题改编)IOFE DCBAP Q图5-24证明 由于外心O 有在ABC △内、外、边上三种情形,故须对α分三种情况讨论. (Ⅰ)当α为锐角时.设ABC △的外接圆半径为R ,内切圆半径为,令BC a =,CA b =,AB c =,连CO ,CI ,则abCP b c=+,ab CQ a c =+,π2OCQ β=-∠,π2OCP α=-∠,cos CD b γ=⋅,cos CE a γ=⋅,sin 2r CI γ=,OCI ICF =∠∠ π22γβ=--(或π22γα+-),π2OCF βγ=--∠(或2πγα+-). 以C 为视点,分别考察△PCQ ,△DCE ,△OCF ,并应用张角定理.P ,O ,Q 共线sin sin sin OCP OCQOC CQ CP γ⇔=+∠∠ []sin ()cos ()cos ab R a c b c γαβ⇔⋅=+⋅++⋅[]224sin sin sin sin 2sin 22sin (cos cos )R R αβγαβγαβ⇔⋅⋅⋅=+++22(sin 2sin 2sin 2)[sin 2sin 22sin (cos cos )]R R αβγαβγαβ⇔++=+++sin 22sin (cos cos )cos cos cos γγαβγαβ⇔=+⇔=+.D ,I ,E 共线()sinsinsin 22sin cos ab r a b CI CD CEγγγγγ⇔=+⇔⋅=+ ()cos ()()(1cos )cos r a b c r a b a b c γγγ⇔++⋅=+⇔+-=⋅(sin sin )(1cos )sin cos αβγγγ⇔+-=⋅22cos cos2sin sin cos 222γαβγγγ-⇔⋅⋅=⋅2sincoscos cos cos cos 22γαβγγαβ-⇔⋅=⇔=+. O ,I ,F 共线sin sin sin OCF OCI ICFCI CF CO⇔=+∠∠∠ ()cos cos sin 2222sin sin 22sin sin CI CI a R R γγβββγγββαβ⎛⎫⎛⎫++ ⎪ ⎪+⎛⎫⎝⎭⎝⎭⇔=+⇔+=+ ⎪⋅⋅⎝⎭2sinsin sin sin22rr R R γγαβ+⋅⋅⋅⋅(注意π22γβ+≠,4sin sin sin 222r R αβγ=⋅⋅) 12sin 4sin sin 2222cos cos 22γαββαβ⎛⎫⇔+=+⋅ ⎪⎝⎭⋅4sin cos cos 12sin sin 222γαββαβ⎛⎫⇔+⋅⋅=+⋅ ⎪⎝⎭sin sin sin sin 22222222222αβγβγααβγαβββ⎛⎫⎛⎫⎛⎫⎛⎫⇔+++++-++++-+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭1cos()cos()αβαβ=+--+cos cos 1cos()1cos()cos cos cos cos βααβαβγγαβ⇔+++-=+-+⇔=+. 因此,D ,I ,E 共线⇔P ,O ,Q 共线⇔O ,I ,F 共线.(Ⅱ)当α为钝角时,注意π2OCP α=-∠,依照(Ⅰ)类似证明. (Ⅲ)当α为直角时,易证点D ,I ,E 共线当且仅当ABC △是等腰直角三角形;点P ,O ,Q 共线当且仅当ABC △是等腰直角三角形;点O ,I ,F 共线当且仅当ABC △是等腰直角三角形.综合即证. 注 在ABC △中,可证得:cos cos cos C A B =+∠∠∠,当且仅当ABC △的外接圆半径等于AB 边上的旁切圆半径.因此本例题还等价于ABC △的外接圆半径等于AB 边上的旁切圆半径,此为例17即1998年全国高中联赛平面几何题结论.5.注意张角定理与斯特瓦尔特定理的等价性例21 如图5-25,设B ,P ,C 依次分别为从A 点引出的三条射线AB ,AP ,AC 上的点.线段BP ,PC 对点A 的张角分别为α,β,且180αβ+<︒,则B ,P ,C 三点共线的下述两个充要条件等价:βαCBA EF P 图5-25(Ⅰ)sin()sin sin AP AC ABαβαβ+=+(张角定理); (Ⅱ)222AB PC AC BP AP BC BP PC BC ⋅+⋅=⋅+⋅⋅(斯特瓦尔特定理). 证明sin()sin sin sin()sin sin AB AC AP AB AP AC AP AC ABαβαβαβαβ+=+⇔⋅⋅+=⋅⋅+⋅⋅ sin cos cos sin sin sin AB AC AB AC AP AB AP AC αβαβαβ⇔⋅⋅⋅+⋅⋅⋅=⋅⋅+⋅⋅.作BE ⊥射线AP 于E ,作CF ⊥射线AP 于F ,则 sin sin AB BE BP k BPAC CF PC k PCαβ⋅⋅===⋅⋅ cos cos AC k BP AB k PC AP k BP AP k PC AP k BC βα⇔⋅⋅⋅+⋅⋅⋅=⋅⋅+⋅⋅=⋅⋅222222222AC AP PC AB AP BP AP AC BP AP AB PC AP BC AC AP AB AP +-+-⇔⋅⋅⋅+⋅⋅⋅=⋅⋅⋅222AB PC AC BP AP BC BP PC BC ⇔⋅+⋅=⋅+⋅⋅.【模拟实战】习题A1.在矩形ABCD 中,AB a =,BC b =,M 为BC 中点,DE ⊥射线AM 于E ,求DE 之长.(用a ,b 表示)2.ABC △中,AB AC =,AD 为BC 边上的高,AD 的中点为M ,CM 的延长线交AB 于K .求证:3AB AK =.3.已知AC AB ⊥,BD AB ⊥,AD 和BC 相交于点E ,EF AB ⊥于F .又AC p =,BD q =,EF r =,AF m =,FB n =.求证:111p q r+=. 4.梯形ABCD (AB DC ∥)的对角线AC ,BD 相交于P ,过P 作梯形下底的平行线交两腰AD 于M ,BC 于N .求证:PM PN =.5.设XOY ∠的平分线上任一点为P ,过P 作两条任意直线AB ,CD ,分别交OX ,OY 于A ,C ,B ,D .求证:OC OA BD OB OD AC ⋅⋅=⋅⋅.6.直线l 的同侧有三个相邻的等边三角形△ADE ,△AFG ,ABC △,且G ,A ,B 都在直线l 上.设这三个三角形的边长依次为b ,c ,a ,连GD 交AE 于N ,连BN 交AC 于L .求证:abcAl ab bc ac =++.7.在O 中,过弦GH 的中点M 作弦AB ,CD ,令AMG α=∠,CMG β=∠.求证:sin sin MB MAMC MDαβ-=-. 8.在平行四边形ABCD 的CD 边上取一点P ,使12CP PD =∶∶,在对角线上取一点Q ,使13CQ QA =∶∶.求证:B ,Q ,P 三点共线. 习题B1.已知四边形ABCD 两组对边的延长线分别交于K ,L .过K ,L 作直线,对角线AC ,BD 之延长线分别交KL 于G ,F .求证:1KF ,1KL ,1KG 成等差数列.2.在锐角三角形ABC 中,AC AB >.求证:B ∠的平分线BD 小于C ∠的平分线CE .3.在O 内,直径AOB ⊥半径OC ,O '与OB ,OC 相切于D ,E ,并与O 内切于F .求证:A ,E ,F 三点共线.4.在Rt ABC △中,90ACB =︒∠,CD AB ⊥于D ,△ADC 和△CDB 的内心分别为1O ,2O ,12O O 与CD 交于K .求证:111BC AC CK+=. 5.设P 为ABC △内任一点,顶点A ,B ,C 与P 的连线分别与BC ,CA ,AB 交于点D ,E ,F .P '为△DEF 周界上任一点,过P '作PD ,PE ,PF 的平行线分别与BC ,CA ,AB 交于D ',E ',F '.证明:在比值P D PD '',P E PE '',P F PF ''中必有一个等于另两个的和.。
