福建省厦门市2020-2021学年高一上学期期末考试数学试题 含答案
福建省厦门市高一化学上学期期末考试题(含答案)
福建省厦门市高一化学上学期期末考试题(含答案)一、单选题(本大题共15小题)1. 下列《科学》杂志评选的2021年十大科学突破中,属于化学研究范畴的是。
A .“洞察”号揭示火星内部结构 B .实现历史性核聚变C .合成抗新冠强效药莫奈拉韦()D .体外胚胎培养取得突破 2. 下列物质不属于分散系的是 A .水 B .碘酒C .空气D .有色玻璃3. 标准状况下,下列物质所占体积最大的是A .236g H OB .21.5mol HC .348g OD .233.0110⨯个2N 4. 管道疏通剂的下列成分中,不属于电解质的是。
A .碳酸钠B .次氯酸钠C .氢氧化钠D .铝粉 5. 下列铜及其化合物的性质实验中,涉及到的反应不属于氧化还原反应的是 A .铜丝在空气中加热 B .用氢气还原氧化铜C .将铁丝插入4CuSO 溶液中D .向4CuSO 溶液中滴加NaOH 溶液6. 积极参加项目学习,提升化学素养。
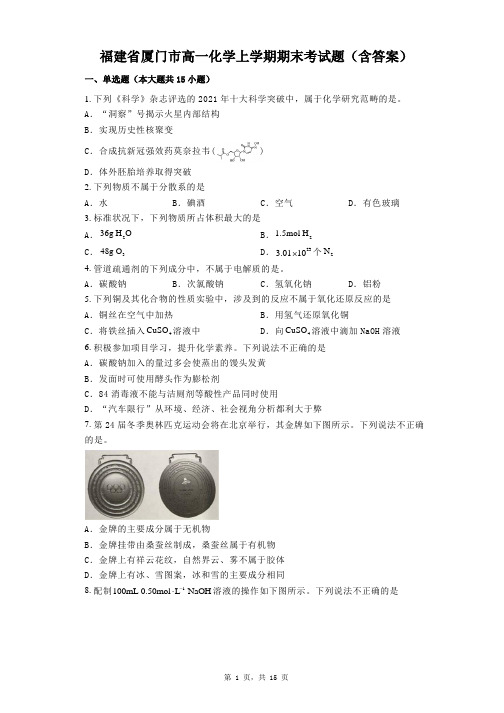
下列说法不正确的是 A .碳酸钠加入的量过多会使蒸出的馒头发黄 B .发面时可使用酵头作为膨松剂C .84消毒液不能与洁厕剂等酸性产品同时使用D .“汽车限行”从环境、经济、社会视角分析都利大于弊7. 第24届冬季奥林匹克运动会将在北京举行,其金牌如下图所示。
下列说法不正确的是。
A .金牌的主要成分属于无机物B .金牌挂带由桑蚕丝制成,桑蚕丝属于有机物C .金牌上有祥云花纹,自然界云、雾不属于胶体D .金牌上有冰、雪图案,冰和雪的主要成分相同8. 配制1100mL 0.50mol L NaOH -⋅溶液的操作如下图所示。
下列说法不正确的是A .操作1前需称取2.0g NaOHB .操作1固体溶解后立即进行操作2C .操作3和操作4分别为洗涤和定容D .操作5后将配制好的溶液倒入试剂瓶9. 离子反应在生产生活中有许多应用。
下列离子方程式正确的是。
A .和面时用小苏打和食醋能使馒头蓬松:-+322HCO +H =H O+CO ↑B .用氨水吸收少量二氧化硫尾气:+2-3224322NH H O+SO =2NH +SO +H O ⋅C .用石灰浆制漂白粉:22Cl 2OH H O Cl ClO ---+=++D .用氯化铁溶液做腐蚀剂印刷电路板:322Fe Cu Fe Cu ++++=+10. 铁及其化合物的“价—类”二维图如图。
福建省福州市福清市高中联合体2020-2021学年高一上学期期末考试数学试题(含解析)

福清市高中联合体2020—12021学年第一学期高一年期末考试数学试卷(完卷时间:120分钟;满分:150分)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分. 注意事项:1.答题前,考生务必在试题卷、答题卡规定的地方填写自己的准考证号、姓名.考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名”与考生本人准考证号、姓名是否一致.2.第Ⅰ卷每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答案标号.第Ⅱ卷用0.5毫米黑色签字笔在答题卡上书写作答.在试题卷上作答,答案无效.3.考试结束,考生必须将试题卷和答题卡一并交回.第Ⅰ卷一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知集合{}1,0,1,2,3A =-,{}31B x x =-<,则A B =( )A. {}3B. {}1,0,1-C.1,0,1,2D. {}1,0,1,2,3-2. 命题“0x ∀≥,sin x x ≤”的否定是( ) A. 0x ∀≥,sin x x > B. 00x ∃<,00sin x x > C. 00x ∃≥,00sin x x >D. 00x ∃≥,00sin x x ≤3. 函数()f x x =是( ) A. 奇函数,且在R 上单调递减 B. 奇函数,且在R 上单调递增 C. 偶函数,且在R 上单调递减D. 偶函数,且在R 上单调递增4. 若角α的顶点与直角坐标系的原点重合,始边与x 轴的非负半轴重合,终边经过点(1,-,则sin 2α=( )A. B. 12-C.12D.25. 函数()38ln f x x x =-+的零点所在区间应是( )A. ()1,2B. ()2,3C. ()3,4D. ()4,56. 要得到函数sin 23y x π⎛⎫=- ⎪⎝⎭的图象,只需将函数sin 24y x π⎛⎫=-⎪⎝⎭图象上所有点的横坐标( ) A. 向左平移12π个单位长度B. 向右平移12π个单位长度C. 向左平移24π个单位长度D. 向右平移24π个单位长度7. 已知51log 4a =,1514b ⎛⎫= ⎪⎝⎭,41log 5c =,则a ,b ,c 的大小关系为( )A. a b c >>B. b c a >>C. b a c >>D. c b a >>8. 月均温全称月平均气温,气象学术语,指一月所有日气温的平均气温.某城市一年中12个月的月均温y (单位:C )与月份x (单位:月)的关系可近似地用函数()sin 36y A x a π⎡⎤=-+⎢⎥⎣⎦(1,2,3,,12x =)来表示,已知6月份的月均温为29C ,12月份的月均温为17C ,则10月份的月均温为( ) A. 20CB. 20.5CC. 21CD. 21.5C二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得3分.9. 下列函数中,最小值是2的有( )A. 1y xx=+B. y =C. 223y x x =++D. e e x x y -=+10. 命题“x R ∀∈,210x ax -+≥”为真命题的一个必要不充分条件可以是( ) A. 22a -≤≤B. 2a ≥-C. 2a ≤D. 22a -<<11. 关于函数()sin cos f x x x =+有下述四个结论,其中正确的是:( ) A. ()f x 的图象关于原点对称 B. ()f x 在区间,4ππ⎛⎫⎪⎝⎭单调递减 C. ()f x 在[],ππ-有2个零点D. ()f x 的最大值为212. 已知定义在R 上的函数()f x 满足()()4f x f x +=,若()1y f x =-的图象关于直线1x =对称,且对任意的[]12,0,2x x ∈,且12x x ≠,都有()()()12120x x f x f x -->⎡⎤⎣⎦,则下列结论正确的是( ) A. ()f x 是偶函数B. ()f x 在()2018,2020上单调递增C. 4是函数()f x 的周期D. ()f x 在()2018,2020上单调递减第Ⅱ卷注意事项: 用0.5毫米黑色签字笔在答题卡上书写作答.在试题卷上作答,答案无效.三、填空题:本大题共4小题,每小题5分,共20分.把答案填在题中的横线上.13. 已知函数()1,12,1x f x x x <⎧=⎨≥⎩则()()0f f =________.14. 已知22tan 31tan αα=--,且α为锐角,则α=________.15. 如图,Rt ABC 的三个顶点A ,B ,C 恰好分别落在函数()21xy x =>,y x =,12log y x =的图象上,且B ,C 两点关于x 轴对称,则点A 的横坐标为________.16. 已知定义在R 上的偶函数()f x ,当0x ≥时,函数()cos ,01,,1,x x f x x x π≤<⎧=⎨-≥⎩则满足()()12f x f x +<的x 的取值范围是________.四、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17. 求下列各式的值: (1)(0312932224-⎛⎫--⨯ ⎪⎝⎭;(2)55251log 3log log 25log 215++⨯. 18. 已知全集U =R ,集合{}20A x x a =+>,()(){}140B x x x =+-≤. (1)当2a =时,求()UA B ;(2)若B A ⊆,求实数a 的取值范围.19. 在①1k =-,②1k =这两个条件中任选一个,补充在下面问题中. 已知函数()kf x kx x=-,且_______, (1)求()f x 的定义域,并判断()f x 的奇偶性;(2)判断()f x 的单调性,并用定义给予证明.20. 已知,2παπ⎛⎫∈ ⎪⎝⎭,且2sin cos 222αα-= (1)求cos α的值; (2)若()4sin 5αβ-=,,2πβπ⎛⎫∈ ⎪⎝⎭,求cos β的值. 21. 某儿童活动中心,为儿童修建一个面积为100平方米的矩形游泳池,为保障儿童生命安全,在其四周都留有宽2米的路面,问所选场地的长和宽各为多少时,才能使占用场地的面积S 最小,并求出该最小值? 22. 已知函数()2sin 36f x x ππ⎛⎫=+⎪⎝⎭.(1)用“五点作图法”在给定的坐标系中,画出函数()f x 在[]0,6上的图象; (2)求()f x 图象的对称轴与单调递增区间; (3)当[]0,x m ∈时,()12f x ≤≤,求实数m 取值范围.福清市高中联合体2020—12021学年第一学期高一年期末考试数学试卷(解析版)(完卷时间:120分钟;满分:150分)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分. 注意事项:1.答题前,考生务必在试题卷、答题卡规定的地方填写自己的准考证号、姓名.考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名”与考生本人准考证号、姓名是否一致.2.第Ⅰ卷每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答案标号.第Ⅱ卷用0.5毫米黑色签字笔在答题卡上书写作答.在试题卷上作答,答案无效.3.考试结束,考生必须将试题卷和答题卡一并交回.第Ⅰ卷一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知集合{}1,0,1,2,3A =-,{}31B x x =-<,则A B =( )A. {}3B. {}1,0,1-C.1,0,1,2D. {}1,0,1,2,3-【答案】A 【解析】 【分析】先求得集合B ,再根据交集定义直接得结果.【详解】因为{}()312B x x =-<=+∞,,又{}1,0,1,2,3A =-,所以{}3A B ⋂=, 故选:A.2. 命题“0x ∀≥,sin x x ≤”的否定是( ) A. 0x ∀≥,sin x x > B. 00x ∃<,00sin x x > C. 00x ∃≥,00sin x x > D. 00x ∃≥,00sin x x ≤【答案】C 【解析】 【分析】由全称命题的否定变换形式即可得出结果. 【详解】命题“0x ∀≥,sin x x ≤” 的否定是00x ∃≥,00sin x x >.故选:C3. 函数()f x x =是( ) A. 奇函数,且在R 上单调递减 B. 奇函数,且在R 上单调递增 C. 偶函数,且在R 上单调递减 D. 偶函数,且在R 上单调递增【答案】B 【解析】 【分析】利用函数的奇偶性定义判断奇偶性,根据函数的解析式判断单调性. 【详解】函数的定义域为R ,关于原点对称,又()(()f x x x f x -=-+=-+=-,所以()f x是奇函数,又,y x y ==R 上的增函数,所以()f x 是R 上的增函数, 故选:B4. 若角α的顶点与直角坐标系的原点重合,始边与x 轴的非负半轴重合,终边经过点(1,-,则sin 2α=( )A. B. 12-C.12D.【答案】D 【解析】 【分析】根据任意角的三角函数的定义,求出sin α和cos α,再由二倍角的正弦公式,即可求出结果.【详解】因为角α的顶点与直角坐标系的原点重合,始边与x轴的非负半轴重合,终边经过点(1,-,所以sin 2α==-,1cos 2α==-,因此1sin 22sin cos 22ααα⎛⎛⎫==⨯⨯-= ⎪ ⎝⎭⎝⎭.故选:D.5. 函数()38ln f x x x =-+的零点所在区间应是( )A. ()1,2B. ()2,3C. ()3,4D. ()4,5【答案】B 【解析】 【分析】利用函数的零点存在定理求解.【详解】由函数()38ln f x x x =-+, 因为()()2ln 220,3ln310f f =-<=+>, 所以函数的零点所在区间应是()2,3 故选:B6. 要得到函数sin 23y x π⎛⎫=- ⎪⎝⎭的图象,只需将函数sin 24y x π⎛⎫=-⎪⎝⎭图象上所有点的横坐标( ) A. 向左平移12π个单位长度B. 向右平移12π个单位长度C. 向左平移24π个单位长度 D. 向右平移24π个单位长度【答案】D 【解析】 【分析】根据sin 2sin 23244y x x πππ⎡⎤⎛⎫⎛⎫=-=-- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,利用平移变换求解. 【详解】因为sin 2sin 23244y x x πππ⎡⎤⎛⎫⎛⎫=-=-- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦, 所以要得到函数sin 23y x π⎛⎫=- ⎪⎝⎭的图象,只需由sin 24y x π⎛⎫=- ⎪⎝⎭图象上所有点横坐标向右平移24π个单位长度,故选:D 7. 已知51log 4a =,1514b ⎛⎫= ⎪⎝⎭,41log 5c =,则a ,b ,c 的大小关系为( )A. a b c >>B. b c a >>C. b a c >>D. c b a >>【答案】C 【解析】 【分析】利用指数函数和对数函数的单调性判断.【详解】因为55510log log 4log 514a >==->-=-,15110144b ⎛⎫⎛⎫<=<= ⎪ ⎪⎝⎭⎝⎭, 4441log log 5log 415c ==-<-=-,所以b a c >> 故选:C8. 月均温全称月平均气温,气象学术语,指一月所有日气温的平均气温.某城市一年中12个月的月均温y (单位:C )与月份x (单位:月)的关系可近似地用函数()sin 36y A x a π⎡⎤=-+⎢⎥⎣⎦(1,2,3,,12x =)来表示,已知6月份的月均温为29C ,12月份的月均温为17C ,则10月份的月均温为( ) A. 20C B. 20.5CC. 21CD. 21.5C【答案】A 【解析】 【分析】由题意得出关于A 、a 的方程组,可得出函数解析式,在函数解析式中令10x =可得结果.【详解】由题意可得sin 2923sin 172A a A a A a a A ππ⎧+=+=⎪⎪⎨⎪+=-=⎪⎩,解得623A a =⎧⎨=⎩,所以,函数解析式为()6sin 3236y x π⎡⎤=-+⎢⎥⎣⎦, 在函数解析式中,令10x =,可得716sin236232062y π⎛⎫=+=⨯-+= ⎪⎝⎭. 因此,10月份的月均温为20C . 故选:A.二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得3分.9. 下列函数中,最小值是2的有( )A. 1y xx=+B. y =C. 223y x x =++D. e e x x y -=+【答案】BCD 【解析】 【分析】根据基本不等式逐一判断即可.【详解】对于A ,1y x x =+,当0x >时,12y x x =+≥=,当且仅当1x =时取等号;当0x <时,12y x x ⎛⎫=--+≤-=- ⎪-⎝⎭, 当且仅当1x =-时取等号,故A 不正确;对于B ,2y=≥=,当且仅当1x =时取等号. 对于C ,()2223122y x x x =++=++≥,当1x =-时,取最小值;对于D ,e e 2x x y -=+≥=,当且仅当0x =时取等号; 故选:BCD【点睛】易错点睛:利用基本不等式求最值时,要注意其必须满足的三个条件: (1)“一正二定三相等”“一正”就是各项必须为正数;(2)“二定”就是要求和的最小值,必须把构成和的二项之积转化成定值;要求积的最大值,则必须把构成积的因式的和转化成定值;(3)“三相等”是利用基本不等式求最值时,必须验证等号成立的条件,若不能取等号则这个定值就不是所求的最值,这也是最容易发生错误的地方10. 命题“x R ∀∈,210x ax -+≥”为真命题的一个必要不充分条件可以是( ) A. 22a -≤≤ B. 2a ≥- C. 2a ≤ D. 22a -<<【答案】BC 【解析】 【分析】根据题意,命题为真可得()240a ∆=--≤,求出a 的取值范围,再根据必要不充分条件即可求解. 【详解】由命题“x R ∀∈,210x ax -+≥”为真命题,可得()240a ∆=--≤,解得22a -≤≤, 对于A ,22a -≤≤是命题为真的充要条件; 对于B ,由2a ≥-不能推出22a -≤≤,反之成立, 所以2a ≥-是命题为真的一个必要不充分条件; 对于C ,2a ≤不能推出22a -≤≤,反之成立, 所以2a ≤也是命题为真的一个必要不充分条件; 对于D ,22a -<<能推出22a -≤≤,反之不成立, 22a -<<是命题为真的一个充分不必要条件.故选:BC11. 关于函数()sin cos f x x x =+有下述四个结论,其中正确的是:( ) A. ()f x 的图象关于原点对称 B. ()f x 在区间,4ππ⎛⎫⎪⎝⎭单调递减C. ()f x在[],ππ-有2个零点 D. ()f x 的最大值为2【答案】BC 【解析】 【分析】分sin 0x ≥,sin 0x <,将函数转化(),224sin cos ,2224x k x k f x x x x k x k πππππππππ⎛⎫+≤≤+ ⎪⎝⎭=+=⎛⎫++<<+ ⎪⎝⎭,再逐项求解判断.【详解】当sin 0x ≥,即22k x k πππ≤≤+时,()sin cos 4f x x x x π⎛⎫=+=+ ⎪⎝⎭,当sin 0x <,即222ππππ+<<+k x k 时,()sin cos 4f x x x x π⎛⎫=-+=+ ⎪⎝⎭,所以(),224sin cos ,2224x k x k f x x x x k x k πππππππππ⎛⎫+≤≤+ ⎪⎝⎭=+=⎛⎫++<<+ ⎪⎝⎭,A.因为函数定义域为R ,关于原点对称,又()()()()sin cos sin cos f x x x x x f x -=-+-=+=,所以()f x 是偶函数,其图象关于y 轴对称,故错误;B.当,4x ππ⎛⎫∈⎪⎝⎭时, 53,,42422x πππππ⎛⎫⎛⎫+∈⊆ ⎪ ⎪⎝⎭⎝⎭,因为sin y x =在3,22ππ⎡⎤⎢⎥⎣⎦上单调递减,所以()f x 在区间,4ππ⎛⎫⎪⎝⎭单调递减,故正确; C. 令()04f x x π⎛⎫=+= ⎪⎝⎭,则4x k ππ+=,因为[]0,x π∈,解得34x π=,又因为()f x 是偶函数,所以函数()f x 在[],ππ-有2个零点,故正确; D. ()f x,故错误; 故选:BC【点睛】关键点点睛:将函数变形为(),224,2224x k x k f x x k x k πππππππππ⎛⎫+≤≤+ ⎪⎝⎭=⎛⎫++<<+ ⎪⎝⎭是本题求解的关键.12. 已知定义在R 上的函数()f x 满足()()4f x f x +=,若()1y f x =-的图象关于直线1x =对称,且对任意的[]12,0,2x x ∈,且12x x ≠,都有()()()12120x x f x f x -->⎡⎤⎣⎦,则下列结论正确的是( ) A. ()f x 是偶函数 B. ()f x 在()2018,2020上单调递增 C. 4是函数()f x 的周期 D. ()f x 在()2018,2020上单调递减【答案】ACD 【解析】 【分析】A. 由()1y f x =-的图象与()y f x =的图象关系判断;C.由()f x 满足()()4f x f x +=判断;BD.由对任意的[]12,0,2x x ∈,且12x x ≠,都有()()()12120x x f x f x -->⎡⎤⎣⎦,得到()f x 在[]0,2上递增,再结合函数的周期性判断.【详解】因为()1y f x =-的图象关于直线1x =对称,所以()y f x =的图象关于直线0x =对称,所以()f x 是偶函数,故A 正确;()f x 满足()()4f x f x +=,所以4是函数()f x 的周期,故C 正确;因为对任意的[]12,0,2x x ∈,且12x x ≠,都有()()()12120x x f x f x -->⎡⎤⎣⎦,所以()f x 在[]0,2上递增,又()()()()20182,20200f f f f == ,所以()f x 在()2018,2020上单调递减,故D 正确B 错误; 故选:ACD第Ⅱ卷注意事项:用0.5毫米黑色签字笔在答题卡上书写作答.在试题卷上作答,答案无效. 三、填空题:本大题共4小题,每小题5分,共20分.把答案填在题中的横线上.13. 已知函数()1,12,1x f x x x <⎧=⎨≥⎩则()()0f f =________.【答案】2 【解析】 【分析】根据分段函数每段的定义域求解.【详解】因为函数()1,12,1x f x x x <⎧=⎨≥⎩所以()01f =, 所以()()()012ff f ==,故答案为:214. 已知22tan 1tan αα=-α为锐角,则α=________. 【答案】3π 【解析】 【分析】根据二倍角的正切公式,求出tan2α,再由α为锐角,即可求出α.【详解】因为22tan tan 21tan ααα==-α为锐角,所以02απ<<, 因此223πα=, 所以3πα=.故答案为:3π.15. 如图,Rt ABC 的三个顶点A ,B ,C 恰好分别落在函数()21xy x =>,y x =,12log y x =的图象上,且B ,C 两点关于x 轴对称,则点A 的横坐标为________.【答案】2 【解析】 【分析】设出点(),2tA t ,根据题意可知//AB x 轴,从而可得出点B ,进而可得点C ,代入对数函数的解析式即可求解.【详解】设出点(),2tA t ,ABC 是直角三角形,且B ,C 两点关于x 轴对称,∴//AB x 轴,A 和B 纵坐标相同,2t x ∴=4t x ∴=,()4,2t t B ∴,则()4,2t t C -,C 在12log y x =的图象上,则12log 42t t=-,整理可得22t t -=-,()1t >,解得2t =. 故答案为:216. 已知定义在R 上的偶函数()f x ,当0x ≥时,函数()cos ,01,,1,x x f x x x π≤<⎧=⎨-≥⎩则满足()()12f x f x +<的x 的取值范围是________. 【答案】113-<<x【解析】 【分析】根据cos y x =和y x =-的单调性,又 cos 1π=-,得到()f x 在 [0,)+∞上递减,再根据()f x 是偶函数,将不等式()()12f x f x +<转化为()()12fx f x +<求解.【详解】当0x ≥时,函数()cos ,01,,1,x x f x x x π≤<⎧=⎨-≥⎩当01x ≤<时, 0x ππ≤<,因为 cos y x =在 []0,π上递减,所以 ()f x 在 [0,1)上递减,当1≥x 时,y x =-递减,又 cos 1π=-,所以()f x 在 [0,)+∞上递减, 又因为()f x 是定义在R 上的偶函数, 则不等式()()12f x f x +<可化为:()()12f x f x +<,所以12x x +>, 解得113-<<x , 故答案为:113-<<x四、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17. 求下列各式的值: (1)(03129324-⎛⎫--⨯ ⎪⎝⎭;(2)55251log 3log log 25log 215++⨯. 【答案】(1)3;(2)1. 【解析】 【分析】(1)根据指数的运算性质即可求解. (2)利用对数的运算性质即可求解. 【详解】(1)原式=33=+=(2)原式51lg 25lg 2log (3)15lg 2lg5=⨯+⨯ 152lg5lg 2log 5lg 2lg5-=+⨯ 12=-+ 1=.18. 已知全集U =R ,集合{}20A x x a =+>,()(){}140B x x x =+-≤. (1)当2a =时,求()UA B ;(2)若B A ⊆,求实数a 的取值范围. 【答案】(1){}|4x x ;(2)()2,+∞. 【解析】 【分析】(1)由2a =得到{}|1A x x =>-,再利用集合的补集和并集运算求解. (2)化简|2a A x x ⎧⎫=>-⎨⎬⎩⎭,{}|14B x x=-,再由B A ⊆求解.【详解】(1)当2a =时,集合{}|1A x x =>-,{}|1UxA x -=,因为()(){}|140B x x x =+-,所以{}|14B x x=-, 所以{}()|4U A B x x=.(2)因为{}|20A x x a =+>, 所以|2a A x x ⎧⎫=>-⎨⎬⎩⎭, 由(1)知,{}|14B x x=-,又因为B A ⊆,所以12a-<-, 解得2a >,所以实数a 的取值范围()2,+∞.19. 在①1k =-,②1k =这两个条件中任选一个,补充在下面问题中. 已知函数()kf x kx x=-,且_______,(1)求()f x 的定义域,并判断()f x 的奇偶性; (2)判断()f x 的单调性,并用定义给予证明. 【答案】(1)答案见解析;(2)答案见解析. 【解析】 【分析】选择①1k =-,可得1()f x x x =-,选择②1k =,可得1()f x x x=-. (1)使函数()f x 有意义,只需0x ≠;再求出()f x -与()f x 的关系即可求解. (2)根据证明函数单调性的步骤:取值、作差、变形、定号即可证明. 【详解】选择①1k =-,因为()kf x kx x =-,所以1()f x x x=-. (1)要使函数()f x 有意义,只需0x ≠, 所以函数()f x 的定义域为(,0)(0,)-∞+∞.因为11()()()f x x x f x x x-=--=--=--, 所以()f x 为奇函数.⑵ 函数()f x 在区间(,0)-∞和(0,)+∞均为增函数. 证明如下: 12,(0,)x x ∀∈+∞,且12x x <, 则12121211()()()f x f x x x x x -=--- 121212()x x x x x x -=-+12121()1)x x x x =-+( ()121212()1x x x x x x -+=,因为120x x <<,所以120x x -<,120x x >,1210x x +>, 所以12())0(f x f x -<,即12()()f x f x <, 故函数()f x 在区间(0,)+∞为增函数; 同理可证,函数()f x 在区间(,0)-∞为增函数;所以函数()f x 在区间(,0)-∞和(0,)+∞均为增函数. 选择②1k =,因为()kf x kx x =-,所以1()f x x x=-. (1)要使函数()f x 有意义,只需0x ≠, 所以函数()f x 的定义域为(,0)(0,)-∞+∞.因为11()()()()f x x x f x x x-=--=--=--, 所以()f x 奇函数.⑵ 函数()f x 在区间(,0)-∞和(0,)+∞均为减函数. 证明如下:12,(0,)x x ∀∈+∞,且12x x <, 则12121211()()()f x f x x x x x -=--- 212112()x x x x x x -=+- 21121()1x x x x ⎛⎫=-+ ⎪⎝⎭()211212()1x x x x x x -+=,因为120x x <<,所以210x x ->,120x x >,1210x x +>, 所以12())0(f x f x ->,即12()()f x f x >, 故函数()f x 在区间(0,)+∞为减函数; 同理可证,函数()f x 在区间(,0)-∞为减函数; 所以函数()f x 在区间(,0)-∞和(0,)+∞均为减函数.20. 已知,2παπ⎛⎫∈ ⎪⎝⎭,且sin cos 222αα-=. (1)求cos α的值; (2)若()4sin 5αβ-=,,2πβπ⎛⎫∈ ⎪⎝⎭,求cos β的值. 【答案】(1);(2. 【解析】 【分析】(1)将已知条件两边平方,求得sin α的值,进而求得cos α的值.(2)先求得()cos αβ-的值,然后利用cos cos[()]βααβ=--,结合两角差的余弦公式,求得cos β的值.【详解】(1)将sincos222αα-=两边同时平方,得11sin 2α-=,则1sin 2α=,又2παπ∈(,),所以cos 2α==-.(2)由(1)知,1sin ,cos 2αα==, 因为2παπ∈(,),2βπ∈π(,),所以22ππαβ-<-<.又因为4sin()5αβ-=,所以3cos()5αβ-,所以cos cos[)]βααβ=--( cos cos()sin sin()ααβααβ=-+-314525=+⨯, 【点睛】关键点点睛:对于三角函数给值求值的问题,关键在于运用已知角的和,差,二倍的运算表示待求的角,再选择相关公式得以求值.21. 某儿童活动中心,为儿童修建一个面积为100平方米的矩形游泳池,为保障儿童生命安全,在其四周都留有宽2米的路面,问所选场地的长和宽各为多少时,才能使占用场地的面积S 最小,并求出该最小值? 【答案】长为14米,宽为14米;196平方米. 【解析】 【分析】先设泳池的长为x 米,宽为y 米,列出式子,再利用基本不等式即可求解.【详解】解:设游泳池的长为x 米,宽为y 米,则场地长为(4)x +米,宽为(4)y +米,()1000,0xy x y =>>,(4)(4)S x y =++ 4()16xy x y =+++ 100164()x y =+++ 1164()x y =++1168xy ≥+11680=+196=,当且仅当“10x y ==”时取等号.∴当10x y ==时,S 取得最小值为196平方米,此时场地长为14米,宽为14米.22. 已知函数()2sin 36f x x ππ⎛⎫=+⎪⎝⎭.(1)用“五点作图法”在给定的坐标系中,画出函数()f x 在[]0,6上的图象; (2)求()f x 图象的对称轴与单调递增区间;(3)当[]0,x m ∈时,()12f x ≤≤,求实数m 的取值范围.【答案】(1)答案见解析;(2)对称轴方程为()31x k k Z =+∈,递增区间为[]()62,61k k k -+∈Z ;(3)[1,2].【解析】 【分析】(1)由[]0,6x ∈,计算出36x ππ+的取值范围,通过列表、描点、连线,可作出函数()f x 在[]0,6上的图象; (2)解方程()362x k k Z ππππ+=+∈可得出函数()f x 的对称轴方程,解不等式()222362k x k k Z ππππππ-≤+≤+∈可得函数()f x 的单调递增区间;(3)利用(1)中的图象结合()12f x ≤≤可得出实数m 的取值范围. 【详解】(1)因为()2sin 36f x x ππ⎛⎫=+ ⎪⎝⎭,当[]0,6x ∈时,13,3666x ππππ⎡⎤+∈⎢⎥⎣⎦, 列表如下:x0 1 524112636xππ+6π2ππ32π2π136πy 1 2 0 2-0 1作图如下:(2)因为()2sin36f x xππ⎛⎫=+⎪⎝⎭,令()362x k k Zππππ+=+∈,解得()31x k k Z=+∈,令()222362k x k k Zππππππ-≤+≤+∈,解得()6261k x k k Z-≤≤+∈,所以()f x的对称轴方程为()31x k k Z=+∈,递增区间为[]()62,61k k k-+∈Z;(3)[]0,x m∈,,36636mxπππππ⎡⎤∴+∈+⎢⎥⎣⎦,又()12f x≤≤,由(1)的图象可知,12m≤≤,m∴的取值范围是[]1,2.【点睛】方法点睛:函数()()sin0y A x Aωϕω=+>>0,的图象的两种作法是五点作图法和图象变换法:(1)五点法:用“五点法”作()()sin0y A x Aωϕω=+>>0,的简图,主要是通过变量代换,设z xωϕ=+,由z取0、2π、π、32π、2π来求出相应的x,通过列表,计算得出五点坐标,描点后得出图象;(2)三角函数图象进行平移变换时注意提取x的系数,进行周期变换时,需要将x的系数变为原来的ω倍,要特别注意相位变换、周期变换的顺序,顺序不同,其变换量也不同.。
2022-2023学年福建省厦门市湖滨中学高一(下)期中数学试卷【答案版】

2022-2023学年福建省厦门市湖滨中学高一(下)期中数学试卷一、单选题(本题共8个小题,每小题5分) 1.已知复数z =(2+i )2,则z 的虚部为( ) A .3B .3iC .4D .4i2.如图所示,观察四个几何体,其中判断正确的是( )A .①是棱台B .②是圆台C .③是棱锥D .④不是棱柱3.已知平面向量a →=(−2,6)与b →=(−4,λ)垂直,则λ的值是( ) A .43B .−43C .12D .﹣124.若O ,M ,N 在△ABC 所在平面内,满足|OA →|=|OB →|=|OC →|,MA →⋅MB →=MB →⋅MC →=MC →•MA →,且NA →+NB →+NC →=0→,则点O ,M ,N 依次为△ABC 的( ) A .重心,外心,垂心 B .重心,外心,内心C .外心,重心,垂心D .外心,垂心,重心5.在△ABC 中,若A =60°,b =1,△ABC 的面积S =√3,则a sinA=( ) A .2√393B .2√293C .26√33D .3√36.如图1,一个正三棱柱容器,底面边长为1,高为2,内装水若干,将容器放倒,把一个侧面作为底面,如图2,这是水面恰好是中截面,则图1中容器水面的高度是( )A .54B .53C .43D .327.圆O 为锐角△ABC 的外接圆,AC =2AB =2,点P 在圆O 上,则BP →⋅AO →的取值范围为( )A .[−12,4)B .[0,2)C .[−12,2)D .[0,4)8.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,若3AC →⋅AB →−BA →⋅BC →=2CA →⋅CB →,2b =b cos C +c cos B ,则cos C 的值为( ) A .13B .−13C .18D .−18二、多选题(共4个小题,每小题5分,全部选对的得5分,选对但不全的得2分,有选错的得0分.) 9.如果平面向量a →=(2,0),b →=(1,1),那么下列结论中正确的是( ) A .|a →|=√2|b →|B .a →⋅b →=2√2C .(a →−b →)⊥b →D .a →∥b →10.△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,a =√7,b =2,A =π3,则( ) A .c =3B .sinB =√217C .sinC =√217D .△ABC 外接圆的面积为7π311.在复平面内,下列说法正确的是( ) A .若复数z 满足z ⋅z =0,则z =0B .若复数z 1,z 2 满足|z 1+z 2|=|z 1﹣z 2|,则z 1z 2=0C .若复数z 1,z 2 满足|z |=|z 2|,则z 12=z 22D .若|z |=1,则|z +1+i |的最大值为√2+112.如图,在棱长为2的正方体ABCD ﹣A 1B 1C 1D 1中,M ,N ,P 分别是AA 1,CC 1,C 1D 1的中点,Q 是线段D 1A 1上的动点,则( )A .存在点Q ,使B ,N ,P ,Q 四点共面 B .存在点Q ,使PQ ∥平面MBNC .经过C ,M ,B ,N 四点的球的表面积为9π2D .过Q ,M ,N 三点的平面截正方体ABCD ﹣A 1B 1C 1D 1所得截面图形不可能是五边形 三、填空题(共4小题,每小题5分,共20分.在答题卡上的相应题目的答题区域内作答) 13.已知复数(m 2﹣3m ﹣1)+(m 2﹣5m ﹣6)i =3(其中i 为虚数单位),则实数m = . 14.一艘船从河岸边出发向河对岸航行.已知船的速度v 1→的大小为|v 1→|=10km/ℎ,水流速度v 2→的大小为|v 2→|=3km/ℎ,那么当航程最短时船实际航行的速度大小为 km /h .15.祖暅(公元前5~6世纪),字景烁,是我国南北朝时期的数学家.他提出了一条原理:“幂势既同,则积不容异.”这句话的意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体的体积相等.该原理在西方直到十七世纪才由意大利数学家卡瓦列利发现,比祖暅晚一千一百多年.如图将某几何体(左侧图)与已被挖去了圆锥体的圆柱体(右侧图)放置于同一平面β上.以平行于平面β的平面于距平面β任意高d 处可横截得到S 圆及S 环两截面,若S 圆=S 环总成立,且图中圆柱体(右侧图)的底面半径为2,高为3,则该几何体(左侧图)的体积是 .16.在锐角△ABC 中,内角A ,B ,C 所对应的边分别是a ,b ,c ,且2c sin (B ﹣A )=2a sin A cos B +b sin2A ,则ca 的取值范围是 .四、解答题(本题共6个小题,共70分,解答应写出必要的文字说明、证明过程或演算步骤) 17.(10分)已知向量a →=(3,2),b →=(x ,−1). (1)已知x =5,求向量a →与b →的夹角θ; (2)若(a →+2b →)⊥(2a →−b →),求实数x 的值.18.(12分)已知复数z =5(1−i)1+2i +(2+i)2,i 为虚数单位. (1)求|z |和z ;(2)若复数z 是关于x 的方程x 2+mx +n =0的一个根,求实数m ,n 的值.19.(12分)如图,某组合体是由正方体ABCD ﹣A 1B 1C 1D 1与正四棱锥P ﹣A 1B 1C 1D 1组成,且PA 1=√32AB . (1)若该组合体的表面积为36(5+√2),求其体积; (2)证明:A 1B ∥平面D 1AC .20.(12分)如图,在平行四边形ABCD 中,AB =1,AD =2,∠BAD =60°,BD ,AC 相交于点O ,M 为BO 中点.设向量AB →=a →,AD →=b →. (1)求|a →−b →|的值; (2)用a →,b →表示BD →和AM →; (3)证明:AB →⊥BD →.21.(12分)在△ABC 中,a =6,sin A =32sin B . (Ⅰ)求b ;(Ⅱ)在下列三个条件中选择一个作为已知,使△ABC 存在且唯一确定,并求△ABC 的面积. 条件①:∠B =2π3; 条件②:BC 边上中线的长为√17; 条件③:sin B =sin2A .注:如果选择多个符合要求的条件分别解答,按第一个解答计分.22.(12分)随着生活水平的不断提高,人们更加关注健康,重视锻炼.通过“小步道”,走出“大健康”,健康步道成为引领健康生活的一道亮丽风景线.如图,A ﹣B ﹣C ﹣A 为某区的一条健康步道,AB 、AC 为线段,BC ̂是以BC 为直径的半圆,AB =2√3km ,AC =4km ,∠BAC =π6. (1)求BĈ的长度; (2)为满足市民健康生活需要,提升城市品位,改善人居环境,现计划新建健康步道A ﹣D ﹣C (B ,D 在AC 两侧),其中AD ,CD 为线段.若∠ADC =π3,求新建的健康步道A ﹣D ﹣C 的路程最多可比原有健康步道A﹣B﹣C的路程增加多少长度?(精确到0.01km)2022-2023学年福建省厦门市湖滨中学高一(下)期中数学试卷参考答案与试题解析一、单选题(本题共8个小题,每小题5分) 1.已知复数z =(2+i )2,则z 的虚部为( ) A .3B .3iC .4D .4i解:∵z =(2+i )2=4+4i +i 2=3+4i ,∴z 的虚部为4. 故选:C .2.如图所示,观察四个几何体,其中判断正确的是( )A .①是棱台B .②是圆台C .③是棱锥D .④不是棱柱解:对于选项A ,不是由棱锥截来的,所以A 不是棱台,故A 错误; 对于选项B ,上、下两个面不平行,所以不是圆台; 对于选项C ,是棱锥.对于选项D ,前、后两个面平行,其他面是平行四边形,且每相邻两个四边形的公共边平行,所以D 是棱柱. 故选:C .3.已知平面向量a →=(−2,6)与b →=(−4,λ)垂直,则λ的值是( ) A .43B .−43C .12D .﹣12解:由题知a →⊥b →,即a →⋅b →=(−2,6)⋅(−4,λ)=8+6λ=0,解得λ=−43. 故选:B .4.若O ,M ,N 在△ABC 所在平面内,满足|OA →|=|OB →|=|OC →|,MA →⋅MB →=MB →⋅MC →=MC →•MA →,且NA →+NB →+NC →=0→,则点O ,M ,N 依次为△ABC 的( ) A .重心,外心,垂心 B .重心,外心,内心C .外心,重心,垂心D .外心,垂心,重心解:因为|OA →|=|OB →|=|OC →|,所以|OA |=|OB |=|OC |, 所以O 为△ABC 的外心;因为MA →⋅MB →=MB →⋅MC →=MC →•MA →, 所以MB →•(MA →−MC →)=0, 即MB →•CA →=0,所以MB ⊥AC , 同理可得:MA ⊥BC ,MC ⊥AB , 所以M 为△ABC 的垂心; 因为NA →+NB →+NC →=0→, 所以NA →+NB →=−NC →,设AB 的中点D ,则NA →+NB →=2ND →, 所以−NC →=2ND →,所以C ,N ,D 三点共线,即N 为△ABC 的中线CD 上的点,且NC =2ND , 所以N 为△ABC 的重心. 故选:D .5.在△ABC 中,若A =60°,b =1,△ABC 的面积S =√3,则a sinA=( ) A .2√393B .2√293C .26√33D .3√3解:因为A =60°,b =1,△ABC 的面积S =√3=12bc sin A =12×1×c ×√32,解得:c =4, 由余弦定理可得a =√b 2+c 2−2bccosA =√1+16−2×1×4×12=√13, 所以a sinA=√13√32=2√393. 故选:A .6.如图1,一个正三棱柱容器,底面边长为1,高为2,内装水若干,将容器放倒,把一个侧面作为底面,如图2,这是水面恰好是中截面,则图1中容器水面的高度是( )A .54B .53C .43D .32解:在图2中,水中部分是四棱柱, 四棱柱底面积为S =12×12×sin60°−12×(12)2×sin60°=3√316,高为2, ∴四棱柱的体积为V =2×3√316=3√38, 设图1中容器内水面高度为h ,则V =12×12×sin60°×ℎ=3√38,解得h =32. ∴图1中容器内水面的高度是32.故选:D .7.圆O 为锐角△ABC 的外接圆,AC =2AB =2,点P 在圆O 上,则BP →⋅AO →的取值范围为( ) A .[−12,4)B .[0,2)C .[−12,2)D .[0,4)解:由△ABC 为锐角三角形,则外接圆圆心在三角形内部,如下图示,又BP →⋅AO →=(BO →+OP →)⋅AO →=BO →⋅AO →+OP →⋅AO →,而AC =2AB =2,若外接圆半径为r , 因为AB sin∠ACB =2r ,∴1sin 12∠AOB=2r ,∴2r ⋅sin 12∠AOB =1, 两边平方得,4r 2⋅1−cos∠AOB2=1,∴2r 2(1﹣cos ∠AOB )=1,则2r 2(1﹣cos ∠AOB )=2r 2(1﹣cos2C )=1, 故cos2C =1−12r 2,且2r >2,即r >1, 由BO →⋅AO →=|BO →||AO →|cos∠AOB =r 2cos2C =r 2−12,对于OP →⋅AO →且P 在圆O 上,当AP 为直径时OP →⋅AO →=r 2,当A ,P 重合时OP →⋅AO →=−r 2, ∴OP →⋅AO →∈[−r 2,r 2],综上,BP →⋅AO →∈[−12,2r 2−12],锐角三角形中∠BAC <90°,则BC <√AC 2+AB 2=√5,即BC =2rsin ∠BAC <√5恒成立, ∴1<r <√52,则2r 2−12<2恒成立,综上所述,BP →⋅AO →的取值范围为[−12,2). 故选:C .8.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,若3AC →⋅AB →−BA →⋅BC →=2CA →⋅CB →,2b =b cos C +c cos B ,则cos C 的值为( ) A .13B .−13C .18D .−18解:由若3AC →⋅AB →−BA →⋅BC →=2CA →⋅CB →可得,3bc cos A ﹣ac cos B =2ab cos C , 由余弦定理得3(b 2+c 2﹣a 2)﹣(a 2+c 2﹣b 2)=2(a 2+b 2﹣c 2),即b 2+2c 2=3a 2,①由正弦定理结合2b =b cos C +c cos B 可得,2sin B =sin B cos C +sin C cos B =sin (B +C )=sin A ,∴2b =a ② 由①②得,11b 2=2c 2,cosC =a 2+b 2−c 22ab =5b 2−c 24b2=1011c 2−c 2811c 2=−18, 故选:D .二、多选题(共4个小题,每小题5分,全部选对的得5分,选对但不全的得2分,有选错的得0分.) 9.如果平面向量a →=(2,0),b →=(1,1),那么下列结论中正确的是( ) A .|a →|=√2|b →|B .a →⋅b →=2√2C .(a →−b →)⊥b →D .a →∥b →解:∵a →=(2,0),b →=(1,1), ∴|a →|=2,|b →|=√2, ∴|a →|=√2|b →|,∴A 正确;a →⋅b →=2,∴B 错误;(a →−b →)⋅b →=(1,−1)⋅(1,1)=1−1=0,∴(a →−b →)⊥b →,∴C 正确; ∵2×1﹣0×1≠0,∴a →∥b →错误,∴D 错误. 故选:AC .10.△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,a =√7,b =2,A =π3,则( ) A .c =3B .sinB =√217C .sinC =√217D .△ABC 外接圆的面积为7π3解:因为a =√7,b =2,A =π3, 由余弦定理得,a 2=7=4+c 2﹣2×2c ×12, 所以c =3,A 正确, 由正弦定理得asinA=b sinB=c sinC=2R ,所以sin B =2×√327=√217,sin C =3√2114,R =√213, 所以△ABC 外接圆的面积S =πR 2=7π3,B 正确,C 错误,D 正确. 故选:ABD .11.在复平面内,下列说法正确的是( ) A .若复数z 满足z ⋅z =0,则z =0B .若复数z 1,z 2 满足|z 1+z 2|=|z 1﹣z 2|,则z 1z 2=0C .若复数z 1,z 2 满足|z |=|z 2|,则z 12=z 22D .若|z |=1,则|z +1+i |的最大值为√2+1解:若复数z 满足z ⋅z =0,则|z |2=0,得z =0,故A 正确;若复数z 1,z 2 满足|z 1+z 2|=|z 1﹣z 2|,不一定有z 1z 2=0,如z 1=1,z 2=i ,故B 错误;若复数z 1,z 2 满足|z 1|=|z 2|,不一定有z 12=z 22,如z 1=1,z 2=i ,故C 错误;若|z |=1,如图:|z +1+i |的几何意义为圆上的动点到定点(﹣1,﹣1)的距离,则|z +1+i |的最大值为√2+1,故D 正确.故选:AD .12.如图,在棱长为2的正方体ABCD ﹣A 1B 1C 1D 1中,M ,N ,P 分别是AA 1,CC 1,C 1D 1的中点,Q 是线段D 1A 1上的动点,则( )A .存在点Q ,使B ,N ,P ,Q 四点共面B .存在点Q ,使PQ ∥平面MBNC .经过C ,M ,B ,N 四点的球的表面积为9π2D .过Q ,M ,N 三点的平面截正方体ABCD ﹣A 1B 1C 1D 1所得截面图形不可能是五边形解:对于A :连接A 1B ,A 1P ,CD 1,如图所示:在棱长为2的正方体ABCD ﹣A 1B 1C 1D 1中,CD 1∥A 1B ,∵P ,N 分别是C 1D 1,C 1C 中点,∴PN ∥CD 1,∴PN ∥A 1B ,故A 1,P ,N ,B 四点共面,当Q 与A 1重合时满足B ,N ,P ,Q 四点共面,故A 正确;对于B :取A 1D 1中点为Q ,连接PQ ,QM ,A 1C 1,如图所示:∵M ,N 分别AA 1,CC 1中点,则A 1M 与C 1N 平行且相等,∴四边形A 1C 1NM 是平行四边形,∴MN ∥A 1C 1,又P 是C 1D 1中点,∴PQ ∥A 1C 1,∴PQ ∥MN ,又MN ⊂平面BMN ,PQ ⊄平面BMN ,故PQ ∥平面BMN ,故B 正确;对C :由图形的对称性易知,经过C ,M ,B ,N 四点的球的球心为矩形AMNC 的中心,∴矩形AMNC 的对角线即为球的直径2R ,又易得矩形AMNC 的对角线长为√1+(2√2)2=3,∴R =32,∴经过C ,M ,B ,N 四点的球的表面积为4πR 2=9π,∴C 错误;对D ,由运动变化思想可得,当Q 与D 1重合时,过Q ,M ,N 三点的平面截正方体的截面为菱形BMD 1N ,当Q 在A 1D 1之间时,由对称性易得:过Q ,M ,N 三点的平面截正方体的截面为六边形,当当Q 与A 1重合时,过Q ,M ,N 三点的平面截正方体的截面为矩形ACC 1A 1,∴D 正确.故选:ABD .三、填空题(共4小题,每小题5分,共20分.在答题卡上的相应题目的答题区域内作答)13.已知复数(m 2﹣3m ﹣1)+(m 2﹣5m ﹣6)i =3(其中i 为虚数单位),则实数m = ﹣1 .解:复数(m 2﹣3m ﹣1)+(m 2﹣5m ﹣6)i =3,则{m 2−3m −1=3m 2−5m −6=0,解得m =﹣1. 故答案为:﹣1.14.一艘船从河岸边出发向河对岸航行.已知船的速度v 1→的大小为|v 1→|=10km/ℎ,水流速度v 2→的大小为|v 2→|=3km/ℎ,那么当航程最短时船实际航行的速度大小为 √91 km /h .解:要使航程最短,则船实际航行应正对着河对岸航行,所以船实际航行的速度大小为√|v 1→|2−|v 2→|2=√91km /h .故答案为:√91.15.祖暅(公元前5~6世纪),字景烁,是我国南北朝时期的数学家.他提出了一条原理:“幂势既同,则积不容异.”这句话的意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体的体积相等.该原理在西方直到十七世纪才由意大利数学家卡瓦列利发现,比祖暅晚一千一百多年.如图将某几何体(左侧图)与已被挖去了圆锥体的圆柱体(右侧图)放置于同一平面β上.以平行于平面β的平面于距平面β任意高d 处可横截得到S 圆及S 环两截面,若S 圆=S 环总成立,且图中圆柱体(右侧图)的底面半径为2,高为3,则该几何体(左侧图)的体积是 8π .解:因为总有S 圆=S 环,圆柱的高为3,底面圆的半径为2,所以该几何体的体积为V 柱−V 锥=22×3π−13π×22×3=8π,故答案为:8π.16.在锐角△ABC 中,内角A ,B ,C 所对应的边分别是a ,b ,c ,且2c sin (B ﹣A )=2a sin A cos B +b sin2A ,则c a 的取值范围是 (1,2) . 解:由正弦定理和正弦二倍角公式可得2sin C sin (B ﹣A )=2sin A sin A cos B +sin B sin2A =2sin A sin A cos B +2sin B sin A cos A =2sin A (sin A cos B +sin B cos A )=2sin A sin (A +B ),因为0<C <π2,π−C =A +B ,所以sin (π﹣C )=sin (A +B )=sin C ≠0,可得sin (B ﹣A )=sin A ,因为0<A <π2,0<B <π2,所以−π2<B −A <π2,所以B =2A ,C =π﹣3A ,由0<B =2A <π2,0<C =π−3A <π2可得π6<A <π4, 所以√22<cosA <√32,12<cos 2A <34, 由正弦定理得c a =sinC sinA =sin3A sinA =sin(2A+A)sinA =sin2AcosA+cos2AsinA sinA = 2cos 2A +cos2A =4cos 2A ﹣1∈(1,2).故答案为:(1,2).四、解答题(本题共6个小题,共70分,解答应写出必要的文字说明、证明过程或演算步骤)17.(10分)已知向量a →=(3,2),b →=(x ,−1).(1)已知x =5,求向量a →与b →的夹角θ;(2)若(a →+2b →)⊥(2a →−b →),求实数x 的值.解:(1)根据题意,向量a →=(3,2),b →=(x ,−1).因为x =5,所以b →=(5,−1),故cosθ=a →⋅b→|a →|⋅|b →|=9+4×25+1=√22, 因为θ∈[0,π],所以向量a →与b →的夹角θ=π4;(2)a →+2b →=(3,2)+(2x ,−2)=(3+2x ,0),2a →−b →=(6,4)−(x ,−1)=(6−x ,5), 由于(a →+2b →)⊥(2a →−b →),所以(a →+2b →)⋅(2a →−b →)=(3+2x ,0)⋅(6−x ,5)=(3+2x)(6−x)=0,解得:x =−32或6,从而x =−32或6.18.(12分)已知复数z =5(1−i)1+2i +(2+i)2,i 为虚数单位.(1)求|z |和z ;(2)若复数z 是关于x 的方程x 2+mx +n =0的一个根,求实数m ,n 的值.解:(1)∵z =5(1−i)1+2i +(2+i)2=5(1−i)(1−2i)(1+2i)(1−2i)+4+4i −1=5(−1−3i)5+3+4i =2+i , ∴|z|=√22+12=√5,z =2−i ;(2)∵复数z 是关于x 的方程x 2+mx +n =0的一个根,∴(2+i )2+m (2+i )+n =0,∴3+4i +2m +mi +n =0,∴(3+2m +n )+(m +4)i =0,∴{3+2m +n =0m +4=0,解得m =﹣4,n =5; 综上,|z|=√5,z =2−i ,m =−4,n =5.19.(12分)如图,某组合体是由正方体ABCD ﹣A 1B 1C 1D 1与正四棱锥P ﹣A 1B 1C 1D 1组成,且PA 1=√32AB .(1)若该组合体的表面积为36(5+√2),求其体积;(2)证明:A 1B ∥平面D 1AC .解:(1)连接A 1C 1、B 1D 1交于点O ,连接PO ,由正棱锥的性质可知PO ⊥平面A 1B 1C 1D 1,设AB =2a ,则PA 1=√3a ,A 1O =12A 1C 1=√2a ,∴PO =√PA 12−A 1O 2=a ,取B 1C 1的中点E ,连接PE ,则PE ⊥B 1C 1,且PE =√PB 12−B 1E 2=√2a , 所以几何体的表面积为5×4a 2+4×12×2a ×√2a =(20+4√2)a 2=36(5+√2),可得a =3, 所以该几何体的体积为(2a)3+13×4a 2×a =8×27+43×33=252;(2)证明:因为BC ∥A 1D 1,且BC =A 1D 1,所以四边形A 1BCD 1是平行四边形,则A 1B ∥D 1C ,A 1B ⊄平面D 1AC ,D 1C ⊂平面D 1AC ,所以A 1B ∥平面D 1AC .20.(12分)如图,在平行四边形ABCD 中,AB =1,AD =2,∠BAD =60°,BD ,AC 相交于点O ,M 为BO 中点.设向量AB →=a →,AD →=b →.(1)求|a →−b →|的值;(2)用a →,b →表示BD →和AM →;(3)证明:AB →⊥BD →.解:(1)在平行四边形ABCD 中,AB =1,AD =2,∠BAD =60°,BD ,AC 相交于点O ,M 为BO 中点.又向量AB →=a →,AD →=b →,则|a →−b →|=√(a →−b →)2=√a →2−2a →⋅b →+b →2=√|a →|2−2|a →|⋅|b →|cos∠BAD +|b →|2=√1−2×1×2×12+4=√3; (2)由题意可得BD →=AD →−AB →=b →−a →,又∵M 为BO 中点,∴BM →=14BD →=14(b →−a →),∴AM →=AB →+BM →=a →+14(b →−a →)=34a →+14b →; (3)证明:∵AB →⋅BD →=a →⋅(b →−a →)=a →⋅b →−a →2,又∵AB =1,AD =2,∠BAD =60°,∴a →⋅b →=1×2×12=1,∴AB →⋅BD →=a →⋅b →−a →2=1−1=0,所以AB →⊥BD →.21.(12分)在△ABC 中,a =6,sin A =32sin B .(Ⅰ)求b ;(Ⅱ)在下列三个条件中选择一个作为已知,使△ABC 存在且唯一确定,并求△ABC 的面积. 条件①:∠B =2π3;条件②:BC 边上中线的长为√17;条件③:sin B =sin2A .注:如果选择多个符合要求的条件分别解答,按第一个解答计分.解:(I )因为sinA =32sinB ,在△ABC 中,由正弦定理a sinA =b sinB , 可得:a =32b ,又因为a =6,所以b =4;(Ⅱ)选择条件①,因为cos B =a 2+c 2−b 22ac, 所以−12=36+c 2−1612c , 则c 2+6c +20=0,无解;选择条件②,设BC 边上的中线为AD ,则AD =√17,CD =3,在△ACD 中,由余弦定理得:cosC =AC 2+CD 2−AD 22⋅AC⋅CD =42+32−(√17)22×4×3=13, 因为cosC =13,C ∈(0,π),所以sinC =√1−cos 2C =2√23, 所以△ABC 的面积为S =12absinC =12×6×4×2√23=8√2;选择条件③,由题设,因为sin2A =2sin A cos A ,所以sin B =2sin A cos A ,因为sinA =32sinB ,所以sin B =3sin B cos A , 因为B ∈(0,π),所以sin B ≠0,所以cosA =13,由余弦定理a 2=b 2+c 2﹣2bc cos A 可得:36=16+c 2−2×4×c ×13,整理得3c 2﹣8c ﹣60=0,解得c =6或−103(舍),因为cosA =13,A ∈(0,π),所以sinA =√1−cos 2A =2√23,所以△ABC 的面积为S =12bcsinA =12×4×6×2√23=8√2.22.(12分)随着生活水平的不断提高,人们更加关注健康,重视锻炼.通过“小步道”,走出“大健康”,健康步道成为引领健康生活的一道亮丽风景线.如图,A ﹣B ﹣C ﹣A 为某区的一条健康步道,AB 、AC为线段,BC ̂是以BC 为直径的半圆,AB =2√3km ,AC =4km ,∠BAC =π6.(1)求BĈ的长度; (2)为满足市民健康生活需要,提升城市品位,改善人居环境,现计划新建健康步道A ﹣D ﹣C (B ,D 在AC 两侧),其中AD ,CD 为线段.若∠ADC =π3,求新建的健康步道A ﹣D ﹣C 的路程最多可比原有健康步道A ﹣B ﹣C 的路程增加多少长度?(精确到0.01km )解:(1)连接BC ,△ABC 中,由余弦定理得BC =√AC 2+AB 2−2AC ⋅ABcos∠BAC =√16+12−2×4×2√3×√32=2, BC ̂=12×2×π×1=π,即π(km ); (2)设AD =a ,CD =b ,△ACD 中,由余弦定理得16=a 2+b 2﹣ab ,所以(a +b )2=16+3ab ≤16+3×(a+b2)2,解得a +b ≤8,当且仅当a =b =4时取得等号,新建健康步道A ﹣D ﹣C 的最长路程8km ,8−π−2√3≈1.39(km ),故新建健康步道A ﹣D ﹣C 的路程最多可比原来有健康步道A ﹣B ﹣C 的路程增加1.39(km ).。
福建省漳州市2020-2021学年学年高一数学上学期期末考试试题(含解析)

福建省漳州市2020-2021学年学年高一数学上学期期末考试试题(含解析)本试卷共5页,22题.全卷满分150分.考试用时120分钟.注意事项:1.答题前,考生务必在试题卷、答题卡规定的地方填写自己的准考证号、姓名.考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名”与考生本人准考证号、姓名是否一致.2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效.3.考试结束,考生必须将试题卷和答题卡一并交回.一.单项选择题:本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知集合{|4}A x x =>,{|2}B x x ,则A B =( )A. (2,)+∞B. (4,)+∞C. (2,4)D. (,4)-∞【答案】B 【解析】 【分析】由交集的定义求解即可. 【详解】{|{|2}4}{|4}x A B x x x x x =>>=>故选:B【点睛】本题主要考查了集合间的交集运算,属于基础题. 2.sin(600)-︒的值是( )A.12B. 12-C.2D. 【答案】C 【解析】 【分析】原式中的角度变形后,利用诱导公式及特殊角的三角函数值计算即可得到结果.【详解】解:()()()sin 600sin 720120sin120sin 18060sin60-︒=-︒+︒=︒=︒-︒=︒= 故选C .【点睛】此题考查了运用诱导公式化简求值,熟练掌握诱导公式是解本题的关键. 3.下列各函数的值域与函数y x =的值域相同的是( ) A. 2yxB. 2xy =C. sin y x =D.2log y x =【答案】D 【解析】 【分析】分别求出下列函数的值域,即可判断. 【详解】函数y x =的值域为R20y x =≥,20x y =>则A ,B 错误;函数sin y x =的值域为[]1,1-,则C 错误; 函数2log y x =的值域为R ,则D 正确; 故选:D【点睛】本题主要考查了求具体函数的值域,属于基础题.4.已知函数42,0,()log ,0,x x f x x x ⎧=⎨>⎩则((1))f f -=( )A. 2-B. 12-C.12D. 2【答案】B 【解析】 【分析】分别计算(1)f -,12f ⎛⎫ ⎪⎝⎭即可得出答案.【详解】121(1)2f --==,241211log log 12222f -⎛⎫===- ⎪⎝⎭所以1((1))2f f -=- 故选:B【点睛】本题主要考查了已知自变量求分段函数的函数值,属于基础题. 5.函数log ||()(1)||a x x f x a x =>图象的大致形状是( )A. B.C. D.【答案】A 【解析】 【分析】判断函数函数()f x 为奇函数,排除BD 选项,取特殊值排除C ,即可得出答案. 【详解】log ||log ||()()||||a a x x x x f x f x x x ---==-=--所以函数()f x 为奇函数,故排除BD.log ||()10||a a a f a a ==>,排除C故选:A【点睛】本题主要考查了函数图像的识别,属于基础题.6.已知0.22log 0.2,2,sin 2a b c ===,则( )A. a b c <<B. a c b <<C. c a b <<D.b c a <<【答案】B【解析】 【分析】分别求出a ,b ,c 的大概范围,比较即可.【详解】因为22log 0.2log 10<=,0sin 21<<,0.20221>= 所以a c b <<. 故选:B【点睛】本题主要考查了指数,对数,三角函数的大小关系,找到他们大概的范围再比较是解决本题的关键,属于简单题.7.已知以原点O 为圆心的单位圆上有一质点P ,它从初始位置01(,22P 开始,按逆时针方向以角速度1/rad s 做圆周运动.则点P 的纵坐标y 关于时间t 的函数关系为 A. sin(),03y t t π=+≥ B. sin(),06y t t π=+≥ C. cos(),03y t t π=+≥D. cos(),06y t t π=+≥【答案】A 【解析】当时间为t 时,点P 所在角的终边对应的角等于3t π+, 所以点P 的纵坐标y 关于时间t 的函数关系为sin(),03y t t π=+≥.8.已知函数()f x 为定义在(0,)+∞的增函数,且满足()()()1f x f y f xy +=+.若关于x 的不等式(1sin )(1)(cos )(1sin )f x f f a x f x --<+-+恒成立,则实数a 的取值范围为( ) A. 1a >- B. 14a >-C. 1a >D. 2a >【答案】D 【解析】 【分析】将题设不等式转化为2(cos )(cos )f x f a x <+,根据函数()f x 的单调性解不等式得出2cos cos x a x <+,通过换元法,构造函数2()g x t t =-,[]1,1t ∈-求出最大值,即可得到实数a 的取值范围.【详解】(1sin )(1)(cos )(1sin )f x f f a x f x --<+-+(1sin )(1sin )(cos )(1)f x f x f a x f ∴-++<++因为()()()2(1sin )(1sin )1sin 1sin 1(cos)1f x f x fx x f x -++=-++=+,(cos )(1)(cos )1f a x f f a x ++=++所以2(cos )(cos )f x f a x <+在(0,)x ∈+∞恒成立故2cos cos x a x <+在(0,)x ∈+∞恒成立,即2cos cos x x a -<在(0,)x ∈+∞恒成立 令[]cos ,1,1x t t =∈-,则22()cos cos g x x x t t =-=-所以函数2()g x t t =-在11,2⎡⎤-⎢⎥⎣⎦上单调递减,在1,12⎛⎤ ⎥⎝⎦上单调递增,(1)2(1)0g g -=>= 所以2a > 故选:D【点睛】利用函数的单调性解抽象不等式以及不等式的恒成立问题,属于中档题.二.多项选择题:本大题共4小题,每小题5分,共20分,在每小题给出的四个选项中,有多个选项符合题目要求,全部选对的得5分,选对但不全的得3分,有选错的得0分.9.设11,,1,32α⎧⎫∈-⎨⎬⎩⎭,则使函数y x α=的定义域是R ,且为奇函数的α值可以是( )A. 1-B.12C. 1D. 3【答案】CD 【解析】 【分析】求出对应α值函数y x α=的定义域,利用奇偶性的定义判断即可.【详解】当α的值为11,2-时,函数y x α=的定义域分别为()(),00,-∞+∞,[)0,+∞当1α=时,函数y x =的定义域为R ,令()f x x =,()()f x x f x -=-=-,则函数y x =为R 上的奇函数当3α=时,函数3y x =的定义域为R ,令3()f x x =,3()()f x x f x -=-=-,则函数3y x=为R 上的奇函数故选:CD【点睛】本题主要考查了判断函数的奇偶性,属于基础题. 10.要得到sin 25y x π⎛⎫=- ⎪⎝⎭的图象,可以将函数sin y x =的图象上所有的点( ) A. 向右平行移动5π个单位长度,再把所得各点的横坐标缩短到原来的12倍B. 向右平行移动10π个单位长度,再把所得各点的横坐标缩短到原来的12倍C. 横坐标缩短到原来的12倍,再把所得各点向右平行移动5π个单位长度D. 横坐标缩短到原来的12倍,再把所得各点向右平行移动10π个单位长度【答案】AD 【解析】 【分析】由正弦函数的伸缩变换以及平移变换一一判断选项即可. 【详解】将函数sin y x =的图象上所有的点向右平行移动5π个单位长度,得到函数n 5si y x π⎛⎫=- ⎪⎝⎭的图象,再把所得各点的横坐标缩短到原来的12倍,得到sin 25y x π⎛⎫=- ⎪⎝⎭的图象,故A 正确;将函数sin y x =的图象上所有的点向右平行移动10π个单位长度,得到函数sin 10y x π⎛⎫=- ⎪⎝⎭的图象,再把所得各点的横坐标缩短到原来的12倍,得到sin 210y x π⎛⎫=- ⎪⎝⎭的图象,故B 错误;将函数sin y x =的图象上所有的点横坐标缩短到原来的12倍,得到sin 2y x =的图象,再把所得各点向右平行移动5π个单位长度,得到25sin 2y x π⎛⎫=-⎪⎝⎭的图象,故C 错误; 将函数sin y x =的图象上所有的点横坐标缩短到原来的12倍,得到sin 2y x =的图象,再把所得各点向右平行移动10π个单位长度,得到sin 25y x π⎛⎫=- ⎪⎝⎭的图象,故D 正确;故选:AD【点睛】本题主要考查了正弦函数的伸缩变换以及平移变换,属于基础题.11.对于函数()sin(cos )f x x =,下列结论正确的是( ) A. ()f x 为偶函数B. ()f x 的一个周期为2πC. ()f x 的值域为[sin1,sin1]-D. ()f x 在[]0,π单调递增【答案】ABC 【解析】 【分析】利用奇偶性的定义以及周期的定义判断A ,B 选项;利用换元法以及正弦函数的单调性判断C 选项;利用复合函数的单调性判断方法判断D 选项. 【详解】函数()f x 的定义域为R ,关于原点对称()()()()sin cos sin cos ()f x x x f x -=-==,则函数()f x 偶函数,故A 正确;()()()sin co 22s sin cos ()f x x x f x ππ+=+==⎡⎤⎣⎦,则函数()f x 的一个周期为2π,故B正确;令[]cos ,1,1t x t =∈-,则()sin f x t =,由于函数sin y t=[]1,1-上单调递增,则()sin 1()sin1sin1()sin1f x f x -≤≤⇒-≤≤,故C 正确;当[]0,x π∈时,函数cos t x =为减函数,由于[]cos 0,1t x =∈,则函数sin y t =在0,1上为增函数,所以函数()f x 在[]0,π单调递减,故D 错误; 故选:ABC【点睛】本题主要考查了判断函数的奇偶性,周期性,求函数值域,复合函数的单调性,属于中档题.12.已知()f x 为R 上的奇函数,且当0x >时,()lg f x x =.记()sin ()cos g x x f x x =+⋅,下列结论正确的是( ) A. ()g x 为奇函数B. 若()g x 的一个零点为0x ,且00x <,则()00lg tan 0x x --=C. ()g x 在区间,2ππ⎛⎫-⎪⎝⎭的零点个数为3个 D. 若()g x 大于1的零点从小到大依次为12,,x x ,则1223x x ππ<+<【答案】ABD 【解析】 【分析】根据奇偶性的定义判断A 选项;将()0g x =等价变形为tan ()x f x =-,结合()f x 的奇偶性判断B 选项,再将零点问题转化为两个函数的交点问题,结合函数()g x 的奇偶性判断C 选项,结合图象,得出12,x x 的范围,由不等式的性质得出12x x +的范围. 【详解】由题意可知()g x 的定义域为R ,关于原点对称因为()()()sin ()cos sin ()cos ()g x x f x x x f x x g x -=-+-⋅-=--⋅=-,所以函数()g x 为奇函数,故A 正确; 假设cos 0x =,即,2x k k Z ππ=+∈时,sin ()co cos s sin 02x k x f x k πππ⎛⎫++⋅==≠ ⎪⎝⎭所以当,2x k k Z ππ=+∈时,()0g x ≠当,2x k k Z ππ≠+∈时,sin ()cos 0tan ()x f x x x f x +⋅=⇔=-当00x <,00x ->,则()000()()lg f x f x x =--=--由于()g x 的一个零点为0x , 则()()00000tan ()lg t lg an 0x x f x x x =-=⇒--=-,故B 正确;当0x >时,令12tan ,lg y x y x ==-,则()g x 大于0的零点为12tan ,lg y x y x ==-的交点,由图可知,函数()g x 在区间()0,π的零点有2个,由于函数()g x 为奇函数,则函数()g x 在区间,02π⎛⎫-⎪⎝⎭的零点有1个,并且(0)sin 0(0)cos00g f =+⋅= 所以函数在区间,2ππ⎛⎫-⎪⎝⎭的零点个数为4个,故C 错误;由图可知,()g x 大于1的零点123,222x x ππππ<<<< 所以1223x x ππ<+< 故选:ABD【点睛】本题主要考查了判断函数的奇偶性以及判断函数的零点个数,属于较难题. 三、填空题:本大题共4题,每小题5分,共20分.13.函数()1xf x a =+(0a >且1a ≠)的图象恒过点__________【答案】()0,2 【解析】分析:根据指数函数xy a =过()0,1可得结果.详解:由指数函数的性质可得xy a =过()0,1,所以1xy a =+过()0,2,故答案为()0,2.点睛:本题主要考查指数函数的简单性质,属于简单题. 14.已知扇形的圆心角为12π,面积为6π,则该扇形的弧长为_______; 【答案】6π 【解析】 【分析】由扇形面积公式求出扇形半径,根据扇形弧长公式即可求解.【详解】设扇形的半径为r 由扇形的面积公式得:216212r ππ=⨯,解得2r该扇形的弧长为2126ππ⨯=故答案为:6π 【点睛】本题主要考查了扇形面积公式以及弧长公式,属于基础题. 15.函数()2sin 23f x x π⎛⎫=- ⎪⎝⎭在区间0,2π⎡⎤⎢⎥⎣⎦上的值域为______;【答案】[2] 【解析】 【分析】由x 的范围,确定23x π-的范围,利用换元法以及正弦函数的单调性,即可得出答案.【详解】0,2x π⎡⎤∈⎢⎥⎣⎦,22,333x πππ⎡⎤∴-∈-⎢⎥⎣⎦令22,333t x πππ⎡⎤=-∈-⎢⎥⎣⎦,函数()2sin g t t =在,32ππ⎡⎤-⎢⎥⎣⎦上单调递增,在2,23ππ⎡⎤⎢⎥⎣⎦上单调递减2si ()(n 33)g ππ--==2si 2()2n 2g ππ==, 222sin (3)3g ππ==所以函数()f x 在区间0,2π⎡⎤⎢⎥⎣⎦上的值域为[2]故答案为:[2]【点睛】本题主要考查了正弦型函数的值域,属于中档题. 16.已知函数1()f x x=,()2sin g x x =,则函数()f x 图象的对称中心为_____,函数()y f x =的图象与函数()y g x =的图象所有交点的横坐标与纵坐标之和为____. 【答案】 (1). (0,0) (2). 0 【解析】 【分析】判断函数()f x ,()g x 为奇函数,即可得出函数()f x ,()g x 图象的对称中心都为原点; 根据对称性即可得出所有交点的横坐标与纵坐标之和. 【详解】1()()f x f x x-=-=-,则函数()f x 为奇函数,即函数()f x 图象的对称中心为(0,0) ()()2sin 2sin ()g x x x g x -=-=-=-,则函数()g x 为奇函数,即函数()g x 的对称中心为(0,0)所以函数()y f x =的图象与函数()y g x =的图象所有交点都关于原点对称 即所有交点的横坐标之和为0,纵坐标之和也为0则函数()y f x =的图象与函数()y g x =的图象所有交点的横坐标与纵坐标之和为0 故答案为:(0,0);0【点睛】本题主要考查了函数奇偶性的应用以及对称性的应用,属于中档题.四、解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤. 17.已知α为锐角,且3cos 5α=. (1)求tan 4πα⎛⎫+ ⎪⎝⎭的值;(2)求cos sin(2)2παπα⎛⎫-+-⎪⎝⎭的值. 【答案】(1)-7(2)4425【解析】 【分析】(1)利用平方关系以及商数关系得出tan α,再利用两角和的正切公式求解即可; (2)利用诱导公式以及二倍角的正弦公式求解即可. 【详解】解:(1)因为α为锐角,且3cos 5α=. 所以24sin 1cos 5αα, 所以sin 4tan cos 3ααα==, 所以41tan tan34tan 7441tan tan 1143παπαπα++⎛⎫+===- ⎪⎝⎭--⨯. (2)因为cos sin 2παα⎛⎫-=⎪⎝⎭, sin(2)sin 2παα-=,所以cos sin(2)sin sin 22παπααα⎛⎫-+-=+ ⎪⎝⎭sin 2sin cos ααα=+4432555=+⨯⨯ 4425= 【点睛】本题主要考查了两角和的正切公式,诱导公式,二倍角的正弦公式,属于中档题. 18.已知集合{}|2216xA x =<<,{|sin 0,(0,2)}B x x x π=>∈. (1)求AB ;(2)集合{|1}C x x a =<<()a ∈R ,若AC C =,求a 的取值范围.【答案】(1){|04}A B x x ⋃=<<(2)4a 【解析】 【分析】(1)利用指数函数以及正弦函数的性质化简集合,A B ,再求并集即可;(2)由题设条件得出C A ⊆,分别讨论集合C =∅和C ≠∅的情况,即可得出答案.【详解】解:(1)依题意{|14}A x x =<<,{|0}B x x π=<<,所以{|04}A B x x ⋃=<<. (2)因为AC C =,所以C A ⊆.①当C =∅时,1a ,满足题意;②当C ≠∅时,1a >,因为C A ⊆,得4a ≤,所以14a <; 综上,4a .【点睛】本题主要考查了集合的并集运算以及根据集合间的包含关系求参数范围,属于中档题.19.已知函数()2sin (sin cos )f x x x x =⋅+. (1)求()f x 的最小正周期; (2)求()f x 的单调区间.【答案】(1)最小正周期为π.(2)单调递增区间为3,()88k k k ππππ⎡⎤-++∈⎢⎥⎣⎦Z ,()f x 的单调递减区间为37,()88k k k ππππ⎡⎤++∈⎢⎥⎣⎦Z .【解析】 【分析】利用倍角公式以及辅助角公式化简函数()f x ,根据周期公式得出第一问;根据正弦函数的单调增区间和减区间求()f x 的单调区间,即可得出第二问. 【详解】解:因为2()2sin 2sin cos f x x x x =+⋅22sin sin 2x x =+1cos2sin2x x =-+ sin2cos21x x =-+214x π⎛⎫=-+ ⎪⎝⎭(1)所以函数()f x 的最小正周期为22T ππ==.(2)由222,242k x k k πππππ-+-+∈Z ,得3222,44k x k k ππππ-++∈Z , 即3,88k xk k ππππ-++∈Z , 所以()f x 的单调递增区间为3,()88k k k ππππ⎡⎤-++∈⎢⎥⎣⎦Z ,同理可得,()f x 的单调递减区间为37,()88k k k ππππ⎡⎤++∈⎢⎥⎣⎦Z .【点睛】本题主要考查了求正弦型函数的最小正周期以及单调区间,属于中档题. 20.已知2()1x af x x bx +=++是定义在[1,1]-上的奇函数. (1)求a 与b 的值;(2)判断()f x 的单调性,并用单调性定义加以证明; (3)若[0,2)απ∈时,试比较(sin )f α与(cos )f α的大小.【答案】(1)0a =. 0b =.(2)()f x 在[1,1]-单调递增.见解析 (3)见解析 【解析】 【分析】(1)根据奇函数的性质得出(0)0f =,(1)(1)f f -=-,求解方程,即可得出a 与b 的值; (2)利用函数单调性的定义证明即可;(3)分别讨论α的取值使得sin cos αα=,sin cos αα<,sin cos αα>,结合函数()f x 的单调性,即可得出(sin )f α与(cos )f α的大小.【详解】解:(1)因为()f x 是定义在[1,1]-上的奇函数,所以(0)0f =,得0a =.又由(1)(1)f f -=-,得到1122b b -=--+,解得0b =. (2)由(1)可知2()1xf x x =+,()f x 在[1,1]-上为增函数.证明如下:任取12,[1,1]x x ∈-且设12x x <, 所以()()1212221211x x f x f x x x -=-++()()22121212221211x x x x x x x x +--=++ ()()()()122112221211x x x x x x x x -+-=++()()()()21122212111x x x x xx --=++由于12x x <且12,[1,1]x x ∈-,所以210x x ->,且2110x x -<,又2110x +>,2210x +>,所以()()()()211222121011x x x x xx --<++,所以()()12f x f x <,从而()f x 在[1,1]-单调递增. (3)当4πα=或54πα=时,sin cos αα=,所以(sin )(cos )f f αα=;当04πα<或524παπ<<时,sin cos αα<, 又因为sin [1,1]α∈-,cos [1,1]α∈-,且()f x 在[1,1]-上为增函数,所以(sin )(cos )f f αα<当544ππα<<时,sin cos αα>,同理可得(sin )(cos )f f αα>; 综上,当4πα=或54πα=时,(sin )(cos )f f αα=;当50,,244ππαπ⎡⎫⎛⎫∈⋃⎪ ⎪⎢⎣⎭⎝⎭时,(sin )(cos )f f αα<;当5,44ππα⎛⎫∈ ⎪⎝⎭时,(sin )(cos )f f αα>.【点睛】本题主要考查由函数的奇偶性求参数,判断函数的单调性以及利用单调性比较函数值大小,属于中档题.21.海水受日月的引力,在一定的时候发生涨落的现象叫潮.一般地,早潮叫潮,晚潮叫汐.在通常情况下,船在涨潮时驶进航道,靠近码头;卸货后,在落潮时返回海洋.下面是某港口在某季节每天的时间与水深关系表: .(1)设港口在x 时刻的水深为y 米,现给出两个函数模型:sin()(0,0,)y A x h A ωϕωπϕπ=++>>-<<和2(0)y ax bx c a =++≠.请你从两个模型中选择更为合适的函数模型来建立这个港口的水深与时间的函数关系式(直接选择模型,无需说明理由);并求出7x =时,港口的水深.(2)一条货船的吃水深度(船底与水面的距离)为4米,安全条例规定至少要有1.5米的安全间隙(船底与洋底的距离),问该船何时能进入港口,何时应离开港口?一天内货船可以在港口呆多长时间?【答案】(1)选择函数模型Asin()y x h ωϕ=++更适合. 水深为3米 (2)货船可以在1时进入港口,在5时出港;或者在13时进港,17时出港.一天内货船可以在港口呆的时间为8小时. 【解析】 【分析】(1)观察表格中水深的变化具有周期性,则选择函数模型Asin()y x h ωϕ=++更适合,由表格数据得出,,,A h ωϕ的值,将7x =代入解析式求解即可; (2)由题意 5.5y 时,船可以进港,解不等式2.5sin4.255.56x π+,得出x 的范围,由x的范围即可确定进港,出港,一天内在港口呆的时间. 【详解】解:(1)选择函数模型Asin()y x h ωϕ=++更适合因为港口在0:00时刻的水深为4.25米,结合数据和图象可知 4.25h =6.75 1.752.52A -==因为12T =,所以22126T πππω===, 所以 2.5sin 4.256y x πϕ⎛⎫=++⎪⎝⎭, 因为0x =时, 4.25y =,代入上式得sin 0ϕ=,因为πϕπ-<<,所以0ϕ=, 所以 2.5sin4.256y x π=+.当7x =时,712.5sin4.25 2.5 4.25362y π⎛⎫=+=⨯-+= ⎪⎝⎭, 所以在7x =时,港口的水深为3米(2)因为货船需要的安全水深是4 1.5 5.5+=米, 所以 5.5y 时,船可以进港, 令2.5sin4.255.56x π+,则1sin62xπ, 因为024x <,解得15x 或1317x ,所以货船可以在1时进入港口,在5时出港;或者在13时进港,17时出港. 因为(51)(173)8-+-=,一天内货船可以在港口呆的时间为8小时. 【点睛】本题主要考查了三角函数在生活中的应用,属于中档题. 22.已知函数3(1)log (1)f x a x +=+,且(2)1f =. (1)求()f x 的解析式;(2)已知()f x 的定义域为[2,)+∞. (ⅰ)求()41xf +的定义域;(ⅱ)若方程()()412xxf f k k x +-⋅+=有唯一实根,求实数k 取值范围.【答案】(1)2()log f x x =(2)(ⅰ)[0,)+∞.(ⅱ)1k = 【解析】 【分析】(1)利用换元法以及(2)1f =,即可求解()f x 的解析式;(2)(ⅰ)解不等式412x +≥,即可得出()41xf +的定义域;(ⅱ)根据()41xf +,()2x f k k ⋅+的定义域得出1k ,结合函数()f x 的解析式将方程化为()2(1)2210x x k k -⋅+⋅-=,利用换元法得出2()(1)1,[1,)g t k t k t t =-+⋅-∈+∞,讨论k的值,结合二次函数的性质即可得出实数k 的取值范围.【详解】解:(1)令1(0)t x t =+>,则3()log f t a t =,所以3()log f x a x =, 因为3(2)log 21f a ==,所以231log 3log 2a ==, 所以3232()log log 3log log f x a x x x ==⨯= (2)(ⅰ)因为()f x 的定义域为[2,)+∞, 所以412x +≥,解得0x , 所以()41xf +的定义域为[0,)+∞.(ⅱ)因为0,22,x x k k ⎧⎨⋅+⎩,所以221xk +在[0,)+∞恒成立, 因为221x y =+在[0,)+∞单调递减,所以221x y =+最大值为1,所以1k .又因为()()412xxf f k k x +-⋅+=,所以()()22log 41log 2xxk k x +-⋅+=, 化简得()2(1)2210xx k k -⋅+⋅-=,令2(1)xt t =,则2(1)10k t k t -⋅+⋅-=在[1,)+∞有唯一实数根, 令2()(1)1,[1,)g t k t k t t =-+⋅-∈+∞,当1k =时,令()0g t =,则1t =,所以21x =,得0x =符合题意,所以1k =; 当1k >时,2440k k ∆=+->,所以只需(1)220g k =-,解得1k ,因为1k >,所以此时无解; 综上,1k =.【点睛】本题主要考查了利用换元法求函数解析式以及根据函数的零点确定参数的范围,属于较难题.。
2022-2023学年福建省厦门市思明区夏门一中数学高一上期末联考试题含解析

要求函数 的对称中心,只需 ,解得 .
所以 的对称中心为 .
21、 (1)答案见解析;(2) 或 .
【解析】(1)利用赋值法计算可得 ,设 ,则 ,
利用 拆项: 即可证得:当 时, ;
(2)结合(1)的结论可证得 是增函数,据此脱去f符号,原问题转化为 在 上恒成立,分离参数有: 恒成立,结合基本不等式的结论可得实数 的取值范围是 或 .
7、C
【解析】关于平面 对称的点 坐标相反,另两个坐标相同,因此结论为
8、C
【解析】求出 长后可得 ,再由弧长公式计算可得
【详解】由题意 ,解得 ,所以 , ,
所以弧 的长为
故选:C
9、C
【解析】取 的中点为 ,连接 ,过 作 的垂线,垂足为 ,可以证明 平面 、 平面 ,求出 的面积后利用公式求出三棱锥 的体积.
1.函数y=log2 的定义域
A.( ,3)B.( ,+∞)
C.( ,3)D.[ ,3]
2.下列函数中,既是偶函数又在区间 上单调递增的函数是
A. B.
C. D.
3.下列函数中,既是偶函数,在 上是增函数的是()
A. B.
C. D.
4.如图所示,在正方体ABCD—A1B1C1D1中,M、N分别是BB1、BC的中点.则图中阴影部分在平面ADD1A1上的正投影为()
故选:A
5、C
【解析】由 为第二象限角,可得 ,再结合 ,化简即可.
【详解】由题意, ,
因为 为第二象限角,所以 ,
所以 .
故选:C.
6、D
【解析】分析:直接利用周期公式求解即可.
详解:∵ , ,
∴ .故选D
点睛:本题主要考查三角函数的图象与性质,属于简单题.由函数 可求得函数的周期为 ;由 可得对称轴方程;由 可得对称中心横坐标.
期末测试卷(二)-2020-2021学年高一数学必修第一册单元提优卷(人教A版(2019))(含答案)

2020-2021学年高一数学第一册单元提优卷(人教A 版(2019))期末测试卷(二)(满分:150分,测试时间:120分钟)一、单选题1.【2020年高考全国Ⅰ卷理数】设集合A ={x |x 2–4≤0},B ={x |2x +a ≤0},且A ∩B ={x |–2≤x ≤1},则a =A .–4B .–2C .2D .42.【2020·广东省高三月考(文)】命题“10,ln 1x x x∀>≥-”的否定是A .10ln 1x x x ∃≤≥-,B .10ln 1x x x ∃≤<-,C .10ln 1x x x∃>≥-,D .10ln 1x x x∃><-,.3.【2020·北京市八一中学高三月考】函数()()213f x ax a x =---在区间[)1,-+∞上是增函数,则实数a 的取值范围是A .1,3⎛⎤-∞ ⎥⎝⎦B .(],0-∞C .10,3⎛⎤ ⎥⎝⎦D .10,3⎡⎤⎢⎥⎣⎦4.【2020·福建省福州第一中学高三其他(理)】已知函数()f x 的定义域为[0,2],则()()21f xg x x =-的定义域为A .[)(]0,11,2B .[)(]0,11,4C .[)0,1D .(]1,45.设函数要想得到函数sin21y x =+的图像,只需将函数cos2y x =的图象()A .向左平移4π个单位,再向上平移1个单位B .向右平移4π个单位,再向上平移1个单位C .向左平移2π个单位,再向下平移1个单位D .向右平移2π个单位,再向上平移1个单位6.【2020·北京高三月考】已知函数()y f x =满足(1)2()f x f x +=,且(5)3(3)4f f =+,则(4)f =A .16B .8C .4D .27.已知3sin(3)cos()0πθπθ-++-=,则sin cos cos 2θθθ=()A .3B .﹣3C .38D .38-8.【2020·南昌市八一中学】已知函数sin (0)y ax b a =+>的图象如图所示,则函数log ()a y x b =-的图象可能A .B .C .D .9.【2020年新高考全国Ⅰ卷】基本再生数R 0与世代间隔T 是新冠肺炎的流行病学基本参数.基本再生数指一个感染者传染的平均人数,世代间隔指相邻两代间传染所需的平均时间.在新冠肺炎疫情初始阶段,可以用指数模型:(e )rtI t =描述累计感染病例数I (t )随时间t (单位:天)的变化规律,指数增长率r 与R 0,T 近似满足R 0=1+rT .有学者基于已有数据估计出R 0=3.28,T =6.据此,在新冠肺炎疫情初始阶段,累计感染病例数增加1倍需要的时间约为(ln2≈0.69)A .1.2天B .1.8天C .2.5天D .3.5天10.【2020年高考北京】已知函数()21x f x x =--,则不等式()0f x >的解集是A .(1,1)-B .(,1)(1,)-∞-+∞C .(0,1)D .(,0)(1,)-∞⋃+∞11.【2020年高考全国Ⅱ卷理数】若2x −2y <3−x −3−y ,则A .ln(y −x +1)>0B .ln(y −x +1)<0C .ln|x −y |>0D .ln|x −y |<012.【2020年高考天津】已知函数3,0,(),0.x x f x x x ⎧≥=⎨-<⎩若函数2()()2()g x f x kx x k =--∈R 恰有4个零点,则k 的取值范围是A .1(,))2-∞-+∞ B .1(,)(0,2-∞-C .(,0)-∞D .(,0))-∞+∞ 二.填空题13.【2020年高考北京】函数1()ln 1f x x x =++的定义域是____________.14.【2020年高考江苏】已知2sin ()4απ+=23,则sin 2α的值是____________.15.【2020·江苏省高三月考】已知函数()2,0228,2x x x f x x x ⎧+<<=⎨-+≥⎩,若()()2f a f a =+,则1f a ⎛⎫⎪⎝⎭的值是____________.16.【2020·六盘山高级中学高三其他(理)】设函数2()2cos ()sin(284f x x x ππ=+++,(0,3π)∈x 则下列判断正确的是____________.①.函数的一条对称轴为6x π=②.函数在区间5,24ππ⎡⎤⎢⎥⎣⎦内单调递增③.0(0,3π)x ∃∈,使0()1f x =-④.∃∈R a ,使得函数()y f x a =+在其定义域内为偶函数三.解答题17.(本题满分10分)已知0a >,0b >.(1)求证:()2232a b b a b +≥+;(2)若2a b ab +=,求ab 的最小值.18.(本题满分12分)已知集合,2|2162xA x ⎧⎫⎪⎪=<<⎨⎬⎪⎪⎩⎭,{|3221}B x a x a =-<<+.(1)当0a =时,求A B ;(2)若A B φ⋂=,求a 的取值范围.19.(本题满分12分)已知函数()21sin sin cos 2f x x x x =+-,x ∈R .(1)求函数()f x 的最大值,并写出相应的x 的取值集合;(2)若()26f α=,3,88ππα⎛⎫∈-⎪⎝⎭,求sin 2α的值.20.(本题满分12分)已知函数()0.52log 2axf x x -=-为奇函数.(1)求常数a 的值;(2)若对任意10,63x ⎡⎤∈⎢⎥⎣⎦都有()3f x t >-成立,求t 的取值范围.21(本题满分12分)【江苏省盐城市第一中学2020届高三下学期6月调研考试数学试题某乡镇响应“绿水青山就是金山银山”的号召,因地制宜的将该镇打造成“生态水果特色小镇”.经调研发现:某珍稀水果树的单株产量W (单位:千克)与施用肥料x (单位:千克)满足如下关系:()253,02()50,251x x W x x x x⎧+≤≤⎪=⎨<≤⎪+⎩,肥料成本投入为10x 元,其它成本投入(如培育管理、施肥等人工费)20x 元.已知这种水果的市场售价大约为15元/千克,且销路畅通供不应求.记该水果树的单株利润为()f x (单位:元).(Ⅰ)求()f x 的函数关系式;(Ⅱ)当施用肥料为多少千克时,该水果树的单株利润最大?最大利润是多少?22.(本题满分12分)已知函数2()2sin cos 0)f x x x x ωωωω=+->的最小正周期为π.(1)求函数()f x 的单调增区间;(2)将函数()f x 的图象向左平移6π个单位,再向上平移1个单位,得到函数()y g x =的图象,若()y g x =在[0,](0)b b >上至少含有10个零点,求b 的最小值.2020-2021学年高一数学第一册单元提优卷期末测试卷(二)(满分:150分,测试时间:120分钟)一、单选题1.【2020年高考全国Ⅰ卷理数】设集合A ={x |x 2–4≤0},B ={x |2x +a ≤0},且A ∩B ={x |–2≤x ≤1},则a =A .–4B .–2C .2D .4【答案】B求解二次不等式240x -≤可得{}2|2A x x -=≤≤,求解一次不等式20x a +≤可得|2a B x x ⎧⎫=≤-⎨⎩⎭.由于{}|21A B x x ⋂=-≤≤,故12a-=,解得2a =-.故选B .2.【2020·广东省高三月考(文)】命题“10,ln 1x x x∀>≥-”的否定是A .10ln 1x x x ∃≤≥-,B .10ln 1x x x ∃≤<-,C .10ln 1x x x ∃>≥-,D .10ln 1x x x∃><-,【答案】D【解析】因为全称命题的否定是特称命题,所以命题“0x ∀>,1ln 1x x ≥-”的否定为“0x ∃>,1ln 1x x<-”.故选D .3.【2020·北京市八一中学高三月考】函数()()213f x ax a x =---在区间[)1,-+∞上是增函数,则实数a 的取值范围是A .1,3⎛⎤-∞ ⎥⎝⎦B .(],0-∞C .10,3⎛⎤ ⎥⎝⎦D .10,3⎡⎤⎢⎥⎣⎦【答案】D【解析】若0a =,则()3f x x =-,()f x 在区间[)1,-+∞上是增函数,符合.若0a ≠,因为()f x 在区间[)1,-+∞上是增函数,故0112a a a>⎧⎪-⎨≤-⎪⎩,解得103a <≤.综上,103a ≤≤.故选:D .4.【2020·福建省福州第一中学高三其他(理)】已知函数()f x 的定义域为[0,2],则()()21f xg x x =-的定义域为A .[)(]0,11,2 B .[)(]0,11,4 C .[)0,1D .(]1,4【答案】C【解析】函数()f x 的定义域是[0,2],要使函数()()21f xg x x =-有意义,需使()2f x 有意义且10x -≠.所以10022x x -≠⎧⎨≤≤⎩,解得01x ≤<.故答案为C .5.设函数要想得到函数sin21y x =+的图像,只需将函数cos2y x =的图象()A .向左平移4π个单位,再向上平移1个单位B .向右平移4π个单位,再向上平移1个单位C .向左平移2π个单位,再向下平移1个单位D .向右平移2π个单位,再向上平移1个单位【答案】B【解析】cos 2sin(2)sin 2()24y x x x ππ==+=+,因此把函数cos 2y x =的图象向右平移4π个单位,再向上平移1个单位可得sin 21y x =+的图象,故选B6.【2020·北京高三月考】已知函数()y f x =满足(1)2()f x f x +=,且(5)3(3)4f f =+,则(4)f =A .16B .8C .4D .2【答案】B【解析】因为(1)2()f x f x +=,且(5)3(3)4f f =+,故()()324442f f =+,解得()48f =.故选:B7.已知3sin(3)cos()0πθπθ-++-=,则sin cos cos 2θθθ=()A .3B .﹣3C .38D .38-【答案】D 【解析】∵3sin(3)cos()0πθπθ-++-=,∴3sin cos 0θθ--=,即cos 3sin θθ=-,∴sin cos cos 2θθθ2222sin cos sin (3sin )3cos sin (3sin )sin 8θθθθθθθθ⋅-===----.故选:D .8.【2020·南昌市八一中学】已知函数sin (0)y ax b a =+>的图象如图所示,则函数log ()a y x b =-的图象可能A .B .C .D .【答案】C【解析】由函数sin (0)y ax b a =+>的图象可得201,23b a πππ<<<<,213a ∴<<,故函数log ()a y xb =-是定义域内的减函数,且过定点(1,0)b +.结合所给的图像可知只有C 选项符合题意.故选:C .9.【2020年新高考全国Ⅰ卷】基本再生数R 0与世代间隔T 是新冠肺炎的流行病学基本参数.基本再生数指一个感染者传染的平均人数,世代间隔指相邻两代间传染所需的平均时间.在新冠肺炎疫情初始阶段,可以用指数模型:(e )rt I t =描述累计感染病例数I (t )随时间t (单位:天)的变化规律,指数增长率r 与R 0,T 近似满足R 0=1+rT .有学者基于已有数据估计出R 0=3.28,T =6.据此,在新冠肺炎疫情初始阶段,累计感染病例数增加1倍需要的时间约为(ln2≈0.69)A .1.2天B .1.8天C .2.5天D .3.5天【答案】B【解析】因为0 3.28R =,6T =,01R rT =+,所以 3.2810.386r -==,所以()0.38rt t I t e e ==,设在新冠肺炎疫情初始阶段,累计感染病例数增加1倍需要的时间为1t 天,则10.38()0.382t t t e e +=,所以10.382t e =,所以10.38ln 2t =,所以1ln 20.691.80.380.38t =≈≈天.故选:B .10.【2020年高考北京】已知函数()21x f x x =--,则不等式()0f x >的解集是A .(1,1)-B .(,1)(1,)-∞-+∞C .(0,1)D .(,0)(1,)-∞⋃+∞【解析】因为()21xf x x =--,所以()0f x >等价于21x x >+,在同一直角坐标系中作出2x y =和1y x =+的图象如图:两函数图象的交点坐标为(0,1),(1,2),不等式21x x >+的解为0x <或1x >.所以不等式()0f x >的解集为:()(),01,-∞⋃+∞.故选:D .11.【2020年高考全国Ⅱ卷理数】若2x −2y <3−x −3−y ,则A .ln(y −x +1)>0B .ln(y −x +1)<0C .ln|x −y |>0D .ln|x −y |<0【答案】A【解析】由2233x y x y ---<-得:2323x x y y ---<-,令()23ttf t -=-,2x y = 为R 上的增函数,3x y -=为R 上的减函数,()f t ∴为R 上的增函数,x y ∴<,0y x ->Q ,11y x ∴-+>,()ln 10y x ∴-+>,则A 正确,B 错误;x y -Q 与1的大小不确定,故CD 无法确定.12.【2020年高考天津】已知函数3,0,(),0.x x f x x x ⎧≥=⎨-<⎩若函数2()()2()g x f x kx x k =--∈R 恰有4个零点,则k 的取值范围是A .1(,))2-∞-+∞ B .1(,(0,2-∞-C .(,0)-∞D .(,0))-∞+∞ 【答案】D【解析】注意到(0)0g =,所以要使()g x 恰有4个零点,只需方程()|2|||f x kx x -=恰有3个实根即可,令()h x =()||f x x ,即|2|y kx =-与()()||f x h x x =的图象有3个不同交点.因为2,0()()1,0x x f x h x x x ⎧>==⎨<⎩,当0k =时,此时2y =,如图1,2y =与()()||f x h x x =有2个不同交点,不满足题意;当k 0<时,如图2,此时|2|y kx =-与()()||f x h x x =恒有3个不同交点,满足题意;当0k >时,如图3,当2y kx =-与2y x =相切时,联立方程得220x kx -+=,令0∆=得280k -=,解得k =k >.综上,k 的取值范围为(,0))-∞+∞ .故选:D .二.填空题13.【2020年高考北京】函数1()ln 1f x x x =++的定义域是____________.【答案】(0,)+∞【解析】由题意得010x x >⎧⎨+≠⎩,0x ∴>故答案为:(0,)+∞14.【2020年高考江苏】已知2sin ()4απ+=23,则sin 2α的值是____________.【答案】13【解析】22221sin ()(cos sin )(1sin 2)4222παααα+=+=+Q 121(1sin 2)sin 2233αα∴+=∴=故答案为:1315.【2020·江苏省高三月考】已知函数()2,0228,2x x x f x x x ⎧+<<=⎨-+≥⎩,若()()2f a f a =+,则1f a ⎛⎫ ⎪⎝⎭的值是____________.【答案】2【解析】由2x ≥时,()28f x x =-+是减函数可知,当2a ≥,则()()2f a f a ≠+,所以02a <<,由()(+2)f a f a =得22(2)8a a a +=-++,解得1a =,则21(1)112f f a ⎛⎫==+= ⎪⎝⎭.故答案为:2.16.【2020·六盘山高级中学高三其他(理)】设函数2()2cos ()sin(2)84f x x x ππ=+++,(0,3π)∈x 则下列判断正确的是_____.①.函数的一条对称轴为6x π=②.函数在区间5,24ππ⎡⎤⎢⎥⎣⎦内单调递增③.0(0,3π)x ∃∈,使0()1f x =-④.∃∈R a ,使得函数()y f x a =+在其定义域内为偶函数【答案】④【解析】函数()1cos 2sin 21244f x x x x ππ⎛⎫⎛⎫=++++=+ ⎪ ⎪⎝⎭⎝⎭,当(0,3π)∈x 时,当6x π=时,23x π=不能使函数取得最值,所以不是函数的对称轴,①错;当5,24x π⎡⎤∈π⎢⎥⎣⎦时,52,2x ⎡⎤∈ππ⎢⎥⎣⎦,函数先增后减,②不正确;若()1f x =-,那么cos 2x =不成立,所以③错;当3 2a =π时,()12f x a x +=函数是偶函数,④正确,三.解答题17.(本题满分10分)已知0a >,0b >.(1)求证:()2232a b b a b +≥+;(2)若2a b ab +=,求ab 的最小值.【答案】(1)证明见解析;(2)1.【解析】证明:(1)∵()()222223220a b b a b a ab b a b +-+=-+=-≥,∴()2232a b b a b +≥+.(2)∵0a >,0b >,∴2ab a b =+≥2ab ≥1≥,∴1≥ab .当且仅当1a b ==时取等号,此时ab 取最小值1.18.(本题满分12分)已知集合,|2162x A x ⎧⎫⎪⎪=<<⎨⎬⎪⎪⎩⎭,{|3221}B x a x a =-<<+.(1)当0a =时,求A B ;(2)若A B φ⋂=,求a 的取值范围.【答案】(1)1|12A B x x ⎧⎫⋂=-<<⎨⎬⎩⎭;(2)3,[2,)4⎛⎤-∞-⋃+∞ ⎥⎝⎦.【解析】(1)1|42A x x ⎧⎫=-<<⎨⎬⎩⎭,0a =时,{|21}B x x =-<<,∴1|12A B x x ⎧⎫⋂=-<<⎨⎬⎩⎭(2)∵A B φ⋂=,∴当B φ=时,3221a a -≥+,即3a ≥,符合题意;当B φ≠时,31213242a a a <⎧⎪⎨+≤--≥⎪⎩或,解得34a ≤-或23a ≤<,综上,a 的取值范围为3,[2,)4⎛⎤-∞-⋃+∞ ⎥⎝⎦.19.(本题满分12分)已知函数()21sin sin cos 2f x x x x =+-,x ∈R .(1)求函数()f x 的最大值,并写出相应的x 的取值集合;(2)若()26f α=,3,88ππα⎛⎫∈- ⎪⎝⎭,求sin 2α的值.【答案】(1)()f x 的最大值为22,此时x 的取值集合为3,8x x k k Z ππ⎧⎫=+∈⎨⎬⎩⎭;(2)4sin 26α=.【解析】(1)因为()()211cos 2111sin sin cos sin 2sin 2cos 222222x f x x x x x x x -=+-=+-=-22sin 2cos cos 2sin sin 224424x x x πππ⎛⎫⎛⎫=-=- ⎪ ⎪⎝⎭⎝⎭,当()2242x k k Z πππ-=+∈,即()38x k k Z ππ=+∈时,函数()y f x =取最大值2,所以函数()y f x =的最大值为22,此时x 的取值集合为3,8x x k k Z ππ⎧⎫=+∈⎨⎬⎩⎭;(2)因为()26f α=,则sin 2246πα⎛⎫-= ⎪⎝⎭,即1sin 243πα⎛⎫-= ⎪⎝⎭,因为3,88ππα⎛⎫∈- ⎪⎝⎭,所以2,422πππα⎛⎫-∈- ⎪⎝⎭,则cos 243πα⎛⎫-= ⎪⎝⎭,所以sin 2sin 2sin 2cos cos 2sin 444444ππππππαααα⎡⎤⎛⎫⎛⎫⎛⎫=-+=-+- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦1432326+=+⋅=.20.(本题满分12分)已知函数()0.52log 2ax f x x -=-为奇函数.(1)求常数a 的值;(2)若对任意10,63x ⎡⎤∈⎢⎥⎣⎦都有()3f x t >-成立,求t 的取值范围.【答案】(1)1a =-;(2)(),1-∞【解析】(1)因为函数()0.52log 2ax f x x -=-为奇函数,所以()()220.50.50.52224log log log 0224ax ax a x f x f x x x x-+-+-=+==----,所以222414a x x-=-,即21a =,1a =或1-,当1a =时,函数()0.50.52log log 12x f x x -==--,无意义,舍去,当1a =-时,函数()0.52log 2x f x x +=-定义域(-∞,-2)∪(2,+∞),满足题意,综上所述,1a =-。
福建省厦门市2021_2021学年高一数学上学期期末考试试题(含解析)

厦门市2021-2021学年度第一学期高一年级质量检测
数学试题
一、选择题:本大题共8个小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合,集合,则()
A. B. C. D.
【答案】A
【解析】
【分析】
根据交集的定义即可求出A∩B.
【详解】∵集合A={-2,-1,0,1,2},集合B={x|-1≤x≤1},∴A∩B={-1,0,1}.
故选A.
【点睛】本题考查交集的求法,是基础题.
2.函数的定义域为()
A. B. C. D.
【答案】B
【解析】
【分析】
使函数有意义的x满足解不等式组即得解.
【详解】使函数有意义的x满足解得即函数的定义域为.
故选B.
【点睛】本题考查了具体函数定义域,属于基础题.
3.已知角的终边经过点,则的值为()
A. B. C. D.
【答案】A
【解析】
【分析】。
福建省厦门市 2020-2021 学年高一上学期期末考试数学试题(含答案解析)

集合 A 是由小于 3 的自然数组成,0 A , 1 A,只有 C 正确,
故选:C.
2.D
【分析】
利用特称命题的否定可得出结论.
【详解】
命题 p 为特称命题,该命题的否定为: x 0, x ex .
故选:D.
3.A
【分析】
利用对数函数的单调性得出 c 0 ,利用指数函数单调性可得出 a 、b 、 0 的大小关系,综合
绝密★启用前
福建省厦门市 2020-2021 学年高一上学期期末考试数学试题
注意事项: 1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上
第 I 卷(选择题)
一、单选题
1.已知集合 A x N x 3 ,则( )
A. 0 A
B. 1 A
C.0 A
D.1 A
2.设命题 p : x 0 , x ex ,则 p 的否定为( )
主要步骤为:作差——变形——判断正负.在所给不等式是积、商、幂的形式时,可考虑比
答案第 3 页,共 14 页
商
9.ABD
【分析】
由诱导公式和商数关系可得.
【详解】
∵ tan 3sin ,∴ sin 3sin ,
cos 若 sin 0 ,则 cos 1或 1, 若 sin 0 ,则 cos 1 .
p2
2 p1 p2 p1 p2
p1 p2 2 4 p1 p2 2 p1 p2
p1 p2 2 2 p1 p2
0 ,所以,
p1 2
p2
2 p1 p2 p1 p2
.
因此,乙方案的平均价格较低.
故选:B.
【点睛】
方法点睛:比较法是不等式性质证明的理论依据,是不等式证明的主要方法之一,作差法的
2020-2021学年高一上学期期末考试数学卷及答案

2020-2021学年高一上学期期末考试数学卷及答案1.集合A和B分别表示y=x+1和y=2两个函数的图像上所有的点,求A和B的交集。
答案:A={(-∞,1]}。
B={2}。
A∩B=A={(-∞,1]}2.已知函数y=(1-x)/(2x^2-3x-2),求函数的定义域。
答案:分母2x^2-3x-2=(2x+1)(x-2),所以函数的定义域为x∈(-∞,-1/2]∪(2,∞)。
3.如果直线mx+y-1=0与直线x-2y+3=0平行,求m的值。
答案:两条直线平行,说明它们的斜率相等,即m=2.4.如果直线ax+by+c=0经过第一、第二,第四象限,求a、b、c应满足的条件。
答案:第一象限中x>0.y>0,所以ax+by+c>0;第二象限中x0,所以ax+by+c0.y<0,所以ax+by+c<0.综上所述,应满足ab<0.bc<0.5.已知两条不同的直线m和n,两个不同的平面α和β,判断下列命题中正确的是哪个。
答案:选项A是正确的。
因为如果m与α垂直,n与β平行,那么m和n的夹角就是α和β的夹角,所以m和n垂直。
6.已知圆锥的表面积为6π,且它的侧面展开图是一个半圆,求这个圆锥的底面半径。
答案:设底面半径为r,侧面的母线长为l,则圆锥的侧面积为πrl。
根据题意,πrl=6π,所以l=6/r。
而侧面展开图是一个半圆,所以底面周长为2πr,即底面直径为2r,所以侧面母线长l=πr。
将上述两个式子代入公式S=πr^2+πrl中,得到r=2.7.已知两条平行线答案:两条平行线的距离等于它们的任意一点到另一条直线的距离。
我们可以先求出l2上的一点,比如(0,7/8),然后带入l1的方程,得到距离为3/5.8.已知函数y=ax-1/(3x^2+5),如果它的图像经过定点P,求点P的坐标。
答案:点P的坐标为(1,2)。
因为当x=1时,y=a-1/8,所以a=17/8.又因为当x=2时,y=1/13,所以17/8×2-1/13=2,解得a=17/8,所以y=17x/8-1/(3x^2+5),当x=1时,y=2.9.已知a=3/5,b=1/3,c=4/3,求a、b、c的大小关系。
福建省厦门市厦门第一中学2023届数学高一上期末综合测试试题含解析

解,得到答案
【详解】由题意,函数 f x ln 1 x2 x 1,
f
lg2
f
lg
1 2
ln
1 (lg2)2 lg2
ln
1
(lg
1)2 2
lg
1 2
2
ln 1 (lg2)2 lg2 ln 1 (lg2)2 lg2 2 ln1 2 2
故选 C 【点睛】本题主要考查了函数值的求法,函数性质等基础知识的应用,其中熟记对数的运算性质是解答的关键,着重
A.1
B. 1
C. 3 2
D.
1 2
8.已知命题 p:x 为自然数,命题 q:x 为整数,则 p 是 q 的()
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
9.已知函数 f x ln
1 x2 x
1,则1 2
A.1
B. lg2
C.2 10.已知函数
D.0
,则
()
A.5
B.2
C.0
D.1
11.下列四个函数中,在其定义域上既是奇函数又是单调递增函数的是
A. y x 1
B. y tan x
C. y x3
D. y 2 x
12.已知向量 a (1, 2) , b (x,3y 5) ,且 a / /b ,若 x , y 均为正数,则 xy 的最大值是
故 D 正确. 故选:D. 2、C 【解析】由已知求得球的半径,再由空间中两点间的距离公式求得|AB|,则答案可求 【详解】∵由已知可得 r 12 22 22 3 ,
而|AB| (1 2)2 (2 2)2 (2 1)2 3 2 ,
∴|AB| 2 r
2023-2024学年福建省厦门市高一上学期期末教学质量数学模拟试题(含解析)

2023-2024学年福建省厦门市高一上学期期末教学质量数学模拟试题考生注意:1.本试卷分选择题和非选择题两部分.满分150分,考试时间120分钟.2.答题前,考生务必用直径0.5毫米黑色墨水签字笔将密封线内项目填写清楚.3.考生作答时,请将答案答在答题卡上.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑;非选择题请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区域内作答,超出答题区域书写的答案无效,在试题卷、草稿纸上作答无效.4.本卷命题范围:人教A 版必修第一册第一章~第五章第4节.一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1 已知集合,,且,则(){}9,3A m ={}2,9B m =A B =m =A. 0B. 3C. D. 3或03±2. 已知扇形的圆心角为,半径为5,则扇形的弧长为( )1rad 5A. B. 1C. 2D. 4123. “”是“”的()1a >0a >A. 充分不必要条件 B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件4. 若,,,则( )ln x π=51log 3y =12z e -=A. B. C. D. x y z<<z x y<<z y x<<y z x<<5. 函数①;②,;③,中,2πcos 2y x x ⎛⎫=- ⎪⎝⎭sin y x =[]0,2πx ∈sin 2y x =[]π,πx ∈-奇函数的个数为( )A 0B. 1C. 2D. 36. 已知幂函数的图象过点,则函数在区间上的()f x x α=15,5⎛⎫ ⎪⎝⎭()(3)()g x x f x =-1,13⎡⎤⎢⎥⎣⎦最小值是( )A. -1B. -2C -4D. -87. 已知函数则的大致图像是( )(),1,ln ,1,x x f x x x ⎧≤⎪=⎨⎪->⎩()2y f x =-A.B.C.D.8. 已知函数在区间上单调递增,则的取值范围是( π()sin (0)4f x x ⎛⎫=+> ⎪⎝⎭ωωπ,π2⎡⎤⎢⎥⎣⎦ω)A. B. C. D. 59,84⎡⎤⎢⎥⎣⎦13,24⎡⎤⎢⎥⎣⎦10,4⎛⎤ ⎥⎝⎦(0,2]二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9. 已知角与角的终边相同,则角可以是( )θ5π3-θA. B. C. D. 7π3-1π34π313π310. 下列说法错误的是()A. 函数与函数表示同一个函数xy x =1y =B. 若是一次函数,且,则()f x ()()165=+f f x x ()41f x x =-C. 函数的图象与y 轴最多有一个交点()f x D. 函数在上是单调递减函数11y x =+()(),11,-∞--+∞ 11. 下列函数中,以为最小正周期,且在上单调递减的为( )ππ,π2⎛⎫ ⎪⎝⎭A. B.C.D.cos 2y x=sin y x=cos y x=tan y x=12. 设函数的定义域为,为奇函数,为偶函数,当时,()f x R ()1f x -()1f x +[]1,1x ∈-,则下列结论正确的是()()21f x x =-+A. 7324f ⎛⎫= ⎪⎝⎭B. 为奇函数()7f x +C.在上为减函数()f x ()6,8D. 方程仅有6个实数解()lg 0f x x +=三、填空题:本题共4小题,每小题5分,共20分.13. 已知且,则的终边在第__________象限.tan 0x <cos 0x <x 14. 函数的零点为______.()32x f x =-15. 已知一元二次不等式对一切实数x 都成立,则k 的取值范围是23208kx kx ++>___________.16. 若函数在区间上的最大值为,最小值为,则()()22211x f x x +=+[]2023,2023-M m ______.M m +=四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17. 已知为钝角,且.α4cos 5α=-(1)求,的值;sin αtan α(2)求的值sin(π)cos(2π)3πcos tan(π)2αααα-+-⎛⎫-++ ⎪⎝⎭18. 已知x >0,y >0,且2x +8y -xy =0,求:(1)xy 的最小值;(2)x +y 的最小值..19. 已知定义在上的偶函数,当时,,且.R ()f x 0x ≥()()3x f x a a =-∈R ()326f -=(1)求的值;a (2)求函数的解析式;()f x (3)解不等式:.()2f x >20. 已知函数.π()sin 213f x x ⎛⎫=++ ⎪⎝⎭(1)求的最小正周期及单调递增区间;()f x (2)当时,求的最大值和最小值及取得最大值、最小值时x 的值.ππ,44x ⎡⎤∈-⎢⎥⎣⎦()f x 21. 深度学习是人工智能的一种具有代表性的实现方法,它是以神经网络为出发点的,在神经网络优化中,指数衰减的学习率模型为,其中L 表示每一轮优化时()()00nG L n L Dn =∈N 使用的学习率,表示初始学习率,D 表示衰减系数,n 表示训练迭代轮数,表示衰减0L 0G 速度.已知某个指数衰减的学习率模型,,且当训练迭代轮数为18时,学()102L =018G =习率衰减为.25(1)求该学习率模型的表达式;(2)要使学习率衰减到以下(不含),至少需训练迭代多少轮?(参考数据1515)lg 20.3010≈22.已知函数.424()log 1,()log f x g x x ⎛⎫=-= ⎪⎝⎭(1)求的定义域,并证明的图象关于点对称;()f x ()f x (2,0)(2)若关于x 的方程有解,求实数a 的取值范围.()()f x g x =数学答案一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. A解析:由得,解得或,A B =23m m =3m =0m =当时,,不满足元素的互异性,舍去;3m =39m =当时,成立.0m =A B =故选:A.2. B解析:因为扇形的圆心角为,半径为5,1rad 5所以由弧长公式得扇形的弧长为.1515l r α=⋅=⨯=故选:B.3. D 解析:因为或,11a a >⇔<-1a >又时,不能得出;1a <-0a >时,不能得出;0a >1a <-所以“”是“”的既不充分也不必要条件.1a >0a >故选: D.4. D解析:,,,ln 1π> 51log 03<120e 1-<<.y z x ∴<<故选:D.5. B解析:根据奇函数定义,②中违背了定义域要关于原点对称这一要求,所以排除[]0,2πx ∈②;对于①,,是奇22πcos sin 2y x x x x ⎛⎫=-= ⎪⎝⎭()()()()22sin sin f x x x x x f x -=--=-=-函数;对于③,,是偶函数.sin 2y x=()()sin 2sin 2f x x x f x -=-==故选:B .6. D解析:因为幂函数的图像过点,所以,得,()f x x α=15,5⎛⎫ ⎪⎝⎭155α=1α=-所以,则显然在区间上单调递增,1()f x x =3()(3)()1g x x f x x =-=-1,13⎡⎤⎢⎥⎣⎦所以所求最小值为.11983g ⎛⎫=-=- ⎪⎝⎭故选:D 7. A解析:函数,则(),1,ln ,1,x x f x x x ⎧≤⎪=⎨⎪->⎩()()2,1,2ln 2, 1.x x y f x x x -⎧≥⎪=-=⎨--<⎪⎩根据复合函数的单调性,当时,函数单调递减;1x ≥()2f x -当时,函数单调递增,只有A 符合1x <()2f x -故选:A.8. C解析:由题意得,则,π,π2x ⎡⎤∈⎢⎥⎣⎦ππππ,4244x ωωπω⎡⎤+∈++⎢⎥⎣⎦则,,πππππ,π2π,2π24422k k ωω⎡⎤⎡⎤++⊆-++⎢⎥⎢⎥⎣⎦⎣⎦Z k ∈当时,由,解得,又,故;0k =πππ242πππ42ωω⎧+≥-⎪⎪⎨⎪+≤⎪⎩3124ω-≤≤0ω>104ω<≤当时,由,得无解,同理当时,无解.1k =ππ3π242π5ππ42ωω⎧+≥⎪⎪⎨⎪+≤⎪⎩ω2,Z k k ≥∈ω故选:C二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9. BD解析:依题意,5π2π,3k k θ=-+∈Z 当时,,1k =π3θ=当时,,3k =13π3θ=所以BD 选项符合,AC 选项不符合.故选:BD 10. ABD解析:A :函数的定义域为,函数的定义域为R ,xy x =(,0)(0,)-∞+∞ 1y =所以这两个函数不表示同一个函数,故A 符合题意;B :设,则,()(0)f x kx b k =+≠2(())()()f f x f kx b k kx b b k x kb b =+=++=++又,所以,解得或,(())165f f x x =+2165k kb b ⎧=⎨+=⎩41k b =⎧⎨=⎩453k b =-⎧⎪⎨=-⎪⎩所以或,故B 符合题意;()41f x x =+5()43f x x =--C :由函数的定义知,函数图象至多与y 轴有一个交点,故C 不符合题意;D :函数在上是单调递减函数,故D 符合题意.11y x =+(,1),(1,)-∞--+∞故选:ABD11. BD解析:作出函数的图象,如图1,显然A 错误;cos 2y x =作函数图象,如图2,故B 正确;sin y x=作函数图象,如图3,故C 错误;cos y x=作函数图象,如图4,故D 正确.tan y x=故选:BD 12. BD 解析:因为为偶函数,所以,()1f x +()()11f x f x +=-+所以,即,(11)((1)1)f x f x -+=--+()(2)f x f x =-+因为为奇函数,所以,()1f x -()()11f x f x -=---所以,即,(31)((3)1)f x f x -+-=---+-(2)(4)f x f x -+=--所以,所以,()(4)f x f x =--(4)(44)(8)f x f x f x -=---=--所以,所以,即函数的一个周期为.()(8)f x f x =-(8)()f x f x +=()f x 8在中,令,得,()(2)f x f x =-+72x =7732222f f f ⎛⎫⎛⎫⎛⎫=-+=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭在中,令,得,()()11f x f x -=---12x =-3111222f f f ⎛⎫⎛⎫⎛⎫-=--=-- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭又,所以,故A 错误;1131244f ⎛⎫-=-+=⎪⎝⎭73132224f f f ⎛⎫⎛⎫⎛⎫=-=--=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭因为,所以,(8)()f x f x +=()()71f x f x +=-所以,从而为奇()()()()()711187f x f x f x f x f x -+=--=--=--+=-+()7f x +函数,故B 正确;因为在区间上是增函数,且的一个周期为,()21f x x =-+(1,0)-()f x 8所以在上单调递增,在上不为减函数.故C 错误;()f x ()7,8()6,8因为为奇函数,所以的图象关于点对称,()1f x -()f x (1,0)-因为为偶函数,所以的图象关于直线对称,()1f x +()f x 1x =又当时,,[]1,1x ∈-()21f x x =-+作出与的大致图象,如图所示.()f x lg y x =-其中单调递减且,所以两函数图象有6个交点,lg y x =-lg121-<-故方程仅有6个实数解,故D 正确.()lg 0f x x +=故选:BD.三、填空题:本题共4小题,每小题5分,共20分.13.二解析:由,得角的终边所在的象限是第二、四象限,tan 0x <x 因为,所以角的终边在第二、三象限或轴非正半轴上,cos 0x <x x 由于上述条件要同时成立,所以的终边在第二象限;x 故答案为:二14. 3log 2解析:令,则,即,()320x f x =-=32x =3log 2x =所以函数的零点为.()32x f x =-3log 2故答案为:3log 215. {}03k k <<解:因为不等式为一元二次不等式,所以,23208kx kx ++>0k ≠又一元二次不等式对一切实数x 都成立,23208kx kx ++>所以有,解得,即,22034208k k k >⎧⎪⎨∆=-⨯⨯<⎪⎩003k k >⎧⎨<<⎩03k <<所以实数k 的取值范围是,{}03k k <<故答案为:.{}03k k <<16. 4解析:因为,()()222222124242111x x x x f x x x x +++===++++令,则,()[]24,2023,20231x g x x x =∈-+()()2f x g x =+又因为,所以函数为奇函数,()()()()224411x x g x g x x x ---===-+-+()g x 因为奇函数的图象关于原点对称,所以在上的最大值和最小值之和为0,即,()g x []2023,2023-max min ()()0g x g x +=所以.max min ()2()24M m g x g x +=+++=故答案为:4四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17. (1)解:因为为钝角,α所以,3sin 5α===故.3sin 35tan 4cos 45ααα===--(2)原式.sin cos sin tan αααα-+=-+将,,代入,3sin 5α=4cos 5α=-3tan 4α=-得原式.342855332754--==--18. (1)∵, , ,0x >0y >280x y xy +-=∴,当且仅当时取等号,28xy x y =+≥=28x y =8≥∴,当且仅当时取等号,64xy ≥416x y ==故的最小值为64.xy (2)∵,则 ,28x y xy +=281y x +=又∵, ,0x >0y >∴,2828()(101018x y x y x y y x y x +=++=++≥+=当且仅当时取等号,212x y ==故的最小值为18.x y +19. (1)因为是定义在上的偶函数,且,()f x R ()326f -=所以,即,()()3326f f =-=3326a -=解得.1a =(2)当时,,0x ≥()31x f x =-设,则,则,0x <0x ->()()31x f x f x -=-=-故()31,031,0x x x f x x -⎧-<=⎨-≥⎩(3)由是偶函数,等价于,即,()f x ()2f x >()2f x >312x->得,得,解得或,33x >1x >1x <-1x >故的解集是.()2f x >()(),11,-∞-⋃+∞20. (1)因为,π()sin 213f x x ⎛⎫=++ ⎪⎝⎭所以函数的周期,2ππ2T ==令,πππ2π22πZ 232k x k k -+≤+≤+∈,得,5ππππ,Z 1212k x k k -+≤≤+∈所以函数的最小正周期为,单调递增区间为.π5ππ[π,π],Z 1212k k k -++∈(2)当时,ππ,44x ⎡⎤∈-⎢⎥⎣⎦则,ππ5π2636x -≤+≤故当,即时,;ππ236x +=-π4x =-min 11()122f x =-+=当,即当时,.ππ232x +=π12x =max ()2f x =即,此时;,此时.max ()2f x =π12x =min 1()2f x =π4x =-21. (1)由条件可得,指数衰减的模型为,()1812n L n D =当时,,代入可得,解得,18n =()25L n =18182152D =45D =所以该学习率模型的表达式()181425n L n ⎛⎫=⨯ ⎪⎝⎭(2)由学习率衰减到以下(不含),可得,151518141255n ⎛⎫⨯< ⎪⎝⎭即,所以,即184255n ⎛⎫< ⎪⎝⎭452log 185n >45218log 5n >,()()452lglg 21lg 22lg 2lg 52lg 21518log 1818181873.9452lg 2lg 52lg 21lg 23lg 21lg 5----=⨯=⨯=⨯=⨯≈----所以,则,即至少需训练迭代74轮.73.9n >74n =22. (1)由题设可得,解得,故的定义域为,410x ->04x <<()f x (0,4)而,4444444()(4)log 1log 1log log 044x x f x f x x x x x -⎛⎫⎛⎫⎛⎫⎛⎫+-=-+-=+= ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭⎝⎭故的图象关于点对称.()f x (2,0)(2)法一:因为关于x 的方程即有()()f x g x=4244log 1log log ()x a x ⎛⎫-==+ ⎪⎝⎭解,故在上有解.41x ax -=+(0,4)x ∈下面求在上有解时实数a 的取值范围.41a x x +=-(0,4)x ∈因为与在区间上都是减函数,4y x =y x =-(0,4)所以函数在区间上也是减函数,4y x x =-(0,4)所以时,的取值范围是.04x <<4xx -(3,)-+∞令,解得.13a +>-4a >-因此,所求实数a 的取值范围是.(4,)-+∞法二:,即,()()f xg x =4244log 1log log ()x a x ⎛⎫-==+ ⎪⎝⎭因为有解,故在上有解,()()f x g x =4x x a x -=+(0,4)整理得到在上有解,2(1)40x a x ++-=(0,4)设,显然,则或2()(1)4h x x a x =++-(0)40h =-<(4)0,104,2h a >⎧⎪⎨+<-<⎪⎩(4)0,10.2h a >⎧⎪⎨+-≤⎪⎩解得.4a >-故实数a 的取值范围为. (4,)-+∞。
福建省厦门市2020-2021学年高一下学期期末考试数学试题参考答案及评分标准

连接 EB , FC . ·····················································································3 分
法一:(存在性证明)因为 EF∥B1C1, BC∥B1C1 , 所以 EF∥BC , ······················································································4 分
所以
n
−
2 3
m
1 3
m
+
1 2
n
+
1 2
r2
=
0
,······················································7
分
即 1 mn + 1 n2 − 2 m2 − 1 mn + 1 r2 = 1 (n2 + r2 ) − 2 m2 = 0 .·························8 分
3
3
因为 F 是 BC 的中点,所以 EF = EB + BF ···················································3 分
= 1 AB + 1 BC = 1 a + 1 b . ···························4 分
3
2
32
(2)因为 ED ⊥ EF ,所以 ED EF = 0 , ···················································5 分
人教版2020-2021学年下学期高一数学期末检测卷及答案(含两套题)

【点睛】一般地,如果 为等差数列, 为其前 项和,则有性质:
(1)若 ,则 ;
(2) 且 ;
(3) 且 为等差数列;
(4) 为等差数列.
6.A
【解析】
【分析】
利用正弦定理将边转化为角得到 ,再由角C的范围可得选项.
【详解】因为 ,
所以由正弦定理得 ,所以 ,即 ,
又因为 为 的内角,
所以 .
解得 , ,
, ;
(2) ,
,
又 ,由题得 ,即 ,
,即
由题知 且 ,故 ,
故 ,
故只需考虑 , 时 , 时 , 时 ,
17.(10分)已知 中,点 .
(1)求直线 的方程;
(2)求 的面积.
18.(12分)已知函数 .
(1)当 时,求不等式 的解集;
(2)若关于x的不等式 的解集为R,求a的取值范围.
19.(12分)己知向量 , .
(1)若 ,其中 ,求 坐标;
(2)若 与 的夹角为 ,求 的值.
20.(12分)自我国爆发新冠肺炎疫情以来,各地医疗单位都加紧了医疗用品的生产,某医疗器械厂统计了口罩生产车间每名工人的生产速度,将所得数据分成五组并绘制出如图所示的频率分布直方图.已知前四组的频率成等差数列,第五组与第二组的频率相等.
故 ,
故答案为:
【点睛】向量的数量积有两个应用:(1)计算长度或模长,通过用 来求;(2)计算角, .特别地,两个非零向量 垂直的等价条件是 .
15.9
【解析】
【分析】
将 变形后利用基本不等式可求其最小值
【详解】 ,
,等号成立时 , .
故答案为:9.
【点睛】应用基本不等式求最值时,需遵循“一正二定三相等”,如果原代数式中没有积为定值或和为定值,则需要对给定的代数变形以产生和为定值或积为定值的局部结构.求最值时要关注取等条件的验证.
福建省厦门市第一中学2020-2021学年高一上学期月考数学试题

福建省厦门市第一中学2020-2021学年高一上学期月考数学试题学校:___________姓名:___________班级:___________考号:___________一、单选题1.若集合{}2,1,0,1,2M =--,211,R 2N y y x x ⎧⎫==-+∈⎨⎬⎩⎭,则M N =( )A .{}2,1,0,1--B .{}2,1,0--C .{}1,2D .{}22.已知幂函数f(x)的图像经过点(9,3),则f(2)-f(1)=( )A .3B .1C -1D .13.下列函数在其定义域上既是奇函数又是减函数的是( ) A .()2xf x =B .3()f x x =C .()1f x x=D .()f x x x =-4.函数()21log f x x x=-+的一个零点落在下列哪个区间( ) A .(0,1)B .(1,2)C .(2,3)D .(3,4)5.已知53()1f x ax bx =++且(5)7,f =则(5)f -的值是( ) A .5-B .7-C .5D .76.已知 5.10.9m =,0.90.95.1,log 5.1n p ==,则这三个数的大小关系是( )A .m<n<pB .m<p<nC .p<m<nD .p<n<m7.已知函数()()()f x x a x b =--(其中)a b >,若()f x 的图象如图所示,则函数()x g x a b =+的图象大致为( )A .B .C .D .8.已知函数()()()2log ,02,0x x x f x x -⎧>⎪=⎨≤⎪⎩,则不等式()1f x >的解集为( ) A .()2,+∞ B .(),0-∞ C .(0,2)D .()(),02,-∞+∞9.一元二次方程2510x x m -+-=的两根均大于2,则实数m 的取值范围是( )A .21,4⎡⎫-+∞⎪⎢⎣⎭B .(,5)-∞-C .21,54⎡⎫--⎪⎢⎣⎭D .21,54⎛⎫-- ⎪⎝⎭10.已知函数()()3log 1f x ax =-,若()f x 在(],2-∞上为减函数,则a 的取值范围为( ) A .()0,∞+B .10,2⎛⎫ ⎪⎝⎭C .()1,2D .(),0-∞11.已知函数()f x 的定义域为R ,()0f x >且满足()()()f x y f x f y +=⋅,且()112f =,如果对任意的x 、y ,都有()()()0x y f x f y ⎡⎤--<⎣⎦,那么不等式()()234f x f x -⋅≥的解集为( )A .(][),12,-∞+∞B .[]1,2C .()1,2D .(],1-∞二、多选题12.(多选题)已知函数()()2220f x x x x =++<与()()2ln g x x x a =++(a R ∈且0a >)的图象上存在关于y 轴对称的点,则a 的取值可以是下列数据中的( )A .21eB .1eC .eD .3e三、填空题13.设集合{}1,2,4A =,{}2|40B x x x m =-+=.若{}1A B ⋂=,则B =__________.14.计算:3112log 2221log 6log 334⎛⎫--+= ⎪⎝⎭______ 15.设函数f (x )=ln(1+|x |)-211x +,则使得f (x )>f (2x -1)成立的x 的取值范围是________.16.已知函数()22log 1a a f x x x x =-+-在31,2⎛⎫⎪⎝⎭内恒小于零,则实数a 的取值范围是_________.四、解答题17.已知()1ln 33x M x f x ⎧⎫⎛⎫==-⎨⎬ ⎪⎝⎭⎩⎭,{}12N x a x a =<<-(1)求M ;(2)若M N M ⋂=,求实数a 的取值范围18.已知函数()113xf x a ⎛⎫=-- ⎪⎝⎭(1)若0a =,画出函数()f x 的图象,并指出函数的单调区间; (2)讨论函数()f x 的零点个数. 19.已知函数()21log 1f x x =+. (1)用定义法证明:()f x 是()1,+∞上的减函数;(2)若对于区间[]3,4上的每一个x 值,不等式()f x x m <+恒成立,求实数m 的取值范围.20.已知二次函数()g x 对一切实数x ∈R ,都有()()11g x g x -=+成立,且()10g =,()01g =,()()()1,h x g x bx c b c R =+++∈.(1)求()g x 的解析式;(2)记函数()h x 在[]1,1-上的最大值为M ,最小值为m ,若4M m -≤,当0b >时,求b 的最大值.21.某创业投资公司拟投资开发某种新能源产品,估计能获得25万元1600万元的投资收益,现准备制定一个对科研课题组的奖励方案:奖金y (单位:万元)随投资收益x (单位:万元)的增加而增加,奖金不超过75万元,同时奖金不超过投资收益的20%.(即:设奖励方案函数模型为()y f x =时,则公司对函数模型的基本要求是:当[]25,1600x ∈时,①()f x 是增函数;②()75f x ≤恒成立;③()5xf x ≤恒成立.) (1)判断函数() 1030x f x =+是否符合公司奖励方案函数模型的要求,并说明理由;(2)已知函数()()51g x a =≥符合公司奖励方案函数模型要求,求实数a 的取值范围.(参考结论:函数()()0af x x a x=+>的增区间为(,-∞、)+∞,减区间为()、() 22.设函数()()()212,xxk f x k x R k Z -=+-⋅∈∈.(1)若()k f x 是偶函数,求k 的值;(2)若存在[]1,2x ∈,使得()()014f mf x x +≤成立,求实数m 的取值范围; (3)设函数()()()0224g x f x f x λ=-+,若()g x 在[)1,x ∈+∞有零点,求实数λ的取值范围.参考答案1.A 【分析】求出二次函数2112y x =-+的值域即为集合N ,两集合取交集即可. 【详解】{}2,1,0,1,2M =--,{}211,R 12N y y x x y y ⎧⎫==-+∈=≤⎨⎬⎩⎭,M N ∴⋂={}2,1,0,1--.故选:A 【点睛】本题考查集合的交集运算,涉及二次函数的值域,属于基础题. 2.C 【解析】设幂函数为f(x)=x α,由f(9)=9α=3,即32α=3,可得2α=1,α=12.所以f(x)=12x故f(2)-f(1)-1. 3.D 【分析】根据基本初等函数的基本性质判断各选项中函数的单调性与奇偶性,即可得出合乎题意的选项. 【详解】对于A 选项,函数()2xf x =是非奇非偶函数且为增函数;对于B 选项,函数()3f x x =是奇函数且为增函数;对于C 选项,函数()1f x x=是奇函数,且在区间(),0-∞和()0,∞+上都是减函数,但在定义域()(),00,-∞⋃+∞上不单调;对于D 选项,函数()f x x x =-的定义域为R ,关于原点对称,且()()()f x x x x x f x -=--⋅-==-,此函数为奇函数,()22,0,0x x f x x x ⎧≤=⎨->⎩,所以,函数()f x x x =-在区间(),0-∞和[)0,+∞上都是减函数,且在R 上连续,则函数()f x x x =-在R 上为减函数. 故选D. 【点睛】本题考查基本初等函数的奇偶性和单调性,熟悉一些常见的基本初等函数的基本性质是解题的关键,考查分析问题和解决问题的能力,属于中等题. 4.B 【分析】求出()1f 、()2f ,由()()120f f ⋅<及零点存在定理即可判断. 【详解】()21log 111f =-+=-,()2112log 222f =-+=,()()120f f ∴⋅<,则函数的一个零点落在区间()1,2上.故选:B 【点睛】本题考查零点存在定理,属于基础题. 5.A 【解析】()()53531,1f x ax bx f x ax bx =++∴-=--+,()()()()2,552f x f x f f +-=∴+-=,()5275f -=-=-,故选A.6.C 【分析】利用指数函数与对数函数的性质即可比较大小. 【详解】设函数f (x )=0.9x ,g (x )=5.1x ,h (x )=log 0.9x 则f (x )单调递减,g (x )单调递增,h (x )单调递减 ∴0<f (5.1)=0.95.1<0.90=1,即0<m <1 g (0.9)=5.10.9>5.10=1,即n >1h (5.1)=log 0.95.1<log 0.91=0,即p <0 ∴p <m <n 故选C . 【点睛】本题考查对数值比较大小,可先从范围上比较大小,当从范围上不能比较大小时,可借助函数的单调性数形结合比较大小.属基础题 7.A 【分析】根据题意,易得()()0x a x b --=的两根为a 、b ,又由函数零点与方程的根的关系,可得()()()f x x a x b =--的零点就是a 、b ,观察()()()f x x a x b =--的图象,可得其与x 轴的两个交点的横坐标分别在区间(,1)-∞-与(0,1)上,又由a b >,可得1b <-,01a <<;根据函数图象变化的规律可得()xg x a b =+的单调性及与y 轴交点的位置,分析选项可得答案. 【详解】解:由二次方程的解法易得()()0x a x b --=的两根为a 、b ;根据函数零点与方程的根的关系,可得()()()f x x a x b =--的零点就是a 、b ,即函数图象与x 轴交点的横坐标;观察()()()f x x a x b =--的图象,可得其与x 轴的两个交点的横坐标分别在区间(,1)-∞-与(0,1)上,又由a b >,可得1b <-,01a <<;在函数()xg x a b =+可得,由01a <<可得其是减函数, 又由1b <-可得其与y 轴交点在x 轴的下方; 分析选项可得A 符合这两点,BCD 均不满足; 故选:A . 【点睛】本题综合考查指数函数的图象与函数零点的定义、性质;解题的关键在于根据二次函数的图象分析出a 、b 的范围.8.D 【分析】当0x >时求解不等式2log 1x >,当0x ≤时求解不等式21x,两段的x 的范围取并集即可. 【详解】当0x >时,不等式()1f x >为2log 1x >,解得2x >; 当0x ≤时,不等式()1f x >为21x,解得0x <.综上所述,()1f x >的解集为()(),02,-∞+∞.故选:D 【点睛】本题考查分段函数不等式,涉及对数不等式、指数不等式,属于基础题. 9.C 【分析】根据条件需满足0∆≥,(2)0f >,对称轴522x =>即可求出m 的取值范围. 【详解】关于x 的一元二次方程2510x x m -+-=的两根均大于2,则Δ25440(2)41010522m f m ⎧⎪=-+≥⎪=-+->⎨⎪⎪>⎩, 解得2154m -<-. 故选C. 【点睛】本题考查一元二次方程根与系数的关系,属于基础题. 10.B 【分析】利用复合函数法可得知内层函数1u ax =-在(],2-∞上为减函数,且10u ax =-≥在(],2-∞上恒成立,由此列出关于实数a 的不等式组,解出即可.【详解】函数()()3log 1f x ax =-的内层函数为1u ax =-,外层函数为3log y u =,由于函数()()3log 1f x ax =-在(],2-∞上为减函数,且外层函数3log y u =为增函数, 则内层函数1u ax =-在(],2-∞上为减函数,0a ∴-<,得0a >, 且10u ax =->在(],2-∞上恒成立,则min 120u a =->,解得12a <. 因此,实数a 的取值范围是10,2⎛⎫ ⎪⎝⎭. 故选B. 【点睛】本题考查复合型对数函数的单调性问题,在利用复合函数法判断内层函数和外层函数的单调性时,还应注意真数在定义域上要恒为正数,考查分析问题和解决问题的能力,属于中等题. 11.B 【分析】计算出()24f -=,并由()()()0x y f x f y ⎡⎤--<⎣⎦可得出函数()y f x =在R 上为减函数,再由()()234f x f x-⋅≥,可得出()()232f xx f -≥-,再由函数()y f x =在R 上的单调性可得出232x x -≤-,解出该不等式即可. 【详解】由于对任意的实数x 、y ,()()()f x y f x f y +=⋅且()0f x >. 令0x y ==,可得()()()000f f f =⋅,且()00f >,解得()01f =. 令y x =-,则()()()01f x f x f ⋅-==,()()1f x f x -=,()()1121f f -==. ()()()211224f f f ∴-=-⋅-=⨯=.设x y <,则0x y -<,由()()()0x y f x f y ⎡⎤--<⎣⎦,得()()f x f y >. 所以,函数()y f x =在R 上为减函数,由()()234f x f x-⋅≥,可得()()232f xx f -≥-.所以232x x -≤-,即2320x x -+≤,解得12x ≤≤. 因此,不等式()()234f x f x -⋅≥的解集为[]1,2.故选B. 【点睛】本题考查抽象函数的单调性解不等式,解题的关键就是将不等式左右两边转化为函数的两个函数值,并利用函数的单调性进行求解,考查分析问题和解决问题的能力,属于中等题. 12.ABC 【分析】根据题意得出()()g x f x -=,可得出22x a e x +=+,于是将问题转化为实数a 的取值范围即为函数()22x h x ex +=+在(),0-∞上的值域,并利用单调性求出函数()y h x =在(),0-∞上的值域,可得出实数a 的取值范围,由此可得出正确选项. 【详解】由题意可得()()g x f x -=,则()()22ln 22x a x x x -+-=++,得()ln 22a x x -=+,22x a e x +∴=+,构造函数()22x h x ex +=+,则实数a 的取值范围即为函数()22x h x e x +=+在(),0-∞上的值域,由于函数()22x h x e x +=+在(),0-∞上单调递增,所以,()()20h x h e <=,2a e ∴<.又0a >,20a e ∴<<,因此,符合条件的选项有A 、B 、C.故选ABC. 【点睛】本题考查函数方程的应用,解题的关键就是将问题转化为函数的零点问题,另外就是利用参变量分离法将参数的取值范围转化为函数的值域问题,考查化归与转化思想的应用,属于中等题. 13.{}1,3 【解析】因为{}1A B ⋂=,所以1x =为方程240x x m -+=的解,则140m -+=,解得3m =,所以2430x x -+=,(1)(3)0x x --=,集合{}1,3B =. 14.1 【分析】根据指数运算律、对数运算律直接计算. 【详解】原式22111log 3log 3122=+--+=. 故答案为:1 【点睛】本题考查指数、对数的运算律,属于基础题. 15.1,13⎛⎫ ⎪⎝⎭【分析】判断()f x 的奇偶性和单调性,据此等价转化不等式,则问题得解. 【详解】由f (x )=ln(1+|x |)-211x+()()()21ln 11x f x x =+--=-+-, 且其定义域为R ,故f (x )为R 上的偶函数, 于是f (x )>f (2x -1)即为f (|x |)>f (|2x -1|). 当x ≥0时,f (x )=ln(1+x )-211x+, ()21ln 1,1y x y x =+=-+在[)0,+∞均是单调增函数, 所以f (x )为[0,+∞)上的增函数, 则由f (|x |)>f (|2x -1|)得|x |>|2x -1|, 两边平方得3x 2-4x +1<0,解得13<x <1. 故答案为:1,13⎛⎫ ⎪⎝⎭【点睛】本题考查函数奇偶性和单调性的判断,涉及利用函数性质解不等式,属综合基础题.16.1,116⎡⎫⎪⎢⎣⎭【分析】由题意得出()()2log 11a x x ->-对任意的31,2x ⎛⎫∈ ⎪⎝⎭恒成立,然后对底数a 分1a >和01a <<两种情况讨论,结合图象找出关键点得出关于a 的不等式(组)求解,可得出实数a 的取值范围.【详解】()()()()2222log 2log log 11log 11aa a a a f x x x x x a x x x x =-+=-+--=----, 则不等式()()2log 11a x x ->-对任意的31,2x ⎛⎫∈ ⎪⎝⎭恒成立.当1a >时,312x <<,则1012x <-<,此时()1log 1log log 102a a a x -<<=,则不等式()()2log 11a x x ->-对任意的31,2x ⎛⎫∈ ⎪⎝⎭不成立; 当01a <<时,如下图所示:由图象可知,若不等式()()2log 11a x x ->-对任意的31,2x ⎛⎫∈ ⎪⎝⎭恒成立,则20113log 122a a <<⎧⎪⎨⎛⎫≥- ⎪⎪⎝⎭⎩,解得1116a ≤<. 因此,实数a 的取值范围是1,116⎡⎫⎪⎢⎣⎭.故答案为1,116⎡⎫⎪⎢⎣⎭. 【点睛】本题考查对数不等式恒成立问题,解题时要注意对底数的取值范围进行分类讨论,并利用数形结合思想得出一些关键点列不等式(组)求解,考查数形结合思想的应用,属于中等题. 17.(1){}12M x x =-<≤;(2)(],1-∞-. 【分析】(1)根据被开方数非负、对数型函数的定义域列出不等式组求解x ,x 的取值集合即为集合M ;(2)由两集合交集的结果可得M N ⊆,即可做出数轴求满足条件的a 的取值范围. 【详解】(1)2603211303x x x x x ⎧--+≥-≤≤⎧⎪⇒⎨⎨>-->⎩⎪⎩,解得12x -<≤, 所以{}12M x x =-<≤; (2)M N M ⋂=,M N ∴⊆,1211122a aa a a <-⎧⎪∴≤-⇒≤-⎨⎪->⎩,即a 的取值范围为(),1-∞-. 【点睛】本题考查函数的定义域、集合的基本运算、根据集合的包含关系求参数的范围,属于基础题. 18.(1)答案见解析;(2)答案见解析. 【分析】(1)当0a =时作出函数()f x 的图像,并根据函数图像写出函数的单调区间;(2)原问题可转化为讨论函数113xy ⎛⎫=- ⎪⎝⎭与函数y a =的交点个数.【详解】(1)若0a =,则()113xf x ⎛⎫=- ⎪⎝⎭,作出函数图像如图所示:函数()f x 的单调增区间为()0,∞+,单调减区间为(),0-∞;(2)函数()113x f x a ⎛⎫=-- ⎪⎝⎭的零点个数即为方程113xa ⎛⎫-= ⎪⎝⎭的解的个数,也即函数113xy ⎛⎫=- ⎪⎝⎭与函数y a =的交点个数,如图所示,当0a <时,函数113xy ⎛⎫=- ⎪⎝⎭与函数y a =没有交点,即()f x 有0个零点;当0a =时,函数113xy ⎛⎫=- ⎪⎝⎭与函数y a =有1个交点,即()f x 有1个零点;当01a <<时,函数113x y ⎛⎫=- ⎪⎝⎭与函数y a =有2个交点,即()f x 有2个零点;当1a ≥时,函数113xy ⎛⎫=- ⎪⎝⎭与函数y a =有1个交点,即()f x 有1个零点.综上所述,当0a <时()f x 有0个零点;当0a =或1a ≥时,()f x 有1个零点;当01a <<时()f x 有2个零点. 【点睛】本题考查函数的图像与性质、利用两函数图像的交点个数判断函数的零点个数,属于中档题. 19.(1)证明见解析;(2)()5,-+∞. 【分析】(1)设121x x >>,利用对数的运算性质以及对数函数的单调性可得出()()12f x f x <,从而得出函数()y f x =在()1+∞,上为减函数; (2)由参变量分离法得出21log 1m x x >-+对任意的[]3,4x ∈上恒成立,然后构造函数()21log 1g x x x =-+,分析函数()y g x =在区间[]3,4上的单调性,求出该函数的最大值,即可求出实数m 的取值范围. 【详解】(1)任取121x x >>,则()()212222121111log log log 111x f x f x x x x +-=-=+++, 121x x >>,则12112x x +>+>,211011x x +∴<<+,22211log log 101x x +∴<=+, 即()()12f x f x <,所以,函数()21log 1f x x =+在()1,+∞上为减函数; (2)对任意的[]3,4x ∈,()f x x m <+,即21log 1x m x <++,得21log 1m x x >-+. 构造函数()21log 1g x x x =-+,其中[]3,4x ∈,则函数()y g x =在区间[]3,4上为减函数, ∴函数()y g x =在区间[]3,4上的最大值为()()2max 13log 354g x g ==-=-,5m ∴>-.因此,实数m 的取值范围是()5,-+∞. 【点睛】本题考查利用定义证明函数的单调性,同时也考查了函数不等式恒成立问题,利用参变量分离法转化为函数的最值问题是解题的关键,考查化归与转化思想的应用,属于中等题. 20.(1)()()21g x x =-;(2)2.【分析】(1)由题意可得出二次函数()y g x =的对称轴为直线1x =,结合()10g =可得出该二次函数的顶点坐标为()1,0,可设()()21g x a x =-,再由()01g =求出实数a 的值,由此可得出函数()y g x =的解析式;(2)求出函数()y h x =的解析式()2h x x bx c =++,分析该二次函数图象的对称轴与区间[]1,1-的位置关系,分析函数()y h x =在区间[]1,1-上的单调性,求出M 和m ,然后解不等式4M m -≤,求出实数b 的取值范围,即可得出实数b 的最大值. 【详解】(1)对一切实数x ∈R ,都有()()11g x g x -=+成立,则二次函数()y g x =的对称轴为直线1x =,又()10g =,则二次函数()y g x =图象的顶点坐标为()1,0, 设()()21g x a x =-,则()01g a ==,因此,()()21g x x =-;(2)()()21h x g x bx c x bx c =+++=++,对称轴为直线2b x =-,0b >,则02b-<. 当12b-≤-时,即当2b ≥时,函数()y h x =在区间[]1,1-上单调递增, 则()11M h b c ==++,()11m h b c =-=-++,则24M m b -=≤,得2b ≤,此时2b =;当102b -<-<时,即当02b <<时,函数()y h x =在区间1,2b ⎡⎫--⎪⎢⎣⎭上单调递减,在区间,12b ⎛⎤- ⎥⎝⎦上单调递增,所以,224b b m f c ⎛⎫=-=-+ ⎪⎝⎭,()11f b c =++,()11f b c -=-++,且()()11f f >-,()11M f b c ∴==++,则2144b M m b -=++≤,整理得24120b b +-≤,解得62b -≤≤,此时,02b <<.因此,02b <≤,则实数b 的最大值为2. 【点睛】本题考查二次函数解析式的求法,同时也考查了二次函数在定区间上最值的求法,当对称轴位置不确定时,需要分析对称轴与定义域的位置关系,结合单调性得出二次函数的最值,考查分类讨论思想的应用,属于中等题.21.(1)函数模型()1030xf x =+,不符合公司要求;详见解析;(2)[]1,2. 【分析】(1)研究函数()1030xf x =+的单调性与值域,验证该函数是否满足题中三个要求,即可得出结论;(2)先求出函数()y g x =的最大值()()max 1600405g x g a ==-,由40575a -≤求出实数a 的范围,在利用参变量分离法求出满足()5xg x ≤恒成立时实数a 的取值范围,由此可得出实数a 的取值范围. 【详解】(1)对于函数模型()1030xf x =+, 当[]25,1600x ∈时,函数()y f x =是单调递增函数,则()()160075f x f ≤≤显然恒成立,若函数()5x f x ≤恒成立,即10305x x +≤,解得60x ≥,则()5xf x ≤不恒成立, 综上所述,函数模型()1030xf x =+,满足基本要求①②,但是不满足③, 故函数模型()1030xf x =+,不符合公司要求;(2)当[]25,1600x ∈时,()()51g x a =≥单调递增,∴函数()y g x =的最大值为()16005405g a ==-,由题意可得40575a -≤,解得2a ≤.设()55x g x =≤恒成立,2255x a x ⎛⎫∴≤+ ⎪⎝⎭恒成立,即225225x a x ≤++, 对于函数2251252525x y x x x ⎛⎫=+=+ ⎪⎝⎭,由题意可知,该函数在25x =处取得最小值, 即min 252522525y =+=,2224a ∴≤+=,1a ≥,12a ∴≤≤. 因此,实数a 的取值范围是[]1,2. 【点睛】本题考查函数模型的选择,本质上就是考查函数基本性质的应用,同时也考查了函数不等式恒成立问题,在求解含单参数的不等式恒成立问题,可充分利用参变量分离法转化为函数最值问题来求解,考查分析问题与解决问题的能力,属于中等题. 22.(1)2k =;(2)54m ≤;(3)1,6⎡⎫+∞⎪⎢⎣⎭. 【分析】(1)由()()k k f x f x -=代入即可求解k ;(2)由已知代入可得2422xxxm -⋅≤-+,分类可得()242242212x x x x xm ----+≤=⋅+-,换元后利用二次函数的性质可求;(3)结合已知,代入可求()g x ,然后结合()g x 在[)1x ∈+∞,有零点利用换元法,结合二次函数的性质可求. 【详解】(1)若()k f x 是偶函数,则()()k k f x f x -=,即()()212212xx x x k k --+-⋅=+-⋅,即()()()()221212122xx x x x x k k k ----=-⋅--⋅=--,则11k -=,即2k =;(2)存在]2[1x ∈,,使得()()014f mf x x +≤成立,即2422x x x m -≤-+, 则()242242212x x x x xm ----+≤=⋅+-, 设2x t -=,∵12x ≤≤, ∴1142t ≤≤, 设()22422141x x t t --⋅+-=+-,则()224125y t t t =+-=+-,∵ 1412t ≤≤,∴当12t =时,函数取得最大值152144y =+-=, 则54m ≤. (3)()022xxf x -=-,()222xxf x -=+, 则()()2222222222xxxx f x --=+=-+,则()()()()()2022422222x x x x g x f x f x λλ--=-+=---+,设22x x t -=-,当1≥x 时,函数22x x t -=-为增函数, 则13222t ≥-=, 若()g x 在[)1,x ∈+∞有零点, 即()()()222220222x x x x g x t t λλ--=---=+-=+在32t ≥上有解, 即22t t λ=-,即2t tλ=-, ∵2t t -在3,2⎡⎫+∞⎪⎢⎣⎭递增,∴341236λ≥-=, 即λ的取值范围是1,6⎡⎫+∞⎪⎢⎣⎭. 【点睛】本题主要综合考查了函数的性质及函数与方程思想的相互转化,培养了学生的逻辑思维能力,属于中档题.。
浙江省台州市2023-2024学年高一上学期期中数学试题含解析

2023年学年第一学期期中考试试卷高一数学(答案在最后)总分:150分考试时间:120分钟一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项符合题目要求.1.已知全集U =R ,集合{}1,0,1,2A =-,{}|210B x x =->,则()A B ⋂R ð等于()A.{}1,0- B.{}1,2C.{}1,0,1- D.{}0,1,2【答案】A 【解析】【分析】先求B R ð,然后由交集运算可得.【详解】因为{}1|210|2B x x x x ⎧⎫=->=>⎨⎬⎩⎭,所以1|2B x x ⎧⎫=≤⎨⎬⎩⎭R ð,所以(){}1,0A B ⋂=-R ð.故选:A2.命题“2000,10x x x ∃∈++<R ”的否定为()A.2000,10x x x ∃∈++≥R B.2000,10x x x ∃∈++>R C.2,10x x x ∀∈++≥R D.2,10x x x ∀∈++>R 【答案】C 【解析】【分析】在写命题的否定中要把存在变任意,任意变存在.【详解】因为特称命题的否定为全称命题,所以2000,10x x x ∃∈++<R 的否定即为2,10x x x ∀∈++≥R .故选:C.3.设x ∈R ,则“220x x -<”是“12x -<”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】A 【解析】【分析】解不等式,再判断不等式解集的包含关系即可.【详解】由220x x -<得()0,2x ∈,由12x -<得()1,3x ∈-,故“220x x -<”是“12x -<”的充分不必要条件.故选:A.4.已知关于x 的不等式20ax bx c ++>的解集为{|2x x <-或}3x >,则下列说法错误的是()A.0a >B.不等式0bx c +>的解集是{}6x x <C.0a b c ++< D.不等式20cx bx a -+<的解集是1|3x x ⎧<-⎨⎩或12x ⎫>⎬⎭【答案】B 【解析】【分析】先求得,,a b c 的关系式,然后对选项进行分析,所以确定正确答案.【详解】由于关于x 的不等式20ax bx c ++>的解集为{|2x x <-或}3x >,所以0a >(A 选项正确),且2323b ac a ⎧-+=-⎪⎪⎨⎪-⨯=⎪⎩,整理得,6b a c a =-=-,由0bx c +>得60,6ax a x --><-,所以不等式0bx c +>的解集是{}6x x <-,所以B 选项错误.660a b c a a a a ++=--=-<,所以C 选项正确.()()22260,6121310cx bx a ax ax a x x x x -+=-++<--=-+<,解得13x <-或12x >,所以D 选项正确.故选:B5.已知函数()y f x =的定义域为{}|06x x ≤≤,则函数()()22f xg x x =-的定义域为()A.{|02x x ≤<或}23x <≤B.{|02x x ≤<或}26x <≤C.{|02x x ≤<或}212x <≤ D.{}|2x x ≠【答案】A 【解析】【分析】由已知列出不等式组,求解即可得出答案.【详解】由已知可得,02620x x ≤≤⎧⎨-≠⎩,解得,02x ≤<或23x <≤.故选:A .6.已知函数5(2),22(),2a x x f x a x x⎧-+≤⎪⎪=⎨⎪>⎪⎩是R 上的减函数,则实数a 的取值范围是()A.()0,2 B.()1,2 C.[)1,2 D.(]0,1【答案】C 【解析】【分析】由题可得函数在2x ≤及2x >时,单调递减,且52(2)22aa -+≥,进而即得.【详解】由题意可知:ay x=在()2,+∞上单调递减,即0a >;5(2)2y a x =-+在(],2-∞上也单调递减,即20a -<;又()f x 是R 上的减函数,则52(2)22aa -+≥,∴02052(2)22a a a a ⎧⎪>⎪-<⎨⎪⎪-+≥⎩,解得12a ≤<.故选:C .7.已知函数()y f x =的定义域为R ,()f x 为偶函数,且对任意12,(,0]x x ∈-∞都有2121()()0f x f x x x ->-,若(6)1f =,则不等式2()1f x x ->的解为()A.()(),23,-∞-⋃+∞ B.()2,3- C.()0,1 D.()()2,01,3-⋃【答案】B 【解析】【分析】由2121()()0f x f x x x ->-知,在(,0]-∞上单调递增,结合偶函数,知其在在[0,)+∞上单调递减即可解.【详解】对120x x ∀<≤,满足()()21210f x f x x x ->-,等价于函数()f x 在(,0]-∞上单调递增,又因为函数()f x 关于直线0x =对称,所以函数()f x 在[0,)+∞上单调递减.则()21f x x ->可化为26x x -<,解得23x -<<.故选:B.8.函数()f x x =,()22g x x x =-+.若存在129,,,0,2n x x x ⎡⎤⋅⋅⋅∈⎢⎥⎣⎦,使得()()()()121n n f x f x f x g x -++⋅⋅⋅++()()()()121n n g x g x g x f x -=++++ ,则n 的最大值是()A.8B.11C.14D.18【答案】C 【解析】【分析】令()222h x x x =-+,原方程可化为存在129,,,0,2n x x x ⎡⎤⋅⋅⋅∈⎢⎥⎣⎦,使得()()()()121n n h x h x h x h x -++⋅⋅⋅+=,算出左侧的取值范围和右侧的取值范围后可得n 的最大值.【详解】因为存在129,,,0,2n x x x ⎡⎤⋅⋅⋅∈⎢⎥⎣⎦,使得()()()()121n n f x f x f x g x -++⋅⋅⋅++()()()()121n n g x g x g x f x -=++++ ,故2221111222222n n n n x x x x x x ---+++-+=-+ .令()222h x x x =-+,90,2x ⎡⎤∈⎢⎥⎣⎦,则()5314h x ≤≤,故()221111531222214n n n x x x x n ---≤-+++-+≤- ,因为()5314n h x ≤≤故5314n -≤,故max 14n =.故选:C.【点睛】本题考查二次函数的最值,注意根据解析式的特征把原方程合理整合,再根据方程有解得到n 满足的条件,本题属于较难题.二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多个选项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9.对实数a ,b ,c ,d ,下列命题中正确的是()A.若a b <,则22ac bc <B.若a b >,c d <,则a c b d ->-C.若14a ≤≤,21b -≤≤,则06a b ≤-≤D.a b >是22a b >的充要条件【答案】BC 【解析】【分析】利用不等式的性质一一判定即可.【详解】对于A ,若0c =,则22ac bc =,故A 错误;对于B ,c d c d <⇒->-,由不等式的同向可加性可得a c b d ->-,故B 正确;对于C ,2121b b -≤≤⇒≥-≥-,由不等式的同向可加性可得06a b ≤-≤,故C 正确;对于D ,若102a b =>>=-,明显22a b <,a b >不能得出22a b >,充分性不成立,故D 错误.故选:BC10.已知函数()42f x x =-,则()A.()f x 的定义域为{}±2x x ≠ B.()f x 的图象关于直线=2x 对称C.()()56ff -=- D.()f x 的值域是()(),00,-∞+∞ 【答案】AC 【解析】【分析】根据解析式可得函数的定义域可判断A ,利用特值可判断,直接求函数值可判断C ,根据定义域及不等式的性质求函数的值域可判断D.【详解】由20x -≠,可得2x ≠±,所以()f x 的定义域为{}±2x x ≠,则A 正确;因为()14f =-,()34f =,所以()()13f f ≠,所以()f x 的图象不关于直线=2x 对称,则B 错误;因为()453f -=,所以()()56f f -=-,则C 正确;因为2x ≠±,所以0x ≥,且2x ≠,所以22x -≥-,且20x -≠,当220x -≤-<时,422x ≤--,即()2f x ≤-,当20x ->时,402x >-,即()0f x >,所以()f x 的值域是(](),20,-∞-+∞ ,故D 错误.故选:AC.11.高斯是德国著名的数学家,近代数学奠基之一,享有“数学王子”的称号,他和阿基米德、牛顿并列为七界三大数学家,用其名字命名的“高斯函数”为:设x ∈R ,用[]x 表示不超过x 的最大整数,则[]y x =称为高斯函数,如:[]1.21=,[]1.22-=-,[]y x =又称为取整函数,在现实生活中有着广泛的应用,诸如停车收费,出租车收费等均按“取整函数”进行计费,以下关于“取整函数”的描述,正确的是()A.x ∀∈R ,[][]22x x =B.x ∀∈R ,[][]122x x x ⎡⎤++=⎢⎥⎣⎦C.x ∀,R y ∈,若[][]x y =,则有1x y ->-D.方程[]231x x =+的解集为【答案】BCD 【解析】【分析】对于A :取12x =,不成立;对于B :设[]x x a =-,[0,1)a ∈,讨论10,2a ⎡⎫∈⎪⎢⎣⎭与1,1)2a ⎡∈⎢⎣求解;对于C :,01x m t t =+≤<,,01y m s s =+≤<,由||x y -=||1t s -<得证;对于D :先确定0x ≥,将[]231x x =+代入不等式[][]()2221x x x ≤<+得到[]x 的范围,再求得x 值.【详解】对于A :取12x =,[][][]1211,2220x x ⎡⎤==⎢⎥⎣⎦==,故A 错误;对于B :设11[],[0,1),[][][]22x x a a x x x x a ⎡⎤⎡⎤=-∈∴++=+++⎢⎥⎢⎥⎣⎦⎣⎦12[]2x a ⎡⎤=++⎢⎥⎣⎦,[2][2[]2]2[][2]x x a x a =+=+,当10,2a ⎡⎫∈⎪⎢⎣⎭时,11,122a ⎡⎫+∈⎪⎢⎣⎭,2[0,1)a ∈,则102a ⎡⎤+=⎢⎥⎣⎦,[2]0a =则1[]2[]2x x x ⎡⎤++=⎢⎣⎦,[2]2[]x x =,故当10,2a ⎡⎫∈⎪⎢⎣⎭时1[]2[]2x x x ⎡⎤++=⎢⎥⎣⎦成立.当1,1)2a ⎡∈⎢⎣时,131,22a ⎡⎫+∈⎪⎢⎣⎭,2[1,,)2a ∈则112a ⎡⎤+=⎢⎥⎣⎦,[2]1a =则1[]2[]1[2]],2[12x x x x x ⎡⎤++=+=+⎢⎣⎦,故当1,1)2a ⎡∈⎢⎣时1[]2[]2x x x ⎡⎤++=⎢⎥⎣⎦成立.综上B 正确.对于C :设[][]x y m ==,则,01x m t t =+≤<,,01y m s s =+≤<,则|||()x y m t -=+-()|||1m s t s +=-<,因此1x y ->-,故C 正确;对于D :由[]231x x =+知,2x 一定为整数且[]310x +≥,所以[]13x ≥-,所以[]0x ≥,所以0x ≥,由[][]()2221x x x ≤<+得[][][]()22311x x x ≤+<+,由[][]231x x ≤+解得[]33 3.322x +≤≤≈,只能取[]03x ≤≤,由[][]()2311x x +<+解得[]1x >或[]0x <(舍),故[]23x ≤≤,所以[]2x =或[]3x =,当[]2x =时x =[]3x =时x =,所以方程[]231x x =+的解集为,故选:BCD.【点睛】高斯函数常见处理策略:(1)高斯函数本质是分段函数,分段讨论是处理此函数的常用方法.(2)由x 求[]x 时直接按高斯函数的定义求即可.由[]x 求x 时因为x 不是一个确定的实数,可设[]x x a =-,[0,1)a ∈处理.(3)求由[]x 构成的方程时先求出[]x 的范围,再求x 的取值范围.(4)求由[]x 与x 混合构成的方程时,可用[][]1x x x ≤<+放缩为只有[]x 构成的不等式求解.12.函数()1f x a x a =+--,()21g x ax x =-+,其中0a >.记{},max ,,m m n m n n m n ≥⎧=⎨<⎩,设()()(){}max ,h x f x g x =,若不等式()12h x ≤恒有解,则实数a 的值可以是()A.1B.12 C.13 D.14【答案】CD 【解析】【分析】将问题转化为()min 12h x ≥;分别在a ≥和0a <<的情况下,得到()f x 与()g x 的大致图象,由此可得确定()h x 的解析式和单调性,进而确定()min h x ,由()min 12h x ≤可确定a 的取值范围,由此可得结论.【详解】由题意可知:若不等式()12h x ≤恒有解,只需()min 12h x ≥即可.()1,21,x x af x a x x a +≤⎧=⎨+-≥⎩,∴令211ax x x -+=+,解得:0x =或2x a=;令2121ax x a x -+=+-,解得:x =或x =;①当2a a≤,即a ≥时,则()f x 与()g x大致图象如下图所示,()()()(),02,02,g x x h x f x x a g x x a ⎧⎪≤⎪⎪∴=<<⎨⎪⎪≥⎪⎩,()h x ∴在(],0-∞上单调递减,在[)0,∞+上单调递增,()()()min 001h x h g ∴===,不合题意;②当2a a>,即0a <<时,则()f x 与()g x大致图象如下图所示,()()()(),0,0,g x x h x f x x g x x ⎧≤⎪∴=<<⎨⎪≥⎩()h x ∴在(],0-∞,a ⎡⎣上单调递减,[]0,a,)+∞上单调递增;又()()001h g ==,21hg a ==,∴若()min 12h x ≥,则需()min h x h =,即1212a ≤,解得:14a -≤;综上所述:实数a的取值集合10,4M ⎛⎤-= ⎥ ⎝⎦,1M ∉ ,12M ∉,13M ∈,14M ∈,∴AB 错误,CD 正确.故选:CD.【点睛】关键点点睛:本题考查函数不等式能成立问题的求解,解题关键是将问题转化为函数最值的求解问题,通过分类讨论的方式,确定()f x 与()g x 图象的相对位置,从而得到()h x 的单调性,结合单调性来确定最值.三、填空题:本题共4小题,每小题5分,共20分.13.若幂函数()f x 过点()42,,则满足不等式()()21f a f a ->-的实数a 的取值范围是__________.【答案】312⎡⎫⎪⎢⎣⎭,【解析】【分析】利用待定系数法求出幂函数()f x 的解析式,再利用函数定义域和单调性求不等式的解集.【详解】设幂函数()y f x x α==,其图像过点()42,,则42α=,解得12α=;∴()12f x x ==,函数定义域为[)0,∞+,在[)0,∞+上单调递增,不等式()()21f a f a ->-等价于210a a ->-≥,解得312a ≤<;则实数a 的取值范围是31,2⎡⎫⎪⎢⎣⎭.故答案为:31,2⎡⎫⎪⎢⎣⎭14.已知0a >,0b >,且41a b +=,则22ab +的最小值是______.【答案】18【解析】【分析】利用基本不等式“1”的妙用求解最小值.【详解】由题意可得24282221018b a b ab a b a ab +=++=⎛⎫⎛⎫ ⎪⎪⎝⎭⎝++≥⎭,当且仅当13a =,6b =时,等号成立.故答案为:1815.若函数()()22()1,,=-++∈f x x xax b a b R 的图象关于直线2x =对称,则=a b +_______.【答案】7【解析】【分析】由对称性得()(4)f x f x =-,取特殊值(0)(4)(1)(3)f f f f =⎧⎨=⎩求得,a b ,再检验满足()(4)f x f x =-即可得,【详解】由题意(2)(2)f x f x +=-,即()(4)f x f x =-,所以(0)(4)(1)(3)f f f f =⎧⎨=⎩,即15(164)08(93)b a b a b =-++⎧⎨=-++⎩,解得815a b =-⎧⎨=⎩,此时22432()(1)(815)814815f x x x x x x x x =--+=-+--+,432(4)(4)8(4)14(4)8(4)15f x x x x x -=--+-----+432232(1696256256)8(644812)14(168)32815x x x x x x x x x x =--+-++-+---+-++432814815x x x x =-+--+()f x =,满足题意.所以8,15a b =-=,7a b +=.故答案为:7.16.设函数()24,()2,ax x a f x x x a-+<⎧⎪=⎨-≥⎪⎩存在最小值,则a 的取值范围是________.【答案】[0,2]【解析】【分析】根据题意分a<0,0a =,02a <≤和2a >四种情况结合二次函数的性质讨论即可》【详解】①当a<0时,0a ->,故函数()f x 在(),a -∞上单调递增,因此()f x 不存在最小值;②当0a =时,()24,0()2,0x f x x x <⎧⎪=⎨-≥⎪⎩,当0x ≥时,min ()(2)04f x f ==<,故函数()f x 存在最小值;③当02a <≤时,0a -<,故函数()f x 在(),a -∞上单调递减,当x a <时,2()()4f x f a a >=-+;当x a ≥时,2()(2)(2)0f x x f =-≥=.若240a -+<,则()f x 不存在最小值,故240a -+≥,解得22a -≤≤.此时02a <≤满足题设;④当2a >时,0a -<,故函数()f x 在(),a -∞上单调递减,当x a <时,2()()4f x f a a >=-+;当x a ≥时,22()(2)()(2)f x x f a a =-≥=-.因为222(2)(4)242(2)0a a a a a a ---+=-=->,所以22(2)4a a ->-+,因此()f x 不存在最小值.综上,a 的取值范围是02a ≤≤.故答案为:[0,2]【点睛】关键点点睛:此题考查含参数的分段函数求最值,考查二次函数的性质,解题的关键是结合二次函数的性质求函数的最小值,考查分类讨论思想,属于较难题.四、解答题:本题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.已知集合{|13}A x x =<<,集合{|21}B x m x m =<<-.(1)若A B ⋂=∅,求实数m 的取值范围;(2)命题p :x A ∈,命题q :x B ∈,若p 是q 的充分条件,求实数m 的取值范围.【答案】(1)[)0,∞+(2)(],2-∞-【解析】【分析】(1)根据B 是否为空集进行分类讨论,由此列不等式来求得m 的取值范围.(2)根据p 是q 的充分条件列不等式,由此求得m 的取值范围.【小问1详解】由于A B ⋂=∅,①当B =∅时,21m m ³-,解得13m ≥,②当B ≠∅时,2111m m m <-⎧⎨-≤⎩或2123m mm <-⎧⎨≥⎩,解得103m ≤<.综上所述,实数m 的取值范围为[)0,∞+.【小问2详解】命题:p x A ∈,命题:q x B ∈,若p 是q 的充分条件,故A B ⊆,所以2113m m ≤⎧⎨-≥⎩,解得2m ≤-;所以实数m 的取值范围为(],2-∞-.18.2018年8月31日,全国人大会议通过了个人所得税法的修订办法,将每年个税免征额由42000元提高到60000元.2019年1月1日起实施新年征收个税.个人所得税税率表(2019年1月1日起执行)级数全年应纳税所得额所在区间(对应免征额为60000)税率(%)速算扣除数1[]0,36000302(]36000,1440001025203(]144000,30000020X 4(]300000,42000025319205(]420000,66000030529206(]660000,96000035859207()960000,+∞45181920有一种速算个税的办法:个税税额=应纳税所得额×税率-速算扣除数.(1)请计算表中的数X ;(2)假若某人2021年税后所得为200000元时,请按照这一算法计算他的税前全年应纳税所得额.【答案】(1)16920X =(2)153850元.【解析】【分析】(1)根据公式“个税税额=应纳税所得额×税率-速算扣除数”计算,其中个税税额按正常计税方法计算;(2)先判断他的全年应纳税所参照的级数,是级数2还是级数3,然后再根据计税公式求解.【小问1详解】按照表格,假设个人全年应纳税所得额为x 元(144000300000x ≤≤),可得:()()20%14400020%1440003600010%360003%x X x -=-⨯+-⨯+⨯,16920X =.【小问2详解】按照表格,级数3,()30000030000020%16920256920-⨯-=;按照级数2,()14400014400010%2520132120-⨯-=;显然1321206000019212020000031692025692060000+=<<=+,所以应该参照“级数3”计算.假设他的全年应纳税所得额为t 元,所以此时()20%1692020000060000t t -⨯-=-,解得153850t =,即他的税前全年应纳税所得额为153850元.19.已知定义在R 上的函数()f x 满足()()()2f x y f x f y +=++,且当0x >时,()2f x >-.(1)求()0f 的值,并证明()2f x +为奇函数;(2)求证()f x 在R 上是增函数;(3)若()12f =,解关于x 的不等式()()2128f x x f x ++->.【答案】(1)(0)2f =-,证明见解析(2)证明见解析(3){1x x <-或}2x >【解析】【分析】(1)赋值法;(2)结合增函数的定义,构造[]1122()()f x f x x x =-+即可;(3)运用题干的等式,求出(3)10f =,结合(2)的单调性即可.【小问1详解】令0x y ==,得(0)2f =-.()2()2(0)20f x f x f ++-+=+=,所以函数()2f x +为奇函数;【小问2详解】证明:在R 上任取12x x >,则120x x ->,所以12()2f x x ->-.又[]11221222()()()()2()f x f x x x f x x f x f x =-+=-++>,所以函数()f x 在R 上是增函数.【小问3详解】由(1)2f =,得(2)(11)(1)(1)26f f f f =+=++=,(3)(12)(1)(2)210f f f f =+=++=.由2()(12)8f x x f x ++->得2(1)(3)f x x f -+>.因为函数()f x 在R 上是增函数,所以213x x -+>,解得1x <-或2x >.故原不等式的解集为{1x x <-或}2x >.20.已知函数()2,R f x x x k x k =-+∈.(1)讨论函数()f x 的奇偶性(写出结论,不需要证明);(2)如果当[]0,2x ∈时,()f x 的最大值是6,求k 的值.【答案】(1)答案见解析(2)1或3【解析】【分析】(1)对k 进行分类讨论,结合函数奇偶性的知识确定正确答案.(2)将()f x 表示为分段函数的形式,对k 进行分类讨论,结合二次函数的性质、函数的单调性求得k 的值.【小问1详解】当0k =时,()f x =||2x x x +,则()f x -=||2x x x --=()f x -,即()f x 为奇函数,当0k ≠时,(1)f =|1|2k -+,(1)|1|2f k -=-+-,(1)(1)|1|2|1|2|1||1|0f f k k k k +-=-+-+-=--+≠,则()f x 不是奇函数,(1)(1)|1|2|1|2|1||1|40f f k k k k --=-++++=-+++≠,则()f x 不是偶函数,∴当0k =时()f x 是奇函数,当0k ≠时,()f x 是非奇非偶函数.【小问2详解】由题设,()f x ()()222,2,x k x x k x k x x k ⎧+-≥⎪=⎨-++<⎪⎩,函数()22y x k x =+-的开口向上,对称轴为2122k kx -=-=-;函数()22y x k x =-++的开口向下,对称轴为2122k k x +=-=+-.1、当1122k k k -<+<,即2k >时,()f x 在(,1)2k-∞+上是增函数,∵122k+>,∴()f x 在[]0,2上是增函数;2、当1122k k k <-<+,即2k <-时,()f x 在1,2k ⎛⎫-+∞ ⎪⎝⎭上是增函数,∵102k-<1,∴()f x 在[]0,2上是增函数;∴2k >或2k <-,在[]0,2x ∈上()f x 的最大值是(2)2|2|46f k =-+=,解得1k =(舍去)或3k =;3、当1122k kk -≤≤+,即22k -≤≤时,()f x 在[]0,2上为增函数,令2246k -+=,解得1k =或3k =(舍去).综上,k 的值是1或3.【点睛】研究函数的奇偶性的题目,如果要判断函数的奇偶性,可以利用奇偶函数的定义()()f x f x -=或()()f x f x -=-来求解.也可以利用特殊值来判断函数不满足奇偶性的定义.对于含有绝对值的函数的最值的研究,可将函数写为分段函数的形式,再对参数进行分类讨论来求解.21.已知函数()2f x x =-,()()224g x x mx m =-+∈R .(1)若对任意[]11,2x ∈,存在[]24,5x ∈,使得()()12g x f x =,求m 的取值范围;(2)若1m =-,对任意n ∈R ,总存在[]02,2x ∈-,使得不等式()200g x x n k -+≥成立,求实数k 的取值范围.【答案】(1)54m ⎡∈⎢⎣(2)(],4∞-【解析】【分析】(1)将题目条件转化为()1g x 的值域包含于()2f x 的值域,再根据[]11,2x ∈的两端点的函数值()()1,2g g 得到()y g x =对称轴为[]1,2x m =∈,从而得到()()min g x g m =,进而求出m 的取值范围;(2)将不等式()200g x x n k -+≥化简得不等式024x n k ++≥成立,再构造函数()0024h x x n =++,从而得到()0max h x k ≥,再构造函数()(){}0max max ,8n h x n n ϕ==+,求出()min n ϕ即可求解.【小问1详解】设当[]11,2x ∈,()1g x 的值域为D ,当[]24,5x ∈,()2f x 的值域为[]2,3,由题意得[]2,3D ⊆,∴()()211243224443g m g m ⎧≤=-+≤⎪⎨≤=-+≤⎪⎩,得5342m ≤≤,此时()y g x =对称轴为[]1,2x m =∈,故()()[]min 2,3g x g m =∈,即()222243g m m m =-+≤≤得1m ≤≤1m ≤≤-,综上可得54m ⎡∈⎢⎣.【小问2详解】由题意得对任意n ∈R ,总存在[]02,2x ∈-,使得不等式024x n k ++≥成立,令()0024h x x n =++,由题意得()0max h x k ≥,而()()(){}{}0max max 2,2max ,8h x h h n n =-=+,设(){}max ,8n n n ϕ=+,则()min n k ϕ≥,而(){},4max ,88,4n n n n n n n ϕ⎧<-⎪=+=⎨+≥-⎪⎩,易得()()min 44n k ϕϕ=-=≥,故4k ≤.即实数k 的取值范围为(],4∞-.22.已知函数()()01ax g x a x =≠+在区间1,15⎡⎤⎢⎥⎣⎦上的最大值为1.(1)求实数a 的值;(2)若函数()()()()()210x b f x b b g x +=-+>,是否存在正实数b ,对区间1,15⎡⎤⎢⎥⎣⎦上任意三个实数r 、s 、t ,都存在以()()f g r 、()()f g s 、()()f g t 为边长的三角形?若存在,求实数b 的取值范围;若不存在,请说明理由.【答案】(1)2a =(2)存在,15153b <<【解析】【分析】(1)由题意()1a g x a x =-+,1,15x ⎡⎤∈⎢⎥⎣⎦,然后分a<0,0a >两种情况讨论函数()g x 的单调性,即可得出结果;(2)由题意()()0bf x x b x=+>,可证得()f x 在(为减函数,在)+∞为增函数,设()u g x =,1,13u ⎡⎤∈⎢⎥⎣⎦,则()()()()0b f g x f u u b u ==+>,从而把问题转化为:1,13u ⎡⎤∈⎢⎥⎣⎦,()()min max2f u f u >时,求实数b 的取值范围.结合()bf u u u=+的单调性,分109b <≤,1193b <≤,113b <<,1b ≥四种情况讨论即可求得答案.【小问1详解】由题意()11ax a g x a x x ==-++,1,15x ⎡⎤∈⎢⎥⎣⎦①当a<0时,函数()g x 在区间1,15⎡⎤⎢⎥⎣⎦上递减,所以()max 151566a ag x g a ⎛⎫==-== ⎪⎝⎭,得6a =(舍去).②当0a >时,函数()g x 在区间1,15⎡⎤⎢⎥⎣⎦上递增,所以()()max 1122a ag x g a ==-==,得2a =.综上所述,2a =.【小问2详解】由题意()22211x g x x x ==-++,又115x ≤≤,由(1)知函数()g x 在区间1,15⎡⎤⎢⎥⎣⎦上递增,∴()()115g g x g ⎛⎫≤≤ ⎪⎝⎭,即()113g x ≤≤,所以函数()g x 在区间1,15⎡⎤⎢⎥⎣⎦上的值域为1,13⎡⎤⎢⎥⎣⎦.又因为()()()()()()()()()2211111x b x x b x b x b f x b b b g x x x++++++=-+=-+=-+,∴()()20x b bf x x b x x+==+>,令120x x <<,则()()()12121212121b b b f x f x x x x x x x x x ⎛⎫⎛⎫⎛⎫-=+-+=-- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,当1x ,(2x ∈时,()121210b x x x x ⎛⎫--> ⎪⎝⎭,所以()()12f x f x >,()f x 为减函数;当1x ,)2x ∈+∞时,()121210b x x x x ⎛⎫--< ⎪⎝⎭,所以()()12f x f x <,()f x 为增函数;∴()f x 在(为减函数,在)+∞为增函数,设()u g x =,由(1)知1,13u ⎡⎤∈⎢⎥⎣⎦,∴()()()()0bf g x f u u b u==+>;所以,在区间1,15⎡⎤⎢⎥⎣⎦上任意三个实数r 、s 、t ,都存在()()f g r 、()()f g s 、()()f g t 为边长的三角形,等价于1,13u ⎡⎤∈⎢⎥⎣⎦,()()min max 2f u f u >.①当109b <≤时,()b f u u u =+在1,13⎡⎤⎢⎥⎣⎦上单调递增,∴()min 133f u b =+,()max 1f u b =+,由()()min max 2f u f u >,得115b >,从而11159b <≤.②当1193b <≤时,()b f u u u =+在13⎡⎢⎣上单调递减,在⎤⎦上单调递增,∴()min f u =,()max 1f u b =+,由()()min max 2f u f u >得77b -<<+1193b <≤.③当113b <<时,()b f u u u =+在13⎡⎢⎣上单调递减,在⎤⎦上单调递增,∴()min f u ==,()max 133f u b =+,由()()min max 2f u f u >得74374399b -+<<,从而113b <<.④当1b ≥时,()b f u u u =+在1,13⎡⎤⎢⎥⎣⎦上单调递减,∴()min 1f u b =+,()max 133f u b =+,由()()min max 2f u f u >得53b <,从而513b ≤<.综上,15153b <<.。
福建省厦门第一中学2021-2022学年高一上学期入学考试数学试题

福建省厦门第一中学2021-2022学年高一上学期入学考试数学试题学校:___________姓名:___________班级:___________考号:___________A.B.C.D.x44415.如图所示,正方形ABCD 的面积为12,ABE V 是等边三角形,点E 在正方形ABCD 内,在对角线AC 上有一点P ,使PD PE +的和最小,则这个最小值为.三、双空题16.如图,在平面直角坐标系xOy 中,把由两条射线AE ,BF 和以AB 为直径的半圆所组成的图形叫做图形C (注:不含AB 线段).已知(1,0),(1,0)A B -,AE ∥BF ,且半圆与y 轴的交点D 在射线AE 的反向延长线上.①当一次函数y=x+b 的图象与图形C 恰好只有一个公共点时,b 的取值范围为; ②已知平行四边形AMPQ (四个顶点A ,M ,P ,Q 按顺时针方向排列)的各顶点都在图形C 上,且不都在两条射线上,则点M 的横坐标x 的取值范围为.四、解答题方案二:圆心O 1、O 2分别在CD 、AB 上,半径分别是O 1C 、O 2A ,锯两个外切的半圆拼成一个圆;方案三: 沿对角线AC 将矩形锯成两个三角形,适当平移三角形并锯一个最大的圆; 方案四:锯一块小矩形BCEF 拼到矩形AFED 下面,利用拼成的木板锯一个尽可能大的圆.(1)写出方案一中圆的半径;(2)通过计算说明方案二和方案三中,哪个圆的半径较大?(3)在方案四中,设CE =x (0<x <1),圆的半径为y .①求y 关于x 的函数解析式;②当x 取何值时圆的半径最大,最大半径为多少?并说明四种方案中哪一个圆形桌面的半径最大.21.已知:直角梯形OABC 中,BC ∥OA ,∠AOC =90°,以AB 为直径的圆M 交OC 于D ,E ,连结AD ,BD ,BE .(1)在不添加其他字母和线的前提下..............,直接..写出图1中的两对相似三角形. (2)直角梯形OABC 中,以O 为坐标原点,A 在x 轴正半轴上建立直角坐标系(如图2), 若抛物线223(0)y ax ax a a =--<经过点A .B .D ,且B 为抛物线的顶点.①求抛物线的解析式.②在x 轴下方的抛物线上是否存在这样的点P :过点P 作PN ⊥x 轴于N ,使得△P AN 与△OAD 相似?若存在,求出点P 的坐标;若不存在,说明理由.22.如图,在矩形ABCD 中,46AB AD E ==,,是AD 边上的一个动点,将四边形BCDE 沿直线BE 折叠,得到四边形BC D E '',连接AC AD '',.。
福建省厦门市2023-2024学年高一上学期10月第一次适应性练习 数学含解析

厦门2023-2024学年高一上学期第一次适应性练习数学试卷(答案在最后)本试卷共4页,满分150分注意事项:1.答题前,考生务必在试题卷、答题卡规定的地方填写自己的班级、座号、姓名.考生要认真核对答题卡上粘贴的条形码的“考号、姓名”与考生本人考号、姓名是否一致.2.回答选择题时,选出答案后用铅笔将答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后再选涂其它答案标号.回答非选择题时,将答案写在答题卡上,写在本卷上无效.3.考试结束,考生只须将答题卡交回.一、单项选择题:本大题8小题,每小题5分,共40分.每小题只有一个正确答案.1.已知集合{|11}A x x =-≤≤,{1,0,2}B =-,则A B = ()A.{1,0}-B.{1,0,1,2}-C.{1,1}- D.{0}2.下列函数中,在区间()0,∞+上是减函数的是()A.1y x=-B.2y x= C.2y x = D.1y x =-3.设,A B 为两个非空集合,“x A ∀∈,都有x B ∈”是“A 是B 的真子集”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件4.下列命题为真命题的是()A.若a b >,则22ac bc >B.若0a b <<,则22a ab b <<C .若0c a b >>>,则a bc a c b >-- D.若0a b c >>>,则a a cb b c+<+5.若函数()1f x -的定义域是[]2,3-,则函数)2f -的定义域是()A.[]1,5 B.[]0,4 C.[]1,16 D.[]0,166.已知实数a b <,关于x 的不等式()210x a b x ab -+++<的解集为()12,x x ,则实数a 、b 、1x 、2x 从小到大的排列是()A.12a x x b <<<B.12x a b x <<<C.12a xb x <<< D.12x a x b<<<7.权方和不等式作为基本不等式的一个变化,在求二元变量最值时有很广泛的应用,其表述如下:设a ,b ,x ,y >0,则()222a b a bx y x y++≥+,当且仅当a b x y =时等号成立.根据权方和不等式,函数291()(0)122f x x x x =+<<-的最小值为()A.16B.25C.36D.498.若函数()f x 的定义域为R ,且(3)5f =.若对任意不相等的实数,x y ,恒有()()2f y f x x y->--,则不等式(21)43f x x -<-的解集为()A .(,1)-∞- B.(1,)-+∞ C.(,2)-∞ D.(2,)+∞二、多项选择题:本大题4小题,每小题5分,全选对得5分,选对但不全得2分,选错或不答得0分.9.已知命题p :R x ∀∈,240x ax ++>,则命题p 成立的一个充分不必要条件可以是下列选项中的()A.[]1,1a ∈-B.()4,4a ∈-C.[]4,4a ∈- D.{}0a ∈10.图中阴影部分用集合符号可以表示为()A.()A B C ⋂⋃B.()A B CC.()U A B C ⋂⋂ðD.()()A B A C ⋂⋃⋂11.甲、乙、丙三名学生同时参加了一次百米赛跑,所用时间(单位:秒)分别为1T ,2T ,3T .甲有一半的时间以速度(单位:米/秒)1V 奔跑,另一半的时间以速度2V奔跑;乙全程以速度奔跑;丙有一半的路程以速度1V 奔跑,另一半的路程以速度2V 奔跑.其中10V >,20V >.则下列结论中一定成立的是()A.123T T T ≤≤ B.123T T T ≥≥ C.2132TT T = D.132111T T T +=12.已知二次函数2y ax bx c =++(0,,,a a b c ≠为常数)的对称轴为1x =,其图像如图所示,则下列选项正确的有()A.0abc abc +=B.当1a x a ≤≤-时,函数的最大值为2c a -C.关于x 的不等式()()2422222ax bx a x b x +>-+-的解为x >或x <D.若关于x 的函数21t x bx =++与关于t 的函数21y t bt =++有相同的最小值,则1b -≥三、填空题:本大题共4小题,每小题5分,共20分.13.命题“[)0,x ∃∈+∞,210x kx -+>”的否定是______.14.设函数()()3,104,10x x f x f x x -≥⎧=⎨+<⎩,则()9f =______.15.已知函数()2,225,2x ax x f x ax x ⎧-+≤=⎨->⎩,若存在1x ,2x R ∈,且12x x ≠,使得()()12f x f x =,则实数a 的取值范围为______.16.已知a ,b 均为正数,且4ab a b =+,则228216a b a b-+-的最小值为__________.四、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤,把解答过程填写在答题卡的相应位置.17.已知集合301x A xx ⎧⎫-=≤⎨⎬+⎩⎭,集合{}22,R B x m x m m =<<∈.(1)当1m =-时,求A B ⋂,U A B U ð;(2)若A B A ⋃=,求实数m 的取值范围.18.已知函数()f x满足:)13f x +=+(1)求()f x 的解析式;(2)判断函数()()2f x xg x x+=在区间[)2,+∞上的单调性,并证明.19.已知函数()()2212f x ax a x =-++.(1)若函数y =的定义域为R ,求实数a 的取值范围;(2)解关于x 的不等式()0f x >.20.已知函数()2f x x =-,()224g x x mx =-+(R m ∈).(1)若对任意x ∈R ,不等式()()g x f x >恒成立,求m 的取值范围;(2)若对任意[]11,2x ∈,存在[]24,5x ∈,使得()()12g x f x =,求m 的取值范围;21.近年来,中美贸易摩擦不断.特别是美国对我国华为的限制.尽管美国对华为极力封锁,百般刁难,并不断加大对各国的施压,拉拢他们抵制华为5G ,然而这并没有让华为却步.华为在2018年不仅净利润创下记录,海外增长同样强劲.今年,我国华为某一企业为了进一步增加市场竞争力,计划在2020年利用新技术生产某款新手机.通过市场分析,生产此款手机全年需投入固定成本250万,每生产x (千部)手机,需另投入成本()R x 万元,且210100,040()100007019450,40x x x R x x x x ⎧+<<⎪=⎨+-≥⎪⎩,由市场调研知,每部手机售价0.7万元,且全年生产的手机当年能全部销售完.(1)求出2020年的利润()W x (万元)关于年产量x (千部)的函数关系式,(利润=销售额—成本);(2)2020年产量为多少(千部)时,企业所获利润最大?最大利润是多少?22.已知函数()(](),,123,1,22x x x f x x x ∞⎧∈-⎪=⎨+∈⎪-⎩.(1)解不等式()20ff x +<;(2)若1x ,()2,2x ∈-∞满足()()12f x f x =,且12x x ≠,求证:122x x +<.厦门2023-2024学年高一上学期第一次适应性练习数学试卷本试卷共4页,满分150分注意事项:1.答题前,考生务必在试题卷、答题卡规定的地方填写自己的班级、座号、姓名.考生要认真核对答题卡上粘贴的条形码的“考号、姓名”与考生本人考号、姓名是否一致.2.回答选择题时,选出答案后用铅笔将答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后再选涂其它答案标号.回答非选择题时,将答案写在答题卡上,写在本卷上无效.3.考试结束,考生只须将答题卡交回.一、单项选择题:本大题8小题,每小题5分,共40分.每小题只有一个正确答案.1.已知集合{|11}A x x =-≤≤,{1,0,2}B =-,则A B = ()A.{1,0}-B.{1,0,1,2}-C.{1,1}-D.{0}【答案】A 【解析】【分析】由交集的概念求解,【详解】集合{|11}A x x =-≤≤,{1,0,2}B =-,则A B = {1,0}-,故选:A2.下列函数中,在区间()0,∞+上是减函数的是()A.1y x=-B.2y x= C.2y x = D.1y x=-【答案】D 【解析】【分析】逐个判断函数的单调性,即可得到结果.【详解】对于A ,函数在区间()0,∞+上是增函数,故A 不正确;对于B ,函数在区间()0,∞+上是增函数,故B 不正确;对于C ,函数在()0,∞+上是增函数,故C 不正确;对于D ,函数在区间()0,∞+上是减函数,故D 正确;故选:D .【点睛】本题考查函数单调性的判断,考查学生分析解决问题的能力,属于基础题.3.设,A B 为两个非空集合,“x A ∀∈,都有x B ∈”是“A 是B 的真子集”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件【答案】B 【解析】【分析】根据集合之间的关系,判断“x A ∀∈,都有x B ∈”和“A 是B 的真子集”的逻辑推理关系,即得答案.【详解】由题意x A ∀∈,都有x B ∈可得A 是B 的子集,推不出A 是B 的真子集;反之,A 是B 的真子集,则必有x A ∀∈,都有x B ∈,故“x A ∀∈,都有x B ∈”是“A 是B 的真子集”的必要不充分条件,故选:B4.下列命题为真命题的是()A.若a b >,则22ac bc >B.若0a b <<,则22a ab b <<C.若0c a b >>>,则a bc a c b >-- D.若0a b c >>>,则a a cb b c+<+【答案】C 【解析】【分析】通过举反例即可判断A ,B ;通过作差法即可判断C ,D .【详解】对于A ,当0c =时,22ac bc =,故A 错误;对于B ,当2,1a b =-=-时,224,2,1a ab b ===,则22a ab b >>,故B 错误;对于C ,()()()()()()()a b a c b b c a c a b c a c b c a c b c a c b -----==------,因为0c a b >>>,所以0,0,0a b c a c b ->->->,所以()0()()c a b c a c b ->--,即a bc a c b>--,故C 正确;对于D ,()()()()()a a c abc b a c c a b b b c b b c b b c ++-+--==+++,因为0a b c >>>,所以()0()c a b b b c ->+,即a a cb b c+>+,故D 错误,故选:C .5.若函数()1f x -的定义域是[]2,3-,则函数)2f -的定义域是()A.[]1,5 B.[]0,4 C.[]1,16 D.[]0,16【答案】D 【解析】【分析】确定[]13,2x -∈-,得到不等式3220x ⎧-≤≤⎪⎨≥⎪⎩,解得答案.【详解】函数()1f x -的定义域是[]2,3-,则[]13,2x -∈-,故3220x ⎧-≤-≤⎪⎨≥⎪⎩,解得016x ≤≤.故选:D6.已知实数a b <,关于x 的不等式()210x a b x ab -+++<的解集为()12,x x ,则实数a 、b 、1x 、2x 从小到大的排列是()A.12a x x b <<<B.12x a b x <<<C.12a x b x <<<D.12x a x b<<<【答案】A 【解析】【分析】由题可知12x x a b +=+,再利用中间量m ,根据12x x +与12x x 之间的关系求出的取值范围,即可判断a 、b 、1x 、2x 之间的关系.【详解】由题可得:12x x a b +=+,121x x ab =+.由a b <,12x x <,设1x a m =+,则2x b m =-.所以212()()()1a m b m ab m b a m ab x x =+-=+--=+,所以2()1m b a m --=,21m m b a+=-.又a b <,所以0b a ->,所以0m >.故1x a >,2x b <.又12x x <,故12a x x b <<<.故选:A.7.权方和不等式作为基本不等式的一个变化,在求二元变量最值时有很广泛的应用,其表述如下:设a ,b ,x ,y >0,则()222a b a b x y x y ++≥+,当且仅当a b x y =时等号成立.根据权方和不等式,函数291()(0)122f x x x x =+<<-的最小值为()A.16B.25C.36D.49【答案】B 【解析】【分析】将给定函数式表示成已知不等式的左边形式,再利用该不等式求解作答.【详解】因a ,b ,x ,y >0,则()222a b a b x y x y++≥+,当且仅当a b x y =时等号成立,又102x <<,即120x ->,于是得22223(23)()252122(12)f x x x x x +=+≥=-+-,当且仅当23122x x =-,即15x =时取“=”,所以函数291()(0)122f x x x x =+<<-的最小值为25.故选:B8.若函数()f x 的定义域为R ,且(3)5f =.若对任意不相等的实数,x y ,恒有()()2f y f x x y->--,则不等式(21)43f x x -<-的解集为()A.(,1)-∞-B.(1,)-+∞ C.(,2)-∞ D.(2,)+∞【答案】D 【解析】【分析】构造函数()()2g x f x x =-,根据题意得()g x 在R 上单调递减,再题意转化为解()()213g x g -<即可.【详解】解:因为对任意不相等的实数,x y ,恒有()()2f y f x x y ->--,所以,对任意不相等的实数,x y ,恒有()()20f y f x x y-+>-,即()()220f y f x x yx y-+->-,令()()2g x f x x =-,所以,对任意不相等的实数,x y ,恒有()()0g y g x x y->-,即()()0g y g x y x-<-,不妨设x y <,则0y x ->,所以,()()0g y g x -<,即()()g x g y >,所以,()g x 在R 上单调递减.所以()()()()2143212211323f x x f x x f -<-⇔---<-=-⨯()()2132132g x g x x ⇔-<⇔->⇔>,所以不等式(21)43f x x -<-的解集为(2,)+∞.故选:D.二、多项选择题:本大题4小题,每小题5分,全选对得5分,选对但不全得2分,选错或不答得0分.9.已知命题p :R x ∀∈,240x ax ++>,则命题p 成立的一个充分不必要条件可以是下列选项中的()A.[]1,1a ∈-B.()4,4a ∈-C.[]4,4a ∈-D.{}0a ∈【答案】AD 【解析】【分析】根据一元二次方程根的判别式,结合充分不必要条件与集合的关系进行求解即可.【详解】若命题p :R x ∀∈,240x ax ++>成立,则2160a ∆=-<,解得44a -<<,故命题p 成立的充分不必要条件是a 属于()4,4-的真子集,因此选项AD 符合要求,故AD 正确.故选:AD.10.图中阴影部分用集合符号可以表示为()A.()A B C ⋂⋃B.()A B CC.()U A B C ⋂⋂ðD.()()A B A C ⋂⋃⋂【答案】AD 【解析】【分析】由图可知,阴影部分是集合B 与集合C 的并集,再由集合A 求交集,或是集A 与B 的交集并上集合A 与C 的交集,从而可得答案【详解】解:由图可知,阴影部分是集合B 与集合C 的并集,再由集合A 求交集,或是集A 与B 的交集并上集合A 与C 的交集,所以阴影部分用集合符号可以表示为()A B C ⋂⋃或()()A B A C ⋂⋃⋂,故选:AD11.甲、乙、丙三名学生同时参加了一次百米赛跑,所用时间(单位:秒)分别为1T ,2T ,3T .甲有一半的时间以速度(单位:米/秒)1V 奔跑,另一半的时间以速度2V 奔跑;乙全程以速度12VV 奔跑;丙有一半的路程以速度1V 奔跑,另一半的路程以速度2V 奔跑.其中10V >,20V >.则下列结论中一定成立的是()A.123T T T ≤≤B.123T T T ≥≥ C.2132TT T = D.132111T T T +=【答案】AC 【解析】【分析】分别计算得到1121002T V V =+,2T =312121002T VV V V =+,根据均值不等式确定A 正确,B 错误,代入计算验证得到C 正确D 错误,得到答案.【详解】甲同学:11121110022TV TV +=,则1121002T V V =+,乙同学:2T =丙同学:312121250501002T VV V V V V =+=+,对于选项A 和B :10V >,20V >,故121212202V V VV V V +≥≥>+,当且仅当12V V =时,等号全部成立,故123T T T ≤≤,故A 正确,B 错误;对于选项C :221321212121210010010022T T T V V VV VV V V ⋅=⋅==++,故C 正确;对于D:121212132112100100VV V V V V T T +++=+≠D 错误.故选:AC.12.已知二次函数2y ax bx c =++(0,,,a a b c ≠为常数)的对称轴为1x =,其图像如图所示,则下列选项正确的有()A.0abc abc +=B.当1a x a ≤≤-时,函数的最大值为2c a -C.关于x 的不等式()()2422222ax bx a x b x +>-+-的解为x >或x <D.若关于x 的函数21t x bx =++与关于t 的函数21y t bt =++有相同的最小值,则1b -≥【答案】ACD 【解析】【分析】A 选项,由开口方向,与y 轴交点,及对称轴,求出,,a b c 的正负,得到A 正确;B 选项,当1a x a ≤≤-时,数形结合得到函数随着x 的增大而减小,从而求出最大值;C 选项,结合2b a =-,化简不等式,求出解集;D 选项,配方得到两函数的最小值,从而得到2124b b -≥-,求出1b -≥【详解】A 选项,二次函数图象开口向上,故0a >,对称轴为12bx a=-=,故20b a =-<,图象与y 轴交点在y 轴正半轴,故0c >,所以<0abc ,故0abc abc abc abc +=-+=,A 正确;B 选项,因为2b a =-,故22y ax ax c =-+,因为0a >,所以11a -<,当11a x a ≤≤-<时,22y ax ax c =-+随着x 的增大而减小,所以x a =时,y 取得最大值,最大值为322y a c a -=+,B 错误;C 选项,因为2b a =-,所以42422ax bx ax ax +=-,()()()2224224222442268a x b x ax ax a a x ax ax a -+-=-+--=-+,故不等式()()2422222ax bx a x b x +>-+-变形为2048ax a >-,因为0a >,22x >,解得:x >x <,故C 正确;D 选项,2224121b t x bx x b ⎛⎫=++=+ +-⎪⎝⎭,当2b x =-时,t 取得最小值,最小值为214b -,2224121b y t bt t b ⎛⎫=++=+ +-⎪⎝⎭,当2b t =-时,y 取得最小值,最小值为214b -,所以2124b b -≥-,即2240b b --≥,所以()215b -≥,即1b -≥D 正确.故选:ACD三、填空题:本大题共4小题,每小题5分,共20分.13.命题“[)0,x ∃∈+∞,210x kx -+>”的否定是______.【答案】[)0,x ∞∀∈+,210x kx -+≤【解析】【分析】利用含有一个量词的命题的否定方法为“改变量词,否定结果”进行作答.【详解】“[)0,x ∃∈+∞,210x kx -+>”为存在量词命题,因此其否定为“[)0,x ∞∀∈+,210x kx -+≤”.故答案为:[)0,x ∞∀∈+,210x kx -+≤14.设函数()()3,104,10x x f x f x x -≥⎧=⎨+<⎩,则()9f =______.【答案】10【解析】【分析】根据分段函数解析式计算可得.【详解】因为()()3,104,10x x f x f x x -≥⎧=⎨+<⎩,所以()()99413310f f =+=-=.故答案为:1015.已知函数()2,225,2x ax x f x ax x ⎧-+≤=⎨->⎩,若存在1x ,2x R ∈,且12x x ≠,使得()()12f x f x =,则实数a 的取值范围为______.【答案】(),4-∞【解析】【分析】先对0,0,0a a a >=<讨论,作示意图后,容易得到0a ≤符合题意,再对0a >分析,可得到答案.【详解】当a<0时,函数()y f x =的示意图如图所示可知在x ∈[,0]a ,必存在1x ,2x R ∈,使()()12f x f x =;当0a =时,则2,2()5,2x x f x x ⎧-≤=⎨->⎩,可知5y =-时存在,符合题意;当0a >时,则22a<,即04a <<时,在2a x =附近,必存在1x ,2x R ∈,使()()12f x f x =;当22a≥时,(2)2445f a a =-<-,故示意图如图所示故不存在1x ,2x R ∈,且12x x ≠,使得()()12f x f x =,综上可得4a <.故答案为:(),4-∞【点睛】本题考查了分段函数存在性问题,分类讨论、数形结合思想的应用,合理分类是解决问题的关键.16.已知a ,b 均为正数,且4ab a b =+,则228216a b a b-+-的最小值为__________.【答案】6【解析】【分析】由已知有411a b +=,则22228221616a ab b a b -+-=+-,利用基本不等式求其最小值,注意取值条件.【详解】由,a b 均为正数,且4ab a b =+,则411a b+=,又2222228282()2161616a a ab b b a b a b -+-=+-+=+-,414()()2224444a a b a b b a b a b +=++=++≥+=,当且仅当44b a a b=,即8,2a b ==取等号,所以2222()()16164a a b b +≥+≥,当且仅当8,2a b ==取等号,则22816a b +≥,所以222616a b +-≥,当且仅当8,2a b ==取等号,目标式最小值为6.故答案为:6四、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤,把解答过程填写在答题卡的相应位置.17.已知集合301x A xx ⎧⎫-=≤⎨⎬+⎩⎭,集合{}22,R B x m x m m =<<∈.(1)当1m =-时,求A B ⋂,U A B U ð;(2)若A B A ⋃=,求实数m 的取值范围.【答案】(1){}11A B x x ⋂=-<<,{2U A B x x ⋃=≤-ð或}1x >-(2)1,22⎡⎤-⎢⎥⎣⎦【解析】【分析】(1)解分式不等式得到{}13A x x =-<≤,进而根据交集,并集和补集概念进行计算;(2)根据并集结果得到B A ⊆,分B =∅与B ≠∅两种情况,得到不等式,求出实数m 的取值范围.【小问1详解】由301x x -≤+等价于()()31010x x x ⎧-+≤⎨+≠⎩,解得:13x -<≤,所以{}13A x x =-<≤,当1m =-时,{}21B x x =-<<,∴{}11A B x x ⋂=-<<;又∵{2U B x x =≤-ð或}1x ≥,∴{2U A B x x ⋃=≤-ð或}1x >-;【小问2详解】因为A B A ⋃=,所以B A ⊆,由(1)可知{}13A x x =-<≤,当B =∅时,22m m ≥,解得:02m ≤≤,当B ≠∅时,要满足题意需222213m m m m ⎧<⎪≥-⎨⎪≤⎩,解得:102m -≤<,综上:实数m 取值范围为1,22⎡⎤-⎢⎥⎣⎦18.已知函数()f x满足:)13f x +=+(1)求()f x 的解析式;(2)判断函数()()2f x xg x x+=在区间[)2,+∞上的单调性,并证明.【答案】(1)2()(1)3,1f x x x =-+≥(2)单调递增,证明见详解.【解析】【分析】(1)换元法求解析式即可,注意中间变量的范围;(2)利用(1)中结果求得()g x ,按照定义法证明函数单调性的基本步骤进行即可:取值,作差,化简变形,定号,下结论.【小问1详解】1t +=,则2(1)x t =-,1t ≥,代入)13fx +=+,得2()(1)3,1f t t t =-+≥,即2()(1)3,1f x x x =-+≥【小问2详解】由(1)可得:()()22(1)324f x xx x g x x xx x+-++===+,()g x 在区间[)2,+∞上单调递增,证明如下:12,[2,)x x ∀∈+∞,且12x x <,则12121212124444()()()()()g x g x x x x x x x x x -=+-+=-+-1212121212124()()(4)()x x x x x x x x x x x x ---=--=因为122x x ≤<,所以12120,4x x x x -<>,所以12()()0g x g x -<,即12()()<g x g x 所以()g x 在区间[)2,+∞上单调递增.19.已知函数()()2212f x ax a x =-++.(1)若函数y =的定义域为R ,求实数a 的取值范围;(2)解关于x 的不等式()0f x >.【答案】(1)22,22⎡⎢⎣⎦(2)答案见解析【解析】【分析】(1)将问题转化为x ∈R 时,()22130ax a x -++≥恒成立,分类讨论a 的值,即可得出范围;(2)分为3种情况讨论,即0a >,0a =,0a <,分别求解不等式即可.【小问1详解】∵函数1y =+的定义域为R ,∴x ∈R 时,()22130ax a x -++≥恒成立.当0a =时,不等式化为:30x -+≥,解得3x ≤,不符合题意,舍去;当0a ≠时,则x ∈R 时,()22130ax a x -++≥恒成立,所以0Δ0a >⎧⎨≤⎩,即20(21)120a a a >⎧⎨+-≤⎩,解得2222a -≤≤,综上所述,实数a 的取值范围是22,22⎡+⎢⎣⎦.【小问2详解】1)当0a >时,关于x 的不等式()22120ax a x -++>化为:()120x x a ⎛⎫--> ⎪⎝⎭,对a 进一步分类讨论:①12a >时,12a<,则不等式的解集为()1,2,a ⎛⎫-∞⋃+∞ ⎪⎝⎭;②12a =时,12a =,则不等式的解集为()(),22,-∞+∞ ;③102a <<时,12a>,则不等式的解集为()1,2,a ⎛⎫-∞⋃+∞ ⎪⎝⎭.2)当0a =时,关于x 的不等式()22120ax a x -++>化为20x ->,则不等式的解集为(),2-∞3)当0a <时,关于x 的不等式()22120ax a x -++>化为:()120x x a ⎛⎫--< ⎪⎝⎭,则不等式的解集为1,2a ⎛⎫ ⎪⎝⎭.综上所述,12a >,不等式的解集为()1,2,a ⎛⎫-∞⋃+∞ ⎪⎝⎭;12a =,不等式的解集为()(),22,-∞+∞ ;102a <<,不等式的解集为()1,2,a ⎛⎫-∞⋃+∞ ⎪⎝⎭;0a =,不等式的解集为(),2-∞,0a <,不等式的解集为1,2a ⎛⎫⎪⎝⎭.20.已知函数()2f x x =-,()224g x x mx =-+(R m ∈).(1)若对任意x ∈R ,不等式()()g x f x >恒成立,求m 的取值范围;(2)若对任意[]11,2x ∈,存在[]24,5x ∈,使得()()12g x f x =,求m 的取值范围;【答案】(1)1122⎛⎫- ⎪⎝⎭(2)54⎡⎢⎣【解析】【分析】(1)变换得到()22160x m x -++>恒成立,计算()221240m ∆=+-<,解得答案.(2)当[]11,2x ∈时,()1g x D ∈,则[]2,3D ⊆,考虑对称轴1x m =≤或2m ≥和对称轴()1,2x m =∈,分别计算函数的最值,计算得到答案.【小问1详解】()()g x f x >恒成立,即()22160x m x -++>恒成立,故()221240m ∆=+-<,解得1122m -<<,m的取值范围为1122⎛⎫- ⎪⎝⎭;【小问2详解】当[]11,2x ∈时,()1g x D ∈,当[]24,5x ∈时,()[]2222,3f x x =-∈,故[]2,3D ⊆,①若()y g x =的对称轴1x m =≤或2m ≥,此时()g x 在区间[]1,2单调,则()g x 在1x =,2x =处取得最值,所以()()2152322843g m g m ⎧≤=-≤⎪⎨≤=-≤⎪⎩,解得5342m ≤≤,解不满足1m £或2m ≥,舍去;②若()y g x =对称轴()1,2x m =∈,故()()[]min 2,3g x g m =∈,即()2243g m m ≤=-+≤,解得1m ≤≤1m ≤≤-,此时,最大值依然在1x =,2x =处取到,故54m ≤≤综上所述:54m ⎡∈⎢⎣.21.近年来,中美贸易摩擦不断.特别是美国对我国华为的限制.尽管美国对华为极力封锁,百般刁难,并不断加大对各国的施压,拉拢他们抵制华为5G ,然而这并没有让华为却步.华为在2018年不仅净利润创下记录,海外增长同样强劲.今年,我国华为某一企业为了进一步增加市场竞争力,计划在2020年利用新技术生产某款新手机.通过市场分析,生产此款手机全年需投入固定成本250万,每生产x (千部)手机,需另投入成本()R x 万元,且210100,040()100007019450,40x x x R x x x x ⎧+<<⎪=⎨+-≥⎪⎩,由市场调研知,每部手机售价0.7万元,且全年生产的手机当年能全部销售完.(1)求出2020年的利润()W x (万元)关于年产量x (千部)的函数关系式,(利润=销售额—成本);(2)2020年产量为多少(千部)时,企业所获利润最大?最大利润是多少?【答案】(1)210600250,040()10000()9200,40x x x W x x x x ⎧-+-<<⎪=⎨-++≥⎪⎩;(2)2020年产量为100千部时,企业所获利润最大,最大利润是9000万元.【解析】【分析】(1)根据给定的函数模型,直接计算作答.(2)利用(1)中函数,借助二次函数最值及均值不等式求出最大值,再比较大小作答.【小问1详解】依题意,销售收入700x 万元,固定成本250万元,另投入成本210100,040()100007019450,40x x x R x x x x ⎧+<<⎪=⎨+-≥⎪⎩万元,因此210600250,040()700()25010000()9200,40x x x W x x R x x x x ⎧-+-<<⎪=--=⎨-++≥⎪⎩,所以2020年的利润()W x (万元)关于年产量x (千部)的函数关系式是210600250,040()10000(9200,40x x x W x x x x ⎧-+-<<⎪=⎨-++≥⎪⎩.【小问2详解】由(1)知,当040x <<时,2()10(30)87508750W x x =--+≤,当且仅当30x =时取等号,当40x ≥时,10000()()920092009000W x x x =-++≤-=,当且仅当10000x x =,即100x =时取等号,而87509000<,因此当100x =时,max ()9000W x =,所以2020年产量为100千部时,企业所获利润最大,最大利润是9000万元.22.已知函数()(](),,123,1,22x x x f x x x ∞⎧∈-⎪=⎨+∈⎪-⎩.(1)解不等式()20f f x +<;(2)若1x ,()2,2x ∈-∞满足()()12f x f x =,且12x x ≠,求证:122x x +<.【答案】(1)1,3⎡⎫--⎪⎢⎪⎣⎭(2)证明见解析【解析】【分析】(1)分段讨论x的取值范围,化简()20f f x +<,分别解一元二次不等式,即可得答案;(2)作出函数()(](),,123,1,22x x x f x x x ∞⎧∈-⎪=⎨+∈⎪-⎩大致图象,结合图像确定12,x x 的范围,讨论当10x ≤,122x x +<成立;1>0x 时,转化为证明()()112f x f x >-,则可构造函数()()()2F x f x f x =--,()0,1x ∈,利用其单调性证明结论.【小问1详解】由题意210x -≥,[]1,1x ∴∈-,①[]1,0x ∈-,不等式()20f f x +<即22120x x --<,,,33x ⎛⎫⎛⎫∴∈-∞-+∞ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,1,3x ⎡⎫∴∈--⎪⎢⎪⎣⎭②(]0,1x ∈,不等式()20f f x +<即22120x x -+<,x ∴∈∅;综上,1,3x ⎡⎫∈--⎪⎢⎪⎣⎭.【小问2详解】函数()(](),,123,1,22x x x f x x x ∞⎧∈-⎪=⎨+∈⎪-⎩大致图象如图,当(],1x ∈-∞时,函数单调递增,当()1,2x ∈时,函数单调递减,∴若1x ,()2,2x ∈-∞满足()()12f x f x =,则1212x x <<<,由图象知,①若10x ≤,则显然122x x +<;②若1>0x ,要证明122x x +<,则要证212x x <-,注意到2x ,121x ->,且()f x 在()1,2递减,则可证明()()212f x f x >-,∵()()12f x f x =,则可证明()()112f x f x >-,构造函数()()()2F x f x f x =--,()0,1x ∈,则()223F x x x ⎛⎫=-- ⎪⎝⎭,1201t t ∀<<<,()()()()2122221212121212222t t F t F t t t t t t t t t --=+--=-+,()()1212122t t t t t t ⎡⎤=-+-⎢⎥⎣⎦,∵122t t +<,121t t <,1222t t >,∴()121220t t t t +-<,∴()()120F t F t ->,∴()F x 在()0,1上单调递减,∵()()()1110F f f =-=,∴()0,1x ∈时,()()10F x F >=,即()()2f x f x >-,∴()()212f x f x >-,从而122x x +<得证.【点睛】难点点睛:解答本题的难点在于证明122x x +<;解答时利用函数()(](),,123,1,22x x x f x x x ∞⎧∈-⎪=⎨+∈⎪-⎩的图像确定12,x x 的范围,再结合范围分类讨论。
