股票期权二叉树定价 excel VBA程序

合集下载

第10章二叉树法期权定价及其Python应用

第10章二叉树法期权定价及其Python应用本章精粹蒙特卡罗模拟法便于处理报酬函数复杂、标的变量多等问题，但是在处理提前行权问题时却表现出明显的不足。

本章将要介绍的二叉树法可以弥补蒙特卡罗模拟法的这种不足。

二叉树的基本原理是：假设变量运动只有向上和向下两个方向，且假设在整个考察期内，标的变量每次向上或向下的概率和幅度不变。

将考察期分为若干阶段，根据标的变量的历史波动率模拟标的变量在整个考察期内所有可能的发展路径，并由后向前以倒推的形式走过所有结点，同时用贴现法得到在0时刻的价格。

如果存在提前行权的问题，必须在二叉树的每个结点处检查在这一点行权是否比下一个结点上更有利，然后重复上述过程。

10.1 二叉树法的单期欧式看涨期权定价假设：(1) 市场为无摩擦的完美市场，即市场投资没有交易成本。

这意味着不支付税负，没有买卖价差(Bid-Ask Spread)、没有经纪商佣金(Brokerage Commission)、信息对称等。

(2) 投资者是价格的接受者，投资者的交易行为不能显著地影响价格。

(3) 允许以无风险利率借入和贷出资金。

(4) 允许完全使用卖空所得款项。

(5) 未来股票的价格将是两种可能值中的一种。

为了建立好二叉树期权定价模型，我们先假定存在一个时期，在此期间股票价格能够从现行价格上升或下降。

下面用实例来说明二叉树期权定价模型的定价方法。

1. 单一时期内的买权定价假设股票今天(t =0)的价格是100美元，一年后(t =1)将分别以120美元或90美元出售，就是1年后股价上升20%或下降10%。

期权的执行价格为110美元。

年无风险利率为8%，投资者可以这个利率放款(购买这些利率8%的债券)或借款(卖空这些债券)。

如图10-1所示。

今天 1年后t =0 t =1u S 0=120 上升20% 1000=Sd S 0=90 下降10%u 0max(u ,0)max(120110,0)10C S X =-=-=?0=Cd 0max(d ,0)max(90110,0)0C S X =-=-=图10-1 买权价格图10-1表示股票买权的二叉树期权定价模型。

运用EXCEL2007制作美式期权二叉树定价模型

全国中文核心期刊·财会月刊□期权是指一种合约，该合约赋予持有人在某一特定日期或该日期之前的任何时间以固定价格购进或售出一种资产的权利。

按期权执行时间，期权可分为欧式期权和美式期权。

欧式期权只能在期权到期日执行，而美式期权可以在到期日或到期日之前任何时间执行。

期权最先在金融领域出现，但它更广泛地被用于投资评价。

期权定价可基于复制原理或风险中性原理，两者比较，根据风险中性原理计算较为简易。

这里，笔者试图根据风险中性原理基于EXCEL2007平台，建立美式期权估价模型。

一、EXCEL2007的相关函数及工具介绍1.单元格绝对引用与相对引用。

例：在A4单元格内输入“=sum （$A1:A $3）”，复制A4单元格，并粘贴至B5单元格，B5格的公式为“=sum （$A2:B $3）”，前面加“$”的为绝对引用，不随移动复制位置的改变而改变。

2.if （Logical_test ，value_if_true ，value_if_false ），判断Logical_test 条件是否为真，为真则执行value_if_true ，为假则执行value_if_false 。

例如：A1单元格输入“50”，A2格内输入“=if （A1>60，”及格”，”不及格”）”，结果A2格内值为“不及格”。

3.sumproduct （array1，array2，array3，….），返回相应的数组或区域乘积的和。

例如：在A1：A3区域分别输入“1，2，3”，在B1：B3区域内输入“2，3，4”，在B4内输入“=sumproduct （A1:A3，B1:B3）”，B4格内的计算实质为“=A1*B1+A2*B2+A3*B3”，结果值为“20”。

4.OR （logical1，logical2，...），在其参数组中，任一参数值为TRUE ，即返回TRUE ；只有当所有参数值均为FALSE 时才返回FALSE 。

例如：在某单元格输入“=OR （D4=“”，D4=“入库”）”，如果D4单元格为空值或“入库”字样，结果为TRUE ；若为其他字符或公式，结果为FALSE 。

ExcelVBA金融工程Section2-美式期权定价

ExcelVBA金融工程Section2-美式期权定价梦特卡罗期权价格计算美式期权指在合约期限内任何时点（直至及包括到期日）均可执行的一种期权，不同于只能在到期日才能执行的欧式期权。

例如，美式看跌期权可以在到期前行使而其内在价值是根據其期权金計算?(S)=max{K-S, 0}。

標的资产价格S t在時间t時，以美式看跌期权計算其公平价值在风险中性時如下F(S t, t)=ê(e?r(τs?t)?(Sτs)|S t(9.39)當隨机资产价格変动從S t開始到首次行使時间ζs。

它的發生可以是在期权到期時或是在期限内任何时点而當它的内在价值大過它的合理价值時。

在期限内任何时点t時，它的最优條款(S t) ≧F(S t, t) (9.40)美式看跌期权的价格应包括以下特性f(S t,t)=max{F(S t, t), ?(S t)} (9.41)公式(9.40)可以用來定義其价格S c(t)在時点t時其行使权的條件需符合S t≦S c(t)。

在此方法下，制定的條款便可輕易地實施只需简單地测試资产價格在特定的價格下便可。

特別注意其公平價值F(S t, t)可以被估計出當所有特定價格，或範圍，在時间t時都被计算出。

即是其特定價格S c(t)都可由倒退法找出開始由期权到期S c(T)=K。

要找出美式看跌期权的現貨價格，需要首先做出整個主要的範圍然后才評估其中性风险的期望値为f0=max{ê(e-rζs?(Sζs)|S0), ?(S0)} (9.42)再者，可以将一個非常大的N分为相等的時间间距Δt=T/N ,那庅便可产生整個期权的生命里當i由0走到N-1为止時每一個時间步骤t i=iΔt。

在時间t i時，試考慮S ti=x同時假設主要遠期時间範圍为{S c(t i+1),… , S c(t N)=K}。

美式看跌期权的公平價格可以用梦特卡罗模拟法中計算出F(S ti=x,t i)= ê(e-r(tζ-ti)?(S tζ )|S ti=x) (9.43)公式(9.43) 可产生资产價格迴路而餘下生命週期的期权则可将公式(9.44) 中的j由i走到N-1为止開始時由S ti=xS tj+1=S tjexp((r-12?σ2)Δt+σ√?tεj(9.44)假如在期权到期前任何时间里其产生價格是S tj+1≤S c(t j+1)的时候，同时当公式(9.43)里的τs=t j+1时該期权便应行使。

第10章二叉树法期权定价及其Python应用

本章将要介绍的二叉树法可以弥补蒙特卡罗模拟法的这种不足。

二叉树的基本原理是：假设变量运动只有向上和向下两个方向，且假设在整个考察期内，标的变量每次向上或向下的概率和幅度不变。

如果存在提前行权的问题，必须在二叉树的每个结点处检查在这一点行权是否比下一个结点上更有利，然后重复上述过程。

10.1 二叉树法的单期欧式看涨期权定价假设：(1) 市场为无摩擦的完美市场，即市场投资没有交易成本。

这意味着不支付税负，没有买卖价差(Bid-Ask Spread)、没有经纪商佣金(Brokerage Commission)、信息对称等。

(2) 投资者是价格的接受者，投资者的交易行为不能显著地影响价格。

(3) 允许以无风险利率借入和贷出资金。

(4) 允许完全使用卖空所得款项。

(5) 未来股票的价格将是两种可能值中的一种。

为了建立好二叉树期权定价模型，我们先假定存在一个时期，在此期间股票价格能够从现行价格上升或下降。

下面用实例来说明二叉树期权定价模型的定价方法。

1. 单一时期内的买权定价假设股票今天(t =0)的价格是100美元，一年后(t =1)将分别以120美元或90美元出售，就是1年后股价上升20%或下降10%。

期权的执行价格为110美元。

年无风险利率为8%，投资者可以这个利率放款(购买这些利率8%的债券)或借款(卖空这些债券)。

如图10-1所示。

使用excel和vba股票操作日志

使用excel和vba股票操作日志使用Excel和VBA进行股票操作日志在进行股票交易时，及时记录并分析交易日志是非常重要的。

利用Excel和VBA编程可以帮助我们更加高效地管理和分析股票操作日志。

本文将介绍如何利用Excel和VBA编写股票操作日志，并提供一些实用的技巧和建议。

一、创建股票操作日志表格我们需要在Excel中创建一个表格，用于记录股票交易的相关信息。

在表格中，我们可以包括以下列：日期、股票代码、股票名称、买入/卖出、交易价格、交易数量、交易金额等信息。

根据实际需要，可以添加其他列来记录更多的交易信息。

在表格中，每一行代表一次交易记录，我们可以根据需要随时添加新的交易记录。

同时，我们可以使用Excel的筛选和排序功能，方便地对交易记录进行筛选和排序。

二、添加VBA宏代码除了手动输入交易记录外，我们还可以利用VBA编写宏代码来自动记录交易信息。

下面是一个示例的VBA代码，用于在表格中添加新的交易记录：```vbaSub AddNewTrade()Dim ws As WorksheetDim lastRow As LongSet ws = ThisWorkbook.Worksheets("交易记录") '将“交易记录”替换为实际的工作表名称lastRow = ws.Cells(ws.Rows.Count, "A").End(xlUp).Row + 1ws.Cells(lastRow, "A").Value = Date '记录当前日期ws.Cells(lastRow, "B").Value = InputBox("请输入股票代码") '输入股票代码ws.Cells(lastRow, "C").Value = InputBox("请输入股票名称") '输入股票名称ws.Cells(lastRow, "D").Value = InputBox("请输入买入/卖出") '输入买入/卖出ws.Cells(lastRow, "E").Value = InputBox("请输入交易价格") '输入交易价格ws.Cells(lastRow, "F").Value = InputBox("请输入交易数量") '输入交易数量ws.Cells(lastRow, "G").FormulaR1C1 = "=RC[-2]*RC[-1]" '计算交易金额MsgBox "交易记录已添加成功！"End Sub```以上代码将在“交易记录”工作表中的下一行添加新的交易记录。

EXCEL VBA 金融工程 Section 2 - BDT二义树及期限结构模型

Black-Derman-Toy 模型Black-Derman-Toy 二义树及期限结构模型与股票期权相似，利率衍生产品都是倚靠其目标物-利率。

而利率期限结构是某个时点不同期限的利率所组成的一条曲线。

它是资产定价、金融产品设计、保值和风险管理、套利以及投机等的基准，也是中央银行控制短期利率变化以影响中长期利率变化的传递机制。

而单因素利率期限结构模型，瞬时短期利率r t 是起着决定性作用的内生变量。

根据市场期望假设，中长期利率等于未来相应时期内瞬时短期利率总和的期望。

而其衍生产品的价格便可根据此短期利率在风险中性下定价f 0=E (e −∫r t dt T 0f T |r 0) (1)在公式(1)，期权的未来收益f T 是会根据产生出来到期利率进行评估。

已近代的方法则会以Health, Jarrow, and Morton 的无套利定价方法进行。

在期权定价上，以上的用树式方法便足够将风险中性的短期利率同现实的利率曲线比较。

而Black-Derman-Toy 因此发展出一个简单的二义树模型校正现实零息债券的利率期限结构及波动率.BDT 模型发展出结合将风险中性的短期利率的二义树及特定时间Δt ，如图1(a) 。

图1：(a) BDT 二义树模型结合树交叉点。

(b) 使用风险中性作为期权定价的单一个BDT 分支树在时间t=i Δt ，由上到下会有t+1个交叉点及短期利率r ij 而j 则由0到i 为止。

而其则代表按年计一个周期利率以最短可以借到的期限Δt 由t 到t+Δt 。

BDT 树则跟从Jarrow and Rudd 到参数设定及概率为p=12。

普遍来说，向上及向下的因素会倚赖时间及其相关短期利率的值。

假设设定为一个non-stochastic 结构的短期利率的波动率，就可表示其关系为时间及每一步骤i 时整个列里的短期利率都可设置为两个因素r ij =αi (βi )j (2)公式(1)，BDT 树提供一个工具用来评估利率期权在风险中性的定价。

使用Excel进行股票投资分析入门教程

使用Excel进行股票投资分析入门教程一、介绍Excel在股票投资分析中的应用股票投资分析是投资者在进行股票交易前对股票市场的研究和分析的过程。

Excel作为一款强大的电子表格软件，可以提供丰富的功能，帮助投资者进行股票投资分析。

本文将详细介绍如何使用Excel进行股票投资分析，以便投资者能够从容应对投资决策。

二、Excel中的股票数据导入与整理在使用Excel进行股票投资分析之前，第一步是将股票数据导入到Excel中并进行整理。

投资者可以通过各种途径获取股票数据，如财经网站、券商软件等。

将获取的数据保存为Excel文件，然后打开Excel进行导入。

在Excel中，投资者可以使用数据导入向导将数据文件导入到工作表中。

导入完成后，可以使用Excel的筛选和排序功能对数据进行整理和分类，以便更好地进行后续的分析。

三、使用Excel进行基本面分析基本面分析是股票投资中的重要一环，它通过分析公司的财务和经营状况来判断公司的价值和发展潜力。

在Excel中，投资者可以利用各种公式和函数进行基本面分析。

1. 利用Excel进行财务分析Excel提供了丰富的财务函数，如SUM、AVERAGE、MAX、MIN等，能够帮助投资者计算财务指标。

例如，可以使用SUM函数计算公司的总资产，使用AVERAGE函数计算公司的平均每股收益。

2. 利用Excel绘制财务图表除了计算财务指标，Excel还可以通过绘制图表来更直观地展示财务情况。

投资者可以借助Excel的图表工具，绘制柱状图、折线图等各种财务图表，以便更好地了解公司的财务状况。

四、使用Excel进行技术分析技术分析是通过研究股票的历史价格和成交量等指标来预测其未来走势的方法。

在Excel中，投资者可以使用各种函数和工具进行技术分析。

1. 利用Excel计算技术指标例如，投资者可以使用Excel的移动平均函数，如AVERAGE、SMA，来计算股票的移动平均线。

移动平均线是技术分析中常用的指标，可以帮助投资者确定股票的趋势。

利用Excel中的宏VBA让股票自动显示当前价格

#NAME? #NAME?
万年青平安银行
#NAME? #NAME? #NAME? #NAME?
#NAME? #NAME?
#NAME? #NAME?
中信银行H股 #NAME? #NAME? #NAME?
#NAME?
开盘价 #NAME? #NAME? #NAME?
单日最高价 #NAME?
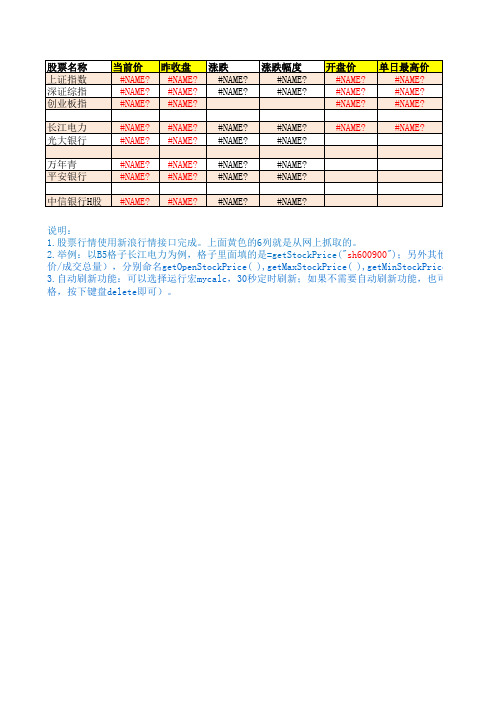
说明： 1.股票行情使用新浪行情接口完成。上面黄色的6列就是从网上抓取的。 2.举例：以B5格子长江电力为例，格子里面填的是=getStockPrice("sh600900")；另外其他4个功能函数价/成交总量），分别命名getOpenStockPrice( ),getMaxStockPrice( ),getMinStockPrice( ),getTra 3.自动刷新功能：可以选择运行宏mycalc，30秒定时刷新；如果不需要自动刷新功能，也可手工触发刷格，按下键盘delete即可）。
股票名称上证指数深证综指创业板指
当前价 #NAME? #NAME? #NAME?
昨收盘 #NAME? #NAME? #NAME?
涨跌 #NAME? #NAME?
涨跌幅度 #NAME? #NAME?
长江电力光大银行
#NAME? #NAME? #NAME? #NAME?
#NAME? #NAME?
当日最低价 #NAME? #NAME? #NAME?
当日成交额(万元) #NAME? #NAME? #NAME?
#NAME?
#NAME?
)；另外其他4个功能函数（开盘价/最高价/最低 nStockPrice( ),getTradeVolume( )。新功能，也可手工触发刷新（在excel上找个空

Excel计算欧式看涨期权的价格二叉树

(下转第157页)Excel 计算欧式看涨期权的价格二叉树鲍世杰（衡水学院数学与计算机学院河北衡水053000）【摘要】：欧式看涨期权是基于标的股票的衍生证券，可以利用股票的二叉树模型通过链锁法求解欧式看涨期权的初始价格，本文主要采用excel 通过股票的二叉树计算欧式看涨期权的初始价格，并且可以把其中的参数设为变量，表单建立后只需修改参数值就可以重新计算欧式看涨期权的价格，因此具有很大的实用性。

【关键词】：欧式看涨期权；衍生证券；二叉树一、引言：随着金融市场的不断发展衍生证券也逐渐的引入中国的证券市场，欧式看涨期权作为基本的衍生证券也进入中国的证券市场，欧式看涨期权的定价主要由标的的股票决定的，【1】股票的二叉树、欧式看涨期权二叉树是其中重要的一种分析方法，本文利用excel 工具计算欧式看涨期权。

二、股票二叉树、期权二叉树【2】欧氏看涨期权：认购期权(call)是一种合约。

合约持有者有权利却无义务在规定的时间或之前按指定的价格买入特定数量的某种标的资产。

建立股票简化二叉树应用【3】链式法则计算欧式看涨期权二叉树三、利用excel 计算欧式看涨期权打开excel 以J1单元格为顶点建立股票的二叉树模型，J11为顶点建立欧氏看涨期权的二叉树模型。

A1键入100，B1键入股价，B 列键入为解释A 列数值代表的意义，以下同理。

A2单元格键入105，B2键入执行价格，A3单元格键入5，B3键入期数，A7键入0.9，B7键入d 值，A8键入1.1，B8键入u 值，A11键入0.95，B11键入，A12键入0.7564，B12键入q ，A13键入0.2436，B13键入1-qJ1中键入公式“=A1”，I2中键入“=J1*$A$7”，在K2中键入公式“=J1*$A$8”，然后选择I2单元格的左下对角单元格复制I2中公式即可，直到E6。

在K2右下单元格中复制K2公式直到Q6，依次类推填满所需要的单元格，从而得到股票的二叉树。

(仅供参考)Excel VBA 金融工程 Section 2 - 期权定价

梦特卡罗期权价格计算欧洲看涨不派息股票期权我会将之前介绍到技巧应用在不派息的欧洲看涨期权上。

分别是控制変量方法CMcEuropeanCall()程序- 请参考源代码OP02，对偶変量法AMcEuropeanCall()程序-请参考源代码OP03及原模拟McEuropeanCall()程序- 请参考源代码OP04，。

当分别输入资料{S0, K, r, σ, T, n}，而经由读取程序readData() -请参考源代码OP01后。

而readData()程序会分别将资料放到以上三个不同方法的程序里，最后结果会输回其期权现价及标准误差到readData()程序。

在全部程序里，随机抽样数ɛ会由StdNormNum()函数产生，并由此根据(FOP.16)带出抽様的到期价格S T(ɛ)。

就对偶変量法，在相同的随机数上加上负数即可S T(-ɛ)。

相同的数值在不同函数，引用不同公式(FOP.18), (FOP.19) 及(FOP.21)里运作后评估。

根据(FOP.2),其均值及方差的现值可将每个抽祥数分别加起来及将其倍乘即可,其可以一个小回路程序由1到n项。

可以更简单的将(FOP.2)的方差计算用以下方式表达S2=1n+1∑gni=12(xi)-nn−1m2(FOP.25)此两个流程都可以在估算期权现价时得出其均值。

在控制变量法，一定要时刻记者将S0包括在均值估算上当为控制变量(FOP.20)的解决方法。

在评估过程里的标准误差可以根据在方差计算时的附加因子1/√n所找出。

Sub readData()Dim assetPrice As Double: assetPrice = Cells(2, 2)Dim strike As Double: strike = Cells(3, 2)Dim maturity As Double: maturity = Cells(4, 2)Dim riskFree As Double: riskFree = Cells(5, 2)Dim sigma As Double: sigma = Cells(6, 2)Dim nsample As Long: nsample = Cells(7, 2)Dim optionPrice As DoubleDim stdEr As Doubleseed = 5678Call McEuropeanCall(assetPrice, strike, riskFree, sigma, maturity, nsample, optionPrice, stdEr)Cells(9, 2) = optionPriceCells(10, 2) = stdErCall CMcEuropeanCall(assetPrice, strike, riskFree, sigma, maturity, nsample, optionPrice, stdEr)Cells(9, 3) = optionPriceCells(10, 3) = stdErCall AMcEuropeanCall(assetPrice, strike, riskFree, sigma, maturity, nsample, optionPrice, stdEr)Cells(9, 4) = optionPriceCells(10, 4) = stdErEnd Sub源代码OP01: 读取基本期权资料程序Sub CMcEuropeanCall(assetPrice As Double, strike As Double, riskFree As Double, sigma As Double, maturity As Double, nsample As Long, ByRef optionPrice As Double, ByRef stdEr As Double)Dim sum01 As Double, sum02 As Double, Vnum As DoubleDim mean As Double, Vd As Double, Vs As LongDim sT As Double, fT As Double, pV As Doublesum01 = 0sum02 = 0For Vs = 1 To nsampleVnum = StdNormNum()sT = assetPrice * Exp((riskFree - 0.5 * sigma ^ 2) * maturity + sigma * Sqr(maturity) * Vnum)fT = CallPayoff(strike, sT) - sTpV = Exp(-riskFree * maturity) * fTsum01 = sum01 + pVsum02 = sum02 + pV * pVNext Vsmean = sum01 / nsampleVd = Sqr(sum02 / (nsample - 1) - (nsample / (nsample - 1)) * mean ^ 2)optionPrice = assetPrice + meanstdEr = Vd / Sqr(nsample)End Sub源代码OP02: 欧州看涨期权控制変量法梦特卡罗模拟程序Sub AMcEuropeanCall(assetPrice As Double, strike As Double, riskFree As Double, sigma As Double, maturity As Double, nsample As Long, ByRef optionPrice As Double, ByRef stdEr As Double)Dim sum01 As Double, sum02 As Double, Vnum As DoubleDim mean As Double, Vd As Double, Vs As LongDim sT As Double, sTa As Double, fT As Double, pV As Doublesum01 = 0sum02 = 0For Vs = 1 To nsampleVnum = StdNormNum()sT = assetPrice * Exp((riskFree - 0.5 * sigma ^ 2) * maturity + sigma * Sqr(maturity) * Vnum)sTa = assetPrice * Exp((riskFree - 0.5 * sigma ^ 2) * maturity + sigma * Sqr(maturity) * (-Vnum))fT = (CallPayoff(strike, sT) + CallPayoff(strike, sTa)) / 2pV = Exp(-riskFree * maturity) * fTsum01 = sum01 + pVsum02 = sum02 + pV * pVNext Vsmean = sum01 / nsampleVd = Sqr(sum02 / (nsample - 1) - (nsample / (nsample - 1)) * mean ^ 2)optionPrice = meanstdEr = Vd / Sqr(nsample)End Sub源代码OP03: 欧州看涨期权对偶変量法梦特卡罗模拟程序Sub McEuropeanCall(assetPrice As Double, strike As Double, riskFree As Double, sigma As Double, maturity As Double, nsample As Long, ByRef optionPrice As Double, ByRef stdEr As Double)Dim sum01 As Double, sum02 As Double, Vnum As DoubleDim mean As Double, Vd As Double, Vs As LongDim sT As Double, fT As Double, pV As Doublesum01 = 0sum02 = 0For Vs = 1 To nsampleVnum = StdNormNum()sT = assetPrice * Exp((riskFree - 0.5 * sigma ^ 2) * maturity + sigma * Sqr(maturity) * Vnum)fT = CallPayoff(strike, sT)pV = Exp(-riskFree * maturity) * fTsum01 = sum01 + pVsum02 = sum02 + pV * pVNext Vsmean = sum01 / nsampleVd = Sqr(sum02 / (nsample - 1) - (nsample / (nsample - 1)) * mean ^ 2)optionPrice = meanstdEr = Vd / Sqr(nsample)End Sub源代码OP04: 欧州看涨期权原梦特卡罗模拟程序Public seed As LongFunction StdNormNum() As DoubleDim v1 As Double, v2 As Double, w As Double, fac As DoubleDim snnUse As DoubleStatic flagSave As Integer: If IsEmpty(flagSave) Then flagSave = 0Static snnSave As DoubleIf (flagSave = 0) ThenNewTrial:v1 = 2# * ran0() - 1#v2 = 2# * ran0() - 1#w = v1 ^ 2 + v2 ^ 2If (w >= 1#) Then GoTo NewTrialfac = Sqr(-2# * Log(w) / w)snnSave = fac * v1snnUse = fac * v2flagSave = 1ElsesnnUse = snnSaveflagSave = 0End IfStdNormNum = snnUseEnd FunctionFunction ran0() As DoubleDim IA As Long: IA = 16807Dim IM As Long: IM = 2147483647Dim IQ As Long: IQ = 127773Dim IR As Long: IR = 2836Dim MASK As Long: MASK = 123459876Dim AM As Double: AM = 1# / IMDim k As Longseed = seed Xor MASKk = seed / IQseed = IA * (seed - k * IQ) - IR * kIf (seed < 0) Then seed = seed + IMran0 = AM * seedseed = seed Xor MASKEnd FunctionFunction CallPayoff(strike As Double, assetPrice As Double) As DoubleCallPayoff = Max(assetPrice - strike, 0)End FunctionFunction Max(x As Double, y As Double) As DoubleIf x > y Then Max = x Else Max = yEnd Function源代码OP05: 随机抽样数函数产生器及看涨期权净值函数m=12n ∑gni=1(x i) and S2=1n+1∑(gni=1(x i)- m)2(FOP.2)S T=S0exp((r-1/2σ2)T+σ√Tɛ(0,1)) (FOP.16) n r(ɛ)=max{S T(ɛ)-K, 0} (FOP.18) ńr(ɛ)=max{S T(ɛ)-K, 0} - S T(ɛ) (FOP.19)n0=S0+Ê(e-rTńr |S0) (FOP.20) ňr(ɛ)=1/2[max{S T(ɛ)-K, 0} +max{S T(-ɛ)-K, 0}] (FOP,21)欧洲看涨派息股票期权现在考虑欧洲看涨派息股票期权的计算方法，假知它支付的股息是{D1, … , D n}而支付时间为{t1, … , t n=T}。

如何在MicrosoftExcel中处理金融数据

如何在MicrosoftExcel中处理金融数据Excel是一种非常强大的工具，可以让您轻松地处理金融数据，包括股票、债券、货币等等。

在本文中，我们将介绍如何使用Excel来处理这些数据，并展示一些实用的技巧和技术，以提高您的工作效率。

1. 数据收集首先，我们需要从可靠的数据源收集数据。

有许多提供基本金融数据的网站，例如雅虎金融、谷歌金融等。

您可以使用它们来获得有关股票、债券、货币等的最新数据。

您也可以使用金融API，如Quandl、Alpha Vantage等，来获取数据。

这些API通常提供一些有用的功能，如历史价格、股息、收益率等。

在本文中，我们将使用Quandl API来获取数据。

2. Excel函数一旦您收集了数据，下一步就是将其导入Excel。

在Excel中，您可以使用不同的函数来处理数据。

以下是一些最常用的函数：- SUM：用于计算一系列数字的总和。

- AVERAGE：用于计算一系列数字的平均值。

- COUNT：用于计算一系列数字中非空单元格的数量。

- MAX：用于找到一组数的最大值。

- MIN：用于找到一组数的最小值。

- ROUND：用于四舍五入数字。

您还可以使用其他函数，如IF函数、VLOOKUP函数等，以更精确地处理数据。

这些函数可以帮助您识别和删除重复项、过滤数据、计算返回率和波动率。

3. 报表和图表Excel还提供了许多报表和图表来展示数据。

这些报表可以帮助您更直观地理解数据和趋势，并支持您做出更好的决策。

以下是一些最常用的报表和图表：- 条形图：用于显示单个或多个数字的比较。

- 饼图：用于显示总数中各组件的占比。

- 散点图：用于显示两个变量之间的关系。

- 折线图：用于显示时间序列数据和趋势。

您还可以使用其他高级图表，如对数图、箱型图等，以深入了解数据。

一些报表和图表可能需要Excel插件才能使用，例如PowerPivot和PowerView插件。

4. 宏宏是Excel的功能之一，它允许用户自动化常见的任务或操作。

期权定价-二叉树模型

期权定价-二叉树模型期权定价是金融市场中的重要内容，它是根据期权的特点和市场条件来确定期权价格的过程。

二叉树模型是一种常用的期权定价方法之一，其基本思想是将时间离散化，并通过构建一个二叉树来模拟标的资产价格的变动。

在二叉树模型中，每个节点代表了一个特定的时刻，而每个节点之间的关系是通过上涨和下跌两种情况进行连接的。

通过调整上涨和下跌的幅度，可以模拟出不同标的资产的价格变动情况。

期权的定价在二叉树模型中可以通过回溯法进行计算。

首先，在最后一个节点上，根据期权的特点以及市场条件来确定期权的价值。

然后，逐步向前回溯，通过考虑不同的路径来计算每个节点上的期权价值。

在回溯过程中，需要考虑每个节点的两个子节点的权重，即上涨和下跌的概率。

这可以根据市场条件来确定，通常是基于历史数据进行估计。

然后，在回溯过程中，可以根据节点上的期权价值和子节点的权重来计算每个节点的期权价格。

通过不断回溯，最终可以得到期权的初始价值，即在当前市场条件下，期权价格应该是多少。

这个初始价值可以用作参考，帮助投资者做出合理的投资决策。

需要注意的是，二叉树模型是一个简化的模型，它有一些假设和限制。

首先，它假设标的资产的价格只有上涨和下跌两种情况，而忽略了其他可能的情况。

其次，它假设市场条件在整个期权有效期内保持不变，而实际情况可能是变化的。

因此，在使用二叉树模型进行期权定价时，需要注意这些假设和限制。

总而言之，期权定价是金融市场中的重要内容，二叉树模型是一种常用的定价方法。

通过构建二叉树模型，并根据回溯法计算每个节点上的期权价值，可以得到期权的初始价格。

然而，需要注意二叉树模型的假设和限制，并结合实际情况进行综合分析和判断。

期权定价是金融市场中的重要内容，其旨在确定期权的合理价格。

期权是一种金融工具，赋予购买者在期权到期时以约定价格购买或出售标的资产的权利。

很多投资者都希望能够在市场上买入或者卖出期权，以便于在未来某个时刻获得利润。

因此，了解期权的合理价格对投资者来说至关重要。

期权二叉树的excel实现总表

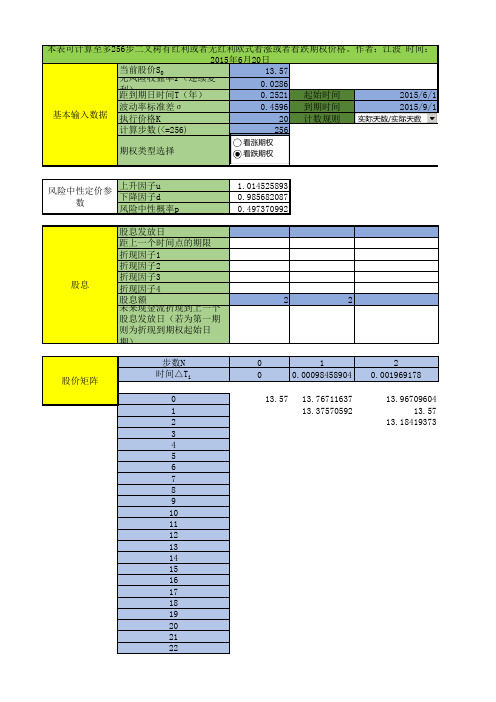
股息发放日将未来的股息折现到该时点，再将该折现值复利到直到下一个股息发放日之间的每一步，并将该值加到对应步数的无红利股价上，得到
有红利的总股价。
3
4
0.002953767 0.003938356
5 0.004922945
6
7
8
9
0.005908 0.006892 0.0078767 0.008861
77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130
12.44518 12.62595 12.809356 12.99542
12.26699 12.445176 12.62595
12.091349 12.26699
11.91823
10
11
12
13
14
15
16
17
18
0.009846 0.01083 0.011815 0.0128 0.013784 0.014769 0.015753 0.016738 0.017723
185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238

股票期权二叉树定价-excel-VBA程序

Sub 期权定价()Dim i As Long'将输入的参数的值赋给相应的变量s0 = Worksheets(1).Cells(1, 2)x = Worksheets(1).Cells(2, 2)r = Worksheets(1).Cells(3, 2)s = Worksheets(1).Cells(4, 2)t = Worksheets(1).Cells(5, 2)n = Worksheets(1).Cells(6, 2)'生成表格Worksheets(1).Cells(1, 4) = "期数" Worksheets(1).Cells(2, 4) = "时间（年）" Worksheets(1).Cells(3, 4) = "上行乘数" Worksheets(1).Cells(4, 4) = "下行乘数" Worksheets(1).Cells(5, 4) = "股票价格" Worksheets(1).Cells(n + 6, 4) = "执行价格" Worksheets(1).Cells(n + 7, 4) = "上行概率" Worksheets(1).Cells(n + 8, 4) = "下行概率" Worksheets(1).Cells(n + 9, 4) = "买入期权价格"'合并相应单元格Set rr1 = Range("D5")For i = 1 To nSet rr1 = Union(Range("D" & (5 + i)), rr1) Nextrr1.SelectWith Selection.HorizontalAlignment = xlGeneral.VerticalAlignment = xlBottom.WrapT ext = False.Orientation = 0.AddIndent = False.IndentLevel = 0.ShrinkToFit = False.ReadingOrder = xlContext.MergeCells = TrueEnd With'设置格式居中With Selection.HorizontalAlignment = xlCenter.VerticalAlignment = xlCenter.WrapT ext = False.Orientation = 0.AddIndent = False.IndentLevel = 0.ShrinkToFit = False.ReadingOrder = xlContext.MergeCells = TrueEnd With'合并相应单元格Set rr2 = Range("D" & (n + 9))For i = 1 To nSet rr2 = Union(Range("D" & (n + 9 + i)), rr2) Nextrr2.SelectWith Selection.HorizontalAlignment = xlGeneral.VerticalAlignment = xlBottom.WrapT ext = False.Orientation = 0.AddIndent = False.IndentLevel = 0.ShrinkToFit = False.ReadingOrder = xlContext.MergeCells = TrueEnd With'设置格式居中With Selection.HorizontalAlignment = xlCenter.VerticalAlignment = xlCenter.WrapT ext = False.Orientation = 0.AddIndent = False.IndentLevel = 0.ShrinkToFit = False.ReadingOrder = xlContext.MergeCells = TrueEnd With'计算表格相应内容'期数Worksheets(1).Cells(1, 5) = 0For i = 1 To nWorksheets(1).Cells(1, 5 + i) = iNext'时间（年）Worksheets(1).Cells(2, 5) = 0For i = 1 To nWorksheets(1).Cells(2, 5 + i) = t / (12 * n) * iNext'上行乘数u = Exp(s * (t / (12 * n)) ^ 0.5)Worksheets(1).Cells(3, 5) = u'下行乘数d = 1 / uWorksheets(1).Cells(4, 5) = d'股票价格For i = 1 To n + 1Worksheets(1).Cells(4 + i, 4 + i) = 50 * d ^ (i - 1)NextFor i = 1 To nFor j = i To nWorksheets(1).Cells(4 + i, 5 + j) = Worksheets(1).Cells(4 + i, 4 + j) * u NextNext'执行价格Worksheets(1).Cells(n + 6, 5 + n) = x'上行概率、下行概率p = ((r * t) / (12 * n) + 1 - d) / (u - d)Worksheets(1).Cells(n + 7, 5 + n) = pWorksheets(1).Cells(n + 8, 5 + n) = 1 - p'买入期权价格'最后一期的期权价值For i = 1 To n + 1q = Worksheets(1).Cells(4 + i, 5 + n) - xIf q > 0 ThenWorksheets(1).Cells(n + 8 + i, 5 + n) = qElseWorksheets(1).Cells(n + 8 + i, 5 + n) = 0End IfNext'由后往前推各期的价值For ii = n To 1 Step -1 '列For jj = 1 To ii '行If Worksheets(1).Cells(n + 8 + jj, 4 + ii + 1) > 0 Or Worksheets(1).Cells(n + 8 + jj + 1,4 + ii + 1) > 0 ThenWorksheets(1).Cells(n + 8 + jj, 4 + ii) = (p * Worksheets(1).Cells(n + 8 + jj, 4 + ii + 1) + (1 - p) * Worksheets(1).Cells(n + 8 + jj + 1, 4 + ii + 1)) / (1 + (r / 12) * (t / n)) ElseWorksheets(1).Cells(n + 8 + jj, 4 + ii) = 0End IfNextNextEnd Sub效果如下：。

金融工程-二叉树模型——期权定价方法实验报告---用于合并

期权定价（二叉树模型）实验报告班级：创金1201 姓名：郑琪瑶学号： 1204200308一、实验目的本实验基于二叉树模型对期权定价。

利用Excel 计算出支付连续红利率资产的期权价格，并探究输入参数（如无风险利率、波动率、期限、时间区间划分方式、收益率等等）对于期权价格的影响，从而巩固二叉树模型这种期权定价的数值方法的相关知识。

二、实验原理当标的资产支付连续收益率为q 的红利时，在风险中性条件下，证券价格的增长率应该为q r -，因此参数p （股票价格上升的概率）、u 、d 应该满足以下式子：d p pue t q r )1()(-+=∆-；同时在一小段时间内股票价格变化的方差满足下式：2222])1([)1(d p pu d p pu t -+--+=∆σ；考克斯、罗斯和鲁宾斯确定参数的第三个条件是du 1=，将三式联列，可以解得（*）三、实验内容1. 假定有一支付连续红利率股票的美式看涨期权，有效期期限为5个月，目前的股票价格和期权执行价格都为50元，无风险利率为10%，波动率为40%，连续收益率为3%，为了使得估计的期权价格比较准确，把时间区间划分成30步，即N=30，利用excel 加载宏可以计算得到相应美式和欧式期权的价格2.探究基于不同红利支付类型：支付已知收益率和支付已知红利数额，计算出相应的美式和欧式期权价格。

3.以支付已知收益率模式下分析期权价格。

使资产连续复利收益率在[1%,10%]变化，保持其余变量不变，分别计算出相应美式f 1和欧式f 2期权的价格4.以支付已知红利数额模式下分析期权价格。

探究下一期的红利支付数额为常数、递增及递减情况下，保持其余变量不变，分别计算出相应美式和欧式期权的价格。

5.根据上述每一步计算得到的当期期权价格的数据绘制折线图，观察折线图，得出结论。

四、实验过程：步骤一：输入已知参数步骤二：根据已知参数及式（*）原理，计算如下参数步骤三：改变参数，确定期权价格（1）以支付已知收益率模式下分析期权价格。