反比例函数 第一节(获一等奖课件)
合集下载
26.1反比例函数 大赛获奖课件 公开课一等奖课件

分析:从组合体中能直接看到的地球表面最远点,是视线与地球相切时的 切点.
如图,本例可以抽象为以地球中心为圆心、地球半径为半径的⊙O 的有关 问题:其中点 F 是组合体的位置,FQ 是⊙O 的切线,切点 Q 是从组合体中观 ︵ 的长就是地球表面上 P,Q 两点间的距离.为计算PQ ︵的 测地球时的最远点,PQ 长需先求出∠POQ(即α)的度数.
【预习导学】
一、自学指导
自学:阅读教材P74-77页,自学两个思考及探究,自学例1,
完成填空。5分钟
正弦值
A的对边 a = 斜边 c
【预习导学】
二、自学检测
4 5
_2
2 2
1
3 2
点拨精讲:正弦值的讨论前提是在直角三角形中,当锐角度数一
定时,它的对边与斜边的比是一个定值。 的正弦,不能把它理解为 。 是一个整体,它表示∠A
【课堂小结】
(学生总结本堂课的收获与困惑)2分钟
【当堂训练】10分钟
28.2 解直角三角形及其应用 28.2.2 应用举例
知识与技能
使学生掌握仰角、俯角的概念,并会正确运用这些概念和 解直角三角形的知识解决一些实际问题. 过程与方法 让学生体验方程思想和数形结合思想在解直角三角形中的
用途.
情感、态度与价值观
(2)∵y1 与 x 成正比例,y2 与(x-2)成反比例, k2 k2 ∴设 y1=k1x,y2= .∴y=k1x- . x-2 x-2 把 x=3,y=5;x=1,y=-1 分别代入上式,得
5=3k1-k2, -1=k1+k2 k1=1, 解之得 k2=-2.
2 ∴函数解析式为:y=x+ . x-2
例 3 如图,一艘海轮位于灯塔 P 的北偏东 65°方向,距离灯塔 80 n mile 的 A 处,它沿正南方向航行一段时间后,到达位于灯塔 P 的南偏东 34°方向 上的 B 处.这时,B 处距离灯塔 P 有多远?(结果取整数)
反比例函数的图像和性质ppt市公开课一等奖省赛课获奖PPT课件

y
0 x (B )
y
0 x (D )
y
0
(B x)
y
0
x
(D )
y 0x y 0x y 0x y 0x
第18页
一、复习:
函数 图象
• 正百分比在函每数个象• 反百分比函数
• y=kx 限内
y —xk
经点 (0,0) ,
关于 原点对
(1,k)直线
称双曲线
k>0
性
质 k<0
y随x增 大而增大
y随x增 大而减小
第14页
练一练 5
若点(-2,y1)、(-1,y2)、(2,y3)在
反百分比函数y 100 x
图象上,则( B )
A、y1>y2>y3
B、y2>y1>y3
C、y3>y1>y2
D、y3>y2>y1
第15页
练一练 6
已知圆柱侧面积是10πcm2,若圆柱底面半径为 rcm,高为hcm,则h与r函数图象大致是( )C.
反百分比函数图像和性质
第1页
回顾与思索1
挑战“记忆”
你还记得一次函数图象与性质吗?
一次函数y=kx+b(k≠0)图象是一条直线, 称直线y=kx+b.
当k>0时,
y
b>0
b=0
பைடு நூலகம்
o
x
b<0
当k<0时,
y
b<0
b=0
o
x
b<0
y随x增大而增大;
y随x增大而减小.
第2页
回顾与思索2
“预见性”,猜一猜
性 两个分支分别在第 两个分支分别在第
全国优质课一等奖初中数学九年级下册《反比例函数》公开课精美课件

2)确定反比例函数解析式。
3)利用反比例函数的意义分析简单的问题。
重点
确定反比例函数的解析式。
难点
利用反比例函数的意义分析简单的问题。
情景导入
下列问题中两个变量间具有函数关系吗?如果有,请直接写出解析式.
[情景一]京沪线铁路全程为1463 km,某次列车的平均速度v(单位:km/h)随此
1463
次列车的全程运行时间t(单位:h)的变化而变化.
3)解这个方程,求出未知系数 ;
4)将求出的未知系数的值代入所设的解析式中。
课堂练习 (利用待定系数法求反比例函数解析式)
例4 已知函数 y = y1 + y2,y1与x 成正比例,y2与x成反比例,且当x=1时,
y=4;当x=2时,y=5。
(1)求y与x的函数关系式;
(2)当x=4时,y 的值。
【详解】∵反比例函数 =
3
− 2
3
=
−2
3
3
,∴反比例函数 = − 2 的比例系数是− 2.
+1
的图象经过点(﹣1,2),则k=_____.
变式 3-1 反比例函数y=
+1
的图象经过点(﹣1,2),∴k+1=(﹣1)×2,解得k=﹣3.
【详解】∵反比例函数y=
变式3-2 已知反比例函数y= (k为常数,且k≠0)的图象经过点(3,4),则该函数图象必不
经过点(
)
A.(2,6)
B.(-1,-12)
C.(0.5,24)
D.(-3,8)
【详解】反比例函数y= (k为常数,且k≠0)的图象经过点(3,4),k=3×4=12;
《反比例函数》一等奖公开课PPT1
课堂导学
2.某种蓄电池的电压为定值,使用此电
源时,电流I(A)与可变电器
的电流为12A时, 第2题
用电器的可变电阻为__3____Ω.
课堂导学
3. 在对物体做功一定的情况下,力F(牛)
与此物体在力的方向上移动的距离s(米)
成反比例函数关系,
其图象如上图所示,
数的表达式. (1)P=9v6
课后巩固
(2)当气体的体积为1.5m3时,气压是多
少? 某气球内充满一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,其图象如下图所示.
【解析】由电压U、电流I及电阻R的关系式I= ,根据已知条件可求出定值电压,即可确定I与R的函数关系.
强P(Pa)和物体与地面的接触面积S(m2) 的函数关系式为_P_=___5S_0___.
课前预习
3.小伟欲用撬棍撬动一块大石头,已 知阻力和阻力臂不变,分别为1 200牛 和0.5米,那么动力F和动力臂L之间的 函数关系式是_F_=__6_0L__0___.
课堂导学
知识点:反比例函数在其他学科的应用
(3)当气球内的气压大于120kPa时,气球将爆炸,为了安全起见,气体的体积应不大于多少? 2 实际问题与反比例函数(二) P(5,1)在图象上, 1.额定电压为220V的电路上电流I(A)与电阻R(Ω)之间的函数关系式为________.
将爆炸,为了安全起见,气体的体积应 5安培时,求电阻R的值;
P(5,1)在图象上,
则当力达到10牛时,
第3题
物体在力的方向上移动的距离是____米.
课堂导学
4.近视眼镜的度数y(度)与镜片焦距
x(米)成反比例.已知200度的近视眼镜
反比例函数公开课一等奖课件省赛课获奖课件

或 y kx1
拟定了K值也 就拟定了反比 例函数的解析 式.环节:设,代, 解,写
检测反馈
▪1.分别写出下列问题中两个变量间的函数关系式,指 出哪些是正比例函数,哪些是反比例函数,哪些既不 是正比例函数也不是反比例函数?
▪ (1)小红一分钟能够制作2朵花,x分钟能够制作y朵 花;
▪ (2)体积为100cm3的长方体,高为hcm时,底面积 为Scm2;
⑶ 已知函数 y = xm -7 是正比例函数,则 m = _8__ ;
已知函数 y = 3xm -7 是反比例函数,则 m = _6__ 。
练习
1、下列函数中,哪些是反比例函数?说出反比例函
数的比例系数
(1)y = -3x; (2)y = 2x+1; (3)y 5 ; x
(4)y =3(x-1)2+1;(5) y 2s (s是常数,s≠0) x
2、已知北京市的总面积为 1.68×104平方 千米,全市总人口为 n 人,人均占有土地面 积为 s 平方千米, s 1.68104 则s有关n的关系式为____n__;
3、京沪线铁路全程为1463 km,某列车平均速
度为 v(km/h),全程运行时间为 t(h), 则v有关t的关系式为__v _14_t63__。
x
x y =6 x y =1661
x y=24
y6 x
y 1661 x
y 24 x
普通地,若变量y与x反比例,则有xy=k
(k为常数,k≠0 ), 也就是
yk
x
上述几个函数都含有 y k 的形式,普通地
x
形如 y k (k是常数,k≠0)的函数叫做反比 x
例函数(proportional function).
拟定了K值也 就拟定了反比 例函数的解析 式.环节:设,代, 解,写
检测反馈
▪1.分别写出下列问题中两个变量间的函数关系式,指 出哪些是正比例函数,哪些是反比例函数,哪些既不 是正比例函数也不是反比例函数?
▪ (1)小红一分钟能够制作2朵花,x分钟能够制作y朵 花;
▪ (2)体积为100cm3的长方体,高为hcm时,底面积 为Scm2;
⑶ 已知函数 y = xm -7 是正比例函数,则 m = _8__ ;
已知函数 y = 3xm -7 是反比例函数,则 m = _6__ 。
练习
1、下列函数中,哪些是反比例函数?说出反比例函
数的比例系数
(1)y = -3x; (2)y = 2x+1; (3)y 5 ; x
(4)y =3(x-1)2+1;(5) y 2s (s是常数,s≠0) x
2、已知北京市的总面积为 1.68×104平方 千米,全市总人口为 n 人,人均占有土地面 积为 s 平方千米, s 1.68104 则s有关n的关系式为____n__;
3、京沪线铁路全程为1463 km,某列车平均速
度为 v(km/h),全程运行时间为 t(h), 则v有关t的关系式为__v _14_t63__。
x
x y =6 x y =1661
x y=24
y6 x
y 1661 x
y 24 x
普通地,若变量y与x反比例,则有xy=k
(k为常数,k≠0 ), 也就是
yk
x
上述几个函数都含有 y k 的形式,普通地
x
形如 y k (k是常数,k≠0)的函数叫做反比 x
例函数(proportional function).
全国优质课微型课比赛一等奖九年级数学下册《反比例函数》获奖课件

∴ቊ
解得:ቊ = 2 或 = −2
≠2
−2≠0
∴ = −2
深层探究 合作交流
五、概念的应用
问题6:已知是的反比例函数,并且当 = 2 时, = 6.
(1)求与之间的函数解析式;
(2)当 =4时,求的值.
.
展示提升 拓展延伸
课堂是个大舞台,每个人既是“演
员”又是听众,“演者”要尽善尽美、
同学们,世界上万事万物时时刻刻都在变
化。“函数”就像我们的生活一样,你笑,它
就笑,你哭,它就哭,你坚强,它就坚强。就
让我们微笑面对生活和学习,把握好生活中的
“自变量”,“函数”还可怕吗?
一、概念的引入
问题1:请分别写出下列各问题中,两个量之间的关系式.
(1)电流,电阻,电压之间满足关系式 = . 当=220 V时,
你能用含有的代数式表示吗?
220
=
(2)京沪线铁路全程为1463,某次列车的平均速度(单位:/)
随此次列车的全程运行时间(单位:)的变化而变化
四、概念的辨析
反比例函数不同的表达形式:
形式一: =
(k 0)
1
形式二:y kx
(k 0)
形式三: =
(k 0)
小贴士
小学曾经学习过反比例关系,即两个相关联的量,
一种量变化,另一种量也随着变化,若这两个量中相对
应的两个数的乘积一定,这两种量就叫做反比例的量,
它们的关系就叫做反比例关系.
1
解得: = −2
−2
∴−1= 2
即:与之间的函数解析式为: = −
2
2
+1
得 = −
反比例函数的图象和性质(1) 大赛获奖课件 公开课一等奖课件

2.练习. 教师多媒体课件出示: (1)如图(1)和(2),根据图中的数据解直角三角形.
师:图(1)中是已知一角和一条直角边解直角三角形的类型,你怎样解决 这个问题呢? AC AC 生 1:根据 cos60°=AB,得到 AB= ,然后把 AC 边的长和 60 cos60° °角的余弦值代入,求出 AB 边的长,再用勾股定理求出 BC 边的长,∠B 的 度数根据直角三角形两锐角互余即可得到.
三、例题讲解 例 1 如图,在 Rt△ABC 中,∠C=90°,AC= 2,BC= 6,解这个 直角三角形.
BC 6 解:∵tanA=AC= = 3, 2 ∴∠A=60°, ∠B=90°-∠A=90°-60°=30°, AB=2AC=2 2.
例 2 如图,在 Rt△ABC 中,∠C=90°,∠B=35°,b=20,解这个直 角三角形.(结果保留小数点后一位)
26.1 反比例函数 26.1.2 反比例函数的图象和性质
第1课时 反比例函数的图象和性质(1)
知识与技能 1.会用描点法画反比例函数的图象. 2.结合图象分析并掌握反比例函数的性质. 过程与方法 体会分类讨论思想、数形结合思想的运用. 情感、态度与价值观 1.体会函数的表示方法,领会数形结合的思想方法. 2.在动手作图的过程中体会其中的乐趣,养成勤于动手、乐 于探索的习惯.
三、例题讲解 例 1 如图,在 Rt△ABC 中,∠C=90°,AC= 2,BC= 6,解这个 直角三角形.
BC 6 解:∵tanA=AC= = 3, 2 ∴∠A=60°, ∠B=90°-∠A=90°-60°=30°, AB=2AC=2 2.
例 2 如图,在 Rt△ABC 中,∠C=90°,∠B=35°,b=20,解这个直 角三角形.(结果保留小数点后一位)
反比例函数的图象和性质 公开课一等奖课件

5 3.(3 分)当 x>0 时,函数 y=-x的图象在( A A.第四象限 B.第三象限 C.第二象限 D.第一象限
)
2k-1 4.(3 分)若双曲线 y= x 位于第二、四象限,则 k 的取值范围是( B ) 1 A.k>2 1 C.k=2 1 B.k<2 D.不确定
5.(4 分)已知 y=(m+1)xm2-5 是反比例函数,若其图象位于第二、四 象限,则 m 的值是( B ) A.2 B.-2 C.± 2 1 D.-2
26.1 反比例函数
26.1.2 反比例函数的图象和性质
第1课时 反比例函数的图象和性质
1.反比例函数的图象是 是: 列表 、
双曲线 ,画反比例函数图象的步骤
、
描点
连线
.
k 2.对于反比例函数 y=x(k≠0),k>0 时,图象的两支分别位于 第 一、三 象限内,在每个象限内,y 随 x 的增大而减小;
k 15.(12 分)一次函数 y=x+1 的图象与反比例函数 y=x(k≠0)的图象都经 过点 A(a,2) (1)求 a 的值及反比例函数的解析式 2 (2)判断点 B(2 2, 2 )是否在该反比例函数的图象上,并说明理由.
解:(1)一次函数 y=x+1 经过点 A(a,2),则有 2=a+1,a=1, k ∴A(1,2),又∵点 A 在 y=x上,则 k=1×2=2 2 2 (2)∵2 2× 2 =2,∴点 B 在反比例函数 y=x的图象上
解:∵坡度为 i=1:2,AC=4 m,∴BC=4×2=8 m
பைடு நூலகம்
(2)作 DS⊥BC,
垂足为 S,且与 AB 相交于 H,∵∠DGH=∠BSH,∠DHG=∠BHS,∴∠ GH 1 GDH=∠SBH,∴GD=2,∵DG=EF=2 m,∴GH=1 m,∴DH= 12+22= 5 m,BH=BF+FH=3.5+(2.5-1)=5 m,设 HS= x m,则 BS=2x m,∴ x2+(2x)2=52,∴x= 5m,∴DS= 5+ 5=2 5≈2×2.236=4.5 m
反比例函数的图像及性质(1)市公开课一等奖省赛课获奖课件
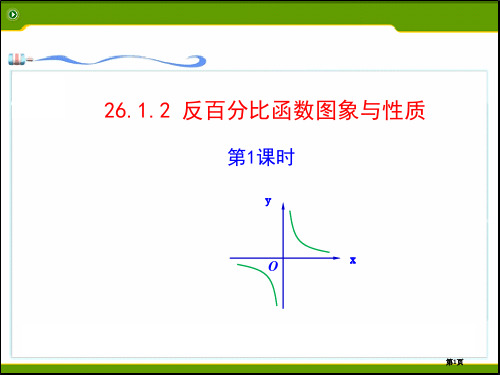
x
函数 两支曲线分别位于第二、四象限内.
第12页
反百分比函数y k
x
答: 由k符号决定.
图象在哪两个象限,由什么确定?
当k>0时,两支曲线分别位于第一,三象限内;
当k<0时,两支曲线分别位于第二,四象限内.
第13页
w归纳: 反百分比函数图象和性质:
1.反百分比函数图象是双曲线;
2.图象性质见下表:
第9页
y
.8
7 6
5 .4
y=—
-4 x
.
.
..
3 2 1
-8 -7 -6 -5 -4 -3 -2 -1 0 -1
1 2 .3 4. 5 6 7 .8
x
-2
.
-3 -4
.
-5 -6
-7 -8 .
第10页
.
y
6
y
5 . y=—4x
6
4
5
3
.
2
..
1
y=— .
-4
.4
x
3
.. .
2 1
x
-6
-5
.-4
26.1.2 反百分比函数图象与性质
第1课时
y x
O
第1页
1.深入熟悉作函数图象步骤,会画反百 分比函数图象. 2.体会函数三种表示方法相互转换,逐 步提升从函数图象获取信息能力,探索 并掌握反百分比函数主要性质.
第2页
1.什么是反百分比函数? k
普通地,形如 y = —x( k是常数, k ≠0 ) 函数叫做反百分比函数. 2.反百分比函数定义中需要注意什么? (1)k 是非零常数. (2)xy = k.
第8页
函数 两支曲线分别位于第二、四象限内.
第12页
反百分比函数y k
x
答: 由k符号决定.
图象在哪两个象限,由什么确定?
当k>0时,两支曲线分别位于第一,三象限内;
当k<0时,两支曲线分别位于第二,四象限内.
第13页
w归纳: 反百分比函数图象和性质:
1.反百分比函数图象是双曲线;
2.图象性质见下表:
第9页
y
.8
7 6
5 .4
y=—
-4 x
.
.
..
3 2 1
-8 -7 -6 -5 -4 -3 -2 -1 0 -1
1 2 .3 4. 5 6 7 .8
x
-2
.
-3 -4
.
-5 -6
-7 -8 .
第10页
.
y
6
y
5 . y=—4x
6
4
5
3
.
2
..
1
y=— .
-4
.4
x
3
.. .
2 1
x
-6
-5
.-4
26.1.2 反百分比函数图象与性质
第1课时
y x
O
第1页
1.深入熟悉作函数图象步骤,会画反百 分比函数图象. 2.体会函数三种表示方法相互转换,逐 步提升从函数图象获取信息能力,探索 并掌握反百分比函数主要性质.
第2页
1.什么是反百分比函数? k
普通地,形如 y = —x( k是常数, k ≠0 ) 函数叫做反百分比函数. 2.反百分比函数定义中需要注意什么? (1)k 是非零常数. (2)xy = k.
第8页
反比例函数的图象与性质浙教版省名师优质课赛课获奖课件市赛课一等奖课件

3、记面积为18cm²旳平行四边形旳一条边长为x(cm),这条 边上旳高为y(cm)。 ⑴ 求y有关x旳函数解析式,以及自变量x旳取值范围; ⑵ 在直角坐标系内,用描点法画出所求函数旳图象; ⑶ 求当边长满足8<x<12时,这条边上旳高y旳取值范围。
LQ @ LQZX
正百分比函数、反百分比函数旳图象与性质比较
影前后紧伴随来到了寿棺前。他们先是犹
LQ @ LQZX
图像旳一种
分支上,过点P作PA⊥x轴于点A、PB⊥y轴于点
B,当点P移动时,△OAB旳面积大小是否变化?
为何?
y
BP
OA
x
LQ @ LQZX
做一做:
1、用“>”或“<”填空:
⑴已知x1,y1和x2,y2是反百分比函数y
=
π x
旳
两对自变量与函数旳相应值。若x1 < x2 <0。
则0 > y1 > y2;
九年级上册 第一章 《反百分比函数》
1.2
LQ @ LQZX
回忆复习
➢画出示意图阐明
➢一次函数y=2x-1,y随x旳增大而__增__大__。
一次函数y=-2x-1,y随x旳增大而_减__小__。
➢想一想:
y
6
反百分比函数
,当x>0时,4 2
y随x旳增大而____。
-6
-4
-2
O
-2
2
4
6
x
-4
-6
LQ @ LQZX
做一做
➢ 用“>”或“<”填空:
⑴已知x1、y1和x2、y2是反百分比函数y
量
6 x
>
旳两对自变
LQ @ LQZX
正百分比函数、反百分比函数旳图象与性质比较
影前后紧伴随来到了寿棺前。他们先是犹
LQ @ LQZX
图像旳一种
分支上,过点P作PA⊥x轴于点A、PB⊥y轴于点
B,当点P移动时,△OAB旳面积大小是否变化?
为何?
y
BP
OA
x
LQ @ LQZX
做一做:
1、用“>”或“<”填空:
⑴已知x1,y1和x2,y2是反百分比函数y
=
π x
旳
两对自变量与函数旳相应值。若x1 < x2 <0。
则0 > y1 > y2;
九年级上册 第一章 《反百分比函数》
1.2
LQ @ LQZX
回忆复习
➢画出示意图阐明
➢一次函数y=2x-1,y随x旳增大而__增__大__。
一次函数y=-2x-1,y随x旳增大而_减__小__。
➢想一想:
y
6
反百分比函数
,当x>0时,4 2
y随x旳增大而____。
-6
-4
-2
O
-2
2
4
6
x
-4
-6
LQ @ LQZX
做一做
➢ 用“>”或“<”填空:
⑴已知x1、y1和x2、y2是反百分比函数y
量
6 x
>
旳两对自变
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1)内容:
反比例函数:意义(表示形式) 解析式的求法
(2)方法:确定反比例函数解析式的条件是已知一对自变量和函 数的对应值,可以利用待定系数法求反比例函数的解析式。
返回
第十七章反比例函数
17.1反比例函数
1、 P47 练习 第3题。 2、已知:y=y1+y2,y1与x成正比例,y2与x成反比例,并 且x=2和x=3时,y的值都等于19,求y与x之间的函数关系 式。 3、预习反比例函数的图象和性质。
返回
第十七章反比例函数
17.1反比例函数
问题
填下列各题中的空格部分,并写出各题的变量间的对应关系的函 数式: 1、京沪线铁路全程为1463km,某次列车的平均速度v(单位: 反比例 关系 Km/h)与此次列车的全程运行时间t(单位:h)成______
v
1463 t
2、某住宅小区要种植一个面积为1000㎡的矩形草坪,草坪的长y (单位:m)与宽x成 反比例 ______ 关系
分析:因为y是x的反比例函数,所以设
y=6代入上式就可求出常数k的值。
k y x
,再把x=2和
返回
第十七章反比例函数
解: k y (1)设 ,因为当x=2时y=6,所以有 x
17.1反比例函数
6
解得 因此 k=12k 212 y xx
(2)把x=4代入 y 12 ,得
y
12 =3 4
返回
第十七章反比例函数
17.1反比例函数
若y与x2-2成反比例,且当x=2时,y=1,则y与 x之间的关系式是?
分析:因为y与x2-2成反比例,所以可设 y=1代入上式就可求出常数k的值。
k y 2 ,再把x=2, x 2
答案是:
2 y 2 x 2
返回
第十七章反比例函数
17.1反比例函数
1.68104 S n
这三个函数表达式有什么共同的特点?
返回
第十七章反比例函数
17.1反比例函数
一般地,形如
反比例函数。
k y x
(k为常数,k≠0)的函数称为
其中X是自变量,y是X的函数,k是函数的比例系数。
自变量x的取值范围是不等于0的一切实数。
返回
第十七章反比例函数
17.1反比例函数
第十七章反比例函数
17.1反比例函数
复习回顾
1、 什么叫函数? 一般地,在一个变化过程中,如果有两个变量X与Y,并且对于X的 每一个确定的值,Y都有唯一确定的值与其对应,那么我们就说X 是自变量,Y是X的函数。 2、什么是一次函数,正比例函数? 一般地,形如y=kx+b(k,b是常数,k≠0)的函数,叫做一次 函数。 即正比例函数是一次函数的特殊形式。 3、什么叫反比例关系? 两个相关联的量,一个量变化,另一个量也随着变化,如果 个数的积一定,这两个数的关系叫做反比例关系。
返回
1000 y x
3、已知北京市的总面积为1.68X104平方千米,人均占有的土地 面积S(单位:平方千米/人)与全市人口n(单位:人)成 反比例 ______关系
1.68104 S n
返回
第十七章反比例函数
17.1反比例函数
1463 v t 1000 y x
k y x
其中(k≠0)
反比例函数
第十七章反比例函数
17.1反比例函数
第一课时
第十七章反比例函数
17.1反比例函数
一、教学目标: 1、经历从实际问题抽象出反比例函数的探索过程,发展学生的抽象力。 2、理解反比例函数的概念,会列出实际问题的反比例函数关系式。
二、教学重点: 理解反比例函数的概念和列出实际问题的反比例函数关系式。 三、教学难点: 列出实际问题的反比例函数关系式。 四、教学过程:
1463 v 如上面的1题中,当路程一定(1463km)时, t
表明速度v就是时间t的反比例函数,当t取某个值时,v就有一个 值与之对应。
总之:
在反比例函数
k y x
中,y会随着自变量x的变化而变化
生活中有哪些量之间是成反比例关系的?
返回
第十七章反比例函数
17.1反比例函数
下列函数中,哪些是反比例函数(x是自变量)?若是, 并说出反比例函数的比例系数。 1、y=-3x 2、y=2x+1
1 3、xy=- 4
(s是常数,s≠0)
4、y=-
3 x
5、y=
3s x
(1、2不是,3、4、5、是反比例函数。它们的比例系数分别是: -
1 ,-3,3s) 4
返回
第十七章反比例函数
17.1反比例函数
例1 已知y是x的反比例函数,当x=2时,y=6。 (1)写出y与x的函数关系式; (2)求当x=4时y的值。
