垃圾运输问题的模型及其求解
垃圾处理的模型

垃圾处理的模型城市垃圾收运是由产生垃圾的源头运送至处理处置场的全过程操作,包括3 个阶段:①收集———垃圾从产生源到公共贮存容器的过程;②清运———指清运车沿一定路线清除贮存容器内垃圾并将其转运到垃圾转运站的过程(在一定情况下,清运车可直接将垃圾运送至处理处置场);③中转———指在转运站将垃圾装载至大容量转运车,远途运输至处理处置场。
前1 个阶段需要对垃圾产生源分布情况、垃圾产生量及成分等进行调查和预测;后2 个阶段需要运用最优化技术对清运线路和转运站垃圾分配运输进行优化。
1 城市生活垃圾产生量预测方法城市生活垃圾收运模式的设计是在对生活垃圾产生量作正确预测的条件下进行的,因为设计的收运模式,不仅应满足当前垃圾产生量的需求,而且应该能够应对未来几年的变化。
目前,国内外较为普遍使用的数理统计方法为单指数平滑法、线性回归分析法、灰色系统模型分析法。
1. 1 单指数平滑法Yt+1=aXt+(1-a)Yt。
(1)式中:t 为时间;a 为指数平滑系数,介于0~1;Xt 为t 时垃圾产生量的实际观测值;Yt 为t 时垃圾产生量的预测值;Yt+1 为t+1 时垃圾产生量的预测值。
1. 2 线形回归分析法Y=a0+a1x1+a2x2+…+amxm。
(2)式中:Y 为垃圾预测产生量;xi 为影响垃圾产生的多个因素(i=1,2,…,m);ai 为回归系数(i=1,2,…,m)。
影响垃圾产生的因素有很多,如人口数量、工资收入、消费水平、生活习惯、燃料结构等。
对于众多因素,可以采用变量聚类法,对数据进行预处理。
据介绍,经过数据处理后多元回归分析法中很多变量都属“同解”,经过变量与处理后,实际运算时,相当于一元回归的“人口模式”预测法〔1〕。
1. 3 灰色系统模型分析法灰色系统模型(GM)包含模型的变量维数m和阶数n,记作GM (n,m)。
在生活垃圾产生量预测中普遍使用GM(1,1)模型。
通过对原始的时间序列数据进行累加处理后,数据便会出现明显的指数规律,通过进一步分析,可以进行垃圾产生量预测。
垃圾运输问题分解

• • • • • • • •
2.2符号说明 1. xi , yi :第i个垃圾站点的坐标 2. w :第i个垃圾站点的垃圾量 i 3. M 1 :运输车的总重载费用 4.M 2 :运输车的总空载费用 5.M 3 :运输车的总费用 6 .N :运输车所需的总车次数 7 . :第j辆车的出车次数
25(15,14)
10
6(0,8)
5(3,11)
31(5,12)
14(10,12) 19(15,12) 13(12,9) 12(14,6) 11(17,3) 10(14,0)
7(7,9) 4(4,7) 3(5,4) 8(9,6)
15(19,9)
5 0 0
2(1,5)ห้องสมุดไป่ตู้
1(3,2) 37(0,0)
9(10,2)
2.模型的假设及符号说明
• • • • • • • • • • • • 2.1模型的假设 (1)运输车装运均正常,不会发生偶然事故; (2)运输车都不存在塞车现象; (3)运输车走直线线路,并可任选路线; (4)忽略运输车行使时的拐弯时间; (5)各垃圾站点每天的垃圾量固定不变; (6)运输车到达每一个站点后必须将该站点的垃圾全部装完; (7)运输车行驶速度不变,固定为40公里/小时; (8)每天每车的工作时间固定不变; (9)运输车使用数量均不受限制; (10)忽略运输车卸垃圾的时间,每站点垃圾装车时间均为10分钟; (11)运营费用里不考虑工人工资、车辆的油费及维修保养费用等。
垃圾运输问题
2008年数学建模竞赛题
小组成员: 袁德琴 周玲玲 张 芳
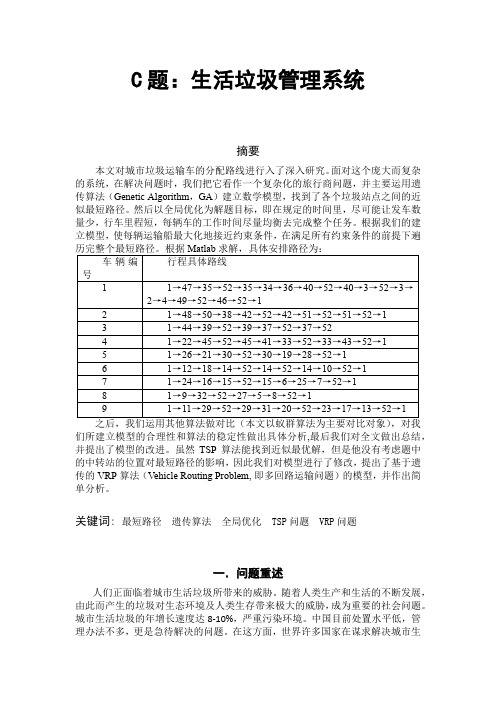
某城区有36个垃圾集中点,每 天都要从垃圾处理厂(第37号节 点)出发将垃圾运回。现有一种 载重 6吨的运输车。每个垃圾点 需要用10分钟的时间装车,运输 车平均速度为40公里/小时(夜 里运输,不考虑塞车现象);每 台车每日平均工作 4小时。运输 车重载运费1.8元/吨公里;运输 车空载费用0.4元/公里;并且假 定街道方向均平行于坐标轴。请 你给出满意的运输调度方案以及 计算程序。
数学模型垃圾运输调度问题和招聘问题

垃圾运输调度问题摘要:本文就生活中垃圾车调度问题进行了研究,通过对垃圾站点之间分布位置的分析,建立单目标规划模型,统筹安排了运输车的调度方案。
首先,应该对题设条件提出一定的假设。
其次,对垃圾站点的位置进行分析,并在图中绘制出其(x,y)散点图。
再次,根据题目要求,建立模型,结合已有的模型,对垃圾点之间的位置分布关系进行讨论及证明,从而确定最基本的行车路线原则。
然后,根据上述建立的单目标模型中的约束条件,编写程序,求解出各运输车辆的数量以及最佳的分配方案。
该模型中包含着运输费用、垃圾量、运输车工作时间的累积计算问题,因此,文中以运输车费用最少为目标函数,以运输车载重量的大小、当天必须将所有垃圾清理完、运输车工作时间等为约束条件,以运输车是否从一个垃圾站点到达另一个垃圾站点为决策变量,建立了使得运输费用最小的单目标的非线性规划模型。
并利用MATLAB编程求解,得到满意方案:载重费:2213.37元,空载费:122.4总共花费2335.77元,花费的总时间:15小时18分,一共发车十次,用4辆车来完成任务。
最后,对模型的优缺点进行了分析,并给出了模型的改进意见,对解决实际问题具有一定的指导意义。
关键词:垃圾运输目标规划运输费用MATLAB编程最优方案1.问题提出1.1 基本情况某城区有36个垃圾集中点,每天都要从垃圾处理厂(第37号节点)出发将垃圾运回。
不考虑垃圾的装车时间。
现有一种载重6吨的运输车,运输车平均速度为40公里/小时(夜里运输,不考虑塞车现象);每台车每日平均工作4小时。
运输车重载运费1.8元/吨公里;运输车空载费用0.4元/公里;并且假定街道方向均平行于坐标轴。
垃圾地理位置坐标如表1所示。
表1 垃圾地理位置坐标数据表1.2 问题要求根据上述基本情况建立的模型中的约束条件,利用计算机编程求解,得出满意的运输车调度方案,包括需要投入多少台运输车,每台车的调度方案以及运营费用。
2.模型建立在建立模型之前,对垃圾车调度问题做一些基本的假设,并给出建立模型时所需要的符号说明,在分析问题的基础上,建立合理优化的模型。
论文_final(垃圾运输路线)
C题:生活垃圾管理系统摘要本文对城市垃圾运输车的分配路线进行入了深入研究。
面对这个庞大而复杂的系统,在解决问题时,我们把它看作一个复杂化的旅行商问题,并主要运用遗传算法(Genetic Algorithm,GA)建立数学模型,找到了各个垃圾站点之间的近似最短路径。
然后以全局优化为解题目标,即在规定的时间里,尽可能让发车数量少,行车里程短,每辆车的工作时间尽量均衡去完成整个任务。
根据我们的建立模型,使每辆运输船最大化地接近约束条件,在满足所有约束条件的前提下遍们所建立模型的合理性和算法的稳定性做出具体分析,最后我们对全文做出总结,并提出了模型的改进。
虽然TSP算法能找到近似最优解,但是他没有考虑题中的中转站的位置对最短路径的影响,因此我们对模型进行了修改,提出了基于遗传的VRP算法(V ehicle Routing Problem, 即多回路运输问题)的模型,并作出简单分析。
关键词:最短路径遗传算法全局优化 TSP问题VRP问题一.问题重述人们正面临着城市生活垃圾所带来的威胁。
随着人类生产和生活的不断发展,由此而产生的垃圾对生态环境及人类生存带来极大的威胁,成为重要的社会问题。
城市生活垃圾的年增长速度达8-10%,严重污染环境。
中国目前处置水平低,管理办法不多,更是急待解决的问题。
在这方面,世界许多国家在谋求解决城市生活垃圾过程中,产生出许多好的办法,并在此过程中总结了经验和教训。
我们知道,城市垃圾自其产生到最终被送到处置场处理,需要环卫部门对其进行收集与运输,这一过程称为城市垃圾的收运。
收运过程可简述如下:某城市有多个行政区,每个区内均有一个车库,假设某一车库拥有最大装载量为w 的垃圾收集车k 辆,并且该区的垃圾收集点(待收集垃圾的点)有n个,该城市共有垃圾中转站p 座。
每天k 辆垃圾车从车库出发,经过收集点收集垃圾,当垃圾负载达到最大装载量时,垃圾车运往中转站,在中转站卸下所有收运的垃圾,然后再出站收集垃圾,如此反复,直到所有收集点的垃圾都被收集完,垃圾车返回车库。
运输问题模型和求解方法的研究(可编辑)

运输问题模型和求解方法的研究摘要运输问题是运筹学的一个分支,是线性规划的特殊形式。
它研究的是如何在物资调运中,制定出一个由若干个产地将物资根据已知的运输交通网运到各个销售地的方案,使得总运费最小。
运输是整个物流活动中的核心,运输管理是物流活动统筹规划和管理的重要部分,对运输环节进行规划和优化,对提高物流活动的效率有着重要意义。
物流被称为“第三利润源泉”,而运输成本又在整个物流成本中占得比例最大。
合理的设计运输方案,可以降低企业的物流成本,也就意味着增加了企业的利润。
本文通过对运输问题模型和求解方法的研究,在产销平衡的条件下,运用不同的方法:表上作业法、Vogel法和Excel软件对运输问题进行求解。
运用表上作业法或Vogel法的基本思路是:初始方案的确定?最优解的检验?调运方案的调整。
其求解步骤相对较为繁琐,所以又介绍了Excel软件的求解方法,该方法相对简单,而且准确快速,但是转换建模相对困难。
总之,各种方法都有其优点和缺点,在解决实际问题中,我们可以根据实际情况选择一种或几种方法进行求解。
关键词:线性规划;运输问题;表上作业法;Excel;Vogel法目录1 前言 11.1 作业背景11.2 选题说明11.2.1 基本思路 11.2.2 作业目标 21.3 工作业绩21.3.1 个人主要工作 21.3.2 主要收获 21.3.3 自我评定 31.3.4 小组成员任务分工情况 32 物流运输概述 42.1 物流与运输 42.2.1 物流运输的概念 42.2.2 运输在物流中的地位 42.2 运输合理化 42.2.1 不合理运输42.2.2 影响运输合理化的因素 53 线性规划与运输问题 63.1 线性规划63.2 运输问题74 运输问题的求解方法104.1 单纯形法104.2 表上作业法104.2.1 初始方案的确定114.2.2 最优解的检验144.2.3 调运方案的改进154.3 Excel规划求解方法165 某物流企业煤炭运输项目方案求解20 结束语22参考文献231 前言1.1 作业背景本文根据《物流系统规划与设计》课程要求而做。
城市垃圾清运调度优化模型研究

城市垃圾清运调度优化模型研究一、引言随着城市化的推进,城市垃圾处理成为一个日益重要的问题。
城市垃圾的清运调度是垃圾处理链条中不可或缺的环节。
传统的清运调度方式存在诸多问题,如低效、不环保等,因此需要建立一种新的城市垃圾清运调度优化模型,以提高清运效率和保护环境。
二、城市垃圾情况分析城市垃圾的来源主要分为居民生活垃圾和商业垃圾,其中居民生活垃圾是城市垃圾的主要来源,占比超过70%。
由于城市化的快速发展,城市垃圾的产生量不断增加,但处理能力却没有同步提高,导致堆积如山的垃圾,加剧了城市环境问题。
三、城市垃圾清运调度传统方法传统的城市垃圾清运调度方法主要是根据经验和时间表来制定清运计划,由于没有充足的数据支持,导致往往存在以下问题:1.清运车辆利用率低,导致清运成本上升;2.清运范围无法全覆盖,导致部分地区积存垃圾;3.清运车辆的行车路线设计不合理,导致清运时间加长。
四、城市垃圾清运调度优化模型为了解决传统的垃圾清运调度方法存在的问题,可以采用优化模型来优化清运调度。
城市垃圾清运调度优化模型主要包括以下几个方面:1.数据采集和建模:利用传感器、监控器等设备收集数据,将城市垃圾的产生量、排放量、处理能力等信息输入优化模型中进行建模。
2.运算优化:将采集到的数据输入优化算法中进行计算,以优化整个清运调度过程,包括清运车辆运行轨迹规划、清运站点设计、清运车辆配备等。
3.结果分析:对优化后的清运调度方案进行分析,评估方案的有效性和可行性,同时对方案进行调整和优化。
五、城市垃圾清运调度优化模型的优点相比传统的城市垃圾清运调度方法,采用优化模型具有如下优点:1.减少清运成本:优化模型能够合理规划清运车辆的行车路线,提高清运车辆的利用率,从而减少清运成本。
2.全覆盖清运:优化模型能够研究每个地区的垃圾产生量和排放量,合理规划清运站点、清运车辆等,从而实现全覆盖清运。
3.保护环境:优化模型能够降低清运车辆的行车里程,从而减少污染物排放,保护环境。
城市垃圾运输问题

在上一个方案中可以发现运输路径9和10都是只运输一个垃圾场的垃圾,运完就会返回, 由图示可以发现路径5和路径7分别可以装载第5号和第37号垃圾集中点的垃圾,且绕路不多, 于是我们考虑到可否将第5号和第37号垃圾集中点分别添入路径5和路径7,具体如下图所示:
图4-3-2
文章题目:城市垃圾运输问题
9
根据此途径我们求的运费为3004.2元,相对上一个方案所用的的钱更少,具体的方案如下 表所示:
4.3问题三
4.3.1问题分析
在本问题中需要解决的是若有载重量为4吨、6吨、8吨三种运输车,又如何调度,以得到 最优的运输方案。在问题一中已求出当只有载重量为6吨的运输车时的合理的运输方案,由于 目标规划的条件是相似的,在这里我们只需将将对运输车载重的约束条件从不大于6吨改为不 大于8吨,在求得各条路线中,对于垃圾量不大于4吨的路线,调用4吨的运输车;对于垃圾量 在(4~6吨)之间的路线,调用6吨的运输车;对于垃圾量在(6~8吨)之间的路线,调用8吨 的运输车。
三、符号说明
四、模型的建立和求解 4.1问题一
根据题目所给的信息,建立合理的模型来调度运输车,使得总的运营费用达到最小。
4.1.1问题的分析
本问题主要是通过分析运输车的路线问题,从而计算出相应的运营费用,通过求得总运营 费用的最小值来确定运输车的调度方案。
4.1.2模型的建立
文章题目:城市垃圾运输问题
4
根据路线所示我们可以求得各个路线运输的垃圾重量,如下表所示:
表4-1-1
运输路线 路线1 路线2 路线3 路线4 路线5 路线6 路线7 路线8 路线9 路线10 路线11 路线12
站点序号 0―30―29―27―0 0―28―26―21―25―20―0 0―36―23―33―0 0―24―18―35―7―0 0―34―17―16―6―0 0―15―13―8―0 0―32―22―10―0 0―19―14―37―4―0 0―12―9―1―0 0―31―5―2―0
城市生活垃圾收运路线优化的数学模型与算法

收稿 日期 :2009一ll一20 基金项 目:国家大学生创新性实验计划项 目 (LA08037);中南大学教
育教学改革研究第五批项 目 作者 简 介 :路 玉龙 (1969一).男 ,中南大学本 科生 ,研究方 向 :应 用数学 。
1 问题描述
城 市生活垃 圾 收运 路 线优 化 问题 可 以描述 为 : 某地 有一 车库 ,假设 该车库 拥有多辆 运输车 ,并 且该
. .
【0 否 则
3 求解 算 法
垃圾 收运 问题可 以看成是 一种带 时间 窗的 车辆 路径 问题 ,当垃圾 收集 点的数量 增大时 ,问题 求解 的 难度 增 长迅速 。其 数学 模 型具 有 变 量多 ,容量 大 等 特点 ,求解其精确解难度极大。因此,在求解这类 大
:第 k辆 车在第 i个 节点 开始 收集 或者 卸载垃 规模 的路 径优 化 问题 时 ,大 多采 用启 发 式 方 法 。启
路 玉龙 ,赵扶摇 ,韩靖 ,张鸿雁
(1.中南大学 数学科学与计算技术学院.湖南 长沙 410083;2.中南大学 信息科学与工程学院 ,湖南 长沙 410083)
摘 要 :给 出了城市生活垃圾收运路线优化问题 的一般描述 ,考虑时间窗、车容量等约束 ,以收运路线总行 程最
短 为 目标。建立 了该优化 问题 的数 学模型。设计 了求解谊问题的单一组合邻域搜 索算法 。随机邻域搜 索算法和
of Municipal Domestic W aste Collection and nsportation
lm Yulong ,Zhao Fuyao ,Han Jing ,Zhang Hongyan
(1.School of Mathematical Science and Computing Technology,Central South UrIiversit)r,Changsha Hunan 410083,China; 2.Schol of Informat ion S c ience and Engineer ing,Central South University,Changsha Htman 410083,China)
城市垃圾运输问题Word版

魅力数模美丽师大浙江师范大学“同梦杯”第八届数学建模竞赛自信创新合作快乐A B论文题目城市垃圾运输问题编号 56组评分监制:浙江师范大学数学建模研究会(2009年5月7日)(说明:评分一栏为评阅人填写,请参赛者不要填写)垃圾运输问题摘要:该题我们的主要解题思路分三阶段:第一阶段,我们先根据题设条件和基本假设画出该题的图。
第二阶段,我们根据图和点的位置关系结合题设,归纳出一些最基本的确定路线的原则:在仔细分析该题后,我们认为该题为一个TSP与VRT相结合的问题。
我们先抛开空载费用,若要把所有的垃圾运回垃圾处理站,这部分有效工的费用为∑2.0*|Xi|*Yi(|Xi|为垃圾点Xi到原点的距离,Yi为垃圾点的垃圾量),是恒定不变的。
只要我们能保证空载路线最小,则所花的时间和费用都最小。
因此解题的关键在于找出一个调度方案,使空载行驶的线路最小。
第三阶段则是编制程序阶段,我们结合下山法逐点搜索,并引入随机生成器。
在出现后继点权值相等难以判断以哪点继续搜索时,由随机生成器确定。
为了让算法更接近人的思维,我们让更靠近父点的子点有更高的几率被作为下一个将去的垃圾点,这也与我们的算法原则对应。
采用计算机模拟搜索的计算方法,搜索出运输车投入辆数以及运输车最佳调配方案,使得在不考虑铲车的情况下运营费用最低。
总运营费用为运输车空载费与实际运输费之和。
问题的解答如下:第一问,求得所需总费用为2496.3元,所需总时间为23小时08分,路线分配图见正文;第二问,求得需4辆铲车,铲车费用为199.0元,分配图及运输车调度表见正文;第三问,运营总费用为:2460.6,其中8吨、6吨、4吨载重量的运输车各需5、2、3辆,路线分配图见正文。
关键词:单目标优化计算机搜索 TSP一、问题的重述某城区有 38 个垃圾集中点,每天都要从垃圾处理厂(第 38 号节点)出发将垃圾运回。
现有一种载重 6 吨的运输车。
每个垃圾点需要用 10 分钟的时间装车,运输车平均速度为 40 公里/小时(夜里运输,不考虑塞车现象);每台车每日平均工作 4 小时。
城市生活垃圾处理数学模型

与我本专业运用
象的数学知识放到大家看得见、摸得着、听得到的生活 情境中,从而让人们感受到生活中处处有数学,生活中 处处要用数学
。
贵州民族大学化学与环境科学学院
贵州民族大学化学与环境科学学院
自Hale Waihona Puke 的想法贵州民族大学化学与环境科学学院
中国城市生活现象
贵州民族大学化学与环境科学学院
贵州民族大学化学与环境科学学院
贵州民族大学化学与环境科学学院
日本的城市现象
贵州民族大学化学与环境科学学院
贵州民族大学化学与环境科学学院
贵州民族大学化学与环境科学学院
垃圾的分类
贵州民族大学化学与环境科学学院
贵州民族大学化学与环境科学学院
(2)运输车到达某个站点后,必须将此站点的所 有垃圾带走: xt,k ut,k(st xk,t);(t 1,2, 36) k1 37 (3)不允许出现自己往自己站点运输垃圾的现象, 即当i j时有: ui,j 0;(i,j 1,2 37)
贵州民族大学化学与环境科学学院
贵州民族大学化学与环境科学学院
三 模型的建立及求解
1 符号说明
• 每天运输前第i个垃圾站点的垃圾量
si
xi,j
• 第i个垃圾站点向第j个垃圾站点运输的垃圾量 • 运输车是否从第i个垃圾站点向第j个垃圾站点运输的01变量 • 第k辆铲车是否从第i条路径向第j条路径运输的0-1变量
贵州民族大学化学与环境科学学院
贵州民族大学化学与环境科学学院
。 五 模型评价 模型的优点
(1)此问题为典型的NP难问题,规划模型的规模较大,共有 2000多个变量,直接求解比较困难。由于在设计算法时采用了一 些技巧,将变量减少到800多个,从而求出了最优的结果。 (2)模型中将各约束条件均考虑在内,对问题的理解较全面, 因此求出的结果为最优。 (3)克服了NP难问题中很难得到最 优解的问题,通过对算法的技巧性设计,使得此问题得以圆满 的解决 模型的缺点 此问题在建模中存在很多难点,因此模型中只考虑了,对于一 个垃圾站点,一旦有运输车到此运输,则必须将所有垃圾带走, 而不能分批次运输,从而导致第8和第10条路径的总垃圾量分 别为3.3和4吨,运输量太少的情况,运输车不能得到充分地利 用。
数学建模:垃圾分类处理与清运方案设计

圆心O
南区 北区
<2>目标函数(最经济): (1)对于各个垃圾站点,只有一辆运输车经过,即每个站点的运进
点和运出点均是有且只有一个,即:
其中, (2)运输车到达某个站点后,必须将此站点的所有垃圾带走:
(3)不允许出现自己往自己站点运输垃圾的现象,即当时有:
(4)不允许从(垃圾转运站)运出垃圾到清运站,即:
1) 假定现有垃圾转运站规模与位置不变条件下,给出大、小型设备 (橱余垃圾)的分布设计,同时在目前的运输装备条件下给出清 运路线的具体方案。以期达到最佳经济效益和环保效果。
2) 假设转运站允许重新设计,请为问题1)的目标重新设计。
(二)问题分析 对于问题一的清运路线问题、路线运输车调度方案的设计,不能仅仅考 虑使运输车的行走路线最短,因为此处还存在着垃圾的累积运输的花费 问题,因此,我们的目标函数应该是使得所有运输的花费最少。在建模 过程中,我们无需考虑投入的运输车台数,只需对各条路径所花费的时 间进行和各运输车载重量约束即可,至于投入的车辆数,在各条路径确 定后,最终便可确定投入运输车数量和花费与收益.
外)站
外
司
1
10
4
12
月亮湾大道站
西部绿化长廊 北端
环卫总站
4
40
16
13
光前站
龙珠三路光前 村旁
环卫总站
1
20
8
14
北头站
前海路北头村 德盈利公
旁
司
1
15
6
15
涌下村站
桃园路涌下村 德盈利公
内
司
1
20
8
白石洲路与石
16
白石洲南站 洲中路交叉东 环卫总站
垃圾分类 数学 模型建立与求解【范本模板】

深圳市南山区垃圾运输问题研究摘要垃圾清运问题具有“产生源高度分散、处置高度集中、产生量和品质随季节变化”的特点。
就南山区垃圾运输的问题的调度方案,我们采用三个标定模型与多个最优化模型,给予了研究:问题一中,分两小问:1)大、小型设备(橱余垃圾)的分布设计;2)在目前的运输装备条件下给出清运路线的具体方案。
在第一小问中,我们首先根据供需关系确定大型设备的个数为3个,小型设备个数为0个.然后我们对所有垃圾中转站的管辖区域进行了有效性分配,确定运输到各垃圾转运站的垃圾数量以及垃圾种类。
最后我们根据各垃圾转运站的垃圾数量,用0—1矩阵采用多目标优化模型求解设备的分布坐标。
在第二小问中,我们根据第一小问确定的转运站管辖区域,优化每个区域的垃圾数量,让每个区域的垃圾转运站达到最高效利用。
同时根据垃圾转运站和垃圾处理设备的分布,采用图论Dijkstra算法,划分为三片区域求出路程最优化。
同时采用多目标优化评价模型对经济效应与环保效果进行评价,通过对路程优化结果的多次调整,对比后最终满足评价模型最优化的结果。
问题二中,要求对垃圾转运站重新设计。
问题一中,在对垃圾转运站的管辖区进行划分时,存在部分垃圾转运站超负荷转运情况严重,部分垃圾转运站利用率较低的不均衡分布问题。
针对此问题我们对垃圾转运站重新设计,均衡分配了各垃圾转运站的利用率。
然后再采用第一问的模型对设备的分布以及路线的选择进行重新划分。
最终求出深圳市南山区垃圾的最优处理方案。
关键字:标定模型影响率函数误差百分比最小二乘法曲线拟合1.问题重述1.1问题的背景:垃圾分类化收集与处理是有利于减少垃圾的产生,有益于环境保护,同时也有利于资源回收与再利用的城市绿色工程。
在发达国家普遍实现了垃圾分类化,随着国民经济发展与城市化进程加快,我国大城市的垃圾分类化已经提到日程上来。
2010年5月国家发改委、住房和城乡建设部、环境保护部、农业部联合印发了《关于组织开展城市餐厨废弃物资源化利用和无害化处理试点工作的通知》,并且在北京、上海、重庆和深圳都取得一定成果,但是许多问题仍然是垃圾分类化进程中需要深入研究的.1.2需要解决的问题用数学建模方法研究解决深圳市南山区垃圾运输问题的问题。
数学建模城市垃圾运输问题

货运公司运输问题数信学院14级信计班魏琮【摘要】本文是针对解决某港口对某地区8个公司所需原材料A、B、C的运输调度问题提出的方案。
首先考虑在满足各个公司的需求的情况下,所需要的运输的最小运输次数,然后根据卸载顺序的约束以及载重费用尽量小的原则,提出了较为合理的优化模型,求出较为优化的调配方案。
针对问题一,在两个大的方面进行分析与优化。
第一方面是对车次安排的优化分析,得出①~④公司顺时针送货,⑤~⑧公司逆时针送货为最佳方案。
第二方面根据车载重相对最大化思想使方案分为两个步骤,第一步先是使每个车次满载并运往同一个公司,第二步采用分批次运输的方案,即在第一批次运输中,我们使A材料有优先运输权;在第二批次运输中,我们使B材料有优先运输权;在第三批次中运输剩下所需的货物。
最后得出耗时最少、费用最少的方案。
耗时为40.3333小时,费用为4864.0元。
针对问题二,加上两个定理及其推论数学模型与问题一几乎相同,只是空载路径不同。
采取与问题一相同的算法,得出耗时最少,费用最少的方案。
耗时为26.3小时,费用为4487.2元。
针对问题三的第一小问,知道货车有4吨、6吨和8吨三种型号。
经过简单的论证,排除了4吨货车的使用。
题目没有规定车子不能变向,所以认为车辆可以掉头。
然后仍旧采取①~④公司顺时针送货,⑤~⑧公司逆时针送货的方案。
最后在满足公司需求量的条件下,采用不同吨位满载运输方案,此方案分为三个步骤:第一,使8吨车次满载并运往同一公司;第二,6吨位车次满载并运往同一公司;第三,剩下的货物若在1~6吨内,则用6吨货车运输,若在7~8吨内用8吨货车运输。
最后得出耗时最少、费用最省的方案。
耗时为19.6833小时,费用为4403.2元。
一、问题重述某地区有8个公司(如图一编号①至⑧),某天某货运公司要派车将各公司所需的三种原材料A,B,C从某港口(编号⑨)分别运往各个公司。
路线是唯一的双向道路(如图1)。
货运公司现有一种载重 6吨的运输车,派车有固定成本20元/辆,从港口出车有固定成本为10元/车次(车辆每出动一次为一车次)。
垃圾转运处理计算公式(从书上复制下来的)

垃圾转运处理计算公式(从书上复制下来的)垃圾处理1.废物转移(1)垃圾容器数量的确定。
? 集装箱数量对成本有很大影响,因此应提前计划和估算。
某一路段需要配置多少集装箱,主要考虑服务范围内的居民人数、人均垃圾产量、垃圾容重、集装箱大小和收集次数。
中国规定的集装箱数量应按照以下方法计算。
首先,根据以下公式计算容器服务范围内的每日垃圾产生量:?w=rca1a2(1)?式中:w―垃圾日产生量,t/d;r―服务范围内居住人口数,人;c―实测的垃圾单位产量,t/人d;a1―垃圾日产量不均匀系数,取1.1~1.15;a2―居住人口变动系数,取1.02~1.05。
? 然后根据方程式(2)和(3)转换每日产生的垃圾量:?vave=w/(a3dave)(2)?vmax=kAve(3)?式中:vave―垃圾平均日产生体积,m3/d;a3―垃圾容重变动系数,取0.7~0.9;dave―垃圾平均容重,t/m3;k―垃圾产生高峰时体积的变动系数,取1.5~1.8;vmax―垃圾高峰时日产生最大体积,m3/d)。
? 最后,使用方程式(4)和(5)计算收集点要设置的垃圾容器数量:?中堂=a4vave/(ef)(4)?nmax=a4vmax/(ef)(5)? 式中:中堂——平时设置的垃圾箱数量,PCs;E——单个垃圾箱容积,m3/件;F——垃圾容器的填充系数,取0.75~0.9;A4——垃圾收集周期,D/时间,每天收集一次时A4=1,每天收集两次时A4=0.5,每两天收集一次时A4=2,依此类推;Nmax——垃圾峰值期间要设置的垃圾容器数量。
?当已知nmax时,可以确定服务区域中垃圾存储容器的数量,然后在每个服务位置正确配置。
容器最好集中在收集点,收集点的服务半径一般不应超过70m。
在规划建造新住宅区时,未设垃圾通道的多层公寓一般每四幢应设置一个容器收集点,并建造垃圾容器间,以利于安置垃圾容器。
(2)清洁运输作业方法①移动容器操作方法:是指将某集装点装满的垃圾连容器一起运往中转卸货后,是否将空集装箱返回至原位置(一般方法)或下一个集装箱装载点?收集成本主要取决于收集时间。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
刘育兴 ,钟剑
(赣南师范学院a.数学与计算机科学学院;b.网络中心,江西赣州341000)
摘要:本文通过垃圾运输问题的模型建立与求解,总结出这类问题的一般性解法,即根据实际问题构造恰当
的有向或无向赋权图,把问题转化成mecq,的TSP问题,通过解决这类TSP问题,从而使原问题获得满意的解答.
例2【2 (工件加工顺序问题).现有l4件工件等待在一台机床上加工.某些工件加工必须安排在另一
些工件完工后才能开始,第j号工件的先期必须完工的工件如表5:
表5 工件加工顺序
维普资讯
第3期 刘育兴,钟剑垃圾运输问题的模型及其求解 55
试设计一个满足条件的加工顺序,使机床花费的总时间最少.
运输车空载费用为:(88+92+84+?+42)jIc 0.4=612 jIc 0.4=244.8(元)
铲车1的空载费用为:(44+l7+7+l3+8+29)jIc 0.4=47.2(元)
铲车2的空载费用为:(46+35+11+22)jIc 0.4=45.6(元)
铲车3的空载费用为:(42+28+6+11+l3+20)jIc0.4=48(元)
维普资讯
赣南师范学院学报 2006年
的行走路线分别为:铲车1:O—l一5 一O;铲车2:O一2—7-÷6一O;铲车3:O一3一l0—8—9一O.由于各
铲车的行走路线已确定且它们花在各条路线上的时间可精确计算出来,因此,根据铲车的情况和各运输车的
行走路线,可安排出如表4所示的较为满意的调度方案:
不要等待铲车,才能使得运输车的工作时间满足题目的要求——每日平均工作4 h.为此,应使铲车跟着运输
车跑完一条线路,也就是说,应使铲车铲完一条线路后再接着铲下一条线路.
问题解答:为叙述方便,每条路线上开始的垃圾集中点称为这条路线的始点,最后的垃圾集中点称为这
条路线的终点.每条线路上运输车行走的路程与花费的时间列表如表2: 莽
— 一3,总权值为45.这恰好就是这l9条H路
中的最短H路.下面考虑将工序1与6插入P2
中,共有8条不同的路,其中最短有向路为P2
8 一1一l4一l2一l3,总权值为29.因此,
所求加工顺序为Pl P2,.4 —ll一1O 一5—3—8 一2一l—l4一l2一l3,机床花费总的准备时间为
ll4.
所以,三辆铲车的总费用为:47.2+45.6+48=140.8(元)
运输车和铲车的总费用为:2216.97+24.8+140.8=2602.57(元)
3 总结与推广
上面通过对垃圾运输问题的解答,我们将其归结为数学建模中的一类较为普遍的问题,即要求经过所有
对象的遍历问题.垃圾运输问题就是这类问题的一个典型代表,这类问题的共同点是,它们都可以通过构造
权等于∞;其次,将原点0用3阶完全有向图来代替,三点分
别为Ol、o2、O3,弧上的权均为∞,Oi(i_1,2,3)与其他各点
之间的弧上权如下确定:Oi分别到点1,2,3的弧上的权等于
铲车由点0分别到路① ,② ,③ 的起点的空载费用,点4,5,
?
,lO分别到点Oi的弧上的权分别等于铲车由路4,5,?。lO
表4 行走路线与时间安排
运输车辆 行走路线及时问安排
1 10:00从点O发车一l1:06到达路线① 的起点一l:02返回点O
2 10:58从点O发车—+o:07到达路线②的起点一l:46返回点O
1O:00从点O发车一l1:03到达路线③ 的起点—加:46返回点O,再次从点O发车一l:l6到
表2 运输路程与时问
根据表2中各路线上运输车花费的时间,各运输车运输路线安排如表3所示:
表3 运输线路时间安排 为了寻找铲车合理的行走路线,构造一有向图D如下:将
各条线路看成一个点,路线① 、② 、?、⑩分别看成点1、2、?、
lO.点i到点j的弧上的权等于铲车由路i的终点到路j的始
点的空载费用,而由点4、5、?、l0分别到点1、2、3的弧上的
又如1998年全国大学生数学建模竞赛题B题《灾情巡视路线》,可将一般网络上多组最优巡视问题转
化为赋权完全图上的多个TsP问题,详细请参见文献[1].
参考文献:
[1】赵肝,但琦.数学建模与数学实验[M】.北京:高等教育出版社,2000.11.149—160.
[2] 李尚志.数学建模竞赛教程[M】.南京:江苏教育出版社。1996.308—312.
(2)含生成圈的图称为哈密顿图或日图.
定义3? 设G是完全(有向或无向)赋权图,在C中寻找权最小闭迹的问题称为TSP问题(即Traveling
Salesman Problem).若此闭迹是日圈,则称此闭迹为最佳日圈.
容易证明:在满足条件t‘}( )+t‘}( , )下,TSP问题可转化为寻找最佳H圈的问题,这可通过构造一
一个恰当的网络(即赋权图)或有向网络,将问题转化成TSP问题或寻找最佳H路的问题,再用合适的方法
求出近似最优解或最优解,问题便可迎刃而解.问题的关键就在于如何构造一个有效的网络,在实际问题中
应具体问题具体分析,有些问题并不是很容易地就能构造出有效的网络,而需要根据自己的经验创造性地构
造合适的网络.下面再举几个例子加以说明.
图2中共有l9条不同的H路,其中的最短
H路可用穷举法,也可用下面的近似方法:先用
Dijkstra算法求出4—3的最短有向路为Pl 4—
7—÷9— —3,总权值为39.ห้องสมุดไป่ตู้将工序lO和11插
人到Pl中,由于弧(10,9)和弧(11,10)的权都
是2,用子路7—11一lO一9替代路Pl冲的弧
(7,9),得最短有向路为Pl,.4—7一l 1一lO一9
个完全图来实现.
2 垃圾运输问题
例l 某城区有若干个垃圾集中点,每天都要从垃圾处理厂(第37号节点)出发将垃圾运回.假定运输
图1 运输车线路图
车的线路已确定下来共lO条(如图1所示).为了
节省费用,运输车在每条线路上总是先从远离处
理厂的垃圾集中点开始运送垃圾.现有6辆载重6
吨的运输车及装垃圾用的铲车,它们的平均速度
达路线⑧ 的起点— :O6返回点O
. 11:43从点O发车—加:14.5到达路线⑩ 的起点一l:06返回点O,再次从点O发车一l:43.5
。 到达路线④ 的起点— :l3返回点O
11:41从点O发车—加:32到达路线⑤的起点一2:
达路线⑨ 的起点— :33返回点O
O:15从点O发车一l:05.5到达路线⑦ 的起点—+2:
工件,弧(i,j)上的权等于tij,并根据各工序之间的加工次序的限制条件画出D中的一条主要路径P:4—7—
1l— 一3—8— 一14一l2一l3,所谓主要路径就是加工所有工件时,必须符合其先后次序而不能调换或改变
这种次序的路径.但主要路径中间可以插人别的在主要路径中未出现的工序.于是问题就变成在满足主要路
为40 kin/h(夜里运输,不考虑塞车现象),每个垃
圾点需要用10 rain的时间装车,每台运输车每日
平均工作4 h.运输车重载运费1.8元/吨km;运
输车和装垃圾用的铲车空载费用0.4 km.并
且假定街道方向均平行于坐标轴.请你给出满意
的运输调度方案(每台运输车的调度方案,每台铲
车的行走路线及总运营费用).
达路线⑥的起点— :o5返回点O
O3返回点O,再次从点O发车一2:33到
l9返回点O,再次从点O发车—+2:52到
铲车 行走路线及时问安排
l lO:00从点O发车—加:32到达路线⑤ 的起点一l:43.5到达路线④ 的起点一3:l3返回点O
1O:58从点O发车一l:O5.5到达路线⑦ 的起点一2:27.5到达路线⑥ 的起点,在此需等待
问题分析:若将工件序号j用点j表示,点i到点J的弧上的权等于加工完第1号工件后再接着加工第i
号工件时机床的准备时间tij,得赋权有向图D,于是问题就转化成:在赋权有向图D中,满足工件加工次序
的限制条件下,寻找最佳H路. ‘
问题解答:如下构造有向图D(V,A):D中的顶点i表示工作序号i,弧(i,j)表示工件i是工件j的前期
的终点分别到点0的空载费用,其余各弧上的权均等于∞.
于是,D是一个完全赋权有向图,问题转化成在D中寻找最
小哈密顿有向圈,可采用对调调优算法,通过编程计算,得到
近似最优哈密顿有向圈(把Oi(i=1,2,3)收缩为点0):O一十1
— -+ 一十7—÷6-+O一十3-+lO-+8 9-+O,因此,3辆铲车
鼍收稿日期:2005一l1一O8
作者简介:刘育兴(1968一),男,江西吉安人,赣南师范学院数学与计算机科学学院讲师,主要从事图论研究.
维普资讯
第3期 刘育兴,钟剑垃圾运输问题的模型及其求解 53
表l 垃圾点地理坐标数据表
问题分析:这是一个遍历问题,此问题的困难之处在于确定铲车的行走路线,并使得运输车工作时尽量
径P的条件下,在D中寻找最佳H路.由表可知:工序lO应在工序5之前,工序9应在工序3之前工序4之
后,工序1应在工序3之后工序l4之前,工序6应在工序8之后工序l4之前,故可将P分成两段:Pl:4—7
一ll— 一3,P2:3—8—2一l4一l2一l3.将工序lO与9插人Pl中可得如下图2:
