2018全国Ⅲ卷高考压轴卷(文科数学 Word版含)答案
2018高中高考全国3卷文科数学带答案

****2018 年一般高等学校招生全国一致考试文科数学注意事项:1.答卷前,考生务必然自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号,回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答案卡一并交回。
一、选择题:本题共12 小题,每题 5 分,共 60 分。
在每题给出的四个选项中,只有一项为哪一项符合题目要求的。
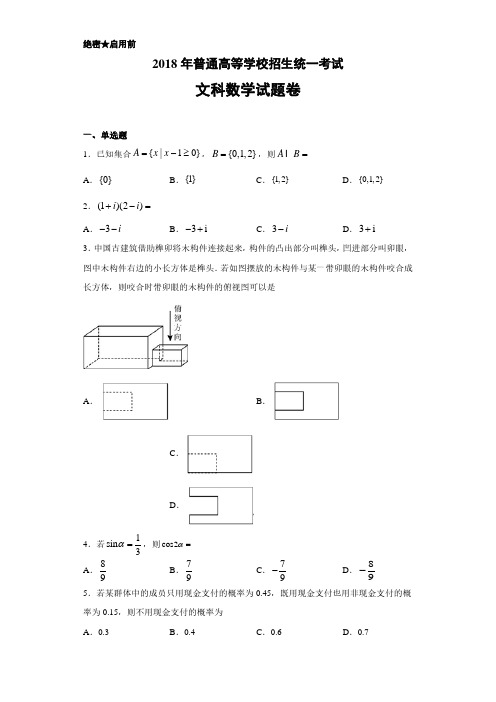
1.已知会集A x | x 1 ≥ 0,B0 ,1,2 ,则A BA.0B.1C.1,2D.0,1,22. 1 i 2 iA . 3 iB . 3 iC . 3 iD . 3 i3.中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫棒头,凹进部分叫卯眼,图中木构件右边的小长方体是棒头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是4.若 sin 1,则 cos2 3877D .8A .B .C .9 9995.若某集体中的成员只用现金支付的概率为0.45 ,既用现金支付也用非现金支付的概率为0.15 ,则不用现金支付的概率为A.B.C.D.6.函数 fx tan x 的最小正周期为21 tanxπ πC . πD . 2 πA .B .427.以下函数中,其图像与函数y ln x 的图像关于直线x 1 对称的是A . y ln 1 xB . y ln 2 xC . y ln 1 xD . y ln 2 x228.直线x y 20 分别与 x 轴, y 轴交于 A ,B 两点,点 P 在圆x 2y 2 上,则 ABP 面积的取值范围是 A . 2,6B . 4,8C . 2,3 2D . 2 2,3 21 / 8----****9.函数422yxx的图像大体为2 210 .已知双曲线x y0 ,b0 )的离心率为2 ,则点4 ,0 到 C 的渐近线的距离为C : 221 ( aa b32A . 2B . 2D .2 2C .22 2211 . ABC 的内角A ,B ,C 的对边分别为a ,b ,c .若ABC 的面积为ab c,则 Cπ π π π 4A .B .C .D .234612 .设A , B , C , D 是同一个半径为4 的球的球面上四点,ABC 为等边三角形且其面积为93 ,则三棱锥D ABC 体积的最大值为A .12 3B .18 3C .24 3D .54 3二、填空题:本题共 4 小题,每题5 分,共 20 分。
2018年高考文科数学全国卷3试题及详细解析(答案)Word版)

2
d
.故答案为D.
11 ABC
的内角A B C的对边分别为a b c 若ABC 的面积为2224
abc 则C
- 4 - A 2 B 3 C 4 D 6
解析 2222cos1
cos
442ABCabcabC
SabC 又1
sin
2ABCSabC 故tan1
C
∴4
C .故答案为C.
12 设A B C D是同一个半径为4的球的球面上四点 ABC
d ∴三棱锥DABC 体积最大值1
93(24)183
3DABCV .故答案为B.
二、填空题 本题共4小题 每小题5分 共20分
13 已知向量
=1,2a
=2,2 b
=1,λc 若
2∥ca+b 则 ________
解析 2(4,2)
ab
∵//(2)
cab
∴1240
解得1
2 .
14 某公司有大量客户 且不同龄段客户对其服务的评价有较大差异 为了解客户的评价
0.15 则不用现金支付的概率为
A 0.3 B 0.4 C 0.6 D 0.7
解析 由题意
10.450.150.4P .故答案为B.
6 函数
2tan
1tan
x
fx
x
的最小正周期为
A 4 B 2 C D 2
解析 2
222
2sin
tansincos1
cos
()sincossin2
sin
1tansincos2
1
cos
x
xxx
x
fxxxx
x
xxx
x
∴()
2018高考全国3卷文科数学带答案

2018高考全国3卷文科数学带答案2018年普通高等学校招生全国统一考试文科数学考试注意事项:1.在答题卡上填写姓名和准考证号。
2.选择题答案用铅笔涂黑,非选择题答案写在答题卡上。
3.考试结束后,将试卷和答题卡一并交回。
一、选择题:1.已知集合A={x|x-1≥2},B={1,2},则A∩B=?A。
∅ B。
{1} C。
{1,2} D。
{ }2.(1+i)(2-i)=?A。
-3-i B。
-3+i C。
3-i D。
3+i3.中国古建筑中,用榫卯连接木构件,凸出部分称为棒头,凹进部分称为卯眼。
如图,若摆放的木构件与带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可能是哪个?图片无法转载)4.若sinα=3/4,则cos2α=?A。
7/9 B。
87/99 C。
-9/8 D。
-95/875.某群体中,只用现金支付的概率为0.45,既用现金支付也用非现金支付的概率为0.15,则不用现金支付的概率为?A。
0.3 B。
0.4 C。
0.5 D。
0.66.函数f(x)=tanx/(1+tan^2x)的最小正周期为?A。
π B。
π/2 C。
π/4 D。
π/67.下列哪个函数的图像关于直线x=1对称于y=lnx的图像?A。
y=ln(1-x) B。
y=ln(2-x) C。
y=ln(1+x) D。
y=ln(2+x)8.直线x+y+2=0分别与x轴、y轴交于A、B两点,点P在圆(x-2)^2+y^2=2上,则△ABP面积的取值范围是?A。
[2,6] B。
[4,8] C。
[3√2,4√2] D。
[2√2,3√2]9.函数y=-x^4+x^2+2的图像大致是?图片无法转载)10.已知双曲线C: (x^2/a^2)-(y^2/b^2)=1(a>0,b>0)的离心率为2,则点(4,2)到C的渐近线的距离为?A。
2 B。
2√3 C。
4 D。
2√511.△ABC的内角A、B、C的对边分别为a、b、c。
若△ABC的面积为S,则C=?A。
2018文科数学全国卷3及其答案

2018年普通高等学校招生全国统一考试文科数学注意事项:1.答卷前,考生务必将自己的姓名和准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分.在每小题给的四个选项中,只有一项是符合题目要求的.1.已知集合{|10}A x x =-≥,{0,1,2}B =,则A B = A .{0}B .{1}C .{1,2}D .{0,1,2}2.(1i)(2i)+-=A .3i--B .3i-+C .3i-D .3i+3.中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫棒头,凹进部分叫卯眼,图中木构件右边的小长方体是棒头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是4.若1sin 3α=,则cos 2α=A .89B .79C .79-D .89-5.若某群体中的成员只用现金支付的概率为0.45,既用现金支付也用非现金支付的概率为0.15,则不用现金支付的概率为A .0.3B .0.4C .0.6D .0.76.函数2tan ()1tan xf x x=+的最小正周期为A .4πB .2πC .πD .2π7.下列函数中,其图像与函数ln y x =的图像关于直线1x =对称的是A .ln(1)y x =-B .ln(2)y x =-C .ln(1)y x =+D .ln(2)y x =+8.直线20x y ++=分别与x 轴,y 轴交于A ,B 两点,点P 在圆22(2)2x y -+=上,则ABP △面积的取值范围是A .[2,6]B .[4,8]C .2,32]D .[22,32]9.函数422y x x =-++的图像大致为10.已知双曲线22221(00)x y C a b a b-=>>:,2,则点(4,0)到C 的渐近线的距离为A 2B .2C .322D .2211.ABC △的内角A ,B ,C 的对边分别为a ,b ,c .若ABC ∆的面积为2224a b c +-,则C =A .2πB .3πC .4πD .6π12.设A ,B ,C ,D 是同一个半径为4的球的球面上四点,ABC △为等边三角形且其面积为,则三棱锥D ABC -体积的最大值为A.B.C.D.二、填空题:本题共4小题,每小题5分,共20分.13.已知向量(1,2)=a ,(2,2)=-b ,(1,)λ=c .若()2+ca b ,则λ=________.14.某公司有大量客户,且不同龄段客户对其服务的评价有较大差异.为了解客户的评价,该公司准备进行抽样调查,可供选择的抽样方法有简单随机抽样、分层抽样和系统抽样,则最合适的抽样方法是________.15.若变量x y ,满足约束条件23024020.x y x y x ++≥⎧⎪-+≥⎨⎪-≤⎩,,则13z x y =+的最大值是________.16.已知函数())1f x x =+,()4f a =,则()f a -=________.三、解答题:共70分,解答应写出文字说明、证明过程或演算步骤,第17~21题为必考题,每个试题考生都必须作答,第22、23题为选考题,考生根据要求作答.(一)必考题:共60分.17.(12分)等比数列{}n a 中,15314a a a ==,.(1)求{}n a 的通项公式;(2)记n S 为{}n a 的前n 项和.若63m S =,求m .18.(12分)某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min )绘制了如下茎叶图:(1)根据茎叶图判断哪种生产方式的效率更高?并说明理由;(2)求40名工人完成生产任务所需时间的中位数m ,并将完成生产任务所需时间超过m 和不超过m 的工人数填入下面的列联表:超过m不超过m第一种生产方式第二种生产方式(3)根据(2)中的列联表,能否有99%的把握认为两种生产方式的效率有差异?附:22()()()()()n ad bc K a b c d a c b d -=++++,2()0.0500.0100.0013.8416.63510.828P K k k ≥.19.(12分)如图,矩形ABCD 所在平面与半圆弧 CD所在平面垂直,M 是 CD 上异于C ,D 的点.(1)证明:平面AMD ⊥平面BMC ;(2)在线段AM 上是否存在点P ,使得MC ∥平面PBD ?说明理由.20.(12分)已知斜率为k 的直线l 与椭圆22143x y C +=:交于A ,B 两点.线段AB 的中点为(1,)(0)M m m >.(1)证明:12k <-;(2)设F 为C 的右焦点,P 为C 上一点,且FP FA FB ++=0 .证明:2||||||FP FA FB =+.21.(12分)已知函数21()exax x f x +-=.(1)求曲线()y f x =在点(0,1)-处的切线方程;(2)证明:当1a ≥时,()e 0f x +≥.(二)选考题:共10分,请考生在第22、23题中任选一题作答。
(完整版)2018年全国卷3文科数学试题及参考答案

年全国卷3文科数学试题及其参考答案 第3页(共13页) 6.函数2tan1tanxfxx的最小正周期为( ) A.4 B.2 C. D.2 【答案】C 【解析】2222tantancos1sincossin2221tan1tancosxxxfxxxxxkxxx,22T(定义域并没有影响到周期) 【考点】切化弦、二倍角、三角函数周期 7.下列函数中,其图像与函数lnyx的图像关于直线1x对称的是 A.ln1yx B.ln2yx C.ln1yx D.ln2yx 【答案】B 【解析】采用特殊值法,在lnyx取一点3,ln3A,则A点关于直线1x的对称点为'1,ln3A应该在所求函数上,排除A,C,D 【考点】函数关于直线对称 8.直线20xy分别与x轴、y轴交于点,AB两点,点P在圆2222xy上,则ABP面积的取值范围是( ) A.2,6 B.4,8 C.2,32 D.22,32 【答案】A 【解析】2,0,0,2AB,22AB,可设22cos,2sinP,则42sin4222sin2,3242PABd 122,62ABPPABPABSABdd
2018年高等学校招生全国统一考试押题卷文科数学试卷(三)及解析

绝密 ★ 启用前2018年普通高等学校招生全国统一考试押题卷文科数学(三)本试题卷共14页,23题(含选考题)。
全卷满分150分。
考试用时120分钟。
★祝考试顺利★注意事项:1、答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
用2B 铅笔将答题卡上试卷类型A 后的方框涂黑。
2、选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3、填空题和解答题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4、选考题的作答:先把所选题目的题号在答题卡上指定的位置用2B 铅笔涂黑。
答案写在答题卡上对应的答题区域内,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
5、考试结束后,请将本试题卷和答题卡一并上交。
第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知全集{}1,2,3,4U =,若{}1,3A =,{}3B =,则()()U U A B 痧等于( )A .{}1,2B .{}1,4C .{}2,3D .{}2,4【答案】D【解析】根据题意得到{} 2,4U A =ð,U B ð{}1,2,4=,故得到()()U U A B 痧{}2,4=.故答案为:D .2.在下列函数中,最小值为2的是( ) A .1y x x=+ B 1sin (0)sin 2y x x xπ=+<<C .2y =D .122x xy =+【答案】D【解析】A 选项x 可以是负数;B 选项2y ≥=,等号成立时sin 1x =,在定义域内班级 姓名 准考证号 考场号 座位号无法满足;C 由基本不等式知D 选项正确.3.从某校高三年级随机抽取一个班,对该班50名学生的高校招生体检表中视力情况进行统计,其结果的频率分布直方图如图所示:若某高校A 专业对视力的要求在0.9以上,则该班学生中能报A 专业的人数为( )A . 30B .25C .22D .20【答案】D【解析】()50 1.000.750.250.220⨯++⨯=,故选D . 4.函数sin 21cos xy x=+的部分图象大致为( )A .B .C .D .【答案】A【解析】因为函数为奇函数,所以其图象关于原点成中心对称,所以选项C ,D 错误;又当0,2x π⎛⎫∈ ⎪⎝⎭时,sin 201cos xy x=>+,所以选项B 错.本题选择A 选项.5.已知等差数列{}n a 的前n 项和为n S ,且233215S S -=,则数列{}n a 的公差为( ) A .3 B .4- C .5- D .6【答案】C【解析】设数列{}n a 的公差为d ,233215S S -=,()()121233215a a a a a ∴+-++=,315d =-,5d =-,故选C .6.某几何体由上、下两部分组成,其三视图如图所示,其俯视图是由一个半圆与其直径组成的图形,则该几何体上部分与下部分的体积之比为( )A .13B .12C .23D .56【答案】C【解析】根据题意得到原图是半个圆锥和半个圆柱构成的图形,圆锥的地面半径为2,圆柱底面半径为2,故得到圆锥的体积为142233⨯π⨯=π,半个圆柱的体积为14122π⨯⨯=π,该几何体上部分与下部分的体积之比为23.故答案为:C . 7.如果函数()()()()2128122f x m x n x m =-+-+>在区间[]2,1--上单调递减,那么mn 的最大值为( ) A .16 B .18 C .25 D .30【答案】B【解析】因为2m >,所以抛物线开口向下,所以822nm---≤,也即是()822n m ---≥,也即是122n m -≤,故()()22122212231818nm m m m m m -=-+=--+≤≤,当且仅当3m =,6n =等号成立,故选B . 8.已知函数()sin cos f x a x b x =+(x ∈R ),若0x x =是函数()f x 的一条对称轴,且0tan 2x =,则()a b ,所在的直线为( )A .20x y -=B .20x y +=C .20x y -=D .20x y +=【答案】C【解析】函数()sin cos f x a x b x =+(x ∈R ),若0x x =是函数()f x 的一条对称轴, 则0x x =是函数()f x 的一个极值点,()cos sin f x a x b x -'=,根据题意有()000c o s s i n 0f x a x b x =-=',又0tan 2x =,故0tan 2a b x b ==,结合选项,点()a b ,所在的直线为20x y -=.故选C .9.在如图所示的程序框图中,若输入的2s =,输出的2018s >,则判断框内可以填入的条件是( )开始输入x结束是否输出s 2s s =1i =1i i =+A .9i >B .10i ≤C .10i ≥D .11i ≥【答案】D【解析】输入2S =,1i =,242S ==;2i =,382S ==;当10i =,1122048S ==; 当10111i =+=,当11i ≥时,满足条件,退出循环,2048S =,故选D .10.函数()()sin (0,0)f x A x A ωϕω=+>>的图像如图所示,则()()()()12318f f f f++++的值等于()A B C 2+ D .1【答案】C【解析】由图知2A =,622T =-,8T ∴=,284ωππ==,2sin 224ϕπ⎛⎫⨯+= ⎪⎝⎭, ()2k k ϕ=π∈Z ,()2sin 4f x x π⎛⎫∴= ⎪⎝⎭, 所以()()()()12318f f f f ++++()()()()()21222812f f f f f =+++++()()1222f f =+=,选C .11.阿波罗尼斯(约公元前262-190年)证明过这样一个命题:平面内到两定点距离之比为常数k (0k >且1k ≠)的点的轨迹是圆.后人将这个圆称为阿氏圆.若平面内两定点A ,B 间的距离为2,动点P 与A ,B 2当P ,A ,B 不共线时,PAB △面积的最大值是( ) A .B 2C 22D 2【答案】A【解析】如图,以经过A ,B 的直线为x 轴,线段AB 的垂直平分线为y 轴,建立直角坐标系,则()1,0A -,()1,0B 设(),P x y ;2PA PB=()()2222121x y x y++-+=,两边平方并整理得:()222261038x y x x y +-+=⇒-+=,PAB △面积的最大值是122222⨯⨯=A .12.已知函数()f x 是定义在R 上的奇函数,其导函数为()f x ',若对任意的正实数x ,都有()()20xf x f x '+>恒成立,且21f =(),则使22x f x <()成立的实数x 的集合为( )A .(()22-∞+∞,B .(22-,C .(-∞D .)+∞【答案】C【解析】构造函数()()2g x x f x =,当0x >时,依题意有()()()20g x x xf x f x ⎡⎤=+⎣'>⎦',所以函数()g x 在0x >上是增函数,由于函数为奇函数,故在0x <时,也为增函数,且()00g =,22gf ==,所以不等式()()22xf xg x g<⇔<,根据单调性有x <C .第Ⅱ卷本卷包括必考题和选考题两部分。
2018高考全国3卷文科数学带答案

2018年普通高等学校招生全国统一考试文科数学注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号,回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答案卡一并交回。
一、选择题:本题共12 小题,每小题 5 分,共60 分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合 A x|x 1≥0 ,B 0,1,2 ,则 A BA.0 B. 1 C.1,2 D.0 ,1,22. 1 i 2 iA. 3 i B. 3 i C.3 i D.3 i3.中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫棒头,凹进部分叫卯眼,图中木构件右边的小长方体是棒头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是4.若sin 13,则cos2A.89B.79C.79D.895.若某群体中的成员只用现金支付的概率为0.45,既用现金支付也用非现金支付的概率为0.15,则不用现金支付的概率为A.0.3 B.0.4 C.0.6 D.0.76.函数 f xtan x21 tan x的最小正周期为A.π4B.π2C.πD.2 π7.下列函数中,其图像与函数y ln x 的图像关于直线x1对称的是A.y ln 1 x B.y ln 2 x C.y ln 1 x D.y ln 2 x2 28.直线x y 2 0 分别与x 轴,y轴交于A,B 两点,点P 在圆x 2 y 2 上,则ABP 面积的取值范围是A.2,6 B. 4 ,8 C. 2 ,3 2 D. 2 2 ,3 21/ 89.函数 4 2 2y x x 的图像大致为10.已知双曲线2 2x yC: 2 2 1(a 0 ,b 0 )的离心率为 2 ,则点 4 ,0 到C 的渐近线的距离为a bA. 2 B.2 C.3 22D.2 211.ABC 的内角 A ,B ,C 的对边分别为a,b ,c .若ABC 的面积为2 2 2a b c4,则CA.π2B.π3C.π4D.π612.设A,B ,C ,D 是同一个半径为 4 的球的球面上四点,ABC 为等边三角形且其面积为9 3 ,则三棱锥D ABC 体积的最大值为A.12 3 B.18 3 C.24 3 D.54 3二、填空题:本题共 4 小题,每小题 5 分,共20 分。
2018全国Ⅲ卷高考压轴卷文科数学(含答案)

2018全国Ⅲ卷高考压轴卷文科数学本试卷共23题(含选考题)。
全卷满分150分。
考试用时120分钟。
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知集合M ={}4x x ≤,N ={}2log x y x =,则M N ⋂=( ) A .[)4,+∞ B .(],4-∞ C .()0,4 D .(]0,4 2. “1a =”是“关于x 的方程230x x a -+=有实数根”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件3. z 为复数z 的共轭复数,i 为虚数单位,且1i z i ⋅=-,则复数z 的虚部为( ) A .i - B .-1 C .i D .14. 下列说法中正确的是A. 先把高三年级的2000名学生编号:1到2000,再从编号为1到50的50名学生中随机抽取1名学生,其编号为m ,然后抽取编号为 150,100,50+++m m m 的学生,这样的抽样方法是分层抽样法B. 线性回归直线a x b yˆˆˆ+=不一定过样本中心点),(y x C. 若两个随机变量的线性相关性越强,则相关系数r 的值越接近于1 D.若一组数据1、a 、3的平均数是2,则该组数据的方差是325. 已知命题p :),0(0+∞∈∃x ,使得00169x x -=,命题q : +∈∀N x ,0)1(2>-x 都有,则下列命题为真命题的是( )A.q p ∧B.q p ∨⌝)( C.()q p ⌝⌝∧)( D.())(q p ⌝⌝∨6. 若3cos()45πα-=,则s 2in α=( )A .725B .37 C.35- D .357. 执行如图所示的程序框图后,输出的值为4,则p 的取值范围是( )A .3748p <≤ B .516p > C .75816p ≤< D .75816p <≤8. 设0.60.3a =,0.60.5b =,3log 4c ππ=,则( )A .b a c >>B .a b c >>C .c b a >>D .c b a >>9. 某几何体的三视图如图所示,其中俯视图中六边形ABCDEF 是边长为1的正六边形,点G 为AF 的中点,则该几何体的外接球的表面积是( )A.316π B. 318π C. 48164π10. 设向量(,1)a x =,(1,3)b =-,且a b ⊥,则向量3a b -与b 的夹角为( ) A .6πB .3π C .23π D .6π511. 已知F 1、F 2是双曲线E :﹣=1(a >0,b >0)的左、右焦点,点M 在E 的渐近线上,且MF 1与x 轴垂直,sin ∠MF 2F 1=,则E 的离心率为( ) A.B.C.D .212. 已知函数()3,02sin cos ,0x x x f x x x x ⎧+>=⎨≤⎩ ,则下列结论正确的是 ( )A .()f x 是奇函数B .()f x 是增函数C .()f x 是周期函数D .()f x 的值域为[1,)-+∞ 二、填空题:本题共4小题,每小题5分,共20分。
2018年高考文科数学全国3卷Word精校版

2018年普通高等学校招生全国统一考试文科数学注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号,回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答案卡一并交回。
一、选择题(本题共12小题,每小题5分,共60分.在每小题给的四个选项中,只有一项符合)1.已知集合{}|10A x x =-≥,{}012B =,,,则A B =( )A .{}0B .{}1C .{}12,D .{}012,,2.()()12i i +-=( ) A .3i --B .3i -+C .3i -D .3i +3.中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫棒头,凹进部分叫卯眼,图中木构件右边的小长方体是棒头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是( )4.若1sin 3α=,则cos2α=( )A .89B .79C .79-D .89-5.若某群体中的成员只用现金支付的概率为0.45,既用现金支付也用非现金支付的概率为0.15,则不用现金支付的概率为( ) A .0.3 B .0.4 C .0.6 D .0.76.函数 ()2tan 1tan xf x x=+的最小正周期为( )A .4π B .2π C .π D .2π7.下列函数中,其图像与函数ln y x =的图像关于直线1x =对称的是( ) A .()ln 1y x =-B .()ln 2y x =-C .()ln 1y x =+D .()ln 2y x =+8.直线20x y ++=分别与x 轴,y 轴交于A ,B 两点,点P 在圆()2222x y -+=上,则ABP ∆面积的取值范围是( )A .[]26,B .[]48,C .D .⎡⎣9.函数422y x x =-++的图像大致为( )10.已知双曲线22221x y C a b-=:(00a b >>,),则点()40,到C 的渐近线的距离为( ) AB .2CD.11.ABC ∆的内角A ,B ,C 的对边分别为a ,b ,c .若ABC ∆的面积为2224a b c +-,则C =( )A .2πB .3πC .4πD .6π12.设A ,B ,C ,D 是同一个半径为4的球的球面上四点,ABC ∆为等边三角形且其面积为则三棱锥D ABC -体积的最大值为( ) A. B. C. D.二、填空题(本题共4小题,每小题5分,共20分)13.已知向量()=1,2a ,()=2,2-b ,()=1,λc .若()2∥c a +b ,则λ=________.14.某公司有大量客户,且不同龄段客户对其服务的评价有较大差异.为了解客户的评价,该公司准备进行抽样调查,可供选择的抽样方法有简单随机抽样、分层抽样和系统抽样,则最合适的抽样方法是________.15.若变量x y ,满足约束条件23024020.x y x y x ++⎧⎪-+⎨⎪-⎩≥,≥,≤则13z x y =+的最大值是________.16.已知函数())ln 1f x x =+,()4f a =,则()f a -=________.三、解答题(共70分,解答应写出文字说明、证明过程或演算步骤,第17~31题为必考题,每个试题考生都必须作答,第22、23题为选考题,考生根据要求作答.) (一)必考题:共60分。
2018高考全国3卷文科数学带答案

2018年普通高等学校招生全国统一考试文科数学注意事项:1答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2•回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡 皮擦干净后,再选涂其它答案标号,回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3 •考试结束后,将本试卷和答案卡一并交回。
一、选择题:本题共 12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合 题目要求的。
1 •已知集合 A 」.x|x _1A 0?, B A.0,1,2?,则 A"B 二A •:、0】 B • 1 C • 〈1 , 2 D • :0 , 1 , 22- 1i 2」二 A • -3 -iB •£ iC •3-i D • 3 i3 •中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫棒头,凹进部分叫卯眼,图中木构件右边的小长方体是棒头•若如图摆放的木构件与某一带卯眼 的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是4•若血'W ,则迹2 '0.45,既用现金支付也用非现金支付的概率为 0.15,则不 用现金支付的概率为A • 0.3B • 0.4C • 0.6D •0.76 •函数f x =tan x 1 tan 2 —的最小正周期为x八 nA • 一B • nC • nD •2 n427 •下列函数中, 其图像与函数 y -1 nx 的图像关于 •直线X =1对称的是A• y =1 n 1-x B • y =ln 2 —xC • y =ln 1 xD • y =ln 22 28 •直线x+y+2=0分别与x 轴,y 轴交于A , B 两点,点P 在圆(x -2)+y 2=2上,则 MBP 面积的取值范围是A • 12, 61B • 4 ,8】C •杠2,3 2D • 2「2 , 3 25 •若某群体中的成员只用现金支付的概率为 A1)9•函数y=_x 4・x 2 2的图像大致为则三棱锥D —ABC 体积的最大值为A . 12.3B . 183 二、填空题:本题共 4小题,每小题5分,共20分。
2018年高考真题全国3卷文科数学(附答案解析)
13.
2
【解析】
【分析】
由两向量共线的坐标关系计算即可.
(1)根据茎叶图判断哪种生产方式的效率更高?并说明理由;
(2)求 40 名工人完成生产任务所需时间的中位数 m ,并将完成生产任务所需时间超 过 m 和不超过 m 的工人数填入下面的列联表:
超过 m
不超过 m
第一种生产方式 第二种生产方式
(3)根据(2)中的列联表,能否有 99%的把握认为两种生产方式的效率有差异?
则 P (A ∪ B=) P (A) + P (B) + P (AB=) 1
= 因为 P (A) 0= .45, P (AB) 0.15
所以 P (B) = 0.4 ,
故选 B. 点睛:本题主要考查事件的基本关系和概率的计算,属于基础题. 6.C 【解析】 【详解】
分析:将函数
f
(
x
)
=
tanx 1+ tan2
Q= SVABC
= 3 AB2 9 3 4
∴AB = 6 , Q 点 M 为三角形 ABC 的中心 ∴BM = 2 BE = 2 3
3 ∴ RtVOMB 中,有 OM = OB2 − BM 2 = 2
∴DM = OD + OM = 4 + 2 = 6
( ) ∴ VD−ABC
= 1×9 max 3
3 × 6 = 18
分析:确定函数 y = lnx 过定点(1,0)关于 x=1 对称点,代入选项验证即可。
详解:函数 y = lnx 过定点(1,0),(1,0)关于 x=1 对称的点还是(1,0),只有=y ln (2 − x )
过此点。 故选项 B 正确 点睛:本题主要考查函数的对称性和函数的图像,属于中档题。 8.A 【解析】
2018年高考真题全国3卷文科数学Word版含解析

2018年高考真题全国3卷文科数学Word版含解析2018年普通高等学校招生全国统一考试(新课标III卷)文科数学注意事项:1.答题前,请先将自己的姓名和准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B铅笔在答题卡上对应题目的答案标号涂黑。
在试题卷和草稿纸上写的答案无效。
3.非选择题的作答:用签字笔直接在答题卡上对应的答题区域内作答。
在试题卷和草稿纸上作答无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
一、选择题(本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是正确的)1.已知集合 $A=\{x|x-1\geq0\}$,$B=\{1,2\}$,则 $A\capB=$()A。
$\varnothing$ B。
$\{1\}$ C。
$\{1,2\}$ D。
$\{1,2\}$2.$(1+i)(2-i)=$()A。
$-3-i$ B。
$-3+i$ C。
$3-i$ D。
$3+i$3.中国古建筑中,利用榫卯将木构件连接起来,构件的凸出部分叫做棒头,凹进部分叫做卯眼。
图中木构件右边的小长方体是棒头。
若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是(删除图)4.若 $\sin\alpha=\frac{3}{8}$,则 $\cos2\alpha=$()A。
$\frac{9}{7}$ B。
$\frac{7}{9}$ C。
$-\frac{9}{8}$ D。
$-\frac{7}{8}$5.若某群体中的成员只用现金支付的概率为0.45,既用现金支付也用非现金支付的概率为0.15,则不用现金支付的概率为()A。
0.3 B。
0.4 C。
0.6 D。
0.76.函数$f(x)=\frac{\tan x}{1+\tan^2x}$ 的最小正周期为()A。
$\frac{\pi}{4}$ B。
$\frac{\pi}{2}$ C。
2018高考全国3卷文科数学带答案

2018年普通高等学校招生全国统一考试文科数学注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号,回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答案卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合{}|10A x x =-≥,{}012B =,,,则A B =A .{}0B .{}1C .{}12,D .{}012,, 2.()()1i 2i +-= A .3i --B .3i -+C .3i -D .3i +3.中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫棒头,凹进部分叫卯眼,图中木构件右边的小长方体是棒头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是4.若1sin 3α=,则cos2α=A .89B .79C .79-D .89-5.若某群体中的成员只用现金支付的概率为0.45,既用现金支付也用非现金支付的概率为0.15,则不用现金支付的概率为 A .0.3 B .0.4C .0.6D .0.76.函数()2tan 1tan xf x x=+的最小正周期为 A .π4B .π2C .πD .2π7.下列函数中,其图像与函数ln y x =的图像关于直线1x =对称的是 A .()ln 1y x =-B .()ln 2y x =-C .()ln 1y x =+D .()ln 2y x =+8.直线20x y ++=分别与x 轴,y 轴交于A ,B 两点,点P 在圆()2222x y -+=上,则ABP ∆面积的取值范围是 A .[]26,B .[]48,C .232⎡⎤⎣⎦,D .2232⎡⎤⎣⎦,9.函数422y x x =-++的图像大致为10.已知双曲线22221x y C a b-=:(00a b >>,2()40,到C 的渐近线的距离为A 2B .2C 32D .2211.ABC ∆的内角A ,B ,C 的对边分别为a ,b ,c .若ABC ∆的面积为2224a b c +-,则C =A .π2B .π3C .π4D .π612.设A ,B ,C ,D 是同一个半径为4的球的球面上四点,ABC ∆为等边三角形且其面积为3则三棱锥D ABC -体积的最大值为A .123B .183C .243D .543二、填空题:本题共4小题,每小题5分,共20分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018全国Ⅲ卷高考压轴卷文科数学本试卷共23题(含选考题)。
全卷满分150分。
考试用时120分钟。
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知集合M ={}4x x ≤,N ={}2log x y x =,则M N ⋂=( )A .[)4,+∞B .(],4-∞C .()0,4D .(]0,42. “1a =”是“关于x 的方程230x x a -+=有实数根”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件 3. z 为复数z 的共轭复数,i 为虚数单位,且1i z i ⋅=-,则复数z 的虚部为( )A .i -B .-1C .i D .14. 下列说法中正确的是A. 先把高三年级的2000名学生编号:1到2000,再从编号为1到50的50名学生中随机抽取1名学生,其编号为m ,然后抽取编号为 150,100,50+++m m m 的学生,这样的抽样方法是分层抽样法B. 线性回归直线a x b yˆˆˆ+=不一定过样本中心点),(y x C. 若两个随机变量的线性相关性越强,则相关系数r 的值越接近于1D.若一组数据1、a 、3的平均数是2,则该组数据的方差是32 5. 已知命题p :),0(0+∞∈∃x ,使得00169x x -=,命题q : +∈∀N x ,0)1(2>-x 都有,则下列命题为真命题的是( )A.q p ∧B.q p ∨⌝)(C.()q p ⌝⌝∧)( D.())(q p ⌝⌝∨6. 若3cos()45πα-=,则s 2in α=( ) A .725 B .37 C.35- D .357. 执行如图所示的程序框图后,输出的值为4,则p 的取值范围是( )A .3748p <≤ B .516p > C .75816p ≤< D .75816p <≤8. 设0.60.3a =,0.60.5b =,3log 4c ππ=,则( )A .b a c >>B .a b c >>C .c b a >>D .c b a >>9. 某几何体的三视图如图所示,其中俯视图中六边形ABCDEF 是边长为1的正六边形,点G 为AF 的中点,则该几何体的外接球的表面积是( )A. 316πB. 318πC. 48164π10. 设向量(,1)a x =,(1,3)b =-,且a b ⊥,则向量3a b -与b 的夹角为( )A .6πB .3πC .23πD .6π511. 已知F 1、F 2是双曲线E:﹣=1(a >0,b >0)的左、右焦点,点M 在E 的渐近线上,且MF 1与x 轴垂直,sin ∠MF 2F 1=,则E 的离心率为( )A. B. C. D .212. 已知函数()3,02sin cos ,0x x x f x x x x ⎧+>=⎨≤⎩ ,则下列结论正确的是 ( )A .()f x 是奇函数B .()f x 是增函数C .()f x 是周期函数D .()f x 的值域为[1,)-+∞二、填空题:本题共4小题,每小题5分,共20分。
13. 已知实数x ,y 满足0010x y x y ≥⎧⎪≥⎨⎪+-≤⎩的最大值为 .14. 函数f (x )=x4cos 1x 4sin +的最小正周期是 . 15. 在平面直角坐标系xOy 中,点()0,3A -,若圆()()22:21C x a y a -+-+=上存在一点M 满足2MA MO =,则实数a 的取值范围是__________.16.函数()f x 的定义域R 内可导,若()()2f x f x =-,且当(),1x ∈-∞时,()()1'0x f x -<,设()()10,,32a f b f c f ⎛⎫=== ⎪⎝⎭,则,,a b c 的大小关系为 三、解答题:共70分。
解答应写出文字说明、证明过程或演算步骤。
第17~21题为必考题,每个试题考生都必须作答。
第22、23题为选考题,考生根据要求作答。
(一)必考题:60分。
17.(12分)已知等比数列{}n a 的所有项均为正数,首项14a =,且324,3,a a a 成等差数列.(1)求数列{}n a 的通项公式;(2)记1n n n b a a λ+=-,数列{}n b 的前n 项和n S ,若122n n S +=-,求实数λ的值.如图,在矩形ABCD 中,2,4,,AD AB E F ==分别为,AB AD 的中点,现将ADE ∆沿DE 折起,得四棱锥A BCDE - .(1)求证: //EF 平面ABC ;(2)若平面ADE ⊥平面BCDE ,求四面体FACE 的体积.19.(12分)《朗读者》栏目在央视一经推出就受到广大观众的喜爱,恰逢4月23日是“世界读书日”,某中学开展了诵读比赛,经过初选有7名同学进行比赛,其中4名女生A 1,A 2,A 3,A 4和3名男生B 1,B 2,B 3.若从7名同学中随机选取2名同学进行一对一比赛.(1)求男生B 1被选中的概率;(2)求这2名同学恰为一男一女的概率.20.(12分)椭圆C : +=1(a >b >0)的短轴两端点为B 1(0,﹣1)、B 2(0,1),离心率e=,点P 是椭圆C 上不在坐标轴上的任意一点,直线B 1P 和B 2P 分别与x 轴相交于M ,N 两点, (Ⅰ)求椭圆C 的方程和|OM|•|ON|的值;(Ⅱ)若点M 坐标为(1,0),过M 点的直线l 与椭圆C 相交于A ,B 两点,试求△ABN 面积的最大值.已知()()x f x e ax a R =-∈(e 为自然对数的底数).(Ⅰ)讨论()f x 的单调性;(Ⅱ)若()f x 有两个零点12,x x ,(1) 求a 的取值范围;(2)在(1)的条件下,求证:122ln x x a +<.(二)选考题:共10分。
请考生在第22、23题中任选一题作答。
如果多做,则按所做的第一题计分。
22.[选修4-4,坐标系与参数方程](10分)已知曲线C 1的参数方程为(t 为参数),以坐标项点为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 2的极坐标方程为ρ=﹣2sin θ.(1)把C 1的参数方程化为极坐标系方程;(2)求C 1与C 2交点的极坐标(ρ≥0,0≤θ<2π).23.[选修4—5:不等式选讲](10分)已知函数f (x )=|x ﹣a|+|2x ﹣1|(a ∈R ).(Ⅰ)当a=1时,求f (x )≤2的解集;(Ⅱ)若f (x )≤|2x+1|的解集包含集合[,1],求实数a 的取值范围.数学(文史类)试卷答案及评分参考一、选择题:1.【答案】D2.【答案】A【解析】关于x 的方程有实数根,则,据此可知:“ a=1”是“关于x 的方程有实数根”的充分不必要条件. 本题选择A 选项.3.【答案】D4.【答案】D5.【答案】D6.【答案】D7.【答案】A8.【答案】A9.【答案】C【解析】由三视图可知,该几何体是一个六棱锥P ABCDEF -,其底面ABCDEF 是边长为1的正六边形,有一个侧面PAF 是底边上的离为2的等腰三角形,且有侧面PAF ⊥底面ABCDEF ,设球心为O ,半径为,R O 到底面的距离为h ,底面正六边形外接球圆半径为()2221,12h h ∴+=-+,解得2215481,1,16256h R h =∴=+=∴此六棱锥P ABCDEF -的外接球表面枳为481481425664ππ⨯=,故选C. 10.【答案】D11.【答案】A【解析】∵MF 1与x 轴垂直,sin ∠MF 2F 1=,∴设MF 1=m ,则MF 2=3m ,由双曲线的定义得3m ﹣m=2a ,即2m=2a ,得m=a ,在直角三角形MF 2F 1中,9m 2﹣m 2=4c 2,即8m 2=4c 2,即8a 2=4c 2,即e=,故选:A . 12.【答案】D二、填空题:13.【答案】214.【答案】【解析】函数f (x )===tan2x .∴最小正周期T=.故答案为. 15. 【答案】[]0,3【解析】设满足2MA MO =的点的坐标为(),M x y ,由题意有:= ()2214x y +-=,即所有满足题意的点M 组成的轨迹方程是一个圆,原问题转化为圆()2214x y +-=与圆()()22:21C x a y a -+-+=有交点,据此可得关于实数a 的不等式组:13≥≤,解得: { 03x R x ∈≤≤,综上可得:实数a 的取值范围是[]0,3.16.【答案】b a c <<三、解答题:(一)必考题:60分。
17.(本小题满分12分)【答案】(1)设数列{}n a 的公比为q ,由条件可知23,3,q q q 成等差数列,所以236q q q =+,解得3q =-或2q =,因为0q >,所以2q =,所以数列{}n a 的通项公式为12()n n a n N ++=∈ .(2)由(1)知,1122(2)2n n n n n n b a a λλλ++=-=-⋅=-⋅,因为122n n S +=-,所以2n n b =,所以1(2)22n n λ+-⋅=,所以32λ=.18.(本小题满分12分)【答案】解:(1)取线段AC 的中点M ,连接,MF MB ,因为F 为AD 的中点,所以MF CD ,且12MF CD =,在折叠前,四边形ABCD 为矩形,E 为AB 的中点,所以BE CD ,且12BE CD =.MF BE ∴,且MF BE =,所以四边形BEFM 为平行四边形,故EF BM ,又EF ⊄平面,ABC BM ⊂平面ABC ,所以EF // 平面ABC .(2) 在折叠前,四边形ABCD 为矩形,2,4,AD AB E ==为AB 的中点,所以,ADE CBE ∆∆都是等腰直角三角形,且2AD AE EB BC ====,所以45DEA CEB ∠=∠=,且DE EC ==.又180,90DEA DEC CEB DEC ∠+∠+∠=∴∠=,又平面ADE ⊥平面BCDE ,平面ADE 平面,BCDE DE CE =⊂平面BCDE ,所以CE ⊥平面ADE ,即CE 为三棱锥C EFD -的高.因为F 为AD 的中点,所以111221224EFA S AD AE ∆=⨯⨯=⨯⨯=,所以四面体FACE 的体积11133EFA V S CE ∆=⨯=⨯⨯=. 19.(本小题满分12分)【答案】(1)经过初选有7名同学进行比赛,其中4名女生A 1,A 2,A 3,A 4和3名男生B 1,B 2,B 3.从7名同学中随机选取2名同学进行一对一比赛.基本事件总数n=,设事件A 表示“男生B 1被选中”,则事件A 包含的基本事件有: (A 1,B 1),(A 2,B 1),(A 3,B 1),(A 4,B 1),(B 1,B 2),(B 1,B 3),共6个,∴男生B 1被选中的概率P (A )=.(2)设事件B 表示“这2名同学恰为一男一女”,则事件B 包含的基本事件有: (A 1,B 1),(A 1,B 2),(A 1,B 3),(A 2,B 1),(A 2,B 2),(A 2,B 3),(A 3,B 1),(A 3,B 2),(A 3,B 3),(A 4,B 1),(A 4,B 2),(A 4,B 3),共12个,∴这2名同学恰为一男一女的概率p=.【解析】(1)先求出基本事件总数n=,设事件A表示“男生B1被选中”,利用列举法求出事件A包含的基本事件个数,由此能求出男生B1被选中的概率.(2)设事件B表示“这2名同学恰为一男一女”,利用列举法求出事件B包含的基本事件个数,由此能求出这2名同学恰为一男一女的概率.20.(本小题满分12分)【答案】(Ⅰ)椭圆C: +=1(a>b>0)焦点在x轴上,由B1(0,﹣1)、B2(0,1),知b=1,由椭圆的离心率e==,则c2=a2,由a2﹣b2=c2,a2﹣1=a2,解得:a2=4,∴椭圆C的方程为:;设点P(x0,y0),则直线B1P方程为y=x﹣1,令y=0,得x M=,同理可得x N=,∴|OM|•|ON|=丨x M丨•丨x N丨=丨丨•丨丨==4,|OM|•|ON|=4;(Ⅱ)当点M坐标为(1,0)时,点N(4,0),丨MN丨=3,设直线AB的方程为x=ty+1,A(x1,y1),B(x2,y2),,整理得(t2+4)y2+2ty﹣3=0,则y1+y2=﹣,y1•y2=﹣,丨y1﹣y2丨===,△ABN面积S=丨MN丨•丨y1﹣y2丨=•=,∵t2≥0,则+≥+=,∴S≤,因此当t=0,即直线AB的方程为x=1时,△ABN面积的最大值是.【解析】(Ⅰ)由b=1,离心率e==,则c2=a2,由a2﹣b2=c2,代入即可求得a和b的值,求得椭圆方程,设点P (x 0,y 0),则直线B 1P 方程为y=x ﹣1,y=0,得x M =,同理可得x N =,∴|OM|•|ON|=丨x M 丨•丨x N 丨==4;(Ⅱ)设直线AB 的方程为x=ty+1,代入椭圆方程,由韦达定理求得丨y 1﹣y 2丨==,S=丨MN 丨•丨y 1﹣y 2丨=,由函数的单调性即可求得△ABN 面积的最大值.21.(本小题满分12分)【答案】(Ⅰ)()f x 的定义域为R ,()x f x e a '=-,(1)当0a ≤时,()0f x '>在R 上恒成立,∴()f x 在R 上为增函数;(2)当0a >时,令()0f x '>得ln x a >,令()0f x '<得ln x a <,∴()f x 的递增区间为(ln ,)a +∞,递减区间为(,ln )a -∞;(Ⅱ)(1)由(Ⅰ)知,当0a ≤时, ()f x 在R 上为增函数,()f x 不合题意; 当0a >时, ()f x 的递增区间为(ln ,)a +∞,递减区间为(,ln )a -∞,又(0)0f e =>,当x →+∞时,()f x →+∞,∴()f x 有两个零点12,x x ,则min ()(ln )ln (1ln )0f x f a a a a a a ==-=-<,解得a e >;(2)由(Ⅱ)(1),当a e >时,()f x 有两个零点12,x x ,且()f x 在(ln ,)a +∞上递增, 在(,ln )a -∞上递减,依题意,12()()0f x f x ==,不妨设12ln x a x <<.要证122ln x x a +<,即证122ln x a x <-,又12ln x a x <<,所以122ln ln x a x a <-<, 而()f x 在(,ln )a -∞上递减,即证12()(2ln )f x f a x >-,又12()()0f x f x ==,即证22()(2ln )f x f a x >-,(2ln x a >). 构造函数2()()(2ln )22ln (ln )x x a g x f x f a x e ax a a x a e =--=--+>,2()220xx a g x e a a e '=+->=,∴()g x 在(ln ,)a +∞单调递增, ∴()(ln )0g x g a >=,从而()(2ln )f x f a x >-,∴22()(2ln )f x f a x >-,(2ln x a >),命题成立.(二)选考题:共10分22.[选修4-4,坐标系与参数方程](10分)【答案】(1)∵曲线C 1的参数方程为(t 为参数),∴曲线C 1的直角坐标方程为(x+4)2+(y+5)2=25,∴x=ρcos θ,y=ρsin θ,∴(ρcos θ+4)2+(ρsin θ+5)2=25,化简,得到C 1的极坐标方程为:ρ2+8ρcos θ+10ρsin θ+16=0.(2)将ρ=﹣2sin θ代入ρ2+8ρcos θ+10ρsin θ+16=0,化简,得:sin 2θ+sin θcos θ﹣1=0,整理,得sin (2θ﹣)=,∴2θ﹣=2k π+或=2k π+,k∈Z ,由ρ≥0,0≤θ<2π,得或,代入ρ=﹣2sin θ,得或,∴C 1与C 2交点的极坐标为(,)或(2,).【解析】(1)先求出曲线C 1的直角坐标方程,再由x=ρcos θ,y=ρsin θ,能求出到C 1的极坐标方程.(2)将ρ=﹣2sin θ代入ρ2+8ρcos θ+10ρsin θ+16=0,得sin (2θ﹣)=,由此能求出C 1与C 2交点的极坐标.23.[选修4—5:不等式选讲](10分)【答案】( I )当a=1时,f (x )=|x ﹣1|+|2x ﹣1|,f (x )≤2⇒|x ﹣1|+|2x ﹣1|≤2,上述不等式可化为或或解得或或∴或或,∴原不等式的解集为.( II)∵f(x)≤|2x+1|的解集包含,∴当时,不等式f(x)≤|2x+1|恒成立,即|x﹣a|+|2x﹣1|≤|2x+1|在上恒成立,∴|x﹣a|+2x﹣1≤2x+1,即|x﹣a|≤2,∴﹣2≤x﹣a≤2,∴x﹣2≤a≤x+2在上恒成立,∴(x﹣2)max≤a≤(x+2)min,∴,所以实数a的取值范围是.【解析】( I)运用分段函数求得f(x)的解析式,由f(x)≤2,即有或或,解不等式即可得到所求解集;(Ⅱ)由题意可得当时,不等式f(x)≤|2x+1|恒成立.即有(x﹣2)max≤a ≤(x+2)min.求得不等式两边的最值,即可得到a的范围.。
