C++实现修正单纯形法优化

合集下载

单纯形法C实现

#include<stdio.h>#define M 5#define N 7float Max(float a[],int n);int k,l;void main(){ float a[M][N];//{{0,2,3,0,0,0,0},{12,2,2,1,0,0,0},{8,1,2,0,1,0,0},{16,4,0,0,0,1, 0},{12,0,4,0,0,0,1}};//初始化单纯形表float cb[M],X[N],z[N],cj[N];//z[M]为检验数准备,jj[M],cj[N]是检验数int jj[M],i,j;int s,p,t=0;float maxcj,Z=0.0;printf("请输入一个%d行%d列的初始单纯形表用于求解%d个约束条件%d个变量的线性规划的原问题！",M,N,M-1,N-1);printf("\n"); printf("请输入初始单纯形表的第1行元素即变量的价值系数（第一个元素应默认为0.0）！");printf("\n");for(j=0;j<N;j++)scanf("%f",&a[0][j]);for(i=1;i<M;i++){printf("请输入初始单纯形表的第%d行元素即限定条件与系数矩阵！",i+1);printf("\n");for(j=0;j<N;j++)scanf("%f",&a[i][j]);}//初始化单纯形表*/for(i=1;i<N;i++) //最优解矩阵的初始化X[i]=0.0;for(j=1;j<N;j++){ s=0;p=0;for(i=1;i<M;i++){if(a[i][j]==1){s++;p=i;}}if(s==1)jj[p]=j;} //确定初始基变量，并标识基变量位置//jj[1]=3;jj[2]=4;jj[3]=5;jj[4]=6;//确定初始基变量，并标识基变量位置for(i=1;i<M;i++) cb[i]=a[0][jj[i]]; //基变量的价值系数for(j=0;j<N;j++)X[j]=0.0;for(i=1;i<M;i++)X[jj[i]]=a[i][0];for(j=1;j<N;j++){ z[j]=0.0;for(i=1;i<M;i++)z[j]+=cb[i]*a[i][j]; }//为寻找出基变量的检验数做准备for(j=1;j<N;j++){ cj[j]=0.0;cj[j]=a[0][j]-z[j];}// 检验数maxcj=Max(cj,N);printf("*********************************\n"); printf("输入的单纯形表如下：\n");for(i=0;i<M;i++){ for(j=0;j<N;j++)printf("%6.2f",a[i][j]);printf("\n");} //输出初始化单纯形表//for(i=1;i<M;i++)//printf("%6.2f",cb[i]);printf("\n");//输出基变量的价值系数//for(i=1;i<N;i++)//printf("%6.2f",X[i]);printf("\n");//输出一个基本可行解矩阵//for(j=1;j<N;j++)//printf("%6.2f",cj[j]);printf("\n");// 输出检验数printf("*********************************\n");while(maxcj>0){float R,alk;R=1000.0;for(i=1;i<M;i++)if(a[i][k]>0){ if(R>a[i][0]/a[i][k]){ R=a[i][0]/a[i][k];l=i;}else if(R==a[i][0]/a[i][k])if(jj[l]<jj[i])l=i;else;}if(R==1000.0){ printf("此问题无解!");t=1;break;}jj[l]=k;alk=a[l][k];for(j=0;j<N;j++)a[l][j]=a[l][j]/alk;for(i=1;i<M;i++)if(i!=l)for(j=0;j<N;j++)if(j!=k)a[i][j]=a[i][j]-a[l][j]/a[l][k]*a[i][k]; for(i=1;i<M;i++)if(i!=l)a[i][k]=0.0;for(i=1;i<M;i++)cb[i]=a[0][jj[i]]; //基变量的价值系数for(j=0;j<N;j++)X[j]=0.0;for(i=1;i<M;i++)X[jj[i]]=a[i][0];for(j=1;j<N;j++){ z[j]=0.0;for(i=1;i<M;i++)z[j]+=cb[i]*a[i][j]; }//为寻找出基变量的检验数做准备for(j=1;j<N;j++){ cj[j]=0.0;cj[j]=a[0][j]-z[j];} // 检验数maxcj=Max(cj,N);}if(t!=1){for(j=0;j<N;j++)Z+=a[0][j]*X[j];for(i=0;i<M;i++){ for(j=0;j<N;j++)printf("%6.2f",a[i][j]);printf("\n");}//输出初始化单纯形表//for(i=1;i<M;i++)//printf("%6.2f",cb[i]);printf("\n");//输出基变量的价值系数printf("满足最优解时，X的取值如下：");printf("\n");for(i=1;i<N;i++)printf("X[%d]=%6.2f,",i,X[i]);printf("\n");//输出一个基本可行解矩阵//for(j=1;j<N;j++)//printf("%6.1f",z[j]);printf("\n");//for(j=1;j<N;j++)//printf("%6.2f",cj[j]);printf("\n");// 输出检验数printf("最优解为Z=%6.2f",Z);printf("\n");}}float Max(float a[],int n){int i,maxjj;float maxaj;maxaj=a[1];maxjj=1;for(i=2;i<n;i++)if(maxaj<a[i]){ maxaj=a[i]; maxjj=i;} k=maxjj;return (maxaj);}。

改进单纯形法讲解1

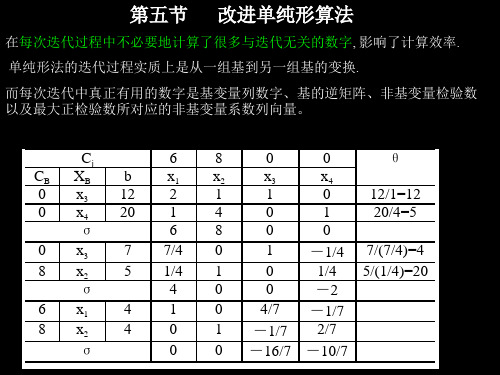
根据矩阵理论，第二步迭代表中的任何数都可由B2－1左乘原始数据得到 1
如：p‘
2＝B2
－1
p2＝
1 0 -
1 0
-
1 0 4 1 4 1 4
p‘3＝B2－1 p3＝
p‘4＝B2－1 p4＝
CB 0 0 0 8 6 8 Cj XB x3 x4 σ x3 x2 σ x1 x2 σ b 12 20 7 5 4 4 6 x1 2 1 6 7/4 1/4 4 1 0 0 8 x2 1 4 8 0 1 0 0 1 0 0 x3 1 0 0 1 0 0 4/7 －1/7 －16/7 0 x4 0 1 0 －1/4 1/4 －2 －1/7 2/7 －10/7 θ 12/1=12 20/4=5 7/(7/4)=4 5/(1/4)=20
例1. 已知: 迭代前的基为: 1 0 0 0 B=( p1, p2, p3, p4 )= 0 1 0 0 0 0 0 1 迭代后的基为: 1 0 0 1 0 0 0 0
1 1
=I
B =(p1, p2, p5, p4) =
-2 0 3 0 5 0 4 1
第r列 -a’1k/a’rk -a’2k/a’rk . . . 1/a’rk . . . . . . -a’mk/a’rk
改进单纯形法的计算步骤可以归结为： (1)在下一步迭代的基变量确定后，求新单纯形表中基矩阵B的逆 θ 矩阵B－1，并求基可行解XB＝B－1 b C XC b x6 x8 x0 x0 0 x 12 2 1 1 0 12/1=12 T -1 0 x 20 1 4 0 1 20/4=5 (2)计算和单纯形乘子Y = CB B 6 8 0 0 σ 0 x 7 7/4 0 1 －1/4 7/(7/4)=4 并计算非基变量的检验数 8 x 5 1/4 1 0 1/4 5/(1/4)=20 4 0 0 σ －2 σN＝CN－CBB－1N＝ CN－ YN 6 x 4 1 0 4/7 －1/7 8 x 4 0 1 2/7 －1/7 － 1 0 0 σ －16/7 －10/7 σj＝Cj－CBB Pj＝ Cj－ Y Pj ，如果有σj ≤0，达到最优解，计算结束。否则转入下一步 (3)根据max {l ∣ l > 0，l∈IN } = k,确定 xk 为换入变量(即为新基的基变量) 计算P‘k＝B－1Pk＝（a1k’、a2k’、…… amk’ ）若aik’ ≤0，线性规划问题有无界解，计算结束。否则转入下一步（4）按最小比值原则来确定第r行基变量xr为换出变量

修正单纯形法

单纯形法的解题思路（一）
在单纯形法计算过程中，我们的目的是求出问题的最优解，判断是否得到最优解的原则是检验数的符号，当求最大值时，要求Zj-Cj≥0；当求最小值时，要求Zj-Cj≤0。如果不满足条件，可根据Zj-Cj的大小找出主元列（∣Zj-Cj∣最大者），找出主元列Pj*后，再计算Qi，而后，根据Qi大小找出主元行（Qi最小者），主元列所对应变量为调入变量，主元行所对应的变量为调出变量，调换基变量后，再重新计算检验数进行判断。
单纯形法的一般解题步骤
改进单纯形法。其基本步骤和单纯形法大致相同，主要区别是在逐次迭代中不再以高斯消去法为基础，而是由旧基阵的逆去直接计算新基阵的逆，再由此确定检验数。这样做可以减少迭代中的累积误差，提高计算精度，同时也减少了在计算机上的存储量。高斯消去法，又称高斯消元法，实际上就是我们俗称的加减消元法。它是线性代数中的一个算法，用于决定线性方程组的解，决定矩阵的秩，以及决定可逆方矩阵的逆。当用于一个矩阵时，高斯消去产生“行消去梯形形式”。
迭代2（4）
求检验数
Z j C j CB Pj C j CB B 1 Pj C j Pj C j
1 2 5 0 1 1 0 1 2 0 1 1 0 0 1
C B B 1
迭代2（5）
1 Z 1 C1 P1 C1 0 1 1 4 3 1 0 2
迭代1（5）
1 Z 1 C1 P1 C1 0 M 2 M 1 4 3 1 0 2 2 Z 2 C 2 P2 C 2 0 M 2 M 1 1 1 M 1 0 0

使用C语言实现单纯形法求解线性规划问题

请输入初始基变量的数字代码 num 矩阵: 0.00 0.00 -1.00 0.00 -0.20
所得解3 已经是最4 优解! 5 --------------------------------------------------------------------------
最优解请为输:入方程组右边的值矩阵 b:
for(j=0;j<n;j++)
printf("%8.2f ",A[i][j]);
printf("\n");
}
printf("\n--------------------------------------------------------------------------\n");
printf("\t\t\t");
第 2 页共 14 页
自动化系上机实验报告（课程名称：运筹学）
学生姓名：
找出初始基可行
解列出初始单纯
形表计算校验数
学号：
计算新的单纯形表
所有δ j<=0?
对于某个δ j>0，是否存在 Pj<=0 确定为入基变量
确定出基变量
已得最优解，结束
无最优解，结束
2、单纯形算法程序的规格说明各段代码功能描述：（1）、定义程序中使用的变量 #include<stdio.h> #include<math.h> #define m 3 /*定义约束条件方程组的个数*/ #define n 5 /*定义未知量的个数*/
4/23/2021 7:33:32 AM
第 9 页共 14 页
自动化系上机实验报告（课程名称：运筹学）

单纯形法C++实现

单纯形法C++实现使⽤单纯型法来求解线性规划，输⼊单纯型法的松弛形式，是⼀个⼤矩阵，第⼀⾏为⽬标函数的系数，且最后⼀个数字为当前轴值下的 z 值。

下⾯每⼀⾏代表⼀个约束，数字代表系数每⾏最后⼀个数字代表 b 值。

算法和使⽤单纯性表求解线性规划相同。

对于线性规划问题：Max x1 + 14* x2 + 6*x3s . t . x1 + x2 + x3 <= 4 x1<= 2 x3 <= 3 3*x2 + x3 <= 6 x1,x2,x3 >= 0我们可以得到其松弛形式：Max x1 + 14*x2 + 6*x3s.t. x1 + x2 + x3 + x4 = 4 x1 + x5 = 2 x3 + x6 = 3 3*x2 + x3 + x7 = 6 x1 , x2 , x3 , x4 , x5 , x6 , x7 ≥ 0我们可以构造单纯性表，其中最后⼀⾏打星的列为轴值。

单纯性表x1x2x3x4x5x6x7bc1=1c2=14c3=6c4=0c5=0c6=0c7=0-z=011110004100010020010010303100016****在单纯性表中，我们发现⾮轴值的x上的系数⼤于零，因此可以通过增加这些个x的值，来使⽬标函数增加。

我们可以贪⼼的选择最⼤的c，再上⾯的例⼦中我们选择c2作为新的轴，加⼊轴集合中，那么谁该出轴呢？其实我们由于每个x都⼤于零，对于x2它的增加是有所限制的，如果x2过⼤，由于其他的限制条件，就会使得其他的x⼩于零，于是我们应该让x2⼀直增⼤，直到有⼀个其他的x刚好等于0为⽌，那么这个x就被换出轴。

我们可以发现，对于约束⽅程1，即第⼀⾏约束，x2最⼤可以为4（4/1），对于约束⽅程4，x2最⼤可以为3(6/3），因此x2最⼤只能为他们之间最⼩的那个，这样才能保证每个x都⼤于零。

因此使⽤第4⾏，来对各⾏进⾏⾼斯⾏变换，使得⼆列第四⾏中的每个x都变成零，也包括c2。

优化设计-单纯形法

x0[1]=0.5*(x0[1]+xe[1]);
x1[0]=0.5*(x1[0]+xe[0]);
x1[1]=0.5*(x1[1]+xe[1]);
x2[0]=0.5*(x2[0]+xe[0]);
x2[1]=0.5*(x2[1]+xe[1]);
}
float max(float x,float y)
{if (x>y)return x;
else {fh=f0; fe=f1; xh=x0; xe=x1; p[0]=0;p[1]=1;p[2]=1;} }
else { fh=f2; fe=f1; xh=x2; xe=x1; p[0]=1;p[1]=1;p[2]=0;} }
else { if(f0<f2)
{ if(f1<f2){fh=f2; fe=f0; xh=x2; xe=x0; p[0]=1;p[1]=1;p[2]=0;}
step3:
{ if(fn4>fh) {sx(); goto step4;}
else {xh[0]=xn4[0];xh[1]=xn4[1];fh=f(xh); goto step4;} }
step4:
eh();
printf("%d\t[%.4f%.4f][%.4f%.4f] [%.4f %.4f] %.4f\n",k,x0[0],x0[1],x1[0],x1[1],x2[0],x2[1],fn1);
1)用单纯形法求法min（x12+2x22-4x1-2x1x2），已知α=1，β=0.5，γ=2，ε=0.005。
程序如下：
#include "stdio.h"
#include "math.h"

单纯形法C程序源代码

单纯形法C程序源代码第一篇：单纯形法C程序源代码单纯形法C程序源代码2008-05-15 15:59 #include #include #define m 3 /*定义约束条件方程组的个数*/ #define n 5 /*定义未知量的个数*/ float M=1000000.0; float A[m][n]; /*用于记录方程组的数目和系数;*/ float C[n]; /*用于存储目标函数中各个变量的系数*/ float b[m]; /*用于存储常约束条件中的常数*/ float CB[m]; /*用于存储基变量的系数*/ float seta[m]; /*存放出基与入基的变化情况*/ float delta[n]; /*存储检验数矩阵*/ float x[n]; int num[m]; /*用于存放出基与进基变量的情况*/ float ZB=0; /*记录目标函数值*/ void input(); void print(); int danchunxing1(); int danchunxing2(int a); void danchunxing3(int a,int b); int danchunxing1() { int i,k=0; int flag=0; float min=0; for(i=0;i=0) flag=1; else {flag=0;break;} if(flag==1) return -1; for(i=0;idelta[i]) {min=delta[i];k=i;} } return k; } int danchunxing2(int a) { int i,k,j; int flag=0; float min; k=a; for(i=0;i0) seta[i]=b[i]/A[i][k]; else seta[i]=M; } min=M; for(i=0;i=seta[i]) {min=seta[i];j=i;} } num[j]=k+1; CB[j]=C[k]; return j; } void danchunxing3(int p,int q) { int i,j,c,l; float temp1,temp2,temp3; c=p;/*行号*/ l=q;/*列号*/ temp1=A[c][l]; b[c]=b[c]/temp1; for(j=0;jvoid print() { int i,j=0; printf("\n------------\n"); for(i=0;iprintf("\n请输入初始基变量的数字代码num矩阵:\n"); for(i=0;i for(i=0;i请输入方程组的系数矩阵A(3行5列): 1 2 1 0 0 4 0 0 1 0 0 4 0 0 1 请输入初始基变量的数字代码num矩阵: 3 4 5 请输入方程组右边的值矩阵b: 8 16 12 请输入目标函数各个变量的系数所构成的系数阵C: -2 -3 0 0 0 ------------ CB XB b X(1) X(2) X(3) X(4) X(5) ------------ 0.00 X(3) 8.00 1.00 2.00 1.00 0.00 0.00 0.00 X(4) 16.00 4.00 0.00 0.00 1.00 0.00 0.00 X(5) 12.00 0.00 4.00 0.00 0.00 1.00 ------------ -2.00 -3.00 0.00 0.00 0.00 ------------ p=2,q=1 ------------ 0.00 X(3) 2.00 1.00 0.00 1.00 0.00 -0.50 0.00 X(4) 16.00 4.00 0.00 0.00 1.00 0.00 -3.00 X(2) 3.00 0.00 1.00 0.00 0.00 0.25 ------------ -2.00 0.00 0.00 0.00 0.75 ------------ p=0,q=0 ------------ -2.00 X(1) 2.00 1.00 0.00 1.00 0.00 -0.50 0.00 X(4) 8.00 0.00 0.00 -4.00 1.00 2.00 -3.00 X(2) 3.00 0.00 1.00 0.00 0.00 0.25 ------------ 0.00 0.00 2.00 0.00 -0.25 ------------ p=1,q=4 ------------ -2.00 X(1) 4.00 1.00 0.00 0.00 0.25 0.00 0.00 X(5) 4.00 0.00 0.00 -2.00 0.50 1.00 -3.00 X(2) 2.00 0.00 1.00 0.50 -0.13 0.00 ------------ 0.00 0.00 1.50 0.13 0.00 ------------ 所得解已经是最优解! 最优解为: x1=4.00 x2=2.00 x3=0.00 x4=0.00 x5=4.00 ZB=14.00Press any key to continue第二篇：单纯形法C语言程序代码长春工业大学课程设计程序代码课程设计名称运筹学课程设计专业信息管理与信息系统班级130506班学生姓名于松南、张鑫蕊、赵改玲、赵海潮指导教师王亚君、王忠吉2015年7月3日#include #includeint m; //记录约束条件方程组的个数int n; //记录未知量的个数float M=1000000.0; float A[100][100];//用于记录方程组的数目和系数float C[100];//用于存储目标函数中各个变量的系数 float b[100];//用于存储常约束条件中的常数 float CB[100];//用于存储基变量的系数 float seta[100];//存放出基与入基的变化情况 float cn[100];//存储检验数矩阵 float x[100]; int num[100];//用于存放出基与进基变量的情况 float Z=0;//记录目标函数值void shuru(); void print(); int mincz(); int find_line(int a); void exchange(int a,int b); int main() {int i,j=0;int p,q,temp; //q：换入，p：换出shuru();printf("\n------------\n");printf(" \tCB\tXB\tb\t");for(i=0; iprintf(" X(%d)\t",i+1);for(i=0; ix[i]=0;printf("\n");while(1) {q=mincz();if(q==-1) {print();printf("\n所得解已经是最优解!\n");printf("\n最优解为:\n");for(j=0; jtemp=num[j]-1;x[temp]=b[j];}for(i=0; iprintf("x%d=%.2f ",i+1,x[i]);Z=Z+x[i]*C[i];}printf("Z=%.2f",Z);}print();p=find_line(q);printf("\np=%d,q=%d",p,q);if(q==-1) break;exchange(p,q);}return 0; } int mincz() {int i,k=0;int flag=0; //检验数标记float min=0;for(i=0; iif(cn[i]>=0)flag=1;else {flag=0;break;}if(flag==1)return -1;//进行到此处，说明存在<0的检验数//找到最小的检验数，作为换入变量for(i=0; iif(min>cn[i]) {min=cn[i];k=i;}}return k; } int find_line(int a) {int flag=0;float min;k=a;for(i=0; iif(A[i][k]<=0)flag=1;else {flag=0;break;}if(flag==1) {printf("\n该线性规划无最优解!\n"); return -1;}for(i=0; iif(A[i][k]>0)seta[i]=b[i]/A[i][k];else seta[i]=M;}min=M;for(i=0; iif(min>=seta[i]) {min=seta[i];j=i;}}num[j]=k+1;CB[j]=C[k];return j; } void exchange(int p,int q) {float temp1,temp2,temp3;c=p; //行号，换出l=q; //列号，换入temp1=A[c][l]; //A[c][l]主元b[c]=b[c]/temp1;for(j=0; jA[c][j]=A[c][j]/temp1; //主元化为1for(i=0; iif(i!=c)if(A[i][l]!=0) {temp2=A[i][l];b[i]=b[i]-b[c]*temp2;//主元所在列，其余元素化为0for(j=0; jA[i][j]=A[i][j]-A[c][j]*temp2;}}temp3=cn[l];for(i=0; icn[i]=cn[i]-A[c][i]*temp3; } void print() {int i,j=0;printf("\n------------\n");for(i=0; iprintf("%8.2f\tX(%d) %8.2f ",CB[i],num[i],b[i]); for(j=0; jprintf("%8.2f ",A[i][j]);printf("\n");}printf("\n------------\n");printf("\t\t\t");for(i=0; iprintf(" %8.2f",cn[i]);printf("\n------------\n"); } void shuru() {int i,j; //循环变量int k;printf("请输入线性规划问题的约束条件个数M：");scanf("%d",&m);printf("请输入线性规划问题的决策变量个数N：");scanf("%d",&n);printf("\n请输入方程组的系数矩阵A(%d行%d列):\n",m,n); for(i=0; ifor(j=0; jscanf("%f",&A[i][j]);printf("\n请输入初始基变量的数字代码矩阵:\n");for(i=0; iscanf("%d",&num[i]);printf("\n请输入方程组右边的值矩阵b:\n");for(i=0; iscanf("%f",&b[i]);printf("\n请输入目标函数各个变量的系数所构成的系数阵C:\n"); for(i=0; iscanf("%f",&C[i]);for(i=0; icn[i]=-C[i];for(i=0; ik=num[i]-1;CB[i]=C[k];}}第三篇：单纯形法matlab程序算法实现与分析算法1．单纯形法具体算例：minz=−3x1+x2+2x3 3x1+2x2−3x3=6 x1−2x2+x3+x5=4x1,x2,x3≥0标准化后：min z=−3x1+x2+2x3+Mx4+Mx53x1+2x2−3x3+x4=6 x1−2x2+x3+x5=4x1,x2,x3,x4,x5≥0用单纯形法求解，程序如下： clear clcM=1000000;A=[3,2,-3,1,0;1,-2,1,0,1];%系数矩阵C=[-3,1,2,M,M,0];%价值矩阵 B=[6;4]; Xt=[4 5];for i=1:length(C)-1 D=0;for j=1:length(Xt)D=D+A(j,i)*C(Xt(j));endxi(i)=C(i)-D; end s=[];for i=1:length(xi)if xi(i)<0 s=[s,i];end endf=length(s); h=1;while(f)for k=1:length(s) j=1; A x=[];for i=1:length(Xt)if A(i,s(k))>0 x(j)=i; j=j+1;end end xif(length(x)+1==1) break; end y=1 xfor i=1:length(x)if B(x(i))/A(x(i),s(k))end end y=x(y); endy1=Xt(y);%»»³ö±äÁ¿ s kaa=A(y,s(k))%s(k)Îª»»Èë±äÁ¿ A(y,:)=A(y,:)./aa; B(y,:)=B(y,:)./aa; z=[];for i=1:length(Xt) z=[z,i]; endz z(y)=[]; z Xtfor i=1:length(z); yz=-A(z(i),s(k))A(z(i),:)=A(z(i),:)+A(y,:).*yz B(z(i)) B(y) yzB(z(i))=B(z(i))+B(y).*yz endfor i=1:length(Xt)if Xt(i)==y1 Xt(i)=s(k); breakend end Xtdisp('×ª»»ºó') A=A B=B AB=[A,B];for i=1:length(C) D=0;for j=1:length(Xt) D=D+AB(j,i)*C(Xt(j));endxi(i)=C(i)-D;end xi s=[];for i=1:length(xi)-1if xi(i)<0 s=[s,i];endend svpa([A,B;C]); f=length(s); h=h+1;if h==5breakend end-xi(length(xi))第四篇：单纯形法的C++实现/*本程序是利用单纯型法来求解线性规划问题输入数据从文本中读入，按照如下的格式：例如：需要求解如下的线性规划问题max z = 2*x1 + 3*x2；约束条件是：x1 + x2<=8;4*x1<=16;4*x2<=12;x1,x2>=0; 则文件中的输入格式是：2 3未知数个数约束条件个数 max2 3 1 1<这里小于符号默认为小于等于， 4 0<注意为零的系数不能省略 0 4<12所需数据从aa.txt中读取*/ #include #include #include #includeusing namespace std;ifstream in("aa.txt");class DanChun { private: doubleMuBiao[100];//目标函数doubleXiShu[100][100];//系数矩阵，最后一列是常数项doubleJianYanShu[100];//检验数，第一个数是最大（或最小）检验数的坐标doubleTheTa[100];//theta doubleCB[100];// intXB[100];// doubleJie[100];//解intBianLian;//变量个数intFangCheng;//方程（约束条件）个数stringMaxMin;//求的是最大值还是最小值？ public:DanChun(int BL,int FC,string MaxOrMin); void Init();void GetJianYanShu(); bool PanDuan(); void Display(); void setXiShu(); void setJie(); void playJie(); };DanChun::DanChun(int BL,int FC,string MaxOrMin) {BianLian = BL;FangCheng = FC;MaxMin = MaxOrMin;int i,j;TheTa[0] = 9999.0;for(i=0;i<100;i++){MuBiao[i]=0;JianYanShu[i]=0;//TheTa[i]=0;//CB[i]=0;//XB[i]=0;//Jie[i]=0;for(j=0;j<100;j++)XiShu[i][j]=0;} }void DanChun::Init() {for(int k=1;k<=BianLian;k++){in>>MuBiao[k];//XB[k]=MuBiao[k];}for(int i=1;i<=FangCheng;i++){char op;//操作符for(int j=1;j<=BianLian;j++){in>>XiShu[i][j];}in>>op;}} if(op=='<') { XiShu[i][0]=0; } else if(op=='>') { XiShu[i][0]=1; } int BL = BianLian + FangCheng;//加上松弛变量后的未知量个数XiShu[i][BianLian+i] = 1;//加上单位矩阵in>>XiShu[i][BL+1]; XB[i]=BianLian+i; void DanChun::GetJianYanShu() { int h=-9999;//记录最大检验数的坐标for(int i=1;i<=BianLian+FangCheng;i++) {double linshi=0;for(int j=1;j<=FangCheng;j++){linshi += (CB[j] * XiShu[j][i]);//cout<<" linshi="<}double ta=MuBiao[i]-linshi;JianYanShu[i]=ta;if(JianYanShu[h]{h=i;} } JianYanShu[0]=h; //for(int w=1;w<6;w++)cout<<"检验数："<for(int i=1;i<=BianLian+FangCheng;i++){if(JianYanShu[i]>0) return 1;}}else if(MaxMin=="min"){for(int i=1;i<=BianLian+FangCheng;i++){if(JianYanShu[i]<0) return 1;}}return 0; }void DanChun::Display() {cout<<"输出系数矩阵："<for(int i=1;i<=FangCheng;i++){cout<for(int j=1;j<=BianLian+1+FangCheng;j++) cout<cout<}cout<<"输出检验数："<for(i=1;i<=FangCheng+BianLian;i++){cout<}cout<void DanChun::setXiShu() {TheTa[0]=9999.0;int kk=0;int j = JianYanShu[0] , i;//确定换位的坐标for(int k=1;k<=FangCheng;k++){if(XiShu[k][ (int)JianYanShu[0] ] != 0){TheTa[k] = XiShu[k][(int)(BianLian+FangCheng+1)] XiShu[k][ (int)(JianYanShu[0]) ];if((TheTa[0] > TheT a[k]) && TheTa[k] > 0){/TheTa[0] = TheTa[k];kk=k;}}//}//得到TheTa值i = kk;//i=3,j=2CB[i]=MuBiao[j];XB[i]=j;//cout<<"TheTa[0]="<//cout<<"得到换处的数据XiShu["<for(int x=1;x<=FangCheng;x++){if(x!=i){double chushu = (-XiShu[x][j]) (XiShu[i][j]);//cout<<"chushu="<for(int y=1;y<=FangCheng+BianLian+1;y++){XiShu[x][y] += XiShu[i][y]*chushu;}}//end ifelse if(x==i){double chushu = XiShu[i][j];for(int y=1;y<=FangCheng+BianLian+1;y++){XiShu[x][y] /= chushu;}}} } void DanChun::setJie() {for(inti=1;i<=FangCheng;i++)Jie[XB[i]]=XiShu[i][BianLian+FangCheng +1]; } void DanChun::playJie() {cout<<"该线性规划问题的最优解为："<for(int i=1;i<=BianLian+FangCheng;i++){cout<}cout<<")t"</} int main() { int x,y;//变量个数和约束条件个数string str;//求max？min？while(in>>x>>y>>str) {DanChun danchun(x,y,str);danchun.Init();danchun.GetJianYanShu();danchun.Display();while(danchun.PanDuan()){danchun.setXiShu();danchun.GetJianYanShu();danchun.Display();}danchun.setJie();danchun.playJie();} return 0; }第五篇：改进单纯形法matlab程序clear clcX=[1 2 3 4 5]; A=[ 1 2 1 0 0; 4 0 0 1 0; 0 4 0 0 1]; C=[2 3 0 0 0 ]; b=[8;16;12]; t=[3 4 5]; B0=A(:,t); while 1CB0=C(:,t); XN01=X;for i=1:length(t);for j=1:length(X);if XN01(j)==t(i)XN01(j)=0;endendend j=1;for i=1:length(X);if XN01(i)~=0XN0(j)=XN01(i);j=j+1;endendfor j=1:length(XN0);CN0(j)=C(XN0(j));end N0=[];for i=1:length(XN0);N0=[N0,A(:,XN0(i))];endxiN0=CN0-CB0*B0*N0; j=1; z=[]; for i=1:length(xiN0)if xiN0(i)>0z(j)=i;j=j+1;endendif length(z)+1==1;break;end n=1;for i=1:length(z)if z(i)>z(n)n=i;endendk=XN0(z(n));%换入变量 B=B0*b; P=B0*A(:,k); j=1;for i=1:length(P)if P(i)>0x(j)=i;j=j+1;endend y=1;for i=1:length(x)if B(x(y))/P(x(y))>B(x(i))/P(x(i))y=i;endendy1=x(y);y=t(y1);%换出变量for i=1:length(t)if t(i)==ym=i;break;endendt(m)=k;P2=B0*A(:,k); q=P2(y1); P2(y1)=-1; P2=-P2./q; E=[1 0 0;0 1 0;0 0 1]; E(:,m)=P2; B0=E*B0; end CB0*B0*b。

修正单纯形法求解约束优化问题

修正单纯形法求解约束优化问题姓名王铎学号2007021271班级机械078日期2010/6/23 一．问题分析求解约束优化问题中，假如目标函数和约束条件都是线性的，像这类约束函数和目标函数都是线性函数的优化问题称作线性规划问题。

从实际问题中建立数学模型一般有以下三个步骤：1. 根据影响所要达到目的的因素找到决策变量；2. 由决策变量和所在大道目的之间的函数关系确定目标函数；3. 有决策变量所受的限制条件确定决策变量所要满足的约束条件；求解线性规划问题的基本方法是单纯形法，而本文研究的是修正单纯形法。

1965 年由J.A.Nelder 等提出。

是在基本单纯形优化法的基础上，引入了反射、扩展与收缩等操作规则，变固定步长推移单纯形为可变步长推移单纯形，在保证优化精度的条件下，加快了优化速度。

是各种单纯形优化法在分析测试中应用最广的一种。

二．数学模型1、线性规划问题的formalization问题(1.1) 称为线性规划问题：x= arg min_x c A T xs.t. Ax=bx>=0 (1.1)其中x为n维列向量，A为m*n的矩阵，b和c分别为m,n维的常数向量。

任意一个线性不等式组约束下求解线性函数的最大最小值问题都可以归结到问题(1.1) 来。

比如A(i,:) x <= b(i)<=>A(i,:) x + y(i) = b(i)y(i)>=0 (1.2)A(i,:) x >= b(i)<=>A(i,:) x - y(i) = b(i)y(i)>=0 (1.3)x<=>x=x'-x"x'>=0x">=0 (1.4)2、单纯形法设m<n即变量个数大于约束的个数。

(否则若m=n则(1.1)的约束可能唯一确定X,最优问题就没有意义，若m>n则可能符合约束的x 不存在，最优问题同样没有意义。

单纯形法C语言程序.

实验：编制《线性规划》计算程序一、实验目的：(1)使学生在程序设计方面得到进一步的训练，掌握Matlab (C 或VB)语言进行程序设计中一些常用方法。

(2)使学生对线性规划的单纯形法有更深的理解.二、实验用仪器设备、器材或软件环境计算机, Matlab R2009a三、算法步骤、计算框图、计算程序等本实验主要编写如下线性规划问题的计算程序:⎩⎨⎧≥≥≤0,0..min b x b Ax t s cx其中初始可行基为松弛变量对应的列组成.对于一般标准线性规划问题:⎩⎨⎧≥≥=0,0..min b x b Ax t s cx１．求解上述一般标准线性规划的单纯形算法（修正）步骤如下：对于一般的标准形式线性规划问题(求极小问题),首先给定一个初始基本可行解。

设初始基为B,然后执行如下步骤：(1).解B Bx b =,求得1B x B b -=，0,N B B x f c x ==令计算目标函数值 1(1,2,...,)i m B b i -=i 以b 记的第个分量(2).计算单纯形乘子w, B wB C =,得到1B w C B -=,对于非基变量，计算判别数1i i i B i i z c c B p c σ-=-=-,可直接计算σ=1B A c c B --令 max{}k i R σσ∈=,R 为非基变量集合若判别数0k σ≤ ,则得到一个最优基本可行解，运算结束；否则，转到下一步(3).解k k By p =,得到1k k y B p -=；若0k y ≤,即k y 的每个分量均非正数，则停止计算，问题不存在有限最优解，否则，进行步骤(4).确定下标r,使 {}:0min ,0t rrk tk tk b b tk y y t y y >=>且r B x 为离基变量,,r k B x p k 为进基变量,用p 替换得到新的基矩阵B,还回步骤(1);２、计算框图为：最优解3．计算程序(Matlab)：A=input('A=');b=input('b=');c=input('c=');format rat%可以让结果用分数输出[m,n]=size(A);E=1:m;E=E';F=n-m+1:n;F=F';D=[E,F]; %创建一个一一映射，为了结果能够标准输出X=zeros(1,n); %初始化Xif(n<m) %判断是否为标准型fprintf('不符合要求需引入松弛变量')flag=0;elseflag=1;B=A(:,n-m+1:n); %找基矩阵cB=c(n-m+1:n); %基矩阵对应目标值的cwhile flagw=cB/B; %计算单纯形乘子，cB/B=cB*inv(B),用cB/B的目的是，为了提高运行速度。

智能优化之下山单纯形法C++

智能优化之下⼭单纯形法C++单纯形法简介在其他⽹站上都可以查到，我就不多说了我们主要说⽅法它主要解决的是局部最优解的问题利⽤多边形进⾏求解的，若有n个变量，则利⽤n+1边形我们这⾥以两个变量为例，求解第三维度的最优解例如解决min f(x,y)=x2 - 4*x + y2 - y - x*ymatlab 图可以看出，差不多是（3，2）附近取得最⼩我们来⽤下⼭单纯形求解我们设⽴三个初始点（0，0），（1.2，0），（0，0.8）我们把它们分别带⼊f中，函数值越⼩的越接近解，我们把它称为最好点，反之，函数值最⼤的点，我们称之为最坏点我们要做的是，利⽤已知点，寻找更加接近解的点我们需要了解⼏种寻找下⼀个点的思想反射 reflect假设三⾓形的三个点是ABP，其中P是最坏点，那么我们寻找⼀个Q点，使得APBQ是⼀个平⾏四边形设向量α为p->A,β为p->B （假设1）那么Q = p + (α+β),其中p和Q是坐标扩张 extern假设，我们得到的新点Q，它⽐原来三⾓形中最好的点还要好，那么，我们可以假定这个探索⽅向是正确的，我们不妨再往前⾛⼀步！其中Q->R = (p->R)/2，我们这⾥称扩张Q点设向量α为Q->A, β为Q->B （假设2）于是，R = Q - (α+β)/2收缩 Shrink我认为收缩有两种因为我们⼀般先做反射点，所以，之后的操作如果针对反射点，那么就是对反射点进⾏收缩基于（假设2），R = Q + (α+β)/4还有⼀种是最优解本来就在三⾓形PAB中，我们对P做收缩基于（假设1），则Q = P + (α+β)/4压缩 compress我们认为，如果上述操作均没有找到更好的点来替代最坏点，那么说明之前的三⾓形是⾮法的，那么我们进⾏压缩操作即，取两边中点与最坏点构成新的三⾓形我们⽤下⼭单纯形法求解步骤如下：求出初始点的最坏点，构成三⾓形重复下述，直到满⾜精度先做⼀次反射如果反射点⽐最好点还要好（更加接近条件：min f(x0,y0)）->做⼀次扩张如果扩张点⽐反射点还要好->扩张点代替之前的最坏点，形成新的三⾓形反之->反射点代替之前的最坏点反之，如果反射点⽐最坏点还要坏->反射点做收缩1 如果收缩点1⽐最坏点好->收缩点1代替最坏点反之->最坏点做收缩2 如果收缩点2⽐最坏点好->收缩点2代替最坏点反之->三⾓形做压缩反之，反射点代替最坏点，形成新的三⾓形C++代码：triangle.h#pragma once#define stds std::#define VEC2_OUT#include "lvgm\lvgm.h"//本⼈博客: https:///lv-anchoret/category/1367052.html#include <vector>#include <algorithm>using namespace lvgm;class Mountain{public:typedef dvec2 valtype;typedef double(*_Fun)(const valtype&);Mountain() { }/*p: three position coordinates(in ordered or not)f: the function Ptrδ: the solution precision*/Mountain(const valtype& p1, const valtype& p2, const valtype& p3, const doubleδ): _δ(δ){_positions.resize(3);_positions[0] = p1;_positions[1] = p2;_positions[2] = p3;sort();}static void setF(_Fun f){_f = f;}void setδ(double delt){_δ = delt;}public:/*origion: the bad positionvec1: bad position -> min positionvec2: bad position -> mid position*/valtype reflect(const valtype& origion, const valtype& vec1, const valtype& vec2){return origion + (vec1 + vec2);}/*origion: the change positionvec1: change position -> left positionvec2: change position -> right position*/valtype shrink(const valtype& origion, const valtype& vec1, const valtype& vec2){return origion + (vec1 + vec2) / 4;}/*origion: the origion positionvec1: origion position -> left positionvec2: origion position -> right position*/void compression(const valtype& origion, const valtype& vec1, const valtype& vec2){_positions[0] = origion + min(vec1, vec2) / 2;_positions[1] = origion + max(vec1, vec2) / 2;}/*origion: the change positionvec1: change position -> left positionvec2: change position -> right position*/valtype exter(const valtype& origion, const valtype& vec1, const valtype& vec2){return origion - (vec1 + vec2) / 2;}void go(){double delt = (_positions[2] - _positions[0]).normal();static int i = 0;while (delt > _δ){stds cout << ++i << "次 " << _positions[0] << "\t" << _positions[1] << "\t" << _positions[2] << stds endl; valtype t = reflect(_positions[2], _positions[1] - _positions[2], _positions[0] - _positions[2]);if (_f(t) < _f(_positions[0])){valtype ex = exter(t, _positions[1] - t, _positions[0] - t);if (_f(ex) < _f(t))_positions[2] = ex;else_positions[2] = t;}else if (_f(t) > _f(_positions[2])){valtype sh = shrink(t, _positions[1] - t, _positions[0] - t);if (_f(sh) < _f(_positions[2])) //反射点收缩_positions[2] = sh;else//三⾓内部内缩{sh = reflect(sh, _positions[1] - sh, _positions[0] - sh);if (_f(sh) < _f(_positions[2]))_positions[2] = sh;else//针对原始点内缩，针对反射点收缩，都不管⽤，那么选择压缩compression(_positions[0], _positions[1] - _positions[2], _positions[0] - _positions[2]);}}else_positions[2] = t;sort();delt = (_positions[2] - _positions[0]).normal();}stds cout << "\n最好点为" << _positions[0] << "\t精度为:" << _δ << stds endl << "函数值为：" << _f(_positions[0]) << stds endl << stds endl; }protected:const valtype& min(const valtype& vec1, const valtype& vec2){return _f(vec1) < _f(vec2) ? vec1 : vec2;}const valtype& max(const valtype& vec1, const valtype& vec2){return _f(vec1) > _f(vec2) ? vec1 : vec2;}friend bool cmp(const valtype& pos1, const valtype& pos2){return Mountain::_f(pos1) < Mountain::_f(pos2);}void sort(){stds sort(_positions.begin(), _positions.end(), cmp);}private:stds vector<valtype> _positions; //min, mid, max or good, mid, baddouble _δ;static _Fun _f;};main.cpp(原错误版本）#include "triangle.h"Mountain::_Fun Mountain::_f=[](const Mountain::valtype& v)->double { return0.; };int main(){auto fun = [](const Mountain::valtype& v)->double{return v.x()*v.x() - 4 * v.x() + v.y()*v.y() - v.y() - v.x()*v.y();};Mountain m(Mountain::valtype(0, 0), Mountain::valtype(1.2, 0), Mountain::valtype(0, 0.8), 0.1);m.setF(fun);m.go();m.setδ(0.01);m.go();m.setδ(0.001);m.go();m.setδ(0.0001);m.go();m.setδ(0.00001);m.go();}error:错在初始化的时候写了⼀个默认函数，创建对象之后才进⾏setF设置内部函数，导致第⼀个三⾓形在构造函数中第⼀次sort的时候，并没有正确排序我们稍微改动⼀下：main.cpp#include "triangle.h"Mountain::_Fun Mountain::_f{ [](const Mountain::valtype& v)->double { return v.x()*v.x() - 4 * v.x() + v.y()*v.y() - v.y() - v.x()*v.y(); } };int main(){Mountain m(Mountain::valtype(0, 0), Mountain::valtype(1.2, 0), Mountain::valtype(0, 0.8), 0.1);m.go();m.setδ(0.01);m.go();m.setδ(0.001);m.go();m.setδ(0.0001);m.go();m.setδ(0.00001);m.go();m.setδ(0.000001);m.go();}这样我们收敛地更好：结果：迭代次数 good medium bad1次 [ 1.2, 0 ] [ 0, 0.8 ] [ 0, 0 ]2次 [ 1.8, 1.2 ] [ 1.2, 0 ] [ 0, 0.8 ]3次 [ 1.8, 1.2 ] [ 3, 0.4 ] [ 1.2, 0 ]4次 [ 3.6, 1.6 ] [ 1.8, 1.2 ] [ 3, 0.4 ]5次 [ 3.6, 1.6 ] [ 2.4, 2.4 ] [ 1.8, 1.2 ]6次 [ 3.6, 1.6 ] [ 2.4, 2.4 ] [ 4.2, 2.8 ]7次 [ 2.4, 1.6 ] [ 3.6, 1.6 ] [ 2.4, 2.4 ]8次 [ 2.7, 2 ] [ 2.4, 1.6 ] [ 3.6, 1.6 ]9次 [ 2.7, 2 ] [ 3.075, 1.7 ] [ 2.4, 1.6 ]10次 [ 2.7, 2 ] [ 3.375, 2.1 ] [ 3.075, 1.7 ]11次 [ 3.01875, 2.225 ] [ 2.7, 2 ] [ 3.375, 2.1 ]12次 [ 3.11719, 2.10625 ] [ 3.01875, 2.225 ] [ 2.7, 2 ]13次 [ 3.11719, 2.10625 ] [ 3.01875, 2.225 ] [ 3.25195, 2.24844 ]14次 [ 3.11719, 2.10625 ] [ 2.88398, 2.08281 ] [ 3.01875, 2.225 ]15次 [ 2.98242, 1.96406 ] [ 3.11719, 2.10625 ] [ 2.88398, 2.08281 ]16次 [ 2.98242, 1.96406 ] [ 3.11719, 2.10625 ] [ 3.13271, 2.01133 ]17次 [ 2.98242, 1.96406 ] [ 2.96689, 2.05898 ] [ 3.11719, 2.10625 ]最好点为[ 2.98242, 1.96406 ] 精度为:0.1函数值为：-6.9990318次 [ 2.98242, 1.96406 ] [ 2.96689, 2.05898 ] [ 2.90339, 1.96416 ]19次 [ 2.98242, 1.96406 ] [ 3.04592, 2.05889 ] [ 2.96689, 2.05898 ]20次 [ 2.98242, 1.96406 ] [ 3.03781, 1.98772 ] [ 3.04592, 2.05889 ]21次 [ 3.02802, 2.01739 ] [ 2.98242, 1.96406 ] [ 3.03781, 1.98772 ]22次 [ 3.02802, 2.01739 ] [ 2.97263, 1.99373 ] [ 2.98242, 1.96406 ]23次 [ 3.00928, 2.02631 ] [ 3.02802, 2.01739 ] [ 2.97263, 1.99373 ]24次 [ 2.99564, 2.00779 ] [ 3.00928, 2.02631 ] [ 3.02802, 2.01739 ]25次 [ 2.99564, 2.00779 ] [ 3.00928, 2.02631 ] [ 2.98968, 2.01688 ]26次 [ 2.99564, 2.00779 ] [ 3.01524, 2.01722 ] [ 3.00928, 2.02631 ]27次 [ 3.0016, 1.9987 ] [ 2.99564, 2.00779 ] [ 3.01524, 2.01722 ]28次 [ 3.0016, 1.9987 ] [ 2.99564, 2.00779 ] [ 2.982, 1.98927 ]29次 [ 3.0016, 1.9987 ] [ 3.00693, 2.01023 ] [ 2.99564, 2.00779 ] 30次 [ 3.0016, 1.9987 ] [ 3.00858, 2.0028 ] [ 3.00693, 2.01023 ]最好点为[ 3.0016, 1.9987 ] 精度为:0.01函数值为：-6.9999931次 [ 3.0016, 1.9987 ] [ 3.00417, 1.99601 ] [ 3.00858, 2.0028 ] 32次 [ 3.0016, 1.9987 ] [ 3.00417, 1.99601 ] [ 2.99719, 1.99191 ] 33次 [ 3.0016, 1.9987 ] [ 3.00573, 2.00008 ] [ 3.00417, 1.99601 ] 34次 [ 3.0016, 1.9987 ] [ 3.00316, 2.00277 ] [ 3.00573, 2.00008 ] 35次 [ 2.99903, 2.00139 ] [ 3.0016, 1.9987 ] [ 3.00316, 2.00277 ] 36次 [ 2.99903, 2.00139 ] [ 3.0016, 1.9987 ] [ 2.99747, 1.99732 ] 37次 [ 3.00174, 2.00141 ] [ 2.99903, 2.00139 ] [ 3.0016, 1.9987 ] 38次 [ 3.00099, 2.00005 ] [ 3.00174, 2.00141 ] [ 2.99903, 2.00139 ] 39次 [ 3.00099, 2.00005 ] [ 3.0002, 2.00106 ] [ 3.00174, 2.00141 ] 40次 [ 2.99945, 1.9997 ] [ 3.00099, 2.00005 ] [ 3.0002, 2.00106 ] 41次 [ 2.99945, 1.9997 ] [ 3.00024, 1.99928 ] [ 3.00099, 2.00005 ]最好点为[ 2.99945, 1.9997 ] 精度为:0.001函数值为：-742次 [ 2.99945, 1.9997 ] [ 2.99927, 1.99921 ] [ 3.00024, 1.99928 ] 43次 [ 2.99945, 1.9997 ] [ 2.9998, 1.99937 ] [ 2.99927, 1.99921 ] 44次 [ 2.99998, 1.99986 ] [ 2.99945, 1.9997 ] [ 2.9998, 1.99937 ] 45次 [ 2.99998, 1.99986 ] [ 2.99945, 1.9997 ] [ 2.99964, 2.00019 ] 46次 [ 2.99998, 1.99986 ] [ 2.99976, 1.99957 ] [ 2.99945, 1.9997 ] 47次 [ 2.99998, 1.99986 ] [ 3.00008, 1.99972 ] [ 2.99976, 1.99957 ] 48次 [ 2.99998, 1.99986 ] [ 3.0003, 2.00001 ] [ 3.00008, 1.99972 ] 49次 [ 2.99998, 1.99986 ] [ 3.00021, 2.00014 ] [ 3.0003, 2.00001 ] 50次 [ 2.99989, 1.99999 ] [ 2.99998, 1.99986 ] [ 3.00021, 2.00014 ] 51次 [ 3.00007, 2.00003 ] [ 2.99989, 1.99999 ] [ 2.99998, 1.99986 ] 52次 [ 3.00007, 2.00003 ] [ 2.99998, 2.00009 ] [ 2.99989, 1.99999 ] 53次 [ 3.00007, 2.00003 ] [ 3.00009, 2.0001 ] [ 2.99998, 2.00009 ]最好点为[ 3.00007, 2.00003 ] 精度为:0.0001函数值为：-754次 [ 3.00007, 2.00003 ] [ 3.00003, 2.00008 ] [ 3.00009, 2.0001 ] 55次 [ 3.00001, 2.00001 ] [ 3.00007, 2.00003 ] [ 3.00003, 2.00008 ] 56次 [ 3.00001, 2.00001 ] [ 3.00004, 2 ] [ 3.00007, 2.00003 ]57次 [ 3.00001, 2.00001 ] [ 2.99998, 1.99998 ] [ 3.00004, 2 ]58次 [ 3.00001, 2.00001 ] [ 2.99998, 1.99998 ] [ 2.99997, 1.99999 ] 59次 [ 3.00001, 2.00001 ] [ 3.00002, 2 ] [ 2.99998, 1.99998 ]60次 [ 3, 1.99999 ] [ 3.00001, 2.00001 ] [ 3.00002, 2 ]61次 [ 3, 1.99999 ] [ 3.00001, 2.00001 ] [ 2.99998, 2.00001 ]62次 [ 3, 1.99999 ] [ 3.00001, 2 ] [ 3.00001, 2.00001 ]最好点为[ 3.00001, 2 ] 精度为:1e-05函数值为：-763次 [ 3.00001, 2 ] [ 3, 1.99999 ] [ 3.00001, 2 ]64次 [ 3.00001, 2 ] [ 2.99999, 2 ] [ 3, 1.99999 ]65次 [ 3.00001, 2 ] [ 3, 2 ] [ 2.99999, 2 ]66次 [ 3, 2 ] [ 3.00001, 2 ] [ 3, 2 ]67次 [ 3, 2 ] [ 3, 2 ] [ 3.00001, 2 ]68次 [ 3, 2 ] [ 3, 2 ] [ 3, 2 ]69次 [ 3, 2 ] [ 3, 2 ] [ 3, 2 ]70次 [ 3, 2 ] [ 3, 2 ] [ 3, 2 ]71次 [ 3, 2 ] [ 3, 2 ] [ 3, 2 ]72次 [ 3, 2 ] [ 3, 2 ] [ 3, 2 ]73次 [ 3, 2 ] [ 3, 2 ] [ 3, 2 ]74次 [ 3, 2 ] [ 3, 2 ] [ 3, 2 ]最好点为[ 3, 2 ] 精度为:1e-06函数值为：-7之前错误版本结果如下结果：1次 [ 0, 0 ] [ 1.2, 0 ] [ 0, 0.8 ]2次 [ 1.2, 0 ] [ 1.2, -0.8 ] [ 0, 0 ]3次 [ 1.2, 0 ] [ 1.2, -0.8 ] [ 2.4, -0.8 ]4次 [ 1.2, 0 ] [ 0.6, -0.2 ] [ 1.2, -0.8 ]5次 [ 1.2, 0 ] [ 0.6, 0.6 ] [ 0.6, -0.2 ]6次 [ 1.5, 1.3 ] [ 1.2, 0 ] [ 0.6, 0.6 ]7次 [ 2.1, 0.7 ] [ 1.5, 1.3 ] [ 1.2, 0 ]8次 [ 2.4, 2 ] [ 2.1, 0.7 ] [ 1.5, 1.3 ]9次 [ 2.4, 2 ] [ 3, 1.4 ] [ 2.1, 0.7 ]10次 [ 2.4, 2 ] [ 3, 1.4 ] [ 3.3, 2.7 ]11次 [ 3, 2.2 ] [ 2.4, 2 ] [ 3, 1.4 ]12次 [ 3, 2.2 ] [ 2.85, 1.75 ] [ 2.4, 2 ]13次 [ 3, 2.2 ] [ 2.85, 1.75 ] [ 3.45, 1.95 ]14次 [ 3, 2.2 ] [ 2.85, 1.75 ] [ 2.6625, 1.9875 ]15次 [ 3, 2.2 ] [ 3.1875, 1.9625 ] [ 2.85, 1.75 ]16次 [ 2.97188, 1.91563 ] [ 3, 2.2 ] [ 3.1875, 1.9625 ]17次 [ 2.97188, 1.91563 ] [ 2.88516, 2.10547 ] [ 3, 2.2 ]18次 [ 2.97188, 1.91563 ] [ 2.85703, 1.82109 ] [ 2.88516, 2.10547 ] 19次 [ 2.97188, 1.91563 ] [ 2.8998, 1.98691 ] [ 2.85703, 1.82109 ] 20次 [ 2.97188, 1.91563 ] [ 3.01465, 2.08145 ] [ 2.8998, 1.98691 ] 21次 [ 2.97188, 1.91563 ] [ 3.01465, 2.08145 ] [ 3.08672, 2.01016 ] 22次 [ 2.94653, 1.99272 ] [ 2.97188, 1.91563 ] [ 3.01465, 2.08145 ] 23次 [ 2.98693, 2.01781 ] [ 2.94653, 1.99272 ] [ 2.97188, 1.91563 ]最好点为[ 2.98693, 2.01781 ] 精度为:0.1函数值为：-6.9992824次 [ 2.98693, 2.01781 ] [ 2.9693, 1.96045 ] [ 2.94653, 1.99272 ] 25次 [ 3.0097, 1.98553 ] [ 2.98693, 2.01781 ] [ 2.9693, 1.96045 ] 26次 [ 3.01282, 2.02228 ] [ 3.0097, 1.98553 ] [ 2.98693, 2.01781 ] 27次 [ 3.01282, 2.02228 ] [ 3.0097, 1.98553 ] [ 3.02342, 1.99696 ] 28次 [ 2.99909, 2.01086 ] [ 3.01282, 2.02228 ] [ 3.0097, 1.98553 ] 29次 [ 3.00782, 2.00105 ] [ 2.99909, 2.01086 ] [ 3.01282, 2.02228 ] 30次 [ 3.00782, 2.00105 ] [ 2.9941, 1.98963 ] [ 2.99909, 2.01086 ] 31次 [ 3.00003, 2.0031 ] [ 3.00782, 2.00105 ] [ 2.9941, 1.98963 ] 32次 [ 3.00003, 2.0031 ] [ 3.00782, 2.00105 ] [ 3.00884, 2.0083 ]最好点为[ 3.00003, 2.0031 ] 精度为:0.01函数值为：-6.9999933次 [ 3.00003, 2.0031 ] [ 2.99901, 1.99585 ] [ 3.00782, 2.00105 ] 34次 [ 3.00003, 2.0031 ] [ 2.99901, 1.99585 ] [ 2.99537, 1.99869 ] 35次 [ 3.00003, 2.0031 ] [ 3.00367, 2.00026 ] [ 2.99901, 1.99585 ] 36次 [ 3.00043, 1.99877 ] [ 3.00003, 2.0031 ] [ 3.00367, 2.00026 ] 37次 [ 3.00043, 1.99877 ] [ 2.99851, 2.00127 ] [ 3.00003, 2.0031 ] 38次 [ 3.00043, 1.99877 ] [ 2.99851, 2.00127 ] [ 2.99891, 1.99693 ] 39次 [ 3.00043, 1.99877 ] [ 2.99975, 2.00156 ] [ 2.99851, 2.00127 ] 40次 [ 3.00043, 1.99877 ] [ 2.99975, 2.00156 ] [ 3.00167, 1.99906 ]最好点为[ 2.9993, 2.00071 ] 精度为:0.001函数值为：-741次 [ 2.9993, 2.00071 ] [ 3.00043, 1.99877 ] [ 2.99975, 2.00156 ] 42次 [ 2.99992, 1.99883 ] [ 2.9993, 2.00071 ] [ 3.00043, 1.99877 ] 43次 [ 2.9992, 2.00028 ] [ 2.99992, 1.99883 ] [ 2.9993, 2.00071 ] 44次 [ 2.99969, 1.99897 ] [ 2.9992, 2.00028 ] [ 2.99992, 1.99883 ] 45次 [ 2.99921, 2.00002 ] [ 2.99969, 1.99897 ] [ 2.9992, 2.00028 ] 46次 [ 2.99958, 1.99911 ] [ 2.99921, 2.00002 ] [ 2.99969, 1.99897 ] 47次 [ 2.99924, 1.99986 ] [ 2.99958, 1.99911 ] [ 2.99921, 2.00002 ] 48次 [ 2.99951, 1.99922 ] [ 2.99924, 1.99986 ] [ 2.99958, 1.99911 ] 49次 [ 2.99928, 1.99975 ] [ 2.99951, 1.99922 ] [ 2.99924, 1.99986 ]最好点为[ 2.99947, 1.9993 ] 精度为:0.0001函数值为：-750次 [ 2.99947, 1.9993 ] [ 2.99928, 1.99975 ] [ 2.99951, 1.99922 ] 51次 [ 2.9993, 1.99968 ] [ 2.99947, 1.9993 ] [ 2.99928, 1.99975 ] 52次 [ 2.9993, 1.99968 ] [ 2.99944, 1.99936 ] [ 2.99947, 1.9993 ] 53次 [ 2.99932, 1.99963 ] [ 2.9993, 1.99968 ] [ 2.99944, 1.99936 ] 54次 [ 2.99938, 1.9995 ] [ 2.99932, 1.99963 ] [ 2.9993, 1.99968 ] 55次 [ 2.99938, 1.9995 ] [ 2.9994, 1.99945 ] [ 2.99932, 1.99963 ] 56次 [ 2.99938, 1.9995 ] [ 2.99936, 1.99955 ] [ 2.9994, 1.99945 ] 57次 [ 2.99938, 1.9995 ] [ 2.99936, 1.99955 ] [ 2.99935, 1.99957 ] 58次 [ 2.99938, 1.9995 ] [ 2.99938, 1.99949 ] [ 2.99936, 1.99955 ] 59次 [ 2.99938, 1.9995 ] [ 2.99937, 1.99953 ] [ 2.99938, 1.99949 ] 60次 [ 2.99938, 1.9995 ] [ 2.99936, 1.99954 ] [ 2.99937, 1.99953 ] 61次 [ 2.99937, 1.99951 ] [ 2.99938, 1.9995 ] [ 2.99936, 1.99954 ] 62次 [ 2.99937, 1.99951 ] [ 2.99938, 1.99949 ] [ 2.99938, 1.9995 ] 63次 [ 2.99938, 1.9995 ] [ 2.99937, 1.99951 ] [ 2.99938, 1.99949 ] 64次 [ 2.99937, 1.99954 ] [ 2.99938, 1.9995 ] [ 2.99937, 1.99951 ] 65次 [ 2.99938, 1.99954 ] [ 2.99937, 1.99954 ] [ 2.99938, 1.9995 ]最好点为[ 2.99938, 1.99954 ] 精度为:1e-05函数值为：-7感谢您的阅读，⽣活愉快~。

用c语言实现单纯形法的编程

用c语言实现单纯形法的编程#include "stdio.h"#include "math.h"#include <iostream>int M,N;float c[100],a[100][100],b[100],CZ[100],Dn[100],th[100],x[100];int Fn[100];int K,L,ths;float zy;int shuru();void findmm();void chang();main(){float max_Z,sum=0,s=0;int i,j,r=0;if(!shuru()) { printf("ERROR!!!\n");return 0;}while(r<N){ r=0;for(j=0;j<N;j++){if(Dn[j]>0){findmm();if(ths==M) {goto loop;}else chang();}else r++;}}loop:if(ths==M){printf("\n此线性规划没有有限最优解!!!\n");printf("\n此线性规划最终迭代结果为：");printf("\n Cj ");for(j=0;j<N;j++)printf("%.3f ",c[j]);printf("\n");printf("Cb Xb b ");for(j=0;j<N;j++)printf(" x%d ",j+1);printf(" th ");for(i=0;i<M;i++){ printf("\n%.1f ",CZ[i]);printf("x%d ",Fn[i]+1);printf("%.3f ",b[i]);for(j=0;j<N;j++){ printf(" %.3f ",a[i][j]);}printf(" %.3f ",th[i]);printf("\n");}printf(" Dn ");for(j=0;j<N;j++)printf(" %.3f ",Dn[j]);printf("\n");printf("\n此时的解为:");sum=0;for(i=0;i<M;i++){ sum+=CZ[i]*b[i];printf("\nx%d=%.3f",Fn[i]+1,b[i]);}max_Z=sum;printf("\n此时目标函数的值为：Z= %.3f\n",max_Z);}else{printf("\n此线性规划最终迭代结果为：");printf("\n Cj ");for(j=0;j<N;j++)printf("%.3f ",c[j]);printf("\n");printf("Cb Xb b ");for(j=0;j<N;j++)printf(" x%d ",j+1);printf(" th ");for(i=0;i<M;i++){ printf("\n%.1f ",CZ[i]);printf("x%d ",Fn[i]+1);printf("%.3f ",b[i]);for(j=0;j<N;j++){ printf(" %.3f ",a[i][j]);}printf(" %.3f ",th[i]);printf("\n");}printf(" Dn ");for(j=0;j<N;j++)printf(" %.3f ",Dn[j]);printf("\n");printf("\n故,目标函数的基解为:");sum=0;for(i=0;i<M;i++){ sum+=CZ[i]*b[i];printf("\nx%d=%.3f",Fn[i]+1,b[i]);}max_Z=sum;printf("\n目标函数的值为：max_Z= %.3f\n",max_Z);}system("pause");return 1;}int shuru(){ int i,j;float sum=0;printf("请输入线性规划问题的约束条件个数M：");scanf("%d",&M);printf("请输入线性规划问题的决策变量个数N：");scanf("%d",&N);printf("请输入目标函数的系数：");for(i=0;i<N;i++)scanf("%f",&c[i]);printf("请输入线性规划问题的约束矩阵：\n");for(i=0;i<M;i++){ for(j=0;j<N;j++)scanf("%f",&a[i][j]);scanf("%f",&b[i]);}printf("请输入线性规划问题的初始基：\n");for(j=0;j<N;j++)scanf("%f",&x[j]);for(i=j=0;j<N;j++){if(x[j]!=0){ Fn[i]=j;CZ[i]=c[j];i++;}}for(j=0;j<N;j++){ sum=0;for(i=0;i<M;i++)sum+=CZ[i]*a[i][j];Dn[j]=c[j]-sum;}return 1;}void findmm(){ int i;int max,min;max=0;K=max;for(i=1;i<N;i++)if(Dn[i]>Dn[K]) max=i;K=max;for(i=0;i<M;i++){if(a[i][K]!=0) {th[i]=b[i]/a[i][K];min=i;} else th[i]=-1;}ths=0;for(i=0;i<M;i++)if(th[i]<0) ths=ths+1;for(i=0;i<M;i++)if((th[i]>0)&&(th[i]<th[min])) min=i;L=min;zy=a[L][K];Fn[L]=K;CZ[L]=c[K];}void chang(){ int i,j;float t;for(j=0;j<N;j++)a[L][j]=a[L][j]/zy;b[L]=b[L]/zy;for(i=0;i<M;i++){if(i==L) continue;t=a[i][K];b[i]=b[L]*(-t)+b[i];for(j=0;j<N;j++)a[i][j]=a[L][j]*(-t)+a[i][j];}t=Dn[K];for(j=0;j<N;j++)Dn[j]=(-t)*a[L][j]+Dn[j];K=0;for(i=1;i<N;i++)if(Dn[i]>Dn[K]) K=i;for(i=0;i<M;i++){if(a[i][K]!=0) {th[i]=b[i]/a[i][K];}else th[i]=-1;}}#include "stdio.h"#include "math.h"#include <iostream>int M,N;float c[100],a[100][100],b[100],CZ[100],Dn[100],th[100],x[100]; int Fn[100];int K,L,ths;float zy;int shuru();void findmm();void chang();main(){float max_Z,sum=0,s=0;int i,j,r=0;if(!shuru()) { printf("ERROR!!!\n");return 0;}while(r<N){ r=0;for(j=0;j<N;j++){if(Dn[j]>0){findmm();if(ths==M) {goto loop;} else chang();}else r++;}}loop:if(ths==M){printf("\n此线性规划没有有限最优解!!!\n");printf("\n此线性规划最终迭代结果为：");printf("\n Cj ");for(j=0;j<N;j++)printf("%.3f ",c[j]);printf("\n");printf("Cb Xb b ");for(j=0;j<N;j++)printf(" x%d ",j+1);printf(" th ");for(i=0;i<M;i++){ printf("\n%.1f ",CZ[i]);printf("x%d ",Fn[i]+1);printf("%.3f ",b[i]);for(j=0;j<N;j++){ printf(" %.3f ",a[i][j]);}printf(" %.3f ",th[i]);printf("\n");}printf(" Dn ");for(j=0;j<N;j++)printf(" %.3f ",Dn[j]);printf("\n");printf("\n此时的解为:");sum=0;for(i=0;i<M;i++){ sum+=CZ[i]*b[i];printf("\nx%d=%.3f",Fn[i]+1,b[i]);}max_Z=sum;printf("\n此时目标函数的值为：Z= %.3f\n",max_Z); }else{printf("\n此线性规划最终迭代结果为：");printf("\n Cj ");for(j=0;j<N;j++)printf("%.3f ",c[j]);printf("\n");printf("Cb Xb b ");for(j=0;j<N;j++)printf(" x%d ",j+1);printf(" th ");for(i=0;i<M;i++){ printf("\n%.1f ",CZ[i]);printf("x%d ",Fn[i]+1);printf("%.3f ",b[i]);for(j=0;j<N;j++){ printf(" %.3f ",a[i][j]);}printf(" %.3f ",th[i]);printf("\n");}printf(" Dn ");for(j=0;j<N;j++)printf(" %.3f ",Dn[j]);printf("\n");printf("\n故,目标函数的基解为:");sum=0;for(i=0;i<M;i++){ sum+=CZ[i]*b[i];printf("\nx%d=%.3f",Fn[i]+1,b[i]);}max_Z=sum;printf("\n目标函数的值为：max_Z= %.3f\n",max_Z);}system("pause");return 1;}int shuru(){ int i,j;float sum=0;printf("请输入线性规划问题的约束条件个数M："); scanf("%d",&M);printf("请输入线性规划问题的决策变量个数N："); scanf("%d",&N);printf("请输入目标函数的系数：");for(i=0;i<N;i++)scanf("%f",&c[i]);printf("请输入线性规划问题的约束矩阵：\n");for(i=0;i<M;i++){ for(j=0;j<N;j++)scanf("%f",&a[i][j]);scanf("%f",&b[i]);}printf("请输入线性规划问题的初始基：\n");for(j=0;j<N;j++)scanf("%f",&x[j]);for(i=j=0;j<N;j++){if(x[j]!=0){ Fn[i]=j;CZ[i]=c[j];i++;}}for(j=0;j<N;j++){ sum=0;for(i=0;i<M;i++)sum+=CZ[i]*a[i][j];Dn[j]=c[j]-sum;}return 1;}void findmm(){ int i;int max,min;max=0;K=max;for(i=1;i<N;i++)if(Dn[i]>Dn[K]) max=i;K=max;for(i=0;i<M;i++){if(a[i][K]!=0) {th[i]=b[i]/a[i][K];min=i;} else th[i]=-1;}ths=0;for(i=0;i<M;i++)if(th[i]<0) ths=ths+1;for(i=0;i<M;i++)if((th[i]>0)&&(th[i]<th[min])) min=i; L=min;zy=a[L][K];Fn[L]=K;CZ[L]=c[K];}void chang(){ int i,j;float t;for(j=0;j<N;j++)a[L][j]=a[L][j]/zy;b[L]=b[L]/zy;for(i=0;i<M;i++){if(i==L) continue;t=a[i][K];b[i]=b[L]*(-t)+b[i];for(j=0;j<N;j++)a[i][j]=a[L][j]*(-t)+a[i][j];}t=Dn[K];for(j=0;j<N;j++)Dn[j]=(-t)*a[L][j]+Dn[j];K=0;for(i=1;i<N;i++)if(Dn[i]>Dn[K]) K=i;for(i=0;i<M;i++){if(a[i][K]!=0) {th[i]=b[i]/a[i][K];} else th[i]=-1;}}/view/579bf98b79563c1ec5da71a4.html /view/560260a8647d27284a73510c.html /view/da495b9b76eeaeaad1f330f9.html//在Visual C++控制台程序中编译执行#include<iostream.h>#include<math.h>#define M 10000//全局变量float kernel[11][31];//核心矩阵表int m=0,n=0,t=0;//m:结构向量的个数//n:约束不等式个数//t:目标函数类型：－1代表求求最小值，1代表求最大值//输入接口函数void input(){//读入所求问题的基本条件cout<<"－－－－－－－－－－参数输入－－－－－－－－－－－"<<endl;cout<<"请按提示输入下列参数："<<endl<<endl;cout<<" 结构向量数m: "<<" m= ";cin>>m;cout<<endl<<" 约束不等式数n:"<<" n= ";cin>>n;int i,j;//初始化核心向量for (i=0;i<=n+1;i++)for (j=0;j<=m+n+n;j++)kernel [i][j]=0;//读入约束条件cout<<endl<<" 约束方程矩阵的系数及不等式方向（1代表<=,-1代表>=）:"<<endl<<endl<<" ";for (i=1;i<=m;i++)cout<<" x"<<i;cout<<" 不等式方向 "<<" 常数项"<<endl;for (i=1;i<=n;i++){cout<<" 不等式"<<i<<" ";for (j=1;j<=m+2;j++)cin>>kernel [i][j];}for (i=1;i<=n;i++){kernel [i][0]=kernel [i][m+2];kernel [i][m+2]=0;}//读入目标条件cout<<endl<<endl<<" 目标函数的系数及类型（求最小值:1；求最大值:-1）:"<<endl<<endl<<" ";for(i=1;i<=m;i++)cout<<"x"<<i<<" ";cout<<"类型"<<endl<<" ";cout<<" 目标函数: ";for (i=1;i<=m;i++)cin>>kernel [0][i];cin>>t;//矩阵调整if(t==-1)for(i=1;i<=m;i++)kernel [0][i]=(-1)*kernel [0][i];for(i=1;i<=n;i++){kernel [i][m+i]=kernel [i][m+1];if(i!=1)kernel [i][m+1]=0;}}//算法函数void comput(){int i,j,flag,temp1,temp2,h,k=0,temp3[10];float a,b[11],temp,temp4[11],temp5[11],f=0,aa,d,c; //初始化for(i=1;i<=n;i++)temp3[i]=0;for(i=0;i<11;i++){ temp4[i]=0;temp5[i]=0;}for(i=1;i<=n;i++){if(kernel [i][m+i]==-1){kernel [i][m+n+i]=1;kernel [0][m+n+i]=M;temp3[i]=m+n+i;}elsetemp3[i]=m+i;}for(i=1;i<=n;i++)temp4[i]=kernel [0][temp3[i]];//循环求解do{for(i=1;i<=m+n+n;i++){a=0;for(j=1;j<=n;j++)a+=kernel [j][i]*temp4[j];kernel [n+1][i]=kernel [0][i]-a; }for(i=1;i<=m+n+n;i++){if(kernel [n+1][i]>=0) flag=1; else{flag=-1;break;}}if(flag==1){ for(i=1;i<=n;i++){if(temp3[i]<=m+n) temp1=1; else{temp1=-1; break;}}//输出结果cout<<endl<<endl;cout<<"－－－－－－－－－－结果输出－－－－－－－－－－－"<<endl<<endl;if(temp1==1){cout<<" 此线性规划的最优解存在!"<<endl<<endl<<" 最优解为："<<endl<<endl<<" ";for(i=1;i<=n;i++)temp5[temp3[i]]=kernel [i][0];for(i=1;i<=m;i++)f+=t*kernel [0][i]*temp5[i];for(i=1;i<=m;i++){cout<<"x"<<i<<" = "<<temp5[i];if(i!=m)cout<<"， ";}cout<<" ;"<<endl<<endl<<" 最优目标函数值f= "<<f<<endl<<endl;return ;}else{cout<<" 此线性规划无解"<<endl<<endl; return ;}}if(flag==-1){temp=100000;for(i=1;i<=m+n+n;i++)if(kernel [n+1][i]<temp){temp=kernel [n+1][i];h=i;}for(i=1;i<=n;i++){if(kernel [i][h]<=0) temp2=1;else {temp2=-1;break;}}}if(temp2==1){cout<<"此线性规划无约束";return ;}if(temp2==-1){c=100000;for(i=1;i<=n;i++){if(kernel [i][h]!=0) b[i]=kernel [i][0]/kernel [i][h]; if(kernel [i][h]==0) b[i]=100000;if(b[i]<0) b[i]=100000;if(b[i]<c){c=b[i];k=i;}}temp3[k]=h;temp4[k]=kernel [0][h];d=kernel [k][h];for(i=0;i<=m+n+n;i++)kernel [k][i]=kernel [k][i]/d;for(i=1;i<=n;i++){ if(i==k)continue;aa=kernel [i][h];for(j=0;j<=m+n+n;j++)kernel [i][j]=kernel [i][j]-aa*kernel [k][j];}}}while(1);return ;}//主函数void main(){ cout<<"-------------------单纯形算法程序----------------------"<<endl<<endl; input();comput();}#include<stdio.h>#include<math.h>#define m 3 /*定义约束条件方程组的个数*/#define n 5 /*定义未知量的个数*/float M=1000000.0;float A[m][n]; /*用于记录方程组的数目和系数;*/float C[n]; /*用于存储目标函数中各个变量的系数*/ float b[m]; /*用于存储常约束条件中的常数*/float CB[m]; /*用于存储基变量的系数*/float seta[m]; /*存放出基与入基的变化情况*/float delta[n]; /*存储检验数矩阵*/float x[n];int num[m]; /*用于存放出基与进基变量的情况*/ float ZB=0; /*记录目标函数值*/void input();void print();int danchunxing1();int danchunxing2(int a);void danchunxing3(int a,int b);int danchunxing1(){int i,k=0;int flag=0;float min=0;for(i=0;i<n;i++)if(delta[i]>=0)flag=1;else {flag=0;break;}if(flag==1)return -1;for(i=0;i<n;i++){if(min>delta[i]){min=delta[i];k=i;}return k;}int danchunxing2(int a){int i,k,j;int flag=0;float min;k=a;for(i=0;i<m;i++)if(A[i][k]<=0)flag=1;else {flag=0;break;}if(flag==1){printf("\n该线性规划无最优解!\n"); return -1;} for(i=0;i<m;i++){if(A[i][k]>0)seta[i]=b[i]/A[i][k];else seta[i]=M;}min=M;for(i=0;i<m;i++){if(min>=seta[i]){min=seta[i];j=i;}}num[j]=k+1;CB[j]=C[k];return j;}void danchunxing3(int p,int q){int i,j,c,l;float temp1,temp2,temp3;c=p;/*行号*/l=q;/*列号*/ temp1=A[c][l];b[c]=b[c]/temp1;for(j=0;j<n;j++)A[c][j]=A[c][j]/temp1;for(i=0;i<m;i++){if(i!=c)if(A[i][l]!=0){temp2=A[i][l];b[i]=b[i]-b[c]*temp2;for(j=0;j<n;j++)A[i][j]=A[i][j]-A[c][j]*temp2;}}temp3=delta[l];for(i=0;i<n;i++)delta[i]=delta[i]-A[c][i]*temp3;}void print(){int i,j=0;printf("\n--------------------------------------------------------------------------\n"); for(i=0;i<m;i++){printf("%8.2f\tX(%d) %8.2f ",CB[i],num[i],b[i]);for(j=0;j<n;j++)printf("%8.2f ",A[i][j]);printf("\n");}printf("\n--------------------------------------------------------------------------\n"); printf("\t\t\t");for(i=0;i<n;i++)printf(" %8.2f",delta[i]);printf("\n--------------------------------------------------------------------------\n"); }void input(){int i,j; /*循环变量*/int k;printf("请输入方程组的系数矩阵A(%d行%d列):\n",m,n);for(i=0;i<m;i++)for(j=0;j<n;j++)scanf("%f",&A[i][j]);printf("\n请输入初始基变量的数字代码num矩阵:\n");for(i=0;i<m;i++)scanf("%d",&num[i]);printf("\n请输入方程组右边的值矩阵b:\n");for(i=0;i<m;i++)scanf("%f",&b[i]);printf("\n请输入目标函数各个变量的系数所构成的系数阵C:\n");for(i=0;i<n;i++)scanf("%f",&C[i]);for(i=0;i<n;i++)delta[i]=C[i];for(i=0;i<m;i++){k=num[i]-1;CB[i]=C[k];}}void main(){int i,j=0;int p,q,temp;input();printf("\n--------------------------------------------------------------------------\n"); printf(" \tCB\tXB\tb\t");for(i=0;i<n;i++)printf(" X(%d)\t",i+1);for(i=0;i<n;i++)x[i]=0;printf("\n");while(1){q=danchunxing1();if(q==-1){print();printf("\n所得解已经是最优解!\n");printf("\n最优解为:\n");for(j=0;j<m;j++){temp=num[j]-1;x[temp]=b[j];}for(i=0;i<n;i++){printf("x%d=%.2f ",i+1,x[i]);ZB=ZB-x[i]*C[i];}printf("ZB=%.2f",ZB);break;}print();p=danchunxing2(q);printf("\np=%d,q=%d",p,q);if(q==-1) break;danchunxing3(p,q);}}。

单纯形法c语言

单纯形法c语言单纯形法（Simplex Algorithm）是一种用于线性规划问题的常用算法。

它的目标是找到线性规划问题的最优解，即满足约束条件下的最大或最小目标函数值。

单纯形法的思想相对简单，但是在实现时需要注意一些细节。

单纯形法的基本原理是通过不断地在可行解空间中移动，逐步逼近最优解。

它通过迭代的方式，每次找到一个更优的可行解，直到找到最优解为止。

这个过程是通过转动问题的一个角点，使其向邻近的角点移动，直到达到最优解。

单纯形法的核心是构造单纯形表（Simplex Tableau）。

单纯形表是一个矩阵，由目标函数和约束条件组成。

表中的每一行代表一个约束条件，而列则代表决策变量。

单纯形表中的元素表示某个变量在约束条件下的系数。

单纯形法的步骤如下：1.将线性规划问题转化为标准形式。

标准形式要求目标函数为最小化形式，约束条件为等式形式，并且决策变量为非负数。

2.构造初始单纯形表。

将约束条件和目标函数转化为单纯形表的形式，并填写初始值。

3.检查单纯形表是否为最优解。

如果表中的目标函数系数均为负数，则可以确定该解为最优解，算法结束。

否则，找到目标函数系数中的最小值所在的列。

4.选择合适的基变量。

在所选列中，找到使约束条件保持满足的最优值所在的行，并将其称为主元行。

将主元行与所选列进行交换，使得目标函数系数中的最小值所在的位置变为主元。

5.进行主元行的消元操作。

通过将主元行除以主元元素，使主元元素变为1，并将其他行的元素都变为0，同时更新单纯形表的其他值。

6.重复第3步到第5步，直到找到最优解或者确定无界问题或者无可行解。

在实现单纯形法的过程中，需要注意以下几点：1.单纯形表的数据结构。

单纯形表可以使用矩阵或数组表示，同时需要记录变量的基变量和非基变量，以及目标函数的最优值。

2.主元行的选取。

可以使用不同的策略选择主元行，例如选取最小比值法或者随机选择法。

3.主元行的消元操作。

消元操作时，需要将主元行的其他元素变为0。

用C语言解决线性规划问题(用单纯形法解)

用C语言解决线性规划问题（用单纯形法解）#include<stdio.h>#include<math.h>#include<iostream.h>#define BORDER -0.00001#define M 100int main(){int k; //初始变量的个数int m; //约束条件的个数;cout<<"输入初始变量的个数"<<endl;cin>>k;cout <<"输入约束条件的个数"<<endl;cin>>m;cout<<"输入约束条件的种类"<<endl;cout<<"0 means <="<<endl;cout<<"1 means >="<<endl;cout<<"2 means ="<<endl;int NGET=0;int NLET=0;int NET =0;int I =0;//人工变量；int *code=new int[m]; //the array of the >= <= =;for(int i=0;i<m;i++){cin>>code[i];if(code[i]==0)NGET++;if(code[i]==1)NLET++;I++ ;if(code[i]==2)NET++;I++ ;}int n; //变量总和；n=k+2*NLET+NGET+NET;float *Index=new float[n+1]; //目标函数的系数;float *c=new float[n+1];int NTYPE;for(i=0;i<n+1;i++)Index[i]=0.0;//为语法要求定初值；cout<<"输入目标函数的系数"<<endl;for(i=0;i<k;i++)cin>>Index[i];for(i=k+NGET+NLET;i<n;i++)//人工变量所在的列；Index[i]=-M; //the initionalization of indexes of manul variable;cout<<"输入所求函数的类型是求最大还是最小"<<endl;cout<<"0 means min"<<endl;cout<<"1 means max"<<endl;cin>>NTYPE;if(NTYPE) //the initionalization of the c[i];{for(i=0;i<n+1;i++)c[i]=-Index[i];//一般情况下只要将目标函数系数的相反数输入；}if(!NTYPE){for(i=0;i<n+1;i++)if(i<k+NGET+NLET)c[i]=Index[i];else c[i]=-Index[i];}delete []Index;float **a=new float*[m+1]; //the array of all the variable to compute;for(i=0;i<m+1;i++)a[i]=new float[n+1];int INDEXG=k;int INDEXL=k+NGET;int INDEXE=k+NGET+NLET;int *ARTV=new int[I]; //保存人工变量；for(i=0;i<m;i++) //the analization of the code[](<= >= = );{if(code[i]==0){a[i][INDEXL]=1.0;INDEXL++;}if(code[i]==1){a[i][INDEXE]=1.0;INDEXE++;a[i][INDEXG]=-1.0;INDEXG++;ARTV[I]=i;I++;}if(code[i]==2){a[i][INDEXE]=1.0;INDEXE++;ARTV[I]=i;I++;}}if( (INDEXG!=k+NLET) || (INDEXL!=k+NGET+NLET) || (INDEXE!=n) )//excption {return -1;}cout<<"输入约束表达式左边的系数"<<endl;for(i=0;i<m;i++)for(int j=0;j<k;j++)cin>>a[i][j];float *b=new float[m];cout<<"输入约束表达式右边的值" <<endl;for(i=0;i<m;i++)cin>>b[i];for(i=0;i<m;i++)a[i][n]=b[i];float *temp=new float[n+1];if(I){for(i=0;i<I;i++)for(int j=0;j<n+1;j++){temp[j]=-a[ARTV[i]][j];c[j]+=M*temp[j];}}for(i=0;i<n+1;i++)a[m][i]=c[i];for(i=0;i<m+1;i++){for(int j=0;j<n+1;j++)cout<<a[i][j]<<" ";cout<<endl;}int flag=0;float temp1;float temp2;int K,J;int index;for(i=0;i<n;i++)if(a[m][i]<0)flag=1; //检验系数;while(flag) //Using a[][] to compute the result; {temp1=0;for(i=0;i<n;i++){if(temp1>a[m][i]){temp1=a[m][i];K=i;}}temp2=M;for(i=0;i<m;i++){if(a[i][K]>0&&(a[i][n]/a[i][K])<temp2){temp2=a[i][n]/a[i][K];J=i;}}if(temp2==M){cout<<"无解!"<<endl;return -1;}float temp3=a[J][K];for(i=0;i<n+1;i++){a[J][i]=a[J][i]/temp3;}for(i=0;i<m+1;i++){if(i!=J){float temp4=a[i][K];for(int j=0;j<n+1;j++){a[i][j]=a[i][j]- a[J][j]*temp4;}}cout<<endl;}flag=0;for(i=0;i<n+1;i++){if(a[m][i]<BORDER)flag=1;}cout<<"**************************************"<<endl;for(i=0;i<m+1;i++){for(int j=0;j<n+1;j++)cout<<a[i][j]<<" ";cout<<endl;}cout<<"***************************************"<<endl;getchar();}if(NTYPE)cout<<"The answer is :"<<a[m][n];if(!NTYPE)cout<<"The answer is :"<<-a[m][n];getchar();return 0;}。

单纯形表计算最优化问题

2、转化为标准型→
max S 2x1 3x2 2x1 2x2 x3 12 x 2 x x 8 1 2 4 s.t.4x1 x5 16 4x x 12 2 6 x1 ~ x6 0
3、写出初始单纯形表→
4、设定程序的初始值： #include"stdio.h" #define M 5 //去掉单存形表第一行（目标函数行）的剩余行数（包括检验数行） #define N 7 //去掉单存形表第一列的剩余列数（包括常数列） 5、运行程序，按照下图依次输入数据，每输入一个数之后按 enter 键再输入下一个，全程不能有输入错误，否则需要重新运行程序与输入数据。
2、转化为标准型→
max S 2 x1 3 x2 x1 x2 x3 2 x1 2 x2 x4 10 3 x1 x2 x5 15 x1 , x2 0
3、写出初始单纯形表→
-S 1 x3 0 x4 0 x5 0
x1 2 1 1 3 2
x2 3 1 2 1 3
5、运行程序，将下图方框中的数据按行依次输入，每输入一个数之后按 enter 键再输入下一个，全程不能有输入错误，否则需要重新运行程序与输入数据。
-S 1 x3 0 x4 0 x5 0
x1 2 1 1 3 2
x2 3 1 2 1 3
x3 0 1 0 0 0
x4 0 0 1 0 0
x5 0 0 0 1 0
输入的第 1 行数据输入的第 2 行数据输入的第 3 行数据输入的第 4 行数据输入的第 5 行数据
6、程序运行结果如下：
因此最终计算得到的最大值为 max=14。此时 X=(4, 2, 0, 0, 0, 4)

c语言实现二阶段单纯形法

c语言实现二阶段单纯形法二阶段单纯形法（Two-Phase Simplex Method）是线性规划的一种求解方法。

它主要分为两个阶段：第一阶段是寻找一个初始解，第二阶段是使用单纯形法进行迭代优化。

以下是一个简单的C语言实现二阶段单纯形法的示例代码：```c#include <stdio.h>#include <stdlib.h>#include <math.h>#define MAX_ITER 1000#define EPSILON 1e-6int main() {int n, m;double a[100][100], b[100], x[100], z, min_x;int phase = 1;int i, j, k;// 输入数据printf("Enter the number of variables (n) and constraints (m): ");scanf("%d %d", &n, &m);printf("Enter the constraint matrix A and the right-hand side vector b:\n");for (i = 0; i < m; i++) {for (j = 0; j < n; j++) {scanf("%lf", &a[i][j]);}scanf("%lf", &b[i]);}printf("Enter the objective function coefficients:\n"); for (j = 0; j < n; j++) {scanf("%lf", &x[j]);}printf("Enter the objective function constant: ");scanf("%lf", &z);// 第一阶段：寻找初始解for (i = 0; i < n; i++) {if (x[i] < 0) { // 如果目标函数的系数小于0，则该变量为基变量min_x = -x[i]; // 计算最小绝对值for (j = 0; j < m; j++) { // 在约束条件中寻找该变量的系数最小值对应的变量if (a[j][i] > EPSILON) { // 如果该变量的系数大于一个很小的值，则该变量为基变量if (fabs(a[j][i]) < min_x) { // 计算最小绝对值min_x = fabs(a[j][i]); // 更新最小绝对值}}}x[i] = -min_x; // 将该变量的值设置为最小绝对值乘以一个很小的正数（使得该变量成为基变量）} else { // 如果目标函数的系数大于等于0，则该变量为非基变量，取值为0x[i] = 0;}}for (i = 0; i < m; i++) { // 判断约束是否满足（无可行解） if (b[i] < z * x[0] + z * x[1] + ... + z * x[n - 1]) { // 如果约束不满足，则无可行解，结束程序printf("No feasible solution.\n");return 0;}}printf("Initial solution: ");for (i = 0; i < n; i++) { // 输出初始解printf("%.2f ", x[i]);}printf("\n");// 第二阶段：使用单纯形法进行迭代优化for (k = 0; k < MAX_ITER; k++) { // 最大迭代次数为1000次，可以根据实际情况进行调整int pivot_index = -1; // 记录pivot变量的下标，初始化为-1表示未找到pivot变量double max_ratio = -1; // 记录最大比值，初始化为-1表示未找到pivot变量对应的比值最大值for (i = 0; i < n; i++) { // 在非基变量中寻找pivot 变量和对应的最大比值if (x[i] > EPSILON) { // 如果该变量的值大于一个很小的正数，则该变量为非基变量，可以作为pivot变量候选者之一 double ratio = b[i] / a[i][n]; // 计算比值（目标函数值/约束条件值）和最大比值比较大小，更新最大比值和对应的pivot变量下标和目标函数值if (ratio > max_ratio) { // 如果当前比值大于最大比值，则更新最大比值和。

改进单纯形法

正检验数换入变量
确定换出变量:
min
B21b B21P5
i i
B21P5
0
min
2 1/
2
,
8 2
,3 1/ 4
4
对应x 4
新的基:
B3 P1, P5, P2 ;
换入变量x5 的系数向量是
1 0 1/ 2 0 1/ 2
B21P5
4
1
2
0
2
主元素
0 0 1/ 4 1 1/ 4
单纯形法的矩阵描述
设线性规划问题可以用如下矩阵形式表示：
目标函数 max z=CX 约束条件 AX≤b 非负条件 X≥0
将该线性规划问题的约束条件加入松弛变量后，得到标准型：
max z=CX+0Xs AX+IXs=b
X，X s≥0
其中，I 是m×m单位矩阵。
若以Xs为基变量，并标记成XB，可将系数矩阵(A，I) 分为 (B，N) 两块。B是基变量的系数矩阵，N是非基变量
8 4
16
4
12 2
目标函数的最优值为：
4
z*
CB B31b
2, 0,3
4
14
2
换入变量
确定换出变量：
min
B11b B11P1
i i
B11P1
0
min
2 1
, 16 4
,
3 0
2
对应x 1
由此得到新的基：
B2 P1, P4 , P2
主元素
1
1
1 0 0
P1
4
0
2
4
E2
4
1
0

c++实现单纯形法现行规划问题的求解

c++实现单纯形法现⾏规划问题的求解在本程序中默认该现⾏规划问题有最优解针对此问题：1 #include<iostream>2using namespace std;34int check(float *sigema, int m) {5for (int i = 1; i <= m ; i++) {6if (sigema[i] > 0) {7return0;8 }9 }10return1;11 }1213//此程序已经化为标准型的线性规划问题中,且默认有最优解14int main(int argc, char* argv[])15 {16//数据输⼊部分17int m, n;18 cout << "请输⼊变量个数：";19 cin >> m;20 cout << "请输⼊不等式个数:";21 cin >> n;22float **matrix = new float*[n + 1]; //系数矩阵23for (int i = 1; i <= n; i++) {24 matrix[i] = new float[m + 2];25 }26float *cj = new float[m + 1];27float *cB = new float[n + 1]; //基变量系数28int *XB = new int[n + 1]; //⽤来标注基变量x的下标29float *b = new float[n + 1];30float *sigema = new float[n + 1];31float *sita = new float[n + 1];32//初始化33for (int i = 0; i <= m; i++) {34 cj[i] = 0;35 }36for (int i = 0; i <= n; i++) {37 cB[i] = 0;38 XB[i] = 0;39 b[i] = 0;40 sigema[i] = 0;41 sita[i] = 0;42 }43 cout << "请输⼊⽬标函数系数(⽤空格间开)：" << endl;44for (int i = 1; i <= m; i++) {45 cin >> cj[i];46 }47 cout << "请输⼊各不等式的系数和常量(⽤空格间开)：" << endl;48for (int i = 1; i <= n; i++) {49 cout << "不等式" << i << ": ";50for (int j = 1; j <= m + 1; j++) {51 cin >> matrix[i][j];52 }53 }54 cout << "请输⼊⽬标函数中基变量下标：" << endl;55for (int i = 1; i <= n; i++) {56 cin >> XB[i];57 cB[i] = cj[XB[i]];58//常量59 b[i] = matrix[i][m + 1];60 }6162//计算检验数63for (int i = 1; i <= m; i++) {64 sigema[i] = cj[i];65for (int j = 1; j <= n; j++) {66 sigema[i] -= cB[j] * matrix[j][i];67 }68 }6970while (check(sigema, m) == 0) {71//寻找⼊基变量72float maxn = sigema[1];73int sigema_xindex = 0;74float sigema_xcoefficient = 0;75for (int i = 1; i <= m; i++) {76if (maxn <= sigema[i]) {77 maxn = sigema[i];78 sigema_xindex = i;79 sigema_xcoefficient = cj[i];80 }81 }82//计算sita83for (int i = 1; i <= n; i++) {84if (matrix[i][sigema_xindex] > 0) {85 sita[i] = b[i] / matrix[i][sigema_xindex];86 }87else {88 sita[i] = 9999; //表⽰sita值为负数89 }90 }91//寻找出基变量92float minn = sita[1];93int sita_xindex = 0;94for (int i = 1; i <= n; i++) {95if (minn >= sita[i] && sita[i] > 0) {96 minn = sita[i];97 sita_xindex = i;98 }99 }100//⼊基出基变换,先⼊基再出基101//⼊基操作102for (int i = 1; i <= n; i++) {103if (i == sita_xindex) {104 XB[i] = sigema_xindex;105 cB[i] = sigema_xcoefficient;106break;107 }108 }109//出基计算110//化1111//cout << endl << "此处为化1的结果------" << endl;112float mul1 = matrix[sita_xindex][sigema_xindex];113for (int i = 1; i <= m; i++) {114 matrix[sita_xindex][i] /= mul1;115 }116 b[sita_xindex] /= mul1;117//化0118//cout << endl << "此处为化0的结果------" << endl;119for (int i = 1; i <= n; i++) {120if (i == sita_xindex) {121continue;122 }123float mul2 = matrix[i][sigema_xindex] / matrix[sita_xindex][sigema_xindex]; 124for (int j = 1; j <= m; j++) {125 matrix[i][j] -= (matrix[sita_xindex][j] * mul2);126 }127 b[i] -= (b[sita_xindex] * mul2);128 }129for (int i = 1; i <= n; i++) {130if (i == sita_xindex) {131continue;132 }133 }134for (int i = 1; i <= m; i++) {135 sigema[i] = cj[i];136for (int j = 1; j <= n; j++) {137 sigema[i] -= cB[j] * matrix[j][i];138 }139 }140 }141float MaxZ = 0;142float *result = new float[m + 1];143for (int i = 0; i <= m; i++) {144 result[i] = 0;145 }146for (int i = 1; i <= n; i++) {147 result[XB[i]] = b[i];148 }149 cout << "最优解为：X = (";150for (int i = 1; i < m; i++) {151 cout << result[i] << ",";152 }153 cout << result[m] << ")" << endl;154for (int i = 1; i <= m; i++) {155 MaxZ += result[i] * cj[i];156 }157 cout << "最优值为：MzxZ = " << MaxZ; 158return0;159 }程序运⾏结果：。

单纯形法C语言程序

单纯形法C语言程序实验:编制《线性规划》计算程序一、实验目的:(1)使学生在程序设计方面得到进一步的训练;，掌握Matlab (C或VB)语言进行程序设计中一些常用方法。

(2)使学生对线性规划的单纯形法有更深的理解.二、实验用仪器设备、器材或软件环境计算机, Matlab R2009a三、算法步骤、计算框图、计算程序等本实验主要编写如下线性规划问题的计算程序:mincxAx,b ,s.t.,x,0,b,0,其中初始可行基为松弛变量对应的列组成.对于一般标准线性规划问题:mincxAx,b ,s.t.,x,0,b,0,,(求解上述一般标准线性规划的单纯形算法(修正)步骤如下:对于一般的标准形式线性规划问题(求极小问题),首先给定一个初始基本可行解。

设初始基为B,然后执行如下步骤:,1Bxb,xBb,令计算目标函数值xfcx,,0,BNBBB(1).解,求得，,1以b(1,2,...,)imBbi,记的第个分量i,1wBC,wCB,BB(2).计算单纯形乘子w, ,得到,对于非基变量，计算判别,1,1,Ac,数,可直接计算令 ,,,,,zccBpciiiBii,cBB,R为非基变量集合 ,,max{}k,,iR,,0k若判别数 ,则得到一个最优基本可行解，运算结束;否则，转到下一步,1yy,0Byp,yBp,kkkkkk(3).解,得到;若,即的每个分量均非正数，则停止计算，问题不存在有限最优解，否则，进行步骤(4).确定下标r,使bbtr,,min,0且y,,x为离基变量,tkyyrktkB:0,tyrtkxp为进基变量,用p替换得到新的基矩阵,B,还回步骤(1)kBkr;12,、计算框图为:开始初始可行基B,1 令x,Bb,x,0,f,cxBNBB1 ,,计算单纯性乘子w,cB,计算判别数,wp,c,j,R(非基变量)Bjjj令,,max{,,j,R}kj是,,0?k否得到最优解,1 解方程By,p,得到y,Bp,kkkk是y,0? k否不存在有限最优解确定下标r,使得,,bbir,min|,0 y,,ikyyrkik,,x为退基变量，x进基变量，以Bkrp代替p,得到新的基矩阵BkBr3: 3(计算程序(Matlab)A=input('A=');b=input('b=');c=input('c=');format rat %可以让结果用分数输出[m,n]=size(A);E=1:m;E=E';F=n-m+1:n;F=F';D=[E,F]; %创建一个一一映射，为了结果能够标准输出 X=zeros(1,n); %初始化Xif(n<m) %判断是否为标准型fprintf('不符合要求需引入松弛变量')flag=0;elseflag=1;B=A(:,n-m+1:n); %找基矩阵cB=c(n-m+1:n); %基矩阵对应目标值的cwhile flagw=cB/B; %计算单纯形乘子，cB/B=cB*inv(B),用cB/B的目的是，为了提高运行速度。