时间序列上机操作题

合集下载

时间序列分析上机操作题

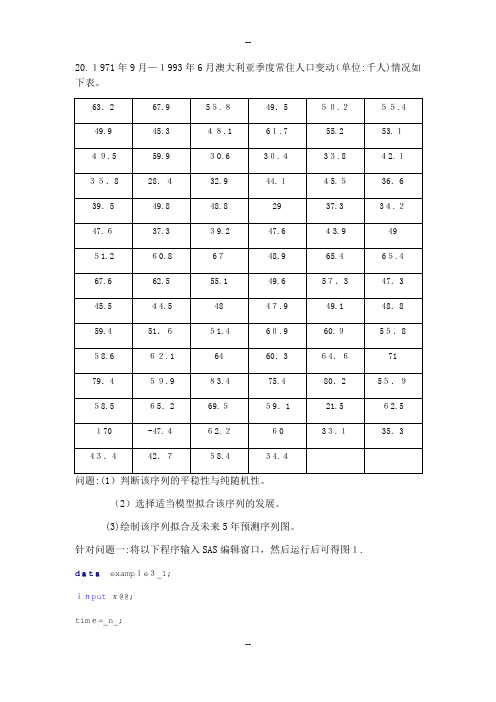
20.１971年9月—１993年6月澳大利亚季度常住人口变动（单位:千人)情况如下表。

问题:(1）判断该序列的平稳性与纯随机性。

（2）选择适当模型拟合该序列的发展。

(3)绘制该序列拟合及未来5年预测序列图。

针对问题一:将以下程序输入SAS编辑窗口，然后运行后可得图１.dａtａ exampｌe３_1;ｉｎputｘ@@;timｅ=_n_;cａｒds;６３.26ﻩ７.95ﻩ５.8 49.5ﻩ50．２55.4ﻩ４９.9 45.３４８.1 6１.755.2ﻩ 53.149.5ﻩ5９．9ﻩ30.4ﻩ30.6ﻩ３３.8 4２.１35.8ﻩ2８.4ﻩ44.1ﻩ32.9ﻩ４5.5 ３6．639.5 4９.8 4８.8 29 3７．33ﻩ４.2 ４7.637ﻩ．339ﻩ．2 47.6 43.9ﻩ４951.2ﻩ６0.8 ６7ﻩ 48.9 ６5.4ﻩ６５.4６7.6 6２.５55.1 49.6ﻩ5７．3 47.３4５.544.5ﻩ 4８47．9 49.1 4８.８５9.451ﻩ.６５1.4 ６0.9 60.9 5５.8 58.６62.1ﻩ64ﻩ 60.3 64.6ﻩ7179.４５9.９８３.４ 75.4 ８０.255ﻩ．9 58.5 ６５.２６9．55ﻩ９.1 2１.5 ６2.5 170 ﻩ－47.462.2ﻩ 60ﻩ3３.135ﻩ.３43.4ﻩ４2.758ﻩ．434ﻩ．4；pｒoｃgｐloｔｄａta＝eｘample3＿1;plotｘ*ｔiｍe=1;symｂｏl1ｃ＝red I=joｉn v=ｓｔａr；ｒun;图１该序列的时序图由图1可读出：除图中17０和－47.４这两个异常数据外，该时序图显示澳大利亚季度常住人口变动一般在在60附近随机波动,没有明显的趋势或周期,基本可视为平稳序列。

再接着输入以下程序运行后可输出五方面的信息。

具体见表１－表5．ｐｒoｃａｒiｍa data＝ｅxａmple3_１;identifyＶａr=x nlag=8;rｕn；表1 分析变量的描述性统计从表1可读出分析变量的名称、该序列的均值;标准差及观察值的个数(样本容量）。

时间序列上机操作

时间序列上机操作第⼀讲：基本的eviews操作（包括试验⼀和实验⼆）实验⼀ EVIEWS中时间序列相关函数操作【实验⽬的】熟悉Eviews的操作：菜单⽅式，命令⽅式；练习并掌握与时间序列分析相关的函数操作。

【实验内容】⼀、EViews软件的常⽤菜单⽅式和命令⽅式；⼆、各种常⽤差分函数表达式；三、时间序列的⾃相关和偏⾃相关图与函数；【实验步骤】⼀、EViews软件的常⽤菜单⽅式和命令⽅式；㈠创建⼯作⽂件⒈菜单⽅式启动EViews软件之后，进⼊EViews主窗⼝在主菜单上依次点击File/New/Workfile，即选择新建对象的类型为⼯作⽂件，将弹出⼀个对话框，由⽤户选择数据的时间频率（frequency）、起始期和终⽌期。

选择时间频率为Annual（年度），再分别点击起始期栏（Start date）和终⽌期栏（End date），输⼊相应的⽇期，然后点击OK按钮，将在EViews软件的主显⽰窗⼝显⽰相应的⼯作⽂件窗⼝。

⼯作⽂件窗⼝是EViews的⼦窗⼝，⼯作⽂件⼀开始其中就包含了两个对象，⼀个是系数向量C（保存估计系数⽤），另⼀个是残差序列RESID（实际值与拟合值之差）。

⒉命令⽅式在EViews软件的命令窗⼝中直接键⼊CREATE命令，也可以建⽴⼯作⽂件。

命令格式为：CREATE 时间频率类型起始期终⽌期则菜单⽅式过程可写为：CREATE A 1985 1998㈡输⼊Y、X的数据⒈DATA命令⽅式在EViews软件的命令窗⼝键⼊DATA命令，命令格式为：DATA <序列名1> <序列名2>…<序列名n>本例中可在命令窗⼝键⼊如下命令：DATA Y X⒉⿏标图形界⾯⽅式在EViews软件主窗⼝或⼯作⽂件窗⼝点击Objects/New Object，对象类型选择Series，并给定序列名，⼀次只能创建⼀个新序列。

再从⼯作⽂件⽬录中选取并双击所创建的新序列就可以展⽰该对象，选择Edit＋/－，进⼊编辑状态，输⼊数据。

(完整word版)时间序列习题(附答案)

一、单项选择题1．时间数列与变量数列（)A都是根据时间顺序排列的B都是根据变量值大小排列的C前者是根据时间顺序排列的，后者是根据变量值大小排列的D前者是根据变量值大小排列的,后者是根据时间顺序排列的2．时间数列中，数值大小与时间长短有直接关系的是（）A平均数时间数列B时期数列C时点数列D相对数时间数列3．发展速度属于( ）A比例相对数B比较相对数C动态相对数D强度相对数4．计算发展速度的分母是( ）A报告期水平B基期水平C实际水平D计划水平5．某车间月初工人人数资料如下:则该车间上半年的平均人数约为( )A 296人B 292人C 295 人D 300人6．某地区某年9月末的人口数为150万人，10月末的人口数为150．2万人,该地区10月的人口平均数为（)矚慫润厲钐瘗睞枥庑赖.A150万人B150．2万人C150．1万人D无法确定7．由一个9项的时间数列可以计算的环比发展速度（）A有8个B有9个C有10个D有7个8．采用几何平均法计算平均发展速度的依据是( )A各年环比发展速度之积等于总速度B各年环比发展速度之和等于总速度C各年环比增长速度之积等于总速度D各年环比增长速度之和等于总速度9．某企业的产值2005年比2000年增长了58．6％，则该企业2001—2005年间产值的平均发展速度为（）聞創沟燴鐺險爱氇谴净.A 5%6.58B 5%6.158158 C 6%6.58 D 6%6.10．根据牧区每个月初的牲畜存栏数计算全牧区半年的牲畜平均存栏数，采用的公式是（）A简单平均法B几何平均法C加权序时平均法D首末折半法11、时间序列在一年内重复出现的周期性波动称为（）A、长期趋势B、季节变动C、循环变动D、随机变动1．C 2．B 3．C 4．B 5．C 6．C 7．A 8．A 9．B 10．D 11、B残骛楼諍锩瀨濟溆塹籟。

二、多项选择题1．对于时间数列,下列说法正确的有( ）A数列是按数值大小顺序排列的B数列是按时间顺序排列的C数列中的数值都有可加性D数列是进行动态分析的基础E编制时应注意数值间的可比性2．时点数列的特点有( ）A数值大小与间隔长短有关B数值大小与间隔长短无关C数值相加有实际意义D数值相加没有实际意义E数值是连续登记得到的3．下列说法正确的有( ）A平均增长速度大于平均发展速度B平均增长速度小于平均发展速度C 平均增长速度=平均发展速度-1D 平均发展速度=平均增长速度-1E 平均发展速度×平均增长速度=14．下列计算增长速度的公式正确的有（） A%100⨯=基期水平增长量增长速度 B %100⨯=报告期水平增长量增长速度C 增长速度= 发展速度—100％D %100⨯-=基期水平基期水平报告期水平增长速度E%100⨯=基期水平报告期水平增长速度5．采用几何平均法计算平均发展速度的公式有（）A 1231201-⨯⨯⨯⨯=n na a a a a a a a nx B 0a a n x n = C1a a nx n = D n R x = E n x x ∑=6．某公司连续五年的销售额资料如下：根据上述资料计算的下列数据正确的有（ ) A 第二年的环比增长速度=定基增长速度=10％ B 第三年的累计增长量=逐期增长量=200万元 C 第四年的定基发展速度为135% D 第五年增长1％绝对值为14万元E第五年增长1%绝对值为13．5万元7．下列关系正确的有（)A环比发展速度的连乘积等于相应的定基发展速度B定基发展速度的连乘积等于相应的环比发展速度C环比增长速度的连乘积等于相应的定基增长速度D环比发展速度的连乘积等于相应的定基增长速度E平均增长速度=平均发展速度—18．测定长期趋势的方法主要有（）A时距扩大法B方程法C最小平方法D移动平均法E几何平均法9．关于季节变动的测定，下列说法正确的是（）A目的在于掌握事物变动的季节周期性B常用的方法是按月（季）平均法C需要计算季节比率D按月计算的季节比率之和应等于400％E季节比率越大，说明事物的变动越处于淡季10．时间数列的可比性原则主要指（）A时间长度要一致B经济内容要一致C计算方法要一致D总体范围要一致E计算价格和单位要一致答案1．BDE 2．BD 3．BC 4．ACD 5．ABD 6．ACE 7．AE8．ACD 9．ABC 10．ABCDE三、判断题1．时间数列中的发展水平都是统计绝对数。

时间序列练习题答案

时间序列练习题答案一、选择题1. 时间序列分析中的自回归模型（AR）是指：A. 模型中的误差项B. 模型预测值依赖于自身过去的值C. 模型预测值依赖于其他变量的值D. 模型预测值依赖于未来的值2. 移动平均模型（MA）的主要特征是：A. 预测值依赖于过去的误差项B. 预测值依赖于过去的观测值C. 预测值依赖于未来的误差项D. 预测值依赖于未来的观测值3. 以下哪个不是时间序列分析中的平稳性检验方法？A. 单位根检验B. 协整检验C. KPSS检验D. 方差比检验4. 时间序列的差分操作通常用于：A. 消除季节性效应B. 消除趋势C. 消除周期性变化D. 消除随机波动5. 季节性调整的目的是：A. 消除随机波动B. 消除季节性效应C. 消除长期趋势D. 消除周期性变化二、简答题1. 简述自回归积分滑动平均模型（ARIMA）的基本组成部分。

2. 解释什么是时间序列的平稳性，并说明为什么在时间序列分析中需要考虑平稳性。

3. 描述季节性时间序列的特点，并说明如何识别和处理季节性效应。

三、计算题1. 给定以下时间序列数据：\[ y_t = \{10, 15, 20, 25, 30, 35, 40, 45, 50, 55\} \] 假设这是一个一阶自回归模型AR(1)，其中自回归系数φ=0.8。

请计算下一个时间点的预测值。

2. 假设一个时间序列模型的ACF（自相关函数）在滞后1时显著不为0，而在滞后2及以后时显著为0。

根据这个信息，推测该时间序列可能属于哪种类型的模型？四、案例分析题1. 某公司销售数据呈现明显的季节性变化，如何在时间序列分析中对数据进行季节性调整？2. 一个时间序列模型的ADF（Augmented Dickey-Fuller）检验结果表明存在单位根，这意味着什么？如何对数据进行处理以消除单位根？五、论述题1. 论述时间序列分析在金融领域中的应用，并举例说明。

2. 讨论时间序列分析中的因果关系检验方法，并说明在实际应用中如何选择合适的方法。

时间序列习题答案

时间序列习题答案时间序列习题答案时间序列分析是一种用来研究随时间变化的数据模式和趋势的方法。

它在经济学、金融学、统计学等领域中被广泛应用。

下面我将给出一些时间序列分析的习题，并附上详细的答案解析。

习题一：某公司过去一年的销售额如下：100, 120, 130, 140, 150, 160, 170, 180, 190, 200。

请计算该公司的平均销售额和年度增长率。

答案解析：首先，计算平均销售额的方法是将所有销售额相加，然后除以销售额的个数。

在这个例子中，销售额的个数为10，总销售额为100+120+130+140+150+160+170+180+190+200=1540。

因此，平均销售额为1540/10=154。

接下来，计算年度增长率的方法是将最后一年的销售额减去第一年的销售额，然后除以第一年的销售额，并乘以100%。

在这个例子中，最后一年的销售额为200，第一年的销售额为100。

因此，年度增长率为(200-100)/100*100%=100%。

习题二：某股票的每日收盘价如下：10.2, 10.5, 10.7, 10.9, 11.1, 11.3, 11.5, 11.7, 11.9, 12.1。

请计算该股票的平均收盘价和收益率。

答案解析：计算平均收盘价的方法与计算平均销售额的方法相同。

将所有收盘价相加，然后除以收盘价的个数。

在这个例子中，收盘价的个数为10，总收盘价为10.2+10.5+10.7+10.9+11.1+11.3+11.5+11.7+11.9+12.1=113.9。

因此，平均收盘价为113.9/10=11.39。

计算收益率的方法是将每日的收盘价减去前一日的收盘价，然后除以前一日的收盘价，并乘以100%。

在这个例子中，第二天的收盘价为10.5，第一天的收盘价为10.2。

因此，第二天的收益率为(10.5-10.2)/10.2*100%=2.94%。

习题三：某城市过去十年的月度平均气温如下：15, 18, 20, 22, 25, 28, 30, 29, 26, 23。

人大(王燕)时间序列课后习题问题详解)2-5(含上机的)

第二章P34 1、（1）因为序列具有明显的趋势，所以序列非平稳。

（2）样本自相关系数：∑∑=-=+---≅=nt tkn t k t tk x xx x x xk 121)())(()0()(ˆγγρ5.10)2021(20111=+++==∑= n t t x n x =-=∑=2201)(201)0(x x t t γ35 =--=+=∑))((191)1(1191x x x x t t t γ29.75 =--=+=∑))((181)2(2181x x x x t t t γ25.9167=--=+=∑))((171)3(3171x x x x t t t γ21.75γ(4)=17.25 γ(5)=12.4167 γ(6)=7.251ρ=0.85（0.85） 2ρ=0.7405（0.702） 3ρ=0.6214（0.556） 4ρ=0.4929（0.415） 5ρ=0.3548（0.280） 6ρ=0.2071（0.153）注：括号的结果为近似公式所计算。

（3）样本自相关图：Autocorrelation Partial Correlation AC PACProb . |*******| . |*******| 1 0.850 0.850 16.732 0.000 . |***** | . *| . | 2 0.702 -0.07628.7610.000 . |**** | . *| . | 3 0.556 -0.07636.7620.000 . |*** | . *| . | 4 0.415 -0.07741.5000.000 . |**. | . *| . | 5 0.280 -0.07743.8000.000 . |* . | . *| . | 6 0.153 -0.07844.5330.000 . | . |. *| . |7 0.034 -0.07744.5720.000. *| . | . *| . | 8 -0.074-0.07744.7710.000 . *| . | . *| . | 9 -0.17-0.07545.9210.000 .**| . | . *| . | 10 -0.252-0.07248.7130.000 .**| . | . *| . | 11 -0.319-0.06753.6930.000 ***| . |. *| . |12 -0.37-0.0661.2200.000该图的自相关系数衰减为0的速度缓慢，可认为非平稳。

时间序列习题(含答案)

一、单项选择题 1．时间数列与变量数列( )A 都是根据时间顺序排列的B 都是根据变量值大小排列的C 前者是根据时间顺序排列的，后者是根据变量值大小排列的D 前者是根据变量值大小排列的，后者是根据时间顺序排列的 2．时间数列中，数值大小与时间长短有直接关系的是( )A 平均数时间数列B 时期数列C 时点数列D 相对数时间数列 3．发展速度属于( )A 比例相对数B 比较相对数C 动态相对数D 强度相对数 4．计算发展速度的分母是( )A 报告期水平B 基期水平C 实际水平D 计划水平 5．某车间月初工人人数资料如下：则该车间上半年的平均人数约为( )A 296人B 292人C 295 人D 300人6．某地区某年9月末的人口数为150万人，10月末的人口数为150．2万人，该地区10月的人口平均数为( )A150万人 B150．2万人 C150．1万人 D 无法确定 7．由一个9项的时间数列可以计算的环比发展速度( ) A 有8个 B 有9个 C 有10个 D 有7个 8．采用几何平均法计算平均发展速度的依据是( )A 各年环比发展速度之积等于总速度B 各年环比发展速度之和等于总速度C 各年环比增长速度之积等于总速度D 各年环比增长速度之和等于总速度 9．某企业的产值2005年比2000年增长了58．6％，则该企业2001—2005年间产值的平均发展速度为( )A 5%6.58 B 5%6.158 C 6%6.58 D 6%6.158 10．根据牧区每个月初的牲畜存栏数计算全牧区半年的牲畜平均存栏数，采用的公式是( )A 简单平均法B 几何平均法C 加权序时平均法D 首末折半法 11、时间序列在一年内重复出现的周期性波动称为（）A 、长期趋势B 、季节变动C 、循环变动D 、随机变动1．C 2．B 3．C 4．B 5．C 6．C 7．A 8．A 9．B 10．D 11、B 二、多项选择题1．对于时间数列，下列说法正确的有( )A 数列是按数值大小顺序排列的B 数列是按时间顺序排列的C 数列中的数值都有可加性D 数列是进行动态分析的基础E 编制时应注意数值间的可比性 2．时点数列的特点有( )A 数值大小与间隔长短有关B 数值大小与间隔长短无关C 数值相加有实际意义D 数值相加没有实际意义E 数值是连续登记得到的3．下列说法正确的有( )A 平均增长速度大于平均发展速度B 平均增长速度小于平均发展速度C 平均增长速度=平均发展速度-1D 平均发展速度=平均增长速度-1E 平均发展速度×平均增长速度=14．下列计算增长速度的公式正确的有( )A %100⨯=基期水平增长量增长速度 B %100⨯=报告期水平增长量增长速度C 增长速度= 发展速度—100％D %100⨯-=基期水平基期水平报告期水平增长速度E %100⨯=基期水平报告期水平增长速度 5．采用几何平均法计算平均发展速度的公式有( )A1231201-⨯⨯⨯⨯=n n a a a a a a a a nx Ba a nx n =C 1a a nx n= D nR x = E n xx ∑=6．某公司连续五年的销售额资料如下：根据上述资料计算的下列数据正确的有( )A 第二年的环比增长速度=定基增长速度=10％B 第三年的累计增长量=逐期增长量=200万元C 第四年的定基发展速度为135％D 第五年增长1％绝对值为14万元E 第五年增长1％绝对值为13．5万元 7．下列关系正确的有( )A 环比发展速度的连乘积等于相应的定基发展速度B 定基发展速度的连乘积等于相应的环比发展速度C 环比增长速度的连乘积等于相应的定基增长速度D 环比发展速度的连乘积等于相应的定基增长速度E 平均增长速度=平均发展速度-1 8．测定长期趋势的方法主要有( )A 时距扩大法B 方程法C 最小平方法D 移动平均法E 几何平均法9．关于季节变动的测定，下列说法正确的是( ) A 目的在于掌握事物变动的季节周期性 B 常用的方法是按月(季)平均法 C 需要计算季节比率D 按月计算的季节比率之和应等于400％E 季节比率越大，说明事物的变动越处于淡季 10．时间数列的可比性原则主要指( )A 时间长度要一致B 经济内容要一致C 计算方法要一致D 总体范围要一致E 计算价格和单位要一致1．BDE 2．BD 3．BC 4．ACD 5．ABD 6．ACE 7．AE8．ACD 9．ABC 10．ABCDE 三、判断题1．时间数列中的发展水平都是统计绝对数。

第五章-时间序列练习试题

d、数列中每个指标数值是通过连续不断的登记而取得的
28.计算序时平均数的方法有( )。
a、简单算术平均法b、加权算术平均法c、简单序时平均法d、加权序时平均法
29.当时间序列中的指标数值存在负数时，不易采用水平法计算平均发展速度，因为计算结果( )。
a、可能为负数b、必须为负数c、可能为虚数d、等于零、
15.说明现象在较长时期内发展的总速度的数值是()。
a、环比发展速度b、平均发展速度c、定基增长速度d、定基发展速度
16.某地区2003－2007年年底生猪存栏头数在2002的基础上分别增加20、30、40、30和50万头，则5年间平均生猪增长量()。
a、10万头b、34万头c、6万头d、13万头
17.已知环比增长速度为8.12％、3.42％、2.91％、5.13％，则定基增长速度为()。
5.时点序列的每一项指标值反映现象在某一段时期达到的水平。
6.时点序列的每一项指标数值的大小和它在时间间隔上的长短没有直接关系。
a、发展速度与1之差
b、扣除基数之后的发展速度
c、报告期比基期水平增长的相对程度
d、报告期比基期水平之差同基期水平之比
12.定基增长速度等于()。
a、累计增长量除以基期水平b、环比增长速度的连乘积
c、环比发展速度的连乘积减1d、定基发展速度减1
13.水平法计算的平均发展速度是一种()。
a、算术平均数b、几何平均数c、序时平均数d、动态平均数
26.编制时间序列应遵循的原则包括( )。
a、指标数值所属的总体范围应该一致b、指标的经济涵义应该相同
c、指标数值的计算方法应该一致d、指标数值的计算价格应该一致
27.时点序列的特点主要有( )。
a、数列中每个指标数值不能相加b、数列中每个指标数值可以相加

(完整版)时间序列习题(含答案)

一、单项选择题1．时间数列与变量数列( )A都是根据时间顺序排列的 B都是根据变量值大小排列的 C前者是根据时间顺序排列的，后者是根据变量值大小排列的D前者是根据变量值大小排列的，后者是根据时间顺序排列的2．时间数列中，数值大小与时间长短有直接关系的是( )A平均数时间数列 B时期数列 C时点数列 D相对数时间数列 3．发展速度属于( )A比例相对数 B比较相对数 C动态相对数 D强度相对数4．计算发展速度的分母是( )A报告期水平 B基期水平 C实际水平 D计划水平5．某车间月初工人人数资料如下：则该车间上半年的平均人数约为( )A 296人B 292人C 295 人D 300人6．某地区某年9月末的人口数为150万人，10月末的人口数为150．2万人，该地区10月的人口平均数为( )A150万人 B150．2万人 C150．1万人 D无法确定7．由一个9项的时间数列可以计算的环比发展速度( )A有8个 B有9个 C有10个 D有7个8．采用几何平均法计算平均发展速度的依据是( )A 各年环比发展速度之积等于总速度B 各年环比发展速度之和等于总速度C 各年环比增长速度之积等于总速度D 各年环比增长速度之和等于总速度9．某企业的产值2005年比2000年增长了58．6％，则该企业2001—2005年间产值的平均发展速度为( )A 5%6.58B 5%6.158C 6%6.58D 6%6.15810．根据牧区每个月初的牲畜存栏数计算全牧区半年的牲畜平均存栏数，采用的公式是( )A 简单平均法B 几何平均法C 加权序时平均法D 首末折半法 11、时间序列在一年内重复出现的周期性波动称为（）A 、长期趋势B 、季节变动C 、循环变动D 、随机变动1．C 2．B 3．C 4．B 5．C 6．C 7．A 8．A 9．B 10．D 11、B二、多项选择题1．对于时间数列，下列说法正确的有( )A 数列是按数值大小顺序排列的B 数列是按时间顺序排列的C 数列中的数值都有可加性D 数列是进行动态分析的基础E 编制时应注意数值间的可比性 2．时点数列的特点有( )A 数值大小与间隔长短有关B 数值大小与间隔长短无关C 数值相加有实际意义D 数值相加没有实际意义E 数值是连续登记得到的3．下列说法正确的有( )A 平均增长速度大于平均发展速度B 平均增长速度小于平均发展速度C 平均增长速度=平均发展速度-1D 平均发展速度=平均增长速度-1E 平均发展速度×平均增长速度=14．下列计算增长速度的公式正确的有( )A%100⨯=基期水平增长量增长速度 B %100⨯=报告期水平增长量增长速度C 增长速度= 发展速度—100％D%100⨯-=基期水平基期水平报告期水平增长速度E%100⨯=基期水平报告期水平增长速度5．采用几何平均法计算平均发展速度的公式有( )A1231201-⨯⨯⨯⨯=n n a a a a a a a a n x K Ba a nx n =C1a a n x n = D nR x = En xx ∑=6．某公司连续五年的销售额资料如下：根据上述资料计算的下列数据正确的有( )A第二年的环比增长速度=定基增长速度=10％B第三年的累计增长量=逐期增长量=200万元C第四年的定基发展速度为135％D第五年增长1％绝对值为14万元E第五年增长1％绝对值为13．5万元7．下列关系正确的有( )A环比发展速度的连乘积等于相应的定基发展速度B定基发展速度的连乘积等于相应的环比发展速度C环比增长速度的连乘积等于相应的定基增长速度D环比发展速度的连乘积等于相应的定基增长速度E平均增长速度=平均发展速度-18．测定长期趋势的方法主要有( )A时距扩大法 B方程法 C最小平方法 D移动平均法 E几何平均法9．关于季节变动的测定，下列说法正确的是( )A目的在于掌握事物变动的季节周期性B常用的方法是按月(季)平均法C需要计算季节比率D按月计算的季节比率之和应等于400％E季节比率越大，说明事物的变动越处于淡季10．时间数列的可比性原则主要指( )A时间长度要一致 B经济内容要一致 C计算方法要一致 D总体范围要一致E计算价格和单位要一致答案1．BDE 2．BD 3．BC 4．ACD 5．ABD 6．ACE 7．AE8．ACD 9．ABC 10．ABCDE三、判断题1．时间数列中的发展水平都是统计绝对数。

时间序列练习题

时间序列练习题时间序列分析是一种用于研究以时间为顺序的数据变动规律的方法。

它可以帮助我们理解和预测未来的趋势，对于决策和规划具有重要的意义。

本文将通过一些时间序列练习题，帮助读者更好地理解和应用时间序列分析。

练习题一：季度销售数据分析某公司的销售数据按照季度记录如下：季度销售额Q1 100Q2 200Q3 300Q4 400请你根据这些数据，进行以下的分析和预测：1. 绘制季度销售额的时间序列图。

2. 计算季度销售额的平均值。

3. 判断季度销售额是否存在趋势性，并进行趋势线的拟合。

4. 判断季度销售额是否存在季节性，如果存在，请进行季节性分解。

5. 使用你认为最适合的模型进行未来一年季度销售额的预测，并给出预测结果。

练习题二：月度股票收益率分析某股票连续12个月的收益率数据如下：月份收益率1 0.032 0.053 -0.024 0.025 -0.016 0.047 -0.038 0.019 0.0210 -0.0511 0.0112 0.03请你根据这些数据，进行以下的分析和预测：1. 绘制月度股票收益率的时间序列图。

2. 计算月度收益率的平均值和标准差。

3. 判断股票收益率是否存在趋势性，并进行趋势线的拟合。

4. 判断股票收益率是否存在季节性，如果存在，请进行季节性分解。

5. 使用你认为最适合的模型进行未来三个月股票收益率的预测，并给出预测结果。

练习题三：年度气温分析某城市过去10年（2011年至2020年）的年度平均气温数据如下：年份平均气温（摄氏度）2011 192012 212013 202014 182015 172016 182017 202018 222019 232020 21请你根据这些数据，进行以下的分析和预测：1. 绘制年度平均气温的时间序列图。

2. 计算年度平均气温的平均值、中位数和极差。

3. 判断气温是否存在趋势性，并进行趋势线的拟合。

4. 判断气温是否存在季节性，如果存在，请进行季节性分解。

时间序列上机作业一

上机作业一程序：习题3.8(a)library(TSA)data(retail)plot(retail,type='l',ylab='sales')points(y=retail,x=time(retail),pch=as.vector(season(retail)))(b)library(TSA)data(retail)retailmonth=season(retail)monthreg=lm(retail~month+time(retail))summary(reg)(c)plot(y=rstudent(reg),x=as.vector(time(retail)),type='l',ylab='Standardized residuals',xlab= ' Time') points(y=rstudent(reg),x=as.vector(time(retail)),pch=as.vector(season(retail)))结果输出：(a)reg=lm(retail~month+time(retail))> summary(reg)Call:lm(formula = retail ~ month + time(retail))Residuals:Min 1Q Median 3Q Max-19.8950 -2.4440 -0.3518 2.1971 16.2045Coefficients:Estimate Std. Error t value Pr(>|t|) (Intercept) -7.249e+03 8.724e+01 -83.099 < 2e-16 *** monthFebruary -3.015e+00 1.290e+00 -2.337 0.02024 * monthMarch 7.469e-02 1.290e+00 0.058 0.95387 monthApril 3.447e+00 1.305e+00 2.641 0.00880 ** monthMay 3.108e+00 1.305e+00 2.381 0.01803 * monthJune 3.074e+00 1.305e+00 2.355 0.01932 * monthJuly 6.053e+00 1.305e+00 4.638 5.76e-06 *** monthAugust 3.138e+00 1.305e+00 2.404 0.01695 * monthSeptember 3.428e+00 1.305e+00 2.626 0.00919 ** monthOctober 8.555e+00 1.305e+00 6.555 3.34e-10 *** monthNovember 2.082e+01 1.305e+00 15.948 < 2e-16 *** monthDecember 5.254e+01 1.305e+00 40.255 < 2e-16 *** time(retail) 3.670e+00 4.369e-02 83.995 < 2e-16 ***---Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1Residual standard error: 4.278 on 242 degrees of freedomMultiple R-squared: 0.9767, Adjusted R-squared: 0.9755F-statistic: 845 on 12 and 242 DF, p-value: < 2.2e-16习题3.14程序：（a）library(TSA)data(retail)retailmonth=season(retail)monthreg=lm(retail~month+time(retail))summary(reg)（b）runs(rstudent(reg))（c）acf(rstudent(reg))（d) qqnorm(rstudent(reg))qqline(rstudent(reg))hist(rstudent(reg),xlab='Standardized Residuals')shapiro.test(rstudent(reg))结果输出：（a）> library(TSA)> data(retail)> retailJan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec 1986 42.4 39.2 42.2 43.9 43.7 45.5 47.1 46.4 47.7 49.4 57.1 75.31987 45.9 44.0 45.0 49.3 47.0 48.9 52.2 51.1 51.5 54.6 62.7 83.51988 53.4 49.0 50.8 53.4 53.8 54.3 58.5 57.3 56.9 60.8 69.2 93.71989 57.8 53.9 56.6 57.5 59.5 57.5 60.1 60.0 60.3 63.5 71.6 99.51990 61.4 58.5 60.0 62.6 63.6 61.4 65.4 63.3 63.1 65.7 72.9 103.41991 61.0 56.7 63.6 63.2 63.7 63.2 67.6 64.1 64.2 68.2 78.2 104.31992 61.9 59.6 60.9 65.3 64.9 64.2 66.2 66.2 66.0 69.7 78.8 106.61993 64.6 62.6 64.7 68.4 66.8 68.4 70.2 69.4 70.5 74.6 84.5 113.81994 69.3 64.8 69.0 70.5 70.6 71.2 72.9 71.9 74.4 77.8 87.3 122.01995 69.5 67.7 69.8 74.1 72.7 73.5 76.7 72.8 76.2 80.0 91.1 126.71996 71.1 70.3 73.4 78.5 77.1 79.7 81.0 78.9 81.6 86.4 101.0 130.61997 76.7 75.8 80.6 82.9 82.0 86.5 88.8 83.9 84.7 92.6 105.7 139.81998 83.0 80.2 82.7 87.0 87.7 86.1 91.5 87.7 87.3 92.5 107.2 139.61999 85.2 81.5 85.1 88.2 90.1 90.1 94.5 91.7 89.7 97.3 111.8 144.52000 91.1 85.3 88.4 92.5 92.8 92.7 97.1 94.0 93.0 100.8 114.0 151.92001 93.9 90.3 92.4 98.6 100.1 99.0 103.5 100.4 101.0 107.4 123.3 164.12002 98.5 97.3 102.7 106.2 105.3 102.0 108.6 103.4 104.1 113.2 131.3 165.32003 100.1 99.3 102.7 108.1 106.3 106.7 111.2 105.9 108.0 116.7 134.0 170.82004 106.3 103.7 107.6 113.5 113.6 113.7 116.6 112.4 113.8 120.4 138.0 172.12005 106.0 102.7 109.1 109.6 110.7 112.7 114.8 111.1 111.5 118.8 136.9 177.52006 105.4 102.6 106.7 114.1 114.7 115.1 116.9 114.7 113.6 122.8 140.5 184.82007 107.6 107.5 113.2> month=season(retail)> month[1] January February March April May June July[8] August September October November December January February [15] March April May June July August September [22] October November December January February March April[29] May June July August September October November [36] December January February March April May June[43] July August September October November December January[50] February March April May June July August[57] September October November December January February March[64] April May June July August September October[71] November December January February March April May[78] June July August September October November December [85] January February March April May June July[92] August September October November December January February [99] March April May June July August September [106] October November December January February March April [113] May June July August September October November [120] December January February March April May June [127] July August September October November December January [134] February March April May June July August [141] September October November December January February March [148] April May June July August September October [155] November December January February March April May [162] June July August September October November December [169] January February March April May June July [176] August September October November December January February [183] March April May June July August September [190] October November December January February March April [197] May June July August September October November [204] December January February March April May June [211] July August September October November December January [218] February March April May June July August [225] September October November December January February March [232] April May June July August September October [239] November December January February March April May [246] June July August September October November December [253] January February March12 Levels: January February March April May June July August ... December> reg=lm(retail~month+time(retail))> summary(reg)Call:lm(formula = retail ~ month + time(retail))Residuals:Min 1Q Median 3Q Max-19.8950 -2.4440 -0.3518 2.1971 16.2045Coefficients:Estimate Std. Error t value Pr(>|t|)(Intercept) -7.249e+03 8.724e+01 -83.099 < 2e-16 ***monthFebruary -3.015e+00 1.290e+00 -2.337 0.02024 *monthMarch 7.469e-02 1.290e+00 0.058 0.95387monthApril 3.447e+00 1.305e+00 2.641 0.00880 **monthMay 3.108e+00 1.305e+00 2.381 0.01803 *monthJune 3.074e+00 1.305e+00 2.355 0.01932 *monthJuly 6.053e+00 1.305e+00 4.638 5.76e-06 ***monthAugust 3.138e+00 1.305e+00 2.404 0.01695 * monthSeptember 3.428e+00 1.305e+00 2.626 0.00919 ** monthOctober 8.555e+00 1.305e+00 6.555 3.34e-10 *** monthNovember 2.082e+01 1.305e+00 15.948 < 2e-16 *** monthDecember 5.254e+01 1.305e+00 40.255 < 2e-16 *** time(retail) 3.670e+00 4.369e-02 83.995 < 2e-16 ***---Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1Residual standard error: 4.278 on 242 degrees of freedomMultiple R-squared: 0.9767, Adjusted R-squared: 0.9755F-statistic: 845 on 12 and 242 DF, p-value: < 2.2e-16（b）> runs(rstudent(reg))$pvalue[1] 9.19e-23$observed.runs[1] 52$expected.runs[1] 127.9333$n1[1] 136$n2[1] 119$k[1] 0(c)(d)> shapiro.test(rstudent(reg))Shapiro-Wilk normality test data: rstudent(reg)W = 0.939, p-value = 8.534e-09>。

时间序列分析习题及答案

时间序列分析第一题：1、绘制时序图：data ex1_1;input x@@ ;time=intnx('month','01jul2004'd,_n_-1);format time date. ;cards;153 134 145 117 187 175 203 178 234 243 189 149 212 227 214 178 300 298 295 248 221 256 220 202 201 237 231 162 175 165 174 135 123 124 119 120 104 106 85 96 85 87 67 90 78 74 75 63;proc gplot data=ex1_1;plot x*time=1;symbol1 c=black v=star i=join;run;时序图：2、绘制自相关图：data ex1_1;input x@@ ;time=intnx('month','01jul2004'd,_n_-1);format time date. ;cards;153 134 145 117 187 175 203 178 234 243 189 149 212 227 214 178 300 298 295 248 221 256 220 202 201 237 231 162 175 165 174 135 123 124 119 120 104 106 85 96 85 87 67 90 78 74 75 63;proc arima data=ex1_1;identify var=x;run;样本自相关图：白噪声检验输出结果：因为P值小于α，所以该序列为非白噪声序列，根据时序图看出数据并不在一个常数值附近随机波动，后期有递减的趋势，所以不是平稳序列。

第二题：1、选择拟合模型方法一：首先绘制该序列的时序图，直观检验序列平稳性。

时间序列习题(含答案)

一、单项选择题1．时间数列与变量数列( >A都是根据时间顺序排列的 B都是根据变量值大小排列的C前者是根据时间顺序排列的，后者是根据变量值大小排列的D前者是根据变量值大小排列的，后者是根据时间顺序排列的2．时间数列中，数值大小与时间长短有直接关系的是( >A平均数时间数列 B时期数列 C时点数列 D相对数时间数列3．发展速度属于( >A比例相对数 B比较相对数 C动态相对数 D强度相对数4．计算发展速度的分母是( >A报告期水平B基期水平C实际水平 D计划水平5．某车间月初工人人数资料如下：则该车间上半年的平均人数约为( >A 296人B 292人C 295 人D 300人6．某地区某年9月末的人口数为150万人，10月末的人口数为150．2万人，该地区10月的人口平均数为( >b5E2RGbCAPA150万人 B150．2万人 C150．1万人 D无法确定7．由一个9项的时间数列可以计算的环比发展速度( >A有8个 B有9个 C有10个 D有7个8．采用几何平均法计算平均发展速度的依据是( >A各年环比发展速度之积等于总速度 B各年环比发展速度之和等于总速度C各年环比增长速度之积等于总速度 D各年环比增长速度之和等于总速度9．某企业的产值2005年比2000年增长了58．6％，则该企业2001—2005年间产值的平均发展速度为( >p1EanqFDPwA B CD10．根据牧区每个月初的牲畜存栏数计算全牧区半年的牲畜平均存栏数，采用的公式是( >A简单平均法 B几何平均法 C加权序时平均法 D首末折半法11、时间序列在一年内重复出现的周期性波动称为< ）A、长期趋势B、季节变动C、循环变动D、随机变动1．C 2．B 3．C 4．B 5．C 6．C 7．A 8．A 9．B 10．D 11、BDXDiTa9E3d二、多项选择题1．对于时间数列，下列说法正确的有( >A数列是按数值大小顺序排列的 B数列是按时间顺序排列的C数列中的数值都有可加性 D数列是进行动态分析的基础E编制时应注意数值间的可比性2．时点数列的特点有( >A数值大小与间隔长短有关 B数值大小与间隔长短无关C数值相加有实际意义 D数值相加没有实际意义 E数值是连续登记得到的3．下列说法正确的有( >A平均增长速度大于平均发展速度 B平均增长速度小于平均发展速度C平均增长速度=平均发展速度-1 D平均发展速度=平均增长速度-1E平均发展速度×平均增长速度=14．下列计算增长速度的公式正确的有( >ABC增长速度= 发展速度—100％DE5．采用几何平均法计算平均发展速度的公式有( >ABCDE6．某公司连续五年的销售额资料如下：根据上述资料计算的下列数据正确的有( >A第二年的环比增长速度=定基增长速度=10％B第三年的累计增长量=逐期增长量=200万元C第四年的定基发展速度为135％D第五年增长1％绝对值为14万元E第五年增长1％绝对值为13．5万元7．下列关系正确的有( >A环比发展速度的连乘积等于相应的定基发展速度B定基发展速度的连乘积等于相应的环比发展速度C环比增长速度的连乘积等于相应的定基增长速度D环比发展速度的连乘积等于相应的定基增长速度E平均增长速度=平均发展速度-18．测定长期趋势的方法主要有( >A时距扩大法B方程法C最小平方法 D移动平均法 E几何平均法9．关于季节变动的测定，下列说法正确的是( >A目的在于掌握事物变动的季节周期性B常用的方法是按月(季>平均法C需要计算季节比率D按月计算的季节比率之和应等于400％E季节比率越大，说明事物的变动越处于淡季10．时间数列的可比性原则主要指( >A时间长度要一致 B经济内容要一致 C计算方法要一致 D总体范围要一致E计算价格和单位要一致答案1．BDE 2．BD 3．BC 4．ACD 5．ABD 6．ACE 7．A E8．ACD 9．ABC 10．ABCDE三、判断题1．时间数列中的发展水平都是统计绝对数。

(完整word版)时间序列分析试题

第九章时间序列分析一、单项选择题1、乘法模型是分析时间序列最常用的理论模型。

这种模型将时间序列按构成分解为（）等四种成分，各种成分之间()，要测定某种成分的变动，只须从原时间序列中（）。

A.长期趋势、季节变动、循环波动和不规则波动；保持着相互依存的关系；减去其他影响成分的变动B.长期趋势、季节变动、循环波动和不规则波动；缺少相互作用的影响力量；减去其他影响成分的变动C.长期趋势、季节变动、循环波动和不规则波动；保持着相互依存的关系；除去其他影响成分的变动D.长期趋势、季节变动、循环波动和不规则波动；缺少相互作用的影响力量；除去其他影响成分的变动答案： C2、加法模型是分析时间序列的一种理论模型。

这种模型将时间序列按构成分解为（）等四种成分，各种成分之间()，要测定某种成分的变动，只须从原时间序列中（）。

A.长期趋势、季节变动、循环波动和不规则波动；保持着相互依存的关系；减去其他影响成分的变动B.长期趋势、季节变动、循环波动和不规则波动；缺少相互作用的影响力量；减去其他影响成分的变动C.长期趋势、季节变动、循环波动和不规则波动；保持着相互依存的关系；除去其他影响成分的变动D..长期趋势、季节变动、循环波动和不规则波动；缺少相互作用的影响力量；除去其他影响成分的变动答案： B3、利用最小二乘法求解趋势方程最基本的数学要求是（）。

A. (Y? 2任意值 B. (Y? 2min Y t ) Y t )C. (Y? 2max D. (Y? 20 Y t ) Y t )答案： B4、从下列趋势方程?125 0.86t 可以得出（）。

Y tA. 时间每增加一个单位，Y 增加 0.86 个单位B. 时间每增加一个单位，Y 减少 0.86 个单位C. 时间每增加一个单位，Y 平均增加0.86 个单位D. 时间每增加一个单位，Y 平均减少0.86 个单位答案： D.5、时间序列中的发展水平（）。

A. 只能是绝对数B. 只能是相对数C.只能是平均数D. 上述三种指标均可以答案： D.6、下列时间序列中，属于时点序列的有（）。

时间序列习题(含答案)

一、单项选择题1．时间数列与变量数列( )A 都是根据时间顺序排列的B 都是根据变量值大小排列的C 前者是根据时间顺序排列的，后者是根据变量值大小排列的D 前者是根据变量值大小排列的，后者是根据时间顺序排列的 2．时间数列中，数值大小与时间长短有直接关系的是( )A 平均数时间数列B 时期数列C 时点数列D 相对数时间数列 3．发展速度属于( )A 比例相对数B 比较相对数C 动态相对数D 强度相对数 4．计算发展速度的分母是( )A 报告期水平B 基期水平C 实际水平D 计划水平5．某车间月初工人人数资料如下：则该车间上半年的平均人数约为( )A 296人B 292人C 295 人D 300人6．某地区某年9月末的人口数为150万人，10月末的人口数为150．2万人，该地区10月的人口平均数为( )A150万人 B150．2万人 C150．1万人 D 无法确定 7．由一个9项的时间数列可以计算的环比发展速度( ) A 有8个 B 有9个 C 有10个 D 有7个 8．采用几何平均法计算平均发展速度的依据是( )A 各年环比发展速度之积等于总速度B 各年环比发展速度之和等于总速度C 各年环比增长速度之积等于总速度D 各年环比增长速度之和等于总速度 9．某企业的产值2005年比2000年增长了58．6％，则该企业2001—2005年间产值的平均发展速度为( )A 5%6.58 B 5%6.158 C 6%6.58 D 6%6.158 10．根据牧区每个月初的牲畜存栏数计算全牧区半年的牲畜平均存栏数，采用的公式是( )A 简单平均法B 几何平均法C 加权序时平均法D 首末折半法 11、时间序列在一年内重复出现的周期性波动称为（）A 、长期趋势B 、季节变动C 、循环变动D 、随机变动1．C 2．B 3．C 4．B 5．C 6．C 7．A 8．A 9．B 10．D 11、B 二、多项选择题1．对于时间数列，下列说法正确的有( )A 数列是按数值大小顺序排列的B 数列是按时间顺序排列的C 数列中的数值都有可加性D 数列是进行动态分析的基础E 编制时应注意数值间的可比性 2．时点数列的特点有( )A 数值大小与间隔长短有关B 数值大小与间隔长短无关C 数值相加有实际意义D 数值相加没有实际意义E 数值是连续登记得到的3．下列说法正确的有( )A 平均增长速度大于平均发展速度B 平均增长速度小于平均发展速度C 平均增长速度=平均发展速度-1D 平均发展速度=平均增长速度-1E 平均发展速度×平均增长速度=14．下列计算增长速度的公式正确的有( )A %100⨯=基期水平增长量增长速度 B %100⨯=报告期水平增长量增长速度C 增长速度= 发展速度—100％D %100⨯-=基期水平基期水平报告期水平增长速度E %100⨯=基期水平报告期水平增长速度 5．采用几何平均法计算平均发展速度的公式有( )A1231201-⨯⨯⨯⨯=n n a a a a a a a a nx Ba a nx n =C 1a a nx n= D nR x = E n x x ∑=6．某公司连续五年的销售额资料如下：根据上述资料计算的下列数据正确的有( )A 第二年的环比增长速度=定基增长速度=10％B 第三年的累计增长量=逐期增长量=200万元C 第四年的定基发展速度为135％D 第五年增长1％绝对值为14万元E 第五年增长1％绝对值为13．5万元 7．下列关系正确的有( )A 环比发展速度的连乘积等于相应的定基发展速度B 定基发展速度的连乘积等于相应的环比发展速度C 环比增长速度的连乘积等于相应的定基增长速度D 环比发展速度的连乘积等于相应的定基增长速度E 平均增长速度=平均发展速度-1 8．测定长期趋势的方法主要有( )A 时距扩大法B 方程法C 最小平方法D 移动平均法E 几何平均法9．关于季节变动的测定，下列说法正确的是( ) A 目的在于掌握事物变动的季节周期性 B 常用的方法是按月(季)平均法 C 需要计算季节比率D 按月计算的季节比率之和应等于400％E 季节比率越大，说明事物的变动越处于淡季 10．时间数列的可比性原则主要指( )A时间长度要一致 B经济内容要一致 C计算方法要一致 D总体范围要一致E计算价格和单位要一致1．BDE 2．BD 3．BC 4．ACD 5．ABD 6．ACE 7．AE8．ACD 9．ABC 10．ABCDE三、判断题1．时间数列中的发展水平都是统计绝对数。

时间序列分析上机操作题

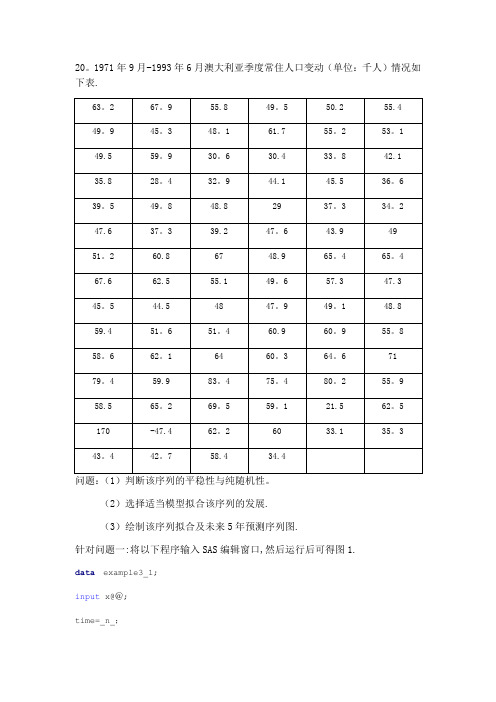
20。

1971年9月-1993年6月澳大利亚季度常住人口变动（单位：千人）情况如下表.问题：（1）判断该序列的平稳性与纯随机性。

（2）选择适当模型拟合该序列的发展.（3）绘制该序列拟合及未来5年预测序列图.针对问题一:将以下程序输入SAS编辑窗口,然后运行后可得图1.data example3_1;input x@＠;time=_n_；cards;63。

2 67。

9 55.8 49。

5 50。

2 55。

4 49。

9 45。

3 48.1 61.7 55.2 53。

1 49.5 59。

9 30。

6 30.4 33.8 42.1 35.8 28。

4 32.9 44.1 45.5 36。

6 39.5 49.8 48。

8 29 37.3 34。

2 47。

6 37.3 39。

2 47。

6 43。

9 49 51.2 60。

8 67 48.9 65.4 65.4 67.6 62.5 55.1 49。

6 57.3 47.3 45。

5 44。

5 48 47.9 49.1 48。

8 59。

4 51。

6 51。

4 60.9 60。

9 55。

8 58.6 62.1 64 60。

3 64.6 71 79.4 59。

9 83.4 75.4 80.2 55.9 58.5 65.2 69.5 59。

1 21。

5 62.5 170 -47.4 62。

2 60 33。

1 35。

3 43.4 42。

7 58。

4 34。

4;proc gplot data=example3_1；plot x＊time=1；symbol1c=red I=join v=star;run;图1 该序列的时序图由图1可读出:除图中170和-47。

4这两个异常数据外,该时序图显示澳大利亚季度常住人口变动一般在在60附近随机波动,没有明显的趋势或周期，基本可视为平稳序列.再接着输入以下程序运行后可输出五方面的信息。

具体见表1-表5.proc arima data= example3_1;identify Var=x nlag=8;run;表1 分析变量的描述性统计从表1可读出分析变量的名称、该序列的均值；标准差及观察值的个数(样本容量）。

时间序列重要习题

时间序列第一次习题
(2)第一季度平均售货员人数；
(3)第一季度平均每售货员的销售额；
(4)第一季度平均每月每个售货员的销售额。

（2）该企业一季度、二季度、和上半年平均每月的商品流转次数。

（提示：商品流转次数=销售额/平均库存额）
3．某企业2010年工业总产值及职工人数资料如下：
2009年末职工人数为2010人。

该企业相关分析人员计算的2010年该企业年平均职工人数和2010年该企业全年劳动生产率的过程如下：
2010年该企业年平均职工人数：
（人）
15754222002120207022018221210=+
++=+++++=-n y y y y y y n n 2010年该企业劳动生产率：
()/5655976146364
年劳动生产率＝
1575
+++=0.38（万元/人）
试问：以上计算过程是否存在问题？为什么？应该如何改进。

（2）1994-2005年该地区人口的平均增长速度.。

时间序列练习题

时间序列练习题时间序列分析是一种对随时间变化的数据进行建模和预测的统计分析方法。

它在经济学、金融学、气象学、环境科学等领域都有着广泛的应用。

为了加深对时间序列分析的理解，以下是一些时间序列练习题，帮助读者巩固相关知识和技能。

1. 下面是某城市某共享单车平台的日订单量数据（单位：订单数）。

请问这组数据属于哪种类型的时间序列数据？日期订单量1月1日 1201月2日 1601月3日 1501月4日 1801月5日 2002. 下面是某公司某产品在2020年1月至6月的月销售额数据（单位：万元）。

请根据给出数据回答以下问题：1月 802月 853月 704月 905月 956月 100（1）请计算该产品在第二季度（4月、5月、6月）的总销售额。

（2）根据给出数据，绘制该产品的销售额趋势图。

3. 下面是某超市某商品每周销量数据（单位：件）。

请计算该商品的季节性指数。

周次销量1 1002 1203 1354 1405 1506 1557 1608 1809 20010 2204. 假设一家公司的销售额数据如下（单位：万元）：日期销售额2019-01 802019-02 852019-03 902019-04 1002019-05 1102019-06 115（1）请计算该公司在2019年第一季度（1月、2月、3月）的平均月销售额。

（2）根据给出数据，绘制该公司的销售额线性趋势图。

5. 下面是某餐厅某菜品2019年1月至6月的月销售量数据（单位：份）。

请根据给出数据，计算该菜品的季节指标和趋势指数。

1月 502月 553月 484月 605月 656月 70以上是时间序列练习题，通过思考和计算这些问题，读者可以进一步巩固和应用时间序列分析的相关知识和方法。

在实际应用中，时间序列分析可以用于预测未来趋势、制定合理的经营策略、评估政策实施效果等。

希望读者通过练习题的探索，能够更好地理解时间序列分析的重要性和实用性。