东北三省四市2018届高考第一次模拟考试数学(文)试题含答案

合集下载

2018年黑龙江省齐齐哈尔市高考数学一模试卷(文科)

2018年黑龙江省齐齐哈尔市高考数学一模试卷（文科）一、选择题：本题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的.1. 设集合A={1, 2, 3}，B={x[3x>4}，则A∩B=()A.{1, 2}B.{2, 3}C.{1, 3}D.{1, 2, 3}2. 设z=3+ii，i是虚数单位，则z的虚部为（）A.1B.−1C.3D.−33. 某校连续12天对同学们的着装进行检查，着装不合格的人数用蒸叶图表示，如图，则该组数据的中位数是（）A.24B.26C.27D.324. 将函数y=sin(2x−π4)的图象向左平移π6个单位后，得到函数f(x)的图象，则f(π12)=()A.√2+√64B.√3+√64C.√32D.√225. 已知等差数列{a n}的前n项和为S n，若a3=3，S4=14．则{a n}的公差为（）A.1B.−1C.2D.−26. 圆x2+y2−2x−4y+3=0的圆心到直线x−ay+1=0的距离为2，则a=()A.−1B.0C.1D.27. 若a，b，c满足2a=3，b=log25，3c=2．则（）A.c<a<bB.b<c<aC.a<b<cD.c<b<a8. 函数f(x)＝(2x−2−x)cosx在区间[−5, 5]上的图象大致为（）A.B.C.D.9. 我国南宋时期的数学家秦九韶（约1202−1261）在他的著作《数书九章》中提出了多项式求值的秦九韶算法．如图所示的框图给出了利用秦九韶算法求多项式的一个实例．若输入的n=5，v=1，x=2，则程序框图计算的是（）A.25+24+23+22+2+1B.25+24+23+22+2+5C.26+25+24+23+22+2+1D.24+23+22+2+110. 如图，网格纸上小正方形的边长为1，图中画出的是某几何体的三视图，则该几何体的表面积为（）A.12√13+6√2+18B.9√13+8√2+18C.9√13+6√2+18D.9√13+6√2+1211. 已知直三棱柱ABC −A 1B 1C 1的底面为等腰直角三角形，∠ABC =90∘，直线A 1C 与平面BCC 1B 1成30∘角，直三棱柱ABC −A 1B 1C 1的外接球的体积为4π3，则三棱柱ABC −A 1B 1C 1的高为（） A.2 B.√3 C.√2D.112. 若x =1是函数f(x)=ax 2+ln x 的一个极值点，则当x ∈[1e ,e]时，f(x)的最小值为（） A.1−e 22B.−e +1eC.−12e 2−1D.e 2−1二、填空题：本题共4小题，每小题5分，共20分．已知实数x ，y 满足{x −y −3≥0x −2y −4≤0x +2y −8≤0 ，则z =2x −y 的最小值为________．已知向量a →=(2, 3)，b →=(m, −6)，若a →⊥b →，则|2a →+b →|=________．已知数列{a n }的前n 项和为S n ，且S n =2a n −1，则数列{1a n}的前6项和为________．已知抛物线y 2=4x 的焦点为F ，准线为l ，点M 在l 上，且在x 轴上方，线段FM 依次与抛物线、y 轴交于点P ，N ，若P 是FN 中点，O 是原点，则直线OM 的斜率为________．三、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.第17～21题为必考题，每个试题考生都必须作答，第22、23题为选考题，考生根据要求作答.（一）必考题：共60分.在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ．满足2acosC +bcosC +ccosB ＝0． (Ⅰ)求角C 的大小；(Ⅱ)若a ＝2，△ABC 的面积为√32，求c 的大小．如图，在直三棱柱ABC −A 1B 1C 1中，BC =BB 1，∠BAC =∠BCA =12∠ABC ，点E 是A 1B 与AB 1的交点，点D 在线段AC 上，B 1C // 平面A 1BD ．（1）求证：BD ⊥A 1C ；（2）求证：AB 1⊥平面A 1BC ．如表是一个容量为20的样本数据分组后的频率分布表：(I)若用组中值代替本组数据的平均数，请计算样本的平均数x ；(II)以频率估计概率，若样本的容量为2000，求在分组[14.5, 17.5)中的频数；(Ⅲ)若从数据在分组[8.5, 11.5)与分组[11.5, 14.5)的样本中随机抽取2个，求恰有1个样本落在分组[11.5, 14.5)的概率．已知椭圆C:x 2a 2+y 2b 2=1(a >b >0)的左、右焦点分别为F 1，F 2．且椭圆C 过点(√3, −√32)，离心率e =12；点P 在椭圆C 上，延长PF 1与椭圆C 交于点Q ，点R 是PF 2中点．(I)求椭圆C 的方程；(II)若O 是坐标原点，记△QF 1O 与△PF 1R 的面积之和为S ，求S 的最大值．已知函数f(x)=x(e x +1)(I)求函数y =f(x)的图象在点（0, f(0)）处的切线方程；(II)若函数g(x)=f(x)−ae x −x ，求函数g(x)在[1, 2]上的最大值．（二）选考题：共10分.请考生在第22、23题中任选一题作答.如果多做，则按所做的第一题计分．[选修4一4：坐标系与参数方程]（10分），已知直线l 过原点且倾斜角为θ0，θ0≠π2，以原点O 为极点，x 轴的非负半轴为极轴建立极坐标系，曲线C 的极坐标方程为ρsin 2θ=4cosθ． (I)写出直线l 的极坐标方程和曲线C 的直角坐标方程； (Ⅱ)已知直线l ´过原点且与直线l 相互垂直，若l ∩C =M ，l ∩C =N ，其中M ，N 不与原点重合，求△OMN 面积的最小值． [选修4-5：不等式选讲]（10分）已知函数f(x)=log 2(|x +1|+|x −1|−a )． (I)当a =3时，求函数f(x)的定义域；(Ⅱ)若不等式f(x)≥2的解集为R ，求实数a 的最大值．参考答案与试题解析2018年黑龙江省齐齐哈尔市高考数学一模试卷（文科）一、选择题：本题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的.1.【答案】B【考点】交集及其运算【解析】可解3x>4得到x>log34，从而求出集合B={x|x>log34}，然后进行交集的运算即可．【解答】B={x|x>log34}，且A={1, 2, 3}；∴A∩B={2, 3}．2.【答案】D【考点】复数的运算【解析】直接利用复数代数形式的乘除运算化简得答案．【解答】解：∵z=3+ii =(3+i)(−i)−i2=1−3i，∴z的虚部为−3．故选D.3.【答案】C【考点】茎叶图【解析】根据茎叶图所给的数据，做出这组数据的中位数．找中位数要把数据按从小到大的顺序排列，位于最中间的一个数或两个数的平均数为中位数．【解答】由茎叶图得：10，11，20，21，22，24，30，33，35，35，37，38，将这组数据从小到大重新排列后，观察数据可知，最中间的两个数为24，30，其平均数即中位数是24+302=27．4.【答案】D【考点】函数y=Asin （ωx+φ）的图象变换【解析】直接利用三角函数的平移变换求出函数的关系式，进一步求出函数的值．【解答】函数y =sin(2x −π4)的图象向左平移π6个单位后，得到函数f(x)=sin(2x +π12)的图象，则：f(π12)=sin(π6+π12)=√22．5.【答案】 B【考点】等差数列的前n 项和【解析】设等差数列{a n }的公差为d ，由a 3=3，S 4=14．可得a 1+2d =3，4a 1+4×32d =14，联立解得d ．【解答】设等差数列{a n }的公差为d ，∵ a 3=3，S 4=14． ∴ a 1+2d =3，4a 1+4×32d =14，联立解得d =−1． 6.【答案】 B【考点】直线与圆的位置关系【解析】x 2+y 2−2x −4y +3=0的圆心(1, 2)，圆心(1, 2)到直线的距离d =2，能求出a ．【解答】x 2+y 2−2x −4y +3=0的圆心(1, 2)，圆心(1, 2)到直线的距离d =√1+a 2=2，解得a =0． 7.【答案】 A【考点】对数的运算性质【解析】利用指数函数与对数函数的单调性即可得出．【解答】2a =3，可得a ∈(1, 2)， b =log 25>2，由3c =2．可得c ∈(0, 1)．∴c<a<b．8.【答案】D【考点】函数的图象与图象的变换【解析】判断函数在[0, 5]之间的零点个数以及特殊点的位置判断选项即可．【解答】当x∈[0, 5]时，f(x)＝(2x−2−x)cosx＝0，可得函数的零点为：0，π2，3π2，排除A，B，当x＝π时，f(π)＝−2π+2−π，<0，对应点在x轴下方，排除选项C，9.【答案】A【考点】程序框图【解析】由题意，模拟程序的运行，依次写出每次循环得到的i，v的值，当i=−1时，不满足条件i≥0，跳出循环，输出v的值为63，即可得解．【解答】解：模拟程序的运行，可得n=5，v=1，x=2，i=4满足条件i≥0，执行循环体，v=3，i=3满足条件i≥0，执行循环体，v=7，i=2满足条件i≥0，执行循环体，v=15，i=1满足条件i≥0，执行循环体，v=31，i=0满足条件i≥0，执行循环体，v=63，i=−1不满足条件i≥0，退出循环，输出v的值为63．由于25+24+23+22+2+1=63．故选A.10.【答案】C【考点】由三视图求体积【解析】画出几何体的图形，利用三视图的数据求解几何体的表面积即可．【解答】作出该几何体的直观图如下所示，故所求几何体的表面积S=2×3×√13+2×12×3×√13+12×4×6+12×3×4+12×4×3√2=9√13+6√2+18．11.【答案】C【考点】棱柱的结构特征【解析】根据棱柱的结构特征可知A1C为球的直径，∠A1CB1为直线A1C与平面BCC1B1成角，根据体积公式和勾股定理即可得出棱柱的高．【解答】由题意可知A1B1⊥平面BB1C1C，∴∠A1CB1为直线A1C与平面BCC1B1成的角，即∠A1CB1=30∘，设AB=BC=x，则A1C=2x．又AC=√2x．∴AA1=√2x．∵棱柱的底面是等腰直角三角形，∠ABC=90∘，∴A1C为棱柱ABC−A1B1C1的外接球的直径，即43π∗(2x2)3=4π3，∴x=1，∴AA1=√2x=√2．12.【答案】A【考点】利用导数研究函数的极值【解析】此题暂无解析【解答】解：由题意得f′(1)=0．∵f′(x)=2ax+1x，∴2a+1=0，a=−12．当x∈[1e,1)时，f′(x)>0，当x∈[1,e)时，f′(x)<0，所以f(x)min=min{f(1e),f(e)}=−12e2+1．故选A．二、填空题：本题共4小题，每小题5分，共20分．【答案】5【考点】简单线性规划【解析】由约束条件作出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，联立方程组求得最优解的坐标，代入目标函数得答案．【解答】实数x，y满足{x−y−3≥0x−2y−4≤0x+2y−8≤0所表示的平面区域如图阴影部分所示，观察可知，由{x −y −3=0x −2y −8=0解得A(2, −1)．当z =2x −y 过点A(2, −1)时，有最小值，最小值为5．【答案】 13【考点】平面向量数量积的性质及其运算【解析】根据题意，由向量的垂直与向量数量积的关系可得若a →⊥b →，则有a →⋅b →=2m −18=0，解可得m 的值，即可得b →的坐标，从而可得向量2a →+b →的坐标，由向量模的计算公式计算可得答案．【解答】根据题意，向量a →=(2, 3)，b →=(m, −6)，若a →⊥b →，则有a →⋅b →=2m −18=0，解可得m =9，则b →=(9, −6)，故2a →+b →=(13, 0)；故|2a →+b →|=13；【答案】63 【考点】数列的求和【解析】由S n =2a n −1(n ∈N ∗)，推导出a 1=1，S n −S n−1=2a n −2a n−1，由此得到a n =2n−1．由求和公式解答即可．【解答】解：∵ a 1=S 1=a 1−1 a 1=1，n >1时，a n =S n −S n−1=2a n −2a n−1， ∴ {a n }是首项为1，公比为2的等比数列． ∴ a n =2n−1， ∴ {1a n}的前6项和为1−1261−12=6332．故答案为：6332.【答案】 −4√2 【考点】抛物线的求解【解析】设N(O, y0)，则P(12, y02)，可得y0|=2√2，k OM=4√2−1=−4√2．【解答】可得F(1, 0)，设N(O, y0)，则P(12, y02)，y024=2，∴|y0|=2√2，从而M(−1, 4√2)，∴k OM=4√2−1=−4√2．三、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.第17～21题为必考题，每个试题考生都必须作答，第22、23题为选考题，考生根据要求作答.（一）必考题：共60分.【答案】（I）在△ABC中，∵2acosC+bcosC+ccosB＝0，∴由正弦定理可得：2sinAcosC+sinBcosC+sinCcosB＝0，∴2sinAcosC+sin(B+C)＝0，又△ABC中，sin(B+C)＝sinA≠0．∴cosC=−12，∵0<C<Π．∴C=2π3，(II)由S=12absinC=√32，a＝2，C=2π3得b＝1，由余弦定理得c2＝4+1−2×2×1×(−12)＝7，∴c=√7．【考点】余弦定理【解析】（I）根据正弦定理将边化角，化简即可得出cosC；(II)根据面积计算b，再利用余弦定理即可得出c的值．【解答】（I）在△ABC中，∵2acosC+bcosC+ccosB＝0，∴由正弦定理可得：2sinAcosC+sinBcosC+sinCcosB＝0，∴2sinAcosC+sin(B+C)＝0，又△ABC中，sin(B+C)＝sinA≠0．∴cosC=−12，∵0<C<Π．∴C=2π3，(II)由S=12absinC=√32，a＝2，C=2π3得b＝1，由余弦定理得c2＝4+1−2×2×1×(−12)＝7，∴c=√7．【答案】连结ED，∵平面AB1C∩平面A1BD=ED，B1C // 平面A1BD，∴B1C // ED，∵E为AB1中点，∴D为AC中点；∵∠BAC=∠BCA=12∠ABC，∴AB=BC，∴BD⊥AC?，由A1A⊥平面ABC，BD⊂平面ABC，得A1A⊥BD‚由?‚A1A、AC是平面A1ACC1内的两条相交直线，得BD⊥平面A1ACC1，∵A1C⊂平面A1ACC1，故BD⊥A1C．由（1）知AB=BC，AB⊥BC，∵BB1=BC，∴四边形ABB1A1是菱形，∴AB1⊥A1B，∵BB1⊥平面ABC，BC⊂平面ABC．∴BC⊥BB1∵AB∩BB1=B，AB，BB1⊂平面ABB1A1．∴BC⊥平面ABB1A∵AB1⊂平面ABB1A1，∴BC⊥AB1，∵BC∩A1B=B，BC，A1B⊂平面A1BC，∴AB1⊥平面A1BC．【考点】直线与平面垂直【解析】（1）连结ED，推导出B1C // ED，D为AC中点，推导出AB=BC，BD⊥AC?，由A1A⊥平面ABC，得A1A⊥BD‚，从而BD⊥平面A1ACC1，由此能证明BD⊥A1C．（2）由AB=BC，AB⊥BC，得四边形ABB1A1是菱形，从而AB1⊥A1B，由BB1⊥平面ABC，得BC⊥BB1，从而BC⊥平面ABB1A，进而BC⊥AB1，由此能证明AB1⊥平面A1BC．【解答】连结ED，∵平面AB1C∩平面A1BD=ED，B1C // 平面A1BD，∴B1C // ED，∵E为AB1中点，∴D为AC中点；∵∠BAC=∠BCA=1∠ABC，∴AB=BC，∴BD⊥AC?，2由A1A⊥平面ABC，BD⊂平面ABC，得A1A⊥BD‚由?‚A1A、AC是平面A1ACC1内的两条相交直线，得BD⊥平面A1ACC1，∵A1C⊂平面A1ACC1，故BD⊥A1C．由（1）知AB=BC，AB⊥BC，∵BB1=BC，∴四边形ABB1A1是菱形，∴AB1⊥A1B，∵BB1⊥平面ABC，BC⊂平面ABC．∴BC⊥BB1∵AB∩BB1=B，AB，BB1⊂平面ABB1A1．∴BC⊥平面ABB1A∵AB1⊂平面ABB1A1，∴BC⊥AB1，∵BC∩A1B=B，BC，A1B⊂平面A1BC，∴AB1⊥平面A1BC．【答案】（I）依题意，整理表格数据如下：故所求平均数为10×0.2+13×0.1+16×0.3+19×0.4=2+1.3+4.8+7.6= 15.7..(Ⅱ)以频率估计概率，样本的容量为2000，分组[14.5, 17.5)的频率为0.3，∴在分组[14.5, 17.5)中的频数为2000×0.3=600(Ⅲ)记[8.5, 11.5)中的样本为A，B，C，D，[11.5, 14.5)中的样本为a，b，则随机抽取2个，所有的情况为：(A, B)，(A, C)，(A, D)，(A, a)，(A, b)，(B, C)，(B, D)，(B, a)，(B, b)，(C, D)，(C, a)，(C, b)，(D, a)，(D, b)，(ab)，共15个其中恰有1个样本落在分组[11.5, 14.5)的为：(A, a)，(A, b)，(B, a)，(B, b)，(C, a)，(C, b)，(D, a)，(D, b)，共8个，..故恰有1个样本落在分组[11.5, 14.5)的概率P=815【考点】频率分布直方图列举法计算基本事件数及事件发生的概率【解析】（I）依题意，整理表格数据，能求出平均数．(Ⅱ)以频率估计概率，样本的容量为2000，分组[14.5, 17.5)的频率为0.3，由此能求出在分组[14.5, 17.5)中的频数．(Ⅲ)记[8.5, 11.5)中的样本为A，B，C，D，[11.5, 14.5)中的样本为a，b，随机抽取2个，利用列举法能求出恰有1个样本落在分组[11.5, 14.5)的概率．【解答】（I）依题意，整理表格数据如下：故所求平均数为10×0.2+13×0.1+16×0.3+19×0.4=2+1.3+4.8+7.6= 15.7..(Ⅱ)以频率估计概率，样本的容量为2000，分组[14.5, 17.5)的频率为0.3，∴在分组[14.5, 17.5)中的频数为2000×0.3=600(Ⅲ)记[8.5, 11.5)中的样本为A，B，C，D，[11.5, 14.5)中的样本为a，b，则随机抽取2个，所有的情况为：(A, B)，(A, C)，(A, D)，(A, a)，(A, b)，(B, C)，(B, D)，(B, a)， (B, b)，(C, D)，(C, a)，(C, b)，(D, a)，(D, b)，(ab)，共15个其中恰有1个样本落在分组[11.5, 14.5)的为：(A, a)，(A, b)，(B, a)，(B, b)，(C, a)，(C, b)，(D, a)，(D, b)，共8个，.. 故恰有1个样本落在分组[11.5, 14.5)的概率P =815 【答案】（I ）依题意，x 2a +y 2b =1，则{3a 2+34b 2=1a 2=b 2+c 2c a =12，解得a =2，b =√3，c =1，故椭圆C 的方程为x 24+y 23=1；(Ⅱ)由O ，R 分别为F 1F 2，PF 2的中点，故OR // PF 1．故△PF 1R 与△PF 1O 同底等高，故S △PF 1R =S △PF 1O ，S =S △PF 1R +S △PF 1O =S △PQO ，当直线PQ 的斜率不存在时，其方程为x =−1，此时S △PQO =12×1×[32−(−32)]=32，当直线PQ 的斜率存在时，设其方程为：y =k(x +1)，设P(x 1, y 1)，Q(x 2, y 2)，显然直线PQ 不与x 轴重合，即k ≠0；联立{y =k(x +1)x 24+y 23=1 解得(3+4k 2)x 2+8k 2x +4k 2−12=0， △=144(k 2+1)>0，故{x 1+x 2=−8k 23+4k 2x 1x 2=4k 2−123+4k 2，故|PQ|=√1+k 2|x 1−x 2|=√1+k 2√(x 1+x 2)2−4x 1x 2=12(1+k 2)3+4k 2，点O 到直线PQ 的距离d =√1+k 2，S =12|PQ|d =6√k (k +1)(3+4k 2)2，令u =3+4k 2∈(3, +∞)，故S =6√u−34∗u+14u2=32√−3u 2−2u +1∈(0,32)，故S 的最大值为32 【考点】椭圆的定义【解析】(Ⅰ)由题意可得{3a 2+34b 2=1a 2=b 2+c 2c a =12，解得即可， (Ⅱ)先判断出S =S △PF 1R +S △PF 1O =S △PQO ，再根据韦达定理和弦长公式和点到直线的距离可得三角形的面积，再利用换元和函数的性质即可求出【解答】（I ）依题意，x 2a 2+y 2b 2=1，则{3a 2+34b 2=1a 2=b 2+c 2c a=12，解得a =2，b =√3，c =1，故椭圆C 的方程为x 24+y 23=1；(Ⅱ)由O ，R 分别为F 1F 2，PF 2的中点，故OR // PF 1．故△PF 1R 与△PF 1O 同底等高，故S △PF 1R =S △PF 1O ，S =S △PF 1R +S △PF 1O =S △PQO ，当直线PQ 的斜率不存在时，其方程为x =−1，此时S △PQO =12×1×[32−(−32)]=32，当直线PQ 的斜率存在时，设其方程为：y =k(x +1)，设P(x 1, y 1)，Q(x 2, y 2)，显然直线PQ 不与x 轴重合，即k ≠0；联立{y =k(x +1)x 24+y 23=1 解得(3+4k 2)x 2+8k 2x +4k 2−12=0， △=144(k 2+1)>0，故{x 1+x 2=−8k 23+4k 2x 1x 2=4k 2−123+4k 2，故|PQ|=√1+k 2|x 1−x 2|=√1+k 2√(x 1+x 2)2−4x 1x 2=12(1+k 2)3+4k 2，点O 到直线PQ 的距离d =√1+k 2，S =12|PQ|d =6√k 2(k 2+1)(3+4k 2)2，令u =3+4k 2∈(3, +∞)，故S =6√u−34∗u+14u2=32√−3u 2−2u +1∈(0,32)，故S 的最大值为32【答案】（I ）依题意，f ´(x)=e 2+1+xe x ，故f ´（0）=e 0+1=2 因为f(0)=0，故所求切线方程为y =2x ； (Ⅱ)依题意，g ´(x)=(x −a +1)⋅e x ，令g ´(x)=0得x =a −1所以当a −1≤1时，x ∈[1, 2]时，g ´(x)≥0恒成立，g(x)单调递增，g(x)最大值为g(2)，当a −1≥2时，x ∈[1, 2]时，g ´(x)≤0恒成立，g(x)单调递减，g(x)最大值为g(1) 当1<a −1<2时，x ∈[1, a −1)时，g ´(x)≤0，g(x)单调递减； x ∈(a −1, 2)时，g ´(x)>0，g(x)单调递增．当x ∈[1, 2]时，g(x)最大值为g(1)或g(2) g(1)=(1−a)e ，g(2)=(2−a)e 2，g(1)−g(2)=(1−a)e −(2−a)e 2=(e 2−e)a −(2e 2−e) ∴ 当a ≥2e 2−e e 2−e=2e−1e−1时，g(1)−g(2)≥0，g(x)max =g(1)=(1−a)e ．当a <2e 2−e e 2−e=2e−1e−1时，g(1)−g(2)<0，g(x)max =g(2)=(2−a)e 2【考点】导数求函数的最值利用导数研究曲线上某点切线方程(Ⅰ)求出函数的导数，计算f(0)，f′(0)，求出切线方程即可；(Ⅱ)求出函数的导数，通过讨论a的范围，结合函数的单调性求出函数的最大值即可．【解答】（I）依题意，f´(x)=e2+1+xe x，故f´（0）=e0+1=2因为f(0)=0，故所求切线方程为y=2x；(Ⅱ)依题意，g´(x)=(x−a+1)⋅e x，令g´(x)=0得x=a−1所以当a−1≤1时，x∈[1, 2]时，g´(x)≥0恒成立，g(x)单调递增，g(x)最大值为g(2)，当a−1≥2时，x∈[1, 2]时，g´(x)≤0恒成立，g(x)单调递减，g(x)最大值为g(1)当1<a−1<2时，x∈[1, a−1)时，g´(x)≤0，g(x)单调递减；x∈(a−1, 2)时，g´(x)>0，g(x)单调递增．当x∈[1, 2]时，g(x)最大值为g(1)或g(2)g(1)=(1−a)e，g(2)=(2−a)e2，g(1)−g(2)=(1−a)e−(2−a)e2=(e2−e)a−(2e2−e)∴当a≥2e2−ee2−e =2e−1e−1时，g(1)−g(2)≥0，g(x)max=g(1)=(1−a)e．当a<2e2−ee2−e =2e−1e−1时，g(1)−g(2)<0，g(x)max=g(2)=(2−a)e2（二）选考题：共10分.请考生在第22、23题中任选一题作答.如果多做，则按所做的第一题计分．[选修4一4：坐标系与参数方程]（10分），【答案】（I）依题意，直线l的极坐标方程为θ=θ0(θ0≠π2, ρ∈R)曲线C:ρSin2θ=4cosθ，ρ2sin2θ=4ρcosθ，直角坐标方程为y2=4x．(Ⅱ)把θ=θ0代入ρsin2θ=4cosθ，得ρM=4cosθ0sin2θ0．直线l´过原点且与直线l相互垂直，可知直线l´的极坐标方程为θ=θ0+π2(ρ∈R)代入ρsin2θ=4cosθ，得ρN cos2θ=−4sinθ0，所以ρN=−4sinθ0cos2θ0，S△OMN=12|OM|⋅|ON|，=2|ρM|⋅|ρN|，=16|2sinθ0cosθ0|=16|sin2θ0|≥16，（当且仅当θ0=π4或3π4时，等号成立）即△OMN面积的最小值为16．【考点】圆的极坐标方程【解析】(Ⅰ)直接利用转换关系，把参数方程和极坐标方程与直角坐标方程进行转化．(Ⅱ)利用直线的极坐标方程建立方程组，进一步利用三角形的面积公式求出结果．（I ）依题意，直线l 的极坐标方程为θ=θ0(θ0≠π2, ρ∈R) 曲线C:ρSin 2θ=4cosθ，ρ2sin 2θ=4ρcosθ，直角坐标方程为y 2=4x ．(Ⅱ)把θ=θ0代入ρsin 2θ=4cosθ，得ρM =4cosθsin 2θ0．直线l ´过原点且与直线l 相互垂直，可知直线l ´的极坐标方程为θ=θ0+π2(ρ∈R) 代入ρsin 2θ=4cosθ，得ρN cos 2θ=−4sinθ0，所以ρN =−4sinθcos 2θ0，S △OMN =12|OM|⋅|ON|， =2|ρM |⋅|ρN |， =16|2sinθ0cosθ0|=16|sin2θ0|≥16，（当且仅当θ0=π4或3π4时，等号成立）即△OMN 面积的最小值为16．[选修4-5：不等式选讲]（10分）【答案】（1）当a =3时，函数f(x)=log 2(|x +1|+|x −1|−a)=log 2(|x +1|+|x −1|−3)， ∴ |x +1|+|x −1|−3>0，即|x +1|+|x −1|>3∴ {x <−1−x −1+1−x >3 或{−1≤x ≤1x +1+1>3 或{x >1x +1+x −1>3 ．解得x <−32或x >32．故函数的定义域为{x|x <−32或x >32}（2）若不等式f(x)≥2的解集为R ，则f(x)≥2恒成立．故|x +1|+|x −1|−a ≥4恒成立．∵ |x +1|+|x −1|≥|x +1−(x −1)|=2，（当且仅当−1≤x ≤1时，取“=”） ∴ 2−a ≥4，故有a ≤−2，故实数a 的最大值为−2 【考点】绝对值三角不等式【解析】（I ）当a =3时，函数f(x)=log 2(|x +1|+|x −1|−a)=log 2(|x +1|+|x −1|−3)，可得|x +1|+|x −1|−3>0，即|x +1|+|x −1|>3，去掉绝对值分别求解， (Ⅱ)若不等式f(x)≥2的解集为R ，则f(x)≥2恒成立．故|x +1|+|x −1|−a ≥4恒成立．求得|x +1|+|x −1|≥|x +1−(x −1)|=2 即可．【解答】（1）当a =3时，函数f(x)=log 2(|x +1|+|x −1|−a)=log 2(|x +1|+|x −1|−3)， ∴ |x +1|+|x −1|−3>0，即|x +1|+|x −1|>3∴ {x <−1−x −1+1−x >3 或{−1≤x ≤1x +1+1>3 或{x >1x +1+x −1>3．解得x <−32或x >32．故函数的定义域为{x|x <−32或x >32}（2）若不等式f(x)≥2的解集为R ，则f(x)≥2恒成立．故|x +1|+|x −1|−a ≥4恒成立．∵ |x +1|+|x −1|≥|x +1−(x −1)|=2，（当且仅当−1≤x ≤1时，取“=”） ∴ 2−a ≥4，故有a ≤−2，故实数a 的最大值为−2。

2018高考数学压轴卷辽宁省大连市2018届高三第一次模拟数学文试题扫描版含答案

2018年大连市高三第一次模拟考试参考答案及评分标准数学（文科）一、选择题（本大题共12小题，每小题5分，共60分）二、填空题（本大题共4小题，每小题5分，共20分）13. 1414. 23 15. （4,0） 16. 7-三、解答题17. (本小题满分12分) 【试题解析】解：（1）由2cos cos cos b Ba C c A =+可得 2sin cos sin cos sin cos sin B B A C C A B =+=，故1cos ,2B =………………………………………………………4分所以3B π=………………………………………………………6分（2）方法一：由2,3b B π==，根据余弦定理可得224ac a c =+- ……………………………………………………………………8分由基本不等式可得22424,ac a c ac =+-≥-所以4ac ≤…………9分当且仅当a c =时，等号成立. ……………………………………10分从而11sin 4222ABC S ac B ∆=≤⨯⨯=，故ABC △…………………………………12分方法二：因为sin sin sin a b c A B C ====所以,a A c C ==…………………………………8分112sin sin sin()2233S ac B A C B A A π==⋅=-)6A π=-+10分当262A ππ-=，即3A π=时，max S =故ABC △…………………………………12分18. (本小题满分12分)【试题解析】解：（1）由散点图可以判断y =c +y 关于年宣传费x 的回归方程类型.…………………………………3分（2）令w =，先建立y 关于w 的线性回归方程 ()()()()()()()88888111118888222211118i i i i i i i i i i ii i i i i ii i i i i i i y y w w w y wy yw wy w y wy w y wy d w w w w w w w w =========----+--====----∑∑∑∑∑∑∑∑∑31280 6.85738681.6-⨯⨯==………………………………………6分 57368 6.8110.6c y dw =-=-⨯=………………………………7分所以y 关于w 的线性回归方程为110.668y w =+所以y 关于x 的线性回归方程为110.6y =+8分（3）（i ）由（2）知，当64x=时，年销售量y 的预报值为110.6654.6y =+= 年利润z 的预报值为654.60.26466.92z =⨯-=…………………9分(ii)根据（2）的结果知，年利润z 的预报值)20.2(110.622.12 6.868.36z x x =⨯+-=-+=-+……………11分6.8=，即46.24x =时，年利润的预报值最大，故年宣传费为46.24千元时，年利润预报值最大.……………12分19.(本小题满分12分)【试题解析】答案：（1）方法一：取PC 中点M ，连接MF DM ,F M , 分别是PB PC ,中点,CB MF CB MF 21,//=∴, E 为DA 中点，ABCD 为正方形，CB DE CB DE 21,//=∴, DE MF DE MF =∴,//,∴四边形DEFM 为平行四边形………3分⊄∴EF DM EF ,//平面PDC ，⊂DM 平面PDC ，//EF ∴平面PDC ………………………………………………5分方法二：取PA 中点N ，连接,NE NF .E 是AD 中点， N 是PA 中点,//NE DP ∴,又F 是PB 中点，N 是PA 中点,//NF AB ∴//AB CD//NF CD ∴又NE NF N =,NE NEF NF NEF ⊂⊂平面平面,DP PCD CD PCD ⊂⊂平面平面//NEF PCD ∴平面平面…………………………………………3分又EF NEF ⊂平面//EF PCD ∴平面………………………………………………5分方法三：取BC 中点G ,连接EG ,FG ,在正方形ABCD 中，E 是AD 中点，G 是BC 中点//GE CD ∴又F 是PB 中点，G 是BC 中点,//GF PC ∴,又PC CD C =,GE GEF GF GEF ⊂⊂平面平面,PC PCD CD PCD ⊂⊂平面平面∴平面GEF //平面PCD ……3分EF ⊂平面GEF//EF ∴平面PCD ……………………………5分（2）方法一：//EF 平面P D C ,F ∴到平面P D C 的距离等于E 到平面P D C 的距离, …………………………6分⊥PA 平面ABCD ，DA PA ⊥∴, 1==AD PA ,在PAD Rt ∆中2=DP ， ⊥PA 平面A B C ，CB PA ⊥∴, 又⊥CB AB , A AB PA =,AB PAB PA PAB ⊂⊂平面，平面⊥∴CB 平面PAB ，又PB ⊂平面PABPB CB ⊥∴,故PC =……………………7分222,PD DC PC ∴+=PDC ∴∆为直角三角形，………………………9分PD E C PD C E V V --=,设E 到平面PDC 的距离为h ，则12121131212131⋅⋅⋅⋅=⋅⋅⋅⋅h …………………………11分 42=∴h∴ F 到平面PDC 的距离42…………………12分方法二：//EF 平面PCD ，∴点F 到平面PCD 的距离等于点E 到平面PCD 的距离，…………………………6分又AD PCD D =平面,E 是AD 中点，∴点A 到平面PCD 的距离等于点E 到平面PCD 距离的2倍.………………………7分取DP 中点H ,连接AH ,由=AD AP 得AH PD ⊥,由AB AP ⊥,AB AD ⊥,AD AP A =,AP PAD ⊂平面AD PAD ⊂平面AB PAD ∴⊥平面,又//AB CD CD PAD ∴⊥平面PCD PAD ∴⊥平面平面……9分又PCD PAD PD =平面平面,,AH PD AH PAD ⊥⊂平面AH PCD ∴⊥平面,AH ∴长即为点A 到平面PCD 的距离，…………………………10分由1,AP AD ==AP AD ⊥,2AH ∴=………………………11分 E ∴点到平面PCD的距离为4，即F 点到平面PCD………………………………12分 20.(本小题满分12分)【试题解析】解：（1）由12c a =可得，2a c =，又因为222b a c =-，所以223b c = 所以椭圆C 方程为2222143x y c c +=，又因为3(1,)2M 在椭圆C 上,所以22223()12143c c += 所以21c =，所以224,3a b ==，故椭圆方程为22143x y +=.………4分（2）方法一：设l 的方程为1x my =+，联立221431x y x my ⎧+=⎪⎨⎪=+⎩，消去x 得22(34)690m y my ++-=，设点1122(,),(,)A x y B x y ，有121222690,,,3434m y y y y m m --∆>+==++………………………6分1234y y m -===+所以14234S m =⨯+1t t =≥，………………8分有224241313t S t t t==++，由函数13y t t=+，[1,)t ∈+∞ [)2130,1,y t t'=->∈+∞ 故函数13y t t =+，在[1,)+∞上单调递增…………………………10分故134t t +≥，故2242461313t S t t t ==≤++当且仅当1t =即0m =时等号成立，四边形APBQ 面积的最大值为6.………………………………12分方法二：设l 的方程为1x my =+，联立221431x y x my ⎧+=⎪⎨⎪=+⎩，消去x 得22(34)690m y my ++-=，设点1122(,),(,)A x y B x y ，有121222690,,,3434m y y y y m m --∆>+==++………………………6分有2212(1)||34m AB m +==+，点(2,0)P -到直线l 点(2,0)Q 到直线l从而四边形APBQ的面积22112(1)234mSm+=⨯=+………………………8分令1t t=≥，有224241313tSt tt==++，函数13y tt=+，[1,)t∈+∞[)2130,1,y tt'=->∈+∞故函数13y tt=+，在[1,)+∞上单调递增……………………10分有134tt+≥，故2242461313tSt tt==≤++当且仅当1t=即0m=时等号成立，四边形APBQ面积的最大值为6.…………………12分方法三：①当l的斜率不存在时，:1l x=此时，四边形APBQ的面积为6S=…………………………6分②当l的斜率存在时，设l为：(1)y k x=-，(0)k≠则22143(1)x yy k x⎧+=⎪⎨⎪=-⎩()22223484120k x k x k∴+-+-=2212122284120,,3434k kx x x xk k-∆>+==++…………………………8分1212()12y y k x x-=-==……………………………………………………………………10分∴四边形APBQ的面积1214242S y y =⨯⨯-= 令 234(3)t k t =+> 则 234t k -=6S =11(0)3t <<116)306S t S ∴=<<∴<< 综上，四边形APBQ 面积的最大值为6.…………………………12分21.(本小题满分12分)【试题解析】解：（1）令()()()l n (0)F x f x g x x x m x =-=-->，有11()1x F x x x -'=-=，当1x >时，()0F x '<，当01x <<时，()0F x '>，所以()F x 在(1,)+∞上单调递减，在(0,1)上单调递增，()F x 在1x =处取得最大值，为1m --，………………………………………2分若()()f x g x ≤恒成立，则10m --≤即1m ≥-.…………………4分（2）方法一：120x x <<，211x x ∴>， 11221122ln 0,ln ln ln 0x x m x x x x x x m --=⎧∴-=-⎨--=⎩，即2121ln ln x x x x -=-21211ln ln x x x x -∴=-，…………………………………………6分欲证：121x x <21211ln ln x x x x -=-，只需证明21ln ln x x -<只需证明21ln x x <.………………………………8分设1t =>，则只需证明12ln ,(1)t t t t <->，即证：12ln 0,(1)t t t t-+<>.………………………………10分设1()2ln (1)H t t t t t =-+>，22221(1)()10t H t t t t -'=--=-<， ()H t ∴在(1,)+∞单调递减，()(1)2ln1110H t H ∴<=-+=，12ln 0t t t∴-+<，所以原不等式成立. ………………………12分方法二：由（1）可知，若函数()()()F x f x g x =- 有两个零点，有(1)0F >，则1m <-，且1201x x <<<………………………………………6分要证121x x <，只需证211x x <，由于()F x 在(1,)+∞上单调递减，从而只需证211()()F x F x >，由12()()0F x F x ==，只需证111111()ln 0F m x x x =--<，………………………………8分又111()ln 0F x x x m =--=，11ln m x x ∴=- 即证1111111111ln ln ln 0m x x x x x x --=-+-< 即证11112ln 0x x x -+-<，1(01)x <<…………………………10分令1()2ln (01)h x x x x x =-+-<<，2221221()10x x h x x x x -+'=+-=>，有()h x 在(0,1)上单调递增，()(1)0h x h <=，11111()2ln 0h x x x x ∴=-+-<. 所以原不等式121x x <成立. ……………………………………12分22.(本小题满分10分)【试题解析】(1) 解：联立⎩⎨⎧==θρθρcos 43cos ，23cos ±=θ，…………2分 20πθ<≤ ，6πθ=………………………………………………3分32=ρ…………………………………………………………4分交点坐标⎪⎭⎫ ⎝⎛6,32π………………………………………………5分（其他形式请酌情给分）(2)设()θρ,P ,()00,θρQ 且004cos ρθ=，⎪⎭⎫⎢⎣⎡∈2,00πθ……………6分由已知23OQ QP =，得⎪⎩⎪⎨⎧==θθρρ0052………………………………8分 θρcos 452=∴，点P 的极坐标方程为 ⎪⎭⎫⎢⎣⎡∈=2,0,cos 10πθθρ…………………………………………10分 23. (本小题满分10分)【试题解析】解：（1）当m =-2时，()()4103223-2=1023452x x f x x x x x x ⎧⎪+≥⎪⎪⎛⎫=++-⎨ ⎪⎝⎭⎪⎪⎛⎫--≤-⎪ ⎪⎝⎭⎩＜＜……………2分当4130x x +≤⎧⎨≥⎩解得12x ≤≤0；当30132x -≤＜＜，恒成立当45332x x --≤⎧⎪⎨≤-⎪⎩解得32x ≤≤--2 此不等式的解集为1-22⎡⎤⎢⎥⎣⎦，………………………………………5分（分三部分分别解f (x )≤3，每部分解对给一分）（2）当x ∈(- ∞，0)时()3302223=3432m x f x x x m x m x ⎧⎛⎫+- ⎪⎪⎪⎝⎭=+++⎨⎛⎫⎪--+≤- ⎪⎪⎝⎭⎩＜＜当302x -＜＜时，不等式化为23+≥+m x x由22[()()]+=--+-≤-=-x x x x 当且仅当2-=-x x即=x. 3∴+≥-m3∴≥--m 7分当32≤-x 时，不等式化为243--+≥+x m x x. 253∴≥++m x x ，令253y x x=++，3(,]2x ∈-∞- 22350,(,]2y x x '=->∈-∞- 253y x x∴=++在3(,]2-∞-上是增函数. ∴当32=-x 时，253=++y x x 取到最大值为356- ∴356m ≥-………………9分综上3m ≥--10分。

东北三省三校(哈师大附中、东北师大附中等)2018届高三第一次模拟考试数学(文)试题含答案

2018年三省三校一模考试文科数学答案一、选择题（本大题共12小题，每小题5分，共60分）1.C2.A3.B4.C5.D6.B7.D8.B9.C 10.C 11.C 12.A二、填空题（本大题共4小题，每小题5分，共20分）13． //l α或l α⊂ 14． []5,2-- 15．丙 16．三、解答题（本大题共70分） 17.（本小题满分12分）解：（Ⅰ）当2≥n 时，3+13232111(22)(22)277n n n n n n a S S ---=-=---= ………4分当1=n 时，112a S ==312=2⨯-，符合上式 ………5分所以32(n n a n -=∈N . (6)分（Ⅱ）由（Ⅰ）得322log 2=32n n b n -=-, ………7分所以=+-++⨯+⨯=++++)13)(23(174141111113221n n b b b b b b n n 13)1311(31)]131231()7141()411[(31+=+-=+--++-+-n n n n n ． ………12分18.（本小题满分12分）解：(Ⅰ) 从使用手机支付的人群中随机抽取1人，抽到青年的概率为710∴使用手机支付的人群中的青年的人数为7604210⨯=人， ………2分则使用手机支付的人群中的中老年的人数为604218-=人，所以22⨯列联表为:………4分2K 的观测值2100(42241816)1800=8.86758426040203k ⨯-⨯=≈⨯⨯⨯ ………6分28.8677.879(7.879)0.005P K >≥= ，， ………7分故有99.5%的把握认为“市场购物用手机支付与年龄有关”. ………8分(Ⅱ) 这100名顾客中采用分层抽样从“使用手机支付”和“不使用手机支付”中抽取得到一个容量为5的样本中：使用手机支付的人有6053100⨯=人，记编号为1,2,3 不使用手机支付的人有2人，记编号为a,b ， ………9分则从这个样本中任选2人有(1,2)(1,3)(1,a)(1,b)(2,3)(2,a)(2,b)(3,a)(3,b)(a,b)共10种其中至少有1人是不使用手机支付的(1,a)(1,b) (2,a)(2,b)(3,a)(3,b)(a,b)共7种， ………11分故7()10P A =. ………12分19.（本小题满分12分）（Ⅰ）证明：∵SO ⊥平面ABC ，∴SO AC ⊥，又∵点M 是圆O 内弦AC 的中点，AC MO∴⊥，………3分又SO MO O = ………4分 AC ∴⊥平面S………5分（Ⅱ）∵SO ⊥平面ABC ，SO 为三棱锥S OCB -的高，111112323S OCB O SCB V V --∴==⨯⨯⨯⨯= ………7分而O EFBC V -与O SCB V -等高，1sin 2215sin 2ESFSCBSE SF ESFS S SC SB CSB ∆∆⨯⨯∠==⨯⨯∠， ∴35SCB EFBC S S ∆=四边形 (10)分因此，33115535O EFBC O SCB V V --==⨯= ………12分20.（本小题满分12分）解：（Ⅰ）2c e a ==，当M 为椭圆C 的短轴端点时，12MF F ∆的面积的最大值为112112c b bc ∴⨯⨯=∴=，而222a b c =+1a b ∴==故椭圆C 标准方程为：2212x y += ………3分（Ⅱ）设112211(,),,),(,)B x y E x y A x y -（，且12x x ≠，2=2a x c= ，(2,0)P ∴由题意知BP 的斜率必存在，设BP ：(2)y k x =-，代入2212x y +=得 2222(21)8820k x k x k +-+-=0∆>得212k <22121222882,2121k k x x x x k k -+=⋅=++ (6)分12x x ≠ ∴AE 斜率必存在，AE ：121121()y y y y x x x x ++=-- ………7分由对称性易知直线AE 过的定点必在x 轴上，则当0y =时，得121122112211121212()(2)(2)()4y x x y x y x k x x k x x x x y y y y k x x k-+-+-=+==+++-2222121221228282222()2121=184421k k x x x x k k k x x k -⋅-⋅-+++==+--+ ………11分即在212k <的条件下，直线AE 过定点（1，0）. ………12分21. （本小题满分12分）解：（Ⅰ）2()12f x x a '=-+.当0a =时，3()4f x x =-在R 上单调递减；当0a <时，2()120f x x a '=-+<，即3()4f x x ax =-+在R 上单调递减； ………2分当0a >时，2()12f x x a '=-+.(,x ∈-∞时，()0f x '<，()f x 在(,-∞上递减；(x ∈时，()0f x '>，()f x 在(上递增；()6x ∈+∞时，()0f x '<，()f x 在(,)6+∞上递减； ………4分综上，当0a ≤时，()f x 在R 上单调递减；当0a >时，()f x 在(,6-∞-上递减；在(66-上递增；,)+∞上递减. ………5分（Ⅱ）∵函数()f x 在[1,1]-上的最大值为1. 即对任意[1,1]x ∈-，()1f x ≤恒成立。

2018年东北三省四市联考模拟文数答案

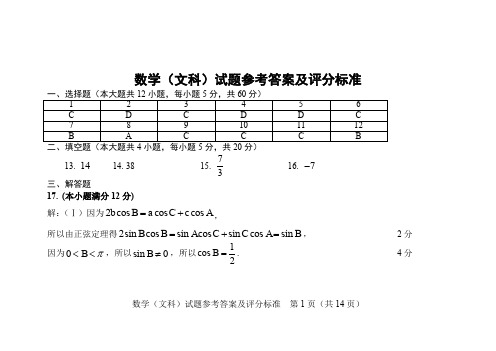
解：（Ⅰ）由 10 0.010 0.015 a 0.030 0.010 1 ，得 a 0.035 . ------------3 分（Ⅱ）平均数为 20 0.1 30 0.15 40 0.35 50 0.3 60 0.1 41.5 岁；数学（文科）试题参考答案及评分标准第 3 页（共 14 页）
1 . 2
数学（文科）试题参考答案及评分标准第 1 页（共 14 页）
因为 0 B ，所以 B （Ⅱ）因为 b 2, B

3
.
2 2
5分

3
，所以，由余弦定理可得 ac a c 4 ，
2 2
8分
因为由基本不等式可得 ac a c 4 2ac 4 ，所以 ac 4 ，当且仅当 a c 时，“等号”成立. （没有说明等号成立条件的扣除 1 分）从而 SABC 10 分
所以 ac
16 8 8 1 sin A sin C cos A C cos A C cos A C ， 3 3 3 2
9分
因为 0 A
2 2 2 2 ，所以， ,0 C AC 3 3 3 3
PA AD 1,在 Rt△PAD 中， DP 2 ， PA 平面 ABCD ， PA CB ,
数学（文科）试题参考答案及评分标准第 5 页（共 14 页）
CB AB , PA AB A , CB 平面 PAB ，CB PB ,
则 PC 3,
设中位数为 x ，则 10 0.010 10 0.015 x 35 0.035 0.5, ------------7 分 x 42.1 岁. （Ⅲ）第 1,2,3 组的人数分别为 20 人,30 人，从第 1,2 组中用分层抽样的方法抽取 5 人，则第 1,2 组抽取的人数分别为 2 人,3 人，分别记为 a1 , a2 , b1 , b2 , b3 . 设从 5 人中随机抽取 3 人，为 (a1 , a2 , b1 ),(a1 , a2 , b2 ),(a1, a2 , b3 ),(a1, b1, b2 ), ，

【高三数学试题精选】2018高考数学(文)第一次模拟考试试题(东北三省四市附答案)

2018高考数学（文）第一次模拟考试试题（东北三省四市
附答案）
c 5不等式选讲
已知函数，．
（1）当时，求不等式的解集；
（2）对于都有恒成立，求实数的取值范围．
10 11、12
二、填空题
13 14 15 16
三、解答题
17解（1）由正弦定理可得，，
∵ ，故，
∵ ，∴ ．
（2）由，，由余弦定理可得，
由基本不等式可得，，
当且仅当时，取得最大值，
故面积的最大值为．
18解（1）由，得．
（2）平均数为岁；
设中位数为，则，∴ 岁．
（3）第1,2组的人数分别为20人，30人，从第1,2组中用分层抽样的方法抽取5人，则第1,2组抽取的人数分别为2人，3人，分别记为，，，，．
设从5人中随机抽取3人，为，，，，，，，，，共10个基本事，
其中第2组恰好抽到2人包含，，，，，共6个基本事，从而第2组中抽到2人的概率．
19解（1）取中点，连接，，
∵ ，分别是，中点，∴ ，，。

黑龙江省齐齐哈尔市2018届高三第一次模拟考试数学(文)试题Word版含详细解析

齐齐哈尔市2018 届高三第一次模拟考试数学试卷（文科）一、选择题:本题共12小题，每小题5分，共60 分，在每小题给出的四个选项中，只有一项是符合题目要求的.1. 设集合A={1,2,3},B={x[>4},则A B=A. {1,2}B. {2,3}C. {1,3}D. {1,2,3}【答案】B【解析】,B={x[>4}选B.2. 设z=，i是虚数单位，则z的虚部为A. 1B. 一1C. 3D. -3【答案】D【解析】因为z=z的虚部为-3，选D.3. 某校连续12天对同学们的着装进行检查，着装不合格的人数用茎叶图表示，如图，则该组数据的中位数是A. 24B. 26C. 27D. 32【答案】C【解析】中位数是选C.4. 将函数y=sin(2x-)的图象向左平移个单位后，得到函数f（x）的图象，则f（）=A. B. C. D.【答案】D【解析】，选D.5. 已知等差数列{a}的前n项和为S.,若a=3,S=14.则{a}的公差为A. 1B. 一1C. 2D. -2【答案】B【解析】由题意得，选B.6. 圆x+y-2x-4y+3=0的圆心到直线x-ay+1=0的距离为2,则a=A. -1B. OC. 1D. 2【答案】B【解析】因为，所以，选B.7. 若a.b.c满足=3,b= 5.=2.则A. c<a<bB. b<c<aC. a<b<cD. c<b<a【答案】A【解析】由题意得，选A.8. 函数f(x)=(2-2)cosx在区间[-5,5]上的图象大致为A. B. C. D.【答案】D【解析】因为当时，；当时，；当时，；所以选D.9. 我国南宋时期的数学家秦九部(约1202-1261)在他的著作《数书九章》中提出了多项式求值的秦九韶算法，如图所示的框图给出了利用秦九韶算法求多项式的一个实例.若输人的n=5,v=1,x=2,则程序框图计算的是A. 2+2+2+2+2+1B. 2+2+2+2+2+5C. 2+2+2+2+2+2+1D. 2+2+2+2+1【答案】A【解析】执行循环得：结束循环，输出选A.点睛：算法与流程图的考查，侧重于对流程图循环结构的考查.先明晰算法及流程图的相关概念，包括选择结构、循环结构、伪代码，其次要重视循环起点条件、循环次数、循环终止条件，更要通过循环规律，明确流程图研究的数学问题，是求和还是求项.10. 如图，网格纸上小正方形的边长为1,图中画出的是某几何体的三视图，则该几何体的表面积为A. 12+6+18B. 9+8+18C. 9+6+18D. 9+6+12【答案】C【解析】几何体如图,表面积为选C.点睛:空间几何体表面积的求法(1)以三视图为载体的几何体的表面积问题，关键是分析三视图确定几何体中各元素之间的位置关系及数量．(2)多面体的表面积是各个面的面积之和；组合体的表面积注意衔接部分的处理．(3)旋转体的表面积问题注意其侧面展开图的应用．11. 已知直三棱柱ABC-ABC的底面为等腰直角三角形，∠ABC-90,直线AC与平面BCCB成30角，直三棱柱ABC-ABC的外接球的体积为，则三棱柱ABC- ABC的高为A. 2B.C.D. 1【答案】C【解析】由题意得A1C中点O为直三棱柱外接球的球心，半径设为R，则由得,因为为直线A1C与平面BCC1B1所成角，所以，选C.点睛：涉及球与棱柱、棱锥的切、接问题时，一般过球心及多面体中的特殊点(一般为接、切点)或线作截面，把空间问题转化为平面问题，再利用平面几何知识寻找几何体中元素间的关系，或只画内切、外接的几何体的直观图，确定球心的位置，弄清球的半径(直径)与该几何体已知量的关系，列方程(组)求解.12. 若x=1是函数f(x)=ax+Inx的一个极值点，则当x[,e]时，f（x）的最小值为A. 1-B. -e+C. --1D. e-1【答案】A【解析】由题意得，当x[,1]时，，当x[,e]时，，所以，选A.点睛：函数极值问题的常见类型及解题策略(1)知图判断函数极值的情况.先找导数为0的点，再判断导数为0的点的左、右两侧的导数符号.(2)已知函数求极值.求→求方程的根→列表检验在的根的附近两侧的符号→下结论.(3)已知极值求参数.若函数在点处取得极值，则，且在该点左、右两侧的导数值符号相反.二.填空题:本题共4小题，每小题5分,共20分。

东北三省四市(沈阳、长春、哈尔滨、大连)教科研联合体2018届高三高考第一次模拟文科综合试卷(含答案)

2018年大连市高三第一次模拟考试参考答案及评分标准思想政治一、选择题(每小题4分，共48分)12.A 13.B 14.C 15.A 16. B 17.C 18.C 19.C 20.B 21.D 22.B 23.B二、非选择题（52分）38. （14分）现状：产业规模大，增长速度快；（2分）专利申请和投资居于世界前列，市场前景广阔。

（2分）影响：一方面，有利于企业降低成本，提高产品产量和经济效益；（3分）有利于满足消费者个性化多样化需求，满足人民对美好生活的需求；（2分）有利于国家转变经济发展方式，调整产业结构，为实体经济发展提供新动能，拉动经济增长。

（3分）另一方面，对劳动力市场造成冲击，一些行业的劳动者有面临失业的风险，对相关行业也会带来冲击。

（2分）39.（12分）①和平与发展是当今时代主题，我国推动构建合作共赢的新型国际关系，顺应时代潮流，有利于促进世界和平与安全；（3分）②国家利益是国际关系的决定因素，共同利益是国家间合作的基础，推动构建合作共赢的新型国际关系，有利于实现金砖各国人民共同利益；（3分）③在多极化趋势下，提升新兴市场国家和发展中国家代表性和发言权，有利于推动建立国际新秩序；（3分）④中国奉行对立自主的和平外交政策，推动构建合作共赢的新型国际关系有利于打造“人类命运共同体”，实现共建共赢共享。

（3分）40.（26分）（1）（10分）①要坚持社会效益与经济效益相统一的原则，始终把社会效益放在首位，取得口碑和票房双赢；（3分）②坚持以人民为中心的创作方向，塑造符合新时代人民群众价值观的英雄形象。

（坚持为人民服务）（3分）③文艺作品应与新时代相匹配、与时代精神相契合，彰显新时代中国精神和中国价值。

（2分）（爱国主义、民族精神）④应立足新时代中华民族伟大复兴的实践活动，塑造社会生活中涌现出来的改革英雄、创业英雄、科技英雄、创新英雄。

（2分）（其它答案言之有理，也可得分。

如实现文化内容形式创新等）（2）①价值观对人们认识世界和改造世界的活动有重要导向作用。

辽宁省沈阳市2018届高三第一次模拟考试数学(文)试题含答案

23. （本小题满分 10 分）选修 4— 5；不等式选讲
已知函数 f ( x) | 2x 1| a | x 1 |
（Ⅰ）当 a 1 时，解关于 x 的不等式 f ( x) 4 ；
（Ⅱ）若 f ( x)
|x
2 | 的解集包含
1 [ ,2] ，求实数
a 的取值范围
.
2
高三第一次模拟考试（数学文科）答案
）
A．充分不必要条件 B ．必要不充分条件
C．充要条件 D．既不充分也不必要条件
12. 已知函数 f x
x
2 2x
1 1
x
sin x ，若正实数 a, b 满 f
4a
fb 9
最小值是 A.1 B.
9
C.9 D.18
2
开始任意输入x(0 x 1)
0 ，则 1
1
的
ab
二. 填空题：本大题共 4 小题，每小题 5 分．
.
1
7
16. 若 sin( x ) ，则 sin(
2x)
.
63
6
三. 解答题：共 70 分。解答应写出文字说明、解答过程或演算步骤。第 17 ~ 21 题为必做题，
每个试题考生都必须作答。第 22、 23 题为选考题，考生根据要求作答。
（一）必考题：共 60 分 . 17. ( 本小题满分 12 分 )
已知数列 { an} 是公差不为 0 的等差数列，首项 a1 1，且 a1、 a2、 a4 成等比数列 . （Ⅰ）求数列 { an} 的通项公式；
（Ⅱ）设数列 { bn} 满足 bn an 2 an ，求数列 {bn} 的前 n项和为 Tn .
18．（本小题满分 12 分）

【统一】黑龙江省2018年普通高等学校招生全国统一考试仿真模拟一数学文试题含Word版含答案

【关键字】统一普通高等学校招生全国统一考试仿真模拟（一）文科数学第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知为纯虚数，且（为虚数单位），则( )A．1B．C．2D．2.（2017·咸阳市二模)若，则的值为( )A．1B．C．D．3.命题“，使得”的否定是( )A．B．C．D．4.（2017·太原二模）如图是某样本数据的茎叶图，则该样本的中位数、众数、极差分别是( )A．32 34 32B．33 45 35C.34 45 32D．33 36 355.（2017·海口市调研）当双曲线的焦距取得最小值时，其渐近线的斜率是( )A．B． C. D．6.一个几何体的三视图如图所示，则该几何体的表面积等于( )A．B． C. D．7.（2017·合肥市质检）点为的重心（三角形三边中线的交点），设，则( )A．B． C. D．8.（2017·太原市二模）设函数的部分图象如图所示，若，且，则( )A．1 B． C. D．9.执行如图所示的程序框图,则输出的值为( )A．2 B． C. D．-110.设等差数列的前项和为，若，则( )A．9 B．10 C. 11 D．1511.（2017·保定市二模）某几何体的三视图如图所示,则该几何体的体积为( )A．6 B．5 C. 4 D．5.512.（2017·济南市二模）设函数是的导函数，，且，则的解集是( )A．B． C. D．第Ⅱ卷（共90分）二、填空题（每题5分，满分20分，将答案填在答题纸上）13.若满足约束条件：则的取值范围是．14.函数为偶函数，则．15.（2017·甘肃省二诊）已知直线与圆交于不同两点，其中为坐标原点，为圆外一点，若四边形是平行四边形，则实数的取值范围为．16.（2017·泰安一模）已知平面向量满足，且与的夹角为120°，则的模的取值范围为．三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17.（2017·成都市二诊）在中，内角所对的边分别为，已知，且.(1)求角的大小；(2)求的最大值.18.（2017·昆明市质检）如图，三棱柱的侧面为正方形，侧面为菱形，.(1)证明：平面平面；(2)若三棱柱的体积为，求点到平面的距离.19.（2017·石家庄模拟）某篮球队对篮球运动员的篮球技能进行统计研究,针对篮球运动员在投篮命中时,运动员在篮筐中心的水平距离这项指标,对某运动员进行了若干场次的统计,依据统计结果绘制如下频率分布直方图:(1)依据频率分布直方图估算该运动员投篮命中时,他到篮筐中心的水平距离的中位数；(2)若从该运动员投篮命中时,他到篮筐中心的水平距离为2到5米的这三组中,用分层抽样的方法抽取7次成绩(单位:米,运动员投篮命中时,他到篮筐中心的水平距离越远越好),并从抽到的这7次成绩中随机抽取2次.规定:这2次成绩均来自到篮筐中心的水平距离为4到5米的这一组,记 1分,否则记0分.求该运动员得1分的概率.20.（2017·唐山市二模）已知点F 为抛物线2:4C x y =的焦点，,,A B D 为抛物线C 上三点，且点A 在第一象限，直线AB 经过点,F BD 与抛物线C 在点A 处的切线平行，点M 为BD 的中点.(1)证明：AM 与y 轴平行； (2)求ABD 面积S 的最小值.21.已知函数2()1x e f x x mx =-+.(1)若(2,2)m ∈-，求函数()y f x =的单调区间；(2)若10,2m ⎛⎤∈ ⎥⎝⎦，则当[0,1]x m ∈+时，函数()y f x =的图象是否总在直线y x =上方？请写出判断过程.请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分. 22.选修4-4：坐标系与参数方程极坐标系与直角坐标系xOy 有相同的长度单位,以坐标原点O 为极点，以x 轴正半轴为极轴.已知曲线1C 的极坐标方程为4πρθ⎛⎫=+⎪⎝⎭，曲线2C 的极坐标方程为sin (0)a a ρθ=>，射线,,,442πππθϕθϕθϕθϕ==+=-=+与曲线1C 分别交异于极点O 的四点,,,A B C D .(1)若曲线1C 关于曲线2C 对称，求a 的值，并把曲线1C 和2C 化成直角坐标方程； (2)求OA OC OB OD +的值.23.选修4-5：不等式选讲设函数()||,0f x x a a =-<. (1)证明：1()2f x f x ⎛⎫+-≥ ⎪⎝⎭； (2)若不等式1()(2)2f x f x +<的解集非空，求a 的取值范围.普通高等学校招生全国统一考试仿真模拟(一)文科数学答案一、选择题1-5:DBABB 6-10:CDDAB 11、12：BB 二、填空题13.33,2⎡⎤--⎢⎥⎣⎦14.1215. (10,5)(5,10)-- 16.0,3⎛ ⎝⎦三、解答题17.解析：(1)由已知223a b c bc =+=+，得222231222b c a bc a bc bc +-+-==. 详解答案即1cos 23A A π=⇒=. (2)由正弦定理，得sin 2sin sin ab B B A==， sin 2sin sin 2sin sin 3b C C B C C π⎛⎫∴==+ ⎪⎝⎭.1sin 2sin sin cos 22b C C C C ⎛⎫=+ ⎪ ⎪⎝⎭2111sin cos 2cos 2sin 222262C C C C C C π⎛⎫==-+=-+ ⎪⎝⎭， ∴当3C π=时，sin b C 取得最大值32. 18.解析：(1)证明：侧面11AA B B 为正方形，知1AB BB ⊥，又1111,AB B C BB B C B ⊥=，所以AB ⊥平面11BB C C ,又AB ⊂平面11AA B B ,所以平面11AA B B ⊥平面11BB C C . (2)设AB a =，A 点到平面111A B C 的距离为h ，由已知，1BB C ∆是边长为a 的等边三角形，在直角三角形ABC 中，AB BC a ==，由(1)知AB ⊥平面1BB C , 则11113ABC A B C A BB C V V --=，即1133ABCBB C Sh S AB ∆=⨯，又已知111ABC A B C V -=,所以221132323a h a =⨯=，得2,a h ==，即A 点到平面111A B C .19. 解析:(１)设该运动员到篮筐的水平距离的中位数为x0.0520.100.200.5⨯++<，且(0.400.20)10.60.5+⨯=>，[]4,5x ∴∈由()0.4050.2010.5x ⨯-+⨯=，解得 4.25x =， ∴ 该运动员到篮筐的水平距离的中位数是4.25(米) ．(2)由题意知,抽到的7次成绩中,有1次来自到篮筐的水平距离为2到3米的这一组,记作1A ；有2次来自到篮筐的水平距离为3到4米的这一组，记作12,B B ；有4次来自到篮筐的水平距离为4到5米的这一组，记作1234,,,C C C C .从7次成绩中随机抽取2次的所有可能抽法如下：1112111213(,),(,),(,),(,),(,)A B A B A C A C A C ,1412111213(,),(),(,),(,),(,)A C B B B C B C B C ,1421(,),(,)B C B C222324121314(,),(,),(,),(,),(,),(,)B C B C B C C C C C C C ,232434(,),(,),(,)C C C C C C 共21个基本事件.其中两次成绩均来自到篮筐的水平距离为4到5米的这一组的基本事件有6个．所以该运动员得1分的概率62=217P =. 20.解析：(1)证明：设220101,,,44x x A x B x ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭，2220,(0)4x D x x ⎛⎫> ⎪⎝⎭.由'2x y =得02BD x k =，又124BD x x k +=，所以01224x x x +=，即1202M x x x x +==，故AM 与y 轴平行.(2)法一：由,,A B F 共线可得AF BF k k =，所以()01014()0x x x x +-=，因010x x -≠，所以014x x =-，即104x x =-. 直线BD 的方程为20011204=()2242x x x x y x x x -+=++，所以2020422M x y x =++.由(1)得30014164x x ⎛⎫=+≥ ⎪⎝⎭，当且仅当004x x =，即02x =时等号成立，故S 的最小值为16. 法二：直线BD 的方程为2011()24x x y x x =-+，20101()24M x x y x x =-+.得2010()4M x x y y --=，则30124ABD ABMx x S S ∆∆-==.设直线:1AB y kx =+，代入24x y =得2440x kx --=，则014x x -=≥，故160ABD S k ∆≥=（时等号成立). 21.解析：(1)函数定义域为R ，222(12)'()(1)x e x mx x m f x x mx -+-+=-+22(1)(1)=(1)x e x x m x mx ----+.①当11m +=，即0m =时，'()0f x ≥,此时()f x 在R 上单调递增； ②当11m +>，即02m <<，(,1)x ∈-∞时，'()0f x >，此时()f x 单调递增，(1,1)x m ∈+时，'()0f x <，此时()f x 单调递减， (1,)x m ∈++∞时，'()0f x >，此时()f x 单调递增.③当11m +<，即20m -<<时，(,1)x m ∈-∞+，'()0f x >，此时()f x 单调递增，(1,1)x m ∈+时，'()0f x <，此时()f x 单调递减， (1,)x ∈+∞时，'()0f x >，此时()f x 单调递增.综上所述，①当0m =时，()f x 在R 上单调递增，②当02m <<时，()f x 在(,1)-∞和(1,)m ++∞上单调递增，()f x 在(1,1)m +上单调递减， ③当20m -<<时，()f x 在(,1)m -∞+和(1,)+∞上单调递增，()f x 在(1,1)m +上单调递减.(2)当10,2m ⎛⎤∈ ⎥⎝⎦时，由(1)知()f x 在(0,1)上单调递增，在(1,1)m +上单调递减. 令()g x x =.①当[0,1]x ∈时，min max ()(0)1,()1f x f g x ===，所以函数()f x 图象在()g x 图象上方.②当[1,1]x m ∈+时，函数()f x 单调递减，所以其最小值为1(1)2m e f m m ++=+，()g x 最大值为1m +，所以下面判断(1)f m +与1m +的大小，即判断x e 与(1)x x +的大小，其中311,2x m ⎛⎤=+∈ ⎥⎝⎦，令()(1),'()21xxm x e x x m x e x =-+=--，令()'()h x m x =，则'()2xh x e =-，因311,2x m ⎛⎤=+∈ ⎥⎝⎦，所以'()20xh x e =->，'()m x 单调递增；所以'(1)30m e =-<，323'402m e ⎛⎫=-> ⎪⎝⎭故存在031,2x ⎛⎤∈ ⎥⎝⎦，使得000'()210xm x e x =--=，所以()m x 在0(1,)x 上单调递减，在03,2x ⎛⎫⎪⎝⎭单调递增，所以022200000000()()=211xm x m x e x x x x x x x ≥=--+--=-++，所以031,2x ⎛⎤∈ ⎥⎝⎦时，2000()10m x x x =-++>，即2(1)e x x >+，也即(1)1f m m +>+，所以函数()f x 的图象总在直线y x =上方.22.解析：(1)21cos 2sin 2cos 22C ρθθρθρθ⎛⎫=+=+ ⎪⎪⎝⎭：，化为直角坐标方程为22(1)(1)2x y -+-=.把2C 的方程化为直角坐标方程为y a =，因为曲线1C 关于曲线2C 对称，故直线y a =经过圆心(1,1)，解得1a =，故2C 的直角坐标方程为1y =.(2)由题意可得，4OA πϕ⎛⎫+⎪⎝⎭，+2OB πϕϕ⎛⎫= ⎪⎝⎭，OC ϕ，4OD πϕ⎛⎫+ ⎪⎝⎭，所以+OA OC OB OD ⋅⋅8sin sin 8cos cos 44ϕπϕϕϕϕ⎛⎫⎛⎫=+++ ⎪ ⎪⎝⎭⎝⎭=8cos84π==23.解析：（1）证明：函数()||,0f x x a a =-<，则1111()||||()f x f x a a x a a x a a x x x x ⎛⎫⎛⎫+-=-+--=-++≥-++ ⎪ ⎪⎝⎭⎝⎭111=|||2||||x x x x x +=+≥= （当且仅当||1x =时取等号）. (2)()(2)|||2|,0f x f x x a x a a +=-+-<.当x a ≤时，()(2)223f x f x a x a x a x +=-+-=-，则()(2)f x f x a +≥-；当2aa x <<时，()(2)2f x f x x a a x x +=-+-=-，则()(2)2af x f x a -<+<-；当2ax ≥时，()(2)232f x f x x a x a x a +=-+-=-，则()(2)2a f x f x +≥-，则()f x 的值域为,2a ⎡⎫-+∞⎪⎢⎣⎭. 不等式1()(2)2f x f x +<的解集非空，即为122a>-，解得，1a >-，由于0a <，则a 的取值范围是(1,0)-.此文档是由网络收集并进行重新排版整理.word 可编辑版本！。

2018年黑龙江省齐齐哈尔市高考一模数学试卷(文科)【解析版】

三、解答题：共 70 分.解答应写出文字说明、证明过程或演算步骤.第 17～21 题为必考题，每个试题考生都必须作答，第 22、23 题为选考题，考生根据要求
第 3 页（共 19 页）
作答.（一）必考题：共 60 分. 17 ．（ 12 分）在△ ABC 中，角 A ， B ， C 所对的边分别为 a ， b ， c ．满足 2acosC+bcosC+ccosB＝0．（Ⅰ）求角 C 的大小；（Ⅱ）若 a＝2，△ABC 的面积为，求 c 的大小．
＝（ B．
） C． D．
5．（5 分）已知等差数列{an}的前 n 项和为 Sn，若 a3＝3，S4＝14．则{an}的公差为（ A．1 ） B．﹣1 C．2 D．﹣2
6．（5 分）圆 x2+y2﹣2x﹣4y+3＝0 的圆心到直线 x﹣ay+1＝0 的距离为 2，则 a＝（） B．0 C．1 D．2 ） D．c＜b＜a ）
2018 年黑龙江省齐齐哈尔市高考数学一模试卷（文科）
一、选择题：本题共 12 小题，每小题 5 分，共 60 分，在每小题给出的四个选项中，只有一项是符合题目要求的. 1．（5 分）设集合 A＝{1，2，3}，B＝{x[3x＞4}，则 A∩B＝（ A．{1，2} 2．（5 分）设 z＝ A．1 B．{2，3} C．{1，3} ） D．﹣3 ）
A．﹣1
7．（5 分）若 a，b，c 满足 2a＝3，b＝log25，3c＝2．则（ A．c＜a＜b B．b＜c＜a C．a＜b＜c
8．（5 分）函数 f（x）＝（2x﹣2﹣x）cosx 在区间[﹣5，5]上的图象大致为（
第 1 页（共 19 页）
A．
B．

东北三省四市2018届高三高考第一次模拟考试数学(文)试题

2018年东北三省四市教研联合体高考模拟试卷（一）数学第I卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的•1.设集合A J.x||x|：：：1? , B J..x|x（x-3）：：：0?，则A U B=（）A. (-1,0)B. (0,1)C. (-1,3) D (1,3)1 +i2.若复数z - 1 I为纯虚则实数a的值为（）1 +aiA. 1B. 0C. -1D. -123.中国有个名句“运城帷幄之中，决胜千里之外. ”其中的“筹”原意是指《孙子算经》中记载的算筹.古代是用算筹来进行计算，算筹是将几寸长的小竹棍摆在平面上进行运算，算筹的摆放形式有纵横两种形式（如图所示）表示一个多位数时，像阿拉伯计数一样，把各个数位的数码从左到右排列，但各位数码的筹式需要纵横相间，个位，百位，万位数用纵式表示，十位，千位，十万位数用横式表示，以此类推，例如3266用算筹表示就是三_ T，则8771用算筹可表示为( )I ---------------------------------------------------------------------- ---- ---- --------- ---- ---------------- ■ -----------------------------------------------------------------------------------------12 3 4 5 6 7 K 9I it in mi IIIII T TT TfTinr 纵式—=三I ］丄丄些才—===二丄士 = zrz 耦此中国古代的算筹孜码A. iXTT I . u 丄叮uIET丄TT_-------- --------- r入及最后输出的n值分别是（）4.如图所示的程序框图是为了求出满足2— n228的最小偶数n,那么在空白框中填入及最后输出的n值分别是（）否B )yX7Tc DBC. 81D. 90A. 9B . 10人冲护结束项之和是（）（单位：cm 3 ）是（）/揃生以6.等差数列〈aj 的公差不为零，首项印=1, a 2是ai 和a 5的等比中项，则数列彷"的前97.某几何体的三视图如图所示（单位: cm ），其俯视图为等边三角形，则该几何体的体积A. n 二 n 1 和 6tan x5.函数f （X ）=1 X 2的部分图象大致为（XC. n 二 n 1 和 8D. n 二 n 2 和 8n = n 2 和 68.已知首项与公比相等的等比数列订昇中，满足a m a n 2二a 4最小值为（）9.已知过曲线y 二e x 上一点P （x 0,y 0）作曲线的切线，若切线在的取值范围是（）10.已知边长为2的等边三角形 ABC ，D 为BC 的中点，以AD 为折痕进行折叠,（2x ）的图象向右平移 a个单位得到函数g （x ）二cos （2x ）f （x ）=si n的图34象，则a 的值可以为（）2x12.已知焦点在x 轴上的双曲线 —m存在一点P 满足PF 1 _ PF 2，且 PF 1F 2的面积为3,则该双曲线的离心率为（19■:41•D.24 y 轴上的截距小于 B .（丄，二）C. （1,使折后的. BDC N ，则过A ,B ,C ,D 四点的球的表面积为（11•将函数 71 =1的左右两个焦点分别为 F ）和F 2，其右支上第U卷(共90 分)二、填空题(每题5分，满分20分，将答案填在答题纸上)［八0,13.设实数x , y满足约束条件《4x-yKO,则z = x+2y+5的最大值为___________________x + y 兰5,14.为了了解居民天气转冷时期电量使用情况，某调查人员由下表统计数据计算出回归直线方程为y 2.11x 61.13，现表中一个数据为污损，则被污损的数据为 ___________________ . (最后结果精确到整数位)15.已知函数f(x)满足f(x 1) = 1 f(X)，当f(1) = 2 时，f (2018) f (2019)的值1-f(x)为__________ .116.已知菱形ABCD的一条对角线BD长为2,点E满足AE ED，点F为CD的中点，2T T T T若AD BE - -2，则CD AF 二_____________ .三、解答题(本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.)17.已知=ABC的内角A , B , C的对边分别为a , b , c，若b=2，且2bcos B 二acosC ccos A .(1 )求B的大小；(2 )求ABC面积的最大值.18.树立和践行“绿水青山就是金山银山，坚持人与自然和谐共生” 的理念越来越深入人心，已形成了全民自觉参与，造福百姓的良性循环. 据此，某网站退出了关于生态文明建设进展情况的调查，调查数据表明，环境治理和保护问题仍是百姓最为关心的热点，参与调查者中关注此问题的约占80% .现从参与关注生态文明建设的人群中随机选出200人，并将这200人按年龄分组：第1组［15,25)，第2组［25,35),第3组［35,45)，第4组［45,55),第5 组［55,65)，得到的频率分布直方图如图所示.(1) 求出a 的值；(2) 求这200人年龄的样本平均数(同一组数据用该区间的中点值作代表)和中位数(精确到小数点后一位)；(3)现在要从年龄较小的第 1,2组中用分层抽样的方法抽取5人，再从这5人中随机抽取 3人进行问卷调查，求这 2组恰好抽到2人的概率. ABCD 是正方形，PA _平面ABCD , E , F 分别是(1)证明:EF // 平面(2)求点F 至U 平面PDC 的距离. 圆C 上.(1)求椭圆C 的方程; (2)已知P(-2,0)与Q(2,0)为平面内的两个定点，过(1,0)点的直线l 与椭圆C 交于A , B两点，求四边形APBQ 面积的最大值. 21.已知函数 f(x)=l nx , g(x)=x m ( m R ).(1 )若f(x) _g(x)恒成立，求实数 m 的取值范围;19.在如图所示的几何体中，四边形线段AD , PB 的中点，PA = AB20.在平面直角坐标系中，椭圆2x 2a+ ；：十30)的离心率为1，点M(1 在椭。

2018届东北三省四市教研协作体高三联合考试文科数学试题及答案精品

东北三省四市教研协作体2018届高三联合考试数学文一、选择题（本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的.）1．已知全集 =N ，集合P ={}，6，4，3，2，1Q={}1,2,3,5,9则()P C Q = A ．{}3,2,1 B ．{}6,4 C ．{}9,5 D {}6,4,3,2,12．如果映射f ：A →B 满足集合B 中的任意一个元素在A 中都有原象，则称为“满射”．若集合A 中有3个元素，集合B 中有2个元素，则从A 到B 的不同满射的个数为 A ．2B ．4C ．6D ．8 3．设 ()212,11,1x x f x x x ⎧--≤⎪=⎨+>⎪⎩，则()()2f f = A ．－2 B ．2 C ．5D ． 264．某几何体的三视图如图，则该几何体的表面积为A．3+ B．8+C ．6+D ．8+5．如果一个几何体的三视图如图所示，则该几何体的表面积为A、21680+ B 、21664+ C 、96 D 、806．已知命题p ：抛物线22x y =的准线方程为21-=y ；命题q ：平面内两条直线的斜率相等是两条直线平行的充分不必要条件；则下列命题是真命题的是A 、q p ∧B 、()q p ⌝∧C 、()()q p ⌝∧⌝D 、q p ∨7．若函数R x x x x f ∈+=,cos sin )(ωω3，又02=-=)(,)(βαf f ，且βα-的最小值为43π，则正数ω的值是 A. 31 B. 32 C.34 D.238．已知)(x f 为定义在),(+∞-∞上的可导函数，且)()('x f x f < 对于任意R x ∈恒成立，则A. )0()2010(),0()2(20102f e f f e f ⋅>⋅>B. )0()2010(),0()2(20102f e f f e f ⋅>⋅<C. )0()2010(),0()2(20102f e f f e f ⋅<⋅>D. )0()2010(),0()2(20102f e f f e f ⋅<⋅<9．已知数列54321,,,,a a a a a 的各项均不等于0和1，此数列前n 项的和为n S ，且满足)51(22≤≤-=n a a S n n n ，则满足条件的数列共有A. 2个B. 6个C. 8个D. 16个10．抛物线px y 22=与直线04=-+y ax 交于A ，B 两点，其中A 点的坐标是),(21．该抛物线的焦点为F ，则=+||||FB FAA.7B.53C. 6D. 511．定义在R 上的奇函数()f x 满足(2)()f x f x -=，当[]0,1x ∈时，()f x =()cos2xg x π=，则集合{}|()()x f x g x =等于A ．1|4,2x x k k z ⎧⎫=+∈⎨⎬⎩⎭B ．1|2,2x x k k z ⎧⎫=+∈⎨⎬⎩⎭C ．1|4,2x x k k z ⎧⎫=±∈⎨⎬⎩⎭D ．{}|21,x x k k z =+∈12. 已知点)1,0(-A ，点B 在圆C ：2222=-+y y x 上运动，则直线AB 斜率的取值范围是 A.]33,33[-B. ),33[]33,(+∞⋃--∞C. ]3,3[-D. ),3[]3,(+∞⋃--∞二、填空题：（本大题共4小题，每小题5分，共20分）13．已知等差数列{}n a 的前n 项和为n S ，且111634a a a +=-，则11S = 。

2018东北三省三校一模联考数学(文)试题

东北三省三校2018 年高三第一次联合模拟考试文科数学试卷本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分,共150 分,考试时间120 分钟。

考试结束后，将本试卷和答题卡一并交回。

注意事项：1．答题前，考生务必先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内。

2．选择题必须使用2B 铅笔填涂；非选择题必须使用0.5 毫米黑色字迹的签字笔书写，字体工整、笔迹清楚。

3．请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效。

4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。

5．保持卡面清洁，不要折叠，不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

第Ⅰ卷（选择题共60 分）一．选择题：本大题共12 小题，每小题5 分，在每小题给出的四个选项中，只有一项是符合题目要求．１．已知集合A {0, b}, B { x Z x23x 0}, 若A B ,则b等于（）A．1 B．2 C．3 D．1 或22i２．复数2 i（）1 2iＡ．i Ｂ．i Ｃ．2（ 2 i）Ｄ．1 i３．ABC的内角A、B、C的对边分别为a、b、c，则“ a b ”是“ cos2 A cos2 B”的（）Ａ．充分不必要条件Ｂ．必要不充分条件Ｃ．充要条件Ｄ．既不充分也不必要条件４．向量a,b满足a 1,b 2,（a b）（2a b）, 则向量a与b的夹角为（）Ａ．45 Ｂ．60 Ｃ．90 Ｄ．120５．实数m是0,6 上的随机数，则关于x的方程x2mx 4 0 有实根的概率为（）Ａ．Ｂ．Ｃ．Ｄ．６．已知三棱锥的三视图，则该三棱锥的体积是f (x) lg(x 1) sin2 x 的零点个数为(A ．63 Ｂ． 2 63Ｃ． 3 6 2 Ｄ． 622 ７．椭圆 x y 2 4 1两个焦点分别是 F 1,F 2 ，任意一点，则 PF 1 PF 2 的取值范围是(点 P 是椭圆上Ａ． 1,4 Ｂ． 1,3 Ｃ． 2,1Ｄ． 1,1８．半径为１的球面上有四个点Ａ，Ｂ，Ｃ，Ｄ，球心为点Ｏ， AB 过点Ｏ，CA C B , DA DB , DC 1, 则三棱锥 A BCD 的体积为( ) Ｂ．Ｃ． 3 Ｄ．已知数列 a n 满足 ln a 1 ln a 2 lna 325 8 a 10 =( )26Ａ． e Ｂ 32 Ｃ． eＤ９． e 35 29 e 3n 1 2 ln a n 3n 2 10．执行如图所示的程序框图，要使输出的 S 的值小于１，则输入的 t 值不能是下面的( ) (n N ) ，则Ａ．8 Ｂ．9 Ｃ． 10 Ｄ． 11 11．若函数 f(x) 2x 3 3mx 2 6x 在区间 2, 上为增函数，则实数 m 的取值范围是Ａ．,2Ｂ． ,2Ｃ．52Ｄ．,5212．函数Ａ．Ｂ．10 Ｃ．11 Ｄ．12 ９第Ⅱ卷(非选择题共 90 分)本卷包括必考题和选考题两部分．第 13 题～第 21 题为必考题，每个试题考生都必须做答，第 22题～第 24题为选考题，考生根据要求做答．二．填空题(本大题共 4小题，每小题 5 分．)13．若等差数列a n 中，满足 a 4 a 6 a 2010 a 2012 8 ，则 S 2015 = _________________________________ ．3 2x y 914．若变量 x,y 满足约束条件，则 z x 2y 的最小值为6xy9下焦点的对称点分别为 A 、B ，点 Q 在双曲线 C 的上支上，点 P 关于点 Q 的对称点为 P 1，则P 1A P 1B = _______ ．16．若函数 f(x)满足 : (ⅰ)函数 f (x)的定义域是 R ； (ⅱ)对任意 x 1,x 2 R 有3f(x 1 x 2) f(x 1 x 2) 2 f (x 1) f (x 2) ；(ⅲ) f(1) 23. 则下列命题中正确的是 __________________________写出所有正确命题的序号)①函数 f (x) 是奇函数；②函数 f (x) 是偶函数；③对任意 n 1,n 2 N ，若 n 1 n 2 ，则f (n 1) f (n 2)；④ 对任意 x R ，有 f(x) 1.三. 解答题(解答应写出文字说明，证明过程或演算步骤)17．(本题满分 12 分)已知 ABC 的面积为 2, 且满足 0 AB AC 4, 设 AB 和 AC 的夹角为． Ⅰ)求的取值范围； Ⅱ)求函数 f( ) 2sin 2() 3cos2 的值域． 418．(本题满分 12 分)空气污染，又称为大气污染，是指由于人类活动或自然过程引起某些物质进入大气中，呈现出足够的浓度，达到足够的时间，并因此危害了人体的舒适、健康和福利或环境的现象．全世界也越来越关注环境保护问题．当空气污染指数(单位：g /m 3)为 0~50时，空气质量级别为一级，空气质量状况属于优；当空气污染指数为50 ~ 100时，空气质量级别为二级，空气质量状况属于良；当空气污染指数为 100 ~150 时，空气质量级别为三级，空气质量状况属于轻度污染；当空气污染指数为 150 ~ 200 时，空气质量级别为四级，空气质量状况属于中度污染；当空气污染指数为 200 ~ 300 时，空气质量15．已知双曲线 C ：2 y16 点 P 与双曲线 C 的焦点不重合．若点Ｐ关于双曲线Ｃ的上、2x4级别为五级，空气质量状况属于重度污染；当空气污染指数为 300 以上时，空气质量级别为六级，空气质量状况属于严重污染． 2018 年１月某日某省 x 个监测点数据统计如 Ⅰ)根据所给统计表和频率分布直方图中的信息求出 x, y 的值，并完成频率分布直方图； Ⅱ)若 A 市共有 5个监测点，其中有 3 个监测点为轻度污染，２个监测点为良．从中任意选取 2 个监测点，事件 A “其中至少有一个为良”发生的概率是多少？19．(本题满分 12 分)如图，多面体 ABCDEF 中，底面 ABCD 是菱形， BCD 60 ，四边形 BDEF 是正方形，且DE 平面 ABCD .( Ⅰ ) 求证 : CF // 平面 AED ；(Ⅱ)若AE 2 ，求多面体 ABCDEF 的体积V .20．(本题满分 12 分)在平面直角坐标系 xOy 中，已知动圆过点 (2,0) ，且被 y 轴所截得的弦长为 4.( Ⅰ ) 求动圆圆心的轨迹 C 1 的方程 ;(Ⅱ) 过点 P (1,2)分别作斜率为 k 1, k 2的两条直线 l 1,l 2 ，交C 1于A, B 两点(点 A,B 异于2 21空气污染指数( 单位： g/m 3)0,5050,100100,150150,200监测点个数1540y100.008 0.007 0.006 0.005频率组距AB点P), 若k1 k2 0，且直线AB与圆C2:(x 2)2y2相切，求△ PAB的面积.21．(本题满分 12 分)已知实数 a 为常数，函数 f(x) xlnx ax 2．Ⅰ)若曲线 y f(x)在 x 1处的切线过点Ａ (0, 2) ，求实数 a 值； Ⅱ)若函数 y f(x) 有两个极值点 x 1, x 2 ( x 1 x 2)．11①求证：2 a 0 ；②求证： f(x 1) 0， f(x 2)2．请从下面所给的 22 , 23 , 24 三题中任选一题做答，并用 2B 铅笔在答题卡上将所选题目对应的题号方框涂黑，按所涂题号进行评分；不涂、多涂均按所答第一题评分；多答按所答第一题评分。