25.3利用频率估计概率ppt
人教版九年级数学上册《用频率估计概率》概率初步PPT优质课件

10
=
小练习
1. 在一次质检抽测中,随机抽取某摊位20袋食盐,测得各袋的质量分别
为(单位:g):492,496,494,495,498,497,501,502,504,
496,497,503,506,508,507,492,496,500,501,499根据
以上抽测结果,任买一袋该摊位的食盐,质量在497.5g~501.5g之间的概
在抛掷一枚硬币时,结果不是“正面向上”,就是“反面向上”
因此,从上面的试验中也能得到相应的“反面向上”的频率。当
“正面向上”的频率稳定于0.5时,“反面向上”的频率也稳定于
0.5.它也与前面用列举法得出的“反面向上”的概率是同一个数值。
探索新知
历史上,有些人曾做过成千上万次抛掷硬币的试验,其中一些
动物1200只,作标记后放回。若干天后,再逮到该种动物1000只,其中
有100只作过标记。按概率方法估算,保护区内这种动物有 12000 只。
【解析】∵该种动物1000只,其中有100只作过标记。∴作过标记的动物占这种动物总
100
数的
1000
=
12000只。
1
1
。∵该种动物共1200只做了标记,∴保护区内这种动物有1200 ÷
试验结果见下表。
探索新知
实际上,从长期实践中,人们观察到,对一般
的随机事件,在做大量重复试验时,随着试验
次数的增加,一个事件出现的频率,总在一个
固定数的附近摆动,显示出一定的稳定性。因
此,我们可以通过大量的重复试验,用一个随
机事件发生的频率去估计它的概率。
探索新知
从抛掷硬币的试验还可以发现,“正面向上”的概率是
植成活的概率为 0.9 。
人教版九年级数学上册《25.3用频率估计概率》课件(共27张PPT)

3 B.在答卷中,喜欢足球的答卷与总问卷的比5为3︰8
C.在答卷中,喜欢足球的答卷占总答卷的
D.在答卷中,每抽出100份问卷,恰有60份答卷是喜欢足球
练习巩固
3.在一个不透明的口袋中装有4个红球和若干个白球,它们除颜色外其他相
同.通过多次摸球试验后发现,摸到红球的频率稳定在25%附近,则口袋中
白球可能有( D ).
在同样条件下,对这种幼树进行大量移植,并统计成活情况,计算成活 的频率.随着移植数n越来越大,频率 m 会越来越稳定,于是就可以把频
n 率作为成活率的估计值.
从表中可以发现,随着移植数的增加,幼树移植成活的频率越来越稳 定.当移植总数为14 000时,成活的频率为0.902,于是可以估计幼树移植 成活的概率为0.9.
转动转盘的次数n
落在“铅笔”的次数m
落在“铅笔”的频率
m n
100 150 200 500 800 1 000 68 111 136 345 546 701
(2) 请估计,当n很大时,频率将会接近多少?
(3) 转动该转盘一次,获得铅笔的概率约是多少?
(4) 在该转盘中,标有“铅笔”区域的扇形的圆心角大
如果随着抛掷次数的增加,“正面向上”的频率的变化在0.5的左右摆动幅度不完全是越来越小,本次实验依然不能称为严格意义上的大量重复实验. 2.某射击运动员在同一条件下的射击成绩记录如下: 902,于是可以估计幼树移植成活的概率为 . 例2 某水果公司以2元/kg的成本价新进了10 000 kg的柑橘.如果公司希望这些柑橘能够获得利润5 000元,那么在出售柑橘(去掉损坏的柑橘)时,每千克大约定价为多少元比较合适 ? 2.某射击运动员在同一条件下的射击成绩记录如下:
约是多少(精确到1°).
25.3用频率估计概率PPT幻灯片
20
随堂练习:
完成下表, 利用你得到的结论解答下列问题:
柑橘总质量(n)/千克
损坏柑橘质量(m)/千克
柑橘损坏的频率(
m n
)
50
投掷次数
正面出现频数
正面出现频率
1
50
2
50
3
50
4
50
5
50
67
5500
8
50
5
在多次试验中,某个事件出现的次 数叫 频数 ,某个事件出现的次 数与试验总次数的比,叫做这个事件 出现的 频率 .
6
历史上曾有人作过抛掷硬币的大量重复实验, 结果如下表所示
抛掷次数(n) 2048 4040 12000 30000 24000 72088
24
问题
概率伴随着我你他
• 1.在有一个10万人的 小镇,随机调查了 2000人,其中有250人 看中央电视台的早间 新闻.在该镇随便问 一个人,他看早间新 闻的概率大约是多少 ?该镇看中央电视台 早间新闻的大约是多 少人?
• 解:
• 根据概率的意义,可以 认为其概率大约等于 250/2000=0.125.
9
从长期的实践中,人们观察到, 对一般的随机事件,在做大量重复 试验时,随着试验次数的增加,一 个事件出现的频率,总在一个固定 数值的附近摆动,显示出一定的稳 定性。因此,我们可以通过大量 的 重复试验,用一个随机事件发生的频 率去 估计它的概率。
10
雅各布·伯努利(1654-1705), 被公认是概率论的先驱之一, 他最早阐明了随着实验次数的 增加,频率稳定在概率附近。
25.3利用频率估计概率课件ppt.

问题2、某水果公司以2 元/千克的成本新进了 10000千克柑橘,销售人员首先从所有的柑橘中随机地抽取若干柑橘,进行了“柑橘损坏率“统计,并把获得的数据记录在下表中了问题1:完好柑橘的实际 2.22 成本为______元/千克问题2:在出售柑橘(已去掉损坏的柑橘)时,希望获利5000元,每千克大约定价为多少元比较合适?约2.8元柑橘总质量损坏柑橘质量柑橘损坏的(n)千克(m)千克频率(m/n 50 100 150 200 250 300 350 400 450 500 5.50 10.50 15.15 19.42 24.35 30.32 35.32 39.24 44.57 0.110 0.105 0.101 0.097 0.097 0.101 0.101 0.098 0.099 0.103 51.54
概率伴随着你我他在有一个10万人的小镇,随机调查解: 了2000人,其中有根据概率的意义,可以 250人看中央电视认为其概率大约等于台的早间新闻.在 250/2000=0.125. 该镇随便问一个人该镇约有他看早间新闻的概
100000×0.125=12500 率大约是多少?该人看中央电视台的早镇看中央电视台早间新闻. 间新闻的大约是多少人?
大家都来做一做从一定的高度落下的图钉,落地后可能图钉尖着地,也可能图钉尖不找地,估计一下哪种事件的概率更大,与同学合作,通过做实验来验证一下你事先估计是否正确?你能估计图钉尖朝上的概率吗?
结束寄语: 概率是对随机现象的一种数学描述,它可以帮助我们更好地认识随机现象,并对生活中的一些不确定情况作出自己的决策. 从表面上看,随机现象的每一次观察结果都是偶然的,但多次观察某个随机现象,立即可以发现:在大量的偶然之中存在着必然的规律. 走啊去完成作业的!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
田家炳中学分部 殷光习
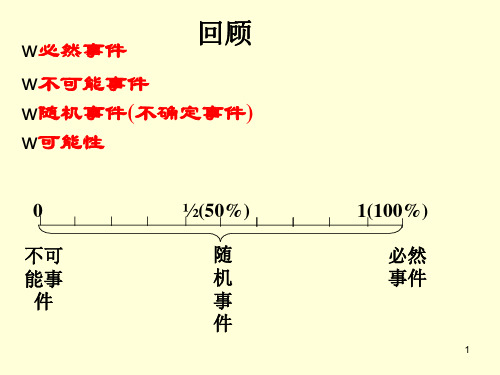
回顾
必然事件 不可能事件 可能性
0 不可 能发 生 可 能 发 生 1 必然 发生
随机事件(不确定事 件)
概率定义: 描述事件发生的可能性的数值, 称为事件发生的概率. 必然事件发生的概率为1 P(必然事件)=1;
不可能事件发生的概率为0, P(不可能事件)=0; 随机事件(不确定事件)发生的概率介于0~1 之 间,如果A为随机事件, 0<P(A)<1.
树状图
钥匙 锁
开始 A A B A B B C A B
所有可能出 (A,A) 现的结果
(A,B) (B,A) (C,B)
B BA BB C CA CB
(B,B)
(C,A)
列表
钥匙
锁
A AA BB
A B
用列举法求概率的条件是什么? (1)实验的所有结果是有限个(n)
(2)各种结果的可能性相等.
填P144页的表格并完成表后的填空.
问题1:某林业部门要考查某种幼树在一定 条件下的移植成活率,应采取什么具体做法?
移植总数 (m) 10 50 270 400 成活数 (m) 8 47 235 369 成活的频 率(m/n) 0.8
从表中可以发现 ,幼树移植成活的频 率在_____左右摆动,
随着统计数据的增 加,这种规律愈加明 显,估计A类幼树移 植成活的概率为____
0.94
0.870
0.923
0.883 0.890 0.915 0.905 0.902
750
1500 3500 7000 14000
662
1335 3203 6335 12628
问题2、某水果公司以2元/千克的成本新进了10000千克柑橘, 销售人员首先从所有的柑橘中随机地抽取若干柑橘,进行 了 “柑橘损坏率“统计,并把获得的数据记录在下表中了
上面两个问题,都不属于结果可能性相等的 类型.移植中有两种情况活或死.它们的可能 性并不相等, 事件发生的概率并不都为50%. 柑橘是好的还是坏的两种事件发生的概率也 不相等.因此也不能简单的用50%来表示它发 生的概率.
材料1:
o.5 则估计抛掷一枚硬币正面朝上的概率为__
材料2:
0.9 则估计油菜籽发芽的概率为___
m P A n
当实验的所有结果不是有限个;或各种可 能结果发生的可能性不相等时.又该如何求 事件发生的概率呢?
问题1:某林业部门要考查某种幼树在一定 条件下的移植成活率,应采取什么具体做法?
问题2:某水果公司以2元/千克的成本新进 了10000千克柑橘,如果公司希望这些柑橘 能够获得利润5000元,那么在出售柑橘时 (去掉坏的),每千克大约定价为多少元?
结
论
瑞士数学家雅各布.伯努利(1654 -1705)最早阐明了可以由频率估计 概率即: 在相同的条件下,大量的重复实验 时,根据一个随机事件发生的频率所逐渐 稳定的常数,可以估计这个事件发生的概 率 随机事件A,用频率估计概率P(A)能小于 0大于1吗?
一般地,在大量重复试验中,如果事件A发生的频率 会稳定在某个常数p附近,那么事件A发生的 概率P(A)=P
你能估计图钉尖朝上的概率吗
?
结束寄语:
概率是对随机现象的一种数学描述,它 可以帮助我们更好地认识随机现象,并对生 活中的一些不确定情况作出自己的决策. 从表面上看,随机现象的每一次观察结 果都是偶然的,但多次观察某个随机现象, 可以发现:在大量的偶然之中存在着必然 的规律.
0.097
0.097
0.101
0.101 0.098
问题2:在出售柑橘( 已去掉损坏的柑橘)时 ,希望获利5000元,每千 克大约定价为多少元比 较合适?
大家都来做一做
从一定的高度落下的图钉,落地后 可能图钉尖着地,也可能图钉尖不找地, 估计一下哪种事件的概率更大,与同学 合作,通过做实验来验证 一下你事先估计是否正确?
柑橘总质量 (n)千克 损坏柑橘质量 (m)千克
50 100
5.50 10.50
柑橘损坏的 频率(m/n) 0.110 0.105 0.101
150 200 250 3ቤተ መጻሕፍቲ ባይዱ0 350 400 450 500
15.15 19.42 24.35 30.32 35.32 39.24 44.57 51.54
问题1:完好柑橘的实 际成本为______元/千 克
m n
需要注意的是:概率是针对大量重复的试验而 言的,大量试验反映的规律并非在每一次试验中出 现. 更一般地,即使试验的所有可能的结果不是有 限个,或各种可能的结果发生的可能性不相等,也 可以通过试验的方法去估计一个随机事件发生的 概率.只要试验次数是足够大的,频率就可以作为 概率的估计值.
P142练习
