2009年5月高三数学模拟测试卷及答案-参考答案

合集下载

2009届高三年第二次模拟考试数学参考答案理科2009.05.24

仙游一中 2009届高三年第二次模拟考试2009.05.24现代中学数学参考答案 (理科)一、选择题：1. C2. A3. D4. D5. A6. B 7．A 8. C 9．C 10. A 二、填空题：11．x y 3±= 12. 2 . 13. ③ ④ 14. 49 15．三、解答题：16．解： (Ⅰ)∵222a cb ac +-=，∴2221cos 22a cb B ac +-==， …………3分又∵0B π<<， ∴3B π=． …………6分（Ⅱ）6sin cos2m n A A ⋅=--223112sin 6sin 12(sin )22A A A =--=--，…10分 ∵203A π<<，∴0sin 1A <≤．∴当sin 1A =时，取得最小值为5-……13分 17.解：（1）设甲选手答对一个问题的正确率为1P ，则211(1)9P -= 故甲选手答对一个问题的正确率123P = 3分（Ⅱ）选手甲答了3道题目进入决赛的概率为32()3=8274分选手甲答了4道题目进入决赛的概率为233218()3327C ⋅= 5分选手甲答了5道题目进入决赛的概率为23242116()()3381C = 6分选手甲可以进入决赛的概率88166427278181P =++= 8分（Ⅲ）ξ可取3，4，5则有33211(3)()()333P ξ==+= 9分22223321212110(4)()()33333327P C C ξ==⋅⋅+⋅⋅= 10分222222442121218(5)()()()()33333327P C C ξ==+= 11分因此有（直接列表也给分）故3453272727E ξ=⋅+⋅+⋅= 13分 18．解：由三视图知，该多面体是底面为直角三角形的直三棱柱,ADE BCF AB BC -==且4,BF =2DE CF CBF π==∠=（1）证明：连续取BE ，易见BE 通过点M ，连接CE 。

2009高考数学模拟试题13套数学5

2009年教师命题比赛数学科试题、选择题：本大题共 8小题，每小题5分，满分30分•在每小题给出的四个选项中，只有一项是符合题目要求的.1•满足 M M {a i , a 2, a 3, a 4）且 M Q{ a !耳，a 3）={ a^a ?}的集合 M 的个数是（） A 1B. 2C 3D 42. “Igx .Igy ”是 “ ..x _ y ”的（）A 充分不必要条件B 必要不充分条件C 充要条件 D既不充分又不必要条件3.若复数Z 满足（2 - i ）Z =2，则Z 所对点所在复平面的象限为 ( ) A 第一象限B第二象限C第三象限D第四象限4设{ a n }是公比为正数的等比数列，若a1=1,a 5=16,则数列{ 「a n}前7项的和为A.63B.64C.127D.128—1兰X 兰1,9.已知实数X 、y 满足条件丿贝U 函数z=3x-y 的最大值是10. 运行下边算法流程，若 x 输入3时，输出y 的值为 __________5.从A 、B 、C 、D 、E 五名短跑运动员中任选 4名，排在标号分别为 1、2、3、4的跑道上，则不同的排法有 A . 24种B . 48种6•右图是一个几何体的三视图，根据图中数据，该几何体的表面积是（ A 9 n C 11 n() C . 120种可得7 .已知 b 0 , b =1, y= b ax 的图象只可能是8、在厶ABC 中，已知向量 10n 12n=0,则函数 y= ax+ b 禾口/7^LiAB 与AC 满足（|AB|輕)BC =0且-AB| AC || AB | | AC |△ ABC ^（）A.三边均不相等的三角形C.直角三角形B. 等腰非等边三角形等边三角形二、填空题（本大题共7小题，每小题30分.其中13~15题是选做题，考生只能选做二题，三题全答的, 只计算前两题得分..）D . 124种X(XXACAB选做题：在下面三道小题中选做两题，三题都选只计算前两题的得分三、解答题（共6个小题，满分80分，解答应写出文字说明、证明过程和演算步骤）16 （本小题满分12分）设"ABC 的内角A , B , C 的对边分别为a,b,c ,且A=60 , c=3b.a 1 1求：（I ）—的值；（n ）求的值.（2008重庆17）c ta nB tanC17（本小题满分12分）甲、乙两个篮球运动员互不影响地在同一位置投球，命中率分别为-2与p ，且乙投球2次均未命中的概率为 -16（I ）求乙投球的命中率 p ；11.已知 f (x) =sin( x 0), f且f （x ）在区间（―，—）有最小值，无最大值, 6 3 贝y 时= _________ . 12. 10.将全体正整数排成一个三角形数阵:1 2 3 6 5 789 15 14 13 4 1012 11按照以上排列的规律，第 2n-1行（n • N 第3个数为|V▼L2y = xy = x +1———13.不等式X+1 +X —2 35的解集为结束14.在直角坐标系xoy 中，已知曲线 c 的参数方程是厂弘厂1 u 是参数），若以o 为X = cosQ极点，x 轴的正半轴为极轴，则曲线C 的极坐标方程可写为15.已知：如图，PT 切O O 于点T ,PA 交O O 于A 、B 两点且与直径 CT 交于点D , CD = 2,AD = 3, BD = 6，贝U PB =开始输入x是否X :::是x _ 1否，且n 》2）从左向右的输出y(n)若甲投球1次，乙投球2次，两人共命中的次数记为 •，求的分布列和数学期望18. (本小题满分14分)如图，在直三棱柱 ABC-A i B i C i 中，平面 ABC 丄侧面A I ABB 1. (I)求证：AB 丄BC ;(n)若直线 AC 与平面A 1BC 所成的角为0，二面角A 1-BC-A 的大小为$的大小关系，并予以证明.19. (本小题满分14分)2设函数 f (x) =2ln (x —1 )-(x —1).(1)求函数f (x)的单调递增区间;(2)若关于x 的方程f x ，x 2-3x-a=0在区间12,4丨内恰有两个相异的实根，求实数a 的取值范围.20、(14分)已知点 H (— 3, 0),点P 在y 轴上，点 Q 在x 轴的正半轴上，点 M 在直线3——PQ 上，且满足 HP PM =0, PMMQ .2(I)当点P 在y 轴上移动时，求点 M 的轨迹C ； D(m,0)( m 0)作直线l 交轨迹C 于A 、B 两点，E 是D 点关于坐标原点(1)求数列3n ?的通项公式;(n)过定点 O 的对称点，求证: (川)在(n) 定值？若存在求出AED "BED ；中，是否存在垂直于x 轴的直线I 被以AD 为直径的圆截得的弦长恒为「的方程；若不存在，请说明理由21.(本题满分14分)已知数列'a * 中，a 1 = 1,且点P a n ,a n 1 n • N ”在直线x - y ■ 1 = 0上.(2) 若函数 f (n) = —1— - 一1一 - 一1— ■■ ■■ - 一1一 n 三 N ,且n _ 2，求函数 f (n)的 n +a t n +a 2 n +a 3 n +a n 最小值；3 七2 • S 3• S n 」.=0-1 Q n 对于一切不小于 2的自然数n 恒成立？若存在，写出g n 的解析式，并加以证明；若不存在，试说明理由. （东莞市2009届高三模拟试题（二））中山市华侨中学 2009年教师命题比赛数学科答案命题教师:赵善兰年级:高二一、选择题1. B 2 A 3 D 4C5C5C 6D7C 8 （改编题）B（本题考查基础知识和基本运算）二、填空题29. 3 ; 10 . 4 ; 11.14/3; 12.（自编题）2n-n-213（—叫一2® [3,+晌4） p = 2si n 015. 15（本题考查基础知识和基本运算）三、解答题16、（2008重庆理数17）（12分）本小题主要考查解三角形、三角变形基本知识，考查学生的变换、化归和运算能力。

安徽省宿州市2009届高三五月联考数学试卷理科(附答案)

安徽省宿州市2009届高三五月联考数学试卷(理)一选择题：1.已知集合{})90sin(,0cos 0-= A ，{}02=+=x x x B ，则B A ⋂为（） {}1,0.-A {}1,1.-B {}1.-C {}0.D 2.i 为虚数单位，则复数=+-)1()1(2i i （）i A 22.+- i B 22.-- i C 22.+ i D 22.-3.设γβα、、为三个不同的平面，给出下列条件：①b a 、为异面直线，βαβα//,//,,a b b a ≠≠⊂⊂ ②α内有三个不共线的点到β的距离相等 ③γβγα⊥⊥, ④γβγα//,//，则其中能使βα//成立的条件为：（）A ①④B ②③C ①③D ②④4.如图是2008年北京奥运会上男子跳台跳水比赛中， 12位评委为某个运动员打出的分数的茎叶统计图，去掉一个最高分和一个最低分之后，所剰数据的平均数和标准差分别为（）16,84.A 4,84.B 16,85.C 4,85.D5．已知变量y x ,满足⎪⎩⎪⎨⎧≤-≤≥,0,2,1y x y x 则2x+y 的最大值是( )A ．3B ．4C ．5D ．66.已知21nx x ⎛⎫+ ⎪⎝⎭的二项展开式的各项系数和为32，则二项展开式中x 系数为( )5.A 10.B 20.C 40.D7.设134:≤-x p ；0)1()12(:2≤+++-a a x a x q .若p ⌝是q ⌝的必要而不充分条件，则实数a 的取值范围是（）⎥⎦⎤⎢⎣⎡21,0.A ⎪⎭⎫ ⎝⎛21,0.B (]⎪⎭⎫⎢⎣⎡+∞⋃∞-,210,.C ()⎪⎭⎫⎝⎛+∞⋃∞-,210,.D8.△ABC 中，AB=AC ，BC=2,则=⋅（）2.-A 2.B 1.-C .D 不确定9.当20π<<x 时，函数xxx x f 2sin sin 82cos 1)(2++=的最小值为（）2.A 32.B 34.C 4.D10.若正四面体SABC 的面ABC 内有一动点P 到平面SAB 、平面SBC 、平面SCA 的距离依次成等差数列，则点P 的轨迹是（）.A 一条线段 .B 一个点 .C 一段圆弧 .D 抛物线的一段11.已知点P 是抛物线x y 42=上一点，设点P 到此抛物线准线的距离为1d ，到直线0102=++y x 的距离为2d ，则21d d +的最小值为（）5.A 4.B 5511.C 511.D12.在数列{}n a 中，对任意*∈N n ，都有k a a a a nn n n =--+++112（k 为常数），则称{}n a 为“等差比数列”，下面对“等差比数列”的判断：①k 不可能为零；②等差数列一定是等差比数列；③等比数列一定是等差比数列；④通项公式为)1,0,0(≠≠+⋅=b a c b a a n n 的数列一定是等差比数列，其中正确的判断为（） .A ① ② .B ② ③ .C ③ ④ .D ① ④二填空题：13.()202x x e dx -=⎰ .14. 执行右边的程序框图，若4p =，则输出的S =15.设M 、N 分别是曲线0sin 2=+θρ和224sin(=+πθρ上的动点，则M 、N 的最小距离是______16.设定义域为R 的函数⎪⎩⎪⎨⎧=≠-=)1(2)1(44)(x x x x f ，若关于x 的方程0)()(2=++c x bf x f 有三个不同的实数解321,,x x x ，则=++232221x x x ____三解答题：17.在锐角ABC ∆中，C B A ,,的对边分别为c b a ,,且A c B b C a cos ,cos ,cos 成等差数列，（1）求B 的值（2）求)cos(sin 22C A A -+的范围18. （12分）一个多面体的直观图如图所示（其中N M ,分别为BC AF ,的中点）（1）求证：//MN 平面CDEF （2）求多面体CDEF A -的体积19.已知某种从太空飞船中带回的植物种子每粒成功发芽的概率都为31，某植物研究所分2个小组分别独立开展该种子的发芽试验，每次实验种一粒种子，如果某次没有发芽，则称该次实验是失败的。

广东省韶关市2009年高三数学五月模拟测试题(理科)(附答案)

广东省韶关市2009年高三第二次模拟测试数学试题(理科)一、选择题（本大题共8小题，每小题5分，满分40分．在每小题给出的四个选项中，只有一项是符合题目要求的1. 复数2(1)i i-（i 是虚数单位）=A ．2B ．2-C ．2iD ．2i -2. 已知等比数列{}n a 的前n 项和为2n n S a =+，则a =A. 0B.-2C.1-D.13 如果指数函数1(),2xy a =-在R 上是增函数，则a 的取值范围是. A ． a ＞2 B ．2＜a ＜3 C. a ＜3 D ．a ＞34. 如图，一个空间几何体的正视图、侧视图、俯视图为全等的等腰直角三角形，如果直角三角形的直角边长为1，那么这个几何体的全面积为A ．32B ．2 正视图侧视图C.3+D俯视图5．北京2008年第29届奥运会开幕式上举行升旗仪式，在坡度 15°的看台上，同一列上的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°，第一排和最后一排的距离为（如图所示），则旗杆的高度为A ．10米B ．30米C ．D ． 6. 以下五个命题①从匀速传递的产品生产流水线上，质检员每10分钟0020从中抽取一件产品进行某项指标检测，这样的抽样是分层抽样②样本方差反映了样本数据与样本平均值的偏离程度③在回归分析模型中，残差平方和越小，说明模型的拟合效果越好④在回归直线方程101.0ˆ+=x y中，当解释变量x 每增加一个单位时，预报变量y ˆ增加0.1个单位 ⑤在一个2×2列联表中，由计算得k 2=13.079,则其两个变量间有关系的可能性是90%以上. 其中正确的是 A ．②③④⑤B ．①③④C ．①③⑤D ．②④F7.下列有关命题的说法正确的是A ．“21x =”是“1=x ”的充分不必要条件B ．“1x =-”是“2560x x --=”的必要不充分条件．C ．命题“x R ∃∈，使得210x x ++<”的否定是：“x R ∀∈，均有210x x ++<”． D ．．命题“若x y =，则sin sin x y =”的逆否命题为真命题． 8.已知函数1(),()12x x f x g x x +==+，若()()f x g x >，则实数x 的取值范围是（） ()A (,1)(0,1)-∞- ()B (,1)-∞- ()C (1,0))-+∞ ()D (1,0)-二.填空题：每小题5分, 共30分.9．已知i 与j 为互相垂直的单位向量，2+=，2b i j λ=+，且a 与b共线，则实数λ= .10．如图，是一程序框图，则输出结果为K =S = .(说明，M N =是赋值语句，也可以写成M N ←，或:M N =)11. 已知可行域0,20,20,y x y x y ≥⎧⎪-+≥⎨⎪+-≤⎩的外接圆C 与x 轴交于点A 1、A 2，双曲线E 以线段A 1A 2为实轴，离心率2e =．则圆C 的方程是；双曲线E 的方程是 . 12. 观察以下几个等式：⑴ 1011021111C C C C C =+； ⑵ 20211204222222C C C C C C C =++；(3)303122130633333333C C C C C C C C C =+++，归纳其特点可以获得一个猜想是：2n n C = ．选做题：在下面三道小题中选做两题，三题都选只计算前两题的得分. 13. （参数方程与极坐标）已知F 是曲线2cos ()1cos 2x R y θθθ=⎧∈⎨=+⎩的焦点，1(,0)2M ，则||MF 的值是 .14（几何证明选讲）如图，P 是圆O 外的一点，PD 为切线，D 为切点，割线PEF经过圆心O ，6,PFPD ==则DFP ∠=__________.15.（不等式选讲）已知(,)P x y 在直线:10l x y --=运动，当函数z =P 点的坐标为三、解答题：本大题共6小题，共80分. 解答应写出文字说明、证明过程或演算步骤.16.(本题满分12分)如图，设A 是单位圆和x 轴正半轴的交点，Q P 、是单位圆上的两点，O 是坐标原点，6π=∠AOP ，[)παα,0,∈=∠AOQ ．（Ⅰ）若34(,)55Q ，求⎪⎭⎫ ⎝⎛-6cos πα的值；（Ⅱ）设函数()f OP OQ α=⋅，求()αf 的值域．17.(本题满分12分)位同学.与方法》的有5人，第二小组选《数学运算》的有2人，现从第一、第二两小组各任选2人分析选课情况.（Ⅰ）求选出的4 人均选《数学解题思想与方法》的概率；（Ⅱ）设ξ为选出的4个人中选《数学运算》的人数，求ξ的分布列和数学期望．18. (本题满分14分)如图，在等腰梯形PDCB 中，3,1,PB DC PD BC ==== A 为PB 边上一点，且1,PA =将PAD ∆沿AD 折起，使平面PAD ⊥平面ABCD ． (Ⅰ)求证：CD ⊥平面PAD ；(Ⅱ) 若M 为PB 的中点，试求异面直线AM 和BC 所成的角的余弦值．(Ⅲ) 试问：在侧棱PB 上是否存在一点Q ，使截面AQC 把几何体分成的两部分的体积之比:7:2PDCQ A Q AC B V V = ？若存在，请求PQ 的长；若不存在，请说明理由.19. (本题满分14分)从社会效益和经济效益出发，某地投入资金进行生态环境建设，并以此发展旅游产业，打算本年度投入800万元，以后每年投入将比上年平均减少20%，本年度旅游收入为400万元，由于该项建设对旅游的促进作用，预计今后的旅游业收入每年会比上年平均增加25%. （Ⅰ）设第n 年（本年度为第一年）的投入为n a 万元，旅游业收入为n b 万元，写出n a ，n b 的表达式；（Ⅱ）至少经过几年旅游业的总收入超过总投入？20. （本题满分14分）已知椭圆的中心在原点，焦点在x轴上，离心率为，且经过点(4,1)M . 直线:l y x m =+交椭圆于,A B 两不同的点. （Ⅰ）求椭圆的方程；（Ⅱ）若直线l 不过点M ,求证：直线,MA MB 与x 轴围成等腰三角形.21. (本题满分14分) 已知x=0是函数)()()(2R x e b ax x x f x ∈++=的一个极值点，且函数()f x 的图象在2x =处的切线的斜率为22e .（Ⅰ）求函数()f x 的解析式并求单调区间.（Ⅱ）设'()()xf xg x e =，其中[2,)x m ∈-，问：对于任意的2m >-,方程()g x =22(1)3m =-在区间(2,)m -上是否存在实数根？若存在，请确定实数根的个数.若不存在，请说明理由.2009年韶关市高三第二次模拟测试数学试题(理科)参考答案及评分标准一、选择题答案 BCBDB ADD 二、填空题9.4； 10.11; 511 （2分，3分）; 11.22224;142x y x y +=-= （2分，3分） 12. 02121202222222n n n n n n n n n n n C C C C C C C -=+++ 或0212222222()()()n n n n n n C C C C=+++13.2;14.30，; 15. (4,3) 三、解答题16.(本题满分12分)如图，设A 是单位圆和x 轴正半轴的交点，Q P 、是单位圆上的两点，O 是坐标原点，6π=∠AOP ，[)παα,0,∈=∠AOQ ．（Ⅰ）若34(,)55Q ，求⎪⎭⎫ ⎝⎛-6cos πα的值；（Ⅱ）设函数()f OP OQ α=⋅，求()αf 的值域．解：（Ⅰ）由已知可得54sin ,53cos ==αα………………………………2分6s i n s i n 6c o s c o s 6c o s παπαπα+=⎪⎭⎫ ⎝⎛-∴ 1043321542353+=⨯+⨯=…………………………4分（Ⅱ）()f OP OQ α=⋅ ()c o s ,s i n c o s ,s i n 66ππαα⎛⎫=⋅ ⎪⎝⎭……………………6分 ααsin 21cos 23+=………………………………7分sin 3πα⎛⎫=+ ⎪⎝⎭………………………………8分[0,)απ∈ 4[,)333πππα∴+∈………………………………9分 s i n 13πα⎛⎫<+≤ ⎪⎝⎭………………………………11分 ()αf ∴的值域是⎛⎤ ⎥ ⎝⎦………………………………12分注：若结果写成闭区间或开区间扣1分 17.(本题满分12分)在高二年级某班学生在数学校本课程选课过程中，已知第一小组与第二小组各有六位同学.每位同学都只选了一个科目，第一小组选《数学运算》的有1人，选《数学解题思想与方法》的有5人，第二小组选《数学运算》的有2人，选《数学解题思想与方法》的有4人，现从第一、第二两小组各任选2人分析选课情况.（Ⅰ）求选出的4 人均选《数学解题思想与方法》的概率；（Ⅱ）设ξ为选出的4个人中选《数学运算》的人数，求ξ的分布列和数学期望．解：（Ⅰ）设“从第一小组选出的2人选《数学解题思想与方法》”为事件 A ，“从第二小组选出的2人选《数学解题思想与方法》”为事件B .由于事件A 、B 相互独立，且25262()3C p A C ==, 24262()5C P B C ==.……4分所以选出的4人均考《数学解题思想与方法》的概率为224()()()3515P A B P A P B ⋅=⋅=⨯= …………………………… 6分（Ⅱ）设ξ可能的取值为0,1,2,3.得4(0)15P ξ==,21112552442222666622(1)45C C C C C P C C C C ξ===+= , 15226611(3).45c p c c ξ===2(2)1(0)(1)(3)9p p p p ξξξξ==-=-=-==…………… 9分ξ的分布列为∴ξ的数学期望 42221012311545945E ξ=⨯+⨯+⨯+⨯= …………12分18.(本题满分14分)如图，在等腰梯形PDCB 中，3,1,PB DC PD BC ====A 为PB 边上一点，且1,PA =将PAD ∆沿AD 折起，使平面PAD ⊥平面ABCD ． (Ⅰ)求证：CD ⊥平面PAD ；(Ⅱ) 若M 为PB 的中点，试求异面直线AM 和BC 所成的角的余弦值．(Ⅲ) 试问：在侧棱PB 上是否存在一点Q ，使截面AQC 把几何体分成的两部分的体积之比:7:2PDCQ A Q AC B V V = ？若存在，请求PQ 的长；若不存在，请说明理由.(Ⅰ)证明：依题意知1,PA =PD =AD AB ⊥，又CD ∥AB CD AD ∴⊥又∵平面PAD ⊥平面ABCD ，平面PAD 平面ABCD AD =，CD ⊥平面PAD …………………4分(Ⅱ) 如图,把四棱锥P ABCD -补成一个长方体，其中,C G 分别为所在棱的中点,则易得AM ∥DF，DG ∥CB ，所以FDG ∠就是异面直线AM 和BC 所成的角…………6分连结FG ，在GBE ∆中，GE === 在GEF∆中，FG ===在FDG ∆中，DG GE DF ====由余弦定理可得：222cos2DF DG FG FDG DF DG +-∠====⋅⋅ (8)分所以异面直线AM 和BC 所成的角的余弦值为…………9分 (Ⅲ) 解：假设在侧棱PB 上存在一点Q ，满足条件 ∵:7:2PDCQ A Q AC B V V =∴29Q ACB P ABCD V V --=………………11分又由90PAD DAB ∠=∠=︒知PA ⊥平面ABCD ，又()()113121,222ABCD S DC AB AD =+=⋅+⋅=ABC S ∆1=．设Q 到平面ABCD 的距离为h ，则 1212231.3939923ABCD ABC ABCD ABC S h S PA S h S ∆⋅=⋅⋅⋅⇒=⋅=⋅=……………………12分又h BQ PA BP = ，1,3BQ BP ∴=故23PQ PB ==14分另解：(Ⅰ)由90PAD DAB ∠=∠=︒知PA ⊥平面ABCD ，如图，分别以,,AD AB AP 所在的直线为x 轴、y 轴、z 轴，建立空间直角坐标系A xyz -，则易得各点的坐标为()0,0,1,P ()1,0,0,D ()1,1,0,C ()0,2,0.B 故()1,0,1,DP =-- ()0,1,0,DC = ()0,2,0AB =．设(),,1n x y =是平面PCD 的一个法向量，由0n DP ⋅=可得()10101x y x y ⋅-+⋅-=⇒-=-由0n DC ⋅= 可得011000x y y ⋅+⋅+⋅=⇒=，∴1,0,x y =-=()1,0,1n ∴=-，()()()1,0,10,2,01002100,n AB ∴⋅=-⋅=-⋅+⋅+⋅=.n AB ∴⊥ 又因为AB是平面PAD 的一个法向量，所以平面PAD ⊥平面PCD ……………4分(Ⅱ)由(Ⅰ)知PB 的中点的坐标为10,1,,2M ⎛⎫ ⎪⎝⎭故10,1,,2AM ⎛⎫= ⎪⎝⎭ 又()1,1,0,CB =-cos ,5AM CB AM CB AM CB⋅∴====⋅所以异面直线AM 和BC所成的角的余弦值为5．……………14分19(本题满分14分)从社会效益和经济效益出发，某地投入资金进行生态环境建设，并以此发展旅游产业，打算本年度投入800万元，以后每年投入将比上年平均减少20%，本年度旅游收入为400万元，由于该项建设对旅游的促进作用，预计今后的旅游业收入每年会比上年平均增加25%.（Ⅰ）设第n 年（本年度为第一年）的投入为n a 万元，旅游业收入为n b 万元，写出n a ，n b 的表达式；（Ⅱ）至少经过几年旅游业的总收入超过总投入？（Ⅰ）解，依题意每年投入构成首项为800万元，公比为45的等比数列，每年旅游业收入组成首项为400万元，公比为54的等比数列。

广西省桂平市2009年5月高考模拟测试文科数学

广西省桂平市2009年5月高考模拟测试文科数学本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．第Ⅰ卷为第1页至第2页．第Ⅱ卷为第3页至第4页．共150分，考试时间120分钟．第Ⅰ卷（选择题共60分）注意事项：1、答卷前，考生先将自己的姓名、考号填写清楚．2、第Ⅰ卷的每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号.第Ⅱ卷的每小题在答题卡上各题的答题区域内作答,在试题卷上作答无效．3、考试结束后，考生只须将答题卡交回．参考公式：如果事件A 、B 互斥，那么球的表面积公式)()()(B P A P B A P +=+ 24R S π=如果事件A 、B 相互独立，那么其中R 表示球的半径)()()(B P A P B A P ⋅=⋅ 球的体积公式如果事件A 在一次试验中发生的概率是P ， 334R V π=那么n 次独立重复试验中恰好发生k 次其中R 表示球的半径的概率k n kk n n P P C k P --=)1()(一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知函数3log )(2+=x x f ，)(1x f -是)(x f 的反函数，若6=+n m ，则)()(11n f m f --的值为)(A 0 )(B 1 )(C 2 )(D 62．已知直线m ⊂平面α，直线n ⊂平面α，“直线m c ⊥，直线n c ⊥”是“直线⊥c 平面α”的条件)(A 充要 )(B 充分而不必要 )(C 必要而不充分 )(D 既不充分也不必要3．某省级标准化高中共有3500名学生，其中高三年级有1400名学生．学校要采用分层抽样的方法从全校学生中抽取一个容量为100的样本做问卷调查，则从高三年级应抽取的学生数为)(A 20 )(B 25 )(C 30 )(D 404．设集合}|||{x y x A ==，}|||{x y y B ==，}|||),({x y y x C ==．则下列关系中正确的是)(A B B A = )(B B C B = )(C ∅=B A )(D C B A =5．在ABC ∆中，2=，2=，若n m +=，则=+n m)(A 1 )(B98)(C 32 )(D 97 6．在等差数列}{n a 中，若2951π=++a a a ，则=+)sin(64a a)(A21)(B 22 )(C 23 )(D 1 7．将函数)32sin(π+=x y 的图象按向量a 平移后所得的图象关于直线4π=x 对称，则向量a 的坐标可能是)(A )2,6(π )(B )1,12(π )(C )1,12(--π )(D )0,6(π- 8．已知双曲线的中心在原点，焦点在x 轴上，它的一条渐近线与x 轴的夹角为α，且34παπ<<，则双曲线的离心率的取值范围是)(A )2,1( )(B )2,2( )(C )2,1( )(D )3,1(9．设函数⎩⎨⎧<>-=)0(1)0(1)(x x x f ，则)(2)()()(b a b a f b a b a ≠-⋅-++的值为)(A a )(B b )(C a 、b 中较小的数 )(D a 、b 中较大的数10．如图是一个44⨯的点阵和圆组成的图形，由这些点所组成的三角形中恰有两个顶点落在圆内的概率是)(A263 )(B 265 )(C 433 )(D 43511．10个完全相同的小球放在标有1、2、3、4号的四个不同盒子里，使每个盒子都不空的放法有（）种)(A 84 )(B 96 )(C 120 )(D 2412．在半径为r 的球内有一内接正三棱锥，它的底面三个顶点恰好都在同一个大圆上，一个动点从三棱锥的一个顶点出发沿球面运动，经过其余三点后返回，则经过的最短路程是)(A r π2 )(B r π37 )(C r π38 )(D r π67第Ⅱ卷（非选择题共90分）二、填空题：本大题共4小题，每小题5分，共20分．请把答案填写在答题卡中的横线上．13．已知0cos sin 2=+αα，则ααα2cos 12sin 2cos ++的值是14．记等比数列}{n a 的前n 项和为n S ，若25=a ，则36S S -的取值范围是15．点P 到点)0,(m A -与到点)0,(m B )0(>m 的距离之差为2，若P 在直线x y =上，则实数m 的取值范围为 16．给出下列命题：第10题①m 、n 为直线，α、β为平面．若α⊂m ，α⊂n ，β//m ，β//n ，则βα//． ②二项式52)1(xx -的展开式中，不存在常数项．③函数x y sin =与x y cos =的图象关于直线4ππ+=k x )(Z k ∈对称．④l 为直线，α、β、γ为三个不同的平面，且l =βα ．若γα⊥，γβ⊥，则γ⊥l ．其中正确命题的序号是（把你认为正确命题的序号都填上）三、解答题：本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤．17．（本小题满分10分）已知A ，R B ∈且22cos 2sin 32cos 2sin 22+--+=B A B A y ，（1）若A 、B 、C 为ABC ∆的三内角，当y 取得最小值时，求C ；（2）当2π=+B A 时，将函数22cos 2sin 32cos 2sin 22+--+=B A B A y 的图象按向量p 平移后得到函数A y 2cos 2=的图象，求出所有满足条件的向量p ．18．（本小题满分12分）从“神七”飞船带回的某种植物种子由于在太空中被辐射，我们把它们称作“太空种子”．这种“太空种子”成功发芽的概率为43，发生基因突变的概率为31，种子发芽与发生基因突变是两个相互独立事件．科学家在实验室对太空种子进行培育，从中选出优良品种．（1）这种太空种子中的某一粒种子既发芽又发生基因突变的概率是多少？（2）四粒这种“太空种子”中至少有两粒既发芽又发生基因突变的概率是多少？19．（本小题满分12分）已知如图①，正三角形ABC 的边长为a 2，CD 是AB 边上的高，E 、F 分别是AC 和BC 边上的点，且满足k CF CE ==，现将ABC ∆沿CD 翻折成直二面角B CD A --，如图②．（1）试判断翻折后直线AB 与平面DEF 的位置关系，并说明理由；（2）求二面角D AC B --的大小；（3）若异面直线AB 与DE 所成角的余弦值为42，求k 的值．AABBC CDEFDEF 第19题图① 图②20．（本小题满分12分）已知a 为实数，函数))(23()(2a x x x f ++=，（1）若函数)(x f 有极值，求a 的取值范围；（2）若0)1(=-'f ，求函数)(x f 的单调区间；并对任意的1x ，]0,1[2-∈x ，求|)()(|21x f x f -的最大值．21．（本小题满分12分）在等比数列}{n a )(*N n ∈中，已知11>a ，0>q ，设n n a b 2l o g =，且6321=++b b b ，0321=b b b ，（1）求数列}{n a 、}{n b 的通项公式n a 、n b ；（2）若数列}{n b 的前n 项和为n S ，试比较n S 与n a 的大小．22．（本小题满分12分）已知焦点在x 轴上，离心率为52的椭圆的一个顶点是抛物线241x y =的焦点，过椭圆右焦点F 的直线l 交椭圆于A 、B 两点，交y 轴于点M ，且AF MA 1λ=，BF MB 2λ=，（1）求椭圆方程；（2）证明：21λλ+为定值．2009年5月份高考模拟测试文科数学答案提示一、选择题：（共12小题，每小题5分，共60分）1．由m x x f =+=3log )(2得32-=m x ，312)(--=∴m m f ，同理得312)(--=n n f ，12222)()(063311===⋅=∴-+----n m n m n f m f ，选)(B2．当n m //时，“直线m c ⊥，直线n c ⊥”≠>“直线⊥c 平面α”，但“直线⊥c 平面α”⇒“直线m c ⊥，直线n c ⊥”，即为必要而不充分条件，选)(C 3．从高三年级应抽取的学生数为4035001400100=⨯，选)(D4．R A =，}0|{≥=y y B ，B B A =∴ ，选)(A5．AB AC AR CA AC CR AC CP AC AP 9431)(3232+=++=+=+=，979431=+=+∴n m ，选)(D6．由2951π=++a a a 得65π=a ，32564π==+∴a a a ，23)sin(64=+∴a a ，选)(C7．设),(t θ=a ，则将函数)32sin(π+=x y 的图象按向量a 平移后所得的图象的函数为t x y ++-=)322sin(πθ，由1)3242sin(±=+-⨯πθπ得23242πππθπ+=+-⨯k ，即62ππθ+-=k ，Z k ∈，当0=k 时，6πθ=，),(t π=a ，选)(A8．)3,1(tan ∈=a b α，3122<<∴a b ，即42222<=<e ac ，22<<∴e ，选)(B9．当b a >时，b b a b a b a f b a b a =-⋅-++=-⋅-++2)1()()(2)()()(，当b a <时，a b a b a b a f b a b a =⨯-++=-⋅-++21)()(2)()()(，选)(C10．所求概率为435410333431611024=--C C C C C ，选)(D 11．挡板法，8439=C 种，选)(A12．设正三棱锥为ABC S -，A 、B 、C 同在一个大圆上，球心为O ，则⊥SO 平面ABC ，经过的最短路程是r r πππππ37)223232(=+++，选)(B二、填空题：（共4小题，每小题5分，共20分）13．由0cos sin 2=+αα得1tan -=α，54tan 1tan 22sin 2-=+=ααα，53tan 1tan 12cos 22=+-=ααα， ααα2cos 12sin 2cos ++12cos 1)12sin 2cos (2=+++=ααα．14．设等比数列}{n a 的公比为q ，则36S S -)11(5654q qa a a a ++=++=，当0>q 时，6)12(2)11(5=+≥++q qa ，1=q 时取等号，当0<q 时，2)12(2)11(5-=+-≤++q q a ，1-=q时取等号，即36S S -的取值范围是),6[]2,(∞+-∞- ．15．点P 的轨迹为11222=--m y x ，渐近线为x m y 12-±=，若P 在直线x y =上，即双曲线与直线x y =有交点，所以112>-m ，即2>m ．第10题16．①当n m //时，命题不成立；②r r rr r r r x C xx C T 31055251)1()1()(--+-=-=，Z r ∈且50≤≤r ，令0310=-r 得Z r ∉=310，命题正确；③设点),(00y x 在函数x y sin =的图象上，关于直线4ππ+=k x 对称的点为),22(00y x k -+ππ，把022x k x -+=ππ代入x y cos =得000sin )22cos(y x x k y ==-+=ππ，即点),22(00y x k -+ππ在函数x y cos =的图象上，命题正确；④课本定理，命题正确．应填：②③④．三、解答题：（共6小题，第17题10分，第18-22题每题12分，共70分） 17．解：（1）1)212cos ()232sin (22+-+-=B A y ， ………………………………………2分由题意：⎪⎩⎪⎨⎧==212cos 232sin B A ，ππ或=∴A ，ππ5或=B ， ………………………………4分又π<+B A ，故ππ322或=C ； …………………………………………5分（2）当2π=+B A 时，π=+B A 22，A B 2cos 2cos -=∴，………………………………6分3)32cos(232sin 32cos ++=+-=∴πA A A y ，…………………………………………8分按向量p 平移后得到函数A y 2cos 2=的图象，故)3,6(-+=ππk p ，Z k ∈． ………10分 18．解：（1）记“这批太空种子中的某一粒种子既发芽又发生基因突变”为事件A ，则413143)(=⨯=A P ； …………………………………………6分（2）25667256108256811)43()41()43()41(131144004=--=--=C C P ． ……………………………12分 19．解法一：（1）//AB 平面DEF ，在ABC ∆中，E 、F 分别是AC 、BC 上的点，且满足k CBCF CACE ==，EF AB //∴，⊄AB 平面DEF ，⊂EF 平面DEF ，//AB ∴平面DEF ； ………………………………………4分（2）过D 点作AC DG ⊥于G ，连结BG ，CD AD ⊥ ，CD BD ⊥，ADB ∠∴是二面角B CD A --的平面角． ︒=∠∴90ADB ，即AD BD ⊥．⊥∴BD 平面ADC ，AC BD ⊥∴，⊥∴AC 平面BGD ，AC BG ⊥∴，BGD ∠∴是二面角D AC B --的平面角， ……6分在ADC Rt ∆中，a AD =，a DC 3=，a AC 2=，23232a a a AC DC AD DG ==⋅=∴，在BDG Rt ∆中，332tan ==∠DGBD BGD ，332arctan =∠∴BGD ，即二面角D AC B --的大小为332arctan ； …………………………………………8分（3）EF AB // ，DEF ∠∴（或其补角）是异面直线AB 与DE 所成的角， a AB 2= ，ak EF 2=∴，又a DC 3=，ak CA k CE 2=⋅=，DE DF =∴ACD CE DC CE DC ∠⋅⋅-+=cos 222k k a k a k a a 64364322222-+=-+=， ………10分ABCDEFG第19题DEF ∠∴cos 4222222==⋅-+=DE EF EF DE DF EF DE ，k k a ak 6432222-+⋅=∴，解得21=k ．……………12分解法二：如图建立空间直角坐标z y x D -，)0,0,(a B ，),0,0(a A ，)0,3,0(a C ，)0,)1(3,(a k a k F -，),)1(3,0(a k a k E -， ………………………………2分（1）设平面DEF 的法向量为),,(z y x =m ，由0=⋅DE m 且0=⋅DF m 得0)1(3=+-z k y k ， 0)1(3=-+y k x k ，令)1(3-=k k y 得)1,)1(3,1(-=k k m ， …………………………4分又),0,(a a -=，0=⋅∴m ，又∉A 平面DEF ，//AB ∴平面DEF ； ………6分（2）设平面ABC 的法向量为),,(111z y x =n ，由0=⋅n 且0=⋅n 得011=-z x ，0311=-y x ，令31=y 得)3,3,3(=n ，……………………………………8分由⊥BD 面ACD 得DB 是平面ACD 的法向量，721213||||,cos =⋅=⋅<∴aa DB DB n n n ，即二面角D AC B --的大小为21arccos ； …………………………………………10分（3）由26128||3642|||||||,cos |222=+-=+-⋅-==><k k k a k k a ka DE AB DE AB 得21=k ． 12分20．解：（1）a x x a x x f 2323)(23+++= ，2323)(2++='∴x a x x f ， ……………2分由函数)(x f 有极值，0)(='∴x f 有两个不等的实数解．0233442>⨯⨯-=∆∴a ，292>∴a ，因此，所求实数a 的取值范围是),223()223,(∞+-∞- ； …………4分（2）0)1(=-'f ，02323=+-∴a ，即49=a ， ………………………………………6分)1)(21(32323)(2++=++='∴x x x a x x f ，由0)(>'x f 得211->-<x x 或，由0)(<'x f 得211-<<-x ，因此，函数)(x f 的单调增区间为]1,(-∞-，),21[∞+-；单调减区间为]21,1[--， …………………………………………8分又825)1(=-f ，1649)21(=-f ，827)0(=f ，所以当]0,1[-∈x 时，1649)21()(min =-=x f ，827)0()(max ==x f ， …………………………………………10分|)()(|21x f x f -∴1631649827|)()(|min max =-=-≤x f x f ，即|)()(|21x f x f -的最大值为83． ……………………………………………………12分 21．解：（1）由题设，有11-=n n q a a ，由11>a ，0>q 知数列}{n a 是单调数列，又n n a b 2log =，由6321=++b b b 得6log 3)(log 223212==a a a a ，即42=a ， …………2分由0321=b b b 及11>a 知，必须13=a ，1423===∴q q a a ，41=∴q ， ……………………………………………………………4分由q a a 12=得161=a ，n n n n q a a ---===∴31114)41(16，n a b n n 26log 2-==；………6分（2）由（1）知，n b n 26-=，)5(2)(1n n b b n S n n -=+=， ……………………………8分当5≥n 时，0≤n S ，0>n a ，n n S a >∴， …………………………………………9分当1=n 时，41=S ，161=a ，n n S a >∴， ……………………………………10分当42≤≤n 时，0444)5(243=-=->--=--a S n n a S n n n ，n n S a <∴， …………11分综上所述，当1=n 或5≥n 时，有n n S a >；当42≤≤n 时，有n n S a <． ……………12分22．解：（1）设椭圆方程)0(12222>>=+b a by a x ，由题意知1=b ， 552)(12=-==a b a c e ，52=∴a ，所以椭圆方程为1522=+y x ； ………………4分（2）由（1）知)0,2(F ，设A 、B 、M 的坐标分别为),(11y x ，),(22y x ，),0(0y ，由1λ=得11112λλ+=x ，1011λ+=y y ， ………………………………………6分由2λ=得22212λλ+=x ，2021λ+=y y ， ………………………………………8分由A 、B 在椭圆上得⎪⎪⎩⎪⎪⎨⎧=+++=+1)1()12(511)()2(1220222210211λλλλλλy y ，即⎪⎩⎪⎨⎧=-++=-++0)55(100)55(102022220221y y λλλλ， ……10分 21,λλ∴是方程0)55(10202=-++y x x 的两根，1021-=+∴λλ是定值．…………12分。

江西省南昌二中2009届高三5月模拟考试数学试题理科2009.5

江西省南昌二中2009届高三5月模拟考试数学试题（理科）一、选择题：本大题共12小题，每小题4分，共60分．1．若z 的共轭复数为z ，()2f z i z i +=+（i 为虚数单位），则)23(i f +等于（）A ．3i -B ．3i +C ．33i +D ．32i -2．已知等比数列{n a }的前n 项和为n S ,且317S a =，则数列{}n a 的公比q 的值为（）A ．2B ．3C ．2或-3D ．2或33．平面向量(,3),(2,1),(1,)a x b c y =-=-=，若(),//()a b c b a c ⊥-+则b 与c 的夹角为（）A ．0B ．4πC ．2π D ．34π4．现从甲、乙、丙等6名学生中安排4人参加4×100m 接力赛跑。

第一棒只能从甲、乙两人中安排1人，第四棒只能从甲、丙两人中安排1人，则不同的安排方案共有（）A ．24种B ．36种C ．48种D ．72种5．能够使圆014222=++-+y x y x 恰有两个点到直线02=++c y x 距离等于1的c 的一个值为（）A ．5B ．53C ．2D ．36．若第一象限内的点),(y x A 落在经过点（6，—2）且方向向量为)2,3(-=a 的直线l 上，则3223log log t y x =-有（）A ．最大值23 B ．最大值1C ．最小值23 D ．最小值17．在三棱锥A —BCD 中，侧棱AB 、AC 、AD 两两垂直，△ABC 、△ACD 、△ADB 的面积分别为2、A —BCD 的外接球的体积为学（）AB ．C ．D ． 8．在243)1(xx +的展开式中,x 的幂的指数是整数的项共有（）A ．3项B ．4项C ．5项D ．6项9．设随机变量ξ服从正态分布N （0，1），若=<<-=>)01(,)1(ξξP p P 则（）A ．p +21B ．p -1C ．p -21D ．p 21-10．如果若干个函数的图象经过平移后能够重合，则称这些函数为“互为生成”函数．给出下列函数：①()s i n c o s fx x x =+；②())s i n c o s fx x x =+；③()s i n f x x=；④()s i n 2fx =其中“互为生成”函数的是（）A ．①②B ．②③C ．③④D ．①④11．f (x )是偶函数，且f (x )在[0，+∞]上是增函数；不等式f (ax + 1)≤f (x –2)对x ∈[12，1]恒成立，则实数a 的取值范围是（） A ．[–2，0] B ．[–5，0] C ．[–5，1] D ．[–2，1]12．对于任意实数a ，要使函数*215cos()()36k y x k N ππ+=-∈在区间[,3]a a +上的值54出现的次数不小于4次，又不多于8次，则k 可以取（）A ．1和2B ．2和3C ．3和4D ．2二、填空题：本大题共4小题，每小题4分，共16分.13．已知52x ⎛- ⎝的展开式中的常数项为T ，()f x 是以T 为周期的偶函数，且当[0,1]x ∈时，()f x x =，若在区间[1,3]-内，函数()()g x f x kx k =--有4个零点，则实数k 的取值范围是 .14．设三角形ABC 的BC 边上的高AD=BC ，c b a 、、分别表示角A 、B 、C 对应的三边，则bcc b +的取值范围是 ;15．已知x 、y 满足1420x x y x y c ≥⎧⎪+≤⎨⎪-+≤⎩且目标函数2z x y =+的最大值为7，则最小值为______;16．给出下列命题：①．函数(2)y f x =-和(2)y f x =-的图象关于直线2x =对称.②．在R 上连续的函数()f x 若是增函数，则对任意0x R ∈均有/0()0f x >成立.③．已知函数2sin()(0,0),2y x y ωθωθπ=+><<=为偶函数其图象与直线的交点的横坐标为1212,.||,2,x x x x πωθ-若的最小值为则的值为的值为2π.④．底面是等边三角形，侧面都是等腰三角形的三棱锥是正三棱锥.⑤．若P 为双曲线2219y x -=上一点，1F 、2F 分别为双曲线的左右焦点，且24PF =，则12PF =或6.其中正确的命题是＿＿＿＿（把所有正确的命题的选项都填上）.三、解答题：本大题共6小题，共75分. 解答应写出文字说明、证明过程或演算步骤. 17．（12分）已知函数2()4sin sin ()cos242xf x x x π=++（1）设0w >为常数，若()y f wx =在区间2,23ππ⎡⎤-⎢⎥⎣⎦上是增函数，求w 的取值范围。

安徽省宿州市2009届高三五月联考数学试卷文科(附答案)

安徽省宿州市2009届高三五月联考数学试卷(文)一、选择（每题5分共60分）1、集合A=﹛x ︱x=n+21,n ∈Z ﹜,B=﹛x ︱x=2k ±21,k ∈Z ﹜则A 与B 的关系为( )A. A ⊇BB.A=BC.A ≠BD. A ⊆B2. 圆x 2+y 2-4x+4y+6=0截直线x-y-5=0所得弦长等于( )A.6 B.3 C.225D. 23. 已知ααcos sin 2=，则ααα2cos 12sin 2cos ++的值是( )A.1 B .2 C. 3 D .4 4. 探索以下规律：则根据规律，从2004到2006，箭头的方向依次是( )A.向下再向右B.向右再向上C.向上再向右D.向右再向下5．已知变量y x ,满足⎪⎩⎪⎨⎧≤-≤≥,0,2,1y x y x 则2x+y 的最大值是( )A ．3B ．4C ．5D ．66、已知函数b a bx ax x f +++=3)(2是定义域为]12,2[--a a 的偶函数，则b a +的值是（）A 、0 B 、31 C 、1 D 、1-7.设F 1、F 2分别是双曲线1922=-y x 的左、右焦点，若点P 在双曲线上，且021=⋅PF PF则=+（） A.10 B.102 C.5 D.528．已知命题:|1|2p x ->“”，命题q ：“x Z ∈”。

如果“p 且q”与“非q”同时为假命题．．．．．．，则满足条件的x 的取值范围为（） A 、{|3,1,}x x x x Z ≥≤-∈或B 、{|13,}x x x Z -≤≤∉C 、{1,0,1,2,3}-D 、{0，1，2}1 2 56 7 9 11 …… ， 3 4 8 09．已知函数()log a f x x =（0a >且1a ≠）满足23()(f f a a >，则1(10f x->的解是A ．01x <<B ．1x <C ．0x >D ．1x >10.一个直棱柱被一平面截去一部分所得几何体的三视图如下，则几何体的体积为（） A .8 B.9 C.10 D.1111．已知)2(log ax y a -=在区间[0,1]上是增函数，则不等式|3|log |1|log ->+x x a a 的解集为 A 、}1|{<x x B 、}1|{-<x x C 、}11|{-≠<x x x 且 D 、}1|{>x x 12．已知x 1是方程x+lgx=3的根, x 2是方程x+10x =3的根, 则x 1+x 2的值是( )A. 6B. 3C. 2D. 1二、填空（每题4分共16分）13. 执行右边的程序框图，若4p =，则输出的S = 14．△ABC 中，AB=AC ，BC=2,则=⋅15. 斜率为1的直线过抛物线y 2=4x 的焦点F,与抛物线交于A 、B 两点,O 为坐标原点，则△ABC 的面积为16．给出下列五个命题：①不等式03422<+-a ax x 的解集为}3|{a x a x <<；②若函数(1)y f x =+为偶函数，则()y f x =的图象关于1x =对称； ③若不等式a x x <-+-|3||4|的解集为空集，必有1≥a ； ④函数)(x f y =的图像与直线a x =至多有一个交点； ⑤若角α，β满足cos α·cos β＝1，则αsin(＋β）＝0. 其中所有正确命题的序号是左视图主视图俯视图三：解答题17、（12分）设向量)cos 22,sin 22(),sin ,(cos x x x x -+==，f(x)=⋅. A 、B 、C 为△ABC 的内角，已知BC=4，且f(4π+A )=2，求ABC 面积的最大值。

09年高考理科数学5月份摸拟试卷

09年高考理科数学5月份摸拟试卷（共8页）(测试120分钟内完成，总分150分，试后交答题卷)一、填空题：（本大题共12小题，每小题5分，满分60分）。

把答案直接填写在答题卷的相应位置上。

1、设全集I R =，集合201x A x x ⎧+⎫=≥⎨⎬-⎩⎭，则I A =ð______________。

2、复数112ii -+的实部与虚部的和为____________。

3、以双曲线221610x y -=的中心为顶点，以右焦点为焦点的抛物线的方程为___________。

4、若tan 24πα⎛⎫+=⎪⎝⎭，则tan 2α=_____________。

5、与直线230x y ++=垂直，且点()2,1P到它的距离_______________________。

6、已知()5a x +的展开式中2x 的系数为1k ，41x a ⎛⎫+ ⎪⎝⎭（,0a R a ∈≠）的展开式中x 的系数为2k ，则12k k ⋅=_____________。

7、某校选派A 、B 两个班参加一次社会活动，其中A 班有学生40名，其中男生24人；B 班有学生50名，其中女生30人，现从A 、B 两班各找一名学生进行问卷调查，则找出的学生是一男一女的概率为_______________。

8、设()()()1,2,,1,,0OA OB a OC b =-=-=-且0,0a b ≥≥，O 为坐标原点，若A 、B 、C 三点共线，则142a b ++的最小值为______________。

9、已知数列{}n a 对于任意的p 、*q N ∈，满足p q p q a a a +=+且22a =，则122320082009111a a a a a a ++⋅⋅⋅+=______________。

10、点P 为双曲线2219x y -=上一点，12,F F 为它的左、右两个焦点，PQ 是12F PF ∠的角分线。

过1F 作PQ 的垂线，垂足为R ，点O 为坐标原点，则OR =_________。

山西省山大附中2009届高三5月模拟(数学理)

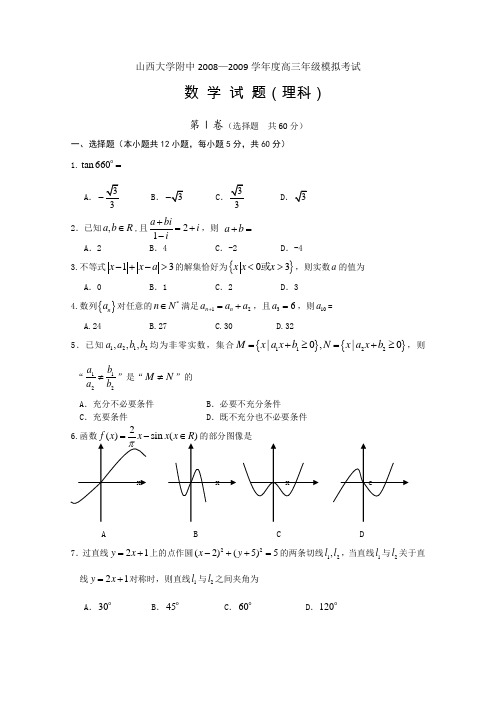
山西大学附中2008—2009学年度高三年级模拟考试数学试题（理科）第Ⅰ卷（选择题共60分）一、选择题（本小题共12小题，每小题5分，共60分） 1.tan 660=A．3-． C．3D2．已知,a b R ∈,且21a bii i+=+-，则 a b += A ．2 B ．4 C ．-2 D ．-43.不等式13x x a -+->的解集恰好为{}03x x x <>或，则实数a 的值为A ．0B ．1C ．2D ．34.数列{}n a 对任意的*n N ∈满足12n n a a a +=+，且36a =，则10a =A.24B.27C.30D.325．已知1212,,,a a b b 均为非零实数，集合{}{}1122|0,|0M x a x b N x a x b =+≥=+≥，则“1122a b a b ≠”是“M N ≠”的 A ．充分不必要条件 B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件 6.函数2sinA B C D7．过直线21y x =+上的点作圆22(2)(5)5x y -++=的两条切线12,l l ，当直线1l 与2l 关于直线21y x =+对称时，则直线1l 与2l 之间夹角为A ．30B ．45C ．60D ．1208．已知向量12(,2),(,)5n n a a b a +==，且11a =，若数列{}n a 的前n 项和为n S ，且a b ∥．则lim n n S →∞=A ．14 B ．45 C ．34 D ．549．已知点P 是以12F F 、为左、右焦点的双曲线22221(0,0)x x a b a b-=>>左支上一点，且满足021=⋅PF PF ，32tan 12=∠F PF ，则此双曲线的离心率为 A2C10.将面积为2的长方形沿对角线折起，使二面角D AC B --的大小为0(0180)αα<<，则三棱锥的外接球的体积的最小值是A. 43π B. 323πD.与α的值有关的数 11.集合A 是集合{|10}B x N x *=∈≤的4元素子集，最小元素为3，最大元素不小于8，则这样的集合A 有A ．21个B ．25个C ．31个D ．45个12.在R 上可导的函数3211()232f x x ax bx c =+++，当(0,1)x ∈时取得极大值，当(1,2)x ∈时取得极小值，则21b a --的取值范围是 A. 11(,)22- B. 11(,)24- C.1(,1)4 D. 1(,1)2第Ⅱ卷（非选择题，共90分）二、填空题（本大题共4小题，每小题5分，共20分）13.设(2,3,4,)n a n =⋅⋅⋅是(2n-的展开式中含x 项的系数，则2007232009122a a a ++⋅⋅⋅+=14.已知函数()s i n (2)(0,0f x A x A ϕϕπ=+><<，若对于任意x R ∈都有5()()12f x f π≥恒成立，则函数f(x)的递减区间是___ __ _.15.已知函数()y f x =是奇函数，且当0x ≥时，()31xf x =-设()y f x =的反函数是()y x ϕ=，则(8)ϕ-=_______16.已知定点(1,0)N ，动点,A B 分别在抛物线24y x =及曲线221(0,0)43x y x y +=>>上，若B 在A 的右侧，且AB ∥x 轴，则ABN ∆的周长的取值范围是．三、解答题（本大题共6小题，共70分.解答应写出必要的文字说明,证明过程或演算步骤） 17.（本小题满分10分）已知函数2()(sin 42)(tan cot )(,)2k f x x x x x x k Z π=++≠∈。

东营市2009年高中招生考试数学模拟试题及答案(5.20)

绝密★启用前试卷类型：A东营市2009年高中招生考试数学模拟试题及答案（5.20）注意事项：1．本试题分第Ⅰ卷和第Ⅱ卷两部分．第Ⅰ卷2页为选择题，36分；第Ⅱ卷8页为非选择题，84分；全卷共12页，满分120分，考试时间为120分钟．2．答第Ⅰ卷前，考生务必将自己的姓名、考号、考试科目涂写在答题卡上，考试结束，试题和答题卡一并收回．3．第Ⅰ卷每题选出答案后，必须用2B 铅笔把答题卡上对应题目的答案标号【ABCD 】涂黑．如需改动，先用橡皮擦干净，再改涂其它答案．4．考试时，不允许使用科学计算器．第Ⅰ卷（选择题共36分）一、选择题：本大题共12小题，在每小题给出的四个选项中，只有一项是正确的，请把正确的选项选出来，每小题选对得3分，选错、不选或选出的答案超过一个均记零分．1、如果－2是一元二次方程x 2＝c 的一个根，那么常数c 是A ．2B ．－2C ．4D ．－42、如图，量角器外缘上有A 、B 两点，它们所表示的读数分别是80°、 50°，则∠ACB 应为 A ．25° B ．15°C ．30°D ．50°3、将如图所示的Rt △ABC 绕直角边AC 旋转一周，所得几何体的主视图是4、下列各组数据中极差最小的是A ．0，1，2，3，4B ．―2，―1，―2，3C ．110，111，112，110，109D ．―100，―200，―300，―400A B C D5．已知方程组⎩⎨⎧=+=+3232y x y x 的解为⎩⎨⎧==11y x ，则函数32+-=x y 与y =－12 x +32的交点坐标为A ．（l ，1）B ．（－1，1）C ．（l ，－1）D ．（－1，－l ）6、“龟兔赛跑”讲述了这样的故事：龟兔同时出发，沿直线向同一目标奔跑，领先的兔子看着缓慢爬行的乌龟，骄傲起来，停下来睡了一觉．当它醒来时，发现乌龟快到终点了，于是急忙追赶，但为时已晚，乌龟还是先到了终点，……. 用s 1，s 2分别表示乌龟和兔子所行的路程，t 为时间，则下列图象中与故事情节相吻合的是（）．A． B ． C ． D ．7、如图是测量一颗玻璃球体积的过程。

浙江省宁波效实中学2009届高三5月模拟考试(数学理)

2009年宁波效实中学高三年纪高考模拟考数学（理科）试卷本试卷分第I 卷和第Ⅱ卷两部分，全卷共4页。

满分150分，考试时间120分钟。

请考生按规定用笔将所有试题的答案涂、写在答题纸上。

参考公式：如果事件,A B 互斥，那么棱柱的体积公式()()()P A B P A P B +=+ V Sh =如果事件,A B 相互独立，那么其中S 表示棱柱的底面积，h 表示棱柱的高 ()()()P A B P A P B ⋅=⋅ 棱锥的体积公式在n 次独立重复实验中事件A 恰好 13V Sh = 发生k 次的概率是(1)k k n k n C p p --，其中S 表示棱锥的底面积，h 表示棱锥的高其中p 表示在一次实验中事件A 发生的概率棱台的体积公式地球的表面积公式 24S R π= 121()3V h S S =球的体积公式43V =3R π 其中12,S S 分别表示棱台的上底、下底面积，其中R 表示球的半径 h 表示棱台的高第I 卷（共50分）一、选择题：本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知复数(2)(1)z i i =-⋅+，则该复数z 的模等于A B C D ．2．已知条件22:(1)(1)0P x y -+-=，条件:(1)(1)0Q x y -⋅-=，那么P 是Q 的A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件3．已知直线l 和两个不同的平面,αβ，则下列命题中，真命题的是A ．若//,l α且//l β，则//αβB ．若.l α⊥且l β⊥，则//αβC ．若l α⊂，且αβ⊥，则l β⊥D ．若//,l α且//αβ，则//l β4．已知92910012910(1)(1)x x a a x a x a x a x -+=+++++，则246810a a a a a ++++=A ．1-B ．0C ．1D ．25．已知函数()f x 满足：1()(1)2,(1)1()f x f f x f x +=+=-，则(2009)f 等于 A ．2 B ．3- C ．12-D ．13 6．已知()2sin(2)6f x x m π=--在[0,]2x π∈上有两个零点，则m 的取值范围为 A ．（1，2） B ．[1，2] C ．[1,2) D ．(1,2]7．已知0a >且1a ≠，则等式log ()log log a a a M N M N +=+A ．对任意正数,M N 都不成立B ．对任意正数,M N 都成立C ．仅对2M N ==成立D ．存在无穷多组正数,M N 成立8．某程序框图如右图所示，现将输出（,)x y 值依次记为：1122(,),(,),,(,),;n n x y x y x y 若程序运行中输出的一个数组是(,10),x -则数组中的x = A ．64 B ．32C ．16D ．89．函数()y f x =在R 上的图象是连续不断的一条曲线，并且在R 上单调递增，已知(1,1),(3,1)P Q --是其图象上的两点，那么|(1)|1f x +<的解集为A ．（0，4）B ．(2,2)-C ．(,0)(4,)-∞+∞D ．(,2)(2,)-∞-+∞10．已知0,0a b ≥≥，且有0(,)|0{(,)|4}22x x y y x y ax by x y ⎧≥⎫⎧⎪⎪⎪≥⊆+≤⎨⎨⎬⎪⎪⎪+≤⎩⎩⎭，则以,a b为坐标的点(,)P a b 所形成的平面区域的面积等于A ．1B ．2C ．4D ．8第Ⅱ卷（共100分）二、填空题：本大题共7小题，每小题4分，共28分。