2010-2018高考数学试题分类汇编文科版专七 不等式 第二十讲 二元一次不等式(组)与简单的线性规划问题答案
2010-2018年高考文科数学真题-集合(含解析)

九年(2010-2018年)高考真题文科数学精选(含解析)专题一 集合与常用逻辑用语第一讲 集合一、选择题1.(2018全国卷Ⅰ)已知集合{0,2}=A ,{21012}=--,,,,B ,则A B =A .{0,2}B .{1,2}C .{0}D .{21012}--,,,, 2.(2018浙江)已知全集{1,2,3,4,5}U =,{1,3}A =,则=U A A .∅ B .{1,3} C .{2,4,5} D .{1,2,3,4,5}3.(2018全国卷Ⅱ)已知集合{}1,3,5,7A =,{}2,3,4,5B =,则AB = A .{3} B .{5}C .{3,5}D .{}1,2,3,4,5,74.(2018北京)已知集合{|||2}A x x =<,{2,0,1,2}B =-,则AB = A .{0,1} B .{–1,0,1}C .{–2,0,1,2}D .{–1,0,1,2}5.(2018全国卷Ⅲ)已知集合{|10}A x x =-≥,{0,1,2}B =,则AB = A .{0} B .{1}C .{1,2}D .{0,1,2}6.(2018天津)设集合{1,2,3,4}A =,{1,0,2,3}B =-,{|12}C x x =∈-<R ≤,则()A B C =A .{1,1}-B .{0,1}C .{1,0,1}-D .{2,3,4}7.(2017新课标Ⅰ)已知集合{|2}A x x =<,{320}B x =->,则A .3{|}2AB x x =< B .A B =∅C .3{|}2A B x x =<D .A B =R 8.(2017新课标Ⅱ)设集合{1,2,3}A =,{2,3,4}B =错误!未找到引用源。
则A B = A .{1,2,3,4} B .{1,2,3} C .{2,3,4} D .{1,3,4}9.(2017新课标Ⅲ)已知集合{1,2,3,4}A =,{2,4,6,8}B =,则A B 中元素的个数为A .1B .2C .3D .410.(2017天津)设集合{1,2,6}A =,{2,4}B =,{1,2,3,4}C =,则()A B C =A .{2}B .{1,2,4}C .{1,2,4,6}D .{1,2,3,4,6}11.(2017山东)设集合{}11M x x =-<,{}2N x x =<,则M N = A .()1,1- B .()1,2- C .()0,2 D .()1,212.(2017北京)已知U =R ,集合{|22}A x x x =<->或,则U A = A .(2,2)- B .(,2)(2,)-∞-+∞ C .[2,2]- D .(,2][2,)-∞-+∞13.(2017浙江)已知集合{|11}P x x =-<<,{|02}Q x x =<<,那么P Q = A .(1,2)- B .(0,1) C .(1,0)- D .(1,2)14.(2016全国I 卷)设集合{1,3,5,7}A =,{|25}B x x =≤≤,则=A BA .{1,3}B .{3,5}C .{5,7}D .{1,7}15.(2016全国Ⅱ卷)已知集合{123}A =,,,2{|9}B x x =<,则A B =A .{210123}--,,,,,B .{21012}--,,,,C .{123},,D .{12},16.(2016全国Ⅲ)设集合{0,2,4,6,8,10},{4,8}A B ==,则A B =A .{48},B .{026},,C .{02610},,,D .{0246810},,,,,17.(2015新课标2)已知集合}21|{<<-=x x A ,}30|{<<=x x B ,则A B =A .)3,1(-B .)0,1(-C .)2,0(D .)3,2( 18.(2015新课标1)已知集合{32,},{6,8,10,12,14}A x x n n N B ==+∈=,则集合A B 中的元素个数为A .5B .4C .3D .219.(2015北京)若集合{|52}A x x =-<<,{|33}B x x =-<<,则A B =A .{|32}x x -<<B .{|52}x x -<<C .{|33}x x -<<D .{|53}x x -<< 20.(2015天津)已知全集{1,2,3,4,5,6}U =,集合{}2,3,5A =,集合{1,3,4,6}B =,则集合U A B =A .{3}B .{2,5}C .{1,4,6}D .{2,3,5}21.(2015陕西)设集合2{|}M x x x ==,{|lg 0}N x x =≤,则M N = A .[0,1] B .(0,1] C .[0,1) D .(-∞,1]22.(2015山东)已知集合{}24A x x =<<,{}(1)(3)0B x x x =--<,则AB = A .()1,3 B .()1,4C .()2,3D .()2,423.(2015福建)若集合{}22M x x =-≤<,{}0,1,2N =,则M N 等于 A .{}0 B .{}1 C .{}0,1,2 D .{}0,124.(2015广东)若集合{}1,1M =-,{}2,1,0N =-,则M N =A .{}0,1-B .{}1C .{}0D .{}1,1-25.(2015湖北)已知集合22{(,)|1,,}A x y x y x y Z =+∈≤,{(,)|||2,B x y x =≤ ||2,,}y x y Z ∈≤,定义集合12121122{(,)|(,),(,)}A B x x y y x y A x y B ⊕=++∈∈,则A B ⊕中元素的个数为A .77B .49C .45D .3026.(2014新课标)已知集合A ={x |2230x x --≥},B ={x |-2≤x <2},则A B = A .[-2, -1] B .[-1,1] C .[-1,2) D .[1,2)27.(2014新课标)设集合M ={0,1,2},N ={}2|320x x x -+≤,则M N = A .{1} B .{2} C .{0,1} D .{1,2}28.(2014新课标)已知集合A ={-2,0,2},B ={x |2x -x -20=},则A B =A . ∅B .{}2C .{}0D .{}2-29.(2014山东)设集合},]2,0[,2{},21{∈==<-=x y y B x x A x 则=B AA . [0,2]B .(1,3)C . [1,3)D . (1,4)30.(2014山东)设集合2{|20},{|14}A x x x B x x =-<=≤≤,则AB =A .(0,2]B .(1,2)C .[1,2)D .(1,4)31.(2014广东)已知集合{1,0,1}M =-,{0,1,2}N =,则MN = A .{0,1} B .{1,0,2}- C .{1,0,1,2}- D .{1,0,1}-32.(2014福建)若集合{|24}P x x =<≤,{|3}Q x x =≥,则P Q 等于A .}{34x x ≤<B .}{34x x <<C .}{23x x ≤<D .}{23x x ≤≤33.(2014浙江)设全集{}2|≥∈=x N x U ,集合{}5|2≥∈=x N x A ,则U A =A .∅B . }2{C . }5{D . }5,2{34.(2014北京)已知集合2{|20},{0,1,2}A x x x B =-==,则AB = A .{0} B .{0,1}C .{0,2}D .{0,1,2}35.(2014湖南)已知集合{|2},{|13}A x x B x x =>=<<,则A B =A .{|2}x x >B .{|1}x x >C .{|23}x x <<D .{|13}x x <<36.(2014陕西)已知集合2{|0},{|1,}M x x N x x x R =≥=<∈,则MN = A .[0,1] B .[0,1) C .(0,1] D .(0,1)37.(2014江西)设全集为R ,集合2{|90},{|15}A x x B x x =-<=-<≤,则()R A B =A .(3,0)-B .(3,1)--C .(3,1]--D .(3,3)-38.(2014辽宁)已知全集,{|0},{|1}U R A x x B x x ==≤=≥,则集合()U A B =A .{|0}x x ≥B .{|1}x x ≤C .{|01}x x ≤≤D .{|01}x x <<39.(2014四川)已知集合2{|20}A x x x =--≤,集合B 为整数集,则AB = A .{1,0,1,2}- B .{2,1,0,1}--C .{0,1}D .{1,0}-40.(2014湖北)已知全集{1,2,3,4,5,6,7}U =,集合{1,3,5,6}A =,则U A = A .{1,3,5,6} B .{2,3,7} C .{2,4,7} D . {2,5,7}41.(2014湖北)设U 为全集,B A ,是集合,则“存在集合C 使得A C ⊆,U B C ⊆”是“∅=B A ”的A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件42.(2013新课标1)已知集合A ={x |x 2-2x >0},B ={x |-5<x <5},则A .A ∩B =∅ B .A ∪B =RC .B ⊆AD .A ⊆B 43.(2013新课标1)已知集合{1,2,3,4}A =,2{|,}B x x n n A ==∈,则AB =A .{}14,B .{}23,C .{}916,D .{}12, 44.(2013新课标2)已知集合(){}2|14,M x x x R =-<∈,{}1,0,1,2,3N =-,则M N =A .{}0,1,2B .{}1,0,1,2- C .{}1,0,2,3- D .{}0,1,2,3 45.(2013新课标2)已知集合{|31}M x x =-<<,{3,2,1,0,1}N =---,则MN = A .{2,1,0,1}-- B .{3,2,1,0}--- C .{2,1,0}-- D .{3,2,1}---46.(2013山东)已知集合B A 、均为全集}4,3,2,1{=U 的子集,且(){4}U A B =,{1,2}B =,则U AB = A .{3} B .{4}C .{3,4}D .∅ 47.(2013山东)已知集合A ={0,1,2},则集合B ={}|,x y x A y A -∈∈中元素的个数是A .1B .3C .5D .948.(2013安徽)已知{}{}|10,2,1,0,1A x x B =+>=--,则()R C A B ⋂=A .{}2,1--B .{}2-C .{}1,0,1-D .{}0,149.(2013辽宁)已知集合{}{}4|0log 1,|2A x x B x x A B =<<=≤=,则A .()01,B .(]02,C .()1,2D .(]12, 50.(2013北京)已知集合{}1,0,1A =-,{}|11B x x =-≤<,则A B =A .{}0B .{}1,0-C .{}0,1D .{}1,0,1-51.(2013广东)设集合2{|20,}S x x x x R =+=∈,2{|20,}T x x x x R =-=∈,则S T =A .{0}B .{0,2}C .{2,0}-D .{2,0,2}-52.(2013广东)设整数4n ≥,集合{}1,2,3,,X n =,令集合{(,,)|,,S x y z x y z X =∈,且三条件,,x y z y z x z x y <<<<<<恰有一个成立},若(),,x y z 和(),,z w x 都在S 中,则下列选项正确的是A .(),,y z w S ∈,(),,x y w S ∉B .(),,y z w S ∈,(),,x y w S ∈C .(),,y z w S ∉,(),,x y w S ∈D .(),,y z w S ∉,(),,x y w S ∉53.(2013陕西)设全集为R , 函数()f x M , 则C M R 为A . [-1,1]B . (-1,1)C .,1][1,)(∞-⋃+∞-D .,1)(1,)(∞-⋃+∞-54.(2013江西)若集合{}2|10A x R ax ax =∈++=中只有一个元素,则a =A .4B .2C .0D .0或4 55.(2013湖北)已知全集为R ,集合112x A x ⎧⎫⎪⎪⎛⎫=≤⎨⎬ ⎪⎝⎭⎪⎪⎩⎭,{}2|680B x x x =-+≤,则R A C B =A .{}|0x x ≤B .{}|24x x ≤≤C .{}|024x x x ≤<>或D .{}|024x x x <≤≥或 56.(2012广东)设集合{1,2,3,4,5,6},{1,3,5}U M ==;则U C M =A .{,,}246B .{1,3,5}C .{,,}124D .U57.(2012浙江)设全集{}1,2,3,4,5,6U =,设集合{}1,2,3,4P =,{}3,4,5Q =,则U P Q ⋂=A .{}1,2,3,4,6B .{}1,2,3,4,5C .{}1,2,5D .{}1,258.(2012福建)已知集合{1,2,3,4}M =,{2,2}N =-,下列结论成立的是A .N M ⊆B .M N M =C .MN N = D .{2}M N = 59.(2012新课标)已知集合2{|20}A x x x =--<,{|11}B x x =-<<,则A .AB B .B AC .A B =D .A B =∅60.(2012安徽)设集合A ={|3213x x --},集合B 为函数)1lg(-=x y 的定义域,则A ⋂B=A .(1,2)B .[1,2]C .[ 1,2)D .(1,2 ]61.(2012江西)若集合{1,1}A =-,{0,2}B =,则集合{|,,}z z x y x A y B =+∈∈中的元素的个数为A .5B .4C .3D .262.(2011浙江)若{|1},{|1}P x x Q x x =<=>-,则A .P Q ⊆B .Q P ⊆C .R C P Q ⊆D .R Q C P ⊆63.(2011新课标)已知集合M ={0,1,2,3,4},N ={1,3,5},P M N =⋂,则P 的子集共有A .2个B .4个C .6个D .8个64.(2011北京)已知集合P =2{|1}x x ≤,{}M a =.若PM P =,则a 的取值范围是A .(-∞, -1]B .[1, +∞)C .[-1,1]D .(-∞,-1][1,+∞) 65.(2011江西)若全集{1,2,3,4,5,6},{2,3},{1,4}U M N ===,则集合{5,6}等于A .M N ⋃B .M N ⋂C .()()n n C M C N ⋃D .()()n n C M C N ⋂66.(2011湖南)设全集{1,2,3,4,5}U M N =⋃=,{2,4}U M C N ⋂=,则N =A .{1,2,3}B .{1,3,5}C .{1,4,5}D .{2,3,4}67.(2011广东)已知集合A ={(,)|,x y x y 为实数,且221}x y +=,B ={(,)|,x y x y 为实数且1}x y +=,则A ⋂B 的元素个数为A .4B .3C .2D .168.(2011福建)若集合M ={-1,0,1},N ={0,1,2},则M ∩N 等于A .{0,1}B .{-1,0,1}C .{0,1,2}D .{-1,0,1,2}69.(2011陕西)设集合{}22||cos sin |,M y y x x x R ==-∈,1{|||N x x i =-<}i x R ∈为虚数单位,,则M N ⋂为A .(0,1)B .(0,1]C .[0,1)D .[0,1]70.(2011辽宁)已知M ,N 为集合I 的非空真子集,且M ,N 不相等,若N I M =∅,则=N MA .MB .NC .ID .∅ 71.(2010湖南)已知集合{}1,2,3M =,{}2,3,4N =,则A .M N ⊆B .N M ⊆C .{}2,3M N =D .{}1,4M N =72.(2010陕西)集合A ={}|12x x -≤≤,B ={}|1x x <,则()R A B ⋂=A .{}|1x x >B .{}|1x x ≥C .{}|12x x <≤D .{}|12x x ≤≤73.(2010浙江)设P ={x ︱x <4},Q ={x ︱2x <4},则A .P Q ⊆B .Q P ⊆C .R P Q ⊆D .R Q P ⊆ 74.(2010安徽)若集合121log 2A x x ⎧⎫⎪⎪=≥⎨⎬⎪⎪⎩⎭,则A =RA .2(,0],2⎛⎫-∞+∞ ⎪ ⎪⎝⎭B .22⎛⎫+∞ ⎪ ⎪⎝⎭C .2(,0][,)2-∞+∞D .2)2+∞ 75.(2010辽宁)已知,A B 均为集合U ={1,3,5,7,9}的子集,且{3}AB =,{9}U B A =,则A =A .{1,3}B .{3,7,9}C .{3,5,9}D .{3,9}二、填空题 76.(2018江苏)已知集合{0,1,2,8}A =,{1,1,6,8}B =-,那么A B = .77.(2017江苏)已知集合{1,2}A =,2{,3B a a =+},若{1}AB =,则实数a 的 值为____.78.(2015江苏)已知集合{}123A =,,,{}245B =,,,则集合AB 中元素的个数为 .79.(2015湖南)已知集合U ={}1,2,3,4,A ={}1,3,B ={}1,3,4,则A (U B )= .80.(2014江苏)已知集合A ={4,3,1,2--},}3,2,1{-=B ,则=B A .81.(2014重庆)设全集{|110}U n N n =∈≤≤,{1,2,3,5,8}A =,{1,3,5,7,9}B =,则()U A B ⋂= .82.(2014福建)若集合},4,3,2,1{},,,{=d c b a 且下列四个关系:①1=a ;②1≠b ;③2=c ;④4≠d 有且只有一个是正确的,则符合条件的有序数组),,,(d c b a 的个数是_________.83.(2013湖南)已知集合{2,3,6,8},{2,3},{2,6,8}U A B ===,则()U A B = .84.(2010湖南)若规定{}1210,,...,E a a a =的子集{}12,,...,n i i i a a a 为E 的第k 个子集,其中k =12111222n i i i ---++⋅⋅⋅+,则(1){}1,3,a a 是E 的第____个子集;(2)E 的第211个子集是_______.85.(2010江苏)设集合{1,1,3}A =-,2{2,4}B a a =++,{3}AB =,则实数a =__.专题一 集合与常用逻辑用语第一讲 集合答案部分1.A 【解析】由题意{0,2}A B =,故选A .2.C 【解析】因为{1,2,3,4,5}U =,{1,3}A =,所以=U A {2,4,5}.故选C .3.C 【解析】因为{}1,3,5,7A =,{}2,3,4,5B =,所以{3,5}A B =,故选C . 4.A 【解析】{|||2}(2,2)A x x =<=-,{2,0,1,2}B =-,∴{0,1}AB =,故选A . 5.C 【解析】由题意知,{|10}A x x =-≥,则{1,2}AB =.故选C . 6.C 【解析】由题意{1,0,1,2,3,4}A B =-,∴(){1,0,1}A B C =-,故选C .7.A 【解析】∵3{|}2B x x =<,∴3{|}2AB x x =<, 选A . 8.A 【解析】由并集的概念可知,{1,2,3,4}AB =,选A . 9.B 【解析】由集合交集的定义{2,4}AB =,选B . 10.B 【解析】∵{1,2,4,6}A B =,(){1,2,4}A BC =,选B .11.C 【解析】{|02}M x x =<<,所以{|02}MN x x =<<,选C . 12.C 【解析】{|22}U A x x =-≤≤,选C .13.A 【解析】由题意可知{|12}P Q x x =-<<,选A .14.B 【解析】由题意得,{1,3,5,7}A =,{|25}B x x =,则{3,5}A B =.选B . 15.D 【解析】易知{|33}B x x =-<<,又{1,2,3}A =,所以{1,2}AB =故选D . 16.C 【解析】由补集的概念,得{0,2,6,10}A B =,故选C .17.A 【解析】∵(1,2)A =-,(0,3)B =,∴(1,3)A B =-.18.D 【解析】集合{|32,}A x x n n N ==+∈,当0n =时,322n +=,当1n =时, 325n +=,当2n =时,328n +=,当3n =时,3211n +=,当4n =时, 3214n +=,∵{6,8,10,12,14}B =,∴A B 中元素的个数为2,选D .19.A 【解析】{|32}AB x x =-<<. 20.B 【解析】{2,5}U B =,∴U A B {2,5}.21.A 【解析】∵{0,1}M =,{|01}N x x ≤=<,∴M N =[0,1]. 22.C 【解析】因为{|13}B x x,所以(2,3)A B =,故选C . 23.D 【解析】∵{0,1}M N . 24.B 【解析】{1}M N =.25.C 【解析】由题意知,22{(,)1,,}{(1,0),(1,0),(0,1),(0,1)}A x y x y x y =+≤∈=--Z ,{(,)||2,||2,,}B x y x y x y =≤≤∈Z ,所以由新定义集合A B ⊕可知,111,0x y =±=或110,1x y ==±.当111,0x y =±=时,123,2,1,0,1,2,3x x +=---,122,1,0,1,2y y +=--,所以此时A B ⊕中元素的个数有:7535⨯=个;当110,1x y ==±时,122,1,0,1,2x x +=--,123,2,1,0,1,2,3y y +=---,这种情形下和第一种情况下除12y y +的值取3-或3外均相同,即此时有5210⨯=,由分类计数原理知,A B ⊕中元素的个数为351045+=个,故应选C .26.A 【解析】{}|13A x x x =-≤或≥,故A B =[-2, -1]. 27.D 【解析】{}|12N x x =≤≤,∴M N ={1,2}. 28.B 【解析】∵{}1,2B =-,∴A B ={}2.29.C 【解析】|1|213x x -<⇒-<<,∴(1,3)A =-,[1,4]B =.∴[1,3)AB =. 30.C 【解析】∵(0,2)A =,[1,4]B =,所以A B =[1,2).31.C 【解析】{}{}{}1,0,10,1,21,0,1,2M N ⋃=-⋃=-,选C .32.A 【解析】P Q =}{34x x ≤<.33.B 【解析】由题意知{|2}U x N x =∈≥,{|A x N x =∈,所以U A ={|2x N x ∈<≤,选B .34.C 【解析】∵{}{}2|200,2A x x x =-==.∴AB =={}0,2. 35.C 【解析】A B ={|23}x x <<.36.B 【解析】∵21x <,∴11x -<<,∴MN ={}|01x x <≤,故选B . 37.C 【解析】{}|3,3A x x =-<,{}|15R B x x x =->≤或, ∴()R A B ={}|31x x --≤≤.38.D 【解析】由已知得,{=0A B x x ≤或}1x ≥,故()U A B ={|01}x x <<.39.A 【解析】{|12}A x x =-≤≤,Z B =,故AB ={1,0,1,2}-. 40.C 【解析】{}2,4,7U A =.41.C 【解析】“存在集合C 使得,U A C B C ⊆⊆”⇔“∅=B A ”,选C . 42.B 【解析】A =(-∞,0)∪(2,+∞),∴AB =R ,故选B . 43.A 【解析】{}1,4,9,16B =,∴{}1,4AB =. 44.A 【解析】∵(1,3)M =-,∴{}0,1,2M N =.45.C 【解析】因为{31}M x x =-<<,{3,2,1,0,1}N =---, 所以M N {2,1,0}=--,选C .46.A 【解析】由题意{}1,2,3AB =,且{1,2}B =,所以A 中必有3,没有4, {}3,4U B =,故U A B ={}3.47.C 【解析】0,0,1,2,0,1,2x y x y ==-=--;1,0,1,2,1,0,1x y x y ==-=-;2,0,1,2,2,1,0x y x y ==-=.∴B 中的元素为2,1,0,1,2--共5个.48.A 【解析】A :1->x ,{|1}R A x x =-≤,(){1,2}R A B =--,所以答案选A49.D 【解析】由集合A ,14x <<;所以(1,2]AB =. 50.B 【解析】集合B 中含-1,0,故{}1,0A B =-.51.A 【解析】∵{}2,0S =-,{}0,2T =,∴ST ={}0. 52.B 【解析】特殊值法,不妨令2,3,4x y z ===,1w =,则()(),,3,4,1y z w S =∈,()(),,2,3,1x y w S =∈,故选B .如果利用直接法:因为(),,x y z S ∈,(),,z w x S ∈,所以x y z <<…①,y z x <<…②,z x y <<…③三个式子中恰有一个成立;z w x <<…④,w x z <<…⑤,x z w <<…⑥三个式子中恰有一个成立.配对后只有四种情况:第一种:①⑤成立, 此时w x y z <<<,于是(),,y z w S ∈,(),,x y w S ∈;第二种:①⑥成立, 此时x y z w <<<,于是(),,y z w S ∈,(),,x y w S ∈;第三种:②④成立, 此时y z w x <<<,于是(),,y z w S ∈,(),,x y w S ∈;第四种:③④成立, 此时z w x y <<<,于是(),,y z w S ∈,(),,x y w S ∈.综合上述四种情况,可得(),,y z w S ∈,(),,x y w S ∈.53.D 【解析】()f x 的定义域为M =[-1,1],故R M =(,1)(1,)-∞-⋃+∞,选D54.A 【解析】当0a =时,10=不合,当0a ≠时,0∆=,则4a =.55.C 【解析】[)0,A =+∞,[]2,4B =,∴[0,2)(4,)R AB =+∞. 56.A 【解析】U M ={,,}246. 57.D 【解析】{}3,4,5Q =,∴U Q ={}1,2,6,∴U P Q ={}1,2.58.D 【解析】由M ={1,2,3,4},N ={-2,2},可知-2∈N ,但是-2∉M ,则N ⊄M ,故A 错误.∵M N ={1,2,3,4,-2}≠M ,故B 错误.M∩N ={2}≠N ,故C 错误,D 正确.故选D .59.B 【解析】A =(-1,2),故B ⊂≠A ,故选B .60.D 【解析】{3213}[1,2]A x x =-≤-≤=-,(1,)(1,2]B A B =+∞⇒=.61.C 【解析】根据题意容易看出x y +只能取-1,1,3等3个数值.故共有3个元素.62.D 【解析】{|1}P x x =< ∴{|1}R P x x =≥,又∵{|1}Q x x =>, ∴R Q P ⊆,故选D .63.B 【解析】{1,3}P MN ==,故P 的子集有4个. 64.C 【解析】因为P M P =,所以M P ⊆,即a P ∈,得21a ≤,解得11a -≤≤,所以a 的取值范围是[1,1]-.65.D 【解析】因为{1,2,3,4}MN =,所以()()U U M N =()U M N ={5,6}. 66.B 【解析】因为U M N ⊂,所以()()()U U U U N N M N M == =[()]U U N M ={1,3,5}.67.C 【解析】由2211x y x y ⎧+=⎨+=⎩消去y ,得20x x -=,解得0x =或1x =,这时1y =或0y =,即{(0,1),(1,0)}A B =,有2个元素.68.A 【解析】集合{1,0,1}{0,1,2}={0,1}MN =-. 69.C 【解析】对于集合M ,函数|cos 2|y x =,其值域为[0,1],所以[0,1]M =,根据复<21x <,所以(1,1)N =-,则[0,1]M N =.70.A 【解析】根据题意可知,N 是M 的真子集,所以MN M =. 71.C 【解析】{}{}{}1,2,32,3,42,3MN ==故选C. 72.D 【解析】{}{}|1,|12R R B x x A B x x ==≥≤≤73.B 【解析】{}22<<x x Q -=,可知B 正确, 74.A 【解析】不等式121log 2x ,得12112201log log ()2x >⎧⎪⎨⎪⎩,得22x , 所以R A =2(,0],2⎛⎫-∞+∞ ⎪ ⎪⎝⎭. 75.D 【解析】因为{3}A B =,所以3∈A ,又因为{9}U B A =,所以9∈A ,所以选D .本题也可以用Venn 图的方法帮助理解.76.{1,8}【解析】由集合的交运算可得A B ={1,8}.77.1【解析】由题意1B ∈,显然1a =,此时234a +=,满足题意,故1a =.78.5【解析】{1,2,3}{2,4,5}{1,2,3,4,5}A B ==,5个元素.79.{1,2,3}【解析】{2}U B ,A (U B )={1,2,3}.80.{}1,3-【解析】=B A {}1,3-.81.{}7,9【解析】{}1,2,3,4,5,6,7,8,9,10U =,{}4,6,7,9,10U A =,{}()7,9U A B =.82.6【解析】因为①正确,②也正确,所以只有①正确是不可能的;若只有②正确,①③④都不正确,则符合条件的有序数组为(2,3,1,4),(3,2,1,4);若只有③正确,①②④都不正确,则符合条件的有序数组为(3,1,2,4);若只有④正确,①②③都不正确,则符合条件的有序数组为(2,1,4,3),(3,1,4,2),(4,1,3,2).综上符合条件的有序数组的个数是6.83.{}6,8【解析】()U A B ={6,8}{2,6,8}{6,8}=.84.【解析】(1)5 根据k 的定义,可知1131225k --=+=;(2)12578{,,,,}a a a a a 此时211k =,是个奇数,所以可以判断所求集中必含元素1a ,又892,2均大于211,故所求子集不含910,a a ,然后根据2j (j =1,2,⋅⋅⋅7)的值易推导出所求子集为12578{,,,,}a a a a a .85.1【解析】考查集合的运算推理.3∈B ,23a +=,1a =.。
不等式(十年全国高考数学真题分类汇编 (文科) )

2012-2021十年全国高考数学真题分类汇编 (文科)不等式(原卷版)一、选择题1.(2021年全国高考乙卷文科)若,x y 满足约束条件4,2,3,x y x y y +≥⎧⎪-≤⎨⎪≤⎩则3z x y =+的最小值为 ( )A .18B .10C .6D .42.(2019年高考数学课标Ⅰ卷文科)已知2log 0.2a =,0.22b =,0.30.2c =,则() ( )A .a b c <<B .a c b <<C .c a b <<D .b c a <<3.(2017年高考数学课标Ⅲ卷文科)设满足约束条件,则的取值范围是( )4.(2017年高考数学课标Ⅱ卷文科)设x 、y 满足约束条件.则的最小值是( )A .B .C . D5.(2017年高考数学课标Ⅰ卷文科)设满足约束条件则的最大值为 ( )A .0B .1C .2D .36.(2014年高考数学课标Ⅱ卷文科)设x ,y 满足约束条件1010330x y x y x y +-⎧⎪--⎨⎪-+⎩≥≤≥,则2z x y =+的最大值为( )A .8B .7C .2D .17.(2014年高考数学课标Ⅰ卷文科)设x ,y 满足约束条件,1,x y a x y +≥⎧⎨-≤-⎩且z x ay =+的最小值为7,则a =( )A .-5B .3x y ,326000x y x y +-≤⎧⎪≥⎨⎪≥⎩z x y =-.A [3,0].B [3,2].C 0,2.D 0,32330233030x y x y y +-≤⎧⎪-+≥⎨⎪+≥⎩= 2 z x y +15-9-19,x y 33,1,0,x y x y y +≤⎧⎪-≥⎨⎪≥⎩z x y =+C .-5或3D .5或-38.(2013年高考数学课标Ⅱ卷文科)设,x y 满足约束条件10,10,3,x y x y x -+≥⎧⎪+-≥⎨⎪≤⎩,则23z x y =-的最小值是( )A .7-B .6-C .5-D .3- 9.(2012年高考数学课标卷文科)已知正三角形ABC 的顶点A (1,1),B (1,3),顶点C 在第一象限,若点(,)x y 在ABC ∆内部,则z x y =-+的取值范围是 ( )A.(1- B .(0,2) C.1,2)D.(0,1+二、填空题10.(2020年高考数学课标Ⅰ卷文科)若x ,y 满足约束条件220,10,10,x y x y y +-≤⎧⎪--≥⎨⎪+≥⎩则z =x +7y 的最大值为______________.11.(2020年高考数学课标Ⅱ卷文科)若x ,y 满足约束条件1121,x y x y x y +≥-⎧⎪-≥-⎨⎪-≤⎩,,则2z x y =+的最大值是__________.12.(2020年高考数学课标Ⅲ卷文科)若x ,y 满足约束条件0,201,x y x y x +≥⎧⎪-≥⎨⎪≤⎩, ,则z =3x +2y 的最大值为_________.13.(2019年高考数学课标Ⅱ卷文科)若变量,x y 满足约束条件23603020x y x y y ⎧⎪⎨⎪⎩+-≥+-≤-≤,,,则3z x y =-的最大值是___________.14.(2018年高考数学课标Ⅲ卷文科)若变量x y ,满足约束条件23024020.x y x y x ++⎧⎪-+⎨⎪-⎩≥,≥,≤则13z x y =+的最大值是________.15.(2018年高考数学课标Ⅱ卷文科)若,x y 满足约束条件250,230,50,x y x y x +-⎧⎪-+⎨⎪-⎩≥≥≤ 则z x y =+的最大值为__________.16.(2018年高考数学课标Ⅰ卷文科)若x y ,满足约束条件220100x y x y y --⎧⎪-+⎨⎪⎩≤≥≤,则32z x y =+的最大值为________.17.(2016年高考数学课标Ⅲ卷文科)设x y ,满足约束条件210,210,1,x y x y x -+⎧⎪--⎨⎪⎩≥≤≤ 则235z x y =+-的最小值为______.18.(2016年高考数学课标Ⅱ卷文科)若,x y 满足约束条件103030x y x y x -+≥⎧⎪+-≥⎨⎪-≤⎩,则2z x y =-的最小值为__________.19.(2016年高考数学课标Ⅰ卷文科)某高科技企业生产产品A 和产品B 需要甲、乙两种新型材料.生产一件产品A 需要甲材料1.5kg ,乙材料1kg ,用5个工时;生产一件产品B 需要甲材料0.5kg ,乙材料0.3kg ,用3个工时,生产一件产品A 的利润为2100元,生产一件产品B 的利润为900元.该企业现有甲材料150kg ,乙材料90kg ,则在不超过600个工时的条件下,生产产品A 、产品B 的利润之和的最大值为 元.20.(2015年高考数学课标Ⅱ卷文科)若,x y 满足约束条件50210210x y x y x y +-≤⎧⎪--≥⎨⎪-+≤⎩,则2z x y =+的最大值为 .21.(2015年高考数学课标Ⅰ卷文科)若x ,y 满足约束条件20,210,220,x y x y x y +-≤⎧⎪-+≤⎨⎪-+≥⎩则3z x y =+的最大值为_________________.22.(2013年高考数学课标Ⅰ卷文科)设,x y 满足约束条件 13,10x x y ≤≤⎧⎨-≤-≤⎩,则2z x y =-的最大值为______.。
2010-2018高考数学试题分类汇编文科版专题七 不等式第二十一讲 不等式综合应用答案

专题七 不等式第二十一讲 不等式综合应用答案部分1.D 【解析】解法一 点(2,1)在直线1x y -=上,4ax y +=表示过定点(0,4),斜率为a-的直线,当0a ≠时,2x ay -=表示过定点(2,0),斜率为1a的直线,不等式2x ay -≤表示的区域包含原点,不等式4ax y +>表示的区域不包含原点.直线4ax y +=与直线2x ay -=互相垂直,显然当直线4ax y +=的斜率0a ->时,不等式4ax y +>表示的区域不包含点(2,1),故排除A ;点(2,1)与点(0,4)连线的斜率为32-,当32a -<-,即32a >时,4ax y +>表示的区域包含点(2,1),此时2x ay -<表示的区域也包含点(2,1),故排除B ;当直线4ax y +=的斜率32a -=-,即32a =时,4ax y +>表示的区域不包含点(2,1),故排除C ,故选D .解法二 若(2,1)A ∈,则21422a a +>⎧⎨-⎩≤,解得32a >,所以当且仅当32a ≤时,(2,1)A ∉.故选D .2.B 【解析】解法一 因为ln 1x x -≤(0x >),所以1234123ln()a a a a a a a +++=++1231a a a ++-≤,所以41a -≤,又11a >,所以等比数列的公比0q <.若1q -≤,则212341(1)(10a a a a a q q +++=++)≤, 而12311a a a a ++>≥,所以123ln()0a a a ++>, 与1231234ln()0a a a a a a a ++=+++≤矛盾,所以10q -<<,所以2131(1)0a a a q -=->,2241(1)0a a a q q -=-<, 所以13a a >,24a a <,故选B .解法二 因为1xe x +≥,1234123ln()a a a a a a a +++=++, 所以123412312341a a a a e a a a a a a a +++=++++++≥,则41a -≤,又11a >,所以等比数列的公比0q <.若1q -≤,则212341(1)(10a a a a a q q +++=++)≤, 而12311a a a a ++>≥,所以123ln()0a a a ++> 与1231234ln()0a a a a a a a ++=+++≤矛盾,所以10q -<<,所以2131(1)0a a a q -=->,2241(1)0a a a q q -=-<, 所以13a a >,24a a <,故选B .3.A 【解析】解法一 函数()f x 的图象如图所示,当||2xy a =+的图象经过点(0,2)时,可知2a =±.当2x y a =+的图象与2y x x =+的图象相切时,由22x a x x+=+,得2240x ax -+=,由0∆=,并结合图象可得2a =,要使()||2xf x a +≥恒成立,当0a ≤时,需满足2a -≤,即20a -≤≤,当0a >时,需满足2a ≤,所以22a -≤≤.解法二 由题意0x =时,()f x 的最小值2,所以不等式()||2xf x a +≥等价于 ||22xa +≤在R 上恒成立. 当a=0x =,得|22x+>,不符合题意,排除C 、D ; 当a =-0x =,得|22x->,不符合题意,排除B ;选A .4.C 【解析】解法一 ∵1x y a b +=(0,0)a b >>过点(1,1),所以111a b+=, 所以111a b =+=≥(当且仅当2a b ==时去等号)2.又a b +≥当且仅当2a b ==时去等号),所以4a b +≥(当且仅当2a b ==时去等号). 解法二∵1x y a b +=(0,0)a b >>过点(1,1),所以111a b+=,所以11()()224a b a b a b a b b a +=++=+++=≥(当且仅当2a b ==时去等号).5.C 【解析】解法一由已知122b aa b ab++==,且0,0a b >>,∴2b a =+≥ab ≥解法二 由题意知0,0a b >>12a b =+≥ab ≥ 6.D 【解析】由已知得34a b ab +=,且0ab >,可知0,0a b >>,所以431a b+= (0,0a b >>),43()()a b a b a b +=++=4377b aa b+++≥ 当且仅当43b aa b=时取等号. 7.D 【解析】本题考查的是均值不等式.因为y x y x 222221⋅≥+=,即222-+≤yx ,所以2-≤+y x ,当且仅当yx22=,即y x =时取等号. 8.B 【解析】由22340x xy y z -+-=,得2234z x xy y =-+.所以2214343xy xy x y z x xy y y x ==-++-1≤=,当且仅当4x y y x =, 即2x y =时取等号此时22y z =,1)(max =zxy. xy y y z y x 2122212-+=-+)211(2)11(2yy x y -=-=1)221121(42=-+≤y y ,故选B. 9.C 【解析】由x 2-3xy +4y 2-z =0得x 2+4y 2-3xy =z ,22443331z x y xyxy xy xy+=-≥-=-=,当且仅当x 2=4y 2即x =2y 时,zxy有最小值1, 将x =2y 代入原式得z =2y 2,所以x +2y -z =2y +2y -2y 2=-2y 2+4y , 当y =1时有最大值2.故选C. 10.C 【解析】 35x y xy +=,135y x+=,113131213(34)()()555x y x y y x y x +⋅+=++≥1132555⨯=. 11.A 【解析】设从甲地到乙地所走路程为S ,则22211S ab v S Sa b a ba b===<=+++ ∵ a b <,∴ 2222ab a v a a b a=>=+,∴a v <<选A. 12.B 【解析】在同一坐标系中作出y m =,y =821m +(0m >),2log y x =图像如下图,由2log x = m ,得122,2m m x x -==,2log x =821m +,得821821342,2m m x x +-+==. 依照题意得8218218218212222,22,22m m m mmm m m b a b a++--+--+-=-=-=-821821222m m mm +++==.8141114312122222m m m m +=++-≥-=++,min ()b a ∴=13.B 【解】(方法一)已知a b <2a b+,比较a22()0a a a b -=-<,所以a <22()0b b b a -=->b <;作差法:022a b b a b +--=>,所以2a bb +<,综上可得2a ba b +<<<;故选B .(方法二)取2a =,8b =4=,52a b +=,所以2a ba b +<<<. 14.D 【解析】对于A 取1a b ==,此时2222a b ab +==,因此A 不正确;对于B 取1a b ==-,此时22a b +=-<=,因此B 不正确;对于C 取1a b ==-,此时1122a b +=-<=,因此C 不正确;对于D ,∵0ab >,∴0b a >,0b a >,∴2b a a b +=≥,D 正确. 15.14【解析】由360a b -+=,得36a b =-,所以36331112222824ab b b --+=+=⨯=≥, 当且仅当363122b b -=,即1b =时等号成立. 16.1[,2]8【解析】当30x -≤≤时,()||f x x ≤恒成立等价于222x x a x ++--≤恒成立,即232a x x --+≤恒成立,所以2min (32)2a x x --+=≤; 当0x >时()||f x x ≤恒成立等价于222x x a x -+-≤恒成立,即22x x a -+≥恒成立,所以2max 1()28x x a -+=≥.综上,a 的取值范围是1[,2]8.17.4【解析】44224141144a b a b ab ab ab ab+++=+≥≥ ,当且仅当222a b =,且12ab =,即2a =2b =时取等号. 18.8【解析】由题意有121a b+=,所以1242(2)()448b a a b a b a b a b +=++=+++=≥.当且仅当4b a a b=,即4b =,2a =时等号成立. 19.30【解析】总费用为600900464()4240x x x x +⨯=+≥⨯,当且仅当900x x=,即30x =时等号成立.20.-1,-2,-3(答案不唯一)【解析】因为“设a ,b ,c 是任意实数.若a b c >>,则a b c +>”是假命题,则它的否定“设a ,b ,c 是任意实数.若a b c >>,则a b c +≤”是真命题, 由于a b c >>,所以2a b c +>,又a b c +≤,所以0c <, 因此a ,b ,c 依次取整数-1,-2,-3,满足a b c +≤.()123,1233->->--+-=->-相矛盾,所以验证是假命题.21.9(,]2-∞【解析】∵[1,4]x ∈,∴4[4,5]x x+∈ ①当5a ≥时,44()2224f x a x a a x a a x x =--+=---=-≤, 所以()f x 的最大值245a -=,即92a =(舍去) ②当4a ≤时,44()5f x x a a x x x=+-+=+≤,此时命题成立.③当45a <<时,max ()max{|4|,|5|}f x a a a a =-+-+,则|4||5||4|5a a a a a a -+-+⎧⎨-+=⎩≥或|4||5||5|5a a a a a a -+<-+-+=,解得92a =或92a <, 综上可得,实数a 的取值范围是9(,]2-∞.22.[-【解析】设(,)P x y ,由20PA PB ⋅≤,得250x y -+≤,x如图由250x y -+≤可知,P 在 MN上, 由2225050x y x y -+=⎧⎨+=⎩,解得(1,7)M ,(5,5)N --, 所以P点横坐标的取值范围为[-.23.24a b =+++92+≤ 9418a b =+++=.当且仅当13a b +=+且5a b +=,即73,22a b ==时等号成立. 24解析】 由新定义运算知,2222(2)4(2)(2)2y x y x y x y x xy --⊗==,因为00x y >>,,所以,22222242(2)22x y y x x y x y y x xy xy xy --+⊗+⊗=+=x 时,(2)x y y x ⊗+⊗250a b c ++=得,a b c =--,则2222()2a b c b c bc =--=++ ()2222222b c b c b c +++=+≤,又2221a b c ++=,所以232a ≤,解得a ,故a26.-1【解析】设|2|a b +最大,则必须,a b 同号,因为22224463()2a b a b ab c ab c +++=++≤, 故有2(2)4a b c +≤,22()2a b c +≥,当且仅当2a b =时取等号,此时2c b =, 所以124a b c ++=2244114()112b b b +=+--≥.27.-2【解析】设2a b t +=,则2a t b =-,因为224240a ab b c -+-=, 所以将2a t b =-代入整理可得22630b tb t c -+-=①, 由0∆≥解得t 2a b +取得最大值时,t =代入①式得b =2a t b =-得a = 所以345a b c -+=55c c =222=--≥. 当且仅当52c =时等号成立. 28.1900 100【解析】(Ⅰ)76000190020 6.0518F v v==⨯++,当且仅当11v = 时等号成立.(Ⅱ)76000200020518F v v==⨯++,当且仅当10v =时等号成立.20001900100-=.29.-2【解析】∵1||2||a a b +=||||4||4||4||a b a a b a a b a a b++=++13114||4||44a a a a +=+-+=≥≥ 当且仅当||,04||b a a a b=<,即2,4a b =-=时取等号 故1||2||a a b+取得最小值时,2a =-. 30.36【解析】因为0,0x a >>,()44a f x x a x =+≥=, 当且仅当4a x x =,即3x ==,解得36a =. 31221x y xy ++=, ∴2()1x y xy +-=,即22()()12x y x y ++-≤, ∴24()3x y +≤,x y +. 32.9【解析】由柯西不等式可知2222211()(4)(12)9x y y x++≥+=.33.①③⑤【解析】令1a b ==,排除②④;由21a b ab =+≥≤,命题①正确;222()2422a b a b ab ab +=+-=-≥,命题③正确;1122a b a b ab ab++==≥,命题⑤正确.。
不等式选讲-2010-2019年高考文科数学真题专题分类汇编训练

专题十五 不等式选讲 第三十五讲 不等式选讲答案部分 2019年1.解:(1)当a =1时,()=|1| +|2|(1)f x x x x x ---. 当1x <时,2()2(1)0f x x =--<;当1x ≥时,()0f x ≥. 所以,不等式()0f x <的解集为(,1)-∞. (2)因为()=0f a ,所以1a ≥.当1a ≥,(,1)x ∈-∞时,()=() +(2)()=2()(1)<0f x a x x x x a a x x -----. 所以,a 的取值范围是[1,)+∞.2.解析 (1)因为2222222,2,2a b ab b c bc c a ac +≥+≥+≥,又1abc =,故有222111ab bc ca a b c ab bc ca abc a b c++++≥++==++.所以222111a b c a b c++≤++. (2)因为, , a b c 为正数且1abc =,故有333()()()a b b c c a +++++≥=3(+)(+)(+)a b b c a c3≥⨯⨯⨯=24.所以333()()()24a b b c c a +++++≥. 3.解析(1)由于2[(1)(1)(1)]x y z -++++222(1)(1)(1)2[(1)(1)(1)(1)(1)(1)]x y z x y y z z x =-+++++-++++++-2223(1)(1)(1)x y z ⎡⎤≤-++++⎣⎦,故由已知得2224(1)(1)(1)3x y z -++++≥,当且仅当x =53,y =–13,13z =-时等号成立. 所以222(1)(1)(1)x y z -++++的最小值为43.(2)由于2[(2)(1)()]x y z a -+-+-222(2)(1)()2[(2)(1)(1)()()(2)]x y z a x y y z a z a x =-+-+-+--+--+--2223(2)(1)()x y z a ⎡⎤-+-+-⎣⎦„,故由已知2222(2)(2)(1)()3a x y z a +-+-+-…,当且仅当43a x -=,13a y -=,223a z -=时等号成立. 因此222(2)(1)()x y z a -+-+-的最小值为2(2)3a +.由题设知2(2)133a +…,解得3a -„或1a -….2010-2018年1.【解析】(1)当1a =时,()|1||1|f x x x =+--,即2,1,()2,11,2, 1.--⎧⎪=-<<⎨⎪⎩≤≥x f x x x x故不等式()1f x >的解集为1{|}2x x >.(2)当(0,1)x ∈时|1||1|x ax x +-->成立等价于当(0,1)x ∈时|1|1ax -<成立. 若0≤a ,则当(0,1)x ∈时|1|1-≥ax ; 若0a >,|1|1ax -<的解集为20x a <<,所以21≥a,故02<≤a . 综上,a 的取值范围为(0,2].2.【解析】(1)当1=a 时,24,1,()2,12,26, 2.+-⎧⎪=-<⎨⎪-+>⎩≤≤x x f x x x x可得()0≥f x 的解集为{|23}-≤≤x x .(2)()1≤f x等价于|||2|4++-≥x a x.而|||2||2|++-+≥x a x a,且当2=x时等号成立.故()1≤f x等价于|2|4+≥a.由|2|4+≥a可得6-≤a或2≥a,所以a的取值范围是(,6][2,)-∞-+∞U.3.【解析】(1)13,,21()2,1,23, 1.x xf x x xx x⎧-<-⎪⎪⎪=+-<⎨⎪⎪⎪⎩≤≥()y f x=的图像如图所示.(2)由(1)知,()y f x=的图像与y轴交点的纵坐标为2,且各部分所在直线斜率的最大值为3,故当且仅当3a≥且2b≥时,()f x ax b+≤在[0,)+∞成立,因此a b+的最小值为5.4.D.【证明】由柯西不等式,得2222222()(122)(22)x y z x y z++++++≥.因为22=6x y z++,所以2224x y z++≥,当且仅当122x y z==时,不等式取等号,此时244333x y z===,,,所以222x y z++的最小值为4.5.【解析】(1)当1a=时,不等式()()f xg x≥等价于2|1||1|40x x x x-+++--≤.①当1x <-时,①式化为2340x x --≤,无解;当11x -≤≤时,①式化为220x x --≤,从而11x -≤≤; 当1x >时,①式化为240x x +-≤,从而1x < 所以()()f x g x ≥的解集为{|1x x -<. (2)当[1,1]x ∈-时,()2g x =.所以()()f x g x ≥的解集包含[1,1]-,等价于当[1,1]x ∈-时()2f x ≥. 又()f x 在[1,1]-的最小值必为(1)f -与(1)f 之一, 所以(1)2f -≥且(1)2f ≥,得11a -≤≤. 所以a 的取值范围为[1,1]-.6.【解析】(1)556556()()a b a b a ab a b b ++=+++3323344()2()a b a b ab a b =+-++ 2224()ab a b =+-4≥(2)∵33223()33a b a a b ab b +=+++23()ab a b =++ 23()2()4a b a b +++≤33()24a b +=+,所以3()8a b +≤,因此2a b +≤.7.【解析】(1)3,1()21,123,2x f x x x x -<-⎧⎪=--⎨⎪>⎩≤≤,当1x <-时,()f x 1≥无解;当x -12≤≤时,由()fx 1≥得,x -211≥,解得x 12≤≤ 当>2x 时,由()f x 1≥解得>2x . 所以()f x 1≥的解集为{}x x 1≥.(2)由()f x x x m -+2≥得m x x x x +---+212≤,而x x x x x x x x +---+--+2212+1+2≤x ⎛⎫ ⎪⎝⎭2355=--+244≤且当32x =时,2512=4x x x x +---+. 故m 的取值范围为5-,4⎛⎤∞ ⎥⎝⎦.8.【解析】证明:由柯西不等式可得:22222()()()ac bd a b c d +++≤,因为22224,16,a b c d +=+= 所以2()64ac bd +≤, 因此8ac bd +≤. 9.【解析】(1)如图所示:(2)()4133212342x x f x x x x x ⎧⎪--⎪⎪=--<<⎨⎪⎪-⎪⎩,≤,,≥,()1f x >.当1x -≤,41x ->,解得5x >或3x <,1x -∴≤. 当312x -<<,321x ->,解得1x >或13x <, 113x -<<∴或312x <<,当32x ≥,41x ->,解得5x >或3x <,332x <∴≤或5x >,综上,13x <或13x <<或5x >,()1f x >∴,解集为()()11353⎛⎫-∞+∞ ⎪⎝⎭U U ,,,. 10.【解析】(I )当12x <-时,()11222f x x x x =---=-,若112x -<<-;当1122x -≤≤时,()111222f x x x =-++=<恒成立;当12x >时,()2f x x =,若()2f x <,112x <<.综上可得,{}|11M x x =-<<.(Ⅱ)当()11a b ∈-,,时,有()()22110a b -->, 即22221a b a b +>+,则2222212a b ab a ab b +++>++, 则()()221ab a b +>+, 即1a b ab +<+,证毕.11.【解析】(Ⅰ)当2a =时,()|22|2f x x =-+.解不等式|22|26x -+„,得13x -剟.因此,()6f x ≤的解集为{|13}x x-剟.(Ⅱ)当x R ∈时,()()|2||12|f x g x x a a x +=-++-|212|x a x a -+-+…|1|a a =-+,当12x =时等号成立, 所以当x R ∈时,()()3f x g x +…等价于|1|3a a -+…. ① 当1a „时,①等价于13a a -+…,无解. 当1a >时,①等价于13a a -+…,解得2a …. 所以a 的取值范围是[2,)+∞.12.【解析】(Ⅰ)当1a =时,不等式()1f x >化为|1|2|1|10x x +--->,当1x -≤时,不等式化为40x ->,无解;当11x -<<时,不等式化为320x ->,解得213x <<; 当1x ≥时,不等式化为20x -+>,解得12x <≤.所以()1f x >的解集为2{|2}3x x <<. (Ⅱ)有题设可得,12,1()312,112,x a x f x x a x a x a x a --<-⎧⎪=+--⎨⎪-++>⎩≤≤,所以函数()f x 图象与x 轴围成的三角形的三个顶点分别为21(,0),(21,0),(,1)3a A B a C a a -++,ABC ∆的面积为22(1)3a +.有题设得22(1)63a +>,故2a >.所以a 的取值范围为(2,)+∞. 13.【解析】(Ⅰ)∵2a b =++2c d =++由题设a b c d +=+,ab cd >得22>.>(Ⅱ)(ⅰ)若||||a b c d -<-,则22()()a b c d -<-, 即22()4()4a b ab c d cd +-<+-.因为a b c d +=+,所以ab cd >>>则22>,即a b c d ++>++ 因为a b c d +=+,所以ab cd >,于是2222()()4()4()a b a b ab c d cd c d -=+-<+-=-. 因此||||a b c d -<-,>||||a b c d -<-的充要条件.14.【解析】(I11a b =+≥,得2ab ≥,且当a b ==故33ab+≥a b ==时取等号.所以33ab +的最小值为(II )由(I)知,23a b +≥≥.由于6>,从而不存在,a b , 使得236a b +=.15.【解析】(I )由0a >,有()f x 111()2x x a x x a a a a a=++-≥+--=+≥. 所以()f x ≥2. (Ⅱ)1(3)33f a a=++-. 当时a >3时,(3)f =1a a+,由(3)f <5得3<a<52+.当0<a ≤3时,(3)f =16a a-+,由(3)f <5<a ≤3.综上,a). 16.【解析】(Ⅰ)当a =-2时,不等式()f x <()g x 化为|21||22|30x x x -+---<,设函数y =|21||22|3x x x -+---,y =15, 212, 1236, 1x x x x x x ⎧-<⎪⎪⎪--≤≤⎨⎪->⎪⎪⎩,其图像如图所示,从图像可知,当且仅当(0,2)x ∈时,y <0,∴原不等式解集是{|02}x x <<.(Ⅱ)当x ∈[2a -,12)时,()f x =1a +,不等式()f x ≤()g x 化为13a x ++≤, ∴2x a -≥对x ∈[2a -,12)都成立,故2a-≥2a -,即a ≤43,∴a 的取值范围为(-1,43].17.【解析】(Ⅰ)2222222,2,2a b ab b c bc c a ca +≥+≥+≥得222a b c ab bc ca ++≥++由题设得()21a b c ++=,即2222221a b c ab bc ca +++++=.所以()31ab bc ca ++≤,即13ab bc ca ++≤(Ⅱ)∵2222,2,2a b c b a c b a c b c a +≥+≥+≥ ∴222()2()a b c a b c a b c b c a+++++≥++ 即222a b c a b c b c a++≥++ ∴2221a b c b c a++≥ 18.【解析】(1)当3a =-时,()3323f x x x ⇔-+-厖2323x x x ⎧⇔⎨-+-⎩„…或23323x x x <<⎧⇔⎨-+-⎩…或3323x x x ⎧⇔⎨-+-⎩…… 1x ⇔„或4x ….(2)原命题()4f x x ⇔-„在[1,2]上恒成立24x a x x ⇔++--„在[1,2]上恒成立 22x a x ⇔---剟在[1,2]上恒成立30a⇔-剟.19.【解析】(Ⅰ)当1a =时,()32f x x ≥+可化为|1|2x -≥.由此可得 3x ≥或1x ≤-.故不等式()32f x x ≥+的解集为{|3x x ≥或1}x ≤-. ( Ⅱ) 由()0f x ≤ 得30x a x -+≤,此不等式化为不等式组30x a x a x ≥⎧⎨-+≤⎩ 或30x aa x x ≤⎧⎨-+≤⎩,即4x a a x ⎧⎪⎨⎪⎩≥≤或2x aa x ⎧⎪⎨-⎪⎩≤≤,因为0a >,所以不等式组的解集为{}|2ax x ≤-,由题设可得2a-=1-,故2a =.专题十五 不等式选讲第三十五讲 不等式选讲2019年1.(2019全国II 文23)已知()|||2|().f x x a x x x a =-+--(1)当1a =时,求不等式()0f x <的解集;(2)若(,1)x ∈-∞时,()0f x <,求a 的取值范围.2.(2019全国1文23)已知a ,b ,c 为正数,且满足abc =1.证明: (1)222111a b c a b c++≤++; (2)333()()()24a b b c c a +++≥++.3.(2019全国III 文23)设,,x y z ∈R ,且1x y z ++=.(1)求222(1)(1)(1)x y z -++++的最小值;(2)若2221(2)(1)()3x y z a -+-+-≥成立,证明:3a ≤-或1a ≥-. 2010-2018年解答题1.(2018全国卷Ⅰ)[选修4–5:不等式选讲](10分)已知()|1||1|f x x ax =+--.(1)当1a =时,求不等式()1f x >的解集;(2)若(0,1)x ∈时不等式()f x x >成立,求a 的取值范围.2.(2018全国卷Ⅱ) [选修4-5:不等式选讲](10分)设函数()5|||2|=-+--f x x a x .(1)当1a =时,求不等式()0≥f x 的解集;(2)若()1≤f x ,求a 的取值范围.3.(2018全国卷Ⅲ) [选修4—5:不等式选讲](10分)设函数()|21||1|f x x x =++-.(1)画出()y f x =的图像;(2)当[0,)x ∈+∞时,()f x ax b +≤,求a b +的最小值.4.(2018江苏)D .[选修4—5:不等式选讲](本小题满分10分)若x ,y ,z 为实数,且226x y z ++=,求222x y z ++的最小值.5.(2017新课标Ⅰ)已知函数2()4f x x ax =-++,()|1||1|g x x x =++-.(1)当1a =时,求不等式()()f x g x ≥的解集;(2)若不等式()()f x g x ≥的解集包含[1,1]-,求a 的取值范围.6.(2017新课标Ⅱ)已知0a >,0b >,332a b +=,证明:(1)55()()4a b a b ++≥;(2)2a b +≤.7.(2017新课标Ⅲ)已知函数()|1||2|f x x x =+--.(1)求不等式()1f x ≥的解集;(2)若不等式2()f x x x m -+≥的解集非空,求m 的取值范围.8.(2017江苏)已知a ,b ,c ,d 为实数,且224a b +=,2216c d +=,证明8ac bd +≤.9.(2016年全国I 高考)已知函数()|1||23|f x x x =+--.(I )在图中画出()y f x =的图像;(II )求不等式|()|1f x >的解集.10.(2016年全国II )已知函数()1122f x x x =-++,M 为不等式()2f x <的解集. (I )求M ;(II )证明:当a ,b M ∈时,1a b ab +<+.11.(2016年全国III 高考)已知函数()|2|f x x a a =-+(Ⅰ)当a =2时,求不等式()6f x ≤的解集;(Ⅱ)设函数()|21|g x x =-,当x ∈R 时,()()3f x g x +≥,求a 的取值范围.12.(2015新课标1)已知函数()|1|2||f x x x a =+--,0a >. (Ⅰ)当1a =时,求不等式()1f x >的解集;(Ⅱ)若()f x 的图像与x 轴围成的三角形面积大于6,求a 的取值范围.13.(2015新课标2)设,,,a b c d 均为正数,且a b c d +=+,证明:(Ⅰ)若ab >cd a b c d >a b c d >||||a b c d -<- 的充要条件.14.(2014新课标1)若0,0a b >>,且11ab a b+=.(Ⅰ) 求33a b +的最小值;(Ⅱ)是否存在,a b ,使得236a b +=?并说明理由.15.(2014新课标2)设函数()f x =1(0)x x a a a++-> (Ⅰ)证明:()f x ≥2;(Ⅱ)若()35f <,求a 的取值范围.16.(2013新课标1)已知函数()f x =|21||2|x x a -++,()g x =3x +.(Ⅰ)当a =-2时,求不等式()f x <()g x 的解集;(Ⅱ)设a >-1,且当x ∈[2a -,12)时,()f x ≤()g x ,求a 的取值范围. 17.(2013新课标2)设,,a b c 均为正数,且1a b c ++=,证明: (Ⅰ)13ab bc ca ++≤ (Ⅱ)2221a b c b c a++≥ 18.(2012新课标)已知函数|2|||)(-++=x a x x f .(Ⅰ)当|3-=a 时,求不等式()3f x …的解集;(Ⅱ)若()|4|f x x -„的解集包含]2,1[,求a 的取值范围.19.(2011新课标)设函数()3f x x a x =-+,其中0a >.(Ⅰ)当1a =时,求不等式()32f x x ≥+的解集;(Ⅱ)若不等式()0f x ≤的解集为{}|1x x ≤- ,求a 的值.。
高考数学十年真题专题解析—不等式选讲
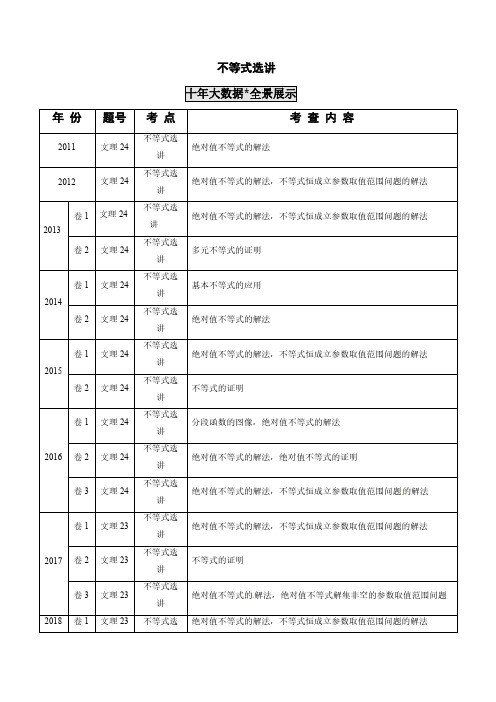
不等式选讲年份题号考点考查内容2011文理24不等式选讲绝对值不等式的解法2012文理24不等式选讲绝对值不等式的解法,不等式恒成立参数取值范围问题的解法2013卷1文理24不等式选讲绝对值不等式的解法,不等式恒成立参数取值范围问题的解法卷2文理24不等式选讲多元不等式的证明2014卷1文理24不等式选讲基本不等式的应用卷2文理24不等式选讲绝对值不等式的解法2015卷1文理24不等式选讲绝对值不等式的解法,不等式恒成立参数取值范围问题的解法卷2文理24不等式选讲不等式的证明2016卷1文理24不等式选讲分段函数的图像,绝对值不等式的解法卷2文理24不等式选讲绝对值不等式的解法,绝对值不等式的证明卷3文理24不等式选讲绝对值不等式的解法,不等式恒成立参数取值范围问题的解法2017卷1文理23不等式选讲绝对值不等式的解法,不等式恒成立参数取值范围问题的解法卷2文理23不等式选讲不等式的证明卷3文理23不等式选讲绝对值不等式的解法,绝对值不等式解集非空的参数取值范围问题2018卷1文理23不等式选绝对值不等式的解法,不等式恒成立参数取值范围问题的解法讲卷2文理23不等式选讲绝对值不等式的解法,不等式恒成立参数取值范围问题的解法卷3文理23不等式选讲绝对值函数的图象,不等式恒成立参数最值问题的解法2019卷1文理23不等式选讲三元条件不等式的证明卷2文理23不等式选讲绝对值不等式的解法,不等式恒成立参数取值范围问题的解法卷3文理23不等式选讲三元条件最值问题的解法,三元条件不等式的证明2020卷1文理23不等式选讲绝对值函数的图像,绝对值不等式的解法卷2文理23不等式选讲绝对值不等式的解法,不等式恒成立参数取值范围问题的解法卷3文理23不等式选讲三元条件不等式的证明考点出现频率2021年预测考点120绝对值不等式的求解23次考4次2021年主要考查绝对值不等式的解法、绝对值不等式的证明,不等式恒成立参数取值范围问题的解法等.考点121含绝对值不等式的恒成立问题23次考12次考点122不等式的证明23次考7次考点120绝对值不等式的求解1.(2020全国Ⅰ文理22)已知函数()3121f x x x =+--.(1)画出()y f x =的图像;(2)求不等式()()1f x f x >+的解集.【解析】(1)∵()3,1151,1313,3x x f x x x x x ⎧⎪+≥⎪⎪=--<<⎨⎪⎪--≤-⎪⎩,作出图像,如图所示:(2)将函数()f x 的图像向左平移1个单位,可得函数()1f x +的图像,如图所示:由()3511x x --=+-,解得76x =-,∴不等式的解集为7,6⎛⎫-∞- ⎪⎝⎭.2.(2020江苏23)设x ∈R ,解不等式2|1|||4x x ++≤.【答案】22,3⎡⎤-⎢⎥⎣⎦【思路导引】根据绝对值定义化为三个不等式组,解得结果.【解析】1224x x x <-⎧⎨---≤⎩ 或10224x x x -≤≤⎧⎨+-≤⎩或0224x x x >⎧⎨++≤⎩,21x ∴-≤<-或10x -≤≤或203x <≤,∴解集为22,3⎡⎤-⎢⎥⎣⎦.3.(2016全国I 文理)已知函数()|1||23|f x x x =+--.(I)在图中画出()y f x =的图像;(II)求不等式|()|1f x >的解集.【解析】(1)如图所示:(2)()4133212342x x f x x x x x ⎧⎪--⎪⎪=--<<⎨⎪⎪-⎪⎩,≤,,≥,()1f x >.当1x -≤,41x ->,解得5x >或3x <,1x -∴≤;当312x -<<,321x ->,解得1x >或13x <,113x -<<∴或312x <<;当32x ≥,41x ->,解得5x >或3x <,332x <∴≤或5x >.综上,13x <或13x <<或5x >,()1f x >∴,解集为()()11353⎛⎫-∞+∞ ⎪⎝⎭ ,,,.4.(2014全国II 文理)设函数()f x =1(0)x x a a a++->(Ⅰ)证明:()f x ≥2;(Ⅱ)若()35f <,求a 的取值范围.【解析】(I)由0a >,有()f x 111()2x x a x x a a a a a=++-≥+--=+≥,∴()f x ≥2.(Ⅱ)1(3)33f a a=++-.当时a >3时,(3)f =1a a+,由(3)f <5得3<a <5212;当0<a ≤3时,(3)f =16a a-+,由(3)f <5得12<a ≤3.综上:a 的取值范围是(152+,5212+).5.(2011新课标文理)设函数()3f x x a x =-+,其中0a >.(Ⅰ)当1a =时,求不等式()32f x x ≥+的解集;(Ⅱ)若不等式()0f x ≤的解集为{}|1x x ≤-,求a 的值.【解析】(Ⅰ)当1a =时,()32f x x ≥+可化为|1|2x -≥,由此可得3x ≥或1x ≤-.故不等式()32f x x ≥+的解集为{|3x x ≥或1}x ≤-.(Ⅱ)由()0f x ≤得30x a x -+≤,此不等式化为不等式组30x ax a x ≥⎧⎨-+≤⎩或30x aa x x ≤⎧⎨-+≤⎩,即4x a a x ⎧⎪⎨⎪⎩≥≤或2x aax ⎧⎪⎨-⎪⎩≤≤,因为0a >,∴不等式组的解集为{}|2a x x ≤-,由题设可得2a-=1-,故2a =.考点121含绝对值不等式的恒成立问题6.(2020全国Ⅱ文理22)已知函数()221f x x a x a =-+-+.(1)当2a =时,求不等式()4f x ≥的解集;(2)若()4f x ≥,求a 的取值范围.【答案】(1)32x x ⎧≤⎨⎩或112x ⎫≥⎬⎭;(2)(][),13,-∞-+∞ .【思路导引】(1)分别在3x ≤、34x <<和4x ≥三种情况下解不等式求得结果;(2)利用绝对值三角不等式可得到()()21f x a ≥-,由此构造不等式求得结果.【解析】(1)当2a =时,()43f x x x =-+-.当3x ≤时,()43724f x x x x =-+-=-≥,解得:32x ≤;当34x <<时,()4314f x x x =-+-=≥,无解;当4x ≥时,()43274f x x x x =-+-=-≥,解得:112x ≥;综上所述:()4f x ≥的解集为32x x ⎧≤⎨⎩或112x ⎫≥⎬⎭.(2)()()()()22222121211f x x a x a x ax a a a a =-+-+≥---+=-+-=-(当且仅当221a x a -≤≤时取等号),()214a ∴-≥,解得:1a ≤-或3a ≥,a ∴的取值范围为(][),13,-∞-+∞ .7.(2019全国II 文理23)[选修4-5:不等式选讲](10分)已知()|||2|().f x x a x x x a =-+--(1)当1a =时,求不等式()0f x <的解集;(2)若(,1)x ∈-∞时,()0f x <,求a 的取值范围.【解析】(1)当a=1时,()=|1| +|2|(1)f x x x x x ---.当1x <时,2()2(1)0f x x =--<;当1x ≥时,()0f x ≥,∴不等式()0f x <的解集为(,1)-∞.(2)因为()=0f a ,∴1a ≥.当1a ≥,(,1)x ∈-∞时,()=() +(2)()=2()(1)<0f x a x x x x a a x x -----∴a 的取值范围是[1,)+∞.8.(2018全国Ⅰ文理)已知()|1||1|f x x ax =+--.(1)当1a =时,求不等式()1f x >的解集;(2)若(0,1)x ∈时不等式()f x x >成立,求a 的取值范围.【解析】(1)当1a =时,()|1||1|f x x x =+--,即2,1,()2,11,2, 1.--⎧⎪=-<<⎨⎪⎩≤≥x f x x x x 故不等式()1f x >的解集为1{|}2x x >.(2)当(0,1)x ∈时|1||1|x ax x +-->成立等价于当(0,1)x ∈时|1|1ax -<成立.若0≤a ,则当(0,1)x ∈时|1|1-≥ax ;若0a >,|1|1ax -<的解集为20x a <<,∴21≥a,故02<≤a .综上,a 的取值范围为(0,2].9.(2018全国Ⅱ文理)设函数()5|||2|=-+--f x x a x .(1)当1a =时,求不等式()0≥f x 的解集;(2)若()1≤f x ,求a 的取值范围.【解析】(1)当1=a 时,24,1,()2,12,26, 2.+-⎧⎪=-<⎨⎪-+>⎩≤≤x x f x x x x 可得()0≥f x 的解集为{|23}-≤≤x x .(2)()1≤f x 等价于|||2|4++-≥x a x .而|||2||2|++-+≥x a x a ,且当2=x 时等号成立.故()1≤f x 等价于|2|4+≥a .由|2|4+≥a 可得6-≤a 或2≥a ,∴a 的取值范围是(,6][2,)-∞-+∞ .10.(2018全国Ⅲ文理)设函数()|21||1|f x x x =++-.(1)画出()y f x =的图像;(2)当[0,)x ∈+∞时,()f x ax b +≤,求a b +的最小值.【解析】(1)13,,21()2,1,23, 1.x x f x x x x x ⎧-<-⎪⎪⎪=+-<⎨⎪⎪⎪⎩≤≥()y f x =的图像如图所示.(2)由(1)知,()y f x =的图像与y 轴交点的纵坐标为2,且各部分所在直线斜率的最大值为3,故当且仅当3a ≥且2b ≥时,()f x ax b +≤在[0,)+∞成立,因此a b +的最小值为5.11.(2018江苏)若x ,y ,z 为实数,且226x y z ++=,求222x y z ++的最小值.【解析】由柯西不等式,得2222222()(122)(22)x y z x y z ++++++≥.因为22=6x y z ++,∴2224x y z ++≥,当且仅当122x y z ==时,不等式取等号,此时244333x y z ===,,,∴222x y z ++的最小值为4.12.(2017全国Ⅰ文理)已知函数2()4f x x ax =-++,()|1||1|g x x x =++-.(1)当1a =时,求不等式()()f x g x ≥的解集;(2)若不等式()()f x g x ≥的解集包含[1,1]-,求a 的取值范围.【解析】(1)当1a =时,不等式()()f x g x ≥等价于2|1||1|40x x x x -+++--≤.①当1x <-时,①式化为2340x x --≤,无解;当11x -≤≤时,①式化为220x x --≤,从而11x -≤≤;当1x >时,①式化为240x x +-≤,从而11712x -+<≤,∴()()f x g x ≥的解集为117{|1}2x x -+-<≤.(2)当[1,1]x ∈-时,()2g x =,∴()()f x g x ≥的解集包含[1,1]-,等价于当[1,1]x ∈-时()2f x ≥.又()f x 在[1,1]-的最小值必为(1)f -与(1)f 之一,∴(1)2f -≥且(1)2f ≥,得11a -≤≤,∴a 的取值范围为[1,1]-.13.(2017全国Ⅲ文理)已知函数()|1||2|f x x x =+--.(1)求不等式()1f x ≥的解集;(2)若不等式2()f x x x m -+≥的解集非空,求m 的取值范围.【解析】(1)3,1()21,123,2x f x x x x -<-⎧⎪=--⎨⎪>⎩≤≤,当1x <-时,()f x 1≥无解;当x -12≤≤时,由()f x 1≥得,x -211≥,解得x 12≤≤;当>2x 时,由()f x 1≥解得>2x .∴()f x 1≥的解集为{}x x 1≥.(2)由()f x x x m -+2≥得m x x x x +---+212≤,而x x x x x x x x +---+--+2212+1+2≤x ⎛⎫ ⎪⎝⎭2355=--+244≤,且当32x =时,2512=4x x x x +---+,故m 的取值范围为5-,4⎛⎤∞ ⎥⎝⎦.14.(2016全国III 文理)已知函数()|2|f x x a a =-+(Ⅰ)当a=2时,求不等式()6f x ≤的解集;(Ⅱ)设函数()|21|g x x =-,当x ∈R 时,()()3f x g x +≥,求a 的取值范围.【解析】(Ⅰ)当2a =时,()|22|2f x x =-+.解不等式|22|26x -+ ,得13x - ,因此()6f x ≤的解集为{|13}x x - .(Ⅱ)当x R ∈时,()()|2||12|f xg x x a a x +=-++-|212|x a x a -+-+ |1|a a =-+,当12x =时等号成立,∴当x R ∈时,()()3f x g x + 等价于|1|3a a -+ .①当1a 时,①等价于13a a -+ ,无解.当1a >时,①等价于13a a -+ ,解得2a .∴a 的取值范围是[2,)+∞.15.(2015全国I 文理)已知函数()|1|2||f x x x a =+--,0a >.(Ⅰ)当1a =时,求不等式()1f x >的解集;(Ⅱ)若()f x 的图像与x 轴围成的三角形面积大于6,求a 的取值范围.【解析】(Ⅰ)当1a =时,不等式()1f x >化为|1|2|1|10x x +--->,当1x -≤时,不等式化为40x ->,无解;当11x -<<时,不等式化为320x ->,解得213x <<;当1x ≥时,不等式化为20x -+>,解得12x <≤.∴()1f x >的解集为2{|2}3x x <<.(Ⅱ)有题设可得,12,1()312,112,x a x f x x a x a x a x a --<-⎧⎪=+--⎨⎪-++>⎩≤≤,∴函数()f x 图象与x 轴围成的三角形的三个顶点分别为21(,0),(21,0),(,1)3a A B a C a a -++,ABC ∆的面积为22(1)3a +.有题设得22(1)63a +>,故2a >.∴a 的取值范围为(2,)+∞.16.(2014全国I 文理)若0,0ab >>,且11a b +=.(Ⅰ)求33a b +的最小值;(Ⅱ)是否存在,a b ,使得236a b +=?并说明理由.【解析】(I)11a b =+≥,得2ab ≥,且当a b ==时取等号.故33ab+≥≥,且当a b ==∴33a b +的最小值为(II)由(I)知,23a b +≥.由于6>,从而不存在,a b ,使得236a b +=.16.(2013全国I 文理)已知函数()f x =|21||2|x x a -++,()g x =3x +.(Ⅰ)当a =-2时,求不等式()f x <()g x 的解集;(Ⅱ)设a >-1,且当x ∈[2a -,12)时,()f x ≤()g x ,求a 的取值范围.【解析】(Ⅰ)当a =-2时,不等式()f x <()g x 化为|21||22|30x x x -+---<,设函数y =|21||22|3x x x -+---,y =15, 212, 1236, 1x x x x x x ⎧-<⎪⎪⎪--≤≤⎨⎪->⎪⎪⎩,其图像如图所示,从图像可知,当且仅当(0,2)x ∈时,y <0,∴原不等式解集是{|02}x x <<.(Ⅱ)当x ∈[2a -,12)时,()f x =1a +,不等式()f x ≤()g x 化为13a x ++≤,∴2x a -≥对x ∈[2a -,12)都成立,故2a -≥2a -,即a ≤43,∴a 的取值范围为(-1,43].17.(2012新课标文理)已知函数|2|||)(-++=x a x x f .(Ⅰ)当|3-=a 时,求不等式()3f x 的解集;(Ⅱ)若()|4|f x x - 的解集包含]2,1[,求a 的取值范围.【解析】(1)当3a =-时,()3323f x x x ⇔-+- 2323x x x ⎧⇔⎨-+-⎩ 或23323x x x <<⎧⇔⎨-+-⎩ 或3323x x x ⎧⇔⎨-+-⎩ 1x ⇔ 或4x .(2)原命题()4f x x ⇔- 在[1,2]上恒成立24x a x x ⇔++-- 在[1,2]上恒成立22x a x ⇔--- 在[1,2]上恒成立30a ⇔- .考点122不等式的证明18.(2020全国Ⅲ文理23)设,,,0,1a b c a b c abc ∈++==R .(1)证明:0ab bc ca ++<;(2)用{}max ,,a b c 表示,,a b c 的最大值,证明:{}3max ,,4a b c ≥【答案】(1)证明见解析(2)证明见解析.【思路导引】(1)根据题设条件,0=++c b a 两边平方,再利用均值不等式证明即可;(2)思路一:不妨设max{,,}a b c a =,由题意得出0,,0a b c ><,由()222322b c b c bc a a a bc bc+++=⋅==,结合基本不等式,即可得出证明.思路二:假设出c b a ,,中最大值,根据反证法与基本不等式推出矛盾,即可得出结论.【解析】(1)证明:().0,02=++∴=++c b a c b a ,0222222=+++++∴ca ac ab c b a 即()222222c b a ca bc ab ++-=++.0,0222<++∴<++∴ca bc ab ca bc ab (2)证法一:不妨设max{,,}a b c a =,由0,1a b c abc ++==可知,0,0,0a b c ><<,1,a b c a bc =--= ,()222322224b c b c bc bc bc a a a bc bc bc++++∴=⋅==≥=,当且仅当b c =时,取等号,a ∴≥,即max{,,}a b c .证法二:不妨设403<<<≤c b a ,则,4,41133>=-->=c b a c ab而1132a b ->--≥>==矛盾,∴命题得证.19.(2019全国I 文理23)已知a ,b ,c 为正数,且满足abc=1.证明:(1)222111a b c a b c++≤++;(2)333()()()24a b b c c a +++≥++.【解析】(1)因为2222222,2,2a b ab b c bc c a ac +≥+≥+≥,又1abc =,故有222111ab bc ca a b c ab bc ca abc a b c ++++≥++==++,∴222111a b c a b c++≤++.(2)因为, , a b c 为正数且1abc =,故有333()()()a b b c c a +++++≥=3(+)(+)(+)a b b c ac 3≥⨯⨯⨯=24.∴333()()()24a b b c c a +++++≥.20.(2019全国III 文理23)设,,x y z ∈R ,且1x y z ++=.(1)求222(1)(1)(1)x y z -++++的最小值;(2)若2221(2)(1)()3x y z a -+-+-≥成立,证明:3a ≤-或1a ≥-.【解析】(1)由于2[(1)(1)(1)]x y z -++++222(1)(1)(1)2[(1)(1)(1)(1)(1)(1)]x y z x y y z z x =-+++++-++++++-2223(1)(1)(1)x y z ⎡⎤≤-++++⎣⎦,故由已知得2224(1)(1)(1)3x y z -++++≥,当且仅当x=53,y=–13,13z =-时等号成立.∴222(1)(1)(1)x y z -++++的最小值为43.(2)由于2[(2)(1)()]x y z a -+-+-222(2)(1)()2[(2)(1)(1)()()(2)]x y z a x y y z a z a x =-+-+-+--+--+--2223(2)(1)()x y z a ⎡⎤-+-+-⎣⎦ ,故由已知2222(2)(2)(1)()3a x y z a +-+-+- ,当且仅当43a x -=,13a y -=,223a z -=时等号成立,因此222(2)(1)()x y z a -+-+-的最小值为2(2)3a +.由题设知2(2)133a + ,解得3a - 或1a - .21.(2017全国Ⅱ文理)已知0a >,0b >,332a b +=,证明:(1)()()554a b a b ++≥;(2)2a b +≤.【解析】(1)556556()()a b a b a ab a b b ++=+++3323344()2()a b a b ab a b =+-++()22244ab a b =+-≥.(2)∵33223()33a b a a b ab b +=+++23()ab a b =++23()2()4a b a b +≤++33()24a b +=+,∴3()8a b +≤,因此2a b +≤.22.(2017江苏)已知a ,b ,c ,d 为实数,且224a b +=,2216c d +=,证明8ac bd +≤.【解析】证明:由柯西不等式可得:22222()()()ac bd a b c d +++≤,因为22224,16,a b c d +=+=∴2()64ac bd +≤,因此8ac bd +≤.23.(2016全国II 文理)已知函数()1122f x x x =-++,M 为不等式()2f x <的解集.(I)求M ;(II)证明:当a ,b M ∈时,1a b ab +<+.【解析】(I)当12x <-时,()11222f x x x x =---=-,若112x -<<-;当1122x -≤≤时,()111222f x x x =-++=<恒成立;当12x >时,()2f x x =,若()2f x <,112x <<.综上可得,{}|11M x x =-<<.(Ⅱ)当()11a b ∈-,,时,有()()22110a b -->,即22221a b a b +>+,则2222212a b ab a ab b +++>++,则()()221ab a b +>+,即1a b ab +<+,证毕.24.(2015全国II 文理)设,,,a b c d 均为正数,且a b c d +=+,证明:(Ⅰ)若ab >cd ,则a b c d +>+;(Ⅱ)a b c d +>+是||||a b c d -<-的充要条件.【解析】(Ⅰ)∵2()2a b a b ab +=++,2()c d c d cd +=++由题设a b c d +=+,ab cd >得22()a b c d >+a b c d +>(Ⅱ)(ⅰ)若||||a b c d -<-,则22()()a b c d -<-,即22()4()4a b ab c d cd +-<+-.因为a b c d +=+,∴ab cd >,由(Ⅰ)得a b c d >(ⅱ)a b c d +>则22(a b c d >+,即a b ab c d cd ++>++因为a b c d +=+,∴ab cd >,于是2222()()4()4()a b a b ab c d cd c d -=+-<+-=-.因此||||a b c d -<-.a b c d +>||||a b c d -<-的充要条件.25.(2013全国II 文理)设,,a b c 均为正数,且1a b c ++=,证明:(Ⅰ)13ab bc ca ++≤;(Ⅱ)2221a b c b c a++≥.【解析】(Ⅰ)2222222,2,2a b ab b c bc c a ca +≥+≥+≥得222a b c ab bc ca ++≥++,由题设得()21a b c ++=,即2222221a b c ab bc ca +++++=,∴()31ab bc ca ++≤,即13ab bc ca ++≤.(Ⅱ)∵2222,2,2a b c b a c b a c b c a +≥+≥+≥,∴222()2()a b c a b c a b c b c a +++++≥++,即222a b c a b c b c a ++≥++,∴2221a b c b c a ++≥.。
2018年数学(文科)高考题分类 真题与模拟题 不等式

E 单元不等式E1 不等式的概念与性质 E2 绝对值不等式的解法 E3 一元二次不等式的解法 E4 简单的一元高次不等式的解法E5 简单的线性规划问题14.E5[2018·全国卷Ⅰ] 若x ,y 满足约束条件{x -2y -2≤0,x -y +1≥0,y ≤0,则z=3x+2y 的最大值为 .14.6 [解析] 不等式组表示的平面区域如图中阴影部分所示,当直线y=-32x+z2经过点A (2,0)时,z 最大,所以z max =3×2+2×0=6.14.E5[2018·全国卷Ⅱ] 若x ,y 满足约束条件{x +2y -5≥0,x -2y +3≥0,x -5≤0,则z=x+y 的最大值为 .14.9 [解析] 作出不等式组表示的可行域如图中阴影部分所示.当直线y=-x+z 经过点A (5,4)时,直线的纵截距z 最大,所以z max =5+4=9.15.E5[2018·全国卷Ⅲ] 若变量x ,y 满足约束条件{2x +y +3≥0,x -2y +4≥0,x -2≤0,则z=x+13y 的最大值是 .15.3 [解析] 作出不等式组表示的可行域如图中阴影部分所示,由图易知目标函数在点A (2,3)处取得最大值,最大值为2+13×3=3.12.E5[2018·浙江卷] 若x ,y 满足约束条件{x -y ≥0,2x +y ≤6,x +y ≥2,则z=x+3y 的最小值是 ,最大值是 . 12.-2 8[解析] 作出如图中阴影部分所示的可行域,易知A (2,2),B (4,-2),C (1,1),目标函数表示斜率为-13的一组平行直线.由图可知,当直线x+3y-z=0经过点A 时,z 取得最大值,最大值为2+3×2=8;当直线x+3y-z=0经过点B 时,z 取得最小值,最小值为4+3×(-2)=-2.13.E5[2018·北京卷] 若x ,y 满足x+1≤y ≤2x ,则2y-x 的最小值是 .13.3 [解析] x ,y 满足的可行域如图中阴影部分所示,联立{y =x +1,y =2x,得交点坐标为(1,2),由图可知,当目标函数z=2y-x 过点(1,2)时,z 有最小值,z min =2×2-1=3.E6 2a b+≤13.C8,E6[2018·江苏卷] 在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,∠ABC=120°,∠ABC 的平分线交AC 于点D ,且BD=1,则4a+c 的最小值为 .13.9 [解析] 方法一:由∠ABC=120°,∠ABC 的平分线交AC 于点D ,得∠ABD=∠CBD=60°.由S △ABC =S △BAD +S △BCD ,得12ac sin 120°=12a ·BD ·sin 60°+12c ·BD ·sin 60°,又BD=1,所以ac=a+c ,则1a +1c=1.而a>0,c>0,所以4a+c=(4a+c )1a +1c=4+4a c +c a +1≥5+2√4a c ·c a =9当且仅当4a c =ca ,即c=2a 时,取等号.因此4a+c 的最小值为9.方法二:以B 为坐标原点,BD 所在直线为x 轴建立直角坐标系,则D (1,0),A c 2,√3c 2,C a 2,-√3a2,故AD⃗⃗⃗⃗⃗ =1-c 2,-√3c2,DC⃗⃗⃗⃗⃗ =a2-1,-√3a 2,又AD ⃗⃗⃗⃗⃗ ∥DC⃗⃗⃗⃗⃗ ,所以1-c 2-√3a2=a 2-1-√3c2,整理得ac=a+c ,以下同方法一.13.E6[2018·天津卷] 已知a ,b ∈R,且a-3b+6=0,则2a +18b 的最小值为 .13.14 [解析] 由已知得a-3b=-6,由基本不等式得2a +18b ≥2√2a -3b =223=14(当且仅当a=-3b=-3时取等号).E7 不等式的证明方法 E8 不等式的综合应用 E9 单元综合8.E9[2018·北京卷] 设集合A={(x ,y )|x-y ≥1,ax+y>4,x-ay ≤2},则 ( ) A . 对任意实数a ,(2,1)∈A B . 对任意实数a ,(2,1)∉A C . 当且仅当a<0时,(2,1)∉A D . 当且仅当a ≤32时,(2,1)∉A8.D [解析] 当a=0时,A 为空集,排除A;当a=2时,(2,1)∈A ,排除B;当a=32时,作出可行域如图中阴影部分所示,由{x -y =1,32x +y =4,得P (2,1),又∵ax+y>4,取不到边界值,∴(2,1)∉A.故选D .1.[2018·北京通州区期末] 已知a ,b ∈R,a>b>0,则下列不等式一定成立的是 ( ) A . 1a >1b B . tan a>tan b C . |log 2a|>|log 2b| D . a ·2-b >b ·2-a1.D [解析] 对于A,a>b>0,则1a <1b ,故不成立;对于B,不妨设a=3π4>b=π4>0,则tan 3π4=-1,tan π4=1,故不成立;对于C,不妨设a=2,b=14,则|log 2a |=1,|log 2b |=2,故不成立.故选D . 2.[2018·唐山五校联考] 已知不等式x 2-bx-a ≥0的解集是{x|x ≤2或x ≥3},则不等式ax 2-bx-1>0的解集是 ( ) A .{x|2<x<3} B .{x |-12<x <-13} C .{x |13<x <12}D .{x |x <13或x <12}2.B [解析] ∵不等式x 2-bx-a ≥0的解集是{x|x ≤2或x ≥3},∴x 2-bx-a=0的解是x 1=2和x 2=3,∴{2+3=b,2×3=-a,解得{a =-6,b =5,则不等式ax 2-bx-1>0即为-6x 2-5x-1>0,解得{x |-12<x <-13}. 3.[2018·遵义联考] 已知O 是坐标原点,点A (-1,1),若点M (x ,y )为平面区域{x +y ≥2,x ≤1,y ≤2上的一个动点,则OA ⃗⃗⃗⃗⃗ ·OM⃗⃗⃗⃗⃗⃗ 的取值范围是 . 3.[0,2] [解析] 设z=OA ⃗⃗⃗ ·OM ⃗⃗⃗⃗ =-x+y.在直角坐标系内作出可行域如图所示.由图可知,当直线z=-x+y 经过可行域内点C (0,2)时,z 有最大值,即(OA ⃗⃗⃗ ·OM ⃗⃗⃗⃗ )max =-0+2=2;当直线z=-x+y 经过可行域内点A (1,1)时,z 有最小值,即(OA ⃗⃗⃗ ·OM ⃗⃗⃗⃗ )min =-1+1=0.所以OA ⃗⃗⃗ ·OM⃗⃗⃗⃗ 的取值范围为[0,2].4. [2018·衡水一中月考] 若x ,y 都是正数,且x+y=3,则4x+1+1y+1的最小值为 .4.95 [解析] 设m=x+1,n=y+1.∵x+y=3,∴{x =m -1,y =n -1,则m+n=5,∴4x+1+1y+1=4m +1n =(4m +1n )(m 5+n 5)=45+4n 5m +m 5n +15≥1+2√4n 5m ·m 5n =95,当且仅当m=103,n=53,即x=73,y=23时取等号.。
高考文科数学2010—2018真题分类 专题一 集合与常用逻辑用语第一讲 集合(带答案)

专题一 集合与常用逻辑用语第一讲 集合一、选择题1.(2018全国卷Ⅰ)已知集合{0,2}=A ,{21012}=--,,,,B ,则A B =A .{0,2}B .{1,2}C .{0}D .{21012}--,,,, 2.(2018浙江)已知全集{1,2,3,4,5}U =,{1,3}A =,则=U A ðA .∅B .{1,3}C .{2,4,5}D .{1,2,3,4,5}3.(2018全国卷Ⅱ)已知集合{}1,3,5,7A =,{}2,3,4,5B =,则AB = A .{3} B .{5}C .{3,5}D .{}1,2,3,4,5,74.(2018北京)已知集合{|||2}A x x =<,{2,0,1,2}B =-,则AB = A .{0,1} B .{–1,0,1}C .{–2,0,1,2}D .{–1,0,1,2}5.(2018全国卷Ⅲ)已知集合{|10}A x x =-≥,{0,1,2}B =,则AB = A .{0} B .{1}C .{1,2}D .{0,1,2}6.(2018天津)设集合{1,2,3,4}A =,{1,0,2,3}B =-,{|12}C x x =∈-<R ≤,则()A B C =A .{1,1}-B .{0,1}C .{1,0,1}-D .{2,3,4}7.(2017新课标Ⅰ)已知集合{|2}A x x =<,{320}B x =->,则A .3{|}2AB x x =< B .A B =∅C .3{|}2A B x x =<D .A B =R 8.(2017新课标Ⅱ)设集合{1,2,3}A =,{2,3,4}B =则A B =A .{1,2,3,4}B .{1,2,3}C .{2,3,4}D .{1,3,4}9.(2017新课标Ⅲ)已知集合{1,2,3,4}A =,{2,4,6,8}B =,则A B 中元素的个数为 A .1 B .2 C .3 D .410.(2017天津)设集合{1,2,6}A =,{2,4}B =,{1,2,3,4}C =,则()A B C =A .{2}B .{1,2,4}C .{1,2,4,6}D .{1,2,3,4,6}11.(2017山东)设集合{}11M x x =-<,{}2N x x =<,则MN = A .()1,1- B .()1,2- C .()0,2 D .()1,212.(2017北京)已知U =R ,集合{|22}A x x x =<->或,则U A ð=A .(2,2)-B .(,2)(2,)-∞-+∞C .[2,2]-D .(,2][2,)-∞-+∞13.(2017浙江)已知集合{|11}P x x =-<<,{|02}Q x x =<<,那么P Q = A .(1,2)- B .(0,1) C .(1,0)- D .(1,2)14.(2016全国I 卷)设集合{1,3,5,7}A =,{|25}B x x =≤≤,则=A BA .{1,3}B .{3,5}C .{5,7}D .{1,7}15.(2016全国Ⅱ卷)已知集合{123}A =,,,2{|9}B x x =<,则A B =A .{210123}--,,,,, B .{21012}--,,,, C .{123},, D .{12}, 16.(2016全国Ⅲ)设集合{0,2,4,6,8,10},{4,8}A B ==,则A B ð=A .{48},B .{026},,C .{02610},,,D .{0246810},,,,, 17.(2015新课标2)已知集合}21|{<<-=x x A ,}30|{<<=x x B ,则A B =A .)3,1(-B .)0,1(-C .)2,0(D .)3,2( 18.(2015新课标1)已知集合{32,},{6,8,10,12,14}A x x n n N B ==+∈=,则集合A B 中的元素个数为A .5B .4C .3D .219.(2015北京)若集合{|52}A x x =-<<,{|33}B x x =-<<,则A B =A .{|32}x x -<<B .{|52}x x -<<C .{|33}x x -<<D .{|53}x x -<< 20.(2015天津)已知全集{1,2,3,4,5,6}U =,集合{}2,3,5A =,集合{1,3,4,6}B =,则集合U A B =ðA .{3}B .{2,5}C .{1,4,6}D .{2,3,5}21.(2015陕西)设集合2{|}M x x x ==,{|lg 0}N x x =≤,则M N = A .[0,1] B .(0,1] C .[0,1) D .(-∞,1]22.(2015山东)已知集合{}24A x x =<<,{}(1)(3)0B x x x =--<,则AB = A .()1,3 B .()1,4C .()2,3D .()2,423.(2015福建)若集合{}22M x x =-≤<,{}0,1,2N =,则M N 等于 A .{}0 B .{}1 C .{}0,1,2 D .{}0,124.(2015广东)若集合{}1,1M =-,{}2,1,0N =-,则M N =A .{}0,1-B .{}1C .{}0D .{}1,1-25.(2015湖北)已知集合22{(,)|1,,}A x y x y x y Z =+∈≤,{(,)|||2,B x y x =≤||2,,}y x y Z ∈≤,定义集合12121122{(,)|(,),(,)}A B x x y y x y A x y B ⊕=++∈∈,则A B ⊕中元素的个数为A .77B .49C .45D .3026.(2014新课标)已知集合A ={x |2230x x --≥},B ={x |-2≤x <2},则A B =A .[-2, -1]B .[-1,1]C .[-1,2)D .[1,2)27.(2014新课标)设集合M ={0,1,2},N ={}2|320x x x -+≤,则M N = A .{1} B .{2} C .{0,1} D .{1,2}28.(2014新课标)已知集合A ={-2,0,2},B ={x |2x -x -20=},则A B =A . ∅B .{}2C .{}0D .{}2-29.(2014山东)设集合},]2,0[,2{},21{∈==<-=x y y B x x A x 则=B AA . [0,2]B .(1,3)C . [1,3)D . (1,4)30.(2014山东)设集合2{|20},{|14}A x x x B x x =-<=≤≤,则AB =A .(0,2]B .(1,2)C .[1,2)D .(1,4) 31.(2014广东)已知集合{1,0,1}M =-,{0,1,2}N =,则M N =A .{0,1}B .{1,0,2}-C .{1,0,1,2}-D .{1,0,1}-32.(2014福建)若集合{|24}P x x =<≤,{|3}Q x x =≥,则P Q 等于A .}{34x x ≤<B .}{34x x <<C .}{23x x ≤<D .}{23x x ≤≤33.(2014浙江)设全集{}2|≥∈=x N x U ,集合{}5|2≥∈=x N x A ,则U A ð=A .∅B . }2{C . }5{D . }5,2{34.(2014北京)已知集合2{|20},{0,1,2}A x x x B =-==,则AB = A .{0} B .{0,1}C .{0,2}D .{0,1,2}35.(2014湖南)已知集合{|2},{|13}A x x B x x =>=<<,则A B =A .{|2}x x >B .{|1}x x >C .{|23}x x <<D .{|13}x x <<36.(2014陕西)已知集合2{|0},{|1,}M x x N x x x R =≥=<∈,则MN = A .[0,1] B .[0,1) C .(0,1] D .(0,1)37.(2014江西)设全集为R ,集合2{|90},{|15}A x x B x x =-<=-<≤,则()R A B =ðA .(3,0)-B .(3,1)--C .(3,1]--D .(3,3)-38.(2014辽宁)已知全集,{|0},{|1}U R A x x B x x ==≤=≥,则集合()U A B =ðA .{|0}x x ≥B .{|1}x x ≤C .{|01}x x ≤≤D .{|01}x x <<39.(2014四川)已知集合2{|20}A x x x =--≤,集合B 为整数集,则AB =A .{1,0,1,2}-B .{2,1,0,1}--C .{0,1}D .{1,0}-40.(2014湖北)已知全集{1,2,3,4,5,6,7}U =,集合{1,3,5,6}A =,则U A =ðA .{1,3,5,6}B .{2,3,7}C .{2,4,7}D . {2,5,7} 41.(2014湖北)设U 为全集,B A ,是集合,则“存在集合C 使得A C ⊆,U B C ⊆ð”是“∅=B A ”的A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件42.(2013新课标1)已知集合A ={x |x 2-2x >0},B ={x |-5<x <5},则A .A ∩B =∅ B .A ∪B =RC .B ⊆AD .A ⊆B43.(2013新课标1)已知集合{1,2,3,4}A =,2{|,}B x x n n A ==∈,则AB =A .{}14,B .{}23,C .{}916,D .{}12, 44.(2013新课标2)已知集合(){}2|14,M x x x R =-<∈,{}1,0,1,2,3N =-,则M N =A .{}0,1,2B .{}1,0,1,2- C .{}1,0,2,3- D .{}0,1,2,3 45.(2013新课标2)已知集合{|31}M x x =-<<,{3,2,1,0,1}N =---,则MN = A .{2,1,0,1}-- B .{3,2,1,0}--- C .{2,1,0}-- D .{3,2,1}---46.(2013山东)已知集合B A 、均为全集}4,3,2,1{=U 的子集,且(){4}U A B =ð,{1,2}B =,则U A B =ðA .{3}B .{4}C .{3,4}D .∅47.(2013山东)已知集合A ={0,1,2},则集合B ={}|,x y x A y A -∈∈中元素的个数是A .1B .3C .5D .948.(2013安徽)已知{}{}|10,2,1,0,1A x x B =+>=--,则()R C A B ⋂=A .{}2,1--B .{}2-C .{}1,0,1-D .{}0,149.(2013辽宁)已知集合{}{}4|0log 1,|2A x x B x x A B =<<=≤=,则A .()01,B .(]02,C .()1,2D .(]12, 50.(2013北京)已知集合{}1,0,1A =-,{}|11B x x =-≤<,则A B =A .{}0B .{}1,0-C .{}0,1D .{}1,0,1-51.(2013广东)设集合2{|20,}S x x x x R =+=∈,2{|20,}T x x x x R =-=∈,则S T =A .{0}B .{0,2}C .{2,0}-D .{2,0,2}-52.(2013广东)设整数4n ≥,集合{}1,2,3,,X n =,令集合{(,,)|,,S x y z x y z X =∈,且三条件,,x y z y z x z x y <<<<<<恰有一个成立},若(),,x y z 和(),,z w x 都在S 中,则下列选项正确的是A .(),,y z w S ∈,(),,x y w S ∉B .(),,y z w S ∈,(),,x y w S ∈C .(),,y z w S ∉,(),,x y w S ∈D .(),,y z w S ∉,(),,x y w S ∉53.(2013陕西)设全集为R , 函数()f x M , 则C M R 为A . [-1,1]B . (-1,1)C .,1][1,)(∞-⋃+∞-D .,1)(1,)(∞-⋃+∞-54.(2013江西)若集合{}2|10A x R ax ax =∈++=中只有一个元素,则a = A .4 B .2 C .0 D .0或455.(2013湖北)已知全集为R ,集合112x A x ⎧⎫⎪⎪⎛⎫=≤⎨⎬ ⎪⎝⎭⎪⎪⎩⎭,{}2|680B x x x =-+≤,则R A C B =A .{}|0x x ≤B .{}|24x x ≤≤C .{}|024x x x ≤<>或D .{}|024x x x <≤≥或 56.(2012广东)设集合{1,2,3,4,5,6},{1,3,5}U M ==;则U C M =A .{,,}246B .{1,3,5}C .{,,}124D .U57.(2012浙江)设全集{}1,2,3,4,5,6U =,设集合{}1,2,3,4P =,{}3,4,5Q =,则U P Q ⋂ð=A .{}1,2,3,4,6B .{}1,2,3,4,5C .{}1,2,5D .{}1,258.(2012福建)已知集合{1,2,3,4}M =,{2,2}N =-,下列结论成立的是A .N M ⊆B .M N M =C .MN N = D .{2}M N = 59.(2012新课标)已知集合2{|20}A x x x =--<,{|11}B x x =-<<,则A .AB Ü B .B A ÜC .A B =D .A B =∅60.(2012安徽)设集合A ={|3213x x --剟},集合B 为函数)1lg(-=x y 的定义域,则A ⋂B= A .(1,2) B .[1,2] C .[ 1,2) D .(1,2 ]61.(2012江西)若集合{1,1}A =-,{0,2}B =,则集合{|,,}z z x y x A y B =+∈∈中的元素的个数为A .5B .4C .3D .262.(2011浙江)若{|1},{|1}P x x Q x x =<=>-,则A .P Q ⊆B .Q P ⊆C .R C P Q ⊆D .R Q C P ⊆63.(2011新课标)已知集合M ={0,1,2,3,4},N ={1,3,5},P M N =⋂,则P 的子集共有A .2个B .4个C .6个D .8个64.(2011北京)已知集合P =2{|1}x x ≤,{}M a =.若PM P =,则a 的取值范围是A .(-∞, -1]B .[1, +∞)C .[-1,1]D .(-∞,-1][1,+∞) 65.(2011江西)若全集{1,2,3,4,5,6},{2,3},{1,4}U M N ===,则集合{5,6}等于A .M N ⋃B .M N ⋂C .()()n n C M C N ⋃D .()()n n C M C N ⋂66.(2011湖南)设全集{1,2,3,4,5}U M N =⋃=,{2,4}U M C N ⋂=,则N =A .{1,2,3}B .{1,3,5}C .{1,4,5}D .{2,3,4}67.(2011广东)已知集合A ={(,)|,x y x y 为实数,且221}x y +=,B ={(,)|,x y x y 为实数且1}x y +=,则A ⋂B 的元素个数为A .4B .3C .2D .168.(2011福建)若集合M ={-1,0,1},N ={0,1,2},则M ∩N 等于A .{0,1}B .{-1,0,1}C .{0,1,2}D .{-1,0,1,2}69.(2011陕西)设集合{}22||cos sin |,M y y x x x R ==-∈,1{|||N x x i =-<}i x R ∈为虚数单位,,则M N ⋂为A .(0,1)B .(0,1]C .[0,1)D .[0,1]70.(2011辽宁)已知M ,N 为集合I 的非空真子集,且M ,N 不相等,若 N I M =∅ð,则=N MA .MB .NC .ID .∅71.(2010湖南)已知集合{}1,2,3M =,{}2,3,4N =,则A .M N ⊆B .N M ⊆C .{}2,3M N =D .{}1,4M N =72.(2010陕西)集合A ={}|12x x -≤≤,B ={}|1x x <,则()R A B ⋂ð=A .{}|1x x >B .{}|1x x ≥C .{}|12x x <≤D .{}|12x x ≤≤73.(2010浙江)设P ={x ︱x <4},Q ={x ︱2x <4},则A .P Q ⊆B .Q P ⊆C .R P Q ⊆ðD .R Q P ⊆ð 74.(2010安徽)若集合121log 2A x x ⎧⎫⎪⎪=≥⎨⎬⎪⎪⎩⎭,则A =R ð A .2(,0],⎛⎫-∞+∞ ⎪ ⎪⎝⎭B .⎫+∞⎪⎪⎝⎭C .2(,0][,)2-∞+∞D .[)2+∞ 75.(2010辽宁)已知,A B 均为集合U ={1,3,5,7,9}的子集,且{3}AB =,{9}U B A =ð,则A =A .{1,3}B .{3,7,9}C .{3,5,9}D .{3,9}二、填空题 76.(2018江苏)已知集合{0,1,2,8}A =,{1,1,6,8}B =-,那么AB = . 77.(2017江苏)已知集合{1,2}A =,2{,3B a a =+},若{1}A B =,则实数a 的 值为____.78.(2015江苏)已知集合{}123A =,,,{}245B =,,,则集合A B 中元素的个数为 .79.(2015湖南)已知集合U ={}1,2,3,4,A ={}1,3,B ={}1,3,4,则A(U B ð)= .80.(2014江苏)已知集合A ={4,3,1,2--},}3,2,1{-=B ,则=B A .81.(2014重庆)设全集{|110}U n N n =∈≤≤,{1,2,3,5,8}A =,{1,3,5,7,9}B =,则()U A B ⋂ð= .82.(2014福建)若集合},4,3,2,1{},,,{=d c b a 且下列四个关系:①1=a ;②1≠b ;③2=c ;④4≠d 有且只有一个是正确的,则符合条件的有序数组),,,(d c b a 的个数是_________.83.(2013湖南)已知集合{2,3,6,8},{2,3},{2,6,8}U A B ===,则()U A B ð= .84.(2010湖南)若规定{}1210,,...,E a a a =的子集{}12,,...,n i i i a a a 为E 的第k 个子集,其中k =12111222n i i i ---++⋅⋅⋅+,则(1){}1,3,a a 是E 的第____个子集;(2)E 的第211个子集是_______.85.(2010江苏)设集合{1,1,3}A =-,2{2,4}B a a =++,{3}AB =,则实数a =__.专题一 集合与常用逻辑用语第一讲 集合答案部分1.A 【解析】由题意{0,2}A B =,故选A .2.C 【解析】因为{1,2,3,4,5}U =,{1,3}A =,所以=U A ð{2,4,5}.故选C .3.C 【解析】因为{}1,3,5,7A =,{}2,3,4,5B =,所以{3,5}A B =,故选C . 4.A 【解析】{|||2}(2,2)A x x =<=-,{2,0,1,2}B =-,∴{0,1}AB =,故选A . 5.C 【解析】由题意知,{|10}A x x =-≥,则{1,2}AB =.故选C . 6.C 【解析】由题意{1,0,1,2,3,4}A B =-,∴(){1,0,1}A B C =-,故选C .7.A 【解析】∵3{|}2B x x =<,∴3{|}2AB x x =<, 选A .8.A 【解析】由并集的概念可知,{1,2,3,4}AB =,选A . 9.B 【解析】由集合交集的定义{2,4}AB =,选B . 10.B 【解析】∵{1,2,4,6}A B =,(){1,2,4}A BC =,选B .11.C 【解析】{|02}M x x =<<,所以{|02}MN x x =<<,选C . 12.C 【解析】{|22}U A x x =-≤≤ð,选C .13.A 【解析】由题意可知{|12}P Q x x =-<<,选A .14.B 【解析】由题意得,{1,3,5,7}A =,{|25}B x x =剟,则{3,5}A B =.选B .15.D 【解析】易知{|33}B x x =-<<,又{1,2,3}A =,所以{1,2}AB =故选D . 16.C 【解析】由补集的概念,得{0,2,6,10}A B =ð,故选C .17.A 【解析】∵(1,2)A =-,(0,3)B =,∴(1,3)A B =-.18.D 【解析】集合{|32,}A x x n n N ==+∈,当0n =时,322n +=,当1n =时,325n +=,当2n =时,328n +=,当3n =时,3211n +=,当4n =时, 3214n +=,∵{6,8,10,12,14}B =,∴A B 中元素的个数为2,选D .19.A 【解析】{|32}A B x x =-<<.20.B 【解析】{2,5}U B ð=,∴U A B =ð{2,5}.21.A 【解析】∵{0,1}M =,{|01}N x x ≤=<,∴M N =[0,1]. 22.C 【解析】因为{|13}B x x =<<,所以(2,3)AB =,故选C . 23.D 【解析】∵{0,1}MN =. 24.B 【解析】{1}M N =.25.C 【解析】由题意知,22{(,)1,,}{(1,0),(1,0),(0,1),(0,1)}A x y x y x y =+≤∈=--Z ,{(,)||2,||2,,}B x y x y x y =≤≤∈Z ,所以由新定义集合A B ⊕可知,111,0x y =±=或110,1x y ==±.当111,0x y =±=时,123,2,1,0,1,2,3x x +=---,122,1,0,1,2y y +=--,所以此时A B ⊕中元素的个数有:7535⨯=个;当110,1x y ==±时,122,1,0,1,2x x +=--,123,2,1,0,1,2,3y y +=---,这种情形下和第一种情况下除12y y +的值取3-或3外均相同,即此时有5210⨯=,由分类计数原理知,A B ⊕中元素的个数为351045+=个,故应选C .26.A 【解析】{}|13A x x x =-≤或≥,故A B =[-2, -1]. 27.D 【解析】{}|12N x x =≤≤,∴M N ={1,2}. 28.B 【解析】∵{}1,2B =-,∴A B ={}2.29.C 【解析】|1|213x x -<⇒-<<,∴(1,3)A =-,[1,4]B =.∴[1,3)AB =. 30.C 【解析】∵(0,2)A =,[1,4]B =,所以A B =[1,2).31.C 【解析】{}{}{}1,0,10,1,21,0,1,2M N ⋃=-⋃=-,选C .32.A 【解析】P Q =}{34x x ≤<.33.B 【解析】由题意知{|2}U x N x =∈≥,{|A x N x =∈,所以U A ð={|2x N x ∈<≤,选B .34.C 【解析】∵{}{}2|200,2A x x x =-==.∴A B =={}0,2.35.C 【解析】A B ={|23}x x <<.36.B 【解析】∵21x <,∴11x -<<,∴MN ={}|01x x <≤,故选B . 37.C 【解析】{}|3,3A x x =-<,{}|15R B x x x =->≤或ð,∴()R A B =ð{}|31x x --≤≤.38.D 【解析】由已知得,{=0AB x x ≤或}1x ≥,故()U A B =ð{|01}x x <<. 39.A 【解析】{|12}A x x =-≤≤,Z B =,故AB ={1,0,1,2}-.40.C 【解析】{}2,4,7U A =ð. 41.C 【解析】“存在集合C 使得,U A C B C ⊆⊆ð”⇔“∅=B A ”,选C . 42.B 【解析】A =(-∞,0)∪(2,+∞),∴A B =R ,故选B .43.A 【解析】{}1,4,9,16B =,∴{}1,4AB =. 44.A 【解析】∵(1,3)M =-,∴{}0,1,2M N =.45.C 【解析】因为{31}M x x =-<<,{3,2,1,0,1}N =---,所以M N {2,1,0}=--,选C .46.A 【解析】由题意{}1,2,3A B =,且{1,2}B =,所以A 中必有3,没有4,{}3,4U B =ð,故U A B =ð{}3. 47.C 【解析】0,0,1,2,0,1,2x y x y ==-=--;1,0,1,2,1,0,1x y x y ==-=-;2,0,1,2,2,1,0x y x y ==-=.∴B 中的元素为2,1,0,1,2--共5个.48.A 【解析】A :1->x ,{|1}R A x x =-≤ð,(){1,2}R A B =--ð,所以答案选A 49.D 【解析】由集合A ,14x <<;所以(1,2]AB =. 50.B 【解析】集合B 中含-1,0,故{}1,0A B =-.51.A 【解析】∵{}2,0S =-,{}0,2T =,∴ST ={}0. 52.B 【解析】特殊值法,不妨令2,3,4x y z ===,1w =,则()(),,3,4,1y z w S =∈,()(),,2,3,1x y w S =∈,故选B .如果利用直接法:因为(),,x y z S ∈,(),,z w x S ∈,所以x y z <<…①,y z x <<…②,z x y <<…③三个式子中恰有一个成立;z w x <<…④,w x z <<…⑤,x z w <<…⑥三个式子中恰有一个成立.配对后只有四种情况:第一种:①⑤成立, 此时w x y z <<<,于是(),,y z w S ∈,(),,x y w S ∈;第二种:①⑥成立,此时x y z w <<<,于是(),,y z w S ∈,(),,x y w S ∈;第三种:②④成立,此时y z w x <<<,于是(),,y z w S ∈,(),,x y w S ∈;第四种:③④成立,此时z w x y <<<,于是(),,y z w S ∈,(),,x y w S ∈.综合上述四种情况,可得(),,y z w S ∈,(),,x y w S ∈.53.D 【解析】()f x 的定义域为M =[-1,1],故R M ð=(,1)(1,)-∞-⋃+∞,选D54.A 【解析】当0a =时,10=不合,当0a ≠时,0∆=,则4a =.55.C 【解析】[)0,A =+∞,[]2,4B =,∴[0,2)(4,)R AB =+∞ð. 56.A 【解析】U M ð={,,}246.57.D 【解析】{}3,4,5Q =,∴U Q ð={}1,2,6,∴U P Q ð={}1,2. 58.D 【解析】由M ={1,2,3,4},N ={-2,2},可知-2∈N ,但是-2∉M ,则N ⊄M ,故A 错误.∵M N ={1,2,3,4,-2}≠M ,故B 错误.M∩N ={2}≠N ,故C 错误,D 正确.故选D .59.B 【解析】A =(-1,2),故B ⊂≠A ,故选B .60.D 【解析】{3213}[1,2]A x x =-≤-≤=-,(1,)(1,2]B A B =+∞⇒=.61.C 【解析】根据题意容易看出x y +只能取-1,1,3等3个数值.故共有3个元素.62.D 【解析】{|1}P x x =< ∴{|1}R P x x =≥ð,又∵{|1}Q x x =>,∴R Q P ⊆ð,故选D .63.B 【解析】{1,3}P MN ==,故P 的子集有4个. 64.C 【解析】因为P M P =,所以M P ⊆,即a P ∈,得21a ≤,解得11a -≤≤,所以a 的取值范围是[1,1]-.65.D 【解析】因为{1,2,3,4}M N =,所以()()U U M N 痧=()U M N ð={5,6}.66.B 【解析】因为U M N ⊂ð,所以()()()U U U U N NM N M ==痧痧 =[()]U U N M 痧={1,3,5}.67.C 【解析】由2211x y x y ⎧+=⎨+=⎩消去y ,得20x x -=,解得0x =或1x =,这时1y = 或0y =,即{(0,1),(1,0)}A B =,有2个元素.68.A 【解析】集合{1,0,1}{0,1,2}={0,1}MN =-. 69.C 【解析】对于集合M ,函数|cos 2|y x =,其值域为[0,1],所以[0,1]M =,根据复<21x <,所以(1,1)N =-,则[0,1]M N =.70.A 【解析】根据题意可知,N 是M 的真子集,所以MN M =. 71.C 【解析】{}{}{}1,2,32,3,42,3M N ==故选C.72.D 【解析】{}{}|1,|12R R B x x A B x x ==痧≥≤≤73.B 【解析】{}22<<x x Q -=,可知B 正确, 74.A 【解析】不等式121log 2x …,得12112201log log ()2x >⎧⎪⎨⎪⎩…,得2x …, 所以R A ð=2(,0],⎛⎫-∞+∞ ⎪ ⎪⎝⎭. 75.D 【解析】因为{3}A B =,所以3∈A ,又因为{9}U B A =ð,所以9∈A ,所以选D .本题也可以用Venn 图的方法帮助理解.76.{1,8}【解析】由集合的交运算可得A B ={1,8}.77.1【解析】由题意1B ∈,显然1a =,此时234a +=,满足题意,故1a =.78.5【解析】{1,2,3}{2,4,5}{1,2,3,4,5}A B ==,5个元素.79.{1,2,3}【解析】{2}U B =ð,A (U B ð)={1,2,3}. 80.{}1,3-【解析】=B A {}1,3-.81.{}7,9【解析】{}1,2,3,4,5,6,7,8,9,10U =,{}4,6,7,9,10U A =ð,{}()7,9U A B =ð. 82.6【解析】因为①正确,②也正确,所以只有①正确是不可能的;若只有②正确,①③④都不正确,则符合条件的有序数组为(2,3,1,4),(3,2,1,4);若只有③正确,①②④都不正确,则符合条件的有序数组为(3,1,2,4);若只有④正确,①②③都不正确,则符合条件的有序数组为(2,1,4,3),(3,1,4,2),(4,1,3,2).综上符合条件的有序数组的个数是6.83.{}6,8【解析】()U A B ð={6,8}{2,6,8}{6,8}=.84.【解析】(1)5 根据k 的定义,可知1131225k --=+=;(2)12578{,,,,}a a a a a 此时211k =,是个奇数,所以可以判断所求集中必含元素1a ,又892,2均大于211,故所求子集不含910,a a ,然后根据2j (j =1,2,⋅⋅⋅7)的值易推导出所求子集为12578{,,,,}a a a a a .85.1【解析】考查集合的运算推理.3∈B ,23a +=,1a =.。
理科数学2010-2018高考真题分类训练:专题七不等式第二十讲二元一次不等式(组)与简单的线性规划问题

A. 7
B. 6
C. 5
D. 3
19.( 2013 陕西)若点 (x, y) 位于曲线 y = |x|与 y = 2 所围成的封闭区域,则 2x- y 的最小值
为
A .- 6
B.- 2
C.0
D.2
x y 8,
2 y x 4,
20.( 2013 四川)若变量 x, y 满足约束条件
唯.一.,则实数 a 的值为(
)
1 A. 或 1
2
1 B. 2或
2
2
16.( 2014 福建)已知圆 C : x a
C. 2 或 1
D. 2或 1
2
y b 1,设平面区域
x y 7 0, x y 7 0, ,若圆 y0
心C
,且圆 C 与 x 轴相切,则 a 2 b2 的最大值为
A . 5 B. 29 C.37
3
2
12
B(吨)
1
2
8
A . 12 万元
B. 16 万元
C.17 万元
D . 18 万元
11.( 2015 天津) 设变量 x, y 满足约束条件
x20 x y 3 0 ,则目标函数 z x 6y 的最大 2x y 3 0
值为
A.3
B.4
C. 18
D . 40
12.( 2015 福建)若变量 x, y 满足约束条件
获取更多数学资源
为
A. 4
B.6
C . 10
D. 17
10.( 2015 陕西) 某企业生产甲、 乙两种产品均需用 A, B 两种原料, 已知生产 1 吨每种产品
需原料及每天原料的可用限额如表所示,如果生产
专题七不等式第二十一讲不等式综合应用十年高考数学(文科)真题题型分类汇编

专题七不等式第二十一讲不等式综合应用2019年1(. 2019天津文13)设x0,y 0,x 2y4 (x1)(2 1)y的最小值为__________.,则xy2010-2018年一、选择题1.(2018北京)设会合A{(x,y)|xy≥1,axy 4,x ay≤2},则 A .对随意实数a ,(2,1)A B .对随意实数a ,(2,1) AC .当且仅当a0时,(2,1)AD .当且仅当a≤3 时, (2,1) A22.(2018浙江)已知a 1,a 2,a 3,a 4成等比数列,且a 1a 2a 3 a 4ln(a 1 a 2 a 3).若 a 11,则A .a1a 3,a 2 a 4B .a 1 a 3,a 2a 4C .a 1 a 3,a 2a 4D .a 1 a 3,a 2 a 4|x | 2,x 1,R ,若对于x 的不等式f(x)≥|xa| 3.(2017天津)已知函数 f(x) x 设a 2,x≥1. 2x在R 上恒建立,则a 的取值范围是A .[ 2,2]B .[ 2 3,2]C .[ 2,23]D .[ 23,2 3] 4.(2015福建)若直线 x y1(a 0,b 0) 过点(1,1),则ab 的最小值等于 a bA .2B .3 C .4 D .55.(2015湖南)若实数 a,b 知足 1 2 ab ,则ab 的最小值为 a bA .2B .2C .22D .4 6.(2014重庆)若log (43a 4b )log 2 ab,则a b 的最小值是A .623B .723C .643D .743.( 2013 福建)若 2 x 2 y 1 ,则 x y 的取值范围是7A .[0,2]B .[2,0]C .[2, )D .(,2]8.(2013 山东)设正实数x,y,z 知足x 2 3xy 4y 2z 0.则当xy获得最大值时, z2 12x y 的最大值为zA .0B .1 9D .3C .49.(2013 山东)设正实数 x,y,z 知足x 23xy 4y 2z 0,则当 z 获得最大值时,x y2yz 的最大值为A .0B . 9C .2D . 98 410 2012 浙江)若正数x,y 知足 x 3y5xy ,则 3x 4y 的最小值是.(24 28 C .5 D .6A .B . 5 5 a 和v , .( 2012 陕西)小王从甲地到乙地的时速分别为 b ( ab ),其全程的均匀时速为 11则A .avab B .v=abC .ab<v<abD .v=ab8 22 12.(2012湖南)已知两条直线l 1:y m 和l 2:y (m0),l 1与函数y log2x的2m 1 图像从左至右订交于点A,B ,l 2与函数y log 2x 的图像从左至右订交于 C,D .记线段AC 和BD 在x 轴上的投影长度分别为 a,b ,当m 变化时,b 的最小值为 aA .162 B.82C.834D.43413.(2011陕西)设0a b ,则以下不等式中正确的选项是A .a b ab a bB .a ab a b2 2 bC .aabb a bD .aba a b b2214.(2011上海)若a,b R,且ab0,则以下不等式中,恒建立的是A.a2b22ab B.a b2abC.112D.b a2a b ab a b二、填空题15.(2018天津)已知a,b R,且a3b60,则2a1的最小值为.b816.(2018天津)已知,函数f(x)x22xa2,x≤0,3,),aR x2若对随意x[2x2a,x0.f(x)≤|x|恒建立,则a的取值范围是____.17.(2017天津)若a,b R,ab0,则a44b41的最小值为.ab18.(2017山东)若直线x y1(a>0,b>0)过点(1,2),则2ab的最小值为.a b19.(2017江苏)某企业一年购置某种货物600吨,每次购置x吨,运费为6万元/次,一年的总储存花费为4x 万元,要使一年的总运费与总储存费之和最小,则x的值是.20.(2017北京)可以说明“设a,b,c是随意实数.若a b c,则ab c”是假命题的一组整数a,b,c的值挨次为____________________.21.(2017浙江)已知a R,函数f(x)|x4a|a在区间[1,4]上的最大值是5,则xa的取值范围是.22.(2017江苏)在平面直角坐标系xOy中,A(12,0),B(0,6),点P在圆O:x2y250上,若PA PB≤20,则点P的横坐标的取值范围是.23.(2015重庆)设a,b0,a b 5,则a1+b+3的最大值为________.24.(2015山东)定义运算“”:x y x2y2(x,y R,xy0).当x0,xyy0时,x y(2y)x的最小值为.25.(2014浙江)已知实数a,b,c知足a bc0,a2b2c21,则a的最大值是__;26.(2014辽宁)对于c 0,当非零实数a,b知足4a22ab b2c0,且使|2a b|最大时,124的最小值为.a b c27 2014c 0 ,当非零实数a , b 4a 22ab 2c 0 |2a b|.(辽宁)对于 知足,且使最大时,345的最小值为.a b c28.(2014湖北)某项研究表示:在考虑行车安全的状况下,某路段车流量F(单位时间内经过丈量点的车辆数,单位:辆/小时)与车流速度v(假定车辆以同样速度v行驶,单位:米/秒)、均匀车长l(单位:米)的值相关,其公式为Fv276000v.18v20l(Ⅰ)假如不限制车型,l,则最大车流量为辆/小时;(Ⅱ)假如限制车型,l5,则最大车流量比(Ⅰ)中的最大车流量增添辆/小时.29.(2013天津)设a+b=2,b>0,则当a=时,1|a|获得最小值.2|a|b302013四川)已知函数f(x)4xa(x0,a0)在x3时获得最小值,则a__..(x31.(2011浙江)若实数x,y知足x2y2xy1,则xy的最大值是____.32.(2011湖南)设x,y R,则(x212)(124y2)的最小值为.y x33.(201安徽)若a0,b0,a b2,则以下不等式对全部知足条件的a,b恒建立的是(写出全部正确命题的编号).①ab1;②a b2;③a2b22;④a3b33;⑤112.a b。
2018年全国各地高考数学分类汇编word版含答案7-不等式

2018年全国各地高考数学分类汇编word版含答案7-不等式一、选择题(共5小题;共25分)1. 设变量x,y满足约束条件x+y≤5,2x−y≤4,−x+y≤1,y≥0,则目标函数z=3x+5y的最大值为 A. 6B. 19C. 21D. 452. 设x∈R,则“x3>8”是“ x >2”的 A. 充分而不必要条件B. 必要而不充分条件C. 充要条件D. 既不充分也不必要条件3. 设x∈R,则“x−12<12”是“x3<1”的 A. 充分而不必要条件B. 必要而不充分条件C. 充要条件D. 既不充分也不必要条件4. 设集合A=x,y x−y≥1,ax+y>4,x−ay≤2,则 A. 对任意实数a,2,1∈AB. 对任意实数a,2,1∉AC. 当且仅当a<0时,2,1∉AD. 当且仅当a≤32时,2,1∉A5. 已知a1,a2,a3,a4成等比数列,且a1+a2+a3+a4=ln a1+a2+a3.若a1>1,则A. a1<a3,a2<a4B. a1>a3,a2<a4C. a1<a3,a2>a4D. a1>a3,a2>a4二、填空题(共7小题;共35分)6. 若变量x,y满足约束条件2x+y+3≥0,x−2y+4≥0,x−2≤0,则z=x+13y的最大值是.7. 若x,y满足约束条件x−2y−2≤0,x−y+1≥0,y≤0,则z=3x+2y的最大值为.8. 若x,y满足约束条件x−y≥0,2x+y≤6,x+y≥2,则z=x+3y的最小值是,最大值是.9. 已知a,b∈R,且a−3b+6=0,则2a+18的最小值为.10. 在△ABC中,角A,B,C所对的边分别为a,b,c,∠ABC=120∘,∠ABC的平分线交AC于点D,且BD=1,则4a+c的最小值为.11. 若x,y满足x+1≤y≤2x,则2y−x的最小值是.12. 已知a∈R,函数f x=x2+2x+a−2,x≤0−x2+2x−2a,x>0.若对任意x∈−3,+∞,f x≤ x 恒成立,则a的取值范围是.三、解答题(共2小题;共26分)13. 某群体的人均通勤时间,是指单日内该群体中成员从居住地到工作地的平均用时.某地上班族 S中的成员仅以自驾或公交方式通勤.分析显示:当 S 中 x % 0<x <100 的成员自驾时,自驾群体的人均通勤时间为 f x = 30,0<x ≤302x +1800x −90,30<x <100(单位:分钟),而公交群体的人均通勤时间不受 x 影响,恒为 40 分钟.试根据上述分析结果回答下列问题:(1)当 x 在什么范围内时,公交群体的人均通勤时间少于自驾群体的人均通勤时间?(2)求该地上班族 S 的人均通勤时间 g x 的表达式;讨论 g x 的单调性,并说明其实际意义.14. 设 a n 是首项为 a 1,公差为 d 的等差数列, b n 是首项为 b 1,公比为 q 的等比数列.(1)设 a 1=0,b 1=1,q =2,若 a n −b n ≤b 1 对 n =1,2,3,4 均成立,求 d 的取值范围;(2)若 a 1=b 1>0,m ∈N ∗,q ∈ 1, 2m,证明:存在 d ∈R ,使得 a n −b n ≤b 1 对n =2,3,⋯,m +1 均成立,并求 d 的取值范围(用 b 1,m ,q 表示).答案第一部分1. C2. A3. A4. D5. B第二部分 6. 37. 68. −2,89. 1410. 911. 312. 18,2第三部分13. (1) 由题意 2x +1800x −90>40,因为 30<x <100,解得 45<x <100.(2) 当 0<x ≤30 时,g x =30⋅x %+40 1−x % =40−x 10; 当 30<x <100 时,g x = 2x +1800−90 ⋅x %+40 1−x % =x 2−13x +58, 所以 g x = 40−x 10,0<x ≤30x 250−1310x +58,30<x <100. 当 0<x <32.5 时,g x 单调递减;当 32.5≤x <100 时,g x 单调递增.说明当 S 中有少于 32.5% 的成员自驾时,通勤时间人均递减;当自驾成员大于 32.5% 时,人均通勤时间递增;当自驾成员为 32.5% 时,人均通勤时间最少.14. (1) 由条件知:a n = n −1 d ,b n =2n−1.因为 a n −b n ≤b 1 对 n =1,2,3,4 均成立,即 n −1 d −2n−1 ≤1 对 n =1,2,3,4 均成立,即1≤1,1≤d≤3,3≤2d≤5,7≤3d≤9,得73≤d≤52.因此,d的取值范围为73,52.(2)由条件知:a n=b1+n−1d,b n=b1q n−1.若存在d,使得a n−b n ≤b1n=2,3,⋯,m+1成立,即b1+n−1d−b1q n−1 ≤b1n=2,3,⋯,m+1,即当n=2,3,⋯,m+1时,d满足q n−1−2n−1b1≤d≤q n−1n−1b1.因为q∈1,2m,则1<q n−1≤q m≤2,从而q n−1−2n−1b1≤0,q n−1n−1b1>0,对n=2,3,⋯,m+1均成立.因此,取d=0时,a n−b n ≤b1对n=2,3,⋯,m+1均成立.下面讨论数列q n−1−2n−1的最大值和数列q n−1n−1的最小值(n=2,3,⋯,m+1).①当2≤n≤m时,q n−2n−q n−1−2n−1=nq n−q n−nq n−1+2n n−1=n q n−q n−1−q n+2n n−1,当1<q≤21时,有q n≤q m≤2,从而n q n−q n−1−q n+2>0 .因此,当2≤n≤m+1时,数列q n−1−2n−1单调递增,故数列q n−1−2n−1的最大值为q m−2m.②设f x=2x1−x,当x>0时,fʹx=ln2−1−x ln22x<0,所以f x单调递减,从而f x<f0=1.当2≤n≤m时,q nnq n−1=q n−1n≤21n1−1n=f1n<1,因此,当2≤n≤m+1时,数列q n−1n−1单调递减,故数列q n−1n−1的最小值为q mm.因此,d的取值范围为b1q m−2m ,b1q mm.。
2018年全国卷文科数学十年真题分类汇编 不等式

不等式一.基础题组1. 【2011全国1,文4】若变量x ,y 满足约束条件,则的最小值为( )(A )17 (B )14 (C )5 (D )3 【答案】C【解析】选C.作出不等式组表示的可行域,从图中不难得到当直线过直线x=1与x-3y=-2的交点(1,1)时取得最小值,所以最小值为5.2. 【2010全国1,文3】若变量x , y 满足约束条件则z =x -2y 的最大值为( )A .4B .3C .2D .1 【答案】:B3. 【2014全国1,文15】设函数则使得成立的的取值范围是________.【答案】63-21x y x y x +≤⎧⎪-≤⎨⎪≥⎩=23z x y +=23z x y +1020y x y x y ≤⎧⎪+≥⎨⎪--≤⎩()113,1,,1,x e x f x x x -⎧<⎪=⎨⎪≥⎩()2f x ≤(,8]-∞【解析】由于题中所给是一个分段函数,则当时,由,可解得:,则此时:;当时,由,可解得:,则此时:,综合上述两种情况可得:4. 【2012全国1,文14】若x ,y 满足约束条件则z =3x -y 的最小值为__________.【答案】:-1【解析】:由题意画出可行域,由z =3x -y 得y =3x -z ,要使z 取最小值,只需截距最大即可,故直线过A (0,1)时,z 最大.∴z max =3×0-1=-1.5. 【2010全国1,文13】不等式>0的解集是__________.,【答案】:{x |-2<x <-1,或x >2}6. 【2008全国1,文13】若满足约束条件则的最大值为 .【答案】9【解析】如图,作出可行域,作出直线l 0:y=2x ,将l 0平移至过点A 处时,函数z=2x-y 有最大值9.1x <12x e-≤1ln 2x ≤+1x <1x ≥132x ≤328x ≤=18x ≤≤(,8]x ∈-∞10,30,330,x y x y x y -+≥⎧⎪+-≤⎨⎪+-≥⎩2232x x x -++x y ,03003x y x y x ⎧+⎪-+⎨⎪⎩,,,≥≥≤≤2z x y =-7. 【2015高考新课标1,文15】若x ,y 满足约束条件 ,则z =3x +y 的最大值为 .【答案】4考点:简单线性规划解法8. 【2017新课标1,文7】设x ,y 满足约束条件则z =x +y 的最大值为,A .0B .1C .2D .3【答案】D 【解析】试题分析:如图,作出不等式组表示的可行域,则目标函数经过时z 取得最大值,故,故选D .20210220x y x y x y +-≤⎧⎪-+≤⎨⎪-+≥⎩33,1,0,x y x y y +≤⎧⎪-≥⎨⎪≥⎩z x y =+(3,0)A max 303z =+=二.能力题组1. 【2014全国1,文11】设,满足约束条件且的最小值为7,则(A )-5 (B )3 (C )-5或3, (D )5或-3 【答案】B【解析】根据题中约束条件可画出可行域如下图所示,两直线交点坐标为:,又由题中可知,当时,z 有最小值:,则,解得:;当时,z 无最小值.故选By ,1,x y a x y +≥⎧⎨-≤-⎩z x ay =+a =11(,)22a a A -+z x ay =+0a >21121222a a a a z a -++-=+⨯=22172a a +-=3a =0a<2. 【2009全国卷Ⅰ,文3】不等式||<1的解集为…( ) A.{x|0<x <1}∪{x|x >1} B.{x|0<x <1} C.{x|-1<x <0} D.{x|x <0} 【答案】:D3. 【2007全国1,文6】下面给出的四个点中,位于表示的平面区域内的点是( )A. B. C. D. 【答案】:C【解析】:将四个点的坐标分别代入不等式组,解可得,满足条件的是(0,-2),故选C .4. 【2013课标全国Ⅰ,文14】设x ,y 满足约束条件则z =2x -y 的最大值为______.,【答案】:3【解析】:画出可行域如图所示.画出直线2x -y =0,并平移,当直线经过点A (3,3)时,z 取最大值,且最大值为z =2×3-3=3.11-+xx 1010x y x y +-<⎧⎨-+>⎩(0,2)(2,0)-(0,2)-(2,0)1010x y x y +-<⎧⎨-+>⎩13,10,x x y ≤≤⎧⎨-≤-≤⎩5. 【2011新课标,文14】若变量满足约束条件,则的最小值为 .【答案】-6【解析】画出不等式组表示的平面区域,平移目标函数表示的直线,不难求出最小值为-6. 三.拔高题组1. 【2012全国1,文11】已知x =ln π,y =log 52,,则( )A .x <y <zB . z <x <yC .z <y <xD .y <z <x 【答案】D【解析】∵x =ln π>1,y =log 52>, ,且<e 0=1,∴y <z <x .2. 【2005全国1,文9】在坐标平面上,不等式组所表示的平面区域的面积为,(A) (B )(C )(D )2【答案】B 【解析】3.【2016新课标1文数】某高科技企业生产产品A 和产品B 需要甲、乙两种新型材料.生产一件产品A 需要,x y 32969x y x y ≤+≤⎧⎨≤-≤⎩2z x y =+12=ez -1log 2=121e2z -==>=12e -131y x y x ≥-⎧⎪⎨≤-+⎪⎩223223甲材料1.5 kg ,乙材料1 kg ,用5个工时;生产一件产品B 需要甲材料0.5 kg ,乙材料0.3 kg ,用3个工时,生产一件产品A 的利润为2100元,生产一件产品B 的利润为900元。
2010-2018年高考文科数学真题-集合(含解析)

九年(2010-2018年)高考真题文科数学精选(含解析)专题一 集合与常用逻辑用语第一讲 集合一、选择题1.(2018全国卷Ⅰ)已知集合{0,2}=A ,{21012}=--,,,,B ,则A B =A .{0,2}B .{1,2}C .{0}D .{21012}--,,,, 2.(2018浙江)已知全集{1,2,3,4,5}U =,{1,3}A =,则=U A ðA .∅B .{1,3}C .{2,4,5}D .{1,2,3,4,5}3.(2018全国卷Ⅱ)已知集合{}1,3,5,7A =,{}2,3,4,5B =,则AB = A .{3} B .{5}C .{3,5}D .{}1,2,3,4,5,74.(2018北京)已知集合{|||2}A x x =<,{2,0,1,2}B =-,则A B =A .{0,1}B .{–1,0,1}C .{–2,0,1,2}D .{–1,0,1,2}5.(2018全国卷Ⅲ)已知集合{|10}A x x =-≥,{0,1,2}B =,则AB = A .{0} B .{1}C .{1,2}D .{0,1,2}6.(2018天津)设集合{1,2,3,4}A =,{1,0,2,3}B =-,{|12}C x x =∈-<R ≤,则()AB C =A .{1,1}-B .{0,1}C .{1,0,1}-D .{2,3,4} 7.(2017新课标Ⅰ)已知集合{|2}A x x =<,{320}B x =->,则A .3{|}2AB x x =< B .A B =∅C .3{|}2A B x x =<D .A B =R8.(2017新课标Ⅱ)设集合{1,2,3}A =,{2,3,4}B =则A B =A .{1,2,3,4}B .{1,2,3}C .{2,3,4}D .{1,3,4}9.(2017新课标Ⅲ)已知集合{1,2,3,4}A =,{2,4,6,8}B =,则A B 中元素的个数为 A .1 B .2 C .3 D .410.(2017天津)设集合{1,2,6}A =,{2,4}B =,{1,2,3,4}C =,则()AB C =A .{2}B .{1,2,4}C .{1,2,4,6}D .{1,2,3,4,6}11.(2017山东)设集合{}11M x x =-<,{}2N x x =<,则M N = A .()1,1- B .()1,2- C .()0,2D .()1,2 12.(2017北京)已知U =R ,集合{|22}A x x x =<->或,则U A ð=A .(2,2)-B .(,2)(2,)-∞-+∞C .[2,2]-D .(,2][2,)-∞-+∞13.(2017浙江)已知集合{|11}P x x =-<<,{|02}Q x x =<<,那么P Q = A .(1,2)- B .(0,1) C .(1,0)- D .(1,2)14.(2016全国I 卷)设集合{1,3,5,7}A =,{|25}B x x =≤≤,则=A BA .{1,3}B .{3,5}C .{5,7}D .{1,7}15.(2016全国Ⅱ卷)已知集合{123}A =,,,2{|9}B x x =<,则A B =A .{210123}--,,,,,B .{21012}--,,,,C .{123},,D .{12},16.(2016全国Ⅲ)设集合{0,2,4,6,8,10},{4,8}A B ==,则A B ð=A .{48},B .{026},,C .{02610},,, D .{0246810},,,,, 17.(2015新课标2)已知集合}21|{<<-=x x A ,}30|{<<=x x B ,则A B =A .)3,1(-B .)0,1(-C .)2,0(D .)3,2( 18.(2015新课标1)已知集合{32,},{6,8,10,12,14}A x x n n N B ==+∈=,则集合A B 中的元素个数为 A .5 B .4 C .3 D .219.(2015北京)若集合{|52}A x x =-<<,{|33}B x x =-<<,则A B =A .{|32}x x -<<B .{|52}x x -<<C .{|33}x x -<<D .{|53}x x -<< 20.(2015天津)已知全集{1,2,3,4,5,6}U =,集合{}2,3,5A =,集合{1,3,4,6}B =,则集合U AB =ð A .{3} B .{2,5}C .{1,4,6}D .{2,3,5}21.(2015陕西)设集合2{|}M x x x ==,{|lg 0}N x x =≤,则M N = A .[0,1] B .(0,1] C .[0,1) D .(-∞,1]22.(2015山东)已知集合{}24A x x =<<,{}(1)(3)0B x x x =--<,则AB =A .()1,3B .()1,4C .()2,3D .()2,423.(2015福建)若集合{}22M x x =-≤<,{}0,1,2N =,则M N 等于 A .{}0 B .{}1 C .{}0,1,2 D .{}0,124.(2015广东)若集合{}1,1M =-,{}2,1,0N =-,则M N =A .{}0,1-B .{}1C .{}0D .{}1,1-25.(2015湖北)已知集合22{(,)|1,,}A x y x y x y Z =+∈≤,{(,)|||2,B x y x =≤ ||2,,}y x y Z ∈≤,定义集合12121122{(,)|(,),(,)}A B x x y y x y A x y B ⊕=++∈∈,则A B ⊕中元素的个数为A .77B .49C .45D .3026.(2014新课标)已知集合A ={x |2230x x --≥},B ={x |-2≤x <2},则A B = A .[-2, -1] B .[-1,1] C .[-1,2) D .[1,2)27.(2014新课标)设集合M ={0,1,2},N ={}2|320x x x -+≤,则M N = A .{1} B .{2} C .{0,1} D .{1,2}28.(2014新课标)已知集合A ={-2,0,2},B ={x |2x -x -20=},则A B =A . ∅B .{}2C .{}0D .{}2-29.(2014山东)设集合},]2,0[,2{},21{∈==<-=x y y B x x A x 则=B AA . [0,2]B .(1,3)C . [1,3)D . (1,4)30.(2014山东)设集合2{|20},{|14}A x x x B x x =-<=≤≤,则AB =A .(0,2]B .(1,2)C .[1,2)D .(1,4) 31.(2014广东)已知集合{1,0,1}M =-,{0,1,2}N =,则MN = A .{0,1} B .{1,0,2}- C .{1,0,1,2}- D .{1,0,1}-32.(2014福建)若集合{|24}P x x =<≤,{|3}Q x x =≥,则P Q 等于A .}{34x x ≤<B .}{34x x <<C .}{23x x ≤<D .}{23x x ≤≤33.(2014浙江)设全集{}2|≥∈=x N x U ,集合{}5|2≥∈=x N x A ,则U A ð= A .∅ B . }2{ C . }5{ D . }5,2{34.(2014北京)已知集合2{|20},{0,1,2}A x x x B =-==,则AB =A .{0}B .{0,1}C .{0,2}D .{0,1,2}35.(2014湖南)已知集合{|2},{|13}A x x B x x =>=<<,则A B =A .{|2}x x >B .{|1}x x >C .{|23}x x <<D .{|13}x x <<36.(2014陕西)已知集合2{|0},{|1,}M x x N x x x R =≥=<∈,则MN = A .[0,1] B .[0,1) C .(0,1] D .(0,1)37.(2014江西)设全集为R ,集合2{|90},{|15}A x x B x x =-<=-<≤,则()R A B =ðA .(3,0)-B .(3,1)--C .(3,1]--D .(3,3)-38.(2014辽宁)已知全集,{|0},{|1}U R A x x B x x ==≤=≥,则集合()U A B =ðA .{|0}x x ≥B .{|1}x x ≤C .{|01}x x ≤≤D .{|01}x x <<39.(2014四川)已知集合2{|20}A x x x =--≤,集合B 为整数集,则AB =A .{1,0,1,2}-B .{2,1,0,1}--C .{0,1}D .{1,0}-40.(2014湖北)已知全集{1,2,3,4,5,6,7}U =,集合{1,3,5,6}A =,则U A =ðA .{1,3,5,6}B .{2,3,7}C .{2,4,7}D . {2,5,7} 41.(2014湖北)设U 为全集,B A ,是集合,则“存在集合C 使得A C ⊆,U B C ⊆ð”是“∅=B A ”的A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件42.(2013新课标1)已知集合A ={x |x 2-2x >0},B ={x |-5<x <5},则A .A ∩B =∅ B .A ∪B =RC .B ⊆AD .A ⊆B 43.(2013新课标1)已知集合{1,2,3,4}A =,2{|,}B x x n n A ==∈,则AB =A .{}14,B .{}23,C .{}916,D .{}12, 44.(2013新课标2)已知集合(){}2|14,M x x x R =-<∈,{}1,0,1,2,3N =-,则M N =A .{}0,1,2B .{}1,0,1,2- C .{}1,0,2,3- D .{}0,1,2,3 45.(2013新课标2)已知集合{|31}M x x =-<<,{3,2,1,0,1}N =---,则MN =A .{2,1,0,1}--B .{3,2,1,0}---C .{2,1,0}--D .{3,2,1}---46.(2013山东)已知集合B A 、均为全集}4,3,2,1{=U 的子集,且(){4}U A B =ð,{1,2}B =,则U A B =ðA .{3}B .{4}C .{3,4}D .∅47.(2013山东)已知集合A ={0,1,2},则集合B ={}|,x y x A y A -∈∈中元素的个数是A .1B .3C .5D .948.(2013安徽)已知{}{}|10,2,1,0,1A x x B =+>=--,则()R C A B ⋂=A .{}2,1--B .{}2-C .{}1,0,1-D .{}0,149.(2013辽宁)已知集合{}{}4|0log 1,|2A x x B x x A B =<<=≤=,则A .()01,B .(]02,C .()1,2D .(]12, 50.(2013北京)已知集合{}1,0,1A =-,{}|11B x x =-≤<,则A B =A .{}0B .{}1,0-C .{}0,1D .{}1,0,1-51.(2013广东)设集合2{|20,}S x x x x R =+=∈,2{|20,}T x x x x R =-=∈,则S T =A .{0}B .{0,2}C .{2,0}-D .{2,0,2}-52.(2013广东)设整数4n ≥,集合{}1,2,3,,X n =,令集合{(,,)|,,S x y z x y z X =∈,且三条件,,x y z y z x z x y <<<<<<恰有一个成立},若(),,x y z 和(),,z w x 都在S 中,则下列选项正确的是A .(),,y z w S ∈,(),,x y w S ∉B .(),,y z w S ∈,(),,x y w S ∈C .(),,y z w S ∉,(),,x y w S ∈D .(),,y z w S ∉,(),,x y w S ∉53.(2013陕西)设全集为R , 函数()f x =M , 则C M R 为A . [-1,1]B . (-1,1)C .,1][1,)(∞-⋃+∞-D .,1)(1,)(∞-⋃+∞-54.(2013江西)若集合{}2|10A x R ax ax =∈++=中只有一个元素,则a =A .4B .2C .0D .0或455.(2013湖北)已知全集为R ,集合112x A x ⎧⎫⎪⎪⎛⎫=≤⎨⎬ ⎪⎝⎭⎪⎪⎩⎭,{}2|680B x x x =-+≤,则R A C B =A .{}|0x x ≤B .{}|24x x ≤≤C .{}|024x x x ≤<>或D .{}|024x x x <≤≥或 56.(2012广东)设集合{1,2,3,4,5,6},{1,3,5}U M ==;则U C M =A .{,,}246B .{1,3,5}C .{,,}124D .U57.(2012浙江)设全集{}1,2,3,4,5,6U =,设集合{}1,2,3,4P =,{}3,4,5Q =,则U P Q ⋂ð=A .{}1,2,3,4,6B .{}1,2,3,4,5C .{}1,2,5D .{}1,258.(2012福建)已知集合{1,2,3,4}M =,{2,2}N =-,下列结论成立的是A .N M ⊆B .M N M =C .MN N = D .{2}M N = 59.(2012新课标)已知集合2{|20}A x x x =--<,{|11}B x x =-<<,则A .AB Ü B .B A ÜC .A B =D .AB =∅ 60.(2012安徽)设集合A ={|3213x x --剟},集合B 为函数)1lg(-=x y 的定义域,则A ⋂B=A .(1,2)B .[1,2]C .[ 1,2)D .(1,2 ]61.(2012江西)若集合{1,1}A =-,{0,2}B =,则集合{|,,}z z x y x A y B =+∈∈中的元素的个数为A .5B .4C .3D .262.(2011浙江)若{|1},{|1}P x x Q x x =<=>-,则A .P Q ⊆B .Q P ⊆C .R C P Q ⊆D .R Q C P ⊆63.(2011新课标)已知集合M ={0,1,2,3,4},N ={1,3,5},P M N =⋂,则P 的子集共有A .2个B .4个C .6个D .8个64.(2011北京)已知集合P =2{|1}x x ≤,{}M a =.若P M P =,则a 的取值范围是A .(-∞, -1]B .[1, +∞)C .[-1,1]D .(-∞,-1][1,+∞) 65.(2011江西)若全集{1,2,3,4,5,6},{2,3},{1,4}U M N ===,则集合{5,6}等于A .M N ⋃B .M N ⋂C .()()n n C M C N ⋃D .()()n n C M C N ⋂66.(2011湖南)设全集{1,2,3,4,5}U M N =⋃=,{2,4}U M C N ⋂=,则N =A .{1,2,3}B .{1,3,5}C .{1,4,5}D .{2,3,4}67.(2011广东)已知集合A ={(,)|,x y x y 为实数,且221}x y +=,B ={(,)|,x y x y 为实数且1}x y +=,则A ⋂B的元素个数为A .4B .3C .2D .168.(2011福建)若集合M ={-1,0,1},N ={0,1,2},则M ∩N 等于A .{0,1}B .{-1,0,1}C .{0,1,2}D .{-1,0,1,2}69.(2011陕西)设集合{}22||cos sin |,M y y x x x R ==-∈,1{|||N x x i =-<}i x R ∈为虚数单位,,则M N ⋂为A .(0,1)B .(0,1]C .[0,1)D .[0,1]70.(2011辽宁)已知M ,N 为集合I 的非空真子集,且M ,N 不相等,若 N I M =∅ð,则=N MA .MB .NC .ID .∅71.(2010湖南)已知集合{}1,2,3M =,{}2,3,4N =,则A .M N ⊆B .N M ⊆C .{}2,3M N =D .{}1,4M N =72.(2010陕西)集合A ={}|12x x -≤≤,B ={}|1x x <,则()R A B ⋂ð=A .{}|1x x >B .{}|1x x ≥C .{}|12x x <≤D .{}|12x x ≤≤73.(2010浙江)设P ={x ︱x <4},Q ={x ︱2x <4},则A .P Q ⊆B .Q P ⊆C .R P Q ⊆ðD .R Q P ⊆ð 74.(2010安徽)若集合121log 2A x x ⎧⎫⎪⎪=≥⎨⎬⎪⎪⎩⎭,则A =R ð A .2(,0],⎛⎫-∞+∞⎪ ⎪⎝⎭ B .⎫+∞⎪⎪⎝⎭C .2(,0][,)-∞+∞ D .)+∞ 75.(2010辽宁)已知,A B 均为集合U ={1,3,5,7,9}的子集,且{3}AB =,{9}U B A =ð,则A =A .{1,3}B .{3,7,9}C .{3,5,9}D .{3,9}二、填空题76.(2018江苏)已知集合{0,1,2,8}A =,{1,1,6,8}B =-,那么A B = .77.(2017江苏)已知集合{1,2}A =,2{,3B a a =+},若{1}AB =,则实数a 的值为____. 78.(2015江苏)已知集合{}123A =,,,{}245B =,,,则集合A B 中元素的个数为 .79.(2015湖南)已知集合U ={}1,2,3,4,A ={}1,3,B ={}1,3,4,则A(U B ð)= . 80.(2014江苏)已知集合A ={4,3,1,2--},}3,2,1{-=B ,则=B A .81.(2014重庆)设全集{|110}U n N n =∈≤≤,{1,2,3,5,8}A =,{1,3,5,7,9}B =,则()U A B ⋂ð= .82.(2014福建)若集合},4,3,2,1{},,,{=d c b a 且下列四个关系:①1=a ;②1≠b ;③2=c ;④4≠d 有且只有一个是正确的,则符合条件的有序数组),,,(d c b a 的个数是_________.83.(2013湖南)已知集合{2,3,6,8},{2,3},{2,6,8}U A B ===,则()U A B ð= .84.(2010湖南)若规定{}1210,,...,E a a a =的子集{}12,,...,n i i i a a a 为E 的第k 个子集,其中k =12111222n i i i ---++⋅⋅⋅+,则(1){}1,3,a a 是E 的第____个子集;(2)E 的第211个子集是_______.85.(2010江苏)设集合{1,1,3}A =-,2{2,4}B a a =++,{3}A B =,则实数a =__.专题一 集合与常用逻辑用语第一讲 集合答案部分1.A 【解析】由题意{0,2}A B =,故选A .2.C 【解析】因为{1,2,3,4,5}U =,{1,3}A =,所以=U A ð{2,4,5}.故选C .3.C 【解析】因为{}1,3,5,7A =,{}2,3,4,5B =,所以{3,5}A B =,故选C .4.A 【解析】{|||2}(2,2)A x x =<=-,{2,0,1,2}B =-,∴{0,1}AB =,故选A .5.C 【解析】由题意知,{|10}A x x =-≥,则{1,2}AB =.故选C . 6.C 【解析】由题意{1,0,1,2,3,4}A B =-,∴(){1,0,1}A B C =-,故选C .7.A 【解析】∵3{|}2B x x =<,∴3{|}2AB x x =<, 选A . 8.A 【解析】由并集的概念可知,{1,2,3,4}AB =,选A . 9.B 【解析】由集合交集的定义{2,4}AB =,选B . 10.B 【解析】∵{1,2,4,6}A B =,(){1,2,4}A BC =,选B .11.C 【解析】{|02}M x x =<<,所以{|02}M N x x =<<,选C .12.C 【解析】{|22}U A x x =-≤≤ð,选C .13.A 【解析】由题意可知{|12}P Q x x =-<<,选A .14.B 【解析】由题意得,{1,3,5,7}A =,{|25}B x x=剟,则{3,5}A B =.选B . 15.D 【解析】易知{|33}B x x =-<<,又{1,2,3}A =,所以{1,2}AB =故选D . 16.C 【解析】由补集的概念,得{0,2,6,10}A B =ð,故选C .17.A 【解析】∵(1,2)A =-,(0,3)B =,∴(1,3)A B =-.18.D 【解析】集合{|32,}A x x n n N ==+∈,当0n =时,322n +=,当1n =时,325n +=,当2n =时,328n +=,当3n =时,3211n +=,当4n =时, 3214n +=,∵{6,8,10,12,14}B =,∴A B 中元素的个数为2,选D .19.A 【解析】{|32}A B x x =-<<.20.B 【解析】{2,5}U B ð=,∴U A B =ð{2,5}. 21.A 【解析】∵{0,1}M =,{|01}N x x ≤=<,∴M N =[0,1]. 22.C 【解析】因为{|13}B x x =<<,所以(2,3)AB =,故选C . 23.D 【解析】∵{0,1}MN =. 24.B 【解析】{1}M N =.25.C 【解析】由题意知,22{(,)1,,}{(1,0),(1,0),(0,1),(0,1)}A x y x y x y =+≤∈=--Z ,{(,)||2,||2,,}B x y x y x y =≤≤∈Z ,所以由新定义集合A B ⊕可知,111,0x y =±=或110,1x y ==±.当111,0x y =±=时,123,2,1,0,1,2,3x x +=---,122,1,0,1,2y y +=--,所以此时A B ⊕中元素的个数有:7535⨯=个;当110,1x y ==±时,122,1,0,1,2x x +=--,123,2,1,0,1,2,3y y +=---, 这种情形下和第一种情况下除12y y +的值取3-或3外均相同,即此时有5210⨯=,由分类计数原理知,A B ⊕中元素的个数为351045+=个,故应选C .26.A 【解析】{}|13A x x x =-≤或≥,故A B =[-2, -1]. 27.D 【解析】{}|12N x x =≤≤,∴M N ={1,2}. 28.B 【解析】∵{}1,2B =-,∴A B ={}2.29.C 【解析】|1|213x x -<⇒-<<,∴(1,3)A =-,[1,4]B =.∴[1,3)AB =. 30.C 【解析】∵(0,2)A =,[1,4]B =,所以A B =[1,2).31.C 【解析】{}{}{}1,0,10,1,21,0,1,2M N ⋃=-⋃=-,选C .32.A 【解析】P Q =}{34x x ≤<.33.B 【解析】由题意知{|2}U x N x =∈≥,{|A x N x =∈,所以U A ð={|2x N x ∈<≤,选B .34.C 【解析】∵{}{}2|200,2A x x x =-==.∴A B =={}0,2.35.C 【解析】A B ={|23}x x <<.36.B 【解析】∵21x <,∴11x -<<,∴M N ={}|01x x <≤,故选B .37.C 【解析】{}|3,3A x x =-<,{}|15R B x x x =->≤或ð,∴()R A B =ð{}|31x x --≤≤.38.D 【解析】由已知得,{=0A B x x ≤或}1x ≥,故()U A B =ð{|01}x x <<.39.A 【解析】{|12}A x x =-≤≤,Z B =,故AB ={1,0,1,2}-. 40.C 【解析】{}2,4,7U A =ð.41.C 【解析】“存在集合C 使得,U A C B C ⊆⊆ð”⇔“∅=B A ”,选C . 42.B 【解析】A =(-∞,0)∪(2,+∞),∴A B =R ,故选B .43.A 【解析】{}1,4,9,16B =,∴{}1,4AB =. 44.A 【解析】∵(1,3)M =-,∴{}0,1,2M N =.45.C 【解析】因为{31}M x x =-<<,{3,2,1,0,1}N =---,所以M N {2,1,0}=--,选C .46.A 【解析】由题意{}1,2,3A B =,且{1,2}B =,所以A 中必有3,没有4,{}3,4U B =ð,故U A B =ð{}3. 47.C 【解析】0,0,1,2,0,1,2x y x y ==-=--;1,0,1,2,1,0,1x y x y ==-=-;2,0,1,2,2,1,0x y x y ==-=.∴B 中的元素为2,1,0,1,2--共5个.48.A 【解析】A :1->x ,{|1}R A x x =-≤ð,(){1,2}R A B =--ð,所以答案选A 49.D 【解析】由集合A ,14x <<;所以(1,2]AB =. 50.B 【解析】集合B 中含-1,0,故{}1,0A B =-.51.A 【解析】∵{}2,0S =-,{}0,2T =,∴ST ={}0. 52.B 【解析】特殊值法,不妨令2,3,4x y z ===,1w =,则()(),,3,4,1y z w S =∈,()(),,2,3,1x y w S =∈,故选B .如果利用直接法:因为(),,x y z S ∈,(),,z w x S ∈,所以x y z <<…①,y z x <<…②,z x y <<…③三个式子中恰有一个成立;z w x <<…④,w x z <<…⑤,x z w <<…⑥三个式子中恰有一个成立.配对后只有四种情况:第一种:①⑤成立,此时w x y z <<<,于是(),,y z w S ∈,(),,x y w S ∈;第二种:①⑥成立,此时x y z w <<<,于是(),,y z w S ∈,(),,x y w S ∈;第三种:②④成立,此时y z w x <<<,于是(),,y z w S ∈,(),,x y w S ∈;第四种:③④成立,此时z w x y <<<,于是(),,y z w S ∈,(),,x y w S ∈.综合上述四种情况,可得(),,y z w S ∈,(),,x y w S ∈.53.D 【解析】()f x 的定义域为M =[-1,1],故R M ð=(,1)(1,)-∞-⋃+∞,选D54.A 【解析】当0a =时,10=不合,当0a ≠时,0∆=,则4a =.55.C 【解析】[)0,A =+∞,[]2,4B =,∴[0,2)(4,)R AB =+∞ð.56.A 【解析】U M ð={,,}246.57.D 【解析】{}3,4,5Q =,∴U Q ð={}1,2,6,∴U P Q ð={}1,2.58.D 【解析】由M ={1,2,3,4},N ={-2,2},可知-2∈N ,但是-2∉M ,则N ⊄M ,故A 错误.∵M N ={1,2,3,4,-2}≠M ,故B 错误.M∩N ={2}≠N ,故C 错误,D 正确.故选D .59.B 【解析】A =(-1,2),故B ⊂≠A ,故选B .60.D 【解析】{3213}[1,2]A x x =-≤-≤=-,(1,)(1,2]B A B =+∞⇒=.61.C 【解析】根据题意容易看出x y +只能取-1,1,3等3个数值.故共有3个元素.62.D 【解析】{|1}P x x =< ∴{|1}R P x x =≥ð,又∵{|1}Q x x =>,∴R Q P ⊆ð,故选D .63.B 【解析】{1,3}P MN ==,故P 的子集有4个. 64.C 【解析】因为P M P =,所以M P ⊆,即a P ∈,得21a ≤,解得11a -≤≤,所以a 的取值范围是[1,1]-.65.D 【解析】因为{1,2,3,4}M N =,所以()()U U M N 痧=()U M N ð={5,6}. 66.B 【解析】因为U M N ⊂ð,所以()()()U U U U N NM N M ==痧痧 =[()]U U N M 痧={1,3,5}.67.C 【解析】由2211x y x y ⎧+=⎨+=⎩消去y ,得20x x -=,解得0x =或1x =,这时1y =或0y =,即{(0,1),(1,0)}AB =,有2个元素. 68.A 【解析】集合{1,0,1}{0,1,2}={0,1}M N =-.69.C 【解析】对于集合M ,函数|cos 2|y x =,其值域为[0,1],所以[0,1]M =,根据复数模的计算方法得不<21x <,所以(1,1)N =-,则[0,1]M N =.70.A 【解析】根据题意可知,N 是M 的真子集,所以MN M =. 71.C 【解析】{}{}{}1,2,32,3,42,3M N ==故选C.72.D 【解析】{}{}|1,|12R R B x x A B x x ==痧≥≤≤73.B 【解析】{}22<<x x Q -=,可知B 正确,74.A 【解析】不等式121log 2x …,得12112201log log ()2x >⎧⎪⎨⎪⎩…,得x … 所以R A ð=2(,0],⎛⎫-∞+∞ ⎪ ⎪⎝⎭.75.D 【解析】因为{3}A B =,所以3∈A ,又因为{9}U B A =ð,所以9∈A ,所以选D .本题也可以用Venn图的方法帮助理解.76.{1,8}【解析】由集合的交运算可得A B ={1,8}.77.1【解析】由题意1B ∈,显然1a =,此时234a +=,满足题意,故1a =.78.5【解析】{1,2,3}{2,4,5}{1,2,3,4,5}A B ==,5个元素.79.{1,2,3}【解析】{2}U B =ð,A (U B ð)={1,2,3}.80.{}1,3-【解析】=B A {}1,3-.81.{}7,9【解析】{}1,2,3,4,5,6,7,8,9,10U =,{}4,6,7,9,10U A =ð,{}()7,9U A B =ð. 82.6【解析】因为①正确,②也正确,所以只有①正确是不可能的;若只有②正确,①③④都不正确,则符合条件的有序数组为(2,3,1,4),(3,2,1,4);若只有③正确,①②④都不正确,则符合条件的有序数组为(3,1,2,4);若只有④正确,①②③都不正确,则符合条件的有序数组为(2,1,4,3),(3,1,4,2),(4,1,3,2).综上符合条件的有序数组的个数是6.83.{}6,8【解析】()U A B ð={6,8}{2,6,8}{6,8}=.84.【解析】(1)5 根据k 的定义,可知1131225k --=+=;(2)12578{,,,,}a a a a a 此时211k =,是个奇数,所以可以判断所求集中必含元素1a ,又892,2均大于211,故所求子集不含910,a a ,然后根据2j(j =1,2,⋅⋅⋅7)的值易推导出所求子集为12578{,,,,}a a a a a . 85.1【解析】考查集合的运算推理.3∈B ,23a +=,1a =.。
文科数学2010-2019高考真题分类训练专题七不等式第二十讲二元一次不等式(组)与简单的线性规划问题答案

专题七 不等式第二十讲 二元一次不等式(组)与简单的线性规划问题答案部分 2019年1.解析 由约束条件23603020x y x y y +-+--⎧⎪⎨⎪⎩,,,………作出可行域如图:化目标函数3z x y =-为3y x z =-,由图可知,当直线3y x z =-过(3,0)A 时, 直线在y 轴上的截距最小,有最大值为9. 2.解析 作出约束条件表示的可行域,如图所示.yx4x-3y+1≥02-1ABO令z y x =-,则y x z =+,当此直线经过可行域内的点B 时,z y x =-取最小值;当此直线经过可行域内的点A 时,z y x =-取最大值.由24310x x y =⎧⎨-+=⎩,得()2,3A ,由12y x =-⎧⎨=⎩,得()2,1B -,所以()min 123y x -=--=-;()max 321y x -=-=.3.解析由约束条件202011x yx yxy+-⎧⎪-+⎪⎨-⎪⎪-⎩…………作出可行域如图:化目标函数4z x y=-+为4y x z=+,由图可知,当直线4y x z=+过A时,有最大值. 联立120xx y=-⎧⎨-+=⎩,解得()1,1A-. 所以的最大值为()()4115-⨯-+=.故选C.4.解析:作出340340x yx yx y-+≥⎧⎪--≤⎨⎪+≥⎩表示的平面区域,如图所示分别联立其中两个方程,得A(2,2),B(-1,1),C(1,-1),则max322210z=⨯+⨯=.故选C.2010-2018年1.D 【解析】解法一 点(2,1)在直线1x y -=上,4ax y +=表示过定点(0,4),斜率为a-的直线,当0a ≠时,2x ay -=表示过定点(2,0),斜率为1a的直线,不等式2x ay -≤表示的区域包含原点,不等式4ax y +>表示的区域不包含原点.直线4ax y +=与直线2x ay -=互相垂直,显然当直线4ax y +=的斜率0a ->时,不等式4ax y +>表示的区域不包含点(2,1),故排除A ;点(2,1)与点(0,4)连线的斜率为32-,当32a -<-,即32a >时,4ax y +>表示的区域包含点(2,1),此时2x ay -<表示的区域也包含点(2,1),故排除B ;当直线4ax y +=的斜率32a -=-,即32a =时,4ax y +>表示的区域不包含点(2,1),故排除C ,故选D .解法二 若(2,1)A ∈,则21422a a +>⎧⎨-⎩≤,解得32a >,所以当且仅当32a ≤时,(2,1)A ∉.故选D .2.C 【解析】不等式组表示的平面区域如图中阴影部分所示,作出直线35y x =-.平移该直线,当经过点C 时,z 取得最大值,由15x y x y -+=⎧⎨+=⎩, 得23x y =⎧⎨=⎩,即(2,3)C ,所以max 325321a =⨯+⨯=,故选C . 3.D 【解析】可行域如图阴影部分,由图可知,目标函数z x y =+过(3,0)点z 取最大值3.选D . 4.A 【解析】如图为可行域结合目标函数的几何意义可得函数在点()6,3B --处取得最小值,最小值为min 12315z =--=-.故选A .5.B 【解析】不等式组的可行域如图,目标函数的几何意义可得函数在点()0,3A 处取得最小值033z =-=- . 在点()2,0B 处取得最大值202z =-=,选B .x6.D 【解析】不等式组可行域如图阴影部分,当2z x y =+过(1,2)A -时取得最大值3,选D .7.D 【解析】如图阴影为可行域,可知在(2,1)A时,min 4z =,无最大值.x所以2z x y =+的取值范围是[4,)+∞.选D . 8.D 【解析】不等式组可行域如图阴影部分,xyCBA –1123–112O目标函数2z x y =+过点(3,3)C 时,取得最大值max 3239z =+⨯=,故选D. 9.C 【解析】作出不等式组所表示的平面区域如图中阴影部分所示,设(,)P x y 为平面区域内任意一点,则22x y +表示2||OP .显然,当点P 与点A 合时,2||OP ,即22x y +取得最大值,由2239x y x y +=⎧⎨-=⎩,解得31x y =⎧⎨=-⎩,故(3,1)A -.所以22x y +的最大值为223(1)10+-=.故选C .10.B 【解析】画出不等式组的平面区域如图所示,由23030x y x y -+=⎧⎨+-=⎩得(1,2)A ,由23030x y x y --=⎧⎨+-=⎩ 得(2,1)B ,由题意可知,当斜率为1的两条直线分别过点A 和点B 时,两直线的距离最小,即22||(12)(21)2AB =-+-=B .11.A 【解析】画出可行域(图略),可知在点(0,1)处z 取得最小值min 2011z =⨯-=-. 12.D 【解析】设该企业每天生产甲、乙两种产品分别为x 、y 吨,则利润34z x y =+.由题意可列32122800x y x y x y +≤⎧⎪+≤⎪⎨≥⎪⎪≥⎩,其表示如图阴影部分区域:当直线340x y z +-=过点(2,3)A 时,z 取得最大值, 所以max 324318z =⨯+⨯=,故选D .13.C 【解析】画出可行域(图略),可知目标函数在点(2,3)处有最大值9.14.B 【解析】由于不等式组2022020x y x y x y m +-≤⎧⎪+-≥⎨⎪-+≥⎩,表示的平面区域为三角形ABC ,且其面积等于43,再注意到直线AB :20x y +-=与直线BC 20x y m -+=互相垂直,所以ΔABC 是直角三角形;易知(2,0)A ,(1,1)B m m -+,C (2422,33m m -+); 从而112222122223ABC m S m m m ∆+=+⋅+-+⋅=43,化简得:2(1)4m +=,解得m =3-,或m =1;检验知当m =3-时,已知不等式组不能表示一个三角形区域,故舍去;所以m =1;故选B .15.B 【解析】作出可行域(图略)可知,目标函数过点(4,1)-时取最大值.16.A 【解析】作出满足条件的可行域,如图中阴影部分所示,易知在点(1,1)A 处,z 取得最大值,故max 2111z =-⨯+=-.17.C 【解析】 将目标函数变形为2y x z =-,当z 取最大值,则直线纵截距最小,故当0m ≤时,不满足题意;当0m >时,画出可行域,如图所示, 其中22(,)2121m B m m --.显然(0,0)O 不是最优解,故只能22(,)2121m B m m --是最优解,代入目标函数得4222121mm m -=--,解得1m =,故选C . 18.A 【解析】根据不等式组作出可行域,如图中阴影部分所示当动点在线段AC 上时xy 取得最大,此时2+y =10.21125(2))2222x y xy x y +=⋅≤=(. 当且仅当52x =,5y =时取等号,对应点落在线段AC 上.故最大值为252.故选A .19.C 【解析】画出可行域如图中阴影部分所示,由图可知,xy A –1–21234–11234O当目标函数2z x y =+经过可行域内的点A (2,1)时,取得最小值0,故20x y +≥,因此12,p p 是真命题,选C .20.D 【解析】画出约束条件表示的平面区域如图,xyx +y -2=0x -2y -2=02x -y +2=022-1-1Oax y z -=取得最大值表示直线ax y z -=向上平移移动最大,a 表示直线斜率,有两种情况:1a =-或2a =.21.C 【解析】平面区域Ω为如图所示的阴影部分的△ABD ,yxDNMy =-x +7y =x +312345–1–2–31234567OAB因圆心(,)C a b ∈Ω,且圆C 与x 轴相切,所以点C 在如图所示的线段MN 上,线段MN 的方程为1y =(2≤x ≤6),由图形得,当点C 在点(6,1)N 处时,22a b +取得最大值226137+=,故选C .22.D 【解析】作出线性约束条件20200x y kx y y +-≥⎧⎪-+≥⎨⎪≥⎩,的可行域.当0k >时,如图(1)所示,此时可行域为y 轴上方、直线20x y +-=的右上方、直线20kx y -+=的右下方的区域,显然此时z y x =-无最小值.当1k <-时.z y x =-取得最小值2;当1k =-时,z y x =-取得最小值-2,均不符合题意,当10k -<<时,如图(2)所示,此时可行域为点A (2,0),B (2k,0),C(0,2)所围成的三角形区域,当直线z y x =-经过点B (2k,0)时,有最小值,即2()4k --=-,所以得12k =-.故选D .23.B 【解析】由23z x y =-得32y x z =-,即233zy x =-.作出可行域如图,平移直线233z y x =-,由图象可知当直线233z y x =-经过点B 时,直线233zy x =-的截距最大,此时z 取得最小值,由103x y x -+=⎧⎨=⎩得34x y =⎧⎨=⎩,即(3,4)B ,代入直线23z x y=-得32346z =⨯-⨯=-,选B .24.A 【解析】2||==y x y 与的图像围成一个三角形区域,3个顶点的坐标分别是 (0,0),(2,2),(2,2).且当取点(2,2)时,2 – y =-6取最小值.所以选A .25.C 【解析】作出可行域,如图,则在A 点取得最大值16,在B 点取得最小值8-,则24a b-=,选C .26.B 【解析】约束条件对应ABC ∆边际及内的区域:53(2,2),(3,2),(,)22A B C则3[8,11]z x y =+∈.27.C 【解析】约束条件对应ABC ∆边际及内的区域:(1,0),(1,2),1,2)A B C ---则2[5,3]z x y =+∈-.28.A 【解析】作出可行域,直线03=-y x ,将直线平移至点)0,2(处有最大值,点)3,21(处有最小值,即362z -剟,应选A .29.B 【解析】由题意,230y xx y =⎧⎨+-=⎩,可求得交点坐标为(1,2)要使直线y =2上存在点(,y )满足约束条件30230x y x y x m +-⎧⎪--⎨⎪⎩………,如图所示.则m m 23≥-可得m ≤1,∴实数m 的最大值为1,故选B .30.B 【解析】做出不等式对应的可行域如图,由y x z 23-=得223zxy -=,由图象可知当直线223z x y -=经过点)2,0(C 时,直线223zx y -=的截距最大,而此时y x z 23-=最小为423-=-=y x z ,选B .31.D 【解析】作出可行域如图中阴影部分所示,由图知目标函数22=+y x 14-=-y x42=+y xO过点()5,15A 时,2+3x y 的最大值为55,故选D .32.B 【解析】画出区域D 如图所示,而=OM ·2x y +,所以2y x z =+,令0l :2y x =,平移直线0l 过点2,2)时,z 取得最大值,故max 2224z =.xy Oy=2x=2yx=233.B 【解析】如图先画出不等式||||1x y +≤表示的平面区域,易知当0x =,1y =时,2x y +取得最大值2,当0,1x y ==-时,2x y +取得最小值-2,选B .xy-22O34.A 【解析】 画出可行域,可知5z x y =+在点1(,)11mm m++取最大值, 由21211m m m+<++解得121m <<. 35.B 【解析】当直线=25y 过点B 时,min 14z =-,当直线=25y 过点D(0,4)时,max 20z =,所以=25y 的取值范围为(-14,20),点D 的坐标亦可利用AB DC =u u u r u u u r求得.xy –4–3–2–11234–11234OACBD36.A 【解析】作出满足约束条件的可行域,如右图所示,可知当直线z=34x y -平移到点(5,3)时,目标函数z=34x y -取得最大值3; 当直线z=34x y -平移到点(3,5)时,目标函数z=34x y -取得最小值11,故选A . 37.6【解析】作出可行域为如图所示的∆ABC 所表示的阴影区域,作出直线320+=x y ,并平移该直线,当直线过点(2,0)A 时,目标函数32z x y =+取得最大值:且max 32206=⨯+⨯=z .xyC BA x -y +1=03x +2y =0x -2y -2=0–1–2–3–4123–1–2–312O38.9【解析】画出不等式组所表示的平面区域,如图中阴影部分所示.作出直线0x y +=,平移该直线,当直线过点(5,4)B 时,z 取得最大值,max 549z =+=.=039.3【解析】易知13z x y =+在可行域的顶点取得最大值,由230240x y x y ++=⎧⎨-+=⎩, 解得21x y =-⎧⎨=⎩,代入13z x y =+,可得53z =-;由23020x y x ++=⎧⎨-=⎩,解得27x y =⎧⎨=-⎩,代入13z x y =+,可得13z =-;由20240x x y -=⎧⎨-+=⎩,解得23x y =⎧⎨=⎩,代入13z x y =+,可得3z =;可知,z 的最大值为3.40.3【解析】作出不等式组21y xx y⎧⎨+⎩≤≤,所表示的平面区域如图中阴影部分所示,yxOy=12x y=x+1y=2xA令2z y x =-,作出直线20y x -=,平移该直线,当直线过点(1,2)A 时,2y x -取得最小值,最小值为2213⨯-=.41.−2;8【解析】由题可得,该约束条件表示的平面区域是以(2,2),(1,1),(4,2)-为顶点的三角形及其内部区域(图略).由线性规划的知识可知,目标函数3z x y =+在点(2,2) 处取得最大值,在点(4,2)-处取得最小值,则最小值min 462z =-=-,最大值max 268z =+=.42.4[,13]5【解析】不等式组所表示的平面区域是以点(0,2),(1,0),(2,3)为顶点的三角形及其内部,如图所示,因为原点到直线220x y +-=的距离为5, 所以22min 4()5x y +=,又当(,)x y 取点(2,3)时,22x y +取得最大值13, 故22x y +的取值范围是4[,13]5.43.216000【解析】由题意,设产品A 生产x 件,产品B 生产y 件,利润2100900z x y =+,线性约束条件为 1.50.51500.390536000,0x y x y x y x y +⎧⎪+⎪⎨+⎪⎪⎩………厖,作出不等式组表示的平面区域如图中阴影部分所示,又由x N ∈,y N ∈,可知取得最大值时的最优解为(60,100), 所以max 210060900100216000z =⨯+⨯=(元).44.10-【解析】作出不等式组表示的平面区域,如图中阴影部分所示,由图知当235z x y =+-经过点(1,1)A --时,z 取得最小值, min 2(1)3(1)510z =⨯-+⨯--=-.45.7 【解析】 由目标函数23z x y =+的可行域为ΔABC 边界及其内部(如图所示).令0z =,即230x y +=,平移直线230x y +=至目标函数的可行域内,可知当23x y z +=过点(2,1)A 时,z 取得最大值,即max 22317z =⨯+⨯=.46.4 【解析】 作出可行域(图略),作出直线0l :30x y +=,平移直线0l ,当直线3z x y =+ 过点A 时,z 取最大值,由2=021=0x y x y +-⎧⎨-+⎩,解得A (1,1),∴3z x y =+的最大值为4.47.4【解析】如图阴影部分,可知12(22)42ABC S ∆=⨯⨯+= xy –2–11212345678O48.3[1,]2【解析】由线性规划的可行域,求出三个交点坐标分别为3(1,0),(1,),(2,1)2,都代入14ax y +≤≤,可得312a ≤≤.49.-2【解析】画出可行域(图略),由题意可知不等式组表示的区域为一三角形,平移参照直线20x y +=,可知在点(,)k k 处2z x y =+取得最小值,故26z k k =+=-. 解得2k =-.50.3【解析】做出可行域可知,当3,3x y ==的时候z 有最大值351.2【解析】此不等式表示的平面区域如图所示y kx z =-+.当k >0时,直线0l :y kx=-平移到A 点时目标函数取最大值,即当4k +4=12 所以k =2 ,当k <0时,直线:y kx =-平移到A 或B 点是目标函数取最大值,可知k 取值是大于零,所以不满足,所以k =2,所以填2.52.6【解析】画出可行区域,即为五边形区域,平移参照直线0x y +=,x y +在点(4,2)处取得最大值,此时()max 426x y +=+=.53.[3,3]-【解析】约束条件对应四边形OABC 边际及内的区域:(0,0),(0,1),(1,2),(3,0)O A B C 则2[3,3]z x y =-∈-.54.3【解析】画出可行域,可知5z x y =+在点1(,)11mm m++取最大值为4,解得3m = 55.1【解析】目标函数2z x y =-,当0x =时,z y =-,所以当y 取得最大值时,z 的值最小;移动直线20x y -=,当直线移动到过点A 时,y 最大,即z 的值最小,此时2111z =⨯-=.56.-6【解析】根据32969x y x y ≤+≤⎧⎨≤-≤⎩得可行域,根据2z x y =+得22x zy =-+,平移2xy =-,易知在点(4,5)-处z 取得最小值-6.57.4【解析】不等式表示的区域是一个四边形,4个顶点是1(0,0),(0,2),(,0),(1,4)2,易见目标函数在(1,4)取最大值8,所以844ab ab =+⇒=,所以24a b ab +≥=,在2a b ==时是等号成立.所以a b +的最小值为4..58.15【解析】设购买铁矿石A 和B 各x ,y 万吨,则购买铁矿石的费用y x z 63+=,x ,y 满足约束条件0.50.7 1.90.520,0x y x y x y +⎧⎪+⎨⎪⎩≥≤≥≥,表示平面区域(图略)则当直线y x z 63+=过点B (1,2)时,购买铁矿石的最少费用=15.59.【解析】(Ⅰ)由已知,,x y 满足的数学关系式为7060600,5530,2,0,0,x y x y x y x y +⎧⎪+⎪⎪⎨⎪⎪⎪⎩≤≥≤≥≥即7660,6,20,0,0,x y x y x y x y +⎧⎪+⎪⎪-⎨⎪⎪⎪⎩≤≥≤≥≥该二元一次不等式组所表示的平面区域为图1中的阴影部分:xx(图1) (图2)(Ⅱ)设总收视人次为万,则目标函数为6025z x y =+.考虑6025z x y =+,将它变形为12525z y x =-+,这是斜率为125-,随变化的一族平行直线.25z 为直线在y 轴上的截距,当25z取得最大值时,的值最大.又因为,x y 满足约束条件,所以由图2可知,当直线6025z x y =+经过可行域上的点M 时,截距25z最大,即最大. 解方程组7660,20,x y x y +=⎧⎨-=⎩得点M 的坐标为(6,3).所以,电视台每周播出甲连续剧6次、乙连续剧3次时才能使总收视人次最多.60.【解析】(Ⅰ)由已知y x ,满足的数学关系式为⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≥≤+≤+≤+003001033605820054y x y x y x y x ,该二元一次不等式组所表示的区域为图1中的阴影部分.(1)(Ⅱ)设利润为z 万元,则目标函数y x z 32+=,这是斜率为32-,随z 变化的一族平行直线.3z 为直线在y 轴上的截距,当3z取最大值时,z 的值最大.又因为y x ,满足约束条件,所以由图2可知,当直线y x z 32+=经过可行域中的点M 时,截距3z的值最大,即z 的值最大.解方程组⎩⎨⎧=+=+30010320054y x y x 得点M 的坐标为)24,20(M ,所以112243202max =⨯+⨯=z .答:生产甲种肥料20车皮,乙种肥料24车皮时利润最大,且最大利润为112万元.(2)61.【解析】设为该儿童分别预订,x y 个单位的午餐和晚餐,共花费元,则 2.54z x y =+,且满足以下条件⎪⎪⎩⎪⎪⎨⎧≥≥+≥+≥+0,54106426664812y x y x y x y x ,即⎪⎪⎩⎪⎪⎨⎧≥≥+≥+≥+0,275371623y x y x y x y x ,做出可行域(图略)作直线:2.540l x y +=,平移直线l 至0l ,当0l 经过C 点时,可使达到最小值.由⎩⎨⎧==⇒⎩⎨⎧=+=+3472753y x y x y x 即(4,3)C , 此时 2.544322z =⨯+⨯=,答 午餐和晚餐分别预定4个单位和3个单位,花费最少=22元.。
高考文科数学2010—18真题 专题七 不等式 第二十讲 二元一次不等式(组)与简单的线性规划问题(带答案)

专题七 不等式第二十讲 二元一次不等式(组)与简单的线性规划问题一、选择题1.(2018北京)设集合{(,)|1,4,2},A x y x y ax y x ay =-+>-≥≤则A .对任意实数a ,(2,1)A ∈B .对任意实数a ,(2,1)A ∉C .当且仅当0a <时,(2,1)A ∉D .当且仅当32a ≤时,(2,1)A ∉ 2.(2018天津)设变量x ,y 满足约束条件5,24,1,0,x y x y x y y +⎧⎪-⎪⎨-+⎪⎪⎩≤≤≤≥ 则目标函数35z x y =+的最大值为A . 6B .19C .21D .453.(2017新课标Ⅰ)设x ,y 满足约束条件3310x y x y y +⎧⎪-⎨⎪⎩≤≥≥,则z x y =+的最大值为A .0B .1C .2D .34.(2017新课标Ⅱ)设x 、y 满足约束条件2330233030x y x y y +-⎧⎪-+⎨⎪+⎩≤≥≥.则2z x y =+的最小值是A .15-B .9-C .1D .95.(2017新课标Ⅲ)设x ,y 满足约束条件326600x y x y +-⎧⎪⎨⎪⎩≤≥≥,则z x y =-的取值范围是A .[–3,0]B .[–3,2]C .[0,2]D .[0,3]6.(2017山东)已知x ,y 满足约束条件250302x y x y -+⎧⎪+⎨⎪⎩≤≥≤,则2z x y =+的最大值是A .-3B .-1C .1D .37.(2017浙江)若x ,y 满足约束条件03020x x y x y ⎧⎪+-⎨⎪-⎩≥≥≤,则2z x y =+的取值范围是A .[0,6]B . [0,4]C .[6,)+∞D .[4,)+∞8.(2017北京)若x ,y 满足32x x y y x ⎧⎪+⎨⎪⎩≤≥≤,则2x y +的最大值为A .1B .3C .5D .99.(2016年山东)若变量,x y 满足2,239,0,x y x y x +≤⎧⎪-≤⎨⎪≥⎩则22x y +的最大值是A .4B .9C .10D .1210.(2016年浙江)若平面区域30,230,230x y x y x y +-≥⎧⎪--≤⎨⎪-+≥⎩夹在两条斜率为1的平行直线之间,则这两条平行直线间的距离的最小值是11.(2015湖南)若变量,x y 满足约束条件111x y y x x +⎧⎪-⎨⎪⎩≥≤≤,则2z x y =-的最小值为A .-1B .0C .1D .212.(2015陕西)某企业生产甲、乙两种产品均需用,A B 两种原料,已知生产1吨每种产品需原料及每天原料的可用限额如表所示,如果生产1吨甲、乙产品可获利润分别为3万元、4万元,则该企业每天可获得最大利润为A .12万元B .16万元C .17万元D .18万元13.(2015天津)设变量,x y 满足约束条件2020280x x y x y -⎧⎪-⎨⎪+-⎩≤≤≤,则目标函数3z x y =+的最大值为.A .7B .8C .9D .1414.(2015重庆)若不等式组2022020x y x y x y m +-⎧⎪+-⎨⎪-+⎩≤≥≥,表示的平面区域为三角形,且其面积等于43,则m 的值为A .-3B .1C .43D .3 15.(2015广东)若变量x ,y 满足约束条件2204x y x y x +⎧⎪+⎨⎪⎩≤≥≤,则23z x y =+的最大值为A .2B .5C .8D .1016.(2015安徽)已知,x y 满足约束条件0401x y x y y -⎧⎪+-⎨⎪⎩≥≤≥,则2z x y =-+的最大值是A .1-B .2-C .5-D .117.(2015福建)变量,x y 满足约束条件02200x y x y mx y +≥⎧⎪-+≥⎨⎪-≤⎩,若2z x y =-的最大值为2,则实数m 等于A .2-B .1-C .1D .218.(2015四川)设实数,x y 满足2102146x y x y x y +⎧⎪+⎨⎪+⎩≤≤≥,则xy 的最大值为A .252B .492C .12D .16 19.(2014新课标1)不等式组124x y x y +≥⎧⎨-≤⎩的解集记为D .有下面四个命题: 1p :(,),22x y D x y ∀∈+≥-, 2p :(,),22x y D x y ∃∈+≥,3p :(,),23x y D x y ∀∈+≤, 4p :(,),21x y D x y ∃∈+≤-.其中真命题是A .2p ,3pB .1p ,4pC .1p ,2pD .1p ,3p20.(2014安徽)y x ,满足约束条件⎪⎩⎪⎨⎧≥+-≤--≤-+02202202y x y x y x ,若ax y z -=取得最大值的最优解不.唯一..,则实数a 的值为( ) A .121-或 B .212或C .2或1D .12-或 21.(2014福建)已知圆()()22:1C x a y b -+-=,设平面区域70,70,0x y x y y +-≤⎧⎪Ω=-+≥⎨⎪≥⎩,若圆心C ∈Ω,且圆C 与x 轴相切,则22a b +的最大值为A .5B .29C .37D .49 22.(2014北京)若,x y 满足20200x y kx y y +-≥⎧⎪-+≥⎨⎪≥⎩且z y x =-的最小值为-4,则k 的值为A .2B .-2C .12D .12- 23.(2013新课标2)设,x y 满足约束条件10,10,3,x y x y x -+≥⎧⎪+-≥⎨⎪≤⎩,则23z x y =-的最小值是A .7-B .6-C .5-D .3-24.(2013陕西)若点(,)x y 位于曲线y = |x |与y = 2所围成的封闭区域,则2x -y 的最小值为A .-6B .-2C .0D .225.(2013四川)若变量,x y 满足约束条件8,24,0,0,x y y x x y +≤⎧⎪-≤⎪⎨≥⎪⎪≥⎩且5z y x =-的最大值为a ,最小值为b ,则a b -的值是A .48B .30C .24D .1626.(2012广东)已知变量,x y 满足约束条件211y x y x y ⎧⎪+⎨⎪-⎩………,则3z x y =+的最大值为A .12B .11C .3D .-127.(2012广东)已知变量,x y 满足约束条件1101x y x x y +≤⎧⎪+≥⎨⎪-≤⎩,则2z x y =+的最小值为A .3B .1C .5-D .6-28.(2012山东)设变量y x ,满足约束条件222441x y x y x y +⎧⎪+⎨⎪--⎩………,则目标函数y x z -=3的取值范围是A .⎥⎦⎤⎢⎣⎡-6,23B .⎥⎦⎤⎢⎣⎡--1,23C .[]6,1-D .⎥⎦⎤⎢⎣⎡-23,6 29.(2012福建)若直线2y x =上存在点(,)x y 满足约束条件30,230,,x y x y x m +-≤⎧⎪--≤⎨⎪≥⎩则实数m 的最大值为( )A .1-B .1C .32D .230.(2012天津)设变量,x y 满足约束条件22024010x y x y x +-⎧⎪-+⎨⎪-⎩………,则目标函数32z x y =-的最小值为A .−5B .−4C .−2D .331.(2012辽宁)设变量,x y 满足-100+20015x y x y y ≤⎧⎪≤≤⎨⎪≤≤⎩,则2+3x y 的最大值为A .20B .35C .45D .5532.(2011广东)已知平面直角坐标系xOy 上的区域D 由不等式⎪⎩⎪⎨⎧≤≤≤≤yx x x 2220给定,若(,)M x y 为D 上的动点,点A的坐标为,则z =OM ·OA 的最大值为A .3B .4C .D .33.(2011安徽)设变量y x y x y x 2,1||||,+≤+则满足的最大值和最小值分别为A .1,-1B .2,-2C .1,-2D .2,-134.(2011湖南)设m >1,在约束条件1y x y mx x y ≥⎧⎪≤⎨⎪+≤⎩下,目标函数z=x+my 的最大值小于2,则m 的取值范围为A .(1,1+ B .(1+∞) C .(1,3 ) D .(3,+∞)35.(2010新课标)已知ABCD 的三个顶点为A (-1,2),B (3,4),C (4,-2),点(x ,y )在ABCD 的内部,则z =2x -5y 的取值范围是A .(-14,16)B .(-14,20)C .(-12,18)D .(-12,20)36.(2010山东)设变量,x y 满足约束条件20510080x y x y x y -+⎧⎪-+⎨⎪+-⎩≥≤≤,则目标函数34z x y =-的最大值和最小值分别为A .3,11-B .3,11--C .11,3-D .11,3二、填空题37.(2018全国卷Ⅰ)若x ,y 满足约束条件220100x y x y y --⎧⎪-+⎨⎪⎩≤≥≤,则32z x y =+的最大值为___.38.(2018全国卷Ⅱ)若,x y 满足约束条件25023050+-⎧⎪-+⎨⎪-⎩≥,≥,≤,x y x y x 则=+z x y 的最大值为___.39.(2018全国卷Ⅲ)若变量x y ,满足约束条件23024020.x y x y x ++⎧⎪-+⎨⎪-⎩≥,≥,≤则13z x y =+的最大值是______.40.(2018北京)若x ,y 满足12x y x +≤≤,则2y x -的最小值是_____.41.(2018浙江)若x ,y 满足约束条件0262x y x y x y -⎧⎪+⎨⎪+⎩≥≤≥,则3z x y =+的最小值是___________,最大值是___________.42.(2016江苏)已知实数,x y 满足240220330x y x y x y -+≥⎧⎪+-≥⎨⎪--≤⎩,则22x y +的取值范围是 .43.(2016全国I 卷)某高科技企业生产产品A 和产品B 需要甲、乙两种新型材料.生产一件产品A 需要甲材料1.5 kg ,乙材料1 kg ,用5个工时;生产一件产品B 需要甲材料0.5 kg ,乙材料0.3 kg ,用3个工时,生产一件产品A 的利润为2100元,生产一件产品B 的利润为900元。
2024年高考数学总复习第七章不等式真题分类28二元一次不等式(组)与简单的线性规划问题

第13页
返回层目录 返回目录
真题分类28 二元一次不等式(组)与简单的线性规划问题
高考·数学
目标函数 z=x+2y,即 y=-12 x+2z ,画出直线 y=-12 x 并平移,当直线 y =-12 x+2z 经过点 A(2,1)时,z 取最小值,无最大值,zmin=2+2×1=4,所以 z 的取值范围为[4,+∞),故选 B.
第12页
返回层目录 返回目录
真题分类28 二元一次不等式(组)与简单的线性规划问题
高考·数学
4.(2020·浙江,3,4 分)若实数 x,y 满足约束条件xx+-y3-y+3≥1≤0,0, 则 z=x+2y
的取值范围是( )
A.(-∞,4]
B.[4,+∞)
C.[5,+∞)
D.(-∞,+∞)
答案:B 由 x,y 满足的约束条件画出可行域, 如图中阴影部分所示(包含边界).
的可行域,
2x+3y-1≤0
如图所示:
第11页
返回层目录 返回目录
真题分类28Leabharlann 二元一次不等式(组)与简单的线性规划问题
高考·数学
目标函数 z=x-12 y 化为 y=2x-2z, 由x2=x+-31y-,1=0, 解得xy==-1. 1, 设 A(-1,1),当直线 y=2x-2z 过 A 点时,z=x-12 y 取得最小值为-32 . 故选 B.
第9页
返回层目录 返回目录
真题分类28 二元一次不等式(组)与简单的线性规划问题
高考·数学
由xy+ =y3=4, 可得点 A(1,3), 转换目标函数 z=3x+y 为 y=-3x+z, 上下平移直线 y=-3x+z,数形结合可得当直线过点 A 时,z 取最小值, 此时 zmin=3×1+3=6. 故选 C.
十年真题(2010)高考数学真题分类汇编专题17不等式选讲理(含解析)

历年考题细目表题型年份考点试题位置解答题2019 不等式选讲2019年新课标1理科23解答题2018 综合测试题2018年新课标1理科23解答题2017 综合测试题2017年新课标1理科23解答题2016 综合测试题2016年新课标1理科24解答题2014 综合测试题2014年新课标1理科24解答题2013 综合测试题2013年新课标1理科24解答题2012 综合测试题2012年新课标1理科24解答题2011 综合测试题2011年新课标1理科24解答题2010 综合测试题2010年新课标1理科24历年高考真题汇编十年真题(2010)高考数学真题分类汇编专题17不等式选讲理(含解析)1.【2019年新课标1理科23】已知a,b,c为正数,且满足abc=1.证明:(1)a2+b2+c2;(2)(a+b)3+(b+c)3+(c+a)3≥24.【解答】证明:(1)分析法:已知a,b,c为正数,且满足abc=1.要证(1)a2+b2+c2;因为abc=1.就要证:a2+b2+c2;即证:bc+ac+ab≤a2+b2+c2;即:2bc+2ac+2ab≤2a2+2b2+2c2;2a2+2b2+2c2﹣2bc﹣2ac﹣2ab≥0(a﹣b)2+(a﹣c)2+(b﹣c)2≥0;∵a,b,c为正数,且满足abc=1.∴(a﹣b)2≥0;(a﹣c)2≥0;(b﹣c)2≥0恒成立;当且仅当:a=b=c=1时取等号.即(a﹣b)2+(a﹣c)2+(b﹣c)2≥0得证.故a2+b2+c2得证.(2)证(a+b)3+(b+c)3+(c+a)3≥24成立;即:已知a,b,c为正数,且满足abc=1.(a+b)为正数;(b+c)为正数;(c+a)为正数;(a+b)3+(b+c)3+(c+a)3≥3(a+b)•(b+c)•(c+a);当且仅当(a+b)=(b+c)=(c+a)时取等号;即:a=b=c=1时取等号;∵a,b,c为正数,且满足abc=1.(a+b)≥2;(b+c)≥2;(c+a)≥2;当且仅当a=b,b=c;c=a时取等号;即:a=b=c=1时取等号;∴(a+b)3+(b+c)3+(c+a)3≥3(a+b)•(b+c)•(c+a)≥3×8••24abc=24;当且仅当a=b=c=1时取等号;故(a+b)3+(b+c)3+(c+a)3≥24.得证.故得证.2.【2018年新课标1理科23】已知f(x)=|x+1|﹣|ax﹣1|.(1)当a=1时,求不等式f(x)>1的解集;(2)若x∈(0,1)时不等式f(x)>x成立,求a的取值范围.【解答】解:(1)当a=1时,f(x)=|x+1|﹣|x﹣1|,由f(x)>1,∴或,解得x,故不等式f(x)>1的解集为(,+∞),(2)当x∈(0,1)时不等式f(x)>x成立,∴|x+1|﹣|ax﹣1|﹣x>0,即x+1﹣|ax﹣1|﹣x>0,即|ax﹣1|<1,∴﹣1<ax﹣1<1,∴0<ax<2,∵x∈(0,1),∴a>0,∴0<x,∴a∵2,∴0<a≤2,故a的取值范围为(0,2].3.【2017年新课标1理科23】已知函数f(x)=﹣x2+ax+4,g(x)=|x+1|+|x﹣1|.(1)当a=1时,求不等式f(x)≥g(x)的解集;(2)若不等式f(x)≥g(x)的解集包含[﹣1,1],求a的取值范围.【解答】解:(1)当a=1时,f(x)=﹣x2+x+4,是开口向下,对称轴为x的二次函数,g(x)=|x+1|+|x﹣1|,当x∈(1,+∞)时,令﹣x2+x+4=2x,解得x,g(x)在(1,+∞)上单调递增,f(x)在(1,+∞)上单调递减,∴此时f(x)≥g(x)的解集为(1,];当x∈[﹣1,1]时,g(x)=2,f(x)≥f(﹣1)=2.当x∈(﹣∞,﹣1)时,g(x)单调递减,f(x)单调递增,且g(﹣1)=f(﹣1)=2.综上所述,f(x)≥g(x)的解集为[﹣1,];(2)依题意得:﹣x2+ax+4≥2在[﹣1,1]恒成立,即x2﹣ax﹣2≤0在[﹣1,1]恒成立,则只需,解得﹣1≤a≤1,故a的取值范围是[﹣1,1].4.【2016年新课标1理科24】已知函数f(x)=|x+1|﹣|2x﹣3|.(Ⅰ)在图中画出y=f(x)的图象;(Ⅱ)求不等式|f(x)|>1的解集.【解答】解:(Ⅰ)f(x),由分段函数的图象画法,可得f(x)的图象,如右:(Ⅱ)由|f(x)|>1,可得当x≤﹣1时,|x﹣4|>1,解得x>5或x<3,即有x≤﹣1;当﹣1<x时,|3x﹣2|>1,解得x>1或x,即有﹣1<x或1<x;当x时,|4﹣x|>1,解得x>5或x<3,即有x>5或x<3.综上可得,x或1<x<3或x>5.则|f(x)|>1的解集为(﹣∞,)∪(1,3)∪(5,+∞).5.【2014年新课标1理科24】若a>0,b>0,且.(Ⅰ)求a3+b3的最小值;(Ⅱ)是否存在a,b,使得2a+3b=6?并说明理由.【解答】解:(Ⅰ)∵a>0,b>0,且,∴2,∴ab≥2,当且仅当a=b时取等号.∵a3+b3 ≥224,当且仅当a=b时取等号,∴a3+b3的最小值为4.(Ⅱ)∵2a+3b≥22,当且仅当2a=3b时,取等号.而由(1)可知,2246,故不存在a,b,使得2a+3b=6成立.6.【2013年新课标1理科24】已知函数f(x)=|2x﹣1|+|2x+a|,g(x)=x+3.(Ⅰ)当a=﹣2时,求不等式f(x)<g(x)的解集;(Ⅱ)设a>﹣1,且当x∈[,]时,f(x)≤g(x),求a的取值范围.【解答】解:(Ⅰ)当a=﹣2时,求不等式f(x)<g(x)化为|2x﹣1|+|2x﹣2|﹣x﹣3<0.设y=|2x﹣1|+|2x﹣2|﹣x﹣3,则y,它的图象如图所示:结合图象可得,y<0的解集为(0,2),故原不等式的解集为(0,2).(Ⅱ)设a>﹣1,且当x∈[,]时,f(x)=1+a,不等式化为1+a≤x+3,故x≥a﹣2对x∈[,]都成立.故a﹣2,解得a,故a的取值范围为(﹣1,].7.【2012年新课标1理科24】已知函数f(x)=|x+a|+|x﹣2|①当a=﹣3时,求不等式f(x)≥3的解集;②f(x)≤|x﹣4|若的解集包含[1,2],求a的取值范围.【解答】解:(1)当a=﹣3时,f(x)≥3 即|x﹣3|+|x﹣2|≥3,即,可得x≤1;,可得x∈∅;,可得x≥4.取并集可得不等式的解集为 {x|x≤1或x≥4}.(2)原命题即f(x)≤|x﹣4|在[1,2]上恒成立,等价于|x+a|+2﹣x≤4﹣x在[1,2]上恒成立,等价于|x+a|≤2,等价于﹣2≤x+a≤2,﹣2﹣x≤a≤2﹣x在[1,2]上恒成立.故当 1≤x≤2时,﹣2﹣x的最大值为﹣2﹣1=﹣3,2﹣x的最小值为0,故a的取值范围为[﹣3,0].8.【2011年新课标1理科24】设函数f(x)=|x﹣a|+3x,其中a>0.(Ⅰ)当a=1时,求不等式f(x)≥3x+2的解集(Ⅱ)若不等式f(x)≤0的解集为{x|x≤﹣1},求a的值.【解答】解:(Ⅰ)当a=1时,f(x)≥3x+2可化为|x﹣1|≥2.由此可得x≥3或x≤﹣1.故不等式f(x)≥3x+2的解集为{x|x≥3或x≤﹣1}.(Ⅱ)由f(x)≤0得|x﹣a|+3x≤0此不等式化为不等式组或即或因为a>0,所以不等式组的解集为{x|x}由题设可得1,故a=29.【2010年新课标1理科24】设函数f(x)=|2x﹣4|+1.(Ⅰ)画出函数y=f(x)的图象:(Ⅱ)若不等式f(x)≤ax的解集非空,求a的取值范围.【解答】解:(Ⅰ)由于f (x ),函数y =f (x )的图象如图所示. (Ⅱ)由函数y =f (x )与函数y =ax 的图象可知,极小值在点(2,1)当且仅当a <﹣2或a 时,函数y =f (x )与函数y =ax 的图象有交点.故不等式f (x )≤ax 的解集非空时,a 的取值范围为(﹣∞,﹣2)∪[,+∞).考题分析与复习建议本专题考查的知识点为:解绝对值不等式、证明不等式、利用不等式恒成立求参数的值或范围,求含有绝对值的函数最值也是考查的热点.求解的一般方法是去掉绝对值,也可以借助数形结合求解.历年考题主要以解答题题型出现,重点考查的知识点为解绝对值不等式、证明不等式、利用不等式恒成立求参数的值或范围,求含有绝对值的函数最值也是考查的热点.预测明年本考点题目会比较稳定,备考方向以知识点解绝对值不等式、利用不等式恒成立求参数的值或范围,证明不等式为重点较佳.最新高考模拟试题1.已知函数()22()f x x a x a R =-+-∈.(1)当2a =时,求不等式()2f x >的解集;(2)若[2,1]x ∈-时不等式()32f x x ≤-成立,求实数a 的取值范围.【答案】(1)2{|3x x <或()4cos(2)6f x x π=-;(2)空集. 【解析】 解:(1)不等式()2f x >,即2222x x -+->.可得22222x x x ≥⎧⎨-+->⎩,或122222x x x <<⎧⎨-+->⎩或12222x x x ≤⎧⎨--+>⎩, 解得23x <或2x >,所以不等式的解集为2{|2}3x x x <>或. (2)当[2,1]x ∈-时,220x -<,所以()22f x x a x =-+-,由()32f x x ≤-得1x a -≤,即11a x a -≤≤+,则1211a a -≤-⎧⎨+≥⎩,该不等式无解, 所以实数a 的取值范围是空集(或者∅).2.已知()221f x x x =-++.(1)求不等式()6f x <的解集;(2)设m 、n 、p 为正实数,且()3m n p f ++=,求证:12mn np pm ++≤.【答案】(1) ()1,3- (2)见证明【解析】(1)①2x ≥时,()24133f x x x x =-++=-,由()6f x <,∴336x -<,∴3x <,即23x ≤<,②12x -<<时,()4215f x x x x =-++=-,由()6f x <,∴56x -<,∴1x >-,即12x -<<, ③1x ≤-时,()42133f x x x x =---=-,由()6f x <,∴336x -<,∴1x >-,可知无解, 综上,不等式()6f x <的解集为()1,3-;(2)∵()221f x x x =-++,∴()36f =,∴()36m n p f ++==,且,,m n p 为正实数∴()222222236m n p m n p mn mp np ++=+++++=,∵222m n mn +≥,222m p mp +≥,222n p np +≥,∴222m n p mn mp np ++≥++,∴()()2222222363m n p m n p mn mp np mn mp np ++=+++++=≥++ 又,,m n p 为正实数,∴可以解得12mn np pm ++≤.3.[选修4—5:不等式选讲]已知函数()|||2|(0)f x x m x m m =--+>.(1)当1m =,求不等式()1f x ≥的解集;(2)对于任意实数,x t ,不等式()21f x t t <++-恒成立,求实数m 的取值范围.【答案】(1)113x x ⎧⎫-≤≤-⎨⎬⎩⎭;(2)()0,2【解析】(1)当1m =时,()1f x ≥为:1211x x --+≥当1x ≥时,不等式为:1211x x ---≥,解得:3x ≤-,无解 当112x -≤<时,不等式为:1211x x -+--≥,解得:13x ≤-,此时1123x -≤≤- 当12x <-时,不等式为:1211x x -+++≥,解得:1x -≥,此时112x -≤<- 综上所述,不等式的解集为113x x ⎧⎫-≤≤-⎨⎬⎩⎭(2)对于任意实数x ,t ,不等式()21f x t t <++-恒成立等价于()()max min |2||1|f x t t <++- 因为|2||1||(2)(1)|3t t t t ++-≥+--=,当且仅当(2)(1)0t t +-≤时等号成立 所以()min |2||1|3t t ++-=因为0m >时,()2f x x m x m =--+=2,23,22,m x m x m x x m x m x m ⎧+<-⎪⎪⎪--≤≤⎨⎪-->⎪⎪⎩, 函数()f x 单调递增区间为(,)2m -∞-,单调递减区间为(,)2m -+∞ ∴当2m x =-时,()max 322m m f x f ⎛⎫=-= ⎪⎝⎭ 332m ∴<,又0m >,解得:02m << ∴实数m 的取值范围()0,24.选修4-5不等式选讲已知关于x 的不等式20x m x -+≤的解集为{|2}x x ≤-,其中0m >.(1)求m 的值;(2)若正数a ,b ,c 满足a b c m ++=,求证:2222b c a a b c++≥. 【答案】(1)2m =(2)见证明【解析】(1)由题意知:20x m x -+≤即20x m x m x ≥⎧⎨-+≤⎩或20x m m x x ≤⎧⎨-+≤⎩ 化简得:3x m m x ≥⎧⎪⎨≤⎪⎩或x m x m ≤⎧⎨≤-⎩ 0m > ∴不等式组的解集为{}x x m ≤-2m ∴-=-,解得:2m =(2)由(1)可知,2a b c ++= 由基本不等式有:22b a b a +≥,22c b c b+≥,22a c a c +≥三式相加可得:222222b c a a b c b c a a b c+++++≥++ 222b c a a b c a b c ∴++≥++,即:2222b c a a b c++≥ 5.选修4-5:不等式选讲 已知函数()13f x x x a =+++(1)当1a =-时,解不等式()2f x ≥;(2)若存在0x 满足00()211f x x ++<,求实数a 的取值范围.【答案】(1) 1|02x x x ⎧⎫≤≥⎨⎬⎩⎭或 (2) 24a << 【解析】(1)当1a =-时,()|1||31|f x x x =++-, 当13x ≥时,不等式等价于1312x x ++-≥,解得12x ≥,12x ∴≥; 当113x -<<时,不等式等价于1312x x +-+≥,解得0x ≤,10x ∴-<≤; 当1x ≤-时,不等式等价于1312x x ---+≥,解得12x ≤-,1x -∴≤. 综上所述,原不等式的解集为1|02x x x ⎧⎫≤≥⎨⎬⎩⎭或. (2)由()00211f x x ++<,得003131x x a +++<, 而()()000000313333333|3|x x a x x a x x a a +++=+++≥+-+=-,(当且仅当()()003330x x a ++≤时等号成立)由题可知min (()2|1|)1f x x ++<,即31a -<,解得实数a 的取值范围是24a <<.6.已知函数()|2|f x ax =-.(Ⅰ)当4a =时,求不等式()|42|8f x x ++≥的解集;(Ⅱ)若[2,4]x ∈时,不等式()|3|3f x x x +-≤+成立,求a 的取值范围.【答案】(I )(,1][1,)-∞-+∞;(II )[1,2]-【解析】(I )当4a =时,原不等式即|42||42|8x x -++≥,即|21||21|4x x -++≥. 当12x ≥时,21214x x -++≥,解得1x ≥,∴1x ≥; 当1122x -≤≤时,12214x x -++≥,无解; 当12x ≤-时,12214x x ---≥,解得1x ≤-,∴1x ≤-; 综上,原不等式的解集为(,1][1,)-∞-+∞(II )由()|3|3f x x x +-≤+得|2||3|3ax x x -+-≤+(*)当[2,3]x ∈时,(*)等价于|2|33|2|2ax x x ax x -+-≤+⇔-≤ 即22a x -≤,所以2222a x x -+≤≤+恒成立,所以813a -≤≤ 当(3,4]x ∈时,(*)等价于|2|33|2|6ax x x ax -+-≤+⇔-≤即48ax -≤≤,所以48a x x-≤≤恒成立,所以12a -≤≤ 综上,a 的取值范围是[1,2]-7.已知函数()21f x x x a =-++,()2g x x =+.(1)当1a =-时,求不等式()()f x g x <的解集;(2)设12a >-,且当1,2x a ⎡⎫∈-⎪⎢⎣⎭,()()f x g x ≤,求a 的取值范围. 【答案】(1)()0,2;(2)11,23⎛⎤-⎥⎝⎦ 【解析】(1)当1a =-时,不等式()()f x g x <化为:21120x x x -+---< 当12x ≤时,不等式化为12120x x x -+---<,解得:102x <≤ 当112x <≤时,不等式化为21120x x x -+---<,解得:112x <≤当1x >时,不等式化为21120x x x -+---<,解得:12x <<综上,原不等式的解集为()0,2(2)由12a x -≤<,得221a x -≤<,21210a x --≤-< 又102x a a ≤+<+ 则()()211f x x x a x a =--++=-++∴不等式()()f x g x ≤化为:12x a x -++≤+得21a x ≤+对1,2x a ⎡⎫∈-⎪⎢⎣⎭都成立 21a a ∴≤-+,解得:13a ≤ 又12a >-,故a 的取值范围是11,23⎛⎤- ⎥⎝⎦8.已知函数()|2|f x x =-.(Ⅰ)求不等式()|1|f x x x <++的解集;(Ⅱ)若函数5log [(3)()3]y f x f x a =++-的定义域为R ,求实数a 的取值范围.【答案】(I )1,3⎛⎫+∞ ⎪⎝⎭(II )(,1)-∞ 【解析】解:(I )由已知不等式()|1|f x x x <++,得|2||1|x x x -<++,当2x ≥时,不等式为21x x x -<++,解得3x >-,所以2x ≥;当12x -<<时,不等式为21x x x -<++,解得13x >,所以123x <<; 当1x ≤-时,不等式为21x x x -<--,解得3x >,此时无解. 综上:不等式的解集为1,3⎛⎫+∞ ⎪⎝⎭.(II )若5log [(3)()3]y f x f x a =++-的定义域为R ,则(3)()30f x f x a ++->恒成立.∵,当且仅当[1,2]x ∈-时取等号.∴330a ->,即1a <.所以实数a 的取值范围是(,1)-∞.9.已知函数()123f x x x =-+-.(Ⅰ)解关于x 的不等式()4f x ≤;(Ⅱ)若()20f x m m -->恒成立,求实数m 的取值范围.【答案】(Ⅰ)111,3⎡⎤⎢⎥⎣⎦;(Ⅱ)()2,1-. 【解析】解:(I )当1x ≤时,不等式为:()1234x x -+-≤,解得1x ≥,故1x =.当13x <<时,不等式为:()1234x x -+-≤,解得1x ≥,故13x <<1<x <3,当3x ≥时,不等式为:()1234x x -+-≤,解得113x ≤,故1133x ≤≤. 综上,不等式()4f x ≤的解集为111,3⎡⎤⎢⎥⎣⎦. (II )由()20f x m m -->恒成立可得()2m m f x +<恒成立.又()37,35,1337,1x x f x x x x x -≥⎧⎪=-+<<⎨⎪-+≤⎩,故()f x 在(],1-∞上单调递减,在()1,3上单调递减,在[)3,+∞上单调递增, ∴()f x 的最小值为()32f =.∴22m m +<,解得21m -<<.即m 的最值范围是()2,1-.10.已知函数()211f x x x =-++.(Ⅰ)解不等式()3f x ≥;(Ⅱ)记函数()f x 的最小值为m ,若,,a b c 均为正实数,且232a b c m ++=,求222a b c ++的最小值.【答案】(Ⅰ){}11x x x ≤-≥或;(Ⅱ)914. 【解析】(Ⅰ)由题意, 3,11()2,1213,2x x f x x x x x ⎧⎪-≤-⎪⎪=--<<⎨⎪⎪≥⎪⎩, 所以()3f x ≥等价于133x x ≤-⎧⎨-≥⎩或11223x x ⎧-<<⎪⎨⎪-≥⎩或1233x x ⎧≥⎪⎨⎪≥⎩. 解得:1x ≤-或1x ≥,所以不等式的解集为{}11x x x ≤-≥或;(Ⅱ)由(1)可知,当12x =时, ()f x 取得最小值32, 所以32m =,即233a b c ++=, 由柯西不等式得2222222()(123)(23)9a b c a b c ++++≥++=, 整理得222914a b c ++≥, 当且仅当123a b c ==时, 即369,,141414a b c ===时等号成立. 所以222a b c ++的最小值为914. 11.已知函数()12f x x a x =+++.(Ⅰ)求1a =时,()3f x ≤的解集;(Ⅱ)若()f x 有最小值,求a 的取值范围,并写出相应的最小值.【答案】(Ⅰ)[3,0]-;(Ⅱ)见解析.【解析】(Ⅰ)当1a =时,232()12121231x x f x x x x x x --≤-⎧⎪=+++=-<<-⎨⎪+≥-⎩∵()3f x ≤当2x -≤时()233f x x =--≤解得32x -≤≤-当21x -<<-时()13f x =≤恒成立当1x -≥时()233f x x =+≤解得10x -≤≤综上可得解集[3,0]-. (Ⅱ)(1)212()12(1)2121(1)211a x a x f x x a x a x a x a x a x -+--≤-⎧⎪=+++=-+--<<-⎨⎪+++≥-⎩当(1)0a -+>,即1a <-时,()f x 无最小值;当(1)0a -+=,即1a =-时,()f x 有最小值1-;当(1)0a -+<且10a -≤,即11a -<≤时, min ()(1)f x f a =-=当(1)0a -+<且10a ->,即1a >时, min ()(2)1f x f =-=综上:当1a <-时,()f x 无最小值;当1a =-时,()f x 有最小值1-;当11a -<≤时, min ()(1)f x f a =-= ;当1a >时, min ()(2)1f x f =-=;12.选修4-5:不等式选讲已知函数()|23||1|f x x x =--+.(1)求不等式()6f x ≤的解集;(2)设集合M 满足:当且仅当x M ∈时,()|32|f x x =-,若,a b M ∈,求证:228223a b a b -++≤. 【答案】(1) {}210x x -≤≤;(2)见解析.【解析】 (1)()4,1323132,1234,2x x f x x x x x x x ⎧⎪-+<-⎪⎪=--+=-+-≤≤⎨⎪⎪->⎪⎩当1x <- 时,46x -+≤ ,得2x -≥ ,故21x -≤<-; 当312x -≤≤ 时,326x -+≤ ,得43x ≥- ,故312x -≤<;当32x > 时,46x -≤ ,得10x ≤ ,故3102x <≤; 综上,不等式()6f x ≤的解集为{}210x x -≤≤(2)由绝对值不等式的性质可知()231(23)(1)32f x x x x x x =--+≤-++=- 等价于23(1)32x x x -≤-++-,当且仅当(23)(1)0x x -+≤, 即213x -≤≤ 时等号成立,故21,3M ⎡⎤=-⎢⎥⎣⎦所以221,133a b -≤≤-≤≤, 所以222510(1),4(1)99a b ≤-≤-≤--≤-, 即228(1)(1)3a b ---≤. 13.[选修4—5:不等式选讲]已知函数()31f x x m x m =----(1)若1m =,求不等式()1f x <的解集.(2)对任意的x R ∈,有()(2)f x f ≤,求实数m 的取值范围.【答案】(1)(,3)-∞;(2)1123m -≤≤ 【解析】(1)()141f x x x =---<, 所以11441(4)11(4)1141x x x x x x x x x <≤≤>⎧⎧⎧⎨⎨⎨---<---<--+<⎩⎩⎩或或 解之得不等式()1f x <的解集为(,3)-∞.(2) 当131,2m m m +>>-时,由题得2必须在3m+1的右边或者与3m+1重合, 所以1231,3m m ≥+∴≤,所以1123m -<≤, 当131,2m m m +==-时,不等式恒成立, 当131,2m m m +<<-时,由题得2必须在3m+1的左边或者与3m+1重合, 由题得1231,3m m ≤+≥,所以m 没有解.综上,1123m -≤≤. 14.已知()21f x x x =+-. (1)证明()1f x x +≥; (2)若,,a b c +∈R ,记33311134abc a b c +++的最小值为m ,解关于x 的不等式()f x m <. 【答案】(1)见证明;(2) 2433x x ⎧⎫-<<⎨⎬⎩⎭【解析】(1)()2212211f x x x x x x +=+-≥-+=.当且仅当()2x 2x 10-≤,等号成立(2)∵333333311131333333234444abc abc abc abc m a b c a b c abc abc +++≥+=+≥⋅==,当且仅当a=b=c 等号成立由不等式()3f x <即()213f x x x =+-<.由()31,01211,02131,2x x f x x x x x x x ⎧⎪-+≤⎪⎪=+-=-<<⎨⎪⎪-≥⎪⎩得:不等式()3f x <的解集为2433x x ⎧⎫-<<⎨⎬⎩⎭. 15.选修4—5:不等式选讲已知函数()11f x x mx =++-,m R ∈。
文科数学高考真题分类汇编 不等式综合应用

专题七不等式第二十一讲不等式综合应用2019年 1.(2019 天津文13)设0x >,0y >,24x y +=,则 (1)(21)x y xy++的最小值为__________.2010-2018年一、选择题1.(2018北京)设集合{(,)|1,4,2},A x y x y ax y x ay =−+>−≥≤则 A .对任意实数a , (2,1)A ∈ B .对任意实数a , (2,1)A ∉C .当且仅当0a <时, (2,1)A ∉D .当且仅当32a ≤时, (2,1)A ∉ 2.(2018)浙江已知1a ,2a ,3a ,4a 成等比数列,且 1234123 ln()a a a a a a a +++=++.若11a >,则A .13a a <,24a a <B .13a a >,24a a <C .13a a <,24a a >D .13a a >,24a a >32017 .(天津)已知函数 ||2,1,()2 , 1.x x f x x x x+<⎧⎪=⎨+⎪⎩≥设a ∈R ,若关于x 的不等式 ()||2x f x a +≥在R 上恒成立,则a 的取值范围是A . [2,2]−B . [23,2]−C . [2,23]−D . [23,23]−4.(2015 福建)若直线 1(0,0)x y a b a b+=>>过点(1,1),则a b +的最小值等于 A 2 B 3 C 4 D 5. . ..52015 .( 湖南)若实数,a b 满足12ab a b+=,则ab 的最小值为 A .2 B 2 C 2..2 D 4.62014 .( 重庆)若 b a ab b a +=+则)(,log 43log 24的最小值是A . 326+B . 327+C . 346+D . 347+7.(2013 福建)若 122=+y x ,则y x +的取值范围是A .]2,0[B .]0,2[−C .),2[+∞− D . ]2,(−−∞ 82013.(山东)设正实数,,x y z 满足22 340x xy y z −+−=.则当xy z取得最大值时, 212x y z+−的最大值为 A 0 B 1 C . . .94D 3 . 9.(2013山东)设正实数z y x ,,满足04322 =−+−z y xy x ,则当z xy取得最大值时,2x y z +−的最大值为A 0B ..98C 2D ..9410.( 2012浙江)若正数,x y 满足35x y xy +=,则34x y +的最小值是A .245B .285C 5D 6 .. 11.(2012 陕西)小王从甲地到乙地的时速分别为a 和b (a b <),其全程的平均时速为v ,则A .a v ab <<B .v =abC .ab <v <2a b + D .v =2a b + 12.(2012 湖南)已知两条直线1l :y m = 和2l :y =821m +(0m >),1l 与函数2log y x =的图像从左至右相交于点,A B ,2l 与函数2log y x =的图像从左至右相交于,C D .记线段AC 和BD 在x 轴上的投影长度分别为,a b ,当m 变化时,b a 的最小值为 A . 162 B.82 C.384 D. 34413.( 2011陕西)设 0a b <<,则下列不等式中正确的是A .2a b a b ab +<<< B .2a b a ab b + <<< C .2a b a ab b + <<< D .2a b ab a b + <<< 14.( 2011上海)若,a b R ∈,且0ab >,则下列不等式中,恒成立的是A .222a b ab +>B .2a b ab +≥C . 112a b ab+> D .2b a a b +≥ 二、填空题15.(2018)天津已知,a b ∈R ,且 360a b −+=,则128a b+ 的最小值为. 16.(2018天津)已知a ∈R ,函数22 220() 220x x a x f x x x a x ⎧ ++−⎪=⎨−+−>⎪⎩ ,≤, ,.若对任意 [3,)x ∈−+∞, ()||f x x ≤恒成立,则a 的取值范围是____.17.( 2017天津)若,a b ∈R ,0ab >,则4441a b ab++ 的最小值为. 18.( 2017山东)若直线 1(00)x y a b a b+=>,>过点(1,2),则2a b +的最小值为. 192017 .(江苏)某公司一年购买某种货物吨,每次购买600 x 吨,运费为万元6 /次,一年的总存储费用为4x 万元,要使一年的总运费与总存储费之和最小,则x 的值是.20.(2017北京)能够说明“设a ,b ,c 是任意实数.若a b c >>,则a b c +>”是假命题的一组整数a ,b ,c 的值依次为____________________.21.(2017浙江)已知a ∈R ,函数4()||f x x a a x=+−+ 在区间,[14]上的最大值是5,则a 的取值范围是.22.(2017 江苏)在平面直角坐标系xOy 中, (12,0)A −,(0,6)B ,点P 在圆O :2250x y +=上,若20PA PB ⋅≤,则点P 的横坐标的取值范围是. 23.( 2015重庆)设,0a b >,5a b +=,则 1++3a b +的最大值为________.24.(2015)山东定义运算“⊗”:22x y x y xy−⊗=(,x y ∈R ,0xy ≠).当0x >, 0y >时, (2)x y y x ⊗+⊗的最小值为.25.( 2014浙江)已知实数,,a b c 满足0a b c ++=, 2221a b c ++=,则a 的最大值是__;26.(2014 辽宁)对于0c > ,当非零实数,a b 满足22 420aab b c −+−=,且使 |2|a b +最大时, 124a b c++的最小值为. 27.(2014 辽宁)对于0c >,当非零实数a ,b 满足224240a ab b c −+−=,且使 |2|a b +最大时, 345a b c−+的最小值为. 28.(2014 湖北)某项研究表明:在考虑行车安全的情况下,某路段车流量F (单位时间内经过测量点的车辆数,单位:辆小时)与车流速度/v (假设车辆以相同速度行驶,单v 位:米秒)、平均车长(单位:米)有关,其公式为/l 的值276000 1820v F v v l=++. ()如果不限定车型,Ⅰ 6.05l = ,则最大车流量为辆小时; /()如果限定车型,Ⅱ5l =,则最大车流量比(Ⅰ)中的最大车流量辆.增加 /小时29.( 2013天津)设a b + = 2,b >0,时, 则当a = 1|| 2||a ab +取得最小值. 30.( 2013四川)已知函数 ()4(0,0)a f x x x a x=+>>在3x =时取得最小值,则a =__.31.( 2011浙江)若实数,x y 满足22 1x y xy ++=,则x y +的最大值是____ . 32.( 2011湖南)设,x y R ∈,则222211 ()(4)x y y x++ 的最小值为. 33.( 2010安徽)若0,0,2a b a b >>+=,则下列不等式对一切满足条件的,a b 恒成立的是写出所有正确命题的编号. ()①1ab ≤;② 2a b +≤;③ 222a b +≥ ; ④333a b +≥;⑤ 112a b +≥.。
2010-2018高考数学试题分类汇编文科版专题七 不等式 第十九讲 不等式的性质与一元二次不等式答案

专题七 不等式第十九讲 不等式的性质与一元二次不等式答案部分1.D 【解析】当0x ≤时,函数()2x f x -=是减函数,则()(0)1f x f =≥,作出()f x 的大致图象如图所示,结合图象可知,要使(1)(2)+<f x f x ,则需102021x x x x +<⎧⎪<⎨⎪<+⎩或1020x x +⎧⎨<⎩≥,所以0x <,故选D .2.A 【解析】由38x >,得2x >,由||2x >,得2x >或2x <-,故“38x >”是“||2x >”的充分而不必要条件,故选A .3.B 【解析】由20x -≥,得2x ≤,由|1|1x -≤,得02x ≤≤,所以“20x -≥”是“|1|1x -≤”的必要而不充分条件.选B . 4.B 【解析】函数()f x 的对称轴为2ax =-, ①当02a-≤,此时(1)1M f a b ==++,(0)m f b ==,1M m a -=+; ②当12a-≥,此时(0)M f b ==,(1)1m f a b ==++,1M m a -=--;③当012a <-<,此时2()24a a m fb =-=-,(0)M f b ==或(1)1M f a b ==++,24a M m -=或214a M m a -=++.综上,M m -的值与a 有关,与b 无关.选B .5.D 【解析】log log 1>=a a b a ,当1>a 时,1>>b a ,10,0∴->->a b a ,(1)()0∴-->a b a ;当01<<a 时,01∴<<<b a ,10,0∴-<-<a b a ,(1)()0∴-->a b a .故选D . 6.A 【解析】由题意得,{}|31P x x x =≥≤或,所以[3,4)P Q = ,故选A . 7.C 【解析】2{|430}{|13},(2,3)A x x x x x A B =-+<=<<= . 8.C 【解析】取满足题意得函数()21f x x =-,若取32k =, 则121()()33f f k ==213k<=,所以排除A . 若取1110k =,则111110()()(10)1911111111111010kf f f k k ===>==----,所以排除D ;取满足题意的函数()101f x x =-, 若取2k =,则1111()()412211f f k k ==>==--,所以排除B , 故结论一定错误的是C .9.A 【解析】{}|13A x x x =-≤或≥,故A B ⋂=[-2, -1]. 10.D 【解析】由1100c d d c<<⇒->->,又 0a b >>,由不等式性质知:0a b d c ->->,所以a bd c<11.D 【解析】由已知得x y >,此时22,x y 大小不定,排除A,B ;由正弦函数的性质,可知C 不成立;故选D .12.B 【解析】不妨设01y x ≤≤≤,当102x y <-≤时,11()()24f x f y x y -<-≤; 当112x y <-≤时,()()()(1)()(0)f x f y f x f f y f -=--- ()(1)f x f -≤()(0)f y f +-111022x y <-+-11111(1)()22224x y y x =-+=+-<,∴14k ≥. 13.C 【解析】如图△ADE ∽△ABC ,设矩形的另一边长为y ,则240()40ADE ABC S y S ∆∆-=, 所以40y x =-,又300xy ≥,所以(40)300x x -≥,即2403000x x -+≤,解得1030x ≤≤.14.A 【解析】∵由22280x ax a --< (0a >),得(4)(2)0x a x a -+<,即24a x a -<<,∴122,4x a x a =-=. ∵214(2)615x x a a a -=--==,∴15562a ==.故选A . 15.A 【解析】解法一 由()()f x a f x +<,得()||1||||a x x a a x a ax x ++++<①当0a ≥,①⇔()||1||||x x a a x a x x ++++<,无解, 即A =Φ,不符合,排除C .取12a =-,①⇔111||1||||222x x x x x -+-->, 符合11,22A ⎡⎤-⊆⎢⎥⎣⎦,排除B 、D .解法二 数形结合,∵()()1||f x x a x =+是奇函数.ⅰ)取1a =,()()1||f x x x =+,如图()()1f x f x +<,无解.排除C .f (x )ⅱ)取12a =-,()11||2f x x x ⎛⎫=- ⎪⎝⎭,()12y f x a f x ⎛⎫=+=- ⎪⎝⎭,满足11,22A ⎡⎤-⊆⎢⎥⎣⎦,排除B 、D解法三 由题意0A ∈,即()()00f a f <=,所以()1||0a aa +<,当0a >时无解,所以0a <,此时210a -<,∴10a -<<.排除C 、D .又111222<-<, ∴取12a =-,①⇔111||1||||222x x x x x -+-->,符合11,22A ⎡⎤-⊆⎢⎥⎣⎦,排除B . 16.C 【解析】验证A ,当332=3>2.7=19.68>1+3+3=13x e 时,,故排除A ;验证B ,当1=2x111113391-+==22441648⨯⨯,故排除B ;验证C ,令()()()21=cos -1+,'=-sin +,''=1-cos 2g x x x g x x x g x x , 显然()''>0g x 恒成立,所以当[)0,+x ∈∞,()()''0=0g x g ≥, 所以[)0,+x ∈∞,()21=cos -1+2g x x x 为增函数,所以()()0=0g x g ≥,恒成立,故选C ;验证D , 令()()()()()2-311=ln 1+-+,'=-1+=8+144+1x x x h x x x x h x x x ,令()'<0h x ,解得0<<3x ,所以当0<<3x 时,()()<0=0h x h ,显然不恒成立,故选C .17.B 【解析】由题可知()11x f x e =->-,22()43(2)11g x x x x =-+-=--+≤,若有()(),f a g b =则()(1,1]g b ∈-,即2431b b -+->-,解得22b < 18.11-(答案不唯一)【解析】由题意知,当1a =,1b =-时,满足a b >,但是11a b>,故答案可以为11-.(答案不唯一,满足0a >,0b <即可)19.(1,4);(1,3](4,)+∞ 【解析】若2λ=,则当2x ≥时,令40x -<,得24x <≤;当2x <时,令2430x x -+<,得12x <<.综上可知14x <<,所以不等式()0f x <的解集为(1,4).令40x -=,解得4x =;令2430x x -+=,解得1x =或3x =.因为函数()f x 恰有2个零点,结合函数的图象(图略)可知13λ<≤或4λ>.20.1(,)4-+∞【解析】当12x >时,不等式为12221x x-+>恒成立;当102x <≤,不等式12112xx +-+>恒成立; 当0x ≤时,不等式为11112x x ++-+>,解得14x >-,即104x -<≤;综上,x 的取值范围为1(,)4-+∞.21.1[,1]2【解析】由题意,22222(1)221u x y x x x x =+=+-=-+,且[0,1]x ∈,又0x =时,221u x y =+=,12x =时,2212u x y =+=,当1x =时,221u x y =+=,所以22x y +取值范围为1[,1]2.22.6 12【解析】设男生数,女生数,教师数为,,a b c ,则2,,,c a b c a b c >>>∈N①84a b >>>,所以max 6b =,②当min 1c =时,21a b >>>,a ,b ∈N ,a ,b 不存在,不符合题意; 当min 2c =时,42a b >>>,a ,b ∈N ,a ,b 不存在,不符合题意; 当min 3c =时,63a b >>>,此时5a =,4b =,满足题意. 所以12a b c ++=. 23.2【解析】111()1111x x f x x x x -+===+---,因为2x ≥,所以11x -≥, 1011x <-≤,所以11(1,2]1x +∈-,故当2x =时,函数()(2)1xf x x x =≥-取得最大值2. 24.()4,1-【解析】由2340x x --+<得:41x -<<,所以不等式2340x x --+>的解集为()4,1-,所以答案应填:()4,1-.25.(2-【解析】由题意可得()0f x <对于[,1]x m m ∈+上恒成立,即22()210(1)230f m m f m m m ⎧=-<⎨+=+<⎩,解得02m -<<.26.36【解析】因为0,0x a >>,()44a f x x a x =+≥=,当且仅当4a x x =,即3x ==,解得36a =. 27.()2,1-【解析】易得不等式220x x +-<的解集为()2,1-.28.(﹣5,0) ∪(5,﹢∞)【解析】做出x x x f 4)(2-= (0>x )的图像,如下图所示.由于)(x f 是定义在R 上的奇函数,利用奇函数图像关于原点对称做出x <0的图像.不等式x x f >)(,表示函数y =)(x f 的图像在y =x 的上方,观察图像易得:解集为(﹣5,0) ∪(5,﹢∞).29.(-7,3)【解析】当x ≥0时,令245x x -<,解得,05x <≤.又因为)(x f 为定义域为R 的偶函数,则不等式(2)5f x +<等价于525x -<+<,即-7<x <3;故解集为(-7,3).30.(0,8)【解析】因为不等式x 2﹣ax +2a >0在R 上恒成立.∴△=2()80a a --<,解得0<a <8.31.9【解析】因为()f x 的值域为[0,+∞),所以,0=∆即24a b =,所以2204a x ax c ++-=的两根,由一元二次方程根与系数的关系得,4)6(,622c a m m a m -=+-=+解得c =9. 32.(3,2)(3,)-⋃+∞【解析】不等式可化为(3)(2)(3)0x x x +-->采用穿针引线法解不等式即可.33.(11)-【解析】2212(1)10x xx x ⎧->⎪⇒∈-⎨->⎪⎩. 34.27【解析】22()[16,81]x y ∈,2111[,]83xy ∈,322421()[2,27]x x y y xy=⋅∈,43y x 的最大值是27.35.1m <-【解析】已知()f x 为增函数且m ≠0若m >0,由复合函数的单调性可知()f mx 和()mf x 均为增函数,此时不符合题意。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题七 不等式第二十讲 二元一次不等式(组)与简单的线性规划问题答案部分1.D 【解析】解法一 点(2,1)在直线1x y -=上,4ax y +=表示过定点(0,4),斜率为a-的直线,当0a ≠时,2x ay -=表示过定点(2,0),斜率为1a的直线,不等式2x ay -≤表示的区域包含原点,不等式4ax y +>表示的区域不包含原点.直线4ax y +=与直线2x ay -=互相垂直,显然当直线4ax y +=的斜率0a ->时,不等式4ax y +>表示的区域不包含点(2,1),故排除A ;点(2,1)与点(0,4)连线的斜率为32-,当32a -<-,即32a >时,4ax y +>表示的区域包含点(2,1),此时2x ay -<表示的区域也包含点(2,1),故排除B ;当直线4ax y +=的斜率32a -=-,即32a =时,4ax y +>表示的区域不包含点(2,1),故排除C ,故选D .解法二 若(2,1)A ∈,则21422a a +>⎧⎨-⎩≤,解得32a >,所以当且仅当32a ≤时,(2,1)A ∉.故选D .2.C 【解析】不等式组表示的平面区域如图中阴影部分所示,作出直线35y x =-.平移该直线,当经过点C 时,z 取得最大值,由15x y x y -+=⎧⎨+=⎩,得23x y =⎧⎨=⎩,即(2,3)C ,所以max 325321a =⨯+⨯=,故选C .3.D 【解析】可行域如图阴影部分,由图可知,目标函数z x y =+过(3,0)点z 取最大值3.选D . 4.A 【解析】如图为可行域结合目标函数的几何意义可得函数在点()6,3B --处取得最小值,最小值为min 12315z =--=-.故选A .5.B 【解析】不等式组的可行域如图,目标函数的几何意义可得函数在点()0,3A 处取得最小值033z =-=- . 在点()2,0B 处取得最大值202z =-=,选B .x6.D 【解析】不等式组可行域如图阴影部分,当2z x y =+过(1,2)A -时取得最大值3,选D .7.D 【解析】如图阴影为可行域,可知在(2,1)A时,min 4z =,无最大值.x所以2z x y =+的取值范围是[4,)+∞.选D . 8.D 【解析】不等式组可行域如图阴影部分,x目标函数2z x y =+过点(3,3)C 时,取得最大值max 3239z =+⨯=,故选D. 9.C 【解析】作出不等式组所表示的平面区域如图中阴影部分所示,设(,)P x y 为平面区域内任意一点,则22x y +表示2||OP .显然,当点P 与点A 合时,2||OP ,即22x y +取得最大值,由2239x y x y +=⎧⎨-=⎩,解得31x y =⎧⎨=-⎩,故(3,1)A -.所以22x y +的最大值为223(1)10+-=.故选C .10.B 【解析】画出不等式组的平面区域如图所示,由23030x y x y -+=⎧⎨+-=⎩得(1,2)A ,由23030x y x y --=⎧⎨+-=⎩ 得(2,1)B ,由题意可知,当斜率为1的两条直线分别过点A 和点B 时,两直线的距离最小,即||AB ==B .11.A 【解析】画出可行域(图略),可知在点(0,1)处z 取得最小值min 2011z =⨯-=-. 12.D 【解析】设该企业每天生产甲、乙两种产品分别为x 、y 吨,则利润34z x y =+.由题意可列32122800x y x y x y +≤⎧⎪+≤⎪⎨≥⎪⎪≥⎩,其表示如图阴影部分区域:当直线340x y z +-=过点(2,3)A 时,z 取得最大值, 所以max 324318z =⨯+⨯=,故选D .13.C 【解析】画出可行域(图略),可知目标函数在点(2,3)处有最大值9.14.B 【解析】由于不等式组2022020x y x y x y m +-≤⎧⎪+-≥⎨⎪-+≥⎩,表示的平面区域为三角形ABC ,且其面积等于43,再注意到直线AB :20x y +-=与直线BC :20x y m -+=互相垂直,所以ΔABC 是直角三角形;易知(2,0)A ,(1,1)B m m -+,C (2422,33m m -+); 从而112222122223ABC m S m m m ∆+=+⋅+-+⋅=43,化简得:2(1)4m +=,解得m =3-,或m =1;检验知当m =3-时,已知不等式组不能表示一个三角形区域,故舍去;所以m =1;故选B .15.B 【解析】作出可行域(图略)可知,目标函数过点(4,1)-时取最大值.16.A 【解析】作出满足条件的可行域,如图中阴影部分所示,易知在点(1,1)A 处,z 取得最大值,故max 2111z =-⨯+=-.17.C 【解析】 将目标函数变形为2y x z =-,当z 取最大值,则直线纵截距最小,故当0m ≤时,不满足题意;当0m >时,画出可行域,如图所示, 其中22(,)2121mB m m --.显然(0,0)O 不是最优解,故只能22(,)2121mB m m --是最优解,代入目标函数得4222121mm m -=--,解得1m =,故选C .18.A 【解析】根据不等式组作出可行域,如图中阴影部分所示当动点在线段AC 上时xy 取得最大,此时2x +y =10.21125(2))2222x y xy x y +=⋅≤=(.当且仅当52x =,5y =时取等号,对应点落在线段AC 上.故最大值为252.故选A .19.C 【解析】画出可行域如图中阴影部分所示,由图可知,当目标函数2z x y =+经过可行域内的点A (2,-1)时,取得最小值0,故20x y +≥,因此12,p p 是真命题,选C .20.D 【解析】画出约束条件表示的平面区域如图,ax y z -=取得最大值表示直线ax y z -=向上平移移动最大,a 表示直线斜率,有两种情况:1a =-或2a =.21.C 【解析】平面区域Ω为如图所示的阴影部分的△ABD ,因圆心(,)C a b ∈Ω,且圆C 与x 轴相切,所以点C 在如图所示的线段MN 上,线段MN 的方程为1y =(-2≤x ≤6),由图形得,当点C 在点(6,1)N 处时,22a b +取得最大值226137+=,故选C .22.D 【解析】作出线性约束条件20200x y kx y y +-≥⎧⎪-+≥⎨⎪≥⎩,的可行域.当0k >时,如图(1)所示,此时可行域为y 轴上方、直线20x y +-=的右上方、直线20kx y -+=的右下方的区域,显然此时z y x =-无最小值.当1k <-时.z y x =-取得最小值2;当1k =-时,z y x =-取得最小值-2,均不符合题意,当10k -<<时,如图(2)所示,此时可行域为点A (2,0),B (-2k,0),C(0,2)所围成的三角形区域,当直线z y x =-经过点B (-2k ,0)时,有最小值,即2()4k --=-,所以得12k =-.故选D .23.B 【解析】由23z x y =-得32y x z =-,即233zy x =-.作出可行域如图,平移直线233z y x =-,由图象可知当直线233z y x =-经过点B 时,直线233zy x =-的截距最大,此时z 取得最小值,由103x y x -+=⎧⎨=⎩得34x y =⎧⎨=⎩,即(3,4)B ,代入直线23z x y=-得32346z =⨯-⨯=-,选B .24.A 【解析】2||==y x y 与的图像围成一个三角形区域,3个顶点的坐标分别是 (0,0),(-2,2),(2,2).且当取点(-2,2)时,2x – y =-6取最小值.所以选A .25.C 【解析】作出可行域,如图,则在A 点取得最大值16,在B 点取得最小值8-,则24a b-=,选C .26.B 【解析】约束条件对应ABC ∆边际及内的区域:53(2,2),(3,2),(,)22A B C则3[8,11]z x y =+∈.27.C 【解析】约束条件对应ABC ∆边际及内的区域:(1,0),(1,2),1,2)A B C ---则2[5,3]z x y =+∈-.28.A 【解析】作出可行域,直线03=-y x ,将直线平移至点)0,2(处有最大值,点)3,21(处有最小值,即362z -剟,应选A .29.B 【解析】由题意,230y xx y =⎧⎨+-=⎩,可求得交点坐标为(1,2)要使直线y =2x 上存在点(x ,y )满足约束条件30230x y x y x m +-⎧⎪--⎨⎪⎩………,如图所示.则m m 23≥-可得m ≤1,∴实数m 的最大值为1,故选B .30.B 【解析】做出不等式对应的可行域如图,由y x z 23-=得223zx y -=,由图象可知当直线223z x y -=经过点)2,0(C 时,直线223zx y -=的截距最大,而此时y x z 23-=最小为423-=-=y x z ,选B .31.D 【解析】作出可行域如图中阴影部分所示,由图知目标函数过点()5,15A 时,2+3x y 的最大值为55,故选D .32.B 【解析】画出区域D 如图所示,而z =·y +,所以y z =+,令0l:y =,平移直线0l 过点2)时,z取得最大值,故max 24z =.33.B 【解析】如图先画出不等式||||1x y +≤表示的平面区域,易知当0x =,1y =时,2x y +取得最大值2,当0,1x y ==-时,2x y +取得最小值-2,选B.34.A 【解析】 画出可行域,可知5z x y =+在点1(,)11mm m++取最大值,由21211m m m+<++解得11m <<. 35.B 【解析】当直线z=2x -5y 过点B 时,min 14z =-,当直线z=2x -5y 过点D(0,-4)时,max 20z =,所以z =2x -5y 的取值范围为(-14,20),点D 的坐标亦可利用AB DC =求得.36.A 【解析】作出满足约束条件的可行域,如右图所示,可知当直线z=34x y -平移到点(5,3)时,目标函数z=34x y -取得最大值3; 当直线z=34x y -平移到点(3,5)时,目标函数z=34x y -取得最小值-11,故选A . 37.6【解析】作出可行域为如图所示的∆ABC 所表示的阴影区域,作出直线320+=x y ,并平移该直线,当直线过点(2,0)A 时,目标函数32z x y =+取得最大值:且max 32206=⨯+⨯=z .38.9【解析】画出不等式组所表示的平面区域,如图中阴影部分所示.作出直线0x y +=,平移该直线,当直线过点(5,4)B 时,z 取得最大值,max 549z =+=.=039.3【解析】易知13z x y =+在可行域的顶点取得最大值,由230240x y x y ++=⎧⎨-+=⎩, 解得21x y =-⎧⎨=⎩,代入13z x y =+,可得53z =-;由23020x y x ++=⎧⎨-=⎩,解得27x y =⎧⎨=-⎩,代入13z x y =+,可得13z =-;由20240x x y -=⎧⎨-+=⎩,解得23x y =⎧⎨=⎩,代入13z x y =+,可得3z =;可知,z 的最大值为3.40.3【解析】作出不等式组21y xx y ⎧⎨+⎩≤≤,所表示的平面区域如图中阴影部分所示,yxOy=12x y=x+1y=2xA令2z y x =-,作出直线20y x -=,平移该直线,当直线过点(1,2)A 时,2y x -取得最小值,最小值为2213⨯-=.41.−2;8【解析】由题可得,该约束条件表示的平面区域是以(2,2),(1,1),(4,2)-为顶点的三角形及其内部区域(图略).由线性规划的知识可知,目标函数3z x y =+在点(2,2) 处取得最大值,在点(4,2)-处取得最小值,则最小值min 462z =-=-,最大值max 268z =+=.42.4[,13]5【解析】不等式组所表示的平面区域是以点(0,2),(1,0),(2,3)为顶点的三角形及其内部,如图所示,因为原点到直线220x y +-=, 所以22min 4()5x y +=,又当(,)x y 取点(2,3)时,22x y +取得最大值13, 故22x y +的取值范围是4[,13]5.43.216000【解析】由题意,设产品A 生产x 件,产品B 生产y 件,利润2100900z x y =+,线性约束条件为 1.50.51500.390536000,0x y x y x y x y +⎧⎪+⎪⎨+⎪⎪⎩………厖,作出不等式组表示的平面区域如图中阴影部分所示,又由x N ∈,y N ∈,可知取得最大值时的最优解为(60,100), 所以max 210060900100216000z =⨯+⨯=(元).44.10-【解析】作出不等式组表示的平面区域,如图中阴影部分所示,由图知当235z x y =+-经过点(1,1)A --时,z 取得最小值,min 2(1)3(1)510z =⨯-+⨯--=-.45.7 【解析】 由目标函数23z x y =+的可行域为ΔABC 边界及其内部(如图所示).令0z =,即230x y +=,平移直线230x y +=至目标函数的可行域内,可知当23x y z +=过点(2,1)A 时,z 取得最大值,即max 22317z =⨯+⨯=.46.4 【解析】 作出可行域(图略),作出直线0l :30x y +=,平移直线0l ,当直线:3z x y =+过点A 时,z 取最大值,由2=021=0x y x y +-⎧⎨-+⎩,解得A (1,1),∴3z x y =+的最大值为4.47.4【解析】如图阴影部分,可知12(22)42ABC S ∆=⨯⨯+=48.3[1,]2【解析】由线性规划的可行域,求出三个交点坐标分别为3(1,0),(1,),(2,1)2,都代入14ax y +≤≤,可得312a ≤≤.49.-2【解析】画出可行域(图略),由题意可知不等式组表示的区域为一三角形,平移参照直线20x y +=,可知在点(,)k k 处2z x y =+取得最小值,故26z k k =+=-. 解得2k =-.50.3【解析】做出可行域可知,当3,3x y ==的时候z 有最大值351.2【解析】此不等式表示的平面区域如图所示y kx z =-+.当k >0时,直线0l :y kx=-平移到A 点时目标函数取最大值,即当4k +4=12 所以k =2 ,当k <0时,直线:y kx =-平移到A 或B 点是目标函数取最大值,可知k 取值是大于零,所以不满足,所以k =2,所以填2.52.6【解析】画出可行区域,即为五边形区域,平移参照直线0x y +=,x y +在点(4,2)处取得最大值,此时()max 426x y +=+=.53.[3,3]-【解析】约束条件对应四边形OABC 边际及内的区域:(0,0),(0,1),(1,2),(3,0)O A B C 则2[3,3]z x y =-∈-.54.3【解析】画出可行域,可知5z x y =+在点1(,)11mm m++取最大值为4,解得3m = 55.1【解析】目标函数2z x y =-,当0x =时,z y =-,所以当y 取得最大值时,z 的值最小;移动直线20x y -=,当直线移动到过点A 时,y 最大,即z 的值最小,此时2111z =⨯-=.56.-6【解析】根据32969x y x y ≤+≤⎧⎨≤-≤⎩得可行域,根据2z x y =+得22x zy =-+,平移2xy =-,易知在点(4,5)-处z 取得最小值-6. 57.4【解析】不等式表示的区域是一个四边形,4个顶点是1(0,0),(0,2),(,0),(1,4)2,易见目标函数在(1,4)取最大值8,所以844ab ab =+⇒=,所以4a b +≥=,在2a b ==时是等号成立.所以a b +的最小值为4..58.15【解析】设购买铁矿石A 和B 各x ,y 万吨,则购买铁矿石的费用y x z 63+=,x ,y 满足约束条件0.50.7 1.90.520,0x y x y x y +⎧⎪+⎨⎪⎩≥≤≥≥,表示平面区域(图略)则当直线y x z 63+=过点B (1,2)时,购买铁矿石的最少费用z =15.59.【解析】(Ⅰ)由已知,,x y 满足的数学关系式为7060600,5530,2,0,0,x y x y x y x y +⎧⎪+⎪⎪⎨⎪⎪⎪⎩≤≥≤≥≥即7660,6,20,0,0,x y x y x y x y +⎧⎪+⎪⎪-⎨⎪⎪⎪⎩≤≥≤≥≥该二元一次不等式组所表示的平面区域为图1中的阴影部分:xx(图1) (图2)(Ⅱ)设总收视人次为z 万,则目标函数为6025z x y =+.考虑6025z x y =+,将它变形为12525z y x =-+,这是斜率为125-,随z 变化的一族平行直线.25z 为直线在y 轴上的截距,当25z取得最大值时,z 的值最大.又因为,x y 满足约束条件,所以由图2可知,当直线6025z x y =+经过可行域上的点M 时,截距25z最大,即z 最大. 解方程组7660,20,x y x y +=⎧⎨-=⎩得点M 的坐标为(6,3).所以,电视台每周播出甲连续剧6次、乙连续剧3次时才能使总收视人次最多.60.【解析】(Ⅰ)由已知y x ,满足的数学关系式为⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≥≤+≤+≤+003001033605820054y x y x y x y x ,该二元一次不等式组所表示的区域为图1中的阴影部分.(1)(Ⅱ)设利润为z 万元,则目标函数y x z 32+=,这是斜率为32-,随z 变化的一族平行直线.3z 为直线在y 轴上的截距,当3z取最大值时,z 的值最大.又因为y x ,满足约束条件,所以由图2可知,当直线y x z 32+=经过可行域中的点M 时,截距3z的值最大,即z 的值最大.解方程组⎩⎨⎧=+=+30010320054y x y x 得点M 的坐标为)24,20(M ,所以112243202max =⨯+⨯=z .答:生产甲种肥料20车皮,乙种肥料24车皮时利润最大,且最大利润为112万元.(2)61.【解析】设为该儿童分别预订,x y 个单位的午餐和晚餐,共花费z 元,则 2.54z x y =+,且满足以下条件⎪⎪⎩⎪⎪⎨⎧≥≥+≥+≥+0,54106426664812y x y x y x y x ,即⎪⎪⎩⎪⎪⎨⎧≥≥+≥+≥+0,275371623y x y x y x y x ,做出可行域(图略)作直线:2.540l x y +=,平移直线l 至0l ,当0l 经过C 点时,可使z 达到最小值. 由⎩⎨⎧==⇒⎩⎨⎧=+=+3472753y x y x y x 即(4,3)C , 此时 2.544322z =⨯+⨯=,答: 午餐和晚餐分别预定4个单位和3个单位,花费最少z=22元.。
