《线性代数》上机作业一(格式)

合集下载

大连理工线代上机实验

基本操作
四则运算、转置、求逆、求秩、求行列式、组合、化为行最简形、求特征值
常见任务
① 矩阵的赋值和其加、减、乘、除（求逆）命令； ② 矩阵化为最简行阶梯型的计算命令；[U0,ip]=rref(A) ③ 多元线性方程组MATLAB求解的几种方法；x=inv(A)*b, U=rref(A) ④ 行列式的几种计算机求解方法； D=det(A),[L,U]=lu(A);D=prod(diag(L)) ⑤ n个m维向量组的相关性及其秩的计算方法和命令; r=rank(A),U=rref(A) ⑥ 求欠定线性方程组的基础解系及超定方程解的MATLAB 命令；xb=null(A) ⑦ 矩阵的特征方程、特征根和特征向量的计算命令； f=poly(A);[P,D]=eig(A) ⑧ 化二次型为标准型的MATLAB命令；yTDy=xTAx; 其中 y=P-1x,
• • • •
-66.5556 25.6667 -18.7778 26.5556
• >>
例三、求秩
• • • • • • • • • • • • >> A=[2,1,-5,1;1,-5,0,7;0,2,1,-1;1,6,-1,-4]; >> r=rank(A); >> r= % = 计算机不显示r的值 ??? r= | Error: Expression or statement is incomplete or incorrect. >> rank(A) ans = 4 >> r r= 4 %不打；则计算机将显示rank(A)的值
例1 用直接解法求解下列线性方程组. 命令如下： A=[2,1,-5,1;1,-5,0,7;0,2,1,-1;1,6,-1,-4]; b=[13,-9,6,0]'; x=A\b

线代作业完整版

作业成绩班级姓名序号第1次作业行列式的性质本次作业目的熟悉行列式的性质；会用化三角法计算简单行列式。

1. 用行列式性质证明下列等式：(1) 1111111122222223333333a kb b c c a b c a kb b c c a b c a kb b c c a b c ++++=++23；证 (2) 2y z z x x y x yz x yy z z x z x y z xx yy z yzx ++++++=+++；证(3)()()()()()()()()()()()()22222222222222221231230123123a a a a b b b b cc c cd d d d ++++++=++++++。

证作业成绩班级姓名序号第2次作业行列式展开克莱姆法则本次作业目的熟悉行列式展开法则和克莱姆法则；会熟练应用展开法则计算行列式；会用克莱姆法则解低阶方程组，讨论方程组的解。

1.1121234134124206D−−=−，求3132342A A A++。

解2. 计算下列行列式：(1) 1111 1111 1111 1111xxyy+−+−；解(2)222b c c a a ba b ca b c+++；解作业成绩班级姓名序号第3次作业矩阵及其运算本次作业目的掌握矩阵的加法、数乘、乘法、转置和方阵的行列式及其运算规律。

1. 计算：(1) ；()123223−⎛⎞⎜⎟−⎜⎟⎜⎟⎝⎠解(2) 111213112312222321332333()a a a x x x x a a a x a a a x ⎛⎞⎜⎟⎜⎟⎜⎟⎝⎠⎛⎞⎜⎟⎜⎟⎜⎟⎝⎠⎞⎟⎟⎟⎠。

解2. 设，求3111123111,124111051⎛⎞⎛⎜⎟⎜=−=−−⎜⎟⎜⎜⎟⎜−⎝⎠⎝A B AB 解3. 已知11(1,2,3),1,,23⎛⎞==⎜⎝⎠αβ⎟，矩阵=A T αβ，其中T α是α的转置，求(为正整数)。

线性代数大作业(一)

线性代数大作业（一）学号：02121443 姓名：惠政成绩：____________1. 设A=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--730005600032001，且B=(E+A)1-(E-A),则(E+B)1-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--45.100033000210001A=[1 0 0 0;-2 3 0 0;0 6 5 0;0 0 -3 7]; B=inv(eye(4)+A)*(eye(4)-A); inv(eye(4)+B) ans =1.0000 0 0 0 -1.00002.0000 0 0 03.0000 3.0000 0 0 0.0000 -1.50004.0000 2. 非齐次线性方程组⎪⎪⎪⎩⎪⎪⎪⎨⎧=+-+--=-++--=-+----=-++--=-++--2101099650074121929543914622517141413235432154321543215432154321x x x x x x x x x x x x x x x x x x x x x x x x x 的解为(3955500,-2477700,-1521800,7075700,2712600)T。

A=[-23 -13 14 14 -7;-2 -2 1 6 -14;-4 -5 -9 2 -9;-4 -7 1 0 -0;9 -1 1 -9 10]; b=[51;-39;121;-65;210]; x=inv(A)*b x =1.0e+006 * 3.9555 -2.4777 -1.5218 7.0757 2.71263. 设行列式D=2235085095234321-c c c c ，则其第4行各余子式分别为M 41=9c 4+72c 2-45c 3 M 42=-24c 4+72c 1 M 43=-15c 4+45c 1 M 44=24c 2-153c +9c 1。

syms c1 c2 c3 c4;D=[3 2 5 9;c1 c2 c3 c4;0 5 8 0;5 3 -2 2]; a=[2 5 9;c2 c3 c4;5 8 0]; b=[3 5 9;c1 c3 c4;0 8 0]; c=[3 2 9;c1 c2 c4;0 5 0]; d=[3 2 5;c1 c2 c3;0 5 8]; det(a),det(b),det(c),det(d); ans =9*c4+72*c2-45*c3 ans =-24*c4+72*c1 ans =-15*c4+45*c1 ans =24*c2-15*c3+9*c1 4. 设R 3的两个基为α1=（1,1,0）T,α2=(0,1,1)T，α3=(0,0,1)Tβ1=(1，-1,2)T,β2=(1,1-1)T,β3=(-2,1，-3)T求解从基α1，α2，α3到基β1，β2，β3的过渡矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡6-1-4302-2-11 B=[1 0 0;1 1 0;0 1 1],C=[1 1 -2;-1 1 1;2 -1 -3]A=inv(B)*C A =1 1 -2 -2 034 -1 -6 5. 非齐次线性方程组⎪⎪⎩⎪⎪⎨⎧=++++=++++=++++=++++12372023244322454323654321543215432154321x x x x x x x x x x x x x x x x x x x x 的通解为k 1⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡00015.0-+k 2⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡15.3-1075.0+⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡7143.102857.0-02143.0- A=[6 3 2 3 4;4 2 1 2 3;4 2 3 2 1;2 1 7 3 2];b=[5;4;0;1]; x0=A\b x=null(A,'r') x0 =-0.2143 0 -0.2857 0 1.7143 x =-0.5000 0.7500 1.0000 0 0 1.0000 0 -3.5000 0 1.0000 6. 其次线性方程组⎪⎪⎩⎪⎪⎨⎧=-+++=+-++-=+--+=+++-0)28(7004)5(2300)3(20442)2(4321432143214321x k x x x x x k x x x x x k x x x x x k 在k 为______1,3,4,6_________时有非零解，其分别对应的基础解系是(0,21,1,-45)T ,(0,-2,0,1)T ,(-3,-7,1,1)T,(35,1,31,65)T 。

线性代数上机作业一

线性代数机算与应用作业题主要练习线性代数课本上所讲函数的用法以及用这些函数解简单的实际问题一、机算题1．利用函数rand 和函数round 构造一个5×5的随机正整数矩阵A 和B 。

（1）计算A ＋B ，A －B 和6A （2）计算()TAB ，TTB A 和()100AB（3）计算行列式A ，B 和AB （4）若矩阵A 和B 可逆，计算1A -和1B - （5）计算矩阵A 和矩阵B 的秩。

2．求解下列方程组（1）求非齐次线性方程组1234123412341234224514171278776652921710x x x x x x x x x x x x x x x x +++=⎧⎪-+-+=⎪⎨+++=⎪⎪--+-=⎩的唯一解。

（2）求非齐次线性方程组123451234512345123455972844228252398881266977x x x x x x x x x x x x x x x x x x x x ++++=⎧⎪++++=⎪⎨++++=⎪⎪++++=⎩的通解。

3．已知向量组134083α⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦，211022α⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦，⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=160323α，⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=212394α，50822110α⎡⎤⎢⎥⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎣⎦，求出它的最大无关组，并用该最大无关组来线性表示其它向量。

4．求向量空间3R 中向量325α⎛⎫ ⎪= ⎪ ⎪⎝⎭在基1231230,1,2001βββ⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪=== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭下的坐标5．求下列矩阵的特征值和特征向量，并判断其正定性。

（1）1232563625A ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦；（2）203131061622B -⎡⎤⎢⎥=--⎢⎥⎢⎥--⎣⎦6．用正交变换法将下列二次型化为标准形。

()222123123112213323,,23f x x x x x x k x x k x x k x x =+++++其中“123k k k ”为自己学号的后三位。

《线性代数》作业

《线性代数》作业第一章1、求排列(2n)(2n-1)…(n+1)1 2…(n -1)n 的逆序数。

解：后面是正常顺序，逆序出现在前n 个数与后n 个数之间，2n 的逆序数是2n-1，2n-1的逆序数是2n-2，……，n+1的逆序数是n ，所以整个排列的逆序数是(2n-1)＋(2n-2)＋……＋n ＝n(3n-1)/22、求排列246......(2n)135……(2n-1)的逆序数。

解析：后一项比前一项的算逆序一次，246......(2n)无逆序，所以从1开始，有246......(2n)共N 个，3开始有46......(2n)有N-1个，.......，.2n-1有一个，所以，加一起得，逆序数为1+2+......+N=N （N+1）/2N=n+(n-1)+......+2+1=n(n+1)/23、试判断655642312314a a a a a a ，662551144332a a a a a a -，662552144332a a a a a a -是否都是六阶行列式中的项。

解a 14a 23a 31a 42a 56a 65 下标的逆序数为 t （431265）=0+1+2+2+0+1=6所以655642312314a a a a a a 是六阶行列式中的项。

662551144332a a a a a a -下标的逆序数为 t （452316）=8所以662551144332a a a a a a -不是六阶行列式中的项。

662552144332a a a a a a -下标的逆序数为t(452316)=8所以662552144332a a a a a a -不是六阶行列式中的项。

4、已知4阶行列式D 中的第3列上的元素分别是3，-4，4，2，第1列上元素的余子式依次为8，2，-10，X ，求X 。

解：X=205、设15234312a a a a a j i 是5阶行列式的一项，若该项的符号为负，则 i= 5 ,j= 4 。

线代上机作业

上机作业（一）随机生成5阶方阵A,B,C及5维列向量b，求：①A+B,A-B.解：在Matlab中输入：A=rand(5,5);B=rand(5,5);C=rand(5,5);b=rand(5,1);得：输入A+B；A-B.得：②A*B+B*A.解：输入A*B+B*A.得：③Ax=b的解,并验证克莱姆法则.解：输入：x=A\b.得：输入：D=A;D1=A;D2=A;D3=A;D4=A;D5=A;D1(:,1)=b;D2(:,2)=b;D3(:,3)=b;D4(:,4)=b;D5(:,5)=b; Y=[det(D1)/det(D);det(D2)/det(D);det(D3)/det(D);det(D4)/det(D);det(D5)/det(D)].得：发现：x=y,故克莱姆法则成立.④A,B的行列式，逆，秩.解：输入：det(A);det(B);inv(A);inv(B);rank(A);rank(B).得：⑤A*B的行列式，逆，秩，并验证det(A*B)=det(A)*det(B).解：输入det(A*B);det(A)*det(B).得：可见det(A*B)=det(A)*det(B).⑥验证(AB)T=B T A T,(AB)−1=B−1A−1,AB≠BA.解：输入(A*B)’;B’*A’;inv(A*B);inv(B)*inv(A);A*B;B*A.由此可见(AB)T =B T A T ,(AB)−1=B −1A −1,AB ≠BA . ⑦求矩阵X 使得AXB=C. 解：输入X=(A\C)/B. 得：上机作业（二）验证：对于一般的方阵A,B,C,D ，若A,C 均为对角矩阵，且A 可逆，则：解：输入：A=rand(3,3);B=rand(3,3);C=rand(3,3);D=rand(3,3);E(1:3,1:3)=A;E(1:3,4:6)=B;E(4:6,1:3)=C;E(4:6,4:6)=D;det(E);det(A)*det(D)-det(B)*det(C).A B A D B CC D≠-A B AD CB C D =-由此可见在Matlab中输入：A=diag(diag(rand(3,3)));B=rand(3,3);C=diag(diag(rand(3,3)));D=rand(3,3);E(1:3,1:3)=A;E(1:3,4:6)= B;E(4:6,1:3)=C;E(4:6,4:6)=D;det(E);det(A*D-C*B).由此可见上机作业（三）N= 201465004共9位 a=最后两位 04. b=第4-5位 46. c=第6-7位 50. d=第4,8位 40. e=第1,8位 20. f=第5,9位 64. g=第4,9位 44. h=第5,7位 60.求A 列向量组的一个最大无关组，并把不属于极大无关组的向量利用极大无关组表示.解：由题意可得该矩阵为：A=[44650123403444312152220644417576080]. 在MAtlab 中输入A=[4,46,50,40,3,4;1,2,3,4,4,3;12,15,22,17,5,7;20,64,44,60,8,0];b=rref(A).所以α1,α2,α3,α4是一个极大无关组，且有：α5=−0.2945α1−1.4863α2−0.0062α3+1.8214α4 α6=−0.0863α1−1.3001α2+0.3643α3+1.1484α4上机作业（四）Ax=b的解在下列不同的取值时变化如何？34123443121522175780a b c dA e f g h ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦解：在Matlab 中输入syms x; syms y; B=[1;2+x;64;50];A=[4,46,50,40;1+y,2+2*y,3+3*y,4+4*y;12,15,22,17;20,64,44,60]; A\B. 得：即X=[(2∗(12597∗ε − 362∗δ + 11873))/(3975∗(ε + 1)) −(3298∗δ − 4563∗ ε+ 2033)/(7950∗(ε + 1))(4791∗ε − 61∗δ + 4669)/(3975∗(ε + 1)) −(4413∗ε − 818∗δ + 2777)/(1590∗(ε + 1))].上机作业（五）随机生成4个5维向量，并进行正交化.解：在Matlab 中输a=rand(5,1);b=rand(5,1);c=rand(5,1);d=rand(5,1);M=[a,b,c,d];N=orth(M). 得：121223344,,121522170.1,0.2,0.5,0.7,0.9,0.95ab c d b A f c ef g h δεεεεδε⎡⎤⎡⎤⎢⎥⎢⎥+++++⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦=--=----即：四个五维向量为: [ 0.78030.38970.24170.40390.0965] 、[ 0.13200.94210.95610.57520.0598] 、[ 0.23480.35320.82120.01540.0430] 、[ 0.16900.64910.73170.64770.4509].正交化向量为: [ −0.2454−0.5709−0.6522−0.4052−0.1559] 、[ 0.8748−0.0664−0.42190.22230.0533] 、[ −0.40650.1428−0.47270.64500.4182] 、[ 0.0895−0.50680.2989−0.12680.7935]. 在Matlab 中输入N’*N 验证答案，得：由结果可知答案正确.上机作业（六）I 、随机生成5阶矩阵，求其特征值及对应特征向量. 解：在Matlab 中输入A=rand(5,5); [X,B]=eig(A).其中B 的对角线元素是特征值, X 的列是相应的特征向量.II 、随机生成5维列向量x ，求矩阵XX′的特征值并观察结果，尝试得出一般性结论.解：在Matlab 中输入syms a; syms b; syms c; syms d; syms e; x=[a;b;c;d;e]; y=x*x’; [X,B]=eig(y).故当a,b,c,d,e 是实数时，矩阵XX′的特征值为(0,0,0,0,a 2+b 2+c 2+d 2+e 2).上机作业（七）化简下列二次型，并判断正定性:()2221231122233,,32fx x x x x x x x x x =+-++()22123121323,,44fx x x x x x x x x =-+-解：在Matlab中输入A=[1,1.5,0;1.5,-1,1;0,1,1];[P,D]=schur(A).得：P就是所求的正交矩阵,使得P’AP=D,所以令X=PY,化简后的二次型为g=−2.0616y12+ y22+2.0616y32.此二次型非正定非负定.在Matlab中输入A=[1,0,2;0,-1,-2;2,-2,0] ;[P,D]=schur(A).得：P就是所求的正交矩阵,使得P’AP=D,所以令X=PY,化简后的二次型为g=−3y12+3y32.此二次型非正定非负定.上机作业（八）某城市共30万人从事农业、工业、商业工作，假定此人数不变，另外，社会调查表明：（1）在此30万人中，目前约15万人从事农业，9万人从事工业，6万人从事商业；（2）农业人员中，每年20%转为工业，10%转为商业；（3）工业人员中，每年20%转为农业，10%转为商业；（4）商业人员中，每年10%转为农业，10%转为工业；预测一、二年后各行业人数，及若干年后各行业人数。

线性代数上机作业

线性代数上机作业一、单项选择题。

1、可逆矩阵用用det()函数求行列式判断，选C 代码如下：A = [2 3 0; 0 -2 -3; -6 -5 6];B = [-3 2 3; 2 2 -1; -1 4 2];C = [3 -2 2;3 -1 2 ; 0 -1 -1];D = [2 1 1; -6 -3 -3; 3 -2 2];det(A)ans =>> det(B)ans =1.1102e-15>> det(C)ans =-3>> det(D)ans =Det(B) 可近似为02、用代数余子式求行列式：C>> 1*(-9)+(-5)*2+5*(-6)+(-9)*(-6)ans =53、n阶线性相关即行列式为0：A>> syms x>> A = [-35 56 x -43;-10 17 21 -14;-5 8 9 -6;20 -31 -34 23] A =[ -35, 56, x, -43][ -10, 17, 21, -14][ -5, 8, 9, -6][ 20, -31, -34, 23]>> det(A)ans =5*x - 320>> x = 320/5x =644、f为正定二次型，用特殊值判断t的范围：At=2行列式大于0和t = 5时行列式小于0A =1 -5 4-5 26 184 -22 22>> det(A)ans =82>> A = [1 -5 -10; -5 26 -52; -10 48 22];>> det(A)ans =-282.00005、因特征值与特征向量对应,选D二、填空题：1、147：由行列式互换行列改变符号，所以|B|=7，>> (-3)^3*(-7)-6*7ans =1472、B = [-2 2 0 ] 由B = 2*(A-E)^-1*A得[-6 6 -2][ 0 -2 4]A = [2 -1 -1; 3 -1 -2; 3 -2 0];>> B = 2*(A-eye(3))^-1*AB =-2.0000 2.0000 0-6.0000 6.0000 -2.00000 -2.0000 4.00003、-13 -7 -13 由f(A)=f(λ) f(x) = -x^2+x-1 所以特征值为f(-3)= -13 ;f(3)=-7; f(4)=-134、10 -4 2 化为行最简型：A = [1 4 4; 0 1 4; 0 0 1];>> a = [2 4 2]';>> rref([A a])ans =1 0 0 100 1 0 -40 0 1 25、>> A = [3 0 2 4; 4 4 0 -3; 4 0 4 4; 2 3 1 0];>> B = [4 -3 4 0; 2 0 4 0; 0 2 -1 2; 0 4 3 1];>> (A*B)^2ans =872 100 1197 34338 1128 471 5341032 128 1432 404404 470 710 3566、-3 求行列式直接用det()即可A = [1 3 2 -3 3; 5 0 1 9 -6; 5 3 3 4 -2; 3 5 1 1 6; 0 0 2 -2 -1];>> det(A)-3.00007、3 求秩用rank()函数。

大连理工大学线性代数实验上机报告材料

大连理工大学线性代数实验上机报告实验一首先随机生成五阶方阵AA=rand(5)A =0.8147 0.0975 0.1576 0.1419 0.6557 0.9058 0.2785 0.9706 0.4218 0.0357 0.1270 0.5469 0.9572 0.9157 0.8491 0.9134 0.9575 0.4854 0.7922 0.9340 0.6324 0.9649 0.8003 0.9595 0.6787>> B=rand(5)随机生成五阶方阵BB =0.7577 0.7060 0.8235 0.4387 0.4898 0.7431 0.0318 0.6948 0.3816 0.4456 0.3922 0.2769 0.3171 0.7655 0.6463 0.6555 0.0462 0.9502 0.7952 0.7094 0.1712 0.0971 0.0344 0.1869 0.7547>> b=rand(1,5)'随机生成列向量bb =0.27600.67970.65510.16260.1190计算A+B>> A+Bans =1.5725 0.8036 0.9811 0.5806 1.1455 1.6489 0.3103 1.6654 0.8033 0.48130.5192 0.8238 1.2743 1.6813 1.49541.5689 1.0037 1.4356 1.5874 1.6434 0.8035 1.0620 0.8347 1.1464 1.4334 计算A-B>> A-Bans =0.0570 -0.6085 -0.6658 -0.2969 0.1660 0.1627 0.2467 0.2758 0.0402 -0.4099 -0.2652 0.2700 0.6401 0.1502 0.2028 0.2579 0.9113 -0.4648 -0.0030 0.2246 0.4612 0.8678 0.7658 0.7726 -0.0760 计算A*B+B*A>> A*B+B*Aans =3.0288 2.3058 3.1439 2.7276 3.10342.9094 2.19673.0040 3.0737 3.25843.3422 2.1423 3.2104 3.5734 3.90494.1446 2.9794 4.3676 4.2354 4.9170 3.1350 1.7787 3.2289 3.1170 3.2815 求Ax=b的解>> x=A\bx =-0.98502.43963.3124-5.65151.7085验证克莱姆法则>> c=A(:,1)c =0.81470.90580.12700.91340.6324>> d=A(:,2)d =0.09750.5469 0.9575 0.9649>> e=A(:,3)e =0.1576 0.9706 0.9572 0.4854 0.8003>> f=A(:,4)f =0.1419 0.4218 0.91570.9595>> g=A(:,5)g =0.65570.03570.84910.93400.6787>> B1=[b';d';e';f';g']'B1 =0.2760 0.0975 0.1576 0.1419 0.6557 0.6797 0.2785 0.9706 0.4218 0.0357 0.6551 0.5469 0.9572 0.9157 0.8491 0.1626 0.9575 0.4854 0.7922 0.9340 0.1190 0.9649 0.8003 0.9595 0.6787>> B2=[c';b';e';f';g']'B2 =0.8147 0.2760 0.1576 0.1419 0.6557 0.9058 0.6797 0.9706 0.4218 0.0357 0.1270 0.6551 0.9572 0.9157 0.8491 0.9134 0.1626 0.4854 0.7922 0.9340 0.6324 0.1190 0.8003 0.9595 0.6787>> B3=[c';d';b';f';g']'B3 =0.8147 0.0975 0.2760 0.1419 0.6557 0.9058 0.2785 0.6797 0.4218 0.0357 0.1270 0.5469 0.6551 0.9157 0.8491 0.9134 0.9575 0.1626 0.7922 0.9340 0.6324 0.9649 0.1190 0.9595 0.6787>> B4=[c';d';e';b';g']'B4 =0.8147 0.0975 0.1576 0.2760 0.6557 0.9058 0.2785 0.9706 0.6797 0.0357 0.1270 0.5469 0.9572 0.6551 0.8491 0.9134 0.9575 0.4854 0.1626 0.9340 0.6324 0.9649 0.8003 0.1190 0.6787>> B5=[c';d';e';f';b']'B5 =0.8147 0.0975 0.1576 0.1419 0.2760 0.9058 0.2785 0.9706 0.4218 0.6797 0.1270 0.5469 0.9572 0.9157 0.6551 0.9134 0.9575 0.4854 0.7922 0.1626 0.6324 0.9649 0.8003 0.9595 0.1190>> x1=det(B1)/det(A)x1 =-0.9850>> x2=det(B2)/det(A) x2 =2.4396>> x3=det(B3)/det(A) x3 =3.3124>> x4=det(B4)/det(A) x4 =-5.6515>> x5=det(B5)/det(A)x5 =1.7085计算A的行列式>> det(A)ans =-0.0250计算B的行列式>> det(B)ans =0.0647求A的逆>> inv(A)ans =3.1375 -0.8078 -1.8788 -4.21945.1680-8.6076 3.5314 2.8907 13.7204 -14.3665 -6.2824 3.7220 3.6132 10.0084 -12.4190 13.6173 -6.8822 -6.3938 -23.5288 27.5825 -2.5292 1.0729 2.4193 5.8870 -7.2671 求B的逆>> inv(B)ans =-0.4430 3.4997 1.3255 -2.6005 -0.4697 1.4047 -1.1626 0.2422 -0.4475 -0.0119 0.7210 -1.8189 -2.0635 2.4434 0.0765 -0.6122 -0.1837 2.0165 0.0375 -1.2564 0.0384 -0.5157 -0.7370 0.5267 1.7407 求A的秩>> rank(A)ans =5求B的秩>> rank(B)ans =5求A*B的行列式>> det(A*B)ans =-0.0016求A*B的逆>> inv(A*B)ans =-74.0649 35.0433 31.2288 121.5740 -137.3442 6.8291 -1.2718 -2.2922 -8.9951 8.6972 63.9620 -31.4202 -29.5061 -105.6918 122.3246 -9.3196 5.7452 4.6259 11.9660 -15.4028 11.9582 -6.3521 -3.3817 -16.7574 18.6360>> rank(A*B)ans =5>> det(A)*det(B)ans =-0.0016验证（1）>> (A*B)'ans =0.9569 1.5566 1.6237 2.2732 2.25520.6922 0.9401 0.4969 0.9371 0.80900.9461 1.6492 1.6875 2.3563 2.38000.7507 1.5887 1.8840 1.9421 2.14811.1399 1.52122.2149 2.4545 2.4497()()111,,T T T AB B A AB B A AB BA---==≠>> B'*A'ans =0.9569 1.5566 1.6237 2.2732 2.2552 0.6922 0.9401 0.4969 0.9371 0.8090 0.9461 1.6492 1.6875 2.3563 2.38000.7507 1.5887 1.8840 1.9421 2.14811.1399 1.52122.2149 2.4545 2.4497 （2）>> inv(B)*inv(A)ans =-74.0649 35.0433 31.2288 121.5740 -137.3442 6.8291 -1.2718 -2.2922 -8.9951 8.6972 63.9620 -31.4202 -29.5061 -105.6918 122.3246 -9.3196 5.7452 4.6259 11.9660 -15.4028 11.9582 -6.3521 -3.3817 -16.7574 18.6360 （3）>> A*Bans =0.9569 0.6922 0.9461 0.7507 1.13991.5566 0.9401 1.6492 1.5887 1.52121.6237 0.4969 1.6875 1.88402.21492.2732 0.9371 2.3563 1.9421 2.4545 2.2552 0.8090 2.3800 2.1481 2.4497>> B*Aans =2.0719 1.6135 2.1978 1.9769 1.9635 1.3528 1.2566 1.3549 1.4850 1.7372 1.7186 1.6454 1.5229 1.6894 1.6900 1.8714 2.0423 2.0113 2.2932 2.4625 0.8797 0.9697 0.8489 0.9690 0.8317 求矩阵X使得AXB=C首先随机生成五阶方阵C>> C=rand(5)C =0.4984 0.7513 0.9593 0.8407 0.35000.9597 0.2551 0.5472 0.2543 0.19660.3404 0.5060 0.1386 0.8143 0.25110.5853 0.6991 0.1493 0.2435 0.61600.2238 0.8909 0.2575 0.9293 0.4733X=A 的逆*B 的逆>> X=inv(A)*C*inv(B)X =3.8432 -13.8858 2.1418 9.4404 -4.5871-9.3312 41.9602 -7.9101 -28.4683 14.8942-7.8738 35.1218 -5.4107 -22.8861 10.158116.7545 -75.6079 14.6784 49.3951 -24.7450-3.5568 17.0848 -2.9018 -11.2670 5.4559实验二1. 验证：对于一般的方阵A,B,C,D ，首先随机生成方阵A,B,C,D A=rand(5)A BA DB CC D ≠-A =0.8258 0.1067 0.8687 0.4314 0.1361 0.5383 0.9619 0.0844 0.9106 0.8693 0.9961 0.0046 0.3998 0.1818 0.5797 0.0782 0.7749 0.2599 0.2638 0.5499 0.4427 0.8173 0.8001 0.1455 0.1450>> B=rand(5)B =0.8530 0.0760 0.4173 0.4893 0.7803 0.6221 0.2399 0.0497 0.3377 0.3897 0.3510 0.1233 0.9027 0.9001 0.2417 0.5132 0.1839 0.9448 0.3692 0.4039 0.4018 0.2400 0.4909 0.1112 0.0965>> C=rand(5)C =0.1320 0.2348 0.1690 0.5470 0.1835 0.9421 0.3532 0.6491 0.2963 0.3685 0.9561 0.8212 0.7317 0.7447 0.6256 0.5752 0.0154 0.6477 0.1890 0.7802 0.0598 0.0430 0.4509 0.6868 0.0811>> D=rand(5)D =0.9294 0.3063 0.6443 0.9390 0.2077 0.7757 0.5085 0.3786 0.8759 0.3012 0.4868 0.5108 0.8116 0.5502 0.4709 0.4359 0.8176 0.5328 0.6225 0.2305 0.4468 0.7948 0.3507 0.5870 0.8443>> Z=[A,B;C,D]Z =0.8258 0.1067 0.8687 0.4314 0.13610.8530 0.0760 0.4173 0.4893 0.78030.5383 0.9619 0.0844 0.9106 0.86930.6221 0.2399 0.0497 0.3377 0.38970.9961 0.0046 0.3998 0.1818 0.57970.3510 0.1233 0.9027 0.9001 0.24170.0782 0.7749 0.2599 0.2638 0.54990.5132 0.1839 0.9448 0.3692 0.40390.4427 0.8173 0.8001 0.1455 0.14500.4018 0.2400 0.4909 0.1112 0.09650.1320 0.2348 0.1690 0.5470 0.18350.9294 0.3063 0.6443 0.9390 0.20770.9421 0.3532 0.6491 0.2963 0.36850.7757 0.5085 0.3786 0.8759 0.30120.9561 0.8212 0.7317 0.7447 0.62560.4868 0.5108 0.8116 0.5502 0.47090.5752 0.0154 0.6477 0.1890 0.78020.4359 0.8176 0.5328 0.6225 0.23050.0598 0.0430 0.4509 0.6868 0.08110.4468 0.7948 0.3507 0.5870 0.8443求Z的行列式>> det(Z)ans =-0.0295求det(A)*det(D)-det(B)*det(C)>> det(A)*det(D)-det(B)*det(C)ans =1.8656e-004随机生成对角矩阵A>> A=diag([rand rand rand rand rand])A =0.1948 0 0 0 0 0 0.2259 0 0 0 0 0 0.1707 0 0 0 0 0 0.2277 0 0 0 0 0 0.4357 随机生成对角矩阵B>> B=diag([rand rand rand rand rand])B =0.3111 0 0 0 0 0 0.9234 0 0 0 0 0 0.4302 0 0 0 0 0 0.1848 0 0 0 0 0 0.9049 随机生成对角矩阵C>> C=diag([rand rand rand rand rand])C =0.9797 0 0 0 0 0 0.4389 0 0 0 0 0 0.1111 0 0 0 0 0 0.2581 0 0 0 0 0 0.4087 随机生成对角矩阵D>> D=diag([rand rand rand rand rand])D =0.5949 0 0 0 00 0.2622 0 0 00 0 0.6028 0 00 0 0 0.7112 00 0 0 0 0.2217>> Z=[A,B;C,D]Z =0.1948 0 0 0 00.3111 0 0 0 00 0.2259 0 0 00 0.9234 0 0 00 0 0.1707 0 00 0 0.4302 0 00 0 0 0.2277 0 0 0 0 0.1848 00 0 0 0 0.4357 0 0 0 0 0.90490.9797 0 0 0 00.5949 0 0 0 00 0.4389 0 0 00 0.2622 0 0 00 0 0.1111 0 00 0 0.6028 0 00 0 0 0.2581 00 0 0 0.7112 00 0 0 0 0.40870 0 0 0 0.2217计算Z的行列式>> det(Z)ans =-1.1243e-004计算det(A)*det(D)-det(B)*det(C)>> det(A)*det(D)-det(B)*det(C)ans =-9.3107e-005计算A*D-B*C的行列式>> det(A*D-B*C)ans =-1.1243e-004实验三求A列向量组的一个最大无关组，并把不属于极大无关组的向量利用极大无关组表示.N= 200865083;a=83;b=86;c=50;d=88;e=28;f=63;g=83;h=60;>>A=[a,b,c,d,3,4;1,2,3,4,4,3;12,15,22,17,5,7;e,f,g,h, 8,0];>> B=rref(A)B =1.0000 0 0 0 -0.3548 0.46560 1.0000 0 0 -1.4905 -2.00200 0 1.0000 0 0.0473 0.39500 0 0 1.0000 1.79841.3383所以a1,a2,a3,a4是一个极大无关组。

200651线性代数作业及答案陕西师范大学网络教育学院高起专、高起本

《线性代数》作业一、选择题1．如果D=333231232221131211a a a a a a a a a ，则行列式33323123222113121196364232a a a a a a a a a 的值应为： A ． 6D B ．12D C ．24D D ．36D 答案：（1）、ylitw2008 （2）↑↑↑微信↑↑↑ （3）智金宝资料库2．设A 为n 阶方阵，R （A ）=r<n,那么：A ．A 的解不可逆B ．0=AC.A 中所有r 阶子式全不为零D. A 中没有不等于零的r 阶子式 3．设n 阶方阵A 与B 相似，那么：A ．存在可逆矩阵P ，使B AP P =-1B ．存在对角阵D ，使A 与B 都相似于DC ．E B E A λλ-=-D ．B A ≠4．如果3333231232221131211==a a a a a a a a a D ，则131211332332223121333231323232a a a a a a a a a a a a ---等于A ． 6B ． -9C ．-3D ．-6 5．设矩阵n m ij a A ⨯=)(，m<n,且R （A ）=r,那么：A ．r<mB ．r<nC ．A 中r 阶子式不为零D ．A 的标准型为⎪⎪⎭⎫⎝⎛0E ，其中E 为r 阶单位阵。

6．A 为n 阶可逆矩阵，λ是A 的一个特征根，则A 的伴随矩阵*A 的特征根之一是：A ．nA1-λ B ．A λ C ．A 1-λD ．nA λ7．如果⎪⎩⎪⎨⎧=--=+=++050403z y kx z y z ky x 有非零解，则k 应为：____________。

A ． k =0B ． k =1C ． k =2D ． k =-2 8．设A 是n 阶方阵，3≥n 且2)(-=n A R ，*A 是A 的伴随阵，那么：___________。

A ． 0≠*AB ． ()0R A *= C ． 1-*=n AA D ． 2)(≤*A R9．设A 为n m ⨯矩阵，齐次线性方程组0=AX 仅有零解的充要条件是：A ． A 的列向量线性无关B ． A 的列向量线性相关C ． A 的行向量线性相关D ． A 的行向量线性相关10．如果⎝⎛=+-=++=+02020z y kx z ky x z kx 有非零解，则k 应为：________。

西南交大大学网络教育学院《线性代数》在线作业

西南交通大学网络教育学院线性代数在线作业本次作业是本门课程本学期的第1次作业，注释如下：一、单项选择题(只有一个选项正确，共8道小题)1. 下列矩阵中，不是初等矩阵。

(A)(B)(C)(D)你选择的答案： B [正确]正确答案：B解答参考：初等矩阵一定是可逆的。

2. 则。

(A)(B)(C)(D)你选择的答案： D [正确]正确答案：D解答参考：A错误，因为m<n ，不能保证R(A)=R(A|b) ；B错误，Ax=0 的基础解系含有n−R( A ) 个解向量；C错误，因为有可能R(A)=n<R(A|b)=n+1 , Ax=b 无解；D正确，因为R(A)=n 。

3. A、B为 n阶方阵,且A、B等价,| A |=0 ，则R(B) 。

(A) 小于n(B) 等于n(C) 小于等于n(D) 大于等于n正确答案：A解答参考：4. 若A为5阶方阵且|A|=2，则|－2A|= 。

(A) 4(B) －4(C) －64(D) 64正确答案：C解答参考：5. 线性方程组{ a 11 x 1 + a 12 x 2 +⋯+ a 1n x n = b 1, a 21 x 1 + a 22 x 2 +⋯+ a 2n x n = b 2, ⋯⋯⋯⋯a m1 x 1 + a m2 x 2 +⋯+ a mn x n = b m }的系数矩阵为A,增广矩阵为A ¯,则它有无穷多个解的充要条件为。

(A) R(A)=R( A ¯)<n(B) R(A)=R( A ¯)<m(C) R(A)<R( A ¯)<m(D) R(A)=R( A ¯)=m正确答案：A解答参考：6. 一个n维向量组α 1 , α 2 ,⋯, α s (s>1) 线性相关的充要条件是(A) 有两个向量的对应坐标成比例(B) 含有零向量(C) 有一个向量是其余向量的线性组合(D) 每一个向量都是其余向量的线性组合正确答案：C解答参考：7. 设3阶矩阵A的特征值为1 , −1 , 2 ，则下列矩阵中可逆矩阵是(A) E−A(B) E+A(C) 2E−A(D) 2E+A正确答案：D解答参考：8. 设α 1 , α 2 , α 3 是齐次方程组Ax=0 的基础解系，则下列向量组中也可作为Ax=0 的基础解系的是(A) α 1 + α 2 , α 2 + α 3 , α 1 +2 α 2 + α 3(B) α 1 + α 2 , α 2 + α 3 , α 3 − α 1(C) α 1 + α 2 , α 2 + α 3 , α 3 + α 1(D) α 1 − α 2 ,0, α 2 − α 3正确答案：C解答参考：二、判断题(判断正误，共6道小题)9.如果行列式有两行元素完全相同，则行列式为零。

《线性代数》作业

《线性代数》作业《线性代数》作业第⼀章1、求排列(2n)(2n-1)…(n+1)1 2…(n -1)n 的逆序数。

解：后⾯是正常顺序，逆序出现在前n 个数与后n 个数之间，2n 的逆序数是2n-1，2n-1的逆序数是2n-2，……，n+1的逆序数是n ，所以整个排列的逆序数是(2n-1)＋(2n-2)＋……＋n ＝n(3n-1)/22、求排列246......(2n)135……(2n-1)的逆序数。

解析：后⼀项⽐前⼀项的算逆序⼀次，246......(2n)⽆逆序，所以从1开始，有246......(2n)共N 个，3开始有46......(2n)有N-1个，.......，.2n-1有⼀个，所以，加⼀起得，逆序数为1+2+......+N=N （N+1）/2N=n+(n-1)+......+2+1=n(n+1)/23、试判断655642312314a a a a a a ，662551144332a a a a a a -，662552144332a a a a a a -是否都是六阶⾏列式中的项。

解a 14a 23a 31a 42a 56a 65 下标的逆序数为 t （431265）=0+1+2+2+0+1=6所以655642312314a a a a a a 是六阶⾏列式中的项。

662551144332a a a a a a -下标的逆序数为 t （452316）=8所以662551144332a a a a a a -不是六阶⾏列式中的项。

662552144332a a a a a a -下标的逆序数为t(452316)=8所以662552144332a a a a a a -不是六阶⾏列式中的项。

4、已知4阶⾏列式D 中的第3列上的元素分别是3，-4，4，2，第1列上元素的余⼦式依次为8，2，-10，X ，求X 。

解：X=205、设15234312a a a a a j i 是5阶⾏列式的⼀项，若该项的符号为负，则 i= 5 ,j= 4 。

《线性代数》上机作业一(格式)

《线性代数》上机作业（一）
课程
《线性代数》
上机
内容
成绩
姓名
雷祥
专业
班级
建筑环境与设备工程
学号
1008020229
教学班
指导
教师
上机
日期
一、上机目的
一、突出教学的பைடு நூலகம்点，减少教学的难点；
二、掌握常用计算方法和处理问题的方法.
二、上机内容
1、向量与矩阵运算。
三、上机作业
1.试分别生成4阶的单位阵和5阶均匀分布的随机矩阵。
2．生成列向量x=[1, 3, 5, 7, 9,…, 15]。
3.试分别生成4阶矩阵A和4阶矩阵B；求A+B，A-B，A*B，A\B，5*B，A^2，A.*B，A.^2及矩阵A的行列式，特征值，特征向量，秩和行最简形.
四、上机心得体会
考试可以带个电脑去就好咯。。。

《线性代数》上机作业

《线性代数》上机作业（一）一、上机目的 1、培养学生运用线性代数的知识解决实际问题的意识、兴趣和能力 2、掌握常用计算方法和处理问题的方法. 二、上机内容 1、求向量组的最大无关组； 2、解线性方程组； 3、解决实际问题举例. 三、上机作业1、设 A=[2 1 2 4; 1 2 0 2; 4 5 2 0; 0 1 1 7];求矩阵A 列向量组的一个最大无关组. 2、用Matlab 解线性方程组|2\ + 4X 2 -= -4參]-+5工？十3屯=10 匕-+ 3x 2 +2x3 - 51、解：在Matlab 中输入:> a=[2 1 2 4; 1 b=rref(a) 解得：b = 1 0 0 0 1 0 0 0 13x-i 41x 262 X 3414x-| 50x 2 3X 3 100 11x 1 38X 2 25X 3501 7];2 0 2; 4 5 2 0; 0 10 0 0 1 所以a1 ，a2,a3,a4 是一个极大无关组2、(1) 解：在Matlab 中输入>> a=[2 4 -6; 1 5 3;1 3 2]; >> b=[-4 10 5]';>> x=a\bx =-321 所以线性方程组的解为x1=-3,x2=2,x3=1 (2) 解：在Matlab 中输入>> a=[3 41 -62;4 50 3;11 38 25]; >> b=[-41 100 50]'; >> x=a\b x = -8.82212.58901.9465>>所以线性方程组的解为x1=-8.8221,x2= 2.5890,x3= 1.9465四、上机心得体会。

数值线性代数上机作业1

0 54.2196 34.8797 23.1669 25.2609 23.2963
0 0 32.4907 -8.9182 -11.2895 -7.9245
0 0 0 7.6283 -3.9114 7.4339
0 0 0 0 3.4197 6.8393
0 0 0 0 0 0.0000
魔方矩阵用matlab内置QR分解：
-0.0710 -0.6424 0.1373 0.4501 0.3329-0.5000
R =
-56.3471 -16.4693 -30.0459 -39.0969 -38.0321 -38.6710
0 -54.2196 -34.8797 -23.1669 -25.2609 -23.2963
0 0 32.4907 -8.9182 -11.2895 -7.9245
-0.0532 -0.5740 -0.4500 -0.2106 -0.64870.0000
-0.5502 0.0011 -0.4460 0.4537 0.20620.5000
-0.1420 -0.4733 0.3763 -0.5034 0.33290.5000
-0.5324 0.0695 0.6287 0.2096 -0.52200.0000
Q =
0.8189 -0.5397 0.1893 -0.0482 0.0090 -0.0011
0.4094 0.3320 -0.7024 0.4489 -0.16170.0332
0.2730 0.4219 -0.1529 -0.5723 0.5854-0.2321
0.2047 0.4067 0.2015 -0.3866 -0.46870.6189
0.2730 0.4219 -0.1529 -0.5723 0.5854-0.2320

线性代数上机作业

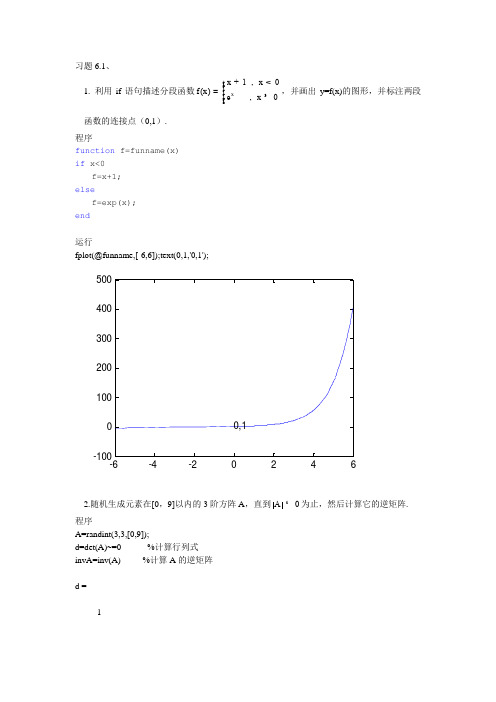
习题6.1、1. 利用if 语句描述分段函数1,0(),0x x x f x e x +<ìïï=íï³ïî，并画出y=f(x)的图形，并标注两段函数的连接点（0,1）.程序function f=funname(x)if x<0f=x+1;elsef=exp(x);end运行fplot(@funname,[-6,6]);text(0,1,'0,1');-6-4-20246-10001002003004005002.随机生成元素在[0，9]以内的3阶方阵A ，直到0A ¹为止，然后计算它的逆矩阵. 程序A=randint(3,3,[0,9]);d=det(A)~=0 %计算行列式invA=inv(A) %计算A 的逆矩阵d =1invA =0.1702 -0.0106 -0.0851-0.0426 0.1277 0.0213-0.0904 -0.1037 0.1702ans =903. 编写一个程序，用以找出10到10000之间的能被5或者17或者47整除的自然数. n=zerosx=10:10000if rem(x,5)|rem(x,17)|rem(x,47)==0n=xend练习 6.21. 下列矩阵为某个线性方程组的增广矩阵，利用MATLAB软件求解该方程组．程序format ratA=[1 2 1 4;2 0 4 3;4 2 2 1;3 1 3 2];b=[13;28;20;6];[R,IP]=rref([A,b])结果R =1 0 0 -3/2 00 1 0 2 00 0 1 3/2 00 0 0 0 1IP =1 2 3 5>> 1 0 0 -3/2 02. 考虑第一章引例3薄板热传导问题，如果希望矩形薄板的左边界温度为0 o C、上边界温度为10 o C、下边界为10 o C、右边界为20 o C，这可能吗？程序format ratA=[4 -1 0 -1 0 0;-1 4 -1 0 -1 0;0 -1 4 0 0 -1;-1 0 0 4 -1 0;0 -1 0 -1 4 -1;0 0 -1 0 -1 4];b=[10;10;30;20;10;30];[U,IP]=rref([A,b])结果U =1 0 0 0 0 0 1212/1610 1 0 0 0 0 1690/1610 0 1 0 0 0 2178/1610 0 0 1 0 0 1548/1610 0 0 0 1 0 1760/1610 0 0 0 0 1 2192/161IP =1 2 3 4 5 63. 已知五个数据点(,cos()),0,0.5,1.0,1.5,2.0t t t=，构造一个四次插值多项式，并计算cos(0.2),cos(0.4),cos(1.4)的近似值．程序A=[0 0 0 0 1;0.0625 0.125 0.25 0.5 1;1 1 1 1 1;5.0625 3.375 2.25 1.5 1;168 4 2 1];b=[1;cos(0.5);cos(1);cos(1.5);cos(2)];[U,IP]=rref([A,b])结果U =1 0 0 0 0 185/85680 1 0 0 0 114/25150 0 1 0 0 -2270/42390 0 0 1 0 67/75400 0 0 0 1 1IP =1 2 3 4 5练习 6.31. 用MA TLAB命令rand随机生成44C D G H，并确定那´的矩阵A和B.求下列指定的,,,些矩阵是相等的.可以利用MATLAB计算两个矩阵的差来测试两个矩阵是否相等.（1）输入：A=randint(4,4,[0,10]);B=randint(4,4,[0,10]);C=A*BD=B*AG=(A'*B')'H=(B'*A')'S1=C-DS2=C-GS3=C-HS4=D-GS5=D-HS6=G-H输出：C =116 48 66 164120 52 50 15677 36 69 126165 128 121 222D =144 124 136 136121 87 126 81145 129 166 12598 60 88 62G =144 124 136 136121 87 126 81145 129 166 12598 60 88 62H =116 48 66 164120 52 50 15677 36 69 126165 128 121 222 S1 =91 13 13 34-13 -34 -51 -894 -53 -82 -2684 61 -45 25 S2 =91 13 13 34-13 -34 -51 -894 -53 -82 -2684 61 -45 25 S3 =0 0 0 00 0 0 00 0 0 00 0 0 0 S4 =0 0 0 00 0 0 00 0 0 00 0 0 0 S5 =-91 -13 -13 -3413 34 51 89-4 53 82 26-84 -61 45 -25S6 =-91 -13 -13 -3413 34 51 89-4 53 82 26-84 -61 45 -25判断是否相等：因为S3=0，S4=0。

（精选）线性代数课后作业及参考答案

（精选）线性代数课后作业及参考答案《线性代数》作业及参考答案一．单项选择题1.设行列式a aa a11122122=m，a aa a13112321=n，则行列式a a aa a a111213212223++等于（）A. m+nB. -(m+n)C. n-mD. m-n2.设矩阵A=100020003，则A-1等于（）A.130012001B.100120013C. 1 3 00 010 00 1 2D. 1 2 00 10013.设矩阵A=312101214---，A*是A的伴随矩阵，则A *中位于（1，2）的元素是（）A. –6B. 6C. 24.设A是方阵，如有矩阵关系式AB=AC，则必有（）A. A =0B. B≠C时A=0C. A≠0时B=CD. |A|≠0时B=C5.已知3×4矩阵A的行向量组线性无关，则秩（A T）等于（）A. 1B. 2C. 3D. 46.设两个向量组α1，α2，…，αs和β1，β2，…，βs均线性相关，则（）A.有不全为0的数λ1，λ2，…，λs使λ1α1+λ2α2+…+λsαs=0和λ1β1+λ2β2+…λsβs=0B.有不全为0的数λ1，λ2，…，λs使λ1（α1+β1）+λ2（α2+β2）+…+λs（αs+βs）=0C.有不全为0的数λ1，λ2，…，λs使λ1（α1-β1）+λ2（α2-β2）+…+λs（αs-βs）=0D.有不全为0的数λ1，λ2，…，λs和不全为0的数μ1，μ2，…，μs使λ1α1+λ2α2+…+λsαs=0和μ1β1+μ2β2+…+μsβs=07.设矩阵A的秩为r，则A中（）A.所有r-1阶子式都不为0B.所有r-1阶子式全为0C.至少有一个r阶子式不等于0D.所有r阶子式都不为08.设Ax=b是一非齐次线性方程组，η1，η2是其任意2个解，则下列结论错误的是（）A.η1+η2是Ax=0的一个解2η1+12η2是Ax=b的一个解C.η1-η2是Ax=0的一个解D.2η1-η2是Ax=b的一个解9.设n阶方阵A不可逆，则必有（）A.秩(A)<n< bdsfid="226" p=""></n<>B.秩(A)=n-1C.A=0D.方程组Ax=0只有零解10.设A是一个n(≥3)阶方阵，下列陈述中正确的是（）A.如存在数λ和向量α使Aα=λα，则α是A的属于特征值λ的特征向量B.如存在数λ和非零向量α，使(λE-A)α=0，则λ是A的特征值C.A的2个不同的特征值可以有同一个特征向量D.如λ1，λ2，λ3是A的3个互不相同的特征值，α1，α2，α3依次是A的属于λ1，λ2，λ3的特征向量，则α1，α2，α3有可能线性相关11.设λ0是矩阵A的特征方程的3重根，A的属于λ0的线性无关的特征向量的个数为k，则必有（）A. k≤3B. k<3C. k=3D. k>312.设A是正交矩阵，则下列结论错误的是（）A.|A|2必为1B.|A|必为1C.A-1=A TD.A的行（列）向量组是正交单位向量组13.设A是实对称矩阵，C是实可逆矩阵，B=C T AC.则（）A.A与B相似B. A与B不等价C. A与B有相同的特征值D. A与B合同15.设有矩阵Ａｍ×ｎ，Ｂｍ×ｓ，Ｃｓ×ｍ，则下列运算有意义的是（）。

西南大学《线性代数》网上作业及参考答案

===================================================================================================1：[论述题]线性代数模拟试题三参考答案：线性代数模拟试题三参考答案 1：[论述题]线性代数模拟试题四参考答案：线性代数模拟试题四参考答案 1：[论述题]线性代数模拟试题五参考答案：线性代数模拟试题五参考答案 1：[论述题]线性代数模拟试题六一、填空题（每小题3分，共15分） 1. 行列式332313322212312111b a b a b a b a b a b a b a b a b a = ( ). 2. 设A 是4×3矩阵，R (A ) = 2，若B = ⎪⎪⎪⎭⎫ ⎝⎛300020201，则R (AB ) = ( ).3. 设矩阵A = ⎪⎪⎪⎭⎫⎝⎛54332221t ，若齐次线性方程组Ax = 0有非零解，则数t = ( ).4. 已知向量,121,3012⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=k βαα与β的内积为2，则数k = ( ).5. 已知二次型232221321)2()1()1(),,(x k x k x k x x x f -+-++=正定，则数k 的取值范围为( ).二、单项选择题（每小题3分，共15分） 1. 设A 为m ×n 矩阵，B 为n ×m 矩阵，m ≠n , 则下列矩阵中为n 阶矩阵的是( ). (A) B T A T (B) A T B T (C) ABA (D) BAB2. 向量组α1，α2，…，αS (s >2)线性无关的充分必要条件是( ). (A) α1，α2，…，αS 均不为零向量(B) α1，α2，…，αS 中任意两个向量不成比例 (C) α1，α2，…，αS 中任意s -1个向量线性无关(D) α1，α2，…，αS 中任意一个向量均不能由其余s -1个向量线性表示===================================================================================================3. 设3元线性方程组Ax = b ，A 的秩为2，η1，η2，η3为方程组的解，η1 + η2 = (2,0,4)T ，η1+ η3 =(1，-2，1)T ，则对任意常数k ，方程组Ax = b 的通解为( ).(A) (1,0,2)T + k (1,-2,1)T (B) (1,-2,1)T + k (2,0,4)T (C) (2,0,4)T + k (1,-2,1)T (D) (1,0,2)T + k (1,2,3)T 4. 设3阶方阵A 的秩为2，则与A 等价的矩阵为( ).(A) ⎪⎪⎪⎭⎫ ⎝⎛000000111(B) ⎪⎪⎪⎭⎫⎝⎛000110111(C) ⎪⎪⎪⎭⎫ ⎝⎛000222111(D) ⎪⎪⎪⎭⎫ ⎝⎛3332221115. 二次型f (x 1,x 2,x 3,x 4,)=43242322212x x x x x x ++++的秩为( ).(A) 1 (B) 2 (C) 3 (D) 4三、判断题（正确的打“√”，错误的打“×”，每小题3分，共15分)1. 设A 为n 阶方阵，n ≥2，则|-5A |= -5|A |. ( )2. 设行列式D =333231232221131211a a a a a a a a a = 3，D 1=333231312322212113121111252525a a a a a a a a a a a a +++，则D 1的值为5. ( ) 3. 设A = ⎪⎪⎭⎫⎝⎛4321, 则|A *| = -2. ( )4. 设3阶方阵A 的特征值为1，-1，2，则E - A 为可逆矩阵. ( )5. 设λ = 2是可逆矩阵A 的一个特征值，则矩阵(A 2)-1必有一个特征值等于41. ( ) 四、(10分) 已知矩阵A = ⎪⎪⎪⎭⎫⎝⎛-210011101，B =⎪⎪⎪⎭⎫⎝⎛410011103， (1) 求A 的逆矩阵A -1. (2) 解矩阵方程AX = B .===================================================================================================五、(10分)设向量组⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=42111α，⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=21302α，⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=147033α，⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=02114α，求向量组的秩和一个极大线性无关组，并将其余向量用该极大线性无关组线性表示.六、(10分) 求线性方程组⎪⎩⎪⎨⎧=++=+++=+++322023143243214321x x x x x x x x x x x 的通解(要求用它的一个特解和导出组的基础解系表示)七、(15分) 用正交变换化二次型f (x 1, x 2, x 3)=2331214x x x x +-为标准形，并写出所用的正交变换.八、(10分) 设a ，b ，c 为任意实数，证明向量组⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=1111a α，⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=0112b α，⎪⎪⎪⎪⎪⎭⎫⎝⎛=0013c α，线性无关.参考答案：线性代数模拟试题六参考答案一、填空题1. 0.2. 23.2.4.32. 5. k > 2. 二、单项选择题1(B). 2(D). 3(D). 4(B). 5(C). 三、判断题1. (⨯). 2(⨯). 3(√). 4(⨯). 5(√).===================================================================================================四、Solution (1)由于⎪⎪⎪⎭⎫ ⎝⎛---→⎪⎪⎪⎭⎫ ⎝⎛-+-100210011110001101100210010011001101211r r⎪⎪⎪⎭⎫ ⎝⎛-----→⎪⎪⎪⎭⎫ ⎝⎛----→+-++111100122010112001111100011110001101132332111r r r r r r ⎪⎪⎪⎭⎫ ⎝⎛-----→-11110012201011200121r ，因此，有⎪⎪⎪⎭⎫ ⎝⎛-----=-1111221121A .(2) 因为B AX =，所以⎪⎪⎪⎭⎫⎝⎛-----=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛-----==-3222342254100111031111221121B A X .五、Solution 因为()⎪⎪⎪⎪⎪⎭⎫⎝⎛-→⎪⎪⎪⎪⎪⎭⎫⎝⎛--=+-+400027120330130101424271210311301,,,4321214321r r r r αααα⎪⎪⎪⎪⎪⎭⎫⎝⎛→⎪⎪⎪⎪⎪⎭⎫ ⎝⎛→⎪⎪⎪⎪⎪⎭⎫⎝⎛→↔+--+-00001000011013011000000001101301100001100110130143324231141312r r r r r r r r ⎪⎪⎪⎪⎪⎭⎫⎝⎛→+-0000100001100301131r r , 于是，421,,ααα是极大无关组且2133ααα+=.===================================================================================================六、Solution 将增广矩阵B 化为行最简形得⎪⎪⎪⎭⎫ ⎝⎛----→⎪⎪⎪⎭⎫ ⎝⎛=+-322103221011111322100112311111213r r B⎪⎪⎪⎭⎫ ⎝⎛-------→⎪⎪⎪⎭⎫ ⎝⎛----→++000003221021101000003221011111123211r r r r ⎪⎪⎪⎭⎫ ⎝⎛---→-00000322102110121r ，这时，可选43,x x 为自由未知量.令0,043==x x 得特解⎪⎪⎪⎪⎪⎭⎫⎝⎛-=0032*η.分别令⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛10,0143x x 得基础解系⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=1021,012121ξξ. 原线性方程组的通解为⎪⎪⎪⎪⎪⎭⎫⎝⎛-+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=00321021012121k k x ，其中21,k k 为任意常数.七、Solution 所给二次型的矩阵为⎪⎪⎪⎭⎫⎝⎛--=102000201A ，)3)(1(122110200201||λλλλλλλλλλ-+=-----=-----=-E A ，===================================================================================================所以A 的特征值为-1，0，3.当1-=λ时，齐次线性方程组=+x E A )(0的基础解系为⎪⎪⎪⎭⎫ ⎝⎛=1011ξ，单位化得⎪⎪⎪⎪⎪⎭⎫⎝⎛=210211p . 当0=λ时，齐次线性方程组=-x E A )0(0的基础解系为⎪⎪⎪⎭⎫⎝⎛=0102ξ，单位化得⎪⎪⎪⎭⎫ ⎝⎛=0102p .当3=λ时，齐次线性方程组=-x E A )3(0的基础解系为⎪⎪⎪⎭⎫ ⎝⎛-=1013ξ，单位化得⎪⎪⎪⎪⎪⎭⎫⎝⎛-=210213p .取()⎪⎪⎪⎪⎪⎭⎫⎝⎛-==2102101021021,,321p p p P ，在正交变换Py x =下得二次型的标准型为23213y y f +-=.===================================================================================================八、Proof 因为()⎪⎪⎪⎪⎪⎭⎫ ⎝⎛→⎪⎪⎪⎪⎪⎭⎫ ⎝⎛→⎪⎪⎪⎪⎪⎭⎫⎝⎛=+-+-001010100001011100001011111,,341311321c b a c b a c b ar r r r ααα ⎪⎪⎪⎪⎪⎭⎫⎝⎛→⎪⎪⎪⎪⎪⎭⎫⎝⎛→⎪⎪⎪⎪⎪⎭⎫⎝⎛→↔↔↔+-+-+-00010*********0000010001001010000100433241212324r r r r r r r cr r br r ar , 于是321,,ααα的秩为3，所以321,,ααα线性无关.1：[论述题]一、填空题(每小题3分，共15分)1. 设A = ⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤411023, B =,010201⎢⎣⎡⎥⎦⎤则AB = ⎪⎪⎪⎭⎫⎝⎛. 2. 设A 为33⨯矩阵, 且方程组Ax = 0的基础解系含有两个解向量, 则R (A ) = ( ). 3. 已知A 有一个特征值-2, 则B = A 2+ 2E 必有一个特征值( ). 4. 若α=(1, -2, x )与),1,2(y =β正交, 则x y = ( ). 5. 矩阵A = ⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤-301012121所对应的二次型是( ).二、单选题(每小题3分，共15分)1. 如果方程⎪⎩⎪⎨⎧=+=-=-+0404033232321kx x x x x kx x 有非零解，则k = ( ).(A) -2 (B) -1===================================================================================================(C) 1 (D) 22. 设A 为n 阶可逆方阵，下式恒正确的是( ). (A) (2A )-1 = 2A -1 (B) (2A )T = 2A T (C) [(A -1)-1]T = [(A T )-1]T (D) [(A T )T ]-1 = [(A -1)-1]T3. 设β可由向量α1 = (1，0，0)，α2 = (0，0，1)线性表示，则下列向量中β只能是( ). (A) (2，1，1) (B) (-3，0，2) (C) (1，1，0) (D) (0，-1，0)4. 向量组α1 ，α2 …，αs 的秩不为s (s 2≥)的充分必要条件是( ). (A) α1 ，α2 …，αs 全是非零向量 (B) α1 ，α2 …，αs 全是零向量(C) α1 ，α2 …，αs 中至少有一个向量可由其它向量线性表出 (D) α1 ，α2 …，αs 中至少有一个零向量 5. 与矩阵A = ⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤200010001相似的是( ).(A) ⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤100020001(B) ⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤200010011(C) ⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤200011001(D) ⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤100020101三、判断题(每小题3分，共15分): 正确打“√”，错误打“×”.1. 设A 为三阶方阵且|A | = -2，则|3A T A | = -108. ( )2. 设A 为四阶矩阵，且|A | = 2，则|A *| = 23. ( ) 3. 设A 为m n ⨯矩阵，线性方程组Ax = 0仅有零解的充分必要条件是A 的行向量组线性无关. ( )4. 设A 与B 是两个相似的n 阶矩阵，则E B E A λλ-=-. ( )5. 设二次型,),(23222132,1x x x x x x f +-=则),(32,1x x x f 负定. ( )四、 (10分) 计算四阶行列式1002210002100021的值.===================================================================================================五、(10分) 设A =⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤-200200011, B =⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤300220011,且A , B , X 满足E X B A B E =--T T 1)( . 求X , X .1-六、(10分) 求矩阵A = ⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤-311111002的特征值和特征向量.七、(15分) 用正交变换化二次型322322213214332),,(x x x x x x x x f +++=为标准型,并写出所作的变换.八、(10分) 设21,p p 是矩阵A 的不同特征值的特征向量. 证明21p p +不是A 的特征向量.参考答案：一、填空题1.⎪⎪⎪⎭⎫ ⎝⎛241010623. 2. 1. 3. 6. 4. 0.5. 2322312121324x x x x x x x +-++. 二、单项选择题1(B). 2(B) . 3(B) . 4(C) . 5(A) . 三、判断题1.( ⨯). 2(√). 3(⨯). 4(√). (5) (⨯). 四、Solution 按第1列展开，得===================================================================================================210021002)1(2100210021)1(110022100021000211411++-⋅+-⋅= 158)1(21-=⋅-⋅+=.五、Solution 由于E X B A B E =--T T 1)(，即[]E X A B E B =--T1)(，进而()E X A B =-T ，所以()[]1T --=A B X .因为()⎪⎪⎪⎭⎫ ⎝⎛=-100020002TA B ，所以⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛=-100021000211000200021X . 六、Solution 因为λλλλλλλ----=----=-3111)2(31111102||E A321)2(3111)2(3212)2(12λλλλλλλ-=--=----=+c c , 所以A 的特征值为2.对于2=λ时，齐次线性方程组=-x E A )2(0与0321=+-x x x 同解，其基础解系为⎪⎪⎪⎭⎫⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛=101,01121ξξ，于是，A 的对应于2的特征向量为⎪⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎪⎭⎫ ⎝⎛10101121k k ，其中21,k k 不全为0. 七、Solution 所给二次型的矩阵⎪⎪⎪⎭⎫ ⎝⎛=320230002A .===================================================================================================因为λλλλλλλ---=---=-3223)2(32023002||E A )1)(5)(2(3121)5)(2(3525)2(121λλλλλλλλλλ---=---=----=+c c , 所以A 的特征值为1, 2, 5.当1=λ时，齐次线性方程组=-x E A )(0的基础解系为⎪⎪⎪⎭⎫ ⎝⎛-=1101ξ，单位化得⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=212101p . 当2=λ时，齐次线性方程组=-x E A )2(0的基础解系为⎪⎪⎪⎭⎫ ⎝⎛=0012ξ，单位化得⎪⎪⎪⎭⎫ ⎝⎛=0012p .当5=λ时，齐次线性方程组=-x E A )5(0的基础解系为⎪⎪⎪⎭⎫ ⎝⎛=1103ξ，单位化得⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=212103p .===================================================================================================取()⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-==2102121021010,,321p p p P ，在正交变换Py x =下得二次型的标准型为23222152y y y f ++=. 八、Proof 令21,p p 是A 的对应于不同特征值21,λλ的特征向量，即111p Ap λ=,222p Ap λ=.假设21p p +是A 的对应于λ的特征向量，即)()(2121p p p p A +=+λ. 由于22112121)(p p Ap Ap p p A λλ+=+=+，所以)(212211p p p p +=+λλλ，于是=-+-2211)()(p p λλλλ0. 根据性质4，知021=-=-λλλλ，进而21λλ=，矛盾.。

河北工业大学2017年春线性代数作业

河北工业大学线性代数作业（1）学院班级姓名学号一. 讨论下列齐次方程组是否有非零解，若有，求出其通解.⎪⎪⎩⎪⎪⎨⎧=+-+-=+-+=+-+-=---0136152032024303524321432143214321x x x x x x x x x x x x x x x x二．求出下列线性方程组的通解.⎪⎩⎪⎨⎧-=+-+=-+-=+-+2534432312432143214321x x x x x x x x x x x x三．用初等变换化下列矩阵为简化梯形矩阵，指出矩阵的秩是多少：1．⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--370320852373812023012．nn 11111001110001100001⨯⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-------四. (1)当λ取什么值时，方程组⎪⎩⎪⎨⎧0=++0=++0=++321321321x x x x x x x x x λλλ 只有零解？有非零解？若有非零解,则确定其通解.(2)当λ分别取什么值时，下面方程组有唯一解？有无穷多解？无解？在它有无穷多解时，求出它的通解.⎪⎩⎪⎨⎧=++=+--=++-2321321321λλλ222x x x x x x x x x河北工业大学线性代数作业（2）学院班级姓名学号一．填空题 1．若行列式0=3333222211111xx x ，则.________,___,=x 2．0100002000010n n=-L L L L L L L L L.3. 1070002000003000000400050= .4. =--nn n 0000000000100002000200010000.5.=0000041323123222114131211a a a a a a a a a a . 6. 当____x 时，0010413=xx x .7.若23013221D 1=，则==ca c ab a b 2033202D 2 . 8.若1333231232221131211-=a a a a a a a a a ，则=---333231312322212113121111324324324a a a a a a a a a a a a . 二．计算下列行列式的值：1．20104110631432111112.333333222222111111b a a c c b b a a c c b b a a c c b +++++++++3．dd c c b b a a d c b a dc b a 3434343412121212111122222222--------4．111222+++γγβγαβγββααγαβα河北工业大学线性代数作业（3）学院班级姓名学号一．选择题1．若()r R =A ，则A 中（）r 阶子式不等于零.()a 任意一个； ()b 只有一个； ()c 至少有一个； ()d 至多有一个.2．克拉默法则仅适用于解（）方程组.()a 非齐次线性方程组； ()b 齐次线性方程组；()c 任何有解的方程组；()d 方程个数=未知量个数，系数矩阵的行列式不等于零.3．设n m ⨯A ，则下列说法不正确的是（）.()a 若()r R =A ，则n m ⨯A 不存在等于零的1-r 阶子式； ()b ()()T R R A A =； ()c (){}min ,R m n ≤A ；()d 当n m =时，若A 为降秩（退化、奇异）方阵，则()n,det 0R <=A A .二．计算下面的n 阶行列式.1．nn n n a x a a a a a x a a a a a x a a a a a x ++++3213213213212.122222222232222n3．nnnnnn n n n n n nn n n n11321221----4．xyy x y x y x 0000000000三．用初等变换法求下面矩阵的秩A =⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--05916410202131412311.河北工业大学线性代数作业（4）学院班级姓名学号一．填空题1．若矩阵X 满足方程()()0=-2+-2X B X A ，则X= . 2. 设A 为3阶矩阵，3=A ，则A 2 =.3．已知[]321=x x x ,,A , ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=B 321x x x ，则=AB ，__________=BA .4. 设B A ,为n 阶方阵，则()()22B A B A B A -=-+成立的条件为_______. 二. 单项选择题1．设有矩阵,,3223⨯⨯B A 33⨯C , 则下列运算可以进行的是（）.()a ABC ；()b TAB； ()c BC AB +； ()d ΒΑ23+.2．设A 为n m ⨯矩阵，则TAA 是（）.()a m 阶方阵； ()b n 阶方阵；()c n m ⨯矩阵；()d m n ⨯矩阵.三. 计算2--3B A C ，已知,,⎥⎦⎤⎢⎣⎡1-1012-7=⎥⎦⎤⎢⎣⎡3021-21=B A C ⎥⎦⎤⎢⎣⎡01726-3-=.四. 计算下列矩阵的乘积（如不符合两矩阵相乘的条件，则说明不能相乘）. 1. ⎥⎦⎤⎢⎣⎡--⎥⎦⎤⎢⎣⎡6234021231 2. ⎥⎦⎤⎢⎣⎡3402⎥⎦⎤⎢⎣⎡104312 3. []⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡321333231232221131211321x x x a a a a a a a a a x x x河北工业大学线性代数作业（5）学院班级姓名学号一. 填空题1. 设A 为n 阶矩阵，且0≠=a A det ，A adj 为其转置伴随阵，则det(adj A )= .2. 设4阶矩阵A 的秩为2，则其转置伴随阵A adj 的秩为 .3. 若⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡740530002=A ，则=1-A .4. 设B A ,为n 阶矩阵，且I AB =，则=BA .5．设A 为n 阶可逆矩阵，则()12T-T ⎡⎤=⎢⎥⎣⎦Α .二.单项选择题1．设B A ,均为n 阶可逆方阵，则=⎥⎦⎤⎢⎣⎡-100B A ( ).()⎥⎦⎤⎢⎣⎡001-1-B A a ； ()⎥⎦⎤⎢⎣⎡001-1-BA b ； ()⎥⎦⎤⎢⎣⎡001-1-AB c ； ()⎥⎦⎤⎢⎣⎡001-1-A B d . 2．设C B A ,,是同阶方阵,且A 可逆，则下列各式中不一定成立的是（）.()a 若AC AB =，则=B C ；()b =ΑΒCA ，则=BC ；()c 若0=AB ，则0=B ； ()d 若CA BA =，则=BC .3．下列矩阵可逆的是（）.()a n 阶对角矩阵； ()b n 阶满秩矩阵；()c n 阶实对称矩阵； ()d n 阶上三角阵.4．设A 为n 阶对称矩阵，且A 可逆，那么有（）.()a T A A =-1； ()b A A T -=；()c IA A T =-1； ()d 以上结论都不对.5．B A,为n 阶矩阵，下列运算正确的是（）.()a ()k k k B A AB =； ()b ()111---=B A AB ；()c A A AA T T= ； ()d AA A A adj adj =.三．设A 满足,O I A A =4--2证明I A I A 2--,,都可逆.四. 设A ，B 均为2阶矩阵，且2=1-=B A det ,det ，求()]2det[21-ΒΑΤ.五．设A 是n 阶矩阵，A adj 是A 的转置伴随阵，若5=A det ，求 det[(5adj A )1-]的值.河北工业大学线性代数作业（6）学院班级姓名学号一．填空题 1.3阶初等阵=12R, ()=12det R,()=-112R .2.3阶初等阵 ()=23R , ()()=2det 3R ,()()=-132R .3.3阶初等阵()=-413R, ()()=-4det 12R，()()=--1134R.4.设⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡3-3-3-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡333231232221331332123111333231232221131211a a a a a a a a a a a a a a a a a a a a a A ，则A = .5.初等矩阵C 31()3-右乘矩阵123[,,]a a a =A ，相当于对A 进行初等变换，结果为______.6.矩阵A 经过有限次初等变换化为矩阵B ，则矩阵A 与B 的秩 .二. 单项选择题1．在下列矩阵中，不是初等矩阵的是（）.()⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡010100001a ；()⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡00101-0100b ；()⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡1000520001.c ；()⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡105010001d . 2．下列说法正确的是（）.()a 对单位阵施行初等变换后所得的矩阵都是初等矩阵； ()b 初等矩阵的乘积还是初等矩阵；()c 可逆阵经过初等变换后仍为可逆阵； ()d 任何矩阵都可以表示有有限个初等阵的乘积.三. 用行初等变换法求下列矩阵的逆矩阵：1．⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡14-52-431-21=A2．⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡11-0000011-000011-00001= A四. 从矩阵方程B AX =中解出X ，其中1.⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡1513-3421-2-=A ，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡311=B2.⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡41-31-351-24=A ，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡4611-31=B河北工业大学线性代数作业（7）学院班级姓名学号一. 填空题 1. 方程组⎩⎨⎧=3++3+3=2++2+22121b x x x ax x x n n 有解的条件为___________.2．二维向量α[]T21=a a ,，β[]T21=b b ,线性相关的充要条件为 .3．若向量组1a ,2a ,a 3线性相关，且123⎡⎤=⎣⎦A aa a ，则R )(A .4．若向量组321a a a ,,线性无关，当常数m l ,满足_______时，向量组 l 1a ，-3a m 2a ，31-a a 线性无关.二. 选择题1.若向量b 可以由向量组m21a ,,a ,a 线性表示，则下列结论正确的是（）.()a 存在常数m k k k ,,, 21，使b =1k 1a +2k 2a ++ m k m a ；()b 存在不全为零的常数m k k k ,,, 21，使b =1k 1a +2k 2a ++ m k m a ；()c 存在唯一的常数m k k k ,,, 21，使b =1k 1a +2k 2a ++ m k m a ； ()d 存在唯一不全为零的常数m k k k ,,21，使b =1k 1a +2k 2a ++ m k m a .2．设b ,a ,,a ,a n21是m 维向量，则关于方程组1k 1a +2k 2a ++ n n a k =b 的说法正确的是（）.()a 若方程组无解，则向量组b ,a ,,a ,a n 21 线性无关； ()b 若方程组有解，则向量组b ,a ,,a ,a n 21 线性相关； ()c 若n 21a ,,a ,a 线性相关，则方程组一定有解；()d 若n 21a ,,a ,a 线性无关，则方程组一定无解.3. 若向量组1a [],,,Τ001=T a ],,[0112=,=3a T cb a ],,[线性无关，则要求（）.()a c b a ==； ()b 0==c b ； ()c 0=c ； ()d 0≠c .三．已知321a a a ,,线性相关，432a a a ,,线性无关，试问：（1）1a 能否由32a a ,线性表示？（2）4a 能否由321a a a ,,线性表示？（3）当上面的表示式成立时，其表示式是否唯一？四．证明:若向量组321a ,a ,a 线性无关，则向量组,,212321122a a b a a a b +=-+=32134+3+2=a a a b也线性无关.河北工业大学线性代数作业（8）学院班级姓名学号一. 填空题1．设向量组r21a ,,a ,a 线性无关，则R {}=21r a a a ,,, .2．设a 为任一n 维向量，n21e ,,e ,e 为n 维单位向量，则向量组,,,21e e a ne , 线性____关.3.由一个方程0=+++21n x x x 构成的方程组的系数矩阵的秩r ____=，该方程组通解为.二.选择题1．向量组1M 和2M 的秩相等，则（）.()a 1M 与2M 等价； ()b 1M 与2M 所含向量个数相等；()c 1M 与2M 所含向量个数不等； ()d 以上结论都不对.2．设A 为n m ⨯矩阵，且R =)(A n m <，则（）.()a A 的行、列向量组均线性无关； ()b A 的行、列向量组均线性相关；()c A 的行向量组线性相关，列向量组线性无关； ()d A 的行向量组线性无关，列向量组线性相关.三. 设[][]T a a a a ],,,[,],,,[,,,,,,,,03121100101010014321=-===T TT.（1）将4a 用321a ,a ,a 线性表示.（2）由定义判定321a ,a ,a 是向量组321a ,a ,a ,4a 的一个最大线性无关向量组.（3）指出向量组321a ,a ,a ,4a 的秩和矩阵=A [321a ,a ,a ,4a ]的秩.四.设向量组为[],,,,T=31211a [],,,,T---=65142a []Ta 74313---=,,,，[]T-=01124,,,a .求该向量组的秩，并具体找出一个最大线性无关组.再把不属于最大线性无关组的向量用最大线性无关组的向量表示出来.河北工业大学线性代数作业（9）学院班级姓名学号一．填空题1．在基[][][]TTT===213132321321,,,,,,,,a a a 下，坐标为210,,的向量为________.2．在n R 中取r 个线性无关的向量r a a a ,,, 21，r<n ，由r21a ,,a ,a 生成的子空间记为S ，则=S dim ，S 的一个基为___________.3. n 阶矩阵Α的秩为r ，则其解空间的维数是 .二．选择题1．设向量组ma a a ,,, 21线性相关，V 为由m21a ,,a ,a 生成的向量空间，则V dim （）.()a m =； ()b m <； ()c m ≤； ()d 无法确定.2. 向量空间W w {=[]},,,,a d cb a dc b a ==++=T0的维数为（）.()a 1 ()b 2； ()c 3； ()d 4.3．若齐次方程组0=x A 有非零解，则其基础解系是（）.()a 唯一的，其中的向量线性相关；()b 唯一的，其中的向量线性无关； ()c 不唯一，其中的向量线性相关；()d 不唯一，其中的向量线性无关.4．设有4⨯3矩阵A ，A 表示非齐次方程组b AX =的增广矩阵，则b AX =有解的充分条件为（）.()a R ()2≤A ； ()b R ()3≤A ； ()c R ()3=A ； ()d R ()3=A .6．设有5⨯5矩阵A ，A 表示非齐次方程组b AX =的增广矩阵，则b AX =有无穷多组解的充分条件是（）.()a ()5<A r ； ()b ()5=r ； ()c ()()5==A A r r ； ()d ()()4≤=A A r r .三．证明[],,,,T=00011a [],,,,T=00112a [][]TT==1111011143,,,,,,,a a 是4R 的一组基，并求向量[]T=4721,,,b 在这组基下的坐标.四试求下列齐次方程组的基础解系，并说明解空间的维数1．⎪⎩⎪⎨⎧=++-=++-=++-01117840246303542432143214321x x x x x x x x x x x x五．求解下列非齐次方程组.⎪⎩⎪⎨⎧-=+-=-+--=+352231232132131x x x x x x x x河北工业大学线性代数作业（10）学院班级姓名学号一．填空题 1．向量[]T11-1-1=,,,a 的规范化向量为=a e _____________.二．选择题1．设A ，B 为正交矩阵，则下列说法错误的是（）.()a 则1-A 和T A 也为正交矩阵，且有T -=A A 1；()b A 的每一行(列)向量都是单位向量，且其中的任意两个行(列)向量正交；()c AB 也为正交矩阵；()d B A +也是正交矩阵.三. 证明x V {=},,,),,(R x x x x x x x x x T ∈=++=3213213210构成3R 的一个子空间,并给出一组基.四．设[][][]TTT=-=-=103211112201,,,,,,,,,,,c b a ，1．求a 、b ，a 与b 的夹角；2．计算c b a b a ),(--23；3．证明c 与b ,a 都正交.五．}|{0==Ax x W 称为矩阵A 的零空间。

《线性代数》上机作业一(格式)

大连理工线代上机实验

线代作业完整版

线性代数 大作业(一)

线性代数上机作业一

《线性代数》作业

线代上机作业

线性代数上机作业

大连理工大学线性代数实验上机报告材料

200651线性代数作业及答案陕西师范大学网络教育学院高起专、高起本

西南交大大学网络教育学院《线性代数》在线作业

《线性代数》作业

最新线性代数上机作业题答案详解

《线性代数》上机作业一(格式)

《线性代数》上机作业

数值线性代数上机作业1

线性代数上机作业

（精选）线性代数课后作业及参考答案

西南大学《线性代数》网上作业及参考答案

河北工业大学2017年春线性代数作业

线性代数大作业(一)