四川省成都市锦江区初2015届九年级二诊数学试题
2015年成都市中考数学试题及答案

成都市二O 一五年高中阶段教育学校统一招生考试(含成都市初三毕业会考)数 学注意事项:1. 全套试卷分为A 卷和B 卷,A 卷满分100分,B 卷满分50分;考试时间120分钟。
2. 在作答前,考生务必将自己的姓名,准考证号涂写在试卷和答题卡规定的地方。
考试结束,监考人员将试卷和答题卡一并收回。
3. 选择题部分必须使用2B 铅笔填涂;非选择题部分也必须使用0.5毫米黑色签字笔书写,字体工整,笔迹清楚。
4. 请按照题号在答题卡上各题目对应的答题区域内作答,超出答题区域书写的答案无效;在草稿纸,试卷上答题均无效。
5. 保持答题卡清洁,不得折叠、污染、破损等。
A 卷(共100分)第I 卷(选择题,共30分)一、选择题(本大题共10个小题,每小题3分,共30分,) 1.3-的倒数是( ) (A )31-(B )31(C )3- (D )32.如图所示的三棱柱的主视图是( )(A ) (B ) (C ) (D )3.今年5月,在成都举行的世界机场城市大会上,成都新机场规划蓝图首次亮相。
新机场建成后,成都将成为继北京、上海之后,国内第三个拥有双机场的城市,按照远期规划, 新机场将新建的4个航站楼的总面积约为126万平方米,用科学计数法表示126万为( )(A )410126⨯ (B )51026.1⨯ (C )61026.1⨯ (D )71026.1⨯ 4.下列计算正确的是( )(A )4222a a a =+ (B )632a a a =⋅ ( C )422)(a a =- (D )1)1(22+=+a a5.如图,在ABC ∆中,BC DE //,6=AD ,3=DB ,4=AE , 则EC 的长为( )(A )1 (B )2 (C )3 (D )4 6.一次函数12+=x y 的图像不经过( )(A )第一象限 (B )第二象限 (C )第三象限 (D )第四象限7.实数a 、b 在数轴上对应的点的位置如图所示,计算b a -的结果为( )(A )b a + (B )b a - (C )a b - (D )b a --8.关于x 的一元二次方程0122=-+x kx 有两个不相等实数根,则k 的取值范围是( ) (A )1->k (B )1-≥k (C )0≠k (D )1->k 且0≠k9.将抛物线2x y =向左平移2个单位长度,再向下平移3个单位长度,得到的抛物线的函数表达式为( ) A 、3)2(2-+=x y B 、3)2(2++=x y C 、3)2(2+-=x y D 、3)2(2--=x y 10.如图,正六边形ABCDEF 内接于圆O ,半径为4,则这个正六边 形的边心距OM 和弧BC 的长分别为( )(A )2、3π(B )32、π (C )3、23π (D )32、43π 二、填空题(本大题共4个小题,每小题4分,共16分,答案写在答题卡上) 11、因式分解:=-92x __________.12、如图,直线n m //,ABC ∆为等腰直角三角形,︒=∠90BAC ,则=∠1________度.13、为响应 “书香成都”建设的号召,在全校形成良好的人文阅读风尚,成都市某中学随机调查了部分学生平均每天的阅读时间,统计结果如图所示,则在本次调查中阅读时间的中位数是_______小时.14、如图,在平行四边形ABCD 中,13=AB ,4=AD ,将平行四边形ABCD 沿AE 翻折后,点B 恰好与点C 重合,则折痕AE 的长为__________.三、解答题(本大题共6个小题,共54分,解答过程写在答题卡上) 15.(本小题满分12分,每小题6分)(1)计算:20)3(45cos 4)2015(8-+︒---π(2)解方程组:⎩⎨⎧-=-=+12352y x y x16. (本小题满分6分) 化简:21)412(2+-÷-++a a a a a CMEDAOFBm n 1B AC17.(本小题满分8分)如图,登山缆车从点A 出发,途经点B 后到达终点C.其中AB 段与BC 段的运行路程均为200m ,且AB 段的运行路线与水平面的夹角为30°,BC 段的运行路线与水平面的夹角为42°,求缆车从点A 运行到点C 的垂直上升的距离.(参考数据:sin42°≈0.67 ,cos42°≈0.74 , tan42°≈0.90)18. (本小题满分8分)国务院办公厅在2015年3月16日发布了《中国足球发展改革总体方案》,这是中国足球史上的重大改革,为进一步普及足球知识,传播足球文化,我市某区在中小学举行了“足球在身边”知识竞赛活动,各类获奖学生人数的比例情况如图所示,其中获得三等奖的学生共50名,请结合图中信息,解答下列问题:(1)求获得一等奖的学生人数;(2)在本次知识竞赛活动中,A ,B ,C ,D 四所学校表现突出,现决定从这四所学校中随机选取两所学校举行一场足球友谊赛.请使用画树状图或列表的方法求恰好选到A ,B 两所学校的概率.19. (本小题满分10分)如图,一次函数4y x =-+的图象与反比例ky x=(k 为常数,且0k ≠)的图象交于()1,A a ,B 两点. (1)求反比例函数的表达式及点B 的坐标;(2)在x 轴上找一点P ,使PA PB +的值最小, 求满足条件的点P 的坐标及PAB ∆的面积.200m 200m 30°42°B ECDA一等奖三等奖优胜奖 40%二等奖 20%xyABO20、(本小题满分10分)如图,在Rt ABC ∆中,90ABC ∠=︒,AC 的垂直平分线分别与AC ,BC 及AB 的延长线相交于点D ,E ,F ,且BF BC =.O e 是BEF ∆的外接圆,EBF ∠的平分线交EF 于点G ,交O e 于点H ,连接BD ,FH .(1)求证:ABC EBF ∆≅∆;(2)试判断BD 与O e 的位置关系,并说明理由; (3)若1AB =,求HG HB ⋅的值.B 卷(共50分)一、填空题(本大题共5个小题,每小题4分,共20分,答案写在答题卡上) 21、比较大小:512-________58.(填"">,""<,或""=) 22、有9张卡片,分别写有1~9这九个数字,将它们背面朝上洗匀后,任意抽出一张,记卡片上的数字为a ,则关于x 的不等式组()431122x x x x a ≥+⎧⎪⎨--<⎪⎩有解的概率为_________. 23、已知菱形A 1B 1C 1D 1的边长为2,∠A 1B 1C 1=60°,对角 线A 1C 1,B 1D 1相交于点O .以点O 为坐标原点,分别以 OA 1,OB 1所在直线为x 轴、y 轴,建立如图所示的直角坐标系.以B 1D 1为对角线作菱形B 1C 2D 1A 2∽菱形A 1B 1C 1D 1,再以A 2C 2为对角线作菱形A 2B 2C 2D 2∽菱形B 1C 2D 1A 2, 再以B 2B 2为对角线作菱形B 2C 3D 2A 3∽菱形A 2B 2C 2D 2,…,按此规律继续作下去,在x 轴的正半轴上得到点A 1,A 2,A 3,…,A n ,则点A n 的坐标为____________.24、如图,在半径为5的O e 中,弦8AB =,P 是弦AB 所对的优弧上的动点,连接AP ,过点A 作AP 的垂线交射线PB 于点C ,当PAB ∆是等腰三角形时,线段BC 的长为 .GHOEDAFCBB 2y B 1C 2 C 3 A 2 A 3 A 1 O C 1D 1 D 2xKHGOCCOCOBAPBAPBAP图(1) 图(2) 图(3)25、如果关于x 的一元二次方程20ax bx c ++=有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”,以下关于倍根方程的说法,正确的是 .(写出所有正确说法的序号) ①方程220x x --=是倍根方程;②若(2)()0x mx n -+=是倍根方程,则22450m mn n ++=; ③若点()p q ,在反比例函数2y x=的图像上,则关于x 的方程230px x q ++=是倍根方程; ④若方程20ax bx c ++=是倍根方程,且相异两点(1)M t s +,,N(4)t s -,都在抛物线2y ax bx c =++上,则方程20ax bx c ++=的一个根为54. 二、解答题(本大题共3个小题,共30分,解答过程写在大题卡上) 26、(本小题满分8分)某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求,商家又用28800元够进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元。
四川省成都市2015年中考数学真题试题(含解析)

成都市二〇一五年高中阶段教育学校统一招生考试数学(含成都市初三毕业会考)A 卷(共100分)第Ⅰ卷(选择题,共30分)一、选择题(本大题共10个小题,每小题3分,共30分,每小题均有四个选项,其中只有一项符合题目要求,答案涂在答题卡上) 1.3-的倒数是 (A )31-(B )31 (C )3- (D )3【答案】:A【解析】:根据倒数的定义,很容易得到3-的倒数是13-,选A 。
2.如图所示的三棱柱的主视图是(A ) (B ) (C ) (D ) 【答案】:B【解析】:本题考查了三视图的知识,主视图是从物体的正面看得到的视图,找到从正面看所得到的图形即可,注意所有的看到的棱都应表现在主视图中。
从正面看易得三棱柱的一条棱位于三棱柱的主视图内,选B 。
3.今年5月,在成都举行的世界机场城市大会上,成都新机场规划蓝图首次亮相。
新机场 建成后,成都将成为继北京、上海之后,国内第三个拥有双机场的城市,按照远期规划, 新机场将新建的4个航站楼的总面积约为126万平方米,用科学计数法表示126万为 (A )410126⨯ (B )51026.1⨯ (C )61026.1⨯ (D )71026.1⨯ 【答案】:C【解析】: 科学记数法的表示形式为10n a ⨯的形式,其中110a ≤<,n 为整数。
确定n 的值时,要看把原数变成a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同。
当原数绝对值>1时,n 是正数; 当原数的绝对值<1时,n 是负数。
将126万用科学记数法表示1.26×106元,选B 。
4.下列计算正确的是(A )4222a a a =+ (B )632a a a =⋅(C )422)(a a =- (D )1)1(22+=+a a【答案】:C【解析】: A 、2a 与 2a 是同类项,能合并,2222a a a +=。
故本选项错误。
B 、2a 与 3a 是同底数幂,根据同底数幂的乘法法则,同底数幂相乘,底数不变,指数相加。
2015年中考二模名校考试数学试题及答案

2015年中考数学二模名校考试数学试题(卷)时间120分钟满分120分2015、2、28一、选择题(1-6小题,每小题2分7-16小题每小题3分,共42分)1.下列各数中,最小的数是()A.﹣2 B.﹣0.1 C.0D.|﹣1| 2.计算(﹣9)2﹣2×(﹣9)×1+12的值为()A.﹣98 B.﹣72 C.64 D.1003.下列式子正确的是()A.﹣(x﹣3)=﹣x﹣3 B. 5a﹣a=5C. 2﹣1=﹣2 D. 2<<34.如图,将一个正六边形分割成六个全等的等边三角形,其中有两个已涂灰,如果再随意涂灰一个空白三角形,则所有涂灰部分恰好成为一个轴对称图形的概率是()A.B.C.D.14题图 5题图 7题图5.如图,直线a、b及木条c在同一平面上,将木条c绕点O旋转到与直线a平行时,其最小旋转角为()A.100°B.90°C.80°D.70°6.下列一元二次方程中,无解的是()A. x2+4x+2=0 B.x2+4x+3=0 C.x2﹣4x+4=0 D.x2﹣4x+5=07.如图,Rt△ABC中,∠C=90°,∠B=45°,AD是∠CAB的平分线,DE⊥AB于E,AB=a,CD=m,则AC的长为()A. 2m B.a﹣m C.a D.a+m8.如图,在正方形网格中,△ABC的三个顶点及点D、E、F、G、H都在格点上,现以D、E、F、G、H中的三点为顶点画三角形,则下列与△ABC面积相等但不全等的三角形是()A.△EHD B.△EGF C.△EFH D.△HDF9.计算(﹣)÷的结果为()A.B.C.D.10.如图,平行四边形ABCD的顶点B,D都在反比例函数y=(x>0)的图象上,点D的坐标为(2,6),AB平行于x轴,点A的坐标为(0,3),将这个平行四边形向左平移2个单位、再向下平移3个单位后点C的坐标为()A.(1,3)B.(4,3)C.(1,4)D.(2,4)8题图 10题图11.张昆早晨去学校共用时15分钟.他跑了一段,走了一段,他跑步的平均速度是250m/分钟,步行的平均速度是80m/分钟;他家离学校的距离是2900m,如果他跑步的时间为x分钟,则列出的方程是()A. 250x+80(﹣x)=2900 B.80x+250(15﹣x)=2900C. 80x+250(﹣x)=2900 D.250x+80(15﹣x)=290012.已知⊙O及⊙O外一点P,过点P作出⊙O的一条切线(只有圆规和三角板这两种工具).以下是甲、乙两同学的作业:甲:①连接OP,作OP的垂直平分线l,交OP于点A;②以点A为圆心、OA为半径画弧、交⊙O于点M;③作直线PM,则直线PM即为所求(如图1).乙:①让直角三角板的一条直角边始终经过点P;②调整直角三角板的位置,让它的另一条直角边过圆心O,直角顶点落在⊙O上,记这时直角顶点的位置为点M;③作直线PM ,则直线PM 即为所求(如图2). 对于两人的作业,下列说法正确的是( ) A .甲对,乙不对 B . 甲不对,乙对 C . 两人都对 D . 两人都不对13.如图,直线l 经过点P (1,2),与坐标轴交于A (a ,0),B (0,b )两点(其中a <b ,如果a+b=6,那么tan∠ABO 的值为( )A .B . 1C .D . 213题图 14题图 16题图 14.如图,在⊙O 中,AB 为直径,点C 为圆上一点,将劣弧沿弦AC 翻折交AB 于点D ,连接CD .如果∠BAC=20°,则∠BDC=( )A . 80°B . 70°C . 60°D . 50° 15.对于实数m ,n ,定义一种运算“※”:m※n=m 2﹣mn ﹣3.下列说法错误的是( ) A . 0※1=﹣3 B . 方程x※2=0的根为x 1=﹣1,x 2=3 C .不等式组无解D . 函数y=x※(﹣2)的顶点坐标是(1,﹣4)16.如图1,S 是矩形ABCD 的AD 边上的一点,点E 以每秒kcm 的速度沿折线BS ﹣SD ﹣DC 匀速运动,同时点F 从点C 出发,以每秒1cm 的速度沿边CB 匀速运动,并且点F 运动到点B 时点E 也运动到点C .动点E ,F 同时停止运动.设点E ,F 出发t 秒时,△EBF的面积为ycm 2.已知y 与t 的函数图象如图2所示.其中曲线OM ,NP 为两段抛物线,MN 为线段.则下列说法:①点E 运动到点S 时,用了2.5秒,运动到点D 时共用了4秒; ②矩形ABCD 的两邻边长为BC=6cm ,CD=4cm ; ③sin∠ABS=;④点E 的运动速度为每秒2cm .其中正确的是( )A .①②③B .①③④C .①②④D . ②③④二、填空题(每小题3分,共12分.)17.在△ABC中,若|sinA﹣|+(1﹣tanB)2=0,则∠C的度数为_________ °.18.如图,已知点A、B、C在⊙O上,CD⊥OB于D,AB=2OD,若∠C=40°,则∠B=_________ °.18题图 19题图 20题图19.如图,一条4m宽的道路将矩形花坛分为一个直角三角形和一个直角梯形,根据图中数据,可知这条道路的占地面积为_________ m2.20.如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2)…根据这个规律,第60个点的横坐标为_________ .三、解答题(共66分)21.(9分)已知关于x,y的二元一次方程x﹣y=3a和x+3y=4﹣a.(1)如果是方程x﹣y=3a的一个解,求a的值;(2)当a=1时,求两方程的公共解;(3)若是已知方程的公共解,当x0≤1时,求y的取值范围.22.(10分)某中学对校园卫生进行清理,某班有13名同学参加这次卫生大扫除,按要求他们需要完成总面积为80m2的三项清扫工作,三项工作的面积比例如图1,每人每分钟完成各项的工作量如图2.(1)从统计图中可知:擦玻璃、擦课桌椅、扫地拖地的面积分别是_________ m2,_________ m2,_________ m2;(2)如果x人每分钟擦玻璃面积ym2,那么y关于x的函数关系式是_________ ;(3)完成扫地拖地的任务后,把13人分成两组,一组去擦玻璃,一组去擦课桌椅,怎样分配才能同时完成任务?23.(10分)河北省赵县A、B两村盛产雪花梨,A村有雪花梨200吨,B村有雪花梨300吨,现将这些雪花梨运到C、D两个冷藏仓库,已知C仓库可储存240吨,D仓库可储存260吨,从A村运往C、D两处的费用分别为40元/吨和45元/吨;从B村运往C、D两处的费用分别为25元/吨和32元/吨,设从A村运往C仓库的雪花梨为x吨,A、B两村往两仓库运雪花梨的运输费用分别为yA 元,yB元.C D 总计A x吨_________ 300吨B _________ _________ 400吨总计240吨260吨500吨(1)请填写下表,并求出yA ,yB与x之间的函数关系式:(2)当x为何值时,A村的运输费用比B村少?(3)请问怎样调运,才能使两村的运费之和最小?求出最小值.24.(11分)(1)如图1,已知△ABC,以AB、AC为边向△ABC外作等边△ABD和等边△ACE,连接BE,CD,请你完成图形,并证明:BE=CD;(尺规作图,不写作法,保留作图痕迹);(2)如图2,已知△ABC,以AB、AC为边向外作正方形ABFD和正方形ACGE,连接BE,CD,BE与CD有什么数量关系?简单说明理由;(3)运用(1)、(2)解答中所积累的经验和知识,完成下题:如图3,要测量池塘两岸相对的两点B,E的距离,已经测得∠ABC=45°,∠CAE=90°,AB=BC=100米,AC=AE,求BE的长.25.(12分)已知,抛物线y=ax2+x+c的顶点为M(﹣1,﹣2),它与x轴交于点B,C(点B在点C左侧).(1)求点B、点C的坐标;(2)将这个抛物线的图象沿x轴翻折,得到一个新抛物线,这个新抛物线与直线l:y=﹣4x+6交于点N.①求证:点N是这个新抛物线与直线l的唯一交点;②将新抛物线位于x轴上方的部分记为G,将图象G以每秒1个单位的速度向右平移,同时也将直线l以每秒1个单位的速度向上平移,记运动时间为t,请直接写出图象G 与直线l有公共点时运动时间t的范围.26.(3分)1)如图1、图2,点P是⊙O外一点,作直线OP,交⊙O于点M、N,则有结论:①点M是点P到⊙O的最近点;②点N是点P到⊙O的最远点.请你从①和②中选择一个进行证明.(注:图1和图2中的虚线为辅助线,可以直接利用)(2)如图,已知,点A、B分别是直角∠XOY的两边上的动点,并且线段AB=4,如果点T是线段AB的中点,则线段TO的长等于_________ ,所以,当点A和B在直角∠XOY 的两边上运动时,点O一定在以点_________ 为圆心,以线段_________ 为直径的圆上.(3)如图,△ABC的等边三角形,AB=4,直角∠XOY的两边OX,OY分别经过点A和点B (点O与点A、点B都不重合),连接OC,求OC的最大值与最小值.(4)如图,在直角坐标系xOy中,点A、B分别是x轴与y轴上的动点,并且线段AB 等于4为一定值.以AB为边作正方形ABCD,连接OC,则OC的最大值与最小值的乘积等于_________ .参考答案三、解答题(本大题共6个小题,共66分.解答应写出文字说明、证明过程或演算步骤)21.解:(1)将代入方程x﹣y=3a得:5+1=3a,∴a=2.(2)当a=1时,两方程为:由①得:x=3+y,代入②得:3+y+3y=3,∴y=0,∴x=3.所以方程组的公共解为:.(3)因为是已知方程的公共解,∴解得:,∵x≤1,∴2a+1≤1,∴a≤0,所以1﹣a≥1,≥1.∴y22.解:(1)擦玻璃的面积:80×20%=16(m2);擦课桌椅的面积:80×25%=20(m2);扫地拖地的面积:80×55%=44(m2);故答案为:16,22,44;(2)由题意可得,每人每分钟擦玻璃的面积为=,得y=x;故答案为:y=x;(3)设擦玻璃的人数为x人,则擦课桌的人数为(13﹣x)人,根据题意得:16÷x=20÷[0.5×(13﹣x)],即=,解得x=8,经检验x=8是原方程的解,则擦课桌椅的有:13﹣8=5(人),答:擦玻璃的8人,擦课桌椅的有5人.23.解:(1)填表如图所示,y=40x+45(200﹣x)=﹣5x+9000,Ay=25(240﹣x)+32(60+x)=7x+7920;B(2)∵A村的运输费用比B村少,∴﹣5x+9000<7x+7920,解得x>90,∵A村有雪花梨200吨,故200≥x>90吨时,A村的运输费用比B村少;(3)A、B两村的运输费用之和为:﹣5x+9000+7x+7920=2x+16920,∵2>0,∴运输费用随x的增大而增大,∵,∴x≤200,∴当x=0时,运输费用最小,为16920元.24.解:(1)完成图形,如图所示:证明:∵△ABD和△ACE都是等边三角形,∴AD=AB,AC=AE,∠BAD=∠CAE=60°,∴∠BAD+∠BAC=∠CAE+∠BAC,即∠CAD=∠EAB,∵在△CAD和△EAB中,,∴△CAD≌△EAB(SAS),∴BE=CD;(2)BE=CD,理由同(1),∵四边形ABFD和ACGE均为正方形,∴AD=AB,AC=AE,∠BAD=∠CAE=90°,∴∠CAD=∠EAB,∵在△CAD和△EAB中,,∴△CAD≌△EAB(SAS),∴BE=CD;(3)由(1)、(2)的解题经验可知,过A作等腰直角三角形ABD,∠BAD=90°,则AD=AB=100米,∠ABD=45°,∴BD=100米,连接CD,则由(2)可得BE=CD,∵∠ABC=45°,∴∠DBC=90°,在Rt△DBC中,BC=100米,BD=100米,根据勾股定理得:CD==100米,则BE=CD=100米.25.解:(1)∵抛物线y=ax2+x+c的顶点为M(﹣1,﹣2),∴该抛物线的解析式为y=a(x+1)2﹣2.即:y=ax2+2ax+a﹣2.∴2a=1.解得 a=.故该抛物线的解析式是:y=x2+x﹣.当y=0时,x2+x﹣=0.解之得 x1=﹣3,x2=1.∴B(﹣3,0),C(1,0);(2)①证明:将抛物线y=x2+x﹣沿x轴翻折后的图象,即新图象,仍过点B、C,其顶点M′与点M关于x轴对称,则M′(﹣1,2).设新抛物线的解析式为:y=a′(x+1)2+2.∵y=a′(x+1)2+2过点C(1,0),∴a′(1+1)2+2=0,解得,a′=﹣.∴翻折后得到的新抛物线的解析式为:y=﹣x2﹣x+.当﹣4x+6=x2+x﹣时,有:x2﹣6x+9=0,解得,x1=x2=3,此时,y=﹣6.∴新抛物线y=﹣x2﹣x+与直线l有唯一的交点N(3,﹣6);②≤t≤6.附解答过程:∵点N是新抛物线y=﹣x2﹣x+与直线l有唯一的交点,∴直线l与新抛物线y=﹣x2﹣x+在x轴上方部分(即G)无交点,∴当直线l经过点C时产生第一个公共点,经过点B时是最后一个公共点,运动t秒时,点B的坐标为(﹣3+t,0),点C的坐标为(1+t,0),直线与x轴交点为(,0).∵当=﹣3+t时,t=6∴图象G与直线l有公共点时,≤t≤6.26.解:(1)①如图1,根据两点之间线段最短可得:PO≤PR+OR.∴PM+MO≤PR+OR.∵MO=RO,∴PM≤PR.∴点M是点P到⊙O的最近点.②如图2,根据两点之间线段最短可得:PS≤PO+OS.∵OS=ON,∴PS≤PO+ON,即PS≤PN.∴点N是点P到⊙O的最远点.(2)如图3,∵∠XOY=90°,点T是线段AB的中点,∴TO=AB=2.∴点O在以点T为圆心,以线段AB为直径的圆上.故答案为:2、T、AB.(3)取AB的中点T,连接TO、CT、OC,如图4.∵∠AOB=90°,点T是线段AB的中点,∴TO=AB=2.∵△ABC的等边三角形,点T是线段AB的中点,∴CT⊥AB,AT=BT=2.∴CT===2.根据两点之间线段最短可得:OC≤OT+CT,即OC≤2+2;CT≤OC+OT,即OC≥CT﹣OT,也即OC≥2﹣2.∴OC的最大值为2+2,OC的最小值为2﹣2.(4)取AB的中点T,连接TO、CO、CT,如图5.∵∠AOB=90°,点T是线段AB的中点,∴TO=AB=2.∵四边形ABCD是正方形,∴BC=AB=4,∠ABC=90°.∵点T是线段AB的中点,∴BT=AB=2.∴CT===2.根据两点之间线段最短可得:OC≤OT+CT,即OC≤2+2;CT≤OC+OT,即OC≥CT﹣OT,也即OC≥2﹣2.∴OC的最大值为2+2,OC的最小值为2﹣2.∵(2+2)(2﹣2)=20﹣4=16.∴OC的最大值与最小值的乘积等于16.故答案为:16.。
2015年成都中考数学(word版_含答案)

成都市2015年高中阶段教育学校统一招生考试(含成都市初三毕业会考)数 学注意事项:全卷分A 卷和B 卷。
A 卷满分100分,B 卷满分50分;考试时间120分钟。
作答前,考生务必将自己的姓名、准考证号涂写在试卷和答题卡规定的地方。
考试结束,监考人员将试卷和答题卡一并收回。
选择题部分必须使用2B 铅笔填涂,非选择题部分必须使用0.5毫米黑色签字笔书写,字体工整,笔迹清楚。
请按照题号在答题卡上各题目对应的答题区域内作答,超出答题区域书写的答案无效。
A 卷(共100分)第I 卷(选择题,共30分)一、选择题(本答题共10个小题,每小题3分,共30分,每小题均有四个选项,其中只有一项符合题目要求。
答案涂在答题卡上)一、选择题(本大题共10个小题,每小题 3分,共30分) 1、3-的倒数是( ) (A)31-(B)31(C)3- (D)3 疯狂解析:此题考查倒数的概念,基础题;答案:A2、如图所示的三棱柱的主视图是( )A B C D疯狂解析:此题考查三视图,基础题;答案:B3、今年5月,在成都举行的世界机场城市大会上,成都新机场规划蓝图首次亮相,新机场建成后,成都将成为继北京、上海之后,国内第三个拥有双机场的城市。
按照远期规划,新机场将建的4个航站楼的总面积约为126万平方米,用科学记数法表示126万为( )(A)410126⨯ (B)41026.1⨯ (C)51026.1⨯ (D)61026.1⨯ 疯狂解析:此题考查科学计数法,基础题;答案:D 4、下列计算正确的是( )(A)4222a a a =+ (B)632a a a =⋅ (C)()422a a =- (D)()1122+=+a a疯狂解析:此题考查整式综合运算,基础题;答案:C5、如图,在△ABC 中,DE//BC ,AD=6,DB=3,AE=4,则EC 的长为( ) (A)1 (B)2 (C)3 (D)4疯狂解析:此题考查相似三角形中的“A ”型相似,基础题;答案:B6、一次函数12+=x y 的图像不经过( )(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限 疯狂解析:此题考查一次函数的图像和性质,基础题;答案:D7、实数a 、b 在数轴上对应的点的位置如图所示,计算b a -的结果为( )(A)b a + (B)b a - (C)a b - (D)b a -- 疯狂解析:此题考查绝对值,基础题;答案:C8、关于x 的一元二次方程0122=-+x kx 有两个不相等的实数根,则k 的取值范围是( ) (A)k >1- (B)k ≥1- (C)k ≠0 (D)k >1-且k ≠0 疯狂解析:此题考查一元二次方程根与系数的关系,基础题;答案:D9、将抛物线2x y =向左平移2个单位长度,再向下平移3个单位长度,得到的抛物线的函数表达式是( ) (A)()322-+=x y (B)()322++=x y (C)()322+-=x y (D)()322--=x y疯狂解析:此题考查函数图像的平移,基础题;答案:A 10、如图,正六边形ABCDEF 内接于☉o ,半径为4,则这个六边形的边心距OM 和弧BC 的长分别为( ) (A)3,2∏ (B)∏,32 (C)32,3∏ (D)34,32∏疯狂解析:此题考查内接多边形,基础题;答案:D 二:填空题(每小题4分,共16分) 11.因式分解: 29______x -=疯狂解析:此题考查平方差公式:()()22a b a b a b -=-+ ,基础题;答案:()()33x x -+12.如图,直线m//n,△ABC 为等腰直角三角形,∠BAC=90°,则∠1=_______度.疯狂解析:此题考查平行线之间的性质及等腰直角三角形的性质,基础题;答案:45o13.为响应”书香成都”建设的号召,在全校形成良好的人文阅读风气,成都市某中学随机调查了部分学生平均每天的阅读时间,统计结果如图,则在本次统计中,阅读时间的中位数是_____小时.疯狂解析:此题考查中位数,基础题;答案:114.如图,在□ABCD 中,AB=13,4AD =,将□ABCD 沿AE 对折,点B 恰好与点C 重合,则折痕AE 的长为_________.疯狂解析:此题考查平行四边形的性质,“三线合一”,勾股定理,简单题;答案:3 解题过程: 将□ABCD 沿AE 对折后,点B 恰好与点C 重合 1113,222AC AB CE BE BC AD ∴====== ∴190,2O AEB AEC BEC ABE ∠=== 是Rt ABE , 由勾股定理知: 222AB AE BE =+()222222132134993AE AB BE AE AE ∴=-=-=-=∴===三.解答题15.(1)计算()()2820154cos 453ooπ---+-疯狂解析:此题考查实数的综合运算:幂的运算,根式运算,基本三角函数,基础题;答案:8 (2)解方程组:25321x y x y +=⎧⎨-=-⎩疯狂解析:此题考查解二元一次方程组的解法,基础题;答案:12x y =⎧⎨=⎩16.化简:211242aa a a a -⎛⎫+÷⎪+-+⎝⎭ 疯狂解析:此题考查分式的化简求值,基础题;答案:(1)(2)a a --17.如图,登山缆车从点A 出发,途径点B 后到达终点C,其中AB 段与BC 段路程均为200m ,且AB 段的运行路线与水平面的夹角为30o,BC 段的运行路线与水平面的夹角为42o,求缆车从点A 到点C 的垂直上升距离.(_参考数据:sin 420.67,cos420.74,tan 420.90ooo≈≈≈)疯狂解析:此题考查直角三角形的边角关系,三角函数,基础题;答案:234m 解题过程:由题易知:,90,90sin ,sin 1sin 2001002sin 2000.67134O OBD AD BE CEADB BEC BD CEBAD CBE AB BEBD AB BAD mCE BE CBE m⊥⊥∴∠=∠=∴∠=∠=∴=∙∠=⨯==∙∠=⨯=所以点A 到点C 的垂直上升距离为:234BD CE m += 。
2015级成都二诊答案_数学(理)

2018四川高考家长QQ群711038213(志愿填报、自主招生、港澳申请、升学规划、兴趣测评等指导)
4 1 ������������������������1 0分 P 2 5 3 3 7 1 1 ( 元) ㊀㊀ X 的数学期望为 E . 8 . ������������������������ 1 2分 X = 1ˑ +2ˑ +3ˑ +4ˑ = 1 1 0 1 0 0 5 2 5 ( 解: 连接 MD , F D. 1 9. Ⅰ) , 为菱形 且 øF 四边形 ȵ B D E F B D =6 0 ʎ, ʑәD B F 为等边三角形 . ������������������������2 分 ʑDM ʅ B ȵM 是 B F 的中点 , F. 又 D 是A ȵA B ʅB C, A B =B C = 2, C 的中点 ,
1 3 ң 1 3 ң ң , ) , , , ) , , ) , ʑA E= ( 1 E F= ( 1 0 0 B F= ( 0 - , - , 2 2 2 2 ң ( , ,) B C = -1 1 0 . ㊀㊀ ������������������������6 分 设平 面 A E F, 平 面 B C F 的 法 向 量 分 别 为 , , ) , ( ( m= x n= x z . 1y 1z 1 . 2y 2, 2) ì 3 ï 1 ң ������ A E m =0 ï- 2x1 +y1 + 2z1 =0 由 ң ⇒í . E F ������m =0 ï1 ï x1 =0 î2
4. D; 1 0. D; 5. C; 1 1. A; 6. B; 1 2. A.
第 Ⅱ 卷( 非选择题 , 共9 0 分)
( 解: 1 7. Ⅰ) x)= f(
1 ; ㊀㊀1 4. 2 4; ㊀㊀1 5. 22; ㊀㊀1 6.பைடு நூலகம்1 1 7 6. 3 ( 三㊁ 解答题 : 共7 0 分)
2015成都市中考数学试卷.doc

成都市二◦一五年高中阶段教育学校统一招生考试(含成都市初三毕业会考)数学A 卷(共100分)第I 卷(选择题,共30 分)2•如图所示的三棱柱的主视图是(A )( B ) (C ) ( D )【答案】:B【解析】:本题考查了三视图的知识,主视图是从物体的正 面看得到的视图,找到从正面看所得到的图形即可,注意所有的看到的棱都应表现在主视图中。
从正面看易得三棱柱的一 条棱位于三棱柱的主视图内,选 B 。
3•今年5月,在成都举行的世界机场城市大会上,成都新机场规划蓝图首次亮相。
新机场 建成后,成都将成为继北京、上海之后,国内第三个拥有双机场的城市,按照远期规划, 新机场将新建的4个航站楼的总面积约为126万平方米,用科学计数法表示 126万为 (A ) 126 104 (B ) 1.26 105(C ) 1.26 106(D ) 1.26 107【答案】:C【解析】:科学记数法的表示形式为 a 10n 的形式,其中1 a <10 , n 为整数。
确定n 的一、选择题(本大题共10个小题,每小题 一项符合题目要求,答案涂在答题卡上) 1.3的倒数是1(A )-3【答案】:A3分,共30分,每小题均有四个选项,其中只有(C )3(D) 3【解析】:根据倒数的定义,很容易得到3的倒数是 -,选 A 。
3值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同。
当原数绝对值〉1时,n是正数;当原数的绝对值< 1时,n是负数。
将126万用科学记数法表示1.26 x 106元,选B。
4•下列计算正确的是(A ) a 22 a 2a 4(B ) 2a 36a a(C)(a 2)24a(D )(a 2 21) a 1【答案】:C【解析】:A 、 2a 2与a 是同类项,能合并, 2 2a a 2a 2。
故本选项错2 3B 、a 与a 是同底数幕,根据同底数幕的乘法法则,同底数幕相乘,底数不 变,指数相加。
2015年中考二模名校联考数学试题

2015年中考二模名校联考数学试题时间 100分钟 满分100分 2015/3/4一、选择题(每小题2分,共20分).1. -2的绝对值是( )A .2B .-2C .0D .21 2. 下列计算正确的是( ).A .325a a a +=B .326a a a ⋅=C .()326aa = D .2222a a ⎛⎫=⎪⎝⎭3. 如图,由三个小立方块搭成的俯视图是( )4. 下列各式计算正确的是( ) A .2222-=-B .a a 482=(a >0)C .)9()4(-⨯-=4-9-⨯D .336=÷5. 如果整式252n x x --+是关于x 的三次三项式,那么n 等于( )A .3B .4C .5D .66. 如图,河堤横断面如图所示,堤高BC =6米,迎水坡AB 的坡比为1:3,则AB 的长为( )米.A .12B .43C .53D .637. 如图,在⊙O 中,弦BC =1,点A 是圆上一点,且∠BAC =30°,则⊙O 半径是( ).A .2B .3C . 1D .5BA第7题图CO正面A B C DABC第6题图8. 把a a a +-232分解因式的结果是( ).A . a a a +-)2(2B . )2(2a a a -C . )1)(1(-+a a aD . 2)1(-a a9. 如图,爸爸从家(点O )出发,沿着扇形AOB 上OA AB BC →→的路径去匀速散步.设爸爸距家(点O )的距离为s ,散步的时间为t ,则下列图形中能大致刻画s 与t 之间函数关系的图象是( )10. 袋子中装有4个黑球和2个白球,这些球的形状、大小、质地等完全相同,在看不到球的条件下,随机地从袋子中摸出三个球.下列事件是必然事件的是( )A .摸出的三个球中至少有一个球是黑球.B .摸出的三个球中至少有一个球是白球.C .摸出的三个球中至少有两个球是黑球.D .摸出的三个球中至少有两个球是白球.二、填空题(每小题3分,共15分)11. 方程0122=--x x 的解是 .12. 截止5月初,受H7N9禽流感的影响,家禽养殖业遭受了巨大的冲击,最新数据显示,损失已超过400亿元,用科学记数法表示为 元.13. 圆锥的底面半径是1,侧面积是2π,则这个圆锥的侧面展开图形的圆心角为__________. 14. 如图,水平放置的圆柱形排水管道的截面直径是1m ,其中水面的宽AB 为0.8m ,则排水管内水的深度为 m .ACDA BC D 第9题图15. 命题“直角三角形的两个锐角互余”的条件是 .三、解答题(在答题卡上作答,写出必要的解题步骤.16~20题每小题7分, 21、22题每小题8分,23题10分,24题14分,共75分.)16. 解不等式组:并将解集在数轴上表示出来。
2024年四川省成都市锦江区中考数学二诊试卷(含解析)

2024年四川省成都市锦江区中考数学二诊试卷一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求,答案涂在答题卡上)1.(4分)某植物种子发芽的最适宜温度是,如果低于最适宜发芽温度记作,那么高于最适宜发芽温度应该记作 A .B .C .D .2.(4分)如图是由六个相同的小正方体搭成的几何体,这个几何体从正面看到的图形是 A .B .C .D .3.(4分)2024年2月,中国载人月球探测任务新飞行器名称已经确定,新一代载人飞船命名为“梦舟”,月面着陆器命名为“揽月”,中国探月工程正向新的目标迈进.已知地球与月球之间的平均距离大约是384000千米,数据384000用科学记数法表示为 A .B .C .D .4.(4分)下列运算正确的是 A .B .C .D .5.(4分)《义务教育课程标准年版)》首次把学生学会炒菜纳入劳动教育课程,并作出明确规定.某班有7名学生已经学会炒的菜品的种数依次为:2,4,3,2,5,2,3.则这组数据的众数和中位数分别是 A .2,2B .2,2.5C .2,3D .3,36.(4分)如图,为了估算河的宽度,小明采用的办法是:在河的对岸选取一点,在近岸取点,,26C ︒1C ︒1C ︒-0.5C ︒()0.5C ︒0.5C ︒-26.5C ︒26.5C︒-()()50.38410⨯60.38410⨯53.8410⨯63.8410⨯()224527a a a +=326(3)9x x -=623422a a a ÷=222()a b a ab b -=-+(2022()A D B使得,,在一条直线上,且与河的边沿垂直,然后又在垂直于的直线上取点,并测得,.如果,则河宽为 A .B .C .D .7.(4分)明代数学家程大位的《算法统宗》中有这样一个问题:隔墙听得客分银,不知人数不知银;七两分之多四两,九两分之少半斤.其大意为:有一群人分银子,如果每人分七两,则剩余四两;如果每人分九两,则还差八两,问有多少人,多少银两(注:明代当时1斤两,故有“半斤八两”这个成语).设有人,银子有两,可列方程组是 A .B .C .D .8.(4分)如图,抛物线的部分图象如图所示,与轴的一个交点坐标为,抛物线的对称轴是直线.下列结论正确的是 A .B .C .关于的方程没有实数根D .若点在该抛物线上,则A D B DE AB C 15BD m =40BC m =30DE m =AD ()30m 35m 40m 45m16=x y ()7498x y x y =-⎧⎨=+⎩7498x y x y =+⎧⎨=-⎩4789y x y x ⎧=-⎪⎪⎨⎪=+⎪⎩4789y x y x ⎧=+⎪⎪⎨⎪=-⎪⎩2(0)y ax bx c a =++≠x (4,0)1x =()abc >420a b c -+>x 22ax bx c ++=(,)P m n 2am bm c a b c++++…二、填空题(本大题共5个小题,每小题4分,共20分,答案写在答题卡上)9.(4分)分解因式: .10.(4分)已知关于的一元二次方程有两个相等的实数根,则的值为 .11.(4分)如图,在菱形中,,分别是,上的点,且,连接,.若,,则的大小为 .12.(4分)如图,正比例函数的图象与反比例函数的图象交于,两点,若点的坐标为,则关于的不等式的解集为 .13.(4分)如图,在中,按以下步骤操作:①分别以点和为圆心,以大于的长为半径作弧,两弧相交于点和;②以点为圆心,以任意长为半径作弧,分别交,于点,;③分别以,为圆心,以大于的长为半径作弧,两弧交于点;④作射线,交直线于点,连接.若,,则 .三、解答题(本大题共5个小题,共48分,解答过程写在答题卡上)14.(12分)(1;(2)解不等式组:.24x y y -=x 22470x x a ++-=a ABCD E F AB BC BE BF =DE DF 140ADC ∠=︒50CDF ∠=︒EDF ∠1y k x =2k y x=A B A (1,2)-x 21k k x x >ABC ∆B C 12BC M N C AC BC E F E F 12EF O CO MN P BP 110BAC ∠=︒7ABP ∠=︒PBC ∠=201tan 60()(3π-︒+---523(1)131722x x x x +>-⎧⎪⎨-≤-⎪⎩15.(8分)“岁岁春草生,踏青二三月”,又到了阳光明媚,适合春季研学的季节.某校数学实践小组就春季研学地点进行了调研:“:非遗博览园;:武侯祠;:杜甫草堂;:大熊猫繁育基地;:金沙遗址博物馆”.实践小组随机抽取了部分同学进行“春季研学最想去的地点”(每人必选且只选一个地点)调查,根据调查结果绘制了如图所示的两幅不完整的统计图.请结合统计图中的信息,解决下列问题:(1)数学实践小组在这次活动中,调查的学生共有 人,在扇形统计图中,地点所对应的圆心角是 度;(2)补全“春季研学最想去的地点统计图”中的条形统计图;(3)若要选出两名研学小组组长,有两名男同学和两名女同学报名,为保证公平决定采取抽签方式抽取两名组长,请用列表或画树状图的方法,求恰好抽到一名男同学和一名女同学担任组长的概率.16.(8分)如图,为了测量山坡的护坡石坝坝顶与坝脚之间的距离,把一根长为6米的竹竿斜靠在石坝旁,量出竿长1米处距离地面的高度为0.6米,又测得石坝与地面的倾斜角为.求石坝坝顶与坝脚之间的距离.(结果精确到,参考数据:,,17.(10分)如图,在中,以边为直径作,交于点,交的延长线于点,连接交于点,且.(1)求证:;(2)如图1,若,求的值;A B C D E D C B AC α72︒C B 0.1m sin 720.95︒≈cos720.31︒≈tan 72 3.08)︒≈ABC ∆AB O BC D CA E DE AB F DE DC =BD DC =23EF FD =EA AC(3)如图2,若,求阴影部分的面积.18.(10分)如图,已知一次函数的图象与反比例函数的图象交于点和点.(1)求反比例函数的表达式及点的坐标;(2)连接,,点为反比例函数图象第一象限上一点,连接,,若,求点的坐标;(3)已知为轴上一点,作直线关于点中心对称的直线,交反比例函数的图象于点,,若,求的值.一、填空题(本大题共5个小题,每小题4分,共20分,答案写在答题卡上)19.(4分)若,则的值为 .20.(4分)如图,将沿方向平移得到,随机在与组成的图形中取点,取到重叠部分(图中阴影部分)的概率为.若,则平移的距离为 .21.(4分)如图,在的正方形网格中,每个小正方形的顶点叫做格点.直线经过格点,,直3EF FD ==23y x =+k y x=(1,)A a B B AO BO P AP BP 2ABP ABO S S ∆∆=P (,0)T t x AB T CD E F EF =t 10m n +=11(2)()n m m n m n++÷+ABC ∆BC DEF ∆ABC ∆DEF ∆176BF =ABC ∆108⨯l A B线经过格点,,直线经过格点,.点,分别在直线,上,连接交直线于点,则的值为 .22.(4分)如图,为了提醒司机安全驾驶,要在隧道中安装电子显示屏.已知隧道截面为抛物线型,水平路面宽米,抛物线顶点到距离为12米.根据计划,安装矩形显示屏的高为1米,为了确保行车安全,显示屏底部距离地面至少8米,若距离左右墙壁各留至少1米的维修空间,则该矩形显示屏的宽的最大长度为 米.23.(4分)如图,在等边中,,点是边上一点,且,过点作于点,连接,则 ;点是的中点,连接,过点作交于点,则 .二、解答题(本大题共3个小题,共30分,解答过程写在答题卡上)24.(8分)2024年3月14日是第五个“国际数学日”,某校数学组在今年“日”举行了数学游园活动,购买了一批钢笔和自动铅笔作为奖品.在前期询价时,通过电话询问文具店了解到,钢笔的价格比自动铅笔贵,且花300元购买的自动铅笔比花400元购买的钢笔多10支.(1)求前期电话询问时钢笔和自动铅笔的单价分别为多少?m C D n E F O Q l n OQ m P OP PQ16AB =C AB MNPQ MQ MNPQ QP ABC ∆9BC =D BC 6BD =D DE AB ⊥E AD AD =F AD CF F FG CF ⊥DE G FG =π60%(2)前往文具店购买时,恰逢商家对价格进行了调整:自动铅笔比之前询问时涨价,而钢笔则按之前询问价格的8.5折出售.若学校最终购买了钢笔和自动铅笔共200支,且购买奖品的费用没有超过1250元,则学校最多购买了多少支钢笔作为奖品?25.(10分)如图,二次函数的图象与轴交于点,(点在点的左侧),与轴交于点,二次函数图象的顶点为.(1)若,求顶点的坐标及线段的长;(2)当时,二次函数的最小值为,求的值;(3)连接,,,若,求点的坐标.26.(12分)已知两个矩形,若其中一个矩形的四个顶点分别在另一个矩形的四条边上(顶点不重合),我们称这个矩形为另一个矩形的“衍生矩形”.【模型探究】(1)如图1,矩形是矩形的“衍生矩形”,不连接其它线段,图中有哪几组全等三角形,请写出并任选一组证明;【迁移应用】(2)如图2,在矩形中,,.点在线段上,且,点是边上的动点,连接,以为边作矩形,点在边上,点落在矩形内.连接,,当面积为时,求的长;【拓展延伸】(3)如图3,在矩形中,,.点是的中点,点是边上的动点,连接,以为边作矩形,点在边上,点始终落在矩形内(不含边界).连接,点是的中点,连接,求长的取值范围(用含,的式子表示).20%2221(0)y x mx m m =--->x A B A B y C D 2m =D AB 14x ……6-m AC BC DC ACB BCD ∠=∠C EFGH ABCD ABCD 7AB =8AD =M AD 5AM =N AB MN MN MNPQ P BC Q ABCD CQ DQ CDQ ∆72AN ABCD 2AB a =2()AD b a b =<N AB M AD MN MN MNPQ P BC Q ABCD MP O MP CO CO a b2024年四川省成都市锦江区中考数学二诊试卷参考答案与试题解析一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求,答案涂在答题卡上)1.(4分)某植物种子发芽的最适宜温度是,如果低于最适宜发芽温度记作,那么高于最适宜发芽温度应该记作 A .B .C .D .【解答】解:低于最适宜发芽温度记作,那么高于最适宜发芽温度应该记作,故选:.2.(4分)如图是由六个相同的小正方体搭成的几何体,这个几何体从正面看到的图形是 A .B .C .D .【解答】解:从正面看,共有三列,左边一列是三个小正方形,中间和右边一列分别是一个小正方形.故选:.3.(4分)2024年2月,中国载人月球探测任务新飞行器名称已经确定,新一代载人飞船命名为“梦舟”,月面着陆器命名为“揽月”,中国探月工程正向新的目标迈进.已知地球与月球之间的平均距离大约是384000千米,数据384000用科学记数法表示为 A .B .C .D .【解答】解:.故选:.4.(4分)下列运算正确的是 A .B.26C ︒1C ︒1C ︒-0.5C ︒()0.5C ︒0.5C ︒-26.5C ︒26.5C︒-1C ︒1C ︒-0.5C ︒0.5C ︒+A ()B ()50.38410⨯60.38410⨯53.8410⨯63.8410⨯5384000 3.8410=⨯C ()224527a a a +=326(3)9x x -=C .D .【解答】解:,故错误,不符合题意;,故正确,符合题意;,故错误,不符合题意;,故错误,不符合题意;故选:.5.(4分)《义务教育课程标准年版)》首次把学生学会炒菜纳入劳动教育课程,并作出明确规定.某班有7名学生已经学会炒的菜品的种数依次为:2,4,3,2,5,2,3.则这组数据的众数和中位数分别是 A .2,2B .2,2.5C .2,3D .3,3【解答】解:这组数据2,2,2,3,3,4,5中2出现3次,次数最多,所以这组数据的众数为2,中位数为3.故选:.6.(4分)如图,为了估算河的宽度,小明采用的办法是:在河的对岸选取一点,在近岸取点,,使得,,在一条直线上,且与河的边沿垂直,然后又在垂直于的直线上取点,并测得,.如果,则河宽为 A .B .C .D .【解答】解:,,,,,即:,623422a a a ÷=222()a b a ab b -=-+222527a a a +=A 326(3)9x x -=B 624422a a a ÷=C 222()2a b a ab b -=-+D B (2022()C AD B A D B DE AB C 15BD m =40BC m =30DE m =AD ()30m 35m 40m 45mAB DE ⊥ BC AB ⊥//DE BC ∴ADE ABC ∴∆∆∽∴AD DE AB BC=301540AD AD =+解得:.故选:.7.(4分)明代数学家程大位的《算法统宗》中有这样一个问题:隔墙听得客分银,不知人数不知银;七两分之多四两,九两分之少半斤.其大意为:有一群人分银子,如果每人分七两,则剩余四两;如果每人分九两,则还差八两,问有多少人,多少银两(注:明代当时1斤两,故有“半斤八两”这个成语).设有人,银子有两,可列方程组是 A .B .C .D .【解答】解:如果每人分七两,则剩余四两,;如果每人分九两,则还差八两,.根据题意可列出方程组.故选:.8.(4分)如图,抛物线的部分图象如图所示,与轴的一个交点坐标为,抛物线的对称轴是直线.下列结论正确的是 A .B.45AD m =D 16=x y ()7498x y x y =-⎧⎨=+⎩7498x y x y =+⎧⎨=-⎩4789y x y x ⎧=-⎪⎪⎨⎪=+⎪⎩4789y x y x ⎧=+⎪⎪⎨⎪=-⎪⎩ 74x y ∴=- 98x y ∴=+∴7498x y x y =-⎧⎨=+⎩A 2(0)y ax bx c a =++≠x (4,0)1x =()abc >420a b c -+>C .关于的方程没有实数根D .若点在该抛物线上,则【解答】解:抛物线开口向下,,对称轴在轴的右侧,、异号,,抛物线与轴交于正半轴,,,故错误;抛物线与轴的一个交点坐标为,且抛物线的对称轴是直线,抛物线与轴的另一个交点坐标为,,故错误;由图象可知抛物线与直线有两个交点,关于的方程有两个不相等的实数根,故错误;当时,该函数取得最大值,此时,当点在该抛物线上,此时,,即,故正确;故选.二、填空题(本大题共5个小题,每小题4分,共20分,答案写在答题卡上)9.(4分)分解因式: .【解答】解:,x 22ax bx c ++=(,)P m n 2am bm c a b c++++… 0a ∴< y a ∴b 0b ∴> y 0c ∴>0abc ∴<A 2(0)y ax bx c a =++≠x (4,0)1x =∴x (2,0)-420a b c ∴-+=B 2(0)y ax bx c a =++≠2y =∴x 22ax bx c ++=C 1x =y a b c =++(,)A m n 2n am bm c =++2am bm c a b c ∴++++…2am bm a b ++…D D 24x y y -=(2)(2)y x x +-24x y y-2(4)y x =-(2)(2)y x x =+-故答案为:.10.(4分)已知关于的一元二次方程有两个相等的实数根,则的值为 2 .【解答】解:根据题意得△,解得,即的值为2.故答案为:2.11.(4分)如图,在菱形中,,分别是,上的点,且,连接,.若,,则的大小为 .【解答】解:四边形是菱形,,,,,,即,在和中,,;,,故答案为:.12.(4分)如图,正比例函数的图象与反比例函数的图象交于,两点,若点的坐标为,则关于的不等式的解集为 或 .(2)(2)y x x +-x 22470x x a ++-=a 224(47)0a =--=2a =a ABCD E F AB BC BE BF =DE DF 140ADC ∠=︒50CDF ∠=︒EDF ∠40︒ ABCD A C ∴∠=∠AB CB =AD DC =BE BF = AB BE CB BF ∴-=-AE CF =ADE ∆CDF ∆AD CD A C AE CF =⎧⎪∠=∠⎨⎪=⎩()ADE CDF SAS ∴∆≅∆50ADE CDF ∴∠=∠=︒140505040EDF ∴∠=︒-︒-︒=︒40︒1y k x =2k y x =A B A (1,2)-x 21k k x x>1x <-01x <<【解答】解:正比例函数的图象与反比例函数的图象交于,两点,点的坐标为,,关于的不等式的解集为或.故答案为:或.13.(4分)如图,在中,按以下步骤操作:①分别以点和为圆心,以大于的长为半径作弧,两弧相交于点和;②以点为圆心,以任意长为半径作弧,分别交,于点,;③分别以,为圆心,以大于的长为半径作弧,两弧交于点;④作射线,交直线于点,连接.若,,则 .【解答】解:由作图过程可知,直线为线段的垂直平分线,为的平分线,,,.,即,,.故答案为:.三、解答题(本大题共5个小题,共48分,解答过程写在答题卡上)14.(12分)(1;1y k x =2k y x =A B A (1,2)-(1,2)B ∴-∴x 21k k x x>1x <-01x <<1x <-01x <<ABC ∆B C 12BC M N C AC BC E F E F 12EF O CO MN P BP 110BAC ∠=︒7ABP ∠=︒PBC ∠=21︒MN BC CP ACB ∠PB PC ∴=ACP BCP ∠=∠PBC BCP ACP ∴∠=∠=∠180BAC ABC ACB ∠+∠+∠=︒ 180BAC ABP PBC BCP ACP ∠+∠+∠+∠+∠=︒11073180PBC ∴︒+︒+∠=︒21PBC ∴∠=︒21︒201tan 60()(3π-︒+---(2)解不等式组:.【解答】解:(1)原式;(2)由得:,由得:,则不等式组的解集为.15.(8分)“岁岁春草生,踏青二三月”,又到了阳光明媚,适合春季研学的季节.某校数学实践小组就春季研学地点进行了调研:“:非遗博览园;:武侯祠;:杜甫草堂;:大熊猫繁育基地;:金沙遗址博物馆”.实践小组随机抽取了部分同学进行“春季研学最想去的地点”(每人必选且只选一个地点)调查,根据调查结果绘制了如图所示的两幅不完整的统计图.请结合统计图中的信息,解决下列问题:(1)数学实践小组在这次活动中,调查的学生共有 200 人,在扇形统计图中,地点所对应的圆心角是 度;(2)补全“春季研学最想去的地点统计图”中的条形统计图;(3)若要选出两名研学小组组长,有两名男同学和两名女同学报名,为保证公平决定采取抽签方式抽取两名组长,请用列表或画树状图的方法,求恰好抽到一名男同学和一名女同学担任组长的概率.【解答】解:(1)调查的总人数为(人,在扇形统计图中,地点所对应的圆心角为;故答案为:200,36;523(1)131722x x x x +>-⎧⎪⎨-≤-⎪⎩91=+-8=523(1)x x +>-52x >-131722x x --...4x (542)x -<…A B C D E D 6030%200÷=)D 2036036200︒⨯=︒(2)组人数为(人,组人数为(人,条形统计图补充为:(3)画树状图为:共有12种等可能的结果,其中一名男同学和一名女同学的结果数为8种,所以恰好抽到一名男同学和一名女同学担任组长的概率.16.(8分)如图,为了测量山坡的护坡石坝坝顶与坝脚之间的距离,把一根长为6米的竹竿斜靠在石坝旁,量出竿长1米处距离地面的高度为0.6米,又测得石坝与地面的倾斜角为.求石坝坝顶与坝脚之间的距离.(结果精确到,参考数据:,,【解答】解:过点作,垂足为,,,,,,C 20015%30⨯=)A ∴2006030204050----=)82123==C B AC α72︒C B 0.1m sin 720.95︒≈cos720.31︒≈tan 72 3.08)︒≈C CF AB ⊥F 90CFB ∴∠=︒DE AB ⊥ 90AED ∴∠=︒90AED AFC ∴∠=∠=︒DAE CAF ∠=∠,,,解得:,在中,,(米,石坝坝顶与坝脚之间的距离约为3.8米.17.(10分)如图,在中,以边为直径作,交于点,交的延长线于点,连接交于点,且.(1)求证:;(2)如图1,若,求的值;(3)如图2,若,求阴影部分的面积.【解答】(1)证明:如图1,连接,,,,,,是的直径,,,.(2)解:如图1,连接,ADE ACF ∴∆∆∽∴AD DE AC CF =∴10.66CF= 3.6CF =Rt CBF ∆72CBF ∠=︒3.6 3.8sin 720.95CF BC ∴=≈≈︒)∴C B ABC ∆AB O BC D CA E DE AB F DE DC =BD DC =23EF FD =EA AC3EF FD ==AD DE DC = C E ∴∠=∠B E ∠=∠ B C ∴∠=∠AB AC ∴=AB O 90ADB ∴∠=︒AD BC ∴⊥BD DC ∴=OD,,,,,,,,,,的值为.(3)解:如图2,连接,,则,是的直径,且,,,由(2)得,,,垂直平分,,是等边三角形,,,,,阴影部分的面积是BD DC = BO OA =//OD AC ∴12OD AC =//AE OD AEF ODF ∴∆∆∽∴23EA EF OD FD ==32OD EA ∴=∴3122EA AC =∴13EA AC =∴EA AC 13OD AD OD OA =AB O 3EF FD ==AB DE ∴⊥90OFD ∴∠=︒AEF ODF ∆∆∽∴1AF EF OF FD==1122OF AF OA OD ∴===DE ∴OA AD OA OD ∴==AOD ∴∆60AOD ∴∠=︒180120BOD AOD ∴∠=︒-∠=︒3FD ==== OB OD ∴==1342BOD BOD S S S π∆∴=-=-⨯=-阴影扇形∴4π-18.(10分)如图,已知一次函数的图象与反比例函数的图象交于点和点.(1)求反比例函数的表达式及点的坐标;(2)连接,,点为反比例函数图象第一象限上一点,连接,,若,求点的坐标;(3)已知为轴上一点,作直线关于点中心对称的直线,交反比例函数的图象于点,,若,求的值.【解答】解:(1)把点代入中得,,点,把点代入得,,反比例函数的表达式为,23y x =+k y x=(1,)A a B B AO BO P AP BP 2ABP ABO S S ∆∆=P (,0)T t x AB T CD E F EF =t (1,)A a 23y x =+235a =+=∴(1,5)A (1,5)A k y x=5k =∴5y x =由,得或,,;(2)延长,交反比例函数的图象于点,则,,,点与点重合,,,,,,,作,交轴于,设直线为,把,代入得,,解得,直线为,由一次函数可知,,将直线向上平移6个单位得到,235y x y x =+⎧⎪⎨=⎪⎩15x y =⎧⎨=⎩522x y ⎧=-⎪⎨⎪=-⎩5(2B ∴-2)-BO k y x =C OB OC =2ABC ABO S S ∆∆∴=2ABP ABO S S ∆∆= P ∴C 5(2B - 2)-5(2C ∴2)5(2P ∴2)//CD AB y D CD 2y x b =+5(2C 2)25b =+3b =-∴CD 23y x =-23y x =+(0,3)E 6DE ∴=23y x =+29y x =+由解得或,,,综上,点的坐标为,或,;(3)设直线为,则,,,,由消去得,,整理得,,是方程的两个根,,,,,295y x y x =+⎧⎪⎨=⎪⎩1210x y ⎧=⎪⎨⎪=⎩51x y =-⎧⎨=-⎩1(2P ∴10)P 5(22)1(210)CD 2y x b =+1(E x 22)x b +2(F x 22)x b +25y x b y x =+⎧⎪⎨=⎪⎩y 52x b x +=2250x bx +-=1x ∴2x 2250x bx +-=122b x x ∴+=-1252x x =-EF ∴===== EF =∴=,直线为,令,则,由可知直线与轴的交点为,,,,的值为一、填空题(本大题共5个小题,每小题4分,共20分,答案写在答题卡上)19.(4分)若,则的值为 10 .【解答】解:;故答案为:10.20.(4分)如图,将沿方向平移得到,随机在与组成的图形中取点,取到重叠部分(图中阴影部分)的概率为.若,则平移的距离为 2 .【解答】解:由平移可得,,,,,,∴210164b +=b ∴=±∴CD 2y x =±0y =x =23y x =+23y x =+x 3(2-0)3(4T ∴-0)t ∴34-34-10m n +=11(2)()n m m n m n ++÷+11(2)()n m m n m n++÷+222n m mn n m mn mn+++=÷2()m n mn mn m n+=⋅+m n=+10=ABC ∆BC DEF ∆ABC ∆DEF ∆176BF =ABC ∆//DE AB BE CF =ABC GEC ∴∆∆∽∴21()4GEC ABC S EC S BC ∆∆==∴12CE BC =设,,,,,解得,,故平移的距离为2.21.(4分)如图,在的正方形网格中,每个小正方形的顶点叫做格点.直线经过格点,,直线经过格点,,直线经过格点,.点,分别在直线,上,连接交直线于点,则的值为 .【解答】解:取格点、、,连接交直线于点,连接、,,,,,,,,连接、、、,则四边形和四边形都是平行四边形,,,,∴CE x =2BC x =2BE CF x x x ∴==-=6BF = 26x x ⨯+=2x =2BE CF ∴==ABC ∆108⨯l A B m C D n E F O Q l n OQ m P OP PQ 54H L K AE m I CH DL //CH DL CHI DLI ∴∆∆∽∴12HI CH LI DL ==13HI ∴=23LI =110333AI ∴=+=28233IE =+=AC KD EC FD AKDC CDFE ////AK CD EF ∴////l m n ∴∴1053843OP AI PQ IE===故答案为:.22.(4分)如图,为了提醒司机安全驾驶,要在隧道中安装电子显示屏.已知隧道截面为抛物线型,水平路面宽米,抛物线顶点到距离为12米.根据计划,安装矩形显示屏的高为1米,为了确保行车安全,显示屏底部距离地面至少8米,若距离左右墙壁各留至少1米的维修空间,则该矩形显示屏的宽的最大长度为 6 米.【解答】解:由题意,如图,建立平面直角坐标系.由顶点为,可设抛物线的解析式为.又,.5416AB =C AB MNPQ MQ MNPQ QP C (0,12)∴212y mx =+(8,0)B 06412m ∴=+.抛物线为.显示屏底部距离地面至少8米,令..或..又显示屏两侧留1米,(米,此时是最大值.故答案为:6.23.(4分)如图,在等边中,,点是边上一点,且,过点作于点,连接,则 是的中点,连接,过点作交于点,则 .【解答】解:,,,,,,,在中,由勾股定理得:.点是的中点,,过点作于,过点作于,过点作于,延长交于,316m ∴=-∴231216y x =-+ ∴819y =+=2391216x ∴=-+4x ∴=4x =-(4,9)D ∴2(41)6PQ MN ∴==⨯-=)ABC ∆9BC =D BC 6BD =D DE AB ⊥E AD AD =F AD CF F FG CF ⊥DE G FG =6BD = 60B ∠=︒90BED ∠=︒3BE ∴=ED =9AB BC AC === 936AE ∴=-=Rt AED ∆AD === F AD 12FD AD ∴==A AL BC ⊥L F FH BC ⊥H G GK BC ⊥K FG BC P是等边三角形,,,,,,,,,,即,,,,,,,,,,,,设,则,,,,,,,即,解得:ABC ∆ 9BC =1922BL CL BC ∴===AL =93622DL BD BL ∴=-=-=FH BC ⊥ AL BC ⊥//FH AL ∴DFH DAL ∴∆∆∽∴DH FH DF DL AL AD ==1322DH =34DH ∴=FH =315344CH CD DH ∴=+=+=CF ∴==90CFP CHP ∠=∠=︒ PCF FCH ∠=∠CPF CFH ∴∆∆∽∴FP CP CF FH CF CH ====FP ∴=395CP =3915815420PH CP CH ∴=-=-=3924355DP CP CD =-=-=GK x =22DG GK x ==DK =245PK DP DK ∴=-=//GK FH PGK PFH ∴∆∆∽∴GK PK FH PH=GK PH PK FH ∴⋅=⋅8124()205x =-x =,,,.二、解答题(本大题共3个小题,共30分,解答过程写在答题卡上)24.(8分)2024年3月14日是第五个“国际数学日”,某校数学组在今年“日”举行了数学游园活动,购买了一批钢笔和自动铅笔作为奖品.在前期询价时,通过电话询问文具店了解到,钢笔的价格比自动铅笔贵,且花300元购买的自动铅笔比花400元购买的钢笔多10支.(1)求前期电话询问时钢笔和自动铅笔的单价分别为多少?(2)前往文具店购买时,恰逢商家对价格进行了调整:自动铅笔比之前询问时涨价,而钢笔则按之前询问价格的8.5折出售.若学校最终购买了钢笔和自动铅笔共200支,且购买奖品的费用没有超过1250元,则学校最多购买了多少支钢笔作为奖品?【解答】解:(1)设前期电话询问时自动铅笔的单价是元,则自钢笔的单价是元,根据题意得:,解得:,经检验,是所列方程的解,且符合题意,(元.答:前期电话询问时钢笔的单价是8元,自动铅笔的单价是5元;(2)设学校购买了支钢笔作为奖品,则购买了支自动铅笔,根据题意得:,解得:,GK ∴=24955PK ==PG ∴===FG FP PG ∴=-==π60%20%x (160%)x +30040010(160%)x x-=+5x =5x =(160%)(160%)58x ∴+=+⨯=)y (200)y -5(120%)(200)80.851250y y ⨯+-+⨯ (1252)y …又为正整数,的最大值为62.答:学校最多购买了62支钢笔作为奖品.25.(10分)如图,二次函数的图象与轴交于点,(点在点的左侧),与轴交于点,二次函数图象的顶点为.(1)若,求顶点的坐标及线段的长;(2)当时,二次函数的最小值为,求的值;(3)连接,,,若,求点的坐标.【解答】解:(1)当时,抛物线的表达式为:,则抛物线的顶点坐标为:;令,则或5,即;(2)由抛物线的表达式知,其对称轴为直线,当时,,同理可得:时,,当时,;当时,函数在时取得最小值,即,解得:(舍去);当时,y y ∴2221(0)y x mx m m =--->x A B A B y C D 2m =D AB 14x ……6-m AC BC DC ACB BCD ∠=∠C 2m =245y x x =--D (2,9)-2450y x x =--=1x =-6AB =x m =1x =22214y x mx m m =---=-4x =1510y m =-x m =221y m m =---4m …4x =15106m -=-2.1m =1m …函数在时取得最小值,即,解得:(舍去);当时,函数在时取得最小值,即,解得:;综上,(3)由抛物线的表达式知,点、、、的坐标分别为、、、,则直线的表达式为:,的表达式为:,过点作交的延长线于点,则直线的表达式为:,联立和的表达式得:,解得:,则点,由中点坐标公式得点的坐标为:,将点的坐标代入得表达式得:,解得:(舍去)或,则点.1x =46m -=-1.5m =14m <<x m =2621m m -=---1m =-1m =-A B C D (1,0)-(21,0)m +(0,21)m --2(,21)m m m ---BC 21y x m =--CD 21y mx m =---A AH BC ⊥CD H AH 1y x =-+AH BC 211x m x --=-+x m =(,1)N m m --H (21,22)m m +--H DC 22(21)21m m m m --=-+--1m =-12(0,2)C -26.(12分)已知两个矩形,若其中一个矩形的四个顶点分别在另一个矩形的四条边上(顶点不重合),我们称这个矩形为另一个矩形的“衍生矩形”.【模型探究】(1)如图1,矩形是矩形的“衍生矩形”,不连接其它线段,图中有哪几组全等三角形,请写出并任选一组证明;【迁移应用】(2)如图2,在矩形中,,.点在线段上,且,点是边上的动点,连接,以为边作矩形,点在边上,点落在矩形内.连接,,当面积为时,求的长;【拓展延伸】(3)如图3,在矩形中,,.点是的中点,点是边上的动点,连接,以为边作矩形,点在边上,点始终落在矩形内(不含边界).连接,点是的中点,连接,求长的取值范围(用含,的式子表示).【解答】解:(1)图中全等三角形有:,.选进行证明,证明:如图1,四边形、是矩形,,,,,EFGH ABCD ABCD 7AB =8AD =M AD 5AM =N AB MN MN MNPQ P BC Q ABCD CQ DQ CDQ ∆72AN ABCD 2AB a =2()AD b a b =<N AB M AD MN MN MNPQ P BC Q ABCD MP O MP CO CO a b AEF CGH ∆≅∆BFG DHE ∆≅∆AEF CGH ∆≅∆ ABCD EFGH 90A B C EFG FGH ∴∠=∠=∠=∠=∠=︒EF GH =90AEF AFE AFE BFG BFG BGF BGF CGH ∴∠+∠=∠+∠=∠+∠=∠+∠=︒AEF CGH ∴∠=∠;选进行证明,证明:四边形、是矩形,,,,,;(2)如图2,过点作于,于,则,四边形、是矩形,,,,,,,,,,,,,四边形是矩形,()AEF CGH AAS ∴∆≅∆BFG DHE ∆≅∆ ABCD EFGH 90A B D EFG FEH ∴∠=∠=∠=∠=∠=︒EH FG =90AEF AFE AFE BFG BFG BGF AEF DEH ∴∠+∠=∠+∠=∠+∠=∠+∠=︒BGF DEH ∴∠=∠()BFG DHE AAS ∴∆≅∆Q QK CD ⊥K QL BC ⊥L 90QKC QLC QLP ∠=∠=∠=︒ ABCD MNPQ 90A B BCD MNP NPQ ∴∠=∠=∠=∠=∠=︒8BC AD ==7CD AB ==MN PQ =90AMN ANM ANM BNP BNP BPN BPN LPQ ∴∠+∠=∠+∠=∠+∠=∠+∠=︒AMN LPQ ∴∠=∠()AMN LPQ AAS ∴∆≅∆5AM LP ∴==AN QL =17722CDQ S QK ∆=⨯⋅= 1QK ∴=90QKC BCD QLC ∠=∠=∠=︒ ∴CKQL,,,,,,即,或5;(3)当点落在边上时,此时,最小,如图3,连接,过点作于,四边形是矩形,经过点,且,,,当点落在矩形的内部,且时,此时最大,如图4,则1CL QK ∴==8512BP BC LP CL ∴=--=--=A B ∠=∠ AMN BNP ∠=∠AMN BNP ∴∆∆∽∴AN AM BP BN =527AN AN=-2AN ∴=Q CD OC NQ O OT BC ⊥T MNPQ NQ ∴O 111222MO NO MP NQ AD b =====CT b ∴=OT a =OC ∴=Q ABCD AM AN a ==OC OC ==CO ∴OC <…。
2015年成都市锦江区初三二诊数学及答案
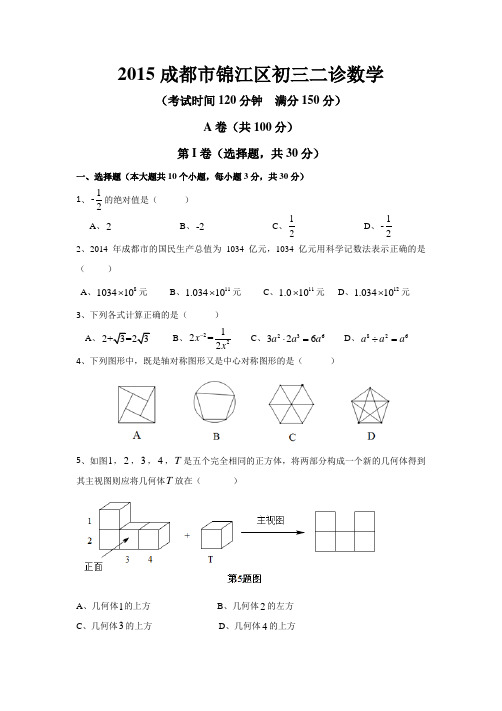
2015成都市锦江区初三二诊数学(考试时间120分钟 满分150分)A 卷(共100分) 第I 卷(选择题,共30分)一、选择题(本大题共10个小题,每小题3分,共30分) 1、1-2的绝对值是( ) A 、2 B 、-2 C 、12 D 、1-22、2014年成都市的国民生产总值为1034亿元,1034亿元用科学记数法表示正确的是( )A 、8103410⨯元B 、111.03410⨯元C 、111.010⨯元D 、121.03410⨯元 3、下列各式计算正确的是( )A 、B 、2212=2x x- C 、236326a a a ⋅= D 、826a a a ÷= 4、下列图形中,既是轴对称图形又是中心对称图形的是( )5、如图1,2,3,4,T 是五个完全相同的正方体,将两部分构成一个新的几何体得到其主视图则应将几何体T 放在( )A 、几何体1的上方B 、几何体2的左方C 、几何体3的上方D 、几何体4的上方6、成都市举行的中学生春季田径运动会上,参加男子跳高的15名运动员的成绩如下表所示:这些运动员跳高成绩的中位数和众数分别是( )A 、1.70,1.65B 、1.70,1.70C 、1.65,1.60D 、3,4 7、下列函数中,自变量x 可以取1和2的函数是( )A 、12y x =- B 、11y x =- C 、y = D 、y =8、如图,若//AB CD ,则E ∠的度数为( )A 、60︒B 、65︒C 、70︒D 、75︒9、如图,在Rt ABC ∆中,90C ︒∠=,4AC =,2BC =,分别以AC ,BC 为半径画圆,则阴影部分的面积为( )A 、542π-B 、104π-C 、108π-D 、582π-10、如图,抛物线21(2)3y a x =+-与221(3)12y x =-+交于点()1,3A ,过点A 作x 轴的平行线,分别交两条抛物线于点B ,C . 则以下结论:①无论x 取何值,2y 的值总是正数;②23a =;③当0x =时,216y y -=;④10AB AC +=;下列结论的是:( )A 、①②④B 、①③④C 、②③④D 、①②③④第II 卷(非选择题,共70分)二、填空题(本大题共4个小题,第小题4分,共16分) 11、因式分解:324y x y -= .12、如图,路灯距离地面8米,身高1.6米的小明站在距离灯的底部(点O )20米的A 处,则小明的影子AM 长 米.13、如果1x ,2x 是一元二次方程2320x x ++=的两个实数根,那么12x x +的值是 .14、如图,一圆与平面直角坐标系中的x 轴切于点(4,0)A ,与y 轴交于点(0,2)B ,(0,8)C ,则该圆的直径为 .三、解答题(本大题共6个小题,共54分) 15、(本题2个小题,共12分)(1)计算:231(2)14sin 603-︒⎛⎫-++- ⎪⎝⎭(2)先化简221111a a a ⎛⎫+÷⎪-+⎝⎭,再在0,1-,12中选取一个适当的数代入求值.16、(6分)如图已知反比例函数(0)ky k x=≠在第一象限的图像上有不同的两点A 、B ,其中(2,6)A ,是原点. 过点B 作BC x ⊥轴于C ,作BD y ⊥轴于D ,四边形OCBD 的周长为14.(1)求反比例函数的解析式; (2)求OB 的长.17、(8分)已知,如图,ABC ∆和ECD ∆都是等腰直角三角形,90ACB DCE ︒∠=∠=,D 为线段AB 上一动点.(1)求证:BD AE =;(2)当D 是线段AB 中点时,求证:四边形AECD 是正方形.18、(8分)如图,小岛A 在港口P 的南偏西45︒方向,距离港口81海里处. 甲船从A 出发,沿AP 方向以9海里/时的速度驶向港口,乙船从港口P 出发,沿南偏东60︒方向,以18海里/时的速度驶离港口. 现两船同时出发, (1)出发后几小时两船与港口P 的距离相等地?(2)出发后几小时乙船在甲船的正东方向?(结果精确到0.1小时)≈1.73)19、(10分)体育课上,小明、小强、小华三人在学习训练踢足球,足球从一人传到另一人就记为踢一次.(1)如果从小强开始踢,经过两次踢后,足球踢到了小华处的概率是多少(用树状图表示或列表说明);(2)如果踢三次后,球踢到了小明处的可能性最小,应从谁开始踢?请说明理由.20、(10分)已知:如图AB 是⊙O 的直径,PB 切⊙O 于点B ,PA 交⊙O 于点C ,PF 分别交AB 、BC 于E 、D ,交⊙O 于F 、G ,且BE 、BD 恰好是关于x 的方程226(413)0x x m m -+++=其中m 为实数)的两根.(1)求证:PBCBAC ∆∆;(2)求证:PF 平分APB ∠;(3)若GE EF ⋅=PBC ∠的度数.B 卷(50分)一、填空题(本大题共5小题,每小题4分,共20分)21、已知220x y -+=,则22114x y xy +--的值为 . 22、若关于x 的方程1(4)333k x x x-+=--无解,则k = . 23、有依次排列的3个数:3,9,8,对任意相邻的两个数,都用右边的数减去左边的数,所得之差在这两个数之间,可产生一个新数串:3,6,9,1-,8,这称为第一次操作;做第二次同样的操作后也可以产生一个新数串:3,3,6,3,9,10-,9,8,依次类推,则从数串3,9,8开始操作第100次以后所产生的那个新数串的所有数之和是 .24、如图,A ,C 是反比例函数3y x=的图象上的两点,连接AC ,过A 、C 分别作y 轴、x 轴的平行线,两线交于B ,那么阴影部分的面积是 .25、在三角形纸片ABC 中,90ABC°?,9AB =,12BC =. 过点A 作直线l 平行于BC ,折叠三角形纸片ABC ,使直角顶点B 落在直线l 上的T 处,折痕为MN . 当点T 在直线l 上移动时,折痕的端点M ,N 也随之移动. 若限定端点M 、N 分别在AB 、BC 边上移动(点M 可以与点A 重合,点N 可以与点C 重合),则线段AT 长度的最大值与最小值之和为 .二、解答题(本大题共3个小题,共30分)26、(8分)随着机构改革工作的深入进行,各单位要减员增效。
四川省成都市武侯区2015届九年级第二次诊断考试数学试题

成都市武侯区2015届九年级第二次诊断考试数学试题 A 卷(共100分)一、选择题(本大题共有10小题,每小题3分,共30分) 1.下列各数比-2小的数是A .-3B .-1C .0D .12.用两块完全相同的长方体搭成如图所示的几何体,这个几何体的主视图是3.花粉的质量很小,一粒某种花粉的质量约为0.000103毫克,那么0.000103用科学计数法表示为 A .510.310-⨯ B .41.0310-⨯ C .30.10.10-⨯ D .31.0310-⨯ 4.下列计算正确的是A .448a a a += B .3(2)32ab a b -=- C .532a a a ÷= D .222(2)4a b a b -=- 5.如图,一个正六边形转盘被分成6个全等的三角形,任意转动这个转盘1次,当转盘停止时,指针指向阴影区域的概率是 A .13 B .14 C .16 D .126.如图,在Rt ABC ∆中,90C ∠=,5AB =,4AC =,那么sin A 的值等于A .45 B .35 C .34 D .437.将下列函数的图象沿y 轴向下平移3个单位长度后,图象经过原点的是 A .3y x =-- B .3y x = C .3y x =+ D .25y x =+8.分式方程3202x x-=-的解为 A .2x = B .3x = C .4x = D .4x =-9.已知在正方形ABCD 中,对角线AC 与BD 相交于点O ,//OE AB 交BC 于点E ,若8AD cm =,则OE 的长为A .3cmB .4cmC .6cmD .8cm 10.如图,在O 中,30C ∠=,2AB =,则弧AB 的长为A .πB .6πC .4πD .23π 二、填空题(本大题共4个小题,每小题4分,共16分) 11.4的算术平方根是_______. 12.在ABC ∆与DEF ∆中,若23AB BC AC DE EF DF ===,且ABC ∆的面积为4,则DEF ∆的面积为________. 13.如图是根据某班50名同学一周的体育锻炼情况绘制的条形统计图,则这个班50名同学一周参加体育锻炼时间的众数是_____小时,中位数是______小时.14.在二次函数2(0)y ax bx c a =++≠中,函数值y 与自变量x 的部分对应值如下表:x ⋅⋅⋅ -2 -1 0 1 2 3 ⋅⋅⋅ y⋅⋅⋅83-13⋅⋅⋅则利用二次函数图象的性质,可知该二次函数2(0)y ax bx c a =++≠图象的对称轴是直线________.三、解答题(本大题共6个小题,共54分) 15.(本小题满分12分,每题6分)(1)计算:101|()4cos 45(3π---+-(2)解不等式组1123(1)5x x x x-⎧-≤⎪⎨⎪-<⎩,在数轴上表示其解集,并写出该不等式组的整数解.16.(本小题满分6分)化简:22()224m m mm m m -÷+--17.(本小题满分8分)如图,大楼AD高50米,和大楼AD相距90米的C处有一塔BC,某人在楼顶D处测塔顶B的仰角∠=,求塔高(结果保留整数,参考数据:2 1.41BDE30=)=,3 1.7318.(本小题满分8分)武侯区某校九年级三班共40名学生,需要参加体育“四选一”自选项目测试,如图是该班学生所报自选项目人数的扇形统计图,请根据图中信息完成下面各题:(1)图中“投掷实心球”所在扇形对应的圆心角的度数为______度;该班自选项目为“投掷实心球”的学生共有_______名;(2)在自选项目为“投掷实心球”的学生中,只有1名女生. 为了了解学生的训练效果,将从自选项目为“投掷实心球”的学生中,随机抽取2名学生进行投掷实心球训练测试,请用树状图或列表法求取所抽取的2名学生中恰好有1名女生的概率.19.(本小题满分10分)如图,一次函数2y x =-+的图象与反比例函数(0)ky k k x=≠为常数且的图象交于点(1,)A m -. (1)求反比例函数的表达式及两个函数图象的另外一个交点B 的坐标; (2)若点C 与点A 关于y 轴对称,连接AC ,BC ,求ABC ∆的面积.20.(本小题满分10分)如图,O 是ABC ∆的外接圆,AB 为直径,过点O 作//OD BC ,交AC 于点D .(1)求ADO ∠的度数; (2)延长DO 交O 于点E ,过点E 作O 的切线,交CB 延长线于点F ,连接DF 交OB 于点G .①试判断四边形CDEF 的形状,并说明理由; ②若2BG =,3AD =,求四边形CDEF 的面积.B 卷(共50分)一、填空题(每小题4分,共20分)21.已知12,x x 是方程22730x x -+=的两根,则1212_______.x x x x +-=22.规定:用符号[]x 表示一个不大于实数x 的最大正数,例如[3.69]3=,[31]2+=,[ 2.56]3-=-,[3]2-=-. 按照这个规定,[131]_____.--=23.三边长均为整数,且周长为18的三角形中,三边都是偶数的概率为_______. 24.如图,矩形ABCD 的顶点A ,B 的坐标分别是(1,0),(0,2)A B --,反比例函数(0)ky k x=≠的图象经过顶点C ,AD 边交y 轴于点E ,若四边形BCDE的面积等于ABE ∆面积的5倍,则k 的值等于_________.25.如图,在ABC ∆中,2AB AC ==,点P 在BC 上:①若点P 为BC 的中点,且2m AP BP PC =+⋅,则m 的值为______;②若BC 边上有2015个不同的点122015,,,P P P ⋅⋅⋅,且相应的有21111m APBP PC =+⋅,22222m AP BP P C =+⋅,⋅⋅⋅,22015201520152015m AP BP P C =+⋅,则122015m m m ++⋅⋅⋅+的值为_______.二、解答题(本大题共3个小题,共30分) 26.(本小题满分8分)如图,在Rt ABC ∆中,90B ∠=,9AB cm =,2BC cm =,点M ,N 分别从A ,B 同时出发,M 在AB 边上沿AB 方向以每秒2cm 的速度匀速运动,N 在BC 边上沿BC 方向以每秒1cm 的速度匀速运动(当点N 运动到点C 时,两点同时停止运动). 设运动时间为x 秒,MBN ∆的面积为2y cm . 的取值范(1)求y 与x 之间的函数关系式,并写出自变量x 围;(2)求MBN ∆的面积的最大值.27.(本小题满分10分)如图,点P 是菱形ABCD 对角线AC 上的一点,连接DP 并延长交AB 于点E ,连接BP 并延长交AD 于点F ,交CD 延长线于点G .(1)求证:PB PD =; (2)若:1:2DF FA =①请写出线段PF 与线段PD 之间满足的数量关系,并说明理由; ②当DGP ∆是等腰三角形时,求tan DAB ∠的值.28.(本小题满分12分)C.如图,在平面直角坐标系xOy中,抛物线与x轴交于,A B两点(点A在点B的左侧),顶点为(0,2)P-.直线DB交y轴于点D,交抛物线于点(43,6)(1)求抛物线的表达式及点D的坐标;A B P E为顶点的四边形仅有一组对边平行,求点E的坐标;(2)点E是抛物线上的动点,若以,,,+(3)连接AP,点F在直线AP上,设点F到直线DB的距离为m,点F到点D的距离为n,求m n 的最小值.参考答案 A 卷一、选择题1~5 ACBCA 6~10 BCDBD 二、填空题11.2 12.9 13.8 9 14.1x = 三、解答题15.(1)-2 (2)312x -<≤ 整数解为1,0,1x =- 16.6m - 17.102米18.36 4 12 19.(1)3,(3,1)y B x=-- (2)4ABC S ∆=20.(1)90(2)①矩形(三个角为直角) ②设半径为r ,OD x =,则22BF GB OD OG r ==- 22BF x r ∴=-作BMDE ⊥于点M ,则BF EM =又1,2OD CB DM CB == OM DO ∴= 即BF r x =- 即22r x x r -=- 又在Rt ADO ∆中,2223x r +=联立解得513,44x r == 92DE x r ∴=+=927322CDEF S ∴=⨯= PS :在解方程组时,可以由20()222r x r rr r x x r x r -=⇒=⇒==+--舍去或 B 卷一、填空题 21. 2 22. -5 23.37解析:三边均为整数的有(2, 7, 9)、(2, 8, 8)、(3, 7, 8)、(4, 6, 8)、(4, 7,7)、(5, 6, 7)、(6, 6, 6),一共有7个,其中均为偶数的有3个. 24.32-解析:如图所示,由5BCDE ABE S S ∆=可以得到2DE AE =,过点D 作y 轴的平行线,与x 轴交于点M ,与过点C 作x 轴的平行线相交于点N 由AEO BAO ∆∆,可以得到12OE =由AEOADM ∆∆,可以得到32,2OM DM ==由DNC BOA ∆≅∆,可以得到2,1DN NC ==∴C 点的坐标为1(3,)2C -133()22k ∴=⨯-=-25. 4;8060解析:如图所示,作ABC ∆的外接圆,并延长AP 交圆于点D 由ABPCDP BP CP AP DP ∆∆⇒⋅=⋅由2APCACD AP AD AC ∆∆⇒⋅=2224m AP BP PC AP AP AD AP AD AC ∴=+⋅=+⋅=⋅==122015420158060m m m ∴++⋅⋅⋅+=⨯=26.(1)29(02)2y x x x =-+<≤ (2)2x =时,取得最大值为527.(1)证明()CDP CBP SAS ∆≅∆(2)①设,PF EP x PD PB y ====,则由12GF GDF BAF x y ∆∆⇒=+ 由GF x y GDP BEP y x +∆∆⇒= 23x y ∴= ②设2,3PF EP t PD PB t ====(I )若DG GP =则52t GF =,92t DG GP ==,9AB t =, 3DF BE t ==,6AF t =在AFB ∆中,作FH AB ⊥于点H ,设AH x =,则22223625(9)t x t t x -=--469x t ∴=,202t FH = 102tan 23DAB ∴∠=(II )若GD PD =则52t GF =,2GD t =,6AB t =,2DF BE t ==,4AF t = 在在AFB ∆中,作FHAB ⊥于点H ,同理可求57tan 9DAB ∴∠= (III )若GP DP = 52t GF =,3DP t = GP DP ∴≠28.(1)212,(0,6)6y x D =-+(2)过点A 作BP 的平行线交抛物线于点1E ,可求130)E -过点B 作AP 的平行线交抛物线于点2E ,可求2(0,2)E过点P 作AB 的平行线交抛物线于点3E ,可求3(6)E --(3)连接DA 并延长DA 至点M ,使得DA AM =,连接,MP MB ,易知DMP ∆为等边三角形,点A 、B 分别为其所在边的中点,故点D 、点M 关于直线AP 对称,MB DP ⊥,∴线段MB 的长度即为m n +的最小值即m n +的最小值为12.。
成都锦江区二诊模拟数学卷含答案

一、选择题(每小题3分,共30分) A 卷(100分) 1、下列各数与-8相等的( )A 、8-B 、8--C 、24-D 、-(-8)2、2017年成都市经济呈现活力增强、稳中向好的发展态势;截止2017年12月,全市实现地区生产 总值约14000亿元,将14000亿元用科学记数法表示是( ) A 、111014⨯元 B 、11104.1⨯元 C 、12104.1⨯元 D 、13104.1⨯元3、如图是由五个大小相同的正方体组成的几何体,从左面看这个几何体,看到的图形是( )4、下列运算正确的是( )A 、532a a a =+B 、532a a a =•C 、632)(a a =-D 、326a a a =÷ 5、在下列四个标志中,既是中心对称图形又是轴对称图形的是( )6、如图,将一块含有30°角的直角三角板的两个顶点放在长方形直尺的一组对边上,如果∠1=30°, 那么∠2的度数为( )A 、60° B 、50° C 、40° D 、30°7、下表记录了甲、乙、丙、丁四名射击运动员最近几次选拔赛成绩的平均数和方差:根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应选择( ) A 、甲 B 、乙 C 、丙 D 、丁8、如图,四边形ABCD 和A'B'C'D'是以点O 为位似中心的位似图形,若OA':A'A=2:1,若四边形A'B'C'D'的面积为122cm ,则四边形ABCD 的面积为( ) A 、242cm B 、272cm C 、362cm D 、542cmABD130°2AB C D OA'B'C'D'第6题图x-11OyABCDE O 第10题图A BC D 6题9、二次函数)0a (c bx ax y 2≠++=的图象如图所示,则下列结论正确的是( ) A 、a<0 B 、c>0 C 、a+b+c>0 D 、b-4ac<010、如图、在矩形ABCD 中、对角线AC 、BD 相交于点O ,AE⊥BD,垂足为E ,AE=3,ED=3BE , 则AB 的值为( ) A 、6 B 、5 C 、32 D 、33 二、填空题(每小题4分,共16分)11、在二次根式x 24-中,x 的取值范围是 ;12、用反证法证明“若a>b>0,则22b a >”,应先假设 ; 13、将抛物3x 2x y 2++=向左平移2个单位长度,再向下平移3个单位长度,得到的抛物线函数表达式为 ;14、如图,在Rt△ABC 中,∠C=90°,以顶点A 为圆心,适当长为半径画弧,分别交AC 、AB 于点M 、N , 再分别以点M 、N 为圆心,大于2MN 的长为半径画弧, 两弧交于点P ,作射线AP 交边BC 于点D ,若CD=4, AB=15,则△ABD 的面积为 。
成都中考数学试卷真题2015

成都中考数学试卷真题20152015年成都市中考数学试卷一、选择题1. 已知一元二次方程$x^2 - 4x + m = 0 (m \in R)$有两个相等的实根,则实数$m$的取值范围是()A. $(-\infty, -1)\cup (4, +\infty)$B. $(-1, 0)\cup (0, 4)$C. $(-\infty, -1)\cup (0, 4)$D. $(-\infty, -1)\cup (0, +\infty)$2. 甲、乙两人共有钱160元。
如果甲拿去自己的$\frac{1}{4}$ ,乙用一半和剩下的甲所有的钱一共买了两本书,每本书20元,那么乙原先有多少钱?()A. 105元B. 115元C. 125元D. 135元3. (2018中国成都中考改编)某超市购进一包贴有“6元”标签的商品24件,它们能否在你现有的数额下全买完?如果能全买完,会多出多少元?如果不能全买完,需要再取多少元才能全买完?()A. 能全买完,多出6元B. 能全买完,多出12元C. 不能全买完,需要再取9元D. 不能全买完,需要再取12元4. 已知一组数据为8,15,23,32,42,一般规律是:后一个数减去前一个数的差是一个等差数列2,3,4,$\dots$,求这个数列第100项的值。
()A. 49B. 50C. 51D. 525. 以下说法正确的是()A. 棱台的高与下底的边垂直B. 锐角三角形的内角和小于180°C. 一个补角是钝角,则这个补角一定小于90°D. 平行四边形的对角线不相等二、填空题6. $ (x + 3)(x − 2) = 9 $的实数解数为\underline{\hphantom{~}},它们的和为\underline{\hphantom{~}}。
7. $ 90° = \underline{\hphantom{~}} $弧度。
8. 若数列$2, 5, 8, 11, \dots$ 的第$ n $项是$ a_n $,则$ a_7 =$ \underline{\hphantom{~}}。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四川省成都市锦江区初2015届九年级二诊数学试题 数学
(考试时间120分钟 满分150分)
A 卷(共100分) 第I 卷(选择题,共30分)
一、选择题(本大题共10个小题,每小题3分,共30分) 1、1
-
2
的绝对值是( ) A 、2 B 、-2 C 、
12 D 、1-2
2、2014年成都市的国民生产总值为1034亿元,1034亿元用科学记数法表示正确的是( ) A 、8
103410⨯元 B 、11
1.03410⨯元 C 、11
1.010⨯元 D 、12
1.03410⨯元 3、下列各式计算正确的是( )
A 、
B 、2
2
12=
2x x - C 、236326a a a ⋅= D 、826
a a a ÷=
4、下列图形中,既是轴对称图形又是中心对称图形的是( )
5、如图,2,3,4,T 是五个完全相同的正方体,将两部分构成一个新的几何体得到其主视图则应将几
何体T 放在( )
A 、几何体的上方
B 、几何体2的左方
C 、几何体3的上方
D 、几何体4的上方
6、成都市举行的中学生春季田径运动会上,参加男子跳高的15名运动员的成绩如下表所示:
这些运动员跳高成绩的中位数和众数分别是( )
A 、1.70,1.65
B 、1.70,1.70
C 、1.65,1.60
D 、3,4 7、下列函数中,自变量x 可以取1和2的函数是( )
A 、12y x =
- B 、11
y x =- C 、y = D 、y =8、如图,若//AB CD ,则E ∠的度数为( ) A 、60︒ B 、65︒ C 、70︒
D 、75︒
9、如图,在Rt ABC ∆中,90C ︒
∠=,4AC =,2BC =,
分
别以AC ,BC 为半径画圆,则阴影部分的面积为( )
A 、542
π
- B 、104π- C 、108π- D 、582
π-
10、如图,抛物线21(2)3y a x =+-与221
(3)12
y x =
-+交于点()1,3A ,过点A 作x 轴的平行线,分别
交两条抛物线于点B ,C . 则以下结论:①无论x 取何值,2y 的值总是正数;②2
3
a =
;③当0x =时,216y y -=;④10AB AC +=;下列结论的是:( )
A 、①②④
B 、①③④
C 、②③④
D 、①②③④
第II 卷(非选择题,共70分)
二、填空题(本大题共4个小题,第小题4分,共16分) 11、因式分解:3
2
4y x y -= .
12、如图,路灯距离地面8米,身高1.6米的小明站在距离灯的底部(点O )
20米的A 处,则小明的影子AM 长 米.
13、如果1x ,2x 是一元二次方程2320x x ++=的两个实数根,那么12x x +的
值是 .
14、如图,一圆与平面直角坐标系中的x 轴切于点(4,0)A ,与y 轴交于点
(0,2)B ,(0,8)C ,则该圆的直径为 .
三、解答题(本大题共6个小题,共54分) 15、(本题2个小题,共12分)
(1)计算:2
3
1(2)14sin 603-︒⎛⎫
-++- ⎪⎝⎭
(2)先化简221111a a a ⎛
⎫+÷
⎪-+⎝⎭
,再在0,1-,2中选取一个适当的数代入求值.
16、(6分)如图已知反比例函数(0)k
y k x
=
≠在第一象限的图像上有不同的两点A 、B ,其中(2,6)A ,是原点. 过点B 作BC x ⊥轴于C ,作BD y ⊥轴于D ,四边形OCBD 的周长为14.
(1)求反比例函数的解析式;
(2)求OB 的长.
四、解答题(每小题8分,共16分)
17、(8分)已知,如图,ABC ∆和ECD ∆都是等腰直角三角形,90ACB DCE ︒∠=∠=,D 为线段AB 上一动点.
(1)求证:BD AE =;
(2)当D 是线段AB 中点时,求证:四边形AECD 是正方形.
18、(8分)如图,小岛A 在港口P 的南偏西45︒
方向,距离港口81海里处. 甲船从A 出发,沿AP 方向以9海里时的速度驶向港口,乙船从港口P 出发,沿南偏东60︒
方向,以18海里时的速度驶离港口. 现
两船同时出发,
(1)出发后几小时两船与港口P 的距离相等地? (2)出发后几小时乙船在甲船的正东方向?(结果
精确到0.1小时) 1.73)
五、解答题(每小题10分,共20分)
19、(10分)体育课上,小明、小强、小华三人在学习训练踢足球,足球从一人传到另一人就记为踢
一次.
(1)如果从小强开始踢,经过两次踢后,足球踢到了小华处的概率是多少(用树状图表示或列表说明); (2)如果踢三次后,球踢到了小明处的可能性最小,应从谁开始踢?请说明理由.
20、(10分)已知:如图AB 是⊙O 的直径,PB 切⊙O 于点B ,PA 交⊙O 于点C ,PF 分别交AB 、BC 于E 、D ,交⊙O 于F 、G ,且BE 、BD 恰好是关于x 的方程226(413)0x x m m -+++=其中m 为实数)的两根.
(1)求证:PBC
BAC ∆∆;
(2)求证:PF 平分APB ∠;
(3)若GE EF ⋅=PBC ∠的度数.
B 卷(50分)
一、填空题(本大题共5小题,每小题4分,共20分)
21、已知220x y -+=,则
2
2114x y xy +--的值为 . 22、若关于x 的方程1(4)333k x x x
-+=--无解,则k = . 23、有依次排列的3个数:3,9,8,对任意相邻的两个数,都用右边的数减去左边的数,所得之差在这两个数之间,可产生一个新数串:3,6,9,1-,8,这称为第一次操作;做第二次同样的操作后也可以产生一个新数串:3,3,6,3,9,10-,9,8,依次类推,则从数串3,9,8开始操作第100次以后所产生的那个新数串的所有数之和是 . 24、如图,A ,C 是反比例函数3
y x
=
的图象上的两点,连接AC ,过A 、C 分别作y 轴、x 轴的平行线,两线交于B ,那么阴影部分的面积是 .
25、在三角形纸片ABC 中,90ABC
°?,9AB =,12BC =. 过点A 作直线平行于BC ,折叠三角形
纸片ABC ,使直角顶点B 落在直线上的T 处,折痕为MN . 当点T 在直线上移动时,折痕的端点M ,N 也随之移动. 若限定端点M 、N 分别在AB 、BC 边上移动(点M 可以与点A 重合,点N 可以与点C 重合),则线段AT 长度的最大值与最小值之和为 .
二、解答题(本大题共3个小题,共30分)
26、(8分)随着机构改革工作的深入进行,各单位要减员增效。
有一家公司现有职员160人,每人每
年可创利10万元. 据评估,在经营条件不变的前提下,每裁员...1人,则留岗职员每人每年可多创利0.1万元,但公司需支付下岗职员每人每年4万元的生活费,并且该公司正常运转所需人数不得小于现有员工的
3
4
,设裁员x 人,可获得的经济效益为y 万元. (1)求y 与x 的函数关系式;
(2)为获得最大的经济效益,该公司应裁员多少人?
27、(10分)已知:在ABC D
中,DBC ACB ? ,2BC AC =,BD BC =,CD 交线段AB 于点E .
(1)如图1,当90ACB
°?时,求证:2DE CE =;
(2)当120ACB °
?时,
①如图2,猜想线段DE 、CE 之间的数量关系并证明你的猜想; ②如图3,点F 是BC 边的中点,连接DF ,DF 与AB 交于G ,求
DG
GF
的值.
28、(12分)在平面直角坐标系xOy 中,抛物线2
y ax bx c =++过点(2,2)且当0x =时y 取得最小值1.
(1)求此抛物线的解析式;
(2)如图,过点(0,2)B 的直线交已知抛物线于P 、Q 两点(P 点为抛物线上不同于A 的一点)过点P 、
Q 分别作x 轴的垂线,垂足分别为S 、R .
①判断SBR D
的形状; ②在线段SR 上求点M ,使得以点P 、S 、M 为顶点的三角形和以点Q 、R 、M 为顶点的三角形相似; (3)已知点(1,3)C 在已知抛物线内部,试探索是否存在满足下列条件的直线:①直线过点(1,3)C ,②直线交抛物线于E 、F 两点且C 点恰好是线段EF 的中点. 若存在,请求出直线的函数解析式;若不存在,请说明理由.。
