理科数学高考真题分类训练专题八 立体几何 第二十三讲 空间中点、直线、平面之间的位置关系
专题八 立体几何 第二十三讲 空间中点、直线、平面之间的位置关系

专题八 立体几何第二十三讲 空间中点、直线、平面之间的位置关系一、选择题1.(2018全国卷Ⅰ)已知正方体的棱长为1,每条棱所在直线与平面α所成的角相等,则α截此正方体所得截面面积的最大值为A B C D2.(2018全国卷Ⅱ)在长方体1111-ABCD A B C D 中,1==AB BC ,1=AA 线1AD 与1DB 所成角的余弦值为A .15B C D 3.(2018浙江)已知平面α,直线m ,n 满足m α⊄,n α⊂,则“m ∥n ”是“m ∥α”的A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件4.(2018浙江)已知四棱锥S ABCD -的底面是正方形,侧棱长均相等,E 是线段AB 上的点(不含端点),设SE 与BC 所成的角为1θ,SE 与平面ABCD 所成的角为2θ,二面角S AB C --的平面角为3θ,则A .123θθθ≤≤B .321θθθ≤≤C .132θθθ≤≤D .231θθθ≤≤5.(2017新课标Ⅱ)已知直三棱柱111ABC A B C -中,120ABC ∠=,2AB =,11BC CC ==,则异面直线1AB 与1BC 所成角的余弦值为A B C D 6.(2017浙江)如图,已知正四面体D ABC -(所有棱长均相等的三棱锥),P ,Q ,R 分别为AB ,BC ,CA 上的点,AP PB =,2BQ CRQC RA==,分别记二面角D PR Q --,D PQ R --,D QR P --的平面角为α,β,γ,则R QPABC DA .γ<α<βB .α<γ<βC .α<β<γD .β<γ<α7.(2016年全国I )平面α过正方体1111ABCD A B C D -的顶点A ,α∥平面11CB D ,αI 平面ABCD =m ,αI 平面11ABB A =n ,则m ,n 所成角的正弦值为A.2 B.2 C.3 D .138.(2015福建)若,l m 是两条不同的直线,m 垂直于平面α ,则“l m ⊥ ”是“l ∥α”的A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件9.(2015浙江)如图,已知ABC ∆,D 是AB 的中点,沿直线CD 将ACD ∆翻折成A CD '∆,所成二面角A CD B '--的平面角为α,则10.(2014广东)若空间中四条两两不同的直线1234,,,l l l l ,满足122334,,l l l l l l ⊥⊥⊥,则下面结论一定正确的是A .14l l ⊥B .14//l lC .14,l l 既不垂直也不平行D .14,l l 的位置关系不确定 11.(2014浙江)设,m n 是两条不同的直线,,αβ是两个不同的平面A .若m n ⊥,//n α,则m α⊥B .若//m β,βα⊥则m α⊥C .若,,m n n ββα⊥⊥⊥则m α⊥D .若m n ⊥,n β⊥,βα⊥,则m α⊥ 12.(2014辽宁)已知m ,n 表示两条不同直线,α表示平面,下列说法正确的是A .若//,//,m n αα则//m nB .若m α⊥,n α⊂,则m n ⊥C .若m α⊥,m n ⊥,则//n αD .若//m α,m n ⊥,则n α⊥13.(2014浙江)如图,某人在垂直于水平地面ABC 的墙面前的点A 处进行射击训练,已知点A 到墙面的距离为AB ,某目标点P 沿墙面的射击线CM 移动,此人为了准确瞄准目标点P ,需计算由点A 观察点P 的仰角θ的大小(仰角θ为直线AP 与平面ABC 所成角).若15AB m =,25AC m =,30BCM ∠=︒则tan θ的最大值ABCD 14.(2014四川)如图,在正方体1111ABCD A B C D -中,点O 为线段BD 的中点.设点P 在线段1CC 上,直线OP 与平面1A BD 所成的角为α,则sin α的取值范围是A1A. B.C .D . 15.(2013新课标Ⅱ)已知,m n 为异面直线,m ⊥平面α,n ⊥平面β.直线l 满足,l m l n ⊥⊥,,l l αβ⊄⊄,则A .α∥β且l ∥αB .α⊥β且l ⊥βC .α与β相交,且交线垂直于lD .α与β相交,且交线平行于l16.(2013广东)设m ,n 是两条不同的直线,α,β是两个不同的平面,下列命题中正确的是A .若αβ⊥,m α⊂,n β⊂,则m n ⊥B .若//αβ,m α⊂,n β⊂,则//m nC .若m n ⊥,m α⊂,n β⊂,则αβ⊥D .若m α⊥,//m n ,//n β,则αβ⊥17.(2012浙江)设l 是直线,,αβ是两个不同的平面A .若l ∥α,l ∥β,则α∥βB .若l ∥α,l ⊥β,则α⊥βC .若α⊥β,l ⊥α,则l ⊥βD .若α⊥β, l ∥α,则l ⊥β18.(2012浙江)已知矩形ABCD ,1AB =,BC =将ABD ∆沿矩形的对角线BD 所在的直线进行翻折,在翻折过程中,A .存在某个位置,使得直线AC 与直线BD 垂直B .存在某个位置,使得直线AB 与直线CD 垂直C .存在某个位置,使得直线AD 与直线BC 垂直D .对任意位置,三对直线“AC 与BD ”,“AB 与CD ”,“AD 与BC ”均不垂直 19.(2011浙江)下列命题中错误..的是 A .如果平面αβ⊥平面,那么平面α内一定存在直线平行于平面β B .如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β C .如果平面αγ⊥平面,平面βγ⊥平面,=l αβ,那么l γ⊥平面D .如果平面αβ⊥平面,那么平面α内所有直线都垂直于平面β20.(2010山东)在空间,下列命题正确的是A .平行直线的平行投影重合B .平行于同一直线的两个平面平行C .垂直于同一平面的两个平面平行D .垂直于同一平面的两条直线平行 二、填空题21.(2018全国卷Ⅱ)已知圆锥的顶点为S ,母线SA ,SB 所成角的余弦值为78,SA 与圆锥底面所成角为45°,若△SAB 的面积为_____. 22.(2016年全国II )α,β是两个平面,m ,n 是两条线,有下列四个命题:①如果m n ⊥,m α⊥,n β∥,那么αβ⊥. ②如果m α⊥,n α∥,那么m n ⊥. ③如果a β∥,m α⊂,那么m β∥.④如果m n ∥,αβ∥,那么m 与α所成的角和n 与β所成的角相等. 其中正确的命题有 .(填写所有正确命题的编号)23.(2015浙江)如图,三棱锥A BCD -中,3AB AC BD CD ====,2AD BC ==,点,M N 分别是,AD BC 的中点,则异面直线,AN CM 所成的角的余弦值是 .24.(2015四川)如图,四边形ABCD 和ADPQ 均为正方形,它们所在的平面互相垂直,动点M 在线段PQ 上,,E F 分别为,AB BC 的中点.设异面直线EM 与AF 所成的角为θ,则θcos 的最大值为_________.25.(2017新课标Ⅲ)a ,b 为空间中两条互相垂直的直线,等腰直角三角形ABC 的直角边AC 所在直线与a ,b 都垂直,斜边AB 以直线AC 为旋转轴旋转,有下列结论: ①当直线AB 与a 成60°角时,AB 与b 成30°角; ②当直线AB 与a 成60°角时,AB 与b 成60°角; ③直线AB 与a 所成角的最小值为45°; ④直线AB 与a 所成角的最小值为60°;其中正确的是________.(填写所有正确结论的编号) 三、解答题26.(2018江苏)在平行六面体1111ABCD A B C D -中,1AA AB =,111AB B C ⊥.D 11B 1A 1DCBA求证:(1)AB ∥平面11A B C ;(2)平面11ABB A ⊥平面1A BC .27.(2018浙江)如图,已知多面体111ABCA B C ,1A A ,1B B ,1C C 均垂直于平面ABC ,120ABC ∠=,14A A =,11C C =,12AB BC B B ===.C 1B 1A 1CBA(1)证明:1AB ⊥平面111A B C ;(2)求直线1AC 与平面1ABB 所成的角的正弦值.28.(2017浙江)如图,已知四棱锥P ABCD -,PAD ∆是以AD 为斜边的等腰直角三角形,BC AD ∥,CD AD ⊥,22PC AD DC CB ===,E 为PD 的中点. (Ⅰ)证明:CE ∥平面PAB ;(Ⅱ)求直线CE 与平面PBC 所成角的正弦值.EDCBAP29.(2017江苏)如图,在三棱锥A BCD -中,AB ⊥AD ,BC ⊥BD ,平面ABD ⊥平面BCD ,点E 、F (E 与A 、D 不重合)分别在棱AD ,BD 上,且EF ⊥AD . 求证:(1)EF ∥平面ABC ;(2)AD ⊥AC .FABCDE30.(2017山东)如图,几何体是圆柱的一部分,它是由矩形ABCD (及其内部)以AB 边所在直线为旋转轴旋转120︒得到的,G 是DF 的中点. (Ⅰ)设P 是CE 上的一点,且AP BE ⊥,求CBP ∠的大小; (Ⅱ)当3AB =,2AD =,求二面角E AG C --的大小.31.(2017江苏)如图,水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ的高均为32cm ,容器Ⅰ的底面对角线AC 的长为cm ,容器Ⅱ的两底面对角线EG ,11E G 的长分别为14cm 和62cm . 分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm . 现有一根玻璃棒l ,其长度为40cm .(容器厚度、玻璃棒粗细均忽略不计)(1)将l 放在容器Ⅰ中,l 的一端置于点A 处,另一端置于侧棱1CC 上,求l 没入水中部分的长度;(2)将l 放在容器Ⅱ中,l 的一端置于点E 处,另一端置于侧棱1GG 上,求l 没入水中部分的长度.32.(2016全国I )如图,在以A ,B ,C ,D ,E ,F 为顶点的五面体中,面ABEF 为正方形,2AF FD =,90AFD ∠=,且二面角D AF E --与二面角C BE F --都是60.(I )证明:平面ABEF ⊥平面EFDC ; (II )求二面角E BC A --的余弦值.33.(2016全国II )如图,菱形ABCD 的对角线AC 与BD 交于点O ,5AB =,6AC =,点E ,F 分别在AD ,CD 上,54AE CF ==,EF 交BD 于点H .将ΔDEF 沿EF折到ΔD EF '的位置,OD '= (I )证明:D H '⊥平面ABCD ; (II )求二面角B D A C '--的正弦值.34.(2016全国III )如图,四棱锥P ABCD -中,PA ⊥底面ABCD ,AD BC ,=3AB AD AC ==,4PA BC ==,M 为线段AD 上一点,2AM MD =, N 为PC 的中点.(Ⅰ)证明MN平面PAB ;(Ⅱ)求直线AN 与平面PMN 所成角的正弦值.BD35.(2014山东)如图,四棱锥P ABCD -中,AP PCD ⊥平面,AD BC ∥,1,,2AB BC AD EF ==分别为线段,AD PC 的中点.(Ⅰ)求证:AP BEF ∥平面; (Ⅱ)求证:BE PAC ⊥平面.36.(2014江苏)如图,在三棱锥ABC P -中,D ,E ,F 分别为棱AB AC PC ,,的中点.已知AC PA ⊥,,6=PA .5,8==DF BC求证:(Ⅰ)直线PA ∥平面DEF ;(Ⅱ)平面BDE ⊥平面ABC .37.(2014新课标Ⅱ)如图,四棱锥P ABCD -中,底面ABCD 为矩形,PA ⊥平面ABCD ,E 为PD 的中点.(Ⅰ)证明:PB ∥平面AEC ;(Ⅱ)设二面角D AE C --为60°,AP =1,AD求三棱锥E ACD -的体积.38.(2014天津)如图四棱锥P ABCD -的底面ABCD是平行四边形,BA BD ==,2AD =,PA PD ==E ,F 分别是棱AD ,PC 的中点.(Ⅰ)证明: EF ∥平面PAB ; (Ⅱ)若二面角P AD B --为60°, (ⅰ)证明:平面PBC ⊥平面ABCD(ⅱ)求直线EF 与平面PBC 所成角的正弦值.39.(2013浙江)如图,在四棱锥P ABCD -中,PA ⊥面ABCD ,2AB BC ==,AD CD ==,PA =120ABC ∠=,G 为线段PC 上的点.PDB(Ⅰ)证明:BD ⊥面APC ;(Ⅱ)若G 是PC 的中点,求DG 与APC 所成的角的正切值; (Ⅲ)若G 满足PC ⊥面BGD ,求PGGC的值. 40.(2013辽宁)如图,AB 是圆O 的直径,PA 垂直圆O 所在的平面,C 是圆O 上的点.(Ⅰ)求证:BC PAC ⊥平面;(Ⅱ)设Q 为PA 的中点,G 为AOC ∆的重心,求证:QG ∥平面PBC .41.(2012江苏)如图,在直三棱柱111ABC A B C -中,1111AB AC =,D E ,分别是棱1BC CC ,上的点(点D 不同于点C ),且AD DE F ⊥,为11B C 的中点.1求证:(Ⅰ)平面ADE ⊥平面11BCC B ;(Ⅱ)直线1//A F 平面ADE .42.(2012广东)如图所示,在四棱锥P ABCD -中,AB ⊥平面PAD ,//,AB CD PD AD =,E 是PB 中点,F 是DC 上的点,且12DF AB =,PH 为PAD ∆中AD 边上的高.(Ⅰ)证明:PH ⊥平面ABCD ; (Ⅱ)若1,1PH AD FC ===,求三棱锥E BCF -的体积;(Ⅲ)证明:EF ⊥平面PAB .43.(2011江苏)如图,在四棱锥ABCD P -中,平面PAD ⊥平面ABCD ,AB AD =,BAD ∠=60°,E 、F 分别是AP 、AD 的中点.C求证:(Ⅰ)直线EF ∥平面PCD ; (Ⅱ)平面BEF ⊥平面PAD .44.(2011广东)如图在椎体P ABCD -中,ABCD是边长为1的棱形,且DAB ∠=60︒,PA PD ==2PB =,E ,F 分别是BC ,PC 的中点.(Ⅰ)证明:AD ⊥平面DEF ;(Ⅱ)求二面角P AD B --的余弦值.45.(2010天津)如图,在五面体ABCDEF 中,四边形ADEF 是正方形,FA ⊥平面ABCD ,BC∥AD ,CD =1,AD =,∠BAD =∠CDA =45°.(Ⅰ)求异面直线CE 与AF 所成角的余弦值; (Ⅱ)证明CD ⊥平面ABF ; (Ⅲ)求二面角B EF A --的正切值.46.(2010浙江)如图,在平行四边形ABCD 中,AB =2BC ,∠ABC =120°.E 为线段AB 的中点,将△ADE 沿直线DE 翻折成△A DE ',使平面A DE '⊥平面BCD ,F 为线段A C '的中点.(Ⅰ)求证:BF ∥平面A DE ';(Ⅱ)设M 为线段DE 的中点,求直线FM 与平面A DE '所成角的余弦值.。
2018年理数真题分类训练专题八立体几何第二十三讲空间中点、直线、平面之间的位置关系答案
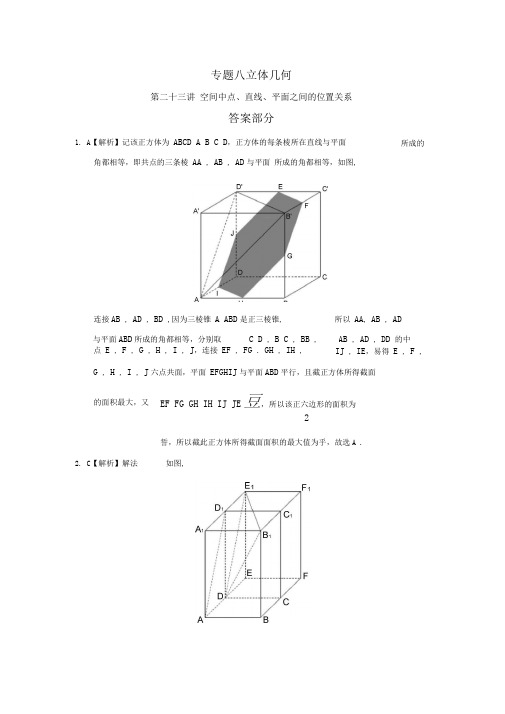
专题八立体几何第二十三讲空间中点、直线、平面之间的位置关系答案部分1. A【解析】记该正方体为ABCD A B C D,正方体的每条棱所在直线与平面角都相等,即共点的三条棱AA , AB , AD与平面所成的角都相等,如图,连接AB , AD , BD ,因为三棱锥A ABD是正三棱锥,点E , F , G , H , I , J,连接EF , FG . GH , IH ,G , H , I , J六点共面,平面EFGHIJ与平面ABD平行,且截正方体所得截面EF FG GH IH IJ JE豆,所以该正六边形的面积为2誓,所以截此正方体所得截面面积的最大值为乎,故选A .与平面ABD所成的角都相等,分别取 C D , B C , BB , AB , AD , DD 的中2. C【解析】解法如图,所成的所以AA, AB , ADIJ , IE,易得E , F , 的面积最大,又4. D 【解析】由题意知四棱锥 SABCD 为正四棱锥,如图,补上一相同的长方体 CDEF C 1D 1E 1F 1,连接DE 1, ^E 1 .B 1E 1 J A B : AE 1271222 75,J 5即异面直线AD 1与DB 1所成角的余弦值为 、一,故选C .5解法二 以D 为坐标原点,DA , DC , DD 1所在直线分别为x 轴, 空间直角坐标系,如图所示.由条件可知 D(0,0,0) , A(1,0,0) , D 1(O,O,73) , B I (1,1,73),UJJJ L UUJJ - 所以 AD 1 ( 1,0, J 3) , DB 1 (1,1, J 3),”的充分不必要条件.故选易知AD i // DE i ,则 BDE i 为异面直线 AD i 与DB i 所成角.因为在长方体 ABCD A 1B 1C 1D 1中,AB BC 1,AA 73,所以 DE 1 J D F —E E 7 J 12(对2DB 1 J 1212(J 3)2亦,在B 1DE 1中,由余弦定理,得 cos B 1DE 122(V 5)2(馮2752 2 75y 轴,z 轴建立ULUU UJLU则由向量夹角公式,得 cos AD 1, DB 1UJLU UJUJ AD 1 DB 1 IAD 1IIDB 112 2^5455即异面直线 AD 1与DB 1所成角的余弦值为—,故选C .53. A 【解析】若m // n ,由线面平行的判定定理知m // .若 m //,不一定推出 m // n ,直线m 与n 可能异面,故// n ”是“ m //连接BD ,记AC I BD O ,连接SO ,则SO 平面ABCD ,取AB 的中点M ,连接SM , OM , OE ,易得AB SM ,则SEO , 3 SMO ,易知3》2 •因5. 40 J 2 【解析】如图所示,设S 在底面的射影为 S ,连接AS , SS . SAB 的面积为1 SA SB Sin ASB寸 SA 2山COS 2 ASBAS SA cos45o4真•••底面周长丨2 AS4J I0 ,•••圆锥的侧面积为 14丁5 4J 1040J 2 .26.【证明】(1)在平行六面体 ABCD AB i C i D i 中,AB为 OM // BC , BC AB , SM AB , 所以3也为OM 与平面SAB 所成的角,即BC 与平面SAB 所成的角,再根据最小角定理知,3 W 1,所以2 W 3 W 1,故选••• SA 280 , SA 4后.••• SA 与底面所成的角为 45o, • SAS 45o,// A i B i .因为AB 平面A iB iC , A| B ]平面 A ] B i C ,又因为AA AB ,所以四边形ABB 1A 1为菱形,因此AB 1丄AB •又因为 AB 」B 1C 1 , BC // BQ , 所以AB 」BC •又因为 A 1B I BC = B ,A 1B 平面 ABC ,BC 平面 ABC , 所以AB 」平面ABC • 因为AB 1 平面ABB 1A 1 , 所以平面ABB 1A 1丄平面A 1BC •AB, A 1B 12/2,所以 A 1B 12AB ,2AA 2•故AB 1 A 1B 1 •由BC 2, BB 1 2, CC 1 1 , BB 1 BC , CC 1 BC 得 B1C 175由AB BC 2,ABC 120o 得 AC273,由CC 1AC ,得 AC 1 713,所以 AB 2B 1C 1 AC 1,故 AB 1 B 1C 1所以AB //平面AB i C •A iB iC iD i 中,四边形 ABB i A i 为平行四边形.(2)在平行六面体ABCD7.【解析】(1)由AB 2 , AA i4,BB i2,AA AB ,BB , AB 得⑵如图,过点G 作C i D A I B I ,交直线A I B I 于点D ,连结AD .由AB I 平面A i B I C I 得平面A i B I C I 平面ABB I , 由 C i D AB 得C i D 平面 ABB I , 所以 GAD 是AC i 与平面ABB I 所成的角. 由 BG 苗,AB I 242,A 1C 1 721^61 得 cos GA B iL , sin CiAB i —,T ?V 7所以 C i D 73,故 sin GAD ClD金J 39因此,直线 AC i 与平面ABB I 所成的角的正弦值是 -一13方法二(1)如图,以AC 的中点0为原点,分别以射线0B ,OC 为x ,y 轴的正半轴, 建立空间直角坐标系 0 xyz.AC i 131Z J M CCx /B由题意知各点坐标如下:A(0, 73,0) , B(1,0,0) , A(0, 73,4)uujr uuju因此 AB 1 (1,73,2) , A 3 (1J 3, 2),所以AB 1 平面A 1B 1C 1 •(2)设直线AG 与平面ABB 1所成的角为uuuu = uuu 厂 Lutr由(1)可知 AC 1 (0,273,1), AB (1V 3,0) , BB, (0,0,2),A iuLur 由AB 1 uuuu AE 0 得 AB 1 A 1B 1 •uLur由AB 1 A 1C 10 得 AB 1 AC 1 •设平面 ABB 1 的法向量 n 二(X, y,z) • uuu AB uuur BB 10,即x0 2z ,可取n (>/3,1,0)•所以sinuuuu I cos AC-i , nujunIAC 1I In I T ao 13 因此,直线 AC 1与平面ABB 1所成的角的正弦值是73913B i (1,0,2) , G(O,73,1),uuuuAC 1 (0,2 圾 3),。
【九年高考理科数学真题分类训练】专题八 立体几何 第二十三讲 空间中点、直线、平面之间的位置关系答案

专题八 立体几何第二十三讲 空间中点、直线、平面之间的位置关系答案部分1.A 【解析】记该正方体为''''-ABCD A B C D ,正方体的每条棱所在直线与平面α所成的角都相等,即共点的三条棱'A A ,''A B ,''A D 与平面α所成的角都相等,如图,连接'AB ,'AD ,''B D ,因为三棱锥'''-A AB D 是正三棱锥,所以'A A ,''A B ,''A D 与平面''AB D 所成的角都相等,分别取''C D ,''B C ,'BB ,AB ,AD ,'DD 的中点E ,F ,G ,H ,I ,J ,连接EF ,FG .GH ,IH ,IJ ,IE ,易得E ,F ,G ,H ,I ,J 六点共面,平面EFGHIJ 与平面''AB D 平行,且截正方体所得截面的面积最大,又2======EF FG GH IH IJ JE,所以该正六边形的面积为26(434⨯=,所以α截此正方体所得截面面积的最大值为4,故选A . 2.C 【解析】解法一 如图,F 1E 1F D 1A 1B 1C 1E C D AB补上一相同的长方体1111-CDEF C D E F ,连接1DE ,11B E . 易知11∥AD DE ,则11∠B DE 为异面直线1AD 与1DB 所成角.因为在长方体1111-ABCD A BC D 中,1==AB BC,1AA所以12===DE,1==DB11===B E ,在11∆B DE中,由余弦定理,得11cos ∠==B DE 即异面直线1AD 与1DB所成角的余弦值为5C . 解法二 以D 为坐标原点,DA ,DC ,1DD 所在直线分别为x 轴,y 轴,z 轴建立空间直角坐标系,如图所示.由条件可知(0,0,0)D ,(1,0,0)A,1D,1(1,1B ,所以1(1=-AD,1(1,1=DB ,则由向量夹角公式,得111111cos ,5||||2⋅<>===AD DB AD DB AD DB即异面直线1AD 与1DB C . 3.A 【解析】若m α⊄,n α⊂,m ∥n ,由线面平行的判定定理知m ∥α.若m ∥α,m α⊄,n α⊂,不一定推出m ∥n ,直线m 与n 可能异面,故“m ∥n ”是“m ∥α”的充分不必要条件.故选A .4.D 【解析】由题意知四棱锥S ABCD -为正四棱锥,如图,EMSODCBA连接BD ,记AC BD O =,连接SO ,则SO ⊥平面ABCD ,取AB 的中点M ,连接SM ,OM ,OE ,易得AB SM ⊥,则2S E O θ=∠,3SMO θ=∠,易知32θθ≥. 因为OM ∥BC ,BC AB ⊥,SM AB ⊥,所以3θ也为OM 与平面SAB 所成的角,即BC 与平面SAB 所成的角,再根据最小角定理知,31θθ≤,所以231θθθ≤≤,故选D .5.C 【解析】如图所示,把三棱柱补成四棱柱,异面直线1AB 与1BC 所成角为11B AD ∠B 1A 1D 1C 1DCBA2111B D===1AD =1AB∴22222211111111cos 25AB AD B D B AD AB AD +-∠===⨯⨯.选C . 6.B 【解析】设O 为三角形ABC 中心,底面如图2,过O 作OE RP ⊥,OF PQ ⊥,OG RQ ⊥,由题意可知tan DO OE α=,tan OD OF β=,tan ODOGγ=,GF EO DC BAPQR图1 图2由图2所示,以P 为原点建立直角坐标系,不妨设2AB =,则(1,0)A -,(1,0)B,C,O ,∵AP PB =,2BQ CR QC RA ==,∴1(3Q,2(3R -,则直线RP的方程为2y x =-,直线PQ的方程为y =,直线RQ的方程为y x =+,根据点到直线的距离公式,知21OE =OF =,13OG =,∴OF OG OE <<,tan tan tan αγβ<<, 因为α,β,γ为锐角,所以αγβ<<.选B7.A 【解析】因为过点A 的平面α与平面11CB D 平行,平面ABCD ∥平面1111A B C D ,所以m ∥11B D ∥BD ,又1A B ∥平面11CB D ,所以n ∥1A B ,则BD 与1A B 所成的角为所求角,所以m ,nA . 8.B 【解析】由“m α⊥且l m ⊥”推出“l α⊂或l α∥”,但由“m α⊥且l α∥”可推出“l m ⊥”,所以“l m ⊥”是“l α∥”的必要而不充分条件,故选B . 9.B 【解析】解法一 设ADC θ∠=,2AB =,则由题意知1AD BD A D '===.在空间图形中,连结A B ',设A B '=t .在ΔA DB '中,2222222112cos 22112A D DB A B t t A DB A D DB ''+-+--'∠==='⨯⨯⨯.过A '作A N DC '⊥,过B 作BM DC ⊥,垂足分别为N M 、. 过N 作//NP MB ,使四边形BPNM 为平行四边形,则NP DC ⊥,连结,A P BP ',则A NP '∠就是二面角A CD B '--的平面角,所以A NP α'∠=. 在ΔRt A ND '中,cos cos DN A D A DC θ''=∠=,sin sin A N A D A DC θ'''=∠=. 同理,sin BM PN θ==,cos DM θ=,故2cos BP MN θ==. 显然BP ⊥平面A NP ',故BP A P '⊥.在ΔRt A BP '中,222222(2cos )4cos A P A B BP t t θθ''=-=-=-.在ΔA NP '中,222cos cos 2A N NP A P A NP A N NPα''+-'=∠='⨯22222sin sin (4cos )2sin t θθθθ+--==222222222cos 2cos 2sin 2sin sin t t θθθθθ+--=+2221cos cos sin sin A DB θθθ'=∠+, 所以2221cos cos cos cos cos sin sin A DB A DB A DB θαθθ'''-∠=∠+-∠ 2222221sin cos cos cos (1cos )0sin sin sin A DB A DB θθθθθθ-''=∠+=+∠≥, 所以cos cos A DB α'∠≥(当2πθ=时取等号),因为α,[0,]A DB π'∠∈,而cos y x =在[0,]π上为递减函数, 所以A DB α'∠≤,故选B .解法二 若CA CB ≠,则当απ=时,A CB π'∠<,排除D ; 当0α=时,0A CB '∠>,0A DB '∠>,排除A 、C ,故选B . 10.D 【解析】利用正方体模型可以看出,1l 与4l 的位置关系不确定.选D .11.C 【解析】选项,,A B D 中m 均可能与平面α平行、垂直、斜交或在平面α内,故选C . 12.B 【解析】对于选项A ,若//,//,m n αα,则m 与n 可能相交、平行或异面,A 错误;显然选项B 正确;对于选项C ,若m α⊥,m n ⊥,则n α⊂或//n α,C 错误;对于选项D ,若//m α,m n ⊥,则//n α或n α⊂或n 与α相交,D 错误.故选B .13.D 【解析】作PH BC ⊥,垂足为H ,设PH x =,则CH =,由余弦定理AH =1tan tan (0)PHPAH AHxθ=∠==>,故当1125x =tan θ取得最大值,最大值为9. 14.B 【解析】直线OP 与平面1A BD 所成的角为α的取值范围是1112AOA C OA π∠→→∠,由于1sin AOA ∠=11sin 2C OA ∠==>,sin 12π= 所以sin α的取值范围是. 15.D 【解析】作正方形模型,α为后平面,β为左侧面可知D 正确.16.D 【解析】A 中,m n 可能平行、垂直、也可能为异面;B 中,m n 还可能为异面;C 中m应与β中两条相交直线垂直时结论才成立,选D .17.B 【解析】利用排除法可得选项B 是正确的,∵l ∥α,l ⊥β,则αβ.如选项A :l ∥α,l ∥β时,α⊥β或α∥β;选项C :若α⊥β,l ⊥α,l ∥β或l β⊂;选项D :若α⊥β, l ⊥α,l ∥β或l ⊥β.18.B 【解析】过点A 作AE BD ⊥,若存在某个位置,使得AC BD ⊥,则BD ⊥面ACE ,从而有BD CE ⊥,计算可得BD 与CE 不垂直,则A 不正确;当翻折到AC CD ⊥时,因为BC CD ⊥,所以CD ⊥面ABC ,从而可得AB CD ⊥;若AD BC ⊥,因为BC CD ⊥,所以BC ⊥面ACD ,从而可得BC AC ⊥,而1AB BC =<=,所以这样的位置不存在,故C 不正确;同理,D 也不正确,故选B .19.D 【解析】对于D ,若平面α⊥平面β,则平面α内的某些直线可能不垂直于平面β,即与平面β的关系还可以是斜交、平行或在平面β内,其余选项易知均是正确的. 20.D 【解析】D 两平行直线的平行投影不一定重合,故A 错;由空间直线与平面的位置关系及线面垂直与平行的判定与性质定理可知B 、C 均错误,故选D . 21.【解析】如图所示,S'SAB设S 在底面的射影为S ',连接AS ',SS '.SAB ∆的面积为2211sin 2216SA SB ASB SA SA ⋅⋅⋅∠=⋅== ∴280SA =,SA =SA 与底面所成的角为45,∴45SAS '∠=,cos 45452AS SA '=⋅==. ∴底面周长2l AS π'=⋅=,∴圆锥的侧面积为12⨯=. 22.②③④【解析】对于命题①,可运用长方体举反例证明其错误:如图,不妨设AA '为直线m ,CD 为 直线n ,ABCD 所在的平面为α.ABC D ''所在的平面为β,显然这些直线和平面满足题目条件,但αβ⊥不成立.命题②正确,证明如下:设过直线n 的某平面与平面α相交于直线l ,则l n ∥, 由m α⊥,有m l ⊥,从知m n ⊥结论正确. 由平面与平面平行的定义知命题③正确. 由平行的传递性及线面角的定义知命题④正确. 23.78【解析】如图连接ND ,取ND 的中点E ,连接,ME CE ,则//ME AN .则异面直线AN ,CM 所成的角为EMC ∠,由题意可知1CN =,AN =∴MECM =DN =,NECE则2227cos 28CM EM CE CME CM EM +-∠===⨯.24.25【解析】AB 为x 轴,AD 为y 轴,AQ 为z 轴建立坐标系, 设正方形边长为2.cos θ=令[]()0,2)f m m =∈()f m '=[]0,2,()0m f m '∈∴<max 2()(0)5f m f ==,即max 2cos 5θ=. 25.②③【解析】如图BDEF 为底面圆的内接正方形,设1AC BC ==,则AB AD AE AF FB FE ED BD ========即侧面均为等边三角形,∵AC ⊥底面BDEF ,FEDCBA假设a FB ∥,由题意b BD ∥,当直线AB 与a 成60°角时,由图可知AB 与b 成60°角,所以①错,②正确;假设a EB ∥,可知③正确,④错.所以正确为②③.26.【证明】(1)在平行六面体1111ABCD A BC D -中,AB ∥11A B . 因为AB ⊄平面11A B C ,11A B ⊂平面11A B C , 所以AB ∥平面11A B C .D 1C 1B 1A 1DCBA(2)在平行六面体1111ABCD A BC D -中,四边形11ABB A 为平行四边形. 又因为1AA AB =,所以四边形11ABB A 为菱形, 因此1AB ⊥1A B .又因为1AB ⊥11B C ,BC ∥11B C , 所以1AB ⊥BC . 又因为1ABBC =B ,1A B ⊂平面1A BC ,BC ⊂平面1A BC ,所以1AB ⊥平面1A BC . 因为1AB ⊂平面11ABB A , 所以平面11ABB A ⊥平面1A BC .27.【解析】(1)由2AB =,14AA =,12BB =,1AA AB ⊥,1BB AB ⊥得111AB AB ==,所以2221111A B AB AA +=.故111AB A B ⊥.由2BC =,12BB =,11CC =,1BB BC ⊥,1CC BC ⊥得11B C = 由2AB BC ==,120ABC ∠=得AC =由1CC AC ⊥,得1AC =,所以2221111AB BC AC +=,故111ABBC ⊥. 因此1AB ⊥平面111A B C .(2)如图,过点1C 作111C D A B ⊥,交直线11A B 于点D ,连结AD . DABCA 1B 1C 1由1AB ⊥平面111A B C 得平面111A B C ⊥平面1ABB ,由111C D A B ⊥得1C D⊥平面1ABB , 所以1C AD ∠是1AC 与平面1ABB 所成的角.由11B C11A B =11AC得111cos C A B ∠=,111sin C A B ∠=,所以1C D =111sin 13C D C AD AC ∠==.因此,直线1AC 与平面1ABB 所成的角的正弦值是13. 方法二 (1)如图,以AC 的中点O 为原点,分别以射线OB ,OC 为x ,y 轴的正半轴,建立空间直角坐标系O xyz -.A由题意知各点坐标如下:(0,A ,(1,0,0)B,1(0,A ,1(1,0,2)B,1)C ,因此1(1AB =,11(12)A B =-,113)AC =-, 由1110AB A B ⋅=得111AB A B ⊥. 由1110AB AC ⋅=得111AB AC ⊥. 所以1AB ⊥平面111A B C .(2)设直线1AC 与平面1ABB 所成的角为θ.由(1)可知1)AC =,(1AB =,1(0,0,2)BB =, 设平面1ABB 的法向量=()x,y,z n .由100AB BB ⎧⋅=⎪⎨⋅=⎪⎩n n,即020x z ⎧+=⎪⎨=⎪⎩,可取(,0)=n .所以111||sin |cos ,|||||AC AC AC θ⋅=<>==⋅n n n因此,直线1AC 与平面1ABB 所成的角的正弦值是1328.【解析】(Ⅰ)如图,设P A 中点为F ,连结EF ,FB .DA因为E ,F 分别为PD ,P A 中点,所以EF ∥AD 且12EF AD =, 又因为BC ∥AD ,12BC AD =,所以 EF ∥BC 且EF =BC ,即四边形BCEF 为平行四边形,所以CE ∥BF , 因此CE ∥平面P AB .(Ⅱ)分别取BC ,AD 的中点为M ,N .连结PN 交EF 于点Q ,连结MQ . 因为E ,F ,N 分别是PD ,P A ,AD 的中点,所以Q 为EF 中点, 在平行四边形BCEF 中,MQ ∥CE . 由PAD ∆为等腰直角三角形得 PN ⊥AD .由DC ⊥AD ,N 是AD 的中点得 BN ⊥AD .所以AD ⊥平面PBN ,由BC ∥AD 得BC ⊥平面PBN , 那么,平面PBC ⊥平面PBN .过点Q 作PB 的垂线,垂足为H ,连结MH .MH 是MQ 在平面PBC 上的射影,所以∠QMH 是直线CE 与平面PBC 所成的角. 设CD =1.在PCD ∆中,由PC =2,CD =1,PD CE在△PBN 中,由PN =BN =1,PB 14QH =,在Rt MQH ∆中,14QH =,MQ所以sin 8QMH ∠=,所以,直线CE 与平面PBC . 29.【解析】证明:(1)在平面ABD 内,因为AB AD ⊥,EF AD ⊥,所以EF AB ∥.又因为EF ⊄平面ABC ,AB ⊂平面ABC ,所以EF ∥平面ABC . (2)因为平面ABD ⊥平面BCD , 平面ABD平面BCD =BD ,BC ⊂平面BCD ,BC BD ⊥,所以BC ⊥平面ABD .因为AD ⊂平面ABD ,所以BC ⊥AD . 又AB AD ⊥,BCAB B =,AB ⊂平面ABC ,BC ⊂平面ABC ,所以AD ⊥平面ABC , 又因为AC ⊂平面ABC , 所以AD AC ⊥.30.【解析】(Ⅰ)因为AP BE ⊥,AB BE ⊥,AB ,AP ⊂平面ABP ,ABAP A =,所以BE ⊥平面ABP , 又BP ⊂平面ABP ,所以BE BP ⊥,又120EBC ∠=︒, 因此30CBP ∠=︒ (Ⅱ)解法一:取EC 的中点H ,连接EH ,GH ,CH . 因为120EBC ∠=︒, 所以四边形BEHC 为菱形,所以AE GE AC GC =====. 取AG 中点M ,连接EM ,CM ,EC . 则EM AG ⊥,CM AG ⊥, 所以EMC ∠为所求二面角的平面角.又1AM =,所以EM CM === 在BEC ∆中,由于120EBC ∠=︒,由余弦定理得22222222cos12012EC =+-⨯⨯⨯︒=,所以EC =EMC ∆为等边三角形, 故所求的角为60︒. 解法二:以B 为坐标原点,分别以BE ,BP ,BA 所在的直线为x ,y ,z 轴,建立如图所示的空间直角坐标系.由题意得(0,0,3)A (2,0,0)E,(1G,(1C -, 故(2,0,3)AE =-,(1AG =,(2,0,3)CG =, 设111(,,)m x y z =是平面AEG 的一个法向量.由00m AE m AG ⎧⋅=⎪⎨⋅=⎪⎩可得1111230,0,x z x -=⎧⎪⎨=⎪⎩取12z =,可得平面AEG的一个法向量(3,=m . 设222(,,)n x y z =是平面ACG 的一个法向量.由00n AG n CG ⎧⋅=⎪⎨⋅=⎪⎩可得22220,230,x x z ⎧+=⎪⎨+=⎪⎩取22z =-,可得平面ACG的一个法向量(3,2)n =-. 所以1cos ,||||2m n m n m n ⋅<>==⋅.因此所求的角为60︒.31.【解析】(1)由正棱柱的定义,1CC ⊥平面ABCD ,所以平面11A ACC ⊥平面ABCD ,1CC AC ⊥. 记玻璃棒的另一端落在1CC 上点M 处.因为AC =40AM =.所以30MN ==,从而3sin 4MAC ∠=. 记AM 与水平的交点为1P ,过1P 作11PQ AC ⊥,1Q 为垂足,则11PQ ⊥平面ABCD ,故1112PQ =,从而11116sin PQ AP MAC==∠.答:玻璃棒l 没入水中部分的长度为16cm .( 如果将“没入水中部分”理解为“水面以上部分”,则结果为24cm)(2)如图,O ,1O 是正棱台的两底面中心. 由正棱台的定义,1OO ⊥平面 EFGH , 所以平面11E EGG ⊥平面EFGH ,1OO ⊥EG . 同理,平面11E EGG ⊥平面1111E FG H ,1OO ⊥11E G . 记玻璃棒的另一端落在1GG 上点N 处.过G 作GK ⊥11E G ,K 为垂足, 则GK =1OO =32. 因为EG = 14,11E G = 62,所以1KG =6214242-=,从而140GG ===. 设1,,EGG ENG αβ==∠∠则114sin sin()cos 25KGG KGG απ=+==∠∠.因为2απ<<π,所以3cos 5α=-.在ENG △中,由正弦定理可得4014sin sin αβ=,解得7sin 25β=. 因为02βπ<<,所以24cos 25β=. 于是sin sin()sin()sin cos cos sin NEG αβαβαβαβ=π--=+=+∠42473(35)525255=⨯+-⨯=. 记EN 与水面的交点为2P ,过2P 作22PQ EG ⊥,2Q 为垂足,则 22P Q ⊥平面EFGH ,故22P Q =12,从而 2EP =2220sin P NEGQ =∠.答:玻璃棒l 没入水中部分的长度为20cm .(如果将“没入水中部分”理解为“水面以上部分”,则结果为20cm) 32.【解析】(Ⅰ)由已知可得AF DF ⊥,AF FE ⊥,所以AF ⊥平面EFDC .又AF ⊂平面ABEF ,故平面ABEF ⊥平面EFDC .(Ⅱ)过D 作DG EF ⊥,垂足为G ,由(Ⅰ)知DG ⊥平面ABEF .以G 为坐标原点,GF 的方向为x 轴正方向,||GF 为单位长度,建立如图所示的空间直角坐标系G xyz -.由(Ⅰ)知DFE ∠为二面角D AF E --的平面角,故60DFE ∠=,则2DF =,DG =(1,4,0)A ,(3,4,0)B -,(3,0,0)E -,D .由已知,AB EF ∥,所以AB ∥平面EFDC . 又平面ABCD平面EFDC DC =,故AB CD ∥,CD EF ∥.由BE AF ∥,可得BE ⊥平面EFDC ,所以CEF ∠为二面角C BE F --的平面角,60CEF ∠=.从而可得(C -.所以(1EC =,(0,4,0)EB =,(3,AC =--,(4,0,0)AB =-. 设(),,n x y z =是平面BCE 的法向量,则C 0n n ⎧⋅E =⎪⎨⋅EB =⎪⎩,即040x y ⎧=⎪⎨=⎪⎩,所以可取(3,0,n =.设m 是平面CD AB 的法向量,则C 0m m ⎧⋅A =⎪⎨⋅AB =⎪⎩,同理可取()0,3,4m =.则219cos ,n m n m n m ⋅==-故二面角C E -B -A 的余弦值为19-.33.【解析】(I )证明:∵54AE CF ==, ∴AE CFAD CD=,∴EF AC ∥. ∵四边形ABCD 为菱形, ∴AC BD ⊥,∴EF BD ⊥,∴EF D H ⊥,∴EF DH'⊥. ∵6AC =,∴3AO =;又5AB =,AO OB ⊥,∴4OB =, ∴1AEOH OD AO=⋅=,∴3DH D H '==, ∴222'OD OH D H '=+,∴'D H OH ⊥. 又∵OH EF H =I ,∴'D H ⊥面ABCD .(Ⅱ)建立如图坐标系H xyz -.()500B ,,,()130C ,,,()'003D ,,,()130A -,,,()430AB =u u u r ,,,()'133AD =-u u u r ,,,()060AC =u u u r,,, 设面'ABD 法向量()1n x y z =,,u r,由1100n AB n AD ⎧⋅=⎪⎨'⋅=⎪⎩得430330x y x y z +=⎧⎨-++=⎩,取345x y z =⎧⎪=-⎨⎪=⎩,∴()1345n =-u r ,,.同理可得面'AD C 的法向量()2301n =u u r,,,∴1212cos n n n n θ⋅=u r u u ru r u u rsin θ=. 34.【解析】(Ⅰ)由已知得232==AD AM , 取BP 的中点T ,连接TN AT ,. 由N 为PC 中点知BC TN //,221==BC TN . 又BC AD //,故TN 平行且等于AM ,四边形AMNT 为平行四边形,于是AT MN //.因为⊂AT 平面PAB ,⊄MN 平面PAB ,所以//MN 平面PAB .(Ⅱ)取BC 的中点E ,连结AE ,由AC AB =得BC AE ⊥,从而AD AE ⊥, 且5)2(2222=-=-=BC AB BE AB AE . 以A 为坐标原点,AE 的方向为x 轴正方向,建立如图所示的空间直角坐标系xyz A -,由题意知,)4,0,0(P ,)0,2,0(M ,)0,2,5(C ,)2,1,25(N , (0,2,4)PM =-,)2,1,25(-=, )2,1,25(=.设(,,)x y z =n 为平面PMN 的法向量,则00PM PN ⎧⋅=⎪⎨⋅=⎪⎩n n ,即⎪⎩⎪⎨⎧=-+=-0225042z y x z x ,可取(0,2,1)n =, 于是||85|cos ,|||||n AN n AN n AN ⋅<>==35.【解析】(Ⅰ)设ACBE O =,连结OF ,EC ,由于E 为AD 的中点,1,//2AB BC AD AD BC ==, 所以//,AE BC AE AB BC ==,因此四边形ABCE 为菱形,所以O 为AC 的中点,又F 为PC 的中点, 因此在PAC ∆中,可得//AP OF .又OF ⊂平面BEF ,AP ⊄平面BEF ,所以AP ∥平面BEF .(Ⅱ)由题意知,//,ED BC ED BC =,所以四边形BCDE 为平行四边形, 因此//BE CD .又AP ⊥平面PCD ,所以AP CD ⊥,因此AP BE ⊥. 因为四边形ABCE 为菱形,所以BE AC ⊥. 又APAC A =,AP ,AC ⊂平面P AC ,所以BE ⊥平面PAC .36.【解析】(Ⅰ)∵D E ,为PC AC ,中点,∴DE ∥P A ∵PA ⊄平面DEF ,DE ⊂平面DEF ,∴P A ∥平面DEF (Ⅱ)∵D E ,为PC AC ,中点,∴132DE PA == ∵E F ,为AC AB ,中点,∴142EF BC == ∴222DE EF DF +=,∴90DEF ∠=°,∴DE ⊥EF∵//DE PA PA AC ⊥,,∴DE AC ⊥ ∵AC EF E =,∴DE ⊥平面ABC∵DE⊂平面BDE,∴平面BDE⊥平面ABC.37.【解析】(Ⅰ)连接BD交AC于点O,连结EO.因为ABCD为矩形,所以O为BD的中点.又E为PD的中点,所以EO∥PB.EO⊂平面AEC,PB⊄平面AEC,所以PB∥平面AEC.(Ⅱ)因为PA⊥平面ABCD,ABCD为矩形,所以AB,AD,AP两两垂直.如图,以A为坐标原点,AB的方向为x轴的正方向,AP为单位长,建立空间直角坐标系A xyz-,则D1),2E1)2AE=.设(,0,0)(0)bm m ,则(c m(AC m=.设1(,,)n x y z=为平面ACE的法向量,则110,0,n ACn AE⎧⋅=⎪⎨⋅=⎪⎩即0,10,2mxy z⎧+=+=,可取1n=-.又2(1,0,0)n=为平面DAE的法向量,由题设121cos,2n n=12=,解得32m=.因为E为PD的中点,所以三棱锥E ACD-的高为12.三棱锥E ACD-的体积113132228V=⨯⨯=.38.【解析】(Ⅰ)证明:如图取PB中点M,连接MF,AM.因为F为PC中点,故MF//BC 且MF=12BC .由已知有BC//AD ,BC=AD .又由于E 为AD 中点, 因而MF//AE 且MF=AE ,故四边形AMFE 为平行四边形,所以EF//AM ,又AM ⊂平面PAB ,而EF ⊄平面PAB ,所以EF//平面PAB .(Ⅱ)(i )证明:连接PE ,BE .因为PA=PD ,BA=BD ,而E 为AD 中点,故PE ⊥AD ,BE ⊥AD ,所以∠PEB 为二面角P-AD-B 的平面角.在三角形PAD 中,由2,AD PA PD ===PE=2.在三角形ABD 中,由BA BD ==BE=1.在三角形PEB 中,PE=2,BE=1,60PEB ∠=,由余弦定理,可解得90PBE ∠=,即BE ⊥PB ,又BC//AD ,BE ⊥AD ,从而BE ⊥BC ,因此BE ⊥平面PBC .又BE ⊂平面ABCD , 所以平面PBC ⊥平面ABCD .(ii )连接BF ,由(i )知BE ⊥平面PBC .所以∠EFB 为直线EF 与平面PBC 所成的角,由,∠ABP 为直角,而MB=12,故,又BE=1,故在直角三角形EBF 中,sin BE EFB EF ∠==所以直线EF 与平面PBC 39.【解析】(Ⅰ)设点O 为AC ,BD 的交点, 由AB =BC ,AD =CD ,得BD 是线段AC 的中垂线.所以O 为AC 的中点,BD ⊥AC .又因为P A ⊥平面ABCD ,BD ⊂平面ABCD ,所以P A ⊥BD .所以BD ⊥平面APC .(Ⅱ)连结OG .由(1)可知OD ⊥平面APC ,则DG 在平面APC 内的射影为OG ,所以∠OGD是DG与平面APC所成的角.由题意得OG=12P A=2.在△ABC中,AC=所以OC=12 AC在直角△OCD中,OD2.在直角△OGD中,tan∠OGD=OD OG=所以DG与平面APC(Ⅲ)连结OG.因为PC⊥平面BGD,OG⊂平面BGD,所以PC⊥OG.在直角△P AC中,得PC所以GC=AC OCPC⋅=从而PG,所以32 PGGC=.40.【解析】(Ⅰ)由AB是圆O的直径,得AC⊥BC.由PA⊥平面ABC,BC⊂平面ABC,得PA⊥BC,又PA∩AC=A,PA⊂平面PAC,AC⊂平面PAC,所以BC⊥平面PAC.(Ⅱ)连OG并延长交AC与M,链接QM,QO.由G为∆AOC的重心,得M为AC中点,由G为PA中点,得QM//PC.又O 为AB 中点,得OM//BC .因为QM∩MO=M,QM ⊂平面QMO .所以QG//平面PBC .41.【解析】(Ⅰ)因为111A B C ABC -是直三棱柱,所以1CC ⊥平面ABC,又AD ⊂平面ABC ,所以1CC AD ⊥,又因为AD 1,,DE CC ⊥DE ⊂平面11BCC B ,1CC ,DE E ⋂=所以AD ⊥平面11BCC B ,又AD ⊂平面ADE,所以平面ADE ⊥平面11BCC B .(Ⅱ)因为1111AB AC =,F 为11C B 的中点,所以111A F BC ⊥.因为1CC ⊥平面111ABC ,且1A F ⊂平面111ABC ,所以1CC 1.A F ⊥又因为1CC ,11B C ⊂平面11BCC B, 1CC ⋂111BC C =,所以1A F ⊥平面11BCC B,所以1//A F AD . 又AD ⊂平面ADE ,1A F ⊄平面ADE ,所以1//A F 平面ADE .42.【解析】(Ⅰ)AB ⊥平面PAD ,PH ⊂面PAD PH AB ⇒⊥又,PH AD AD AB A PH ⊥=⇒⊥面ABCD(Ⅱ)E 是PB 中点⇒点E 到面BCF 的距离1122h PH == 三棱锥E BCF -的体积11111133262BCF V S h FC AD h ∆=⨯=⨯⨯⨯⨯=⨯= (Ⅲ)取PA 的中点为G ,连接,DG EG ,PD AD DG PA =⇒⊥,又AB ⊥平面PAD ⇒面PAD ⊥面PAB DG ⇒⊥面PAB ,点,E G 是棱,PB PA 的中点11//,//////22EG AB DF AB EG DF DG EF ⇒⇒⇒,得:EF ⊥平面PAB .43.【证明】:(Ⅰ)在△PAD 中,因为E 、F 分别为AP ,AD 的中点,所以EF//PD .又因为EF ⊄平面PCD ,PD ⊂平面PCD ,所以直线EF//平面PCD .(Ⅱ)连结DB ,因为AB=AD ,∠BAD=60°,所以△ABD 为正三角形,因为F 是AD 的中点,所以BF ⊥AD .因为平面PAD ⊥平面ABCD ,BF ⊂平面ABCD ,平面PAD 平面ABCD=AD ,所以BF ⊥平面PAD .又因为BF ⊂平面BEF ,所以平面BEF ⊥平面PAD .44.【解析】法一:(Ⅰ)证明:取AD 中点G ,连接PG ,BG ,BD .因PA=PD ,有PG AD ⊥,在ABD ∆中,1,60AB AD DAB ==∠=︒,有ABD ∆为等边三角形,因此,BG AD BG PG G ⊥⋂=,所以AD ⊥平面PBG ,.AD PB AD GB ⇒⊥⊥又PB//EF ,得AD EF ⊥,而DE//GB 得AD ⊥DE ,又FE DE E ⋂=,所以AD ⊥平面DEF .(Ⅱ),PG AD BG AD ⊥⊥,PGB ∴∠为二面角P —AD —B 的平面角,在2227,4Rt PAG PG PA AG ∆=-=中 在3sin 602Rt ABG BG AB ∆⋅中,==222734cos 222PG BG PB PGB PG BG +-+-∴∠===⋅法二:(Ⅰ)取AD 中点为G ,因为,.PA PD PG AD =⊥又,60,AB AD DAB ABD =∠=︒∆为等边三角形,因此,BG AD ⊥,从而AD ⊥平面PBG .延长BG 到O 且使得PO ⊥OB ,又PO ⊂平面PBG ,PO ⊥AD ,,AD OB G ⋂=所以PO ⊥平面ABCD .以O 为坐标原点,菱形的边长为单位长度,直线OB ,OP 分别为x 轴,z 轴,平行于AD 的直线为y 轴,建立如图所示空间直角坐标系. 设11(0,0,),(,0,0),(,,0),(,,0).22P m G n A n D n -则||||sin 60GB AB=︒=11(((,0),(,).22222422n m B n Cn E n F ∴++++ 由于3(0,1,0),(,0,0),()2242n m AD DE FE ===+- 得0,0,,,AD DE AD FE AD DE AD FE DE FE E ⋅=⋅=⊥⊥⋂=AD ∴⊥平面DEF .(Ⅱ)1(,,),()2PA nm PB n m =--=+-22,1,m m n ====解之得 取平面ABD 的法向量1(0,0,1),n =-设平面PAD 的法向量2(,,)n a b c =由2230,0,0,0,22b b PA n ac PD n c ⋅=--=⋅=+-=得由取2(1,0,2n =12cos ,n n ∴<>== 45.【解析】(Ⅰ)因为四边形ADEF 是正方形,所以FA //ED .故CED ∠为异面直线CE与AF 所成的角.因为FA ⊥平面ABCD ,所以FA ⊥CD .故ED ⊥CD .在Rt △CDE 中,CD =1,ED=CE故cos CED ∠=ED CE=3. 所以异面直线CE 和AF所成角的余弦值为3. (Ⅱ)证明:过点B 作BG //CD ,交AD 于点G ,则45BGA CDA ∠=∠=.由45BAD ∠=,可得BG ⊥AB ,从而CD ⊥AB ,又CD ⊥FA ,FA ⋂AB =A ,所以CD ⊥平面ABF .(Ⅲ)解:由(Ⅱ)及已知,可得AG即G 为AD 的中点.取EF 的中点N ,连接GN ,则GN ⊥EF ,因为BC //AD ,所以BC //EF .过点N 作NM ⊥EF ,交BC 于M ,则GNM ∠为二面角B -EF -A 的平面角.连接GM ,可得AD ⊥平面GNM ,故AD ⊥GM .从而BC ⊥GM .由已知, 可得GM=2.由NG //FA ,FA ⊥GM ,得NG ⊥GM . 在Rt △NGM 中,tan GM 1NG 4GNM ∠==, 所以二面角B -EF -A 的正切值为14. 46.【解析】 (Ⅰ)取A D '的中点G ,连结GF ,CE ,由条件易知FG CD ∥,12FG CD =.BE CD ∥,12BE CD =.所以FG BE ∥,FG BE =. 故四边形BEGF 为平行四边形,所以BF EG ∥因为EG ⊂平面'A DE ,BF ⊄平面'A DE ,所以BF //平面'A DE (Ⅱ)在平行四边形ABCD 中,设BC a =,则2AB CD a ==, AD AE EB a ===,连CE ,因为0120ABC ∠=在△BCE 中,可得CE a ,在△ADE 中,可得DE =a ,在△CDE 中,因为222CD CE DE =+,所以CE DE ⊥,在正三角形'A DE 中,M 为DE 中点,所以A M '⊥DE .由平面'A DE ⊥平面BCD ,可知A M '⊥平面BCD , A M '⊥CE .取A E '的中点N ,连线NM 、NF ,所以NF ⊥DE ,NF ⊥A M '.因为DE 交A M '于M ,所以NF ⊥平面'A DE ,则∠FMN 为直线FM 与平面'A DE 所成角.在Rt △FMN 中,NF a , MN =12a ,FM =a , 则cos FMN ∠=12. 所以直线FM 与平面'A DE 所成角的余弦值为12.。
秒杀真题之十年高考真题分类训练与答案(理科)空间中点、直线、平面之间的位置关系

秒杀真题之十年高考真题分类训练与答案(理科)空间中点、直线、平面之间的位置关系2019年1.(2019全国Ⅲ理8)如图,点N 为正方形ABCD 的中心,△ECD 为正三角形,平面ECD ⊥平面ABCD ,M 是线段ED 的中点,则A .BM =EN ,且直线BM 、EN 是相交直线B .BM ≠EN ,且直线BM ,EN 是相交直线C .BM =EN ,且直线BM 、EN 是异面直线D .BM ≠EN ,且直线BM ,EN 是异面直线2.(2019全国Ⅱ理7)设α,β为两个平面,则α∥β的充要条件是A .α内有无数条直线与β平行B .α内有两条相交直线与β平行C .α,β平行于同一条直线D .α,β垂直于同一平面3.(2019江苏16)如图,在直三棱柱ABC -A 1B 1C 1中,D ,E 分别为BC ,AC 的中点,AB =BC . 求证:(1)A 1B 1∥平面DEC 1;(2)BE ⊥C 1E .4.(2019北京理12)已知l ,m 是平面a 外的两条不同直线.给出下列三个论断: ①l m ⊥; ②m a P ; ③l a ⊥以其中的两个论断作为条件,余下的一个论断作为结论,写出一个正确的命题: ______.2010-2018年一、选择题1.(2018全国卷Ⅰ)已知正方体的棱长为1,每条棱所在直线与平面α所成的角相等,则α截此正方体所得截面面积的最大值为A B C D2.(2018全国卷Ⅱ)在长方体1111-ABCD A B C D 中,1==AB BC ,1=AA 线1AD 与1DB 所成角的余弦值为A .15B .6C .5D .23.(2018浙江)已知平面α,直线m ,n 满足m α⊄,n α⊂,则“m ∥n ”是“m ∥α”的A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件4.(2018浙江)已知四棱锥S ABCD -的底面是正方形,侧棱长均相等,E 是线段AB 上的点(不含端点),设SE 与BC 所成的角为1θ,SE 与平面ABCD 所成的角为2θ,二面角S AB C --的平面角为3θ,则A .123θθθ≤≤B .321θθθ≤≤C .132θθθ≤≤D .231θθθ≤≤5.(2017新课标Ⅱ)已知直三棱柱111ABC A B C -中,120ABC ∠=,2AB =,11BC CC ==,则异面直线1AB 与1BC 所成角的余弦值为A B C D 6.(2017浙江)如图,已知正四面体D ABC -(所有棱长均相等的三棱锥),P ,Q ,R 分别为AB ,BC ,CA 上的点,AP PB =,2BQ CR QC RA==,分别记二面角D PR Q --,D PQ R --,D QR P --的平面角为α,β,γ,则RQ P AB C DA .γ<α<βB .α<γ<βC .α<β<γD .β<γ<α 7.(2016年全国I )平面α过正方体1111ABCD A B C D -的顶点A ,α∥平面11CB D ,αI 平面ABCD =m ,αI 平面11ABB A =n ,则m ,n 所成角的正弦值为A.2 B.2 C.3 D .138.(2015福建)若,l m 是两条不同的直线,m 垂直于平面α ,则“l m ⊥ ”是“l ∥α”的A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件9.(2015浙江)如图,已知ABC ∆,D 是AB 的中点,沿直线CD 将ACD ∆翻折成A CD '∆,所成二面角A CD B '--的平面角为α,则10.(2014广东)若空间中四条两两不同的直线1234,,,l l l l ,满足122334,,l l l l l l ⊥⊥⊥,则下面结论一定正确的是A .14l l ⊥B .14//l lC .14,l l 既不垂直也不平行D .14,l l 的位置关系不确定11.(2014浙江)设,m n 是两条不同的直线,,αβ是两个不同的平面A .若m n ⊥,//n α,则m α⊥B .若//m β,βα⊥则m α⊥C .若,,m n n ββα⊥⊥⊥则m α⊥D .若m n ⊥,n β⊥,βα⊥,则m α⊥12.(2014辽宁)已知m ,n 表示两条不同直线,α表示平面,下列说法正确的是A .若//,//,m n αα则//m nB .若m α⊥,n α⊂,则m n ⊥C .若m α⊥,m n ⊥,则//n αD .若//m α,m n ⊥,则n α⊥13.(2014浙江)如图,某人在垂直于水平地面ABC 的墙面前的点A 处进行射击训练,已知点A 到墙面的距离为AB ,某目标点P 沿墙面的射击线CM 移动,此人为了准确瞄准目标点P ,需计算由点A 观察点P 的仰角θ的大小(仰角θ为直线AP 与平面ABC 所成角).若15AB m =,25AC m =,30BCM ∠=︒则tan θ的最大值ABCD 14.(2014四川)如图,在正方体1111ABCD A B C D -中,点O 为线段BD 的中点.设点P 在线段1CC 上,直线OP 与平面1A BD 所成的角为α,则sin α的取值范围是A1A. B.C .D . 15.(2013新课标Ⅱ)已知,m n 为异面直线,m ⊥平面α,n ⊥平面β.直线l 满足,l m l n ⊥⊥,,l l αβ⊄⊄,则A .α∥β且l ∥αB .α⊥β且l ⊥βC .α与β相交,且交线垂直于lD .α与β相交,且交线平行于l16.(2013广东)设m ,n 是两条不同的直线,α,β是两个不同的平面,下列命题中正确的是A .若αβ⊥,m α⊂,n β⊂,则m n ⊥B .若//αβ,m α⊂,n β⊂,则//m nC .若m n ⊥,m α⊂,n β⊂,则αβ⊥D .若m α⊥,//m n ,//n β,则αβ⊥17.(2012浙江)设l 是直线,,αβ是两个不同的平面A .若l ∥α,l ∥β,则α∥βB .若l ∥α,l ⊥β,则α⊥βC .若α⊥β,l ⊥α,则l ⊥βD .若α⊥β, l ∥α,则l ⊥β18.(2012浙江)已知矩形ABCD ,1AB =,BC =将ABD ∆沿矩形的对角线BD 所在的直线进行翻折,在翻折过程中,A .存在某个位置,使得直线AC 与直线BD 垂直B .存在某个位置,使得直线AB 与直线CD 垂直C .存在某个位置,使得直线AD 与直线BC 垂直D .对任意位置,三对直线“AC 与BD ”,“AB 与CD ”,“AD 与BC ”均不垂直19.(2011浙江)下列命题中错误..的是A .如果平面αβ⊥平面,那么平面α内一定存在直线平行于平面βB .如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面βC .如果平面αγ⊥平面,平面βγ⊥平面,=l αβ,那么l γ⊥平面D .如果平面αβ⊥平面,那么平面α内所有直线都垂直于平面β20.(2010山东)在空间,下列命题正确的是A .平行直线的平行投影重合B .平行于同一直线的两个平面平行C .垂直于同一平面的两个平面平行D .垂直于同一平面的两条直线平行二、填空题21.(2018全国卷Ⅱ)已知圆锥的顶点为S ,母线SA ,SB 所成角的余弦值为78,SA 与圆锥底面所成角为45°,若△SAB 的面积为_____.22.(2016年全国II )α,β是两个平面,m ,n 是两条线,有下列四个命题:①如果m n ⊥,m α⊥,n β∥,那么αβ⊥.②如果m α⊥,n α∥,那么m n ⊥.③如果a β∥,m α⊂,那么m β∥.④如果m n ∥,αβ∥,那么m 与α所成的角和n 与β所成的角相等.其中正确的命题有 .(填写所有正确命题的编号)23.(2015浙江)如图,三棱锥A BCD -中,3AB AC BD CD ====,2AD BC ==,点,M N 分别是,AD BC 的中点,则异面直线,AN CM 所成的角的余弦值是 .24.(2015四川)如图,四边形ABCD 和ADPQ 均为正方形,它们所在的平面互相垂直,动点M 在线段PQ 上,,E F 分别为,AB BC 的中点.设异面直线EM 与AF 所成的角为θ,则θcos 的最大值为_________.25.(2017新课标Ⅲ)a ,b 为空间中两条互相垂直的直线,等腰直角三角形ABC 的直角边AC 所在直线与a ,b 都垂直,斜边AB 以直线AC 为旋转轴旋转,有下列结论: ①当直线AB 与a 成60°角时,AB 与b 成30°角;②当直线AB 与a 成60°角时,AB 与b 成60°角;③直线AB 与a 所成角的最小值为45°;④直线AB 与a 所成角的最小值为60°;其中正确的是________.(填写所有正确结论的编号)三、解答题26.(2018江苏)在平行六面体1111ABCD A B C D -中,1AA AB =,111AB B C ⊥.D 11B 1A 1DC B A求证:(1)AB ∥平面11A B C ; (2)平面11ABB A ⊥平面1A BC .27.(2018浙江)如图,已知多面体111ABCA B C ,1A A ,1B B ,1C C 均垂直于平面ABC ,120ABC ∠=,14A A =,11C C =,12AB BC B B ===.C 1B 1A 1C BA(1)证明:1AB ⊥平面111A B C ;(2)求直线1AC 与平面1ABB 所成的角的正弦值.28.(2017浙江)如图,已知四棱锥P ABCD -,PAD ∆是以AD 为斜边的等腰直角三角形,BC AD ∥,CD AD ⊥,22PC AD DC CB ===,E 为PD 的中点.(Ⅰ)证明:CE ∥平面PAB ;(Ⅱ)求直线CE 与平面PBC 所成角的正弦值.ED B AP29.(2017江苏)如图,在三棱锥A BCD -中,AB ⊥AD ,BC ⊥BD ,平面ABD ⊥平面BCD ,点E 、F (E 与A 、D 不重合)分别在棱AD ,BD 上,且EF ⊥AD .求证:(1)EF ∥平面ABC ;(2)AD ⊥AC .F AB C DE30.(2017山东)如图,几何体是圆柱的一部分,它是由矩形ABCD (及其内部)以AB 边所在直线为旋转轴旋转120︒得到的,G 是DF 的中点.(Ⅰ)设P 是CE 上的一点,且AP BE ⊥,求CBP ∠的大小;(Ⅱ)当3AB =,2AD =,求二面角E AG C --的大小.31.(2017江苏)如图,水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ的高均为32cm ,容器Ⅰ的底面对角线AC 的长为cm ,容器Ⅱ的两底面对角线EG ,11E G 的长分别为14cm 和62cm . 分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm . 现有一根玻璃棒l ,其长度为40cm .(容器厚度、玻璃棒粗细均忽略不计)(1)将l 放在容器Ⅰ中,l 的一端置于点A 处,另一端置于侧棱1CC 上,求l 没入水中部分的长度;(2)将l 放在容器Ⅱ中,l 的一端置于点E 处,另一端置于侧棱1GG 上,求l 没入水中部分的长度.32.(2016全国I )如图,在以A ,B ,C ,D ,E ,F 为顶点的五面体中,面ABEF 为正方形,2AF FD =,90AFD ∠=,且二面角D AF E --与二面角C BE F --都是60.(I )证明:平面ABEF ⊥平面EFDC ;(II )求二面角E BC A --的余弦值.33.(2016全国II )如图,菱形ABCD 的对角线AC 与BD 交于点O ,5AB =,6AC =,点E ,F 分别在AD ,CD 上,54AE CF ==,EF 交BD 于点H .将ΔDEF 沿EF折到ΔD EF '的位置,OD '=(I )证明:D H '⊥平面ABCD ;(II )求二面角B D A C '--的正弦值.34.(2016全国III )如图,四棱锥P ABCD -中,PA ⊥底面ABCD ,AD BC ,=3AB AD AC ==,4PA BC ==,M 为线段AD 上一点,2AM MD =, N 为PC 的中点.(Ⅰ)证明MN 平面PAB ;(Ⅱ)求直线AN 与平面PMN 所成角的正弦值.BD35.(2014山东)如图,四棱锥P ABCD -中,AP PCD ⊥平面,AD BC ∥,1,,2AB BC ADE F ==分别为线段,AD PC 的中点.(Ⅰ)求证:AP BEF ∥平面; (Ⅱ)求证:BE PAC ⊥平面.36.(2014江苏)如图,在三棱锥ABC P -中,D ,E ,F 分别为棱AB AC PC ,,的中点.已知AC PA ⊥,,6=PA .5,8==DF BC求证:(Ⅰ)直线PA ∥平面DEF ;(Ⅱ)平面BDE ⊥平面ABC .37.(2014新课标Ⅱ)如图,四棱锥P ABCD -中,底面ABCD 为矩形,PA ⊥平面ABCD ,E 为PD 的中点.(Ⅰ)证明:PB ∥平面AEC ;(Ⅱ)设二面角D AE C --为60°,AP =1,AD求三棱锥E ACD -的体积.38.(2014天津)如图四棱锥P ABCD -的底面ABCD是平行四边形,BA BD ==,2AD =,PA PD ==E ,F 分别是棱AD ,PC 的中点.(Ⅰ)证明: EF ∥平面PAB ; (Ⅱ)若二面角P AD B --为60°, (ⅰ)证明:平面PBC ⊥平面ABCD(ⅱ)求直线EF 与平面PBC 所成角的正弦值.39.(2013浙江)如图,在四棱锥P ABCD -中,PA ⊥面ABCD ,2AB BC ==,AD CD ==,PA =120ABC ∠=,G 为线段PC 上的点.PDB(Ⅰ)证明:BD ⊥面APC ;(Ⅱ)若G 是PC 的中点,求DG 与APC 所成的角的正切值; (Ⅲ)若G 满足PC ⊥面BGD ,求PGGC的值. 40.(2013辽宁)如图,AB 是圆O 的直径,PA 垂直圆O 所在的平面,C 是圆O 上的点.(Ⅰ)求证:BC PAC ⊥平面;(Ⅱ)设Q 为PA 的中点,G 为AOC ∆的重心,求证:QG ∥平面PBC .41.(2012江苏)如图,在直三棱柱111ABC A B C -中,1111AB AC =,D E ,分别是棱1BC CC ,上的点(点D 不同于点C ),且AD DE F ⊥,为11B C 的中点.1求证:(Ⅰ)平面ADE ⊥平面11BCC B ;(Ⅱ)直线1//A F 平面ADE .42.(2012广东)如图所示,在四棱锥P ABCD -中,AB ⊥平面PAD ,//,AB CD PD AD =,E 是PB 中点,F 是DC 上的点,且12DF AB =,PH 为PAD ∆中AD 边上的高.(Ⅰ)证明:PH ⊥平面ABCD ; (Ⅱ)若1,1PH AD FC ===,求三棱锥E BCF -的体积;(Ⅲ)证明:EF ⊥平面PAB .43.(2011江苏)如图,在四棱锥ABCD P -中,平面PAD ⊥平面ABCD ,AB AD =,BAD ∠=60°,E 、F 分别是AP 、AD 的中点.C求证:(Ⅰ)直线EF ∥平面PCD ; (Ⅱ)平面BEF ⊥平面PAD .44.(2011广东)如图在椎体P ABCD -中,ABCD 是边长为1的棱形,且DAB ∠=60︒,PA PD ==2PB =,E ,F 分别是BC ,PC 的中点.(Ⅰ)证明:AD ⊥平面DEF ;(Ⅱ)求二面角P AD B --的余弦值.45.(2010天津)如图,在五面体ABCDEF 中,四边形ADEF 是正方形,FA ⊥平面ABCD ,BC∥AD ,CD =1,AD =,∠BAD =∠CDA =45°.(Ⅰ)求异面直线CE 与AF 所成角的余弦值; (Ⅱ)证明CD ⊥平面ABF ; (Ⅲ)求二面角B EF A --的正切值.46.(2010浙江)如图,在平行四边形ABCD 中,AB =2BC ,∠ABC =120°.E 为线段AB 的中点,将△ADE 沿直线DE 翻折成△A DE ',使平面A DE '⊥平面BCD ,F 为线段A C '的中点.(Ⅰ)求证:BF ∥平面A DE ';(Ⅱ)设M 为线段DE 的中点,求直线FM 与平面A DE '所成角的余弦值.答案部分2019年1.解析 如图所示,联结BE ,BD .因为点N 为正方形ABCD 的中心,ECD △为正三角形,平面ECD ⊥平面ABCD ,M 是线段ED 的中点,所以BM ⊂平面BDE ,EN ⊂平面BDE ,因为BM 是BDE △中DE 边上的中线,EN 是BDE △中BD 边上的中线,直线BM,EN 是相交直线,设DE a =,则BD=,BE==, 所以BM =,EN a ==,所以BM EN ≠.故选B .2.解析:对于A ,α内有无数条直线与β平行,则α与β相交或βα∥,排除; 对于B ,α内有两条相交直线与β平行,则βα∥;对于C ,α,β平行于同一条直线,则α与β相交或βα∥,排除; 对于D ,α,β垂直于同一平面,则α与β相交或βα∥,排除. 故选B .3.证明:(1)因为D ,E 分别为BC ,AC 的中点, 所以ED ∥AB .在直三棱柱ABC-A 1B 1C 1中,AB ∥A 1B 1, 所以A 1B 1∥ED .又因为ED ⊂平面DEC 1,A 1B 1⊄平面DEC 1, 所以A 1B 1∥平面DEC 1.(2)因为AB =BC ,E 为AC 的中点,所以BE ⊥AC . 因为三棱柱ABC-A 1B 1C 1是直棱柱,所以CC 1⊥平面ABC . 又因为BE ⊂平面ABC ,所以CC 1⊥BE .因为C 1C ⊂平面A 1ACC 1,AC ⊂平面A 1ACC 1,C 1C ∩AC =C , 所以BE ⊥平面A 1ACC 1.因为C 1E ⊂平面A 1ACC 1,所以BE ⊥C 1E .4.解析:由l ,m 是平面α外的两条不同直线,知: 由线面平行的判定定理得: 若l l m α⊥⊥,,则m αP . 由线面平行、垂直的性质定理得m αP ,l α⊥,则l m ⊥.2010-2018年1.A 【解析】记该正方体为''''-ABCD A B C D ,正方体的每条棱所在直线与平面α所成的角都相等,即共点的三条棱'A A ,''A B ,''A D 与平面α所成的角都相等,如图,连接'AB ,'AD ,''B D ,因为三棱锥'''-A AB D 是正三棱锥,所以'A A ,''A B ,''A D 与平面''AB D 所成的角都相等,分别取''C D ,''B C ,'BB ,AB ,AD ,'DD 的中点E ,F ,G ,H ,I ,J ,连接EF ,FG .GH ,IH ,IJ ,IE ,易得E ,F ,G ,H ,I ,J 六点共面,平面EFGHIJ 与平面''AB D 平行,且截正方体所得截面的面积最大,又======EF FG GH IH IJ JE,所以该正六边形的面积为26(434⨯⨯=,所以α截此正方体所得截面面积的最大值为4,故选A . 2.C 【解析】解法一 如图,F 1E 1F D 1A 1B 1C 1E C D AB补上一相同的长方体1111-CDEF C D E F ,连接1DE ,11B E . 易知11∥AD DE ,则11∠B DE 为异面直线1AD 与1DB 所成角. 因为在长方体1111-ABCD A B C D 中,1==AB BC,1=AA所以12===DE,1==DB11===B E ,在11∆B DE中,由余弦定理,得11cos ∠==B DE , 即异面直线1AD 与1DB所成角的余弦值为5,故选C . 解法二 以D 为坐标原点,DA ,DC ,1DD 所在直线分别为x 轴,y 轴,z 轴建立空间直角坐标系,如图所示.由条件可知(0,0,0)D ,(1,0,0)A,1D,1(1B ,所以1(1=-AD,1(1,1=DB ,则由向量夹角公式,得111111cos ,||||2⋅<>===AD DB AD DB AD DB即异面直线1AD 与1DB C . 3.A 【解析】若m α⊄,n α⊂,m ∥n ,由线面平行的判定定理知m ∥α.若m ∥α,m α⊄,n α⊂,不一定推出m ∥n ,直线m 与n 可能异面,故“m ∥n ”是“m ∥α”的充分不必要条件.故选A .4.D 【解析】由题意知四棱锥S ABCD -为正四棱锥,如图,EMSODCBA连接BD ,记AC BD O =,连接SO ,则SO ⊥平面ABCD ,取AB 的中点M ,连接SM ,OM ,OE ,易得AB SM ⊥,则2S E O θ=∠,3SMO θ=∠,易知32θθ≥.因为OM ∥BC ,BC AB ⊥,SM AB ⊥,所以3θ也为OM 与平面SAB 所成的角,即BC 与平面SAB 所成的角,再根据最小角定理知,31θθ≤,所以231θθθ≤≤,故选D .5.C 【解析】如图所示,把三棱柱补成四棱柱,异面直线1AB 与1BC 所成角为11B AD ∠B 1A 1D 1C 1DCBA2111B D===1AD =1AB ,∴22222211111111cos 25AB AD B D B AD AB AD +-∠===⨯⨯.选C . 6.B 【解析】设O 为三角形ABC 中心,底面如图2,过O 作OE RP ⊥,OF PQ ⊥,OG RQ ⊥,由题意可知tan DO OE α=,tan OD OF β=,tan ODOGγ=,GF EO DC BAPQR图1 图2由图2所示,以P 为原点建立直角坐标系,不妨设2AB =,则(1,0)A -,(1,0)B,C,(0,3O ,∵AP PB =,2BQ CR QC RA==,∴1(,33Q,2(,33R -,则直线RP的方程为2y x =-,直线PQ的方程为y =,直线RQ的方程为39y x =+,根据点到直线的距离公式,知21OE =39OF =,13OG =,∴OF OG OE <<,tan tan tan αγβ<<, 因为α,β,γ为锐角,所以αγβ<<.选B7.A 【解析】因为过点A 的平面α与平面11CB D 平行,平面ABCD ∥平面1111A B C D ,所以m ∥11B D ∥BD ,又1A B ∥平面11CB D ,所以n ∥1A B ,则BD 与1A B 所成的角为所求角,所以m ,nA . 8.B 【解析】由“m α⊥且l m ⊥”推出“l α⊂或l α∥”,但由“m α⊥且l α∥”可推出“l m ⊥”,所以“l m ⊥”是“l α∥”的必要而不充分条件,故选B . 9.B 【解析】解法一 设ADC θ∠=,2AB =,则由题意知1AD BD A D '===.在空间图形中,连结A B ',设A B '=t .在ΔA DB '中,2222222112cos 22112A D DB A B t t A DB A D DB ''+-+--'∠==='⨯⨯⨯.过A '作A N DC '⊥,过B 作BM DC ⊥,垂足分别为N M 、. 过N 作//NP MB ,使四边形BPNM 为平行四边形,则NP DC ⊥,连结,A P BP ',则A NP '∠就是二面角A CD B '--的平面角,所以A NP α'∠=. 在ΔRt A ND '中,cos cos DN A D A DC θ''=∠=,sin sin A N A D A DC θ'''=∠=. 同理,sin BM PN θ==,cos DM θ=,故2cos BP MN θ==. 显然BP ⊥平面A NP ',故BP A P '⊥.在ΔRt A BP '中,222222(2cos )4cos A P A B BP t t θθ''=-=-=-.在ΔA NP '中,222cos cos 2A N NP A P A NP A N NPα''+-'=∠='⨯22222sin sin (4cos )2sin t θθθθ+--==222222222cos 2cos 2sin 2sin sin t t θθθθθ+--=+2221cos cos sin sin A DB θθθ'=∠+, 所以2221cos cos cos cos cos sin sin A DB A DB A DB θαθθ'''-∠=∠+-∠ 2222221sin cos cos cos (1cos )0sin sin sin A DB A DB θθθθθθ-''=∠+=+∠≥, 所以cos cos A DB α'∠≥(当2πθ=时取等号),因为α,[0,]A DB π'∠∈,而cos y x =在[0,]π上为递减函数, 所以A DB α'∠≤,故选B .解法二 若CA CB ≠,则当απ=时,A CB π'∠<,排除D ; 当0α=时,0A CB '∠>,0A DB '∠>,排除A 、C ,故选B . 10.D 【解析】利用正方体模型可以看出,1l 与4l 的位置关系不确定.选D .11.C 【解析】选项,,A B D 中m 均可能与平面α平行、垂直、斜交或在平面α内,故选C . 12.B 【解析】对于选项A ,若//,//,m n αα,则m 与n 可能相交、平行或异面,A 错误;显然选项B 正确;对于选项C ,若m α⊥,m n ⊥,则n α⊂或//n α,C 错误;对于选项D ,若//m α,m n ⊥,则//n α或n α⊂或n 与α相交,D 错误.故选B .13.D 【解析】作PH BC ⊥,垂足为H ,设PH x =,则CH =,由余弦定理AH =1tan tan (0)PHPAH AHxθ=∠==>,故当1125x =时,tan θ取得最大值,最大值为9. 14.B 【解析】直线OP 与平面1A BD 所成的角为α的取值范围是1112AOA C OA π∠→→∠,由于1sin AOA ∠=11sin 2C OA ∠==>,sin 12π= 所以sin α的取值范围是. 15.D 【解析】作正方形模型,α为后平面,β为左侧面可知D 正确.16.D 【解析】A 中,m n 可能平行、垂直、也可能为异面;B 中,m n 还可能为异面;C 中m应与β中两条相交直线垂直时结论才成立,选D .17.B 【解析】利用排除法可得选项B 是正确的,∵l ∥α,l ⊥β,则αβ.如选项A :l ∥α,l ∥β时,α⊥β或α∥β;选项C :若α⊥β,l ⊥α,l ∥β或l β⊂;选项D :若α⊥β, l ⊥α,l ∥β或l ⊥β.18.B 【解析】过点A 作AE BD ⊥,若存在某个位置,使得AC BD ⊥,则BD ⊥面ACE ,从而有BD CE ⊥,计算可得BD 与CE 不垂直,则A 不正确;当翻折到AC CD ⊥时,因为BC CD ⊥,所以CD ⊥面ABC ,从而可得AB CD ⊥;若AD BC ⊥,因为BC CD ⊥,所以BC ⊥面ACD ,从而可得BC AC ⊥,而1AB BC =<=,所以这样的位置不存在,故C 不正确;同理,D 也不正确,故选B .19.D 【解析】对于D ,若平面α⊥平面β,则平面α内的某些直线可能不垂直于平面β,即与平面β的关系还可以是斜交、平行或在平面β内,其余选项易知均是正确的. 20.D 【解析】D 两平行直线的平行投影不一定重合,故A 错;由空间直线与平面的位置关系及线面垂直与平行的判定与性质定理可知B 、C 均错误,故选D . 21.【解析】如图所示,S'SAB设S 在底面的射影为S ',连接AS ',SS '.SAB ∆的面积为2211sin 22SA SB ASB SA SA ⋅⋅⋅∠=⋅==, ∴280SA =,SA =.∵SA 与底面所成的角为45,∴45SAS '∠=,cos 45452AS SA '=⋅==. ∴底面周长2l AS π'=⋅=,∴圆锥的侧面积为12⨯=. 22.②③④【解析】对于命题①,可运用长方体举反例证明其错误:如图,不妨设AA '为直线m ,CD 为 直线n ,ABCD 所在的平面为α.ABC D ''所在的平面为β,显然这些直线和平面满足题目条件,但αβ⊥不成立.命题②正确,证明如下:设过直线n 的某平面与平面α相交于直线l ,则l n ∥, 由m α⊥,有m l ⊥,从知m n ⊥结论正确. 由平面与平面平行的定义知命题③正确. 由平行的传递性及线面角的定义知命题④正确. 23.78【解析】如图连接ND ,取ND 的中点E ,连接,ME CE ,则//ME AN .则异面直线AN ,CM 所成的角为EMC ∠,由题意可知1CN =,AN =∴ME.又CM =DN =NECE =则2227cos 28CM EM CE CME CM EM +-∠===⨯. 24.25【解析】AB 为x 轴,AD 为y 轴,AQ 为z 轴建立坐标系, 设正方形边长为2.cos θ=令[]()0,2)f m m =∈()f m '=[]0,2,()0m f m '∈∴< max 2()(0)5f m f ==,即max 2cos 5θ=. 25.②③【解析】如图BDEF 为底面圆的内接正方形,设1AC BC ==,则AB AD AE AF FB FE ED BD ========,即侧面均为等边三角形,∵AC ⊥底面BDEF ,FEDCBA假设a FB ∥,由题意b BD ∥,当直线AB 与a 成60°角时,由图可知AB 与b 成60°角,所以①错,②正确;假设a EB ∥,可知③正确,④错.所以正确为②③. 26.【证明】(1)在平行六面体1111ABCD A B C D -中,AB ∥11A B .因为AB ⊄平面11A B C ,11A B ⊂平面11A B C , 所以AB ∥平面11A B C .D 1C 1B 1A 1DCBA(2)在平行六面体1111ABCD A B C D -中,四边形11ABB A 为平行四边形. 又因为1AA AB =,所以四边形11ABB A 为菱形, 因此1AB ⊥1A B .又因为1AB ⊥11B C ,BC ∥11B C , 所以1AB ⊥BC . 又因为1ABBC =B ,1A B ⊂平面1A BC ,BC ⊂平面1A BC ,所以1AB ⊥平面1A BC . 因为1AB ⊂平面11ABB A , 所以平面11ABB A ⊥平面1A BC .27.【解析】(1)由2AB =,14AA =,12BB =,1AA AB ⊥,1BB AB ⊥得111AB A B ==,所以2221111A B AB AA +=.故111AB A B ⊥.由2BC =,12BB =,11CC =,1BB BC ⊥,1CC BC ⊥得11B C = 由2AB BC ==,120ABC ∠=得AC =由1CC AC ⊥,得1AC =2221111AB B C AC +=,故111AB B C ⊥.因此1AB ⊥平面111A B C .(2)如图,过点1C 作111C D A B ⊥,交直线11A B 于点D ,连结AD .DABCA 1B 1C 1由1AB ⊥平面111A B C 得平面111A B C ⊥平面1ABB , 由111C D A B ⊥得1C D ⊥平面1ABB , 所以1C AD ∠是1AC 与平面1ABB 所成的角.由11B C =11A B =,11AC得111cos C A B ∠=,111sin C A B ∠=,所以1C D,故111sin C D C AD AC ∠==.因此,直线1AC 与平面1ABB. 方法二 (1)如图,以AC 的中点O 为原点,分别以射线OB ,OC 为x ,y 轴的正半轴,建立空间直角坐标系O xyz -.A由题意知各点坐标如下:(0,A ,(1,0,0)B,1(0,A ,1(1,0,2)B,1C ,因此1(1AB =,11(12)A B =-,113)AC =-,由1110AB A B ⋅=得111AB A B ⊥. 由1110AB AC ⋅=得111AB AC ⊥. 所以1AB ⊥平面111A B C .(2)设直线1AC 与平面1ABB 所成的角为θ.由(1)可知1AC =,AB =,1(0,0,2)BB =, 设平面1ABB 的法向量=()x,y,z n .由100AB BB ⎧⋅=⎪⎨⋅=⎪⎩n n,即020x z ⎧+=⎪⎨=⎪⎩,可取(=n .所以111||sin |cos ,|13||||AC AC AC θ⋅=<>==⋅n n n .因此,直线1AC 与平面1ABB28.【解析】(Ⅰ)如图,设P A 中点为F ,连结EF ,FB .DA因为E ,F 分别为PD ,P A 中点,所以EF ∥AD 且12EF AD =, 又因为BC ∥AD ,12BC AD =,所以 EF ∥BC 且EF =BC ,即四边形BCEF 为平行四边形,所以CE ∥BF , 因此CE ∥平面P AB .(Ⅱ)分别取BC ,AD 的中点为M ,N .连结PN 交EF 于点Q ,连结MQ . 因为E ,F ,N 分别是PD ,P A ,AD 的中点,所以Q 为EF 中点, 在平行四边形BCEF 中,MQ ∥CE . 由PAD ∆为等腰直角三角形得 PN ⊥AD .由DC ⊥AD ,N 是AD 的中点得 BN ⊥AD .所以AD ⊥平面PBN ,由BC ∥AD 得BC ⊥平面PBN , 那么,平面PBC ⊥平面PBN .过点Q 作PB 的垂线,垂足为H ,连结MH .MH 是MQ 在平面PBC 上的射影,所以∠QMH 是直线CE 与平面PBC 所成的角. 设CD =1.在PCD ∆中,由PC =2,CD =1,PD CE在△PBN 中,由PN =BN =1,PB 得14QH =,在Rt MQH ∆中,14QH =,MQ ,所以sin 8QMH ∠=,所以,直线CE 与平面PBC 所成角的正弦值是8. 29.【解析】证明:(1)在平面ABD 内,因为AB AD ⊥,EF AD ⊥,所以EF AB ∥.又因为EF ⊄平面ABC ,AB ⊂平面ABC ,所以EF ∥平面ABC . (2)因为平面ABD ⊥平面BCD , 平面ABD平面BCD =BD ,BC ⊂平面BCD ,BC BD ⊥,所以BC ⊥平面ABD .因为AD ⊂平面ABD ,所以BC ⊥AD . 又AB AD ⊥,BCAB B =,AB ⊂平面ABC ,BC ⊂平面ABC ,所以AD ⊥平面ABC , 又因为AC ⊂平面ABC , 所以AD AC ⊥.30.【解析】(Ⅰ)因为AP BE ⊥,AB BE ⊥,AB ,AP ⊂平面ABP ,ABAP A =,所以BE ⊥平面ABP , 又BP ⊂平面ABP ,所以BE BP ⊥,又120EBC ∠=︒, 因此30CBP ∠=︒ (Ⅱ)解法一:取EC 的中点H ,连接EH ,GH ,CH . 因为120EBC ∠=︒, 所以四边形BEHC 为菱形,所以AE GE AC GC ===== 取AG 中点M ,连接EM ,CM ,EC . 则EM AG ⊥,CM AG ⊥, 所以EMC ∠为所求二面角的平面角.又1AM =,所以EM CM === 在BEC ∆中,由于120EBC ∠=︒,由余弦定理得22222222cos12012EC =+-⨯⨯⨯︒=,所以EC =EMC ∆为等边三角形, 故所求的角为60︒. 解法二:以B 为坐标原点,分别以BE ,BP ,BA 所在的直线为x ,y ,z 轴,建立如图所示的空间直角坐标系.由题意得(0,0,3)A (2,0,0)E,G,(C -,故(2,0,3)AE =-,AG =,(2,0,3)CG =,设111(,,)m x y z =是平面AEG 的一个法向量.由00m AE m AG ⎧⋅=⎪⎨⋅=⎪⎩可得1111230,0,x z x -=⎧⎪⎨+=⎪⎩ 取12z =,可得平面AEG的一个法向量(3,2)=m .设222(,,)n x y z =是平面ACG 的一个法向量.由00n AG n CG ⎧⋅=⎪⎨⋅=⎪⎩可得22220,230,x x z ⎧+=⎪⎨+=⎪⎩ 取22z =-,可得平面ACG的一个法向量(3,2)n =-. 所以1cos ,||||2m n m n m n ⋅<>==⋅. 因此所求的角为60︒.31.【解析】(1)由正棱柱的定义,1CC ⊥平面ABCD ,所以平面11A ACC ⊥平面ABCD ,1CC AC ⊥.记玻璃棒的另一端落在1CC 上点M 处.因为AC =40AM =.所以30MN ==,从而3sin 4MAC ∠=. 记AM 与水平的交点为1P ,过1P 作11PQ AC ⊥,1Q 为垂足,则11PQ ⊥平面ABCD ,故1112PQ =, 从而11116sin PQ AP MAC==∠. 答:玻璃棒l 没入水中部分的长度为16cm .( 如果将“没入水中部分”理解为“水面以上部分”,则结果为24cm)(2)如图,O ,1O 是正棱台的两底面中心.由正棱台的定义,1OO ⊥平面 EFGH ,所以平面11E EGG ⊥平面EFGH ,1OO ⊥EG .同理,平面11E EGG ⊥平面1111E F G H ,1OO ⊥11E G .记玻璃棒的另一端落在1GG 上点N 处.过G 作GK ⊥11E G ,K 为垂足, 则GK =1OO =32.因为EG = 14,11E G = 62,所以1KG =6214242-=,从而140GG ===. 设1,,EGG ENG αβ==∠∠则114sin sin()cos 25KGG KGG απ=+==∠∠. 因为2απ<<π,所以3cos 5α=-. 在ENG △中,由正弦定理可得4014sin sin αβ=,解得7sin 25β=. 因为02βπ<<,所以24cos 25β=. 于是sin sin()sin()sin cos cos sin NEG αβαβαβαβ=π--=+=+∠42473(35)525255=⨯+-⨯=. 记EN 与水面的交点为2P ,过2P 作22P Q EG ⊥,2Q 为垂足,则 22P Q ⊥平面EFGH ,故22P Q =12,从而 2EP =2220sin P NEGQ =∠. 答:玻璃棒l 没入水中部分的长度为20cm .(如果将“没入水中部分”理解为“水面以上部分”,则结果为20cm)32.【解析】(Ⅰ)由已知可得AF DF ⊥,AF FE ⊥,所以AF ⊥平面EFDC .又AF ⊂平面ABEF ,故平面ABEF ⊥平面EFDC .(Ⅱ)过D 作DG EF ⊥,垂足为G ,由(Ⅰ)知DG ⊥平面ABEF .以G 为坐标原点,GF 的方向为x 轴正方向,||GF 为单位长度,建立如图所示的空间直角坐标系G xyz -.由(Ⅰ)知DFE ∠为二面角D AF E --的平面角,故60DFE ∠=,则2DF =,DG =,可得(1,4,0)A ,(3,4,0)B -,(3,0,0)E -,D .由已知,AB EF ∥,所以AB ∥平面EFDC .又平面ABCD 平面EFDC DC =,故AB CD ∥,CD EF ∥.由BE AF ∥,可得BE ⊥平面EFDC ,所以CEF ∠为二面角C BE F --的平面角, 60CEF ∠=.从而可得(C -.所以EC =,(0,4,0)EB =,(3,AC =--,(4,0,0)AB =-. 设(),,n x y z =是平面BCE 的法向量,则C 00n n ⎧⋅E =⎪⎨⋅EB =⎪⎩,即040x y ⎧+=⎪⎨=⎪⎩,所以可取(3,0,n =. 设m 是平面CD AB 的法向量,则C 00m m ⎧⋅A =⎪⎨⋅AB =⎪⎩, 同理可取()0,3,4m =.则219cos ,19n m n m n m ⋅==-.故二面角C E-B -A 的余弦值为.33.【解析】(I )证明:∵54AE CF ==, ∴AE CF AD CD=,∴EF AC ∥. ∵四边形ABCD 为菱形,∴AC BD ⊥,∴EF BD ⊥,∴EF DH ⊥,∴EF D H '⊥.∵6AC =,∴3AO =;又5AB =,AO OB ⊥,∴4OB =, ∴1AE OH OD AO =⋅=,∴3DH D H '==, ∴222'OD OH D H '=+,∴'D H OH ⊥.又∵OH EF H =I ,∴'D H ⊥面ABCD .(Ⅱ)建立如图坐标系H xyz -.()500B ,,,()130C ,,,()'003D ,,,()130A -,,,()430AB =uu u r ,,,()'133AD =-uuur ,,,()060AC =uuu r ,,,设面'ABD 法向量()1n x y z =,,u r ,由1100n AB n AD ⎧⋅=⎪⎨'⋅=⎪⎩得430330x y x y z +=⎧⎨-++=⎩,取45y z ⎪=-⎨⎪=⎩,∴()1345n =-u r ,,. 同理可得面'AD C 的法向量()2301n =u u r ,,,∴1212cos n n n n θ⋅==u r u u r u r u u r,∴sin θ. 34.【解析】(Ⅰ)由已知得232==AD AM , 取BP 的中点T ,连接TN AT ,.由N 为PC 中点知BC TN //,221==BC TN . 又BC AD //,故TN 平行且等于AM ,四边形A M NT 为平行四边形,于是AT MN //.因为⊂AT 平面PAB ,⊄MN 平面PAB ,所以//MN 平面PAB .(Ⅱ)取BC 的中点E ,连结AE ,由AC AB =得BC AE ⊥,从而AD AE ⊥, 且5)2(2222=-=-=BC AB BE AB AE . 以A 为坐标原点,AE 的方向为x 轴正方向,建立如图所示的空间直角坐标系xyz A -,由题意知,)4,0,0(P ,)0,2,0(M ,)0,2,5(C ,)2,1,25(N , (0,2,4)PM =-,)2,1,25(-=PN , )2,1,25(=.设(,,)x y z =n 为平面PMN 的法向量,则00PM PN ⎧⋅=⎪⎨⋅=⎪⎩n n ,即⎪⎩⎪⎨⎧=-+=-0225042z y x z x , 可取(0,2,1)n =, 于是||85|cos ,|25||||n AN n AN n AN ⋅<>== 35.【解析】(Ⅰ)设AC BE O =,连结OF ,EC ,由于E 为AD 的中点,1,//2AB BC AD AD BC ==, 所以//,AE BC AE AB BC ==,因此四边形ABCE 为菱形,所以O 为AC 的中点,又F 为PC 的中点,因此在PAC ∆中,可得//AP OF .又OF ⊂平面BEF ,AP ⊄平面BEF ,所以AP ∥平面BEF .(Ⅱ)由题意知,//,ED BC ED BC =,所以四边形BCDE 为平行四边形, 因此//BE CD .又AP ⊥平面PCD ,所以AP CD ⊥,因此AP BE ⊥. 因为四边形ABCE 为菱形,所以BE AC ⊥.又AP AC A =,AP ,AC ⊂平面P AC ,所以BE ⊥平面PAC .36.【解析】(Ⅰ)∵D E ,为PC AC ,中点,∴DE ∥P A ∵PA ⊄平面DEF ,DE ⊂平面DEF ,∴P A ∥平面DEF(Ⅱ)∵D E ,为PC AC ,中点,∴132DE PA == ∵E F ,为AC AB ,中点,∴142EF BC == ∴222DE EF DF +=,∴90DEF ∠=°,∴DE ⊥EF∵//DE PA PA AC ⊥,,∴DE AC ⊥∵AC EF E =,∴DE ⊥平面ABC∵DE⊂平面BDE,∴平面BDE⊥平面ABC.37.【解析】(Ⅰ)连接BD交AC于点O,连结EO.因为ABCD为矩形,所以O为BD的中点.又E为PD的中点,所以EO∥PB.EO⊂平面AEC,PB⊄平面AEC,所以PB∥平面AEC.(Ⅱ)因为PA⊥平面ABCD,ABCD为矩形,所以AB,AD,AP两两垂直.如图,以A为坐标原点,AB的方向为x轴的正方向,AP为单位长,建立空间直角坐标系A xyz-,则D1),2E1(0,)2AE=.设(,0,0)(0)bm m ,则(c m(AC m=.设1(,,)n x y z=为平面ACE的法向量,则110,0,n ACn AE⎧⋅=⎪⎨⋅=⎪⎩即0,10,2mxy z⎧+=+=,可取1nm=-.又2(1,0,0)n=为平面DAE的法向量,由题设121cos,2n n=12=,解得32m=.因为E为PD的中点,所以三棱锥EACD-的高为12.三棱锥E ACD-的体积11313222V=⨯⨯=.38.【解析】(Ⅰ)证明:如图取PB中点M,连接MF,AM.因为F为PC中点,故MF//BC 且MF=12BC .由已知有BC//AD ,BC=AD .又由于E 为AD 中点, 因而MF//AE 且MF=AE ,故四边形AMFE 为平行四边形,所以EF//AM ,又AM ⊂平面PAB ,而EF ⊄平面PAB ,所以EF//平面PAB .(Ⅱ)(i )证明:连接PE ,BE .因为PA=PD ,BA=BD ,而E 为AD 中点,故PE ⊥AD ,BE ⊥AD ,所以∠PEB 为二面角P-AD-B 的平面角.在三角形PAD 中,由2,AD PA PD ===PE=2.在三角形ABD 中,由BA BD ==,可解得BE=1.在三角形PEB 中,PE=2,BE=1,60PEB ∠=,由余弦定理,可解得90PBE ∠=,即BE ⊥PB ,又BC//AD ,BE ⊥AD ,从而BE ⊥BC ,因此BE ⊥平面PBC .又BE ⊂平面ABCD , 所以平面PBC ⊥平面ABCD .(ii )连接BF ,由(i )知BE ⊥平面PBC .所以∠EFB 为直线EF 与平面PBC 所成的角,由,∠ABP 为直角,而MB=12,可得,故,又BE=1,故在直角三角形EBF 中,sin BE EFB EF ∠==所以直线EF 与平面PBC 39.【解析】(Ⅰ)设点O 为AC ,BD 的交点,由AB =BC ,AD =CD ,得BD 是线段AC 的中垂线.所以O 为AC 的中点,BD ⊥AC .又因为P A ⊥平面ABCD ,BD ⊂平面ABCD ,所以P A ⊥BD .所以BD ⊥平面APC .(Ⅱ)连结OG .由(1)可知OD ⊥平面APC ,则DG 在平面APC 内的射影为OG ,所以∠OGD是DG与平面APC所成的角.由题意得OG=12P A在△ABC中,AC所以OC=12 AC在直角△OCD中,OD2.在直角△OGD中,tan∠OGD=3ODOG=.所以DG与平面APC.(Ⅲ)连结OG.因为PC⊥平面BGD,OG⊂平面BGD,所以PC⊥OG.在直角△P AC中,得PC所以GC=5AC OCPC⋅=.从而PG,所以32 PGGC=.40.【解析】(Ⅰ)由AB是圆O的直径,得AC⊥BC.由PA⊥平面ABC,BC⊂平面ABC,得PA⊥BC,又PA∩AC=A,PA⊂平面PAC,AC⊂平面PAC,所以BC⊥平面PAC.(Ⅱ)连OG并延长交AC与M,链接QM,QO.由G为∆AOC的重心,得M为AC中点,由G为PA中点,得QM//PC.又O 为AB 中点,得OM//BC .因为QM∩MO=M,QM ⊂平面QMO .所以QG//平面PBC .41.【解析】(Ⅰ)因为111A B C ABC -是直三棱柱,所以1CC ⊥平面ABC,又AD ⊂平面ABC ,所以1CC AD ⊥,又因为AD 1,,DE CC ⊥DE ⊂平面11BCC B ,1CC ,DE E ⋂=所以AD ⊥平面11BCC B ,又AD ⊂平面ADE,所以平面ADE ⊥平面11BCC B .(Ⅱ)因为1111AB AC =,F 为11C B 的中点,所以111A F B C ⊥.因为1CC ⊥平面111ABC ,且1A F ⊂平面111ABC ,所以1CC 1.A F ⊥又因为1CC ,11B C ⊂平面11BCC B , 1CC ⋂111B C C =,所以1A F ⊥平面11BCC B ,所以1//A F AD .又AD ⊂平面ADE ,1A F ⊄平面ADE ,所以1//A F 平面ADE .42.【解析】(Ⅰ)AB ⊥平面PAD ,PH ⊂面PAD PH AB ⇒⊥又,PH AD AD AB A PH ⊥=⇒⊥面ABCD(Ⅱ)E 是PB 中点⇒点E 到面BCF 的距离1122h PH == 三棱锥E BCF -的体积1111113326212BCF V S h FC AD h ∆=⨯=⨯⨯⨯⨯=⨯= (Ⅲ)取PA 的中点为G ,连接,DG EG ,PD AD DG PA =⇒⊥,又AB ⊥平面PAD ⇒面PAD ⊥面PAB DG ⇒⊥面PAB ,点,E G 是棱,PB PA 的中点11//,//////22EG AB DF AB EG DF DG EF ⇒⇒⇒,得:EF ⊥平面PAB .43.【证明】:(Ⅰ)在△PAD 中,因为E 、F 分别为AP ,AD 的中点,所以EF//PD .又因为EF ⊄平面PCD ,PD ⊂平面PCD ,所以直线EF//平面PCD .(Ⅱ)连结DB ,因为AB=AD ,∠BAD=60°,所以△ABD 为正三角形,因为F 是AD 的中点,所以BF ⊥AD .因为平面PAD ⊥平面ABCD ,BF ⊂平面ABCD ,平面PAD 平面ABCD=AD ,所以BF ⊥平面PAD .又因为BF ⊂平面BEF ,所以平面BEF ⊥平面PAD .44.【解析】法一:(Ⅰ)证明:取AD 中点G ,连接PG ,BG ,BD .因PA=PD ,有PG AD ⊥,在ABD ∆中,1,60AB AD DAB ==∠=︒,有ABD ∆为等边 三角形,因此,BG AD BG PG G ⊥⋂=, 所以AD ⊥平面PBG ,.AD PB AD GB ⇒⊥⊥又PB//EF ,得AD EF ⊥,而DE//GB 得AD ⊥DE ,又FE DE E ⋂=, 所以AD ⊥平面DEF .(Ⅱ),PG AD BG AD ⊥⊥,PGB ∴∠为二面角P —AD —B 的平面角,在2227,4Rt PAG PG PA AG ∆=-=中 在3sin 60Rt ABG BG AB ∆⋅中,==222734cos 27PG BG PB PGB PG BG +-+-∴∠===-⋅法二:(Ⅰ)取AD 中点为G ,因为,.PA PD PG AD =⊥又,60,AB AD DAB ABD =∠=︒∆为等边三角形,因此,BG AD ⊥, 从而AD ⊥平面PBG .延长BG 到O 且使得PO ⊥OB ,又PO ⊂平面PBG ,PO ⊥AD ,,AD OB G ⋂=所以PO ⊥平面ABCD .以O 为坐标原点,菱形的边长为单位长度,直线OB ,OP 分别为x 轴,z 轴,平行于AD 的直线为y 轴,建立如图所示空间直角坐标系. 设11(0,0,),(,0,0),(,,0),(,,0).22P m G n A n D n -则||||sin 60GB AB=︒=11(((,0),(,).2222n m B nC n E n F ∴++++ 由于3(0,1,0),(,0,0),()2242n mAD DE FE ===+- 得0,0,,,AD DE AD FE AD DE AD FE DE FE E⋅=⋅=⊥⊥⋂=AD ∴⊥平面DEF .(Ⅱ)1(,,),()22PA n mPB n m =--=+-22,1,m m n ====解之得 取平面ABD 的法向量1(0,0,1),n =- 设平面PAD 的法向量2(,,)n a b c = 由2230,0,0,0,2222b bPA n a c PD n a c ⋅=--=⋅=+-=得由得取2n=12cos,7n n∴<>==-45.【解析】(Ⅰ)因为四边形ADEF是正方形,所以FA//ED.故C E D∠为异面直线CE 与AF所成的角.因为FA⊥平面ABCD,所以FA⊥CD.故ED⊥CD.在Rt△CDE中,CD=1,ED=,CE故cos CED∠=EDCE=3.所以异面直线CE和AF所成角的余弦值为3.(Ⅱ)证明:过点B作BG//CD,交AD于点G,则45BGA CDA∠=∠=.由45BAD∠=,可得BG⊥AB,从而CD⊥AB,又CD⊥FA,FA⋂AB=A,所以CD⊥平面ABF.(Ⅲ)解:由(Ⅱ)及已知,可得AG,即G为AD的中点.取EF的中点N,连接GN,则GN⊥EF,因为BC//AD,所以BC//EF.过点N作NM⊥EF,交BC于M,则GNM∠为二面角B-EF-A的平面角.连接GM,可得AD⊥平面GNM,故AD⊥GM.从而BC⊥GM.由已知,可得GM=2.由NG//FA,FA⊥GM,得NG⊥GM.在Rt△NGM中,tanGM1NG4GNM∠==,所以二面角B-EF-A的正切值为14.46.【解析】(Ⅰ)取A D'的中点G,连结GF,CE,由条件易知。
专题八 立体几何 第二十三讲 空间中点、直线、平面之间的位置关系专题训练

专题八 立体几何第二十三讲 空间中点、直线、平面之间的位置关系一、选择题1.(2018全国卷Ⅰ)已知正方体的棱长为1,每条棱所在直线与平面α所成的角相等,则α截此正方体所得截面面积的最大值为A B C D2.(2018全国卷Ⅱ)在长方体1111-ABCD A B C D 中,1==AB BC ,1=AA 线1AD 与1DB 所成角的余弦值为A .15BCD 3.(2018浙江)已知平面α,直线m ,n 满足m α⊄,n α⊂,则“m ∥n ”是“m ∥α”的A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件4.(2018浙江)已知四棱锥S ABCD -的底面是正方形,侧棱长均相等,E 是线段AB 上的点(不含端点),设SE 与BC 所成的角为1θ,SE 与平面ABCD 所成的角为2θ,二面角S AB C --的平面角为3θ,则A .123θθθ≤≤B .321θθθ≤≤C .132θθθ≤≤D .231θθθ≤≤5.(2017新课标Ⅱ)已知直三棱柱111ABC A B C -中,120ABC ∠=,2AB =,11BC CC ==,则异面直线1AB 与1BC 所成角的余弦值为A B C D 6.(2017浙江)如图,已知正四面体D ABC -(所有棱长均相等的三棱锥),P ,Q ,R 分别为AB ,BC ,CA 上的点,AP PB =,2BQ CR QC RA==,分别记二面角D PR Q --,D PQ R --,D QR P --的平面角为α,β,γ,则RQ P AB C DA .γ<α<βB .α<γ<βC .α<β<γD .β<γ<α 7.(2016年全国I )平面α过正方体1111ABCD A B C D -的顶点A ,α∥平面11CB D ,αI 平面ABCD =m ,αI 平面11ABB A =n ,则m ,n 所成角的正弦值为A.2 B.2 C.3 D .138.(2015福建)若,l m 是两条不同的直线,m 垂直于平面α ,则“l m ⊥ ”是“l ∥α”的A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件9.(2015浙江)如图,已知ABC ∆,D 是AB 的中点,沿直线CD 将ACD ∆翻折成A CD '∆,所成二面角A CD B '--的平面角为α,则10.(2014广东)若空间中四条两两不同的直线1234,,,l l l l ,满足122334,,l l l l l l ⊥⊥⊥,则下面结论一定正确的是A .14l l ⊥B .14//l lC .14,l l 既不垂直也不平行D .14,l l 的位置关系不确定11.(2014浙江)设,m n 是两条不同的直线,,αβ是两个不同的平面A .若m n ⊥,//n α,则m α⊥B .若//m β,βα⊥则m α⊥C .若,,m n n ββα⊥⊥⊥则m α⊥D .若m n ⊥,n β⊥,βα⊥,则m α⊥12.(2014辽宁)已知m ,n 表示两条不同直线,α表示平面,下列说法正确的是A .若//,//,m n αα则//m nB .若m α⊥,n α⊂,则m n ⊥C .若m α⊥,m n ⊥,则//n αD .若//m α,m n ⊥,则n α⊥13.(2014浙江)如图,某人在垂直于水平地面ABC 的墙面前的点A 处进行射击训练,已知点A 到墙面的距离为AB ,某目标点P 沿墙面的射击线CM 移动,此人为了准确瞄准目标点P ,需计算由点A 观察点P 的仰角θ的大小(仰角θ为直线AP 与平面ABC 所成角).若15AB m =,25AC m =,30BCM ∠=︒则tan θ的最大值ABCD 14.(2014四川)如图,在正方体1111ABCD A B C D -中,点O 为线段BD 的中点.设点P在线段1CC 上,直线OP 与平面1A BD 所成的角为α,则sin α的取值范围是A1A. B.C .D . 15.(2013新课标Ⅱ)已知,m n 为异面直线,m ⊥平面α,n ⊥平面β.直线l 满足,l m l n ⊥⊥,,l l αβ⊄⊄,则A .α∥β且l ∥αB .α⊥β且l ⊥βC .α与β相交,且交线垂直于lD .α与β相交,且交线平行于l16.(2013广东)设m ,n 是两条不同的直线,α,β是两个不同的平面,下列命题中正确的是A .若αβ⊥,m α⊂,n β⊂,则m n ⊥B .若//αβ,m α⊂,n β⊂,则//m nC .若m n ⊥,m α⊂,n β⊂,则αβ⊥D .若m α⊥,//m n ,//n β,则αβ⊥17.(2012浙江)设l 是直线,,αβ是两个不同的平面A .若l ∥α,l ∥β,则α∥βB .若l ∥α,l ⊥β,则α⊥βC .若α⊥β,l ⊥α,则l ⊥βD .若α⊥β, l ∥α,则l ⊥β18.(2012浙江)已知矩形ABCD ,1AB =,BC =将ABD ∆沿矩形的对角线BD 所在的直线进行翻折,在翻折过程中,A .存在某个位置,使得直线AC 与直线BD 垂直B .存在某个位置,使得直线AB 与直线CD 垂直C .存在某个位置,使得直线AD 与直线BC 垂直D .对任意位置,三对直线“AC 与BD ”,“AB 与CD ”,“AD 与BC ”均不垂直19.(2011浙江)下列命题中错误..的是A .如果平面αβ⊥平面,那么平面α内一定存在直线平行于平面βB .如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面βC .如果平面αγ⊥平面,平面βγ⊥平面,=l αβ,那么l γ⊥平面D .如果平面αβ⊥平面,那么平面α内所有直线都垂直于平面β20.(2010山东)在空间,下列命题正确的是A .平行直线的平行投影重合B .平行于同一直线的两个平面平行C .垂直于同一平面的两个平面平行D .垂直于同一平面的两条直线平行二、填空题21.(2018全国卷Ⅱ)已知圆锥的顶点为S ,母线SA ,SB 所成角的余弦值为78,SA 与圆锥底面所成角为45°,若△SAB 的面积为_____.22.(2016年全国II )α,β是两个平面,m ,n 是两条线,有下列四个命题:①如果m n ⊥,m α⊥,n β∥,那么αβ⊥.②如果m α⊥,n α∥,那么m n ⊥.③如果a β∥,m α⊂,那么m β∥.④如果m n ∥,αβ∥,那么m 与α所成的角和n 与β所成的角相等.其中正确的命题有 .(填写所有正确命题的编号)23.(2015浙江)如图,三棱锥A BCD -中,3AB AC BD CD ====,2AD BC ==,点,M N 分别是,AD BC 的中点,则异面直线,AN CM 所成的角的余弦值是 .24.(2015四川)如图,四边形ABCD 和ADPQ 均为正方形,它们所在的平面互相垂直,动点M 在线段PQ 上,,E F 分别为,AB BC 的中点.设异面直线EM 与AF 所成的角为θ,则θcos 的最大值为_________.25.(2017新课标Ⅲ)a ,b 为空间中两条互相垂直的直线,等腰直角三角形ABC 的直角边AC 所在直线与a ,b 都垂直,斜边AB 以直线AC 为旋转轴旋转,有下列结论: ①当直线AB 与a 成60°角时,AB 与b 成30°角;②当直线AB 与a 成60°角时,AB 与b 成60°角;③直线AB 与a 所成角的最小值为45°;④直线AB 与a 所成角的最小值为60°;其中正确的是________.(填写所有正确结论的编号)三、解答题26.(2018江苏)在平行六面体1111ABCD A B C D -中,1AA AB =,111AB B C ⊥.D 11B 1A 1DC B A求证:(1)AB ∥平面11A B C ; (2)平面11ABB A ⊥平面1A BC .27.(2018浙江)如图,已知多面体111ABCA B C ,1A A ,1B B ,1C C 均垂直于平面ABC ,120ABC ∠=,14A A =,11C C =,12AB BC B B ===.C 1B 1A 1C BA(1)证明:1AB ⊥平面111A B C ;(2)求直线1AC 与平面1ABB 所成的角的正弦值.28.(2017浙江)如图,已知四棱锥P ABCD -,PAD ∆是以AD 为斜边的等腰直角三角形,BC AD ∥,CD AD ⊥,22PC AD DC CB ===,E 为PD 的中点.(Ⅰ)证明:CE ∥平面PAB ;(Ⅱ)求直线CE 与平面PBC 所成角的正弦值.ED B AP29.(2017江苏)如图,在三棱锥A BCD -中,AB ⊥AD ,BC ⊥BD ,平面ABD ⊥平面BCD ,点E 、F (E 与A 、D 不重合)分别在棱AD ,BD 上,且EF ⊥AD .求证:(1)EF ∥平面ABC ;(2)AD ⊥AC .F AB C DE30.(2017山东)如图,几何体是圆柱的一部分,它是由矩形ABCD (及其内部)以AB 边所在直线为旋转轴旋转120︒得到的,G 是DF 的中点.(Ⅰ)设P 是CE 上的一点,且AP BE ⊥,求CBP ∠的大小;(Ⅱ)当3AB =,2AD =,求二面角E AG C --的大小.31.(2017江苏)如图,水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ的高均为32cm ,容器Ⅰ的底面对角线AC 的长为cm ,容器Ⅱ的两底面对角线EG ,11E G 的长分别为14cm 和62cm . 分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm . 现有一根玻璃棒l ,其长度为40cm .(容器厚度、玻璃棒粗细均忽略不计)(1)将l 放在容器Ⅰ中,l 的一端置于点A 处,另一端置于侧棱1CC 上,求l 没入水中部分的长度;(2)将l 放在容器Ⅱ中,l 的一端置于点E 处,另一端置于侧棱1GG 上,求l 没入水中部分的长度.32.(2016全国I )如图,在以A ,B ,C ,D ,E ,F 为顶点的五面体中,面ABEF 为正方形,2AF FD =,90AFD ∠=,且二面角D AF E --与二面角C BE F --都是60.(I )证明:平面ABEF ⊥平面EFDC ;(II )求二面角E BC A --的余弦值.33.(2016全国II )如图,菱形ABCD 的对角线AC 与BD 交于点O ,5AB =,6AC =,点E ,F 分别在AD ,CD 上,54AE CF ==,EF 交BD 于点H .将ΔDEF 沿EF折到ΔD EF '的位置,OD '(I )证明:D H '⊥平面ABCD ;(II )求二面角B D A C '--的正弦值.34.(2016全国III )如图,四棱锥P ABCD -中,PA ⊥底面ABCD ,AD BC ,=3AB AD AC ==,4PA BC ==,M 为线段AD 上一点,2AM MD =,N 为PC 的中点.(Ⅰ)证明MN 平面PAB ;(Ⅱ)求直线AN 与平面PMN 所成角的正弦值.B D35.(2014山东)如图,四棱锥P ABCD -中,AP PCD ⊥平面,AD BC ∥,1,,2AB BC ADE F ==分别为线段,AD PC 的中点.(Ⅰ)求证:AP BEF ∥平面;(Ⅱ)求证:BE PAC ⊥平面.36.(2014江苏)如图,在三棱锥ABC P -中,D ,E ,F 分别为棱AB AC PC ,,的中点.已知AC PA ⊥,,6=PA .5,8==DF BC求证:(Ⅰ)直线PA ∥平面DEF ;(Ⅱ)平面BDE ⊥平面ABC .37.(2014新课标Ⅱ)如图,四棱锥P ABCD -中,底面ABCD 为矩形,PA ⊥平面ABCD ,E 为PD 的中点.(Ⅰ)证明:PB ∥平面AEC ;(Ⅱ)设二面角D AE C --为60°,AP =1,AD求三棱锥E ACD -的体积.38.(2014天津)如图四棱锥P ABCD -的底面ABCD是平行四边形,BA BD ==,2AD =,PA PD ==E ,F 分别是棱AD ,PC 的中点.(Ⅰ)证明: EF ∥平面PAB ; (Ⅱ)若二面角P AD B --为60°, (ⅰ)证明:平面PBC ⊥平面ABCD(ⅱ)求直线EF 与平面PBC 所成角的正弦值.39.(2013浙江)如图,在四棱锥P ABCD -中,PA ⊥面ABCD ,2AB BC ==,AD CD ==,PA =120ABC ∠=,G 为线段PC 上的点.PDB(Ⅰ)证明:BD ⊥面APC ;(Ⅱ)若G 是PC 的中点,求DG 与APC 所成的角的正切值; (Ⅲ)若G 满足PC ⊥面BGD ,求PGGC的值. 40.(2013辽宁)如图,AB 是圆O 的直径,PA 垂直圆O 所在的平面,C 是圆O 上的点.(Ⅰ)求证:BC PAC ⊥平面;(Ⅱ)设Q 为PA 的中点,G 为AOC ∆的重心,求证:QG ∥平面PBC .41.(2012江苏)如图,在直三棱柱111ABC A B C -中,1111AB AC =,D E ,分别是棱1BC CC ,上的点(点D 不同于点C ),且AD DE F ⊥,为11B C 的中点.1求证:(Ⅰ)平面ADE ⊥平面11BCC B ;(Ⅱ)直线1//A F 平面ADE .42.(2012广东)如图所示,在四棱锥P ABCD -中,AB ⊥平面PAD ,//,AB CD PD AD =,E 是PB 中点,F 是DC 上的点,且12DF AB =,PH 为PAD ∆中AD 边上的高.(Ⅰ)证明:PH ⊥平面ABCD ; (Ⅱ)若1,1PH AD FC ===,求三棱锥E BCF -的体积;(Ⅲ)证明:EF ⊥平面PAB .43.(2011江苏)如图,在四棱锥ABCD P -中,平面PAD ⊥平面ABCD ,AB AD =,BAD ∠=60°,E 、F 分别是AP 、AD 的中点.C求证:(Ⅰ)直线EF ∥平面PCD ; (Ⅱ)平面BEF ⊥平面PAD .44.(2011广东)如图在椎体P ABCD -中,ABCD是边长为1的棱形,且DAB ∠=60︒,PA PD ==2PB =,E ,F 分别是BC ,PC 的中点.(Ⅰ)证明:AD ⊥平面DEF ;(Ⅱ)求二面角P AD B --的余弦值.45.(2010天津)如图,在五面体ABCDEF 中,四边形ADEF 是正方形,FA ⊥平面ABCD ,BC∥AD ,CD =1,AD =,∠BAD =∠CDA =45°.(Ⅰ)求异面直线CE 与AF 所成角的余弦值; (Ⅱ)证明CD ⊥平面ABF ; (Ⅲ)求二面角B EF A --的正切值.46.(2010浙江)如图,在平行四边形ABCD 中,AB =2BC ,∠ABC =120°.E 为线段AB 的中点,将△ADE 沿直线DE 翻折成△A DE ',使平面A DE '⊥平面BCD ,F 为线段A C '的中点.(Ⅰ)求证:BF ∥平面A DE ';(Ⅱ)设M 为线段DE 的中点,求直线FM 与平面A DE '所成角的余弦值.专题八 立体几何初步第二十二讲 空间几何体的三视图、表面积和体积答案部分1.C 【解析】解法一 将三视图还原为直观图,几何体是底面为直角梯形,且一条侧棱和底面垂直的四棱锥,如图所示,DCBA P易知,BC AD ∥,1BC =,2AD AB PA ===,AB AD ⊥,PA ⊥平面ABCD ,故PAD ∆,PAB ∆为直角三角形,∵PA ⊥平面ABCD ,BC ⊂平面ABCD ,PA BC ⊥,又BC AB ⊥,且PA AB A =,∴BC ⊥平面PAB ,又PB ⊂平面PAB .BC PB ⊥,∴PBC ∆为直角三角形,容易求得3PC =,CD =,PD =,故PCD ∆不是直角三角形,故选C .解法二 在正方体中作出该几何体的直观图,记为四棱锥P ABCD -,如图,由图可知在此四棱锥的侧面中,直角三角形的个数为3,故选C .PDCBA2.B 【解析】由三视图可知,该几何体为如图①所示的圆柱,该圆柱的高为2,底面周长16.画出该圆柱的侧面展开图,如图②所示,连接MN ,则2=MS ,4=SN ,则从M 到N=B .SNM图① 图②3.A 【解析】由题意知,在咬合时带卯眼的木构件中,从俯视方向看,榫头看不见,所以是虚线,结合榫头的位置知选A .4.B 【解析】设等边三角形ABC 的边长为x ,则21sin 60932x =6x =. 设ABC ∆的外接圆半径为r ,则62sin 60r =,解得r =,所以球心到ABC ∆所在平面的距离2d ==,则点D 到平面ABC 的最大距离146d d =+=,所以三棱锥D ABC -体积的最大值max 116633ABC V S ∆=⨯=⨯=B .5.D 【解析】如图以1AA 为底面矩形一边的四边形有11AAC C 、11AA B B 、11AA D D 、11AA E E 4个,每一个面都有4个顶点,所以阳马的个数为16个.故选D .E 1E AA 1D CD 1C 1B 1B6.C 【解析】由三视图可知,该几何体是一个底面为直角梯形的直四棱柱,所以该几何体的体积1(12)2262V =⨯+⨯⨯=.故选C . 7.B 【解析】由题意可知,该几何体是由一个三棱锥和一个三棱柱构成,则表面所有梯形之和为12(24)2122⨯+⨯=.选B .8.B 【解析】解法一 由题意,该几何体是一个组合体,下半部分是一个底面半径为3,高为4的圆柱,其体积213436V =π⨯⨯=π,上半部分是一个底面半径为3,高为6的圆柱的一半, 其体积221(36)272V =⨯π⨯⨯=π, 故该组合体的体积12362763V V V =+=π+π=π.故选B .解法二 该几何体可以看作是高为14,底面半径为3的圆柱的一半,所以体积为21(3)14632ππ⨯⨯=.选B . 9.B 【解析】圆柱的轴截面如图,1AC =,12AB =,所以圆柱底面半径2r BC ==,那么圆柱的体积是22314V r h πππ==⨯⨯=,故选B . 10.A 【解析】该几何体是由一个高为3的圆锥的一半,和高为3的三棱锥组成(如图),其体积为:21111(13)(213)132322ππ⨯⨯⨯+⨯⨯⨯=+.选A .11.B 【解析】借助正方体可知粗线部分为该几何体是四棱锥,2=B .12.C 【解析】由三视图可知,四棱锥的底面是边长为1的正方形,高为1,其体积21111133V =⨯⨯=.设半球的半径为R,则2R =2R =,所以半球的体积32142326V π=⨯⨯=.故该几何体的体积1213V V V =+=+.故选C . 13.A 【解析】由三视图可得此几何体为一个球切割掉18后剩下的几何体, 设球的半径为r ,故37428833r ππ⨯=,所以2r =, 表面积227341784S r r πππ=⨯+=,选A .14.C 【解析】该几何体是圆锥与圆柱的组合体,设圆柱底面圆半径为r ,周长为c ,圆锥母线长为l ,圆柱高为h . 由图得2r =,2π4πc r ==,由勾股定理得:4l =,21π2S r ch cl =++表4π16π8π=++28π=,故选C .15.B 【解析】由三视图可得该几何体是平行六面体,上下底面是边长为3的正方形,故面积都是9,前后两个侧面是平行四边形,一边长为3、该边上的高为6,故面积都为18,左右两个侧面是矩形,边长为3,故面积都为2(9 +18+16.C 【解析】由题意得,该几何体为一立方体与四棱锥的组合,∴体积3322231223=⨯⨯+=V ,故选C . 17.D 【解析】由三视图知:该几何体是半个圆柱,其中底面圆的半径为1,母线长为2,所以该几何体的表面积是()1211222342ππ⨯⨯⨯++⨯=+,故选D . 18.A 【解析】这是一个三棱锥与半个圆柱的组合体,2111112(12)12323V ππ=⨯⨯+⨯⨯⨯⨯⨯=+,选A .19.D 【解析】如图,设正方形的棱长为1,则截取部分为三棱锥111A A B D -,其体积为16,又正方体的体积为1,则剩余部分的体积为56,故所求比值为15.A 1AC20.B【解析】 在长、宽、高分别为2、1、1的长方体中,该四面体是如图所示的三棱锥P ABC -,表面积为211222224⨯⨯⨯+⨯=+21.A 【解析】由圆锥的对称性可知,要使其内接长方体最大,则底面为正方形,令此长方体底面对角线长为2x ,高为h ,则由三角形相似可得,212x h-=,所以22h x =-, (0,1)x ∈,长方体体积2232216)2(22)2()327x x x V h x x ++-==-=长方体≤, 当且仅当22x x =-,即23x =时取等号,2121233V ππ=⨯⨯=圆锥,故材料利用率为16827293ππ=,选A .22.B 【解析】由三视图可知,此组合体是由半个圆柱与半个球体组合而成,其表面积为22222422016r r r r ππππ+++=+,所以2r =.23.B 【解析】如图,设辅助正方体的棱长为4,三视图对应的多面体为三棱锥A - BCD,最长的棱为6AD ==,选B .24.C 【解析】原毛坯的体积2(3)654V ππ=⨯⨯=,由三视图可知该零件为两个圆柱的组合体,其体积2212(2)4(3)234V V V πππ'=+=⨯⨯+⨯⨯=,故所求比值为10127V V '-=. 25.A 【解析】如图,将边长为2的正方体截去两个角,∴21226112212S =⨯⨯-⨯⨯+=+表26.A 【解析】圆柱的正视图是矩形,∴选A .27.D 【解析】由三视图画出几何体的直观图,如图所示,则此几何体的表面积1232S S S S S S =-+++正方形斜面,其中1S 是长方体的表面积,2S 是三棱柱的水平放置的一个侧面的面积,3S 是三棱柱的一个底面的面积,可求得2138()S cm =,选D .28.C 【解析】由题意可知AD BC ⊥,由面面垂直的性质定理可得AD ⊥平面11DB C ,又2sin 603AD =⋅=111111121332A B DC B DC V AD S -∆=⋅=⨯, 故选C .29.A 【解析】圆柱的底面半径为1,母线长为1,2112S ππ=⨯⨯=侧. 30.B 【解析】直观图为棱长为2的正方体割去两个底面半径为l 的14圆柱,所以该几何体的体积为321221284ππ-⨯⨯⨯⨯=-. 31.C 【解析】由几何体的形成过程知所得几何体为圆柱,底面半径为1,高为1,其侧面积22S rh ππ==.32.B 【解析】由直观图可知,该几何体由一个长方体和一个截角三棱柱组成.从上往下看,外层轮廓线是一个矩形,矩形内部有一条线段连接的两个三角形.33.A 【解析】由三视图知,该几何体为放到的半个圆柱底面半径为2高为4,上边放一个长为4宽为2高为2长方体,故其体积为21244222π⨯⨯+⨯⨯ =168π+,故选A . 34.A 【解析】还原后的直观图是一个长宽高依次为10,6 ,5的长方体上面是半径为3高为2的半个圆柱.35.C 【解析】几何体是圆柱与圆锥叠加而成它的体积为221353573V πππ=⨯⨯+⨯=36.B 【解析】由三视图可知该几何体的体积:221121232V πππ=⨯⨯+⨯⨯⨯=. 37.D 【解析】通过正视图及俯视图可看出该几何体为半个圆锥和一个三棱锥的组合体,故侧视图可以为D .38.C 【解析】由三视图可知该几何体是底面为等腰梯形的放倒的一个直四棱柱,如图,所以该四棱柱的表面积12(24)444242S =⨯⨯+⨯+⨯+⨯24+48=+39.D 【解析】选项A 正确,∵SD ⊥平面ABCD ,而AC 在平面ABCD 内,所以AC SD ⊥.因为ABCD 为正方形,所以AC BD ⊥,而BD 与SD 相交,所以AC ⊥平面SBD ,所以AC SB ⊥;选项B 正确,因为AB CD ,而CD 在平面SCD 内,AB 不在平面SCD 内,所以AB平面SCD ;选项C 正确,设AC 与BD 的交点为O ,连结SO ,则SA 与平面SBD 所成的角ASO ∠,SC 与平面SBD 所成的角CSO ∠,易知这两个角相等;选项D 错误,AB 与SC 所成的角等于SCD ∠,而DC 与SA 所成的角等于SAB ∠,易知这两个角不相等.40.C 【解析】该几何体由两个长方体组合而成,其表面积等于下面长方体的全面积加上面长方体的4个侧面积之和.2(10810282)2(6882)360S =⨯+⨯+⨯+⨯+⨯=. 41.B 【解析】该几何体上半部是底面边长为4cm ,高为2cm ,的正四棱柱,其体积为344232()cm ⨯⨯=;下半部分是上、下底面边长分别为4cm ,8cm ,高为2cm 的正四棱台,其体积为1224(164864)233⨯+⨯+⨯=,故其总体积为2243203233+=. 42.112【解析】连接1AD ,1CD ,1B A ,1B C ,AC ,因为E ,H 分别为1AD ,1CD 的中点,所以EH ∥AC ,12EH AC =,因为F ,G 分别为1B A ,1B C 的中点,所以FG ∥AC ,12FG AC =,所以EH FG ∥,EH FG =,所以四边形EHGF 为平行四边形,又EG HF =,EH HG =,所以四边形EHGF 为正方形,又点M 到平面EHGF 的距离为12,所以四棱锥M EFGH -的体积为21113212⨯⨯=. 43.43【解析】正方体的棱长为2,以其所有面的中心为顶点的多面体是正八面体,其中正,则该正八面体的体积为214233⨯⨯=.44.OE 交AC 于G ,由题意OE AC ⊥,设等边三角形ABC 的边长为x (05x <<),则OG x =,5GE x =. G ODFECBA由题意可知三棱锥的高h ===底面24ABC S x ∆=,三棱锥的体积为2134V x =⨯=设45()53h x x x =-,则34()203h x x x '=-(05x <<), 令()0h x '=,解得x =(0,x ∈时,()0h x '>,()h x 单调递增;当x ∈时,()0h x '<,()h x 单调递减,所以x =()h x取得最大值4h =所以2max 1212V === 45.9π2【解析】设正方体边长为a ,由2618a =,得23a =,外接球直径为23R ==,344279πππ3382V R ==⨯=. 46.22π+【解析】由三视图可知,长方体的长、宽、高分别为2,1,1,圆柱的高为1,底面圆半径为1,所以2π1π21121242V ⨯=⨯⨯+⨯⨯=+.47.32【解析】设球的半径为r ,则213223423V r r V r ππ⨯==. 48.2【解析】根据三视图可知该四棱锥的底面是底边长为2m ,高为1m 的平行四边形,四棱锥的高为3m ,故其体积为121323⨯⨯⨯=(3m ). 49.83π【解析】由三视图可知,该几何体是中间为一个底面半径为1,高为2的圆柱,两端是底面半径为1,高为1的圆锥,所以该几何体的体积22181221133V πππ=⨯⨯+⨯⨯⨯⨯=.50.12【解析】由题意知,该六棱锥是正六棱锥,设该六棱锥的高为h ,则216234h ⨯⨯⨯=,解得1h =,2=,该六棱锥的侧面积为1122122⨯⨯=. 51.PA ⊥平面ABC ,2PA =,AB BC ==2CA =,所以PB ==,PC ==52.32【解析】设甲、乙两个圆柱的底面半径分别是12,r r ,母线长分别是12,l l . 则由1294S S =,可得1232r r =.又两个圆柱的侧面积相等,即112222rl r l ππ=, 则112223l r l r ==,所以111222923432V S l V S l ==⨯=. 53【解析】设正方体的棱长为a2r =,即球半径r =.若球的体积为92π,即349)32ππ=,解得a =54.1:24【解析】三棱锥ADE F -与三棱锥ABC A -1的 相似比为1:2,故体积之比为1:8.又因三棱锥ABC A -1与三棱柱ABC C B A -111的体积之比 为1:3.所以,三棱锥ADE F -与三棱柱ABC C B A -111的体积之比为1:24. 另:112211111334224ADE ABC V S h S h V ==⨯⨯=,所以121:24V V =. 55.38【解析】由三视图知,此几何体为一个长为4,宽为3,高为1的长方体中心,去除一个半径为1的圆柱,所以表面积为()243+41+31+2-2=38ππ⨯⨯⨯⨯. 56.92【解析】该几何体是底面是直角梯形,高为4的直四棱柱几何体的表面积是12(25)4(2544922S =⨯⨯+⨯++++⨯=.57111322sin 603332ABC V PA S ∆=⋅=⋅⋅⋅⋅⋅=.58.13【解析】由圆锥底面面积是这个球面面积的316,得223416r R ππ=,所以r R =,则小圆锥的高为2R,大圆锥的高为32R ,所以比值为13.59.【解析】(Ⅰ)证明:PD ⊥平面,,ABCD PD PCD ⊂∴平面PCD ⊥平面ABCD ,平面PCD平面ABCD CD =,MD ⊂平面ABCD ,MD CD ⊥,∴MD ⊥平面PCD ,,,,,,CF PCD CF MD CF MF MD MF MDF ⊂∴⊥⊥⊂平面又平面MD MF M =,∴CF MDF ⊥平面.(Ⅱ)00,,60,30,CF MDF CF DF PCD CDF ⊥∴⊥∠=∴∠=平面又易知11==,22CF CD 从而12,,,2DE CF EF DC DE PE DP CP ∴=∴=∴=∥12CDE S CD DE ∆=⋅=,22MD ====11.338216M CDE CDE V S MD -∆∴=⋅=⋅=60.【解析】(Ⅰ)由已知得ABC DBC ∆≅∆,因此AC DC =,又G 为AD 的中点,CG AD ⊥;同理BG AD ⊥;因此AD ⊥平面BCG ,又EF AD ∥,∴EF ⊥平面BCG .CD(Ⅱ)在平面ABC 内,做AO CB ⊥,交CB 的延长线于O ,由平面ABC ⊥平面BCD ,知AO ⊥平面BCD ,又G 为AD 的中点,因此G 到平面BCD 的距离h 是AO 的一半,在AOB ∆中,sin 603AO AB =⋅=1132D BCG G BCD DBG V V S h --∆==⨯⨯=. 61.【解析】(Ⅰ)连结1AC ,交1A C 于点O ,连结DO ,则O 为1AC 的中点,因为D 为AB的中点,所以OD ∥1BC ,又因为OD ⊂平面1A CD ,1BC ⊄平面1A CD , 所以1BC //平面1A CD ;(Ⅱ)由题意知 CD ⊥平面11ABB A .再由12AA AC CB ===,AB =90ACB ∠=,CD =1A D =DE =13A E =.故22211A D DE A E +=,即1DE A D ⊥所以111132C A DE V -=⨯=. 62.【解析】(Ⅰ)证明:连接AC ,交于BD 于O 点,连接PO .因为底面ABCD 是菱形,所以,AC BD BO DO ⊥=,由PB PD =知,PO BD ⊥.再由PO AC O ⋂=知,BD ⊥面APC ,因此BD PC ⊥.(Ⅱ)解:因为E 是P A 的中点,所以1122P BCE C PEB C PAB B APC V V V V ----=== 由2PB PD AB AD ====知,ABD PBD ≅ 因为60BAD ∠=,所以1PO AO AC BO ====.又222,PA PO AO PA PO AC =+=⊥即.故132APCSPO AC =∙=. 由(1)知,1111,2232P BCE B APC APCBO APC V V BO S --⊥==∙∙∙=面因此. 63.【解析】(1)由已知可得AE =3,BF =4,则折叠完后EG =3,GF =4,又因为EF =5,所以可得EG GF ⊥,又因为CF EGF ⊥底面,可得CF EG ⊥,即EG CFG ⊥面所以平面DEG ⊥平面CFG .(2)过G 作GO 垂直于EF ,GO 即为四棱锥G -EFCD 的高, 所以所求体积为11124516335CDEF S GO ⋅=⨯⨯⨯=. 64.【解析】(I )由条件知PDAQ 为直角梯形因为QA ⊥平面ABCD ,所以平面PDAQ ⊥平面ABCD ,交线为AD .又四边形ABCD 为正方形,DC ⊥AD ,所以DC ⊥平面PDAQ ,可得PQ ⊥DC .在直角梯形PDAQ 中可得DQ =PQ =2PD ,则PQ ⊥QD 所以PQ ⊥平面DCQ .(II )设AB =a .由题设知AQ 为棱锥Q —ABCD 的高,所以棱锥Q —ABCD 的体积311.3V a =由(I )知PQ 为棱锥P —DCQ 的高,而PQ ,△DCQ 的面积为22a , 所以棱锥P —DCQ 的体积为321.3V a =故棱锥Q —ABCD 的体积与棱锥P —DCQ 的体积的比值为1.。
文科数学高考真题分类汇编 空间中点、直线、平面之间的位置关系

(1)证明:MN∥平面 C1DE; (2)求点 C 到平面 C1DE 的距离.
15.(2019 天津文 17)如图,在四棱锥 P − ABCD 中,底面 ABCD 为平行四边形, PCD 为等边三角形,平面 PAC ⊥平面 PCD, PA ⊥ CD , CD = 2, AD = 3,
下面结论一定正确的是
A. l1 ⊥ l4 B.l1 / /l4 C. l1 , l4 既不垂直也不平行 D. l1 , l4 的位置关系不确定
12.(2014 浙江)设m, n 是两条不同的直线,, 是两个不同的平面
A.若 m ⊥ n , n// ,则 m ⊥
B.若 m // , ⊥ 则m ⊥
点.若三棱锥 O − ABC体积的最大值为 36,则球 O 的表面积为
A. 36
B. 64
C.144
D.256
9.(2015 广东)若直线l1 和l2 是异面直线,l1在平面 内,l2 在平面 内,l 是平面 与平
面 的交线,则下列命题正确的是
A. l 与l1, l2 都不相交
B. l 与l1 ,l2 都相交
放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为 8 尺,米堆的高为 5 尺,
问米堆的体积和堆放的米各为多少?”已知 1 斛米的体积约为 1.62 立方尺,圆周率约为 3,
估算出堆放的米约有
A.14斛
B. 22 斛
C. 36 斛
D. 66 斛
8.(2015 新课标 2)已知 A 、 B是球O 的球面上两点, AOB = 90 ,C 为该球面上的动
13.(2019 全国 1 文 16)已知∠ACB=90°,P 为平面 ABC 外一点,PC=2,点 P 到∠ACB 两边
理科数学2010-2019高考真题分类训练专题八立体几何第二十三讲空间中点、直线、平面之间的位置关系答案

专题八 立体几何第二十三讲 空间中点、直线、平面之间的位置关系答案部分2019年1.解析 如图所示,联结BE ,BD .因为点N 为正方形ABCD 的中心,ECD △为正三角形,平面ECD ⊥平面ABCD ,M 是线段ED 的中点,所以BM ⊂平面BDE ,EN ⊂平面BDE ,因为BM 是BDE △中DE 边上的中线,EN 是BDE △中BD 边上的中线,直线BM ,EN 是相交直线,设DE a =,则2BD a =,2235244BE a a a =+=, 所以6BM a =,223144EN a a a =+=, 所以BM EN ≠.故选B .2.解析:对于A ,α内有无数条直线与β平行,则α与β相交或βα∥,排除; 对于B ,α内有两条相交直线与β平行,则βα∥;对于C ,α,β平行于同一条直线,则α与β相交或βα∥,排除;对于D ,α,β垂直于同一平面,则α与β相交或βα∥,排除.故选B .3.证明:(1)因为D ,E 分别为BC ,AC 的中点,所以ED ∥AB .在直三棱柱ABC-A 1B 1C 1中,AB ∥A 1B 1,所以A 1B 1∥ED .又因为ED ⊂平面DEC 1,A 1B 1⊄平面DEC 1,所以A 1B 1∥平面DEC 1.(2)因为AB =BC ,E 为AC 的中点,所以BE ⊥AC .因为三棱柱ABC-A 1B 1C 1是直棱柱,所以CC 1⊥平面ABC .又因为BE ⊂平面ABC ,所以CC 1⊥BE .因为C 1C ⊂平面A 1ACC 1,AC ⊂平面A 1ACC 1,C 1C ∩AC =C ,所以BE ⊥平面A 1ACC 1.因为C 1E ⊂平面A 1ACC 1,所以BE ⊥C 1E.4.解析:由l ,m 是平面α外的两条不同直线,知:由线面平行的判定定理得: 若l l m α⊥⊥,,则m αP .由线面平行、垂直的性质定理得m αP ,l α⊥,则l m ⊥.2010-2018年1.A 【解析】记该正方体为''''-ABCD A B C D ,正方体的每条棱所在直线与平面α所成的角都相等,即共点的三条棱'A A ,''A B ,''A D 与平面α所成的角都相等,如图,D'B'IJGF E D连接'AB ,'AD ,''B D ,因为三棱锥'''-A AB D 是正三棱锥,所以'A A ,''A B ,''A D 与平面''AB D 所成的角都相等,分别取''C D ,''B C ,'BB ,AB ,AD ,'DD 的中点E ,F ,G ,H ,I ,J ,连接EF ,FG .GH ,IH ,IJ ,IE ,易得E ,F ,G ,H ,I ,J 六点共面,平面EFGHIJ 与平面''AB D 平行,且截正方体所得截面的面积最大,又2======EF FG GH IH IJ JE,所以该正六边形的面积为26(434⨯⨯=,所以α截此正方体所得截面面积的最大值为4,故选A . 2.C 【解析】解法一 如图,F 1E 1F D 1A 1B 1C 1EC DA B补上一相同的长方体1111-CDEF C D E F ,连接1DE ,11B E .易知11∥AD DE ,则11∠B DE 为异面直线1AD 与1DB 所成角.因为在长方体1111-ABCD A B C D 中,1==AB BC,1=AA所以12===DE,1==DB11===B E ,在11∆B DE中,由余弦定理,得22211cos 5∠==B DE , 即异面直线1AD 与1DBC . 解法二 以D 为坐标原点,DA ,DC ,1DD 所在直线分别为x 轴,y 轴,z 轴建立空间直角坐标系,如图所示.由条件可知(0,0,0)D ,(1,0,0)A,1D,1(1B ,所以1(1=-u u u u r AD,1(1,1=u u u u r DB ,则由向量夹角公式,得111111cos ,5||||⋅<>===u u u u r u u u u r u u u u r u u u u r u u u u u r u u u u r AD DB AD DB AD DB , 即异面直线1AD 与1DB所成角的余弦值为5,故选C . 3.A 【解析】若m α⊄,n α⊂,m ∥n ,由线面平行的判定定理知m ∥α.若m ∥α,m α⊄,n α⊂,不一定推出m ∥n ,直线m 与n 可能异面,故“m ∥n ”是“m ∥α”的充分不必要条件.故选A .4.D 【解析】由题意知四棱锥S ABCD -为正四棱锥,如图,E M SODC B A连接BD ,记AC BD O =I ,连接SO ,则SO ⊥平面ABCD ,取AB 的中点M ,连接SM ,OM ,OE ,易得AB SM ⊥,则2SEO θ=∠,3SMO θ=∠,易知32θθ≥. 因为OM ∥BC ,BC AB ⊥,SM AB ⊥,所以3θ也为OM 与平面SAB 所成的角,即BC 与平面SAB 所成的角,再根据最小角定理知,31θθ≤,所以231θθθ≤≤,故选D .5.C 【解析】如图所示,把三棱柱补成四棱柱,异面直线1AB 与1BC 所成角为11B AD ∠B 1A 1D 1C 1D CB A11B D ===1AD =1AB =∴22222211111111cos 25AB AD B D B AD AB AD +-∠===⨯⨯.选C . 6.B 【解析】设O 为三角形ABC 中心,底面如图2,过O 作OE RP ⊥,OF PQ ⊥,OG RQ ⊥,由题意可知tan DO OE α=,tan OD OF β=,tan OD OGγ=, G FE O DC B AP QR 图1 图2由图2所示,以P 为原点建立直角坐标系,不妨设2AB =,则(1,0)A -,(1,0)B,C,O ,∵AP PB =,2BQ CR QC RA==,∴1(3Q,2(3R -,则直线RP的方程为2y x =-,直线PQ的方程为y =,直线RQ 的方程为39y x =+,根据点到直线的距离公式,知21OE =,39OF =,13OG =,∴OF OG OE <<,tan tan tan αγβ<<,因为α,β,γ为锐角,所以αγβ<<.选B7.A 【解析】因为过点A 的平面α与平面11CB D 平行,平面ABCD ∥平面1111A B C D ,所以m ∥11B D ∥BD ,又1A B ∥平面11CB D ,所以n ∥1A B ,则BD 与1A B 所成的角为所求角,所以m ,n A . 8.B 【解析】由“m α⊥且l m ⊥”推出“l α⊂或l α∥”,但由“m α⊥且l α∥”可推出“l m ⊥”,所以“l m ⊥”是“l α∥”的必要而不充分条件,故选B .9.B 【解析】解法一 设ADC θ∠=,2AB =,则由题意知1AD BD A D '===.在空间图形中,连结A B ',设A B '=t .在ΔA DB '中,2222222112cos 22112A D DB A B t t A DB A D DB ''+-+--'∠==='⨯⨯⨯. 过A '作A N DC '⊥,过B 作BM DC ⊥,垂足分别为N M 、.过N 作//NP MB ,使四边形BPNM 为平行四边形,则NP DC ⊥,连结,A P BP ',则A NP '∠就是二面角A CD B '--的平面角,所以A NP α'∠=. 在ΔRt A ND '中,cos cos DN A D A DC θ''=∠=,sin sin A N A D A DC θ'''=∠=. 同理,sin BM PN θ==,cos DM θ=,故2cos BP MN θ==.显然BP ⊥平面A NP ',故BP A P '⊥.在ΔRt A BP '中,222222(2cos )4cos A P A B BP t t θθ''=-=-=-. 在ΔA NP '中,222cos cos 2A N NP A P A NP A N NPα''+-'=∠='⨯ 22222sin sin (4cos )2sin t θθθθ+--==222222222cos 2cos 2sin 2sin sin t t θθθθθ+--=+ 2221cos cos sin sin A DB θθθ'=∠+,所以2221cos cos cos cos cos sin sin A DB A DB A DB θαθθ'''-∠=∠+-∠ 2222221sin cos cos cos (1cos )0sin sin sin A DB A DB θθθθθθ-''=∠+=+∠≥, 所以cos cos A DB α'∠≥(当2πθ=时取等号),因为α,[0,]A DB π'∠∈,而cos y x =在[0,]π上为递减函数,所以A DB α'∠≤,故选B .解法二 若CA CB ≠,则当απ=时,A CB π'∠<,排除D ;当0α=时,0A CB '∠>,0A DB '∠>,排除A 、C ,故选B .10.D 【解析】利用正方体模型可以看出,1l 与4l 的位置关系不确定.选D .11.C 【解析】选项,,A B D 中m 均可能与平面α平行、垂直、斜交或在平面α内,故选C .12.B 【解析】对于选项A ,若//,//,m n αα,则m 与n 可能相交、平行或异面,A 错误;显然选项B 正确;对于选项C ,若m α⊥,m n ⊥,则n α⊂或//n α,C 错误;对于选项D ,若//m α,m n ⊥,则//n α或n α⊂或n 与α相交,D 错误.故选B .13.D 【解析】作PH BC ⊥,垂足为H ,设PH x =,则CH =,由余弦定理AH =1tan tan (0)PH PAH AH xθ=∠==>,故当1x =tan θ. 14.B 【解析】直线OP 与平面1A BD 所成的角为α的取值范围是1112AOA C OA π∠→→∠,由于1sin AOA ∠=,11sin 2C OA ∠==>,sin 12π= 所以sin α的取值范围是.15.D 【解析】作正方形模型,α为后平面,β为左侧面可知D 正确.16.D 【解析】A 中,m n 可能平行、垂直、也可能为异面;B 中,m n 还可能为异面;C 中m应与β中两条相交直线垂直时结论才成立,选D .17.B 【解析】利用排除法可得选项B 是正确的,∵l ∥α,l ⊥β,则αβ.如选项A :l ∥α,l ∥β时,α⊥β或α∥β;选项C :若α⊥β,l ⊥α,l ∥β或l β⊂; 选项D :若α⊥β, l ⊥α,l ∥β或l ⊥β.18.B 【解析】过点A 作AE BD ⊥,若存在某个位置,使得AC BD ⊥,则BD ⊥面ACE ,从而有BD CE ⊥,计算可得BD 与CE 不垂直,则A 不正确;当翻折到AC CD ⊥时,因为BC CD ⊥,所以CD ⊥面ABC ,从而可得AB CD ⊥;若AD BC ⊥,因为BC CD ⊥,所以BC ⊥面ACD ,从而可得BC AC ⊥,而1AB BC =<=,所以这样的位置不存在,故C 不正确;同理,D 也不正确,故选B .19.D 【解析】对于D ,若平面α⊥平面β,则平面α内的某些直线可能不垂直于平面β,即与平面β的关系还可以是斜交、平行或在平面β内,其余选项易知均是正确的.20.D 【解析】D 两平行直线的平行投影不一定重合,故A 错;由空间直线与平面的位置关系及线面垂直与平行的判定与性质定理可知B 、C 均错误,故选D .21.【解析】如图所示,S'SA B设S 在底面的射影为S ',连接AS ',SS '.SAB ∆的面积为2221115sin 1cos 5152216SA SB ASB SA ASB SA ⋅⋅⋅∠=⋅⋅-∠=⋅=, ∴280SA =,45SA =.∵SA 与底面所成的角为45o ,∴45SAS '∠=o ,2cos 45452102AS SA '=⋅=⨯=o . ∴底面周长2410l AS ππ'=⋅=,∴圆锥的侧面积为1454104022ππ⨯⨯=. 22.②③④【解析】对于命题①,可运用长方体举反例证明其错误:如图,不妨设AA '为直线m ,CD 为直线n ,ABCD 所在的平面为α.ABC D ''所在的平面为β,显然这些直线和平面满足题目条件,但αβ⊥不成立.命题②正确,证明如下:设过直线n 的某平面与平面α相交于直线l ,则l n ∥, 由m α⊥,有m l ⊥,从知m n ⊥结论正确.由平面与平面平行的定义知命题③正确.由平行的传递性及线面角的定义知命题④正确.23.78【解析】如图连接ND ,取ND 的中点E ,连接,ME CE ,则//ME AN .则异面直线AN ,CM 所成的角为EMC ∠,由题意可知1CN =,22AN =, ∴2ME =.又22CM =,22DN =,2NE =,∴3CE =,则2227cos 282222CM EM CE CME CM EM +-∠===⨯⨯⨯.24.25【解析】AB 为x 轴,AD 为y 轴,AQ 为z 轴建立坐标系, 设正方形边长为2.cos θ=令[]()0,2)f m m =∈()f m '= []0,2,()0m f m '∈∴<Qmax 2()(0)5f m f ==,即max 2cos 5θ=. 25.②③【解析】如图BDEF 为底面圆的内接正方形,设1AC BC ==,则AB AD AE AF FB FE ED BD ========,即侧面均为等边三角形,∵AC ⊥底面BDEF , FED C B A假设a FB ∥,由题意b BD ∥,当直线AB 与a 成60°角时,由图可知AB 与b 成60°角,所以①错,②正确;假设a EB ∥,可知③正确,④错.所以正确为②③.26.【证明】(1)在平行六面体1111ABCD A B C D -中,AB ∥11A B .因为AB ⊄平面11A B C ,11A B ⊂平面11A B C ,所以AB ∥平面11A B C .D 1C 1B 1A 1DCBA(2)在平行六面体1111ABCD A B C D -中,四边形11ABB A 为平行四边形. 又因为1AA AB =,所以四边形11ABB A 为菱形, 因此1AB ⊥1A B .又因为1AB ⊥11B C ,BC ∥11B C , 所以1AB ⊥BC .又因为1A B I BC =B ,1A B ⊂平面1A BC ,BC ⊂平面1A BC , 所以1AB ⊥平面1A BC . 因为1AB ⊂平面11ABB A , 所以平面11ABB A ⊥平面1A BC .27.【解析】(1)由2AB =,14AA =,12BB =,1AA AB ⊥,1BB AB ⊥得111AB A B ==,所以2221111A B AB AA +=.故111AB A B ⊥.由2BC =,12BB =,11CC =,1BB BC ⊥,1CC BC ⊥得11B C =由2AB BC ==,120ABC ∠=o得AC =由1CC AC ⊥,得1AC =2221111AB B C AC +=,故111AB B C ⊥.因此1AB ⊥平面111A B C .(2)如图,过点1C 作111C D A B ⊥,交直线11A B 于点D ,连结AD .DABCA 1B 1C 1由1AB ⊥平面111A B C 得平面111A B C ⊥平面1ABB , 由111C D A B ⊥得1C D ⊥平面1ABB , 所以1C AD ∠是1AC 与平面1ABB 所成的角.由11B C =11A B =,11AC得111cos C A B ∠=,111sin C A B ∠=,所以1C D,故111sin C D C AD AC ∠==. 因此,直线1AC 与平面1ABB. 方法二 (1)如图,以AC 的中点O 为原点,分别以射线OB ,OC 为x ,y 轴的正半轴,建立空间直角坐标系O xyz -.A由题意知各点坐标如下:(0,A ,(1,0,0)B,1(0,A ,1(1,0,2)B,1C ,因此1(1AB =u u u r,11(12)A B =-u u u u r,113)AC =-u u u u r , 由1110AB A B ⋅=u u u r u u u u r得111AB A B ⊥. 由1110AB AC ⋅=u u u r u u u u r得111AB AC ⊥. 所以1AB ⊥平面111A B C .(2)设直线1AC 与平面1ABB 所成的角为θ.由(1)可知1AC =u u u u r,AB =u u u r ,1(0,0,2)BB =u u u r,设平面1ABB 的法向量=()x,y,z n .由100AB BB ⎧⋅=⎪⎨⋅=⎪⎩u u u r u u u r n n,即020x z ⎧+=⎪⎨=⎪⎩,可取(=n .所以111||sin |cos ,|||||AC AC AC θ⋅=<>==⋅u u u u ru u u u r u u u u r n n n . 因此,直线1AC 与平面1ABB28.【解析】(Ⅰ)如图,设P A 中点为F ,连结EF ,FB .D A因为E,F分别为PD,P A中点,所以EF∥AD且12EF AD=,又因为BC∥AD,12BC AD=,所以EF∥BC且EF=BC,即四边形BCEF为平行四边形,所以CE∥BF,因此CE∥平面P AB.(Ⅱ)分别取BC,AD的中点为M,N.连结PN交EF于点Q,连结MQ.因为E,F,N分别是PD,P A,AD的中点,所以Q为EF中点,在平行四边形BCEF中,MQ∥CE.由PAD∆为等腰直角三角形得PN⊥AD.由DC⊥AD,N是AD的中点得BN⊥AD.所以AD⊥平面PBN,由BC∥AD得BC⊥平面PBN,那么,平面PBC⊥平面PBN.过点Q作PB的垂线,垂足为H,连结MH.MH是MQ在平面PBC上的射影,所以∠QMH是直线CE与平面PBC所成的角.设CD=1.在PCD∆中,由PC=2,CD=1,PD得CE,在△PBN中,由PN=BN=1,PB14QH=,在Rt MQH ∆中,14QH =,MQ ,所以sin QMH ∠=所以,直线CE 与平面PBC 所成角的正弦值是8. 29.【解析】证明:(1)在平面ABD 内,因为AB AD ⊥,EF AD ⊥,所以EF AB ∥.又因为EF ⊄平面ABC ,AB ⊂平面ABC ,所以EF ∥平面ABC . (2)因为平面ABD ⊥平面BCD , 平面ABD I 平面BCD =BD ,BC ⊂平面BCD ,BC BD ⊥,所以BC ⊥平面ABD .因为AD ⊂平面ABD ,所以BC ⊥AD .又AB AD ⊥,BC AB B =I ,AB ⊂平面ABC ,BC ⊂平面ABC , 所以AD ⊥平面ABC , 又因为AC 平面ABC , 所以AD AC ⊥.30.【解析】(Ⅰ)因为AP BE ⊥,AB BE ⊥,AB ,AP 平面ABP ,AB AP A =I ,所以BE ⊥平面ABP , 又BP ⊂平面ABP ,所以BE BP ⊥,又120EBC ∠=︒, 因此30CBP ∠=︒ (Ⅱ)解法一:取»EC的中点H ,连接EH ,GH ,CH . 因为120EBC ∠=︒, 所以四边形BEHC 为菱形,所以223213AE GE AC GC ====+=. 取AG 中点M ,连接EM ,CM ,EC . 则EM AG ⊥,CM AG ⊥, 所以EMC ∠为所求二面角的平面角.又1AM =,所以13123EM CM ==-=. 在BEC ∆中,由于120EBC ∠=︒,由余弦定理得22222222cos12012EC =+-⨯⨯⨯︒=, 所以23EC =,因此EMC ∆为等边三角形, 故所求的角为60︒. 解法二:以B 为坐标原点,分别以BE ,BP ,BA 所在的直线为x ,y ,轴,建立如图所示的空间直角坐标系.由题意得(0,0,3)A (2,0,0)E,G,(C -,故(2,0,3)AE =-u u u r,AG =u u u r ,(2,0,3)CG =u u u r,设111(,,)m x y z =是平面AEG 的一个法向量.由00m AE m AG ⎧⋅=⎪⎨⋅=⎪⎩u u u r u u u r可得1111230,0,x z x -=⎧⎪⎨+=⎪⎩ 取12z =,可得平面AEG的一个法向量(3,2)=m . 设222(,,)n x y z =是平面ACG 的一个法向量.由00n AG n CG ⎧⋅=⎪⎨⋅=⎪⎩u u u ru u u r可得22220,230,x x z ⎧+=⎪⎨+=⎪⎩ 取22z =-,可得平面ACG的一个法向量(3,2)n =-. 所以1cos ,||||2m n m n m n ⋅<>==⋅.因此所求的角为60︒.31.【解析】(1)由正棱柱的定义,1CC ⊥平面ABCD ,所以平面11A ACC ⊥平面ABCD ,1CC AC ⊥. 记玻璃棒的另一端落在1CC 上点M 处.因为AC =40AM =.所以30MN ==,从而3sin 4MAC ∠=. 记AM 与水平的交点为1P ,过1P 作11PQ AC ⊥,1Q 为垂足, 则11PQ ⊥平面ABCD ,故1112PQ =, 从而11116sin PQ AP MAC==∠.答:玻璃棒l 没入水中部分的长度为16cm .( 如果将“没入水中部分”理解为“水面以上部分”,则结果为24cm)(2)如图,O ,1O 是正棱台的两底面中心. 由正棱台的定义,1OO ⊥平面 EFGH , 所以平面11E EGG ⊥平面EFGH ,1OO ⊥EG . 同理,平面11E EGG ⊥平面1111E F G H ,1OO ⊥11E G . 记玻璃棒的另一端落在1GG 上点N 处.过G 作GK ⊥11E G ,K 为垂足, 则GK =1OO =32. 因为EG = 14,11E G = 62,所以1KG =6214242-=,从而222211 243240GG KG GK =+=+=. 设1,,EGG ENG αβ==∠∠则114sin sin()cos 25KGG KGG απ=+==∠∠.因为2απ<<π,所以3cos 5α=-.在ENG △中,由正弦定理可得4014sin sin αβ=,解得7sin 25β=. 因为02βπ<<,所以24cos 25β=. 于是sin sin()sin()sin cos cos sin NEG αβαβαβαβ=π--=+=+∠42473(35)525255=⨯+-⨯=. 记EN 与水面的交点为2P ,过2P 作22P Q EG ⊥,2Q 为垂足,则 22P Q ⊥平面EFGH ,故22P Q =12,从而 2EP =2220sin P NEGQ =∠.答玻璃棒l 没入水中部分的长度为20cm .(如果将“没入水中部分”理解为“水面以上部分”,则结果为20cm) 32.【解析】(Ⅰ)由已知可得AF DF ⊥,AF FE ⊥,所以AF ⊥平面EFDC .又AF ⊂平面ABEF ,故平面ABEF ⊥平面EFDC .(Ⅱ)过D 作DG EF ⊥,垂足为G ,由(Ⅰ)知DG ⊥平面ABEF .以G 为坐标原点,GF u u u r 的方向为x 轴正方向,||GF uuu r为单位长度,建立如图所示的空间直角坐标系G xyz -.由(Ⅰ)知DFE ∠为二面角D AF E --的平面角,故60DFE ∠=o,则2DF =,DG =,可得(1,4,0)A ,(3,4,0)B -,(3,0,0)E -,D .由已知,AB EF ∥,所以AB ∥平面EFDC .又平面ABCD I 平面EFDC DC =,故AB CD ∥,CD EF ∥.由BE AF ∥,可得BE ⊥平面EFDC ,所以CEF ∠为二面角C BE F --的平面角,60CEF ∠=o.从而可得(C -.所以EC =u u u r ,(0,4,0)EB =u u u r,(3,AC =--u u u r ,(4,0,0)AB =-u u u r.设(),,n x y z =r是平面BCE 的法向量,则C 00n n ⎧⋅E =⎪⎨⋅EB =⎪⎩u u u r r u u ur r,即040x y ⎧=⎪⎨=⎪⎩,所以可取(3,0,n =r.设m r 是平面CD AB 的法向量,则C 0m m ⎧⋅A =⎪⎨⋅AB =⎪⎩u u u r r u u u rr ,同理可取()4m =r.则cos ,19n m n m n m ⋅==-r r r r r r .故二面角C E-B -A 的余弦值为21919-.33.【解析】(I )证明:∵54AE CF ==, ∴AE CFAD CD=,∴EF AC ∥. ∵四边形ABCD 为菱形, ∴AC BD ⊥,∴EF BD ⊥, ∴EF DH ⊥,∴EF D H '⊥. ∵6AC =,∴3AO =;又5AB =,AO OB ⊥,∴4OB =, ∴1AEOH OD AO=⋅=,∴3DH D H '==, ∴222'OD OH D H '=+,∴'D H OH ⊥. 又∵OH EF H =I ,∴'D H ⊥面ABCD .(Ⅱ)建立如图坐标系H xyz -.()500B ,,,()130C ,,,()'003D ,,,()130A -,,, ()430AB =uu u r ,,,()'133AD =-uuur ,,,()060AC =uuu r,,, 设面'ABD 法向量()1n x y z =,,u r,由1100n AB n AD ⎧⋅=⎪⎨'⋅=⎪⎩u u r u u u r u u r u u u u r得430330x y x y z +=⎧⎨-++=⎩,取345x y z =⎧⎪=-⎨⎪=⎩,∴()1345n =-u r ,,. 同理可得面'AD C 的法向量()2301n =u u r,,, ∴12129575cos5210n n n n θ⋅+===⋅u r u u ru r u u r ,∴295sin θ=. 34.【解析】(Ⅰ)由已知得232==AD AM , 取BP 的中点T ,连接TN AT ,. 由N 为PC 中点知BC TN //,221==BC TN . 又BC AD //,故TN 平行且等于AM ,四边形AMNT 为平行四边形,于是AT MN //.因为⊂AT 平面PAB ,⊄MN 平面PAB ,所以//MN 平面PAB .(Ⅱ)取BC 的中点E ,连结AE ,由AC AB =得BC AE ⊥,从而AD AE ⊥, 且5)2(2222=-=-=BC AB BE AB AE . 以A 为坐标原点,AE u u u r的方向为x 轴正方向,建立如图所示的空间直角坐标系xyz A -,由题意知,)4,0,0(P ,)0,2,0(M ,)0,2,5(C ,)2,1,25(N , (0,2,4)PM =-u u u u r ,)2,1,25(-=,)2,1,25(=.设(,,)x y z =r n 为平面PMN 的法向量,则00PM PN ⎧⋅=⎪⎨⋅=⎪⎩r u u u u r r u u u rn n ,即⎪⎩⎪⎨⎧=-+=-0225042z y x z x , 可取(0,2,1)n =r,于是||85|cos ,|||||n AN n AN n AN ⋅<>==r u u u rr u u u r r u u u r .35.【解析】(Ⅰ)设AC BE O =I ,连结OF ,EC ,由于E 为AD 的中点,1,//2AB BC AD AD BC ==, 所以//,AE BC AE AB BC ==,因此四边形ABCE 为菱形,所以O 为AC 的中点,又F 为PC 的中点, 因此在PAC ∆中,可得//AP OF .又OF ⊂平面BEF ,AP ⊄平面BEF ,所以AP ∥平面BEF .(Ⅱ)由题意知,//,ED BC ED BC =,所以四边形BCDE 为平行四边形, 因此//BE CD .又AP ⊥平面PCD ,所以AP CD ⊥,因此AP BE ⊥. 因为四边形ABCE 为菱形,所以BE AC ⊥.又AP AC A =I ,AP ,AC ⊂平面P AC ,所以BE ⊥平面PAC . 36.【解析】(Ⅰ)∵D E ,为PC AC ,中点,∴DE ∥P A∵PA ⊄平面DEF ,DE 平面DEF ,∴P A ∥平面DEF (Ⅱ)∵D E ,为PC AC ,中点,∴132DE PA ==∵E F ,为AC AB ,中点,∴142EF BC ==∴222DE EF DF +=,∴90DEF ∠=°,∴DE ⊥EF ∵//DE PA PA AC ⊥,,∴DE AC ⊥ ∵AC EF E =I ,∴DE ⊥平面ABC∵DE 平面BDE ,∴平面BDE ⊥平面ABC . 37.【解析】(Ⅰ)连接BD 交AC 于点O ,连结EO .因为ABCD 为矩形,所以O 为BD 的中点. 又E 为PD 的中点,所以EO ∥PB .EO ⊂平面AEC,PB ⊄平面AEC ,所以PB ∥平面AEC .(Ⅱ)因为PA ⊥平面ABCD ,ABCD 为矩形,所以AB ,AD ,AP 两两垂直.如图,以A 为坐标原点,AB u u u r的方向为轴的正方向,AP u u u r 为单位长,建立空间直角坐标系A xyz -,则D 1),2E 1)2AE =uu u r . 设(,0,0)(0)b m m f ,则(c m (AC m =u u u r.设1(,,)n x y z =为平面ACE 的法向量,则110,0,n AC n AE ⎧⋅=⎪⎨⋅=⎪⎩u u u r u u u r 即0,10,2mx y z ⎧=+=,可取1n m =-. 又2(1,0,0)n =为平面DAE 的法向量,由题设121cos ,2n n =12=,解得32m =. 因为E 为PD 的中点,所以三棱锥E ACD-的高为12.三棱锥E ACD -的体积113132228V =⨯⨯=. 38.【解析】(Ⅰ)证明:如图取PB 中点M ,连接MF ,AM .因为F 为PC 中点,故MF//BC 且MF=12BC .由已知有BC//AD ,BC=AD .又由于E 为AD 中点, 因而MF//AE 且MF=AE ,故四边形AMFE 为平行四边形, 所以EF//AM ,又AM 平面PAB ,而EF ⊄平面PAB , 所以EF//平面PAB .(Ⅱ)(i )证明:连接PE ,BE .因为PA=PD ,BA=BD ,而E 为AD 中点,故PE ⊥AD ,BE ⊥AD ,所以∠PEB 为二面角P-AD-B 的平面角.在三角形PAD 中,由2,AD PA PD ===PE=2.在三角形ABD 中,由BA BD ==,可解得BE=1.在三角形PEB 中,PE=2,BE=1,60PEB ∠=o ,由余弦定理,可解得90PBE ∠=o ,即BE ⊥PB ,又BC//AD ,BE ⊥AD ,从而BE ⊥BC ,因此BE ⊥平面PBC .又BE 平面ABCD , 所以平面PBC ⊥平面ABCD .(ii )连接BF ,由(i )知BE ⊥平面PBC .所以∠EFB 为直线EF 与平面PBC 所成的角,由,∠ABP 为直角,而MB=12,可得故,又BE=1,故在直角三角形EBF 中,sin BE EFB EF ∠==所以直线EF 与平面PBC 39.【解析】(Ⅰ)设点O 为AC ,BD 的交点,由AB =BC ,AD =CD ,得BD 是线段AC 的中垂线. 所以O 为AC 的中点,BD ⊥AC .又因为P A ⊥平面ABCD ,BD ⊂平面ABCD , 所以P A ⊥BD .所以BD ⊥平面APC .(Ⅱ)连结OG .由(1)可知OD ⊥平面APC ,则DG 在平面APC 内的射影为OG ,所以∠OGD是DG与平面APC所成的角.由题意得OG=12P A在△ABC中,AC所以OC=12 AC在直角△OCD中,OD2.在直角△OGD中,tan∠OGD=3ODOG=.所以DG与平面APC.(Ⅲ)连结OG.因为PC⊥平面BGD,OG⊂平面BGD,所以PC⊥OG.在直角△P AC中,得PC所以GC=AC OCPC⋅=从而PG,所以32 PGGC=.40.【解析】(Ⅰ)由AB是圆O的直径,得AC⊥BC.由PA⊥平面ABC,BC⊂平面ABC,得PA⊥BC,又PA∩AC=A,PA⊂平面PAC,AC⊂平面PAC,所以BC⊥平面PAC.(Ⅱ)连OG并延长交AC与M,链接QM,QO.由G为∆AOC的重心,得M为AC中点,由G为PA中点,得QM//PC.又O 为AB 中点,得OM//BC . 因为QM∩MO=M,QM ⊂平面QMO . 所以QG//平面PBC .41.【解析】(Ⅰ)因为111ABC A B C -是直三棱柱,所以1CC ⊥平面ABC,又AD ⊂平面ABC ,所以1CC AD ⊥,又因为AD 1,,DE CC ⊥DE ⊂平面11BCC B ,1CC ,DE E ⋂=所以AD ⊥平面11BCC B ,又AD ⊂平面ADE,所以平面ADE ⊥平面11BCC B .(Ⅱ)因为1111A B AC =,F 为11C B 的中点,所以111A F B C ⊥.因为1CC ⊥平面111A B C ,且1A F ⊂平面111A B C ,所以1CC 1.A F ⊥又因为1CC ,11B C ⊂平面11BCC B ,1CC ⋂111B C C =,所以1A F ⊥平面11BCC B ,所以1//A F AD .又AD ⊂平面ADE ,1A F ⊄平面ADE ,所以1//A F 平面ADE . 42.【解析】(Ⅰ)AB ⊥平面PAD ,PH ⊂面PAD PH AB ⇒⊥又,PH AD AD AB A PH ⊥=⇒⊥I 面ABCD (Ⅱ)E 是PB 中点⇒点E 到面BCF 的距离1122h PH == 三棱锥E BCF -的体积11111133262BCF V S h FC AD h ∆=⨯=⨯⨯⨯⨯=⨯= (Ⅲ)取PA 的中点为G ,连接,DG EG ,PD AD DG PA =⇒⊥, 又AB ⊥平面PAD ⇒面PAD ⊥面PAB DG ⇒⊥面PAB , 点,E G 是棱,PB PA 的中点11//,//////22EG AB DF AB EG DF DG EF ⇒⇒⇒,得:EF ⊥平面PAB .43.【证明】:(Ⅰ)在△PAD 中,因为E 、F 分别为AP ,AD 的中点,所以EF//PD .又因为EF ⊄平面PCD ,PD ⊂平面PCD ,所以直线EF//平面PCD .C(Ⅱ)连结DB ,因为AB=AD ,∠BAD=60°,所以△ABD 为正三角形,因为F 是AD 的中点,所以BF ⊥AD .因为平面PAD ⊥平面ABCD ,BF ⊂平面ABCD ,平面PAD I 平面ABCD=AD ,所以BF ⊥平面PAD .又因为BF ⊂平面BEF ,所以平面BEF ⊥平面PAD .44.【解析】法一:(Ⅰ)证明:取AD 中点G ,连接PG ,BG ,BD .因PA=PD ,有PG AD ⊥,在ABD ∆中,1,60AB AD DAB ==∠=︒,有ABD ∆为等边 三角形,因此,BG AD BG PG G ⊥⋂=, 所以AD ⊥平面PBG ,.AD PB AD GB ⇒⊥⊥又PB//EF ,得AD EF ⊥,而DE//GB 得AD ⊥DE ,又FE DE E ⋂=, 所以AD ⊥平面DEF .(Ⅱ),PG AD BG AD ⊥⊥Q ,PGB ∴∠为二面角P —AD —B 的平面角, 在2227,4Rt PAG PG PA AG∆=-=中 在sin 60Rt ABG BG AB ∆⋅o中,=222734cos 27PG BG PB PGB PG BG +-+-∴∠===-⋅法二:(Ⅰ)取AD 中点为G ,因为,.PA PD PG AD =⊥又,60,AB AD DAB ABD =∠=︒∆为等边三角形,因此,BG AD ⊥, 从而AD ⊥平面PBG .延长BG 到O 且使得PO ⊥OB ,又PO ⊂平面PBG ,PO ⊥AD ,,AD OB G ⋂=所以PO ⊥平面ABCD .以O 为坐标原点,菱形的边长为单位长度,直线OB ,OP 分别为x 轴,轴,平行于AD 的直线为y 轴,建立如图所示空间直角坐标系. 设11(0,0,),(,0,0),(,,0),(,,0).22P m G n A n D n -则||||sin 60GB AB=︒=u u ur u u u rQ11(((,,0),(,).22222422n m B nC n E n F ∴++++ 由于(0,1,0),(()2242n mAD DE FE ===+-u u u r u u u r u u u r 得0,0,,,AD DE AD FE AD DE AD FE DE FE E ⋅=⋅=⊥⊥⋂=u u u r u u u ru u u r u u u rAD ∴⊥平面DEF .(Ⅱ)1(,,),()22PA n m PBn m =--=+-u u u r u u u rQ22,1,m m n ====解之得 取平面ABD 的法向量1(0,0,1),n =- 设平面PAD 的法向量2(,,)n a b c =由220,0,0,0,2222b bPA n a c PD n a c ⋅=--=⋅=+-=u u u r u u u r 得由得取2(1,0,2n =12cos ,7n n ∴<>==- 45.【解析】(Ⅰ)因为四边形ADEF 是正方形,所以FA //ED .故CED ∠为异面直线CE与AF 所成的角.因为FA ⊥平面ABCD ,所以FA ⊥CD .故ED ⊥CD . 在Rt △CDE 中,CD =1,ED=CE故cos CED ∠=ED CE=3.所以异面直线CE 和AF所成角的余弦值为3. (Ⅱ)证明:过点B 作BG //CD ,交AD 于点G ,则45BGA CDA ∠=∠=o.由45BAD ∠=o ,可得BG ⊥AB ,从而CD ⊥AB ,又CD ⊥FA ,FA ⋂AB =A ,所以CD ⊥平面ABF .(Ⅲ)解:由(Ⅱ)及已知,可得AG,即G 为AD 的中点.取EF 的中点N ,连接GN ,则GN ⊥EF ,因为BC //AD ,所以BC //EF .过点N 作NM ⊥EF ,交BC 于M ,则GNM ∠为二面角B -EF -A 的平面角.连接GM ,可得AD ⊥平面GNM ,故AD ⊥GM .从而BC ⊥GM .由已知, 可得GM=2.由NG //FA ,FA ⊥GM ,得NG ⊥GM . 在Rt △NGM 中,tan GM 1NG 4GNM ∠==, 所以二面角B -EF -A 的正切值为14.46.【解析】 (Ⅰ)取A D '的中点G ,连结GF ,CE ,由条件易知FG CD ∥,12FG CD =.BE CD ∥,12BE CD =.所以FG BE ∥,FG BE =.故四边形BEGF 为平行四边形,所以BF EG ∥因为EG ⊂平面'A DE ,BF ⊄平面'A DE ,所以BF //平面'A DE (Ⅱ)在平行四边形ABCD 中,设BC a =,则2AB CD a ==,AD AE EB a ===,连CE ,因为0120ABC ∠=在△BCE 中,可得CE a , 在△ADE 中,可得DE =a ,在△CDE 中,因为222CD CE DE =+,所以CE DE ⊥, 在正三角形'A DE 中,M 为DE 中点,所以A M '⊥DE . 由平面'A DE ⊥平面BCD ,可知A M '⊥平面BCD , A M '⊥CE . 取A E '的中点N ,连线NM 、NF , 所以NF ⊥DE ,NF ⊥A M '. 因为DE 交A M '于M , 所以NF ⊥平面'A DE ,则∠FMN 为直线FM 与平面'A DE 所成角. 在Rt △FMN 中,NF a , MN =12a ,FM =a , 则cos FMN ∠=12. 所以直线FM 与平面'A DE 所成角的余弦值为12.。
高考理科数学真题分类 专题八 立体几何 第二十三讲 空间中点、直线、平面之间的位置关系(带答案)
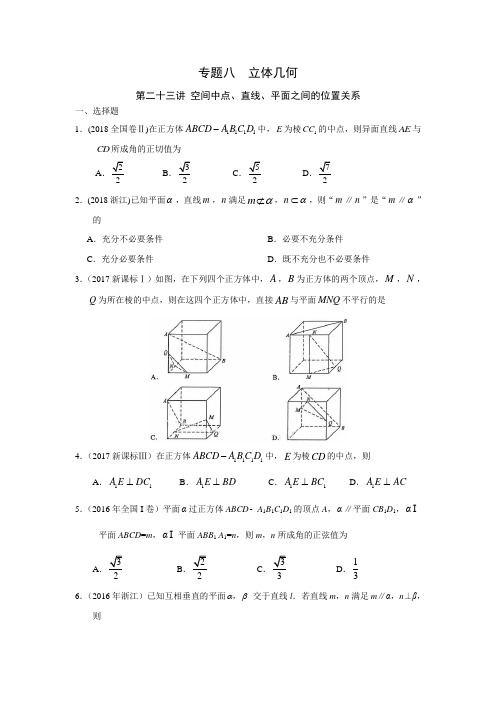
专题八 立体几何第二十三讲 空间中点、直线、平面之间的位置关系一、选择题1.(2018全国卷Ⅱ)在正方体1111-ABCD A BC D 中,E 为棱1CC 的中点,则异面直线AE 与CD 所成角的正切值为A B C D 2.(2018浙江)已知平面α,直线m ,n 满足m α⊄,n α⊂,则“m ∥n ”是“m ∥α”的A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件3.(2017新课标Ⅰ)如图,在下列四个正方体中,A ,B 为正方体的两个顶点,M ,N ,Q 为所在棱的中点,则在这四个正方体中,直接AB 与平面MNQ 不平行的是4.(2017新课标Ⅲ)在正方体1111ABCD A BC D -中,E 为棱CD 的中点,则 A .11A E DC ⊥ B .1A E BD ⊥ C .11A E BC ⊥ D .1A E AC ⊥ 5.(2016年全国I 卷)平面α过正方体ABCD -A 1B 1C 1D 1的顶点A ,α∥平面CB 1D 1,αI平面ABCD =m ,αI 平面ABB 1 A 1=n ,则m ,n 所成角的正弦值为A B .2 C D .136.(2016年浙江)已知互相垂直的平面αβ, 交于直线l .若直线m ,n 满足m ∥α,n ⊥β,则A .m ∥lB .m ∥nC .n ⊥lD .m ⊥n7.(2015新课标1)《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺,问”积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有A .14斛B .22斛C .36斛D .66斛8.(2015新课标2)已知A 、B 是球O 的球面上两点, 90=∠AOB ,C 为该球面上的动点.若三棱锥ABC O -体积的最大值为36,则球O 的表面积为 A .π36 B .π64 C .π144 D .π2569.(2015广东)若直线1l 和2l 是异面直线,1l 在平面α内,2l 在平面β内,l 是平面α与平面β的交线,则下列命题正确的是A .l 与1l ,2l 都不相交B .l 与1l ,2l 都相交C .l 至多与1l ,2l 中的一条相交D .l 至少与1l ,2l 中的一条相交10.(2015浙江)如图,已知ABC ∆,D 是AB 的中点,沿直线CD 将ACD ∆翻折成A CD '∆,所成二面角A CD B '--的平面角为α,则11.(2014广东)若空间中四条两两不同的直线1234,,,l l l l ,满足122334,,l l l l l l ⊥⊥⊥,则下面结论一定正确的是A .14l l ⊥B .14//l lC .14,l l 既不垂直也不平行D .14,l l 的位置关系不确定 12.(2014浙江)设,m n 是两条不同的直线,,αβ是两个不同的平面A .若m n ⊥,//n α,则m α⊥B .若//m β,βα⊥则m α⊥C .若,,m n n ββα⊥⊥⊥则m α⊥D .若m n ⊥,n β⊥,βα⊥,则m α⊥ 13.(2014辽宁)已知m ,n 表示两条不同直线,α表示平面,下列说法正确的是A .若//,//,m n αα则//m nB .若m α⊥,n α⊂,则m n ⊥C .若m α⊥,m n ⊥,则//n αD .若//m α,m n ⊥,则n α⊥14.(2014浙江)如图,某人在垂直于水平地面ABC 的墙面前的点A 处进行射击训练,已知点A 到墙面的距离为AB ,某目标点P 沿墙面的射击线CM 移动,此人为了准确瞄准目标点P ,需计算由点A 观察点P 的仰角θ的大小(仰角θ为直线AP 与平面ABC 所成角)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中复习系列资料专题八 立体几何第二十三讲 空间中点、直线、平面之间的位置关系2019年1.(2019全国Ⅲ理8)如图,点N 为正方形ABCD 的中心,△ECD 为正三角形,平面ECD ⊥平面ABCD ,M 是线段ED 的中点,则A .BM =EN ,且直线BM 、EN 是相交直线B .BM ≠EN ,且直线BM ,EN 是相交直线C .BM =EN ,且直线BM 、EN 是异面直线D .BM ≠EN ,且直线BM ,EN 是异面直线2.(2019全国Ⅱ理7)设α,β为两个平面,则α∥β的充要条件是A .α内有无数条直线与β平行B .α内有两条相交直线与β平行C .α,β平行于同一条直线D .α,β垂直于同一平面3.(2019江苏16)如图,在直三棱柱ABC -A 1B 1C 1中,D ,E 分别为BC ,AC 的中点,AB =BC . 求证:(1)A 1B 1∥平面DEC 1;(2)BE ⊥C 1E .4.(2019北京理12)已知l ,m 是平面a 外的两条不同直线.给出下列三个论断:①l m ⊥; ②m a P ; ③l a ⊥以其中的两个论断作为条件,余下的一个论断作为结论,写出一个正确的命题: ______.2010-2018年一、选择题1.(2018全国卷Ⅰ)已知正方体的棱长为1,每条棱所在直线与平面α所成的角相等,则α截此正方体所得截面面积的最大值为A B C D2.(2018全国卷Ⅱ)在长方体1111-ABCD A B C D 中,1==AB BC ,1=AA 线1AD 与1DB 所成角的余弦值为A .15B .6C .5D .23.(2018浙江)已知平面α,直线m ,n 满足m α⊄,n α⊂,则“m ∥n ”是“m ∥α”的A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件4.(2018浙江)已知四棱锥S ABCD -的底面是正方形,侧棱长均相等,E 是线段AB 上的点(不含端点),设SE 与BC 所成的角为1θ,SE 与平面ABCD 所成的角为2θ,二面角S AB C --的平面角为3θ,则A .123θθθ≤≤B .321θθθ≤≤C .132θθθ≤≤D .231θθθ≤≤ 5.(2017新课标Ⅱ)已知直三棱柱111ABC A B C -中,120ABC ∠=o ,2AB =,11BC CC ==,则异面直线1AB 与1BC 所成角的余弦值为A B C D 6.(2017浙江)如图,已知正四面体D ABC -(所有棱长均相等的三棱锥),P ,Q ,R 分别为AB ,BC ,CA 上的点,AP PB =,2BQ CR QC RA==,分别记二面角D PR Q --,D PQ R --,D QR P --的平面角为α,β,γ,则RQ PAB CDA.γ<α<βB.α<γ<βC.α<β<γD.β<γ<α7.(2016年全国I)平面α过正方体1111ABCD A B C D-的顶点A,α∥平面11CB D,αI平面ABCD=m,αI平面11ABB A=n,则m,n所成角的正弦值为A.32B.22C.33D.138.(2015福建)若,l m是两条不同的直线,m垂直于平面α,则“l m⊥”是“l∥α”的A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件9.(2015浙江)如图,已知ABC∆,D是AB的中点,沿直线CD将ACD∆翻折成A CD'∆,所成二面角A CD B'--的平面角为α,则10.(2014广东)若空间中四条两两不同的直线1234,,,l l l l,满足122334,,l l l l l l⊥⊥⊥,则下面结论一定正确的是A.14l l⊥B.14//l l C.14,l l既不垂直也不平行D.14,l l的位置关系不确定11.(2014浙江)设,m n是两条不同的直线,,αβ是两个不同的平面A .若m n ⊥,//n α,则m α⊥B .若//m β,βα⊥则m α⊥C .若,,m n n ββα⊥⊥⊥则m α⊥D .若m n ⊥,n β⊥,βα⊥,则m α⊥12.(2014辽宁)已知m ,n 表示两条不同直线,α表示平面,下列说法正确的是A .若//,//,m n αα则//m nB .若m α⊥,n α⊂,则m n ⊥C .若m α⊥,m n ⊥,则//n αD .若//m α,m n ⊥,则n α⊥13.(2014浙江)如图,某人在垂直于水平地面ABC 的墙面前的点A 处进行射击训练,已知点A 到墙面的距离为AB ,某目标点P 沿墙面的射击线CM 移动,此人为了准确瞄准目标点P ,需计算由点A 观察点P 的仰角θ的大小(仰角θ为直线AP 与平面ABC 所成角).若15AB m =,25AC m =,30BCM ∠=︒则tan θ的最大值ABCD 14.(2014四川)如图,在正方体1111ABCD A B C D -中,点O 为线段BD 的中点.设点P 在线段1CC 上,直线OP 与平面1A BD 所成的角为α,则sin α的取值范围是A1A. B.C .D . 15.(2013新课标Ⅱ)已知,m n 为异面直线,m ⊥平面α,n ⊥平面β.直线l 满足,l m l n ⊥⊥,,l l αβ⊄⊄,则A .α∥β且l ∥αB .α⊥β且l ⊥βC .α与β相交,且交线垂直于lD .α与β相交,且交线平行于l16.(2013广东)设m ,n 是两条不同的直线,α,β是两个不同的平面,下列命题中正确的是A .若αβ⊥,m α⊂,n β⊂,则m n ⊥B .若//αβ,m α⊂,n β⊂,则//m nC .若m n ⊥,m α⊂,n β⊂,则αβ⊥D .若m α⊥,//m n ,//n β,则αβ⊥17.(2012浙江)设l 是直线,,αβ是两个不同的平面A .若l ∥α,l ∥β,则α∥βB .若l ∥α,l ⊥β,则α⊥βC .若α⊥β,l ⊥α,则l ⊥βD .若α⊥β, l ∥α,则l ⊥β18.(2012浙江)已知矩形ABCD ,1AB =,BC =将ABD ∆沿矩形的对角线BD 所在的直线进行翻折,在翻折过程中,A .存在某个位置,使得直线AC 与直线BD 垂直B .存在某个位置,使得直线AB 与直线CD 垂直C .存在某个位置,使得直线AD 与直线BC 垂直D .对任意位置,三对直线“AC 与BD ”,“AB 与CD ”,“AD 与BC ”均不垂直19.(2011浙江)下列命题中错误..的是A .如果平面αβ⊥平面,那么平面α内一定存在直线平行于平面βB .如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面βC .如果平面αγ⊥平面,平面βγ⊥平面,=l αβI ,那么l γ⊥平面D .如果平面αβ⊥平面,那么平面α内所有直线都垂直于平面β 20.(2010山东)在空间,下列命题正确的是A .平行直线的平行投影重合B .平行于同一直线的两个平面平行C .垂直于同一平面的两个平面平行D .垂直于同一平面的两条直线平行二、填空题21.(2018全国卷Ⅱ)已知圆锥的顶点为S ,母线SA ,SB 所成角的余弦值为78,SA 与圆锥底面所成角为45°,若△SAB 的面积为515,则该圆锥的侧面积为_____.22.(2016年全国II )α,β是两个平面,m ,n 是两条线,有下列四个命题:①如果m n ⊥,m α⊥,n β∥,那么αβ⊥.②如果m α⊥,n α∥,那么m n ⊥.③如果a β∥,m α⊂,那么m β∥.④如果m n ∥,αβ∥,那么m 与α所成的角和n 与β所成的角相等.其中正确的命题有 .(填写所有正确命题的编号)23.(2015浙江)如图,三棱锥A BCD -中,3AB AC BD CD ====,2AD BC ==,点,M N 分别是,AD BC 的中点,则异面直线,AN CM 所成的角的余弦值是 .24.(2015四川)如图,四边形ABCD 和ADPQ 均为正方形,它们所在的平面互相垂直,动点M 在线段PQ 上,,E F 分别为,AB BC 的中点.设异面直线EM 与AF 所成的角为θ,则θcos 的最大值为_________.25.(2017新课标Ⅲ)a ,b 为空间中两条互相垂直的直线,等腰直角三角形ABC 的直角边AC 所在直线与a ,b 都垂直,斜边AB 以直线AC 为旋转轴旋转,有下列结论: ①当直线AB 与a 成60°角时,AB 与b 成30°角;②当直线AB 与a 成60°角时,AB 与b 成60°角;③直线AB 与a 所成角的最小值为45°;④直线AB 与a 所成角的最小值为60°;其中正确的是________.(填写所有正确结论的编号)三、解答题26.(2018江苏)在平行六面体1111ABCD A B C D -中,1AA AB =,111AB B C ⊥.D 11B 1A 1DC B A求证:(1)AB ∥平面11A B C ; (2)平面11ABB A ⊥平面1A BC .27.(2018浙江)如图,已知多面体111ABCA B C ,1A A ,1B B ,1C C 均垂直于平面ABC ,120ABC ∠=o ,14A A =,11C C =,12AB BC B B ===.C 1B 1A 1C BA(1)证明:1AB ⊥平面111A B C ;(2)求直线1AC 与平面1ABB 所成的角的正弦值.28.(2017浙江)如图,已知四棱锥P ABCD -,PAD ∆是以AD 为斜边的等腰直角三角形,BC AD ∥,CD AD ⊥,22PC AD DC CB ===,E 为PD 的中点.(Ⅰ)证明:CE ∥平面PAB ;(Ⅱ)求直线CE 与平面PBC 所成角的正弦值.ED C B AP29.(2017江苏)如图,在三棱锥A BCD -中,AB ⊥AD ,BC ⊥BD ,平面ABD ⊥平面BCD ,点E 、F (E 与A 、D 不重合)分别在棱AD ,BD 上,且EF ⊥AD .求证:(1)EF ∥平面ABC ;(2)AD ⊥AC .F AB C DE30.(2017山东)如图,几何体是圆柱的一部分,它是由矩形ABCD (及其内部)以AB 边所在直线为旋转轴旋转120︒得到的,G 是»DF的中点. (Ⅰ)设P 是»CE上的一点,且AP BE ⊥,求CBP ∠的大小; (Ⅱ)当3AB =,2AD =,求二面角E AG C --的大小.31.(2017江苏)如图,水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ的高均为32cm ,容器Ⅰ的底面对角线AC 的长为107cm ,容器Ⅱ的两底面对角线EG ,11E G 的长分别为14cm 和62cm . 分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm . 现有一根玻璃棒l ,其长度为40cm .(容器厚度、玻璃棒粗细均忽略不计)(1)将l 放在容器Ⅰ中,l 的一端置于点A 处,另一端置于侧棱1CC 上,求l 没入水中部分的长度;(2)将l 放在容器Ⅱ中,l 的一端置于点E 处,另一端置于侧棱1GG 上,求l 没入水中部分的长度.32.(2016全国I )如图,在以A ,B ,C ,D ,E ,F 为顶点的五面体中,面ABEF 为正方形,2AF FD =,90AFD ∠=o ,且二面角D AF E --与二面角C BE F --都是60o .(I )证明:平面ABEF ⊥平面EFDC ; (II )求二面角E BC A --的余弦值.33.(2016全国II )如图,菱形ABCD 的对角线AC 与BD 交于点O ,5AB =,6AC =,点E ,F 分别在AD ,CD 上,54AE CF ==,EF 交BD 于点H .将ΔDEF 沿EF折到ΔD EF '的位置,10OD '=. (I )证明:D H '⊥平面ABCD ; (II )求二面角B D A C '--的正弦值.34.(2016全国III )如图,四棱锥P ABCD -中,PA ⊥底面ABCD ,AD BC P ,=3AB AD AC ==,4PA BC ==,M 为线段AD 上一点,2AM MD =, N 为PC 的中点.(Ⅰ)证明MN P 平面PAB ;(Ⅱ)求直线AN 与平面PMN 所成角的正弦值.PABDCNM35.(2014山东)如图,四棱锥P ABCD-中,AP PCD⊥平面,AD BC∥,1,,2AB BC AD E F==分别为线段,AD PC的中点.(Ⅰ)求证:AP BEF∥平面;(Ⅱ)求证:BE PAC⊥平面.36.(2014江苏)如图,在三棱锥ABCP-中,D,E,F分别为棱ABACPC,,的中点.已知ACPA⊥,,6=PA.5,8==DFBCPAFDE求证:(Ⅰ)直线PA∥平面DEF;(Ⅱ)平面BDE⊥平面ABC.37.(2014新课标Ⅱ)如图,四棱锥P ABCD-中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.(Ⅰ)证明:PB∥平面AEC;(Ⅱ)设二面角D AE C--为60°,AP=1,AD=3,求三棱锥E ACD-的体积.38.(2014天津)如图四棱锥P ABCD-的底面ABCD是平行四边形,2BA BD==,2AD=,5PA PD==E,F分别是棱AD,PC的中点.(Ⅰ)证明: EF∥平面PAB;(Ⅱ)若二面角P AD B--为60°,(ⅰ)证明:平面PBC⊥平面ABCD(ⅱ)求直线EF与平面PBC所成角的正弦值.PCDBF39.(2013浙江)如图,在四棱锥P ABCD-中,PA⊥面ABCD,2AB BC==,7AD CD==,3PA=120ABC∠=o,G为线段PC上的点.PDABG(Ⅰ)证明:BD⊥面APC;(Ⅱ)若G是PC的中点,求DG与APC所成的角的正切值;(Ⅲ)若G满足PC⊥面BGD,求PGGC的值.40.(2013辽宁)如图,AB是圆O的直径,PA垂直圆O所在的平面,C是圆O上的点.(Ⅰ)求证:BC PAC⊥平面;(Ⅱ)设Q为PA的中点,G为AOC∆的重心,求证:QG∥平面PBC.41.(2012江苏)如图,在直三棱柱111ABC A B C-中,1111A B AC=,D E,分别是棱1BC CC,上的点(点D不同于点C),且AD DE F⊥,为11B C的中点.DF1BC1B1求证:(Ⅰ)平面ADE⊥平面11BCC B;(Ⅱ)直线1//A F平面ADE.42.(2012广东)如图所示,在四棱锥P ABCD-中,AB⊥平面PAD,//,AB CD PD AD=,E是PB中点,F是DC上的点,且12DF AB=,PH为PAD∆中AD边上的高.(Ⅰ)证明:PH ⊥平面ABCD ; (Ⅱ)若1,1PH AD FC ===,求三棱锥E BCF -的体积;(Ⅲ)证明:EF ⊥平面PAB .43.(2011江苏)如图,在四棱锥ABCD P -中,平面PAD ⊥平面ABCD ,AB AD =,BAD ∠=60°,E 、F 分别是AP 、AD 的中点.C求证:(Ⅰ)直线EF ∥平面PCD ; (Ⅱ)平面BEF ⊥平面PAD .44.(2011广东)如图在椎体P ABCD -中,ABCD是边长为1的棱形,且DAB ∠=60︒,PA PD ==2PB =,E ,F 分别是BC ,PC 的中点.(Ⅰ)证明:AD ⊥平面DEF ;(Ⅱ)求二面角P AD B --的余弦值.45.(2010天津)如图,在五面体ABCDEF 中,四边形ADEF 是正方形,FA ⊥平面ABCD ,BC ∥AD ,CD =1,AD =,∠BAD =∠CDA =45°.(Ⅰ)求异面直线CE 与AF 所成角的余弦值; (Ⅱ)证明CD ⊥平面ABF ; (Ⅲ)求二面角B EF A --的正切值.46.(2010浙江)如图,在平行四边形ABCD 中,AB =2BC ,∠ABC =120°.E 为线段AB 的中点,将△ADE 沿直线DE 翻折成△A DE ',使平面A DE '⊥平面BCD ,F 为线段A C '的中点.(Ⅰ)求证:BF ∥平面A DE ';(Ⅱ)设M 为线段DE 的中点,求直线FM 与平面A DE '所成角的余弦值.。
