4-2《图形的初步认识》全章复习与巩固 知识讲解
图形的初步认识全章复习与巩固

符号
1 颗星 1 面旗
旁白
1 颗星 1 面旗
同学摆擂台!(写在黑板上)
要求:(1)出自网校资源(靠旁白)、非难偏怪题 (2)标明出处、奖励规则。 (3)擂主会解题。
一、师生问好
同学们好!
课前就位
• 发测评截图的同学:…..加3颗星星 截屏快捷键:Ctrl + PrntScr ; 截图Ctrl + Alt+A) 有高清课堂观看笔记 的 加3颗星星 • 上周积分情况汇报
老师摆擂
10. 如图所示, AB AC (1)AC=BC+______; (2)CD=AD-______; BD (3)CD=______-BC; (4)AB+BC=______-CD. AD
课堂小结及点评
1、合上学案,回想一下这节课我们都复习了 哪些知识点和类型题? 2、各小组积分情况点评。
布置学案
D
5、点评:理解概念,掌握概念与概念的本质区别
例2.(天门、潜江、仙桃)如图所示,是每个面上都有一个 汉字的正方体的一种展开图,那么在原正方体的表面上, 与“看”相对的面上的汉字是 ( ) A.南 B.世 C.界 D.杯
解题思路:由图形可以判定“南”与“世”相对, “看”与“界”相对,“非”与“杯”相对 点评:判断两个面是对面的根据是:展开图的对面没有公共边 或公共顶点
要点梳理——检测
知识点一:多姿多彩的图形 2.立体图形与平面图形的相互转化
抢答
(1)立体图形的平面展开图: 把立体图形按一定的方式展开就 平面图形 会得到-------- ----,把平面图形按一定的途径进行折叠就 会得
到相应的立体图形
正 左、右 上
抢答 知识点二:直线、射线、线段的区别与联系
华东师大初中七年级上册数学图形的初步认识全章复习与巩固提高知识讲解精选
图形的初步认识《》全章复习与巩固(提高)知识讲解【学习目标】 1.认识一些简单的几何体的平面展开图及三视图,初步培养空间观念和几何直观; 2.掌握直线、射线、线段、角这些基本图形的概念、性质、表示方法和画法;.初步学会应用图形与几何的知识解释生活中的现象及解决简单的实际问题;3.逐步掌握学过的几何图形的表示方法,能根据语句画出相应的图形,会用语句描述简单4 的图形.【知识网络】【要点梳理】要点一、立体图形与平面图形1.几何图形的分类要点诠释:在给几何体分类时,不同的分类标准有不同的分类结果..立体图形与平面图形的相互转化2.(1)立体图形的平面展开图:把立体图形按一定的方式展开就会得到平面图形,把平面图形按一定的途径进行折叠就会得到相应的立体图形,通过展开与折叠能把立体图形和平面图形有机地结合起来.要点诠释:①对一些常见立体图形的展开图要非常熟悉,例如正方体的 11种展开图,三棱柱,圆柱等的展开图.②不同的几何体展成不同的平面图形,同一几何体沿不同的棱剪开,可得到不同的平面图形,那么排除障碍的方法就是:联系实物,展开想象,建立“模型”,整体构想,动手实践.(2)三视图:正视图--------------从正面看?几何体的三视图左视图--------------从侧边看??俯视图--------------从上面看要点诠释:①会判断简单物体(直棱柱、圆柱、圆锥、球)的三视图.②三视图的画法原则:高平齐宽相等长对正.③能根据三视图描述基本几何体或实物原型. )几何体的构成元素及关系:3(点动成线,线与线相交成点;线动成面,面与面相交. 、面构成的几何体是由点、线.成线;面动成体,体是由面组成要点二、直线、射线、线段直线,射线与线段的区别与联系1.2. 基本性质(1)直线的性质:两点确定一条直线. (2)线段的性质:两点之间,线段最短.要点诠释:①本知识点可用来解释很多生活中的现象. 如:要在墙上固定一个木条,只要两个钉子就可以了,因为如果把木条看作一条直线,那么两点可确定一条直线..②连接两点间的线段的长度,叫做两点的距离3.画一条线段等于已知线段(1)度量法:可用直尺先量出线段的长度,再画一条等于这个长度的线段.(2)用尺规作图法:用圆规在射线AC上截取AB=a,如下图:.线段的比较与运算4)线段的比较:(1.比较两条线段的长短,常用两种方法,一种是度量法;一种是叠合法 2)线段的和与差:( AD=AB-BD。
第四章图形的初步认识知识点总结

第四章图形的初步认识知识点总结1、生活中常见的立体图形(1)球体(2)柱体:包括圆柱和棱柱。
1)圆柱:有两个底面是圆,侧面是曲面。
2)棱柱:上下两个底面是两个平行且相同的多边形,侧面是平行四边形。
棱柱可按底面多边形边数分为三棱柱、四棱柱、五棱柱等。
(3)椎体:包括圆锥和棱锥。
1)圆锥:有一个底面是圆,侧面是曲面。
2)棱锥:底面是多边形,侧面是三角形。
棱锥可按底面多边形边数分为三棱锥、四棱锥、五棱锥等。
(4)多面体:由平的面围成的立体图形。
2、画立体图形(1)视图:就是从正面、上面、和侧面(左面或右面)三个不同的方向看一个物体,然后描绘三张所看到的图,即视图。
正视图:从正面看到的图形。
俯视图:从上面看到的图形。
侧视图:从侧面看到的图形。
依观看方向不同,有左视图、右视图。
三视图:通常把正视图、俯视图、与左(或右)视图称作一个物体的三视图。
(2)球体的三视图都是圆。
正方体的三视图都是正方形圆柱体的正视图和左视图都是长方体,俯视图是圆。
圆锥体的正视图和左视图都是三角形,俯视图是圆,中心有一个点。
3、由视图到立体图形主视图:可分清物体的长与高。
俯视图:可分清物体的长与宽。
左视图:可分清物体的宽与高。
口诀:主俯长对正,主左高齐平,俯左宽相等。
4、立体图形的表面展开图多面体是由平面图形围成的的立体图形,沿着多面体的一些棱将它剪开,可以把多面体的表面展开成一个平面图形,这个平面图形叫做多面体的表面展开图。
正方体的表面展开图:有“一四一型”、“一三二型”、“二二二型”、“三三型”口诀:一行不过四,“田”“凹”应弃之,相间、Z端是对面。
5、平面图形(1)圆是由曲线围成的封闭图形。
(2)多边形:由在同一平面且不在同一直线上的三条或三条以上的线段首尾顺次连结所组成的封闭图形叫做多边形。
按照组成多边形的边的个数,多边形可分为三角形、四边形、五边形、六边形……在多边形里,三角形是最基本的图形,每个n边形都可以分割成(n-2)个三角形。
几何图形初步全章复习与巩固知识讲解.doc

《几何图形初步》全章复习与巩固(基础)知识讲解【学习目标】1.认识一些简单的几何体的平面展开图及三视图,初步培养空间观念和几何直观;2.掌握直线、射线、线段、角这些基本图形的概念、性质、表示方法和画法;3.初步学会应用图形与几何的知识解释生活中的现象及解决简单的实际问题;4.逐步掌握学过的几何图形的表示方法,能根据语句画出相应的图形,会用语句描述简单的图形.【知识网络】【要点梳理】要点一、多姿多彩的图形1.几何图形的分类立体图形:棱柱、棱锥、圆柱、圆锥、球等.几何图形平面图形:三角形、四边形、圆等 ..要点诠释:在给几何体分类时,不同的分类标准有不同的分类结果2.立体图形与平面图形的相互转化(1)立体图形的平面展开图:把立体图形按一定的方式展开就会得到平面图形,把平面图形按一定的途径进行折叠就会得到相应的立体图形,通过展开与折叠能把立体图形和平面图形有机地结合起来.要点诠释:①对一些常见立体图形的展开图要非常熟悉,例如正方体的11 种展开图,三棱柱,圆柱等的展开图;②不同的几何体展成不同的平面图形,同一几何体沿不同的棱剪开,可得到不同的平面图形,那么排除障碍的方法就是:联系实物,展开想象,建立“模型”,整体构想,动手实践. (2)从不同方向看:几何体的三视图主(正)视图---------从正面看左视图 -----从左(右)边看俯视图 ---------------从上面看要点诠释:①会判断简单物体(直棱柱、圆柱、圆锥、球)的三视图.②能根据三视图描述基本几何体或实物原型.(3)几何体的构成元素及关系几何体是由点、线、面构成的 . 点动成线,线与线相交成点;线动成面,面与面相交成线;面动成体,体是由面组成.要点二、直线、射线、线段1.直线,射线与线段的区别与联系2.基本性质(1)直线的性质 : 两点确定一条直线. (2) 线段的性质 : 两点之间,线段最短.要点诠释:①本知识点可用来解释很多生活中的现象. 如:要在墙上固定一个木条,只要两个钉子就可以了,因为如果把木条看作一条直线,那么两点可确定一条直线.②连接两点间的线段的长度,叫做两点间的距离.3.画一条线段等于已知线段(1)度量法:可用直尺先量出线段的长度 , 再画一条等于这个长度的线段 .(2)用尺规作图法:用圆规在射线 AC上截取 AB=a,如下图:4.线段的比较与运算(1)线段的比较:比较两条线段的长短,常用两种方法,一种是度量法;一种是叠合法. (2)线段的和与差:如下图,有AB+BC=AC,或 AC=a+b; AD=AB-BD。
《图形的初步认识》全章复习与巩固(提高)知识讲解

《图形的初步认识》全章复习与巩固(提高)知识讲解【学习目标】1. 经历从现实世界抽象几何图形的过程,能说出常见的几何体和平面图形;2.掌握直线、射线、线段、角这些基本图形的概念、表示方法、性质、及画法;3.初步学会应用图形与几何的知识解释生活中的现象及解决简单的实际问题.【知识网络】【要点梳理】要点一、几何图形1.几何图形的分类要点诠释:在给几何体分类时,不同的分类标准有不同的分类结果.2.几何体的构成元素几何体是由点、线、面构成的.点动成线,线与线相交成点;线动成面,面与面相交成线;面动成体,体是由面组成.要点二、线段、射线、直线1.直线,射线与线段的区别与联系2. 基本事实(1)直线:两点确定一条直线. (2)线段:两点之间线段最短. 要点诠释:①本知识点可用来解释很多生活中的现象. 如:要在墙上固定一个木条,只要两个钉子就可以了,因为如果把木条看作一条直线,那么两点可确定一条直线. ②连接两点间的线段的长度,叫做两点的距离.3.画一条线段等于已知线段(1)度量法:可用直尺先量出线段的长度,再画一条等于这个长度的线段. (2)用尺规作图法:用圆规在射线AC 上截取AB =a,如下图:4.线段的比较与运算(1)线段的比较:①度量法;②叠合法;③估算法.(2)线段的和与差:如下图,有AB+BC =AC ,或AC =a+b ;AD =AB-BD.(3)线段的中点:把一条线段分成两条相等线段的点,叫做线段的中点.如下图,有:12AM MB AB ==.要点诠释:①线段中点的等价表述:如上图,点M 在线段上,且有12AM AB =,则点M 为线段AB 的中点.②除线段的中点(即二等分点)外,类似的还有线段的三等分点、四等分点等. 如下图,点M,N,P 均为线段AB 的四等分点,则有AB PB NP MN AM 41====. PN要点三、角1.角的概念及其表示(1)角的定义:从一点引出的两条射线所形成的图形叫做角,这个点叫做角的顶点,这两条射线是角的边;此外,角也可以看作由一条射线绕着它的端点旋转而形成的图形.(2)角的表示方法:角通常有三种表示方法:一是用三个大写英文字母表示,二是用角的顶点的一个大写英文字母表示,三是用一个小写希腊字母或一个数字表示.例如下图:要点诠释:①角的两种定义是从不同角度对角进行的定义.②当一个角的顶点有多个角的时候,不能用顶点的一个大写字母来表示. 2.角的分类3.角的度量1周角=360°,1平角=180°,1°=60′,1′=60″. 要点诠释:①度、分、秒的换算是60进制,与时间中的小时分钟秒的换算相同. ②度分秒之间的转化方法:由度化为度分秒的形式(即从高级单位向低级单位转化)时用乘法逐级进行;由度分秒的形式化成度(即低级单位向高级单位转化)时用除法逐级进行. ③同种形式相加减:度加(减)度,分加(减)分,秒加(减)秒;超60进一,减一 成60.4.角的比较与运算(1)角的比较方法: ①度量法;②叠合法;③估算法.(2)角的平分线:从一个角的顶点出发,把这个角分成相等的两个角的射线,叫做这个角的平分线,例如:如下图,因为OC 是∠AOB 的平分线,所以∠1=∠2=12∠AOB ,或∠AOB=2∠1=2∠2. 类似地,还有角的三等分线等.5.余角、补角(1)定义:若∠1+∠2=90°,则∠1与∠2互为余角.其中∠1是∠2的余角,∠2是∠1的余角. 若∠1+∠2=180°,则∠1与∠2互为补角.其中∠1是∠2的补角,∠2是∠1的补角. (2)性质:同角(或等角)的余角相等;同角(或等角)的补角相等.要点诠释:①余角(或补角)是两个角的关系,是成对出现的,单独一个角不能称其为余角(或补角).②一个角的余角(或补角)可以不止一个,但是它们的度数是相同的.③只考虑数量关系,与位置无关.④“等角是相等的几个角”,而“同角是同一个角”.6.方位角以正北、正南方向为基准,描述物体运动的方向,这种表示方向的角叫做方位角.要点诠释:(1)方位角还可以看成是将正北或正南的射线旋转一定角度而形成的.所以在应用中一要确定其始边是正北还是正南.二要确定其旋转方向是向东还是向西,三要确定旋转角度的大小. (2)北偏东45 °通常叫做东北方向,北偏西45 °通常叫做西北方向,南偏东45 °通常叫做东南方向,南偏西45 °通常叫做西南方向.(3)方位角在航行、测绘等实际生活中的应用十分广泛.【典型例题】类型一、几何图形1.对于棱柱体而言,不同的棱柱体由不同的面构成:三棱柱由2个底面,3个侧面,共5个面构成;四棱柱由2个底面,4个侧面,共6个面构成;五棱柱由2个底面,5个侧面,共7个面构成;六棱柱由2个底面,6个侧面,共8个面构成;(1)根据以上规律判断,十二棱柱共有多少个面?(2)若某个棱柱由24个面构成,那么这个棱柱是什么棱柱?(3)棱柱底面多边形的边数为n,则侧面的个数为多少?棱柱共有多少个面?(4)底面多边形边数为n的棱柱,其顶点个数为多少个?有多少条棱?【答案与解析】解:(1)十二棱柱由2个底面,12个侧面,共14个面构成.(2)这个棱柱有24个面,由于底面有2个,故其侧面共有22个,从而这个棱柱是二十二棱柱.(3)棱柱底面多边形的边数与侧面的个数是相等的,即底面多边形的边数为n,则侧面的个数也为n,棱柱的面数为(n+2).(4)底面多边形的边数为n的棱柱,其顶点个数为2n个,共有3n条棱.【总结升华】根据立体图形的特点,从特殊到一般,寻找规律.举一反三:【变式】如图把一个圆绕虚线旋转一周,得到的几何体是()A. B. C. D.【答案】B类型二、线段和角的概念或性质2.下列判断错误的有( )①延长射线OA;②直线比射线长,射线比线段长;③如果线段PA=PB,则点P是线段AB的中点;④连接两点间的线段,叫做两点间的距离.A.0个B.2个C.3个D.4个【答案】D【解析】①由于射线向一方无限延伸,因此,不能延长射线;②由于直线向两方无限延伸,射线向一方无限延伸,因此它们都是不能度量的,所以它们不存在相等或不相等的关系,而线段是可以度量的,可以比较线段的长短;③线段PA=PB,只有当点P在线段AB上时,才是线段AB的中点,否则就不是;④两点间的距离是表示大小的量,而线段是图形,二者的本质属性不同.【总结升华】本题考查的是基本概念,要抓住概念间的本质区别.举一反三:【变式】下列说法正确的个数有( )①若∠1+∠2+∠3=90°,则∠1,∠2,∠3互余.②互补的两个角一定是一个锐角和一个钝角.③因为钝角没有余角,所以,只有当角为锐角时,“一个角的补角比这个角的余角大”这个说法才正确.A.0个B.1个C.2个D.3个【答案】B 提示:③正确3. (安徽芜湖)如图所示的4×4正方形网格中,∠1+∠2+∠3+∠4+∠5+∠6+∠7等于().A.330°B.315°C.310°D.320°【答案】B【解析】通过网格的特征首先确定∠4=45°.由图形可知:∠l与∠7互余,∠2与∠6互余,∠3与∠5互余,所以∠l+∠2+∠3+∠4+∠5+∠6+∠7=90°+90°+90°+45°=315°.【总结升华】互余的两个角只与数量有关,而与位置无关.举一反三:【变式】如图所示,AB和CD都是直线,∠AOE=90°,∠3=∠FOD,∠1=27°20′,求∠2,∠3.【答案】解:因为∠AOE =90°,所以∠2=90°-∠1=90°-27°20′=62°40′. 又∠AOD =180°-∠1=152°40′,∠3=∠FOD .所以∠3=12∠AOD =76°20′. 答:∠2为62°40′,∠3为76°20′.4. 如图所示,时钟的时针由3点整的位置(顺时针方向)转过多少度时,与分针第一次重合.【答案与解析】解:设时针转过的度数为x °时,与分针第一次重合,依题意有: 12x =90+x 解得9011x =答:时针转过9011⎛⎫⎪⎝⎭°时,与分针第一次重合. 【总结升华】在相同时间里,分针转过的度数是时针的12倍,此外此问题可以转化为追及问题来解决. 举一反三:【变式】125°÷4= °= ° ′ 【答案】31.25,31、15类型三、利用数学思想方法解决有关线段或角的计算 1.方程的思想方法5. 如图所示,B 、C 是线段AD 上的两点,且32CD AB =,AC =35cm ,BD =44cm ,求线段AD 的长.【答案与解析】解:设AB =x cm ,则3cm 2CD x =(35)cm BC x =-或3(44)cm 2x -于是列方程,得335442x x -=-解得:x =18,即AB =18(cm ) 所以BC =35-x =35-18=17(cm )33182722CD x ==⨯=(cm ) 所以AD =AB+BC+CD =18+17+27=62(cm )【总结升华】根据题中的线段关系,巧设未知数,列方程求解. 2.分类的思想方法6. 同一直线上有A 、B 、C 、D 四点,已知AD =59DB ,AC =95CB ,且CD =4cm ,求AB 的长.【思路点拨】先根据题意画出图形,再从图上直观的看出各线段的关系及大小. 【答案与解析】 解:利用条件中的AD =59DB ,AC =95CB ,设DB =9x ,CB =5y , 则AD =5x ,AC =9y ,分类讨论:(1)当点D ,C 均在线段AB 上时,如图所示:∵ AB =AD+DB =14x ,AB =AC+CB =14y ,∴ x =y∵ CD =AC -AD =9y -5x =4x =4,∴ x =1,∴ AB =14x =14(cm ). (2)当点D ,C 均不在线段AB 上时,如图所示:方法同上,解得87AB =(cm ).(3)如图所示,当点D 在线段AB 上而点C 不在线段AB 上时,方法同上,解得11253AB =(cm ).(4)如图所示,当点C 在线段AB 上而点D 不在线段AB 上时,方法同上,解得11253AB =(cm ).综上可得:AB的长为14cm,87cm,11253cm.【总结升华】解决没有图形的题目时,一要注意满足条件下的图形的多样性;二要注意解决的方法,注意方程法在解决图形问题中的应用. 在正确答案中,(3)与(4)的答案虽然相同,但作为图形上的差别应了解.。
word完整版几何图形初步全章复习与巩固提高知识讲解
《几何图形初步》全章复习与巩固(提高)知识讲解【学习目标】 1.认识一些简单的几何体的平面展开图及三视图,初步培养空间观念和几何直观; 2.掌握直线、射线、线段、角这些基本图形的概念、性质、表示方法和画法;.初步学会应用图形与几何的知识解释生活中的现象及解决简单的实际问题;3.逐步掌握学过的几何图形的表示方法,能根据语句画出相应的图形,会用语句描述简单4 的图形.【知识网络】【要点梳理】要点一、多姿多彩的图形1.几何图形的分类立体图形:棱柱、棱锥、圆柱、圆锥、球等. ?几何图形??平面图形:三角形、四边形、圆等.要点诠释:在给几何体分类时,不同的分类标准有不同的分类结果.2.立体图形与平面图形的相互转化(1)立体图形的平面展开图:把立体图形按一定的方式展开就会得到平面图形,把平面图形按一定的途径进行折叠就会得到相应的立体图形,通过展开与折叠能把立体图形和平面图形有机地结合起来.要点诠释:①对一些常见立体图形的展开图要非常熟悉,例如正方体的 11种展开图,三棱柱,圆柱等的展开图;②不同的几何体展成不同的平面图形,同一几何体沿不同的棱剪开,可得到不同的平面图形,那么排除障碍的方法就是:联系实物,展开想象,建立“模型”,整体构想,动手实践.(2)从不同方向看:主(正)视图----------从正面看?几何体的三视图左视图----------------从左边看??俯视图----------------从上面看要点诠释:①会判断简单物体(直棱柱、圆柱、圆锥、球)的三视图.②能根据三视图描述基本几何体或实物原型. )几何体的构成元素及关系(3点动成线,线与线相交成点;线动成面,面与面相交、面构成的.几何体是由点、线.成线;面动成体,体是由面组成要点二、直线、射线、线段直线,射线与线段的区别与联系1.2. 基本性质(1)直线的性质:两点确定一条直线. (2)线段的性质:两点之间,线段最短.要点诠释:①本知识点可用来解释很多生活中的现象. 如:要在墙上固定一个木条,只要两个钉子就可以了,因为如果把木条看作一条直线,那么两点可确定一条直线。
华东师大版七年级数学上册第四章《图形的初步认识》知识点汇总

华东师大版七年级数学上册
第四章《图形的初步认识》知识点汇总
复习内容:立体图形的三视图、展开图,最基本的图形——点和线,角,相交线,平行线.
(一)立体图形的三视图:正视图、左视图、俯视图
(二)立体图形的展开图
(三)最基本的图形——点和线
1、两点之间,线段最短.
2、连结两点的线段的长度,叫做这两点的距离.
3、经过两点有一条直线,并且只有一条直线.(两点确定一条直线)
4、把一条线段分成两条相等线段的点叫做线段的中点.(四)角
1、一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线.
2、⑴如果两个角的和是90º,这两个角叫做互为余角.
⑵如果两个角的和是180º,这两个角叫做互为补角.
说明:①若∠1与∠2互余,则∠1+∠2=90º.
②若∠1与∠2互补,则∠1+∠2=180º.
3、⑴同角(或等角)的余角相等.
⑵同角(或等角)的补角相等.
4、用角度表示方向: 一般以正北、正南为基准,向东旋转的角度表示方向.如图,OA 示为北偏西60º.
5、对顶角相等.。
《几何图形初步》全章复习与巩固(提高)知识讲解
《几何图形初步》全章复习与巩固(提高)知识讲解【知识网络】【要点梳理】要点一、多姿多彩的图形1.几何图形的分类要点诠释:在给几何体分类时,不同的分类标准有不同的分类结果.2.立体图形与平面图形的相互转化(1)立体图形的平面展开图:把立体图形按一定的方式展开就会得到平面图形,把平面图形按一定的途径进行折叠就会得到相应的立体图形,通过展开与折叠能把立体图形和平面图形有机地结合起来.要点诠释:①对一些常见立体图形的展开图要非常熟悉,例如正方体的11种展开图,三棱柱,圆柱等的展开图;②不同的几何体展成不同的平面图形,同一几何体沿不同的棱剪开,可得到不同的平面图形,那么排除障碍的方法就是:联系实物,展开想象,建立“模型”,整体构想,动手实践.立体图形:棱柱、棱锥、圆柱、圆锥、球等.⎧⎨⎩平面图形:三角形、四边形、圆等.几何图形⎧⎨⎩(2)从不同方向看:主(正)视图----------从正面看几何体的三视图左视图----------------从左边看俯视图----------------从上面看要点诠释:①会判断简单物体(直棱柱、圆柱、圆锥、球)的三视图.②能根据三视图描述基本几何体或实物原型.(3)几何体的构成元素及关系几何体是由点、线、面构成的.点动成线,线与线相交成点;线动成面,面与面相交成线;面动成体,体是由面组成.要点二、直线、射线、线段1.直线,射线与线段的区别与联系2.基本性质(1)直线的性质:两点确定一条直线.(2)线段的性质:两点之间,线段最短.要点诠释:①本知识点可用来解释很多生活中的现象.如:要在墙上固定一个木条,只要两个钉子就可以了,因为如果把木条看作一条直线,那么两点可确定一条直线。
②连接两点间的线段的长度,叫做两点间的距离.3.画一条线段等于已知线段(1)度量法:可用直尺先量出线段的长度,再画一条等于这个长度的线段.(2)用尺规作图法:用圆规在射线AC 上截取AB=a,如下图:4.线段的比较与运算(1)线段的比较:比较两条线段的长短,常用两种方法,一种是度量法;一种是叠合法.(2)线段的和与差:如下图,有AB+BC=AC,或AC=a+b;AD=AB-BD。
《几何图形初步》全章复习与巩固(基础)知识讲解及练习巩固
⎧⎨⎩①对一些常见立体图形的展开图要非常熟悉,例如正方体的 11种展开图,三棱柱,圆柱等的展开图;②不同的几何体展成不同的平面图形,同一几何体沿不同的棱剪开,可得到不同的平面图形,那么排除障碍的方法就是:联系实物,展开想象,建立“模型”,整体构想,动手实践.(2)从不同方向看:主(正)视图---------从正面看 几何体的三视图 左视图-----从左(右)边看俯视图---------------从上面看要点诠释:①会判断简单物体(直棱柱、圆柱、圆锥、球)的三视图.②能根据三视图描述基本几何体或实物原型.(3)几何体的构成元素及关系几何体是由点、线 、面构成的.点动成线,线与线相交成点;线动成面,面与面相交成线;面动成体,体是由面组成.要点二、直线、射线、线段1. 直线,射线与线段的区别与联系2. 基本性质(1)直线的性质:两点确定一条直线. (2)线段的性质:两点之间,线段最短.要点诠释:①本知识点可用来解释很多生活中的现象. 如:要在墙上固定一个木条,只要两个钉子就可以了,因为如果把木条看作一条直线,那么两点可确定一条直线.②连接两点间的线段的长度,叫做两点间的距离.3.画一条线段等于已知线段(1)度量法:可用直尺先量出线段的长度,再画一条等于这个长度的线段.(2)用尺规作图法:用圆规在射线AC 上截取AB=a,如下图:4.线段的比较与运算(1)线段的比较:比较两条线段的长短,常用两种方法,一种是度量法;一种是叠合法.(2)线段的和与差:如下图,有AB+BC=AC ,或AC=a+b ;AD=AB-BD 。
(3)线段的中点:把一条线段分成两条相等线段的点,叫做线段的中点.如下图,有:12AMMB AB ==要点诠释:①线段中点的等价表述:如上图,点M 在线段上,且有12AM AB =,则点M 为线段AB 的中点. ②除线段的中点(即二等分点)外,类似的还有线段的三等分点、四等分点等.如下图,点M,N,P 均为线段AB 的四等分点.P NAB PB NP MN AM 41==== 要点三、角1.角的度量 (1)角的定义:有公共端点的两条射线组成的图形叫做角,这个公共端点是角的顶点,这两条射线是角的两条边;此外,角也可以看作由一条射线绕着它的端点旋转而形成的图形.(2)角的表示方法:角通常有三种表示方法:一是用三个大写英文字母表示,二是用角的顶点的一个大写英文字母表示,三是用一个小写希腊字母或一个数字表示.例如下图:C b a M B A要点诠释:①角的两种定义是从不同角度对角进行的定义;②当一个角的顶点有多个角的时候,不能用顶点的一个大写字母来表示.(3)角度制及角度的换算1周角=360°,1平角=180°,1°=60′,1′=60″,以度、分、秒为单位的角的度量制,叫做角度制.要点诠释:①度、分、秒的换算是60进制,与时间中的小时分钟秒的换算相同.②度分秒之间的转化方法:由度化为度分秒的形式(即从高级单位向低级单位转化)时用乘法逐级进行;由度分秒的形式化成度(即低级单位向高级单位转化)时用除法逐级进行. ③同种形式相加减:度加(减)度,分加(减)分,秒加(减)秒;超60进一,减一 成60.(4)角的分类(5)画一个角等于已知角(1)借助三角尺能画出15°的倍数的角,在0~180°之间共能画出11个角.(2)借助量角器能画出给定度数的角.(3)用尺规作图法.2.角的比较与运算(1)角的比较方法: ①度量法;②叠合法.(2)角的平分线:从一个角的顶点出发,把这个角分成相等的两个角的射线,叫做这个角的平分线,例如:如下图,因为OC 是∠AOB 的平分线,所以∠1=∠2=12∠AOB ,或∠AOB=2∠1=2∠2. 类似地,还有角的三等分线等.3.角的互余互补关系余角补角(1)若∠1+∠2=90°,则∠1与∠2互为余角.其中∠1是∠2的余角,∠2是∠1的余角.(2)若∠1+∠2=180°,则∠1与∠2互为补角.其中∠1是∠2的补角,∠2是∠1的补角. ∠β锐角 直角 钝角 平角 周角 范围 0<∠β<90° ∠β=90° 90°<∠β<180° ∠β=180° ∠β=360°(3)结论: 同角(或等角)的余角相等;同角(或等角)的补角相等.要点诠释:①余角(或补角)是两个角的关系,是成对出现的,单独一个角不能称其为余角(或补角).②一个角的余角(或补角)可以不止一个,但是它们的度数是相同的.③只考虑数量关系,与位置无关.④“等角是相等的几个角”,而“同角是同一个角” .4.方位角以正北、正南方向为基准,描述物体运动的方向,这种表示方向的角叫做方位角.要点诠释:(1)方位角还可以看成是将正北或正南的射线旋转一定角度而形成的.所以在应用中一要确定其始边是正北还是正南.二要确定其旋转方向是向东还是向西,三要确定旋转角度的大小.(2)北偏东45 °通常叫做东北方向,北偏西45 °通常叫做西北方向,南偏东45 °通常叫做东南方向,南偏西45 °通常叫做西南方向.(3)方位角在航行、测绘等实际生活中的应用十分广泛.【典型例题】类型一、概念或性质的理解1.下列说法正确的是( )A.射线AB与射线BA表示同一条射线.B.连结两点的线段叫做两点之间的距离.C.平角是一条直线.D.若∠1+∠2=90°,∠1+∠3=90°,则∠2=∠3. 【答案】D【解析】选项A中端点和延伸方向不同,所以是两条射线;选项B中两点之间的距离是指线段的长度,是一个数值,而不是图形;C中角和直线是两种不同的概念,不能混淆.【总结升华】理解概念,掌握概念与概念的本质区别,并进行“比较”性分析和记忆.举一反三:【变式】下列结论中,不正确的是().A.两点确定一条直线B.两点之间,直线最短C.等角的余角相等D.等角的补角相等【答案】B类型二、立体图形与平面图形的相互转化2.(2015•泰州)一个几何体的表面展开图如图所示,则这个几何体是()A.四棱锥B.四棱柱C.三棱锥D.三棱柱【答案】A.【总结升华】此题主要考查了几何体的展开图,熟记常见立体图形的平面展开图的特征是解决此类问题的关键.举一反三:【变式】(瞿州模拟)下面形状的四张纸板,按图所示的线经过折叠可以围成一个直三棱柱的是().【答案】C3. (浙江金华)如图所示几何体的主视图是()【答案】A【解析】从正面看球位于桌面右方,故选A.【总结升华】从正面看所得到的图形是主视图,先得到球体的主视图,再得到长方体的主视图,再根据球体在长方体的右边可得出答案.类型三、互余互补的有关计算4. 已知∠A=53°27′,则∠A的余角等于().A.37°B.36°33′C.63°D.143°【思路点拨】根据互为余角的定义求解.【答案】B【解析】∠A的余角为90°-53°27′=36°33′.【总结升华】本题考查角互余的概念:和为90度的两个角互为余角.举一反三:(2015•东莞模拟)一个角的余角比这个角的补角的一半小40°,则这个角为度.【变式】【答案】80.解:设这个角为x,则它的余角为(90°﹣x),补角为(180°﹣x),由题意得,(180°﹣x)﹣(90°﹣x)=40°,解得x=80°.类型四、方位角5.如图,射线OA的方向是:________;射线OB的方向是:_________;射线OC的方向是:________ .【思路点拨】OA表示的方向是北偏东,再加上其偏转的角度即可,同理OB、OC也是如此.【答案】北偏东15°;北偏西40°;南偏东45°.【解析】根据方位角的定义解答.【总结升华】熟知方位角的定义结合图形便可解答.类型五、钟表上的角6. (广西钦州)钟表分针的运动可看作是一种旋转现象,一只标准时钟的分针匀速旋转,经过15分钟旋转了________度.【答案】90【解析】根据钟表的特征;整个钟面是360°,分针每5分钟旋转30°,所以经过15分钟旋转了90°.【总结升华】在钟表问题中,常利用时针与分针转动的度数关系:时钟上的分针匀速旋转一分钟时的度数为6°,时针一分钟转过的度数为0.5°;两个相邻数字间的夹角为30°,每个小格夹角为6°,并且利用起点时间时针和分针的位置关系建立角的图形.类型六、利用数学思想方法解决有关线段或角的计算1.方程的思想方法7.如图所示,在射线OF上,顺次取A、B、C、D四点,使AB:BC:CD=2:3:4,又M、N分别是AB、CD的中点,已知AD=90cm,求MN的长.【思路点拨】有关比例问题,可设每一份为x,列方程求解,再利用中点定义,找出线段的和、差.【答案与解析】解:设线段AB,BC,CD的长分别是2x cm,3x cm,4x cm,∵AB+BC+CD=AD=90 cm,∴2x+3x+4x=90,x=10,∴AB=20 cm,BC=30 cm,CD=40 cm,∴MN=MB+BC+CN=12AB+BC+12CD=10+30+20=60(cm).【总结升华】当已知某线段被分成的几条线段的长度比时,可根据比设未知数x,用x的式子表示相关的线段的长度,列方程求出x的值,进而求出线段的长.举一反三:【变式】如图所示,已知∠AOC=∠BOD=100°,且∠AOB:∠AOD=2:7,求∠BOC和∠COD的度数.【答案】解:设∠AOB的度数为2x,则∠AOD的度数为7x.由∠AOD=∠AOB+∠BOD及∠BOD=100°,可得7x=2x+100°.解得x=20°,所以∠AOB=2x=40°.所以∠BOC=∠AOC-∠AOB=100°-40°=60°,∠COD=∠BOD-∠BOC=100°-60°=40°.2.分类的思想方法8.以∠AOB的顶点O为端点的射线OC,使∠AOC:∠BOC=5:4.(1)若∠AOB=18°,求∠AOC与∠BOC的度数;(2)若∠AOB=m,求∠AOC与∠BOC的度数.【答案与解析】解:(1)分两种情况:①OC在∠AOB的外部,可设∠AOC=5x,则∠BOC=4x得∠AOB=x,即x=18°所以∠AOC=90°,∠BOC=72°②OC在∠AOB的内部,可设∠AOC=5x,则∠BOC=4x∠AOB=∠AOC+∠BOC=9x所以9x=18°,则x=2°所以∠AOC=10°,∠BOC=8°(2)仿照(1),可得:若∠AOB=m,则∠AOC=59m,∠BOC=49m,或∠AOC=5m,∠BOC=4m.【总结升华】本题中的已知条件没有明确地说明OC在∠AOB的内部或外部,所以两个问题都必须分类讨论.举一反三:【变式1】已知线段AB=8cm,在直线AB上画线段BC=3cm,求线段AC的长.【答案】解:分两种情况:(1)如图(1),AC=AB-BC=8-3=5(cm);(2)如图(2),AC=AB+BC=8+3=11(cm).所以线段AC的长为5cm或11cm.【变式2】下列判断正确的个数有( )①已知A、B、C三点,过其中两点画直线一共可画三条②过已知任意三点的直线有1条③三条直线两两相交,有三个交点A.0个B.1个C.2个D.3个【答案】A3.类比的思想方法9.(1)如图,线段AD上有两点B、C,图中共有______条线段.(2)如图,在∠AOD的内部有两条射线OB、OC,则图中共有个角.【答案】(1)6;(2)6.【解析】(1)以A为端点的线段有3条,同样以B,C,D为一个端点的线段也各有3条,又因为所有线段均重复了一次,所以共有线段条数:3462⨯=(条).(2)以射线OA为一边的角有3个,同样以OB,OC,OD为一边的角也各有3个,又因为所有角均重复一次,所以共有角的个数:3462⨯=(个).【总结升华】用同样的方法解决了不同的问题,用已知的知识类比地学习未知的内容. 【巩固练习】一、选择题1.从左边看图1中的物体,得到的是图2中的().2.如图所示是正方体的一种平面展开图,各面都标有数,则标有数“-4”的面与其对面上的数之积是().A.4 B.12 C.-4 D.03.在下图中,是三棱锥的是().4.如图所示,点O在直线AB上,∠COB=∠DOE=90°,那么图中相等的角的对数是().A.3 B.4 C.5 D.75.如图所示的图中有射线().A.3条B.4条C.2条D.8条6.(2015•宝应县校级模拟)在地理课堂上,老师组织学生进行寻找北极星的探究活动时,李佳同学使用了如图所示的半圆仪,则下列四个角中,最可能和∠AOB互补的角为()A.B.C.D.7.十点一刻时,时针与分针所成的角是().A.112°30′B.127°30′C.127°50′D.142°30′8.在海面上有A和B两个小岛,若从A岛看B岛是北偏西42°,则从B岛看A岛应是().A.南偏东42°B.南偏东48°C.北偏西48°D.北偏西42°二、填空题9.把一条弯曲的公路改为直道,可以缩短路程,其理由是________.10.已知∠α=30°18′,∠β=30.18°,∠γ=30.3°,则相等的两角是________.11.用平面去截一个几何体,如果得出的横截面是圆形,那么被截的几何体是________(填一个答案即可).12.(2015秋•泾阳县期中)如图是一个正方体的展开图,和C面的对面是 面.13.若∠1+∠2=90°,∠1+∠3=90°,则∠2=∠3,其根据是________.14.若∠α是它的余角的2倍,∠β是∠α的2倍,那么把∠α和∠β拼在一起(有一条边重合)组成的角是________度.15.一副三角板如图摆放,若∠BAE=135 °17′,则∠CAD 的度数是 .16.如下图,点A 、B 、C 、D 代表四所村庄,要在AC 与BD 的交点M 处建一所“希望小学”,请你说明选择校址依据的数学道理 .三、解答题 17. (2015春•淄博校级期中)如图,已知点C 为AB 上一点,AC=12cm ,CB=AC ,D 、E 分别为AC 、AB 的中点,求DE 的长.18.如图所示,已知∠COB =2∠AOC ,OD 平分∠AOB ,且∠COD =19°,求∠AOB 的度数.19.在一张城市地图上,如图所示,有学校、医院、图书馆三地,图书馆被墨水染黑,具体位置看不清,但知道图书馆在学校的北偏东45°方向,在医院的南偏东60°方向,你能确定图书馆的位置吗?MB C DA20.如图所示,线段AB =4,点O 是线段AB 上一点,C 、D 分别是线段OA 、OB 的中点,小明据此很轻松地求得CD =2.在反思过程中突发奇想:若点O 运动到AB 的延长线上,原来的结论“CD =2”是否仍然成立?请帮小明画出图形并说明理由.【答案与解析】一、选择题1.【答案】B【解析】从左边看,圆台被遮住一部分,故选B .2.【答案】B【解析】由正方体的平面展开图可知,标有数-4的面的对面是标有数-3的面,故两个数之积为12.3.【答案】B【解析】A 选项是四棱锥,B 选项是三棱锥,C 、D 两项都是三棱柱,故选B .4.【答案】C【解析】因为∠COB =90°,所以∠BOD+∠COD =90°,即∠BOD =90°-∠COD .因为∠DOE =90°,所以∠EOC+∠COD =90°,即∠EOC =90°-∠COD ,所以∠BOD =∠EOC .同理∠AOE =∠COD .又因为∠AOC =∠COB =∠DOE =90°(∠AOC =∠COB ,∠AOC =∠DOE ,∠COB =∠DOE ),所以图中相等的角有5对,故选C .5.【答案】D6.【答案】D .【解析】根据图形可得∠AOB 大约为135°,∴与∠AOB 互补的角大约为45°,综合各选项D 符合.7.【答案】D【解析】一刻是15分钟,十点一刻,即10点15分时,时针与分针所成的角为:34304⎛⎫+⨯ ⎪⎝⎭°=142.5°=142°30′,故选D . 8.【答案】A【解析】方位角存在这样的规律:甲、乙两地之间的方位角,方向相反,角度相等.由此可知从B 岛看A 岛的方向为南偏东42°,故选A .二、填空题9. 【答案】两点之间,线段最短【解析】本题是应用线段的性质解释生活中的现象,由于这是两点之间连线长度的比较,符合“两点之间,线段最短”.10.【答案】∠α和∠γ【解析】30.3601810︒''=⨯=,于是∠α=∠γ.11.【答案】圆柱(圆锥、圆台、球体等)【解析】答案不唯一,例如用平面横截圆锥即可得到圆形.12.【答案】F.【解析】这是一个正方体的平面展开图,共有六个面,其中面“B”与面“D”相对,面“A”与面“E”相对,“C”与面“F”相对.13.【答案】同角的余角相等【解析】根据余角的性质解答问题.14.【答案】60度或180【解析】先求出∠α=60°,∠β=120°;再分∠α在∠β内部和外部两种情况来讨论.15.【答案】44°43′;【解析】∠BAD+∠CAE=180°,即∠BAE+∠CAD=180°,所以∠CAD=180°-135°17′=44°43′.16.【答案】两点之间,线段最短.三、解答题17.【解析】解:∵AC=12cm,CB=AC,∴CB=6cm,∴AB=AC+BC=12+6=18cm,∵E为AB的中点,∴AE=BE=9cm,∵D为AC的中点,∴DC=AD=6cm,所以DE=AE﹣AD=3cm.18.【解析】解:设∠AOC=x°,则∠COB=2x°.因为OD平分∠AOB,所以∠AOD=12∠AOB=12(∠AOC+∠BOC)=32x°.又因为∠DOC=∠AOD-∠AOC,所以3192x x=-.解得x=38,所以∠AOB=3x°=114°.19.【解析】解:如图所示.在医院A处,以正南方向为始边,逆时针转60°角,得角的终边射线AC.在学校B处,以正北方向为始边,顺时针旋转45°角,得角的终边射线BD.AC与BD的交点为点O,则点O就是图书馆的位置.20.【解析】解:原有的结论仍然成立,理由如下:当点O在AB的延长线上时,如图所示,CD=OC-OD=12(OA-OB)=12AB=142 2⨯=.。
浙教版初中数学七年级上册《图形的初步认识》全章复习与巩固(基础)知识讲解

浙教版初中数学七年级上册《图形的初步认识》全章复习与巩固(基础)知识讲解本文讲述了几何图形的初步认识,包括常见的几何体和平面图形的分类和构成元素。
同时,讲解了直线、射线、线段、角等基本图形的概念、表示方法、性质和画法,并介绍了应用图形与几何的知识解释生活中的现象及解决简单的实际问题的能力。
在几何体的分类中,不同的分类标准会得到不同的分类结果。
而几何体是由点、线、面构成的,点可以动成线,线与线相交成点,线动成面,面与面相交成线,面动成体,体是由面组成。
在线段、射线和直线的区别与联系中,直线由两点确定,线段是两点之间的最短距离,而射线则是从一个点出发,延伸出去的线段。
在画一条线段等于已知线段时,可以用度量法或尺规作图法。
而线段的比较与运算可以通过度量法、叠合法或估算法来实现。
同时,线段的中点可以将一条线段分成两条相等的线段。
最后,本文介绍了角的概念及其表示方法。
角是由两条射线共同确定的,可以用度数或弧度来表示。
角是由两条射线或一条射线绕着端点旋转形成的图形,其中端点称为角的顶点,射线称为角的边。
角的表示方法有三种:用三个大写字母表示、用顶点的一个大写字母表示、用一个小写希腊字母或数字表示。
角可以根据其大小和范围进行分类,包括锐角、直角、钝角、平角和周角。
角的度量单位是度,一周角等于360度,一平角等于180度,一度等于60分,一分等于60秒。
度、分、秒之间的转换方法是逐级进行乘除法,超过60进一或减一成60.角的比较和运算有三种方法:度量法、叠合法和估算法。
角的平分线是从角的顶点出发,将角分成相等的两个或三个角的射线。
余角和补角是两个角的关系,同角(或等角)的余角和补角相等。
方位角是以正北、正南方向为基准,描述物体运动方向的角。
2024年图形的初步认识复习 课件 浙教版

2024年图形的初步认识复习课件浙教版一、教学内容本节课我们将复习《2024年图形的初步认识》一章节,详细内容包括:平面几何图形的基本概念、图形的识别与分类、图形的属性(周长、面积)、图形的对称性及简单组合图形的识别。
二、教学目标1. 巩固对平面几何图形的基本概念的理解,能准确识别和分类各种图形。
2. 掌握图形的周长和面积计算方法,并能运用到实际问题中。
3. 理解图形的对称性,能够判断图形是否具有对称性。
三、教学难点与重点教学难点:图形的组合识别、图形的对称性判断。
教学重点:图形的基本概念、周长和面积的计算、图形的分类。
四、教具与学具准备教具:PPT课件、黑板、粉笔。
学具:练习本、铅笔、直尺、圆规。
五、教学过程1. 导入:通过PPT展示一组生活中的几何图形,引导学生观察并说出这些图形的名称,激发学生对图形的兴趣。
2. 知识回顾:a. 请学生回顾平面几何图形的基本概念、分类及图形的周长、面积计算方法。
b. 教师通过PPT进行讲解,强调重点内容。
3. 实践情景引入:a. 设计一个简单的图形组合问题,让学生分组讨论并解答。
b. 学生展示解答过程,教师点评并给出正确答案。
4. 例题讲解:a. 选取一道图形周长和面积计算的例题,详细讲解解题步骤。
b. 学生跟随教师一起解答,巩固所学知识。
5. 随堂练习:a. 设计一些图形识别、周长和面积计算的练习题,让学生独立完成。
b. 教师对学生的练习进行批改和反馈。
b. 强调图形的对称性判断方法。
六、板书设计1. 《2024年图形的初步认识》复习2. 内容:a. 图形的基本概念、分类b. 图形的周长、面积计算c. 图形的对称性3. 例题及解答过程七、作业设计1. 作业题目:2. 答案:(见附件)八、课后反思及拓展延伸1. 反思:本节课学生对图形的基本概念和计算方法掌握较好,但对图形的对称性判断还有待加强,需要在今后的教学中加强练习。
2. 拓展延伸:a. 引导学生思考:如何计算组合图形的周长和面积?b. 课后查阅资料,了解更多关于几何图形的知识。
《图形认识初步》章节全面复习 课件

类似地,还有角的三等分线等.
练习:如图所示,OE,OD分别平分∠AOB 和∠BOC,且∠AOB=90º. (1)如果∠BOC=40º,求∠EOD的度数; (2)如果∠EOD=70º,求∠BOC的度数.
【变式】如图所示,已知∠AOC= ∠BOD=100°,且∠AOB:∠AOD= 2:7,求∠BOC和∠COD的度数.
①度、分、秒的换算是60进制,与时间中的小时分钟秒的换算相同. ②度分秒之间的转化方法:由度化为度分秒的形式(即从高级单位向低级 单位转化)时用乘法逐级进行;由度分秒的形式化成度(即低级单位向高级单位转化)时 用除法逐级进行. ③同种形式相加减:超60进一,减一成60.
2.角的比较与运算 (1)角的比较方法: ①度量法;②叠合法. (2)角的平分线: 从一个角的顶点出发,把这个角分成相等的两个角的射 线,叫做这个角的平分线.例如:如下图,
归纳: ①余角(或补角)是两个角的关系,是成对出现的,单独一个角不能称其为余角(或补角). ②一个角的余角(或补角)可以不止一个,但是它们的度数是相同的, ③只考虑数量关系,与位置无关. ④“等角是相等
4.方位角
以正北、正南方向为基准,描述物体运动的方向, 这 种表示方向的角叫做方位角.
练习:1.如图射线OA表示的方向是( )
aa
b
b
A
Aa
Ba b CB
bC
A
D
B
A
D
B
(3)线段的中点、三等分点、四等分点等
把一条线段分成两条相等线段的点,叫做线段的中点.如下图,
有:
A
AM
M
MB
图形的初步认识复习

图形的初步认识复习3.图形变换思想。
在研究⾓的概念时,要充分体会对射线旋转的认识。
在处理图形时应注意转化思想的应⽤,如⽴体图形与平⾯图形的互相转化。
4.化归思想。
在进⾏直线、线段、⾓以及相关图形的计数时,总要划归到公式n(n-1)/2的具体运⽤上来。
⼀、本章的知识结构图⼆、知识回顾本章的主要内容是图形的初步认识,从⽣活周围熟悉的物体⼊⼿,对物体的形状的认识从感性逐步上升到抽象的⼏何图形。
通过从不同⽅向看⽴体图形和展开⽴体图形,初步认识⽴体图形与平⾯图形的联系。
在此基础上,认识⼀些简单的平⾯图形——直线、射线、线段和⾓。
⼀、⽴体图形与平⾯图形例1 (1)如图1所⽰,上⾯是⼀些具体的物体,下⾯是⼀些⽴体图形,试找出与下⾯⽴体图形相类似的物体。
(2)如图2所⽰,写出图中各⽴体图形的名称。
图1图2解:(1)①与d类似,②与c类似,③与a类似,④与b类似。
(2)①圆柱,②五棱柱,③四棱锥,④长⽅体,⑤五棱锥。
例2 如图3所⽰,讲台上放着⼀本书,书上放着⼀个粉笔盒,指出右边三个平⾯图形分别是左边⽴体图形的哪个视图。
图3解:(1)左视图,(2)俯视图,(3)正视图练习1.下图是⼀个由⼩⽴⽅体搭成的⼏何体由上⽽看得到的视图,⼩正⽅形中的数字表⽰该位置⼩⽴⽅块的个数,则从正⾯看它的视图为()2.如图,把左边的图形折叠起来,它会变成右边的正⽅体是右边的()3.如图,下⾯三个正⽅体的六个⾯按相同规律涂有红、黄、蓝、⽩、⿊、绿六种颜⾊,那么涂黄⾊、⽩⾊、红⾊的对⾯分别是()A.蓝、绿、⿊ B.绿、蓝、⿊ C.绿、⿊、蓝 D.蓝、⿊、绿4.若如下平⾯展开图折叠成正⽅体后,相对⾯上的两个数之和为5,求x+y+z的值。
5.⼀个物体从不同⽅向看的视图如下,画出该物体的⽴体图形。
⼆、直线、射线、线段(⼀).直线、射线、线段的区别与联系:从图形上看,直线、射线可以看做是线段向两边或⼀边⽆限延伸得到的,或者也可以看做射线、线段是直线的⼀部分;线段有两个端点,射线有⼀个端点,直线没有端点;线段可以度量,直线、射线不能度量。
图形认识初步复习
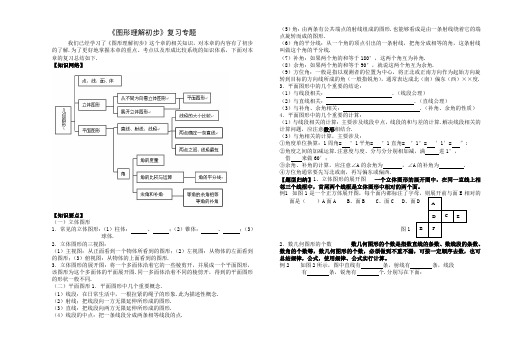
《图形理解初步》复习专题我们已经学习了《图形理解初步》这个章的相关知识,对本章的内容有了初步的了解.为了更好地掌握本章的重点、考点以及形成比较系统的知识体系,下面对本章的复习总结如下.【知识网络】【知识要点】(一)立体图形1.常见的立体图形:(1)柱体:、;(2)锥体:、;(3)球体.2.立体图形的三视图:(1)主视图:从正面看到一个物体所看到的图形;(2)左视图:从物体的左面看到的图形;(3)俯视图:从物体的上面看到的图形.3.立体图形的展开图:将一个多面体沿着它的一些棱剪开,并展成一个平面图形,该图形为这个多面体的平面展开图.同一多面体沿着不同的棱剪开,得到的平面图形的形状一般不同.(二)平面图形1.平面图形中几个重要概念.(1)线段:在日常生活中,一根拉紧的绳子的形象.此为描述性概念.(2)射线;把线段向一方无限延伸所形成的图形.(3)直线:把线段向两方无限延伸所形成的图形.(4)线段的中点:把一条线段分成两条相等线段的点. (5)角:由两条有公共端点的射线组成的图形.也能够看成是由一条射线绕着它的端点旋转而成的图形.(6)角的平分线:从一个角的顶点引出的一条射线,把角分成相等的角,这条射线叫做这个角的平分线.(7)补角:如果两个角的和等于180°,这两个角互为补角.(8)余角:如果两个角的和等于90°,就说这两个角互为余角.(9)方位角:一般是指以观测者的位置为中心,将正北或正南方向作为起始方向旋转到目标的方向线所成的角(一般指锐角),通常表达成北(南)偏东(西)××度. 3.平面图形中的几个重要的结论:(1)与线段相关: .(线段公理)(2)与直线相关: .(直线公理)(3)与补角、余角相关: .(补角、余角的性质)4.平面图形中的几个重要的计算:(1)与线段相关的计算:主要涉及线段中点,线段的和与差的计算.解决线段相关的计算问题,应注意数形相结合.(3)与角相关的计算,主要涉及:①角度单位换算:1周角= °1平角= °1直角= °1°= ′1′= ″;②角度之间的加减运算.注意度与度、分与分分别相加减,满进1°,借来做60′;③余角、补角的计算,应注意∠A的余角为,∠A的补角为 .④方位角通常要先写北或南,再写偏东或偏西.【题型归纳】1、立体图形的展开图一个立体图形的展开图中,在同一直线上相邻三个线框中,首尾两个线框是立体图形中相对的两个面。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《图形的初步认识》全章复习与巩固【知识网络】【要点梳理】要点一、立体图形与平面图形1.几何图形的分类要点诠释:在给几何体分类时,不同的分类标准有不同的分类结果.2.立体图形与平面图形的相互转化(1)立体图形的平面展开图:把立体图形按一定的方式展开就会得到平面图形,把平面图形按一定的途径进行折叠就会得到相应的立体图形,通过展开与折叠能把立体图形和平面图形有机地结合起来.要点诠释:①对一些常见立体图形的展开图要非常熟悉,例如正方体的 11种展开图,三棱柱,圆柱等的展开图.②不同的几何体展成不同的平面图形,同一几何体沿不同的棱剪开,可得到不同的平面图形,那么排除障碍的方法就是:联系实物,展开想象,建立“模型”,整体构想,动手实践. (2)三视图:⎧⎨⎩正视图--------------从正面看几何体的三视图 左视图--------------从侧边看俯视图--------------从上面看要点诠释:①会判断简单物体(直棱柱、圆柱、圆锥、球)的三视图. ②三视图的画法原则:高平齐宽相等长对正. ③能根据三视图描述基本几何体或实物原型. (3)几何体的构成元素及关系:几何体是由点、线 、面构成的.点动成线,线与线相交成点;线动成面,面与面相交成线;面动成体,体是由面组成.要点二、直线、射线、线段1. 直线,射线与线段的区别与联系2. 基本性质(1)直线的性质:两点确定一条直线. (2)线段的性质:两点之间,线段最短. 要点诠释:①本知识点可用来解释很多生活中的现象. 如:要在墙上固定一个木条,只要两个钉子就可以了,因为如果把木条看作一条直线,那么两点可确定一条直线. ②连接两点间的线段的长度,叫做两点的距离.3.画一条线段等于已知线段(1)度量法:可用直尺先量出线段的长度,再画一条等于这个长度的线段. (2)用尺规作图法:用圆规在射线AC 上截取AB=a,如下图:4.线段的比较与运算 (1)线段的比较:比较两条线段的长短,常用两种方法,一种是度量法;一种是叠合法.(2)线段的和与差:如下图,有AB+BC=AC ,或AC=a+b ;AD=AB-BD 。
(3)线段的中点:把一条线段分成两条相等线段的点,叫做线段的中点.如下图,有12AM MB AB ==,或AB =2AM =2MB .要点诠释:①线段中点的等价表述:如上图,点M 在线段上,且有12AM AB =,则点M 为线段AB 的中点.②除线段的中点(即二等分点)外,类似的还有线段的三等分点、四等分点等.如下图,点M,N,P 均为线段AB 的四等分点.PNAB PB NP MN AM 41==== 要点三、角1.角的相关概念(1)角的定义:有公共端点的两条射线组成的图形叫做角,这个公共端点是角的顶点,这两条射线是角的两条边;此外,角也可以看作由一条射线绕着它的端点旋转而形成的图形.其中起始位置的射线叫做角的始边,终止位置的射线叫做角的终边.(2)角的表示方法:角通常有四种表示方法:一是用三个大写英文字母表示,二是用角的顶点的一个大写英文字母表示,三是用一个小写希腊字母,四是用一个数字表示.例如下图:要点诠释:①角的两种定义是从不同角度对角进行的定义;②当一个角的顶点有多个角的时候,不能用顶点的一个大写字母来表示.(3)角度制及角度的换算1周角=360°,1平角=180°,1°=60′,1′=60″,以度、分、秒为单位的角的度量制,Bba MBA叫做角度制. 要点诠释:①度、分、秒的换算是60进制,与时间中的小时分钟秒的换算相同.②度分秒之间的转化方法:由度化为度分秒的形式(即从高级单位向低级单位转化)时用乘法逐级进行;由度分秒的形式化成度(即低级单位向高级单位转化)时用除法逐级进行. ③同种形式相加减:度加(减)度,分加(减)分,秒加(减)秒;超60进一,减一 成60. (4)角的分类(5)画一个角等于已知角(1)借助一副三角尺能画出15°的倍数的角,在0~180°之间共能画出11个角. (2)借助量角器能画出给定度数的角. (3)用尺规作图法. 2.角的比较与运算(1)角的比较方法: ①度量法;②叠合法.(2)角的平分线:从一个角的顶点出发,把这个角分成相等的两个角的射线,叫做这个角的平分线,例如:如下图,因为OC 是∠AOB 的平分线,所以∠1=∠2=12∠AOB ,或∠AOB=2∠1=2∠2. 类似地,还有角的三等分线等.3.角的互余互补关系(1)若∠1+∠2=90°,则∠1与∠2互为余角.其中∠1是∠2的余角,∠2是∠1的余角. (2)若∠1+∠2=180°,则∠1与∠2互为补角.其中∠1是∠2的补角,∠2是∠1的补角. (3)结论: 同角(或等角)的余角相等;同角(或等角)的补角相等. 要点诠释:①余角(或补角)是两个角的关系,是成对出现的,单独一个角不能称其为余角(或补角). ②一个角的余角(或补角)可以不止一个,但是它们的度数是相同的. ③只考虑数量关系,与位置无关.④“等角是相等的几个角”,而“同角是同一个角” . 4.方位角以正北、正南方向为基准,描述物体运动的方向,这种表示方向的角叫做方位角. 要点诠释:(1)方位角还可以看成是将正北或正南的射线旋转一定角度而形成的.所以在应用中一要确定其始边是正北还是正南.二要确定其旋转方向是向东还是向西,三要确定旋转角度的大小.(2)北偏东45 °通常叫做东北方向,北偏西45 °通常叫做西北方向,南偏东45 °通常叫做东南方向,南偏西45 °通常叫做西南方向.(3)方位角在航行、测绘等实际生活中的应用十分广泛.【典型例题】类型一、概念或性质的理解1.下列判断错误的有( )①延长射线OA;②直线比射线长,射线比线段长;③如果线段PA=PB,则点P是线段AB的中点;④连接两点间的线段,叫做两点间的距离.A.0个B.2个C.3个D.4个【答案】D【解析】①由于射线向一方无限延伸,因此,不能延长射线;②由于直线向两方无限延伸,射线向一方无限延伸,因此它们都是不能度量的,所以它们不存在相等或不相等的关系,而线段是可以度量的,可以比较线段的长短;③线段PA=PB,只有当点P在线段AB上时,才是线段AB的中点,否则就不是;④两点间的距离是表示大小的量,而线段是图形,二者的本质属性不同.【总结升华】本题考查的是基本概念,要抓住概念间的本质区别.举一反三:【变式】下列说法正确的个数有( ).①若∠1+∠2+∠3=90°,则∠1,∠2,∠3互余.②互补的两个角一定是一个锐角和一个钝角.③因为钝角没有余角,所以,只有当角为锐角时,“一个角的补角比这个角的余角大”这个说法才正确.A.0个B.1个C.2个D.3个【答案】B 提示:③正确类型二、立体图形与平面图形的相互转化1. 展开与折叠问题2.如图所示,它们的平面展开图是由5个大小相同的正方形组成,其中沿正方形的边不能折成无盖小方盒的是().【答案】B【解析】图形B无论怎样折叠都有一个侧面重合,这样就缺少一个侧面,所以图形B不能折成无盖小方盒.【总结升华】解题时勿忘记四棱柱的特征及正方体展开图的各种情形.举一反三:【变式】已知O为圆锥的顶点,M为圆锥底面圆上一点,点P在OM上.一只蜗牛从P点出发,绕圆锥侧面爬行,回到P点时,所爬过的最短路线的痕迹如图所示.若沿OM将圆锥侧面剪开并展平,所得侧面展开图(如图)是().【答案】D2.从不同方向看3. (河北)将正方体骰子(相对面上的点数分别为1和6,2和5,3和4)放置于水平桌面上,如图1所示.在图2中,将骰子向右翻滚90°,然后在桌面上按逆时针方向旋转90°,则完成一次变换.若骰子的初始位置为图1所示的状态,那么按上述规则连续完成10次变换后,骰子朝上一面的点数是().A.6 B.5 C.3 D.2【答案】B【解析】第一次变换:将骰子向右翻滚90°,正面向上的应当是5,右面的是3,正面是1,再在桌面上按逆时针方向旋转90°,面向上的应当是5,右面的是1,正面是4;第二次变换:将骰子向右翻滚90°,正面向上的应当是6,右面的是5,正面是4,再在桌面上按逆时针方向旋转90°,面向上的应当是6,右面的是4,正面是2;第三次变换:将骰子向右翻滚90°,正面向上的应当是3,右面的是6,正面是2,再在桌面上按逆时针方向旋转90°,正面向上的应当是3,右面的是2,正面是1,就回到了初始状态.所以每完成三次变换即可回到原来的位置,所以第十次变换后的状态与第一次变换后的状态相同,所以朝上一面的点数是5.【总结升华】先找到规律再从上面看便得答案.举一反三:【变式1】(南昌)沿圆柱体上底面直径截去一部分后的物体如图所示,它的俯视图是().【答案】D【高清课堂:图形认识初步章节复习399079 多姿多彩的图形例2】【变式2】如图,是由一些完全相同的小立方块搭成的几何体的三种视图,那么搭成这个几何体所用的小立方块的个数是()A. 5个B. 6个C. 7个D. 8个 【答案】D类型三、互余互补的有关计算4. (安徽芜湖)如图所示的4×4正方形网格中,∠1+∠2+∠3+∠4+∠5+∠6+∠7等于( )A .330°B .315°C .310°D .320° 【答案】B【解析】通过网格的特征首先确定∠4=45°.由图形可知:∠l 与∠7互余,∠2与∠6互余,∠3与∠5互余,所以∠l+∠2+∠3+∠4+∠5+∠6+∠7=90°+90°+90°+45°=315°. 【总结升华】互余的两个角只与数量有关,而与位置无关. 举一反三:【变式】如图所示,AB 和CD 都是直线,∠AOE =90°,∠3=∠FOD ,∠1=27°20′,求∠2,∠3.【答案】解:因为∠AOE =90°,所以∠2=90°-∠1=90°-27°20′=62°40′. 又∠AOD =180°-∠1=152°40′,∠3=∠FOD .所以∠3=12∠AOD =76°20′. 答:∠2为62°40′,∠3为76°20′. 类型四、方位角5. (山东潍坊)用A 、B 、C 分别表示学校、小明家、小红家,已知学校在小明家的南偏东25°,小红家在小明家正东,小红家在学校北偏东35°,则∠ACB 等于( )A.35°B.55°C.60°D.84°【思路点拨】根据方位角的概念,分清方向,正确地画出图形,即可求解.【答案】B【解析】根据题意画出图形如下:∵∠ACB与35°互余,∴∠ACB=90°-35°=55°【总结升华】解答此类题需要从运动的角度,正确画出方位角,找准中心是解答此类题的关键.举一反三:【变式】(张家界模拟)考点办公室设在校园中心O点,带队老师休息室A位于O点的北偏东45°,某考室B位于O点南偏东60°,请在图(1)中画出射线OA、OB,并计算∠AOB 的度数.【答案】解:如图(2),以O为顶点,正北方向线为始边向东旋转45°,得OA;以O为顶点,正南方向线为始边向东旋转60°,得OB,则∠AOB=180°-(45°+60°)=75°.类型五、利用数学思想方法解决有关线段或角的计算1.方程的思想方法6. 如图所示,B 、C 是线段AD 上的两点,且32CD AB =,AC =35cm ,BD =44cm ,求线段AD 的长.【答案与解析】解:设AB =x cm ,则3cm 2CD x =(35)cm BC x =-或3(44)cm 2x -于是列方程,得335442x x -=-解得:x =18,即AB =18(cm ) 所以BC =35-x =35-18=17(cm )33182722CD x ==⨯=(cm ) 所以AD =AB+BC+CD =18+17+27=62(cm )【总结升华】根据题中的线段关系,巧设未知数,列方程求解. 2.分类的思想方法7. 同一直线上有A 、B 、C 、D 四点,已知AD =59DB ,AC =95CB ,且CD =4cm ,求AB 的长.【思路点拨】先根据题意画出图形,再从图上直观的看出各线段的关系及大小. 【答案与解析】 解:利用条件中的AD =59DB ,AC =95CB ,设DB =9x ,CB =5y , 则AD =5x ,AC =9y ,分类讨论:(1)当点D ,C 均在线段AB 上时,如图所示:∵ AB =AD+DB =14x ,AB =AC+CB =14y ,∴ x =y∵ CD =AC -AD =9y -5x =4x =4,∴ x =1,∴ AB =14x =14(cm ). (2)当点D ,C 均不在线段AB 上时,如图所示:方法同上,解得87AB =(cm ).(3)如图所示,当点D 在线段AB 上而点C 不在线段AB 上时,方法同上,解得11253AB =(cm ).(4)如图所示,当点C 在线段AB 上而点D 不在线段AB 上时,方法同上,解得11253AB =(cm ).综上可得:AB 的长为14cm ,87cm ,11253cm . 【总结升华】解决没有图形的题目时,一要注意满足条件下的图形的多样性;二要注意解决的方法,注意方程法在解决图形问题中的应用. 在正确答案中,(3)与(4)的答案虽然相同,但作为图形上的差别应了解. 类型六、钟表上的角8. 如图所示,时钟的时针由3点整的位置(顺时针方向)转过多少度时,与分针第一次重合.【答案与解析】解:设时针转过的度数为x °时,与分针第一次重合,依题意有 12x =90+x 解得9011x =答:时针转过9011⎛⎫⎪⎝⎭°时,与分针第一次重合. 【总结升华】在相同时间里,分针转过的度数是时针的12倍,此外此问题可以转化为追及问题来解决.。
