第九讲 一笔画
合集下载
一笔画 课件
感谢聆听
制作单位：建德市实验小学 制作日期：2019年3月28日
BE
FD
C
4个偶点，2个奇点 是一笔画
D K
H A
C J
I B
4个奇点 不是一笔画
下图至少要画几笔才能画成?
D K
C J
H A
I B
4个奇点 不是一笔画
下图如何改造一下就能变成一笔画?
D K
C J
H A
I B
4个奇点 不是一笔画
下图是邮递员李阿姨每天所要走的路 线图，你有办法帮李阿姨设计一条路线让 她不走重复路线吗?
1.下列各图至少要用几笔画完?
2.某儿童公园游乐场平面图如右 图所示，其中A，B，C，E，E，F 均表示园中的六处景观。为了方 便游客，今打算修出(入)口两处 。为了让游客可以从某入(出)口 进去后，可以不重复地走完图中 所有通道后从另一出(入)口出园 。问游乐场的两个出(入)口应修 在何处?
3.下图是博物馆展厅，由 六间展室组成，每相邻两 室间有一扇门相通，请你 设计一个出口，使参观者 能够从入口处（A处）进 去，一次不重复地经过所 有的门，最后由出口走出。
有2个奇点
有4个奇点
①凡是由偶点组成的连通
A
图，一定可以一笔画成；画时可
以任一偶点为起点，最后一定能
以这个点为终点画完此图。
C
D
②凡是只有两个奇点的连通 图，一定可以一笔画完；画时必
须以一个奇点为起点，另一个奇
点为终点。
B 有4个奇点
③其他情况的图，都不能一 笔画出。
判断：下面图形是一笔画吗？
A
下图是邮递员李阿姨每天所要走的路 线图，你有办法帮李阿姨设计一条路线让 她不走重复路线吗?
第九讲 一笔画问题 PPT
• 解答：图（1）中无奇点，能一笔画出，从任意点开始再回到这一点， 仅举一例：A→B→C→N→F→G→H→M→D→N→E→M→H；
• 图（2）有两个奇点，可以从B开始到E结束，也可以从E开始到B结束， 如：B→C→D→E→A→B→E；
• 图（3）不能一笔画出有4个奇点，要想一笔画出至少应该添一笔，可 以连接A、B，如图1，其它的任何两个奇点都可以。共有多少连法呢， 你能列举出来吗？共有6种分别为AB、AC、AD、BC、BD、CD；
重复.从上图中容易看出：能一笔画出的图首先必须是连
通图.但是否所有的连通图都可以一笔画出呢？下面，我
们就来探求解决这个问题的方法。
•
为了叙述的方便，我们把与奇数条边相连的结点叫做
奇点，把与偶数条边相连的点称为偶点.如上图（a）中的
八个结点全是奇点，上图（b）中E、F为奇点，G为偶点。
•
容易知道，上图（b）可以一笔画出，即从奇点E出发，
得出了一个非常重要的结论，你想知道吗？其实
这就是“一笔画”问题，也是一种数学游戏，学
完了下面的内容，也许你就能像欧拉那样解决
“七桥问题”了。
• 欧拉解决这个问题的方法非常巧妙.他认为： 人们关心的只是一次不重复地走遍这七座桥，而 并不关心桥的长短和岛的大小，因此，岛和岸都 可以看作一个点，而桥则可以看成是连接这些点 的一条线.这样，一个实际问题就转化为一个几何 图形能否一笔画出的问题了.
都有一条通路（即可以从其中一点出发，沿着图 的边走到另一点，如A到I的通路为A→H→I或 A→D→I…），这样的图，我们称为连通图；而 下图中（c）的一些结点之间却不存在通路（如M 与N），像这样的图就不是连通图。
•
所谓图的一笔画，指的就是：从图的一点出发，笔不
一笔画原理
一笔画原理
一笔画原理是指只用一条笔画，不抬笔、不重复，将图形或文字一气呵成的绘画方法。
这种绘画方法要求绘画者在开始时要仔细观察，构思出合理的笔画顺序和路径。
只有通过准确而连贯的笔画，才能完成整个图形。
一笔画原理在绘画艺术中被广泛应用，它既是一种技术要求，也是一种艺术表现方式。
这种绘画方法对绘画者的技巧、耐心和思维逻辑要求都非常高。
在实际绘画过程中，绘画者需要善于观察和构思，将整个图形清晰地在脑海中形成，然后才能准确地用一条笔画表达出来。
一笔画原理还可以培养绘画者细心观察、抽象思维和创造力等方面的能力。
通过不断的练习和挑战，绘画者能够提高细节把握能力和笔触的稳定性，使自己在绘画时更具有独特的风格和韵味。
这种绘画方式不仅局限于图形的描绘，还可以运用到书法、漫画等领域。
通过一笔画原理，书法家可以用一条笔画表达出自己独特的书法风格和气质；漫画家则可以用一笔画勾勒出丰富的卡通形象和有趣的场景。
总之，一笔画原理是一种非常具有挑战性和创造性的绘画方式。
通过运用一笔画原理，绘画者可以在限制中发挥自己的想象力和创造力，创作出独特而有趣的作品。
小学数学一笔画课件
THANKS FOR WATCHING
感谢您的观看
03
一笔画问题的解题方法
逐步推理法
总结词
通过逐步推理，按照一定的逻辑顺序，确定笔画的路径。
详细描述
逐步推理法是一种常用的解题方法，它通过逐步分析图形的特点和规律，推断出 笔画的路径。这种方法需要有一定的逻辑推理能力，对于一些较为复杂的图形， 需要仔细分析其结构，找出正确的笔画路径。
奇偶点分析法
拉回路是指一条通过图形的每条边且每条边只通过一次的闭合路径。
02
奇点与偶点
在图形中，如果一个节点发出的线条数是奇数，则该节点称为奇点；如
果一个节点发出的线条数是偶数，则该节点称为偶点。
03
哈密顿路径和哈密顿回路
哈密顿路径是指一条通过图形的每条边且每条边只通过一次的路径，但
不一定是闭合路径；哈密顿回路是指一条通过图形的每条边且每条边只
计算机科学
一笔画问题在计算机科学 中也有广泛应用，例如在 计算机图形学、算法设计 等领域。
实际应用
一笔画问题在现实生活中 也有很多应用，如地图的 绘制、电路设计、交通规 划等。
02
一笔画问题的数学原理
欧拉公式
欧拉公式
对于一个连通图，其边数和顶点数的关系可以用公式(V - E + F = 2)来表示，其中(V)表示顶点数，(E)表示边数，(F)表示面 数。这个公式是解决一笔画问题的重要依据。
问题的能力。
创新的一笔画问题
总结词
创意问题，挑战性
VS
详细描述
创新的一笔画问题通常涉及更为复杂和创 意的图形，如不规则多边形、立体图形等 ，这类问题旨在激发学生的创造力和挑战 精神。同时，这类问题也可能涉及到数学 中的其他知识点，如平面几何、立体几何 等。
一笔画ppt(1)
专题活动：一笔画
“一笔画”是指笔不离开纸，而且 每条线都只画一次不准重复而画成 的图形。
“一笔画”是一种有趣的数学游 戏，那么什么样的图形可以一笔 画成呢？试一试，画一画，发挥 你的想象力，发现一笔画的规律。
你能用一笔画出下列图形吗？
（ 4 ）个
（ 2 ）个
（ 9 ）个
（ 5 ）个
交点分为两种图1来自图3图5图2
图4
图6
下面是一笔画故事： 事情发生在公元18世纪普鲁士的哥尼斯堡城.一条河从这个城市穿过，河中
有两个小岛把主流分成了两半.河上有七座桥连接两岛同河的两岸沟通（如图）. 这是个风景秀丽的地方，吸引了许多游人.人们在这里参观、散步.不知谁最先提 出了一个问题：一个散步者怎样能一次走遍这七座桥，最后又回到出发点，而 每座桥只走过一次，不许重复.
⒉凡是只有两个奇点的连通图（其余都为偶点），一 定可以一笔画成。画时必须把一个奇点为起点，另一 个奇点终点。
⒊其他情况的图都不能一笔画出。
观察下列图形，试着画一画。
图1
图2
图3
图4
图5
图6
根据今天学习知识，先判断下列图形能不能 一笔画成？再想一想该从哪里开始画？最后 再动手画画看。
判断下列图形能否一笔画。
（1）从这点出发的线的数目 是双数的，叫双数点（偶点）。 （2）从这点出发的线的数目 是单数的，叫单数点（奇点）。
①从这点出发的线的数目是单数的，叫单数点（奇点）。 如：
●
●
●
②从这点出发的线的数目是双数的，叫双数点（偶点）。 如：
●
●
●
数学家欧拉找到一笔画的规律是：
⒈凡是都由偶点组成的连通图，一定可以一笔画成。 画时可以把任一偶点为起点，最后一定能以这个点为 终点画完此图。
“一笔画”是指笔不离开纸，而且 每条线都只画一次不准重复而画成 的图形。
“一笔画”是一种有趣的数学游 戏，那么什么样的图形可以一笔 画成呢？试一试，画一画，发挥 你的想象力，发现一笔画的规律。
你能用一笔画出下列图形吗？
（ 4 ）个
（ 2 ）个
（ 9 ）个
（ 5 ）个
交点分为两种图1来自图3图5图2
图4
图6
下面是一笔画故事： 事情发生在公元18世纪普鲁士的哥尼斯堡城.一条河从这个城市穿过，河中
有两个小岛把主流分成了两半.河上有七座桥连接两岛同河的两岸沟通（如图）. 这是个风景秀丽的地方，吸引了许多游人.人们在这里参观、散步.不知谁最先提 出了一个问题：一个散步者怎样能一次走遍这七座桥，最后又回到出发点，而 每座桥只走过一次，不许重复.
⒉凡是只有两个奇点的连通图（其余都为偶点），一 定可以一笔画成。画时必须把一个奇点为起点，另一 个奇点终点。
⒊其他情况的图都不能一笔画出。
观察下列图形，试着画一画。
图1
图2
图3
图4
图5
图6
根据今天学习知识，先判断下列图形能不能 一笔画成？再想一想该从哪里开始画？最后 再动手画画看。
判断下列图形能否一笔画。
（1）从这点出发的线的数目 是双数的，叫双数点（偶点）。 （2）从这点出发的线的数目 是单数的，叫单数点（奇点）。
①从这点出发的线的数目是单数的，叫单数点（奇点）。 如：
●
●
●
②从这点出发的线的数目是双数的，叫双数点（偶点）。 如：
●
●
●
数学家欧拉找到一笔画的规律是：
⒈凡是都由偶点组成的连通图，一定可以一笔画成。 画时可以把任一偶点为起点，最后一定能以这个点为 终点画完此图。
关于一笔画问题的经典探讨PPT培训课件
段。
一笔画定理及其证明
一笔画定理
一个连通图形可以一笔画成当且仅当该图形中奇数个顶点的度数之和为2。
证明过程
首先，根据连通性规则，图形必须是连通的。然后，根据奇偶性规则，如果图 形中奇数个顶点的度数之和为2，则该图形可以一笔画成；如果图形中奇数个顶 点的度数之和不为2，则该图形不能一笔画成。
一笔画定理的应用实例
应用
一笔画问题在计算机科学、电子工 程、运筹学等领域都有广泛的应用。
一笔画问题的重要性和应用领域
理论价值
一笔画问题在数学理论中具有重 要的价值，是图论、组合数学等 领域的重要研究课题之一。
应用价值
一笔画问题在计算机图形学、电 路设计、物流规划等领域都有广 泛的应用，可以帮助人们解决一 系列实际问题。
06
一笔画问题的实际应用案例
地图着色问题
算法设计
解决地图着色问题需要设计一种有效的算法，能够判断给定的地图是否可以一笔画成，并找出最少所需的颜色数 量。常用的算法包括贪心算法、回溯算法等。
实例分析
地图着色问题可以通过实例来分析，例如给定一个包含多个国家的地图，如何使用最少的颜色对各个国家进行着 色，使得相邻的国家颜色不同。
判断一笔画图形
通过计算图形中奇数个顶点的度数之 和，可以判断该图形是否可以一笔画 成。
设计一笔画图案
解决实际问题
一笔画定理在计算机科学、电子工程、 机械工程等领域都有广泛的应用，例 如在电路设计和布线、机器人路径规 划等方面。
利用一笔画定理，可以设计出具有特 定形状和结构的一笔画图案。
03
一笔画问题的经典问题解析
THANKS
感谢观看
一个顶点的度数为奇数，意味着该顶点是起点或 终点。
一笔画定理及其证明
一笔画定理
一个连通图形可以一笔画成当且仅当该图形中奇数个顶点的度数之和为2。
证明过程
首先，根据连通性规则，图形必须是连通的。然后，根据奇偶性规则，如果图 形中奇数个顶点的度数之和为2，则该图形可以一笔画成；如果图形中奇数个顶 点的度数之和不为2，则该图形不能一笔画成。
一笔画定理的应用实例
应用
一笔画问题在计算机科学、电子工 程、运筹学等领域都有广泛的应用。
一笔画问题的重要性和应用领域
理论价值
一笔画问题在数学理论中具有重 要的价值，是图论、组合数学等 领域的重要研究课题之一。
应用价值
一笔画问题在计算机图形学、电 路设计、物流规划等领域都有广 泛的应用，可以帮助人们解决一 系列实际问题。
06
一笔画问题的实际应用案例
地图着色问题
算法设计
解决地图着色问题需要设计一种有效的算法，能够判断给定的地图是否可以一笔画成，并找出最少所需的颜色数 量。常用的算法包括贪心算法、回溯算法等。
实例分析
地图着色问题可以通过实例来分析，例如给定一个包含多个国家的地图，如何使用最少的颜色对各个国家进行着 色，使得相邻的国家颜色不同。
判断一笔画图形
通过计算图形中奇数个顶点的度数之 和，可以判断该图形是否可以一笔画 成。
设计一笔画图案
解决实际问题
一笔画定理在计算机科学、电子工程、 机械工程等领域都有广泛的应用，例 如在电路设计和布线、机器人路径规 划等方面。
利用一笔画定理，可以设计出具有特 定形状和结构的一笔画图案。
03
一笔画问题的经典问题解析
THANKS
感谢观看
一个顶点的度数为奇数，意味着该顶点是起点或 终点。
《一笔画》 ppt课件
画时以任一点为起点， 最后仍回到该点
画时以一个单数点为 起点，另一个为终点
例3：判断下列图形能否一笔画
图1
图3
图5
图2
图4
图6
例4：下图是一个公园的平面图， 要使游人走遍每一条路不重复，出 口和入口应设在哪儿？
甲、乙两个邮递员去送信，两人以同样的速度走遍 所有的街道，甲从A点出发，乙从B点出发，最后都回 到邮局（C）。如果要选择最短的线路，谁先回到邮局？
邮局
乙
甲
欧拉（ 公元1707-1783年）
总结：
一个图形能否一笔画成，关键在于图中单数点的多少。
(1)一笔画必须是连通的(图形的各部分之间连接在一 起) （2）凡是图形中没有单数点的一定可以一笔画成。可 选任一个点做起点，且一笔画后可以回到出发点。 （3）凡是图形中只有两个单数点，一定可以一笔画成。 画时必须从一个单数点为起点，以另一单数点为终点。 （4）凡是图形中单数点的个数多于两个时，此图肯定 是不能一笔画成。
例1：判断下列图形能否一笔画
不连通的图形不能一笔画
图1
图2
图3
连通的图形有可能一笔画
Hale Waihona Puke 图4图5两条相交的线处都有一个交点。
数一数下列图形各有几个交点？
（ 4 ）个
（ 2 ）个
（ 9 ）个
（ 5 ）个
交点分为两种
①从这点出发的线的数目是单数的，叫单数点。 如：
●
●
●
②从这点出发的线的数目是双数的，叫双数点。
如：
●
●
●
例2：观察下列图形，完成统计表
图1
图2
图3
图4
图5
图6
图7
一笔画的定理和画法
一笔画定理
一个图形要能一笔画完成必须符合两个条件： 图形是联通的；图形中的奇点（与奇数条边 相连的点）个数为0或2。
一笔画画法
由偶点组成的连通图，一笔画时，可以把任一 偶点为起点，最后一定能以这个点为终点画完 此图。
只有两个奇点的连通图（其余都为偶点），一笔 画时，必须我家小同学的学习记录
小学奥数
一笔画
一笔画 A 定义 C 定理
B 规律 D 画法
一笔画问题是研究平面上由线段构成的一个图形 能不能一笔画成，且使得画笔在每条线段上都不 重复。
一笔画的规律
凡是由偶点组成的连通图，一定可以一笔画成。
凡是只有两个奇点的连通图（其余都为偶点）， 一定可以一笔画成。
其他情况的图都不能一笔画出。（有偶数个奇点 除以二可以算出此图至少需几笔画成。）
一笔画课件
超市
电器城
文具店
菜市场
服装城
2、 下图是一个公园的平面图，能不能使游 人走遍每一条路不重复？入口和出口又应设 在哪儿？ E ● D● C●
F ●
●G
● B
●A
3、 甲乙两个邮递员去送信，两人同时出发以 同样的速度走遍所有的街道，甲从A点出发， 乙从B点出发，最后都回到邮局（C点）。如果 要选择最短的线路，谁先回到邮局？
脑筋急转弯： 想一想 一笔能写出1000吗？
18世纪风景秀丽的哥尼斯堡（位于立陶宛与波兰之间，现属 俄罗斯）中有一条河，河的中间有两个小岛，河的两岸与两岛之间 共建有七座桥（如图），城中的居民经常沿河过桥散步，不知从什 么时候起，脚下的桥梁触发了人们的灵感，一个有趣的问题在居民 中传开了：谁能够一次走遍所有的７座桥，而且每座桥都只通过一 次？最后是否仍能回到出发点？ 这就是数学史上著名的七桥问题。
不重复的路
——一笔画
“ 一笔画”是指笔不离开纸， 而且每条线都只画一次 不 准重复而画成的图形。
你能用一笔画出下列图形吗？
下列哪些图形能一笔画出来，哪些不能？
课堂练习
1、 一辆洒水车要给某城市的街道洒水，街道地图 如下：你能否设计一条洒水车洒水的路线，使洒水 车不重复地走过所有的街道，再回到出发点？ 小广场
D
B
A
C
欧拉解决这个问题的方法非常巧妙。他认为：人们关 心的只是一次不重复地走遍这七座桥，而并不关心桥的长 而桥则可 短和岛的大小，因此，岛和岸都可以看作一个点， 以看成是连接这些点的一条线。这样，一个实际问题就转 化为一个几何图形（如下图）能否一笔画出的问题了。
A
B
交点分为两种
（ 1 ）从这点出发的线的数目 是双数的，叫双数点（偶点）。 图形能否一笔画成，关键在于图 中单数点的多少。 （1）凡是图形中没有单数点的一定可以 一笔画成。 （2）凡是图形中只有一个或者两个单数 点，一定可以一笔画成。画时必须从一个 单数点为起点，以另一单数点为终点。 （3）凡是图形中单数点的个数多于两个 时，此图肯定是不能一笔画成。
奥数第九讲作业
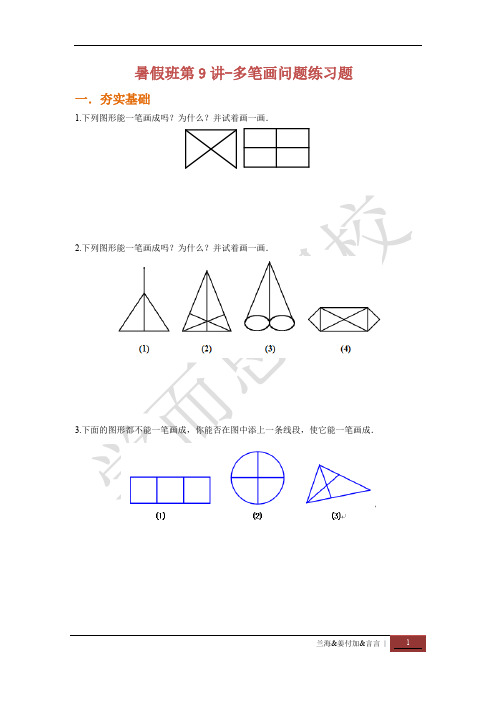
7.解析：把每个展室看作一个点，整个展厅的外部也看作一个点，两室之间有门相通，可以 看作两点之间有线相连．这样，展厅的平面图就转化成 b 图，一个实际问题也就转 化为这个图能否一笔画成的问题了，即能否从 A 出发，一笔画完此图，最后再回到 A ．图( b )中，所有的点都是偶点，因此，一定可以以 A 作为起点和终点而一笔画 完此图． 即游人可以从入口进， 一次不重复地穿过所有的门， 最后从出口出来． 下 面仅给出一种参观路线： A E B C E F C D F A ．
9.下图为某邮递员负责的邮区街道图，图中交叉点为邮户，每个小长方形的长为 180 米、宽 为 150 米． 如果邮递员每分钟行 200 米， 在每个邮户停留半分钟， 从邮局出发走遍所有邮户， 再回到邮局，最少要用 分钟．
150 邮局 180
兰海&姜付加&言言 |
3
四．杯赛演练：
10. “春蕾杯”小学数学邀请赛决赛 下面的图形，要求画过的线段不能重复画，那么这个图形最少 笔才能画出．
50m 60m 70m 300m 100m 图1 400m
A
兰海&姜付加&言言 |
6
11.(中国台湾小学数学竞赛选拔赛复赛) 有一个城市的街道图是由一些矩形所构成，如下图．一位警察要从 A 点出发巡逻，行经每一 条路段至少一次后回到 A 点．请问他至少要行走多少米？50m 60m 70m 30m 100m 第12题 400m
A
兰海&姜付加&言言 |
4
答案： 1.解析：第一个图形可以一笔画，第二个图形有 4 个奇点不可以一笔画。 2.解析：⑴、⑷可以，⑵、⑶不可以；其实我们不必把所有奇点都找出来，只要发现图中的 奇点多于 2 个就不能一笔画成了． 3.解析：⑴ 图中有四个点是奇点，所以不能一笔画成，要想使这个图形一笔画成，就要添 加一笔，使这个图形的奇点变成两个．如下图： （答案不唯一）
一笔画的由来和规律
一笔画的由来和规律一、一笔画的由来一笔画，又称为一笔绘画或一笔画艺术，是一种以一笔连续不断的动作完成的绘画方式。
它起源于中国传统绘画，并在现代艺术中得到了广泛的应用。
一笔画的由来可以追溯到古代的中国绘画传统。
中国绘画历史悠久，源远流长，经历了漫长的发展过程。
在古代，绘画被视为一种高雅的艺术形式，被广泛应用于宫廷艺术和文人雅士的创作中。
传统的中国绘画注重笔墨的运用和表现技巧，强调意境的抒发和情感的表达。
在这样的背景下，一笔画应运而生。
它起初是作为传统绘画的一种技法，用于表现瞬间的动态和氛围。
一笔画的特点是以一笔勾勒出整个画面，不做任何修改，力求捕捉瞬间的神韵和气息。
这种绘画方式要求画家具备高超的技巧和快速的反应能力，同时也强调画家的个人风格和创造力。
二、一笔画的规律一笔画虽然看似简单，但却有着一定的规律和技巧。
在进行一笔画创作时，画家需要遵循以下几个基本原则：1. 结构先行：一笔画的创作要从整体结构出发，先勾勒出整个画面的轮廓和大致形状。
这样可以保持画面的整体平衡和协调，为后续的细节填充奠定基础。
2. 动态表现：一笔画注重捕捉瞬间的动态和气息，因此画家需要运用流畅的线条和变化的笔触来表现物体的运动和变化。
通过线条的曲直、粗细和方向的变化，能够有效地传达物体的形态和动感。
3. 线与面的结合：一笔画中的线条并不是孤立存在的，它们与画面中的各种形状和面积相互关联。
画家需要通过线条的勾勒和填充来创造出物体的形状和质感，使画面更加生动和立体。
4. 简约而不简单：一笔画强调以简洁的线条表现复杂的事物，画家需要通过精准的勾勒和准确的笔触来表达出物体的本质和特征。
简约并不意味着简单，画家需要通过细腻的技巧和丰富的想象力来展现画面的深度和内涵。
5. 快意而不浮躁：一笔画追求的是速度与灵感的结合，画家在创作时需要保持快速而流畅的笔触，但又不能过于急躁和随意。
只有在快意的同时保持对画面整体的把握和细节的处理，才能使一笔画达到艺术的境界。
第九讲 一笔画问题
•
所谓图的一笔画，指的就是：从图的一点出发，笔不 离纸，遍历每条边恰好一次，即每条边都只画一次，不准 重复.从上图中容易看出：能一笔画出的图首先必须是连 通图.但是否所有的连通图都可以一笔画出呢？下面，我 们就来探求解决这个问题的方法。 • 为了叙述的方便，我们把与奇数条边相连的结点叫做 奇点，把与偶数条边相连的点称为偶点.如上图（a）中的 八个结点全是奇点，上图（b）中E、F为奇点，G为偶点。 • 容易知道，上图（b）可以一笔画出，即从奇点E出发， 沿箭头所指方向，经过F、G、E，最后到达奇点F；同理， 从奇点F出发也可以一笔画出，最后到达奇点E.而从偶点 G出发，却不能一笔画出.
• 4．下图是一公园的平面图，要使游客走遍 每一条路且不重复，问出入口应设在哪里？
• 【例题2】 下面各图能不能一笔画成？如 果能应该怎样画？如果不能，最少需要添 几笔使它能够一笔画出？
分析：图（1）全是偶点，无奇点，能一笔画成，从任意点开始即可；图（2） 只有B、E两个奇点，其它均为偶点，可以一笔画出，注意从一奇点开始到另 一奇点结束；图（3）有A、B、C、D四个奇点，不能一笔画出，要想一笔画 出，至少应该减少两个奇点，所以应该将上述四点中，任两点之间加一条线， 使之成为偶点；图（4）中有A、B、C、D、E、F、G、H八个奇点，不能一 笔画出，至少应该减少6个奇点，所以应该从8个奇点中选出6个，两两一组， 连三条线，使它们变为偶点。
• 【例题5】 下图是一个公园的平面图.要使游客走 遍每条路而不重复，问出入口应设在哪里？
分析与解答 本题实际上是这个图 以哪两点为起点和终点一 笔画出的问题.观察左图， 可以发现仅有两个奇点：H 与B点.因此，出入口应分 别设在H点与B点.
• 【例题6】一张纸上画有如下图所示的图， 你能否用剪刀一次连续剪下图中的三个正 方形和两个三角形？
第九讲 学习一笔画
第九讲学习一笔画【研究目标】一笔画，就是从图形某点出发，笔不离开纸，而且每条线都只画一次不重复，它是一种有趣的数学游戏，那么，哪些图形不能一笔画成，哪些图形可以一笔画成呢？一个图形能否一笔画成，关键在于单数点的多少，有2个或0个单数点的图形就能够一笔画成，单数点在一笔画中只能作为起点和终点。
例题1：一些平面图形是又点和线构成的，这里的“线”可以是线段，也可以是一段曲线，每个图中的每个点和线的连接情况如何？例题2：观察下列图形，那个图形可以一笔画成？怎么画？例题3：下图是某地区所有街道的平面图，甲、乙两人同时分别从A、B出发，以相同的速度走遍所有的街道，最后到达C。
那么两人谁最先到达？例题4：下图（图1）能否一笔画成，若不能，你能用什么方法把它改成能够一笔画成的图形？例题5：邮递员叔叔要向一个居民小区送信，怎么样走才能少走重复路，使每天走的路尽可能短？课堂练习：练习一：1.任意找一个平面图形，数一数图中有几个单数点，几个双数点。
2.数一数下面图形有几个双数点？分别是哪些点？练习二：1.下面图形能不能一笔画成，如果能，请说明画法，如果不能请说明理由。
2.观察下列图形，哪个图形可以一笔画成？怎么画？练习三：1.下图是某新村小区主干道平面图。
甲、乙两人同时分别从A、B出发，以相同的速度走遍的所有主干道，最后到达C。
问谁能最先到达C？2.一只蚂蚁分别从A点和B点出发，爬遍所有的小路。
如果每次爬行的速度相同，那么从哪一点出发所用的时间少？练习四：将下图改成一笔画。
练习五：1.下图是一个小区中花园的平面图，你能一次不重复地走完所有的路吗？入口和出口应该设计在哪儿呢？2.下面是“儿童乐园”平面图，出口应没在哪里才能不重复地走遍每条路？课外练习：练习一：数一数下面图形有几个单数点？练习二：下列图形能一笔画成吗？为什么？练习三：甲、乙两辆车同时以相同的速度分别从A、B出发，哪辆车能最先行驶完所有的路线？练习四：园林工人在花园浇花，怎样才能不重复地走遍每一条小路？。
第九讲 一笔画ppt课件
2
例2:18世纪的欧洲有个哥尼斯堡城，瑞格尔河穿过这个城市，河上有两个岛，在岛与岛之间及 陆地B、C与岛之间有7座桥，不少人热衷于一个有趣的数学游戏:一个游人怎样才能走遍七座 桥，每座桥只能经过一次，最后又回到出发点？
点拨 考虑一笔画问题，若奇点超过2个就不行。 解答 把两个岛A，D和陆地B，C缩小为4个点，把7座桥变成连接 A、B、C、D的7条线，如右图所示。显然A、B、C、D都是奇点， 不能将图一笔画成，也就是说不能没有重复地一次走遍七座桥。
5
热身1 能否一笔画出一条线路，使它和下图中的八条线段都相交一次，且不准在端点相 交？ 不能，因为图中有四个奇点。
6
热身2 在六面体的顶点B上有一只蚂蚁，它与顶点E上的另一只蚂蚁约定，在爬速相同时爬过 所有的棱线之后，最后到终点D，问哪知蚂蚁获胜？
D
A
C
B
E E蚂蚁先到达D，因为图中只有D与E是奇点，B蚂蚁是从偶点出发必走重复路。
3
ቤተ መጻሕፍቲ ባይዱ
迁移1 公园有9块花园，水源在A处（如图所示），现在要修渠引水浇地，修的水渠不许 交叉，路线要最简捷，还要浇遍9块地，你说这条水渠怎样修？
A
A
4
迁移2 下图中有A、B、C、D、E、F六个小岛，各岛之间共有15座桥，现在要从A岛出发， 不重复地走遍十五座桥，能走吗？若能则该怎么走？
ABCBDBEDEFDADCAF
7
拓展1 农技试验田里用纵横的田埂划分成9个作物对比区（见图所示）。农技员过桥后，能不 能不走重复的路，把试验田的田埂走一遍？若不能，请找出一条走重复路线最少的捷径来。
桥
桥
不能。因为有8个奇点。捷径设计如图（虚线表示重复路）
8
拓展2一位邮递员每天骑自行车去送信，他投送信件的街道如下图所示，图上数字表示街道的 千米数，他从邮局出发，走遍街道后回到邮局，问走什么样的路线最合理？最少走的是千 米？
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
例2:18世纪的欧洲有个哥尼斯堡城，瑞格尔河穿过这个城市， 河上有两个岛，在岛与岛之间及陆地B、C与岛之间有7座桥， 不少人热衷于一个有趣的数学游戏:一个游人怎样才能走遍七座 桥，每座桥只能经过一次，最后又回到出发点？
点拨 考虑一笔画问题，若奇点超过2个就不行。 解答 把两个岛A，D和陆地B，C缩小为4个点，把7 座桥变成连接A、B、C、D的7条线，如右图所示。 显然A、B、C、D都是奇点，不能将图一笔画成， 也就是说不能没有重复地一次走遍七座桥。
拓展1 农技试验田里用纵横的田埂划分成9个作物对比区（见 图所示）。农技员过桥后，能不能不走重复的路，把试验田的 田埂走一遍？若不能，请找出一条走重复路线最少的捷径来。
桥
桥
不能。因为有8个奇点。捷径设计如图（虚线表示重复路）
拓展2一位邮递员每天骑自行车去送信，他投送信件的 街道如下图所示，图上数字表示街道的千米数，他 从邮局出发，走遍街道后回到邮局，问走什么样的 路线最合理？最少走的是千米？
例1: 下图是一个公园的平面图①，要使游客通过每条路且 不重复，问出入口应设在哪里？
I G
F J
E A B 图① C
J 出口
D
图② B 入口
点拨 这个问题实质上是一笔画问题，数一数奇点与偶点各多少。 解答 因为图中只有B和J处两个奇点，因此只要把出入口分别 设在这两个奇点处，游客就能从入口处进入公园，不重复地 走遍所有的路后从出口处离开公园，图②所示是其中的一种 走法。
热身1 能否一笔画出一条线路，使它和下图中的八条线段 都相交一次，且不准在端点相交？
不能，因为图中有四个奇点。
热身2 在六面体的顶点B上有一只蚂蚁，它与顶点E 上的另一只蚂蚁约定，在爬速相同时爬过所有的棱 线之后，最后到终点D，问哪知蚂蚁获胜？
D
A B E
C
E蚂蚁先到达D，因为图中只有D与E是奇点，B 蚂蚁是从偶点出发必走重复路。
迁移1 公园有9块花园，水源在A处（如图所示），现在要 修渠引水浇地，修的水渠不许交叉，路线要最简捷，还要浇 遍9块地，你说这条水渠怎样修？
A
A
迁移2 下图中有A、B、C、D、E、F六个小岛，各 岛之间共有15座桥，现在要从A岛出发，不重复地走 遍十五座桥，能走吗？若能则该怎么走？
A B C B D B E D E F D A D C A F
最短路线设计如图，图中虚线连接的路线是重复走的最短路 线。全程最少走（0.5×2＋1×2＋2）×2＋3×6＋1×4=32 （千米）