北京市各区县2014-2015学年高一上学期期末试题分类汇编——函数
北京市各区县2014-2015学年高一上学期期末试题分类汇编——幂指对

2015年北京市各区县高一期末试题分类汇编——幂指对(2015年1月·西城期末·2.若幂函数y x =α的图象过点(4,2),则=α_____.12(2015年1月·延庆期末·7.函数()log 21a y x =++的图像过定点 A . ()2,1- B .()2,1 C . ()1,1-D .)1,1((2015年1月·东城期末·13. 求值:⎝⎛⎭⎫1681-34+log 354+log 345=________.278(2015年1月·顺义期末·10.函数y =_____[1,)+∞_______ .(2015年1月·顺义期末·9.函数()f x =的定义域为 (]0,3 .(2015年1月·顺义期末·11.2lg 2lg 25+的值等于 2 .(2015年1月·石景山期末·2.下列算式正确的是 ( )A .222log (3)log 3log ππ=+B 2==-C .lg 62lg3= D . 3322555-==(2015年1月·石景山期末·13. 若函数()f x 的图象与2x y =的图象关于___y 轴_____对称,则函数()f x =__2x -__.(注:填上你认为正确的一种情形即可,不必考虑所有可能的情形)(2015年1月·昌平期末·3)已知函数2()log f x x =,当[1,4]x ∈时,函数()f x 的值域是(A )[0,1] (B )[0,2] (C )[1,2] (D )[1,4] (2015年1月·昌平期末·9)设函数()f x 是定义在R 上的奇函数,当0x ≥时,()23x f x x k =-+(k 为常数),则(1)f -= (A )2 (B )1 (C )2- (D )1-(2015年1月·昌平期末·10)设正数a ,b 满足23log log a b =,则下列结论中,不可能...成立的是(A )1a b << (B )01b a <<< (C )a b = (D )1b a << (2015年1月·昌平期末·11)函数()f x x α=的图象过点(2,4),则(1)f -=_____ . 1(2015年1月·石景山期末·14. 三个变量123,,y y y 随x 的变化情况如下表:三个变量123,,y y y 中,变量___3y ____随x 呈对数函数型变化,变量__2y _____随x 呈指数函数型变化,变量___1y ____随x 呈幂函数变化.(2015年1月·丰台期末·9.已知变量y 随变量x 变化的数据如下表:则能基本反映这一变化规律的函数模型是( ) A . x y 2=B .2x y =C .x y 2log =D .137.0--=x y(2015年1月·延庆期末·13.不等式212>x的解集为____ ___.),1(+∞-(2015年1月·密云期末·6. 函数log =a y x (0>a 且1≠a )的图象经过点)1,2(-,函数=xy b (0>b 且1≠b )的图象经过点)2,1(,则下列关系式中正确的是 A . 22b a >B . ba 22>C . b a )21()21(> D . 2121b a >(2015年1月·顺义期末·11.已知 4.10.9m =,0.94.1n =,0.9log 4.1p =,则这三个数从小到大用“<”连接的顺序是p m n <<_______________ .(2015年1月·昌平期末·4)设 2.50 2.51(),(2.5),22a b c ===,则(A )a b c >> (B )b a c >> (C )c b a >> (D )b c a >> (2015年1月·东城期末·6.设2log πa =,12log πb =,2πc -=,则A .a b c >> B. b a c >> C. a c b >>D. c b a >>(2015年1月·房山期末·6)设3log 2a =,0.3eb =,8cos7c π=,则(A )b a c << (B )b c a << (C )c a b <<(D )c b a <<(2015年1月·丰台期末·6.已知3π=m ,3log π=n ,πtan =p ,则这三个数的大小关系是( )A .p n m >>B .m p n >>C . n m p >>D .n m p >>(2015年1月·海淀期末·7.设10.52,e ,0.5a b c -===,其中e 2.71828≈,则,,a b c 的大小顺序为 DA.a b c >>B.a c b >>C.b a c >>D.b c a >>(2015年1月·延庆期末·17.已知3.0222,3.0log ,3.0===c b a ,则c b a ,,大小关系是_____ __. b a c >>(2015年1月·昌平期末·7)定义运算,,,,a ab a b b a b ≤⎧⊕=⎨>⎩则函数()12xf x =⊕的图象是(A ) (B ) (C ) (D )(2015年1月·海淀期末·9.已知函数()f x ax b =+的图象如右图所示,则函数()x g x a b =+的图象 可能是 BA. B. C. D.(2015年1月·海淀期末·12.右图中有五个函数的图象,依据图象用“<”表示出以下五个量,,,,1a b c d 的大小关系,正确的是 CA. 1a c b d <<<<B. 1a d c b <<<<2xxC. 1a c b d <<<<D. 1a c d b <<<<(2015年1月·东城期末·5. 若函数y =log a x (a >0,且a ≠1)的图象如图所示,则下列函数图象正确的是( )A B C D(2015年1月·房山期末·14)已知()f x =ln , 0,2,0,x x x x >⎧⎨+⎩≤ 若0()0f x =,则0x =__________.2-或1(2015年1月·西城期末·3.函数2lg ,0,()4,0,x x f x x x >⎧=⎨-<⎩的零点是_____.2-,1;(2015年1月·房山期末·15)如果函数()f x 的定义域为R ,(2)(1)()f x f x f x +=+-,若(3)lg3lg 2f =-, (2)lg3lg5f =+,则(1)f(2015年1月·丰台期末·10.已知函数22(),1()3(1),1xx x f x f x x ⎧-≤⎪=⎨⎪->⎩,则()f x 在区间(,2015)-∞内的零点个数为( ) A .2015B .2016C .2017D .无数个(2015年1月·密云期末·12. 已知函数21,(01),()2,(10),x x x f x x ⎧+<≤⎪=⎨-≤≤⎪⎩且5()4f m =,则m 的值为 . 12(2015年1月·顺义期末·14.定义在R 上的函数()f x 满足2,(0()(1)(2),(0)x x f x f x f x x ⎧≤=⎨--->⎩.则(2015)________.f = 12(2015年1月·顺义期末·5.函数131()3xf x x ⎛⎫=- ⎪⎝⎭的零点一定位于下列的哪个区间A. (-1,0)B. (0,1)C. (1, 2)D. (2, 3)(2015年1月·延庆期末·12.已知函数)(x f 是定义在R 上的偶函数,且在区间),0[+∞上单调递增,若实数a 满足)1(2)(log )(log 212f a f a f ≤+,则a 的取值范围是A .]221[ B . ]2,1[ C . )21,0(D .]2,0((2015年1月·石景山期末·10.设函数()log (2)a f x x a =-+在区间(1,)+∞上恒为正值,则实数a 的取值范围是( )A .(1,2]B .(1,2)C .(0,1)(1,2)⋃D . 5(1,)2(2015年1月·延庆期末·19.(本题8分)求下列各式的植:(Ⅰ)0323321)12(])2[(2)41(-+-⨯+-;(Ⅱ)2lg 31025lg 4lg 27log +++ . 解:解:(Ⅰ)原式148121+⨯+=2=. ………………………………4分 (Ⅱ)原式2100lg 3log 33++=7223=++=. …………………8分(2015年1月·密云期末·15. (本小题满分13分) 已知函数2()1+log 1=--()f x x . (I )求函数()f x 的定义域;(II )求(5)f 的值; (III )求函数()f x 的零点.解:(I )由题:10x ->, ----------------2分1.x ∴>∴函数()f x 的定义域{}1x x >. ----------------4分(II )2(5)1log (51)121f =-+-=-+= ----------------8分 (III )令2()1+log 1=--()=0f x x , 2log (1) 1.x ∴-=1 2.x ∴-=3.x ∴=∴函数()f x 的零点为3. ----------------13分(2015年1月·西城期末·7.(本小题满分10分)已知函数()23x x f x a b =⋅+⋅,其中,a b 为常数. (Ⅰ)若0ab >,判断()f x 的单调性,并加以证明; (Ⅱ)若0ab <,解不等式:(1)()f x f x +>. (Ⅰ)解:当0,0a b >>时,()f x 在R 上是增函数;当0,0a b <<时,()f x 在R 上是减函数; 【 1分】 证明如下:当0,0a b >>时,任取12,x x ∈R ,且12x x <,则210x x x ∆=->, 则 212121()()(22)(33)x x x xy f x f x a b ∆=-=-+-.因为 122122,0(22)0xxxxa a <>⇒->;又122133,0(33)0xxxxb b <>⇒->, 所以 21()()0y f x f x ∆=->,所以,当0,0a b >>时,()f x 在R 上是增函数.当0,0a b <<时,同理可得,()f x 在R 上是减函数. 【 5分】 (Ⅱ)解:由(1)()2230xxf x f x a b +-=⋅+⋅>,得 32()2xb a >-. (*) 【 6分】 ① 当0,0a b <>时,(*)式化为3()22xa b->, 解得32log ()2ax b>-. 【 8分】② 当0,0a b ><时,(*)式化为3()22xab-<, 解得32log ()2ax b<-.【10分】(2015年1月·东城期末·19.(本题满分9分)已知函数x x x f -+=e e )(,其中e 是自然对数的底数. (Ⅰ)证明:)(x f 是R 上的偶函数;(Ⅱ)判断)(x f 在(0,)+∞上的单调性,并证明. 19.(本题满分9分)解:(Ⅰ)因为函数)(x f 的定义域是R ,且()e e x x f x --=+=)(x f , 所以)(x f 是偶函数. (Ⅱ))(x f 在(0,)+∞上是单调递增函数. 设210x x <<,则112212()()()x x x x f x f x e e e e ---=+-+=1212(e -e )(1)x xx x e---.由210x x <<,得12e <e xx,所以12e -e0xx <.又由210x x <<得210x x --<,所以121x x e--<,所以1210x x e --->.所以,12()()0f x f x -<,即12()()f x f x <.所以,)(x f 在(0,)+∞上是单调递增函数. (2015年1月·房山期末·21)(本小题满分12分)已知函数()log (21)x a f x =-(0a >,1a ≠). (Ⅰ)求函数()f x 的定义域;(Ⅱ)当1a >时,判断函数()f x 的单调性,并用单调性的定义证明;(Ⅲ)若()1f x >,求x 的取值范围. 解:(Ⅰ)由()log (21)x a f x =-,要使函数有意义,则210x-> -----------------2分解得0x >. -----------------2分 ∴函数()f x 的定义域为(0,)+∞ -----------------1分 (Ⅱ)当1a >时,函数()f x 在定义域(0,)+∞上单调递增 -----------------1分证明:任取12,(0,)x x ∈+∞,设12x x <,则22112121log (21)log (21)log 21x x x a a a x y y y -∆=-=---=-210x x >>,21221x x ∴>>,即2121210x x->->.∴2121121x x->- 又1a >,所以2121log 021x a x->-,即0y ∆> -----------------2分 因此,函数()f x 在(0,)+∞上是增函数.(Ⅲ)由()log (21)1x a f x =->得 ()log (21)log x a a f x a =->当1a >时,得21xa ->,解得2log (1)x a >+ -----------------2分当01a <<时,得21xa -<,解得20log (1)x a <<+ -----------------2分 综上,当1a >时,x 的取值范围为2(log (1),)a ++∞,当01a <<时,x 的取值范围为2(0,log (1))a +.(2015年1月·丰台期末·17.(本小题满分8分) 已知对数函数()f x 图象经过点()3,8 (Ⅰ)求函数()f x 的解析式; (Ⅱ)若()1f x >,求x 的范围.解:(Ⅰ)设()x x f a log =(其中0>a 且1≠a )因为函数()x f 图象经过点()3,8,有()38=f 即38log =a 得2=a所以此函数的解析式为()x x f 2l o g = ┄┄┄┄┄┄┄┄┄┄┄4分(Ⅱ)由()1>x f 即2log 1log 22=>x ,解得2>x 所以x 的范围是()+∞,2 ┄┄┄┄┄┄┄┄┄┄┄8分 (2015年1月·丰台期末·20. (本小题满分9分) 已知函数2()21x f x a =-+(Ⅰ)求出函数()f x 的定义域; (Ⅱ)若()f x 是奇函数,求实数a 的值;(Ⅲ)设()(41)()(0)x g x f x x =-≥,且函数()g x 的最小值为21-,求实数a 的值. 解:(Ⅰ)()x f 的定义域为R ┄┄┄┄┄┄┄┄┄2分 (Ⅱ)因为()x f 是奇函数,则 ()()x f x f -=-即⎪⎭⎫ ⎝⎛+--=+--122122xx a a 于是212221221221222=+++⨯=+++=-x x x x xa 得1=a ┄┄┄┄┄┄┄┄┄┄┄5分 (或由()x f 的定义域为R ,又()x f 是奇函数,则 ()()00f f -=得()00=f 于是01220=+-a 得1=a ,此时()()x f x f -=-满足条件,所以1=a ) (3)由()()()()2222142+-⨯-=-=a a x f x g xxx ()0≥x设()12≥=t t x ,令()222+--=a t at t h当0=a 时,()()122≥+-=t t t h ,无最小值,舍;当0<a 时,()2112+--⎪⎭⎫⎝⎛-=a a a t a t h ,无最小值,舍;当0>a 时,()2112+--⎪⎭⎫⎝⎛-=a a a t a t h若1≥a 即110≤<a,()t h 在[)+∞,1单调递增,()()01min ==h t h 不符合舍 若10≤<a 即11≥a ,()21211min -=+--=⎪⎭⎫⎝⎛=a a a h t h 即02522=+-a a 解得2=a (舍)或21=a 综上,a 值为21┄┄┄┄┄┄┄┄┄┄┄9分。
《解析》北京市西城区2014-2015学年高一上学期期末数学试卷Word版含解析

北京市西城区2014-2015学年高一上学期期末数学试卷一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合要求的.1.(4分)已知α∈(0,2π),且sinα<0,cosα>0,则角α的取值范围是()A.B.C.D.2.(4分)已知向量=(2,8),=(﹣4,2).若=2﹣,则向量=()A.(0,18)B.(8,14)C.(12,12)D.(﹣4,20)3.(4分)已知角α的终边经过点P(3,﹣4),那么sinα=()A.B.C.D.4.(4分)在△ABC中,D是BC的中点,则=()A.B.C.D.5.(4分)函数y=(sinx﹣cosx)2的最小正周期为()A.2πB.C.πD.6.(4分)如果函数y=cos(x+φ)的一个零点是,那么φ可以是()A.B.C.D.7.(4分)如图,在矩形ABCD中,AB=2,,E是CD的中点,那么=()A.4B.2C.D.18.(4分)当x∈[0,π]时,函数f(x)=cosx﹣sinx的值域是()A.[﹣2,1]B.[﹣1,2]C.[﹣1,1]D.9.(4分)为得到函数的图象,只需将函数y=sinx的图象()A.向左平移个长度单位B.向右平移个长度单位C.向左平移个长度单位D.向右平移个长度单位10.(4分)已知,为单位向量,且•=m,则|+t|(t∈R)的最小值为()A.B.1C.|m| D.二、填空题:本大题共6小题,每小题4分,共24分.把答案填在题中横线上.11.(4分)若向量=(1,2)与向量=(λ,﹣1)共线,则实数λ=.12.(4分)设α是第二象限角,,则cosα=.13.(4分)若,且tanθ>1,则θ的取值范围是.14.(4分)已知向量=(1,3),=(2,﹣1),=(1,1).若=λ+μ(λ,μ∈R),则=.15.(4分)函数f(x)=sin2x+sinx•cosx的最大值是.16.(4分)关于函数,给出下列三个结论:①对于任意的x∈R,都有;②对于任意的x∈R,都有;③对于任意的x∈R,都有.其中,全部正确结论的序号是.三、解答题:本大题共3小题,共36分.解答应写出文字说明,证明过程或演算步骤. 17.(12分)已知tanα=﹣2,其中.(Ⅰ)求的值;(Ⅱ)求sin2α的值.18.(14分)已知向量=(cosα,sinα),=(﹣,),其中α是锐角.(Ⅰ)当α=30°时,求|+|;(Ⅱ)证明:向量+与﹣垂直;(Ⅲ)若向量与夹角为60°,求角α.19.(10分)已知函数f(x)=asinx+bcosx,其中a∈Z,b∈Z.设集合A={x|f(x)=0},B={x|f (f(x))=0},且A=B.(Ⅰ)证明:b=0;(Ⅱ)求a的最大值.一、填空题:本大题共5小题,每小题4分,共20分.把答案填在题中横线上.20.(4分)已知集合A={a,b},则满足A∪B={a,b,c}的不同集合B的个数是.21.(4分)已知幂函数f(x)=xα的图象过点(4,2),则α=.22.(4分)函数f(x)=的零点是.23.(4分)设f(x)是定义在R上的偶函数,且f(x)在[0,+∞)上是减函数.若f(m)>f(2),则实数m的取值范围是.24.(4分)已知函数f(x)的定义域为D.若对于任意的x1∈D,存在唯一的x2∈D,使得=M成立,则称函数f(x)在D上的几何平均数为M.已知函数g(x)=3x+1(x∈[0,1]),则g(x)在区间[0,1]上的几何平均数为.二、解答题:本大题共3小题,共30分.解答应写出文字说明,证明过程或演算步骤. 25.(10分)已知函数f(x)=(x﹣2)(x+a),其中a∈R.(Ⅰ)若f(x)的图象关于直线x=1对称,求a的值;(Ⅱ)求f(x)在区间[0,1]上的最小值.26.(10分)已知函数f(x)=a•2x+b•3x,其中a,b为常数.(Ⅰ)若ab>0,判断f(x)的单调性,并加以证明;(Ⅱ)若ab<0,解不等式:f(x+1)>f(x).27.(10分)定义在R上的函数f(x)同时满足下列两个条件:①对任意x∈R,有f(x+2)≥f(x)+2;②对任意x∈R,有f(x+3)≤f(x)+3.设g(x)=f(x)﹣x.(Ⅰ)证明:g(x+3)≤g(x)≤g(x+2);(Ⅱ)若f(4)=5,求f的值.北京市西城区2014-2015学年高一上学期期末数学试卷参考答案与试题解析一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合要求的.1.(4分)已知α∈(0,2π),且sinα<0,cosα>0,则角α的取值范围是()A.B.C.D.考点:三角函数值的符号.专题:三角函数的求值.分析:直接由sinα<0,cosα>0可得α为第四象限的角,结合α∈(0,2π)得到选项.解答:解:由sinα<0,cosα>0,可得α为第四象限的角,又α∈(0,2π),∴α∈.故选:D.点评:本题考查了三角函数的象限符号,是基础的会考题型.2.(4分)已知向量=(2,8),=(﹣4,2).若=2﹣,则向量=()A.(0,18)B.(8,14)C.(12,12)D.(﹣4,20)考点:平面向量数量积的运算.专题:计算题;平面向量及应用.分析:运用向量的加减和数乘坐标运算,计算即可得到所求向量.解答:解:向量=(2,8),=(﹣4,2),若=2﹣,则=(4,16)﹣(﹣4,2)=(8,14).故选B.点评:本题考查平面向量的坐标运算,考查向量的加减和数乘运算,属于基础题.3.(4分)已知角α的终边经过点P(3,﹣4),那么sinα=()A.B.C.D.考点:任意角的三角函数的定义.专题:三角函数的求值.分析:由条件利用任意角的三角函数的定义,求得sinα的值.解答:解:由于角α的终边经过点P(3,﹣4),∴x=3,y=﹣4,r=|OP|=5,∴sinα==﹣,故选:B.点评:本题主要考查任意角的三角函数的定义,属于基础题.4.(4分)在△ABC中,D是BC的中点,则=()A.B.C.D.考点:向量的加法及其几何意义.专题:平面向量及应用.分析:利用向量的平行四边形法则、中点的性质即可得出.解答:解:∵D是BC的中点,∴=,故选:A.点评:本题考查了向量的平行四边形法则,属于基础题.5.(4分)函数y=(sinx﹣cosx)2的最小正周期为()A.2πB.C.πD.考点:三角函数中的恒等变换应用;三角函数的周期性及其求法.专题:三角函数的求值.分析:化简可得y=1﹣sin2x,由周期公式可得答案.解答:解:化简可得y=(sinx﹣cosx)2=1﹣sin2x,∴由周期公式可得T==π,故选:C点评:本题考查三角函数的恒等变换,涉及三角函数的周期性,属基础题.6.(4分)如果函数y=cos(x+φ)的一个零点是,那么φ可以是()A.B.C.D.考点:余弦函数的图象.专题:三角函数的图像与性质.分析:根据余弦函数的性质即可得到结论.解答:解:若y=cos(x+φ)的一个零点是,则cos(+φ)=0,即+φ=kπ+,k∈Z即φ=kπ+,当k=0时,φ=,故选:A点评:本题主要考查余弦函数的求值,根据函数零点的定义结合余弦函数的性质是解决本题的关键.7.(4分)如图,在矩形ABCD中,AB=2,,E是CD的中点,那么=()A.4B.2C.D.1考点:平面向量数量积的运算.专题:计算题;平面向量及应用.分析:运用向量的三角形法则和向量的平方即为模的平方,以及向量垂直的条件即数量积为0,计算即可得到.解答:解:=(+)•=+=+=0+==2.故选B.点评:本题考查平面向量的数量积的定义和性质,考查向量的垂直的条件和向量的平方与模的平方的关系,考查运算能力,属于基础题.8.(4分)当x∈[0,π]时,函数f(x)=cosx﹣sinx的值域是()A.[﹣2,1]B.[﹣1,2]C.[﹣1,1]D.考点:两角和与差的正弦函数;正弦函数的图象.专题:三角函数的求值;三角函数的图像与性质.分析:化简解析式可得f(x)=2cos(x+),当x∈[0,π]时,x+∈[,],由正弦函数的图象和性质可知:2cos(x+)∈[﹣2,1].解答:解:∵f(x)=cosx﹣sinx=2cos(x+)∴当x∈[0,π]时,x+∈[,]∴由正弦函数的图象和性质可知:2cos(x+)∈[﹣2,1]故选:A.点评:本题主要考察了两角和与差的正弦函数公式的应用,正弦函数的图象和性质,属于基本知识的考查.9.(4分)为得到函数的图象,只需将函数y=sinx的图象()A.向左平移个长度单位B.向右平移个长度单位C.向左平移个长度单位D.向右平移个长度单位考点:函数y=Asin(ωx+φ)的图象变换.专题:计算题.分析:将y=sinx化为y=cos(x﹣),再根据三角函数的图象变换知识确定平移的方向和长度即可.解答:解:y=sinx=cos(x﹣),,故只需将函数y=sinx的图象向左平移个长度单位.故选C.点评:本题考查了三角函数的图象变换,中间用到了诱导公式,属于常考题型.10.(4分)已知,为单位向量,且•=m,则|+t|(t∈R)的最小值为()A.B.1C.|m| D.考点:平面向量数量积的运算.专题:计算题;平面向量及应用.分析:运用向量的数量积的性质,向量的平方即为模的平方,配方整理,再由二次函数的最值求法,即可得到所求最值.解答:解:,为单位向量,且•=m,则|+t|2=+t2+2t=1+t2+2tm=(t+m)2+1﹣m2,当t=﹣m时,|+t|2取得最小值1﹣m2,则|+t|(t∈R)的最小值为.故选D.点评:本题考查平面向量的数量积的性质,考查二次函数的最值求法,考查运算能力,属于基础题.二、填空题:本大题共6小题,每小题4分,共24分.把答案填在题中横线上.11.(4分)若向量=(1,2)与向量=(λ,﹣1)共线,则实数λ=.考点:平面向量共线(平行)的坐标表示.专题:计算题.分析:利用向量共线的充要条件列出方程,解方程求出λ的值.解答:解:∵∴﹣1=2λ∴故答案为:.点评:解决有关向量共线的问题,应该利用向量共线的充要条件:坐标交叉相乘相等.12.(4分)设α是第二象限角,,则cosα=.考点:同角三角函数间的基本关系.专题:计算题;三角函数的求值.分析:利用sin2α+cos2α=1,结合α是第二象限角,即可求得cosα.解答:解:∵sinα=,α是第二象限角,∴cosα=﹣=﹣=﹣.故答案为:﹣.点评:本题考查同角三角函数间的基本关系,属于基础题.13.(4分)若,且tanθ>1,则θ的取值范围是(,).考点:三角函数线;任意角的三角函数的定义.专题:三角函数的求值.分析:由条件利用正切函数的图象特征求得θ的取值范围.解答:解:若,且tanθ>1,则θ∈(,),故答案为:(,).点评:本题主要考查正切函数的图象特征,属于基础题.14.(4分)已知向量=(1,3),=(2,﹣1),=(1,1).若=λ+μ(λ,μ∈R),则=.考点:平面向量的基本定理及其意义.专题:平面向量及应用.分析:利用向量的线性运算、向量相等即可得出.解答:解:∵向量=(1,3),=(2,﹣1),=(1,1).=λ+μ(λ,μ∈R),∴,解得,∴=.故答案为:.点评:本题考查了向量运算性质、向量基本定理,考查了推理能力与计算能力,属于中档题.15.(4分)函数f(x)=sin2x+sinx•cosx的最大值是.考点:三角函数中的恒等变换应用.专题:三角函数的求值.分析:化简可得f(x)=sin(2x﹣)+,易得其最大值.解答:解:化简可得f(x)=sin2x+sinx•cosx=+sin2x=sin(2x﹣)+,∴当sin(2x﹣)=1时函数取最大故答案为:点评:本题考查三角函数的最值,属基础题.16.(4分)关于函数,给出下列三个结论:①对于任意的x∈R,都有;②对于任意的x∈R,都有;③对于任意的x∈R,都有.其中,全部正确结论的序号是①②③..考点:正弦函数的图象.专题:三角函数的图像与性质.分析:根据三角函数的图象和性质进行判断即可.解答:解:①f(x)=cos[﹣(2x﹣)]=cos(﹣2x)=cos(2x﹣),故①正确,②f(x+)=sin[2(x+)﹣)]=﹣sin(2x﹣)],f(x﹣)=sin[2(x﹣)﹣)]=﹣sin(2x﹣),则f(x+)=f(x﹣)故②正确③f()=sin(2×﹣)=sin=1为最大值,故x=是函数的对称轴,故③正确,故答案为:①②③.点评:本题主要考查三角函数的图象和性质,利用三角函数的诱导公式以及三角函数变换是解决本题的关键.三、解答题:本大题共3小题,共36分.解答应写出文字说明,证明过程或演算步骤. 17.(12分)已知tanα=﹣2,其中.(Ⅰ)求的值;(Ⅱ)求sin2α的值.考点:同角三角函数基本关系的运用;两角和与差的正切函数.专题:三角函数的求值.分析:(Ⅰ)原式利用两角和与差的正切函数公式化简,把tanα的值代入计算即可求出值;(Ⅱ)由tanα的值求出sinα与cosα的值,原式利用二倍角的正弦函数公式化简,把各自的值代入计算即可求出值.解答:解:(Ⅰ)∵tanα=﹣2,∴tan(α﹣)===3;(Ⅱ)∵α∈(,π),tanα=﹣2,∴cosα=﹣=﹣,sinα==,则sin2α=2sinαcosα=﹣.点评:此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.18.(14分)已知向量=(cosα,sinα),=(﹣,),其中α是锐角.(Ⅰ)当α=30°时,求|+|;(Ⅱ)证明:向量+与﹣垂直;(Ⅲ)若向量与夹角为60°,求角α.考点:平面向量数量积的运算.专题:平面向量及应用.分析:(Ⅰ)当α=30°时,求得+的坐标,可得|+|的值.(Ⅱ)由条件求得(+)•(﹣)=0,从而证得向量+与﹣垂直.(Ⅲ)若向量与夹角为60°,根据两个向量的数量积公式、两个向量的数量积的定义,求得,从而得到角α的值.解答:(Ⅰ)解:当α=30°时,=(,),所以,+=(,),所以,|+|==.(Ⅱ)证明:由向量=(cosα,sinα),=(﹣,),得+=(cosα﹣,sinα+),﹣=(cosα+,sinα﹣),由,得向量+,﹣均为非零向量.因为(+)•(﹣)=﹣=(cos2α+sin2α)﹣(+)=0,所以向量+与向量﹣垂直.(Ⅲ)解:因为||=||=1,且向量与夹角为60°,所以=||•||•cos60°=,所以,即.因为,所以,所以,即.点评:本题主要考查两个向量的数量积公式、两个向量的数量积的定义,两个向量坐标形式的运算,两个向量垂直的条件,根据三角函数的值求角,属于基础题.19.(10分)已知函数f(x)=asinx+bcosx,其中a∈Z,b∈Z.设集合A={x|f(x)=0},B={x|f (f(x))=0},且A=B.(Ⅰ)证明:b=0;(Ⅱ)求a的最大值.考点:集合的相等.专题:集合.分析:(Ⅰ)利用集合相等得到f(0)=0,从而求b;(Ⅱ)讨论a与0的关系,在a≠0时,因为A=B,对于任意x∈R,必有asinx≠kπ(k∈Z,且k≠0)成立,结合正弦函数的有界性得到,求得a的最大值.解答:(Ⅰ)证明:显然集合A≠∅.设x0∈A,则f(x0)=0.(1分)因为A=B,所以x0∈B,即f(f(x0))=0,所以f(0)=0,(3分)所以b=0.(4分)(Ⅱ)解:由(Ⅰ)得f(x)=asinx,a∈Z.①当a=0时,显然满足A=B.(5分)②当a≠0时,此时A={x|asinx=0};B={x|asin(asinx)=0},即B={x|asinx=kπ,k∈Z}.(6分)因为A=B,所以对于任意x∈R,必有asinx≠kπ(k∈Z,且k≠0)成立.(7分)所以对于任意x∈R,,所以,(8分)即|a|<|k|•π,其中k∈Z,且k≠0.所以|a|<π,(9分)所以整数a的最大值是3.(10分)点评:本题考查集合相等的运用以及正弦函数的有界性的运用,属于中档题.一、填空题:本大题共5小题,每小题4分,共20分.把答案填在题中横线上.20.(4分)已知集合A={a,b},则满足A∪B={a,b,c}的不同集合B的个数是4.考点:并集及其运算.专题:集合.分析:根据题意和并集的运算,按照B中元素的个数依次写出满足条件的集合即可.解答:解:因为集合A={a,b},满足A∪B={a,b,c},所以B={c}、{a,c}、{b,c}、{a,b,c}共4个,故答案为:4.点评:本题考查并集及其运算,注意列举时按一定的顺序做到不重不漏,属于基础题.21.(4分)已知幂函数f(x)=xα的图象过点(4,2),则α=.考点:幂函数的性质.专题:函数的性质及应用.分析:根据幂函数的图象过点(4,2),代入幂函数的解析式求得即可.解答:解:∵4α=2,解得,故答案为:点评:本题主要考查幂函数的图象和性质,属于基础题.22.(4分)函数f(x)=的零点是﹣2或1.考点:函数零点的判定定理.专题:函数的性质及应用.分析:转化为或求解即可.解答:解:∵函数f(x)=∴或解得:x=1,或x=﹣2故答案:﹣2,1;点评:本题考查了分段函数的解析式的求解,函数的零点的求解属于中档题.23.(4分)设f(x)是定义在R上的偶函数,且f(x)在[0,+∞)上是减函数.若f(m)>f(2),则实数m的取值范围是(﹣2,2).考点:奇偶性与单调性的综合.专题:函数的性质及应用.分析:根据函数奇偶性和单调性之间的关系,将不等式进行转化即可得到结论.解答:解:∵f(x)是定义在R上的偶函数,且f(x)在[0,+∞)上是减函数,∴不等式f(m)>f(2),等价为f(|m|)>f(2),即|m|<2,解得﹣2<m<2,故答案为:(﹣2,2);点评:本题主要考查不等式的求解,根据函数奇偶性和单调性之间的关系,将不等式进行等价转化是解决本题的关键.24.(4分)已知函数f(x)的定义域为D.若对于任意的x1∈D,存在唯一的x2∈D,使得=M成立,则称函数f(x)在D上的几何平均数为M.已知函数g(x)=3x+1(x∈[0,1]),则g(x)在区间[0,1]上的几何平均数为2.考点:平均值不等式.专题:不等式的解法及应用.分析:我们易得若函数在区间D上单调递增,则C应该等于函数在区间D上最大值与最小值的几何平均数,由g(x)=x,D=[0,1],代入即可得到答案.解答:解:根据已知中关于函数g(x)在D上的几何平均数为C的定义,结合g(x)=3x+1在区间[0,1]单调递增则x1=0时,存在唯一的x2=1与之对应C==2,故答案为:2.点评:本题考查的知识点是函数单调性的性质,其中根据函数在区间上的几何平均数的定义,判断出C等于函数在区间D上最大值与最小值的几何平均数,是解答本题的关键.二、解答题:本大题共3小题,共30分.解答应写出文字说明,证明过程或演算步骤. 25.(10分)已知函数f(x)=(x﹣2)(x+a),其中a∈R.(Ⅰ)若f(x)的图象关于直线x=1对称,求a的值;(Ⅱ)求f(x)在区间[0,1]上的最小值.考点:二次函数的性质;二次函数在闭区间上的最值.专题:函数的性质及应用.分析:(Ⅰ)先求出函数的对称轴,得到,解出即可;(Ⅱ)先求出函数的对称轴,通过讨论对称轴的位置,从而得到答案.解答:(Ⅰ)解法一:因为f(x)=(x﹣2)(x+a)=x2+(a﹣2)x﹣2a,所以,f(x)的图象的对称轴方程为.由,得a=0.解法二:因为函数f(x)的图象关于直线x=1对称,所以必有f(0)=f(2)成立,所以﹣2a=0,得a=0.(Ⅱ)解:函数f(x)的图象的对称轴方程为.①当,即a≥2时,因为f(x)在区间(0,1)上单调递增,所以f(x)在区间[0,1]上的最小值为f(0)=﹣2a.②当,即0<a<2时,因为f(x)在区间上单调递减,在区间上单调递增,所以f(x)在区间[0,1]上的最小值为.③当,即a≤0时,因为f(x)在区间(0,1)上单调递减,所以f(x)在区间[0,1]上的最小值为f(1)=﹣(1+a).点评:本题考查了二次函数的性质,考查了函数的最值问题,是一道中档题..26.(10分)已知函数f(x)=a•2x+b•3x,其中a,b为常数.(Ⅰ)若ab>0,判断f(x)的单调性,并加以证明;(Ⅱ)若ab<0,解不等式:f(x+1)>f(x).考点:函数单调性的性质;函数单调性的判断与证明.专题:函数的性质及应用.分析:(Ⅰ)当a>0,b>0时,f(x)在R上是增函数;当a<0,b<0时,f(x)在R上是减函数.再利用函数的单调性的定义进行证明.(Ⅱ)解:由f(x+1)﹣f(x)=a•2x+2b•3x>0,得,再分类讨论求得它的解集.解答:(Ⅰ)解:当a>0,b>0时,f(x)在R上是增函数;当a<0,b<0时,f(x)在R上是减函数.证明如下:当a>0,b>0时,任取x1,x2∈R,且x1<x2,则△x=x2﹣x1>0,则.因为;又,所以△y=f(x2)﹣f(x1)>0,所以,当a>0,b>0时,f(x)在R上是增函数.当a<0,b<0时,同理可得,f(x)在R上是减函数.(Ⅱ)解:由f(x+1)﹣f(x)=a•2x+2b•3x>0,得.(*)①当a<0,b>0时,(*)式化为,解得.②当a>0,b<0时,(*)式化为,解得.点评:本题主要考查函数的单调性的判断和证明,利用函数的单调性解指数、对数不等式,体现了转化、分类讨论的数学思想,属于中档题.27.(10分)定义在R上的函数f(x)同时满足下列两个条件:①对任意x∈R,有f(x+2)≥f(x)+2;②对任意x∈R,有f(x+3)≤f(x)+3.设g(x)=f(x)﹣x.(Ⅰ)证明:g(x+3)≤g(x)≤g(x+2);(Ⅱ)若f(4)=5,求f的值.考点:抽象函数及其应用.专题:函数的性质及应用.分析:(Ⅰ)通过g(x)=f(x)﹣x,利用x+2,x+3分别代替x推出方程,由条件①,②转化,即可推出g(x+3)≤g(x)≤g(x+2).(Ⅱ)由(Ⅰ)g(x+2)≥g(x),然后推出g(x+3)≤g(x),说明g(x)是以6为周期的周期函数所然后求解函数值.解答:(本小题满分10分)(Ⅰ)证明:因为g(x)=f(x)﹣x,所以g(x+2)=f(x+2)﹣x﹣2,g(x+3)=f(x+3)﹣x﹣3.由条件①,②可得g(x+2)=f(x+2)﹣x﹣2≥f(x)+2﹣x﹣2=f(x)﹣x=g(x);【(2分)】③g(x+3)=f(x+3)﹣x﹣3≤f(x)+3﹣x﹣3=f(x)﹣x=g(x).④【(4分)】所以g(x+3)≤g(x)≤g(x+2).(Ⅱ)解:由③得g(x+2)≥g(x),所以g(x+6)≥g(x+4)≥g(x+2)≥g(x).【(6分)】由④得g(x+3)≤g(x),所以g(x+6)≤g(x+3)≤g(x).【(7分)】所以必有g(x+6)=g(x),即g(x)是以6为周期的周期函数.【(8分)】所以g=g(335×6+4)=g(4)=f(4)﹣4=1.【(9分)】所以f=g+2014=2015.【(10分)】点评:本题考查抽象函数的应用,函数的周期性以及不等式的证明,难度比较大.。
北京市西城区2014-2015学年度高三第一学期期末试数学理-含答案
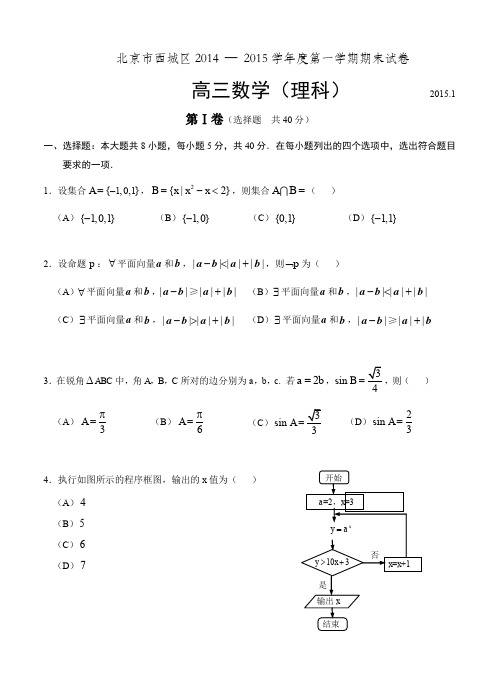
北京市西城区2014 — 2015学年度第一学期期末试卷高三数学(理科) 2015.1第Ⅰ卷(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.设集合1,0,1{}A -=,2{|2}B x x x =-<,则集合A B =( )(A ){1,0,1}-(B ){1,0}-(C ){0,1}(D ){1,1}-3.在锐角∆ABC 中,角A ,B ,C 所对的边分别为a ,b ,c . 若2a b =,sin B =,则( ) (A )3A π= (B )6A π=(C)sin A =(D )2sin 3A =4.执行如图所示的程序框图,输出的x 值为( ) (A )4 (B )5 (C )6 (D )72.设命题p :∀平面向量a 和b ,||||||-<+a b a b ,则p ⌝为( )(A )∀平面向量a 和b ,||||||-+≥a b a b (B )∃平面向量a 和b ,||||||-<+a b a b (C )∃平面向量a 和b ,||||||->+a b a b (D )∃平面向量a 和b ,||||||-+≥a b a b5.设函数()3cos f x x b x =+,x ∈R ,则“0b =”是“函数()f x 为奇函数”的( ) (A )充分而不必要条件 (B )必要而不充分条件 (C )充分必要条件 (D )既不充分也不必要条件8. 设D 为不等式组1,21,21x y x y x y ---+⎧⎪⎨⎪⎩≤≥≤表示的平面区域,点(,)B a b 为坐标平面xOy 内一点,若对于区域D内的任一点(,)A x y ,都有1OA OB ⋅≤成立,则a b +的最大值等于( ) (A )2 (B )1 (C )0(D )36.一个四棱锥的三视图如图所示,那么对于这个四棱锥,下列说法中正确的是( ) (A(B )最长棱的棱长为3(C )侧面四个三角形中有且仅有一个是正三角形 (D )侧面四个三角形都是直角三角形7. 已知抛物线2:4C y x =,点(,0)P m ,O 为坐标原点,若在抛物线C 上存在一点Q ,使得90OQP?o ,则实数m 的取值范围是( )(A )(4,8) (B )(4,)+? (C )(0,4)(D )(8,)+?侧(左)视图正(主)视图俯视图第Ⅱ卷(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分. 9. 复数2i12iz -=+,则||z = _____.10.设12,F F 为双曲线C :2221(0)16x y a a -=>的左、右焦点,点P 为双曲线C 上一点,如果12||||4PF PF -=,那么双曲线C 的方程为____;离心率为____.11.在右侧的表格中,各数均为正数,且每行中的各数从左到右成等差数列,每列中的各数从上到下成等比数列,那么x y z ++=______.12. 如图,在ABC ∆中,以BC 为直径的半圆分别交AB ,AC 于点E ,F ,且2AC AE =,那么AFAB=____;A ∠= _____.13.现要给4个唱歌节目和2个小品节目排列演出顺序,要求2个小品节目之间恰好有3个唱歌节目,那么演出顺序的排列种数是______. (用数字作答)14. 设P ,Q 为一个正方体表面上的两点,已知此正方体绕着直线PQ 旋转()角后能与自身重合,那么符合条件的直线PQ 有_____条.三、解答题:本大题共6小题,共80分.解答应写出必要的文字说明、证明过程或演算步骤. 15.(本小题满分13分)已知函数()cos cos 442x x xf x =+, x ∈R 的部分图象如图所示. (Ⅰ)求函数()f x 的最小正周期和单调递增区间;(Ⅱ) 设点B 是图象上的最高点,点A 是图象与x 轴的交点,求BAO ∠tan 的值.16.(本小题满分13分)现有两种投资方案,一年后投资盈亏的情况如下: (1)投资股市:(2)购买基金:(Ⅰ)当4p =时,求q 的值; (Ⅱ)已知甲、乙两人分别选择了“投资股市”和“购买基金”进行投资,如果一年后他们中至少有一人获利的概率大于45,求p 的取值范围; (Ⅲ)丙要将家中闲置的10万元钱进行投资,决定在“投资股市”和“购买基金”这两种方案中选择一种,已知12p =,16q =,那么丙选择哪种投资方案,才能使得一年后投资收益的数学期望较大?给出结果并说明理由.如图,在四棱柱1111D C B A ABCD -中,A A 1⊥底面A B CD ,90BAD ∠=,BC AD //,且122A A AB AD BC ==== ,点E 在棱AB 上,平面1A EC 与棱11C D 相交于点F .(Ⅰ)证明:1A F ∥平面1B CE ;(Ⅱ)若E 是棱AB 的中点,求二面角1A EC D --的余弦值; (Ⅲ)求三棱锥11B A EF -的体积的最大值.18.(本小题满分13分)已知函数2()(0)f x ax bx a =->和()ln g x x =的图象有公共点P ,且在点P 处的切线相同.(Ⅰ)若点P 的坐标为1(,1)e-,求,a b 的值; (Ⅱ)已知a b =,求切点P 的坐标.19.(本小题满分14分)已知椭圆C :2211612x y +=的右焦点为F ,右顶点为A ,离心率为e ,点(,0)(4)P m m >满足条件||||FA e AP =. (Ⅰ)求m 的值;(Ⅱ)设过点F 的直线l 与椭圆C 相交于M ,N 两点,记PMF ∆和PNF ∆的面积分别为1S ,2S ,求证:12||||S PM S PN =.B CDA B 1C 1E FA 1 D 1设函数()(9)f x x x =-,对于任意给定的m 位自然数0121m m n a a a a -=(其中1a 是个位数字,2a 是十位数字,),定义变换A :012()()()()m A n f a f a f a =+++. 并规定(0)0A =.记10()n A n =,21()n A n =,, 1()k k n A n -=,.(Ⅰ)若02015n =,求2015n ;(Ⅱ)当3m ≥时,证明:对于任意的*()m m ∈N 位自然数n 均有1()10m A n -<; (Ⅲ)如果*010(,3)m n m m <∈≥N ,写出m n 的所有可能取值.(只需写出结论)北京市西城区2014 — 2015学年度第一学期期末高三数学(理科)参考答案及评分标准2015.1一、选择题:本大题共8小题,每小题5分,共40分.1.C 2.D 3.A 4.C 5.C 6.D 7.B 8.A 二、填空题:本大题共6小题,每小题5分,共30分.9.1 10.221416x y -=11.17412.12 π313.9614.13注:第10,12题第一问2分,第二问3分.三、解答题:本大题共6小题,共80分. 其他正确解答过程,请参照评分标准给分. 15.(本小题满分13分) (Ⅰ)解:因为()cos cos 442x x xf x =+cos 22x x=+ ……………… 2分=π2sin()26x +, ……………… 4分所以 2π4π12T ==. 故函数()f x 的最小正周期为4π. ……………… 6分由题意,得πππ2π2π2262x k k -++≤≤, 解得4π2π4π4π+33k x k -≤≤,所以函数()f x 的单调递增区间为4π2π[4π,4π+],()33k k k -∈Z . ……………… 9分(Ⅱ)解:如图过点B 作线段BC 垂直于x由题意,得33π4TAC ==,2=BC , 所以2tan 3πBC BAO AC ∠==.16.(本小题满分13分)(Ⅰ)解:因为“购买基金”后,投资结果只有“获利”、“不赔不赚”、“亏损”三种,且三种投资结果相互独立, 所以p +13+q =1. ……………… 2分 又因为14p =, 所以q =512. ……………… 3分 (Ⅱ)解:记事件A 为 “甲投资股市且盈利”,事件B 为“乙购买基金且盈利”,事件C 为“一年后甲、乙两人中至少有一人投资获利”, ……………… 4分则C AB AB AB =U U ,且A ,B 独立. 由上表可知, 1()2P A =,()P B p =.所以()()()()P C P AB P AB P AB =++ ……………… 5分 111(1)222p p p =?+?? 1122p =+. ……………… 6分因为114()225P C p =+>,所以35p >. ……………… 7分 又因为113p q ++=,0q ≥,所以23p ≤.所以3253p ≤<. ……………… 8分(Ⅲ)解:假设丙选择“投资股票”方案进行投资,且记X 为丙投资股票的获利金额(单位:万元),所以随机变量X 的分布列为:…………… 9分则113540(2)2884EX =⨯+⨯+-⨯=. ……………10 分假设丙选择“购买基金”方案进行投资,且记Y 为丙购买基金的获利金额(单位:万元),所以随机变量Y 的分布列为:…………… 11分则111520(1)2366EY =⨯+⨯+-⨯=. …………… 12分因为EX EY >,所以丙选择“投资股市”,才能使得一年后的投资收益的数学期望较大.……… 13分17.(本小题满分14分)(Ⅰ)证明:因为1111D C B A ABCD -是棱柱,所以平面ABCD ∥平面1111A B C D .又因为平面ABCD 平面1A ECF EC =,平面1111A B C D 平面11A ECF A F =,所以1A F ∥EC . …………………2分 又因为1A F ⊄平面1B CE ,EC ⊂平面1B CE ,所以1A F ∥平面1B CE . …………………4分 (Ⅱ)解:因为1AA ⊥底面ABCD ,90BAD ∠=,所以1AA ,AB ,AD 两两垂直,以A 为原点,以AB ,AD ,1AA 分别为x 轴、y 轴和z 轴,如图建立空间直角坐标系. …………………5分则1(0,0,2)A ,(1,0,0)E ,(2,1,0)C , 所以 1(1,0,2)A E =-,1(2,1,2)AC =-. 设平面1A ECF 的法向量为(,,),m x y z = 由10A E m ⋅=,10AC m ⋅=, 得20,220.x z x y z -=⎧⎨+-=⎩令1z =,得(2,2,1)m =-. …………………7分 又因为平面DEC 的法向量为(0,0,1)n =, …………………8分所以1cos ,3||||m n m n m n ⋅<>==⋅,由图可知,二面角1A EC D --的平面角为锐角,所以二面角1A EC D --的余弦值为13. …………………10分(Ⅲ)解:过点F 作11FM A B ⊥于点M ,因为平面11A ABB ⊥平面1111A B C D ,FM ⊂平面1111A B C D , 所以FM ⊥平面11A ABB ,所以11111113B A EF F B A E A B E V V S FM --∆==⨯⨯ …………………12分1222323FM FM ⨯=⨯⨯=. 因为当F 与点1D 重合时,FM 取到最大值2(此时点E 与点B 重合), 所以当F 与点1D 重合时,三棱锥11B A EF -的体积的最大值为43. ………………14分18.(本小题满分13分) (Ⅰ)解:由题意,得21()1e e ea bf =-=-, …………………1分 且()2f x ax b '=-,1()g x x'=, …………………3分 由已知,得11()()e ef g ''=,即2e eab -=, 解得22e a =,3e b =. …………………5分 (Ⅱ)解:若a b =,则()2f x ax a '=-,1()g x x'=, 设切点坐标为(,)s t ,其中0s >,由题意,得 2ln as as s -=, ① 12as a s-=, ② …………………6分 由②,得 1(21)a s s =-,其中12s ≠,代入①,得 1ln 21s s s -=-. (*) …………………7分因为 10(21)a s s =>-,且0s >,所以 12s >. …………………8分 设函数 1()ln 21x F x x x -=--,1(,)2x ∈+∞, 则 2(41)(1)()(21)x x F x x x ---'=-. …………………9分 令()0F x '= ,解得1x =或14x =(舍). …………………10分当x 变化时,()F x '与()F x 的变化情况如下表所示,…………………12分所以当1x =时,()F x 取到最大值(1)0F =,且当1(,1)(1,)2x ∈+∞时()0F x <.因此,当且仅当1x =时()0F x =. 所以方程(*)有且仅有一解1s =. 于是 ln 0t s ==,因此切点P 的坐标为(1,0). …………………13分19.(本小题满分14分)(Ⅰ)解:因为椭圆C 的方程为 2211612x y +=,所以 4a =,b =2c =, ………………2分 则 12c e a ==,||2FA =,||4AP m =-. ………………3分 因为||21||42FA AP m ==-, 所以 8m =. ………………5分(Ⅱ)解:若直线l 的斜率不存在, 则有 21S S =,||||PM PN =,符合题意. …………6分若直线l 的斜率存在,则设直线l 的方程为)2(-=x k y ,),(11y x M ,),(22y x N . 由 ⎪⎩⎪⎨⎧-==+),2(,1121622x k y y x 得 2222(43)1616480k x k x k +-+-=, ……………… 7分可知 0>∆恒成立,且 34162221+=+k k x x ,3448162221+-=k k x x . ……………… 8分因为 8)2(8)2(8822112211--+--=-+-=+x x k x x k x y x y k k PN PM ……………… 10分 )8)(8()8)(2()8)(2(211221----+--=x x x x k x x k)8)(8(32)(102212121--++-=x x kx x k x kx0)8)(8(323416103448162212222=--++⋅-+-⋅=x x k k k k k k k ,所以 MPF NPF ∠=∠. ……………… 12分 因为PMF ∆和PNF ∆的面积分别为11||||sin 2S PF PM MPF =⋅⋅∠, 21||||sin 2S PF PN NPF =⋅⋅∠, ……………… 13分 所以12||||S PM S PN =. ……………… 14分20.(本小题满分13分)(Ⅰ)解:114082042n =+++=,2201434n =+=,3182038n =+=,418826n =+=,5141832n =+=,6181432n =+=,……所以 201532n =. ……………… 3分(Ⅱ)证明:因为函数2981()(9)()24f x x x x =-=--+,所以对于非负整数x ,知()(9)20f x x x =-≤.(当4x =或5时,取到最大值)… 4分 因为 12()()()()m A n f a f a f a =+++,所以 ()20A n m ≤. ……………… 6分 令 1()1020m g m m -=-,则31(3)102030g -=-⨯>.当3m ≥时,11(1)g()1020(1)1020910200m m m g m m m m --+-=-+-+=⨯->, 所以 (1)g()0g m m +->,函数()g m ,(m ∈N ,且3m ≥)单调递增. 故 g()g(3)0m >≥,即11020()m m A n ->≥.所以当3m ≥时,对于任意的m 位自然数n 均有1()10m A n -<. …………………9分 (Ⅲ)答:m n 的所有可能取值为0,8,14,16,20,22,26,28,32,36,38.…………………14分。
北京市各区县2014-2015学年高一上学期期末试题分类汇编——三角函数

2015年北京市各区县高一期末试题分类汇编——三角函数(2015年1月·昌平期末·14)某蒸汽机上的飞轮直径为20cm ,每分钟按顺时针...方向旋转180转,则飞轮每秒钟...转过的弧度数是_________;轮周上的一点每秒钟...经过的弧长为_________.6π- ,60cm π(2015年1月·延庆期末·8.若x x f 3cos )(cos =,则)3(sinπf 的值为A . 1-B .23 C .0D .1(2015年1月·西城期末·1.已知(0,2π)α∈,且sin 0<α,cos 0>α,则角α的取值范围是( ) (A )π(0,)2(B )π(,π)2(C )3π(π,)2(D )3π(,2π)2(2015年1月·西城期末·3.已知角α的终边经过点(3,4)P -,那么sin =α( ) (A )3 (B )4-(C )3 (D )3-(A )3 (B )3(C )5π3(D )7π3(2015年1月·海淀期末·10.为了得到函数sin(2)2y x π=-的图象,可以将函数sin 2y x =的图象 AA. 向右平移4π个单位长度 B. 向左平移4π个单位长度 C. 向右平移2π个单位长度 D. 向左平移2π个单位长度(2015年1月·西城期末·9.为得到函数πcos()6y x =+的图象,只需将函数sin y x =的图象( )(A )向左平移π3个单位 (B )向右平移π3个单位 (C )向左平移2π3个单位(D )向右平移2π3个单位(2015年1月·海淀期末·11.已知(,)αππ∈-,且sin cos7πα=-,则α= AA. 514π-或914π- B. 914π-或914π C. 514π或514π- D. 514π或914π (2015年1月·密云期末·2.sin 240=A .B .12-C .12D (2015年1月·顺义期末·2.sin120的值等于A .12B .12-CD .(2015年1月·海淀期末·2. 7sin6π=DA.B. C. 12D. 12-(2015年1月·延庆期末·2.已知)2,0[πα∈,与角3π-终边相同的角是A .3π B .32π C .34π D .35π (2015年1月·延庆期末·3.若0sin >α ,且0cos <α ,则角α是 A .第一象限角B .第二象限角C .第三象限角D .第四象限角(2015年1月·延庆期末·4.若角α的终边经过点)4,3(-P ,则tan =α A .54 B .53-C .34-D. 43-(2015年1月·延庆期末·11. 要得到)42sin(π+=x y 的图象只需将x y 2sin =的图象A .向左平移4π个单位 B .向右平移4π个单位 C .向右平移8π个单位D .向左平移8π个单位(2015年1月·海淀期末·6.若直线x a =是函数()sin f x x =的一条对称轴,则()f a = DA.0B.1C. 1-D. 1或1- (2015年1月·密云期末·5.函数)32sin(2π+=x y 的一个对称中心A .)0,6(πB .)0,6(π-C .)0,12(πD .)0,12(π-(2015年1月·西城期末·6.如果函数cos()y x =+ϕ的一个零点是3π,那么ϕ可以是( ) (A )6π(B )6π-(C )3π (D )3π-(2015年1月·东城期末·2. 已知sin 0,cos 0θθ<>,则角θ是 A .第一象限角B .第二象限角C .第三象限角D .第四象限角(2015年1月·房山期末·7)要得到函数cos 2y x =的图象,只需将函数cos(2)5y x π=+的图象(A )向左平移5π个单位 (B )向右平移5π个单位 (C )向左平移10π个单位(D )向右平移10π个单位(2015年1月·房山期末·8)函数πsin 2()6y x =+的图象(A )关于点π(,0)6对称 (B )关于点π(,0)3对称 (C )关于直线π6x =-对称 (D )关于直线π3x =对称(2015年1月·丰台期末·4.已知135sin =α,α是第一象限角,则cos(π)α-的值为( ) A .513-B .513C .1213-D . 1213(2015年1月·顺义期末·6.先将函数sin 2y x =的图象向右平移3π个长度单位,再作所得图象关于x 轴的对称图形,此时函数的解析式为 A.sin(2)3y x π=- B .sin(2)3y x π=-+ C.2sin(2)3y x π=-- D.2sin(2)3y x π=-+(2015年1月·昌平期末·6)将函数cos 2y x =的图象上所有的点向右平移12个单位,得到的图象所对应的函数解析式为(A )1cos(2)2y x =- (B )1cos(2)2y x =+ (C )cos(21)y x =- (D )cos(21)y x =+(2015年1月·顺义期末·8.如图,现要在一块半径为1m 圆心角为3π的扇形金属板AOB 上,A剪出一个平行四边形MNPQ ,使点P 在弧AB 上,点Q 在OA 上,点,M N 在OB 上,记MNPQ Y 的面积为S ,则S 的最大值为2 2m2 2(2015年1月·昌平期末·2)已知角α的终边经过点(1P -,则cos α=(A (B ) (C )12 (D )12-(2015年1月·丰台期末· 7.已知函数sin()y A x ωϕ=+ππ,(0,0,)22A ωϕ>>-<<的图象如下,则ω与ϕ的值分别为( ) A .2,3π B .2,6π C .1,23π D .1,26π(2015年1月·密云期末·4.在下列函数中,既是偶函数又在区间0,1()上单调递减的函数为A .xy 1= B .x y lg = C .x y cos = D .2x y =(2015年1月·丰台期末·8. 关于π()3cos(2),R 6f x x x =-∈,下列叙述正确的是( )A . 若12()()3==f x f x ,则12-x x 是2π的整数倍B . 函数()f x 的图象关于点π(,0)6-对称 C . 函数()f x 的图象关于直线π6x =对称D . 函数()f x 在区间π(0,)4上为增函数(2015年1月·密云期末·8.已知函数11()sin cos =+f x x x,在下列结论中: ①π是()f x 的一个周期;②()f x 的图象关于直线x 4π=对称;③()f x 在(,0)2π-上单调递减.正确结论的个数为 A. 0B.1C. 2D. 3(2015年1月·西城期末·12.已知α是第二象限的角,且5sin 13α=,则cos =α1213-. (2015年1月·西城期末·13.若(,)22ππ∈-θ,且tan 1>θ,则θ的取值范围是_(,)42ππ.(2015年1月·石景山期末·11.若cos 2α=,且α的终边过点(,2)P x ,则x = (2015年1月·石景山期末·12.sin α=3cos α,则tan α= 3 .(2015年1月·房山期末·12)若角α的终边经过点(2,1)P ,则tan =α ,πtan()4+=α12;3(2015年1月·丰台期末·12.已知点3(,)5P m -为角α的终边与单位圆的交点,则=αcos ;35- (2015年1月·顺义期末·9.已知角α的终边经过点()3,4P ,则sin α的值为____45___. (2015年1月·西城期末·16.关于函数()sin(2)()6f x x x π=-∈R ,给出下列三个结论:① 对于任意的x ∈R ,都有2()cos(2)3f x x π=-; ② 对于任意的x ∈R ,都有()()22f x f x ππ+=-;③ 对于任意的x ∈R ,都有()()33f x f x ππ-=+.其中,全部正确结论的序号是_____. ① ② ③(2015年1月·房山期末·13)已知3cos 5=-α,且α为第二象限的角,则sin()α-= 45- . (2015年1月·顺义期末·12.函数2sin(2)6y x π=+图像的对称中心是_________;对称轴方程是_______. (,0),,21226k k x k Z ππππ-=+∈ (2015年1月·延庆期末·16.已知B A ,是圆O 上两点,2=∠AOB 弧度,2=OA ,则劣弧AB 长度是__ ____.4(2015年1月·东城期末·12. 已知1tan(3)2απ-=-,则πcos()cos()2sin(π+)2cos(π)αααα++---的值是13. (2015年1月·东城期末·15. 函数1π2s i n ()36y x=-的单调递减区间是__[6π2π,6π2π](Z)k k k ++∈_.(2015年1月·丰台期末·14.函数)3πsin(2+=x y )2π0(≤≤x 的值域是 ;[1,2] (2015年1月·顺义期末·12.不等式cos 0x >的解集为_________ππ{|2π2π+,}22x k x k k -<<∈Z _______ .(2015年1月·海淀期末·17. 已知函数sin()y A t ωϕ=+(其中0,0,||2A πωϕ>><)的图象如右图所示,它刻画了质点P 做匀速圆周运动(如图2)时,质点相对水平直线l 的位置值y (||y 是质点与直线l 的距离(米),质点在直线l 上方时,y 为正,反之y 为负)随时间t (秒)的变化过程. 则(1)质点P 运动的圆形轨道的半径为________米; (2)质点P 旋转一圈所需的时间T =_________秒; (3)函数()f t 的解析式为:__________________; (4)图2中,质点P 首次出现在直线l 上的时刻t =_______秒.(1)2;(2)2;(3)()f t =π2sin(π)6t -;(4)16第17题(图2)(2015年1月·延庆期末·18.设函数)32sin(ππ+=x y ,若对任意R x ∈,存在x 1,x 2使)()()(21x f x f x f ≤≤恒成立,则21x x -的最小值是_______.2(2015年1月·房山期末·16)已知函数()sin()f x x ωϕ=+(0ω>,0πϕ<<)的图象与直线y b =(10b -<<)的三个相邻交点的横坐标分别为1,3,7,则()f x 的最小正周期为 ,()f x 取得最大值时x;56,k k +∈Z(2015年1月·丰台期末·18)(本小题满分9分) 已知θ为锐角(Ⅰ)若tan 2θ=,求sin cos sin cos θθθθ+-的值;(Ⅱ)若1)cos (sin sin 2=+θθθ,求θ的值. 解:(Ⅰ)sin cos tan 1213sin cos tan 121θθθθθθ+++===--- ┄┄┄┄┄┄┄┄┄┄┄4分(Ⅱ)22sin (sin cos )2sin 2sin cos 1cos2sin 21θθθθθθθθ+=+=-+=s i n 2c o sθθ= 由π(0,)2θ∈得2(0,π)θ∈故π24θ=所以π8θ= ┄┄┄┄┄┄┄┄┄┄┄9分(2015年1月·丰台期末·19. (本小题满分10分) 已知函数()sin(2)sin(2)cos 233f x x x x a ππ=++-++的最大值是(Ⅰ)求常数a 的值;(Ⅱ)求函数()f x 的最小正周期和单调递增区间. 解:(Ⅰ)()sin(2)sin(2)cos 233f x x x x a ππ=++-++sin 2cos 2π)4x x ax a=++=++a =a ∴= ┄┄┄┄┄┄┄┄┄┄┄6分(Ⅱ)2ππ2T == 令πππ2π-22π+,242k x k k Z ≤+≤∈解得3πππ-π+,88k x k k Z ≤≤∈ 所以函数()=y f x 的单调递增区间为3ππ[π-,π+],88k k k Z ∈┄┄┄┄┄10分(2015年1月·顺义期末·15.(本小题满分13分)已知4sin 5α=,且02απ<<. (Ⅰ)求tan α的值; (Ⅱ)求cos 2sin()2ααπ++的值. 15.(本小题满分13分) 解:(Ⅰ)因为4sin 5α=,02απ<<, 故3cos 5α=,所以34tan =α. -------------6分(Ⅱ)23238cos 2sin()12sin cos 1225525ααααπ++=-+=-+=. --------------13分(2015年1月·昌平期末·18)(本小题共14分)在平面直角坐标系xOy 中,角,(0)2παβαβπ<<<<的顶点与原点O 重合,始边与x轴的正半轴重合,终边分别与单位圆交于,A B 两点,,A B 两点的横坐标分别为54,135-. (I )写出cos ,cos αβ的值;(只需写出结果) (II )求tan β的值; (III )求AOB ∠的余弦值.解:(Ⅰ)5cos 13α=;4cos 5β=-.(Ⅱ)因为4cos 5β=-,2πβπ<<,所以3sin 5β=. ……………………4分 所以3sin 35tan 4cos 45βββ===--. ……………………6分(Ⅲ) 因为5cos 13α=,02πα<<,所以12sin 13α=. ……………………8分所以cos cos()AOB βα∠=- ……………………9分cos cos sin sin βαβα=+ …………………11分45312513513=-⨯+⨯ 1665=. ……………………14分(2015年1月·延庆期末·21.(本题10分)设函数xxx f tan sin )(=. (Ⅰ)求函数)(x f 的定义域; (Ⅱ)已知)2,0(πα∈,且135)(=αf ,求)4(πα+f 的值. 解:解:(Ⅰ)要使函数)(x f 有意义,只要使0tan ≠x , ∴函数)(x f 的定义域为,|{R x x ∈且},2Z k k x ∈≠π. ………………3分 (Ⅱ)由x x x cos sin tan =,得x x f cos )(=,∴135cos )(==ααf . …………5分 ∵)2,0(πα∈,∴1312cos 1sin 2=-=αα. ………………7分∴4sinsin 4coscos )4cos()4(παπαπαπα-=+=+f262722131222135-=⨯-⨯=. ………………10分 (2015年1月·石景山期末·17.(本题满分9分)已知02απ<<,4sin 5α=. (I )求cos α的值;(II )求tan()4πα+的值;(III )求sin()cos()tan()2cos()ππαααπα---+的值.解:(I )02απ<<,4sin 5α=,3cos 5α∴=; …………2分 (II )4tan 3α=…………4分 tan()74πα+=- …………6分(III )sin()cos()tan()2cos()ππαααπα---+=sin cos cot cos αααα-=3sin cot cos 5ααα-=-=-. …………9分(2015年1月·石景山期末·18. (本题满分8分)函数()2sin(2)3f x x π=-的部分图象如右图所示.(I )写出()f x 的最小正周期及图中0x ,0y 的值; (II )求()f x 在区间[,]46ππ-上的最大值和最小值.解:(I ) ()f x 的最小正周期为π,0512x π=,02y =. …………4分 (II )因为[,]46x ππ∈-,所以52[,0]36x ππ-∈-. 于是,当203x π-=,即6x π=时,()f x 取得最大值0;当232x ππ-=-,即12x π=-时,()f x 取得最大值2- …………8分yOx0x0y(2015年1月·延庆期末·22.(本题10分)已知函数x x x x f 22cos 32sin sin )(++=. (Ⅰ)求)(x f 的最小正周期; (Ⅱ)求函数的单调减区间; (Ⅲ)当]44[ππ-∈x 时,求函数)(x f 的最小值.解:解:(Ⅰ)∵1cos 22sin )(2++=x x x fx x 2cos 2sin +=)42sin(2π+=x , ……………………2分∴)(x f 的最小正周期πωπ==2T . ……………………4分(Ⅱ)由πππππk x k 2234222+≤+≤+得ππππk x k +≤≤+858)(Z k ∈ ∴函数的单调减区间]85,8[ππππk k ++)(Z k ∈. …………………7分(Ⅲ)由]43,4[42]2,2[2]4,4[πππππππ-∈+⇒-∈⇒-∈x x x . ∴当442ππ-=+x 时,即4π-=x 时,)(x f 取得最小值0. …………10分(2015年1月·昌平期末·20)(本小题共16分)已知函数()()12cos2f x x x =+. (I )求函数()f x 的定义域; (II )求函数()f x 在区间[,]66ππ-上的最大值和最小值; (III )求函数()f x 的单调递增..区间. 解:(Ⅰ)要使函数有意义,只需22x k ππ≠+,即24k x ππ≠+. ………………2分 所以函数()f x 的定义域为,24k x x k ππ⎧⎫≠+∈⎨⎬⎩⎭Z . ………………3分(Ⅱ)()(12)cos2f x x x =(12x = ………………4分cos22x x = ………………5分2sin(2)6x π=+. ………………7分因为66x ππ-≤≤,所以2662x πππ-≤+≤. ………………8分所以1sin(2)126x π-≤+≤.即12sin(2)26x π-≤+≤.所以当262x ππ+=,即6x π=时,函数()f x 的最大值为2; ……10分当266x ππ+=-;即6x π=-时,函数()f x 的最小值为1-. ……12分(Ⅲ) 因为222262k x k πππππ-≤+≤+, ………………14分所以36k x k ππππ-≤≤+. ………………15分结合定义域,可知函数()f x 单调递增区间为,,,()3446k k k k k ππππππππ⎡⎫⎛⎤---+∈⎪ ⎢⎥⎣⎭⎝⎦Z . ………………16分 (2015年1月·东城期末·18.(本题满分10分)已知函数2()22cos 1f x x x ==+-.(Ⅰ)求()f x 的最小正周期;(Ⅱ)求()f x 在区间,64ππ⎡⎤-⎢⎥⎣⎦上的最大值和最小值.18.(本题满分10分)解:(Ⅰ)因为2()22cos 1f x x x =+-x x 2cos 2sin 3+=)62sin(2π+=x .所以)(x f 的最小正周期为π.(Ⅱ)因为.32626,46πππππ≤+≤-≤≤-x x 所以 于是,当6,262πππ==+x x 即时,)(x f 取得最大值2;当)(,6,662x f x x 时即πππ-=-=+取得最小值—1.(Ⅰ)根据函数()sin()f x A x =+ωϕ (0A >,0>ω,π02<<ϕ)的部分图象可得 2A =,------------------1分 5πππ41264T =-=,由此可得()f x 的最小正周期为π, ------------------1分 0>ω,2T π==πω,∴2ω= ------------------2分又π()26f =,∴ππ22π,62k k ϕ⨯+=+∈Z -----------------2分 ∴π2π,6k k ϕ=+∈Z ,而π02<<ϕ∴π6ϕ= ------------------1分∴函数()f x 的解析式为π()2sin(2)6f x x =+ -----------------1分(Ⅱ) ∵ππ[,]212x ∈--,∴π5π2[,0]66x +∈-∴当π206x +=,即π12x =-时,()f x 取得最大值0, ------------------2分当ππ262x +=-,即π3x =-时,()f x 取得最小值2- ------------------2分 (2015年1月·顺义期末·18.(本小题满分已知函数2()cos cos f x x x x =. (Ⅰ)求()f x 的最小正周期; (Ⅱ)求()f x 在区间[,]122ππ(Ⅲ)作出()f x 在一个周期内的图象.解:(Ⅰ)因为()f x 1cos 222x x +=π1sin(2)62x =++. ---------------------------------------------------4分所以函数()f x 的最小正周期为π.---------------------------------5分(Ⅱ)π1()sin(2)62f x x =++. 因为122x ππ≤≤,所以ππ7π2366x ≤+≤, 所以1πsin(2)126x -+≤≤,因此π130sin(2)622x ++≤≤,即()f x 的取值范围为3[0]2,-----------------------------10分(Ⅲ)()f x 在[,]1212π11π-上的图象如图所示. ----------------------------14分(其它周期上的图象同等给分) (个别关键点错误酌情给分)(2015年1月·顺义期末·19.(本小题满分13分)已知函数2()cos2sin f x x x =-. (I )求(0)f 的值;(II )求函数()f x 的最大值和最小值,并分别写出使函数取得最大值和最小值时的x 值.解:(I )2(0)cos0sin 01f =-=. ------------------------------------------------------------------6分 (II )2222()cos2sin 12sin sin 3sin 1f x x x x x x =-=--=-+, -------------------8分所以)(x f 最大值是1,最小值是2-. ------------------------------------------------10分 当sin 0x =时,即()x k k Z π=∈时函数()f x 取得最大值1, 当sin 1x =±时,即()2x k k Z ππ=+∈时函数()f x 取得最小值2-.-------13分(2015年1月·顺义期末·20.(本小题共14分)已知向量1,cos )a x x =-r ,(1,2cos )b x =r ,设函数()f x a b =⋅r r .(Ⅰ)求函数()f x 的最小正周期及最值;(Ⅱ)若,2x ππ⎡⎤∈⎢⎥⎣⎦,求函数()f x 的单调递增区间; (Ⅲ)若不等式|()|1f x m -<在,43x ππ⎡⎤∈⎢⎥⎣⎦上恒成立求实数m 的取值范围.解:(Ⅰ))()()21,cos 1,2cos f x a b x x x =⋅=-⋅r r2212cos x x -+2cos 2x x +2sin(2)6x π=+.————4分∴最小正周期T π=当2262x k πππ+=+即6x k ππ=+时()max 2f x =,当2262x k πππ+=-即3x k ππ=-时()min 2f x =-.()k z ∈———7分(Ⅱ)由()2sin 26f x x π⎛⎫=+⎪⎝⎭, 222262k x k πππππ-≤+≤+,k Z ∈∴()f x 的单调递增区间为36k x k ππππ-≤≤+k Z ∈.令上式1k = ∴2736x ππ≤≤()'1.又Q ,2x ππ⎡⎤∈⎢⎥⎣⎦()'2 又()'1()'2得的 ()f x 的单调递增区间为2,3ππ⎡⎤⎢⎥⎣⎦————11分(Ⅲ)由43x ππ≤≤∴252366x πππ≤+≤1sin 2262x π⎛⎫∴≤+≤ ⎪⎝⎭;∴12sin 26x π⎛⎫≤+≤ ⎪⎝⎭——————————12分要()||1f x m -<恒成立 ,即()||1m f x -<恒成立,∴2sin 212sin 2166x m x ππ⎛⎫⎛⎫+-<<++ ⎪ ⎪⎝⎭⎝⎭∴2sin 2162sin 216m x m x ππ⎧⎛⎫>+- ⎪⎪⎪⎝⎭⎨⎛⎫⎪<++ ⎪⎪⎝⎭⎩恒成立∴12m m ⎧>⎪⎨<⎪⎩; 即)1,2m ∈————14分(2015年1月·房山期末·20)(本小题共12分)已知函数()2cos (sin cos )1f x x x x =+-. (Ⅰ)求()f x 的单调递增区间; (Ⅱ)若函数()()g x f x k =-在[0,]2π上有两个不同的零点,求实数k 的取值范围.(20)(本小题共12分) 解:(Ⅰ)由()2cos (sin cos )1f x x x x =+-(1)(1)sin 2 cos 2 x x =+分分 -------------------2分)4x π=+ -------------------2分由222()242k x k k Z πππππ-+≤+≤+∈ -------------------2分解得:3()88k x k k Z ππππ-+≤≤+∈ -------------------2分 所以函数)(x f 的递增区间为3[,]()88k k k Z ππππ-++∈. (Ⅱ)由0,2x π⎡⎤∈⎢⎥⎣⎦,得24x π+∈5,44ππ⎡⎤⎢⎥⎣⎦, 可知函数)(x f 在0,8π⎡⎤⎢⎥⎣⎦上单调递增,()[1f x ∈,在,82ππ⎛⎤⎥⎝⎦上单调递减,()[1f x ∈-, -------------------2分 所以若函数()()g x f x k =-在0,2π⎡⎤⎢⎥⎣⎦上有两个不同的零点,则[1k ∈.(2015年1月·海淀期末·18.本题满分13分已知函数2()2sin()36f x x ππ=+.(Ⅰ)请用“五点法”画出函数()f x 在一个 周期上的图象(先列表,再画图); (Ⅱ)求()f x 的单调增区间;(Ⅲ)求()f x 在13[,]24-上的取值范围.18.本题满分13分解:(Ⅰ)函数2()2sin()36f x x ππ=+的周期3T =,-----------------------------------1分)第17题(图1)描点画图如图所示. --------------------------------------------------5分(Ⅱ)函数sin y x =的单调增区间为ππ[2π,2π]()22k k k -+∈Z .-----------------------6分由π2π2π2π()2362k x k k ππ-≤+≤+∈Z , 得1313()2k x k k -≤≤+∈Z .所以()f x 单调增区间为1[31,3]()2k k k -+∈Z .----------------------------------------------9分(Ⅲ)因为13[,]24x ∈-,所以2πππ2π[,]3663x +∈-, 所以2ππ1sin()[,1]362x +∈- 所以2ππ2sin()[1,2]36x +∈-,即()f x 在13[,]24-上的取值范围是[1,2]-.-------------13分 说明:(Ⅱ)(Ⅲ)问,如果最终结果错误,可细化解题步骤给过程分;如果仅有最终正确结果,无步骤每问各扣1分。
北京市密云县2014-2015学年度第一学期高一数学期末试题

密云县2014—2015学年度第一学期期末考试 高一数学试卷 2015.1第一部分 (选择题 共40分)一、选择题.共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项. 1.已知集合}9,7,5,3,1{=U ,}7,5,1{=A ,则=A C UA .}3,1{B .}9,7,3{C .}9,5,3{D .}9,3{2.sin 240=A .B .12-C .12D 3.已知△ABC 三个顶点的坐标分别为(0,0)A ,(2,2)B ,(0,)C c ,若AB BC ⊥,那么 c 的值是A.1-B.3C.3-D.44.在下列函数中,既是偶函数又在区间0,1()上单调递减的函数为A .xy 1=B .x y lg =C .x y cos =D .2x y = 5.函数)32sin(2π+=x y 的一个对称中心A .)0,6(πB .)0,6(π-C .)0,12(πD .)0,12(π- 6. 函数log =a y x (0>a 且1≠a )的图象经过点)1,2(-,函数=xy b (0>b 且1≠b )的图象经过点)2,1(,则下列关系式中正确的是 A . 22b a >B . ba 22>C . b a )21()21(> D . 2121b a >7.如图,点P 在边长为1的正方形的边上运动,设M 是CD 的中点,则当P 沿着路径--B A M C -运动时,点P 经过的路程x 与△APM 的面积y 的函数关系为)(x f y =,则)(x f y =的图象是8.已知函数11()sin cos =+f x x x,在下列结论中: ①π是()f x 的一个周期;②()f x 的图象关于直线x 4π=对称;③()f x 在(,0)2π-上单调递减.正确结论的个数为A. 0B.1C. 2D. 3第二部分 (非选择题 共110分)二、填空题共6小题,每小题5分,共30分.9. 如果向量(4,2)=-a ,(,1)x =b ,且a ,b 共线,那么实数x = .10. 已知集合{}{}2|1,|230=>=--<A x x B x x x ,则=AB .11.sin15o sin75o 的值是____________.12. 已知函数21,(01),()2,(10),x x x f x x ⎧+<≤⎪=⎨-≤≤⎪⎩且5()4f m =,则m 的值为 .13. 已知ABC ∆是正三角形,若AC AB λ=-a 与向量AC 的夹角大于90,则实数λ的取值范围是__________. 14.给出定义:若11< +22m x m -≤ (其中m 为整数),则m 叫做离实数x 最近的整数,记作{}x ,即{}=x m . 在此基础上给出下列关于函数()={}f x x x -的四个判断:①=()y f x 的定义域是R ,值域是11(,]22-; ②点(,0)k 是=()y f x 的图象的对称中心,其中k Z ∈; ③函数=()y f x 的最小正周期为1; ④函数=()y f x 在13]22(,上是增函数.则上述判断中正确的序号是 .(填上所有正确的序号)三、解答题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. 15. (本小题满分13分) 已知函数2()1+log 1=--()f x x . (I )求函数()f x 的定义域; (II )求(5)f 的值; (III )求函数()f x 的零点.16. (本小题满分14分)已知sin θ=其中θ是第三象限角. (Ⅰ)求cos ,tan θθ的值;(Ⅱ)求⎪⎭⎫⎝⎛π-θ4tan 的值; (III) 求πθπθθ⎛⎫+-++ ⎪⎝⎭sin 2sin()cos 22的值.17. (本小题满分13分)已知向量(cos )θθ=a ,(sin ,0)θ=b ,其中θ∈R .(Ⅰ)当π3θ=时,求⋅a b 的值; (Ⅱ)当π[0,]2θ∈时,求2(+)a b 的最大值.18. (本小题满分14分)函数f (x )=A sin(ωx +φ) (A >0,ω>0, |φ|<π2)的部分图象如图所示.(Ⅰ)求函数()f x 的解析式;(Ⅱ)将y =f (x )的图象向右平移π6个单位后得到新函数()g x 的图象,求函数()g x 的解析式;(Ⅲ)求函数2()()-f x g x 的单调增区间.19. (本小题满分13分)设二次函数2()f x ax bx c =++0,a x R ≠∈满足条件: ①21()(1)2≤≤+x f x x , ②(1)(1)-+=--f x f x ; ③()f x 在R 上的最小值为0. (I )求(1)f 的值; (II )求()f x 的解析式;(III )求最大值(1)m m >,使得存在t R ∈,只要[]1,x m ∈,都有()f x t x +≤成立.20.(本小题满分13分)若函数)(x f 对任意的x ∈R ,均有)(2)1()1(x f x f x f ≥++-,则称函数)(x f 具有性质P . (Ⅰ)判断下面两个函数是否具有性质P ,并说明理由.①2x y =; ②3y x =.(Ⅱ)若函数)(x f 具有性质P ,且(0)()0f f n ==(2,n >n ∈*N ),求证:对任意{1,2,3,,1}i n ∈-有()0f i ≤;(Ⅲ)在(Ⅱ)的条件下,是否对任意[0,]x n ∈均有0)(≤x f .若成立给出证明,若不成立给出反例.密云县2014—2015学年度第一学期期末考试高一数学试卷参考答案及评分参考2015.01一、选择题共8小题,每小题5分,共40分.二、填空题共6小题,每小题5分,共30分.9.-2 10.(1,3) 11.1412.1213.2λ> 14.①③④ 三、解答题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. 15. (本小题满分13分)解:(I )由题:10x ->, ----------------2分1.x ∴>∴函数()f x的定义域{}1x x >. --4分(II )2(5)1log (51)121f =-+-=-+= ----------------8分 (III )令2()1+log 1=--()=0f x x , 2log (1) 1.x ∴-=1 2.x ∴-= 3.x ∴= ∴函数()f x 的零点为3. -----------13分16. (本小题满分14分) 解:(Ⅰ)sin 5θ=-且θ是第三象限角, cos θ∴== ------2分sin tan 2.cos θθθ∴== ----------------4分 (Ⅱ)由(Ⅰ),tan tan 4tan()41tan tan4πθπθπθ--=+⋅----------------6分211.1213-==+⨯----------------9分(III)πθπθθ⎛⎫+-++ ⎪⎝⎭sin 2sin()cos 22θθθ=++-2cos 2sin 2cos 1 -----12分=-+-+--22(2(1555=-3.5 ---------14分17. (本小题满分13分) 解:(Ⅰ)当π3θ=时,163(,),(,0)2a b ==,---------------2分1302a b ∴⋅=⨯= ----------------5分(Ⅱ)由题: 2()a b +222a a b b =+⋅+2222cos )2(cos sin 0)sin 0θθθθθθ=++⋅⋅++22cos sin 2sin 1θθθ=⋅++sin 22cos 2θθ=+-)24πθ=-+. -----10分02πθ≤≤, 32444πππθ∴-≤-≤.∴当242ππθ-=即38πθ=时, ----------------11分2()a b +2. --------------- ----13分18. (本小题满分14分)解:(Ⅰ)由所给图象知A =1, ---------------1分34T =11π12-π6=3π4,T =π,所以ω=2πT =2.----------------2分 由sin ⎝ ⎛⎭⎪⎫2×π6+φ=1,|φ|<π2得π3+φ=π2,解得φ=π6,-------4分所以f (x )=sin ⎝ ⎛⎭⎪⎫2x +π6. ----------------5分(Ⅱ)f (x )=sin ⎝⎛⎭⎪⎫2x +π6的图象向右平移π6个单位后得到的图象对应的函数解 析式为()g x =sin ⎣⎢⎡⎦⎥⎤2⎝⎛⎭⎪⎫x -π6+π6 ----------------7分 =sin ⎝ ⎛⎭⎪⎫2x -π6. --------------9分(Ⅲ)由题: 2()()f x g x -2sin(2)sin(2)66x x ππ=+--12cos 22cos 222x x x x =+-+32cos 222x x =+)3x π=+. -------------12分222,(),232k x k k Z πππππ-≤+≤+∈令 ----------------13分5,(),1212k x k k Z ππππ-≤≤+∈则 ∴函数f(x)的增区间为5()1212k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦,.------14分19.(本小题满分13分)解:(I) ∵在上恒成立,∴即. -----------------2分(II )∵(1)(1)-+=--f x f x ,∴函数图象关于直线对称,∴∵,∴ ---------------------------4分又∵在上的最小值为,∴,即,由解得,∴; -------------7分(III )∵当时, 恒成立,∴且,由得,解得---------------9分由得:,解得,……………(10分)∵,∴,---------------11分当时,对于任意,恒有,∴的最大值为. -------------------12分另解:(酌情给分)且在上恒成立∵在上递减,∴,∵在上递减,∴∴,∴,,∵,∴,∴,∴的最大值为20.(本小题满分13分)21)21)m =4-1max min 1)(1)x -+⎪⎩1t x ≤-+x t ++2100x -≤(-1-22t +14+12b ⎨⎪=⎪⎩a bc ⎨⎪-+⎩.2)1=)2x(Ⅰ)证明:①函数()2x f x =具有性质P .11(1)(1)2()222220x x x x f x f x f x -+-++-=+-⋅=>,……………1分即)(2)1()1(x f x f x f ≥++-,此函数为具有性质P .……………2分 ②函数3)(x x f =不具有性质P . ……………3分例如,当1x =-时,(1)(1)(2)(0)8f x f x f f -++=-+=-,2()2f x =-, 所以,)1()0()2(-<+-f f f ,……………4分 此函数不具有性质P . (Ⅱ)假设)(i f 为(1),(2),,(1)f f f n -中第一个大于0的值,则0)1()(>--i f i f ,因为函数()f x 具有性质P ,所以,对于任意n ∈*N ,均有(1)()()(1)f n f n f n f n +-≥--, 所以0)1()()2()1()1()(>--≥≥---≥--i f i f n f n f n f n f , 所以()[()(1)][(1)()]()0f n f n f n f i f i f i =--+++-+>,与0)(=n f 矛盾,所以,对任意的{1,2,3,,1}i n ∈-有()0f i ≤. ……………9分(Ⅲ)不成立.例如2()()x x n x f x xx -⎧=⎨⎩为有理数,为无理数.……………10分证明:当x 为有理数时,1,1x x -+均为有理数,222(1)(1)2()(1)(1)2(112)2f x f x f x x x x n x x x -++-=-++---++-=,当x 为无理数时,1,1x x -+均为无理数,22)1()1()(2)1()1(222=-++-=-++-x x x x f x f x f所以,函数)(x f 对任意的x ∈R ,均有)(2)1()1(x f x f x f ≥++-,即函数)(x f 具有性质P . ……………12分 而当],0[n x ∈(2n >)且当x 为无理数时,0)(>x f .所以,在(Ⅱ)的条件下,“对任意[0,]x n ∈均有0)(≤x f ”不成立.……………13分 (其他反例仿此给分,如0()1x x f x ⎧=⎨⎩为有理数,为无理数,,,0,()1,x x f x ⎧=⎨⎩为整数,为非整数,20,(),x x f x x ⎧=⎨⎩为整数,为非整数,等.)。
北京市西城区2014-2015学年度第一学期期末高中一年级数学试题

市西城区2014 — 2015学年度第一学期期末 高一数学2015.1A 卷 [必修 模块4] 本卷总分值:100分一、选择题:本大题共10小题,每题4分,共40分.1.(0,2π)α∈,且sin 0<α,cos 0>α,那么角α的取值围是〔 〕 〔A 〕π(0,)2〔B 〕π(,π)2〔C 〕3π(π,)2〔D 〕3π(,2π)22.向量(2,8)=a ,(4,2)=-b .假设2=-c a b ,那么向量=c 〔 〕 〔A 〕(0,18)〔B 〕(12,12)〔C 〕(8,14)〔D 〕(4,20)-3.角α的终边经过点(3,4)P -,那么sin =α〔 〕 〔A 〕35〔B 〕34〔C 〕34-〔D 〕45-4.函数sin y x =和cos y x =在区间M 上都是增函数,那么区间M 可以是〔 〕 〔A 〕π(0,)2〔B 〕π(,π)2〔C 〕3π(π,)2〔D 〕3π(,2π)25.在△ABC 中,D 是BC 的中点,那么AB AC +=〔 〕 〔A 〕2AD〔B 〕2DA〔C 〕2BD〔D 〕2DB6.以下函数中,偶函数是〔 〕 〔A 〕()sin()f x x =π+ 〔B 〕()tan()f x x =π- 〔C 〕()sin()2f x x π=+ 〔D 〕()cos()2f x x π=-7.为得到函数πcos()6y x =+的图象,只需将函数cos y x =的图象〔 〕〔A 〕向左平移π3个单位 〔B 〕向右平移π3个单位 〔C 〕向左平移π6个单位〔D 〕向右平移π6个单位8.如图,在矩形ABCD 中,2AB =,3BC =, E 是CD 的中点,那么AE DC ⋅=〔 〕 〔A 〕4〔B 〕2〔C 〕3〔D 〕19.函数2sin y x =的最小正周期为〔 〕 〔A 〕2π〔B 〕π〔C 〕π2〔D 〕π410.向量(1,sin )θ=a ,(cos θ=b ,其中R θ∈,那么||-a b 的最大值是〔 〕 〔A 〕4〔B 〕3〔C 〕2〔D 〕1二、填空题:本大题共6小题,每题4分,共24分. 把答案填在题中横线上. 11.假设(0,)∈πα,且α与角53π-终边一样,那么=α_____. 12.假设向量(1,2)=a 与向量(,1)=-λb 共线,那么实数=λ_____. 13.α是第二象限的角,且5sin 13α=,那么cos =α_____. 14. 向量(1,3)=a ,(2,1)=-b ,(1,1)=c .假设(,)=∈R c a +b λμλμ,那么=λμ_____. 15.函数2()(sin cos )f x x x =+的最大值是_____.16.关于函数()sin(2)()6f x x x π=-∈R ,给出以下三个结论:① 函数()f x 的图象与2()cos(2)3g x x π=-的图象重合; ② 函数()f x 的图象关于点(,0)12π对称; ③ 函数()f x 的图象关于直线3x π=对称.其中,全部正确结论的序号是_____.三、解答题:本大题共3小题,共36分. 解答应写出文字说明,证明过程或演算步骤. 17.〔本小题总分值12分〕tan 2=-α,且(,)2π∈πα. 〔Ⅰ〕求πtan()4-α的值;〔Ⅱ〕求sin 2α的值.18.〔本小题总分值12分〕向量(cos ,sin )=ααa ,1(,22=-b ,其中α是锐角. 〔Ⅰ〕证明:向量+a b 与-a b 垂直; 〔Ⅱ〕当|2||2|+=-a b a b 时,求角α.19.〔本小题总分值12分〕函数()sin 221f x x x =+. 〔Ⅰ〕求()f x 的单调递减区间;〔Ⅱ〕假设对于任意ππ[,]42x ∈,都有()2f x m -<成立,数m 的取值围.B 卷 [学期综合] 本卷总分值:50分一、填空题:本大题共5小题,每题4分,共20分. 把答案填在题中横线上. 1.函数1lg y x=的定义域是_____. 2.假设幂函数y x =α的图象过点(4,2),那么=α_____.3.662log 2log 9+=_____.4.函数21,0,()4,0,x x f x x x ->⎧=⎨-<⎩的零点是_____.5.设()f x 是定义在R 上的偶函数,且()f x 在[0,)+∞上是减函数.假设(21)()f m f m ->,那么实数m 的取值围是_____.二、解答题:本大题共3小题,共30分.解答应写出文字说明,证明过程或演算步骤. 6.〔本小题总分值10分〕全集U =R ,集合{|(2)0}P x x x =-≥,{|26}M x a x a =<<+. 〔Ⅰ〕求集合UP ;〔Ⅱ〕假设UP M ⊆,数a 的取值围.7.〔本小题总分值10分〕函数()(2)()f x x x a =-+,其中a ∈R .〔Ⅰ〕假设()f x 的图象关于直线1x =对称,求a 的值; 〔Ⅱ〕求()f x 在区间[0,1]上的最小值.8.〔本小题总分值10分〕函数()23xxf x a b =⋅+⋅,其中,a b 为常数. 〔Ⅰ〕假设0ab >,判断()f x 的单调性,并加以证明; 〔Ⅱ〕假设0ab <,解不等式:(1)()f x f x +>.市西城区2014 — 2015学年度第一学期期末试卷高一数学参考答案与评分标准 2015.1A 卷 [必修 模块4] 总分值100分一、选择题:本大题共10小题,每题4分,共40分.1.D ;2.C ;3.D ;4. D ;5. A ;6. C ;7. C ;8.B ;9. B ; 10.B . 二、填空题:本大题共6小题,每题4分,共24分.11.3π; 12.12-; 13.1213-; 14.32; 15.2; 16. ①②③.注:16题,少解不给分.三、解答题:本大题共3小题,共36分. 17.〔本小题总分值12分〕 〔Ⅰ〕解:因为 tan 2=-α,所以 πtan tanπ4tan()π41tan tan 4--=+⋅ααα【 3分】 3=.【 6分】〔Ⅱ〕解:由π(,π)2∈α,tan 2α=-, 得sin α=, 【 8分】cos α=【10分】 所以 4sin 22sin cos 5==-ααα. 【12分】18.〔本小题总分值12分〕〔Ⅰ〕证明:由向量(cos sin )αα=,a,1(2=-b ,得1(cos ,sin 22+=-+ααa b,1(cos ,sin 22-=+-ααa b , 【 1分】由π(0,)2∈α,得向量+a b ,-a b 均为非零向量. 【 2分】 因为222213()()||||(sincos )()044+⋅-=-=+-+=ααa b a b a b , 【 5分】所以向量+a b 与-a b 垂直. 【 6分】 〔Ⅱ〕解:将|2||2|+=-a b a b 两边平方,化简得223(||||)80-+⋅=a b a b . 【 8分】 由||||1==a b , 得 0⋅=a b , 【 9分】所以 1cos 02αα-+=,所以 tan =α. 【11分】 注意到 π(0,)2∈α, 所以 π6α=.【12分】19.〔本小题总分值12分〕〔Ⅰ〕解:()sin 221f x x x =+π12sin(2)3x =+-. 【 2分】 因为函数sin y x =的单调递减区间为π3π[2π,2π]()22k k k ++∈Z .由 ππ3π2π22π232k x k +≤-≤+()k ∈Z ,【 4分】 得 5π11πππ1212k x k +≤≤+()k ∈Z . 所以()f x 的单调递减区间为5π11π[π,π]1212k k ++()k ∈Z . 【 6分】 〔Ⅱ〕解: 因为 ππ[,]42x ∈, 所以 ππ2π2633x -≤≤,由〔Ⅰ〕得 π212sin(2)33x +-≤≤,所以 ()f x 的值域是[23],. 【 8分】()2()2()2f x m f x m f x -<⇔-<<+,ππ[,]42x ∈. 【10分】所以 max ()2m f x >-,且 min ()2m f x <+,所以 14m <<, 即m 的取值围是(1,4). 【12分】B 卷 [学期综合] 总分值50分一、填空题:本大题共5小题,每题4分,共20分.1.{|01x x ∈<<R ,或1}x >;2.12; 3.2; 4.2-,1; 5.1(,1)3.注:4题,少解得2分,有错解不给分. 二、解答题:本大题共3小题,共30分. 6.〔本小题总分值10分〕〔Ⅰ〕解:因为全集U =R ,集合{|(2)0}P x x x =-≥,所以 {|(2)0}UP x x x =-<, 【 2分】即集合{|02}UP x x =<<.【 4分】〔Ⅱ〕解:因为UP M ⊆,所以 0,262,a a ≤⎧⎨+≥⎩【 6分】 解得 0,2.a a ≤⎧⎨≥-⎩【 8分】所以 [2,0]a ∈-.【10分】 注:第〔Ⅱ〕小问没有等号扣1分. 7.〔本小题总分值10分〕〔Ⅰ〕解法一:因为2()(2)()(2)2f x x x a x a x a =-+=+--, 所以,()f x 的图象的对称轴方程为22ax -=. 【 2分】 由212a-=,得0a =. 【 4分】 解法二:因为函数()f x 的图象关于直线1x =对称,所以必有(0)(2)f f =成立, 【 2分】 所以 20a -=, 得0a =. 【 4分】〔Ⅱ〕解:函数()f x 的图象的对称轴方程为22ax -=. ① 当202a-≤,即 2a ≥时, 因为()f x 在区间(0,1)上单调递增,所以()f x 在区间[0,1]上的最小值为(0)2f a =-. 【 6分】② 当2012a-<<,即 02a <<时, 因为()f x 在区间2(0,)2a -上单调递减,在区间2(,1)2a-上单调递增, 所以()f x 在区间[0,1]上的最小值为222()()22a a f -+=-.【 8分】 ③ 当212a -≥,即 0a ≤时,因为()f x 在区间(0,1)上单调递减,所以()f x 在区间[0,1]上的最小值为(1)(1)f a =-+. 【10分】 8.〔本小题总分值10分〕〔Ⅰ〕解:当0,0a b >>时,()f x 在R 上是增函数;当0,0a b <<时,()f x 在R 上是减函数; 【 1分】证明如下:当0,0a b >>时,任取12,x x ∈R ,且12x x <,那么210x x x ∆=->, 那么212121()()(22)(33)xxxxy f x f x a b ∆=-=-+-.因为 122122,0(22)0xxxxa a <>⇒->;又122133,0(33)0xxxxb b <>⇒->, 所以 21()()0y f x f x ∆=->,所以,当0,0a b >>时,()f x 在R 上是增函数.当0,0a b <<时,同理可得,()f x 在R 上是减函数. 【 5分】 〔Ⅱ〕解:由(1)()2230xxf x f x a b +-=⋅+⋅>,得 32()2xb a >-. 〔*〕 【 6分】 ①当0,0a b <>时,〔*〕式化为3()22xa b->,. . . .11 / 11 解得32log ()2a x b>-.【 8分】 ②当0,0a b ><时,〔*〕式化为3()22x a b -<, 解得32log ()2a x b<-. 【10分】。
2015年北京市各区县高一期末试题分类汇编-三角函数

2015年北京市各区县高一期末试题分类汇编——三角函数1.(2015年1月·延庆期末·8.若x x f 3cos )(cos =,则)(sin 3πf 的值为 A . 1-B .23 C .0 D .12.(2015年1月·西城期末·1.已知(0,2π)α∈,且sin 0<α,cos 0>α,则角α的取值范围是( ) (A )π(0,)2(B )π(,π)2(C )3π(π,)2(D )3π(,2π)23.(2015年1月·西城期末·3.已知角α的终边经过点(3,4)P -,那么sin =α( ) (A )35(B )45-(C )34(D )34-4.(2015年1月·房山期末·2)下列各角中,与角π3-终边相同的角是 (A )2π3 (B )4π3(C )5π3(D )7π35.(2015年1月·海淀期末·10.为了得到函数sin(2)2y x π=-的图象,可以将函数sin 2y x =的图象 AA. 向右平移4π个单位长度 B. 向左平移4π个单位长度 C. 向右平移2π个单位长度 D. 向左平移2π个单位长度6.(2015年1月·西城期末·9.为得到函数πcos()6y x =+的图象,只需将函数sin y x =的图象( )(A )向左平移π3个单位 (B )向右平移π3个单位 (C )向左平移2π3个单位(D )向右平移2π3个单位7.(2015年1月·海淀期末·11.已知(,)αππ∈-,且sin cos7πα=-,则α= AA. 514π-或914π- B. 914π-或914π C. 514π或514π- D. 514π或914π 8.(2015年1月·密云期末·2.sin 240=A.32-B .12-C .12D .329.(2015年1月·顺义期末·2.sin120的值等于A .12B .12-C .32D .32-10.(2015年1月·海淀期末·2. 7sin6π= A.32 B.32-C. 12D. 12- 11.(2015年1月·延庆期末·2.已知)2,0[πα∈,与角3π-终边相同的角是 A .3π B .32π C .34π D .35π12.(2015年1月·延庆期末·3.若0sin >α ,且0cos <α ,则角α是A .第一象限角B .第二象限角C .第三象限角D .第四象限角13.(2015年1月·延庆期末·4.若角α的终边经过点)4,3(-P ,则tan =α A .54 B .53-C .34-D. 43-14.(2015年1月·延庆期末·11. 要得到)42sin(π+=x y 的图象只需将x y 2sin =的图象A .向左平移4π个单位 B .向右平移4π个单位 C .向右平移8π个单位D .向左平移8π个单位15.(2015年1月·海淀期末·6.若直线x a =是函数()sin f x x =的一条对称轴,则()f a = DA.0B.1C. 1-D. 1或1- 16.(2015年1月·密云期末·5.函数)32sin(2π+=x y 的一个对称中心A .)0,6(πB .)0,6(π-C .)0,12(πD .)0,12(π-17.(2015年1月·西城期末·6.如果函数cos()y x =+ϕ的一个零点是3π,那么ϕ可以是( )(A )6π (B )6π- (C )3π (D )3π-18.(2015年1月·东城期末·2. 已知sin 0,cos 0θθ<>,则角θ是 A .第一象限角B .第二象限角C .第三象限角D .第四象限角19.(2015年1月·房山期末·7)要得到函数cos 2y x =的图象,只需将函数cos(2)5y x π=+的图象(A )向左平移5π个单位 (B )向右平移5π个单位(C )向左平移10π个单位 (D )向右平移10π个单位 20.(2015年1月·房山期末·8)函数πsin 2()6y x =+的错误!未找到引用源。
2014-2015学年高一上学期期末考试数学 试题

2014-2015学年高一上学期期末考试数学试题一、选择题(每小题4分,共40分) 1.函数)13lg(13)(2++-=x xx x f 的定义域是( )A.),31(+∞- B.)1,31(- C. )31,31(- D.)31,(--∞2.已知21{|log ,2},{|(),1}2x A y y x x B y y x ==<==<,则A∩B =( )A.1(,)2+∞ B.(2,21) C. )21,0( D.1(,1)23.设α、β为钝角且sin α=,cos β=,则αβ+的值为( ) A.π43B.π45C. π47D.π45或π474.设函数)(x f 是定义在R 上的以5为周期的奇函数,若33)2013(,1)2(-+=>a a f f ,则a 的取值范围是( )A.)0,(-∞B.)3,0(C.),0(+∞D.),3()0,(+∞-∞ 5.要得到函数的图象,只需将函数的图象( )A.向左平移个单位B.向左平移个单位C.向右平移个单位D.向右平移个单位6.设函数()1()cos 2f x x ωϕ=+,对任意x ∈R 都有33f x f x ππ⎛⎫⎛⎫-=+ ⎪ ⎪⎝⎭⎝⎭,若函数()()3sin 2g x x ωϕ=+-,则3g π⎛⎫⎪⎝⎭的值为 ( )A. B. 5-或3 C. 2- D.217.设()f x 为定义在R 上的奇函数,且0x >时,()()12xf x =,则函数()()sin F x f x x=-在[]ππ-,上的零点个数为 ( ) A.2 B.3 C. 4 D.58.已知函数)1,0)(3(log )(2≠>+-=a a ax x x f a 且满足:对任意实数21,x x ,当221ax x ≤<时,总有,0)()(21>-x f x f 则实数a 的取值范围是 ( )A.(0,3)B.(1,3)C.(2,23)D.(1,23)二、填空题(每小题4分,共20分)11.sin168sin 72sin102sin198-=12.已知函数f x x x x x ()()c o s ()=≤<<⎧⎨⎪⎩⎪2020π,若f f x (())02=,则x 0的值是____________ 13.已知=-+--=-<<αααααπαtan 112cos 2sin ,55sin cos ,20则____________ 14.设为实常数,是定义在R 上的奇函数,当时,,若对一切成立,则的取值范围为________15. 设,40,2cos ,2sin πθθθ<<==b a 给出)4tan(πθ+值的四个答案;①a b -1;②ba-1; ③a b +1;④ba+1. 其中正确的是 .三、解答题(本大题共4题,共40分)数学答题卷2015.1二、填空题(本大题共5小题,每小题4分,共20分.)11. 12. 13._________________14. _____________ 15.三、解答题(本大题共4小题,共40分,解答应写出文字说明、证明过程或演算步骤)17.函数12--=x xy 的定义域为集合A ,关于x 的不等式)0)(lg(2lg >+<a x a ax 的解集为B ,求使A B A =成立的实数a 的取值范围.19.已知函数a xax x f -+=)( (1)若方程0)(=x f 有正根,求实数a 的取值范围; (2)设函数|)(sin sin |)(x f x x g ⋅=,且)(x g 在区间]2,0[π上不单调,求实数a 的取值范围。
【精品】2014-2015年北京市朝阳区高一(上)期末数学试卷带解析

2014-2015学年北京市朝阳区高一(上)期末数学试卷一、选择题(共10小题,每小题5分,满分50分)1.(5分)已知全集U=R,集合A={0,1,2,3,4,5},B={x|x≥2},则A∩(∁B)=()UA.{1}B.{0,1}C.{1,2}D.{0,1,2}2.(5分)函数f(x)=+lg(x+1)的定义域为()A.(﹣1,1)B.(﹣1,+∞)C.(1,+∞)D.(﹣∞,1)3.(5分)下列函数中,既是奇函数又是增函数的为()A.y=x+1 B.y=﹣x2C.y= D.y=x|x|4.(5分)偶函数f(x)的图象如图所示,则f(﹣1),f(﹣),f()的大小关系是()A.f(﹣1)<f(﹣)<f() B.f(),f(﹣),f(﹣1)C.f(﹣),f(),f(﹣1)D.f(﹣1),f(),f(﹣)5.(5分)函数f(x)=lnx﹣的零点所在的大致区间是()A.(1,2) B.(2,3) C.(1,)D.(e,+∞)6.(5分)从某小学随机抽取100分学生,将们们的身高(单位:厘米)数据绘制成频率分布直方图(如图),若要从身高在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取20人参加一项活动,则身高在[120,130)内的学生中选取的人数应为()A.8 B.12 C.10 D.307.(5分)已知a,b∈R,下列命题正确的是()A.若a>b,则|a|>|b|B.若a>b,则C.若|a|>b,则a2>b2D.若a>|b|,则a2>b28.(5分)f(x)是R上的奇函数,当x>0时,f(x)=2x,则当x<0时,f(x)=()A.﹣()x B.()x C.﹣2x D.2x9.(5分)在股票买卖过程中,经常用两种曲线来描述价格变化情况,一种是即时价格曲线y=f(x),另一种是平均价格曲线y=g(x),如f(2)=3表示股票开始买卖后2小时的即时价格为3元;g(2)=3表示2小时内的平均价格为3元,下面给出了四个图象,实线表示y=f(x),虚线表示y=g(x),其中正确的是()A.B.C.D.10.(5分)函数f(x)满足对定义域内的任意x,都有f(x+2)+f(x)<2f(x+1),则函数f(x)可以是()A.f(x)=2x+1 B.f(x)=x2﹣2x C.f(x)=e x D.f(x)=lnx二、填空题(共6小题,每小题5分,满分30分)11.(5分)为了了解1000名学生的学习情况,采用系统抽样的方法,从中抽取容量为40的样本,则分段的间隔为.12.(5分)已知幂函数y=f(x)图象过点(2,8),则f(3)=.13.(5分)执行如图所示的程序框图,若输入n的值为8,则输出的s的值为.14.(5分)当x>﹣1时,函数y=x+的最小值为.15.(5分)如图,矩形ABCD中,AB=2,BC=1,以点C为圆心,CB为半径的圆与边DC交于点E,F是上任意一点(包括端点),在矩形ABCD内随机取一点M,则点M落在△AFD内部的概率的取值范围是.16.(5分)对于集合A={a1,a2,…a n}(n≥2,n∈N*),如果a1•a2…•a n=a1+a2+…+a n,则称集合A具有性质P,给出下列结论:①集合{,}具有性质P;②若a1,a2∈R,且{a1,a2}具有性质P,则a1a2>4③若a1,a2∈N*,则{a1,a2}不可能具有性质P;④当n=3时,若a i∈N*(i=1,2,3),则具有性质P的集合A有且只有一个.其中正确的结论是.三、解答题(共4小题,满分40分)17.(9分)已知集合A={x2﹣3x﹣10≤0},B={x|m﹣1<x<2m+1}(Ⅰ)当m=3时,求A∩B.(Ⅱ)若B⊆A,求实数m的取值范围.18.(9分)某车间将10名技工平均分成甲、乙两组加工某种零件,在单位时间内每个技工加工的合格零件数,按十位数学为茎,个位数学为叶得到的茎叶图如图所示,已知甲、乙两组数据的平均数都为10.(Ⅰ)求m,n的值;(Ⅱ)别求出甲、乙两组数据的方差S甲2和S乙2,并由此分析两组技工的加工水平;(Ⅲ)质检部门从该车间甲、乙两组技工中各随机抽取一名技工,对其加工的零件进行检测,若两人加工的合格零件数之和大于17,则称该车间“质量合格”,求该车间“质量合格”的概率.(注:为数据x1,x2,…x n的平均数,方差S2=[(x1﹣)2+(x2﹣)2+…+(x n ﹣)2])19.(10分)已知函数f(x)=ax2+bx﹣a+2(1)若关于x的不等式f(x)>0的解集是(﹣1,3),求实数a,b的值;(2)若b=2,a>0,解关于x的不等式f(x)>0.20.(12分)对于函数f(x),g(x),φ(x)如查存在实数a,b使得φ(x)=a•f (x)+b•g(x),那么称φ(x)为f(x),g(x)的线性组合函数,如对于f(x)=x+1,g(x)=x2+2x,φ(x)=2﹣x2存在a=2,b=﹣1使得φ(x)=2f(x)=g(x),此时φ(x)就是f(x),g(x)的线性组合函数.(Ⅰ)设f(x)=x2+1,g(x)=x2﹣x,φ(x)=x2﹣2x+3,试判断φ(x)是否为f(x),g(x)的线性组合函数?关说明理由;(Ⅱ)设f(x)=log 2x,g(x)=log x,a=2,b=1,线性组合函数为φ(x),若不等式3φ2(x)﹣2φ(x)+m<0在x∈[,4]上有解,求实数m的取值范围;(Ⅲ)设f(x)=x,g(x)=(1≤x≤9),取a=1,b>0,线性组合函数φ(x)使φ(x)≥b恒成立,求b的取值范围,(可利用函数y=x+(常数k>0)在(0,]上是减函数,在[,+∞)上是增函数)2014-2015学年北京市朝阳区高一(上)期末数学试卷参考答案与试题解析一、选择题(共10小题,每小题5分,满分50分)1.(5分)已知全集U=R,集合A={0,1,2,3,4,5},B={x|x≥2},则A∩(∁B)=()UA.{1}B.{0,1}C.{1,2}D.{0,1,2}【解答】解:∵B={x|x≥2},∴∁U B={x|x<2},则A∩(∁U B)={0,1},故选:B.2.(5分)函数f(x)=+lg(x+1)的定义域为()A.(﹣1,1)B.(﹣1,+∞)C.(1,+∞)D.(﹣∞,1)【解答】解:由题意得:,解得:﹣1<x<1,故选:A.3.(5分)下列函数中,既是奇函数又是增函数的为()A.y=x+1 B.y=﹣x2C.y= D.y=x|x|【解答】解:A.y=x+1为非奇非偶函数,不满足条件.B.y=﹣x2是偶函数,不满足条件.C.y=是奇函数,但在定义域上不是增函数,不满足条件.D.设f(x)=x|x|,则f(﹣x)=﹣x|x|=﹣f(x),则函数为奇函数,当x>0时,y=x|x|=x2,此时为增函数,当x≤0时,y=x|x|=﹣x2,此时为增函数,综上在R上函数为增函数.故选:D.4.(5分)偶函数f(x)的图象如图所示,则f(﹣1),f(﹣),f()的大小关系是()A.f(﹣1)<f(﹣)<f() B.f(),f(﹣),f(﹣1)C.f(﹣),f(),f(﹣1)D.f(﹣1),f(),f(﹣)【解答】解:根据图象f().故选:B.5.(5分)函数f(x)=lnx﹣的零点所在的大致区间是()A.(1,2) B.(2,3) C.(1,)D.(e,+∞)【解答】解:函数的定义域为:(0,+∞),有函数在定义域上是递增函数,所以函数只有唯一一个零点.又∵f(2)﹣ln2﹣1<0,f(3)=ln3﹣>0∴f(2)•f(3)<0,∴函数f(x)=lnx﹣的零点所在的大致区间是(2,3).故选:B.6.(5分)从某小学随机抽取100分学生,将们们的身高(单位:厘米)数据绘制成频率分布直方图(如图),若要从身高在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取20人参加一项活动,则身高在[120,130)内的学生中选取的人数应为()A.8 B.12 C.10 D.30【解答】解:根据频率分布直方图,得;身高在[120,130)的频率为0.030×10=0.3,频数是0.3×100=30;身高在[130,140)的频率为0.020×10=0.2,频数是0.2×100=20;身高在[140,150]的频率为0.010×10=0.1,频数是0.1×100=10;在这三组学生中,用分层抽样的方法选取20人参加一项活动,身高在[120,130)内的学生中选取的人数为20×=10.故选:C.7.(5分)已知a,b∈R,下列命题正确的是()A.若a>b,则|a|>|b|B.若a>b,则C.若|a|>b,则a2>b2D.若a>|b|,则a2>b2【解答】解:A.错误,比如3>﹣4,便得不到|3|>|﹣4|;B.错误,比如3>﹣4,便得不到;C.错误,比如|3|>﹣4,得不到32>(﹣4)2;D.正确,a>|b|,则a>0,根据不等式的性质即可得到a2>b2.故选:D.8.(5分)f(x)是R上的奇函数,当x>0时,f(x)=2x,则当x<0时,f(x)=()A.﹣()x B.()x C.﹣2x D.2x【解答】解:设x<0,﹣x>0;∴.故选:A.9.(5分)在股票买卖过程中,经常用两种曲线来描述价格变化情况,一种是即时价格曲线y=f(x),另一种是平均价格曲线y=g(x),如f(2)=3表示股票开始买卖后2小时的即时价格为3元;g(2)=3表示2小时内的平均价格为3元,下面给出了四个图象,实线表示y=f(x),虚线表示y=g(x),其中正确的是()A.B.C.D.【解答】解:刚开始交易时,即时价格和平均价格应该相等,A,D错误;开始交易后,平均价格应该跟随即时价格变动,即时价格与平均价格同增同减,故A,B,D均错误.故选:C.10.(5分)函数f(x)满足对定义域内的任意x,都有f(x+2)+f(x)<2f(x+1),则函数f(x)可以是()A.f(x)=2x+1 B.f(x)=x2﹣2x C.f(x)=e x D.f(x)=lnx【解答】解:由f(x+2)+f(x)<2f(x+1)得,f(x+2)﹣f(x+1)<f(x+1)﹣f(x)①,∵(x+2)﹣(x+1)=(x+1)﹣x,∴①说明自变量变化相等时,当自变量越大时,对应函数值的变化量越来越小,对于A、f(x)=2x+1是一次函数,且在R上直线递增,函数值的变化量是相等的,A错;对于B、f(x)=x2﹣2x在定义域上不是单调函数,在(﹣∞,1)上递减,在(1,+∞)递增,B错;对于C、f(x)=e x是增长速度最快﹣呈爆炸式增长的指数函数,当自变量越大时,对应函数值的变化量越来越大,C错;对于D、f(x)=lnx是增长越来越慢的对数函数,当自变量越大时,对应函数值的变化量越来越小,D正确.故选:D.二、填空题(共6小题,每小题5分,满分30分)11.(5分)为了了解1000名学生的学习情况,采用系统抽样的方法,从中抽取容量为40的样本,则分段的间隔为25.【解答】解:由已知得:分段的间隔为:=25.故答案为:25.12.(5分)已知幂函数y=f(x)图象过点(2,8),则f(3)=27.【解答】解:设幂函数y=f(x)=x a,其图象过点(2,8),∴2a=8;解得a=3,∴f(x)=x3,∴f(3)=33=27.故答案为:27.13.(5分)执行如图所示的程序框图,若输入n的值为8,则输出的s的值为8.【解答】解:当i=2,k=1时,s=2,;当i=4,k=2时,s=(2×4)=4;当i=6,k=3时,s=(4×6)=8;当i=8,k=4时,不满足条件“i<8”,退出循环,则输出的s=8故答案为:814.(5分)当x>﹣1时,函数y=x+的最小值为1.【解答】解:∵x>﹣1,∴x+1>0,∴y=x+=x+1+﹣1≥2﹣1=1当且仅当x+1=即x=0时取等号,故答案为:1.15.(5分)如图,矩形ABCD中,AB=2,BC=1,以点C为圆心,CB为半径的圆与边DC交于点E,F是上任意一点(包括端点),在矩形ABCD内随机取一点M,则点M落在△AFD内部的概率的取值范围是[] .【解答】解:由题意,设△AFD的高为h,因为F是上任意一点(包括端点),所以h∈[1,2],所以△AFD的面积范围为[,1],又矩形ABCD的面积为2,由几何概型的公式可得点M落在△AFD内部的概率的取值范围[];故答案为:[].16.(5分)对于集合A={a1,a2,…a n}(n≥2,n∈N*),如果a1•a2…•a n=a1+a2+…+a n,则称集合A具有性质P,给出下列结论:①集合{,}具有性质P;②若a1,a2∈R,且{a1,a2}具有性质P,则a1a2>4③若a1,a2∈N*,则{a1,a2}不可能具有性质P;④当n=3时,若a i∈N*(i=1,2,3),则具有性质P的集合A有且只有一个.其中正确的结论是①③④.【解答】解:∵•=+=﹣1,故①是正确的;②不妨设a1+a2=a1a2=t,则由韦达定理知a1,a2是一元二次方程x2﹣tx+t=0的两个根,由△>0,可得t<0,或t>4,故②错;③不妨设A中a1<a2<a3<…<a n,由a1a2…a n=a1+a2+…+a n<na n,得a1a2…a n﹣1<n,当n=2时,即有a1<2,∴a1=1,于是1+a2=a2,a2无解,即不存在满足条件的集合A,故③正确.当n=3时,a1a2<3,故只能a1=1,a2=2,求得a3=3,于是具有性质P的集合A 只有一个,为{1,2,3}.当n≥4时,由a1a2…a n﹣1≥1×2×3×…×(n﹣1),即有n>(n﹣1)!,也就是说具有性质P的集合A存在的必要条件是n>(n﹣1)!,事实上,(n﹣1)!≥(n﹣1)(n﹣2)=n2﹣3n+2=(n﹣2)2﹣2+n>2,矛盾,∴当n≥4时不存在具有性质P的集合A,故④正确.故答案为:①③④.三、解答题(共4小题,满分40分)17.(9分)已知集合A={x2﹣3x﹣10≤0},B={x|m﹣1<x<2m+1}(Ⅰ)当m=3时,求A∩B.(Ⅱ)若B⊆A,求实数m的取值范围.【解答】解:(Ⅰ)当m=3时,A={x2﹣3x﹣10≤0}=[﹣2,5],B=(2,7);则A∩B=(2,5].(Ⅱ)∵B⊆A,当B≠∅时,;解得,﹣1≤m≤2;当B=∅时,由m﹣1≥2m+1得,m≤﹣2;故实数m的取值范围为{m|m≤﹣2或﹣1≤m≤2}.18.(9分)某车间将10名技工平均分成甲、乙两组加工某种零件,在单位时间内每个技工加工的合格零件数,按十位数学为茎,个位数学为叶得到的茎叶图如图所示,已知甲、乙两组数据的平均数都为10.(Ⅰ)求m,n的值;(Ⅱ)别求出甲、乙两组数据的方差S甲2和S乙2,并由此分析两组技工的加工水平;(Ⅲ)质检部门从该车间甲、乙两组技工中各随机抽取一名技工,对其加工的零件进行检测,若两人加工的合格零件数之和大于17,则称该车间“质量合格”,求该车间“质量合格”的概率.(注:为数据x1,x2,…x n的平均数,方差S2=[(x1﹣)2+(x2﹣)2+…+(x n ﹣)2])【解答】解:(I)由题意可得=(7+8+10+12+10+m)=10,解得m=3.再由=(n+9+10+11+12)=10,解得n=8.(Ⅱ)分别求出甲、乙两组技工在单位时间内加工的合格零件数的方差,S甲2=[(7﹣10)2+(8﹣10)2+(10﹣10)2+(12﹣10)2+(13﹣10)2]=5.2,S乙2=[(8﹣10)2+(9﹣10)2+(10﹣10)2+(11﹣10)2+(12﹣10)2]=2,并由,S甲2<S乙2,可得两组的整体水平相当,乙组的发挥更稳定一些.(Ⅲ)质检部门从该车间甲、乙两组技工中各随机抽取一名技工,对其加工的零件进行检测,设两人加工的合格零件数分别为(a,b),则所有的(a,b)有(7,8)、(7,9)、(7,10)、(7,11)、(7,12)、(8,8)、(8,9)、(8,10)、(8,11)、(8,12)、(10,8)、(10,9)、(10,10)、(10,11)、(10,12)、(12,8)、(12,9)、(12,10)、(12,11)、(12,12)、(13,8)、(13,9)、(13,10)、(13,11)、(13,12),共计25个,而满足a+b≤17的基本事件有(7,8)、(7,9)、(7,10)、(8,8)、(8,9),共计5个基本事件,故满足a+b>17的基本事件个数为25﹣5=20,即该车间“质量合格”的基本事件有20个,故该车间“质量合格”的概率为P==.19.(10分)已知函数f(x)=ax2+bx﹣a+2(1)若关于x的不等式f(x)>0的解集是(﹣1,3),求实数a,b的值;(2)若b=2,a>0,解关于x的不等式f(x)>0.【解答】解:(1)∵不等式f(x)>0的解集是(﹣1,3)∴﹣1,3是方程ax2+bx﹣a+2=0的两根,∴可得,解之得﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(5分)(2)当b=2时,f(x)=ax2+2x﹣a+2=(x+1)(ax﹣a+2),∵a>0,∴①若,即a=1,解集为{x|x≠﹣1}.②若,即0<a<1,解集为.③若,即a>1,解集为.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(14分)20.(12分)对于函数f(x),g(x),φ(x)如查存在实数a,b使得φ(x)=a•f (x)+b•g(x),那么称φ(x)为f(x),g(x)的线性组合函数,如对于f(x)=x+1,g(x)=x2+2x,φ(x)=2﹣x2存在a=2,b=﹣1使得φ(x)=2f(x)=g(x),此时φ(x)就是f(x),g(x)的线性组合函数.(Ⅰ)设f(x)=x2+1,g(x)=x2﹣x,φ(x)=x2﹣2x+3,试判断φ(x)是否为f(x),g(x)的线性组合函数?关说明理由;(Ⅱ)设f(x)=log 2x,g(x)=log x,a=2,b=1,线性组合函数为φ(x),若不等式3φ2(x)﹣2φ(x)+m<0在x∈[,4]上有解,求实数m的取值范围;(Ⅲ)设f(x)=x,g(x)=(1≤x≤9),取a=1,b>0,线性组合函数φ(x)使φ(x)≥b恒成立,求b的取值范围,(可利用函数y=x+(常数k>0)在(0,]上是减函数,在[,+∞)上是增函数)【解答】解:(Ⅰ)设a•(x2+1)+b•(x2﹣x)=x2﹣2x+3,即(a+b)x2﹣bx+a=x2﹣2x+3,则,此时方程组无解,故不存在a,b使得φ(x)=a•f(x)+b•g(x),则φ(x)不是f(x),g(x)的线性组合函数.(Ⅱ)∵a=2,b=1,∴φ(x)=2f(x)+g(x)=2log 2x+log x=2log2x﹣log2x=log2x,若不等式3φ2(x)﹣2φ(x)+m<0在x∈[,4]上有解,即m<﹣3(log2x)2+2log2x在x∈[,4]上有解,设t=log2x,则∵x∈[,4],∴t∈[,2],则不等式等价为m<﹣3t2+2t,∵y=﹣3t2+2t=﹣3(t﹣)2+,∴当t=时,函数y取得最大值,则m<,实数m的取值范围是m<.(Ⅲ)由题意φ(x)=x+,(1≤x≤9),①若∈(1,9),则φ(x)在[1,)上递减,在(,9]上递增,故φ(x)min=φ()=2,由,解得1<b≤4.②若≤1,则φ(x)在[1,9]上递增,故φ(x)min=φ(1)=1+b,由,解得1<b≤1.③若≥9,则φ(x)在[1,9]上递减,故φ(x)min=φ(9)=9+,由,此时不等式组无解.综上b的取值范围是(0,4].赠送初中数学几何模型【模型三】双垂型:图形特征:60°运用举例:1.在Rt△ABC中,∠ACB=90°,以斜边AB为底边向外作等腰三角形PAB,连接PC. (1)如图,当∠APB=90°时,若AC=5,PC=62,求BC的长;(2)当∠APB=90°时,若AB=45APBC的面积是36,求△ACB的周长.2.已知:如图,B、C、E三点在一条直线上,AB=AD,BC=CD.(1)若∠B=90°,AB=6,BC=23,求∠A的值;(2)若∠BAD+∠BCD=180°,cos∠DCE=35,求ABBC的值.3.如图,在四边形ABCD中,AB=AD,∠DAB=∠BCD=90°,(1)若AB=3,BC+CD=5,求四边形ABCD的面积(2)若p= BC+CD,四边形ABCD的面积为S,试探究S与p之间的关系。
2015年北京市各区县高一期末试题分类汇编——幂指对

2015年北京市各区县高一期末试题分类汇编——幂指对1.(2015年1月·延庆期末·7.函数()log 21a y x =++的图像过定点 A . ()2,1- B .()2,1 C . ()1,1-D .)1,1(2.(2015年1月·石景山期末·2.下列算式正确的是 ( )A .222log (3)log 3log ππ=+B .236(8)82-=-=-C .lg 62lg 3= D .3322555-==3.(2015年1月·昌平期末·3)已知函数2()log f x x =,当[1,4]x ∈时,函数()f x 的值域是 (A )[0,1] (B )[0,2] (C )[1,2] (D )[1,4]4.(2015年1月·昌平期末·9)设函数()f x 是定义在R 上的奇函数,当0x ≥时,()23xf x x k =-+(k为常数),则(1)f -=(A )2 (B )1 (C )2- (D )1-5.(2015年1月·昌平期末·10)设正数a ,b 满足23log log a b =,则下列结论中,不可能...成立的是 (A )1a b << (B )01b a <<< (C )a b = (D )1b a << 6(2015年1月·丰台期末·9.已知变量y 随变量x 变化的数据如下表:x 6.0 4.1 2.2 0.3 4.3 y 737.0- 485.0 138.1 585.1 766.1 则能基本反映这一变化规律的函数模型是( ) A . xy 2=B .2x y =C .x y 2log =D .137.0--=x y7.(2015年1月·密云期末·6. 函数log =a y x (0>a 且1≠a )的图象经过点)1,2(-,函数=xy b (0>b 且1≠b )的图象经过点)2,1(,则下列关系式中正确的是 A . 22b a >B . ba 22>C . b a )21()21(> D . 2121b a >8.(2015年1月·昌平期末·4)设 2.50 2.51(),(2.5),22a b c ===,则(A )a b c >> (B )b a c >> (C )c b a >> (D )b c a >>9.(2015年1月·东城期末·6.设2log πa =,12log πb =,2πc -=,则A .a b c >> B. b a c >> C. a c b >>D. c b a >>10.(2015年1月·房山期末·6)设3log 2a =,0.3eb =,8cos7c π=,则 (A )b a c << (B )b c a << (C )c a b <<(D )c b a <<11.(2015年1月·丰台期末·6.已知3π=m ,3log π=n ,πtan =p ,则这三个数的大小关系是( )A .p n m >>B .m p n >>C . n m p >>D .n m p >>12.(2015年1月·海淀期末·7.设110.522,e ,0.5a b c -===错误!未找到引用源。
【历年高一数学期末试题】北京市西城区(普通校)2014-2015学年高一上学期期末考试数学试题Word版含答案

高一数学
试卷满分: 150 分 考试时间: 120 分钟
2015.1
A 卷 [必修 模块 4] 本卷满分: 100 分
三
题号
一
二
本卷总分
17
18
19
分数
一、选择题:本大题共 10 小题,每小题 4 分,共 40 分 .在每小题给出的四个选项中,只有一 项是符合要求的 .
( A) 1 m2
( B) 1
( C) | m |
( D) 1 m2
二、填空题:本大题共 6 小题,每小题 4 分,共 24 分 . 把答案填在题中横线上 .
11.若向量 a (1,2) 与向量 b ( , 1) 共线,则实数
_____.
12.已知 是第二象限的角,且 sin
5 ,则 cos
13
_____.
(Ⅰ)若 ab 0 ,判断 f (x) 的单调性,并加以证明; (Ⅱ)若 ab 0 ,解不等式: f ( x 1) f ( x) .
( B) (8,14)
( C) (12,12)
( D) ( 4,20)
3.已知角 的终边经过点 P(3, 4) ,那么 sin ( )
( A) 3 5
4
( B)
5
3
( C)
4
4.在△ ABC 中, D 是 BC 的中点,则 AD ( )
( A) 1 ( AB 2 1
( C) ( AB 2
AC ) BC )
13.若
( , ) ,且 tan 1,则 的取值范围是 _____. 22
14.已知向量 a (1,3) , b (2, 1) , c (1,1).若 c a + b ( , R ) ,则
北京市各区县2014-2015学年高一上学期期末试题分类汇编 向量

2015年北京市各区县高一期末试题分类汇编——向量(2015年1月·延庆期末·6.已知向量)0,1(),2,1(=-=b a,那么向量a b -3的坐标是A. (4,2)-B. (4,2)--C. (4,2)D. (4,2)-(2015年1月·西城期末·2.已知向量(2,8)=a ,(4,2)=-b .若2=-c a b ,则向量=c ( ) (A )(0,18)(B )(8,14)(C )(12,12)(D )(4,20)-(2015年1月·西城期末·4.在△ABC 中,D 是BC 的中点,则AD =( )(A )1()2AB AC + (B )1()2AB AC - (C )1()2AB BC +(D )1()2AB BC -(2015年1月·西城期末·7.如图,在矩形ABCD 中,2AB =,3BC =, E 是CD的中点,那么AE DC ⋅=( ) (A )4(B )2(C )3(D )1(2015年1月·西城期末·10.已知a ,b 为单位向量,且m ⋅=a b ,则||t +a b ()t ∈R 的最小值为( ) (A )21m +(B )1(C )||m(D )21m -(2015年1月·石景山期末·4.已知a 与b 均为单位向量,它们的夹角为60,那么||a b -等于( )A .1B .2C .3D .2(2015年1月·石景山期末·6.已知向量a ,b ,且2AB a b =+,56BC a b =-+,72CD a b =-,则一定共线的三点是 ( )A .,,A C DB .,,A B CC .,,B C DD .,,A B D(2015年1月·顺义期末·3.已知(0,3)AB =,那么AB 等于A .2B .3C .4D .5(2015年1月·顺义期末·6.已知向量(42)=,a ,(1)m =-,b ,若a ⊥b ,则m 的值为 A .21 B .2 C .21- D .2- (2015年1月·房山期末·4)在△ABC 中,D 是BC 的中点,则AB AC +等于(A )12AD(B )AD (C )DA(D )2AD(2015年1月·海淀期末·3.若向量(0,1)=a ,(2,1)=-b ,(1,1)=c ,则BA.()//-a b cB. ()-⊥a b cC. ()0-⋅>a b cD. |||-=a b c |(2015年1月·顺义期末·5.如图,在平行四边形ABCD 中,下列结论中正确的是CA .AB CD = B .AB AD BD -=C .AD AB AC += D .AD BC +=0(2015年1月·顺义期末·2.若向量(0,1)a =-,(3,2)b =,,则向量2a b -的坐标是 A. (3,4)- B.(3,4)- C. (3,4)-- D. (3,4)(2015年1月·顺义期末·6.已知向量(42)=,a ,(1)m =-,b ,若a ⊥b ,则m 的值为B A .21 B .2 C .21- D .2- (2015年1月·密云期末·3.已知△ABC 三个顶点的坐标分别为(0,0)A ,(2,2)B ,(0,)C c ,若AB BC ⊥,那么c 的值是A.1-B.3C.3-D.4(2015年1月·顺义期末·8. 设向量2222(cos ,sin ),(cos ,sin )x x x x ==-a b ,函数()f x =⋅a b ,则函数()f x 的图象CA. 关于点(π,0)中心对称B. 关于点π(,0)2中心对称C. 关于点π(,0)4中心对称 D. 关于点(0,0)中心对称(2015年1月·密云期末·9如果向量(4,2)=-a ,(,1)x =b ,且a ,b 共线,那么实数x = . -2(2015年1月·密云期末·13已知ABC ∆是正三角形,若AC AB λ=-a 与向量AC 的夹角大于90,则实数λ的取值范围是__________.2λ>(2015年1月·顺义期末·10.已知()4,2a =-,(),5b x =且//a b ,则x 的值为10-_________.(2015年1月·顺义期末·13.已知||4a =,||3b =,a 与b 的夹角为0120,则||________.a b +=(2015年1月·延庆期末·15.已知向量),3(),3,1(x b a -=-=,若b a //,则=x _____;若b a ⊥,则x =_____.9;1-(2015年1月·西城期末·11.若向量(1,2)=a 与向量(,1)=-λb 共线,则实数=λ__12-___. (2015年1月·西城期末·14.已知向量(1,3)=a ,(2,1)=-b ,(1,1)=c .若(,)=∈R c a +b λμλμ,则=λμ_32_. (2015年1月·房山期末·11)设向量(,1)m =a ,(2,3)=-b ,若满足//a b ,则m =(2015年1月·海淀期末·15.如图,正方形ABCD 的边长为2,P 是线段DC 上的动点(含端点),则BP AC ⋅的取值范围是_[0,4]__.(2015年1月·石景山期末·16.(本题满分9分)已知向量(4,2)=-a ,(,1)x =b .A B(I ) 若a ,b 共线,求x 的值; (II )若a ⊥b ,求x 的值;(III )当2x =时,求a 与b 的夹角θ的余弦值. 解:(I )a ,b 共线,412x ∴⨯=-,2x ∴=-; …………3分(II )a ⊥b ,420x ∴-=,12x ∴=; …………6分(III )当2x =时,42216b ⋅=⨯-⨯=a ,||25,||5==a b ,3cos 5||||a b a b θ⋅∴==. …………9分(2015年1月·顺义期末·16. (本小题满分13分)已知非零向量a 、b 满足1=a ,且1()()2-=a b a +b ⋅. (Ⅰ)求b ; (Ⅱ)当12a b =⋅时,求向量a 与b 的夹角θ的值. 解:(Ⅰ)因为1()()2-=a b a +b ⋅ ,即2212-=a b ,所以221111222=-=-=b a ,故2=b . ---------------------6分 (Ⅱ)因为cos θ=a ba b ⋅=22, 又0180θ≤<︒, 故45θ=. -----------------------------------------------------------------------------13分 (2015年1月·密云期末·17. (本小题满分13分)已知向量(cos )θθ=a ,(sin ,0)θ=b ,其中θ∈R .(Ⅰ)当π3θ=时,求⋅a b 的值; (Ⅱ)当π[0,]2θ∈时,求2(+)a b 的最大值.解:(Ⅰ)当π3θ=时,163(,),(,0)2a b ==,---------------2分1302224a b ∴⋅=⨯+= ----------------5分(Ⅱ)由题: 2()a b +222a a b b =+⋅+2222cos )2(cos sin 0)sin 0θθθθθθ=++⋅⋅++22cos sin 2sin 1θθθ=⋅++sin 22cos2θθ=+-)24πθ=-+. ----------------10分02πθ≤≤,32444πππθ∴-≤-≤. ∴当242ππθ-=即38πθ=时, ----------------11分2()a b +2. --------------- ----13分(2015年1月·西城期末·18.(本小题满分14分)已知向量(cos ,sin )=ααa ,1(2=-b ,其中α是锐角. (Ⅰ)当30︒=α时,求||+a b ; (Ⅱ)证明:向量+a b 与-a b 垂直; (Ⅲ)若向量a 与b 夹角为60︒,求角α.(Ⅰ)解:当30︒=α时,1)2=a , 【 1分】所以 +a b =, 【 2分】所以 ||+=a b = 【 4分】(Ⅱ)证明:由向量(cos sin )αα=,a ,1(,22=-b , 得 1(cos ,sin )22+=-+ααa b ,1(cos ,sin )22-=+-ααa b , 由 π(0,)2∈α,得向量+a b ,-a b 均为非零向量. 【 5分】 因为 222213()()||||(sincos )()044+⋅-=-=+-+=ααa b a b a b , 【 7分】所以向量+a b 与-a b 垂直. 【 8分】 (Ⅲ)解:因为||||1==a b ,且向量a 与b 夹角为60︒, 所以 1||||cos 602︒⋅=⋅=a b a b . 【10分】所以 11cos 22-=αα, 即 π1sin()62-=α. 【12分】 因为 π02<<α, 所以 πππ663-<-<α, 【13分】 所以 ππ66-=α, 即3π=α. 【14分】 (2015年1月·顺义期末·16.(本小题共13分)在平面直角坐标系xoy 中,已知(0,0)O ,(1,3)A ,(2,5)B , (5,2)C -OP OA t AB =+.(Ⅰ)当1,t =- 1时分别求点P 的坐标; (Ⅱ)证明:当1t =时OP OC ⊥. 解:(Ⅰ)()1,3OA =()1,2AB =()()1,31,2OP OA t AB t =+=+————4分∴当1t =-时()0,1OP = 即:()0,1P ——————————6分同样可求当1t =时 ()2,5P —————8分∴所求P 点坐标分别为:()()0,1,2,5———————10分(Ⅱ)当1t =时,(2,5)OP =,又(5,2)OC =-,∴255(2)0OP OC ⋅=⨯+⨯-=,∴OP OC ⊥—————13分(2015年1月·房山期末·18)(本小题共12分)如图,矩形ABCD 中,1AB =,2BC =,P 是BC 的中点,Q 是CD 上的动点.(Ⅰ)求AP AQ ⋅的最小值; (Ⅱ)求()AP AQ AD +⋅的值.解:法一:(Ⅰ)如图,以AB 所在直线为x 轴,A 为坐标原点建立直角坐标系, ------------------1分因为1AB =,2BC =,P 是BC 的中点, 所以(1,1)P ------------------1分 设(,2)Q x ,01x ≤≤ ------------------1分(1,1)(,2)2AP AQ x x ⋅=⋅=+ ------------------ 2分当0x =时,AP AQ ⋅取得最小值2 ------------------1分 所以,AP AQ ⋅的最小值为2(Ⅱ)因为2AD =,所以(0,2)D ------------------1分()AP AQ AD AP AD AQ AD +⋅=⋅+⋅(1,1)(0,2)(,2)(0,2)246x =⋅+⋅=+= ------------------5分法二:(Ⅰ)由||||cos AP AQ AP AQ PAQ ⋅=∠ ------------------2分要使AP AQ ⋅最小,则需||cos AQ PAQ ∠最小,可知当点Q 与点D 重合时,||AQ 最小,cos PAQ ∠最小------------------1分||||cos 222AP AD AP AD PAD ⋅=∠=⨯= 所以,AP AQ ⋅的最小值为2 ------------------3分 (直接求AP AD ⋅,未说明理由扣2分) (Ⅱ)()AP AQ AD AP AD AQ AD +⋅=⋅+⋅ 2||||cos AQ AD DAQ =+⋅∠22||6AD =+= ------------------6分或()()()AP AQ AD AB BP AD AD DQ AD +⋅=+⋅++⋅246BP AD AD AD =⋅+⋅=+= ------------------ 6分B(2015年1月·延庆期末·23.(本题12分)如图,点P 是以AB 为直径的圆O 上动点,P '是点P 关于AB 的对称点,)0(2>=a a AB .(Ⅰ)当点P 是弧AB 上靠近点B 的三等分点时,求⋅的值; (Ⅱ)求P O '⋅的最大值和最小值.解:23.(本题12分)解法一:(Ⅰ)连接OP ,PB ,∵P 是弧AB 靠近点B 的三等分点,)0(2>=a a AB ∴a AP PAB 3,6==∠π. ……………………2分∴232336cosa a a AB OP AB AP =⨯⨯=⋅=⋅π………………………4分 (Ⅱ)设θ=∠PAB , 则θθcos 2,2a AP POB ==∠,此时向量AP 与OP 的夹角为θ3, ………………………6分 ∴)2cos(cos 23cos cos 222θθθθθ+=⋅='⋅a a P O )sin 2sin cos 2(cos cos 22θθθθθ-=a )cos sin 22sin cos 22(cos 22θθθθθ⨯-⨯=a ]2sin )12(cos 2[cos 22θθθ-+=a )12cos 2cos 2(22-+=θθa]89)412(cos 2[22-+=θa , ………………………10分 ∴ 当412cos -=θ时,P O '⋅的最小值为289a -. 当12cos =θ时,P O '⋅的最大值为22a . ………………12分 解法二:(Ⅰ)以直径AB 所在直线为x 轴,以O 为坐标原点建立平面直角坐标系. ∵P 是弧AB 靠近点B 的三等分点,连接OP ,则3BOP π∠=, …………1分 ∴点P坐标为1(,)22a a .又点A 坐标是(,0)a -,点B 坐标是(,0)a ,∴3(,)22AP a a =,(2,0)AB a =, ∴23AP AB a ⋅=.(Ⅱ)设POB θ∠=,[0,2)θπ∈,则(cos ,sin )P a a θθ,(cos ,sin )P a a θθ'- ∴(cos ,sin )AP a a a θθ=+,(cos ,sin )OP a a θθ'=-. ………………6分 ∴22222cos cos sin AP OP a a a θθθ'⋅=+- 22(2cos cos 1)a θθ=+-2221192(cos cos )2168a a θθ=++-222192(cos )48a a θ=+-. ………10分当1cos 4θ=-时,AP OP '⋅有最小值298a -,当cos 1θ=时,AP OP '⋅有最大值22a . …………………12分。
2014--2015年西城区高一数学期末试题及答案

北京市西城区2014 — 2015学年度第一学期期末试卷高一数学 2015.1试卷满分:150分 考试时间:120分钟A 卷 [必修 模块4] 本卷满分:100分一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合要求的.1.已知(0,2π)α∈,且sin 0<α,cos 0>α,则角α的取值范围是( ) (A )π(0,)2(B )π(,π)2(C )3π(π,)2(D )3π(,2π)22.已知向量(2,8)=a ,(4,2)=-b .若2=-c a b ,则向量=c ( ) (A )(0,18)(B )(12,12)(C )(8,14)(D )(4,20)-3.已知角α的终边经过点(3,4)P -,那么sin =α( ) (A )35(B )34(C )34-(D )45-4.已知函数sin y x =和cos y x =在区间M 上都是增函数,那么区间M 可以是( ) (A )π(0,)2(B )π(,π)2(C )3π(π,)2(D )3π(,2π)25.在△ABC 中,D 是BC 的中点,则AB AC +=( ) (A )2AD(B )2DA(C )2BD(D )2DB6.下列函数中,偶函数是( ) (A )()sin()f x x =π+ (B )()tan()f x x =π- (C )()sin()2f x x π=+ (D )()cos()2f x x π=-7.为得到函数πcos()6y x =+的图象,只需将函数cos y x =的图象( )(A )向左平移π3个单位 (B )向右平移π3个单位 (C )向左平移π6个单位(D )向右平移π6个单位8.如图,在矩形ABCD 中,2AB =,BC , E 是CD 的中点,那么AE DC ⋅=( )(A )4(B )2(C (D )19.函数2sin y x =的最小正周期为( ) (A )2π(B )π(C )π2(D )π410.已知向量(1,sin )θ=a ,(cos θ=b ,其中R θ∈,则||-a b 的最大值是( ) (A )4(B )3(C )2(D )1二、填空题:本大题共6小题,每小题4分,共24分. 把答案填在题中横线上. 11.若(0,)∈πα,且α与角53π-终边相同,则=α_____. 12.若向量(1,2)=a 与向量(,1)=-λb 共线,则实数=λ_____. 13.已知α是第二象限的角,且5sin 13α=,则cos =α_____. 14. 已知向量(1,3)=a ,(2,1)=-b ,(1,1)=c .若(,)=∈R c a +b λμλμ,则=λμ_____. 15.函数2()(sin cos )f x x x =+的最大值是_____.16.关于函数()sin(2)()6f x x x π=-∈R ,给出下列三个结论:① 函数()f x 的图象与2()cos(2)3g x x π=-的图象重合; ② 函数()f x 的图象关于点(,0)12π对称; ③ 函数()f x 的图象关于直线3x π=对称.其中,全部正确结论的序号是_____.三、解答题:本大题共3小题,共36分. 解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分12分)已知tan 2=-α,且(,)2π∈πα. (Ⅰ)求πtan()4-α的值; (Ⅱ)求sin 2α的值.18.(本小题满分12分)已知向量(cos ,sin )=ααa ,1(,22=-b ,其中α是锐角. (Ⅰ)证明:向量+a b 与-a b 垂直; (Ⅱ)当|2||2|+=-a b a b 时,求角α.19.(本小题满分12分)已知函数()sin 21f x x x =+. (Ⅰ)求()f x 的单调递减区间;(Ⅱ)若对于任意ππ[,]42x ∈,都有()2f x m -<成立,求实数m 的取值范围.B 卷 [学期综合] 本卷满分:50分一、填空题:本大题共5小题,每小题4分,共20分. 把答案填在题中横线上. 1.函数1lg y x=的定义域是_____. 2.若幂函数y x =α的图象过点(4,2),则=α_____. 3.662log 2log 9+=_____. 4.函数21,0,()4,0,x x f x x x ->⎧=⎨-<⎩的零点是_____.5.设()f x 是定义在R 上的偶函数,且()f x 在[0,)+∞上是减函数.若(21)()f m f m ->,则实数m 的取值范围是_____.二、解答题:本大题共3小题,共30分.解答应写出文字说明,证明过程或演算步骤. 6.(本小题满分10分)已知全集U =R ,集合{|(2)0}P x x x =-≥,{|26}M x a x a =<<+. (Ⅰ)求集合U P ð;(Ⅱ)若U P M ⊆ð,求实数a 的取值范围.7.(本小题满分10分)已知函数()(2)()f x x x a =-+,其中a ∈R . (Ⅰ)若()f x 的图象关于直线1x =对称,求a 的值; (Ⅱ)求()f x 在区间[0,1]上的最小值.8.(本小题满分10分)已知函数()23x x f x a b =⋅+⋅,其中,a b 为常数. (Ⅰ)若0ab >,判断()f x 的单调性,并加以证明; (Ⅱ)若0ab <,解不等式:(1)()f x f x +>.北京市西城区2014 — 2015学年度第一学期期末试卷高一数学参考答案及评分标准 2015.1A 卷 [必修 模块4] 满分100分一、选择题:本大题共10小题,每小题4分,共40分.1.D ;2.C ;3.D ;4. D ;5. A ;6. C ;7. C ;8.B ;9. B ; 10.B . 二、填空题:本大题共6小题,每小题4分,共24分.11.3π; 12. 12-; 13. 1213-; 14.32; 15. 2; 16. ① ② ③.注:16题,少解不给分.三、解答题:本大题共3小题,共36分. 17.(本小题满分12分) (Ⅰ)解:因为 tan 2=-α,所以 πtan tanπ4tan()π41tan tan 4--=+⋅ααα 【 3分】3=. 【 6分】(Ⅱ)解:由π(,π)2∈α,tan 2α=-, 得sin α=, 【 8分】cos α=. 【10分】所以 4sin 22sin cos 5==-ααα. 【12分】18.(本小题满分12分)(Ⅰ)证明:由向量(cos sin )αα=,a ,1(,)22=-b ,得1(cos ,sin 2+=-+ααa b,1(cos ,sin 2-=+-ααa b , 【 1分】 由π(0,)2∈α,得向量+a b ,-a b 均为非零向量. 【 2分】 因为222213()()||||(sin cos )()044+⋅-=-=+-+=ααa b a b a b , 【 5分】所以向量+a b 与-a b 垂直. 【 6分】 (Ⅱ)解:将|2||2|+=-a b a b 两边平方,化简得223(||||)80-+⋅=a b a b . 【 8分】 由||||1==a b , 得 0⋅=a b , 【 9分】所以 1cos 02αα-=,所以 tan =α. 【11分】 注意到 π(0,)2∈α, 所以 π6α=. 【12分】19.(本小题满分12分)(Ⅰ)解:()sin 21f x x x =+π12sin(2)3x =+-. 【 2分】因为函数sin y x =的单调递减区间为π3π[2π,2π]()22k k k ++∈Z . 由 ππ3π2π22π232k x k +≤-≤+()k ∈Z , 【 4分】 得 5π11πππ1212k x k +≤≤+()k ∈Z . 所以()f x 的单调递减区间为5π11π[π,π]1212k k ++()k ∈Z . 【 6分】 (Ⅱ)解: 因为 ππ[,]42x ∈, 所以 ππ2π2633x -≤≤,由(Ⅰ)得 π212sin(2)33x +-≤≤,所以 ()f x 的值域是[23],. 【 8分】 ()2()2()2f x m f x m f x -<⇔-<<+,ππ[,]42x ∈. 【10分】所以 max ()2m f x >-,且 min ()2m f x <+,所以 14m <<, 即m 的取值范围是(1,4). 【12分】B 卷 [学期综合] 满分50分一、填空题:本大题共5小题,每小题4分,共20分.1. {|01x x ∈<<R ,或1}x >;2. 12; 3. 2; 4. 2-,1; 5. 1(,1)3.注:4题,少解得2分,有错解不给分. 二、解答题:本大题共3小题,共30分. 6.(本小题满分10分)(Ⅰ)解:因为全集U =R ,集合{|(2)0}P x x x =-≥,所以 {|(2)0}U P x x x =-<ð, 【 2分】 即集合{|02}U P x x =<<ð. 【 4分】(Ⅱ)解:因为 U P M ⊆ð,所以 0,262,a a ≤⎧⎨+≥⎩【 6分】解得 0,2.a a ≤⎧⎨≥-⎩ 【 8分】所以 [2,0]a ∈-. 【10分】 注:第(Ⅱ)小问没有等号扣1分. 7.(本小题满分10分)(Ⅰ)解法一:因为2()(2)()(2)2f x x x a x a x a =-+=+--, 所以,()f x 的图象的对称轴方程为22ax -=. 【 2分】 由212a-=,得0a =. 【 4分】 解法二:因为函数()f x 的图象关于直线1x =对称,所以必有(0)(2)f f =成立, 【 2分】 所以 20a -=, 得0a =. 【 4分】 (Ⅱ)解:函数()f x 的图象的对称轴方程为22ax -=. ① 当202a-≤,即 2a ≥时,因为()f x 在区间(0,1)上单调递增,所以()f x 在区间[0,1]上的最小值为(0)2f a =-. 【 6分】② 当2012a-<<,即 02a <<时, 因为()f x 在区间2(0,)2a -上单调递减,在区间2(,1)2a-上单调递增, 所以()f x 在区间[0,1]上的最小值为222()()22a a f -+=-. 【 8分】 ③ 当212a-≥,即 0a ≤时, 因为()f x 在区间(0,1)上单调递减,所以()f x 在区间[0,1]上的最小值为(1)(1)f a =-+. 【10分】 8.(本小题满分10分)(Ⅰ)解:当0,0a b >>时,()f x 在R 上是增函数;当0,0a b <<时,()f x 在R 上是减函数; 【 1分】证明如下:当0,0a b >>时,任取12,x x ∈R ,且12x x <,则210x x x ∆=->, 则212121()()(22)(33)x x x xy f x f x a b ∆=-=-+-.因为 122122,0(22)0x x x x a a <>⇒->;又122133,0(33)0x x x xb b <>⇒->, 所以 21()()0y f x f x ∆=->,所以,当0,0a b >>时,()f x 在R 上是增函数.当0,0a b <<时,同理可得,()f x 在R 上是减函数. 【 5分】 (Ⅱ)解:由(1)()2230x xf x f x a b +-=⋅+⋅>,得 32()2xb a >-. (*) 【 6分】 ① 当0,0a b <>时,(*)式化为3()22xa b->, 解得32log ()2ax b>-. 【 8分】② 当0,0a b ><时,(*)式化为3()22xa b-<, 解得32log ()2ax b<-.【10分】。
北京市石景山区2014-2015学年度第一学期高一数学期末试题带答案

石景山区2014—2015学年第一学期期末考试试卷高一数学一、选择题:本大题共10个小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的,把所选项前的字母填在题后括号内.1. 对于任意的R α∈,sin 2α= ( )A .2sin αB .2sin cos ααC .2cos αD .22cos sin αα-2.下列算式正确的是 ( )A .222log (3)log 3log ππ=+B2=-C .lg 62lg3= D .3322555-==3.设集合,A B 为全集U 的子集,则右图中阴影部分表示的集合是( )A .AB ⋂C .U B A ⋂ðB .U A B ⋂ð D . ()()U U A B ⋃痧4.已知a 与b 均为单位向量,它们的夹角为60,那么||a b -等于( )A .1BCD .25. 若函数32()22f x x x x =+--的一个正数零点附近的函数值用二分法逐次计算, 参考数据如下表:那么方程32220x x x +--=的一个近似根(精确到)为( )A .1.2B .1.3C .1.4D . 1.56.已知向量a ,b ,且2AB a b =+,56BC a b =-+,72CD a b =-,则一定共线的三点是 ( )A .,,A C DB .,,A B CC .,,B C DD .,,A B D7. 设方程20ax bx c ++=的两根为12,x x ,且12x x <,0a <,那么20ax bx c ++>的解集是( )A .1{|}x x x < C .12{|}x x x x <<B .2{|}x x x > D .12{|}x x x x x <>或8. 下列函数中,既是偶函数,又在[0,1]上单调递增的是 ( )A .cos y x =B .2y x =-C .2sin cos y x x =D .|sin |y x =9.将函数sin 2y x =的图象向左平移4π个单位,再向上平移1个单位,所得图象的函数解析式是 ( )A .cos 2y x =B .22cos y x =C .sin(2)4y x π=+D .22sin y x =10.设函数()log (2)a f x x a =-+在区间(1,)+∞上恒为正值,则实数a 的取值范围是( )A .(1,2]B .(1,2)C .(0,1)(1,2)⋃D . 5(1,)2二、填空题:本大题共4个小题,每小题3分,共12分.把答案填在题中横线上. 11.若cos 2α=,且α的终边过点(,2)P x ,则x = . 12.sin α=3cos α,则tan α= .13. 若函数()f x 的图象与2x y =的图象关于________对称,则函数()f x =_________. (注:填上你认为正确的一种情形即可,不必考虑所有可能的情形) 14. 三个变量123,,y y y 随x 的变化情况如下表:三个变量123,,y y y 中,变量_______随x 呈对数函数型变化,变量_______随x 呈指数函数型变化,变量_______随x 呈幂函数变化.三、解答题:本大题共6个小题,共48分.应写出文字说明,证明过程或演算步骤. 15.(本题满分8分)已知集合{|37}A x x =≤≤,{|0}B x x a =<<. (Ⅰ)若5a =,求A B ⋃和A B ⋂; (Ⅱ)若A B φ⋂≠,求a 的取值范围.16.(本题满分9分)已知向量(4,2)=-a ,(,1)x =b . (I ) 若a ,b 共线,求x 的值; (II )若a ⊥b ,求x 的值;(III )当2x =时,求a 与b 的夹角θ的余弦值.17.(本题满分9分)已知02απ<<,4sin 5α=. (I )求cos α的值; (II )求tan()4πα+的值;(III )求sin()cos()tan()2cos()ππαααπα---+的值.18. (本题满分8分)函数()2sin(2)3f x x π=-的部分图象如右图所示.(I )写出()f x 的最小正周期及图中0x ,0y 的值; (II )求()f x 在区间[,]46ππ-上的最大值和最小值.19. (本题满分7分) (Ⅰ)证明:函数4()f x x x=+在(0,2]上是减函数; (Ⅱ)已知函数()af x x x=+有如下性质:如果常数0a >,那么该函数在上是减函数,在)+∞上是增函数.设常数(1,9)a ∈,求函数()af x x x=+在[1,3]x ∈上的最大值和最小值.20. (本题满分7分)对于函数12(),(),()f x f x h x ,如果存在实数,a b 使得12()()()h x a f x b f x =⋅+⋅,那么称()h x 为12(),()f x f x 的生成函数.(Ⅰ)下面给出两组函数,()h x 是否分别为12(),()f x f x 的生成函数?并说明理由; 第一组:12()sin ,()cos ,()sin()3f x x f x x h x x π===+;第二组:1)(,1)(,)(22221+-=++=-=x x x h x x x f x x x f ;(Ⅱ)设 ,生成函数()h x . 若不等式23()2()0h x h x t ++<在[2,4]x ∈上有解,求实数t 的取值范围.12212()log ,()log ,2,1f x xf x x a b ====yOx0x 0y石景山区2014—2015学年第一学期期末考试试卷高一数学参考答案一、选择题:本大题共10个小题,每小题4分,共40分.二、填空题:本大题共4个小题,每小题3分,共12分.三、解答题:本大题共6个小题,共48分.解答题应写出文字说明,证明过程或演算步骤. 15.(本题满分8分)解:2{|10210}{|37}A x x x x x =-+≤=≤≤ …………2分 (Ⅰ)5a =,{|05}B x x ∴=<<{|07}A B x x ∴⋃=<≤, …………4分 {|35}A B x x ⋂=≤< …………5分(Ⅱ)若A B φ⋂≠,则3a > …………8分16.(本题满分9分)解:(I )a ,b 共线,412x ∴⨯=-,2x ∴=-; …………3分(II )a ⊥b ,420x ∴-=,12x ∴=; …………6分(III )当2x =时,42216b ⋅=⨯-⨯=a ,||25,||5==a b ,3cos 5||||a b a b θ⋅∴==. …………9分17. (本题满分9分) 解:(I )02απ<<,4sin 5α=,3cos 5α∴=; …………2分(II )4tan 3α=…………4分 tan()74πα+=- …………6分(III )sin()cos()tan()2cos()ππαααπα---+=sin cos cot cos αααα-=3sin cot cos 5ααα-=-=-. …………9分18. (本题满分8分)解:(I ) ()f x 的最小正周期为π,0512x π=,02y =. …………4分 (II )因为[,]46x ππ∈-,所以52[,0]36x ππ-∈-. 于是,当203x π-=,即6x π=时,()f x 取得最大值0;当232x ππ-=-,即12x π=-时,()f x 取得最大值2- …………8分19.(本题满分7分)(Ⅰ)证明:设12,x x 是(0,2]内的任意两个不相等的实数,且12x x <,则210x x x ∆=->,2121212121121221212121214444()()()()()4()(4)4()()(1)y f x f x x x x x x x x x x x x x x x x x x x x x x x x ∆=-=+-+=-+---=-+=--=∆⋅1202x x <<≤,1204x x ∴<<,1240x x ∴-<, 0y ∴∆<.因此,函数4()f x x x=+在(0,2]是减函数. …………3分 (Ⅱ)(1,9)a ∈,13∴<< …………4分所以,函数()af x x x=+在上是减函数,在上是增函数.x ∴=当()f x有最小值 …………5分又(1)1,(3)33a f a f =+=+, 最大值进行如下分类讨论:(ⅰ)当(1)(3)f f ≥时,即39a ≤<时,当1x =时,函数()f x 有最大值1a +;……6分 (1)(3)f f <13a <<3x =()f x 3a+20.(本题满分7分)解:(Ⅰ)① 设sin cos sin()3a x b x x π+=+,即1sin cos sin 2a x b x x x +=+,取1,2a b ==,所以()h x 是12(),()f x f x 的生成函数. …………2分② 设222()(1)1a x x b x x x x -+++=-+,即22()()1a b x a b x b x x +--+=-+,则111a b a b b +=⎧⎪-+=-⎨⎪=⎩,该方程组无解.所以()h x 不是12(),()f x f x 的生成函数. …4分 (Ⅱ)122122()2()()2log log log h x f x f x x x x =+=+=若不等式23()2()0h x h x t ++<在[2,4]x ∈上有解,23()2()0h x h x t ++<,即22223()2()3log 2log t h x h x x x <--=-- 设2log s x =,则[1,2]s ∈,22223log 2log 32y x x s s =--=--,max 5y =-,故,5t <-. ………7分【如有不同解法,请参考评分标准酌情给分】。
2015年北京市各区县高一期末试题分类汇编-函数

1.(2015年1月·延庆期末·5.函数x x y -+-=31的定义域为A .)3,1(B .]3,1[C .),3()1,(+∞-∞D .),0()0,1(+∞2.(2015年1月·丰台期末·2.函数()lg(1)f x x x =+-的定义域为( )A .(]1,0B .[)1,0C .[]1,0D .()1,03.(2015年1月·顺义期末·3.下列各组函数中表示同一函数的是 A. 2y x =和2()y x = B. ||y x =和33y x =C.2log a y x =和2log a y x =(0,1)a a >≠D.y x =和log x a y a =(0,1)a a >≠ 4.(2015年1月·顺义期末·7.有下列四个命题: ①||,y x ={}2,1,0,1,2x ∈--,则它的值域为{}0,1,4; ②2,2,y x x x R =≠∈,则它的值域为{}|0,4y y y ≥≠,③211x y x -=-,则它的值域为{}|,2y y R y ∈≠;④1y x =-,则它的值域为{}|0y y ≥.其中正确命题的个数为A.1B.2C.3D. 45.(2015年1月·海淀期末·4.下列函数中,既是奇函数又是(1,1)-上的增函数的是A. 2x y =B. tan y x =C. 1y x -=D. cos y x = 6.(2015年1月·海淀期末·5.函数1,0,1,0x x y x x -≥⎧=⎨-<⎩的值域是A. RB. [0,)+∞C. [1,)-+∞D. (1,)-+∞7.(2015年1月·丰台期末·3.下列函数中是偶函数且在区间(0,)+∞内为单调递增函数的是( )A .x y cos =B .12y x =C .2x y -=D .23log y x =8.(2015年1月·东城期末·3. 下列函数中,在区间(0,+∞)上为增函数的是A .1y x=B .y =(x -1)2C .y =2-x D .2log (1)y x =+ 10.(2015年1月·东城期末·16.对于任意两个实数1x ,2x ,定义11212212,,max(,),.x x x x x x x x ≥⎧=⎨<⎩若2()2,()f x x g x x =-=-,则max((),())f x g x 的最小值为________.11.(2015年1月·昌平期末·13)已知函数3, 1,(),1,x x f x x x ⎧<=⎨-≥⎩则((1))f f =_______ ;若()2f x =,则x = .12.(2015年1月·昌平期末·15)已知函数2()23f x x x =-+在闭区间[0,]m 上有最大值3,最小值2,则m 的取值范围是 __________ .13.(2015年1月·西城期末·4.设()f x 是定义在R 上的偶函数,且()f x 在[0,)+∞上是减函数.若()(2)f m f >,则实数m 的取值范围是_____.14.(2015年1月·海淀期末·13. 函数22y x x =-在区间[1,2)-上的值域为___.15.(2015年1月·顺义期末·13.已知二次函数()f x 满足(0)3f =-,(1)(3)0f f =-=,那么()f x = .16.(2015年1月·顺义期末·14.定义在R 上的偶函数cx bax x f ++=2)(的图象如图所示,则实数a 、b 、c 的大小关系是____________ .17.(2015年1月·海淀期末·14. 方程3221x x +=的解的个数为_____,若有解,则将其解按四舍五入精确到个位,得到的近似解为______.18.(2015年1月·海淀期末·16.已知函数:2y x =,2log y x =,2x y =, sin y x =,cos y x =,tan y x =.从中选出两个函数记为()f x 和()g x ,若()()()F x f x g x =+的 图象如图所示,则()F x =_____.19.(2015年1月·昌平期末·16)已知函数2()sin 11xf x x x =+++的最大值为M,最小值为m ,则m M +=_______ .20.(2015年1月·石景山期末·5. 若函数32()22f x x x x =+--的一个正数零点附近的函数值用二分法逐次计算,参考数据如下表:(1)2f =- (1.5)0.625f = (1.25)0.984f =-(1.375)0.260f =-(1.438)0.165f =(1.4065)0.052f =-那么方程32220x x x +--=的一个近似根(精确到0.1)为( )A .1.2B .1.3C .1.4D . 1.5xy1 O第16题图22.(2015年1月·丰台期末·15.已知定义域为R 的函数()f x 的图象关于原点对称.当0>x 时,()ln f x x =,则(e)f -= ;23.(2015年1月·密云期末·14.给出定义:若11< +22m x m -≤ (其中m 为整数),则m 叫做离实数x 最近的整数,记作{}x ,即{}=x m . 在此基础上给出下列关于函数()={}f x x x -的四个判断:①=()y f x 的定义域是R ,值域是11(,]22-; ②点(,0)k 是=()y f x 的图象的对称中心,其中k Z ∈; ③函数=()y f x 的最小正周期为1;④函数=()y f x 在13]22(,上是增函数. 则上述判断中正确的序号是 .(填上所有正确的序号)24.(2015年1月·丰台期末·16. 如图,某机器人的运动轨道是边长为1米的正三角形ABC .开机后它从A点出发,沿轨道先逆时针运动再顺时针运动,每运动6米改变一次运动方向(假设按此方式无限运动下去).运动过程中随时记录逆时针运动的总路程1s 和顺时针运动的总路程2s .x为该机器人的“运动状态参数”,规定:逆时针运动时 x =1s ,顺时针运动时x =2s -.机器人到A 点的距离d 与x 满足函数关系d =()f x .现有如下结论: ①()f x 的值域为[0,1]; ②()f x 是以3为周期的函数; ③()f x 是定义在R 上的奇函数; ④()f x 在区间[3,2]--上单调递增. 其中正确的有 (写出所有正确结论的编号).25.(2015年1月·顺义期末·17.(本题满分13分) 已知函数1()f x kx x=-,且(1)1f =. (Ⅰ)求实数k 的值;(Ⅱ)判断函数在),0(+∞上的单调性,并用定义加以证明.26.(2015年1月·延庆期末·24.(本题12分)设函数54)(2--=x x x f . (Ⅰ)在区间]6,2[-上画出函数)(x f 的图像;(Ⅱ)当2>k 时,求证:在区间]5,1[-上,k kx y 3+=的图像位于函数)(x f 图像的上方.解:27.(2015年1月·西城期末·6.(本小题满分10分)已知函数()(2)()f x x x a =-+,其中a ∈R . (Ⅰ)若()f x 的图象关于直线1x =对称,求a 的值; (Ⅱ)求()f x 在区间[0,1]上的最小值.28.(2015年1月·顺义期末·18.(本小题共13分) 已知函数()mf x x x=+,且此函数图象过点(1,5) . (Ⅰ)求实数m 的值并判断()f x 的奇偶性;(Ⅱ)判断函数()f x 在[)2,+∞上的单调性,并用定义证明你的结论.29.(2015年1月·顺义期末·19.(本小题共14分)1y (毫克)为了预防冬季流感,某学校对教室用药熏消毒法 进行消毒.已知药物释放过程中室内每立方米空气 中的含药量y (毫克)与时间t (小时)成正比, 药物释放完毕后y 与t 的函数关系式为:1()4t a y -=,(a 为常数),根据图中提供的信息,回答下列问题:(Ⅰ)写出从药物释放开始,每立方米空气中的含药量y (毫克)与时间t (小时)之间的函数关系式; (Ⅱ)据测定当空气中每立方米的含药量降低到0.5 毫克以下时,学生方可进入教室,那么从药物释放完毕,至少需要经过多少小时后,学生才能回到教室.30.(2015年1月·石景山期末·19. (本题满分7分) (Ⅰ)证明:函数4()f x x x=+在(0,2]上是减函数; (Ⅱ)已知函数()af x x x=+有如下性质:如果常数0a >,那么该函数在(0,]a 上是减函数,在[,)a +∞上是增函数.设常数(1,9)a ∈,求函数()af x x x=+在[1,3]x ∈上的最大值和最小值.31.(2015年1月·密云期末·19. (本小题满分13分) 设二次函数2()f x ax bx c =++0,a x R ≠∈满足条件: ①21()(1)2≤≤+x f x x ,②(1)(1)-+=--f x f x ;③()f x 在R 上的最小值为0. (I )求(1)f 的值; (II )求()f x 的解析式;(III )求最大值(1)m m >,使得存在t R ∈,只要[]1,x m ∈,都有()f x t x +≤成立.32.(2015年1月·石景山期末·20. (本题满分7分)对于函数12(),(),()f x f x h x ,如果存在实数,a b 使得12()()()h x a f x b f x =⋅+⋅,那么称()h x 为12(),()f x f x 的生成函数.(Ⅰ)下面给出两组函数,()h x 是否分别为12(),()f x f x 的生成函数?并说明理由; 第一组:12()sin ,()cos ,()sin()3f x x f x x h x x π===+;第二组:1)(,1)(,)(22221+-=++=-=x x x h x x x f x x x f ;(Ⅱ)设 ,生成函数()h x . 若不等式23()2()0h x h x t ++<在[2,4]x ∈上有解,求实数t 的取值范围.33.(2015年1月·昌平期末·19)(本小题共15分)已知函数()2f x x x x =-.(I )判断函数()f x 的奇偶性并求函数()f x 的零点; (II )写出()f x 的单调区间;(只需写出结果) (III )试讨论方程()f x m =的根的情况.34.(2015年1月·昌平期末·21)(本小题共13分)已知函数()f x 对任意,a b ∈R ,都有()()2()()f a b f a b f a f b ++-=⋅,且(0)0f ≠. (I ) 求(0)f ;(II )证明:函数()f x 为偶函数;(Ⅲ) 存在正数m ,使得()0f m =,求满足()()f x T f x +=的1个T 值(0)T ≠.35.(2015年1月·东城期末·21.(本题满分8分)已知函数2()43f x x x a =-++,a ∈R .(Ⅰ)若函数()y f x =的图象与x 轴无交点,求a 的取值范围; (Ⅱ)若函数()y f x =在[1,1]-上存在零点,求a 的取值范围;(Ⅲ)设函数()52g x bx b =+-,b ∈R .当0a =时,若对任意的1[1,4]x ∈,总存在2[1,4]x ∈,使得12212()log ,()log ,2,1f x xf x x a b ====36.(2015年1月·房山期末·22)(本小题满分12分)设)(x f 和()g x 都是定义在集合M 上的函数,对于任意的x M ∈,都有(())(())f g x g f x =成立,称函数)(x f 与()g x 在M 上互为“H 函数”.(Ⅰ)若函数()21f x x =+,()32g x x =+,判断)(x f 与()g x 在R 上是否互为“H 函数”; (Ⅱ)若函数()2f x x =与()sin g x x =在M 上互为“H 函数”,求集合M ;(Ⅲ)若函数xa x f =)((0a >,1a ≠)与1)(+=x x g 在集合M 上互为“H 函数”,求a 的取值范围.(2015年1月·西城期末·8.(本小题满分10分)定义在R 上的函数()f x 同时满足下列两个条件:① 对任意x ∈R ,有(2)()2f x f x +≥+;② 对任意x ∈R ,有(3)()3f x f x +≤+. 设()()g x f x x =-.(Ⅰ)证明:(3)()(2)g x g x g x +≤≤+; (Ⅱ)若(4)5f =,求(2014)f 的值.37.(2015年1月·密云期末·20.(本小题满分13分)若函数)(x f 对任意的x ∈R ,均有)(2)1()1(x f x f x f ≥++-,则称函数)(x f 具有性质P . (Ⅰ)判断下面两个函数是否具有性质P ,并说明理由.①2x y =; ②3y x =.(Ⅱ)若函数)(x f 具有性质P ,且(0)()0f f n ==(2,n >n ∈*N ),求证:对任意{1,2,3,,1}i n ∈-有()0f i ≤;(Ⅲ)在(Ⅱ)的条件下,是否对任意[0,]x n ∈均有0)(≤x f .若成立给出证明,若不成立给出反例.38.(2015年1月·海淀期末·19.本题满分12分已知定义在R 上的奇函数()f x 满足:“对于区间(0,)+∞上的任意,a b ,都有()()f a b f b +>成立”. (Ⅰ)求(0)f 的值,并指出()f x 在区间(0,)+∞上的单调性; (Ⅱ)用增函数的定义证明:函数()f x 是(,0)-∞上的增函数;(Ⅲ)判断()f x 是否为R 上的增函数,如果是,请给出证明;如果不是,请举出反例.yO x1 1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2015年北京市各区县高一期末试题分类汇编——函数(2015年1月·延庆期末·5.函数x x y -+-=31的定义域为A .)3,1(B .]3,1[C .),3()1,(+∞-∞D .),0()0,1(+∞(2015年1月·丰台期末·2.函数()lg(1)f x x -的定义域为( ) A .(]1,0 B .[)1,0C .[]1,0D .()1,0(2015年1月·顺义期末·3.下列各组函数中表示同一函数的是A. y =2y = B. ||y x =和y =C.2log a y x =和2log a y x =(0,1)a a >≠D.y x =和log x a y a =(0,1)a a >≠ (2015年1月·顺义期末·7.有下列四个命题: ①||,y x ={}2,1,0,1,2x ∈--,则它的值域为{}0,1,4; ②2,2,y x x x R =≠∈,则它的值域为{}|0,4y y y ≥≠,③211x y x -=-,则它的值域为{}|,2y y R y ∈≠;④y ={}|0y y ≥.其中正确命题的个数为A.1B.2C.3D. 4(2015年1月·海淀期末·4.下列函数中,既是奇函数又是(1,1)-上的增函数的是BA. 2x y =B. tan y x =C. 1y x -=D. cos y x = (2015年1月·海淀期末·5.函数1,0,1,0x x y x x -≥⎧=⎨-<⎩的值域是CA. RB. [0,)+∞C. [1,)-+∞D. (1,)-+∞(2015年1月·丰台期末·3.下列函数中是偶函数且在区间(0,)+∞内为单调递增函数的是( )A .x y cos =B .12y x =C .2x y -=D .23log y x =(2015年1月·东城期末·3. 下列函数中,在区间(0,+∞)上为增函数的是A .1y x=B .y =(x -1)2C .y =2-x D .2log (1)y x =+ (2015年1月·房山期末·9)心理学家发现,在特定条件下,学生对概念的接受能力y 与提出概念所用的时间t (单位:分)满足函数关系2y at bt c =++(a ,b ,c 是常数),下表记录了三次实验的数据,根据上述函数模型和实验数据,若要学生达到最强接受能力,提出概念所用的时间为 (A )10分钟 (B )12分钟 (C )13分钟 (D )14分钟(2015年1月·东城期末·16.对于任意两个实数1x ,2x ,定义11212212,,max(,),.x x x x x x x x ≥⎧=⎨<⎩若2()2,()f x x g x x =-=-,则max((),())f x g x 的最小值为________.1-(2015年1月·昌平期末·13)已知函数3, 1,(),1,x x f x x x ⎧<=⎨-≥⎩则((1))f f =_______ ;若()2f x =,则x = .13, 3log 2 (2015年1月·昌平期末·15)已知函数2()23f x x x =-+在闭区间[0,]m 上有最大值3,最小值2,则m 的取值范围是 __________ .[1,2](2015年1月·西城期末·4.设()f x 是定义在R 上的偶函数,且()f x 在[0,)+∞上是减函数.若()(2)f m f >,则实数m 的取值范围是_____.(2,2)-(2015年1月·海淀期末·13. 函数22y x x =-在区间[1,2)-上的值域为__[1,3]- _. (2015年1月·顺义期末·13.已知二次函数()f x 满足(0)3f =-,(1)(3)0f f =-=,那么()f x = 223x x +- . (2015年1月·顺义期末·14.定义在R 上的偶函数cx bax x f ++=2)(的图象如图所示, 则实数a 、b 、c 的大小关系是____a c b >>__ ______ .(2015年1月·海淀期末·14. 方程3221x x +=的解的个数为_____,若有解,则将其解按四舍五入精确到个位,得到的近似解为____ 1 , 3 __.(2015年1月·海淀期末·16.已知函数:2y x =sin y x =,cos y x =,tan y x =.从中选出两个函数记为()f x 和()g x ,若()()()F x f x g x =+的 图象如图所示,则()F x =__2sin x x +___.(2015年1月·昌平期末·16)已知函数2()sin 11f x x x =+++的最大值为M,最小值为m ,则m M +=_______ . 2(2015年1月·石景山期末·5. 若函数32()22f x x x x =+--的一个正数零点附近的函数值用二分法逐次计算, 参考数据如下表:那么方程32220x x x +--=的一个近似根精确到为 A .1.2 B .1.3C .1.4D . 1.5(2015年1月·密云期末·7.如图,点P 在边长为1的正方形的边上运动,设M 是CD 的中点,则当P 沿着路径--B A M C -运动时,点P 经过的路程x 与△APM 的面积y 的函数关系为)(x f y =,则)(x f y =的图象是 A(2015年1月·丰台期末·15.已知定义域为R 的函数()f x 的图象关于原点对称.当0>x 时,()ln f x x =,则(e)f -= ; 1-(2015年1月·密云期末·14.给出定义:若11< +22m x m -≤ (其中m 为整数),则m 叫做离实数x 最近的整数,记作{}x ,即{}=x m . 在此基础上给出下列关于函数()={}f x x x -的四个判断:①=()y f x 的定义域是R ,值域是11(,]22-; ②点(,0)k 是=()y f x 的图象的对称中心,其中k Z ∈; ③函数=()y f x 的最小正周期为1;④函数=()y f x 在13]22(,上是增函数. 则上述判断中正确的序号是 .(填上所有正确的序号) ①③④(2015年1月·丰台期末·16. 如图,某机器人的运动轨道是边长为1米的正三角形ABC .开机后它从A点出发,沿轨道先逆时针运动再顺时针运动,每运动6米改变一次运动方向(假设按此方式无限运动下去).运动过程中随时记录逆时针运动的总路程1s 和顺时针运动的总路程2s .x 为该机器人的“运动状态参数”,规定:逆时针运动时 x =1s ,顺时针运动时x =2s -.机器人到A 点的距离d 与x 满足函数关系d =()f x .现有如下结论:①()f x 的值域为[0,1]; ②()f x 是以3为周期的函数;③()f x 是定义在R 上的奇函数; ④()f x 在区间[3,2]--上单调递增.其中正确的有 (写出所有正确结论的编号).①②④ (2015年1月·顺义期末·17.(本题满分13分) 已知函数1()f x kx x=-,且(1)1f =. (Ⅰ)求实数k 的值;(Ⅱ)判断函数在),0(+∞上的单调性,并用定义加以证明.解:(Ⅰ)由(1)1f =得2k =;-----------------------------------------6分(Ⅱ)为增函数.在),0(+∞任取两数1x ,2x .设210x x >>,则2121212112111()()(2)(2)()(2)f x f x x x x x x x x x -=---=-+因为210x x >>,所以210x x ->,21120x x +>, 所以21()()0f x f x ->,即21()()f x f x >,所以()f x 为增函数.------13分(2015年1月·延庆期末·24.(本题12分)设函数54)(2--=x x x f .(Ⅰ)在区间]6,2[-上画出函数)(x f 的图像;(Ⅱ)当2>k 时,求证:在区间]5,1[-上,k kx y 3+=的图像位于函数)(x f 图像的上方.解:24.(本题12分) 解]:(Ⅰ)…………………………3分(Ⅱ)当]5,1[-∈x 时,54)(2++-=x x x f .)54()3()(2++--+=x x x k x g )53()4(2-+-+=k x k x436202422+--⎪⎭⎫ ⎝⎛--=k k k x , ………………………5分 ∵ 2>k ,∴124<-k. ………………………6分 ① 当1241<-≤-k ,即62≤<k 时,取24kx -=, min )(x g ()[]6410414362022---=+--=k k k . ∵ ,64)10(162<-≤k ,∴064)10(2<--k 则0)(min >x g .………9分② 当124-<-k,即6>k 时,取1-=x ,min )(x g =02>k . 由 ①、②可知,当2>k 时,在]5,1[-∈x 上0)(>x g ,∴在区间]5,1[-上,)3(+=x k y 的图像位于函数)(x f 图像的上方.……12分(2015年1月·西城期末·6.(本小题满分10分)已知函数()(2)()f x x x a =-+,其中a ∈R . (Ⅰ)若()f x 的图象关于直线1x =对称,求a 的值; (Ⅱ)求()f x 在区间[0,1]上的最小值.(Ⅰ)解法一:因为2()(2)()(2)2f x x x a x a x a =-+=+--, 所以,()f x 的图象的对称轴方程为22ax -=. 【 2分】由212a-=,得0a =. 【 4分】 解法二:因为函数()f x 的图象关于直线1x =对称,所以必有(0)(2)f f =成立, 【 2分】 所以 20a -=, 得0a =. 【 4分】 (Ⅱ)解:函数()f x 的图象的对称轴方程为22ax -=. ① 当202a-≤,即 2a ≥时, 因为()f x 在区间(0,1)上单调递增,所以()f x 在区间[0,1]上的最小值为(0)2f a =-. 【 6分】② 当2012a-<<,即 02a <<时, 因为()f x 在区间2(0,)2a -上单调递减,在区间2(,1)2a-上单调递增, 所以()f x 在区间[0,1]上的最小值为222()()22a a f -+=-. 【 8分】 ③ 当212a-≥,即 0a ≤时, 因为()f x 在区间(0,1)上单调递减,所以()f x 在区间[0,1]上的最小值为(1)(1)f a =-+. 【10分】(2015年1月·顺义期末·18.(本小题共13分) 已知函数()mf x x x=+,且此函数图象过点(1,5) . (Ⅰ)求实数m 的值并判断()f x 的奇偶性;(Ⅱ)判断函数()f x 在[)2,+∞上的单调性,并用定义证明你的结论. 解:(Ⅰ)Q ()f x 过点()1,5 ∴4m =.————————2分 ∴()4fx x x =+定义域是()(),00,-∞+∞U , Q ()4f x x x-=--()f x =- ∴()f x 是奇函数 ;————6分(Ⅱ)()f x 在[)2,+∞上单调递增.———8分 证明:任取[)12,2,x x ∈+∞,,不妨设122x x ≤<,()()21212144f x f x x x x x ⎛⎫⎛⎫-=+-+ ⎪ ⎪⎝⎭⎝⎭()()2112124x x x x x x --=;——————10分 当122x x ≤<时,Q 1240x x ->,210x x ->,120x x >,∴()()210f x f x ->∴()()21f x f x >;∴()f x 在[)2,+∞上单调递增.————————————13分(2015年1月·顺义期末·19.(本小题共14分) 为了预防冬季流感,某学校对教室用药熏消毒法 进行消毒.已知药物释放过程中室内每立方米空气 中的含药量y (毫克)与时间t (小时)成正比, 药物释放完毕后y 与t 的函数关系式为:1()4t a y -=,(a 为常数),根据图中提供的信息,回答下列问题:(Ⅰ)写出从药物释放开始,每立方米空气中的含药量y (毫克)与时间t (小时)之间的函数关系式;(Ⅱ)据测定当空气中每立方米的含药量降低到0.5 毫克以下时,学生方可进入教室,那么从药物释放完毕,至少需要经过多少小时后,学生才能回到教室.19. (本小题共14分) (Ⅰ)由图形可设y kt =(00.1)t ≤≤,———2分把点(0.1,1)分别代入y kt =和1()4t ay -=,解得10,0.1k a ==.———8分∴0.110,(00.1)1(),(0.1)4t t t y t -≤≤⎧⎪=⎨>⎪⎩.———10分 (Ⅱ)依题意0.111()0.542t -<=,解得0.6t > ,又 0.60.10.5-= ∴药物释放完毕0.5小时后学生才能回到教室.———14分))(2015年1月·石景山期末·19. (本题满分7分) (Ⅰ)证明:函数4()f x x x=+在(0,2]上是减函数; (Ⅱ)已知函数()af x x x=+有如下性质:如果常数0a >,那么该函数在上是减函数,在)+∞上是增函数.设常数(1,9)a ∈,求函数()af x x x=+在[1,3]x ∈上的最大值和最小值. (Ⅰ)证明:设12,x x 是(0,2]内的任意两个不相等的实数,且12x x <,则210x x x ∆=->,2121212121121221212121214444()()()()()4()(4)4()()(1)y f x f x x x x x x x x x x x x x x x x x x x x x x x x ∆=-=+-+=-+---=-+=--=∆⋅1202x x <<≤,1204x x ∴<<,1240x x ∴-<, 0y ∴∆<.因此,函数4()f x x x=+在(0,2]是减函数. …………3分 (Ⅱ)(1,9)a ∈,13∴<< …………4分所以,函数()af x x x=+在上是减函数,在上是增函数. x ∴=当()f x有最小值 …………5分又(1)1,(3)33a f a f =+=+, 最大值进行如下分类讨论:(ⅰ)当(1)(3)f f ≥时,即39a ≤<时,当1x =时,函数()f x 有最大值1a +;……6分 (ⅱ)当(1)(3)f f <时,即13a <<时,当3x =时,函数()f x 有最大值33a+. ……7分 (2015年1月·密云期末·19. (本小题满分13分)设二次函数2()f x ax bx c =++0,a x R ≠∈满足条件:①21()(1)2≤≤+x f x x , ②(1)(1)-+=--f x f x ; ③()f x 在R 上的最小值为0.(I )求(1)f 的值; (II )求()f x 的解析式;(III )求最大值(1)m m >,使得存在t R ∈,只要[]1,x m ∈,都有()f x t x +≤成立. 解:(I) ∵)1(21)(2x x f x +≤≤在R 上恒成立, ∴211(1)(11)12f ≤≤+= 即(1)1f =. ---------------------------2分 (II )∵(1)(1)-+=--f x f x ,∴函数图象关于直线1x =-对称,∴1,2.2bb a a-=-= ∵(1)1f =,∴1a b c ++= ---------------------------4分 又∵()f x 在R 上的最小值为0,∴(1)0f -=,即0a b c -+=, 由210b a a b c a b c =⎧⎪++=⎨⎪-+=⎩解得1412a cb ⎧==⎪⎪⎨⎪=⎪⎩, ∴2111()424f x x x =++; -------------7分 (III )∵当[1,]x m ∈时, ()f x t x +≤恒成立,∴(1)1f t +≤且()f m t m +≤,由(1)1f t +≤得240t t +≤,解得40t -≤≤ ---------------9分由()f m t m +≤得:222(1)210m t m t t --+++≤,解得11t m t -≤≤-……………(10分)∵40t -≤≤,∴11(4)9m t ≤-≤--=,---------------11分 当4t =-时,对于任意[1,9]x ∈,恒有211(4)(109)(9)(1)044f x x x x x x --≤-+=--≤, ∴m 的最大值为9. -------------------12分 另解:(酌情给分)2()(1)4f x t x x t x +≤⇔++≤且[1,]x m ∈⇔11t x t x ⎧≥--⎪⎨≤-+⎪⎩在[1,]m 上恒成立⇔max min(1)(1)t x t x ⎧≥--⎪⎨≤-+⎪⎩∵1y x =--在[1,]m上递减,∴max (1)4x --=-,∵1y x =-+在[1,]m 上递减,∴2min (1)11)x m -+=-+=-∴241)t -≤≤-,∴21)4-≥-,21)4≤,∵1m >12≤,∴9m ≤,∴m 的最大值为9(2015年1月·石景山期末·20. (本题满分7分)对于函数12(),(),()f x f x h x ,如果存在实数,a b 使得12()()()h x a f x b f x =⋅+⋅,那么称()h x 为12(),()f x f x 的生成函数.(Ⅰ)下面给出两组函数,()h x 是否分别为12(),()f x f x 的生成函数?并说明理由;第一组:12()sin ,()cos ,()sin()3f x x f x x h x x π===+; 第二组:1)(,1)(,)(22221+-=++=-=x x x h x x x f x x x f ;(Ⅱ)设 ,生成函数()h x . 若不等式23()2()0h x h x t ++<在[2,4]x ∈上有解,求实数t 的取值范围.解:(Ⅰ)① 设sin cos sin()3a x b x x π+=+,即1sin cos sin 2a x b x x x +=,取1,2a b ==,所以()h x 是12(),()f x f x 的生成函数. …………2分 ② 设222()(1)1a x x b x x x x -+++=-+,即22()()1a b x a b x b x x +--+=-+, 则111a b a b b +=⎧⎪-+=-⎨⎪=⎩,该方程组无解.所以()h x 不是12(),()f x f x 的生成函数. …4分 (Ⅱ)122122()2()()2log log log h x f x f x x x x =+=+=12212()log ,()log ,2,1f x x f x x a b ====若不等式23()2()0h x h x t ++<在[2,4]x ∈上有解,23()2()0h x h x t ++<,即22223()2()3log 2log t h x h x x x <--=--设2log s x =,则[1,2]s ∈,22223log 2log 32y x x s s =--=--,max 5y =-,故,5t <-. ………7分(2015年1月·昌平期末·19)(本小题共15分) 已知函数()2f x x x x =-.(I )判断函数()f x 的奇偶性并求函数()f x 的零点;(II )写出()f x 的单调区间;(只需写出结果)(III )试讨论方程()f x m =的根的情况.解:(Ⅰ)因为()()2()f x x x x -=----2x x x =-+(2)x x x =--()f x =-,…………………2分 所以()f x 为奇函数.…………………3分 令()0f x =,即20x x x -=,(2)0x x -=.解得:0,=2, 2.x x x ==-所以函数的零点为2,0,2-.…………………6分 (Ⅱ)函数()f x 的单调递增区间为(,1),(1,)-∞-+∞;单调递减区间为(1,1)-.…………………9分 (Ⅲ)当1>1m m <-或时,方程()f x m =有一个根;…………………11分 当1m =±时,方程()f x m =有两个根;…………………13分 当11m -<<时,方程()f x m =有三个根.…………………15分(2015年1月·昌平期末·21)(本小题共13分)已知函数()f x 对任意,a b ∈R ,都有()()2()()f a b f a b f a f b ++-=⋅,且(0)0f ≠. (I ) 求(0)f ;(II )证明:函数()f x 为偶函数;(Ⅲ) 存在正数m ,使得()0f m =,求满足()()f x T f x +=的1个T 值(0)T ≠.解:(Ⅰ)令0a b ==.则(0)(0)2(0)(0)f f f f +=⋅.因为(0)0f ≠,所以(0)1f =. ………………3分 (Ⅱ)令0,a b x ==.则()()2(0)()2()f x f x f f x f x +-=⋅=.所以()()f x f x -=.所以函数()f x 为偶函数. ………………7分(Ⅲ)令,a x b m ==.因为()0f m =,所以()()2()()0f x m f x m f x f m ++-=⋅=. ………………9分即 ()()f x m f x m +=--.………………10分 所以(2)()f x m f x +=-. ………………11分所以(4)(2)()f x m f x m f x +=-+=.所以满足(+)()f x T f x =的一个T 值为4m . ………………13分 (2015年1月·东城期末·21.(本题满分8分)已知函数2()43f x x x a =-++,a ∈R .(Ⅰ)若函数()y f x =的图象与x 轴无交点,求a 的取值范围;(Ⅱ)若函数()y f x =在[1,1]-上存在零点,求 a 的取值范围;(Ⅲ)设函数()52g x bx b =+-,b ∈R .当0a =时,若对任意的1[1,4]x ∈,总存在2[1,4]x ∈,使得12()()f x g x =,求b 的取值范围.21.(本题满分8分)解:(Ⅰ)若函数()y f x =的图象与x 轴无交点,则方程()0f x = 的判别式0∆<,即164(3)0a -+<,解得1a >.(Ⅱ)2()43f x x x a =-++的对称轴是2x =,所以()y f x =在[1,1]-上是减函数,()y f x =在[1,1]-上存在零点,则必有:(1)0(1)0f f ≤⎧⎨-≥⎩,即080a a ≤⎧⎨+≥⎩, 解得:80a -≤≤,故实数 的取值范围为80a -≤≤;(Ⅲ)若对任意的1[1,4]x ∈,总存在2[1,4]x ∈,使12()()f x g x =,只需函数()y f x =的值域为函数()y g x =值域的子集.当0a =时,2()43f x x x =-+的对称轴是2x =,所以()y f x =的值域为[1,3]-. 下面求()52g x bx b =+-,[1,4]x ∈的值域.① 0b =时,()5g x =,不合题意,舍去.② 0b >时,()52g x bx b =+-的值域为[5,52]b b -+,只需要5152 3.b b -≤-⎧⎨+≥⎩, 解得6b ≥. ③ 0b <时,()52g x bx b =+-的值域为[52,5]b b +-,只需要5215 3.b b +≤-⎧⎨-≥⎩,解得3b ≤-. 综上:实数b 的取值范围6b ≥或3b ≤-.(2015年1月·房山期末·22)(本小题满分12分)设)(x f 和()g x 都是定义在集合M 上的函数,对于任意的x M ∈,都有(())(())f g x g f x =成立,称函数)(x f 与()g x 在M 上互为“H 函数”.(Ⅰ)若函数()21f x x =+,()32g x x =+,判断)(x f 与()g x 在R 上是否互为“H 函数”; (Ⅱ)若函数()2f x x =与()sin g x x =在M 上互为“H 函数”,求集合M ;(Ⅲ)若函数x a x f =)((0a >,1a ≠)与1)(+=x x g 在集合M 上互为“H 函数”,求a的取值范围.解:(Ⅰ))(x f 与()g x 在R 上互为“H 函数” -----------------1分x ∀∈R ,由()21f x x =+,()32g x x =+,则(())2(32)1f g x x =++, -----------------1分(())3(21)2g f x x =++ -----------------1分(())(())f g x g f x = -----------------1分所以)(x f 与()g x 互为“H 函数”(Ⅱ)由))(()((x f g x g f =得x x 2sin sin 2= -----------------1分化简得,0)cos 1(sin 2=-x x ,0sin =x 或1cos =x -----------------1分 解得πk x =或πk x 2=,Z k ∈, -----------------1分 即集合{|,}M x x k k Z ==π∈ -----------------1分 (Ⅲ)由))(()((x f g x g f =得11+=+x x a a (0>a 且1≠a )变形得,1)1(=-a a x , -----------------2分由于0>a 且1≠a ,11-=a a x , 因为0>x a ,所以011>-a ,即1>a -----------------2分 (2015年1月·西城期末·8.(本小题满分10分)定义在R 上的函数()f x 同时满足下列两个条件:① 对任意x ∈R ,有(2)()2f x f x +≥+;② 对任意x ∈R ,有(3)()3f x f x +≤+. 设()()g x f x x =-.(Ⅰ)证明:(3)()(2)g x g x g x +≤≤+;(Ⅱ)若(4)5f =,求(2014)f 的值.(Ⅰ)证明:因为()()g x f x x =-,所以(2)(2)2g x f x x +=+--,(3)(3)3g x f x x +=+--.由条件①,②可得(2)(2)2()22()()g x f x x f x x f x x g x +=+--≥+--=-=; ③ 【 2分】 (3)(3)3()33()()g x f x x f x x f x x g x +=+--≤+--=-=. ④ 【 4分】 所以(3)()(2)g x g x g x +≤≤+.(Ⅱ)解:由③得 (2)()g x g x +≥,所以(6)(4)(2)()g x g x g x g x +≥+≥+≥. 【 6分】由④得 (3)()g x g x +≤,所以(6)(3)()g x g x g x +≤+≤. 【 7分】 所以必有(6)()g x g x +=,即()g x 是以6为周期的周期函数. 【 8分】 所以(2014)(33564)(4)(4)41g g g f =⨯+==-=. 【 9分】 所以(2014)(2014)20142015f g =+=. 【10分】 (2015年1月·密云期末·20.(本小题满分13分)若函数)(x f 对任意的x ∈R ,均有)(2)1()1(x f x f x f ≥++-,则称函数)(x f 具有性质P .(Ⅰ)判断下面两个函数是否具有性质P ,并说明理由.①2x y =; ②3y x =.(Ⅱ)若函数)(x f 具有性质P ,且(0)()0f f n ==(2,n >n ∈*N ), 求证:对任意{1,2,3,,1}i n ∈-有()0f i ≤;(Ⅲ)在(Ⅱ)的条件下,是否对任意[0,]x n ∈均有0)(≤x f .若成立给出证明,若不成立给出反例.(Ⅰ)证明:①函数()2x f x =具有性质P .11(1)(1)2()222220x x x x f x f x f x -+-++-=+-⋅=>,……………1分即)(2)1()1(x f x f x f ≥++-,此函数为具有性质P .……………2分②函数3)(x x f =不具有性质P . ……………3分例如,当1x =-时,(1)(1)(2)(0)8f x f x f f -++=-+=-,2()2f x =-,所以,)1()0()2(-<+-f f f ,……………4分此函数不具有性质P .(Ⅱ)假设)(i f 为(1),(2),,(1)f f f n -中第一个大于0的值,则0)1()(>--i f i f ,因为函数()f x 具有性质P ,所以,对于任意n ∈*N ,均有(1)()()(1)f n f n f n f n +-≥--,所以0)1()()2()1()1()(>--≥≥---≥--i f i f n f n f n f n f , 所以()[()(1)][(1)()]()0f n f n f n f i f i f i =--+++-+>, 与0)(=n f 矛盾,所以,对任意的{1,2,3,,1}i n ∈-有()0f i ≤. ……………9分(Ⅲ)不成立. 例如2()()x x n x f x x x -⎧=⎨⎩为有理数,为无理数.……………10分 证明:当x 为有理数时,1,1x x -+均为有理数,222(1)(1)2()(1)(1)2(112)2f x f x f x x x x n x x x -++-=-++---++-=, 当x 为无理数时,1,1x x -+均为无理数,22)1()1()(2)1()1(222=-++-=-++-x x x x f x f x f所以,函数)(x f 对任意的x ∈R ,均有)(2)1()1(x f x f x f ≥++-,即函数)(x f 具有性质P . ……………12分 而当],0[n x ∈(2n >)且当x 为无理数时,0)(>x f .所以,在(Ⅱ)的条件下,“对任意[0,]x n ∈均有0)(≤x f ”不成立.……………13分 (其他反例仿此给分,如0()1x x f x ⎧=⎨⎩为有理数,为无理数,,,0,()1,x x f x ⎧=⎨⎩为整数,为非整数,20,(),x x f x x ⎧=⎨⎩为整数,为非整数,等.)(2015年1月·海淀期末·19.本题满分12分已知定义在R 上的奇函数()f x 满足:“对于区间(0,)+∞上的任意,a b ,都有()()f a b f b +>成立”.(Ⅰ)求(0)f 的值,并指出()f x 在区间(0,)+∞上的单调性;(Ⅱ)用增函数的定义证明:函数()f x 是(,0)-∞上的增函数;(Ⅲ)判断()f x 是否为R 上的增函数,如果是,请给出证明;如果不是,请举出反例.19.本题满分12分解:(Ⅰ)因为()f x 是定义在R 上的奇函数, 所以(0)(0)f f =--,即(0)0f =.----------------------------------------------------2分 ()f x 在区间(0,)+∞上单调递增.------------------------------------------------------4分 (Ⅱ)法1:任取12,x x ∈(,0)-∞,且120x x x ∆=->,则120,0x x ->->,----------------5分 因为对于区间(0,)+∞上的任意,a b ,都有()()f a b f b +>成立, 所以211()()()f x f x x f x -=-+∆>-,即21()()0f x f x --->.-------------------7分 因为()f x 是定义在R 上的奇函数, 所以1221()()()()0y f x f x f x f x ∆=-=--->---------------------------------------8分 所以函数()f x 是(,0)-∞上的增函数.--------------------------------------------------9分 法2:任取12,x x ∈(,0)-∞,且120x x <<,则120x x ->->,且210x x ->,------5分 因为对于区间(0,)+∞上的任意,a b ,都有()()f a b f b +>成立, 所以2212[()]()f x x x f x -+->-,即12()()f x f x ->-.-----------------------------7分 因为()f x 是定义在R 上的奇函数, 所以12()()f x f x ->-,即12()()f x f x <,--------------------------------------------8分 所以函数()f x 是(,0)-∞上的增函数. --------------------------------------------------9分 (Ⅲ)()f x 不一定是R 上的增函数. ---------------------------------------------10分 反例如下: 令1,0,()0,0.x f x x x ⎧-≠⎪=⎨⎪=⎩或者1,0,()0,0,1,0.x x f x x x x ->⎧⎪==⎨⎪+<⎩-----------------------------------------12分。
