[配套K12]2017年中考数学专题练习 一元二次方程2(答案不全)
2017年中考数学专题训练一元二次方程.doc

一元二次方程一、选择1. 方程(m2 1)x2 mx 5 0 是关于x的一元二次方程,则m 的值不能是()A.0 B .12C . 1D .122. 一元二次方程 22x x 1的常数项为()A.-1 B .1 C .0 D .± 13. 一元二次方程 2(x1) 2 的解是()A. x1 1 2 ,x2 1 2B. x1 1 2 ,x2 1 2C. x1 3,x2 1D. x1 1,x2 32 x4. 把方程x 6 4 0的左边配成完全平方,正确的变形是()A.(x 3)2 9 B .(x3)2 13 C .(x3)2 5 D .( x 3)2 55. 方程(3x 1)( x 1)(4x 1)( x1) 的解是()A.x1 1,x 0 B .x1 1, x2 2 C .x1 2, x2 1 D .无解26. 若关于x 的方程2x2 ax a 2 0 有两个相等的实根,则a的值是()A.-4 B .4 C .4 或-4 D .27. 方程2x 3 x 1 1的解的情况是()A.有两个不相等的实数根 B .没有实数根C.有两个相等的实数根 D .有一个实数根8. 某商品原价200 元,连续两次降价a%后售价为148 元,下列所列方程正确的是()A. 200(1+a%) 2=148B. 200(1 -a%)2=148C. 200(1 -2a%)=148D. 200(1 -a2%)=148二、 填空题29. 一元二次方程 2x 1 6x的一般形式是,其中一次项系数是 .10. 认真观察下列方程,指出使用何种方法解比较适当:(1)22 1x + x = - ,应选用法;(2)2 x 2 x 1 x 2 x 4 ,应选用法;(3) 2x 2 3x 7 0 ,应选用 法.1211. xx2配成完全平方式需加上.12. 若关于 x 的方程 2 2x x k的一个根是 1,则另一个根是. 13. 若关于 x 的一元二次方程22xx k没有实数根,则k 的取值范是. 14. 以-3 和 7 为根且二次项系数为 1 的一元二次方程是 .215. 从正方形的铁皮上,截去2cm 宽的一条长方形,余下的面积是48cm,则原来的正方形铁皮的面积是.16.在实数范围内定义一种运算“*” ,其规则为2b 2a *b a,根据这个规则,方程(x 2 )*5 0的解为.三、解答题17. 用适当的方法解下列方程:(1)2 2x(x 1)4(2) 3x 64 0(3)(x 2)( x 3) 12 (4)23y 1 2 3y18.22 kx k已知方程(k 1)x 2 3 0.(1)k 取何值时,方程有一个实数根;(2)k 取何值时,方程有两个不相等的实数根;19.若关于x 的方程 2 4 3 0x x a 有实数根.(1)求a 的取值范围;(2)若a 为符合条件的最小整数,求此时方程的根.20.为了解决老百姓看病难的问题,卫生部门决定下调药品的价格.某种药品经过两次连续降价后,由每盒100 元下调至64 元,求这种药品平均每次降价的百分率是多少?21.百货商店服装柜在销售中发现:某品牌童装平均每天可售出20 件,每件盈利40 元.为3了迎接“六一决定采取适当的降价措售量,增加盈利,减 :如果每件童装降价 1 元,那么平均每天就可多售出 2 件.要 想平均种童装盈利 1200 元,那么每件降价多少元?22. 已知关于 x 的一元二次方程 2 2 2 0 x ax b , a 0, b 0 . (1)若方数确定a ,b的大小关系;(2)若 a ∶ b =2∶ 3 ,且 2x x 2 ,求 a ,b 的值. 1 2 参考答案一、选择题: 1.C ; 2. A ; 3.B ; 4.C ; 5.B ;6. B ;7.A ;8.B2x二、: 9. 2x 6 1 0 , 6; 10. (1)配方法;(2)因式分解法; (3)公式法; 11. 1 16; 12. 3; 13. k 1; 14.24 21 0xx ; 15. 64cm2;16.7, 3x 1x.2三、解答题:4317.(1)x 1 1,x 3 ;(2)方根;( 3) 1, 6 x 1 x;(4)y 1 y. 222318. (1)方程要有数根,是一元一次方程,因此系数是 0,即当 k ,方程是一元一次方程,它有根; (2)方程要有两个不相数根,此是一元二次方程,式0, 所以2 (2k) 4(k 1)(k 3) 0,即当3 k 且 k ,方程有两个不等 2 实根. 19. (1) 24 4(3 a) 4 4a . ∵该方程有实数根, ∴ 4 4a ≥ 0. 解得 a ≥1.(2)当符合条件的最小, a = 1. 2 4 4 0 方x x ,方程x 1 x 2 2 .2品平均每次降价的百分率是 x , 2意,得 100 1 x 64 . 2则1 x 0.64 . 1 x 0.8. x 0.2, x 2 1.8(意,舍去) .1 品平均每次降价 20%. x2每件降价x (40 ) 20 8 1200 x,解得 x 120,x 210 .4要尽快存,所以 x =20. 答:每件降价 20 元.22. (1) ∵ 关于 x 的一元二次方程22 2 0xax b 有实数根 ,∴ Δ= 2 2 (2a) 4b 0 ,有22a b , (a b)( a b) 0 .∵a 0,b 0 , ∴ a b 0, a b 0. ∴ a b .5。
【配套K12】山东省潍坊市2017年中考数学二模试卷(含解析)

2017年山东省潍坊市中考数学二模试卷一、选择题(本大题共12小题,在每个小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来,每小题选对得3分,错选、不选或选出的答案超过一个均记0分.)1.下列运算正确的是()A.a n•a2=a2n B.a3•a2=a6C.a n•(a2)n=a2n+2D.a2n﹣3÷a﹣3=a2n2.人工智能AlphaGo因在人机大战中大胜韩国围棋手李世石九段而声名显赫.它具有自我对弈学习能力,决战前已做了两千万局的训练(等同于一个人近千年的训练量).此处“两千万”用科学记数法表示为()A.0.2×107B.2×107C.0.2×108D.2×1083.如图,厂房屋顶人字形(等腰三角形)钢架的跨度BC=10米,∠B=36°,则中柱AD(D 为底边中点)的长是()A.5sin36°米B.5cos36°米C.5tan36°米D.10tan36°米4.已知关于x的分式方程+=1的解是非负数,则m的取值范围是()A.m>2 B.m≥2 C.m≥2且m≠3 D.m>2且m≠35.若关于x的方程x2﹣+cosα=0有两个相等的实数根,则锐角α为()A.30° B.45° C.60° D.75°6.已知一个圆锥体的三视图如图所示,则这个圆锥体的侧面积是()A.40π B.24π C.20 πD.12π7.如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为()A.35° B.40° C.50° D.65°8.如图,矩形ABCD中,AB=,BC=,点E在对角线BD上,且BE=1.8,连接AE并延长交DC于F,则等于()A.B.C.D.9.二次函数y=﹣x2+1的图象与x轴交于A、B两点,与y轴交于点C,下列说法错误的是()A.点C的坐标是(0,1) B.线段AB的长为2C.△ABC是等腰直角三角形D.当x>0时,y随x增大而增大10.如图,⊙C过原点,与x轴、y轴分别交于A、D两点.已知∠OBA=30°,点D的坐标为(0,2),则⊙C半径是()A.B.C. D.211.如图,在菱形ABCD中,∠B=45°,以点A为圆心的扇形与BC,CD相切,向这样一个靶子上随意抛一枚飞镖,则飞镖插在阴影区域的概率为()A .1﹣B .C .1﹣D .12.如图,边长分别为1和2的两个等边三角形,开始它们在左边重合,大三角形固定不动,然后把小三角形自左向右平移直至移出大三角形外停止.设小三角形移动的距离为x ,两个三角形重叠面积为y ,则y 关于x 的函数图象是( )A .B .C .D .二、填空题(本大题共6小题,共18分.只要求填写最后结果,每小题填对得3分.)13.分解因式:x 2﹣y 2﹣3x ﹣3y= .14.计算﹣|2﹣2cos30°|+()﹣1﹣(1﹣π)0的结果是 . 15.如图,已知函数y=ax+b 与函数y=kx ﹣3的图象交于点P (4,﹣6),则不等式ax+b ≤kx ﹣3<0的解集是 .16.计算: = .17.如图,已知正方形ABCD 的对角线交于点O ,过O 点作OE ⊥OF ,分别交AB 、BC 于E 、F ,若AE=4,CF=3,则EF 等于 .18.手机上常见的wifi标志如图所示,它由若干条圆心相同的圆弧组成,其圆心角为90°,最小的扇形半径为1.若每两个相邻圆弧的半径之差为1,由里往外的阴影部分的面积依次记为S1、S2、S3…,则S1+S2+S3+…+S20= .三、解答题(本大题共7小题,共66分.解答要写出文字说明、证明过程或演算步骤)19.某校数学课题学习小组在“测量教学楼高度”的活动中,设计了以下两种方案:请你选择其中的一种方法,求教学楼的高度(结果保留整数)20.目前中学生带手机进校园现象越来越受到社会关注,针对这种现象,某校数学兴趣小组的同学随机调查了学校若干名家长对“中学生带手机”现象的态度(态度分为:A.无所谓;B.基本赞成;C.赞成;D.反对),并将调查结果绘制成频数折线统计图1和扇形统计图2(不完整).请根据图中提供的信息,解答下列问题:(1)此次抽样调查中,共调查了多少名中学生家长;(2)求出图2中扇形C所对的圆心角的度数,并将图1补充完整;(3)根据抽样调查结果,请你估计1万名中学生家长中有多少名家长持反对态度;(4)在此次调查活动中,初三(1)班和初三(2)班各有2位家长对中学生带手机持反对态度,现从这4位家长中选2位家长参加学校组织的家校活动,用列表法或画树状图的方法求选出的2人来自不同班级的概率.21.小明早晨从家里出发匀速步行去上学,小明的妈妈在小明出发后10分钟,发现小明的数学课本没带,于是她带上课本立即匀速骑车按小明上学的路线追赶小明,结果与小明同时到达学校.已知小明在整个上学途中,他出发后t分钟时,他所在的位置与家的距离为s 千米,且s与t之间的函数关系的图象如图中的折线段OA﹣AB所示.(1)试求折线段OA﹣AB所对应的函数关系式;(2)请解释图中线段AB的实际意义;(3)请在所给的图中画出小明的妈妈在追赶小明的过程中,她所在位置与家的距离s(千米)与小明出发后的时间t(分钟)之间函数关系的图象.(友情提醒:请对画出的图象用数据作适当的标注)22.LED灯具有环保节能、投射范围大、无频闪、使用寿命较长等特点,在日常生活中,人们更倾向于LED灯的使用,某校数学兴趣小组为了解LED灯泡与普通白炽灯泡的销售情况,进行了市场调查:某商场购进一批30瓦的LED灯泡和普通白炽灯泡进行销售,其进价与标价如下表:(1)该商场购进了LED灯泡与普通白炽灯泡共300个,LED灯泡按标价进行销售,而普通白炽灯泡打九折销售,当销售完这批灯泡后可以获利3200元,求该商场购进LED灯泡与普通白炽灯泡的数量分别为多少个?(2)由于春节期间热销,很快将两种灯泡销售完,若该商场计划再次购进两种灯泡120个,在不打折的情况下,请问如何进货,销售完这批灯泡时获利最多且不超过进货价的30%,并求出此时这批灯泡的总利润为多少元?23.如图1,若△ABC和△ADE为等边三角形,M,N分别为EB,CD的中点,易证:CD=BE,△AMN是等边三角形:(1)当把△ADE绕点A旋转到图2的位置时,CD=BE吗?若相等请证明,若不等于请说明理由;(2)当把△ADE绕点A旋转到图3的位置时,△AMN还是等边三角形吗?若是请证明,若不是,请说明理由(可用第一问结论).24.如图,在Rt△ABC中,∠C=90°,sinA=,AB=10,点O为AC上一点,以OA为半径作⊙O交AB于点D,BD的中垂线分别交BD,BC于点E,F,连结DF.(1)求证:DF为⊙O的切线;(2)若AO=x,DF=y,求y与x之间的函数关系式.25.如图,在等腰三角形ABC中,AB=AC,以底边BC的垂直平分线和BC所在的直线建立平面直角坐标系,抛物线y=﹣x2+x+4经过A、B两点.(1)写出点A、点B的坐标;(2)若一条与y轴重合的直线l以每秒2个单位长度的速度向右平移,分别交线段OA、CA 和抛物线于点E、M和点P,连接PA、PB.设直线l移动的时间为t(0<t<4)秒,求四边形PBCA的面积S(面积单位)与t(秒)的函数关系式,并求出四边形PBCA的最大面积;(3)在(2)的条件下,抛物线上是否存在一点P,使得△PAM是直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.2017年山东省潍坊市中考数学二模试卷参考答案与试题解析一、选择题(本大题共12小题,在每个小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来,每小题选对得3分,错选、不选或选出的答案超过一个均记0分.)1.下列运算正确的是()A.a n•a2=a2n B.a3•a2=a6C.a n•(a2)n=a2n+2D.a2n﹣3÷a﹣3=a2n【考点】48:同底数幂的除法;46:同底数幂的乘法;47:幂的乘方与积的乘方;6F:负整数指数幂.【分析】根据同底数幂的除法法则、同底数幂的乘法法则计算,判断即可.【解答】解:a n•a2=a2+n,A选项错误;a3•a2=a5,B选项错误;a n•(a2)n=a3n,C选项错误;a2n﹣3÷a﹣3=a2n,D选项正确,故选:D.2.人工智能AlphaGo因在人机大战中大胜韩国围棋手李世石九段而声名显赫.它具有自我对弈学习能力,决战前已做了两千万局的训练(等同于一个人近千年的训练量).此处“两千万”用科学记数法表示为()A.0.2×107B.2×107C.0.2×108D.2×108【考点】1I:科学记数法—表示较大的数.【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.【解答】解:将“两千万”用科学记数法表示为:2×107,故选:B3.如图,厂房屋顶人字形(等腰三角形)钢架的跨度BC=10米,∠B=36°,则中柱AD(D为底边中点)的长是()A.5sin36°米B.5cos36°米C.5tan36°米D.10tan36°米【考点】T8:解直角三角形的应用.【分析】根据等腰三角形的性质得到DC=BD=5米,在Rt△ABD中,利用∠B的正切进行计算即可得到AD的长度.【解答】解:∵AB=AC,AD⊥BC,BC=10米,∴DC=BD=5米,在Rt△ADC中,∠B=36°,∴tan36°=,即AD=BD•tan36°=5tan36°(米).故选:C.4.已知关于x的分式方程+=1的解是非负数,则m的取值范围是()A.m>2 B.m≥2 C.m≥2且m≠3 D.m>2且m≠3【考点】B2:分式方程的解.【分析】分式方程去分母转化为整式方程,求出整式方程的解表示出x,根据方程的解为非负数求出m的范围即可.【解答】解:分式方程去分母得:m﹣3=x﹣1,解得:x=m﹣2,由方程的解为非负数,得到m﹣2≥0,且m﹣2≠1,解得:m≥2且m≠3.故选:C5.若关于x的方程x2﹣+cosα=0有两个相等的实数根,则锐角α为()A.30° B.45° C.60° D.75°【考点】AA:根的判别式;T5:特殊角的三角函数值.【分析】根据根与系数的关系,将原式转化为关于cosα的方程,然后根据特殊角的三角函数值解答.【解答】解:∵关于x的方程x2﹣+cosα=0有两个相等的实数根,∴△=0,即﹣4×1×cosα=0,∴cosα=,∴α=60°.故选C.6.已知一个圆锥体的三视图如图所示,则这个圆锥体的侧面积是()A.40π B.24π C.20 πD.12π【考点】U3:由三视图判断几何体;MP:圆锥的计算.【分析】先利用三视图得到底面圆的半径为4,圆锥的高为3,再根据勾股定理计算出母线长l为5,然后根据圆锥的侧面积公式:S侧=πrl代入计算即可.【解答】解:根据三视图得到圆锥的底面圆的直径为8,即底面圆的半径r为4,圆锥的高为3,所以圆锥的母线长l==5,所以这个圆锥的侧面积是π×4×5=20π.故选C.7.如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为()A.35° B.40° C.50° D.65°【考点】R2:旋转的性质.【分析】根据两直线平行,内错角相等可得∠ACC′=∠CAB,根据旋转的性质可得AC=AC′,然后利用等腰三角形两底角相等求∠CAC′,再根据∠CAC′、∠BAB′都是旋转角解答.【解答】解:∵CC′∥AB,∴∠ACC′=∠C AB=65°,∵△ABC绕点A旋转得到△AB′C′,∴AC=AC′,∴∠CAC′=180°﹣2∠ACC′=180°﹣2×65°=50°,∴∠CAC′=∠BAB′=50°.故选C.8.如图,矩形ABCD中,AB=,BC=,点E在对角线BD上,且BE=1.8,连接AE并延长交DC于F,则等于()A.B.C.D.【考点】S9:相似三角形的判定与性质;LB:矩形的性质.【分析】根据勾股定理求出BD,得到DE的长,根据相似三角形的性质得到比例式,代入计算即可求出DF的长,求出CF,计算即可.【解答】解:∵四边形ABCD是矩形,∴∠BAD=90°,又AB=,BC=,∴BD==3,∵BE=1.8,∴DE=3﹣1.8=1.2,∵AB∥CD,∴=,即=,解得,DF=,则CF=CD﹣DF=,∴==,故选A.9.二次函数y=﹣x2+1的图象与x轴交于A、B两点,与y轴交于点C,下列说法错误的是()A.点C的坐标是(0,1) B.线段AB的长为2C.△ABC是等腰直角三角形D.当x>0时,y随x增大而增大【考点】HA:抛物线与x轴的交点;H3:二次函数的性质.【分析】判断各选项,点C的坐标可以令x=0,得到的y值即为点C的纵坐标;令y=0,得到的两个x值即为与x轴的交点坐标A、B;且AB的长也有两点坐标求得,对函数的增减性可借助函数图象进行判断.【解答】解:A,令x=0,y=1,则C点的坐标为(0,1),正确;B,令y=0,x=±1,则A(﹣1,0),B(1,0),|AB|=2,正确;C,由A、B、C三点坐标可以得出AC=BC,且AC2+BC2=AB2,则△ABC是等腰直角三角形,正确;D,当x>0时,y随x增大而减小,错误.故选D.10.如图,⊙C过原点,与x轴、y轴分别交于A、D两点.已知∠OBA=30°,点D的坐标为(0,2),则⊙C半径是()A.B.C. D.2【考点】M2:垂径定理;D5:坐标与图形性质;M5:圆周角定理.【分析】连接AD.根据90°的圆周角所对的弦是直径,得AD是直径,根据等弧所对的圆周角相等,得∠D=∠B=30°,运用解直角三角形的知识即可求解.【解答】解:连接AD.∵∠AOD=90°,∴AD是圆的直径.在直角三角形AOD中,∠D=∠B=30°,OD=2,∴AD==.则圆的半径是.故选B.11.如图,在菱形ABCD中,∠B=45°,以点A为圆心的扇形与BC,CD相切,向这样一个靶子上随意抛一枚飞镖,则飞镖插在阴影区域的概率为()A.1﹣B.C.1﹣D.【考点】X5:几何概率;MC:切线的性质.【分析】根据切线的性质得到AE⊥BC,根据投资研究得到AE=BE=AB,根据求概率的公式即可得到结论.【解答】解:如图,设切点为E,F,连接AE,∵以点A为圆心的扇形与BC,CD相切,∴AE⊥BC,∵∠B=45°,∴AE=BE=AB,∠BAC=135°,∴S菱形ABCD=BC•AE=AB2,S阴影=S菱形﹣S扇形=AB2﹣=πAB2,∴飞镖插在阴影区域的概率=1﹣,故选A.12.如图,边长分别为1和2的两个等边三角形,开始它们在左边重合,大三角形固定不动,然后把小三角形自左向右平移直至移出大三角形外停止.设小三角形移动的距离为x,两个三角形重叠面积为y,则y关于x的函数图象是()A.B.C.D.【考点】E7:动点问题的函数图象.【分析】根据题目提供的条件可以求出函数的解析式,根据解析式判断函数的图象的形状.【解答】解:①x≤1时,两个三角形重叠面积为小三角形的面积,∴y=×1×=,②当1<x≤2时,重叠三角形的边长为2﹣x,高为,y=(2﹣x)×=x2﹣x+,③当x=2时,两个三角形没有重叠的部分,即重叠面积为0,故选:B.二、填空题(本大题共6小题,共18分.只要求填写最后结果,每小题填对得3分.)13.分解因式:x2﹣y2﹣3x﹣3y= (x+y)(x﹣y﹣3).【考点】56:因式分解﹣分组分解法.【分析】根据观察可知,此题有4项且前2项适合平方差公式,后2项可提公因式,分解后也有公因式(x+y),直接提取即可.【解答】解:x2﹣y2﹣3x﹣3y,=(x2﹣y2)﹣(3x+3y),=(x+y)(x﹣y)﹣3(x+y),=(x+y)(x﹣y﹣3).14.计算﹣|2﹣2cos30°|+()﹣1﹣(1﹣π)0的结果是2+1 .【考点】2C:实数的运算;6E:零指数幂;6F:负整数指数幂;T5:特殊角的三角函数值.【分析】原式利用二次根式性质,绝对值的代数意义,零指数幂、负整数指数幂法则计算即可得到结果.【解答】解:原式=3﹣+2﹣1=2+1,故答案为:2+115.如图,已知函数y=ax+b与函数y=kx﹣3的图象交于点P(4,﹣6),则不等式ax+b≤kx ﹣3<0的解集是﹣4<x≤4 .【考点】FD:一次函数与一元一次不等式.【分析】先把P点坐标代入y=kx﹣3得k=﹣,则可确定函数y=﹣x﹣3与x轴的交点坐标,然后利用函数图象写出在x轴下方,且直线y=ax+b不在直线y=kx﹣3上方所对应的自变量的范围即可.【解答】解:如图,把P(4,﹣6)代入y=kx﹣3得4k﹣3=﹣6,解得k=﹣,则y=0时,y=﹣x﹣3=0,解得x=﹣4,所以不等式ax+b≤kx﹣3<0的解集为﹣4<x≤4.故答案为﹣4<x≤4.16.计算: = .【考点】6B:分式的加减法.【分析】原式通分并利用同分母分式的加减法则计算即可得到结果.【解答】解:原式===,故答案为:17.如图,已知正方形ABCD的对角线交于点O,过O点作OE⊥OF,分别交AB、BC于E、F,若AE=4,CF=3,则EF等于 5 .【考点】LE:正方形的性质;KD:全等三角形的判定与性质.【分析】由△BOF全等于△AOE,得到BF=AE=4,在直角△BEF中,从而求得EF的值.【解答】解:解:∵正方形ABCD中,OB=OC,∠BOC=∠EOF=90°,∴∠EOB=∠FOC,在△BOE和△COF中,,∴△BOE和COF全等(ASA),∴BF=AE=4,∵AB=BC,∴BE=CF=3,在Rt△BEF中,BF=4,BE=3,∴EF=5.故答案为5;18.手机上常见的wifi标志如图所示,它由若干条圆心相同的圆弧组成,其圆心角为90°,最小的扇形半径为1.若每两个相邻圆弧的半径之差为1,由里往外的阴影部分的面积依次记为S1、S2、S3…,则S1+S2+S3+…+S20= 195π.【考点】MO:扇形面积的计算.【分析】先利用扇形的面积公式分别计算出S1=π;S2=π+π;S3=π+2π,则利用此规律得到S20=π+19π,然后把它们相加即可.【解答】解:S1=π•12=π;S2=π•(32﹣22)=π+π;S3=π•(52﹣42)=π+2π;…S 20=π+19π;∴S 1+S 2+S 3+…+S 20=5π+(1+2+3+…+19)π=195π. 故答案为195π.三、解答题(本大题共7小题,共66分.解答要写出文字说明、证明过程或演算步骤) 19.某校数学课题学习小组在“测量教学楼高度”的活动中,设计了以下两种方案:请你选择其中的一种方法,求教学楼的高度(结果保留整数) 【考点】T8:解直角三角形的应用.【分析】若选择方法一,在Rt △BGC 中,根据CG=即可得出CG 的长,同理,在Rt △ACG 中,根据tan ∠ACG=可得出AG 的长,根据AB=AG+BG 即可得出结论.若选择方法二,在Rt △AFB 中由tan ∠AFB=可得出FB 的长,同理,在Rt △ABE 中,由tan∠AEB=可求出EB 的长,由EF=EB ﹣FB 且EF=10,可知﹣=10,故可得出AB的长.【解答】解:若选择方法一,解法如下:在Rt △BGC 中,∠BGC=90°,∠BCG=13°,BG=CD=6.9,∵CG=≈=30,在Rt△ACG中,∠AGC=90°,∠ACG=22°,∵tan∠ACG=,∴AG=30×tan22°≈30×0.40=12,∴AB=AG+BG=12+6.9≈19(米).答:教学楼的高度约19米.若选择方法二,解法如下:在Rt△AFB中,∠ABF=90°,∠AFB=43°,∵tan∠AFB=,∴FB=≈,在Rt△ABE中,∠ABE=90°,∠AEB=32°,∵tan∠AEB=,∴EB=≈,∵EF=EB﹣FB且EF=10,∴﹣=10,解得AB=18.6≈19(米).答:教学楼的高度约19米.20.目前中学生带手机进校园现象越来越受到社会关注,针对这种现象,某校数学兴趣小组的同学随机调查了学校若干名家长对“中学生带手机”现象的态度(态度分为:A.无所谓;B.基本赞成;C.赞成;D.反对),并将调查结果绘制成频数折线统计图1和扇形统计图2(不完整).请根据图中提供的信息,解答下列问题:(1)此次抽样调查中,共调查了多少名中学生家长;(2)求出图2中扇形C所对的圆心角的度数,并将图1补充完整;(3)根据抽样调查结果,请你估计1万名中学生家长中有多少名家长持反对态度;(4)在此次调查活动中,初三(1)班和初三(2)班各有2位家长对中学生带手机持反对态度,现从这4位家长中选2位家长参加学校组织的家校活动,用列表法或画树状图的方法求选出的2人来自不同班级的概率.【考点】X6:列表法与树状图法;V5:用样本估计总体;V9:频数(率)分布折线图;VB:扇形统计图.【分析】(1)用B类的人数除以它所占的百分比即可得到调查的总人数;(2)用360°乘以C类所占的百分比得到扇形C所对的圆心角的度数,再计算出C类人数,然后补全条形统计图;(3)用10000乘以D类的百分比可估计持反对态度的家长的总数;(4)画树状图展示所有12种等可能的结果数,再找出2人来自不同班级的结果数,然后根据概率公式求解.【解答】解:(1)共调查的中学生家长数是:40÷20%=200(人);(2)扇形C所对的圆心角的度数是:360°×(1﹣20%﹣15%﹣60%)=18°,C类的人数是:200×(1﹣20%﹣15%﹣60%)=10(人),补图如下:(3)根据题意得:10000×60%=6000(人),答:10000名中学生家长中有6000名家长持反对态度;(4)设初三(1)班两名家长为A1,A2,初三(2)班两名家长为B1,B2,画树状图为:共有12种等可能的结果数,其中2人来自不同班级共有8种,所以选出的2人来自不同班级的概率==.21.小明早晨从家里出发匀速步行去上学,小明的妈妈在小明出发后10分钟,发现小明的数学课本没带,于是她带上课本立即匀速骑车按小明上学的路线追赶小明,结果与小明同时到达学校.已知小明在整个上学途中,他出发后t分钟时,他所在的位置与家的距离为s 千米,且s与t之间的函数关系的图象如图中的折线段OA﹣AB所示.(1)试求折线段OA﹣AB所对应的函数关系式;(2)请解释图中线段AB的实际意义;(3)请在所给的图中画出小明的妈妈在追赶小明的过程中,她所在位置与家的距离s(千米)与小明出发后的时间t(分钟)之间函数关系的图象.(友情提醒:请对画出的图象用数据作适当的标注)【考点】FH:一次函数的应用.【分析】(1)OA为正比例函数图象,可以用待定系数法求出;(2)AB段离家距离没发生变化说明在以家为圆心做曲线运动;(3)妈妈的速度正好是小明的2倍,所以妈妈走弧线路用(20﹣12)÷2=4分钟.【解答】解:(1)线段OA对应的函数关系式为:s=t(0≤t≤12)线段AB对应的函数关系式为:s=1(12<t≤20);(2)图中线段AB的实际意义是:小明出发12分钟后,沿着以他家为圆心,1千米为半径的圆弧形道路上匀速步行了8分钟;(3)由图象可知,小明花20分钟到达学校,则小明的妈妈花20﹣10=10分钟到达学校,可知小明妈妈的速度是小明的2倍,即:小明花12分钟走1千米,则妈妈花6分钟走1千米,故D(16,1),小明花20﹣12=8分钟走圆弧形道路,则妈妈花4分钟走圆弧形道路,故B (20,1).妈妈的图象经过(10,0)(16,1)(20,1)如图中折线段CD﹣DB就是所作图象.22.LED灯具有环保节能、投射范围大、无频闪、使用寿命较长等特点,在日常生活中,人们更倾向于LED灯的使用,某校数学兴趣小组为了解LED灯泡与普通白炽灯泡的销售情况,进行了市场调查:某商场购进一批30瓦的LED灯泡和普通白炽灯泡进行销售,其进价与标价如下表:(1)该商场购进了LED灯泡与普通白炽灯泡共300个,LED灯泡按标价进行销售,而普通白炽灯泡打九折销售,当销售完这批灯泡后可以获利3200元,求该商场购进LED灯泡与普通白炽灯泡的数量分别为多少个?(2)由于春节期间热销,很快将两种灯泡销售完,若该商场计划再次购进两种灯泡120个,在不打折的情况下,请问如何进货,销售完这批灯泡时获利最多且不超过进货价的30%,并求出此时这批灯泡的总利润为多少元?【考点】FH:一次函数的应用;9A:二元一次方程组的应用.【分析】(1)设该商场购进LED灯泡x个,普通白炽灯泡的数量为y个,利用该商场购进了LED灯泡与普通白炽灯泡共300个和销售完这批灯泡后可以获利3200元列方程组,然后解方程组即可;(2)设该商场购进LED灯泡a个,则购进普通白炽灯泡个,这批灯泡的总利润为W元,利用利润的意义得到W=(60﹣45)a+(30﹣25)=10a+600,再根据销售完这批灯泡时获利最多且不超过进货价的30%可确定a的范围,然后根据一次函数的性质解决问题.【解答】解:(1)设该商场购进LED灯泡x个,普通白炽灯泡的数量为y个,根据题意得,解得,答:该商场购进LED灯泡与普通白炽灯泡的数量分别为200个和100个;(2)设该商场购进LED灯泡a个,则购进普通白炽灯泡个,这批灯泡的总利润为W元,根据题意得W=(60﹣45)a+(30﹣25)=10a+600,∵10a+600≤[45a+25]×30%,解得a≤75,∵k=10>0,∴W随a的增大而增大,∴a=75时,W最大,最大值为1350,此时购进普通白炽灯泡=45个.答:该商场购进LED灯泡75个,则购进普通白炽灯泡45个,这批灯泡的总利润为1350元.23.如图1,若△ABC和△ADE为等边三角形,M,N分别为EB,CD的中点,易证:CD=BE,△AMN是等边三角形:(1)当把△ADE绕点A旋转到图2的位置时,CD=BE吗?若相等请证明,若不等于请说明理由;(2)当把△ADE绕点A旋转到图3的位置时,△AMN还是等边三角形吗?若是请证明,若不是,请说明理由(可用第一问结论).【考点】KM:等边三角形的判定与性质;KD:全等三角形的判定与性质;R2:旋转的性质.【分析】(1)CD=BE.利用“等边三角形的三条边相等、三个内角都是60°”的性质证得△ABE≌△ACD;然后根据全等三角形的对应边相等即可求得结论CD=BE;(2)△AMN是等边三角形.首先利用全等三角形“△ABE≌△ACD”的对应角相等、已知条件“M、N分别是BE、CD的中点”、等边△ABC的性质证得△ABM≌△ACN;然后利用全等三角形的对应边相等、对应角相等求得AM=AN、∠NAM=∠NAC+∠CAM=∠MAB+∠CAM=∠BAC=60°,所以有一个角是60°的等腰三角形的正三角形.【解答】解:(1)CD=BE.理由如下:∵△ABC和△ADE为等边三角形,∴AB=AC,AD=AE,∠BAC=∠EAD=60°,∵∠BAE=∠BAC﹣∠EAC=60°﹣∠EAC,∠DAC=∠DAE﹣∠EAC=60°﹣∠EAC,∴∠BAE=∠DAC,在△ABE和△ACD中,,∴△ABE≌△ACD(SAS)∴CD=BE;(2)△AMN是等边三角形.理由如下:∵△ABE≌△ACD,∴∠ABE=∠ACD.∵M、N分别是BE、CD的中点,∴BM=CN∵AB=AC,∠ABE=∠ACD,在△ABM和△ACN中,,∴△ABM≌△ACN(SAS).∴AM=AN,∠MAB=∠NAC.∴∠NAM=∠NAC+∠CAM=∠MAB+∠CAM=∠BAC=60°∴△AMN是等边三角形.24.如图,在Rt△ABC中,∠C=90°,sinA=,AB=10,点O为AC上一点,以OA为半径作⊙O交AB于点D,BD的中垂线分别交BD,BC于点E,F,连结DF.(1)求证:DF为⊙O的切线;(2)若AO=x,DF=y,求y与x之间的函数关系式.【考点】ME:切线的判定与性质;KG:线段垂直平分线的性质;T7:解直角三角形.【分析】(1)连接OD,由于EF是BD的中垂线,DF=BF.从而可知∠FDB=∠B,又因为OA=OD,所以∠OAD=∠ODA,从而可证明∠ODF=90°;(2)连接OF,由题意可知:AO=x,DF=y,OC=6﹣x,CF=8﹣y,然后在Rt△COF中与Rt△ODF 中利用勾股定理分别求出OF,化简原式即可求出答案.【解答】(1)连接OD.∵OA=OD,∴∠OAD=∠ODA,∵EF是BD的中垂线,∴DF=BF.∴∠FDB=∠B,∵∠C=90°,∴∠OAD+∠B=90°.∴∠ODA+∠FDB=90°.∴∠ODF=90°,又∵OD为⊙O的半径,∴DF为⊙O的切线,(2)连接OF.在Rt△ABC中,∵∠C=90°,sinA=,AB=10,∴AC=6,BC=8,∵AO=x,DF=y,∴OC=6﹣x,CF=8﹣y,在Rt△COF中,OF2=(6﹣x)2+(8﹣x)2在Rt△ODF中,OF2=x2+y2∴(6﹣x)2+(8﹣x)2=x2+y2,∴y=﹣x+(0<x≤6)25.如图,在等腰三角形ABC中,AB=AC,以底边BC的垂直平分线和BC所在的直线建立平面直角坐标系,抛物线y=﹣x2+x+4经过A、B两点.(1)写出点A、点B的坐标;(2)若一条与y轴重合的直线l以每秒2个单位长度的速度向右平移,分别交线段OA、CA 和抛物线于点E、M和点P,连接PA、PB.设直线l移动的时间为t(0<t<4)秒,求四边形PBCA的面积S(面积单位)与t(秒)的函数关系式,并求出四边形PBCA的最大面积;(3)在(2)的条件下,抛物线上是否存在一点P,使得△PAM是直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.【考点】HF:二次函数综合题.【分析】(1)抛物线的解析式中,令x=0,能确定点B的坐标;令y=0,能确定点A的坐标.(2)四边形PBCA可看作△ABC、△PBA两部分;△ABC的面积是定值,关键是求出△PBA的面积表达式;若设直线l与直线AB的交点为Q,先用t表示出线段PQ的长,而△PAB的面积可由(PQ•OA)求得,在求出S、t的函数关系式后,由函数的性质可求得S的最大值.(3)△PAM中,∠APM是锐角,而PM∥y轴,∠AMP=∠ACO也不可能是直角,所以只有∠PAC 是直角一种可能,即直线AP、直线AC垂直,此时两直线的斜率乘积为﹣1,先求出直线AC 的解析式,联立抛物线的解析式后可求得点P的坐标.【解答】解:(1)抛物线y=﹣x 2+x+4中:令x=0,y=4,则 B (0,4);令y=0,0=﹣x 2+x+4,解得 x 1=﹣1、x 2=8,则 A (8,0);∴A (8,0)、B (0,4).(2)△ABC 中,AB=AC ,AO ⊥BC ,则OB=OC=4,∴C (0,﹣4).由A (8,0)、B (0,4),得:直线AB :y=﹣x+4;依题意,知:OE=2t ,即 E (2t ,0);∴P (2t ,﹣2t 2+7t+4)、Q (2t ,﹣t+4),PQ=(﹣2t 2+7t+4)﹣(﹣t+4)=﹣2t 2+8t ;S=S △ABC +S △PAB =×8×8+×(﹣2t 2+8t )×8=﹣8t 2+32t+32=﹣8(t ﹣2)2+64; ∴当t=2时,S 有最大值,且最大值为64.(3)∵PM ∥y 轴,∴∠AMP=∠ACO <90°;而∠APM 是锐角,所以△PAM 若是直角三角形,只能是∠PAM=90°;由A (8,0)、C (0,﹣4),得:直线AC :y=x ﹣4;所以,直线AP 可设为:y=﹣2x+h ,代入A (8,0),得:﹣16+h=0,h=16∴直线AP :y=﹣2x+16,联立抛物线的解析式,得:,解得、 ∴存在符合条件的点P ,且坐标为(3,10).。
初三数学一元二次方程应用题及答案(K12教育文档)

初三数学一元二次方程应用题及答案(word版可编辑修改)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(初三数学一元二次方程应用题及答案(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为初三数学一元二次方程应用题及答案(word版可编辑修改)的全部内容。
第1章(九上)一元二次方程解决问题一、选择1、某电视机厂计划用两年的时间把某种型号的电视机的成本降低36%, 若每年下降的百分数相同,则这个百分数为 ( )A 、10% B 、20% C 、120% D 、180%2、某超市一月份的营业额为200万元,已知第一季度的总营业额共1000万元, 如果平均每月增长率为x ,则由题意列方程应为 ( )A 、200(1+x )2=1000 B 、200+200×2x=1000 C 、200+200×3x=1000 D 、200[1+(1+x )+(1+x)2]=10003、某农户种植花生,原来种植的花生亩产量为200千克,出油率为50%(即每100千克花生可加工成花生油50千克).现在种植新品种花生后,每亩收获的花生可加工成花生油132千克,其中花生出油率的增长率是亩产量的增长率的21.则新品种花生亩产量的增长率为 ( )A 、20% B 、30% C 、50% D 、120%4、若两个连续整数的积是56,则它们的和是 ( ) A 、±15 B、15 C 、-15 D 、11二、填空5、市政府为了解决市民看病难的问题,决定下调药品的价格.某种药品经过连续两次降价后,由每盒200元下调至128元,求这种药品平均每次降价的百分率是 。
2017-2018年中考数学专题复习题一元二次方程(含解析)

2017-2018年中考数学专题复习题:一元二次方程、选择题1.若一元二次方程」J 的常数项是0,则m 等于,2. 已知m 是方程'1 , . 1_匚的一个根,则:川一扛仁“厶的值为| ,mna 4-i3.一元二次方程.1 —的两个实数根中较大的根是,5.若关于x 的一元二次方程^ . ' [ - ■有实数根,则k 的取值范围是C )A.; _ 16.若a ,b 是方程.一.J,i L.- 的两根,则 …7.给出一种运算:对于函数A ':,规定 -_-例如:若函数T ,则有厂-I '■已知函数-',则方程’I 的解是||A. 一 dB. 3C. 二D. 9A. 2016B. 2015C.3D 17 116D.3D 16 3D IS4. A. C. D.-L1-V5将方程•:.; - \配方后,原方程变形为A . -iB. I ' - I C .D.C. ::A. 2016B. 2015C.2014D.2012形的周长可以是I II ■ - ■' D.- - I :公园有一块正方形的空地, 后来从这块空地上划出部分区域栽种鲜花(如图〉,原空地一边减少了 i m 另一边减少了 2m剩余空地的面积为亠.,求原正方形空地的边长,设原正方形的空地的边长为xm ,则可列方程为A. I ■' - I : B. ..- <C. I .- I :D.上:;、填空题11. 已知实数m 满足+ ,则代数式 + .的值等于•12.方程jc z - 1- 0的根为 13.若 兀二次方程伍卅十b 尤+ c = 0( 口、b 、c 为吊数,口 = 0】有解,则解为 14. 已知实数 m n 满足.- 一,则代数式」..1 :1的最小值等于A.B.「】•, X -;:C.D. _;•.、, 「一 / ■ ?8.已知等腰三角形的腰和底的长分别是一元二次方程.:-〔I 的根,则该三角A. 5B. 7C. 5 或 7D. 109.有x 支球队参加篮球比赛,共比赛了45场,每两队之间都比赛一场,则下列方程A.丨一B. : 「—人C.10.15.若关于x的一元二次方程.[一有两个相等的实数根,则k的值为16.17.18.19.20. 刘谦的魔术表演风靡全国,小明也学起了刘谦发明了一个魔术盒,当任意实数对..进入其中时,会得到一个新的实数:,例如把放入其中,就会得到■: ■- | . “现将实数对:二-勺:■:放入其中,得到实数2,贝y用= _________ •已知一元二次方程x2+ 3x —4= 0的两根为莖]、莖之,则工:+井化+ £ =_____________________ 设•;、是方程_ - 的两根,则J ■: I I . ■■- ■[「一________已知「,一二是关于x的一元二次方程];.-■_的两个实数根,且则艮= _________ .O1=22如图,在边长为6cm正方形ABCD^,点P从点A开始沿AB边向点B以丨,「的速度移动,点Q从点B开始沿BC和CD边向D点以•的速度移动,如果点P、Q分别从AB同时出发,其中一点到终点,另一点也随之停止•过了_______ 秒钟后,匕卩RQ的面积等于&C3F! H•三、计算题21.在实数范围内定义一种新运算,规定: - .求方程':.■ 2- 5 G的解.22. 已知关于x的一元二次方程;I . :一■:.I.】求证:无论m取何值,原方程总有两个不相等的实数根;当m为何整数时,原方程的根也是整数.23. 先阅读理解下面的例题,再按要求解答下列问题:例题:求代数式严一J ;: 41;的最小值.解:,■.;—・1・丨丨一•^ :v (y + 2)2>0;.(y+2)2 + 4 > 4■■- - i / - V的最小值是4..求代数式:-::亠:亠'的最小值;求代数式4 /「小的最大值;(3某居民小区要在一块一边靠墙(墙长15冏的空地上建一个长方形花园ABCD花园一边靠墙,另三边用总长为20m的栅栏围成’如图,设1 「,请问:当x取何值时,花园的面积最大?最大面积是多少?24. 某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量I千克与每千克售价.元■满足一次函数关系,部分数据如下表:I求y与x之间的函数表达式;丄设商品每天的总利润为.•元,则当售价x定为多少元时,厂商每天能获得最大利润?最大利润是多少?J.如果超市要获得每天不低于1350元的利润,且符合超市自己的规定,那么该商品每千克售价的取值范围是多少?请说明理由.11. 914. 4 15. 616. 3 或一 117. 1318. —「■产22..证明:- 】. -. | - I . 一 '■■ - | -,-. I •;,则无论m 取何实数时,原方程总有两个不相等的实数根; (V 解:关于x 的一元二次方程-::,:.-■.,利用公式法解得:•- ■- :要使原方程的根是整数,必须使得 W 了卜彳是完全平方数, 设 I -.,变形得:j . -■,「一 一丄和■-.- 一的奇偶性相同,【答案】1. B2. C 8. B9. A3. B4. A5. D6. C7. B 10. C13.可得•或I口一771-1—2 ・lei —朋一丄=一2将;,-1代入__________ '宀― 7,得•,,:符合题意,2 '当;=- 一时,原方程的根是整数.23.解:. —,?,5+ 护",'_ 〔L「,则=::亠心亠4的最小值是1匸;411' I,1 ■:; I;,则-!.厂「宀的最大值为5;(V由题意,得花园的面积是•「- ■:,7-2jc2+20jt = -2(r-5)2+S0'■ I ■ I,■-「:•/./.工的最大值是50,此时=F ,则当「= 5 ;.时,花园的面积最大,最大面积是「.24.解:;.T_;设丁一,卜丄八;将栄工洛、心曲代入,得:T:..::: ,解得:.._..屮.1- ':1 '- :;⑺用匸40)(- 2x + 200)二-2x: + 280x-8000二一2(x- 7Cf)24-180C,当二气时,W取得最大值为1800,答:售价为70元时获得最大利润,最大利润是1800元. :当…二1辽)时,得:--.一:」:.「.一.让.,解得:55或=壬5,该抛物线的开口向上,所以当■- 时,m -',又每千克售价不低于成本,且不高于80元,即4 —- :-0,该商品每千克售价的取值范围是'-…1.。
【配套K12】江苏省南通市通州区金沙镇2017届中考数学专题复习 专题9-1 一元二次方程(无答案)

专题9-1 一元二次方程(满分100分,答卷时间90分钟)一、选择题:本大题共8小题,每小题2分,共16分.在每小题给出的四个选项中,恰有一项是符合题目要求的,请将正确选项的字母代号填在题后括号内.1. 下列方程中是一元二次方程的是 【 】A .2x +1=0B .y 2+x =1C .x 2+1=0D .x1+x 2=1 2. 一元二次方程x 2-2x -3=0的两个根分别为【 】A .x 1=1,x 2=3B .x 1=1,x 2=-3C .x 1=-1,x 2=3D .x 1=-1,x 2=-3 3. 用配方法解方程x 2+4x +1=0,经过配方,得到【 】A .(x +2)2=5B .(x -2)2=5C .(x -2)2=3D .(x +2)2=34. 若三角形的两边分别是3和6,第三边的长是方程x 2-6x +8=0的一个根,则这个三角形的周长是 【 】A .9B .11C .13D .11或13 5. 一元二次方程3x 2+4x -2=0的根的情况是【 】A .有两个不相等的实数根B .只有一个实数根C .有两个相等的实数根D .没有实数根6. 一元二次方程x 2-3x +1=0的两个根分别是x 1,x 2,则x 12x 2+x 1x 22的值是 【 】A .3B .-3C .13D .-137. 某城市计划经过两年的时间,将城市绿地面积从今年的144万平方米提高到225万平方米,则每年平均增长【 】A .15%B .20%C .25%D .30%8. 关于x 的一元二次方程x 2-mx +2m -1=0的两个实数根分别是x 1,x 2,且x 12+x 22=7,则(x 1-x 2)2的值是 【 】A .1B .12C .13D .25二、填空题:本大题共10小题,每小题2分,共20分.不需写出解答过程,请把答案直接填写在题中横线.9. 将一元二次方程2(x -1)2=7x 化成一般式是__________.10.已知关于x 的方程x 2-5x +m =0的一个根是1,则m 的值是__________.11.当c =__________时,关于x 的方程2x 2+8x +c =0有两个实数根.(只需填一个符合要求的数)12.若关于x的方程2x2+4x+k=0有两个相等的实数根,则k的值是__________.13.某小区准备在每两幢楼房之间,开辟面积为300平方米的一块长方形绿地,并且长比宽多10 米,设长方形绿地的宽为x米,则可列方程为__________.14.已知关于x的一元二次方程的两个根分别是1和-3,则该方程为__________.15.一元二次方程x2-mx+6=0的一个实数根x1=2,则另一个实数根x2=__________.16.若方程x2+(m2-1)x+m=0的两根互为相反数,则m=__________.17.要组织一次篮球联赛,赛制为单循环形式(每两队之间都赛一场),计划安排21场比赛,应邀请__________个球队参加比赛.18.如果m,n是两个不相等的实数,且满足23m m-=,23n n-=,那么代数式2222016n mn m-++=__________.三、解答题:本大题共8小题,共64分.解答时应写出文字说明、证明过程或演算步骤.19.(本小题满分8分)解方程:(1)2x2-2x-1=0;(2)x2-6x+3=0.(配方法)20.(本小题满分6分)已知x=1是一元二次方程ax2+bx-40=0的一个解,且a≠b,求2222a ba b--的值.21.(本小题满分6分)市人民政府为了解决群众看病难的问题,决定下调药品的价格,某种药品,经过连续两次降价后,由每盒200元调至128元,求这种药品平均每次降价的百分率是多少?22.(本小题满分8分)已知关于x的方程x2+(m+2)x+2m-1=0(m为实数).(1)求证:方程有两个不相等的实数根;(2)当m为何值时,方程的两根互为相反数并求出此时方程的解.23.(本小题满分8分)关x的一元二次方程(x-2)(x-3)=m有两个实数根x1,x2.(1)求m的取值范围;(2)若x1,x2满足等式x1x2-x1-x2+1=0,求m的值.24.(本小题满分10分)商场某种新商品每件进价是120元,在试销期间发现,当每件商品售价为130元时,每天可销售70件,当每件商品售价高于130元时,每涨价1元,日销售量就减少1件.(1)当每件商品售价定为170元时,每天可销售多少件商品商场获得的日盈利是多少?(2)在上述条件不变,商品销售正常的情况下,每件商品的销售价定为多少元时,商场日盈利可达到1600元?(提示:盈利=售价-进价)25.(本小题满分8分)阅读下列材料,并用相关的思想方法解决问题.计算:111111111111111123423452345234⎛⎫⎛⎫⎛⎫⎛⎫---⨯+++-----⨯++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭.令111234++=t ,则原式=()2211114111555555t t t t t t t t t ⎛⎫⎛⎫-+---=+---+= ⎪ ⎪⎝⎭⎝⎭.解方程(x 2+5x +1)(x 2+5x +7)=7.26.(本小题满分10分)如图1,为美化校园环境,某校计划在一块长为60米,宽为40米的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的通道,设通道宽为a 米. (1)如果通道所占面积是整个长方形空地面积的83,求出此时通道的宽; (2)已知某园林公司修建通道、花圃的造价y 1(元),y 2(元)与修建面积x (m 2)之间的函数关系如图2所示,如果学校决定由该公司承建此项目,并要求修建的通道的宽度不少于2米且不超过10米,那么通道宽为多少时,修建的通道和花圃的总造价最低,最低总造价为多少元?图1 图2。
中考数学《一元二次方程》专题训练(附带答案)

中考数学《一元二次方程》专题训练(附带答案)一、单选题1.关于x的方程x2-2x+k=0有两个不相等的实数根,则k的取值范围是()A.k<1B.k>1C.k<-1D.k>-12.关于x的一元二次方程x2+4x+k=0有两个相等的实数根,则k的值为()A.k=4B.k=﹣4C.k≥﹣4D.k≥43.关于x的一元二次方程方程(m-1)x2-2x-1=0有两个实数根,则实数m的取值范围是()A.B.C.D.4.方程x2﹣5x=0的解是()A.x1=0,x2=﹣5B.x=5C.x1=0,x2=5D.x=05.用配方法解一元二次方程x2+6x−10=0,此方程可变形为()A.(x+3)2=1B.(x−3)2=1C.(x−3)2=19D.(x+3)2=19 6.已知b2﹣4ac是一元二次方程ax2+bx+c=0(a≠0)的一个实数根,则ab的取值范围为()A.ab≥18B.ab≤18C.ab≥14D.ab≤147.已知A=x2+3,B=2x+1,则A,B的大小关系正确的是()A.A>B B.A<BC.A=B D.与x的大小有关8.已知关于x的一元二次方程2x²+4x·sinα+1=0有两个相等的实数根,则锐角α的度数为()A.30°B.45°C.60°D.75°9.用配方法解方程x2﹣x﹣1=0时,配方结果正确的是()A.(x﹣1)2=2B.(x −12)2=54C.(x −12)2=1D.(x −12)2=3410.某种品牌的手机经过四、五月份连续两次降价,每部售价由3200元降到了2500元.设平均每月降价的百分率为x,根据题意列出的方程是()A.2500(1+x)2=3200B.2500(1−x)2=3200C.3200(1−x2)=2500D.3200(1−x)2=250011.用配方法解方程x2﹣4x﹣3=0,下列配方结果正确的是()A.(x﹣4)2=19B.(x﹣2)2=7C.(x+2)2=7D.(x+4)2=1912.下列关于x的方程中,没有实数解的是()A.x2﹣4x+4=0B.x2﹣2x﹣3=0C.x2﹣2x=0D.x2﹣2x+5=0二、填空题13.某企业2018年底缴税80万元,2020 年底缴税96.8万元,设这两年该企业交税的年平均增长率为x根据题意,可得方程为。
中考数学专题练习 一元二次方程2(答案不全)(2021年整理)

2017年中考数学专题练习一元二次方程2(答案不全)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2017年中考数学专题练习一元二次方程2(答案不全))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2017年中考数学专题练习一元二次方程2(答案不全)的全部内容。
一元二次方程一、填空题1.若分式的值为0,则x的值为.2.已知方程(x+a)(x﹣3)=0和方程x2﹣2x﹣3=0的解相同,则a= .3.方程x2=|x|的根是.4.一小球以15m/s的速度竖直向上弹出,它在空中的高度h( m)与时间t(s)满足关系式:h=15t﹣5t2,当t= s时,小球高度为10m,小球所能达到的最大高度为.5.已知(x2+y2﹣2)(x2+y2)=3,则x2+y2= .6.若a2+b2+a﹣2b+=0,则= .7.将方程化成二次项系数为1的一般形式,则一次项系数是,常数项是.8.方程(3x﹣1)2=(2﹣x)2的根是.9.把化成ax2+bx+c=0(a≠0)的形式后,则a= ,b= ,c= .10.请写出一个一元二次方程,使其一根为﹣1,你写的方程是.二、选择题11.下列方程不是整式方程的是( )A.B.0。
2x2﹣0.4x3=0C.D.12.在下列方程中,一元二次方程的个数是( )①3x2+7=0,②ax2+bx+c=0,③(x+2)(x﹣3)=x2﹣1,④x2﹣+4=0,⑤x2﹣(+1)x+=0,⑥3x2﹣+6=0A.1个B.2个C.3个D.4个13.已知关于x的一元二次方程(m﹣1)x2+x+m2+2m﹣3=0的一个根为0,则m的值为()A.1 B.﹣3C.1或﹣3 D.不等于1的任意实数14.已知2y2+y﹣2的值为3,则4y2+2y+1的值为()A.10 B.11 C.10或11 D.3或1115.已知一元二次方程ax2+bx+c=0中二次项系数,一次项系数和常数项之和为0,那么方程必有一根为( )A.0 B.1 C.﹣1 D.±116.若b(b≠0)是方程x2+cx+b=0的根,则b+c的值为()A.1 B.﹣1 C.2 D.﹣217.从正方形的铁片上,截去2cm宽的一条长方形,余下的面积是48cm2,则原来的正方形铁片的面积是()A.96cm2B.64cm2C.54cm2D.52cm218.若方程x2+ax﹣2a=0的一根为1,则a的取值和方程的另一根分别是()A.1,﹣2 B.﹣1,2 C.1,2 D.﹣1,﹣219.若a,b,c为三角形ABC的三边,且a,b,c满足(a﹣b)(a﹣c)=0,则△ABC为()A.直角三角形B.钝角三角形C.等边三角形D.等腰三角形或等边三角形20.一元二次方程x2﹣3x﹣1=0与x2﹣x+3=0的所有实数根的和等于( )A.2 B.﹣4 C.4 D.3三、解答题21.选用适当的方法解下列方程:(1)(3﹣x)2+x2=9(2)(2x﹣1)2+(1﹣2x)﹣6=0(3)(3x﹣1)2=4(1﹣x)2(4)(x﹣1)2=(1﹣x)22.解下列关于x的方程:(1)x2+(1+2)x+3+=0;(2)x2﹣3|x|﹣4=0(3)(x﹣3)2+(x+4)2﹣(x﹣5)2=17x+24.23.已知2+是方程x2﹣4x+c=0的一个根,求方程的另一个根及c的值.24.一元二次方程ax2+bx+c=0(a≠0)有两根x1,x2,则,,则x1+x2= ,x1x2= .请运用上面你发现的结论,解答问题:已知x1,x2是方程x2﹣x﹣1=0的两根,不解方程求下列式子的值:①x12+x22;②;③(x1+1)(x2+1).25.解方程,有一位同学解答如下:解:这里a=,b=,c=∴b2﹣4ac=(﹣∴=∴请你分析以上解答有无错误,如有错误,指出错误的地方,并写出正确的结果.26.已知等腰三角形两边长分别是x2﹣8x+15=0的两根,求此等腰三角形的周长.27.如图,一个长为15m的梯子斜靠在墙上,梯子的顶端距地面的距离为12m,如果梯子的顶端下滑了1m,那么梯子的底端也向后滑动1m吗?试列出方程解答此问题,并论证前面的结论.参考答案一、填空题(共10小题,每小题2分,满分20分)1.1;2.1;3.x1=0,x2=1,x3=﹣1;4.1或2;;5.3;6.﹣3;7.﹣;;8.;9.1;;;10.x2+x=0;二、选择题(共10小题,每小题2分,满分20分)11.D;12.B;13.B;14.B;15.B;16.B;17.B;18.A;19.D;20.D;三、解答题(共7小题,满分58分)21.;22.;23.;24.﹣;;25.;26.;27.;。
【配套K12】2017年中考数学试题分项版解析汇编第02期专题16压轴题含解析
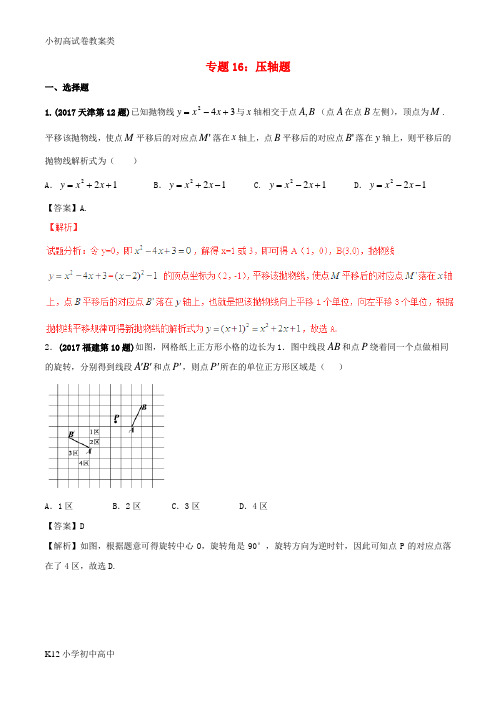
专题16:压轴题一、选择题1.(2017天津第12题)已知抛物线342+-=x x y 与x 轴相交于点B A ,(点A 在点B 左侧),顶点为M .平移该抛物线,使点M 平移后的对应点'M 落在x 轴上,点B 平移后的对应点'B 落在y 轴上,则平移后的抛物线解析式为( )A .122++=x x yB .122-+=x x y C. 122+-=x x y D .122--=x x y【答案】A.2.(2017福建第10题)如图,网格纸上正方形小格的边长为1.图中线段AB 和点P 绕着同一个点做相同的旋转,分别得到线段A B ''和点P ',则点P '所在的单位正方形区域是( )A .1区B .2区C .3区D .4区【答案】D【解析】如图,根据题意可得旋转中心O ,旋转角是90°,旋转方向为逆时针,因此可知点P 的对应点落在了4区,故选D.3.(2017河南第10题)如图,将半径为2,圆心角为120︒的扇形OAB 绕点A 逆时针旋转60︒,点O ,B 的对应点分别为'O ,'B ,连接'BB ,则图中阴影部分的面积是( )A .23πB .3π C.23π D .23π 【答案】C.【解析】考点:扇形的面积计算.4.(2017湖南长沙第12题)如图,将正方形ABCD 折叠,使顶点A 与CD 边上的一点H 重合(H 不与端点D C ,重合),折痕交AD 于点E ,交BC 于点F ,边AB 折叠后与边BC 交于点G ,设正方形ABCD 的周长为m ,CHG ∆的周长为n ,则mn 的值为( ) A .22 B .21 C .215- D .随H 点位置的变化而变化【答案】B【解析】试题分析:设正方形ABCD 的边长为2a ,正方形的周长为m=8a ,设CM=x ,DE=y ,则DM=2a-x ,EM=2a-y ,∵∠EMG=90°,∴∠DME+∠CMG=90°.∵∠DME+∠DEM=90°,∴∠DEM=∠CMG ,又∵∠D=∠C=90°△DEM ∽△CMG , ∴CG CM MG DM DE EM ==,即22CG x MG a x y a y==-- ∴CG=(2)(2)=,x a x x a y CG MG y y--= △CMG 的周长为CM+CG+MG=24ax x y- 在Rt △DEM 中,DM 2+DE 2=EM 2即(2a-x )2+y 2=(2a-y )2整理得4ax-x 2=4ay ∴CM+MG+CG=2444ax x ay a y y-===n . 所以12n m =故选:B .考点:1、正方形,2、相似三角形的判定与性质,3、勾股定理5. (2017广东广州第10题) 0a ≠,函数a y x=与2y ax a =-+在同一直角坐标系中的大致图象可能是( )【答案】D【解析】考点: 二次函数与反比例函数的图像的判断.6. (2017山东临沂第14题)如图,在平面直角坐标系中,反比例函数k y x=(0x >)的图象与边长是6的正方形OABC 的两边AB ,BC 分别相交于M ,N 两点,OMN V 的面积为10.若动点P 在x 轴上,则PM PN +的最小值是( )A .B .10C .D .【答案】C【解析】试题分析:由正方形OABC 的边长为6可得M 的坐标为(6,6k ),N 的坐标为(6k ,6),因此可得BN=6-6k ,BM=6-6k ,然后根据△OMN 的面积为10,可得21116666(6)10262626k k k ⨯-⨯⨯-⨯⨯-⨯-=,解得k=24,得到M (6,4)和N (4,6),作M 关于x 轴的对称点M ′,连接NM ′交x 轴于P ,则M ′N 的长=PM+PN 的值最小,最后由AM=AM ′=4,得到BM ′=10,BN=2,根据勾股定理求得NM ′故选:C考点:1、反比例函数与正方形,2、三点之间的最小值7. (2017山东青岛第8题)一次函数)0(≠+=k b kx y 的图像经过点A (4,1--),B (2,2)两点,P 为反比例函数xkb y =图像上的一个动点,O 为坐标原点,过P 作y 轴的垂线,垂足为C ,则△PCO 的面积为( ) A 、2 B 、4 C 、8 D 、不确定【答案】【解析】试题分析:如下图,把点A (4,1--),B (2,2)代入)0(≠+=k b kx y 得22--=x y ,即k=-2,b=-2 所以反比例函数表达式为x y 4=设P (m ,n ),则nm 4=,即mn=4△PCO 的面积为21OCPC=21mn=2 考点: 1、一次函数,2、反比例函数图像与性质8. (2017四川泸州第12题)已知抛物线214y x =+1具有如下性质:给抛物线上任意一点到定点(0,2)F 的距离与到x 轴的距离相等,如图,点M 的坐标为,P 是抛物线2114y x =+上一动点,则PMF ∆周长的最小值是( )A .3B .4C .5D .6【答案】C.9. (2017山东滨州第12题)在平面直角坐标系内,直线AB 垂直于x 轴于点C (点C 在原点的右侧),并分别与直线y =x 和双曲线y =1x 相交于点A 、B ,且AC +BC =4,则△OAB 的面积为( )A .3或 3B 1 1C . 3D 1【答案】A.【解析】如图,分线段AB在双曲线1yx=和直线y=x交点的左右两侧两种情况,设点C的坐标为(m,0),则点A的坐标为(m,m),点B的坐标为(m,1m ),因AC+BC=4,所以m+1m=4,解得m=2,当时,即线段AB在双曲线1yx=和直线y=x交点的左侧,求得所以即可求得△OAB的面积为1(232⨯-=;当线段AB在双曲线1yx=和直线y=x交点的右侧,求得所以即可求得△OAB的面积为1(232⨯+=,故选A.10.(2017山东日照第12题)已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标为(4,0),其部分图象如图所示,下列结论:①抛物线过原点;②4a+b+c=0;③a﹣b+c<0;④抛物线的顶点坐标为(2,b);⑤当x<2时,y随x增大而增大.其中结论正确的是()A .①②③B .③④⑤C .①②④D .①④⑤【答案】C .考点:抛物线与x 轴的交点;二次函数图象与系数的关系.11.(2017江苏宿迁第8题)如图,在Rt C ∆AB 中,C 90∠=,C 6A =cm ,C 2B =cm .点P 在边C A 上,从点A 向点C 移动,点Q 在边C B 上,从点C 向点B 移动,若点P 、Q 均以1cm/s 的速度同时出发,且当一点移动到终点时,另一点也随之停止,连接Q P ,则线段Q P 的最小值是A .20cmB .18cm C.cm D .cm【答案】C.【解析】试题分析:设运动时间为t 秒,则AP=t ,CQ=t ,所以CP=6-t ,根据勾股定理可得222PQ PC CQ =+,即222(6)PQ t t =-+,所以222212362(3)18PQ t t t =-+=-+,因t ≤2,根据二次函数的性质可得当t=2时,2PQ 的值最小为20,即可得线段Q P 的最小值是,故选C.12.(2017江苏苏州第10题)如图,在菱形CD AB 中,60∠A =,D 8A =,F 是AB 的中点.过点F 作F D E ⊥A ,垂足为E .将F ∆AE 沿点A 到点B 的方向平移,得到F '''∆A E .设P 、'P 分别是F E 、F ''E 的中点,当点'A 与点B 重合时,四边形CD 'PP 的面积为A .B ..8【答案】A.【解析】试题分析:作,,DH AB PK AB FL AB ⊥⊥⊥在菱形CD AB 中,60∠A =,D 8A =,F 是AB 的中点4AF EF EL ∴==∴=,P 是F E 的中点,PK ∴= DH =1PP CD ∴=高为8S ∴==L K H故答案选A. 考点:平行四边形的面积,三角函数.13. (2017山东菏泽第8题)一次函数b ax y +=和反比例函数xc y =在同一个平面直角坐标系中的图象如图所示,则二次函数c bx ax y ++=2的图c 象可能是( )A .B . C. D .【答案】C.14. (2017浙江台州第10题) 如图,矩形EFGH 的四个顶点分别在菱形ABCD 的四条边上,BE BF =,将,AEH CFG ∆∆分别沿,EH FG 折叠,当重叠部分为菱形且面积是菱形ABCD 面积的116时,则AE EB为 ( )A.53B.2 C.52D.4【答案】A【解析】试题分析:依题可得阴影部分是菱形.设S菱形ABCD=16,BE=x.从而得出AB=4,阴影部分边长为4-2x.根据(4-2x)2=1求出x=32或x=52,从而得出3452332AEEB-==.故选:A.考点:1、菱形的性质,2、翻折变换(折叠问题)15. (2017浙江金华第10题)如图,为了监控一不规则多边形艺术走廊内的活动情况,现已在,A B两处各安装了一个监控探头(走廊内所用探头的观测区为圆心角最大可取到180的扇形),图中的阴影部分是A处监控探头观测到的区域,要使整个艺术走廊都能被监控到,还需要安装一个监控探头,则安装的位置是()A.E处 B.F处 C.G处 D.H处【答案】D.【解析】试题分析:根据两点确定一条直线,观察可以摄像头应安装在点H的位置,故选D.16.(2017浙江湖州第10题)在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点.从44⨯的正方形网格图形中(如图1),从点A经过一次跳马变换可以到达点B,C,D,E等处.现有2020⨯的正方形网格图形(如图2),则从该正方形的顶点M经过跳马变换到达与其相对的顶点N,最少需要跳马变换的次数是()A.13 B.14 C.15 D.16【答案】B考点:1、勾股定理,2、规律探索17. (2017浙江舟山第10题)下列关于函数1062+-=x x y 的四个命题:①当0=x 时,y 有最小值10;②n 为任何实数,n x +=3时的函数值大于n x -=3时的函数值;③若3>n ,且n 是整数,当1+≤≤n x n 时,y 的整数值有)42(-n 个;④若函数图象过点),(0y a 和)1,(0+y b ,则b a <.其中真命题的序号是( )A .①B .② C.③ D .④【答案】C.【解析】试题分析:①错,理由:当x=6321--=⨯时,y 取得最小值;②错,理由:因为332n n ++-=3, 即横坐标分别为x=3+n , x=3−n 的两点的纵坐标相等,即它们的函数值相等;③对,理由:若n>3,则当x=n 时,y=n 2− 6n+10>1,当x=n+1时,y=(n+1)2− 6(n+1)+10=n 2−4n+5,则n 2−4n+5-(n 2− 6n+10)=2n-5,因为当n 为整数时,n 2− 6n+10也是整数,2n-5也是整数,n 2−4n+5也是整数,故y 有2n-5+1=2n-4个整数值;④错,理由:当x<3时,y 随x 的增大而减小,所以当a<3,b<3时,因为y 0<y 0+1,所以a>b ,故错误;故选C. 考点:二次函数图象上点的坐标特征.二、填空题1.(2017北京第16题)下图是“作已知直角三角形的外接圆”的尺规作图过程已知:0,90Rt ABC C ∆∠=,求作Rt ABC ∆的外接圆.作法:如图.(1)分别以点A 和点B 为圆心,大于12AB 的长为半径作弧,两弧相交于,P Q 两点; (2)作直线PQ ,交AB 于点O ;(3)以O 为圆心,OA 为半径作O . O 即为所求作的圆.请回答:该尺规作图的依据是 .【答案】到线段两端点距离相等的点在线段的垂直平分线上;两点确定一条直线;垂直平分线的定义;90°的圆周角所对弦为直径.不在同一条直线上的三个点确定一个圆.(答案不唯一)【解析】找到外接圆的圆心和半径是解本题的关键,由题意得:圆心是线段AB 的中点,半径是AB 长的一半,所以只需作出AB 的中垂线,找到交点O 即可.考点:作图-基本作图;线段垂直平分线的性质2. (2017天津第18题)如图,在每个小正方形的边长为1的网格中,点C B A ,,均在格点上.(1)AB 的长等于 ;(2)在ABC ∆的内部有一点P ,满足2:1:::=∆∆∆PCA PBC PAB S S S ,请在如图所示的网格中,用无刻度...的直尺,画出点P ,并简要说明点P 的位置是如何找到的(不要求证明) .【答案】(1;(2)详见解析.【解析】试题分析:(1)根据勾股定理即可求得(2)如图,AC 与网络线相交,得点D 、E ,取格点F ,连结FB 并延长,与网格线相交,得点M 、N ,连结DN 、EM ,DN 与EM 相交于点P ,点P 即为所求.3.(2017福建第16题) 已知矩形ABCD 的四个顶点均在反比例函数1y x=的图象上,且点A 的横坐标是2,则矩形ABCD 的面积为 .【答案】7.5【解析】因为双曲线既关于原点对称,又关于直线y=±x 对称,矩形既是轴对称图形又是中心对称图形,所以可知点C 与点A 关于原点对称,点A 与点B 关于直线y=x 对称,由已知可得A (2,0.5),∴C (-2,-0.5)、B (0.5,2),从而可得D (-0.5,-2),继而可得S 矩形ABCD =7.5.【答案】1或12. 考点:折叠(翻折变换).5. (2017湖南长沙第18题)如图,点M 是函数x y 3=与xk y =的图象在第一象限内的交点,4=OM ,则k 的值为 .【答案】考点:一次函数与反比例函数6. (2017广东广州第16题)如图9,平面直角坐标系中O 是原点,OABC 的顶点,A C 的坐标分别是()()8,0,3,4,点,D E 把线段OB 三等分,延长,CD CE 分别交,OA AB 于点,F G ,连接FG ,则下列结论:①F 是OA 的中点;②OFD ∆与BEG ∆相似;③四边形DEGF 的面积是203;④OD =;其中正确的结论是 .(填写所有正确结论的序号)【答案】①③【解析】试题分析:如图,分别过点A 、B 作AN OB ⊥ 于点N ,BM x ⊥ 轴于点M在OABC 中,(80)(34)(114)A C B OB ∴=,,,,,D E 、 是线段AB 的三等分点, 12OD BD ∴= ,CB OF ODFBDC ∴∆∆111222OF OD OF BC OA BC BD ∴==∴==, F ∴ 是OA 的中点,故①正确.(34)5C OC OA ∴=≠,,OABC ∴ 不是菱形.,DOF COD EBG ODF COD EBG ∴∠≠∠=∠∠≠∠=∠(40),F CF OC CFO COF ∴<∴∠>∠,,DFO EBG ∴∠≠∠故OFD ∆ 和BEG ∆ 不相似.则②错误;由①得,点G 是AB 的中点,FG ∴ 是OAB ∆ 的中位线1,2FG OB FG OB ∴==D E 、 是OB 的三等分点,DE ∴=1118416222OAB S OB AN OA BM ∆=⋅=⋅=⨯⨯= 解得:1162AN OB= ,DF FG ∴ 四边形DEGH 是梯形()551202121223DEGF DE FG h S OB h OB AN -∴==⋅=⋅=四边形 则③正确13OD OB == ,故④错误. 综上:①③正确.考点: 平行四边形和相似三角形的综合运用7. (2017山东临沂第19题)在平面直角坐标系中,如果点P 坐标为(),m n ,向量OP uu u r 可以用点P 的坐标表示为(),OP m n =uu u r .已知:()11,OA x y =uu r ,()22,OB x y =uu u r ,如果12120x x y y ⋅+⋅=,那么OA uu r 与OB uu u r 互相垂直.下列四组向量:①()2,1OC =uuu r ,()1,2OD =-uuu r ;②()cos30,tan 45OE =︒︒uu u r ,()1,sin 60OF =︒uu u r ;③)2OG =-uuu r,12OH ⎫=⎪⎭uuu r ; ④()0,2OM π=uuu r ,()2,1ON =-uuu r .其中互相垂直的是 (填上所有正确答案的序号).【答案】①③④【解析】试题分析:根据向量垂直的定义:② 因为2×(﹣1)+1×2=0,所以OC 与OD 互相垂直;③ 因为cos30°×1+tan45°•sin60°=21+1×20,所以OE 与OF 不互相垂直; ④+(﹣2)×12=3﹣2﹣1=0,所以OG 与OH 互相垂直; ④因为π0×2+2×(﹣1)=2﹣2=0,所以OM 与ON 互相垂直.综上所述,①③④互相垂直.故答案是:①③④.考点:1、平面向量,2、零指数幂,3、解直角三角形8. (2017四川泸州第16题)在ABC ∆中,已知BD 和CE 分别是边,AC AB 上的中线,且BD CE ⊥,垂足为O ,若2,4OD cm OE cm ==,则线段AO 的长为 cm .【答案】【解析】试题分析:如图,由BD 和CE 分别是边,AC AB 上的中线,可得DE ∥BC ,且12DE OD OE BC OB OC === , 因BD CE ⊥,2,4OD cm OE cm ==,根据勾股定理可得,又因12DE OD OE BC OB OC ===,可得AO 并延长AO 交BC 于点M ,由BD 和CE 分别是边,AC AB 上的中线交于点M ,可知AM 也是△ABC 的边BC 上的中线,在Rt △BOC 中,根据斜边的中线等于斜边的一半可得OM=12三角形重心的性质可得9. (2017山东滨州第18题)观察下列各式:2111313=-⨯, 2112424=-⨯ 2113535=-⨯ ……请利用你所得结论,化简代数式213⨯+224⨯+235⨯+…+2(2)n n +(n ≥3且为整数),其结果为__________. 【答案】2354(1)(2)n n n n +++ . 【解析】根据题目中所给的规律可得,原式=12222(...)2132435(2)n n ++++⨯⨯⨯+ =111111111(1...)23243512n n n -+-+-+-+-++=111113(1)(2)2(2)2(1)(1)221222(1)(2)n n n n n n n n ++-+-++--=⨯++++=2354(1)(2)n n n n +++ . 10. (2017江苏宿迁第16题)如图,矩形C ABO 的顶点O 在坐标原点,顶点B 、C 分别在x 、y 轴的正半轴上,顶点A 在反比例函数k y x=(k 为常数,0k >,0x >)的图象上,将矩形C ABO 绕点A 按逆时针方向旋转90得到矩形C '''AB O ,若点O 的对应点'O 恰好落在此反比例函数图象上,则C OB O 的值是 .【解析】试题分析:设点A 的坐标为(a ,b ),即可得OB=a ,OC=b,已知矩形C ABO 绕点A 按逆时针方向旋转90得到矩形C '''AB O ,可得点C 、A 、B ’在一条直线上,点A 、C ’、B 在一条直线上,AC ’=a ,AB ’=b ,所以点O ’的坐标为)(a+b , b -a ),根据反比例函数k 的几何意义可得ab=(a+b )(b-a ),即可得220b ab a --=,解这个以b为未知数的一元二次方程得11,b b ==(舍去),所以,b =所以C OB ===O 11. (2017辽宁沈阳第16题)如图,在矩形ABCD 中,53AB BC ==,,将矩形ABCD 绕点B 按顺时针方向旋转得到矩形GBEF ,点A 落在矩形ABCD 的边CD 上,连接CE ,则CE 的长是.【答案】5. 【解析】考点:四边形与旋转的综合题.12. (2017山东日照第16题)如图,在平面直角坐标系中,经过点A的双曲线y=(x>0)同时经过点B,且点A在点B的左侧,点A的横坐标为,∠AOB=∠OBA=45°,则k的值为.【答案】试题分析:过A作AM⊥y轴于M,过B作BD选择x轴于D,直线BD与AM交于点N,如图所示:则OD=MN,DN=OM,∠AMO=∠BNA=90°,∴∠AOM+∠OAM=90°,∵∠AOB=∠OBA=45°,∴OA=BA,∠OAB=90°,∴∠OAM+∠BAN=90°,∴∠AOM=∠BAN,在△AOM和△BAN中,AOM BANAMO BNA OA BA∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△AOM≌△BAN(AAS),∴,∴∴B,∴双曲线y=(x>0)同时经过点A和B,=k,整理得:k2﹣2k﹣4=0,解得:k=1,∴考点:反比例函数图象上点的坐标特征.13. (2017江苏苏州第18题)如图,在矩形CDAB中,将C∠AB绕点A按逆时针方向旋转一定角度后,CB的对应边C''B交CD边于点G.连接'BB、CC',若D7A=,CG4=,G''AB=B,则CC'='BB(结果保留根号).【解析】试题分析:连接AG,设DG=x,则 G=4+x ''AB =B在'Rt AB G ∆ 中,22492(4)1x x x +=+⇒= ,则5,7AB BC ==''CC BB ∴==考点:旋转的性质 ,勾股定理 .14. (2017山东菏泽第14题)如图,y AB ⊥轴,垂足为B ,将ABO ∆绕点A 逆时针旋转到11O AB ∆的位置,使点B 的对应点1B 落在直线x y 33-=上,再将11O AB ∆绕点1B 逆时针旋转到111O B A ∆的位置,使点1O 的对应点2O 落在直线x y 33-=上,依次进行下去......若点B 的坐标是)1,0(,则点12O 的纵坐标为 .【答案】()3333+【解析】15. (2017浙江金华第16题)在一空旷场地上设计一落地为矩形ABCD 的小屋,10AB BC m +=.拴住小狗的10m 长的绳子一端固定在B 点处,小狗在不能进人小屋内的条件下活动,其可以活动的区域面积为()2S m .(1)如图1,若4BC m =,则S = 2m .(2)如图2,现考虑在(1)中的矩形ABCD 小屋的右侧以CD 为边拓展一正CDE ∆区域,使之变成落地为五边ABCDE 的小屋,其它条件不变.则在BC 的变化过程中,当S 取得最小值时,边长BC 的长为 m .【答案】52. 【解析】试题分析:(1)在B 点处是以点B 为圆心,10为半径的34个圆;在A 处是以A 为圆心,4为半径的14个圆;在C 处是以C 为圆心,6为半径的14个圆;所以S=222113641088444ππππ⨯+⨯+⨯= ;(2)设BC=x,则AB=10-x ,222330110(10)43604S x x πππ=⨯+⨯-+⨯ =3π(-10x+250),当x=52时,S 最小,即BC=52. 16. (2017浙江湖州第16题)如图,在平面直角坐标系x y O 中,已知直线y kx =(0k >)分别交反比例函数1y x =和9y x =在第一象限的图象于点A ,B ,过点B 作D x B ⊥轴于点D ,交1y x=的图象于点C ,连结C A .若C ∆AB 是等腰三角形,则k 的值是 .【解析】试题分析:令B 点坐标为(a ,9a )或(a ,ka ),则C 点的坐标为(a ,1a),令A 点的坐标为(b ,kb )或(b ,1b ),可知BC=8a ,ka=9a ,kb=1b ,可知29a k =,21b k =,然后可知8a ,解得. 考点:反比例函数与k 的几何意义17. (2017湖南湘潭第16题)阅读材料:设11(,)a x y =,22(,)b x y =,如果//a b ,则2121x y x y ⋅=⋅.根据该材料填空:已知(2,3)a =,(4,)b m =,且//a b ,则m = .【答案】6.【解析】试题分析:利用新定义设11(,)a x y =,22(,)b x y =,如果//a b ,则2121x y x y ⋅=⋅,2m=4×3,m=6.18. (2017浙江台州第16题)如图,有一个边长不定的正方形ABCD ,它的两个相对的顶点,A C 分别在边长为1的正六边形一组平行的对边上,另外两个顶点,B D 在正六边形内部(包括边界),则正方形边长a 的取值范围是 .3a ≤≤a ≤≤ ) 【解析】试题分析:因为AC 为对角线,故当AC 最小时,正方形边长此时最小.①当 A 、C 都在对边中点时(如下图所示位置时),显然AC 取得最小值,∵正六边形的边长为1,∴∴a 2+a 2=AC 2=2.∴②当正方形四个顶点都在正六边形的边上时,a 最大(如下图所示).设A ′(. ∵OB ′⊥OA ′.∴B ′(-2,t ) 设直线MN 解析式为:y=kx+b,M (-1,0),N (-12,(如下图)∴0122k b k b -+=⎧⎪⎨-+=-⎪⎩.∴k b ⎧=⎪⎨=⎪⎩.∴直线MN 的解析式为:x+1),将B ′(t )代入得:t=32此时正方形边长为A ′B ′取最大.∴3a ≤≤.考点:1、勾股定理,2、正多边形和圆,3、计算器—三角函数,4、解直角三角形三、解答题1.(2017北京第29题)在平面直角坐标系xOy 中的点P 和图形M ,给出如下的定义:若在图形M 上存在一点Q ,使得P Q 、两点间的距离小于或等于1,则称P 为图形M 的关联点.(1)当O 的半径为2时,①在点123115,0,,,0222P P P ⎛⎛⎫⎛⎫ ⎪ ⎪ ⎝⎭⎝⎭⎝⎭中,O 的关联点是_______________. ②点P 在直线y x =-上,若P 为O 的关联点,求点P 的横坐标的取值范围. (2)C 的圆心在x 轴上,半径为2,直线1y x =-+与x 轴、y 轴交于点A B 、.若线段AB 上的所有点都是C 的关联点,直接写出圆心C 的横坐标的取值范围【答案】(1)①23,P P ≤x ≤-2 或2 ≤x ≤2,(2)-2≤x ≤1或2≤x ≤【解析】本题解析:(1)12315,01,22OP P OP ===, 点1P 与⊙的最小距离为32 ,点2P 与⊙的最小距离为1,点3P 与⊙的最小距离为12, ∴⊙的关联点为2P 和3P .②根据定义分析,可得当直线y=-x 上的点P 到原点的距离在1到3之间时符合题意;∴ 设点P 的坐标为P (x ,-x) ,当OP=1时,由距离公式可得,1= ,解得x = ,当OP=3时,由距离公式可得,3= ,229x x +=,解得2x =±,∴ 点的横坐标的取值范围为-2≤x ≤-2 或2 ≤x ≤2(2)∵y=-x+1与轴、轴的交点分别为A 、B 两点,∴ 令y=0得,-x+1=0,解得x=1, 令得x=0得,y=0,∴A(1,0) ,B (0,1) ,分析得:如图1,当圆过点A 时,此时CA=3,∴ 点C 坐标为,C ( -如图2,当圆与小圆相切时,切点为D ,∴CD=1 ,又∵直线AB所在的函数解析式为y=-x+1,∴直线AB与x轴形成的夹角是45°,∴ RT△°ACD中,,∴ C点坐标为x≤∴ C点的横坐标的取值范围为;-2≤c如图3,当圆过点A时,AC=1,C点坐标为(2,0)如图4,当圆过点 B 时,连接 BC ,此时 BC =3,在 Rt△OCB中,由勾股定理得=点坐标为.∴ C 点的横坐标的取值范围为2≤c x ≤;∴综上所述点C ≤c x ≤-2 或2 ≤c x ≤2. 考点:切线,同心圆,一次函数,新定义.2.(2017天津第25题)已知抛物线32-+=bx x y (b 是常数)经过点)0,1(-A .(1)求该抛物线的解析式和顶点坐标;(2)P(m ,t)为抛物线上的一个动点,P 关于原点的对称点为'P .①当点'P 落在该抛物线上时,求m 的值;②当点'P 落在第二象限内,2'A P 取得最小值时,求m 的值.【答案】(1)223y x x =--,顶点的坐标为(1,-4);(2)12m m ==;(3)22m +=. 【解析】试题解析:(1)∵抛物线32-+=bx x y 经过点)0,1(-A ,∴0=1-b-3,解得b=-2.∴抛物线的解析式为223y x x =--,∵2223(1)4y x x x =--=--,∴顶点的坐标为(1,-4).(2)①由点P(m ,t)在抛物线223y x x =--上,有223t m m =--.∵P 关于原点的对称点为'P ,有P’(-m ,-t ).∴2()2()3t m m -=----,即223t m m =--+∴222323m m m m --=--+解得12m m ==②由题意知,P’(-m ,-t )在第二象限,∴-m<0,-t>0,即m>0,t<0.又抛物线223y x x =--的顶点的坐标为(1,-4),得-4≤t<0.过点P’作P’H⊥x 轴,H 为垂足,有H (-m ,0).又)0,1(-A ,223t m m =--,则22222',(1)214P H t AH m m m t ==-+=-+=+当点A 和H 不重合时,在Rt △P’AH 中,222''P A P H AH =+当点A 和H 重合时,AH=0, 22''P A P H =,符合上式.∴222''P A P H AH =+,即22'4(40)P A t t t =++-≤≤记2'4(40)y t t t =++-≤≤,则2115'()24y t =++, ∴当t=-12时,y’取得最小值. 把t=-12代入223t m m =--,得21232m m -=--解得122222m m +==由m>0,可知22m -=不符合题意∴m =3.(2017福建第25题)已知直线m x y +=2与抛物线2y ax ax b =++有一个公共点(1,0)M ,且a b <. (Ⅰ)求抛物线顶点Q 的坐标(用含a 的代数式表示);(Ⅱ)说明直线与抛物线有两个交点;(Ⅲ)直线与抛物线的另一个交点记为N . (ⅰ)若211-≤≤-a ,求线段MN 长度的取值范围; (ⅱ)求QMN ∆面积的最小值.【答案】(Ⅰ)抛物线顶点Q 的坐标为(-12,-94a );(Ⅱ)理由见解析;(Ⅲ)(i )MN ≤(ii )△QMN 面积的最小值为2742+. 【解析】 试题分析:(Ⅰ)由抛物线过点M (1,0),可得b=-2a ,将解析式y=ax 2+ax+b=ax 2+ax-2a 配方得y=a(x+ 12)2- 94a ,从而可得抛物线顶点Q 的坐标为(- 12,- 94a ). (Ⅱ)由直线y=2x+m 经过点M (1,0),可得m=-2.由y=2x-2、y=ax 2+ax-2a ,可得ax 2+(a-2)x-2a+2=0,(*),由根的判别式可得方程(*)有两个不相等的实数根,从而可得直线与抛物线有两个交点. (Ⅲ)由y=2x-2、y=ax 2+ax-2a ,可得点N (2a -2,4a-6). (i )根据勾股定理得,MN 2=20(132a -)2,再由-1≤a ≤-12,可得-2≤1a ≤-1,从而可得132a -<0,继而可得,从而可得MN 的取值范围. (ii )作直线x=-12 交直线y=2x-2于点E ,得 E (-12,-3), 从而可得△QMN 的面积S=S △QEN +S △QEM =2732748a a -- ,即27a 2+(8S-54)a+24=0,(*)因为关于a 的方程(*)有实数根, 从而可和S ≥2742+,继而得到面积的最小值.(Ⅲ)把y=2x-2代入y=ax 2+ax-2a ,得ax 2+(a-2)x-2a+2=0, 即x 2+(1-2a )x-2+2a =0,所以(x-1)(x+2-2a)=0, 解得x 1=1,x 2 =2a -2,所以点N (2a -2,4a-6). (i )根据勾股定理得,MN 2=[(2a -2)-1]2+(4a -6)2=20(132a -)2, 因为-1≤a ≤-12,由反比例函数性质知-2≤1a ≤-1,所以132a -<0,所以(312a - ),所以MN ≤(ii )作直线x=-12 交直线y=2x-2于点E ,把x=-12代入y=2x-2得,y=-3,即E (-12,-3), 又因为M (1,0),N (2a -2,4a -6),且由(Ⅱ)知a<0, 所以△QMN 的面积S=S △QEN +S △QEM =()12921324a a ⎛⎫----- ⎪⎝⎭ =2732748a a -- , 即27a 2+(8S-54)a+24=0,(*)因为关于a 的方程(*)有实数根,所以△=(8S-54)2-4×27×24≥0,即(8S-54)2≥()2, 又因为a<0,所以S=2732748a a -- >274,所以8S-54>0,所以8S-54>0,所以8S-54≥S ≥2742+ ,当S=274+*)可得满足题意.故当a=-3,b =3时,△QMN 面积的最小值为2742+.4.(2017河南第23题)如图,直线23y x c =-+与x 轴交于点(3,0)A ,与y 轴交于点B ,抛物线243y x bx c =-++经过点A ,B .(1)求点B 的坐标和抛物线的解析式;(2)M (m ,0)为x 轴上一个动点,过点M 垂直于x 轴的直线与直线AB 和抛物线分别交于点P 、N , ①点M 在线段OA 上运动,若以B ,P ,N 为顶点的三角形与APM ∆相似,求点M 的坐标;②点M 在x 轴上自由运动,若三个点M ,P ,N 中恰有一点是其它两点所连线段的中点(三点重合除外),则称M ,P ,N 三点为“共谐点”.请直接写出使得M ,P ,N 三点成为“共谐点”的m 的值.【答案】(1)B (0,2),2410233y x x =-++;(2)①点M 的坐标为(118,0)或M (52,0);②m=-1或m=14-或m=12. 【解析】 试题分析:(1) 把点(3,0)A 代入23y x c =-+求得c 值,即可得点B 的坐标;抛物线243y x bx c =-++经过点(3,0)A ,即可求得b 值,从而求得抛物线的解析式;(2)由MN x ⊥轴,M (m ,0),可得N(2410,233m m m -++ ),①分∠NBP=90°和∠BNP =90°两种情况求点M 的坐标;②分N 为PM 的中点、P 为NM 的中点、M 为PN 的中点3种情况求m 的值.试题解析:(1)直线23y x c =-+与x 轴交于点(3,0)A , ∴2303c -⨯+=,解得c=2 ∴B (0,2), ∵抛物线243y x bx c =-++经过点(3,0)A , ∴2433203b -⨯++=,∴b=103∴抛物线的解析式为2410233y x x =-++; (2)∵MN x ⊥轴,M (m ,0),∴N(2410,233m m m -++ ) ①有(1)知直线AB 的解析式为223y x =-+,OA=3,OB=2 ∵在△APM 中和△BPN 中,∠APM=∠BPN, ∠AMP=90°,若使△APM 中和△BPN 相似,则必须∠NBP=90°或∠BNP =90°,分两种情况讨论如下:(I )当∠NBP=90°时,过点N 作NC y ⊥轴于点C ,则∠NBC+∠BNC=90°,NC=m , BC=22410410223333m m m m -++-=-+ ∵∠NBP=90°,∴∠NBC+∠ABO=90°,∴∠BNC=∠ABO ,∴Rt △NCB ∽ Rt △BOA ∴NC CB OB OA = ,即24103323m m m -+= ,解得m=0(舍去)或m=118 ∴M (118,0); (II )当∠BNP=90°时, BN ⊥MN ,∴点N 的纵坐标为2, ∴24102233m m -++= 解得m=0(舍去)或m=52∴M (52,0); 综上,点M 的坐标为(118,0)或M (52,0); ②m=-1或m=14-或m=12. 考点:二次函数综合题.5. (2017广东广州第25题)如图14,AB 是O 的直径,,2AC BC AB ==,连接AC .(1)求证:045CAB ∠=; (2)若直线l 为O 的切线,C 是切点,在直线l 上取一点D ,使,B D A B B D =所在的直线与AC 所在的直线相交于点E ,连接AD .①试探究AE 与AD 之间的数量关系,并证明你的结论; ②EB CD是否为定值?若是,请求出这个定值;若不是,请说明理由. 【答案】(1)详见解析;(2)①AE AD = ②2BE CD = 【解析】试题分析:(1)直径所对的圆周角是圆心角的一半,等弧所对的圆周角是圆心角的一半;(2)①等角对等边;②试题解析:(1)证明:如图,连接BC.222BE EI AE ==⨯= 是O 的直径, 90ACB ∴∠=︒ AC BC CAB CBA =∴∠=∠18090452CAB CBA ︒-︒∴∠=∠==︒ (2)①如图所示,作BF l ⊥ 于F由(1)可得,ACB ∆ 为等腰直角三角形. O 是AB 的中点. CO AO BO ∴== ACB ∴∆ 为等腰直角三角形.又l 是O 的切线,OC l BF l ∴⊥⊥∴ 四边形OBEC 为矩形 22AB BFBD BF ∴=∴= 303075BDF DBA BDA BAD ∴∠=︒∴∠=︒∠=∠=︒,15901575CBE CEB DEA ∴∠=︒∠=︒-︒=︒=∠,,ADE AED AD AE ∴∠=∠∴=②当ABD ∠ 为钝角时,如图所示,同样,1,302BF BD BDC =∴∠=︒ 1801501509015152ABD AEB CBE ADB ︒-︒∴∠=︒∠=︒-∠=︒∠==︒,, AE AD ∴=(3)当D 在C 左侧时,由(2)知CD AB ,,30ACD BAE DAC EBA ∠=∠∠=∠=︒,AC CD CAD BAE AB AE ∴∆∆∴==,,15AE BA BD BAD BDA ∴=∠=∠=︒30IBE ∴∠=︒,在Rt IBE ∆ 中,2222BE EI AE CD ==⨯== 2BE CD∴=当D 在C 右侧时,过E 作EI AB ⊥ 于I由(2)得,15ADC BEA ∠=∠=︒AB CDEAB ACD ∴∠=∠AC CD ACD BAE AB AE ∴∆∆∴== AE ∴= ,15BA BD BAD BDA =∠=∠=︒ 30IBE ∴∠=︒在Rt IBE ∆ 中,2222BE EI AE CD ==⨯== 2BE CD∴= 考点:圆的相关知识的综合运用6. (2017湖南长沙第26题)如图,抛物线21648(0)y mx mx m m =-+>与x 轴交于A,B 两点(点B 在点A 左侧),与y 轴交于点C ,点D 是抛物线上的一个动点,且位于第四象限,连接OD 、BD 、AC 、AD ,延长AD 交y 轴于点E 。
中考数学专题训练 一元二次方程(答案不全)(2021年整理)

2017年中考数学专题训练一元二次方程(答案不全)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2017年中考数学专题训练一元二次方程(答案不全))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2017年中考数学专题训练一元二次方程(答案不全)的全部内容。
一元二次方程一、选择题1.已知关于x的一元二次方程3x2+4x﹣5=0,下列说法正确的是( )A.方程有两个相等的实数根B.方程有两个不相等的实数根C.没有实数根D.无法确定2.若一元二次方程x2﹣2x﹣m=0无实数根,则一次函数y=(m+1)x+m﹣1的图象不经过第()象限.A.四B.三C.二D.一3.有两个一元二次方程M:ax2+bx+c=0;N:cx2+bx+a=0,其中a•c≠0,a≠c.下列四个结论中,错误的是( )A.如果方程M有两个相等的实数根,那么方程N也有两个相等的实数根B.如果方程M的两根符号相同,那么方程N的两根符号也相同C.如果5是方程M的一个根,那么是方程N的一个根D.如果方程M和方程N有一个相同的根,那么这个根必是x=14.方程x2﹣2x+3=0的根的情况是( )A.有两个相等的实数根B.只有一个实数根C.没有实数根D.有两个不相等的实数根5.一元二次方程x2+x+=0的根的情况是()A.有两个不相等的实数根B.有两个相等的实数根C.无实数根D.无法确定根的情况6.一元二次方程4x2+1=4x的根的情况是()A.没有实数根B.只有一个实数根C.有两个相等的实数根D.有两个不相等的实数根7.方程(m﹣2)x2﹣x+=0有两个实数根,则m的取值范围()A.m>B.m≤且m≠2 C.m≥3 D.m≤3且m≠28.关于x的一元二次方程(m﹣2)x2+(2m+1)x+m﹣2=0有两个不相等的正实数根,则m的取值范围是()A.m>B.m>且m≠2 C.﹣<m<2 D.<m<29.若关于x的一元二次方程x2+(2k﹣1)x+k2﹣1=0有实数根,则k的取值范围是( ) A.k≥B.k>C.k<D.k≤10.关于x的一元二次方程x2+x+m=0有实数根,则m的取值范围是()A.m≥B.m≤C.m≥D.m≤11.下列方程有两个相等的实数根的是()A.x2+x+1=0 B.4x2+2x+1=0 C.x2+12x+36=0 D.x2+x﹣2=012.下列一元二次方程中有两个不相等的实数根的方程是( )A.(x﹣1)2=0 B.x2+2x﹣19=0 C.x2+4=0 D.x2+x+l=013.若关于x的一元二次方程x2﹣2x+kb+1=0有两个不相等的实数根,则一次函数y=kx+b的大致图象可能是()A.B.C.D.14.关于x的一元二次方程(m﹣2)x2+2x+1=0有实数根,则m的取值范围是()A.m≤3 B.m<3 C.m<3且m≠2 D.m≤3且m≠215.若关于x的一元二次方程x2﹣4x+5﹣a=0有实数根,则a的取值范围是()A.a≥1 B.a>1 C.a≤1 D.a<1二、填空题16.若关于x的一元二次方程x2﹣3x+m=0有两个相等的实数根,则m= .17.若关于x的一元二次方程x2﹣x+m=0有两个不相等的实数根,则m的值可能是(写出一个即可).18.关于x的方程mx2+x﹣m+1=0,有以下三个结论:①当m=0时,方程只有一个实数解;②当m ≠0时,方程有两个不等的实数解;③无论m取何值,方程都有一个负数解,其中正确的是(填序号).19.若关于x的一元二次方程ax2+3x﹣1=0有两个不相等的实数根,则a的取值范围是.20.关于x的方程x2+2x﹣m=0有两个相等的实数根,则m= .21.已知关于x的一元二次方程x2+x﹣1=0有两个不相等的实数根,则k的取值范围是.22.关于x的一元二次方程(k﹣1)x2﹣2x+1=0有两个不相等的实数根,则实数k的取值范围是.23.关于x的一元二次方程2x2﹣4x+m﹣1=0有两个相等的实数根,则m的值为.24.若关于x的一元二次方程ax2+2x﹣1=0无解,则a的取值范围是.三、解答题25.关于x的一元二次方程x2+(2k+1)x+k2+1=0有两个不等实根x1,x2.(1)求实数k的取值范围.(2)若方程两实根x1,x2满足|x1|+|x2|=x1•x2,求k的值.26.已知关于x的一元二次方程x2﹣4x+m=0.(1)若方程有实数根,求实数m的取值范围;(2)若方程两实数根为x1,x2,且满足5x1+2x2=2,求实数m的值.27.已知:关于x的方程x2+2mx+m2﹣1=0(1)不解方程,判别方程根的情况;(2)若方程有一个根为3,求m的值.28.已知关于x的一元二次方程(x﹣3)(x﹣2)=|m|.(1)求证:对于任意实数m,方程总有两个不相等的实数根;(2)若方程的一个根是1,求m的值及方程的另一个根.29.已知关于x的一元二次方程x2﹣(2m+3)x+m2+2=0.(1)若方程有实数根,求实数m的取值范围;(2)若方程两实数根分别为x1、x2,且满足x12+x22=31+|x1x2|,求实数m的值.30.已知关于x的一元二次方程(x﹣1)(x﹣4)=p2,p为实数.(1)求证:方程有两个不相等的实数根;(2)p为何值时,方程有整数解.(直接写出三个,不需说明理由)湘教版九年级(上)中考题单元试卷:第1章一元二次方程(05)参考答案一、选择题(共15小题)1.B;2.D;3.D;4.C;5.B;6.C;7.B;8.D;9.D;10.D;11.C;12.B;13.B;14.D;15.A;二、填空题(共9小题)16.;17.0;18.①③;19.a>﹣且a≠0;20.﹣1;21.k≥1;22.k<2且k≠1;23.3;24.a <﹣1;三、解答题(共6小题)25.;26.;27.;28.;29.;30.;。
2017年中考数学专题练习一元二次方程(含解析)(1)

一元二次方程一、选择题1 .方程x2-2x-5=0, x3=x, y2- 3x=2, x2=0,其中一元二次方程的个数是()A. 1个B. 2个C. 3个D. 4个2. x2- 6x=1,左边配成一个完全平方式得()2 2 2 2A. (x - 3)=10B.(x - 3)=9C.(x - 6)=8D.(x- 6)=103 .方程(x - 1)(x+3)=5 的根为()A. X1=- 1, X2= - 3B. X1=1, X2= - 3C. X1=- 2, X2=4D. X1=2, X2=—44 .若关于x的方程3x2- 2x+m=0的一个根是-1,贝U m的值为()A. - 5B.- 1C. 1D. 55.用公式法解-x2+3x=1时,先求出a、b、c的值,贝U a、b、c依次为()A. - 1, 3,- 1B. 1 , - 3, - 1C.- 1,- 3, - 1D. 1,- 3, 16 .方程x2=0与3x2=3x的解为()A. 都是x=0B. 有一个相同,且这个相同的解为x=0C. 都不相同D. 以上答案都不对2 27. 已知x - 8xy+15y =0,那么x是y的()倍.A. 3B. 5C. 3 或5D. 2 或4&已知x=1是方程x2- ax+1=0的根,化简,打:-_;得()A. 1B. 0C.- 1D. 29. 方程x (x+1)=x+1的根为()A.- 1B. 1C.- 1或1D.以上答案都不对10. 某产品的成本两年降低了75%平均每年递降()A. 50%B. 25%C. 37.5%D.以上答案都不对、填空题11 .方程3x2- 5x=0的二次项系数是_____ .12. _________________________________________ 5X2+5=26X化成一元二次方程的一般形式为.13. _____________________________________________________ 一元二次方程ax +bx+c=O,若有一个根为-1,则a- b+c= ________________________________________ ;如果a+b+c=O,则有一根为_____214. _____________________________________________________ 一元二次方程ax +bx+c=0 (0)有一根为零的条件是 __________________________________________________ .15. 关于x的方程2x m’T-3=0是一元二次方程,则m __________ .三、解答题16. 用适当的方法解方程:2(1)2x - 4x+1=0;(2)x2- 5x - 6=0;(3)( x - 2)( x- 3) =12;(4)9 (x- 3) 2- 4 (x- 2) 2=0.17 .用配方法推导一元二次方程ax2+bx+c=0 (a丰0)的求根公式.18 .已知下列n (n为正整数)个关于x的一元二次方程:x2-仁0,2x +x - 2=0,X2+2X - 3=0,2x + (n- 1) x - n=0.(1)请解上述一元二次方程;(2)请你指出这n个方程的根具有什么共同特点,写出一条即可.19.如图,有33米长的竹篱笆,要围成一边(墙长15米)面积为130平方米的长方形鸡场,求鸡场的长和宽各为多少?/ / / / 彳鸡场一元二次方程参考答案与试题解析一、选择题1 .方程x2-2x-5=0, x3=x, y2- 3x=2, x2=0,其中一元二次方程的个数是()A.1 个B.2 个C.3 个D.4 个【考点】一元二次方程的定义.【分析】直接根据一元二次方程的定义可得到在所给的方程中x2- 2x- 5=0,x2=0 是一元二次方程. 【解答】解:方程x2- 2x- 5=0, x3=x, y2- 3x=2, x2=0,其中一元二次方程是x2- 2x - 5=0, x2=0. 故选B. 【点评】本题考查了一元二次方程的定义:只含有一个未知数,并且未知数的最高次数为 2 的整式方程叫一元二次方程.2. x2- 6x=1 ,左边配成一个完全平方式得()2 2 2 2A.(x- 3)2=10B.(x- 3)2=9C.(x- 6)2=8D.(x- 6)2=10【考点】解一元二次方程-配方法.【专题】计算题.【分析】给方程左右两边都加上9,左边化为完全平方式,右边合并为一个常数,即可得到正确的选项.【解答】解:x2- 6x=1 ,方程左右两边都加上9得:x2- 6x+9=10,即(x - 3)2=10.故选A【点评】此题考查了解一元二次方程-配方法,利用此方法解方程时,首先将方程的二次项系数化3方程(x- 1)(x+3)=5 的根为()A. x1=- 1 , x2=- 3B. x1=1 , x2=- 3C. x1=- 2, x2=4D. x1=2, x2=- 4【考点】解一元二次方程-因式分解法.分析】首先把方程转化为一般形式,再利用因式分解法即可求解.为1,同时将常数项移到方程右边,然后方程左右两边都加上一次项系数一半的平方,左边化为完全平方式,右边合并为一个非负常数,开方转化为两个一元一次方程来求解.【解答】解:(x - 1)( x+3) =5,2x2+3x- x- 3- 5=0,x2+2x- 8=0,( x- 2)( x+4) =0,解得x1=2,x2=- 4.故选D.【点评】本题考查了一元二次方程的解法.解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.4 .若关于x的方程3x2- 2x+m=0的一个根是-1,贝U m的值为( )A.- 5 B.- 1 C.1 D.5【考点】一元二次方程的解.【专题】方程思想.【分析】根据一元二次方程解的定义,将x=1代入原方程,然后解关于m的一元一次方程即可.【解答】解:T关于x的方程3x2- 2x+m=0的一个根是-1,•••当x= - 1时,由原方程,得3+2+m=0,解得m=- 5;故选A.【点评】本题考查的是一元二次方程的根即方程的解的定义.本题逆用一元二次方程解的定义易得出m的值.5.用公式法解- x2+3x=1 时,先求出a、b、c 的值,贝a、b、c 依次为( )A.- 1 , 3,- 1B. 1 ,- 3,- 1C.- 1 ,- 3,- 1D. 1 ,- 3, 1【考点】解一元二次方程-公式法.【分析】先移项,化成一般形式,再得出答案即可.【解答】解:•••- x2+3x=1,2•- x +3x- 1=0,2• x2- 3x+1=0,• a=- 1, b=3, c=- 1(或a=1, b=- 3, c=1), 故选A.【点评】本题考查了解一元二次方程和一元二次方程的一般形式的应用,解此题的关键是能把方程化成一般形式.6.方程x2=0 与3x2=3x 的解为( )A. 都是x=0B. 有一个相同,且这个相同的解为x=0C. 都不相同D. 以上答案都不对【考点】解一元二次方程-因式分解法.【专题】计算题.【分析】解x2=0得X i=X2=0;变形3X2=3X得x2- x=0,左边分解得到x (x - 1) =0,则X i=0, X2=1.2【解答】解:••• X =0/• X i=X2=0;■/ X2- X=0 ,••• X (X - 1) =0,二X i=0, X2=1 .故选B.【点评】本题考查了解一元二次方程-因式分解法:先把方程右边变形为0,然后把方程左边进行因式分解,这样把一元二次方程转化为两个一元一次方程,再解一次方程可得到一元二次方程的解.227.已知X - 8Xy+15y =0,那么X 是y 的( )倍.A. 3B. 5C. 3 或5D. 2 或4【考点】解一元二次方程-因式分解法.【专题】计算题.【分析】先把等式左边分解因式得到(X - 3y) (X- 5y) =0,则X- 3y=0或X- 5y=0 ,即可得到x=3y或X=5y.【解答】解:T( X - 3y) ( X - 5y) =0,•X- 3y=0 或X- 5y=0,•X=3y 或X=5y.故选c.【点评】本题考查了解一元二次方程-因式分解法:先把方程右边变形为0,然后把方程左边进行因式分解,这样把一元二次方程转化为两个一元一次方程,再解一次方程可得到一元二次方程的解.8. 已知x=1是方程x?- ax+仁0的根,化简,.广.一一-二一:「亠广得( )A. 1B. 0C.- 1D. 2【考点】一元二次方程的解;二次根式的性质与化简.【分析】先将x=1代入方程x2- ax+1=0,可得关于a的方程,解方程求出a的值,再根据二次根式的性质化简即可.【解答】解:T x=1是方程x2- ax+1=0的根,21 - a x 1+1=0,二a=2,.'J J n-也fC=■ - I ,-■-=a - 1 -( 3 - a)=2a - 4=2X 2 - 4=0.故选B.【点评】本题主要考查了方程的解的定义,二次根式的性质与化简,解题关键是将已知的根代入方程,正确求出a的值. 44方程x (x+1) =x+1的根为( )A. - 1B. 1•••( x+1) ( x - 1) =0,解得:X i=- 1 , X2=1 .故选C.【点评】此题考查了因式分解法解一元二次方程•此题难度不大,注意因式分解法解一元二次方程的一般步骤:①移项,使方程的右边化为零;②将方程的左边分解为两个一次因式的乘积;③令每个因式分别为零,得到两个一元一次方程;④解这两个一元一次方程,它们的解就都是原方程的解.10. 某产品的成本两年降低了75%平均每年递降( )A. 50%B. 25%C. 37.5%D.以上答案都不对【考点】一元二次方程的应用.【专题】增长率问题.【分析】设平均每年降低x,根据经过两年使成本降低75%可列方程求解.【解答】解:设平均每年降低x,2(1 - x) =1 - 75%解得x=0.5=50%或x=1.5 (舍去).故平均每年降低50%故选A.【点评】本题考查理解题意的能力,关键设出降低的百分率,然后根据现在的成本,可列方程求解.二、填空题211 .方程3x - 5x=0的二次项系数是 3 .【考点】一元二次方程的一般形式.C.- 1或1D.以上答案都不对【考点】解一元二次方程-因式分解法.【分析】首先提取公因式,可得( x+1)( x - 1) =0,继而可求得答案.【解答】解:••• x (x+1) =x+1,.x (x+1) -( x+1) =0,【分析】先找出方程的二次项,再找出项的系数即可.【解答】解:方程3x2- 5x=0的二次项系数是3,故答案为:3.【点评】本题考查了一元二次方程的一般形式的应用,主要考查学生的理解能力.12. 5X2+5=26X化成一元二次方程的一般形式为5x2- 26x+5=0 .【考点】一元二次方程的一般形式.【专题】计算题.【分析】将方程右边的式子移项,并按照x的降幕排列,即可得到一元二次方程的一般形式.【解答】解:5X2+5=26X,2移项得:5X - 26x+5=0.故答案为:5X2-26X+5=0【点评】此题考查了一元二次方程的一般形式,一元二次方程的一般形式为ax2+bx+c=0 (a, b, c 为常数,且0).13. —元二次方程ax2+bx+c=0 ,若有一个根为-1,则a- b+c= 0 ;如果a+b+c=O,则有一根为1 . 【考点】一元二次方程的解.【分析】由一元二次方程解的意义把方程的根X= - 1代入方程,得到 a - b+c=O;由a+b+c=O,可知a x 12+b x 1+c=0,故方程ax2+bx+c=0 有一根为1.2【解答】解:把X= - 1代入一元二次方程ax +bx+c=O得:a - b+c=O;i " I 2如果a+b+c=O,那么a x 1 +b x 1+c=0,所以方程ax2+bx+c=0有一根为1.故答案是:0; 1.【点评】本题考查的是一元二次方程的解的定义,属于基础题型,比较简单.14. 一元二次方程ax2+bx+c=0 (0)有一根为零的条件是c=0 .【考点】一元二次方程的解.【专题】计算题.【分析】根据一元二次方程的定义和根与系数的关系解答.【解答】解:T一元二次方程ax2+bx+c=0 (a丰0)的二次项系数是a,常数项是c,/• X1?X2 = 一,a又•• •该方程有一根为零,••• X1?X2=—=0;a•/0,•- c=0.故答案为:0.【点评】本题主要考查了一元二次方程的解,在解答此题时,禾U用了根与系数的关系.15 .关于x的方程2x ;-3=0是一元二次方程,则m= ±二【考点】一元二次方程的定义.【分析】根据一元二次方程的概念,可得出卅-仁2,解得m即可.【解答】解:•••关于x的方程2x . - 3=0是一元二次方程,••• m-仁2,解得m=± 二.故答案为:士二【点评】本题考查了一元二次方程的概念,二次项系数不为0,未知数的最高次数为2.三、解答题16.用适当的方法解方程:(1)2x2- 4x+1=0;(2)x2- 5x - 6=0;(3)( x - 2)( x- 3) =12;(4)9 (x- 3) 2- 4 (x- 2) 2=0.【考点】解一元二次方程-因式分解法;解一元二次方程-配方法.【分析】(1)找出a, b, c的值,计算出根的判别式的值大于0,代入求根公式即可求出解;(2)利用因式分解法求解即可;(3)先将方程整理为一般形式,再利用因式分解法求解;(4)利用因式分解法求解即可.【解答】解:(1) 2x2- 4x+仁0,这里a=2, b=- 4, c=1,=16 - 4x 2x 1=8,4±Vs= 2 + V22X2 2^~(2)x2- 5x - 6=0,(x- 6)( x+1) =0,/• x - 6=0 或x+1=0,解得x i=6, X2=- 1 ;(3)( x - 2)( x- 3) =12,整理,得x2- 5x- 6=0,(x- 6)( x+1) =0,/• x - 6=0 或x+1=0,解得X1=6, X2=- 1;(4)9 (x- 3) 2- 4 (x- 2) 2=0,[3 (x - 3) +2 (x - 2) ][3 ( x- 3)- 2 (x- 2) ]=0 ,(5x- 13)( x - 5) =0,1 ?解得X1= I , X2=5.5【点评】本题考查了一元二次方程的解法•解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.17 .用配方法推导一元二次方程ax2+bx+c=0 (a丰0)的求根公式.【考点】解一元二次方程-公式法;配方法的应用.【专题】计算题.【分析】由a不为0,在方程左右两边同时除以a,并将常数项移到方程右边,方程左右两边都加上一次项系数一半的平方,左边化为完全平方式,右边通分并利用同分母分式的减法法则计算,当b2-4ac> 0时,开方即可推导出求根公式.2【解答】解:ax +bx+c=0 (0),方程左右两边同时除以a得:x2+" x+' =0,a a移项得:x2+ " x=- 一a a2 - 2 J 'A:配万得:X + X+ = -= ,,即(X^—)= .,自4a 4 a 自4a 4a当b2- 4ac> 0时,x「.=±【点评】此题考查了一元二次方程的求根公式,以及配方法的应用,学生在开方时注意这个条件的运用.18 .已知下列n (n为正整数)个关于x的一元二次方程:x2-仁0,2x +x - 2=0,2x +2x- 3=0,2x + (n- 1) x - n=0.(1)请解上述一元二次方程;(2)请你指出这n个方程的根具有什么共同特点,写出一条即可.【考点】解一元二次方程-因式分解法;一元二次方程的解.【专题】规律型.【分析】(1)分别利用因式分解法解各方程;(2)根据方程根的特征易得这n个方程都有一个根为1,另外一根等于常数项.【解答】解:(1) x2-仁0,解得X1=1, X2=- 1,x2+x - 2=0,解得X1=1, X2=- 2,2x +2x- 3=0,解得X1=1, X2=- 3,…x2+ (n —1) x- n=0,解得X1=1, X2=- n;(2)这n个方程都有一个根为1,另外一根等于常数项.【点评】本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).19.如图,有33米长的竹篱笆,要围成一边(墙长15米)面积为130平方米的长方形鸡场,求鸡场的长和宽各为多少?/ / / /〈鸡场【考点】一元二次方程的应用.【专题】几何图形问题.【分析】首先设鸡场的长为x米,则宽为一米,根据题意可得等量关系:鸡场的长X宽=130平2方米,列出方程,解出x的值.【解答】解:设鸡场的长为x米,则宽为米,由题意得:2;;P — Vx X =130,2解得:X1=25, X2=13,•••墙长15 米,25 > 15,••• 25不合题意舍去,••• x=13,则:一二=10 (米).2答:鸡场的长为13米,则宽为10米.【点评】此题主要考查了一元二次方程的应用,关键是弄懂题意,找出题目中的等量关系,此题根据鸡场的面积列出方程即可.。
2017中学考试真题分类——一元二次方程

2017中考真题分类——一元二次方程一、选择题(每题只有一个最佳答案,请将其填在括号内!)1. (2017·山东泰安·7)一元二次方程2660x x --=配方后化为( )A .2(3)15x -= B .2(3)3x -= C. 2(3)15x += D .2(3)3x +=2. (2017·浙江舟山·8)用配方法解方程0122=-+x x 时,配方结果正确的是( )A .2)2(2=+xB .2)1(2=+x C. 3)2(2=+x D .3)1(2=+x3. (2017·江苏苏州·4)关于x 的一元二次方程220x x k -+=有两个相等的实数根,则k 的值为( )A .1B .1- C.2 D .2-4. (2017·江苏扬州·3)一元二次方程2720x x --=的实数根的情况是( ) A .有两个不相等的实数根 B .有两个相等的实数根 C .没有实数根D .不能确定5. (2017·四川宜宾·4)一元二次方程 的根的情况是( ) A. 有两个不相等的实数根 B. 有两个相等的实数根 B. 没有实数根 D.无法判断6. (2017·广东广州·5)关于x 的一元二次方程280x x q ++=有两个不相等的实数根,则q 的取值范围是( )A .16q <B .16q > C. 4q ≤ D .4q ≥7. (2017·甘肃兰州·6)如果一元二次方程2230x x m ++=有两个相等的实数根,那么是实数m 的取值为( )A.98m >B.89m >C.98m =D.89m =8. (2017·山东滨州·2)一元二次方程x 2-2x =0根的判别式的值为A .4B .2C .0D .-49. (2017·安徽·8)一种药品原价每盒25元,经过两次降价后每盒16元.设两次降价的百分率都为x ,则x 满足( )A .16(12)25x +=B .25(12)16x -= C.216(1)25x += D .225(1)16x -=214204x x -+=10. (2017·浙江杭州·7)某景点的参观人数逐年增加,据统计,2014年为10.8万人次,2016年为16.8万人次,设参观人次的平均年增长率为x ,则( ) A .10.8(1+x )=16.8 B .16.8(1-x )=10.8C .10.8(1+x )2=16.8 D .10.8[(1+x )+(1+x )²]=16.811. (2017·江苏无锡·7)商店今年1月份的销售额是2万元,3月份的销售额是4.5万元,从1月份到3月份,该店销售额平均每月的增长率是( ) A .20% B .25% C.50% D .62.5%12. (2017·湖南衡阳·9)中国“一带一路”战略给沿线国家和地区带来很大的经济效益,沿线某地区居民2015年年收入200美元,预计2017年年收入将达到1000美元,设2015年到2017年该地区居民年人均收入平均增长率为x ,可列方程为:( ) A .()200121000x += B .()220011000x += C.()220011000x +=D .20021000x +=13. (2017·甘肃庆阳·9)如图,某小区计划在一块长为32m ,宽为20m 的矩形空地上修建三条同样宽的道路,剩余的空地上种植草坪,使草坪的面积为2570m ,若设道路的宽为m x ,则下面所列方程正确的是( ) A.()()32220570x x --=B.32203220570x x +??C.()()32203220570x x --?D.2322202570x x x +?=14. (2017·江苏南京·5)若方程()2519x -=的两根为a 和b ,且a b >,则下列结论中正确的是 ( ) A .a 是19的算术平方根 B .b 是19的平方根 C.5a -是19的算术平方根D .5b +是19的平方根15. (2017·浙江温州·8)我们知道方程2230x x +-=的解是11x =,23x =-,现给出另一个方程2(23)2(23)30x x +++-=,它的解是( )A .11x =,23x =B .11x =,23x =-C .11x =- ,23x = D .11x =-,23x =- 16. (2017·江西·5)已知一元二次方程22510x x -+=的两个根为12,x x ,下列结论正确的是( ) A . 1252x x +=-B .121x x = C. 12,x x 都是有理数 D .12,x x 都是正数17. (2017·湖南益阳·6)关于x 的一元二次方程20(0)ax bx c a ++=≠的两根为11x =,21x =-,那么下列结论一定成立的是( )A .240b ac ->B .240b ac -=C .240b ac -<D .240b ac -≤18. (2017·四川绵阳·7)关于x 的方程022=++n mx x 的两个根是2-和1,则mn 的值为( )A .8-B .8 C. 16 D .16-二、填空题(请将正确答案全部填写在横线上,多填、漏填、错填都不得分!)19. (2017·山东潍坊·16)已知关于x 的一元二次方程0122=+-x kx 有实数根,则k 的取值范围是 .20. (2017·山东德州·15)方程()()3121x x x -=- 的根为 .21. (2017·山东泰安·22)关于x 的一元二次方程22(21)(1)0x k x k +-+-=无实数根,则k 的取值范围为 .22. (2017·山东枣庄·14)已知关于的一元二次方程有两个不相等的实数根,则的取值范围是 .23. (2017·甘肃庆阳·15)若关于x 的一元二次方程()21410k x x -++=有实数根,则k 的取值范围是.24. (2017·江苏淮安·14)若关于x 的一元二次方程210x x k -++=有两个不相等的实数根,则k 的取值范围是 .25. (2017·江苏扬州·18)若关于x的方程240200x -+=存在整数解,则正整数m 的所有取值的和为 .26. (2017·山东菏泽·10)关于x 的一元二次方程06)1(22=-++-k k x x k 的一个根式0,则k 的值是_______.27. (2017·江苏南京·12)已知关于x 的方程20x px q ++=的两根为-3和-1,则p = ;q = .28. (2017·江苏泰州·12)方程22310x x +-=的两个根为1x 、2x ,则1211x x +等于___ x 2210ax x --=a29. (2017·江苏盐城·13)若方程2410x x -+=的两根是1x ,2x ,则()1221x x x ++的值为___________.30. (2017·四川成都·22)已知12,x x 是关于x 的一元二次方程250x x a -+=的两个实数根,且221210x x -=,则a =___________.31. (2017·四川眉山·15)已知一元二次方程x 2-3x -2=0的两个实数根为x 1,x 2,则(x 1-1)(x 2-1)的值是________.32. (2017·四川内江·22,24)若实数x 满足2210x x --=,则322742017x x x -+-=____设,αβ是方程(1)(4)5x x +-=-的两实数根,则22βααβ+= ________ 33. (2017·甘肃兰州·21(2))解方程:22410x x --=.34. (2017·浙江丽水·18)解方程:(3)(1)3x x --=.35. (2017·湖南湘潭·22)由多项式乘法:2()()()x a x b x a b x ab ++=+++,将该式从右到左使用,即可得到“十字相乘法”进行因式分解的公式:2()()()x a b x ab x a x b +++=++示例:分解因式:256x x ++=2(23)23x x +++⨯=(2)(3)x x ++(1)尝试:分解因式:268x x ++=(x +___)(x +___); (2)应用:请用上述方法....解方程:2340x x --=.36. (2017·湖北黄冈·17)已知关于x 的一元二次方程()22210x x x k +++=①有两个不相等的实数根. ⑴求k 的取值范围;⑵设方程①的两个实数根分别为12,x x ,当k =1时,求2212x x +的值.37. (2017·山东滨州·20) 根据要求,解答下列问题. (1)根据要求,解答下列问题.①方程x 2-2x +1=0的解为________________________;②方程x 2-3x +2=0的解为________________________;③方程x 2-4x +3=0的解为________________________; …… ……(2)根据以上方程特征及其解的特征,请猜想:①方程x 2-9x +8=0的解为________________________;②关于x 的方程________________________的解为x 1=1,x 2=n .(3)请用配方法解方程x 2-9x +8=0,以验证猜想结论的正确性.38. (2017·山东潍坊·23节选)工人师傅用一块长为10dm ,宽为6dm 的矩形铁皮制作一个无盖的长方体容器,需要将四角各裁掉一个正方形,(厚度不计) (1)在图中画出裁剪示意图,用实线表示裁剪线,虚线表示折痕;并求长方体底面面积为212dm 时,裁掉的正方形边长多大?39.(2017·山东菏泽·19)列方程解应用题:某玩具厂生产一种玩具,按照控制固定成本降价促销的原则,使生产的玩具能够及时售出,据市场调查:每个玩具按480元销售时,每天可销售160个;若销售单价每降低1元,每天可多售出2个.已知每个玩具的固定成本为360元,问这种玩具的销售单价为多少元时,厂家每天可获利润20000元?40.(2017·四川眉山·24)东坡某烘焙店生产的蛋糕礼盒分为六个档次,第一档次(即最低档次)的产品每天生产76件,每件利润10元.调查表明:生产提高一个档次的蛋糕产品,该产品每件利润增加2元.⑴若生产的某批次蛋糕每件利润为14元,此批次蛋糕属第几档次产品;⑵由于生产工序不同,蛋糕产品每提高一个档次,一天产量会减少4件.若生产的某档次产品一天的总利润为1080元,该烘焙店生产的是第几档次的产品?41.(2017·浙江衢州·20)根据衢州市统计局发布的统计数据显示,衢州市近5年国民生产总值数据如图1所示,2016年国民生产总值中第一产业、第二产业、第三产业所占比例如图2所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一元二次方程
一、填空题
1.若分式的值为0,则x的值为.
2.已知方程(x+a)(x﹣3)=0和方程x2﹣2x﹣3=0的解相同,则a= .
3.方程x2=|x|的根是.
4.一小球以15m/s的速度竖直向上弹出,它在空中的高度h( m)与时间t(s)满足关系式:h=15t ﹣5t2,当t= s时,小球高度为10m,小球所能达到的最大高度为.
5.已知(x2+y2﹣2)(x2+y2)=3,则x2+y2= .
6.若a2+b2+a﹣2b+=0,则= .
7.将方程化成二次项系数为1的一般形式,则一次项系数是,常数项是.
8.方程(3x﹣1)2=(2﹣x)2的根是.
9.把化成ax2+bx+c=0(a≠0)的形式后,则a= ,b= ,c= .
10.请写出一个一元二次方程,使其一根为﹣1,你写的方程是.
二、选择题
11.下列方程不是整式方程的是()
A. B.0.2x2﹣0.4x3=0
C. D.
12.在下列方程中,一元二次方程的个数是()
①3x2+7=0,②ax2+bx+c=0,③(x+2)(x﹣3)=x2﹣1,④x2﹣+4=0,⑤x2﹣(+1)x+=0,⑥3x2﹣+6=0 A.1个B.2个C.3个D.4个
13.已知关于x的一元二次方程(m﹣1)x2+x+m2+2m﹣3=0的一个根为0,则m的值为()
A.1 B.﹣3
C.1或﹣3 D.不等于1的任意实数
14.已知2y2+y﹣2的值为3,则4y2+2y+1的值为()
A.10 B.11 C.10或11 D.3或11
15.已知一元二次方程ax2+bx+c=0中二次项系数,一次项系数和常数项之和为0,那么方程必有一根为()
A.0 B.1 C.﹣1 D.±1
16.若b(b≠0)是方程x2+cx+b=0的根,则b+c的值为()
A.1 B.﹣1 C.2 D.﹣2
17.从正方形的铁片上,截去2cm宽的一条长方形,余下的面积是48cm2,则原来的正方形铁片的面积是()
A.96cm2B.64cm2C.54cm2D.52cm2
18.若方程x2+ax﹣2a=0的一根为1,则a的取值和方程的另一根分别是()
A.1,﹣2 B.﹣1,2 C.1,2 D.﹣1,﹣2
19.若a,b,c为三角形ABC的三边,且a,b,c满足(a﹣b)(a﹣c)=0,则△ABC为()A.直角三角形B.钝角三角形
C.等边三角形D.等腰三角形或等边三角形
20.一元二次方程x2﹣3x﹣1=0与x2﹣x+3=0的所有实数根的和等于()
A.2 B.﹣4 C.4 D.3
三、解答题
21.选用适当的方法解下列方程:
(1)(3﹣x)2+x2=9
(2)(2x﹣1)2+(1﹣2x)﹣6=0
(3)(3x﹣1)2=4(1﹣x)2
(4)(x﹣1)2=(1﹣x)
22.解下列关于x的方程:
(1)x2+(1+2)x+3+=0;
(2)x2﹣3|x|﹣4=0
(3)(x﹣3)2+(x+4)2﹣(x﹣5)2=17x+24.
23.已知2+是方程x2﹣4x+c=0的一个根,求方程的另一个根及c的值.
24.一元二次方程ax2+bx+c=0(a≠0)有两根x1,x2,则,,则x1+x2= ,x1x2= .
请运用上面你发现的结论,解答问题:
已知x1,x2是方程x2﹣x﹣1=0的两根,不解方程求下列式子的值:
①x12+x22;
②;
③(x1+1)(x2+1).
25.解方程,有一位同学解答如下:
解:这里a=,b=,c=
∴b2﹣4ac=(﹣
∴=
∴
请你分析以上解答有无错误,如有错误,指出错误的地方,并写出正确的结果.
26.已知等腰三角形两边长分别是x2﹣8x+15=0的两根,求此等腰三角形的周长.
27.如图,一个长为15m的梯子斜靠在墙上,梯子的顶端距地面的距离为12m,如果梯子的顶端下滑了1m,那么梯子的底端也向后滑动1m吗?试列出方程解答此问题,并论证前面的结论.
参考答案
一、填空题(共10小题,每小题2分,满分20分)
1.1;2.1;3.x1=0,x2=1,x3=﹣1;4.1或2;;5.3;6.﹣3;7.﹣;;8.;9.1;;;10.x2+x=0;
二、选择题(共10小题,每小题2分,满分20分)
11.D;12.B;13.B;14.B;15.B;16.B;17.B;18.A;19.D;20.D;
三、解答题(共7小题,满分58分)
21.;22.;23.;24.﹣;;25.;26.;27.;。
