北师大版必修1 3.2.2指数运算的性质讲稿

合集下载

《3.2.2指数运算的性质》课件1-优质公开课-北师大必修1精品

2
= 3 100 1 ( 3)
2
2
=99.
(2)原式=
1 ( 3)2

(
27
)
2 3
(
1
1
)2
33
2
8 100
= 1 ( 2)2 ( 3)2 10 27
32
=1+1-10+27
=19.
【补偿训练】(2014·成都高一检测)计算：
0.751 (
3
)
1 2
[1
3

211 115
1]a b 3 2 6 2 3 6

9a1b0

9a.
3
(2)①原式=
a2 b3 { g[
ba
(
a b3
)
1 2
1
]2
1
}2
1
3
=
a2 b3 [ g(
ba

a2
3
11
)2 ]2
a2 [
b
b2 (1
11
)2 ]2
b2
a2
3
=
a2 [
b
b4 (1
1
)]2

2 1 3 1 1
【自主解答】(1)①原式=
(
64

)
2 3

(
27
)
2 3

[(
3
)3
2
]3
(3)2

9
.
27
64
4
4 16
②原式

22
23
3
24
7
24

高中数学第3章 §2 2.2 指数运算的性质优质课件北师大版必修1

第五页，共28页。
思考：上节指数已经由正整数扩充到实数，那么正整数幂的运算(yùn suàn)法则是否可以扩充到实数指数幂呢？
当 a 0, b 0 时，对任意实数 m, n 都满足
上述性质，可以归纳如下：
am an amn (am )n a mn (ab)n anbn
第六页，共28页。
102 ，10 5 ．
解：10 10 10 3 4 12 ；
10
10 10
3； 4
102 10 2 32 1 ；
9
1
1
10 5 10 5 45 ．
第十三页，共28页。
【变式练习(liànxí)】
求下列各式的值：
（1）100000.75
（2）
(125
)
2 3
27
解：(1)
3
100000.75 (104 )4
y
1 2
)
1 3
·
( xy )
1 2
第十一页，共28页。
【提升(tíshēng) 总结】含字母的幂的运算是高中数学中的基本运算之一, 可以仿照单项式乘除法进行，首先是系数相乘(xiānɡ chénɡ) 除，然后是同底数幂相乘(xiānɡ chénɡ)除，并且要注意符号．
第十二页，共28页。
例 3.已知10 3,10 4 ．求10 ，10 ，
巩固
((习g1ǒ)n3 g g__ù(_)_113练_)_3 ____121_7_____2_7_____
3
(2x)5 ___(_2_1_x_)_5____3_2_1_x_5___
化为同底的指数 (zhǐshù)运算
35 ( 1) ___3_5__(__3__2_)_____3__5 __3__2_____3_3_____2_7_____

数学：3.2.2《指数运算的性质》课件(北师大版必修1)

10 5 .
点评：运用整体思想和运算性质是解决本题的关键，要深刻理解这种方法. 练习3.已知10α=2，10β=3，把下面的数写成底数是10的幂的形式： 2 3
（ 1）；（ 2） 8；（ 3） 24；（ 4） . 3 2
例4. 已知
a a
1
1 2

1 2
3, 求下列各式的值：
2 2 3 2 3 2
五、小
结
1.无理数指数幂的意义一般地，无理数指数幂aα(a>0, α是无理数）是一个确定的实数. 2.实数指数幂的运算性质对任意的实数 r, s, 均有下面的运算性质：（1）ar· as=ar+s （a>0, r, s ∈R）（2）(ar)s=ars （a>0, r, s ∈R）（3）(a· b)r=arbr（a>0, b>0, r ∈R ） 3.逼近的思想，体会无限接近的含义.
a
n
n n
n
a
(n>1,n∈N+),
②
a （n为奇数） (n>1,n∈N+). a a (n为偶数)
2.有理数指数幂运算性质
对任意的有理数 r, s,均有下面的运算性质：（1）ar· as=ar+s （a>0, r, s ∈Q）（2）(ar)s=ars （a>0, r, s ∈Q ）（3）(a· b)r=arbr（a>0, b>0, r ∈Q ）
四、例题与练习
n b b （ ) n n （其中a>0, 例1.在实数范围内，对比(ab)n=anbn和 a a b>0, b≠0),说明后者可以归入前者.
当a 练习1.在实数范围内，对比性质（1），

秋北师大版必修1示范教案322指数运算的性质

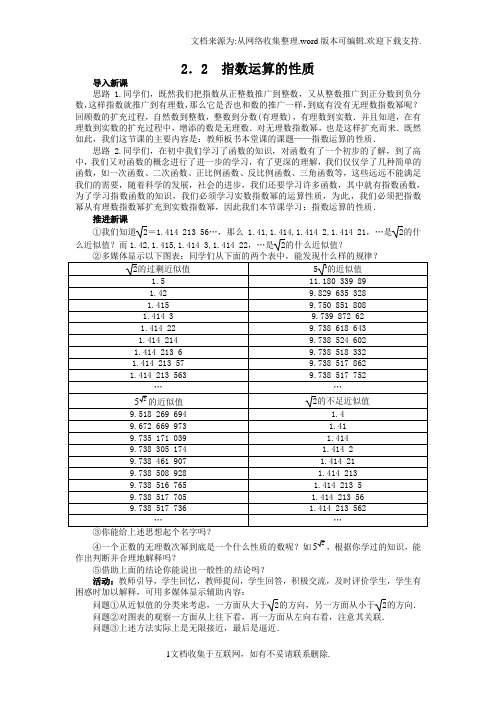
2．2 指数运算的性质导入新课思路1.同学们，既然我们把指数从正整数推广到整数，又从整数推广到正分数到负分数，这样指数就推广到有理数，那么它是否也和数的推广一样，到底有没有无理数指数幂呢？回顾数的扩充过程，自然数到整数，整数到分数(有理数)，有理数到实数．并且知道，在有理数到实数的扩充过程中，增添的数是无理数．对无理数指数幂，也是这样扩充而来．既然如此，我们这节课的主要内容是：教师板书本堂课的课题——指数运算的性质．思路 2.同学们，在初中我们学习了函数的知识，对函数有了一个初步的了解，到了高中，我们又对函数的概念进行了进一步的学习，有了更深的理解，我们仅仅学了几种简单的函数，如一次函数、二次函数、正比例函数、反比例函数、三角函数等，这些远远不能满足我们的需要，随着科学的发展，社会的进步，我们还要学习许多函数，其中就有指数函数，为了学习指数函数的知识，我们必须学习实数指数幂的运算性质，为此，我们必须把指数幂从有理数指数幂扩充到实数指数幂，因此我们本节课学习：指数运算的性质．推进新课①我们知道2＝1.414 213 56…，那么1.41,1.414,1.414 2,1.414 21，…是2的什么近似值？而1.42,1.415,1.414 3,1.414 22，…是2的什么近似值？2的过剩近似值52的近似值1.511.180 339 891.429.829 635 3281.4159.750 851 8081.414 39.739 872 621.414 229.738 618 6431.414 2149.738 524 6021.414 213 69.738 518 3321.414 213 579.738 517 8621.414 213 5639.738 517 752……25的近似值2的不足近似值9.518 269 694 1.49.672 669 973 1.419.735 171 039 1.4149.738 305 174 1.414 29.738 461 907 1.414 219.738 508 928 1.414 2139.738 516 765 1.414 213 59.738 517 705 1.414 213 569.738 517 736 1.414 213 562……5，根据你学过的知识，能④一个正数的无理数次幂到底是一个什么性质的数呢？如2作出判断并合理地解释吗？⑤借助上面的结论你能说出一般性的结论吗？活动：教师引导，学生回忆，教师提问，学生回答，积极交流，及时评价学生，学生有困惑时加以解释，可用多媒体显示辅助内容：问题①从近似值的分类来考虑，一方面从大于2的方向，另一方面从小于2的方向．问题②对图表的观察一方面从上往下看，再一方面从左向右看，注意其关联．问题③上述方法实际上是无限接近，最后是逼近．问题④对问题给予大胆猜测，从数轴的观点加以解释．问题⑤在③④的基础上，推广到一般的情形，即由特殊到一般．讨论结果：①1.41,1.414,1.414 2,1.414 21，…，这些数都小于2，称2的不足近似值，而1.42,1.415,1.414 3,1.414 22，…，这些数都大于2，称2的过剩近似值．②第一个表：从大于2的方向逼近2时，25就从51.5,51.42,51.415,51.414 3,51.414 22，…，即大于25的方向逼近25.第二个表：从小于2的方向逼近2时，25就从51.4,51.41,51.414,51.414 2,51.414 21，…，即小于25的方向逼近25.从另一角度来看这个问题，在数轴上近似地表示这些点，数轴上的数字表明一方面25从51.4,51.41,51.414,51.414 2,51.414 21，…，即小于25的方向接近25，而另一方面25从51.5,51.42,51.415,51.414 3,51.414 22，…，即大于52的方向接近52，可以说从两个方向无限地接近25，即逼近25，所以25是一串有理数指数幂51.4,51.41,51.414,51.414 2,51.414 21，…和另一串有理数指数幂51.5,51.42,51.415,51.414 3,51.414 22，…，按上述变化规律变化的结果，事实上表示这些数的点从两个方向向表示25的点靠近，但这个点一定在数轴上，由此我们可得到的结论是25一定是一个实数，即51.4＜51.41＜51.414＜51.414 2＜51.414 21＜…＜25＜…＜51.414 22＜51.414 3＜51.415＜51.42＜51.5.充分表明25是一个实数，再如⎝ ⎛⎭⎪⎫123，3π等都是实数．③逼近思想，事实上里面含有极限的思想，这是以后要学的知识．④根据②③我们可以推断25是一个实数，猜测一个正数的无理数次幂是一个实数． ⑤无理数指数幂的意义：一般地，无理数指数幂a α(a ＞0，α是无理数)是一个确定的实数．也就是说无理数可以作为指数，并且它的结果是一个实数，这样指数概念又一次得到推广，在数的扩充过程中，我们知道有理数和无理数统称为实数．我们规定了无理数指数幂的意义，知道它是一个确定的实数，结合前面的有理数指数幂，那么，指数幂就从有理数指数幂扩充到实数指数幂．1为什么在规定无理数指数幂的意义时，必须规定底数是正数？2无理数指数幂的运算法则是怎样的？是否与有理数指数幂的运算法则相通呢？ 3你能给出实数指数幂的运算法则吗？活动：教师组织学生互助合作，交流探讨，引导他们用反例说明问题，注意类比，归纳．对问题(1)回顾我们学习分数指数幂的意义时对底数的规定，举例说明．对问题(2)结合有理数指数幂的运算法则，既然无理数指数幂a α(a ＞0，α是无理数)是一个确定的实数，那么无理数指数幂的运算法则应当与有理数指数幂的运算法则类似，并且相通．对问题(3)有了有理数指数幂的运算法则和无理数指数幂的运算法则，实数的运算法则自然就得到了．讨论结果：(1)底数大于零的必要性，若a ＝－1，那么a α是＋1还是－1就无法确定了，这样就造成混乱，规定了底数是正数后，无理数指数幂a α是一个确定的实数，就不会再造成混乱．(2)因为无理数指数幂是一个确定的实数，所以能进行指数的运算，也能进行幂的运算，有理数指数幂的运算性质，同样也适用于无理数指数幂．类比有理数指数幂的运算性质可以得到无理数指数幂的运算法则：①a r ·a s ＝a r ＋s(a ＞0，r ，s 都是无理数)．②(a r )s ＝a rs(a ＞0，r ，s 都是无理数)．③(a ·b )r ＝a r b r(a ＞0，b ＞0，r 是无理数)．(3)指数幂扩充到实数后，指数幂的运算性质也就推广到了实数指数幂．实数指数幂的运算性质：对任意的实数r ，s ，均有下面的运算性质： ①a r ·a s ＝a r ＋s(a ＞0，r ，s ∈R )．②(a r )s ＝a rs(a ＞0，r ，s ∈R )．③(a ·b )r ＝a r b r(a ＞0，b ＞0，r ∈R )．思路1例1 在实数范围内，对比(ab )n＝a n b n和⎝ ⎛⎭⎪⎫a b n ＝anbn (其中a ＞0，b ＞0，b ≠0)，说明后者可以归入前者．解：⎝ ⎛⎭⎪⎫a b n ＝(ab －1)n ＝a n b －n ＝a n b n ，因此，性质⎝ ⎛⎭⎪⎫a b n ＝a nbn 可以归入性质(ab )n ＝a n b n.例2 化简(式中字母均为正实数)：(1)3x 2(2x －2yz )；(2)(1ax y )α(4y －α)．活动：学生观察，思考，所谓化简，即若能化为常数则化为常数，若不能化为常数则应使所化式子达到最简，对既有分数指数幂又有根式的式子，应该把根式统一化为分数指数幂的形式，便于运算，教师有针对性地提示引导，对(1)(2)由里向外，要紧扣分数指数幂的意义和运算性质，并对学生作及时的评价，注意总结解题的方法和规律．解：(1)3x 2(2x －2yz )＝(3×2)x 2－2yz ＝6yz ；(2)(1ax y )α(4y －α)＝14ax ·α·y α·y －α＝4xyα－α＝4x .点评：注意运算性质的应用．例3 已知10α＝3,10β＝4，求10α＋β，10α－β，10－2α，510β.活动：学生思考，观察题目的特点，从整体上看，应利用运算性质，然后再求值，要有预见性，教师引导学生考虑问题的思路，必要时给予提示．解：10α＋β＝10α×10β＝3×4＝12；10α－β＝10α10β＝34；10－2α＝(10α)－2＝3－2＝19；510β＝(10β)15＝154.点评：运用整体思想和运算法则是解决本题的关键，要深刻理解这种做法．思路2 例1 计算：(1)614＋3338＋40.062 5＋(5π)0－2－1； (2)23125＋⎝ ⎛⎭⎪⎫12－2＋13343－⎝ ⎛⎭⎪⎫12713-；(3)(11342x y--)(21323x y )；(4)(1122x y -)÷(1144x y -)．活动：学生观察、思考，根式化成分数指数，利用幂的运算性质解题，另外要注意整体的意识，教师有针对性地提示引导，对(1)根式的运算常常化成幂的运算进行，对(2)充分利用指数幂的运算法则来进行，对(3)则要根据单项式乘法和幂的运算法则进行，对(4)要利用平方差公式先因式分解，并对学生作及时的评价．解：(1)614＋3338＋40.062 5＋(5π)0－2－1＝1123252748⎛⎫⎛⎫+⎪ ⎪⎝⎭⎝⎭＋(0.062 5)14＋1－12＝112312344 531(0.5)222⨯⨯⨯⎛⎫⎛⎫+++ ⎪ ⎪⎝⎭⎝⎭＝52＋32＋0.5＋12＝5.(2)23125＋⎝⎛⎭⎪⎫12－2＋13343－13127-⎛⎫⎪⎝⎭＝(53)233(5)＋(2－1)－2＋133(7)－133(3)--＝2335⨯＋2－2×(－1)＋1337⨯－313()3-⨯-＝25＋4＋7－3＝33.(3)(11342x y--)(21323x y)＝(－2×3)(12113342x x y y-⋅)＝121 113333 424 66x y x y-++-⋅=-＝－64x33y.(4)(1122x y-)÷(1144x y-)＝[(14x)2－(14y)2]÷(1144x y-)＝(1144x y+)(1144x y-)÷(1144x y-)＝1144x y+.点评：在指数运算中，一定要注意运算顺序和灵活运用乘法公式．例2 化简下列各式：(1)222233x yx y----++－222233x yx y-----+；(2)(a3＋a－3)(a3－a－3)÷[(a4＋a－4＋1)(a－a－1)]．活动：学生观察式子的特点，特别是指数的特点，教师引导学生考虑题目的思路，这两题要注意分解因式，特别是立方和和立方差公式的应用，对有困难的学生及时提示：对(1)考查x2与23x的关系可知x2＝(23x)3，立方关系就出来了，公式便可运用，对(2)先利用平方差，再利用幂的乘方转化为立方差，再分解因式，组织学生讨论交流．解：(1)原式＝2233332233()()x yx y----++－2233332233()()x yx y------＝(23x-)2－2233x y--＋(23y-)2－[(23x-)2＋(23x-)(23y-)＋(23y-)2]＝424424 333333 ()()x xy y x xy y -------+---＝2332()xy xy--=-(2)原式＝[(a3)2－(a－3)2]÷[(a4＋a－4＋1)(a－a－1)]＝a 23－a －23a 4＋a －4＋1a －a －1＝a 2－a －2a 4＋a －4＋1a 4＋a －4＋1a －a －1＝a 2－a －12a －a－1＝a ＋a －1. 点评：注意立方和、立方差公式在分数指数幂当中的应用，因为二项和、差公式，平方差公式一般在使用中一目了然，而对立方和、立方差公式却一般不易观察到，32a ＝(12a )3还容易看出，对其中夹杂的数字m 可以化为m ·1122a a -＝m ，需认真对待，要在做题中不断地提高灵活运用这些公式的能力．1．化简：(1＋1322-)(1＋1162-)(1＋182-)(1＋142-)(1＋122-)的结果是( )．A ．12(1－1322-)－1B ．(1－1322-)－1C ．1－1322- D ．12(1－1322-)解析：根据本题的特点，注意到它的整体性，特别是指数的规律性，我们可以进行适当的变形．因为(1＋1322-)(1－1322-)＝1－1162-，所以原式的分子、分母同乘(1－1322-)，依次类推，所以1122132(12)(12)12----+-＝11321212----＝11321(12)2---. 答案：A2．计算⎝ ⎛⎭⎪⎫2790.5＋0.1－2＋2310227-⎛⎫ ⎪⎝⎭－3π0＋9－0.5＋490.5×2－4.解：原式＝12259⎛⎫ ⎪⎝⎭＋100＋232764⎛⎫ ⎪⎝⎭－3＋1214916⨯＝53＋100＋916－3＋13＋716＝100. 3．计算a ＋2a －1＋a －2a －1(a ≥1)．解：原式＝a －1＋12＋a －1－12＝a －1＋1＋|a －1－1|(a ≥1)．本题可以继续向下做，去掉绝对值，作为思考留作课下练习．4．设a ＞0，x ＝12(11n n a a --)，则(x ＋1＋x 2)n的值为__________．解析：1＋x 2＝1＋14(11n n a a --)2＝14(11n n a a -+)2.这样先算出1＋x 2，再算出1＋x 2，将x ＝12(11n n a a --)代入1＋x 2，得1＋x 2＝1＋14(11n n a a --)2＝14(11n n a a -+)2.所以(x ＋1＋x 2)n ＝1111211()()24nn n n n a a a a --⎡-+⎢⎢⎣ ＝111111()()22nn n n n a a a a --⎡⎤-++⎢⎥⎣⎦＝a .答案：a参照我们说明无理数指数幂的意义的过程，请你说明无理数指数幂32的意义．活动：教师引导学生回顾无理数指数幂25的意义的过程，利用计算器计算出3的近似值，取它的过剩近似值和不足近似值，根据这些近似值计算32的过剩近似值和不足近似值，利用逼近思想，“逼出”32的意义，学生合作交流，在投影仪上展示自己的探究结果．解：3＝1.732 050 80…，取它的过剩近似值和不足近似值如下表． 3的过剩近似值32的过剩近似值3的不足近似值32的不足近似值1.8 3.482 202 253 1.7 3.249 009 585 1.74 3.340 351 678 1.73 3.317 278 183 1.733 3.324 183 446 1.731 3.319 578 342 1.732 1 3.322 110 36 1.731 9 3.321 649 849 1.732 06 3.322 018 252 1.732 04 3.321 972 2 1.732 051 3.321 997 529 1.732 049 3.321 992 923 1.732 050 9 3.321 997 298 1.732 050 7 3.321 996 838 1.732 050 813.321 997 0911.732 050 793.321 997 045…… ……我们把用2作底数，3的不足近似值作指数的各个幂排成从小到大的一列数： 21．7,21.73,21.731,21.731 9，…，同样把用2作底数，3的过剩近似值作指数的各个幂排成从大到小的一列数： 21．8,21.74,21.733,21.732 1，…，不难看出3的过剩近似值和不足近似值相同的位数越多，即3的近似值精确度越高，以其过剩近似值和不足近似值为指数的幂2α会越来越趋近于同一个数，我们把这个数记为32，即21.7＜21.73＜21.731＜21.731 9＜…＜23＜…＜21.732 1＜21.733＜21.74＜21.8.也就是说32是一个实数，23＝3.321 997 …也可以这样解释：当3的过剩近似值从大于3的方向逼近3时，32的近似值从大于32的方向逼近32；当3的不足近似值从小于3的方向逼近3时，32的近似值从小于32的方向逼近32.所以32就是一串有理指数幂21.7,21.73,21.731,21.731 9，…和另一串有理指数幂21.8,21.74,21.733,21.732 1，…，按上述规律变化的结果，即32≈3.321 997. (1)无理数指数幂的意义．一般地，无理数指数幂a α(a ＞0，α是无理数)是一个确定的实数． (2)实数指数幂的运算性质：对任意的实数r ，s ，均有下面的运算性质： ①a r ·a s ＝a r ＋s(a ＞0，r ，s ∈R )．②(a r )s ＝a rs(a ＞0，r ，s ∈R )．③(a ·b )r ＝a r b r(a ＞0，b ＞0，r ∈R )． (3)逼近的思想，体会无限接近的含义．习题3—2 A 组6,8.无理数指数是指数概念的又一次扩充，教学中要让学生通过多媒体的演示，理解无理数指数幂的意义，教学中也可以让学生自己通过实际情况去探索，自己得出结论，加深对概念的理解，本堂课内容较为抽象，又不能进行推理，只能通过多媒体的教学手段，让学生体会，特别是逼近的思想、类比的思想，多做练习，提高学生理解问题、分析问题的能力．[备用习题]1．以下各式中成立且结果为最简根式的是( )．A.a ·5a 3a ·10a 7＝10a 4B.3xy 2xy 2＝y 3x 2C.a 2b b 3aa b 3＝8a 7b 15 D ．(35－125)3＝5＋125125－235·125 答案：B2．对于a ＞0，r ，s ∈Q ，以下运算中正确的是( )．A ．a r ·a s ＝a rsB ．(a r )s ＝a rsC ．⎝ ⎛⎭⎪⎫a b r ＝a r ·b sD ．a r b s ＝(ab )r ＋s答案：B 3．式子x －2x －1＝x －2x －1成立的充要条件是( )． A.x －2x －1≥0B ．x ≠1C ．x ＜1D ．x ≥2解析：方法一：要使式子x －2x －1＝x －2x －1成立，需x －1＞0，x －2≥0，即x ≥2.若x ≥2，则式子x －2x －1＝x －2x －1成立．从而x ≥2是式子x －2x －1＝x －2x －1成立的充要条件．故选D. 方法二：对A ，式子x －2x －1≥0连式子成立也保证不了，尤其x －2≤0，x －1＜0时式子不成立．对B ，x －1＜0时式子不成立．对C ，x ＜1时x －1无意义．对D ，正确．答案：D 4．化简b －2b －1(1＜b ＜2)．解：b －2b －1＝b －12＝b －1(1＜b ＜2)．5．计算32＋5＋32－ 5.解：令x ＝32＋5＋32－5，两边立方，得x 3＝2＋5＋2－5＋332＋5·32－5·(32＋5＋32－5)，即x 3＝4－3x ，x 3－3x ＋4＝0.∴(x －1)(x 2＋x ＋4)＝0.∵x 2＋x ＋4＝(x ＋12)2＋154＞0，∴x －1＝0，即x ＝1.∴32＋5＋32－5＝1.(设计者：郑芳鸣)。

高中数学北师大版必修1课件3.2.2 指数运算的性质精选ppt课件

an (5)(ab)n＝____b_n____________ (b≠0)．
(其中 m，n∈N＋)
2．实数指数幂的运算性质 (1)am·an＝_____a_m_＋_n_______；(2)(am)n＝_____a_m_n_______； (3)(ab)n＝_____a_n_b_n _____．
(其中 a>0，b>0，m，n∈R)
4
x4＋y4＝(x＋y)3
D. 4 4＝4 2
解析：对 A，ba5＝a－5b5；对 B，12 （－3）4＝12 34＝3 3；
11
对 C，令 x＝y＝1 知不成立；对 D， 4 4＝48＝24＝ 4 2，故选 D.
3．计算－61－2＋160.75＝__4_4_____．解析：原式＝－61－2＋24×34＝36＋8＝44.
4．若 x＜0，则|x|－ x2＝____0____．
在运算性质中，特别要注意幂的底数是正数的规定，如果改
变等式成立的条件，则有可能不成立，如 a＝－2，b＝－4
1
1
1
1
时，(ab)2＝[(－2)×(－4)]2＝(－2)2×(－4)2则无意义．
探究点一指数幂的化简
化简：(1) 3 ab2（ ab）3(a，b>0)；
[解] (1)原式＝1＋14×4912－110012
＝1＋16－110 ＝1165.
(2)原式＝29512＋110－2＋2674－23－3＋3478
＝53＋100＋196－3＋4387＝100.
利用指数幂的运算性质化简求值的方法 (1)数的转化：①对幂底数是小数的先将小数化为分数，②分数化最简，带分数化为假分数，③根式化分数指数幂，④幂底数为负数的先确定幂的符号． (2)运算顺序：有括号先算括号内的，无括号先算指数运算.

高中数学北师大版必修一3.2.2【教学课件】《指数运算的性质》

( ab ) a b
n
n
a n an ( ) n b b
其中 m,n∈ N
北京师范大学出版社 | 必修一
探索新知
阅读课本,无理数 2 =1．414 213 562 373 095 048 801 688 724 210… 的不足近似值和过剩近似值,从两边逼近 2
1.4 1.41 1.414 1.4142 2 1.4143 1.415 1.42 1.5
得到 10
2
的近似值
2
101.4 101.41 101.414 101.4142 10
101.4143 101.415 101.42 101.5
10 2 应该是个确定的实数 10
2
25.9545535195
北京师范大学出版社 | 必修一
1.4 25.118 864 31... 1.41 25.703 957 82... 1.414 25.941 793 62... 1.414 2 25. 953 743 00... 1.414 21 25.954 340 62... … ...
31.622 776 60... 1.5 26.302 679 91... 1.42 26.001 595 63... 1.415 25.959 719 76... 1.414 3 25.954 938 25... 1.414 22 ... ...
例 3 已知 10

3,10 4, 求10 ， 10

+

， 10
2
， 10
5
解： 10

10 10 3 4 12
10

北师大版高中数学必修一3.2.2指数运算的性质课件

37 48
(x≠0).
64 -3
2
25 1 解 :(1)原式= + 2+ 9 27 0.1 5 9 37 = +100+ -3+ =100. 3 16 48 1 1 2 1 1 (2)原式=2�� 3 × �� 3 -2�� 3 ×2�� 3 2 4 =1-4x-1=1- . ��
(2)∵
1 (��2
− ��
1 2=
-
1 2 )2=a+a-1-2=5-2=3,
∴ ∴
1 |��2 1 ��2
− ��
1 2 |=
3,
− ��
± 3.
(3)a3+a-3=(a+a-1)(a2-aa-1+a-2) =(a+a-1)(a2+2aa-1+a-2-3) =(a+a-1)[(a+a-1)2-3] =5×(25-3)=110.
1 2
37 -3+ 48
-7-
2.2 指数运算的性质
题型一题型二题型三
目标导航
Z 知识梳理 D典例透析
HISHISHULI
IANLITOUXI
S随堂演练
UITANGYANLIAN
− �� (3)a3+a-3. 分析:应设法寻找所求式子与条件a+a-1=5的联系,进而整体代入求值.
1 (2)��2
-3-
2.2 指数运算的性质
目标导航
Z 知识梳理 D典例透析
HISHISHULI
IANLITOUXI

高中数学第三章指数函数和对数函数2.2指数运算的性质课件北师大版必修

§2 指数扩充及其运算性质指数概念的扩充
2.2 指数运算的性质
分数指数幂
1.定义:给定① 正实数 a,对于任意给定的整数m,n(m,n② 互素 ),存在唯一
的③
正实数
b,使得④
bn=am
,我们把b叫作a的
m n
次幂,记作b=
a
m n
.
前提条件结论
正分数指数幂
负分数指数幂
0的分数指数幂
a>0,m,n均为正整数,m,n互素,n>1
∴a+a-1=14,
将化简所得结论代入求值.
∴原式=15.
1
1
1
1
(2)
x2
1
y2
1
=
(x2 y2 )2
1
11
1
x 2 y 2 (x 2 y 2 )(x 2 y 2 )
1
= x y 2(xy)2 .①
x y
∵x+y=12,xy=9,②
∴(x-y)2=(x+y)2-4xy=122-4×9=108,
判断正误,正确的画“√”,错误的画“✕”.
a的n次方根有且只有一个. ( ✕ )
2. 4 16 的运算结果是±2. ( ✕ )
n为大于1的奇数时, 对n 任a 意a∈R都有意义. ( √ )
n为大于1的偶数时, 只n 有a a≥0时才有意义. ( √ ) 5. n an =( n a)n. ( ✕ )
∴a= 4 3.
指数式条件求值问题的解法指数式条件求值问题的解题步骤: (1)审题:从整体上把握已知条件和所求代数式的特点; (2)化简:化简已知条件与所求代数式; (3)代入:把已知条件代入求值.
(1)已知

高中数学3.2.2指数扩充及其运算性质1课件北师大版必修

当n 是偶数时，正数a的n次方根用符号±n a 表示.
式子 n a 叫做根式，其中
n叫做根指数，a叫做被开方数
分数指数幂
给定正实数a，对于任意给定的整数m,n
(m,n互素），存在唯一的正实数b，使得
bn am,
则称b为a的
m n
次幂.
记作
m
b an.
把正分数指数幂写成根式形式，
m
即
a n n am a 0, m, n N,且n 1
1
A. x x2 x 0
1
B.x 5
5
x
C.
x y
5 6
6
y x
5
x,
y
0
1
D.6 y2 y3 y 0
问题：
n
n
（1）、
a
的含义是什
么？结果呢？
a （2）、n n 的含义是什
么？结果呢？
三、根式的运算性质：
a 1)、(n a )n
2)、n an
a, n为奇数 a ，n为偶数
（3）( a b ) n = a m b n
a m ÷a n = a m ×b －n = a m－n
a b
n
=
(
a
×b
－1
)
n
=
a
n
×
b
－n
an bn
将根式转化分数指数幂的形式。（a>0,b>0)
a 1, a a3 a
5 6
2, 3 ( 3a3 )4
3
8 3
a
4b
4
27b3
a b 9
3, 4
(a b)3
3
(a b)4 4.

新版高中数学北师大版必修1课件3.2.2指数运算的性质

2
=x,
1
��2
2=y.于是联想到用完全平方公式,把公式 ��12-��21的分
��2+��2
子、分母同乘分母的有理化因式后,分式的分子就变成了用 x+y,xy
表示的代数式.
解:∵x+y=12,xy=9,∴(x-y)2=(x+y)2-4xy=122-4×9=108.又 x<y,
·��
=
��
��
·
��
��
=
��
��
·
��
-��
=
��
�� -��
.
答案:C
-17-
2.2 指数运算的性质
=(a+a-1)[(a+a-1)2-3].因为 a+a-1=7,
所以 a3+a-3=7×(72-3)=322.
1
(4)因为(��4
+
��-14
1
)2=��2
1
+2��4
��-14
+
��-12
=
1
��2
+
��-12+2=3+2=5,
1
且��4
123456
首页
课前篇自主预习
课堂篇探究学习
当当堂堂检检测测
4.(0.001)-13+2723 −

高中数学北师大版必修一 3.2.1-2指数概念的扩充、指数运算的性质课件(33张)

【解析】 (1) －23＝－2； 4 4 (2) －32＝ 32＝ 3； 8 (3) 3－π8＝|3－π|＝π－3； (4)原式＝ x－y2＋y－x＝|x－y|＋y－x. 当 x≥y 时，原式＝x－y＋y－x＝0；当 x<y 时，原式＝y－x＋y－x＝2(y－x)． 0，x≥y，所以原式＝ 2y－x，x<y.
2．1 指数概念的扩充 2．2 指数运算的性质
【课标要求】 1.理解分数指数幂的含义，了解实数指数幂的意义. ]2.掌握分数指数幂与根式的互化. 3.掌握幂的运算性质. 4.能熟练地运用性质进行化简或求值．
自主学习 |新知预习| 1．分数指数幂 (1)定义：给定正实数 a，对于任意给定的整数 m，n(m，n 互素)， m n m 存在唯一的正实数 b，使得 b ＝a ，我们把 b 叫作 a 的次幂，记作 b n ＝a .
n 【思路点拨】根式与分数指数幂互化的依据是 a ＝ am(a>0， m，n∈N＋，且 n>1)．当所求根式含有多重根号时，由里向外用分数指数幂写出，然后再利用运算性质化简．
m n
【解析】 (1)－ x＝－x 6
2
1 2 6 1 3
1 2
(x>0)；
3 4 1 －3 4
4 1 y ＝(|y| ) ＝－y (y<0)；x ＝(x ) ＝ x 3(x>0)； 1 3 1 1 1 x 3 ＝x 3 ＝ x(x≠0)．故选 C.
m n
(2)意义：
2.无理数指数幂无理数指数幂 aα(a>0，α 是无理数)是一个确定的正实数． 3．指数运算性质：当 a>0，b>0 时，对任意实数 m，n 满足以下三条运算性质： (1)am· an＝am＋n. (2)(am)n＝amn. (3)(ab)n＝anbn.

3.2指数扩充及其运算性质3.2.2指数运算的性质教案1北师大版必修1

3.2指数扩充及其运算性质3.2.2指数运算的性质教案1北师
大版必修1
3.2.2 指数运算的性质
本节教材分析
本节课是分数指数幂的意义的引出及应用，分数指数是指数概念的又一次扩充，要让学生反复理解分数指数幂的意义.
三维目标
1、知识与技能：（1）在前面学习有理指数幂的运算的基础上引入了实数指数的概念及运算．（2）能够利用实数指数幂的运算性质进行运算、化简．
2、过程与方法：（1）让学生了解指数幂的扩展,进一步体会数域的扩充对于数学知识的发展的重要意义．（2）随着数的扩展,相应的运算性质也要延用和拓展,引入指数函数．
3、情感．态度与价值观：使学生通过学习无理指数幂的确定,了解数学中的无限逼近的思想,体会学习指数扩展的重要意义,增强学习数学的积极性和自信心．
教学重点：运用有理数指数幂性质进行化简求值.
教学难点：有理数指数幂性质的灵活应用.
教学建议：教学中可以通过根式与分数指数幂的互化来巩固加深对这一概念的理解，用观察、归纳和类比的方法完成，由于是硬性的规定，没有合理的解释，因此安排一些练习，强化训练，巩固知识，要辅助以信息技术的手段来完成大容量的课堂教学任务.
新课导入设计
导入一:同学们，既然我们把指数从正整数推广到整数，又从整数推广到正分数到负分数，这样就推广到有理数，那么它是否和数的推广一样，到底有没有无理数指数幂呢？回归数的扩充过程中，自然数到整数，整数到有理数，有理数到实数.同样指数的扩充和数域扩充一致，教师接着点题.
导入二：引导学生回归初中正整数指数幂运算及性质导出课题.
1。

2.指数运算的性质-北师大版必修1教案

2.指数运算的性质-北师大版必修1教案一、知识背景在代数运算中，指数运算是一种常见且重要的运算。

掌握指数运算的性质可以帮助我们更好地理解、应用指数运算，同时也是进一步学习代数与数学的基础。

二、教学目标1.熟练掌握指数运算的基本概念和符号表示；2.理解指数运算的基本法则，并能够运用加、减、乘、除和幂运算等法则进行简单计算；3.掌握指数运算的性质，能够灵活使用指数化乘、指数化除、指数运算中的分配律等性质进行数值计算和代数运算；4.培养学生的数学思维和逻辑推理能力，提高学生的解决问题的综合能力。

三、教学内容本节课主要涉及指数运算的性质，包括：1.指数化乘法、指数化除法；2.指数运算中的分配律、幂的乘方和除方；四、教学方法1.讲授法：教师通过板书及PPT等形式讲解指数运算的性质，引导学生理解求证；2.对话式教学法：教师与学生之间互动问答，让学生思考问题、讲解问题；3.小组合作学习法：学生分组进行讨论、合作学习，实现彼此合作，解决问题。

五、教学过程5.1 指数化乘法和指数化除法•教学目标：学生应该能够理解指数化乘法和指数化除法的规律，并能够独立运用规律进行数值和代数的计算。

•教学过程：1.引入：通过一个小实验进行引入，学生玩变幻数字的游戏，猜测规律，并总结出指数化乘法和指数化除法的规律，让学生直观感受指数运算。

2.讲解：通过对规律的表述和举例，让学生理解指数化乘法和指数化除法的规律。

同时，提供一些例题进行讲解。

3.练习：让学生通过课堂练习和课后作业进行适当练习，巩固所学知识。

5.2 指数运算中的分配律、幂的乘方和除方•教学目标：学生应该理解指数运算中的分配律、幂的乘方和除方的性质，并能够灵活地使用它们进行数值计算和代数运算。

•教学过程：1.讲解：通过对分配律、乘方和除方的实际应用举例进行讲解，引导学生理解并掌握这些性质的运用方法。

2.练习：提供一些例题进行练习和讲解，并让学生自己思考和解决一些问题，巩固所学知识。

数学北师大版高中必修1指数运算的性质

必修一第三章第 2 节第 2课时指数运算的性质学案一，学习目标（1）了解随着数的扩展,相应的运算性质也要延用和拓展（2能够利用实数指数幂的运算性质进行运算、化简二．学习重点: 实数指数幂的运算性质．学习难点：实数指数的运算与化简．三、课前预习1.你知道有哪些正整数指数幂的运算性质？请填出下列结果：m,n N +∈（1）．m n a a = ；（2）．m n (a )= （3）．n (ab)= ；（4）．当a 0≠时,有mn a a=2. 实数指数幂的运算性质： (1)a r a s ＝ (2)(a r )s＝(a>0，) (3)(ab)r＝ (a>0，b>0，)．（4） n n a a-=1 （a 0≠ ）（5） n mn m a a = (a>0)（6）当0,,,1a m n N n *>∈>m na -=四、堂中互动(先将根式写成分数指数幂的形式，再利用幂的运算性质化简即可．) 例156ba 和mm 3用分数指数幂形式表示分别为和。

例2化简（式子中的字母都是正实数）（点拨：再利用幂的运算性质和乘法公式即可）（1）; （2）1(x y)(4y )α-αα（3）11112424(2x3y )(2x 3y )--+-例3:已知103,104αβ==,求10α+β,10α-β,210-α,510β （点拨：利用幂的运算性质即可）例4．已知42121=+-aa,求下列各式的值（点拨：形如1x x a -+=的式子要两边平方）（1）1-+a a （2）22-+a a五、即学即练：1.5x =3 5y =2则5x-2y=3、若1,0a b ><,且b b a a -+=则b b a a --的值等于（）A 、6B 、2±C 、2-D 、24、2x +2-x =5 求4x +4-x 与4x -4-x的值练案A 组基础达标1. 下列各式计算正确的是（） A 1)1(0=- B a a a=⋅221C 8432=D 211333aaa-÷=2、44等于（）A 、16aB 、8aC 、4aD 、2a3.对任意实数x ，下列等式正确的是（）a a a ab a b a 9.D 9.C .B 6.A )()31()(.2241612134---÷的结果是化简4．设5x ＝4,5y ＝2，则52x －y ＝________.5. 计算（1）211511336622(2)(6)(3)a b a b a b -÷-6计算2932-7，已知32121=+-a a ，求下列各式的值：（1）1-+a a ；（2）22-+a aB 组能力提高、探究创新8。