代数式1
7年级上册数学第四章《代数式1》讲义

第四章《代数式》讲义考点一:代数式的有关概念:(1)代数式:代数式是由运算符号(加、减、乘、除、乘方、开方)把数或表示数的字母连结而成的式子.单独的一个数或者一个字母也是代数式.带有“<(≤)”“>(≥)”“=”“≠”等符号的不是代数式。
② 书写代数式时,a ×b 通常写作ab ;1÷a 通常写作a1;数字通常写在字母的前面,带分数要先化成 假分数;数字与数字相乘仍用“×”号。
③ 当实际问题中含有单位时,若运算结果是和的形式时,则要把整个的代数式括起来再写单位。
(2)代数式的值:用数值代替代数式里的字母,计算后所得的结果p 叫做代数式的值.求代数式的值可以直接代入、计算.如果给出的代数式可以化简,要先化简再求值.(3)用代数式表达简单的数量关系:1、应特别注意数学语言中的关键词语。
2、要分清代数式中数量关系的运算层次和顺序,必要时要正确地添加括号。
3、有多种运算关系时,一般按“先读先写”的原则进行列式。
4、分清代数式、等式和不等式。
【典型例题】类型一:若正方形的边长为a ,则4a 表示的实际意义为类型二: ① 甲,乙两地相距15km ,小刚骑自行车从甲地用了t h ,那么他骑车的速度是每小时 千米。
② 某村去年梨的产量是a kg ,今年比去年增产30%,那么今年梨的产量是 千克。
类型三:如图所示,搭一个正方形需要4根火柴棒,按图中方式: ...... n=1 n=2 n=31、搭2个正方形需要 根火柴棒;2、搭3个正方形需要 根火柴棒;3、搭100个正方形需要 根火柴棒;4、若用n 表示所搭正方形的个数,则搭n 个正方形需要 根火柴棒;5、用2011根火柴棒能搭 个正方形 类型四:下列各式中哪些是代数式,哪些不是代数式2x -1 a =1 π a 0.5 S =πr 0.5>0.3类型五:当的值。
时,求代数式,)23)(32(43n m n m n m +-=-=【课堂练习题】1、某校学生总数是m 人,其中男生占52%,则女生人数为 。
代数式(1)

代数式(1)【活动宗旨】能通过具体例子认识用字母表示数的优越性,会用字母表示简单数量关系式中的数量,能用代数式表示一些简单的实际问题中的数量关系。
【内容简析】用字母表示数是跨入代数大门的第步,是数学发展中飞跃性的进步,是代数与算术的一个重要区别。
本节从小学学过的加法、乘法交换这两个运算律以及行程问题中的公式s=vt 入手,引出用字母表示数所具有的简明、一般化的优越性,在讲解时从具体的数过渡到字母表示数,很好地渗透了抽象概括、由特殊到一般的思维方法。
课本没有直接给出代数式的概念,而是通过实例中出现的各种式子自然引出的,学习的关键在于准确理解所给式子的形式特点。
重点是字母表示数的意义并能根据题意列出简单代数式;难点是代数式的书写规定,正确理解代数式中字母的抽象性与任意性以及列简单代数式。
【流程设计】一、情境创设进入中学后我们学的数学分为“代数”与“几何”,代数的重要特点是广泛地应用字母来表示数,它是数学发展的一个飞跃进步,是我们进一步研究和解决许多数量关系的基础。
我国古代“代数思想”的出现是领先世界的,如:金元时代的李治(1192—1279)创造的“天元术”,李治在他的著作《测圆海镜》一书中,介绍了方程的创法。
其中有“立天元一某某”,这几乎和现在的“设x 为某某”一样了,还有我国古代第一个以数学为专业的职业数学家朱世杰(13—14世纪)和数学教育家,在他的著作《四元玉鉴》中,以天、地、人、物为未知量,相当于现在的x 、y 、z 、w ,这些都蕴含着极其宝贵的代数思想。
而欧洲的数学家们,直到16、17世纪才达到他们于13世纪末的水平,但无论如何,他们都没有用一个符号或字母来表示未知数,因而始终受到局限。
二、新知探索1.对于加法有:3+5=5+3;21313121+=+; 这是小学学过的加法交换律,也就是说:两数相加,交换加数的位置,和不变。
如果a 、b 分别表示任意两个数,加法交换律可以表示成 a+b=b+a 。
5.2 代数式 一

范海中学(年级学科)教学案学科数学年级七年级时间总序号课题 5.1 代数式(一)备课人洪晓琳学习目标能在具体情境中,进一步体会字母表示数的意义。
能根据简单的数量关系列代数式;能用自然语言表示代数的意义,并能解释一些简单代数式的实际背景或几何意义,发展符号感。
重点代数式的含义。
难点理解描述数量关系的语句,正确列出代数式。
师生互动过程教学内容和学生活动教师活动一、创设情境,引入新课多媒体展示练习,让学生完成1、香蕉每千克售价3元,m千克售价元。
2、温度由5 0c 上升t 0c后是0c 。
3、每台电脑售价X元,降价10%后,每台售价为元。
4、m袋大米的质量是w千克,x袋大米的质量是千克。
指导学生理解题目中的数量关系正确列出算式生口答:(1)3m (2) 5+t (3) (1-10%) (4) wx/m以上列出式子,有哪些具体特点,这些式子是什么?二、引导学生探究代数式1、问题导读:(1)、什么是代数式,单独一个数或字母是代数式吗?(2)、怎样判断代数式?下列各式哪些是代数式,哪些不是?通过对上节课的回顾与练习,引出代数式的意义和代数式的特点。
师生互动过程教学内容和学生活动教师活动①x23②a=2 ③m ④s=πR2⑤37⑥π⑦5>3 ⑧89 ⑨5352(3)、试做例1、例2,思考:列代数式时应注意什么?(4)、是自然语言,为数学语言,在描述问题时比更简单明确,更具有一般性。
(5)、试做例3。
2、合作交流:代数式:像上面这样的式子都叫代数式,即用运算符号把数和表示数的字母连接而成的式子。
单独一个数或一个表示数的字母也是代数式。
判断方法:判断是不是代数式的唯一方法,即看它是不是由运算符号连接而成的式子。
注:①、单独一个数或一个字母可以看成是这个数或这个字母与数“1”的乘积,因此单独一个数或一个字母也是代数式。
②、“=”不是运算符号,不能将等式与代数式混淆。
③、代数式的乘号常用“•”代替,或省略不写。
代数式1

5
(3)(a+b)(a-b)可以解释为 (4)(1+8%)x可以解释为
; ;
; .
练习: 判断下列式子哪些是代数式,哪些不是。
(1)、a2+b2 (3)、13
s
(2)、 t (4)、x=2
(5)、3×4 -5
(6)、 3×4 -5 =7
(7)、x-1≤0 (9)、10x+5y=15
a; (3)
1 2
(
x
;y
)
(4)a3; (5) - 8 3 a2bc;
4
解:符合书写要求的有:(1)(3)
练一练:1.用代数式表示
(1)f的11倍再加上2可以表示为 11f+2 ;9 a
(2)数a的 1与这个数的和可以表示为 8
;
8
(3)一个2n教室有2扇门4n和4扇窗户,n个这样的教
室有
扇门和
扇窗户;(1+ 15﹪)m
(4)产量由mkg增长15﹪后,达到___ _____ kg.
(5)一个三位数,个位数字为a,十位数字为b,百位数字 为c,则这个三位数是_______.
例1 门票:成人10元/人;学生5元/人.
(1)一个旅游团有成人x人,学生y人,请你根据上图确定该旅 游团应付多少门票费?
(2)如果该旅游团有37个成人,15个学生,那么门票费是多少 呢?
解:(1)该旅游团应付的门票费是(10x+5y)元. (2)把x=37,y=15代入代数式得 10x+5y =10×37+5×15 =445.
10x+5y还能表示什么意义?
(1)如果用x(元/kg)表示大米的价格,用y(元/kg) 表示食油的价格,那么10x+5y就表示小强的妈妈 购买10kg大米和5kg食油所用的费用;
数学自学指南--代数式-1

自学资料一天,唐僧命徒弟悟空、八戒、沙僧三人去花果山摘些桃子。
不长时间,徒弟三人摘完桃子高高兴兴回来。
师父唐僧问:你们每人各摘回多少个桃子?八戒憨笑着说:师父,我来考考你。
我们每人摘的一样多,我筐里的桃子不到100个,如果3个3个地数,数到最后还剩1个。
你算算,我们每人摘了多少个?沙僧神秘地说:师父,我也来考考你。
我筐里的桃子,如果4个4个地数,数到最后还剩1个。
你算算,我们每人摘了多少个?悟空笑眯眯地说:师父,我也来考考你。
我筐里的桃子,如果5个5个地数,数到最后还剩1个。
你算算,我们每人摘多少个?一、用字母表示数【知识探索】1.用字母表示数,字母和数一样可以参与运算,可以用式子把数量关系简明地表示出来.【说明】字母可以表示任意的数,也可以表示特定意义的公式,还可以表示符合条件的某一个数,甚至可以表示具有某些规律的数.2.(1)在省略乘号时,要把数字写在字母的前面;(2)当数字是带分数时,常写成假分数;(3)数字和字母之间的乘号用“· ”或省略不写;(4)数字和字母的除法通常用“”表示;(5)是数字不是字母.【错题精练】例1.用代数式表示:“a,b两数的平方和与a,b乘积的差”,正确的是()A. a2+b2﹣abB. (a+b)2﹣abC. a2b2﹣abD. (a2+b2)ab例2.一个数倍5除,商为,余数为2,则这个数是__________ .第1页共10页自学七招之日计划护体神功:每日计划安排好,自学规划效率高非学科培训例3.某商店在甲批发市场以每包m元的价格进了20包茶叶,又在乙批发市场以每包n元(m>n)的价格进了同样的40包茶叶,如果商家以每包m+n元的价格卖出这种茶叶,卖完后,这家商店()2A. 盈利了;B. 亏损了;C. 不赢不亏;D. 盈亏不能确定.例4.一个两位数,十位数上的数字是a,各位数上的数字是b,则这两位数可以表示为()A. ab;B. a+b;C. 10a+b;D. 10b+a.例5.用12m长的铝合金做成一个长方形的窗框(如图),设长方形窗框横条的长度为x(m),则长方形窗框的面积为()A. x(12−x)m2B. x(6−x)m2C. x(6−1.5x)m2D. x(6−2x)m2【举一反三】1.用代数式表示“a的3倍与b的差的平方”,正确的是()A. (3a-b)2B. 3(a-b)2C. 3a-b2D. (a-3b)22.某数为,用表示:某数与1的和的绝对值__________ .3.设为整数,用表示被3除以2的整数是__________ .4.丁丁比昕昕小,丁丁今年a岁,昕昕今年b岁,2年后丁丁比昕昕小__________ 岁第2页共10页自学七招之预习轻身术:预习习惯培养好,课堂轻松没烦恼非学科培训第3页 共10页自学七招之举一反三剑:总结归纳典型题,多种解法开脑洞非学科培训5.果园里有苹果树和梨树共45棵,其中梨树有a 棵,苹果树比梨树多__________ 棵6.磁悬浮列车是一种科技含量很高的新型交通工具,它有速度快,爬坡能力强,能耗低等优点,它每个座位的平均能耗仅为飞机每个座位平均能耗的三分之一,汽车每个座位平均能耗的70%,那么,汽车每个座位的平均能耗是飞机每个座位平均能耗的( ) A. 37; B. 73; C. 1021;D. 2110.7.某企业今年1月份产值为x 万元,2月份比1月份增加了10%,3月份比2月份减少了20%,则3月份的产值是( )万元. A. (1+10%)(1−20%)x ; B. (1+10%+20%)x ; C. (x +10%)(x −20%); D. (1+10%−20%)x .8.在两个形状、大小完全相同的大长方形内,分别互不重叠地放入四个如图③的小长方形后得图①,图②,已知大长方形的长为a ,两个大长方形未被覆盖部分分别用阴影表示,则图①阴影部分周长与图②阴影部分周长的差是( )(用a 的代数式表示)A. −a ;B. a ;C. −12a ;D. 12a .二、求代数式的值【知识探索】1.用数值代替代数式里的字母,按照代数式中的运算关系计算得出的结果叫做代数式的值.【错题精练】例1.当x =1时,代数式x 3+x +m 的值是7,则当x =−1时,这个代数式的值是( ) A. 7; B. 3; C. 1; D. ﹣7.例2.已知代数式x﹣3y的值是4,则代数式(x﹣3y)2﹣2x+6y﹣1的值是()A. 7B. 9C. 23D. -1例3.若a=-2,b=8,则__________ ; .例4.已知3a2-2a-3=0,则7+4a-6a2的值是__________例5.如图所示是一个运算程序的示意图,若开始输入x的值为81,则第2017次输出的结果为.【举一反三】1.x2-3x-4的值是7,则6x-2x2+2的值是__________2.当x=1时,代数式x3+x+m的值是7,则当x=−1时,这个代数式的值是()A. 7;B. 3;C. 1;D. ﹣7.3.已知代数式2x2﹣3x+9的值为7,则的值为()A.B.C.8D.10第4页共10页自学七招之预习轻身术:预习习惯培养好,课堂轻松没烦恼非学科培训4.已知,则=__________ .5.已知时,代数式的值是5,求当时,的值;6.如果那么=__________ .7.已知A=2a2 +3ab-2a-1 ,B=-a2+ab-1,若3A+6B的值与a的值无关,求b=__________三、列代数式【错题精练】例1.如图,将6张长为a,宽为b的矩形纸板无重叠地放置在一个矩形纸盒内,盒底未被覆盖的两个矩形面积分别记为S1、S2,当S2=2S1时,则a与b的关系为()A. a=0.5b;B. a=b;C. a=1.5b;D. a=2b.【举一反三】1.如图1,将一个边长为a的正方形纸片剪去两个小长方形,得到一个“”的图案,如图2所示,再将剪下的两个小长方形拼成一个新的长方形,如图3所示,则新长方形的周长可表示为.(用含a,b的代数式表示)第5页共10页自学七招之举一反三剑:总结归纳典型题,多种解法开脑洞非学科培训四、拓展:列代数式(数字变化类规律)【错题精练】例1.小林按如图所示的程序输入一个正数x,最后输出的结果是277,则满足条件的所有x的值为.例2.如下表,从左到右在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等,则第2018个格子中的数为()A. 4;B. 3;C. 0;D. -2.【举一反三】1.在求1+4+42+43+44+45+46+47的值时,小聪发现:从第二个加数起每一个加数都是前一个加数的4倍,于是他设:x=1+4+42+43+44+45+46+47①,然后在①式的两边都乘以4,得:4x= 4+42+43+44+45+46+47+48②,②-①得:4x−x=48−1,即3x=48−1,从而得到x= 47.3探索:若把“4”换成字母a(a≠0且a≠1),则计算1+a+a2+a3+a4+⋯+a2017=.2.某市出租车收费标准:3 km以内(含3 km)起步价为8元,超过3 km后每1 km加收1.8元.(1)若小明坐出租车行驶了6 km,则他应付多少元车费?(2)如果用s表示出租车行驶的路程,m表示出租车应收的车费,请你表示出s与m之间的数量关系第6页共10页自学七招之预习轻身术:预习习惯培养好,课堂轻松没烦恼非学科培训(s>3).五、拓展:列代数式(几何变化类规律)【错题精练】例1.观察下列一组图形,其中图形①中共有2颗星,图形②中共有6颗星,图形③中共有11颗星,图形④中共有17颗星,…,按此规律,图形⑧中星星的颗数是()A. 43;B. 45;C. 51;D. 53.例2.“分块计数法”:对有规律的图形进行计数时,有些题可以采用“分块计数”的方法.例如:图1有6个点,图2有12个点,图3有18个点,……,按此规律,求图10、图n有多少个点?(1)我们将每个图形分成完全相同的6块,每块黑点的个数相同(如上图),这样图1中黑点个数是6×1=6个;图2中黑点个数是6×2=12个:图3中黑点个数是6×3=18个;……;所以容易求出图10、图n中黑点的个数分别是个、个.(2)请你参考以上“分块计数法”,先将上面的点阵进行分块(画在答题卷上),再完成以下问题:①第5个点阵中有个圆圈;②第n个点阵中有多少个圆圈?【举一反三】第7页共10页自学七招之举一反三剑:总结归纳典型题,多种解法开脑洞非学科培训1.如图图案是用长度相同的火柴棒按一定规律拼搭而成,图案①需8根火柴棒,图案②需15根火柴棒,…,(1)按此规律,图案⑦需根火柴棒;第n个图案需根火柴棒.(2)用2017根火柴棒能按规律拼搭而成一个图案?若能,说明是第几个图案:若不可能,请说明理由.2.下面每个正方形中的五个数之间都有相同的规律,根据这种规律,则第4个正方形中间数字m 为,第n个正方形的中间数字为.(用含n的代数式表示)1.由于受H7N9禽流感的影响,我市某城区今年2月份鸡的价格比1月份下降a%,3月份比2月份下降b%,已知1月份鸡的价格为24元/千克.设3月份鸡的价格为m元/千克,则()A. m=24(1−a%−b%);B. m=24(1−a%)b%;C. m=24−a%−b%;D. m=24(1﹣a%)(1﹣b%).2.某商店的一商品因需求量大,经营者对该商品进行了两次提价,每次提价10%;后经市场物价调整,又一次降价20%,已知提价前的商品价格为a,则该商品的最终价格为()A. 1.04a;B. a;C. 0.96a;D. 0.968a.3.下列用字母表示数的写法中,规范的是()yx;A. 123B. x×5y×1;3第8页共10页自学七招之预习轻身术:预习习惯培养好,课堂轻松没烦恼非学科培训C. 5xy;3D. 5xy÷3.4.甲乙两地相距a(km),一辆汽车从甲地出发,行驶了t(h)后,距离乙地还有b(km),则汽车的行驶速度可表示为__________5.在矩形ABCD内,将两张边长分别为a和b(a>b)的正方形纸片按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),矩形中未被这两张正方形纸片覆盖的部分用阴影表示,若图1中阴影部分为S1,图2中阴影部分的面积和为S2.则关于S1,S2的大小关系表述正确的是()A. S1>S2;B. S1<S2;C. S1=S2;D. 无法确定.6.已知S1=x,S2=3S1−2,S3=3S2−2,S4=3S3−2,…,S2014=3S2013−2,则S2014=(结果用含x的代数式表示).7.按照如图所示的操作步骤,若输入x的值为2,则输出的值为__________8.观察下列一组图形中点的个数,其中第1个图形中共有4个点,第2个图形中共有10个点,第3个图形中共有19个点,…按此规律第5个图形中共有点的个数是.第9页共10页自学七招之举一反三剑:总结归纳典型题,多种解法开脑洞非学科培训9.当x=2时,代数式1x−1的值是210.已知x−3y=2,则代数式3x−9y+5=.● 实数的运算第10页共10页自学七招之预习轻身术:预习习惯培养好,课堂轻松没烦恼非学科培训。
3.2_代数式(1)

想一想 (1)小红去买笔记本,笔记 本每本2.5元,她买了m本, 一共用去 元? (2)小明100 m赛跑用了t s,
那么平均速度是
m/s.
定义: 用运算符号把数和字母连接而成 的式子称为代数式.
单独一个数或一个字母也是代数式. 例如:0、-9、1.5、a、x等也是代数式.
下列各式中,哪些是代数式?
③
4
х+ху+у
2
2
④ m ⑤ 2ху
⑥ ab+bc+ac
④ ⑤ ⑦
⑦
8
单项式: ① ② 多项式: ③ ⑥
随堂练习
1. 下列整式哪些是单项式,哪些是多项式? 它们的次数分别是多少?
a, 1 x 2 y, 2 x 1, x 2 xy y 2 . 3 单项式有 a. 1 x 2 y ,
3 x 是 1 次的, 2 是 3 次的; 注 意 是圆周 例如 ah 5 率的代号,不是单项式 概念中的字母。 1 mn 是 2 次的, b2 是 2 次的 16 2 单项式概念中的字母具
有可任意取值的含义。
注意:
(1)圆周率是常1。 如单项式 c的系数是1。
3 2 2
4
3
(2) 3n
2n 1
2
3 2 2 3
a 3, a 2 b, (1)多项式 a a b ab b 的项有 解: ab2, b 3 ;次数是 3 .
(1)多项式 3n
4 2
4
2n 1的项有3n , 2n ,
2
1 ;次数是
4 .
仔细观察下列哪些是单项式,哪些是 多项式,并将序号添写在下面的横线上。 ① abc -3х 2 ②
3.2 代数式(1)(苏科版)(解析版)

3.2 代数式(1)1.下列各式中,是代数式的有( ) ①12,②2a ﹣1>0,③ab=ba ,④12(a 2﹣b 2),⑤a ,⑥0. A .1个B .2个C .3个D .4个 【答案】D【解析】根据代数式的概念,可知①12,④12(a 2﹣b 2),⑤a ,⑥0是代数式,共有4个. 故选D. 2.用语言叙述3a ﹣15的数量关系,其中错误的是( )A .a 的3倍与l5的差B .3a 与15的相反数的和C .a 与5差的3倍D .a 与l5的差的3倍 【答案】D【解析】A 、a 的3倍与l5的差,列式为3a-15,故正确;B 、3a 与15的相反数的和,列式为3a+(-15)=3a-15,故正确;C 、a 与5差的3倍,列式为3(a-5)=3a-15,故正确;D 、a 与l5的差的3倍,列式为3(a-15)=3a-45,故不正确.故选D.3.下列各式书写正确的是( )A .x 2y 23B .112mnC .x÷13y D .14(a+b ) 【答案】D【解析】A 、应把数字放在前面,即32 x 2y ,故本选项不符合题意; B 、当出现带分数时,要化为假分数,故本选项不符合题意;C 、当表示除法时,要用分数的形式表示,故本选项不符合题意;D 、41(a+b )是代数式,故本选项符合题意. 故选D .4.关于代数式a 2﹣1的意义,下列说法中不正确的是( )A .比a 的平方少1的数B .a 与1的差的平方C .a 、1两数的平方差D .a 的平方与1的差【答案】B【解析】A、a2-1表示:比a的平方少1的数,说法正确,故错误;B、a与1的差的平方应为:(x-1)2,故错误.C、a2-1表示为a的平方与1的平方差,说法正确,故正确;D、a2-1表示为:a的平方与1的差,说法正确,故错误;故选B.5.我们知道,用字母表示的代数式是具有一般意义的,请仔细分析下列赋予3a实际意义的例子中不正确的是()A.若葡萄的价格是3元/千克,则3a表示买a千克葡萄的金额B.若a表示一个等边三角形的边长,则3a表示这个等边三角形的周长C.将一个小木块放在水平桌面上,若3表示小木块与桌面的接触面积,a表示桌面受到的压强,则3a表示小木块对桌面的压力D.若3和a分别表示一个两位数中的十位数字和个位数字,则3a表示这个两位数【答案】D【解析】A. 若葡萄的价格是3元/千克,则3a表示买a千克葡萄的金额,故正确;B. 若a表示一个等边三角形的边长,则3a表示这个等边三角形的周长,故正确;C. 将一个小木块放在水平桌面上,若3表示小木块与桌面的接触面积,a表示桌面受到的压强,则3a表示小木块对桌面的压力,故正确;D. 若3和a分别表示一个两位数中的十位数字和个位数字,则30+a表示这个两位数,故不正确;故选D.6.某中学组织九年级学生春游,有m名师生租用45座的大客车若干辆,共有2个空座位,那么租用大客车的辆数是________(用m的代数式表示).【答案】2 45 m+【解析】解:共有2个空座位,那么一共可以坐(m+2)人,∴租用大客车的辆数是2 45m+,故答案为:2 45m+.7.现有5元面值人民币m张,10元面值人民币n张,共有人民币________元(用含m、n的代数式表示).【答案】()510m n +【解析】解:由题意得:共有人民币()510m n +元,故答案为:()510m n +8.体育委员小金带了500元钱去买体育用品,已知一个足球x 元,一个篮球y 元,则代数式50032x y --表示的实际意义是______.【答案】小金用500元买3个足球和2个篮球后剩下的钱数【解析】∵一个足球x 元,一个篮球y 元,∴3x 表示三个足球的价格,2y 表示两个篮球的价格,∴50032x y --表示小金用500元买3个足球和2个篮球后剩下的钱数,故答案为:小金用500元买3个足球和2个篮球后剩下的钱数.9.下列各式哪些是代数式?哪些不是代数式?(1)3>2;(2)a+b=5;(3)a ;(4)3;(5)5+4﹣1;(6)m 米;(7)5x ﹣3y【答案】代数式有(3)(4)(5)(7);(1)(2)(6)不是代数式.【解析】(1)、(2)中的“>”、“=”它们不是运算符号,因此(1)、(2)不是代数式.(3)、(4)中a 、3是代数式,因为单个数字和字母是代数式.(5)中是加减运算符号把5、4、1连接起来,因此是代数式.(6)m 米含有单位名称,故不是代数式.(7)5x ﹣3y 中由乘、减两种运算联起5、x 、3、y ,因此是代数式.答:代数式有(3)(4)(5)(7);(1)(2)(6)不是代数式.10.某公园准备修建一块长方形草坪,长为30米,宽为20米.并在草坪上修建如图所示的十字路,已知十字路宽x 米.回答下列问题:(1)修建的十字路面积是多少平方米?(2)如果十字路宽2米,那么草坪(阴影部分)的面积是多少?【答案】(1)修建十字路的面积是(50x -x 2)平方米;(2)草坪(阴影部分)的面积为504平方米.【解析】(1)由题意得:两条路的总长为50米,两条路相交处正方形面积为x 2,∴修建的十字路面积=,(2)草坪的面积==当x=2时,上式==504答:草坪的面积为50411.下列语句正确的是()A.1+a不是一个代数式B.0是代数式C.S=πr2是一个代数式D.单独一个字母a不是代数式【答案】B【解析】A、1+a是一个代数式,故本选项不符合题意;B、0是代数式,故本选项符合题意;C、S=πr2是等式,不是一个代数式,故本选项不符合题意;D、单独一个字母a是代数式,故本选项不符合题意.故选B.12.下列关于“代数式3x+2y”的意义叙述不正确的有()个.①x的3倍加上y的2倍的和;②小明跑步速度为x千米/小时,步行的速度为y千米/时,则小明跑步3小时后步行2小时,走了(3x+2y)千米;③某小商品以每个3元卖了x个,又以每个2元卖了y个,则共卖了(3x+2y)元.A.3 B.2 C.1 D.0【答案】D【解析】∵ “代数式3x+2y”的意义是x的3倍与y的2倍的和,∴①正确;而将“代数式3x+2y”赋予实际意义,可以是:(1)小明跑步速度为x千米/小时,步行的速度为y千米/时,则小明跑步3小时后步行2小时,共走了(3x+2y)千米,故②正确;也可以是(2)某小商品以每个3元卖了x个,又以每个2元卖了y个,则共卖了(3x+2y)元,故③正确.即上述叙述中不正确的有0个.故选D . 13.2a b a b -+的意义是( ) A .a 与b 差的2倍除以a 与b 的和B .a 的2倍与b 的差除以a 与b 和的商C .a 的2倍与b 的差除a 与b 的和D .a 与b 的2倍的差除以a 与b 和的商【答案】B【解析】2a b a b -+的意义是a 的2倍与b 的差除以a 与b 和的商, 故选B.14.a 与x 的平方差的倒数,用代数式表示为( )A .21a x -B .22()a x -C .221a x -D .2222a x - 【答案】C【解析】a 与x 的平方差为22a x -,所以a 与x 的平方差的倒数为221a x -. 故选:C .15.下图中表示阴影部分面积的代数式是 ( )A .ab +bcB .c(b -d)+d(a -c)C .ad +c(b -d)D .ab -cd【答案】C【解析】 解:把图形补成一个大矩形,则阴影部分面积=ab ﹣(a ﹣c )(b ﹣d )=ab ﹣[ab ﹣ad ﹣c (b ﹣d )]=ab ﹣ab+ad+c (b ﹣d )=ad+c (b ﹣d ).故选C .16.苹果每千克a 元,梨每千克b 元,则代数式2a+b 表示购买___________________________【答案】2千克苹果和1千克梨的钱数【解析】2a 表示购买2千克苹果的钱数,b 表示购买1千克梨的钱数.答案为2千克苹果和1千克梨的钱数.17.赋予式子“ab”一个实际意义: .【答案】边长分别为a ,b 的矩形面积【解析】一个长为a ,宽为b 的长方形的面积是ab .故答案为边长分别为a ,b 的矩形面积.18.用完全一样的火柴棍按如图所示的方法拼成“金鱼”形状的图形,则按照这样的方法拼成第4个图形需要火柴棍________根,拼成第n 个图形(n 为整数)需要火柴棍________根(用含n 的代数式表示).【答案】30 7n+2【解析】解:观察发现:搭1条金鱼需要火柴9根,搭2条金鱼需要16根, 搭3条金鱼需要火柴23根,即发现了每多搭1条金鱼,需要多用7根火柴,那么搭n 条金鱼需要火柴:9+7(n-1)=7n+2;当n=4时, 7n+2=7×4+2=30; 故答案为:30,7n+2.19.用字母表示阴影部分的面积:图(1)______;图(2)______;图(3)_____;图(4)______;图(5)______;【答案】ab mn - ()a x b -212ab r π- 214ab b π- 2214R R π-; 【解析】(1). ab mn - ;(2). ()a x b -;(3). 212ab r π- ;(4). 214ab b π- ;(5). 2214R R π-.20.某市居民使用自来水接如下标准收费(水费按月缴纳) 居民月用水量 不超过310m 的部分 超过310m 但不超过318m 的部分 超过318m 的部分单价 2元/3m 3元/3m 4元/3m(1)某用户一个月用了315m 水,求该用户这个月应缴纳的水费;(2)设某户月用水量为n 立方米,当18n 时,求该用户应缴纳的水费(用含n 的代数式表示);(3)甲、乙两用户一个月共用水336m ,已知甲用户缴纳的水费超过了20元,设甲用户这个月用水3m x ,则甲、乙两用户一个月共缴纳的水费为________元(用含x 的代数式表示直接写出答案).【答案】(1)35元;(2)4n-28元;(3)106-x 或2x+44或x+70【解析】解:(1)10×2+(15-10)×3=20+15=35元,∴该用户这个月应缴纳水费35元;(2)∵n >18,∴该用户应缴纳的水费为:10×2+(18-10)×3+(n-18)×4=4n-28(元);(3)∵甲用户缴纳的水费超过了20元,∴甲用户的用水量大于10m 3,当10<x≤18时,则18≤36-x ,此时共缴纳的水费为:10×2+(x-10)×3+4×(36-x )-28=106-x (元);当x >18时,即0<36-x≤10,此时共缴纳的水费为:4x-28+(36-x )×2=2x+44(元);当x >18时,即10<36-x <18,此时共缴纳的水费为:4x-28+10×2+(36-x-10)×3=x+70(元).21.如图,根据你发现的规律,计算1816248n +++++(n 是正整数)的结果为( )① ② ③18+=?1816++=? 181624+++=? A .2(21)n +B .2(21)n -C .2(2)n +D .2n 【答案】A【解析】∵1+8=9=32,1+8+16=25=52,1+8+16+24=49=72,∴1816248n +++++=2(21)n + 故选A.22.若a 是不为1的有理数,我们把11a-称为a 的差倒数,如:2的差倒数是1112=--,1-的差倒数是111(1)2=--,已知121,3a a =-是1a 的差倒数,3a 是2a 的差倒数,4a 是3a 的差倒数,…,依次类推. (1)分别求出234,,a a a 的值.(2)求1232016a a a a ++++的值. 【答案】(1)234a =,34a =,413a =-;(2)2968 【解析】解:(1)∵113a =-,∴2131413a ==⎛⎫-- ⎪⎝⎭, 314314a ==-,411143a ==--; (2)根据(1)可知,每三个数为一个循环组循环,∵a 1+a 2+a 3=135343412-++=,2016÷3=672,∴1232016a a a a ++++=5367212⨯=2968.。
代数式(1)

1、写明字母所取的值,即“当……时”。 2、写明所要求值的代数式。
3、将字母所取的值代入该代数式中的相同字母 中,根据运算关系求出计算结果。
1、也可先代入后计算,代入步骤必不可少。
2、在将数字代入字母过程中,有时要适当地加入运算符号
或括号,如数字间相乘关系要加入乘号,当幂的底数是分数、 负数时,它的底数一定要加括号。
。
思考: 当x= -4, -3, -2, -1, 1, 2, 3, 4
求出
x 3
2
解: 当 x=-4时
x 3 ( 4) 3 16 3 13
2 2
时,分别 的值.你发现了什么?
x 3 ( 3) 3 9 3 6
2 2
x=-3时
x=-2时
x 3 ( 2) 3 4 3 1
有意义。
±1 时,
x 有最
无意义。 ),最
( 2)代数式
小 值 ( 填“大”或“小” 大 值,是 0
。 5 x 3 有最 值,是
2
小 值是 0 5 4
。
代数式 - x - 3 有最 当x
3
2
时,代数式
大
。
值,是
。
( 3)代数式 x 有最 当x
小
0
0
时,代数式
3 x 4 有最
小
值,是
x 的值,求代数式 (2)x -3.5
4 x 5的值。 (3)x 2 1 2
解:当x 2时,x 5 4 2 5 4 13
当x 3.5时,x 5 4 ( 3.5) 5 4 9
当x 2 1 2 15 时,x 5 4 2 4 1 2 5
第3课时代数式1

根据上述规律解决下列问题:
(1)完成第四个等式: 92 4 _4__ 2 17
(2)写出你猜想的第n个等式(用含n的式子表示),
并验证其正确性.
如果把“6”换成字母“a”(a 0且a 1),能否求出
1 a a2 a3 a4 a2018的值?你的答案是(B )
a 2018 1 A.
a1
a 2019 1 B.
a1
a 2018 1 C.
a
D.a2018 1
4.为落实“阳光体育”工程,某校计划购买m个篮球
和n个排球,已知篮球每个80元,排球每个60元,则
输
y x 4(x 1)
输
入
出
x
y x 4(x 1)
y
题型3 探究数、式及图形的变化规律 【例3】将一些半径相同的小圆按如图所示的规律摆放,
请仔细观察,第n个图形有__n__2 ___n____4__个小圆。
(用含n的代数式表示)
第1个图形 第2个图形
第3个图形
第4个图形
备考训练
1.某工厂第一年生产a件产品,第二年比第一年增产了20%,
S 1 6 62 63 64 65 66 67 68 69, ① 然后在①式的两边都乘以6,得:
6S 6 62 63 64 65 66 67 68 69 610. ② ②-①得 6S S 610 1,即5S 610 1,所以S 610 1.
5
得出答案后,爱动脑筋的小林想:
购买这些篮球和排球的总费用为(___8_0_m____6__0_n_)__元。
5.如图是一组有规律的图案,它们是由边长相同的 正方形和正三角形镶嵌而成,第1个图案有4个三角 形,第2个图案有7个三角形,第3个图案有10个三角 形,… ,依此规律,第n个图案有(__3_n_+_1_)__个三角 形(用含n的代数式表示)
3.2代数式(1)
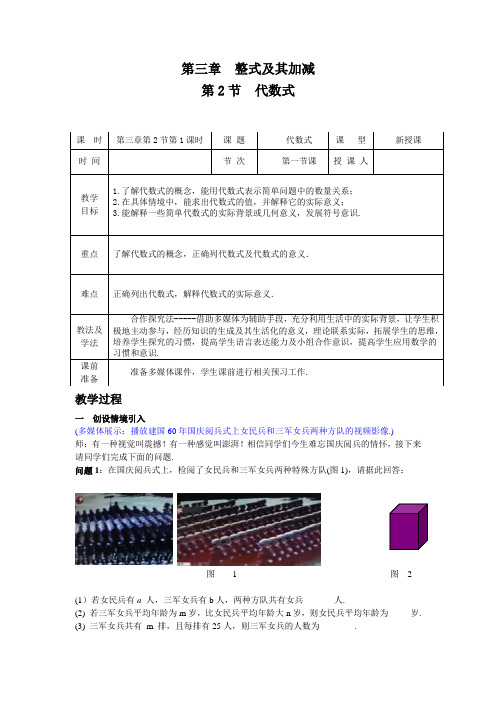
第三章 整式及其加减第2节 代数式教学过程一 创设情境引入(多媒体展示:播放建国60年国庆阅兵式上女民兵和三军女兵两种方队的视频影像.)师:有一种视觉叫震撼!有一种感觉叫澎湃!相信同学们今生难忘国庆阅兵的情怀,接下来请同学们完成下面的问题.问题1:在国庆阅兵式上,检阅了女民兵和三军女兵两种特殊方队(图1),请据此回答:图 1 图 2(1)若女民兵有a 人,三军女兵有b 人,两种方队共有女兵_______人.(2) 若三军女兵平均年龄为m 岁,比女民兵平均年龄大n 岁,则女民兵平均年龄为_____岁.(3) 三军女兵共有 m 排,且每排有25人,则三军女兵的人数为________.(4)女民兵方队用t 秒钟走了s 米,她们的平均速度可以表示为_______米/秒.生1:(a+b );生2:()m n -;生3:25m ;生4:st ;(教师对每位答案正确的学生都给予积极的评价和鼓励,如:好!很棒!这位同学思维敏捷!很扎实等,进一步调动学生的积极性.)师:前面的同学表现很出色,请大家继续完成下面问题.问题2:(如图2)市政府准备在人工湖中心建一个大型雕塑,设计雕塑的底座为正方体,已知它的棱长是 a ,则它的表面积是_______;它的体积是_______.生5:26a ,3a .师:前面同学们的表现都很出色.我们把上面的这些式子叫做代数式.--------教师板书课题. (设计意图:通过阅兵式的情境再现,激励学生的斗志,激发学生的学习热情.通过两个问题既复习上节课所学的用字母表示数知识,也是为学习代数式做铺垫.学生回答问题中的5个式子包含有+、-、×、÷、乘方等多种运算,学生口答过程中,教师顺势板书好答案,为下一步学生观察、理解和引出代数式,埋下了伏笔.)二 探究新知师:请同学们观察并思考: 23,,25,,6,......s a b m n m a a t +- 这些式子有哪些共同点? 生1:都含有数字或字母.师:除了数字和字母外,还有什么?生2:还有运算符号(+、-、×、÷、乘方).师:运算符号在数字和字母之间起到什么样的作用?生3:把数或字母连接起来了.师:回答很好!同学们,这就是代数式!现在你能用自己的语言叙述一下什么是代数式吗? (学生交流2分钟后,找不同学生语言叙述,互相补充,教师加以引导.然后投影展示代数式的定义.)(投影展示)定义:像23,,25,,6,......s a b m n m a a t +-这样,用运算符号把数和字母连接起来的式子叫做代数式. 单独的一个数或字母也是代数式 .(知识点1----教师板书.) 例如: a, b, m , n , 25 , ……师:你能举个代数式的例子吗?(找几个同学进行举例,教师做好板书并给予积极的评价.)(设计意图:通过学生观察、思考、小组合作交流等活动,让学生加深对知识的认识和理解,从而生成新知识,体验探究成功的快乐感,也克服机械的背诵学习知识.)师:接下来,我想考验一下大家对新知识的理解,请完成下面的题目.巩固练习(多媒体投影):1. 下列式子中哪些是代数式?哪些不是?为什么?a , 0 , ab b a +=+ ,7x y + , 8pq -, 2()m n + ,1t t +> ,π .(让学生口答判断结果,对有困难的学生引导其根据代数式的定义作出判断,从而强调定义中的“运算符号”知识.)2. 用代数式表示.1)一个练习本的价格是m元,买n个练习本需要_____元;2)买n斤苹果花了p元钱,每斤苹果_____元钱;3)乙数a的123倍是_____;4)甲身高a厘米,乙比甲矮2厘米,则乙身高为____厘米.(让4名学生上黑板板演完成.教师引导学生进行评价和纠正,并强调代数式的书写规范①字母与字母相乘,“×”号通常简写作“•”,或省略不写;②除法运算时,“÷”号要转化成分数线;③数字与字母相乘,数字写在字母前,“×”可省略;遇到带分数要写成假分数;④代数式是和或差的形式,后面有单位,在书写代数式时应加括号.)(设计意图:两个练习既检测和促进学生学习新知识,同时也为学习代数式的值做铺垫.)师:上面(4)中,若a=160,乙的身高是多少米?a=170呢?150呢?生:158厘米.师:158,你怎样知道的?学生:用160-2得来.师:原来的a呢?生:用160来替换了.师:158就是a=160时,代数式a-2的值.(学生阅读课本p81,课本第二自然段.了解什么是代数式的值,并完成a=170、150时代数式的值. -----教师板书知识点2.)(设计意图:通过学生亲身经历计算引出新知识,结合看书自学,从而领会新知识,培养学生的动手和动脑习惯.)师:同学们现在也会列代数式和求代数式的值了,下面的问题该如何解决呢?例1 列代数式,并求值.(-----多媒体展示)(1)某公园的门票价格是:成人票每张10元,学生票每张5元.一个旅游团有成人x人、学生y人,那么该旅游团应付多少门票费?(2)如果该旅游团有37个成人、15个学生,那么他们应付多少门票费?解:(1)该旅游团应付的门票费是(105x y+)元.(2)当x=37, y=15 时;105x y+=10×37+5×15=445.因此,他们应付445元门票费.(学生上黑板进行板演过程,教师巡视,对有困难的学生进行指导.根据学生的解题情况,教师进一步规范学生的解题格式规范.)(设计意图:通过例题示范巩固前面的知识,进一步规范学生的解题格式,同时体会代数式在现实背景中的意义,也为下一个环节打下基础.)师:在这个问题中,105x y+表示旅游团付给公园的门票费.在不同的生活情境中还可以表示其它的意义,你能联系实际说说它的其它意义吗?生1:一支钢笔10元钱,一个笔记本5元钱,买了x支钢笔和y个笔记本一共花的钱数. 生2:苹果的单价是x元,橘子的单价是y元,买了10斤苹果和5斤橘子,一共花了多少钱.生3:一副羽毛球拍x元。
代数式1课件

例2、根据题意,列代数式:
(1)把a本书分给若干名学生,若每人5本,尚余
a- 3
3本,则有学生
5
人。
(2)一项工程,甲队单独完成需a天,乙队单独
1
完成需b天,若两队合做,需 (3)a的3倍与b的一半的差 :
1 a
+
1 b
天完成。
b
2
3 a-
1 2
。
(4)a与b两数和的平方: ( a+ b )
。
例3、填空:
(2a2 + 12a) c㎡ 。 的表面积为:
大家练一练: 2、观察一组数
1 2 , 2 3 , 3 4 , 4 5 , 5 6 , ......
这组数的第n个数是:
。
3、教材第62页“思考”的2、3两个问题。
大家说说看: 1、在本节课中,你有哪些收获? 2、书写代数式要注意哪些问题?
2、列代数式时要注意哪些问题?
正方形 个数 火柴 根数
1 4
2
3
4
……
n
7
10
13
…… 3n+1
大家练一练:n支铅笔售价为
10n m
元;
(2)某工厂去年产值a万元,今年预计要比去年增产
(1+m%)a 万元; m%,今年的产值预计为: a2 + b2 (3)a、b两数的平方和为:
。
(4)长方体的长为3㎝,宽和高都为a ㎝,则长方体
2.2代数式(1)
温故而知新:
1、用字母表示数有哪些优点?
用字母表示数,可以把一些数量关系更简明地表示出 来,把具体的数换成抽象的字母,使所得式子反映的 规律具有普遍意义,从而为叙述和研究问题带来方便.
2.1.1 代数式(一)(解析版)
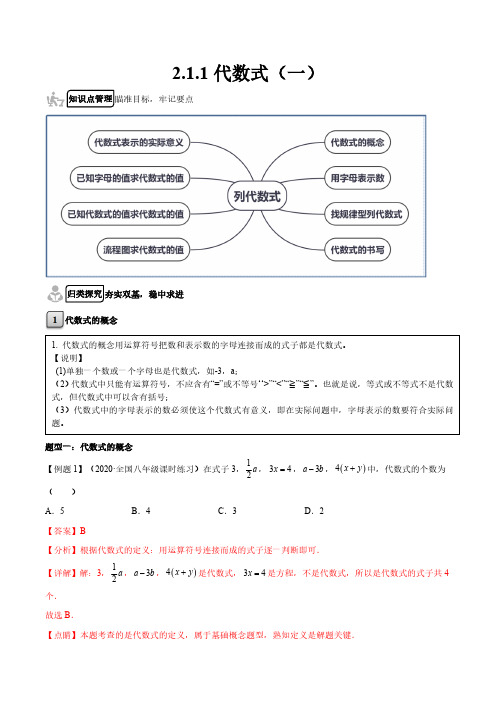
2.1.1代数式(一)代数式的概念题型一:代数式的概念【例题1】(2020·全国八年级课时练习)在式子3,12a ,34x =,3ab -,()4x y +中,代数式的个数为()A .5B .4C .3D .2【答案】B【分析】根据代数式的定义:用运算符号连接而成的式子逐一判断即可.【详解】解:3,12a ,3ab -,()4x y +是代数式,34x =是方程,不是代数式,所以是代数式的式子共4个.故选B .【点睛】本题考查的是代数式的定义,属于基础概念题型,熟知定义是解题关键.变式训练【变式1-1】(2018·河北沧州市·七年级期末)下列说法正确的是( )A .2a 是代数式,1不是代数式B .代数式2a b -表示2﹣a 除bC .当x =4时,代数式413x -的值为0D .零是最小的整数【答案】C【分析】根据代数式的定义、代数式表示的意义、代数式求值等知识点判断各项【详解】2a 是代数式,单独的数字也是代数式,故A 不正确;代数式2a b -表示2-a 除以b ,故B 不正确;当x=4时,代数式413x -的值为0,故C 正确;零是绝对值最小的整数,故D 不正确.故选C .【点睛】此题主要考查代数式的定义、代数式表示的意义、代数式求值等知识点.用数值代替代数式里的字母解题的关键【变式1-2】(2019·上海市西延安中学七年级月考)下列各式中,代数式有()个(1)a+b=b+a;(2)1;(3)2x-1 ;(4)23x x +;(5) s = πr 2;(6) -6k A .2B .3C .4D .5【答案】C【分析】根据代数式的定义即可求解.【详解】(1)a+b=b+a 为等式,故错误;(2)1为代数式,正确;(3)2x-1为代数式,正确;(4)23x x +为代数式,正确;(5) s = πr 2为等式,故错误;(6) -6k 为代数式,正确故选C.【点睛】此题主要考查代数式的识别,解题的关键是熟知代数式的定义.【变式1-3】(2020·正安县思源实验学校七年级期中)下列式子①23´②210x -=③y ④s vt =⑤ 3.14π>⑥1a ⑦()()x y x y +-⑧452x x +,其中代数式有( )A .3个B .4个C .5个D .6个【答案】C【分析】代数式是运算符号把数和表示数的字母连接而成的式子,据此确定解答即可.【详解】解:代数式是运算符号把数和表示数的字母连接而成的式子,所以以上八个式子中,是代数式的有①③⑥⑦⑧五个.故选:C【点睛】本题考查了代数式的定义,准确理解代数式的定义是解题关键.题型二:用字母表示数【例题2】三个连续整数中,中间一个是m ,则最大的一个是()A .m+1B .m+2C .m+3D .m+4【答案】A【分析】根据三个连续的自然数两两之间相差1,可知中间一个是m ,那么最大的一个数就是m+1.【详解】解:三个连续的自然数两两之间相差1,中间一个是m ,最大的一个数就是m+1.故选A .【点睛】明确相邻的两个自然数之间相差1是解决此题关键.变式训练【变式2-1】下列说法正确的是( )A .-a 一定是负数B .a 的倒数是1aC .2a 一定是分数D .a 2一定是非负数【答案】D【解析】【分析】本题考查的是负数、倒数、分数、非负数的定义,根据负数、倒数、分数、非负数的定义依次判断各项即可.A 、当a 是负数时,-a 是正数,故本选项错误;B 、当a 是0时,a 没有倒数,故本选项错误;C 、当a=4时,a 2=2,是整数,故本选项错误; D 、2a 一定是非负数,本选项正确,故选D.【点睛】本题考查了用字母表示数,解题的关键是掌握好负数、倒数、分数、非负数的定义.【变式2-2】a +1的相反数是()A .-a +1B .-(a +1)C .a -1D .11a +【答案】B【详解】1a +的相反数是:(1)a -+.点睛:表示一个式子的相反数只需把这个式子用括号括起来,再在括号前面添上一个“-”即可.【变式2-3】(2019·山东)甲数比乙数的3倍大2,若甲数为x ,则乙数为( )A .3x -2B .3x+2C .23x +D .23-x 【答案】D【分析】本题主要考查列代数式,根据甲数比乙数的3倍大2,可知甲数减去2是乙数的3倍,再除以3即可得到结果.【详解】根据题意,得乙数为23x -.选D.【点睛】本题考查了列代数式,解题的关键是正确理解文字语言中的关键词,从而明确其中的运算关系,正确地列出代数式.题型三:找规律型列代数式【例题3】(2020·江西省于都中学七年级期中)观察如图所示图形,则第n 个图形中三角形的个数是( )A .2n +2B .4n +4C .4nD .4n -4【分析】由已知的三个图可得到一般的规律,即第n个图形中三角形的个数是4n,根据一般规律解题即可.【详解】解:根据给出的3个图形可以知道:第1个图形中三角形的个数是4,第2个图形中三角形的个数是8,第3个图形中三角形的个数是12,从而得出一般的规律,第n个图形中三角形的个数是4n.故选C.【点睛】此题考查了学生由特殊到一般的归纳能力.解此题时要注意寻找各部分间的联系,找到一般规律.变式训练【变式3-1】(2020·广州市育才中学七年级期中)用棋子摆出下列一组“口”字,按照这种方法摆下去,则第n个“口”字需要用棋子( )A.(4n﹣4)枚B.4n枚C.(4n+4)枚D.n2枚【答案】B【分析】观察图形可知,构成每个“口”字的棋子数量,等于构成边长为(n+1)的正方形所需要的棋子数量减去构成边长为(n+1-2)的正方形所需要的棋子数量.【详解】解:由图可知第n个“口”字需要用棋子的数量为(n+1)2-(n+1-2)2=4n,故选择B.【点睛】本题考查了规律的探索.【变式3-2】(2020·广东七年级期末)下列图案由边长相等的黑、白两色正方形按一定的规律拼接而成,依此规律,第n个图形中白色正方形的个数为( )A .4n +1B .4n ﹣1C .3n ﹣2D .3n +2【答案】D 【分析】第一个图形中有5个白色正方形;第2个图形中有531+´个白色正方形;第3个图形中有532+´个白色正方形;…由此得出第n 个图形中有53(1)32nn +´+﹣=个白色正方形.【详解】解:第一个图形中有5个白色正方形;第2个图形中有531+´个白色正方形;第3个图形中有532+´个白色正方形;…第n 个图形中有53(1)32nn +´+﹣=个白色正方形.故选:D 。
3.代数式_1PPT课件(北师大版)

A.5
B.4
C.3
D.2
【点拨】由代数式的定义知,3x=4 不是代数式,其他均是代数
式.故选 B.
夯实基础逐点练
2.【2018·柳州】苹果原价是每斤 a 元,现在按 8 折出售,假如现
在要买一斤,那么需要付费( A )
A.0.8a 元
B.0.2a 元
C.1.8a 元
D.(a+0.8)元
夯实基础逐点练
(3)在(2)的情况下,李明从 A 地到 B 地比原计划少用的时间是多
少?
28v0-v+28100 h乘车里程不超过 3 km 的收费是起 步价加出租汽车燃油附加费,共 8 元;乘车里程超过 3 km 的, 除了照收 8 元以外,超过部分每千米加收 1.5 元(不足 1 km 按 1 km 计算).
设 n 是整数,三个连续的偶数可分别表示为 2n-2,2n,2n+2, 它们的和为(2n-2)+2n+(2n+2).
整合方法提升练
11.【2018·贵阳】如图,将边长为 m 的正方形纸板沿虚线剪成两 个小正方形和两个长方形,拿掉边长为 n 的小正方形纸板后, 将剩下的三块拼成新的长方形.
(1)用含 m 或 n 的式子表示拼成的长方形的周长;
夯实基础逐点练
10.由题意写出代数式. (1)a 除以 b 的商与 c 的和;
ab+c (2)比 a 的 2 倍与 b 的差小 6 的数;
(2a-b)-6
整合方法提升练
(3)a,b 两数和的平方与它们差的平方的和; (a+b)2+(a-b)2
(4)用含同一个字母的代数式分别表示三个连续的偶数,并写出它 们的和.
初中数学-代数式(一)

2 3
分母中、被 开方数中均 不含字母的 代数式。
2、单项式及其系数:
1 2 2 形如:2 a b , m n , 3 xy, 1 3 ,a 的整式叫单项式。 2 5
1 1 1 1 1 1 =- a- b+( c-2d) =- a- b+ c-2d 2 2 2 2 2 2
括号前有系数 则先将系数乘 进括号,再去 括号。
例8:去括号并合并同类项
=(-1+6)mn+(-9) =5mn-9
不急不燥, 先组合(符 号跟后走), 后并项。
2 y+3x2 y)-1 =(-xy-2xy)+(x
=-3xy+4x2 y-1
(1)括号前面是“+”号,去括号及前面的加 号后,括号里面每一项都不变号。 (2)括号前面是“-”号,去括号及前面的 减加号后,括号里面每一项都改变符号。
3、同类项:除了系数,字母及相应字母 的指数完全相同的单项式叫同类项。
例如:3ab与 4ab; 5x y 与x y;5m与 m。
4、合并同类项:就是将同类项的系数相加 作为新系数,字母及字母指数完全不变。
例 如 : 8a 3a ( 8 3) a 11a; 7x y 4x y ( 7 4) x y 3x y ; 1 1 3 mn mn ( 1 ) mn mn。 2 2 2
m 1 mn 例5:已知 n 5 ,求 m n
m 1 解:由 ,可得n 5 m n 5
的值。
m n m 5m 故 m n m 5m 6m 4m 6 3 . 4 2
代数式(1)

四、拓展提升: ( 1 )一个两位数的个位数字是 a , 十位数字是b,用代数式表示这个 两位数; 10b+a (2)你能用代数式表示一个三位 数吗?试一试。 100a+10b+c
五、课堂总结:
这节课你学会了哪些新知识?
你还有哪里不懂的地方吗?
1、代数式的定义。依据定义判断是否为代数式。
2、(1)x的3倍与3的差 3x-3 1 2x+ y (2)x的2倍与y的 1 的和 2 2 (3)b的3倍相反数 -3b 1 (4)a的倒数与1的差 -1 a (5)a与b的和的平方 (a+b)2 a b2 (6)a与b的平方的和 a2 b2 (7)a、b两数的平方和
列代数式的一般方法: 1、抓住关键字,由关键字确定相应的运算符号 2、理清运算顺序,一般是先读的先写, 必要时添上括号
3.2 代数式(1)
预习任务:
• 1、代数式的定义。 • 2、判断是否为代数式。 • 3、能根据实际列代数式。
一、概念
用运算符号和括号把数字或表示 数字的字母连接而成的式子叫做 代数式.
思考:代数式由什么组成?
一个代数式由数,表示数的字母和运算符号组成;
这里的运算包括加、减、乘、除、乘方等。
规定:单独一个的数或一个字母也称为代数式。
1 (比如: 3,0,x,h都是代数式.)
练习:判断下列式子哪些是代数式,哪
些不是。
(1)-3x (3)10x+5y=15 (5)13 (7)(a+b)2
(2)ab (4)a2+b2 (6)x≤2 (8) |ab|
答: (1)、(2)、(4)、(5)、(7)是 代数式。 (3)、(6)、(8)不是代数式。
巩固练习:
代数式(1)教学设计

2. 代数式(一)教学目标:1.了解代数式的概念,能用代数式表示简单问题中的数量关系;2.在具体情境中,能求出代数式的值,并解释它的实际意义;3.能解释一些简单代数式的实际背景或几何意义,发展符号感;教学重点:列代数式。
教学难点:正确列出代数式表示现实问题中的数量关系;从不同的角度给代数式赋予实际意义。
教学方法:探究合作教学用具:多媒体教学教学过程:第一环节 旧知归纳,直奔主题内容:承接先前的若干实例,回顾具体代数式所表达的含义。
归纳它们的基本特征。
学生在通过上一节知识的回顾,知道4+3(x -1),x +x +(x -1),a +b ,ab ,2(m +n ),ts ,a 3 …… 这样一些式子都具有一定的实际意义,而探求当x =200时4+3(x -1)的代数式的值,不仅理解了代数式和代数式的值的意义,而且了解到学习这些知识的重要性。
目的:极大地调动了学生学习数学的积极性.同时滲透了把实际问题抽象成数学问题的一般思想方法.第二环节 创设背景,理解概念代数式:用运算符号把数和字母连接而成的式子.(单独一个数或一个字母也是代数式) 内容:讲解教材中的例1 列代数式,并求值.参观花展:门票:成人10元/人;学生5元/人.(1)一个旅游团有成人x 人、学生y 人,请你根据上图确定该旅游团应付多少门票费?(2)如果该旅游团有37个成人,15个学生,那么门票费是多少呢?解:(1)该旅游团应付的门票费是(10x +5y )元.(2)把x=37,y=15代入代数式得10x+5y=10×37+5×15 =445.目的:经过多媒体展示实际背景,学生演板、师生交流,让学生从实际问题想出数学问题,学会列代数式和求代数式的值,体验数学来源于生活,又为现实活服务,极大地调动学生学习的主动性、积极性;规定代数式的书写要求,代数式求值的格式并用多媒体展示,目的在于让学生体会数学的规范性,严密性,进一步培养学生的数感和符号感.第三环节反设探究,意义升华内容:承接上面的例子,继续提出问题:前面10x+5y表示的是x个成人、y个学生进公园的门票费,那么它还可以表示什么呢?请大家想一想后,写出一种或两种表示的内容.要求学生在独立思考的基础之上,做小组交流,随后全班交流。
代数式(1)

2.035
1
5 6
9
1
3
3
2
1
6
4
注 意 当单项式的系数为1或 –1时,这个“1”应省略 不写。
课堂小结
代数式的概念 由运算符号将数与表示数的字母链接而成的式子。 代数式的书写规范 1.数字与字母、字母与字母相乘,乘号通常用“·”表示或省略不写,并 且把数字写在字母前面,若数字是带分数应写成假分数. 2.除法运算通常写成分数的形式. 3.结果是和或差的形式时,应将式子用括号括起来,再写上单位名称. 单项式的概念、系数、次数
像a-1,a+6,a+7, am+bn m+n 等式子都是 代数式(algebraic expression).
“代数式”是由运算符号将数、表 示数的字母连接而成的式子.
单独一个数或一个字母也是代数式
你认为a+b=b+a、a<b是代数式吗? 不是,a+b=b+a是等式,a<b是不 等式,它们分别表示两个代数式的相等关 系、大小关系. “代数式”是由运算符号将数、表 示数的字母连接而成的式子.
天8:00到21:00为用电高峰段(简称“峰时”),
峰时电价为0.55元/千瓦时;21:00到次日8:00 为用电低谷段(简称“谷时”),谷时电价为0.35 元/千瓦时.该地某用户上月峰时用电a千瓦时,谷 时用电b千瓦时,该用户上月的峰时电费、谷时电 费和总电费分别为多少?
像
0.55a、0.35b、0.15m、2a2、 0.8a和abc
作业
课堂作业 数学书 第72页 练一练 第2题 家庭作业 《学习与评价》 3.2 代数式 第一课时
单独的一个数或一个字母也是单项式; 单独一个数 (常数项) 的次数是 0 。
例如 3 x 是 1 次的,
专题07代数式(1)

专题07代数式(1)(全国一年)学校:___________姓名:___________班级:___________考号:___________一、单选题1.(2020·西藏中考真题)观察下列两行数: 1,3,5,7,9,11,13,15,17,… 1,4,7,10,13,16,19,22,25,…探究发现:第1个相同的数是1,第2个相同的数是7,…,若第n 个相同的数是103,则n 等于( ) A .18 B .19C .20D .21【答案】A【解析】根据探究发现:第1个相同的数是1,第2个相同的数是7,⋯,第n 个相同的数是6(1)165n n -+=-,进而可得n 的值.【详解】解:第1个相同的数是1061=⨯+, 第2个相同的数是7161=⨯+, 第3个相同的数是13261=⨯+, 第4个相同的数是19361=⨯+,⋯,第n 个相同的数是6(1)165n n -+=-, 所以65103n -=, 解得18n =.答:第n 个相同的数是103,则n 等于18. 故选:A .【点睛】此题主要考查了数字变化规律,确定出相同数的差值,从而得出相同数的通式是解题的关键. 2.(2020·广西河池中考真题)下列运算,正确的是( ) A .a (﹣a )=﹣a 2 B .(a 2)3=a 5 C .2a ﹣a =1 D .a 2+a =3a【答案】A【解析】利用单项式乘单项式、积的乘方的运算法则,合并同类项的运算法则分别计算后即可确定正确的选项.【详解】解:A 、a (﹣a )=﹣a 2,原计算正确,故此选项符合题意; B 、(a 2)3=a 6,原计算错误,故此选项不符合题意;C 、2a ﹣a =a ,原计算错误,故此选项不符合题意;D 、a 2与a 不是同类项,不能合并,原计算错误,故此选项不符合题意; 故选:A .【点睛】本题考查了单项式乘单项式、积的乘方,合并同类项.解题的关键是能够熟练掌握有关的运算法则,难度不大.3.(2020·湖北黄石中考真题)下列运算正确的是( ) A .835a b ab -= B .()325a a =C .933a a a ÷=D .23a a a ⋅=【答案】D【解析】根据整式的加减、幂的乘方、同底数幂的乘除法逐项判断即可. 【详解】A 、8a 与3b 不是同类项,不可合并,此项错误 B 、()23236a a a ⨯==,此项错误C 、93936a a a a -÷==,此项错误D 、2213a a a a +⋅==,此项正确 故选:D .【点睛】本题考查了整式的加减、幂的乘方、同底数幂的乘除法,熟记各运算法则是解题关键. 4.(2020·内蒙古通辽中考真题)下列说法不正确...的是( ) A .2a 是2个数a 的和 B .2a 是2和数a 的积 C .2a 是单项式 D .2a 是偶数【答案】D【解析】根据2a 的意义,分别判断各项即可.【详解】解:A 、2a =a+a ,是2个数a 的和,故选项正确; B 、2a =2×a ,是2和数a 的积,故选项正确; C 、2a 是单项式,故选项正确;D 、当a 为无理数时,2a 是无理数,不是偶数,故选项错误; 故选D.【点睛】本题考查了代数式的意义,注意a 不一定为整数是解题的关键. 5.(2020·广东深圳中考真题)下列运算正确的是( ) A .a+2a=3a 2B .235a a a ⋅=C .33()ab ab = D .326()a a -=-【答案】B【解析】根据合并同类项、同底数幂的乘法、幂的乘方、积的乘方逐项分析即可. 【详解】A .a +2a =3a ,该选项错误; B .235a a a ⋅=,该选项正确; C .333()ab a b =,该选项错误; D .326()a a -=,该选项错误; 故选B .【点睛】本题考查了整式的运算,熟练掌握幂的运算法则是解答本题的关键. 6.(2020·山东东营中考真题)下列运算正确的是( ) A .()235x x =B .()222x y x y -=+ C .2323522x y xy x y -⋅=- D .()33x y x y -+=-+【答案】C【解析】根据幂的乘方,完全平方,同底数幂的乘法法则逐一判断即可.【详解】A :326(x )x =,故此选项错误B :222(x y)=x 2xy+y --,故此选项错误C :23235x y 2xy 2x y -⋅=-,故此选项正确D :(3x+y)=3x y ---,故此选项错误 答案故选C【点睛】本题主要考查了幂的乘方,整式的乘法和完全平方的运算,熟记运算法则是解题的关键.7.(2020·甘肃金昌中考真题)下列各式中计算结果为6x 的是( ) A .24x x + B .82x x -C .24x x ⋅D .122x x ÷【答案】C【解析】根据合并同类项,同底数幂的乘法、除法,即可解答.【详解】解:A. 24x x ,不是同类项,不能合并,不符合题意; B 82x x ,不是同类项,不能合并,不符合题意; C .24x x ⋅=x 6,符合题意; D. 122x x ÷=x 10,不符合题意; 故选:C.【点睛】本题考查了合并同类项,同底数幂的乘法、除法,解决本题的关键是熟记合并同类项,同底数幂的乘法、除法的法则.8.(2020·山东淄博中考真题)下列运算正确的是( ) A .a 2+a 3=a 5 B .a 2•a 3=a 5 C .a 3÷a 2=a 5 D .(a 2)3=a 5【答案】B【解析】【详解】A .根据合并同类项的定义即可判断; B .根据同底数幂的乘法,底数不变,指数相加即可判断; C .根据同底数幂的除法,底数不变,指数相减即可判断; D .根据幂的乘方,底数不变,指数相乘即可判断.【解答】解:A .a 2+a 3≠a 5,所以A 选项错误;B .a 2•a 3=a 5,所以B 选项正确; C .a 3÷a 2=a ,所以C 选项错误;D .(a 2)3=a 6,所以D 选项错误; 故选:B .【点评】本题考查了同底数幂的乘法和除法、合并同类项、幂的乘方与积的乘方,解决本题的关键是综合掌握以上知识.9.(2020·辽宁营口中考真题)下列计算正确的是( ) A .x 2•x 3=x 6 B .xy 2﹣14xy 2=34xy 2C .(x +y )2=x 2+y 2D .(2xy 2)2=4xy 4【答案】B【解析】根据完全平方公式、同底数幂的乘法、合并同类项、积的乘方的运算法则分别进行计算后,可得到正确答案.【详解】解:A 、x 2•x 3=x 5,原计算错误,故此选项不符合题意; B 、xy 2﹣14xy 2=34xy 2,原计算正确,故此选项符合题意; C 、(x +y )2=x 2+2xy +y 2,原计算错误,故此选项不符合题意; D 、(2xy 2)2=4x 2y 4,原计算错误,故此选项不符合题意. 故选:B .【点睛】本题考查完全平方公式、同底数幂的乘法、合并同类项、积的乘方的运算法则,关键在于熟练掌握基础运算方法.10.(2020·辽宁沈阳中考真题)下列运算正确的是( ) A .235a a a += B .236a a a ⋅=C .()3328a a =D .33a a a ÷=【答案】C【解析】根据同底数幂乘法法则,积的乘方法则,同底数幂的除法法则以及合并同类项的法则,对各选项计算后利用排除法求解.【详解】A 、23a a +,不能进行底数不变,指数相加运算,故错误; B 、235a a a ⋅=,同底数幂相乘,底数不变,指数相加,故错误; C 、利用积的乘方法则()3328a a =,故正确;D 、32a a a ÷=,同底数幂相除,底数不变,指数相减,故错误. 故选:C .【点睛】题主要考查同底数幂相乘,底数不变,指数相加;积的乘方,等于把积中的每一个因式分别乘方,再把所得的幂相乘;合并同类项,只把系数相加减,字母和字母的指数不变;同底数幂相除,底数不变,指数相减.熟练掌握性质是解题的关键.11.(2020·江苏无锡中考真题)若2x y +=,3z y -=-,则x z +的值等于( ) A .5 B .1C .-1D .-5【答案】C【解析】将两整式相加即可得出答案. 【详解】∵2x y +=,3z y -=-,∴()()1x y z y x z ++-=+=-, ∴x z +的值等于1-, 故选:C .【点睛】本题考查了整式的加减,熟练掌握运算法则是解本题的关键. 12.(2020·内蒙古呼伦贝尔中考真题)下列计算正确的是( ) A .236a a a ⋅= B .222()x y x y +=+ C .()2526a a a ÷= D .22(3)9xy xy -=【答案】C【解析】根据同底数幂的乘法,完全平方公式,同底数幂的除法,幂的乘方与积的乘方法则逐项判断即可. 【详解】解:A 、235a a a ⋅=,故选项错误; B 、222()2x y x y xy +=++,故选项错误; C 、()2526a a a ÷=,故选项正确;D 、222(3)9xy x y -=,故选项错误; 故选C .【点睛】本题考查了同底数幂的乘法,完全平方公式,同底数幂的除法,幂的乘方与积的乘方,掌握运算法则是解题的关键.13.(2020·辽宁丹东中考真题)下面计算正确的是( ) A .3332a a a ⋅= B .22423a a a += C .933a a a ÷= D .()326327a a -=-【答案】D【解析】根据整式的计算法则依次计算即可得出正确选项. 【详解】解:A. 336a a a ⋅=,所以A 错误; B.22223a a a +=,所以B 错误; C.936a a a ÷=,所以C 错误; D.()326327a a -=-,所以D 正确;故答案选:D.【点睛】本题考查整式乘除法的简单计算,注意区分同底数幂相乘,底数不变,指数相加,而幂的乘方是底数不变,指数相乘,这两个要区分清楚;合并同类项的时候字母部分不变,系数进行计算.14.(2020·广西玉林中考真题)观察下列按一定规律排列的n 个数:2,4,6,8,10,12,…;若最后三个数之和是3000,则n 等于( ) A .499 B .500 C .501 D .1002【答案】C【解析】根据题意列出方程求出最后一个数,除去一半即为n 的值. 【详解】设最后三位数为x -4,x -2,x . 由题意得: x -4+x -2+x =3000, 解得x =1002. n =1002÷2=501. 故选C .【点睛】本题考查找规律的题型,关键在于列出方程简化步骤. 15.(2020·广西玉林中考真题)下列计算正确的是( ) A .87a a -= B .2242a a a += C .2236a a a ⋅= D .623a a a ÷=【答案】C【解析】根据整式的加减乘除运算法则逐个运算即可求解. 【详解】解:选项A :87a a a -=,故选项A 错误; 选项B :2222a a a +=,故选项B 错误; 选项C :2236a a a ⋅=,故选项C 正确; 选项D :624a a a ÷=,故选项D 错误. 故选:C .【点睛】本题考查了整式的加减乘除运算法则,熟练掌握运算法则是解决此类题的关键. 16.(2020·宁夏中考真题)下列各式中正确的是( ) A .326a a a ⋅= B .321ab ab -=C .261213a a a+=+ D .2(3)3a a a a -=-【答案】D【解析】利用整式的计算法则对四个选项一一验证即可得出答案. 【详解】解:A. 325a a a ⋅=,所以A 错误;B. 32ab ab ab -=,所以B 错误;C. 2611233a a a a+=+ ,所以C 错误;D. 2(3)3a a a a -=-,所以D 正确; 故答案选D.【点睛】本题考查整式乘除法的简单计算,注意区分同底数幂相乘,底数不变,指数相加,而幂的乘方是底数不变,指数相乘,这两个要区分清楚;合并同类项的时候字母部分不变,系数进行计算,只有当系数计算结果为0时,整体为0.17.(2020·吉林中考真题)下列运算正确的是( ) A .236a a a ⋅= B .()325a a = C .22(2)2a a =D .32a a a ÷=【答案】D【解析】根据同底数幂的乘除法、幂的乘方、积的乘方逐项判断即可. 【详解】A 、23235a a a a +⋅==,此项错误 B 、()23236a a a ⨯==,此项错误C 、22(2)4a a =,此项错误D 、3232a a a a -÷==,此项正确 故选:D .【点睛】本题考查了同底数幂的乘除法、幂的乘方、积的乘方,熟记整式的运算法则是解题关键. 18.(2020·广西中考真题)下列运算正确的是( ) A .22422x x x += B .3232x x x ⋅=C .()322xx =D .75222x x x ÷=【答案】D【解析】根据合并同类项法则,幂的乘方与积的乘方,同底数幂的乘法以及单项式除以单项式分别求出每个式子的值,再判断即可.【详解】A.22223x x x +=,故本选项不符合题意; B.325x x x ,故本选项不符合题意;C.()326x x =,故本选项不符合题意;D.75222x x x ÷=,正确. 故选:D .【点睛】本题考查了合并同类项法则,幂的乘方与积的乘方,同底数幂的乘法以及单项式除以单项式等知识点,能正确求出每个式子的值是解答此题的关键. 19.(2020·山东威海中考真题)下列运算正确的是( ) A .32533x x x ⋅= B .236(2)6x x =C .222()x y x y +=+D .325x x x +=【答案】A【解析】分别进行同底数幂的乘法、幂的乘方、完全平方公式、合并同类项等运算,然后选出正确选项即可.【详解】A 、32533x x x ⋅=,本选项正确; B 、236(2)8x x =,本选项错误;C 、222+2()x x y x y y +=+,本选项错误;D 、3232+x x x x +=,本选项错误; 故选:A .【点睛】此题考查合并同类项、完全平方公式、幂的乘方、同底数幂的乘法,掌握运算法则是解题关键. 20.(2020·重庆中考真题)已知a +b =4,则代数式122a b++的值为( ) A .3 B .1C .0D .-1【答案】A【解析】通过将所求代数式进行变形,然后将已知代数式代入即可得解. 【详解】由题意,得411132222a b a b +++=+=+= 故选:A.【点睛】此题主要考查已知代数式求代数式的值,熟练掌握,即可解题. 21.(2020·四川雅安中考真题)下列式子运算正确的是( ) A .2235x x x += B .()x y x y -+=- C .235x x x D .44x x x +=【答案】C【解析】根据合并同类项、去括号、同底数幂的乘法进行计算即可求解.【详解】解:A 、235x x x +=,故选项错误; B 、()x y x y -+=--,故选项错误; C 、235x x x ,故选项正确;D 、44x x x +=和x 不是同类项,不能合并,故选项错误; 故选C.【点睛】本题考察了合并同类项、去括号、同底数幂的乘法,要掌握运算法则.22.(2020·|2|0b a -=,则2+a b 的值是( ) A .4 B .6 C .8 D .10【答案】D【解析】直接利用绝对值和二次根式的性质分别化简得出答案.|2|0b a -=, ∴a-2=0,b-2a=0, 解得:a=2,b=4, 故a+2b=10. 故选:D .【点睛】此题主要考查了非负数的性质,正确得出a ,b 的值是解题关键.23.(2020·黑龙江大庆中考真题)若2|2|(3)0x y ++-=,则x y -的值为( )A .-5B .5C .1D .-1【答案】A【解析】根据绝对值和平方的非负性可求出x ,y 的值,代入计算即可; 【详解】∵2|2|(3)0x y ++-=, ∴20x +=,30y -=, ∴2x =-,3y =, ∴235-=--=-x y . 故答案选A .【点睛】本题主要考查了绝对值和平方的非负性,准确计算是解题的关键. 24.(2020·四川眉山中考真题)下列计算正确的是( )A .222()x y x y +=+B .2233235x y xy x y +=C .()326328a b a b -=-D .523()x x x -÷=【答案】C【解析】根据完全平方公式、同类项的合并以及幂的四则运算法则依次判断即可.【详解】解:A 选项222()2x y x xy y +=++而不是22xy +,故A 选项错误;B 选项22x y 和23xy 不是同类项,不能进行加减运算,故B 选项错误;C 选项()32363632(2)8a ba b a b -=-=-,故C 选项正确;D 选项22355()x x x x x =--÷÷=-而不是3x ,故D 选项错误. 故选:C.【点睛】本题主要考查了整式乘法的综合,涉及了完全平方公式、同类项的合并及幂的四则运算,熟练掌握相应的运算法则并灵活应用是解题的关键.25.(2020·云南昆明中考真题)下列运算中,正确的是( )A 2B .6a 4b ÷2a 3b =3abC .(﹣2a 2b )3=﹣8a 6b 3D .22111-+⋅=--a a a a a a【答案】C【解析】直接利用二次根式的加减运算法则和整式的除法运算法则、分式的乘法运算法则、积的乘方运算法则分别化简得出答案.【详解】解:A B 、6a 4b ÷2a 3b =3a ,此选项错误,不合题意; C 、(﹣2a 2b )3=﹣8a 6b 3,正确;D 、22111a a a a a -+⨯--=()2111a a a a-⨯--=-a ,故此选项错误,不合题意; 故选:C .【点睛】此题主要考查了二次根式的加减运算和整式的除法运算、分式的乘法运算、积的乘方运算,正确掌握相关运算法则是解题关键.A 2=±B .1122-⎛⎫=- ⎪⎝⎭C .()3339a a -=- D .633(0)a a a a ÷=≠【答案】D【解析】根据算术平方根、负整数指数幂、积的乘方、同底数幂的除法法则判断即可.【详解】A.2=,故本选项错误;B. 1122-⎛⎫= ⎪⎝⎭,故本选项错误; C. ()33327a a -=-,故本选项错误; D. 633(0)a a a a ÷=≠,故本选项正确; 故选:D .【点睛】本题主要考查了算术平方根、负整数指数幂、积的乘方、同底数幂的除法法则,牢记法则是解题的关键.27.(2020·江苏无锡中考真题)下列选项错误的是( )A .1cos602︒= B .235a a a ⋅=C 2=D .2(2)22x y x y -=-【答案】D【解析】分别根据特殊角的三角函数值,同底数幂的乘法法则,二次根式的除法法则以及去括号法则逐一判断即可.【详解】解:A .1cos602︒=,本选项不合题意; B .235a a a ⋅=,本选项不合题意;C2=1,本选项不合题意; D .2(x−2y )=2x−4y ,故本选项符合题意; 故选:D .【点睛】本题主要考查了特殊角的三角函数值,同底数幂的乘法,二次根式的除法以及去括号与添括号,28.(2020·江苏镇江中考真题)下列计算正确的是( ) A .a 3+a 3=a 6 B .(a 3)2=a 6C .a 6÷a 2=a 3 D .(ab )3=ab 3【答案】B【解析】根据合并同类项、同底数幂的乘除法、幂的乘方、积的乘方的计算法则进行计算即可. 【详解】解:3332a a a +=,因此选项A 不正确;32326()a a a ⨯==,因此选项B 正确;62624a a a a -÷==,因此选项C 不正确;333()ab a b =,因此选项D 不正确;故选:B .【点睛】本题考查合并同类项、同底数幂的乘除法、幂的乘方、积的乘方的计算方法,掌握相关运算方法是解题的关键.29.(2020·黑龙江鹤岗中考真题)下列各运算中,计算正确的是( ) A .22423a a a += B .826x x x -= C .222()x y x xy y -=-+ D .()326327x x -=-【答案】D【解析】直接利用完全平方公式以及整式的加减、幂的运算法则分别化简得出答案. 【详解】A 、结果是23a ,故本选项不符合题意; B 、8x 和2x -不能合并,故本选项不符合题意; C 、结果是222x xy y -+,故本选项不符合题意; D 、结果是627x -,故本选项符合题意; 故选:D .【点睛】此题主要考查了整式的混合运算,正确掌握相关运算法则是解题关键.30.(2020·江苏泰州中考真题)点(),P a b 在函数32y x =+的图像上,则代数式621a b -+的值等于( ) A .5 B .3 C .3- D .1-【答案】C【详解】把(),P a b 代入函数解析式32y x =+得:32=+b a , 化简得到:32-=-a b ,∴()()621=231=221=-3-+-+⨯-+a b a b . 故选:C .【点睛】本题主要考查了通过函数解析式与已知点的坐标得到式子的值,求未知式子的值,准确化简式子是解题的关键.31.(2020·辽宁朝阳中考真题)下列运算正确的是( ) A .326a a a ⋅= B .()235aa =C .3222a a a ÷=D .2235x x x +=【答案】C【解析】根据同底数幂的乘法法则、同底数幂的除法法则、幂的乘方法则、合并同类项逐项计算即可. 【详解】A. 325a a a ⋅=,故不正确; B. ()236a a =,故不正确;C. 3222a a a ÷=,正确;D. 235x x x +=,故不正确; 故选C .【点睛】本题考查了整式的运算,熟练掌握运算法则是解答本题的关键.同底数的幂相乘,底数不变,指数相加;同底数幂相除,底数不变指数相减;幂的乘方,底数不变,指数相乘;合并同类项时,把同类项的系数相加,所得和作为合并后的系数,字母和字母的指数不变.32.(2020·山东枣庄中考真题)图(1)是一个长为2a ,宽为2b (a >b )的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是A. abB.()2a b + C. ()2a b - D. 22a b -【解析】试题分析:由题意可得,正方形的边长为a b +,故正方形的面积为()2a b +。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例1
指出下列代数式的意义: (1) 2a+5; (3) (5) a2+b2 1 a (2) 2(x+5) (4) (a+b)2 1 (6) a + a
用代数式表示: (1)x的3倍与3的差; (2)x的2倍与y的倒数的和; (3)a与b的和的平方; (4)2a的立方。 ( 5) a与b的差与c的平方的和 ( 6) 百位数字是a,十位数字是b,个位数字 是c的三位数 ( 7) 用含一个字母的代数式表示三个连 续的整数,并写出它们的和.
4
(2)一五彩花圃的形状 如下图,花圃的面积 为_____/千克,食油 y元/千克,妈
妈买10千克大米、2千克食油共需 ________ ( 10x+2y) 元
学习目标
1掌握代数式的概念及其书写要
求; 2能用语言表述代数式的含义; 3根据问题中的数量关系列出所 要求的代数式
代数式的组成:
<1 >
一个代数式由数、表示数的字母和运算符号
组成.单独一个数或者一个字母也称代数式. <2>这里的运算符号是指加、减、乘、除、乘方。 式子不含“=”、“>”、“<”、“≤”、“≥”。
做一做
在x,1,x2 -2,s=ab, 代数式的个数是( B )个
A. 5 B. 4 C. 3 D. 2
代 数 式 的 规 范 写 法
:
(1) a×b (2) 1÷a
通常写作 a· b 或 ab ;
1 通常写作 a
;
(3) 数字通常写在字母前面; (4)带分数一般写成假分数. 1 6 如: 1 ×a 通常写作 a 5 5
课内练习
1 1 (1)a与b的 的和; a+ b 2 2
(2)a与b的平方的差;a b
2
2
(3)m与n的差的平方; m n (4)v1,v2的和除s所得的商;
s v1 v 2
一试身手
用文字叙述下列代数式的意义;
(1) 2a-3
(3)
(2) ( a b )
2
3
a b
2
1)已知甲数比乙数的2倍少1.设乙数为X, 用关于X 的代数式表示甲数
2)甲种日记本每本x元,乙种日记本每本y元, 用代数式表示购买10本甲种日记本和5本乙 种日记本的总钱数是多少? 3)甲乙两人加工同一种产品,甲每天加工x 只产品,乙每天加工y只产品,甲加工了 10天,乙加工了5天,试用代数式表示加 工产品的总数?
售票处
成 人 票 价 10 元 学 生 票 价 5 元
一个旅游团有成人37人,学生15人,那么 该旅游团应付多少门票费? 若该旅游团有成人x人,学生y人,那么 该旅游团应付多少门票费?
5.2 代 数 式
看下面的问题,填空:
(1)日平均气温是指一天中2:00,8:00,14:00,20:00四个时刻 气温的平均值.若上述四个时刻气温的摄氏度数分别 abcd 是a,b,c,d,则日平均气温的摄氏度数_____________ 。
,v=sh中
辨一辨 下列各式是代数式吗?
(1)2x+3y
(3)5x=4y-2 (5) -7 (7) x 2 y
3
(2)3xy-5 (4) m (6) x﹥y3
用语言叙述下列代数式的实际意义: (1)苹果每千克的价格是x元,则 可以怎样解释? (2)8a3可以怎样解释?
1 x 2
(3)10x+5y可以怎样解释?
下面的图形你能摆出来吗?
1、按上图方式,围4个正六边形, 需要多少根小棒? 21根 2、围100个正六边形,需要多少根 小棒,你是怎样算出来的? 501根 3、如用m来表示正六边形的个数, 那么围m个正六边形需要多少根小棒
A=X+Y+Z
其中:
A代表成功,X代表艰苦 的学习,
Y代表正确的方法,Z代表少说空话
自学提示
阅读课本143页-144页(5分钟)
(1)哪些符号是运算符号?代数式是怎样
的式子?写法有什么要求? (2)代数式与等式有怎样的区别与联系? (3)代数式中的数量关系如何表述? (4)列代数式要经历哪些步骤?
像 数式。
abcd 10x+2y、 4
、2a2 等的式子是代
