北邮复变函数课件2-1
合集下载
复变函数第4讲PPT课件

§2.1 解析函数的概念
1.复变函数的导数
1)导数概念:
设函数f (z)在点z0及其邻域内有定义,如果极限
lim f (z0 z) f (z0 )
z 0
z
存在, 那么就说f (z)在点z0可导. 这个极限值称
为f (z)在点z0的导数.
记作
f
'(z0 )
dw dz
z z0
lim
z 0
f
( z0
u e x cos y, x v e x si n y, x
u e x si ny u v
y v
e x cos y
x y v u
y
x y
故 f (z) e x (cos y i siny)在 全 平 面 可 导 , 解 析 。
f '(z) u i v e x cos y ie x si ny f (z). x x
条件是 u(x, y) 和 v(x, y)在D内可微,且
满足Cauchy-Rieman方程
u v ,
v
u .
x y x y
并且在解析的条件下
f (z) ux ivx vy iuy
第18页/共26页
例1 判定下列函数在何处可导,在何处解析:
(1) f (z) ex (cosy i siny); 解:(1) u e x cos y, v e x siny,
第7页/共26页
例如
f
(z)
1 z2
z
,则当z
0,
1时 ,f
'(z)
2z 1 (z2 z)2
.
思考题
实 函 数 中, f ( x) x 2 在( , )内 可 导;
1.复变函数的导数
1)导数概念:
设函数f (z)在点z0及其邻域内有定义,如果极限
lim f (z0 z) f (z0 )
z 0
z
存在, 那么就说f (z)在点z0可导. 这个极限值称
为f (z)在点z0的导数.
记作
f
'(z0 )
dw dz
z z0
lim
z 0
f
( z0
u e x cos y, x v e x si n y, x
u e x si ny u v
y v
e x cos y
x y v u
y
x y
故 f (z) e x (cos y i siny)在 全 平 面 可 导 , 解 析 。
f '(z) u i v e x cos y ie x si ny f (z). x x
条件是 u(x, y) 和 v(x, y)在D内可微,且
满足Cauchy-Rieman方程
u v ,
v
u .
x y x y
并且在解析的条件下
f (z) ux ivx vy iuy
第18页/共26页
例1 判定下列函数在何处可导,在何处解析:
(1) f (z) ex (cosy i siny); 解:(1) u e x cos y, v e x siny,
第7页/共26页
例如
f
(z)
1 z2
z
,则当z
0,
1时 ,f
'(z)
2z 1 (z2 z)2
.
思考题
实 函 数 中, f ( x) x 2 在( , )内 可 导;
复变函数课件1-2
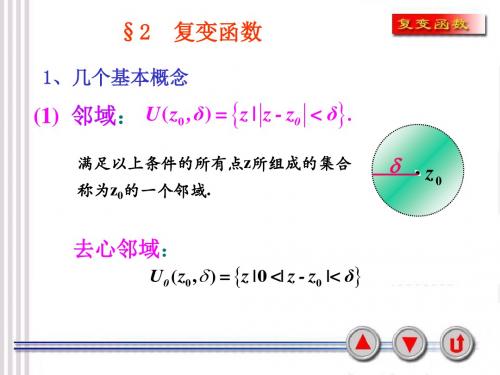
定义域
函数值集合
称w为z的象点(映象),而z称为w的原象。
y
(z)
v
(w)
w=f(z)
G
z
原象
w=f(z)
G* w象
o
x
o
u
14
2) 函数 w z2 构成的映射.
显然将 z 平面上的点z1 i, z2 1 2i, z3 1 映射成 w平面上的点w1 1, w2 3 4i, w3 1.
单连通区域
多连通区域
11
§1.5 复变函数的极限与连续性
1、 复变函数的定义
定义 设 GD 是一个复数 z = x + iy 的集合, 如果有 一个确定的法则存在, 按照这一法则, 对于集合 GD
中 的 每 一 个 复 数 z, 就 有 一 个 或 几 个 复 数
w = u + iv 与之对应, 则称复变数 w 是复变数 z 的
惟一性
与实变函数的极限性质类似.
复合运算等
22
5、函数的连续性
连续的定义:
如果
lim
z z0
f (z)
f (z0 ),
那么我们就说
f (z) 在 z0 处连续.
(1) f(z)在z0处有定义
连续的 三要素:
(2)f(z)在z0处有极限 (3)f(z)在z0处的极限值等于函 数值
如果f(z)在区域D内处处连续,则称f(z)在D内连续.
5
课堂练习 判断下列区域是否有界?
(1) 圆环域: r1 z z0 r2; (2) 上半平面: Im z 0;
(3) 角形域: 0 arg z ;
(4) 带形域: a Im z b.
课02-第一章复变函数2ppt课件

直线 x的象的参数: 方程为
u2y2, v2 y. (y为参 ) 数 消去参y数 得: v24 2(2u ),
以原点为焦点,开口相左的抛物线.(图中红色曲线)
同理y 直 的 线 象 : 为
v24 2(2u ),
以原点为焦点,开口相右的 抛物线.(图中蓝色曲线)
12
4. 反函数的定义: 设wf(z)的定义集 z平合 面为 上的 G, 集
2
这个映射通常函简数 w称 f为 (z) 由 所构成的 . 映射
如G 果 中的 z被 点 映 w射 f(z)映射 G*成 中的 w,那 点 w 末 称z为 的(映 象)象 而 , z称w 为 的原 . 象
5
3. 两个特殊的映射:
(1)函数 wz构成的 . 映射
将 z平面 z a 上 i映 b的 w 射 平 点 成 面
2 s i n s i n 2 ic o s s i n
22
22
2 s i 2 n s i 2 n ic o 2 s
30
2 s i 2 n cπ o 2 s isπ i n 2
因0 为 2 πs,in 0,
2 上式就 ei是 ei的 复三 数角 . 表示式
4
解 设z rei ,
y
还是线段.
v
w ei ,
w z2
则 r2, 2 , o
x
o
u
故0 线 r 2 , 段 π 映 0 射 4 , 为 π ,
4
2
16
例1 在映w射 z2下求下列平w面 平点 面集
上的: 象
(2)双曲 x2线 y24;
解 令 z x i,y w u i,v
y
zz3 1o z 2
x
u2y2, v2 y. (y为参 ) 数 消去参y数 得: v24 2(2u ),
以原点为焦点,开口相左的抛物线.(图中红色曲线)
同理y 直 的 线 象 : 为
v24 2(2u ),
以原点为焦点,开口相右的 抛物线.(图中蓝色曲线)
12
4. 反函数的定义: 设wf(z)的定义集 z平合 面为 上的 G, 集
2
这个映射通常函简数 w称 f为 (z) 由 所构成的 . 映射
如G 果 中的 z被 点 映 w射 f(z)映射 G*成 中的 w,那 点 w 末 称z为 的(映 象)象 而 , z称w 为 的原 . 象
5
3. 两个特殊的映射:
(1)函数 wz构成的 . 映射
将 z平面 z a 上 i映 b的 w 射 平 点 成 面
2 s i n s i n 2 ic o s s i n
22
22
2 s i 2 n s i 2 n ic o 2 s
30
2 s i 2 n cπ o 2 s isπ i n 2
因0 为 2 πs,in 0,
2 上式就 ei是 ei的 复三 数角 . 表示式
4
解 设z rei ,
y
还是线段.
v
w ei ,
w z2
则 r2, 2 , o
x
o
u
故0 线 r 2 , 段 π 映 0 射 4 , 为 π ,
4
2
16
例1 在映w射 z2下求下列平w面 平点 面集
上的: 象
(2)双曲 x2线 y24;
解 令 z x i,y w u i,v
y
zz3 1o z 2
x
《复变函数与积分变换》PPT课件

z = z1 + t(z2 z1 ),
(0 ≤ t ≤ 1)
(2)过两点 z1 和z2的直线L的参数方程为
z = z1 + t(z2 z1 ),
(∞ < t < +∞)
(3)z1、z2,z3 三点共线得充要条件为
z3 z1 = t, z2 z1
(t为 非 实 ) 一 零 数
浙江大学
例: 考察下列方程(或不等式)在平面上所描绘的几何图形。 (1) z 2i = z + 2 该方程表示到点2i和-2距离相等的点的轨迹,所以方程 表示的曲线就是连接点2i 和-2的线段的垂直平分线, 它的方程为y = -x。
复变函数与积分变换
贾厚玉 mjhy@
浙江大学
第一章 复数与复变函数 第二章 解析函数 第三章 复变函数的积分 第四章 级数 第五章 留数 第六章 保角映射 Laplace变换 第七章 Laplace变换
浙江大学
第一章 复数与复变函数
复数及其代数运算 复数的表示 复数的乘幂与方根 复平面点集与区域 复变函数 复变函数的极限与连续
浙江大学
例:已知正三角形的两个顶点为 求三角形的另一个顶点。
z1 = 1, z2 = 2 + i
y
z3 z1 = (z2 z1 )e 3 1 3 = (1+ i)( + i) 2 2 1 3 1 + 3 i = + 2 2
3 3 1+ 3 z3 = i + 2 2
i
π
z3
z2
x
O
z1
3 + 3 1 3 ′ z3 = i + 2 2
Re z 2 ≤ 1
z 2 = (x + iy)2 = (x2 y2 ) + 2ixy
复变函数课件:2_1极限与连续

映射 如果用 z 平面上的点表示自变量 z 的值, 而用另一个平面 w 平面上的点表示函数 w 的 值, 那末函数 w f (z) 在几何上就可以看作 是把 z 平面上的一个点集 E (定义集合) 变到 w 平面上的一个点集 A (函数值集合)的映射 (或变换).
如果 E 中的点 z 被映射 w f (z) 映射成 A 中的点 w, 那末 w 称为 z 的象 (映象), 而 z 称为 w 的原象.
由二元实函数极限的定义,
lim u(x, y) a, lim v(x, y) b.
xx0 y y0
xx0 y y0
充分性() 若 lim u(x, y) a, lim v(x, y) b,
xx0
xx0
y y0
y y0
0, 0,使得当0 x x0 2 y y0 2 时
| u(x, y) a | , | v(x, y) b | ,
例3 函数 w z2, 令 z x iy, w u iv, 则 u iv ( x iy)2 x2 y2 2xyi, 于是函数 w z2 对应于两个二元实变函数 : u x2 y2, v 2xy.
3. 映射的概念
对于复变函数,由于它反映了两对变量u, v 和 x, y 之间的对应关系,因而无法用同一平面内 的几何图形表示出来, 必须看成是两个复平面上 的点集之间的对应关系.
2. 复变函数极限与实函数极限的关系
定理2.1.1 设 f (z) u(x, y) iv(x, y)在点集E 上
有定义,z0 x0 iy0为E的一个聚点, a ib,
则 lim f (z) a ib z z0
lim u(x, y) a, lim v(x, y) b.
若有一法则 f ,使对E中的每一个点 z x iy, 存在多个 w u iv 和它对应, 则称 f 为在 E 上定义了一个复变数(多值)函数 .
复变函数第二章课件

9
例 判断下列函数的解析性.
1) w z ;2) f ( z ) e x (cos y i sin y );3)w z Re( z )
例 设函数
f ( z ) x 2 axy by 2 i (cx 2 dxy y 2 ).
问:常数 a, b, c, d 取何值时, ( z ) 在复平面 f 内处处解析?
注
Lnz n nLnz n 1 Ln z n Lnz
不成立!!
18
对数函数的解析性 y z
z e
w
v
i
O
w
O
x
w ln z
u
i
arg z v
ln z 在除去原点和负实轴的平面内解析,且有
d ln z 1 1 w de dz z dw (Lnz )k (k Z) 在除去原点和负实轴的平面内解析.
19
3.3 幂函数
对 z 0, ; C
w z e Lnz e (ln z 2k i ) w0e2k i (k Z), 其中 w0 e ln z 是 z 的一个主值.
(sin z )' cos z, (cos z )' sin z
iz
(3)遵从通常的三角恒等式;
22
(4)周期为 2 ; (5) sin z 0 z n , n Z; ; 1 ; ; cos z 0 z (n ) , n Z; ; 2 (6) sin z 1 和 cos z 1不成立; (7) cos( z ) cos z , sin( z ) sin z ; (8) e cos z i sin z.
例 判断下列函数的解析性.
1) w z ;2) f ( z ) e x (cos y i sin y );3)w z Re( z )
例 设函数
f ( z ) x 2 axy by 2 i (cx 2 dxy y 2 ).
问:常数 a, b, c, d 取何值时, ( z ) 在复平面 f 内处处解析?
注
Lnz n nLnz n 1 Ln z n Lnz
不成立!!
18
对数函数的解析性 y z
z e
w
v
i
O
w
O
x
w ln z
u
i
arg z v
ln z 在除去原点和负实轴的平面内解析,且有
d ln z 1 1 w de dz z dw (Lnz )k (k Z) 在除去原点和负实轴的平面内解析.
19
3.3 幂函数
对 z 0, ; C
w z e Lnz e (ln z 2k i ) w0e2k i (k Z), 其中 w0 e ln z 是 z 的一个主值.
(sin z )' cos z, (cos z )' sin z
iz
(3)遵从通常的三角恒等式;
22
(4)周期为 2 ; (5) sin z 0 z n , n Z; ; 1 ; ; cos z 0 z (n ) , n Z; ; 2 (6) sin z 1 和 cos z 1不成立; (7) cos( z ) cos z , sin( z ) sin z ; (8) e cos z i sin z.
复变函数-工科复变2-1

( 3 ) w z R z ) e ; ( ( 4 f ( z ) z 2 .
与一元函数类似地, 记
由该定理 f(z, )u (x 可 ,y)得 iv (x,y函 )在数 点 z0x0i0 y处的导 : 数公式
(1 )w z ;
(2 )f(z) e x (cy o issiy )n ;
(3 )w zR z)e;((4 f(z) z2 .
(1 )w z; (2)f(z)ex(cy oissiy)n; (3)w zRz)e;((4 f(z)z2.
16
2. 充要条件
Cauchy-Rieman简介
17
定理1 复变函数 f(z)u (x ,y 点)v(x ,y)i z0x0y0i 可导的充分必要条件是:
(1 )w z ;
(2 )f(z) e x (cy o issiy )n ;
(3 )w zR z)e;((4 f(z ) z2 .
9
(3) 求导法则 由于复变函数中导数的定义与一元实函数
中导数的定义在形式上完全一致,同时,复变 函数中的极限运算法则也和实函数中一样,因 而实函数中的求导法则可推广到复变函数中, 且证明方法相同,此处略.
z 0
z
A
复变函数可微的概念在形式上与一元实变 函数的微分概念完全一致。
复变函数可微与可导是否也具有一元实变
函数可微与可导的关系?
13
f ( z 0 z ) f ( z 0 ) A z
f ( z 0 z ) f ( z 0 ) A z z
2x3yi lim z0 xyi
再l由 i m ( z)0, x0
lim2x2
z 0
复变函数课件第二节复平面上的点集优质文档

远 点的一个邻域的并集。 注意:加上无穷远点后,许多性质将有很多
变化。
曲线:
设已给 z z(t)(a , t b )
如果Rez(t)和Imz(t)都是闭区间[a,b]上连续函数 ,则称这些点组成集合为一条连续曲线。如
果对上任意不同两点t及s,但不同时是的端点
,我们有: z(t)z(s)
即是一条除端点外不自交的连续曲线,那么上
段所构成的折线连起来,而使这条折 线上的所有点完全属于D。 则称D是一个区域。 结合前面的定义,可以定义有有界区域、无界 区域。
连通性:
性质(2)我们称为连通性,即区域是连通的 开集。 区域D内及其边界上全部点所组成的集称为 闭区域。
扩充复平面:
在扩充复平面上,不含无穷远点的区域的定 义同上; 含无穷远点的区域是C上的一个区域与无穷
为一角形,它是一个单连通无界区域 ,其边界为半射线:
arzg i)(2 arzg i()3
例4、集合:
{ z|2 |z i|3 }
为一个圆环,它是一个多连通有Hale Waihona Puke 区 域其边界|z为i圆|:3
|zi|2
例5、在扩充复平面上,集合
{z|2|z|}
为单连通的无界区域,其边界分别为
{|z|2}
而集合 {z|2|z|}
区域的连通性:
设D是一个区域,在复平面C上,如果D内 中既有属于E的点,又有不属于E的点,则称
区域D内及其边界上全部点所组成的集称为
任何简单闭曲线所围成的内区域中每一点 区域D内及其边界上全部点所组成的集称为
集合称为E的边界,记为 则称a为的E孤立点(是边界点但不是聚点); 注意:加上无穷远点后,许多性质将有很多
述集合称为一条简单连续曲线,或若尔当曲线
变化。
曲线:
设已给 z z(t)(a , t b )
如果Rez(t)和Imz(t)都是闭区间[a,b]上连续函数 ,则称这些点组成集合为一条连续曲线。如
果对上任意不同两点t及s,但不同时是的端点
,我们有: z(t)z(s)
即是一条除端点外不自交的连续曲线,那么上
段所构成的折线连起来,而使这条折 线上的所有点完全属于D。 则称D是一个区域。 结合前面的定义,可以定义有有界区域、无界 区域。
连通性:
性质(2)我们称为连通性,即区域是连通的 开集。 区域D内及其边界上全部点所组成的集称为 闭区域。
扩充复平面:
在扩充复平面上,不含无穷远点的区域的定 义同上; 含无穷远点的区域是C上的一个区域与无穷
为一角形,它是一个单连通无界区域 ,其边界为半射线:
arzg i)(2 arzg i()3
例4、集合:
{ z|2 |z i|3 }
为一个圆环,它是一个多连通有Hale Waihona Puke 区 域其边界|z为i圆|:3
|zi|2
例5、在扩充复平面上,集合
{z|2|z|}
为单连通的无界区域,其边界分别为
{|z|2}
而集合 {z|2|z|}
区域的连通性:
设D是一个区域,在复平面C上,如果D内 中既有属于E的点,又有不属于E的点,则称
区域D内及其边界上全部点所组成的集称为
任何简单闭曲线所围成的内区域中每一点 区域D内及其边界上全部点所组成的集称为
集合称为E的边界,记为 则称a为的E孤立点(是边界点但不是聚点); 注意:加上无穷远点后,许多性质将有很多
述集合称为一条简单连续曲线,或若尔当曲线
北邮复变函数课件2-1

z0 z z0
z
y0 x iy i
x0
当点沿不同的方向使z 0时,极限值不同,
故f (z) Im z在复平面上处处不可导.
7
例3 问f (z) x 2 yi是否可导?
解 lim f lim f (z z) f (z)
z0 z z0
设z z沿着平行于 y 轴的直线趋向于 z,
lim x 2yi lim 2yi 2, z0 x yi y0 yi
所以f (z) x 2 yi的导数 不存在.
x 0 y
z o
y 0 x
9
2.可导与连续:
函数 f (z) 在 z0 处可导则在 z0 处一定连续, 但 函数 f(z) 在 z0 处连续不一定在 z0 处可导. 证 根据在 z0 可导的定义,
dw dz f (z0 ) z z,
dw f (z0 ) z f (z0 ) dz, 即
f
( z0
)
dw dz
z z0
函数 w f (z)在 z0 可导与在 z0 可微是等价的.
如果函数 f (z)在区域 D内处处可微, 则称
f (z)在区域 D内可微.
两个互为反函数的单值函数, 且(w) 0
13
二.复函数的微分:
1.定义 设函数w f (z)在 z0 可导, 则 w f (z0 z) f (z0 ) f (z0 ) z (z)z, 式中 lim (z) 0, (z)z 是 z 的高阶无穷
0, 0, 使得当 0 | z | 时,
有
f
( z0
z) z
f
(z0 )
复变函数课件1-2

下页
结束
铃
( 5 ) 0 arg
zi zi
4
,
当 z x iy 时 ,
zi zi
x y 1
2 2
x ( y 1)
2
2
i
2x x ( y 1)
2 2
,
由 0 arg
2 2
zi zi
2
4
知
2x x ( y 1)
2 2
x y 1 x ( y 1)
2
0,
0,
18
首页
上页
返回
下页
结束
铃
因为 x ( y 1 ) 0 ,
2 2
2 x 0, 2 2 于是 x y 1 0 , 2 2 2 x x y 1,
x 0, 2 2 x y 1, 2 2 ( x 1) y 2 .
(1)彼此不相交
边界
y
I(C)
o
E(C)
x
(2)I(C) 是一个有界区域 (称为C的内部). (3)E(C) 是一个无界区域(称为C的外部). (4)若简单折线P的一个端点属于I(C),另一个 端点属于E(C) ,则P必与C有交点.
10
首页
上页
返回
下页
结束
铃
光滑曲线:
如果在 t 上 , x ( t ) 和 y ( t ) 都是连续的 , 且对于 t 的每一个值 , 有 [ x ( t ) ] [ y ( t ) ] 0, 那末
重点
重点
没有重点的连续曲线 C 称为简单曲线(或若尔当曲 线).
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
如果函数 f ( z )在 区域 D内处处可微, 则称 f ( z )在 区域 D内可微.
15
三.可微(可导)的充要条件
1.在一点可导或可微
Th 1 : 设 f ( z ) u ( x , y ) iv ( x , y ) 在区域 D 内有定义, 则 f ( z ) 在 D 内一点 z x iy 可微
( g(z) 0)
12
(6)
f [ g ( z )] f ( w ) g ( z ).
f ( z ) 1
其中 w g ( z )
(7 )
( w )
,
其中 w f ( z ) 与 z ( w ) 是 函数 , 且 ( w ) 0
两个互为反函数的单值
1 ik x 1 ik x i y 1 i y z x
z
x i y
1i
y
25
由于 k 的任意性
,
z z
1 ki 1 ki
不趋于一个确定的值
.
z 0
lim
h( z0 z ) h( z0 ) z
2
不存在 .
因此 h ( z ) z
小, f ( z0 ) z 是函数 w f ( z ) 的改变量 w 的 线性部分.
f ( z 0 ) z 称为函数 记作
w f ( z ) 在点 z 0 的微分 ,
dw f ( z 0 ) z . 如果函数在 z 0 的微分存在 , 则称函数 f (z)
z 0
lim f ( z 0 z ) f ( z 0 ) ,
即 f ( z ) 在 z 0 连续 .
[证毕]
11
3.求导公式与法则:
(1 ) (2)
(3) (4)
( c ) 0 , 其中 c 为复常数
n ( z ) nz n 1
. .
,
其中 n 为正整数
f (z)
lim
x x
x 0
1,
设 z z 沿着平行于
y 轴的直线趋向于
z,
x 0
z 0
lim
x 2 yi x yi
lim
2 yi yi
y 0
2,
y
所以 f ( z ) x 2 yi 的导数 不存在 .
o
z
y 0
即 z 0 z 在区域 D 内以任意方式趋于 比值 f ( z0 z ) f ( z0 ) z 都趋于同一个数
z 0时 , .
如果函数 f ( z ) 在区域 D 内处处可导, 我们 就称 f ( z ) 在区域内 D 可导.
4
例1 解
求 f ( z ) z 的导数 .
2
z 0
lim
( x x ) 2 ( y y ) i x 2 yi z
x 2 yi x yi
z
o
z 0
y
lim
y 0
x
z 0
设 z z 沿着平行于
x 轴的直线趋向于
z,
8
z 0
lim
x 2 yi x yi
存在 ,
f ( z ) 在 z0
f ( z ) 在 z 0 可导 . 这个极限值称为
记作
f ( z 0 )
dw dz
z z0
lim
f ( z0 z ) f ( z0 ) z
z 0
.
3
在定义中应注意:
z 0 z z 0 (即 z 0 )的方式是任意的 .
20
四.解析函数的概念
1. 解析函数的定义
(1) 如果函数 那末称 f ( z ) 在 z 0 及 z 0 的邻域内处处可导 , f ( z ) 在 z 0 解析 .
( 2)如果函数 f ( z ) 在 区域 D 内每一点解析 , 则称 f ( z ) 在 区域 D 内解析 .或称 f ( z )是 区域 D 内的一个解析函数 (全纯函数或正则函数 ).
g ( z ) f ( z ) g ( z ). f ( z ) g ( z ) f ( z ) g ( z ).
f ( z ) g ( z )
(5)
f ( z ) g ( z ) f ( z ) g ( z ) f (z) . 2 g(z) g (z)
解
研究函数
f ( z ) z Re( z ) 的可导性与解析性
.
(1 ) z 0 ,
z 0
lim
f (0 z ) f (0) z
lim
z Re( z ) z
z 0
0,
故 f ( z ) z Re( z ) 在 z 0 处可导 .
(2) z 0,
23
例4
研究函数
2
f ( z ) z , g ( z ) x 2 yi 和
2
h ( z ) z 的解析性
.
解
由本节例1和例3知:
f ( z ) z 在复平面内是解析的
2
;
;
g ( z ) x 2 yi 处处不解析
下面讨论
h ( z ) z 的解析性
2
,
2
h( z0 z ) h( z0 ) z
在 z 0 可微 .
14
特别地,
当 f (z) z 时 ,
d w d z f ( z 0 ) z z ,
d w f ( z 0 ) z f ( z 0 ) d z , 即
f ( z 0 )
dw dz
z z0
函数 w f ( z )在 z0 可导与在 z0 可微是等价的 .
仅在 z 0 处可导 , 而在其他点都 , 它在复平面内处处不解 析.
不可导 , 根据定义
26
例5 解
研究函数
w
1 z
的解析性
.
因为 w 且 dw dz
1 z
在复平面内除 1 z
2
z 0 处处可导
,
,
z 0 外处处解析
.
所以 w 在复平面内除
z 0 为它的奇点
,
27
例6
Im( z z ) Im z z
Im z Im z Im z z
Im z z
Im( x i y ) x i y
y x i y
,
当点沿平行于实轴的方
向 ( y 0 ) 而使 z 0 时 ,
6
z 0
lim
f z
19
Th3
设 f ( z ) u ( x , y ) iv ( x , y ) 在区域 D 内有定义, 则 f ( z ) 在 D 内一点 z x iy 可微
的必要条件
( )
(1) u x , u y , v x , v y 存在; ( 2 ) u x v y , u y -v x .
17
注意到二元函数可微,偏导,连续 的性质
xy , 2 2 x y f (x, y) 0, x y
2 2 2
连续
0
2
x y
0
偏导连续
2 2 ( x y ) sin 2 2 x y f ( x, y) 0 1
可微分
偏导存在
xy 2 2 f (x, y) x y 0 x y 0
y x i y
,
y 0 x0
1 i
,
当点沿不同的方向使
z 0 时 , 极限值不同 .
故 f ( z ) Im z 在复平面上处处不可导
7
例3 解
问 f ( z ) x 2 yi 是否可导?
z 0
lim
f z
lim
f (z z) f (z) z
2011. 9. 28
1
第二章 解析函数
§1 解析函数的概念及充要条件
2
一、复变函数的导数—“差商的极限”
1.定义:
设函数 w f ( z ) 定义于区域 D , z 0 为 D 中的一 点 , 点 z 0 z 不出 D 的范围 ,
如果极限
那末就称 的导数 ,
z 0Βιβλιοθήκη limf ( z0 z ) f ( z0 ) z
13
二.复函数的微分:
1.定义
设函数 w f ( z )在 z0 可导, 则 w f ( z0 z ) f ( z0 ) f ( z0 ) z ( z )z , 式中 lim ( z ) 0, ( z )z 是 z 的高阶无穷
z 0
2 2
x y 0
2 2
x y 0
2 2
x y 0
2 2
18
Th2
设 f ( z ) u ( x , y ) iv ( x , y ) 在区域 D 内有定义, 则 f ( z ) 在 D 内一点 z x iy 可微
的充分条件
( )
(1 ) u x , u y , v x , v y 在 ( x , y ) 连续; ( 2 ) u x v y , u y -v x ,
z0 z
z0
2
z
24
( z 0 z )( z 0 z ) z 0 z 0
15
三.可微(可导)的充要条件
1.在一点可导或可微
Th 1 : 设 f ( z ) u ( x , y ) iv ( x , y ) 在区域 D 内有定义, 则 f ( z ) 在 D 内一点 z x iy 可微
( g(z) 0)
12
(6)
f [ g ( z )] f ( w ) g ( z ).
f ( z ) 1
其中 w g ( z )
(7 )
( w )
,
其中 w f ( z ) 与 z ( w ) 是 函数 , 且 ( w ) 0
两个互为反函数的单值
1 ik x 1 ik x i y 1 i y z x
z
x i y
1i
y
25
由于 k 的任意性
,
z z
1 ki 1 ki
不趋于一个确定的值
.
z 0
lim
h( z0 z ) h( z0 ) z
2
不存在 .
因此 h ( z ) z
小, f ( z0 ) z 是函数 w f ( z ) 的改变量 w 的 线性部分.
f ( z 0 ) z 称为函数 记作
w f ( z ) 在点 z 0 的微分 ,
dw f ( z 0 ) z . 如果函数在 z 0 的微分存在 , 则称函数 f (z)
z 0
lim f ( z 0 z ) f ( z 0 ) ,
即 f ( z ) 在 z 0 连续 .
[证毕]
11
3.求导公式与法则:
(1 ) (2)
(3) (4)
( c ) 0 , 其中 c 为复常数
n ( z ) nz n 1
. .
,
其中 n 为正整数
f (z)
lim
x x
x 0
1,
设 z z 沿着平行于
y 轴的直线趋向于
z,
x 0
z 0
lim
x 2 yi x yi
lim
2 yi yi
y 0
2,
y
所以 f ( z ) x 2 yi 的导数 不存在 .
o
z
y 0
即 z 0 z 在区域 D 内以任意方式趋于 比值 f ( z0 z ) f ( z0 ) z 都趋于同一个数
z 0时 , .
如果函数 f ( z ) 在区域 D 内处处可导, 我们 就称 f ( z ) 在区域内 D 可导.
4
例1 解
求 f ( z ) z 的导数 .
2
z 0
lim
( x x ) 2 ( y y ) i x 2 yi z
x 2 yi x yi
z
o
z 0
y
lim
y 0
x
z 0
设 z z 沿着平行于
x 轴的直线趋向于
z,
8
z 0
lim
x 2 yi x yi
存在 ,
f ( z ) 在 z0
f ( z ) 在 z 0 可导 . 这个极限值称为
记作
f ( z 0 )
dw dz
z z0
lim
f ( z0 z ) f ( z0 ) z
z 0
.
3
在定义中应注意:
z 0 z z 0 (即 z 0 )的方式是任意的 .
20
四.解析函数的概念
1. 解析函数的定义
(1) 如果函数 那末称 f ( z ) 在 z 0 及 z 0 的邻域内处处可导 , f ( z ) 在 z 0 解析 .
( 2)如果函数 f ( z ) 在 区域 D 内每一点解析 , 则称 f ( z ) 在 区域 D 内解析 .或称 f ( z )是 区域 D 内的一个解析函数 (全纯函数或正则函数 ).
g ( z ) f ( z ) g ( z ). f ( z ) g ( z ) f ( z ) g ( z ).
f ( z ) g ( z )
(5)
f ( z ) g ( z ) f ( z ) g ( z ) f (z) . 2 g(z) g (z)
解
研究函数
f ( z ) z Re( z ) 的可导性与解析性
.
(1 ) z 0 ,
z 0
lim
f (0 z ) f (0) z
lim
z Re( z ) z
z 0
0,
故 f ( z ) z Re( z ) 在 z 0 处可导 .
(2) z 0,
23
例4
研究函数
2
f ( z ) z , g ( z ) x 2 yi 和
2
h ( z ) z 的解析性
.
解
由本节例1和例3知:
f ( z ) z 在复平面内是解析的
2
;
;
g ( z ) x 2 yi 处处不解析
下面讨论
h ( z ) z 的解析性
2
,
2
h( z0 z ) h( z0 ) z
在 z 0 可微 .
14
特别地,
当 f (z) z 时 ,
d w d z f ( z 0 ) z z ,
d w f ( z 0 ) z f ( z 0 ) d z , 即
f ( z 0 )
dw dz
z z0
函数 w f ( z )在 z0 可导与在 z0 可微是等价的 .
仅在 z 0 处可导 , 而在其他点都 , 它在复平面内处处不解 析.
不可导 , 根据定义
26
例5 解
研究函数
w
1 z
的解析性
.
因为 w 且 dw dz
1 z
在复平面内除 1 z
2
z 0 处处可导
,
,
z 0 外处处解析
.
所以 w 在复平面内除
z 0 为它的奇点
,
27
例6
Im( z z ) Im z z
Im z Im z Im z z
Im z z
Im( x i y ) x i y
y x i y
,
当点沿平行于实轴的方
向 ( y 0 ) 而使 z 0 时 ,
6
z 0
lim
f z
19
Th3
设 f ( z ) u ( x , y ) iv ( x , y ) 在区域 D 内有定义, 则 f ( z ) 在 D 内一点 z x iy 可微
的必要条件
( )
(1) u x , u y , v x , v y 存在; ( 2 ) u x v y , u y -v x .
17
注意到二元函数可微,偏导,连续 的性质
xy , 2 2 x y f (x, y) 0, x y
2 2 2
连续
0
2
x y
0
偏导连续
2 2 ( x y ) sin 2 2 x y f ( x, y) 0 1
可微分
偏导存在
xy 2 2 f (x, y) x y 0 x y 0
y x i y
,
y 0 x0
1 i
,
当点沿不同的方向使
z 0 时 , 极限值不同 .
故 f ( z ) Im z 在复平面上处处不可导
7
例3 解
问 f ( z ) x 2 yi 是否可导?
z 0
lim
f z
lim
f (z z) f (z) z
2011. 9. 28
1
第二章 解析函数
§1 解析函数的概念及充要条件
2
一、复变函数的导数—“差商的极限”
1.定义:
设函数 w f ( z ) 定义于区域 D , z 0 为 D 中的一 点 , 点 z 0 z 不出 D 的范围 ,
如果极限
那末就称 的导数 ,
z 0Βιβλιοθήκη limf ( z0 z ) f ( z0 ) z
13
二.复函数的微分:
1.定义
设函数 w f ( z )在 z0 可导, 则 w f ( z0 z ) f ( z0 ) f ( z0 ) z ( z )z , 式中 lim ( z ) 0, ( z )z 是 z 的高阶无穷
z 0
2 2
x y 0
2 2
x y 0
2 2
x y 0
2 2
18
Th2
设 f ( z ) u ( x , y ) iv ( x , y ) 在区域 D 内有定义, 则 f ( z ) 在 D 内一点 z x iy 可微
的充分条件
( )
(1 ) u x , u y , v x , v y 在 ( x , y ) 连续; ( 2 ) u x v y , u y -v x ,
z0 z
z0
2
z
24
( z 0 z )( z 0 z ) z 0 z 0
