【数学】2010届高三数学一轮复习：解三角形1

合集下载

解三角形是高中数学重点和难点也是历年高考必考点和命题热点题型

解三角形是高中数学重点和难点也是历年高考必考点和命题热点题型
高一到高三数学必刷基础题型全归纳解已更新完成解三角形专题，而三角形是高中数学教学中的重点和难点，也是历年高考的必考点和命题热点。

其中，正弦定理和余弦定理及解三角形更是重中之重，但面对利用正余弦定理或三角函数关系所产生的各类解，学生往往缺乏必要的甄别意识和区分技能，从而造成“会而不对，对而不全”的现象时有发生。

利用这些题型掌握可以轻松提高
1．掌握正弦定理、余弦定理，并能解决一些简单的三角形度量问题
2．本部分是高考中的重点考查内容，主要考查利用正、余弦定理解三角形、判断三角形的形状，求三角形的面积等
3．命题形式多种多样，解答题以综合题为主，常与三角恒等变换、平面向量相结合
Word文档资料，微信：1989450104，其实，学习一定是有捷径和方法的，不是一味的苦学到半夜，清华北大数名学霸耗精心总结《高分其实很简单》，学霸们晒方法、晒技巧、晒笔记、晒心得、晒智慧！更有高考“必考点”、易考点、分析，让你做题，解题学会举一反三！。

高考数学第一轮章节复习课件第三章三角函数解三角形

2.已知角α的终边所在的直线方程，则可先设出终边上一点的坐标，求出此点到原点的距离，然后用三角函数的定义来求相关问题，若直线的倾斜角为特殊角，也可直接写出角α的值.
【注意】若角α的终边落在某条直线上，一般要分类讨论.
已知角α的终边在直线3x＋4y＝0上，求sinα， cosα，tanα的值.
.
解析：tan= 答案：
5.某时钟的秒针端点A到中心点O的距离为5 cm，秒针均匀地绕点O旋转，当时间t＝0时，点A与钟面上标12的点B
重
合.将A、B两点间的距离d(cm)表示成t(s)的函数，则d
＝
，其中t∈[0,60].
解析：∵经过t(s)秒针转了弧度
d
5. t
, d
t
10 sin
.
2 60
)内的单调性.
知识点
考纲下载
考情上线
函数y＝ Asin(ωx ＋φ)的图象
1.考查图象的变换和 1.了解函数y＝Asin(ωx＋φ)
解析式的确定，以的
及通过图象描绘，物理意义；能画出y＝
观察讨论有关性质. Asin(ωx＋φ)的图象，了解
2.以三角函数为载体，参数A、ω、φ对函数图象
考查数形结合的思想. 变化的影响.
当且仅当α＝，即α＝2时取等号，此时故当半径r＝1 cm，圆心角为2弧度时，扇形面积最大，其最大值为1 cm2.
法二：设扇形的圆心角为α(0<α<2π)，半径为r，面积为S，
则扇形的弧长为rα，由题意有：2r＋rα＝4⇒α＝
×r2＝2r－r2＝－(r－1)2＋1，
∴当r＝1(cm)时，S有最大值1(cm2)，
为余弦线
有向线段 AT 为正切线

高三数学一轮复习精品学案3：4.6 正弦定理、余弦定理及解三角形

4.6 正弦定理、余弦定理及解三角形导学目标1．掌握正弦定理、余弦定理，并能解决一些简单的三角形度量问题．2．能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的实际问题．主要考查有关定理的应用、三角恒等变换的能力、运算能力及转化的数学思想．解三角形常常作为解题工具用于立体几何中的计算或证明，或与三角函数联系在一起求距离、高度以及角度等问题，且多以应用题的形式出现．考点梳理1．正弦定理(1)正弦定理：在一个三角形中，各边和它所对角的正弦的比相等，即．其中R是三角形外接圆的半径．(2)正弦定理的其他形式：①a＝2R sin A，b＝，c＝；②sin A＝a2R，sin B＝，sin C＝；③a∶b∶c＝______________________.2．余弦定理(1)余弦定理：三角形中任何一边的平方等于其他两边的平方的和减去这两边与它们的夹角的余弦的积的两倍．即a2＝，b2＝，c2＝.若令C＝90°，则c2＝，即为勾股定理．(2)余弦定理的变形：cos A＝，cos B＝，cos C ＝.若C为锐角，则cos C>0，即a2＋b2______c2；若C为钝角，则cos C<0，即a2＋b2______c2.故由a2＋b2与c2值的大小比较，可以判断C为锐角、钝角或直角．(3)正、余弦定理的一个重要作用是实现边角____________，余弦定理亦可以写成sin2A＝sin 2B ＋sin 2C －2sin B sin C cos A ，类似地，sin 2B ＝____________；sin 2C ＝__________________.注意式中隐含条件A ＋B ＋C ＝π.3．解斜三角形的类型(1)已知三角形的任意两个角与一边，用____________定理．只有一解．(2)已知三角形的任意两边与其中一边的对角，用____________定理，可能有___________________．如在△ABC 中，已知a ，b 和A 时，解的情况如表：A 为锐角A 为钝角或直角图形关系式 a ＝b sin A b sin A <a <ba ≥ba >b解的个数① ② ③ ④(3)已知三边，用____________定理．有解时，只有一解． (4)已知两边及夹角，用____________定理，必有一解． 4．三角形中的常用公式或变式(1)三角形面积公式S △＝＝＝____________＝____________＝____________．其中R ，r 分别为三角形外接圆、内切圆半径．(2)A ＋B ＋C ＝π，则A ＝__________， A2＝__________，从而sin A ＝____________， cos A ＝____________，tan A ＝____________； sin A 2＝__________，cos A2＝__________， tan A2＝________.tan A ＋tan B ＋tan C ＝__________. (3)若三角形三边a ，b ，c 成等差数列，则2b ＝____________⇔2sin B ＝____________⇔2sin B 2＝cos A －C 2⇔2cos A ＋C 2＝cos A －C 2⇔tan A 2tan C 2＝13.类型一正弦定理的应用△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知A －C ＝90°，a ＋c ＝2b ，求C .在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c .已知A ＝π4，b sin ⎝⎛⎭⎫π4＋C －c sin ⎝⎛⎭⎫π4＋B ＝a .(1)求证：B －C ＝π2；(2)若a ＝2，求△ABC 的面积．类型二余弦定理的应用在△ABC 中，a ，b ，c 分别是角A ，B ，C 的对边，且cos B cos C ＝－b2a ＋c. (1)求B 的大小；(2)若b ＝13，a ＋c ＝4，求△ABC 的面积．若△ABC 的内角A ，B ，C 所对的边a ，b ，c 满足(a ＋b )2－c 2＝4，且C ＝60°，则ab 的值为( )A.43B ．8－4 3C ．1 D.23类型三正、余弦定理的综合应用△ABC 的内角A 、B 、C 的对边分别为a ，b ，c ，已知a ＝b cos C ＋c sin B . (1)求B ；(2)若b ＝2，求△ABC 面积的最大值．设△ABC 的内角A ，B ，C 所对的边分别为a ，b ，c ，且a ＋c ＝6，b ＝2，cos B＝79. (1)求a ，c 的值； (2)求sin(A －B )的值．类型四判断三角形的形状在三角形ABC 中，若tan A ∶tan B ＝a 2∶b 2，试判断三角形ABC 的形状．在△ABC 中，若sin 2A ＋sin 2B <sin 2C ，则△ABC 的形状是( )A ．锐角三角形B ．直角三角形C ．钝角三角形D ．不能确定类型五解三角形应用举例某港口O 要将一件重要物品用小艇送到一艘正在航行的轮船上．在小艇出发时，轮船位于港口O 北偏西30°且与该港口相距20 n mile 的A 处，并以30 n mile/h 的航行速度沿正东方向匀速行驶．假设该小艇沿直线方向以v n mile/h 的航行速度匀速行驶，经过t h 与轮船相遇．(1)若希望相遇时小艇的航行距离最小，则小艇航行速度的大小应为多少？(2)假设小艇的最高航行速度只能达到30 n mile/h ，试设计航行方案(即确定航行方向和航行速度的大小)，使得小艇能以最短时间与轮船相遇，并说明理由．如图，渔船甲位于岛屿A的南偏西60°方向的B处，且与岛屿A相距12海里，渔船乙以10海里/小时的速度从岛屿A出发沿正北方向航行，若渔船甲同时从B处出发沿北偏东α的方向追赶渔船乙，刚好用2小时追上．(1)求渔船甲的速度；(2)求sinα的值．1．已知两边及其中一边的对角解三角形时，要注意解的情况，谨防漏解．2．在判断三角形的形状时，一般将已知条件中的边角关系利用正弦定理或余弦定理转化为角角关系(注意应用A＋B＋C＝π这个结论)或边边关系，再用三角变换或代数式的恒等变形(如因式分解、配方等)求解，注意等式两边的公因式不要约掉，要移项提取公因式，否则有可能漏掉一种形状．3．要熟记一些常见结论，如三内角成等差数列，则必有一角为60°；若三内角的正弦值成等差数列，则三边也成等差数列；内角和定理与诱导公式结合产生的结论：sin A＝sin(B＋C)，cos A＝－cos(B＋C)，sin A2＝cosB＋C2，sin2A＝－sin2(B＋C)，cos2A＝cos2(B＋C)等．4．应用正、余弦定理解斜三角形应用题的一般步骤：(1)分析：理解题意，分清已知与未知，画出示意图；(2)建模：根据已知条件与求解目标，把已知量与求解量尽量集中到一个三角形中，建立一个解斜三角形的模型；(3)求解：利用正、余弦定理有序地解出三角形，求得数学模型的解；(4)检验：检验上述所求得的解是否符合实际意义，从而得出实际问题的解．5．正、余弦定理是应用极为广泛的两个定理，它将三角形的边和角有机地联系起来，从而使三角与几何产生联系，为求与三角形有关的量(如面积、外接圆、内切圆半径和面积等)提供了理论依据，也是判断三角形形状、证明三角形中有关等式的重要依据．主要方法有：化角法，化边法，面积法，运用初等几何法．注意体会其中蕴涵的函数与方程思想、等价转化思想及分类讨论思想．在△ABC 中，A >B 是sin A >sin B 的( ) A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件在△ABC 中，已知b ＝6，c ＝10，B ＝30°，则解此三角形的结果有( ) A ．无解 B ．一解 C ．两解D ．一解或两解(2013·陕西)设△ABC 的内角A, B, C 所对的边分别为a, b, c, 若b cos C ＋c cos B ＝a sin A, 则△ABC 的形状为( )A ．锐角三角形B ．直角三角形C ．钝角三角形D ．不确定(2012·陕西)在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c .若a ＝2，B ＝π6，c＝23，则b ＝________．在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，若a ＝2，b ＝2，sin B ＋cos B ＝2，则角A 的大小为________．答案考点梳理1．(1)a sin A ＝b sin B ＝csin C ＝2R(2)①2R sin B 2R sin C ②b 2R c2R③sin A ∶sin B ∶sin C2．(1)b 2＋c 2－2bc cos A c 2＋a 2－2ca cos B a 2＋b 2－2ab cos C a 2＋b 2(2)b 2＋c 2－a 22bc c 2＋a 2－b 22ca a 2＋b 2－c 22ab > <(3)互化 sin 2C ＋sin 2A －2sin C sin A cos B sin 2A ＋sin 2B －2sin A sin B cos C3．(1)正弦 (2)正弦一解、两解或无解 ①一解 ②二解 ③一解 ④一解 (3)余弦 (4)余弦4．(1)12ab sin C 12bc sin A 12ac sin B abc 4R 12(a ＋b ＋c )r(2)π－(B ＋C ) π2－B ＋C 2sin(B ＋C ) －cos(B ＋C )－tan(B ＋C ) cos B ＋C 2 sin B ＋C21tanB ＋C 2tan A tan B tan C (3)a ＋c sin A ＋sin C解：由a ＋c ＝2b 及正弦定理可得sin A ＋sin C ＝2sin B .又由于A －C ＝90°，B ＝180°－(A ＋C )，故cos C ＋sin C ＝sin A ＋sin C ＝2sin(A ＋C )＝2sin(90°＋2C )＝2sin2(45°＋C )．∴2sin(45°＋C )＝22sin(45°＋C )cos(45°＋C )，即cos(45°＋C )＝12.又∵0°＜C ＜90°，∴45°＋C ＝60°，C ＝15°.『评析』利用正弦定理将边边关系转化为角角关系，这是解此题的关键．解：(1)证明：对b sin ⎝⎛⎭⎫π4＋C －c sin ⎝⎛⎭⎫π4＋B ＝a 应用正弦定理得sin B sin ⎝⎛⎭⎫π4＋C －sin C sin ⎝⎛⎭⎫π4＋B ＝sin A ，即sin B ⎝⎛⎭⎫22sin C ＋22cos C －sin C⎝⎛⎭⎫22sin B ＋22cos B ＝22，整理得sin B cos C －sin C cos B ＝1，即sin ()B －C ＝1.由于B ，C ∈⎝⎛⎭⎫0，3π4，∴B －C ＝π2. (2)∵B ＋C ＝π－A ＝3π4，又由(1)知B －C ＝π2，∴B ＝5π8，C ＝π8.∵a ＝2，A ＝π4，∴由正弦定理知b ＝a sin B sin A ＝2sin 5π8，c ＝a sin C sin A ＝2sin π8.∴S △ABC ＝12bc sin A ＝12×2sin 5π8×2sin π8×22＝2sin5π8sin π8＝2cos π8sin π8＝22sin π4＝12.解：(1)由余弦定理知，cos B ＝a 2＋c 2－b 22ac ，cos C ＝a 2＋b 2－c 22ab ，将上式代入cos B cos C ＝－b2a ＋c 得a 2＋c 2－b 22ac ·2ab a 2＋b 2－c 2＝－b2a ＋c ，整理得a 2＋c 2－b 2＝－ac . ∴cos B ＝a 2＋c 2－b 22ac ＝－ac 2ac ＝－12.∵B 为三角形的内角，∴B ＝23π.(2)将b ＝13，a ＋c ＝4，B ＝23π代入b 2＝a 2＋c 2－2ac cos B ，得13＝42－2ac －2ac cos 23π，解得ac ＝3.∴S △ABC ＝12ac sin B ＝334.『评析』①根据所给等式的结构特点利用余弦定理将角化边进行变形是迅速解答本题的关键．②熟练运用余弦定理及其推论，同时还要注意整体思想、方程思想在解题过程中的运用．解：由余弦定理得c 2＝a 2＋b 2－2ab cos C ＝a 2＋b 2－ab ，代入(a ＋b )2－c 2＝4中得(a ＋b )2－(a 2＋b 2－ab )＝4，即3ab ＝4，∴ab ＝43.故选A .解：(1)由已知及正弦定理得sin A ＝sin B cos C ＋sin C sin B .① 又A ＝π－(B ＋C )，故sin A ＝sin(B ＋C )＝sin B cos C ＋cos B sin C .② 由①，②和C ∈(0，π)得sin B ＝cos B . 又B ∈(0，π)，所以B ＝π4.(2)△ABC 的面积S ＝12ac sin B ＝24ac .由已知及余弦定理得4＝a 2＋c 2－2ac cos π4.又a 2＋c 2≥2ac ，故ac ≤42－2，当且仅当a ＝c 时，等号成立．因此△ABC 面积的最大值为2＋1.『评析』(1)化边为角与和角或差角公式的正向或反向多次联用是常用的技巧；(2)已知边及其对角求三角形面积最值是高考中考过多次的问题，既可用三角函数求最值，也可以用余弦定理化边后用不等式求最值．解：(1)由余弦定理b 2＝a 2＋c 2－2ac cos B ，得b 2＝(a ＋c )2－2ac (1＋cos B )，又a ＋c ＝6，b ＝2， cos B ＝79，所以ac ＝9，解得a ＝3，c ＝3.(2)在△ABC 中，sin B ＝1－cos 2B ＝429，由正弦定理得sin A ＝a sin B b ＝223.因为a ＝c ，所以A 为锐角，所以cos A ＝1－sin 2A ＝13.因此sin(A －B )＝sin A cos B －cos A sin B ＝10227.解法一：由正弦定理，得a 2b 2＝sin 2Asin 2B ，所以tan A tan B ＝sin 2A sin 2B，所以sin A cos B cos A sin B ＝sin 2A sin 2B，即sin2A ＝sin2B .所以2A ＝2B ，或2A ＋2B ＝π，因此A ＝B 或A ＋B ＝π2，从而△ABC 是等腰三角形或直角三角形．解法二：由正弦定理，得a 2b 2＝sin 2A sin 2B ，所以tan A tan B ＝sin 2A sin 2B ，所以cos B cos A ＝sin Asin B ，再由正、余弦定理，得a 2＋c 2－b 22ac b 2＋c 2－a 22bc＝ab，化简得(a 2－b 2)(c 2－a 2－b 2)＝0，即a 2＝b 2或c 2＝a 2＋b 2.从而△ABC 是等腰三角形或直角三角形．『评析』由已知条件，可先将切化弦，再结合正弦定理，将该恒等式的边都化为角，然后进行三角函数式的恒等变形，找出角之间的关系；或将角都化成边，然后进行代数恒等变形，可一题多解，多角度思考问题，从而达到对知识的熟练掌握．解：在△ABC中，∵sin 2A ＋sin 2B <sin 2C ，∴由正弦定理知a 2＋b 2<c 2.∴cos C ＝a 2＋b 2－c 22ab<0，即∠C 为钝角，△ABC 为钝角三角形．故选C .解法一：(1)设相遇时小艇航行的距离为S n mile ，则 S ＝900t 2＋400－2·30t ·20·cos （90°－30°）＝900t 2－600t ＋400＝900⎝⎛⎭⎫t －132＋300，故当t ＝13时，S min ＝103，此时v ＝10313＝30 3.即小艇以30 3 n mile/h 的速度航行，相遇时小艇的航行距离最小． (2)设小艇与轮船在B 处相遇，则v 2t 2＝400＋900t 2－2·20·30t ·cos(90°－30°)，故v 2＝900－600t ＋400t 2.∵0<v ≤30，∴900－600t ＋400t 2≤900，即2t 2－3t≤0，解得t ≥23.又t ＝23时，v ＝30.故v ＝30时，t 取得最小值，且最小值等于23. 此时，在△OAB 中，有OA ＝OB ＝AB ＝20，故可设计航行方案如下：航行方向为北偏东30°，航行速度为30 n mile/h ，小艇能以最短时间与轮船相遇．解法二：(1)若相遇时小艇的航行距离最小，又轮船沿正东方向匀速行驶，则小艇航行方向为正北方向．设小艇与轮船在C 处相遇．在Rt △OAC 中，OC ＝20cos30°＝103，AC ＝20sin30°＝10.又AC ＝30t ，OC ＝vt ，此时，轮船航行时间t ＝1030＝13，v ＝10313＝30 3. 即小艇以30 3 n mile/h 的速度航行，相遇时小艇的航行距离最小．(2)假设v ＝30时，小艇能以最短时间与轮船在D 处相遇，此时AD ＝DO ＝30t .又∠OAD ＝60°，所以AD ＝DO ＝OA ＝20，解得t ＝23. 据此可设计航行方案如下：航行方向为北偏东30°，航行速度的大小为30 n mile/h.这样，小艇能以最短时间与轮船相遇．证明如下：如图，由(1)得OC ＝103，AC ＝10，故OC >AC ，且对于线段AC 上任意点P ，有OP ≥OC >AC .而小艇的最高航行速度只能达到30 n mile/h ，故小艇与轮船不可能在A ，C 之间(包含C )的任意位置相遇．设∠COD ＝θ(0°<θ<90°)，则在Rt △COD 中，CD ＝103tan θ，OD ＝103cos θ. 由于从出发到相遇，轮船与小艇所需要的时间分别为t ＝10＋103tan θ30和t ＝103v cos θ，所以10＋103tan θ30＝103v cos θ. 由此可得，v ＝153sin （θ＋30°）. 又v ≤30，故sin(θ＋30°)≥32，从而，30°≤θ<90°. 由于θ＝30°时，tan θ取得最小值，且最小值为33. 于是，当θ＝30°时，t ＝10＋103tan θ30取得最小值，且最小值为23. 『评析』①这是一道有关解三角形的实际应用题，解题的关键是把实际问题抽象成纯数学问题，根据题目提供的信息，找出三角形中的数量关系，然后利用正、余弦定理求解．②解三角形的方法在实际问题中，有广泛的应用．在物理学中，有关向量的计算也要用到解三角形的方法．近年的高考中我们发现以解三角形为背景的应用题开始成为热点问题之一．③不管是什么类型的三角应用问题，解决的关键都是充分理解题意，将问题中的语言叙述弄明白，画出帮助分析问题的草图，再将其归结为属于哪类可解的三角形．④本题用几何方法求解也较简便．解：(1)依题意，∠BAC ＝120°，AB ＝12，AC ＝10×2＝20，在△ABC 中，由余弦定理知BC 2＝AB 2＋AC 2－2AB ·AC ·cos ∠BAC ＝122＋202－2×12×20×cos120°＝784，BC ＝28.所以渔船甲的速度为v ＝282＝14(海里/小时)． (2)在△ABC 中，AB ＝12，∠BAC ＝120°，BC ＝28，∠BCA ＝α，由正弦定理得AB sin α＝BC sin ∠BAC ，即12sin α＝28sin120°，从而sin α＝12sin120°28＝3314.解：因为在同一三角形中，角大则边大，边大则正弦大，反之也成立，故是充要条件．故选C .解：由正弦定理知sin C ＝c ·sin B b ＝56，又由c >b >c sin B 知，C 有两解．也可依已知条件，画出△ABC ，由图知有两解．故选C .解：由已知和正弦定理可得sin B cos C ＋sin C cos B ＝sin A ·sin A ，即sin(B ＋C )＝sin A sin A ，亦即sin A ＝sin A sin A .因为0<A <π，所以sin A ＝1，所以A ＝π2.所以三角形为直角三角形．故选B .解：由余弦定理知b 2＝a 2＋c 2－2ac cos B ＝22＋()232－2×2×23×cos π6＝4，b ＝2.故填2.解：∵sin B ＋cos B ＝2，∴2sin ⎝⎛⎭⎫B ＋π4＝2，即sin ⎝⎛⎭⎫B ＋π4＝1. 又∵B ∈(0，π)，∴B ＋π4＝π2，B ＝π4. 根据正弦定理a sin A ＝b sin B ，可得sin A ＝a sin B b ＝12. ∵a ＜b ，∴A ＜B .∴A ＝π6.故填π6.。

高三数学三角函数三角恒等变换解三角形试题答案及解析

高三数学三角函数三角恒等变换解三角形试题答案及解析1.已知函数的图象上关于轴对称的点至少有3对，则实数的取值范围是（）A．B．C．D．【答案】A【解析】原函数在轴左侧是一段正弦型函数图象，在轴右侧是一条对数函数的图象，要使得图象上关于轴对称的点至少有对，可将左侧的图象对称到轴右侧，即，应该与原来轴右侧的图象至少有个公共点如图，不能满足条件，只有此时，只需在时，的纵坐标大于，即，得．【考点】分段函数，函数图象，正弦型函数，对数函数2.若，则函数的最大值是___________．【答案】【解析】由题意因为，所以，所以函数的最大值是．【考点】求最大值．3.已知，，则下列不等式一定成立的是A．B．C．D．【答案】D【解析】,【考点】三角函数的性质4.若，且为第二象限角，则（）A．B．C．D．【答案】B【解析】由得又为第二象限角，所以，选B．【考点】两角差余弦公式5.设函数对任意的，都有，若函数，则的值是（）A．1B．-5或3C．-2D．【答案】C【解析】根据题意有是函数图像的对称轴，从而有，所以有，故选C．【考点】三角函数的性质．6.设的最小值为，则．【答案】【解析】，根据题意，结合二次函数在某个区间上的最值问题，对参数进行讨论，当时，其最小值为，所以不合题意，当时，其最小值为，解得，当时，其最小值为，无解，所以．【考点】倍角公式，二次函数在给定区间上的最值问题．7.设函数对任意的，都有，若函数，则的值是（）A．1B．-5或3C．D．-2【答案】D【解析】根据题意有是函数图像的对称轴，从而有，所以有，故选D．【考点】三角函数的性质．8.下列函数中，以为最小正周期的偶函数是（）A．y=sin2x+cos2xB．y=sin2xcos2xC．y=cos（4x+）D．y=sin22x﹣cos22x【答案】D【解析】因为A项为非奇非偶函数，B项是奇函数，C项是奇函数，只有D项是符合题意的，故选D．【考点】诱导公式，倍角公式，三角函数的奇偶性和周期．9.函数的最大值为．【答案】【解析】解析式表示过的直线的斜率，由几何意义，即过定点（4，3）与单位圆相切时的切线斜率为最值．所以设切线得斜率为k，则直线方程为，即 ,【考点】三角函数最值【方法点睛】本题主要考查三角函数最值问题及转化的思想，解决问题的根据是根据所给函数式子转化为直线与圆的位置关系问题，即将所给式子看做定点与单位圆上点的连线的斜率的范围问题，通过模型转化使问题定点巧妙解决，属于经典试题．10.（本题满分12分）如图，在中，边上的中线长为3，且，．（1）求的值；（2）求边的长．【答案】（1）（2）4【解析】（1）利用角的关系，再结合两角差正弦公式展开就可求解（2）先在三角形ABD中，由正弦定理解出BD长，即CD长：由正弦定理，得，即，解得…故；再在三角形ADC中由余弦定理解出AC：；AC= 4试题解析：（1）（2）在中，由正弦定理，得，即，解得…故，从而在中，由余弦定理，得；AC= 4 ；【考点】正余弦定理11.中，，则的最大值为．【答案】【解析】设，由余弦定理的推论，所以，设，代入上式得，，故，当时，此时，符合题意，因此最大值为，故答案为：．【考点】解三角形．【思路点睛】首先假设，然后再根据余弦定理的推论，可得，找到与的关系，再设，代入上式得，利用根的判别式，进而求出结果．本题的关键是利用余弦定理的推论．12.已知函数的部分图象如图所示．（1）求函数的解析式；（2）若，求函数在区间上的单调减区间．【答案】（1）；（2），．【解析】（1）由图象中的最高点和最低点的纵坐标得到关于的方程组求得，再利用图象得到函数的周期，进而得到值，最后代入最低点坐标或最高点坐标结合的范围求出，即得到函数的解析式；（2）先求出，利用两角和差的正弦公式将其化为的形式，再利用整体思想求其单调递减区间．试题解析：（1）由图知，解得，又，所以，所以，将点代入，得，再由，得，所以；（2）因为由，解得；又，故所求的单调减区间为，．【考点】1.三角函数的图象与性质；2.三角恒等变形．13.已知角的终边经过点（-4，3），则= ，= ；【答案】;【解析】由题意可得.【考点】任意角三角函数的定义.14.在△ABC中，a、b、c分别是角A、B、C的对边，且．（Ⅰ）求角B的大小；（Ⅱ）若，求△ABC的面积．【答案】（Ⅰ）；（Ⅱ）．【解析】（Ⅰ）在解三角形的背景下，考查正弦定理，余弦定理，知值求值．（Ⅱ）综合余弦定理，求三角形的面积公式，需要把作为整体求之．试题解析：（Ⅰ）由正弦定理得将上式代入已知即，即．∵∵∵B为三角形的内角，∴．（Ⅱ）由余弦定理得，结合，可得，所以△ABC的面积．【考点】正弦定理，余弦定理，三角形的面积公式．15.在△中，角，，所对的边分别为，，，表示△的面积，若，，则．【答案】【解析】∵，∴，∴，∴，．∵，∴，∴，∴，∴．【考点】解三角形．【思路点睛】先利用余弦定理和三角形的面积公式可得，可得，再用正弦定理把中的边换成角的正弦，利用两角和公式化简整理可求得，最后根据三角形内角和，进而求得．16.中，角A，B，C的对边分别为a，b，c，若的面积，则 .【答案】【解析】由余弦定理，，又，，，即，，．【考点】1、余弦定理；2、同角三角函数的基本关系；3、三角形面积公式.【思路点睛】本题主要考查的是余弦定理、同角三角函数基本关系、三角形的面积公式，属于容易题.因为题目求，且的面积，边的平方的形式一般想到余弦定理，面积展开后利用余弦定理即可求得与的关系，从而利用同角三角函数的基本关系求得.17.（2012•安徽）设△ABC的内角A、B、C所对边的长分别为a、b、c，且有2sinBcosA=sinAcosC+cosAsinC．（Ⅰ）求角A的大小；（Ⅱ）若b=2，c=1，D为BC的中点，求AD的长．【答案】（Ⅰ）；（Ⅱ）【解析】（Ⅰ）根据2sinBcosA=sinAcosC+cosAsinC，可得2sinBcosA=sin（A+C），从而可得2sinBcosA=sinB，由此可求求角A的大小；（Ⅱ）利用b=2，c=1，A=，可求a的值，进而可求B=，利用D为BC的中点，可求AD的长．解：（Ⅰ）∵2sinBcosA=sinAcosC+cosAsinC∴2sinBcosA=sin（A+C）∵A+C=π﹣B∴sin（A+C）=sinB＞0∴2sinBcosA=sinB∴cosA=∵A∈（0，π）∴A=；（Ⅱ）∵b=2，c=1，A=∴a2=b2+c2﹣2bccosA=3∴b2=a2+c2∴B=∵D为BC的中点，∴AD=．【考点】余弦定理；三角函数的恒等变换及化简求值．18.在中，已知．（Ⅰ）求sinA与角B的值；（Ⅱ）若角A,B,C的对边分别为的值．【答案】（Ⅰ）；（Ⅱ），．【解析】（I）给出了关于角的两个三角函数值，利用诱导公式和同角三角函数的基本关系式可求得其正弦、余弦，再根据三角形的性质可求得的值；（II）在第一问的基础上，利用正弦定理可求得边，再由余弦定理求边，注意利用三角形基本性质舍解．试题解析：（Ⅰ）∵，，又∵，．∵，且，．（Ⅱ）由正弦定理得，，另由得，解得或（舍去），，．【考点】三角函数的诱导公式，同角三角函数的基本关系式及利用正、余弦定理在解三角形．19.已知，则的值为．【答案】．【解析】，故填：．【考点】三角恒等变形．20.在中，角A，B，C的对边分别为，，，若，则角的值为（）A．或B．或C．D．【答案】A．【解析】，，∴或，故选A．【考点】余弦定理．【思路点睛】由已知条件，可先将切化弦，再结合正弦定理，将该恒等式的边都化为角，然后进行三角函数式的恒等变形，找出角之间的关系；或将角都化成边，然后进行代数恒等变形，可一题多解，多角度思考问题，从而达到对知识的熟练掌握．21.为了得到函数的图象，只需把函数图象上的所有点（）A．横坐标缩短到原来的倍，纵坐标不变B．横坐标伸长到原来的2倍，纵坐标不变C．纵坐标缩短到原来的倍，横坐标不变D．纵坐标缩短到原来的2倍，横坐标不变【答案】A【解析】这是一个三角函数的图象变换问题，一般的为了得到函数的图象，只需把函数的图象上所有点的横坐标伸长（）或缩短（）到原来的倍（纵坐标不变）即可，因此为了得到函数的图象，只需把函数图象上的所有点横坐标缩短到原来的倍，纵坐标不变，故选A.【考点】三角函数的图象变换．【方法点睛】本题是一个三角函数的图象变换问题，属于容易题.一般的要得到函数（其中）的图像可按以下步骤进行：先把的图象向左（）或向右（）平移个单位，再将所得函数的图象上各点的横坐标扩大（）或缩小（）为原来的（纵坐标不变），再把所得函数图象上各点的纵坐标扩大（）或缩小（）为原来的倍（横坐标不变），最后再将所得图像向上（）或向下（）平移个单位，即可得到函数的图象.22.如图，在中，，，点在边上，且，.（I）求；（II）求的长.【答案】（Ⅰ）；（Ⅱ），.【解析】（Ⅰ）由图可知，所以，又，所以，再由两角差的正弦公式可求得；（Ⅱ）由题意可用正弦定理、余弦定理即可求出、的长，在中，有，又从而可求得；在中，由余弦定理得，，从而可求出.试题解析：（Ⅰ）在中，因为，所以，所以（Ⅱ）在中，由正弦定理得，在中，由余弦定理得，所以【考点】1.解三角形；2.两角差的正弦公式.23.设的内角对边分别为，已知，且.（1）求角的大小；（2）若向量与共线，求的值.【答案】(1);(2)。

2010高三数学高考第一轮复习向量复习教案：空间向量及其运算

第十三章空间向量与立体几何一、知识网络：二．考纲要求：（1）空间向量及其运算① 经历向量及其运算由平面向空间推广的过程；② 了解空间向量的概念，了解空间向量的基本定理及其意义，掌握空间向量的正交分解及其坐标表示；③ 掌握空间向量的线性运算及其坐标表示；④ 掌握空间向量的数量积及其坐标表示，能运用向量的数量积判断向量的共线与垂直。

（2）空间向量的应用① 理解直线的方向向量与平面的法向量；② 能用向量语言表述线线、线面、面面的垂直、平行关系；③ 能用向量方法证明有关线、面位置关系的一些定理（包括三垂线定理）；④ 能用向量方法解决线线、线面、面面的夹角的计算问题，体会向量方法在研究几何问题中的作用。

三、命题走向本章内容主要涉及空间向量的坐标及运算、空间向量的应用。

本章是立体几何的核心内容，高考对本章的考查形式为：以客观题形式考查空间向量的概念和运算，结合主观题借助空间向量求夹角和距离。

预测10年高考对本章内容的考查将侧重于向量的应用，尤其是求夹角、求距离，教材上淡化了利用空间关系找角、找距离这方面的讲解，加大了向量的应用，因此作为立体几何解答题，用向量法处理角和距离将是主要方法，在复习时应加大这方面的训练力度。

第一课时空间向量及其运算一、复习目标：1．理解空间向量的概念；掌握空间向量的加法、减法和数乘； 2．了解空间向量的基本定理； 3．掌握空间向量的数量积的定义及其性质；理解空间向量的夹角的概念；掌握空间向量的数量积的概念、性质和运算律；了解空间向量的数量积的几何意义；能用向量的数量积判断向量的共线与垂直。

二、重难点：理解空间向量的概念；掌握空间向量的运算方法三、教学方法：探析类比归纳，讲练结合四、教学过程（一）、谈最新考纲要求及新课标高考命题考查情况，促使积极参与。

学生阅读复资P128页，教师点评，增强目标和参与意识。

（二）、知识梳理，方法定位。

（学生完成复资P128页填空题，教师准对问题讲评）。

高三数学解三角形试题答案及解析

高三数学解三角形试题答案及解析1.已知的内角，面积满足所对的边，则下列不等式一定成立的是A．B．C．D．【答案】A【解析】由题设得：（1）由三角形面积公式及正弦定理得：所以又因为，所以所以恒成立，所以故选A.【考点】1、两角和与差的三角函数；2、正弦定理；3、三角形的面积公式.2.某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上，在小艇出发时，轮船位于港口O北偏西30°且与该港口相距20海里的A处，并正以30海里/小时的航行速度沿正东方向匀速行驶，假设该小艇沿直线方向以v海里/小时的航行速度匀速行驶，经过t小时与轮船相遇．(1)若希望相遇时小艇的航行距离最小，则小艇航行速度的大小应为多少？(2)假设小艇的最高航行速度只能达到30海里/小时，试设计航行方案(即确定航行方向和航行速度的大小)，使得小艇能以最短时间与轮船相遇，并说明理由．＝10，此时v＝＝30【答案】（1）当t＝时，Smin（2）航行方向为北偏东30°，航行速度为30海里/小时，小艇能以最短时间与轮船相遇．【解析】解：(1)设相遇时小艇航行的距离为S海里，则S＝＝＝．＝10，此时v＝＝30．故当t＝时，Smin答：小艇以30海里/小时的速度航行，相遇时小艇的航行距离最小．(2)设小艇与轮船在B处相遇，如图，则v2t2＝400＋900t2－2·20·30t·cos(90°－30°)，故v2＝900－＋．∵0<v≤30，∴900－＋≤900，即－≤0，解得t≥．又t＝时，v＝30．故v＝30时，t取最小值，且最小值等于．此时，在△OAB中，有OA＝OB＝AB＝20，故可设计航行方案如下：航行方向为北偏东30°，航行速度为30海里/小时，小艇能以最短时间与轮船相遇．3.（2011•浙江）在△ABC中，角A，B，C，所对的边分别为a，b，c．已知sinA+sinC=psinB （p∈R）．且ac=b2．（1）当p=，b=1时，求a，c的值；（2）若角B为锐角，求p的取值范围．【答案】（1）a=1，c=或a=，c=1 （2）＜p＜【解析】（1）解：由题设并利用正弦定理得故可知a，c为方程x2﹣x+=0的两根，进而求得a=1，c=或a=，c=1（2）解：由余弦定理得b2=a2+c2﹣2accosB=（a+c）2﹣2ac﹣2accosB=p2b2﹣b2cosB﹣，即p2=+cosB，因为0＜cosB＜1，所以p2∈（，2），由题设知p∈R，所以＜p＜或﹣＜p＜﹣又由sinA+sinC=psinB知，p是正数故＜p＜即为所求4.E，F是等腰直角斜边AB上的三等分点，则tan ECF=（ )A．B．C．D．【答案】D【解析】作CD⊥AB于D,则D为EF的中点．令CB=CA=3,则AB=6,CD=3,∴ED=FD=1∴tan ECF=∴tan ECF==5.已知点是的重心,且,则实数的值为( )A．B．C．D．【答案】B【解析】由已知得，，延长分别交于点，由重心的性质，设，，则，，，代入得，【考点】1、重心的性质；2、勾股定理；3、正弦定理和余弦定理.6.在△ABC中，若0＜tan A·tan B＜1，那么△ABC一定是( )A．锐角三角形B．钝角三角形C．直角三角形D．形状不确定【答案】B【解析】由0＜tan A·tan B＜1，可知tan A＞0，tan B＞0，即A，B为锐角，tan(A＋B)＝＞0，即tan(π－C)＝－tan C＞0，所以tan C＜0，所以C为钝角，所以△ABC为钝角三角形．故选B7.线段AB外有一点C,∠ABC=60°,AB=200km,汽车以80km/h的速度由A向B行驶,同时摩托车以50km/h的速度由B向C行驶,则运动开始几小时后,两车的距离最小()A．B．1C．D．2【答案】C【解析】如图所示,设过xh后两车距离为ykm,则BD=200-80x,BE=50x,∴y2=(200-80x)2+(50x)2-2×(200-80x)·50x·cos 60°,整理得y2=12900x2-42000x+40000(0≤x≤2.5),∴当x=时y2最小,即y最小.8.若△ABC的三个内角满足sin A∶sin B∶sin C＝4∶5∶7，则△ABC()A．一定是锐角三角形B．一定是直角三角形C．一定是钝角三角形D．可能是锐角三角形，也可能是钝角三角形【答案】C【解析】由正弦定理可设a＝4k，b＝5k，c＝7k，则cos C＝<0，因此三角形为钝角三角形．9.某旅游景点有一处山峰，游客需从景点入口A处向下沿坡角为α的一条小路行进a百米后到达山脚B处，然后沿坡角为β的山路向上行进b百米后到达山腰C处，这时回头望向景点入口A处俯角为θ，由于山势变陡到达山峰D坡角为γ，然后继续向上行进c百米终于到达山峰D处，游览风景后，此游客打算乘坐由山峰D直达入口A的缆车下山结束行程，如图所示，假设A，B，C，D四个点在同一竖直平面．(1)求B，D两点的海拔落差h；(2)求AD的长【答案】（1）b sin β＋c sin γ（2）【解析】(1)h＝b sin β＋c sin γ.(2)方法一：联结AC.在△ABC中，由余弦定理得AC2＝a2＋b2＋2ab cos(α＋β)，在△ACD中，由余弦定理得AD2＝AC2＋c2－2cAC cos(π－γ＋θ)，所以AD＝.方法二：联结AC.在△ABC中，由正弦定理得，所以AC＝，以下同方法一．10.在△中，所对边分别为、、．若，则．【答案】【解析】三角形中问题在解决时要注意边角的互化，本题求角，可能把边化为角比较方便，同时把正切化为正弦余弦，由正弦定理可得，，所以有，即，在三角形中，于是有，，．【考点】解三角形．11.在△ABC中，边角，过作，且，则.【答案】【解析】依题意，，由余弦定理得，，由三角形的面积公式得，即，，又，，，即，又点、、三点共线，则，解方程组，解得，.【考点】余弦定理，三角形的面积公式，向量的数量积.12.设△ABC的内角A，B，C的对边分别为a，b，c，(a＋b＋c)(a－b＋c)＝ac．（Ⅰ）求B；（Ⅱ）若sinAsinC＝，求C．【答案】（I）；（II）或.【解析】（I）已知等式右边利用多项式乘多项式法则计算，整理后得到关系式，利用余弦定理表示出，将关系式代入求出的值，由为三角形的内角，利用特殊角的三角函数值即可求出的度数；（II）由（I）得的度数，；利用利用两角和与差的余弦函数公式化简，变形后将及的值代入求出的值，利用特殊三角函数的值求出的值，与的值联立即可求出的度数.试题解析：（I）为三角形的内角(II)由（I）得:或或【考点】1.余弦定理；2.两角的和差公式.13.在中，，.（Ⅰ）求的值；（Ⅱ）求的值.【答案】（Ⅰ）.（Ⅱ）.【解析】（Ⅰ）根据已知条件，建立的方程组即可得解.（Ⅱ）应用余弦定理可首先.进一步应用正弦定理即得.试题解析：（Ⅰ）由和可得, 2分所以， 3分又所以. 5分（Ⅱ）因为,,由余弦定理可得 7分，即. 9分由正弦定理可得 11分， 12分所以. 13分【考点】正弦定理、余弦定理的应用，三角形面积.14.在中，已知（1）求；（2）若，的面积是，求.【答案】（1）；（2）2.【解析】（1）用三角形三内角和定理及特殊角的三角函数值求解；（2）利用余弦定理与三角形的面积公式，得到关于、的方程组，解出即得.（1）在中，，，，.（2）由余弦定理，则，又的面积是，则，即，，即，.【考点】三角形三内角和定理，余弦定理，三角形的面积.15.在中,角的对边分别为,且满足（1）求证：；（2）若的面积,,的值.【答案】（1）详见解析，（2）【解析】（1）转化三角形问题中的边角关系式，首先要选择定理.由正弦定理，将等式中的边化为对应角的正弦，由内角和定理，得，再利用诱导公式、两角和差的正弦公式得，在三角形中即证；（2）解三角形问题应灵活应用边角的计算公式.在（1）的条件下，；由三角形的面积公式及余弦定理可求.试题解析：（1）由，根据正弦定理，得： 2分又在△ABC中，，则，所以即 4分所以，即又为三角形内角，所以。

高三数学第一轮复习解三角形教案

高三数学第一轮复习解三角形教案三角形是几何学中研究的一个重要的图形，它拥有许多特征和性质，因此在数学中被广泛地研究和应用。

在高三数学第一轮复习中，对于三角形的解题方法和相关知识的掌握是非常重要的。

本文将为大家介绍三角形的基本概念、常用定理和解题技巧。

一、三角形的基本概念1. 三角形的定义：三角形是由三条线段组成的图形，其中任意两条线段的长度之和大于第三条线段的长度。

2. 三角形的分类：(1) 根据边长分类：等边三角形、等腰三角形、一般三角形。

(2) 根据角度分类：锐角三角形、直角三角形、钝角三角形。

(3) 根据边角关系分类：外角、内角、对角、邻角等。

3. 三角形的元素：三角形的边、角和顶点。

二、三角形的常用定理1. 三角形内角和定理：一个三角形的三个内角的和为180°。

2. 直角三角形的性质：(1) 斜边平方等于两直角边平方和的定理（勾股定理）。

(2) 直角三角形内角的关系：直角对顶角为90°，直角三角形的其它两个内角为锐角。

三、三角形的解题技巧1. 判断三角形的类型：(1) 根据边长关系判断三角形的类型：边长相等的三角形为等边三角形，两边相等的三角形为等腰三角形，其余为一般三角形。

(2) 根据角度关系判断三角形的类型：有一个角大于90°的三角形为钝角三角形，有一个角等于90°的三角形为直角三角形，其余为锐角三角形。

2. 运用三角形的性质和定理解题：(1) 利用三角形内角和定理解决求角度的问题。

(2) 运用勾股定理解决用已知信息求三角形边长的问题。

(3) 利用等腰三角形的性质解决求角度或边长的问题。

四、三角形解题的思路1. 首先，根据问题中给出的已知条件判断三角形的类型，并利用已知信息列写方程。

2. 其次，根据三角形的性质和定理对三角形进行推导和运算，求解未知量。

3. 最后，验证解答的合理性，并作出结论。

通过掌握三角形的基本概念、常用定理和解题技巧，我们不仅可以更好地理解三角形的属性和性质，还能够灵活运用这些知识解决实际问题。

高三数学一轮课件第四章三角函数与解三角形 4.2 同角三角函数的基本关系及诱导公式

=
25.
5
关闭关闭
解析答案
知识梳理双基自测
12345
-11-
自测点评
1.平方关系和商数关系式中的角都是同一个角,且商数关系式中
α≠
π 2
+kπ,k∈Z.
2.利用平方关系式解决问题时,要注意开方运算结果的符号,需要
根据角α的范围确定.
3.公式化简求值时,要利用公式化任意角的三角函数为锐角三角
函数,其步骤:去负—脱周—化锐,特别注意函数名称和符号的确定.
(2)若 α∈R,则 tan α=csoins��恒成立. (
)
(3)sin(π+α)=-sin α成立的条件是α为锐角. ( )
(4)若 cos(nπ-θ)=13(n∈Z),则 cos θ=13. ( )
(1)× (2)× (3)× (4)×
关闭
答案
-7-
知识梳理双基自测
12345
什(1)么1 ? (2) 3
答案
考点1
考点2
考点3
-25-
解析: (1)原式=-sin 1 200°·cos 1 290°-cos 1 020°sin 1 050°
=-sin(3×360°+120°)cos(3×360°+210°)-
cos(2×360°+300°)sin(2×360°+330°)
=
-
4 5
,
cos��
=
3 5
,
于是 1
cos ��-sin ��
=
1 35- -45
= 57.
考点1
考点2
考点3

高三数学一轮复习第四章三角函数与解三角形培优专题8三角形中的最值问题课件

第四章三角函数与解三角形高考培优8 三角形中的最值问题
[培优技法] 在解三角形专题中，求其“范围与最值”的问题，一直都是这部分内容的重点、难点．解决这类问题，通常有下列五种解题技巧： (1)利用基本不等式求范围或最值； (2)利用三角函数求范围或最值； (3)利用三角形中的不等关系求范围或最值； (4)根据三角形解的个数求范围或最值； (5)利用二次函数求范围或最值．要建立所求量(式子)与已知角或边的关系，然后把角或边作为自变量，所求量(式子)的值作为函数值，转化为函数关系，将原问题转化为求函数的值域问题．这里要利用条件中的范围限制，以及三角形自身范围限制，要尽量把角或边的范围(也就是函数的定义域)找完善，避免结果的范围过大．
点拨本例由于含有附加条件“△ABC为锐角三角形”，故不能采用基本不等式法求解，应转化为三角函数后，利用函数求最值，要注意角度范

高三数学一轮复习解三角形教案

芯衣州星海市涌泉学校解三角形〔1〕一、课前检测1.设函数.sin )32cos()(2x x x f ++=π〔Ⅰ〕求函数)(x f 的最大值和最小正周期；〔Ⅱ〕设C B A ,,为ABC ∆的三个内角，假设31cos =B ，41)2(-=C f ，且C 为锐角，求A sin 的值. 解：〔Ⅰ〕x x x f 2sin )32cos()(++=π 22cos 13sin 2sin 3cos2cos x x x -+-=ππ……4分 .2sin 2321x -=……5分所以函数)(x f 的最大值为231+,最小正周期为π.7分〔Ⅱ〕41sin 2321)2(-=-=C C f ，所以，23sin =C ，9分因为C 为锐角,所以.3π=C …10分又因为在ABC ∆中，31cos =B ，所以332sin =B ，所以……11分 C B C B C B A sin cos cos sin )sin(sin +=+=.6322233121232+=⨯+⨯=13分 2.函数()sin()(0,||)f x x ωϕωϕπ=+><的图象如下列图.〔Ⅰ〕求,ωϕ的值；〔Ⅱ〕设()()()4g x f x f x π=-，求函数()g x 的单调递增区间. 解：〔Ⅰ〕由图可知πππ=-=)42(4T ,22==T πω，………2分又由1)2(=πf 得，1)sin(=+ϕπ，又(0)1f =-，得sin 1ϕ=- πϕ<||2πϕ-=∴，…4分〔Ⅱ〕由〔Ⅰ〕知：x x x f 2cos )22sin()(-=-=π…6分因为()(cos 2)[cos(2)]cos 2sin 22g x x x x x π=---=1sin 42x =…9分所以，24222k x k ππππ-≤≤+，即 (Z)2828k k x k ππππ-≤≤+∈.……12分故函数()g x 的单调增区间为[,] (Z)2828k k k ππππ-+∈.……13分 3.α为锐角，且tan()24πα+=.〔Ⅰ〕求tan α的值；〔Ⅱ〕求sin 2cos sin cos 2αααα-的值. 解：〔Ⅰ〕1tan tan()41tan πααα++=-，…………2分所以1tan 21tan αα+=-，1tan 22tan αα+=-，所以1tan 3α=.……………5分〔Ⅱ〕2sin 2cos sin 2sin cos sin cos 2cos 2αααααααα--= 2sin (2cos 1)sin cos 2sin cos 2cos 2ααααααα-===.……8分因为1tan 3α=，所以cos 3sin αα=，又22sin cos 1αα+=，所以21sin 10α=，………10分又α为锐角，所以sin α=，所以sin 2cos sin cos 2αααα-=.………12分二、知识梳理〔一).三角形中的各种关系设△ABC 的三边为a 、b 、c ，对应的三个角为A 、B 、C ．1．角与角关系：A+B+C=π，由A ＝π－〔B ＋C 〕可得：1〕sinA ＝sin 〔B ＋C 〕，cosA ＝－cos 〔B ＋C 〕．2〕222C B A +-=π．有：2cos 2sin C B A +=，2sin 2cos C B A +=．2．边与边关系：a+b>c ，b+c>a ，c+a>b ，a －b<c ，b －c<a ，c －a>b ．3．边与角关系：1〕正弦定理R Cc B b A a 2sin sin sin === 变式有：①C B A cb a sin :sin :sin ::=； ②C Rc B R b A R asin 2,sin 2,sin 2===； ③CB A c b aC c B b A a sin sin sin sin sin sin ++++===； ④C B A c b a sin :sin :sin ::=。

高三文科数学一轮复习之三角函数和解三角形

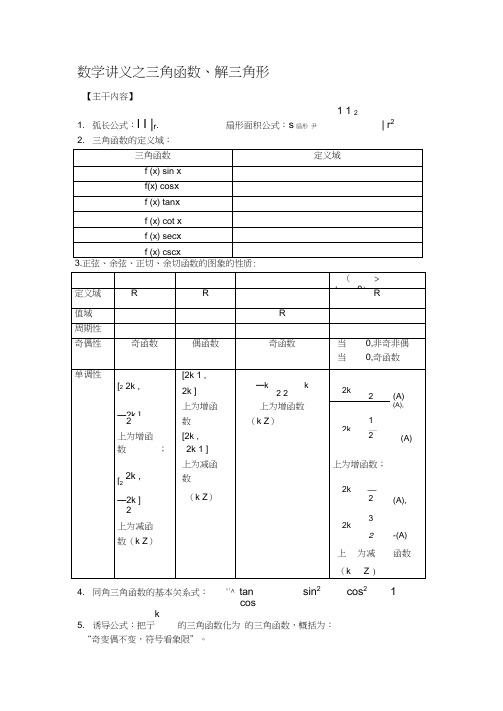
数学讲义之三角函数、解三角形【主干内容】1 1 21. 弧长公式：l I |r. 扇形面积公式：s扇形尹| r22. 三角函数的定义域：4. 同角三角函数的基本关系式：si^ tan sin2cos21cosk5. 诱导公式：把亍的三角函数化为的三角函数，概括为：“奇变偶不变，符号看象限”。

重要公式：cos（） cos cos sin sin6•三角函数图象的作法：描点法及其特例一一五点作图法（正、余弦曲线）三点二线作图法（正切曲线）【注意！！！】本专题主要思想方法1. 等价变换。

熟练运用公式对问题进行转化，化归为熟悉的基本问题；2. 数形结合。

充分利用单位圆中的三角函数线及三角函数图象帮助解题；3. 分类讨论。

【题型分类】题型一：三角运算，要求熟练使用各种诱导公式、倍角公式等。

〖例1〗（10全国卷I文）cos300A.31-C1n .3B.— D. 2222C【命题意图】本小题主要考查诱导公式、特殊三角函数值等三角函数知识【解析】cos300cos36601cos602〖例2〗（10全国卷n文）已知sin2，则cos(x 2 )3A. JB.1C.1D V5D.3993【解析】B:本题考查了二倍角公式及诱导公式，•••SINA=2/3 , cos( 2 )cos2(12sin 2) -9〖例3〗（10福建文）计算12sin 22.5的结果等于（）A.-B.豆C.D.迈2232【答案】B2故选B.【解原式=cos 45 - 51例4〗（10浙江文）函数f（x） sin2（2x -）的最小正周期是 ___________4最小正周期为2，本题主要考察了二倍角余弦公式的灵活运用，属容易题。

题型二：三角函数的图象：三角函数图象从“形”上反应了三角函数的性质。

是（）D解析：对解析式进行降幕扩角，转化为f x】cos 4x —1，可知其2 2 21例1〗（10重庆文）下列函数中，周期为，且在［壬，？］上为减函数的是A. y sin(2x -)B. y cos(2x )C. y sin(x 【答案】AD.cos(x —)1例2〗（09浙江文）已知 a 是实数，则函数 f （x ） 1 a sin ax 的图象不可能1例3〗为得到y sin2x 的图象A.向左平移丸个长度单位12C.向左平移4个长度单位6分析：先统一函数名称，在根据平移的法则解决.B .向右平移个长度单位12D.向右平移士个长度单位6n解析：函数 y cos 2x sin 2x — —33 2sin 2xsin2 x512故要将函数y sin2x的图象向左平移丸个长度单位，选择答案A.121例4〗(10江西文)四位同学在同一个坐标系中分别选定了一个适当的区间,y sin(x ), y sin(x )各自作出三个函数y sin2x,63的图像如下,结果发现恰有一位同学作出的图像有错误，那么有错误的图像是【答案】C【命题意图】考查三角函数的图像与性质•【解析】作出三个函数图像对比分析即可选择 Co2最小正周期为 -.3(I)求的最小正周期.〖例6〗(11浙江文)已知函数 f(x) As in (§x ) , x R , A 0 ,0 -. y f (x)的部分图像，如图所示， P 、Q 分别为该图像的最高点和最低点，点P 的坐标为(1, A).(I)求f (x)的最小正周期及 (n)若点R 的坐标为(1,0),1例5〗(09重庆文)设函数f(x )2 2(sin x cos x) 2cos x( 0)的(n)若函数y g(x)的图像是由y f(x)的图像向右平移三个单位长度得到，求y g(x)的单调增区间.解：(I)2 2依题意得————，故2 3的最小正周期为由2k 2 解得三k3依题意得：5w 3x w 2k24 2 w x w k 4 3-(kZ) 寻(kZ)\故y g(x)的单调增区间为:拿的值；PRQ —，求A 的值.题型三：三角函数的最值：最值是三角函数最为重要的内容之一，其主要方法是利用正余弦函数的有界性，通过三角换元或者是其它的三角恒等变换转化问题。

高三数学一轮复习课件第四章 4.2 同角三角函数基本关系式及诱导公式

A.{1，－1,2，－2}
B.{－1,1}
√C.{2，－2}
D.{1，－1,0,2，－2}
解析当 k 为偶数时，A＝ssiinn αα＋ccooss αα＝2；
当 k 为奇数时，A＝－sisninαα－ccooss αα＝－2.
(2)(2018·太原质检)化简：tanπ＋αcos2π＋αsinα－32π＝－1 . cos－α－3πsin－3π－α
A.－
2 6
B.
2 6
C.－23
√D.23
(2)已知 sin α＝25 5，则 tan(π＋α)＋csoins5522ππ＋－αα＝
52或－52
.
3 课时作业
PART THREE
基础保分练
1.已知 α 是第四象限角，tan α＝－152，则 sin α 等于
1 A.5
(2)商数关系：
sin cos
αα＝tan
αα≠π2＋kπ，k∈Z
.
2.三角函数的诱导公式
公式
一
角 2kπ＋α(k∈Z)
二 π＋α
三
四
－α π－α
正弦
sin α
－__s_i_n_α_ _－__s_in__α_ __s_in__α_
五 π2－α
_c_o_s__α_
六 π2＋α
__c_o_s_α__
α＝tan
－sin α α·cos α·tan
α＝－tan1
α＝2
1
6＝
6 12 .
1 2 3 4 5 67
2 题型分类深度剖析
PART TWO
自主演练
题型一同角三角函数基本关系式的应用
1.已知 α 是第四象限角，sin α＝－1123，则 tan α 等于

2013-2014学年高三数学一轮复习导学案：解三角形(1)

abc sin A sin B sinC
。
5.已知△ABC 的三边满足 (a b c)(a b c) 3ab ，求角 C=
6.设△ABC 中内角 A，B，C 所对的边分别为 a, b, c ，已知 tan A △ABC 的最长的边长为 1，求△ABC 的最短的边长。
课题
解三角形（1）
姓名：
一、学习目标：
1.掌握正弦定理、余弦定理，并能初步运用正弦定理、余弦定理解斜在△ABC 中，已知， a
4 3 , b 4, A 300 , 则 sin B 3
2. 在△ABC 中，A，B，C 对应三边分别为 a, b, c ，若 a2 (b c)2 bc ，则 A 的大小等于 3. 已知在△ABC 中， a 5, c 7, sin A
课外作业：解三角形（1）
姓名：
3
1.在 ABC 中，已知 b c 1, C 450 , B 300 ，则 b 2.在等腰三角形 ABC 中，若顶角 A 的余弦值为
。。。。
3 ，则其底角 B 的正弦值为 5
3.在△ABC 中，若 a2 b2 c2 bc, 2b 3c, a 3 19 ，则△ABC 的面积为 4.在△ABC 中，已知 A 600 , b 1, SABC 3 ，则
5 3 ，则角 C= 14
4. 在△ABC 中，已知 AC 3, AB 3, B 300 ，则 BC 的值为
三、【课堂研讨】
例 1 已知下列三角形中两边及其一边的对角，先判别三角形是否有解？有解的作出解答： ① a 7, b 8, A 1050 ； ③ b 10, c 5 6, C 600 ； ② a 10, b 20, A 800 ； ④ a 2 3, b 6, A 300 。

高三数学：解三角形专题

高三数学：解三角形专题知识回顾】1.正弦定理：$\frac{a}{\sin A} = \frac{b}{\sin B} =\frac{c}{\sin C} = 2R$。

cos A = \frac{b^2 + c^2 - a^2}{2bc}$。

cos B = \frac{a^2 + c^2 - b^2}{2ac}$。

cos C = \frac{a^2 + b^2 - c^2}{2ab}$。

2.余弦定理：$b^2 = a^2 + c^2 - 2ac\cos B$。

c^2 = a^2 + b^2 - 2ab\cos C$。

a^2 = b^2 + c^2 - 2bc\cos A$。

3.推论：正余弦定理的边角互换功能①$a = 2R\sin A$，$b = 2R\sin B$，$c = 2R\sin C$；②$\sin A = \frac{a}{2R}$，$\sin B = \frac{b}{2R}$，$\sinC = \frac{c}{2R}$；③$\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2R$；④$a:b:c = \sin A:\sin B:\sin C$；⑤$\sin^2 A = \sin^2 B + \sin^2 C - 2\sin B\sin C\cos A$；sin^2 B = \sin^2 C + \sin^2 A - 2\sin C\sin A\cos B$；sin^2 C = \sin^2 A + \sin^2 B - 2\sin A\sin B\cos C$。

4.三角形中的基本关系式：$\sin(B+C) = \sin A$，$\cos(B+C) = -\cos A$。

sin\frac{B+C}{2} = \sqrt{\frac{1-\cos A}{2}}$，$\cos\frac{B+C}{2} = \sqrt{\frac{1+\cos A}{2}}$。

高三数学复习专题练习题：解三角形（含答案）

⾼三数学复习专题练习题：解三⾓形（含答案）⾼三数学复习专题练习：解三⾓形（含答案）⼀. 填空题（本⼤题共15个⼩题，每⼩题5分，共75分）1.在△ABC 中，若2cosBsinA=sinC,则△ABC ⼀定是三⾓形.2.在△ABC 中，A=120°,AB=5,BC=7，则CBsin sin 的值为 . 3.已知△ABC 的三边长分别为a,b,c,且⾯积S △ABC =41（b 2+c 2-a 2），则A= . 4.在△ABC 中，BC=2，B=3π，若△ABC 的⾯积为23，则tanC 为 . 5.在△ABC 中，a 2-c 2+b 2=ab,则C= .6.△ABC 中，若a 4+b 4+c 4=2c 2(a 2+b 2),则C= .7.在△ABC 中，⾓A ，B ，C 所对的边分别为a,b,c ，若a=1,b=7,c=3,则B= . 8.在△ABC 中，若∠C=60°，则c b a ++ac b+= . 9.如图所⽰，已知两座灯塔A 和B 与海洋观察站C 的距离都等于a km, 灯塔A 在观察站C 的北偏东20°，灯塔B 在观察站C 的南偏东40°，则灯塔A 与灯塔B 的距离为 km.10.⼀船⾃西向东匀速航⾏，上午10时到达⼀座灯塔P 的南偏西75°距塔68海⾥的M 处，下午2时到达这座灯塔的东南⽅向的N 处，则这只船的航⾏速度为海⾥/⼩时. 11. △ABC 的内⾓A 、B 、C 的对边分别为a 、b 、c ，若c=2，b=6，B=120°,则a= .12. 在△ABC 中,⾓A 、B 、C 的对边分别为a 、b 、c ，若（a 2+c 2-b 2）tanB=3ac ，则⾓B 的值为 . 13. ⼀船向正北航⾏，看见正西⽅向有相距10 海⾥的两个灯塔恰好与它在⼀条直线上，继续航⾏半⼩时后，看见⼀灯塔在船的南偏西600，另⼀灯塔在船的南偏西750，则这艘船是每⼩时航⾏________ 海⾥.14.在△ABC 中，A=60°，AB=5，BC=7，则△ABC 的⾯积为 .15.在△ABC 中，⾓A 、B 、C 所对的边分别为a 、b 、c.若（3b-c ）cosA=acosC ，则cosA= .（资料由“⼴东考神”上传，如需更多⾼考复习资料，请上 tb ⽹搜“⼴东考神”）⼆、解答题（本⼤题共6个⼩题，共75分）1、已知△ABC 中，三个内⾓A ，B ，C 的对边分别为a,b,c,若△ABC 的⾯积为S ，且2S=（a+b ）2-c 2，求tanC 的值. （10分）2、在△ABC 中，⾓A ，B ，C 所对的边分别为a,b,c ，并且a 2=b(b+c). （11分）（1）求证：A=2B ；（2）若a=3b,判断△ABC 的形状.3、在△ABC 中，a 、b 、c 分别是⾓A ，B ，C 的对边，且C B cos cos =-ca b+2. (12分)（1）求⾓B 的⼤⼩；（2）若b=13，a+c=4，求△ABC 的⾯积.4、△ABC 中，⾓A ，B ，C 的对边分别为a ，b ，c ，且b 2+c 2-a 2+bc=0. (12分) （1）求⾓A 的⼤⼩；（2）若a=3，求bc 的最⼤值；（3）求cb C a --?)30sin(的值.5、已知△ABC 的周长为)12(4+，且sin sin B C A +=． (12分)（1）求边长a 的值；（2）若A S ABC sin 3=?，求A cos 的值．6、在某海岸A 处，发现北偏东 30⽅向，距离A 处）（13+n mile 的B 处有⼀艘⾛私船在A 处北偏西 15的⽅向，距离A 处6n mile 的C 处的缉私船奉命以35n mile/h 的速度追截⾛私船. 此时，⾛私船正以5 n mile/h 的速度从B 处按照北偏东 30⽅向逃窜，问缉私船⾄少经过多长时间可以追上⾛私船，并指出缉私船航⾏⽅向. (12分)ACB3015· ·参考答案：⼀、填空题：1、等腰；2、53；3、45°；4、33；5、60°；6、45°或135°；7、65π；8、1；9、3a ；10、2617；11、2；12、3π或32π；13、10；14、103；15、33。

高三数学一轮复习第四章三角函数、解三角形第一节三角函数的概念、同角三角函数的关系式和诱导公式课

＝tanα.
4.能利用单位圆中的三角函数线推导出π2±α，π±α 的正弦、余弦、正切的诱导公式.
h
3
•关注热点
•1.三角函数的定义及应用是本节考查重点，注意三角函数值符号的确定．
•2.同角三角函数关系式常用来化简、求值，是高考热点．
•3.利用诱导公式求值或化简三角函数式是考查重点．
•4.主要以选择题、填空题的形式考查.
－α)＝
－.tanα
•(5)公式五
cosα，tan( －c，osαtan(π
sin(π2－α)＝ cosα ，cos(2π－α)＝ sinα .
h
11
(6)公式六 sin(π2＋α)＝ cosα ，cos(2π＋α)＝－sinα .
即 α＋k·2π(k∈Z)，－α，π±α 的三角函数值，等于 α 的同名函数值，前面加上一个把 α 看成锐角时原函数值的符号；π2±α 的正弦(余弦)函数值，分别等于 α 的余弦(正弦) 函数值，前面加上一个把 α 看成锐角时原函数值的符号．
∴－sinα＝－2cosα.
∴sinα＝2cosα，即 tanα＝2.
(1)原式＝5ttaannαα－＋42＝5×2－2＋4 2＝－16.
h
32
(2)原式＝sin2α＋2sinαcosα＝sins2iαn＋2α＋2sicnoαsc2αosα ＝tanta2αn＋2α＋2ta1nα＝85.
h
33
化简ssiinn[kkπ＋－1απc＋osα[]kc－os1kππ－＋αα](k∈Z)．
终边在 y 轴上的角的集合为{α|α＝kπ＋π2，k∈Z}；
终边在坐标轴上的角的集合为{α|α＝k2π，k∈Z}．
h
14

新高考数学一轮复习考点知识归类讲义第29讲解三角形应用举例及综合问题

新高考数学一轮复习考点知识归类讲义第29讲解三角形应用举例及综合问题1.仰角和俯角在同一铅垂平面内的水平视线和目标视线的夹角，目标视线在水平视线上方叫仰角，目标视线在水平视线下方叫俯角(如图1).2.方位角从正北方向起按顺时针转到目标方向线之间的水平夹角叫做方位角.如B点的方位角为α(如图2).3.方向角正北或正南方向线与目标方向线所成的锐角，如南偏东30°，北偏西45°等.4.坡度：坡面与水平面所成的二面角的正切值.➢考点1 解三角形应用举例[名师点睛]1.距离问题的类型及解法(1)类型：两点间既不可达也不可视，两点间可视但不可达，两点都不可达.(2)解法：选择合适的辅助测量点，构造三角形，将问题转化为求某个三角形的边长问题，从而利用正、余弦定理求解.2.高度问题的类型及解法（1）在测量高度时，要理解仰角、俯角的概念，仰角和俯角都是在同一铅垂面内，视线与水平线的夹角.（2）准确理解题意，分清已知条件与所求，画出示意图.（3）运用正、余弦定理，有序地解相关的三角形，逐步求解问题的答案，注意方程思想的运用.3.角度问题的类型及解法（1）测量角度问题的关键是在弄清题意的基础上，画出表示实际问题的图形，并在图形中标出有关的角和距离，再用正弦定理或余弦定理解三角形，最后将解得的结果转化为实际问题的解.（2）方向角是相对于某点而言的，因此在确定方向角时，必须先弄清楚是哪一个点的方向角.[典例]1.（2022·湖北·华中师大一附中模拟预测）为了测量一个不规则公园,C D 两点之间的距离，如图，在东西方向上选取相距1km 的,A B 两点，点B 在点A 的正东方向上，且,,,A B C D 四点在同一水平面上．从点A 处观测得点C 在它的东北方向上，点D 在它的西北方向上；从点B 处观测得点C 在它的北偏东15︒方向上，点D 在它的北偏西75方向上，则,C D 之间的距离为______km.【答案】2 【分析】由题意确定相应的各角的度数，在ABC 中，由正弦定理求得BC ,同理再求出DB ，解DBC △，求得答案.【详解】由题意可知，904545,9045135,9015105CAB DAB CBA ∠=-=∠=+=∠=+=,157590,15CDB DBA ∠=+=∠= ,故在ABC 中，1804510530ACB ∠=--=，故sin sin BD AB DAB ADB =∠∠ ，1sin 452sin 30BC ⨯==在ABD △中，1801513530ADB ∠=--=，故sin sin BC AB CAB ACB =∠∠ ，1sin1352sin 30BD ⨯==，所以在DBC △中，90CBD ∠=，则22222CD BC DB =+=+= ,故答案为：22. (2021·全国甲卷)2020年12月8日，中国和尼泊尔联合公布珠穆朗玛峰最新高程为8 848.86(单位：m).三角高程测量法是珠峰高程测量方法之一，如图是三角高程测量法的一个示意图，现有A ，B ，C 三点，且A ，B ，C 在同一水平面上的投影A ′，B ′，C ′满足∠A ′C ′B ′＝45°，∠A ′B ′C ′＝60°.由C 点测得B 点的仰角为15°，BB ′与CC ′的差为100；由B 点测得A 点的仰角为45°，则A ，C 两点到水平面A ′B ′C ′的高度差AA ′－CC ′约为(3≈1.732)( )A.346B.373C.446D.473答案 B解析如图所示，根据题意过C 作CE ∥C ′B ′，交BB ′于E ，过B 作BD ∥A ′B ′，交AA ′于D ，则BE ＝100，C ′B ′＝CE ＝100tan 15°.在△A ′C ′B ′中，∠C ′A ′B ′＝180°－∠A ′C ′B ′－∠A ′B ′C ′＝75°，则BD ＝A ′B ′＝C ′B ′·sin 45°sin 75°，又在B 点处测得A 点的仰角为45°，所以AD ＝BD ＝C ′B ′·sin 45°sin 75°，所以高度差AA ′－CC ′＝AD ＋BE＝C ′B ′·sin 45°sin 75°＋100＝100tan 15°·sin 45°sin 75°＋100＝100sin 45°sin 15°＋100＝100×2222×⎝ ⎛⎭⎪⎫32－12＋100＝100(3＋1)＋100≈373.3．（2022·全国·高三专题练习）公路北侧有一幢楼，高为60米，公路与楼脚底面在同一平面上.一人在公路上向东行走，在点A 处测得楼顶的仰角为45°，行走80米到点B 处，测得仰角为30°，再行走80米到点C 处，测得仰角为θ.则tan θ=______________.【答案】37777【解析】首先得到60,603OA OB ==，然后由余弦定理得：2222cos OA AB OB AB OB ABO =+-⋅∠，2222cos OC BC OB BC OB OBC =+-⋅∠，然后求出OC 即可【详解】如图，O 为楼脚，OP 为楼高，则60OP =，易得：60,603OA OB ==由余弦定理得：2222cos OA AB OB AB OB ABO =+-⋅∠，2222cos OC BC OB BC OB OBC =+-⋅∠，两式相加得：()22222230800OA OC AB OB OC +=+⇒=，则77OC =故377tan 2077θ=377[举一反三] 1．（2022·山东师范大学附中模拟预测）魏晋时期刘徽撰写的《海岛算经》是关于测量的数学著作，其中第一题是测量海岛的高．一个数学学习兴趣小组研究发现，书中提供的测量方法甚是巧妙，可以回避现代测量器械的应用．现该兴趣小组沿用古法测量一山体高度，如图点E 、H 、G 在水平线AC 上，DE 和FG 是两个垂直于水平面且等高的测量标杆的高度，记为h ，EG 为测量标杆问的距离，记为d ，GC 、EH 分别记为,a b ，则该山体的高AB =（）A ．hd h a b +-B ．hd h a b--C ．hd d a b +-D ．hd d a b -- 【答案】A【分析】根据所给数据，利用解直角三角形先求出BM ，即可得解.【详解】连接FD ，并延长交AB 于M 点，如图，因为在Rt BMD △中tan h BDM b ∠=，所以||||||tan BM BM b MD BDM h ==∠；又因为在Rt BMF △中tan h BFM a∠=，所以||||||tan BM BM a MF BFM h ==∠，所以||||||||BM a BM b MF MD d h h-=-=，所以||hd BM a b =-，即||hd AB BM h h a b =+=+-，故选：A ．2．（2022·江苏南通·高三期末）某校数学建模社团学生为了测量该校操场旗杆的高AB ，先在旗杆底端的正西方点C 处测得杆顶的仰角为45°，然后从点C 处沿南偏东30°方向前进20m 到达点D 处，在D 处测得杆顶的仰角为30°，则旗杆的高为（）A ．20mB ．10mC ．103mD ．1033m 【答案】B 【分析】根据条件确定相关各角的度数，表示出AB ，,AD AC 等边的长度，然后在ACD △中用余弦定理即可解得答案.【详解】如图示，AB 表示旗杆，由题意可知：45,0,630ACB ACD ADB ∠=∠=∠=︒︒︒，所以设AB x = ，则3,AD x AC x ==，在ACD △ 中，2222cos AD AC CD AC CD ACD =+-⨯⨯⨯∠ ,即2221(3)()(20)2202x x x =+-⨯⨯⨯ ，解得10x = ，（20x =-舍去），故选：B.3．（2022·辽宁·沈阳二中模拟预测）沈阳二中北校区坐落于风景优美的辉山景区，景区内的一泓碧水蜿蜒形成了一个“秀”字，故称“秀湖”．湖畔有秀湖阁()A 和临秀亭()B 两个标志性景点，如图．若为测量隔湖相望的A 、B 两地之间的距离，某同学任意选定了与A 、B 不共线的C 处，构成ABC ，以下是测量数据的不同方案： ①测量A ∠、AC 、BC ；②测量A ∠、B 、BC ；③测量C ∠、AC 、BC ；④测量A ∠、C ∠、B ．其中一定能唯一确定A 、B 两地之间的距离的所有方案的序号是_____________．【答案】②③【分析】利用正弦定理可判断①②，利用余弦定理可判断③，根据已知条件可判断④不满足条件.【详解】对于①，由正弦定理可得sin sin AC BC B A =，则sin sin AC A B BC =，若AC BC >且A ∠为锐角，则sin sin sin AC A B A AB=>，此时B 有两解，则C ∠也有两解，此时AB 也有两解；对于②，若已知A ∠、B ，则C ∠确定，由正弦定理sin sin BC AB A C=可知AB 唯一确定；对于③，若已知C ∠、AC 、BC ，由余弦定理可得222cos AB AC BC AC BC C =+-⋅ 则AB 唯一确定；对于④，若已知A ∠、C ∠、B ，则AB 不确定.故答案为：②③.4．（2022·辽宁·大连市一0三中学模拟预测）如图所示，遥感卫星发现海面上有三个小岛，小岛 B 位于小岛A 北偏东75距离60海里处，小岛B 北偏东15距离330海里处有一个小岛 C .(1)求小岛A 到小岛C 的距离；(2)如果有游客想直接从小岛A 出发到小岛 C ，求游船航行的方向.解：(1)在ABC 中，6030330，==AB BC1807515120ABC ∠=-+=，根据余弦定理得：.2222cos AC AB BC AB BC ABC =+-⋅⋅∠2260(30330)260(30330)cos1205400=+-⨯⨯⋅=306=AC 所以小岛A 到小岛 C 的最短距离是306.(2)根据正弦定理得：sin sin AC AB ABC ACB =∠∠ 30660120sin ACB=∠ 解得2sin ACB ∠=在ABC ∆中，,<BC ACACB ∴∠为锐角45ACB ∴∠=1801204515CAB ∴∠=--=. 由751560-=得游船应该沿北偏东60的方向航行答:小岛A 到小岛 C 的最短距离是306;游船应该沿北偏东60的方向航行. 5．（2022·广东·高三开学考试）如图，测量河对岸的塔高AB 时，可以选取与塔底B 在同一水平面内的两个测量基点C 与D ．现测得30BCD ∠=︒，135BDC ∠=︒，50CD =米，在点C 测得塔顶A 的仰角为45°，求塔高AB ．【解】在BCD △中，1801803013515CBD BCD BDC ∠=︒-∠-∠=︒-︒-︒=︒，∵()sin sin15sin 4530CBD ∠=︒=︒-︒sin 45cos30cos45sin30=︒︒-︒︒62-=由正弦定理sin sin BC CD BDC CBD =∠∠得()sin 5031sin 62CD BDC BC CBD ⋅∠===∠-.在Rt ABC △中45ACB ∠=︒．∴)5031AB BC ==．所以塔高AB 为)5031米．➢考点2 求解平面几何问题[名师点睛]平面几何中解三角形问题的求解思路(1)把所提供的平面图形拆分成若干个三角形，然后在各个三角形内利用正弦、余弦定理求解；(2)寻找各个三角形之间的联系，交叉使用公共条件，求出结果.1.(2021·新高考八省联考)在四边形ABCD 中，AB ∥CD ，AD ＝BD ＝CD ＝1.(1)若AB ＝32，求BC ； (2)若AB ＝2BC ，求cos ∠BDC . 解(1)如图所示，在△ABD 中，由余弦定理可知，cos ∠ABD ＝AB 2＋BD 2－AD 22AB ·BD ＝⎝ ⎛⎭⎪⎫322＋12－122×32×1＝34.∵AB ∥CD ，∴∠BDC ＝∠ABD ，即cos ∠BDC ＝cos ∠ABD ＝34. 在△BCD 中，由余弦定理可得，BC 2＝BD 2＋CD 2－2BD ·CD cos ∠BDC ＝12＋12－2×1×1×34，∴BC ＝22. (2)设BC ＝x ，则AB ＝2BC ＝2x .由余弦定理可知， cos ∠ABD ＝AB 2＋BD 2－AD 22AB ·BD ＝（2x ）2＋12－122×2x ×1＝x ，①cos ∠BDC ＝CD 2＋BD 2－BC 22CD ·BD ＝12＋12－x 22×1×1＝2－x 22.②∵AB ∥CD ，∴∠BDC ＝∠ABD ，即cos ∠BDC ＝cos ∠ABD .联立①②，可得2－x 22＝x ，整理得x 2＋2x －2＝0，解得x 1＝3－1，x 2＝－3－1(舍去).将x 1＝3－1代入②，解得cos ∠BDC ＝3－1.2.（2022·湖北·襄阳四中模拟预测）在ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，角A 的平分线AD 交BC 边于点D . (1)证明：AB DBAC DC=，2AD AB AC DB DC =⋅-⋅；(2)若1AD =，23A π=，求DB DC ⋅的最小值. 解：(1)在ABD △和BCD △中，可得BAD CAD ∠=∠，ADB ADC π∠+∠=，所以sin sin BAD CAD ∠=∠，sin sin ADB ADC ∠=∠，由正弦定理，得sin sin AB BDADB BAD =∠∠，sin sin AC DC ADC CAD=∠∠，两式相除得AB DB AC DC =，可得ABBD BC AB AC=+，AC DC BC AB AC =+，又由cos cos ABD ABC ∠=∠，根据余弦定理得22222222AB BD AD AB BC AC AB BD AB BC+-+-=⋅⋅ 所以()()22222222BD DC BDAD AB BD AB BC AC AB AC BD BC BD BC BC BC=+-+-=+-- 代入可得222AC AB AD AB AC BD DC AB AC AB AC=+-⋅++ABAC AB AC BD DC AB AC BD DC AB AC AB AC ⎛⎫=⋅+-⋅=⋅-⋅ ⎪++⎝⎭.(2)由1AD =，23A π=及ABD ACD ABC S S S +=△△△，可得b c bc += 根据基本不等式得2bc b c bc=+≥，解得4bc ≥，当且仅当2b c ==时等号成立，又由1AD =，2AD AB AC DB DC =⋅-⋅，可得13DB DC bc ⋅=-≥，所以DB DC ⋅的最小值是3. [举一反三]1．（2022·山东·济南市历城第二中学模拟预测）如图，已知在ABC 中，M 为BC 上一点，2AB AC BC =≤，π0,2B ⎛⎫∈ ⎪⎝⎭且15sin 8B =．(1)若AM BM =，求ACAM的值； (2)若AM 为BAC ∠的平分线，且1AC =，求ACM △的面积．解：（1）因为15sin B =π0,2B ⎛⎫∈ ⎪⎝⎭,所以27cos 1sin 8B B -=，因为2AB AC =，所以由正弦定理知sin 2sin C ABB AC==，即sin 2sin C B =，因为AM BM =，所以2AMC B ∠=∠，sin sin 22sin cos AMC B B B ∠==，在AMC 中，sin 2sin cos 7cos sin 2sin 8AC AMC B B B AM C B ∠====．（2）由题意知22AB AC ==，设BC x =，由余弦定理得222217cos 48x B x +-==，解得2BC =或32BC =．因为2AC BC ≤，所以2BC =，因为AM 为BAC ∠的平分线，BAM CAM ∠=∠所以11sin 2211sin 22ABM ACMAB AM BAM BM hS SAC AM CAM CM h⋅∠⨯==⋅∠⨯（h 为底边BC 的高）所以2BM AB CMAC ==，故1233CM BC ==，而由（1）知sin 2sin C B ==112sin 1223ACM S AC CM C =⋅⋅=⨯⨯=△． 2．（2022·福建省福州第一中学三模）已知ABC 的内角A 、B 、C 所对的边分别为a 、b 、c ，sinsin2A Bb c B +=. (1)求角C ；(2)若AB 边上的高线长为ABC 面积的最小值. 解：(1)由已知A B C π++=，所以sin sin cos 222A B C Cb b b π+-==，所以cossin 2C b c B =，由正弦定理得sin cos sin sin 2CB C B =，因为B 、()0,C π∈，则sin 0B >，022C π<<，cos 02C>，所以，cos sin 2C C =，则cos 2sin cos 222C C C =，所以1sin 22C =，所以26C π=，则3C π=.(2)由11sin 22ABCSc ab C =⋅=，得4ab c =，由余弦定理222222cos 2c a b ab C a b ab ab ab ab =+-=+-≥-=，即24c c ≥，因为0c >，则4c ≥，当且仅当4a b c ===取等号，此时ABC 面积的最小值为3．（2022·山东师范大学附中模拟预测）在①2sin cos sin b C B c B =+，②cos cos 2B bC a c=-两个条件中任选一个，补充在下面的问题中，并解答该问题.在ABC 中，内角A 、B 、C 所对的边分别是a 、b 、c ，且________. (1)求角B ；(2)若a c +=D 是AC 的中点，求线段BD 的取值范围.解：(1)选①，由2sin cos sin b C B c B =+及正弦定理可得2sin sin cos sin sin B C C B C B =+，所以，sin sin cos C B C B =，因为B 、()0,C π∈，所以，sin 0C >，则sin 0B B =>，所以，tan B =3B π∴=；选②，由cos cos 2B bC a c=-及正弦定理可得()sin cos 2sin sin cos B C A C B =-，所以，()2sin cos sin cos cos sin sin sin A B B C B C B C A =+=+=，A 、()0,B π∈，sin 0A ∴>，所以，1cos 2B =，则3B π=.(2)因为a c +=0a <<由已知AD DC =，即BD BA BC BD -=-，所以，2BD BA BC =+，所以，()222242BD BA BC BA BC BA BC =+=++⋅，即())22222242cos33BD c a ac c a ac a c ac aa π=++=++=+-=-22993,344a a ⎛⎡⎫=+=+∈ ⎪⎢ ⎣⎭⎝⎭，所以，34BD ≤<➢考点3 三角函数与解三角形的交汇问题（2022·浙江省新昌中学模拟预测）已知函数21()cos sin 2f x x x x ωωω=-+，其中0>ω，若实数12,x x 满足()()122f x f x -=时，12x x -的最小值为2π． (1)求ω的值及()f x 的对称中心；(2)在ABC 中，a ，b ，c 分别是角A ，B ，C的对边，若()1,f A a =-=ABC 周长的取值范围．解：(1)211cos 21()cos sin 2222x f x x x x x ωωωωω-=-+=-+12cos 2sin 226x x x πωωω⎛⎫=+=+ ⎪⎝⎭，显然()f x 的最大值为1，最小值为1-，则()()122f x f x -=时，12x x -的最小值等于2T，则22T π=，则22ππω=，1ω=；令2,6x k k ππ+=∈Z ，解得,122k x k ππ=-+∈Z ，则()f x 的对称中心为,0,122k k ππ⎛⎫-+∈ ⎪⎝⎭Z ； (2)()sin(2)16f A A π=+=-，22,62A k k πππ+=-+∈Z ，又()0,A π∈，则23A π=，由正弦定理得2sin sin sina b cA B C====，则2sin ,2sin b B c C ==，则周长为2sin 2sin 2sin 2sin 3a b c B C B B π⎛⎫++=+=+- ⎪⎝⎭3sin 3cos 32sin()3B B B π=++=++，又03B π<<，则2333B πππ<+<，则32sin()23B π<+≤，故周长的取值范围为(23,23⎤+⎦.[举一反三]1．（2022·浙江湖州·模拟预测）已知函数()sin(),0,0,02f x A x x R A πωϕωϕ⎛⎫=+∈>><< ⎪⎝⎭的部分图像如图所示．(1)求()f x 的解析式；(2)在锐角ABC 中，若边1BC =，且3212Af π⎛⎫-= ⎪⎝⎭，求ABC 周长的最大值．解：(1)由图得2A =，32ππ3π43124T ⎛⎫=--= ⎪⎝⎭，又2πT ω=，所以2ω=，将点π,012⎛⎫- ⎪⎝⎭代入()2sin(2)f x x ϕ=+，得πsin 06ϕ⎛⎫-+= ⎪⎝⎭，即π,6k k Z ϕπ=+∈，考虑到π02ϕ<<，故π6ϕ=，即()f x 的解析式为π()2sin 26f x x ⎛⎫=+ ⎪⎝⎭(2)由π3212A f ⎛⎫-= ⎪⎝⎭3sin A =及π0,2A ⎛⎫∈ ⎪⎝⎭，故π3A =，因为ABC 为锐角三角形，且π3A =，故ππ,62B ⎛⎫∈ ⎪⎝⎭由正弦定理，得sin sin sin a b c A B C ===所以2π1sin )1sin sin3a b c B C B B ⎤⎛⎫++=+=+- ⎪⎥⎝⎭⎦1π12sin cos 12sin 26B B B ⎛⎫⎛⎫=+⋅=++ ⎪ ⎪⎝⎭⎝⎭又ππ2π,633B ⎛⎫+∈ ⎪⎝⎭，故π2sin 6B ⎛⎫+∈ ⎪⎝⎭，故ABC 周长的最大值为3.2.（2022·山东淄博·三模）已知函数21()cos cos (0)2f x x x x ωωωω=-+>，其图像上相(1)求函数()f x 的解析式；(2)记ABC 的内角,,A B C 的对边分别为,,a b c ，4a =，12bc =，()1f A =．若角A 的平分线AD交BC 于D ，求AD 的长．解：(1)因为()211cos cos 2cos 222f x x x x x x ωωωωω=-+=-πsin 26x ω⎛⎫=- ⎪⎝⎭，设函数()f x 的周期为T ，由题意222444πT ⎛⎫+=⎪+ ⎝⎭，即2224ππω⎛⎫= ⎪⎝⎭，解得1ω=，所以()πsin 26f x x ⎛⎫=- ⎪⎝⎭.(2)由()1f A =得：sin 216A π⎛⎫-= ⎪⎝⎭，即22,Z 62A k k πππ-=+∈，解得,Z 3A k k ππ=+∈，因为[0,]A π∈，所以π3A =，因为A 的平分线AD 交BC 于D ，所以ABCABDACDSSS=+，即111sinsin sin 232626bc c AD b AD πππ=⋅⋅+⋅⋅，可得AD = 由余弦定理得：，()22222cos 3a b c bc A b c bc =+-=+-，而12bc =，得()252b c +=，因此AD ==。