2020年乌鲁木齐高考模拟理科数学试题及答案
新疆2020年数学高三理数第一次模拟考试试卷(II)卷

新疆2020年数学高三理数第一次模拟考试试卷(II)卷姓名:________ 班级:________ 成绩:________一、填空题 (共14题;共15分)1. (2分) (2019高一上·鸡东月考) 设集合,,则________, ________.2. (1分)(2017·成都模拟) 已知复数z=1﹣2i,那么复数的虚部是________.3. (1分) (2018高二下·溧水期末) 某校共有400名学生参加了一次数学竞赛,竞赛成绩都在[50,100]内,且频率分布直方图如图所示(成绩分组为[50,60),[60,70),[70,80),[80,90),[90,100],则在本次竞赛中,得分不低于80分的人数为________.4. (1分)(2016·江西模拟) 运行如图语句,则输出的结果T=________.5. (1分) (2017高一下·苏州期末) 集合A={1,2,3,4},B={1,2,3},点P的坐标为(m,n),m∈A,n∈B,则点P在直线x+y=5上的概率为________.6. (1分) (2019高三上·洛阳期中) 已知点P是曲线上任意一点,过点P向y轴引垂线,垂足为H,点Q是曲线上任意一点,则|PH|+|PQ|的最小值为________.7. (1分)已知集合A={a,b},B={a,b,c,d,e},满足条件A⊆M⊆B的集合M的个数为________.8. (1分) (2016高三上·天津期中) 若 =3,tan(α﹣β)=2,则tan(β﹣2α)=________.9. (1分) (2018高三上·酉阳期末) 函数的单调递增区间是________.10. (1分) (2020·新课标Ⅱ·文) 记为等差数列的前n项和.若,则________.11. (1分) (2019高一上·南昌月考) 以下说法中,正确的是________.(填上所有正确说法的序号):①已知角终边上一点,则;②函数的最小正周期是;③把函数的图象向右平移个单位长度可以得到的图象;④数的图象关于对称;⑤函数在上有零点,则实数的取值范图是 .12. (1分) (2017高二上·大庆期末) 圆x2+y2﹣2x﹣2y+1=0上的动点Q到直线3x+4y+8=0距离的最小值为________.13. (1分) (2019高一下·延边月考) 在中,,,为的三等分点,则 ________ .14. (1分) (2018高二下·泸县期末) 已知直三棱柱(侧棱垂直于底面的棱柱)各顶点都在同一球面上,且,,若此球的表面积等于,则 ________.二、解答题 (共12题;共105分)15. (10分)如图,在直四棱柱ABCD﹣A1B1C1D1中,底面ABCD是边长为2的正方形,E,F分别为线段DD1 ,BD的中点.(1)求证:EF∥平面ABC1D1;(2)四棱柱ABCD﹣A1B1C1D1的外接球的表面积为16π,求异面直线EF与BC所成的角的大小.16. (5分)(2017·辽宁模拟) 已知是函数f(x)=msinωx﹣cosωx(m>0)的一条对称轴,且f (x)的最小正周期为π(Ⅰ)求m值和f(x)的单调递增区间;(Ⅱ)设角A,B,C为△ABC的三个内角,对应边分别为a,b,c,若f(B)=2,,求的取值范围.17. (10分)(2017·湖北模拟) 已知函数f(x)=8a2lnx+x2+6ax+b(a,b∈R)(1)若曲线y=f(x)在点(1,f(1))处的切线方程为y=2x,求a,b的值;(2)若a≥1,证明:∀x1 ,x2∈(0,+∞),且x1≠x2 ,都有>14成立.18. (10分) (2019高二下·南昌期末) 已知椭圆的左焦点为,短轴的两个端点分别为A,B,且满足:,且椭圆经过点(1)求椭圆的标准方程;(2)设过点M 的动直线 (与X轴不重合)与椭圆C相交于P,Q两点,在X轴上是否存在一定点T,无论直线如何转动,点T始终在以PQ为直径的圆上?若有,求点T的坐标,若无,说明理由。
2020年新疆高考数学模拟试卷(理科)(4月份)

2020年新疆高考数学模拟试卷(理科)(问卷)(4月份)一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中只有一项是符合题目要求的.1.(5分)已知全集U R =,集合2{|340}A x x x =--<,{|10}B x x =-„,则集合(U A B =I ð)A .{|41}x x -<<B .{|11}x x -<„C .{|14}x x -<<D .{|14}x x <<2.(5分)若3(12z i i=+表示虚数单位),则复数z 在复平面内对应的点位于( ) A .第一象限B .第二象限C .第三象限D .第四象限3.(5分)若1sin(),(,0)232ππαα+=∈-,则tan (cos21)(αα+= )A .89-B .42-C .42D .894.(5分)设x ,y 满足约束条件2330,2330,10,x y x y y +-⎧⎪-+⎨⎪+⎩„……,则z x y =+的最大值是( ) A .4- B .1 C .2 D .45.(5分)已知,0(),0x lgx x f x a b x ->⎧=⎨+⎩„且(0)3f =,(1)4f -=,则((3))(f f -= )A .1-B .3lg -C .0D .16.(5分)一个几何体的三视图如图所示,若这个几何体的体积为205,则该几何体的外接球的表面积为( )A .36πB .64πC .81πD .100π7.(5分)下面四个条件中,是a b >成立的充分而不必要的条件为( )A .ac bc >B .1a b >-C .33a b >D .22log log a b >8.(5分)已知1A ,2A 分别是双曲线2222:1x y C a b -=的左,右顶点,F 为左焦点,以12A A 为直径的圆与双曲线C 的两条渐近线在x 轴上方,从左至右依次交于M ,N 两点,若//FM ON ,则该双曲线的离心率为( )A .2B .2C .233D .62 9.(5分)如图,正方形ABCD 中,M 、N 分别是BC 、CD 的中点,若AC AM BN λμ=+u u u r u u u u r u u u r ,则(λμ+= )A .2B .83C .65 D .8510.(5分)函数()cos()(0,)22f x A x ππωϕωϕ=+>-<<的部分图象如图中实线所示,图中圆C 与()f x 的图象交于M ,N 两点,且M 在y 轴上,则下列说法中正确的是( )A .函数()f x 的最小正周期是2πB .函数()f x 的图象关于点5(,0)3π成中心对称C .函数()f x 在5(,)1212ππ-单调递增D .将函数()f x 的图象向左平移3π后得到的关于y 轴对称 11.(5分)蜂巢是由工蜂分泌蜂蜡建成的从正面看,蜂巢口是由许多正六边形的中空柱状体连接而成,中空柱状体的底部是由三个全等的菱形面构成,菱形的一个角度是10928'︒,这样的设计含有深刻的数学原理、我国著名数学家华罗庚曾专门研究蜂巢的结构著有《谈谈与蜂房结构有关的数学问题》.用数学的眼光去看蜂巢的结构,如图,在六棱柱ABCDEF A B C D E -'''''的三个顶点A ,C ,E 处分别用平面BFM ,平面BDO ,平面DFN截掉三个相等的三棱锥M ABF -,O BCD -,N DEF -,平面BFM ,平面BDO ,平面DFN 交于点P ,就形成了蜂巢的结构.如图,设平面PBOD 与正六边形底面所成的二面角的大小为θ,则有:( )A .3tan 5444θ'=︒ B .3sin 5444θ=︒' C .3cos 44θ=︒'D .以上都不对 12.(5分)已知()cos ()2x xe e f x x x R -+=+∈,[1x ∀∈,4],(2)2f mx lnx f -- (2)(2)f lnx mx -+-,则实数m 的取值范围是( )A .212[,]22ln ln + B .12[,1]2ln e +C .22[,1]22ln ln + D .112[,]2ln e +二、填空题:本大题共4小题,每小题5分.13.(5分)二项式5()ax x+的展开式中x 的系数为10,则a = .14.(5分)根据公共卫生传染病分析中心的研究,传染病爆发疫情期间,如果不采取任何措施,则会出现感染者基数猛增,重症挤兑,医疗资源负荷不堪承受的后果.如果采取公共卫生强制措施,则会导致峰值下降,峰期后移.如图,设不采取措施、采取措施情况下分别服从正态分布(35,2)N ,(70,8)N ,则峰期后移了 天,峰值下降了 %(注:正态分2πσ15.(5分)如图,椭圆2222:1(0)x y C a b a b +=>>,与两条平行直线1:l y x b =+,2:l y x b=-分别交于四点A ,B ,C ,D ,且四边形ABCD 的面积为23b ,则直线AD 的斜率为16.(5分)在ABC ∆中,已知6AB =,60A ∠=︒,BC 边上的中线19AD =,则sin B = . 三、解答题:第17~21题每题12分,解答应在答卷的相应各题中写出文字说明,证明过程或演算步骤.17.(12分)如图,在多面体ABCDEF 中,底面ABCD 是正方形,梯形ADEF ⊥底面ABCD ,且12AF EF DE AD ===. (Ⅰ)证明:平面ABF ⊥平面CDF ; (Ⅱ)求直线AF 与平面CDE 所成角的大小.18.(12分)设n S 是公差不为零的等差数列{}n a 的前n 项和.已知2a 是1a 与5a 的等比中项,636S =.(Ⅰ)求{}n a 的通项公式;(Ⅱ)设12n a n n b a +=g ,求{}n b 的前n 项和n T .19.(12分)已知抛物线2:2(0)C y px p =>的焦点为F ,Q 是抛物线上的一点,(1,22)FQ =u u u r.。
2020届新疆乌鲁木齐市高考数学三诊试卷(理科)(有答案)(已审阅)

新疆乌鲁木齐市高考数学三诊试卷(理科)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合A={x|x2﹣3x+2<0},B={x|1<x<3},则()A.A=B B.A⊇B C.A⊆B D.A∩B=∅2.若复数为纯虚数(i为虚数单位),则实数m等于()A.﹣1 B.C.D.13.等差数列{a n}中,已知a1=2,a3+a5=10,则a7等于()A.5 B.6 C.8 D.104.“log2a>log2b”是“”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件5.明朝数学家程大位将“孙子定理”(也称“中国剩余定理”)编成易于上口的《孙子歌诀》:三人同行七十稀,五树梅花廿一支,七子团圆正半月,除百零五便得知.已知正整数n被3除余2,被5除余3,被7除余4,求n的最小值.按此歌诀得算法如图,则输出n的结果为()A.53 B.54 C.158 D.2636.下列函数中,以为最小正周期的偶函数是()A.B.y=sin22x﹣cos22xC.y=sin2x+cos2x D.y=sin2xcos2x7.已知实数x,y满足,则z=﹣3x﹣y的最大值为()A.﹣19 B.﹣7 C.﹣5 D.﹣48.已知x,y∈R,x2+y2+xy=315,则x2+y2﹣xy的最小值是()A.35 B.105 C.140 D.2109.某几何体的三视图如图所示,则该几何体的表面积为()A.8+2πB.8+3πC.10+2πD.10+3π10.已知双曲线的左,右焦点分别为F1,F2,点A在双曲线上,且AF2⊥x轴,若△AF1F2的内切圆半价为,则其离心率为()A.B.2 C.D.11.球O与棱长为2的正方体ABCD﹣A1B1C1D1的各个面都相切,点M为棱DD1的中点,则平面ACM截球O所得截面的面积为()A.B.πC.D.12.已知对任意实数k>1,关于x的不等式在(0,+∞)上恒成立,则a的最大整数值为()A.0 B.﹣1 C.﹣2 D.﹣3二、填空题(每题5分,满分20分,将答案填在答题纸上)13.若单位向量满足,则向量的夹角的余弦值为.14.学校拟安排六位老师至5 月1日至5月3日值班,要求每人值班一天,每天安排两人,若六位老师中王老师不能值5月2日,李老师不能值5月3日的班,则满足此要求的概率为.15.若P是抛物线y2=8x上的动点,点Q在以点C(2,0)为圆心,半径长等于1的圆上运动.则|PQ|+|PC|的最小值为.16.已知定义在R上的奇函数f(x)满足,S n为数列{a n}的前n项和,且S n=2a n+n,则f(a5)+f(a6)=.三、解答题(本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.△ABC中,角A,B,C的对边分别是a,b,c,已知(2a+b)sinA+(2b+a)sinB=2csinC.(Ⅰ)求C的大小;(Ⅱ)若,求△ABC周长的最大值.18.如图,在直三棱柱ABC﹣A1B1C1中,△ABC是正三角形,E是棱BB1的中点.(Ⅰ)求证平面AEC1⊥平面AA1C1C;(Ⅱ)若AA1=AB,求二面角C﹣AE﹣C1的平面角的余弦值.19.对某地区儿童的身高与体重的一组数据,我们用两种模型①y=bx+a,②y=ce dx拟合,得到回归方程分别为,,作残差分析,如表:身高x(cm)60708090100110体重y(kg)68101415180.410.01 1.21﹣0.190.41﹣0.360.070.12 1.69﹣0.34﹣1.12(Ⅰ)求表中空格内的值;(Ⅱ)根据残差比较模型①,②的拟合效果,决定选择哪个模型;(Ⅲ)残差大于1kg的样本点被认为是异常数据,应剔除,剔除后对(Ⅱ)所选择的模型重新建立回归方程.(结果保留到小数点后两位)附:对于一组数据(x1,y1),(x2,y2),…(x n,y n),其回归直线y=bx+a的斜率和截距的最小二乘法估计分别为,.20.在平面直角坐标系xOy中,M,N是x轴上的动点,且|OM|2+|ON|2=8,过点M,N分别作斜率为的两条直线交于点P,设点P的轨迹为曲线E.(Ⅰ)求曲线E的方程;(Ⅱ)过点Q(1,1)的两条直线分别交曲线E于点A,C和B,D,且AB∥CD,求证直线AB的斜率为定值.21.设函数.(Ⅰ)讨论f(x)的单调性;(Ⅱ)当a<﹣2时,讨论f(x)的零点个数.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.[选修4-4:坐标系与参数方程]22.已知直线l的参数方程为(t为参数,),以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,圆C的极坐标方程为ρ=2cosθ.(Ⅰ)讨论直线l与圆C的公共点个数;(Ⅱ)过极点作直线l的垂线,垂足为P,求点P的轨迹与圆C相交所得弦长.[选修4-5:不等式选讲]23.已知函数f(x)=|2x﹣1|+|x+a|.(Ⅰ)当a=1时,求y=f(x)图象与直线y=3围成区域的面积;(Ⅱ)若f(x)的最小值为1,求a的值.新疆乌鲁木齐市高考数学三诊试卷(理科)参考答案与试题解析一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合A={x|x2﹣3x+2<0},B={x|1<x<3},则()A.A=B B.A⊇B C.A⊆B D.A∩B=∅【考点】15:集合的表示法.【分析】化简集合A,即可得出集合A,B的关系.【解答】解:∵集合A={x|x2﹣3x+2<0}=(1,2),B={x|1<x<3},∴A⊆B.故选:C.2.若复数为纯虚数(i为虚数单位),则实数m等于()A.﹣1 B.C.D.1【考点】A5:复数代数形式的乘除运算.【分析】利用复数代数形式的乘除运算化简,由实部为0且虚部不为0列式求得m值.【解答】解:∵为纯虚数,∴,得m=1.故选:D.3.等差数列{a n}中,已知a1=2,a3+a5=10,则a7等于()A.5 B.6 C.8 D.10【考点】84:等差数列的通项公式.【分析】根据题意和等差数列的性质得到:a1+a7=a3+a5,代入数据求出a7的值.【解答】解:∵等差数列{a n}中,a1=2,a3+a5=10,∴由等差数列的性质得,a1+a7=a3+a5=10,解得a7=8,故选:C.4.“log2a>log2b”是“”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【考点】2L:必要条件、充分条件与充要条件的判断.【分析】利用指数函数与对数函数的单调性即可得出.【解答】解:∵.反之不成立,可能0>a>b.故选:A.5.明朝数学家程大位将“孙子定理”(也称“中国剩余定理”)编成易于上口的《孙子歌诀》:三人同行七十稀,五树梅花廿一支,七子团圆正半月,除百零五便得知.已知正整数n被3除余2,被5除余3,被7除余4,求n的最小值.按此歌诀得算法如图,则输出n的结果为()A.53 B.54 C.158 D.263【考点】EF:程序框图.【分析】【方法一】根据正整数n被3除余2,被5除余3,被7除余4,求出n的最小值.【方法二】按此歌诀得算法的程序框图,按程序框图知n的初值,代入循环结构求得n的值.【解答】解:【方法一】正整数n被3除余2,得n=3k+2,k∈N;被5除余3,得n=5l+3,l∈N;被7除余4,得n=7m+4,m∈N;求得n的最小值是53.【方法二】按此歌诀得算法如图,则输出n的结果为按程序框图知n的初值为263,代入循环结构得n=263﹣105﹣105=53,即输出n值为53.故选:A.6.下列函数中,以为最小正周期的偶函数是()A.B.y=sin22x﹣cos22xC.y=sin2x+cos2x D.y=sin2xcos2x【考点】H1:三角函数的周期性及其求法.【分析】利用诱导公式、二倍角公式化简函数的解析式,再利用三角函数的奇偶性、周期性,得出结论.【解答】解:∵cos(2x+)=﹣sin2x,是奇函数,故排除A;∵y=sin22x﹣cos22x=﹣cos4x,是偶函数,且,故B满足条件;∵y=sin2x+cos2x=sin(2x+)是非奇非偶函数,故排除C;∵y=sin2xcos2x=sin4x是奇函数,故排除D,故选:B.7.已知实数x,y满足,则z=﹣3x﹣y的最大值为()A.﹣19 B.﹣7 C.﹣5 D.﹣4【考点】7C:简单线性规划.【分析】由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,联立方程组求得最优解的坐标,代入目标函数得答案.【解答】解:由约束条件作出可行域如图所示,联立,解得A(2,﹣1),化目标函数z=﹣3x﹣y为y=﹣3x﹣z,由图可知,当直线z=﹣3x﹣y过点A(2,﹣1)时,z=﹣3x﹣y有最大值,最大值为﹣5.故选:C.8.已知x,y∈R,x2+y2+xy=315,则x2+y2﹣xy的最小值是()A.35 B.105 C.140 D.210【考点】7F:基本不等式.【分析】x,y∈R,x2+y2+xy=315,可得x2+y2=315﹣xy≥2xy,因此xy≤105.即可得出.【解答】解:∵x,y∈R,x2+y2+xy=315,∴x2+y2=315﹣xy,315﹣xy≥2xy,当且仅当x=y=±时取等号.∴xy≤105.∴x2+y2﹣xy=315﹣2xy≥315﹣210=105.故选:B.9.某几何体的三视图如图所示,则该几何体的表面积为()A.8+2πB.8+3πC.10+2πD.10+3π【考点】L!:由三视图求面积、体积.【分析】根据三视图可得该几何体为一个长方体和半个圆柱结合所成,即可求出表面积.【解答】解:根据三视图可得该几何体为一个长方体和半个圆柱结合所成,所以表面积.故选D.10.已知双曲线的左,右焦点分别为F1,F2,点A在双曲线上,且AF2⊥x轴,若△AF1F2的内切圆半价为,则其离心率为()A.B.2 C.D.【考点】KC:双曲线的简单性质.【分析】由题意可得A在双曲线的右支上,由双曲线的定义可得|AF1|﹣|AF2|=2a,设Rt△AF1F2内切圆半径为r,运用等积法和勾股定理,可得r=c﹣a,结合条件和离心率公式,计算即可得到所求值.【解答】解:由点A在双曲线上,且AF2⊥x轴,可得A在双曲线的右支上,由双曲线的定义可得|AF1|﹣|AF2|=2a,设Rt△AF1F2内切圆半径为r,运用面积相等可得S=|AF2|•|F1F2|=r(|AF1|+|AF2|+|F1F2|),由勾股定理可得|AF2|2+|F1F2|2=|AF1|2,解得r=,,则离心率e==,故选A.11.球O与棱长为2的正方体ABCD﹣A1B1C1D1的各个面都相切,点M为棱DD1的中点,则平面ACM截球O所得截面的面积为()A.B.πC.D.【考点】LG:球的体积和表面积.【分析】求出圆心到截面距离,利用d2+r2=1求出截面半径,即可求出截面的面积.【解答】解:设圆心到截面距离为d,截面半径为r,由V O﹣ACM =V M﹣AOC,即,∴,又d2+r2=1,∴,所以截面的面积为.故选D.12.已知对任意实数k>1,关于x的不等式在(0,+∞)上恒成立,则a的最大整数值为()A.0 B.﹣1 C.﹣2 D.﹣3【考点】6E:利用导数求闭区间上函数的最值.【分析】求出函数的导数,得到函数的单调区间,画出函数的大致图象,结合图象求出a的范围,从而确定a的最大整数值即可.【解答】解:令,依题意,对任意k>1,当x>0时,y=f(x)图象在直线y=k(x﹣a)下方,,x,f′(x),f(x)的变化如下表:x(0,1)1(1,+∞)f′(x)+0﹣f(x)递增递减y=f(x)的大致图象:则当a=0时,∵f'(0)=2,∴当1<k<2时不成立;当a=﹣1时,设y=k0(x+1)与y=f(x)相切于点(x0,f(x0)).则,解得.∴,故成立,∴当a∈Z时,a max=﹣1.故选:B.二、填空题(每题5分,满分20分,将答案填在答题纸上)13.若单位向量满足,则向量的夹角的余弦值为.【考点】9R:平面向量数量积的运算.【分析】设向量,的夹角为θ,根据向量的数量积公式计算即可.【解答】解:∵,∴,∵为单位向量,即,∴4﹣4cosθ+1=2,∴.故答案为:.14.学校拟安排六位老师至5 月1日至5月3日值班,要求每人值班一天,每天安排两人,若六位老师中王老师不能值5月2日,李老师不能值5月3日的班,则满足此要求的概率为.【考点】CB:古典概型及其概率计算公式.【分析】六位老师值班每天两人的排法有种,求出满足要求的排法有42种,即可求出概率.【解答】解:六位老师值班每天两人的排法有种,满足要求的排法有:第一种情况,王老师和李老师在同一天值班,则只能排在5月1号,有种;第二种情况,王老师和李老师不在同一天值班,有种,故共有42种.因此满足此要求的概率.故答案为.15.若P是抛物线y2=8x上的动点,点Q在以点C(2,0)为圆心,半径长等于1的圆上运动.则|PQ|+|PC|的最小值为3.【考点】K8:抛物线的简单性质.【分析】先根据抛物线方程求得焦点坐标,根据抛物线的定义可知P到准线的距离等于点P 到焦点的距离,进而问题转化为求点P到点Q的距离与点P到抛物线的焦点距离之和的最小值,根据图象可知当P,Q,F三点共线时P到点Q的距离与点P到抛物线的焦点距离之和的最小,为圆心到焦点F的距离减去圆的半径.【解答】解:由于点C为抛物线的焦点,则|PC|等于点P到抛物线准线x=﹣2的距离d.又圆心C到抛物线准线的距离为4,则|PQ|+|PC|=|PQ|+d≥3.当点P为原点,Q为(1,0)时取等号.故|PQ|+|PC|得最小值为3.故答案为:3.16.已知定义在R上的奇函数f(x)满足,S n为数列{a n}的前n项和,且S n=2a n+n,则f(a5)+f(a6)=3.【考点】8E:数列的求和.【分析】由已知求得函数周期,再由数列递推式求出数列通项,求得a5、a6的值,则答案可求.【解答】解:∵f(x)为奇函数,∴f(﹣x)=﹣f(x),又∵,∴.∴.∴f(x)是以3为周期的周期函数.∵数列{a n}满足a1=﹣1,且S n=2a n+n,∴当n≥2时,S n﹣1=2a n﹣1+n﹣1,则a n=2a n﹣2a n﹣1+1,即a n=2a n﹣1﹣1,∴a n﹣1=2(a n﹣1﹣1)(n≥2),则,∴.上式对n=1也成立.∴a5=﹣31,a6=﹣63.∴f(a5)+f(a6)=f(﹣31)+f(﹣63)=f(2)+f(0)=f(2)=﹣f(﹣2)=3.故答案为:3.三、解答题(本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.△ABC中,角A,B,C的对边分别是a,b,c,已知(2a+b)sinA+(2b+a)sinB=2csinC.(Ⅰ)求C的大小;(Ⅱ)若,求△ABC周长的最大值.【考点】HT:三角形中的几何计算.【分析】(Ⅰ)由正弦定理得到a2+b2﹣c2=﹣ab,由此利用余弦定理能求出.(Ⅱ)由正弦定理求出a=2sinA,b=2sinB.由此利用正弦加法定理求出周长l=,由此能求出△ABC周长的最大值.【解答】解:(Ⅰ)∵△ABC中,角A,B,C的对边分别是a,b,c,(2a+b)sinA+(2b+a)sinB=2csinC.∴由已知,得,即a2+b2﹣c2=﹣ab,∴,由0<C<π,∴.(Ⅱ)∵,∴,∴a=2sinA,b=2sinB.设周长为l,则==∵,∴2<2sin(A+)+≤2+,∴△ABC周长的最大值为.18.如图,在直三棱柱ABC﹣A1B1C1中,△ABC是正三角形,E是棱BB1的中点.(Ⅰ)求证平面AEC1⊥平面AA1C1C;(Ⅱ)若AA1=AB,求二面角C﹣AE﹣C1的平面角的余弦值.【考点】MT:二面角的平面角及求法;L Y:平面与平面垂直的判定.【分析】(Ⅰ)分别取AC,AC1的中点O,F,推导出四边形OBEF是平行四边形,从而OB ∥EF.推导出OB⊥面ACC1A1,从而EF⊥平面ACC1A1,由此能证明平面AEC1⊥平面AA1C1C.(Ⅱ)建立空间直角坐标系,利用向量法能求出二面角C﹣AE﹣C1的平面角的余弦值.【解答】证明:(Ⅰ)分别取AC,AC1的中点O,F,连结OB,OF,EF,则OF BE,∴四边形OBEF是平行四边形,∴OB∥EF.∵ABC﹣A1B1C1是直三棱柱,ABC是正三角形,O是AC的中点,∴OB⊥面ACC1A1,∴EF⊥平面ACC1A1,∴平面AEC1⊥平面AA1C1C.(Ⅱ)建立如图O﹣xyz空间直角坐标系,设AA1=AB=2,则,,设平面AEC的法向量为,平面AEC1的法向量为,则有,,得,设二面角C﹣AE﹣C1的平面角为θ,则.∴二面角C﹣AE﹣C1的平面角的余弦值为.19.对某地区儿童的身高与体重的一组数据,我们用两种模型①y=bx+a,②y=ce dx拟合,得到回归方程分别为,,作残差分析,如表:身高x(cm)60708090100110体重y(kg)68101415180.410.01 1.21﹣0.190.41﹣0.360.070.12 1.69﹣0.34﹣1.12(Ⅰ)求表中空格内的值;(Ⅱ)根据残差比较模型①,②的拟合效果,决定选择哪个模型;(Ⅲ)残差大于1kg的样本点被认为是异常数据,应剔除,剔除后对(Ⅱ)所选择的模型重新建立回归方程.(结果保留到小数点后两位)附:对于一组数据(x1,y1),(x2,y2),…(x n,y n),其回归直线y=bx+a的斜率和截距的最小二乘法估计分别为,.【考点】BK:线性回归方程.【分析】(Ⅰ)根据残差分析,把x=80代入得.10﹣10.39=﹣0.39,即可求表中空格内的值;(Ⅱ)求出残差的绝对值和,即可得出结论;(Ⅲ)确定残差大于1kg的样本点被剔除后,剩余的数据,即可求出回归方程.【解答】解:(Ⅰ)根据残差分析,把x=80代入得.10﹣10.39=﹣0.39.所以表中空格内的值为﹣0.39.(Ⅱ)模型①残差的绝对值和为0.41+0.01+0.39+1.21+0.19+0.41=2.62,模型②残差的绝对值和为0.36+0.07+0.12+1.69+0.34+1.12=3.7.2.62<3.7,所以模型①的拟合效果比较好,选择模型①.(Ⅲ)残差大于1kg的样本点被剔除后,剩余的数据如表由公式:,.得回归方程为y=0.24x﹣8.76.20.在平面直角坐标系xOy中,M,N是x轴上的动点,且|OM|2+|ON|2=8,过点M,N分别作斜率为的两条直线交于点P,设点P的轨迹为曲线E.(Ⅰ)求曲线E的方程;(Ⅱ)过点Q(1,1)的两条直线分别交曲线E于点A,C和B,D,且AB∥CD,求证直线AB的斜率为定值.【考点】J3:轨迹方程.【分析】(Ⅰ)求出M,N的坐标,利用|OM|2+|ON|2=8求曲线E的方程;(Ⅱ)利用点差法,求出CD的斜率,即可证明结论.【解答】(Ⅰ)解:设P(m,n),直线,令y=0,得,直线,令y=0,得.∴.∴曲线E的方程是;(Ⅱ)证明:∵AB∥CD,设,A(x A,y A),B(x B,y B),C (x C,y C),D(x D,y D),则(1﹣x A,1﹣y A)=λ(x C﹣1,y C﹣1),即x A=1+λ﹣λx C,y A=1+λ﹣λy C①,同理x B=1+λ﹣λx D,y B=1+λ﹣λy D②将A(x A,y A),B(x B,y B),代入椭圆方程得,化简得3(x A+x B)(x A﹣x B)=﹣4(y A+y B)(y A﹣y B)③把①②代入③,得3(2+2λ)(x C﹣x D)﹣3λ(x C+x D)(x C﹣x D)=﹣4(2+2λ)(y C﹣y D)+4λ(2+2λ)(y C+y D)(y C﹣y D)将C(x C,y C),D(x D,y D),代入椭圆方程,同理得3(x C+x D)(x C﹣x D)=﹣4(y C+y D)(y C ﹣y D)代入上式得3(x C﹣x D)=﹣4(y C﹣y D).即,∴直线AB的斜率为定值21.设函数.(Ⅰ)讨论f(x)的单调性;(Ⅱ)当a<﹣2时,讨论f(x)的零点个数.【考点】6B:利用导数研究函数的单调性;6D:利用导数研究函数的极值.【分析】(Ⅰ)求出函数的导数,通过讨论a的范围求出函数的单调区间即可;(Ⅱ)求出f(e﹣a),由f(1)>0,f(e﹣a)<0,及f(x)的单调性,可知f(x)在(1,e﹣a)上有唯一零点,取,则,根据函数的零点存在定理讨论即可.【解答】解:(Ⅰ)f'(x)=2(x﹣1)(lnx+a)(x>0).①当a=0时,f'(x)=2(x﹣1)lnx,当0<x<1时,f'(x)>0,当x>1时,f'(x)>0.当x=1时,f'(x)=0.∴f(x)在(0,+∞)递增;②当a>0时,令f'(x)=0,得,此时e﹣a<1.易知f(x)在(0,e﹣a)递增,(e﹣a,1)递减,(1,+∞)递增;③当a<0时,e﹣a>1.易知f(x)在(0,1)递增,(1,e﹣a)递减,(e﹣a,+∞)递增.(Ⅱ)当a<﹣2时,由(Ⅰ)知f(x)在(0,1)上递增,(1,e﹣a)上递减,(e﹣a,+∞)上递增,且,将x=e﹣a代入f(x),得,∵a<﹣2,∴f(e﹣a)<0.下面证明当x∈(0,1)时存在x0,使f(x0)<0.首先,由不等式lnx<x﹣1,∴,∴,∴.考虑到x2﹣2x=x(x﹣2)<0,∴.再令,可解出一个根为,∵a<﹣2,∴,∴,就取.则有f(x0)<0.由零点存在定理及函数f(x)在(0,1)上的单调性,可知f(x)在(0,1)上有唯一的一个零点.由f(1)>0,f(e﹣a)<0,及f(x)的单调性,可知f(x)在(1,e﹣a)上有唯一零点.下面证明在x∈(e﹣a,+∞)上,存在x1,使f(x1)>0,就取,则,∴,由不等式e x>x+1,则e﹣a+a>(﹣a+1)+a>0,即f(x1)>0.根据零点存在定理及函数单调性知f(x)在(e﹣a,+∞)上有一个零点.综上可知,f(x)当a<﹣2时,共有3个零点.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.[选修4-4:坐标系与参数方程]22.已知直线l的参数方程为(t为参数,),以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,圆C的极坐标方程为ρ=2cosθ.(Ⅰ)讨论直线l与圆C的公共点个数;(Ⅱ)过极点作直线l的垂线,垂足为P,求点P的轨迹与圆C相交所得弦长.【考点】Q4:简单曲线的极坐标方程.【分析】(Ⅰ)直线l为过定点A(0,1),倾斜角在内的一条直线,圆C的方程为(x﹣1)2+y2=1,即可讨论直线l与圆C的公共点个数;(Ⅱ)过极点作直线l的垂线,垂足为P,联立得,即可求点P的轨迹与圆C相交所得弦长.【解答】解:(Ⅰ)直线l为过定点A(0,1),倾斜角在内的一条直线,圆C的方程为(x﹣1)2+y2=1,∴当时,直线l与圆C有1个公共点;当时,直线l与圆C有2个公共点(Ⅱ)依题意,点P在以OA为直径的圆上,可得轨迹极坐标方程为.联立得.∴点P的轨迹与圆C相交所得弦长是.[选修4-5:不等式选讲]23.已知函数f(x)=|2x﹣1|+|x+a|.(Ⅰ)当a=1时,求y=f(x)图象与直线y=3围成区域的面积;(Ⅱ)若f(x)的最小值为1,求a的值.【考点】5B:分段函数的应用;R4:绝对值三角不等式.【分析】(Ⅰ)当a=1时可写出f(x)的解析式,进而可从图象上看出围成的区域即为三角形,计算即得结论;(Ⅱ)分与两种情况讨论即可.【解答】解:(Ⅰ)当a=1时,f(x)=|2x﹣1|+|x+1|=,其图象如图所示,易知y=f(x)图象与直线y=3交点坐标,所以围成区域的面积为 [1﹣(﹣1)]×(3﹣)=.(Ⅱ)当,即时,.所以,所以﹣a﹣1=1,解得a=﹣,满足题意;当,即时,,所以f(x)min=f()=|+a|=+a=1,解得a=,满足题意;综上所述,或.。
乌鲁木齐地区2020年高三年级第一次质量监测理科数学高三

乌鲁木齐地区2020年高三年级第一次质量监测理科数学问卷(卷面分值:150分;考试时间:120分钟)第Ⅰ卷(选择题 共60分)一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中只有一项是符合题目要求的。
1. 若集合}082|{2<--=x x x A ,}09|{2≤-=x x B ,则集合=B A .A ]3,2(- .B ]3,4(- .C )2,3[- .D )4,3[-2. 已知复数z 满足|43|)21(i i z +=+(i 是虚数单位),则z 的共轭复数z = .A i 21+ .B i 21- .C i 21+- .D i 21--3. 已知双曲线)0,0(12222>>=-b a by a x 的两条渐近线互相垂直,焦距为26,则该双曲线的实轴长为.A 3 .B 6 .C 9 .D 124. 已知m,n 为两条不同的直线,γβα,,为三个不同的平面,则下列命题正确的是.A 若αα//,//n m ,则n m //.B 若βγβα⊥⊥,且m =γα ,则β⊥m .C 若αα⊂⊂n m ,,ββ//,//n m ,则βα// .D 若βαβα⊥⊥,//,n m ,则n m ⊥5. 数列}{n a 是公差为2的等差数列,n S 为其前n 项和,且1341,,a a a 成等比数列,则=4S.A 8 .B 12 .C 16 .D 246. 若正整数n 除以正整数m 的余数为r ,则记为m n r mod =,例如5mod 122=,如图程序框图的算法源于我国古代著名的中国剩余定理,执行该程序框图,则输出的i 等于 .A 2 .B 4 .C 8 .D 167. 为了解某市居民用水情况,通过抽样,获得了100位居民某年的月均用水量(单位:吨),将该数据按照]5.4.4[),1,5.0[),5.0,0[ 分成9组,绘制了如图所示的频率分布直方图,政府要试行居民用水定额管理,制定了一个用水量标准a ,使85%的居民用水量不超过a ,按平价收水费,超出a 的部分按议价收费,则以下比较适合作为标准a 的是.A 2.5吨 .B 3吨 .C 3.5吨 .D 4吨8. 天文学中为了衡量星星的明暗程度,古希腊天文学家喜帕恰斯(Hipparchus ,又名依巴谷)在公元前二世纪首先提出了星等这个概念。
2020年新疆高考数学一模试卷(理科)
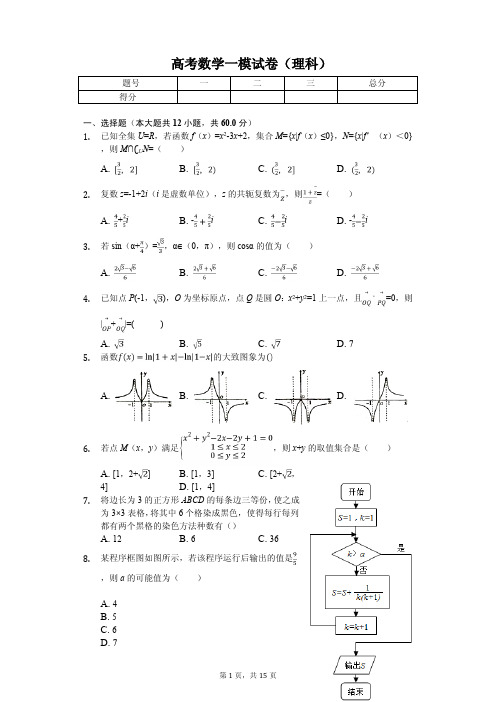
23. 设函数 f(x)=|x-2|+|3x-4|. (Ⅰ)解不等式 f(x)>5x;
(Ⅱ)若 f(x)的最小值为 m,若实数 a,b 满足 2a+3b=3m,求证:a2+b2 .
第 4 页,共 15 页
1.【答案】A
答案和解析
【解析】【分析】 本题主要考查集合的简单运算及导数的运算.属于基础题.先求出函数的导数后,解两 个不等式化简集合 M、N,后求补集 CUN,最后求交集 M∩CUN 即得. 【解答】 解:∵f(x)=x2-3x+2, ∴f′(x)=2x-3, 由 x2-3x+2≤0 得 1≤x≤2,
由 2x-3<0 得 x< ,
∴CUN=[ ,+∞),
∴M∩CUN=
.
故选 A.
2.【答案】B
【解析】解:∵z=-1+2i,
∴=
.
故选:B.
把 z=-1+2i 代入 ,再由复数代数形式的乘除运算化简得答案.
本题考查复数代数形式的乘除运算,考查复数的基本概念,是基础题.
B. [-3,-1]
C. (-∞,-3]
D. (-∞,-1]
10. 已知点 A 是抛物线 C:x2=4y 的对称轴与准线的交点,过点 A 作抛物线 C 的两条切
线,切点分别为 P,Q,则△APQ 的面积为( )
A. 2
B. 3
C. 4
D. 5
11. 已知三棱柱 ABC-A1B1C1 的侧棱与底面垂直,AA1=2,BC=2,∠BAC= ,则三棱柱
19. 港珠澳大桥是中国建设史上里程最长,投资最多,难度最大的跨海桥梁项目大桥建 设需要许多桥染构件.从某企业生产的桥梁构件中抽取 100 件测量这些桥梁构件的 质量指标值,由测量结果得到如图所示的频率分布直方图,质量指标值落在区间[55 ,65),[65,75),[75,85]内的频率之比为 4:2:1. (Ⅰ)求这些桥梁构件质量指标值落在区间[75,85]内的频率; (Ⅱ)若将频率视为概率,从该企业生产的这种桥梁构件中随机抽取 3 件,记这 3 件桥梁构件中质量指标值位于区间[45,75)内的桥梁构件件数为 X,求 X 的分布 列与数学期望.
2020年新疆乌鲁木齐市高考数学三模试卷1(问卷) (含答案解析)

2020年新疆乌鲁木齐市高考数学三模试卷1(问卷)一、选择题(本大题共12小题,共60.0分) 1. 设i 为虚数单位,则复数3−4i i=( )A. −4−3iB. −4+3iC. 4+3iD. 4−3i 2. 集合A ={x |−2<x <3},B ={x ∈Z |x 2−5x <0},则A ∩B =( )A. {1,2}B. {2,3}C. {1,2,3}D. {2,3,4}3. 命题“∀x ∈(0,π2),tanx >0”的否定是( )A. ∃x 0∈(0,π2),tanx 0≤0 B. ∃x 0∉(0,π2),tanx 0≤0 C. ∀x ∈(0,π2),tanx ≤0 D. ∃x 0∈(0,π2),tanx 0>0 4. 在等差数列{a n }中,a 1+a 5=8,a 4=7,则a 5=( )A. 11B. 10C. 7D. 3 5. 若角A 的终边过点(−4,−3),则sin2A 的值为( )A. −2425B. −725C. 2425D. 7256. 某校5人参加头脑奥林匹克竞赛选拔考试,已知这5人的平均考试成绩为81分,其中4人的成绩分别为73分、82分、82分、84分,由这5人得分所组成的一组数据的中位数是( )A. 81B. 82C. 83D. 847. 如图,在正方体ABCD −A 1B 1C 1D 1中,E,F,G,H 分别为A 1D 1,C 1D 1,BC,C 1C 的中点,则异面直线EF 与GH 所成的角大小等于( ).A. 45°B. 60°C. 90°D. 120°8. 在正三角形ABC 中,D 是BC 上的点,且AB =4,BD =1,则AB ⃗⃗⃗⃗⃗ ⋅AD⃗⃗⃗⃗⃗⃗ =( ) A. 4 B. 2 C. 2√3 D. 14 9. 设A(x 1,y 1),B(x 2,y 2)是抛物线y 2=2px(p >0)上的两点,并且满足OA ⊥OB.则y 1y 2等于( ) A. −4p 2B. 4p 2C. −2p 2D. 2p 210. 四面体ABCD 的外接球为O ,AD ⊥平面ABC ,AD =2,∠ACB =30°,AB =√3,则球O 的表面积为( )A. 32πB. 16πC. 12πD.223π11. 已知F 1,F 2分别是双曲线E :x 2a 2−y2b 2=1(a >0,b >0)的左、右焦点,若E 上存在一点P 使得|PF 1⃗⃗⃗⃗⃗⃗⃗ +PF 2⃗⃗⃗⃗⃗⃗⃗ |=b ,则E 的离心率的取值范围是( )A. [√52,+∞) B. (1,√52] C. [√5,+∞) D. (1,√5]12. 若函数f(x)=|4x −x 2|+2a −8至少有3个零点,则实数a 的取值范围是( )A. (−∞,3)B. (−∞,3]C. [2,3)D. [2,3]二、填空题(本大题共4小题,共20.0分)13. 今有四张卡片上分别写有“好”、“好”、“学”、“习”四个字,现将其随机排成一行,则恰好排成“好好学习”的概率是 _______.14. 已知 f(x)是定义在R 上的奇函数,当 x <0时,f(x)=log 2(2−x),则f(0)+f(2)=______. 15. 若函数y =2cosωx 在区间[0,2π3]上递减,且有最小值1,则ω的值可以是____. 16. 设等差数列{a n }满足a 2=5,a 6+a 8=30,则数列{1a n 2−1}的前n 项的和等于______.三、解答题(本大题共7小题,共82.0分)17. 在△ABC 中,cosA =√33,c =√3,a =3√2. (Ⅰ)求sin C 的值; (Ⅱ)求△ABC 的面积.18. 某学校在高二年级学生中进行了一次有关数学学习时长与学习效果的跟踪调查,为期一个月,共调查了120人.其中日平均学习数学时间超过40分钟的有70人,不超过40分钟的有50人.在一个月后的月考成绩中,日平均学习数学时间超过40分钟的学生中有42人成绩提升,不超过40分钟的学生中有18人成绩提升. (Ⅰ)根据以上数据建立一个2×2的列联表; 2×2的列联表:有提升没有提升合计超过40分钟不超过40分钟合计(Ⅱ)画出等高条形图;(Ⅲ)检验学习时长是否与成绩提升有关,可靠性有多大.P(K2≥k)0.1000.0500.0250.0100.001k 2.7063.8415.0246.63510.828,其中n=a+b+c+d.附:K2=2(a+b)(c+d)(a+c)(b+d)19.如图,三棱柱ABC−A1B1C1中,AC=CB,AB=AA1,∠BAA1=60°(1)证明:AB⊥A1C(2)若平面ABC⊥平面AA1B1B,AB=CB=2,求点A到平面BB1C1C的距离.20.已知椭圆x2a2+y2b2=1(a>b>0)的右焦点为F2(1,0),离心率为e=12.(1)求椭圆的方程:(2)设直线y=kx+1与椭圆相交于A.B两点.M,N分别为线段AF2,BF2的中点,若坐标原点O在以MN为直径的圆上,求k的值.21.已知函数f(x)=2x−e x+1(Ⅰ)求f(x)的最大值;(Ⅱ)已知x∈(0,1),af(x)<tanx,求a的取值范围。
2020年新疆乌鲁木齐市高考数学三模试卷(理科)(问卷) (解析版)

解: = .
故选:A.
2.已知集合A={x|(x﹣2)(x+2)≤0},B={﹣2,﹣1,0,1,2,3},则A∩B=( )
A.∅B.{0,1,2}
C.{﹣1,0,1}D.{﹣2,﹣1,0,1,2}
【分析】求出集合A,B,由此能求出A∩B.
解:∵集合A={x|(x﹣2)(x+2)≤0}={x|﹣2≤x≤2},
A. B.
C. D.
【分析】作出y=f(x)的函数图象,根据y=f(x)和y=logax的图象有5个交点列不等式组得出a的范围.
解:当x∈[0,2]时,f(x)=42﹣|x﹣1|﹣4,
故f(x)在[0,2]上的函数图象关于直线Байду номын сангаас=1对称,
又任意实数x∈[2k﹣2,2k+1﹣2](k∈N,k≥2),都有 ,
A. B. C. D.
6.某校有甲、乙两个数学建模兴趣班.其中甲班有40人,乙班有50人.现分析两个班的一次考试成绩,算得甲班的平均成绩是90分,乙班的平均成绩是81分,则这两个数学建模兴趣班所有同学的平均成绩是( )
A.85B.85.5C.86D.86.5
7.正方体ABCD﹣A′B′C′D′中,AB的中点为M,DD′的中点为N,则异面直线B′M与CN所成角的大小为( )
3.命题P:∀x∈R,x2+1≥1,则¬P是( )
A.∀x∈R,x2+1<1B.∀x∈R,x2+1≥1
C. D.
4.已知等差数列{an}满足a1+a3+a5=18,a3+a5+a7=30,则a2+a4+a6=( )
A.20B.24C.26D.28
2020年新疆乌鲁木齐市高考数学一诊试卷(理科)

2020年新疆乌鲁木齐市高考数学一诊试卷(理科)一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的第Ⅰ卷(选择题共60分)1.(5分)设集合2{|30}A x x x =-<,{|14}B x x =<<,则(A B =I ) A .(0,4)B .(1,4)C .(3,4)D .(1,3)2.(5分)若复数z 满足131iz i i+=--(其中i 为虚数单位),则||(z = )A .2B .3CD .43.(5分)已知m ,n 是两条不同的直线,α,β,γ是三个不同的平面,则下列命题正确的是( )A .若//m α,//n α,则//m nB .若αγ⊥,βγ⊥,则//αβC .若//m α,//n α,且m β⊂,n β⊂,则//αβD .若m α⊥,n β⊥,且αβ⊥,则m n ⊥4.(5分)设0.62a =,0.3log 0.6b =,3log 0.6c =,则有( ) A .c b a <<B .a b c <<C .b c a <<D .c a b <<5.(5分)已知向量,a b r r 满足||2,||3a b ==r r ,且a r 与b r 的夹角为3π,则(2)(2)(a b a b +-=r r r r) A .3-B .1-C .1D .36.(5分)已知双曲线22221(0,0)x y a b a b-=>>的左、右焦点分别为1F ,2F ,B 为虚轴的一个端点,且12120F BF ∠=︒,则双曲线的离心率为( )A .2B C .32D 7.(5分)执行如图所示的程序框图,则输出的(n = )A .3B .4C .5D .68.(5分)从数字1,2,3,4,5这五个数中,随机抽取2个不同的数,则这2个数的和为偶数的概率是( ) A .15B .25 C .35D .459.(5分)已知等比数列{}n a 的前n 项和为n S ,且14a ,22a ,3a 依次等差数列,若11a =,则5(S = ) A .16B .31C .32D .6310.(5分)将奇函数()3)cos(2)(0)f x x x ϕϕϕπ=+-+<<的图象向右平移ϕ个单位长度后得到函数()y g x =的图象,则下列关于()g x 的一个单调递减区间是( ) A .5(,)1212ππ-B .5(,)1212ππ-C .7(,)1212ππD .511(,)1212ππ 11.(5分)已知抛物线2:2(0)C y px p =>的焦点F ,点00(,66)()2pM x x >是抛物线上一点,以M 为圆心的圆与直线2p x =交于A 、B 两点(A 在B 的上方),若5sin 7MFA ∠=,则抛物线C 的方程为( ) A .24y x =B .28y x =C .212y x =D .216y x =12.(5分)已知函数22,0(),0x x f x x x ⎧=⎨<-⎩…,若对任意[,3]22m mx ∈+,都有()3()f x m f x +…,则实数m 的取值范围是( ) A .[4,)+∞B .[23,)+∞C .[3,)+∞D .[22,)+∞二、填空题:本大题共4个小题,每小题5分13.(5分)若x ,y 满足约束条件220100x y x y y --⎧⎪-+⎨⎪⎩„…„,则32z x y =+的最大值为 .14.(5分)已知4cos()35πα+=-,α为锐角,则sin α= .15.(5分)已知数列{}n a 满足:1112,(12,n n n n n a a a a n a a a +⎧==⎨+<⎩…,2,)⋯,若33a =,则1a = . 16.(5分)如图,已知在长方体1111ABCD A B C D -中,3AB =,4AD =,15AA =,点E 为1CC 上的一个动点,平面1BED 与棱1AA 交于点F ,给出下列命题:①四棱锥11B BED F -的体积为20;②存在唯一的点E ,使截面四边形1BED F 的周长取得最小值274;③当E 点不与C ,1C 重合时,在棱AD 上均存在点G ,使得//CG 平面1BED ; ④存在唯一一点E ,使得1B D ⊥平面1BED ,且165CE =. 其中正确的命题是 (填写所有正确的序号)三、解答题:第17~21题每题12分,解答应写出文字说明、证明过计算步骤17.(12分)ABC ∆的内角A ,B ,C 的对边分别是a ,b ,c ,且sin 3sin sin sin c C b AA B a b++=+.(Ⅰ)求C ∠的值;(Ⅱ)若2c =ABC ∆面积的最大值.18.(12分)如图,四棱锥P ABCD -中,PA ⊥底面ABCD ,//AD BC ,90BAD ∠=︒,2AD BC =,M 为PD 的中点.(Ⅰ)证明://CM 平面PAB ;(Ⅱ)若PBD ∆是等边三角形,求二面角A PB M --的余弦值.19.(12分)“团购”已经渗透到我们每个人的生活,这离不开快递行业的发展,如表是20132017-年全国快递业务量(x 亿件:精确到0.1)及其增长速度(%)y 的数据.(Ⅰ)试计算2012年的快递业务量;(Ⅱ)分别将2013年,2014年,⋯,2017年记成年的序号:1t ,2,3,4,5;现已知y 与t 具有线性相关关系,试建立y 关于t 的回归直线方程ˆˆˆybx a =+; (Ⅲ)根据(Ⅱ)问中所建立的回归直线方程,估算2019年的快递业务量.附:回归直线的斜率和截距地最小二乘法估计公式分别为:1221ˆni ii nii x ynxy bxnx ==-=-∑∑,ˆˆay bx =-20.(12分)已知椭圆2222:1(0)x y C a b a b+=>>过点2),左焦点(2,0)F -.(Ⅰ)求椭圆C 的标准方程;(Ⅱ)过点F 作于x 轴不重合的直线l ,l 与椭圆交于A ,B 两点,点A 在直线4x =-上的投影N 与点B 的连线交x 轴于D 点,D 点的横坐标0x 是否为定值?若是,请求出定值;若不是,请说明理由.21.(12分)已知函数221()()x f x alnx a R x-=-∈.(Ⅰ)讨论()f x 的单调性;(Ⅱ)若方程()2f x x =有两个不相等的实数根,求证:2()2af a e <+. 选考题:共10分,二选一22.(10分)在平面直角坐标系xOy 中,曲线221:40C x y x +-=,直线l 的参数方程为cos (sin x t t y t αα=⎧⎨=⎩为参数),其中(0,)6πα∈,以坐标原点O 为极点,x 轴非负半轴为极轴,建立极坐标系.(Ⅰ)求曲线1C 的极坐标方程和直线l 的普通方程;(Ⅱ)设(4,0)M ,2C 的极坐标方程ρθ=,A ,B 分别为直线l 与曲线1C ,2C 异于原点的公共点,当30AMB ∠=︒时,求直线l 的斜率. 23.函数()|22||3|f x x x =-++. (Ⅰ)求不等式()25f x x +…的解集;(Ⅱ)若()f x 的最小值为k ,且实数a ,b ,c 满足()a b c k +=,求证:22228a b c ++….2020年新疆乌鲁木齐市高考数学一诊试卷(理科)参考答案与试题解析一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的第Ⅰ卷(选择题共60分)1.(5分)设集合2{|30}A x x x =-<,{|14}B x x =<<,则(A B =I ) A .(0,4)B .(1,4)C .(3,4)D .(1,3)【解答】解:Q 集合2{|30}{|03}A x x x x x =-<=<<, {|14}B x x =<<,{|13}(1,3)A B x x ∴=<<=I .故选:D .2.(5分)若复数z 满足131iz i i+=--(其中i 为虚数单位),则||(z = )A .2B .3CD .4【解答】解:21(1)233321(1)(1)2i i iz i i i i i i i ++=-=-=-=---+,则|||2|2z =-=. 故选:A .3.(5分)已知m ,n 是两条不同的直线,α,β,γ是三个不同的平面,则下列命题正确的是( )A .若//m α,//n α,则//m nB .若αγ⊥,βγ⊥,则//αβC .若//m α,//n α,且m β⊂,n β⊂,则//αβD .若m α⊥,n β⊥,且αβ⊥,则m n ⊥【解答】解:由m ,n 是两条不同的直线,α,β,γ是三个不同的平面,知: 在A 中,若//m α,//n α,则m 与n 相交、平行或异面,故A 错误; 在B 中,若αγ⊥,βγ⊥,则α与β相交或平行,故B 错误;在C 中,若//m α,//n α,且m β⊂,n β⊂,则α与β相交或平行,故C 错误; 在D 中,若m α⊥,n β⊥,且αβ⊥,则线面垂直、面面垂直的性质定理得m n ⊥,故D 正确.。
2020届新疆乌鲁木齐一模数学(理科)试卷及答案

2020年新疆乌鲁木齐市高考数学一诊试卷(理科)一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的第Ⅰ卷(选择题共60分)1.(5分)设集合2{|30}A x x x =-<,{|14}B x x =<<,则(A B = )A .(0,4)B .(1,4)C .(3,4)D .(1,3)2.(5分)若复数z 满足131iz i i+=--(其中i 为虚数单位),则||(z =)A .2B .3CD .43.(5分)已知m ,n 是两条不同的直线,α,β,γ是三个不同的平面,则下列命题正确的是()A .若//m α,//n α,则//m nB .若αγ⊥,βγ⊥,则//αβC .若//m α,//n α,且m β⊂,n β⊂,则//αβD .若m α⊥,n β⊥,且αβ⊥,则m n⊥4.(5分)设0.62a =,0.3log 0.6b =,3log 0.6c =,则有()A .c b a<<B .a b c<<C .b c a<<D .c a b<<5.(5分)已知向量,a b 满足||2,||3a b == ,且a 与b 的夹角为3π,则(2)(2)(a b a b +-= )A .3-B .1-C .1D .36.(5分)已知双曲线22221(0,0)x y a b a b-=>>的左、右焦点分别为1F ,2F ,B 为虚轴的一个端点,且12120F BF ∠=︒,则双曲线的离心率为()A .2B C .32D 7.(5分)执行如图所示的程序框图,则输出的(n =)A .3B .4C .5D .68.(5分)从数字1,2,3,4,5这五个数中,随机抽取2个不同的数,则这2个数的和为偶数的概率是()A .15B .25C .35D .459.(5分)已知等比数列{}n a 的前n 项和为n S ,且14a ,22a ,3a 依次等差数列,若11a =,则5(S =)A .16B .31C .32D .6310.(5分)将奇函数())cos(2)(0)f x x x ϕϕϕπ=+-+<<的图象向右平移ϕ个单位长度后得到函数()y g x =的图象,则下列关于()g x 的一个单调递减区间是()A .5(,)1212ππ-B .5(,1212ππ-C .7(,)1212ππD .511(,1212ππ11.(5分)已知抛物线2:2(0)C y px p =>的焦点F ,点00()2pM x x >是抛物线上一点,以M 为圆心的圆与直线2p x =交于A 、B 两点(A 在B 的上方),若5sin 7MFA ∠=,则抛物线C 的方程为()A .24y x=B .28y x =C .212y x =D .216y x=12.(5分)已知函数22,0(),0x x f x x x ⎧=⎨<-⎩ ,若对任意[,3]22m mx ∈+,都有()3()f x m f x + ,则实数m 的取值范围是()A .[4,)+∞B.)+∞C .[3,)+∞D.)+∞二、填空题:本大题共4个小题,每小题5分13.(5分)若x ,y 满足约束条件220100x y x y y --⎧⎪-+⎨⎪⎩,则32z x y =+的最大值为.14.(5分)已知4cos()35πα+=-,α为锐角,则sin α=.15.(5分)已知数列{}n a 满足:1112,(12,n n n nn a a a a n a a a +⎧==⎨+<⎩ ,2,)⋯,若33a =,则1a =.16.(5分)如图,已知在长方体1111ABCD A B C D -中,3AB =,4AD =,15AA =,点E 为1CC 上的一个动点,平面1BED 与棱1AA 交于点F ,给出下列命题:①四棱锥11B BED F -的体积为20;②存在唯一的点E ,使截面四边形1BED F的周长取得最小值③当E 点不与C ,1C 重合时,在棱AD 上均存在点G ,使得//CG 平面1BED ;④存在唯一的点E ,使得1B D ⊥平面1BED ,且165CE =.其中正确的命题是(填写所有正确的序号)三、解答题:第17~21题每题12分,解答应写出文字说明、证明过计算步骤17.(12分)ABC ∆的内角A ,B ,C 的对边分别是a ,b ,c ,且sin 3sin sin sin c C b AA B a b++=+.(Ⅰ)求C ∠的值;(Ⅱ)若c =ABC ∆面积的最大值.18.(12分)如图,四棱锥P ABCD -中,PA ⊥底面ABCD ,//AD BC ,90BAD ∠=︒,2AD BC =,M 为PD 的中点.(Ⅰ)证明://CM 平面PAB ;(Ⅱ)若PBD ∆是等边三角形,求二面角A PB M --的余弦值.19.(12分)“团购”已经渗透到我们每个人的生活,这离不开快递行业的发展,如表是20132017-年全国快递业务量(x 亿件:精确到0.1)及其增长速度(%)y 的数据.(Ⅰ)试计算2012年的快递业务量;(Ⅱ)分别将2013年,2014年,⋯,2017年记成年的序号:1t ,2,3,4,5;现已知y 与t 具有线性相关关系,试建立y 关于t 的回归直线方程ˆˆˆybx a =+;(Ⅲ)根据(Ⅱ)问中所建立的回归直线方程,估算2019年的快递业务量.附:回归直线的斜率和截距地最小二乘法估计公式分别为:1221ˆniii nii x ynxy bxnx ==-=-∑∑,ˆˆay bx =-20.(12分)已知椭圆2222:1(0)x y C a b a b+=>>过点2),左焦点(2,0)F -.(Ⅰ)求椭圆C 的标准方程;(Ⅱ)过点F 作于x 轴不重合的直线l ,l 与椭圆交于A ,B 两点,点A 在直线4x =-上的投影N 与点B 的连线交x 轴于D 点,D 点的横坐标0x 是否为定值?若是,请求出定值;若不是,请说明理由.21.(12分)已知函数221()()x f x alnx a R x-=-∈.(Ⅰ)讨论()f x 的单调性;(Ⅱ)若方程()2f x x =有两个不相等的实数根,求证:2()2af a e <+.选考题:共10分,二选一22.(10分)在平面直角坐标系xOy 中,曲线221:40C x y x +-=,直线l 的参数方程为cos (sin x t t y t αα=⎧⎨=⎩为参数),其中(0,)6πα∈,以坐标原点O 为极点,x 轴非负半轴为极轴,建立极坐标系.(Ⅰ)求曲线1C 的极坐标方程和直线l 的普通方程;(Ⅱ)设(4,0)M ,2C 的极坐标方程ρθ=,A ,B 分别为直线l 与曲线1C ,2C 异于原点的公共点,当30AMB ∠=︒时,求直线l 的斜率.23.函数()|22||3|f x x x =-++.(Ⅰ)求不等式()25f x x + 的解集;(Ⅱ)若()f x 的最小值为k ,且实数a ,b ,c 满足()a b c k +=,求证:22228a b c ++ .2020年新疆乌鲁木齐市高考数学一诊试卷(理科)一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的第Ⅰ卷(选择题共60分)1.(5分)设集合2{|30}A x x x =-<,{|14}B x x =<<,则(A B = )A .(0,4)B .(1,4)C .(3,4)D .(1,3)【解答】解: 集合2{|30}{|03}A x x x x x =-<=<<,{|14}B x x =<<,{|13}(1,3)A B x x ∴=<<= .故选:D .2.(5分)若复数z 满足131iz i i+=--(其中i 为虚数单位),则||(z =)A .2B .3CD .4【解答】解:21(1)233321(1)(1)2i i iz i i i i i i i ++=-=-=-=---+,则|||2|2z =-=.故选:A .3.(5分)已知m ,n 是两条不同的直线,α,β,γ是三个不同的平面,则下列命题正确的是()A .若//m α,//n α,则//m nB .若αγ⊥,βγ⊥,则//αβC .若//m α,//n α,且m β⊂,n β⊂,则//αβD .若m α⊥,n β⊥,且αβ⊥,则m n⊥【解答】解:由m ,n 是两条不同的直线,α,β,γ是三个不同的平面,知:在A 中,若//m α,//n α,则m 与n 相交、平行或异面,故A 错误;在B 中,若αγ⊥,βγ⊥,则α与β相交或平行,故B 错误;在C 中,若//m α,//n α,且m β⊂,n β⊂,则α与β相交或平行,故C 错误;在D 中,若m α⊥,n β⊥,且αβ⊥,则线面垂直、面面垂直的性质定理得m n ⊥,故D 正确.故选:D .4.(5分)设0.62a =,0.3log 0.6b =,3log 0.6c =,则有()A .c b a<<B .a b c<<C .b c a<<D .c a b<<【解答】解:0.621a => ,0.3log 0.6(0,1)b =∈,3log 0.60c =<,则有c b a <<.故选:A .5.(5分)已知向量,a b 满足||2,||3a b == ,且a 与b 的夹角为3π,则(2)(2)(a b a b +-= )A .3-B .1-C .1D .3【解答】解: ||2,||3,,3a b a b π==<>=,∴221(2)(2)223242932312a b a b a b a b +-=-+=⨯-⨯+⨯⨯⨯=-.故选:B .6.(5分)已知双曲线22221(0,0)x y a b a b-=>>的左、右焦点分别为1F ,2F ,B 为虚轴的一个端点,且12120F BF ∠=︒,则双曲线的离心率为()A .2B C .32D 【解答】解:双曲线22221(0,0)x y a b a b-=>>的左、右焦点分别为1F ,2F ,B 为虚轴的一个端点,且12120F BF ∠=︒,可得c b =,22233c a c -=,2ce a===.故选:D .7.(5分)执行如图所示的程序框图,则输出的(n =)A .3B .4C .5D .6【解答】解:模拟程序的运行,可得0S =,1n =2S =,2n =满足条件30S <,执行循环体,246S =+=,3n =满足条件30S <,执行循环体,6814S =+=,4n =满足条件30S <,执行循环体,141630S =+=,5n =此时,不满足条件30S <,退出循环,输出n 的值为5.故选:C .8.(5分)从数字1,2,3,4,5这五个数中,随机抽取2个不同的数,则这2个数的和为偶数的概率是()A .15B .25C .35D .45【解答】解:由题意知本题是一个古典概型,从五个数中随机抽取2个不同的数有25C 种不同的结果,而这2个数的和为偶数包括2、4,1、3,1、5,3、5,四种取法,由古典概型公式得到25442105P C ===,故选:B .9.(5分)已知等比数列{}n a 的前n 项和为n S ,且14a ,22a ,3a 依次等差数列,若11a =,则5(S =)A .16B .31C .32D .63【解答】解:14a ,22a ,3a 依次等差数列,可得21344a a a =+,显然公比q 不为1,则211144a q a a q =+,即为2440q q -+=,解得2q =,则551(1)12531112a q S q --===--.故选:B .10.(5分)将奇函数())cos(2)(0)f x x x ϕϕϕπ=+-+<<的图象向右平移ϕ个单位长度后得到函数()y g x =的图象,则下列关于()g x 的一个单调递减区间是()A .5(,)1212ππ-B .5(,1212ππ-C .7(,)1212ππD .511(,1212ππ【解答】解: 奇函数())cos(2)2sin[(2)]6f x x x x πϕϕϕ=+-+=+-,06πϕ∴-=,6πϕ∴=,()2sin 2f x x =.把()f x 的图象向右平移6πϕ=个单位长度后得到函数()2sin(23y g x x π==-的图象,令3222232k x k πππππ+-+ ,求得5111212k x k ππππ++,故函数()g x 的单调递减区间为5[12k ππ+,11]12k ππ+,k Z ∈,故选:D .11.(5分)已知抛物线2:2(0)C y px p =>的焦点F ,点00()2pM x x >是抛物线上一点,以M 为圆心的圆与直线2p x =交于A 、B 两点(A 在B 的上方),若5sin 7MFA ∠=,则抛物线C 的方程为()A .24y x =B .28y x =C .212y x =D .216y x=【解答】解:如图所示,过M 点作CM ⊥直线22p px ==,垂足为C ,交准线于D ,∴5sin 7MCMFA MF∠==,由抛物线定义可得:MF MD =,∴005272px MC p MF x -==+00575722x p x p +=-03x p∴=点00()2pM x x >是抛物线上一点,∴202px =23666p ⨯=6p ∴=212y x∴=故选:C.12.(5分)已知函数22,0(),0x x f x x x ⎧=⎨<-⎩ ,若对任意[,3]22m mx ∈+,都有()3()f x m f x + ,则实数m 的取值范围是()A .[4,)+∞B.)+∞C .[3,)+∞D.)+∞【解答】解:22,0()(),0x x f x f x x x ⎧--==-⎨<⎩ ,∴函数22,0(),0x x f x x x ⎧=⎨<-⎩,为R 上的奇函数,又0x 时,2()f x x =为增函数,()f x ∴为定义域R 上的增函数.又3f =,()3())f x m f x f ∴+= , 对任意[,3]22m mx ∈+,()3())f x m f x f += ,()f x 为定义域R上的增函数,1)]1)(3)2max mm x ∴-=+ ,即13(11)22m ---=,解得:m .即实数m的取值范围是,)+∞,故选:B .二、填空题:本大题共4个小题,每小题5分13.(5分)若x ,y 满足约束条件220100x y x y y --⎧⎪-+⎨⎪⎩,则32z x y =+的最大值为6.【解答】解:作出不等式组对应的平面区域如图:由32z x y =+得3122y x z =-+,平移直线3122y x z =-+,由图象知当直线3122y x z =-+经过点(2,0)A 时,直线的截距最大,此时z 最大,最大值为326z =⨯=,故答案为:614.(5分)已知4cos()35πα+=-,α为锐角,则sin α=310+.【解答】解:因为4cos()35πα+=-,α为锐角,所以13sin()35απ+=,故11111sin sin()))33233ααππαπαπ=+-=+-+=故答案为:310+15.(5分)已知数列{}n a 满足:1112,(12,n n n n n a a a a n a a a +⎧==⎨+<⎩ ,2,)⋯,若33a =,则1a =34.【解答】解:由1112,2,n n n nn a a a a a a a +⎧=⎨+<⎩ ,①若31a a ,则3232a a ==,232a =,又21a a <与212a a =+相矛盾,21a a ∴ ,21322a a ==,得134a =;②若31a a <,则322a a =+,21a ∴=,由2112a a ==,112a =,与31a a <不符.∴134a =.故答案为:34.16.(5分)如图,已知在长方体1111ABCD A B C D -中,3AB =,4AD =,15AA =,点E 为1CC 上的一个动点,平面1BED 与棱1AA 交于点F ,给出下列命题:①四棱锥11B BED F -的体积为20;②存在唯一的点E ,使截面四边形1BED F 的周长取得最小值③当E 点不与C ,1C 重合时,在棱AD 上均存在点G ,使得//CG 平面1BED ;④存在唯一的点E ,使得1B D ⊥平面1BED ,且165CE =.其中正确的命题是①②③④(填写所有正确的序号)【解答】解:①由题意可得1//D F BE,1111111111111111111[](543543)2032232B BED F B BED B BFD D BEB D BFB V V V V V BB BC AB BBD A AB -----=+=+=+=⨯⨯+⨯⨯= ,所以①正确;②将长方体展开,如图所示,恰好过B 点时,截面的周长为12BD ,而在1BDD ∆中,1BD ==,所以最小值为1BED F 为平行四边形,且E 为展开图中唯一的点所以②正确;③E 嗲不与C ,1C 重合,则F 不会为A ,即CG 不在面1EBD 内,可作出CG 的平面与1EBD 平行,所以在棱AD 上均有相应的G ,使得//CG 面1EBD ,故③正确;④因为1BB BD =,可得对角面11BB D D 为正方形,可得11B D BD ⊥,若1BE B C ⊥时,由三垂线定理可得1B D BE ⊥,即有1B D ⊥面1EBD ,在矩形11BB C C 中,1BE B C ⊥,所以1CE BC BC CC =,所以1165BC BC CE CC ==,故④正确综上可得:正确为①②③④.故答案为:①②③④.三、解答题:第17~21题每题12分,解答应写出文字说明、证明过计算步骤17.(12分)ABC ∆的内角A ,B ,C 的对边分别是a ,b ,c ,且sin 3sin sin sin c C b AA B a b++=+.(Ⅰ)求C ∠的值;(Ⅱ)若c =ABC ∆面积的最大值.【解答】解:()I 由题意结合正弦定理可得,22()3a b ab c +=+,即222a b c ab +-=,所以2221cos 22a b c C ab +-==,(0,)C π∈ ,故13C π=,()II 由余弦定理可得,222a b ab =+-,所以,2222a b ab ab +=+ ,故2ab ,则1sin 22ABC S ab C ∆=,当且仅当a b ==时,面积取得最大值2.18.(12分)如图,四棱锥P ABCD -中,PA ⊥底面ABCD ,//AD BC ,90BAD ∠=︒,2AD BC =,M 为PD 的中点.(Ⅰ)证明://CM 平面PAB ;(Ⅱ)若PBD ∆是等边三角形,求二面角A PB M --的余弦值.【解答】解:(Ⅰ)证明:如图,取AD 中点N ,连结MN ,CN ,M 为PD 的中点,//MN AP ∴,2AD BC = ,AN BC ∴=,//BC AD ,∴四边形ABCN 是平行四边形,//AB CN ∴,CN NM N = ,BA AP A = ,∴平面//CMN 平面PAB ,CM ⊂ 平面MNC ,//CM ∴平面PAB .(Ⅱ)解:以A 为原点,AB 为x 轴,AD 为y 轴,AP 为z 轴,建立空间直角坐标系,PBD ∆ 为等边三角形,AB AD AP ∴==,设2AB =,则(0A ,0,0),(2B ,0,0),(0D ,2,0),∴(2BD =- ,2,0),(2BP =-,0,2),设平面BDP 的法向理(n x =,y ,)z ,则220220n BD x y n BP x z ⎧=-+=⎪⎨=-+=⎪⎩ ,令1z =,得(1n = ,1,1),AD ⊥ 平面PAB ,∴平面PAB 的法向量(0n =,1,0),||3cos ||||3n m n m θ∴== .∴二面角A PB M --的余弦值为3.19.(12分)“团购”已经渗透到我们每个人的生活,这离不开快递行业的发展,如表是20132017-年全国快递业务量(x 亿件:精确到0.1)及其增长速度(%)y 的数据.(Ⅰ)试计算2012年的快递业务量;(Ⅱ)分别将2013年,2014年,⋯,2017年记成年的序号:1t ,2,3,4,5;现已知y 与t 具有线性相关关系,试建立y 关于t 的回归直线方程ˆˆˆybx a =+;(Ⅲ)根据(Ⅱ)问中所建立的回归直线方程,估算2019年的快递业务量.附:回归直线的斜率和截距地最小二乘法估计公式分别为:1221ˆniii nii x ynxy bxnx ==-=-∑∑,ˆˆay bx =-【解答】解:(Ⅰ)设2012年的快递业务量为a ,则9261%aa-=,解得57.1a ≈;即2012年的快递业务量为57.1亿件;(Ⅱ)由题意列表得,t12345y6152485128计算1(12345)35t =⨯++++=,1(6152485128)485y =⨯++++=,512222222515(161252348451528)5348ˆ 6.712345535ii i i it ytybtt==-⨯+⨯+⨯+⨯+⨯-⨯⨯===-++++-⨯-∑∑,ˆˆ48(6.7)368.1ay bt =-=--⨯=,所以y 关于t 的线性回归方程是ˆ 6.768.1yt =-+;(Ⅲ)令6t =,计算2018年比上半年增长率是ˆ 6.7668.127.9(%)y=-⨯+=;所以2018年快递业务增长量为399.9(127.9%)511.5⨯+≈(亿件);令7t =,计算2018年比上半年增长率是ˆ 6.7768.121.2(%)y=-⨯+=;所以2019年快递业务增长量为511.5(121.2%)619.9⨯+≈(亿件).20.(12分)已知椭圆2222:1(0)x y C a b a b+=>>过点,左焦点(2,0)F -.(Ⅰ)求椭圆C 的标准方程;(Ⅱ)过点F 作于x 轴不重合的直线l ,l 与椭圆交于A ,B 两点,点A 在直线4x =-上的投影N 与点B 的连线交x 轴于D 点,D 点的横坐标0x 是否为定值?若是,请求出定值;若不是,请说明理由.【解答】解:(Ⅰ)椭圆2222:1(0)x y C a b a b+=>>过点,左焦点(2,0)F -,可得2c =,2a =a =,2b =,可得椭圆的方程为22184x y +=;(Ⅱ)D 点的横坐标为定值3-.理由如下:直线l 的斜率不为0,设:2AB x my =-,联立椭圆方程2228x y +=,可得22(2)440m y my +--=,设1(A x ,1)y ,2(B x ,2)y ,1y ,20y ≠,12242m y y m +=+,12242y y m=-+,两式相除可得1212y y m y y +=-,由1(4,)N y -,可设BN 的方程为2112(4)4y y y y x x --=++,令0y =,可得121122122021212144(2)44y x y y x y y my y x y y y y y y -------=-==---12121212122121212424333my y y y y y y y y y y y y y y y -+-++--===----.则D 点的横坐标为定值3-.21.(12分)已知函数221()()x f x alnx a R x-=-∈.(Ⅰ)讨论()f x 的单调性;(Ⅱ)若方程()2f x x =有两个不相等的实数根,求证:2()2af a e <+.【解答】解:2221()()x ax I f x x -+'=,0x >,对于221y x ax =-+,△28a =-,对称轴为4a x =,当△0时,即[a ∈-时,()0f x ' ,()f x 在(0,)+∞递增;当△0>时,即(a ∈-∞,-⋃,)+∞,方程有两个不同的根84a a m =,n =m n <,由于(0)1y =,当a <-,m ,0n <,函数在(0,)+∞递增;当a >,m ,0n >,函数()f x 在(0,)m ,(,)n +∞递增,(,)m n 递减;综上,a - 时,()f x 在(0,)+∞递增;a >时,()f x 在8(0,4a a --,8(4a a +-,)+∞上递增;在递减;()II 令1()()2g x f x x alnx x=-=--,0x >,方程()2f x x =有两个不相等的实数根,相当于函数()g x 由两个零点,222111()a ax axg x x x x x--'=-=-=,当0a 时,()0g x '>,()g x 在(0,)+∞递增,则()g x 至多只有一个零点,不成立;当0a >时,1(0,)x a ∈时,()g x 递增;1(x a ∈,)+∞递减,所以1()()min g x g a alna a==-+,由0a alna -+>,又0a >,所以a e >,因为1a是()g x 的极大值点,由11a>,g (1)10=-<,由a e >,a e a >,1a e a -<,21()a a a a g e alne e a e---=--=-+,对于2x y e x =-,易知y 在(,)e +∞递增,因为指数函数比幂函数增长的快,所以20a e a ->,()0a g e -<,所以函数()g x 在1(,)a e a -与1(a,1)各有一个零点,所以a e >,要证明2()2a f a e <+,即证明a e >时,211(22a alna e a---<成立,设h (a )211(2()a alna a e e a =--->,h'(a )22111lna a e =+--,由于h '(a )在(,)e +∞递减,所以h '(a )h '<(e )0=,所以h (a )在(,)e +∞递减;所以h (a )h <(e )22e e=-<,故原命题成立.选考题:共10分,二选一22.(10分)在平面直角坐标系xOy 中,曲线221:40C x y x +-=,直线l 的参数方程为cos (sin x t t y t αα=⎧⎨=⎩为参数),其中(0,)6πα∈,以坐标原点O 为极点,x 轴非负半轴为极轴,建立极坐标系.(Ⅰ)求曲线1C 的极坐标方程和直线l 的普通方程;(Ⅱ)设(4,0)M ,2C的极坐标方程ρθ=,A ,B 分别为直线l 与曲线1C ,2C 异于原点的公共点,当30AMB ∠=︒时,求直线l 的斜率.【解答】解:(Ⅰ)曲线221:40C x y x +-=,转换为极坐标方程为4cos ρθ=.直线l 的参数方程为cos (sin x t t y t αα=⎧⎨=⎩为参数),转换为直角坐标方程为tan y x α=,(0,6πα∈.(Ⅱ)由已知可得:θα=,则||4cos AB αα=-,1||tan 4sin AM ραα==,由于|||AM AB =,所以4sin )ααα=-,解得tan k α==所以直线的斜率为23.函数()|22||3|f x x x =-++.(Ⅰ)求不等式()25f x x + 的解集;(Ⅱ)若()f x 的最小值为k ,且实数a ,b ,c 满足()a b c k +=,求证:22228a b c ++ .【解答】解:(Ⅰ)31,1()|22||3|5,3131,3x x f x x x x x x x +>⎧⎪=-++=-+-⎨⎪--<-⎩.()25f x x + ,∴31251x x x ++⎧⎨>⎩ 或52531x x x -++⎧⎨-⎩ 或31253x x x --+⎧⎨<-⎩,4x ∴ 或30x - 或3x <-,0x ∴ 或4x ,∴不等式的解集为{|0x x 或4}x .(Ⅱ)由(Ⅰ)知()4min f x k ==.()4a b c k ∴+==,4ab ac ∴+=,22222222()()228a b c a b a c ab ac ∴++=++++= ,当且仅当a b c ===22228a b c ∴++ .。
2020年新疆高考数学(理科)模拟试卷(1)

2020年新疆高考数学(理科)模拟试卷(1)一.选择题(共12小题,满分60分,每小题5分)1.(5分)据记载,欧拉公式e ix =cos x +i sin x (x ∈R )是由瑞士著名数学家欧拉发现的,该公式被誉为“数学中的天桥”.特别是当x =π时,得到一个令人着迷的优美恒等式e πi +1=0,将数学中五个重要的数(自然对数的底e ,圆周率π,虚数单位i ,自然数的单位1和零元0)联系到了一起,有些数学家评价它是“最完美的数学公式”.根据欧拉公式,若复数e π4i 的共轭复数为z ,则z =( ) A .−√22−√22i B .−√22+√22i C .√22+√22i D .√22−√22i 2.(5分)已知集合A ={0,1,2,3},集合B ={x ||x |≤2},则A ∩B =( ) A .{0,3}B .{0,1,2}C .{1,2}D .{0,1,2,3}3.(5分)函数f (x )=x 2+e |x |的图象只可能是( )A .B .C .D .4.(5分)已知向量a →=(1,3),b →=(3,﹣2),则向量2a →•b →=( ) A .12B .﹣3C .3D .﹣65.(5分)已知F 2为双曲线C :x 2a 2−y 2b 2=1(a >0,b >0)的右焦点,且F 2在C 的渐近线上的射影为点H ,O 为坐标原点,若|OH |=|F 2H |,则C 的渐近线方程为( ) A .x ±y =0B .√3x ±y =0C .x ±√3y =0D .x ±2y =06.(5分)△ABC 的三个内角A ,B ,C 所对的边分别为a ,b ,c ,M 在边AB 上,且AM =13AB ,b =2,CM =2√73,2sinA−sinB sin2B=cb,则S △ABC =( )A .3√34B .√3C .2√3D .8√337.(5分)中国古代用算筹来进行记数,算筹的摆放形式有纵横两种形式(如图所示),表示一个多位数时,像阿拉伯记数﹣样,把各个数位的数码从左到右排列,但各位数码的筹式需要纵横相间,其中个位、百位、万…用纵式表示,十位、千位、十万位用横式表示,例如6613用算筹表示就是,则8335可用算筹表示为( )A .B .C .D .8.(5分)甲、乙两位同学将高三6次物理测试成绩做成如图所示的茎叶图加以比较(成绩均为整数满分100分),乙同学对其中一次成绩记忆模糊,只记得成绩不低于90分且不是满分,则甲同学的平均成绩超过乙同学的平均成绩的概率为( )A .25B .12C .35D .459.(5分)如图,在菱形ABCD 中,∠ABC =2π3,线段AD ,BD 的中点分别E ,F .现将 MBD 沿对角线BD 翻折,当二面角A ﹣BD ﹣C 的余弦值为13时,异面直线BE 与CF 所成角的正弦值是( )A .√356B .16C .2√65 D .1510.(5分)已知函数f(x)=|cos(ωx +π6)|(ω>0)在[0,π2]上单调递减,则ω的最大值为( )A .13B .23C .43D .5311.(5分)已知函数f (x )是定义在R 上的奇函数,f(32+x)=f(x −32),且x ∈(−32,0)时,f (x )=log 2(﹣3x +1),则f (2020)=( ) A .4B .log 27C .2D .﹣212.(5分)已知F 1,F 2是椭圆C :x 2a +y 2b =1(a >b >0)的左、右焦点,A 是C 的左顶点,点P 在过A 且斜率为√36的直线上,△PF 1F 2为等腰三角形,∠F 1F 2P =120°,则C 的离心率为( ) A .23B .12C .13D .14二.填空题(共4小题,满分20分,每小题5分)13.(5分)曲线f (x )=2x 3﹣x ﹣1在点(0,f (0))处的切线在x 轴上的截距为 . 14.(5分)若实数x ,y 满足|x ﹣3|+|y ﹣2|≤1,则z =yx 的最小值是 .15.(5分)已知正三棱锥S ﹣ABC 的侧棱长为4√3,底面边长为6,则该正三棱锥外接球的表面积是 .16.(5分)已知函数f (x )=ax −2x−3lnx ,其中a 为实数.若函数f (x )在区间(1,+∞)上有极小值,无极大值,则a 的取值范围是 . 三.解答题(共5小题,满分60分,每小题12分)17.(12分)在等比数列{a n }中,公比q ∈(0,1),且满足a 3=2,a 1a 3+2a 2a 4+a 3a 5=25. (1)求数列{a n }的通项公式;(2)设b n =log 2a n ,数列{b n }的前n 项和为S n ,当S 11+S 22+⋯+S n n取最大值时,求n的值.18.(12分)如图1,四边形PBCD 是等腰梯形,BC ∥PD ,PB =BC =CD =2,PD =4,A 为PD 的中点,将△ABP 沿AB 折起,如图2,点M 是棱PD 上的点. (1)若M 为PD 的中点,证明:平面PCD ⊥平面ABM ;(2)若PC =√6,试确定M 的位置,使二面角M ﹣AB ﹣D 的余弦值等于√55.19.(12分)某医院体检中心为回馈大众,推出优惠活动:对首次参加体检的人员,按200元/次收费,并注册成为会员,对会员的后续体检给予相应优惠,标准如下: 体检次序 第一次 第二次 第三次 第四次 第五次及以上收费比例10.950.900.850.8该休检中心从所有会员中随机选取了100位对他们在本中心参加体检的次数进行统计,得到数据如表: 检次数 一次 两次 三次 四次 五次及以上频数60201244假设该体检中心为顾客体检一次的成本费用为150元,根据所给数据,解答下列问题: (Ⅰ)已知某顾客在此体检中心参加了3次体检,求这3次体检,该体检中心的平均利润;(Ⅱ)该体检中心要从这100人里至少体检3次的会员中,按体检次数用分层抽样的方法抽出5人,再从这5人中抽取2人,每人发放现金200元.用5表示体检3次的会员所得现金和,求ξ的分布列及E (ξ). 20.(12分)已知曲线f(x)=mx−m e x 在点(1,f (1))处的切线斜率为−1e. (1)求m 的值,并求函数f (x )的极小值;(2)当x ∈(0,π)时,求证:e x sin x ﹣x +e x ﹣2+1>e x x cos x .21.(12分)已知椭圆C :x 2a +y 2=1(a >1)的离心率是√22. (Ⅰ)求椭圆C 的方程;(Ⅱ)已知F 1,F 2分别是椭圆C 的左、右焦点,过F 2作斜率为k 的直线l ,交椭圆C 于A ,B 两点,直线F 1A ,F 1B 分别交y 轴于不同的两点M ,N .如果∠MF 1N 为锐角,求k 的取值范围.四.解答题(共1小题,满分10分,每小题10分)22.(10分)在直角坐标系xOy 中,参数方程{x =cosθy =sinθ(其中θ为参数)的曲线经过伸缩变换φ:{x′=2xy′=y 得到曲线C ,以原点O 为极点,x 轴正半轴为极轴建立极坐标系,曲线D 的极坐标方程为ρsin(θ+π4)=3√102. (Ⅰ)求曲线C 的普通方程及曲线D 的直角坐标方程;(Ⅱ)设M 、N 分别为曲线C 和曲线D 上的动点,求|MN |的最小值. 五.解答题(共1小题)23.已知函数f (x )=|x ﹣a 2|+|x ﹣2a +3|,g (x )=x 2+ax +3. (1)当a =1时,解关于x 的不等式f (x )≤6;(2)若对任意x 1∈R ,都存在x 2∈R ,使得不等式f (x 1)>g (x 2)成立,求实数a 的取值范围.2020年新疆高考数学(理科)模拟试卷(1)参考答案与试题解析一.选择题(共12小题,满分60分,每小题5分)1.(5分)据记载,欧拉公式e ix=cos x+i sin x(x∈R)是由瑞士著名数学家欧拉发现的,该公式被誉为“数学中的天桥”.特别是当x=π时,得到一个令人着迷的优美恒等式eπi+1=0,将数学中五个重要的数(自然对数的底e,圆周率π,虚数单位i,自然数的单位1和零元0)联系到了一起,有些数学家评价它是“最完美的数学公式”.根据欧拉公式,若复数e π4i的共轭复数为z,则z=()A.−√22−√22i B.−√22+√22i C.√22+√22i D.√22−√22i【解答】解:复数e π4i=cosπ4+i sinπ4=√22+√22i,则共轭复数为z=√22−√22i,故选:D.2.(5分)已知集合A={0,1,2,3},集合B={x||x|≤2},则A∩B=()A.{0,3}B.{0,1,2}C.{1,2}D.{0,1,2,3}【解答】解:A={0,1,2,3},B={x|﹣2≤x≤2},∴A∩B={0,1,2}.故选:B.3.(5分)函数f(x)=x2+e|x|的图象只可能是()A.B.C.D.【解答】解:因为对于任意的x∈R,f(x)=x2+e|x|>0恒成立,所以排除A,B,由于f(0)=02+e|0|=1,则排除D,故选:C .4.(5分)已知向量a →=(1,3),b →=(3,﹣2),则向量2a →•b →=( ) A .12B .﹣3C .3D .﹣6【解答】解:向量a →=(1,3),b →=(3,﹣2), 则向量2a →=(2,6),所以2a →•b →=2×3+6×(﹣2)=﹣6. 故选:D .5.(5分)已知F 2为双曲线C :x 2a −y 2b =1(a >0,b >0)的右焦点,且F 2在C 的渐近线上的射影为点H ,O 为坐标原点,若|OH |=|F 2H |,则C 的渐近线方程为( ) A .x ±y =0B .√3x ±y =0C .x ±√3y =0D .x ±2y =0【解答】解:双曲线C :x 2a −y 2b =1(a >0,b >0)的渐近线方程为y =±b ax ,若|OH |=|F 2H |,可得在直角三角形OHF 2中,∠HOF 2=45°, 可得C 的渐近线方程为x ±y =0. 故选:A .6.(5分)△ABC 的三个内角A ,B ,C 所对的边分别为a ,b ,c ,M 在边AB 上,且AM =13AB ,b =2,CM =2√73,2sinA−sinB sin2B=cb,则S △ABC =( )A .3√34B .√3C .2√3D .8√33【解答】解:△ABC 中,2sinA−sinB sin2B=c b,∴2sinA−sinB sin2B=sinC sinB,∴2sin C cos B =2sin A ﹣sin B ,∴2sin C cos B =2(sin B cos C +cos B sin C )﹣sin B , ∴cos C =12,又C ∈(0°,180°), ∴C =60°; 又 AM →=13AB →,∴CM →=CA →+AM →=CA →+13AB →=CA →+13(CB →−CA →)=23CA →+13CB →, ∴3CM →=2CA →+CB →,∴9CM →2=4CA →2+CB →2+4CA →•CB →;∴28=16+a 2+4a ,解得a =2或a =﹣6(不合题意,舍去),∴△ABC 的面积为S △ABC =12×2×2sin60°=√3. 故选:B .7.(5分)中国古代用算筹来进行记数,算筹的摆放形式有纵横两种形式(如图所示),表示一个多位数时,像阿拉伯记数﹣样,把各个数位的数码从左到右排列,但各位数码的筹式需要纵横相间,其中个位、百位、万…用纵式表示,十位、千位、十万位用横式表示,例如6613用算筹表示就是,则8335可用算筹表示为( )A .B .C .D .【解答】解:∵个位、百位、万…用纵式表示,十位、千位、十万位用横式表示, ∴8335用算筹表示的话,千位上的8是横式,百位上的3是纵式,十位上的3是横式,个位上的5时纵式, 故选:B .8.(5分)甲、乙两位同学将高三6次物理测试成绩做成如图所示的茎叶图加以比较(成绩均为整数满分100分),乙同学对其中一次成绩记忆模糊,只记得成绩不低于90分且不是满分,则甲同学的平均成绩超过乙同学的平均成绩的概率为( )A .25B .12C .35D .45【解答】解:由题意可得x 甲=16(88+87+85+92+93+95)=90, 设被污损的数字为x ,则x 乙=16(85+86+88+90+99+x )=89+x6, 满足题意时,x 甲>x 乙. 即:90>89+x6,解得x <6,即x 可能的取值为0,1,2,3,4,5,结合古典概型计算公式可得满足题意的概率为:p =610=35. 故选:C .9.(5分)如图,在菱形ABCD 中,∠ABC =2π3,线段AD ,BD 的中点分别E ,F .现将 MBD 沿对角线BD 翻折,当二面角A ﹣BD ﹣C 的余弦值为13时,异面直线BE 与CF 所成角的正弦值是( )A .√356B .16C .2√65D .15【解答】解:设菱形边长为2,过E 作EH ⊥BD ,交BD 于H 点, 设BE 与CF 的夹角为θ,则θ∈[0,π2], 记A ﹣BD ﹣C =α,则cos α=13, CF →⋅BE →=CF →⋅(BH →+HE →)=CF →⋅HE →,即CF →⋅BE →=|CF →|⋅|HE →|cos(π−α)=√3×√32×(−13)=−12, 则|CF →||BE →|cosθ=12, ∴cosθ=16,即sinθ=√356,故选:A .10.(5分)已知函数f(x)=|cos(ωx +π6)|(ω>0)在[0,π2]上单调递减,则ω的最大值为( ) A .13B .23C .43D .53【解答】解:当0≤x ≤π2时,0≤ωx ≤π2ω,π6≤ωx +π6≤π2ω+π6, ∵y =|cos x |在[0,π2]上为减函数,∴要使f (x )在[0,π2]上单调递减, 则π2ω+π6≤π2得π2ω≤π3,即0<ω≤23,即ω的最大值为23,故选:B .11.(5分)已知函数f (x )是定义在R 上的奇函数,f(32+x)=f(x −32),且x ∈(−32,0)时,f (x )=log 2(﹣3x +1),则f (2020)=( ) A .4B .log 27C .2D .﹣2【解答】解:根据题意,f (x )满足f(32+x)=f(x −32),即f (x +3)=f (x ),函数f (x )是周期为3的周期函数,则f (2020)=f (1+2019)=f (1),又由f (x )为奇函数,则f (1)=﹣f (﹣1)=﹣log 2(3+1)=﹣2, 故选:D .12.(5分)已知F 1,F 2是椭圆C :x 2a 2+y 2b 2=1(a >b >0)的左、右焦点,A 是C 的左顶点,点P 在过A 且斜率为√36的直线上,△PF 1F 2为等腰三角形,∠F 1F 2P =120°,则C 的离心率为( ) A .23B .12C .13D .14【解答】解:由题意可知:A (﹣a ,0),F 1(﹣c ,0),F 2(c ,0), 直线AP 的方程为:y =√36(x +a ),由∠F 1F 2P =120°,|PF 2|=|F 1F 2|=2c ,则P (2c ,√3c ), 代入直线AP :√3c =√36(2c +a ),整理得:a =4c , ∴题意的离心率e =ca =14. 故选:D .二.填空题(共4小题,满分20分,每小题5分)13.(5分)曲线f (x )=2x 3﹣x ﹣1在点(0,f (0))处的切线在x 轴上的截距为 ﹣1 . 【解答】解:f ′(x )=6x 2﹣1, ∴k =f ′(0)=﹣1,而f (0)=﹣1, ∴切线方程为y +1=﹣x , 令y =0得x =﹣1, 故答案为:﹣1.14.(5分)若实数x ,y 满足|x ﹣3|+|y ﹣2|≤1,则z =yx的最小值是13.【解答】解:不等式|x ﹣3|+|y ﹣2|≤1可表示为如图所示的平面区域.z =y x为该区域内的点与坐标原点连线的斜率,显然,当x =3,y =1时,z =y x取得最小值13.故答案为:13.15.(5分)已知正三棱锥S﹣ABC的侧棱长为4√3,底面边长为6,则该正三棱锥外接球的表面积是64π.【解答】解:如图所示:由正棱锥得,顶点在底面的投影是三角形ABC的外接圆的圆心O',外接圆的半径r,正三棱锥的外接球的球心在高SO'所在的直线上,设为O,连接OA得:r=6 sinπ3,所以r=2√3,即O'A=2√3,所以三棱锥的高h=√SA2−O′A2=√(4√3)2−(2√3)2=6,由勾股定理得,R2=r2+(R﹣h)2,解得:R=4,所以外接球的表面积S=4πR2=64π.故答案为:64π.16.(5分)已知函数f(x)=ax−2x−3lnx,其中a为实数.若函数f(x)在区间(1,+∞)上有极小值,无极大值,则a的取值范围是(0,1).【解答】解:∵函数f(x)=ax−2x−3lnx,∴f'(x)=a+2x2−3x=ax2−3x+2x2,∵函数在区间(1,+∞)上有极小值无极大值,∴f '(x )=0即ax 2﹣3x +2=0在区间(1,+∞)上有1个变号实根,且x <1时,f ′(x )<0,x >1时,f ′(x )>0,结合二次函数的性质可知,{a >0a −1<0,单调递减,解可得,0<a <1. 当a =1时,f ′(x )=(x−1)(x−2)x 2,因为x >1,所以x ﹣1>0,x 2>0,故当x >2时,f ′(x )>0,函数单调递增,当1<x <2时,f ′(x )<0,函数单调递减,故当x =2时,函数取得极小值,满足题意,当a =0时,f (x )在(1,+∞)单调递减,没有极值. 故答案为:(0,1].三.解答题(共5小题,满分60分,每小题12分)17.(12分)在等比数列{a n }中,公比q ∈(0,1),且满足a 3=2,a 1a 3+2a 2a 4+a 3a 5=25. (1)求数列{a n }的通项公式;(2)设b n =log 2a n ,数列{b n }的前n 项和为S n ,当S 11+S 22+⋯+S n n取最大值时,求n的值.【解答】解:(1)a 1a 3+2a 2a 4+a 3a 5=25, 可得a 22+2a 2a 4+a 42=(a 2+a 4)2=25,由a 3=2,即a 1q 2=2,①,可得a 1>0,由0<q <1,可得a n >0, 可得a 2+a 4=5,即a 1q +a 1q 3=5,② 由①②解得q =12(2舍去),a 1=8, 则a n =8•(12)n ﹣1=24﹣n ;(2)b n =log 2a n =log 224﹣n =4﹣n ,可得S n =12n (3+4﹣n )=7n−n 22, S n n=7−n 2, 则S 11+S 22+⋯+S nn=3+52+⋯+7−n2=12n (3+7−n2)=13n−n 24=−14(n −132)2+16916, 可得n =6或7时,S 11+S 22+⋯+S n n取最大值212.则n 的值为6或7.18.(12分)如图1,四边形PBCD 是等腰梯形,BC ∥PD ,PB =BC =CD =2,PD =4,A 为PD 的中点,将△ABP 沿AB 折起,如图2,点M 是棱PD 上的点. (1)若M 为PD 的中点,证明:平面PCD ⊥平面ABM ;(2)若PC =√6,试确定M 的位置,使二面角M ﹣AB ﹣D 的余弦值等于√55.【解答】解:(1)证明:由题意,AD =BC ,且AD ∥BC ,故四边形ABCD 是平行四边形, 又PB =BC =CD =2,PD =4,∴△PBA 是正三角形,四边形ABCD 是菱形,取AB 的中点E ,连接PE ,CE ,易知△ABC 是正三角形,则AB ⊥PE ,AB ⊥EC , 又PE ∩EC =E , ∴AB ⊥平面PEC , ∴AB ⊥PC ,取PC 的中点N ,连接MN ,BN ,则MN ∥CD ∥AB ,即A ,B ,N ,M 四点共面, 又PB =BC =2,则BN ⊥PC , 又AB ∩BN =B , ∴PC ⊥平面ABM , 又PC 在平面PCD 内, ∴平面PCD ⊥平面ABM ;(2)∵PE =CE =2×√32=√3,PC =√6, ∴PE ⊥EC ,又AB ⊥PE 且AB ⊥EC ,则可以EB ,EC ,AB 所在直线为x 轴,y 轴,z 轴建立空间直角坐标系,则A(−1,0,0),B(1,0,0),D(−2,√3,0),P(0,0,√3),设DM →=λMP →(λ>0),则M(−21+λ,√31+λ,√3λ1+λ),易知平面ABD 的一个法向量为n →=(0,0,1),设平面MAB 的一个法向量为m →=(x ,y ,z),又AB →=(2,0,0),AM →=(−1+λ1+λ,√31+λ,√3λ1+λ), ∴{m →⋅AB →=2x =0m →⋅AM →=−1+λ1+λx +√31+λy +√3λ1+λz =0,则可取m →=(0,−λ,1), 由题意,|n →⋅m →|n →||m →||=√λ+1=√55,解得λ=2,故DM =2MP .19.(12分)某医院体检中心为回馈大众,推出优惠活动:对首次参加体检的人员,按200元/次收费,并注册成为会员,对会员的后续体检给予相应优惠,标准如下: 体检次序 第一次 第二次 第三次 第四次 第五次及以上收费比例10.950.900.850.8该休检中心从所有会员中随机选取了100位对他们在本中心参加体检的次数进行统计,得到数据如表: 检次数 一次 两次 三次 四次 五次及以上频数60201244假设该体检中心为顾客体检一次的成本费用为150元,根据所给数据,解答下列问题: (Ⅰ)已知某顾客在此体检中心参加了3次体检,求这3次体检,该体检中心的平均利润;(Ⅱ)该体检中心要从这100人里至少体检3次的会员中,按体检次数用分层抽样的方法抽出5人,再从这5人中抽取2人,每人发放现金200元.用5表示体检3次的会员所得现金和,求ξ的分布列及E (ξ).【解答】解:(1)医院3次体检的收入为200×(1+0.95+0.9)=570, 三次体验的成本为150×3=450, 故平均利润为(570﹣450)÷3=40元;(2)根据题意抽取的5个人中3人体检三次,1人体检四次,1人体验5次及以上, ξ=0,200,400, P (ξ=0)=1C 52=110, P (ξ=200)=C 31C 21C 53=35. P (ξ=400)=C 32C 21C 53=310,分布列如下:ξ 0 200 400 P0.10.60.3E (ξ)=0+200×0.6+400×0.3=120+120=240. 20.(12分)已知曲线f(x)=mx−m e x 在点(1,f (1))处的切线斜率为−1e. (1)求m 的值,并求函数f (x )的极小值;(2)当x ∈(0,π)时,求证:e x sin x ﹣x +e x ﹣2+1>e x x cos x .【解答】解:(1)由题意,f (x )的定义域为R . ∵f ′(x)=−m(x−2)e x ,∴f ′(1)=m e =−1e,∴m =﹣1. ∴f(x)=1−xe x ,∴f ′(x)=x−2e x , 当x >2时,f '(x )>0,f (x )单调递增; 当x <2时,f '(x )<0,f (x )单调递减, x =2是f (x )的极小值点, ∴f (x )的极小值为f(2)=−1e 2. (2)证明:要证e x sin x ﹣x +e x ﹣2+1>e x x cos x ,两边同除以e x , 只需证1−x e +1e>xcosx −sinx 即可.即证f(x)+1e 2>xcosx −sinx , 由(1)可知,f(x)+1e 2在x =2处取得最小值0;设g (x )=x cos x ﹣sin x ,x ∈(0,π),则g '(x )=cos x ﹣x sin x ﹣cos x =﹣x sin x , ∵x ∈(0,π),∴g '(x )<0,∴g (x )在区间(0,π)上单调递减,从而g (x )<g (0)=0, ∴f(x)+1e 2>xcosx −sinx , 即e x sin x ﹣x +e x ﹣2+1>e x x cos x . 21.(12分)已知椭圆C :x 2a +y 2=1(a >1)的离心率是√22. (Ⅰ)求椭圆C 的方程;(Ⅱ)已知F 1,F 2分别是椭圆C 的左、右焦点,过F 2作斜率为k 的直线l ,交椭圆C 于A ,B 两点,直线F 1A ,F 1B 分别交y 轴于不同的两点M ,N .如果∠MF 1N 为锐角,求k 的取值范围.【解答】解:(Ⅰ)由题意,{c a =√22b 2=1a 2=b 2+c 2,解得a 2=2.∴椭圆C 的方程为x 22+y 2=1;(Ⅱ)由已知直线l 的斜率不为0,设直线l 的方程为y =k (x ﹣1), 直线l 与椭圆C 的交点A (x 1,y 1),B (x 2,y 2), 联立{y =k(x −1)x 22+y 2=1,得(2k 2+1)x 2﹣4k 2x +2k 2﹣2=0.由已知,△>0恒成立,且x 1+x 2=4k22k 2+1,x 1x 2=2k 2−22k 2+1,①直线F 1A 的方程为y =y1x 1+1(x +1),令x =0,得M (0,y 1x 1+1),同理可得N (0,y 2x 2+1).∴F 1M →⋅F 1N →=1+y 1y 2(x 1+1)(x 2+1)=1+k 2(x 1−1)(x 2−1)(x 1+1)(x 2+1)=(1+k 2)x 1x 2+(1−k 2)(x 1+x 2)+1+k2x 1x 2+x 1+x 2+1, 将①代入并化简得:F 1M →⋅F 1N →=7k 2−18k 2−1,依题意,∠MF 1N 为锐角,则F 1M →⋅F 1N →=7k 2−18k 2−1>0,解得:k 2>17或k 2<18.综上,直线l 的斜率的取值范围为(﹣∞,−√77)∪(−√24,0)∪(0,√24)∪(√77,+∞).四.解答题(共1小题,满分10分,每小题10分)22.(10分)在直角坐标系xOy 中,参数方程{x =cosθy =sinθ(其中θ为参数)的曲线经过伸缩变换φ:{x′=2xy′=y 得到曲线C ,以原点O 为极点,x 轴正半轴为极轴建立极坐标系,曲线D 的极坐标方程为ρsin(θ+π4)=3√102. (Ⅰ)求曲线C 的普通方程及曲线D 的直角坐标方程;(Ⅱ)设M 、N 分别为曲线C 和曲线D 上的动点,求|MN |的最小值.【解答】解:(Ⅰ)参数方程{x =cosθy =sinθ(其中θ为参数)的曲线经过伸缩变换φ:{x′=2xy′=y 得到曲线C :x 24+y 2=1;曲线D 的极坐标方程为ρsin(θ+π4)=3√102.转化为直角坐标方程为:x +y −3√5=0; (Ⅱ)设点P (2cos θ,sin θ)到直线x +y ﹣3√5=0的距离d =√5|2=√5sin(θ+α)−3√5|2,当sin (θ+α)=1时,d min =√10. 五.解答题(共1小题)23.已知函数f (x )=|x ﹣a 2|+|x ﹣2a +3|,g (x )=x 2+ax +3. (1)当a =1时,解关于x 的不等式f (x )≤6;(2)若对任意x 1∈R ,都存在x 2∈R ,使得不等式f (x 1)>g (x 2)成立,求实数a 的取值范围.【解答】解:(1)当a =1时,不等式f (x )≤6即为|x ﹣1|+|x +1|≤6, 等价为{x ≥12x ≤6或{−1<x <12≤6或{x ≤−1−2x ≤6,解得1≤x ≤3或﹣1<x <1或﹣3≤x ≤﹣1, 则原不等式的解集为[﹣3,3];(2)若对任意x 1∈R ,都存在x 2∈R ,使得不等式f (x 1)>g (x 2)成立, 可得f (x 1)min >g (x 2)min ,由f (x )=|x ﹣a 2|+|x ﹣2a +3|≥|x ﹣a 2﹣x +2a ﹣3|=a 2﹣2a +3,当且仅当(x ﹣a 2)(x ﹣2a +3)≥0取得等号,可得f(x)的最小值为a2﹣2a+3,g(x)=x2+ax+3的最小值为12−a24,则a2﹣2a+3>12−a24,即5a2﹣8a>0,解得a>85或a<0.。
2020年新疆乌鲁木齐高三一模数学试卷(理科)

2020年新疆乌鲁木齐高三一模数学试卷(理科)一、选择题(本大题共12小题,每小题5分,共60分)1.若集合,,则集合( ).A. B. C. D.2.已知复数满足(是虚数单位),则的共轭复数( ).A. B. C. D.3.已知双曲线的两条渐近线互相垂直,焦距为,则该双曲线的实轴长为( ).A. B. C. D.4.已知,为两条不同的直线,,,为三个不同的平面,则下列命题正确的是( ).A.若,,则B.若,且,则C.若,,,,则D.若,,,则5.数列是公差为的等差数列,为其前项和,且,,成等比数列,则( ).A.B.C.D.6.若正整数除以正整数的余数为,则记为,例如,如图程序框图的算法源于我国古代著名的《中国剩余定理》,执行该程序框图,则输出的等于( ).开始否??否是是输出结束A.B.C.D.7.为了解某市居民用水情况,通过抽样,获得了位居民某年的月均用水量(单位:吨),将数据按照,,,分成组,绘制了如图所示的频率分布直方图,政府要试行居民用水定额管理,制定一个用水量标准,使的居民用水量不超过,按平价收水费,超出的部分按议价收费,则以下比较适合做为标准的是( ).月均用水量吨频率组距A.吨B.吨C.吨D.吨8.天文学中为了衡量星星的明暗程度,古希腊天文学家喜帕恰斯(,又名依巴谷)在公元前二世纪首先提出了星等这个概念.星等的数值越小,星星就越亮;星等的数值越大,它的光就越暗.到了年,由于光度计在天体光度测量中的应用,英国天文学家普森()又提出了衡量天体明暗程度的亮度的概念,天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足,其中星等为的星的亮度为().已知“心宿二”的星等是,“天津四”的星等是,“心宿二”的亮度是“天津四”的倍,则与最接近的是(当较小时,)( ).A.B.C.D.9.已知函数,则下列判断正确的是( ).A.的图象关于对称B.为奇函数C.的值域为D.在上是增函数10.已知,,,,则,,的大小关系是().A.B.C.D.11.已知抛物线的焦点为,准线为,过点且斜率为的直线交抛物线于点(在第一象限),于点,直线交轴于点,则( ).A.B.C.D.12.已知函数,若且,则的取值范围是( ).A.B.C.D.二、填空题(本大题共4小题,每小题5分,共20分)13.已知单位向量,满足,则向量与的夹角的大小为 .14.已知点在圆上,点在直线上,则的最小值为 .15.造纸术是我国古代四大发明之一.纸张的规格是指纸张制成后,经过修整切边,裁成一定的尺寸,现在我国采用国际标准,规定以、、、;、、、等标记来表示纸张的幅面规格.复印纸幅面规格只采用系列和系列,其中系列的幅面规格为:①规格的纸张的幅宽(以表示)和长度(以表示)的比例关系为;②将纸张沿长度方向对开成两等分,便成为规格,纸张沿长度方向对开成两等分,便成为规格,,如此对开至规格.现有、、、、纸各一张.若纸的面积为,则这张纸的面积之和等于 .16.如图,正方体的棱长为,有下列四个命题:①与平面所成角为;②三棱锥与三棱锥的体积比为 ;③过点作平面,使得棱,,在平面上的正投影的长度相等,则这样的平面有且仅有一个;④过作正方体的截面,设截面面积为,则的最小值为.上述四个命题中,正确命题的序号为 .三、解答题(本大题共5小题,每小题12分,共60分)(1)(2)17.如图,在四棱锥中,平面,是正方形,是中点,点在上,且.证明平面.若,求平面与平面所成二面角的正弦值.(1)(2)18.已知的面积为,边上的高是,.求外接圆的半径.求和的长.19.在统计调查中,问卷的设计是一门很大的学问,特别是对一些敏感性问题.例如学生在考试中有无作弊现象,社会上的偷税漏税等.更要精心设计问卷,设法消除被调查者的顾虑,使他们能够如实回答问题,否则被调查者往往会拒绝回答,或不提供真实情况,为了调查中学生中的早恋现象,随机抽出名学生,调查中使用了两个问题.①你的学籍号的最后一位数是奇数(学籍号的后四位是序号);②你是否有早恋现象,让被调查者从装有个红球,个黑球(除颜色外完全相同)的袋子中随机摸取两个球,摸到两球同色的学生如实回答第一个问题,摸到两球异色的学生如实回答第二个问题,回答“是”的人往一个盒子中放一个小石子,回答“否”的人什么都不放,后来在盒子中收到了个小石子.【答案】解析:∵集合(1)(2)你能否估算出中学生早恋人数的百分比?若从该地区中学生中随机抽取一个班(人),设其中恰有个人存在早恋的现象,求的分布列及数学期望.(1)(2)20.已知函数().当时,求曲线在点处的切线方程.若在定义域内为单调函数,求实数的取值范围.(1)(2)21.点与定点的距离和它到直线的距离的比是常数,设点的轨迹为曲线.求曲线的方程.过点的直线与曲线交于,两点,设的中点为,,两点为曲线上关于原点对称的两点,且(),求四边形面积的取值范围.四、选做题(本大题共2小题,选做1题,共10分)(1)(2)22.在直角坐标系中,以坐标原点为极点,轴正半轴为极轴建立极坐标系,曲线的极坐标方程为,四边形的四个顶点都在曲线上.求曲线的直角坐标方程.若,相交于点,求的值.(1)(2)23.已知函数.求不等式的解集.若不等式的解集包含,求实数的取值范围.D1.,,∴即.故选.解析:∵,∴.,故正确.故选.解析:∵双曲线,两条渐近线垂直,令,则,∴,则,又∵双曲线焦距为,则,,∴,所以该双曲线长轴长为,故正确.解析:数列为公差为的等差数列,A 2.B 3.B 4.D 5.∵,,成等比数列,则,,解得:,∴,,所以.故选.解析:如图程序框图中,初始值,,第次循环:,,,则?不成立;第次循环:,,,则?成立;,则?不成立;第次循环:,,,则?不成立;第次循环:,,,则?成立;,D 6.则?成立;循环终止,输出.故正确.解析:如频率分布直方图中,此位居民月均用水量在各组间频率为:在频率为,频率为, 频率为, 频率为, 频率为, 频率为, 频率为, 频率为, 频率为,由在频率为,在频率为,则吨比较适合做为标准.故选.解析:∵,而,,∴,∴,又天津四为,则心宿二为,∴.B 7.C 8.故选.解析:,,,,,由,则,则,,,如图可得,则,综上所述,.故选.解析:A 9.A 10.C 11.D=-1由抛物线定义知,∴为等腰三角形,∵, ∴点为中点,又∵, ∴直线方程为,联立得,即,∵,∴,即,∴,.∴.故选.解析:若且,时,即与矛盾,舍.②时,即与矛盾,舍.③时,即,∵,则,则,,令,,则,时,,单调递减;时,,单调递增,故,又,,且,∴,∴,B 12.即.故选.13.解析:设单位向量与夹角为,∵,,∴.则,故.故答案为:.14.解析:圆,变形为,圆心为,半径,则圆心到直线距离为,由题意最小值为.15.解析:设纸张长度为,(),则又∵,∴纸张宽度为,又纸面积为,∴,∴,,,又,∴,,∴,又,∴,∴,故这张纸面积之和构成一个以为首项,为公比的等比数列,∴面积之和为.解析:对于①:连接,∵平面,设与交于点,连接,则即为直线与平面的夹角,则,故①正确;对于②:连接,设与交于点,①②④16.∵平面,,平面,,又,平面,故,,,故点为线段 的三等分点,则,故②正确;对于③:由②知,平面符合要求,注意到: ,,(1) ,则平面、平面、平面也符合要求,只需将四个平面平移至点即可,∴一共有这样的平面个,故③错误;对于④:设 ,作交于点,则平面,作,则有,连接,平面,,∵, ,即 ,,则,由柯西不等式有:,“”当且仅当 时取得,故,故④正确.综上,命题①②④正确.解析:∵平面,(1)证明见解析.(2).17.(2)(1)(2)∴,又∵是正方形,是中点,,∴﹐∴,∴,∴,∴,∴,∴平面.建立如图空间直角坐标系,不妨设,则,由题意得,,,,,设平面的法向量为,∴,得,易得平面的法向量为,∴,∵二面角的正弦值为.解析:设角 ,,的对边分别为 ,, , 由,得由, 求出,.设外接圆的半径为 , 由 ,求得.由,得…①(1)(2),,或,18.(1)(2)(1)(2)由,得,∴…②由①②联立可解得,或∴,,或,.解析:摸到同色球的概率为,摸到异色球的概率为,据此可估计人中有人摸到同色球,人摸到异色球,因此有人回答了问题①,人回答了问题②;因为学生学籍号的后四位是序号,最后一位数是奇数的概率为,因此回答问题①的人有人回答了“是”,据此估计有人在问题②中回答了“是”,∴估计中学生的早恋人数的百分比为.依题意,分布列为,,∴.解析:由,∴,∴,,∴,∴切线方程为,即.由,(1).(2)分布列为,;.19.(1).(2).20.(1)(2)设,则.①当时,,∴递减,由,,∴在不恒正或恒负,∴在不为单调函数,不符合.②当时,,,显然不能恒正或恒负,不符合.③当时,,得,且在上递增,在上递增,∴,,∴要使恒成立,则,即,∴,即时,在定义域不单调:时,在定义域内为单调递增.综上:从如成两为单调函数,则.解析:由题意得,即,∴曲线的方程为.①当直线斜率为零时,点与点重合,不满足,∴直线不与轴重合.②当直线斜率不为零时,设,代入得,整理得设,,,,则,,∴,(1).(2).21.(1)(2)(1)∵,∴,又点在曲线上,代入,即,化简得,①点到的距离为,设四边形的面积为,的面积为,∴,∴,由①得,∵,当时取得最小值,∴,四边形的取值范围为.解析:曲线的直角坐标方程为.设直线的倾斜角为,则该直线的参数方程为,其中为参数.与联立得,,则,设方程的根为,,则由直线参数方程的几何意义可得,同理.∴.解析:不等式可化为,或,或,解得,或,或,(1)曲线的直角坐标方程为.(2).22.(1)的解集为.(2)实数的取值范围为.23.(2)所以的解集为.由题可知,即当时,不等式恒成立,即,即时,恒成立,令,所以,即,所以实数的取值范围为.。
2020年新疆乌鲁木齐市高考数学一诊试卷(理科)(含解析)

2020年新疆乌鲁木齐市高考数学一诊试卷(理科)一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的第Ⅰ卷(选择题共60分)1.设集合A ={x|x 2−3x <0},B ={x|1<x <4},则A ∩B =( ) A.(0, 4) B.(1, 4) C.(3, 4) D.(1, 3)2.若复数z 满足z =1+i1−i −3i (其中i 为虚数单位),则|z|=( ) A.2 B.3 C.√10 D.43.已知m ,n 是两条不同的直线,α,β,γ是三个不同的平面,则下列命题正确的是()A.若m // α,n // α,则m // nB.若α⊥γ,β⊥γ,则α // βC.若m // α,n // α,且m ⊂β,n ⊂β,则α // βD.若m ⊥α,n ⊥β,且α⊥β,则m ⊥n4.设a =20.6,b =log 0.30.6,c =log 30.6,则有( ) A.c <b <a B.a <b <c C.b <c <a D.c <a <b5.已知向量a →,b →满足|a →|=2,|b →|=3,且a →与b →的夹角为π3,则(a →+2b →)(2a →−b →)=( ) A.−3 B.−1 C.1 D.36.已知双曲线x 2a 2−y 2b 2=1(a >0, b >0)的左、右焦点分别为F 1,F 2,B 为虚轴的一个端点,且∠F 1BF 2=120∘,则双曲线的离心率为( )A.2B.√3C.32D.√627.执行如图所示的程序框图,则输出的n=()A.3B.4C.5D.68.从数字1,2,3,4,5这五个数中,随机抽取2个不同的数,则这2个数的和为偶数的概率是()A.15B.25C.35D.459.已知等比数列{a n}的前n项和为S n,且4a1,2a2,a3依次等差数列,若a1=1,则S5=()A.16B.31C.32D.6310.将奇函数f(x)=√3sin(2x+φ)−cos(2x+φ)(0<φ<π)的图象向右平移φ个单位长度后得到函数y=g(x)的图象,则下列关于g(x)的一个单调递减区间是()A.(−π12,5π12) B.(−5π12,π12)C.(π12,7π12)D.(5π12,11π12)11.已知抛物线C:y 2=2px(p >0)的焦点F ,点M(x 0,6√6)(x 0>p2)是抛物线上一点,以M 为圆心的圆与直线x =p2交于A 、B 两点(A 在B 的上方),若sin∠MFA =57,则抛物线C 的方程为( ) A.y 2=4x B.y 2=8x C.y 2=12x D.y 2=16x12.已知函数f(x)={x 2−x 2 ,x ≥0#/DEL/#,x <0#/DEL/#,若对任意x ∈[m 2,m 2+3],都有f(x +m)≥3f(x),则实数m 的取值范围是( ) A.[4, +∞) B.[2√3,+∞) C.[3, +∞) D.[2√2,+∞)二、填空题:本大题共4个小题,每小题5分若x ,y 满足约束条件{x −2y −2≤0,x −y +1≥0,y ≤0,则z =3x +2y 的最大值为________.已知cos(α+π3)=−45,α为锐角,则sinα=________.已知数列{a n }满足:a n+1={2a n ,a n ≥a 1a n +2,a n <a 1(n =1, 2,…),若a 3=3,则a 1=________34.如图,已知在长方体ABCD −A 1B 1C 1D 1中,AB =3,AD =4,AA 1=5,点E 为CC 1上的一个动点,平面BED 1与棱AA 1交于点F ,给出下列命题: ①四棱锥B 1−BED 1F 的体积为20;②存在唯一的点E ,使截面四边形BED 1F 的周长取得最小值2√74;③当E点不与C,C1重合时,在棱AD上均存在点G,使得CG // 平面BED1;.④存在唯一的点E,使得B1D⊥平面BED1,且CE=165其中正确的命题是________(填写所有正确的序号)三、解答题:第17~21题每题12分,解答应写出文字说明、证明过计算步骤△ABC的内角A,B,C的对边分别是a,b,c,且sinA+sinB=csinC+3bsinA.a+b (Ⅰ)求∠C的值;(Ⅱ)若c=√2,求△ABC面积的最大值.如图,四棱锥P−ABCD中,PA⊥底面ABCD,AD // BC,∠BAD=90∘,AD=2BC,M为PD的中点.(Ⅰ)证明:CM // 平面PAB;(Ⅱ)若△PBD是等边三角形,求二面角A−PB−M的余弦值.“团购”已经渗透到我们每个人的生活,这离不开快递行业的发展,如表是2013−2017年全国快递业务量(x亿件:精确到0.1)及其增长速度(y%)的数据.(Ⅰ)试计算2012年的快递业务量;(Ⅱ)分别将2013年,2014年,…,2017年记成年的序号t:1,2,3,4,5;现已知y 与t 具有线性相关关系,试建立y 关于t 的回归直线方程y =b x +a ; (Ⅲ)根据(Ⅱ)问中所建立的回归直线方程,估算2019年的快递业务量. 附:回归直线的斜率和截距地最小二乘法估计公式分别为:b =∑−i=1n xiyi nx ¯y ¯∑−i=1n xi 2nx ¯2,a =y ¯−b x ¯已知椭圆C:x 2a 2+y 2b 2=1(a >b >0)过点(2,√2),左焦点F(−2, 0). (Ⅰ)求椭圆C 的标准方程;(Ⅱ)过点F 作于x 轴不重合的直线l ,l 与椭圆交于A ,B 两点,点A 在直线x =−4上的投影N 与点B 的连线交x 轴于D 点,D 点的横坐标x 0是否为定值?若是,请求出定值;若不是,请说明理由.已知函数f(x)=2x 2−1x−alnx(a ∈R).(Ⅰ)讨论f(x)的单调性;(Ⅱ)若方程f(x)=2x 有两个不相等的实数根,求证:f(a)<ae 2+2.选考题:共10分,二选一在平面直角坐标系xOy 中,曲线C 1:x 2+y 2−4x =0,直线l 的参数方程为{x =tcosαy =tsinα (t 为参数),其中α∈(0, π6),以坐标原点O 为极点,x 轴非负半轴为极轴,建立极坐标系.(Ⅰ)求曲线C 1的极坐标方程和直线l 的普通方程;(Ⅱ)设M(4, 0),C 2的极坐标方程ρ=4√3sinθ,A ,B 分别为直线l 与曲线C 1,C 2异于原点的公共点,当∠AMB =30∘时,求直线l 的斜率.函数f(x)=|2x −2|+|x +3|. (Ⅰ)求不等式f(x)≥2x +5的解集;(Ⅱ)若f(x)的最小值为k ,且实数a ,b ,c 满足a(b +c)=k ,求证:2a 2+b 2+c 2≥8.2020年新疆乌鲁木齐市高考数学一诊试卷(理科)一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的第Ⅰ卷(选择题共60分)1.设集合A={x|x2−3x<0},B={x|1<x<4},则A∩B=()A.(0, 4)B.(1, 4)C.(3, 4)D.(1, 3)【解答】∵集合A={x|x2−3x<0}={x|0<x<3},B={x|1<x<4},∴A∩B={x|1<x<3}=(1, 3).2.若复数z满足z=1+i1−i−3i(其中i为虚数单位),则|z|=()A.2B.3C.√10D.4【解答】z=1+i1−i −3i=(1+i)2(1−i)(1+i)−3i=2i2−3i=−2i,则|z|=|−2|=2.3.已知m,n是两条不同的直线,α,β,γ是三个不同的平面,则下列命题正确的是()A.若m // α,n // α,则m // nB.若α⊥γ,β⊥γ,则α // βC.若m // α,n // α,且m⊂β,n⊂β,则α // βD.若m⊥α,n⊥β,且α⊥β,则m⊥n【解答】解:由m,n是两条不同的直线,α,β,γ是三个不同的平面,知:在A中,若m // α,n // α,则m与n相交、平行或异面,故A错误;在B中,若α⊥γ,β⊥γ,则α与β相交或平行,故B错误;在C中,若m // α,n // α,且m⊂β,n⊂β,则α与β相交或平行,故C错误;在D中,若m⊥α,n⊥β,且α⊥β,则线面垂直、面面垂直的性质定理得m⊥n,故D正确.故选D .4.设a =20.6,b =log 0.30.6,c =log 30.6,则有( ) A.c <b <a B.a <b <c C.b <c <a D.c <a <b【解答】∵a =20.6>1,b =log 0.30.6∈(0, 1),c =log 30.6<0, 则有c <b <a .5.已知向量a →,b →满足|a →|=2,|b →|=3,且a →与b →的夹角为π3,则(a →+2b →)(2a →−b →)=( ) A.−3 B.−1 C.1 D.3【解答】∵|a →|=2,|b →|=3,<a →,b →>=π3,∴(a →+2b →)⋅(2a →−b →)=2a →2−2b →2+3a →⋅b →=2×4−2×9+3×2×3×12=−1.6.已知双曲线x 2a 2−y 2b 2=1(a >0, b >0)的左、右焦点分别为F 1,F 2,B 为虚轴的一个端点,且∠F 1BF 2=120∘,则双曲线的离心率为( ) A.2 B.√3C.32D.√62【解答】双曲线x 2a 2−y 2b 2=1(a >0, b >0)的左、右焦点分别为F 1,F 2,B 为虚轴的一个端点,且∠F 1BF 2=120∘,可得cb =√3,3c 2−3a 2=c 2,e =ca =√32=√62. 7.执行如图所示的程序框图,则输出的n =( )A.3B.4C.5D.6【解答】模拟程序的运行,可得S=0,n=1S=2,n=2满足条件S<30,执行循环体,S=2+4=6,n=3满足条件S<30,执行循环体,S=6+8=14,n=4满足条件S<30,执行循环体,S=14+16=30,n=5此时,不满足条件S<30,退出循环,输出n的值为(5)8.从数字1,2,3,4,5这五个数中,随机抽取2个不同的数,则这2个数的和为偶数的概率是()A.15B.25C.35D.45【解答】由题意知本题是一个古典概型,∵从五个数中随机抽取2个不同的数有C52种不同的结果,而这2个数的和为偶数包括2、4,1、3,1、5,3、5,四种取法,由古典概型公式得到P=4C52=410=25,9.已知等比数列{a n}的前n项和为S n,且4a1,2a2,a3依次等差数列,若a1=1,则S5=()A.16B.31C.32D.63【解答】解:4a1,2a2,a3依次等差数列,可得4a2=4a1+a3,显然公比q不为1,则4a1q=4a1+a1q2,即为q2−4q+4=0,解得q=2,则S5=a1(1−q5)1−q =1−251−2=31.故选B.10.将奇函数f(x)=√3sin(2x+φ)−cos(2x+φ)(0<φ<π)的图象向右平移φ个单位长度后得到函数y=g(x)的图象,则下列关于g(x)的一个单调递减区间是()A.(−π12,5π12) B.(−5π12,π12) C.(π12,7π12) D.(5π12,11π12)【解答】∵奇函数f(x)=√3sin(2x+φ)−cos(2x+φ)=2sin[(2x+φ)−π6],∴φ−π6=0,∴φ=π6,f(x)=2sin2x.把f(x)的图象向右平移φ=π6个单位长度后得到函数y=g(x)=2sin(2x−π3)的图象,令2kπ+π2≤2x−π3≤2kπ+3π2,求得kπ+5π12≤x≤kπ+11π12,故函数g(x)的单调递减区间为[kπ+5π12, kπ+11π12],k∈Z,11.已知抛物线C:y2=2px(p>0)的焦点F,点M(x0,6√6)(x0>p2)是抛物线上一点,以M为圆心的圆与直线x=p2交于A、B两点(A在B的上方),若sin∠MFA=57,则抛物线C的方程为()A.y2=4xB.y2=8xC.y2=12xD.y2=16x【解答】如图所示,过M点作CM⊥直线x=p2=p2,垂足为C,交准线于D,∴sin∠MFA =57=MCMF , 由抛物线定义可得:MF =MD , ∴MCMF =x 0−p 2x 0+p 2=575x 0+52p =7x 0−72p∴x 0=3p∵点M(x 0,6√6)(x 0>p2)是抛物线上一点, ∴(6√6)2=2px 0 36×6=6p 2 ∴p =6 ∴y 2=12x12.已知函数f(x)={x 2−x 2 ,x ≥0#/DEL/#,x <0#/DEL/#,若对任意x ∈[m 2,m2+3],都有f(x +m)≥3f(x),则实数m 的取值范围是( ) A.[4, +∞) B.[2√3,+∞) C.[3, +∞) D.[2√2,+∞)【解答】∵f(−x)={−x 2x 2 ,x ≥0#/DEL/#,x <0#/DEL/#=−f(x), ∴函数f(x)={x 2−x2 ,x ≥0#/DEL/#,x <0#/DEL/#,为R 上的奇函数,又x ≥0时,f(x)=x 2为增函数, ∴f(x)为定义域R 上的增函数. 又f(√3)=3,∴f(x +m)≥3f(x)=f(√3x),∵对任意x ∈[m 2,m2+3],f(x +m)≥3f(x)=f(√3x),f(x)为定义域R 上的增函数,∴m ≥[(√3−1)x]max =(√3−1)(m2+3), 即(1−√3−12)m =3−√32m ≥3(√3−1),解得:m ≥2√3.即实数m 的取值范围是[2√3, +∞),二、填空题:本大题共4个小题,每小题5分若x ,y 满足约束条件{x −2y −2≤0,x −y +1≥0,y ≤0,则z =3x +2y 的最大值为________.【解答】解:作出不等式组对应的平面区域如图:由z =3x +2y 得y =−32x +12z , 平移直线y =−32x +12z ,由图象知当直线y =−32x +12z 经过点A(2, 0)时,直线的截距最大,此时z 最大,最大值为z =3×2=6, 故答案为:6已知cos(α+π3)=−45,α为锐角,则sinα=________. 【解答】因为cos(α+π3)=−45,α为锐角, 所以sin(α+13π)=35,故sinα=sin(α+13π−13π)=12sin(α+13π)−√32cos(α+13π)=3+4√310. 已知数列{a n }满足:a n+1={2a n ,a n ≥a 1a n +2,a n <a 1(n =1, 2,…),若a 3=3,则a 1=________34. 【解答】 由a n+1={2a n ,a n ≥a 1a n +2,a n <a 1,①若a3≥a1,则a3=3=2a2,a2=32,又a2<a1与a2=a1+2相矛盾,∴a2≥a1,a2=32=2a1,得a1=34;②若a3<a1,则a3=a2+2,∴a2=1,由a2=1=2a1,a1=12,与a3<a1不符.∴a1=34.如图,已知在长方体ABCD−A1B1C1D1中,AB=3,AD=4,AA1=5,点E 为CC1上的一个动点,平面BED1与棱AA1交于点F,给出下列命题:①四棱锥B1−BED1F的体积为20;②存在唯一的点E,使截面四边形BED1F的周长取得最小值2√74;③当E点不与C,C1重合时,在棱AD上均存在点G,使得CG // 平面BED1;④存在唯一的点E,使得B1D⊥平面BED1,且CE=165.其中正确的命题是________(填写所有正确的序号)【解答】①由题意可得D1F // BE,V B1−BED1F =V B1−BED1+V B1−BFD1=V D1−BEB1+V D1−BFB1=13[12⋅BB1⋅BC⋅AB+12⋅BB1⋅D1A1⋅AB]=13⋅12(5×4×3+5×4×3)=20,所以①正确;②将长方体展开,如图所示,恰好过B点时,截面的周长为2BD1,而在△BDD1中,BD1=√52+(3+4)2=√74,所以最小值为2√74,由面面平行的性质可得四边形BED1F为平行四边形,且E为展开图中唯一的点所以②正确;③E嗲不与C,C1重合,则F不会为A,即CG不在面EBD1内,可作出CG的平面与EBD1平行,所以在棱AD上均有相应的G,使得CG // 面EBD1,故③正确;④因为BB1=BD,可得对角面BB1D1D为正方形,可得B1D⊥BD1,若BE⊥B1C时,由三垂线定理可得B1D⊥BE,即有B1D⊥面EBD1,在矩形BB1C1C中,BE⊥B1C,所以CEBC =BCCC1,所以CE=BC⋅BCCC1=165,故④正确综上可得:正确为①②③④.三、解答题:第17~21题每题12分,解答应写出文字说明、证明过计算步骤△ABC的内角A,B,C的对边分别是a,b,c,且sinA+sinB=csinC+3bsinAa+b.(Ⅰ)求∠C的值;(Ⅱ)若c=√2,求△ABC面积的最大值.【解答】(I)由题意结合正弦定理可得,(a+b)2=3ab+c2,即a2+b2−c2=ab,所以cosC=a 2+b2−c22ab=12,∵C∈(0, π),故C=13π,(II)由余弦定理可得,2=a2+b2−ab,所以,a2+b2=2+ab≥2ab,故ab≤2,则S△ABC=12absinC≤√32,当且仅当a=b=√2时,面积取得最大值√32.如图,四棱锥P−ABCD中,PA⊥底面ABCD,AD // BC,∠BAD=90∘,AD =2BC,M为PD的中点.(Ⅰ)证明:CM // 平面PAB;(Ⅱ)若△PBD是等边三角形,求二面角A−PB−M的余弦值.【解答】(1)证明:如图,取AD 中点N ,连结MN ,CN , ∵M 为PD 的中点,∴MN // AP , ∵AD =2BC ,∴AN =BC ,∵BC // AD ,∴四边形ABCN 是平行四边形,∴AB // CN , ∵CN ∩NM =N ,BA ∩AP =A ,∴平面CMN // 平面PAB , ∵CM ⊂平面MNC ,∴CM // 平面PAB .(2)以A 为原点,AB 为x 轴,AD 为y 轴,AP 为z 轴,建立空间直角坐标系, ∵△PBD 为等边三角形,∴AB =AD =AP , 设AB =2,则A(0, 0, 0),B(2, 0, 0),D(0, 2, 0), ∴BD →=(−2, 2, 0),BP →=(−2, 0, 2), 设平面BDP 的法向理n →=(x, y, z),则{n →⋅BD →=−2x +2y =0n →⋅BP →=−2x +2z =0 ,令z =1,得n →=(1, 1, 1), ∵AD ⊥平面PAB ,∴平面PAB 的法向量n →=(0, 1, 0), ∴cosθ=|n →⋅m →||n →|⋅|m →|=√3×1=√33. ∴二面角A −PB −M 的余弦值为√33.“团购”已经渗透到我们每个人的生活,这离不开快递行业的发展,如表是2013−2017年全国快递业务量(x 亿件:精确到0.1)及其增长速度(y%)的数据.(Ⅰ)试计算2012年的快递业务量;(Ⅱ)分别将2013年,2014年,…,2017年记成年的序号t:1,2,3,4,5;现已知y 与t 具有线性相关关系,试建立y 关于t 的回归直线方程y =b x +a ; (Ⅲ)根据(Ⅱ)问中所建立的回归直线方程,估算2019年的快递业务量. 附:回归直线的斜率和截距地最小二乘法估计公式分别为:b =∑−i=1n xiyi nx ¯y ¯∑−i=1n xi 2nx ¯2,a =y ¯−b x ¯【解答】(1)设2012年的快递业务量为a , 则92−a a=61%,解得a ≈57.1;即2012年的快递业务量为57.1亿件; (2)由题意列表得,计算t ¯=15×(1+2+3+4+5)=3,y ¯=15×(61+52+48+51+28)=48, b =∑ 5i=1t i y i −5t ¯y¯∑ 5i=1t i 2−5t¯2=(1×61+2×52+3×48+4×51+5×28)−5×3×4812+22+32+42+52−5×32=−6.7,a =y ¯−b t ¯=48−(−6.7)×3=68.1,所以y 关于t 的线性回归方程是y =−6.7t +68.1;(Ⅲ)令t=6,计算2018年比上半年增长率是y=−6.7×6+68.1=27.9(%);所以2018年快递业务增长量为399.9×(1+27.9%)≈511.5(亿件);令t=7,计算2018年比上半年增长率是y=−6.7×7+68.1=21.2(%);所以2019年快递业务增长量为511.5×(1+21.2%)≈619.9(亿件).已知椭圆C:x 2a2+y2b2=1(a>b>0)过点(2,√2),左焦点F(−2, 0).(Ⅰ)求椭圆C的标准方程;(Ⅱ)过点F作于x轴不重合的直线l,l与椭圆交于A,B两点,点A在直线x=−4上的投影N与点B的连线交x轴于D点,D点的横坐标x0是否为定值?若是,请求出定值;若不是,请说明理由.【解答】(1)椭圆C:x 2a2+y2b2=1(a>b>0)过点(2,√2),左焦点F(−2, 0),可得c=2,2a=√42+(√2)2+√0+(√2)2=4√2,即a=2√2,b=√a2−c2=2,可得椭圆的方程为x 28+y24=1;(2)D点的横坐标为定值−(3)理由如下:直线l的斜率不为0,设AB:x=my−2,联立椭圆方程x2+2y2=8,可得(2+m2)y2−4my−4=0,设A(x1, y1),B(x2, y2),y1,y2≠0,y1+y2=4m2+m2,y1y2=−42+m2,两式相除可得y1+y2y1y2=−m,由N(−4, y1),可设BN的方程为y−y1=y2−y1x2+4(x+4),令y=0,可得x0=−y1x2−4y1y2−y1−4=−y1x2−4y2y2−y1=−y1(my2−2)−4y2y2−y1=−my1y2+2y1−4y2y2−y1=y1+y2+2y1−4y2y2−y1=3y1−3y2y2−y1=−(3)则D点的横坐标为定值−(3)已知函数f(x)=2x 2−1x−alnx(a∈R).(Ⅰ)讨论f(x)的单调性;(Ⅱ)若方程f(x)=2x有两个不相等的实数根,求证:f(a)<ae+2.【解答】 (I)f ′(x)=2x 2−ax+1x 2,x >0,对于y =2x 2−ax +1,△=a 2−8,对称轴为x =a4,当△≤0时,即a ∈[−2√2,2√2]时,f ′(x)≥0,f(x)在(0, +∞)递增; 当△>0时,即a ∈(−∞, −2√2)∪(2√2, +∞),方程有两个不同的根m =a−√a 2−84,n =a+√a 2−84,m <n ,由于y(0)=1,当a <−2√2,m ,n <0,函数在(0, +∞)递增;当a >2√2,m ,n >0,函数f(x)在(0, m),(n, +∞)递增,(m, n)递减; 综上,a ≤−2√2时,f(x)在(0, +∞)递增;a >2√2时,f(x)在(0, a−√a 2−84),(a+√a 2−84, +∞)上递增;在(a−√a 2−84,a+√a 2−84)递减;(II)令g(x)=f(x)−2x =−1x −alnx ,x >0,方程f(x)=2x 有两个不相等的实数根,相当于函数g(x)由两个零点, g ′(x)=1x 2−ax =−ax−1x 2=1−ax x 2,当a ≤0时,g ′(x)>0,g(x)在(0, +∞)递增,则g(x)至多只有一个零点,不成立;当a >0时,x ∈(0, 1a )时,g(x)递增;x ∈(1a , +∞)递减, 所以g(x)min =g(1a )=−a +alna ,由−a +alna >0,又a >0,所以a >e ,因为1a 是g(x)的极大值点, 由1>1a ,g(1)=−1<0,由a >e ,e a >a ,e −a <1a ,g(e −a )=−1e −a −alne −a =−e a +a 2, 对于y =e x −x 2,易知y 在(e, +∞)递增,因为指数函数比幂函数增长的快, 所以e a −a 2>0,g(e −a )<0,所以函数g(x)在(e −a ,1a )与(1a , 1)各有一个零点,所以a >e ,要证明f(a)<ae 2+2,即证明a >e 时,a(2−1e 2)−1a −alna <2成立, 设ℎ(a)=a(2−1e 2)−1a −alna(a >e),ℎ′(a)=1+1a 2−lna −1e 2,由于ℎ′(a)在(e, +∞)递减,所以ℎ′(a)<ℎ′(e)=0, 所以ℎ(a)在(e, +∞)递减; 所以ℎ(a)<ℎ(e)=e −2e <2, 故原命题成立.选考题:共10分,二选一在平面直角坐标系xOy 中,曲线C 1:x 2+y 2−4x =0,直线l 的参数方程为{x =tcosαy =tsinα (t 为参数),其中α∈(0, π6),以坐标原点O 为极点,x 轴非负半轴为极轴,建立极坐标系.(Ⅰ)求曲线C 1的极坐标方程和直线l 的普通方程;(Ⅱ)设M(4, 0),C 2的极坐标方程ρ=4√3sinθ,A ,B 分别为直线l 与曲线C 1,C 2异于原点的公共点,当∠AMB =30∘时,求直线l 的斜率. 【解答】(1)曲线C 1:x 2+y 2−4x =0,转换为极坐标方程为ρ=4cosθ. 直线l 的参数方程为{x =tcosαy =tsinα (t 为参数),转换为直角坐标方程为y =tanαx ,α∈(0, π6). (2)由已知可得:θ=α,则|AB|=4cosα−4√3sinα,|AM|=ρ1tanα=4sinα, 由于|AM|=√3|AB|,所以4sinα=√3(4cosα−4√3sinα), 解得k =tanα=√34. 所以直线的斜率为√34. 函数f(x)=|2x −2|+|x +3|. (Ⅰ)求不等式f(x)≥2x +5的解集;(Ⅱ)若f(x)的最小值为k ,且实数a ,b ,c 满足a(b +c)=k ,求证:2a 2+b 2+c 2≥8. 【解答】(1)f(x)=|2x −2|+|x +3|={3x +1,x >1−x +5,−3≤x ≤1−3x −1,x <−3.∵f(x)≥2x +5,∴{3x +1≥2x +5x >1或{−x +5≥2x +5−3≤x ≤1 或{−3x −1≥2x +5x <−3 ,∴x ≥4或−3≤x ≤0或x <−3, ∴x ≤0或x ≥4,∴不等式的解集为{x|x ≤0或x ≥4}. (2)由(Ⅰ)知f(x)min =k =4. ∴a(b +c)=k =4,∴ab +ac =4,∴2a 2+b 2+c 2=(a 2+b 2)+(a 2+c 2)≥2ab +2ac =8, 当且仅当a =b =c =±√2时取等号, ∴2a 2+b 2+c 2≥8.。
2020年新疆乌鲁木齐市高考数学一模试卷(理科)(问卷)(含解析)

2020年新疆乌鲁木齐市高考数学一模试卷(理科)一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中只有一项是符合题目要求的.1.若集合A={x|x2−2x−8<0},B={x|x2−9≤0},则集合A∪B=()A.(−2, 3]B.(−4, 3]C.[−3, 2)D.[−3, 4)2.已知复数z满足z(1+2i)=|3+4i|(i是虚数单位),则z的共轭复数()A.1+2iB.1−2iC.−1+2iD.−1−2i3.已知双曲线x 2a2−y2b2=1(a>0,b>0)的两条渐近线互相垂直,焦距为6√2,则该双曲线的实轴长为()A.3B.6C.9D.124.已知m,n为两条不同的直线,α,β,γ为三个不同的平面,则下列命题正确的是()A.若m // α,n // α,则m // nB.若α⊥β,γ⊥β且α∩γ=m,则m⊥βC.若m⊂α,n⊂α,m // β,n // β,则α // βD.若m⊥α,n // β,α⊥β,则m⊥n5.数列{a n}是公差为2的等差数列,S n为其前n项和,且a1,a4,a13成等比数列,则S4=()A.8B.12C.16D.246.若正整数n除以正整数m的余数为r,则记为r=nbmodm,例如2=12bmod5,如图程序框图的算法源于我国古代著名的中国剩余定理,执行该程序框图,则输出的i等于()A.2B.4C.8D.167.为了解某市居民用水情况,通过抽样,获得了100位居民某年的月均用水量(单位:吨),将该数据按照[0, 0.5),[0.5, 1),…[4.4.5]分成9组,绘制了如图所示的频率分布直方图,政府要试行居民用水定额管理,制定了一个用水量标准a,使85%的居民用水量不超过a,按平价收水费,超出a的部分按议价收费,则以下比较适合作为标准a的是()A.2.5吨B.3吨C.3.5吨D.4吨8.天文学中为了衡量星星的明暗程度,古希腊天文学家喜帕恰斯(Hipparcℎus,又名依巴谷)在公元前二世纪首先提出了星等这个概念.星等的数值越小,星星就越亮;星等的数值越大它的光就越暗.到了1850年,由于光度计在天体光度测量中的应用,英国天文学家普森(M.R.Pogson)又提出了衡量天体明暗程度的亮度的概念,天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足m1−m2=2.5(lgE2−lgE1),其中星等为m k的星的亮度为E k(k=1, 2)已知“心宿二”的星等是1.00,“天津四”的星等是1.25,“心宿二”的亮度是“天津四”的r倍,则与r最接近的是(当|x|较小时,10x≈1+2.3x+2.7x2)()A.1.24B.1.25C.1.26D.1.279.已知函数f(x)=2sin2(x+π6)+√3sin(2x+π3)−1,则下列判断正确的是()A.f(x)的图象关于x=π6对称 B.f(x)为奇函数C.f(x)的值域为[−3, 1]D.f(x)在[0,π3]上是增函数10.已知α∈(0,π4),a=(sinα)sinα,b=(sinα)cosα,c=(cosα)sinα,则a,b,c的大小关系()A.b<a<cB.b<c<aC.a<b<cD.c<b<a11.已知抛物线y2=4x的焦点F,准线为l,过点F且斜率为√3的直线交抛物线于点M(M在第一象限),MN⊥l于点N,直线NF交y轴于点D,则|MD|=()A.4B.2√3C.2D.√312.已知函数f(x)={lnx−1,x≥113(x+2),x<1,若α<β且f(α)=f(β),则β−α的取值范围是()A.[8−3ln3, 6]B.[8−3ln3, e2−1]C.[9−4ln3, 6]D.[9−4ln3, e2−1]二、填空题:本大题共4小题,每小题5分已知单位向量a →,b →满足a →⋅(a →+2b →)=2,则向量a →,b →夹角的大小为________.已知点N 在圆x 2+y 2−4x +4y +7=0上,点M 在直线3x −4y +6=0上,则|MN|的最小值为________.造纸术是我国古代四大发明之一.纸张的规格是纸张制成之后,经过修整切边,裁成一定的尺寸.现在我国采用国际标准,规定以A0,A1,…,A10;B0,B1,…,B10等标记来表示纸张的幅面规格.复印纸幅面规格只采用A 系列和B 系列,其中A 系列的幅面规格为:①A0规格的纸张幅宽(以x 表示)和长度(以y 表示)的比例关系为x:y =1:√2,②将A0纸张沿长度方向对开成两等份,便成为A1规格,A1纸张沿长度方向对开成两等份,便成为A2规格,…,如此对开至A8规格,现有A0,A1,A2,A3,…,A8纸各一张,若A4纸的面积为624cm 2,这九张纸的面积之和等于________(cm 2)如图,正方体ABCD −A 1B 1C 1D 1的棱长为1,有下列四个命题:①BC 1与平面BCD 1A 1所成的角为30∘;②三棱锥A −A 1BD 与三棱锥C 1−A 1BD 的体积比为1:2;③过点A 作平面α,使得棱AB ,AD ,AA 1在平面α上的正投影的长度相等,则这样的平面α有且只有一个;④过BD 1作正方体的截面,设截面面积为S ,则S 的最小值为√62;上述四个命题中,正确命题的序号为________三、解答题:第17~21题每题12分,解答应写出文字说明、证明过程或演算步骤.如图,在四棱锥P−ABCD中,PA⊥平面ABCD,ABCD是正方形,E是CD的中点,点F在BC上,且BF=3FC.(Ⅰ)证明:EF⊥平面PAE;AB,求平面PAB与平面PEF所成的二面角的正弦值.(Ⅱ)若PA=54已知△ABC的面积为3,BC边上的高是2,tanA=3.(Ⅰ)求△ABC外接圆的半径;(Ⅱ)求AB和AC的长.在统计调查中,问卷的设计是一门很大的学问,特别是对一些敏感性问题.例如学生在考试中有无作弊现象,社会上的偷税漏税等,更要精心设计问卷,设法消除被调查者的顾虑,使他们能够如实回答问题,否则被调查者往往会拒绝回答,或不提供真实情况,为了调查中学生中的早恋现象,随机抽出300名学生,调查中使用了两个问题.①你的学籍号的最后一位数是奇数(学籍号的后四位是序号);②你是否有早恋现象,让被调查者从装有4个红球,6个黑球(除颜色外完全相同)的袋子中随机摸取两个球,摸到两球同色的学生如实回答第一个问题,摸到两球异色的学生如实回答第二个问题,回答“是”的人往一个盒子中放一个小石子,回答“否”的人什么都不放,后来在盒子中收到了78个小石子.(Ⅰ)你能否估算出中学生早恋人数的百分比?(Ⅱ)若从该地区中学生中随机抽取一个班(40人),设其中恰有X 个人存在早恋的现象,求X 的分布列及数学期望已知函数f(x)=ax 2−xlnx −x(a ∈R).(Ⅰ)当a =1e 时,求曲线y =f(x)在点(e, f(e))处的切线方程;(Ⅱ)若f(x)在定义域内为单调函数,求实数a 的取值范围.点P(x, y)与定点F(−1, 0)的距离和它到直线l:x =−3的距离的比是常数√33,设点P 的轨迹为曲线E .(Ⅰ)求曲线E 的方程;(Ⅱ)过点F 的直线l 与曲线E 交于A ,B 两点,设AB 的中点为M ,C 、D 两点为曲线E 上关于原点O 对称的两点,且CO →=λOM →(λ>0),求四边形ACBD 面积的取值范围.选考题:共10分,请考生在22、23两题中任选一题作答,如果多做,则按所做的第题计分作答时用2B 铅笔在答题卡上把所选题目的题号涂黑在直角坐标系xOy 中,以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,曲线E 的极坐标方程为ρ=2,四边形ABCD 的四个顶点都在曲线E 上.(Ⅰ)求曲线E的直角坐标方程;(Ⅱ)若AC,BD相交于点P(1, 1)求|PA|⋅|PB|⋅|PC|⋅|PD|的值.已知函数f(x)=|x−1|+|x+2|.(Ⅰ)求不等式f(x)≤5的解集;(Ⅱ)若不等式f(x)≥x2−ax+1的解集包含[−1, 1],求实数a的取值范围.2020年新疆乌鲁木齐市高考数学一模试卷(理科)(问卷)一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中只有一项是符合题目要求的.1.若集合A ={x|x 2−2x −8<0},B ={x|x 2−9≤0},则集合A ∪B =( )A.(−2, 3]B.(−4, 3]C.[−3, 2)D.[−3, 4) 【解答】∵集合A ={x|x 2−2x −8<0}={x|−2<x <4},B ={x|x 2−9≤0}={x|−3≤x ≤3},∴集合A ∪B ={x|−3≤x <4}=[−3, 4).2.已知复数z 满足z(1+2i)=|3+4i|(i 是虚数单位),则z 的共轭复数z ¯=()A.1+2iB.1−2iC.−1+2iD.−1−2i 【解答】由z(1+2i)=|3+4i|=5,得z =51+2i =5(1−2i)(1+2i)(1−2i)=1−2i ,∴z ¯=1+2i .3.已知双曲线x 2a 2−y 2b 2=1(a >0,b >0)的两条渐近线互相垂直,焦距为6√2,则该双曲线的实轴长为( )A.3B.6C.9D.12【解答】双曲线x 2a 2−y 2b 2=1(a >0,b >0)则双曲线的渐近线方程为y =±b a x∵两条渐近线互相垂直,∴b a ×(−b a )=−1,∴a 2=b 2,∵焦距为6√2,∴2c =6√2,∴c =3√2,∴a 2=18−a 2,∴a 2=9,∴a =3,∴双曲线的实轴长为:(6)4.已知m ,n 为两条不同的直线,α,β,γ为三个不同的平面,则下列命题正确的是()A.若m // α,n // α,则m // nB.若α⊥β,γ⊥β且α∩γ=m,则m⊥βC.若m⊂α,n⊂α,m // β,n // β,则α // βD.若m⊥α,n // β,α⊥β,则m⊥n【解答】A.若m // α,n // α,则m // n,相交,或为异面直线,因此不正确;B.若α⊥β,γ⊥β且α∩γ=m,则m⊥β,因此正确;C.若m⊂α,n⊂α,m // β,n // β,则α与β不一定平行,因此不正确;D.若m⊥α,n // β,α⊥β,则m与n不一定垂直,因此不正确.5.数列{a n}是公差为2的等差数列,S n为其前n项和,且a1,a4,a13成等比数列,则S4=()A.8B.12C.16D.24【解答】数列{a n}是公差d为2的等差数列,S n为其前n项和,且a1,a4,a13成等比数列,可得a42=a1a13,即(a1+6)2=a1(a1+24),解得a1=3,则S4=4a1+6d=4×3+6×2=(24)6.若正整数n除以正整数m的余数为r,则记为r=nbmodm,例如2=12bmod5,如图程序框图的算法源于我国古代著名的中国剩余定理,执行该程序框图,则输出的i等于()A.2B.4C.8D.16【解答】模拟程序的运行,可得i=1,n=7,第一次执行循环体,得i=2,n=9,此时9mod3=0,不满足第一条件;第二次执行循环体,得i=4,n=13,此时13mod3=1,但13mod5=3,不满足第二条件;第三次执行循环体,得i=8,n=21,此时21mod3=0,不满足第一条件;第四次执行循环体,得i=16,n=37,此时37mod3=1,且37mod5=2,满足第二条件,此时退出循环.所以输出i的值为(16)7.为了解某市居民用水情况,通过抽样,获得了100位居民某年的月均用水量(单位:吨),将该数据按照[0, 0.5),[0.5, 1),…[4.4.5]分成9组,绘制了如图所示的频率分布直方图,政府要试行居民用水定额管理,制定了一个用水量标准a,使85%的居民用水量不超过a,按平价收水费,超出a的部分按议价收费,则以下比较适合作为标准a的是()A.2.5吨B.3吨C.3.5吨D.4吨【解答】[0, 0.5)的频数为0.08×0.5×100=4,[0.5, 1)的频数为0.16×0.5×100=8,[1, 1.5)的频数为0.3×0.5×100=15,[1.5, 2)的频数为0.44×0.5×100=22,[2, 2.5)的频数为0.5×0.5×100=25,[2.5, 3)的频数为0.28×0.5×100=14,[3, 3.5)的频数为0.12×0.5×100=6,[3.5, 4)的频数为0.08×0.5×100=4,[4.4.5]的频数为0.04×0.5×100=(2)4+8+15+22+25+14=86故前六组占86%,a为3吨.8.天文学中为了衡量星星的明暗程度,古希腊天文学家喜帕恰斯(Hipparcℎus,又名依巴谷)在公元前二世纪首先提出了星等这个概念.星等的数值越小,星星就越亮;星等的数值越大它的光就越暗.到了1850年,由于光度计在天体光度测量中的应用,英国天文学家普森(M.R.Pogson)又提出了衡量天体明暗程度的亮度的概念,天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足m1−m2=2.5(lgE2−lgE1),其中星等为m k的星的亮度为E k(k=1, 2)已知“心宿二”的星等是1.00,“天津四”的星等是1.25,“心宿二”的亮度是“天津四”的r倍,则与r最接近的是(当|x|较小时,10x≈1+2.3x+2.7x2)()A.1.24B.1.25C.1.26D.1.27【解答】设“心宿二”的星等是m1,“天津四”的星等是m2,“心宿二”的亮度是E1,“天津四”的亮度是E2,则m1=1.00,m2=1.25,E1=rE2,∵两颗星的星等与亮度满足m1−m2=2.5(lgE2−lgE1),∴1−1.25=2.5(lgE2−lgrE2),即:lgr=0.1,∴r=100.1≈1+2.3×0.1+2.7×(0.1)2=1+0.23+0.027=1.257,∴与r最接近的是1.26,9.已知函数f(x)=2sin2(x+π6)+√3sin(2x+π3)−1,则下列判断正确的是()A.f(x)的图象关于x=π6对称 B.f(x)为奇函数C.f(x)的值域为[−3, 1]D.f(x)在[0,π3]上是增函数【解答】∵f(x)=2sin2(x+π6)+√3sin(2x+π3)−1=√3sin(2x+13π)−cos(2x+13π)=2sin(2x+π6),由于x=π6时,函数值为2为函数的最大值,满足对称的性质,故A正确,10.已知α∈(0,π4),a=(sinα)sinα,b=(sinα)cosα,c=(cosα)sinα,则a,b,c的大小关系()A.b<a<cB.b<c<aC.a<b<cD.c<b<a【解答】因为α∈(0,π4),∴0<sinα<cosα<1;∴y=(sinα)x单调递减;y=x sinα单调递增;∴(sinα)sinα>(sinα)cosα;(sinα)sinα<(cosα)sinα;∴a>b,a<c.即c>a>b.(也可以取30∘直接带入比较)11.已知抛物线y 2=4x 的焦点F ,准线为l ,过点F 且斜率为√3的直线交抛物线于点M (M 在第一象限),MN ⊥l 于点N ,直线NF 交y 轴于点D ,则|MD|=( ) A.4 B.2√3C.2D.√3【解答】由题意,可知:F(1, 0). 直线l FM :y =√3(x −1). 联立{y =√3(x −1)y 2=4x, 整理,得3x 2−10x +3=(0) 解得x =13,或x =(3) 当x =13时,y =−2√33;当x =3时,y =2√3. ∴点M 坐标为(3, 2√3).∵准线l:x =−(1)∴点N 坐标为(−1, 2√3). ∴直线FN 斜率k NF =2√3−1−1=−√3. ∴l FN :y =−√3(x −1), ∴点D 坐标为(0, √3).∴|MD|=√(3−0)2+(2√3−√3)2=2√3. 故选:B .12.已知函数f(x)={lnx −1,x ≥113(x +2),x <1 ,若α<β且f(α)=f(β),则β−α的取值范围是( )A.[8−3ln3, 6]B.[8−3ln3, e 2−1]C.[9−4ln3, 6]D.[9−4ln3, e 2−1] 【解答】作出函数f(x)的图象,如图所示,由α<β且f(α)=f(β),可得lnβ−1=13(α+2), 由题意可得,lnβ−1<1即1≤β<e 2, 故α=3lnβ−5, 则β−α=β−3lnβ+5,令ℎ(x)=x −3lnx +5,1≤x <e 2, 则ℎ′(x)=1−3x =x−3x,易得ℎ(x)在[1, 3)上单调递减,[3, e 2)上单调递增, 故当x =3时函数取得极小值,也是最小值ℎ(3)=8−3ln3, 而ℎ(e 2)=e 2−1>ℎ(1)=6, 故8−3ln3≤ℎ(x)≤(6) 故选:A .二、填空题:本大题共4小题,每小题5分已知单位向量a →,b →满足a →⋅(a →+2b →)=2,则向量a →,b →夹角的大小为________. 【解答】 ∵|a →|=|b →|=1,∴a →⋅(a →+2b →)=a →2+2a →⋅b →=1+2a →⋅b →=2, ∴a →⋅b →=12, ∴cos <a →,b →>=a →⋅b→|a →||b →|=12,且0≤<a →,b →>≤π,∴<a →,b →>=π3.已知点N 在圆x 2+y 2−4x +4y +7=0上,点M 在直线3x −4y +6=0上,则|MN|的最小值为________.【解答】化圆x2+y2−4x+4y+7=0为(x−2)2+(y+2)2=1,则圆心坐标为(2, −2),半径为(1)圆心到直线3x−4y+6=0的距离d=√32+(−4)2=4>1,∴直线与圆相离,如图:由图可知,|MN|的最小值为4−1=(3)故答案为:(3)造纸术是我国古代四大发明之一.纸张的规格是纸张制成之后,经过修整切边,裁成一定的尺寸.现在我国采用国际标准,规定以A0,A1,…,A10;B0,B1,…,B10等标记来表示纸张的幅面规格.复印纸幅面规格只采用A系列和B系列,其中A系列的幅面规格为:①A0规格的纸张幅宽(以x 表示)和长度(以y表示)的比例关系为x:y=1:√2,②将A0纸张沿长度方向对开成两等份,便成为A1规格,A1纸张沿长度方向对开成两等份,便成为A2规格,…,如此对开至A8规格,现有A0,A1,A2,A3,…,A8纸各一张,若A4纸的面积为624cm2,这九张纸的面积之和等于________(cm2)【解答】可设Ai纸张的面积分别为S i,i=0,1,…,8,则{S i}为等比数列,公比q= 12,∵S4=624=S0×(12)4,解得S0=99(84)可得这9张纸的面积之和=9984[1−(12)9]1−12=19929cm2.如图,正方体ABCD−A1B1C1D1的棱长为1,有下列四个命题:①BC1与平面BCD1A1所成的角为30∘;②三棱锥A−A1BD与三棱锥C1−A1BD的体积比为1:2;③过点A 作平面α,使得棱AB ,AD ,AA 1在平面α上的正投影的长度相等,则这样的平面α有且只有一个;④过BD 1作正方体的截面,设截面面积为S ,则S 的最小值为√62; 上述四个命题中,正确命题的序号为________【解答】如图所示,①BC 1与平面BCD 1A 1所成的角θ为锐角,满足:sinθ=OC1BC 1=√222=12,θ=30∘,正确;②三棱锥A −A 1BD 的体积=13×12×12=16,三棱锥C 1−A 1BD 的体积=13−4×16=13,因此体积比=1:2,正确;③过点A 作平面α,使得棱AB ,AD ,AA 1在平面α上的正投影的长度相等,则这样的平面α有且只有一个,是经过点A 且与直线AC 1垂直的平面,正确. ④过BD 1作正方体的截面,设截面面积为S ,截面为BFD 1E ,其中E ,F 为分别为棱AA 1,CC 1的中点,此时面积S =√12+(12)2×1=√52<√62,因此不正确.上述四个命题中,正确命题的序号为①②③.三、解答题:第17~21题每题12分,解答应写出文字说明、证明过程或演算步骤.如图,在四棱锥P −ABCD 中,PA ⊥平面ABCD ,ABCD 是正方形,E 是CD 的中点,点F 在BC 上,且BF =3FC . (Ⅰ)证明:EF ⊥平面PAE ;(Ⅱ)若PA =54AB ,求平面PAB 与平面PEF 所成的二面角的正弦值.【解答】(1)证明:以A 为原点,AB 为x 轴,AD 为y 轴,AP 为z 轴,建立空间直角坐标系,设AB =a ,AP =b ,则E(a2, a, 0),F(a, 34a, 0),A(0, 0, 0),P(0, 0, b), EF →=(a2, −a4, 0),AE →=(a2,a, 0),AP →=(0, 0, b),则EF →⋅AE →=0,EF →⋅AP →=0,∴EF ⊥AE ,EF ⊥AP , ∵AE ∩AP =A ,∴EF ⊥平面PAE . (2)∵PA =54AB ,设AB =4,则AP =5, 则P(0, 0, 5),E(2, 4, 0),F(4, 3, 0), PE →=(2, 4, −5),PF →=(4, 3, −5), 设平面PEF 的法向量m →=(x, y, z),则{m →⋅PE →=2x +4y −5z =0m →⋅PF →=4x +3y −5z =0 ,取x =1,得m →=(1, 2, 2), 平面PAB 的法向量n →=(0, 1, 0),设平面PAB 与平面PEF 所成的二面角的平面角为θ, 则cosθ=|m →⋅n →||m →|⋅|n →|=23,∴平面PAB 与平面PEF 所成的二面角的正弦值为: sinθ=√1−(23)2=√53.已知△ABC 的面积为3,BC 边上的高是2,tanA =3. (Ⅰ)求△ABC 外接圆的半径; (Ⅱ)求AB 和AC 的长. 【解答】(1)由题意,设AB =c ,AC =b ,BC =a ,tanA =3>(0) ∴cosA =√11+tan 2A =√11+9=√1010,sinA =√1−cos 2A =3√1010, ∵△ABC 的面积S 为3,BC 边上的高ℎ是2, ∴3=12aℎ=12×a ×2,解得a =3,∴设△ABC 外接圆的半径为R ,则由正弦定理可得2R =asinA =3√1010,解得△ABC 外接圆的半径R =√102. (2)∵由(Ⅰ)可得sinA =3√1010,△ABC 的面积S 为3=12bcsinA =bc3√1020, ∴解得bc =2√10,①∵由(Ⅰ)可得a =3,cosA =√1010,利用余弦定理可得9=b 2+c 2−2bc ×√1010=b 2+c 2−4√10×√1010,可得b 2+c 2=13,②∴由①②联立解得{b =2√2c =√5,或{b =√5c =2√2 .在统计调查中,问卷的设计是一门很大的学问,特别是对一些敏感性问题.例如学生在考试中有无作弊现象,社会上的偷税漏税等,更要精心设计问卷,设法消除被调查者的顾虑,使他们能够如实回答问题,否则被调查者往往会拒绝回答,或不提供真实情况,为了调查中学生中的早恋现象,随机抽出300名学生,调查中使用了两个问题.①你的学籍号的最后一位数是奇数(学籍号的后四位是序号);②你是否有早恋现象,让被调查者从装有4个红球,6个黑球(除颜色外完全相同)的袋子中随机摸取两个球,摸到两球同色的学生如实回答第一个问题,摸到两球异色的学生如实回答第二个问题,回答“是”的人往一个盒子中放一个小石子,回答“否”的人什么都不放,后来在盒子中收到了78个小石子. (Ⅰ)你能否估算出中学生早恋人数的百分比?(Ⅱ)若从该地区中学生中随机抽取一个班(40人),设其中恰有X 个人存在早恋的现象,求X 的分布列及数学期望 【解答】(1)摸到同色球的概率为p 1=C 42+C 62C 102=715,摸到异色球的概率为p 2=C 41C61C 102=815,由此可估计300人中有300×715=140人摸到同色球,160人摸到异色球, ∴有140人回答了问题①,160人回答了问题②,∵学生学籍号的后四位是顺序号,∴最后一位是奇数的概率为12, 因此回答问题①的140人有70人回答了“量”, 据此估计有8人在问题②中回答了“是”, ∴估计中学生的早恋人数的百分比为8160=5%. (2)依题意X ∼B(40, 0.05),分布列为P(X =k)=C 40k (120)k (1920)20−k ,k =0,1,2,…,(40)∴E(X)=40×0.05=(2)已知函数f(x)=ax 2−xlnx −x(a ∈R).(Ⅰ)当a =1e 时,求曲线y =f(x)在点(e, f(e))处的切线方程; (Ⅱ)若f(x)在定义域内为单调函数,求实数a 的取值范围. 【解答】(I )当a =1e 时,f(x)=x 2e−xlnx −x ,f ′(x)=2x e−lnx −2,∴f(e)=e −e −e =−e ,f ′(e)=−1,所以切线方程为y +e =−(x −e),即x +y =0;(II)由f ′(x)=2ax −lnx −2,x >0,设g(x)=2ax −lnx −2,x >0,则g ′(x)=2a −1x ,当a <0时,g ′(x)<0,g(x)在(0, +∞)单调递减,由g(e 2a−2)=2ae 2a−2−2a =2a(e 2a−2−1)>0,g(1)=2a −2<0, ∴g(x)在(0, +∞)不恒正或恒负,∴f(x)在(0, +∞)不为单调函数,不符合条件; 当a =0时,g(x)=−lnx −2,x >0,显然不满足条件; 当a >0时,由g ′(x)=0,得x =12a ,当x ∈(0, 12a )时,g(x)递减,当x ∈(12a , +∞)时,g(x)递增; ∴g(x)min =g(12a )=ln2a −1,根据题意要使g(x)≥0恒成立,则ln2a ≥1,即a ≥e2, 综上,a ≥e2.点P(x, y)与定点F(−1, 0)的距离和它到直线l:x =−3的距离的比是常数√33,设点P 的轨迹为曲线E . (Ⅰ)求曲线E 的方程;(Ⅱ)过点F 的直线l 与曲线E 交于A ,B 两点,设AB 的中点为M ,C 、D 两点为曲线E 上关于原点O 对称的两点,且CO →=λOM →(λ>0),求四边形ACBD 面积的取值范围. 【解答】 (1)由条件得√(x+1)2+y 2|x+3|=√33,整理得2x 2+3y 2=6,即曲线E 的方程为x 23+y 22=1;(2)①当直线l 的斜率为0时,点M 与O 重合,不满足CO →=λOM →(λ>0),故斜率不为0;②当直线斜率不为0时,设AB:x =my −1,代入E 得2(my −1)2+3y 2−6=0,整理得(2m 2+3)y 2−4my −4=0,设A(x 1, y 1)B(x 2, y 2),则y 1+y 2=4m2m 2+3,y 1y 2=−42m 2+3, 所以AB =2|y 1−y 2|=√1+m 2√16m 2(2m 2+3)2+162m 2+3=4√3(1+m 2)2m 2+3,x 1+x 2=m(y 1+y 2)−2=4m 22m 2+3−2=−62m 2+3, 所以M(−32m +3, 2m2m +3),因为CO →=λOM →(λ>0),所以C(3λ2m 2+3, −2λm2m 2+3), 又因为C 在曲线E 上,代入得9λ2(2m 2+3)23+4λ2m 2(2m 2+3)22=1,整理得λ2=2m 2+3, 因为点O 到直线AB 的距离d =√2,设四边形ACBD 面积为S ,△ABO 的面积为S 1, 则S 1=12AB ⋅d =12×4√3(1+m 2)2m 2+3×√1+m 2=2√3⋅√1+m 22m 2+3,所以S =S △ABC +S △ABD =(λ+1)S 1+(λ−1)S 1=2λS 1=4√3λ⋅√1+m 22m 2+3, 将λ2=2m 2+3代入得S =4√3⋅√1+m 22m 2+3=4√3⋅√12+1m 2+1,因为m ∈R ,所以当m =0时S 取最小值为4,所以4≤S <2√6 故四边形的取值范围为[4, 2√6).选考题:共10分,请考生在22、23两题中任选一题作答,如果多做,则按所做的第题计分作答时用2B 铅笔在答题卡上把所选题目的题号涂黑 在直角坐标系xOy 中,以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,曲线E 的极坐标方程为ρ=2,四边形ABCD 的四个顶点都在曲线E 上. (Ⅰ)求曲线E 的直角坐标方程;(Ⅱ)若AC ,BD 相交于点P(1, 1)求|PA|⋅|PB|⋅|PC|⋅|PD|的值. 【解答】(1)曲线E 的极坐标方程为ρ=2,转换为直角坐标方程为:x 2+y 2=(4) (2)设经过点P(1, 1)的直线AC 的参数方程为{x =1+cosθty =1+sinθt (t 为参数) 把直线AC 的参数方程代入圆的方程为(1+cosθt)2+(1+sinθt)2=4,整理得t 2+2(cosθ+sinθ)t −2=0, 所以t 1t 2=−(2)所以|PA||PC|=|t 1t 2|=(2)同理经过点P(1, 1)的直线BD 的参数方程为{x =1+cos(π−θ)ty =1+sin(π−θ)t (t 为参数)整理得{x =1−cosθty =1+sinθt (t 为参数),把直线BD 的参数方程代入圆的方程为(1−cosθt)2+(1+sinθt)2=4,整理得t 2+2(sinθ−cosθ)t −2=0, 所以t 3t 4=−2,所以|PB||PD|=|t 3t 4|=(2) 故:|PA|⋅|PB|⋅|PC|⋅|PD|=(4) 已知函数f(x)=|x −1|+|x +2|. (Ⅰ)求不等式f(x)≤5的解集;(Ⅱ)若不等式f(x)≥x 2−ax +1的解集包含[−1, 1],求实数a 的取值范围. 【解答】(1)函数f(x)=|x −1|+|x +2|={−2x −1,x ≤−24,−2<x <12x +1,x ≥1;当x ≤−2时,不等式f(x)≤5为−2x −1≤5,解得x ≥−3,即−3≤x ≤−2;当−2<x <1时,不等式f(x)≤5为4≤5恒成立,即−2<x <1; 当x >1时,不等式f(x)≤5为2x +1≤5,解得x ≤2,即1≤x ≤2; 综上知,不等式f(x)≤5的解集为{x|−3≤x ≤2}; (2)不等式f(x)≥x 2−ax +1的解集包含[−1, 1], 即x ∈[−1, 1]时,不等式4≥x 2−ax +1恒成立; 即x ∈[−1, 1]时,不等式x 2−ax −3≤0恒成立; 设g(x)=x 2−ax −3,x ∈[−1, 1], 则{g(−1)≤0g(1)≤0 ,即{1+a −3≤01−a −3≤0,解得−2≤a ≤2;所以实数a 的取值范围是[−2, 2].。
新疆2020年高考理科数学模拟试题及答案(一)

新疆2020年高考理科数学模拟试题及答案(一)(满分150分,考试时间120分钟)一、选择题(本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的。
)1. 已知集合2{|2}A x x =<,则R C A =( )A.{|22}x x -≤≤B.{|22}x x x ≤-≥或C.{|22}x x -≤≤D.{|22}x x x ≤-≥或2. 若()12z i i +=,则z =( )A.1i --B.1i -+C.1i -D.1i +3. 已知3a e =,33log 5log 2b =-,2ln 3c =,则a ,b ,c 的大小关系为( ) A .a c b >> B .b c a >> C .c a b >>D .c b a >>4. 已知10,2sin cos 2R ααα∈-=,则tan(2)4πα-=( ) A .43 B .7- C .34- D .175. 已知某几何体的三视图如图所示,网格中小正方形的边长为1,则该几何体的表面积为( )A. 20B. 22C. 24D.6. 已知函数()f x 和(2)f x +都是定义在R 上的偶函数,当[0,2]x ∈时,()2xf x =,则20192f ⎛⎫-= ⎪⎝⎭( )A. 2B. 2C.32227. 直线2130x ay a -+-=,当a 变动时,所有直线所过的定点为( ) A.1(,3)2-B. 1(,3)2--C. 1(,3)2D.1(,3)2- 8. 三棱锥V ABC -的底面三角形ABC 为正三角形,侧面VAC 垂直于底面,VA VC =,已知其正视图VAC ∆面积为23,则其侧视图的面积为 ( ) A.32 B. 36 C. 34 D.339. 如图,已知直四棱柱中,,,且,则直线与直线所成角的余弦值为( )A.B. C. D.10. 已知中,内角所对的边分别是,若,且,则当取到最小值时,( ) A.B.C.D. 11. 定义在上的偶函数满足:当时,,.若函数有6个零点,则实数的取值范围是( )A.B.C.D.12. 已知抛物线的焦点为,且到准线的距离为2,直线与抛物线交于两点(点在轴上方),与准线交于点,若,则( ) A.B.C.D.二、填空题(本题共4小题,每小题5分,共20分。
理科数学答案 新疆维吾尔自治区2020年普通高考第三次适应性检测试卷答案

因为 CE⊂平面 COE,所以 AB⊥CE,
取 CE 的中点 G,连接 AG,PG,
因为 P 为 CD 中点,所以 PG∥DE,
又菱形 ABDE 中,AB∥DE,
树人·优升 2020 年普通高考第三次适应性检测 理科数学答案 第 2 页 共 6 页
所以 PG∥AB,故 A,B,P,G 四点共面, 由 EA = CA 可得 AG⊥CE, 又 AB∩AG = A,所以 CE⊥平面 ABP. ……………………………………… 6 分 (2) 由(1) 可知,AB,OC,OE 两两垂直,以 OC,OB,OE 所在直线分别为 x,y,z 轴建立如 图所示空间直角坐标系,
P( X
=
1200) =
1
-C
1 3
p(
1
-p)
2
故
E(
X)=
1200
×[
1
-C
1 3
p(
1
-p)
2]
+2000×C13
p(1-p)
2
=
1200 + 2400p( 1 -p)
2
令 f (p)= p(1-p) 2,p∈(0, 1)
则 f ′( p)= (1-p) 2 -2p(1-p)= ( p-1) (3p-1) ……………………………… 10 分
,
∴
1 ∈(0, tan B
3),
∴
c∈(1,4) .
∴ c 的取值范围为(1,4) . ……………………………………………………… 12 分
树人·优升 2020 年普通高考第三次适应性检测 理科数学答案 第 1 页 共 6 页
18. ( Ⅰ) 依题意,(0. 005+a+b+0. 035+0. 028) ×10 = 1,
2020年新疆乌鲁木齐市高考数学三模试卷(一)(有答案解析)
2020年新疆乌鲁木齐市高考数学三模试卷(一)一、选择题(本大题共12小题,共60.0分)1.已知集合A={x|x2-x>0},B={x|-},则()A. A∩B=∅B. A∪B=RC. A⊆BD. B⊆A2.若=2-i(其中i是虚数单位),则实数a=()A. -3B. -1C. 1D. 33.当0<a<1时,在同一坐标系中,函数y=a-x与y=log a x的图象是()A. B.C. D.4.已知直线l⊥平面α,直线m⊂平面β,有下列命题:①α∥β⇒l⊥m,②α⊥β⇒l∥m③l∥m⇒α⊥β④l⊥m⇒α∥β正确的命题是()A. ①与②B. ③与④C. ②与④D. ①与③5.从1,2,3,4,5,6中任意取出两个不同的数,其和为7的概率为()A. B. C. D.6.设等差数列{n}的前n项和为若,则( )A. 45B. 54C. 72D. 817.在下列区间中,函数f(x)=e x+3x-4的零点所在的区间为()A. (0,)B. ()C. ()D. (1,)8.若函数f(x)=A sin(ωx+φ)(A>0,ω>0,|φ|<)的部分图象如图所示,则函数f(x)的解析式为()A. f(x)=sin(2x+)B. f(x)=cos(2x+)C. f(x)=cos(2x+)D. f(x)=sin(2x+)9.正方体的全面积为6,它的顶点都在球面上,则这个球的表面积是()A. 3πB. 4πC. 6πD. 8π10.高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的称号,用其名字命名的“高斯函数”为:设x∈R,用[x]表示不超过x的最大整数,则y=[x]称为高斯函数.例如:[-2.1]=-3,[3.1]=3,已知函数,则函数y=[f(x)]的值域为()A. B. (0,2] C. {0,1,2} D. {0,1,2,3}11.已知抛物线C:y2=8x的焦点为F,直线l过焦点F与抛物线C分别交于A,B两点,且直线l不与x轴垂直,线段AB的垂直平分线与x轴交于点P(10,0),则△AOB 的面积为()A. 4B. 4C. 8D. 812.已知函数f(x)是定义在R上的奇函数,当x<0时,f(x)=e x(x+1),给出下列命题:①当x>0时,f(x)=e-x(x-1)②函数f(x)有3个零点③f(x)>0的解集为(-1,0)∪(1,+∞)④∀x1,x2∈R,都有|f(x1)-f(x2)|<2其中正确命题的个数是()A. 4B. 3C. 2D. 1二、填空题(本大题共4小题,共20.0分)13.若变量x,y满足约束条件则z=x+y的最大值是______.14.在△ABC中,D为BC的中点,E为AD的中点,F为BE的中点,若=,则λ+μ=______.15.已知双曲线=1(a>0,b>0)的右焦点为F,以F为圆心,焦距为半径的圆交y轴正半轴于点M,线段FM交双曲线于点P,且|FM|=2|FP|,则双曲线的离心率为______.16.已知数列{a n}中,前n项和为S n,且,则的最大值为______.三、解答题(本大题共7小题,共84.0分)17.在△ABC中,角A,B,C的对边分别为a,b,c,已知(2a-b)cos C+2c sin2=c.(Ⅰ)求角C的大小;(Ⅱ)若a+b=4,c=,求△ABC的面积.18.如图,在三棱锥P-ABC中,PA=PB=,PA⊥PB,AC⊥平面PAB,D、E分别是AC,BC上的点,DE∥平面PAB.(Ⅰ)求证:AB∥平PDE;(Ⅱ)若D为线段AC中点,PA=2.求点B到平面PDE的距离.19.十九大提出,坚决打赢脱贫攻坚战,某帮扶单位为帮助定点扶贫村真脱贫,坚持扶贫同扶智相结合,帮助贫困村种植蜜柚,并利用电商进行销售,为了更好地销售,现从该村的蜜柚树上随机摘下了100个蜜柚进行测重,其质量分别在[1500,1750),[1750,2000),[2000,2250),[2250,2500),[2500,2750),[2750,3000](单位:克)中,其频率分布直方图如图所示,(Ⅰ)已经按分层抽样的方法从质量落在[1500,1750),[2000,2500)的蜜柚中抽取了5个,现从这5个蜜柚中随机抽取2个.求这2个蜜柚质量均小于2000克的概率:(Ⅱ)以各组数据的中间值代表这组数据的平均水平,以频率代表概率,已知该贫困村的蜜柚树上大约还有5000个蜜柚等待出售,某电商提出了两种收购方案:方案一:所有蜜柚均以30元/千克收购;方案二:低于2250克的蜜柚以60元/个收购,高于或等于2250克的以80元/个收购.请你通过计算为该村选择收益最好的方案.20.已知F是椭圆=1的右焦点,过点F的直线交椭圆于A,B两点.M是AB的中点,直线OM与直线x=2交于点N.(Ⅰ)求征:=0;(Ⅱ)求四边形OANB面积的最小值.21.已知函数f(x)=ln x+.(Ⅰ)若a=-2,求函数f(x)的单调区间;(Ⅱ)若函数f(x)有两个极值点x1,x2,求证:f(x1)+f(x2)<0.22.在平面直角坐标系xoy中,直线l的参数方程为(t为参数).以坐标原点为极点,x轴的非负半轴为极轴的极坐标系中.曲线C的极坐标方程为cos ().(Ⅰ)写出直线l的普通方程和曲线C的直角坐标方程;(Ⅱ)判断直线l与曲线C的位置关系,并说明理由.23.已知函数f(x)=|2x+1|-|x-3|(Ⅰ)求不等式f(x)≥0的解集;(Ⅱ)若关于x的不等式f(x)≥|x-3|+a恒成立,求实数a的取值范围.-------- 答案与解析 --------1.答案:B解析:解:∵集合A={x|x2-x>0}={x|x<0或x>1},B={x|-},∴A∪B=R.故选:B.先分别求出集合A={x|x2-x>0}={xx|x<0或x>1},B={x|-},再求出A∪B,能求出结果.本题考查集合的运算及关系,考查并集定义、不等式性质等基础知识,考查运算求解能力,属于基础题.2.答案:A解析:【分析】本题考查复数代数形式的乘除运算,考查复数相等的条件,属于基础题.把已知等式变形,利用复数代数形式的乘除运算化简,再由复数相等的条件求得a值.【解答】解:∵=2-i,∴1+ai=(2-i)(1-i)=1-3i,∴a=-3,故选:A.3.答案:C解析:解:∵函数y=a-x与可化为函数y=,其底数大于1,是增函数,又y=log a x,当0<a<1时是减函数,两个函数是一增一减,前增后减.故选:C.先将函数y=a-x化成指数函数的形式,再结合函数的单调性同时考虑这两个函数的单调性即可判断出结果本题考查函数的图象,考查同学们对对数函数和指数函数基础知识的把握程度以及数形结合的思维能力.4.答案:D解析:解:∵l⊥α,α∥β,∴l⊥β,又直线m⊂β,故有l⊥m,即①正确;∵l⊥α,α⊥β,∴l∥β,或l⊂β,此时l与m可能平行,相交或异面,即②错误;∵l⊥α,l∥m,∴m⊥α,又m⊂β,故有α⊥β,即③正确.∵l⊥α,l⊥m,∴又m⊂β,此时α与β可能相交可能平行,故④错误;故选:D.本题应逐个判断:①④需用熟知的定理即线线垂直,面面垂直来说明,②③可举出反例来即可.本题考查直线的平行于垂直关系,熟练运用性质定理是解决问题的关键,属基础题.5.答案:B解析:【分析】本题考查古典概型及其概率公式,属基础题.列出所有的基本事件和随机事件中含有的基本事件,两者的比值为所求的概率.【解答】解:从1,2,3,4,5,6中任意取出两个不同的数,共有15种不同的取法,它们分别是(1,2),(1,3),(1,4),(1,5),(1,6),(2,3),(2,4),(2,5),(2,6),(3,4),(3,5),(3,6),(4,5),(4,6),(5,6),从1,2,3,4,5,6中任意取出两个不同的数,它们的和为7,则不同的取法为:(1,6),(2,5),(3,4),共有3种情形,故所求的概率为,故选:B.6.答案:B解析:【分析】由等差数列的性质可得:S3,S6-S3,S9-S6成等差数列.即可得出.本题考查了等差数列的求和公式及其性质,考查了推理能力与计算能力,属于中档题.【解答】解:由等差数列的性质可得:S3,S6-S3,S9-S6成等差数列.∴2×(27-9)=9+S9-27,解得S9=54.故选:B.7.答案:C解析:解:f′(x)=e x+3>0,f(x)为R上的增函数,f()==,因为,所以,所以f()<0,但f(1)=e+3-4>0,∴f()•f(1)<0所以f(x)的零点在区间(,1),故选:C.先判断函数的单调性,再利用零点存在定理判断零点所在的区间,属于基础题.函数零点所在区间的判断,需利用函数的单调性和零点存在定理来判断,选择怎样的点来计算其函数值且函数值异号是关键,可根据解析的特点选点,如对于对数lg x,ln x等,应选x=10n或x=e n等,对于指数a x,应选x=log a m(如0,1等)等形式的数来计算.8.答案:D解析:解:由函数的部分图象可知A=1,=,故T=π,所以=π,即:ω=2.由函数图象的对称轴为x=,所以:2×+φ=+2kπ,k∈Z,因|φ|<,故φ=,所以f(x)=sin(2x+).故选:D.根据图象得到函数的振幅和周期,从而得到A,ω的值,再根据对称轴得到φ的值后可得函数的解析式.已知y=A sin(ωx+φ)的图象,求其解析式时可遵循“两看一算”,“两看”指从图象上看出振幅和周期,“一算”指利用最高点或最低点的坐标计算φ.9.答案:A解析:解:因为正方体的全面积为6,所以正方体的棱长为:1,正方体的对角线为:.因为正方体的顶点都在球面上,所以正方体的对角线就是外接球的直径,所以外接球的半径为:.外接球的表面积为:=3π.故选:A.通过正方体的表面积求出棱长,然后求出正方体的外接球的半径,即可求解表面积.本题考查正方体的外接球的表面积的求法,求出外接球的半径是解题的关键,考查计算能力.10.答案:C解析:解:因为,所以f(x)==,又1+2x+1∈(1,+∞),所以f(x)∈(,3),由高斯函数的定义可得:函数y=[f(x)]的值域为,故选:C.由分式函数值域的求法得:f(x)==,又1+2x+1∈(1,+∞),所以f(x)∈(,3),由高斯函数定义的理解得:函数y=[f(x)]的值域为,得解.本题考查了分式函数值域的求法及对即时定义的理解,属中档题.11.答案:C解析:解:设直线l:x=ty+2,A(x1,y1),B(x2,y2),则由,可以得到y2-8ty-16=0,所以AB的中点M(4t2+2,4t),线段AB的垂直平分线与x轴交于点P(10,0),故t≠0.所以AB的中垂线的方程为:y=-(x-4t2-2)+4t=+8t+,令y=0可得x=8t2+2,解方程10=8t2+2,得t=±1.此时|AB|==8=16,O到AB的距离为d==,所以=8.故选:C.设直线l:x=ty+2,联立直线方程和抛物线方程可求得中垂线的方程,再利用P的坐标求出t,最后算出AB的长和O到AB的距离后可得所求的面积.直线与圆锥曲线相交时的产生的对称问题,应利用两个几何性质来构造不同变量之间的关系,这个两个几何性质就是中点和垂直.12.答案:A解析:解:对于①,f(x)为R上的奇函数,设x>0,则-x<0,∴f(-x)=e-x(-x+1)=-f(x),∴f(x)=e-x(x-1),①正确;对于②,∵f(-1)=0,f(1)=0,且f(0)=0,∴f(x)有3个零点,②正确;对于③,x<0时,f(x)=e x(x+1),易得-1<x<0时,f(x)>0;x>0时,f(x)=e-x(x-1),易得x>1时,f(x)>0;∴f(x)>0的解集为(-1,0)∪(1,+∞),③正确;对于④,x<0时,f′(x)=e x(x+2),x<-2时,f′(x)<0,-2<x<0时,f′(x)>0;∴f(x)在(-∞,0)上单调递减,在(-2,0)上单调递增;∴x=-2时,f(x)取最小值-e-2,且x<-2时,f(x)<0;∴f(x)<f(0)=1;即-e-2<f(x)<1;x>0时,f′(x)=e-x(2-x);∴f(x)在(0,2)上单调递增,在(2,+∞)上单调递减;x=2时,f(x)取最大值e-2,且x>2时,f(x)>0;∴f(x)>f(0)=-1;∴-1<f(x)≤e-2;∴f(x)的值域为(-1,e-2]∪[-e-2,1);∴∀x1,x2∈R,都有|f(x1)-f(x2)|<2;④正确.故选:A.根据f(x)为奇函数,设x>0,得-x<0,可求出f(x)=e-x(x-1)判定①正确;由f(x)解析式求出-1,1,0都是f(x)的零点,判定②正确;由f(x)解析式求出f(x)>0的解集,判断③正确;分别对x<0和x>0时的f(x)求导,根据导数符号判断f(x)的单调性,根据单调性求f(x)的值域,可得∀x1,x2∈R,有|f(x1)-f(x2)|<2,判定④正确.本题考查了奇函数的定义与应用问题,也考查了函数的零点以及不等式的解集、根据导数符号判断函数单调性和求函数最值、求函数值域的方法,是综合性题目.13.答案:7解析:解:不等式组对应的可行域所示:其中A(3,4),当动直线x+y-z=0过A时,z有最大值为7.故答案为:7.画出不等式组对应的可行域后平移动直线x+y-z=0可得z的最大值.二元一次不等式组条件下的二元函数的最值问题,常通过线性规划来求最值,求最值时往往要考二元函数的几何意义,比如3x+4y表示动直线3x+4y-z=0的横截距的三倍,而则表示动点P(x,y)与(1,-2)的连线的斜率.14.答案:解析:解:如图,∵D为BC的中点,E为AD的中点,F为BE的中点;∴==;又;∴根据平面向量基本定理得,;∴.故答案为:.可画出图形,根据D为BC的中点,E为AD的中点,F为BE的中点即可得出,而根据平面向量基本定理即可求出λ,μ,从而得出λ+μ.考查向量加法的平行四边形法则,以及向量数乘的几何意义,平面向量基本定理.15.答案:解析:解:因为|FM|=2c,|FO|=c,所以|OM|=,因为|FM|=2|FP|,所以P为FM的中点,P(,),设左焦点为F'(-c,0),根据定义有|PF'|=|PF|+2a=2a+c,即,整理得到,所以e=,故答案为:.本题考查圆锥曲线中的离心率的计算,关键是利用题设条件构建关于a,b,c的一个等式关系,属于中档题.16.答案:2解析:解:根据题意,数列{a n}满足,①则有S n-1=a n-1,②①-②可得:(n-1)a n=na n-1,则有==1+,又由f(n)=1+(n>1且n∈Z)为减函数,则当n=2时,取得最大值,其最大值为1+=2;故答案为:2.根据题意,由变形可得S n-1=a n-1,两式相减可得变形可得==1+,结合f(n)=1+(n>1且n∈Z)的单调性分析可得当n=2时,取得最大值,计算可得答案.本题考查数列的递推公式的应用,注意分析a n与a n-1的关系,属于基础题.17.答案:解:(Ⅰ)因为(2a-b)cos C+2c sin2=c,所以(2a-b)cos C+c(1-cos B)=c,即(2a-b)cos C=c cos B,由正弦定理得到:2sin A cos C-sin B cos C=sin C cos B,即2sin A cos C=sin A,因为A∈(0,π),故sin A>0,所以cos C=,又C∈(0,π),可得C=.(Ⅱ)由(Ⅰ)得由余弦定理可得cos C==,所以=,由于a+b=4,c=,整理得ab=3,可得S△ABC=ab sin C==.解析:本题考查二倍角公式的应用,三角恒等变换、正余弦定理的应用,三角形面积公式,属于中档题.(Ⅰ)利用降幂公式和正弦定理化简(2a-b)cos C+2c sin2=c,可得2sin A cos C=sin A,从而得到cos C=,即C=.(Ⅱ)利用余弦定理得到=,再利用a+b=4,c=,可得ab=3,利用面积公式计算即可.18.答案:证明:(Ⅰ)∵DE∥平面PAB,DE⊂平面ABC,平面ABC∩平面PAB=AB,∵DE∥AB,又AB⊄平面PDE,∴AB∥平面PDE.解:(Ⅱ)取AB的中点为F,连接EF,∵PA=PB,∴PF⊥AB,∵AC⊥平面PAB,AC⊂平面ABC,∴平面PAB⊥平面ABC,平面PAB∩平面ABC=AB,PF⊂平面PAB,∴PF⊥平面ABC,又PA=PB=2,PB⊥PA,故PF为等腰直角三角形斜边AB上的高,故PF=,∴点P到平面ABC的距离为,∵D为线段AC中点,DE∥AB,故E为BC的中点,故DE=AB=,∵AC⊥平面PAB,PA⊂平面PAB,∴AC⊥PA,同理AC⊥AB,∵PC=4,∴AC==2,故AD=,而EF∥AC,故EF⊥AB,∵EF∩PF=F,故AB⊥平面PEF,而PE⊂平面PEF,∴AB⊥PE,故DE⊥PE,在Rt△PAD中,∵PA=2,AD=,故PD=,在Rt△PEF中,∵PF=,EF=,故PE=,故=,又=,设点B到平面PDE的距离为d,则V B-PDE==,解得d=.解析:本题考查线面平行的判定,考查利用等体积法求解点到平面的距离,属于中档题. (Ⅰ)由DE∥平面PAB,可得DE∥AB,从而可证AB∥平面PDE.(Ⅱ)利用等体积法可求点B到平面PDE的距离.19.答案:解:(Ⅰ)质量落在[1500,1750)和[2000,2250)中的频率分别是0.1和0.15,分层抽样的方法抽取5个蜜柚,则[1500,1750)中抽取2个,[2000,2250)中抽取3个,2个蜜柚质量均小于2000的概率为;(Ⅱ)根据题意,方案一收益为:30×(1.625×500+1.875×500+2.125+2.375×750×2000+2.625×1000+2.875×250=343125(元)方案二收益为:500+500+750×60+2000+1000+250×80=365000 (元)∵365000>343125,∴选择方案二.解析:(Ⅰ)利用频率分布直方图可得质量落在[1500,1750)和[2000,2250)中的频率,从而可得抽取的5个蜜柚中落在[1500,1750)和[2000,2250)中的个数,利用古典概型的概率计算公式可得概率.(Ⅱ)利用频率分布直方图中的数据计算出各组的频率,再利用组中值计算出5000只蜜柚在各组中分布的个数,最后按各自方案计算出收益,我们选择收益较大的方案即可.本题考查频率分布直方图的应用和古典概型的计算,属于基础题.20.答案:证明:(Ⅰ)当直线AB斜率不存在时,直銭AB与x轴垂直,∴AB⊥FN,∴=0,当直线AB斜率存在时,设斜率为k,则直线AB的方程为y=k(x-1),设A(x1,y1),B(x2,y2),M(x0,y0),则x0=,y0=,联立得(1+2k2)x2-4k2x+2k2-2=0得x1+x2=,x1x2=,∴x0=,y0=,所以直线的方程为y=-,∴N(2,-),又∵F(1,0),∴k FN=-,∴AB⊥FN,∴=0;解:(Ⅱ)当直线AB斜率不存在时,直銭AB与x轴垂直,∴S四边形OANB=|AB|•|ON|=××2=,当直线AB斜率存在时,S四边形OANB=S OAB+S NAB,设点O到直线AB的距离为d1,点N到直线AB的距离为d2,则d1=,d2=|FN|=,|AB|=•=,∴S四边形OANB=S OAB+S NAB=d1|AB|+d2|AB|=|AB|(d1+d2)=×(+)==>所以四边形OANB面积的最小值为.解析:(Ⅰ)当直线AB斜率存在时,设出直线的方程,联立直线方程和抛物线方程后可得AB中点坐标,故可用直线的斜率表示N的坐标,求出FN的斜率后可证=0.注意直线AB斜率不存在的情形.(Ⅱ)当直线AB斜率存在时,利用韦达定理弦长公式点到直线的距离可以计算S四边形═>,当直线AB斜率不存在时,S四边形OANB=,故可得四边形OANB面OANB积的最小值.圆锥曲线的位置关系中的定点、定值、最值问题,一般可通过联立方程组并消元得到关于x或y的一元二次方程,再把要求解的目标代数式化为关于两个的交点横坐标或纵坐标的关系式,该关系中含有x1+x2,x1x2或y1+y2,y1y2,最后利用韦达定理把关系式转化为若干变量的方程(或函数),从而可求定点、定值、最值问题.21.答案:(Ⅰ)解:当a=-2时,f(x)=ln x--x+5,f′(x)=+-1==,当0<x<2时,f′(x)>0,当x>2时,f′(x)<0,∴f(x)的增区间为(0,2),减区间为(2,+∞).(Ⅱ)证明:f′(x)=--1=(x>0),∵f(x)有两个极值点x1,x2,故x1,x2为-x2+x-a=0的两个正数解,∴,∴0<a<,∴f(x1)+f(x2)=ln(x1x2)+-(x1+x2)-4a+2=ln a-4a+2,令g(a)=ln a-4a+2,则当0<a<时,g′(a)=-4=>0,∴g(a)在(0,)上单调递增,∴当0<a<时,g(a)<g()=ln-1+2=1-ln4<0,∴f(x1)+f(x2)<0.解析:本题考查了导数与函数单调性的关系,利用导数研究函数的极值,属于中档题.(Ⅰ)求出f′(x)后讨论其符号可得函数的单调区间;(Ⅱ)利用导数可得两个极值点为-x2+x-a=0的两个根,利用韦达定理可把而f(x1)+f (x2)化为ln a-4a+2,其中0<a<,利用函数单调性可证结论.22.答案:解(Ⅰ)消去参数t,则直线l的普通方程为x-2y+2=0,因为ρ=2cos(θ+),故ρ=2cosθ-2sinθ即ρ2=2ρcosθ-2ρsinθ,曲线C的直角坐标方程为x2+y2-2x+2y=0.(Ⅱ)圆心(1,-1)到直线x-2y+2=0的距离d=>,直线l与曲线C是相离的位置关系.解析:(Ⅰ)消去参数t后可得直线的普通方程.把ρ=2cos(θ+)化成ρ2=2ρcosθ-2ρsinθ再利用化简后可得曲线C的直角坐标方程.(Ⅱ)利用圆心到直线的距离可判断直线与曲线的位置关系.本题考查了极坐标方程与直角方程的互化,关键是,必要时须在给定方程中构造ρcosθ,ρsinθ.直线与圆的位置关系可用圆心到直线的距离与半径的大小来判断,属中档题.23.答案:解:(Ⅰ)函数f(x)=|2x+1|-|x-3|=;画出函数f(x)的图象,如图所示,根据函数图象知,当f(x)≥0时,x的取值范围是x≤-4,或x≥;所以不等式f(x)≥0的解集为(-∞,-4]∪[,+∞);(Ⅱ)f(x)≥|x-3|+a恒成立,即|2x+1|-2|x-3|≥a恒成立,令g(x)=|2x+1|-2|x-3|,则g(x)=,所以f(x)的最小值为-7,则a的取值范围是a≤7.解析:(Ⅰ)利用零点分段讨论可得不等式的解集.(Ⅱ)不等式恒成立等价于|2x+1|-2|x-3|≥a,令g(x)=|2x+1|-2|x-3|,求出g(x)的最小值后可得实数a的取值范围.本题考查了含有绝对值不等式的解法与应用问题,解题时有零点分段讨论法、图象法、平方法等,利用零点分段讨论法时注意分类点的合理选择,利用平方去掉绝对值符号时注意代数式的正负,利用图象法求解时注意图象的正确刻画.。
2020年新疆乌鲁木齐市高考数学一诊试卷(理科)(有解析)

2020年新疆乌鲁木齐市高考数学一诊试卷(理科)一、单项选择题(本大题共12小题,共60.0分)1.设集合A={x|x2−2x−3≤0},B={x|0<x<4},则A∩B=()A. [−1,4)B. [−1,3)C. (0,3]D. (0,4)2.|1−2i2+i|=()A. 1B. √2C. −iD. 23.设α,β,γ是三个互不重合的平面,m,n是两条不重合的直线,则下列命题中正确的是()A. 若α⊥β,β⊥γ,则α⊥γB. 若α⊥β,m⊥α,则m//βC. 若α//β,m⊄β,m//α,则m//βD. 若m//α,n//β,α⊥β,则m⊥n4.已知a=log35,b=log95,则有()A. a>b>0B. 0<a<bC. a<b<0D. 0>a>b5.已知向量a⃗=(1,√3),向量a⃗,c⃗的夹角是π3,a⃗⋅c⃗=2,则|c⃗|等于()A. −2B. 4C. 2D. −46.设F1、F2分别是双曲线C:x2a2−y2b2=1(a>0,b>0)的左、右焦点,以F1为圆心、|F1F2|为半径的圆与双曲线左支的其中一个交点为A,若∠AF1F2=120°,则该双曲线的离心率是()A. √2B. √3C. √3+1D. √3+127.执行如图所示的程序框图,则输出的数的个数是()A. 7B. 6C. 5D. 48.从1,2,3,4,5,6这6个数字中,不放回地任取两数,两数都是偶数的概率是()A. 12B. 13C. 14D. 159.已知S n是等差数列{a n}的前n项和,a2=4,S4=20,若a1,a k,S k+2成等比数列,则正整数k=()A. 3B. 4C. 5D. 610.已知函数f(x)的图象可由函数y=3sin(2x+π3)的图象向右平移π3个单位长度得到,则下列结论错误的是A. f(x)的一个周期可为−2πB. 函数f(x)在区间(−π12,5π12)上是增函数C. 函数f(x)的图象关于直线x=π12对称D. 函数f(x)的一个零点为x=π611.已知抛物线y2=4x的焦点为F,准线与x轴相交于点M,N为抛物线上的一点且NF=12MN,则)A. 30∘B. 90∘C. 60∘D. 45∘12.已知f(x)是定义域为R的偶函数,当x⩽0时,f(x)=x2+4x,则f(x+2)>5的解集为()A. B.C. D.二、填空题(本大题共3小题,共15.0分)13.已知α为锐角,cosα=45,则sin(π6+α)=______ .14.已知数列{a n}满足a n=(−1)na n−1+1(n≥2),若a7=711,则a5=______ .15.如图,正方体ABCD−A1B1C1D1的棱长为2,P,Q,R分别是棱BC,CD,DD1的中点.下列命题:①过A1C1且与CD1平行的平面有且只有一个;②平面PQR截正方体所得截面图形是等腰梯形;③AC1与QR所成的角为60°;④线段MN与GH分别在棱A1B1和CC1上运动,则三棱锥M−NGH体积是定值;⑤线段MN 是该正方体内切球的一条直径,点O 在正方体表面上运动,则OM ⃗⃗⃗⃗⃗⃗⃗ ⋅ON ⃗⃗⃗⃗⃗⃗ 的最大值是2.其中真命题的序号是______ (写出所有真命题的序号). 三、解答题(本大题共8小题,共87.0分)16. 已知x,y 满足{x −4y +3≤03x +5y −25≤0x ≥1,设z =yx ,求z 的最大值与最小值.17. 在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,且2a −c =2bcos C .(1)求sin(A+C 2+B)的值;(2)若b =√3,求c −a 的取值范围.18. 如图,四棱锥P −ABCD 中,已知PA ⊥平面ABCD ,△ABC 为等边三角形,PA =2AB =2,AC ⊥CD ,PD 与平面PAC 所成角的正切值为C 2.(Ⅰ)证明:BC//平面PAD ;(Ⅱ)若M 是BP 的中点,求二面角P −CD −M 的余弦值.19. 某班5名学生的数学和物理成绩如下表:(1)求物理成绩y 对数学成绩x 的回归直线方程; (2)一名学生的数学成绩是96,试预测他的物理成绩.附:回归直线的斜率和截距的最小二乘法估计公式分别为:b ̂=∑x i ni=1y i −nxy ∑x i 2n i=1−nx i2,a ̂=y −b ̂x .20. 已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)过点A(2,0),且离心率为√32. (Ⅰ)求椭圆C 的方程;(Ⅱ)设直线y =kx +√3与椭圆C 交于M ,N 两点,若直线x =3上存在点P ,使得四边形PAMN 是平行四边形,求k 的值.21. 已知函数f(x)=2x 2+alnx(a ∈R).⑴讨论函数f(x)的单调性;⑴若g(x)=f(x)−4x +2存在两个极值点,且x 0是函数g(x)的极小值点,求证:g(x 0)>12−ln222. 在平面直角坐标系xOy 中,倾斜角为α的直线l 的参数方程为{x =tcosαy =1+tsinα(其中t 为参数).在以O 为极点、x 轴的非负半轴为极轴的极坐标系(两种坐标系的单位长度相同)中,曲线C :ρ(1+cos2θ)=λsinθ的焦点F 的极坐标为(1,π2). (Ⅰ)求常数λ的值;(Ⅱ)设l 与C 交于A 、B 两点,且|AF|=3|FB|,求α的大小.23. 已知函数f(x)=|ax −3|,不等式f(x)≤2的解集为{x|1≤x ≤5}.(1)解不等式f(x)<2f(x+1)−1;(2)若m≥3,n≥3,f(m)+f(n)=3,求证:1m +4n≥1.【答案与解析】1.答案:C解析:解:∵集合A={x|x2−2x−3≤0}={x|−1≤x≤3},B={x|0<x<4},∴A∩B={x|0<x≤3}=(0,3].故选:C.先分别求出集合A,B,由此能求出A∩B.本题考查交集的求法,考查交集定义、不等式性质等基础知识,考查运算求解能力,考查函数与方程思想,是基础题.2.答案:A=1.解析:解:原式=√12+(−2)2√22+12故选:A.利用复数模的计算公式及其性质即可得出.本题考查了复数的模的运算性质,考查了推理能力与计算能力,属于基础题.3.答案:C解析:本题考查空间直线与直线的关系,直线与平面的关系,考查空间想象能力和推理能力,属于基础题.解析:α与γ可能相交或平行,故A错;m可能平行于β或m在β内,故B错;由直线与平面平行的判断定理得m//β,故C正确;m与n可能相交、平行或异面,故D错.解:若α⊥β,β⊥γ,则α与γ相交或平行,故A错;若α⊥β,m⊥α,则m平行于β或m在β内,故B错;若α//β,m⊄β,m//α,则由直线与平面平行的判断定理的m//β,故C正确;若m//α,n//β,α⊥β,则m与n相交、平行或异面,故D错.故选C.4.答案:A解析:本题考查了比较大小,结合对数函数的单调性即可,属于基础题.解:∵a=log35>1>log95=b>0,∴a>b>0.故选:A.5.答案:C解析:本题考查了平面向量数量积的应用问题,是基础题目.根据平面向量数量积运算的定义,即可求出对应的模长.解:∵向量a⃗=(1,√3),∴|a⃗|=√12+(√3)2=2;又向量a⃗,c⃗的夹角是π3,a⃗⋅c⃗=2,∴|a⃗|⋅|c⃗|⋅cosπ3=2|c⃗|⋅12=2,∴|c⃗|=2.故选:C.6.答案:D解析:解:F1、F2分别是双曲线C:x2a2−y2b2=1(a>0,b>0)的左、右焦点,以F为圆心、|F1F2|为半径的圆与双曲线左支的其中一个交点为A,若∠AF1F2=120°,A不妨在第二象限,|AF1|=2c,可得A(−2c,√3c),可得4c2a2−3c2b2=1,可得:4e2−3e2e2−1=1,e>1,解得e2=2+√32.可得e=√3+12.故选:D.利用已知条件求出A的坐标,代入双曲线方程然后求解离心率即可.本题考查双曲线的简单性质的应用,是基本知识的考查.7.答案:A解析:本题考查了程序框图中的循环结构的应用,解题的关键是由框图的结构判断出框图的计算功能由题意,即求n≤100(n∈N),满足log2n∈N的n的个数.解:由题意,即求n≤100(n∈N),满足log2n∈N的n的个数,∴n=1,2,4,8,16,32,64,共7个.故选:A.8.答案:D解析:解:从1,2,3,4,5,6这6个数中,不放回地任意取两个数,共有C62=15种结果,其中满足条件两个数都是偶数的有(2,4),(2,6),(4,6)共3种情况不放回地任意取两个数,两个数都是奇数的概率P=315=15故选D.根据已知中从1,2,3,4,5,6这6个数中,不放回地任意取两个数,由C62种结果,及列举出满足条件两个数都是偶数的基本事件个数,代入概率公式,即可得到答案.本题考查的知识点是等可能事件的概率,处理方法是:计算出基本事件总数N,则满足条件A的基本事件总数A(N),代入P=A(N)÷N求了答案.9.答案:D解析:解:设等差数列{a n}的公差为d,a2=4,S4=20,可得a1+d=4,4a1+6d=20,解得a1=d=2,则a n=2+2(n−1)=2n,a1,a k,S k+2成等比数列,可得a1S k+2=a k2,即2⋅12(k+2)(2+2k+4)=4k2,解得k=6,故选:D.设等差数列的公差为d,运用等差数列通项公式和求和公式,解方程可得首项和公差,再由等比数列中项性质,解方程可得k的值.本题考查等差数列的通项公式和求和公式的运用,考查等比数列中项性质,以及方程思想和运算能力,属于基础题.10.答案:C解析:求出平移后的图象对应的函数解析式,再由正弦函数的图象与性质求解.解:函数y=3sin(2x+π3)的图象向右平移π3个单位长度得到f(x)=3sin[2(x−π3)+π3]=3sin(2x−π3)的图象,f(−2π+x)=f(x),故A正确;当−π12<x<5π12,−π2<2x−π3<π2,f(x)递增,B正确;当x=π12时,f(π12)=3sin(−π6),显然图象不关于直线x=π12对称,C错误;f(π6)=0,D正确,故选C.11.答案:C解析:本题考查抛物线的几何性质,属于中档题.过N作NE垂直于准线与E,由抛物线的定义得NE=NF,在Rt△ENM中求出∠EMN=30°.即可得到结论.解答:解:过N作NE垂直于准线与E.由抛物线的定义得:NE=NF,MN.在Rt△ENM中因为EN=NF=12所以∠EMN=30∘,故∠NMF=90∘−∠EMN=60∘.故选C.12.答案:C解析:本题主要考查函数解析式的求解以及不等式的解法,利用偶函数的对称性是解决本题的关键.由单调性与奇偶性可得|x+2|>5,求解即可.解:由题意,若x>0,则−x<0,∵当x ⩽0时,f(x)=x 2+4x , ∴当−x <0时,f(−x)=x 2−4x , ∵f(x)是定义域为R 的偶函数, ∴f(−x)=x 2−4x =f(x),即当x >0时,f(x)=x 2−4x ,可知当x ∈(2,+∞)时函数单调递增, 令f(x)=x 2−4x =5,x >0,解得x =5, 则f(x +2)>5⇔f(|x +2|)>f(5),当x ∈(0,2)时,函数单调递减,当x ∈[2,+∞)时函数单调递增, 可知|x +2|>5,解得x <−7或x >3. 故选C .13.答案:4+3√310解析:解:∵α为锐角,cosα=45,则sinα=35, ∴sin(π6+α)=sin π6cosα+cos π6sinα=12×45+√32×35=4+3√310, 故答案为:4+3√310. 由条件利用同角三角函数的基本关系求得sinα的值,再利用两角和的正弦公式求得sin(π6+α)的值. 本题主要考查同角三角函数的基本关系、两角和的正弦公式,属于基础题.14.答案:47解析:本题考查数列的第5项的求法,是中档题,解题时要认真审题,注意数列的递推公式的合理运用. 由已知得711=−1a 6+1,解得a 6=114,再由114=1a 5+1,能求出a 5. 解:∵数列{a n }满足a n =(−1)n a n−1+1(n ≥2),a 7=711,∴711=−1a 6+1,解得a 6=114,∴114=1a 5+1,解得a 5=47. 故答案为:47.15.答案:①⑤解析:解:对于①,∵CD 1//A 1B ,A 1B ∩A 1C 1=A 1,∴过A 1C 1且与CD 1平行的平面为A 1BC 1,有且只有一个,故①正确;对于②,如图,平面PQR 截正方体所得截面图形是正六边形,不是等腰梯形,故②错误;对于③,∵QR//CD 1,而CD 1//̲A 1B ,又AC 1在平面AA 1B 1B 中的射影为AB 1,A 1B ⊥AB 1,由三垂线定理可知,A 1B ⊥AC 1,即QR ⊥AC 1,故③错误; 对于④,如图,由图可知,V M−NGH =V G−MNH =V G−MNC 1−V H−MNC 1=13×2MN ⋅GH ,由于MN ⋅GH 不是定值,故④错误;对于⑤,设点P 为此正方体的内切球的球心,半径R =1.∵OM⃗⃗⃗⃗⃗⃗⃗ ⋅ON ⃗⃗⃗⃗⃗⃗ ≤|OM ⃗⃗⃗⃗⃗⃗⃗ |⋅|ON ⃗⃗⃗⃗⃗⃗ |,∴当点O ,M ,N 三点共线时,OM ⃗⃗⃗⃗⃗⃗⃗ ⋅ON ⃗⃗⃗⃗⃗⃗ 的取得最大值. 此时,OM ⃗⃗⃗⃗⃗⃗⃗ ⋅ON ⃗⃗⃗⃗⃗⃗ ≤(|OP ⃗⃗⃗⃗⃗ |+|PM ⃗⃗⃗⃗⃗⃗ |)⋅(|OP ⃗⃗⃗⃗⃗ |−|PN ⃗⃗⃗⃗⃗⃗ |),而|PM ⃗⃗⃗⃗⃗⃗ |=|PN⃗⃗⃗⃗⃗⃗ |=1, ∴OM ⃗⃗⃗⃗⃗⃗⃗ ⋅ON⃗⃗⃗⃗⃗⃗ ≤|PO|2−1,当且仅当点P 为正方体的一个顶点时上式取得最大值,又正方体的对角线长为2√3, ∴(OM⃗⃗⃗⃗⃗⃗⃗ ⋅ON ⃗⃗⃗⃗⃗⃗ )max =(2√32)2−1=2,故答案为:①⑤.①,利用线面平行的性质,过A 1C 1且与CD 1平行的平面为A 1BC 1,可判断① ②,作图可知,平面PQR 截正方体所得截面图形是正六边形,可判断②; ③,利用三垂线定理可知,QR ⊥AC 1,可判断③;④,作图,可知V M−NGH =V G−MNH =V G−MNC 1−V H−MNC 1=13×2MN ⋅GH ,由于MN ⋅GH 不是定值,可判断④;⑤,利用向量数量积的概念及性质,可知当点O ,M ,N 三点共线时,OM ⃗⃗⃗⃗⃗⃗⃗ ⋅ON ⃗⃗⃗⃗⃗⃗ 的取得最大值,继而可求得该最大值,可判断⑤.本题考查空间线面、面面之间的位置关系,考查作图能力、推理运算能力,考查平面向量的数量积的概念及性质的应用,属于难题.16.答案:z max =225,z min =25解析:由约束条件{x −4y +3≤03x +5y −25≤0x ≥1作出点(x,y)的可行域如图所示,∵z =y x =y−0x−0,∴z 的值就是可行域中的点与原点O(0,0)连线的斜率,由图形可知:z max =k OA ,z min =k OB ,由{x −4y +3=0x =1,解得A(1,225),k OA =225,由{x −4y +3=03x +5y −25=0,解得B(5,2),k OB =25,故z max =225,z min =25. 17.答案:解:(1)由余弦定理可得:2a −c =2bcosC =a 2+b 2−c 22ab×2b ,整理可得,a 2+c 2−b 2=ac ,cosB =a 2+c 2−b 22ac=12,又,故,,所以;(2)由(1)得sinB =√32,所以a sinA =c sinC =bsinB =2,从而a =2sin A ,c =2sin C . 所以c −a =2sinC −2sinA =2sin(2π3−A)−2sinA=√3cosA −sinA =2sin(π3−A).因为A +C =2π3,所以0<A <2π3,从而−π3<π3−A <π3, 所以−√3<2sin(π3−A)<√3, 故c −a 的取值范围为(−√3,√3).解析:本题主要考查了正弦定理,余弦定理及和差角公式及辅助角公式在求解三角形中的应用,属于中档试题.(1)由已知结合余弦定理进行化简求解cos B ,进而可求B ,代入即可求解;(2)由已知结合正弦定理可表示c −a ,然后结合和差角公式及正弦函数的性质即可求解.18.答案:证明:(Ⅰ)∵PA ⊥平面ABCVD ,∴PA ⊥CD ,又AC ⊥CD ,CA ∩PA =A ,∴CD ⊥平面PAC , ∴∠DPC 为PD 与平面PAC 所成角,在Rt △PAC 中,tan∠DPC =CDPC =√155, 在Rt △PAC 中,PC =√1+4=√5,∴CD =√3, 在Rt △ACD 中,AD =2,∠CAD =60°,∵∠BCA =60°,∴在底面ABCD 中,BC//AD ,AD ⊂平面PAD , BC ⊄平面PAD ,∴BC//平面PAD .解:(Ⅱ)设BC 的中点为N ,连结AN ,则AN ⊥BC , 由(Ⅰ)知BC//AD ,∴AN ⊥AD ,分别以AN ,AD ,AP 为x ,y ,z 轴,建立空间直角坐标系,则P(0,0,2),C(√32,12,0),D(0,2,0),M(√34,−14,1),则CD ⃗⃗⃗⃗⃗ =(−√32,32,0),PD ⃗⃗⃗⃗⃗ =(0,2,−2),DM ⃗⃗⃗⃗⃗⃗⃗ =(√34,−94,1), 设平面PCD 的法向量为n ⃗ =(x,y ,z), 则{n ⃗ ⋅CD ⃗⃗⃗⃗⃗ =−√3x +3y =0n ⃗ ⋅PD ⃗⃗⃗⃗⃗ =2y −2z =0, 令y =1,n ⃗ =(√3,1,1),设平面CDM 的法向量为m⃗⃗⃗ =(x,y ,z), 则{m ⃗⃗⃗ ⋅CD ⃗⃗⃗⃗⃗ =−√3x +3y =0m⃗⃗⃗ ⋅MD ⃗⃗⃗⃗⃗⃗⃗ =√3x −9y +4z =0,令y =1,得m⃗⃗⃗ =(√3,1,32),设二面角P −CD −M 的平面角为θ, 则cosθ=|m ⃗⃗⃗ ⋅n ⃗⃗ ||m ⃗⃗⃗ |⋅|n ⃗⃗ |=3+1+32√5⋅√3+1+94=11√525.故二面角P −CD −M 的余弦值为11√525.解析:(Ⅰ)推导出PA ⊥CD ,CD ⊥平面PAC ,∠DPC 为PD 与平面PAC 所成角,由此能证明BC//平面PAD .(Ⅱ)设BC 的中点为N ,连结AN ,则AN ⊥BC ,分别以AN ,AD ,AP 为x ,y ,z 轴,建立空间直角坐标系,利用向时法能求出二面角P −CD −M 的余弦值.本题考查线面平行的证明,考查二面角的余弦值的求法,考查空间中线线、线面、面面间的位置关系等基础知识,意在考查学生的转化能力和计算求解能力,是中档题.19.答案:解:(1)根据表中数据,计算x =15×(88+76+73+66+63)=73.4,y =15×(78+65+71+64+61)=67.8,∑x i 5i=1y i =88×78+76×65+73×71+66×64+63×61=25054,∑x i 25i=1=882+762+732+662+632=27174, ∴b ̂=∑x i ni=1y i −nxy ∑x i 2n i=1−nx i2=25054−5×73.4×67.827174−5×73.42≈0.73, â=y −b ̂x =67.8−0.73×73.4≈14.22, ∴回归直线方程为y ̂=0.73x +14.22; (2)利用(1)中回归方程,令x =96,则ŷ=0.73×96+14.22=84.3, ∴一名学生的数学成绩是96时,试预测他的物理成绩是84.3.解析:(1)根据表中数据,计算x 、y ,求出回归系数b ^、a ^,即可写出回归直线方程; (2)利用(1)中回归方程,计算x =96时y ^的值即可.本题考查了回归直线方程的求法与应用问题,也考查了计算能力,是中档题.20.答案:解:(Ⅰ)由题意得a =2,e =c a =√32,所以c =√3.因为a 2=b 2+c 2, 所以b =1,所以椭圆C 的方程为x 24+y 2=1.(Ⅱ)若四边形PAMN 是平行四边形, 则 PA//MN ,且|PA|=|MN|. 所以 直线PA 的方程为y =k(x −2), 所以 P(3,k),|PA| =√k 2+1. 设M(x 1,y 1),N(x 2,y 2). 由{y =kx +√3x 2+4y 2=4得 (4k 2+1)x 2+8√3kx +8=0, 由Δ>0,得 k 2>12, 且x 1+x 2=−8√3k4k +1,x 1x 2=84k 2+1.所以|MN|=√(k 2+1)[(x 1+x 2)2−4x 1x 2] =√(k 2+1)64k 2−32(4k 2+1)2.因为|PA|=|MN|, 所以 √(k 2+1)64k −32(4k 2+1)2=√k 2+1.整理得 16k 4−56k 2+33=0,解得 k =±√32,或 k =±√112.经检验均符合Δ>0,但k =− √32时不满足PAMN 是平行四边形,舍去. 所以 k =√32,或 k =±√112.解析:本题考查椭圆方程的求法,直线与椭圆的位置关系的应用,考查转化思想以及计算能力,属于中档题.(Ⅰ)利用已知条件求出a ,b ,即可得到椭圆的方程;(Ⅱ)直线PA 的方程为y =k(x −2),得到 P(3,k),求出|PA| =√k 2+1,设M(x 1,y 1),N(x 2,y 2),联立直线与椭圆方程,利用韦达定理以及弦长公式转化求解即可.21.答案:解:函数的定义域为(0,+∞),(1)f′(x)=4x +ax=4x 2+a x,当a ≥0,f′(x)>0恒成立, ∴函数f(x)在(0,+∞)上单调递增;当a <0时,令f′(x)=0,得x =√−a2或x =−√−a2(不合题意,舍去),则当x ∈(0,√−a2)时,f′(x)<0,函数f(x)在(0,√−a2)上单调递减,当x ∈(√−a 2,+∞)时,f′(x)>0,函数f(x)在(√−a2,+∞)上单调递增. (2)∵g(x)=2x 2−4x +2+alnx , ∴g′(x)=4x −4+ax =4x 2−4x+ax,∵函数g(x)存在两个极值点,设两个极值点为x 1,x 0, ∴x 1,x 0是方程4x 2−4x +a =0的两根, ∴△=16−16a >0,0<a <1,且x 1+x 0=1,∵函数y =4x 2−4x +a 开口向上,与x 轴交于两点,x 0是函数g(x)的极小值点, ∴x 1<x 0,从而12<x 0<1,由4x 02−4x 0+a =0,得a =−4x 02+4x 0,x 0∈(12,1), g(x 0)=2(x 0−1)2+(4x 0−4x 02)lnx 0,设ℎ(t)=2(t −1)2+(4t −4t 2)lnt(12<t <1), ∵ℎ′(t)=4(1−2t)lnt >0, ∴ℎ(t)在(12,1)上递增, ∴ℎ(t)>ℎ(12)=12−ln2,∴g(x 0)>12−ln2.解析:本题的考点是利用导数研究函数的单调性,以及函数的极值问题.对于参数问题要注意进行分类讨论,属于中档题.(1)对函数求导,利用导函数与函数单调性的关系即可求解.(2)利用条件x 0是函数f(x)的极值点,确定a 的数值,然后证明:g(x 0)>12−ln2.22.答案:解:(Ⅰ)曲线C :ρ(1+cos2θ)=λsinθ,转换为:2ρ2cos 2θ=λρsinθ, 即:x 2=λ2y ,由于:曲线C 的焦点F 的极坐标为(1,π2). 即:F(0,1), 所以:λ8=1, 故:λ=8.(Ⅱ)把倾斜角为α的直线l 的参数方程为{x =tcosαy =1+tsinα(其中t 为参数)代入x 2=4y . 得到:cos 2αt 2−4sinαt −4=0. 所以:t 1+t 2=4sinαcos 2α,t 1⋅t 2=−4cos α<0, 且|AF|=3|FB|, 故:t 1=6sinαcos 2α,t 2=−2sinαcos 2α,整理得−12sin 2αcos 4α=−4cos 2α,解得:tanα=±√33, 由于:0<α≤π, 故:α=π6或5π6.解析:本题考查的知识要点:参数方程极坐标方程和直角坐标方程之间的转换一元二次方程根和系数关系式的应用,三角函数关系式的恒等变换,主要考察学生的运算能力和转换能力,属于基础题型.(Ⅰ)直接利用转换关系式,把参数方程极坐标方程和直角坐标方程之间进行转换. (Ⅱ)利用一元二次方程关系式的应用和三角函数关系式的变换的应用求出结果.23.答案:(1)解:因为不等式f(x)≤2的解集为{x|1≤x ≤5},则x =1和x =5是方程f(x)=|ax −3|=2的解,即{|a −3|=2|5a −3|=2,所以实数a 的值为1. 不等式f(x)<2f(x +1)−1可化为|x −3|<2|x −2|−1,则{x ≥3x −3<2(x −2)−1或{2≤x <3−(x −3)<2(x −2)−1或x <2−(x −3)<−2(x −2)−1,解得x≥3或83<x<3或x<0,所以原不等式的解集为{x|x<0或x>83}.(2)证明:因为m≥3,n≥3,所以f(m)+f(n)=|m−3|+|n−3|=m−3+n−3=3,即m+n=9.所以1m +4n=19(m+n)(1m+4n)=19(1+4+nm+4mn)≥19(5+2√nm⋅4mn)=1,当且仅当nm =4mn,即m=3,n=6时取等号.解析:(1)利用不等式f(x)≤2的解集为{x|1≤x≤5},说明x=1和x=5是方程f(x)=|ax−3|=2的解,求出a,然后转化不等式f(x)<2f(x+1)−1为|x−3|<2|x−2|−1,通过分类讨论转化求解即可.(2)化简f(m)+f(n)=3,得到m+n=9.利用基本不等式证明即可.本题考查解绝对值不等式和利用基本不等式证明不等式.是中档题.。
