2018届中考数学《锐角三角函数》专题复习练习含答案
2018年中考数学《锐角三角函数》专题练习含答案

2018中考数学专题练习《锐角三角函数》(时间:100分钟 满分:120分)一、选择题(本大题共10小题,每小题3分,共30分)1.下列各数是有理数的是( )A. B. 4πC. sin 45︒D.1cos60︒ 2一个公共房门前的台阶高出地面1.2米,台阶拆除并改造成供轮椅行走的斜坡,数据如图1所示,则下列关系或说法正确的是( )A.斜坡AB 的坡度是10ºB.斜坡AB 的坡度是tan10︒C. 1.2tan10AC =︒米D. 1.2cos10AB =︒米3.在ABC ∆中,A ∠,B ∠都是锐角,且1sin 2A =,cos 2B =,则ABC ∆三个角的大小关系是( )A. C A B ∠>∠>∠B. B C A ∠>∠>∠C. A B C ∠>∠>∠D. C B A ∠>∠>∠4.如图2,在R t A B C ∆中,90A ∠=︒,AD BC ⊥于点D ,:3:2BD CD =,则t a n B 的值是( )A. 32B. 23C. D. 5.如图3,AB 是⊙O 的直径,C 是⊙O 上的点,过点C 作⊙O 的切线,交AB 的延长线于点E ,30A ∠=︒,则s sin E 的值为( )A. 12B. 2C.D.6.数学社团的同学们对某塔的高度进行了测量,如图4,他们在A 处仰望塔顶,测得仰角为30º,再往楼的方向前进60 m 至B 处,测得仰角为60º,若学生的身高忽略不计,1.7≈,结果精确到1m ,则该楼的高度CD 为( )A.47 mB.51 mC.53 mD.54 m7.如图5,点O 是摩天轮的圆心,长为110米的AB 是其垂直地面的直径,小莹在地面C 点处利用测角仪测得摩天轮的最高点A 的仰角为33º,测得圆心O 的仰角为21º,则小莹所在C 点到直径AB 所在直线的距离约为(参考数据:tan330.65︒≈,tan 210.38︒≈)( )图 5A.169米B.204米C.240米D.407米8.如图6,在ABC ∆中,已知90ABC ∠=︒,点D 沿BC 自B 向C 运动(点D 与点B , C 不重合),作BE AD ⊥于E ,CF AD ⊥交AD 的延长线于F ,则BE CF +的值( )A.不变B.增大C.减小D.先变大,再变小9.如图7,轮船从B 处以每小时50海里的速度沿南偏东30º方向匀速航行,在B 处观测灯塔A 位于南偏东75º的方向上,轮船航行半小时到达C 处,在C 处观测灯塔A 位于北偏东60º的方向上,则C 处与灯塔A 的距离是( )A. B.C. 50海里D. 25海里10.某数学兴趣小组的同学进行测量大树CD 高度的综合实践活动,如图8,在点A 处测得直立于地面的大树顶端C 的仰角为36º,然后沿在同一剖面的斜坡AB 行走13米至坡顶B 处,然后沿水平方向行走6米至大树脚底点D 处,斜面AB 的坡度(或坡比)1:2.4i =,那么大树CD 的高度约为(参考数据:sin360.59︒≈,cos360.81︒≈,tan360.73︒≈)( )A.8.1米B.17.2米C.19.7米D.25.5米二、填空题(本大题共8小题,每小题3分,共24分)11.若θ为三角形的一个锐角,且2sin 0θ=,则tan θ= .12.在Rt ABC ∆中,90C ∠=︒,4tan 3A =,8BC =,则ABC ∆的面积为 . 13.在平面直角坐标系中,已知点P 在第一象限内,点P 与原点O 的距离2OP =,点P 与原点O 的连线与x 轴的正半轴的夹角为60º,则点P 的坐标是 .14.如图9,某景区从游客中心A 处修建通往百米观景长廊BC 的两条栈道AB ,AC .若56B ∠=︒,45C ∠=︒,则游客中心A 到观景长廊BC 的距离AD 的长度约为 米.(参考数据:sin560.8︒≈,tan56 1.5︒≈ )15.如图10,6个形状、大小完全相同的菱形组成网格,菱形的顶点称为格点.已知菱的一个角(O ∠)为60º,A ,B ,C 都在格点上,则tan ABC ∠的值是 .16.如图11,一艘渔船位于灯塔P 的北偏东30º方向,距离灯塔18海里的A 处,它沿正南方向航行一段时间后,到达位于灯塔P 的南偏东55º方向上的B 处,此时渔船与灯塔P 的距离约为 海里.(结果取整数,参考数据:sin550.8︒≈,cos550.6︒≈,tan55 1.4︒≈)17.如图12,以边长为20 cm 的正三角形纸板的各顶点为端点,在各边上分别截取4 cm 长的六条线段,过截得的六个端点作所在边的垂线,形成三个有两个直角的四边形,把它们沿图中的虚线剪掉,用剩下的纸板折成一个底为正三角形的无盖柱形盒子,则它的容积为 cm 3.18.图13是我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”,图中的四个直角三角形是全等的,如果大正方形ABCD 的面积是小正方形EFGH 面积的13倍,那么tan ADE ∠的值为 .三、解答题(本大题共6小题,共66分)19. ( 8分)计算2145cos 302sin 602tan 60︒+︒-+︒︒.20.(10分)在Rt ABC ∆中,90C ∠=︒,30A B ∠-∠=︒,2a b -=,试解该直角三角形.21. (10分)如图14,物理实验室有一个单摆在左右摆动,摆动过程中选取了两个瞬时状态,从C 处测得E ,F 两点的俯角分别为60ACE ∠=︒,45BCF ∠=︒,这时点F 相对于点E 升高了3cm ,求该摆绳CD 的长度.(参考数据 1.7≈ 1.4≈)22. (12分)太阳能光伏发电因其清洁、安全、便利、高效等特点。
普通中学2018届初三中考数学复习锐角三角函数专题综合练习含答案

天津市和平区普通中学2018届初三中考数学复习锐角三角函数专题综合练习 1. 计算4sin60°-3tan30°的值为( ) A.3 B .23 C .33 D .0 2.计算sin 245°+cos 245°的值为( ) A .2 B .1 C .0 D .33. 为测量如图所示的上山坡道的倾斜度,小明测得数据如图所示,则该坡道倾斜角α的正切值是( )A.117B .4 C.14 D.4174. sin α=0.231 6,cos β=0.231 6,则锐角α与锐角β之间的关系是( ) A .α=β B .α+β=180° C .α+β=90° D .α-β=90°5. 在△ABC 中,∠C =90°,下列各式中不正确的是( )A .b =a ·tanB B .a =b ·cosAC .c =b sinBD .c =acosB6. 如图,小雅家(图中点O 处)门前有一条东西走向的公路,现测得有一水塔(图中点A 处)在她家北偏东60°方向500 m 处,那么水塔所在的位置到公路的距离AB 长是( )A .250 mB .250 3 m C.500 33m D .250 2 m7.王师傅在楼顶上的点A 处测得楼前一棵树CD 的顶端C 的俯角为60°,已知水平距离BD =10 m ,楼高AB =24 m ,则树CD 的高度为( )A .(24-1033)m B .(24-103) m C .(24-53) m D .9 m8. 使用计算器计算:sin 52°18′≈________.(精确到0.001)9.已知cos β=0.741 6,利用计算器求出β的值约为________.(精确到1°) 10. 在Rt △ABC 中,∠C =90°,c =10,b =53,则∠A =________,S △ABC =________. 11. 如图,在Rt △ABC 中,∠C =90°,求sinA 和sinB 的值.12. 如图,在Rt △ABC 中,∠C =90°,AB =10,BC =6,求sinA ,cosA ,tanA 的值.13. 如图(1),在Rt △ABC 中,∠C =90°,AB =6,BC =3,求∠A 的度数;14. 如图(2),AO是圆锥的高,OB是底面半径,AO=3OB,求α的度数.15. 如图,在Rt△ABC中,∠C=90°,AC=2,BC=6,解这个直角三角形.16. 如图,在Rt△ABC中,∠C=90°,∠B=35°,b=20,解这个直角三角形.(结果保留小数点后一位)。
2018年中考数学真题汇编 锐角三角函数-精选

中考数学真题汇编:锐角三角函数一、选择题1.的值等于()A. B.C. 1D.【答案】B2.如图,过点,,,点是轴下方上的一点,连接,,则的度数是()A. B.C.D.【答案】B3.如图,一把直尺,的直角三角板和光盘如图摆放,为角与直尺交点,,则光盘的直径是( )A.3B.C.D.【答案】D4.如图,旗杆及升旗台的剖面和教学楼的剖面在同一平面上,旗杆与地面垂直,在教学楼底部E点处测得旗杆顶端的仰角,升旗台底部到教学楼底部的距离米,升旗台坡面CD的坡度,坡长米,若旗杆底部到坡面CD的水平距离米,则旗杆AB的高度约为()(参考数据:,,)A. 12.6米B. 13.1米 C. 14.7米 D. 16.3米【答案】B5.一艘在南北航线上的测量船,于A点处测得海岛B在点A的南偏东30°方向,继续向南航行30海里到达C点时,测得海岛B在C点的北偏东15°方向,那么海岛B离此航线的最近距离是(结果保留小数点后两位)(参考数据:)()A. 4.64海里B. 5.49海里 C. 6.12海里 D. 6.21海里【答案】B6.如图,两根竹竿AB和AD斜靠在墙CE上,量得∠ABC=α,∠ADC=β,则竹竿AB与AD的长度之比为()A. B.C.D.【答案】B7. 如图,已知在中,,,,则的值是()A. B. C.D.【答案】A8. 如图,电线杆CD的高度为h,两根拉线AC与BC相互垂直,∠CAB=α,则拉线BC的长度为(A、D、B 在同一条直线上)()A. B.C.D. h•cosα【答案】B二、填空题9.如图.一-艘渔船正以60海里/小时的速度向正东方向航行,在处测得岛礁在东北方向上,继续航行1.5小时后到达处此时测得岛礁在北偏东方向,同时测得岛礁正东方向上的避风港在北偏东方向为了在台风到来之前用最短时间到达处,渔船立刻加速以75海里/小时的速度继续航行________小时即可到达 (结果保留根号)【答案】10.如图,旗杆高AB=8m,某一时刻,旗杆影子长BC=16m,则tanC=________。
2018年中考数学真题分类汇编第二期专题27锐角三角函数与特殊角试题含解析

锐角三角函数与特殊角一.选择题1.2018•山东烟台市•3分)利用计算器求值时,小明将按键顺序为显示结果记为a,的显示结果记为b.则a,b的大小关系为()A.a<b B.a>b C.a=b D.不能比较【分析】由计算器的使用得出A.b的值即可.【解答】解:由计算器知a=(sin30°)﹣4=16.b==12,∴a>b,故选:B.【点评】本题主要考查计算器﹣基础知识,解题的关键是掌握计算器的使用.. 2(2018•金华、丽水•3分)如图,两根竹竿AB和AD斜靠在墙CE上,量得∠ABC=α,∠ADC=β,则竹竿AB与AD的长度之比为()A.B.C.D.【解析】【解答】解:设AC=x,在Rt△ABC中,AB= .在Rt△ACD中,AD= ,则,故答案为:B。
【分析】求AB与AD的比,就不必就求AB和AD的具体的长度,不妨设AB=x,用含x的代数式分别表示出AB,AD的长,再求比。
3. (2018·黑龙江大庆·3分)2cos60°=()A.1 B. C. D.【分析】直接利用特殊角的三角函数值进而计算得出答案.【解答】解:2cos60°=2×=1.二.填空题1. (2018·湖北江汉油田、潜江市、天门市、仙桃市·3分)我国海域辽阔,渔业资源丰富.如图,现有渔船B在海岛A,C附近捕鱼作业,已知海岛C位于海岛A的北偏东45°方向上.在渔船B上测得海岛A位于渔船B的北偏西30°的方向上,此时海岛C恰好位于渔船B的正北方向18(1+)n mile处,则海岛A,C之间的距离为18n mile.【分析】作AD⊥BC于D,根据正弦的定义、正切的定义分别求出BD.CD,根据题意列式计算即可.【解答】解:作AD⊥BC于D,设AC=x海里,在Rt△ACD中,AD=AC×sin∠ACD=x,则CD=x,在Rt△ABD中,BD=x,则x+x=18(1+),解得,x=18,答:A,C之间的距离为18海里.故答案为:18【点评】本题考查的是解直角三角形的应用,掌握方向角的概念、锐角三角函数的定义是解题的关键.2.(2018•江苏宿迁•3分)如图,将含有30°角的直角三角板ABC放入平面直角坐标系,顶点A,B分别落在x、y轴的正半轴上,∠OAB=60°,点A的坐标为(1,0),将三角板ABC 沿x轴向右作无滑动的滚动(先绕点A按顺时针方向旋转60°,再绕点C按顺时针方向旋转90°,…)当点B第一次落在x轴上时,则点B运动的路径与坐标轴围成的图形面积是________.【答案】+π【分析】在Rt△AOB中,由A点坐标得OA=1,根据锐角三角形函数可得AB=2,OB=,在旋转过程中,三角板的角度和边的长度不变,所以点B运动的路径与坐标轴围成的图形面积:S=,计算即可得出答案.【详解】在Rt△AOB中,∵A(1,0),∴OA=1,又∵∠OAB=60°,∴cos60°=,∴AB=2,OB=,∵在旋转过程中,三角板的角度和边的长度不变,∴点B运动的路径与坐标轴围成的图形面积:S==π,故答案为:π.【点睛】本题考查了扇形面积的计算,锐角三角函数的定义,旋转的性质等,根据题意正确画出图形是解题的关键.3. (2018•广西北海•3分)如图,从甲楼底部A 处测得乙楼顶部 C 处的仰角是 30°,从甲楼顶部B 处测得乙楼底部D 处的俯角是45°.已知甲楼的高AB 是120m ,则乙楼的高CD 是m (结果保留根 号)。
2018-2019学年初三中考数学专题复习锐角三角函数(含答案)
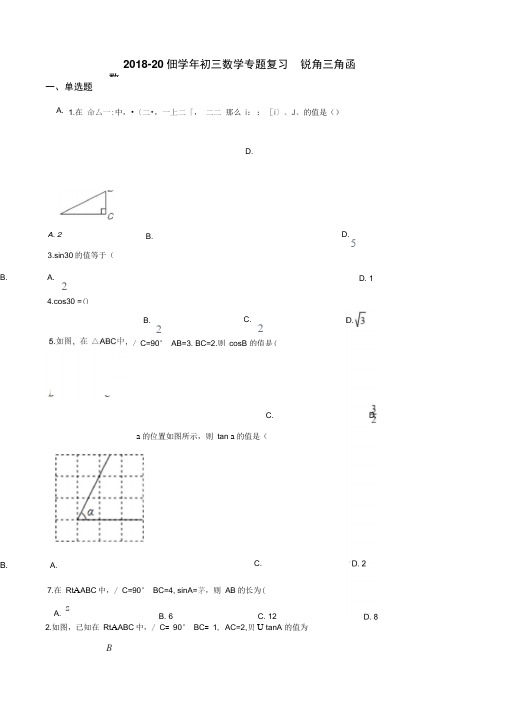
2018-20佃学年初三数学专题复习 锐角三角函数一、单选题1.在 命厶一:中,•〔二•,一上二「, 二二 那么 i ::[i 〕、J 、的值是()D.2.如图,已知在 Rt A ABC 中,/ C = 90° BC = 1, AC=2,贝U tanA 的值为A. A. 2B.3.sin30的值等于(A.24.cos30 =()B.D.5D. 1C.2B.2/ C=90° AB=3, BC=2,则 cosB 的值是(C.a 的位置如图所示,则 tan a 的值是(A.B.C.7.在 Rt A ABC 中,/ C=90° BC=4, sinA=茅,则 AB 的长为(s A.B. 6C. 12 B8.如图,铁路路基横断面为一个等腰梯形,若腰的坡度为下i=3:2,顶宽是7米,路基高是6米,则路基的底宽是()14•如图,钓鱼竿 AC 长6m ,露在水面上的鱼线 BC 长3 m ,某钓者想看看鱼钓上的情况,把鱼竿 AC 转动到AC'的位置,此时露在水面上的鱼线B'为3 m ,则鱼竿转过的角度是()A. 7米B. 1米 9.三角形在正方形网格纸中的位置如图所示,则C. 1米 sin a 的值是(D. 1米 B.C.D.10.在三角形ABC 中,/ C 为直角,sinA=,则tanB 的值为(B.C.11.游客上歌乐山山有两种方式:一种是如图,先从 是沿着盘山公路开车上山到C,已知在A 处观铡到A 沿登山步道走到B ,再沿索道乘座缆车到C ,另一种C ,得仰角/ CAD=3°,且A 、B 的水平距离 AE=430米,A 、B 的竖直距离 BE=210米,索道 BC 的坡度i=1: 米;(参考数据:tan310.6cos3l °~).91.5, CD 丄AD 于D , BF 丄CD 于F ,则山篙 CD 为() C. 686D. 69312.在 Rt A ABC 中,/ C=90° 如果/ A=a, BC=a,那么AC 等于()A. a • tan aB. a • cot aC. 13.化简等于( A. sin28 — °cos28 °B. 0C. cos28— sin28D.以上都不对A. 60 °B. 45 °C.15 °D. 9015.如图在 Rt A ABC 中,/ C=90° AB=15,sinA=g ,贝U BC 等于()16•如图1,是工人将货物搬运上货车常用的方法,把一块木板斜靠在货车车厢的尾部,形成一个斜坡,货 物通过斜坡进行搬运•根据经验,木板与地面的夹角为20° (即图2中/ ACB=20 )时最为合适,已知货车车厢底部到地面的距离 AB=1.5m ,木板超出车厢部分 AD=0.5m ,则木板CD 的长度为 ____________ •(参考数据:sin20 °~ 0.34,2Gbos20°~ 0.9397精确到 0.1m ).17. 已知 cosB=』(,则/ B=18. 如图,在一次数学课外实践活动中,小聪在距离旗杆 10m 的A 处测得旗杆顶端 B 的仰角为60 °测角仪高AD 为1m ,则旗杆高BC 为 __________ m (结果保留根号).■rf|FJ 1 f J 1 f *c fA. 45B. 5二、填空题C.D.A f:侧....lw ___ _ __ CD <io?«—M19. 一山坡的坡比为3: 4,一人沿山坡向上走了_ 20米,那么这人垂直高度上升了米.20•如图,如果在坡度i=1: 2.4的斜坡上两棵树间的水平距离AC 为3米,那么两树间的坡面距离 AB 是21•如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口 C 测得教学楼顶中D 的仰角为18°教学楼底部B 的俯角为20°量得实验楼与教学楼之间的距离 AB=30m.(结果精确到 0.1m 。
2018年全国各地中考数学真题汇编:锐角三角函数(及答案)

中考数学真题汇编:锐角三角函数一、选择题1.的值等于()A. B. C. 1 D.【答案】B2.如图,过点,,,点是轴下方上的一点,连接,,则的度数是()A. B. C. D.【答案】B3.如图,一把直尺,的直角三角板和光盘如图摆放,为角与直尺交点,,则光盘的直径是( )A.3B.C.D.【答案】D4.如图,旗杆及升旗台的剖面和教学楼的剖面在同一平面上,旗杆与地面垂直,在教学楼底部E点处测得旗杆顶端的仰角,升旗台底部到教学楼底部的距离米,升旗台坡面CD的坡度,坡长米,若旗杆底部到坡面CD的水平距离米,则旗杆AB的高度约为()(参考数据:,,)A. 12.6米B. 13.1米C. 14.7米D. 16.3米【答案】B5.一艘在南北航线上的测量船,于A点处测得海岛B在点A的南偏东30°方向,继续向南航行30海里到达C点时,测得海岛B在C点的北偏东15°方向,那么海岛B离此航线的最近距离是(结果保留小数点后两位)(参考数据:)()A. 4.64海里B. 5.49海里C. 6.12海里D. 6.21海里【答案】B6.如图,两根竹竿AB和AD斜靠在墙CE上,量得∠ABC=α,∠ADC=β,则竹竿AB与AD的长度之比为()A. B. C. D.【答案】B7. 如图,已知在中,,,,则的值是()A. B. C. D.【答案】A8. 如图,电线杆CD的高度为h,两根拉线AC与BC相互垂直,∠CAB=α,则拉线BC的长度为(A、D、B 在同一条直线上)()A. B. C. D. h•cosα【答案】B二、填空题9.如图.一-艘渔船正以60海里/小时的速度向正东方向航行,在处测得岛礁在东北方向上,继续航行1.5小时后到达处此时测得岛礁在北偏东方向,同时测得岛礁正东方向上的避风港在北偏东方向为了在台风到来之前用最短时间到达处,渔船立刻加速以75海里/小时的速度继续航行________小时即可到达(结果保留根号)【答案】10.如图,旗杆高AB=8m,某一时刻,旗杆影子长BC=16m,则tanC=________。
2018年中考数学真题汇编 锐角三角函数

中考数学真题汇编:锐角三角函数一、选择题1.的值等于()A. B.C.1 D.【答案】B2.如图,过点,,,点是轴下方上的一点,连接,,则的度数是()A. B.C.D.【答案】B3.如图,一把直尺,的直角三角板和光盘如图摆放,为角与直尺交点,,则光盘的直径是( )A.3B.C.D.【答案】D4.如图,旗杆及升旗台的剖面和教学楼的剖面在同一平面上,旗杆与地面垂直,在教学楼底部E点处测得旗杆顶端的仰角,升旗台底部到教学楼底部的距离米,升旗台坡面CD的坡度,坡长米,若旗杆底部到坡面CD的水平距离米,则旗杆AB的高度约为()(参考数据:,,)A. 12.6米B. 13.1米 C. 14.7米 D. 16.3米【答案】B5.一艘在南北航线上的测量船,于A点处测得海岛B在点A的南偏东30°方向,继续向南航行30海里到达C点时,测得海岛B在C点的北偏东15°方向,那么海岛B离此航线的最近距离是(结果保留小数点后两位)(参考数据:)()A. 4.64海里B. 5.49海里 C. 6.12海里 D. 6.21海里【答案】B6.如图,两根竹竿AB和AD斜靠在墙CE上,量得∠ABC=α,∠ADC=β,则竹竿AB与AD的长度之比为()A. B.C.D.【答案】B7. 如图,已知在中,,,,则的值是()A.B.C.D.【答案】A8. 如图,电线杆CD的高度为h,两根拉线AC与BC相互垂直,∠CAB=α,则拉线BC的长度为(A、D、B 在同一条直线上)()A. B.C.D. h•cosα【答案】B二、填空题9.如图.一-艘渔船正以60海里/小时的速度向正东方向航行,在处测得岛礁在东北方向上,继续航行1.5小时后到达处此时测得岛礁在北偏东方向,同时测得岛礁正东方向上的避风港在北偏东方向为了在台风到来之前用最短时间到达处,渔船立刻加速以75海里/小时的速度继续航行________小时即可到达 (结果保留根号)【答案】10.如图,旗杆高AB=8m,某一时刻,旗杆影子长BC=16m,则tanC=________。
2018年中考数学真题分类汇编第二期专题27锐角三角函数与特殊角试题含解析

锐角三角函数与特殊角一.选择题1.2018•山东烟台市•3分)利用计算器求值时,小明将按键顺序为显示结果记为a,的显示结果记为b.则a,b的大小关系为()A.a<b B.a>b C.a=b D.不能比较【分析】由计算器的使用得出A.b的值即可.【解答】解:由计算器知a=(sin30°)﹣4=16.b==12,∴a>b,故选:B.【点评】本题主要考查计算器﹣基础知识,解题的关键是掌握计算器的使用.. 2(2018•金华、丽水•3分)如图,两根竹竿AB和AD斜靠在墙CE上,量得∠ABC=α,∠ADC=β,则竹竿AB与AD的长度之比为()A.B.C.D.【解析】【解答】解:设AC=x,在Rt△ABC中,AB= .在Rt△ACD中,AD= ,则,故答案为:B。
【分析】求AB与AD的比,就不必就求AB和AD的具体的长度,不妨设AB=x,用含x的代数式分别表示出AB,AD的长,再求比。
3. (2018·黑龙江大庆·3分)2cos60°=()A.1 B.C.D.【分析】直接利用特殊角的三角函数值进而计算得出答案.【解答】解:2cos60°=2×=1.二.填空题1. (2018·湖北江汉油田、潜江市、天门市、仙桃市·3分)我国海域辽阔,渔业资源丰富.如图,现有渔船B在海岛A,C附近捕鱼作业,已知海岛C位于海岛A的北偏东45°方向上.在渔船B上测得海岛A位于渔船B的北偏西30°的方向上,此时海岛C恰好位于渔船B的正北方向18(1+)n mile处,则海岛A,C之间的距离为18n mile.【分析】作AD⊥BC于D,根据正弦的定义、正切的定义分别求出BD.CD,根据题意列式计算即可.【解答】解:作AD⊥BC于D,设AC=x海里,在Rt△ACD中,AD=AC×sin∠ACD=x,则CD=x,在Rt△ABD中,BD=x,则x+x=18(1+),解得,x=18,答:A,C之间的距离为18海里.故答案为:18【点评】本题考查的是解直角三角形的应用,掌握方向角的概念、锐角三角函数的定义是解题的关键.2.(2018•江苏宿迁•3分)如图,将含有30°角的直角三角板ABC放入平面直角坐标系,顶点A,B分别落在x、y轴的正半轴上,∠OAB=60°,点A的坐标为(1,0),将三角板ABC 沿x轴向右作无滑动的滚动(先绕点A按顺时针方向旋转60°,再绕点C按顺时针方向旋转90°,…)当点B第一次落在x轴上时,则点B运动的路径与坐标轴围成的图形面积是________.【答案】+π【分析】在Rt△AOB中,由A点坐标得OA=1,根据锐角三角形函数可得AB=2,OB=,在旋转过程中,三角板的角度和边的长度不变,所以点B运动的路径与坐标轴围成的图形面积:S=,计算即可得出答案.【详解】在Rt△AOB中,∵A(1,0),∴OA=1,又∵∠OAB=60°,∴cos60°=,∴AB=2,OB=,∵在旋转过程中,三角板的角度和边的长度不变,∴点B运动的路径与坐标轴围成的图形面积:S==π,故答案为:π.【点睛】本题考查了扇形面积的计算,锐角三角函数的定义,旋转的性质等,根据题意正确画出图形是解题的关键.3. (2018•广西北海•3分)如图,从甲楼底部A 处测得乙楼顶部 C 处的仰角是 30°,从甲楼顶部B 处测得乙楼底部D 处的俯角是 45°.已知甲楼的高 AB 是 120m ,则乙楼的高 CD 是 m (结果保留根号)。
2018届湘教版数学中考专项训练(四)锐角三角函数(含答案)

1.(2016·怀化中考)在△Rt ABC中,∠C=90°,sin A=,AC=6cm,则BC的长度为A.sin B=B.sin B=C.sin B=D.sin B=1251313A.米2B.米2C.⎝4+tanθ⎭米2D.(4+4tanθ)米26.如图,在菱形ABCD中,DE⊥AB,cos A=,BE=2,则tan∠DBE的值是()225专项训练四锐角三角函数一、选择题45()A.6cmB.7cmC.8cmD.9cm2.(2016·乐山中考)如图,在△Rt ABC中,∠BAC=90°,AD⊥BC于点D,则下列结论不正确的是()AD AC AD CDAB BC AC AC第2题图第4题图△3.在ABC中,若三边BC,CA,AB满足BC∶CA∶AB=5∶12∶13,则cos B的值为()512512A. B. C. D.△4.数学活动课上,小敏、小颖分别画了ABC和△DEF,尺寸如图.如果两个三角形的面积分别记作△SABC,△SDEF,那么它们的大小关系是()A.△SABC>△SDEFB.△SABC<△SDEFC.△SABC=△SDEFD.不能确定5.(2016·金华中考)一座楼梯的示意图如图所示,BC是铅垂线,CA是水平线,BA与CA的夹角为θ.现要在楼梯上铺一条地毯,已知C A=4米,楼梯宽度1米,则地毯的面积至少需要()44sinθcosθ⎛4⎫第5题图第6题图35155A. B.2 C. D.7.(2016·长沙中考)如图,热气球的探测器显示,从热气球A处看一栋楼顶部B处的仰角为30°,看这栋楼底部C处的俯角为60°,热气球A处与楼的水平距离为120m,则这栋楼的高度为()A.1603mB.1203mC.300mD.1602m2455在△9.ABC中,∠A,∠B都是锐角,且⎝cos A-2⎭+|1-tan B|=0,则∠C=于点E,BC=6,sin A=,则DE=.15.(2016·盐城中考)已知△ABC中,tan B=,BC=6,过点A作BC边上的高,垂足第7题图第8题图8.(2016·攀枝花中考)如图,点D(0,3),O(0,0),C(4,0)在⊙A上,BD是⊙A的一条弦,则sin∠OBD的值为()1343A. B. C. D.二、填空题⎛1⎫2.10.(2016·岳阳中考)如图,一山坡的坡度为i=1∶3,小辰从山脚A出发,沿山坡向上走了200米到达点B,则小辰上升了米.第10题图第11题图第12题图11.(2016·娄底新化县一模)如图,△ABC的顶点都在正方形网格的格点上,则cos C =.12.如图,以O为圆心,任意长为半径画弧,与射线OM交于点A,再以A为圆心,AO 长为半径画弧,两弧交于点B,画射线OB,则cos∠AOB的值为.13.如图,在△Rt ABC中,∠ACB=90°,D是AB的中点,过D点作AB的垂线交AC35第13题图第14题图14.(2016·西宁中考)如图,为保护门源百里油菜花海,由“芬芳浴”游客中心A处修建通往百米观景长廊BC的两条栈道AB,AC.若∠B=56°,∠C=45°,BC=100米,则游客中心A到观景长廊BC的距离AD的长约为米(参考数据:sin56°≈0.8,tan56°≈1.5).23为点D,且满足BD∶CD=2∶△1,则ABC的面积为.三、解答题(1)2(2cos45°-sin60°)+2417.如图,AD是△ABC的中线,tan B=,cos C=,AC= 2.求:16.计算:4;(2)(-2)0-3tan30°+|3-2|.1232(1)BC的长;(2)sin∠ADC的值.18.(2016·衡阳中考)在某次海上军事演习期间,我军为确保△OBC海域内的安全,特派遣三艘军舰分别在O,B,C处监控△OBC海域,在雷达显示图上,军舰B在军舰O的正东方向80海里处,军舰C在军舰B的正北方向60海里处,三艘军舰上装载有相同的探测雷达,雷达的有效探测范围是半径为r的圆形区域(只考虑在海平面上的探测).(△1)若三艘军舰要对OBC海域进行无盲点监控,则雷达的有效探测半径r至少为多少海里?(2)现有一艘敌舰A从东部接近△OBC海域,在某一时刻军舰B测得A位于北偏东60°方向上,同时军舰C测得A位于南偏东30°方向上,求此时敌舰A离△OBC海域的最短距离为多少海里?(3)若敌舰A沿最短距离的路线以202海里△/时的速度靠近OBC海域,我军军舰B 沿北偏东15°的方向行进拦截,问B军舰速度至少为多少才能在此方向上拦截到敌舰A?=5.连接 CD ,如图所示.∵∠OBD =∠OCD ,∴sin ∠OBD =sin ∠OCD = = .故选 D.9.75° 10.100 11. 12. 13.14.60×6× = 8 ;如图②,△ ABC 为钝角三角形时,∵ BC = 6 , BD ∶CD = 2∶1 ,∴ BD =8 ,∴CE =AC ·cos C = =1,∴AE =CE =1.在 △Rt ABE 中,∵tan B = ,∴BE = =3×1=3,∴BC =BE (2)∵AD 是△ABC 的中线,∴CD = BC =2,∴DE =CD -CE =1.∵AE ⊥BC ,DE =AE=1,∴∠DAE =∠ ADC =45°,∴sin ∠ADC = 2.OB 2+BC 2= 802+602=100( 海里).∵ OC = ×100=50(海里),∴雷达的有效探测半径(2)作 AM ⊥BC 于 M .∵∠ACB =30°,∠CBA =60°,∴∠CAB =90°,∴AB = BC =30 海里.在 △Rt ABM 中,∵∠AMB =90°,AB =30 海里,∠BAM =30°,∴BM = AB =15 海里,参考答案与解析1.C 2.C 3.C 4.C 5.D 6.B 7.A8.D 解析:∵D (0,3),C (4,0),∴OD =3,OC =4.∵∠COD =90°,∴CD = 32+42OD 3CD 52 5 1 155 2 415. 或 24 解析:可分两种情况:如图①,△ABC 为锐角三角形时,∵BC =6,BD ∶CD2 2 8 1 1=2∶1,∴BD =4.∵AD ⊥BC ,tan B =3,∴AD =BD ·tan B =4×3=3,∴△S ABC =2BC · AD =2832 2 1 112.∵ AD ⊥BC ,tan B =3,∴AD =BD ·tan B =12×3=8,∴△S ABC =2BC · AD =2×6×8=24.综上所述,△ABC 的面积为 8 或 24.16.解:(1)原式=2; (2)原式=3-2 3.17.解:(1)过点 A 作 AE ⊥BC 于点 E .在 △Rt ACE 中,∵cos C =222× 2 1 AE 23 tan B+CE =4;12218.解:(1)在 Rt △OBC 中,∵BO =80 海里,BC =60 海里,∠OBC =90°,∴OC =1 12 2r 至少为 50 海里;121 2AM =AB ·cos ∠BAM =15 3海里,∴此时敌舰 A 离△OBC 海域的最短距离为 15 3海里;a20 2(3)假设 B 军舰在点 N 处拦截到敌舰.在 BM 上取一点 H ,使得 HB =HN .设 MN =x 海 里.∵∠HBN =∠HNB =15°,∴∠MHN =∠HBN +∠HNB =30°,∴HN =HB =2x 海里,MH = 3x 海里.∵BM =15 海里,∴15= 3x +2x ,x =30-15 3,∴AN =AM -MN =(30 3 -30)海里, B N = MN 2+BM 2=15( 6- 2) 海里.设 B 军舰速度为 a 海里/时,由题意15( 6- 2) 30 3-30≤ ,解得 a ≥20.∴B 军舰速度至少为 20 海里/时,才能在此方向上拦截到敌舰 A .。
中考数学复习《锐角三角函数》专题训练-附带有答案

中考数学复习《锐角三角函数》专题训练-附带有答案一、选择题1.已知α是锐角,若sinα= 12,则α的度数是()A.30°B.45°C.60°D.75°2.如图,在Rt△ABC中,BC=3,斜边AC=5,则下列等式正确的是()A.sinC=35B.cosC=43C.tanA=34D.sinA=453.在Rt△ABC中,∠C=90°,sinA= 513,则tanB的值为()A.1213B.512C.1312D.1254.如图所示,河堤横断面迎水坡AB的坡比是1:2,堤高BC=4m,则坡面AB的长度是()mA.8 B.16 C.4√5D.4√35.如图,在正方形网格中.每个小正方形的边长都是1,小正方形的顶点称为格点,△ABC的顶点都在格点上,则∠BAC的正切值是()A.√55B.15C.2√55D.126.如图,河堤的横断面迎水坡AB的坡比是1:√2,堤高BC=6m,则坡面AB的长度是()A.10m B.12√2m C.6√3m D.6√2m7.如图,在菱形ABCD中,延长AB于E并且CE⊥AE,AC=2CE,则∠CBE的度数为()A.50°B.40°C.30°D.60°8.如图,在▱ABCD中AB=8,∠ABC=60°,BE平分∠ABC,交边AD于点E,连接CE,若AE=2ED,则CE的长为()A.6 B.4 C.4√3D.2√6二、填空题9.计算:2sin30°−tan45°=.10.如图,在平面直角坐标系内有一点P(5,12),那么OP与x轴正半轴的夹角α的正弦值.11.如图,Rt△ABC中,∠C=90°,BC=15,tanA= 15,则AB= .812.如图,某无人机兴趣小组在操场上开展活动,此时无人机在离地面20√3米的D处,无人机测得操控者A的俯角为30°,测得点C处的俯角为45°.又经过人工测量操控者A和教学楼BC之间的水平距离为80米,教学楼BC的高度米.(注:点A、B、C、D都在同一平面上,参考数据:√3≈1.7结果保留整数).13.如图,在△ABC中AB=AC,D是△ABC外一点,连接BD和DC,BD=AB,∠BDC+12∠BAC=180°,DC=1,tan∠ABC=2√33则线段BC的长为.三、解答题14.计算:2sin45°+tan30°·cos30°−√2.15.已知:如图在△ABC中,AD是边BC上的高,E为边AC的中点,BC=14,AD=12,4sin5B=求:(1)线段DC的长;(2)tan∠EDC的值.16.小明学了《解直角三角形》内容后,对一条东西走向的隧道AB进行实地测量.如图所示,他在地面上点C处测得隧道一端点A在他的北偏东15︒方向上,他沿西北方向前进D,此时测得点A在他的东北方向上,端点B在他的北偏西60︒方向上,(点A、B、C、D在同一平面内)(1)求点D与点A的距离;(2)求隧道AB的长度.(结果保留根号)17.如图1,在等腰三角形ABC中AB=AC,O为底边BC的中点,AB切⊙O于点D,连接OD,⊙O交BC于点M,N.(1)求证:AC是⊙O的切线;(2)∠B=42°,①若OD=4,求劣弧DM的长;②如图2,连接DM,若DM=4,直接写出OD的长.(参考数据:sin24°取0.4,cos24°取0.9,tan24°取0.45)18.如图,在边长为9的正方形ABCD中,等腰Rt△CEF的直角顶点与正方形ABCD的顶点C重合,斜边EF与正方形ABCD的对角线交于点E,射线FE与AD交于点P,与BC交于点Q且BQCQ =45.(1)求证:△CDE≌△CBF;(2)求CF的长;(3)求tan∠BCF的值.参考答案1.A2.C3.D4.C5.D6.C7.D8.C9.010.121311.1712.1413.2√314.解:原式=2×√22+√33×√32-√2 =√2+12-√2=1215.(1)解:在△ABC 中,∵AD 是边BC 上的高∴AD ⊥BC .∴sin B =45AD AB =. ∵AD =12 ∴5154AB AD ==. 在Rt △ABD 中,∵222215129BD AB AD --∴CD =BC ﹣BD =14﹣9=5.(2)解:在Rt △ADC 中,E 是AC 的中点∴DE =EC∴∠EDC =∠C .∴tan EDC ∠=tan C ∠=125AD CD =.16.(1)由题意可知:154560ACD ∠=︒+︒=︒ 180454590ADC ∠=︒-︒-︒=︒ 在Rt ADC 中 ∴tan 1003tan 6010033300AD DC ACD =⨯∠=︒==(米)答:点D 与点A 的距离为300米.(2)过点D 作DE AB ⊥于点E .∵AB 是东西走向∴45,60ADE BDE ∠=︒∠=︒在Rt ADE △中 ∴2sin 300sin 453001502DE AE AD ADE ==⨯∠=⨯︒==在Rt BDE 中 ∴tan 1502tan 60231506BE DE BDE =⨯∠=︒==∴26AB AE BE =+=答:隧道AB 的长为(15021506)米17.(1)证明:过点 O 作 OE ⊥AC 于点 E ,连接 OA ,如图∵AB =AC , O 为底边 BC 的中点∴AO 为 ∠BAC 的平分线∵OD ⊥AB∴OD =OE∵OD 为 ⊙O 的半径∴OE为⊙O的半径∴直线AC到圆心O的距离等于圆的半径∴AC是⊙O的切线(2)解:①∵AB切⊙O于点D∴∠ODB=90°∵∠B=42°∴∠BOD=48°∵OD=4∴劣弧DM的长为48×π×4180=16π15;②过点O作OF⊥DM于点F,如图∵OF⊥DM∴DF=MF=12DM=2∵OD=OM∴OF为∠DOM的平分线∴∠DOF=12∠BOD=24° .在Rt△ODF中∵sin∠DOF=DFOD∴sin24°=2OD∴OD=2sin24°≈20.4=5 .18.(1)证明:∵四边形ABCD是正方形,△CEF是等腰直角三角形∴∠BCD=∠ECF=90°,CD=CB,CE=CF∴∠DCE=∠BCF在△CDE与△CBF中∵{CD=CB∠DCE=∠BCFCE=CF∴△CDE≌△CBF;(2)解:∵∠CEQ=∠CBE=45°,∠ECQ=∠BCE∴△CEQ∽△CBE∴CECB=CQCE∵BQCQ=45,BC=9∴BQ=4,CQ=5∴CE=3√5∵CF=CE∴CF=3√5;(3)解:过点F作FR⊥BC于R∵△CDE≌△CBF∴∠FBR=∠EDC=45°∴△BRF是等腰直角三角形∴RF=RB在Rt△CRF中∵CF2=CR2+FR2∴(3√5)2=RF2+(9−RF)2∴RF=3∴BR=3∴CR=6∴tan∠BCF=RFCR =12.。
2018年全国各地中考数学真题汇编:锐角三角函数(含答案)-数学备课大师【全免费】

中考数学真题汇编:锐角三角函数一、选择题1.的值等于()A. B. C. 1 D.【答案】B2.如图,过点,,,点是轴下方上的一点,连接,,则的度数是()A. B. C. D.【答案】B3.如图,一把直尺,的直角三角板和光盘如图摆放,为角与直尺交点,,则光盘的直径是( )A.3B.C.D.【答案】D4.如图,旗杆及升旗台的剖面和教学楼的剖面在同一平面上,旗杆与地面垂直,在教学楼底部E点处测得旗杆顶端的仰角,升旗台底部到教学楼底部的距离米,升旗台坡面CD的坡度,坡长米,若旗杆底部到坡面CD的水平距离米,则旗杆AB的高度约为()(参考数据:,,)A. 12.6米B. 13.1米C. 14.7米D. 16.3米【答案】B5.一艘在南北航线上的测量船,于A点处测得海岛B在点A的南偏东30°方向,继续向南航行30海里到达C点时,测得海岛B在C点的北偏东15°方向,那么海岛B离此航线的最近距离是(结果保留小数点后两位)(参考数据:)()A. 4.64海里B. 5.49海里C. 6.12海里D. 6.21海里【答案】B6.如图,两根竹竿AB和AD斜靠在墙CE上,量得∠ABC=α,∠ADC=β,则竹竿AB与AD的长度之比为()A. B. C. D.【答案】B7. 如图,已知在中,,,,则的值是()A. B. C. D.【答案】A8. 如图,电线杆CD的高度为h,两根拉线AC与BC相互垂直,∠CAB=α,则拉线BC的长度为(A、D、B 在同一条直线上)()A. B. C. D. h•cosα【答案】B二、填空题9.如图.一-艘渔船正以60海里/小时的速度向正东方向航行,在处测得岛礁在东北方向上,继续航行1.5小时后到达处此时测得岛礁在北偏东方向,同时测得岛礁正东方向上的避风港在北偏东方向为了在台风到来之前用最短时间到达处,渔船立刻加速以75海里/小时的速度继续航行________小时即可到达(结果保留根号)【答案】10.如图,旗杆高AB=8m,某一时刻,旗杆影子长BC=16m,则tanC=________。
18年中考数学《锐角三角函数》回归考点练习试卷含答案

锐角三角函数练习卷1.tan 60︒的值等于()(A )1(B(C (D )22.Rt △ABC 中,∠C=90°,AC ∶BC=1∶3,则cosA=_______,tanA=_________.3.设α、β为锐角,若sin α=23,则α=________;若tan β=33,则β=_________. 4.已知α是锐角,且sin α=54,则cos(90°-α)=( ) A.54 B.43 C.53 D.51 5.三角形在正方形网格纸中的位置如图所示,则sin α的值是( ) A.43 B.34 C.53 D.546.如图,⊙O 是△ABC 的外接圆,AD 是⊙O 的直径,连接CD ,若⊙O 的半径23=r ,AC=2,则cosB 的值是( )A.23 B.35 C.25 D.327.如图,若∠A =60°,AC =20m ,则BC 大约是(结果精确到0.1m)( ) A .34.64m B .34.6m C .28.3m D .17.3mB8.在△ABC 中,∠C=90°,AB=15,sinA=31,则BC=( ) A.45 B.5 C.51 D.4519.如图,CD 是Rt △ABC 斜边上的高,AC=4,BC=3,则cos ∠BCD=( ) A.53 B.43 C.34 D.5410.计算:(02cos 45=︒.11.计算:()102 3.142sin 603π-︒⎛⎫+--- ⎪⎝⎭12.已知:如图,△ABC 内接于⊙O ,点D 在OC 的延长线上,sinB=21,∠CAD=30°. (1)求证:AD 是⊙O 的切线; (2)若OD ⊥AB ,BC=5,求AD 的长.13.计算:2sin60º+12--02008–|1–3|O14.计算:101(2013)3452-⎛⎫--- ⎪⎝⎭15.如图是一个半圆形桥洞截面示意图,圆心为O ,直径AB 是河底线,弦CD 是水位线,CD ∥AB ,且CD = 24 m ,OE ⊥CD 于点E .已测得sin ∠DOE =.(1)求半径OD ;(2)根据需要,水面要以每小时0.5 m 的速度下降,则经过多长时间才能将水排干?16.如图,在△中,∠=90°,sin=,=15,求△的周长和tan的值.参考答案 1 .C 2 .21,3 3 .60°,30° 4 . A 5. C 6. B 7. B8 . B 9 .D 10. 1- 11 .3212答案思路解析:圆的切线问题跟过切点的半径有关,连接OA ,证∠OAD=90°.由sinB=21可以得到∠B=30°,由此得到圆心角∠AOD=60°,从而得到△ACO 是等边三角形,由此∠OAD=90°.AD 是Rt △OAD 的边,有三角函数可以求出其长度.(1)证明:如图,连接OA. ∵sinB=21,∴∠B=30°.∴∠AOD=60°. ∵OA=OC ,∴△ACO 是等边三角形. ∴∠OAC=60°.∴∠OAD=90°.∴AD 是⊙O 的切线. (2)解:∵OD ⊥AB ∴ OC 垂直平分AB. ∴ AC=BC=5.∴OA=5.在Rt △OAD 中,由正切定义,有tan ∠AOD=OAAD. ∴ AD=35.13.2114. 2 15.(1)∵OE ⊥CD 于点E ,CD =24(m ),∴ED ==12(m ).在Rt △DOE 中,∵sin ∠DOE = =,∴OD =13(m ). (2)OE ==(m )∴将水排干需:5÷0.5=10(小时). 16.在中, ∠=90°,=15==, ∴∴周长为36,BC 124tan A .AC 93===。
锐角三角函数(解析版)2018年数学全国中考真题-2

2018年数学全国中考真题锐角三角函数(试题二)解析版一、选择题1. (2018广西省柳州市,7,3分)如图,在Rt△ABC 中,△C =90°,BC =4,AC =3,则sinB =ACAB=( )第7题图 A .35B .45C .37D .34【答案】A【解析】由勾股定理,得:AB =22AC BC +=2234+=5.根据正弦的定义,得:sinB =AC AB =35. 【知识点】锐角的三角函数 2. 的值等于( △ A.B.C. 1D.【答案】B【解析】分析:根据特殊角的三角函数值直接求解即可. 详解:cos30°=. 故选:B .点睛:本题考查特殊角的三角函数值的记忆情况.特殊角三角函数值计算在中考中经常出现,要熟练掌握.3. (2018湖南娄底,10,3)如图,往竖直放置的在A 处山短软管连接的粗细均匀细管组成的“U 形装置中注入一定量的水,水面高度为6cm ,现将右边细管绕A 处顺时针方向旋转60到AB 位置,则AB 中水柱的长度约为( )A .4cmB .63cmC .8cmD .12cm【答案】C4C A x2xx【解析】右边细管绕 A 处顺时针方向旋转 60°后,左右两侧液面的竖直高度相等,且竖直方向和 AB 方向的总长度不变。
根据 AB 与水平方向成 30°夹角,可知此时AB 中水柱的长度为右边竖直高度的2倍,而为总长度仍然为 12cm 。
利用方程易得:AB 中水柱长度为 8cm ,故选B 【知识点】特殊角的三角函数、综合物理中连通器知识4. (2018湖南娄底,9,3)如图,由四个全等的直角三角形围成的大正方形的面积是169,小正方形的面积为49,则sincos( )A .513B .513C .713D .713【答案】D【解析】根据大正方形面积为169得到直角三角形斜边为13,小正方形面积为49得直角边的差为7,想到直角边为12个和5,得到1371312135cos sin -=-=-αα,故选D 【知识点】弦图,勾股定理、锐角三角函数5. (2018江苏常州,8,2)某数学研究性学习小组制作了如下的三角函数计算图尺:在半径为1的半圆形量角器中,画一个直径为1的圆,把刻度尺CA 的0刻度固定在半圆的圆心O 处,刻度尺可以绕点O 转,从图中所示的图尺可读出sin ∠AOB 的值是( ) A .85 B .87 C .107 D .54【答案】D 【解析】 如图,连接EF ,由题意可知OF =8,OE =OH =10, ∵∠OEF +∠EOF =∠EOF +∠BOF ,∴∠OEF =∠AOB, ∵OE 是直径,∴∠EFO =90゜, ∴sin ∠AOB =84105OF OE ==,故选D .6.(2018辽宁葫芦岛,9,3分) 如图, AB 是⊙O 的直径, C , D 是⊙O 上AB 两侧的点,若∠D =30°,则tan ∠ABC 的值为( ) A .12BCD【答案】C ,【解析】∵AB 是⊙O 的直径,∴∠ACB =90°,∵∠A =∠D =30°,∴∠ABC =60°,∵tan 60°tan ∠ABC故选C .7. (2018广西南宁,12,3)如图,矩形纸片ABCD ,AB =4,BC =3,点P 在BC 上,将△CDP 沿DP 折叠,点C 落在点E 处,PE 、DE 分别交AB 于点O 、F ,且OP =OF ,则cos ∠ADF 的值为( )A .1113B .1315C .1517D .1719【答案】C ,【解析】由题意得:Rt △DCP ≌Rt △DEP ,∴DC =DE =4,CP =EP 在Rt △OEF 和Rt △OBP 中,∠EOF =∠BOP ,∠B =∠E ,OP =OF Rt △OEF ≌Rt △OBP (AAS ),∴OE =OB ,EF =BP 设EF 为x ,则BP =x ,DF -EF =4-x ,又∵BF =OF +OB =OP +OE =PE =PC ,PC =BC -BP =3-x ∴AF =AB -BF =4-(3-x )=1+xAEHDP在Rt △DAF 中,AF 2+DF 2=DF 2,即(1+x )2+32=(4-x )2 解得x =35,∴EF =35,DF =4-35 = 175∴在Rt △DAF 中,cos ∠ADF =AD DF =1517.8. (2018贵州贵阳,7,3分)如图,A 、B 、C 是小正方形的顶点,且每个小正方形的边长为1,则tan ∠BAC 的值为( )A .12B .1 CD【答案】B【解析】连接BC ,则BC ⊥AB .在Rt △ABC 中,AB =BC tan ∠BAC =BCAB=1.9.(2018黑龙江大庆,1,3) 2cos 60°=( )A .1B .3C .2D .21 【答案】A ,【解析】根据cos 60°=21,计算即可.10. (2018云南,12,4分)在Rt △ABC 中,∠C =90°,AC =1,BC =3,则∠A 的正切值为 ··· ( )A .3B .13C D 【答案】A .【解析】根据正切的意义得tan A =BC AC =31.二、填空题1. (2018黑龙江省齐齐哈尔市,题号16,分值3,AB=20,BC=10,AD=13,则线段CD=________.【答案】172分)【解析】过点A 作BD ⊥AE 交于点E ,AB=20,设AE=3x ,BE=4x ,∴AB ²=25x²=400,解得x=4,即AE=12,BE=16.∵AD=13,∴过点D 作DF ⊥BC 于点F ,∴DF ∥AB ,即∠ABD=∠BDF ,当四边形ABCD 是凸四边形时,BD=BE+DE=21,tan ∠BDF=34,可得DF=845,BF=635,又∵CF=BF-BC=135 ,∴17 当四边形ABCD 是凹四边形时,BD=BE-DE=11, ,tan ∠BDF=34,可得DF=445,BF=335,又∵CF=BC-BF=175,∴故答案为17 【知识点】锐角三角函数的性质,平行线的性质,勾股定理.2. (2018青海,10,2分)在△ABC 中,若|sin A −12|+(cos B −12)2=0,则∠C 的度数是 .【答案】90°.【解析】∵|sin A −12|+(cos B −12)2=0,∴sinA=21,cosB=21,∴∠A=30°,∠B=60°,∴∠C=180°﹣30°﹣60°=90°.【知识点】特殊角的锐角三角函数值3. (2018江苏苏州,17,3分)如图,在Rt △ABC 中,∠B =90°,AB =BC .将△ABC 绕点A 按逆时针方向旋转90°得到△AB C '',连接B C ',则sin ∠ACB '= .【答案】45【解析】 本题解答时要过B ’作B ’D ⊥AC 于D ,利用用等角的三角函数值相等中,旋转的性质,直角三角形三边的关系以及勾股定理来进行计算.过点B ’作B ’D ⊥AC 于D ,由旋转可知:∠B ’AB =90゜,AB ’=AB∴∠AB ’D +∠B ’AD =∠B ’AD +∠CAB ,∴∠AB ’D =∠CAB . ∵ABBC=AC =5∴B ’D =AB ’sin 'AB D ∠ ==AB ’sin CAB ∠=2=, ∴CD =5-2=3,∴B ’D4, ∴B ’C =5, ∴sin ∠ACB ’='4'5B D BC =.4. (2018江苏镇江,11,2分)如图,△ABC 中,∠BAC >90°,BC =5,将△ABC 绕点C 按顺时针方向旋转90°,点B 对应点B ′落在BA 的延长线上,若sin ∠B ′AC =910,则AC =________.【解析】如答图所示.因为将△ABC 绕点C 按顺时针方向旋转90°得到△A ′B ′C ,所以∠BCB ′=90°,B ′C =BC =5,所以∠BB ′C =45°.过点C 作CD ⊥BB ′于点D ,则△CDB ′是等腰直角三角形,所以CDRt △△ACD 中,因为sin ∠B ′AC =CD AC =910,即2AC =910,解得ACA(第11题图)CA BB 'A '5. (2018山东莱芜,17,9分)如图,若△ABC 内一点P 满足∠P AC =∠PCB =∠PBA ,则称点P 为△ABC 的布罗卡尔点.三角形的布罗卡尔点是法国数学家和数学教育家克雷尔首次发现,后来被数学爱好者法国军官布罗卡尔重新发现,并用他的名字命名,布罗卡尔点的再次发现,引发了研究“三角形几何”的热潮. 已知△ABC 中,CA =CB ,∠ACB =120°,P 为△ABC 的布罗卡尔点,若P A =3,则PB +PC =___________.【答案】1+33【思路分析】由“布罗卡尔点”的定义,得到∠P AC =∠PCB =∠PBA ,又∠ABC =∠BAC =30°,可证△BCP ∽△ABP 即可. 【解题过程】解:如图,由“布罗卡尔点”的定义,设∠P AC =∠PCB =∠PBA =α,又CA =CB ,∠ACB =120°,∴∠ABC =∠BAC =30°,∴∠CBP =∠P AB =30°-α=β,∴△BCP ∽△ABP ,∴PB /P A =BC /AB =PC /PB ,而在△ABC 中,作CD ⊥AB 于D ,则BD =12AB ,而cos B =BD BC =32,∴BC AB =13,∴PB 3=13=PCPB ,∴PB =1,PC =33,∴PB +PC =1+33.故答案为1+33.【知识点】新定义问题;相似三角形的性质与判定;解直角三角形6.(2018山东莱芜,13,3分)计算:(π-3.14)0+2cos60°=_______. 【答案】2【解析】原式=1+2×12=1+1=2.故答案为2.【知识点】特殊角的三角函数值;零指数幂7. (2018四川眉山,17,3分)如图,在边长为1的小正方形网格中,点A 、B 、C 、D 都在这些小正方形的顶点上,AB 、CD 相交于点O ,则tan ∠AOD = .B(第11题答图)CA BB 'A 'D【答案】2,【解析】如图所示,连接AE 、BE ,易证CD ∥BE ,∴∠AOD =∠ABE ,显然△ABE 是直角三角形,∴tan ∠AOD =tan ∠ABE =2AE BE ==.三、解答题1. (2018山西省,19题,8分) 祥云桥位于省城太原南部,该桥塔主体由三根曲线塔柱组合而成,全桥共设13对直线型斜拉索,造型新颖,是“三晋大地”的一种象征。
2018年中考数学《锐角三角函数》同步提分训练(有答案)

2018年中考数学提分训练: 锐角三角函数一、选择题1.在Rt△ABC中,∠C=90°,AC=4,AB=5,则tanA的值是()A. B. C. D.2.如图,在△ABC中,AC=8,∠ABC=60°,∠C=45°,AD⊥BC,垂足为D,∠ABC的平分线交AD于点E,则AE的长为()A. B. 2 C. D. 33.在下列网格中,小正方形的边长为1,点A,B,O都在格点上,则∠A的正弦值是()A. B. C. D.4.已知是等腰直角三角形的一个锐角,则的值为()A. B. C. D. 15.一辆小车沿着如图所示的斜坡向上行驶了100米,其铅直高度上升了15米.在用科学计算器求坡角α的度数时,具体按键顺序是()A. B.C. D.6.在△ABC中,∠C=90°,AB=6,cosA= ,则AC等于().A. 18B. 2C.D.7.如图,小强从热气球上测量一栋高楼顶部B的仰角为30°,测量这栋高楼底部C的俯角为60°,热气球与高楼的水平距离为45米,则这栋高楼高为()米A.15B.30C.45D.608.△ABC中,∠A,∠B均为锐角,且(tanB﹣)(2sinA﹣)=0,则△ABC一定是()A.等腰三角形B.等边三角形C.直角三角形D.有一个角是60°的三角形9.如图,矩形ABCD中,O为AC的中点,过点O的直线分别与AB,CD交于点E,F,连接BF交AC于点M,连接DE,BO.若∠COB=60°,FO=FC,则下列结论:①FB⊥OC,OM=CM;②△EOB≌△CMB;③四边形EBFD 是菱形;④MB∶OE=3∶2.其中正确结论的个数是()A. 1B. 2C. 3D. 410.如图,在半径为5的⊙O中,弦AB=6,点C是优弧上一点(不与A,B重合),则cosC的值为()A. B. C. D.11.如图,四边形ABCD,A1B1BA,…,A5B5B4A4都是边长为1的小正方形.已知∠ACB=a,∠A1CB1=a1,…,∠A5CB5=a5.则tana•tana1+tana1•tana2+…+tana4•tana5的值为()A. B. C. 1 D.二、填空题12.计算:tan60°﹣cos30°=________.13.已知∠A是锐角,且tanA= ,则∠A=________.14.坡角为α=60°,则坡度i=________.15.如图,在平面直角坐标系中,点A的坐标为(﹣2,),以原点O为中心,将点A顺时针旋转165°得到点A′,则点A′的坐标为________.16.如图,在△ABC中,AB=AC,AH⊥BC,垂足为点H,如果AH=BC,那么sin∠BAC的值是________.17.在Rt△ABC中,∠C=90°,AB=2,BC= ,则sinA=________.18.已知△ABC,AB=AC,BC=8,点D、E分别在边BC、AB上,将△ABC沿着直线DE翻折,点B落在边AC上的点M处,且AC=4AM,设BD=m,那么∠ACB的正切值是________.(用含m的代数式表示)19.如图,为了测量河的宽度AB,测量人员在高21m的建筑物CD的顶端D处测得河岸B处的俯角为45°,测得河对岸A处的俯角为30°(A,B,C在同一条直线上),则河的宽度AB约为________.三、解答题20.计算:2cos45°﹣tan60°+sin30°﹣|﹣|.21.某游乐场一转角滑梯如图所示,滑梯立柱均垂直于地面,点在线段上.在点测得点的仰角为,点的俯角也为,测得间的距离为10米,立柱高30米.求立柱的高(结果保留根号).22.如图,为了测量建筑物的高度,在处树立标杆,标杆的高是.在上选取观测点、,从测得标杆和建筑物的顶部、的仰角分别为、,从测得、的仰角分别为、.求建筑物的高度(精确到).(参考数据:,,.)23.如图1,水坝的横截面是梯形ABCD,∠ABC=37°,坝顶DC=3m,背水坡AD的坡度i(即tan∠DAB)为1:0.5,坝底AB=14m.(1)求坝高;(2)如图2,为了提高堤坝的防洪抗洪能力,防汛指挥部决定在背水坡将坝顶和坝底同时拓宽加固,使得AE=2DF,EF⊥BF,求DF的长.(参考数据:sin37°≈ ,cos37°≈ ,tan37°≈ )答案解析一、选择题1.【答案】C【解析】:∵在Rt△ABC中,∠C=90°,AC=4,AB=5,∴BC==3∴tanA==故答案为:C【分析】利用勾股定理先求出BC的长,再利用锐角三角形函数的定义,即可求出tanA的值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初三中考数学复习 锐角三角函数 专题复习练习题
1.已知在△ABC 中,若∠C=90°,sin A =1
3,则cos B 等于( )
A.13 B .1 C.23 D.223
2.在△ABC 中,a ,b ,c 分别是∠A ,∠B,∠C 的对边,如果a 2+b 2=c 2,那么下列结论正确的是( )
A .csin A =a
B .bcos B =c
C .atan A =b
D .ctan B =b 3.如图,已知AD 是△ABC 的外接圆的直径,AD =13 cm ,cos B =5
13,则AC 的长等
于( )
A .5 cm
B .6 cm
C .12 cm
D .10 cm
4.在△ABC 中,若|sin A -3
2|+⎝
⎛⎭⎪⎫cos B -122=0,则△ABC 是( )
A .不等边的等腰三角形
B .等边三角形
C .不等腰的直角三角形
D .等腰直角三角形 5.如图,∠1的正切值是( )
A .2 B.13 C. 5 D.5
2
6.为了测量被池塘隔开的A ,B 两点之间的距离,根据实际情况,作出如图所示的图形,其中AB ⊥BE ,EF ⊥BE ,AF 交BE 于点D ,点C 在BD 上.有四位同学分别测量出以下四组数据:①BC ,∠ACB ;②CD ,∠ACB ,∠ADB ;③EF ,DE ,BD ;④DE ,DC ,BC.根据所测数据,能求出A ,B 间距离的有( ).
A .1组
B .2组
C .3组
D .4组0
7.在一次数学活动中,李明利用一根拴有小锤的细线和一个半圆形量角器制作了一个测角仪,去测量学校内一座假山的高度CD.如图,已知李明距假山的水平距离BD 为12 m ,他的眼睛距地面的高度为1.6 m ,李明的视线经过量角器零刻度线OA 和假山的最高点C ,此时,铅垂线OE 经过量角器的60°刻度线,则假山的高度为( )
A .(43+1.6)m
B .(123+1.6)m
C .(42+1.6)m
D .43m
8.如图,在一个房间内,有一架梯子斜靠在墙上,梯子顶端距地面的垂直距离MA 为a m ,此时梯子的倾斜角为60°,若梯子顶端距离地面的垂直距离NB 为b m ,梯子的倾斜角为45°,则这间房子的宽AB 是( )
A.3a +b 2 m
B.3a -b 2
m
C.⎝ ⎛⎭⎪⎪⎫33a -b m
D.⎝
⎛⎭
⎪⎪⎫33a +b m 9.在△ABC 中,∠C =90°,a ,b ,c 分别是∠A,∠B ,∠C 的对边,且有c 2+4b 2-4bc =0,则sin A +cos A 的值为( )
A .1 B.1+32 C.1+22 D.3+22
10.如图,两个高度相等的圆柱形水杯,甲杯装满液体,乙杯是空杯,若把甲杯中的液体全部倒入乙杯,则乙杯中的液面与图中点P 的距离是( )
A .2 cm
B .4 3 cm
C .6 cm
D .8 cm
11.计算:12+2sin 60°=________.
12.如图,在△ABC 中,AB =5,BC =13,AD 是BC 边上的高,AD =4,则CD =______,
sin C =________.
13.如图,在菱形ABCD 中,DE ⊥AB ,垂足为点E ,DE =6 cm ,sin A =3
5,则菱形ABCD
的面积是________cm 2.
14.如图所示的是市民广场到地下通道的手扶电梯示意图,其中AB ,CD 分别表示地下通道、市民广场电梯口处地面的水平线,∠ABC =135°,BC 的长是5 2 m ,则乘电梯从点B 到点C 上升的高度h 是________m.
15.如图,△ABC 的内心在y 轴上,点C 的坐标为(2,0),点B 的坐标为(0,2),直线AC 的解析式为y =1
2
x -1,则tan A 的值是________.
16.某厂家新开发的一种电动车如图,它的大灯A 射出的光线AB ,AC 与地面MN 所夹的角分别为8°和10°,大灯A 与地面的距离为1 m ,则该车大灯照亮地面的宽度BC 是________m .(不考虑其他因素,参考数据:sin 8°≈425,tan 8°≈17,sin 10°
≈950,tan 10°≈5
28
)
17.如图,将以点A 为直角顶点的等腰直角三角形ABC 沿直线BC 平移得到△A′B′C′,使点B′与点C 重合,连接A′B,则tan ∠A′BC′=________.
18.如图,矩形ABCD 的对角线AC ,BD 相交于点O.过点O 作OE⊥AC 交AB 于点E ,若BC =4,△AOE 的面积为5,则sin ∠BOE 的值为________.
19.当x =2sin 45°+tan 60°时,先将代数式x
x 2-1÷⎝
⎛⎭⎪⎫1+
1x -1化简,后求值.
20.如图,在平面直角坐标系内,点O 为原点,点A 的坐标为(10,0),点B 在第一象限内,且BO =5,sin ∠BOA =3
5
.
求:(1)点B 的坐标; (2)cos ∠BAO 的值.
21.如图,在矩形ABCD 中,E 是BC 边上的一点,AE =BC ,DF⊥AF,垂足为点F ,连接DE.
(1)求证:AB =DF ;
(2)若AD =10,AB =6,求tan ∠EDF 的值.
22.一个长方体木箱沿斜面下滑,当木箱滑至如图所示的位置时,AB=3 m,已知木箱高BE= 3 m,斜面坡角为30°,求木箱端点E距地面AC的高度EF.
23.如图,马路的两边CF,DE互相平行,线段CD为人行横道,马路两侧的A,B两点分别表示车站和超市,CD与AB所在直线互相平行,且都与马路的两边垂直,马路宽20米,A,B相距62米,∠A=67°,∠B=37°.
(1)求CD与AB之间的距离;
(2)某人从车站A出发去超市B,求他沿折线A→D→C→B到达超市比直接横穿马路多走多少米?
(参考数据:sin 67°≈1213,cos 67°≈513,tan 67°≈125,sin 37°≈3
5,cos 37°
≈45,tan 37°≈3
4)
答案:
1---10 AACCB CADBC 11. 3 3
12. 10 229
29
13. 60 14. 5 15. 13
16. 75
17. 13
18. 35
19. 解:原式=x x 2-1÷x x -1=x (x +1)(x -1)·x -1x =1
x +1.
又∵x=2sin 45°+tan 60°=2×
22+3=1+3,∴原式=1
2+3
=2- 3. 20. 解:(1)过点B 作BC⊥OA 于点C ,图略.
∵sin ∠BOA =35,∴BC =BO·sin ∠BOA =5×3
5=3.
∴OC =BO 2-BC 2=4.∴点B 的坐标为(4,3).
(2)∵BC=3,OC =4,OA =10,∴AC =6,∴AB =62+32=35, ∴cos ∠BAO =6
35=2
5
5.
21. 解:(1)证明:∵四边形ABCD 是矩形,∴AD ∥BC ,AD =BC ,
∴∠DAF =∠AEB.∵AE =BC ,∴AE =AD ,又∵∠B=∠DFA=90°, ∴△EAB ≌△ADF ,∴AB =DF.
(2)在Rt △ABE 中,BE =AE 2-AB 2=102-62=8.
∵△EAB ≌△ADF ,∴DF =AB =6,AF =EB =8,∴EF =AE -AF =10-8=2, ∴tan ∠EDF =EF DF =26=1
3.
22. 解:连接AE ,图略.
在Rt △ABE 中,AB =3,BE =3,则AE =AB 2+BE 2=2 3. ∵tan ∠EAB =BE AB =3
3
,∴∠EAB =30°.
在Rt △AEF 中,∠EAF =∠EAB+∠BAC=30°+30°=60°, ∴EF =AE×sin ∠EAF =23×
3
2
=3(m ). 答:木箱端点E 距地面AC 的高度EF 为3 m . 23. 解:(1)设CD 与AB 之间的距离为x 米,
则在Rt △BCF 和Rt △ADE 中, ∵CF BF =tan 37°,DE
EA
=tan 67°,
∴BF =CF tan 37°≈43x ,AE =DE tan 67°≈512
x. 又∵AB=62,CD =EF =20,
∴43x +512
x +20≈62,解得x≈24, 故CD 与AB 之间的距离约为24米.
(2)在Rt △BCF 和Rt △ADE 中,
∵BC =CF sin 37°≈2435
=40(米), AD =DE sin 67°≈241213
=26(米), ∴AD +DC +CB -AB≈26+20+40-62=24(米).
答:他沿折线A→D→C→B 到达超市比直接横穿马路多走约24米.。
