飞行动力学与控制大作业
飞行控制系统大作业

《飞行控制系统》课程实验报告班级 0314102学号 ********* 姓名孙旭东成绩南京航空航天大学2017年4月(一)飞机纵向飞行控制系统的设计与仿真1、分析飞机纵向动力学模态,求飞机的长周期与短周期阻尼与自然频率。
在MATLAB环境下导入数据文件,输入damp(alon),得出结果:Eigenvalue Damping Freq. (rad/s)-2.29e+000 + 4.10e+000i 4.88e-001 4.69e+000-2.29e+000 - 4.10e+000i 4.88e-001 4.69e+000-3.16e-002 1.00e+000 3.16e-002-7.30e-003 + 3.35e-002i 2.13e-001 3.42e-002-7.30e-003 - 3.35e-002i 2.13e-001 3.42e-002长周期的根为 -7.30e-003 + 3.35e-002i 和 -7.30e-003 - 3.35e-002i阻尼为 2.13e-001自然频率为 3.42e-002(rad/s)短周期的根为 -2.29e+000 + 4.10e+000i 和 -2.29e+000 - 4.10e+000i阻尼为 4.88e-001自然频率为 4.69e+000(rad/s)2、对升降舵及油门单位阶跃输入下的飞机自然特性进行仿真,画出相应的状态曲线。
sys=ss(alon,blon,clon,dlon)[y,t]=step(sys,500)subplot(221)plot(t,y(:,1,1))xlabel('t(s)')ylabel('\Deltau(m/s)')subplot(222)plot(t,y(:,1,2))xlabel('t(s)')ylabel('\Deltau(m/s)')subplot(223)plot(t,y(:,2,1))xlabel('t(s)')ylabel('\Delta\alpha(deg)')subplot(224)plot(t,y(:,2,2))xlabel('t(s)')ylabel('\Delta\alpha(deg)')200400600-10-505t(s)∆q (d e g /s )200400600-4-2024t(s)∆q (d e g /s )200400600-150-100-50050t(s)∆θ(d e g )0200400600-50050100t(s)∆θ(d e g )200400600-2000200400t(s)∆u (m /s )0200400600-6-4-2t(s)∆α(d e g )200400600-2000200400t(s)∆u (m /s )0200400600-2024t(s)∆α(d e g )subplot(221) plot(t,y(:,3,1)) xlabel('t(s)')ylabel('\Deltaq(deg/s)') subplot(222) plot(t,y(:,3,2)) xlabel('t(s)')ylabel('\Deltaq(deg/s)') subplot(223) plot(t,y(:,4,1)) xlabel('t(s)')ylabel('\Delta\theta(deg)') subplot(224) plot(t,y(:,4,2)) xlabel('t(s)')ylabel('\Delta\theta(deg)')subplot(121) plot(t,y(:,5,1)) xlabel('t(s)')ylabel('\Deltah(m)') subplot(122) plot(t,y(:,5,2)) xlabel('t(s)')ylabel('\Deltah(m)')2004006004t(s)∆h (m )200400600-2.5-2-1.5-1-0.54t(s)∆h (m )以上各图为升降舵及油门单位阶跃输入下的飞机自然特性行仿真,左边一列为升降舵的阶跃输入,右边一列为油门的阶跃输入。
飞控大作业(蔡云鹏)
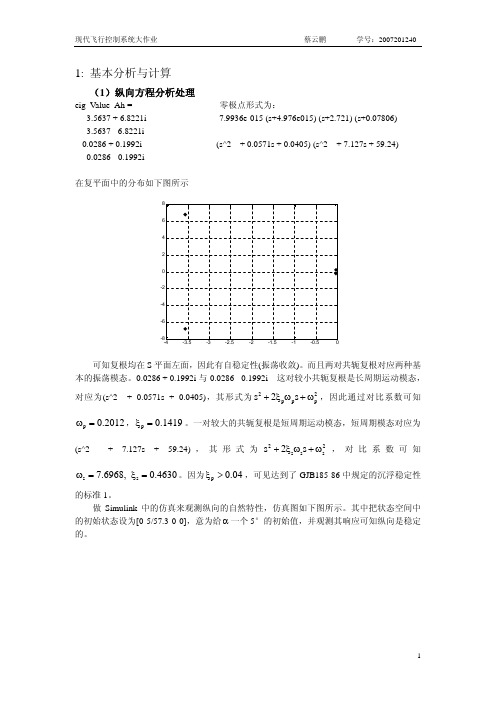
1: 基本分析与计算(1)纵向方程分析处理eig_Value_Ah = 零极点形式为: -3.5637 + 6.8221i -7.9936e-015 (s+4.976e015) (s+2.721) (s+0.07806) -3.5637 - 6.8221i ---------------------------------------------------------------------- -0.0286 + 0.1992i (s^2 + 0.0571s + 0.0405) (s^2 + 7.127s + 59.24) -0.0286 - 0.1992i在复平面中的分布如下图所示可知复根均在S 平面左面,因此有自稳定性(振荡收敛)。
而且两对共轭复根对应两种基本的振荡模态。
-0.0286 + 0.1992i 与-0.0286 - 0.1992i 这对较小共轭复根是长周期运动模态,对应为(s^2 + 0.0571s + 0.0405),其形式为22p p s 2s p +ξω+ω,因此通过对比系数可知,。
一对较大的共轭复根是短周期运动模态,短周期模态对应为p 0.2012ω=p 0.1419ξ=(s^2 + 7.127s + 59.24),其形式为2s s s s 2s 2+ξω+ω,对比系数可知。
因为s s 7.6968, 0.4630ω=ξ=p 0.04ξ>,可见达到了GJB185-86中规定的沉浮稳定性的标准1。
做Simulink 中的仿真来观测纵向的自然特性,仿真图如下图所示。
其中把状态空间中的初始状态设为[0 5/57.3 0 0],意为给α一个5°的初始值,并观测其响应可知纵向是稳定的。
上图中右图是空速V 的响应,左图是迎角α的响应。
可以看出其纵向自然特性是随着时间而自稳定的。
在讨论纵向操纵性时,给定升降舵偏角一个幅值为5=°e δ,宽度为1秒的一个脉冲,其中脉冲可用signal builder 来构造,Simulink 框图和各状态变量的响应的输出如下图所示:Vαqθ可见,,,V q αθ在升降舵受到脉冲干扰后,其均随时间而收敛,其中空速V 和仰俯角θ的变换范围较大,其稳定所需时间较长。
复旦 飞行力学与飞行控制大作业

ixt jyt kzt 。设飞机有一角速度 ix j y kz ,它会引起质量元 dm 产生一
t t t
牵连速度 Vdm 。牵连速度的向量值可按下式计算:
第3页
i Vdm xt xt
j
k
t
y
yt
z
zt
t
i ( yt zt zt yt ) j ( zt xt xt zt ) k ( xt yt yt xt ) iVdmx jVdmy kVdmz
R rt (t rt )t
上式除以 t ,并令 t 0 ,可得:
(A.1)
dr drt t rt dt dt
上式中
(A.2)
dr dr 为向量相对于地坐标系变化率 (即绝对运动) , t 为向量相对于动坐标系的 dt dt
变化率(即相对运动) ,t rt 为由动坐标系转动而引起的向量变化率(即牵连运动) 。上式 可以推广到任意向量的情况。对于 H t 、 Vt 向量有:
A.2 运动学方程组的建立 A.2.1 角位置运动学方程组
永远是沿垂直轴的, 永远是沿水平轴的。唯有 在飞机的三个姿态角的角速度中,
、 向机体三轴投影, xt 、 yt 、 是绕机体轴 OX t 的。 因些, 把 、 只有 xt 包含 的全部,
第4页
z 都会含有 、 的投影分量。因此,用坐标变换可得 x 、 y 、 z 和 、 、 之间
(A.21)
dH Vxt sin Vyt cos cos Vzt cos sin (A.22) dt dZ Vxt sin cos Vyt (sin sin sin cos cos ) Vzt (cos cos sin sin sin ) dt
北航研究生飞行力学大作业

1.1.2 体轴系下的质心动力学方程
与风轴系下质心加速度类似:
2
飞行力学计算实习作业
~ E E VCB aCB WBBVCB 0 r q u u 0 p v v r 0 w w q p vr wq u ur v wp uq vp w
力 fW 分为可控力 AW 和重力 mgW ,可控力分为气动力和推力
D TxW AW C Ty 1 0 cos W 0 sin W cos W sin W 0 cos W sin W 0 0 sin W 0 1 0 0 0 cos W g
于是
~W E E CW aCW LWEWE LEW VCW V
又
~W ~W WW LWEWE LEW
则
1
飞行力学计算实习作业
~W E E VCW V aCW WW CW rW 0 0 rW pW qW V VrW VqW qW V V 0 0 pW 0 0 0
2
飞行力学计算实习作业
第 1 章 在平面地球假设条件下推导方程
1.1 质心动力学方程推导
1.1.1 风轴系下质心动力学方程。
基于大地平面假设、无风( w 0 ) ,取 FW 为动系,质心 C 为动点。由于质心 C 始 终与 FW 原点重合, 因此 r w 0 , 进而 aCW aOW 。 其中 aCW 为 C 点的绝对加速度在 FW 下 的表示。 由于绝对速度在风轴系中有
V
于是加速度为:
E CW
飞控大作业

《飞行控制系统》课程实验报告班级 0314103学号 031410329 姓名嵇程成绩南京航空航天大学2017年4月《飞行控制系统》课程实验(8学时)一、目标通过本实验,学生能够掌握基本的飞行控制系统的结构,设计的方法,仿真验证方法及控制性能的分析,加深对课堂教学内容的理解。
二、环境在windows操作系统下,matlab/simulink下进行设计与仿真。
三、内容(一)飞机纵向飞行控制系统的设计与仿真(4学时)1、飞机纵向自然特性的分析与仿真,包括短周期模态,长周期模态的分析,求解阻尼与自然频率,分析开环响应特性。
2、飞机俯仰角控制系统的设计;3、飞机速度控制系统的设计;4、飞机纵向运动的仿真与分析(二)飞机侧向飞行控制系统的设计与仿真(4学时)1、飞机纵向自然特性的分析与仿真,包括滚转模态,荷兰滚及螺旋模态的分析,求解阻尼与自然频率,分析开环响应特性。
2、飞机滚转角控制系统的设计;3、飞机航向控制系统的设计;4、飞机侧向航向协调控制仿真与分析四.要求1.在matlab下进行编程,系统设计与仿真;2.撰写实验报告,要求给出设计的参数,实验结果及曲线。
3.报告封面采用模板给定格式。
4.报告需提交打印稿,沿左侧装订。
(一)飞机纵向俯仰角与速度控制系统设计 某飞机的纵向线性小扰动方程为:lon lon xA xB u =+& 其中 状态[]T x u q h αθ=∆∆∆∆∆,控制量[]T e T u δδ=∆∆ 问题:1、 分析飞机纵向动力学模态,求飞机的长周期与短周期阻尼与自然频率。
输入:[W n ,z,p]=damp(alon)%系统的自然频率、阻尼比和闭环极点输出:W n z p 2.7127 2.7127 0.0708 0.0708 0.0030 0.3890 0.3890 0.0875 0.0875 1.0000 -1.0553 + 2.4990i -1.0553 - 2.4990i -0.0062 + 0.0706i -0.0062 - 0.0706i -0.0030 + 0.0000i表1-1-1p 1p 2ζ W n 长周期 -0.0062 + 0.0706i -0.0062 - 0.0706i 0.0875 0.0708 短周期 -1.0553+2.4990i -1.0553 - 2.4990i0.3890 2.7127表1-1-22、 对升降舵及油门单位阶跃输入下的飞机自然特性进行仿真,画出相应的状态曲线。
飞行器设计中的动力学及控制技术研究

飞行器设计中的动力学及控制技术研究一、引言飞行器设计中的动力学及控制技术研究是航空航天领域的重要研究方向之一。
飞行器的动力学与控制技术涉及飞行器的运动学、动力学模型建立与仿真、控制系统设计与优化等方面。
本文将重点介绍飞行器设计中的动力学与控制技术研究的相关内容。
二、飞行器的动力学建模飞行器的动力学建模是指通过数学模型描述飞行器的运动规律、特性及相互作用。
常用的飞行器动力学模型有刚体模型和弹性模型两种。
1. 刚体模型刚体模型是指将飞行器看作一个质点或刚体,忽略其形变与挠曲变化。
通过力学平衡原理和牛顿第二定律建立动力学方程,描述飞行器的运动状态。
刚体模型适用于飞行器速度相对较小、运动较为简单的情况。
2. 弹性模型弹性模型是指考虑飞行器的形变和挠曲变化对其运动规律的影响。
通过使用有限元分析等方法建立飞行器的弹性模型,并结合刚体模型进行综合仿真与分析。
弹性模型适用于考虑飞行器变形和振动等复杂运动情况。
三、飞行器的动力学仿真与优化飞行器的动力学仿真与优化是指在动力学模型的基础上,通过数值计算方法模拟飞行器运动,并优化控制策略、参数等,以实现飞行器运动的稳定性和精度。
1. 动力学仿真采用数值方法求解飞行器的动力学方程,模拟飞行器在不同工况下的运动轨迹、动力响应等。
常用的数值计算方法有欧拉法、龙格-库塔法、四阶龙格-库塔法等。
动力学仿真可以评估飞行器的稳定性和控制性能,在设计阶段优化系统参数,提高飞行器的运动性能。
2. 控制系统设计与优化飞行器的控制系统设计是指根据飞行器的动力学特性和要求,设计合适的控制器结构和算法,并优化控制参数,以实现飞行器的稳定控制。
常用的控制器设计方法有比例积分微分(PID)控制、模糊控制、自适应控制等。
控制系统设计与优化可以提高飞行器的稳定性、精度和鲁棒性。
四、飞行器动力学与控制应用研究飞行器动力学与控制技术的研究应用广泛,包括飞行器的操纵性与操纵质量评估、飞行器的自主导航与引导、飞行器的姿态稳定与控制等。
航天飞行动力学作业及答案(1)

航天飞行动力学作业(1)1. 动坐标系矢量导数已知火箭相对于地面坐标系的速度5500/v m s =,弹道倾角10θ=,并在纵向平面内运动,俯仰角速度为 1.5/s ω=,火箭俯仰角为30。
整流罩质心距离火箭质心为20m ,质心整流罩分离时相对于火箭箭体的相对速度为2m/s r v =,速度倾角(与火箭纵轴夹角)为45,求整流罩相对于地面坐标系的速度矢量。
解答: c =+r r ρ,c r 为整流罩在地面坐标系下的矢径,r 为火箭质心在地面坐标系下的矢径,ρ为整流罩质心距离火箭质心距离。
c d d d dt dt dt =+r r ρ d dt t δδ=+⨯ρρωρ c d d dt dt tδδ=++⨯r r ρωρ111111cx x rx x x cy y ry y y cz z rz z z v v v v v v v v v ωρωρωρ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=++⨯⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦ 5500*cos102*cos 450205417.95500*sin102*sin 4500956.900 1.5/57.300cx cy cz v v v ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=++⨯=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦ 2. 变质量质点动力学方程设火箭发动机秒耗量100kg/s m =,相对喷气速度为3000m/s e μ=,俯仰角速度为 1.5/s ω=,转动惯量变化率1000kg m/s z I =⋅,喷口距离质心距离为10m ρ=,求火箭发动机工作产生的附件哥氏力、附加相对力,附加哥氏力矩,附加相对力矩。
解答:附加哥氏力:0100221000052.3561.5/57.300k T e F m -⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥'=-⨯=-⨯⨯⨯=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦ωρ 附加相对力:30003000001000000rele F m -⎡⎤⎡⎤⎢⎥⎢⎥'=-⨯=-⨯=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦μ 附加哥氏力矩:0000100100()00001000000001000 1.5/57.30 1.5/57.30287.96kT e T e M m tδδ--⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥'=-⋅-⨯⨯=--⨯⨯⨯=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦Iωρωρ 附加相对力矩:0rele e M m '=-⨯=ρμ3. 引力和重力及其夹角将地球视为标准椭球模型,编程求解地表处地心维度分别为=306090φ,,时的:(1)引力加速度,r g g φ;(2)重力加速,r k k φ;(3)离心惯性加速度,er e a a ϕ''; (4)引力加速度与地心矢径夹角1μ;(5)重力加速度与地心矢径夹角μ;(6)地理纬度0B 。
飞行动力学与控制大作业

飞行动力学与控制大作业报告院(系)航空科学与工程学院专业名称飞行器设计学号学生姓名目录一.飞机本体动态特性计算分析 (2)1.1飞机本体模型数据 (2)1.2模态分析 (2)1.3传递函数 (3)1.4升降舵阶跃输入响应 (3)1.5频率特性分析 (5)1.6短周期飞行品质分析 (6)二.改善飞行品质的控制器设计 (7)2.1SAS控制率设计 (7)2.1.1控制器参数选择 (8)2.1.2数值仿真验证 (12)2.2CAS控制率设计 (13)三.基于现代控制理论的飞行控制设计方法 (16)3.1特征结构配置问题描述 (16)3.1.1特征结构的可配置性 (16)3.1.2系统模型 (16)3.2系统的特征结构配置设计 (17)3.2.1设计过程 (17)3.2.2具体的设计数据 (17)3.2.3结果与分析 (18)四.附录 (20)一. 飞机本体动态特性计算分析1.1飞机本体模型数据本文选取F16飞机进行动态特性分析及控制器设计,飞机的纵向状态方程形式如下:.x =Ax +Bu y =Cx (1.1)状态变量为:[]Tu q αθ=x控制变量为:e δ=u基准状态选择为120,2000V m s H m ==的定直平飞。
选取状态向量()Tu q αθ=x ,控制量为升降舵偏角,则在此基准状态下线化全量方程所得到的矩阵数据如下:-0.0312 -1.1095 -9.8066 -0.5083-0.0013 -0.6543 0 0.9185 0 0 0 1.00000 -0.3828 0 -0.6901⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦Α (1.2)[]-0.0167-0.0014-0.0956T=B(1.3)[]1.000057.295857.295857.2958diag =C(1.4)1.2模态分析矩阵A 的特征值算出为:1,23,4-0.6778 + 0.5926i-0.0100 + 0.0769iλλ==对应的特征向量如下:0.9874 0.9874 -1.0000 -1.0000 0.1137 - 0.0053i 0.1137 + 0.0053i 0.0011 - 0.0000i 0.0011 + 0.0000i 0.0521 - 0.0629i 0.0521 + 0.0629i 0.002=V 1 + 0.0078i 0.0021 - 0.0078i 0.0019 + 0.0735i 0.0019 - 0.0735i -0.0006 + 0.0001i -0.0006 - 0.0001i ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦由系统特征值可知,系统具有两对共轭复根,也即具有两种运动模态:长周期模态与短周期模态,其对应的模态频率及阻尼比如下:表一 飞机长短周期模态特征可以看出,在此飞行状态下,飞机纵向具有明显的长周期模态,但不具备明显的短周期的模态特征,模态频率过低,需要使用纵向增稳系统,改善阻尼比和自然频率。
飞行动力学作业题

1. 平衡曲线 根据~e L C δ曲线说明为什么静稳定的飞机符合操纵习惯,静不稳定的飞机不符合操纵习惯
2. 平衡曲线 根据~e V δ曲线说明为什么静稳定的飞机符合操纵习惯,静不稳定的飞机不符合操纵习惯
3. 为什么L C =0时,m C ≠0?
4. 详细说明要增加飞机迎角飞行员如何操作,飞机的舵面如何变化,气动力与力矩如何变化
5. 什么是定载静稳定性导数,应如何设计风洞试验来获得定载静稳定性导数?画出定载时的~m L C C 关系曲线。
6. 根据图1-10分析勺形区域下降段为什么会出现自动俯冲和反操纵。
7. 试分析为什么在起飞着陆时要对重心前限进行限制,还有哪些因素限制了重心的前限,为什么?
8. 分析真实的飞机从定常直线平飞转入拉升运动并完整一个完整筋斗的完整过程中飞机迎角和驾驶杆位移的变化情况。
9. 分析正常情况下重心与焦点、握杆机动点之间的关系。
如果重心不满足正常的与焦点、握杆机动点的位置关系会有什么后果。
10 课本P43作业题第一道。
航空飞行器飞行动力学答案

航空飞行器飞行动力学答案航空飞行器飞行动力学答案【篇一:尔雅航空与航天考试答案】class=txt>a、脱壳而出b、气垫着陆c、乘伞而降d、网捕而归正确答案:d 我的答案:d2第一颗人造卫星发射于()。
1.0 分a、1957年8月4日b、1958年8月4日c、1957年10月4日d、1958年10月4日正确答案:c 我的答案:c3鱼鹰属于()1.0 分a、歼击机b、无人机c、运输机d、轰炸机正确答案:c 我的答案:c4飞机低速飞行时的马赫数可能是()。
1.0 分a、5b、3c、0.3d、正确答案:c 我的答案:c5在飞机飞行速度约为每小时800-900公里时()。
1.0 分a、涡扇发动机油耗率高于涡轮发动机b、涡轮发动机油耗率高于涡扇发动机c、涡轮发动机和涡扇发动机油耗率基本相等d、涡轮发动机和涡扇发动机的油耗率波动较大正确答案:b 我的答案:b6脱离速度是()。
1.0 分a、第一宇宙速度b、第二宇宙速度c、第三宇宙速度d、第四宇宙速度正确答案:b 我的答案:b7飞机的外部部件连接的方式主要以()为主。
1.0 分a、拼接b、胶水c、焊接d、铆接正确答案:d 我的答案:d8关于采用无线遥控方式操作的无人机,下列说法错误的是()。
1.0 分a、飞机成本较高b、飞机灵活性较高c、受到距离限制d、存在电子干扰正确答案:a 我的答案:a9我国的高级教练机包括()。
0.0 分“运-8”b、c、“歼-10”d、“猎鹰”正确答案:d 我的答案:c10惯性导航平台能够精确给出的数据不包括()。
1.0 分a、速度b、姿态c、方位数据d、加速度正确答案:d 我的答案:d11飞机机身是通过()区分上下结构的。
1.0 分a、支柱横梁c、地板d、桁梁正确答案:c 我的答案:c12扰动源在静止空气中以亚音速做等速直线运动,那么m值0.0 分a、等于0b、大于0小于1c、等于1d、大于1正确答案:b 我的答案:a13旋翼系统由()构成。
飞行控制系统大作业

飞行控制系统大作业一、 飞机纵向俯仰角与速度控制系统设计 某飞机的纵向线性小扰动方程为: lon lon x A x B u =+其中 状态[]T x u q h αθ=∆∆∆∆∆,控制量[]T eT u δδ=∆∆问题:1、 分析飞机纵向动力学模态,求飞机的长周期与短周期阻尼与自然频率。
2、 对升降舵及油门单位阶跃输入下的飞机自然特性进行仿真,画出相应的状态曲线。
3、 采用短周期简化方法,求出传递函数()e qG s δ∆∆。
采用根轨迹方法设计飞机的俯仰角控制系统,并进行仿真。
4、 基于长周期简化方法,求出传递函数()T uG s δ∆∆,设计飞机的速度控制系统,并进行仿真。
5、 基于纵向线性模型(状态方程),分别对速度控制与俯仰角控制进行仿真。
假设作动器特性为1010s +。
要求:给出相应的传递函数,画出相应的结构图根轨迹图及仿真曲线。
二、 飞机侧向滚转角控制系统设计 某飞机的侧向线性小扰动方程为: lat lat x A x B u =+其中 状态[]T x p rβφψ=∆∆∆∆∆,控制量[]T ar u δδ=∆∆问题:1、 求出侧向运动方程的特征根,及对应的模态,求出荷兰滚模态的阻尼及自然频率。
2、 对副翼与方向舵单位阶跃输入下的自然特性进行仿真。
3、 采用简化方法,求出传递函数()a pG s δ∆∆。
采用根轨迹方法设计飞机的滚转角控制系统,并进行仿真。
4、 设计飞机航向控制系统,并进行仿真。
5、设计飞机方向舵协调控制律,基于侧向线性模型(状态方程),进行航向控制系统的仿真。
假设作动器特性为1010s +。
要求:给出相应的传递函数,画出相应的结构图根轨迹图及仿真曲线,提交word 打印稿。
1. 数据文件在文件中,按照学号的最后一位选择相应的数据文件。
如学号最后一位为5,则选择文件作为你设计的数据。
2. 在matlab 中 输入load data5 则可将数据导入, 其中 alon 为纵向系统阵,blon 为纵向控制输入阵alat 为侧向系统阵,blat 为侧向控制输入阵控制量的单位为deg ,状态变量的单位为(deg ,deg/s , m ) 3、由状态方程求传递函数用ss2tf ()函数。
飞行动力学作业

飞行动力学与控制课程总结姓名:学号:时间: 2015/6/30飞行动力学是一门综合多学科知识,飞行器总体设计和控制设计过程中必不可少的知识基础。
飞行动力学中弹道学部分建立了导弹飞行的六自由度数学模型和弹目相对运动方程即制导律,为总体设计中制导和控制部分提供了数学模型和导引方法。
动态分析部分则深入研究导弹在飞行过程中的动态特性,根据这些特性,导弹设计过程中可以合理安排气动布局,结构以及控制律的参数,分析导弹的稳定性、操纵性和机动性能。
导弹总体设计看中导弹的性能,包括飞行性能(射程、速度、高度、机动性)、制导精度、突防能力、可靠性、成本等等,下面我就飞行力学和动态分析在部位安排、气动布局、制导控制部分的应用作简要的分析。
一、 气动外形和结构布局影响1. 导弹的稳定性首先考虑导弹的稳定性,在导弹运动过程中,受到外力扰动是指偏离原来的飞行状态。
干扰消失的最初状态,若导弹具有恢复到原来飞行状态的趋势,称为具有静稳定性;干扰消失后导弹运动恢复到原来状态,则具有动稳定性。
导弹的静稳定性对导弹部位安排与气动布局有指导作用。
首先纵向静稳定性指标为 0<-=A F g y z b X X C m αα(1)若使导弹具有纵向静稳定性,焦点必须在重心的后面,改变方案有两种:➢ 改变导弹气动布局,从而改变焦点的位置,如改变弹翼的外形、面积以及相对弹身的安装位置,改变尾翼面积,添置小前翼等。
➢ 改变导弹内部器件的部位安排,以调整重心的位置。
考虑到导弹横向静稳定性,横向静稳定性条件为0<βxm ,弹翼(弹翼后掠角和上反角)和垂直尾翼对其影响最大。
➢ 弹翼后掠角χ: 当受到干扰使导弹有一个正的侧滑角0>β,在左侧弹翼实际后掠角变为βχ+,垂直于弹翼前缘的速度减小,升力减小;右侧变为βχ-,垂直于弹翼前缘的速度增加,升力增加;这样就产生了负的滚转力矩,即0<βx m 。
(气动布局的设计,尤其是弹翼翼型的选取)➢ 上反角w ψ: 当受干扰使导弹有一个正的侧滑角0>β,当弹翼有个正上反角0>w ψ时,右侧弹翼有个正的攻角增量0>∆α,相应的右翼上升力增加,相反左侧弹翼有个负的攻角增量0<∆α,左侧升力减小。
航空航天工程师的飞行器动力学和控制

航空航天工程师的飞行器动力学和控制航空航天工程师扮演着推动现代航空航天技术发展的重要角色。
他们的工作范围涉及到飞行器动力学和控制领域,旨在研究和设计高效、稳定、安全的航空航天系统。
本文将探讨航空航天工程师在飞行器动力学和控制方面的工作内容和挑战。
一、动力学的研究与应用动力学是研究运动及其变化的学科,对于飞行器来说,动力学研究是基于牛顿力学的力的平衡和运动定律去分析和计算飞行器的运动状态。
航空航天工程师需要获取飞行器的运动数据,并基于这些数据进行分析,以确保飞行器在瞬息万变的环境中能安全、高效地运行。
在动力学的研究中,航空航天工程师需要掌握与飞行器运动相关的知识,如质量、力、加速度、速度和位移等。
他们还需要了解飞行器在不同空气动力环境中的性能表现,以及如何优化飞行器以提高其运动性能。
二、控制系统的设计与优化航空航天工程师还需要进行飞行器控制系统的设计与优化工作。
控制系统是为了使飞行器能够按照特定的轨迹和条件进行稳定、安全地运行。
航空航天工程师在设计控制系统时需要考虑飞行器的属性,如质心位置、惯性矩阵、气动参数等。
为了设计出高效且稳定的控制系统,航空航天工程师需要运用现代控制理论和方法,如PID控制器、状态空间方法等。
他们还需要运用数学建模和仿真软件来评估控制系统的性能,以使飞行器具有良好的稳定性和操纵性。
三、飞行器动力学与控制的挑战航空航天工程师在飞行器动力学和控制领域面临着许多挑战。
首先,不同类型的飞行器,如飞机、直升机、火箭等,其动力学特性和控制要求都有所不同,要求工程师有针对性地进行研究和设计。
其次,飞行器的非线性特性和不确定性因素,如外部气动因素、动力系统失效等,给飞行器的动力学和控制带来了很大的复杂性。
航空航天工程师需要运用先进的控制理论和方法,以应对这些复杂性,并确保飞行器的安全运行。
最后,随着航空航天技术的不断发展,新的飞行器设计和控制技术不断涌现,这也对航空航天工程师的专业知识和技能提出了更高的要求。
飞行器的动力学与控制分析

飞行器的动力学与控制分析随着科技的不断发展和进步,飞行器已经成为了人们生活中不可或缺的一部分。
在现代化的军用和民用交通领域,飞行器已经成为了必备的交通工具。
掌握飞行器的动力学与控制分析,可以更好地了解飞行器的运动规律,掌握其稳定性和可控性,并且能够更好地理解飞行器所运用的各种技术。
一、飞行器的动力学飞行器的运动可以分为三个方向:平面运动、垂直运动和自旋。
平面运动是指飞行器在平面内进行的运动,主要包括飞行器的升降、俯仰和滚转三个方向。
垂直运动是指飞行器在三维空间中进行的上升和下降、盘旋和飞行的运动。
自旋是指飞行器绕其自身中心轴线旋转的运动。
在这三个方向中,最复杂的是垂直运动。
因为这种运动不仅需要考虑重力的影响,还需要考虑空气阻力和方向稳定性等因素。
所以,在掌握飞行器的运动规律时,我们需要对各个运动方向下的动力学进行更深入地了解和掌握。
二、飞行器的控制分析飞行器的控制分析是指对飞行器进行控制的方法和技术进行分析研究。
对于现代飞行器而言,控制系统可以分为两类:自动控制系统和手动控制系统。
自动控制系统是指在机载电脑的控制下,飞行器可以自主进行一系列的操作和控制,具有稳定性和准确性的特点。
例如,自动驾驶系统可以在飞行过程中根据预设航路的要求自动地控制飞行器的运动和方向。
而手动控制系统则是由飞行员通过手动操作控制飞行器,更具有操作性和灵活性的特点。
对于飞行器的控制分析,关键的方法是设计和实现控制算法和控制策略。
掌握好这些技术,可以使飞行器更好的进行运动和变化。
三、飞行器的稳定性分析飞行器的稳定性是指在不受外界干扰的情况下,飞行器系统自身能够保持所需状态的性质。
对于飞行器而言,稳定性是其最为基本的特性之一。
在稳定性分析中,人们主要关注的是飞行器的回转半径和飞行速度的变化,以及在不同飞行条件下的姿态调节。
四、飞行器机载控制系统的主要构成飞行器的控制系统主要由一些传感器、执行机构和控制器几部分构成。
传感器通常用于检测飞行器的姿态、速度、高度和其它各种参数,而执行机构则用于控制飞行器在空中进行各种姿态调节和变化。
航空航天工程师的飞行器动力学和控制

航空航天工程师的飞行器动力学和控制航空航天工程师在航空航天领域发挥着重要的作用,其中飞行器动力学和控制是他们的核心职责。
本文将讨论航空航天工程师在飞行器动力学和控制方面的工作内容以及所面临的挑战。
一、飞行器动力学飞行器动力学研究的是飞行器的运动规律和力学特性。
航空航天工程师在飞行器动力学中扮演着重要的角色,他们负责设计和分析飞行器的动力系统,确保其安全而高效的运行。
在飞行器动力学方面,航空航天工程师需要了解飞行器的气动特性,包括升力、阻力和侧向力等。
他们还需要研究飞行器的动力装置,包括发动机、推力和燃料系统等。
通过分析和计算这些因素,航空航天工程师可以确定飞行器的性能参数,如速度、加速度和续航能力。
除了设计和分析,航空航天工程师还需要进行飞行试验和性能评估。
他们会利用模拟器和飞行器试验平台进行实验研究,验证设计的有效性和准确性。
通过这些试验,航空航天工程师可以获取真实飞行器的数据,并对其进行进一步分析和优化。
二、飞行器控制飞行器控制是航空航天工程师的另一个关键工作领域。
在飞行器控制中,航空航天工程师致力于实现对飞行器运动的精确控制和稳定。
他们负责设计和实施飞行器的自动控制系统,以确保飞行器在各种条件下的安全飞行。
在飞行器控制方面,航空航天工程师需要了解控制系统的原理和方法,包括传感器、执行器和控制算法等。
他们会利用数学模型和控制理论来分析和设计飞行器的控制系统,使其能够对飞行器的姿态、位置和速度等进行精确控制。
航空航天工程师还需要进行飞行器控制系统的调试和优化。
他们会利用模拟器和实际飞行器进行试验,对控制系统进行测试和验证。
通过实验数据的分析和反馈,航空航天工程师可以对控制系统进行调整和改进,以提高飞行器的控制性能。
三、挑战和前景在飞行器动力学和控制方面,航空航天工程师面临着许多挑战。
首先,飞行器的复杂性和多变性使得对其动力学和控制的研究变得更加困难。
其次,航空航天工程师需要不断更新自己的知识和技术,以适应新技术和新材料的发展。
航空航天工程师的飞行器动力学和控制

航空航天工程师的飞行器动力学和控制航空航天工程师是一项充满挑战性和魅力的职业,他们负责设计、开发和改进各种类型的飞行器。
在这个岗位上,飞行器动力学和控制是必不可少的知识领域。
本文将介绍航空航天工程师在飞行器动力学和控制方面的工作内容和技术要求。
一、飞行器动力学飞行器动力学是研究飞行器在空气中运动规律的科学,主要包括力学、空气动力学和运动学三个方面。
作为航空航天工程师,对于飞行器的动力学性能有着深入的理解是必不可少的。
首先,航空航天工程师需要掌握力学的基本原理,包括牛顿定律和质心力学等。
这些原理将帮助工程师了解飞行器在加速、转弯和停止过程中所受到的力和力矩。
其次,空气动力学是飞行器动力学的核心内容。
航空航天工程师需要了解空气动力学的基本原理,包括空气动力学力学和气动力学的相关知识。
他们需要通过数值模拟、实验测试和经验公式等方法来研究飞行器在不同飞行状态下的气动特性,以便优化设计并提高飞行性能。
最后,运动学是研究飞行器运动轨迹和姿态的学科。
航空航天工程师需要掌握运动学的基本概念,如欧拉角、姿态稳定性和航线规划等。
这些知识将帮助工程师设计飞行器的姿态控制系统和飞行计划。
二、飞行器控制飞行器控制是确保飞行器安全、稳定和精确操控的关键技术。
航空航天工程师需要在飞行器动力学的基础上,熟悉各种控制理论和方法,并将其应用于飞行器控制系统的设计和优化。
首先,航空航天工程师需要了解传统控制理论,如PID控制和根轨迹法。
这些理论为设计主动控制系统提供了基础,可以使飞行器自动地控制其姿态、速度和航向等。
其次,现代控制理论也是飞行器控制的重要组成部分。
航空航天工程师需要熟悉状态空间表示法、H∞控制和模糊控制等。
这些理论可以提高控制系统的性能和鲁棒性,以应对飞行器在不同飞行环境下的扰动和不确定性。
最后,航空航天工程师还需要掌握飞行器导航和制导技术。
导航是确定飞行器位置和航向的过程,而制导则是根据导航信息指导飞行器的飞行路径。
飞行控制系统大作业模板

飞行控制系统大作业一、飞机纵向俯仰角与速度控制系统设计 某飞机的纵向线性小扰动方程为: lon lon x A x B u =+其中 状态[]T x u q h αθ=∆∆∆∆∆,控制量[]T e T u δδ=∆∆ 问题:1、分析飞机纵向动力学模态,求飞机的长周期与短周期阻尼与自然频率。
输入指令:damp(alon),即可得到结果:长周期的两个根为:-8.36e-003 + 4.90e-002i ,-8.36e-003 - 4.90e-002i 阻尼为1.68e-001角频率为4.97e-002(rad/s)短周期的两个根为:-1.97e+000 + 3.21e+000i ,-1.97e+000 - 3.21e+000i 阻尼为5.24e-001角频率为3.77e+000 (rad/s)2、对升降舵及油门单位阶跃输入下的飞机自然特性进行仿真,画出相应的状态曲线。
输入如下代码,分三次进行输出: sys=ss(alon,blon,clon,dlon) [y,t]=step(sys,500) 第一次输出 subplot(221) plot(t,y(:,1,1)) xlabel('t(s)') ylabel('\Deltau(m/s)') subplot(222) plot(t,y(:,1,2)) xlabel('t(s)') ylabel('\Deltau(m/s)') subplot(223) plot(t,y(:,2,1)) xlabel('t(s)') ylabel('\Delta\alpha(deg)') subplot(224) plot(t,y(:,2,2)) xlabel('t(s)') ylabel('\Delta\alpha(deg)') 第二次输出 subplot(221) plot(t,y(:,3,1)) xlabel('t(s)') ylabel('\Deltaq(deg/s)') subplot(222) plot(t,y(:,3,2)) xlabel('t(s)') ylabel('\Deltaq(deg/s)') subplot(223) plot(t,y(:,4,1)) xlabel('t(s)') ylabel('\Delta\theta(deg)') subplot(224) plot(t,y(:,4,2)) xlabel('t(s)') ylabel('\Delta\theta(deg)') 第三次输出 subplot(121) plot(t,y(:,5,1)) xlabel('t(s)') ylabel('\Deltah(m)') subplot(122) plot(t,y(:,5,2)) xlabel('t(s)') ylabel('\Deltah(m)')输出曲线中左侧为 加入阶跃信号产生的输出,右侧为 加入阶跃信号。
飞行控制原理大作业

综合设计1:针对所给出的飞机纵向简化运动模型,设计纵向增稳控制系统,给出系统原理结构,并对增加控制系统前后的纵向品质特性进行对比分析,并通过仿真验证阶跃和脉冲操纵输入响应。
1纵向方程[∆V ∆α̇∆θq̇][−0.020244−0.8761−2.5373E −4−1.0189−0.32169−0.650200.90484007.9472E −11−2.4982010−1.3861][∆V ∆α∆θq ]+[0 1.22−4.132060−0.14325000][δe δT]2纵向模态分析 2.1 飞行品质要求根据品质规范GJB 185-86 有人驾驶飞机(固定翼)飞行品质的要求:根据飞行品质要求对短周期的指标进行限定,要求如表2.2:表2.1 长短周期模态参数范围表2.1 纵向特征值由特征值可以看到,不论是短周期还是长周期,都是具有负实部的特征根,因而短周期和长周期都是稳定收敛的,并且满足前述飞行品质要求。
2.3 稳定性分析根据所得到的4个具有负实部的特征值知,该系统为稳定的。
现根据系统根轨迹来判断其稳定性。
以速度—升降舵传递函数为例:上图为其开环传递函数根轨迹图。
由图可以看出,所有四个极点均位于纵轴的左侧区域,说明该系统确实稳定。
2.3系统原理结构图图示为方向舵变化脉冲输入、油门变化零输入时的仿真系统结构。
3仿真验证3.1升降舵阶跃响应曲线状态及输出量相对于升降舵通道的阶跃宽度为1s,幅值1∘的响应曲线如下。
从图中可以看出在阶跃信号作用下,各输出变量一开始均有一个阶跃值,随着时间的增加,各个输出量逐渐趋于稳定状态。
飞机纵向运动短周期和长周期均是稳定的。
3.2升降舵脉冲响应曲线状态及输出量相对于升降舵通道的脉冲宽度为1s,幅值1的响应曲线如下。
综合设计2:利用上述运动模型,设计自动导航控制系统,实现下列自动飞行过程:自高度3000m,速度600km/h开始,以不小于-10deg的航迹俯仰角俯冲增速,在500m高度拉起并完成1个筋斗,之后恢复3000m高度、600km/h速度的飞行状态,控制策略自行设计。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
飞行动力学与控制大作业报告院(系)航空科学与工程学院专业名称飞行器设计学号学生姓名目录一.飞机本体动态特性计算分析.............. 错误!未定义书签。
飞机本体模型数据...................... 错误!未定义书签。
模态分析.............................. 错误!未定义书签。
传递函数.............................. 错误!未定义书签。
升降舵阶跃输入响应.................... 错误!未定义书签。
频率特性分析.......................... 错误!未定义书签。
短周期飞行品质分析.................... 错误!未定义书签。
二.改善飞行品质的控制器设计.............. 错误!未定义书签。
SAS控制率设计........................ 错误!未定义书签。
控制器参数选择........................ 错误!未定义书签。
数值仿真验证.......................... 错误!未定义书签。
CAS控制率设计........................ 错误!未定义书签。
三.基于现代控制理论的飞行控制设计方法.... 错误!未定义书签。
特征结构配置问题描述.................. 错误!未定义书签。
特征结构的可配置性.................... 错误!未定义书签。
系统模型.............................. 错误!未定义书签。
系统的特征结构配置设计................ 错误!未定义书签。
设计过程.............................. 错误!未定义书签。
具体的设计数据........................ 错误!未定义书签。
结果与分析............................ 错误!未定义书签。
四.附录.................................. 错误!未定义书签。
一. 飞机本体动态特性计算分析1.1飞机本体模型数据本文选取F16飞机进行动态特性分析及控制器设计,飞机的纵向状态方程形式如下:.x =Ax +Bu y =Cx(1.1)状态变量为:[]Tu q αθ=x控制变量为:e δ=u基准状态选择为120,2000V m s H m ==的定直平飞。
选取状态向量()Tu q αθ=x ,控制量为升降舵偏角,则在此基准状态下线化全量方程所得到的矩阵数据如下:-0.0312 -1.1095 -9.8066 -0.5083-0.0013 -0.6543 0 0.9185 0 0 0 1.00000 -0.3828 0 -0.6901⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦Α (1.2)[]-0.0167-0.0014-0.0956T=B(1.3)[]1.000057.295857.295857.2958diag =C(1.4)1.2模态分析矩阵A 的特征值算出为:1,23,4-0.6778 + 0.5926i-0.0100 + 0.0769iλλ==对应的特征向量如下:0.9874 0.9874 -1.0000 -1.0000 0.1137 - 0.0053i 0.1137 + 0.0053i 0.0011 - 0.0000i 0.0011 + 0.0000i 0.0521 - 0.0629i 0.0521 + 0.0629i 0.002=V 1 + 0.0078i 0.0021 - 0.0078i 0.0019 + 0.0735i 0.0019 - 0.0735i -0.0006 + 0.0001i -0.0006 - 0.0001i ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦由系统特征值可知,系统具有两对共轭复根,也即具有两种运动模态:长周期模态与短周期模态,其对应的模态频率及阻尼比如下:表一 飞机长短周期模态特征可以看出,在此飞行状态下,飞机纵向具有明显的长周期模态,但不具备明显的短周期的模态特征,模态频率过低,需要使用纵向增稳系统,改善阻尼比和自然频率。
1.3传递函数飞机迎角与俯仰角速度对应于升降舵输入下的传递函数如下:()324320.08021 5.0880.16150.069831.3760.84360.024320.00488s s s s s s s G s α----++=++ (1.5)()324325.477 3.7240.10349.5360161.3760.84360.024320.00488q G s s s s e s s s s ----++=-++(1.6)1.4 升降舵阶跃输入响应由上述传递函数可得迎角与俯仰角速度在升降舵单位阶跃输入下的响应分别如下:图1 升降舵单位阶跃输入迎角时域响应上面阶跃响应的性能指标为:稳态值为- ,调节时间为,超调量是%,上升时间是。
图2 升降舵单位阶跃输入俯仰角速度时域响应上面阶跃响应的性能指标为:稳态值为0,调节时间为,超调量是0,上升时间是。
1.5频率特性分析迎角与俯仰角速度对应的传递函数的Bode图如下:图3 迎角对升降舵响应传递函数Bode图图4 俯仰角速度对升降舵响应传递函数Bode图1.6短周期飞行品质分析飞机在当前状态下不具备短周期模态特征,短周期模态响应过大且频率过低,操纵特性不符合飞行品质的要求,因此需要添加SAS控制器来改善短周期模态阻尼,提高短周期模态频率,使操纵品质满足要求。
二.改善飞行品质的控制器设计2.1SAS控制率设计增稳装置是在阻尼器的基础上发展而来的。
阻尼器的作用主要是增加飞机的俯仰阻尼,从而在一定程度上改善了飞机的短周期反应特性,但它不能改变飞机的纵向静稳定性,这时不能仅仅依靠阻尼器,必须借助于纵向增稳系统(SAS)。
纵向增稳装置除了俯仰角速度反馈回路之外,还有对迎角或法向过载的反馈回路,因而不仅能增加飞机俯仰阻尼,而且还能增加飞机的纵向静稳定性,提高飞机的短周期振荡频率,可以在更广阔的飞行范围内改善飞机的飞行品质。
下图为纵向增稳装置的工作原理图。
其中迎角变化是通过迎角传感器感受,其信号输入经放大器放大后,再经舵机及助力器,推动舵面朝着减小迎角变化的方向偏转。
图5 纵向增稳系统原理框图在本文中,对上述结构图做出如下简化:图6 纵向增稳系统简化图2.1.1 控制器参数选择在图6中,暂时忽略滤波器的作用,可得如下控制方程:e q K q K αδα∆=+(2.1)附加的气动导数增量为:,q q e e M K M M K M δααδ∆=∆=(2.2)从力学观点出发,通过迎角反馈,飞机的静稳定性增加,通过俯仰角速度反馈,飞机的俯仰阻尼增加,从而可以改变飞机短周期的运动模态。
为了使控制器设计更具实用价值,将迎角传感器与助力器的动力学特性分别表示为带宽10/rad s 和20.2/rad s 的一阶惯性环节,即:()1010G s s α=+,()20.220.2G s s δ=+ 首先考虑只有迎角反馈时的情况,即在原理图中k α≠0,k q =0。
取系统动态方程的状态变量为:[]T e f x u p αθδα=,则系统的动态方程如下:00000000000020.2020.2010000100e e f v A B x u q αθδα⋅⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥-⎢⎥⎣⎦⎣⎦⎣⎦(2.3)057.296000000057.296000000057.296y x ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦(2.4)迎角反馈回路的开环传递函数如下:()22216.2033(63.39)(0.031530.01373)(20.2)(10)(0.019930.00602)( 1.3560.8106)f s s s s s s s s G s s α++++++++=+ (2.5) 迎角反馈回路闭环后的根轨迹如下图所示:图7 迎角反馈回路的根轨迹由于相较于助力器与迎角传感器,短周期模态对应的极点较小,因此将短周期极点局部放大,局部放大后的根轨迹图如下:图8 迎角反馈回路的根轨迹局部放大图由图7可见,迎角传感器和助力器极点在左半平面离原点很远处,对其他模态影响较小。
由图8可见,迎角反馈使短周期模态的频率逐渐增加但是阻尼比逐渐降低,其中,频率的增加为主要变化。
对短周期的影响基本可以忽略。
因此,可以通过选取适当的反馈增益使短周期的模态频率达到理想的值。
选取 1.62k α=,此时,短周期的频率为s ,阻尼比为,因此,当前的短周期阻尼比偏低,需要引入俯仰角速度反馈增加短周期模态的阻尼比。
当 1.62k α=时,以反馈迎角后的系统作为新的被控对象,此时俯仰角速度反馈回路的开环传递函数如下:()22(19.89)(11.35)(0.029440.01307)(0.30888.078 110.6455 s (s+10) (s+0.6509) (s+0.02901))fq s s s s s s G s ++++++=(2.6)从开环传递函数中可知迎角反馈对助力器与迎角传感器的极点几乎没有影响,在俯仰角反馈时也有相同的结论,此时,俯仰角速度反馈回路闭环后的根轨迹如下所示:图9 俯仰角速度反馈回路的根轨迹图10俯仰角速度反馈回路的根轨迹局部放大图由上图可知,当选取0.824q k =时,短周期模态具有最佳阻尼比,此时模态频率为s 。
可见,在 1.62k α=,0.824q k =时,短周期模态得到了很大的改善,具有良好的阻尼比和自然频率,满足良好的操纵性能要求。
采用SAS 控制器后,长短周期模态的特征值,自然频率及阻尼比如下:表二 采用SAS 控制器后飞行器长短周期模态特性通过上述分析可以看出,迎角反馈增益主要影响短周期模态的自然频率,俯仰角速度反馈增益主要影响短周期的阻尼比。
选取适合的迎角反馈增益和俯仰角速度反馈增益进行组合,可以得到满意的自然频率和阻尼比,进而在很大程度上改善飞机的纵向短周期模态特征。
2.1.2 数值仿真验证当上述SAS 控制器参数选为 1.62k α=,0.824q k =时,迎角与俯仰角速度对升降舵单位阶跃输入的响应如下所示:图11改善纵向稳定性后α的阶跃响应上面阶跃响应的性能指标为:稳态值为,调节时间为,超调量是%,上升时间是。
图12改善纵向稳定性后q 的阶跃响应上面阶跃响应的性能指标为:稳态值为0,调节时间为,超调量是0,上升时间是。
由图可以看出,对飞机本体进行SAS 控制律设计后,短周期模态得到了很好的改善,受到扰动后的震荡能够迅速收敛且响应适中,飞行品质较好。
