一、常量
VF教案第2章第1节

第二章 Visual Foxpro 程序设计基础
格式 1:SCATTER [F1ELDS<字段名表>] [MEMO] TO <数组名>? [BLANK] 功能:复制表的当前记录的指定字段到数组元素,若不指定字段 ,则复制除备注型 M 和通用型 G 之外的全 部字段。 格式 2:SCATTER [F1ELDS LIKE<通配符>|FIELDS EXCEPT<通配符>][MEMO]TO<数组名>[BLANK] 功能:复制用通配符指定包括或排除的字段 ②将数组数据复制到表的当前记录。 格式 1:GATHER FROM <数组名>[FIELDS <字段名表>][MEMO] 功能:将数组中的数据作为一个记录复制到表的当前记录中,若数组元素个数多于记录中字段的个数,则 多余部分被忽略。 格式 2:GATHER FROM <数组名>[FIELDS LIKE<通配符>|FIELDS EXCEPT<通配符>][MEMO] 功能:复制用通配符指定包括或排除的字段
4
酒泉职业技术学院 VF 教案
说明:①选用 LIKE 只显示与通配符相匹配的内存变量。 ②[TO PRINTER]显示的同时送往打印机; [TO FILE] 存入给定文件名的文本文件.TXT 中。 ③ LIST 滚动显示,DISP 分页显示 4.内存变量的清除 格式 1:CLEAR MEMORY 格式 2:RELEASE<内存变量名表> 格式 3:RELEASE ALL [EXTENDED] 格式 4:RELEASE ALL [LIKE<通配符>|EXCEPT<通配符>] 5.表中数据与数组数据之间的交换 ①将表的当前记录复制到数组
高等数学 第一章

数列中的每一个数称为数列的项,第 n 项 xn 称 为数列的一般项或通项.
(一)数列极限的概念
定义 2 对于数列 {xn} ,当 n 无限增大时,如果数列的一般项 xn 无限地接近于某一确定的数
值
a,则称常数
a
是数列 {xn} 的极限,或称数列 {xn} 收敛,其收敛于
(二)指数函数
y ax (a 0 ,a 1) 为指数函数,它的定义域为 ( , ) ,值域为 (0 , ) .当 a 1 时,y ax 单调增加;当 0 a 1 时, y ax 单调减少.指数函数的图形都经过点 (0 ,1) ,且均在 x 轴上方。
(三)对数函数
y loga x (a 0 ,a 1) 为对数函数,它是指数函数 y ax 的反函数,其定义域为 (0 , ) ,值 域为 ( , ) .当 a 1 时, y loga x 单调增加;当 0 a 1 时, y loga x 单调减少.对数函数 的图形都经过点 (1,0) ,且均在 y 轴的右方.
其中,D 称为函数的定义域,x 称为自变量,y 称为因变量.
(三)函数的定义
当 x 取定义域 D 内的某一定值 x0 时,按照对应法则 f ,所得的对应值 y0 称为函数 y f (x) 在
x0 处的函数值,记作
y0
y x x0
f (x0 ) ,
当 x 取遍定义域 D 中的所有数值时,按照对应法则 f ,所得的所有对应值 y 构成的集合称为函 数的值域,记作 M {y | y f (x) ,x D}.
则称函数 f (x) 在区间 I 上是单调增加的,区间 I 称为单调增区间;如果对于区间 I 内的任意两 点 x1 ,x2 ,当 x1 x2 时,恒有 f (x1) f (x2 ) ,
数字电路第一章
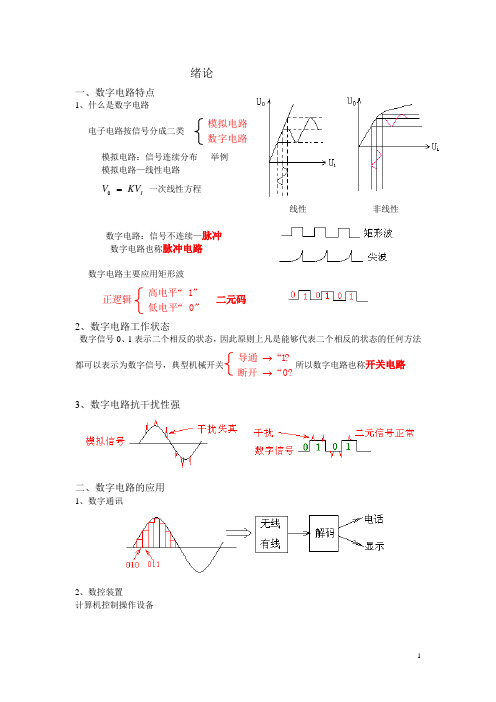
绪论一、数字电路特点1、什么是数字电路电子电路按信号分成二类模拟电路数字电路模拟电路:信号连续分布 举例模拟电路—线性电路 0IV K V = 一次线性方程 线性 非线性数字电路:信号不连续—脉冲数字电路也称脉冲电路数字电路主要应用矩形波正逻辑高电平 1低电平 0“”“”二元码2、数字电路工作状态数字信号0、1表示二个相反的状态,因此原则上凡是能够代表二个相反的状态的任何方法都可以表示为数字信号,典型机械开关 导通“1 断开“0→→所以数字电路也称开关电路3、数字电路抗干扰性强二、数字电路的应用1、数字通讯2、数控装置 计算机控制操作设备3、数字计算机(最广泛、最杰出的应用)算盘1857年,Hill计数器1890年人口普查使用的制表机第二代1951年,IBM开始决定开发商用电脑,聘请冯·诺依曼担任公司的科学顾问,1952年12月研制出IBM第一台存储程序计算机,也是通常意义上的电脑,这是IT历史上一个重要的里程碑。
它叫IBM 701。
第一代1946年启动“埃尼阿克”(ENIAC)计算机1958年8月16日第一个集成电路第三代1964年4月7日,IBM主席Tom Watson,System 360。
Jr.亲自发布System 360。
超级计算机IBM蓝色基因落户德日计算相当于1.5万台PC( 2006年)第一章逻辑代数基础前面二进制数表示方法不讲,其它学科介绍,本书不用这些概念。
二进制逢二进一1101,110 ++右面给出常用的四位二进制逐一递增的8.4.2.1码。
§1.1 基本概念公式和定理1.1.1 基本和常用逻辑运算一、三种基本逻辑运算1、 与逻辑(与运算、逻辑乘)与逻辑—全部条件具备,事件发生。
下图用机械开关来表示与逻辑运算。
功能表开、关,亮、灭是一个二元状态,可以用0、1码表示 ②真值表 ①赋值合,亮断10,灭→→③与逻辑式 YA B =⋅④逻辑图(符号)多端输入(多个开关) Y ABC =上述逻辑运算的器件称“门” 对应与逻辑称“与门”2、 或逻辑(逻辑加)或逻辑— 一个或一个以上条件具备,事件发生。
浙教版数学八年级上册《5.1常量与变量》说课稿1

浙教版数学八年级上册《5.1 常量与变量》说课稿1一. 教材分析浙教版数学八年级上册《5.1 常量与变量》这一节主要介绍常量和变量的概念。
教材通过生活中的实例,让学生感受常量和变量的存在,进而引导学生探究常量和变量的数学定义。
本节课的内容是学生学习函数的基础,对于学生理解函数的实质,以及后续学习一次函数、二次函数等函数知识具有重要意义。
二. 学情分析八年级的学生已经掌握了实数、代数式等基础知识,对于生活中的变化和规律有一定的认识。
但是,对于数学中的常量和变量概念,学生可能还比较陌生。
因此,在教学过程中,我将以生活中的实例为导入,引导学生感受常量和变量的存在,再逐步引入数学定义,帮助学生理解和掌握常量和变量的概念。
三. 说教学目标1.知识与技能目标:让学生理解常量和变量的概念,能够正确地识别常量和变量。
2.过程与方法目标:通过生活中的实例,培养学生从实际问题中抽象出常量和变量的能力。
3.情感态度与价值观目标:激发学生学习数学的兴趣,培养学生的数学思维。
四. 说教学重难点1.教学重点:让学生理解常量和变量的概念,能够正确地识别常量和变量。
2.教学难点:如何引导学生从实际问题中抽象出常量和变量的概念。
五. 说教学方法与手段1.教学方法:采用情境教学法、问题教学法和小组合作学习法。
2.教学手段:利用多媒体课件、实物模型等辅助教学。
六. 说教学过程1.导入:通过展示生活中的一些实例,如气温变化、商品价格变动等,让学生感受常量和变量的存在。
2.新课导入:引导学生从实例中抽象出常量和变量的概念,给出常量和变量的数学定义。
3.实例分析:通过一系列的实例,让学生进一步理解和掌握常量和变量的概念。
4.练习巩固:让学生进行一些相关的练习题,巩固所学知识。
5.课堂小结:对本节课的内容进行总结,引导学生理解常量和变量在数学中的重要性。
七. 说板书设计板书设计如下:常量:数值不变的量变量:数值可变的量八. 说教学评价教学评价主要通过学生的课堂表现、作业完成情况和课后反馈来进行。
《高等数学》 第一章(上)

25
1 005
5
超过 35 000 元至 55 000 元的部分
30
2 755
6
超过 55 000 元至 80 000 元的部分
35
5 505
7
超过 80 000 元的部分
45
13 505
第一节 函数的概念
个人所得税=(工资-五险一金-个税起征点)×税率-速算扣除数,用分段函 数可表示为
3%x ,
y0 y |xx0 f (x0 ) .
函数 y f (x) 的定义域 D 是自变量 x 的取值范围,而函数值 y 又是由对应 法则 f 来确定的,所以函数实质上是由其定义域 D 和对应法则 f 所确定的.通 常称函数的定义域 D 和对应法则 f 为函数的两要素.只要函数的定义域相同, 对应法则也相同,它们就是相同的函数,而与变量用什么字母或符号表示无关.
第一节 函数的概念
三、函数的概念
函数的记号通常记作 y f (x) ,在后续内容或后续课程中可能有下列记号, 也表示函数.例如
y F(x),y g(x) ,y G(x) ,y (x) , s s(t),v v(t) ,a a(t) ,r r( ) .
又如,经济学中的成本函数就是表示企业总成本与产量之间关系的公式,它 分为短期成本函数和长期成本函数,其中,短期成本函数 C C(q) 可分为固定成 本 b 与可变成本 f (q) ,即 C b f (q) .经济学中除了成本函数外,还有收入函 数 R R(q) 和利润函数 L L(q) ,其中, L R C ,这里 q 表示产品的数量.
y f (x) ,x D . 其中,变量 x 称为自变量,变量 y 称为因变量,集合 D 称为函数的定义域, f 称为函数的对应法则.
VFP常量与变量

一. 常量:在程序运行过程中保持不变的量称为常量。
vfp中,共有5种类型的常量:数值型常量,字符型常量,逻辑型常量,日期型常量和日期时间型常量。
1.数值型常量:数值型常量可以是整数或实数,例如:56,69.8等都是数值型常量。
字符型常量:字符型常量是用定界符括起来的由字符、空格和数字所组成的字符串。
定界符可以是单引号、双引号和方括号。
当某一种定界符本身是字符型常量的组成部分时,就应选用另一种定界符。
例如:“abcd”,…教授‟,[王明]都是正确写法的字符型常量。
逻辑型常量:逻辑型常量只有2个值:“真”与“假”。
用.T.,.t.,.Y.,.y.,表示“真”,用.F.,.f.,.N.,.n.,表示“假”。
注意:两边的点不可去掉但可用空格代替。
日期型常量:日期型常量必须用花括号括起来,例如:{^95.01.12}、{^01/12/95}都是日期型常量的正确写法。
大括号中的“^”键盘符,是为了解决“千年虫”问题而加入的。
日期时间型常量:日期时间型常量也必须用花括号括起来,例如:{^2005/12/06 11:12: 32pm}、{2005.12.06 11:12:32pm}、{^2005-12-06 11:12:32pm}都是正确的日期时间型常量的写法。
注意:日期和时间数据间必须有空格。
二. 变量:在程序运行过程中还会发生变化的量称为变量。
vfp中,共有3种变量:字段变量、内存变量和系统内存变量。
前两种变量的名称由1~个字母、下划线和数字表示,且必须以字母打头;而系统内存变量由系统规定。
1. 字段变量:字段变量是表文件结构中的数据项,vfp中共有13种字段变量。
在本章第一节中已有叙述。
字段变量是一种多值变量,比如“职工档案”表中的“姓名”字段,对应第一条记录中的值是“张三”,对应第二条记录中的值是“李四”,表中有多少条记录,就对应有多少个值。
移动记录指针到所需记录,即可找出字段变量的当前值。
内存变量:内存变量是独立存在于内存中的变量,一般随程序结束或退出vfp而释放,也可在程序代码中使用命令释放内存变量。
高数1(函数)

关于坐标原点对称的。
例如 cos x 是偶函数,sin x 是奇函数,但
y = sin x + cos x 是既不是奇函数也不是偶函数。
y
y = f (x)
偶函数的图像是 关于y轴对称
f (-x)
f (x)
-x
o x 偶函数 y
x y = f (x) f (x)
(3)图像法:图像法是把变量之间的函数关系借助图 形表示出来的方法,它可形象地表示出函数变化的性态。 优点是鲜明直观,但不便于作理论分析。 如图1-1 表示温度T 与时间 t 的函数关系。
T
T= f (t )
0
t
分段函数(piecewise function):用解析式表示函 数时,有些函数在其定义域的不同范围内采用不同的 1 表达式。 x0 x sin 例1-4 函数 y 是一个分段 x 函数,它的定义域为全体实数。 例1-5 静脉注射G 钠盐100000单位后,血清中的药 C 物浓度C 为时间 t 的函数,
自变量 (independent variable) 定义域 (domain of definition)
{y y=f (x) , xD}称为函数的值域(domain of y fuction value),记为 f (D) 单值函数(one-valued function): f ( x) 如果定义域 D 中的每一个x值所 对应的函数值都是唯一的。 a x b 多值函数(multiple valued function): ( D [a, b] ) 如果有的x值所对应的函数值不止一个。 例1-2 函数 y2= x ,它的定义域为x>0。但是,对于 定义域内的每一个 x值,对应的 y 值有两个: y = ±√x 为多值函数。 ※ 没有特别说明时,函数指的都是单值函数。
2_1_2程序设计语言VB的基础

在了解、熟悉了VB程序设计语言的开发环境以后, 一起来体验VB程序的运行调试! 求s=1×2×3×…×n问题的VB程序:(文件名为 lx1.frm) Private Sub Command1_Click() n=inputbox(“请输入n的值:”,“输入”) s=1 for i=1 to n s=s*I next I msgbox “s=”+str(s),0,”计算结果” end sub 验证:当N=22时,运行的结果是:
第二章 程序设计初步
一、常量、变量、标准函数与表达式
1.常量(constant) 是指在程序运行过程中保持不变的量, 在 Visual Basic中,常量一般分为: ⑴ 数值常量 ⑵ 字符串常量 ⑶ 符号常量
⑴ 数值常量 :数值常量就是数学中说的常数,
数值常量有整型常量和实型常量两种。 实型常量又分为定点数和浮点数两种。 如1、10、3.14159、2e6(2*10^6)
②关系表达式与字符串表达式: 关系表达式与字符串表达式: A、关系运算符: = < > >= <= <> 字符串运算符:= < > >= <= &(特别要注意与数学中大于 与小于的区别) B、关系表达式: 3>1 x>2 且 X<4 字符串表达式:“syty”>“Tcte” A65B66T84Y89”啊” “汉”a han C、优先级:相同 D、取值:T F 类型:逻辑值 例: 数学式 VB式 1<3 1<3 2<x<3 x>2且x<3 且 x≤3 x<=3 例: “syty”>“Tcte” 取值:T “勤劳” & “中国人民” 取值: “勤劳中国人民”
(完整word版)高等数学讲义(一)

高等数学基础高等数学基础课程的学习内容微积分学,它是创建于十七世纪的一门数学学科,创始人是英国数学家牛顿(Newton )和德国数学家莱布尼茨(Leibniz )。
用著名学者的话来形容“微积分、或者数学分析,是人类思维的伟大成果之一。
它处于自然科学与人文科学之间的地位,使它成为高等教育的一种特别有效的工具”。
“微积分的创立,与其说是数学史上,不如说是人类历史上的一件大事。
时至今日,它对工程技术的重要性就像望远镜之于天文学,显微镜之于生物学一样。
第1讲 函数1.2 函数要知道什么是函数,需要先了解几个相关的概念。
一、常量与变量先看几个例子:圆的面积公式2πr S =自由活体的下落距离2021gt t v s += 在上述讨论的问题中,g v ,,π0是常量,t s r S ,,,是变量。
变量可以视为实属集合(不止一个元素)。
二、函数的定义定义1.1 设D 是一个非空数集。
如果有一个对应规则f ,使得对每一D x ∈,都能对应于唯一的一个数y ,则此对应规则f 称为定义在集合D 上的一个函数,并把数x 与对应的数y 之间的对应关系记为)(x f y =并称x 为该函数的自变量,y 为函数值或因变量,D 为定义域。
实数集合},)(;{D x x f y y Z ∈==称为函数f 的值域。
看看下面几个例子中哪些是函数:}6,3,1{=Xf}9,8,6,2{=Yf 是函数,且2)1(=f ,8)3(=f ,6)6(=f定义域}6,3,1{=D ,值域}8,6,2{=Z ,一般地Y Z ⊂。
}7,6,3,1{=X}9,8,6,2{=Yf 不是函数。
}6,3,1{=X}9,8,6,2{=Yf 是函数,且2)1(=f ,8)3(=f ,8)6(=f定义域}6,3,1{=D ,值域}8,2{=Z 。
}6,3,1{=X}9,8,6,2{=Yf 不是函数。
由函数定义可以得出,函数的对应规则和定义域是确定函数的两个要素,用解析法表示的函数的对应规则就是由表达式确定的,而定义域就是使表达式有意义的所有x 轴上的点。
Basic讲稿(1-4)

第三章 用BASIC来帮你做数学题
FB中的数和表达式
数学中的数有自然数、小数和分数等
FB中只有两种数,即整数和实数 负数和数轴的概念 整数:12,876,-12,0等都是整数
实数:带有小数部分的数即实数,在FB
中有两种格式:定点格式和浮点格式
定点格式:用这种格式表示的小数,其
运算顺序
在FB中,各算术运算符的优先级是这样
规定的(从左往右优先级顺序降低): ^ →*、/ →\ →MOD →+、 例:表达式 7-2*5 MOD 3 ^2\2*(1+1) 7-0=7
的运算顺序和结果是什么?
一些FB源程序的例子
看一些FB源程序例子;
说明一些基本概念,包括程序及编程是
程序设计语言的种类
编写计算机软件所用的程序设计语言有
很多种,根据其发展情况,可以分为以 下几种:
机器语言
汇编语言 高级语言
机器语言
在机器语言中,所有的指令和数据都由0
和1组成,能被计算机直接识别和理解, 因此,用机器语言编写的程序,无需经 过任何翻译,就可以在计算机上直接运 行 机器语言程序又称为目标程序 每种机器所能理解的机器语言可能不尽 相同
FB中的算术表达式
加号:+
减号: 乘号:* 除号:/
FB中没有大小括号之分,统一用()来表示。
例如,[2*(3+1)-3]/5在Basic中表示为:
(2*(3+1)-3)/5
当算式中有多层括号时,先计算最里层
的括号 在FB中,这样的式子叫做算术表达式 例3-3:将下列数学式转化成FB的算术表 达式: 35 5 1) 2A+3C 2) 2 3 3)9÷(3+1) 4) (B+3) ÷ B *2
一元一次方程的变量与常量教学介绍

一元一次方程的变量与常量教学介绍一元一次方程是初中数学中的基础知识之一,也是解决实际问题的有力工具。
本文将介绍一元一次方程中的变量与常量的概念,并探讨如何在教学中有效地介绍这一内容。
一、变量与常量的概念在学习一元一次方程前,学生需要首先了解变量与常量的概念。
变量是指在方程中表示未知数的字母或符号,常常用x来表示。
常量是指在方程中已知数,其数值是固定不变的。
变量和常量的概念有助于学生理解方程中的数学关系。
二、变量与常量的表示方式变量和常量在方程中的表示方式可以有多种形式。
例如,我们可以用一个未知数加上一个已知数来表示一个一元一次方程。
具体表达形式如下:ax + b = c其中,a表示未知数的系数,b表示已知数的系数,c表示方程的常量。
通过这样的表示方式,学生能够清晰地看到方程中的变量和常量的不同。
三、变量与常量的应用举例在实际问题中,一元一次方程的变量与常量有着广泛的应用。
以下是一些常见的应用举例:1. 速度问题:假设一辆汽车以每小时60公里的速度行驶,已知行驶时间为t小时,求行驶的距离。
在这个问题中,速度是常量,时间是变量,距离则是方程的解。
2. 价格问题:某商品原价为p元,现在打折后降价c元,求现在的价格。
在这个问题中,原价是常量,降价和现价是变量,我们需要通过方程求解现价。
3. 比例问题:某材料中A和B两种分子的比例为a:b,假设总共有c个分子,求A和B各有多少个分子。
在这个问题中,比例是常量,分子数是变量,我们可以通过方程求解A和B的个数。
通过这些实际应用举例,学生能够更好地理解方程中变量和常量的概念,并将其应用到解决实际问题中。
四、教学设计与方法为了有效地教授一元一次方程的变量与常量,教师可以采用以下教学设计与方法:1. 引入问题:通过具体实例或问题,引导学生思考在实际情境中如何使用方程来描述相关的数学关系。
2. 示范演示:教师可以通过具体计算步骤的示范演示,让学生清楚地了解变量和常量在方程中的表示和应用。
新教科版高中信息技术选修一:2.1 常量、变量的定义 知识要点复习

第二章程序设计基础第一节常量、变量的定义一、常量:在程序进行过程中不变的量,在VB中一般分数值常量与字符常量两种。
数值常量:就是数学中说的常数,分整型常量和实型常量两种整型常量:即整数,指不带小数点的数值如1、0、-10、+35等都是合法的整数实型常量:即实数,指带小数点的数值。
实型常量又分为定点数和浮点数两种。
例:定点数:3.14159和-6.8,1.99浮点数:2E6、1E5例:1.2345×103 可表示为1.2345E3,字母E表示底数10浮点数就是数学上的科学计数法。
字符串常量:被一对双引号括起来的若干个合法的字符称为字符串常量。
例如:”China”、”Visual Basic”、”18”、”3.1415”等。
符号常量:如果多次用到同一个常量,则可用一个有意义的名字表示这个常量。
二、变量:在程序执行过程中,其值可以改变的量称为变量变量命名注意要点:1、必须以字母开头,不能以数字或其他字符开头。
2、只能由字母、汉字、数字学或下划线组成,不能含有小数点、空格等字符。
3、最长不超过255个字符4、不能以VB保留字作变量名,如语句定义符、函数名等。
5、VB不区分变量名中字母大小写。
如HELLO和Hello是同一个变量。
三、常量和变量的定义1、符号常量的声明:Const 常量名[As 常量类型] = 常量值如:Const pi = 3.14 常量名为pi2、变量的声明:Dim <变量名>As <变量类型>如:Dim a As Integer定义一个整型变量,变量名为a3、变量的赋值:变量 = 表达式例:Private Sub Form_Click()Dim a As Integer, b As Integer, c As IntegerDim str As Stringa = 54b = 114c = a + bstr = "Hello World"Print "a="; a, "b="; b, "c="; cPrint strEnd Sub四、运算符例:5 / 2 = 2.5 \ 整除例: 5 \ 2 = 2 Mod 求余数例:5 Mod 2 = 1注意:关系表达式的运算结果为布尔值True 或 False例:3 > 2 结果为 True(真或是)3、逻辑运算Not(取反)And(与) Or(或)运算结果为布尔型(Boolean)True 或 False逻辑运算符的优先级为:Not > And > Or例如:t or true and false4、日期运算符与日期表达式日期表达式是用日期运算符“+”或“-”将算式表达式、日期型常量、日期型变量、日期函数等连接起来的式子,如表达式“#2003/09/01# +30”的运算结果是“2003-10-1”;表达式“#2003/10/20# - #2003/10/10#”的运算结果为整数105、字符运算字符串连接符为“+”和“&”“123” + “45” = “12345”“123” & “45” = “12345”123 + “45” = 168“123” & 45 = “12345”6、运算符的执行顺序:算术运算符 > 字符串运算符 > 关系运算符 > 逻辑运算符例如:“123”+ 321 &“abcd”=”444abcd”。
高等数学第一章函数与极限

两个函数 f 与 g 构成复合函数的关键在于内函
数的值域要包含在外函数的定义域中。
例2 分析下列复合函数的结构:
⑴ y = cot x
2
解 ⑴ y= u, ⑵ y = eu ,
; u cot v ,
u sin v ,
单调递增或单调递减函数统称为单调函数。
(3)有界性 设函数 y = f ( x ) 定义在区间 (a,b) 上,若存在
一个常 数 k , 使得当 x ∈ (a,b) 时,恒有 f (x) k
( f (x) k) 成立,则称f ( x )在 (a,b)有上界(下界)。
若 f ( x )在 (a,b)既有上界又有下界, 则称f (x )在 (a,b)上有界。 如果函数 f ( x ) 在其定义域内有界,则称f ( x ) 为有界函数。
指数函数
y ax (a >0,a ≠1,a 为常数)
对数函数 三角函数 反三角函数
y =loga x (a >0,a ≠1,a 为常数)
y = sin x , y =cos x , y =tan x , y =cot x y =secx, y =csc x
y = arcsin x , y arccotx
y arccos x ,
y arctan x
这六种函数统称为基本初等函数,这些函数的性质、 图形必须熟悉.
1.2.2 复合函数
设 y f (u),其中 u (x) ,且 (x) 的值全部或部分落
在 f (u)的定义域内,则称 y f (x)为 x 的复合函数,而 u
1 x0
y
第一节 函数的概念

例如U 1,1.5 = x 0 < x - 1 <1.5
o
表示以点x0 = 1为中心, 以 =1.5为半径的邻域, 即 -0.5,1 1, 2.5
三、函数
• 引例1:圆的面积A与其半径r之间的相互关 系为: A = r 2 ,当r在(0,+∞)内任 意取定一个数值时,就可由上式确定圆面积 A的对应数值。 • 引例2:某商品的销售单价为k元,销售数 量x与销售收入R之间的相互关系为:R=kx, 当x在自然数集1,2,3,…中任意取定一个 数值时,就可由上式确定销售收入R的对应 数值。
二、区间与集合
•集合与集合的元素 集合是指具有某种特定性质的事物的总体. 集合可 用大写的字母A, B, C, D 等表示. 组成集合的事物称为集合的元素. 集合的元素可用 小写的字母a, b, c, d 等表示. a是集合M的元素记为aM, 读作a属于M. a不是集合M的元素记为aM, 读作a不属于M. •集合的表示 A={a, b, c, d, e, f, g}是用列举法表示的. M={(x, y)|x, y为实数, x2+y2=1}是用描述法表示的.
三、 函数
• 引例3:某百货商店记录了毛线历年来的月销售量 (单位:百公斤),并将近10年来的平均月销售 量列成下表。
月份t 平均月 销售量s 1 2 3 4 5 6 7 8 9 10 11 12
81 84 45 49 9 5 6 17 94 161 144 123
• 该表表示了该商店毛线的销售量与月份之间的相 互关系,且当t在1,2,3,…,12中任意确定一个 数值时,从表中就可确定一个平均月销售量s的对 应数值。
•几个数集 所有自然数构成的集合记为N, 称为自然数集. 所有实数构成的集合记为R, 称为实数集.
1等于多少度角

1等于多少度角
1等于多少度角?这是一个非常有趣的问题,即使它似乎有点让人困惑。
事实上,这个问题可以从不同的角度来理解,并由此产生不同的答案。
首先,我们可以从数学的角度看待这个问题。
在数学中,“1”是一个常量,它可以代表任何数字,但不构成角度。
因此,在数学上,“1”不能等于任何度数角。
然而,“1”也可以用来作为一周360度的基本单位,这也就意味着“1”等于1度。
在这种情况下,我们可以得出结论:1等于1度。
此外,还有另外一种角度,即“1”可以表示一个特殊的角度,如90度,180度和360度。
在这种情况下,“1”可以是90度,180度或360度,但不能等于其他度数角。
最后,“1”还可以用于表示某种数学和物理相对应的概念,例如,1弧度等于57.3度,1度角等于0.0174弧度,360度角等于2π弧度等。
这些概念都会影响“1”的大小和确定它等于多少度角。
总的来说,“1”可以代表不同的度数角,但答案取决于你如何使用“1”。
如果你将“1”看作一周360度的基本单位,那么它就等于1度。
如果你将“1”用于表示90度,180度和360度之类的特殊角度,那么它也可以等于其中任意一个角度。
此外,“1”还可以用于表示特定的数学和物理概念,确定它等于多少度角也取决于这些概念。
因此,从数学和物理的角度来看,“1”等于多少度角的答案并不是一个固定的数字,而是跟你如何使用它有关系的。
一 常量和变量

一常量和变量在一个变化过程中,我们称数值发生变化的量为变量,数值保持不变的量为常量.二函数概念一般地,在一个变化过程中,如果有两个变量X和Y,并且对于X的每一个给定的值,Y都有确定的值与它相对应,那么我们就说X是自变量,Y是X的函数.对函数感念的理解,主要抓住以下三点:1 有两个变量.;2 一个变量的每一个数值随着另一个变量的数值变化而变化;;3自变量每一个确定的值,函数有一个且只有一个值与之对应;. 三函数值对于自变量在取值范围内的某个确定的值,函数所对应的值,函数有唯一确定的对应值这个对应值就叫做当自变量的值为A时的函数值,求函数值的实质是求代数式的值.四函数的表示形式(1) 列表法;(2)图像法;(3)代数法.一次函数概念若两个变量X,Y之间的关系可以表示为y=kx+b(k,b为常数k不等于o)的形式,则称y是x的一次函数.特别地,当b=o时,称y是x 的正比例函数.一次函数与正比例函数的联系正比例函数是特殊的一次函数, 正比例函数一定是一次函数,但一次函数不一定是正比例函数.;一次函数图像: 一条过(o,b) (- ,o)的直线.函数的图像: 把一个函数的自变量x与对应的因变量y的值分别作为点的横坐标和纵坐标在直角坐标系中描出它的对应点,所有这些点组成的图形叫做该函数的图像;.作函数图像的一般步骤是:列表|描点|连线.待定系数法要确定变量间的函数关系式,设出某些未知系数,然后根据所给条件利用方程或者是方程组\来确定这些未知系数的方法叫待定系数法.用待定系数法确定一次函数表达式的一般步骤1设函数表达式为y=kx+b,其中包含待定的系数k,b;2根据所给条件列方程(组);3解方程(组),求出待定系数k与b的值;4将待定系数k,b的值代入所设的函数表达式中,得到一次函数表达式;。
福州大学大学物理(上)01-1预备知识(微积分)

确定的极限I , 我们称这个极限I 为函数 f ( x ) 记为 在区间[a , b]上的定积分,
积分上限
f ( i )xi a f ( x )dx I lim 0 i 1
被 积 函 数
被 积 表 达 式
b
n
积分和
一点 i ( i x i ), 作乘积 f ( i )x i ( i 1,2,)
并作和 S f ( i )x i ,
n
记 max{x1 , x 2 , , x n }, 如果不论对[a , b]
i 1
18
怎样的分法,也不论在小区间[ xi 1 , xi ] 上
2
解
例4 解
原式 2 sin x cos x x 0 求 2
1
3 . 2
1 当 x 0 时, 的一个原函数是ln | x | , x 1 1 1 dx 2 x ln | x |2 ln1 ln 2 ln 2.
1 dx . x
8
(二)不定积分
定义函数f(x)的所有原函数叫作f(x)的不定积分 记作 f ( x )dx
用F(x)表示f(x)的一个原函数,则f(x)的不定 积分可写作
f(x) —— 被积函数 不定积分的性质: f (x)dx —— 被积式 ' X——积分变量 1.( f ( x )dx) f ( x ) ∫——积分符号 ' C——积分常数 2. F ( x )dx F( x ) C
a a c
b
c
b
23
牛顿—莱布尼茨公式 N-L公式
如果 F ( x ) 是连续函数 f ( x ) 在区间[a , b ]上的
c中定义常量

在C语言中,常量是指在程序中固定不变的值。
常量可以是整数、浮点数、字符或字符串等。
与变量不同,常量的值在程序执行期间是不可更改的。
在C语言中定义常量的方法主要有两种:
1.使用#define预处理器指令。
这是在C语言中定义常量最常用的方法。
例如:
c复制代码
#define PI 3.14159
#define MAX_VALUE 100
使用#define定义的常量不需要指定数据类型,编译器会自动根据后面的值进行推断。
预处理器会在编译前将程序中所有出现的常量替换为对应的值。
2.使用const关键字。
const关键字可以用于定义常量变量,即变量的值不能被修改。
例如:
c复制代码
const int MAX_VALUE = 100;
const float PI = 3.14159;
使用const定义的常量必须指定数据类型,并且变量的值在初始化后不能被修改。
编译时会对const定义的常量进行类型检查,确保其值符合对应的数据类型要求。
需要注意的是,使用#define定义的常量在预处理阶段进行简单的文本替换,不占用内存空间,而使用const定义的常量在程序运行时会占用内存空间。
另外,从C++开始,推荐使用constexpr关键字来定义编译时常量,这可以提供更好的类型安全性和可读性。
新函数(一)

函数(一)知识要点一、函数的概念:1变量与常量:在问题研究的过程中,可以取不同数值的量叫做变量,保持数值不变的量叫做常量(或常数)2、函数的定义:在某个变化过程中有两个变量,设x为和y,如果在变量x的允许取值范围内,变量y随着x的变化而变化,那么变量y叫做变量x的函数,x叫做自变量.3、函数的定义域与函数值:函数的自变量允许取值的范围,叫做这个函数的定义域.如果变量y是自变量x的函数,那么对于x在定义域内取定的一个值a,变量y的对应值叫做当x=a 时的函数值.“y是x的函数”用记号y=f(x)来表示.这里括号内的字母x表示自变量,括号外的字母f表示y随着x变化而变化的规律。
在函数用记号y=f(x)表示时,f(a)表示x=a时的函数值.二正比例函数:1正比例函数的定义:一般地,形如y =kx (其中k = 0)的函数叫做正比例函数,其中k叫做比例系数。
正比例函数的定义域是一切实数.2、正比例函数的图像:一般地,正比例函数y=kx (k丰0)的图像是经过原点(0,0)和点(1, k)的一条直线,. 我们把正比例函数y=kx的图像叫做直线y=kx.3、正比例函数的性质:(1 )当k>0时,正比例函数的图像经过第一、三象限;自变量x的值逐渐增大时,y的值也随着逐渐增大.(2)当k<0时,正比例函数的图像经过第二、四象限;自变量x的值逐渐增大时,y的值也随着逐渐减小.三、反比例函数:1、反比例函数的定义:k函数y , (k = 0 )叫做反比例函数,其中k也叫比例系数.x反比例函数的定义域为不等于零的一切实数2、反比例函数的图像与性质:反比例函数的图像是双曲线(1)当k > 0时,函数图像的两个分支分别分布在第一、三象限内,在每一个象限中,y随x的增大而减小;(2)当k V0时,两个分支分别分布在第二、四象限内,在每一个象限中,y随X的增大而增大。
(3 )两个分支都无限接近但永远不能达到x轴和y轴。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二、变量
• 变量是指在程序执行过程中其值可以改变的量。 与常量不同,要存储可变的数据时就要用到变量。 变量由变量名和数据类型两部分组成。 • 1.变量的命名规则 变量的命名规则同常量名命名规则相同。 • 2.变量声明 变量的声明分为显式声明和隐式声明。 (1)显式声明 显式声明是在变量使用之前先声明变量。
ቤተ መጻሕፍቲ ባይዱ
• • •
语法格式:
{Dim} <变量名> [As <类型>][,<变量名2> [As <类型2>]]…
<变量名>遵循标准的变量命名约定。 <类型>用来定义被声明<变量名>的数据类型或对象类型。 使用声明语句建立一个变量后,VB自动将数值型的变量赋初值0,将字符型或变体类型的变量赋空串,将布尔型的变量赋False。 例如: Dim a as integer Dim b as long Dim c as single 上面的3个语句可以写为: Dim a as integer,b as long,c as single 缺省 [As类型]为可变类型。 另外,若把多个变量都定义成同一类型,例如:把X,Y,Z都定义成双精度型,必须写成: Dim X as double,Y as double,Z as double 如果写成:Dim x,y,z as double 则x,y定义成变体类型,z定义成双精度。 (2)隐式声明 VB中使用未加说明的变量时,系统默认为可变类型(Variant),这种方式称为隐式说明。建议初学者养成对变量显示说明的习惯,以避免 一些不必要的错误。 Dim r as single,s as single Const PI=3.14 S=PI*r^2 C=2*PI*r Print S,C 程序中未对C进行变量定义,但也可以正常使用这个变量,这个变量的类型是变体类型(Variant)。
• 2、字符串运算符 • 字符串只有连接运算,在VB中可以用“+”或“&”。建议尽量使用“&”, 使程序看起来更明了。 • 注意:“+”和“&”的区别。当两个被连接的数据都是字符型时,它们的 作用相同。当数字型和字符型连接时,“&”把数据都转化成字符型然 后连接;“+”把数据都转化成数字型然后连接。 • 例如: • "ABC"+"DEF" 结果为:"ABCDEF"。 • "姓名:" & "张三" 结果为:"姓名:张三"。 • 23 & "7" 结果为:"237"。 • 23+"7" 结果为:30。 • 23+"7abc" 则会出现类型不匹配的错误 •
•
(一)运算符: 运算符是用来对运算对象进行各 种运算的操作符。 表达式用来表示某个求值规则, 它由运算符和配对的圆括号将常 量、变量、函数、对象等操作数 以合理的形式组合而成。
• 1、算术运算符 • 用来进行简单的算术运算,运算结果是一 个数值。 • 单目运算符: • 运算符的后面只有一个操作数,例如:-5。 • 双目运算符: • 运算符的前后有两个操作数,例如:a+b。
• • •
Const <常量名> [As <数据类型>]=<表达式>… <常量名>名由1-255个字符组成,可以包含数字、英文字母(大小写均可) 或下划线,不能有“• ”或其他类型说明字符,并且必须以英文字母开头。 例如: xm、Room1、xy_2、name是合法的常量名 in.sum、75ab是非法的常量名 常量名不能是VB的关键字。 例如:If、While、String都是非法的常量名,如果常量名是VB的关键字,VB 编辑器会显示出错信息。常量名在同一程序区域内必须惟一。 <表达式>由数值、字符串等常量及运算符组成。 如果在一行中声明多个常量可用逗号进行分隔。 例如: Const PI as Double=3.1415926 „声明PI为一个双精度的常量’ Const S=”北京” ‘声明S为一个字符型的常量’ Const PI=3.1415926, S=”北京”
一、常量
•
常量是指在程序运行过程中始终保持不变的常数、字符串等。在VB 中,有两种形式的常量:一种是系统提供的内部常量,另一种是用户 自定义的符号常量。
• 1.内部常量 系统内部常量是指VB内置的一些便于记忆的常量。是应用程序和控 件提供的。例如: Form1.BackColor=vbRed „将窗体的背景颜色设为红色,vbRed代表 红色,为内部常量 • 2.符号常量 为了方便开发,有时程序员还需要创建自己的符号常量。声明常量的 语法格式为:
