中考数学模拟测试(二)新人教版【含解析】

合集下载

2022年人教版中考第二次模拟考试《数学卷》含答案解析

人教版数学中考综合模拟检测试题学校________ 班级________ 姓名________ 成绩________一、选择题(本大题共16小题，共42分,本大题有16个小题，共42分，1-10小题各3分，11-16小题各2分，在每小题给出的四个选项中，只有一项是符合题目要求的)1.3-的相反数是( ) A. 3-B. 3C.13D. 13-2.下列各式中，计算正确的是( ) A. 235x y xy +=B. 623x x x ÷=C. ()33926x x -=-D. 325a a a ⋅=3.成人每天维生素D 的摄入量约为0.0000046克．数据”0.0000046”用科学记数法表示为( ) A. 74610-⨯B. 74.610-⨯C. 64.610-⨯D. 50.4610-⨯4.由若干个大小形状完全相同的小立方块所搭几何体的俯视图如图所示，其中小正方形中的数字表示在该位置的小立方块的个数，则这个几何体的主视图是( )A. B. C. D.5.如图，已知1130∠=︒，250∠=︒，3105∠=︒，则4∠=A. 75︒B. 65︒C. 55︒D. 50︒6.如图所示，在A ，B 处观测到C 处方位分别是( )A. 北偏东60°，北偏西40°B. 北偏东30°，北偏西40°C. 北偏东30°，北偏西50°D. 北偏东60°，北偏西50°7.解不等式组3422133xx x-≥⎧⎪⎨+>-⎪⎩①②时，不等式①②的解集在同一条数轴上表示正确的是( )A B.C. D.8.如图，有一块菱形纸片ABCD，沿高DE剪下后拼成一个矩形，矩形的相邻两边DC和DE的长分别是5，3．则EB的长是( )A. 0.5B. 1C. 1.5D. 29.如图，⊙O的半径为5，AB为弦，点C为AB的中点，若∠ABC=30°，则弦AB的长为( )A. 12B. 5C.53310.下列说法正确的是( )A. 检测某批次灯泡使用寿命，适宜用全面调查B. “367人中有2人同月同日生”为必然事件C. 可能性是1%的事件在一次试验中一定不会犮生D. 数据3，5，4，1，﹣2的中位数是411.1832( )A. 1到2之间B. 2到3之间C. 3到4之间D. 4到5之间12.如图，在22⨯的方格中，小正方形的边长是1，点、、都在格点上，则AC边上的高为()A. 5B.322C.355D.3213.如图是二次函数y=ax 2+bx+c 图象的一部分，且过点A(3，0)，二次函数图象的对称轴是x=1，下列结论正确的是A. b 2>4acB. ac>0C. a –b+c>0D. 4a+2b+c<014.如图，有一张三角形纸片ABC ，已知∠B ＝∠C ＝x°，按下列方案用剪刀沿着箭头方向剪开，可能得不到全等三角形纸片的是( )A. B.C. D.15.如图，在等腰三角形ABC ∆中，AB AC =，图中所有三角形均相似，其中最小的三角形面积为1，ABC ∆的面积为42，则四边形DBCE 的面积是( )A. 20B. 22C. 24D. 2616.如图，直线1y =与反比例函数(0)k y x x=<，2(0)y x x =>的图象分别交于点A 和点B ，线段AB 的长是8，若直线()()20=+≠y n x n 与2(0)y x x =>的图象有交点，与(0)k y x x=<无交点，则n 的取值范围为( )A. 60-<<nB. 06n <<C. 60-<<n 或06n <<D. 02n <<二、填空题(本大题共3小题，共11分本大题有3个小题，共11分，17小题3分：18～19小题各有2个空，每空2分，把答案写在题中横线上)17.若a ﹣b ＝3，a +b ＝﹣2，则a 2﹣b 2＝_____． 18.如图，已知点坐标为()3,1，为轴正半轴上一动点，则AOB ∠度数为_________，在点运动的过程中12AB OB +的最小值为________．19.(2013年四川自贡4分)如图，在函数()8y x>0x=的图象上有点P 1、P 2、P 3…、P n 、P n+1，点P 1的横坐标为2，且后面每个点的横坐标与它前面相邻点的横坐标的差都是2，过点P 1、P 2、P 3…、P n 、P n+1分别作x 轴、y 轴的垂线段，构成若干个矩形，如图所示，将图中阴影部分的面积从左至右依次记为S 1、S 2、S 3…、S n ，则S 1=，S n = ．(用含n 的代数式表示)三、解答题(本大题有7个小题，共67分．解答应写出文字说明、证明过程或演算步骤)20.解密数学魔术：魔术师请观众心想一个数，然后将这个数按以下步骤操作：魔术师能立刻说出观众想的那个数．(1)如果小玲想的数是3-，请你通过计算帮助她告诉魔术师的结果;(2)如果小明想了一个数计算后，告诉魔术师结果为85，那么魔术师立刻说出小明想的那个数是：__________;(3)观众又进行了几次尝试，魔术师都能立刻说出他们想的那个数．若设观众心想的数为，请你按照魔术师要求的运算过程列代数式并化简，再用一句话说出这个魔术的奥妙．21.两个边长分别为和的正方形如图放置(图1)，其未叠合部分(阴影)面积为1S ;若再在图1中大正方形的右下角摆放一个边长为的小正方形(如图2)，两个小正方形叠合部分(阴影)面积为2S ．(1)用含、的代数式分别表示1S 、2S ; (2)若10a b +=，22ab =，求12S S +的值;(3)当1232S S +=时，求出图3中阴影部分的面积3S ．22.为弘扬遵义红色文化，传承红色文化精神，某校准备组织学生开展研学活动．经了解，有A ．遵义会议会址、B ．苟坝会议会址、C ．娄山关红军战斗遗址、D ．四渡赤水纪念馆共四个可选择的研学基地．现随机抽取部分学生对基地的选择进行调查，每人必须且只能选择一个基地．根据调查结果绘制如下不完整的条形统计图和扇形统计图．(1)统计图中m ＝，n ＝ ;(2)若该校有1500名学生，请估计选择B 基地的学生人数;(3)某班在选择B 基地的4名学生中有2名男同学和2名女同学，需从中随机选出2名同学担任”小导游”，请用树状图或列举法求这2名同学恰好是一男一女的概率． 23.如图，A B ∠=∠，AE BE =，点D 在AC 边上，12∠=∠．()1求证：AEC ≌BED ;()2若75C ∠=︒，求AEB ∠的度数; ()3若90AEC ∠=︒，当AEC 的外心在直线DE 上时，2CE =，求AE 的长．24.如图，在平面直角坐标系中，过点B (6，0)的直线AB 与直线OA 相交于点A (4，2)，动点M 在线段OA 和射线AC 上运动． (1)求直线AB 的解析式． (2)求△OAC 的面积．(3)是否存在点M ，使△OMC 的面积是△OAC 的面积的14?若存在求出此时点M 的坐标;若不存在，说明理由．25.如图1，在ABC ∆中，AB AC =，O 是ABC ∆的外接圆，过点作BCD ACB ∠=∠交O 于点，连接AD 交BC 于点，延长DC 至点，使CF AC =，连接AF .(1)求证：ED EC =; (2)求证：AF 是O 切线;(3)如图2，若点是ACD ∆的内心，25BC BE ⋅=，求BG 的长. 26.如图，在平面直角坐标系中，抛物线y ＝x (x ﹣b )﹣12与y 轴相交于A 点，与x 轴相交于B 、C 两点，且点C 在点B 右侧，设抛物线的顶点为P ． (1)若点B 与点C 关于直线x ＝1对称，求b 的值; (2)若OB ＝OA ，求△BCP 的面积;(3)当﹣1≤x ≤1时，该抛物线上最高点与最低点纵坐标的差为h ，求出h 与b 的关系;若h 有最大值或最小值，直接写出这个最大值或最小值．答案与解析一、选择题(本大题共16小题，共42分,本大题有16个小题，共42分，1-10小题各3分，11-16小题各2分，在每小题给出的四个选项中，只有一项是符合题目要求的)1.3-相反数是( ) A. 3- B. 3C.13D. 13-【答案】B 【解析】【分析】根据只有符号不同的两个数叫做互为相反数解答．【详解】解：-3的相反数是3，故选B.【点睛】本题考查了相反数的定义，是基础题，熟记概念是解题的关键． 2.下列各式中，计算正确的是( ) A. 235x y xy += B. 623x x x ÷=C. ()33926x x -=-D. 325a a a ⋅=【答案】D 【解析】【分析】根据合并同类项，同底数幂的除法、积的乘方，单项式乘单项式分别求出每个式子的结果，再判断即可．【详解】A 、2x 和3y 不能合并，故本选项错误; B 、x 6÷x 2＝x 4，故本选项错误; C 、()33928x x -=-，故本选项错误;D 、325a a a ⋅=，故本选项正确; 故选：D ．【点睛】本题考查了合并同类项，同底数幂的除法、积的乘方，单项式乘单项式的应用，主要考查学生的计算能力和辨析能力．3.成人每天维生素D 的摄入量约为0.0000046克．数据”0.0000046”用科学记数法表示为( ) A. 74610-⨯ B. 74.610-⨯C. 64.610-⨯D. 50.4610-⨯【答案】C 【解析】【分析】本题用科学记数法的知识即可解答．【详解】解：60.0000046 4.610-=⨯．故选C ．【点睛】本题用科学记数法的知识点，关键是很小的数用科学记数法表示时负指数与0的个数的关系要掌握好．4.由若干个大小形状完全相同的小立方块所搭几何体的俯视图如图所示，其中小正方形中的数字表示在该位置的小立方块的个数，则这个几何体的主视图是( )A. B. C. D.【答案】A 【解析】【分析】由俯视图知该几何体共3列，其中第1列前一排3个正方形、后1排1个正方形，第2列只有前排2个正方形，第三列只有1个正方形，据此可得．【详解】解：由俯视图知该几何体共3列，其中第1列前一排3个正方形、后1排1个正方形，第2列只有前排2个正方形，第三列只有1个正方形，所以其主视图为：故选A ．【点睛】本题考查了三视图的知识，主视图是从物体的正面看得到的视图． 5.如图，已知1130∠=︒，250∠=︒，3105∠=︒，则4∠=A. 75︒B. 65︒C. 55︒D. 50︒【答案】A 【解析】【分析】先证明两直线平行，再根据平行的性质即可求出∠4. 【详解】∵1130∠=︒，250∠=︒ ∴∠1+∠2=180°， ∴两直线平行 ∴∠4=180°-∠3=75°，故选A.【点睛】此题主要考查平行线的判定与性质，解题的关键是熟知同旁内角互补，两直线平行. 6.如图所示，在A ，B 处观测到C 处的方位分别是( )A 北偏东60°，北偏西40° B. 北偏东30°，北偏西40° C. 北偏东30°，北偏西50° D. 北偏东60°，北偏西50°【答案】D 【解析】【分析】根据方向角的定义进行求解即可得答案.【详解】A 处观测到的C 处的方位角是：北偏东60°， B 处观测到的C 处的方位角是：北偏西50°，故选D ．【点睛】本题考查了方向角，正确理解方向角的定义是解题的关键.7.解不等式组3422133x x x -≥⎧⎪⎨+>-⎪⎩①②时，不等式①②的解集在同一条数轴上表示正确的是( )A. B.C. D.【答案】D【解析】【分析】先求出不等式组中各个不等式的解集，再利用数轴确定不等式组的解集．x≤-，【详解】解不等式①得：1x<，解不等式②得：5将两不等式解集表示在数轴上如下：故选D．【点睛】本题考查了解一元一次不等式组，在数轴上表示不等式的解集解不等式组时要注意解集的确定原则：同大取大，同小取小，大小小大取中间，大大小小无解了．8.如图，有一块菱形纸片ABCD，沿高DE剪下后拼成一个矩形，矩形的相邻两边DC和DE的长分别是5，3．则EB的长是( )A. 0.5B. 1C. 1.5D. 2【答案】B【解析】【分析】直接利用菱形的性质得出AD的长，再利用勾股定理得出AE的长，进而利用平移的性质得出答案．【详解】解：∵有一块菱形纸片ABCD，DC＝5，∴AD＝BC＝5，∵DE＝3，∠DEA＝90°，∴AE＝4，则BE＝5﹣4＝1．故选B．【点睛】此题主要考查了图形的剪拼以及菱形的性质，正确得出AE的长是解题关键．9.如图，⊙O的半径为5，AB为弦，点C为AB的中点，若∠ABC=30°，则弦AB的长为( )A. 12B. 5C.532D. 53【答案】D【解析】【分析】连接OC、OA，利用圆周角定理得出∠AOC=60°，再利用垂径定理得出AB即可．【详解】连接OC、OA，∵∠ABC=30°，∴∠AOC=60°，∵AB为弦，点C为AB的中点，∴OC⊥AB，在Rt△OAE中，53∴AB=53，故选D．【点睛】此题考查圆周角定理，关键是利用圆周角定理得出∠AOC=60°．10.下列说法正确的是( )A. 检测某批次灯泡的使用寿命，适宜用全面调查B. “367人中有2人同月同日生”为必然事件C. 可能性是1%的事件在一次试验中一定不会犮生D. 数据3，5，4，1，﹣2的中位数是4【答案】B【解析】【分析】根据可能性大小、全面调查与抽样调查的定义及中位数的概念、必然事件、不可能事件、随机事件的概念进行判断．【详解】检查某批次灯泡的使用寿命调查具有破坏性，应采用抽样调查，A错;一年有366天所以367个人中必然有2人同月同日生，B对;可能性是1％的事件在一次试验中有可能发生，故C错;3，5，4，1，-2按从小到大排序为-2，1，3，4，5，3在最中间故中位数是3，D错．故选B.【点睛】区分并掌握可能性、全面调查与抽样调查的定义及中位数的概念、必然事件、不可能事件、随机事件的概念．11.估计1832⨯+的运算结果应在( )A. 1到2之间B. 2到3之间C. 3到4之间D. 4到5之间【答案】C【解析】【分析】先计算出原式=2+3，再进行估算即可.【详解】1832⨯+=122+3=2+32⨯，3的数值在1-2之间，所以2+3的数值在3-4之间．故选C．12.如图，在22⨯的方格中，小正方形的边长是1，点、、都在格点上，则AC边上的高为()A. 5B. 322C. 355D. 32【答案】C【解析】【分析】先用间接法求出△ABC 的面积，然后求出AC 的长度，根据面积公式即可求出AC 边上的高.【详解】解：根据题意，得：11132211212422222ABC S ∆=⨯-⨯⨯-⨯⨯⨯=--=， ∵22125AC =+=，又12ABC S AC h ∆=•， ∴AC 边上的高：32235255ABC S h AC∆⨯===;故选：C.【点睛】本题考查了勾股定理与网格问题，解题的关键是利用勾股定理求出AC 的长度，以及间接法求出△ABC 的面积.13.如图是二次函数y=ax 2+bx+c 图象的一部分，且过点A(3，0)，二次函数图象的对称轴是x=1，下列结论正确的是A. b 2>4acB. ac>0C. a –b+c>0D. 4a+2b+c<0【答案】A【解析】【分析】略【详解】根据抛物线与x 轴有两个交点有b 2﹣4ac ＞0可对A 进行判断;由抛物线开口向下得a ＜0，由抛物线与y轴的交点在x轴上方得c＞0，则可对B进行判断;根据抛物线的对称性得到抛物线与x轴的另一个交点为(﹣1，0)，所以a﹣b+c=0，则可对C选项进行判断;由于x=2时，函数值大于0，则有4a+2b+c＞0，于是可对D选项进行判断．∵抛物线与x轴有两个交点，∴b2﹣4ac＞0，即b2＞4ac，所以A选项正确;∵抛物线开口向下，∴a＜0，∵抛物线与y轴的交点在x轴上方，∴c＞0，∴ac＜0，所以B选项错误;∵抛物线过点A(3，0)，二次函数图象的对称轴是x=1，∴抛物线与x轴的另一个交点为(﹣1，0)，∴a﹣b+c=0，所以C选项错误;∵当x=2时，y＞0，∴4a+2b+c＞0，所以D选项错误．故选A.【点睛】二次函数图象与系数的关系．14.如图，有一张三角形纸片ABC，已知∠B＝∠C＝x°，按下列方案用剪刀沿着箭头方向剪开，可能得不到全等三角形纸片的是( )A. B.C. D.【答案】C【解析】【分析】根据全等三角形的判定定理进行判断．【详解】解：A、由全等三角形的判定定理SAS证得图中两个小三角形全等，故本选项不符合题意;B、由全等三角形的判定定理SAS证得图中两个小三角形全等，故本选项不符合题意;C 、如图1，∵∠DEC ＝∠B +∠BDE ，∴x °+∠FEC ＝x °+∠BDE ， ∴∠FEC ＝∠BDE ，所以其对应边应该是BE 和CF ，而已知给的是BD ＝FC ＝3，所以不能判定两个小三角形全等，故本选项符合题意;D 、如图2，∵∠DEC ＝∠B +∠BDE ，∴x °+∠FEC ＝x °+∠BDE ， ∴∠FEC ＝∠BDE ，∵BD ＝EC ＝2，∠B ＝∠C ，∴△BDE ≌△CEF ，所以能判定两个小三角形全等，故本选项不符合题意;由于本题选择可能得不到全等三角形纸片的图形，故选C ．【点睛】本题考查了全等三角形的判定，注意三角形边和角的对应关系是关键．15.如图，在等腰三角形ABC ∆中，AB AC =，图中所有三角形均相似，其中最小的三角形面积为1，ABC ∆的面积为42，则四边形DBCE 的面积是( )A. 20B. 22C. 24D. 26【答案】D【解析】【分析】利用AFH ADE ∆~∆得到2916AHF ADE S FH S DE ∆∆⎛⎫== ⎪⎝⎭，所以9,16,AFH ADE S x S x ∆∆==则1697x x -=，解得1x =，从而得到16ADE S ∆=，然后计算两个三角形的面积差得到四边形DBCE 的面积．【详解】如图，根据题意得AFH ADE ∆~∆，∴2239416AHF ADE S FH S DE ∆∆⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭ 设9AFH S x ∆=，则16ADE S x ∆=，∴1697x x -=，解得1x =，∴16ADE S ∆=，∴四边形DBCE 的面积421626=-=．故选D ．【点睛】本题考查了相似三角形的判定：有两组角对应相等的两个三角形相似．也考查了相似三角形的性质． 16.如图，直线1y =与反比例函数(0)k y x x=<，2(0)y x x =>的图象分别交于点A 和点B ，线段AB 的长是8，若直线()()20=+≠y n x n 与2(0)y x x =>的图象有交点，与(0)k y x x =<无交点，则n 的取值范围为( )A. 60-<<nB. 06n <<C. 60-<<n 或06n <<D. 02n <<【答案】B【解析】分析】先确定()2,1B ，再确定A 点的坐标为()6,1-，接着求出反比例函数解析式为6y x =-．结合图像，当0n <时，不合题意;当0n >时，直线2=+y nx n 与2(0)y x x=>有交点，要满足直线2=+y nx n 与(0)k y x x =<无交点，即方程62+=-nx n x无解，方程化为2260++=nx nx ，利用根的判别式得到24460=-⨯<n n ，最后解关于n 的不等式即可．【详解】解：当1y =时，21=x，解得2x =，则()2,1B ，线段AB 的长是8， A ∴点的坐标为()6,1-， A 点()6,1-在反比例函数k y x=的图像上， 616∴=-⨯=-k ，反比例函数解析式为6y x=-，当0n <时，直线2=+y nx n 与(0)k y x x=<有交点，不合题意，当0n >时，直线2=+y nx n 与2(0)y x x=>有交点，此时当方程62+=-nx n x 无解时，直线2=+y nx n 与(0)k y x x =<无交点，方程整理得2260++=nx nx ，24460∴=-⨯<n n ，解得6n <，满足条件的n 的范围为06n <<．故答案为B ．【点睛】本题考查了反比例函数与一次函数的交点问题、待定系数法求函数解析式，把求反比例函数与一次函数的交点坐标问题转换成解成方程组是解答本题的关键．二、填空题(本大题共3小题，共11分本大题有3个小题，共11分，17小题3分：18～19小题各有2个空，每空2分，把答案写在题中横线上)17.若a ﹣b ＝3，a +b ＝﹣2，则a 2﹣b 2＝_____．【答案】-6【解析】【分析】先利用平方差公式分解因式，进而将已知代入求出答案．【详解】∵a 2﹣b 2＝(a +b )(a ﹣b )，∴把a ﹣b ＝3，a +b ＝﹣2代入得：原式＝3×(﹣2)＝﹣6．故答案为：﹣6．【点睛】本题考查平方差公式，解题关键是利用平方差公式，将a 2﹣b 2变形为(a +b )(a ﹣b )．18.如图，已知点坐标为()3,1，为轴正半轴上一动点，则AOB ∠度数为_________，在点运动的过程中12AB OB +的最小值为________．【答案】 (1). 30° (2).3【解析】【分析】过点A 作A 关于x 轴的对称点C ，交x 轴于点D ，过点C 作CM ⊥OA 于点M ，交x 轴于点B ，根据A 点坐标，写出AD 和OD 长，根据三角函数知识求出∠AOB 即可，证BM=1OB 2，AB=BC ，得到1=BC+BM 2+AB OB ，然后在Rt △ACM 中，根据三角函数知识求出CM 即可. 【详解】解：过点A 作A 关于x 轴的对称点C ，交x 轴于点D ，过点C 作CM ⊥OA 于点M ，交x 轴于点B ，∵点坐标为()3,1，AD⊥x轴，∴AD=1，3∴在Rt△AOD中，AD3tan AOB==OD3∠，∴∠AOB=30°;∵CM⊥OA，∴∠OMB=∠AMB=90°，∴BM=1OB 2，∵∠OBM=∠DBC，∴∠ACM=30°，∵A，C关于x轴对称，∴AB=BC，AD=CD=1，∴AC=2，∴1=BC+BM2+AB OB，∴当C，B，M三点共线时，12AB OB+有最小值，即CM长，在Rt△ACM中，CM=3AC cos30=2=3⨯⨯故答案为：30°3【点睛】本题是对解直角三角形的考查，熟练掌握三角函数知识和证明当C，B，M三点共线时，1 2AB OB+有最小值，是解决本题的关键.19.(2013年四川自贡4分)如图，在函数()8y x>0x=的图象上有点P 1、P 2、P 3…、P n 、P n+1，点P 1的横坐标为2，且后面每个点的横坐标与它前面相邻点的横坐标的差都是2，过点P 1、P 2、P 3…、P n 、P n+1分别作x 轴、y 轴的垂线段，构成若干个矩形，如图所示，将图中阴影部分的面积从左至右依次记为S 1、S 2、S 3…、S n ，则S 1=，S n = ．(用含n 的代数式表示)【答案】4;()8n n 1+．【解析】【详解】当x=2时，P 1的纵坐标为4，当x=4时，P 2的纵坐标为2当x=6时，P 3纵坐标为43，当x=8时，P 4的纵坐标为1，当x=10时，P 5的纵坐标为：45， … ∴()188S 2424221211⎡⎤=⨯-==-⎢⎥⨯⨯+⎢⎥⎣⎦（）; ()24288S 22223322221⎡⎤=⨯-=⨯=-⎢⎥⨯⨯+⎢⎥⎣⎦（）; ()24188S 21223323231⎡⎤=⨯-=⨯=-⎢⎥⨯⨯+⎢⎥⎣⎦（）; …()()n 888S 22n 2n 1n n 1⎡⎤=-=⎢⎥++⎢⎥⎣⎦．三、解答题(本大题有7个小题，共67分．解答应写出文字说明、证明过程或演算步骤) 20.解密数学魔术：魔术师请观众心想一个数，然后将这个数按以下步骤操作：魔术师能立刻说出观众想的那个数．(1)如果小玲想的数是3-，请你通过计算帮助她告诉魔术师的结果;(2)如果小明想了一个数计算后，告诉魔术师结果为85，那么魔术师立刻说出小明想的那个数是：__________;(3)观众又进行了几次尝试，魔术师都能立刻说出他们想的那个数．若设观众心想的数为，请你按照魔术师要求的运算过程列代数式并化简，再用一句话说出这个魔术的奥妙．【答案】(1)2;(2)80;(3)见解析【解析】【分析】(1)把-3代入操作步骤计算即可得到结果;(2)设这个数为x，然后列出方程;(3)把a代入，然后化简代数式即可．【详解】解：(1)(﹣3×3﹣6)÷3+7＝2;(2)设这个数为x，(3x﹣6)÷3+7＝85，解得：x＝80，故答案为：80;(3)设观众想的数为a，∴3675 3aa-+=+，因此，魔术师只要将最终结果减去5，就能得到观众想的数了．【点睛】本题是对代数式运算的考查，熟练掌握代数式化简求值是解决本题的关键.21.两个边长分别为和的正方形如图放置(图1)，其未叠合部分(阴影)面积为1S;若再在图1中大正方形的右下角摆放一个边长为的小正方形(如图2)，两个小正方形叠合部分(阴影)面积为2S．(1)用含、的代数式分别表示1S 、2S ;(2)若10a b +=，22ab =，求12S S +的值;(3)当1232S S +=时，求出图3中阴影部分的面积3S ．【答案】(1)S 1＝a 2−b 2，S 2＝2b 2−ab (2)34(3)16【解析】【分析】(1)由图中正方形和长方形的面积关系，可得答案;(2)根据S 1＋S 2＝a 2−b 2＋2b 2−ab ＝a 2＋b 2−ab ，将a ＋b ＝10，ab ＝22代入进行计算即可;(3)根据S 3＝a 2＋b 2−12b (a ＋b )−12a 2＝12(a 2＋b 2−ab )和S 1＋S 2＝a 2＋b 2−ab ＝32，可求得图3中阴影部分的面积S 3．【详解】(1)由图可得，S 1＝a 2−b 2，S 2＝2b 2−ab ．(2)∵a ＋b ＝10，ab ＝22∴S 2＋S 2＝a 2−b 2＋2b 2−ab＝a 2＋b 2−ab＝(a ＋b )2−3ab＝100−3×22＝34∴S 1＋S 2的值为34．(3)由图可得：S 3＝a 2＋b 2−12b (a ＋b )−12a 2＝12(a 2＋b 2−ab ) ∵S 1＋S 2＝a 2＋b 2−ab ＝32∴S 3＝12×32＝16， ∴图3中阴影部分的面积S 3为16．【点睛】本题考查了完全平方公式的几何背景，数形结合、恰当进行代数式变形是解答本题的关键． 22.为弘扬遵义红色文化，传承红色文化精神，某校准备组织学生开展研学活动．经了解，有A ．遵义会议会址、B ．苟坝会议会址、C ．娄山关红军战斗遗址、D ．四渡赤水纪念馆共四个可选择的研学基地．现随机抽取部分学生对基地的选择进行调查，每人必须且只能选择一个基地．根据调查结果绘制如下不完整的条形统计图和扇形统计图．(1)统计图中m＝，n＝;(2)若该校有1500名学生，请估计选择B基地的学生人数;(3)某班在选择B基地的4名学生中有2名男同学和2名女同学，需从中随机选出2名同学担任”小导游”，请用树状图或列举法求这2名同学恰好是一男一女的概率．【答案】(1)56，15;(2)555人;(3)23．【解析】【分析】(1)先由C类别人数及其所占百分比求出总人数，再进一步求解可得;(2)用总人数乘以样本中选择B基地的学生人数所占比例即可得;(3)根据题意画出树状图得出所有等情况数，找出选出的2名学生恰好是一男一女的情况数，然后根据概率公式即可得出答案．【详解】解：(1)由题意可知：总人数为40÷20%＝200(人)所以m＝200×28%＝56(人)，n%＝30200×100%＝15%，即n＝15，故答案为：56，15;(2)估计选择B基地的学生人数1500×200564030200---＝555(人);(3)根据题意画出树状图如下：一共有12种情况，恰好是1男1女的情况有8种，∴这2名同学恰好是一男一女的概率为812＝23．【点睛】本题考查了列表法与树状图法：利用列表法或树状图法展示所有等可能的结果n，再从中选出符合事件A 或B 的结果数目m ，然后利用概率公式计算事件A 或事件B 的概率．也考查了统计图的综合． 23.如图，A B ∠=∠，AE BE =，点D 在AC 边上，12∠=∠．()1求证：AEC ≌BED ;()2若75C ∠=︒，求AEB ∠的度数;()3若90AEC ∠=︒，当AEC 的外心在直线DE 上时，2CE =，求AE 的长．【答案】(1)见解析;(2)30AEB ∠=︒;(3)AE 23=【解析】【分析】()1由三角形的外角的性质可得DCE BDE ∠=∠，由”AAS ”可证BDE ≌ACE △;()2由全等三角形的性质可求DE EC =，BED AEC ∠=∠，可得75∠=∠=︒EDC C ，即可求解;()3由直角三角形的外心是斜边的中点，可得点D 是AC 的中点，可证ECD 是等边三角形，可得60C ∠=°，即可求解．【详解】证明：()112∠=∠+∠=∠+∠ADE DCE BDE ，且12∠=∠，DCE BDE ∴∠=∠，A B ∠=∠，AE BE =，AEC ∴≌()BED AAS()2AEC ≌BED ，DE EC ∴=，BED AEC ∠=∠，75∴∠=∠=︒EDC C ，118027530∴∠=︒-⨯︒=︒，∠=∠BED AEC ，130∴∠=∠=︒AEB ;()390AEC∠=︒，AEC∴的外心是斜边AC的中点，AEC的外心在直线DE上，点D是AC中点，∴==AD CD DE，又DE EC=，∴==CD EC DE，ECD∴是等边三角形，60C∴∠=︒，323∴==AE EC．【点睛】本题考查了三角形的外接圆和外心，全等三角形的判定和性质，直角三角形的性质，等腰三角形的判定和性质，灵活运用这些性质进行推理是本题的关键．24.如图，在平面直角坐标系中，过点B(6，0)的直线AB与直线OA相交于点A(4，2)，动点M在线段OA 和射线AC上运动．(1)求直线AB的解析式．(2)求△OAC的面积．(3)是否存在点M，使△OMC的面积是△OAC的面积的14?若存在求出此时点M的坐标;若不存在，说明理由．【答案】(1)y＝﹣x+6;(2)S△OAC＝12;(3)存在，M的坐标是：M1(1，12)或M2(1，5)或M3(﹣1，7)【解析】【分析】(1)利用待定系数法即可求得函数的解析式;(2)求得C的坐标，即OC的长，利用三角形的面积公式即可求解;(3)当△OMC的面积是△OAC的面积的14时，根据面积公式即可求得M的横坐标，然后代入解析式即可求得M的坐标．【详解】解：(1)设直线AB 的解析式是y kx b =+，根据题意得：4260k b k b +=⎧⎨+=⎩，解得：16k b =-⎧⎨=⎩，则直线的解析式是：y x 6=-+;(2)在y ＝﹣x +6中，令x ＝0，解得：y ＝6，OAC 1S 64122∆=⨯⨯=; (3)设OA 的解析式是y ＝mx ，则4m ＝2，解得：1m 2=，则直线的解析式是：12y x =， ∵当△OMC 的面积是△OAC 的面积的14时， ∴当M 的横坐标是1414⨯=，在12y x =中，当x ＝1时，y ＝12，则M 的坐标是1(1,)2; 在y x 6=-+中，x ＝1则y ＝5，则M 的坐标是(1，5)．则M 的坐标是：M 1(1，12)或M 2(1，5)．当M 的横坐标是：﹣1，在y x 6=-+中，当x ＝﹣1时，y ＝7，则M 的坐标是(﹣1，7);综上所述：M 的坐标是：M 1(1，12)或M 2(1，5)或M 3(﹣1，7)．【点睛】本题主要考查了用待定系数法求函数的解析式以及三角形面积求法等知识，利用M 点横坐标为±1分别求出是解题关键．25.如图1，在ABC ∆中，AB AC =，O 是ABC ∆的外接圆，过点作BCD ACB ∠=∠交O 于点，连接AD 交BC 于点，延长DC 至点，使CF AC =，连接AF .(1)求证：ED EC =;(2)求证：AF 是O 的切线;(3)如图2，若点是ACD ∆的内心，25BC BE ⋅=，求BG 的长.【答案】(1)证明见解析;(2)证明见解析;(3)BG=5.【解析】【分析】(1)根据等腰三角形的性质可得A ABC CB =∠∠，再根据圆周角定理以及ACB BCD ∠=∠可得BCD ADC ∠=∠，即可得ED=EC ;(2)连接OA ，可得OA BC ⊥，继而根据CA CF =以及三角形外角的性质可以推导得出CAF ACB ∠=∠，可得//BC AF ，从而可得OA AF ⊥，问题得证;(3)证明ABE CBA ∆∆，可得2AB BC BE =⋅，从而求得5AB =，连接AG ，结合三角形内心可推导得出BAG BGA ∠=∠，继而根据等腰三角形的判定可得5BG AB ==.【详解】(1)∵AB AC =，∴A ABC CB =∠∠，又∵ACB BCD ∠=∠，ABC ADC ∠=∠，∴BCD ADC ∠=∠，∴ED EC =;(2)连接OA ，∵AB AC =，∴AB AC =，∴OA BC ⊥，∵CA CF =，∴CAF CFA ∠=∠，∴2ACD CAF CFA CAF ∠=∠+∠=∠，∵ACB BCD ∠=∠，∴2ACD ACB ∠=∠，∴CAF ACB ∠=∠，∴//BC AF ，∴OA AF ⊥，∴AF 为O 的切线;(3)∵ABE CBA ∠=∠，BAD BCD ACB ∠=∠=∠，∴ABE CBA ∆∆，∴AB BE BC AB=， ∴2AB BC BE =⋅，∵25BC BE ⋅=，∴5AB =，连接AG ，∴BAG BAD DAG ∠=∠+∠，BGA GAC ACB ∠=∠+∠，∵点为内心，∴DAG GAC ∠=∠，又∵BAD BCD ACB ∠=∠=∠，∴BAD DAG GAC ACB ∠+∠=∠+∠，∴BAG BGA ∠=∠，∴5BG AB ==.【点睛】本题考查了等腰三角形的判定与性质，切线的判定，相似三角形的判定与性质，三角形的内心等知识，正确添加辅助线，熟练掌握和灵活运用相关知识是解题的关键.26.如图，在平面直角坐标系中，抛物线y ＝x (x ﹣b )﹣12与y 轴相交于A 点，与x 轴相交于B 、C 两点，且点C 在点B 的右侧，设抛物线的顶点为P ．(1)若点B 与点C 关于直线x ＝1对称，求b 的值;(2)若OB ＝OA ，求△BCP 的面积;(3)当﹣1≤x ≤1时，该抛物线上最高点与最低点纵坐标的差为h ，求出h 与b 的关系;若h 有最大值或最小值，直接写出这个最大值或最小值．【答案】(1)2(2)2764(3)h 存在最小值，最小值为1 【解析】【分析】 (1)由点B 与点C 关于直线x ＝1对称，可得出抛物线的对称轴为直线x ＝1，再利用二次函数的性质可求出b 值;(2)利用二次函数图象上点的坐标特征可求出点A 的坐标，结合OA ＝OB 可得出点B 的坐标，由点B 的坐标利用待定系数法可求出抛物线的解析式，由抛物线的解析式利用二次函数图象上点的坐标特征可求出点C 的坐标，利用配方法可求出点P 的坐标，再利用三角形的面积公式即可求出△BCP 的面积;(3)分b≥2，0≤b ＜2，﹣2＜b ＜0和b≤﹣2四种情况考虑，利用二次函数图象上点的坐标特征结合二次函数的图象找出h 关于b 的关系式，再找出h 的最值即可得出结论．【详解】解：(1)∵点B 与点C 关于直线x ＝1对称，y ＝x (x ﹣b )﹣12＝x 2﹣bx ﹣12， ∴﹣2b ＝1，解得：b ＝2． (2)当x ＝0时，y ＝x 2﹣bx ﹣12＝﹣12， ∴点A 的坐标为(0，﹣12)．又∵OB ＝OA ，∴点B 的坐标为(﹣12，0)．将B (﹣12，0)代入y ＝x 2﹣bx ﹣12，得：0＝14+12b ﹣12，解得：b ＝12， ∴抛物线的解析式为y ＝x 2﹣12x ﹣12．∵y ＝x 2﹣12x ﹣12＝(x ﹣14)2﹣916， ∴点P 的坐标为(14，﹣916)．当y ＝0时，x 2﹣12x ﹣12＝0，解得：x 1＝﹣12，x 2＝1， ∴点C 的坐标为(1，0)．∴S △BCP ＝12×[1﹣(﹣12)]×|﹣916|＝2764． (3)y ＝x 2﹣bx ﹣12＝(x ﹣2b )2﹣12﹣24b ．当2b ≥1，即b≥2时，如图1所示， y 最大＝b+12，y 最小＝﹣b+12， ∴h ＝2b ;当0≤2b ＜1，即0≤b ＜2时，如图2所示， y 最大＝b+12，y 最小＝﹣12﹣24b ， ∴h ＝1+b+24b ＝(1+2b )2; 当﹣1＜2b ＜0，﹣2＜b ＜0时，如图3所示 y 最大＝12﹣b ，y 最小＝﹣12﹣24b ， ∴h ＝1﹣b+24b ＝(1﹣2b )2; 当2b ≤﹣1，即b≤﹣2时，如图4所示， y 最大＝﹣b+12，y 最小＝b+12， h ＝﹣2b ．。

2022年中考数学模拟卷二习题课件新版新人教版

上一栏目解答题 19 20 21 22 23 24 25 下一栏目
21．(8分)如图，某小区规划在长32米，宽20米的矩形场地ABCD上修建三条同样宽的3条小路，使其中两条与AD平行，一条与AB平行，其余部分种草．若草坪的面积为566平方米，问小路应为多宽？解：设小路宽为x米．依题意，可得(32－2x)(20－x)＝566，整理，得x2－36x＋37＝0，解得x1＝18＋ 28(7舍去)， x2＝18－ 2.87 答：小路宽应为(18－ 28)米7 ．
2
2
上一栏目解答题 19 20 21 22 23 24 25 下一栏目
∴S＝S△ACM＋S△ADM＋S△BDM＝4＋2x－2－x2＋4x＋5＝－x2＋6x＋7， ∴S关于x的函数解析式为S＝－x2＋6x＋7(1＜x＜5)． ∵S＝－x2＋6x＋7＝－(x－3)2＋16， ∴当x＝3时，四边形ADBC的面积S有最大值，最大值为16.
＝ 3 (x＞0)和y＝－ 6 (x＞0)的图象交于B，A两点．若C是y轴上任意一点，
x
x
则△ABC的面积为( D)
A．3
B．6
C．9
D. 9
2
选择题 1 2 3 4 5 6 7 8 9 10 下一栏目
10．如图1，在矩形ABCD中，AB＞AD，对角线AC，BD相交于点O，动点P由
点A出发，沿AB→BC→CD向点D运动．设点P的运动路程为x，△AOP的
上一栏目附加题
附加题(20分)
如图，直线y＝mx＋1与x轴、y轴分别相交于A，B两点，与双曲线y＝x(k)(x＞0)
相交于点P，PC⊥x轴于点C，且PC＝2，点A的坐标为(－2，0)．
(1)求双曲线的解析式；
解：把A(－2，0)代入y＝mx＋1中，得m＝ 1 ，∴y＝1 x＋1.

2022年人教版九年级数学中考模拟试卷2(含答案解析)

2022年人教版九年级数学中考模拟试卷2一．选择题（共12小题，满分48分，每小题4分）1．计算|﹣2|+2﹣1的结果是（）A．﹣1B．0C．1D．22．下面各式计算正确的是（）A．（a5）2＝a7B．a8÷a2＝a6C．3a3•2a3＝6a9D．（a+b）2＝a2+b23．如图，直线AB∥CD∥EF，点O在直线EF上，下列结论正确的是（）A．∠α+∠β﹣∠γ＝90°B．∠α+∠γ﹣∠β＝180°C．∠γ+∠β﹣∠α＝180°D．∠α+∠β+∠γ＝180°4．如图，在长方体中，AB＝4，BC＝3，AA1＝5，若以BDD1B1为主（正）视平面，则该长方体左视图的面积为（）A．12B．C．25D．245．如图，在△ABC与△ADE中，∠BAC＝∠D，要使△ABC与△ADE相似，还需满足下列条件中的（）A．＝B．＝C．＝D．＝6．在一元一次不等式组的解集中，整数解的个数是（）A．4B．5C．6D．77．某地近年来持续干旱，为了倡导节约用水，该地一家庭记录了去年12个月的月用水量如表，m取1≤m≤3的整数，用水量x/吨34567频数1254﹣m m下列关于用水量的统计量不会发生变化的统计量是（）A．平均数、中位数B．众数、中位数C．平均数、方差D．众数、方差8．如图，A、B、C是⊙O上的三个点，∠AOB＝58°，则∠BCA的度数是（）A．58°B．42°C．32°D．29°9．如图，二次函数y＝ax2+bx+c的对称轴是直线x＝1，且经过点（﹣1，0），则下列结论：①abc＜0；②2a﹣b＝0；③a＜﹣；④若方程ax2+bx+c﹣2＝0的两个根为x1和x2，则（x1+1）（x2﹣3）＜0，正确的有（）个．A．1B．2C．3D．4。

初三模拟二数学试卷答案

一、选择题（每题5分，共50分）1. 若m+n=2，m^2+n^2=5，则m-n的值为（）A. 1B. -1C. 3D. -3答案：B解析：根据平方差公式，(m+n)^2 = m^2 + 2mn + n^2，代入m+n=2和m^2+n^2=5，得4 = 5 + 2mn，解得mn=-0.5。

再根据完全平方公式，(m-n)^2 = m^2 - 2mn +n^2，代入mn=-0.5，得(m-n)^2 = 5 + 1 = 6，所以m-n=±√6。

由于m+n=2，所以m-n不能为正数，故m-n=-√6，即m-n=-1。

2. 若a、b、c是等差数列的前三项，且a+b+c=12，则b的值为（）A. 4B. 6C. 8D. 10答案：B解析：等差数列的前三项之和等于中间项的三倍，即a+b+c=3b，代入a+b+c=12，得3b=12，解得b=4。

3. 若一个等比数列的公比为q，且q≠1，若前三项分别为a、ar、ar^2，则该数列的第四项为（）A. ar^3B. ar^4C. ar^5D. ar^6答案：B解析：等比数列的通项公式为an = a1 q^(n-1)，所以第四项为ar^3 q = ar^4。

4. 在直角坐标系中，点A(2,3)，点B(-1,-4)，则线段AB的中点坐标为（）A. (1,1)B. (1,-1)C. (3,1)D. (3,-1)答案：A解析：线段AB的中点坐标为((x1+x2)/2, (y1+y2)/2)，代入点A(2,3)和点B(-1,-4)，得中点坐标为((2-1)/2, (3-4)/2)，即(1,1)。

5. 若函数f(x) = ax^2 + bx + c的图象开口向上，且a>0，则下列说法正确的是（）A. b>0B. b<0C. c>0D. c<0答案：C解析：二次函数的开口方向由二次项系数a决定，a>0时开口向上。

对于开口向上的二次函数，顶点坐标为(-b/2a, c-b^2/4a)，因为a>0，所以顶点的y坐标c-b^2/4a>0，即c>0。

2022年人教版中考第二次模拟检测《数学卷》含答案解析

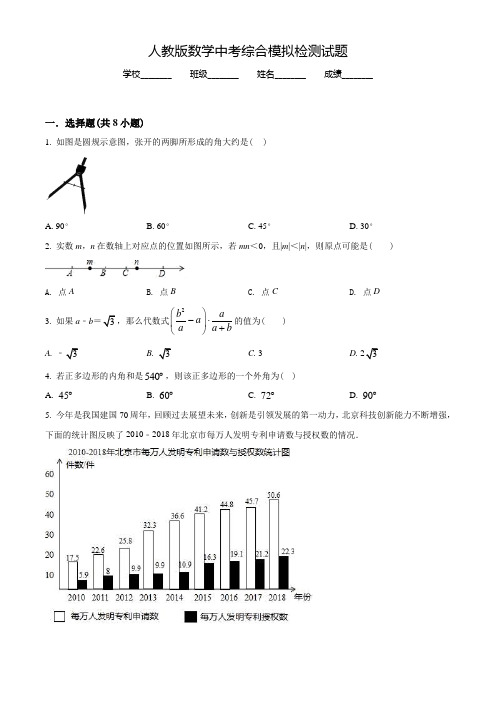
人教版数学中考综合模拟检测试题学校________ 班级________ 姓名________ 成绩________一．选择题(共8小题)1. 如图是圆规示意图，张开的两脚所形成的角大约是()A. 90°B. 60°C. 45°D. 30°2. 实数m，n在数轴上对应点的位置如图所示，若mn＜0，且|m|＜|n|，则原点可能是( )A. 点AB. 点BC. 点CD. 点D3. 如果a﹣b＝3，那么代数式2b aaa a b⎛⎫-⋅⎪+⎝⎭的值为( )A. ﹣3B. 3C. 3D. 234. 若正多边形的内角和是540︒，则该正多边形的一个外角为( )A. 45︒B. 60︒C. 72︒D. 90︒5. 今年是我国建国70周年，回顾过去展望未来，创新是引领发展的第一动力，北京科技创新能力不断增强，下面的统计图反映了2010﹣2018年北京市每万人发明专利申请数与授权数的情况．根据统计图提供的信息，下列推断合理的是( ) A. 2010﹣2018年，北京市毎万人发明专利授权数逐年增长B. 2010﹣2018年，北京市毎万人发明专利授权数的平均数超过10件C. 2010年申请后得到授权的比例最低D. 2018年申请后得到授权的比例最高6. 弹簧原长(不挂重物)15cm ，弹簧总长L (cm )与重物质量x (kg )的关系如下表所示：弹簧总长L (cm ) 16 17 18 19 20 重物重量x (kg )0.51.01.52.02.5当重物质量为5kg (在弹性限度内)时，弹簧总长L (cm )是( ) A. 22.5B. 25C. 27.5D. 307. 如图，抛物线2815y x x =-+与轴交于、两点，对称轴与轴交于点，点(0,2)D -，点(0,6)E -，点是平面内一动点，且满足90DPE ∠=︒，M 是线段PB 的中点，连结CM ．则线段CM 的最大值是( )．A. 3B.412C.72D. 58. 如图，点A ，B ，C 是⊙O 上的三个点，点D 在BC 的延长线上.有如下四个结论：①在∠ABC 所对的弧上存在一点E ，使得∠BCE =∠DCE ;②在∠ABC 所对的弧上存在一点E ，使得∠BAE =∠AEC ;③在∠ABC 所对的弧上存在一点E ，使得EO 平分∠AEC ;④在∠ABC 所对的弧上任意取一点E (不与点A ，C 重合) ，∠DCE=∠ABO +∠AEO 均成立.上述结论中，所有．．正确结论的序号是( )A. ①②③B. ①③④C. ②④D. ①②③④二．填空题(共8小题)9. 质地均匀的正方体骰子，其六个面上分别刻有1，2，3，4，5，6六个数字，投掷这个骰子一次，则向上一面的数字是偶数的概率为10. 用一组，，的值说明命题”若ac bc =，则a b =“是错误的，这组值可以是a =__________，b =__________，c =__________．11. 如图，某人从点A 出发，前进5m 后向右转60°，再前进5m 后又向右转60°，这样一直走下去，当他第一次回到出发点A 时，共走了_____m ．12. 如图所示的网格是正方形网格，△ABC 是_____三角形．(填”锐角”“直角”或”钝角”)13. 如图，过⊙O 外一点P 作⊙O 的两条切线P A ，PB ，切点分别为A ，B ，作直线BC ，连接AB ，AC ，若∠P ＝80°，则∠C ＝_____°．14. 如图，在矩形ABCD 中，过点B 作对角线AC 的垂线，交AD 于点E ，若AB ＝2，BC ＝4，则AE ＝_____．15. 2019年2月，全球首个5G 火车站在上海虹桥火车站启动.虹桥火车站中5G 网络峰值速率为4G 网络峰值速率的10倍.在峰值速率下传输8千兆数据，5G 网络比4G 网络快720秒，求这两种网络的峰值速率.设4G 网络的峰值速率为每秒传输x 千兆数据，依题意，可列方程为___.16. ▱ABCD 中，对角线AC 、BD 相交于点O ，E 是边AB 上的一个动点(不与A 、B 重合)，连接EO 并延长，交CD 于点F ，连接AF ，CE ，下列四个结论中： ①对于动点E ，四边形AECF 始终是平行四边形;②若∠ABC ＜90°，则至少存在一个点E ，使得四边形AECF 是矩形; ③若AB ＞AD ，则至少存在一个点E ，使得四边形AECF 菱形; ④若∠BAC ＝45°，则至少存在一个点E ，使得四边形AECF 是正方形．以上所有正确说法的序号是_____．三．解答题(共12小题)17.计算：052sin 60(2019)π-︒--18. 解不等式组: 4(21)31385x x x x -<+⎧⎪-⎨<⎪⎩19. 已知：如图1，直线，所成的角跑到画板外面去了，你有什么办法作出这两条直线所成角的角平分线? 小明的做法是： (1)如图2，画PC a ∥;(2)以为圆心，任意长为半径画圆弧，分别交直线，PC 于点，; (3)连结AD 并延长交直线于点;请你先完成下面的证明，然后完成第(4)步作图： ∵PC a ∥∴1PDA ∠=∠( )∵以圆心，任意长为半径画圆弧，分别交直线，PC 于点， ∴PA PD =∴PAB ∠=∠ ∴1PAB ∠=∠∴以直线，的交点和点、为顶点所构成的三角形为等腰三角形( ) 根据上面的推理证明完成第(4)步作图(4)请在图2画板内作出”直线，所成的跑到画板外面去的角”的平分线(画板内的部分)，尺规作出图形，并保留作图痕迹．第(4)步这么作图的理论依据是：．20. 已知关于的方程mx2+(2m-1)x+m-1=0(m≠0) .(1)求证：方程总有两个不相等的实数根;(2)若方程的两个实数根都是整数，求整数的值.21. 如图，在△ABC中，AB＝AC，D为BC中点，AE∥BD，且AE＝BD．(1)求证：四边形AEBD是矩形;(2)连接CE交AB于点F，若∠ABE＝30°，AE＝2，求EF的长．22. 在平面直角坐标系xOy中，直线l：y＝x+b与x轴交于点A(﹣2，0)，与y轴交于点B．双曲线ykx =与直线l交于P，Q两点，其中点P的纵坐标大于点Q的纵坐标(1)求点B的坐标;(2)当点P的横坐标为2时，求k的值;(3)连接PO，记△POB的面积为S．若112S＜＜，结合函数图象，直接写出k的取值范围．23. 如图，AB是O的直径，CB与O相切于点B．点D在O上，且BC BD=，连接CD交O于点E．过点E作EF⊥AB于点H，交BD于点M，交O于点F．(1)求证：∠MED=∠MDE．(2)连接BE，若3ME=，MB=2．求BE的长．24. 为了推动全社会自觉尊法学法守法用法，促进全面依法治国，某区每年都举办普法知识竞赛，该区某单位甲、乙两个部门各有员工200人，要在这两个部门中挑选一个部门代表单位参加今年的竞赛，为了解这两个部门员工对法律知识的掌握情况，进行了抽样调查，从甲、乙两个部门各随机抽取20名员工，进行了法律知识测试，获得了他们的成绩(百分制)，并对数据(成绩)进行整理，描述和分析，下面给出了部分信息．a．甲部门成绩的频数分布直方图如下(数据分成6组：40≤x＜50，50≤x＜60，60≤x＜70，70≤x＜80，80≤x ＜90，90≤x≤100)b．乙部门成绩如下：40 52 70 70 71 73 77 78 80 8182 82 82 82 83 83 83 86 91 94c．甲、乙两部门成绩的平均数、方差、中位数如下：平均数方差中位数甲79.6 36.84 78.5乙77 147.2 md．近五年该单位参赛员工进入复赛的出线成绩如下：2014年2015年2016年2017年2018年出线成绩(百79 81 80 81 82分制)根据以上信息，回答下列问题：(1)写出表中m值;(2)可以推断出选择部门参赛更好，理由为;(3)预估(2)中部门今年参赛进入复赛的人数为．25. 如图，P是直径AB上的一点，AB=6，CP⊥AB交半圆AB于点C，以BC为直角边构造等腰Rt△BCD，∠BCD=90°，连接OD．小明根据学习函数的经验，对线段AP，BC，OD的长度之间的关系进行了探究．下面是小明的探究过程，请补充完整：(1)对于点P在AB上的不同位置，画图、测量，得到了线段AP，BC，OD的长度的几组值，如下表：位置1 位置2 位置3 位置4 位置5 位置6 位置…AP 0.00 1.00 2.00 3.00 4.00 5.00 …BC 6.00 5.48 4.90 4.24 3.46 2.45 …OD 6.71 7.24 7.07 6.71 6.16 5.33 …在AP，BC，OD的长度这三个量中，确定________的长度是自变量，________的长度和________的长度都是这个自变量的函数;(2)在同一平面直角坐标系xOy中，画出(1)中所确定的函数的图象;(3)结合函数图象，解决问题：当OD=2BC时，线段AP的长度约为________．26. 在平面直角坐标系xOy中，抛物线y＝mx2﹣6mx+9m+1(m≠0)．(1)求抛物线的顶点坐标;(2)若抛物线与x轴的两个交点分别为A和B点(点A在点B的左侧)，且AB＝4，求m的值．(3)已知四个点C(2，2)、D(2，0)、E(5，﹣2)、F(5，6)，若抛物线与线段CD和线段EF都没有公共点，请直接写出m的取值范围．27. 已知C为线段AB中点，∠ACM＝α．Q为线段BC上一动点(不与点B重合)，点P在射线CM上，连接P A，PQ，记BQ＝kCP．(1)若α＝60°，k＝1，①如图1，当Q为BC中点时，求∠P AC的度数;②直接写出P A、PQ的数量关系;(2)如图2，当α＝45°时．探究是否存在常数k，使得②中的结论仍成立?若存在，写出k的值并证明;若不存在，请说明理由．28. 对于平面直角坐标系xOy中的点P，Q，给出如下定义：若P，Q为某个三角形的顶点，且边PQ上的高h，满足h＝PQ，则称该三角形为点P，Q的”生成三角形”．(1)已知点A(4，0);①若以线段OA为底的某等腰三角形恰好是点O，A的”生成三角形”，求该三角形的腰长;②若Rt△ABC是点A，B“生成三角形”，且点B在x轴上，点C在直线y＝2x﹣5上，则点B的坐标为;(2)⊙T的圆心为点T(2，0)，半径为2，点M的坐标为(2，6)，N为直线y＝x+4上一点，若存在Rt△MND，x的取值范围．是点M，N的”生成三角形”，且边ND与⊙T有公共点，直接写出点N的横坐标N答案与解析一．选择题(共8小题)1. 如图是圆规示意图，张开的两脚所形成的角大约是()A. 90°B. 60°C. 45°D. 30°【答案】B【解析】【分析】观察图形，直接判断结果．【详解】解：观察图形，张开的两脚所形成的角大约是60，故选B．【点睛】本题考查了角的概念，正确的识别图形是解题的关键．2. 实数m，n在数轴上对应的点的位置如图所示，若mn＜0，且|m|＜|n|，则原点可能是( )A. 点AB. 点BC. 点CD. 点D【答案】B【解析】【分析】由若mn＜0可知，m、n异号，所以原点可能是点B或点C，而又由|m|＜|n|即可根据距离正确判断．【详解】解：∵mn＜0∴m、n异号∴原点可能是点B或点C又由|m|＜|n|，观察数轴可知，原点应该是点B．故选B．【点睛】本题考查的是绝对值的意义，利用数形结合的思想研究绝对值会让问题更加明确清晰，是一种常用的方法．3. 如果a ﹣b 2b a a a a b ⎛⎫-⋅ ⎪+⎝⎭的值为( )A. C. 3 D. 【答案】A【解析】【分析】先化简分式，然后将a ﹣b ＝代入计算即可．【详解】解：原式＝22b a a a a b⋅-+ ＝()()a b a b a a a b-+-⋅+ ＝﹣(a ﹣b )，∵a ﹣b，故选A ．【点睛】本题考查了分式的化简求值，熟练掌握分式混合运算法则是解题的关键．4. 若正多边形的内角和是540︒，则该正多边形的一个外角为( )A. 45︒B. 60︒C. 72︒D. 90︒【答案】C【解析】【分析】根据多边形的内角和公式()2180n -•︒求出多边形的边数，再根据多边形的外角和是固定的360︒，依此可以求出多边形的一个外角．【详解】正多边形的内角和是540︒，多边形的边数为54018025︒÷︒+＝，多边形的外角和都是360︒，多边形的每个外角360572÷︒＝＝．故选．【点睛】本题主要考查了多边形的内角和与外角和之间的关系，关键是记住内角和的公式与外角和的特征，难度适中．5. 今年是我国建国70周年，回顾过去展望未来，创新是引领发展第一动力，北京科技创新能力不断增强，下面的统计图反映了2010﹣2018年北京市每万人发明专利申请数与授权数的情况．根据统计图提供的信息，下列推断合理的是( )A. 2010﹣2018年，北京市毎万人发明专利授权数逐年增长B. 2010﹣2018年，北京市毎万人发明专利授权数的平均数超过10件C. 2010年申请后得到授权的比例最低D. 2018年申请后得到授权的比例最高【答案】B【解析】【分析】根据统计图得出各年的具体数据，依据增长情况和百分比概念逐一判断即可得．【详解】解：A ．2010﹣2018年，北京市毎万人发明专利授权数在2012﹣2013年不变，此选项错误; B ．2010﹣2018年，北京市毎万人发明专利授权数的平均数为5.989.99.910.916.319.121.222.39++++++++≈13.7，超过10件，此选项正确; C ．2014年申请后得到授权的比例最低，此选项错误;D ．2017年申请后得到授权的比例最高，此选项错误;故选B ．【点睛】本题考查条形统计图、用样本估计总体，解答本题的关键是明确题意，利用数形结合的思想解答．6. 弹簧原长(不挂重物)15cm ，弹簧总长L (cm )与重物质量x (kg )的关系如下表所示：弹簧总长L (cm )16 17 18 19 20 重物重量x (kg ) 0.5 1.0 1.5 2.0 2.5当重物质量为5kg (在弹性限度内)时，弹簧总长L (cm )是( )A. 22.5B. 25C. 27.5D. 30【答案】B【解析】【分析】根据表格数据，建立数学模型，进而利用待定系数法可得函数关系式，当x ＝5时，代入函数解析式求值即可．【详解】设弹簧总长L (cm )与重物质量x (kg )的关系式为L ＝kx +b ，将(0.5，16)、(1.0，17)代入，得：0.51617k b k b +=⎧⎨+=⎩，解得：k 2b 15=⎧⎨=⎩， ∴L 与x 之间的函数关系式为：L ＝2x +15;当x ＝5时，L ＝2×5+15＝25(cm ) 故重物为5kg 时弹簧总长L 是25cm ，故选B ．【点睛】此题主要考查根据实际问题列一次函数关系式，解决本题的关键是得到弹簧长度的关系式，难点是得到x 千克重物在原来基础上增加的长度．7. 如图，抛物线2815y x x =-+与轴交于、两点，对称轴与轴交于点，点(0,2)D -，点(0,6)E -，点是平面内一动点，且满足90DPE ∠=︒，M 是线段PB 的中点，连结CM ．则线段CM 的最大值是( )．A. 3B. 412C.72D. 5【答案】C【解析】【分析】解方程x2−8x＋15＝0得A(3，0)，利用抛物线的性质得到C点为AB的中点，再根据圆周角定理得到点P 在以DE为直径的圆上，圆心Q点的坐标为(−4，0)，接着计算出AQ＝5，⊙Q的半径为2，延长AQ交⊙Q于F，此时AF的最大值为7，连接AP，利用三角形的中位线性质得到CM＝12AP，从而得到CM的最大值．【详解】解方程x2−8x＋15＝0得x1＝3，x2＝5，则A(3，0)，∵抛物线的对称轴与x轴交于点C，∴C点为AB的中点，∵∠DPE＝90°，∴点P在以DE为直径的圆上，圆心Q点的坐标为(−4，0)，AQ＝2234＝5，⊙Q的半径为2，延长AQ交⊙Q于F，此时AF最大，最大值为2＋5＝7，连接AP，∵M是线段PB的中点，∴CM为△ABP为中位线，∴CM＝12 AP，∴CM的最大值为72．故选：C．【点睛】本题考查了抛物线与x轴的交点：把求二次函数y＝ax2＋bx＋c(a，b，c是常数，a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程．也考查了二次函数的性质和圆周角定理．8. 如图，点A，B，C是⊙O上的三个点，点D在BC的延长线上.有如下四个结论：①在∠ABC所对的弧上存在一点E，使得∠BCE=∠DCE;②在∠ABC所对的弧上存在一点E，使得∠BAE=∠AEC;③在∠ABC所对的弧上存在一点E，使得EO平分∠AEC;④在∠ABC所对的弧上任意取一点E(不与点A，C重合)，∠DCE=∠ABO +∠AEO均成立.上述结论中，所有．．正确结论的序号是( )A. ①②③B. ①③④C. ②④D. ①②③④【答案】D【解析】【分析】①当BE是⊙O的直径时，根据圆周角定理和邻补角的定义得到结论;②当AE∥BC时，得到弧AB=弧CE，根据圆周角定理得到结论;③当点E是弧AC的中点时，根据角平分线的定义得到结论;④根据圆内接四边形的性质和四边形的内角和得到结论．【详解】解：①当BE是⊙O的直径时，∠BCE=∠DCE=90°，故①正确;②当AE∥BC时，弧AB=弧CE，∴弧BCE=弧ABC，∴∠BAE=∠AEC;故②正确;③当点E是弧AC的中点时，EO平分∠AEC;故正确;④如图2，∵∠A=∠ECD，∠A+12∠BOE=180°，∴∠ABO+∠AEO=360°-∠A-∠BOE=360°-∠DCE-2(180°-∠COE)，∴∠DCE=∠ABO+∠AEO，故正确;故选D ．【点睛】本题考查圆周角定理，解题关键是正确的理解题意．二．填空题(共8小题)9. 质地均匀的正方体骰子，其六个面上分别刻有1，2，3，4，5，6六个数字，投掷这个骰子一次，则向上一面的数字是偶数的概率为【答案】12 【解析】【分析】向上一面的数字是偶数的情况数除以总情况数6即为所求的概率．【详解】解：正方体骰子，六个面上分别刻有的1，2，3，4，5，6六个数字中，偶数为2，4，6，则向上一面的数字是偶数的概率为3162=．【点睛】明确概率的意义是解答的关键，用到的知识点为：概率等于所求情况数与总情况数之比． 10. 用一组，，的值说明命题”若ac bc =，则a b =“是错误的，这组值可以是a =__________，b =__________，c =__________．【答案】 (1). -1 (2). -2 (3). 0【解析】【分析】根据题意选择a 、b 、c 的值即可．【详解】当c ＝0，a ＝−1，b ＝−2，所以ac ＝bc ，但a ≠b ，当c ＝0，a ＝3，b ＝−2，所以ac ＝bc ，但a ≠b ，故答案不唯一;故答案为：-1;-2，0．【点睛】本题考查了命题与定理，要说明一个命题的正确性，一般需要推理、论证，而判断一个命题是假命题，只需举出一个反例即可．11. 如图，某人从点A出发，前进5m后向右转60°，再前进5m后又向右转60°，这样一直走下去，当他第一次回到出发点A时，共走了_____m．【答案】30【解析】【分析】从A点出发，前进5m后向右转60°，再前进5m后又向右转60°，…，这样一直走下去，他第一次回到出发点A时，所走路径为正多边形，根据正多边形的外角和为360°，判断多边形的边数，再求路程．【详解】解：依题意可知，某人所走路径为正多边形，设这个正多边形的边数为n，则60n＝360，解得n＝6，∴他第一次回到出发点A时一共走了：5×6＝30(m)，故答案为30．【点睛】本题考查了多边形的外角和，正多边形的判定与性质．关键是根据每一个外角判断多边形的边数．12. 如图所示的网格是正方形网格，△ABC是_____三角形．(填”锐角”“直角”或”钝角”)【答案】锐角【解析】【分析】根据三边的长可作判断．【详解】解：∵AB2＝32+12＝10，AC2＝12+42＝17，BC2＝32+42＝25，∴AB2+AC2＞BC2，∴△ABC为锐角三角形，故答案为锐角．【点睛】本题考查了三边的关系，会利用三边关系确定三角形的形状：若三角形的三边分别为a、b、c，①当a2+b2＞c2时，△ABC为锐角三角形;②当a2+b2＜c2时，△ABC为钝角三角形;③当a2+b2＝c2时，△ABC为直角三角形．13. 如图，过⊙O外一点P作⊙O的两条切线P A，PB，切点分别为A，B，作直线BC，连接AB，AC，若∠P＝80°，则∠C＝_____°．【答案】50【解析】【分析】根据切线的性质得出∠P AO＝∠PBO＝90°，求出∠AOB的度数，根据圆周角定理求出∠C即可．【详解】解：连接OA，∵过⊙O外一点P作⊙O的两条切线P A，PB，切点分别为A，B，∴∠P AO＝∠PBO＝90°，∵∠P＝80°，∴∠AOB＝360°﹣90°﹣90°﹣80°＝100°，∴∠C＝12AOB＝50°，故答案为50．【点睛】本题考查了切线的性质，圆周角定理等知识点，能求出∠AOB的度数和根据圆周角定理得出∠C＝12AOB是解此题的关键．14. 如图，在矩形ABCD中，过点B作对角线AC的垂线，交AD于点E，若AB＝2，BC＝4，则AE＝_____．【答案】1【解析】【分析】根据矩形的性质得到∠DAB＝∠ABC＝90°，AD＝BC＝4，根据勾股定理得到AC＝22AB BC+＝25，设AC与BE交于F，根据相似三角形的性质即可得到结论．【详解】解：∵四边形ABCD是矩形，∴∠DAB＝∠ABC＝90°，AD＝BC＝4，∴AC＝22AB BC+＝25，设AC与BE交于F，∵BE⊥AC，∴AB2＝AF•AC，∴AF＝2225525=，∴CF＝AC﹣AF＝855，∵AE∥BC，∴△AEF∽△CBF，∴AE AF BC CF=，∴255 4855AE=，∴AE＝1，故答案为1．【点睛】本题考查了矩形的性质，相似三角形的判定和性质，勾股定理，熟练掌握正方形的性质是解题的关键．15. 2019年2月，全球首个5G火车站在上海虹桥火车站启动.虹桥火车站中5G网络峰值速率为4G网络峰值速率的10倍.在峰值速率下传输8千兆数据，5G网络比4G网络快720秒，求这两种网络的峰值速率.设4G网络的峰值速率为每秒传输x千兆数据，依题意，可列方程为___.【答案】8872010x x-=【解析】【分析】设4G网络的峰值速率为每秒传输x千兆，则5G网络的峰值速率为每秒传输10x千兆，根据在峰值速率下传输8千兆数据，5G网络快720秒列出方程即可．【详解】解：设4G网络的峰值速率为每秒传输x千兆，则5G网络的峰值速率为每秒传输10x千兆，根据题意，得8872010x x-=．故答案为8872010x x-=．【点睛】本题考查了由实际问题抽象出分式方程，理解题意，找到等量关系列出方程是解题的关键．16. ▱ABCD中，对角线AC、BD相交于点O，E是边AB上的一个动点(不与A、B重合)，连接EO并延长，交CD于点F，连接AF，CE，下列四个结论中：①对于动点E，四边形AECF始终是平行四边形;②若∠ABC＜90°，则至少存在一个点E，使得四边形AECF是矩形;③若AB＞AD，则至少存在一个点E，使得四边形AECF是菱形;④若∠BAC＝45°，则至少存在一个点E，使得四边形AECF是正方形．以上所有正确说法的序号是_____．【答案】①③④【解析】分析】①根据平行四边形的性质得AB∥DC，OA＝OC，再由平行线的性质和对顶角相等可得∠OAE＝∠OCF，∠AOE＝∠COF，根据ASA来判定△AOE≌△COF，推出AE=CF,由此可判断四边形为平行四边形;②根据矩形的判定定理可知，当CE⊥AB时，四边形AECF为矩形，而图2-2中，AB<AD时，点E不在线段AB上;③根据菱形的判定定理可知：当EF⊥AC时，四边形AECF为菱形;④当CE⊥AB且∠BAC＝45°时，四边形AECF为正方形，在AB上一定存在一点E【详解】解：(1)如图1，∵四边形ABCD为平行四边形，对角线AC与BD交于点O，∴AB∥DC，AB＝DC，OA＝OC，OB＝OD，∴∠OAE＝∠OCF，∵∠AOE＝∠COF，∴△AOE≌△COF(ASA)，∴AE＝CF，又∵AE∥CF，∴四边形AECF为平行四边形，即E在AB上任意位置(不与A、B重合)时，四边形AECF恒为平行四边形，故选项①正确;(2)如图2，当∠ABC＜90°,当CE⊥AB时，四边形AECF为矩形，在图2中，AB>AD时，存在一点E, 使得四边形AECF是矩形;而图2-2中，AB<AD时，点E不在线段AB上;故选项②不正确．(3)如图3，当EF⊥AC时，四边形AECF为菱形，∵AB＞AD，∴在AB 上一定存在一点E, 使得四边形AECF 是矩形;故选项③正确．(4)如图4，当CE ⊥AB 且∠BAC ＝45°时，四边形AECF 为正方形，故选项④正确．故答案为：①③④．【点睛】本题主要考查平行四边形以及几种特殊平行四边形的判定．熟悉平行四边形、矩形、菱形、正方形的判定方法是解答此题的关键．三．解答题(共12小题)17. 计算：05122sin 60(2019)π-︒-- 【答案】4 3.+【解析】【分析】原式第一项利用绝对值的代数意义化简，第二项化为最简二次根式，第三项利用利用特殊角的三角函数值计算，第四项利用零指数幂法则计算，最后进行加减运算即可. 【详解】()05122sin602019π-︒--， =35321+-， =4 3.【点睛】此题考查了实数的运算，熟练掌握运算法则是解本题的关键． 18. 解不等式组: 4(21)31385x x x x -<+⎧⎪-⎨<⎪⎩ 【答案】4x 1-<<.【解析】【分析】分别解出两不等式的解集，再求其公共解．【详解】()42131385x x x x ⎧-+⎪⎨-⎪⎩＜①＜② 解不等式①得：x ＜1，解不等式②得：x ＞-4，所以不等式组的解集为：-4＜x ＜1．【点睛】此题考查解一元一次不等式组，求不等式组的解集应遵循以下原则：同大取较大，同小取较小，小大大小中间找，大大小小解不了．19. 已知：如图1，直线，所成的角跑到画板外面去了，你有什么办法作出这两条直线所成角的角平分线? 小明的做法是：(1)如图2，画PC a ∥;(2)以为圆心，任意长为半径画圆弧，分别交直线，PC 于点，;(3)连结AD 并延长交直线于点;请你先完成下面的证明，然后完成第(4)步作图：∵PC a ∥∴1PDA ∠=∠( )∵以为圆心，任意长为半径画圆弧，分别交直线，PC 于点，∴PA PD =∴PAB ∠=∠∴1PAB ∠=∠∴以直线，的交点和点、为顶点所构成的三角形为等腰三角形( )根据上面的推理证明完成第(4)步作图(4)请在图2画板内作出”直线，所成的跑到画板外面去的角”的平分线(画板内的部分)，尺规作出图形，并保留作图痕迹．第(4)步这么作图的理论依据是：．【答案】两直线平行，同位角相等;PDA ;等角对等边;等腰三角形三线合一【解析】【分析】根据平行线的性质及圆的特点得到1PAB ∠=∠，故可得以直线，的交点和点、为顶点所构成的三角形为等腰三角形，然后根据等腰三角形三线合一即可作图．【详解】(1)如图2，画PC a ∥;(2)以为圆心，任意长为半径画圆弧，分别交直线，PC 于点，;(3)连结AD 并延长交直线于点;请你先完成下面的证明，然后完成第(4)步作图：∵PC a ∥∴1PDA ∠=∠(两直线平行，同位角相等)∵以为圆心，任意长为半径画圆弧，分别交直线，PC 于点，∴PA PD =∴PAB ∠=∠PDA∴1PAB ∠=∠∴以直线，的交点和点、为顶点所构成的三角形为等腰三角形(等角对等边)根据上面的推理证明完成第(4)步作图(4)请在图2画板内作出”直线，所成的跑到画板外面去的角”的平分线(画板内的部分)，尺规作出图形，并保留作图痕迹．第(4)步这么作图的理论依据是：等腰三角形三线合一故答案为：两直线平行，同位角相等;PDA ;等角对等边;等腰三角形三线合一．【点睛】此题主要考查复杂尺规作图，解题的关键是熟知平行线的性质、圆的基本性质及等腰三角形的判定与性质．20. 已知关于的方程mx 2+(2m-1)x+m-1=0(m≠0) .(1)求证：方程总有两个不相等的实数根;(2)若方程的两个实数根都是整数，求整数的值.【答案】(1)证明见解析(2)m=1或m=-1【解析】试题分析：(1)由于m≠0，则计算判别式的值得到1=，从而可判断方程总有两个不相等的实数根;(2)先利用求根公式得到1211,1x xm=-=-，然后利用有理数的整除性确定整数的值．试题解析：(1)证明：∵m≠0，∴方程为一元二次方程，2(21)4(1)10m m m=---=>，∴此方程总有两个不相等的实数根;(2)∵(21)12mxm--±=，1211,1x xm∴=-=-，∵方程的两个实数根都是整数，且m是整数，∴m=1或m=−1.21. 如图，在△ABC中，AB＝AC，D为BC中点，AE∥BD，且AE＝BD．(1)求证：四边形AEBD是矩形;(2)连接CE交AB于点F，若∠ABE＝30°，AE＝2，求EF的长．【答案】(1)证明见解析27．【解析】【分析】(1)由AE∥BD，且AE＝BD可得四边形AEBD是平行四边形,再根据AB＝AC，D为BC中点,可知AD⊥BC 即可得出四边形AEBD是矩形.(2)根据30°所对的直角边是斜边的一半即可求出EB,再根据矩形的性质求出BC即可利用勾股定理求出EC,由题意可证△AEF∽△BCF,再根据对应边成比例即可求出结果.【详解】(1)证明：∵AE∥BD，AE＝BD，∴四边形AEBD是平行四边形，∵AB＝AC，D为BC的中点，∴AD⊥BC，∴∠ADB＝90°，∴四边形AEBD是矩形．(2)解：∵四边形AEBD是矩形，∴∠AEB＝90°，∵∠ABE＝30°，AE＝2，∴BE＝23，BC＝4，∴EC＝27，∵AE∥BC，∴△AEF∽△BCF，∴12 EF AECF BC，∴EF13=EC=273．【点睛】本题为矩形与等腰三角形的结合题型,关键在于熟练掌握矩形与等腰三角形的性质.22. 在平面直角坐标系xOy中，直线l：y＝x+b与x轴交于点A(﹣2，0)，与y轴交于点B．双曲线ykx =与直线l交于P，Q两点，其中点P的纵坐标大于点Q的纵坐标(1)求点B的坐标;(2)当点P的横坐标为2时，求k的值;(3)连接PO，记△POB的面积为S．若112S＜＜，结合函数图象，直接写出k的取值范围．【答案】(1)点B的坐标为(0，2);(2)k的值为8;(3)54＜k＜3.【解析】【分析】(1)有点A的坐标，可求出直线的解析式，再由解析式求出B点坐标．(2)把点P的横坐标代入直线解析式即可求得点P的纵坐标，然后把点P代入反比例函数解析式即可得k值．(3)根据△POB的面积为S的取值范围求点P的横坐标取值，然后把横坐标代入直线解析式，即可求得点P 纵坐标的取值范围，进而求得k的取值范围．【详解】解：(1)∵直线l：y＝x+b与x轴交于点A(﹣2，0)∴﹣2+b＝0∴b＝2∴一次函数解析式为：y＝x+2∴直线l与y轴交于点B为(0，2)∴点B的坐标为(0，2);(2)∵双曲线ykx=与直线l交于P，Q两点∴点P在直线l上∴当点P的横坐标为2时，y＝2+2＝4 ∴点P的坐标为(2，4)∴k＝2×4＝8∴k的值为8(3)如图：S△BOP12=⨯2×x p＝x p，∵11 2S＜＜，∴12＜x p＜1，∴52＜y p＜3，∴54＜k＜3【点睛】本题主要涉及一次函数与反比例函数相交的知识点．根据交点既在一次函数上又在反比例函数上，即可解决问题．23. 如图，AB 是O 的直径，CB 与O 相切于点B ．点D 在O 上，且BC BD =，连接CD 交O 于点E ．过点E 作EF ⊥AB 于点H ，交BD 于点M ，交O 于点F ． (1)求证：∠MED=∠MDE ．(2)连接BE ，若3ME =，MB=2．求BE 的长．【答案】(1)证明见解析;(2)10【解析】【分析】(1)由题意得//EF BC ，则C DEM ∠=∠，又C MDE ∠=∠，则结论得证;(2)连BE ，BE BF =，可得BEF D ∠=∠，可证BEM BDE ∆∆∽，则2BE BM BD =，可求BE 的长．【详解】(1)证明：CB 与O 相切于点，OB BC ∴⊥，EF AB ⊥，//EF BC ∴，DEM C ∴∠=∠，BC BD =，C MDE ∴∠=∠，MED MDE ∴∠=∠;(2)EF AB ⊥，AB 是O 的直径，BE BF =，D BEF ∴∠=∠，EBM DBE ∠=∠，BEM BDE ∆∆∽，BE BD BM BE=，即2BE BM BD =， MED MDE ∠=∠3∴==ME MDBM=,2BD MB MD∴=+=5BE=．10【点睛】本题主要考查了等腰三角形和平行线之间的角度转化以及圆周角定理和相似综合，熟练的在圆中找出对应的相似三角形是求解本题的关键.24. 为了推动全社会自觉尊法学法守法用法，促进全面依法治国，某区每年都举办普法知识竞赛，该区某单位甲、乙两个部门各有员工200人，要在这两个部门中挑选一个部门代表单位参加今年的竞赛，为了解这两个部门员工对法律知识的掌握情况，进行了抽样调查，从甲、乙两个部门各随机抽取20名员工，进行了法律知识测试，获得了他们的成绩(百分制)，并对数据(成绩)进行整理，描述和分析，下面给出了部分信息．a．甲部门成绩的频数分布直方图如下(数据分成6组：40≤x＜50，50≤x＜60，60≤x＜70，70≤x＜80，80≤x ＜90，90≤x≤100)b．乙部门成绩如下：40 52 70 70 71 73 77 78 80 8182 82 82 82 83 83 83 86 91 94c．甲、乙两部门成绩的平均数、方差、中位数如下：平均数方差中位数甲79.6 36.84 78.5乙77 147.2 md．近五年该单位参赛员工进入复赛的出线成绩如下：2014年2015年2016年2017年2018年出线成绩(百79 81 80 81 82分制)。

人教版中考二模测试《数学试卷》含答案解析

人教版数学中考综合模拟检测试题学校________ 班级________ 姓名________ 成绩________一、选择题1.的相反数是( ) A. 7B. 17-C. D. 12.使3x -有意义的的取值范围是( ) A. 3x >B. 3x <C. 3x ≥D. 3x ≠3.掷一枚质地均匀的硬币10次，下列说法正确的是( ) A. 每两次必有1次正面向上 B. 可能有5次正面向上 C. 必有5次正面向上D. 不可能有10次正面向上4.下列图形中，不是轴对称图是( )A. B. C. D.5.如图是下面哪个图形俯视图( )A. B.C. D.6.经过某十字路口的汽车，可能直行，也可能向左转或向右转，如果这三种可能性大小相同，则两辆汽车经过这个十字路口时，一辆向右转，一辆向左转的概率是( )A.23B.29C.13D.197.我国古代数学名著《孙子算经》中记载了一道题，大意是：有100匹马恰好拉了100片瓦，已知1匹大马能拉3片瓦，3匹小马能拉1片瓦，问有多少匹大马、多少匹小马?设大马有匹，小马有匹，可列方程组为( )A. 10033100x y x y +=⎧⎨+=⎩B. 1003100x y x y +=⎧⎨+=⎩C. 1003100x y x y +=⎧⎨+=⎩D. 100131003x y x y +=⎧⎪⎨+=⎪⎩8.已知()11,A x y 、()22,B x y 两点在反比例函数()10ky x x+=>的图象上，下列三个命题：①若12x y =，则12y x =;②若12019x =，22020x =，则12y y >;③过、两点的直线与轴、轴分别交于、两点，连接OA 、OB ，则AOC BOD S S =△△．其中真命题个数是( )A. 0B. 1C. 2D. 39.已知整数1a 、2a 、3a 、4a 、……满足下列条件：10a =，211a a =-+，322a a =-+，433a a =-+，……，1n n a a n +=-+(为正整数)依此类推，则2020a 的值为( )A 1008-B. 1009-C. 1010-D. 1011-10.如图，PA 、PB 是O 的切线，、为切点，是劣弧AB 的中点，连接BC 并延长交PA 于，若23PD AD =，则CDCB的值为( )A.13B.23C.35D.25二、填空题11.12的结果是______．12.自从”新冠病毒”爆发以来，胖胖同学每周且每天3次自测体温．结果统计如下表：体温(°C ) 36.1 36.2 36.3 36.4 36.5 36.6 367 次数 2346312则这些体温的众数是______°C ． 13.计算22111m m m +--的结果是______． 14.如图，将菱形纸片ABCD 折叠，使点落在AD 边的点处，折痕为CE ，若70D ∠=︒，则AEF ∠的度数是______．15.二次函数()20y ax bx c a =++≠的图象经过点()2,0-，()0,0x ，012x <<，与轴的负半轴相交，且交点在()0,2-的上方．下列四个结论中一定正确的是______． ①0b >;②210a b --<;③20a c +<;④3a b <．(填序号即可)16.【问题探究】如图1，//a b ，直线MN a ⊥，垂足为M ，交于点，点到直线的距离为2，点到的距离为1，1MN =，5AB =，则AM BN +的最小值是______;(提示：将线段BN 沿NM 方向平移1个单位长度即可解决，如图2所示．)【关联运用】如图3，在等腰Rt ABC 和等腰Rt DEF △中，90ACB DFE ∠=∠=︒，EF 在直线AB 上，24BC DF ==，连接CE 、CF ，则CE CF +的最小值是______．三、解答题17.计算：()2248233a a a a a -÷+．18.如图，已知AC ⊥AE ，BD ⊥BF ，∠1＝∠2，求证：AE ∥BF ．19.2020年2月10日，光明中学团委利用网络平台组织八年级600名学生参加”全民抗疫”知识大赛．为了了解本次大赛的成绩，随机抽取了部分学生的成绩作为样本，按，，，四个等级进行统计，制成如下不完整的统计图．(说明：级80分-100分，级70分-79分，级60-69分，级0分-59分)根据所给信息，解答以下问题：(1)在扇形统计图中，级对应的扇形的圆心角是______度; (2)补全条形统计图;(3)所抽取学生的足球运球测试成绩的中位数会落在______等级;(4)若成绩达到等级的学生可以选为志愿者，请估计该校八年级600名学生中可以选为志愿者学生有多少人? 20.请仅用无刻度直尺完成下列画图，不写画法，保留画图痕迹．(1)如图1，在77⨯的正方形网格中，每个小正方形的边长为1，小正方形的顶点叫做格点．ABC 的顶点在格点上，过点画一条直线．．平分ABC 的面积; (2)如图2，点在正方形ABCD 的内部，且EB EC =，过点画一条射线．．平分BEC ∠; (3)如图3，点、、均在O 上，且120BAC ∠=︒，在优弧BC 上画M 、两点．．，使60MAN ∠=︒．21.在等边ABC 中，点在边BC 上，以OC 为半径的O 交AC 于点，过点作DE AB ⊥于点．(1)如图1，求证：DE 为O 的切线;(2)如图2，连接AO 交DE 于点，若为DE 中点，求tan CAO ∠的值．22.某超市销售一种文具，进价为 5(元/件)，售价为6(元/件)时，当天的销售量为100件，在销售过程中发现：售价每上涨0.5元，当天的销售量就减少5件，设当天销售单价统一为 (元/件)(6x ≥，且是按0.5元的倍数上涨)，当天销售利润为元．(1)求与函数关系式(不要求写出自变量的取值范围); (2)要使当天销售利润不低于240元，求当天销售单价的范围;(3)若每件文具的利润不超过60%，要使当天获得利润最大，每件文具售价为多少元?并求出最大利润. 23.在ABC 中，AB AC =，点在底边BC 上，EDF ∠的两边分别交AB 、AC 所在直线于、两点，2EDF ABC ∠=∠，BD nCD =．(1)如图1，若45ABC ∠=︒，1n =，求证：DE DF =;(2)如图2，求DEDF的值(含的式子表示);(3)如图3，连接EF ，若tan 1B ∠=，//EF BC ，且58EF BC =，直接写出的值为______．24.抛物线：2y ax c =+与轴交于点、两点，与轴交于点()0,1C -，且4AB OC =． (1)直接写出抛物线的解析式;(2)如图1，点M 在轴左侧的抛物线上，将点M 先向右平移4个单位长度，再向下平移()0n n ≥个单位长度，得到的对应点恰好落在抛物线上，若2MNC S =△，求点M 的坐标;(3)如图2，将抛物线向上平移2个单位长度得到抛物线1C ，一次函数y kx b =+的图象与抛物线1C 只有一个公共点，与轴交于点，探究：轴上是否存在定点满足90EGF ∠=︒?若存在，求出点的坐标;否则，说明理由．答案与解析一、选择题1.的相反数是( ) A. 7 B. 17-C. D. 1【答案】A 【解析】【分析】根据相反数的代数意义：只有符号不同的两个数,互为相反数，即可得出结论．【详解】解：的相反数是7 故选A ．【点睛】此题考查的是求一个数的相反数，掌握相反数的代数意义是解决此题的关键．2.有意义的的取值范围是( ) A. 3x > B. 3x <C. 3x ≥D. 3x ≠【答案】C 【解析】分析：根据被开方数是非负数，可得答案．详解：由题意，得 x-3≥0，解得x≥3，故选C ．点睛：本题考查了二次根式有意义的条件，利用得出不等式是解题关键． 3.掷一枚质地均匀的硬币10次，下列说法正确的是( ) A. 每两次必有1次正面向上 B. 可能有5次正面向上 C. 必有5次正面向上 D. 不可能有10次正面向上【答案】B 【解析】【分析】根据概率的意义即可判断选项正否，排除法求解.【详解】ACD 都将概率的意义理解错，概率不代表必有或不可能，故ACD 错误，选B.【点睛】本题考查了概率的判断，解题的关键是清楚概率不代表几次中一定发生或者不发生某个事件.4.下列图形中，不是轴对称图的是()A. B. C. D.【答案】D【解析】【分析】根据轴对称图形的定义：在平面内，如果一个图形沿一条直线折叠，直线两旁的部分能够完全重合，这样的图形叫做轴对称图形，即可得出结论．【详解】解：A选项是轴对称图形，故本选项不符合题意;B选项是轴对称图形，故本选项不符合题意;C选项是轴对称图形，故本选项不符合题意;D选项不是轴对称图形，故本选项符合题意．故选D．【点睛】此题考查的是轴对称图形的识别，掌握轴对称图形的定义是解决此题的关键．5.如图是下面哪个图形的俯视图( )A. B.C. D.【答案】D【解析】【分析】根据各选项的俯视图进行判断即可．【详解】解：A．球的俯视图为一个圆(不含圆心)，不合题意;B．圆柱的俯视图为一个圆(不含圆心)，不合题意;C．圆台的俯视图为两个同心圆，不合题意;D．圆锥的俯视图为一个圆(含圆心)，符合题意;故选D．【点睛】本题主要考查了简单几何体的三视图，俯视图是从上往下看得到的平面图形．6.经过某十字路口的汽车，可能直行，也可能向左转或向右转，如果这三种可能性大小相同，则两辆汽车经过这个十字路口时，一辆向右转，一辆向左转的概率是( )A. 23B.29C.13D.19【答案】B【解析】【分析】可以采用列表法或树状图求解．可以得到一共有9种情况，一辆向右转，一辆向左转有2种结果数，根据概率公式计算可得．【详解】画”树形图”如图所示：∵这两辆汽车行驶方向共有9种可能的结果，其中一辆向右转，一辆向左转的情况有2种，∴一辆向右转，一辆向左转的概率为29;故选B．【点睛】此题考查了树状图法求概率．解题的关键是根据题意画出树状图，再由概率＝所求情况数与总情况数之比求解7.我国古代数学名著《孙子算经》中记载了一道题，大意是：有100匹马恰好拉了100片瓦，已知1匹大马能拉3片瓦，3匹小马能拉1片瓦，问有多少匹大马、多少匹小马?设大马有匹，小马有匹，可列方程组为()A.10033100x yx y+=⎧⎨+=⎩B.1003100x yx y+=⎧⎨+=⎩C.1003100x yx y+=⎧⎨+=⎩D.100131003x yx y+=⎧⎪⎨+=⎪⎩【答案】D 【解析】【分析】根据题意，列出二元一次方程组即可．【详解】解：由题意可得100131003x y x y +=⎧⎪⎨+=⎪⎩故选D ．【点睛】此题考查的是二元一次方程组的应用，掌握实际问题中的等量关系是解决此题的关键． 8.已知()11,A x y 、()22,B x y 两点在反比例函数()10ky x x+=>的图象上，下列三个命题：①若12x y =，则12y x =;②若12019x =，22020x =，则12y y >;③过、两点的直线与轴、轴分别交于、两点，连接OA 、OB ，则AOC BOD S S =△△．其中真命题个数是( )A. 0B. 1C. 2D. 3【答案】D 【解析】【分析】将点A 、B 的坐标代入反比例函数解析式中即可判断①;然后利用反比例函数的增减性即可判断②;设1=+m k ，直线CD 的解析式为y=ax ＋b ，然后利用待定系数法求出直线CD 的解析式，从而求出点C 和点D 的坐标，然后根据点A 、B 的位置分类讨论，分别画出对应的图形，根据三角形的面积公式即可判断③．【详解】解：将A 、B 的坐标代入()10ky x x+=>中，得 111+=k y x ，221+=ky x 变形可得221+=kx y 若12x y = ∴111+=k y x =221+=kx y ，故①正确;∵1+k ＞0，x ＞0∴反比例函数图象在第一象限，y 随x 的增大而减小 ∵当12019x =＜22020x =， ∴12y y >，故②正确;设1=+m k ，直线CD 的解析式为y=ax ＋b ， ∴反比例函数的解析式为()0my x x=> ∴11,⎛⎫ ⎪⎝⎭m A x x 、22,⎛⎫ ⎪⎝⎭m B x x ，将点A 、B 的坐标代入y=ax ＋b 中，得1122max b x m ax bx ⎧=+⎪⎪⎨⎪=+⎪⎩ 解得：()121212m a x x m x x b x x ⎧=-⎪⎪⎨+⎪=⎪⎩∴直线CD 的解析式为121212+=-+m mx mx y x x x x x 当x=0时，y=1212+mx mx x x ;当y=0时，x=12x x +∴点D 的坐标为(0，1212+mx mx x x )，点C 的坐标为(12x x +，0)当点B 在点A 左侧时，过点B 作BE ⊥y 轴于E ，过点A 作AF ⊥x 轴于F ，如下图所示∴AF=1mx ，BE=2x ，OC=12x x +，OD=1212+mx mx x x∴S △AOC =12OC ·AF=12()12x x +·1m x =1212+mx mx x S △BOD =12OD ·BE=12·1212+mx mx x x ·2x =1212+mx mx x ∴S △AOC = S △BOD ;当点B 在点A 右侧时，过点A 作AE ⊥y 轴于E ，过点B 作BF ⊥x 轴于F ，如下图所示∴BF=2m x ，AE=1x ，OC=12x x +，OD=1212+mx mx x x ∴S △AOD =12OD ·AE=12·1212+mx mx x x ·1x =1222+mx mx x S △BOC =12OC ·BF=12·()12x x +·2m x =1222+mx mx x ∴S △AOD = S △BOC∴S △AOD ＋S △AOB = S △BOC ＋S △AOB ∴S △AOC = S △BOD ，故③正确．综上：正确的有结论有3个故选D ．【点睛】此题考查的是反比例函数和一次函数的综合题型，掌握利用待定系数法求一次函数解析式、反比例函数的图象及性质是解决此题的关键．9.已知整数1a 、2a 、3a 、4a 、……满足下列条件：10a =，211a a =-+，322a a =-+，433a a =-+，……，1n n a a n +=-+(为正整数)依此类推，则2020a 的值为( )A. 1008-B. 1009-C. 1010-D. 1011-【答案】C 【解析】【分析】根据题意，分别求出1a 、2a 、3a 、4a 、5a ，然后总结规律即可推出2020a 的值．【详解】解：由题意可知：10a =;2011a =-+=-;3121a =--+=-;4132a =--+=-;5242a =--+=-……(2020－1)÷2=1009……1 故()2020100911010a =-+=- 故选C ．【点睛】此题考查的是探索规律题，找到运算规律是解决此题的关键． 10.如图，PA 、PB 是O 的切线，、为切点，是劣弧AB 的中点，连接BC 并延长交PA 于，若23PD AD =，则CDCB的值为( )A.13B.23C.35D.25【答案】D 【解析】【分析】连接OA 、OB 、OP ，过点D 作DE ∥PB 交OP 于点E ，根据切线长定理可得PA=PB ，∠APO=∠BPO ，∠AOP=∠BOP ，利用等角对等边证出DE=PD ，然后证出△DEC ∽△BPC ，列出比例式即可求出结论．【详解】解：连接OA 、OB 、OP ，过点D 作DE ∥PB 交OP 于点E∵PA 、PB 是O 的切线，∴PA=PB ，∠APO=∠BPO ，∠AOP=∠BOP ∵是劣弧AB 的中点，23PD AD = ∴PO 必过点C ，25=PD PA ∵DE ∥PB∴△DEC ∽△BPC ，∠DEC=∠BPO ∴=CD DECB PB，∠DEC=∠APO ∴DE=PD ∴25===CD DE PD CB PB PA 故选D ．【点睛】此题考查的是切线长定理、等腰三角形的判定和相似三角形的判定及性质，掌握切线长定理、等腰三角形的判定和相似三角形的判定及性质是解决此题的关键．二、填空题11.的结果是______．【答案】【解析】【分析】根据二次根式的乘法公式化简即可．==故答案为：【点睛】此题考查的是二次根式的化简，掌握二次根式的乘法公式是解决此题的关键． 12.自从”新冠病毒”爆发以来，胖胖同学每周且每天3次自测体温．结果统计如下表：则这些体温众数是______°C ．【答案】36.4 【解析】【分析】根据众数的定义：是一组数据中出现次数最多的数值，叫众数，即可得出结论．【详解】解：由表格可知：这些体温的众数是36.4°C 故答案为：36.4．【点睛】此题考查的是求一组数据的众数，掌握众数的定义是解决此题的关键．13.计算22111m m m +--的结果是______．【答案】11m + 【解析】【分析】根据分式的加法法则计算即可．【详解】解：22111m m m+-- =22111-+--m m m =()()111--+m m m=11m + 故答案为：11m +．【点睛】此题考查的是分式的加法运算，掌握分式的加法法则是解决此题的关键．14.如图，将菱形纸片ABCD 折叠，使点落在AD 边的点处，折痕为CE ，若70D ∠=︒，则AEF ∠的度数是______．【答案】30° 【解析】【分析】根据菱形的性质可得CB=CD ，∠B=∠D=70°，∠A=180°－∠B=110°，然后根据折叠的性质可得CB=CF ，∠B=∠CFE=70°，根据等边对等角证出∠CFD=∠D=70°，根据平角的定义求出∠AFE ，再根据三角形内角和定理即可求出结论．【详解】解：∵四边形ABCD 为菱形，∠D=70°∴CB=CD ，∠B=∠D=70°，∠A=180°－∠B=110° 由折叠的性质可得CB=CF ，∠B=∠CFE=70° ∴CF=CD∴∠CFD=∠D=70°∴∠AFE=180°－∠CFE －∠CFD=40° ∴∠AEF=180°－∠A －∠AFE=30° 故答案为：30°．【点睛】此题考查的是菱形的性质、折叠的性质、等腰三角形的性质和三角形内角和定理，掌握菱形的性质、折叠的性质、等腰三角形的性质和三角形内角和定理是解决此题的关键．15.二次函数()20y ax bx c a =++≠的图象经过点()2,0-，()0,0x ，012x <<，与轴的负半轴相交，且交点在()0,2-的上方．下列四个结论中一定正确的是______． ①0b >;②210a b --<;③20a c +<;④3a b <．(填序号即可) 【答案】①②③ 【解析】【分析】根据题意，画出图形，由图象易知：a ＞0，对称轴为直线x=2ba-＜0，-2＜c ＜0，从而判断①;将()2,0-代入2y ax bx c =++中，可得24c b a =-，结合c 的取值范围即可判断②;结合②可知42+=a cb ，然后将x=1代入二次函数解析式中可得0y a bc =++<，从而判断③;化简32-a ba即可判断④．【详解】解：根据题意，画图如下由图象易知：a ＞0，对称轴为直线x=2ba-＜0，-2＜c ＜0 ∴b ＞0，故①正确;将()2,0-代入2y ax bx c =++中，得420a b c -+= ∴24c b a =- ∴-2＜24b a - ∴422--a b ＜0∴210a b --<，故②正确; ∵420a b c -+= ∴42+=a cb 由图象可知，当x=1时，0y a bc =++< ∴402+++<a ca c 变形，得20a c +<，故③正确;由图象可知，当x=13-时，11093=-+<y a b c3113322262-⎛⎫=-⨯=- ⎪⎝⎭a b b b a a a ∵无法判断2ba -和16-的大小 ∴无法判断162-b a 的符号 ∴无法判断32-a ba的符号 ∴无法比较a 和3b 的大小，故④错误．综上：正确的有①②③．故答案为：①②③．【点睛】此题考查的是二次函数的图象及性质，掌握二次函数的图象及性质与各项符号的关系是解决此题的关键．16.【问题探究】如图1，//a b ，直线MN a ⊥，垂足为M ，交于点，点到直线的距离为2，点到的距离为1，1MN =，5AB =，则AM BN +的最小值是______;(提示：将线段BN 沿NM 方向平移1个单位长度即可解决，如图2所示．)【关联运用】如图3，在等腰Rt ABC 和等腰Rt DEF △中，90ACB DFE ∠=∠=︒，EF 在直线AB 上，24BC DF ==，连接CE 、CF ，则CE CF +的最小值是______．【答案】(1). 32(2). 213【解析】【分析】[问题探究]过点A作AH⊥b于H，过点B作BK⊥b于K，作BJ⊥AH交AH的延长线于J，连接MK、AB+=AM＋MK≥AK(当且仅当A、M、K共线时，取等号)，然和AK，根据两点之间线段最短可得AM BN后利用勾股定理求出AK即可;[关联运用]过点F作直线l∥BA，交CA的延长线于点N，取AC的中点G，作C关于直线l的对称点M，连接MF、GF、MN，根据对称性和平行四边形的判定及性质推出CF=MF，GF=CE，根据两点之间线段最+=GF＋MF≥MG(当且仅当G、F、M共线时，取等号)，然后利用勾股定理求出MG即可．短可得CE CF【详解】解：[问题探究]过点A作AH⊥b于H，过点B作BK⊥b于K，作BJ⊥AH交AH的延长线于J，连接MK、AB和AK由图易知，四边形HJBK为矩形，MN=BK=1，MN∥BK，AH=2＋1=3，AJ=2＋1＋1=4∴四边形MNBK为平行四边形，HK=BJ∴BN=MK+=AM＋MK≥AK(当且仅当A、M、K共线时，取等号)∴AM BN在Rt△ABJ中，223AB AJ-=∴HK=3∴2232AH HK+=+≥32∴AM BN+的最小值是32即AM BN故答案为：32;[关联运用]过点F 作直线l ∥BA ，交CA 的延长线于点N ，取AC 的中点G ，作C 关于直线l 的对称点M ，连接MF 、GF 、MN由对称性可得CF=MF ，CN=MN ，∠CNF=∠MNF ∵在等腰Rt ABC 和等腰Rt DEF △中，24BC DF == ∴∠FED=∠BAC=45°，EF=DF=2，AC=BC=4 ∴EF ∥AC ，CG=AG=12AC=2=EF ∴四边形CEFG 为平行四边形 ∴GF=CE∴CE CF +=GF ＋MF ≥MG (当且仅当G 、F 、M 共线时，取等号) ∵直线l ∥BA∴四边形EFNA 为平行四边形，∠CNF=∠BAC=45° ∴AN=EF=2，∠CNF=∠MNF=45°∴GN=AG ＋AN=4，MN=CN=AC ＋AN=6，∠MNC=∠CNF ＋∠MNF=90° 根据勾股定理可得22213+=GN MN ∴CE CF +≥213即CE CF +的最小值为213 故答案为：13【点睛】此题考查的是两点之间线段最短的应用、勾股定理、平行四边形的判定及性质、矩形的判定及性质和轴对称的性质，掌握两点之间线段最短、勾股定理、平行四边形的判定及性质、矩形的判定及性质和轴对称的性质是解决此题的关键．三、解答题17.计算：()2248233a a a a a -÷+．【答案】69a 【解析】【分析】根据同底数幂的乘法、同底数幂的除法、积的乘方和合并同类项法则计算即可．【详解】解：原式6669=-+a a a69a =【点睛】此题考查的是幂的运算性质和合并同类项，掌握同底数幂的乘法、同底数幂的除法、积的乘方和合并同类项法则是解决此题的关键．18.如图，已知AC ⊥AE ，BD ⊥BF ，∠1＝∠2，求证：AE ∥BF ．【答案】见解析【解析】【分析】由垂直的定义可知∠EAC ＝∠FBD ＝90°，然后由等式的性质可求∠EAG ＝∠FBG 从而根据同位角相等，两直线平行可证AE ∥BF .【详解】∵AC ⊥AE ，BD ⊥BF ， ∴∠EAC ＝∠FBD ＝90°，又∵∠1＝∠2， ∴∠EAG ＝∠FBG ， ∴AE ∥BF .【点睛】本题考查了垂直的定义及平行线的判定方法，熟练掌握同位角相等，两直线平行是解答本题的关键.19.2020年2月10日，光明中学团委利用网络平台组织八年级600名学生参加”全民抗疫”知识大赛．为了了解本次大赛的成绩，随机抽取了部分学生的成绩作为样本，按，，，四个等级进行统计，制成如下不完整的统计图．(说明：级80分-100分，级70分-79分，级60-69分，级0分-59分)根据所给信息，解答以下问题：(1)在扇形统计图中，级对应的扇形的圆心角是______度;(2)补全条形统计图;(3)所抽取学生的足球运球测试成绩的中位数会落在______等级;(4)若成绩达到等级的学生可以选为志愿者，请估计该校八年级600名学生中可以选为志愿者学生有多少人? 【答案】(1)117;(2)见解析;(3);(4)60人【解析】【分析】(1)利用B级人数除以其所占调查总人数的百分比即可求出调查总人数，然后利用调查人数减去A级、B级、D级的人数即可求出C级人数，求出C级人数占调查人数的百分比，再乘360°即可求出结论;(2)根据C级人数补全条形统计图即可;(3)根据中位数的定义即可求出结论;(4)求出A级所占调查总人数的百分比，再乘600即可求出结论．【详解】解：(1)调查总人数为18÷45%=40(人)C级人数有40－4－18－5=13(人)级对应的扇形的圆心角是13360117 40⨯︒=︒故答案为：117;(2)补全条形统计图如下：(3)∵本次抽取了40名同学∴所抽取学生的足球运球测试成绩的中位数会落在B 等级故答案为：B ;(4)46006040⨯=(人) 答：该校八年级600名学生中可以选为志愿者学生有60人．【点睛】此题考查的是条形统计图和扇形统计图，结合条形统计图和扇形统计图得出有用信息是解决此题的关键．20.请仅用无刻度直尺完成下列画图，不写画法，保留画图痕迹．(1)如图1，在77⨯的正方形网格中，每个小正方形的边长为1，小正方形的顶点叫做格点．ABC 的顶点在格点上，过点画一条直线．．平分ABC 的面积; (2)如图2，点在正方形ABCD 的内部，且EB EC =，过点画一条射线．．平分BEC ∠; (3)如图3，点、、均在O 上，且120BAC ∠=︒，在优弧BC 上画M 、两点．．，使60MAN ∠=︒．【答案】(1)见解析;(2)见解析;(3)见解析【解析】【分析】(1)找出以BC 为对角线的矩形BECD ，连接DE ，交BC 于点O ，作直线AO 即可;(2)连接AC 、BD 交于点O ，作射线EO 即可;(3)连接BO 并延长交O 于点N ，连接AN ，连接CO 并延长交O 于点M ，连接AM ，根据直径所对的圆周角是直角即可得出结论．【详解】解：(1)如图所示，找出以BC 为对角线的矩形BECD ，连接DE ，交BC 于点O ，作直线AO ，根据矩形的性质可得O 为BC 的中点，根据中线的性质可得直线AO 平分ABC 的面积，故AO 即为所求;(2)连接AC 、BD 交于点O ，作射线EO ，根据正方形性质可得OB=OC∵四边形ABCD 为正方形∴OB=OC∴点O 在BC 的中垂线上，∵EB=EC∴点E 在BC 的中垂线上∴EO 垂直平分BC∴射线EO 平分BEC ∠，射线EO 即为所求;(3)连接BO 并延长交O 于点N ，连接AN ，连接CO 并延长交O 于点M ，连接AM∵BN 和CM 都为O 的直径，∴∠BAN=∠CAM=90°∵120BAC ∠=︒∴∠BAM=∠BAC －∠CAM=30°，∴∠MAN=∠BAN －∠BAM=60°∴点M 、N 即为所求．【点睛】此题考查的是根据三角形中线性质、矩形的性质和圆周角的推论作图，掌握矩形的性质、正方形的性质、三角形中线的性质、三线合一和直径所对的圆周角是直角是解决此题的关键．21.在等边ABC 中，点在边BC 上，以OC 为半径的O 交AC 于点，过点作DE AB ⊥于点． (1)如图1，求证：DE 为O 的切线;(2)如图2，连接AO 交DE 于点，若为DE 中点，求tan CAO ∠的值．【答案】(1)见解析;(2)3tan 5CAO ∠=．【解析】【分析】 (1)连接OD ，根据等边三角形的性质可得60∠=∠=∠=︒B C A ，然后根据等边对等角和平行线的判定可知//OD AB ，然后根据平行线的性质可证90ODE ∠=︒，最后根据切线的判定定理即可证出结论;(2)过点作OG AC ⊥于，根据锐角三角函数求出33OG CG DG ==，然后利用AAS 证出FEA FDO △△≌，求出AG=5DG ，利用锐角三角函数即可求出结论．【详解】(1)证明：连接OD ，ABC 等边三角形，60B C A ∴∠=∠=∠=︒，∵OC=OD60∴∠=∠=︒C ODC ，//OD AB ∴，△OCD 为等边三角形而DE AB ⊥，90DEB ∴∠=︒，90ODE ∴∠=︒，∴OD DE ⊥，∴DE 为O 的切线．(2)解：过点作OG AC ⊥于，∵OC=OD∴CG=DG在Rt OCG △中，tanC==OG CG∴OG ==，由(1)知：OD DE ⊥，又有点为DE 中点，∴AF=OF在△FEA 和△FDO 中90AEF ODF AFE OFDAF OF ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩∴FEA FDO △△≌，22AE OD CG DG ∴===，在Rt AED 中，AD AE =·cos ∠DAE=2AE ，4AD DG ∴=，∴AG=5DG在Rt AOG中，tan ∠===OG OAG AG ，即tan CAO ∠=【点睛】此题考查的是等边三角形的判定及性质、切线的判定、锐角三角函数和全等三角形的判定及性质，掌握等边三角形的判定及性质、切线的判定、锐角三角函数和全等三角形的判定及性质是解决此题的关键． 22.某超市销售一种文具，进价为 5(元/件)，售价为6(元/件)时，当天的销售量为100件，在销售过程中发现：售价每上涨0.5元，当天的销售量就减少5件，设当天销售单价统一为 (元/件)(6x ≥，且是按0.5元的倍数上涨)，当天销售利润为元．(1)求与的函数关系式(不要求写出自变量的取值范围);(2)要使当天销售利润不低于240元，求当天销售单价的范围;(3)若每件文具的利润不超过60%，要使当天获得利润最大，每件文具售价为多少元?并求出最大利润.【答案】(1)210210800=-+-y x x ;(2)当天销售单价所在的范围为813≤≤x ;(3)每件文具售价为8元时，最大利润为240元．【解析】【分析】(1)根据当天销售利润等于每件利润乘以当天销量，找到当天销量与单价的关系即可得出答案;(2)先求出利润等于240元时的单价，再根据二次函数图像的性质确定范围;(3)先确定单价范围，再根据二次函数的性质求最值．【详解】(1)由题意6(5)10050.5-⎛⎫=--⨯ ⎪⎝⎭x y x ∴与的函数关系式为：210210800=-+-y x x(2)要使当天利润不低于240元，则240y ≥.221021080010(10.5)302.5240y x x x ∴=-+-=--+=解得，18x =，213x =100-<，抛物线的开口向下，当天销售单价所在的范围为813≤≤x(3)每件文具利润不超过60%550.6x ∴-≤⨯，得68x ≤≤文具的销售单价为68x ≤≤由(1)得221021080010(10.5)302.5y x x x =-+-=--+对称轴为10.5x =68x ≤≤在对称轴的左侧，且随着的增大而增大当8x =时，取得最大值，此时()21010.5302.5240y x =--+=，即每件文具售价为8元时，最大利润为240元.【点睛】本题考查了二次函数的应用，熟练掌握销售问题中的等量关系，以及二次函数的性质是解题的关键．23.在ABC 中，AB AC =，点在底边BC 上，EDF ∠的两边分别交AB 、AC 所在直线于、两点，2EDF ABC ∠=∠，BD nCD =．(1)如图1，若45ABC ∠=︒，1n =，求证：DE DF =;(2)如图2，求DE DF 的值(含的式子表示);(3)如图3，连接EF ，若tan 1B ∠=，//EF BC ，且58EF BC =，直接写出的值为______．【答案】(1)见解析;(2)=DE n DF;(3)3或13 【解析】【分析】 (1)连接AD ，根据等腰直角三角形的性质可得45B C ∠=∠=︒，然后根据三线合一可得90ADB ADC ∠=∠=︒，从而得出BD CD AD ==，34∠=∠，利用ASA 即可证出DEA DFC △△≌，从而得出结论;(2)过点D 作DG AB ⊥于，DH AC ⊥于，根据相似三角形判定定理分别证出DGB DHC △△∽，DGE DHF △△∽，列出比例式即可求出结论;(3)过点E 作EG ⊥BC 于G ，过点F 作FH ⊥BC 于H ，根据平行线可证△AEF ∽△ABC ，列出比例式可设AE=AF=5a ，则AB=AC=8a ，利用锐角三角函数用a 表示各个线段，然后根据相似三角形的判定定理证出△GED ∽△HDF ，列出比例式即可列出关于n 的方程，从而求出结论．【详解】(1)证明：连接AD ，AB AC =，45B C ∴∠=∠=︒，又1n =，BD CD ∴=，90ADB ADC ∴∠=∠=︒，145∴∠=︒=∠B ，BD CD AD ∴==，而290EDF B ∠=∠=︒，34∴∠=∠DEA DFC ∴△△≌DE DF ∴=;(2)解：过点D 作DG AB ⊥于，DH AC ⊥于，90DGB DHC ∴∠=∠=︒，AB AC =，B C ∴∠=∠DGB DHC ∴△△∽， DG DB DH DC ∴=①由(1)可知：180A EDF ∠+∠=︒，GED HFD ∴∠=∠，DGE DHF ∴△△∽，DGDEDH DF ∴=②由①式、②式知：DE DBn DF DC ==．(3)过点E 作EG ⊥BC 于G ，过点F 作FH ⊥BC 于H∵tan 1B ∠=∴∠B=45°∴∠B=∠C=45°，△ABC 、△GBE 和△HCF 都为等腰直角三角形，2EDF ABC ∠=∠=90°∴GE=GB ，HC=HF∵//EF BC ，且58EFBC =，∴∠AEF=∠B=45°，∠AFE=∠C=45°，△AEF ∽△ABC∴AE=AF ，58===AE AF EF AB AC BC 设AE=AF=5a ，则AB=AC=8a∴BE=FC=3a∴GE=GB=BE ·cos ∠B=2，HF=HC=FC ·cos ∠C=2，= ∵∠EGD=∠DHF=∠EDF=90°∴∠GED ＋∠EDG=90°，∠HDF ＋∠EDG=90°∴∠GED=∠HDF∴△GED ∽△HDF ∴===GE DG DE n DH HF DF即2===DE n DH DF ∴DH=2a n，DG=2an ∵GB ＋DG ＋DH ＋HC=BC＋2n= 整理，得231030-+=n n解得：n=3或13故答案为：3或13．【点睛】此题考查的是相似三角形的判定及性质、全等三角形的判定及性质、锐角三角函数和等腰直角三角形的性质，掌握相似三角形的判定及性质、全等三角形的判定及性质、锐角三角函数和等腰直角三角形的性质是解决此题的关键．24.抛物线：2y ax c =+与轴交于点、两点，与轴交于点()0,1C -，且4AB OC =．(1)直接写出抛物线的解析式;(2)如图1，点M 在轴左侧的抛物线上，将点M 先向右平移4个单位长度，再向下平移()0n n ≥个单位长度，得到的对应点恰好落在抛物线上，若2MNC S =△，求点M 的坐标;(3)如图2，将抛物线向上平移2个单位长度得到抛物线1C ，一次函数y kx b =+的图象与抛物线1C 只有一个公共点，与轴交于点，探究：轴上是否存在定点满足90EGF ∠=︒?若存在，求出点的坐标;否则，说明理由．【答案】(1)2114y x =-;(2)()2,0M -或(222,222--+;(3)存在，()0,2G 【解析】【分析】 (1)根据题意，求出点B 的坐标，然后将点B 、C 的坐标代入抛物线的解析式中即可求出结论;(2)设21,14M m m ⎛⎫- ⎪⎝⎭，则()214,414N m m ⎛⎫++- ⎪⎝⎭，利用待定系数法求出直线MC 的解析式，过点作//NE y 轴交CM 于，根据点N 与y 轴的位置关系分类讨论，利用”铅垂高，水平宽”列出方程，即可求出结论;(3)根据题意可得平移后的二次函数解析式为2114y x =+，设21,14E m m ⎛⎫+ ⎪⎝⎭，求出直线l 的解析式，然后联立方程，令△=0即可求出12k m =，过点作EH AB ⊥于，记定点()0,G t ，连接EG 、FG ，利用相似三角形的判定证出OGF HEG △△∽，列出比例式即可求出结论．。

精品人教版中考第二次模拟检测《数学卷》含答案解析

人教版中考数学仿真模拟测试题一．选择题1.2020的相反数是( )A. 2020B. ﹣2020C. 12020D. 12020- 2.新冠病毒(2019﹣nCoV )是一种新的Sarbecovirus 亚属的β冠状病毒，它是一类具有囊膜的正链单股RNA 病毒，其遗传物质是所有RNA 病毒中最大的，也是自然界广泛存在的一大类病毒．其粒子形状并不规则，直径约60﹣220nm ，平均直径为100nm (纳米)．1米＝109纳米，100nm 可以表示为( )米．A. 0.1×10﹣6B. 10×10﹣8C. 1×10﹣7D. 1×1011 3.如图所示的几何体是由六个相同的小正方体组合而成的，它的俯视图是( )A. B.C. D.4.下列计算正确的是( )A. 5510a a a +=B. 3()33a b a b --=--C. 33()mn mn --=D. 624a a a ÷= 5.若点A (m-4,1-2m )在第三象限,那么m 的值满足 ( )A. m>12 B. m<4 C. 12<m<4 D. m>4 6.下列说法中，正确的是( )A. 对载人航天器零部件的检查适合采用抽样调查的方式B. 某市天气预报中说“明天降雨概率是80%”，表示明天该市有80%的地区降雨C. 通过抛掷1枚质地均匀的硬币，确定谁先发球的比赛规则是公平的D. 掷一枚骰子，点数为3的面朝上是确定事件7.如图，AB∥CD，则根据图中标注的角，下列关系中成立的是 ( )A. ∠1＝∠3B. ∠2＋∠3＝180°C. ∠2＋∠4＜180°D. ∠3＋∠5＝180° 8.如图，从圆O 外一点P 引圆O 的两条切线PA ，PB ，切点分别为A ，B ，如果60APB ∠=， 8PA =，那么弦AB 的长是( )A. 4B. 43C. 8D. 83 9.如图，某风景区为了方便游人参观，计划从主峰A 处架设一条缆车线路到另一山峰C 处，若在A 处测得C 处的俯角为30°，两山峰的底部BD 相距900米，则缆车线路AC 的长为( ) 3 3 3D. 1800米 10.设x 1，x 2是一元二次方程x 2﹣2x ﹣5＝0的两根，则x 12+x 22的值为( ) A. 6 B. 8 C. 14D. 16 11.已知M 、N 两点关于y 轴对称，且点M 在反比例函数12y x =的图象上，点N 在一次函数3y x 的图象上，设点M 的坐标为(a ，b)，则二次函数2()y abx a b x =++( )A. 有最小值，且最小值是92-B. 有最大值，且最大值是92- C. 有最大值，且最大值是92 D. 有最小值，且最小值是9212.如图，若抛物线y＝﹣12x2+3与x轴围成封闭区域(边界除外)内整点(点的横、纵坐标都是整数)的个数为k，则反比例函数y＝kx(x＞0)的图象是()A. B.C. D. 二．填空题13.使分式43x有意义的x的取值范围______．14.不透明袋子中装有5个红色球和3个蓝色球，这些球除了颜色外没有其他差别.从袋子中随机摸出一个球，摸出蓝色球的概率为_______．15.若△ABC∽△DEF，且相似比为3：1，△ABC的面积为54，则△DEF的面积为_____．16.如图，CD 为圆O的直径，弦AB⊥CD，垂足为E，若∠BCD＝22.5°，AB＝2cm，则圆O的半径为______．17.如图，直线y＝kx与双曲线y＝3x交于A、B两点，BC⊥y轴于点C，则△ABC的面积为______．18.如图，△ABC 中，∠BAC ＝45°，∠ACB ＝30°，将△ABC 绕点A 顺时针旋转得到△A 1B 1C 1，当C ，B 1，C 1三点共线时，旋转角α，连接BB 1，交于AC 于点D ，下面结论：①△AC 1C 为等腰三角形；②CA ＝CB 1；③α＝135°；④△AB 1D ∽△ACB 1；⑤1AB B C ＝622-中，正确的结论的序号为______．三．解答题19.计算：(﹣12)﹣2+(π﹣3)0+|1﹣2|+tan45° 20.先化简再求值：2(32)(32)5()(2)x y x y x x y x y +-----其中13x =-，1y =-21.为响应“书香学校，书香班级”的建设号召，平顶山市某中学积极行动，学校图书角的新书、好书不断增加．下面是随机抽查该校若干名同学捐书情况统计图：请根据下列统计图中的信息，解答下列问题：(1)此次随机调查同学所捐图书数的中位数是，众数是；(2)在扇形统计图中，捐2本书的人数所占的扇形圆心角是多少度？(3)若该校有在校生1600名学生，估计该校捐4本书的学生约有多少名？22.如图，矩形ABCD 中，CE ⊥BD 于E ，CF 平分∠DCE 与DB 交于点F ．(1)求证：BF ＝BC ；(2)若AB ＝4cm ，AD ＝3cm ，求CF 的长．23.今年义乌市准备争创全国卫生城市，某小区积极响应，决定在小区内安装垃圾分类的温馨提示牌和垃圾箱，若购买2个温馨提示牌和3个垃圾箱共需550元，且垃圾箱的单价是温馨提示牌单价的3倍． (1)求温馨提示牌和垃圾箱的单价各是多少元？(2)该小区至少需要安放48个垃圾箱，如果购买温馨提示牌和垃圾箱共100个，且费用不超过10000元，请你列举出所有购买方案，并指出哪种方案所需资金最少？最少是多少元？24.如图，AB 为⊙O 的直径，AC 切⊙O 于点A ，连结BC 交O 于点D ，E 是⊙O 上一点，且与点D 在AB 异侧，连结DE(1)求证：∠C ＝∠BED ；(2)若∠C ＝50°，AB ＝2，则BD 的长为(结果保留π)25.对某一个函数给出如下定义：对于函数y ，若当a x b ，函数值y 满足m y n ，且满足()n m k b a -=-，则称此函数为“k 属和合函数”例如：正比例函数3y x =-，当13x 时，93y --，则()()3931k ---=-，求得：3k =，所以函数3y x =-“3属和合函数”.(1)①一次函数()2115y x x =-为“k 属和合函数”，则k 的值为______，②若一次函数()115y ax x =-为“1属和合函数”，求a 的值；(2)反比例函数k y x=(0k >，a x b 且0a b <<)是“k 属和合函数”，且2020a b +，请求出22a b +的值； (3)已知二次函数22362y x ax a a =-+++，当11x -时，y 是“k 属和合函数”，求k 的取值范围.26.如图，抛物线y=ax2+bx+c(a＜0，a、b、c为常数)与x轴交于A、C两点，与y轴交于B点，A(﹣6，0)，C(1，0)，B(0，163)．(1)求该抛物线的函数关系式与直线AB的函数关系式；(2)已知点M(m，0)是线段OA上的一个动点，过点M作x轴的垂线l，分别与直线AB和抛物线交于D、E 两点，当m为何值时，△BDE恰好是以DE为底边的等腰三角形？(3)在(2)问条件下，当△BDE恰妤是以DE为底边的等腰三角形时，动点M相应位置记为点M'，将OM'绕原点O顺时针旋转得到ON(旋转角在0°到90°之间)；①探究：线段OB上是否存在定点P(P不与O、B重合)，无论ON如何旋转，NPNB始终保持不变，若存在，试求出P点坐标：若不存在，请说明理由；②试求出此旋转过程中，(NA34NB)的最小值．答案与解析一．选择题1.2020的相反数是( )A. 2020B. ﹣2020C.12020D.12020【答案】B【解析】【分析】直接利用相反数的定义得出答案．【详解】解：2020的相反数是：﹣2020．故选：B．【点睛】此题主要考查了相反数，正确把握相反数的定义是解题关键．2.新冠病毒(2019﹣nCoV)是一种新的Sarbecovirus亚属的β冠状病毒，它是一类具有囊膜的正链单股RNA 病毒，其遗传物质是所有RNA病毒中最大的，也是自然界广泛存在的一大类病毒．其粒子形状并不规则，直径约60﹣220nm，平均直径为100nm(纳米)．1米＝109纳米，100nm可以表示为()米．A. 0.1×10﹣6B. 10×10﹣8C. 1×10﹣7D. 1×1011【答案】C【解析】【分析】绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10﹣n，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．【详解】解：100nm＝100×10﹣9m＝1×10﹣7m，故选：C．【点睛】本题是对科学记数法知识的考查，熟练掌握负指数幂知识是解决本题的关键.3.如图所示的几何体是由六个相同的小正方体组合而成的，它的俯视图是( )A. B. C.D.【答案】D【解析】【分析】根据从上面看得到的图形是俯视图, 可得答案.【详解】解：从上面看第一层是两个小正方形, 第二层是三个小正方形,故选:D.【点睛】本题主要考查三视图的定义，其中俯视图为从上面看得到的图形.4.下列计算正确的是( )A. 5510a a a +=B. 3()33a b a b --=--C. 33()mn mn --=D. 624a a a ÷=【答案】D【解析】【分析】根据合并同类项的法则，积的乘方，同底数幂的除法即可作出判断．【详解】解：A 、5552a a a +=，故选项错误； B 、()333a b a b --=-+，故选项错误；C 、()333mn m n ---=，则选项错误；D 、正确．故选D ．【点睛】本题考查同底数幂的除法，合并同类项，同底数幂的乘法，积的乘方很容易混淆，一定要记准法则才能做题．5.若点A (m-4,1-2m )在第三象限,那么m 的值满足 ( )A. m>12 B. m<4 C. 12<m<4 D. m>4 【答案】C【解析】【分析】根据第三象限内点的横坐标与纵坐标都是负数列出不等式组，然后求解即可．【详解】∵点A(m-4,1-2m)在第三象限，∴40?120?mm-<⎧⎨-<⎩①②，解不等式①得，m<4，解不等式②得,m>12，所以,m的取值范围是12<m<4.故选C.【点睛】本题考查解一元一次不等式组, 象限及点的坐标.6.下列说法中，正确的是( )A. 对载人航天器零部件的检查适合采用抽样调查的方式B. 某市天气预报中说“明天降雨的概率是80%”，表示明天该市有80%的地区降雨C. 通过抛掷1枚质地均匀的硬币，确定谁先发球的比赛规则是公平的D. 掷一枚骰子，点数为3的面朝上是确定事件【答案】C【解析】【分析】根据不同的数据调查方式，可能事件，确定事件，判断比赛怎么公平去解答即可.【详解】A中，载人航天器属于精密仪器，零部件必须全面检查以确保安全，不能用抽样调查，排除A；B 中，天气预报中的降雨概率不是指降雨的范围，排除B；D中，掷骰子属于随机事件，不能确定，排除D. 故选C【点睛】此题重点考察学生对概率、可能事件，确定事件的理解，掌握其定义是解题的关键.7.如图，AB∥CD，则根据图中标注的角，下列关系中成立的是( )A. ∠1＝∠3B. ∠2＋∠3＝180°C. ∠2＋∠4＜180°D. ∠3＋∠5＝180°【答案】D【解析】试题分析：根据平行线的性质对各选项分析判断利用排除法求解：A 、∵OC 与OD 不平行，∴∠1=∠3不成立，故本选项错误；B 、∵OC 与OD 不平行，∴∠2+∠3=180°不成立，故本选项错误；C 、∵AB ∥CD ，∴∠2+∠4=180°，故本选项错误；D 、∵AB ∥CD ，∴∠3+∠5=180°，故本选项正确．故选D ．考点：平行线的性质．8.如图，从圆O 外一点P 引圆O 的两条切线PA ，PB ，切点分别为A ，B ，如果60APB ∠=， 8PA =，那么弦AB 的长是( )A. 4B. 3C. 8D. 83【答案】C【解析】【分析】先利用切线长定理得到PA PB =，再利用60APB ∠=可判断APB 为等边三角形，然后根据等边三角形性质求解．【详解】解：PA ，PB 为O 的切线，PA PB ∴=，60APB ∠=，APB ∴为等边三角形，8AB PA ∴==．故选C ．【点睛】本题考查切线长定理，掌握切线长定理是解题的关键．9.如图，某风景区为了方便游人参观，计划从主峰A 处架设一条缆车线路到另一山峰C 处，若在A 处测得C 处的俯角为30°，两山峰的底部BD 相距900米，则缆车线路AC 的长为( )A. 3003米B. 6003米C. 9003米D. 1800米【答案】B 【解析】【分析】过点C 作CO ⊥AB ，垂足为O ，由图可看出，三角形OAC 为一直角三角形，已知一直角边和一角，则可求斜边．【详解】解：过点C 作CO ⊥AB ，垂足为O ，∵BD=900， ∴OC=900， ∵∠EAC=30°， ∴∠ACO=30°．在Rt △AOC 中，则AC ＝cos30OC＝3米)．故选：B ．【点睛】本题考查解直角三角形的应用-仰角俯角问题，锐角三角函数等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题，学会用构建方程的思想思考问题． 10.设x 1，x 2是一元二次方程x 2﹣2x ﹣5＝0的两根，则x 12+x 22的值为( ) A. 6 B. 8C. 14D. 16【答案】C 【解析】【分析】根据根与系数的关系得到x 1+x 2=2，x 1•x 2=-5，再变形x 12+x 22得到(x 1+x 2)2-2x 1•x 2，然后利用代入计算即可．【详解】∵一元二次方程x 2-2x-5=0的两根是x 1、x 2， ∴x 1+x 2=2，x 1•x 2=-5，∴x 12+x 22=(x 1+x 2)2-2x 1•x 2=22-2×(-5)=14．故选C ．【点睛】考查了一元二次方程ax 2+bx+c=0(a≠0)的根与系数的关系：若方程的两根为x 1，x 2，则x 1+x 2=-ba，x 1•x 2=c a． 11.已知M 、N 两点关于y 轴对称，且点M 在反比例函数12y x=的图象上，点N 在一次函数3y x 的图象上，设点M 的坐标为(a ，b)，则二次函数2()y abx a b x =++( )A. 有最小值，且最小值是92-B. 有最大值，且最大值是92-C. 有最大值，且最大值是92D. 有最小值，且最小值是92【答案】A 【解析】分析：先用待定系数法求出二次函数的解析式，再根据二次函数图象上点的坐标特点求出其最值即可．解答：解：因为M ，N 两点关于y 轴对称，所以设点M 的坐标为(a ，b)，则N 点的坐标为(-a ，b)，又因为点M 在反比例函数12y x=的图象上，点N 在一次函数y=x+3的图象上，所以1b 2a b a 3==-+，整理得1ab 2a b 3=+=故二次函数y=abx 2+(a+b)x 为y=12x 2+3x ，所以二次项系数为12＞0，故函数有最小值，最小值为y=23142-⨯=-．故选A ．12.如图，若抛物线y ＝﹣12x 2+3与x 轴围成封闭区域(边界除外)内整点(点的横、纵坐标都是整数)的个数为k ，则反比例函数y ＝kx(x ＞0)的图象是( )A. B.C. D.【答案】A【解析】【分析】找到函数图象与x轴、y轴的交点，得出k＝8，即可得出答案．【详解】解：抛物线y＝﹣12x2+3，当y＝0时，x＝±6；当x＝0时，y＝3，则抛物线y＝﹣12x2+3与x轴围成封闭区域(边界除外)内整点(点的横、纵坐标都是整数)为(﹣1，2)，(0，1)，(0，2)，(1，1)，(1，2)，(2，1)；共有8个，∴k＝6；故选：A．【点睛】此题考查二次函数图象和性质、反比例函数的图象，解题的关键是求出k的值．二．填空题13.使分式43x有意义的x的取值范围______．【答案】x≠3【解析】【分析】根据分母不为零分式有意义，可得答案．【详解】解：根据题意，得 x ﹣3≠0，解得x≠3，故答案为：x≠3．【点睛】本题考查了分式有意义的条件：分母不为零；按此条件解题即可．14.不透明袋子中装有5个红色球和3个蓝色球，这些球除了颜色外没有其他差别.从袋子中随机摸出一个球，摸出蓝色球的概率为_______．【答案】38【解析】分析：根据概率的求法，找准两点：①全部情况的总数；②符合条件的情况数目；二者的比值即其发生的概率.详解：由于共有8个球，其中篮球有5个，则从袋子中摸出一个球，摸出蓝球的概率是38，故答案是38．点睛：此题主要考查了概率的求法，如果一个事件有n 种可能，而且这些事件的可能性相同，其中事件 A 出现m 种结果，那么事件A 的概率P(A)=m n． 15.若△ABC ∽△DEF ，且相似比为3：1，△ABC 的面积为54，则△DEF 的面积为_____．【答案】6 【解析】【分析】根据相似三角形的面积比等于相似比的平方计算，得到答案．【详解】解：∵△ABC ∽△DEF ，相似比为3：1，∴ABC DEFS S＝32，即54DEFS＝9，解得，△DEF 的面积＝6，故答案为：6．【点睛】本题考查的知识点是相似三角形的性质，解题关键是掌握相似三角形的面积比等于相似比的平方这一定理．16.如图，CD 为圆O 的直径，弦AB ⊥CD ，垂足为E ，若∠BCD ＝22.5°，AB ＝2cm ，则圆O 的半径为______．【答案】2【解析】【分析】连接OB，根据垂径定理以及勾股定理即可求出OB的长度．【详解】如图，连接OB，∵OC＝OB，∠BCD＝22.5°，∴∠EOB＝45°，∵AB⊥CD，CD是直径，AB=2，∴EB＝12AB＝1，∴OE＝EB＝1，∴OB＝22OE BE=2，故答案为：2【点睛】本题考查垂径定理、勾股定理及三角形外角性质，垂直弦直径平分弦，并且平分弦这条弦所对的两条弧；熟练掌握垂径定理是解题关键．17.如图，直线y＝kx与双曲线y＝3x交于A、B两点，BC⊥y轴于点C，则△ABC的面积为______．【答案】3【解析】【分析】根据反比例函数的图象与正比例函数图象的对称性，可判断点A与点B关于原点对称，则S△BOC＝S△AOC，再利用反比例函数k的几何意义得到S△BOC＝1.5，则易得S△ABC＝3．【详解】∵直线y＝kx与双曲线y＝3 x交于A，B两点，∴点A与点B关于原点对称，∴S△BOC＝S△AOC，∵S△BOC＝12×3＝1.5，∴S△ABC＝2S△BOC＝3．故答案为：3．【点睛】本题主要考查反比函数与一次函数的综合，熟练掌握反比例函数比例系数的几何意义，是解题的关键．18.如图，△ABC中，∠BAC＝45°，∠ACB＝30°，将△ABC绕点A顺时针旋转得到△A1B1C1，当C，B1，C1三点共线时，旋转角为α，连接BB1，交于AC于点D，下面结论：①△AC1C为等腰三角形；②CA＝CB1；③α＝135°；④△AB1D∽△ACB1；⑤1ABB C＝62中，正确的结论的序号为______．【答案】①②④⑤【解析】【分析】首先根据旋转的性质得出AC1＝AC，从而结论①可判断；再通过三角形内角和定理及旋转角的计算对②③作出判断；通过∠AB1D＝∠ACB1=30°，∠B1AD＝∠CA B1，，判定△AB1D∽△ACB1；通过证明△ABD∽△B1CD，利用相似三角形的性质列式计算对⑤作出判断．【详解】由旋转的性质可知：AC1＝AC，∴△AC1C为等腰三角形，即①正确；∵∠ACB＝30°，∴∠C1＝∠ACB1＝30°，又∵B 1AC 1＝∠BAC ＝45°， ∴∠AB 1C ＝75°，∴∠CAB 1＝180°﹣75°﹣30°＝75°， ∴CA ＝CB 1；即②正确；∵∠CAC 1＝∠CAB 1+∠B 1AC 1＝120°， ∴旋转角α＝120°，故③错误； ∵∠BAC ＝45°，∴∠BAB 1＝45°+75°＝120°， ∵AB ＝AB 1，∴∠AB 1B ＝∠ABD ＝30°，在△AB 1D 与△ACB 1中，∵∠AB 1D ＝∠ACB 1=30°，∠B 1AD ＝∠CA B 1， ∴△AB 1D ∽△ACB 1，即④正确；在△ABD 与△B 1CD 中，∵∠ABD ＝∠ACB 1，∠ADB ＝∠CDB 1， ∴△ABD ∽△B 1CD ， ∴1AB B C ＝1ADB D， ∴∠DB 1C=∠DAB=45°，过点D 作DM ⊥B 1C ，设DM ＝x ，则B 1M ＝x ，B 1D ＝2x ，DC ＝2x ， CM ＝3x ， ∴AC ＝B 1C ＝(3+1)x ， ∴AD ＝AC ﹣CD ＝(3﹣1)x ，∴1AB B C ＝1AD B D ＝(31)2x x-＝622-，即⑤正确．故答案为：①②④⑤．【点睛】本题主要考查旋转的性质，等腰三角形的性质定理，等腰直角三角形的性质，含30°角的直角三角形的性质，相似三角形的判定和性质，添加合适的辅助线，构造直角三角形，熟练掌握相似三角形的判定和性质定理，是解题的关键．三．解答题19.计算：(﹣12)﹣2+(π﹣3)0+|1+5．【解析】【分析】第一项利用负指数幂法则计算，第二项利用零指数幂法则计算，第三项化简绝对值，最后一项利用特殊角的三角函数值计算，最后合并即可得出结论．【详解】解：(﹣12)﹣2+(π﹣3)0+|1|+tan45°＝﹣1+1+5．【点睛】本题考查实数的混合运算，主要考查负指数幂，化简绝对值，零指数幂，特殊角的三角函数．熟练掌握各运算的运算法则是解题的关键.20.先化简再求值：2(32)(32)5()(2)x y x y x x y x y +-----其中13x =-，1y =- 【答案】259y xy -+；-2 【解析】【分析】先利用平方差公式，单项式乘多项式，完全平方公式的法则进行计算，然后去括号，合并同类项化简，最后代入求值．【详解】解：2(32)(32)5()(2)x y x y x x y x y +----- =222229455(44)x y x xy x xy y --+--+ =2222294554+4x y x xy x xy y --+-- =259y xy -+当13x =-，1y =-时，原式=215(1)9()(1)5323-⨯-+⨯-⨯-=-+=-【点睛】本题考查整式的混合运算及化简求值，掌握平方差公式和完全平方公式正确计算是解题关键．21.为响应“书香学校，书香班级”的建设号召，平顶山市某中学积极行动，学校图书角的新书、好书不断增加．下面是随机抽查该校若干名同学捐书情况统计图：请根据下列统计图中的信息，解答下列问题：(1)此次随机调查同学所捐图书数的中位数是，众数是；(2)在扇形统计图中，捐2本书的人数所占的扇形圆心角是多少度？(3)若该校有在校生1600名学生，估计该校捐4本书的学生约有多少名？【答案】(1)4本；2本；(2)108°；(3)该校捐4本书的学生约有416名．【解析】【分析】(1)根据捐2本的学生数所占的百分比和人数可以求得本次调查的学生数，从而可以得到中位数和众数；(2)根据扇形统计图中的数据，利用“扇形圆心角度数=360°×所占百比例”即可得出结果；(3)根据样本估计总体的方法，利用学生总人数×捐4本书的学生人数所占的百分比可得出结果．【详解】解：(1)本次调查的人数为：15÷30%＝50(人)，捐书4本的学生人数为：50﹣9﹣15﹣7﹣6＝13(人)，将所捐图书数按照从小到大的顺序排列，则处在第25，26位的捐书数都为4本，∴此次随机调查同学所捐图书数的中位数是4本；根据统计图可知捐2本书的人数最多，∴众数是2本，故答案为：4本；2本；(2)根据题意得，360°×30%＝108°，答：捐2本书的人数所占的扇形圆心角是108°；(3)根据题意得，1600×1350＝416(名)，答：该校捐4本书的学生约有416名．【点睛】本题考查的是条形统计图和扇形统计图，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据，扇形统计图能清楚地表示出每个项目占总体的百分比．同时考查了是众数、中位数的定义．22.如图，矩形ABCD中，CE⊥BD于E，CF平分∠DCE与DB交于点F．(1)求证：BF＝BC；(2)若AB＝4cm，AD＝3cm，求CF的长．【答案】(1)见解析；(2)CF＝655cm．【解析】【分析】(1)要求证BF＝BC只要证明∠CFB＝∠FCB就可以，从而转化为证明∠BCE＝∠BDC就可以；(2)已知AB＝4cm，AD＝3cm，就是已知BC＝BF＝3cm，CD＝4cm，在直角△BCD中，根据三角形的面积等于12BD•CE＝12BC•DC，就可以求出CE的长．要求CF的长，可以在直角△CEF中用勾股定理求得．其中EF＝BF﹣BE，BE在直角△BCE中根据勾股定理就可以求出，由此解决问题．【详解】证明：(1)∵四边形ABCD是矩形，∴∠BCD＝90°，∴∠CDB+∠DBC＝90°．∵CE⊥BD，∴∠DBC+∠ECB＝90°．∴∠ECB＝∠CDB．∵∠CFB＝∠CDB+∠DCF，∠BCF＝∠ECB+∠ECF，∠DCF＝∠ECF，∴∠CFB＝∠BCF∴BF＝BC(2)∵四边形ABCD是矩形，∴DC＝AB＝4(cm)，BC＝AD＝3(cm)．在Rt △BCD 中，由勾股定理得BD 5．又∵BD•CE ＝BC•DC ，∴CE ＝125BC DC BD ⋅=．∴BE 95==． ∴EF ＝BF ﹣BE ＝3﹣9655=．∴CF ==cm ．【点睛】本题考查矩形的判定与性质，等腰三角形的判定定理，等角对等边，以及勾股定理，三角形面积计算公式的运用，灵活运用已知，理清思路，解决问题．23.今年义乌市准备争创全国卫生城市，某小区积极响应，决定在小区内安装垃圾分类的温馨提示牌和垃圾箱，若购买2个温馨提示牌和3个垃圾箱共需550元，且垃圾箱的单价是温馨提示牌单价的3倍． (1)求温馨提示牌和垃圾箱的单价各是多少元？(2)该小区至少需要安放48个垃圾箱，如果购买温馨提示牌和垃圾箱共100个，且费用不超过10000元，请你列举出所有购买方案，并指出哪种方案所需资金最少？最少是多少元？【答案】(1)温馨提示牌和垃圾箱的单价各是50元和150元；(2)答案见解析【解析】【分析】(1)根据“购买2个温馨提示牌和3个垃圾箱共需550元”，建立方程求解即可得出结论；(2)根据“费用不超过10000元和至少需要安放48个垃圾箱”，建立不等式即可得出结论．【详解】(1)设温情提示牌的单价为x 元，则垃圾箱的单价为3x 元，根据题意得，2x +3×3x =550， ∴x =50，经检验，符合题意，∴3x =150元，即：温馨提示牌和垃圾箱的单价各是50元和150元；(2)设购买温情提示牌y 个(y 为正整数)，则垃圾箱为(100﹣y )个，根据题意得，意，()100485015010010000.y y y -≥⎧⎨+-≤⎩∴5052y ≤≤，∵y 为正整数，∴y 为50，51，52，共3中方案；有三种方案：①温馨提示牌50个，垃圾箱50个，②温馨提示牌51个，垃圾箱49个，③温馨提示牌52个，垃圾箱48个，设总费用为w 元W=50y +150(100﹣y )=﹣100y +15000，∵k=-1000<，∴w 随y 的增大而减小∴当y =52时，所需资金最少，最少是9800元．【点睛】此题主要考查了一元一次不等式组，一元一次方程的应用，正确找出相等关系是解本题的关键． 24.如图，AB 为⊙O 的直径，AC 切⊙O 于点A ，连结BC 交O 于点D ，E 是⊙O 上一点，且与点D 在AB 异侧，连结DE(1)求证：∠C ＝∠BED ；(2)若∠C ＝50°，AB ＝2，则BD 的长为(结果保留π)【答案】(1)证明见解析；(2)BD 的长度＝59π．【解析】【分析】 (1)连接AD ，根据圆周角定理得到∠ADB ＝90°，根据切线的性质得到∠BAC ＝90°，则利用等角的余角相等得到∠DAB ＝∠C ，然后根据圆周角定理和等量代换得到结论；(2)连接OD ，利用(1)中结论得到∠BED ＝∠C ＝50°，再利用圆周角定理得到∠BOD 的度数，然后根据弧长公式计算BD 的长度．【详解】(1)证明：连接AD ，如图，∵AB 为⊙O 的直径，∴∠ADB ＝90°，∵AC 切⊙O 于点A∴CA ⊥AB ，∴∠BAC ＝90°，∴∠C+∠ABD ＝90°，而∠DAB+∠ABD ＝90°，∴∠DAB ＝∠C ，∵∠DAB ＝∠BED ，∴∠C ＝∠BED ；(2)解：连接OD ，如上图，∵∠BED ＝∠C ＝50°，∴∠BOD ＝2∠BED ＝100°，又∵⊙O 的半径为1，∴根据弧长计算公式得到：BD 的长度＝1001180π⋅⋅＝59π．【点睛】本题主要考查了切线的性质：圆的切线垂直于经过切点的半径．若出现圆的切线，必连过切点的半径，构造定理图，得出垂直关系．也考查了圆周角定理和弧长公式，熟练掌握各知识点是解题的关键． 25.对某一个函数给出如下定义：对于函数y ，若当a x b ，函数值y 满足m y n ，且满足()n m k b a -=-，则称此函数为“k 属和合函数”例如：正比例函数3y x =-，当13x 时，93y --，则()()3931k ---=-，求得：3k =，所以函数3y x =-为“3属和合函数”.(1)①一次函数()2115y x x =-为“k 属和合函数”，则k 的值为______，②若一次函数()115y ax x =-为“1属和合函数”，求a 的值；(2)反比例函数k y x=(0k >，a x b 且0a b <<)是“k 属和合函数”，且a b +，请求出22a b +的值； (3)已知二次函数22362y x ax a a =-+++，当11x -时，y 是“k 属和合函数”，求k 的取值范围.【答案】(1)①2；②1a =±；(2)2018；(3)若a ＞1时，6k >；若0＜a ≤1时，362k <≤；若﹣1＜a ≤0时，362k ≤<；若a ＜﹣1时，6k >. 【解析】【分析】(1)①根据“k 属和合函数”的定义即可求出k 的值；②根据a 的取值范围分类讨论，然后再根据“1属和合函数”的定义分别求a 的值即可；(2)根据反比例函数的增减性，求出y 的取值范围，然后根据“k 属和合函数”的定义即可求出ab 的值，然后利用完全平方公式的变形即可求出22a b +的值；(3)根据对称轴与x 的取值范围的相对位置分类讨论：(i )若a ＞1时，即11x -在对称轴左侧，根据二次函数的增减性求出y 的取值范围，然后根据“k 属和合函数”的定义即可求出k 与a 的关系，根据a 的取值求出k 的取值即可；(ii )若0＜a ≤1时，即11x -含对称轴，且x=﹣1离对称轴最远，原理同上；(iii )若﹣1＜a ≤0时，即11x -含对称轴，且x=1离对称轴最远，原理同上；(iiii )若a ＜﹣1时，即11x -在对称轴右侧，原理同上.【详解】解：(1)①∵一次函数21y x =-当15x 时19y ≤≤，根据“k 属和合函数”的定义：()9151k -=-，解得：k=2；②当a ＞0时，∵1y ax =-当15x 时，151a y a -≤≤-，根据“1属和合函数”的定义：()()()511151a a ---=⨯-，解得：1a =；当a ＜0时，∵1y ax =-当15x 时，511a y a -≤≤-，根据“1属和合函数”的定义：()()()151151a a ---=⨯-，解得：1a =-，综上所述：1a =±；(2)∵k y x =(0k >，a x b 且0a b <<)， ∴当a x b 时，y 随x 的增大而减小，∴k k y b a≤≤，根据“k 属和合函数”的定义：()b a a k k b k =--，解得：1ab =，∵2020a b +=，∴()22222018a b a b ab =+-=+；(3)二次函数22362y x ax a a =-+++的对称轴为：()623a x a =-=⨯-， (i )若a ＞1时，即11x -在对称轴左侧，如下图所示：不难发现，当x=1时，y 最大值为：283y a a =+-，当x=﹣1时，y 最小值为：243y a a =--，根据“k 属和合函数”的定义：()()()22834311a a a a k +----=⨯--⎡⎤⎣⎦，解得：6k a =，∵a ＞1，∴6k >；(ii )若0＜a ≤1时，即11x -含对称轴，且x=﹣1离对称轴最远，如下图所示：不难发现：当x=a 时，y 最大值为：242y a a =+，当x=﹣1时，y 最小值为：243y a a =--，根据“k 属和合函数”的定义：()()()22424311a a a a k +---=⨯--⎡⎤⎣⎦，解得：()2312k a =+，此函数的对称轴为：a=﹣1，开口向上， ∴0＜a ≤1在对称轴的右侧，k 随a 的增大而增大，∴当0＜a ≤1时，解得：362k <≤； (iii )若﹣1＜a ≤0时，即11x -含对称轴，且x=1离对称轴最远，如下图所示：不难发现：当x=a 时，y 最大值为：242y a a =+，当x=1时，y 最小值：283y a a =+-，根据“k 属和合函数”的定义：()()()22428311a a a a k +-+-=⨯--⎡⎤⎣⎦解得：()2312k a =-，此函数对称轴为：a=1，开口向上， ∴﹣1＜a ≤0在对称轴的左侧，k 随a 的增大而减小∴当﹣1＜a ≤0时，解得：362k ≤<； (iiii )若a ＜﹣1时，即11x -在对称轴右侧，如下图所示：不难发现，当x=1时，y 最小值为：283y a a =+-，当x=﹣1时，y 最大值为：243y a a =--，根据“k 属和合函数”的定义：()()()22438311a a a a k ---+-=⨯--⎡⎤⎣⎦解得：6k a =-∵a ＜﹣1，∴6k >；综上所述：若a ＞1时，6k >；若0＜a ≤1时，362k <≤；若﹣1＜a ≤0时，362k ≤<；若a ＜﹣1时，6k >. 【点睛】此题考查的是新定义类问题、一次函数的性质、反比例函数的性质和二次函数的性质，读懂新定义类问题的定义、掌握各类函数的增减性和分类讨论的数学思想是解决此题的关键.26.如图，抛物线y =ax 2+bx +c (a ＜0，a 、b 、c 为常数)与x 轴交于A 、C 两点，与y 轴交于B 点，A (﹣6，0)，C (1，0)，B (0，163)． (1)求该抛物线的函数关系式与直线AB 的函数关系式；(2)已知点M (m ，0)是线段OA 上的一个动点，过点M 作x 轴的垂线l ，分别与直线AB 和抛物线交于D 、E 两点，当m 为何值时，△BDE 恰好是以DE 为底边的等腰三角形？(3)在(2)问条件下，当△BDE 恰妤是以DE 为底边的等腰三角形时，动点M 相应位置记为点M '，将OM '绕原点O 顺时针旋转得到ON (旋转角在0°到90°之间)；①探究：线段OB 上是否存在定点P (P 不与O 、B 重合)，无论ON 如何旋转，NP NB始终保持不变，若存在，试求出P 点坐标：若不存在，请说明理由；②试求出此旋转过程中，(NA 34+NB )的最小值．【答案】y 89=-x 2409-x 163+，直线AB 的解析式为：y 89=x 163+；(2)当m =﹣4时，△BDE 恰好是以DE为底边的等腰三角形；(3)①存在，P (0，3)；②．【解析】【分析】(1)根据A 和C 的坐标设出两点式，再代入点B 的坐标，即可求出抛物线的解析式；设直线AB 的解析式为y=kx+n ，将A 和B 的坐标代入求解，即可得出直线AB 的解析式；(2)根据点M 的坐标写出点D 的坐标，作BG ⊥DE 于点D 得出GM=OB 163=，代入求解即可得出答案； (3)①假设存在，证出△NOP ∽△BON 得出34OP NP ON ON NB OB ===即可得出答案；②结合①得出(NA 34+NB )的最小值=NA+NP ，此时N ，A ，P 三点共线，计算即可得出答案.【详解】解：(1)设抛物线解析式为y= a(x+6)(x ﹣1)，(a≠0)．将B (0，163)代入，得163=a(x+6)(x ﹣1)，解得：a 89=-， ∴该抛物线解析式为y 89=-(x+6)(x ﹣1)或y 89=-x 2409-x 163+．设直线AB 的解析式为y=kx+n (k≠0)．将点A (﹣6，0)，B (0，163)代入，得 06163k n n =-+⎧⎪⎨=⎪⎩，解得89163k n ⎧=⎪⎪⎨⎪=⎪⎩，则直线AB 的解析式为：y 89=x 163+； (2)∵点M (m ，0)，过点M 作x 轴的垂线l 分别与直线AB 和抛物线交于D 、E 两点，∴D (m ，89m 163+)，当DE 为底时，如图1，作BG ⊥DE 于G ，则EG=GD 12=ED ，GM=OB 163=， ∵DM+DG=GM=OB ， ∴89m 16132++(89-m 2409-m 16839+-m 163-)163=，解得：m 1=﹣4，m 2=0(不合题意，舍去)，∴当m=﹣4时，△BDE 恰好是以DE 为底边的等腰三角形；。

人教版中考二模测试《数学试题》含答案解析

人教版数学中考综合模拟检测试题学校________ 班级________ 姓名________ 成绩________一．选择题(共15小题)1.下列四个实数中，最小是( ) A. 2-B. -5C. 1D. 42.若式子3x +在实数范围内有意义，则的取值范围是( ) A. 3x ≤-B. 3x ≥-C. 3x <-D. 3x >-3.下列说法正确的是( )A. 为了解一批灯泡使用寿命，宜采用普查方式B. 掷两枚质地均匀的硬币，两枚硬币都是正面朝上这一事件发生的概率为12C. 掷一枚质地均匀的正方体骰子，骰子停止转动后，5点朝上是必然事件D. 甲乙两人在相同条件下各射击10次，他们成绩的平均数相同，方差分别是S 甲2＝0.4，S 乙2＝0.6，则甲的射击成绩较稳定4.下列四个图案中，是中心对称图形的是( )A. B.C. D.5.如图，在下列四个几何体中，它的三视图(主视图、左视图、俯视图)完全相同的是 ( )A. ①②B. ②③C. ①④D. ②④6.《九章算术》是我国古代数学的经典著作，书中有一个问题：”今有黄金九枚，白银一十一枚，称之重适等．交易其一，金轻十三两．问金、银一枚各重几何?”．意思是：今有甲种袋子中装有黄金9枚(每枚黄金重量相同)，乙种袋子中装有白银11枚(每枚白银重量相同)，称重两袋相等．两袋互相交换1枚后，甲种袋子比乙种袋子轻了13两(袋子重量忽略不计)．问黄金、白银每枚各重多少两?设每枚黄金重x 两，每枚白银重y 两，则可建立方程为( )A. 11x 9y (8x y)(10y x)13=⎧⎨+++=⎩B. 11x 9y(10y x)(8x y)13=⎧⎨+-+=⎩C. 911(10)(8)13x yy x x y =⎧⎨+-+=⎩D. 911(8)(10)13x yx y y x =⎧⎨+++=⎩7.从﹣1、2、3、﹣6这四个数中任取两数，分别记为、，那么点(),m n 在函数6y x =图象的概率是( ) A.12B.13C.14D. 188.正方形ABCD 的边AB 上有一动点，以EC 为边作矩形ECFG ，且边FG 过点，在点从点移动到点的过程中，矩形ECFG 的面积( )A. 先变大后变小B. 先变小后变大C. 一直变大D. 保持不变9.反比例函数1k y x-=与一次函数y ＝k (x+1)(其中x 为自变量，k 为常数)在同一坐标系中的图象可能是( )A. B. C. D.10.已知有理数1a ≠，我们把11a-称为a 的差倒数，如：2的差倒数是1=-112-，-1的差倒数是11=1(1)2--．如果12a =-，a 2是a 1的差倒数，a 3是a 2的差倒数，a 4是a 3的差倒数……依此类推，那么12100a a a +++的值是( )A. -7.5B. 7.5C. 5.5D. -5.511.计算：32﹣18的结果是( ) A.2 B. 22C.3 D. 2312.计算：22x x -﹣42x -＝( ) A 1B. 2C.22x x +- D.22x - 13.如图，矩形DEFG 的边EF 在△ABC 的边BC 上，顶点D ，G 分别在边AB ，AC 上，AH ⊥BC ，垂足为H ，AH 交DG 于点P ，已知BC ＝6，AH ＝4．当矩形DEFG 面积最大时，HP 的长是( )A. 1B. 2C. 3D. 414.抛物线23y x bx =++的对称轴为直线1x =．若关于的一元二次方程230x bx t ++-=(为实数)在14x -<<的范围内有实数根，则的取值范围是( )A. 211t ≤<B. 2t ≥C. 611t <<D. 26t ≤<15.如图，A ，B ，C ，D 为一直线上4个点，BC ＝3，△BCE 为等边三角形，⊙O 过A ，D ，E 三点，且∠AOD ＝120°，设AB ＝x ，CD ＝y ，则y 与x 的函数关系式是( )A. y ＝3xB. y ＝19x C. y ＝3x +3 D. y ＝9x二．填空题(共1小题)16.定义：等腰三角形的顶角与其一个底角的度数的比值k 称为这个等腰三角形的特征值．若等腰△ABC 中，∠A ＝80°，则等腰△ABC 的特征值k ＝_____．(多选) A .85B .58C .14D .4三．解答题(共8小题)17.计算x•x3+(2x2)2﹣2x5÷x18.如图，已知：在△AFD和△CEB中，点A、E、F、C在同一直线上，AE=CF，∠B=∠D，AD∥BC．求证：AD=BC．19.某同学进行社会调查，随机抽查了某个小区的200户家庭的年收入，并绘制成统计图(如图)．请你根据统计图给出的信息回答：(1)样本数据的中位数是_____，众数是_____;(2)这200户家庭的平均年收入为_____万元;(3)在平均数、中位数两数中，_____更能反映这个小区家庭的年收入水平．(4)如果该小区有1200户住户，请你根据抽样调查的结果估计该小区有_____户家庭的年收入低于1.3万元?20.如图，在下列18×7的网格中，横、纵坐标均为整数的点叫做格点，例如A(﹣8，0)、B(﹣4.3)都是格点．(1)直接写出△ABO的形状：(2)要求在图中仅用无刻的直尺画图：将△ABO绕点O顺时针旋转得△DEO，且点B的对应点E落在x轴正半轴上．操作如下：第一步：在x正半轴上找一个格点E，使OE＝OB;第二步：找一个格点F，使∠EOF＝∠AOB;第三步：找一个格点M，作直线AM交直线OF于D，连DE，则△DEO即为所作出的图形．请你按以上操作完成画图．并直接写出点E，F，M三点的坐标．21.如图，△ABC内接于⊙O，BC是⊙O的直径，弦AF交BC于点E，∠CAF＝2∠B．(1)求证：AE＝AC;(2)若⊙O的半径为4，E是OB的中点，求EF的长．22.公司以10元/千克的价格收购一批产品进行销售，经过市场调查获悉，日销售量y(千克)是销售价格x(元/千克)的一次函数，部分数据如表：销售价格x(元/千克) 10 15 20 25 30日销售量y(千克) 300 225 150 75 0(1)直接写出y与x之间的函数表达式;(2)求日销售利润为150元时的销售价格;(3)若公司每销售1千克产品需另行支出a元(0＜a＜10)的费用，当20≤x≤25时，公司的日获利润的最大值为1215元，求a的值．23.如图1，AB⊥BC，分别过点A，C作BM的垂线，垂足分别为M，N．(1)求证：BM•BC＝AB•CN;(2)若AB＝BC．①如图2，若BM＝MN，过点A作AD∥BC交CM的延长线于点D，求DN：CN的值;②如图3，若BM＞MN，延长BN至点E，使BM＝ME，过点A作AF∥BC交CE延长线于点F，若E是CF 的中点，且CN＝1，直接写出线段AF的长．24.抛物线y＝﹣x2+bx+c与x轴交于A，B两点(点A在B左边)，与y轴交于点C．(1)如图1，已知A(﹣1，0)，B(3，0)．①直接写出抛物线的解析式;②点H在x轴上，D(1，0)，连接AC，DC，HC，若CD平分∠ACH，求点H的坐标;(2)如图2，直线y＝﹣1与抛物线y＝﹣x2+bx+c交于点D，点E，D关于x轴对称．①若点D在抛物线对称轴的右侧，求证：DB⊥AE;②若点D在抛物线对称轴左侧，请直接判断，BD是否垂直AE?答案与解析一．选择题(共15小题)1.下列四个实数中，最小的是( )A. B. -5C. 1D. 4【答案】B 【解析】【分析】正实数都大于0，负实数都小于0，正实数大于一切负实数，两个负实数绝对值大的反而小，据此判断即可．【详解】根据实数大小比较的方法，可得514-<<，所以四个实数中，最小的数是-5．故选B ．【点睛】此题主要考查了实数大小比较的方法，要熟练掌握，解答此题的关键是要明确：正实数0>>负实数，两个负实数绝对值大的反而小．2.( ) A. 3x ≤- B. 3x ≥-C. 3x <-D. 3x >-【答案】B 【解析】【分析】根据二次根式的性质，被开方数大于或等于0．【详解】解：依题意有x+3≥0，即x≥-3时，二次根式有意义．故选：B ．【点睛】主要考查了二次根式的意义和性质，二次根式中的被开方数必须是非负数，否则二次根式无意义． 3.下列说法正确的是( )A. 为了解一批灯泡的使用寿命，宜采用普查方式B. 掷两枚质地均匀的硬币，两枚硬币都是正面朝上这一事件发生的概率为12C. 掷一枚质地均匀的正方体骰子，骰子停止转动后，5点朝上是必然事件D. 甲乙两人在相同条件下各射击10次，他们成绩的平均数相同，方差分别是S 甲2＝0.4，S 乙2＝0.6，则甲的射击成绩较稳定【答案】D【解析】【分析】根据全面调查与抽样调查的特点对A进行判断;利用画树状图求概率可对B进行判断;根据必然事件和随机事件的定义对C进行判断;根据方差的意义对D进行判断．【详解】解：A.为了解一批灯泡的使用寿命，宜采用抽样调查的方式，所以A选项错误;B.利用树状图得到共有正正、正反、反正、反反四种可能的结果数，所以两枚硬币都是正面朝上这一事件发生的概率为14，所以B选项错误;C.掷一枚质地均匀的正方体骰子，骰子停止转动后，5点朝上是随机事件，所以C选项错误;D.因为S甲2＝0.4，S乙2＝0.6，所以甲的方差小于乙的方差，所以甲的射击成绩较稳定，所以D选项正确．故选：D【点睛】本题考查了调查的方式、概率的意义、随机事件的意义以及方差的意义，难点在于理解概率的意义反映的只是这一事件发生的可能性的大小．4.下列四个图案中，是中心对称图形的是( )A. B.C. D.【答案】C【解析】【分析】根据中心对称图形的概念求解．【详解】解：A.不是中心对称图形，故本选项错误;B.不是中心对称图形，故本选项错误;C.是中心对称图形，故本选项正确;D.不是中心对称图形，故本选项错误;故选：C【点睛】本题考查了中心对称图形的概念，如果一个图形绕某一点旋转180°后能够与自身重合，那么这个图形就叫做中心对称图形，这个点叫做对称中心．5.如图，在下列四个几何体中，它的三视图(主视图、左视图、俯视图)完全相同的是( )A. ①②B. ②③C. ①④D. ②④【答案】C【解析】【分析】根据从正面看得到的图形是主视图，从左面看得到的图形是左视图，从上面看得到的图形是俯视图，可得答案．【详解】解：①正方体的三视图都是正方形，④球的三视图都是圆;②圆柱的主视图、左视图都是长方形，俯视图是圆形;③锥的主视图是三角形、左视图是三角形，俯视图是圆形．故选：C【点睛】本题考查了简单几何体的三视图，难度不大，熟悉主视图、左视图、俯视图的概念是解决问题的关键．6.《九章算术》是我国古代数学经典著作，书中有一个问题：”今有黄金九枚，白银一十一枚，称之重适等．交易其一，金轻十三两．问金、银一枚各重几何?”．意思是：今有甲种袋子中装有黄金9枚(每枚黄金重量相同)，乙种袋子中装有白银11枚(每枚白银重量相同)，称重两袋相等．两袋互相交换1枚后，甲种袋子比乙种袋子轻了13两(袋子重量忽略不计)．问黄金、白银每枚各重多少两?设每枚黄金重x两，每枚白银重y 两，则可建立方程为( )A.11x9y(8x y)(10y x)13=⎧⎨+++=⎩B.11x9y(10y x)(8x y)13=⎧⎨+-+=⎩C.911(10)(8)13x yy x x y=⎧⎨+-+=⎩D.911(8)(10)13x yx y y x=⎧⎨+++=⎩【答案】C【解析】【分析】设每枚黄金重x 两，每枚白银重y 两，根据”黄金9枚和白银11枚的重量相等，黄金8枚和白银1枚的重量比黄金1枚白银10枚轻13两”，即可得出关于x ，y 的二元一次方程，此题得解．【详解】解：设每枚黄金重x 两，每枚白银重y 两，依题意，得：911(10)(8)13x yy x x y =⎧⎨+-+=⎩故选：C ．【点睛】本题考查了由实际问题抽象出二元一次方程组，找准等量关系，正确列出二元一次方程组是解题的关键．7.从﹣1、2、3、﹣6这四个数中任取两数，分别记为、，那么点(),m n 在函数6y x =图象的概率是( ) A.12B.13C.14D. 18【答案】B 【解析】【分析】根据反比例函数图象上点的坐标特征可得出 mn ＝6，列表找出所有 mn 的值，根据表格中 mn ＝6所占比例即可得出结论．【详解】点(),m n 在函数6y x=的图象上， 6mn ∴=．列表如下：mn 的值为6的概率是41123=．故选．【点睛】本题考查了反比例函数图象上点的坐标特征以及列表法与树状图法，通过列表找出mn＝6的概率是解题的关键．8.正方形ABCD的边AB上有一动点，以EC为边作矩形ECFG，且边FG过点，在点从点移动到点的过程中，矩形ECFG的面积( )A. 先变大后变小B. 先变小后变大C. 一直变大D. 保持不变【答案】D【解析】【分析】连接DE，△CDE的面积是矩形CFGE的一半，也是正方形ABCD的一半，则矩形与正方形面积相等．【详解】连接DE，∵S△CDE＝12S四边形CEGF，S△CDE＝12S正方形ABCD，∴矩形ECFG与正方形ABCD的面积相等．故选D．【点睛】此题考查了正方形的性质、矩形的性质，连接DE由面积关系进行转化是解题的关键．9.反比例函数1kyx-=与一次函数y＝k(x+1)(其中x为自变量，k为常数)在同一坐标系中的图象可能是( )A. B. C. D.【答案】C【解析】【分析】分别根据反比例函数与一次函数的性质对各选项进行逐一分析即可．【详解】解：一次函数()1y k x +＝可化为y kx k +＝，即一次函数在y 轴上的截距为k ，A 、由反比例函数的图象可知，k ＞0，由一次函数的图象可知k ＜0，由一次函数在y 轴上的截距可知k ＜0，两结论矛盾，故本选项错误;B 、由反比例函数的图象可知，k-1>0，即k ＞1，由一次函数的图象可知0＜k ＜1，两结论矛盾，故本选项错误;C 、由反比例函数的图象可知k-1＜0，即k ＜1，由一次函数的图象可知k ＞0，当x=-1时，y=0，故0＜k ＜1，两结论一致，故本选项正确确;D 、由反比例函数的图象可知，k ＜0，由一次函数的图象可知k ＜0，由一次函数在y 轴上的截距可知k ＞0，两结论矛盾，故本选项错误．故选C ．【点睛】本题考查的是反比例函数的图象与一次函数的图象，熟知以上知识是解答此题的关键． 10.已知有理数1a ≠，我们把11a-称为a 的差倒数，如：2的差倒数是1=-112-，-1的差倒数是11=1(1)2--．如果12a =-，a 2是a 1的差倒数，a 3是a 2的差倒数，a 4是a 3的差倒数……依此类推，那么12100a a a +++的值是( ) A. -7.5B. 7.5C. 5.5D. -5.5 【答案】A【解析】【分析】求出数列的前4个数，从而得出这个数列以2-，13，32依次循环，且1312326-++=-，再求出这100个数中有多少个周期，从而得出答案．【详解】解：∵12a=-，∴211 1(2)3a==--，3131213a==-，412312a==--，……∴这个数列以-2，13，32依次循环，且1312326-++=-，∵1003331÷=，∴12100115 3327.562a a a ⎛⎫+++=⨯--=-=-⎪⎝⎭，故选A．【点睛】本题考查了规律型：数字的变化类：通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素，然后推广到一般情况．11.( )B.D.【答案】A【解析】【分析】根据二次根式的性质把各个二次根式化简，合并同类二次根式得到答案．【详解】解：==故选：A【点睛】本题考查了二次根式的加减，把二次根式化成最简二次根式是解决问题的关键．12.计算：22xx-﹣42x-＝( )A. 1B. 2C.22xx+-D.22x-【答案】B【解析】【分析】根据同分母分式加减法法则计算，得到答案．【详解】解： 2422x x x --- 242x x -=- ()222x x -=- 2=．故选：B【点睛】本题考查了同分母分式的加减运算，较为简单，注意最后结果要化为最简分式或者整式． 13.如图，矩形DEFG 的边EF 在△ABC 的边BC 上，顶点D ，G 分别在边AB ，AC 上，AH ⊥BC ，垂足为H ，AH 交DG 于点P ，已知BC ＝6，AH ＝4．当矩形DEFG 面积最大时，HP 的长是( )A. 1B. 2C. 3D. 4【答案】B【解析】【分析】首先设HP x =，将AP 用含x 的代数式表示出来，运用矩形的性质、相似三角形的判定与性质表示出DG ，根据矩形DEFG 的面积S ＝DG ×DE ，得到二次函数，用配方法求出函数的最大值．【详解】解：设HP ＝x ，则DE ＝GF ＝x ，∵四边形DEFG 是矩形，∴DG ＝EF ，DE ＝GF ＝HP ＝x ，DG ∥EF ，∵AH ⊥BC ，∴AH ⊥DG ，∵DG ∥EF ，∴△ADG ∽△ABC ，∴DG AP BC AH=， ∴446DG x =-，解得：DG ＝362x -， ∴矩形DEFG 的面积S ＝DG ×DE ＝3(6)2x -x ＝-32(x -2)2+6， ∵-32＜0， ∴S 有最大值，当x ＝2时，S 的最大值是6，即当HP ＝2时，矩形DEFG 的面积最大，故选：B ．【点睛】本题主要考察了相似三角形的判定和性质、矩形的性质、二次函数的性质，解题的关键是建立二次函数模型解决最值问题.14.抛物线23y x bx =++的对称轴为直线1x =．若关于的一元二次方程230x bx t ++-=(为实数)在14x -<<的范围内有实数根，则的取值范围是( )A. 211t ≤<B. 2t ≥C. 611t <<D. 26t ≤<【答案】A【解析】【分析】根据给出的对称轴求出函数解析式为223y x x =-+，将一元二次方程230x bx t ++-=的实数根可以看做223y x x =-+与函数y t =的有交点，再由14x -<<的范围确定的取值范围即可求解; 【详解】∵23y x bx =++的对称轴为直线1x =，∴2b =-，∴223y x x =-+，∴一元二次方程230x bx t ++-=的实数根可以看做223y x x =-+与函数y t =的有交点，∵方程在14x -<<的范围内有实数根，当1x =-时，6y =，当4x =时，11y =，函数223y x x =-+在1x =时有最小值2，∴211t ≤<，故选A ．【点睛】本题考查二次函数的图象及性质;能够将方程的实数根问题转化为二次函数与直线的交点问题，借助数形结合解题是关键．15.如图，A，B，C，D为一直线上4个点，BC＝3，△BCE为等边三角形，⊙O过A，D，E三点，且∠AOD ＝120°，设AB＝x，CD＝y，则y与x的函数关系式是( )A. y＝3xB. y＝19x C. y＝3x+3 D. y＝9x【答案】D【解析】【分析】连接AE，DE，根据同弧所对的圆周角等于圆心角的一半，求得∠AED＝120°，然后求得△ABE∽△ECD．根据相似三角形的对应边对应成比例即可表示出x与y的关系，从而不难求解．【详解】解：连接AE，DE，∵∠AOD＝120°，∴AmD为240°，∴∠AED＝120°，∵△BCE等边三角形，∴∠BEC＝60°;∴∠AEB+∠CED＝60°;又∵∠EAB+∠AEB＝∠EBC＝60°，∴∠EAB＝∠CED，∵∠ABE＝∠ECD＝120°;∴△ABE∽△ECD，∴AB BE EC CD=，即33x y =， ∴()906y x x=<<．故选：D【点睛】此题主要考查了圆周角定理、相似三角形的判定与性质、等边三角形的判定和性质、求反比例函数的解析式，熟练掌握相似三角形的判定和性质是解题的关键．二．填空题(共1小题)16.定义：等腰三角形的顶角与其一个底角的度数的比值k 称为这个等腰三角形的特征值．若等腰△ABC 中，∠A ＝80°，则等腰△ABC 的特征值k ＝_____．(多选)A .85B .58C .14D .4 【答案】A 、C【解析】【分析】可知等腰三角形的两底角相等，则可求得底角的度数．从而可求解．【详解】解：①当∠A 为顶角时，等腰三角形两底角的度数为：18080502︒-︒=︒ ∴特征值808505k ︒==︒ ②当∠A 为底角时，顶角的度数为：180°﹣80°﹣80°＝20° ∴特征值201804k ︒==︒，综上所述，特征值k 为85或14．故答案是：A ，C 【点睛】此题为新定义问题，考查了等腰三角形的性质和三角形的内角和定理，能够对已知角进行分类讨论是解决问题的关键．三．解答题(共8小题)17.计算x •x 3+(2x 2)2﹣2x 5÷x【答案】3x 4【解析】【分析】根据整式的运算法则即可求出答案．【详解】解：原式＝x 4+4x 4﹣2x 4＝3x 4．故答案是：43x【点睛】本题考查了整式混合运算，按照先算乘方，再算乘除，最后计算加减的运算顺序进行计算，熟练掌握运算法则是解题的关键．18.如图，已知：在△AFD 和△CEB 中，点A 、E 、F 、C 在同一直线上，AE=CF ，∠B=∠D ，AD ∥BC ．求证：AD=BC ．【答案】证明见解析．【解析】【分析】因为AE=CF ，所以AE+EF=CF+EF ，即AF=CE ，因为AD ∥BC ，所以∠A=∠C ，再有∠B=∠D ，根据”AAS ”即得△AFD ≌△BEC ，于是AD=CB ．【详解】解： AE=CF ，AE+EF=CF+EF ，即AF=CE ，AD ∥BC ，∠A=∠C ，在△AFD 与△BEC 中A CB D AF CE ∠=∠⎧⎪∠=∠⎨⎪=⎩△AFD ≌△BEC ，∴AD=CB ．【点睛】本题考查的是平行线的性质、全等三角形的判定与性质．19.某同学进行社会调查，随机抽查了某个小区的200户家庭的年收入，并绘制成统计图(如图)．请你根据统计图给出的信息回答：(1)样本数据的中位数是_____，众数是_____;(2)这200户家庭的平均年收入为_____万元;(3)在平均数、中位数两数中，_____更能反映这个小区家庭的年收入水平．(4)如果该小区有1200户住户，请你根据抽样调查的结果估计该小区有_____户家庭的年收入低于1.3万元? 【答案】(1)1.2，1.3;(2)1.6;(3)中位数;(4)660【解析】【分析】(1)根据众数和中位数的定义分别进行解答即可;(2)根据加权平均数的计算公式分别进行计算即可;(3)根据平均数，中位数两数的意义分别进行分析，即可得出答案;(4)用总户数乘以200户中家庭的年收入低于1.3万元所占的百分比即可求得答案．【详解】解：(1)因为共有20个数，数据中的第10和11个数据的平均数是中位数，所以中位数是1.2(万元);(2)根据图示可知：平均收入为(20×0.05×0.6+20×0.05×0.9+20×0.1×1.0+20×0.15×1.1+20×0.2×1.2+20×0.25×1.3+20×0.15×1.4+20×0.05×9.7)÷2 0＝32÷20＝1.6(万元);因为众数是一组数据中出现次数最多的数，所以众数是1.3(万元);(3)在平均数，中位数两数中平均数受到极端值的影响较大，所以中位数更能反映这个地区家庭的年收入水平;(4)1200×(5%+5%+10%+15%+20%)＝660户．故答案是：1.2，1.3;1.6;中位数，660．【点睛】本题考查条形统计图、平均数、中位数、众数以及用样本估计总体，解题的关键是明确题意，找出所求问题需要的条件．20.如图，在下列18×7的网格中，横、纵坐标均为整数的点叫做格点，例如A(﹣8，0)、B(﹣4.3)都是格点．(1)直接写出△ABO的形状：(2)要求在图中仅用无刻的直尺画图：将△ABO绕点O顺时针旋转得△DEO，且点B的对应点E落在x轴正半轴上．操作如下：第一步：在x正半轴上找一个格点E，使OE＝OB;第二步：找一个格点F，使∠EOF＝∠AOB;第三步：找一个格点M，作直线AM交直线OF于D，连DE，则△DEO即为所作出的图形．请你按以上操作完成画图．并直接写出点E，F，M三点的坐标．【答案】(1)△ABO是等腰三角形;(2)图见解析，E(5，0)，F(4，3)，M(1，3)【解析】【分析】(1)利用勾股定理求出AB，OB即可判断．(2)根据要求作出点E(5，0)，点F(4，3)，取格点M(1，3)，使得AM平分∠BAO，直线AM交OF于D，连接DE，△ODE即为所求．【详解】解：(1)∵22345==+=，AB OB∴ABO是等腰三角形．(2)如图，△ODE即为所求．E(5，0)，F(4，3)，M(1，3)．故答案是：(1)△ABO是等腰三角形;(2)图见解析，E(5，0)，F(4，3)，M(1，3)【点睛】本题考查了勾股定理、等腰三角形的判定和性质、利用旋转的性质画图以及平面直角坐标系中点的坐标，能利用勾股定理求坐标系中两点间的距离、利用旋转的性质画图是解决问题的关键．21.如图，△ABC内接于⊙O，BC是⊙O的直径，弦AF交BC于点E，∠CAF＝2∠B．(1)求证：AE＝AC;(2)若⊙O的半径为4，E是OB的中点，求EF的长．【答案】(1)见解析;(2)EF6【解析】【分析】(1)过A作AH⊥CE于H，结合直径所对的圆周角是直角，得到∠ACB的余角∠CAH＝∠ABC，结合∠CAF ＝2∠ABC，得到∠EAH＝∠CAH，依据ASA证明△ACH≌△AEH，依据全等的性质即可;(2)连接BF，先根据半径是4，及E是OB的中点，求出CE、BE;然后利用第(1)问∠CAH＝∠ABC，及公共角∠C证明△CAH∽△CBA，依据相似的性质求得AC、AE，再依据同弧所对的圆周角相等，得到证明△CAE∽△FBE的条件，依据相似的性质即可求得EF的长．【详解】(1)证明：过A作AH⊥CE于H，又∵BC是⊙O的直径，∴∠CAB＝∠AHC＝∠AHE＝90°，∴∠ACB+∠ABC＝∠ACB+∠CAH＝90°，∴∠CAH＝∠ABC，又∵∠CAF＝2∠ABC，∴∠EAH＝∠CAH，又∵AH＝AH，∴△ACH≌△AEH(ASA)，∴AC＝AE;(2)解：连接BF，∵⊙O的半径为4，∴BC＝8，∵E是OB的中点，∴BE＝OE＝2，∴CE＝6，∴CH＝12CE＝3，∵∠CAH＝∠ABC，∠C＝∠C，∴△CAH∽△CBA，∴AC CH CB AC=,∴AC2＝CH∙CB＝3×8＝24，∴AE＝AC＝6，∵∠F＝∠C，∠FBE＝∠CAE，∴△CAE∽△FBE，∴AE CE BE EF=，266EF=，∴EF6．【点睛】本题考查了圆和相似、全等的综合，主要包含：直径所对的圆周角是直角，同弧所对的圆周角相等、全等的判定与性质、相似的判定与性质，作辅助线构造相似模型，及求出AE，是解题的关键．22.公司以10元/千克的价格收购一批产品进行销售，经过市场调查获悉，日销售量y(千克)是销售价格x(元/千克)的一次函数，部分数据如表：(1)直接写出y 与x 之间的函数表达式;(2)求日销售利润为150元时的销售价格;(3)若公司每销售1千克产品需另行支出a 元(0＜a ＜10)的费用，当20≤x ≤25时，公司的日获利润的最大值为1215元，求a 的值．【答案】(1)y ＝﹣15x +450;(2)销售价格为()元或(20﹣)元;(3)a 的值为2【解析】【分析】(1)设一次函数解析式为y ＝kx +b (≠0)，任选两点求表达式，求得k 便可;(2)根据题意列出日销售利润w 与销售价格x 之间的函数关系式，根据二次函数的性质确定最大值即可;(3)根据题意列出日销售利润w 与销售价格x 之间的函数关系式，依据二次函数的最大值列出a 的一元二次方程求得a 的值．【详解】解：(1)设一次函数解析式为y ＝kx +b (≠0)，把x ＝10，y ＝300和x ＝20，y ＝150代入得1030020150k b k b +=⎧⎨+=⎩ 解得：15450k b =-⎧⎨=⎩， ∴y ＝﹣15x +450;(2)设日销售利润w ＝y (x ﹣10)＝(﹣15x +450)(x ﹣10)即w ＝﹣15x 2+600x ﹣4500，当w ＝150时，150＝﹣15x 2+600x ﹣4500，解得，20x =±答：日销管利润为150元时的销售价格为(20+元或(20-元;(3)日获利w ＝y (x ﹣10﹣a )＝(﹣15x +450)(x ﹣10﹣a )，即w ＝﹣15x 2+(600+15a )x ﹣(450a +4500)，对称轴为()156001202152a x a +=-=+⨯-， ∵0＜a ＜10， ∴12020252a <+<， ∴当1202x a =+时，w 有最大值， w 215150150012154a a =-+=，解得a 1＝2，a 2＝38＞10(舍去)，综上所述，a 的值为2．故答案是：(1)y ＝﹣15x +450;(2)销售价格为(20+310)元或(20﹣310)元;(3)a 值为2【点睛】本题主要考查了一次函数与二次函数的综合应用，一元二次方程，解题时要利用图表中的信息，学会用待定系数法求解一次函数解析式，并将实际问题转化为求函数最值问题，从而来解决实际问题． 23.如图1，AB ⊥BC ，分别过点A ，C 作BM 的垂线，垂足分别为M ，N ．(1)求证：BM •BC ＝AB •CN ;(2)若AB ＝BC ．①如图2，若BM ＝MN ，过点A 作AD ∥BC 交CM 的延长线于点D ，求DN ：CN 的值;②如图3，若BM ＞MN ，延长BN 至点E ，使BM ＝ME ，过点A 作AF ∥BC 交CE 的延长线于点F ，若E 是CF 的中点，且CN ＝1，直接写出线段AF 的长．【答案】(1)见解析;(2)①DN ：CN ＝32;②AF ＝3﹣2 【解析】【分析】(1)根据两角对应相等的两个三角形相似证明即可．(2)如图2中，连接AN ，延长AN 交BC 的延长线于H ，作BK ⊥AN 于K ．，设CN ＝m ，则BM ＝CN ＝MN ＝m ，BN ＝AM ＝2m ，想办法用m 表示AN ，NH 即可解决问题．(3)如图3中，连接AE ，延长AE 交BC 的延长线于H ．△AFE ≌△HCE (ASA )，推出AE ＝EH ，AF ＝CH ，利用直角三角形斜边中线的性质求出AE ，EH ，再利用勾股定理求出BH 即可解决问题．【详解】解：(1)证明：如图1中，∵AM ⊥BN ，CN ⊥BN ，AB ⊥BC ，∴∠AMB ＝∠N ＝∠ABC ＝90°，∴∠A +∠ABM ＝90°，∠ABM +∠CBN ＝90°，∴∠A +∠CBN ＝90°，∴△ABM ∽△BCN ， ∴BM AB CN BC=， ∴BM •BC ＝AB •CN ．(2)解：①如图2中，连接AN ，延长AN 交BC 的延长线于H ，作BK ⊥AN 于K ．由(1)可知：△ABM ∽△BCN ，∴AB BM BC CN= ∵AB ＝BC ，∴AM ＝BN ，BM ＝CN ，设CN ＝m ，∵BM ＝MN ，∴BM ＝CN ＝MN ＝m ，BN ＝AM ＝2m ，∵AM ⊥BN ，BM ＝MN ， ∴5AB AN m ==， ∵1122ABN S BN AM AN BK =⋅⋅=⋅⋅． ∴455BK m==， ∴22221635555AK AB BK m m m =-=-=， ∵∠BAK ＝∠BAH ，∠ABH ＝∠AKB ＝90°，∴△ABK∽△AHB，∴AK AB AB AH=，∴35555m mAHm=，∴553AH m=，∴5525533HN AH AN m m m =-=-=，∵AD∥CH，∴532253DN AN mCN NHm===．②如图3中，连接AE，延长AE交BC的延长线于H．∵AF∥CH，∴∠F＝∠ECH，∵∠AEF＝∠CEH，EF＝CF，∴△AFE≌△HCE(ASA)，∴AE＝EH，AF＝CH，∵AM⊥BE，BM＝ME，∴AB＝AE，∵∠ABH＝90°，∴BE＝AE＝EH，∵CN＝BM＝ME＝1，∴BE＝AE＝EH＝2，∴AB＝BC＝AE＝2，∴2223BH AH AB=-=∴232CH BH BC =-=-，∴AF ＝23﹣2．故答案是：(1)见解析;(2)①DN ：CN ＝32;②AF ＝23﹣2 【点睛】本题考查了相似三角形的判定和性质、勾股定理、等腰三角形的性质、平行线分线段成比例定理、三角形的面积公式、全等三角形的判定和性质、线段垂直平分线的性质、直角三角形斜边上的中线的性质等知识点，综合性较强，熟练掌握相关知识点是解题的关键．24.抛物线y ＝﹣x 2+bx +c 与x 轴交于A ，B 两点(点A 在B 左边)，与y 轴交于点C ．(1)如图1，已知A (﹣1，0)，B (3，0)．①直接写出抛物线的解析式;②点H 在x 轴上，D (1，0)，连接AC ，DC ，HC ，若CD 平分∠ACH ，求点H 的坐标;(2)如图2，直线y ＝﹣1与抛物线y ＝﹣x 2+bx +c 交于点D ，点E ，D 关于x 轴对称．①若点D 在抛物线对称轴的右侧，求证：DB ⊥AE ;②若点D 在抛物线对称轴的左侧，请直接判断，BD 是否垂直AE ?【答案】(1)①y ＝﹣x 2+2x +3;②点H 的坐标为(133，0);(2)①见解析;②DB ⊥AE 【解析】【分析】(1)①用待定系数法解答便可;②过D 作DE ⊥AC 于点E ，DF ⊥CH 于点F ，求出DF ，设H (m ，0)，再由三角形的面积公式列出m 的方程进行解答;(2)①设DE 与x 轴的交点为G 点，连接DB ，并延长DB 与AE 交于点H ，运用求函数图象的交点坐标的方法求出A 、B ，D 点坐标，求得DG 、BG 、AG 、EG ，再证明△DBG ∽△AGE 便可得结论;②仿照上面方法便可得结论．详解】解：(1)①把A (﹣1，0)，B (3，0)代入y ＝﹣x 2+bx +c ，得10930b c b c --+=⎧⎨-++=⎩， ∴23b c =⎧⎨=⎩， ∴抛物线的解析式为：y ＝﹣x 2+2x +3;②过D 作DE ⊥AC 于点E ，DF ⊥CH 于点F ，如图1，∵y ＝﹣x 2+2x +3∴C (0，3)，∴OC ＝3，∵A (﹣1，0)，B (3，0)，D (1，0)，∴OA ＝1，OB ＝3，OD ＝1，AD ＝2， ∴2210AC OA OC =+， ∵1122ACD SAD OC AC DE =⋅⋅=⋅⋅， ∴3105AD OC DE AC ⋅== ∵CD 平分∠ACH ， ∴3105DF DE == 设点H 的坐标为(m ，0)，则DH ＝m ﹣1，29CH m =+， ∵1122CDH SCH DF DH OC =⋅⋅=⋅⋅， ()23910315m m +=-， ∴m ＝﹣1(舍去)，或133m =， ∴点H 的坐标为(133，0); (2)①设DE 与x 轴的交点为G 点，连接DB ，并延长DB 与AE 交于点H ，如图2，∵抛物线y＝﹣x2+bx+c与x轴交于A，B两点(点A在B左边)，∴24b b cA⎫-+⎪⎪⎝⎭，24b b cB⎫++⎪⎪⎝⎭，∵直线y＝﹣1与抛物线y＝﹣x2+bx+c交于点D，点D在抛物线对称轴的右侧，∴D点的坐标为2441b b c⎫+++-⎪⎪⎝⎭，∵点E，D关于x轴对称，∴244,12b b cE⎛⎫+++⎪⎪⎝⎭，DG＝EG＝1，∴2222444444b bc b b c b c b c AG+++-+++++ ==2222444444222b bc b b c b c b cBG++++++++ =-=∴22224442444DG b c b cAG b c b c+++==++++，224442BG b c b cEG+++=，∴DG BG AG EG=，∵∠DGB＝∠AGE＝90°，∴△DGB∽△AGE，∴∠BDG＝∠EAG，∵∠EAG+∠AEG＝90°，∴∠BDG+∠AEG＝90°，∴∠DHE＝90°，∴DB⊥AE;②BD⊥AE．如图3，∵抛物线y＝﹣x2+bx+c与x轴交于A，B两点(点A在B左边)，∴24b b cA⎫-+⎪⎪⎝⎭，24b b cB⎫++⎪⎪⎝⎭，∵直线y＝﹣1与抛物线y＝﹣x2+bx+c交于点D，点D在抛物线对称轴的左侧，∴D点的坐标为2441b b c⎫+++-⎪⎪⎝⎭，∵点E，D关于x轴对称，∴244,12b b cE⎛⎫+++⎪⎪⎝⎭，DG＝EG＝1，∴2222444444b bc b b c b c b c AG-+-++++-+ ==2222444444 222b bc b b c b c b cBG++-+++++=-=，∴EG AG BG DG=，∵∠DGB＝∠AGF＝90°，∴△DGB∽△AGE，∴∠BDG＝∠EAG，∵∠EAG+∠AEG＝90°，∴∠BDG+∠AEG＝90°，∴∠DHE＝90°，∴DB⊥AE．故答案是：(1)①y＝﹣x2+2x+3;②点H的坐标为(133，0);(2)①见解析;②DB⊥AE【点睛】此题考查了三角形面积公式、利用待定系数法求函数的解析式、相似三角形的判定和性质、函数图象交点坐标的求法以及数形结合的数学思想等知识点，是一道综合题．也是中考中的压轴题．。

模拟测评中考数学二模试题(含答案及解析)

中考数学二模试题考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I 卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I 卷（选择题 30分）一、单选题（10小题，每小题3分，共计30分）1、不等式72x -＋1<322x -的负整数解有( )A ．1个B ．2个C ．3个D ．4个2、在下列选项的四个几何体中，与其他类型不同的是（） A ． B ． C ． D ．3、如图，在数轴上有三个点A 、B 、C ，分别表示数5-， 3.5-，5，现在点C 不动，点A 以每秒2个单位长度向点C 运动，同时点B 以每秒1.5个单位长度向点C 运动，则先到达点C 的点为（）A ．点AB ．点BC ．同时到达D ．无法确定4、已知∠A 与∠B 的和是90°，∠C 与∠B 互为补角，则∠C 比∠A 大（） ·线○封○密○外A ．180°B ．135°C ．90°D ．45°5、关于x ，y 的方程组225x y mx m+=⎧⎨+=⎩的解满足x ＋y ＜6，则m 的最小整数值是( )A ．－1B ．0C ．1D ．26、已知455'1A ∠=︒，451'''218B ∠=︒，45.15C ∠=︒，则（） A ．A B C >>∠∠∠ B ．B A C ∠>∠>∠ C ．A C B ∠>∠>∠D ．C A B ∠>∠>∠7、日历表中竖列上相邻三个数的和一定是（）． A ．3的倍数B ．4的倍数C ．7的倍数D ．不一定8、下列命题与它的逆命题都为真命题的是（） A ．已知非零实数x ，如果30x为分式，那么它的倒数也是分式． B ．如果x 的相反数为7，那么x 为-7．C ．如果一个数能被8整除，那么这个数也能被4整除．D ．如果两个数的和是偶数，那么它们都是偶数． 9、下列运算中，正确的是（） A ．()326x x =B ．326x x x ⋅=C ．22456x x x +=D ．()33xy xy =10、如图，反比例函数3(0)y x x=->图象经过矩形OABC 边AB 的中点E ，交边BC 于F 点，连接EF 、OE 、OF ，则OEF 的面积是（）A ．32B ．94C ．73D ．52第Ⅱ卷（非选择题 70分）二、填空题（5小题，每小题4分，共计20分） 1、已知1530A '∠=︒，那么它的余角是________，它的补角是________． 2、双曲线()251m y m x -=-，当0x >时，y 随x 的增大而减小，则m =________．3、边长为a 、b 的长方形，它的周长为14，面积为10，则22a b ab +的值为__．4、比较大小(填“＞”或“＜”): 32- __________43-.5、以下说法：①两点确定一条直线；②两点之间直线最短；③若||a a =-，则0a <；④若a ，b 互为相反数，则a ，b 的商必定等于1-．其中正确的是_________．（请填序号）三、解答题（5小题，每小题10分，共计50分） 1、如图1，在平面直角坐标系中，抛物线2y x x =+与x 轴交于A 、B 两点（点A 在点B 的左侧），与y 轴交于点C ．（1）求A 、C 两点的坐标；（2）连接AC ，点P 为直线AC 上方抛物线上（不与A 、C 重合）的一动点，过点P 作PD AC ⊥交AC 于点D ，PE x ⊥轴交AC 于点E ，求PD DE +的最大值及此时点P 的坐标； ·线○封○密○外（3）如图2，将原抛物线沿射线CB 方向平移y '，点M 为新抛物线y '对称轴上一点，在新抛物线y '上是否存在一点N ，使以点C 、A 、M 、N 为顶点的四边形为平行四边形，若存在，请直接写出点M 的坐标，并选择一个你喜欢的点写出求解过程；若不存在，请说明理由． 2、如图，抛物线2y x bx c =-++与x 轴交于点()1,0A -，()3,0B 两点．点P 是直线BC 上方抛物线上一动点，过点P 作PE x ⊥轴于点E ，交直线BC 于点D ．设点P 的横坐标为m ．（1）求抛物线的解析式；（2）求PCB 的最大面积及点P 的坐标； 3、已知抛物线222y x mx m =--．（1）求证：对任意实数m ，抛物线与x 轴总有交点．（2）若该抛物线与x 轴交于1,0A ，求m 的值．4、鱼卷是泉州十大名小吃之一，不但本地人喜欢，还深受外来游客的赞赏．小张从事鱼卷生产和批发多年，有着不少来自零售商和酒店的客户，当地的习俗是农历正月没有生产鱼卷，客户正月所需要的鱼卷都会在农历十二月底进行一次性采购．2018年年底小张的“熟客”们共向小张采购了5000箱鱼卷，到2020年底“熟客”们采购了7200箱．（1）求小张的“熟客"们这两年向小张采购鱼卷的年平均增长率；（2）2020年底小张“熟客”们采订购鱼卷的数量占小张年底总销售量的45，由于鱼卷受到游客们的青睐，小张做了一份市场调查，决定今年年底是否在网上出售鱼卷，若没有在网上出售鱼卷，则按去年的价格出售，每箱利润为15元，预计销售量与去年持平；若计划在网上出售鱼卷，则需把每箱售价下4至5元，且每下调1元销售量可增加1000箱，求小张在今年年底能获得的最大利润是多少元？5、已知关于x 的方程6332x m mxx +-=-的解是非正整数，则符合条件的所有整数m 的和是（） A ．8- B ．2- C ．2 D ．4-参考答案-一、单选题 1、A 【分析】先求出不等式组的解集，再求不等式组的整数解．【详解】去分母得：x ﹣7+2＜3x ﹣2，移项得：﹣2x ＜3，解得：x 32-＞．故负整数解是﹣1，共1个．故选A ．【点睛】本题考查了不等式的解法，并会根据未知数的范围确定它所满足的特殊条件的值．一般方法是先解不等式，再根据解集求其特殊值． 2、B 【分析】根据立体图形的特点进行判定即可得到答案．【详解】解：A 、C 、D 是柱体，B 是锥体，所以，四个几何体中，与其他类型不同的是B ．故选B ． ·线○封○密·○外【点睛】本题主要考查了立体图形的识别，解题的关键在于能够准确找到立体图形的特点 3、A 【分析】先分别计算出点A 与点C 之间的距离为10，点B 与点C 之间的距离为8.5，再分别计算出所用的时间．【详解】解：点A 与点C 之间的距离为：5(5)5510--=+=，点B 与点C 之间的距离为：5( 3.5)5 3.58.5--=+=，点A 以每秒2个单位长度向点C 运动，所用时间为5210=÷（秒）；同时点B 以每秒1.5个单位长度向点C 运动，所用时间为1728.5 1.5533÷==（秒）；故先到达点C 的点为点A ，故选：A ．【点睛】本题考查了数轴，解决本题的关键是计算出点A 与点C ，点B 与点C 之间的距离． 4、C 【分析】根据补角的定义进行分析即可. 【详解】解：∵∠A +∠B ＝90°，∠B +∠C ＝180°， ∴∠C ﹣∠A ＝90°，即∠C 比∠A 大90°，故选C ．【点睛】考核知识点：补角.理解补角的数量关系是关键. 5、B 【解析】【分析】先解方程组，得出x ，y 的值，再把它代入x +y ＜6即可得出m 的范围．由此即可得出结论．【详解】解方程组225x y m x m +=⎧⎨+=⎩，得：5249x m y m =-⎧⎨=-⎩． ∵x +y ＜6，∴5m ﹣2+（4﹣9m ）＜6，解得：m ＞﹣1，∴m 的最小整数值是0．故选B ．【点睛】本题考查了二元一次方程组的解以及求一元一次不等式的整数解，解答此题的关键是解方程组． 6、A【分析】先把∠C ＝45.15°化成15°9′的形式，再比较出其大小即可．【详解】解：∵455'1A ∠=︒，451'''218B ∠=︒，45.15C ∠=︒， ∴45.15450.1560459''C ∠=︒=︒+⨯=︒，∴4515451218''459'''︒>︒>︒，即A B C >>∠∠∠．故选：A ·线○封○密·○外【点睛】本题考查的是角的大小比较，熟知度、分、秒的换算是解答此题的关键7、A【分析】设中间的数字为x，表示出前一个与后一个数字，求出和即可做出判断．【详解】解：设日历中竖列上相邻三个数的中间的数字为x，则其他两个为x-7，x+7，则三个数之和为x-7+x+x+7=3x，即三数之和为3的倍数．故选：A．【点睛】本题考查列代数式，解题的关键是知道日历表中竖列上相邻三个数的特点．8、B【分析】先判断原命题的真假，然后分别写出各命题的逆命题，再判断逆命题的真假. 【详解】解：A. 30x的倒数是30x，不是分式，原命题是假命题，不符合题意；B. 如果x的相反数为7，那么x为-7是真命题，逆命题为：如果x为-7，那么x的相反数为7，是真命题，符合题意；C. 如果一个数能被8整除，那么这个数也能被4整除是真命题，逆命题为：如果一个数能被4整除，那么这个数也能被8整除，是假命题，不符合题意；D.因为两个奇数的和也是偶数，所以原命题是假命题，不符合题意；故选B.【点睛】本题主要考查命题的逆命题和命题的真假判断，正确的命题叫真命题，错误的命题叫做假命题．判断命题的真假关键是要熟悉课本中的性质定理．9、A 【分析】根据 “幂的乘方”“同底数幂乘法”“合并同类项”“积的乘方”的运算法则，即可选出正确选项. 【详解】 A 选项，幂的乘方，底数不变，指数相乘，()326x x =，所以A 选项正确.B 选项，同底数幂相乘，底数不变，指数相加，325x xx ，所以B 选项错误.C 选项，合并同类项，字母和字母指数不变，系数相加，22256x x x +=，所以C 选项错误. D 选项，积的乘方，积中每一个因式分别乘方，()333xy x y =，所以D 选项错误. 故选A 【点睛】整式计算基础题型，掌握运算法则，熟练运用. 10、B 【分析】连接OB ．首先根据反比例函数的比例系数k 的几何意义，得出S △AOE =S △COF =1.5，然后由三角形任意一边的中线将三角形的面积二等分及矩形的对角线将矩形的面积二等分，得出F 是BC 的中点，则S △BEF =12S △OCF =0.75，最后由S △OEF =S 矩形AOCB ﹣S △AOE ﹣S △COF ﹣S △BEF ，得出结果．【详解】连接OB ． ∵E 、F 是反比例函数y =﹣3x （x ＞0）图象上的点，EA ⊥x 轴于A ，FC ⊥y 轴于C ，∴S △AOE =S △COF=1.5． ∵矩形OABC 边AB 的中点是E ，∴S △BOE =S △AOE =1.5，S △BOC =S △AOB =3，∴S △BOF =S △BOC ﹣S △COF =3﹣1.5=1.5，∴F·线○封○密○外是BC 的中点，∴S △OEF =S 矩形AOCB ﹣S △AOE ﹣S △COF ﹣S △BEF =6﹣1.5﹣1.5﹣0.5×1.5=94．故选B ．【点睛】本题主要考查了反比例函数的比例系数k 与其图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S 的关系，即S =12|k |．得出点F 为BC 的中点是解决本题的关键．二、填空题1、7430'︒ 16430'︒ 【分析】根据余角、补角的性质即可求解．【详解】解：901530896015307430''''︒-︒=︒-︒=︒， 180153017960153016430''''︒-︒=︒-︒=︒故答案为7430'︒，16430'︒．【点睛】此题考查了补角和余角的性质，理解余角和补角的性质是解题的关键． 2、2- 【分析】根据反比例函数的定义列出方程求解，再根据它的性质决定解的取舍．【详解】根据题意得：25110m m ⎧-=-⎨-⎩＞，解得：m =﹣2．故答案为﹣2．【点睛】本题考查了反比例函数的性质．对于反比例函数y =kx ，当k ＞0时，在每一个象限内，函数值y 随自变量x 的增大而减小；当k ＜0时，在每一个象限内，函数值y 随自变量x 增大而增大． 3、70 【分析】直接利用长方形的周长和面积公式结合提取公因式法分解因式计算即可．【详解】解：依题意：2a +2b =14，ab =10，则a +b =7∴a 2b +ab 2=ab （a+b ）=70；故答案为：70 【点睛】此题主要考查了提取公因式法分解因式，正确得出a +b 和ab 的值是解题关键． 4、＜．【分析】根据两个负数比较大小，其绝对值大的反而小比较即可．【详解】 ·线○封○密·○外解：∵339226-== ，448336-== ，9866＞， ∴ 32-<43-．故答案为：＜．【点睛】本题考查有理数的大小比较，能熟记有理数的大小比较的内容是解此题的关键，注意：正数都大于0，负数都小于0，正数大于一切负数，两个负数比较大小，其绝对值大的反而小． 5、① 【分析】分别利用直线的性质以及线段的性质和相反数、绝对值的性质分别分析得出答案．【详解】①两点确定一条直线，正确；②两点之间直线最短，错误，应为两点之间线段最短；③若||a a =-，则0a ≤，故③错误；④若a ，b 互为相反数，则a ，b 的商等于1-（a ，b 不等于0），故④错误．故答案为：①. 【点睛】此题主要考查了直线的性质以及线段的性质和相反数、绝对值，正确掌握相关定义是解题关键．三、解答题 1、（1）(3,0)A -，C ；（23(2P -（3）(2,或(2, 【分析】（1）分别令0x =和0y =即可求出函数图象与坐标轴相应的交点坐标；（2）运用待定系数法求出直线AC的解析式，设2(,30)3P m m m -+-<<，求出2PE =，证明△~PDE AOC ∆可求出2)PD =，2)DE，得23)2PD DE m +=+ 根据二次函数的性质可得结论；（3）在射线CB 上取一点Q，使CQ =Q 作QG y ⊥轴于点G ，证明△QGC BOC ∆∽得3,QG CG ==（1）在2y =中，令0x =，y =C ∴，令0y =，即2x 解得，13x =-，21x =，A B x x <，(3,0)A ∴- （2）设直线AC 的解析式为(0)y kx b k =+≠把(3,0),A C -两点的坐标分别代入(0)y kx b k =+≠中，得，·线○封○密·○外30k b b -+=⎧⎪⎨=⎪⎩解得，k b ⎧=⎪⎨⎪=⎩∴直线AC的解析式为：y x =∵点P 为直线AC 上方抛物线上（不与A 、C 重合）的一动点，∴设2(,30)P m m -<< ∵PE x ⊥轴∴(E m ，PE //y 轴 ∴∠PED ACO =∠，2PE =2= ∵PD AC ⊥ ∴∠90PDE ︒=∵(3,0),A C -∴3OA =，OC =∵∠90AOC ︒=∴AC ==90PDE AOC PED ACO ︒∠=∠==∠∠，∴△~PDE AOC ∆∴PD DE PEAO OC AC==即23PD ==∴2)113PD m =-，2)DE =∴2(3)113⎛+=⋅-+ ⎝⎭PD DE m m23()33244m =-++∵0<当32m =-时，PD DE +有最大值，PD DE +当32m =-时，233()()22--∴此时，3(2P -（3）在射线CB 上取一点Q，使CQ =Q 作QG y ⊥轴于点G ，则∠90QGC ︒=，如图，·线○封·○密○外(1,0),B C∴1OB =，OC =∵∠90BOC ︒=∴BC =∵∠90QGC BOC ︒=∠=，∠QCG BCO =∠ ∴△QGC BOC ∆∽ ∴QG CG CQBO CO CB==即1QG =∴3,QG CG ==∵221)y x x ==+将抛物线2y =CB 方向平移y '∴相当于抛物线y=21)x +3个单位，再向下平移∴213)y x '=+-22)x =- ∴新抛物线的对称轴为x =2，∵点M 为新抛物线y '对称轴上一点 ∴点M 的横坐标为2 当四边形ACMN 为平行四边形时，如图，根据平行四边形的性质可知，AC //NM ，AC =NM 由图可知，将点C 先向右平移2个单位，再向下平移若干个单位得到点M ，∴将点(3,0)A -先向右平移2个单位，再向下平移若干个单位得到点N ， ∴点N 的横坐标为：321-+=- 当1x =-时，212)y '=--=·线○封○密○外此时，点N 的坐标为(1,-将点(3,0)A -先向右平移2个单位得到点(1,N -，将点C 先向右平移2M ，∴此时点M 的坐标为(2, 当四边形ACNM 为平行四边形时，如图根据平行四边形的性质可知，AC //MN ，AC =MN由嵊可知，将点(3,0)A -先向右平移5个单位，再向下平移若干个单位得到点M ，∴将点C 先向右平移5个单位，再向下平移若干个单位得到点N ， ∴点N 的横坐标为055+=当5x =时，22)y '=-∴此时点N 的坐标为(5,∴将点(3,0)A -先向右平移5(2,M ， ∴此时点M的坐标为(2,综上所述，点M的坐标为：(2,或(2, 【点睛】本题主要考查了二次函数与坐标轴的交点，二次函数的平移和对称轴、一次函数的解析式等知识点．要会利用数形结合的思想把代数和几何图形结合起来，利用点的坐标的意义表示线段的长度，从而求出线段之间的关系．2、（1）2y x 2x 3=-++；（2）32m =时，PCB S △最大278=，此时315,24P ⎛⎫⎪⎝⎭【分析】（1）待定系数法直接将函数图象上已知坐标点代入函数表达式解方程即可；（2）先求出直线BC 的解析式，根据题意用含m 的表达式分别表示出P ，D 的坐标，再用含m 的表达式表示出PCB 的面积，根据二次函数求最值知识求解即可．【详解】解：（1）将点A 、B 坐标代入抛物线解析式，得10930b c b c --+=⎧⎨-++=⎩，解得23b c =⎧⎨=⎩，∴抛物线的解析式为2y x 2x 3=-++．（2）当0x =时，3y =， ∴()0,3C ，·线○封○密○外设直线BC 的解析式为()0y kx b k =+≠， ∵直线BC 经过点B 、点C ，∴将点B 、C 坐标代入直线BC 解析式得：330b k b =⎧⎨+=⎩，解得：13k b =-⎧⎨=⎩，∴直线BC 的解析式为3y x =-+． ∵点P 的横坐标为()03m m <<，PE x ⊥，∴点D 的横坐标也为()03m m <<，将P ，D 分别代入抛物线和直线BC 解析式，∴()2,23P m m m -++，(),3D m m -+，∴()()222333PD m m m m m =-++--+=-+，∴()2233392222B CPCB m m PD x x S m m ⨯-+⋅-===-+△， ∴2239332727m 222288PCBSm m ⎛⎫=-+=--+≤⎪⎝⎭， ∴当32m =时，PCB S △最大278=， ∴此时315,24P ⎛⎫⎪⎝⎭．【点睛】此题考查一次函数求解析式和二次函数求解析式及二次函数图像，求最值等，此题还涉及到结合图像列出三角形面积公式，有一定难度． 3、（1）见解析（2）122,1m m =-= 【分析】（1）令0y =，得到关于x 的一元二次方程，根据一元二次方程根的判别式判断即可；（2）令1x =，0y =，解一元二次方程即可求得m 的值（1）令0y =，则有2220x mx m --= 222890m m m ∆=+=≥ 即，对于任意实数方程2220x mx m --=总有两个实数根， ∴对任意实数m ，抛物线与x 轴总有交点．（2）解：∵抛物线222y x mx m =--与x 轴交于1,0A ， ∴202m m =-- 解得122,1m m =-= 【点睛】本题考查了二次函数与坐标轴交点问题，掌握一元二次方程根的判别式以及解一元二次方程是解题的关键． 4、（1）20% ·线○封○密○外（2）小张在今年年底能获得的最大利润是143000元.【分析】（1）设小张的“熟客”们这两年向小张采购鱼卷的年平均增长率为,x 则可得方程2500017200,x 再解方程即可得到答案；（2）先求解今年的总的销量为9000箱，设今年总利润为w 元，价格下调x 元，则可建立二次函数为1590001000w x x ，再利用二次函数的性质求解最大值即可. （1）解：设小张的“熟客”们这两年向小张采购鱼卷的年平均增长率为,x 则2500017200,x 整理得：2361,25x 解得：121120%,5x x （负根不合题意舍去）答：小张的“熟客”们这两年向小张采购鱼卷的年平均增长率为20%. （2）解： 2020年底小张“熟客”们采订购鱼卷的数量占小张年底总销售量的45，2020年小张年总销量为：47200=90005（箱），设今年总利润为w 元，价格下调x 元，则1590001000w x x令0,w 则1215,9,x x所以抛物线的对称轴为：1593,2x10000,a所以函数有最大值， 45,x当4x =时，1113000143000w 最大值（元），所以小张在今年年底能获得的最大利润是143000元. 【点睛】本题考查的是一元二次方程的应用，二次函数的应用，掌握“确定相等关系建立一元二次方程，建立二次函数模型”是解本题的关键. 5、A 【分析】将m 看作一个常数，先求关于x 的一元一次方程的解，再根据方程的解是非正整数求出符合条件的所有整数m 的值，最后求和即可．【详解】解：6332x m mx x +-=- 两边同乘以3，得3(2)6x x m mx -+=-去括号，得326x x m mx --=-移项合并同类项，得()16m x m +=+因为方程有解，所以10m +≠，所以65151111m m x m m m +++===++++ 要使方程的解是非正整数，则整数m 满足： 511m ≥-+且51m +为整数所以51m+的值为：-1或-5 解得：m =-6或-2 ·线○封○密·○外则符合条件的所有整数m的和是：-6+（-2）=-8故选：A【点睛】本题考查了一元一次方程的解法、以及解的应用，正确求解方程是解题关键．。

2022年人教版中考二模考试《数学试题》含答案解析

人教版数学中考综合模拟检测试题学校________ 班级________ 姓名________ 成绩________一、选择题(本大题共6小题，每小题3分，共18分)1.19的相反数是( ) A. ﹣19B. -119C.119D. 192.如图所示，把图1中正方体的一个角切掉，形成了如图2的几何体，则图2的俯视图是( )．A. B. C. D.3.下列各式计算正确的是( )． A. 2222a a a -= B. 22(3)3a a = C. 2(1)21a a --=-+D. 222()a b a b +=+4.对于一列数据，如果去掉一个最大值和一个最小值，那么这列数据分析一定不受影响的是( )． A. 平均数B. 中位数C. 众数D. 方差5.如图，在34⨯的正方形网格中，能画出与”格点ABC “面积相等的”格点正方形”有( )个．A. 2B. 4C. 6D. 86.对于二次函数2(12)(0)y ax a x a =+->，下列说法错误的是( )． A. 该二次函数图象的对称轴可以是轴 B. 该二次函数图象的对称轴不可能是1x = C. 当2x >时，的值随的值增大而增大 D. 该二次函数图象的对称轴只能在轴的右侧二、填空题(本大题共6小题，每小题3分，共24分)7.计算：43-=________．8.据北晚新视觉网3月20日报道，”新冠肺炎肆虐全球，意大利尤其严重，据民防都门预计，该国日前每月急需9000万只口罩．其中9000万用科学记数法表示为________．9.《九章算术》是中国古代数学著作之一，书中有这样一个问题：五只雀、六只燕共重一斤，雀重燕轻，互换其中一只，恰好一样重．问：每只雀、燕的重量各为多少?设一只雀的重量为斤，一只燕的重量为斤，则可列方程为________．10.已知α、β是方程x 2﹣2x ﹣3=0两个实数根，则α2﹣3α﹣αβ的值为____．11.已知菱形OABC 在坐标系中如图放置，点C 在x 轴上，若点A 坐标为(3，4)，经过A 点的双曲线交BC 于D ，则△OAD 的面积为____．12.在Rt △ABC 中，AC=3，BC=4，点P 是斜边AB 上一点，若△PAC 是等腰三角形，则线段AP 的长可能为____．三、解答题13.(1)化简：(2x +1)(2x ﹣1)+(x +1)(1﹣2x )．(2)如图，在四边形ABCD 中，AB ⊥BC ，E ，F ，M 分别是AD ，DC ，AC 的中点，连接EF ，BM ，求证：EF =BM ．14.先化简，再求值：224442x xxx x x-+⎛⎫÷-⎪-⎝⎭，其中232x=-．15.如图，在矩形ABCD中，E、F分别是BC，AD边上的点，且AE=CF，若AC⊥EF，试判断四边形AECF 的形状，请说明理由．16.《小猪佩奇》这部动画片，估计同学们都非常喜欢．周末，小猪佩奇一家4口人(小猪佩奇，小猪乔治，小猪妈妈，小猪爸爸)到一家餐厅就餐，包厢有一圆桌，旁边有四个座位(，，，)．(1)小猪佩奇随机坐到座位的概率是________;(2)若现在由小猪佩奇，小猪乔治两人先后选座位，用树状图或列表的方法计算出小猪佩奇和小猪乔治坐对面的概率．17.如图，在67⨯的正方形的网格图中，点，，均为格点，仅用无刻度直尺按要求作图．(1)在图1中，画一条射线AM ，使45BAM ∠=︒; (2)在图2中，在线段AB 上求点，使45CPA ∠=︒．18.为了增强学生的疫情防控意识，响应”停课不停学”号召，某校组织了一次”疫情防控知识”专题网上学习，并进行了一次全校2500名学生都参加的网上测试．阅卷后，教务处随机抽取了100份答卷进行分析统计，发现考试成绩(分)的最低分为51分，最高分为满分100分，并绘制了如下不完整的统计图表．请根据图表提供的信息，解答下列问题：分数段(分)频数(人) 频率 5161x ≤< 01 6171x ≤<18 018 7181x ≤< 8191x ≤< 35 0.35 91101x ≤<12 012 合计 1001(1)填空：a =________，b =________，n =________; (2)将频数分布直方图补充完整;(3)该校对成绩为91100x ≤≤的学生进行奖励，按成绩从高分到低分设一、二、三等奖，并且一、二、三等奖的人数比例为1:3:6，请你估算全校获得二等奖的学生人数;(4)结合调查的情况，为了提高疫情防控意识，请你给学校提一条合理性建议．19.如图1，是某保温杯的实物图和平面抽象示意图．点，是保温杯上两个固定点，与两活动环相连，把手CD 与两个活动环AD ，BC 相连，现测得 2.6cm AD BC ==，17cm AB =，如图2，当，，三点共线时，恰好AC BC ⊥． (1)请求把手CD 的长;(2)如图3，当//CD AB 时，求ADC ∠的度数．(参考数据：sin57.50.843︒=，cos57.50.538︒=，tan57.5 1.570︒=)20.如果，⊙O 是△ABC 的外接圆，∠A =45°，BD ∥OC 交AC 的延长线于点D ． (1)求证：BD 是⊙O 的切线; (2)若∠D =30°，OC =2． ①求∠ABC 的度数; ②求AB 的长．21.数学活动课上，小明同学根据学习函数的经验，对函数的图像、性质进行了探究，下面是小明同学探究过程，请补充完整：如图1，已知在Rt ABC △，90ACB ︒∠=，30A ︒∠=，2cm BC =，点为AB 边上的一个动点，连接PC ．设cm BP x =，cm CP y =．【初步感知】⊥时，则①x=________，②y=________;(1)当CP AB【深入思考】(2)试求与之间的函数关系式并写出自变量的取值范围;(3)通过取点测量，得到了与的几组值，如下表：/cmx0 0.5 1 1.5 2. 2.5 3 3.5 4y 2 1.8 1.7 _____ 2 2.3 2.6 3.0 _____/cm(说明：补全表格时相关数值保留一位小数)1)建立平面直角坐标系，如图2，描出已补全后的表中各对应值为坐标的点，画出该函数的图象;2)结合画出函数图象，写出该函数的两条性质：①________________________________;②________________________________．22.已知：在Rt△ABC中，∠B=90°，∠ACB=30°，点D为BC边上一动点，以AD为边，在AD的右侧作等边三角形ADE．(1)当AD平分∠BAC时，如图1，四边形ADCE是形;(2)过E作EF⊥AC于F，如图2，求证：F为AC的中点;(3)若AB=2，①当D为BC的中点时，过点E作EG⊥BC于G，如图3，求EG的长;②点D从B点运动到C点，则点E所经过路径长为．(直接写出结果)23.已知点P 为抛物线y 12x 2上一动点，以P 为顶点，且经过原点O 的抛物线，记作”y p ”，设其与x 轴另一交点为A ，点P 的横坐标为m ．(1)①当△OP A 为直角三角形时，m = ; ②当△OP A 为等边三角形时，求此时”y p ”的解析式;(2)若P 点的横坐标分别为1，2，3，…n (n 为正整数)时，抛物线”y p ”分别记作”1p y “、”2p y “…，”n p y “，设其与x 轴另外一交点分别为A 1，A 2，A 3，…A n ，过P 1，P 2，P 3，…P n 作x 轴的垂线，垂足分别为H 1，H 2，H 3，…H n ．1)① P n 的坐标为 ;OA n = ;(用含n 的代数式来表示) ②当P n H n ﹣OA n =16时，求n 的值．2)是否存在这样的A n ，使得∠OP 4A n =90°，若存在，求n 的值;若不存在，请说明理由．答案与解析一、选择题(本大题共6小题，每小题3分，共18分)1.19的相反数是( ) A. ﹣19 B. -119C.119D. 19【答案】A 【解析】【分析】根据相反数的定义即可求解.【详解】解：19的相反数是：﹣19．故选A ．【点睛】此题主要考查相反数，解题的关键是熟知相反数的定义.2.如图所示，把图1中正方体一个角切掉，形成了如图2的几何体，则图2的俯视图是( )．A. B. C. D.【答案】C 【解析】【分析】根据俯视图是从上面看得到的视图，进行判断即可．【详解】解：图2的俯视图是带有一条对角线的正方形，故选：C ．【点睛】此题主要考查了三视图，注意：看得见的棱用实线表示，看不见的棱用虚线表示． 3.下列各式计算正确的是( )． A. 2222a a a -=B. 22(3)3a a =C. 2(1)21a a --=-+D. 222()a b a b +=+【答案】A 【解析】【分析】根据合并同类项法则、积的乘方法则、单项式乘多项式法则及完全平方公式逐一判断即可．【详解】解：A ．2222a a a -=，正确; B ．22(3)9a a =，原式错误; C ．2(1)22a a --=-+，原式错误; D ．222()2a b a b ab +=++，原式错误;故选：A ．【点睛】本题主要考查整式的运算，解题的关键是掌握合并同类项法则、积的乘方法则、单项式乘多项式法则及完全平方公式．4.对于一列数据，如果去掉一个最大值和一个最小值，那么这列数据分析一定不受影响的是( )． A. 平均数 B. 中位数C. 众数D. 方差【答案】B 【解析】【分析】根据平均数、中位数、众数和方差的求法分析即可【详解】解：由于中位数是位于最中间的一个数或中间两数的平均数，所以去掉一个最大值和一个最小值，中位数一定不受影响，而其余的统计量，有可能会发生变化，故选：B ．【点睛】此题主要考查统计的有关知识，主要包括平均数、中位数、众数、方差的意义，此题关键是了解中位数的定义．5.如图，在34⨯的正方形网格中，能画出与”格点ABC “面积相等的”格点正方形”有( )个．A. 2B. 4C. 6D. 8【答案】C 【解析】【分析】求出ABC 的面积为4，然后作出面积为4的格点正方形即可．【详解】解：12442ABCS=⨯⨯=，则可画出的格点正方形如图：共有6个，故选：C ．【点睛】本题考查了格点图形的面积计算，掌握基本图形的性质是解题的关键． 6.对于二次函数2(12)(0)y ax a x a =+->，下列说法错误的是( )． A. 该二次函数图象的对称轴可以是轴 B. 该二次函数图象的对称轴不可能是1x =C. 当2x >时，的值随的值增大而增大D. 该二次函数图象的对称轴只能在轴的右侧【答案】D【解析】【分析】求出该抛物线的对称轴为112x a=-，然后对各项进行判断即可．【详解】解：该抛物线的对称轴为：121122a x a a-=-=-， A. 当1102a -=即12a =时，该二次函数图象的对称轴是轴，正确; B. 由1112a -≠可知该二次函数图象的对称轴不可能是1x =，正确; C. ∵0a >， ∴1112a-<， ∴当2x >时，的值随的值增大而增大，正确;D. 该二次函数图象的对称轴可以在轴的左侧，错误，故选：D ．【点睛】本题考查了二次函数的图象和性质，熟练掌握二次函数的对称轴公式是解题的关键．二、填空题(本大题共6小题，每小题3分，共24分)7.3=________．【答案】【解析】【分析】根据算术平方根的意义进行计算即可．3231=-=-，故答案为：－1．【点睛】本题考查了算术平方根的意义，熟练掌握基础知识是解题关键．8.据北晚新视觉网3月20日报道，”新冠肺炎肆虐全球，意大利尤其严重，据民防都门预计，该国日前每月急需9000万只口罩．其中9000万用科学记数法表示为________．【答案】7910⨯【解析】【分析】科学记数法的表示形式为a×10n 的形式，其中1≤|a|＜10，n 为整数．确定n 的值时，要看把原数变成a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相同．当原数绝对值＞10时，n 是正数;当原数的绝对值＜1时，n 是负数．【详解】解：9000万用科学记数法表示为：7910⨯，故答案为：7910⨯．【点睛】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n 的形式，其中1≤|a|＜10，n 为整数，表示时关键要正确确定a 的值以及n 的值．9.《九章算术》是中国古代数学著作之一，书中有这样一个问题：五只雀、六只燕共重一斤，雀重燕轻，互换其中一只，恰好一样重．问：每只雀、燕的重量各为多少?设一只雀的重量为斤，一只燕的重量为斤，则可列方程为________．【答案】56145x y x y y x +=⎧⎨+=+⎩【解析】【分析】根据五只雀、六只燕共重一斤可得561x y +=，根据互换其中一只，恰好一样重可得45x y y x +=+，据此可得答案．【详解】解：设一只雀的重量为斤，一只燕的重量为斤，由题意得：56145x y x y y x +=⎧⎨+=+⎩，故答案为：56145x y x y y x +=⎧⎨+=+⎩．【点睛】本题考查由实际问题抽象出二元一次方程组，解答本题的关键是明确题意，列出相应的方程组． 10.已知α、β是方程x 2﹣2x ﹣3=0的两个实数根，则α2﹣3α﹣αβ的值为____．【答案】3或7．【解析】【分析】先根据一元二次方程解的定义和根与系数的关系可得α2﹣2α=3，αβ=﹣3，然后求出一元二次方程的两根，即可求出结论．【详解】解：∵α、β是方程x 2﹣2x ﹣3=0的两个实数根，∴α2﹣2α=3，αβ=﹣3，∴α2﹣3α﹣αβ=α2﹣2α﹣α﹣αβ=3﹣α﹣(﹣3)=6﹣α．∵x2﹣2x﹣3=0，即(x+1)(x﹣3)=0，解得：x1=﹣1，x2=3，∴α=3或﹣1，∴6﹣α=3或7．故答案为：3或7．【点睛】本题考查了根与系数的关系以及一元二次方程的解，熟练掌握一元二次方程的根与系数的关系和一元二次方程的解法是解题的关键．11.已知菱形OABC在坐标系中如图放置，点C在x轴上，若点A坐标为(3，4)，经过A点的双曲线交BC于D，则△OAD的面积为____．【答案】10．【解析】【分析】根据三角形的面积公式，S△AOD＝12底×高，而S菱形OABC＝底×高，它们等底同高，因此S△AOD＝12S菱形OABC，据此进行求解即可得答案．【详解】∵点A坐标为(3，4)，∴OA2234+=5．∵四边形ABCO为菱形，∴OC＝OA，S菱形ABCO＝5×4＝20，∴S△OAD12=S菱形ABCO12=⨯20＝10．故答案为：10．【点睛】本题考查了菱形的性质，反比例函数的知识，正确把握相关知识是解题的关键．12.在Rt△ABC中，AC=3，BC=4，点P是斜边AB上一点，若△PAC是等腰三角形，则线段AP的长可能为____．【答案】3，2.5或185．【解析】【分析】分三种情况讨论，再利用等腰三角形的性质进行计算即可．【详解】若△PAC是等腰三角形，则分以下三种情况：①PA=AC=3;②AP=PC时，则∠A=∠ACP，∵∠A+∠B=90°，∠ACP+∠BCP=90°，∴∠B=∠BCP，∴PC=PB，∴AP=PB=PC，∴P为AB的中点，∵在Rt△ABC中，22345AB=+=，∴AP=2.5;③PC=AC时，过C作CD⊥AB于D，则AP=2AD，∵在Rt△ACD中，AD=AC•cosA，∴AP=2AC•cosA，又∵在Rt△ABC中，3 cos5ACAAB==，∴3182355 AP=⨯⨯=，综上所述，AP的长为3，2.5或185．故答案：3，2.5或185．【点睛】本题考查等腰三角形，熟练应用等腰三角形的性质及锐角三角函数是解题关键．三、解答题13.(1)化简：(2x+1)(2x﹣1)+(x+1)(1﹣2x)．(2)如图，在四边形ABCD中，AB⊥BC，E，F，M分别是AD，DC，AC的中点，连接EF，BM，求证：EF=BM．【答案】(1)2x2﹣x;(2)证明见解析．【解析】【分析】(1)原式利用平方差公式，以及多项式乘以多项式法则计算，合并即可得到结果;(2)根据三角形的中位线定理和直角三角形斜边中线的性质可得结论．【详解】(1)解：(2x+1)(2x-1)+(x+1)(1-2x)．=4x2-1+x-2x2+1-2x，=2x2-x;(2)证明：∵E，F分别是AD，DC的中点，∴EF是△ADC的中位线，∴EF=12 AC，∵AB⊥BC，M是AC的中点，∴BM=12 AC，∴EF=BM．【点睛】本题属于计算和几何的综合题，考查了整式的混合运算，三角形的中位线定理，直角三角形斜边中线的性质等知识，熟练掌握定理和性质是关键．14.先化简，再求值：224442x x x x x x -+⎛⎫÷- ⎪-⎝⎭，其中232x =-．【答案】12x +，36【解析】【分析】根据分式的混合运算法则进行化简，然后代入x 的值计算即可．【详解】解：原式2(2)(2)(2)(2)x x x x x x-+-=÷-2(2)(2)x x x x x -=⋅+-12x =+，当232x =-时，原式1136232223===-+．【点睛】本题考查了分式的化简求值以及分母有理化，熟练掌握运算法则是解题的关键．15.如图，在矩形ABCD 中，E 、F 分别是BC ，AD 边上的点，且AE =CF ，若AC ⊥EF ，试判断四边形AECF 的形状，请说明理由．【答案】四边形AECF 是菱形，理由见解析．【解析】【分析】由矩形的性质得出∠B=∠D=90°，AB=CD ，AD=BC ，AD ∥BC ，由HL 证明Rt △ABE ≌Rt △CDF ，即可BE=DF ，得出CE=AF ，由CE ∥AF ，证出四边形AECF 是平行四边形，再由AC ⊥EF ，即可得出四边形AECF 是菱形．【详解】四边形AECF 是菱形，理由如下：∵四边形ABCD 是矩形，∴∠B =∠D =90°，AB =CD ，AD =BC ，AD ∥BC ，在Rt △ABE 和Rt △CDF 中，AE CF AB CD =⎧⎨=⎩， ∴Rt △ABE ≌Rt △CDF (HL )，∴BE=DF．∵BC=AD，∴CE=AF．∵CE∥AF，∴四边形AECF是平行四边形，又∵AC⊥EF，∴四边形AECF是菱形．【点睛】本题考查了矩形的性质、全等三角形的判定与性质、菱形的判定、平行四边形的判定;熟练掌握矩形的性质和菱形的判定，证明三角形全等是解题的关键．16.《小猪佩奇》这部动画片，估计同学们都非常喜欢．周末，小猪佩奇一家4口人(小猪佩奇，小猪乔治，小猪妈妈，小猪爸爸)到一家餐厅就餐，包厢有一圆桌，旁边有四个座位(，，，)．(1)小猪佩奇随机坐到座位的概率是________;(2)若现在由小猪佩奇，小猪乔治两人先后选座位，用树状图或列表的方法计算出小猪佩奇和小猪乔治坐对面的概率．【答案】(1)14;(2)13【解析】【分析】(1)根据概率公式可得答案;(2)画出树状图，得出所有情况数以及小猪佩奇和小猪乔治坐对面的情况数，然后根据概率公式求解．【详解】解：(1)∵有4个座位，∴小猪佩奇随机坐到座位的概率是14;(2)树状图如下：∴共有12种结果，其中与或与为对面，共有4种， ∴小猪佩奇和小猪乔治坐对面的概率41123==．【点睛】本题考查了列表法或树状图法求概率，利用列表法或树状图法展示所有等可能的结果n ，再从中选出符合事件A 或B 的结果数目m ，然后利用概率公式求事件A 或B 的概率．17.如图，在67⨯的正方形的网格图中，点，，均为格点，仅用无刻度直尺按要求作图．(1)在图1中，画一条射线AM ，使45BAM ∠=︒;(2)在图2中，在线段AB 上求点，使45CPA ∠=︒．【答案】(1)见解析;(2)见解析【解析】【分析】(1)根据勾股定理，通过构造等腰直角三角形作图即可;(2)根据网格特点，通过构造平行线作图即可．【详解】解：(1)如图1，射线1AM 或2AM 即为所求;(2)如图2，点即为所求．【点睛】本题考查了勾股定理与网格问题，平行线的性质，熟练掌握网格特点和勾股定理是解题的关键． 18.为了增强学生的疫情防控意识，响应”停课不停学”号召，某校组织了一次”疫情防控知识”专题网上学习，并进行了一次全校2500名学生都参加的网上测试．阅卷后，教务处随机抽取了100份答卷进行分析统计，发现考试成绩(分)的最低分为51分，最高分为满分100分，并绘制了如下不完整的统计图表．请根据图表提供的信息，解答下列问题：分数段(分) 频数(人)频率 5161x ≤<0.1 6171x ≤< 180.18 7181x ≤<8191x ≤< 350.35 91101x ≤< 120.12 合计100 1(1)填空：a =________，b =________，n =________;(2)将频数分布直方图补充完整;(3)该校对成绩为91100x ≤≤的学生进行奖励，按成绩从高分到低分设一、二、三等奖，并且一、二、三等奖的人数比例为1:3:6，请你估算全校获得二等奖的学生人数;(4)结合调查的情况，为了提高疫情防控意识，请你给学校提一条合理性建议．【答案】(1)10，25，0.25;(2)见解析;(3)90人;(4)见解析【解析】【分析】(1)根据频数、频率、总数之间的关系计算即可;(2)根据a ，b 的值补全频数分布直方图即可;(3)用该校总人数乘以成绩为91100x ≤≤的频率，再乘以二等奖的比例即可;(4)建议学校开展疫情防控的专题讲座，让同学们更加充分的了解疫情【详解】解：(1)1000.110a =⨯=，1001018351225b =----=，250.25100n ==; 故答案为：10，25，0.25;(2)补全频数分布直方图如图所示：(3)325000.129010⨯⨯=(人)，答：估计全校获得二等奖的学生人数约为90人;(4)建议学校开展疫情防控的专题讲座，让同学们更加充分的了解疫情．【点睛】本题考查了频数分布表、频数分布直方图、样本估计总体，直方图能清楚地表示出每个项目的数据，从统计图中得到必要的信息是解决问题的关键．19.如图1，是某保温杯的实物图和平面抽象示意图．点，是保温杯上两个固定点，与两活动环相连，把手CD 与两个活动环AD ，BC 相连，现测得 2.6cm AD BC ==，17cm AB =，如图2，当，，三点共线时，恰好AC BC ⊥．(1)请求把手CD 的长;(2)如图3，当//CD AB 时，求ADC ∠的度数．(参考数据：sin57.50.843︒=，cos57.50.538︒=，tan57.5 1.570︒=)【答案】(1)14.2=CD cm ;(2)122.5︒∠=ADC 【解析】【分析】(1)在Rt ABC △中，利用勾股定理求出AC 即可解决问题;(2)分别过，作CE AB ⊥于，DF AB ⊥于，易得四边形CDFE 是矩形，Rt Rt ADF BCE ≌，求出AF ，计算出cos DAF ∠的值即可得到DAF ∠的度数，进而可得ADC ∠的度数．【详解】解：(1)如图2，在Rt ABC △中，222217 2.616.8cm AC AB BC =-=-=，∴16.8 2.614.2cm CD AC AD =-=-=;(2)如图3，分别过，作CE AB ⊥于，DF AB ⊥于，∵CD AB ，∴90CDF DFE CEF ︒∠==∠=∠， ∴四边形CDFE 是矩形， ∴DF CE =，EF CD =， ∵AD BC =，∴Rt Rt ADF BCE ≌，∴()2(1714.2)2 1.4cm AF BE AB EF ==-÷=-÷=，∴ 1.47cos 0.5382.613AF DAF AD ∠===≈， ∴57.5DAF ∠=︒， ∵CDAB ，∴18057.5122.5ADC ︒︒∠=-=︒．【点睛】本题考查了勾股定理的应用以及解直角三角形的应用，熟练掌握勾股定理和三角函数是解题的关键．20.如果，⊙O 是△ABC 的外接圆，∠A =45°，BD ∥OC 交AC 的延长线于点D ． (1)求证：BD 是⊙O 的切线; (2)若∠D =30°，OC =2． ①求∠ABC 的度数; ②求AB 的长．【答案】(1)证明见解析;(2)①60°;62【解析】【分析】(1)先利用同弧所对的圆周角和圆心角的关系证明∠BOC=90°，再由平行线的性质得出OBD=90°，按照切线的判定定理可得答案;(2)延长CO 交⊙O 于点E ，连接AE ，过C 作CH ⊥AB 于H ．①平行线的性质可得∠ACE=∠D=30°，由直径所对的圆周角为直角可得∠EAC=90°，从而可得∠E=60°，再利用同弧所对的圆周角相等可得答案;②由半径的长求得直径的长，利用30°角所对直角边等于斜边的一半，可得AE 的长，由勾股定理求得AC 的长，利用含45°角的直角三角形和含60°角的直角三角形，可分别求得AH 和BH 的长，两者相加即可得出AB 的长．【详解】(1)证明：∵∠BAC=45°， ∴∠BOC=2∠BAC=90°， ∵BD ∥OC ，∴∠BOC+∠OBD=180°，∴∠OBD=90°，∴BD是⊙O的切线;(2)延长CO交⊙O于点E，连接AE，过C作CH⊥AB于H．①∵BD∥OC，∠D=30°，∴∠ACE=∠D=30°，∵CE为直径，∴∠EAC=90°，∴∠E=60°，∴∠ABC=∠E=60°;②∵OC=2，∴CE=4，∵∠EAC=90°，∠ACE=30°，∴AE12=CE=2，∴AC2242=-=3∵∠BAC=45°，∴AH=CH22=AC22=⨯36=∵∠ABC=60°，∴BH3=CH362==，∴AB=AH+BH62=【点睛】本题考查了切线的判定与性质、圆中的有关计算等知识点，熟练掌握相关性质及定理是解题的关键．21.数学活动课上，小明同学根据学习函数的经验，对函数的图像、性质进行了探究，下面是小明同学探究过程，请补充完整：如图1，已知在Rt ABC △，90ACB ︒∠=，30A ︒∠=，2cm BC =，点为AB 边上的一个动点，连接PC ．设cm BP x =，cm CP y =．【初步感知】(1)当CP AB ⊥时，则①x =________，②y =________; 【深入思考】(2)试求与之间的函数关系式并写出自变量的取值范围; (3)通过取点测量，得到了与的几组值，如下表：/cm x0 0.5 1 1.5 2. 2.5 3 3.5 4 /cm y21.81.7_____22.32.63.0_____(说明：补全表格时相关数值保留一位小数)1)建立平面直角坐标系，如图2，描出已补全后的表中各对应值为坐标的点，画出该函数的图象; 2)结合画出的函数图象，写出该函数的两条性质：①________________________________;②________________________________．【答案】(1)①;3;(2)224(04)y x x x =-+≤≤;(3)1.8，3.5;1)作图见解析;2)①的最小值为3(或1.7)，②当01x ≤≤时，随增大而减小．【解析】【分析】(1)根据含30度直角三角形的性质求出BP ，CP 即可;(2)过作CD AB ⊥于，分两种情况：①当01x ≤≤时，②当14x <≤时，分别利用勾股定理计算即可; (3)分别求出x ＝1.5和x ＝4时y 的值，即可补全表格; 1)描点、连线即可;2)根据函数图象，可从最值和增减性方面写出函数的性质．【详解】解：(1)当CP AB ⊥时，BP ＝12BC ＝1，CP ＝2221=3-，故答案：①;②3; (2)过作CD AB ⊥于，由(1)可知，1BD =，3CD =，①当01x ≤≤时，如图1-1，1PD x =-，22222(1)(3)24PC PD CD x x x =+=-+=-+，∴224y x x =-+;②当14x <≤时，如图1-2，1PD x =-，22222(1)(3)24PC PD CD x x x =+=-+=-+，综合①②可得：224y x x =-+(04)x ≤≤;(3)当x ＝1.5时，224 3.25 1.8y x x ==-+≈，当x ＝4时，22412 3.5y x x ==-+≈，/cm x0 0.5 1 1.5 2. 2.5 3 3.5 4 /cm y21.81.71.822.32.63.03.51)函数图象如图所示：2)由函数图象得：①的最小值为3(或1.7);②当01x ≤≤时，随增大而减小．【点睛】本题考查了函数图象和性质的探究，含30度直角三角形的性质，勾股定理等，熟练掌握函数图象的画法及数形结合的思想是解题的关键．22.已知：在Rt △ABC 中，∠B =90°，∠ACB =30°，点D 为BC 边上一动点，以AD 为边，在AD 的右侧作等边三角形ADE ．(1)当AD 平分∠BAC 时，如图1，四边形ADCE 是形; (2)过E 作EF ⊥AC 于F ，如图2，求证：F 为AC 的中点; (3)若AB =2，①当D 为BC 的中点时，过点E 作EG ⊥BC 于G ，如图3，求EG 的长; ②点D 从B 点运动到C 点，则点E 所经过路径长为．(直接写出结果)【答案】(1)菱形;(2)证明见解析;(3)①EG 52=;②3 【解析】【分析】(1)根据平行四边形的判定定理得到四边形ADCE 为平行四边形，证明AD=AE ，根据菱形的判定定理证明结论;(2)证明△BAD ≌△FAE ，根据全等三角形的性质得到AB=AF ，根据直角三角形的性质得到AC=2AB ，证明结论;(3)①作EF ⊥AC 于F ，连接EC ，根据勾股定理求出BC ，根据等腰三角形的性质求出CG ，根据勾股定理计算，得到答案; ②根据线段垂直平分线的判定定理得到E'E''垂直平分AC ，证明△E'AE''≌△BAC ，得到E'E''=BC=23．【详解】解：(1)在Rt △ABC 中，∠B =90°，∠ACB =30°， ∴∠BAC =60°． ∵AD 平分∠BAC ， ∴∠BAD =∠DAC =30°． ∵△ADE 为等边三角形， ∴∠DAE =60°， ∴∠EAC =30°，∴∠EAC =∠ACB ，∠DAC =∠ACB ， ∴AE ∥DC ，AD =DC ． ∵AE =AD ，∴AE =CD ， ∴四边形ADCE 为平行四边形． ∵AD =AE ，∴平行四边形ADCE 为菱形．故答案为：菱形; (2)60,BAC DAE ∠=∠=︒,BAD FAE ∴∠=∠在△BAD 和△F AE 中，90BAD FAE ABD AFE AD AE ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩， ∴△BAD ≌△F AE (AAS )，∴AB=AF，在Rt△ABC中，∠B=90°，∠ACB=30°，∴AC=2AB，∴AC=2AF，∴F为AC的中点;(3)①如图3，作EF⊥AC于F，连接EC，在Rt△ABC中，∠B=90°，∠ACB=30°，∴AC=2AB=4，∴BC22AC AB-=3∵D为BC的中点，∴BD12=BC3=∴AD227AB BD+=∵AF=FC，EF⊥AC，∴EC=AE=AD7=∵EC=EA=ED，EG⊥DC，∴CG12=CD32=∴EG 2252EC CG =-=; ②如图4，当点D 与点B 重合时，点E 在E '处，点E '是AC 中点; 当点D 与点C 重合时，点E 在E ''处，其中△ACE ''是等边三角形，由(1)得：AE =CE ，∴点E 始终落在线段AC 的垂直平分线上， ∴E 'E ''垂直平分AC ，∴点E 的运动路径是从AC 的中点E '，沿着AC 垂直平分线运动到E ''处，在△E 'AE ''和△BAC 中，''''''''CAB E AE ABC AE E AC AE ∠=∠⎧⎪∠=∠⎨⎪=⎩， ∴△E 'AE ''≌△BAC (AAS )， ∴E 'E ''=BC =23．故答案为：23．【点睛】本题考查是等边三角形的性质、菱形的判定、直角三角形的性质，掌握全等三角形的判定定理和性质定理是解题的关键． 23.已知点P 为抛物线y 12=x 2上一动点，以P 为顶点，且经过原点O 的抛物线，记作”y p ”，设其与x 轴另一交点为A ，点P 的横坐标为m ．(1)①当△OP A 为直角三角形时，m = ; ②当△OP A 为等边三角形时，求此时”y p ”的解析式;(2)若P 点的横坐标分别为1，2，3，…n (n 为正整数)时，抛物线”y p ”分别记作”1p y “、”2p y “…，”n p y “，设其与x 轴另外一交点分别为A 1，A 2，A 3，…A n ，过P 1，P 2，P 3，…P n 作x 轴的垂线，垂足分别为H 1，H 2，H 3，…H n ．1)① P n 的坐标为 ;OA n = ;(用含n 的代数式来表示) ②当P n H n ﹣OA n =16时，求n 的值．2)是否存在这样的A n ，使得∠OP 4A n =90°，若存在，求n 的值;若不存在，请说明理由．【答案】(1)① 2;② y 12=-x 23;(2)1)：① (n ，12n 2);2n ;② n =8;2)：存在，n =10．【解析】【分析】(1)①由△OP A 为直角三角形时．得到△OP A 为以点P 为顶点的等腰直角三角形，从而可得答案，②由△OP A 为等边三角形，过P 作PH OA ⊥于，利用三角函数与抛物线的解析式212y x =，求点,P A 的坐标，从而可得答案，(2)1)①利用P n 的横坐标为n ，结合抛物线的对称性可得答案，②由 P n H n ﹣OA n =16，建立方程求解即可，2) 画出图形，证明Rt △OP 4H 4∽Rt △P 4A n H 4即可得到答案．【详解】解：(1)①当△OP A 为直角三角形时．∵PO =P A ，故△OP A 为以点P 为顶点的等腰直角三角形， ∴点P 的横坐标和纵坐标相同，故点P (m ，m )，将点P 的坐标代入y 12=x 2得：m 12=m 2，解得：m =0或2(舍去0)．故答案为：2;②当△OP A 为等边三角形时，如图，过P 作PH OA ⊥于，,60,OH m POH ∴=∠=︒3,PH m ∴=P (m 3)，将点P 的坐标代入抛物线表达式212y x =, 解得：m 3故点P 的坐标为(36)，故”y p ”的解析式为：y =a (x ﹣3)2+6，点A 的坐标为(2m ，0)，即(3，0)，将点A 的坐标代入y =a (x ﹣3)2+6并解得：a 12=-，故”y p ”的解析式为：y 12=-(x ﹣32+612=-x 23; (2)1)① 由题意得：P n 的横坐标为n ，则其坐标为(n ，12n 2)，由抛物线对称性得：A n =2n ．故答案为：(n ，12n 2);2n ; ②由题意得：P n H n ﹣OA n 12=n 2﹣2n =16，解得：n =8或﹣4(舍去﹣4)，∴n =8;2)存在，理由：如下图所示，由1)知，点P 4的坐标为(4，8)，A n =2n ，即OH 4=4，P 4H 4=8，H 4A n =2n ﹣4，∵∠OP 4A n =90°，∴∠OP 4H 4+∠H 4P 4A n =90°．∵∠H 4P 4A n +∠P 4A n H 4=90°，∴∠OP 4H 4=∠P 4A n H 4，∴Rt △OP 4H 4∽Rt △P 4A n H 4，444444,n P H OH A H P H ∴= ∴P 4H 42=OH 4•H 4A n ，即82=4×(2n ﹣4)，解得：n =10．当10n =时，使得∠410OP A =90°．【点睛】本题考查的是二次函数的性质，等腰直角三角形，等边三角形的性质，三角形的相似的判定与性质，掌握以上知识是解题的关键．。

精品人教版中考二模检测《数学卷》含答案解析

人教版中考数学仿真模拟测试题一、选择题(共12小题，每小题3分，共36分)1. 12--的相反数的倒数是( ) A.12B. 12-C. 2D. 2-2. 一种新病毒的半径仅有0.000009毫米，将0.000009用科学记数法表示应是( ) A. 6910-⨯B. 5910-⨯C. 60.910-⨯D. 50.910-⨯3. 选择计算22(43) (43)x y x y -++的最佳方法是( ) A. 运用多项式乘多项式法则 B. 运用平方差公式 C. 运用单项式乘多项式法则D. 运用完全平方公式4. 如图，∠BCD ＝95°，AB ∥DE ，则∠α与∠β满足( )A. ∠α+∠β＝95°B. ∠β﹣∠α＝95°C. ∠α+∠β＝85°D. ∠β﹣∠α＝85°5. 图2是图1中长方体的三视图，若用S 表示面积，222S x x S x x ++主左＝，＝，则S 俯＝( )A. 232x x ++B. 22x +C. 221x x ++D. 223x x +6. 如图，在Rt ABC ∆中，90B =∠，以点A 为圆心，适当长为半径画弧，分别交AB AC 、于点,D E ，再分别以点D E 、为圆心，大于12DE 为半径画弧，两弧交于点F ，作射线AF 交边BC 于点1,4BG AC ==，则ACG ∆的面积是( )A. 1B.32C. 2D.527. 若一次函数y kx b =+的图象不经过第二象限，则关于x 的方程20x kx b ++=的根的情况是( ) A. 有两个不相等的实数根 B. 有两个相等的实数根 C. 无实数根D. 无法确定8. 已知点A (-13)，O 为坐标原点，连接OA ．将线段OA 绕点O 按逆时针方向旋转30得到线段OA '，则点A '的坐标为( ) A. (1，3)-B. ( 2-3)C. ( 3-2)D. (3-1)9. 为了了解某班同学一周的课外阅读量，任选班上15名同学进行调查，统计如表，则这组数据的中位数和众数分别是( ) 阅读量(单位：本/周)123人数(单位：人) 1 464A. 1，2B. 2，2C. 4，6D. 6，610. 已知分式方程312(1)(2)x kx x x +=++-+的解为非负数，求k 的取值范围( ) A. 5k ≥B. 1k ≥-C. 5k ≥且6k ≠D. 1k ≥-且0k ≠11. 已知一扇形的圆心角为60︒，半径为5，则以此扇形为侧面的圆锥的底面圆的周长为( ) A.53π B. 10πC. 56πD. 16π12. 已知抛物线y ＝ax 2+3x+c (a ，c 为常数，且a≠0)经过点(﹣1，﹣1)，(0，3)，有下列结论： ①ac ＜0；②当x ＞1时，y 值随x 值的增大而减小； ③3是方程ax 2+2x+c ＝0的一个根；④当﹣1＜x ＜3时，ax 2+2x+c ＞0 其中正确结论的个数是( ) A. 1B. 2C. 3D. 4二、填空题(共5小题，每小题3分，共15分)13. 计算：011123tan30(π2020)()2--︒+--=______．14. 若关于x 的一元二次方程22(2)0x m x m +-+=的两个实数根互为倒数，则m 的值是_____． 15. 如图，∠AOB ＝90°，∠B ＝30°，以点O 为圆心，OA 为半径作弧交AB 于点C ，交OB 于点D ，若OA ＝4，则阴影部分的面积为_____．16. 如图，已知直线323y x =+与x 轴，y 轴分别交于点A ，B ，将△ABO 沿直线AB 翻折后得到△ABC ，若反比例函数ky x=(x ＜0)的图象经过点C ，则k ＝______．17. 如图，在正方形ABCD 中，M 、N 是对角线AC 上的两个动点，P 是正方形四边上的任意一点，且4AB =，2MN =．关于下列结论：①当△P AN 是等腰三角形时，P 点有6个；②当△PMN 是等边三角形时，P 点有4个；③DM+DN 的最小值等于6．其中，一定正确的结论的序号是_______．三、解答题(共7小题，满分69分)18. 先化简(1﹣32x +)÷22214x x x -+-，然后从不等式2x ﹣6＜0的非负整数解中选取一个合适的解代入求值．19. (1)问题发现：如图1，△ABC是等腰直角三角形，四边形ADEF是正方形，点D、F分别在边AB、AC 上，请直接写出线段BD、CF的数量和位置关系；(2)拓展探究：如图2，当正方形ADEF绕点A逆时针旋转锐角θ时，上述结论还成立吗？若成立，请给予证明；若不成立，请说明理由．20. 为提升学生的艺术素养，学校计划开设四门艺术选修课：A．书法；B．绘画；C．乐器；D．舞蹈．为了解学生对四门功课的喜欢情况，在全校范围内随机抽取若干名学生进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门)．将数据进行整理，并绘制成如下两幅不完整的统计图，请结合图中所给信息解答下列问题：(1)本次调查的学生共有多少人？扇形统计图中∠α的度数是多少？(2)请把条形统计图补充完整；(3)学校为举办2018年度校园文化艺术节，决定从A．书法；B．绘画；C．乐器；D．舞蹈四项艺术形式中选择其中两项组成一个新的节目形式，请用列表法或树状图求出选中书法与乐器组合在一起的概率．21. 如图，小明在大楼30米高(即PH＝30米)的窗口P处进行观测，测得山坡上A处的俯角∠APQ为15°，山脚B处的俯角∠BPQ为60°，已知该山坡的坡度i(即tan∠ABC)为13，点P，H，B，C，A在同一个平面上，点H、B、C在同一条直线上，且PH丄HC．(1)求出山坡坡角(∠ABC)大小；(2)求A、B两点间的距离(结果精确到0.131.732)．22. 如图，⊙O 是△ABC 的外接圆，点O 在BC 边上，∠BAC 的平分线交⊙O 于点D ，连接BD 、CD ，过点D 作BC 的平行线与AC 的延长线相交于点P ．(1)求证：PD 是⊙O 的切线； (2)求证：AB CP BD CD =；(3)若tan 2ABC ∠=，5AB =DP 的长．23. 随着《流浪地球》的热播，其同名科幻小说的销量也急剧上升．为应对这种变化，某网店分别花20000元和30000元先后两次增购该小说，第二次的数量比第一次多500套，且两次进价相同． (1)该科幻小说第一次购进多少套？(2)根据以往经验：当销售单价是25元时，每天的销售量是250套；销售单价每上涨1元，每天的销售量就减少10套．网店要求每套书的利润不低于10元且不高于18元．①直接写出网店销售该科幻小说每天的销售量y (套)与销售单价x (元)之间的函数关系式及自变量x 的取值范围；②网店决定每销售1套该科幻小说，就捐赠a (0＜a ＜7)元给困难职工，每天扣除捐赠后可获得的最大利润为1960元，求a 的值．24. 如图，在平面直角坐标系中，菱形ABCD 的三个顶点A ，B ，D 在坐标轴上，且已知点A (3-，0)，点B (0，4)，现有抛物线m 经过点B ，C 和OD 的中点．(1)求抛物线m 的解析式；(2)在抛物线m 上是否存在点P ，使得PBC PDC S S =△△？若存在，求出点P 的坐标，若不存在，请说明理由； (3)抛物线m 与x 轴的另一交点为F ，M 是线段AC 5 MF MC +的最小值．答案与解析一、选择题(共12小题，每小题3分，共36分)1. 12--的相反数的倒数是( ) A.12B. 12-C. 2D. 2-【答案】C 【解析】【分析】根据绝对值，相反数及倒数的计算方法进行计算即可得解. 【详解】根据题意，1122--=-，12-的相反数是12，12的倒数是2，故选：C.【点睛】本题主要考查了绝对值，相反数，倒数的计算方法，熟练掌握相关知识点是解决本题的关键. 2. 一种新病毒的半径仅有0.000009毫米，将0.000009用科学记数法表示应是( ) A. 6910-⨯ B. 5910-⨯C. 60.910-⨯D. 50.910-⨯【答案】A 【解析】【分析】根据科学记数法的定义：把一个数表示成10n a ⨯的形式，(其中110a ≤<，n 为整数)，这种记数的方法叫做科学记数法，即可表示．【详解】解：∵60.000009=910-⨯．故选A ．【点睛】本题考查科学记数法，较容易，熟练掌握科学记数法的表示方法是顺利解题的关键． 3. 选择计算22(43) (43)x y x y -++的最佳方法是( ) A. 运用多项式乘多项式法则 B. 运用平方差公式 C. 运用单项式乘多项式法则 D. 运用完全平方公式【答案】B 【解析】【分析】直接利用平方差公式计算得出答案．【详解】选择计算(-4x 2+3y )(4x 2+3y )的最佳方法是：运用平方差公式．故选：B ．【点睛】此题主要考查了多项式乘法，正确应用公式是解题关键． 4. 如图，∠BCD ＝95°，AB ∥DE ，则∠α与∠β满足( )A. ∠α+∠β＝95°B. ∠β﹣∠α＝95°C. ∠α+∠β＝85°D. ∠β﹣∠α＝85°【答案】D 【解析】【分析】过点C 作CF∥AB，然后利用两直线平行，内错角相等；两直线平行，同旁内角互补进行推理证明即可. 【详解】解：过点C 作CF∥AB∵AB ∥DE ，CF∥AB ∴AB ∥DE ∥CF ∴∠BCF=∠α ∠DCF+∠β=180° ∴∠BCD ＝∠BCF +∠DCF ∴∠α+180°-∠β=95° ∴∠β﹣∠α＝85° 故选：D【点睛】本题考查平行线的性质，熟练掌握平行线的性质进行推理证明是本题的解题关键.5. 图2是图1中长方体的三视图，若用S 表示面积，222S x x S x x ++主左＝，＝，则S 俯＝( )A. 232x x ++B. 22x +C. 221x x ++D. 223x x +【答案】A 【解析】【分析】由主视图和左视图的宽为x ，结合两者的面积得出俯视图的长和宽，从而得出答案．【详解】∵S 主=x 2+2x =x (x +2)，S 左=x 2+x =x (x +1)，∴俯视图的长为x +2，宽为x +1，则俯视图的面积S 俯=(x +2)(x +1)=x 2+3x +2．故选A ．【点睛】本题考查了由三视图判断几何体，解题的关键是根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状，以及几何体的长、宽、高．6. 如图，在Rt ABC ∆中，90B =∠，以点A 为圆心，适当长为半径画弧，分别交AB AC 、于点,D E ，再分别以点D E 、为圆心，大于12DE 为半径画弧，两弧交于点F ，作射线AF 交边BC 于点1,4BG AC ==，则ACG ∆的面积是( )A. 1B.32C. 2D.52【答案】C 【解析】【分析】利用基本作图得到AG 平分∠BAC ，利用角平分线的性质得到G 点到AC 的距离为1，然后根据三角形面积公式计算△ACG 的面积．【详解】解：由作法得AG 平分BAC ∠，G ∴点到AC 的距离等于BG 的长，即G 点到AC 的距离为1，所以ACG ∆的面积14122=⨯⨯=．故选C ．【点睛】本题考查了作图-基本作图：熟练掌握基本作图(作一条线段等于已知线段；作一个角等于已知角；作已知线段的垂直平分线；作已知角的角平分线；过一点作已知直线的垂线)．也考查了交平分线的性质． 7. 若一次函数y kx b =+的图象不经过第二象限，则关于x 的方程20x kx b ++=的根的情况是( ) A. 有两个不相等的实数根 B. 有两个相等的实数根C. 无实数根D. 无法确定【答案】A 【解析】【分析】利用一次函数性质得出k ＞0，b ≤0，再判断出△=k 2-4b ＞0，即可求解. 【详解】解：一次函数y kx b =+的图象不经过第二象限，0k ∴>，0b ≤，240k b ∴∆=->，∴方程有两个不相等的实数根．故选A ．【点睛】本题考查的是一元二次方程的根的判别式，熟练掌握一次函数的图像和一元二次方程根的判别式是解题的关键.8. 已知点A (-1)，O 为坐标原点，连接OA ．将线段OA 绕点O 按逆时针方向旋转30得到线段OA '，则点A '的坐标为( ) A. (1，- B. ( 2-C. (-2)D. (-1)【答案】D 【解析】【分析】如图，作AH ⊥x 轴于H ，作A′E ⊥x 轴于E ．解直角三角形求出A′E ，OE 即可．【详解】如图，作AH ⊥x 轴于H ，作A′E ⊥x 轴于E ．∵A (-13，∴OH=1，3∴tan ∠AOH=AH OH 3 ∴∠AOH=60°，∠OAH=30°，∴OA=OA′=2OH=2，∵∠AOA′=30°，∴∠A′OE=30°，∴A′E=12OA′=1，33 ∴A′(31)，故选：D ．【点睛】本题考查坐标与图形的变化，解直角三角形，旋转变换等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题．9. 为了了解某班同学一周的课外阅读量，任选班上15名同学进行调查，统计如表，则这组数据的中位数和众数分别是( )阅读量(单位：本/周)1 2 3 人数(单位：人) 14 6 4A. 1，2B. 2，2C. 4，6D. 6，6【答案】B【解析】【分析】根据众数，中位数的定义即可解决问题．【详解】解：15名同学一周的课外阅读量为0，1，1，1，1，2，2，2，2，2，2，3，3，3，3， ∵2出现了6次，它的次数最多，∴众数为2．∵随机调查了15名同学，∴根据表格数据可以知道中位数为2，故选：B ．【点睛】本题考查了确定一组数据的中位数和众数的能力．要明确定义，一些学生往往对这个概念掌握不清楚，计算方法不明确而误选其它选项，注意找中位数的时候一定要先排好顺序，然后再根据奇数和偶数个来确定中位数，如果数据有奇数个，则正中间的数字即为所求，如果是偶数个则找中间两位数的平均数． 10. 已知分式方程312(1)(2)x k x x x +=++-+的解为非负数，求k 的取值范围( ) A. 5k ≥B. 1k ≥-C. 5k ≥且6k ≠D. 1k ≥-且0k ≠【答案】D【解析】【分析】先把分式方程转化为整式方程求出用含有k 的代数式表示的x ，根据x 的取值求k 的范围．【详解】解：分式方程转化为整式方程得，(3)(1)k (1)(2)x x x x +-=+-+解得：k 1x =+解为非负数，则k+10≥，∴k -1≥又∵x≠1且x≠-2，∴k+11k+1-2≠≠，∴k -1≥ ，且k 0≠故选D【点睛】本题考查了分式方程的解，解答本题的关键是先把分式方程转化为整式方程，求出方程的解，再按要求列不等式，解不等式．11. 已知一扇形的圆心角为60︒，半径为5，则以此扇形为侧面的圆锥的底面圆的周长为( )A. 53π B. 10π C.56π D.16π【答案】A【解析】【分析】利用弧长公式计算出扇形的弧长，以此扇形为侧面的圆锥的底面圆的周长即是扇形的弧长.【详解】解：扇形的弧长＝60?••55= 180?3，以此扇形为侧面的圆锥的底面圆的周长为53π．故选：A．【点睛】本题考查了弧长的计算：••180n r l.12. 已知抛物线y＝ax2+3x+c(a，c为常数，且a≠0)经过点(﹣1，﹣1)，(0，3)，有下列结论：①ac＜0；②当x＞1时，y的值随x值的增大而减小；③3是方程ax2+2x+c＝0的一个根；④当﹣1＜x＜3时，ax2+2x+c＞0其中正确结论的个数是( )A. 1B. 2C. 3D. 4【答案】C【解析】【分析】先由抛物线y＝ax2+3x+c(a，c为常数，且a≠0)经过点(﹣1，﹣1)，(0，3)，列方程组求出a，c，从而解得其解析式，进而求得其对称轴，再根据二次函数与方程和二次函数与不等式的关系可解．【详解】把点(﹣1，﹣1)，(0，3)代入y＝ax2+3x+c得：133a cc-=-+⎧⎨=⎩∴13 ac=-⎧⎨=⎩∴y＝﹣x2+3x+3 ∴①ac＜0正确；该抛物线的对称轴为：322b x a =-=， ∴②当x ＞1时，y 的值随x 值的增大而减小是错误的；方程ax 2+2x+c ＝0可化为：方程ax 2+3x+c ＝x ，把x ＝3代入y ＝﹣x 2+3x+3得y ＝3，∴﹣x 2+2x+3＝0，故③正确；∴(3，3)在该抛物线上，又∵抛物线y ＝ax 2+3x+c (a ，c 为常数，且a≠0)经过点(﹣1，﹣1)，∴抛物线y ＝ax 2+3x+c 与y ＝x 的交点为(﹣1，﹣1)和(3，3)，当﹣1＜x ＜3时，ax 2+3x+c ＞x ，即ax 2+2x+c ＞0④当﹣1＜x ＜3时，ax 2+2x+c ＞0，故④正确．综上，①③④正确．故选C ．【点睛】本题考查了二次函数解析式、二次函数的对称轴、二次函数与方程、二次函数与不等式的关系，综合性较强，难度较大．二、填空题(共5小题，每小题3分，共15分)13. 0113tan30(π2020)()2-︒+--=______．1【解析】【分析】原式第一项运用算术平方根的性质进行化简，第二项代入特殊角三角函数值，第三项运用零指数幂运算法则计算，第四项运用负整数指数幂的运算法则进行计算，最后根据实数的运算法则得出结果即可.0113tan30(π2020)()2-︒+--=3123⨯+-11【点睛】此题考查了实数的混合运算，掌握运算法则是解答此题的关键.14. 若关于x 的一元二次方程22(2)0x m x m +-+=的两个实数根互为倒数，则m 的值是_____．【答案】-1【解析】【分析】利用根与系数的关系结合方程的两个实数根互为倒数，可求出m 的值，再将其代入原方程，取使得原方程根的判别式0∆≥的值即可．【详解】解：∵关于x 的一元二次方程2220x m x m +-+=（）的两个实数根互为倒数，21m ∴=，1m ∴=±．当1m =时，原方程为210x x =-+，∴21)4113<0=∆=(-⨯⨯-﹣，不符合题意， ∴1m =舍去；当1m =-时，原方程为2310x x =-+， 23)41150=∴∆=(-⨯⨯>﹣，符合题意．故答案为1-．【点睛】本题考查了根与系数的关系以及根的判别式，牢记两根之积等于c a是解题的关键． 15. 如图，∠AOB ＝90°，∠B ＝30°，以点O 为圆心，OA 为半径作弧交AB 于点C ，交OB 于点D ，若OA ＝4，则阴影部分的面积为_____．【答案】43π．【解析】【分析】连接OC ，作CH ⊥OB 于H ，根据直角三角形的性质求出AB ，根据勾股定理求出BD ，证明△AOC 为等边三角形，得到∠AOC ＝60°，∠COB ＝30°，根据扇形面积公式、三角形面积公式计算即可．【详解】解：连接OC ，作CH ⊥OB 于H ，∵∠AOB＝90°，∠B＝30°，∴∠OAB＝60°，AB＝2OA＝8，由勾股定理得，OB＝22AB OA-＝43，∵OA＝OC，∠OAB＝60°，∴△AOC为等边三角形，∴∠AOC＝60°，∴∠COB＝30°，∴CO＝CB，CH＝12OC＝2，∴阴影部分的面积＝2604360⨯π﹣12×4×4×32+12×43×2﹣2304360π⨯＝43π，故答案为：43π．【点睛】本题考查扇形的面积计算、等边三角形的判定与性质、三角形的面积公式，利用了分割法，解题的关键是掌握扇形的面积公式．16. 如图，已知直线323y x=+与x轴，y轴分别交于点A，B，将△ABO沿直线AB翻折后得到△ABC，若反比例函数kyx=(x＜0)的图象经过点C，则k＝______．【答案】33-【解析】【分析】先由直线解析式求出A、B两点坐标，进而得到∠A、∠B的度数，连接OC交AB于D，求出OD的长，由轴对称性可得OC 的长，过C作CE⊥x轴于点E，通过解直角三角形求出OE、CE的长即可.【详解】对于323y x=+，当x=0时，y=2；当y=0时，x=-23，∴A(-23，0)，B(0，2) ∴AO=23,OB=2, ∴tan∠OAB=3OB OA=, ∴∠OAB=30°∴∠OBA=60°, 连接OC，过点C作CE⊥x轴，垂足为E，由翻折得，OD⊥AB，OD=CD，∴OD=123AOD=60°, ∴3OCE=30°∴OE=123∴223OC OE-=∴3∴k=33-故答案为：33-【点睛】考查折叠得性质、直角三角形的勾股定理、解直角三角形，反比例函数图象上点的坐标特征等知识，求出点C的坐标是解决问题的关键．．17. 如图，在正方形ABCD中，M、N是对角线AC上两个动点，P是正方形四边上的任意一点，且4AB=，2MN=．关于下列结论：①当△P AN是等腰三角形时，P点有6个；②当△PMN是等边三角形时，P点有4个；③DM+DN的最小值等于6．其中，一定正确的结论的序号是_______．【答案】①②③【解析】【分析】①②利用图象法即可解决问题.③连接DB，与AC相交于点O，利用正方形的性质求出相应线段的长，并根据二次函数的性质即可得解.【详解】①如图，△P AN是等腰三角形时，P点有6个；故正确；②如图2，当△PMN是等边三角形时，P点有4个；故正确；③连接DB，与AC相交于点O，如图，∵四边形ABCD 是正方形，且AB=4；42,DB DB AC ∴=⊥22DO ∴=设OM x =，则2ON x =-222222DM DN OM DO ON DO ∴+=+++，即()()222282821DM DN x x x ∴+=++-+=-2+18， 1MO ∴=时，DM=DN=3最小336DM DN ∴+=+=即DM DN +的最小值为6，故③正确故答案为：①②③．【点睛】本题考查正方形的性质、等腰三角形的判定和性质、等边三角形的判定和二次函数的性质等知识，解题的关键是灵活运用所学知识解决问题．三、解答题(共7小题，满分69分)18. 先化简(1﹣32x +)÷22214x x x -+-，然后从不等式2x ﹣6＜0的非负整数解中选取一个合适的解代入求值．【答案】21x x --，2. 【解析】【分析】原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约分得到最简结果，解不等式求出x 的值，代入计算即可求出值．【详解】原式=()()()22223·21x x x x x +-+-+- =()()()2221·21x x x x x +--+- =21x x --，由不等式2x ﹣6＜0，得到x ＜3，∴不等式2x﹣6＜0的非负整数解为x=0，1，2，由题意可知x≠2、x≠1，所以x=0，当x=0时，原式=2．【点睛】本题考查了分式的化简求值，熟练掌握分式混合运算的运算顺序以及运算法则是解题的关键.19. (1)问题发现：如图1，△ABC是等腰直角三角形，四边形ADEF是正方形，点D、F分别在边AB、AC 上，请直接写出线段BD、CF的数量和位置关系；(2)拓展探究：如图2，当正方形ADEF绕点A逆时针旋转锐角θ时，上述结论还成立吗？若成立，请给予证明；若不成立，请说明理由．【答案】(1)BD＝CF，BD⊥CF，理由见解析；(2)成立，理由见解析.【解析】【分析】(1)根据等腰直角三角形的性质和正方形的性质解答即可；(2)△ABC是等腰直角三角形，四边形ADEF是正方形，易证得△BAD≌△CAF，根据全等三角形的对边相等，即可证得BD＝CF，进而证明BD⊥CF【详解】(1)BD＝CF，BD⊥CF，理由如下：∵△ABC是等腰直角三角形，四边形ADEF是正方形，∴AB＝AC，AD＝AF，∠BAC＝∠DAF＝90°，∴BD＝CF，BD⊥CF；(2)成立，理由如下：∵△ABC是等腰直角三角形，四边形ADEF是正方形，∴AB＝AC，AD＝AF，∠BAC＝∠DAF＝90°，∵∠BAD＝∠BAC﹣∠DAC，∠CAF＝∠DAF﹣∠DAC，∴∠BAD＝∠CAF，在△BAD与△CAF中，AB AC BAD CAF AD AF =⎧⎪∠=∠⎨⎪=⎩，∴△BAD ≌△CAF (SAS )，∴BD ＝CF ，延长BD ，分别交直线AC 、CF 于点M ，G ，如图，∵△BAD ≌△CAF ，∴∠ABM ＝∠GCM ，∵∠BMA ＝∠CMG ，∴∠BGC ＝∠BAC ＝90°，∴BD ⊥CF ．【点睛】本题考查了正方形的性质、全等三角形的判定与性质、等腰直角三角形的性质等知识，解题的关键在于正确寻找全等三角形解决问题．20. 为提升学生的艺术素养，学校计划开设四门艺术选修课：A ．书法；B ．绘画；C ．乐器；D ．舞蹈．为了解学生对四门功课的喜欢情况，在全校范围内随机抽取若干名学生进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门)．将数据进行整理，并绘制成如下两幅不完整的统计图，请结合图中所给信息解答下列问题：(1)本次调查的学生共有多少人？扇形统计图中∠α的度数是多少？(2)请把条形统计图补充完整；(3)学校为举办2018年度校园文化艺术节，决定从A ．书法；B ．绘画；C ．乐器；D ．舞蹈四项艺术形式中选择其中两项组成一个新的节目形式，请用列表法或树状图求出选中书法与乐器组合在一起的概率．【答案】(1)本次调查的学生总人数为40人，∠α=108°；(2)补图见解析；(3)书法与乐器组合在一起的概率为16．【解析】【分析】(1)用A科目人数除以其对应的百分比可得总人数，用360°乘以C对应的百分比可得∠α的度数；(2)用总人数乘以C科目的百分比即可得出其人数，从而补全图形；(3)画树状图展示所有12种等可能的结果数，再找出恰好是“书法”“乐器”的结果数，然后根据概率公式求解．【详解】(1)本次调查的学生总人数为4÷10%=40人，∠α=360°×(1﹣10%﹣20%﹣40%)=108°；(2)C科目人数为40×(1﹣10%﹣20%﹣40%)=12人，补全图形如下：(3)画树状图为：共有12种等可能的结果数，其中恰好是书法与乐器组合在一起的结果数为2，所以书法与乐器组合在一起的概率为21 126．【点睛】本题考查了条形统计图、扇形统计图、列表法与树状图法求概率，读懂统计图、熟练掌握列表法或树状图法求概率是解题的关键.21. 如图，小明在大楼30米高(即PH＝30米)的窗口P处进行观测，测得山坡上A处的俯角∠APQ为15°，山脚B处的俯角∠BPQ为60°，已知该山坡的坡度i(即tan∠ABC)为13，点P，H，B，C，A在同一个平面上，点H、B、C在同一条直线上，且PH丄HC．(1)求出山坡坡角(∠ABC)的大小；(2)求A、B两点间的距离(结果精确到0.131.732)．【答案】(1)∠ABC ＝30°；(2)AB ≈34.6米．【解析】【分析】(1)根据俯角以及坡度的定义即可求解；(2)在直角△PHB 中，根据三角函数即可求得PB 的长，然后在直角△PBA 中利用三角函数即可求解．【详解】解：(1)∵tan ∠ABC ＝1：3，∴∠ABC ＝30°； (2)由题意得：∠PBH ＝60°，∵∠ABC ＝30°，∴∠ABP ＝90°，又∵∠APB ＝45°，∴△PAB 为等腰直角三角形，在直角△PHB 中，PB ＝==203sin 3∠PH PBH 米．在直角△PBA 中，AB ＝PB ＝203≈34.6米．【点睛】本题主要考查了解直角三角形的应用﹣俯角的问题以及坡度的定义，正确利用三角函数是解题的关键． 22. 如图，⊙O 是△ABC 的外接圆，点O 在BC 边上，∠BAC 的平分线交⊙O 于点D ，连接BD 、CD ，过点D 作BC 的平行线与AC 的延长线相交于点P ．(1)求证：PD 是⊙O 的切线；(2)求证：AB CP BD CD =；(3)若tan 2ABC ∠=， 2 5AB =，求线段DP 的长．【答案】(1)见解析；(2)见解析；(3)15【解析】【分析】(1)先判断出∠BAC=2∠BAD ，进而判断出∠BOD=∠BAC=90°，得出PD ⊥OD 即可得出结论；(2)先判断出∠ADB=∠P ，再判断出∠DCP=∠ABD ，即可证明△ABD ∽△DCP ，进一步可得出结论；(3)首先求出BC=10，从而得出OD=5，作CG ⊥DP ，则可得四边形ODGC 是正方形，故可得CG=5，由tan tan CPG ACB ∠=∠可求出GP=10，从而可得结论.【详解】(1)如图，连接OD ，∵BC 是⊙O 的直径，∴∠BAC=90°，∵AD 平分∠BAC ，∴∠BAC=2∠BAD ，∵∠BOD=2∠BAD ，∴∠BOD=∠BAC=90°，∵DP ∥BC ，∴∠ODP=∠BOD=90°，∴PD ⊥OD ，∵OD 是⊙O 半径，∴PD 是⊙O 的切线；(2)∵PD ∥BC ，∴∠ACB=∠P ，∵∠ACB=∠ADB ，∴∠ADB=∠P ，∵∠ABD+∠ACD=180°，∠ACD+∠DCP=180°，∴∠DCP=∠ABD ，∴△ABD ∽△DCP ， ∴AB BD CD CP = ∴AB•CP=BD•CD ．(3)在Rt ABC ∆中，∵tan 2ABC ∠=，25AB =，∴245AC AB ==，∴2210BC AB AC =+=，∴5OD =，过点C 作CG DP ⊥，垂足为G ，则四边形ODGC 为正方形，∴5DG CG OD ===，∵BC PD ∥，∴CPG ACB ∠=∠，tan tan CPG ACB ∴∠=∠，∴CG AB GP AC=，即52545GP =，解得，10GP =，∴15DP DG GP =+=．【点睛】此题是圆的综合题，主要考查了圆的性质，切线的性质和判定，勾股定理，相似三角形的判定和性质，同角的余角相等，判断出△ABD ∽△DCP 是解本题的关键．23. 随着《流浪地球》的热播，其同名科幻小说的销量也急剧上升．为应对这种变化，某网店分别花20000元和30000元先后两次增购该小说，第二次的数量比第一次多500套，且两次进价相同．(1)该科幻小说第一次购进多少套？(2)根据以往经验：当销售单价是25元时，每天的销售量是250套；销售单价每上涨1元，每天的销售量就减少10套．网店要求每套书的利润不低于10元且不高于18元．①直接写出网店销售该科幻小说每天的销售量y (套)与销售单价x (元)之间的函数关系式及自变量x 的取值范围；②网店决定每销售1套该科幻小说，就捐赠a (0＜a ＜7)元给困难职工，每天扣除捐赠后可获得的最大利润为1960元，求a 的值．【答案】(1)该科幻小说第一次购进1000套；(2)①y ＝﹣10x +500(30≤x ≤38)；②a ＝2【解析】【分析】(1)设该科幻小说第一次购进m 套，根据题意列方程即可得到结论；(2)根据题意列函数关系式即可；(3)设每天扣除捐赠后可获得利润为w 元．根据题意得到w ＝(x -20-a )(-10x +500)＝-10x 2+(10a +700)x ﹣500a ﹣10000(30≤x ≤38)求得对称轴为x ＝35+12a ， ①若0＜a ＜6，则13035382a <+，则当x ＝35+12a 时，w 取得最大值，解方程得到a 1＝2，a 2＝58，于是得到a ＝2；②若6＜a ＜7，则38＜3512+a ，则当30≤x ≤38时，w 随x 的增大而增大；解方程得到a ＝53，但6＜a ＜7，故舍去．于是得到结论．【详解】解：(1)设该科幻小说第一次购进m 套，则3000020000500m m=+， 1000m ∴=，经检验，当1000m =时，(500)0m m +≠，则1000m =是原方程的解，答：该科幻小说第一次购进1000套；(2)根据题意得，25010(25)10500(3038)y x x x =--=-+；(3)设每天扣除捐赠后可获得利润为w 元．2(20)(10500)10(10700)50010000(3038)w x a x x a x a x =---+=-++--对称轴为1352x a =+， ①若06a <<，则13035382a <+，则当1352x a =+时，w 取得最大值， 113520[1035500]196022a a x a ⎛⎫⎛⎫∴+---++= ⎪ ⎪⎝⎭⎝⎭ 12a ∴=，258a =，又06a <，则2a =；②若67a <<，则138352a <+，则当3038x 时，w 随x 的增大而增大； ∴当38x =时，w 取得最大值，则(3820)(1038500)1960a ---⨯+=，53a ∴=，但67a <<，故舍去．综上所述，2a =．【点睛】本题考查了二次函数的应用，难度较大，最大销售利润的问题常利用函数的增减性来解答，正确的理解题意，确定变量，建立函数模型，然后结合实际选择最优方案．24. 如图，在平面直角坐标系中，菱形ABCD 的三个顶点A ，B ，D 在坐标轴上，且已知点A (3-，0)，点B (0，4)，现有抛物线m 经过点B ，C 和OD 的中点．(1)求抛物线m 的解析式；(2)在抛物线m 上是否存在点P ，使得PBC PDC S S =△△？若存在，求出点P 的坐标，若不存在，请说明理由；(3)抛物线m 与x 轴的另一交点为F ，M 是线段AC 5 MF MC +的最小值．【答案】(1)254y x x =-+；(2)存在满足条件的点P ，使得PBC PDC S S =△△，理由见解析；(3)5【解析】【分析】(1)先求出点C 和点D 的坐标，再求出点E 的坐标，设出函数m 的解析式，把B 、E 、C 三点坐标代入解析式进行求解即可；(2)P 点是抛物线m 和直线AC 的交点，求出AC 的解析式，联立方程组，解出方程组进行取舍即可得点P 坐标；(3)过C 作⊥CH x 轴于H ，过M 作MN BC ⊥于N ，证明△AOG ∽△CNM，可得)MC MF MN +=+，从而可得结论.【详解】(1)∵(3,0)A -，(0,4)B∴OA 3=，4OB =∴5AB =，即菱形的长为5，∴5AD =，5BC =∴(2,0)D ，(5,4)C∴OD 的中点坐标为：(1,0)设抛物线的解析式为：2y ax bx c =++，则 042554a b c c a b c ++=⎧⎪=⎨⎪++=⎩，解得154a b c =⎧⎪=-⎨⎪=⎩∴抛物线m 的解析式为254y x x =-+． (2)存在满足条件的点P ，使得PBC PDC S S =△△．理由如下：①当点P 在BC 下方时，∵BC CD =，PBC PDC S S =△△，∴P 点在菱形ABCD 的对角线上，∴P 点是抛物线m 和直线AC 的交点，设直线AC 的解析式为y kx n =+，∵(3A -，0)，(5C ，4)，∴3054k n k n -+=⎧⎨+=⎩，解得1232k n ⎧=⎪⎪⎨⎪=⎪⎩， ∴直线AC 的解析式为1322y x =+，由2132254y x y x x ⎧=+⎪⎨⎪=-+⎩解得1274x y ⎧=⎪⎪⎨⎪=⎪⎩或54x y =⎧⎨=⎩(舍去)， ∴1(2P ，7)4． (3)过C 作⊥CH x 轴于H ，过M 作MN BC ⊥于N ，∵BC x ∥轴，∴NCM MAO ∠=∠，又∵90AOG CNM ∠=∠=︒，∴△AOG ∽△CNM ， ∴5OG MN AG CM == 55()5()5MF MC MF MF MN +==+， ∵点F 到BC 最小距离为CH ，∴MF MN +的最小值为CH 的长度4，5MF MC +的最小值为45【点睛】此题主要考查了利用待定系数法求二次函数的解析式，并利用方程组的解求直线和抛物线的交点坐标，也考查了菱形的性质，综合性较强．。

人教版中考第二次模拟测试《数学试题》含答案解析

人教版数学中考综合模拟检测试题学校________ 班级________ 姓名________ 成绩________一、填空题(每小题3分，共24分)1.如果|a |＋a ＝0，则22(1)a a -+＝______．2.已知x 2-x -1＝0，则代数式-x 3＋2x 2＋2002的值为______．3.若由你选择一个喜欢的数值m ，使一次函数()2y m x m =-+的图象经过第一、二、四象限，则m 的值可以是___________．4.升国旗时，某同学站在离旗杆底部18米处行注目礼，当国旗升至旗杆顶端时，该同学视线的仰角恰为45°，若该同学双眼离地面1.6米，则旗杆高度为_______米．5.如图，某涵洞截面是抛物线型，现测得水面宽AB ＝1.6m ，涵洞顶点O 到水面的距离CO ＝2.4m ，在图中直角坐标系内涵洞截面所在抛物线的表达式是______________．6.已知一个圆的弦切角等于40°，那么这个弦切角所夹的弧所对的圆心角的度数是______．7.如图，在Rt △ABC 中，腰AC ＝BC ＝1，按下列方法折叠Rt △ABC ，点B 不动，使BC 落在AB 上，点A 不动，使AB 落在AC 的延长线上;点C 不动，使CA 落在CB 上，设点A 、B 、C 对应的落点分别为A ′、B ′、C ′，则△A ′B ′C ′的面积是______．8.如图，⊙O 1的半径是⊙O 2的直径，⊙O 1的半径O 1C 交⊙O 2于B ，若AB 的度数是48°，那么AC 的度数是______．二、选择题(每小题3分，共18分)9.已知一个多边形的内角和是它的外角和的2倍，那么这个多边形的边数是( )A. 3B. 4C. 5D. 610.在一次汽车性能测试中，型号不同甲、乙两辆汽车同时从A 地出发，匀速向距离560千米的B 地行驶，结果甲车7小时到达，乙车8小时到达，则两车行驶时离A 地的距离s (千米)与行驶时间t (小时)的函数关系对应的图象大致是( )A B.C. D.11.两圆的圆心坐标分别为(3，0)、(0，4)，直径分别为4和6，则这两圆的位置关系是( )A. 外离B. 相交C. 外切D. 内切12.在Rt ABC 中，C Rt ∠=∠，若30A ∠=，则cos sin A B +等于( ) A. 312 B. 1 3 D. 21213.在直角坐标系中，O 为坐标原点，A (1，1)，在x 轴上确定点P ，使△AOP 为等腰三角形，则符合条件的点P 的个数共有( )A. 4个B. 3个C. 2个D. 1个14.当今材料科学已发展到纳米时代，1纳米等于1米的十亿分之一，我国科学家已研制成功直径为0.4纳米的碳米管，如果用科学记数法表示这种碳米管的直径，应为()A. 4×10-9米B. 0.4×10-8米C. 4×10-10米D. 0.4×10-9米三、解答题(15～19每小题8分，共40分)15.解方程21023x xx x-+=-．16.某校初二年级四个班的同学外出植树一天，已知每小时5个女生种3棵树，3个男生种5棵树，各班人数如图所示，则植树最多的是初二几班．17.声音在空气中传播的速度y(米/秒)是气温x (摄氏度)的一次函数，下表列出了一组不同气温时的音速．气温x/摄氏度0 5 10 15 20音速y/(米/秒) 331 334 337 340 343(1)求y 与x之间的函数关系式(2)气温x=22(摄氏度)时，某人看到烟花燃放5秒后才听到声响，那么此人与燃放的烟花所在地相距多远?18.某广场有一块长50米、宽30米的空地，现要将它改造为花园，请你设计一个修建方案，使满足下列条件：(1)正中间留出一条宽2米的道路(如图);(2)道路两旁修建花坛，且花坛总面积占整个面积(不包括道路)的一半;(3)设计好的整个图形既是轴对称图形，又是中心对称图形．(计算结果精确到0.1米)．19.已知：△ABC 是⊙O 的内接三角形，BT 为⊙O 的切线，B 为切点，P 为直线AB 上一点，过P 作BC 的平行线交直线BT 于点E ，交直线AC 于点F ．(1)如图 (1)所示，当P 在线段AB 上时，求证：P A ·PB ＝PE ·PF ;(2)如图 (2)所示，当P 为线段BA 延长线上一点时，第(1)题的结论还成立吗?如果成立，请给出证明;如果不成立，请说明理由．四、解答题(每题9分，共18分)20.先仔细阅读下列材料，然后回答问题：如果a ＞0，b ＞0，那么(a -b )2≥0，即a ＋b -2ab ≥0 得2a b +≥ab ，其中，当a ＝b 时取等号，我们把2a b +称为a 、b 算术平均数， ab 称为a 、b 的几何平均数．如果a ＞0，b ＞0，c ＞0，同样可以得到3a b c ++≥3abc ，其中，当a ＝b ＝c 时取等号于是就有定理：几个正数的算术平均数不小于它们的几何平均数．请用上述定理解答问题：把边长为30 cm 的正方形纸片的4角各剪去一个小正方形，折成无盖纸盒(如图)(1)设剪去的小正方形边长为x cm ，无盖纸盒的容积为V ，求V 与x 的函数关系式及x 的取值范围．(2)当x 为何值时，容积V 有最大值，最大值是多少?21.以△ABC 的边AC 为直径的半圆交AB 边于D 点，∠A 、∠B 、∠C 所对边长为a 、b 、c ，且二次函数y ＝12(a ＋c )x 2-bx ＋12(c -a )顶点在x 轴上，a 是方程z 2＋z -20＝0的根． (1)证明：∠ACB ＝90°;(2)若设b ＝2x ，弓形面积S 弓形AED ＝S 1，阴影面积为S 2，求(S 2-S 1)与x 的函数关系式;(3)在(2)条件下，当BD为何值时，(S2-S1)最大?答案与解析一、填空题(每小题3分，共24分)1.如果|a |＋a ＝0______．【答案】-2a ＋1【解析】【分析】由0a a +=得到0,a ≤ 根据0a ≤ 【详解】解：0,a a +=,a a ∴=-0,a ∴≤10,a ∴-＜1112.a a a a a =-+=--=-故答案为：12.a -a =是解题的关键．2.已知x 2-x -1＝0，则代数式-x 3＋2x 2＋2002值为______．【答案】2003【解析】【分析】由210x x --=得到221,1,x x x x -==+把原多项式降次处理，进而可得答案．【详解】解：210,x x --=221,1,x x x x ∴-==+32222002(1)22002x x x x x ∴-++=-+++22002120022003.x x =-+=+=故答案为：2003.【点睛】本题考查的是代数式的值，把待求值的代数式进行降次处理是解题的关键．3.若由你选择一个喜欢的数值m ，使一次函数()2y m x m =-+的图象经过第一、二、四象限，则m 的值可以是___________．【答案】1 (答案不唯一，满足02m <<均可)【解析】【分析】一次函数()2y m x m =-+的图象经过第一、二、四象限，列出不等式组200,m m -<⎧⎨>⎩求解即可．【详解】解：一次函数()2y m x m =-+的图象经过第一、二、四象限，200m m -<⎧⎨>⎩解得：02m <<m 值可以是1．故答案为：1(答案不唯一，满足02m <<均可)．【点睛】此题主要考查了一次函数图象，一次函数y kx b =+的图象有四种情况：①当0,0k b >>时，函数y kx b =+的图象经过第一、二、三象限;②当0,0k b ><时，函数y kx b =+的图象经过第一、三、四象限;③当0,0k b <>时，函数y kx b =+的图象经过第一、二、四象限;④当0,0k b <<时，函数y kx b =+的图象经过第二、三、四象限．4.升国旗时，某同学站在离旗杆底部18米处行注目礼，当国旗升至旗杆顶端时，该同学视线的仰角恰为45°，若该同学双眼离地面1.6米，则旗杆高度为_______米．【答案】19.6【解析】【分析】由题意可知，在直角三角形中，已知角和邻边，要求出对边，直接用正切即可解答．【详解】解：根据题意可得：旗杆高度为1.6+18×tan45°=1.6+18=19.6(m )．故答案为：19.6．【点睛】本题考查仰角的定义，要求学生能借助仰角构造直角三角形并解直角三角形．5.如图，某涵洞的截面是抛物线型，现测得水面宽AB ＝1.6m ，涵洞顶点O 到水面的距离CO ＝2.4m ，在图中直角坐标系内涵洞截面所在抛物线的表达式是______________．【答案】y ＝－154x 2 【解析】【详解】解：设涵洞所在抛物线的解析式为y=ax 2，由题意可知点B 坐标为(0．8，-2．4)，代入得-2．4=a×0．82 解得a=-154，所以y=-154x 2 故答案为：y ＝－154x 2 【点睛】本题考查二次函数的应用．6.已知一个圆的弦切角等于40°，那么这个弦切角所夹的弧所对的圆心角的度数是______．【答案】80°【解析】【分析】根据题意画出图形，利用切线的性质与等腰三角形的性质可得答案．【详解】解：如图，AB 为O 的切线，切点为，40,DAB ∠=︒,OA AB ∴⊥90,OAB ∴∠=︒50,OAD ∴∠=︒,OA OD =50,OAD ODA ∴∠=∠=︒80.AOD ∴∠=︒故答案为：80°．【点睛】本题考查了切线的性质定理，等腰三角形的性质，掌握以上知识点是解题的关键．7.如图，在Rt △ABC 中，腰AC ＝BC ＝1，按下列方法折叠Rt △ABC ，点B 不动，使BC 落在AB 上，点A 不动，使AB 落在AC 的延长线上;点C 不动，使CA 落在CB 上，设点A 、B 、C 对应的落点分别为A ′、B ′、C ′，则△A ′B ′C ′的面积是______．【答案】12【解析】分析】过'C 作''C H AB ⊥，利用轴对称的性质求解''',,,BC AB AC 利用勾股定理求解',C H 由''''''A B C ABB AB C S S S ∆∆∆=-可得答案．【详解】解：如图：过'C 作''C H AB ⊥，结合题意知：'AC H ∆是等腰直角三角形，由对折知：'1,BC BC ==Rt△ABC 中，腰AC ＝BC ＝1， 2,AB ∴='21,AC ∴=-'22(21)1,22C H ∴=-=- ''12212(1),2222AC B S ∆∴=⨯-=- 由对折知：'2,AB AB =='1221,22ABB S ∆∴=⨯⨯= ''''''2211(),2222A B C ABB AB C S S S ∆∆∆∴=-=--= 故答案为：12．【点睛】本题考查的是轴对称的性质，勾股定理，图形面积的计算，掌握轴对称的性质是解题的关键． 8.如图，⊙O 1的半径是⊙O 2的直径，⊙O 1的半径O 1C 交⊙O 2于B ，若AB 的度数是48°，那么AC 的度数是______．【答案】24°【解析】【分析】连接2BO ，得到等腰21O O B ∆，结合已知条件求解21O O B ∠，从而可得答案．【详解】解：如图，连接2,BOAB 的度数是48°， 248,AO B ∴∠=︒212,O O O B =212124,O O B O BO ∴∠=∠=︒AC ∴的度数是24︒,故答案是：24.︒【点睛】本题考查的是等腰三角形的性质，弧的度数等于它所对的圆心角的度数，掌握以上知识点是解题的关键．二、选择题(每小题3分，共18分)9.已知一个多边形的内角和是它的外角和的2倍，那么这个多边形的边数是( )A. 3B. 4C. 5D. 6【答案】D【解析】【分析】本题主要考查了多边形内角与外角．n 边形的内角和可以表示成(n-2)•180°，外角和为360°，根据题意列方程求解．【详解】解：设多边形的边数为n ，依题意，得(n-2)•180°=2×360°，解得n=6，故选D【点睛】错因分析较易题.失分原因：没有掌握多边形的内角和与外角和公式.逆袭突破多边形的性质，详见逆袭必备P24必备23.10.在一次汽车性能测试中，型号不同的甲、乙两辆汽车同时从A地出发，匀速向距离560千米的B地行驶，结果甲车7小时到达，乙车8小时到达，则两车行驶时离A地的距离s(千米)与行驶时间t(小时)的函数关系对应的图象大致是()A. B.C. D.【答案】C【解析】【分析】由甲乙列车同时出发，符合条件的有,C D，又因为甲车7小时到达，乙车8小时到达，所以甲车所花的时间少于乙车所花的时间，从而可得答案．【详解】解：因为甲乙列车同时出发，所以两个图像都经过原点，符合条件的有,C D，又因为甲车7小时到达，乙车8小时到达，所以甲车所花的时间少于乙车所花的时间，而图表示乙车还没有到达地，不符合题意，所以正确答案为C．故选C．【点睛】本题考查的是实际问题中的一次函数图像问题，掌握自变量的范围对函数图像的影响，以及路程与时间图像中，速度的大小对图像的影响，掌握以上知识是解题的关键．11.两圆的圆心坐标分别为(3，0)、(0，4)，直径分别为4和6，则这两圆的位置关系是()A. 外离B. 相交C. 外切D. 内切【答案】C【解析】【分析】根据两圆的位置关系的判定：外切(两圆圆心距离等于两圆半径之和)，内切(两圆圆心距离等于两圆半径之差)，外离(两圆圆心距离大于两圆半径之和)，相交(两圆圆心距离小于两圆半径之和大于两圆半径之差)，内含(两圆圆心距离小于两圆半径之差)．【详解】解：∵两圆直径分别为4和6，∴两圆的半径分别为2和3.∵两圆的圆心坐标分别为(3，0)、(0，4)，∴根据勾股定理,得两圆的圆心距离为5.∵2+3=5，即两圆圆心距离等于两圆半径之和, ∴这两圆的位置关系是是外切．故选C ．【点睛】本题考查勾股定理，两圆的位置关系．12.在Rt ABC 中，C Rt ∠=∠，若30A ∠=，则cos sin A B +等于( )B. 1 【答案】C【解析】解：∠B =90°﹣∠A =90°﹣30°=60°，则cos A +sin B =22+．故选C ． 13.在直角坐标系中，O 为坐标原点，A (1，1)，在x 轴上确定点P ，使△AOP 为等腰三角形，则符合条件的点P 的个数共有( )A. 4个B. 3个C. 2个D. 1个【答案】A【解析】【分析】有三种情况：当OA=OP 时，以O 为圆心，以OA 为半径画弧交x 轴于两点;当OA=AP 时，以A 为圆心，以OA 为半径画弧交x 轴于一点;当OP=AP 时，根据线段垂直平分线的性质作OA 的垂直平分线，交x 轴于点P ，综上即可得答案.【详解】如图，当OA=OP 时，以O 为圆心，以OA 为半径画弧交x 轴于两点(P 2、P 3)，当OA=AP 时，以A 为圆心，以OA 为半径画弧交x 轴于一点(P 1)，当OP=AP 时，作OA 的垂直平分线，交x 轴于一点(P 4).∴符合使△AOP 为等腰三角形的点P 有4个，故选A.【点睛】本题考查了坐标与图形的性质及等腰三角形的判定;对于底和腰不等的等腰三角形，若条件中没有明确哪边是底哪边是腰时，应在符合三角形三边关系的前提下分类讨论．14.当今材料科学已发展到纳米时代，1纳米等于1米的十亿分之一，我国科学家已研制成功直径为0.4纳米的碳米管，如果用科学记数法表示这种碳米管的直径，应为( )A. 4×10-9米B. 0.4×10-8米C. 4×10-10米D. 0.4×10-9米【答案】C【解析】【分析】科学记数法的形式是：10n a ⨯ ，其中110,a ≤＜为整数，所以4,a =，取决于原数小数点的移动位数与移动方向，是小数点的移动位数，往左移动，为正整数，往右移动，为负整数，本题小数点往右移动到4的后面，所以10.n =-【详解】解：0.4纳米910810.40.4104101010--=⨯=⨯=⨯⨯ 米．故选C ．【点睛】本题考查的知识点是用科学记数法表示绝对值较小的数，关键是在理解科学记数法的基础上确定好,a n 的值，同时掌握小数点移动对一个数的影响．三、解答题(15～19每小题8分，共40分)15.解方程21023x x x x -+=-．【答案】x 1＝-1，x 2＝3．【解析】【分析】去分母把方程化为整式方程，得到整式方程的解，检验可得答案．【详解】解：21023x x x x -+=- 223(2)310(2),x x x x ∴-+=-2230,x x ∴--=(3)(1)0,x x ∴-+=121, 3.x x ∴=-=经检验：121,3x x =-=都是原方程的根，所以原方程的根是121,3x x =-=．【点睛】本题考查的是分式方程的解法，掌握把分式方程化为整式方程再求解，并检验是解题关键． 16.某校初二年级四个班的同学外出植树一天，已知每小时5个女生种3棵树，3个男生种5棵树，各班人数如图所示，则植树最多的是初二几班．【答案】三班．【解析】【分析】由条形统计图得到各班的男女学生人数，由每班男、女生种树的速度相同，所以每班人数减去相同的女生数和男生数，计算剩下的男生与女生种的数的数量即可得到答案．【详解】解：由图可知一班二班三班四班女生数(人)22 18 13 15 男生数(人)18 20 22 21因为每班男、女生种树的速度相同，所以每班人数减去相同的女生数和男生数，比较结果不变，每个班减去13个女生和18个男生，一班余下女生9人，可植树35×9＝525(棵)．二班余下女生5人和男生2人，可植树35×5＋53×2＝613(棵)．三班余下男生4人，可植树53×4＝623(棵)．四班余下女生2人和男生3人，可植树35×2＋53×3＝615(棵)．所以种树最多的班级是三班．【点睛】本题考查的是条形统计图的应用，掌握条形统计图的特点是解题的关键．17.声音在空气中传播的速度y (米/秒)是气温x (摄氏度)的一次函数，下表列出了一组不同气温时的音速．(1)求y 与 x 之间的函数关系式(2)气温x=22(摄氏度)时，某人看到烟花燃放5秒后才听到声响，那么此人与燃放的烟花所在地相距多远?【答案】(1)33315y x =+(2)1721 【解析】【分析】(1)由表中的数据可知，温度每升高5℃，声速就提高3米/秒，所以y 是x 的一次函数，利用待定系数法即可求出该函数解析式;(2)令x=22，求出此时的声速y ，然后利用路程=速度×时间即可求出该距离．【详解】(1)根据表中数据可知y 与x 成一次函数关系，故设y=kx+b ，取两点(0，331)，(5，334)代入关系式得 3313345b k b =⎧⎨=+⎩，解得35331k b ⎧=⎪⎨⎪=⎩， ∴函数关系式为y=35x+331; (2)把x=22代入y=35x+331，得y=35×22+331=344.2， 334.2×5=1721m ，∵光速非常快，传播时间可以忽略，故此人与燃放烟花的所在地相距约1721m ．【点睛】本题考查了一次函数的应用，解题的关键是仔细分析表中的数据，利用待定系数法求出函数解析式．18.某广场有一块长50米、宽30米的空地，现要将它改造为花园，请你设计一个修建方案，使满足下列条件：(1)正中间留出一条宽2米的道路(如图);(2)道路两旁修建花坛，且花坛总面积占整个面积(不包括道路)的一半;(3)设计好的整个图形既是轴对称图形，又是中心对称图形．(计算结果精确到0.1米)．【答案】x 的值约取3.9米．【解析】【分析】如图，设计成下图所示，设设花坛的边与空地之间的距离为米，由题意列出方程求解即可．【详解】解：设计成如下图方案．设花坛的边与空地之间的距离为米，由题意可列方程： (502)30(5024)(302),2x x -⨯---=227900,x x ∴-+= 解得： 123.93,2.1x x ≈≈(舍去)，x 的值约取3.9米．花坛四周与空地的距离，中间与道路的距离都约为3.9米．【点睛】本题考查轴对称图形与中心对称图形，考查了一元二次方程的解法，掌握以上知识是解题的关键． 19.已知：△ABC 是⊙O 的内接三角形，BT 为⊙O 的切线，B 为切点，P 为直线AB 上一点，过P 作BC 的平行线交直线BT 于点E ，交直线AC 于点F ．(1)如图 (1)所示，当P 在线段AB 上时，求证：P A ·PB ＝PE ·PF ;(2)如图 (2)所示，当P 为线段BA 延长线上一点时，第(1)题的结论还成立吗?如果成立，请给出证明;如果不成立，请说明理由．【答案】(1)证明见解析;(2)对谁成立，证明见解析【解析】【分析】(1)利用圆周角、弦切角间的关系证明△APF ∽△BPE ，根据相似三角形的性质证明 PA •PB=PE •PF 成立．(2)当点P 在线段BA 的延长线上时，(1)的结论仍成立．先证明∠AFP=∠PBE ，再由∠BPE=∠FPA ，可得△PAF ∽△PEB ，根据成比例线段证明 PA •PB=PE •PF 成立．【详解】证明：(1) 如图1，连接,BO 延长BO 与圆交于,H∵EB 为⊙O 的切线，90,ABE HBA ∴∠+∠=︒ BH 为⊙O 的直径，90,BAH ∴∠=︒90,AHB ABH ∴∠+∠=︒,AHB ACB ∠=∠90,ACB ABH ∴∠+∠=︒∴∠ACB=∠ABE ，∵EF ∥BC ，∴∠AFP=∠ACB ，故∠AFP=∠ABE ．∠APF=∠EPB ，∴△APF ∽△BPE ， ,PA PF PE PB∴= ∴PA•PB=PE•PF ．(2)结论成立，理由如下：∵EB 为⊙O 的切线，结合(1)问：∴∠ACB=∠ABT ，∵EF ∥BC ，∴∠ACB =∠AFP ，,ACB ABT AFP ∴∠=∠=∠∴∠AFP=∠PBE ．∠BPE=∠FPA ，△PAF ∽△PEB ，,PA PF PE PB ∴= ∴PA•PB=PE•PF ．当点P 在线段BA 的延长线上时，(1)的结论仍成立．【点睛】本题主要考查圆的相交弦及切线的性质，用三角形全等证明线段间的关系，体现了数形结合的数学思想，属于中档题．四、解答题(每题9分，共18分)20.先仔细阅读下列材料，然后回答问题：如果a ＞0，b ＞0，那么(a -b )2≥0，即a ＋b -2ab ≥0 得2a b +≥ab ，其中，当a ＝b 时取等号，我们把2a b +称为a 、b 的算术平均数， ab 称为a 、b 的几何平均数．如果a ＞0，b ＞0，c ＞0，同样可以得到3a b c ++≥3abc ，其中，当a ＝b ＝c 时取等号于是就有定理：几个正数的算术平均数不小于它们的几何平均数．请用上述定理解答问题：把边长为30 cm 的正方形纸片的4角各剪去一个小正方形，折成无盖纸盒(如图)(1)设剪去的小正方形边长为x cm ，无盖纸盒的容积为V ，求V 与x 的函数关系式及x 的取值范围．(2)当x 为何值时，容积V 有最大值，最大值多少?【答案】(1)V ＝4x (15-x )2(0＜x ＜15);(2)当剪去的小正方形边长为5 cm 时，无盖空盒的容积最大为2×103 cm 3 【解析】【分析】(1)由剪去的小正方形边长为x cm ，表示纸盒的底边与高，利用容积公式得到答案，(2)利用3a b c ++3abc 【详解】解：(1) 设剪去的小正方形边长为x cm ，纸盒底边为(302),x cm -纸盒的高是,xcmV ＝x (30-2x )(30-2x )＝4x (15-x )2(0＜x ＜15)，(2) V ＝332(15)(15)22(15)(15)2210,3x x x x x x +-+-⎡⎤••--≤=⨯⎢⎥⎣⎦这时，当2x ＝15-x ，即x ＝5时取等号．∴ 当剪去的小正方形边长为5 cm 时，无盖空盒的容积最大为2×103 cm 3 【点睛】本题考查的是阅读题型，掌握题干给的信息解决实际问题，同时考查了列函数关系式，求函数的最大值等问题，知识迁移能力是解题关键．21.以△ABC 的边AC 为直径的半圆交AB 边于D 点，∠A 、∠B 、∠C 所对边长为a 、b 、c ，且二次函数y ＝12(a ＋c )x 2-bx ＋12(c -a )顶点在x 轴上，a 是方程z 2＋z -20＝0的根． (1)证明：∠ACB ＝90°;(2)若设b ＝2x ，弓形面积S 弓形AED ＝S 1，阴影面积为S 2，求(S 2-S 1)与x 的函数关系式;(3)在(2)的条件下，当BD 为何值时，(S 2-S 1)最大?【答案】(1)证明见解析;(2)S 2-S 1＝-2πx 2＋4x ;(3)BD 244ππ+．【解析】【分析】(1)由抛物线的顶点在轴上，得到0,∆= 从而可得结论．(2)利用a 是z 2＋z -20＝0的根，求解的值，再利用S 2-S 1＝S △ABC -(S 半圆-S 1)-S 1＝S △ABC -S 半圆，从而可得答案，(3)由(2)的函数关系式求解(21S S -)最大时,,a b c ，利用直径所对的圆周角是直角，得到,BCD BAC ∆∆利用相似三角形的性质可得答案．【详解】(1)因为二次函数y ＝12(a ＋c )x 2-bx ＋12(c -a )的顶点在x 轴上， ∴ Δ＝0，即：b 2-4×12(a ＋c )×12(c -a )＝0， ∴ c 2＝a 2＋b 2，得∠ACB ＝90°．(2)∵ z 2＋z -20＝0．∴ z 1＝-5，z 2＝4，∵ a ＞0，得a ＝4．设b ＝AC ＝2x ，有S △ABC ＝12AC ·BC ＝4x ，S 半圆＝12π x 2∴ S 2-S 1＝S △ABC -(S 半圆-S 1)-S 1＝S △ABC -S 半圆＝-2πx 2＋4x (3) S 2-S 1＝-2π(x -4π)2＋8π， ∴ 当x ＝4π时，(S 2-S 1)有最大值8π．这时，b ＝8π，a ＝4，c ＝244ππ+, 如图，连接,CDAC 为圆的直径，90,90,ADC CDB ∴∠=︒∠=︒90,ACB ∠=︒,BCD BAC ∴∆∆,BC BD BA BC∴= BD ＝22244BC a BA c ππ+==．当BD 为22444ππ++时，(S 2-S 1)最大．【点睛】本题考查二次函数与轴只有一个交点的性质，考查一元二次方程的解法，二次函数的最值，三角形相似的判定与性质，直径所对的圆周角是直角等知识点，掌握相关的知识点是解题的关键．。

人教版中考二模检测《数学试卷》含答案解析

人教版数学中考综合模拟检测试题学校________ 班级________ 姓名________ 成绩________一、选择题(每小题3分，共计30分)1.的相反数是()A. B. 17- C. 7 D. 172.下列运算一定正确的是()A 2224x x x += B. 236x x x ⋅= C. ()()22a b a b a b +-=- D. ()32626a a = 3.下列图形中，是中心对称图形但不是轴对称图形的是()A. B. C. D. 4.如图所示的几何体是由一些小立方块搭成的，则这个几何体的俯视图是( )A. B. C. D. 5.如图，PA 、PB 分别与O 相切于、两点，点为O 上一点，连接AC 、BC ，若70P ∠=︒，则ACB∠的度数为()A. 60︒B. 115︒C. 125︒D. 165︒ 6.将抛物线2y x 向上平移3个单位长度，再向右平移2个单位长度，所得到的抛物线为()A. ()223y x =++B. ()223y x =-+C. ()223y x =--D. ()223y x =+- 7.某商品经过连续两次提价，售价由原来的每件16元提高到每件25元，则平均每次提价的百分率为()A. 25%B. 40%C. 18%D. 36% 8.方程2332x x =-的解为() A. 311x = B. 113x = C. 67x = D. 76x = 9.点()1,4--在反比例函数2k y x -=的图象上，则下列各点在此函数图象上的是() A. ()1,4- B. ()4,1--C. ()41-,D. ()4,1- 10.如图，在平行四边形ABCD 中，点在对角线BD 上，EMAD ，交AB 于点M ，EN AB ，交AD于点，则下列式子不正确的是()A. AM DE BM BE =B. AM DN AB AD =C. BC BE ME BD =D. BD BC BE EM= 二、填空题(每小题3分，共计30分)11.将数6360000用科学记数法表示为____________．12.在函数23x y x -=-中，自变量的取值范围是__________． 13.分解因式：32269a a b ab -+=__________．14.不等式组302321x x -⎧≤⎪⎨⎪+≥⎩的解集是__________．15.二次函数()239y x =+-的最小值是__________．16.如图，将ABC ∆绕点逆时针旋转得到A B C ∆''，其中点与是对应点，点与是对应点，点落在边AC 上，连接A B '，若45ACB ∠=︒，6AC =，4BC =，则A B '的长为___________．17.一个扇形的弧长是13cm π，半径是18cm ，则此扇形的面积是________2cm ．18.在ABC 中，50A ∠=︒，30B ∠=︒，点在AB 边上，连接CD ，若ACD 为直角三角形，则BCD ∠的度数为_______________度.19.同时掷两枚质地均匀的骰子，每枚骰子的六个面上分别刻有1到6的点数，则这两枚骰子向上的一面出现的点数不相同的概率为__________．20.(原创)如图，在四边形ABCD 中，AB AD =，连接AC ，180BAC ADC ∠+∠=︒，1tan 2ACD ∠=，52AC =，则ABC ∆的面积为___________．三、解答题(共60分)21.先化简，再求代数式22m n mn n m m m ⎛⎫--÷- ⎪⎝⎭值，其中2tan30tan 45m =︒+︒，2cos 45n =︒ 22.如图，在每个小正方形的边长均为1的方格纸中，有线段AB 和线段CD ，点、、、均在小正方形的顶点上．(1)在方格纸中画以AB 为一边等腰ABE ∆;(2)在方格纸中画以CD 为一边的三角形CDF ，点在小正方形的顶点上，且三角形CDF 的面积为5，连接EF ，并直接写出EFC ∠的正切值．23.某中学对全校六年级学生进行了一次数学模拟考试，并随机抽取了部分学生的测试成绩作为样本进行分析，绘制成了如下两幅不完整的统计图，请你根据统计图中提供的信息解答下列问题：(1)扇形统计图中，优秀部分对应的圆心角的度数为____________;(2)通过计算，补全条形统计图;(3)若该中学六年级共有1000人参加了这次数学考试，估计该校六年级共有多少名学生的数学成绩可以达到良好及良好以上?24.已知：在矩形ABCD 中，BD 是对角线，AE BD ⊥于点，CF BD ⊥于点．(1)如图1，求证：BE DF =;(2)如图2，当2BD AB =时，连接AF 、CE ，在不添加任何辅助线情况下，请直接写出图2中四个三角形，使写出的每个三角形的面积都等于矩形ABCD 面积的38． 25.某中学为了丰富学生的课余生活，计划购买排球和篮球供球类兴趣小组活动使用，若购买4个篮球和3个排球需用94元;若购买16个篮球和5个排球需用306元;(1)求一个篮球和一个排球各多少元;(2)该中学决定购买排球和篮球共40个，总费用不超过550元，那么该中学至少可以购买多少个排球? 26.如图，PA ，PB 分别与O 相切于点和点，点为弧AB 上一点，连接PC 并延长交O 于点，为弧AF 上一点，连接BD 交FC 于点，连接AD ，且2180APB PEB ∠+∠=︒．(1)如图1，求证：//PF AD ;(2)如图2，连接AE ，若90APB ∠=︒，求证：PE 平分AEB ∠;(3)如图3，在(2)的条件下，连接AB 交PE 于点，连接OE ，8AD =，4sin 5ABD ∠=，求PH 的长． 27.如图，抛物线25y ax bx =+-交轴于点、 (在的左侧)，交轴于点，且OB OC =，()2,0A -．(1)求抛物线的解析式;(2)点为第四象限抛物线上一点，过点作轴的平行线交BC 于点，设点横坐标为，线段PD 的长度为，求与的函数关系式．(不要求写出的取值范围)(3)在(2)的条件下，为BP 延长线上一点，且45PFC ∠=︒，连接OF 、CP 、PB ，FOB ∆的面积为3600169，求PBC ∆的面积．答案与解析一、选择题(每小题3分，共计30分)1.的相反数是()A. B. 17- C. 7 D. 17 【答案】C【解析】【分析】直接根据相反数的定义求解．【详解】由相反数的定义知：-7的相反数为7．故选：C ．【点睛】本题考查了相反数的定义：a 的相反数为-a ，掌握相反数的定义是解答此题的关键. 2.下列运算一定正确的是()A. 2224x x x +=B. 236x x x ⋅=C. ()()22a b a b a b +-=-D. ()32626a a =【答案】C【解析】分析】利用合并同类项，同底数幂的乘法，幂的乘方与积的乘法法则，平方差公式解题即可.【详解】2x ＋2x ＝4x ，A 错误;235x x x ，B 错误; ()()22a b a b a b +-=-，C 正确;()32628a a =，D 错误; 故选：C ．【点睛】本题考查整式的运算;熟练掌握同底数幂的乘法，幂的乘方与积的乘法法则，平方差公式是解题的关键．3.下列图形中，是中心对称图形但不是轴对称图形的是()A. B. C. D.【答案】B【解析】【分析】根据轴对称图形与中心对称图形的概念结合各图形的特点求解即可．【详解】A 、是轴对称图形，不是中心对称图形，故此选项错误;B 、不是轴对称图形，是中心对称图形，故此选项正确;C 、是轴对称图形，并不是中心对称图形，故此选项错误;D 、是轴对称图形，不是中心对称图形，故此选项错误;故选：B ．【点睛】本题考查了中心对称图形和轴对称图形的知识，注意掌握好中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后与原图重合．4.如图所示的几何体是由一些小立方块搭成的，则这个几何体的俯视图是( )A. B. C. D.【答案】D【解析】试题分析：根据三视图中，从左边看得到的图形是左视图,因此从左边看第一层是两个小正方形，第二层左边一个小正方形，故选D考点：简单组合体的三视图5.如图，PA 、PB 分别与O 相切于、两点，点为O 上一点，连接AC 、BC ，若70P ∠=︒，则ACB∠的度数为()A. 60︒B. 115︒C. 125︒D. 165︒【答案】C【解析】【分析】由于AP 、BP 是切线，那么∠OAP ＝∠OBP ＝90°，利用四边形内角和可求∠AOB ＝110°，再利用圆周角定理可求∠ADB ＝55°，再根据圆内接四边形对角互补可求∠ACB ．【详解】如图所示，连接OA ，OB ，∠ADB 是AB 所对的圆周角，∵AP 、BP 是切线，∴∠OAP ＝∠OBP ＝90°，∴∠AOB ＝360°−90°−90°−70°＝110°，∴∠ADB ＝55°，又∵圆内接四边形的对角互补，∴∠ACB ＝180°−∠ADB ＝180°−55°＝125°．故选：C ．【点睛】本题考查了切线的性质、圆周角定理、圆内接四边形的性质．解题的关键是连接OA 、OB ，求出∠AOB ．6.将抛物线2y x 向上平移3个单位长度，再向右平移2个单位长度，所得到的抛物线为()A. ()223y x =++B. ()223y x =-+C. ()223y x =--D. ()223y x =+- 【答案】B【解析】【分析】根据”左加右减、上加下减”的原则进行解答即可．【详解】将抛物线y=x 2向上平移3个单位长度，再向右平移2个单位长度后，得到的抛物线的解析式为y=(x-2)2+3，故选：B【点睛】本题考查的是二次函数的图象与几何变换，熟练掌握平移的规律”左加右减，上加下减”是解答此题7.某商品经过连续两次提价，售价由原来的每件16元提高到每件25元，则平均每次提价的百分率为()A. 25%B. 40%C. 18%D. 36% 【答案】A【解析】【分析】设提价的百分率为x ，根据增长率的公式a (1+x )2=b 建立方程，求解即可．【详解】设提价的百分率为x ，根据题意可列方程为16(1+x )2=25，解方程得x 1＝0.25，x 2＝-2.25(舍)∴每次降价得百分率为25%故选：A ．【点睛】本题考查了一元二次方程实际应用问题关于增长率的类型问题，按照公式a (1+x )2=b 对照参数位置代入值即可，公式的记忆与运用是本题的解题关键．8.方程2332x x=-的解为() A. 311x = B. 113x = C. 67x = D. 76x = 【答案】C【解析】【分析】分式方程去分母转化为整式方程，求出整式方程的解得到x 的值，经检验即可得到分式方程的解．【详解】去分母得：2x ＝9x−6，解得：67x =，经检验67x =是分式方程的解，故选：C ．【点睛】此题考查了解分式方程，利用了转化的思想，解分式方程注意要检验．9.点()1,4--在反比例函数2k y x -=的图象上，则下列各点在此函数图象上的是() A. ()1,4-B. ()4,1--C. ()41-,D. ()4,1- 【答案】B【分析】根据点(-1，-4)在反比例函数2kyx-=的图象上，可以求得k的值，从而可以判断各个选项是否正确．【详解】∵点(-1，-4)在反比例函数2kyx-=的图象上，∴k＝-2，∴4yx =，∵(-1)×4＝-4≠4，故选项A不符合题意;(−4)×(−1)＝4，故选项B符合题意;4×(−1)＝-4≠4，故选项C不符合题意;(−4)×1＝−4≠4，故选项D符合题意，故选：B．【点睛】本题考查反比例函数图象上点的坐标特征，解答本题的关键是明确题意，利用反比例函数的性质解答．10.如图，在平行四边形ABCD中，点在对角线BD上，EM AD，交AB于点M，EN AB，交AD 于点，则下列式子不正确的是()A. AM DEBM BE= B.AM DNAB AD= C.BC BEME BD= D.BD BCBE EM=【答案】C【解析】【分析】根据平行四边形的性质以及相似三角形的性质解答即可．【详解】∵在▱ABCD中，EM∥AD，EN AB，∴易证四边形AMEN为平行四边形，∴易证△BEM∽△BAD∽△END，AM NE DE BM BM BE==，A 项正确; AM DN AB AD=，B 项正确; BC AD BD ME ME BE==，C 项错误; BD AD BC BE EM EM==，D 项正确. 故选：C ．【点睛】此题主要考查相似三角形的性质及平行四边形的性质，本题关键是要懂得找相似三角形，利用相似三角形的性质求解．二、填空题(每小题3分，共计30分)11.将数6360000用科学记数法表示为____________．【答案】66.3610⨯【解析】【分析】科学记数法的表示形式为a×10n 的形式，其中1≤|a|＜10，n 为整数．确定n 的值时，要看把原数变成a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n 是正数;当原数的绝对值＜1时，n 是负数．【详解】6360000=66.3610⨯．故答案为：66.3610⨯．【点睛】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n 的形式，其中1≤|a|＜10，n 为整数，表示时关键要正确确定a 的值以及n 的值．12.在函数23x y x -=-中，自变量的取值范围是__________．【答案】32x ≠ 【解析】【分析】根据分母不等于0列式计算即可得解．【详解】∵2x−3≠0， ∴32x ≠，故答案为：32x ≠．【点睛】本题考查了函数自变量的范围，一般从三个方面考虑：(1)当函数表达式是整式时，自变量可取全体实数;(2)当函数表达式是分式时，考虑分式的分母不能为0;(3)当函数表达式是二次根式时，被开方数非负数．13.分解因式：32269a a b ab -+=__________．【答案】()23a a b -【解析】【分析】因式分解时有公因式先提公因式，然后再考虑用公式法.继续分解.【详解】解：32269a a b ab -+ ()22 69a a ab b =-+()23a a b =-．故答案为()23a a b =-．【点睛】本题主要考查了因式分解，熟练掌握提公因式法和公式法是解题的关键. 14.不等式组302321x x -⎧≤⎪⎨⎪+≥⎩的解集是__________．【答案】3x ≥．【解析】【分析】先求出两个不等式的解集，取两个解集的公共部分即为不等式组的解集. 【详解】解：解不等式302x -≤，得：3x ≥，解不等式321x +≥，得：13x ≥-， ∴不等式组的解集为3x ≥，故答案为3x ≥．【点睛】本题考查了一元一次不等式组的解法，确定两个不等式解集的公共部分是解题的关键.15.二次函数()239y x =+-的最小值是__________．【答案】9-【解析】【分析】根据顶点式，可直接得到．【详解】二次函数y ＝2(x ＋3)2−5中，当x ＝−3时，取得最小值−9，故答案为：−9．【点睛】本题考查二次函数的基本性质，解题的关键是正确掌握二次函数的顶点式，若题目给出是一般式则需进行配方化为顶点式或者直接运用顶点公式．16.如图，将ABC ∆绕点逆时针旋转得到A B C ∆''，其中点与是对应点，点与是对应点，点落在边AC 上，连接A B '，若45ACB ∠=︒，6AC =，4BC =，则A B '的长为___________．【答案】13【解析】【分析】由旋转的性质可得AC ＝A C '＝6，∠ACB ＝ACA '∠＝45°，可得A CB '∠＝90°，由勾股定理可求解．【详解】∵将△ABC 绕点C 逆时针旋转得到△A′B′C ，∴AC ＝A C '＝6，∠ACB ＝ACA '∠＝45°，∴A CB '∠＝90°，∴A B '22BC A C +'2246+=13 故答案为：13【点睛】本题考查了旋转的性质，勾股定理，熟练掌握旋转的性质是本题的关键．17.一个扇形的弧长是13cm π，半径是18cm ，则此扇形的面积是________2cm ．【答案】117π【解析】【分析】直接代入S 扇形＝12lR ，进行计算即可．【详解】由题意得，l ＝13πcm ，R ＝18cm ，故S 扇形＝12×13π×18＝117πcm 2．故答案为：117π．【点睛】本题考查了扇形面积的计算，解答本题的关键是掌握扇形的面积计算公式，难度一般． 18.在ABC 中，50A ∠=︒，30B ∠=︒，点在AB 边上，连接CD ，若ACD 为直角三角形，则BCD ∠的度数为_______________度.【答案】60︒或10︒【解析】【分析】当ACD ∆为直角三角形时，有两种情况90ADC ∠=︒或90ACD ∠=︒，依据三角形内角和定理，结合具体图形分类讨论求解即可.详解】解：分两种情况：①如图1，当90ADC ∠=︒时，∵30B ∠=︒，∴903060BCD ∠=︒-︒=︒;②如图2，当90ACD ∠=︒时，∵50A ∠=︒，30B ∠=︒，∴1803050100ACB ∠=︒-︒-︒=︒，∴1009010BCD ∠=︒-︒=︒，综上，则BCD ∠的度数为60︒或10︒;故答案为60︒或10︒;【点睛】本题主要考查了三角形内角和定理以及数学的分类讨论思想，能够正确进行分类是解题的关键. 19.同时掷两枚质地均匀的骰子，每枚骰子的六个面上分别刻有1到6的点数，则这两枚骰子向上的一面出现的点数不相同的概率为__________．【答案】56 【解析】【分析】首先根据题意列出表格，然后由表格即可求得所有等可能的结果与两枚骰子点数不相同的情况，再利用概率公式即可求得答案．【详解】列表得：(1，6) (2，6) (3，6) (4，6) (5，6) (6，6)(1，5) (2，5) (3，5) (4，5) (5，5) (6，5)(1，4) (2，4) (3，4) (4，4) (5，4) (6，4)(1，3) (2，3) (3，3) (4，3) (5，3) (6，3)(1，2) (2，2) (3，2) (4，2) (5，2) (6，2)(1，1) (2，1) (3，1) (4，1) (5，1) (6，1)由表可知一共有36种情况，两枚骰子点数不相同的有30种，所以两枚骰子点数相同的概率为3036=56，故答案为：56【点睛】本题考查了列表法与树状图法求随机事件的概率，列表法可以不重复不遗漏的列出所有可能的结果，适合于两步完成的事件;解题时还要注意是放回试验还是不放回试验．用到的知识点为：概率=所求情况数与总情况数之比．20.(原创)如图，在四边形ABCD 中，AB AD =，连接AC ，180BAC ADC ∠+∠=︒，1tan 2ACD ∠=，52AC =，则ABC ∆的面积为___________．【答案】58 【解析】【分析】过作AE CD ⊥交CD 延长线于点，过作BF AC ⊥，由AAS 可证DEA AFB ∆∆≌，由此AE BF =，在Rt AEC ∆中，52AC =，由1tan 2ACD ∠=及勾股定理可求得12AE =，即12BF =，继而根据三角形面积公式求解即可．【详解】过作AE CD ⊥交CD 延长线于点，过作BF AC ⊥，则90AFB AED ∠=∠=︒，180BAC ADC ∠+∠=︒，180ADE ADC ∠+∠=︒，∴ADE BAC ∠=∠，在DEA ∆和AFB ∆中，90ADE BAC AED AFB AD BA ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩，∴DEA AFB ∆∆≌，∴AE BF =，在Rt AEC ∆中，1tan 2AE ACD CE ∠==，设AE=x ，则CE=2x ，52AC =，由勾股定理，得222AE CE AC +=，即2225(2)(2x x +=，解得12AE =， ∴12BF =，∴ABC ∆的面积1528AC BF =⨯⨯= 故答案为：58．【点睛】此题考查了三角形的面积计算，全等三角形的判定与性质，勾股定理及正切的定义．作辅助线构造全等三角形是解答此题的关键．三、解答题(共60分)21.先化简，再求代数式22m n mn n m m m ⎛⎫--÷- ⎪⎝⎭的值，其中2tan30tan 45m =︒+︒，2cos 45n =︒ 【答案】1m n -，32【解析】【分析】先根据分式的混合运算顺序和运算法则化简原式，再根据特殊锐角三角函数值求得m 的值，代入计算可得．【详解】原式=222m n m mn n m m m ⎛⎫--÷- ⎪⎝⎭2()1m n m n m m m n --=÷=-， 322tan 30tan 45213133m ︒︒=+=⨯+=+，22cos 45212n ︒==⨯=， ∴113322233113m n ===-+- 【点睛】本题主要考查分式的化简求值，解题的关键是熟练掌握分式的混合运算顺序和运算法则． 22.如图，在每个小正方形的边长均为1的方格纸中，有线段AB 和线段CD ，点、、、均在小正方形的顶点上．(1)在方格纸中画以AB 为一边的等腰ABE ∆;(2)在方格纸中画以CD 为一边三角形CDF ，点在小正方形的顶点上，且三角形CDF 的面积为5，连接∠的正切值．EF，并直接写出EFC【答案】(1)见解析;(2)图见解析，2【解析】【分析】(1)根据题意可画出相应图形;∠的正切值．(2)根据题意可以画出相应图形以及EFC【详解】(1)如图：∆为所求;ABE(2)如图，tan2∠=(画图答案不唯一)EFC【点睛】本题考查作图、勾股定理、三角形的面积、等腰三角形的性质，解题的关键是画出相应的图形，找出所求问题需要的条件．23.某中学对全校六年级学生进行了一次数学模拟考试，并随机抽取了部分学生的测试成绩作为样本进行分析，绘制成了如下两幅不完整的统计图，请你根据统计图中提供的信息解答下列问题：(1)扇形统计图中，优秀部分对应的圆心角的度数为____________;(2)通过计算，补全条形统计图;(3)若该中学六年级共有1000人参加了这次数学考试，估计该校六年级共有多少名学生的数学成绩可以达到良好及良好以上?【答案】(1)72º;(2)见解析;(3)640名【分析】(1)先根据良好的学生数和所占的百分比可以求得本次调查的学生数，再求出扇形统计图中表示成绩类别为”优”的扇形所对应的圆心角的度数;(2)根据(1)中的结果和条形统计图中的数据可以求得成绩为”中”的学生数，从而可以将条形统计图补充完整;(3)根据统计图中数据可以求得该校六年级约有多少名学生的数学成绩可以达到良好及良好以上．【详解】(1)00224450÷=(人)，103607250⨯︒=︒，故答案为：72º;(2)5020%10⨯=，补图如下：(3)1022100064050+⨯=人答：估计该校六年级共有640名学生的数学成绩可达到优秀及以上．【点睛】本题考查条形统计图、扇形统计图、用样本估计总体，解答本题的关键是明确题意，利用数形结合的思想解答．24.已知：在矩形ABCD 中，BD 是对角线，AE BD ⊥于点，CF BD ⊥于点．(1)如图1，求证：BE DF =;(2)如图2，当2BD AB =时，连接AF 、CE ，在不添加任何辅助线的情况下，请直接写出图2中四个三角形，使写出的每个三角形的面积都等于矩形ABCD 面积的38．【答案】(1)见解析;(2)ABF ∆，AED ∆，BCF ∆，ECD ∆【解析】(1)由AAS 证明△ABE ≌△CDF ，即可得出结论;(2)连接AC ，交BD 于点O ，由矩形的对角线相等且互相平分以及2BD AB =得到AOB ∆是等边三角形，，由AE BD ⊥于点，得到BE=OE ，OF=DF ，进而BF=34BD,故3348ABF ABD ABCD S S S ==矩形，由等底等高的三角形面积相等，得到ABF S ∆=AED S ∆=BCF S ∆=∆ECD S =38ABCDS 矩形. 【详解】(1)∵在矩形ABCD 中，AB CD =，AB CD ∥，∴ABE CDF ∠=∠，∵AE BD ⊥，CF BD ⊥，∴90AEB CFD ∠=∠=︒，∴ABE CDF ∆∆≌，∴BE DF =;(2)如图：连接AC ，交BD 于点O ，∵四边形ABCD 是矩形，∴OA=OB=OC=OD ，∵2BD AB =，∴AB=OB=OA ，∴AOB ∆是等边三角形，∵AE BD ⊥于点，∴BE=OE ，同理OF=DF ，∴BE=OE=OF=DF ，∴BF=34BD, ∴3348ABF ABD ABCD S S S ==矩形 ∴BF=DE,由(1)知，AE=CF ，∴ABF S ∆=AED S ∆=BCF S ∆=∆ECD S =38ABCDS 矩形【点睛】本题考查了矩形的性质、全等三角形的判定与性质、含30°角的直角三角形的性质、平行线的性质、三角形面积公式等知识;熟练掌握矩形的性质和含30°角的直角三角形的性质，证明三角形全等是解题的关键．25.某中学为了丰富学生的课余生活，计划购买排球和篮球供球类兴趣小组活动使用，若购买4个篮球和3个排球需用94元;若购买16个篮球和5个排球需用306元;(1)求一个篮球和一个排球各多少元;(2)该中学决定购买排球和篮球共40个，总费用不超过550元，那么该中学至少可以购买多少个排球?【答案】(1)购买一个篮球16元，购买一个排球10元;(2)15个【解析】【分析】(1)设每个排球x 元，每个篮球y 元，根据”购买4个篮球和3个排球需用94元;购买16个篮球和5个排球需用306元”，即可得出关于x ，y 的二元一次方程组，解之即可得出结论;(2)设购买篮球a 个，则购买排球(40-a )个，根据总价=单价×数量结合购买排球和篮球的总费用不超过550元，即可得出关于a 的一元一次不等式，解之取其中的最小值整数值即可得出结论．【详解】(1)设购买一个排球元，购买一个篮球元：4394165306x y x y +=⎧⎨+=⎩，解得1610x y =⎧⎨=⎩，答：设购买一个篮球16元，购买一个排球10元;(2)设该中学可以购买个排球，则购买篮球()40a -个：()101640550a a +-≤，解得15a ≥，答：该中学至少可以购买15个排球．【点睛】本题考查了二元一次方程组的应用、一元一次不等式的应用以及二元一次方程的应用，解题的关键是：(1)找准等量关系，正确列出二元一次方程组;(2)根据各数量之间的关系，正确列出一元一次不等式． 26.如图，PA ，PB 分别与O 相切于点和点，点为弧AB 上一点，连接PC 并延长交O 于点，为弧AF 上的一点，连接BD 交FC 于点，连接AD ，且2180APB PEB ∠+∠=︒．(1)如图1，求证：//PF AD ;(2)如图2，连接AE ，若90APB ∠=︒，求证：PE 平分AEB ∠;(3)如图3，在(2)的条件下，连接AB 交PE 于点，连接OE ，8AD =，4sin 5ABD ∠=，求PH 的长．【答案】(1)见解析;(2)见解析;(3)257【解析】【分析】 (1)连接OA 、OB ，由切线的性质可得90OAP OBP ∠=∠=︒，由四边形内角和是360︒，得180∠+∠=︒P AOB ，由同弧所对的圆心角是圆周角的一半，得到2AOB ADB ∠=∠，等量代换得到ADB PEB ∠=∠，由同位角相等两直线平行，得到//PF AD ;(2)过点做PK PF ⊥交EB 延长线于点，由90APB ∠=︒得290PEB ∠=︒，从而45PEB ∠=︒，由切线的性质，得PA PB =，由PK PE ⊥，45PEK ∠=︒，得PE PK =，从而90APE EPB ︒∠=-∠，进而APE BPK ∠=∠，即可证得APE BPK ∆∆≌由此45K AEP ∠=∠=︒，得到AEP PEB ∠=∠，即可证得PE 平分AEB ∠;(3)连接AO 并延长交圆于点M ，连接OB 、OH 、OP 、OD 、DM ，由45ADE ∠=︒，90AED ∠=︒，可得DE AE =，由OA 、OD 为半径，可得OA OD =，即可证出DEO AEO ∆∆≌，由直径所对的圆周角是直角，可得90ADM ∠=︒，在Rt ADM ∆中，由正弦定义可得10AM =，由此5OA OB ==，由OAPB 为正方形，对角线AB 垂直平分OP ，从而，OH PH =.在Rt OAP ∆中，252OP OA ==.延长EO 交AD 于，在Rt OEP ∆中，由勾股定理得7PE =，在Rt OEH ∆中，由勾股定理得257PH =. 【详解】(1)连接OA 、OB∵PA 、PB 与圆相切于点、，且OA 、OB 为半径，∴OA AP ⊥，OB BP ⊥，∴90OAP OBP ∠=∠=︒，∴在四边形AOBP 中，360180180P AOB ∠+∠=︒-︒=︒，∵AB AB =，∴2AOB ADB ∠=∠，∴2180P ADB ∠+∠=︒，∵2180P PEB ∠+∠=︒，∴ADB PEB ∠=∠，∴//PF AD(2)过点做PK PF ⊥交EB 延长线于点∵90APB ∠=︒，∴21809090PEB ∠=︒-︒=︒，∴45PEB ∠=︒，∵PA 、PB 为圆的切线，∴PA PB =，∵PK PE ⊥，45PEK ∠=︒，∴PE PK = ，∵9090APE EPB KPB EPB ︒︒∠=-∠=∠=-∠，∴APE BPK ∠=∠，∴APE BPK ∆∆≌，∴45K AEP ∠=∠=︒，∴AEP PEB ∠=∠，∴PE 平分AEB ∠;(3)连接AO 并延长交圆于点M ，连接OB 、OH 、OP 、OD 、DM∵45ADE ∠=︒，90AED ∠=︒，∴DE AE =，∵OA 、OD 为半径，∴OA OD =，∵OE OE =，∴DEO AEO ∆∆≌， ∴1452AEO OED AED ∠=∠=∠=︒， ∴90OEP ∠=︒，∵AM 为圆的直径，∴90ADM ∠=︒，∵弧AD =弧AD ，∴ABD AMD ∠=∠，在Rt ADM ∆中，8AD =，4sin 5AMD ∠=，则10AM =， ∴5OA OB ==，由题易证四边形OAPB 为正方形，∴对角线AB 垂直平分OP ，AB OP =，∵在AB 上，∴OH PH =，在Rt OAP ∆中，252OP OA ==延长EO 交AD 于，∵DE AE =，可证OK AD ⊥，DOK ABD ∠=∠，∴4DK KE ==，3OK =，1OE =∴在Rt OEP ∆中，227PE OP OE =-=在Rt OEH ∆中，222OH OE EH =+∵OH PH =，7EH PE HP PH =-=-∴()22217PH PH =+- ∴257PH =．【点睛】本题考查了圆的综合题，圆的性质，等腰三角形的性质，相交弦定理，正弦定理，勾股定理，灵活运用这些性质定理解决问题是本题的关键．27.如图，抛物线25y ax bx =+-交轴于点、 (在的左侧)，交轴于点，且OB OC =，()2,0A -．(1)求抛物线的解析式;(2)点为第四象限抛物线上一点，过点作轴的平行线交BC 于点，设点横坐标为，线段PD 的长度为，求与的函数关系式．(不要求写出的取值范围)(3)在(2)的条件下，为BP 延长线上一点，且45PFC ∠=︒，连接OF 、CP 、PB ，FOB ∆的面积为3600169，求PBC ∆的面积．【答案】(1)213522y x x =--;(2)21522d t t =-+;(3)7710 【解析】【分析】(1)对于25y ax bx =+-，令0x =，得5y =，从而点()0,5C -，由OB OC =得到点()5,0B 将()5,0B 、()2,0A -代入25y ax bx =+-，由待定系数法即可抛物线的解析式为213522y x x =--; (2)设213,522P t t t ⎛⎫-- ⎪⎝⎭由()5,0B ，()0,5C -可得直线BC 的解析式为5y x =-，由PD y 轴，故(),15D t -，由此可得213(5)522DP t t t ⎛⎫=---- ⎪⎝⎭，从而21522d t t =-+; (3)过点作CB 的垂线交轴于点，过点作CF 的垂线交PB 于点，过点做OM PB ⊥，延长PD 交轴于点，连接KE 交BC 于点，过点作CQ PN ⊥．由已知可得FCE ∆、KCB ∆均为等腰直角三角形，从而CK CB =，CE CF =，由等式的性质可得KCE BCF ∠=∠，进而KCE BCF ∆∆≌，由可得全等三角形的性质CKE CBF ∠=∠，KE BF =，所以90KEB ∠=︒，90OMB KEB ∠=∠=︒，所以BOM BKE ∆∆∽.由相似三角形的性质可得2KE OM =，由三角形的面积可求得OM 的值，在Rt OBM ∆中，由正切的定义可求得t 的值，由PBC CPD PDB S S S ∆∆∆=+即可得解.【详解】(1)∵对于25y ax bx =+-,令0x =，则5y =，∴()0,5C -，5OB OC ==，∴()5,0B ，将()5,0B 、()2,0A -代入25y ax bx =+-，∴255504250a b a b +-=⎧⎨--=⎩，解得，1232a b ⎧=⎪⎪⎨⎪=-⎪⎩∴抛物线的解析式为213522y x x =--; (2)∵在抛物线213522y x x =--上，设213,522P t t t ⎛⎫-- ⎪⎝⎭， ∵()5,0B ，()0,5C -，∴直线BC 的解析式为5y x =-，∵//PD y 轴，∴点的横坐标与点横坐标相同，∴(),15D t -， ∴213(5)522DP t t t ⎛⎫=----⎪⎝⎭， ∴21522d t t =-+; (3)过点作CB 的垂线交轴于点，过点作CF 的垂线交PB 于点，过点做OM PB ⊥，延长PD 交轴于点，连接KE 交BC 于点，过点作CQ PN ⊥．∵90KCB FCE ∠=∠=︒，45CFE CBO ∠=∠=︒，∴FCE ∆、KCB ∆均为等腰直角三角形，∴CK CB =，CE CF =，KCB BCE FCE BCE ∠+∠=∠+∠，∴KCE BCF ∠=∠，∴KCE BCF ∆∆≌，∴CKE CBF ∠=∠，KE BF =，∴90KHC CKH BHE HBE ∠+∠=∠+∠=︒，∴90KEB ∠=︒，∴90OMB KEB ∠=∠=︒，∵OBM KBM ∠=∠，∴BOM BKE ∆∆∽， ∴12OB OM KB KE ==， ∴2KE OM =， ∴2136002169BOF S BF OM OM ∆=⨯==， ∴6013OM =， ∴在Rt OBM ∆中，2513BM =， ∴12tan tan 5OBM PBN ∠=∠=， ∴1(5)(2)122tan 55t t PN PBN BN t --+∠===-， ∴145t =， ∴211111577522222210PBC CPD PDB S S S PD CQ PD BN PD OB t t ∆∆∆⎛⎫=+=⨯+⨯=⨯=⨯⨯-+= ⎪⎝⎭【点睛】本题考查的是二次函数综合运用，涉及到一次函数、解直角三角形、面积的计算等，本题综合性强，但是难度不大．。

人教版中考第二次模拟检测《数学试题》含答案解析

人教版数学中考综合模拟检测试题学校________ 班级________ 姓名________ 成绩________一、选择题(每题3分，共30分) 1. 3-2的绝对值是( ) A. 23-B. 32-C. 3D. 1 2. 下列运算正确的是( )A. 224x x x +=B. 235a a a =C. ()2236x x =D. ()()54mn mn mn ÷= 3. 下列所给的汽车标志图案中，既是轴对称图形，又是中心对称图形的是( )A. B.C. D.4. 如果点(),2m m -在双曲线k y x =上，那么双曲线k y x =图像在第( )象限 A. 一、二 B. 三、四C. 一、三D. 二、四 5. 如图，由5个完全相同的小正方体组合成一个立体图形，它的左视图是( )A. B. C. D. 6. 如图将两块三角板的直角顶点重叠在一起，DOB ∠与DOA ∠的比是2:11，则BOC ∠的度数为( )A. 45︒B. 60︒C. 70︒D. 40︒7. 如图，在Rt ABC 中，CD 是斜边AB 上的中线，已知 1.52CD BC ==，，则cos B 的值是( )A. 23B.32C.34D.438. 如图，在⊙O中，点A、B、C在⊙O上，且∠ACB＝110°，则∠α＝( )A. 70°B. 110°C. 120°D. 140°9. 如图，在ABC中，点D，E分别为AB，AC边上的点，且//DE BC，CD、BE相较于点O，连接AO 并延长交DE于点G，交BC边于点F，则下列结论中一定正确的是()A. AD AEAB EC= B.AG AEGF BD= C.OD AEOC AC= D.AG ACAF EC=10. 如图，2020D次哈尔滨至幸福镇动车需要匀速通过一条隧道(隧道长大于火车长)，火车在隧道内的长度与火车进入隧道的时间之间的关系用图象描述大致是()A. B. C. D.二、填空题(每题3分，共30分)11. 禽流感病毒的形状一般为球形，直径大约为0.000000102m，将0.000000102用科学记数法表示为_____．12. 在函数3||3xyx-=+中，自变量的取值范围是________．13. 化简计算：12842-=_______． 14. 分解因式：33327a b ab -=_________．15. 不等式组131722523(1)x x x x ⎧-≤-⎪⎨⎪+>-⎩的整数解的个数是_________．16. 在一个口袋中有4个完全相同的小球，把它们分别标号为1，2，3，4，随机地摸出一个小球不放回，再随机地摸出一个小球，则两次摸出的小球的标号的和为奇数的概率是_____________.17. 一个扇形半径为2cm ，面积为22cm π，则此扇形的圆心角为________．18. 纸片ABC 中，60,16,14B AB cm AC m ∠=︒==，将它折叠使与重合，折痕MN 交AB 于点M ，则线段AM 的长为________． 19. 如图，O 的半径OD ⊥弦AB 于点，连结AO 并延长交O 于点，连结EC .若8AB =，CD =，则EC的长为_______．20. 如图,在ABC 中，60C ∠=°，D E 、分别在边BC AC 、上，,AD AB EAB EBA =∠=∠，23AB =,1DE =，则线段AE 的长为______．三、解答题(21、22题各7分，23、24题各8分，25-27题各10分，共计60分)21. 先化简，再求值：(1﹣x+31x +)÷2441x x x +++，其中x=tan45°+(12)﹣1． 22. 如图，在106⨯的正方形网格中，每个小正方形的边长均为1，线段AB 、线段EF 的端点均在小正方形的项点上．(1)在图中以AB 为边画Rt ABC ，使点在小正方形的顶点上，且90BAC ∠=︒，2tan 3ACB ∠=;(2)在(1)的条件下，在图中画以EF 为边且面积为3的DEF ，使点在小正方形的顶点上，且45CBD ∠=︒，连结CD ，直接写出线段CD 的长．23. 为了解某校学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况，随杋抽取了名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目)，并将调查结果绘制成如图统计图表：学生最喜爱的节目人数统计表节目人数(名) 百分比最强大脑10% 朗读者%b 中国诗词大会40% 出彩中国20%根据以上提供的信息，解答下列问题：(1)x =______，a =_____，b =____;(2)补全上面条形统计图;(3)若该校共有学生5000名，根据抽样调查结果，估计该校最喜爱《中国诗词大会》节目的学生有多少名． 24. 已知点是平行四边形ABCD 的边CD 的中点，BD 是对角线，AG BD 交CB 的延长线于，连接DG 交AB 于点．(1)如图1，求证：BF GE =;(2)如图2，当四边形AGBD 是矩形时，请你确定四边形BEDF 的形状并说明．25. 某服装加工厂甲、乙两个车间共同加工一款休闲装，且每人每天加工的件数相同，甲车间比乙车间少10人，甲车间每天加工服装400件，乙车间每天加工服装600件．(1)求甲、乙两车间各有多少人;(2)甲车间更新了设备，平均每人每天加工的件数比原来多了10件，乙车间的加工效率不变，在两个车间总人数不变的情况下，加工厂计划从乙车间调出一部分人到甲车间，使每天两个车间加工的总数不少于1314件，求至少要从乙车间调出多少人到甲车间．26. 已知ABD △内接于圆，点为弧BD 上一点，连接BC AC AC 、，交BD 于点，CED ABC ∠=∠．(1)如图1，求证：弧AB =弧AD ;(2)如图2，过作BF AC ⊥于点，交圆点，连接AG 交BD 于点，且222EH BE DH =+，求CAG ∠的度数;(3)如图3，在(2)条件下，圆上一点M 与点关于BD 对称，连接ME ，交AB 于点，点为弧AD 上一点，PQ BG ∥交AD 于点Q ，交BD 的延长线于点，AQ BN =，ANE 的周长为20，52DR =，求圆半径． 27. 在平面直角坐标系中，抛物线27287y ax x a =-+-经过原点，交轴正半轴于点，顶点为，对称轴交轴于点．(1)如图1，求点的坐标;(2)如图2，点为抛物线在第一象限上一点，连接OP 交对称轴于点，设点的横坐标为，DE 的长为，求与之间的函数解析式，不要求写出自变量的取值范围;、，(3)如图3，在(2)的条件下，点为BD上一点，连接OF，点为OF上一点，连接EG BG=，若BG=∠+∠=︒，EG EOBOF BGE60答案与解析一、选择题(每题3分，共30分) 1. 3-2的绝对值是( ) A. 23-B. 32-C. 3D. 1【答案】A【解析】【分析】根据差的绝对值是大数减小数，可得答案．【详解】3-2的绝对值是2-3．故选A ．【点睛】本题考查了实数性质，差的绝对值是大数减小数．2. 下列运算正确的是( )A. 224x x x +=B. 235a a a =C. ()2236x x =D. ()()54mn mn mn ÷= 【答案】B【解析】【分析】根据合并同类项，同底数幂的乘除以及积的乘方逐一计算即可.【详解】A. 2222x x x += ，此选项错误;B. 235·a a a = ，此选项正确;C. ()2239x x = ，此选项错误;D. ()()544mn mn m n ÷=，此选项错误.故选B【点睛】本题考查了合并同类项，同底数幂的乘除，积的乘方，熟练掌握运算法则是解题的关键. 3. 下列所给的汽车标志图案中，既是轴对称图形，又是中心对称图形的是( )A. B. C. D.分析：根据轴对称图形与中心对称图形的概念求解即可．详解：A ．是轴对称图形，不是中心对称图形;B ．是轴对称图形，也是中心对称图形;C ．是轴对称图形，不是中心对称图形;D ．是轴对称图形，不是中心对称图形．故选B ．点睛：本题考查了中心对称图形和轴对称图形的知识，关键是掌握好中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，图形旋转180°后与原图重合．4. 如果点(),2m m -在双曲线k y x =上，那么双曲线k y x =的图像在第( )象限 A. 一、二B. 三、四C. 一、三D. 二、四【答案】D【解析】【分析】将点代入，可判定k ＜0，然后再判定双曲线的图像位置【详解】∵点(m ，-2m)在双曲线上，代入得：k=22m -≤0∵k≠0∴k ＜0∴双曲线经过二、四象限故选：D【点睛】本题考查双曲线图像的性质，解题关键是判定出k 的符号5. 如图，由5个完全相同的小正方体组合成一个立体图形，它的左视图是( )A. B. C. D.试题分析：从左面看易得第一层有2个正方形，第二层最左边有一个正方形．故选B ．考点：简单组合体的三视图．6. 如图将两块三角板的直角顶点重叠在一起，DOB ∠与DOA ∠的比是2:11，则BOC ∠的度数为( )A. 45︒B. 60︒C. 70︒D. 40︒【答案】C【解析】【分析】设∠DOB=2x ，则∠DOA=11x ，可推导得到∠AOB=9x=90°，从而得到角度大小【详解】∵∠DOB 与∠DOA 的比是2:11∴设∠DOB=2x ，则∠DOA=11x∴∠AOB=9x∵∠AOB=90°∴x=10°∴∠BOD=20°∴∠COB=70°故选：C【点睛】本题考查角度的推导，解题关键是引入方程思想，将角度推导转化为计算的过程，以便简化推导 7. 如图，在Rt ABC 中，CD 是斜边AB 上的中线，已知 1.52CD BC ==，，则cos B 的值是( )A. 23B. 32C. 34D. 43【答案】A根据CD是Rt△ABC的中线，可得AD=DB=DC，进而得到斜边AB的长，已知BC，可直接求出cosB的大小【详解】∵CD是Rt△ABC斜边上的中线，CD=1.5∴AD=DB=DC=1.5，∴AB=3∵BC=2∴cosB=2 3故选：A【点睛】本题考查锐角三角函数，解题关键是利用直角三角形斜边中线是斜边长一半来求解8. 如图，在⊙O中，点A、B、C在⊙O上，且∠ACB＝110°，则∠α＝( )A. 70°B. 110°C. 120°D. 140°【答案】D【解析】【分析】作AB所对的圆周角∠ADB，如图，利用圆内接四边形的性质得∠ADB＝70°，然后根据圆周角定理求解．【详解】解：作AB所对的圆周角∠ADB，如图，∵∠ACB+∠ADB＝180°，∴∠ADB＝180°﹣110°＝70°，∴∠AOB＝2∠ADB＝140°．故选D．【点睛】本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半9. 如图，在ABC 中，点D ，E 分别为AB ，AC 边上的点，且//DE BC ，CD 、BE 相较于点O ，连接AO 并延长交DE 于点G ，交BC 边于点F ，则下列结论中一定正确的是( )A. AD AE AB EC =B. AG AE GF BD =C. OD AE OC AC =D. AG AC AF EC= 【答案】C【解析】【分析】由//DE BC 可得到DEO ∽CBO ，依据平行线分线段成比例定理和相似三角形的性质进行判断即可．【详解】解：A.∵//DE BC ， ∴AD AE AB AC= ,故不正确; B. ∵//DE BC ， ∴AG AE GF EC = ,故不正确; C. ∵//DE BC ，∴ADE ∽ABC ，DEO ∽CBO ,DE AE BC AC ∴=，DE OD BC OC= ． OD AE OC AC∴= ，故正确; D. ∵//DE BC ， ∴AG AE AF AC = ,故不正确; 故选C ．【点睛】本题主要考查的是相似三角形的判定和性质，熟练掌握相似三角形的性质和判定定理是解题的关键．10. 如图，2020D 次哈尔滨至幸福镇的动车需要匀速通过一条隧道(隧道长大于火车长)，火车在隧道内的长度与火车进入隧道的时间之间的关系用图象描述大致是( )A. B. C. D.【答案】A【解析】【分析】火车通过隧道分为3个过程：逐渐进入隧道，完全进入隧道并在其中行驶，逐渐出隧道【详解】火车在逐渐进入隧道的过程中，火车在隧道内的长度逐渐增加;火车完全进入隧道后，还在隧道内行驶一段时间，因此在隧道内的长度是火车长，且保持一段时间不变; 火车在逐渐出隧道的过程中，火车在隧道内的长度逐渐减少;符合上述分析过程的为：A故选：A【点睛】本题考查函数图像在生活中的应用，解题关键是分析事件变化的过程，并能够匹配对应函数图像变化二、填空题(每题3分，共30分)11. 禽流感病毒的形状一般为球形，直径大约为0.000000102m ，将0.000000102用科学记数法表示为_____．【答案】71.0210⨯﹣ 【解析】【分析】绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10-n ，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．【详解】0.000000102=1.02×10-7．故答案为1.02×10-7．【点睛】本题考查用科学记数法表示较小的数，一般形式为a×10-n ，其中1≤|a|＜10，n 为由原数左边起第一个不为零的数字前面的0的个数所决定．12. 在函数3||3x y x -=+中，自变量的取值范围是________．【答案】3x ≠-【解析】【分析】分式的分母不能为0【详解】函数要想有意义，则分式的分母不能为0，即：x+3≠0∴x≠－3故答案为：x≠－3【点睛】本题考查求函数自变量的取值，通常关注3个点：(1)分数(式)分母不为0;(2)二次根式内的式子非负;(3)符合生活实际13. 化简计算：-=_______．【答案】【解析】【分析】先化简二次根式，然后同类项合并【详解】原式=故答案为：【点睛】本题考查二次根式的减法计算，解题过程中，我们一般先将二次根式化为最简二次根式，然后再进行后续计算14. 分解因式：33327a b ab -=_________．【答案】3(3)( 3 )ab a b a b -+【解析】【分析】先提取公因式，然后利用平方差公式进一步分解【详解】原式=22223ab(a -9b )=3ab[a -(3b)]=3(3)( 3 )ab a b a b -+故答案为：3(3)( 3 )ab a b a b -+【点睛】本题考查因式分解，因式分解常见的方法有：(1)提取公因式;(2)利用乘法公式分解因式;(3)十字相乘法分解因式(4)分组法分解因式15. 不等式组131722523(1)x x x x ⎧-≤-⎪⎨⎪+>-⎩的整数解的个数是_________．【答案】【解析】【分析】分别求解两个不等式，得到不等式组的解集，判断解集内整数的个数【详解】解不等式131722x x -≤-得：x≤4 解不等式523(1)x x +>-得：x ＞52- ∴52-＜x≤4 ∴整数解有：－2、－1、0、1、2、3、4共7个故答案为：7【点睛】本题考查求不等式的整数解，解答过程和解不等式是完全相同的过程，最后只需分析解集中的整数解即可16. 在一个口袋中有4个完全相同的小球，把它们分别标号为1，2，3，4，随机地摸出一个小球不放回，再随机地摸出一个小球，则两次摸出的小球的标号的和为奇数的概率是_____________. 【答案】23; 【解析】试题解析：列表得：所有等可能的情况有12种，其中之和为奇数的情况有8种，则82.123P == 故答案为:2.317. 一个扇形的半径为2cm ，面积为22cm π，则此扇形的圆心角为________．【答案】180︒【解析】【分析】设圆心角为n°，直接代入求扇形面积公式可得到【详解】设扇形的圆心角为n°则扇形面积为：222360n ππ︒=︒解答：n=180故答案为：180°【点睛】本题是扇形面积公式的考查，该公式可理解为圆的面积乘扇形圆心角与圆周角的比例 18. 纸片ABC 中，60,16,14B AB cm AC m ∠=︒==，将它折叠使与重合，折痕MN 交AB 于点M ，则线段AM 的长为________．【答案】6或10【解析】【分析】如下图，过点A 作BC 垂线交BC 于点D ，△ABD 是含有30°的直角三角形，已知AB ，则可得到AD 的长;根据折叠的性质，可得△BCM 是正三角形，设MB=x ，则可得到DC=x-8;在Rt △ADC 中，利用勾股定理可得到一个关于x 的方程，解得结果即为BM 长，进而得出MA 长【详解】情况一：如下图，△ABC 是锐角三角形，过点A 作BC 垂线交BC 于点D∵∠B=60°，AB=16，AD ⊥BC∴在Rt △ABD 中，BD=8，AD=3∵△MCN 是△MBN 折叠得到，∴∠MCB=∠B=60°∴△MBC 为正三角形，∴MB=BC设MB=x ，则BC=x ，DC=x-8∵AC=14∴在Rt △ADC 中，222AD DC AC +=，即()()22283814x +-= 解得：x=6(舍)或x=10，∴AM=6情况二：如下图，当△ABC 是钝角三角形，过点A 作BC 垂线交BC 于点D同理，BD=8，AD=83，△MBC 正三角形设MB=x ，则BC=x ，CD=8－x∵AC=14∴在Rt △ADC 中，222AD DC AC +=，即()()22283814x +-= 解得：x=6或x=10(舍)，∴AM=10综上得：AM=10或AM=6故答案为：6或10【点睛】本题考查勾股定理和折叠的性质，解题的关键是设未知边为x ，寻找直角三角形，利用勾股定理建立等式方程19. 如图，O 的半径OD ⊥弦AB 于点，连结AO 并延长交O 于点，连结EC .若8AB =，CD =，则EC的长为_______．【答案】13【解析】如下图，连接EB.根据垂径定理，设半径为r ，在Rt △AOC 中，可求得r 的长;△AEB ∽△AOC ，可得到EB 的长，在Rt △ECB 中，利用勾股定理得EC 的长【详解】如下图，连接EB∵OD ⊥AB ，AB=8，∴AC=4设O 的半径为r∵CD=2，∴OC=r-2在Rt △ACO 中，222AC OC AO +=，即()22242r r +-=解得：r=5，∴OC=3∵AE 是O 的直径，∴∠EBA=90° ∴△OAC ∽△EAB ∴EB AE OC AO =，∴EB=6 在Rt △CEB 中，222BC BE CE +=，即22246CE +=解得：CE=213故答案为：213【点睛】本题考查垂径定理、相似和勾股定理，需要强调，垂径定理中五个条件”知二推三”，本题知道垂直和过圆心这两个条件20. 如图,在ABC 中，60C ∠=°，D E 、分别在边BC AC 、上，,AD AB EAB EBA =∠=∠，23AB =,1DE =，则线段AE 的长为______．7【解析】如下图，构造△ABC的外接圆，利用圆周角与圆心角的关系，求得∠AHF=30°，从而得到△AGH与△AGF 是含有30°的直角三角形，进而得到三角形各边长;然后证△AHE≌△ADE，在△AEH中利用余弦定理可求得AE长【详解】如下图，作△ABC的外接圆，圆心为点O，过点E作AB的垂线，交AB于点F，交O于点G，反向延长EF交O于点H，连接AG、BG、AH∵∠ABE=∠BAE，EF⊥AB，23AB∴3O在AB的垂直平分线上，即点O在GH上∴GH是O的直径，点G是AB的中点∴∠HAG=90°∵∠C=60°∴∠AHG=30°∴∠AGH=60°在Rt△AGF中，∵3∴GF=1，AG=2∴在Rt△AGH中，GH=4，AH=23∴AH=AD设∠ABD=∠ADB=x根据AB=AD和∠ABE=∠BAE可推导得：∠BAD=180-2x，∠DAE=x-60，∠AEB=2x-60，∠ABE=∠BAE=120-x，∠EBC=2x-120∴∠HAE=∠HAG－∠GAF-∠BAD－∠DAE=x-60∴∠HAE=∠DAE在△AHE与△ADE中60AH AD HAE DAE x AE AE ⎧==⎪∠=∠=-⎨⎪=⎩∴△AHE ≌△ADE∴EH=ED=1∵EH=1，GF=1，HG=4，∴F E=2∴在Rt △AEF 中，【点睛】本题考查了等腰三角形的性质、圆心角与圆周角之间的关系、全等的证明，解题关键是构造出△ABC 的外接圆，然后寻找全等三角形三、解答题(21、22题各7分，23、24题各8分，25-27题各10分，共计60分)21. 先化简，再求值：(1﹣x+31x +)÷2441x x x +++，其中x=tan45°+(12)﹣1．【答案】-15【解析】【分析】先根据分式混合运算顺序和运算法则化简原式，再根据三角函数值、负整数指数幂得出x 的值，最后代入计算可得．【详解】原式=(21311x x x -+++)÷()221x x ++ =()()()2221·12x x x x x +-+++ =22x x-+，当x=tan45°+(12)﹣1=1+2=3时，原式=231235-=-+．【点睛】本题考查了分式的化简求值，熟练掌握分式混合运算的运算顺序、特殊角的三角函数值、负指数幂的运算是解题的关键.22. 如图，在106⨯的正方形网格中，每个小正方形的边长均为1，线段AB 、线段EF 的端点均在小正方形的项点上．(1)在图中以AB 为边画Rt ABC ，使点在小正方形的顶点上，且90BAC ∠=︒，2tan 3ACB ∠=; (2)在(1)的条件下，在图中画以EF 为边且面积为3的DEF ，使点在小正方形的顶点上，且45CBD ∠=︒，连结CD ，直接写出线段CD 的长．【答案】(1)画图见解析;(2)画图见解析;26CD =．【解析】【分析】(1)根据90BAC ∠=︒，2tan 3ACB ∠=，确定点C 的位置，进而画出Rt ABC ，即可; (2)根据45CBD ∠=︒，以EF 为边且面积为3的DEF ，确定出点D 的位置，即可画出DEF ．【详解】(1)如图，Rt ABC 即为所求;(2)如图，DEF 即为所求，221526CD =+=．【点睛】本题主要考查直角三角形的定义以及锐角三角函数的定义，掌握锐角三角函数的定义，是解题的关键．23. 为了解某校学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况，随杋抽取了名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目)，并将调查结果绘制成如图统计图表：学生最喜爱的节目人数统计表节目人数(名) 百分比最强大脑10% 朗读者%b 中国诗词大会40% 出彩中国20%根据以上提供的信息，解答下列问题：(1)x =______，a =_____，b =____;(2)补全上面的条形统计图;(3)若该校共有学生5000名，根据抽样调查结果，估计该校最喜爱《中国诗词大会》节目的学生有多少名．【答案】(1)50530x a b ===，，;(2)补全条形统计图见解析;(3)2000人．【解析】【分析】(1)读取”出彩中国”的数据，可得到样本容量x 的值，再利用样本容量×百分比=人数的公式，分别计算a 、b 、c 的值;(2)根据求出的c 的值绘制图形;(3)诗词大会百分比×总人数即可【详解】(1)读取”出彩中国”的数据，10人对应的比例为20%∴样本容量x=10÷20%=50人 a=50×10%=5人;b%=15÷50=30%，b=30c=50×40%=20人(2)图形如下：(3)喜爱《中国诗词大会》人数约为：5000×40%=2000人【点睛】本题考查调查统计，解题关键是通过残缺图表信息，先求解出样本容量，后续再根据题干要求相应求解24. 已知点是平行四边形ABCD的边CD的中点，BD是对角线，AG BD交CB的延长线于，连接DG 交AB于点．;(1)如图1，求证：BF GE(2)如图2，当四边形AGBD是矩形时，请你确定四边形BEDF的形状并说明．【答案】(1)见解析;(2)菱形【解析】【分析】(1)证四边形ADBG是平行四边形，得到BG=AD=BC，得点B是GC中点，证BF是△CDG的中位线即可;(2)先证四边形BFDE是平行四边形，在利用矩形ADBG对角线相等的性质证BE=ED即可【详解】(1)∵四边形ABCD是平行四边形，∴BC=AD，BC∥AD∵AG∥BD，∴四边形ADBG是平行四边形，GE=ED∴BG=AD=BC∴点B是CG的中点∵点F是CD的中点∴BF是△CDG的中位线∴BF=GE(2)∵四边形ABCD是平行四边形，∴EB∥FD根据(1)知，BF∥GD∴四边形BFDE 是平行四边形∵四边形ADBG 是矩形∴AB=DG ，BE=ED∴平行四边形BEDF 是菱形【点睛】本题考查了平行四边形、矩形的性质，并利用性质证明菱形.常见解题思路是先得到平行四边形，再利用菱形的特点证平行四边形是菱形25. 某服装加工厂甲、乙两个车间共同加工一款休闲装，且每人每天加工的件数相同，甲车间比乙车间少10人，甲车间每天加工服装400件，乙车间每天加工服装600件．(1)求甲、乙两车间各有多少人;(2)甲车间更新了设备，平均每人每天加工的件数比原来多了10件，乙车间的加工效率不变，在两个车间总人数不变的情况下，加工厂计划从乙车间调出一部分人到甲车间，使每天两个车间加工的总数不少于1314件，求至少要从乙车间调出多少人到甲车间．【答案】(1)甲车间有20人，乙车间有30人;(2)从乙车间至少调12人到甲车间．【解析】【分析】(1)设甲车间x 人，则乙车间(x+10)人，根据等量关系：甲车间每人生产件数=乙车间每人生产件数得到分式方程;(2)设调a 人到甲车间，则不等关系为：(甲车间原人数+a)×生产效率+(乙车间原人数-a)×生产效率≥1314，列写不等式求解即可【详解】(1)解：设甲车间有人，乙车间有()10x +人; 则：40060010x x =+ 解得：20x ，经检验：20x 是原分式方程的解.x+10=30(人).答：甲车间有20人，乙车间有30人.(2)设从乙车间调人到甲车间; 则：400400(20)10(30)13142020a a ⎛⎫+⨯++-⨯≥ ⎪⎝⎭，解得：11.4a ≥.因为为正整数，所以的最小值为12.答：从乙车间至少调12人到甲车间.【点睛】本题考查分式方程和不等式的应用，应用题解题关键是通过题干抽取出等量(不等)关系，根据这个关系列写方程即可26. 已知ABD △内接于圆，点为弧BD 上一点，连接BC AC AC 、，交BD 于点，CED ABC ∠=∠．(1)如图1，求证：弧AB =弧AD ;(2)如图2，过作BF AC ⊥于点，交圆点，连接AG 交BD 于点，且222EH BE DH =+，求CAG ∠的度数;(3)如图3，在(2)的条件下，圆上一点M 与点关于BD 对称，连接ME ，交AB 于点，点为弧AD 上一点，PQ BG ∥交AD 于点Q ，交BD 的延长线于点，AQ BN =，ANE 的周长为20，52DR =求圆半径．【答案】(1)见解析;(2)∠CAG=45°;(3)r=62【解析】【分析】(1)证∠ABD=∠ACB 可得;(2)如下图，△AHD 绕点A 旋转至△ALE 处，使得点D 与点B 重合，证△ALE ≌△AHE ，利用勾股定理逆定理推导角度;(3)如下图，延长QR 交AB 于点T ，分别过点N 、Q 作BD 的垂线，交于点V ，I ，取QU=AE ，过点U 作UK 垂直BD.先证△AEN ≌△QUD ，再证△NVE ≌△RKU ，可得到NV=KR=DK ，进而求得OB 的长.【详解】(1)∵∠CED 是△BEC 的外角，∴∠CED=∠EBC+∠BCA∵∠ABC=∠ABD+∠EBC又∵∠CED=∠ABC∴∠ABD=∠ACB∴弧AB=弧AD(2)如下图，△AHD 绕点A 旋转至△ALE 处，使得点D 与点B 重合∵△ALB是△AHD旋转所得∴∠ABL=∠ADB，AL=AH设∠CAG=a，则∠CBG=a∵BG⊥AC∴∠BCA=90°-a，∴∠ADB=∠ABD=90°-a∴在△BAD中，BAE+∠HAD=180-a-(90°-a)-(90°-a)=a∴∠LAE=∠EAH=a∵LA=AH，AE=AE∴△ALE≌△AHE，∴LE=EH∵HD=LB，222EH BE DH=+∴△LBE为直角三角形∴∠LBE=(90°-a)+(90°-a)=90°，解得：a=45°∴∠CAG=45°(3)如下图，延长QR交AB于点T，分别过点N、Q作BD的垂线，交于点V，I，取QU=AE，过点U作UK垂直BD由(2)得∠BAD=90°∴点O在BD上设∠R=n ，则∠SER=∠BEC=∠MEB=90°-n ∴∠AEN=2n∵SQ ⊥AC∴∠TAS=∠AQS=∠DQR ，AN=QD∵QU=AE∴△AEN ≌△QUD∴∠QUD=∠AEN=2n∴UD=UR=NE ，∵△ANE 的周长为20∴QD+QR=20在△DQR 中，QD=7∵∠ENR=∠UDK=∠R=n∴△NVE ≌△RKU∴NV=KR=DK=522 ∴BN=5∴BD=122，OB=62r =【点睛】本题考查了圆的证明，涉及到全等、旋转和勾股定理，解题关键是结合图形特点，适当构造全等三角形27. 在平面直角坐标系中，抛物线27287y ax x a =-+-经过原点，交轴正半轴于点，顶点为，对称轴交轴于点．(1)如图1，求点的坐标;(2)如图2，点为抛物线在第一象限上一点，连接OP 交对称轴于点，设点横坐标为，DE 的长为，求与之间的函数解析式，不要求写出自变量的取值范围;(3)如图3，在(2)的条件下，点为BD 上一点，连接OF ，点为OF 上一点，连接EG BG 、，60BOF BGE ∠+∠=︒，EG EO =，若23BG =，求点横坐标的值．【答案】(1)(27,7)D -;(2)772d t =-;(3)43473t =+．【解析】【分析】(1)代入点(0，0)，先求出a 的值，然后将二次函数配成顶点式，求出点D 坐标;(2)过点P 作x 轴垂线，交x 轴于点K ，ED 交x 轴于点B ;设点21,74P t t t ⎛⎫- ⎪⎝⎭，△PKO ∽△EBO ，可得到EB 的长，加上BD 的长即为ED 的长;(3)如下图，连接AG 、AE ，过点B 、G 分别作AG 、x 轴垂线，交于点M 、N.先利用Rt △BGM 求得BM 、GM 的长，在利用Rt △ABM 得到tan ∠BAG ，然后结合Rt △ANG 得到AN 、GN 的长，从而推导出ON 的长，接着便可证△OGB 是直角三角形，从而推导出∠EOB=30°，得出结论【详解】(1)∵抛物线过点(0，0)，代入抛物线得：0=0-0+28a-7，解得：14a =则抛物线为：222211117=(7(728(27)4444)4)747y x x x x x -=--=+---= ∴(27,7)D -(2)如下图，过点P 作x 轴垂线，交x 轴于点K ，ED 交x 轴于点B设21,74P t t t ⎛⎫ ⎪⎝⎭∴PK=2174t t -，OK=t ∵7,7)D -∴(27,0)B∴OB=27∵PK∥EB，∴△PKO ∽△EBO ∴PK EB OK OB =，即：217427t t EB t -= 解得：7142EB t =- ∴77147722d EB BD t t =+=-+=- (3)如下图，连接AG 、AE ，过点B 、G 分别作AG 、x 轴垂线，交于点M 、N设,60BGE BOF αα∠=∠=︒-则，∠GEA=120°α-∵EB 是AO 的垂直平分线,∴EA=EO,∴EA EO EG ==∴在△GEA 中，∠EGA=∠EAG=()1180120302αα⎡⎤︒-︒-=︒+⎣⎦ ∴∠BGA=30° ∵抛物线解析式为：2174y x x = 可得：77∵3Rt △BGM 中，3GM=3∴在Rt △ABM 中，MA=5∴3tan BAG ∠=∵AG=3+5=8∴在Rt △AGN 中，421207∴NB=AN-AB=7，∴ON=OB-BN=7 ∴在Rt △ONG 中，OG=4∴在△OGB 中，三边满足勾股定理逆定理，即∠BGO=90°∴EOG 90α∠=︒-，EOA 30∴∠=︒∵14EB =-，，∠EOB=30°解得：t =+ 【点睛】本题是二次函数和三角函数的综合，解题关键是利用二次函数的性质，得到线段的长度，然后利用三角函数和勾股定理推导求得。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

中考模拟测试(二)(满分：120分时间：120分钟)一、选择题(每小题3分，共30分) 1．－2的倒数是( D )A ．－ 2 B.22 C. 2 D ．－222．(2016·桂林)下列几何体的三视图相同的是( B )A ．圆柱B ．球C ．圆锥D ．长方体3．(2016·玉林)下列命题是真命题的是( B ) A ．必然事件发生的概率等于0.5B ．5名同学二模的数学成绩是92，95，95，98，110，则他们的平均分是98，众数是95C ．射击运动员甲、乙分别射击10次且击中环数的方差分别是5和18，则乙较甲稳定D ．要了解金牌获得者的兴奋剂使用情况，可采用抽样调查的方法 4．(2016·抚顺)下列运算正确的是( D )A ．a 2＋4a －4＝(a ＋2)2B ．a 2＋a 2＝a 4C ．(－2ab )2＝－4a 2b 2D ．a 4÷a ＝a 35．(2016·咸宁)如图，直线l 1∥l 2，CD ⊥AB 于点D ，∠1＝50°，则∠BCD 的度数为( C ) A ．50° B ．45° C ．40° D ．30°,第5题图) ,第8题图) ,第9题图),第10题图)6．(2016·襄阳)不等式组⎩⎪⎨⎪⎧2x －1≤1，－12x<1的整数解的个数为( C )A ．0个B ．2个C ．3个D ．无数个7．(2016·深圳)施工队要铺设一段全长2000米的管道，因在中考期间需停工两天，实际每天施工需比原计划多50米，才能按时完成任务，求原计划每天施工多少米．设原计划每天施工x 米，则根据题意所列方程正确的是( A )A.2000x －2000x ＋50＝2B.2000x ＋50－2000x ＝2C.2000x －2000x －50＝2D.2000x －50－2000x＝28．(2016·内江)如图，点A ，B ，C 在⊙O 上，若∠BAC＝45°，OB ＝2，则图中阴影部分的面积为( C )A ．π－4 B.23π－1 C ．π－2 D.2π3－29．已知二次函数的图象如图，则下列结论中正确的有( B ) ①a ＋b ＋c ＞0；②a －b ＋c ＜0；③b ＞0；④b ＝2a ；⑤abc ＜0. A ．5个 B ．4个 C ．3个 D ．2个10．(2016·威海)如图，在△ABC 中，∠B ＝∠C＝36°，AB 的垂直平分线交BC 于点D ，交AB 于点H ，AC 的垂直平分线交BC 于点E ，交AC 于点G ，连接AD ，AE ，则下列结论错误的是( A )A.BD BC＝5－12B ．AD ，AE 将∠BAC 三等分 C ．△ABE ≌△ACD D ．S △ADH ＝S △CEG 二、填空题(每小题3分，共24分)11．红细胞是人体中血液运输氧气的主要媒介，人体中红细胞的直径约为0.0000077 m ，将0.0000077用科学记数法表示为__7.7×10－6__．12．(2016·淮安)点A(3，－2)关于x 轴对称的点的坐标是__(3，2)__．13．函数y ＝11－x中，自变量x 的取值范围是__x<1__．14．(2016·常德)如图，把平行四边形ABCD 折叠，使点C 与点A 重合，这时点D 落在D 1，折痕为EF ，若∠BAE＝55°，则∠D 1AD ＝__55°__．15.(2016·枣庄)如图，是矗立在高速公路水平地面上的交通警示牌，经测量得到如下数据：AM ＝4米，AB ＝8米，∠MAD ＝45°，∠MBC ＝30°，则警示牌的高CD 为__2.9__米．(结果精确到0.1米，参考数据：2≈1.41，3≈1.73),第14题图) ,第15题图) ,第16题图)16．如图，圆内接四边形ABCD 中两组对边的延长线分别相交于点E ，F ，且∠A＝55°，∠E ＝30°，则∠F ＝__40°__．17．某果园有100棵橘子树，平均每一棵树结600个橘子，根据经验估计，每多种一棵树，平均每棵树就会少结5个橘子，设果园增种x 棵橘子树，果园橘子总个数为y 个，则果园里增种__10__棵橘子树，橘子总个数最多．18．(2016·包头)如图，已知△ABC 是等边三角形，点D ，E 分别在边BC ，AC 上，且CD ＝CE ，连接DE 并延长至点F ，使EF ＝AE ，连接AF ，CF ，连接BE 并延长交CF 于点G.下列结论：①△ABE≌△ACF；②BC＝DF ；③S △ABC ＝S △ACF ＋S △DCF ；④若BD ＝2DC ，则GF ＝2EG.其中正确的结论是__①②③④__．(填写所有正确结论的序号)三、解答题(共66分)19．(6分)先化简，再求值：(a ＋1－4a －5a －1)÷(1a －1a 2－a)，其中a ＝2＋ 3.解：原式＝a (a －2)，当a ＝2＋3时，原式＝(2＋3)(2＋3－2)＝3＋2320．(7分)(2015·青岛)如图，△ABC 中，AB ＝AC ，AD 是BC 边上的中线，AE ∥BC ，CE⊥AE ，垂足为E.(1)求证：△ABD≌△CAE；(2)连接DE ，线段DE 与AB 之间有怎样的位置和数量关系？请证明你的结论．解：(1)∵AB ＝AC ，∴∠B ＝∠ACB ，又∵AD 是BC 边上的中线，∴AD ⊥BC ，即∠ADB ＝90°，∵AE ∥BC ，∴∠EAC ＝∠ACB ，∴∠B ＝∠EAC ，∵CE ⊥AE ，∴∠CEA ＝90°，∴∠CEA ＝∠ADB ，又∵AB ＝AC ，∴△ABD ≌△CAE(2)由△ABD≌△CAE 可得AE ＝BD ，又∵AE∥BD ，∴四边形ABDE 是平行四边形，∴AB ∥DE 且AB ＝DE21．(7分)(2016·巴中)如图，一次函数y ＝kx ＋b(k ，b 为常数，k ≠0)的图象与x 轴、y 轴分别交于A ，B 两点，且与反比例函数y ＝nx(n 为常数且n≠0)的图象在第二象限交于点C ，CD ⊥x 轴，垂足为D ，若OB ＝2OA ＝3OD ＝6.(1)求一次函数与反比例函数的解析式； (2)求两函数图象的另一个交点坐标；(3)直接写出不等式kx ＋b≤nx的解集．解：(1)∵OB ＝2OA ＝3OD ＝6，∴OB ＝6，OA ＝3，OD ＝2，∵CD ⊥OA ，∴DC ∥OB ，∴OB CD ＝AOAD，∴6CD ＝35，∴CD ＝10，∴C (－2，10)，B (0，6)，A (3，0)，可求一次函数为y ＝－2x ＋6，反比例函数解析式为y ＝－20x (2)由⎩⎪⎨⎪⎧y ＝－2x ＋6，y ＝－20x 解得⎩⎪⎨⎪⎧x ＝－2，y ＝10或⎩⎪⎨⎪⎧x ＝5，y ＝－4，故另一个交点坐标为(5，－4) (3)－2≤x ＜0或x≥522．(7分)(2016·安徽)一袋中装有形状大小都相同的四个小球，每个小球上各标有一个数字，分别是1，4，7，8.现规定从袋中任取一个小球，对应的数字作为一个两位数的个位数；然后将小球放回袋中并搅拌均匀，再任取一个小球，对应的数字作为这个两位数的十位数．(1)写出按上述规定得到所有可能的两位数；(2)从这些两位数中任取一个，求其算术平方根大于4且小于7的概率．解：(1)按规定得到所有可能的两位数为：11，14，17，18，41，44，47，48，71，74，77，78，81.84，87，88 (2)这些两位数共有16个，其中算术平方根大于4且小于7的共有6个，分别为17，18，41，44，47，48，则所求概率P ＝616＝3823．(7分)(2016·苏州)某高校学生会向全校2900名学生发起了“爱心一日捐”捐款活动，为了解捐款情况，学生会随机调查了部分学生的捐款金额，并用得到的数据绘制了如下统计图①和图②，请根据相关信息，解答下列问题：(1)本次接受随机抽样调查的学生人数为__50__，图①中m 的值是__32__； (2)求本次你调查获取的样本数据的平均数、众数和中位数；(3)根据样本数据，估计该校本次活动捐款金额为10元的学生人数．解：(2)平均数是4×5＋16×10＋12×15＋10×20＋8×3050＝16(元)，众数是10元，中位数是15元 (3)该校本次活动捐款金额为10元的学生人数是2900×32%＝928(人)24．(8分)(2016·贺州)某地区2014年投入教育经费2900万元，2016年投入教育经费3509万元．(1)求2014年至2016年该地区投入教育经费的年平均增长率； (2)按照义务教育法规定，教育经费的投入不低于国民生产总值的百分之四，结合该地区国民生产总值的增长情况，该地区到2018年需投入教育经费4250万元，如果按(1)中教育经费投入的增长率，到2018年该地区投入的教育经费是否能达到4250万元？请说明理由．(参考数据： 1.21＝1.1， 1.44＝1.2， 1.69＝1.3， 1.96＝1.4) 解：(1)设增长率为x ，根据题意得2900(1＋x )2＝3509，解得x 1＝0.1＝10%，x 2＝－2.1(不合题意，舍去)，则这两年投入教育经费的平均增长率为10%(2)2018年该地区投入的教育经费是3509×(1＋10%)2＝4245.89(万元)，∵4245.89＜4250，∴不能达到25．(12分)(2016·贵港)如图1，在正方形ABCD 内作∠EAF＝45°，AE 交BC 于点E ，AF 交CD 于点F ，连接EF ，过点A 作AH⊥EF，垂足为H.(1)如图2，将△ADF 绕点A 顺时针旋转90°得到△ABG. ①求证：△AGE≌△AFE；②若BE ＝2，DF ＝3，求AH 的长．(2)如图3，连接BD 交AE 于点M ，交AF 于点N.请探究并猜想：线段BM ，MN ，ND 之间有什么数量关系？并说明理由．解：(1)①由旋转的性质可知：AF ＝AG ，∠DAF ＝∠BAG.∵四边形ABCD 为正方形，∴∠BAD ＝90°.又∵∠EAF ＝45°，∴∠BAE ＋∠DAF ＝45°，∴∠BAG ＋∠BAE ＝45°，∴∠GAE ＝∠FAE ，由SAS 可证△GAE≌△FAE②∵△GAE ≌△FAE ，AB ⊥GE ，AH ⊥EF ，∴AB ＝AH ，GE ＝EF ＝5.设正方形的边长为x ，则EC ＝x －2，FC ＝x －3，在Rt △EFC 中，由勾股定理得EF 2＝FC 2＋EC 2，即(x －2)2＋(x －3)2＝25，解得x 1＝6，x 2＝－1(不符合题意，舍去)，∴AB ＝6.∴AH ＝6(2)将△ABM 逆时针旋转90°得△ADM′.∵四边形ABCD 为正方形，∴∠ABD ＝∠ADB ＝45°.由旋转的性质可知∠ABM ＝∠ADM′＝45°，BM ＝DM′，∴∠NDM ′＝90°，∴NM ′2＝ND2＋DM′2.∵∠EAM ′＝90°，∠EAF ＝45°，∴∠EAF ＝∠FAM′＝45°.由SAS 可证△AMN≌△ANM′，∴MN ＝NM′.又∵BM ＝DM′，∴MN 2＝ND 2＋BM 226．(12分)(2016·乐山)在直角坐标系xOy 中，A(0，2)，B(－1，0)，将△ABO 经过旋转、轴对称变化后得到如图1所示的△BCD.(1)求经过A ，B ，C 三点的抛物线的解析式； (2)连接AC ，点P 是位于线段BC 上方的抛物线上一动点，若直线PC 将△ABC 的面积分成1∶3两部分，求此时点P 的坐标；(3)现将△ABO，△BCD 分别向下、向左以1∶2的速度同时平移，求出在此运动过程中△ABO 与△BCD 重叠部分面积的最大值．解：(1)y ＝－32x 2＋12x ＋2(2)如图1，设直线PC 与AB 交于点E.∵直线PC 将△ABC 的面积分成1∶3两部分，∴AEBE＝13或AEBE＝3. 过E 作EF⊥OB 于点F ，则EF∥OA ，∴△BEF ∽△BAO ，∴EF AO ＝BE BA ＝BF BO ，∴当AE BE ＝13时，EF2＝34＝BF 1，∴EF ＝32，BF ＝34，∴E (－14，32)，∴直线PC 解析式为y＝－25x ＋75，∴－32x 2＋12x ＋2＝－25x ＋75，∴x 1＝－25，x 2＝1(舍去)，∴P 1(－25，3925)；当AE BE ＝3时，同理可得P 2(－67，2349) (3)设△ABO 平移的距离为t ，△A 1B 1O 1与△B 2C 1D 1重叠部分的面积为S.由平移得，A 1B 1的解析式为y ＝2x ＋2－t ，A 1B 1与x 轴交点坐标为(t －22，0)．C 1B 2的解析式为y ＝12x ＋t ＋12，C 1B 2与y 轴交点坐标为(0，t ＋12)．①如图2，当0＜t ＜35时，△A 1B 1O 1与△B 2C 1D 1重叠部分为四边形．设A 1B 1与x 轴交于点M ，C 1B 2与y 轴交于点N ，A 1B 1与C 1B 2交于点Q ，连接OQ ，由⎩⎪⎨⎪⎧y ＝2x ＋2－t ，y ＝12x ＋12＋t 得⎩⎪⎨⎪⎧x ＝4t －33，y ＝5t3，∴Q (4t －33，5t 3)，∴S ＝S △QMO ＋S △QON ＝12×2－t 2×5t 3＋12×(t ＋12)×3－4t 3＝－1312t 2＋t ＋14＝－1312(t －613)2＋2552，∴当t ＝613时，S 的最大值为2552； ②如图3，当35≤t ＜45时，△A 1B 1O 1与△B 2C 1D 1重叠部分为直角三角形．设A 1B 1与x 轴交于点H ，A 1B 1与C 1D 1交于点G ，∴G (1－2t ，4－5t )，∴D 1H ＝2－t 2＋1－2t ＝4－5t2，D 1G ＝4－5t ，∴S ＝12D 1H ×D 1G ＝12×4－5t 2×(4－5t )＝14(5t －4)2.∴当35≤t<45时，S 的最大值为14.。