已知右面的两个正方形边长分别为6分米和4分米
组合图形题及答案

组合图形题及答案【篇一:五年级组合图形面积练习题】class=txt>2、求下面图形的面积。
(单位:cm)4、计算下面图形中阴影部分的面积。
30dm25dm 5m5、求下列阴影部分的面积。
②已知s平=48dm2,求s阴。
16cm8dm③已知:阴影部分的面积为24平方厘米,求梯形的面积。
④求s阴。
8dm4dm12cm6、求下面各图形的面积。
(单位:分米)7、“实践操作”显身手:10分2、求下面图形的面积。
16cm一、已知右面的两个正方形边长分别为6分米和4分米,求图中阴影部分的面积。
二、右图是两个相同的直角三角形叠在一起,求阴影部分的面积。
(单位:厘米)三、如图,这个长方形的长是9厘米,宽是8厘米,a和b是宽的中点,求长方形内阴影部分的面积。
四、在右图中,三角形edf的面积比三角形abe的面积大6平方厘米,已知长方形abdc的长和宽分别为6厘米、4厘米,df 的长是多少厘米?五、右图是一块长方形公园绿地,绿地长24米,宽16米,中间有一条宽为2米的道路,求草地(阴影部分)的面积。
六、如图,三角形abc的面积是24平方厘米,且dc=2ad,e、f分别是af、bc的中点,那么阴影部分的面积是多少?七、如图,三角形abc的面积是90平方厘米,ef平行于bc,ab=3ae,那么三角形甲、乙、丙的面积各是多少平方厘米?八、如图长方形,长18厘米,宽12厘米,ae、af两条线段把长方形面积三等分,求三角形aef的面积。
九如图,abcd是一个长12厘米,宽5厘米的长方形,求阴影部分三角形ace的面积。
十已知正方形甲的边长是8厘米,正方形乙的面积是36平方厘米,那么图中阴影部分的面积是多少?【篇二:圆组合图形练习题】复习练习题1、求下列各图阴影部分的面积(单位:厘米)2、计算下面图形的面积。
(单位:厘米)3、计算下面图形中涂色部分的面积。
(单位:厘米)4、求下面图形中涂色部分的面积。
(单位:厘米)①②5、如下图示,ab=46、计算下图中涂色部分的面积。
五年级奥数组合图形的面积

五年级奥数组合图形的面积Document number:NOCG-YUNOO-BUYTT-UU986-1986UT组合图形的面积1.基本平面图形特征及面积公式特征面积公式正方形①四条边都相等。
②四个角都是直角。
③有四条对称轴。
S=a2长方形①对边相等。
②四个角都是直角。
③有二条对称轴。
S=ab平行四边形①两组对边平行且相等。
②对角相等,相邻的两个角之和为180°③平行四边形容易变形。
S=ah三角形①两边之和大于第三条边。
②两边之差小于第三条边。
③三个角的内角和是180°。
④有三条边和三个角,具有稳定性。
S=ah÷2梯形①只有一组对边平行。
②中位线等于上下底和的一半。
S=(a+b)h÷22.基本解题方法:由两个或多个简单的基本几何图形组合成的组合图形,要计算这样的组合图形面积,先根据图形的基本关系,再运用分解、组合、平移、割补、添辅助线等几种方法将图形变成基本图形分别计算。
1.已知右面的两个正方形边长分别为6分米和4分米,求图中阴影部分的面积。
2.右图是两个相同的直角三角形叠在一起,求阴影部分的面积。
(单位:厘米)3.如图,这个长方形的长是9厘米,宽是8厘米,A和B是宽的中点,求长方形内阴影部分的面积。
4.在右图中,三角形EDF的面积比三角形ABE的面积大6平方厘米,已知长方形ABDC的长和宽分别为6厘米、4厘米,DF的长是多少厘米5.正方形ABCD的面积是100平方厘米,AE=8厘米,CF=6厘米,求阴影部分的面积。
6.右图是一块长方形公园绿地,绿地长24米,宽16米,中间有一条宽为2米的道路,求草地(阴影部分)的面积。
7.如图,三角形ABC的面积是24平方厘米,且DC=2AD,E、F分别是AF、BC的中点,那么阴影部分的面积是多少8.如下图,是一块长方形草地,长方形的长是16米,宽是10米,中间有两条宽2米的道路,一条是长方形,一条是平行四边形,那么有草部分(阴影部分)的面积有多大9.如图,一个三角形的底长5米,如果底延长1米,那么面积就增加2平方米。
组合图形的面积练习题5道

组合图形的面积练习题5道2、求下面图形的面积。
你能想出几种方法。
、求下面图形的面积。
2、计算下面图形中阴影部分的面积。
30dm25dmm七、求下列阴影部分的面积。
③已知:阴影部分的面积为24平方厘米,求梯形的面积。
8dm16cm8dm②已知S平=48dm2,求S阴。
④求S阴。
312cm三、“实践操作”显身手:10分16cm2、求下面图形的面积。
组合图形面积计算练习姓名:1、计算下列组合图形的面积2、求下列阴影部分的面积。
③已知:阴影部分的面积为24平方厘米,求梯形的面积。
12cm②已知S平=48dm2,求S阴。
dm ④求S阴。
dm组合图形面积计算练习姓名:1、求下面各图形的面积。
3、求下面图形的面积。
16cm4、已知右面的两个正方形边长分别为6分米和4分米,求图中阴影部分的面积。
5、计算右边图形的面积。
发展题:如图,ABCD是一个长12厘米,宽5厘米的长方形,求阴影部分三角形ACE的面积。
组合图形的面积如图,ABCD是直角梯形,求阴影部分的面积和。
下图1的长方形是一块草坪,中间有两条宽1米的走道,求植草的面积。
下图2中,边长为10和15的两个正方体并放在一起,求三角形ABC的面积。
下图3中,三角形ABC的面积是36平方厘米,三角形ABE与三角形AEC的面积相等,如果AB=9厘米,FB=FE,求三角形AFE的面积。
下图1中两个正方形的边长分别是10厘米和6厘米,求阴影部分的面积。
下图2中三角形ABC面积是36平方厘米,AC长8厘米,DE长3厘米,求阴影的面积。
下图3中BC=10厘米,EC=8厘米,且阴影部分面积比三角形EFG的面积大10平方厘米。
求平行四边形的面积。
下图1求四边形ABCD的面积。
下图2已知正方形ABCD的边长是7厘米,求正方形EFGH的面积。
下图3图中两个正方形的边长分别是6厘米和4厘米,求阴影部分的面积。
下图4中两个完全一样的三角形重叠在一起,求阴影部分的面积。
下图1中,甲三角形的面积比乙三角形的面积大多少平方厘米?下图2中正方形的边长为8厘米,CE为20厘米,梯形BCDF的面积是多少平方厘米?如下图3,正方形ABCD 中,AB=4厘米,EC=10厘米,求阴影部分的面积。
(完整版)五年级上册数学组合图形面积练习题

五上数学组合图形拓展练习题姓名学号1,已知正方形ABCD的边长是7 厘米,求正方形EFGH的面积。
2、小两个正方形组成下图所示的组合图形厘米,求阴影部分的面积。
3、如图,已知四条线段的长分别是:AB=2厘米,厘米,并且有两个直角。
求四边形ABCD 的面积。
CE=6厘米,CD=5厘米,AF=47、如图:正方形ABCD的边长为 6 厘米,三角形ABE,三角形ADF与四边形AECF的面积彼此相等。
求三角形AEF的面积8、cm)4102012 9、计算下面图形中阴影部分的面积。
12dm10、求下列阴影部分的面积16cm ②已知S 平=48dm2,求S阴。
8dm③已知:阴影部分的面积为24 平方厘米,求梯形的面积7cm 12cm 8dm4dm11、求下面各图形的面积单位:分米)12、“实践操作”显身手:10分1、求下面图形中阴影部分的面积。
13、已知右面的两个正方形边长分别为 6 分米和4 分米,求图中阴影部分的面积。
④求S 阴14、右图是两个相同的直角三角形叠在一起,求阴影部分的面积。
单位:厘米)15、如图,这个长方形的长是9厘米,宽是8厘米,A 和B是宽的中点,求长方形内阴影部分的面积。
24 米,宽16 米,中间有一条宽为2 米17、右图是一块长方形公园绿地,绿地长的道路,求草地(阴影部分)的面积。
18、如图,三角形ABC 的面积是24 平方厘米,且BC 的中点,那么阴影部分的面积是多少?如图,三角形 ABC 的面积是 90 平方厘米, EF 平行于 BC ,AB=3AE ,那么九 如图, ABCD 是一个长 12 厘米, 宽 5 厘米的长方形, 阴影部分三角形 ACE 的面积。
十 已知正方形甲的边长是 8 厘米,正方形乙的面积是36 平方厘米,那么图中阴影部分的面积是多少? 三角形甲、乙、丙的面积各是多少平方厘米?20、 如图长方形,长 18厘米,宽 12厘米, AE 、AF 两条线段把长方形面积三等 分,求三角形 AEF 的面积。
五年级奥数--组合图形的面积

组合图形的面积姓名知识、规律、方法1、常见的几种规则图形。
(1)三角形:有三条线段首位相接围成的图形。
分类:(2)四边形2、面积计算公式。
三角形:S=ah÷2 长方形:S=ab正方形:S=a2 平行四边形:S=ah梯形:S=(a+b)h÷2【例题1】正图正方形中套着一个长方形,正方形的边长是12厘米,长方形的四个角的顶点把正方形的四条边各分成两段,其中长的一段是短的2倍。
求中间长方形的面积。
【例题2】四边形ABCD和四边形DEFG都是正方形,已知三角形AFH的面积是7平方厘米。
三角形CDH的面积是多少平方厘米?【例题3】下图中正方形的边长为8厘米,CE为20厘米,梯形BCDF的面积是多少平方厘米?【例题4】图中ABCD是长方形,三角形EFD的面积比三角形ABF的面积大6平方厘米,求ED的长。
练习:一、已知右面的两个正方形边长分别为6分米和4分米,求图中阴影部分的面积。
二、右图是两个相同的直角三角形叠在一起,求阴影部分的面积。
(单位:厘米)三、如图,这个长方形的长是9厘米,宽是8厘米,A和B是宽的中点,求长方形内阴影部分的面积。
四、右图是一块长方形公园绿地,绿地长24米,宽16米,中间有一条宽为2米的道路,求草地(阴影部分)的面积。
五、如图,三角形ABC的面积是90平方厘米,EF平行于BC,AB=3AE,那么三角形甲、乙、丙的面积各是多少平方厘米?六、在等腰梯形ABCD中,AD=12厘米,高DF=10厘米。
三角形CDE的面积是24平方厘米。
求梯形面积。
七、在右图中,三角形EDF的面积比三角形ABE的面积大75平方厘米,已知正方形ABCD的边长为15厘米,DF的长是多少厘米?八、如图,ABCD是一个长12厘米,宽5厘米的长方形,求阴影部分三角形ACE的面积。
九、如图,A、B两点是长方形长和宽的中点,长为8,宽为6,那么阴影部分占长方形的面积是多少?十、在正方形ABCD中,AB是4厘米,三角形BCF比三角形DEF的面积多2平方厘米,求DE的长。
举一反三--六年级奥数面积计算(1)

组合图形的面积(1)
13、图中BO=2DO,阴影部分 的面积是4平方厘米,求梯形 ABCD的面积是多少平方厘米?
14、如图,正方形ABCD的边长 是12厘米,CE=4厘米。求阴影 部分的面积。
组合图形的面积(1)
15、图中三角形ABC的面积是 36平方厘米,AC长8厘米,DE 长3厘米,求阴影部分的面积 (ADFC不是正方形)。 16、有两种自然的放法将正 方形内接于等腰直角三角形。 已知等腰直角三角形的面积 是36平方厘米,两个正方形 的面积分别是多少?
六年奥数——举一反三 面积计算(一)
组合图形的面积(1)
1、已知右面的两个正方形边长 分别为6分米和4分米,求图中阴 影部分的面积。
2、如图,这个长方形的长是9厘 米,宽是8厘米,A和B是宽的中 点,求长方形内阴影部分的面积。
组合图形的面积(1)
3、右图是两个相同的直角三 角形叠在一起,求阴影部分的 面积。(单位:厘米)
4、如图,长方形长18厘米, 宽12厘米,AE、AF两条线段 把长方形面积三等分,求三 角形AEF的面积。
组合图形的面积(1)
5、如图,三角形ABC的面积是 24平方厘米,且DC=2AD,E、 F分别是AF、BC的中点,那么 阴影部分的面积是多少?
6、如图,三角形ABC的面积是 90平方厘米,EF平行于BC, AB=3AE,那么三角形甲、乙、 丙的面积各是多少平方厘米?
组合图形的面积(1)
7、在等腰梯形ABCD中,AD=12 厘米,高DF=10厘米。三角形 CDE的面积是12平方厘米。求梯 形面积。
8、如图,三角形EDF的面积比三 角形ABE的面积大6平方厘米,已 知长方形ABDC的长和宽分别为6 厘米、4厘米,DF的长多少厘米?
六年级组合图形面积

∴S△BCE=2/3S△ABC=60cm²
S△AEC=1/33S△ABC=30cm²
∵EF平行于BC
答:甲的面积10cm², ∴AF:AC=AE:AB=1:3
乙的面积20cm²,丙 的面积60cm²。
∴S△AEF=1/3S△AEC=10cm²
∴S△EFC=30-10=20cm²
7、在等腰梯形ABCD中,AD=12 厘米,高DF=10厘米。三角形CDE 的面积是12平方厘米。求梯形面 积。
“EF平行于BC,AB=3AE”可得:AE:AB=1:3,AF:AC=1:3,
再据“等高不等底的三角形的面积比就等于其对应底的比”, 所 又 据以因此S甲解△答=A13S即E△C可=A13ES.△C,解A乙B:C=于∵S,是32A△B就=A3E可ACE,以丙求=出S三△32 角AB形C,甲、乙、丙的面积,
8、如图,三角形EDF的面积比三 角形ABE的面积大6平方厘米,已 知长方形ABDC的长和宽分别为6厘 米、4厘米,DF的长多少厘米?
解:S正=6*4=24cm²
S(ACDE)=S(ABCD)-S(ABE)=S(ACF)-S(EDF) S(ACF)=S(ABCD)+[S(EDF)-S(ACF)] =24+6 =30 CF=30×2÷4=15cm DF=CF-CD=15-6=9cm
六年奥数——举一反三 组合图形的面积
组合图形的面积(1)
1、已知右面的两个正方形边长 分别为6分米和4分米,求图中阴 影部分的面积。
阴影面积=两个正方形面积-△ACB-△BGF
6²+4²-6×6÷2-4×10÷2=22dm²
2、如图,这个长方形的长是9厘 米,宽是8厘米,A和B是宽的中 点,求长方形内阴影部分的面积。
小学数学《组合图形面积计算》综合练习试题

组合图形(一)一、考点、热点回顾二、典型例题【典型例题】(一)、基础图形(割补、整体-空白)【例1】已知平行四边表的面积是28平方厘米,求阴影部分的面积。
练习、如果用铁丝围成如下图一样的平行四边形,需要用多少厘米铁丝?(单位:厘米)【例2】下图中甲和乙都是正方形,求阴影部分的面积。
(单位:厘米)练习、1 、已知右面的两个正方形边长分别为6分米和4分米,求图中阴影部分的面积。
2、求图中阴影部分的面积。
(单位:厘米)【例3】将如图(1)所示的三角形纸片沿粗虚线折叠,成如图(2)所示的图形.。
已知图(1)三角形的面积是图(2)图形面表的1.5倍,图(2)中阴影部分的面积之和为1平方厘米。
求重叠部分的面积。
练习、将如图所示的三角形沿虚线折叠,得到如图所示的多边形。
这个多边5,已知图中阴影部分的面积和为6平方厘米,求形面积是原三角形面积的7原三角形的面积。
(二)、差不变【例4】如图所示,甲三角形的面积比乙三角形的面积大6平方厘米,求CE 的长度。
练习、1、右图是两个相同的直角三角形叠在一起,求阴影部分的面积。
(单位:厘米)2、平行四边形ABCD的边长,BC=10厘米,直角三角形BCE的直角边EC长8厘米,已知阴影部分的面积比三角形EFG的面积大10平方厘米。
求CF的长。
(三)、三角形等积变换我们已经掌握了三角形面积的计算公式:三角形面积=底×高÷2这个公式告诉我们:三角形面积的大小,取决于三角形底和高的乘积.如果三角形的底不变,高越大(小),三角形面积也就越大(小).同样若三角形的高不变,底越大(小),三角形面积也就越大(小).为便于实际问题的研究,我们还会常常用到以下结论:①等底等高的两个三角形面积相等.②底在同一条直线上并且相等,该底所对的角的顶点是同一个点或在与底平行的直线上,这两个三角形面积相等.③若两个三角形的高(或底)相等,其中一个三角形的底(或高)是另一个三角形的几倍,那么这个三角形的面积也是另一个三角形面积的几倍.【例5】已知三角形ABC的面积为1,BE= 2AB,BC=CD,求三角形BDE的面积?练习、1、如图,已知平行四边形ABCD的面积是60平方分米,E、F分别是AB、AD边上的中点,图中阴影部分的面积是多少平方分米?2、右图中的长方形ABCD的长是20厘米,宽是12厘米,AF=BE,图中阴影部分的面积是多少平方厘米?【例6】用三种不同的方法,把任意一个三角形分成四个面积相等的三角形.【例7】在三角形ABC中,DC=2BD,CE=3AE,阴影部分的面积是20平方厘米,求三角形ABC的面积。
五年级奥数第14讲——平面图形面积计算

学生课程讲义课程名称五年级奥数上课时间任课老师沈老师第14 讲,本讲课题:平面图形面积计算内容概要如何将一般多边形及组合图形转化为基本图形。
本讲所指平面图形面积计算主要指多边形及其组合图形面积的计算,这些图形面积计算一般都可以转化成三角形、长方形、平行四边形和梯形的面积计算,后者的计算公式都是我们在课内已经学过并且应该熟记的。
主要的技巧在于如何将一般多边形及其组合图形“转化”为基本图形。
【例1】在梯形中阴影部分面积是150平方厘米,求梯形面积。
随堂练习11.已知平行四边形的的面积是28平方厘米,求阴影图形的面积。
2.如果用铁丝围成如下图一样的平行四边形,需要用多少厘米铁丝?(单位:厘米)【例2】如图,两个完全相同的直角三角形叠在一起,求阴影部分的面积。
(单位分米)随堂练习21.下图中两个完全一样的三角形重叠在一起,求阴影部分的面积。
(单位:厘米)2.图中两个正方形的边长分别是6厘米和4厘米,求阴影部分的面积。
【例3】如图,将长为9厘米,宽为6厘米的长方形划分成四个三角形,其面积分别为S 1、S 2、S 3、S 4、,且S 1=S 2=S 3+S 4,求S 4 。
随堂练习31.如图,四边形ABCD 是直角梯形,其中AD =12厘米,AB =8厘米,BC =15厘米,且△ADE 、四边形DEBF 及△CDF 的面积相等,求三角形EBF 的面积。
2. 已知大正方形的边长是5厘米,小正方形的边长是4厘米,求阴影部分的面积。
3. 正方形的边长分别是10厘米、6厘米,阴影部分的面积是多少平方厘米?ABC EFDG【例4】如图,ABCD 是边长为4分米的正方形,长方形DEFG 的长是5分米,求长方形DEFG 的宽。
随堂练习4如图,ABCD 是正方形,EDGF 是长方形,CD=6厘米,DG=8厘米,求宽ED=?FA B GCD E 86【例5】如图,已知四边形ABCD 被它的两条对角线分成四个三角形,其中甲的面积是1,乙的面积是2,丙的面积是3,求丁的面积。
小学奥数阴影部分面积计算 PPT 演示文稿

二、等量代换法求阴影部分的面积
• 练2、下图中两个完全一样的三角形重叠在 一起,求阴影部分的面积。(单位:厘米)
每个大三角形的面积=小三角形CDE的面积十梯形面积
二、等量代换法求阴影部分的面积
• 练3:在右图中,平行四边形ABCD的边BC 长10厘米,直角三角形ECB的直角边EC长8 厘米。已知阴影部分的总面积比三角形EFG 的面积大10平方厘米,求平行四边形ABCD 的面积。
练2.求图中阴影部分的面积。(单位:厘米)
三、平移法求面积
练3.求图中阴影部分的面积。(单位:厘米)
四、等高求面积法
• 例4:求下图中阴影部分的面积。
四、等高求面积
• 练1.把下图三角形的底边BC四等分,在下 面括号里填上“>”、“<”或“=”。
甲的面积( )乙的面积。
四、等高求面积法
• 练2:两条对角线把梯形ABCD分割成四个 三角形。已知两个三角形的面积(如图所 示),求另两个三角形的面积各是多少? (单位:平方厘米)
大、小正方形的面积和: 三角形BGF的面积:
两部分面积差:
一、直接和间接方法求阴影部分面积
• 练1、如图,ABDC是一个长12厘米,宽5 厘米的长方形,已知DE长3厘米,求阴影 部分三角形ACE的面积。
一、直接和间接方法求阴影部分面积
• 练1、如图,ABDC是一个长12厘米,宽5 厘米的长方形,已知DE长3厘米,求阴影 部分三角形ACE的面积。
根据图形可知:把所有的空白处拼 起来等于4个与阴影部分相同的正 方形,也就是说阴影部分的正方形 是大正方形的1/5,所以大正方形 的面积是25,所以边长是5. 故答案为:5.
五年级 图形题面积计算(必练题题库)
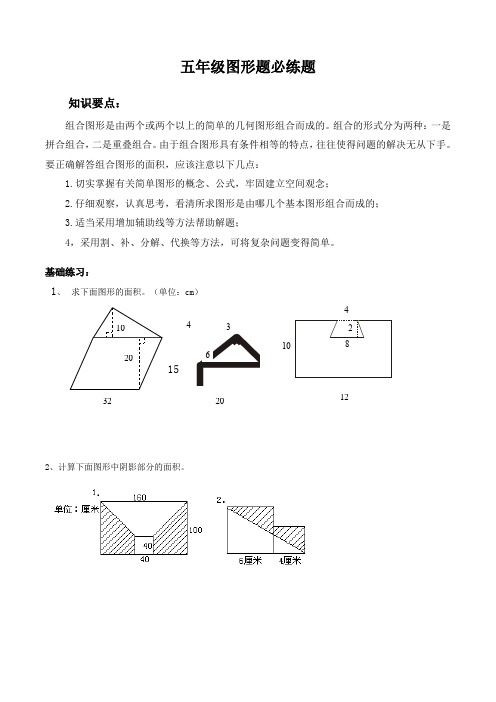
五年级图形题必练题知识要点:组合图形是由两个或两个以上的简单的几何图形组合而成的。
组合的形式分为两种:一是拼合组合,二是重叠组合。
由于组合图形具有条件相等的特点,往往使得问题的解决无从下手。
要正确解答组合图形的面积,应该注意以下几点:1.切实掌握有关简单图形的概念、公式,牢固建立空间观念;2.仔细观察,认真思考,看清所求图形是由哪几个基本图形组合而成的;3.适当采用增加辅助线等方法帮助解题;4,采用割、补、分解、代换等方法,可将复杂问题变得简单。
基础练习:1、 求下面图形的面积。
(单位:cm )152、计算下面图形中阴影部分的面积。
2010643482 1032 201230dm12dm 5m25dm 5m3、求下列阴影部分的面积。
① ②已知S 平=48dm 2,求S 阴。
③已知:阴影部分的面积为24④求S 阴。
平方厘米,求梯形的面积。
4、求下面各图形的面积。
(单位:分米)3m13cm 16cm8dm3dm12cm 7cm4dm8dm5、“实践操作”显身手:10分6、已知右面的两个正方形边长分别为6分米和4分米,求图中阴影部分的面积。
7、右图是两个相同的直角三角形叠在一起,求阴影部分的面积。
(单位:厘米)8、如图,这个长方形的长是9厘米,宽是8厘米,A 和B 是宽的中点,求长方形内阴影部分的面积。
9、在右图中,三角形EDF 的面积比三角形ABE 的面积大6平方厘米,已知长方形ABDC 的长和宽分别为6厘米、4厘米,DF 的长是多少厘米?16cm12cm14cm 24m10m8m1、求下面图形中阴影部分的面积。
2、求下面图形的面积。
10、右图是一块长方形公园绿地,绿地长24米,宽16米,中间有一条宽为2米的道路,求草地(阴影部分)的面积。
11、如图,三角形ABC的面积是24平方厘米,且DC=2AD,E、F分别是AF、BC的中点,那么阴影部分的面积是多少?12、如图,三角形ABC的面积是90平方厘米,EF平行于BC,AB=3AE,那么三角形甲、乙、丙的面积各是多少平方厘米?13、如图长方形,长18厘米,宽12厘米,AE、AF两条线段把长方形面积三等分,求三角形AEF的面积。
多边形的面积

例1.图中的甲和乙都是正方形,求阴影部分的面积。
(单位:厘米)例2.计算右图的面积。
(单位:厘米)例3.如图,已知四条线段的长分别是:AB=2厘米,CE=6厘米,CD=5厘米,AF=4厘米,并且有两个直角。
求四边形ABCD的面积。
例4.右图是两面三刀个相同的直角三角形叠在一起,求阴影部分的面积。
(单位:分米)例5.下页左图是一块长方形草地,长方形的长是16,宽是10,中间有两条道路,一条是长方形,一条是平行四边形,那么,有草部分(阴影部分)的面积有多大?(单位:米)练习与思考1.求图中阴影部分的面积。
2.求图中阴影部分的面积。
3.下左图的长方形中,三角形ADE与四边形DEBF和三角形CDF的面积分别相等,求三角形DEF的面积。
4.四中平等四边形ABCD的边BC长10厘米,直角三角形BCE的直角边EC长8厘米,已知阴影部分的面积比三角形EFG的面积大10平方厘米,求CF的长。
5.图中三角形的高为4,面积为16;长方形的宽为6,长方形的面积是三角形面积的多少倍?6.如图,长方形的长是8,宽是6,A和B是宽的中点,求长方形内阴影部分的面积。
7.如图,BC长为5,求画斜线的两个三角形的面积之和。
8.上右图是两个一样的直角三角形重叠在一起,按照图上标出的数,计算阴影部分的面积。
9.右图是一块长方形草地,长方形长为16,宽为12,中间有一条宽为2的道路,求草地(阴影部分)的面积。
例1.一个正方形,如果它的边长增加5厘米,那么,所成的正方形比原来正方形的面积多95平方厘米。
原来的正方形的面积是多少平方厘米?例2.右图中由9个小长方形组成的一个大长方形。
按图中的编号,1号、2号、3号、4号、5号长方形的面积依次为1平方厘米、2平方厘米、3平方厘米、4平方厘米、5平方厘米。
求6号长方形的面积。
例3.右图中三角形ABC为等边三角形,D为AB边上的中点。
已知三角形BDE的面积为5平方厘米。
求等边三角形ABC的面积。
例4.右图中长方形的长为12厘米,宽为6厘米。
求阴影部分的面积

求阴影部分的面积计算平面图形的面积问题是常见题型,求平面阴影部分的面积是这类问题的难点。
不规则阴影面积常常由三角形、四边形、弓形、扇形和圆、圆弧等基本图形组合而成的,在解此类问题时,要注意观察和分析图形,会分解和组合图形。
现介绍几种常用的方法。
我们已经学习过三角形、正方形、长方形、平行四边形、梯形的面积公式以后还要学圆、扇形等基本图形的面积计算,图形及计算公式如下:三角形面积= 正方形面积=长方形面积= 平行四边形面积=梯形面积= 圆面积=半径×半径×π=πr2,扇形面积=半径×半径×π×圆心角的度数÷360°【例1】直接运用公式求阴影面积【练习一】【例2】拼接法如图6,在一块长为8米、宽为4米的矩形草地上,有一条弯曲的柏油小路(小路任何地方的水平宽都是1个单位),求阴影部分草地的面积。
【练习二】右图是一块长方形公园绿地,绿地长24米,宽16米,中间有一条宽为2米的道路,求草地(阴影部分)的面积。
【例3】加减法如图长方形,长18厘米,宽12厘米,AE、AF两条线段把长方形面积三等分,求三角形AEF的面积。
细心点哦,不要【练习三】【强化练习】1.如图,三角形ABC 的面积是90平方厘米,EF 平行于BC ,AB=3AE ,那么三角形甲、乙、丙的面积各是多少平方厘米?2.右图正方形边长为12厘米,四边形EFGH 面积是6平方厘米,那么阴影面积是多少平方厘米?3.如图,A 、B 两点是长方形长和宽的中点,那么阴影部分占长方形的面积是多少?4.计算右边图形的面积。
(至少用3种方法)(单位:米)5.ABCD 是正方形,BE=EC ,AB=12厘米,阴影面积是多少?6.【过手训练】1求阴影部分的面积2.已知正方形乙的边长是8厘米,正方形甲的面积是36平方厘米,那么图中阴影部分的面积是多少?3.如图,正方形ABCD 的边长是12厘米,CE=4厘米。
组合图形面积计算 -基础

戴氏教育精品堂培训学校名校冲刺组合图形(一)一、考点、热点回顾戴氏教育温馨提醒:致亲爱的学子:每个人都有梦想,但不是每个人都能实现梦想。
实现梦想的人因为他们懂得坚持。
什么是坚持:坚持就是在不能坚持时咬紧牙关再坚持一下!时刻记住:坚持,坚持,再坚持!!!二、典型例题【典型例题】(一)、基础图形(割补、整体-空白)【例1】已知平行四边表的面积是28平方厘米,求阴影部分的面积。
练习、如果用铁丝围成如下图一样的平行四边形,需要用多少厘米铁丝?(单位:厘米)【例2】下图中甲和乙都是正方形,求阴影部分的面积。
(单位:厘米)练习、1 、已知右面的两个正方形边长分别为6分米和4分米,求图中阴影部分的面积。
2、求图中阴影部分的面积。
(单位:厘米)【例3】将如图(1)所示的三角形纸片沿粗虚线折叠,成如图(2)所示的图形.。
已知图(1)三角形的面积是图(2)图形面表的1.5倍,图(2)中阴影部分的面积之和为1平方厘米。
求重叠部分的面积。
练习、将如图所示的三角形沿虚线折叠,得到如图所示的多边形。
这个多边形面积是原三角形面积的75,已知图中阴影部分的面积和为6平方厘米,求原三角形的面积。
(二)、差不变【例4】如图所示,甲三角形的面积比乙三角形的面积大6平方厘米,求CE 的长度。
练习、1、右图是两个相同的直角三角形叠在一起,求阴影部分的面积。
(单位:厘米)2、平行四边形ABCD的边长,BC=10厘米,直角三角形BCE的直角边EC长8厘米,已知阴影部分的面积比三角形EFG的面积大10平方厘米。
求CF的长。
(三)、三角形等积变换我们已经掌握了三角形面积的计算公式:三角形面积=底×高÷2这个公式告诉我们:三角形面积的大小,取决于三角形底和高的乘积.如果三角形的底不变,高越大(小),三角形面积也就越大(小).同样若三角形的高不变,底越大(小),三角形面积也就越大(小).为便于实际问题的研究,我们还会常常用到以下结论:①等底等高的两个三角形面积相等.②底在同一条直线上并且相等,该底所对的角的顶点是同一个点或在与底平行的直线上,这两个三角形面积相等.③若两个三角形的高(或底)相等,其中一个三角形的底(或高)是另一个三角形的几倍,那么这个三角形的面积也是另一个三角形面积的几倍.【例5】已知三角形ABC的面积为1,BE=2AB,BC=CD,求三角形BDE的面积?练习、1、如图,已知平行四边形ABCD的面积是60平方分米,E、F分别是AB、AD边上的中点,图中阴影部分的面积是多少平方分米?2、右图中的长方形ABCD的长是20厘米,宽是12厘米,AF=BE,图中阴影部分的面积是多少平方厘米?【例6】用三种不同的方法,把任意一个三角形分成四个面积相等的三角形.【例7】在三角形ABC中,DC=2BD,CE=3AE,阴影部分的面积是20平方厘米,求三角形ABC的面积。
苏教版五年级上册数学组合图形面积练习题
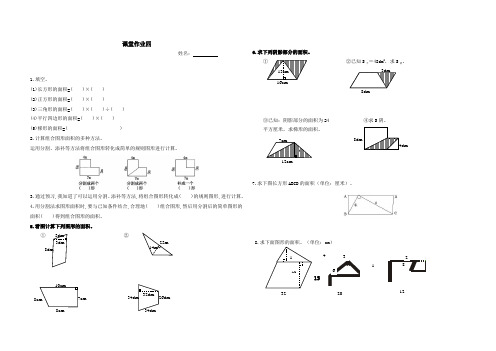
课堂作业四姓名:1.填空。
(1)长方形的面积=( )×( )(2)正方形的面积=( )×( )(3)三角形的面积=( )×( )÷( )(4)平行四边形的面积=( )×( )(5)梯形的面积=( )2.计算组合图形面积的多种方法。
运用分割、添补等方法将组合图形转化成简单的规则图形进行计算。
3.通过预习,我知道了可以运用分割、添补等方法,将组合图形转化成( )的规则图形,进行计算。
4.用分割法求图形面积时,要与已知条件结合,合理地( )组合图形,然后用分割后的简单图形的面积( )得到组合图形的面积。
5.看图计算下列图形的面积。
①②6.求下列阴影部分的面积。
①②已知S平=48dm2,求S阴。
③已知:阴影部分的面积为24 ④求S阴。
平方厘米,求梯形的面积。
7.求下图长方形ABCD的面积(单位:厘米)。
8.求下面图形的面积。
(单位:cm)153dm5dm8dm25m14m32dm26dm34dm34dm10cm7cm8cm8cm13cm16cm8dm3dm20164 382132 20 1212cm7cm4dm8dm9.一块梯形地,上底是30米,下底减少10米变成一个平行四边形,它的面积就是1500平方米,原来梯形的面积是多少?10.一块平行四边形地,长280米,宽50米,这块地的面积是多少公顷?11.一条高速公路全长48千米,宽50米,这条高速公路占地多少公顷?合多少平方千米?12.一块占地4公顷的长方形地,宽80米,长是多少米?13.一块长方形菜地。
长280米,宽150米,如果每公顷蔬菜收入10万元,这块菜地共可收入多少万元?14.已知右面的两个正方形边长分别为6分米和4分米,求图中阴影部分的面积。
北师大版五年级上册数学-组合图形拓展练习题

五上数学组合图形拓展练习题1,已知正方形ABCD的边长是7厘米,求正方形EFGH的面积。
2、小两个正方形组成下图所示的组合图形。
已知组合图形的周长是52厘米,DG=4厘米,求阴影部分的面积。
3、如图,已知四条线段的长分别是:AB=2厘米,CE=6厘米,CD=5厘米,AF=4厘米,并且有两个直角。
求四边形ABCD的面积。
4、求下图长方形ABCD的面积(单位:厘米)。
5、下图中,甲三角形的面积比乙三角形的面积大多少平方厘米?6、如图,正方形ABCD 的边长是8cm,BO=6.4cm,BO⊥AE,那么AE 的长度是多少cm?7、如图:正方形ABCD的边长为6厘米,三角形ABE,三角形ADF与四边形AECF的面积彼此相等。
求三角形AEF的面积。
8、 求下面图形的面积。
(单位:cm )159、计算下面图形中阴影部分的面积。
30dm12dm 5m25dm 5m10、求下列阴影部分的面积。
① ②已知S 平=48dm 2,求S 阴。
③已知:阴影部分的面积为24④求S 阴。
平方厘米,求梯形的面积。
3m2010643482 1032 201213cm 16cm8dm3dm12cm7cm4dm8dm11、求下面各图形的面积。
(单位:分米)12、“实践操作”显身手:13、已知右面的两个正方形边长分别为6分米和4分米,求图中阴影部分的面积。
14、右图是两个相同的直角三角形叠在一起,求阴影部分的面积。
(单位:厘米)15、如图,这个长方形的长是9厘米,宽是8厘米,A 和B 是宽的中点,求长方形内阴影部分的面积。
16、在右图中,三角形EDF 的面积比三角形ABE 的面积大6平方厘米,已知长方形ABDC 的长和宽分别为6厘米、4厘米,DF 的长是多少厘米?16cm12cm14cm 24m10m8m①求下面图形中阴影部分的面积。
②求下面图形的面积。
17、右图是一块长方形公园绿地,绿地长24米,宽16米,中间有一条宽为2米的道路,求草地(阴影部分)的面积。
盐城市第二小学五年级数学国庆假期作业

盐城市第二小学五年级数学国庆假期作业纸班级学号姓名一、仔细斟酌,认真填写。
1.平行四边形的面积是32平方厘米,和它等底等高的三角形的面积是()。
2.有一个三角形的面积是45平方分米,底是15分米,那么它的高是()厘米。
3.一个三角形的面积比与它等底等高的平行四边形的面积少12平方分米,平行四边形的面积是()平方分米,三角形的面积是()平方分米。
4.三角形的面积是4平方米,与它等底等高的平行四边形的面积是()平方米。
5.一个直角梯形,下底长6厘米,如果将上底增加2厘米,就变成正方形。
原来的这个梯形的面积是()平方厘米。
6.一个三角形和一个平行四边形的面积相等,底也相等,如果三角形的高是8厘米,那么平行四边形的的高是()。
7.等腰三角形的周长是16分米,腰长5分米,底边的高4分米,它的面积是()。
8.三角形有一条边的底是4分米,这条边上的高是3分米;另一边的长是6分米,另一边上的高是()分米。
9.直角三角形的三条边分别是3厘米、4厘米和5厘米,它的面积是()。
10.一个三角形的底扩大4倍,要想面积不变,高应该()。
11.两个完全相同的梯形拼成一个平行四边形,这个平行四边形的底长30厘米,高是6厘米。
每个梯形的面积是()平方厘米。
12.一个三角形与一个平行四边形面积相等,底也相等。
如果平行四边形的高是22厘米,那么三箭形的高是()厘米。
13.一个直角梯形,如果上底增加2厘米,就成为一个边长为4厘米的正方形,这个梯形的面积是()平方厘米。
14. 一个三角形与一个平行四边形面积相等,底也相等。
如果三角形的高是22厘米,那么平行四边形的高是()厘米。
15.8公顷=()平方米 50000平方米=()公顷6000公顷=()平方千米 352公顷=()平方千米()公顷16.用小数表示。
3角=()元 4角5分=()元 7克=()千克32公项=()平方千米 125平方米=()平方千米二、组合图形练习题。
1、计算下面图形中阴影部分的面积。
北师大版五年级数学上册专项练习题20——组合图形拓展练习题

专项练习题20——组合图形拓展练习题姓名1、已知正方形ABCD的边长是7厘米,求正方形EFGH的面积。
2、小两个正方形组成下图所示的组合图形。
已知组合图形的周长是52厘米,DG=4厘米,求阴影部分的面积。
3、如图,已知四条线段的长分别是:AB=2厘米,CE=6厘米,CD=5厘米,AF=4厘米,并且有两个直角。
求四边形ABCD的面积。
4、求下图长方形ABCD的面积(单位:厘米)。
5、下图中,甲三角形的面积比乙三角形的面积大多少平方厘米?6、如图,正方形ABCD 的边长是8cm,BO=6.4cm,BO⊥AE,那么AE 的长度是多少cm?7、如图:正方形ABCD的边长为6厘米,三角形ABE,三角形ADF与四边形AECF的面积彼此相等。
求三角形AEF的面积。
8、 求下面图形的面积。
(单位:cm )9、计算下面图形中阴影部分的面积。
30dm12dm 5m25dm 5m10、求下列阴影部分的面积。
②已知S 平=48dm 2,求S 阴。
16cm8dm③已知:阴影部分的面积为24④求S 阴。
平方厘米,求梯形的面积。
11、求下面各图形的面积。
(单位:分米)12、“实践操作”显身手13、已知右面的两个正方形边长分别为6分米和4分米,求图中阴影部分的面积。
14、右图是两个相同的直角三角形叠在一起,求阴影部分的面积。
(单位:厘米)12cm 4dm8dm16cm(2)求下面图形的面15、如图,这个长方形的长是9厘米,宽是8厘米,A和B是宽的中点,求长方形内阴影部分的面积。
16、在右图中,三角形EDF的面积比三角形ABE的面积大6平方厘米,已知长方形ABDC 的长和宽分别为6厘米、4厘米,DF的长是多少厘米?17、右图是一块长方形公园绿地,绿地长24米,宽16米,中间有一条宽为2米的道路,求草地(阴影部分)的面积。
18、如图,三角形ABC的面积是24平方厘米,且DC=2AD,E、F分别是AF、BC的中点,那么阴影部分的面积是多少?19、如图,三角形ABC的面积是90平方厘米,EF平行于BC,AB=3AE,那么三角形甲、乙、丙的面积各是多少平方厘米?20、如图长方形,长18厘米,宽12厘米,AE、AF两条线段把长方形面积三等分,求三角形AEF的面积。
