工程力学第六章答案 梁的变形
工程力学课后习题答案(2-6章-版本2)

3.3 图3.3所示钢架的点B 作用一个水平力F ,钢架重量忽略不计。
求支座A 、D 的约束力。
解:由图3.3可以确定D 点受力的方向,这里将A 点的力分解为x 、y 方向,如图3.3.1 根据力与矩平衡有)2(:)(0:)(0:)(=-=-=-∑∑∑FL L F A M F F y F F F x F Dy Dx (1)解上面三个方程得到 )(2),(2),(↑=↓=←=F F F F F F D y x3.5如图3.5铰链四杆机构ABCD 的CD 边固定,在铰链A 、B 处有力F1、F2作用,如图所示。
该机构在图示位置平衡,杆重忽略不计。
求力F1和力F2的关系。
解:(1)对A 点分析,如图3.5.1,设AB 杆的内力为T ,则将力投影到垂直于AC 方向的AM 上有0)15cos()30cos(:)(1=︒-︒∑T F AM F ①图3.5(2)对B 点分析,如图3.5.2,将力投影到垂直于BD 方向的BN 有 0)30cos()60cos(:)B N (2=︒-︒∑T F F ②由①、②可得 22108593790.64395055332F F F ≈+=3.8如图3.8有5根杆件组成的结构在A 、B 点受力,且CA 平行于DB ,CA DE BE DB ===。
F=20kN,P=12kN 。
求BE 杆的受力。
解:(1)对A 点受力分析,将力投影到垂直于AC 方向的AN 上有060sin :)(=-︒∑F FAN F AB①(2)对B 点受力分析,如图3.8.2.将力投影到垂直于BD 方向的BM 上有060cos 60sin 30cos :)B M (=︒-︒-︒∑P F FF BE AB②由①、②可得373095kN 16.1658075kN 328≈=BE F (方向斜向上)3.9如图(见书上)所示3根杆均长2.5m ,其上端铰结于K 处,下端A 、B 、C 分别与地基铰结,且分布在半径r=1.5m 的圆周上,A 、B 、C 的相对位置如图所示。
工程力学习题答案6廖明成

工程力学习题答案6廖明成第六章 杆类构件的内力分析习 题6.1 试求图示结构1-1和2-2截面上的内力,指出AB 和CD 两杆的变形属于哪类基本变形,并说明依据。
(a )(b )题6.1图解:(a )应用截面法:对题的图取截面2-2以下部分为研究对象,受力图如图一所示:BM图一图二由平衡条件得:0,AM=∑6320N F ⨯-⨯=解得:NF =9KNCD 杆的变形属于拉伸变形。
应用截面法,取题所示截面1-1以右及2-2以下部分作为研究对象,其受力图如图二所示,由平衡条件有: 0,OM =∑ 6210NF M ⨯-⨯-= (1)0,yF =∑ 60NSF F --=(2)将NF =9KN 代入(1)-(2)式,得:M=3 kN·mSF =3 KNAB 杆属于弯曲变形。
(b )应用截面法 ,取1-1以上部分作为研究对象,受力图如图三所示,由平衡条件有:0,Fx =∑20NF -=图三F NMNF =2KN0,DM =∑ 210M -⨯=M=2KNAB 杆属于弯曲变形6.2 求图示结构中拉杆AB 的轴力。
设由AB 连接的1和2两部分均为刚体。
题6.2图解:首先根据刚体系的平衡条件,求出AB杆的内力。
刚体1的受力图如图一所示D图一 图二平衡条件为:0,CM=∑104840D N F F ⨯-⨯-⨯=(1)刚体2受力图如图二所示,平衡条件为:0,EM =∑ 240NDF F ⨯-⨯=(2)解以上两式有AB 杆内的轴力为:NF =5KN6.3 试求图示各杆件1-1、2-2和3-3截面上的轴力,并做轴力图。
(a )C(b )(c )(d )题6.3图解:(a ) 如图所示,解除约束,代之以约束反力,做受力图,如图1a 所示。
利用静力平衡条件,确定约束反力的大小和方向,并标示在图1a 中,作杆左端面的外法线n ,将受力图中各力标以正负号,轴力图是平行于杆轴线的直线,轴力图线在有轴向力作用处要发生突变,突变量等于该处总用力的数值,对于正的外力,轴力图向上突变,对于负的外力,轴力图向下突变,轴力图如2a 所示,截面1和截面2上的轴力分别为1N F =-2KN2N F =-8KN ,(a )nkN(a 1)(2)C(b )CBkNb 1)(b 2)((b )解题步骤和(a )相同,杆的受力图和轴力图如(1b )(2b )所示,截面1和截面2上的轴力分别为1N F =4KN 2N F =6KN(c )解题步骤和(a )相同,杆的受力图和轴力图如(1c )(2c )所示,截面1,截面2和截面3上的轴力分别为1N F =3F 2N F =4F ,3NF =4FB C(c )4F(c 1)(c 2)(d)A D(d 1)(d 2)(d )解题步骤和(a )相同,杆的受力图和轴力图如(1d )(2d )所示,截面1和截面2上的轴力分别为1N F =2KN 2N F =2KN6.4 求图示各轴1-1、2-2截面上的扭矩,并做各轴的扭矩图。
工程力学:弯曲变形 习题与答案

一、单选题1、研究梁的变形的目的是()。
A.进行梁的正应力计算B.进行梁的刚度计算C.进行梁的稳定性计算D.进行梁的剪应力计算正确答案:B2、图示圆截面悬臂梁,若直径d增大1倍(其它条件不变),则梁的最大正应力、最大挠度分别降至原来的()。
A.1/2 1/4B.1/4 1/8C.1/8 1/8D.1/8 1/16正确答案:D3、下面关于梁、挠度和转角的讨论中,正确的结论是()。
A.挠度最大的截面转角为零B.挠度最大的截面转角最大C.转角为零的截面挠度最大D.挠度的一阶导数等于转角正确答案:D4、已知两悬臂梁的抗弯截面刚度EI相同,长度分别为l和2l,在自由端各作用F1和F2,若二者自由端的挠度相等,则F1/F2=()。
A.2B.4C.6D.8正确答案:D5、梁上弯矩为零处()。
A.梁的转角一定为零B.梁的挠度一定为零C.挠度一定为零,转角不一定为零D.梁的挠曲线的曲率一定为零正确答案:D6、已知等直梁在某段上的挠曲轴方程w(x)=–Cx4,C为常量,则在该段梁上()。
A.分布载荷是x的一次函数B.分布载荷是x的二次函数C.无分布载荷作用D.有均匀分布载荷作用正确答案:D7、在等直梁弯曲变形中,挠曲线曲率最大值发生在()。
A.剪力最大处B.转角最大处C.弯矩最大处D.挠度最大处正确答案:C8、材料相同的(a)悬臂梁和(b)悬臂梁,长度也相同,在自由端各作用2P和P,截面形状分别是b(宽)×2b(高)、b×b。
关于它们的最大挠度正确的是()。
A.(a)梁最大挠度是(b)梁的1/4倍B.(a)梁最大挠度是(b)梁的1/2倍C.(a)梁最大挠度与(b)梁的相等D.(a)梁最大挠度是(b)梁的2倍正确答案:A9、已知简支梁的EI为常数,在梁的左端和右端分别作用一力偶m1和m2今欲使梁的挠曲线在x=l/3处出现一拐点,则比值m1/m2为()。
A.2B.3C.1/2D.1/3正确答案:C10、两根梁尺寸,受力和支承情况完全相同,但材料不同,弹性模量分别为E1和E2,且E1=7E2,则两根梁的挠度之比y1/y2为()。
工程力学知到章节答案智慧树2023年重庆大学

工程力学知到章节测试答案智慧树2023年最新重庆大学第一章测试1.变形固体的基本假设是()。
参考答案:连续、均匀性假设和各向同性假设;2.要使构件安全、正常地工作,必须满足()。
参考答案:强度要求、刚度要求、稳定性要求第二章测试1.平衡是指物体相对于惯性参考系保持静止或作匀速转动的状态。
()参考答案:错2.根据力的平行四边形法,作用于同一物体上的两个力都可以合成为一个合力。
()参考答案:错3.变形体在两个大小相等、方向相反、作用线沿同一直线的力作用下不一定能维持平衡。
()参考答案:对4.受力图中各约束反力的作用线方位及指向(除柔索和光滑接触面约束外)一般自己假定。
()参考答案:对5.下列关于刚体的描述,不正确的是()。
参考答案:变形极小的物体就可视为刚体6.下列关于约束反力的表述中,不正确的是()。
参考答案:约束反力的大小和方向由约束构造特点确定7.如题图所示体系,构件自重不计,则支座A处约束反力作用线方位正确的是()。
参考答案:沿AE8.如题图所示体系,构件自重不计,则受力分析图不正确的是()。
参考答案:第三章测试1.在任何坐标系中,力都可以用其在坐标轴上的投影解析表示。
()参考答案:错2.力对某轴之矩等于力对轴上任一点之矩在该轴上的投影。
()参考答案:对3.只要保持力偶矩不变,力偶可在其作用面内任意移动和转动,都不会改变原力偶对物体的作用效应。
()参考答案:错4.力系向某点简化,其主矢和主矩都不为零,且主矢和主矩正交,则该力系可以继续简化为一合力。
()参考答案:错5.作用在一个刚体上的两力,满足的条件,则该二力可能是()。
参考答案:一对平衡的力或一个力偶6.某平面力系向其平面内A点简化的结果为:,则该力系向其平面内任选的另一点B简化的结果为()。
参考答案:7.下列关于力平移的表述中,正确的是()。
参考答案:作用在刚体上的力可以沿其作用线平移到该刚体上任一点,其作用效应不变8.各力作用位置如图所示的平面力系中,已:F1=4kN,F2=3kN,q=2kN/m,M1=100N·m,M2=200N·m。
工程力学第六章 弯曲变形

荷情况有关,而且还与梁的材料、截面尺寸、形
状和梁的跨度有关。所以,要想提高弯曲刚度,
就应从上述各种因素入手。
一、增大梁的抗弯刚度EI 二、减小跨度或增加支承 三、改变加载方式 48EI
作 业
1、2、4(a、e)
§6-3 用叠加法计算梁的变形 梁的刚度计算
一、用叠加法计算梁的变形
在材料服从胡克定律、且变形很小的前提下, 载荷与它所引起的变形成线性关系。 当梁上同时作用几个载荷时,各个载荷所引 起的变形是各自独立的,互不影响。若计算几个 载荷共同作用下在某截面上引起的变形,则可分 别计算各个载荷单独作用下的变形,然后叠加。
例: 梁AB,横截面为边长为a的正方形,
弹性模量为E1;杆BC,横截面为直径为d的圆 形,弹性模量为E2。试求BC杆的伸长及AB梁 中点的挠度。
例:用叠加法求图示梁B端的挠度和转角。
解:
二、梁的刚度计算
刚度条件:
max [ ] max [ ]
[w]、[θ]是构件的许可挠度和转角,它们决定
q
B
x
l
由边界条件: x 0时, 0 x l时, 0
ql 3 , D0 得: C 24
梁的转角方程和挠曲线方程分别为:
y
q 2 3 3 (6lx 4 x l ) 24 EI
q
B
x
l
A qx (2lx 2 x 3 l 3 ) 24 EI
ql 3 24 EI
l 2
x
P AC 解: 段:M ( x ) x 2 y P EI " x 2 A P 2 EI ' x C x 4 l 2 P 3 EI x Cx D 12
工程力学课后习题答案

工程力学练习册学校学院专业学号教师姓名第一章静力学基础1-1 画出下列各图中物体A,构件AB,BC或ABC的受力图,未标重力的物体的重量不计,所有接触处均为光滑接触。
(a)(b)(c)(d)(e)(f)(g)1-2 试画出图示各题中AC杆(带销钉)和BC杆的受力图(a)(b)(c)(a)1-3 画出图中指定物体的受力图。
所有摩擦均不计,各物自重除图中已画出的外均不计。
(a)(b)(c)(d)(e)(f)(g)第二章 平面力系2-1 电动机重P=5000N ,放在水平梁AC 的中央,如图所示。
梁的A 端以铰链固定,另一端以撑杆BC 支持,撑杆与水平梁的夹角为30 0。
如忽略撑杆与梁的重量,求绞支座A 、B 处的约束反力。
题2-1图解得: N P F F B A 5000===2-2 物体重P=20kN ,用绳子挂在支架的滑轮B 上,绳子的另一端接在绞车D 上,如图所示。
转动绞车,物体便能升起。
设滑轮的大小及轴承的摩擦略去不计,杆重不计,A 、B 、C 三处均为铰链连接。
当物体处于平衡状态时,求拉杆AB 和支杆BC 所受的力。
题2-2图解得: P F PF AB BC 732.2732.3=-=2-3 如图所示,输电线ACB 架在两电线杆之间,形成一下垂线,下垂距离CD =f =1m ,两电线杆间距离AB =40m 。
电线ACB 段重P=400N ,可近视认为沿AB 直线均匀分布,求电线的中点和两端的拉力。
题2-3图以AC 段电线为研究对象,三力汇交2-4 图示为一拔桩装置。
在木桩的点A 上系一绳,将绳的另一端固定在点C ,在绳的点B 系另一绳BE ,将它的另一端固定在点E 。
然后在绳的点D 用力向下拉,并使绳BD 段水平,AB 段铅直;DE 段与水平线、CB 段与铅直线成等角α=0.1rad (弧度)(当α很小时,tan α≈α)。
如向下的拉力F=800N ,求绳AB 作用于桩上的拉力。
题2-4图作BD 两节点的受力图 联合解得:kN F F F A 80100tan 2=≈=α2-5 在四连杆机构ABCD 的铰链B 和C 上分别作用有力F 1和F 2,,机构在图示位置平衡。
工程力学c材料力学部分第六章 弯曲变形

A l/2
C l
B
解:此梁上的荷载可视为 正对称和反对称荷载的叠加, 正对称和反对称荷载的叠加, 如图所示。 如图所示。 正对称荷载作用下:
q/2
5(q / 2)l 4 5ql 4 wC1 = − =− 384 EI 768 EI
B
(q / 2)l 3 ql 3 θ A1 = −θ B1 = =− 24 EI 48EI
w P A a D
a
A C a H a B
EI
Pl 3 wB = − 3 EI
P
B
l
Pl 2 θB = − 2 EI
P A a 2a 2a C B
P/2
P/2 B
P/2
=
A
+
P/2
力分解为关于中截面的对称和反对称力( )之和的形式。 解:将P力分解为关于中截面的对称和反对称力(P/2)之和的形式。 力分解为关于中截面的对称和反对称力 显然,在反对称力( / )作用下, 显然,在反对称力(P/2)作用下,wc=0 对称力作用的简支梁, 对称力作用的简支梁,可以等效为悬臂梁受到两个力的作用 的问题。 的问题。
wA=0 θA=0
B
②、变形连续条件 变形连续条件: 连续条件
P A C θC左 wC左= wC右, =θ C右 B
的悬臂梁, 例1:图示一弯曲刚度为 的悬臂梁,在自由端受一集中力 作 :图示一弯曲刚度为EI的悬臂梁 在自由端受一集中力F 试求梁的挠曲线方程,并求最大挠度及最大转角。 用,试求梁的挠曲线方程,并求最大挠度及最大转角。 解:① 建立坐标系并写出弯矩方程 ①
在小变形情况下, 曲线弯曲平缓, 在小变形情况下,挠曲线弯曲平缓,
∴ w′ ≪ 1
2
工程力学26 梁弯曲时的变形和刚度计算

式中, x为梁变形前轴线上任一点的横坐标, w为该点的挠度。
工 程力 学
ENGINEERING MECHANICS
工 程力 学
ENGINEERING MECHANICS
2 挠曲线的近似微分方程
纯弯曲时曲率与弯矩的关系为
1M
EI
横力弯曲时, M和都是x的函数。略去剪力对梁的位移
工 程力 学
ENGINEERING MECHANICS 梁弯曲时的变形和刚度计算
工 程力 学
ENGINEERING MECHANICS
一、工程中的弯曲变形问题
弯曲构件除了要满足强度条件外, 还需满足刚度条件。如车床主 轴的过大弯曲引起加工零件的误差。
工 程力 学
ENGINEERING MECHANICS
工 程力 学
ENGINEERING MECHANICS
取梁的左端点为坐标原点, 梁变形前的轴线为x轴, 横截面的
铅垂对称轴为y轴, xy平面为纵向对称平面。
y
A
挠度符号?
C
B
x
C1 w
B'
挠度
挠度(w): 横截面形心(即轴线上的点)在垂直于x轴
方向的线位移, 称为该截面的挠度(Deflection) 。
3 2
M (x) EI
工 程力 学
ENGINEERING MECHANICS
w (1 w2 )32
M (x) EI
由于挠曲线是一条非常平坦的曲线, w'2远比1小, 可以略去不计,
于是上式可写成 w M (x) EI
此式称为 梁的挠曲线近似微分方程。
(Approximately differential equation of the deflection curve)
《工程力学》课后习题答案全集

工程力学习题答案第一章 静力学基础知识思考题:1. ×;2. √;3. √;4. √;5. ×;6. ×;7. √;8. √习题一1.根据三力汇交定理,画出下面各图中A 点的约束反力方向。
解:(a )杆AB 在A 、B 、C 三处受力作用。
由于力和的作用线交于点O 。
如图(a )所示,根据三力平衡汇交定理, 可以判断支座A 点的约束反力必沿 通过A 、O 两点的连线。
(b )同上。
由于力和的作用线 交于O 点,根据三力平衡汇交定理, 可判断A 点的约束反力方向如 下图(b )所示。
2.不计杆重,画出下列各图中AB 杆的受力图。
解:(a )取杆AB 为研究对象,杆除受力外,在B 处受绳索作用的拉力,在A 和E 两处还受光滑接触面约束。
约束力和的方向分别沿其接触表面的公法线,并指向杆。
其中力与杆垂直,力通过半圆槽的圆心O 。
AB 杆受力图见下图(a )。
(b)由于不计杆重,曲杆BC 只在两端受铰销B 和C 对它作用的约束力和,故曲杆BC 是二力构件或二力体,此两力的作用线必须通过B 、C 两点的连线,且=。
研究杆AB ,杆在A 、B 两点受到约束反力和,以及力偶m 的作用而平衡。
根据力偶的性质,和必组成一力偶。
(d)由于不计杆重,杆AB 在A 、C 两处受绳索作用的拉力和,在B 点受到支座反力。
和相交于O 点,根据三力平衡汇交定理,可以判断必沿通过pB RpB Rp B T A N E N E N A N B N C N BN CN A N B N A N B N A T C T B N A T C TB NB、O两点的连线。
见图(d).第二章 力系的简化与平衡思考题:1. √;2. ×;3. ×;4. ×;5. √;6. ×;7. ×;8. ×;9. √.1. 平面力系由三个力和两个力偶组成,它们的大小和作用位置如图示,长度单位为cm ,求此力系向O 点简化的结果,并确定其合力位置。
工程力学--材料力学(北京科大、东北大学版)第4版第六章习题答案

第六章习题6—1用积分法求以下各梁的转角方程、挠曲线方程以及指定的转角和挠度。
已知抗弯刚度EI为常数。
6-2、用积分法求以下各梁的转角方程、挠曲线方程以及指定的转角和挠度。
已知抗弯刚度EI为常数。
6-3、用叠加法求图示各梁中指定截面的挠度和转角。
已知梁的抗弯刚读EI为常数。
6-4阶梯形悬臂梁如图所示,AC段的惯性矩为CB段的二倍。
用积分法求B端的转角以及挠度。
6-5一齿轮轴受力如图所示。
已知:a=100mm,b=200mm,c=150mm,l=300mm;材料的弹性模量E=210Pa;轴在轴承处的许用转角[]=0.005rad。
近似的设全轴的直径均为d=60mm,试校核轴的刚度。
回答:6-6一跨度为4m的简支梁,受均布载荷q=10Kn/m,集中载荷P=20Kn,梁由两个槽钢组成。
设材料的许用应力[]=160Ma,梁的许用挠度[]=。
试选择槽钢的号码,并校核其刚度。
梁的自重忽略不计。
m壁厚=4mm,单位长度重量6-7两端简支的输气管道,外径D=114m。
q=106N/m,材料的弹性模量E=210Gpa。
设管道的许用挠度试确定管道的最大跨度。
6-845a号工字钢的简支梁,跨长l=10m,材料的弹性模量E-210Gpa。
若梁的最大挠度不得超过,求梁所能承受的布满全梁的最大均布载荷q。
6-9一直角拐如图所示,AB段横截面为圆形,BC段为矩形,A段固定,B段为滑动轴承。
C端作用一集中力P=60N。
有关尺寸如图所示。
材料的弹性模量E=210Gpa,剪切弹性模量G=0.4E。
试求C端的挠度。
提示:由于A端固定,B端为滑动轴承,所以BC杆可饶AB杆的轴线转动。
C端挠度由二部分组成;(1)把BC杆当作悬臂梁,受集中力P作用于C端产生的挠度,;(2)AB杆受扭转在C锻又产生了挠度,。
最后,可得C端的挠度6-10、以弹性元件作为测力装置的实验如图所示,通过测量BC梁中点的挠度来确定卡头A处作用的力P,已知,梁截面宽b=60mm,高h=40mm,材料的弹性模量E=210Gpa。
工程力学-梁的变形

(12-2)
12.1 基 本 概 念
12.1.3 梁的挠曲线近似微分方程
为了求得梁的挠曲线方程,首先应建立挠曲线的近似微分方程。
在模块10中推导纯弯曲时梁横截面上的正应力过程中,已经导
出了梁在纯弯曲时的曲率表达式(10-5)。对于等截面直梁,在纯
弯曲时,因为M和EIz均为常数,所以曲率1/ρ也是常数。而在横力
图12-3 静定单跨梁的边界条件
12.2 梁的变形计算
【例12-1】
如图12-4所示,悬臂梁AB的长度为l,自由端受集中力FP的作
用,试求梁的挠曲线方程和转角方程,并计算梁的最大挠度和最
大转角。
【解】 (1)列出弯矩方程。
M x FP l x
(2)列出挠曲线近似微分方程。
d 2 y M x FP l x
dx 2
EI
EI
(3)积分。一次积分得转角方程
图12-4 【例12-1】图
dy dx
d2 dx
y
2
dx
FPlx EI
FP x 2 2EI
C
(12-10)
12.2 梁的变形计算
【例12-1】
(4)确定积分常数。悬臂梁在固定端A的约束条件为转角和
A端移动和转动),这一约束条件的表达式
为:当x=0,θ=0时,代入式(12-10)得C=0
式(12-7)就是梁的挠曲线近似微分方程。它是计算梁变形的基本 方程,只适用于弹性范围内的小变形情况。
12.2 梁的变形计算
12.2.1 二次积分法计算梁的变形
将挠曲线近似微分方程两边积分,得到转角方程和挠曲线方程,然 后把梁的横截面位置坐标x代入方程,从而求得任一截面上的转角和挠 度。这种求梁变形的方法称为积分法。
大学工程力学试题及答案

大学工程力学试题及答案一、选择题(每题2分,共20分)1. 以下哪项不是材料力学中的基本假设?A. 均匀性假设B. 连续性假设C. 各向同性假设D. 各向异性假设答案:D2. 梁的弯曲应力公式为:A. σ = (M/I) * (y/R)B. σ = (M/I) * (R/y)C. σ = (M/I) * (y/R)D. σ = (M/I) * (R/y)答案:C3. 弹性模量E的单位是:A. N/mB. N/m²C. PaD. J/m³答案:C4. 以下哪种材料不属于脆性材料?A. 玻璃B. 陶瓷C. 橡胶D. 混凝土答案:C5. 根据能量守恒定律,以下说法不正确的是:A. 机械能守恒B. 能量可以无中生有C. 能量可以转化为其他形式D. 能量守恒定律适用于所有物理过程答案:B6. 静定结构与超静定结构的主要区别在于:A. 材料种类B. 受力情况C. 几何形状D. 约束数量答案:D7. 以下哪种情况不属于平面力系的平衡条件?A. 合力为零B. 合力矩为零C. 合外力为零D. 合外力矩为零答案:C8. 梁的剪力图和弯矩图可以用来确定:A. 梁的变形B. 梁的内力C. 梁的自重D. 梁的外力答案:B9. 梁的挠度与弯矩之间的关系是:A. 线性关系B. 非线性关系C. 没有关系D. 反比关系答案:B10. 以下哪种方法不适用于解决超静定结构问题?A. 弯矩分配法B. 力法C. 位移法D. 能量法答案:A二、填空题(每题2分,共20分)1. 材料的弹性模量E与泊松比μ之间的关系是E = _______。
答案:2G(1+μ)2. 梁在纯弯矩作用下,其横截面上的应力分布为_______。
答案:线性分布3. 在静力平衡状态下,一个物体的合力为_______。
答案:零4. 材料力学中的胡克定律表明,在弹性范围内,材料的应力与应变之间存在_______关系。
答案:线性5. 梁的弯矩与截面的惯性矩I成_______关系。
工程力学材料力学部分习题

工程力学——材料力学部分习题第六章变形体力学基础是非判断题1.材料力学是研究构件承载能力的一门学科。
()2.材料力学的任务是尽可能使构件安全地工作。
()3.材料力学主要研究弹性范围内的小变形情况。
()4.因为构件是变形固体,在研究构件的平衡时,应按变形后的尺寸进行计算。
()5.外力就是构件所承受的载荷。
()6.材料力学研究的内力是构件各部分间的相互作用力。
()7.用截面法求内力时,可以保留截开后构件的任一部分进行平衡计算。
( )8.压强是构件表面的正应力。
()9.应力是横截面上的平均内力。
()10.材料力学只研究因构件变形引起的位移。
()11.线应变是构件中单位长度的变形量。
()12.构件内一点处各方向线应变均相等。
()13.切应变是变形后构件中任意两根微线段夹角角度的变化量。
()14.构件上的某一点,若任何方向都无应变,则该点无位移。
()15.材料力学只限于研究等截面直杆。
()16.杆件的基本变形只是拉(压)、剪、扭、和弯四种,如果还有另一种变形,必定是这四种变形的某种组合。
()填空题17.构件的承载能力包括____________、___________和____________三个方面;根据材料的主要性能作如下三个基本假设___________、___________、____________。
18.构件的强度是指___________________________________________________________;刚度是指_________________________________________________________________________;稳定性是指_______________________________________________________________________。
19.在材料力学中分析杆件内力的基本方法是__________,步骤是_____________________。
工程力学2第六章 弯曲变形

§6-4 用叠加法求弯曲变形
设梁上有n 个载荷同时作用,任意截面上的弯矩 为M(x),转角为 ,挠度为y,则有:
d2y EI 2 EIy'' M ( x ) dx n
由弯矩的叠加原理知: 所以, 即,
§6–3 用积分法求弯曲变形 (Beam deflection by integration )
一、微分方程的积分 (Integrating the differential equation )
M ( x) w EI
若为等截面直梁, 其抗弯刚度EI为一常量上式可改写成
EIw M ( x )
代入求解,得
1 Fb 3 C1 C 2 Fbl 6 6l D1 D2 0
FAy x1
ymax
x2
a
b
目录
§6-3 用积分法求弯曲变形
5)确定转角方程和挠度方程
AC 段: 0 x1 a
Fb 2 Fb 2 EI 1 x1 (l b2 ) 2l 6l
Fb 3 Fb 2 EIy1 x1 ( l b 2 ) x1 6l 6l
转角
4、挠度与转角的关系 ( Relationship between deflection and slope): w
A
tg w ' w '( x )
B
x
C C'
转角
w挠度
挠曲线
B
5、挠度和转角符号的规定
(Sign convention for deflection and slope) 挠度 向上为正,向下为负. 转角 自x 转至切线方向,逆时针转为正,顺时针转为负. w
工程力学第六章答案 梁的变形

第五章 梁的变形测试练习判断改错题梁上弯矩最大的截面 挠度也最大 弯矩为零的截面 转角亦为零 ( )两根几何尺寸、支承条件完全相同的静定梁,只要所受荷栽相同,则两梁所对应的截面的挠度及转角相同,而与梁的材料是否相同无关。
( )悬臂梁受力如图所示,若 点上作用的集中力 在 段上作等效平移,则 截面的转角及挠度都不变。
( )图示均质等直杆(总重量为 ),放置在水平刚性平面上,若 端有一集中力 作用,使 部分被提起, 部分仍与刚性上剪力和弯矩均为零。
( )挠曲线近似微分方程不能用于求截面直梁的位移。
( )等截面直梁在弯曲变形时,挠度曲线的曲率最大值发生在转角等于零的截面处。
( ) 两简支梁的抗刚度 及跨长 均相同,受力如图所示,则两梁跨中截面的挠度不等而转角是相等的。
题 图题图( )简支梁在图示任意荷载作用下,截面 产生挠度和转角,若在跨中截面 又加上一个集中力偶 作用,则梁的截面 的挠度要改变,而转角不变。
一铸铁简支梁,在均布载荷作用下,当其横截面相同且分别按图示两种情况放置时,梁同一截面的应力及变形均相同。
( )图示变截面梁,当用积分法求挠曲线方程时,因弯矩方程有三个,则通常有 个积分常量。
( ).填空题挠曲线近似微分方程EIx M x y )()("-= 的近似性表现在 和 。
已知图示二梁的抗弯度 相同,若使二者自由端的挠度相等,则=21P P。
题 图 题图题 图题 图题应用叠加原理求梁的变形时应满足的条件是: 。
在梁的变形中挠度和转角之间的关系是 。
用积分法求图示的外伸梁( 为拉杆)的挠曲线方程时,求解积分常量所用到的边界条件是 ,连续条件是 。
用积分法求图示外伸梁的挠曲线方程时,求解积分常量所用到边界条件是 ,连续条件是 。
图示结构为 次超静定梁。
纯弯曲梁段变形后的曲率与外力偶矩 的关系为 ,其变形曲线为 曲线。
两根 值相同、跨度之比为 : 的简支梁,当承受相同的均布荷载 作用时,它们的挠度之比为 。
工程力学复习题及答案

1.力是物体间相互的机械作用,这种作用使物体的机械运动状态发生改变。
2.物体受力发生变形的过程,属于机械运动状态改变的过程。
3.受力物体和施力物体间的相互作用力的性质相同。
4.刚体是受力作用而不变形的物体。
5.在所研究的机械运动问题中,物体的变形可以不考虑,那么此物体可视为刚体。
1.力系中各力的作用线汇交于一点的力系,称为汇交力系;力系中各力的作用线在同一个平面内且汇交于一点,这样的力系称为平面汇交力系。
2.平面汇交力系平衡的必要和充分条件是:该力系的合力等于零。
3.平面汇交力系平衡的几何条件是:该力系的力多边形是自行封闭的。
4.刚体在三力作用下平衡,其中两力的作用线汇交于一点,则该三力组成的平衡力系一定是平面汇交力系。
5.在正交的力系中,力沿某轴的分力的大小于同一力在该轴上的投影的绝对值相等。
1.力偶是大小相等、方向相反且不共线的两个平行力。
2.力偶在任何坐标轴上的投影的代数和恒等于零。
3.力偶矩相等是作用在刚体上的两个力偶等效的充分必要条件。
4.力偶使刚体转动的效果与矩心位置无关,完全由力偶矩决定。
5.力偶于力都是物体间相互的机械作用,力偶的作用效果是改变物体转动的状态。
1.平面任意力系向一点的简化,需要将力系中各力都等效的平移到作用面内任意选定的一点上,该点称为简化中心。
2.对于给定的任意力系,其主矢与简化中心的位置无关。
但在一般情况下,简化中心的位置不同时,对应的力系的主矩则不相同。
3.平面任意力系平衡的必要和充分条件是平面任意力系的主矢和主矩同时为零。
4.平面任意力系的平衡方程可写成三种形式,一矩式、二矩式和三矩式,其中二矩式和三矩式对矩心位置必须附加条件。
5.平面平行力系平衡时,只有两个独立的平衡方程。
1.两个物体间具有不光滑接触面时,接触面处会产生阻碍两物体间的相对滑动或相对滑动趋势的机械作用,这种作用称为滑动摩擦力。
其方向沿接触面公切线,与物体相对滑动相反。
2.临界平衡状态下,静滑动摩擦力的值称为最大静摩擦力,以Fmax表示。
工程力学(第二版)课后答案
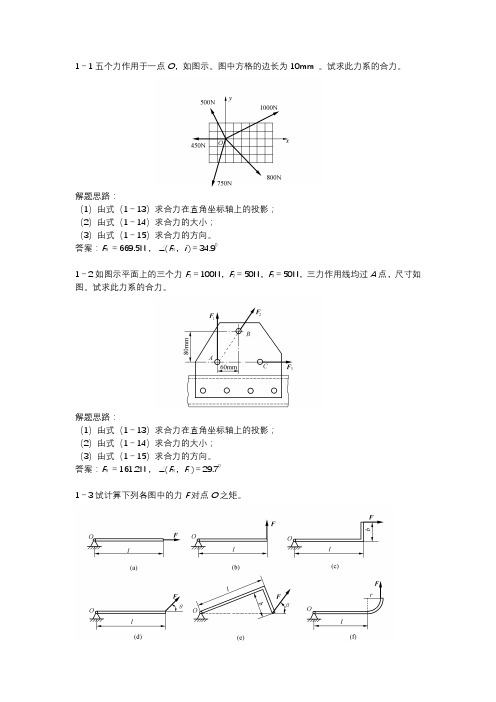
1-1五个力作用于一点O,如图示。
图中方格的边长为10mm 。
试求此力系的合力。
解题思路:(1)由式(1-13)求合力在直角坐标轴上的投影;(2)由式(1-14)求合力的大小;(3)由式(1-15)求合力的方向。
答案:F R =669.5N , ∠(F R,i )=34.901-2如图示平面上的三个力F1=100N,F2=50N,F3=50N,三力作用线均过A点,尺寸如图。
试求此力系的合力。
解题思路:(1)由式(1-13)求合力在直角坐标轴上的投影;(2)由式(1-14)求合力的大小;(3)由式(1-15)求合力的方向。
答案:F R =161.2N , ∠(F R,F i)=29.701-3试计算下列各图中的力F对点O之矩。
解题思路:各小题均由式(1-16)求力矩。
答案:略1-4如图所示的挡土墙重G 1=75 kN ,铅直土压力G 2=120 kN ,水平土压力F p =90 kN 。
试求三力对前趾A 点之矩的和,并判断挡土墙是否会倾倒。
解题思路:(1)由式(1-16)求三力对前趾A 点之矩的代数和; (2)若其值为负(顺时针转),则挡土墙不会翻倒。
答案:∑M A =-180kN.m ,不会倾倒。
1-5如图所示,边长为a 的正六面体上沿对角线AH 作用一力F 。
试求力F 在三个坐标轴上的投影,力F 对三个坐标轴之矩以及对点O 之矩矢。
解题思路:(1)由式(1-13)、(1-14)、(1-15)求合力的大小和方向; (2)由式(1-25)求力对三个坐标轴之矩; (3)由式(1-26)求力对坐标原点之矩。
答案:M x =0,Fa M y 33=,Fa M 33z =-, k Fa j Fa M O 3333-=1-7试画出下列各图中物体A ,构件AB 的受力图。
未画重力的物体重量不计,所有接触面均为光滑接触。
解题思路:(1)画出研究对象的轮廓形状; (2)画出已知的主动力;(3)在解除约束处按约束的性质画出约束力。
工程力学

工程力学[单项选择题]1、力对点之矩和力偶对点之矩,与矩心位置的关系是()。
A.都与矩心的位置无关B.都与矩心的位置有关C.力对点之矩与矩心的位置有关,力偶对点之矩与矩心的位置无关D.无法确定参考答案:C[单项选择题]2、已知构件受力如图所示,不计自重,支座A的约束力方向是()。
A.沿AB的连线B.沿AC的连线C.沿AD的连线D.无法确定方向参考答案:B[单项选择题]3、铰接三杆机构OABO1在图示位置平衡,各杆自重不计。
已知OA=40cm,O1B=60cm,作用在OA上的力偶矩M=1N.M。
力偶矩M2的大小是()。
1A.1N.MB.2N.MC.3N.MD.5N.M参考答案:C[单项选择题]4、力偶对物体的作用效应决定于()。
A.力偶矩的大小B.力偶的转向C.力偶的作用平面D.力偶矩的大小、力偶的转向、力偶的作用平面参考答案:D[单项选择题]5、已知梁上作用一力偶M,梁长为l,梁重不计,支座A和B的约束力为()。
A.AB.BC.CD.D参考答案:B[单项选择题]6、曲柄连杆活塞机构的活塞上受力F=400N。
如不计所有构件的重量,在曲柄上应加多大的力偶矩M是()才能使机构在图示位置平衡。
A.AB.BC.CD.D参考答案:C[单项选择题]7、两个共点力可合成一个力,一个力也可分解为两个相交的力。
一个力分解为两个相交的力可以有()个解。
A.1B.2C.3D.无穷参考答案:D[单项选择题]8、水平梁受三角形载荷作用,分布载荷的最大值为qkN/m,梁长为1,与之等效合力的大小和位置分别是()。
A.AB.BC.CD.D参考答案:B[单项选择题]9、图所示重为P=100N的物体放在水平面上,静摩擦系数F=0.3,动摩擦系数F=0.25,水平推力P=10N,则摩擦力等于()。
A.0NB.10NC.25ND.30N参考答案:B[单项选择题]10、已知某平面力系简化的最后结果为一合力,若将此平面力系向作用面内其它任一点0简化,则主矢FR 和主矩M()。
工程力学课后习题答案第六章 杆类构件的内力分析

第六章 杆类构件的内力分析6.1。
(a )(b )题6.1图解:(a )应用截面法:对题的图取截面2-2以下部分为研究对象,受力图如图一所示:BM图一图二由平衡条件得:0,AM=∑6320N F ⨯-⨯=解得: N F =9KN CD 杆的变形属于拉伸变形。
应用截面法,取题所示截面1-1以右及2-2以下部分作为研究对象,其受力图如图二所示,由平衡条件有:0,OM=∑6210N F M ⨯-⨯-=(1)0,yF=∑60N S F F --=(2)将N F =9KN 代入(1)-(2)式,得: M =3 kN·m S F =3 KN AB 杆属于弯曲变形。
(b )应用截面法 ,取1-1以上部分作为研究对象,受力图如图三所示,由平衡条件有:0,Fx =∑20NF-=图三MNF =2KN0,DM=∑210M -⨯= M =2KNAB 杆属于弯曲变形 6.2题6.2图解:首先根据刚体系的平衡条件,求出AB 杆的内力。
刚体1的受力图如图一所示D2m图一图二平衡条件为:0,CM=∑104840D N F F ⨯-⨯-⨯=(1) 刚体2受力图如图二所示,平衡条件为:0,EM=∑240N D F F ⨯-⨯= (2)解以上两式有AB 杆内的轴力为:N F =5KN6.3(a )(c )题6.3图解:(a ) 如图所示,解除约束,代之以约束反力,做受力图,如图1a 所示。
利用静力平衡条件,确定约束反力的大小和方向,并标示在图1a 中,作杆左端面的外法线n ,将受力图中各力标以正负号,轴力图是平行于杆轴线的直线,轴力图线在有轴向力作用处要发生突变,突变量等于该处总用力的数值,对于正的外力,轴力图向上突变,对于负的外力,轴力图向下突变,轴力图如2a 所示,截面1和截面2上的轴力分别为1N F =-2KN 2N F =-8KN ,n (b 2 (面N F题6.4图解(a )如图所示,分别沿1-1,2-2截面将杆截开,受力图如1a 所示,用右手螺旋法则,并用平衡条件可分别求得:1T =16 kN·m 2T =-20 kN·m ,根据杆各段扭矩值做出扭矩图如2a 所示。
工程力学_浙江大学中国大学mooc课后章节答案期末考试题库2023年

工程力学_浙江大学中国大学mooc课后章节答案期末考试题库2023年1.关于磁悬浮列车减小摩擦的方法,正确的说法是参考答案:使摩擦面脱离接触2.材料不同的两物块A和B叠放在水平面上,其中物块A放在物块B上,物块B放在地面上。
在物块B上作用一力,已知物块A重0.5kN,物块B重0.2kN,物块A、B间的摩擦系数f1=0.25,物块B与地面间的摩擦系数f2=0.2,拉动B物块所需要的最小力为参考答案:0.14kN3.一物块重600N,放在不光滑的平面上,静摩擦因数fs=0.3,动摩擦因数f=0.2,在左侧有一推力150N,物块有向右滑动的趋势。
则其此时所受的摩擦力以及最大静摩擦力分别是多少参考答案:150N、180N4.零杆不受力,所以它是桁架中不需要的杆,可以撤除参考答案:错误5.用10N的力拉着木箱在水平面上运动时,木箱受到的摩擦力是10N参考答案:错误6.用50N的力推桌子没有推动,是因为推力小于摩擦力参考答案:错误7.重心和形心是否重合取决于材料是否匀质参考答案:正确8.物体越重受到的摩擦力就越大参考答案:错误9.材料经过冷作硬化后,其比例极限和塑性分别参考答案:提高,下降10.假设一拉伸杆件的弹性模量E=300GPa,比例极限为 sp=300MPa,杆件受一沿轴线的拉力,测得轴向应变为e=0.0015,则该拉应力s的大小为参考答案:300MPa£s£450MPa11.受轴向拉伸的杆件,其最大切应力与轴线的角度为4512.一等直拉杆在两端承受拉力作用,若其一段为钢,另一段为铝,则两段的参考答案:应力相同,变形不同13.脆性材料与塑性材料相比,其拉伸性能的最大特点是参考答案:没有明显的屈服阶段和塑性变形14.现有一两端固定、材料相同的阶梯杆,其大径与小径的横截面积之比为4:1,杆的大径与小径长度相同,在大径与小径交界处施加一轴向力P,则杆的大径与小径所受轴力之比为参考答案:4:115.在低碳钢的拉伸实验中,材料的应力变化不大而变形显著增加的是参考答案:屈服阶段16.下列结论中哪些是正确的?①若压杆中的实际应力不大于该压杆的临界应力,则杆件不会失稳;②受压杆件的破坏均由失稳引起;③压杆临界应力的大小可以反映压杆稳定性的好坏;④若压杆中的实际应力大于scr=πE2/λ2,则压杆必定破坏。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五章 梁的变形测试练习1. 判断改错题5-1-1 梁上弯矩最大的截面,挠度也最大,弯矩为零的截面,转角亦为零. ( ) 5-1-2 两根几何尺寸、支承条件完全相同的静定梁,只要所受荷栽相同,则两梁所对应的截面的挠度及转角相同,而与梁的材料是否相同无关。
( ) 5-1-3 悬臂梁受力如图所示,若A 点上作用的集中力P 在A B 段上作等效平移,则A 截面的转角及挠度都不变。
( ) 5-1-4 图示均质等直杆(总重量为W ),放置在水平刚性平面上,若A 端有一集中力P 作用,使A C 部分被提起,C B 部分仍与刚性平面贴合,则在截面C 上剪力和弯矩均为零。
( ) 5-1-5 挠曲线近似微分方程不能用于求截面直( ) 5-1-6 等截挠度曲线的等于零的截面处。
( )5-1-7两简2a 均相同,受力如图所示,则两梁跨中截面的挠度不等而转角是相等的。
( )5-1-8 简支梁在图示任意荷载作用下,截面C 产生挠度和转角,若在跨中截面C 又加上一个集中力偶M 0作用,则梁的截面C 的挠度要改变,而转角不变。
( )5-面相,梁 ) 5-,因积分常 )EIx M x y )()("-= 的近。
5-2-2 已知图示二梁的抗弯度E I 相同,若使二者自由端的挠度相等,则=21P 。
5-2-3 应用叠加。
5-2-4 在梁的变5-2-5 用积分法时,求解积分常量所用到的边界条件是 ,连续条件是 。
5-2-6 用积分法求图示外伸梁的挠曲线方程时,求解积分常量所用到边界条件是 ,连续条件是 。
5-2-7 图示结构为 次超静定梁。
5-2-8 曲率与变形曲线为 曲线。
5-2-9 之比为它们的挠 5-2-10 载时,的 次方力时,挠曲线方程是x 的 次方程。
梁上作用有力偶矩时,挠曲线方程是x 的 次方程。
5-2-11 图示外伸梁,若A B 段作用有均布荷载,B C 段上无荷载,则A B 段挠曲线方程是x题5-1-3图 题5-1-4图 题5-1-8图题5-1-7图题5-1-9图 题5-2-2图 题5-2-7图 题5-2-6图 x C的 次方程;B C 段挠曲线方程是x 的 次方程。
5-2-12 减小梁变形的主要。
5-2-13已知梁的挠度曲线方程为)6x EI,则该梁的弯矩方程为 。
5-2-14 梁的变形中,挠度和截面弯矩M 的关系是 ,挠度和截面剪力Q 的关系是。
5-2-15 为使图示A B 段的挠曲线为一直线,则x = 。
5-2-16要使图示简支梁的挠曲线的拐点位于距A 端l /3处,则M 1:M 2=。
5-2-17 图示静定梁,其B D 上无荷载作用,若已知B 截面的挠度y B ,则C 截面的挠度y C = ,D 截面的转角θD = 。
中点最大挠 A .EI 48 B .EI 484 C .EI 384 D .EI335-3-2 悬臂梁长为l ,梁上作用有均布荷载q ,则自由端截面的挠度为。
( )A .EI ql 64B .EI ql 63C .EI ql 84D .EIql 835-3-3 两梁尺寸及材料均相同,而受力如图示,则两梁的A . 弯矩相同,挠曲线形状不相同B . 弯矩相同,挠曲线形状相同C . 弯矩不相同,挠曲线形状不相同D . 弯矩不相同,挠曲线形状相同5-3-4 图示(a )、(b )两梁,长度、截面尺寸及约束均相同,图(a )梁的外力偶矩作用在C 截面,图(b )梁的外力偶矩作用在B 支座的右作侧,则两梁A B 段的内力和弯曲变形的比较是 ( )。
A 。
内力相同,变形不相同B .内力及变形均相同C .内力及变形均不相同D .内力不相同,变形相同5-3-5 当用积分法求图示梁的挠度曲线方程时条件中,除x =0, θA =0;是 ( ) 。
A =(θC )右BC .D .5-3-6 荷载q (x )=f (x )作用下,梁的挠度曲线方程为⎰⎰++-=,)()(D Cx dxdx x M x EIy ,其中,积分常量 ( )。
A .0,0==D CB .0,0≠=D C题5-2-11图 题5-2-17图 2 题5-2-16图 题5-2-15图题5-3-4图C 0 (a )(b )题5-3-3图C .0,0≠≠D C D .0,0=≠D C5-3-7要反映A . 对B . 剪C . 约束条件对变形的影响D . 梁的轴向位移对变形的影响5-3-8 图示悬臂梁在B 、C 两截面上各承受一个力偶矩作用,两力偶矩大小相等,转向相反,使梁产生弯曲变形。
B 截面的变形为()。
A .0,0≠=θy B . 0,0=≠θyC .0,0≠≠θyD 。
0,0==θy5-3-9图示简支梁受集中力作用,其最大挠度f 发生在( )。
A .集中力作用处 B 。
跨中截面 C .转角为零处 D 。
转角最大处5-3-10 两简支梁E I 及l 均相同,作用荷载如图所示。
跨中截面C 分别产生挠度y C 和转角θC ,则两梁C 点的挠度及两梁C 点的转角有 ( )。
A .θC 相等,y C 不相等 B 。
θC 不相等,y C 相等 C .θC 和都不相等 D 。
θC 和y C 都相等 4.计算题5-4-1 试画出图示各梁挠曲线的大致形状 5-4布知)(设E I =常量5-4-常试求方程中的积分常量。
5-4-4 试用叠加法求图示梁B 点的挠度和转角。
(E I =常量)5作 5多少时,面的抗拉与5A B ,截面为矩形,宽度为b ,高度为h ,钢板放在刚硬地面上时原有曲率半径为ρ,在两端受力P 作用使其平直,则将有均布压力作用于刚硬地面C -C 上。
已知刚梁E (弹性模量),试求所需的P 力及其在压平时梁内的最大正应力。
5-4-8 长度为l 、抗弯刚度荷载的示刚点、钢条的一端伸出水平面一小段C D ,如图所示。
若伸出长度为a ,试求刚条翘起而不与水平面接触的C D 段的长度b 。
题5-3-5图 B题5-3-6图 题5-3-8图 (a ) (c ) (b ) 题5-4-1图题5-4-4图 题5-4-3图题5-4-6图 题5-4-5图 题5-4-7图 C5-4-10 超静定梁如图所示,A B 段内作用有均布荷载q ,当C 支座向下沉陷EIql 964=∆时,试求梁的反力。
5-4-11 矩形截面悬臂梁如图所示,梁长为l ,在沿其截面高度高度变形如图所示,若A B 梁和C D 梁的抗(2) 当B C 杆长为2,2lEI =时。
5-4-13 A B 示。
0k N /m ,,试求B 点的约束力5-4-14 悬臂相同。
已与C D 梁中点之间的间隙Δ(垂直距离),如图所示,当受P 力于Δ,试求各梁的支座反力。
5-4-15 具有初始挠度的A B 梁如图所示,梁的E I 和l 均为已知。
当梁上作用有三角形分布荷载时(q 0已知),梁便呈直线形状。
试求梁的初始挠曲线方程。
5-4-16 试根据对称性求图示梁的5-4-17 两端固定的等截面梁,梁力15-1-1 ×。
挠度和转角不仅与弯矩有关,而且,例如,当悬臂梁自由端作用有集中力P 时,自由端的M =0,但挠度和转角都是最大值。
5-1-2 ×。
凡弹性变形均与材料的弹性模量值有关。
5-1-3 √。
外力在研究的梁段以外,用等效力系代替不影响研究段的内力及变形。
5-1-4 ×。
在C 截面上弯矩为零而剪力不为力零。
5-1-5 ×。
可以用于变截面梁,只是分母中的I z 不同。
5-1-6 ×。
根据,)()("1EI x M x y =±=ρ可知曲率ρ1最大值应在M 最大的截面处(E I =常量时)。
5-1-7 √。
若将2q 分解成正对称和反对称两组,就可明显看出,在正对称的q 作用下C 点有挠度,转角等于零。
5-1-8 ×。
在C 截面加上一力偶矩后C 截面的挠度不变,而转角改变。
题5-4-10图 题5-4-11图 2 题5-4-12图2 题5-4-16图 题5-4-14图 题5-4-9解图85-1-9 ×。
应力不同,变形相同。
因为变形只与I z 有关,而T 形截面无论┬是┴还是,其惯性矩I z 是相等的。
而应力不仅与I z 有关而且还与y m a x (上下边缘到中性轴的距离)有关,┬这种方法的最大拉应力比┴这种方法的最大拉应力要大。
5-1-10 ×弯矩方程式有三个,但积分时要分成四段,因截面改变处要分段。
2.填空题5-2-1 忽略剪力Q 的影响;1)(1'≈+y5-2-2 8。
因33231)2(3a a P EI a P =,所以8)2(3321==aa P P 5-2-3 小变形及材料为线弹性 5-2-4 )()('x x y θ= 5-2-5 ;,0,0BD B A l y l x y x ∆====5-2-6AA A AB A y y y y ))(,)()(;0,02121====θθ5-2-7 二次 5-2-8EIM±=ρ1;圆弧线 5-2-9 1:16。
因16/1384)2(5/384)(544=EIl q EI l q 5-2-10 4;3;2 5-2-11 4;15-2-12 合理安排受力,减小M ;减小l ;加大E I 5-2-13 )()(x l P x M -= 5-2-14 EIx Q x y EIx M x y )()(;)()('''"-=-= 5-2-15 l -a 5-2-16 1/2 5-2-17 a y y B C 2/21=3.选择题5-3-1 A 5-3-2 C 5-3-3 A 5-3-4 B 5-3-5 B 5-3-6 D 5-3-7 C 5-3-8 D 5-3-9 C 5-3-10 B 4 计算题5-4-2 梁的挠曲线方程为(1) 求分布荷载的合力 ⎰==tKl dx x q P 033)(求合力作用点到点的距离:l P x dx x q d t43)(0=⋅=⎰ (2) 求反力:443,12433Kl P R Kl P R B A ==== (3) 列43)(3xKx x R x M A ⋅-⋅= (4) 代入EIx M y )("-=中并积分,由边界条件确定0,905=-=D Kl C 所以 )45(360)(5523l x x l EIKxx y --=5-4-3 (1)边界条件:,0,011'1===θy x 解出01=C,0,011==y x ,解出01=D(2)连续光滑条件:,)()(,22'1'21C C y y l x x ===解出 02=C ,)()(,22121C C y y lx x ===,解出02=D5-4-4 (1)只有q 作用时,EIql y EI ql q B q B 8)(,6)(43==θ (2)只有P =q l 作用时:(3)然后两者叠加: 5-4-5 (1)只有2021ql M =作用时,())(2)(,)(3)(0000↑⋅=↵=ly EI l M M B MC M A θθ(2)只有q 作用时,q A 1()(2=θ)EIl q lEI l ql y q C 8)2(23)81()(42+⋅⋅=(3)叠加:5-4-6 (1)将B 约束解除,用反力R B 代替。
