进位制
1.3.2 进位制(共31张PPT)

4.把 98(5)转化为九进制数为 解析:98(5)=9×51+8×50=53,
.
故 98(5)=58(9). 答案:58
5.127(8)化为六进制数的最高位数字是 解析:∵127(8)=1×82+2×8+7=87,
.
∴127(8)=223(6). 答案:2
应用示例 例 1 把二进制数 110011(2)化为十进制数. 解:110011(2)=1×25+1×24+0×23+0×22+1×21+1×20=1×32+1×1 6+1×2+1=51. 点评:先把二进制数写成不同位上数字与 2 的幂的乘积之和的 形式,再按照十进制的运算规则计算出结果.
题型二
k 进制数化为十进制数
【例题 2】将下列各数化成十进制数. (1)11001000(2); (2)310(8). 分析:解答本题可按其他进制转化为十进制的方法,先写成不同 位上的数乘以基数的幂的形式,再相加求和. 解:(1)11001000(2)=1×27+1×26+0×25+0×24+1×23+0×22+0×21+ 0×20=200; (2)310(8)=3×82+1×81+0×80=200.
程序框图如图所示.
程序: INPUT “a,k,n=”;a,k,n b=0 i=1 t=a MOD 10 DO b=b+t������k (i-1) a=a\10 t=a MOD 10 i=i+1 LOOP UNTIL i>n PRINT b END
^
(3)十进制数 a 化为非十进制的 k 进制数 b 的算法是除 k 取余 法. 算法步骤: 第一步,给定十进制正整数 a 和转化后的数的基数 k. 第二步,求出 a 除以 k 所得的商 q,余数 r. 第三步,将得到的余数依次从右到左排列. 第四步,若 q≠0,则 a=q,返回第二步;否则,输出全部余数 r 排列得 到的 k 进制数.
数字进位制

数字进位制一、十进制(Decimal System)十进制是我们日常生活中最常用的进位制。
它由0-9这10个数字组成。
每一位的权值都是10的幂次方,从右往左依次为10^0、10^1、10^2...以此类推。
在十进制中,数字的数值大小由高位到低位依次递增,方便人们理解和计算。
二、二进制(Binary System)二进制是计算机系统中最基础的进位制。
它只由0和1这两个数字组成。
每一位的权值都是2的幂次方,从右往左依次为2^0、2^1、2^2...以此类推。
二进制中的数值大小由高位到低位递增,与十进制不同的是,每一位只能是0或1,所以运算更加简单高效。
三、八进制(Octal System)八进制是一种较为少见的进位制,它由0-7这8个数字组成。
每一位的权值都是8的幂次方,从右往左依次为8^0、8^1、8^2...以此类推。
八进制在计算机领域中用得较少,但在Unix系统中经常使用,例如文件权限的表示就是用八进制。
四、十六进制(Hexadecimal System)十六进制是计算机系统中常见的进位制之一。
它由0-9和A-F这16个数字组成,其中A-F分别表示10-15。
每一位的权值都是16的幂次方,从右往左依次为16^0、16^1、16^2...以此类推。
十六进制在计算机领域中广泛应用,例如表示颜色、内存地址等。
五、三进制(Ternary System)三进制是一种基于3的进位制。
它由0-2这3个数字组成。
每一位的权值都是3的幂次方,从右往左依次为3^0、3^1、3^2...以此类推。
三进制在现实生活中较少使用,但在某些领域如电子工程中有一定应用,例如存储器中的三值逻辑。
六、五进制(Quinary System)五进制是一种基于5的进位制。
它由0-4这5个数字组成。
每一位的权值都是5的幂次方,从右往左依次为5^0、5^1、5^2...以此类推。
五进制在现实生活中较少使用,但在某些领域如音乐理论中有一定应用,例如五线谱的音符表示就是用五进制。
进位制

a=rnrn-1„r1r0(2)
思考 你会把三进制数10221(3)化为二进制数吗? 解:第一步:先把三进制数化为十进制数: 10221(3)=1×34+0×33+2×32+2×31+1×30 =81+18+6+1=106.
第二步:再把十进制数化为二进制数: 106=1101010(2).
∴10221(3)=106=1101010(2).
思考:那么二进制数与十进制数之间是如 何转化的呢?
例1:把二进制数110011(2)化为十进制数.
分析:先把二进制数写成不同位上数字与2的 幂的乘积之和的形式,再按照十进制数的运算规 则计算出结果. 解:110011(2) =1×25+1×24+0×23+0×22+1×21+1×20 =1×32+1×16+1×2+1=51. [引申]你会把三进制数10221(3)化为十进制数吗? 解:10221(3)=1×34+0×33+2×32+2×31 +1×30 =81+18+6+1=106.
如十进制可使用的数字有0 ~ 9十个数字,基数是10; 二进制可使用的数字有0和1,基数是2; 十六进制可使用的数字或符号有0 ~ 9等10个数字以 及A ~ F等6个字母(规定字母A ~ F对应10~15),十六进制的 基数是16.
注意:为了区分不同的进位制,常在数字的 右下脚标明基数. 如111001(2)表示二进制数,34(5)表示5进制数. 十进制数一般不标注基数.
意思是:(1)第一个数字an不能等于0; (2)每一个数字an,an-1,…,a1,a0都须小于k.
进位制

小学数学必知二进制及其应用知识点讲解
十进制:用 0~9 十个数字表示,逢 10 进 1;不同数位上的数字表示不同的含义,十位上的 2 表示 20,百位上的 2 表示 200。
所以 234=200+30+4=2 ×102+3×10+4。
=An × 10n-1+An-1 × 10n-2+An-2 × 10n-3+An-3 × 10n-4+An-4 × 10n-5+An-6×10n-7+……+A3×102+A2×101+A1×100
注意:N0=1;N1=N(其中 N 是任意自然数)
二进制:用 0~1 两个数字表示,逢 2 进 1;不同数位上的数字表示不同的含义。
( 2 ) =An × 2n-1+An-1 × 2n-2+An-2 × 2n-3+An-3 × 2n-4+An-4 × 2n-5+An-6×2n-7
+……+A3×22+A2×21+A1×20
注意:An 不是 0 就是 1。
十进制化成二进制:
①根据二进制满 2 进 1 的特点,用 2 连续去除这个数,直到商为 0,然后把每次所得的余数按自下而上依次写出即可。
②先找出不大于该数的 2 的 n 次方,再求它们的差,再找不大于这个差的 2 的 n 次方,依此方法一直找到差为 0,按照二进制展开式特点即可写出。
数学练习:进制。
2.23. 进位制

b an பைடு நூலகம்k
n 1
an 1 k
n 2
ai k a1 k
i 1
0
1.从右到左依次取k进制数各位上的数字,乘以相 应k的幂,k的幂从0开始取值,每次增加1,递增到n 2.把得到的乘积加起来,所得的结果就是相应的十 进制数.
2、十进制数转化为二进制数
例 把89化为二进制数
a02(3)=a×32+2=9a+2
即9a-2b=7.
∴2b+9=9a+2,
∵a∈{1,2},b∈{0,1},
∴当a=1时,b=1符合题意
当a=2时,b=
11 2
不合题意
∴a=1,b=1.
3.已知a=12(16),b=25(7),c=33(4),则a,b,c的大 小关系是( (A)a<b<c (C)c<a<b ) (B)c<b<a (D)b<c<a
除2取余法
所以:89=1011001(2) 1.最后一步商为0 2.将上式各步所得的余数从下到上排列,得 到:89=1011001(2)
9.若二进制数10b1(2)和三进制数a02(3)相等,求正
整数a,b.
【提示】把10b1(2)和a02(3)化成十进制数,
【解析】∵10b1(2)=1×23+b×2+1=2b+9
52014(60) 5 60 2 60 0 60 1 60 4 60 64800000 432000 0 60 4 65232064(10)
4 3 2 1
0
k进制的数 anan1an 2 ai a2a1a0( k ) 转化位十进制数的算法
5 4 3 2 1
20150908-进位制

数学学习的基本方法是 思考、总结、练习
数学学习的基本方法是 思考、总结、练习
为了区分不同的进位制,常在数的右下角标明基数, 十进制一般不标注基数.
例如十进制的133.59,写成133.59(10)
七进制的13,写成13(7);二进制的10,写成10(2)
一般地,若k是一个大于1的整数,那么以k
为基数的k进制可以表示为一串数字连写在一起
例:4FCH = 4×162 + 15× R1 + 12× R0
= 1024 + 240 + 12 = 1276D
⒊ 二进制 十六进制
转换方法:以小数点为界,利用4位二进制数与1位 十六进制数的对应关系转换。 例:1011011.100111B ?H 0101 1011.1001 1100 B 5B9CH (逆转换成立)
an an 1 a1a0( k ) an k an 1 k
n n 1
a1 k a0 k
1
0 (10)
其它进制数化成十进制数公式
二进制
数学学习的基本方法是 思考、总结、练习
在电子计算机中,数是以二进制的形式表示的。二 进制数每个数位只可能取两个不同的数码,0和1。
十进制数转化成二进制数
数学学习的基本方法是 思考、总结、练习
整数的转换可采用除2取余法,即把要转换 的十进制数的整数部分不断除以2,并记下 每次除所得余数,直到商为0为止,将所得 余数,从最后一次除得余数读起,就是这个 十进制整数所对应的二进制整数。小数部分 的转换采用乘2取整法,被转换的小数部 分,每次相乘后,所得乘积的整数部分就为 对应的十进制数,将所得小数从第一次乘得 整数读起,就是这个十进制小数所对应的二 进制小数。
四年级数论进位制
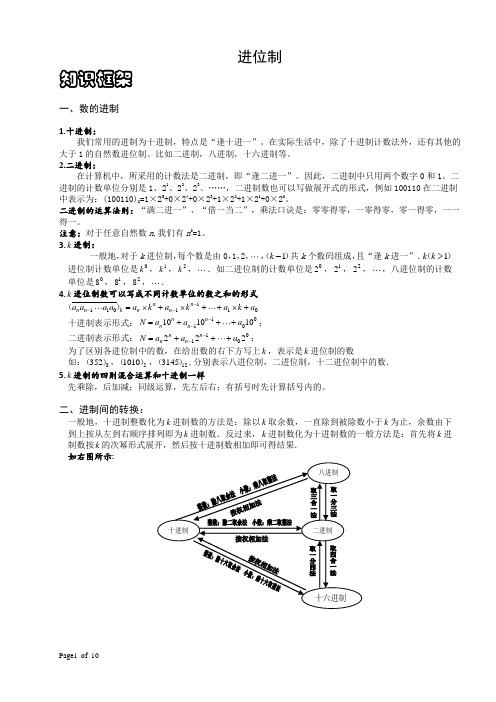
进位制知识框架一、数的进制1.十进制:我们常用的进制为十进制,特点是“逢十进一”。
在实际生活中,除了十进制计数法外,还有其他的大于1的自然数进位制。
比如二进制,八进制,十六进制等。
2.二进制:在计算机中,所采用的计数法是二进制,即“逢二进一”。
因此,二进制中只用两个数字0和1。
二进制的计数单位分别是1、21、22、23、……,二进制数也可以写做展开式的形式,例如100110在二进制中表示为:(100110)2=1×25+0×24+0×23+1×22+1×21+0×20。
二进制的运算法则:“满二进一”、“借一当二”,乘法口诀是:零零得零,一零得零,零一得零,一一得一。
注意:对于任意自然数n ,我们有n 0=1。
3.k 进制:一般地,对于k 进位制,每个数是由0,1,2,,1k -()共k 个数码组成,且“逢k 进一”.1k k >()进位制计数单位是0k ,1k ,2k ,.如二进位制的计数单位是02,12,22,,八进位制的计数单位是08,18,28,.4.k 进位制数可以写成不同计数单位的数之和的形式 1110110n n n n k n n a a a a a k a k a k a ---=⨯+⨯++⨯+()十进制表示形式:1010101010n n n n N a a a --=+++; 二进制表示形式:1010222n n n n N a a a --=+++;为了区别各进位制中的数,在给出数的右下方写上k ,表示是k 进位制的数如:8352(),21010(),123145(),分别表示八进位制,二进位制,十二进位制中的数.5.k 进制的四则混合运算和十进制一样先乘除,后加减;同级运算,先左后右;有括号时先计算括号内的。
二、进制间的转换:一般地,十进制整数化为k 进制数的方法是:除以k 取余数,一直除到被除数小于k 为止,余数由下到上按从左到右顺序排列即为k 进制数.反过来,k 进制数化为十进制数的一般方法是:首先将k 进制数按k 的次幂形式展开,然后按十进制数相加即可得结果.如右图所示:例题精讲【例 1】 把9865转化成二进制、五进制、八进制,看看谁是最细心的。
进位制

二,概念介绍
进位制:进位制是人们为了计数和运算方便而约定的 计数系统。 比如:满二进一,就是二进制;满十进一,就是十进 制;满十六进一,就是十六进制。 基数: “满几进一”就是几进制,几进制的基数就是几 例如:满二进一,就是二进制,二进制的基数就是二
三,探究新知
哪位同学能描述一下十进制的有关内容呢?(从下面 几个方面描述)
• 89=2*44+1 44=2*22+0 22=2*11+0 11=2*5+1 5=2*2+1
2
44
2 22 2 11 2 5 2 2 21 0
1
0 0
1 1
0
1
练习:一组同学把89转化为4进制的数 二组同学把89转化为5进制的数
三组同学把89转化为6进制的数制数的算法,称为除K取余法
获胜组的奖励是: 将你的算法用程序框图表示出来,并把它设计为程序 ,明天上课展示给大家。 我们在使用计算机的时,我们输入的一般是10进制的 数,计算机把它们要转化为2进制的数,然后再进行 运算,那么怎样把10进制的数化为2进制的数呢?
k进制 转化为十进制
例1、把89化为二进制数.
2 89
余数
一,知识背景
我们平时在数数的时候,19后面是20,29后面是 30,等等,也就是说,当数数时候,每当个位数满十, 十位数上就进一位,由1变成2,由2变成3,等等,其 他各位数上都是如此。在此过程中,我们已经用到了进 位制中的十进制。 我们常见的数字都是十进制的,传说,这与古人曾经以手 指计数有关,比如十两等于一斤,十厘米等于一分米等 但是并不是生活中的每一种数字都是十进制的,同学们, 你们能不能举一些生活中其它进位制的例子,同时说一 说他们的应用呢?
进位制与计算

进位制与计算在数学和计算机科学中,进位制是一种基数系统,用于计数和表示数字。
常见的进位制有十进制、二进制、八进制和十六进制。
每种进位制都有其特定的表示方法和计算规则。
一、十进制十进制是最常用的进位制,使用了0-9这10个数字。
它的计算规则是每个数字的位权是10的幂次方,从右往左逐位相加。
例如,数字123的计算方法如下:1 × 10^2 + 2 × 10^1 +3 × 10^0 = 100 + 20 + 3 = 123二、二进制二进制是计算机系统中最基本的进位制,只使用了0和1这两个数字。
它的计算规则与十进制类似,只是每个数字的位权是2的幂次方。
例如,数字101的计算方法如下:1 × 2^2 + 0 × 2^1 + 1 × 2^0 = 4 + 0 + 1 = 5在计算机中,二进制广泛用于表示和存储数据。
由于计算机内部使用的是二进制,将数据转化为二进制可以更便于计算和处理。
三、八进制八进制使用了0-7这8个数字。
它的计算规则与十进制和二进制类似,每个数字的位权是8的幂次方。
例如,数字47的计算方法如下:4 × 8^1 + 7 × 8^0 = 32 + 7 = 39在计算机领域,八进制不如二进制广泛使用,但在某些特定场景下仍然起到重要作用。
四、十六进制十六进制使用了0-9和A-F这16个数字,其中A-F分别代表10-15。
它的计算规则与其他进位制相同,每个数字的位权是16的幂次方。
例如,数字3A的计算方法如下:3 × 16^1 + 10 × 16^0 = 48 + 10 = 58十六进制在计算机领域中被广泛使用,特别是在表示存储地址和颜色等方面。
总结:进位制是一种基数系统,用于计数和表示数字。
十进制、二进制、八进制和十六进制是常见的进位制。
每种进位制都有其特定的表示方法和计算规则。
十进制是最常用的,二进制是计算机系统中最基本的。
高中数学知识点:进位制

高中数学知识点:进位制
进位制是一种记数方式,用有限的数字在不同的位置表示不同的数值.可使用数字符号的个数称为基数,基数为n ,即可称n 进位制,简称n 进制.现在最常用的是十进制,通常使用10个阿拉伯数字0-9进行记数.
对于任何一个数,我们可以用不同的进位制来表示.比如:十进数57,可以用二进制表示为111001,也可以用八进制表示为71、用十六进制表示为39,它们所代表的数值都是一样的.
表示各种进位制数一般在数字右下角加注来表示,如111001(2)表示二进制数,34(5)表示5进制数.
1.k 进制转换为十进制的方法:
012211)(0121a k a k a k a k a a a a a a a n n n n k n n +⨯+⨯++⨯+⨯=--- ,
把k 进制数a 转化为十进制数b 的算法程序为:
INPUT “ a,k,n=”;a,k,n
i=1
b=0
WHILE i<=n
t=GET a[i]
b=b+t*k^(i-1)
i=i+1
WEND
PRINT b
END
2.十进制转化为k进制数b的步骤为:
第一步,将给定的十进制整数除以基数k,余数便是等值的k进制的最低位;
第二步,将上一步的商再除以基数k,余数便是等值的k进制数的次低位;
第三步,重复第二步,直到最后所得的商等于0为止,各次所得的余数,便是k进制各位的数,最后一次余数是最高位,即除k取余法.
要点诠释:
1、在k进制中,具有k个数字符号.如二进制有0,1两个数字.
2、在k进制中,由低位向高位是按“逢k进一”的规则进行计数.
3、非k进制数之间的转化一般应先转化成十进制,再将这个十进制数转化为另一种进制的数,有的也可以相互转化.。
数的进位知识点

数的进位知识点进位是数学中非常基础的概念,它涉及到整数的表示和运算。
在日常生活和各个学科都会涉及到进位的概念,尤其在计算机科学和金融领域中更为重要。
本文将介绍数的进位的相关知识点,包括进位制、进位运算和进位的应用。
一、进位制进位制是一种计数的方法,根据不同的进位基数,可以分为十进制、二进制、八进制和十六进制等。
具体如下:1. 十进制:十进制是我们常用的计数方式,以0-9的十个数字为基础。
每当个位到达9时,就需要进位到十位,十位到达9时就需要进位到百位,以此类推。
2. 二进制:二进制是计算机中最常用的进位制,只包含0和1两个数字。
每当个位到达1时,就需要进位到十位,十位到达1时就需要进位到百位,以此类推。
3. 八进制:八进制以0-7的八个数字为基础。
每当个位到达7时,就需要进位到十位,十位到达7时就需要进位到百位,以此类推。
4. 十六进制:十六进制以0-9和A-F的共十六个数字表示。
其中A代表10,B代表11,依此类推。
每当个位到达F时,就需要进位到十位,十位到达F时就需要进位到百位,以此类推。
进位制的转换非常常见,可以通过多种方法进行计算和转换。
例如,将十进制转换为二进制可以使用除以2取余法,将十进制转换为八进制可以使用除以8取余法,将十进制转换为十六进制可以使用除以16取余法。
二、进位运算进位运算是指在进行数学运算中,当某一位的结果超过了进位制的基数时,需要把多余的进位向高位进行传递的过程。
进位运算的常见形式包括加法进位和乘法进位。
1. 加法进位:在两个数相加的过程中,当某一位的结果超过了进位制的基数时,就会产生进位。
例如,对于十进制数相加时,当个位相加的结果大于10时,就会产生进位,将个位的进位加到十位上。
2. 乘法进位:在两个数相乘的过程中,当某一位的结果超过了进位制的基数时,也会产生进位。
例如,对于十进制数相乘时,当个位相乘的结果大于10时,就会产生进位,将个位的进位加到十位上。
进位运算在数学计算过程中非常常见,可以通过列竖式的方法进行演算和解决。
进位制

二进制:
在电子计算机中,数是以二进制的形式表示的。二 进制数每个数位只可能取两个不同的数码,0和1。
二进制数与十进制数的转换:
(1)二进制数化为十进制数:
例1 把二进制数110011(2)化为十进制数.
110011 1 25 1 24 0 23 0 22 1 21 1 20 (2)
A)
an an1 a1a0( k ) (0 an k ,0 an1 ,, a1 , a0 k ).
751 7 16 5 16 116 1873 (16) (10)
2 1 0
110011 1 25 1 24 0 23 0 22 1 21 1 20 (2) =51
——进位制
一、进位制
进位制是人们为了计数和运算方便而约定的计数 系统。
比如:
满二进一,就是二进制; 满十进一,就是十进制; 满十二进一,就是十二进制; 满六十进一,就是六十进制
基数: “满几进一”就是几进制,几进制的基数就是几.
十进制: 我们最常用最熟悉的就是十进制数,它 的数值部分是十个不同的数字符号0,1,2, 3,4,5,6,7,8,9来表示的。
探究:P34
若an an 1 a1a0( k ) 表示一个k 进制数,请你把它写成各位 上数字与k的幂的乘积之和的形式。
an an 1 a1a0( k ) an k an 1 k
n n 1
a1 k a0 k
1
0 (10)
其它进制数化成十进制数公式
n
n 1
a1 k a0 k
1
0 (10)
2、十进制数化成k进制数
除k取余法
数字的进制和进位制

数字的进制和进位制数字是人类思维和交流的基础,而数字的进制和进位制是数字世界中的重要概念。
从古至今,人们使用不同的进制和进位制来表达数字,使得数字能够更好地在不同领域和文化中得到应用。
本文将介绍数字的进制和进位制的基本概念、不同进制的应用以及进位制对数字表达的影响。
一、进制和进位制的基本概念进制是指数字所使用的基数,即数字系统中使用的符号数量。
常见的数字进制有十进制、二进制、八进制和十六进制等。
在不同的进制中,每个进位的权值是不同的。
例如,在十进制中,每个进位的权值是10的倍数(1、10、100、1000……),而在二进制中,每个进位的权值是2的倍数(1、2、4、8……)。
进位制是指数位之间的位置关系,它决定了数字的位值以及进位的方式。
常见的进位制有逢十进一、逢二进一、逢八进一和逢十六进一等。
比如在十进制中,逢十进一,即当个位达到10时,向左进一位,变为十位。
二、不同进制的应用1. 十进制十进制是我们最常使用的一种进制系统,它使用0-9共10个数字来表示任意数值。
在十进制中,我们使用了阿拉伯数字,它是现代数字系统的基础。
2. 二进制二进制是计算机中最基础和最常用的进制系统。
它只使用0和1两个数字来表示任意数值。
在二进制中,每个位上的数值都是2的倍数(1、2、4、8……),通过不同位的组合,可以表示复杂的数值和字符。
3. 八进制八进制使用0-7共8个数字来表示任意数值。
在计算机科学中,八进制通常用于表示特定的位串,如文件权限和内存地址等。
4. 十六进制十六进制使用0-9和A-F共16个字符来表示任意数值。
在计算机领域中,十六进制常常用于表示颜色值、内存地址等。
不同进制有不同的应用场景,例如,二进制在计算机领域中被广泛使用,八进制和十六进制常用于表示编码或地址,而十进制则是我们日常生活和商业交易中最常用的进制。
三、进位制对数字表达的影响进位制决定了数字的位值以及进位的方式,对数字表达有重要影响。
在十进制中,进位制为逢十进一,这使得大数的表达变得更加简洁。
进位制

思考5:一般地,如何将k进制数 anan-1„a1a0(k)写成各数位上的数字与基 数k的幂的乘积之和的形式?
an an1...a1a0( k ) an k an1 k
n n 1
... a1 k a0 k
1
0
知识探究(二):k进制化十进制的算法
思考1:二进制数110011(2)化为十进制 数是什么数? 110011(2) =1×25+1×24+0×23+0×22+1×21+1×20 =32+16+2+1=51.
思考2:在十进制中10表示十,在二进制 中10表示2.一般地,若k是一个大于1的 整数,则以k为基数的k进制数可以表示 为一串数字连写在一起的形式: anan-1„a1a0(k). 其中各个数位上的数字an,an-1,„,a1, a0的取值范围如何?
思考4:十进制数4528表示的数可以写成 4×103+5×102+2×101+8×100,依此类 比,二进制数110011(2),八进制数 7342(8)分别可以写成什么式子? 110011(2) =1×25+1×24+0×23+0×22+1×21+1×20 7342(8)=7×83+3×82+4×81+2×80.
anan - 1 L a2a1(k ) = an ? k n - 1 an - 1 ? k n - 2 L + a2 ? k 1 a1 k0
知识探究(三):除k取余法
解: 根据“逢二进一”的原则,有 89=2×44+1 89=2×44+1 44= 2×22+0 = 2× (2×22+0)+1 22= 2×11+0 = 2× (2× (2× (2× 5+1)+0)+0)+1 11= 2× 5+1 5= 2× 2+1 = 2× (2× (2× (2× (2× 2+1)+1)+0)+0)+1
进位制

例1 将十进制数458分别转化为四进制 数和六进制数.
4 4
4 4 4 458 余数
6
6 6 6
458 76 12 2 0
余数 2 4 0 2
114
28 7 1
2 2 0 3
1
0
458=13022(4)=2042(6)
例2 将五进制数3241(5)转化为七进制数.
30241(5)=3×54+2×52+4×5+1 =1946.
思考2:十进制数4528表示的数可以写成 4×103+5×102+2×101+8×100,依此类比, 二进制数110011(2),八进制数 7342(8)分别
可以写成什么式子?
110011(2) =1×25+1×24+0×23+0×22+1×21+1×20=51 7342(8)=7×83+3×82+4×81+2×80=3810
十进制数一般不标注基数.
一般地,若k是一个大于1的整数,则以k为 基数的k进制数可以表示为一串数字连写在一起 的形式:
a n a n1 a1a0( k ) (an , an1 , , a1 , a0 N ,0 a n k , 0 an1, , a1 , a0 k ).
1
0
理论迁移
例1 将下列各进制数化为十进制数. (1)10303(4) ; (2)1234(5). 10303(4)=1×44+3×42+3×40=307.
1234(5)=1×53+2×52+3×51+4×50=194.
理论迁移
例2 已知10b1(2)=a02 (3),求数字a,b的值. 10b1(2)=1×23+b×2+1=2b+9. a02(3)=a×32+2=9a+2.
进位制概念及应用

进位制概念及应用一、数的进制1.十进制:我们常用的进制为十进制,特点是“逢十进一”。
在实际生活中,除了十进制计数法外,还有其他的大于1的自然数进位制。
比如二进制,八进制,十六进制等。
2.二进制:在计算机中,所采用的计数法是二进制,即“逢二进一”。
因此,二进制中只用两个数字0和1。
二进制的计数单位分别是1、21、22、23、……,二进制数也可以写做展开式的形式,例如100110在二进制中表示为:(100110)2=1×25+0×24+0×23+1×22+1×21+0×20。
二进制的运算法则:“满二进一”、“借一当二”,乘法口诀是:零零得零,一零得零,零一得零,一一得一。
注意:对于任意非零自然数n ,我们有n 0=1。
3.k 进制:一般地,对于k 进位制,每个数是由0,1,2,L ,1k -()共k 个数码组成,且“逢k 进一”.1k k >()进位制计数单位是0k ,1k ,2k ,L .如二进位制的计数单位是02,12,22,L ,八进位制的计数单位是08,18,28,L .4.k 进位制数可以写成不同计数单位的数之和的形式1110110n n n n k n n a a a a a k a ka k a ---=⨯+⨯++⨯+L L () 十进制表示形式:1010101010n n n n N a a a --=+++L ;二进制表示形式:1010222n n n n N a a a --=+++L ;为了区别各进位制中的数,在给出数的右下方写上k ,表示是k 进位制的数如:8352(),21010(),123145(),分别表示八进位制,二进位制,十二进位制中的数.5.k 进制的四则混合运算和十进制一样先乘除,后加减;同级运算,先左后右;有括号时先计算括号内的。
二、进制间的转换:一般地,十进制整数化为k 进制数的方法是:除以k 取余数,一直除到被除数小于k 为止,余数由下到上按从左到右顺序排列即为k 进制数.反过来,k 进制数化为十进制数的一般方法是:首先将k 进制数按k 的次幂形式展开,然后按十进制数相加即可得结果.如右图所示:1. 将下面的数转化为十进制的数:()21111 ()21010010 ()54301 ()1608B巩固:请将十进制数90转化成二进制、七进制和十六进制。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 3.十进制数转化为k进制数的方法:(除k 取余法) 用k连续去除该十进制数或所得的商,直到 商为零为止,然后把每次所得的余数倒着 排成一个数,就是相应的k进制数。
作业:
1、P47 3
2、P50 A3 B1
(用10个数字来记数,称基数为10) 第二、它有“数位”,即从右往左为个位、十位、 百位、千位等等。 例如:3721 表示有:1个1,2个十, 7个百即7个10的平方,3 个千即3个10的立方
3721 3 10 7 10 2 10 110
3 2 1
0
其它进位制的数又是如何的呢?
0, 则a=q, 返回第二步;否则,执
第四步,将依次得到的余数从右到左排列,得到k 进制数。
(2)程序框图:
开始 输入a,k 求a除以k的商q 求a除以k的余数r 输出r a=q q=0? 是 否
将依次输出的r从右到左排列 结束
(3)程序:
INPUT “a,k=”;a,k b=0
i=0
DO q=a\k
其它进制:
实际上,十进制数只是计数法中的一种,但它不是唯一 记数法。除了十进制数,生产生活中还会遇到非十进制的 记数制。如时间:60秒为1分,60分为1小时,它是六十进 制的。两根筷子一双,两只手套为一副,它们是二进制的。
二进制、七进制、八进制、十二进制、 六十进制…… 二进制只有0和1两个数字,七进制用0~6七个数字 十六进制有0~9十个数字及ABCDEF六个字母.
所以,110011(2)=51.
练习 1、将下面的二进制数化为十进制数? (1)11 (2)110 2、把其他进位制的数化为十进制数的公式是什么?
an an 1 a1a0( k ) an k an 1 k
n n 1
a1 k a0 k
1
0 (10)
其它进制数化成十进制数公式
比如:
满二进一,就是二进制; 满十进一,就是十进制; 满十二进一,就是十二进制; 满六十进一,就是六十进制
基数: “满几进一”就是几进制,几进制的基数就是几.
2、最常见的进位制是什么?除此之外还有哪 些常见的进位制?请举例说明. • 最常见的进位制应该是我们数学中的十进 制,比如一般的数值计算,但是并不是生活 中的每一种数字都是十进制的. • 古人有半斤八两之说,就是十六进制与十 进制的转换. • 比如时间和角度的单位用六十进位制, 计算 “一打”数值时是12进制的。 • 电子计算机用的是二进制 。
**上面的程序如采用get函数,可简化为:
INPUT a,k,n i=1 b=0 WHILE i<=n t=GET a[i] b=t*k^(i-1)+b i=i+1 WEND PRINT b END
备注:GET函数用于取出a的右数第i位数
2、十进制转换为二进制
方法:除2取余法,即用2连续去除89或所得的商,然后取余数。 例、 把89化为二进制数 解: 根据“逢二进一”的原则,有 89=2×44+1 89=2×44+1 = 2× (2×22+0)+1 44= 2×22+0 = 2×( 2×( 2×11+0)+0)+1 22= 2×11+0 = 2× (2× (2× (2× 5+1)+0)+0)+1 11= 2× 5+1 = 2× (2× (2× (2× (2× 2+1)+1)+0)+0)+1 5= 2× 2+1 所以89=2×(2×(2×(2×(2 × 2 +1)+1)+0)+0)+1 =2×(2×(2×(2×(22+1)+1)+0)+0)+1 =2×(2×(2×(23+2+1)+0)+0)+1 =2×(2×(24+22+2+0)+0)+1 =2×(25+23+22+0+0)+1 =26+24+23+0+0+20 89=1×26+0×25+1×24+1×23+0×22+0×21+1×20 所以:89=1011001(2)
探究:P43
若an an1 a1a0( k ) 表示一个k 进制数,请你把它写成各位 上数字与k的幂的乘积之和的形式。
an an 1 a1a0( k ) an k an 1 k
n n 1
a1 k a0 k
1
0 (10)
其它进制数化成十进制数公式
算法案例
(第三课时)
复习引入:
1、秦九韶算法的方法和步骤?
2、秦九韶算法的程序框图?
3、举例说明日常生活中的进位制。
新课讲解:
一、进位制
1、什么是进位制?
进位制是人们为了计数和运算方便而约定的记数系统。
进位制是一种记数方式,用有限的数字在不同的位 置表示不同的数值。可使用数字符号的个数称为基 数,基数为n,即可称n进位制,简称n进制。
二、 二进制
二进制的表示方法
二进制是用0、1两个数字来描述的.如11001
区分的写法:11001(2)或者 (11001)2 4 3 2 1 0 11001(2) 1 2 1 2 0 2 0 2 1 2
如7342(8) 八进制呢?
k进制呢? anan-1an-2„a1(k)?
例2、设计一个算法,将k进制数a(共有n位)转换为十进制 数b。
(1)算法步骤: 第一步,输入a,k和n的值; 第二步,将b的值初始化为0,i的值初始化为1; 第三步,b=b+ai*ki-1, i=i+1 第四步,判断i>n是否成立.若是,则执行第五步,否则, 返回第三步; 第五步,输010111(2)=
(3);
(4)。
小结
• 1.进位制是一种记数方式,用有限的数 字在不同的位置表示不同的数值。可使 用数字符号的个数称为基数,基数为k, 即可称k进位制,简称k进制。k进制需要 使用k个数字; • 2.十进制与二进制之间转换的方法; 先把这个k进制数写成用各位上的数字与 k的幂的乘积之和的形式,再按照十进制 数的运算规则计算出结果。
为了区分不同的进位制,常在数的右下角标明基数, 十进制一般不标注基数.
例如十进制的133.59,写成133.59(10)
七进制的13,写成13(7);二进制的10,写成10(2)
一般地,若k是一个大于1的整数,那么以k
为基数的k进制可以表示为一串数字连写在一起
的形式:
anan1 a1a0(k ) (0 an k,0 an1,, a1, a0 k ).
另解(除2取余法的另一直观写法): 2 2 2 2 2 2 2
注意: 1.最后一步商为0, 2.将上式各步所得的余数从下到上排列,得到: 89=1011001(2) 练习 将下面的十进制数化为二进制数? (1)10 (2)20
89 44 22 11 5 2 1 0
余数 1 0 0 1 1 0 1
3、十进制转换为其它进制
例1:把89化为五进制数。 解:根据除k取余法 以5作为除数,相应的除法算式为:
5 5
89 17 5 3 0
余数
4 2 3
所以,89=324(5)
例2、设计一个程序,实现“除k取余法”。
(1)、 算法步骤: 第一步,给定十进制正整数a和转化后的数的基数k; 第二步,求出a 除以k 所得的商q ,余数r; 第三步,若q 行第四步;
开始 输入a,k,n b=0 把a的右数第i位数字赋给t
b=b+t*ki-1
i=i+1
i>n?
i=1 是 输出b 结束
否
(3)程序:
INPUT “a,k,n=”;a,k,n
b=0 i=1
t=a MOD 10
DO b=b+t*k^(i-1) a=a\10 t=a MOD 10
i=i+1
LOOP UNTIL i>n PRINT b END
r=a MOD k
b=b+r*10^i i=i+1 a=q LOOP UNTIL q=0 PRINT b END
练习: 完成下列进位制之间的转化: (1)10231(4)= (2)235(7)= (3)137(10)= (4)1231(5)=
(10); (10); (6); (7);
(5)213(4)=
练习:下列写法正确的是: ( A ) A、751 (16) B、751 (7) C、095 (12) D、901 (2)
an an1 a1a0(k ) (0 an k ,0 an1,, a1, a0 k ).
3、十进制的构成 十进制由两个部分构成
十进制:“满十进一”
第一、它有0~9十个数字;
三、二进制与十进制的转换
1、二进制数转化为十进制数
例1:将二进制数110011(2)化成十进制数。
解:根据进位制的定义可知
110011( 2) 1 2 1 2 0 2 0 2 1 2 1 2
5 4 3 2 1
0
51
1 32 116 1 2 1
十进制:
我们最常用最熟悉的就是十进制数,它的数值部分是十个不 同的数字符号0,1,2,3,4,5,6,7,8,9来表示的。
例如133.59,它可用一个多项式来表示:
133.59=1*102+3*101+3*100 +5*10-1+9*10-2
式中1处在百位,第一个3所在十位,第二个3所在 个位,5和9分别处在十分位和百分位。十进制数是逢 十进一的。
