除数是小数的除法法则
整数小数分数的计算方法

整数的除法法则
1)从被除数的高位起,先看除数有几位,再用除数试除被除数的前几位,如果它比除数小,再试除多一位数;
2)除到被除数的哪一位,就在那一位上面写上商;
3)每次除后余下的数必须比除数小。
除数是整数的小数除法法则:
1)按照整数除法的法则去除,商的小数点要和被除数的小数点对齐;
2)如果除到被除数的末尾仍有余数,就在余数后面补零,再继续除。
除数是小数的小数除法法则:
1)先看除数中有几位小数,就把被除数的小数点向右移动几位,数位不够的用零补足;2)然后按照除数是整数的小数除法来除。
分数的除法法则:
1)用被除数的分子与除数的分母相乘作为分子;
2)用被除数的分母与除数的分子相乘作为分母。
(即被除数不变,乘除数的倒数)。
小数除法

(一)小数除法运算法则:1、小数除以整数的运算法则:(1)按照整数除法的法则去除(2)商的小数点要和被除数的小数点对齐(3)如果除到被除数的末尾仍有余数就在后面添上0再继续除。
(4)除得的商的哪一位上不够商1就要在那一位上写0占位。
2、小数除以小数的运算法则:(1)一看:看清被除数有几位小数(2)二移:把除数和被除数的小数点同时向右移动相同的位置,使除数变成整数,当被除数位数不足时,用“0”补足。
(3)三算:按照小数除整数的计算法则进行计算。
3、竖式中的小数点和数位的对齐方式:在加法和减法中,必须小数点对齐;在乘法中,要末尾对齐,在除法时,商的小数点要和被除数的小数点对齐。
(二)商与除数以及被除数之间的相互关系:1、商不变规律:被除数扩大a 倍(或缩小),除数也扩大(或缩小)a 倍,商不变。
简言之,被除数和除数同时扩大或者同时缩小相同的倍数,商不变。
2、商变化规律:被除数不变,除数扩大(或缩小)a 倍,商缩小(或扩大)a 倍。
被除数扩大(或缩小)a 倍,除数不变,商扩大(或缩小)a 倍。
3、一个数(0除外)除以另一个数(非零数),当除数大于1时,商小于被除数;当除数等于1时,商等于被除数;当除数小于1时,商大于被除数。
(三)近似值的相关内容:1、求商的近似值:计算时要比保留的小数多一位。
2、求积的近似值:计算出整个积的值后再去近似值。
3、保留的近似值,小数末尾的0不能去掉。
4、取商的近似值的方法:“四舍五入”法、“进一法”和“去尾法”在解决问题的时候,可以根据实际情况选择“进一法”和“去尾法”取商的近似值。
(四)循环小数的相关内容:1、小数可以分为无限小数和有限小数。
小数部分位数有限的叫有限小数,小数部分位数无限的叫无限小数。
2、 循环小数的定义:一个数的小数部分,从某一位起,一个数字或者几个数字依次不断重复出现,这样的小数叫做循环小数。
3、 是循环小数必须满足的条件:(1)、必须是无限小数。
(2)、一个数字或者几个数字依次不断重复出现4、 一个循环小数的小数部分,依次不断重复出现的一个数字或者几个数字,叫做这个循环小数的循环节;如5.33……循环节是3。
除法运算规律

除法运算规律在数学运算中,除法是一种常见的运算方式,用于将一个数分成若干等分。
除法运算规律是数学中有关除法运算的一些基本规则和性质。
本文将介绍除法运算的规律和相关概念。
一、整除和余数在进行除法运算时,可能会出现两种结果:整除和余数。
整除指的是除法的结果能够整除,没有余数;余数指的是除法的结果不能整除,还剩下的部分。
例如,对于整数18除以整数5的运算,可以得到商为3,余数为3,即18÷5=3余3。
二、除法运算法则除法运算有以下几个基本规律:1. 除以0没有意义:任何数除以0都是没有意义的,因为0不能作为除数。
2. 0除以任何数等于0:无论被除数是多少,0除以任何数的结果都是0。
3. 除数为1时,商等于被除数:当除数为1时,商等于被除数。
例如,12除以1的结果为12,即12÷1=12。
4. 商乘除数等于被除数:被除数可以由商和除数的乘积得出。
例如,12除以3等于4,即4×3=12。
5. 除数乘商加余数等于被除数:除数乘以商再加上余数等于被除数。
例如,18除以5等于3余3,即3×5+3=18。
6. 若除数和被除数的正负性相同,商为正;若除数和被除数的正负性相反,商为负。
例如,(-12)除以3等于-4,即(-12)÷3=-4。
7. 除数的倍数关系:若一个数是另一个数的倍数,则它们之间的除法结果是整数。
例如,10除以2的结果是5,即10÷2=5。
三、小数除法在除法运算中,还存在小数除法。
小数除法指的是被除数或除数中存在小数部分的除法运算。
例如,5÷2=2.5,2.5就是一个小数除法的结果。
在小数除法中,需要将两个数都转换成小数后再进行运算。
当除数为小数时,可以通过移动小数点的位置,将小数转化为整数,然后按照整数除法的规则进行运算。
当被除数为小数时,可以将小数转化为分数,然后按照分数除法的规则进行运算。
四、除法运算的应用除法运算在日常生活中有很多应用。
小数除法规律总结

小数除法规律总结 TTA standardization office【TTA 5AB- TTAK 08- TTA 2C】
1.一个数(0除外),除以一个大于1的数,商小于被除数。
一个数(0除外),除以一个小于1的数,商大于被除数。
一个数(0除外),除以一个等于1的数,商等于被除数。
2.当被除数不变时,除数扩大a倍,商缩小a倍;
当被除数不变时,除数缩小a倍,商扩大a倍。
3.当除数不变时,被除数扩大a倍,商扩大a倍;
当除数不变时,被除数缩小a倍,商缩小a倍;
4.当被除数和除数同时扩大或缩小相同的倍数,商不变。
5.当被除数大于除数时,商大于1;
当被除数小于除数时,商小于1;
当被除数等于除数时,商等于1.
6.小数除法的计算方法:
(1)用商不变定律,同时扩大
(2)按整数除法的方法去除
(3)商的小数点要和被除数的小数点对齐
(4)整数部分不够除,商0,点上小数点
(5)如果有余数,要添0再除
7.整数除法计算法则:
先从被除数的高位除起,除数是几位数,就看被除数的前几位;如果不够除,就多看一位,除到被除数的哪一位,商就写在哪一位的上面。
如果哪一位上不够商1,要补“0”占位。
每次除得的余数要小于除数。
小数除法规律总结

小数除法规律总结1.一个数(0除外),除以一个大于1的数,商小于被除数。
一个数(0除外),除以一个小于1的数,商大于被除数。
一个数(0除外),除以一个等于1的数,商等于被除数。
2.当被除数不变时,除数扩大a倍,商缩小a倍;
当被除数不变时,除数缩小a倍,商扩大a倍。
3.当除数不变时,被除数扩大a倍,商扩大a倍;
当除数不变时,被除数缩小a倍,商缩小a倍;
4.当被除数和除数同时扩大或缩小相同的倍数,商不变。
5.当被除数大于除数时,商大于1;
当被除数小于除数时,商小于1;
当被除数等于除数时,商等于1.
6.小数除法的计算方法:
(1)用商不变定律,同时扩大
(2)按整数除法的方法去除
(3)商的小数点要和被除数的小数点对齐
(4)整数部分不够除,商0,点上小数点
(5)如果有余数,要添0再除
7. 整数除法计算法则:
先从被除数的高位除起,除数是几位数,就看被除数的前几位;如果不够除,就多看一位,除到被除数的哪一位,商就写在哪一位的上面。
如果哪一位上不够商1,要补“0”占位。
每次除得的余数要小于除数。
11。
小数除法重要知识点总结

小数除法重要知识点总结要掌握小数除法的知识,首先需要了解小数的概念。
小数是整数和分数之间的一种数表示方法,它包括整数部分和小数部分。
小数部分由小数点和小数点后的数字组成,表示比一个整数大但比下一个整数小的数。
小数的概念是小数除法的基础,因此我们需要先掌握小数的概念。
在进行小数除法运算时,有一些重要的知识点需要注意:1.小数除法的基本定义。
在小数除法中,除数、被除数和商都可以是整数或者小数。
小数除法的基本定义是:被除数除以除数得商。
例如,5.6除以0.2等于28。
2.小数点的处理。
在小数除法中,小数点的位置非常重要。
当进行小数除法运算时,我们需要确保小数点的位置正确,并且在计算商的时候也需要正确地保留小数点的位置。
3.无限循环小数的处理。
在进行小数除法运算时,如果出现了无限循环小数,我们需要通过一定的方法将其化为有限循环小数或者分数表示。
4.小数除法的应用。
小数除法在日常生活中有着广泛的应用,比如计算时间、速度、价格等等。
因此,掌握小数除法的知识可以帮助我们解决很多实际生活中的问题。
在进行小数除法运算时,我们需要注意以下几点:1.确定小数点的位置。
在进行小数除法运算时,我们需要确定小数点的位置,并将其对齐。
比如,如果被除数和除数的小数点位置不同,我们需要通过移动小数点的位置将它们对齐。
2.运用除法法则。
小数除法和整数除法在运算方法上是一样的,我们仍然可以运用除法法则进行计算。
比如,我们可以先将被除数和除数都乘以相同的倍数,使得被除数变为整数,然后再进行除法运算。
3.处理无限循环小数。
在进行小数除法运算时,如果出现了无限循环小数,我们需要通过一定的方法将其化为有限循环小数或者分数表示。
这样可以使计算更加简单和准确。
当然,小数除法还有一些特殊情况需要注意:1.如果除数是小数,我们需要将其转化为整数。
在进行小数除法运算时,如果除数是小数,我们需要将其转化为整数。
比如,5.6除以0.2等于28,等价于5.6乘以10除以2。
(完整版)小数除法知识点总结

第一单元小数除法1、除数是整数的小数除法计算法则:除数是整数的小数除法,按照整数除法的法则去除,商的小数点要和被除数的小数点对齐;如果除到被除数的末尾仍有余数,就在余数后面添0再继续除。
2、除数是小数的小数除法计算法则:除数是小数的除法,先移动除数的小数点,使它变成整数;除数的小数点向右移动几位,被除数的小数点也向右移动几位(位数不够的,在被除数末尾用0补足),然后按照除数是整数的小数除法进行计算。
3、连除的算式可以写成被除数除以几个数的积,但除以几个数的积时,必须给这个相乘的式子加上小括号。
4、在小数除法中的发现:①当除数不为0时,除数大于1时,商小于被除数。
如:3.5÷5=0.7②当除数不为0时,除数小于1时,商大于被除数。
如:3.5÷0.5=7当除数不为0时,除数等于1时,商等于被除数。
如:3.5÷1=3.55、小数除法的验算方法:①商×除数=被除数(通用) ②被除数÷商=除数6、商的近似数:根据要求要保留的小数位数,决定商要除出几位小数,再根据“四舍五入”法保留一定的小数位数,求出商的近似数。
例如:要求保留一位小数的,商除到第二位小数可停下来;要求保留两位小数的,商除到第三位小数停下来……如此类推。
7、循环小数:A、小数部分的位数是有限的小数,叫做有限小数。
如,0.37、1.4135等。
B、小数部分的位数是无限的小数,叫做无限小数。
如5.3… 7.145145…等。
C、一个数的小数部分,从某位起,一个数字或者几个数字依次不断重复出现,这样的小数叫做循环小数。
(如5.3… 3.12323… 5.7171…)D、一个循环小数的小数部分,依次不断重复的数字,叫做小数的循环节。
(如5.333… 的循环节是3, 4.6767…的循环节是67,6.9258258…的循环节是258)E、用简便方法写循环小数的方法:①只写一个循环节,并在这个循环节的首位和末位上面记一个小圆点②例如:只有一个数字循环节的,就在这个数字上面记一个小圆点,5.333…写作5.3 ;有两位小数循环的,就在这两位数字上面,记上小圆点,7.4343…写作7.4 3 ;有三位或以上小数循环的,在首位和末位记上小数点,10.732732…写作10.7328、除法中的变化规律:①商不变性质:被除数和除数同时扩大或缩小相同的倍数( 0除外),商不变。
小数除法知识点总结

第一单元小数除法1、除数是整数的小数除法计算法则:除数是整数的小数除法,按照整数除法的法则去除商的小数点要和( )的小数点对齐;如果除到被除数的末尾仍有余数,就在余数后面添( )再继续除。
2、除数是小数的小数除法计算法则:除数是小数的除法,先移动除数的小数点,使它变成( );除数的小数点向右移动几位,( )的小数点也向右移动几位(位数不够的,在被除数末尾用0补足),然后按照除数是整数的小数除法进行计算。
3、在小数除法中的发现:①当除数大于1时,商小于被除数。
如:3.5÷5=0.7②当除数小于1时,商大于被除数。
如:3.5÷0.5=7练习1:4.5÷ 4.5÷ 4.5 4.5÷ 4.54、小数除法的验算方法:商×除数=被除数(通用)5、商的近似数:四舍五入、进一法、去尾法取积、商的近似值,究竟要保留几位小数,一般是根据题目要求决定。
如果题目要求保留一位小数,就要看第( )位小数;如果要求保留两位小数,就要看第( )位小数……然后按( )法取近似值。
1、在实际生活中,如果以“元”为单位,只要保留两位小数即可。
2、在实际情况中,取近似值时还可能用到“进一法”如:装油,铺地砖。
“去尾法”如做衣服,做蛋糕等。
3、取商的近似值时,要除到比需要保留的小数位数多一位,然后再四舍五入。
6、循环小数问题:1、小数部分的位数是有限的小数,叫做( )例如:5.67854。
2、小数部分的位数是无限的小数,叫做( )。
例如:5.67245...,5.6767...3、一个数的小数部分,从某位起,一个数字或者几个数字依次不断重复出现,这样的小数叫做( )例如:0.33...,5.6767...,4.123123...4、一个循环小数的小数部分,依次不断重复的数字,叫做小数的( )5、用简便方法写循环小数的方法:①只写一个循环节,并在这个循环节的首位和末位上面记一个小圆点。
小数除法的意义和法则

小数除法的意义和法则小数除法是数学中的基本运算之一,它是用来解决两个小数的除法运算的方法。
小数除法的意义在于帮助我们计算两个小数之间的商,并且可以应用到日常生活和各种实际问题中。
在进行小数除法时,需要遵循一定的法则和步骤,以确保计算的准确性和有效性。
小数除法的意义:小数除法的意义在于解决两个小数之间的除法运算。
在日常生活中,我们经常会遇到需要计算两个小数之间的商的情况,比如购物时计算折扣、计算比率、计算利息等。
小数除法可以帮助我们准确地计算出这些商,从而帮助我们更好地理解和处理实际问题。
此外,小数除法还可以帮助我们理解和应用数学中的各种概念和定理,比如分数、百分数、比率、比例等。
通过小数除法的运算,我们可以更好地理解这些概念,并且可以将它们应用到各种实际问题中,从而提高我们的数学素养和解决问题的能力。
小数除法的法则:小数除法有一些基本的法则和步骤,需要遵循才能确保计算的准确性和有效性。
下面是小数除法的基本法则:1. 将小数除法转化为整数除法:在进行小数除法时,可以将小数转化为整数,然后进行整数除法的运算。
具体做法是将被除数和除数都乘以一个适当的倍数,使得除数变为整数,然后进行整数除法的运算,最后将商转化为小数。
2. 对齐小数点:在进行小数除法时,需要确保被除数和除数的小数点对齐,以便进行准确的计算。
3. 补零:如果被除数的小数位数少于除数的小数位数,需要在被除数的末尾补零,以便进行准确的计算。
4. 进行除法运算:按照整数除法的步骤进行计算,得出商和余数。
5. 将商转化为小数:将得到的商转化为小数,并且保留适当的小数位数,以满足实际问题的要求。
小数除法的法则和步骤需要我们严格遵守,以确保计算的准确性和有效性。
通过掌握小数除法的法则和步骤,我们可以更好地进行小数除法的运算,从而解决各种实际问题。
总之,小数除法是数学中的基本运算之一,它的意义在于帮助我们解决两个小数之间的除法运算,并且可以应用到日常生活和各种实际问题中。
(精心整理)小数除法知识点
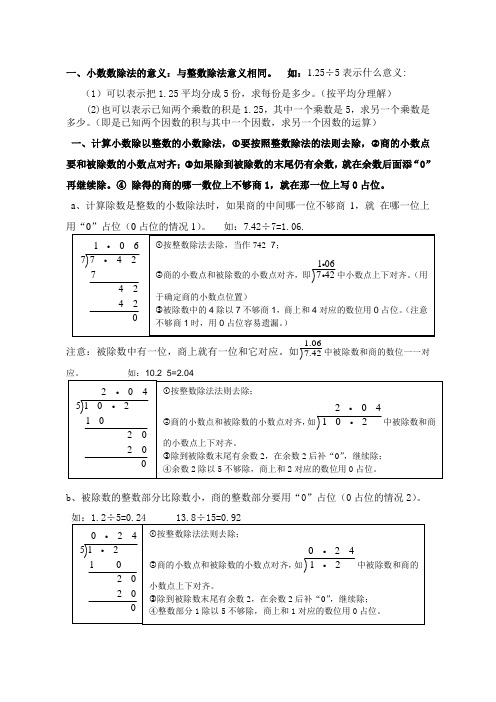
一、小数数除法的意义:与整数除法意义相同。
如:1.25÷5表示什么意义: (1)可以表示把1.25平均分成5份,求每份是多少。
(按平均分理解) (2)也可以表示已知两个乘数的积是1.25,其中一个乘数是5,求另一个乘数是多少。
(即是已知两个因数的积与其中一个因数,求另一个因数的运算) 一、计算小数除以整数的小数除法,①要按照整数除法的法则去除,②商的小数点要和被除数的小数点对齐;③如果除到被除数的末尾仍有余数,就在余数后面添“0”再继续除。
④ 除得的商的哪一数位上不够商1,就在那一位上写0占位。
a 、计算除数是整数的小数除法时,如果商的中间哪一位不够商1,就 在哪一位上用“0”占位(0占位的情况1)。
如:7.42÷7=1.06.注意:被除数中有一位,商上就有一位和它对应。
如 1.067.42中被除数和商的数位一一对应。
如:10.2÷5=2.04b 、被除数的整数部分比除数小,商的整数部分要用“0”占位(0占位的情况2)。
06424242 106742中小数点上下对齐。
对应的数位用0422020042中被除数和商,继续除; 0占位。
24202020 242中被除数和商的0”,继续除;对应的数位用0占位。
二、整数除以整数的计算方法与小数除以整数的计算方法一样,商的小数点仍旧和总结:整数除以整数商为小数的除法和小数除以整数的除法完全相同,不同的是整数做被除数时小数点没有显出来,商的小数点和被除数小数点对齐时要知道在哪里对齐;如:36÷5;36的小数点在6后面没有显示出来,因为36.0=36。
三、除数是小数的除法:商的小数点要和被除数移动后的小数点对齐。
1、除数是小数的除法,先移动除数的小数点,使它变成整数;除数的小数点向右移动几位,被除数的小数点也向右移动几位(利用的是商不变规律)(位数不够的,在被除数的末尾用“0”补足),然后按除数是整数的小数除法进行计算。
五年级数学小数除法知识点归纳(附习题及解析),一定要给孩子看

五年级数学小数除法知识点归纳(附习题及解析),一定要给孩子看《小数除法》要点知识1、小数除法的意义:已知两个因数的积与其中的一个因数,求另一个因数的运算。
如:0.6÷0.3表示已知两个因数的积0.6,一个因数是0.3,求另一个因数是多少。
2、小数除以整数的计算方法:小数除以整数,按整数除法的方法去除,商的小数点要和被除数的小数点对齐。
整数部分不够除,商0,点上小数点。
如果有余数,要添0再除。
3、除数是小数的除法的计算方法:先将除数和被除数扩大相同的倍数,使除数变成整数,再按“除数是整数的小数除法”的法则进行计算。
注意:如果被除数的位数不够,在被除数的末尾用0补足。
4、在实际应用中,小数除法所得的商也可以根据需要用“四舍五入”法保留一定的小数位数,求出商的近似数。
5、除法中的变化规律:①商不变性质:被除数和除数同时扩大或缩小相同的倍数(0除外),商不变。
②除数不变,被除数扩大(缩小),商随着扩大(缩小)。
③被除数不变,除数缩小,商反而扩大;被除数不变,除数扩大,商反而缩小。
6、(P28)循环小数:一个数的小数部分,从某一位起,一个数字或者几个数字依次不断重复出现,这样的小数叫做循环小数。
循环节:一个循环小数的小数部分,依次不断重复出现的数字。
如6.3232……的循环节是32.简写作6.327.小数部分的位数是有限的小数,叫做有限小数。
小数部分的位数是无限的小数,叫做无限小数。
小数分为有限小数和无限小数。
易错题解析1、9.97÷4.21的商保留两位小数是( )保留整数是()。
2.37 22.去掉0.25的小数点,就是把这个数扩大();把50.4的小数点向左移动两位,就是把它缩小到原来的()。
100倍百分之一3、125缩小到它的()是0.125;()扩大到它的100倍是0.3。
千分之一 0.0034、0.25除以0.15,当商是1.6时,余数是();0.79÷0.04,商是19,余数是()。
小数除法的计算方法

小数除法的计算方法
小数除法是一种常见的计算方法,它用于计算两个小数的商。
在进行小数除法时,我们需要先确定小数点的位置,然后进行计算。
例如,我们要计算 2.4 除以 0.6 的结果。
首先,我们需要对两个小数的小数点进行对齐。
在这个例子中,我们可以将 0.6 的小数点移动一位,变为 6。
这样,我们就可
以将 2.4 和 6 进行除法运算。
接下来,我们将 2.4 除以 6,得到 0.4。
所以,2.4 除以 0.6 的
结果是 0.4。
小数除法的计算方法就是这样简单。
我们只需要对两个小数的小数点进行对齐,然后进行普通的除法运算即可。
无论小数是何种形式,都可以使用这种方法进行计算。
除法的运算法则

除法的运算法则除法是数学运算中的一种基本运算,它主要用于计算两个数的商。
除法的运算法则是指在进行除法运算时需要遵守的一些规则和原则。
本文将详细介绍除法的运算法则,包括整数除法、小数除法和混合数除法的运算规则。
通过学习和理解这些法则,我们可以更好地掌握除法的计算方法,并能在实际问题中正确运用。
一、整数除法的运算法则整数除法是指两个整数相除的运算。
在进行整数除法时,需要注意以下几个运算法则:1. 商的正负号当除数和被除数的符号相同时,商为正数;当除数和被除数的符号不同时,商为负数。
2. 商的绝对值和余数整数除法中的商取两数相除后的整数部分,余数为两数相除后的余数。
例如,对于整数除法10 ÷ 3,商为3,余数为1。
3. 除数和被除数的因子关系在整数除法中,除数和被除数的因子关系必须满足:除数是被除数的因子。
即如果a ÷ b = c,则a必须是b的倍数。
二、小数除法的运算法则小数除法是指两个小数相除的运算。
与整数除法不同,小数除法需要注意以下几个运算法则:1. 被除数和除数的小数位数小数除法中,被除数和除数的小数位数可以不相同,但计算结果的小数位数应根据题目要求加以控制。
2. 商的小数位数在小数除法中,商的小数位数由除数和被除数的小数位数决定。
通常情况下,商的小数位数不宜超过两位或三位,可以根据实际情况进行取舍。
3. 除法运算中的小数点对齐小数除法中,需要将被除数的小数点和除数的小数点对齐,以便进行除法运算。
对齐后,可以将小数除法转化为整数除法运算,再根据结果确定小数点的位置。
三、混合数除法的运算法则混合数除法是指由整数和小数组成的数与整数或小数相除的运算。
在进行混合数除法时,需注意以下几个运算法则:1. 将混合数转化为带分数或假分数形式在混合数除法中,首先需要将混合数转化为带分数或假分数形式,以便进行计算。
例如,将3 1/2转化为7/2。
2. 除法运算的整数部分和小数部分混合数除法中,可以先计算除法运算的整数部分,再计算除法运算的小数部分。
小数除法法则是

小数除法法则是小数除法是数学中的一个基本运算法则,它用于计算小数之间的除法。
在小数除法中,我们需要遵循一定的步骤和规则,以确保我们得到正确的答案。
本文将介绍小数除法的基本法则,并通过一些例子来帮助读者更好地理解这一概念。
首先,让我们回顾一下小数的基本概念。
小数是指那些不是整数的数,它们可以被写成整数和分数的形式,其中分数的分母是10的幂。
例如,0.5可以写成1/2,0.75可以写成3/4。
小数除法就是要计算两个小数之间的商,即一个小数除以另一个小数。
在进行小数除法时,我们需要按照以下步骤进行:1. 将除数和被除数写成分数的形式。
如果它们已经是分数的形式,那就不需要转换了。
2. 将除数的分母乘以一个适当的倍数,使其变成整数。
同时,将被除数的分子和分母乘以相同的倍数,保持它们的比值不变。
3. 进行分数除法,即将被除数的分数除以除数的分数。
这相当于将被除数乘以除数的倒数。
4. 将得到的分数化简为最简形式,即约分。
让我们通过一个例子来说明小数除法的具体步骤。
假设我们要计算0.6除以0.2。
首先,我们将这两个小数写成分数的形式,得到6/10除以2/10。
然后,我们将除数2/10乘以5,得到10/10,同时将被除数6/10乘以5,得到30/10。
接下来,我们进行分数除法,即30/10除以10/10,得到3。
最后,我们将得到的分数3化简为最简形式,即3。
除了上面的例子,我们还可以通过其他例子来进一步说明小数除法的法则。
例如,0.75除以0.25,0.9除以0.3等等。
通过这些例子,读者可以更好地理解小数除法的步骤和规则。
总之,小数除法是数学中的一个基本运算法则,它用于计算小数之间的除法。
在进行小数除法时,我们需要按照一定的步骤和规则来进行,以确保我们得到正确的答案。
希望本文能够帮助读者更好地理解小数除法的概念和方法。
小 数 除 法

小数除法一、数学知识与方法:1、小数除法法则1-1、除数是小数的除法,先移动()的小数点,使它变成()数,除数的小数点向右移动几位,()的小数点也向()移动几位,位数不够的,在()的末尾用()补足,然后按照除数是()数的小数除法进行计算。
1-2、计算2.025÷1.47时,先将1.47的小数点去掉,相当于把小数点向()移动()位,使它变成()数,再将除数2.205的小数点向()移动()位,最后按除数是整数的除法进行计算。
1-3、两个数相除时,如果除数扩大100倍,要使商不变,被除数应扩大()倍。
1-4、两个数的商是1.8,如果被除数和除数同时扩大到原来的10倍,则商是()。
1-5、两个不为0的数相除,除数()时,商就大于被除数;除数()时,商就小于被除数。
1-5、由21.45÷15=1.43,可知2.145÷15=(),214.5÷0.15=()。
1-6、两个因数的积是3.56,如果两个因数同时扩大到原来的10倍,则积是()。
1-9、0.25时()分 3.75千米=()米560千克=()吨1-10、在下列括号内填上适当的数0.56÷0.7=()÷7=()0.56÷0.07=()÷7=()8.64÷3.6=()÷36=()8.64÷0.36=()÷36=( )1-11、除法中,如果除数扩大10倍,要使商不变,被除数也要()。
1-112、两个数相除的商是256,被除数是128,那么除数是()。
1-12、用竖式计算75.6÷0.18 57.38÷9.5 35.1÷7.8 9.6÷0.320.396÷1.2= 0.756÷0.36= 27.5÷0.025=70.3-17.48÷7.6 3.64÷5.2×23.32、循环小数2-1一个小数,从小数部分的某一位起,或依次不断地出现,这样的小数叫做()。
