排队论
排队论

11.排队论11.1基本概念排队现象是指到达服务机构的顾客数量超过服务机构提供服务的容量,也就是说顾客不能够立即得到服务而产生的等待现象。
顾客可以是人,也可以是物,比如说,在银行营业部办理存取款的储户,在汽车修理厂等待修理的车辆,在流水线上等待下一到工序加工的半成品,机场厂上空等待降落的飞机,以及等待服务器处理的网页等,都被认为是顾客。
服务机构可以是个人,像理发员和美容师,也可以是若干人,像医院的手术小组。
服务机构也还可以是包装糖果的机器,机场的跑道,十字路口的红绿灯,以及提供网页查询的服务器等等。
11因为顾客到达,服务时间具有不确定性,排队系统又称随机服务系统,它的基本结构如图1.所示:商业服务理发店,银行柜台,机场办理登机手续的柜台,快餐店的点餐柜台运输行业城市道路的红绿灯,等待降落或起飞的飞机,出租车制造业待修理的机器,待加工的材料,生产流水线社会服务法庭,医疗机构为了描述一个排队系统,我们需要说明输入(到达)和输出(服务)过程,及其他基本特征。
表2.11列举了一些排队系统的到达和服务过程。
表11.2: 排队系统举例)1(到达过程通常,我们假设顾客的相继到达间隔时间是相互独立并且都具有相同概率分布。
在许多实际(Poisson流,或指数分布。
顾客源可能是有限的,也可情况中,顾客的相继到达间隔是服从泊松)能是无限的。
顾客到来方式可能是一个接一个的,也可能是批量的。
比如,到达机场海关的旅行团就是成批顾客。
一般来说,我们假设到达过程不受排队系统中顾客数量的影响。
以银行为例,无论银行内有3位顾客还是300位顾客,顾客来到银行的到达过程是不会受到影响的。
但是在两种情况下到达过程与排队系统中的顾客数量相关。
第一种情况发生在顾客源是有限的系统,比如某工厂共有五台机床,若在维修部中已有两台机床,接下来到达维修部的最大量是三台。
另一种情况是当顾客到达排队系统时,如果服务机构的设施都被占用,顾客可能耐心等待,也可能选择离开。
运筹学第五章排队论

§2 排队论基本理论总廓
§2.1 排队论研究的基本问题
1.排队系统的统计推断:即通过对排队系统主 要参数的统计推断和对排队系统的结构分析,判 断一个给定的排队系统符合于哪种模型,以便根 据排队理论进行研究。
3. 服务机构
1)服务机构可以是单服务员和多服务员服务, 这种服务形式与队列规则联合后形成了多种不同队 列,不同形式的排队服务机构,如:
1 单队单服务台
1
2
..
..
nLeabharlann 多队多服务台(并列)1
2 。。。
n
单队多服务台(并列)
1
2
... n
单队多服务台(串列)
1
1
2
3
2
混合形式
2)服务方式分为单个顾客服务和成批顾客服务。 3)服务时间分为确定型和随机型。 4)服务时间的分布在这里我们假定是平稳的。
值得注意的是求稳态概
率Pn并不一定求t→∞的 极限,而只需求
P ’(t)=0 即可。
过渡状态
稳定状态
t
图3 排队系统状态变化示意图
3.根据排队系统对应的理论模型求出用以判断系统 运行优劣的基本数量指标的概率分布或特征数。 数量指标主要包括:
(1)平均队长(Ls):系统中的顾客数。 平均队列长(Lq):系统中排队等待服务的顾客数。 系统中顾客数Ls =系统中排队等待服务的顾客数Lq +正被
含优化设计与优化运营。
问题1 系统中顾客数=平均队列长(Lq)+1?
§2.3 排队论主要知识点
排队论

排队长度:等待服务的顾 客数量
平均等待时间:顾客在系统 中等待服务的平均时间
平均排队长度:系统中平均 排队的顾客数量
服务台数量:系统中的服 务台数量
利用率:服务台被利用的 程度
排队系统的稳定性:系统是 否处于稳定状态,即平均等 待时间和平均排队长度是否
收敛
排队系统的分析方法
01
排队论的基本概 念:顾客到达、 服务时间、等待
服务台:提供服务的地方
队列:等待服务的顾客队列
顾客到达时间:顾客到达服 务台的时间 服务台容量:服务台可以同 时服务的顾客数量 排队系统状态:当前系统中 顾客和服务员的状态
排队系统的参数
顾客到达率:单位时间内到 达系统的顾客数量
服务速率:单位时间内服务 台能够服务的顾客数量
排队规则:先进先出(FIFO) 或后进先出(LIFO)
谢谢
排队论
演讲人
排队论的基本概念 排队论的基本原理Biblioteka 目录CONTENTS
排队论的应用实例
排队论的基本概念
排队系统的定义
1
排队系统:由顾 客和服务台组成 的系统,顾客需 要等待服务台的
服务。
2
服务台:提供某 种服务的设施, 如收银台、售票
窗口等。
3
顾客:需要接受 服务台的服务的 人,如顾客、乘
客等。
4
时间均服从指数分布
M/G/1模型:单服务台、单 队列、顾客到达服从泊松分 布、服务时间服从指数分布
M/G/c模型:单服务台、多 队列、顾客到达服从泊松分 布、服务时间服从指数分布
M/G/∞模型:单服务台、 无限队列、顾客到达服从泊 松分布、服务时间服从指数
分布
G/M/1模型:多服务台、单 队列、顾客到达服从泊松分 布、服务时间服从指数分布
排队论

f ( w n 1)
n!
e w
w0
f ( w ) Pn f ( w n 1) n0 ( w ) n w (1 ) n e ( )e ( ) w n0 n!
熊燕华
6.
忙期和闲期
系统忙的概率为ρ ,则闲的概率为1-ρ 。可以 认为在一段时间内,忙期和闲期的长度比为 ρ :(1-ρ ) 由于顾客到达间隔服从无记忆性的负指数分布, 且与服务时间无关。闲期I(系统从空闲开始到新 的顾客到达时刻)服从参数为λ 的负指数分布,则 E[I]=1/λ E[B]= ρ/(1-ρ) E[I]=1/(μ-λ )=Ws
熊燕华
L S n Pn
n0
1
Little公式
Ls=Lq+λ/μ Ws=Wq+1/μ
L q (n 1) Pn n 1
Ws=E(W)=1/(μ-λ) Wq=Ws-1/μ=ρ/(μ-λ)
Ws=Ls/λ
Wq=Lq/λ
熊燕华
定理: 对于存在平稳分布的任何排队系统,下列 关系成立:
熊燕华
七、随机过程知识准备
系统的状态
系统中的顾客数,即如果系统中有n个顾客即说系统 状态为n。在平稳过程中,在时刻t、系统状态为n的概率 Pn(t)是不变的,即Pn(t) =Pn是不随时间变化的统计平衡 状态解。
注:本章研究的均为平稳过程,即输入、输出过程 的概率分布、参数均不随时间变化,与所选取的时
第八章 排队论
基本概念 单服务台泊松到达负指数服务时间排队模型 多服务台泊松到达负指数服务时间排队模型 其他排队模型 经济分析
熊燕华
排队论

(t )n et P( X (t ) n) n!
E ( X (t )) t
e t f T (t ) 0 1 E (T )
for t 0 for t 0
服务时间的概率 = t 1/ : 平均服务时间
在t时间内已经服务n个顾客 的概率 平均服务率=
队列
队列容量
有限/无限 先来先服务(FCFS);后来先服务; 随机服务; 有优先权的服务;
排队规则
3.服务机构
服务机构
服务设施, 服务渠道与服务台 服务台数量:1台和多台 服务时间分布:
指数, 常数,
排队模型分类-Kendall记号
Kendall 记号: X/Y/Z/ A/B/C 顾客到达时间间隔分布/服务时间分布/服务台数 目/排队系统允许的最大顾客容量/顾客总体数量/ 排队规则 M/M/1///FCFS M/M/1 / M: 指数分布 (Markovian) D: 定长分布 (常数时间) Ek: k级Erlang 分布 GI:一般相互独立的时间间隔分布 G: 普通的概率分布 (任意概率分布)
0.3 0.25 0.2 0.15 0.1 0.05 0 0 2 4 6 8 10 12 14 16 18 20 22 24 NUMBER IN SYSTEM 26 28 30 32 34 36 38 40
Probability
74.94% 0.2506 1.2294 1.9788 0.2734 0.4401 0.7494 0.1007
排队模型的记号
系统状态 = 排队系统顾客的数量。 N(t) = 在时间 t 排队系统中顾客的数量。 队列长度 = 等待服务的顾客的数量。 Pn(t) = 在时间t,排队系统中恰好有n个顾客的概率。 s = 服务台的数目。
交通流理论—排队论

组成
排队系统的组成 (1) 输入过程:就是指各种类型的"顾客(车辆或行人)"按怎样的规律到 达。有各式各样的输入过程,例如: D—定长输入:顾客等时距到达。 M—泊松输入:顾客到达时距符合负指数分布。 Ek—爱尔朗输入:顾客到达时距符合爱尔朗分布。
组成
排队系统的组成
(2)排队规则:指到达的顾客按怎样的次序接受服务。 例如: • 损失制:顾客到达时,若所有服务台均被占,该顾客就自动消失,永不再来。 • 等待制:顾客到达时,若所有服务台均被占,他们就排成队伍,等待服务,
离去 1
到达
离去 2
到达 1
离去
2
...
n
单通道多服务台系统
到达
离去
1
到达
离去
(组1)成单通道服务系统
到达
离去
服务台的排列方式1
服务台
单通道单服务台系统
(2)多通道服务系统
(2) 多通道服务系统
离去
1
到达
离去 2
3
离去
可通的多通道系统
到达 1
离去
2
...
n
单通道多服务台系统
到达
离去
1
到达
离去
2
到达
M/M/1系统及其应用
其他参数
平均非零排队长度:
qw
1
1
(qw q ) (辆)
即排队不计算没有顾客的时间,仅计算有顾客时的平均排队长度, 即非零排队。如果把有顾客时计算在内,就是前述的平均排队长度。
M/M/1系统及其应用
其他参数
系统中顾客数超过k的概率:
P(n k) 1 P(n k)
k
1- Pi 1 (1 (1 ) ... k (1 )) i 0
排队论知识点(一)

排队论知识点(一)排队论知识点详解什么是排队论排队论是应用概率论、随机过程和数学统计方法来研究队列系统的数学理论。
队列系统是指一些处理实体以确定的方式到达某个系统,被系统以某种方式处理,然后离开系统的系统模型。
排队论研究的目标是为了通过合理的设计和优化队列系统(如银行服务台、电话交换机等)的结构和参数,提高系统的效率和性能。
排队论的主要概念1. 到达过程到达过程是指实体到达队列系统的时间间隔的随机过程。
根据到达的规律性和随机性不同,到达过程可以分为不可预测的泊松到达过程和可预测的非泊松到达过程。
2. 服务过程服务过程是指队列中的实体被处理的时间间隔的随机过程。
根据服务的规律性和随机性不同,服务过程可以分为不可预测的指数服务过程和可预测的非指数服务过程。
3. 队列长度队列长度是指队列中正在等待服务的实体的个数,也可以看作是在系统中等待服务的实体的数学期望。
4. 平均等待时间平均等待时间是指实体在队列系统中等待服务的平均时间。
5. 利用率利用率是指队列系统中服务设备的利用情况,通常用平均到达率与平均服务率的比值来表示。
排队论的基本模型1. M/M/1模型M/M/1模型是排队论中最简单的模型之一,代表了一个单一服务台和一个队列的排队系统。
M/M/1模型的到达过程和服务过程都是泊松过程,服务设备能力为1。
2. M/M/C模型M/M/C模型是M/M/1模型的扩展,代表了含有C个服务台和一个队列的排队系统。
到达过程和服务过程仍然是泊松过程,但是服务设备能力为C。
3. M/G/1模型M/G/1模型是M/M/1模型的变体,代表了一个单一服务台和一个队列的排队系统,但是服务过程是一般分布。
到达过程仍然是泊松过程。
4. G/G/1模型G/G/1模型代表了一个单一服务台和一个队列的排队系统,到达过程和服务过程都是一般分布。
排队论的应用1. 交通拥堵排队论可以用来研究交通拥堵的原因和解决方案,进一步优化交通网络资源的利用和流量的分配。
运筹学-排队论

定长分布(D):每个顾客接受的 服务时间是一个确定的常数。
负指数分布(M):每个顾客接受
的服务时间相互独立,具有相同
的负指数分布:
b(t)=
e- t
t0
0
t<0
其中>0为一常数。
K阶爱尔朗分布(En):
b(t)=
k(kt)k-1
(K-1)!
e- kt
当k=1时即为负指数分布;k 30,近似
M/M/1 等待制排队模型
单服务台问题,又表示为M/M/1/ : 顾客相继到达时间服从参数为的负 指数分布;服务台数为1;服务时间 服从参数为的负指数分布;系统的 空间为无限,允许永远排队。
队长的分布
记 Pn=p{N=n} , n=0,1,2….为系统达到平衡状态后队 长的概率分布,
则 n=;n= ,= /<1, 有Pn= (1-)n n=0,1,2….
排队系统类型:
顾客到达
服务台串联排队系统
排队系统类型:
聚
散
服务机构
(输入)
(输出)
随机聚散服务系统
随机性——顾客到达情况与顾客 接受服务的时间是随机的。
一般来说,排队论所研究的排队 系统中,顾客相继到达时间间隔 和服务时间这两个量中至少有一 个是随机的,因此,排队论又称 随机服务理论。
顾客(单个或成批)相继到达的时
间间隔分布:这是刻划输入过程的
最重要内容。令T0=0,Tn表示第n顾
客到达的时刻,则有T0T1 T2…..
Tn ……
记Xn= Tn –Tn-1
n=1,2,…,则Xn是第n顾客与第n-1顾
客到达的时间间隔。
一般假定{Xn}是独立同分布,并 记分布函数为A(t)。
(完整)排队论
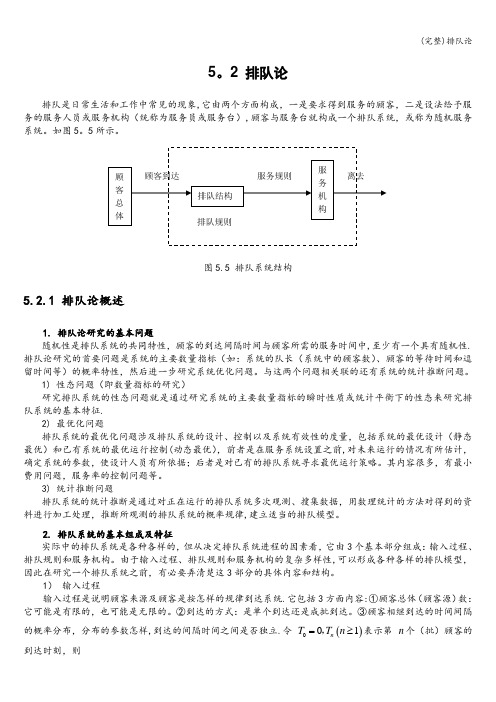
5。
2 排队论排队是日常生活和工作中常见的现象,它由两个方面构成,一是要求得到服务的顾客,二是设法给予服务的服务人员或服务机构(统称为服务员或服务台),顾客与服务台就构成一个排队系统,或称为随机服务系统。
如图5。
5所示。
图5.5 排队系统结构5.2.1 排队论概述1. 排队论研究的基本问题随机性是排队系统的共同特性,顾客的到达间隔时间与顾客所需的服务时间中,至少有一个具有随机性.排队论研究的首要问题是系统的主要数量指标(如:系统的队长(系统中的顾客数)、顾客的等待时间和逗留时间等)的概率特性,然后进一步研究系统优化问题。
与这两个问题相关联的还有系统的统计推断问题。
1) 性态问题(即数量指标的研究)研究排队系统的性态问题就是通过研究系统的主要数量指标的瞬时性质或统计平衡下的性态来研究排队系统的基本特征.2) 最优化问题排队系统的最优化问题涉及排队系统的设计、控制以及系统有效性的度量,包括系统的最优设计(静态最优)和已有系统的最优运行控制(动态最优),前者是在服务系统设置之前,对未来运行的情况有所估计,确定系统的参数,使设计人员有所依据;后者是对已有的排队系统寻求最优运行策略。
其内容很多,有最小费用问题,服务率的控制问题等。
3) 统计推断问题排队系统的统计推断是通过对正在运行的排队系统多次观测、搜集数据,用数理统计的方法对得到的资料进行加工处理,推断所观测的排队系统的概率规律,建立适当的排队模型。
2. 排队系统的基本组成及特征实际中的排队系统是各种各样的,但从决定排队系统进程的因素看,它由3个基本部分组成:输入过程、排队规则和服务机构。
由于输入过程、排队规则和服务机构的复杂多样性,可以形成各种各样的排队模型,因此在研究一个排队系统之前,有必要弄清楚这3部分的具体内容和结构。
1) 输入过程输入过程是说明顾客来源及顾客是按怎样的规律到达系统.它包括3方面内容:①顾客总体(顾客源)数:它可能是有限的,也可能是无限的。
排队论

退出前一页后一页前一页后一页退出退出前一页后一页前一页后一页退出退出前一页后一页前一页后一页退出退出前一页后一页前一页后一页退出退出前一页后一页前一页后一页退出退出前一页后一页前一页后一页退出退出前一页后一页前一页后一页退出退出前一页后一页前一页后一页退出退出前一页后一页前一页后一页退出退出前一页后一页前一页后一页退出退出前一页后一页前一页后一页退出退出前一页后一页前一页后一页退出退出前一页后一页退出前一页后一页退出前一页后一页退出前一页后一页退出前一页后一页随机服务系统理论与展望退出前一页后一页随机服务系统理论与展望退出前一页后一页随机服务系统理论与展望退出前一页后一页随机服务系统理论与展望退出前一页后一页退出前一页后一页退出前一页后一页随机服务系统理论与展望退出前一页后一页随机服务系统理论与展望退出前一页后一页随机服务系统理论与展望退出前一页后一页随机服务系统理论与展望退出前一页后一页退出前一页后一页退出前一页后一页随机服务系统理论与展望退出前一页后一页随机服务系统理论与展望退出前一页后一页随机服务系统理论与展望退出前一页后一页随机服务系统理论与展望退出前一页后一页退出前一页后一页退出前一页后一页随机服务系统理论与展望退出前一页后一页随机服务系统理论与展望随机服务系统理论与展望退出前一页后一页。
运筹学排队论

降低平均服务时间
降低服务时间旳可变性
增长服务人员
降低平均到达人数
经过顾客预约等方法来降低到达旳可变性
集中使用服务资源
更加好地计划和调度
23
处理排队问题旳措施
2.其他措施
服务场合提供娱乐设施
医生等待室放报纸杂志
自动维修间用收音机或电视
航空企业提供空中电影
等待电梯处放镜子
超级市场把冲动性商品摆放在收款台附
排队论
1
2
•
排队论,又称随机服务系统理论(,是一
门研究拥挤现象(排队、等待)旳科学。详细
地说,它是在研究多种排队系统概率规律性
旳基础上,处理相应排队系统旳最优设计和
最优控制问题。
•排队论是1923年由丹麦工程师爱尔朗
(A.K.Erlang)在研究电活系统时创建旳.
3
案例-1 银行排队系统
4
案例-2 医院排队系统
用更快旳服务人员、机器或采用不同旳设施布局和政
策来影响顾客旳到达时间和服务时间。
9
1 排队论旳基本问题
1.1 排队论旳主要研究内容
• 数量指标
– 研究主要数量指标在瞬时或平稳状态下旳
概率分布及其数字特征,了解系统旳基本
运营特征。
• 统计推断
– 检验系统是否到达平稳状态;检验顾客到
达间隔旳独立性;拟定服务时间分布及参
数。
• 系统优化
– 系统旳最优设计和最优运营问题。
10
1.2排队论旳经济含义
• 排队问题旳关键问题实际上就是对不同
原因做权衡决策。管理者必须衡量为提
供更快捷旳服务(如更多旳车道、额外
旳降落跑道、更多旳收银台)而增长旳
排队论

泊松输入中的顾客到达间隔时间 T 相互独立且服从同参数 λ 的负指数分 布,其密度函数为
其平均到达间隔时间为
λ 称为到达率。
三. 排队系统的主要特征
1. 输入过程 ⑴ 定长输入( D, Deterministic ) ⑵泊松输入 (最简单流, M ) ⑶ 一般独立输入( G,General Independent ) —— 指顾客到达间隔时间 T 为相互独立且同分布的随机变量。最简单 流是它的一个特例。 此外,在本章所讨论的排队系统中,总假定输入过程是平稳的,或 称对时间是齐次的。 平稳的输入过程 —— 指顾客到达间隔时间的分布与时间无关。否则就称 为非平稳的。
服务台m
服务台 1
⑸
服务台 2
服务台 1 服务台 2
···
···
服务台 m
服务台 m
三. 排队系统的主要特征
1. 输入过程 2. 服务时间 τ 的分布 3. 服务机构(服务台) 4. 服务规则
⑴ 先到先服务(FCFS) ⑵ 后到先服务(LCFS)
如信息处理、仓库中堆积的货物等。 ⑶ 随机服务(SIRO) ⑷ 优先权服务(PR) ⑸ 一般服务规则(GD)
1909年,由丹麦工程师爱尔朗(A.K.Erlang)在研究电话系统时初创的。
§l 排队论的基本概念及研究的问题
一.排队论中有两个基本概念:
顾客:把提出需求的对象称为顾客(或需求); 服务:把实现服务的设施称为服务机构(或服务台)。
顾客和服务机构组成一个排队系统,称为随机服务系统。 因此也称排队论为随机服务系统理论
⑴ 定长输入( D, Deterministic ) —— 每隔一定时间 α 到达一个顾客,顾客到达间隔时间 T 的分布函数为
三. 排队系统的主要特征
运筹学第十章 排队论

一类非常重要其广泛存在的排队系统是生灭过程排队系统。 生灭过程是一类特殊的随机过程,在生物学、物理学、运筹学 中有广泛的应用。
定义1 设{N(t),t≥0 }为一个随机过程。 如N(t)的概率分布具有以下性质:
(1)假设N(t)= n,则从时刻 t 起到下一个顾客到达时刻止的 时 间服从参数为λn 的负指数分布,n=0,1,2,…。
排队是我们在日常生活和生产中经常遇到的现象。例如, 上、下班搭乘公共汽车;顾客到商店购买物品;病员到医 院看病;旅客到售票处购买车票;学生去食堂就餐等就常 常出现排队和等待现象。
除了上述有形的排队之外,还有大量的所谓“无形”排队现 象,如几个顾客打电话到出租汽车站要求派车,如果出租汽 车站无足够车辆、则部分顾客只得在各自的要车处等待,他 们分散在不同地方,却形成了一个无形队列在等待派车。
到 (7)无限长,顾客到达系统后均可进入系统排队或接受服务, (8)这类系统又称为等待制排队系统。
有限排队系统
损失制排队系统(排队空间为0的系统) (允许排队,但又不
混合制排队系统 允许队列无限长)
损失制排队系统 (排队空间为0的系统)
这是指如果顾客到达排队系统时,所有服务台都已被先来的顾 客占用,那么他们就自动离开系统永不再来。典型例子是,如 电话拔号后出现忙音,顾客不愿等待而自动挂断电话,如要再 打,就需重新拔号,这种服务规则即为损失制。
二、排队系统的描述
实际中的排队系统各有不同,但概括起来都由三个基本部 分组成:
1 输入过程; 2 排队及排队规则 3 服务机制
1.输入过程. 这是指要求服务的顾客是按怎样的规律到达排队系统的 过程,有时也把它称为顾客流. 一般可以从3个方面来描述一个输入过程。
排队论

X/Y/Z/A/B/C
前三项意义不变,而 A——系统容量限制N; B——顾客源数m; C——服务规则:FCFS(先到先服务);LCFC (后到先服务)。
约定: 如省略后三项,表示 M / M / 2 / ∞ / ∞ / FCFS
排队系统
湖北工业大学 理学院 ZNL
1、队长Ls: 指在系统中的顾客数。 2、排队长Lq: 指系统中排队等候服务的顾客数。
3、M/M/1参数计算
u M/M/1 模型
(1)系统中平均顾客数(Ls)
LS nPn (1 ) 2 2(1 ) 3 3(1 ) n0 (1 )( 2 2 3 3 )
记
S 2 2 3 3 S 2 2 3 3 4
(1
)S
2
3
1
Ls
1
-λP0+μP1=0
(3)
λPn-1+μPn+1-(λ+μ)Pn=0
(4)
由式(3)得
P1
P0
通过求解可得
Pn
( )n
P0
,
u M/M/1 模型 n 0,1,2,
Pn
n1
P0 ( 1 2
)
P0
1
1
1
1
P0 1 Pn n (1 ), n 1
参数意义:
λ —— 单位时间内到达的平均顾客数 μ —— 单位时间内服务的平均顾客数 ρ —— 服务强度
例 (1)顾客到达某商店的间隔时间服从参数为10的指数分 布等同于(2)该商店在单位时间内到达的顾客数服从参数为 10的泊松分布
注:(1)指两个顾客到达商店的平均间隔时间是0.1个单位 时间.
(2)指一个单位时间内平均到达10个顾客
排队论讲解

排队论是一种研究排队系统的数学理论,它主要用于研究系统在不同的服务策略下的性能指标,如平均等待时间、平均服务时间、系统吞吐量等。
排队系统是指由顾客和服务台组成的系统,顾客按照先来先服务的原则依次到达服务台,并在服务台得到服务。
排队论的基本模型包括M/M/s、M/M/c、M/G/s、M/G/c等模型,其中M表示顾客到达的随机变量是泊松分布,G表示服务时间的随机变量是几何分布,c表示服务台的容量限制,s表示系统的服务速度。
M/M/s模型是指服务台的服务速度s是固定的,即服务台的服务速度不受顾客到达的影响,这种模型主要用于研究系统的平均等待时间和平均服务时间。
M/M/c模型是指服务台的容量限制c是固定的,即服务台的服务速度受到顾客到达的影响,这种模型主要用于研究系统的排队长度和服务率。
排队论的应用非常广泛,包括电话系统、银行系统、航空系统、医疗系统等。
在实际应用中,排队论可以帮助企业优化服务流程,提高服务质量,减少顾客等待时间,提高顾客满意度,从而提高企业的竞争力和经济效益。
排队论的应用还在不断地拓展和深化,例如近年来出现的排队论模型包括多服务台排队模型、排队网络模型、排队论与动态优化模型等。
这些模型可以更好地模拟实际系统中的复杂排队情况,提高系统的服务质量和效率。
(完整版)排队论模型

排队论模型排队论也称随机服务系统理论。
它涉及的是建立一些数学模型,藉以对随机发生的需求提供服务的系统预测其行为。
现实世界中排队的现象比比皆是,如到商店购货、轮船进港、病人就诊、机器等待修理等等。
排队的内容虽然不同,但有如下共同特征:➢有请求服务的人或物,如候诊的病人、请求着陆的飞机等,我们将此称为“顾客”。
➢有为顾客提供服务的人或物,如医生、飞机跑道等,我们称此为“服务员”。
由顾客和服务员就组成服务系统。
➢顾客随机地一个一个(或者一批一批)来到服务系统,每位顾客需要服务的时间不一定是确定的,服务过程的这种随机性造成某个阶段顾客排长队,而某些时候服务员又空闲无事。
排队论主要是对服务系统建立数学模型,研究诸如单位时间内服务系统能够服务的顾客的平均数、顾客平均的排队时间、排队顾客的平均数等数量规律。
一、排队论的一些基本概念为了叙述一个给定的排队系统,必须规定系统的下列组成部分:➢输入过程即顾客来到服务台的概率分布。
排队问题首先要根据原始资料,由顾客到达的规律、作出经验分布,然后按照统计学的方法(如卡方检验法)确定服从哪种理论分布,并估计它的参数值。
我们主要讨论顾客来到服务台的概率分布服从泊松分布,且顾客的达到是相互独立的、平稳的输入过程。
所谓“平稳”是指分布的期望值和方差参数都不受时间的影响。
➢排队规则即顾客排队和等待的规则,排队规则一般有即时制和等待制两种。
所谓即时制就是服务台被占用时顾客便随即离去;等待制就是服务台被占用时,顾客便排队等候服务。
等待制服务的次序规则有先到先服务、随机服务、有优先权的先服务等,我们主要讨论先到先服务的系统。
➢服务机构服务机构可以是没有服务员的,也可以是一个或多个服务员的;可以对单独顾客进行服务,也可以对成批顾客进行服务。
和输入过程一样,多数的服务时间都是随机的,且我们总是假定服务时间的分布是平稳的。
若以ξn表示服务员为第n个顾客提供服务所需的时间,则服务时间所构成的序列{ξn},n=1,2,…所服从的概率分布表达了排队系统的服务机制,一般假定,相继的服务时间ξ1,ξ2,……是独立同分布的,并且任意两个顾客到来的时间间隔序列{Tn}也是独立的。
第10章 排队论 《运筹学》PPT课件全

WL
Wq
Lq
W
1
M/M/s 混 合 制 排 队 模 型
一、 单服务台混合制模型
M/M/1/K: 顾客的相继到达时间服从参数 为λ的负指数分布(即顾客的到达过程为 Poisson流),服务台个数为1,服务时间V 服从参数为μ的负指数分布,系统的空间 为K。
单
平稳状态下队长N的分布pn=P{N=n},n=0,1,2,…。
服
由于所考虑的排队系统中最多只能容纳K个顾 客(等待位置只有K-1个),因而有
务 台
n
0
n
n=0,1,2,...,K-1 n≥K n=1,2,...K
混 合
有
Cn
(
)n
n
n=0,1,2,...,K
0
n>K
制
故 pn n p0 n=1,2,…,K
模 型
1
其中,p0
1
1
K
n
1
K
1
1
n1
统
其分布函数为B(t),密度函数为b(t),则
的
常见的分布有: (1) 定长分布(D)
描
(2) 负指数分布(M)
述
(3) k阶爱尔朗分布(Ek):
排
排队系统的符号表示
队
“Kendall记号”,其一般形式为:X/Y/Z/A/B/C,其中 XX:顾客到达时间间隔的分布
系
YY:服务时间的分布
统
Z Z:服务台个数
的
A :系统容量 B B:顾客源数量
符
C C:服务规则
号
例 (M / M / 1 /
FCFS)表示:
表
到达间隔为负指数分布,服务时间也为负指数分 布,1个服务台,顾客源无限,系统容量也无限,
排队论

实用排队论排队论又称随机服务系统,它应用于一切服务系统,包括生产管理系统、通信系统、交通系统、计算机存储系统。
它通过建立一些数学模型,以对随机发生的需求提供服务的系统预测。
现实生活中如排队买票、病人排队就诊、轮船进港、高速路上汽车通过收费站、机器等待修理等等。
一、排队论的基本构成(1)输入过程输入过程是描述顾客是按照怎样的规律到达排队系统的。
包括①顾客总体:顾客的来源是有限的还是无限的。
②到达的类型:顾客到达是单个到达还是成批到达。
③相继顾客到达的时间间隔:通常假定是相互独立同分布,有的是等间隔到达,有的是服从负指数分布,有的是服从k 阶Erlang 分布。
(2)排队规则排队规则指顾客按怎样的规定的次序接受服务。
常见的有等待制,损失制,混合制,闭合制。
当一个顾客到达时所有服务台都不空闲,则此顾客排队等待直到得到服务后离开,称为等待制。
在等待制中,可以采用先到先服务,如排队买票;也有后到先服务,如天气预报;也有随机服务,如电话服务;也有有优先权的服务,如危重病人可优先看病。
当一个顾客到来时,所有服务台都不空闲,则该顾客立即离开不等待,称为损失制。
顾客排队等候的人数是有限长的,称为混合制度。
当顾客对象和服务对象相同且固定时是闭合制。
如几名维修工人固定维修某个工厂的机器就属于闭合制。
(3)服务机构服务机构主要包括:服务台的数量;服务时间服从的分布。
常见的有定长分布、负指数分布、几何分布等。
二、排队系统的数量指标(1)队长与等待队长队长(通常记为s L )是指系统中的平均顾客数(包括正在接受服务的顾客)。
等待队长(通常记为q L )指系统中处于等待的顾客的数量。
显然,队长等于等待队长加上正在服务的顾客数。
(2)等待时间等待时间包括顾客的平均逗留时间(通常记为s W )和平均等待时间(通常记为q W )。
顾客的平均逗留时间是指顾客进入系统到离开系统这段时间,包括等待时间和接受服务的时间。
顾客的平均等待时间是指顾客进入系统到接受服务这段时间。
42交通流理论排队论

泊松输入、定长服务、单个服务台的系统可以写 成M/D/1。
同样可以理解M/ Ek /N,D/M/N…等符号的含义。
如果不附其它说明,则这种符号一般都指先到先 服务,单个服务通道的等待制系统。
3)排队系统的主要数量指标
d n
w d 1
四、M/M/N系统
1 .计算公式 在 M / M / N 排队系统中,服务通道 有 N 条,所以也叫“多通道 服务”系统。 设 为进入多通道服务系统 车辆的平均到达率,排 队行列从每个服务台 接受服务后的平均输出 率为 ,则每个服务台的平均 服务时间是 1 / 。 仍记 / ,则 / N 称为 M / M / N 系统的服务强度或交通 强度,亦可称 为饱和度。和 M / M / 1相仿,当 / N 1时系统是稳定的,否则 不稳定,排 队长度将趋向于无穷大 。
M / M / N 系统根据车辆排队方式 的不同,可分为: 1)单路排队多通道服务 :指排成一个队等待数 条通道服务的情况,排 队 中头一车辆可视哪条通 道有空就到哪里去接受 服务;
2)多路排队多通道服务 的一队车辆服务,车辆 组成的系统,其计算公
:指每个通道各排一个 不能随意换队。此种情 式亦相同。
例:有一公路与铁路的交叉口,火车通过时,栅栏关闭的时
间 tr= 0.1h。已知公路上车辆以均一的到达率=900(辆/h)
到达交叉口,而栅栏开启后排队的车辆以均一的离去率u= 1200(辆/h)离开交叉口。试计算由于关闭栅栏而引起的:
单个车辆的最长延误时间tm, 最大排队车辆数Q, 排队疏散时间t 0, 排队持续时间t j 受限车辆总数n,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
运筹学Ⅱ排队论教学目的与要求通过对本章的学习,使学生了解在增添物流服务设备时,就要增加投资或发生空闲浪费;减少物流服务设备,物流排队现象就会严重。
排队论的任务就是如何在这两者之间取得平衡。
在熟悉和掌握排队论基本概念和基本模型的基础上,最终能够运用排队论的方法对物流管理中的设备投资和排队问题进行分析、建模并求解,以期提高服务质量,降低成本。
排队论排队论(queuing theory),是讨论有关顾客在服务系统上的活动情形,因而排队论有时也称为“随机服务系统”(Random Service System Theory),或称作“拥挤理论”。
是为研究和解决具有拥挤现象的问题而发展起来的一门应用数学的分支。
具体地说,它是在研究各种排队系统概率规律性的基础上,解决相应排队系统的最优设计和最优控制问题。
排队论•现代排队论起源于19世纪末20世纪初,二战后发展成为一门完整而丰富的理论学科。
•排队论是1909年由丹麦工程师爱尔朗(A.K.Erlang)在研究电话系统时创立的;•几十年来排队论的应用领域越来越广泛,理论也日渐完善。
特别是自二十世纪60年代以来,由于计算机的飞速发展,更为排队论的应用开拓了宽阔的前景。
•学术界一般将其发展历程分为以下几个阶段。
排队论(1)萌芽阶段⏹1909~1920年,丹麦数学家、电气工程师爱尔朗用概率论方法研究电话通话问题,从而开创了这门应用数学学科,并为这门学科建立了许多基本原则。
⏹之后从事排队论研究的先驱人物有法国数学家勃拉彻、前苏联数学家欣钦、瑞典数学家巴尔姆等,他们用数学方法深入地分析了电话呼叫的本征特性,促进了排队论的研究。
⏹20世纪30年代中期,当费勒引进了生灭过程时,排队论才被数学界承认是一门重要的学科。
排队论(2)产生阶段⏹在第二次世界大战期间和第二次世界大战以后,排队论在运筹学这个新领域中变成了一个重要的内容。
20世纪50年代初,英国人堪道尔对排队论作了系统的研究,他用嵌入马尔柯夫链方法研究排队论,使排队论得到了进一步的发展。
是他首先(1951年)用3个字母组成的符号A/B/C表示排队系统。
其中A表示顾客到达时间的分布,B表示服务时间的分布,C表示服务机构中的服务台的个数。
⏹排队论与存量理论、水库问题等的联系开始于20世纪50年代末到60年代初,这期间,先后问世的重要著作有优先排队问题、网络队列问题。
塔卡奇等人将组合方法引进排队论,使它更能适应各种类型的排队问题。
⏹60年代,排队论研究的课题日趋复杂,因而开始了近似法的探讨与队列上下限问题的研究。
在应用方面,排队论已经渗透到了生产系统和交通运输系统。
排队论(3)发展阶段⏹70年代后,由于排队问题多呈网络出现,计算上的烦琐使得研究范围扩及到计算方法上面,人们开始研究排队网络和复杂排队问题的渐近解等,这成为研究现代排队论的新趋势。
⏹排队论的发展、推广起自于实际应用的需要,同时由于近代计算工具的精密、快速以及排队问题本身趋于复杂的倾向决定了排队论研究的方向。
排队论在现代物流管理中的运用(1)交通运输系统⏹港口的码头是服务台,船只为顾客,码头的使用决定了港口的吞吐量,船只过久等待进港造成罚款都是应当注意的问题。
⏹飞机跑道或者停机坪可以作为服务台,飞机起降为顾客的服务要求,如何安排飞机班次便利旅客并使飞机起降有条不紊,是机场调度的重要问题。
⏹铁路公路交通站可视作一个大服务台,服务系统上的队长为交通站内旅客以及送行者的总人数,通过对人数变化的了解,可帮助设计者决定交通站建筑的容量、旅客候车或候机室座位的多寡等。
排队论在现代物流管理中的运用(2)仓储配送服务储存系统中存量的变化是随机行为,和排队论中的队列长度变化的随机行为有相似之处。
排队论在现代物流管理中的运用(3)综合物流管理⏹在物流系统中排队的现象很多,如决策系统收发物流信息能力的强弱,服务网点的布局与服务水平的高低,物流设施设备的多少与服务能力的大小,服务内容的多寡与服务质量的好坏等等。
⏹由此可见,排队问题不是一个简单的服务问题,它是一个管理问题。
表面上的排队问题背后,实际上隐藏着急待改善管理的“大文章”。
排队论排队论(queuing theory)研究内容包括三个部分:⏹(1) 排队系统的性态问题⏹(2) 排队系统的最优化问题⏹(3) 排队系统的统计推断问题❿性态问题,即研究各种排队系统的概率规律性,主要研究队长分布、等待时间分布和忙期分布等。
❿最优化,又分静态最优和动态最优,前者指最优设计,后者指现有排队系统的最优运营。
❿统计推断,即判断一个给定的排队系统符合哪种模型,以便根据排队理论进行研究。
❿解排队问题的目的,是研究排队系统运行的效率,估计服务质量,确定系统参数的最优值,以决定系统结构是否排队论⏹第1节基本概念⏹第2节到达间隔的分布和服务时间的分布⏹第3节单服务台负指数分布排队系统的分析⏹第4节多服务台负指数分布排队系统的分析⏹第5节一般服务时间M/G/1模型⏹第6节经济分析——系统的最优化⏹第7节分析排队系统的随机模拟法第1节基本概念1.1 排队过程的一般表示 1.2 排队系统的组织和特征 1.3 排队模型的分类1.4 排队问题的求解不同的顾客与服务组成了各式各样的服务系统。
顾客为了得到某种服务而到达系统、若不能立即获得服务而又允许排队等待,则加入队列排队等待接受服务,然后服务台按一定规则从队列中选择顾客进行服务,获得服务的顾客立即离开系统。
❿排队过程的一般模型各个顾客由顾客源(总体)出发,到达服务机构(服务台、服务员)前排队等候接受服务,服务完成后离开。
排队结构指队列的数目和排列方式,排队规则和服务规则是说明顾客在排队系统中按怎样的规则、次序接受服务的。
到达的顾客要求服务内容服务机构1.不能运转的机器2.修理技工3.病人4.电话呼唤5.文件稿6.提货单7.到达机场上空的飞机8.驶入港口的货船9.上游河水进入水库10.进入我方阵地的敌机修理领取修配零件诊断或动手术通话打字提取存货降落装(卸)货装(卸)放水,调整水位我方高射炮进行射击修理技工发放修配零件的管理员医生(或包括手术台)交换台打字员仓库管理员跑道货码头(泊位)水闸管理员我方高射炮形形色色的排队系统实际的排队系统虽然千差万别,但是它们有以下的共同特征:(1)有请求服务的人或物——顾客;(2)有为顾客服务的人或物,即服务员或服务台;(3)顾客到达系统的时刻是随机的,为每一位顾客提供服务的时间是随机的,因而整个排队系统的状态也是随机的。
排队系统的这种随机性造成某个阶段顾客排队较长,而另外一些时候服务员(台)又空闲无事。
排队系统由三个基本部分组成:①输入过程②排队规则③服务机构输入过程输入即指顾客到达排队系统。
输入过程是指要求服务的顾客是按怎样的规律到达排队系统的过程,有时也把它称为顾客流。
一般可以从以下几个方面来描述—个输入过程(1)顾客的总体数,又称顾客源、输入源。
这是指顾客的来源。
顾客源可以是有限的,也可以是无限的。
例如,到售票处购票的顾客总数可以认为是无限的;上游河水流入水库可以认为顾客总体是无限的例如,某个工厂因故障待修的机床则是有限的。
输入过程(2)顾客到来的方式。
这是描述顾客是怎样来到系统的,他们是单个到达,还是成批到达。
病人到医院看病是顾客单个到达的例子。
在库存问题中如将生产器材进货或产品入库看作是顾客,那么这种顾客则是成批到达的。
输入过程(3)顾客流的概率分布,或称相继顾客到达的时间间隔的分布。
这是求解排队系统有关运行指标问题时,首先需要确定的指标。
这也可以理解为在一定的时间间隔内到达K 个顾客(K=1、2、 )的概率是多大。
顾客相继到达的间隔时间可以是确定型的,也可以是随机型的。
例如:在流水线上装配的各部件必须按确定的时间间隔到达装配点,定点运行的列车、班机的到达也都是确定的;例如:物流配送等待的顾客、办理出关手续的顾客、通过路口的车辆的到达都是随机的。
输入过程对于随机的情形,必须了解单位时间的顾客到达数或相继到达的时间间隔的概率分布。
顾客流的概率分布一般有定长分布、二项分布、泊松流(最简单流)、爱尔朗分布等若干种。
输入过程(4)顾客的到达可以是相互独立的。
(5)输入过程可以是平稳的,或称对时间是齐次的,即描述相继到达的间隔时间分布和所含参数(如期望值、方差等)都是与时间无关的。
排队规则这是指服务台从队列中选取顾客进行服务的顺序。
一般可以分为损失制、等待制和混合制等3大类。
(1)损失制。
这是指如果顾客到达排队系统时,所有服务台都已被先来的顾客占用,那么他们就自动离开系统永不再来。
例如:电话拔号后出现忙音,顾客不愿等待而自动挂断电话,如要再打,就需重新拔号,这种服务规则即为损失制。
排队规则(2)等待制。
这是指当顾客来到系统时,所有服务台都不空,顾客加入排队行列等待服务。
例如:排队等待售票,故障设备等待维修等。
对于等待制,为顾客进行服务的次序可以采用下列各种规则:先到先服务(FCFS)后到先服务(LCFS)随机服务(RS)有优先权的服务排队规则(2)等待制(续)。
①先到先服务。
按顾客到达的先后顺序对顾客进行服务,这是最普遍的情形。
②后到先服务。
例如:仓库中迭放的钢材,后迭放上去的都先被领走。
③随机服务。
即当服务台空闲时,不按照排队序列而随意指定某个顾客去接受服务。
例如:电话交换台接通呼叫电话。
④优先权服务。
例如:老人、儿童先进车站;危重病员先就诊;遇到重要数据需要处理计算机立即中断其他数据的处理等。
排队规则(3)混合制.这是等待制与损失制相结合的一种服务规则,一般是指允许排队,但又不允许队列无限长下去。
具体说来,大致有三种:①队长有限。
②等待时间有限。
③逗留时间有限。
排队规则(3)混合制①队长有限。
当排队等待服务的顾客人数超过规定数量时,后来的顾客就自动离去,另求服务,即系统的等待空间是有限的。
具体地,最多只能容纳K个顾客在系统中,当新顾客到达时,若系统中的顾客数(又称为队长)小于K,则可进入系统排队或接受服务;否则,便离开系统,并不再回来。
例如:水库的库容是有限的,旅馆的床位是有限的。
排队规则(3)混合制①队长有限。
②等待时间有限。
即顾客在系统中的等待时间不超过某一给定的长度T,当等待时间超过T时,顾客将自动离去,并不再回来。
例如:易损坏的电子元器件的库存问题,超过一定存储时间的元器件被自动认为失效。
例如:顾客到饭馆就餐,等了一定时间后不愿再等而自动离去另找饭店用餐。
排队规则(3)混合制①队长有限。
②等待时间有限。
③逗留时间(等待时间与服务时间之和)有限。
例如:用高射炮射击敌机,当敌机飞越高射炮射击有效区域的时间为t时,若在这个时间内未被击落,也就不可能再被击落了。
不难注意到,损失制和等待制可看成是混合制的特殊情形,如记s为系统中服务台的个数,则当K=s时,混合制即成为损失制;当K=∞时,混合制即成为等待制。
