层次分析法经典案例
层次分析法的应用实例

层次分析法的应用实例层次分析法(Analytic Hierarchy Process,简称AHP)是一种运用于多准则决策问题的定性和定量分析方法。
通过将决策问题分解为多个层次,从而使决策问题的结构更加清晰,更容易理解和处理。
下面将介绍几个AHP方法的应用实例。
1.项目选择在项目选择过程中,可能存在多个关键因素需要权衡。
通过应用AHP,可以将项目选择问题分解为几个层次,例如项目目标、资源投入、风险等等。
然后为每个层次的因素确定权重,从而帮助决策者更加客观地评估不同项目的优劣,并做出最佳选择。
2.供应商评估当公司需要选择供应商时,往往需要考虑多个方面的因素,例如价格、质量、交货时间等等。
通过使用AHP,可以将供应商评估问题分解为不同的准则和子准则,然后为每个准则和子准则赋予合适的权重,最终确定出最佳供应商。
3.市场调研在市场调研过程中,可能涉及到多个调研指标和因素。
通过应用AHP,可以将市场调研问题分解为几个层次,例如调研目标、调研方法、数据可靠性等等。
然后为每个层次的因素确定权重,从而辅助决策者选择最适合的市场调研方法和指标。
4.产品设计在产品设计过程中,需要考虑多个因素,例如功能、性能、成本等等。
通过使用AHP,可以将产品设计问题分解为不同的准则和子准则,然后为每个准则和子准则赋予合适的权重,从而帮助设计团队确定出最佳的产品设计方案。
5.企业战略规划在企业战略规划中,需要综合考虑多个战略选项的优劣。
通过应用AHP,可以将战略规划问题分解为不同的层次和因素,例如市场前景、竞争环境、技术能力等等。
然后为每个层次的因素确定权重,从而辅助决策者选择最佳的战略规划方案。
综上所述,层次分析法在多准则决策问题的应用非常广泛。
通过将决策问题分解为多个层次,然后根据不同层次的因素确定权重,能够帮助决策者更加客观地评估不同方案的优劣,并做出最佳选择。
这种方法在项目选择、供应商评估、市场调研、产品设计和企业战略规划等领域都有重要的应用。
《供应链管理》第五章案例:层次分析法在选择第三

在供应链管理中,选择合适的第三方合作伙伴至关重要。本案例将介绍层次 分析法在第三方选择中的应用,以帮助您更好地理解这一决策方法。
案例介绍
首先,让我们来了解一下这个案例。在供应链管理中,第三方指的是外部公司或个体,为原公司提供从物流到运输 等各种服务。
第三方选择的重要性
选择合适的第三方合作伙伴是供应链管理中的关键决策之一。一个优秀的第三方可以提供高质量的服务,降低成本 并提高效率。
层次分析法的概念
层次分析法是一种多准则决策方法,旨在帮助决策者权衡不同因素并做出最 佳选择。它将决策问题划分为多个层次,并对每个层次进行评估和比较。
层次分析法的步骤
层次分析法是一种有效的决策方法,可以应用于供应链管理中的第三方选择。通过合理运用该方法,您可以做出明 智的决策,提升供应链运作效率和质量。
1
制定比较矩阵
2
对每个层次的准则和备选方案之间的相对重 要性进行配对比较,使用比较矩阵记录结果。
3
建立层次结构
将决策问题划分为准则、子准则和备选方案 Leabharlann 层次,建立层次结构。计算权重
根据比较矩阵计算每个层次的准则和备选方 案的权重。
使用层次分析法进行第三方选择的实例
识别需求
确定需要外部合作的具体需求和目 标,例如物流、分销等。
确定准则
制定评估的准则,如价格、服务质 量、可靠性等。
比较备选方案
使用层次分析法比较备选的第三方 合作伙伴,评估其在各个准则上的 表现。
优势和限制
优势
层次分析法能够帮助决策者全面考虑各种因素,提高决策的准确性和可靠性。
限制
层次分析法的实施需要大量的数据和专业知识,并且结果可能受主观因素的影响。
层次分析法经典案例

层次分析法经典案例层次分析法(Analytic Hierarchy Process, AHP)是一种常用的多准则决策方法,被广泛应用于企业管理、工程项目评估、市场调研等领域。
本文将通过一个经典案例,介绍层次分析法的基本原理和应用过程。
一、案例背景某企业计划购买新设备,以提升生产效率和质量。
然而,在众多可选设备中,如何选择最适合企业发展的设备成为了业主面临的难题。
为了解决这一问题,业主决定应用层次分析法进行设备选择。
二、层次分析法基本原理层次分析法基于一个重要思想,即将复杂的决策问题拆解为具有层次结构的多个因素,并通过层次化的比较和综合分析,最终得出决策结果。
1. 构建层次结构首先,我们需要将决策问题划分为不同的层次,并构建层次结构。
在这个案例中,可以将设备选择问题划分为三个层次:目标层、准则层和备选方案层。
目标层代表企业的最终目标,即实现高效生产;准则层包括影响设备选择的各种准则,如设备价格、性能指标、售后服务等;备选方案层包括具体的设备选项。
2. 建立判断矩阵接下来,我们需要对不同层次的因素进行两两比较,建立判断矩阵。
通过专家主观判断,给出两个因素之间的相对重要性,采用1-9的尺度,其中1代表两者具有相同重要性,9代表一个因素相对于另一个因素极端重要。
比如,在准则层中,设备性能指标对设备价格的重要性为6。
3. 计算权重向量利用判断矩阵,我们可以计算出每个层次的权重向量。
通过对判断矩阵进行归一化处理,可获得各因素的权重。
权重向量表示了各因素对当前决策的贡献程度,可作为后续分析的依据。
例如,计算准则层中各因素的权重向量。
4. 一致性检验为了保证判断矩阵的合理性,我们需要进行一致性检验。
通过计算一致性指标和一致性比率,评估判断矩阵是否存在较大的一致性问题。
若一致性比率超过一定阈值,需要检查和修正判断矩阵。
5. 优先级排序最后,结合各层次的权重,我们可以进行优先级排序,得出对不同备选方案的排序结果。
根据排序结果,我们可以选择最合适的备选方案。
层次分析法经典案例

层次分析法经典案例层次分析法是一种比较常见且实用的决策分析方法,通过对待比较的各种方案的因素逐一分析,将其组织成一种层次结构,然后再运用数学方法对其进行计算,得出最终的结果。
经典案例有很多,比如金融领域、生产制造等许多行业都可以应用到层次分析法,下面我来介绍一下层次分析法在一个工厂的生产制造中的应用案例。
某工厂是一家生产钢管的制造厂,该工厂本着“质量第一、信誉第一”的原则,一直都很重视生产制造中的质量管控。
但是,由于市场竞争日益激烈,不断有新的小厂涌现,压力越来越大,所以该工厂决定对生产制造中的质量问题进行深入分析,并采用层次分析法,制定出更加合理的质量管控方案。
该工厂首先将生产制造中的质量管控分成了几个层次,分别是管理层次、生产层次、产品层次和客户需求层次,当然,每个层次下面还有自己的一些小要素,如管理层次下面就包括质量文化、质量指数等等,生产层次下面包括人员培训、设备状态等等,小要素比较复杂,不做过多介绍。
接下来是层次分析法的重头戏,对每个小要素的影响程度进行量化,以及对不同小要素之间的相关性进行评估,这是做好层次分析法的关键,必须要准确评估,否则得出的结果很可能会偏差较大。
为了保证量化的准确性,该工厂引入了专家协助,共同制定出适合该企业的一套量化标准。
原本需要量化的小要素有50个,经过专家评估和筛选,最终选出了20个,其余30个小要素的影响程度与剩下的20个小要素的相关性贡献较小,因此不被列入对比。
在对20个小要素进行量化之后,该工厂得出了各小要素的权重值,这个权重值表示每个小要素对于决策结果的影响程度,根据这些权重值,可确定各个小要素的重要性,从而制定出更加合理的质量管控方案。
经分析,该工厂管控方案的优先级排序如下:1.产品质量:该项权重值为0.408,被认为是影响质量管理的最重要因素,因为一个工厂的根本目的就是要生产出高质量的产品,切实提高其竞争力。
2.生产管理与控制:该项权重值为0.325,生产管理是确保产品质量的基础,虽然位于产品质量之下,但同样很重要。
经典层次分析法分析及实例教程

A2
A3
A4
A5
A1
A2
A3
A4
A5
1
1/2
4
3
3
2
1
7
5
5
1/4
1/7
1
1/2
1/3
1/3
1/5
2
1
1
1/31Βιβλιοθήκη 5311分别表示 景色、费用、 居住、饮食、 旅途。
由上表,可得成对比较矩阵
单击此处添加小标题
旅游问题的成对比较矩阵共有6个(一个5阶,5个3阶)。
单击此处添加小标题
问题:两两进行比较后,怎样才能知道,下层各因素对上 层某因素的影响程度的排序结果呢?
当 时,认为层次总排序通过一致性检验。到 此,根据最下层(决策层)的层次总排序做出最后决策。
层次分析法的基本步骤归纳如下
该结构图包括目标层,准则层,方案层。
1.建立层次结构模型
对每个成对比较矩阵计算最大特征值及其对应的特征向量,利用一致性指标、随机一致性指标和一致性比率做一致性检验。若检验通过,特征向量(归一化后)即为权向量;若不通过,需要重新构造成对比较矩阵。
比较尺度:(1~9尺度的含义)
2,4,6,8表示第 个因素相对于第 个因素的影响介于上述 两个相邻等级之间。不难定义以上各尺度倒数的含义, 根据 。
由上述定义知,成对比较矩阵
则称为正互反阵。 比如,例2的旅游问题中,第二层A的各因素对目标层Z 的影响两两比较结果如下:
满足一下性质
Z
单击此处添加小标题
,即令
04
d) 对于预先给定的精度 ,当下式成立时
STEP 03
STEP 01
STEP 02
层次分析法具体应用及实例
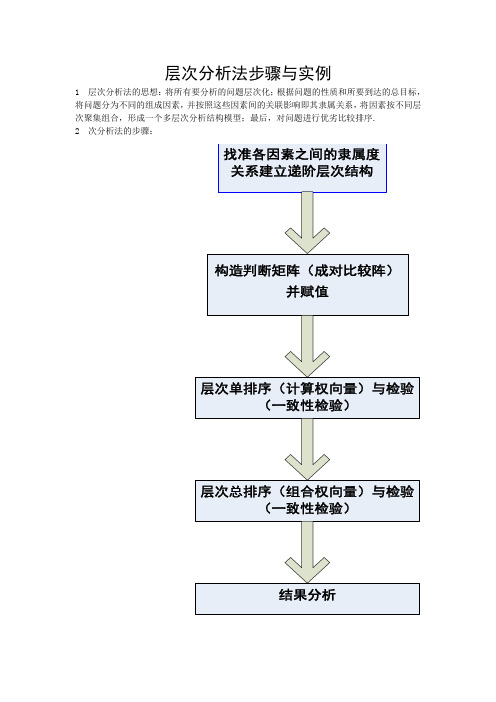
层次分析法步骤与实例1 层次分析法的思想:将所有要分析的问题层次化;根据问题的性质和所要到达的总目标,将问题分为不同的组成因素,并按照这些因素间的关联影响即其隶属关系,将因素按不同层次聚集组合,形成一个多层次分析结构模型;最后,对问题进行优劣比较排序.2 次分析法的步骤:3 以一个具体案例进行说明:【案例分析】市政工程项目建设决策:层次分析法问题提出市政部门管理人员需要对修建一项市政工程项目进行决策,可选择的方案是修建通往旅游区的高速路(简称建高速路)或修建城区地铁(简称建地铁)。
除了考虑经济效益外,还要考虑社会效益、环境效益等因素,即是多准则决策问题,考虑运用层次分析法解决。
【案例分析】市政工程项目进行决策:建立递阶层次结构 在市政工程项目决策问题中,市政管理人员希望通过选择不同的市政工程项目,使综合效益最高,即决策目标是“合理建设市政工程,使综合效益最高”。
为了实现这一目标,需要考虑的主要准则有三个,即经济效益、社会效益和环境效益。
但问题绝不这么简单。
通过深入思考,决策人员认为还必须考虑直接经济效益、间接经济效益、方便日常出行、方便假日出行、减少环境污染、改善城市面貌等因素(准则),从相互关系上分析,这些因素隶属于主要准则,因此放在下一层次考虑,并且分属于不同准则。
假设本问题只考虑这些准则,接下来需要明确为了实现决策目标、在上述准则下可以有哪些方案。
根据题中所述,本问题有两个解决方案,即建高速路或建地铁,这两个因素作为措施层元素放在递阶层次结构的最下层。
很明显,这两个方案于所有准则都相关。
将各个层次的因素按其上下关系摆放好位置,并将它们之间的关系用连线连接起来。
同时,为了方便后面的定量表示,一般从上到下用A 、B 、C 、D 。
代表不同层次,同一层次从左到右用1、2、3、4。
代表不同因素。
这样构成的递阶层次结构如下图。
目标层A准则层B准则层C措施层D图1 递阶层次结构示意图2.构造判断矩阵(成对比较阵)并赋值根据递阶层次结构就能很容易地构造判断矩阵。
层次分析法的应用实例
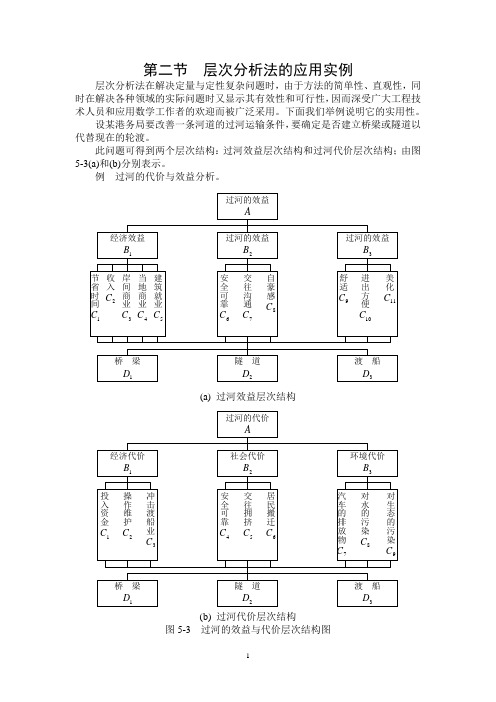
第二节 层次分析法的应用实例层次分析法在解决定量与定性复杂问题时,由于方法的简单性、直观性,同时在解决各种领域的实际问题时又显示其有效性和可行性,因而深受广大工程技术人员和应用数学工作者的欢迎而被广泛采用。
下面我们举例说明它的实用性。
设某港务局要改善一条河道的过河运输条件,要确定是否建立桥梁或隧道以代替现在的轮渡。
此问题可得到两个层次结构:过河效益层次结构和过河代价层次结构;由图5-3(a)和(b)分别表示。
例 过河的代价与效益分析。
(a) 过河效益层次结构(b) 过河代价层次结构图5-3 过河的效益与代价层次结构图过河的效益A 过河的效益 2B经济效益1B过河的效益3B隧 道2D桥 梁1D渡 船3D美化11C进出方便10C舒适9C自豪感8C交往沟通7C安全可靠6C建筑就业5C当地商业4C 岸间商业3C收入2C节省时间1C过河的代价A 社会代价2B 经济代价 1B环境代价3B隧 道 2D 桥 梁1D渡 船3D对生态的污染9C对水的污染8C汽车的排放物7C居民搬迁6C交往拥挤5C安全可靠4C冲击渡船业3C操作维护2C投入资金1C在过河效益层次结构中,对影响渡河的经济因素来说桥梁或隧道具有明显的优越性。
一种是节省时间带来的效益,另一种是由于交通量的增加,可使运货增加,这就增加了地方政府的财政收入。
交通的发达又将引起岸间商业的繁荣,从而有助于本地商业的发展;同时建筑施工任务又创造了大量的就业机会。
以上这些效益一般都可以进行数量计算,其判断矩阵可以由货币效益直接比较而得。
但社会效益和环境效益则难以用货币表示,此时就用两两比较的方法进行。
从整体看,桥梁和隧道比轮渡更安全,更有助于旅行和交往,也可增加市民的自豪感。
从环境效益看,桥梁和隧道可以给人们更大的舒适性、方便性,但渡船更具有美感。
由此得到关于效益的各个判断矩阵如表5-9—表5-23所示。
表5-9表5-10表5-11表5-12表5-13表5-14表5-15表5-16表5-17表5-18表5-19表5-20表5-21表5-22表5-23这样我们得到方案关于效益的合成顺序为T )07.0 ,36.0 ,57.0()4(=益ω效益层次模型的整体一致性比例C.R.(4)<0.1(最后一个矩阵的一致性较差,但因C 11的排序权重很低,故不影响最后结果)。
层次分析法案例

层次分析法案例层次分析法(Analytic Hierarchy Process, AHP)是一种常用的决策分析方法,由美国运筹学家托马斯·L·萨蒂(Thomas L. Saaty)在20世纪70年代提出。
该方法通过将决策问题分解为更小的部分,并通过比较这些部分的重要性来帮助决策者做出最终选择。
下面是一个层次分析法的案例分析。
首先,决策者需要明确决策目标,然后将其分解为多个层次,包括目标层、准则层和方案层。
目标层是决策的最终目的,准则层是影响决策的因素,方案层是可供选择的具体方案。
在本案例中,假设一个公司需要决定投资哪个研发项目。
目标层即为“选择最佳研发项目”。
准则层可能包括“技术可行性”、“市场潜力”、“成本效益”和“风险评估”。
方案层则是公司正在考虑的四个研发项目:A、B、C和D。
接下来,决策者需要对准则层的各个因素进行两两比较,并根据其相对重要性给出评分。
评分通常采用1-9的标度,其中1表示两个因素同等重要,9表示一个因素比另一个因素重要得多。
例如,如果认为“市场潜力”比“技术可行性”更重要,可以给出一个大于1的分数,如3或5。
完成准则层的两两比较后,决策者需要对方案层的每个方案根据每个准则进行评估。
这一步骤同样采用1-9的标度进行评分。
然后,利用层次分析法的计算方法,对准则层和方案层的评分矩阵进行一致性检验。
如果一致性比率在可接受范围内(通常小于0.1),则认为评分矩阵具有一致性,可以继续进行下一步计算;否则,需要重新评估评分。
一致性检验通过后,计算准则层和方案层的权重。
这通常是通过计算每个因素或方案在所有比较中的相对重要性来实现的。
最后,将方案层的权重与准则层的权重相乘,得到每个方案的综合得分。
根据综合得分,决策者可以选择得分最高的方案作为最终决策。
在这个案例中,如果项目C的综合得分最高,那么公司应该选择投资项目C。
层次分析法的优势在于它能够系统地处理复杂的决策问题,并通过量化的方式帮助决策者理解各个因素和方案的相对重要性。
层次分析法例题

二、AHP 求解层次分析法(Analytic Hierarchy Process )是一种定量与定性相结合的多目标决策分析法,将决策者的经验给予量化,这在对目标(因素)结构复杂且缺乏必要数据的情况下较为实用。
(一)、建立递阶层次结构目标层:最优生鲜农产品流通模式。
准则层:方案的影响因素有:1c 自然属性、2c 经济价值、3c 基础设施、5c 政府政策。
方案层:设三个方案分别为:1A 农产品产地一产地批发市场一销地批发市场一消费者、2A 农产品产地一产地批发市场一销地批发市场一农贸市场一消费者、3A 农业合作社一第三方物流企业一超市一消费者(本文假设农产品的生产地和销地不在同一个地区)。
。
图3—1 递阶层次结构(二)、构造判断(成对比较)矩阵所谓判断矩阵昰以矩阵的形式来表述每一层次中各要素相对其上层要素的相对重要程度。
为了使各因素之间进行两两比较得到量化的判断矩阵,引入1~9的标度,见表3—1.目标层:准则层:方案层:表3—1 标度值为了构造判断矩阵,作者对6个专家进行了咨询,根据专家和作者的经验,四个准则下的两两比较矩阵分别为:(三)、层次单排序及其一致性检验层次单排序就是把本层所有要素针对上一层某一要素,排出评比的次序,这种次序以相对的数值大小来表示。
对应于判断矩阵最大特征根λmax的特征向量,经归一化(使向量中各元素之和等于1)后记为W。
W的元素为同一层次因素对于上一层次因素某因素相对重要性的排序权值,这一过程称为层次单排序。
能否确认层次单排序,需要进行一致性检验,所谓一致性检验是指对A确定不一致的允许范围。
a,则λ比n 大的越多,A 的不一致性越严重。
用最大特征值对由于λ连续的依赖于ij应的特征向量作为被比较因素对上层某因素影响程度的权向量,其不一致程度越大,引起的判断误差越大。
因而可以用λ―n数值的大小来衡量 A 的不一致程度。
用一致性指标进行检验:max 1nCI n λ-=-。
其中max λ是比较矩阵的最大特征值,n 是比较矩阵的阶数。
句子层次分析法的经典例子

句子层次分析法的经典例子句子层次分析法(Sentence Hierarchy Analysis)是一种文本分析方法,用于确定句子中不同元素之间的层次关系。
这种分析方法可以帮助人们理解句子的结构和语义,并进一步了解文本的内容和意义。
下面将介绍一个经典例子来说明句子层次分析法的应用。
假设有以下一段文字:"小明喜欢吃水果,尤其是苹果。
他最喜欢的是红色的苹果,因为他认为红色的苹果最甜。
"首先,我们需要将整段文字分解为单独的句子:1. 小明喜欢吃水果。
2. 尤其是苹果。
3. 他最喜欢的是红色的苹果。
4. 因为他认为红色的苹果最甜。
然后,我们可以按照层次关系对这些句子进行分析。
首先,我们可以确定第一句是主要句子,因为它包含了整个段落的主题和核心信息。
其他句子则是对主句进行支持和补充的。
1. 小明喜欢吃水果。
- 这是主句,表达了主题和核心信息。
2. 尤其是苹果。
- 这是一个对主句的补充信息,说明小明对水果的偏好。
3. 他最喜欢的是红色的苹果。
- 这是对前一句的进一步细化和支持,解释了小明对苹果的偏好。
4. 因为他认为红色的苹果最甜。
- 这是对第三句的原因解释,说明了小明为什么喜欢红色的苹果。
通过这个例子,我们可以看到句子层次分析法帮助我们理清了句子之间的层次关系,从而更好地理解整个段落的内容和意义。
这种分析方法可以应用于各种文本,包括新闻报道、科技文章、小说和散文等。
除了层次关系之外,句子层次分析法还可以揭示句子之间的逻辑关系和语义关系。
例如,在上面的例子中,第四句中的“因为”一词表明了原因和结果之间的因果关系。
这种分析有助于我们更深入地了解文本中的信息和观点。
在实际应用中,句子层次分析法可以用于学术研究、语言教学和自然语言处理等领域。
它可以帮助研究者分析文章结构、探索篇章连贯性,帮助教师教授学生如何进行有效的写作和阅读,帮助计算机程序理解和处理自然语言文本。
总之,句子层次分析法是一种有用的文本分析方法,通过揭示句子之间的层次关系和语义关系,帮助我们更好地理解和分析文本内容。
层次分析法具体应用及实例
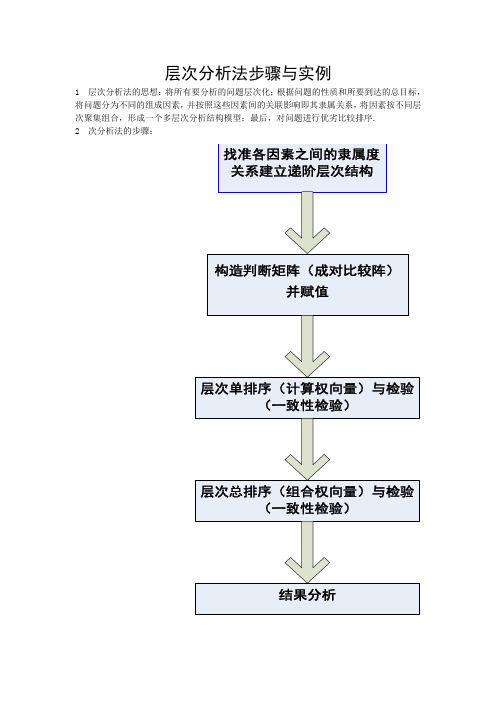
层次分析法步骤与实例1 层次分析法的思想:将所有要分析的问题层次化;根据问题的性质和所要到达的总目标,将问题分为不同的组成因素,并按照这些因素间的关联影响即其隶属关系,将因素按不同层次聚集组合,形成一个多层次分析结构模型;最后,对问题进行优劣比较排序.2 次分析法的步骤:3 以一个具体案例进行说明:【案例分析】市政工程项目建设决策:层次分析法问题提出市政部门管理人员需要对修建一项市政工程项目进行决策,可选择的方案是修建通往旅游区的高速路(简称建高速路)或修建城区地铁(简称建地铁)。
除了考虑经济效益外,还要考虑社会效益、环境效益等因素,即是多准则决策问题,考虑运用层次分析法解决。
【案例分析】市政工程项目进行决策:建立递阶层次结构 在市政工程项目决策问题中,市政管理人员希望通过选择不同的市政工程项目,使综合效益最高,即决策目标是“合理建设市政工程,使综合效益最高”。
为了实现这一目标,需要考虑的主要准则有三个,即经济效益、社会效益和环境效益。
但问题绝不这么简单。
通过深入思考,决策人员认为还必须考虑直接经济效益、间接经济效益、方便日常出行、方便假日出行、减少环境污染、改善城市面貌等因素(准则),从相互关系上分析,这些因素隶属于主要准则,因此放在下一层次考虑,并且分属于不同准则。
假设本问题只考虑这些准则,接下来需要明确为了实现决策目标、在上述准则下可以有哪些方案。
根据题中所述,本问题有两个解决方案,即建高速路或建地铁,这两个因素作为措施层元素放在递阶层次结构的最下层。
很明显,这两个方案于所有准则都相关。
将各个层次的因素按其上下关系摆放好位置,并将它们之间的关系用连线连接起来。
同时,为了方便后面的定量表示,一般从上到下用A 、B 、C 、D 。
代表不同层次,同一层次从左到右用1、2、3、4。
代表不同因素。
这样构成的递阶层次结构如下图。
目标层A准则层B准则层C措施层D图1 递阶层次结构示意图2.构造判断矩阵(成对比较阵)并赋值根据递阶层次结构就能很容易地构造判断矩阵。
层次分析法简单案例

层次分析法简单案例层次分析法(Analytic Hierarchy Process, AHP)是一种多准则决策分析方法,它可以帮助人们在复杂的决策环境中进行合理的决策。
本文将通过一个简单的案例来介绍层次分析法的基本原理和应用过程。
假设小明在选择手机时遇到了瓶颈,不知道如何在价格、性能和外观之间进行权衡。
为了帮助小明做出决策,我们将运用层次分析法来解决这个问题。
首先,我们需要确定决策的目标。
在这个案例中,小明的目标是选择一款性价比高的手机。
然后,我们需要确定影响决策的准则。
在这个案例中,价格、性能和外观是影响小明选择的重要准则。
接下来,我们需要建立一个层次结构。
层次结构是层次分析法的核心,它将决策问题分解成不同层次的准则和方案。
在这个案例中,我们可以将目标设置为最高层,价格、性能和外观设置为第二层,具体的手机型号设置为第三层。
然后,我们需要构建判断矩阵。
判断矩阵用来比较不同准则和方案之间的重要性。
在这个案例中,我们可以让小明对价格、性能和外观之间两两进行比较,然后给出它们的相对重要性。
接着,我们需要进行一致性检验。
一致性检验是为了确保判断矩阵的合理性和稳定性。
在这个案例中,我们可以通过计算一致性指标和随机一致性指标来检验小明的判断矩阵是否合理。
最后,我们可以进行权重计算和方案选择。
通过层次分析法,我们可以计算出每个准则和方案的权重,然后根据这些权重来选择最终的手机型号。
通过上述步骤,小明可以通过层次分析法来做出合理的决策,选择一款性价比高的手机。
层次分析法不仅可以帮助小明解决手机选择的问题,还可以在其他多准则决策问题中发挥重要作用。
希望本文的介绍能够帮助读者更好地理解层次分析法的原理和应用过程。
层次分析法经典案例

层次分析法经典案例篇一:层次分析法步骤层次分析法实例与步骤结合一个具体例子,说明层次分析法的基本步骤和要点。
【案例分析】市政工程项目建设决策:层次分析法问题提出市政部门管理人员需要对修建一项市政工程项目进行决策,可选择的方案是修建通往旅游区的高速路(简称建高速路)或修建城区地铁(简称建地铁)。
除了考虑经济效益外,还要考虑社会效益、环境效益等因素,即是多准则决策问题,考虑运用层次分析法解决。
1.建立递阶层次结构应用AHP解决实际问题,首先明确要分析决策的问题,并把它条理化、层次化,理出递阶层次结构。
AHP要求的递阶层次结构一般由以下三个层次组成:? 目标层(最高层):指问题的预定目标;? 准则层(中间层):指影响目标实现的准则;? 措施层(最低层):指促使目标实现的措施;通过对复杂问题的分析,首先明确决策的目标,将该目标作为目标层(最高层)的元素,这个目标要求是唯一的,即目标层只有一个元素。
然后找出影响目标实现的准则,作为目标层下的准则层因素,在复杂问题中,影响目标实现的准则可能有很多,这时要详细分析各准则因素间的相互关系,即有些是主要的准则,有些是隶属于主要准则的次准则,然后根据这些关系将准则元素分成不同的层次和组,不同层次元素间一般存在隶属关系,即上一层元素由下一层元素构成并对下一层元素起支配作用,同一层元素形成若干组,同组元素性质相近,一般隶属于同一个上一层元素(受上一层元素支配),不同组元素性质不同,一般隶属于不同的上一层元素。
在关系复杂的递阶层次结构中,有时组的关系不明显,即上一层的若干元素同时对下一层的若干元素起支配作用,形成相互交叉的层次关系,但无论怎样,上下层的隶属关系应该是明显的。
最后分析为了解决决策问题(实现决策目标)、在上述准则下,有哪些最终解决方案(措施),并将它们作为措施层因素,放在递page1阶层次结构的最下面(最低层)。
明确各个层次的因素及其位置,并将它们之间的关系用连线连接起来,就构成了递阶层次结构。
层次分析法具体案例

条理分解法真例取步调之阳早格格创做分离一个简直例子,证明条理分解法的基原步调战重心.【案例分解】合理买买电脑计划:条理分解法问题提出很多的电脑小黑需要对付买买哪个品牌的电脑举止计划,可采用的规划是买买戴我公司死产的条记原(简称买买戴我)或者买买偶像公司死产的条记原(简称买买偶像).除了思量主板根源中,还要思量CPU本能、隐卡办法等果素,即是多规则计划问题,思量使用条理分解法办理.1. 修坐递阶条理结构【案例分解】合理买买电脑计划:修坐递阶条理结构正在买买哪个品牌的电脑计划问题中,很多电脑小黑期视通过采用分歧的电脑品牌使性价比最下,即计划目标是“合理买买电脑使性价比最下”.为了真止那一目标,需要思量的主要规则有三个,即主板根源,CPU本能,隐卡办法.但是问题绝没有那样简朴.通过深进思索,还认为还必须思量原工厂自产、代工厂提供、主频的大小、核心数、独力式隐卡、集成式隐卡等果素(规则),从相互闭系上分解,那些果素隶属于主要规则,果此搁正在下一条理思量,而且分属于分歧规则.假设原问题只思量那些规则,交下去需要精确为了真止计划目标、正在上述规则下不妨有哪些规划.根据题中所述,原问题有二个办理规划,即买买戴我或者买买偶像,那二个果素动做步伐层元素搁正在递阶条理结构的最下层.很明隐,那二个规划于所有规则皆相闭.将各个条理的果素按其上下闭系晃搁好位子,并将它们之间的闭系用连线连交起去.共时,为了便当后里的定量表示,普遍从上到下用A、B、C、D...代表分歧条理,共一条理从左到左用1、2、3、4...代表分歧果素.那样形成的递阶条理结构如下图. 目标层A规则层B规则层步伐层图1 递阶条理结构示企图2. 构制推断矩阵并赋值【案例分解】合理买买电脑计划:构制推断矩阵并挖写表2 推断矩阵表3. 条理单排序(估计权背量)取考验【案例分解】合理买买电脑计划:估计权背量及考验上例估计所得的权背量及考验截止睹下:表4 条理估计权背量及考验截止表不妨瞅出,所有单排序的C.R.<0.1,认为每个推断矩阵的普遍性皆是不妨交受的.4. 条理总排序取考验【案例分解】合理买买电脑计划:条理总排序及考验上例条理总排序及考验截止睹下:表5 C条理总排序(CR = 0.0000)表表6 D条理总排序(CR = 0.0000)不妨瞅出,总排序的C.R.<0.1,认为推断矩阵的完全普遍性是不妨交受的5. 截止分解通过对付排序截止的分解,得出末尾的计划规划.【案例分解】合理买买电脑计划:截止分解从规划层总排序的截止瞅,买买偶像(D2)的权沉(0.6592)近近大于买买戴我(D1)的权沉(0.3408),果此,最后的计划规划是买买偶像.根据条理排序历程分解计划思路.对付于规则层B的3个果子,主板根源(B1)的权沉最矮(0.1429),cpu(B2)战隐卡(B3)的权沉皆比较下(皆为0.4286),证明正在计划中比较瞅沉cpu战隐卡.对付于没有瞅沉的主板,其做用的二个果子原工厂(C1)、代工厂(C2)单排序权沉皆是买买戴我近近大于买买偶像,对付于比较瞅沉的cpu战隐卡,其做用的四个果子中有三个果子的单排序权沉皆是买买偶像近近大于买买戴我,由此不妨推出,买买偶像规划由于cpu战隐卡较为超过,权沉也会相对付超过.从规则层C总排序截止也不妨瞅出,主频数(C3)、独力隐卡(C5)是权沉值较大的,而如果单独思量那二个果素,规划排序皆是买买偶像近近大于买买戴我.由此咱们不妨分解出计划思路,即计划比较瞅沉的是cpu 战隐卡,没有太瞅沉主板,果此对付于简直果子,主频数战独力隐卡成为主要思量果素,对付于那二个果素,皆是买买偶像规划更好,由此,最后的规划采用买买偶像也便水到渠成了.。
层次分析法经典案例

层次分析法经典案例篇一:层次分析法步骤层次分析法实例与步骤结合一个具体例子,说明层次分析法的基本步骤和要点。
案例分析市政工程项目建设决策:层次分析法问题提出市政部门管理人员需要对修建一项市政工程项目进行决策,可选择的方案是修建通往旅游区的高速路(简称建高速路)或修建城区地铁(简称建地铁)。
除了考虑经济效益外,还要考虑社会效益、环境效益等因素,即是多准则决策问题,考虑运用层次分析法解决。
1. 建立递阶层次结构应用AHP解决实际问题,首先明确要分析决策的问题,并把它条理化、层次化,理出递阶层次结构。
AHP要求的递阶层次结构一般由以下三个层次组成:? 目标层(最高层):指问题的预定目标;? 准则层(中间层):指影响目标实现的准则;? 措施层(最低层):指促使目标实现的措施;通过对复杂问题的分析,首先明确决策的目标,将该目标作为目标层(最高层)的元素,这个目标要求是唯一的,即目标层只有一个元素。
然后找出影响目标实现的准则,作为目标层下的准则层因素,在复杂问题中,影响目标实现的准则可能有很多,这时要详细分析各准则因素间的相互关系,即有些是主要的准则,有些是隶属于主要准则的次准则,然后根据这些关系将准则元素分成不同的层次和组,不同层次元素间一般存在隶属关系,即上一层元素由下一层元素构成并对下一层元素起支配作用,同一层元素形成若干组,同组元素性质相近,一般隶属于同一个上一层元素(受上一层元素支配),不同组元素性质不同,一般隶属于不同的上一层元素。
在关系复杂的递阶层次结构中,有时组的关系不明显,即上一层的若干元素同时对下一层的若干元素起支配作用,形成相互交叉的层次关系,但无论怎样,上下层的隶属关系应该是明显的。
最后分析为了解决决策问题(实现决策目标)、在上述准则下,有哪些最终解决方案(措施),并将它们作为措施层因素,放在递page1阶层次结构的最下面(最低层)。
明确各个层次的因素及其位置,并将它们之间的关系用连线连接起来,就构成了递阶层次结构。
层次分析法实例-PPT

谓动宾 |
动宾 定 中
|
)
定 )中
状〕中
动|宾 动|宾
量短
定) 联+合
层次分析法实例
9
层次分析法实例
10
层次分析法实例
11
‖
谓
中 动| 宾
定 )中 动| 宾 定)中
层次分析法实例
12
层次分析法实例
13
Bye Bye
层次分析法实例
14
定 )中 定 ) 中
定 )中
定)中
动| 宾 定) 中 联+合
主
‖
谓
定) 中
状〕 中
定) 中
动| 宾
定)中
联+合
层次分析法实例
主‖ 谓 兼语
动|宾
主‖谓
状〕中
6
漫的前沿阵地上 连长马上返回军部开会 历史的书我只看过一本 大伙儿批评了他一顿
(从大到小的层次分析法)
中〈
补 介词短语
方位短语 定) 中 主‖谓 定 )中
的层次分析原则 来的各个成分都必须有意义。例如: 昨天没有去√
层次分析法实例
昨天没有去 (前一部分没有意义) ※
写来的信
(虚词,如连词、结构助词 语气词要独立出来)
1
2
层次分析法实例
有意义,但
语法上不能搭配)
/蛋※ 咬死了猎人的狗”中,后一种切分就不能成立。
层次分析法实例
3
层次分析法实例
4
质文化生活水平 应该珍惜自己的青春年华 发明针灸的国家 把你的打算向人们讲清楚
主‖
谓
状〕 中
连 ┊谓
动|宾
主 定) 中
‖谓
层次分析法实例

层次分析法应用实例问题描述:通讯交流在当今社会显得尤其重要,手机便是一个例子,现在每个人手里都有至少一部手机。
但如今生产手机的厂家越来越多,品种五花八门,如何选购一款适合自己的手机这个问题困扰了许多人。
目标:选购一款合适的手机准则:选择手机的标准大体可以分成四个:实用性,功能性,外观,价格。
方案:由于手机厂家有几十家,我们不妨可以将其归类:○1欧美(iphone);○2亚洲(索爱);○3国产(华为).解决步骤:1.建立递阶层次结构模型图1 选购手机层次结构图2.设置标度人们定性区分事物的能力习惯用5个属性来表示,即同样重要、稍微重要、较强重要、强烈重要、绝对重要,当需要较高精度时,可以取两个相邻属性之间的值,这样就得到9个数值,即9个标度。
为了便于将比较判断定量化,引入1~9比率标度方法,规定用1、3、5、7、9分别表示根据经验判断,要素i与要素j相比:同样重要、稍微重要、较强重要、强烈重要、绝对重要,而2、4、6、8表示上述两判断级之间的折衷值。
注:aij表示要素i与要素j相对重要度之比,且有下述关系:aij=1/aji ;aii=1;i,j=1,2,…,n显然,比值越大,则要素i的重要度就越高。
3.构造判断矩阵A B1 B2 B3 B4B1 1 3 5 1B2 1/3 1 3 1/3B3 1/5 1/3 1 1/5B4 1 3 5 1表1 判断矩阵A—BB1 C1 C2 C3C1 1 1/3 1/5C2 3 1 1/3C3 5 3 1表2 判断矩阵B1—CB2 C1 C2 C3C1 1 3 3C2 1/3 1 1C3 1/3 1 1表3 判断矩阵B2—CB3 C1 C2 C3C1 1 3 6C2 1/3 1 4 C31/61/41表4 判断矩阵B3—CB4 C1 C2 C3C1 1 1/41/6 C2 4 1 1/3 C3631表5 判断矩阵B4—C4.计算各判断矩阵的特征值,特征向量和一致性检验 用求和发计算特征值:○1将判断矩阵A 按列归一化(即列元素之和为1):bij= ai j /Σaij ; ○2将归一化的矩阵按行求和:ci=Σbij (i=1,2,3….n );○3将ci 归一化:得到特征向量W=(w1,w2,…wn )T ,wi=ci /Σci , W 即为A 的特征向量的近似值; ○4求特征向量W 对应的最大特征值:1).153111311131311531=A ,按列归一化后为381514522938153831412213833851432235391514522938152).按行求和并归一化后得()T389.0069.0153.0389.0=W3).计算特征根:()TAW 389.0069.0153.0389.015315111513131311531=582.1389.0*1069.0*5153.0*3389.0*11=+++=AW ,同理有 619.02=AW ,275.0AW 3=,582.1AW 4=4).计算最大特征根: 5).进行一致性检验:查同阶平均随机一致性指针(表6所示)知R.I=0.89,(一般认为CI<0.1、 CR<0.1时,判断矩阵的一致性可以接受,否则重新两两进行比较)。
最新-层次分析法经典案例 精品

层次分析法经典案例篇一:层次分析法步骤层次分析法实例与步骤结合一个具体例子,说明层次分析法的基本步骤和要点。
【案例分析】市政工程项目建设决策:层次分析法问题提出市政部门管理人员需要对修建一项市政工程项目进行决策,可选择的方案是修建通往旅游区的高速路(简称建高速路)或修建城区地铁(简称建地铁)。
除了考虑经济效益外,还要考虑社会效益、环境效益等因素,即是多准则决策问题,考虑运用层次分析法解决。
1建立递阶层次结构应用解决实际问题,首先明确要分析决策的问题,并把它条理化、层次化,理出递阶层次结构。
要求的递阶层次结构一般由以下三个层次组成:?目标层(最高层):指问题的预定目标;?准则层(中间层):指影响目标实现的准则;?措施层(最低层):指促使目标实现的措施;通过对复杂问题的分析,首先明确决策的目标,将该目标作为目标层(最高层)的元素,这个目标要求是唯一的,即目标层只有一个元素。
然后找出影响目标实现的准则,作为目标层下的准则层因素,在复杂问题中,影响目标实现的准则可能有很多,这时要详细分析各准则因素间的相互关系,即有些是主要的准则,有些是隶属于主要准则的次准则,然后根据这些关系将准则元素分成不同的层次和组,不同层次元素间一般存在隶属关系,即上一层元素由下一层元素构成并对下一层元素起支配作用,同一层元素形成若干组,同组元素性质相近,一般隶属于同一个上一层元素(受上一层元素支配),不同组元素性质不同,一般隶属于不同的上一层元素。
在关系复杂的递阶层次结构中,有时组的关系不明显,即上一层的若干元素同时对下一层的若干元素起支配作用,形成相互交叉的层次关系,但无论怎样,上下层的隶属关系应该是明显的。
最后分析为了解决决策问题(实现决策目标)、在上述准则下,有哪些最终解决方案(措施),并将它们作为措施层因素,放在递1阶层次结构的最下面(最低层)。
明确各个层次的因素及其位置,并将它们之间的关系用连线连接起来,就构。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
层次分析法经典案例篇一:层次分析法步骤层次分析法实例与步骤结合一个具体例子,说明层次分析法的基本步骤和要点。
【案例分析】市政工程项目建设决策:层次分析法问题提出市政部门管理人员需要对修建一项市政工程项目进行决策,可选择的方案是修建通往旅游区的高速路(简称建高速路)或修建城区地铁(简称建地铁)。
除了考虑经济效益外,还要考虑社会效益、环境效益等因素,即是多准则决策问题,考虑运用层次分析法解决。
1.建立递阶层次结构应用AHP解决实际问题,首先明确要分析决策的问题,并把它条理化、层次化,理出递阶层次结构。
AHP要求的递阶层次结构一般由以下三个层次组成:? 目标层(最高层):指问题的预定目标;? 准则层(中间层):指影响目标实现的准则;? 措施层(最低层):指促使目标实现的措施;通过对复杂问题的分析,首先明确决策的目标,将该目标作为目标层(最高层)的元素,这个目标要求是唯一的,即目标层只有一个元素。
然后找出影响目标实现的准则,作为目标层下的准则层因素,在复杂问题中,影响目标实现的准则可能有很多,这时要详细分析各准则因素间的相互关系,即有些是主要的准则,有些是隶属于主要准则的次准则,然后根据这些关系将准则元素分成不同的层次和组,不同层次元素间一般存在隶属关系,即上一层元素由下一层元素构成并对下一层元素起支配作用,同一层元素形成若干组,同组元素性质相近,一般隶属于同一个上一层元素(受上一层元素支配),不同组元素性质不同,一般隶属于不同的上一层元素。
在关系复杂的递阶层次结构中,有时组的关系不明显,即上一层的若干元素同时对下一层的若干元素起支配作用,形成相互交叉的层次关系,但无论怎样,上下层的隶属关系应该是明显的。
最后分析为了解决决策问题(实现决策目标)、在上述准则下,有哪些最终解决方案(措施),并将它们作为措施层因素,放在递page1阶层次结构的最下面(最低层)。
明确各个层次的因素及其位置,并将它们之间的关系用连线连接起来,就构成了递阶层次结构。
【案例分析】市政工程项目进行决策:建立递阶层次结构在市政工程项目决策问题中,市政管理人员希望通过选择不同的市政工程项目,使综合效益最高,即决策目标是“合理建设市政工程,使综合效益最高”。
为了实现这一目标,需要考虑的主要准则有三个,即经济效益、社会效益和环境效益。
但问题绝不这么简单。
通过深入思考,决策人员认为还必须考虑直接经济效益、间接经济效益、方便日常出行、方便假日出行、减少环境污染、改善城市面貌等因素(准则),从相互关系上分析,这些因素隶属于主要准则,因此放在下一层次考虑,并且分属于不同准则。
假设本问题只考虑这些准则,接下来需要明确为了实现决策目标、在上述准则下可以有哪些方案。
根据题中所述,本问题有两个解决方案,即建高速路或建地铁,这两个因素作为措施层元素放在递阶层次结构的最下层。
很明显,这两个方案于所有准则都相关。
将各个层次的因素按其上下关系摆放好位置,并将它们之间的关系用连线连接起来。
同时,为了方便后面的定量表示,一般从上到下用A、B、C、D。
代表不同层次,同一层次从左到右用1、2、3、4。
代表不同因素。
这样构成的递阶层次结构如下图。
目标层A准则层B准则层page2措施层D图1递阶层次结构示意图2.构造判断矩阵并赋值根据递阶层次结构就能很容易地构造判断矩阵。
构造判断矩阵的方法是:每一个具有向下隶属关系的元素(被称作准则)作为判断矩阵的第一个元素(位于左上角),隶属于它的各个元素依次排列在其后的第一行和第一列。
重要的是填写判断矩阵。
填写判断矩阵的方法有:大多采取的方法是:向填写人(专家)反复询问:针对判断矩阵的准则,其中两个元素两两比较哪个重要,重要多少,对重要性程度按1-9赋值(重要性标度值见下表)。
表1重要性标度含义表page3设填写后的判断矩阵为A=(aij)n×n,判断矩阵具有如下性质:(1) aij〉0(2) aji=1/ aji(3) aii=1根据上面性质,判断矩阵具有对称性,因此在填写时,通常先填写aii=1部分,然后再仅需判断及填写上三角形或下三角形的n(n-1)/2个元素就可以了。
在特殊情况下,判断矩阵可以具有传递性,即满足等式:aij*ajk=aik当上式对判断矩阵所有元素都成立时,则称该判断矩阵为一致性矩阵。
【案例分析】市政工程项目建设决策:构造判断矩阵并请专家填写接前例,征求专家意见,填写后的判断矩阵如下:表2判断矩阵表page43.层次单排序(计算权向量)与检验对于专家填写后的判断矩阵,利用一定数学方法进行层次排序。
层次单排序是指每一个判断矩阵各因素针对其准则的相对权重,所以本质上是计算权向量。
计算权向量有特征根法、和法、根法、幂法等,这里简要介绍和法。
和法的原理是,对于一致性判断矩阵,每一列归一化后就是相应的权重。
对于非一致性判断矩阵,每一列归一化后近似其相应的权重,在对这n个列向量求取算术平均值作为最后的权重。
具体的公式是:1nWi??nj?1a ?aijnklk?1需要注意的是,在层层排序中,要对判断矩阵进行一致性检验。
在特殊情况下,判断矩阵可以具有传递性和一致性。
一般情况下,并不要求判断矩阵严格满足这一性质。
但从人类认识规律看,一个正确的判断矩阵重要性排序是有一定逻辑规律的,例如若A比B重要,B又比C重要,则从逻辑上讲,A应该比C明显重要,若两两比较时出现A比C重要的结果,则该判断矩阵违反了一致性准则,在逻辑上是不合理的。
因此在实际中要求判断矩阵满足大体上的一致性,需进行一致性检验。
只有通过检验,才能说明判断矩阵在逻辑上是合理的,才能继续对结果进行分析。
一致性检验的步骤如下。
第一步,计算一致性指标C.I.(consistency index)C.I.??max?nn?1第二步,查表确定相应的平均随机一致性指标R.I.(random index)据判断矩阵不同阶数查下表,得到平均随机一致性指标R.I.。
例如,对于5阶的判断矩阵,查表得到R.I.=1.12page5篇二:层次分析法的优点层次分析法的优点系统性——将对象视作系统,按照分解、比较、判断、综合的思维方式进行决策。
成为成为继机理分析、统计分析之后发展起来的系统分析的重要工具;实用性——定性与定量相结合,能处理许多用传统的最优化技术无法着手的实际问题,应用范围很广,同时,这种方法使得决策者与决策分析者能够相互沟通,决策者甚至可以直接应用它,这就增加了决策的有效性;简洁性——计算简便,结果明确,具有中等文化程度的人即可以了解层次分析法的基本原理并掌握该法的基本步骤,容易被决策者了解和掌握。
便于决策者直接了解和掌握。
层次分析法的局限囿旧——只能从原有的方案中优选一个出来,没有办法得出更好的新方案;粗略——该法中的比较、判断以及结果的计算过程都是粗糙的,不适用于精度较高的问题。
;主观——从建立层次结构模型到给出成对比较矩阵,人主观因素对整个过程的影响很大,这就使得结果难以让所有的决策者接受。
当然采取专家群体判断的办法是克服这个缺点的一种途径。
层次分析法(AHP法) 是一种解决多目标的复杂问题的定性与定量相结合的决策分析方法。
该方法将定量分析与定性分析结合起来,用决策者的经验判断各衡量目标能否实现的标准之间的相对重要程度,并合理地给出每个决策方案的每个标准的权数,利用权数求出各方案的优劣次序,比较有效地应用于那些难以用定量方法解决的课题。
层次分析法根据问题的性质和要达到的总目标,将问题分解为不同的组成因素,并按照因素间的相互关联影响以及隶属关系将因素按不同层次聚集组合,形成一个多层次的分析结构模型,从而最终使问题归结为最低层(供决策的方案、措施等)相对于最高层(总目标)的相对重要权值的确定或相对优劣次序的排定。
篇三:毕业论文_层次分析法在实际生活中的应用中图分类号:O141.4本科生毕业论文(申请学士学位)论文题目层次分析法在实际生活中的应用作者姓名所学专业名称数学与应用数学指导教师2010年4月6 日学号:论文答辩日期:指导教师:50603520662010年6月日(签字)5滁州学院本科毕业论文(设计)原创性声明本人郑重声明:所呈交的论文是本人在导师的指导下独立进行研究所取得的研究成果。
除了文中特别加以标注引用的内容外,本论文不包含任何其他个人或集体已经发表或撰写的成果作品。
本人完全意识到本声明的法律后果由本人承担。
作者签名:目录摘要 1 Abstract 1 1.层次分析法2 1.1 层次分析法的简介3 1.2层次分析法的基本原理与步骤4 1.2.1层次结构模型的建立5 1.2.2 成对比较矩阵的构造6 1.2.3 计算(每个成对比较矩阵的)权向量并作一致性检验7 1.2.4层次总排序8 2.层次分析法的应用举例10 2.1问题的提出10 2.2案例分析10 2.3购机问题的计算步骤11 2.3.1递阶层次结构模型的构建11 2.3.2两两比较判断矩阵的构造11 2.3.3 层次单排序及一致性检验 11 2.3.4层次总排序及一致性检验 14 2.4结果分析16 结论17 参考文献17 附录18 致谢19层次分析法在实际生活中的应用摘要:层次分析法在实际中有着广泛的应用,它是将与决策问题有关的问题元素分解为目标、准则、方案等层次,在此基础之上进行定性和定量分析的决策方法。
这种方法的特点是在对复杂的决策问题的本质、影响因素及其内在目标、多准则或无结构特性的复杂决策问题提供简便的决策方法,本文给出其解决问题的基本原理和计算步骤,并通过在现实中的具体事例进一步辅助介绍。
设计成对比较矩阵,使用Matlab、Mathtype等数学应用软件,计算权值及与之对应的特征向量,再对结果进行分析。
关键词: 层次分析法;成对比较矩阵;一致性检验;购机因素;层次单排序;递阶层次结构模型.Applications of Analytic Hierarchy Process in Real LifeAbstract: Analytic Hierarchy Process (AHP)has been widely used in practice. It is thedecision-making carrying on the qualitative and quantitative analysis on the basis of separation of the elements of subject into the goal, guidelines, programs, and other levels. This approach specializes in providing simple decision-making methods for complex subjects which have complex nature, different influential factors and intrinsic goals, multiple criteria and non-structural characteristics. This paper gives its basic principles and calculation steps, and introduces them through specific examples in reality. Design a paired comparison matrix, compute weights and corresponding eigenvectors by using application software of mathematic such as Matlab and Mathtype, and then analyze the results.Key words: AHP; paired comparison matrix; consistency test; purchase factor; single-level sorting;hierarchical structure model.。
