冀教版2019-2020年八年级数学下册15.微专题:正方形中的典型模型问题
八年级数学下册课件(冀教版)正方形

正方形(square)是我们熟悉的几何图形,它的四 条边都相等,四个角都是直角.因此,正方形既是矩形, 又是菱形.它既有矩形的性质,又有菱形的性质.
正方形的定义:有一组邻边相等且有一个角是直角的 平行四边形叫做正方形. 要点精析 (1)正方形的四条边都相等,说明正方形是特殊的菱形; (2)正方形的四个角都是直角,说明正方形是特殊的矩 形.即:正方形既是特殊的矩形,又是特殊的菱形.
3 已知在四边形ABCD 中,∠A=∠B=∠C=90°,
如果添加一个条件,即可推出该四边形是正方形,
那么这个条件可以是( D )
A.∠D=90°
B.AB=CD
C.AD=BC
D.BC=CD
4 ▱ABCD 的对角线AC 与BD 相交于点O,且AC⊥BD, 请添加一个条件:A__C_=__B__D_,使得▱ABCD 为正方形.
证明:∵四边形ABCD 是正方形, ∴∠AOE=∠DOF=90°,AO=DO,∠OBA=45°. 又∵DG⊥AE, ∴∠EAO+∠AEO=∠EDG+∠GED=90°. ∵∠AEO=∠GED,∴∠EAO=∠EDG=∠FDO. ∴△AEO ≌△DFO (ASA).∴OE=OF. ∴∠OEF=45°. ∴∠OEF=∠OBA. ∴EF∥AB.
AC=BD,AD∥BC,
∠DAC=∠ACD=45°.
∵BD=CE,∴AC=CE.∴∠CAE=∠CEA.
∵AD∥CE,∴∠DAF=∠AEC. ∴∠DAF=∠CAE= 1 ∠DAC=22.5°.
2
又∵∠ACF=45°,∴∠AFC=112.5°.
3 如图是边长为10 cm的正方形铁片,过两个顶点 剪掉一个三角形,以下四种剪法中,裁剪线长度 所标的数据(单位:cm)不正确的是( A )
2正方形课件冀教版八年级数学下册

知识点1 正方形的定义和性质
定义:有一组邻边相等且有一个角是直角 的平行四边形叫做正方形.
大家谈谈
1.正方形是不是轴对称图形?如果是轴对称图形,那么它有几条 对称轴,都是哪些直线?
是轴对称图形,有四条对称轴
2.正方形与平行四边形、矩形和菱形的关系
两组对边
分别平行
四边形
平行四边形
正 矩形 方 菱形
知识点2
正方形的判定
判定一个四边形是正方形, 只要这个四边形既是矩形又是菱形即可.
判定定理1:有一组邻边相等的矩形是正方形. 判定定理2:对角线垂直的矩形是正方形. 判定定理3:有一个角是直角的菱形是正方形. 判定定理4:对角线相等的菱形是正方形.
1.已知:如图,在正方形ABCD中,点E在对角线AC上.
1.了解正方形的有关概念,了解正方形与平行四边形、矩形、菱形的关系. 2.理解并掌握正方形的性质、判定方法.能运用正方形的性质解决有关计 算和证明问题.
重点
理解并掌握正方形的性质、判定方法.
难点
理解并掌握正方形的性质、判定方法.
菱形
定义 性质定理
判定定理
有一个邻边相等的平行四边形叫做菱形. 菱形既是中心对称图形,也是轴对称图形 菱形的四条边都相等 菱形的两条对角线互相垂直 菱形的每条对角线平分一组对角 四条边相等的四边形是菱形 两条对角线互相垂直的平行四边形是菱形
正方形
定义 性质定理 判定定理
有一个邻边相等且有一个角是直角的 平行四边形叫做菱形.
正方形具有平行四边形、矩形和菱形 的一切性质
判定一个四边形是正方形,只要判定 这个四边形既是矩形又是菱形即可.
2. 如图,P为AB上任意一点,分别以AP,PB 为边在AB同侧作正方形APCD,正方形 PBEF,设∠CBE=α,则∠AFP为 ( B ) A. 2α
八年级数学下册 微专题:正方形中的典型模型问题
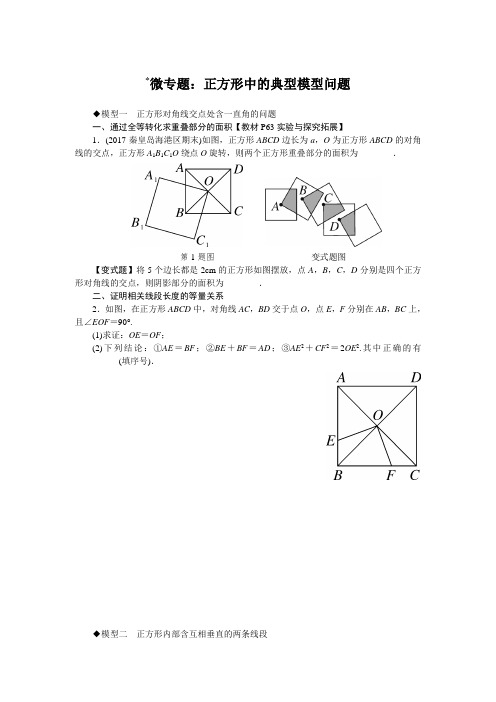
*微专题:正方形中的典型模型问题◆模型一正方形对角线交点处含一直角的问题一、通过全等转化求重叠部分的面积【教材P63实验与探究拓展】1.(2017·秦皇岛海港区期末)如图,正方形ABCD边长为a,O为正方形ABCD的对角线的交点,正方形A1B1C1O绕点O旋转,则两个正方形重叠部分的面积为________.第1题图变式题图【变式题】将5个边长都是2cm的正方形如图摆放,点A,B,C,D分别是四个正方形对角线的交点,则阴影部分的面积为________.二、证明相关线段长度的等量关系2.如图,在正方形ABCD中,对角线AC,BD交于点O,点E,F分别在AB,BC上,且∠EOF=90°.(1)求证:OE=OF;(2)下列结论:①AE=BF;②BE+BF=AD;③AE2+CF2=2OE2.其中正确的有__________(填序号).◆模型二正方形内部含互相垂直的两条线段3.(2017·石家庄新华区期末)如图,点E,F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE与BF相交于点O.下列结论:①AE=BF;②AE⊥BF;③AD=OE;④S△AOB =S四边形DEOF.其中正确的有()A.4个B.3个C.2个D.1个◆模型三含一外角平分线问题4.如图,四边形ABCD是正方形,点E是BC的中点,∠AEF=90°,EF交正方形外角的平分线CF于F.求证:AE=EF.【变式题】如图,正方形ABCD中,E为BC上一点,过B作BG⊥AE于G,延长BG 至点F使∠CFB=45°.(1)求证:∠BAG=∠CBF;(2)求证:AG=FG.参考答案与解析 1.14a 2 【变式题】4cm 2 2.(1)证明:∵BD ,AC 为正方形ABCD 的对角线,∴OB =OC ,∠EBO =∠FCO =45°,∠BOF +∠FOC =90°.∵∠EOF =∠EOB +∠BOF =90°,∴∠EOB =∠FOC .在△EOB 和△FOC 中,⎩⎪⎨⎪⎧∠EBD =∠FCO ,BO =CO ,∠EOB =∠FOC ,∴△EOB ≌△FOC (ASA),∴OE =DF .(2)解:①②③3.B4.证明:如图,取AB 的中点H ,连接EH .∵∠AEF =90°,∴∠2+∠AEB =90°.∵四边形ABCD 是正方形,∴∠1+∠AEB =90°,∴∠1=∠2.∵E 是BC 的中点,H 是AB 的中点,∴BH =BE ,AH =CE ,∴∠BHE =45°.∵CF 是∠DCG 的平分线,∴∠FCG =45°,∴∠AHE=∠ECF =135°.在△AHE 和△ECF 中,⎩⎪⎨⎪⎧∠1=∠2,AH =EC ,∠AHE =∠ECF ,∴△AHE ≌△ECF (ASA),∴AE=EF .【变式题】(1)证明:∵BG ⊥AE ,∴∠AGB =90°,∴∠ABG +∠BAG =90°.∵∠CBF +∠ABG =90°,∴∠BAG =∠CBF .(2)证明:如图,过点C 作CH ⊥BF 于H 点.∵∠CFB =45°,∴CH =HF .∵AG ⊥BF ,CH ⊥BF ,∴∠AGB =∠BHC =90°.在△AGB 和△BHC 中,⎩⎪⎨⎪⎧∠AGB =∠BHC ,∠BAG =∠CBH ,AB =BC ,∴△AGB ≌△BHC ,∴AG =BH ,BG =CH =HF .∵BH =BG +GH ,∴BH =HF +GH =FG ,∴AG =FG .。
(优选)2019年八年级数学下册12微专题平行四边形中的典型模型问题习题(新版)冀教版

微专题:平行四边形中的典型模型问题◆模型一平行四边形+内角平分线→等腰三角形1.(2017·石家庄长安区期末)如图,在▱ABCD中,AB=4,AD=7,∠ABC的平分线BE交AD 于点E,则DE的长为( )A.4 B.3 C.3.5 D.2第1题图第2题图2.如图,在▱ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E.若AB=3,EF=1,则BC长为( )A.4 B.5 C.6 D.73.如图,在平行四边形ABCD中,P是CD边上一点,且AP和BP分别平分∠DAB和∠CBA.若AD=5,AP=8,则△APB的周长是________.◆模型二平行四边形中求面积或判断全等三角形模型(根据中心对称性或等高求面积)4.如图,平行四边形的两条对角线将平行四边形的面积分成四部分,分别记作S1,S2,S3,S4,下列关系式成立的是( )A.S1<S2<S3<S4 B.S1=S2=S3=S4C.S1+S2>S3+S4 D.S1=S3<S2=S4第4题图第5题图5.如图,已知▱ABCD的面积为24,点E为AD边上一点,则图中阴影部分的面积是( ) A.6 B.9 C.12 D.156.如图,在平行四边形ABCD中,直线EF经过其对角线的交点O,且分别交AD,BC于点M,N,交BA,DC的延长线于点E,F,下列结论:①AO=BO;②OE=OF;③△EAM≌△FCN;④△EAO≌△CNO,其中正确的是( )A.①② B.②③ C.②④ D.③④第6题图第7题图7.如图,AC,BD为▱ABCD的对角线,已知BC=6,BC边上的高为4,则阴影部分的面积为________.8.如图,在平行四边形ABCD中,对角线AC,BD交于点O,过点O的直线分别交AD,BC于点M,N.若△CON的面积为2,△DOM的面积为3,则△AOB的面积为________.第8题图第9题图9.(2017·南充中考)如图,在▱ABCD中,过对角线BD上一点P作EF∥BC,GH∥AB.若CG =2BG,S△BPG=1,则S▱AEPH=________.◆模型三平行四边形中利用面积法求高的问题10.(2017·邢台县校级期末)如图,平行四边形ABCD的邻边AD∶AB=5∶4,过点A作AE⊥BC,AF⊥CD,垂足分别为点E,F.若AE=2cm,则AF=________cm.第10题图变式题图【变式题】高在内部→高在外部如图,▱ABCD的周长是103+62,AB的长是5 3 ,DE⊥AB于E,DF⊥CB交CB的延长线于点F,DE的长是3,则DF的长为________.参考答案与解析1.B 2.B3.24 解析:∵四边形ABCD 是平行四边形,∴AD ∥CB ,AB ∥CD ,∴∠DAB +∠CBA =180°.又∵AP 和BP 分别平分∠DAB 和∠CBA ,∴∠PAB +∠PBA =12(∠DAB +∠CBA )=90°.∴∠APB =90°.∵AP 平分∠DAB ,∴∠DAP =∠PAB .∵AB ∥CD ,∴∠PAB =∠DPA ,∴∠DAP =∠DPA ,∴DP =AD =5.同理PC =CB =5,则AB =DC =DP +PC =10.在Rt△APB 中,AB =10,AP =8,∴BP =102-82=6,∴△APB 的周长为6+8+10=24.4.B5.C6.B7.128.59.4 解析:∵EF ∥BC ,GH ∥AB ,∴四边形HPFD 、BEPG 为平行四边形,∴S △PHD =S △DFP ,S △PEB =S △BGP .∵四边形ABCD 为平行四边形,∴S △ABD =S △CDB ,∴S △ABD -S △PEB -S △PHD =S △CDB -S △BGP -S △DFP ,即S 四边形AEPH =S 四边形PFCG .∵CG =2BG ,S △BPG =1,∴S 四边形AEPH =S 四边形PFCG =4S △BPG =4×1=4.10.2.5 【变式题】562 解析:∵▱ABCD 的周长是103+62,∴CD =AB =53,AD =BC =(103+62-2×53)÷2=32.∵S ▱ABCD =AB ·DE =BC ·DF ,即53×3=32·DF ,∴DF =562.。
冀教版八年级数学下册2《正方形》课件

情景二
A
D
A
D
B
C
问题:
B
C
图中CD在移动时,这个图形始终是怎样的图形? (CD在移动的过程中始终保持与AB平行)
当CD移动到CD位置,且 AD =AB时,此 时是什么图形啊?
当AD=AB这个四边形是矩形,它是特殊的矩形, 是一组邻边相等的矩形也是正方形.
正方形的概念:
有__一__组__邻__边__相__等__且__有__一__个__角__是__直__角__的_
理由。
A
D
F G
BE
C
学以致用
由三条公路围成的一个区域为直角三 角形形状.工程队要想在区域内划一块 正方形的地块作为新小区,且让小区足 够大,请你来帮工程队设计一下
A
F E
B
D
C
例2.如图四边形ABCD和DEFG都是正方形,
试说明AE=CG
A
D
解:因为四边形ABCD是正方形
根据正方形的四边相等,得 AD=CD
C
即AC平分∠BAD,BD平分∠ABC
∴
∠ABD=∠DAC=
1 2
×
90°=45°
又∵正方形的两条对角线互相垂直 即AC⊥BD
∴∠DOC=90°
例2
如图:在正方形ABCD中,点E在对角线AC 上,那么BE与DE相等吗?为什么?
解: BE = DE
因为 对角线所在的
D
C
直线是正方形ABCD的一条
E
对称轴,而点E在对称轴上,
两组对边平行且相等,两组对角相等,对角线互
相平分
A
D
2.具有矩形的一切特征
O
四个角都是直角,对角线相等
翼教版八年级数学下册微专题矩形中的典型模型问题

微专题:矩形中的典型模型问题◆模型一面积问题1.(2017·北京中考)现代数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所得两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证.请根据该图完成这个推论的证明过程.证明:S矩形NFGD=S△ADC-(S△ANF+S△FGC),S矩形EBMF=S△ABC-(________+ ________).易知,S△ADC=S△ABC,________=________,________=________.可得S矩形NFGD=S矩形EBMF.2.如图,在矩形ABCD中,点E,F分别是AB,CD的中点,连接DE,BF,分别取DE,BF的中点M,N,连接AM,CN,MN.若AB=2 3 ,BC=25,则图中阴影部分图形的面积和为________.第2题图第3题图3.如图,点P是矩形ABCD内任意一点,连接PA,PB,PC,PD,得到的四个三角形的面积分别为S1,S2,S3,S4,其中S1=2,S4=6,则S3-S2=________.◆模型二矩形中根据面积法求两垂线段的定值问题4.如图,P是矩形ABCD的边AD上一点,PE⊥AC于E,PF⊥BD于F(P与A,D不重合),若AB=2,BC=23,则PE+PF的值为( )A.2 B.1 C. 3 D.无法确定第4题图第5题图5.如图,在矩形ABCD中,AB=3,BC=2,点E为AD的中点,点F为BC边上任一点,过点F分别作EB,EC的垂线,垂足分别为点G,H,则FG+FH的值为________.【变式题】含角平分线,本质不同如图,四边形ABCD是矩形,E为AD上一点,且∠CBD=∠EBD,P为对角线BD上一点,PN⊥BE于点N,PM⊥AD于点M.(1)求证:BE=DE;(2)判断AB和PM,PN的数量关系并说明理由.◆模型三矩形内部含45°角的问题6.(2017·包头中考)如图,在矩形ABCD中,点E是CD的中点,点F是BC上一点,且FC=2BF,连接AE,EF.若AB=2,AD=3,则∠AEF的度数为________.参考答案与解析1.S △AEF S △FCM S △ANF S △AEF S △FGC S △FMC 2.2153.4 解析:∵四边形ABCD 是矩形,∴AB =CD ,AD =BC .设点P 到AD ,AB ,BC ,CD 的距离分别为h 1,h 2,h 3,h 4,则S 1=12AD ·h 1,S 2=12AB ·h 2,S 3=12BC ·h 3,S 4=12CD ·h 4.∵12AD ·h 1+12BC ·h 3=12BC ·CD ,12AB ·h 2+12CD ·h 4=12AB ·BC ,∴12AD ·h 1+12BC ·h 3=12AB ·h 2+12CD ·h 4,即∴S 2+S 4=S 1+S 3,∴S 3-S 2=S 4-S 1=6-2=4. 4.C5.3105解析:连接EF .∵四边形ABCD 是矩形,∴CD =AB =3,AD =BC =2,∠A =∠D =90°.∵点E 为AD 的中点,∴AE =DE =1.在Rt △ABE 中,BE =AE 2+AB 2=12+32=10,在Rt △DCE 中,CE =DE 2+DC 2=12+32=10,∴BE =CE =10.∵S △BCE =S △BEF +S △CEF ,∴12BC ·AB =12BE ·FG +12CE ·FH ,即BE (FG +FH )=BC ·AB ,∴10(FG +FH )=2×3,解得FG +FH =3105.【变式题】(1)证明:∵四边形ABCD是矩形,∴AD∥BC,∴∠ADB=∠CBD,∵∠CBD=∠EBD,∴∠ADB=∠EBD,∴BE=DE.(2)解:AB=PM+PN.理由如下:如图,延长MP交BC于Q.∵AD∥BC,PM⊥AD,∴PQ⊥BC.∵∠CBD=∠EBD,PN⊥BE,∴PQ=PN,∴AB=MQ=PM+PQ=PM+PN.6.45°解析:连接AF.∵四边形ABCD是矩形,∴∠B=∠C=90°,CD=AB=2,BC=AD=3.∵FC=2BF,∴BF=1,FC=2,∴AB=FC.∵E是CD的中点,∴CE=12CD=1,∴BF=CE.在△ABF和△FCE中,⎩⎪⎨⎪⎧AB=FC,∠B=∠C,BF=CE,∴△ABF≌△FCE(SAS),∴∠BAF=∠CFE,AF=FE.∵∠BAF+∠AFB=90°,∴∠CFE+∠AFB=90°,∴∠AFE =180°-90°=90°,∴△AEF是等腰直角三角形,∴∠AEF=45°.易错专题:求二次函数的最值或函数值的范围——类比各形式,突破给定范围求最值◆类型一 没有限定自变量的取值范围求最值 1.函数y =-(x +1)2+5的最大值为________.2.已知二次函数y =3x 2-12x +13,则函数值y 的最小值是【方法12】( )A .3B .2C .1D .-13.函数y =x(2-3x),当x 为何值时,函数有最大值还是最小值?并求出最值. ◆类型二 限定自变量的取值范围求最值4.在二次函数y =x 2-2x -3中,当0≤x ≤3时,y 的最大值和最小值分别是【方法12】( )A .0,-4B .0,-3C .-3,-4D .0,05.已知0≤x ≤32,则函数y =x 2+x +1( )A .有最小值34,但无最大值B .有最小值34,有最大值1C .有最小值1,有最大值194D .无最小值,也无最大值6.已知二次函数y =-2x 2-4x +1,当-5≤x ≤0时,它的最大值与最小值分别是( )A .1,-29B .3,-29C .3,1D .1,-37.已知0≤x ≤12,那么函数y =-2x 2+8x -6的最大值是________.◆类型三 限定自变量的取值范围求函数值的范围8.从y =2x 2-3的图像上可以看出,当-1≤x ≤2时,y 的取值范围是( )A .-1≤y ≤5B .-5≤y ≤5C .-3≤y ≤5D .-2≤y ≤19.(贵阳中考)已知二次函数y =-x 2+2x +3,当x ≥2时,y 的取值范围是( )A .y ≥3B .y ≤3C .y >3D .y <310.二次函数y =x 2-x +m(m 为常数)的图像如图所示,当x =a 时,y <0;那么当x =a -1时,函数值CA .y <0B .0<y <mC .y >mD .y =m11.二次函数y=2x2-6x+1,当0≤x≤5时,y的取值范围是______________.◆类型四已知函数的最值,求自变量的取值范围或待定系数的值12.当二次函数y=x2+4x+9取最小值时,x的值为( )A.-2 B.1 C.2 D.913.已知二次函数y=ax2+4x+a-1的最小值为2,则a的值为( )A.3 B.-1 C.4 D.4或-114.已知y=-x2+(a-3)x+1是关于x的二次函数,当x的取值范围在1≤x≤5时,y在x=1时取得最大值,则实数a的取值范围是( )A.a=9 B.a=5 C.a≤9 D.a≤515.已知a≥4,当1≤x≤3时,函数y=2x2-3ax+4的最小值是-23,则a=________.16.若二次函数y=x2+ax+5的图像关于直线x=-2对称,已知当m≤x≤0时,y有最大值5,最小值1,则m的取值范围是_____________.参考答案与解析1.5 2.C3.解:∵y =x (2-3x )=-3⎝ ⎛⎭⎪⎫x 2-23x =-3⎝ ⎛⎭⎪⎫x -132+13,∴该抛物线的顶点坐标是⎝ ⎛⎭⎪⎫13,13.∵-3<0,∴该抛物线的开口方向向下,∴当x =13时,该函数有最大值,最大值是13. 4.A 5.C6.B 解析:首先看自变量的取值范围-5≤x ≤0是否包含了顶点的横坐标.由于y =-2x 2-4x +1=-2(x +1)2+3,其图像的顶点坐标为(-1,3),所以在-5≤x ≤0范围内,当x =-1时,y 取最大值,最大值为3;当x =-5时,y 取最小值,最小值为y =-2×(-5)2-4×(-5)+1=-29.故选B.7.-2.5 解析:∵y =-2x 2+8x -6=-2(x -2)2+2,∴该抛物线的对称轴是直线x =2,当x <2,y随x 的增大而增大.又∵0≤x ≤12,∴当x =12时,y 取最大值,y 最大=-2×⎝ ⎛⎭⎪⎫12-22+2=-2.5. 8.C9.B 解析:当x =2时,y =-4+4+3=3.∵y =-x 2+2x +3=-(x -1)2+4,∴当x >1时,y 随x 的增大而减小,∴当x ≥2时,y 的取值范围是y ≤3.故选B.10.C 解析:当x =a 时,y <0,则a 的范围是x 1<a <x 2,又对称轴是直线x =12,所以a -1<0.当x <12时,y 随x 的增大而减小,当x =0时函数值是m .因此当x =a -1<0时,函数值y 一定大于m . 11.-72≤y ≤21 解析:二次函数y =2x 2-6x +1的图像的对称轴为直线x =32.在0≤x ≤5范围内,当x =32时,y 取最小值,y 最小=-72;当x =5时,y 取最大值,y 最大=21.所以当0≤x ≤5时,y 的取值范围是-72≤y ≤21.12.A13.C 解析:∵二次函数y =ax 2+4x +a -1有最小值2,∴a >0,y 最小值=4ac -b 24a =4a (a -1)-424a =2,整理得a 2-3a -4=0,解得a =-1或4.∵a >0,∴a =4.故选C.14.D 解析:第一种情况:当二次函数的对称轴不在1≤x ≤5内时,∵在1≤x ≤5时,y 在x =1时取得最大值,∴对称轴一定在1≤x ≤5的左边,∴对称轴直线x =a -32<1,即a <5;第二种情况:当对称轴在1≤x ≤5内时,∵-1<0,∴对称轴一定是在顶点处取得最大值,即对称轴为直线x =1,∴a -32=1,即a =5.综上所述,a≤5.故选D.15.5 解析:抛物线的对称轴为直线x=3a4.∵a≥4,∴x=3a4≥3.∵抛物线开口向上,在对称轴的左侧,y随x的增大而减小,∴当1≤x≤3时,函数取最小值-23时,x=3.把x=3代入y=2x2-3ax+4中,得18-9a+4=-23,解得a=5.16.-4≤m≤-2 解析:∵二次函数图像关于直线x=-2对称,∴-a2×1=-2,∴a=4,∴y=x2+4x +5=(x+2)2+1.当y=1时,x=-2;当y=5时,x=0或-4.∵当m≤x≤0时,y有最大值5,最小值1,∴-4≤m≤-2.。
2020春冀教版初中数学八年级下册习题课件--小专题(十) 正方形中与旋转有关的计算与证明

解:(1)BD=CF 成立. 证明:∵四边形 ADEF 是正方形,
∴AD=AF,∠FAD=90°.∴∠FAB+∠BAD=90°.
∵∠CAF+∠FAB=90°,∴∠BAD=∠CAF.
AB=AC,
(2)如果正方形 EFGH 的边长为 b(b>a),(1)中的结论是否仍然成 立?请作出判断并给予证明.
【解答】 解:(1)AF 与 BH 的大小关系为:AF=BH.当正方形 EFGH 绕点 E 旋转变化时,这种关系保持不变.
(2)结论仍然成立. 证明:∵四边形 ABCD 是正方形, ∴AE=BE,∠AEH+∠BEH=90°. ∵四边形 EFGH 是正方形, ∴EF=EH,∠AEH+∠AEF=90°.
4.如图 1,△ABC 是等腰直角三角形,∠BAC=90°,AB=AC, 四边 BD=CF, BD⊥CF 成立.
(1)当△ABC 绕点 A 逆时针旋转 θ(0°<θ<90°)时,如图 2,BD =CF 成立吗?若成立,请证明;若不成立,请说明理由.
在△ABD 和△ACF 中,∠BAD=∠CAF, AD=AF,
∴△ABD≌△ACF(SAS).∴BD=CF.
(2)证明:由(1)得△ABD≌△ACF, ∴∠HFN=∠ADN. 又∵∠HNF=∠AND,∴∠NHF=∠NAD=90°. ∴HD⊥HF,即 BD⊥CF.
模型归纳:如图,在正方形 ABCD 中,O 为对角线的交点,直角 ∠EOF 绕点 O 旋转,若 OE,OF 分别与 DA,AB 延长线交于点 G, H,则△AOE≌△BOF,△AOG≌△BOH,△OGH 是等腰直角三角 形,且 S 四边形 OEBF=14S 正方形 ABCD.
八年级数学下册 微专题:正方形中的典型模型问题

八年级数学下册微专题:正方形中的典型模型问题介绍本文档介绍了八年级数学下册的微专题,主题为“正方形中的典型模型问题”。
正方形作为一种常见的几何图形,在数学中有着广泛的应用。
通过研究和探究正方形中的典型模型问题,可以帮助同学们巩固和深化对正方形特性的理解,提高问题解决能力。
主要内容本专题主要包括以下几个方面的内容:1. 正方形的特性介绍正方形的定义、性质以及相关公式,帮助同学们全面了解正方形的基本特性,如边长、对角线、面积等。
2. 与正方形相关的模型问题探究在日常生活中与正方形相关的典型模型问题。
例如:如何利用正方形铺砖,如何计算正方形围栏的长度等。
通过这些实际问题的应用,培养同学们运用正方形特性解决实际问题的能力。
3. 解决模型问题的方法和思路介绍解决模型问题的一般方法和思路,引导同学们分析问题、建立数学模型、推导解答过程。
通过实际案例的讲解,帮助同学们掌握解决模型问题的基本技巧。
教学目标通过研究本微专题,同学们应能达到以下目标:1. 掌握正方形的定义和基本特性。
2. 理解正方形在模型问题中的应用。
3. 培养解决模型问题的能力和思维方式。
4. 提高数学问题分析和数学建模能力。
教学方法与活动设计针对本微专题的教学,建议采用以下教学方法和活动设计:1. 课堂讲解:通过讲解正方形的定义、性质和相关公式,夯实基础知识。
2. 实例演练:给同学们提供一些典型的正方形模型问题,引导他们进行分析和解答。
3. 小组讨论:组织同学们在小组内互相交流,讨论和解决正方形模型问题。
4. 探究活动:引导同学们自主探究实际生活中的正方形模型问题,发现其中的数学规律。
总结通过学习八年级数学下册微专题“正方形中的典型模型问题”,同学们能够深入了解正方形的特性以及在实际问题中的应用。
同时,通过解决模型问题的过程,同学们能够培养数学思维和解决问题的能力。
希望同学们能够通过本专题的学习,对正方形有更深入的认识,并能运用所学知识解决实际问题。
《正方形》PPT-冀教版八年级数学下册

引入新课
小红在店里看到一块漂亮的方纱巾, 非常想 买。但她拿起来看时感觉不太方。商店老板看 她犹豫的样子, 马上过来拉起一组对角, 让 小红看这组对角是否对齐, 小红还有些犹豫, 老板又拉起另一组对角, 让小红检验。小红 终于买了这块纱巾。你认为小红买的这块纱巾 真是正方形吗?你能帮她检验吗?
情景二
A
D
A
D
B
C
B
C
问题:
图中CD在移动时, 这个图形始终是怎样的图形? (CD在移动的过程中始终保持与AB平行)
当CD移动到CD位置, 且 AD =AB时, 此 时是什么图形啊?
当AD=AB这个四边形是矩形,它是特殊的矩形, 是一组邻边相等的矩形也是正方形.
正方形的概念:
有__一__组__邻__边__相__等__且__有__一__个__角__是__直__角__的_
四个角都是直角, 对角线相等 (3)具有菱形的一切性质
对角线互相平
四条边相等; 对角线互相垂直, 每条对角线平分一组对角
学一学
例题解析
例1. 如图, 在正方ABCD中, 求∠ABD、
∠DAC、∠DOC的度数。
A
解: ∵ 四边形ABCD是正方形
D
根据正方形的四个内角都为直角
O
得∠DAB=∠ABC=90°
22.6 正方形
(1)平行四边形有哪些性质?矩形与平行四边 形比较有哪些特殊的性质?
边: 对边平行且相等
平行四边形 角: 对角相等邻角互补
矩形
对角线: 对角线互相平分 对称性: 轴对称图形
角: 四个角是直角 对角线: 对角线相等
菱形的性质
菱形的性质
具有平行四边形一切性质
冀教版2019-2020年八年级数学下册教案:22.6 正方形

22.6 正方形1.掌握正方形的概念、性质,并会运用;(重点) 2.理解正方形与平行四边形、矩形、菱形的联系和区别;(难点)3.掌握正方形的判定条件;(重点) 4.合理地利用正方形的判定进行有关的论证和计算.(难点)一、情境导入做一做:用一张长方形的纸片(如图所示)折出一个正方形.学生在动手过程中对正方形产生感性认识,并感知正方形与矩形的关系.问题:什么样的四边形是正方形?二、合作探究探究点一:正方形的性质【类型一】 利用正方形的性质求线段长或证明如图所示,正方形ABCD 的边长为1,AC是对角线,AE 平分∠BAC ,EF ⊥AC 于点F .(1)求证:BE =CF ; (2)求BE 的长.解析:(1)由角平分线的性质可得到BE =EF ,再证明△CEF 为等腰直角三角形,可证明BE =CF ;(2)设BE =x ,在△CEF 中可表示出CE ,由BC =1,可列出方程,可求得BE .(1)证明:∵四边形ABCD 为正方形,∴∠B =90°,∵EF ⊥AC ,∴∠EF A =90°,∵AE 平分∠BAC ,∴BE =EF ,又∵AC 平分∠BCD ,∴∠ACB =45°,∴∠FEC =∠FCE ,∴EF =FC ,∴BE =CF ;(2)解:设BE =x ,则EF =CF =x ,在Rt △CEF 中,CE =EF 2+CF 2=2x ,∵BC =1,∴x +2x =1,解得x =2-1,即BE 的长为2-1.方法总结:矩形被每条对角线分成两个直角三角形,被两条对角线分成四个等腰直角三角形,因此正方形的计算问题可以转化到直角三角形和等腰直角三角形中去解决.【类型二】 利用正方形的性质求角度或证明在正方形ABCD 中,点F 是边AB 上一点,连接DF ,点E 为DF 中点.连接BE 、CE 、AE .(1)求证:△AEB ≌△DEC ;(2)当EB =BC 时,求∠AFD 的度数.解析:(1)根据正方形的四条边都相等可得AB =CD ,每一个角都是直角可得∠BAD =∠ADC =90°,再根据直角三角形斜边上的中线等于斜边的一半可得AE =EF =DE =12DF ,根据等边对等角可得∠EAD =∠EDA ,再求出∠BAE =∠CDE ,然后利用“边角边”证明即可;(2)根据全等三角形对应边相等可得EB =EC ,再求出△BCE 是等边三角形,根据等边三角形的性质可得∠EBC =60°,然后求出∠ABE =30°,再根据等腰三角形两底角相等求出∠BAE ,然后根据等边对等角可得∠AFD =∠BAE .(1)证明:在正方形ABCD 中,AB =CD ,∠BAD =∠ADC =90°,∵点E 为DF 的中点,∴AE =EF =DE =12DF ,∴∠EAD =∠EDA ,∵∠BAE =∠BAD -∠EAD ,∠CDE =∠ADC -∠EDA ,∴∠BAE =∠CDE ,在△AEB 和△DEC 中,⎩⎪⎨⎪⎧AB =CD ,∠BAE =∠CDE ,AE =DE ,∴△AEB ≌△DEC (SAS);(2)解:∵△AEB ≌△DEC ,∴EB =EC ,∵EB =BC ,∴EB =BC =EC ,∴△BCE 是等边三角形,∴∠EBC =60°,∴∠ABE =90°-60°=30°,∵EB =BC =AB ,∴∠BAE =12(180°-30°)=75°,又∵AE =EF ,∴∠AFD =∠BAE =75°.方法总结:正方形是最特殊的平行四边形,在正方形中进行计算时,要注意计算出相关的角的度数,要注意分析图形中有哪些相等的线段.探究点二:正方形的判定【类型一】 利用“一组邻边相等的矩形是正方形”判定已知:如图,在Rt △ABC 中,∠ACB =90°,CD 为∠ACB 的平分线,DE ⊥BC 于点E ,DF ⊥AC 于点F .求证:四边形CEDF 是正方形.解析:要证四边形CEDF 是正方形,则要先证明四边形DECF 是矩形,再证明一组邻边相等即可.证明:∵CD 平分∠ACB ,DE ⊥BC ,DF ⊥AC ,∴DE =DF ,∠DFC =90°,∠DEC =90°,又∵∠ACB =90°,∴四边形DECF 是矩形,∵DE =DF ,∴矩形DECF 是正方形.方法总结:要注意判定一个四边形是正方形,必须先证明这个四边形为矩形或菱形.利用“有一个角是直角的菱形是正方形”判定如图,已知在四边形ABFC 中,∠ACB =90°,BC 的垂直平分线EF 交BC 于点D ,交AB 于点E ,且CF =AE ;(1)试判断四边形BECF 是什么四边形?并说明理由;(2)当∠A 的大小满足什么条件时,四边形BECF 是正方形?请回答并证明你的结论.解析:(1)根据中垂线的性质:中垂线上的点到线段两个端点的距离相等,有BE =EC ,BF =FC ,又因为CF =AE ,可得出BE =EC =BF =FC ,根据四边相等的四边形是菱形,所以四边形BECF 是菱形;(2)由菱形的性质知,对角线平分一组对角,即当∠ABC =45°时,∠EBF =90°,得出菱形EBFC 为正方形,根据直角三角形中两个锐角互余得∠A =45°.解:(1)四边形BECF 是菱形.理由如下:∵EF 垂直平分BC ,∴BF =FC ,BE =EC ,∴∠3=∠1,∵∠ACB =90°,∴∠3+∠4=90°,∠1+∠2=90°,∴∠2=∠4,∴EC =AE ,∴BE =AE ,∵CF =AE ,∴BE =EC =CF =BF ,∴四边形BECF 是菱形;(2)当∠A =45°时,菱形BECF 是正方形.证明:∵∠A =45°,∠ACB =90°,∴∠CBA =45°,∴∠EBF =2∠CBA =90°,∴菱形BECF 是正方形.方法总结:正方形的判定方法:①先判定四边形是矩形,再判定这个矩形有一组邻边相等;②先判定四边形是菱形,再判定这个矩形有一个角为直角;③还可以先判定四边形是平行四边形,再用①或②进行判定.探究点三:正方形的性质与判定的综合已知:如图,△ABC 中,点O 是AC 上的一动点,过点O 作直线MN ∥BC ,设MN 交∠BCA 的平分线于点E ,交∠BCA 的外角∠ACG 的平分线于点F ,连接AE 、AF .(1)求证:∠ECF =90°;(2)当点O 运动到何处时,四边形AECF 是矩形?请说明理由;(3)在(2)的条件下,△ABC 应该满足条件:________________________,则四边形AECF 为正方形.(直接添加条件,无需证明)解析:(1)由已知CE 、CF 分别平分∠BCO 和∠GCO ,可推出∠BCE =∠OCE ,∠GCF =∠OCF ,所以得∠ECF =90°;(2)由(1)可得出EO =CO =FO ,点O 运动到AC 的中点时,则有EO =CO =FO =AO ,所以这时四边形AECF 是矩形;(3)由已知和(2)得到的结论,点O 运动到AC 的中点时,且△ABC 满足∠ACB 为直角的直角三角形时,则推出四边形AECF 是矩形且对角线垂直,所以四边形AECF 是正方形.(1)证明:∵CE 平分∠BCO ,CF 平分∠GCO ,∴∠OCE =∠BCE ,∠OCF =∠GCF ,∴∠ECF =12×180°=90°;(2)解:当点O 运动到AC 的中点时,四边形AECF 是矩形.理由如下:∵MN ∥BC ,∴∠OEC =∠BCE ,∠OFC =∠GCF ,又∵CE 平分∠BCO ,CF 平分∠GCO ,∴∠OCE =∠BCE ,∠OCF =∠GCF ,∴∠OCE =∠OEC ,∠OCF =∠OFC ,∴EO =CO ,FO =CO ,∴OE =OF .又∵当点O 运动到AC 的中点时,AO =CO ,∴四边形AECF 是平行四边形,∵∠ECF =90°,∴四边形AECF 是矩形;(3)解:当点O 运动到AC 的中点时,且满足∠ACB为直角时,四边形AECF 是正方形.∵由(2)知,当点O 运动到AC 的中点时,四边形AECF 是矩形,已知MN ∥BC ,当∠ACB =90°,则∠AOF =∠COE =∠COF =∠AOE =90°,即AC ⊥EF ,∴四边形AECF 是正方形.故答案为:∠ACB 为直角.方法总结:此题考查的是正方形和矩形的判定,角平分线的定义,平行线的性质,等腰三角形的判定等知识.解题的关键是由已知得出EO =FO ,确定(2)(3)的条件.如图,AE 是正方形ABCD 中∠BAC 的平分线,AE 分别交BD 、BC 于F 、E ,AC 、BD 相交于O .求证:(1)BE =BF ;(2)OF =12CE .解析:(1)根据正方形的性质可求得∠ABE =∠AOF =90°.由于AE 是正方形ABCD 中∠BAC 的平分线,根据“等角的余角相等”即可求得∠AFO =∠AEB .根据“对顶角相等”即可求得∠BFE =∠AEB ,BE =BF ;(2)连接O 和AE 的中点G .根据三角形的中位线的性质即可证得OG ∥BC ,OG =12CE .根据平行线的性质即可求得∠OGF =∠FEB ,从而证得∠OGF =∠AFO ,OG =OF ,进而证得OF =12CE .证明:(1)∵四边形ABCD 是正方形,∴AC ⊥BD ,∴∠ABE =∠AOF =90°.∵∠CAE =∠BAE ,∴∠AFO =∠AEB ,又∵∠AFO =∠BFE ,∴∠BFE =∠AEB ,∴BE =BF ;(2)连接O 和AE 的中点G .∵AO =CO ,AG =EG ,∴OG ∥BC ,OG =12CE ,∴∠OGF =∠FEB .∵∠AFO=∠AEB ,∴∠OGF =∠AFO ,∴OG =OF ,∴OF =12CE .方法总结:在正方形的条件下证明线段的关系,通常的方法是连接对角线构造垂直平分线,利用垂直平分线的性质、中位线定理、角平分线、等腰三角形等知识来证明,有时也利用全等三角形来解决.三、板书设计 1.正方形的性质对边平行,四条边都相等; 四个角都是直角;对角线互相垂直、平分且相等,并且每一条对角线平分一组对角.2.正方形的判定方法一组邻边相等的矩形是正方形; 有一个角是直角的菱形是正方形.本节课采用探究式教学,让学生产生学习兴趣,通过实践活动调动学生的积极性,给学生动手动脑的机会,变被动学习为主动学习,引导通过感官的思维去观察、探究、分析知识形成的过程,以此深化知识、更深刻理解知识、主动获取知识,养成良好的学习习惯.。
冀教版数学八下课件正方形

证明: ∵ 四边形ABCD是正方形
A
D
∴∠B=900 ∠ACB=450
∵∠AEF=900 AB=AE
∴△ABF≌△AFE(HL)
∴BF=EF
又∵∠FEC=900
E
∴∠EFC=450
∴EC=EF(等角对等边)
B F
C
∴BF=EF=EC
灿若寒星
构建与证明
∴∠A=∠B=∠C=900.
A
D
∴四边形ABCD是矩形.
∵AB=BC,
∴四边形ABCD是正方形. 灿若寒星
B
C
正方形的判定
定理:对角线相等的菱形是正方形.
已知:四边形ABCD是菱形,且对角线AC=BD.
求证:四边形ABCD是正方形. 分析:要证明四边形ABCD是正方形,可转化为证明有 一组邻边相等的矩形(或有一个角是直角的菱形)即可.
如图,分别延长等腰直角三角形OAB的两条直 角边AO和BO,使AO=OC,BO=OD
求证:四边形ABCD是正方形。
A
D
O
B
C
灿若寒星
轴对称
灿若寒星
思维拓展
如何设计花坛?
在一块正方形的花坛上,欲修建两条直的小路,使得两条直的 小路将花坛平均分成面积相等的四部分(不考虑道路的宽度), 你有几种方法?(至少说出三种)
初中数学课件
金戈铁骑整理制作
正方形
灿若寒星
学习目标
1.理解正方形与平行四边形、矩形、菱形概 念之间的联系和区别;
2.能用正方形的定义、性质进行推理与计算.
学习重点
正方形与平行四边形、矩形、菱形的联系.
灿若寒星
八年级数学下册 12 微专题 平行四边形中的典型模型问题习题 (新版)冀教版
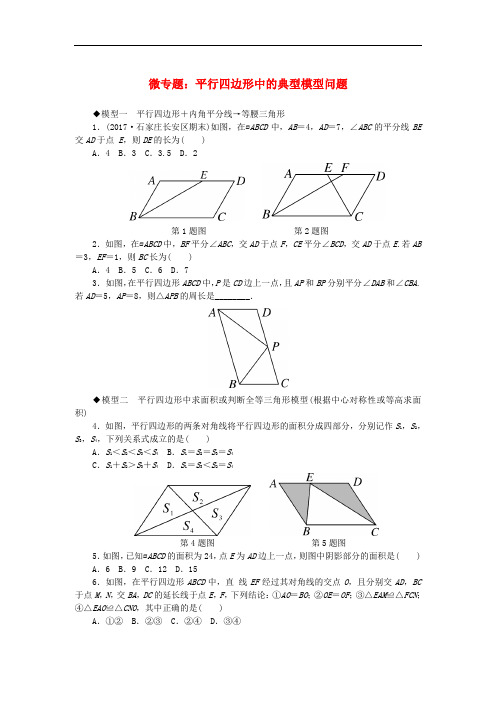
微专题:平行四边形中的典型模型问题◆模型一平行四边形+内角平分线→等腰三角形1.(2017·石家庄长安区期末)如图,在▱ABCD中,AB=4,AD=7,∠ABC的平分线BE 交AD于点E,则DE的长为( )A.4 B.3 C.3.5 D.2第1题图第2题图2.如图,在▱ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E.若AB =3,EF=1,则BC长为( )A.4 B.5 C.6 D.73.如图,在平行四边形ABCD中,P是CD边上一点,且AP和BP分别平分∠DAB和∠CBA.若AD=5,AP=8,则△APB的周长是________.◆模型二平行四边形中求面积或判断全等三角形模型(根据中心对称性或等高求面积)4.如图,平行四边形的两条对角线将平行四边形的面积分成四部分,分别记作S1,S2,S3,S4,下列关系式成立的是( )A.S1<S2<S3<S4 B.S1=S2=S3=S4C.S1+S2>S3+S4 D.S1=S3<S2=S4第4题图第5题图5.如图,已知▱ABCD的面积为24,点E为AD边上一点,则图中阴影部分的面积是( ) A.6 B.9 C.12 D.156.如图,在平行四边形ABCD中,直线EF经过其对角线的交点O,且分别交AD,BC 于点M,N,交BA,DC的延长线于点E,F,下列结论:①AO=BO;②OE=OF;③△EAM≌△FCN;④△EAO≌△CNO,其中正确的是( )A.①② B.②③ C.②④ D.③④第6题图第7题图7.如图,AC,BD为▱ABCD的对角线,已知BC=6,BC边上的高为4,则阴影部分的面积为________.8.如图,在平行四边形ABCD中,对角线AC,BD交于点O,过点O的直线分别交AD,BC于点M,N.若△CON的面积为2,△DOM的面积为3,则△AOB的面积为________.第8题图第9题图9.(2017·南充中考)如图,在▱ABCD中,过对角线BD上一点P作EF∥BC,GH∥AB.若CG=2BG,S△BPG=1,则S▱AEPH=________.◆模型三平行四边形中利用面积法求高的问题10.(2017·邢台县校级期末)如图,平行四边形ABCD的邻边AD∶AB=5∶4,过点A作AE⊥BC,AF⊥CD,垂足分别为点E,F.若AE=2cm,则AF=________cm.第10题图变式题图【变式题】高在内部→高在外部如图,▱ABCD的周长是103+62,AB的长是5 3 ,DE⊥AB于E,DF⊥CB交CB的延长线于点F,DE的长是3,则DF的长为________.参考答案与解析1.B 2.B3.24 解析:∵四边形ABCD 是平行四边形,∴AD ∥CB ,AB ∥CD ,∴∠DAB +∠CBA =180°.又∵AP 和BP 分别平分∠DAB 和∠CBA ,∴∠PAB +∠PBA =12(∠DAB +∠CBA )=90°.∴∠APB =90°.∵AP 平分∠DAB ,∴∠DAP =∠PAB .∵AB ∥CD ,∴∠PAB =∠DPA ,∴∠DAP =∠DPA ,∴DP =AD =5.同理PC =CB =5,则AB =DC =DP +PC =10.在Rt△APB 中,AB =10,AP =8,∴BP =102-82=6,∴△APB 的周长为6+8+10=24.4.B5.C6.B7.128.59.4 解析:∵EF ∥BC ,GH ∥AB ,∴四边形HPFD 、BEPG 为平行四边形,∴S △PHD =S △DFP ,S △PEB =S △BGP .∵四边形ABCD 为平行四边形,∴S △ABD =S △CDB ,∴S △ABD -S △PEB -S △PHD =S △CDB -S △BGP -S △DFP ,即S 四边形AEPH =S 四边形PFCG .∵CG =2BG ,S △BPG =1,∴S 四边形AEPH =S 四边形PFCG =4S △BPG =4×1=4.10.2.5 【变式题】562 解析:∵▱ABCD 的周长是103+62,∴CD =AB =53,AD =BC =(103+62-2×53)÷2=32.∵S ▱ABCD =AB ·DE =BC ·DF ,即53×3=32·DF ,∴DF =562.。
初二数学笔记详解-正方形几个基本模型

本次课程椺 9 week
对⻆线性质相关模型 辅助线 僻线
辅助线20 连顶点
il
鯯
2 半⻆模型
3 构造正方形
4 最值专题
一 垂直类模型
1 对⻆线性质
A
D
0连接对⻆线
得4个⻢腰直⻆三⻆形
0
20 对⻆线上的点
B
陘作垂线 连接端点
C
找等量关系
①等腰直⻆三⻆形
A
E
F
102个全乳
此 证 将 ADF旋转至 0ABG 在0时和 0AEG中 胩 AG
40截取MEAN
LfAt 二LEAG二450
At AE
可证 ABN E oADN
o ANNE 0AMN
OAEFEOAzGL SAD
i DFBN MN二MN
in GFEF
膙可得
iDFtBE
50日吓 坑
Ff
䏎
50时
i CM3N f
iBNElDN2
A
D
1
3 P5
papi的最值 mini
B
4 EN C
A
NBD i
BHA ANE.toCHAEOMG V AH GQAH V GQ
137SoABC二 t.BC
SoAGE二So Am ENT AmUS
12 思路 ENEMG.CANMÉOGQM
TEN GKAH
BE BHtHC
SoABC i.AH.BE
2AM.GQ ci YBH二AN HEAll 3H ANtAQ 2AM
B
C
za
H
iOABEEODAI in 吼 暅
ioADIEOHCILSM
i AKDAIBl
in 斜中战CG二 BEAD
冀教版数学八年级下册 正方形

第15讲正方形一.教学目标掌握正方形的性质和判定。
二.知识点梳理1.正方形的性质(1)正方形的定义:有一组邻边相等并且有一个角是直角的平行四边形叫做正方形.(2)正方形的性质①正方形的四条边都相等,四个角都是直角;②正方形的两条对角线相等,互相垂直平分,并且每条对角线平分一组对角;③正方形具有四边形.平行四边形.矩形.菱形的一切性质.④两条对角线将正方形分成四个全等的等腰直角三角形,同时,正方形又是轴对称图形,有四条对称轴.2.正方形的判定正方形的判定方法:①先判定四边形是矩形,再判定这个矩形有一组邻边相等;②先判定四边形是菱形,再判定这个菱形有一个角为直角.③还可以先判定四边形是平行四边形,再用1或2进行判定.3.正方形的判定与性质(1)正方形的性质:正方形具有平行四边形.矩形.菱形的所有性质.(2)正方形的判定正方形的判定没有固定的方法,只要判定既是矩形又是菱形就可以判定.三.典型例题例1 下列说法中正确的是()A.对角线相等且有一个角是直角的平行四边形是正方形B.对角线互相垂直且一组邻边相等的平行四边形是正方形C.四个角都相等的菱形是正方形D.对角线互相垂直平分且有一组邻边相等的四边形是正方形例2 如图,四边形ABCD是正方形,延长AB到E,使AE=AC,则∠BCE的大小是()A.67.5°B.22.5°C.30°D.45°例3 如图,正方形ABCD中,AE=AB,直线DE交BC于点F,则∠BED的度数是()A.105°B.120°C.135°D.150°例4 如图,正方形ABCD中,点E.F分别是BC.CD上的点,且CE=CF,点P.Q分别是AF.EF的中点,连接PD.PQ.DQ,则△PQD的形状是()A.等腰三角形B.直角三角形C.等腰非直角三角形D.等腰直角三角形例5 如图,已知正方形ABCD的边长为4,P是对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接AP,EF.给出下列结论:①PD=EC;②四边形PECF的周长为8;③△APD 一定是等腰三角形;④AP=EF;⑤EF的最小值为2;⑥AP⊥EF.其中正确结论的序号为()A.①②④⑤⑥B.①②④⑤C.②④⑤D.②④⑤⑥例6 如图,▱ABCD中,对角线AC,BD相交于点O,∠OBC=∠OCB.(1)求证:▱ABCD是矩形;(2)请添加一个条件使矩形ABCD为正方形并说明理由.例7 已知:如图,在矩形ABCD中,M,N分别是边AD.BC的中点,E,F分别是线段BM,CM的中点.(1)求证:BM=CM;(2)判断四边形MENF是什么特殊四边形,并证明你的结论;(3)当矩形ABCD的长和宽满足什么条件时,四边形MENF是正方形?为什么?例8 如图,已知在正方形ABCD中,点E是BC边上的一点,F为AB延长线上一点,连结AE.EF.CF,且满足△ABE≌△CBF.(1)若∠BAE=20°,求∠EFC的度数;(2)试判断AE与CF之间的位置关系,并说明理由.四.课堂练习1.下列判定正确的是()A.一组对边相等且一组对角相等的四边形是平行四边形B.对角线相等且一组对边平行的四边形是矩形C.对角线相等的矩形是正方形D.有一条对角线平分一个内角的平行四边形是菱形2.如图,在正方形ABCD中,点E在边BC上,点F在线段DE上,若AB=AF,则∠BFE=()A.45°B.30°C.60°D.55°3.如图,面积为16的正方形ABCD中,有一个小正方形EFGH,其中E.F.G分别在AB.BC.FD 上.若BF=1,则小正方形的周长为()A.7 B.6 C.5 D.44.如图4,过正方形ABCD的顶点B作直线l,过A,C作直线l的垂线,垂足分别为E,F,若AE=1,CF=3,则AB的长为()A.B.10 C.3 D.5.如图,在△ABC中,∠ABC=90°,分别以△ABC的边向外作正方形,连接EC.BF,过B 作BM⊥FG于M,交AC于N,下列结论:=2S△AEC;③S四边形AFMN=2S△ABF;④S正方形ABDE=S四边形AFMN,其①△ABF≌△AEC;②S四边形ABDE中正确的是()A.①②B.①②③C.①D.①②③④6.如图,已知E是正方形ABCD的边CD的中点,点F在BC上,且∠DAE=∠FAE,求证:AF=AD+CF.7.如图,BD是边长为1的正方形ABCD的对角线,BE平分∠DBC交DC于点E,延长BC到点F,使CF=CE,连接DF,交BE的延长线于点G.(1)求证:△BCE≌△DCF;(2)求CF的长.8.如图示,正方形ABCD的顶点A在等腰直角三角形DEF的斜边EF上,EF与BD相交于点H,连接CF.①求证:△DAE≌△DCF.②求证:AH2=AE2+HF2.9.如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN与E,垂足为F,连接CD,BE.(1)求证:CE=AD;(2)当D在AB中点时,四边形CDBE是什么特殊四边形?说明理由;(3)在满足(2)的条件下,当△ABC满足什么条件时,四边形CDBE是正方形?请说明你的理由.10.如图①,正方形ABCD中,M是AB的中点,E是延长线上一点.MN⊥DM,且交∠CBE的平分线于N.(1)若点F是AD的中点,求证:MD=MN;(2)若将上述条件中的“M是AB的中点”改为“M是AB上的任意一点”,其它条件不变.如图②所示,则结论“MD=MN”是否成立.若成立,给出证明;若不成立,请说明理由.五.课后作业1.在四边形ABCD中,两对角线交于点O,若OA=OB=OC=OD,则这个四边形()A.可能不是平行四边形B.一定是菱形C.一定是正方形D.一定是矩形2.如图,在▱ABCD中,E为BC边上一点,以AE为边作正方形AEFG,若∠BAE=45°,∠CEF=15°,则∠D的度数是()A.55°B.60°C.65°D.70°3.如图,在矩形ABCD内有一点F,FB与FC分别平分∠ABC和∠BCD,点E为矩形ABCD 外一点,连接BE,CE.现添加下列条件:①EB∥CF,CE∥BF;②BE=CE,BE=BF;③BE∥CF,CE⊥BE;④BE=CE,CE∥BF,其中能判定四边形BECF是正方形的共有()A.1个B.2个C.3个D.4个4.如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为(,1),则点C 的坐标为()A.(,1)B.(﹣1,)C.(,1)D.(﹣,﹣1)5.如图,正方形ABCD的边长为4,点E在对角线BD上,且∠DAE=67.5°,EF⊥AB,垂足为F,则EF的长为()A.1 B.C.4D.36.如图,正方形ABCD的边长为6,在各边上顺次截取AE=BF=CG=DH=4,则四边形EFGH 的面积是()A.14 B.16 C.18 D.207.如图,以Rt△ABC的斜边BC为边,在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO.若AB=4,AO=6,则AC的长等于()A.12B.16 C.8+6D.4+68.如图,四边形ABCD与四边形OEFG都是正方形,O是正方形ABCD的中心,OE交BC 于点M,OG交CD于点N,下列结论:①△ODG≌△OCE;②GD=CE;③OG⊥CE;④若正方形ABCD的边长为2,则四边形OMCN的面积等于1,其中正确的结论有()A.1个B.2个C.3个D.4个9.如图,四边形ABCD和四边形CEFG都是正方形,且BC=CD,CE=CG,∠BCD=∠GCE=90°.(1)求证:△BCG≌△DCE;(2)求证:BG⊥DE.10.已知:如图,正方形ABCD中,P是边BC上一点,BE⊥AP,DF⊥AP,垂足分别是点E.F.(1)求证:EF=AE﹣BE;(2)连接BF,若AD=5,AF=3,求BF的长.11.已知:如图,在矩形ABCD中,M.N分别是AD.BC的中点,P.Q分别是BM.DN 的中点.(1)求证:BM∥DN;(2)求证:四边形MPNQ是菱形;(3)矩形ABCD的边长AB与AD满足什么数量关系时四边形MPNQ为正方形,请说明理由.12.已知:在正方形ABCD和正方形DEFG中,顶点B.D.F在同一直线上,H是BF的中点.(1)如图①,若AB=1,DG=2,求BH的长;(2)如图②,连接AH.GH,求证:AH=GH且AH⊥GH.13.如图,在正方形ABCD中,点F是BC延长线上一点,BE⊥DF,垂足为E,BE交CD于点G.(1)求证:BG=DF;(2)求证:EF+EG=CE.14.如图,正方形ABCD中,AB=4,点E是对角线AC上的一点,连接DE.过点E作EF⊥ED,交AB于点F,以DE.EF为邻边作矩形DEFG,连接AG.(1)求证:矩形DEFG是正方形;(2)求AG+AE的值;(3)若F恰为AB中点,连接DF交AC于点M,请直接写出ME的长.15.(1)如图1的正方形ABCD中,点E,F分别在边BC,CD上,∠EAF=45°,延长CD到点G,使DG=BE,连接EF,AG.求证:EF=FG;(2)如图2,等腰Rt△ABC中,∠BAC=90°,AB=AC,点M,N在边BC上,且∠MAN=45°.若BM=1,CN=3,求MN的长.16.如图,正方形ABCD中,点E是BC延长线上一点,连接DE,过点B作BF⊥DE于点F,连接FC.(1)求证:∠FBC=∠CDF;(2)作点C关于直线DE的对称点G,连接CG,FG,猜想线段DF,BF,CG之间的数量关系,并证明你的结论.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
*微专题:正方形中的典型模型问题
◆模型一正方形对角线交点处含一直角的问题
一、通过全等转化求重叠部分的面积【教材P63实验与探究拓展】
1.(2017·秦皇岛海港区期末)如图,正方形ABCD边长为a,O为正方形ABCD的对角线的交点,正方形A1B1C1O 绕点O旋转,则两个正方形重叠部分的面积为________.
第1题图变式题图
【变式题】将5个边长都是2cm的正方形如图摆放,点A,B,C,D分别是四个正方形对角线的交点,则阴影部分的面积为________.
二、证明相关线段长度的等量关系
2.如图,在正方形ABCD中,对角线AC,BD交于点O,点E,F分别在AB,BC上,且∠EOF=90°.
(1)求证:OE=OF;
(2)下列结论:①AE=BF;②BE+BF=AD;③AE2+CF2=2OE2.其中正确的有__________(填序号).
◆模型二正方形内部含互相垂直的两条线段
3.(2017·石家庄新华区期末)如图,点E,F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE与BF 相交于点O.下列结论:①AE=BF;②AE⊥BF;③AD=OE;④S△AOB=S四边形DEOF.其中正确的有()
A.4个
B.3个
C.2个
D.1个
◆模型三含一外角平分线问题
4.如图,四边形ABCD是正方形,点E是BC的中点,∠AEF=90°,EF交正方形外角的平分线CF于F.求证:AE=EF.
【变式题】如图,正方形ABCD中,E为BC上一点,过B作BG⊥AE于G,延长BG至点F使∠CFB=45°.
(1)求证:∠BAG=∠CBF;
(2)求证:AG=FG.
参考答案与解析
1.1
4
a 2 【变式题】4cm 2 2.(1)证明:∵BD ,AC 为正方形ABCD 的对角线,∴OB =OC ,∠EBO =∠FCO =45°,∠BOF +∠FOC =90°.∵∠EOF =∠EOB +∠BOF =90°,∴∠EOB =∠FOC .在△EOB 和△FOC 中,⎩⎪⎨⎪⎧∠EBD =∠FCO ,BO =CO ,
∠EOB =∠FOC ,∴△EOB ≌△FOC (ASA),∴OE =DF .
(2)解:①②③ 3.B
4.证明:如图,取AB 的中点H ,连接EH .∵∠AEF =90°,∴∠2+∠AEB =90°.∵四边形ABCD 是正方形,∴∠1+∠AEB =90°,∴∠1=∠2.∵E 是BC 的中点,H 是AB 的中点,∴BH =BE ,AH =CE ,∴∠BHE =45°.∵CF 是∠DCG 的平分线,∴∠FCG =45°,∴∠AHE =∠ECF =135°.在△AHE 和△ECF 中,⎩⎪⎨⎪⎧∠1=∠2,AH =EC ,
∠AHE =∠ECF ,∴△AHE ≌△ECF (ASA),∴AE =EF .
【变式题】
(1)证明:∵BG ⊥AE ,∴∠AGB =90°,∴∠ABG +∠BAG =90°.∵∠CBF +∠ABG =90°,∴∠BAG =∠CBF . (2)证明:如图,过点C 作CH ⊥BF 于H 点.∵∠CFB =45°,∴CH =HF .∵AG ⊥BF ,CH ⊥BF ,∴∠AGB =∠BHC =90°.在△AGB 和△BHC 中,⎩⎪⎨⎪⎧∠AGB =∠BHC ,∠BAG =∠CBH ,AB =BC ,∴△AGB ≌△BHC ,∴AG =BH ,BG =CH =HF .∵BH =BG +GH ,
∴BH =HF +GH =FG ,∴AG =FG .。
