第四章 求解水动力弥散方程的有限单元法2
有限单元法课后习题全部解答_王勖成

d 2w dx2
δ
dw dx
−
d 3w dx3
δ
w
L 0
= 0
∫ 1.5 如有一问题的泛函= 为 Π(w)
L
EI
0 2
d 2w dx2
2
+
kw2 2
+ qwdx ,其中 E,
I,
k 是常数,q
是给定函数,w 是未知函数,试导出原问题的微分方程和边界条件.
∫ = δΠ(w)
L 0
x3 L2
)
+
a2 (x2
−
x3 L
)
+
x3 L3
(1)
x3 上式中的最后一项 L3 前面没有待定系数,这是由于使用了在 x=L 处φ=1 的强制边界条件。
从物理意义上说,相当于给定边界条件的解为齐次方程的通解加一个特解的缘故。将(1)
式代入教材(1.2.26)式,得到残量:
R(
x)
=
a1 (−6
x L2
+
Q
δφ
dΩ
+
Γ−Γq
k
∂φ ∂n
δφ
dΩ
−
Γq
αφ
−
q
−
k
∂φ ∂n
δφ d
Γ
欧拉方程: k
∂2φ ∂x2
+
k
∂2φ ∂y 2
+
Q
=0
Γφ
自然边界: αφ
−
q
−
k
∂φ ∂n
=0
Γ
−
Γq
强制边界:
k
∂φ ∂n
=0
习题 1.8: 板弯曲问题的平衡方程为:
工程流体水力学第四章习题答案
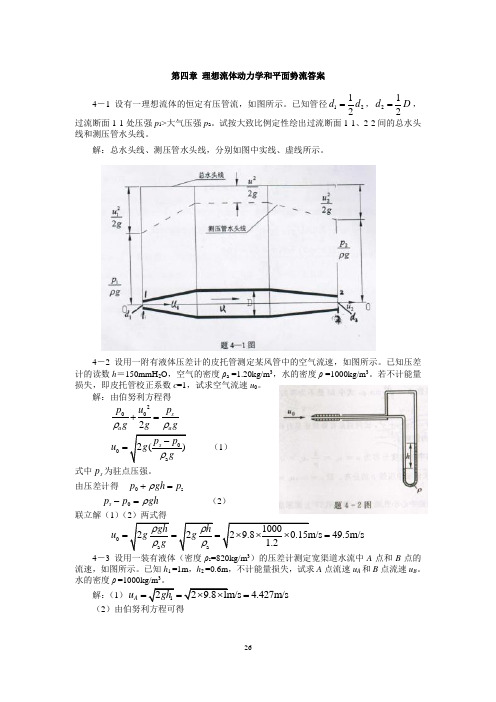
第四章 理想流体动力学和平面势流答案4-1 设有一理想流体的恒定有压管流,如图所示。
已知管径1212d d =,212d D =,过流断面1-1处压强p 1>大气压强p a 。
试按大致比例定性绘出过流断面1-1、2-2间的总水头线和测压管水头线。
解:总水头线、测压管水头线,分别如图中实线、虚线所示。
4-2 设用一附有液体压差计的皮托管测定某风管中的空气流速,如图所示。
已知压差计的读数h =150mmH 2O ,空气的密度ρa =1.20kg/m 3,水的密度ρ =1000kg/m 3。
若不计能量损失,即皮托管校正系数c =1,试求空气流速u 0。
解:由伯努利方程得2002s a a p u p g g gρρ+= 00a 2()s p p u g gρ-=(1) 式中s p 为驻点压强。
由压差计得 0s p gh p ρ+=0s p p gh ρ-= (2)联立解(1)(2)两式得0a a 10002229.80.15m/s 49.5m/s 1.2gh h u gg g ρρρρ===⨯⨯⨯= 4-3 设用一装有液体(密度ρs =820kg/m 3)的压差计测定宽渠道水流中A 点和B 点的流速,如图所示。
已知h 1 =1m ,h 2 =0.6m ,不计能量损失,试求A 点流速u A 和B 点流速u B 。
水的密度ρ =1000kg/m 3。
解:(1)1229.81m/s 4.427m/s A u gh ==⨯⨯= (2)由伯努利方程可得22A AA u p h g gρ+= (1)22B BB u p h g gρ+= (2)式中A h 、A p 和B h 、B p 分别为A 点和B 点处的水深和驻点压强。
由(1)、(2)式可得2222A B A BA B p p u u h h g g gρ-=+-- (3) 由压差计得,22ρρρρ--++=A A s B B p gh gh gh gh p ,所以220.82A BA B p p h h h h gρ-=+-- (4) 由(3)式、(4)式得2222 4.427(10.82)0.6(10.82)0.8922229.8B A u u h g g =--=--=⨯ 29.80.892m/s 4.18m/s B u =⨯⨯=。
水动力学基本微分方程

流出: (Q Qy dy)dt y
y 2
沿z方向流入单元体的水量: v2 dx dy dt 流出:v1 dx dy dt
流入量-流出量=:
Q x x方向: dxdt x
y方向: Q y y dydt
2 H 2 H 2 H s H 2 2 2 K t x y z
2.对于二维的情况,常用 和T表示(
各项均乘以m)
H H H (Tx ) (Ty ) , x x y y t 2 H 2 H H 当Tx Ty T时, 则 2 2 x y T t
上述分析表明:H降低,承压含水层释 放部分地下水;H增大,承压含水层贮存部 分地下水,这部分水量称为弹性贮存量。
弹性贮水量的大小与含水层的岩性和 结构有关,为了表征含水层弹性释水(储 水)的能力,下面将给出弹性贮水率和贮 水系数的概念。
2.含水层的贮水率和贮水系数
1.贮水率(Specific storativity)用 s 表示
H H H H ( K xx ) ( K yy ) ( K zz ) s x x y y z z t
上式就是非均质各向异性承压含水层中地下水三 维非稳定运动的基本微分方程。对各向异性介质,取 坐标轴方向与主渗透方向一致。
(二)方程的化简和讨论
1.对于均质各向同性含水层,K为常数,这时 简化为:
a
o
b a dy
x y Qx为单位时间内通过abcd断面流入的水量。在dt内,
沿x方向通过abcd断面流入均衡单元的水量 a'b'c'd'断面从均衡单元流出的水量为
Qx (Qx dx)dt x
溶质运移理论水动力散方程的解析解法-精选文档

,浓度为原点的1%
随时间推移,弥散 晕范围逐步扩大
11
一、基本解-空间瞬时无限线源与平面瞬时点源
一口承压完整井中瞬 时注入示踪剂,求浓 度时空分布规律
映射
三维空间一条无 限长瞬时线源
12
一、基本解-空间瞬时无限线源与平面瞬时点源
取三维空间上z轴与瞬时线源重合,假定单位长度线 源瞬时注入示踪剂的质量为ml,在线源上任意位置 z ' 处 取一分为线源段 d z ',将其视为点源的作用,其瞬时注入 ' m d z 示踪剂质量为 l ,在瞬时点源空间上任意点(x,y,z) 产生的微分浓度
mM ml M
对应解为
15
一、基本解-空间瞬时无限面源与平面瞬时无限线源与一维瞬时点源
空间直角坐标系中,取yoz坐标面与面源重合,并设 单位面源瞬时注入质量为mf 的示踪剂 无限面源可以视为无数连 续排列的无限线源组成
mM
16
一、基本解-空间瞬时无限线源与平面瞬时点源
' y 从无限面源中分割出一根平行于z轴,在 处,宽 ' dy 度为 的窄长型微分面源,对空间上任意(x,y,z)处 的作用,与空间瞬时无限线源想当,后者单位长度注 ' m dy 入量与前者的 相当,有 f
积分得
浓度与y、z无关,实质为一维弥散问题
17
一、基本解-有限空间(平面)问题
' y 对于边界简单的情况,可用反映法转化为无限空 间问题在叠加求解
,相当于水流问题中的隔水边界。假设点(x0,y0) 对半无限含水层中瞬时注入质量为m的示踪剂
C 0 n
18
二、一维水动力弥散问题
设有一无限长均质砂柱,原有溶液浓C0=0,在t=0, x=0处瞬时注入质量为m的示踪剂,取砂柱中心轴为x 轴,流速方向为正,求浓度C(x,t) 分布
求解半无限长多孔介质柱体水动力弥散系数的一种最小二乘法

定存 在误 差 , 且误差 随着 x的变 化 而变 化 。苏 里坦 等 初 而
U 引 舌
在 用水 动力 弥散 理论 解 决 实 际 的环 境 地质 问题 时 , 先 首
步推 导 了不 带 不 可 积 积 分 的 ef( 的 逼 近 公 式 , 以求 解 r ) c 可 “ 已知 x求 e c ) 的 问题 , 是 很难 求 解 “ 知 e c ) r ( ” f 但 已 r ( 求 f x 的 问题 , 给反 求 参 数 带 来 困难 。MA L B软件 中 的 ef ” 即 TA r c
W A N G o Y ng — e —f ng
( c ol f n i n na Su i ,C iaU i r t o G ocec s W u a 3 0 4, u e) Sh o o v o metl tde E r s hn nv sy f e sin e , h n4 0 7 H bi e i
水动 力 弥散 系数 。 最后 将 该方 法应 用 于一个 实例 , 算 结果 表 明该 方 法 比 e c ) 似公 式法 、 计 r( 近 f 配线 法 、 态分 布 函 正
数 法等传 统方 法要好 。
[ 键词 ] 水动 力 弥散 系数 ; 余误 差 函数 ; 关 补 最小二 乘法 [ 中图分 类号 ] P 4 . 6 18 [ 文献标 识码 ] A [ 文章 编号 ] 10 0 4—1 8 2 l 0 14(0 0) 3—0 0 0 6—0 3
The Le s ua e M e ho a ni g t yd o yna i ipe so a t Sq r t d G i n he H r d m cD s r in
Co f ce ft m i— i in t e i into he Se — nf ie Por e u y i e M di m S lnde r
溶质运移理论-(一)水动力弥散的基本概念与弥散方程共34页

若由于化学反应或生物化学反应而使示踪剂在单位体积溶液中的消耗速率
或产生速率与其浓度成正比,也可以用上述式子表示。
20
七、源汇项:吸附与解吸
在一定条件下,溶液中某些溶质在多孔介质的固相表 面产生吸附、解吸或者离子交换等物理化学作用。如果这 些溶质属于我们的研究对象,则这些作用的结果应该综合 到源汇项中,如果固相表面吸附示踪剂,视为汇,否则, 称为解吸,视为源,而离子交换即可视为汇也可视为源。
水动力弥散现象 多孔介质中,当存在两种或两种以上可混溶的流体 时,在流体运动作用下,期间发生过渡带,并使浓 度区域平均化的现象
4
三、 水动力弥散现象
水动力弥散
分子扩散
两部分
机械弥散
由浓度高的方 向向浓度底 的方向运动, 趋于均一
由于微观多孔介质中流 速分布的不均一而引起 的示踪剂(水质点)浓 度在地下水含水层中不 均匀分布的现象。
一、流体类型
可混溶流体 两种或两种以上的流体在同一储集空间中不存
在明显的突变界面,见下图。如滨海含水层中海水 入侵地下淡水。(示踪剂) 不可混溶流体
多种(两种或两种以上)的流体在同一储集空 间中存在着明显的突变界面,见下图。如油、气、 水或其它有机物流体。(多相流体)
1
一、流体类型
可混溶流体
不可混溶流体
简化成
(1)
多孔介质中溶质的分子扩散通量
(2)
多孔介质分子扩散系数,数值上小于
溶质的对流量
机械弥散通量
联立上述两式,得
16
六、水动力弥散方程
将所有平均号“-”略去
17
六、水动力弥散方程
18
七、源汇项
源汇项指在单位时间液相体积中由于化学反 应、生物化学作用或抽注水等产生减少α组 分质量的速率。
溶质运移理论-(四)水动力弥散系数的计算方法-PPT精选文档

二、二维水动力弥散-瞬时投放示踪剂
3.代入上述公式求DL、u
4.利用不在x轴上的观测孔资料,求出其tm’,根据
(5-23)求出DT
18
二、二维水动力弥散-瞬时投放示踪剂
算例 在某次瞬时投放示踪剂室内弥散试验中,测得一 距投放井80cm且位于x轴上的观测点处的电导率和时 间数据(见课本P62),相应的实测曲线见图5-5
0 2 . 135 C 利用 C ,可类似求解出DL m ax 0 C 3 . 011 C m ax
4
一、一维水动力弥散-连续注入示踪剂
(2)连续注入示踪剂 其解为 当t较大或者x较长时,
换元,令
得
5
一、一维水动力弥散-连续注入示踪剂
对给定t,为关于x的正态分布函数
直线法将高斯浓度 转化为简单直线。 不足: 1.两个观测孔资料,其 中一个位于x轴; 2.转化X、Y数据时,计 算量大
21
二、二维水动力弥散-瞬时投放示踪剂
3.标准曲线法
若分子扩散可忽略,有
式 改成 若y=0(主流线上) 当 因 时, ,故计算得u偏大。
22
二、二维水动力弥散-瞬时投放示踪剂
x是测得Cm的位置,此时
11
二、二维水动力弥散-瞬时投放示踪剂
瞬时投放示踪剂 1.逐点求参法
3个时刻t1、t2、t3对应浓度C1、C2、C3 ,由式
(4-65)
当y=0时,有 联立,
(5-16)
12
二、二维水动力弥散-瞬时投放示踪剂
若只考虑(5-16)式 则
令y=0,由(4-65)导出横向弥散系数
理论上,每3组浓度-时间数据可求出u、DL、DT
地下水溶质运移理论及模型
计算水动力学2009重点

◎非守恒型控制方程的推导:几点说明:从微元体的角度看,控制方程的守恒型与非守恒型是等价的,都是物理守恒定律的数学表示。
但对有限大小的计算体积,两个形式是有区别的。
不论节点布置的疏密程度如何,根据控制方程导出的离散方程也具有对任意大小容积守恒的特性。
非守恒型方程便于对离散方程进行理论分析,而守恒型控制方程能保持物理量守恒的性质,便于克服对流项非线性引起的问题。
第七章双边界法第八章SIMPLE算法自1972年问世以来,在计算流体力学及传热学中得到了广泛的应用,同时也得到了不断的改进与发展。
近年来,SIMPLE改进算法的研究成果主要有:Patankar于1980年提出的SIMPLER算法,Spalding于1981年提出的SIMPLEST算法和Doormal与Raithby于1984年提出的SIMPLEC算法[29]等。
(一)(一)SIMPLER算法由SIMPLE算法得出的值对修正速度而言是相当好的,但对修正压力则是过分了。
虽然对采用了亚松驰处理,也未必能恰到好处。
这样就使速度场的改进与压力场的改进不能较好的同步进行,最终影响了整个流场的迭代收敛速度。
于是就产生了这样的想法:只用来修正速度,压力场的改进则另谋更合适的方法。
此外,在SIMPLE算法中,为了确定动量离散方程的系数,一开使就假设了一个速度分布,那么与这一速度分布相协调的压力场即可由动量方程计算而得,不必在单独假定一个压力场。
把以上两个思想结合起来,就构成了SIMPLER算法。
在SIMPLER算法中,初始的压力场和速度场是相协调的,算出的压力场不必亚松驰,使迭代层次数减少。
但另一方面,每一层次计算中所花的时间则较SIMPLE多,因为SIMPLER算法中要多解一个Poisson方程。
但就总的计算时间来说,SIMPLER算法一般较SIMPLE少。
(二)(二)SIMPLEST算法与SIMPLE算法相比,它主要有以下两个特点:(1)对流项采用迎风格式,因为这是一个绝对稳定的格式,且扩散项与对流项的影响系数可以分离开来,不像指数(或乘方)格式那样综合在一起。
第四章 水动力学基础(完整版)

水轮机的 作用水头 水轮机效 水轮机的 率 H1 H t H 2 hw12 出力
ห้องสมุดไป่ตู้
gQH P P N P
P N P HP gQ
Nt t gQH t
Z2 Z1
0
0
表明:在不可压缩理想液体恒定流情况下,微小流束内不同过水断
面上,单位重量液体所具有的机械能保持相等(守恒)。
第四章
水动力学基础
4.1.3 毕托管测流速原理
其原理如下:
2 uA A点处水流的总能量为 h1 2g
根据伯诺里方程可得:
2 uA h2 g h1g 2
求得:
u A 2 g (h2 h1 ) 2 gh
2
2
1
1
2
2
(Z
Q
p ) gudA g
均匀流或渐变 流过水断面上
p ( Zg ) C
(Z
p p ) g dA ( Z ) gQ g g A
3 u dA A
2 g gudA
A
2
u gdA 2g
3 A
v3 A
v 2
2g
gQ
动能修正系数,1.05~1.1
第四章
水动力学基础
授课内容:
4.1 理想液体元流的能量方程 4.2 实际液体元流的能量方程 4.3 实际液体总流的能量方程 4.4 恒定总流动量方程
4.5 理想液体运动微分方程及其积分
4.6 实际液体的微分方程
4.7 恒定平面势流
4.1 理想液体元流的能量方程
4.1.1 理想液体元流的能量方程 取过水断面1–1及2–2为控 制面液体从断面1–1流向断面 2–2。 两端面之间没有汇流或分流
溶质运移理论-(四)水动力弥散系数的计算方法-PPT精选文档

(5-61)
30
二、二维水动力弥散-瞬时投放示踪剂
4.弥散晕面积求参法 表明t时刻的一系列浓度与对应的椭圆面积在半对数 坐标上为一直线,斜率为
(5-62)
联立,可得DL、DT
求出横轴截距d,有(5-61)得
可求有效孔隙度
由(5-60)得 求出浓度C等值线围成的椭圆面积随时间变化值,则 31 S/t与t在半对数坐标中呈直线。同理可求上述参数
13
二、二维水动力弥散-瞬时投放示踪剂
实际中,仅用3组数组求出的参数具有一定随机 性甚至失去物理意义,故需要一些列C-t数据。可先 去掉不符合物理意义的数值,再将其余参数算术平均 值即可视作待求参数的近似值。如下表:
14
二、二维水动力弥散-瞬时投放示踪剂
2.直线图解法
(5-23)
15
一、二维水动力弥散-瞬时投放示踪剂
参数计算步骤:
(1)若已知流向 在注入孔正下游设一取样孔(x1,0),偏离正下游 设孔(x2,y2)
26
二、二维水动力弥散-瞬时投放示踪剂
参数计算步骤:
1.作lgCD-lgt实测曲线; 2.与标准曲线拟合,得rD1和rD2; 3.根据(5-45)、(5-42)与(5-43),易知
若观测孔偏离流向,会出现弥散度偏低
实测曲线与理论曲线形状相同,只发生坐标平移
(1)作对应不同β值的标准曲线族,做出实测曲线 与标准曲线进行拟合;
(2)找出拟合最好的β0 ; (3)找出与A=1,WC=1相对应的C0、t0 ;
40
二、二维水动力弥散-连续投放示踪剂
将u、DT、DL视作待求参 数,联立上述3式可得结果
41
二、二维水动力弥散-连续投放示踪剂
11
溶质运移理论-(三)水动力弥散方程的解析解法-文档资料

23
无限长多孔介质砂柱,初试示踪剂呈阶梯函数分布
求解思路:
初始浓度的分布视为沿x轴连续分布的瞬 时变强度点源,利用点源基本解积分求取
取浓度坐标与阶梯相重合,线源的坐标用x’表示,有
C表示示踪剂浓度,n为有效 孔隙率;ω 为砂柱横截面积
24
无限长多孔介质砂柱,初试示踪剂呈阶梯函数分布
考虑与u等速的动坐标系,在位于x’处强度为 ' dm C n dx f 的瞬时点源作用下,任意点处的微分浓 度为:
对于式(4-11),令
8
一、基本解
(4-15)
代入(4-15)
讨论并计算得 代入得最终结果
9
一、基本解
(4-20)
空间瞬时点源的解
分析上式得 等浓度面为圆心位于原点处的球面; 浓度空间分布情况如图所示;
10
一、基本解
任何时刻处浓度最大值在原点 随时间增加,原点处浓度减少 由于
或
对于式
19
二、一维水动力弥散问题
此时有
简化成 采取动坐标,令 则
比静止流场多了一个对流项
,让坐标原点跟着流速一起前进
20
二、一维水动力弥散问题
将X、T反变换
21
二、一维水动力弥散问题
与正态分布密度函数对比
浓度曲线出现峰值的x坐标
曲线在点 ut处对称;
当x 时, C 0;
积分得
浓度与y、z无关,实质为一维弥散问题
17
一、基本解-有限空间(平面)问题
' y 对于边界简单的情况,可用反映法转化为无限空 间问题在叠加求解
,相当于水流问题中的隔水边界。假设点(x0,y0) 对半无限含水层中瞬时注入质量为m的示踪剂
有限单元法课后习题全部答案-王勖成

Ω
=0
∫ ∫ = Ω w j R dΩ
∂
Ω
∂a
j
AT
(
N i
(
x)ai
)δ
(
x
−
x k
)
[
A(
N i
(
x)ai
)
−
f (x)]dΩ
∫ =
Ω
AT
(N
j (x))δ
(x
−
x k
)
[
A(
Ni
(
x)ai
)
−
f
( x)]d Ω
∑{ } m
=
k =1
AT
(
N
j
(
xk
))
[
A(
N i
(
xk
)ai )
= R( L) 3
0= , R( 2L) 3
0 ,从而可以解出待定系数 a1, a2 。带入(1)式可以得到φ 。
配点法仅考虑了有限个点的局部特性,子域法则要求在有限个子域 Ωi 内残量的积分
∫ R(x)dx = 0 为零,子域的个数仍然取决于未知函数个数,通常选取各子域的并集为整个 Ωi
待求区域,一般情况可以选择各子域大小相同,但对于某些局部变化较复杂的区域,可以缩 小子域的大小,使得子域分布更合理。例如取子域为
−
f
( xk
)]
m
m
∑ ∑ = =k
1= AT (N j )A (N i )ai − k
1
AT
(N
j)f
= Ka-P
(写成矩阵形式)
m
∑ = 因此, kij k= =1 AT (N j )A (N i ) k ji , 系数矩阵对称,且无需积分。
溶质运移理论-水动力弥散方程的数值解法

一、有限差分法-导数的有限差分近似
图中,去x轴上任意一点i,其坐标为 xi ix 在改点左右相聚为 x处分别取(i-1)和
(i+1),其坐标分别为 xi-1i-1x和xi1i1 x
以i为中心,泰勒展开C(x)
3
一、有限差分法-导数的有限差分近似
整理并略去余项
(6-1)-(6-2),再除以 2x 略去余项
一、有限差分法-二维水动力弥散的差分解法
二维水动力弥散方程
(4-56)
(1)显格式
式(4-56)中的对流项取中心差分
C i,jn , 1 tC i,j,nD LC i 1 , j,n2 C x i,j2 ,n C i 1 ,j,n D TC i, j 1 ,n 2 C y i,j2 ,n C i,j 1 ,n-u C i 1 , j,2 n x C i,j 1 ,n
式中仅有一个未知数
10
一、有限差分法-二维水动力弥散的差分解法
化简后,有
C i,j,n 1 D L x 2 t-2 u x t C i 1 ,j,n 1 2 D L x 2 t 2 D T y 2 t C i,j,n D L x 2 t-2 u x t C i-1 ,j,n D T y 2 tC i,j 1 ,n D T y 2 tC i,j-1 ,n
涉及以(i,j)为中 心的5个网格点在tn 时刻的已知浓度
11
一、有限差分法-二维水动力弥散的差分解法
(2)隐格式
式(4-56)中右端的对流项取中心差分, 右端个C的时阶均取n+1水平
C ij,n , 1 tC i,j,n D LC i 1 , j 1 ,n 2 C ix ,j 2 1 ,n C i 1 ,j,n 1 D TC i, j 1 ,n 2 C i,y j,n 2 1 C i,j 1 ,n 1-u C i 1 , j,n 2 1 x C i,j,n 1
水动力学基础课件:第四章 实际流体动力学(7)
(4) 求解流量时,一般要结合一维流动的连续性方程求解。伯努利 方程的p1和p2应为同一度量单位,同为绝对压强或者同为相对压强,p1和 p2的问题与静力学中的处理完全相同。
该物体上的所有外力的矢量和。
F
dk
dt
k mu
在此先建立控制体的概念:所谓控制体是空间的一个固定不变的
区域,它的边界面称为控制面。
如图,现以总流的一段管段为例。取断面1和2以及其间管壁 表面所组成的封闭曲面为控制面,内部的空间为控制体。流体 从控制面1流入控制体,从控制面2流出,管壁可看成流管,无 流体进出。
Q
Q
方程式的物理意义:
Z1
p1
g
1V12
2g
Z2
p2
g
2V22
2g
hw
H1 H2 hw E1 E2 hw
实际液体恒定总流的能量方程式表明:水流总是从水头大处流向水头
小处;或水流总是从单位机械能大处流向单位机械能小处。
实际液体总流的总水头线必定是一条 逐渐下降的线,而测压管水头线则可能是 下降的线也可能是上升的线甚至可能是一 条水平线。
B C 0.2m
A
3m
泵
例题示意图
[解] 取A、C两断面写能量方程:
zA
pA
g
2 A
2g
zC
pC
g
C2
2g
hAC
通过A点的水平面为基准面,则 zA 0, zC 3.2m;
pA 2at 1.96 108 Pa, pc 0(在大气中);水的重度g 9800 m3 ,
水动力模型基本方程及边界条件

一般情况下河流海岸水流运动特征可用“近水平流”来表 示。水平尺度>>垂向尺度 ,水平动量>>垂向动量。 从“近水平流” 特征可得出静压假定。 垂向动量方程中已采用近乎水平流假定, 垂向加速度<<垂 向压力梯度。
p g
z
pg(z)
1 p g x x
1 p g y y
第二讲、水动力模型基本方程及边界条件
u v v v w v ( u v w )v u v v2 vw x y z x y z x y z
第二讲、水动力模型基本方程及边界条件 四、平面二维方程(垂向积分模式)
将方程沿深度积分,利用自由面运动学边界条件和床面运 动学边界条件,可得到垂向积分的平面二维控制方程。
v t u x v v y v w v z 1 p y f u x ( A h x v ) y ( A h y v ) z ( A v v z )
p g
z
z
ζ
y
x
h
第二讲、水动力模型基本方程及边界条件 一、三维不可压缩流体运动的基本方程
x
y
四、平面二维方程(垂向积分模式)
对于守恒型动量方程,取垂线平均
U ( h t) x[xU x2(h) ] y[yU x (h V ) ] g(h) xfV (h) sx b x A h( 2 x U 2 2 y U 2)(h)
,
V (h t ) x[yU x (h V ) ] y[yV y2(h ) ] g (h ) yfU (h ) sy by A h( x 2 V 2 y 2 V 2)(h)
二、边界条件
2. 底部边界条件
➢无滑动条件(粘附条件) uvw0床面上
➢底部应力定律,将近底速度(离底小距离)与近底速度梯
有限单元法-20130524

对该内积进行分部积分形成与其对应的另一个
内积
u, L
*
(v) ,如果 L 与 L* 在形式上相
同,则称算子 L( ) 为自共轭算子。
自共轭算子
如果一个线性算子形成一个方程组,
* L (u), v u, L (v) s F (v)G(u) F (u)G (v) ds *
L(u) 与 L*(v)在形式上完全相同
函数F(v), G(u), F(u), G*(v) 为是分部积分过程中
得到的对 u 和 v 的导数项。
函数 F(u) : 本征边界条件 (Essential boundary condition)
函数 G(u) : 自然边界条件 (Natural boundary condition)
连续函数空间
所有定义在区间[a, b] 上的连续函数集 合,按函数加法和数与函数乘法构成数域
R 上的线性空间,此线性空间称为连续函
数空间,记作 C [a, b]。 连续函数空间满足线性空间的八条计
算规律。
内积 (Inner Product)
连续函数空间C [a, b]中两个函数的内积可
定义为
1 , 2
du * dv 本征边界条件: F (v) v F (u ) u 自然边界条件: G (u ) G (v ) dx dx
例题解答
2. 判断算子的正定性
1 du du L (u), u 0 u 2 dx 0 ud dx dx 1 2
du du du du u dx dx 0 0 dx dx 0 0 dx dx
1 0 为空间R中的零元素
范数 (Normal Number)
水动力学及习题经典讲解

x x(a,b,c,t) 空间坐标: y y ( a , b , c , t )
z z(a,b,c,t)
若给定a,b,c,即为某一质点的运 动轨迹线方程。
z (t)
其中:a,b,c为t=t0起始时刻质点所
M/(x,y,z)
§3.1 流体运动的描述方法
研究流体流动的两种方法:拉格朗日法和欧拉法
• 拉格朗日法 ——以研究单个液体质点的运动过程作为 基础,综合所有质点的运动,构成整个液体的运动。
• 拉格朗日方法(lagrangian method)是以流场中每一流 体质点作为描述对象的方法,它以流体个别质点随时 间的运动为基础,通过综合足够多的质点(即质点系) 运动求得整个流动。——质点系法
(3)注意 a.在非恒定流情况下,流线的位置随时间而 变;流线与迹线不重合。 b.在恒定流情况下,流线的位置不随时间而 变,且与迹线重合。
c.在非恒定流情况下,位变加速度(迁移加 速度)与时变加速度(局地加速度)都不为 零。 d.在恒定流情况下,时变加速度(局地加速 度)为零,位变加速度(迁移加速度)可以 不为零。
!流线能反映瞬时的流动方向 流线不能相交,不能为折线。
流线的性质:
a.同一时刻的不同流线,不能相交。因为根据
流线定义, 在交点的液体质点的流速向量 应同时与这两条流线相切,即一个质点有两个 速度向量,这显然矛盾的、不成立的。
b.流线不能是折线,而是一条光滑的曲 线。因为流体是连续介质,各运动要素 是空间的连续函数。
p d A ( p d p ) d A g d A d n c o s 0 ,d n c o s d zdpgdz0
水动力弥散方程解析解的适用条件和优缺点

水动力弥散方程解析解的适用条件和优缺点尽管解析解法在求解复杂的水动力弥散方程定解中存在一定缺陷,但仍然不可忽略它所起的作用。
室内或野外试验都要根据解析解的实用条件来进行设计,并用解析解去拟合观测资料以求得水动力弥散系数。
解析解中将瞬时注入点源问题的解称为基本解。
由基本解出发,利用叠加原理导出线源、面源、多点源及连续注入问题的解。
因此,点源问题的解是一切解的根本,需十分重视。
(1)空间瞬时点源的解其基本条件是:①均质各向同性介质;②静止流场0=u ,弥散系数为常数,流体密度为常数(ρ=常数);③0=t 时,在原点处瞬时注入溶质的质量为m 。
以瞬时点源的位置为原点,可以得出浓度C 是相对于原点对称的。
可简化出纯弥散方程:)(222222zC y C x CD t C ∂∂+∂∂+∂∂=∂∂ 式中,D 代表多孔介质的分子扩散系数。
该式可看出,是球对称的,有利于纯弥散方式的应用讨论。
取半径为R 和R+d R 的两个球面所构成的单元体为均衡段,根据质量均衡有:tC V J n W J n W V dR RD R D ∂∂=∙∙-∙∙+ 式中,W 为球面积;n 为有效孔隙率;J D 为弥散通量,且R C DJ D ∂∂-=,V V 为均衡段空隙体积。
忽略高阶微量,化简后得:)(122R C R R RD t C ∂∂∂∂∙∙=∂∂ 于是该点源的定解问题可以写成:⎪⎭⎫ ⎝⎛∂∂∂∂∙=∂∂R C R R R D t C 22 (R ≧0,t>0) 0),(0==t t R C (R>0)0),(=∞→R t R C (t>0)0),(0==R t R C (t>0) m dR R n C =∙∙⎰∞024π (t>0)(该式将点源处浓度限制在有限区域)通过Boltzmann 变换,将原来的偏微分方程定解问题转变为常微分方程定解问题,可求得空间瞬时点源的解为:Dt R e Dt n mt R C 4232)(8),(-=π从上式可得出:①等浓度面为圆心位于原点处的球面;②任何时候的浓度最大值都在原点处,且随着时间的增加,原点处的浓度减小。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章 求解水动力弥散方程的有限单元法里兹法有限元和加权余量法有限元都能有效地用于求解地下水运动问题。
但里兹法仅适用于对称正定算子,因此用里兹法求解水动力弥散方程时,寻求相应的泛函比较困难,常要求对方程进行适当交换,去掉一阶导数数项,使变换后的方程为自伴的,用有限元求得的方程组对称正定,易于求解。
但是,这种变换多为指数变换,当Peclet 数较大时,变换会引入较大误差,有时由于指数过大,数值处理会产生溢出。
加权余量法可以不加限制地将一般的微分方程通过方程余量和权函数正交化途径,化为代数方程组而获得近似解。
由于它不要求寻找与微分方程相应的泛函,无论对自伴、非自伴或非线性问题都可以求解。
因此,加权余量法,尤其迦辽金法有限元在求解水动力弥散方程中应用较广。
有关有限单元法的一些基本概念,已在前两章节中做了介绍,本章将主要介绍迦辽金有限单无法在求解水动力弥散方程中的应用求解对水动力弥散方程的几种特殊解法。
第一节 用迦辽金有限元求解水质模型的基本方法如前所述,为求得计算区域溶质浓度的变化,应首先建立相应的数学模型,并给出相应的初始和边界条件。
由第一章可知,对非均质流体,该数学模型由以下方程组成:()5713))((--∂∂+∂∂-=j j j s iji x z g x p k v ρμθ重力加速度g j 是矢量,所以g j ;只在x j =z 对取值。
()5813),(),,(--==p c p c μμρρ对低浓度不可压缩流体,可用其一阶近似式;()()6013)()(5913)(),(0000--∂∂-∂∂∂∂=∂∂---+=-+=i ii ij i cv x x c D x t c c c c c βμμαρρ或()()6213)])([(6113)())(()(1--∂∂+∂∂∂∂=∂∂--∂∂-∂∂∂∂=∂∂jj j ij i i i j c ij i c x z g x p k x t p C v x x D x t ρμρμθθθ对均质流体该模型由以下方程组成:()()()63136513))((6413))((--∂∂-=--∂∂∂∂=∂∂--∂∂∂∂=∂∂ii ii di i s x h k v x h kh x t h x h KM x t h θμμ潜水承压水对流弥散方程同式(3-l -60)或式(3-l -61)。
式中各符号意义同第一章说明。
在均质流体中,由于ρ和μ为常数,浓度分布不影响流速分布,水流问题和浓度问题可以分别独立求解。
即首先由水流方程求得流速分布,再将流速作为已知量,代人对流一弥散方程求得浓度分布。
而在非均质流体情况下,由于ρ和μ与浓度c 有关,浓度变化亦影响流速,因此水流问题和溶质运移问题必须联立求解,其中最常用的是迭代求解法。
在这种求解过程中,首先给出密度ρ和粘度μ,由运动方程求出流速公布,再求出浓度分布,然后代入状态方程求出ρ、μ,与初值比较,进一步修正ρ、μ值。
在一个计算时段内重复上述计算过程,直到收敛为止。
由上述介绍可见,无论对均质还是非均质流体,都须分别计算流速分布和浓度分布。
以下具体介绍迦辽金有限元解法。
一、压力p 的计算根据迦辽金有限元法的概念,将压力p 的试函数p ~通过基函数的线性组合来表示,即 ()()143,...,2,1--=Φ=≈N J p p p j j式中,J Φ为终点J 的基函数。
将水流连续方程(3-l -62)写成迦辽金积分表达式,即()2430}))(({1--=ΩΦ∂∂-⎥⎥⎦⎤⎢⎢⎣⎡+∂∂∂∂⎰Ωd t pg x p k x L i j ij jμρμρ上式二阶导数应用分部积分和格林公式,并将积分转化到各个单元上进行,可得到下式:()()343,....,3,2,10~~~21--==Φ⎪⎪⎭⎫ ⎝⎛+∂∂⎪⎪⎭⎫ ⎝⎛+Ω⎥⎦⎤Φ∂∂-∂Φ∂⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+∂∂⎪⎪⎭⎫ ⎝⎛-∑∑⎰ΓΩN I dL n g x p k d t p x g x p k L i i j ij i L L i j ij ρμρμρμρ式中,n i 为边界民的外法向分量;L 为单元e 中二类边界长度。
将压力p 的试函数J J p p Φ=~代入立式得:()443~1--Φ⎪⎪⎭⎫ ⎝⎛+∂∂-Ω∂Φ∂+Ω∂Φ∂∂Φ∂+ΩΦΦ∂∂∑⎰∑⎰∑⎰∑⎰ΓΩΓΩΩdL n g x p k d x g k d p x x k d t p I i j j ij Ij ij J i J j J ij I J Jρμρρμρμρμ在相应定解条件下求解上式,可得到区域Ω内各节点的压力分布P J :二、流速分布的计算流速计算有两种方法。
第一种方法是将求得的压力p j 代入式(3-4-1),再代人运动方程(3-l -57)即得:()543--⎪⎪⎭⎫ ⎝⎛+∂Φ∂⎪⎪⎭⎫ ⎝⎛-=j j jJ iiji g x p k v ρμθ由上式求得的流速在单元内部是常数,但在单元与单元之间交界处不连续,这对用某些方法计算浓度会有一定影响。
第二种方法是对运动方程(3-1-57)进行迦辽金有限元求解。
首先将流速用基函数的()643~--Φ==Jij i i v v v线性组合来表示,即然后将运动方程写成迦辽金积分表达式:⎰Ω==ΩΦ+∂∂+Φ) ..., ,2 ,1( 0)]~)(([n i g g x pk v I i j i ijJ ij ρμθ (3-4-7)把式(3-4-l )代入式(3-4-7),并在各单元上进行积分即得到计算各结点流速的有限元方程:0=ΩΦ⎪⎪⎭⎫ ⎝⎛+∂Φ∂+ΩΦΦ∑⎰∑⎰ΓΩΓΩd g x p k d v I j j JJ i ij I J ij ρμθ 三、水动力弥散方程的求解为进行有限元计算::同样将浓度C 写成基函数的线性组合,即()n J C C C J J ,...,2,1~=Φ=≈将对流一弥散方程写成迦辽金积分表达式;()()()1043,...,2,10~~~--==ΩΦ⎥⎥⎦⎤⎢⎢⎣⎡∂∂-∂∂-⎪⎪⎭⎫ ⎝⎛∂∂∂∂⎰Ωn I d t c c v x x C D x I i i j ij i对上式二阶导数应用分部积分和格林公式,则有()1143~~~--Φ∂∂+Ω∂Φ∂∂∂-=ΩΦ⎪⎪⎭⎫ ⎝⎛∂∂∂∂⎰⎰⎰ΓΓΩdL n x c D d x x c D d x c D x I i j ij i I j ij I j ij i式中, Γ为区域Ω的二类或三类边界段; n i 为边界Γ的外法向矢量。
将武(3-4--11)代入式(3-4~10),并将积分转为在单元上进行,则得到;()()12430~~~~--=Φ∂∂+Ω⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧∂Φ∂∂∂-Φ⎥⎦⎤⎢⎣⎡∂∂-∂∂-∑⎰∑⎰ΓΓΓΩdL n x c D d x x c D t c C v x I i j ij i I j ij I i i上式左侧最后一项面积积分表示弥散通量的边界条件。
Γ表示单元e 与二类边界Γ相交的部分,若两者不相交,则该线积分为零。
对于包含有三类边界,即已知对流一弥散通量的边界,为了边界条件处理方便,可以对弥散方程中的二阶和一阶导教体应用格林公式,即有:()()1343~~~~--Φ⎪⎪⎭⎫ ⎝⎛-∂∂+Ω∂Φ∂-=ΩΦ⎥⎥⎦⎤⎢⎢⎣⎡∂∂-⎪⎪⎭⎫ ⎝⎛∂∂∂∂⎰⎰⎰ΓΩΩdL n C v x c D d x D d C v x x c D x I i i jij j I ij I i i j ij i此式代入式(3-4-10),并在单元中进行积分,则得:()14430~~~2--=Φ⎪⎪⎭⎫ ⎝⎛-∂∂+Ω⎥⎥⎦⎤⎢⎢⎣⎡∂Φ∂⎪⎪⎭⎫ ⎝⎛-∂∂-Φ∂∂-∑⎰∑⎰ΓΩdL n C v x c D d x C v x c D t c I i i j ij i I i j ij I 将近似函数J J c C Φ=~代人式(3-4-12)和式(3-4-14),分别得到二类和三类边界的迦辽金有限元积分或为二类边界:()()15430~--=∂∂-Ω∂∂+Ω⎥⎥⎦⎤⎢⎢⎣⎡∂∂∂∂+∂∂∑⎰∑⎰∑⎰ΩΩΓe e e I i j j J J I J i I j J ij I J i i e e dL n x cDi d t C d C x x D v x φφφφφφφ三类边界:()()16430~--=∂∂-Ω∂∂+Ω⎥⎥⎦⎤⎢⎢⎣⎡∂∂∂∂+∂∂∑⎰∑⎰∑⎰ΓΩΩdL n x cD d t c d C x x D v x I i j ij j J I j i I j J ij i j i i φφφφφφφ式(3-4-16)所表示的处理方法对流速的求解比较敏感。
三类边界问题还可以用以下处理办法。
如三类边界条件表示为()1743)(''3--=-∂∂ΓC n v n C v x cD i i i i jij其中C’’表示自边界外侧区域进入边界处的液体浓度。
由此可得:''C n v n C v n x cD i i J i j i i jij+=∂∂φ 此式代人式(3-4-16),整理后得到三类边界的另一种计算式:()()18430''3--=-Ω∂∂+-Ω⎥⎥⎦⎤⎢⎢⎣⎡∂∂∂∂+∂∂∑⎰∑⎰∑⎰∑⎰ΩΓΓΩεεεφφφφφφφφφdL C n v d t C dL C n v d C x x D v x I i i JJ I J J I i i J j J i I ij I J i i 上述式(3-4-4)、式(3-4-5)[或式(3-4-8)]、式(3-4-15)及式(3-4-16)或式(3-4-18)即是对水质模型进行迦辽金有限元计算的基本公式。
在具体应用中,由于剖分单元的形状和单元基函数的类型不同,由上述基本算式可以得到相应的有限元方程。
关于水流方程的有限元计算问题,已在第一篇第五章作了介绍,以下仅就二维对流一弥散方程的有限元计算方法作一说明。
设剖分单元为三角形,单元编号用e 表示,单元中三个结点编号分别以i 、j 、m 表示。
因是二维问题,j i x x ,的下标i 、j=1,2,相应x 1=x ,x 2=y ,由此式(3-4-12)变为()()()()1943,....,2,10~~~~~~~~~~--==Γ⎥⎥⎦⎤⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+⎭⎬⎫⎩⎨⎧⎪⎪⎭⎫ ⎝⎛∂∂∂∂+∂∂∂∂+∂∂∂∂+∂∂∂∂-⎥⎦⎤⎢⎣⎡∂∂-∂∂-∂∂-∑⎰∑⎰Γ∆n i d n y cD x c D n y c D x c D y y c D y x c D x y c D x x c D t c C v y C v x i y yy yx x xy xx t iyy i yx i xy i xx i y x φφφφφφε为了进行有限单元的计算,需构造三角形单元的基函数,其中最简单的是线性插值。
