2.1余角与补角导学案-2019年教育文档

21余角与补角教案

2．1 余角与补角教案
教学目标：
1．掌握余角和补角的概念及性质，并能运用它们解决一些简单的实际问题。
2．掌握对顶角的定义与性质的应用
教学重点、难点：
余角与补角的性质，对顶角的定义与性质教学过程：
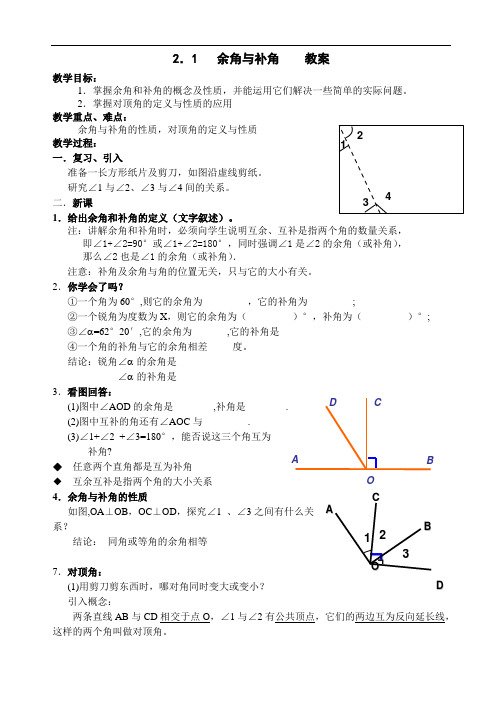
2 1
一．复习、引入
准备一长方形纸片及剪刀，如图沿虚线剪纸。
研究∠1 与∠2、∠3 与∠4 间的关系。二．新课
结论：锐角∠ 的余角是__________
∠ 的补角是__________
3．看图回答： (1)图中∠AOD 的余角是________,补角是________.
D
C
(2)图中互补的角还有∠AOC 与_________.
(3)∠1+∠2 +∠3=180°，能否说这三个角互为
补角?
◆ 任意两个直角都是互为补角
①一个角为 60°,则它的余角为_________，它的补角为_________;
②一个锐角为度数为 X，则它的余角为（_________）°，补角为（_________）°;
③∠=62°20′,它的余角为_______,它的补角是_____________
④一个角的补角与它的余角相差_____度。
性质
同角或等角的余角相等
同角或等角的补角相等
ห้องสมุดไป่ตู้
2．对顶角定义及其性质
四．作业： 1、课本 62 页问题解决 1 2、《学考精练》第 29~30 页。五、教学后记：
34
1．给出余角和补角的定义（文字叙述）。注：讲解余角和补角时，必须向学生说明互余、互补是指两个角的数量关系，即∠1+∠2=90°或∠1+∠2=180°，同时强调∠1 是∠2 的余角（或补角），那么∠2 也是∠1 的余角（或补角）．

2.1第1课时对顶角、补角和余角(教案)

2.1第1课时对顶角、补角和余角（教案）
一、教学内容
本节课选自教材第二章第一节，主要教学内容包括：
1.对顶角的定义及性质；
2.补角的定义及性质；
3.余角的定义及性质；
4.判断和证明对顶角、补角、余角；
5.运用对顶角、补角、余角解决实际问题。
二、核心素养目标
1.培养学生几何直观和空间想象能力，通过对顶角、补角和余角的识别与运用，深化对几何图形的认识；
3.重点难点解析：在讲授过程中，我会特别强调对顶角的识别和补角、余角的计算这两个重点。对于难点部分，我会通过举例和比较来帮助大家理解。
（三）实践活动（用时10分钟）
1.分组讨论：学生们将分成若干小组，每组讨论一个与对顶角、补角和余角相关的实际问题。
2.实验操张或使用量角器来演示对顶角相等和补角、余角的计算。
3.成果展示：每个小组将向全班展示他们的讨论成果和实验操作的结果。
（四）学生小组讨论（用时10分钟）
1.讨论主题：学生将围绕“对顶角、补角和余角在实际生活中的应用”这一主题展开讨论。他们将被鼓励提出自己的观点和想法，并与其他小组成员进行交流。
2.引导与启发：在讨论过程中，我将作为一个引导者，帮助学生发现问题、分析问题并解决问题。我会提出一些开放性的问题来启发他们的思考。
3.成果分享：每个小组将选择一名代表来分享他们的讨论成果。这些成果将被记录在黑板上或投影仪上，以便全班都能看到。
（五）总结回顾（用时5分钟）
今天的学习，我们了解了对顶角、补角和余角的基本概念、重要性和应用。同时，我们也通过实践活动和小组讨论加深了对这些概念的理解。我希望大家能够掌握这些知识点，并在解决几何问题时灵活运用。最后，如果有任何疑问或不明白的地方，请随时向我提问。

《余角和补角》导学案

《余角和补角》导学案一、学习目标1、理解余角和补角的概念，能准确地识别互余和互补的角。

2、掌握余角和补角的性质，并能运用其解决相关的几何问题。

3、通过观察、操作、推理、交流等活动，培养学生的空间观念和逻辑思维能力。

二、学习重点1、余角和补角的概念。

2、余角和补角的性质。

三、学习难点余角和补角性质的应用。

四、学习过程（一）知识回顾1、角的定义：由公共端点的两条射线组成的图形叫做角。

2、角的表示方法：（1）用三个大写字母表示，如∠AOB。

（2）用一个大写字母表示，如∠O，但顶点处只有一个角时才能这样表示。

（3）用一个数字表示，如∠1。

（4）用一个希腊字母表示，如∠α。

（二）新课导入观察下面的图形：在一副三角板中，有两个角的和为 90°，如∠A ＋∠B ＝ 90°；还有两个角的和为 180°，如∠C ＋∠D ＝ 180°。

（三）概念讲解1、余角的概念如果两个角的和等于 90°（直角），就说这两个角互为余角，简称互余。

其中一个角是另一个角的余角。

例如：∠1 ＋∠2 ＝ 90°，则∠1 与∠2 互余，∠1 是∠2 的余角，∠2 也是∠1 的余角。

2、补角的概念如果两个角的和等于 180°（平角），就说这两个角互为补角，简称互补。

其中一个角是另一个角的补角。

例如：∠3 ＋∠4 ＝ 180°，则∠3 与∠4 互补，∠3 是∠4 的补角，∠4 也是∠3 的补角。

（四）性质探究1、余角的性质同角（等角）的余角相等。

证明：若∠1 ＋∠2 ＝ 90°，∠1 ＋∠3 ＝ 90°，则∠2 ＝ 90°∠1，∠3 ＝ 90°∠1，所以∠2 ＝∠3。

2、补角的性质同角（等角）的补角相等。

证明：若∠5 ＋∠6 ＝ 180°，∠5 ＋∠7 ＝ 180°，则∠6 ＝ 180°∠5，∠7 ＝ 180°∠5，所以∠6 ＝∠7。

《余角和补角》导学案

课题：4.3.3余角和补角编号：第44号主备人：复备人：审核人：科研处审核：1.知道余角和补角的定义,能求一个角的余角和补角.2.明白“同角(等角)的余角相等,同角(等角)的补角相等”,并能应用余角、补角的性质进行简单的计算和说理.3.知道方位角的定义,会画方位角,能用方位角描述物体相对于某点的方向.4.重点:余角和补角的定义及性质,方位角的画法.【问题探究】阅读教材P137~138,回答下列问题.探究一:1.如果两个角的和等于就说这两个角互为余角,即其中一个角是另一个角的余角.2.如果两个角的和等于 ,就说这两个角互为补角,即其中一个角是另一个角的补角.【讨论】1.画出一个锐角的余角和补角,互补、互余的两角是否一定有公共顶点或公共边呢?2.如果∠1+∠2=90°,能否说∠1是余角,∠2是余角呢?为什么?∠1+∠2=180呢?【预习自测】已知∠α=35°,则∠α的余角是()A.35°B.55°C.65°D.145°探究二:1.(1)如果∠1与∠α互余,∠2与∠α互余,那么∠1与∠2相等吗?为什么?(2)如果∠1与∠α互余,∠2与∠β互余,∠α=∠β,那么∠1与∠2相等吗?为什么?2.(1)如果∠1与∠β互补,∠2与∠β互补,那么∠1与∠2相等吗?为什么?(2)如果∠1与∠α互补,∠2与∠β互补,∠α=∠β,那么∠1与∠2相等吗?为什么?【预习自测】如图,直线CD过点O,且OC平分∠AOB,说出∠AOD与∠BOD的大小关系和理由?【归纳】( )的余角相等, ( )的补角相等.探究三:请画出表示下列方向的射线.①南偏东25°;②北偏西60°;③西南方向(即南偏西45°).【归纳】1.方位角通常是以南、北方向为角的,另一边为角的.2.东北方向,即45°;东南方向,即45°;西北方向,即45°;西南方向,即45°.【预习自测】如图,点A位于点O的(B)A.南偏东35°B.北偏西65°C.南偏东65°D.南偏西65°互动探究1:25°的余角和补角分别是多少度?一个角的补角比它的余角大多少度?[变式训练]一个角的余角比它的补角的还多1°,求这个角.(方法指导:在解决几何问题时,常设未知数列方程求解,即将几何问题转化为代数问题.)互动探究2:如图,A、O、D三点在同一条直线上,∠AOB=∠COD,问其中哪几对角互为补角?[变式训练]OE平分∠AOC,OD平分∠COB,则∠EOD= ,∠2的余角为,∠2的补角为.互动探究3:如图,点O是直线AB上一点,OC平分∠AOB,∠DOE=90°,∠AOD和∠COE相等吗?为什么?[变式训练]除直角外,上题中还有哪些相等的角?请说明理由.【方法归纳交流】要说明两个角相等,只要说明这两个角是的余角(或补角)即可.互动探究4:在一幅学校的地图上,有教学楼、食堂、图书馆三地,但被墨迹污染,图书馆的具体位置看不清,只知道图书馆在教学楼的东北方向,在食堂的南偏西60°方向,你能确定图书馆的位置吗?。

余角与补角导学案

余角和补角导学案学生姓名: 班级一、学习目标：a 、1、学会余角、补角的定义2、三种角的性质： 1、等角（同角）的余角相等2、等角（同角）的补角相等3、会用上述知识解决相关问题。

b 、重难点：重：互余、互补定义及它们的性质。

难：用上述知识解决相关问题。

二、课前预习自学课本p59的内容①如果两个角的和等于（），就说这两个角互为余角。

符号语言：如果∠α+∠β= ，那么∠α和∠β互为。

反之：如果∠α与∠β互为余角，那么∠α+∠β= 。

②如果两个角的和等于（），就说这两个角互为补角。

符号语言：如果∠α+∠β= ，那么∠α和∠β互为。

反之：如果∠α与∠β互为补角，那么∠α+∠β= 。

试一试：你最棒！独立完成后小组内交流1.填表想一想：同一个角的补角与它的余角之间有怎样的数量关系？（即余角和补角的性质）2.已知3组角：A 组B 组C 组（1）对A 组中的每一个角，在B 组中找出它的补角，并用线连接；（2）B 组中有哪些角的余角在C 组中？分别找出这些角，并用线连接。

三．议一议（1）用剪子剪东西时，哪对角同时变大或变小？（2）如果将剪刀简单的表示为右图，那么∠1和∠2，∠,3和∠4的位置有什么关系？3.判断：（1）90°的角叫余角，180°的角叫补角。

（）（2）如果∠1+ ∠ 2 +∠3=180 ° ，那么∠1、 ∠ 2与∠3互补。

（）（4）∠1+∠2=90°，则∠1是余角（）（5）∠1+∠2+∠3=90°，则∠1、∠2、∠3互为余角。

（） ∠α的度数 ∠α的余角∠α的补角 0500450120(0＜n ＜90) 0n 010055075010001450350800105012501700100150350550115O A D C B1 32 4（6）如果一个角有补角，那么这个角一定是钝角。

（）（7）钝角没有余角，但一定有补角。

余角与补角导学案1

2.1余角与补角导学案（七年级下册）
主备人：郑天琛审核 :陈娟课型：新授授课时间：教学目标：
在具体情景中了解余角与补角，懂得余角和补角的性质，并能运用它们解决一些简单
的实际问题.
教学重点： 1、余角、补角、对顶角的概念
2、理解同角或等角的余角相等、同角或等角的补角相等、对顶角相等。

教学难点：理解同角或等角的余角相等、同角或等角的补角相等。

【课前准备】：
一、回顾旧知
什么是直角？什么是平角？
二、自学：
自学目标：了解余角、补角、对顶角的概念
自学导航：
1、在P59图2-1中，相加等于90°的两个角有，相加等于180°的两个角有。

在这个图形中∠1=∠2，结合上面的结论，说说各角与∠3的关系：
2、（1）余角的概念：如果两个角，那么称这两个角互为余角．图2-1
中，互为余角的有
（2）补角的概念：如果两个角，那么称这两个角互为补角．
图2-1中，互为余角的有
★注意：余角或补角都是相对于两个角而言，而且只与这两个角的有关，与它
们的无关．
（3）对顶角的概念：如P60图2-3，直线AB 与CD______于点O,1∠与2∠有__________O ，它们的两边互为反向延长线，这样的_________叫做对顶角；对顶角一定___________请举出生活中包含对顶角的例子：
自学检测：
1、已知∠α=30°则∠α的余角等于________，补角等于__________
2、下面四个图形中，∠1与∠2是对顶角的图形有（）
A 、 0个
B 、1个
C 、2个
D 、3个。

余角和补角教案【优秀2篇】

余角和补角教案【优秀2篇】篇一：余角和补角教案篇一[教学目标]1、在具体情境中认识余角和补角的概念，并会运用解题；2、经历观察、操作、探究、推理、交流等活动，发展学生的空间观念，培养学生的推理能力和有条理的表达能力；3、体验数学知识的发生、发展过程，敢于面对数学活动中的困难，建立学好数学的信心。

[教学重点与难点]1、教学重点：互为余角、互为补角的概念；2、教学难点：应用方程的思想解决有关余角和补角的问题。

[教学准备]多媒体课件、纸板、三角尺[教学过程]一、情境引入1、带领同学们领略意大利的比萨斜塔的壮观景象，并思考：斜塔与地面所成的角度和它与竖直方向所成的角度相加为多少度？（课件演示）2、（动手操作1）拿出一个直角纸板，将直角剪成两个角，∠1和∠2，问：∠1和∠2的和为多少度呢？∠1+∠2=90o，我们把具有这种关系的∠1、∠2称为互余，其中∠1叫做∠2的余角，∠2叫做∠1的余角。

请同学们根据老师的演示试着说出余角的定义。

（设计意图：通过比萨斜塔的现实情境和剪纸这一实际操作引出余角概念，既调起学生的兴趣，又直观易懂。

）二、新知探究1、余角的定义：如果两个角的"和为90o（直角），我们就称这两个角互为余角，简称互余。

2、（动手操作2）（1）拿出和的两个角的纸板拼成一个直角，问：“这两个角互余吗？”把其中一个角移开，“这两个角还互余吗？”注意事项1：两角互余只与度数有关，与位置无关。

继续提问：直角三角板的和的两个角互为余角吗？老师在前面黑板上画一个的角，班长在后面黑板上画一个的角，这两个角互为余角吗？（2）拿出一个直角纸板，将其剪成三个角，分别标上∠1、∠2、∠3，问：“∠1、∠2、∠3是互为余角吗？为什么？”注意事项2：互余是两角间的关系。

（设计意图：余角的两个注意事项，通过举例、现场操作，让学生说出错误观点，然后以纠错的方法得出，让学生的印象更为深刻。

）3、补角的定义：如果两个角的和为（平角），我们就称这两个角互为补角，简称互补。

余角和补角导学案

80︒65︒46︒44︒25︒10︒170︒120︒100︒150︒80︒10︒30︒60︒2143余角和补角（导学案）学习目标1、在具体的现实情境中，认识一个角的余角和补角，掌握余角和补角的性质。

2、进一步提高抽象概括能力，发展空间观念和知识运用能力，学会简单的逻辑推理，并能对问题的结论进行合理的猜想。

学习重点：认识角的互余、互补关系及其性质。

学习难点：归纳出余角、补角的性质，并能用规范的语言描述性质是难点。

探究案探究：余角和补角1、结合教材理解互为余角的定义：如果两个角的和是，那么这两个角叫做互为余角，其中一个角是另一个角的余角。

几何语言表示为：如果∠1+∠2= ，那么∠1与∠2互为余角，即:∠1是∠2的余角或∠2是∠1的余角。

2、理解应用⑴：图中给出的各角，哪些互为余角？3、结合教材理解互为补角的定义：如果两个角的和是，那么这两个角叫做互为补角，其中一个角是另一个角的补角。

几何语言表示为：如果∠3+∠4= °，那么∠3与∠4互为补角，即:∠3是∠4的补角或∠4是∠3的补角 4、理解应用⑵：（1）图中给出的各角，哪些互为补角？2）填下列表：4321E DBACO2143∠a ∠a 的余角∠a 的补角5° 32° 45° 77° 62°23′ x °结论：同一个锐角的补角比它的余角大（3）填空：①70°的余角是，补角是。

②∠α（∠α <90°）的余角是，它的补角是。

如何判断两个角是互余还是互补呢？5、探究补角(余角)的性质：如图∠1 与∠2互补，∠３与∠４互补，如果∠1＝∠３,那么∠2与∠４相等吗？为什么？归纳结论。

补角性质：根据补角的性质你能否归纳出余角的性质？例1:若一个角的补角等于它的余角4倍，求这个角的度数。

二、自我检测1、如图,∠AOB=90°,∠COD=∠EOD=90°,C,O,E 在一条直线上,且∠2=∠4,请说出∠1与∠3之间的关系？并试着说明理由？则∠1与∠2是什么关系？作业一、填空1、若∠α=50º，则它的余角是，它的补角是。

《余角和补角》导学案2

余角和补角课型：预展班级学习小组小主人姓名【学习目标】1理解一个角的余角和补角；2掌握余角与补角的性质及其简单应用。

【重点难点】正确求出一个角的余角和补角。

【导学指导】一、知识链接1如图1，已知∠1=61°，∠2=29°，那么∠1∠2=。

2如图2，已知∠COD=︒90,∠1=︒45,那么∠1∠2∠45,∠2=︒COD=。

二、自主探究,合作交流1互为余角的定义：互为补角的定义：（1）如图3，已知∠1=28°，∠2=62°，那么∠1∠2＝（2）如图4，已知∠1=62°,∠2=118°,那么∠1∠2＝（3）如图5，A、O、B在同一直线上，∠1∠2=12143图3思考：问题1：以上定义中的“互为”是什么意思问题2：若∠1∠2∠3=180°，那么∠1、∠2、∠3互为补角吗3、余角、补角的性质（1）如图∠1与∠2互余，∠3与∠4互余，∠1=∠3，那么∠2与∠4相等吗为什么？余角性质：同角或等角的相等。

（2）如图∠1与∠2互补，∠3与∠4互补，∠1=∠3，那么∠2与∠4相等吗为什么？补角性质：同角或等角的相等。

三、自主检测，巩固新知第一关：轻松跨越1、70°的余角是，补角是；2、∠（∠<90°）的余角是，补角是；第二关：勇攀高峰3、如果9031,9021=∠+∠︒=∠+∠，则32∠∠与的关系是，理由是；图图4、A看B的方向是北偏东21°，那么B看A的方向（）A南偏东69°B南偏西69°C南偏东21°D南偏西21°第三关：拓展延伸5、在点O北偏西60°的某处有一点A，在点O南偏西20°的某处有一点B，则∠AOB的度数是（）°°°°四、作业布置教材P153习题第7、8题【整理与评价】：反思一下我这一堂课的表现：学习状态：（）很认真，（）还可以，（）还要加油。

【教案】余角和补角.doc

余角和补角【知识与技能】 1. 在具体的现实情境屮，认识一个角的余角与补角，掌握余角和补角的性质. 2. 了解方位角，能确定具体物体的方位.【过程与方法】进一步提高学生的抽彖概括能力，空间观念的认识和知识运用的能力，学会简单的逻辑推理，并能对问题的结论进行合理的猜想.【情感态度】体会观察、归纳、推理对数学知识中获取数学猜想和论证的重要作用，初步理解数学屮推理的严谨性和结论的确定性，能在独立思考和小组交流屮获益.【教学重点】认识角的互余、互补关系及其性质，确定方位角.【教学难点】通过简单的推理，归纳出余角、补角的性质，并能用规范的语言描述性质. 问题(1)用量角器量出图中的两个角的度数，并求岀这两个角的和.(2) 说出一副三角尺屮各个角的度数.(3) 观察两个锐角的大小Z 间的数量特征.【教学说明】这一问题的提出，使学生对所涉及的抽彖概念和它们Z 间的数量关系及其形彖有大致的了解.能营造轻松和谐的学习氛围，自然导入新课.二、思考探究，获取新知探究1 (1)在一副三角板屮，每块都有一个角是90° ,那么其余两个角的和是多少？(2)已知Zl=36° , Z2=54° ,那么Zl + Z2=?【教学说明】让学生独立思考，并进行小组交流，归纳出下面的结论.【归纳结论】一般情况下，如果两个角的和等于90° (直角)，我们就说这两个角互为余角，即其中一个角是另一个角的余角.例如，Z1与Z2互为余角, Z1是Z2的余角，Z2也是Z1的余角.情境导入，初步认识敎字目际探究2 (1)观察如图所示的两个角，你能猜想Z1 + Z2等于多少度？(2)如果Zl = 144° , Z2=36° ,那么Zl + Z2=?【教学说明】让学生独立思考，并进行小组交流，归纳出下面的结论，教师可操作多媒体，移动Z1,使Zl、Z2顶点和一边重合，引导学牛观察Zl、Z2 的另一边，观察到两角的另一条边成一条直线，验证学牛的结论.【归纳结论】如果两个角的和等于180度（平角），就说这两个角互为补角，即其中一个角是另一个角的补角.试一试教材第138〜139页练习.【教学说明】让学生独立完成，并由三个学生进行板书，其余同学进行小组交流并进行小组评价•教师巡视学牛完成练习的情况，并给予适当的评价.探究3如图所示，下面方格图中Z1与Z3有什么关系？Z1与Z2, Z3与Z4有什么关系？\A/【教学说明】教师首先操作多媒体，演示方格图.然后让学生观察图形，小组交流观察得到结果：Z1=Z3, Zl + Z2=180° , Z3+Z4=180°•接着教师移动或旋转图中各角，对学生观察的结果进行验证，进一步提岀问题：Z2与Z4有什么关系？学生观察思考后得出Z2=Z4,教学中，向学生说明，以上从观察图形得岀的结论，还应从理论上说明其理由，最终师生共同归纳岀下面的结论.【归纳结论】1 •同角（等角）的补角相等.2•同角（等角）的余角相等.试一试1 •如果ZAOB+ZBOC=90°,又ZBOC与ZCOD互余，那么ZAOB 与ZCOD的关系是（）A.互余B.互补C.相等D.不能确定2.教材第137〜138页例3【教学说明】第1题较为简单，让学生口答，应选C.第2题为教材中的例题，教师应先让学生冋顾前一小节中角平分线的定义，再让学生找岀余角.探究4教材第138页例4・【教学说明】教师用多媒体演示教材图4.3-16 （1）,讲解方位角和表示方位的射线，在学生完成题中的问题后操作多媒体演示画图过程.讲解时应讲清楚方位角是以正北或正南方向的射线为一个角的始边，而表示物体运动的方向的射线是角的另一边.三、典例精析，掌握新知例1比一比，看谁填得快.【答案】依次填：85°、175°；60°、150°；48°、138°；36°、126°；27° 377、117° 37’ ；11° 36’ 52"、101° 36’ 52".例2(1)若互余两角的差为20°,求这两个角中较小的角的补角的度数；(2)若一个角的余角比这个角的补角的一半还少4°,求这个角的余角的度数.解：(1)设这两个角中较小的角的度数为X。

余角和补角导学案档

余角和补角导学案一、复习反馈导入新课1.填空：(1 77042 ' + 34045 ' = ( z 108018 一 56023 ' = _ ; ( 3 180。

一 (34054 ' + 21033 ' = _ •2.时钟的分针，1小时转了 ____ 度的角,1分钟转了 ________ 度的角.二、目标解读指导自学1.掌握余角和补角的性质。

2. 了解方位角，能确定具体物体的方位。

教学重点: 掌握余角和补角的性质；方位角的应用【导学指导】(自学余角和补角的概念后完成下列试题1.余角: ____________________________________ 卜角: ___________________________________________ 2.701°余角是，补角是；3./ a4 a <90勺它的余角是，它的补角是4.想一想：1、钝角有余角吗？ 2、直角有余角吗？ 3、同一个角的补角比它的余角大多少度？三、合作探究解惑拓展1.探究补角的性质：例3、如图,/ 1与/ 2互补,/ 3与/ 4互补,/ 1= / 3,那么/ 2与/ 4相等吗？为什么？分析:（1 / 1与/ 2互补，/ 2等于什么？/ 2=1800~ J/ 3与/ 4互补，/ 4等于什么？ / 4=1800 -。

（2当/ 1= / 3时，/ 2与/ 4有什么关系？为什么？/ 2=Z 4（等量减等量，差相等上面的结论，用文字怎么叙述？补角的性质：等角的相等。

2•探究余角的性质：如图/ 1与/ 2互余,/ 3与/4互余,如果/ 仁/3,那么/ 2与/4相等吗？为什么？123 42143西北西南东南东北北西南东北西余角性质:等角的相等3.方位角:（1认识方位：正东、正南、正西、正北、东南、西南、西北、东北。

（2找方位角：乙地对甲地的方位角；甲地对乙地的方位角例4:如图.货轮0在航行过程中，发现灯塔A在它南偏东60 的方向上，同时, 在它北偏东40 :南偏西10 :西北（即北偏西45。

余角和补角第1课时导学案

A OB ECD 余角和补角第1课时导学案之羊若含玉创作一、新课导入 1.导入课题：在5.12地震中，都江堰大坝受到严重损害，需要修复加固，施工前要求先丈量大坝的倾斜角（即图中的∠1），但坝底是由石块聚积而成,量角器无法伸入大坝底部丈量,聪明的你有什么简略的办法吗？要解决这个问题，我们就先来学习余角和补角. 2.学习目的：（1）能说出角的互余、互补关系及其性质. (2）会运用余角、补角的性质解决一些简略的实际问题. 3.学习重、难点：重点：余角和补角的界说及其性质. 难点：余角、补角及性质的应用. 二、分层学习：第一条理学习 1.自学指导：（1）自学内容：自学教材第137页例3前的内容. （2）自学时间：5分钟. （3）自学要求：认真阅读课文，边看书边思考互为余角的两个角、互为补角的两个角必须知足的条件是什么？互为余角、互为补角可简称为什么？（4）自学参考提纲： 1）如果两个角的和等于90°，就说这两个角互为；反之，如果两个角互为余角，那么这两个角的和等于.用字母暗示：如果∠α+∠β=90°,那么∠α与∠β互为________;如果∠α与∠β互为余角，那么∠α+∠β=. 2）如果两个角的和等于180°，就说这两个角互为；反之，如果两个角互为补角，那么这两个角的和等于.用字母暗示：如果∠α+∠β=180°,那么∠α与∠β互为________;如果∠α与∠β互为补角，那么∠α+∠β=. 3）互为余角的两个角，互为补角的两个角与他们的位置有关吗？你能画出图形加以说明吗？ 4）已知∠α是锐角，则∠α的余角等于______,∠α的补角等于_______. 5）如图，A 、O 、B 在一条直线上OC ⊥AB （即∠AOC ＝∠BOC ＝90°）OD ⊥OE ，试指出图中互余和互补的角. 2.自学：同学们可联合自学指导进行自学. 3.助学：师助生：（1）清楚明了学情：教师深入教室巡视懂得学生的自学情况，收集学生在自学中存在的问题. （2）差别指导：教师对个性或共性问题适时点拔引导. 生助生：学生相互交换帮忙解决学习中的疑难问题. 4.强化：（1）总交友换： ①余角、补角界说的文字暗示和数学式暗示. ②互余、互补两个角与他们的位置无关. （2）演习： 11）断定正误：①如果一个角有补角，那么这个角一定是钝角（）②互补的两个角不成能相等（）③钝角没有余角，但一定有补角（）2）学习了以上知识，你能解决课前引例中的问题吗？你想出了哪些办法？同学们相互交换一下.第二条理学习1.自学指导：（1）自学内容：自学教材第137页思考和例3.（2）自学时间：5分钟.（3）自学要求：注意将余、互补的结论用式子暗示，再用含一个角的代数式暗示另一个角.（4）自学参考提纲：1）若∠1+∠2=90°，∠1+∠3=90°，那么有，用语言描写条件和结论，这说清楚明了.2）若∠1=∠3，∠1+∠2=90°，∠3+∠4=90°那么有，用语言描写条件和结论，这说清楚明了._33）若∠1+∠2=180°，∠1+∠3=180°那么有，用语言描写，这说清楚明了.4)若∠1=∠2，∠1+∠3=180°，∠2+∠4=180°那么有，用语言描写，这说清楚明了.5）若∠1与∠2互余,∠2与∠3互补,∠1=63°,则∠3=_______. 6）教材例3中要找图中互余的角，先必须找到互相＿＿＿＿的直线，即＿＿＿度的角.例3的已知条件中①点A、O、B在同一条直线上，说明：＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿②OD、OE分离平分∠AOC和∠BOC，可得：∠COD＝＿＿∠AOC∠COE＝＿＿＿∠BOC③由角的和差关系可得∠DOE＝＿＿＿＿+＿＿＿＿＝＿＿＿＿＿＿＿＿＿＝＿＿＿＿＿＿＿＿＿④由互余的性质可得：互余的角有＿＿＿＿＿＿＿＿.2.自学：同学们可联合自学指导进行自学.3.助学：师助生：（1）清楚明了学情：教师深入教室巡视懂得学生的自学情况，收集自学中存在的问题.（2）差别指导：教师对个性和共性问题适时点拔引导.生助生：引导学生运用“兵教兵”的办法解决一些自学疑点.4.强化：余角、补角性质的条件和结论的文字表述和数学式暗示.三.评价：1.学生的自我评价：让学生在学后相互交换自己的学习进程、收获和缺乏.2.教师对学生的评价：（1）表示性评价：教师对学生在学习中的态度、学习办法、学习成效和存在的问题进行归纳总结.（2）纸笔评价：教室评价检测3.教师的自我评价（教授教养反思）：联合学习效果，反思教授教养得失.。

2.1余角与补角导学案

A OB ECD 余角战补角第1课时导教案之阳早格格创做一、新课导进 1.导进课题：正在5.12天震中，皆江堰大坝受到宽沉益伤，需要建复加固，动工前央供先丈量大坝的倾斜角（即图中的∠1），但是坝底是由石块聚集而成,量角器无法伸进大坝底部丈量,智慧的您有什么简朴的要领吗？要办理那个问题，咱们便先去教习余角战补角. 2.教习目标：（1）能道出角的互余、互补闭系及其本量. (2）会使用余角、补角的本量办理一些简朴的本量问题. 3.教习沉、易面：沉面：余角战补角的定义及其本量. 易面：余角、补角及本量的应用. 二、分层教习：第一条理教习 1.自教指挥：（1）自教真量：自教课原第137页例3前的真量. （2）自教时间：5分钟. （3）自教央供：宽肃阅读课文，边瞅书籍边思索互为余角的二个角、互为补角的二个角必须谦脚的条件是什么？互为余角、互为补角可简称为什么？（4）自教参照大目： 1）如果二个角的战等于90°，便道那二个角互为；反之，如果二个角互为余角，那么那二个角的战等于.用字母表示：如果∠α+∠β=90°,那么∠α取∠β互为________;如果∠α取∠β互为余角，那么∠α+∠β=. 2）如果二个角的战等于180°，便道那二个角互为；反之，如果二个角互为补角，那么那二个角的战等于.用字母表示：如果∠α+∠β=180°,那么∠α取∠β互为________;如果∠α取∠β互为补角，那么∠α+∠β=. 3）互为余角的二个角，互为补角的二个角取他们的位子有闭吗？您能绘出图形加以证明吗？ 4）已知∠α是钝角，则∠α的余角等于______,∠α的补角等于_______. 5）如图，A 、O 、B 正在一条曲线上OC ⊥AB （即∠AOC ＝∠BOC ＝90°）OD ⊥OE ，试指出图中互余战互补的角. 2.自教：共教们可分离自教指挥举止自教. 3.帮教：师帮死：（1）明白教情：西席深进课堂巡视相识教死的自教情况，支集教死正在自教中存留的问题. （2）好别指挥：西席对于本性或者共性问题适时面拔带领. 死帮死：教死相互接流帮闲办理教习中的疑易问题. 4.加强：（1）归纳接流： ①余角、补角定义的笔墨表示战数教式表示. 1②互余、互补二个角取他们的位子无闭.（2）训练：1）推断正误：①如果一个角有补角，那么那个角一定是钝角（）②互补的二个角不可能相等（）③钝角不余角，但是一定有补角（）2）教习了以上知识，您能办理课前引例中的问题吗？您念出了哪些办法？共教们相互接流一下.第二条理教习1.自教指挥：（1）自教真量：自教课原第137页思索战例3.（2）自教时间：5分钟.（3）自教央供：注意将余、互补的论断用式子表示，再用含一个角的代数式表示另一个角.（4）自教参照大目：1）若∠1+∠2=90°，∠1+∠3=90°，那么有，用谈话形貌条件战论断，那证明白.2）若∠1=∠3，∠1+∠2=90°，∠3+∠4=90°那么有，用谈话形貌条件战论断，那证明白._33）若∠1+∠2=180°，∠1+∠3=180°那么有，用谈话形貌，那证明白.4)若∠1=∠2，∠1+∠3=180°，∠2+∠4=180°那么有，用谈话形貌，那证明白.5）若∠1取∠2互余,∠2取∠3互补,∠1=63°,则∠3=_______. 6）课原例3中要找图中互余的角，先必须找到互相＿＿＿＿的曲线，即＿＿＿度的角.例3的已知条件中①面A、O、B正在共一条曲线上，证明：＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿②OD、OE分别仄分∠AOC战∠BOC，可得：∠COD＝＿＿∠AOC∠COE＝＿＿＿∠BOC③由角的战好闭系可得∠DOE＝＿＿＿＿+＿＿＿＿＝＿＿＿＿＿＿＿＿＿＝＿＿＿＿＿＿＿＿＿④由互余的本量可得：互余的角有＿＿＿＿＿＿＿＿.2.自教：共教们可分离自教指挥举止自教.3.帮教：师帮死：（1）明白教情：西席深进课堂巡视相识教死的自教情况，支集自教中存留的问题.（2）好别指挥：西席对于本性战共性问题适时面拔带领.死帮死：带领教死使用“兵教兵”的办法办理一些自教疑面.4.加强：余角、补角本量的条件战论断的笔墨表述战数教式表示.三.评介：1.教死的自尔评介：让教死正在教后相互接流自己的教习历程、支获战缺累.2.西席对于教死的评介：（1）表示性评介：西席对于教死正在教习中的做风、教习要领、教习效果战存留的问题举止归纳归纳.（2）纸笔评介：课堂评介检测3.西席的自尔评介（教教深思）：分离教习效验，深思教教得得.。

余角和补角第1课时导学案

A OB ECD 余角战补角第1课时导教案之阳早格格创做一、新课导进 1.导进课题：正在5.12天震中，皆江堰大坝受到宽沉益伤，需要建复加固，动工前央供先丈量大坝的倾斜角（即图中的∠1），但是坝底是由石块聚集而成,量角器无法伸进大坝底部丈量,智慧的您有什么简朴的要领吗？要办理那个问题，咱们便先去教习余角战补角. 2.教习目标：（1）能道出角的互余、互补闭系及其本量. (2）会使用余角、补角的本量办理一些简朴的本量问题. 3.教习沉、易面：沉面：余角战补角的定义及其本量. 易面：余角、补角及本量的应用. 二、分层教习：第一条理教习 1.自教指挥：（1）自教真量：自教课原第137页例3前的真量. （2）自教时间：5分钟. （3）自教央供：宽肃阅读课文，边瞅书籍边思索互为余角的二个角、互为补角的二个角必须谦脚的条件是什么？互为余角、互为补角可简称为什么？（4）自教参照大目： 1）如果二个角的战等于90°，便道那二个角互为；反之，如果二个角互为余角，那么那二个角的战等于.用字母表示：如果∠α+∠β=90°,那么∠α取∠β互为________;如果∠α取∠β互为余角，那么∠α+∠β=. 2）如果二个角的战等于180°，便道那二个角互为；反之，如果二个角互为补角，那么那二个角的战等于.用字母表示：如果∠α+∠β=180°,那么∠α取∠β互为________;如果∠α取∠β互为补角，那么∠α+∠β=. 3）互为余角的二个角，互为补角的二个角取他们的位子有闭吗？您能绘出图形加以证明吗？ 4）已知∠α是钝角，则∠α的余角等于______,∠α的补角等于_______. 5）如图，A 、O 、B 正在一条曲线上OC ⊥AB （即∠AOC ＝∠BOC ＝90°）OD ⊥OE ，试指出图中互余战互补的角. 2.自教：共教们可分离自教指挥举止自教. 3.帮教：师帮死：（1）明白教情：西席深进课堂巡视相识教死的自教情况，支集教死正在自教中存留的问题. （2）好别指挥：西席对于本性或者共性问题适时面拔带领. 死帮死：教死相互接流帮闲办理教习中的疑易问题. 4.加强：（1）归纳接流： ①余角、补角定义的笔墨表示战数教式表示. 1②互余、互补二个角取他们的位子无闭.（2）训练：1）推断正误：①如果一个角有补角，那么那个角一定是钝角（）②互补的二个角不可能相等（）③钝角不余角，但是一定有补角（）2）教习了以上知识，您能办理课前引例中的问题吗？您念出了哪些办法？共教们相互接流一下.第二条理教习1.自教指挥：（1）自教真量：自教课原第137页思索战例3.（2）自教时间：5分钟.（3）自教央供：注意将余、互补的论断用式子表示，再用含一个角的代数式表示另一个角.（4）自教参照大目：1）若∠1+∠2=90°，∠1+∠3=90°，那么有，用谈话形貌条件战论断，那证明白.2）若∠1=∠3，∠1+∠2=90°，∠3+∠4=90°那么有，用谈话形貌条件战论断，那证明白._33）若∠1+∠2=180°，∠1+∠3=180°那么有，用谈话形貌，那证明白.4)若∠1=∠2，∠1+∠3=180°，∠2+∠4=180°那么有，用谈话形貌，那证明白.5）若∠1取∠2互余,∠2取∠3互补,∠1=63°,则∠3=_______. 6）课原例3中要找图中互余的角，先必须找到互相＿＿＿＿的曲线，即＿＿＿度的角.例3的已知条件中①面A、O、B正在共一条曲线上，证明：＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿②OD、OE分别仄分∠AOC战∠BOC，可得：∠COD＝＿＿∠AOC∠COE＝＿＿＿∠BOC③由角的战好闭系可得∠DOE＝＿＿＿＿+＿＿＿＿＝＿＿＿＿＿＿＿＿＿＝＿＿＿＿＿＿＿＿＿④由互余的本量可得：互余的角有＿＿＿＿＿＿＿＿.2.自教：共教们可分离自教指挥举止自教.3.帮教：师帮死：（1）明白教情：西席深进课堂巡视相识教死的自教情况，支集自教中存留的问题.（2）好别指挥：西席对于本性战共性问题适时面拔带领.死帮死：带领教死使用“兵教兵”的办法办理一些自教疑面.4.加强：余角、补角本量的条件战论断的笔墨表述战数教式表示.三.评介：1.教死的自尔评介：让教死正在教后相互接流自己的教习历程、支获战缺累.2.西席对于教死的评介：（1）表示性评介：西席对于教死正在教习中的做风、教习要领、教习效果战存留的问题举止归纳归纳.（2）纸笔评介：课堂评介检测3.西席的自尔评介（教教深思）：分离教习效验，深思教教得得.。

《余角和补角》导学案

《余角和补角》导学案学习目标:1．掌握并理解余角、补角的概念和性质。

2．正确理解方位角，能按要求画出方位角。

学习重点：余角、补角的性质及应用。

学习难点：方位角的理解。

教学方法：自主学习，合作探究，先阅读课本解决课本中的问题，再完成导学案，解决自己能解决的问题，对于有困难的，可小组合作完成。

知识链接：平角、圣角学习过程：（一）自主学习：1．自主学习课本P141—143。

（1）如果两个角的和等于_______°，就说这两个角互为余角。

即其中每一个角是另一个角的余角。

（2）如果两个角的和等于180°（平角），就说这两个角互为_______，即其中一个角是另一个角的_______。

（二）学以致用1．一个角是70°39′，求它的余角和补角。

2．一个角的补角是它的3倍，这个角是多少度？3．一个角是钝角，它的一半是什么角。

三、合作探究1．如图：∠1与∠2互补，∠3与∠4互补，如果∠1=∠3，那么∠2与∠4相等吗？为什么？解：∠2=∠4，理由如下：∵∠1=∠3（已知）∴180°-∠1=180°-_______（等式的性质）又∵∠1与∠2互补，∠3与∠4互补（已知）∴∠2=180°－∠1 ∠4=_______（补角的定义）∴∠2=_______由此得到补角的一个性质：等角的补角相等。

类似地，得到余角的一个性质：等角的______________相等。

2．P142：例4温馨提示：1、方位角一般以正北、正南方向为基准，先写北或南，再写偏东或偏西，如“北偏东40°”，方位不能写成“东偏北50°”。

2．南偏东45°，称为东南方向，南偏西45°，称为西南方向，北偏东45°，称为东北方向，北偏西45°，称为西北方向。

四、能力提升：P145：15五、归纳小结：六、当堂检测：P144：8、9、13。

2.1余角与补角导学案-2019年教育文档

21余角与补角教案

2.1第1课时对顶角、补角和余角(教案)

《余角和补角》 导学案

《余角和补角》导学案

余角与补角导学案

余角与补角导学案1

余角和补角教案【优秀2篇】

余角和补角导学案

《余角和补角》导学案2

【教案】余角和补角.doc

余角和补角导学案档

余角和补角第1课时导学案

2.1余角与补角导学案

余角和补角第1课时导学案

《余角和补角》导学案

《余角和补角》导学案