【物理】匀变速直线运动的速度与位移的关系-优质课件
合集下载
高中物理精品课件:匀变速直线运动的速度和位移关系

动,在水平上滑行时,做末速度为 0 的匀减速直线运动,由平均速度
+
公式 = = 0 2 1 可得滑行分析运动过程可知:
1 =
则整个过程有
2
=
解得: = 18/
2
⋅ 1 ,2 =
1 + 2
1 + 2
=
2
⋅ 2
54+40.5
10.5
= 9/
A.A、B两个物体的加速度大小都在不断减小
B.A物体的加速度不断增大,B物体的加速度不断减小
C. A、B物体的位移都不断增大
D. A、B两个物体的平均速度大小都大于 v1
本题答案: AC
v
v2
2
v2
v1
0
A
B
t0
t
【2013广东高考】.如图7,游乐场中,从高处A到水面B处有
两条长度相同的光滑轨道。甲、乙两小孩沿不同轨道同时从A处
B
[答案]
ACD
某型号的舰载飞机在航空母舰上的跑道上加速时,发动机产生的最
大加速度为5 m/s2,所需的起飞速度为50m/s,跑道长100m 。
(1)通过计算判断,飞机能否靠自身的发动机从舰上起飞?
(2)为使飞机在开始滑行时就有一定的初速度,航空母舰装有弹射
装置。对于该型号的舰载飞机,弹射系统必须使它具有多大的初速
2
02 + 2
2
v2
O
2
x
x
物体由静止开始做匀加速直线运动
(1)在1T末、2T末、3T末、……nT末的瞬时速度之比
(2)在1T内、2T内、3T内、……nT内的位移之比
+
公式 = = 0 2 1 可得滑行分析运动过程可知:
1 =
则整个过程有
2
=
解得: = 18/
2
⋅ 1 ,2 =
1 + 2
1 + 2
=
2
⋅ 2
54+40.5
10.5
= 9/
A.A、B两个物体的加速度大小都在不断减小
B.A物体的加速度不断增大,B物体的加速度不断减小
C. A、B物体的位移都不断增大
D. A、B两个物体的平均速度大小都大于 v1
本题答案: AC
v
v2
2
v2
v1
0
A
B
t0
t
【2013广东高考】.如图7,游乐场中,从高处A到水面B处有
两条长度相同的光滑轨道。甲、乙两小孩沿不同轨道同时从A处
B
[答案]
ACD
某型号的舰载飞机在航空母舰上的跑道上加速时,发动机产生的最
大加速度为5 m/s2,所需的起飞速度为50m/s,跑道长100m 。
(1)通过计算判断,飞机能否靠自身的发动机从舰上起飞?
(2)为使飞机在开始滑行时就有一定的初速度,航空母舰装有弹射
装置。对于该型号的舰载飞机,弹射系统必须使它具有多大的初速
2
02 + 2
2
v2
O
2
x
x
物体由静止开始做匀加速直线运动
(1)在1T末、2T末、3T末、……nT末的瞬时速度之比
(2)在1T内、2T内、3T内、……nT内的位移之比
匀变速直线运动的位移与速度的关系 课件

匀变速直线运动的速度与位移的
预习导引
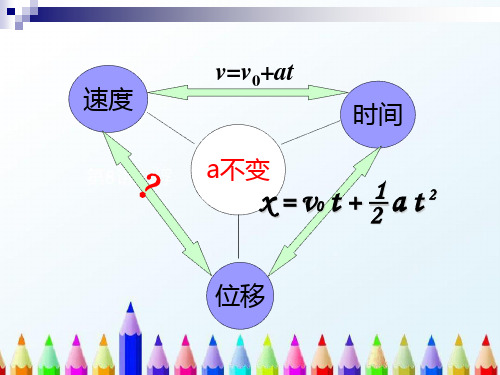
1.匀变速直线运动的速度公式为 v=v 0+at,位移公式为
1
x=v0t+ at2,由以上两个公式消去时间 t,就可以得出匀变速直线运动
2
的位移与速度的关系式 v 2-0 2 =2ax。
预习交流 1
应用 v2-0 2 =2ax 分析匀变速直线运动有何优势?
答案:因公式 v2-0 2 =2ax 不涉及物体运动的时间,故在不要求计
未知量的正负。对于无法确定方向的未知量。可以先假设为正方
向,待求解后,再根据正负确定所求物理量的方向。
(4)根据物理量特点及求解需要选用适当的公式列方程。
(5)计算结果并判断其是否符合题意和实际情况。
思考探究
探究初速度为零的匀变速直线运动的几个重要推论。
初速度为零的匀加速直线运动,将时间 t 等分
典题例解
【例 1】 “歼-15”战机是我国自行设计研制的首型舰载多用途
歼击机,短距离起飞能力强大。若“歼-15”战机正常起飞过程中加速
度为 a,经 s 距离就达到起飞速度腾空而起。现已知“辽宁号”航空母
舰起飞甲板长为 L(L<s),且起飞过程可简化为匀加速直线运动。现
有两种方法助其正常起飞,方法一是在航空母舰静止的情况下,用弹
v1∶v2∶v3∶ …∶vn=
;
④第 1 m,第 2 m,第 3 m……第 n m 所用的时间之比
为
。
解答:由图象法可得
①1 s 内,2 s 内,3 s 内……n s 内物体的位移之比 x 1∶x 2∶
x3∶…∶xn=1∶ 4∶ 9∶…∶n2
②第 1 s 内,第 2 s 内,第 3 s 内……第 n s 内的位移之比 x1' ∶
预习导引
1.匀变速直线运动的速度公式为 v=v 0+at,位移公式为
1
x=v0t+ at2,由以上两个公式消去时间 t,就可以得出匀变速直线运动
2
的位移与速度的关系式 v 2-0 2 =2ax。
预习交流 1
应用 v2-0 2 =2ax 分析匀变速直线运动有何优势?
答案:因公式 v2-0 2 =2ax 不涉及物体运动的时间,故在不要求计
未知量的正负。对于无法确定方向的未知量。可以先假设为正方
向,待求解后,再根据正负确定所求物理量的方向。
(4)根据物理量特点及求解需要选用适当的公式列方程。
(5)计算结果并判断其是否符合题意和实际情况。
思考探究
探究初速度为零的匀变速直线运动的几个重要推论。
初速度为零的匀加速直线运动,将时间 t 等分
典题例解
【例 1】 “歼-15”战机是我国自行设计研制的首型舰载多用途
歼击机,短距离起飞能力强大。若“歼-15”战机正常起飞过程中加速
度为 a,经 s 距离就达到起飞速度腾空而起。现已知“辽宁号”航空母
舰起飞甲板长为 L(L<s),且起飞过程可简化为匀加速直线运动。现
有两种方法助其正常起飞,方法一是在航空母舰静止的情况下,用弹
v1∶v2∶v3∶ …∶vn=
;
④第 1 m,第 2 m,第 3 m……第 n m 所用的时间之比
为
。
解答:由图象法可得
①1 s 内,2 s 内,3 s 内……n s 内物体的位移之比 x 1∶x 2∶
x3∶…∶xn=1∶ 4∶ 9∶…∶n2
②第 1 s 内,第 2 s 内,第 3 s 内……第 n s 内的位移之比 x1' ∶
匀变速直线运动的位移与速度的关系 课件

【答案】 BD
2.位移公式 x=v0t+12at2. (1)公式中 x、v0、a 均是 矢量 ,应用公式解题前应先根据正 方向明确它们的正、负值.一般规定初速度的方向为正方向. (2)当 v0=0 时,x=12at2,表示初速度为零的匀加速直线运动的 _位__移____与时间的关系.
一、由速度图象求匀变速直线运动的位移=( 3- 2)∶( 2-1)∶1,故 D 正确.
由 x=12at2 知,子弹运动的逆过程由右向左穿过第 1 块、前 2 块、前 3 块的时间之比 t1∶t2∶t3=1∶ 2∶ 3,再根据 v=at 知,子弹由右向左依 次“穿出”3 个木块的速度之比为 1∶ 2∶ 3.则子弹实际运动依次穿入 每个木块时的速度之比 v1∶v2∶v3= 3∶ 2∶1,故 B 正确.
推导:设物体的初速度为 v0,做匀变速运动的加速度为 a,t 秒末的速度为 v.由 x =v0t+12at2 得①
x
1
平均速度 v =t=v0+2at②
t 由速度公式 v=v0+at,当 t′=2时
t
t
v2=v0+a2③
由②③得 v =vt2④
又 v=vt2+at2⑤ 由③④⑤解得 vt2=v0+2 v⑥
值
相同
若位移的计算结果为负 说明这段时间内位移的方向与规定的正方向
值
相反
2.公式 x=v0t+12at2 是匀变速直线运动位移的一般表达形式,它表明质点在 各个时刻相对初始时刻的位移 x 跟时间 t 的关系.当物体做匀减速直线运动时, 公式的表达形式不变,a 取负值;当初速度为零时,公式简化为 x=12at2.
3.初速度为零的匀加速直线运动的几个比例 (1)1T 末、2T 末、3T 末、……、nT 末瞬时速度之比为 v1∶v2∶v3∶……∶vn= 1∶2∶3∶……∶n (2)1T 内、2T 内、3T 内、……、nT 内的位移之比 x1∶x2∶x3……∶xn=1∶22∶32∶……∶n2 (3)第一个 T 内、第二个 T 内、第三个 T 内,……,第 n 个 T 内位移之比 xⅠ∶xⅡ∶xⅢ∶……∶xn=1∶3∶5∶……∶(2n-1) (4)通过前 x、前 2x、前 3x……时的速度比 v1∶v2∶v3∶……∶vn=1∶ 2∶ 3∶……∶ n (5)通过前 x、前 2x、前 3x……的位移所用时间的比. t1∶t2∶t3∶……∶tn=1∶ 2∶ 3∶……∶ n (6)通过连续相等的位移所用的时间之比 tⅠ∶tⅡ∶tⅢ∶……∶tn=1∶( 2-1)∶( 3- 2)∶……∶( n- n-1).
2.位移公式 x=v0t+12at2. (1)公式中 x、v0、a 均是 矢量 ,应用公式解题前应先根据正 方向明确它们的正、负值.一般规定初速度的方向为正方向. (2)当 v0=0 时,x=12at2,表示初速度为零的匀加速直线运动的 _位__移____与时间的关系.
一、由速度图象求匀变速直线运动的位移=( 3- 2)∶( 2-1)∶1,故 D 正确.
由 x=12at2 知,子弹运动的逆过程由右向左穿过第 1 块、前 2 块、前 3 块的时间之比 t1∶t2∶t3=1∶ 2∶ 3,再根据 v=at 知,子弹由右向左依 次“穿出”3 个木块的速度之比为 1∶ 2∶ 3.则子弹实际运动依次穿入 每个木块时的速度之比 v1∶v2∶v3= 3∶ 2∶1,故 B 正确.
推导:设物体的初速度为 v0,做匀变速运动的加速度为 a,t 秒末的速度为 v.由 x =v0t+12at2 得①
x
1
平均速度 v =t=v0+2at②
t 由速度公式 v=v0+at,当 t′=2时
t
t
v2=v0+a2③
由②③得 v =vt2④
又 v=vt2+at2⑤ 由③④⑤解得 vt2=v0+2 v⑥
值
相同
若位移的计算结果为负 说明这段时间内位移的方向与规定的正方向
值
相反
2.公式 x=v0t+12at2 是匀变速直线运动位移的一般表达形式,它表明质点在 各个时刻相对初始时刻的位移 x 跟时间 t 的关系.当物体做匀减速直线运动时, 公式的表达形式不变,a 取负值;当初速度为零时,公式简化为 x=12at2.
3.初速度为零的匀加速直线运动的几个比例 (1)1T 末、2T 末、3T 末、……、nT 末瞬时速度之比为 v1∶v2∶v3∶……∶vn= 1∶2∶3∶……∶n (2)1T 内、2T 内、3T 内、……、nT 内的位移之比 x1∶x2∶x3……∶xn=1∶22∶32∶……∶n2 (3)第一个 T 内、第二个 T 内、第三个 T 内,……,第 n 个 T 内位移之比 xⅠ∶xⅡ∶xⅢ∶……∶xn=1∶3∶5∶……∶(2n-1) (4)通过前 x、前 2x、前 3x……时的速度比 v1∶v2∶v3∶……∶vn=1∶ 2∶ 3∶……∶ n (5)通过前 x、前 2x、前 3x……的位移所用时间的比. t1∶t2∶t3∶……∶tn=1∶ 2∶ 3∶……∶ n (6)通过连续相等的位移所用的时间之比 tⅠ∶tⅡ∶tⅢ∶……∶tn=1∶( 2-1)∶( 3- 2)∶……∶( n- n-1).
匀变速直线运动的位移与时间位移与速度的关系公开课一等奖课件省赛课获奖课件

解:依题有t=5s,x=150m,vB=45m/s, 由 v x v0 v
t2
有
vA
2x t
vB
2 150 5
m
/
s
45m
/
s
15m
/
s
故物体通过A点的速度为15m/s。
知识拓展3
一物体以v0做匀变速直线运动中,通过时 间t速度变为v,位移为x,这段时间t内中间位 置x/2的瞬时速度等于多少?
v1:v2:v3:…:vn=1:2:3:…:n (由v=at知 v∝t)
⑵在持续相等的时间间隔内的位移之比为
x1:x2:x3:…:xn=1:3:5:…:(2n-1)
在持续相等的时间间隔内的位移之比为
v x1:x2:x3:…:xn=1:3:5:…:(2n-1)
1
V6
91
V5
7
V4
5
V3
3
V2
1
V1
t
(1)小球的加速度 ; (2)拍摄时B球的速度vB; (3)拍摄时SCD; (4)A球上面滚动的小球尚有几颗?
例3 在“测定匀变速直线运动的加速度” 的实验中,某一次实验得到如图所示的 纸带中间的一段,在持续的四个计数点A、 B、C、D中C点的位置没有打上,测出A、 B间距离为x1,B、D间距离为x,如图所 示,试拟定B、C间的距离x2。
t1x : t2x : t3x :…:tnx 1: 2 : 3 :…: n
⑸通过持续相似位移所用时间之比为
t1 : t2 : t3 :…:tn 1(: 2 1)(: 3 2):…(: n n 1)
例13 一列火车由静止开始做匀加速直线 运动,一种人站在第1节车厢前端旁的站 台前观察,第1节车厢通过他历时2s,全 部车厢通过他历时8s,无视车厢之间的距 离,车厢长度相等,则这列火车共有____
人教版高一物理必修1第二章第4节匀变速直线运动的速度与位移的关系课件(共19张PPT)

9.一个质点做匀变速直线运动,依次经过a、b、c、d四点, 质点ab、bc、cd三段的时间之比为2:1:1,已知ab段的长度 为L,cd段的长度也为L,质点经过b点时的速度大小为v, 则下列说法正确的是( ABD ) A.bc段的长度为4L/5 B.质点从a点运动到d点所用的时间为14L/5v C.质点运动的加速度大小为10v2/49L D.质点在c点的速度大小为9v/7
6.质点从静止开始做匀加速直线运动在第1个2s、第2个2s
和第2s内三段位移比为( C )
A.2:6:5
B.2:8:7
C.4:12:3
D.2:2:1
7.某质点做直线运动,其位移一时间图象如图所示,图中 PQ为抛物线,P为抛物线的顶点,QR为抛物线过Q点的切线, 与t轴的交点为R.下列说法正确的是( BD ) A.t=0时,质点的速度大小为2m/s B.PQ段表示质点做匀加速直线运动 C.0-2s内质点的平均速度大小为1m/s D.R点对应的时刻为t=3s
高一物理必修1 第二章匀变速直线运动的研究 第3节匀变速直线运动的速度与位移的关系
一、匀变速直线运动的位移与速度的关系
1.公式推导:利用公式
v v0 at
和
x
v0t
1 2
at 2
,消去公式中
的t,从而直接得到速度v与位移x的关系式。
2.匀变速直线运动的位移与速度公式为
v2-v02=2ax
3.如果问题的已知量和所求量都不涉及时间,利用此公式求
a=4m/s2,v=34m/s
12.一物体由静止开始做匀加速直线运动,在某段时间t 内位移为x,物体在前一半时间和后一半时间的位移之 比为2:3。求: (1)质点加速度的大小; a=4x/5t2 (2)质点在这段时间之前已经发生位移的大小。
匀变速直线运动的速度与位移的关系 PPT

两者速度相等,往往是物体间能否追上, 或两者距离最大、最小的临界条件,是分析 判断的切入点。
试求:汽车从路口开动后,在追上自行车之前经 过多长时间两车相距最远?此时距离是多少?
x汽
△x
x自
解:已知汽车 v汽0 0,a ,3自m 行/ s车2 当汽车的速度与自行车的
速度相等时,两车之间的距离
最大。设此时经时间t,则
v 汽 at v自
t
v自 a
6s
3
2s
x
x自 x 汽
v自t
v汽 t
- 0.25
24s
x汽
vt
v汽
2
v自
Hale Waihona Puke t1024
24m
168m
自行车:x自= v自t = 4 × 24s = 96m
x汽﹥ x自+ x0
因而发生了车祸。
小结
讨论追及问题,其实质就是分析讨论两物 体在相同时间内能否到达相同的空间位置的 问题。
1、两个关系:时间关系和位移关系
2、一个条件:两者速度相等
2
6 2m
6 2
2m
6m
v自 6m / s
x汽
△ x
x自
例2:汽车以10 m/s的速度行驶,司机发现前方60 m处有一自行车以4 m/s的速度与汽车在同一条直线 同向行驶,司机以大小为0.25 m/s2的加速度开始刹车 制动。假设自行车速度不变,请判断能不能发生车祸。
X0
x自
x汽
汽车
v 汽 10m / s
a 0.25m / s 2
自行车 v自 4m / s
x0 60m
解:已知汽车 v汽 10m / s,a 0.25m / s2
试求:汽车从路口开动后,在追上自行车之前经 过多长时间两车相距最远?此时距离是多少?
x汽
△x
x自
解:已知汽车 v汽0 0,a ,3自m 行/ s车2 当汽车的速度与自行车的
速度相等时,两车之间的距离
最大。设此时经时间t,则
v 汽 at v自
t
v自 a
6s
3
2s
x
x自 x 汽
v自t
v汽 t
- 0.25
24s
x汽
vt
v汽
2
v自
Hale Waihona Puke t1024
24m
168m
自行车:x自= v自t = 4 × 24s = 96m
x汽﹥ x自+ x0
因而发生了车祸。
小结
讨论追及问题,其实质就是分析讨论两物 体在相同时间内能否到达相同的空间位置的 问题。
1、两个关系:时间关系和位移关系
2、一个条件:两者速度相等
2
6 2m
6 2
2m
6m
v自 6m / s
x汽
△ x
x自
例2:汽车以10 m/s的速度行驶,司机发现前方60 m处有一自行车以4 m/s的速度与汽车在同一条直线 同向行驶,司机以大小为0.25 m/s2的加速度开始刹车 制动。假设自行车速度不变,请判断能不能发生车祸。
X0
x自
x汽
汽车
v 汽 10m / s
a 0.25m / s 2
自行车 v自 4m / s
x0 60m
解:已知汽车 v汽 10m / s,a 0.25m / s2
4 匀变速直线运动的位移与速度的关系(课件)

(1)均只适用于匀变速直线运动
(2)均为矢量式,要规定正方向后,代入正负进行计算
【例1】发射子弹时,子弹在枪筒中的运动可以看作是匀 加速运动,如果枪弹在枪筒中的加速度大小是5×105 m/s2 ,枪筒长0.64m,枪弹射出枪口时的速度是多大?
v0=0 a=5×105m/s2 x=0.64m 0 解:以子弹射出枪口时速度v方向为正方向 根据题意得: v0 =0 x =0.64m a=5×10: x v0t at 2 1 带入数据得: 0.64 m 0 5 10 5 m s 2 t 2 2 解得: t 1.6 103 s t 1.6 103 s 舍去
代入:
解得:
v v0 at v 800 m / s
还有其它什么更好的方法吗?
【例1】发射子弹时,子弹在枪筒中的运动可以看作是匀 加速运动,如果枪弹在枪筒中的加速度大小是5×105 m/s2 ,枪筒长0.64m,枪弹射出枪口时的速度是多大?
v0=0 a=5×105m/s2 x=0.64m 0 解:以子弹射出枪口时速度v方向为正方向 根据题意得: v0 =0 x =0.64m a=5×105m/s2 由位移公式: 0.64 x/m
26m
1s
v v0 at a 4m s 2
分析:在上面的案例中,无论是已知条件还是所要求解的问题都不 包含时间t,而我们学过速度公式和位移公式(均含t):
v v0 at
1 x v0 t at 2 2
消去时间t
v v 2ax
2 2 0
位移公式(3)
注意:
1、矢量表达式:建立正方向。 2、适用范围:仅适用于匀变速直线运动。 3、何时选取公式:不涉及时间t时。所有公式选取原则: 4、 v0 0 时,原始公式直接写为 v 2 2ax
高中物理 第二章 2.4匀变速直线运动的位移和速度关系 课件(共38张PPT)
B
3、甲、乙两物体同时从同一点出发,同方向做匀加速直线运动,它们的速度图线如图所示
② t > t ,AB运动时间不等 A (3)适用范围:匀变速直线运动.
0 D.在t=10 s时两车在公路上相遇
② t t t 例机3停、车小并光以准5m备/去s的车速站度乘匀车速去追广赶州,,司当机小看光到到信达号车经站1前. 的流沙大道时,发现汽车在离自己10m处正以10m/s匀速行驶,A小光立即示意司
初关速于1度 两0为车m零之的间/匀的s加位匀速置直关线系速运,动下行的列规说驶律法正确,的是小光立即示意司机停车并以5m/s的
逆看车行方向考虑时 就把原来的一个匀减速运动转化为一个初速为零的匀加速运动.
速度匀速追赶,司机看到信号经反应时间后,立即刹
车,加速度为2m/s2问:小光追上汽车所需时间? (t=10s)
匀变速直线运动规律:
1、速度与时间关系: v=v0+at
2、位移与时间关系 :
x
v0t
1 2
at2
3、位移与速度关系 : v2 v02 2ax
1、适用于匀变速直线运动
2、规定正方向,矢量正负值代入公式中运算, 最后说明方向
匀变速直线运动规律
一、两个基本公式xx0 00tt a 12at③2t①②
0 1 : s1v0t1 2a2 ; tv1v0at
1 2 : s 2 v 1 t 1 2 a 2 v t 0 a t 1 2 t a 2 v 0 t 2 3 a 2 ; v 2 t v 1 a v 0 t 2 a 2 3 : s 3 v 2 t 1 2 a 2 v t 0 2 a t 1 2 t a 2 v 0 t 5 2 a 2 ; v 3 t v 2 a v 0 t 3 a 3 4 : s 4 v 3 t 1 2 a 2 v t 0 3 a t 1 2 t a 2 v 0 t 7 2 a 2 ; v 4 t v 3 a v 0 t 4 a
高中物理第4节《匀变速直线运动的位移与速度的关系》教学课件

课堂讲义
解析 机械波由振动产生;电磁波由周期性 变化的电场(或磁场)产生,机械波是能量波, 传播需要介质,速度由介质决定,电磁波是 物质波,波速由介质和自身的频率共同决定; 机械波有横波,也有纵波,而电磁波一定是 横波,它们都能发生反射、折射、干涉和衍 射等现象,故选项B、C、D正确.
答案 BCD 借题发挥 机械波的传播速度完全由介质决
§2.4 匀变速直线运动的位移与速 度的关系
匀变速直线运动规律:
1、速度公式: v=v0+at
2、位移公式:
x
v0t
1 2
at
2
3、平均速度:v
1 2
(v0
v)
练习:推动弹头加速运动。若把子弹在枪筒中
的运动看做匀加速直线运动,设子弹的加速度 a=5×105m/s2,枪筒长x=0.64m,求子弹射出枪 口时的速度。
实验证实了电磁波的存在.
还运用自己
精湛的实验技术测定了电磁波的波长和频率,
预习导学
(3)电磁波的波长λ,波速v和周期T、频率f的 关系:
v
f
λ=vT=
. c≈3×108 m/s
(4) 电 磁 波 在 真 空 中 的 传 播 速 度 v
=
.
课堂讲义
一、电磁振荡中各物理量的变化情况 如图3-1-2所示
作 用 , 放 电 电 流 由 零逐逐渐渐增强增 大 , 线 圈 产 生 的
磁场
,电容器里的电场电逐场渐能 减弱,
电全磁部场场转能能化逐为渐
转
化
为
磁场 .
能
.
放
电
完
毕
后
,
人教版必修1 2.4匀变速直线运动的位移与速度的关系 (共13张PPT)[优质实用版课件]
![人教版必修1 2.4匀变速直线运动的位移与速度的关系 (共13张PPT)[优质实用版课件]](https://img.taocdn.com/s3/m/efe7cc4608a1284ac85043b4.png)
末速度 (4)据上述分析,你准备选用哪个公式求解?
请同学们画出子弹加速运动的示意图
v0=0 a=5×105m/s2 v=?
x=0.64m
0
0.64
x/m
可先求解出时间t
这个过程也可以这样处理:
} x
v0t
1 2
at 2
联立求解两式消去t,得
此式即为:匀变速直线运动位移与速度的关系式
说明:
1. 公式适用范围:匀变速直线运动
2. 此式优点:不需计算时间t 。
例1:如图所示,一辆正以8 m/s速度沿直线行驶的汽车,突 然以1 m/s2的加速度加速行驶,则汽车行驶了18 m时的速度
为( C ) ?
A.8 m/s B.12 m/s C.10 m/s
D.14 m/s
例2:某飞机着陆时的速度时216km/h,随后匀减速滑行, 加速度大小是2m/s2,机场的跑到至少要多长才能使飞机安 全地停下来。
解:规定飞机着陆时运 动的方向为正方向。 根据公式 v 2 v02 2ax 则有 x v 2 v02
2a 代入数据,得 技术标准如下: 汽车载重标准为4.5 t≤质量≤12 t 空载检测的制动距离(车速20 km/h)≤3.8 m 满载检测的制动距离(车速30 km/h)≤8.0 m 该型号的汽车空载和满载时的制动加速度应该满足什 么要求?
2.4匀变速直线运动的 位移与速度的关系
第二章 匀变速直线运动的研究
学习目标
(1)通过对公式推导过程的学习,掌握速度与位移关系公式。
(2)会应用速度与位移关系式v2-v02=2ax 分析解决有关问
题。 (3)培养学生运用数学知识合理选择公式建立方程或方程组 的能力。
请同学们画出子弹加速运动的示意图
v0=0 a=5×105m/s2 v=?
x=0.64m
0
0.64
x/m
可先求解出时间t
这个过程也可以这样处理:
} x
v0t
1 2
at 2
联立求解两式消去t,得
此式即为:匀变速直线运动位移与速度的关系式
说明:
1. 公式适用范围:匀变速直线运动
2. 此式优点:不需计算时间t 。
例1:如图所示,一辆正以8 m/s速度沿直线行驶的汽车,突 然以1 m/s2的加速度加速行驶,则汽车行驶了18 m时的速度
为( C ) ?
A.8 m/s B.12 m/s C.10 m/s
D.14 m/s
例2:某飞机着陆时的速度时216km/h,随后匀减速滑行, 加速度大小是2m/s2,机场的跑到至少要多长才能使飞机安 全地停下来。
解:规定飞机着陆时运 动的方向为正方向。 根据公式 v 2 v02 2ax 则有 x v 2 v02
2a 代入数据,得 技术标准如下: 汽车载重标准为4.5 t≤质量≤12 t 空载检测的制动距离(车速20 km/h)≤3.8 m 满载检测的制动距离(车速30 km/h)≤8.0 m 该型号的汽车空载和满载时的制动加速度应该满足什 么要求?
2.4匀变速直线运动的 位移与速度的关系
第二章 匀变速直线运动的研究
学习目标
(1)通过对公式推导过程的学习,掌握速度与位移关系公式。
(2)会应用速度与位移关系式v2-v02=2ax 分析解决有关问
题。 (3)培养学生运用数学知识合理选择公式建立方程或方程组 的能力。
物理2 4《匀变速直线运动的速度与位移的关系》课件
xⅠ∶xⅡ∶xⅢ∶…∶xN=1∶3∶5∶…∶(2n-1)。
(4)通过前 x、前 2x、前 3x…位移时的速度之比 v1∶v2∶v3∶…∶vn=1∶ 2∶ 3∶…∶ n。 (5)通过前 x、前 2x、前 3x…的位移所用时间之比 t1∶t2∶t3∶…∶tn= 1∶ 2∶ 3∶…∶ n
(6)通过连续相等的位移所用时间之比 tⅠ∶tⅡ∶tⅢ∶…∶tn=1∶( 2-1)∶( 3- 2)∶…∶( n- n-1)。
由图知10~40 s内汽车匀速行驶,因此 v2=v1=20 m/s 运动学公式得60 s末汽车的速度
①
②
由图知40~60 s内汽车以加速度1 m/s2匀减速行驶,由
v3=(20-1× m/s=0③ 20) 根据①②③式,可画出汽车在 0~60 s 内 的 v-t 图线,如图所示。 (2)由图可知,在这 60 s 内汽车行驶的路 程为 30+60 s= × m=900 m。④ 20 2 [答案] (1)见解析图 (2)900 m
v1 解析:由 v1=at1 得,a= =1 m/s2 t1 1 所以第 1 s 内的位移 x1= a×12 m=0.5 m 2 (1)由于第 4 s 末与第 6 s 末的速度之比 v1∶v2=4∶6=2∶3 3 故第 6 s 末的速度 v2= v1=6 m/s 2
(2)第1 s内与前6 s内的位移之比x1∶x6=12∶62
2
x2
解方程得:vx= 2
答案:
vA 2+vB 2 2
[例2]
汽车由静止开始在平直的公路
上行驶,0~60 s内汽车的加速度随时间变 化的图线如图2-4-2所示。 (1)画出汽车在0~60 s内的v-t图线; (2)求在这60 s内汽车行驶的路程。 [思路点拨] (1)首先由图像确定汽车的运动情况。确定 图2-4-2
匀变速直线运动的速度与位移的关系课件

(3)第一个T内,第二个T内,第三个T内,…,第n个T内位移之 比
xⅠ∶xⅡ∶xⅢ∶…∶xn=1∶3∶5∶…∶(2n-1). (4)通过前x、前2x、前3x…位移时的速度之比 v1∶v2∶v3∶…∶vn=1∶ 2∶ 3∶…∶ n. (5)通过前x、前2x、前3x…的位移所用时间之比 t1∶t2∶t3∶…∶tn=1∶ 2∶ 3∶…∶ n.
)
A.此公式只适用于匀加速直线运动
B.此公式适用于匀变速直线运动
C.此公式只适用于位移为正的情况
D.此公式不可能出现a、x同时为负值的情况
B
[公式x=
v2-v20 2a
适用于匀变速直线运动,既适用于匀加速直
线运动,也适用于匀减速直线运动,既适用于位移为正的情况,也
适用于位移为负的情况,选项B正确,选项A、C错误;当物体做反
速度与位移的关系式 1.适用条件:公式表述的是匀变速直线运动的速度与 位移的关系,适用于匀变速直线运动. 2.公式的矢量性:公式中v0、v、a、x都是矢量,应用时必须 选取统一的正方向,一般选v0方向为正方向. (1)物体做加速运动时,a取正值;做减速运动时,a取负值. (2)x>0,说明物体位移的方向与初速度的方向相同;x<0,说明 物体位移的方向与初速度的方向相反.
(1)火车做匀减速运动的最小加速度的大小; (2)火车全部通过隧道的最短时间.
思路点拨:①火车匀减速运动的位移为200 m,而匀速通过隧 道的位移为100 m+500 m=600 m.
②火车到达隧道口的速度为108 km/h时匀减速运动的加速度为 最小.
[解析] (1)火车减速过程中 v0=144 km/h=40 m/s,x=200 m, v=108 km/h=30 m/s 当车头到达隧道口速度恰为108 km/h时加速度最小,设为a 由v2-v20=2ax 得a=v2- 2xv20=320×2-240002 m/s2=-1.75 m/s2.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
都有中间位置的瞬时速度大于中间时刻的
瞬时速度.
vx vt
2
2
v
vx
vt2
2 >x/2
x
v
vx vt
2
2
vx
vt 2
2
x
<x/2
O
t 2
t
t
Ott t 2
学习目标 知识储备 学习探究 典例精析 课堂小结 自我检测
三 . 重要推论Δx =aT2 的推导及应用 【问题设计】 物体做匀变速直线运动,加速度为a,从某时刻起T 时间内的位 移为x1,紧接着第二个T 时间内的位移为x2.试证明:x2-x1=aT2.
答案 根据v = v0+ at ① x = v0t + at2/2 ② 由①得 t = (v-v0)/a ③
把③代入②得
x
v0
v
v0 a
1 a( v v0 )2 2a
整理得:v2-v02=2ax
将v0= 0,v = 50 m/s,x = 195 m 代入上式得:a≈6.41 m/s2.
学习目标 知识储备 学习探究 典例精析 课堂小结 自我检测
学习目标 知识储备 学习探究 典例精析 课堂小结 自我检测
学习目标 知识储备 学习探究 典例精析 课堂小结 自我检测
1.(速度与位移关系的简单应 用)两个小车在水平面上做 加速度相同的匀减速直线运
动,若它们的初速度之比为
1∶2,它们运动的最大位移 之比为( B ) A.1∶2 B.1∶4 C.1 : 2 D.2∶1
x
v0t
1 at 2 2
前4
s
内:48 4v0
1 a 42 2
前8
s
内:48
80
8v0
1 2
a
82
解得: v0 8m/s a 2m/s 2
学习目标 知识储备 学习探究 典例精析 课堂小结 自我检测
三、对Δx aT 2的灵活应用
例3:做匀加速直线运动的物体,从开始计时起连续两个4 s的时 间间隔内通过的位移分别是48 m和80 m,则这个物体的初速度和 加速度各是多少?
( BD ) A.加速度大小之比为3∶1
a1 : a2 2 :1
B.位移大小之比为1∶2 C.平均速度大小之比为2∶1 D.平均速度大小之比为1∶1
x1 : x2 1: 2
v1
: v2
0 v : 2
v0 2
1:1
学习目标 知识储备 学习探究 典例精析 课堂小结 自我检测
三、对Δx aT 2的灵活应用
v0
4
1 2
2
42
v0 8m/s
学习目标 知识储备 学习探究 典例精析 课堂小结 自我检测
三、对Δx aT 2的灵活应用
例3:做匀加速直线运动的物体,从开始计时起连续两个4 s的时 间间隔内通过的位移分别是48 m和80 m,则这个物体的初速度和 加速度各是多少?
解析
解法二:利用两个基本公式
由
学习目标 知识储备 学习探究 典例精析 课堂小结 自我检测
一、速度与位移关系的简单应用
解析
例1:A、B、C 三点在同一条
直线上,一物体从A 点由静止 开始做匀加速直线运动,经过 初速度为0
B 点的速度是v,到C 点的速度 是3v,则xAB∶xBC等于( A ) A.1∶8
速度—位移公式 v2 v02 2ax 从A到B: v2 0 2axAB
证明
设物体的初速度为v0
自计时起T 时间内的位移 x1= v0T+aT2/2
①
在第2个T时间内的位移
x2= v0·2T+a(2T)2/2-x1= v0T+3aT2/2
②
由①②两式得连续相等时间内的位移差为
Δx= x2 - x1= v0T +3aT2/2- v0T-aT2/2 = aT2 即Δx = aT2.
x < 0说明物体通过的位移方向与初速度方向 相反
2.两种特殊情况
(1)当v0= 0时, v2=2ax
.
(2)当v = 0时, -v20=2ax
.
3.公式特点:该公式不涉及 时间 .
学习目标 知识储备 学习探究 典例精析 课堂小结 自我检测
二 . 中间时刻的瞬时速度与平均速度
【问题设计】 一质点做匀变速直线运动的v-t 图象如图所示.已知一段时间内的
初速度为v0,末速度为v. 位移/时间
(1)这段时间内的平均速度(用v0、v表示)
(2)中间时刻的瞬时速度 v t
2
(3)这段位移中间位置的瞬时速度
v
x
2
答案 (1)v-t 图像与t 轴所围面积表示位移
位移:x v0 v t 2
平均速度:v x v0 v t2
(2)由图中可知:中间时刻的瞬时 速度大小等于梯形中位线长度
解析 解法三:利用平均速度公式
第2
s
时速度:v1
x1 T
48 4
m / s 12 m / s
第6
s
时速度: v2
x2 T
80 4
m / s 20
m/s
物体的加速度:a v2 v1 20 12 m/s 2 2m/s 2
t
4
物体的初速度:v0
v1
a
T 2
12
m / s 22
m/s8
m/s
解析
小球释放后做匀加速直线运动,且每相邻的两个小球的 时间间隔相 等,均为0.1 s,可以认为A、B、C、D各点 是一个小球在不同时刻的位置
(1)由推论Δx =aT2 ,小球的加速度
a x xBC xAB 0.2 0.15 m/s2 5m/s2
T2
T2
0.12
学习目标 知识储备 学习探究 典例精析 课堂小结
2
v02 v 2 2
3.平均速度公式总结:
v x ,适用条件: 任意运动
.
t
v v0 v ,适用条件: 匀变速直线运动 .
2
v vt
,适用条件: 匀变速直线运动 .
注意
2
对匀变速直线运动有v源自vt2v0 2
v
学习目标 知识储备 学习探究 典例精析 课堂小结
自我检测
【延伸思考】 在匀变速直线运动中,中间时刻的瞬时速度vt/2 与中间位置的 瞬时速度vx/2 哪一个大?结论:无论匀加速还是匀减速直线运动,
学习目标 知识储备 学习探究 典例精析 课堂小结 自我检测
一. 速度位移公式的推导及应用 【问题设计】
我国第一艘航空母舰“辽宁号”已有能力同时起飞3架歼15战机,如图 为辽宁舰上3个起飞点示意图,1、2号位置为短距起飞点,起飞线长 105米;3号位置为远距起飞点,起飞线长195 米.如果歼15 战机起飞 速度为50 m/s,起飞时航母静止不动,且不使用弹射系统,则战机由 3号起飞点起飞的加速度至少是多少?(设跑道水平)
自我检测
3.(对Δx=aT2 的理解和应用) 从斜面上某一位置每隔0.1 s释放一个相同的小球,释放后小球 做匀加速直线运动,在连续释放几个后,对在斜面上滚动的小球
答案
(3)对前一半位移:v
2 x
2
v
2 0
2a
x 2
对后一半位移:v 2
-
v
2 x
2
2a x 2
解得:v x
2
v02 v 2 2
x 2
x 2
v0
vx
v
2
学习目标 知识储备 学习探究 典例精析 课堂小结 自我检测
【要点提炼】
1.中间时刻的瞬时速度
vt
2
v0 v 2
2.中间位置的瞬时速度 v x
例3:做匀加速直线运动的物体,从开始计时起连续两个4 s的时 间间隔内通过的位移分别是48 m和80 m,则这个物体的初速度和 加速度各是多少?
解析
解法一:利用关系式Δx =aT2
x aT 2 a x 80 48 m/s 2 2m/s 2
T2
42
前4s内的位移:x
v0t
1 2
at 2
48
学习目标 知识储备 学习探究 典例精析 课堂小结 自我检测
匀变速直线运动的速度与位移关系式 1.公式:v2 - v02= 2ax 2.推导:物体以加速度a 做匀变速直线运动时,设其初
速度为v0 ,末速度为v,则由 速度公式:v = v0+at 位移公式:x = v0t+at2/2 消去时间 t 得位移与速度的关系式为 v2 – v02 = 2ax.
9s
解析
从P 到Q : x vP vQ 60 vP 15
t
2
6
2
vP 5m/s
a vQ vP 15 5 m / s2 5 m / s2
t
6
3
从O 到P :
vP2
0
2axOP
xOP
52 2 5
m 7.5 m
从O 到Q :
3
vQ
atOQ
tOQ
15 5
s9
s
OP
Q
3
学习目标 知识储备 学习探究 典例精析 课堂小结 自我检测
学习目标 知识储备 学习探究 典例精析 课堂小结 自我检测
一辆汽车从静止开始由甲地出 解析
发,沿平直公路开往乙地,汽车
先做匀加速直线运动,接着做匀
减速直线运动,开到乙地刚好停 止,其速度—时间图象如图所示, 那么0 ~t 和 t ~3t 两段时间内
v-t 图中斜率:表示加速度 v-t 图中面积:表示位移
vt
2
v0 v 2
学习目标 知识储备 学习探究 典例精析 课堂小结 自我检测
二 . 中间时刻的瞬时速度与平均速度 【问题设计】 一质点做匀变速直线运动的v-t 图象如图所示.已知一段时间内的 初速度为v0,末速度为v. (1)这段时间内的平均速度(用v0、v表示) (2)中间时刻的瞬时速度v (3)这段位移中间位置的瞬时速度v
瞬时速度.
vx vt
2
2
v
vx
vt2
2 >x/2
x
v
vx vt
2
2
vx
vt 2
2
x
<x/2
O
t 2
t
t
Ott t 2
学习目标 知识储备 学习探究 典例精析 课堂小结 自我检测
三 . 重要推论Δx =aT2 的推导及应用 【问题设计】 物体做匀变速直线运动,加速度为a,从某时刻起T 时间内的位 移为x1,紧接着第二个T 时间内的位移为x2.试证明:x2-x1=aT2.
答案 根据v = v0+ at ① x = v0t + at2/2 ② 由①得 t = (v-v0)/a ③
把③代入②得
x
v0
v
v0 a
1 a( v v0 )2 2a
整理得:v2-v02=2ax
将v0= 0,v = 50 m/s,x = 195 m 代入上式得:a≈6.41 m/s2.
学习目标 知识储备 学习探究 典例精析 课堂小结 自我检测
学习目标 知识储备 学习探究 典例精析 课堂小结 自我检测
学习目标 知识储备 学习探究 典例精析 课堂小结 自我检测
1.(速度与位移关系的简单应 用)两个小车在水平面上做 加速度相同的匀减速直线运
动,若它们的初速度之比为
1∶2,它们运动的最大位移 之比为( B ) A.1∶2 B.1∶4 C.1 : 2 D.2∶1
x
v0t
1 at 2 2
前4
s
内:48 4v0
1 a 42 2
前8
s
内:48
80
8v0
1 2
a
82
解得: v0 8m/s a 2m/s 2
学习目标 知识储备 学习探究 典例精析 课堂小结 自我检测
三、对Δx aT 2的灵活应用
例3:做匀加速直线运动的物体,从开始计时起连续两个4 s的时 间间隔内通过的位移分别是48 m和80 m,则这个物体的初速度和 加速度各是多少?
( BD ) A.加速度大小之比为3∶1
a1 : a2 2 :1
B.位移大小之比为1∶2 C.平均速度大小之比为2∶1 D.平均速度大小之比为1∶1
x1 : x2 1: 2
v1
: v2
0 v : 2
v0 2
1:1
学习目标 知识储备 学习探究 典例精析 课堂小结 自我检测
三、对Δx aT 2的灵活应用
v0
4
1 2
2
42
v0 8m/s
学习目标 知识储备 学习探究 典例精析 课堂小结 自我检测
三、对Δx aT 2的灵活应用
例3:做匀加速直线运动的物体,从开始计时起连续两个4 s的时 间间隔内通过的位移分别是48 m和80 m,则这个物体的初速度和 加速度各是多少?
解析
解法二:利用两个基本公式
由
学习目标 知识储备 学习探究 典例精析 课堂小结 自我检测
一、速度与位移关系的简单应用
解析
例1:A、B、C 三点在同一条
直线上,一物体从A 点由静止 开始做匀加速直线运动,经过 初速度为0
B 点的速度是v,到C 点的速度 是3v,则xAB∶xBC等于( A ) A.1∶8
速度—位移公式 v2 v02 2ax 从A到B: v2 0 2axAB
证明
设物体的初速度为v0
自计时起T 时间内的位移 x1= v0T+aT2/2
①
在第2个T时间内的位移
x2= v0·2T+a(2T)2/2-x1= v0T+3aT2/2
②
由①②两式得连续相等时间内的位移差为
Δx= x2 - x1= v0T +3aT2/2- v0T-aT2/2 = aT2 即Δx = aT2.
x < 0说明物体通过的位移方向与初速度方向 相反
2.两种特殊情况
(1)当v0= 0时, v2=2ax
.
(2)当v = 0时, -v20=2ax
.
3.公式特点:该公式不涉及 时间 .
学习目标 知识储备 学习探究 典例精析 课堂小结 自我检测
二 . 中间时刻的瞬时速度与平均速度
【问题设计】 一质点做匀变速直线运动的v-t 图象如图所示.已知一段时间内的
初速度为v0,末速度为v. 位移/时间
(1)这段时间内的平均速度(用v0、v表示)
(2)中间时刻的瞬时速度 v t
2
(3)这段位移中间位置的瞬时速度
v
x
2
答案 (1)v-t 图像与t 轴所围面积表示位移
位移:x v0 v t 2
平均速度:v x v0 v t2
(2)由图中可知:中间时刻的瞬时 速度大小等于梯形中位线长度
解析 解法三:利用平均速度公式
第2
s
时速度:v1
x1 T
48 4
m / s 12 m / s
第6
s
时速度: v2
x2 T
80 4
m / s 20
m/s
物体的加速度:a v2 v1 20 12 m/s 2 2m/s 2
t
4
物体的初速度:v0
v1
a
T 2
12
m / s 22
m/s8
m/s
解析
小球释放后做匀加速直线运动,且每相邻的两个小球的 时间间隔相 等,均为0.1 s,可以认为A、B、C、D各点 是一个小球在不同时刻的位置
(1)由推论Δx =aT2 ,小球的加速度
a x xBC xAB 0.2 0.15 m/s2 5m/s2
T2
T2
0.12
学习目标 知识储备 学习探究 典例精析 课堂小结
2
v02 v 2 2
3.平均速度公式总结:
v x ,适用条件: 任意运动
.
t
v v0 v ,适用条件: 匀变速直线运动 .
2
v vt
,适用条件: 匀变速直线运动 .
注意
2
对匀变速直线运动有v源自vt2v0 2
v
学习目标 知识储备 学习探究 典例精析 课堂小结
自我检测
【延伸思考】 在匀变速直线运动中,中间时刻的瞬时速度vt/2 与中间位置的 瞬时速度vx/2 哪一个大?结论:无论匀加速还是匀减速直线运动,
学习目标 知识储备 学习探究 典例精析 课堂小结 自我检测
一. 速度位移公式的推导及应用 【问题设计】
我国第一艘航空母舰“辽宁号”已有能力同时起飞3架歼15战机,如图 为辽宁舰上3个起飞点示意图,1、2号位置为短距起飞点,起飞线长 105米;3号位置为远距起飞点,起飞线长195 米.如果歼15 战机起飞 速度为50 m/s,起飞时航母静止不动,且不使用弹射系统,则战机由 3号起飞点起飞的加速度至少是多少?(设跑道水平)
自我检测
3.(对Δx=aT2 的理解和应用) 从斜面上某一位置每隔0.1 s释放一个相同的小球,释放后小球 做匀加速直线运动,在连续释放几个后,对在斜面上滚动的小球
答案
(3)对前一半位移:v
2 x
2
v
2 0
2a
x 2
对后一半位移:v 2
-
v
2 x
2
2a x 2
解得:v x
2
v02 v 2 2
x 2
x 2
v0
vx
v
2
学习目标 知识储备 学习探究 典例精析 课堂小结 自我检测
【要点提炼】
1.中间时刻的瞬时速度
vt
2
v0 v 2
2.中间位置的瞬时速度 v x
例3:做匀加速直线运动的物体,从开始计时起连续两个4 s的时 间间隔内通过的位移分别是48 m和80 m,则这个物体的初速度和 加速度各是多少?
解析
解法一:利用关系式Δx =aT2
x aT 2 a x 80 48 m/s 2 2m/s 2
T2
42
前4s内的位移:x
v0t
1 2
at 2
48
学习目标 知识储备 学习探究 典例精析 课堂小结 自我检测
匀变速直线运动的速度与位移关系式 1.公式:v2 - v02= 2ax 2.推导:物体以加速度a 做匀变速直线运动时,设其初
速度为v0 ,末速度为v,则由 速度公式:v = v0+at 位移公式:x = v0t+at2/2 消去时间 t 得位移与速度的关系式为 v2 – v02 = 2ax.
9s
解析
从P 到Q : x vP vQ 60 vP 15
t
2
6
2
vP 5m/s
a vQ vP 15 5 m / s2 5 m / s2
t
6
3
从O 到P :
vP2
0
2axOP
xOP
52 2 5
m 7.5 m
从O 到Q :
3
vQ
atOQ
tOQ
15 5
s9
s
OP
Q
3
学习目标 知识储备 学习探究 典例精析 课堂小结 自我检测
学习目标 知识储备 学习探究 典例精析 课堂小结 自我检测
一辆汽车从静止开始由甲地出 解析
发,沿平直公路开往乙地,汽车
先做匀加速直线运动,接着做匀
减速直线运动,开到乙地刚好停 止,其速度—时间图象如图所示, 那么0 ~t 和 t ~3t 两段时间内
v-t 图中斜率:表示加速度 v-t 图中面积:表示位移
vt
2
v0 v 2
学习目标 知识储备 学习探究 典例精析 课堂小结 自我检测
二 . 中间时刻的瞬时速度与平均速度 【问题设计】 一质点做匀变速直线运动的v-t 图象如图所示.已知一段时间内的 初速度为v0,末速度为v. (1)这段时间内的平均速度(用v0、v表示) (2)中间时刻的瞬时速度v (3)这段位移中间位置的瞬时速度v
