【数学】重庆十一中2009届高三临考模拟(理)

合集下载

重庆十一中高级高三数学下高考模拟试题(14,理数)

高2009级高三下数学高考模拟试题14时间：120分钟满分：150分一、填空题：（本大题共10个小题，每小题5分，共50分） 1．设函数y =M ，集合{}2|,N y y x x R ==∈，则MN 等于A ．φB ．NC ．[1,)+∞D ．M2．汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车，若把这一过程中汽车的行驶路程s 看作时间t 的函数，其图象可能是3已知函数()sin126sin(36)cos54cos(36),f x x x x x =-+-则()f x 是 A ．单调递增函数 B ．单调递减函数C ．奇函数 D ．偶函数4．若数列{}n a 满足221n n a a d +-=（d 为正常数，n N +∈）,则称{}n a 为“等方差数列”.甲：数列{}n a 为等方差数列；乙：数列{}n a 为等差数列，则甲是乙的A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件5．若函数1()axf x e b=-的图象在0x =处的切线l 与圆22:1C x y +=相离，则(,)P a b 与圆C 的位置关系是A ．在圆外B ．在圆内C ．在圆上D ．不能确定 6．函数sin y x =和cos y x =的图象在[0,8]π内的所有交点中，能确定的不同直线的条数是A ．28B ．18C ．16D ．6 7．已知函数()2ln38,f x x x =+则0(12)(1)limx f x f x∆→-∆-∆的值为（）A ．10B ．-10C ．-20D ．208．正四棱锥ABCD V -的五个顶点在同一个球面上,若其底面边长为4,侧棱长为62,则此球的表面积为 ( )A ．π18B ．π36C ． π72D ． π99．已知双曲线E 的离心率为e ，左、右两焦点分别为F 1、F 2，抛物线C 以F 2为顶点，F 1为焦点,点P 为抛物线与双曲线右支上的一个交点，若a|PF 2|＋c|PF 1|＝8a 2（其中a 、c 分别为双曲线的实半轴长和半焦距），则e 的值为 ( ) A. 3 B. 3 C. 2 D. 6sA ．sss B ． C ． D ．10．设D 为ABC ∆的边AB 上一点，P 为ABC ∆内一点，且满足,AD AB =,01AP AD BC λλλ=+>+，则APDABCS S ∆∆有 ( ) A．最小值为12+B．最大值为12+ C．最小值为12- D．最大值为12- 二、填空题：本大题共5个小题，每小题5分，共25分.11. 641)1)的展开式中x 的系数是 .12.如果ξ～B （20,31），则使P （ξ=k ）取最大值的k 的值是____________. 13．已知i 是虚数单位，m 和n 都是实数，且ni i m +=+11)1(，则2009)(nim ni m -+= 14．设连续掷两次骰子得到的点数分别为m ．n ，则直线y=m nx 与圆(x －3)2+y 2=1相交的概率是_____．15．定义在实数集R 上的函数()f x ，如果存在函数()()g x Ax B A B =+、为常数，使得()()f x g x ≥对一切实数x 都成立，那么称()g x 为函数()f x 的一个承托函数．下列说法正确的有：_____(写序号)．①函数()f x =存在无数个承托函数； ②函数22()1xf x x x =-+不存在承托函数；③()||g x x =-为函数()1xf x e =-的一个承托函数； ④函数21()5411f x x x =--+，若函数()g x 的图象恰为()f x 在点1(1,)12P -处的切线，则()g x 为函数()f x 的一个承托函数三、解答题（6个小题，共75分）16.已知()f x 是定义在[]ππ2,2-上的偶函数,当[]π,0 时,()x x f cos =；(]ππ2,∈x 时,()x f y =的图像是斜率为π2且在y 轴上的截距为2-的直线在相应区间上的部分.⑴求()π2-f 、⎪⎭⎫⎝⎛-3πf 的值； ⑵写出函数()x f y =的表达式,作出其图像,并根据图像写出函数的单调区间.17．将一个半径适当的小球放入如图所示的容器上方入口处，小球将自由下落，小球在下落的过程中，将3次遇到黑色障碍物，最后落入A 袋或B 袋。

重庆市2009届高三数学模拟试题分类汇编——立体几何

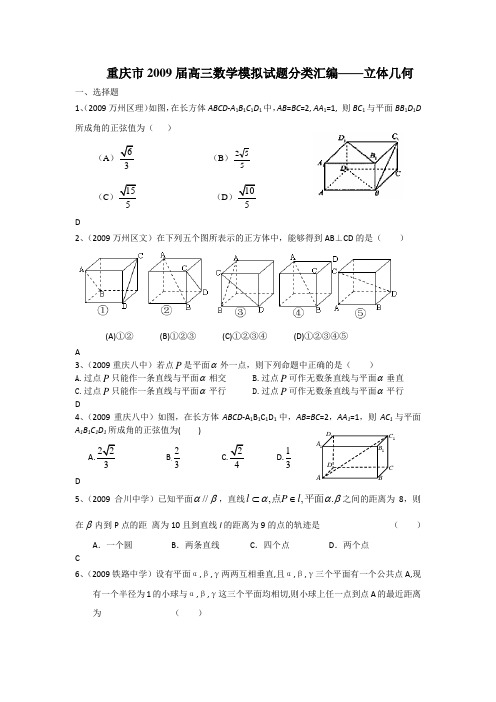
重庆市2009届高三数学模拟试题分类汇编——立体几何一、选择题1、（2009万州区理）如图，在长方体ABCD -A 1B 1C 1D 1中，AB =BC =2, AA 1=1, 则BC 1与平面BB 1D 1D 所成角的正弦值为（）（A ）63（B ）552（C ）155 （D ）105D2、（2009万州区文）在下列五个图所表示的正方体中，能够得到AB ⊥CD 的是（）(A)①② (B)①②③ (C)①②③④ (D)①②③④⑤ A3、（2009重庆八中）若点P 是平面α外一点，则下列命题中正确的是（）A.过点P 只能作一条直线与平面α相交B.过点P 可作无数条直线与平面α垂直C.过点P 只能作一条直线与平面α平行D.过点P 可作无数条直线与平面α平行 D4、（2009重庆八中）如图，在长方体ABCD -A 1B 1C 1D 1中，AB=BC =2，AA 1=1，则AC 1与平面A 1B 1C 1D 1所成角的正弦值为( ) A.223 B 23 C.24D.13D5、（2009合川中学）已知平面βα//，直线βαα.,,平面点l P l ∈⊂之间的距离为8，则在β内到P 点的距离为10且到直线l 的距离为9的点的轨迹是（）A ．一个圆B ．两条直线C ．四个点D ．两个点C6、（2009铁路中学）设有平面α,β,γ两两互相垂直,且α,β,γ三个平面有一个公共点A,现有一个半径为1的小球与α,β,γ这三个平面均相切,则小球上任一点到点A 的最近距离为（）1A ABC D 1D1C 1BA ．21 B ．22 C ．3 D ．2－1C二、填空题1、（2009重庆八中）14.已知各顶点都在一个球面上的正四棱柱底面边长为1，体积为2，则这个球的表面积是________________ 4π2、（2009重庆八中）已知三棱锥P ABC -的三条侧棱PA 、PB 、PC 的长分别为a 、b 、c ，且两两垂直，并满足22()6a b c += ,当三棱锥体积最大时，侧面PAB 与底面ABC 成060，则三棱锥体积最大时a =__________________ 13、（2009合川中学）已知正四面体的棱长为6，则这个正四面体的外接球的体积是 .29π4、（2009合川中学）已知直线α⊂a ，直线l 与平面α所成的角为3π，则两直线a 、l 所成的角的范围是 .]2,3[ππ 5、（2009铁路中学）现有4个条件：（其中a,b 表示不同的直线，α,β,γ表示不同的平面）①γ⊥α，γ⊥β ②a //b ，a ⊥α，b ⊥β③a ,b 异面，a ⊂α，b ⊂β，且a //β,b//α④α内距离为d 的两平行直线在β内的射影仍为两条距离为d 的平等行线其中能推出 α//β的条件是（写出所有满足题意的条件的序号） ②③三、解答题 1、（2009重庆八中）17．如图，在四棱锥O ABCD -中，底面ABCD 是边长为2的菱形，OA ABCD ⊥底面, 2OA =,M 为OA 的中点，N 为BC 的中点,060ABC ∠= （1）证明：直线MN OCD 平面‖；（2）求异面直线AB 与MD 所成角的余弦值；（3）求点B 到平面OCD 的距离。

重庆十一中高级高三数学下学期临考模拟试题(理数,五月)

（3）求证：不等式对于恒成立。
20．如图，设抛物线（）的准线与轴交于，焦点为；以、为焦点，离心率的椭圆与抛物线在轴上方的一个交点为 .
（Ⅰ）当时，求椭圆的方程及其右准线的方程；
（Ⅱ）在（Ⅰ）的条件下，直线经过椭圆的右焦点，与抛物线交于，如果以线段为直径作圆，试判断点与圆的位置关系，并说明理由；
（Ⅰ）求该人在4次投掷中恰有三次投入红袋的概率;
（Ⅱ）求该人两次投掷后得分的数学期望
18．如图，平面平面ABCD，四边形ABEF与ABCD都是直角梯形, ，
（1）证明：C、D、F、E四点共面；
（2）设，求二面角A—ED—B的大小。
19.已知数列中，，且
（1）求证：；
（2）设，是数列的前n项和，求的解析式；
①动点在平面上的射影是线段
②三棱锥的体积有最大值；
③恒有平面平面；
④异面直线与不可能互相垂直；
⑤异面直线与所成角的取值范 .
三、解答题（共75分）
16．函数
（1）求函数的最小正周期；
（2）若存在，使不等式成立，求函数m的取值范围。
17．投掷飞碟的游戏中，飞碟投入红袋记2分，投入蓝袋记1分，未投入袋记0分.现知某人在以前投掷1000次的试验中，有500次入红袋，250次入蓝袋，其余不能入袋
C． D．
7．已知三棱柱的侧棱与底面边长都相等，在底面ABC内的射影为的中心，则与底面ABC所成的角的正弦值为（）
A． B． C． D．
8．设函数，且，则（）
A． B． C．0D．不存在
9．设椭圆的离心率为e＝，右焦点为F（c，0），方程ax2＋bx－c＝0的两个实根分别为x1和x2，则点P（x1，x2）（）

重庆十一中高2009级高三下月考数学理科试题4

重庆十一中高2009级高三下月考数学理科试题4时间：120分钟满分：150分命题：潘文荣一、选择题：本大题共10小题，每小题5分，共50分 1．=+-ii i 1)1( ( ) A ．i B ．i -C ．1D ．-12. m=3”是“直线（m-1）x+2my+1=0与直线(m+3)x-(m-1)y+3=0相互垂直”的 ( ) A ．充分不必要条件 B.必要不充分条件C ．充要条件 D.既不充分也不必要条件3．已知3sin()45x π-=，则sin 2x 的值为 ( )A ．1925B ．1625C ．1425D ．7254．已知m 、n 是不重合的直线，α、β是不重合的平面，给出下列四个命题①βαβα//,,则若⊥⊥m m ②βαβα//,//,,则若n m n m ⊂⊂ ③若αα⊥⊥n m n m 则,,//④βαβα⊥⊂⊥则若,,m m其中正确命题的个数为（）A ．1个B ．2个C ．3个D ．4个5．设函数)(x f 的图象关于点（1，23）对称，且存在反函数)(1x f -，若0)3(=f ，则)3(1-f等于（）A ．－1B ．1C ．－2D ．26．已知数列{log 3(a n +1)}(n ∈N *)为等差数列，且a 1=2,a 2=8，则213243111lim(x a a a a a a →∞+++---…+11)n n a a +=- ( )A ．14 B.34 C.12 D.17．一个幼儿园的母亲节联谊会上，有5个小孩分别给妈妈画了一幅画作为礼物，放在了5个相同的信封里，可是忘了做标记，现在妈妈们随机的任取一个信封，则恰好有两个妈妈拿到了自己孩子的画的概率为 ( ) A ．121 B ．81 C ．61 D ．41 8．已知两个正数,x y 满足45x y xy ++=，则xy 取最小值时,x y 的值分别为（）A ．5,5B ．510,2C ．10,5D ．10,109．如果以原点为圆心的圆经过双曲线)0,0(12222>>=-b a by a x 的焦点，而且被该双曲线的右准线分成弧长为2：1的两段圆弧，那么该双曲线的离心率e 等于（）A ．5B ．25 C ．3 D ．210．二次函数)(x f 的二次项系数为正数，且对任意项R x ∈都有)4()(x f x f -=成立，若)21()21(22x x f x f -+<-，则x 的取值范围是()A 2>x ()B 2-<x 或20<<x ()C 02<<-x ()D 2-<x 或0>x二、填空题：本大题共6小题，每小题4分，共24分11．1023)21(xx -展开式中的常数项为 . 12. 设若1=a，,2=b b a c -=，且a c ⊥，则向量a 与b 的夹角为 .13．不等式组⎪⎪⎩⎪⎪⎨⎧≥+-≥+≤∈∈0503,y x y x x Z y N x 表示平面区域A ，点),(y x 满足y x z +=3，则z 的最大为： .14．霓虹灯的一个部位由一串七个小灯泡组成，每个灯泡均可亮出红色或黄色．现设计每次变换只闪亮其中三个灯泡，且相邻两个不同时亮，则一共可呈现种不同的变换形式 15.正六棱柱ABCDEF-A 1B 1C 1D 1E 1F 1的侧面是正方形，若底面边长为a,则该正六棱柱外接球的表面积为 .16、符号[]x 表示不超过x 的最大整数，如[][]208.1,3-=-=π，定义函数{}[]x x x -=，那么下列命题中正确的是。

2009届重庆高三学生学业第二次质量调研抽测理

2009届重庆市高三学生学业第二次质量调研抽测数学试卷（理科）本试卷分第第 I 卷（选择题）和第n 卷（非选择题）两部分。

共150分，考试时间120分钟。

参考公式：如果事件AB 互斥，那么 P(A B) P(A) P (B)如果事件AB 相互独立，那么P(A B)P (A) P (B)如果事件A 在一次实验中发生的概率是 P,那么它在n 次独立重复实验中恰好发生 k 此的概率P n （k ） C ：P k （1 P ）n k球的表面积公式S 4 R 2其中R 表示球的半径43球的体积公式 v - R 3其中R 表示球的半径3注意事项：1 •答题前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。

2•选择题没小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，不能答在试题上。

3•填空题的答案和解答题的解答过程直接写在答题卡n 上。

4 •考试结束，监考人将本试题和答题卡一并收回。

第I 卷（选择题，共50 分）、选择题：（本大题10个小题，每小题5分，共50分）各题答案必须答在答题卡上。

A • -2B • 0C • 2D • 42 •若复数z 1 2，则z 的虚部为i( )A • 1B • -1C • iD • i3.已知函数f （x ）2x 3(x 1)2(x 1)' 则下列结论正确的是( )A • f (x)在 x 1处连续B • f (1) 5C . lim f (x)x 15D • lim f (x)2x 14•若命题甲：AUB=A 为假命题，命题乙：A B A 也为假命题，U 为全集，则下列四个用文氏形反应集合 A 与B 的关系中可能正确的是1.lim^C . 5设数列｛a n ｝是以2为首项，1为公差的等差数列，｛b n ｝是以1为首项，2为公比的等比点，O 为坐标原点，且I OP I | PQ |，则此椭圆的离心率为9. 如图，在120°的二面角a l 内，半径为1的圆O 1与半径为2的圆。

2009年重庆高考预测试卷四理

5.2009年重庆高考预测卷理科数学试题(四)说明：本试题满分 150分，考试时间120分钟。

参考公式：如果事件A 、B 互斥，那么P(A B) = P(A) P(B) 如果事件A 、B 相互独立，那么 P(A ・B) = P(A) P(B) 如果事件A 在一次试验中发生的概率是p ，那么在n 次独立重复试验中，事件A 恰好C . 2的直线的倾斜角的大小为5■:发生k 次的概率为 P n (k)=C ：p k (1-p 严、选择题(本大题共一项符合题目要求。

第I 卷(选择题共50 分)10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有1. 如果复数2 - bi(b ・R)的实数部分与虚数部分互为相反数，则 1 i b 的值等于2. 已知 P:.x :：: 1，则Q 是P 的( )条件充分不必要 B •必要不充分 3. 4. C . 充要等差数列｛a n ｝中，若 A . 14 D •既不充分又不必要a 4 ' a 6 ' a 8 ' a® ' a 12 = 120，则1a 9 an 3的值为B . 15C . 16D . 17从点P (1,3 )向圆 2 2x - y =1作两条切线PA 、PB ,切点为A 、 B ，则弦AB 所在AB=12 26.设双曲线冷-笃=1 (a . 0, b . 0)的离心率为,3，且它的一条准线与抛物线 a b2y =4x 的准线重合，则此双曲线的方程为2一 2sin a+sin 2a.，-兀、血•/ 兀\”,+9.已知k(0 ：：： a )，则 sin(a )的值1 +ta n a4 4A .随k 的增大而增大B .有时随k 的增大而增大，有时随 k 的增大而减小c .随k 的增大而减小 D .是一个与k 无关的常数2 2x y— -^=1 (a>0, b>0)右支上一点P ,满足PF , =3，实轴长为1,a bF 1、F 2分别是双曲线的左、右焦点，M 为y 轴上一点，则PM '(PF — PFJ =1 3 5 7 A.-B .c .D .2222第n 卷(非选择题共100分)、填空题(本大题共 5个小题，每小题5分，共25分。

重庆11中高级高三上数学试题(理科实验班)4

重庆十一中高2009级高三上(理科实验班)数学测试题4满分：150分时间：120分钟命题：潘文荣内容 (集合与简易逻辑、函数、导数、数列、三角函数）一、选择题：本大题共10小题，每小题5分，共50分。

1、已知全集{}11,7,5,3,2=I ，{}7,5,2-=a A ，{}11,5=A C I ，则a 的值为（）A ．2B ．8C ．2或8D ．2-或82、设)(x f =⎪⎩⎪⎨⎧〈+≥--11112|2|2x x x x 则=)]21([f f （）A ．21 B ．134 C ．59- D ．41253、若x x f 2)(=的反函数为)(1x f-，且4)()(11=+--b f a f ，则ba 11+的最小值是( ). A ．1B ．21C ．31D ．414、已知等差数列｛a n ｝的前n 项和为S n ，且S 4=3，S 8=7，则S 12的值是 ( )A 8B 11C 12D 15 5、函数)]3)(1lg[(x x y -+=的单调减区间为（）A. ]1,1(-B. ]1,(-∞C. )3,1[D. ),1[+∞ 6、若,53)22sin(,54)2sin(=+=+θπθπ则θ角的终边在（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限7、、函数a x y -=2log 图象的对称轴为2=x ，则a 的值为（） A ．21 B ．21- C ．2 D ．2- 8、下列命题中，正确的是（）①数列{(－1)n 3}没有极限；②数列{(－1)nn2}的极限为0； ③数列{n )23(3-+}的极限为3； ④数列{nn)3(2}没有极限．A ．①②B ．①②③C ．②③④D ．①②③④9、若函数2cos 3sin )(++==x x x f y 0[∈x , )2π，且关于x 的方程m x f =)(有2个不等实数根α、β，则=+)sin(βαA ．21 B ．23 C ．21或23D ．无法确定10、已知两个等差数列{}n a 和{}n b 的前n 项和分别为A n 和n B ，且7453n n A n B n +=+，则使得n na b 为整数的正整数n 的个数是（） A ．2 B ．3 C ．4 D ．5二、填空题：本大题共6小题，每小题4分，共24分．11、定义在R 上的奇函数f (x )以4为周期，则f (2005)+ f (2006)+ f (2007)的值为 . 12、已知数列1, a 1, a 2, 4成等差数列，1, b 1, b 2, b 3, 4成等比数列，则=+221b a a _______． 13、函数21432-+--=x x x y 的定义域是 14、已知21)sin(=+βα，31)sin(=-βα，则=βαt a n :t a n _． 15、已知正项数列{}n a 满足：11a =，且1(*)21nn nn a a n N a +=∈⋅+，k a 是数列{}n a 的第k 项，则2121lim k nk n k a k k →∞=-⋅=+∑ . 16、关于函数))(32sin(4)(R x x x f ∈+=π，有下列命题：①由f (x 1) = f (x 2)=0可得x 1－x 2必是π的整数倍； ②若)12,6(,21ππ-∈x x ，且21211),6()(2x x x x f x f <++=则π； ③函数的图象关于点)0,6(π-对称； ④函数y = f (－x )的单调递增区间可由不等式)(223222Z k k x k ∈+≤+-≤-πππππ求得。

重庆11中高2009级高三上数学试题(理科实验班)3

专心
21、已知二次函数 y f ( x) 的图像经过坐标原点，其导函数为 f ( x) 6 x 2 ，数列 {an } 的前 n 项和
'
为 S n ，点 ( n, S n )( n N ) 均在函数 y f ( x) 的图像上。
（Ⅰ）、求数列 {an } 的通项公式；使得 Tn
ab 1 ab 1 ab lg 1 ab a b lg (1 a )(1 b) ， f lg ab 1 ab a b (1 a )(1 b) 1 ab 1 1 ab
所以 f ( a ) f (b) f
20、已知函数 f ( x) ax 2ax 2 b( a 0) ，在区间 2, 3 上有最大值 5，最小值 2。
2
（1）求 a，b 的值。（2）若 b 1 , g ( x) f ( x) ( 2 ) x 在2, 4 上单调，求 m 的取值范围。
m
用心
爱心
13、解析：直线 x y 1 0 与抛物线 y ax 相切，将 y=x－1 代入抛物线方程得 ax x 1 0 ， ∴
2
2
用心
爱心
专心
1 4a 0 ，a=
14、解析： lim (
x 2
1 。 4
4 1 1 1 ) lim 2 x 2 2 x 2 x 4 4 x
（Ⅱ）、设 bn
1 ， Tn 是数列 {bn } 的前 n 项和，求 an an 1
m 对所有 n N 都成立的最小正整数 m； 20
22、已知数列｛an｝满足：a1＝
3na n－1 3 ，且 an＝（n 2，n N） 2 2a n－1＋n－1

重庆十一中高级高三上(理科实验班)数学测试题1

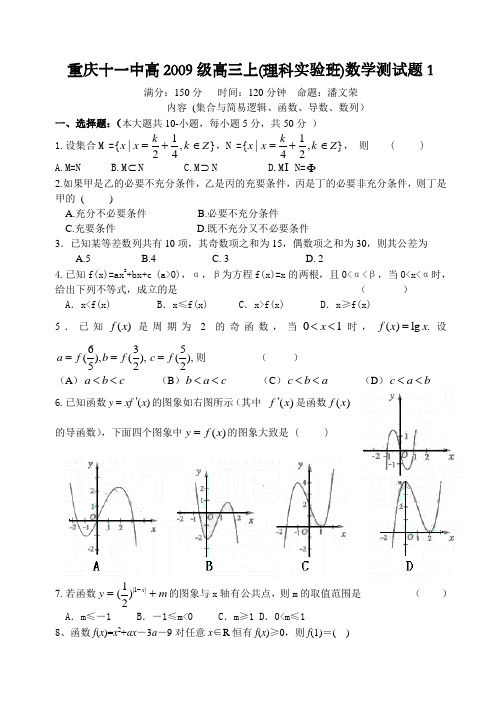
重庆十一中高2009级高三上(理科实验班)数学测试题1满分：150分时间：120分钟命题：潘文荣内容 (集合与简易逻辑、函数、导数、数列）一、选择题：（本大题共10-小题，每小题5分，共50分）1.设集合M =},412|{Z k k x x ∈+=，N =},214|{Z k k x x ∈+=，则 ( ) A.M=N B.M ⊂N C.M ⊃N D.M N=Φ2.如果甲是乙的必要不充分条件，乙是丙的充要条件，丙是丁的必要非充分条件，则丁是甲的 ( ) A. B.必要不充分条件C.充要条件D.既不充分又不必要条件3．已知某等差数列共有10项，其奇数项之和为15，偶数项之和为30，则其公差为A.5B.4C. 3D. 24.已知f(x)=ax 2+bx+c (a>0)，α，β为方程f(x)=x 的两根，且0<α<β，当0<x<α时，给出下列不等式，成立的是（） A ．x<f(x) B ．x ≤f(x) C ．x>f(x) D ．x ≥f(x) 5．已知()f x 是周期为2的奇函数，当01x <<时，()l g .f x x =设63(),(),52a f b f ==5(),2c f =则（）（A ）a b c << （B ）b a c << （C ）c b a << （D ）c a b <<6.已知函数)(x f x y '=的图象如右图所示（其中 )(x f '是函数)(x f 的导函数），下面四个图象中)(x f y =的图象大致是 ( )7.若函数m y x +=-|1|)21(的图象与x 轴有公共点，则m 的取值范围是（）A ．m ≤－1B ．－1≤m<0C ．m ≥1D ．0<m ≤18、函数f (x )=x 2+ax －3a －9对任意x ∈R 恒有f (x )≥0，则f (1)＝( )A ．6B ．5C ．4D ．39、已知正实数x 1,x 2及函数f(x),满足4x =)(1)(1x f x f -+,且f(x 1)+f(x 2)=1,则f(x 1+x 2)的最小值A.4B.2C.54 D.41 10．已知数列}{n a 、}{n b 都是公差为1的等差数列，其首项分别为1a 、1b ，且511=+b a ，*11,N b a ∈．设n b n a c =（*N n ∈），则数列}{n c 的前10项和等于（） A ．55 B ．70 C ．85 D ．100二、填空题：本大题共6小题，每小题4分，共24分．11.已知非空集合M 满足：M ⊆{1,2,3,4,5}且若x ∈M 则6-x ∈M ,则满足条件的集合M 有个.12在曲线y =x 3+3x 2+6x －10的切线斜率中斜率最小的切线方程是 . 13.设二次函数)0()(2≠++=a c bx ax x f ，若)()(21x f x f =（其中21x x ≠），则)2(21x x f +等于 . 14.已知244)(+=x xx f ，则和)10011000()10012()10011(f f f +++ ＝。

2009届重庆高三学生学业质量调研抽测一理

2009届重庆市高三学生学业质量调研抽测（一）数学试卷（理科）第I 卷（选择题，共50分）一、选择题：（本大题10个小题，每小题5分，共50分）在每小题给出的四个备选项中，只有一项是符合题目要求的.1．函数sin cos y x x =⋅的最小正周期为（）A ．2π B ．π C ．2π D ．4π 2．已知全集,U R =集合{}{}2,1,A x x B x x =>=≤则()()U U A C B B C A =（）A ．∅B ．{}12x x x <≥或C ．{}12x x ≤<D ．{}12x x <≤3．函数22(0)y x x x =-<的反函数为（）A ．11)y x =≥-B ．10)y x =+>C ．11)y x =+≥D ．10)y x =->4．若0,0,a b >>且1,a ≠则log 0a b >是(1)(1)0a b -⋅->的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件5．将直线1:2l y x =绕原点逆时针旋转60得直线2l ，则直线2l 到直线3:230l x y +-=的角为（）A ．30B ．60C ．120D ．1506．已知点P 在抛物线24x y =上，且点P 到x 轴的距离与点P 到焦点的距离之比为13，则点P 到x 轴的距离为（）A ．12B ．1C ．14D ．2 7．将函数()cos y f x x =的图象按向量(,1)4a π=平移得到22sin y x =的图象，那么函数()f x 可以是（）A ．sin xB ．cos xC ．2sin xD ．2cos x8．若点P 为共焦点的椭圆1C 和双曲线2C 的一个交点,1F 、2F 分别是它们的左右焦点.设椭圆离心率为1e ，双曲线离心率为2e ，若120PF PF ⋅=,则221211e e +=（） A ．1 B ．2 C ．3 D ．49．在平行四边形ABCD 中，11,,34AE AB AF AD ==CE 与BF 相交于G 点.若,,AB a AD b ==则AG =（）A ．2177a b +B ．2377a b +C ．3177a b +D ．4277a b + 10．如图，坐标纸上的每个单元格的边长为1，由下往上的六个点：1，2，3，4，5，6的横纵坐标分别对应数列{}*()n a n N ∈的前12项，如下表所示：按如此规律下去，则200920102011a a a ++=（）A ．1003B ．1005C ．1006D ．2011第II 卷（非选择题，共100分）二．填空题：（本大题共6小题，每小题4分，共24分）将每小题正确的答案填在相应的横线上.11．函数()f x =________________________.12．方程2222210x y mx my m m +++++-=表示圆，则m 的取值范围是___________;13．已知数列{}n a 是等比数列，且45678910128,a a a a a a a ∙∙∙∙∙∙=则21510________;a a a ∙= 14．已知实数,x y 满足1210x x y x y m ≥⎧⎪-+≤⎨⎪+≤⎩，如果目标函数y Z x =的最大值为2，则实数___________m =;15．定义在实数集R 上的偶函数()f x 满足(1)(1)f x f x -=+.当[]2,3x ∈时，()f x x =，则[]2,0x ∈-时，()____________f x =；16．如图，以AB 为直径的圆有一内接梯形ABCD ，且//AB CD .若双曲线1C 以A 、B 为焦点，且过C 、D 两点，则当梯形的周长最大时，双曲线的离心率为_____________.三、解答题：（本大题共6小题，共76分）.解答应写出文字说明，演算步骤或证明过程.17．（13分）已知33(cos ,sin ),(cos ,sin ),2222x x a x x b ==-若2().f x a b a b =⋅-+ （I ）求函数()f x 的单调减区间；（II ）若,,34x ππ⎡⎤∈-⎢⎥⎣⎦求函数()f x 的最大值和最小值. 18．（13分）设数列{}n a 满足12323...2(*).n n a a a na n N ++++=∈（I ）求数列{}n a 的通项；（II ）设2,n n b n a =求数列{}n b 的前n 项和n S .19．（13分）某厂家拟在2009年举行促销活动，经调查测算，该产品的年销量（即该厂的年产量）x 万件与年促销费用(0)t t ≥万元满足4(21k x k t =-+为常数）。

重庆十一中高三数学试卷(理科含答案)

重庆十一中高三数学试卷（理科）一、选择题（本大题共12小题，每小题5分，满分60分．在每小题给出的四个选项中，只有一项是符合题目要求的）．1．已知全集U=R，集合A={x|0＜x＜9，x∈R}和B={x|﹣4＜x＜4，x∈Z}关系的韦恩图如图所示，则阴影部分所示集合中的元素共有（）A．3个 B．4个 C．5个 D．无穷多个2．在公差不为零的等差数列{a n}中，2a3﹣a72+2a11=0，数列{b n}是等比数列，且b7=a7，则log2（b6b8）的值为（）A．2 B．4 C．8 D．13．与曲线=1共焦点，而与曲线=1共渐近线的双曲线方程为（）A．=1 B．=1 C．=1 D．=14．已知f（x）是定义在R上的奇函数，当x≥0时，f（x）=5x+m（m为常数），则f（﹣log57）的值为（）A．4 B．﹣4 C．6 D．﹣65．设函数f（x）的定义域为R，x0（x0≠0）是f（x）的极大值点，以下结论一定正确的是（）A．∀x∈R，f（x）≤f（x0）B．﹣x0是f（﹣x）的极小值点C．﹣x0是﹣f（x）的极小值点D．﹣x0是﹣f（﹣x）的极小值点6．“0≤a＜2”是“ax2+2ax+1＞0的解集是实数集R”的（）A．充分而非必要条件B．必要而非充分条件C．充要条件D．既非充分也非必要条件7．设关于x，y的不等式组表示的平面区域内存在点P（x0，y0），满足x0﹣2y0=2，求得m的取值范围是（）A．B．C．D．8．定义在R上的函数f（x）的图象关于点（﹣，0）成中心对称，且对任意的实数x都有，f（﹣1）=1，f（0）=﹣2，则f（1）+f（2）+…+f（2 017）=（）A．0 B．﹣2 C．1 D．﹣49．已知某几何体的三视图（单位：cm）如图所示，则该几何体的体积是（）A．100 cm3B．108 cm3C．84 cm3D．92 cm310．已知F1，F2分别是双曲线﹣=1（a＞0，b＞0）的左、右焦点，点P在双曲线上且不与顶点重合，过F2作∠F1PF2的角平分线的垂线，垂足为A．若|OA|=b，则该双曲线的离心率为（）A．B．C．D．11．已知△ABC中，BC=1，AB=，AC=，点P是△ABC的外接圆上的一个动点，则•的最大值是（）A．2 B．C．D．12．如图，已知点E为平行四边形ABCD的边AB上一点，=2，F n（n∈N*）﹣为边DC上的一列点，连接AF n交BD于G n，点G n（n∈N*）满足=a n+1（3a n+2），其中数列{a n}是首项为1的正项数列，则a4的值为（）A．45 B．51 C．53 D．61二、填空题（本大题共4小题，每小题5分，满分20分）13．已知全集U={a1，a2，a3，a4}，集合A是集合U的恰有两个元素的子集，且满足下列三个条件：①若a1∈A，则a2∈A；②若a3∉A，则a2∉A；③若a3∈A，则a4∉A．则集合A=．（用列举法表示）14．若双曲线x2﹣y2=1右支上一点A（a，b）到直线y=x的距离为，则a+b=．15．在△ABC中，内角A、B、C所对的边分别是a、b、c，若sinC+sin（B﹣A）=sin2A，则△ABC的形状为．16．在（1+x﹣x2）6的展开式中x5的系数为．三、解答题（本大题共6小题，满分70分，第17题为10分外其余均为12分，）17．如图所示，在四边形ABCD中，∠D=2∠B，且AD=1，CD=3，cos∠B=（1）求△ACD的面积；（2）若BC=2，求AB的长．18．某企业通过调查问卷（满分50分）的形式对本企业900名员土的工作满意度进行调查，并随机抽取了其中30名员工（16名女员工，14名男员工）的得分，如下表：（1）根据以上数据，估计该企业得分大于45分的员工人数；（2）现用计算器求得这30名员工的平均得分为40.5分，若规定大于平均得分为‘满意’，否则为“不满意”，请完成下列表格：〔3）根据上述表中数据，利用独立性检验的方法判断，能否在犯错误的概率不超过1%的前提下，认为该企业员工“性别”与“工作是否满意”有关？参考数据：19．已知递增的等比数列{a n}中，a1，a2，a3分别为下表中第一、二、三行中某一个数，且a1，a2，a3中的任何两个数不在下表中同一行和同一列，（1）求数列{a n}通项公式；（2）若数列{b n}满足，若n为偶数，求数列{b n}的前n项和．20．已知矩形ABCD中，，BC=1，现沿对角线BD折成二面角C﹣BD﹣A，使AC=1（I）求证：DA⊥面ABC（II）求二面角A﹣CD﹣B的大小．21．抛物线C1：x2=4y在点A，B处的切线垂直相交于点P，直线AB与椭圆C2：+=1相交于C，D两点．（1）求抛物线C1的焦点F与椭圆C2的左焦点F1的距离；（2）设点P到直线AB的距离为d，试问：是否存在直线AB，使得|AB|，d，|CD|成等比数列？若存在，求直线AB的方程；若不存在，请说明理由．22．已知函数．（Ⅰ）若p=2，求曲线f（x）在点（1，f（1））处的切线方程；（Ⅱ）若函数f（x）在其定义域内为增函数，求正实数p的取值范围；（Ⅲ）设函数，若在[1，e]上至少存在一点x0，使得f（x0）＞g（x0）成立，求实数p的取值范围．重庆十一中高三数学试卷（理科）参考答案与试题解析一、选择题（本大题共12小题，每小题5分，满分60分．在每小题给出的四个选项中，只有一项是符合题目要求的）．1．已知全集U=R，集合A={x|0＜x＜9，x∈R}和B={x|﹣4＜x＜4，x∈Z}关系的韦恩图如图所示，则阴影部分所示集合中的元素共有（）A．3个 B．4个 C．5个 D．无穷多个【考点】Venn图表达集合的关系及运算．【分析】由阴影部分可知对应的集合为B∩∁U A，然后根据集合的基本运算进行求解即可．【解答】解：由阴影部分可知对应的集合为B∩∁U A，∵A={x|0＜x＜9，x∈R}，∴∁U A={x|x≥9或x≤0}，∵B={x|﹣4＜x＜4，x∈Z}={﹣3，﹣2，﹣1，0，1，2，3}∴B∩∁U A={﹣3，﹣2，﹣1，0，1，2，3}∩{x|x≥9或x≤0}={﹣3，﹣2，﹣1，0}，共有4个元素．故选：B．2．在公差不为零的等差数列{a n}中，2a3﹣a72+2a11=0，数列{b n}是等比数列，且b7=a7，则log2（b6b8）的值为（）A．2 B．4 C．8 D．1【考点】等差数列的性质．【分析】根据数列{a n}为等差数列可知2a7=a3+a11，代入2a3﹣a72+2a11=0中可求得a7，再根据{b n}是等比数列可知b6b8=b72=a72代入log2（b6b8）即可得到答案．【解答】解：∵数列{a n}为等差数列，∴2a7=a3+a11，∵2a3﹣a72+2a11=0，∴4a7﹣a72=0∵a7≠0∴a7=4∵数列{b n}是等比数列，∴b6b8=b72=a72=16∴log2（b6b8）=log216=4故选：B3．与曲线=1共焦点，而与曲线=1共渐近线的双曲线方程为（）A．=1 B．=1 C．=1 D．=1【考点】双曲线的标准方程．【分析】根据椭圆方程先求出焦点坐标，再由渐近线相同设出双曲线方程为，根据c值列出方程求出λ的值即可．【解答】解：由题意得，曲线=1是焦点在y轴上的椭圆，且c===5，所以双曲线焦点的坐标是（0、5）、（0，﹣5），因为双曲线与曲线=1共渐近线，所以设双曲线方程为，即，则﹣64λ﹣36λ=25，解得λ=，所以双曲线方程为，故选：A．4．已知f（x）是定义在R上的奇函数，当x≥0时，f（x）=5x+m（m为常数），则f（﹣log57）的值为（）A．4 B．﹣4 C．6 D．﹣6【考点】抽象函数及其应用；函数奇偶性的性质．【分析】根据奇函数的性质，可得f（0）=0，代入构造关于m的方程，解得当x≥0时函数解析式，进而得到答案．【解答】解：∵f（x）是定义在R上的奇函数，∴f（0）=0，∵当x≥0时，f（x）=5x+m，∴f（0）=1+m=0，解得：m=﹣1，故f（x）=5x﹣1，∴f（﹣log57）=﹣f（log57）=﹣（7﹣1）=﹣6，故选：D5．设函数f（x）的定义域为R，x0（x0≠0）是f（x）的极大值点，以下结论一定正确的是（）A．∀x∈R，f（x）≤f（x0）B．﹣x0是f（﹣x）的极小值点C．﹣x0是﹣f（x）的极小值点D．﹣x0是﹣f（﹣x）的极小值点【考点】函数在某点取得极值的条件；函数的图象与图象变化．【分析】A项，x0（x0≠0）是f（x）的极大值点，不一定是最大值点，故不正确；B项，f（﹣x）是把f（x）的图象关于y轴对称，因此，﹣x0是f（﹣x）的极大值点；C项，﹣f（x）是把f（x）的图象关于x轴对称，因此，x0是﹣f（x）的极小值点；D项，﹣f（﹣x）是把f（x）的图象分别关于x轴、y轴做对称，因此﹣x0是﹣f （﹣x）的极小值点．【解答】解：对于A项，x0（x0≠0）是f（x）的极大值点，不一定是最大值点，因此不能满足在整个定义域上值最大，故A错误；对于B项，f（﹣x）是把f（x）的图象关于y轴对称，因此，﹣x0是f（﹣x）的极大值点，故B错误；对于C项，﹣f（x）是把f（x）的图象关于x轴对称，因此，x0是﹣f（x）的极小值点，故C错误；对于D项，﹣f（﹣x）是把f（x）的图象分别关于x轴、y轴做对称，因此﹣x0是﹣f（﹣x）的极小值点，故D正确．故选：D．6．“0≤a＜2”是“ax2+2ax+1＞0的解集是实数集R”的（）A．充分而非必要条件B．必要而非充分条件C．充要条件D．既非充分也非必要条件【考点】必要条件、充分条件与充要条件的判断．【分析】求出ax2+2ax+1＞0的解集是实数集R的充要条件，根据集合的包含关系判断即可．【解答】解：若ax2+2ax+1＞0的解集是实数集R，则a=0时，1＞0成立，a≠0时，则，解得：0＜a＜1，综上，0≤a＜1，故“0≤a＜2“是“0≤a＜1“的必要不充分条件，故选：B．7．设关于x，y的不等式组表示的平面区域内存在点P（x0，y0），满足x0﹣2y0=2，求得m的取值范围是（）A．B．C．D．【考点】简单线性规划．【分析】先根据约束条件画出可行域．要使可行域存在，必有m＜﹣2m+1，要求可行域包含直线y=x﹣1上的点，只要边界点（﹣m，1﹣2m）在直线y=x﹣1的上方，且（﹣m，m）在直线y=x﹣1的下方，从而建立关于m的不等式组，解之可得答案．【解答】解：先根据约束条件画出可行域，要使可行域存在，必有m＜﹣2m+1，要求可行域包含直线y=x﹣1上的点，只要边界点（﹣m，1﹣2m）在直线y=x﹣1的上方，且（﹣m，m）在直线y=x﹣1的下方，故得不等式组，解之得：m＜﹣．故选C．。

重庆市部分重点中学高2009级一诊模拟试题(理)数学

重庆市数学试题卷一．选择题1.已知集合(){}(){},2, ,2M x y x y N x y x y =+==-=-，那么集合M N 为（）A ．0,2x y ==B ．()0,2C ．{}0,2D ．(){}0,22.函数()y f x =为偶函数，则函数()1y f x =+的一条对称轴是（） A ．0x = B ．1x =- C ．1x = D ．2x =3.正项等比数列{}n a 满足：152,8a a ==，则3a 的值为（） A ．4 B ．3 C ．－3 D ．4±4.直线y x =截圆()2224x y -+=所得的弦长为（）A ．1 B． C ．2 D5.若直线1l ，2l 的斜率分别是22730x x -+=的两根，则1l 与2l 的夹角为（）A ．3π B ．4π C ．23π D ．34π6.函数344+-=x x y 在区间[]2,3-上的最小值为（）A ．72B ．36C ．12D ．07．已知正四棱锥S —ABCD 侧棱长为2，底面边长为3，E 是SA 的中点，则异面直线BE 与SC 所成角的大小为（） A ．90°B ．60°C ．45°D ．30°8.已知椭圆()222210x y a b a b +=>>，直线y x =与椭圆交于,A B两点，若AB =（其中c =，则该椭圆的离心率为（）ABCD ．129.设变量x ，y 满足约束条件：3123x y x y x y +≥⎧⎪-≥-⎨⎪-≤⎩.则目标函数z=2x+3y 的最小值为（A ）6 （B ）7 （C ）8 （D ）2310.某校高三年级共有六个班,现从外校转入4名学生,要安排到该年级的两个班级且每班安排2名,则不同的安排方案种数为( )A. 2426C AB. 2426A AC. 262A D. 242621C A 二．填空题11.某学校共有师生2400人，现用分层抽样的方法，从所有师生中抽取一个容量为160的样本，已知从学生中抽取的人数为150，那么该学校的教师人数是 .12.在ABC ∆中，角A B C 、、所对的边长分别为,,a b c ，且()22a c a b b -=-，则A C B ∠=_______.13.在数列中，对于任意自然数，都有1221n n a a a +++=-…，则22212n a a a +++=…_______. 14.已知,A B 为椭圆22222519x y a a +=上的两点，2F 为椭圆的右焦点，若2285AF BF a +=，AB 中点到椭圆左准线的距离为32，则a 的值为______.15.设实数x 、y满足条件⎪⎩⎪⎨⎧≥-≤≤+013y x y y x ，则x y 的最大值为 ______.三．解答题 16.设函数2()sin cos f x x x x = （1）求()f x 的最小正周期和值域；（2）将函数()y f x =的图象按向量1(,)122a π→=-平移后得到函数()y g x =的图象，求函数()y g x =的解析式。

重庆市部分重点中学高2009级一诊模拟试题(理)数学

秘密★启用前重庆市部分重点中学高2009级一诊模拟试题数学试题卷（理科） 2008.12数学试题共3页。

满分150分。

考试时间120分钟。

注意事项：1.答题前，务必将自己的姓名、准考证号填写在答题卡规定的位置上。

2.答选择题时，必须使用2B 铅笔将答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦擦干净后，再选涂其他答案标号。

3.答非选择题时，必须使用0.5毫米黑色签字笔，将答案书写在答题卡规定的位置上。

4.所有题目必须在答题卡上作答，在试题卷上答题无效。

一．选择题（本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的）1.已知集合(){}(){},2, ,2M x y x y N x y x y =+==-=-，那么集合M N 为（）A ．0,2x y ==B ．()0,2C ．{}0,2D ．(){}0,2 2.函数()y f x =为偶函数，则函数()1y f x =+的一条对称轴是（）A ．0x =B ．1x =-C ．1x =D ．2x =3.正项等比数列{}n a 满足：152,8a a ==，则3a 的值为（）A ．4B ．3C ．－3D ．4±4.直线y x =截圆()2224x y -+=所得的弦长为（）A ．1B ．C ．2D 5.若直线1l ，2l 的斜率分别是22730x x -+=的两根，则1l 与2l 的夹角为（）A ．3πB ．4π C ．23π D ．34π 6.关于x 的不等式2032x a x x -≥-+的解集为(]()1,2,a +∞ ，则实数a 的取值范围是（） A ．()1,2 B ．[]1,2 C ．()2,+∞ D ．(),1-∞- 7.在ABC ∆的内角满足sin cos 0A A +>且tan sin 0A A -<，则角A 的取值范围是（）A ．0,4π⎛⎫ ⎪⎝⎭B ．,42ππ⎛⎫⎪⎝⎭ C ．3,24ππ⎛⎫ ⎪⎝⎭ D ．3,44ππ⎛⎫ ⎪⎝⎭8.已知椭圆()222210x y a b a b +=>>，直线2y x =与椭圆交于,A B 两点，若AB =（其中c =，则该椭圆的离心率为（）A ．2B ．3C ．2D ．12 9.已知,,A B C 是平面上不共线上三点，O 为ABC ∆外心，动点P 满足：()()()111123OP OA OB OC λλλ⎡⎤=-+-++⎣⎦ （R λ∈且0λ≠），则P 的轨迹一定通过ABC ∆的（）A ．内心B ．垂心C ．重心D ．AB 边的中点10.已知椭圆()2222:10x y C a b a b+=>>的左焦点为F ，椭圆C 与直线y x =在第一象限的交点为P ，椭圆C 在P 点的切线为l ，过原点O 作直线平行于l 交FP 于M ，则PM 的长为（）A ．222ab a b +B ．aCD ．222a b a b +二．填空题（每小题4分，共24分，请将正确答案填到答题纸指定的空白处） 11.若向量()()()1,1,1,1,1,2a b c ==-=- ，用,a b 表示c = ______________.12.在ABC ∆中，角A B C 、、所对的边长分别为,,a b c ，且()22a c a b b -=-，则ACB ∠=_______. 13.在数列中，对于任意自然数，都有1221n n a a a +++=-…，则22212n a a a +++=…_______. 14.已知,A B 为椭圆22222519x y a a +=上的两点，2F 为椭圆的右焦点，若2285AF BF a +=，AB 中点到椭圆左准线的距离为32，则a 的值为______. 15.已知直线()2:22,1x y l a b a b+=>>与曲线222210x y x y +--+=相切且直线l 交与x 轴交于A 点，交y 轴于点B ，则AOB ∆面积的最小值为______.16.已知关于x 的方程20x ax b ++=的两根均在区间()1,1-内，则21a b a +-+的取值范围是______.三．解答题（本大题共6个小题，共76分，请将正确且必要的解题过程规范地书写到答题纸的指定位置处）17.（13分）求函数21cos cos 122y x x x =++的最小正周期，最大值和最小值。

重庆十一中高三数学高考模拟试题

高2009级高三下数学试题10时间；120分钟满分；150分一、选择题（本大题共10个小题，每小题5分，共50分1、设全集R U =,{}A x x y y B x x x A ∈==⎭⎬⎫⎩⎨⎧<+-=,cos |,012|，则=B A IA ．]1,2(cosB ．]1,2[cosC ．)2,1(-D ．]2cos ,1(-2、已知函数⎩⎨⎧≤>=)0(3)0(log )(2x x x x f x ，则)]41([f f 的值是A ． 9B ．91C ．－9D ．－913、锐角三角形ABC 中，边长,a b 是方程220x -+=的两个根，且2sin()0A B +-=，则c 边的长是A.4C.D.4、已知双曲线2222by a x -＝1的左焦点为F 1，左、右顶占为A 1、A 2，P 为双曲线上任意一点，则分别以线段PF 1，A 1A 2为直径的两个圆的位置关系为A ．相交B ．相切C ．相离D ．以上情况都有可能5、若x ∈R ，n ∈N *，定义：nx M =x(x+1)(x+2)…(x+n-1),例如M 3-5=(-5)·(-4)(-3)=-60,则函数f(x)=M 7x-3cosx 20062005A.是偶函数不是奇函数B.是奇函数不是偶函数C.既是奇函数又是偶函数D.既不是奇函数也不是偶函数6、一机器狗每秒钟前进或后退一步，程序设计师让机器狗以前进3步，再后退2步的规律移动，如果将此机器狗放在数轴的原点，面向正方向，以一步的距离为一个单位长，令P(n)表示第n 秒时机器狗所在位置的坐标，且P(0)=0，那么下列结论中错误的是A. P (3)=3B. P (5)=1C. P (101)=21D. P (103)<P(104)7、某市组织一次高三调研考试，考试后统计的数学成绩服从正态分布，其密度函数为)(1021)(200)80(2R x ex f x ∈⋅=-π，则下列命题不正确的是（）A ．该市这次考试的数学平均成绩为80分；B ．分数在120分以上的人数与分数在60分以下的人数相同；C ．分数在110分以上的人数与分数在50分以下的人数相同；D ．该市这次考试的数学成绩标准差为10.8、四面体ABCD 的外接球球心在CD 上，且2CD =，3=AB ，在外接球面上A B ，两点间的球面距离是（）Ａ．π6Ｂ．π3Ｃ．2π3Ｄ．5π69．关于函数)42sin()(π-=x x f ，有下列命题:① 其表达式可写成⎪⎭⎫ ⎝⎛+=42cos )(πx x f ； ② 直线)(8x f x 是π-=图象的一条对称轴；③ )(x f 的图象可由x x g 2sin )(=的图象向右平移4π个单位得到； ④ 存在),0(πα∈，使)3()(αα+=+x f x f 恒成立则其中真命题为A ．②③B ．①②C ．②④D ．③④10、一系列椭圆都以一定直线l 为准线，所有椭圆的中心都在定点M ，且点M 到l 的距离为2，若这一系列椭圆的离心率组成以43为首项，31为公比的等比数列，而椭圆相应的长半轴长为a i (i =1，2，…，n ),则a 1+a 2+…+a n =A.⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛--132149nB. ⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛--131149nC. ⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-n32149D. ⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-n 31149二、填空题（每题5分，共25分）11、用系统抽样法要从160名学生中抽取容量为20的样本，将160名学生从1——160编号。

2009年高考重庆数学(理科)试题及参考答案

2009年高考重庆数学(理科)试题及参考答案
板块吸筹完毕一般发生在大盘启动初期，其主要特征是该板块大部分股票前期套牢筹码基本消失，股票启动时获利比例高于，板块大部分股票有启动迹象。

年月日——月日航天军工启动
凌云股份北方国际
二、板块洗盘完毕必将拉升
板块洗盘完毕一般发生在大盘拉升中期，是指该板块大部分股票拉升一波后进入洗盘阶段，主要特
板块二次吸筹后启动是指该板块经过一轮上涨后，大部分股票主力几乎全部出货，然后经过大幅下跌后（一般是大盘中期回调引起的）新的主力重新吸筹，吸筹完毕的特征是该板块大部分股票前期套牢
盘几乎割肉出局，上方套牢筹码消失转移到下方，股票经过的换手。

年月——月日发电设备启动
深圳惠程智光电气
板块，从该板块中寻找强势整理即将启动的个股。

、同步选股
大盘经过一波拉升后进入洗盘阶段的选股步骤：点击报价→点击热门板块分析→点鼠标右键→点
击区间热门板块→设置起止日期（上面填大盘启动日期，下面填大盘滞涨最后一天的日期）→点击确定→点击均涨幅，然后选取涨幅最大的板块，从该板块中寻找强势股，等待洗盘完毕后二次拉升时介入。

重庆市江北十一中-高三数学12月月考(理科)

重庆市江北十一中2008-2009学年高三12月月考数学（理科）试题第Ⅰ卷（选择题，共60分）一．选择题（本大题共12小题，每小题5分，共60分） 1．设集合{}{}=⋂-+-==≤-=B A x x y y B x x A 则,22|,4|3||A ．{0}B ．{2}C ．OD ．{}72|≤≤x x2．如果复数)1)((2mi i m ++是实数，则实数m=A ．1B ．－1C ．2D ．2-3．已知函数)5(,)0)(3()0(2)(f x x f x x f x 则⎩⎨⎧>-≤==A ．32B ．16C ．21 D ．321 4．如果=-⎪⎭⎫ ⎝⎛+=⎪⎭⎫⎝⎛∈απααππαcos 224sin ,54sin ,,2那么且A ．522B ．522-C ．524 D ．－524 5．已知各顶点都在一个球面上的正四棱柱高为4体积为16，则这个球的表面积为A ．16πB ．20πC ．24πD ．32π6．一工厂生产了某种产品24000件，它们来自甲．乙．丙三条生产线，现采用分层抽样的方法对这批产品进行抽样检查，已知从甲．乙．丙三条生产线依次抽取的个体数恰好组成一个等差数列，则这批产品中乙生产线的产品数量是A ．12000B ．6000C ．4000D ．80007．已知正数数列{a n }中，a 1=3，且对于任意大于1的整数n ，点),(1-n n a a 总在直线 2)1(lim 03+=--∞→n a y x nn 上，则=A ．0B ．1C ．2D ．38．若圆),(110122222a a C x y y x y ax y x --==+=++-+对称，过点关于直线和圆的圆P 与y 轴相切，则圆心P 的轨迹方程是 A ．08442=++-y x y B ．02222=+-+y x yC ．08442=+-+y x yD ．0122=+--y x y9．已知函数)(1)(1x f a x xa x f ----=的反函数的图像的对称中心是（－1，3），则不等式f （x ）＞0的解集是 A ．（2，3） B ．（－∞，2）∪（3，+∞）C ．（－3，4）D ．（－∞，－3）∪（4，+∞）10．设,1)1(4)1(6)1(4)1(234+-+-+-+-=x x x x S 与它相等的是A ．（4)2-xB ．4)1(-xC ．x 4D ．(4)1+x11．如右图直角梯形OABC 中，AB//OC ，AB=1，OC=BC=2，直线l ：x=t 截此梯形所得位于l 左方图形的面积为S ，则函数)(t f S =的图象大致是A B C D12．已知点O ABC O ∆+==+为且,所在平面内一点，则点O 一定是△ABC 的 A ．外心B ．内心C ．垂心D ．重心第Ⅱ卷（非选择题，共90分）二．填空题（本大题共4个小题，每小题4分，共16分，将答案填在题后的横线上） 13．在抛物线5442-==x y x y 线上求一点，使该点到直的距离最短，该点的坐标是14．若y x S y x 4,1422+==+则的最大值为 . 15．在1，2，3，4，5这五个数字组成的无重复数字的三位数中，各位数字之和为奇数的共有个。

重庆十一中高2009级高三上(理科实验班)数学测试题2

重庆十一中高2009级高三上(理科实验班)数学测试题2(集合、函数、导数、数列、数归、极限) 满分：150分时间：120分钟命题；潘文荣一、选择题（本大题共10小题，每小题5分，共50分）1．1、若集合M={y ︱x 2=y ，x }R ∈，集合N={y ︱x+y=0，x R ∈}，则M N 等于（）A.{y ︱y R ∈}B.{(-1,1),(0,0)}C.{(0,0)}D.{x ︱x ≥0} 2．“p 或q 是假命题”是“非p 为真命题”的（）A ．充分而不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件 3．设)(x f 是定义在R 上的偶函数，且)()2(x f x f -=+，当]2,0(∈x ，1)(2-=x x f 则 =)7(fA .48B.24C. 8D.04、已知数列}{n a 满足)(133,0*11N n a a a a n n n ∈+-==+，则20a = （）A 0B 3-C3D235、已知2 3 , 1() 2 , 1x x f x x +≠⎧=⎨=⎩，下面结论正确的是（A ）()f x 在1x =处连续（B ）(1)5f = （C ） 1lim ()2x f x -→= （D ）5)(lim 1=→x f x 6．设f 1(x)=∣x-1∣,f 56)(22-+-=x x x ,函数g(x)是这样定义的:当f )()(21x f x ≥时，g(x)= f 1(x),当f 1(x)<f )(2x 时，g(x)= f )(2x ,若方程g(x)=a 有四个不同的实数解,则实数a 的取值范围是( )A.a<4B.0<a<4C.0<a<3D.3<a<47、=--=--→→)22(1lim ,11)1(lim11x f x x x f x x 则若( )A ．－1B ．1C ．－21D ．21 8．设f(x)、g(x)分别是定义在R 上的奇函数和偶函数,当x ＜0时,)()()()(x g x f x g x f '+'＞0.且g(3)=0.则不等式f(x)g(x)＜0的解集是 ( )A ．(-3,0)∪(3,+∞)B (-3,0)∪(0, 3) C(-∞,- 3)∪(3,+∞) D(-∞,- 3)∪(0, 3)9．定义新运算⊕：当a b ≥时，a b a ⊕=；当a b <时, 2a b b ⊕=，则函数()(1)(2)f x x x x =⊕-⊕， []2,2x ∈-的最大值等于（）A ．-1B ．1C ．6D ．12 10、已知等差数列｛a n ｝与｛b n ｝的前n 项和分别为S n 与T n , 若1223+-=n n T S n n , 则lim ∞→n b n b a 的值是A32 B 26C 23D 49 二、填空题（本大题共6小题，每小题4分，满分24分）11．在等差数列｛a n ｝中，前n 项和为S n ，若S 19=31，S 31=19，则S 50的值是______12．已知函数1(),2()2(1),2xx f x f x x ⎧≥⎪=⎨⎪+<⎩，则函数2(log 3)f 的值为___________。