2013年第十三届中环杯决赛五年级试题和答案解析
第十三届中环杯五年级初赛试题附答案分析 2
第十三届“中环杯”小学生思维能力训练活动五年级选拔赛1.计算:31.3×7.7+11×8.85+0.368×230=()。
2.宠物商店有狃狸犬和西施犬共2012只,其中母犬1110只,狐狸犬1506 只,公西施犬202只。
那么母狐狸犬有_( )只。
3.一个数A为质数,并且A+14, A+18, A+32, A+36也是质数。
那A的值是( )4.一个口袋中有50个编上号码的相同的小球,其中编号为1,2,3,4,5的小球分别有2,6,10,12,20个。
任意从口袋中取球,至少要取出()个小球,才能保证其中至少有7个号码相同的小球。
5.表格中定义了关于“*”的运算,如3*4=2。
(1*2)*(1*2)*……(1*2)=()。
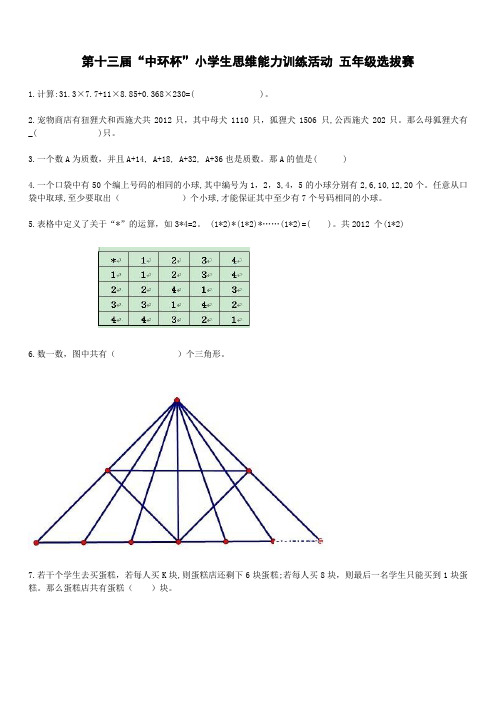
共2012 个(1*2)6.数一数,图中共有()个三角形。
7.若干个学生去买蛋糕,若每人买K块,则蛋糕店还剩下6块蛋糕;若每人买8块,则最后一名学生只能买到1块蛋糕。
那么蛋糕店共有蛋糕()块。
8.—张正方形纸,如图所示折叠后,构成的图形中,角x的度数是()。
9.A、B两地相距66千米,甲、丙两人从A地向B地行走,乙从B地向AI地行走。
甲每小时行12千米,乙每小时行10千米,丙每小时行8千米。
三人同时出发()小时后, 乙刚好走到甲、丙两人距离的中点。
10.有()个形如abcdabcd的数能被18769 整除。
11.小明带24个自制的纪念品去伦敦奥运会卖。
早上每个纪念品卖7英镑,卖出的纪念品不到总数的一半。
下午他对每个纪念品的价格进行打折,折后的价格仍是—个整数。
下午他卖完了剩下的纪念品。
全天共收入120英镑。
那么早上他卖出了()个纪念品。
12.如图,在一个四边形ABCD中,AC,BD相交于点O。
作三角形DBC的高DE,联结AE。
若三角形ABO的面积与三角形DCO的面积相等,且DC=17厘米,DE=15厘米,则阴影部分的面积为( )平方厘米。
13.五名选手在一次数学竞赛中共得414分;毎人得分互不相等且都是整数,并且其中得分最高的选手得了92分,那么得分最低的选手至少得()分,最多得()分。
十三届五年级中环杯选拔赛答案

7. 【答案】 97 块
3 能被 8 K 整除。 先用盈亏问题思考, 人数 6 7 8 K , 即1 所以 K 7 ,
即学生人数是 13 人。所以蛋糕共有 13 8 7 97 块 8. 【答案】 75 9. 【答案】 3.3
66 12 8 2 10 3.3 (小时)
所以 a3 28 。所以 a2 a3 8 。 17. 【答案】 623
2012 y 6 x y 2012 y x y 6 。 6 x 7 y 2012 7 x y 2012 x x y 2012 x 7
1 1 DE EC 15 8 60cm 2 。 2 2
13. 【答案】52,79 如果要考虑最低的得分,那么其余几人的得分要尽量高,则为 91、90、89, 则得解为 52。 如要考虑最多得分, 那要用平均思想解答。 414-92=322, 322 ÷4=80.5,则其余四人的分数分别为 82、81、80、79。 14. 【答案】 C 由 D 与 E 所讲的话可判断出 D 与 E 两人间至少有一人是说谎者;若 C 说实 话,则 AB 两人均说谎,说谎人数超过两人,矛盾,故 C 是说谎者,因此 AB 两人都说实话,可推知写字的人是 C 。 15. 【答案】18.75 或 6.25 此题两解。第二次相遇,可能在中点的左面,也可能在中点的右面。 首先求出 AB 两地的距离:300×2÷(60-40)=30 分钟,(60+40)×30 =3000 米。 再求第二次相遇两人分别走的时间之差,得到两个结果:18.75 分钟或 6.25 分钟。 16. 【答案】 8 首先当 m 2 时,要使得
(1)根据 x y
2013第十三届中环杯五年级决赛详解

计算: 3第十三届“中环杯”小学生思维能力训练活动五年级决赛1、我们有下列公式: 21n( n 2 22n1)(2 n 1)6231 332 n n ( n1) 223 23 2(1 3 1 3 1) (2 99 (99 1)3 2 32) (99 3 99 399) 。
299 (99 1) (299 1) 99 (991)【分析】原式225502400336 22、有一类四位数,除以 5 余 1,除以 7 余 4,除以 11 余 9。
这类四位数中最小的一个是多 少?【分析】设所求数为 5a1,则有 5 a 14(mod 7) a 2(mod 7) ,设a 7b 2 ,则所求数为 35b11 ,则有 35 b119(mod11) b 10(mod11) ,设 b 11 c 10 ,则所求数为 385c361 ,故最小的四位数为 3852 3611131 。
3、有 A 、B 、C 、D 、E 五个人,其中每个人永远说谎话或者永远说真话,并且他们彼此都 互相知道对方的行为。
A 说 B 是说谎者 ,B 说 C 是说谎者,C 说 D 是说谎者,D 说 E 是说 谎者。
那么,这五个人中最多有多少个说谎者?【分析】若 A 说真话,由 A 所说的话可知 B 说谎话,由 B 所说的话可知 C 说真话,继续推 知 D 说谎话,E 说真话,有 2 人说谎。
若 A 说谎话,则 B 说真话,C 说谎话,D 说真话,E 说谎话,有 3 人说谎。
由此,最多有 3 个说谎者。
4、在 1 到 200 之间,有多少个数,其所有不同的素因数之和为 16?(比如:12 的所有不 同素因数为 2、3,其和为 2+3=5)【分析】由于 2 3 5 7 17 16 ,所以所求数至多有 3 个不同素因数。
且由于 16 为偶 数,若拆成 3 个素数之和,其中必有 2。
1、16 2 3 11 ,有 66、132、198 共 3 个 2、16 3 13 ,有 39、117 共 2 个3、16 5 11,有 55 共 1 个 综上,共有 6 个。
13届中环杯决赛四年级(详解)

还是 HI 上,都满足这个相似模型,所以速度比都是
v老鼠 AL 17 ,所以 v捕鼠器 8cm / s 。 v捕鼠器 LK 8
4/4
(2) v捕鼠器 8cm / s
C B
L A DK E F G H I J
如图,将立体图形放置到平面中来,容易知道图中的虚线 AB 就是老鼠要走的最短 路径。如果智能捕鼠器开始的时候在 DE 上的 K 点,则 KL 就是其要走的路径。由于 老鼠与智能捕鼠器同时启动,所以两者走的时间相同,路程比就是速度比,所以
1/4
第十三届“中环杯”中小学生思维能力训练活动四年级决赛答案
6. 答:6 因为 13|123123,且 2013÷2=1006„„1,所以 13| 123123 123 。
2012 个123
又 123÷13=9„„6,所以 123123 123 ÷13 的余数是 6。
4. 答:648
ABC =(A+B+C)×36,所以 36| ABC ,9|(A+B+C)。
若 A+B+C=9,则 ABC =9×36=324,不符题意; 若 A+B+C=18,则 ABC =18×36=648,符合题意; 若 A+B+C =27,则 ABC =27×36=972,不符题意。 所以 ABC =648。 5. 答:酒 如图,由 a、b、c 可知,(6)是书店, (3)是花店,(2)是面包店。由 e、f 可知,酒 店、文具店、E 店在同一侧,所以只能在(4)、(5)、(6)的位置,那么 A 不是酒店就 是文具店。E 肯定在(4)或(6)处,不论(4)或(6)哪个是 E 店,酒店都在其旁边。则 中间是酒店,所以 A 是酒店。
第十三届中环杯四年级决赛试题

第十三届“中环杯”小学生思维能力训练活动四年级决赛题一、填空题(每小题5分,共50分):1、计算:999999÷185185×20=( )。
2、从1开始做乘法:1×2×3…,当乘到( )时,乘积的最后100个数字第一次全部是0。
3、如图所示网格中,要从A到B,方向只能向右或向上,不能经过C以及D,有( )条不同的路径。
4、一个介于500-800之间的三位自然数,正好等于它各位数字和的36倍,则这个自然数是( )。
5、如图所示,有A、B、C、D、E、F共6家商店位于某一条街的两边,商店A位于街上的阴影部分,其他商店的位置关系如下:a、A店的右边是书店;学习奥数的优点1、激发学生对数学学习的兴趣,更容易让学生体验成功,树立自信。
2、训练学生良好的数学思维习惯和思维品质。
要使经过奥数训练的学生,思维更敏捷,考虑问题比别人更深层次。
3、锻炼学生优良的意志品质。
可以培养持之以恒的耐心和克服困难的信心,以及战胜难题的勇气。
可以养成坚韧不拔的毅力4、获得扎实的数学基本功,发挥创新精神和创造力的最大空间。
b、书店的对面是花店;c、花店的旁边是面包店;d、E店在D店的对面;e、酒店在E店的旁边;f、E店和文具店在街道的同一侧。
那么,A店是( )店。
6、123123…123÷13的余数是( )。
(2013个123)7、李老师要在下午3时出门去探望朋友。
他估计时间快到了,一看家里的时钟,发现时钟早在中午12时10分就已经停了。
他给钟换好电池没有拨针就离开家了(换电池时间不计)。
到朋友家时,得知当时时间离3时还差10分。
晚上11时,李老师从朋友家出来,回到家看见家中的时钟才9时。
如果李老师来回路上用时相同,他家的钟停了( )小时( )分钟。
8、某商场在春节有促销抽奖活动,规则如下:在暗箱内有四种颜色的小球各若干个,购物每满100元可以摸球一次。
如果消费者能凑齐同样颜色的小球两个就可以参加一次抽奖,若参加抽奖5次都没有中奖则可获得安慰奖一份。
第十三届中环杯中小学生思维能力训练活动四年级决赛试卷及解析

淤
于 榆
盂
4. 在一个 2011伊4024 的棋盘上袁从下到上每行分别标上从 1 至 2011 的编号袁从左 到右每列分别标上从 1 至 4024 的编号遥 一只蜗牛从位于第 1 列第 1 行的格子开始袁沿 着第 1 行爬行袁每次前进一格遥 每当蜗牛快要爬出棋盘或遇到已经爬过的格子时袁它必 须向左拐袁然后沿着直线继续爬行遥 这样袁它沿着一条螺旋状的路径爬行袁直到爬完所有 的格子为止遥 请问蜗牛最后停留的格子袁行的编号与列的编号之和为多少钥 渊图为 4伊5 棋 盘的示例袁蜗牛最后停留的格子所在的行的编号与列的编号之和为 3垣2越5遥 冤 渊本题 10 分冤
4
3
2
1 1 2 34 5
图1
图2
渊2冤 图 3 所示是一个立体的四级台阶袁每级台阶的长尧宽尧高都分别相 等遥 已知高 A D=h=3 厘米袁宽 DE=b=1 厘米袁长 A C=a=8 厘米遥 一只聪明的老 鼠沿着台阶表面从 A 点往 B 点爬行渊假设在垂直面它可垂直爬行冤袁且走的 是最短路径遥 另有一个智能捕鼠器袁它可以放在线段 DE尧FG尧HI 中的任意一 条上的任意一点遥 如果它放在 DE 上袁那么它走动的路线一定垂直于 DE遥 同 理袁如果它放在 FG 或 HI 上袁那么它走动的路线一定垂直于 FG 或 HI遥 已知 老鼠与智能捕鼠器同时启动袁老鼠的速度 v=17 厘米/秒遥 求证院为了正好捕 捉到老鼠袁智能捕鼠器的速度与它放置的位置没有关系袁并求出其速度遥
位于某一条街的两边袁 商店 A 位于街上的阴影
部分袁其他商店的位置关系如下院Βιβλιοθήκη a援 A 店的右边是书店曰
b援 书店的对面是花店曰
五年级中环杯历届试题

五年级中环杯历届试题五年级中环杯历届试题导语:在所有好的,不好的情绪里,毫无预兆地想念你,是我不可告人的隐疾。
以下小编为大家介绍五年级中环杯历届试题文章,欢迎大家阅读参考!五年级中环杯历届试题一、单项选择题(在下列每题的四个选项中,只有一个选项是符合试题要求的。
请把答案填入答题框中相应的题号下。
每小题1分,共23分)1. 健康牛的体温为( )。
A. 38~39.5°CB. 37~39°CC. 39~41°CD. 37.5~39.5°C2. 动物充血性疾病时,可视黏膜呈现( )。
A. 黄染B. 潮红C. 苍白D. 发绀3. 心肌细胞脂肪变性是指( )。
A. 心肌间质脂肪浸润B. 心肌脂肪组织变性C. 心外膜脂肪细胞堆积D. 心肌细胞胞质中出现脂滴4. 化脓菌入血、生长繁殖、产生毒素、形成多发性脓肿,该病是( )。
A. 脓毒血症B. 毒血症C. 败血症D. 菌血症5. 细胞坏死过程中,核变小、染色质浓聚,被称之为( )。
A. 核溶解B. 核分裂C. 核固缩D. 核碎裂6. 在慢性炎症组织中,最多见的炎症细胞是( )。
A.中性粒细胞 B.嗜酸性粒细胞C.淋巴细胞 D.肥大细胞7. 商品蛋鸡中暑时的胸肌颜色( )。
A.暗红色 B.鲜红色 C.浅白色 D.基本正常8. 甲硝唑主要用于下列哪种情况( )。
A. 大肠杆菌病B. 抗滴虫和厌氧菌C. 需氧菌感染D. 真菌感染9. 下列动物专用抗菌药是( )。
A.环丙沙星 B.氧氟沙星 C.强力霉素 D.泰乐菌素10.被病毒污染的场地,进行消毒时,首选的消毒药是( )。
A.烧碱 B.双氧水 C.来苏儿 D.新洁尔灭11.解救弱酸性药物中毒时加用NaHCO3的目的是( )。
A. 加快药物排泄B. 加快药物代谢C. 中和药物作用D. 减少药物吸收12.国家强制免疫的动物疫病不含( )。
A.禽流感 B.蓝耳病 C.猪瘟 D.新城疫13.鸭传染性浆膜炎的病原为( )。
2013世奥赛五年级a卷

---------------------------------- 世界奥林匹克数学竞赛(中国区)选拔赛 第十届世界奥林匹克数学竞赛(中国区)选拔赛 最后他做完所有题目得了 80 分。
则奥斑马答对了 题。
---------------------------------------------------------------------------------7. 奥斑马参加数学比赛,一共有三十道题,答对一题得 7 分,答错一题扣 3 分。
世界奥林匹克数学竞赛(中国区)选拔赛---------------------------------------装-----------------------------订---------------------------线---------------------------------- 2.阿傻和阿瓜看同一本书,阿傻从 2011 年 8 月 1 日开始看,每天看 20 页,阿瓜则从 2011 年 8 月 9 日开始看,每天看 36 页。
过了若干天后,两人恰好同时把书看完,那么这本书 共有多少页?3. 带领 39 只小羊到一块青草地上准备过冬。
已知青草地上的草匀速生长,如果每只羊(包含喜羊羊)每天吃青草 1 千克,24 天可以吃完;如果每只羊每天吃 2 千克青草,8 天就吃完全部青草。
如果喜羊羊要求整个冬天每天都有青草吃,而且要保持青草既不增加也不减少。
那么每天每只羊只能吃多少千克青草?4.如图以右图的 10 个黑点作为顶点,可以作出多少个三角形? 三、综合素质题。
(10 分) 某校师生共为舟曲灾区捐款 46200 元,经统计发现,他们各自所捐的钱数,共 有 10 种不同档次,最低档次共有 10 人,而每上升一个档次,捐款人数就减少 1 人;且从第二档次开始,以后各档次每人捐款的钱数,分别为最低档次每人捐款钱数的 2 倍、3 倍、4 倍、……10 倍,那么捐款最多的人捐款多少元? 四、数学与生活。
2013第十三届中环杯五年级初赛详解

A O
D
B
E
C
【分析】平行线,三角形等积变形,勾股定理; 中等难度题, 要对平行线的判定较为熟悉,同时看到高要想到垂直,顺势使用勾股 定理求直角三角形边长 【解析】因为 S S S ABO DCO ,所以 S ABC DCB ,由于两个三角形共用底边 BC ,所以两 个三角形 BC 边上的高相等,于是 AD 与 BC 平行,所以三角形 ACE 中, CE 边上 的高为 15 厘米。 又在直角三角形 CDE 中,由勾股定理,可知
137 72 9864 , 137 73 10001 ,所以共有 72 8 1 65 个满足要求的数。
11. 小明带 24 个自制的纪念品去伦敦奥运会卖。 早上每个纪念品卖 7 英镑, 卖出的纪念品不 到总数的一半。下午他对每个纪念品的价格进行打折,折后的价格仍是一个整数。下午 他卖完了剩下的纪念品,全天共收入 120 英镑。那么早上他卖出了( )个纪念品? 【分析】不定方程整数解,因数分解; 中等难度题, 有耐心的选手可以直接枚举出答案, 对不定方程掌握得比较熟练的也 可通过不定方程迅速解出答案。 【解析】法一:枚举法 早上最多卖出 11 个
8 K 1 ,共有 13 个学生,蛋糕店有 13 8 7 97 或 13 7 6 97 块蛋糕。
8. 一个正方形纸,如图所示折叠后,构成的图形中角 x 的度数是(
)度?
x
【分析】角,正方形、等边三角形,特殊的直角三角形; 此题略有难度,需要对基本图形比较熟悉,同时对特殊的直角三角形有了解。 【解析】
43 120 11 7 43 11 7 13 13 25 10 7 50 10 7 14 7 9 7 57 9 7 15 3.8
2013年5年级世奥赛试题与详细答案

参考答案(六六老师详解版本)一、填空题1、2×(99+97+……+3+1)=2×250=50002、4.6×4.9=22.543、设6次的平均分为a ,则后4次的平均分为a +4.8,第一、二、六次的平均分为a -3.2 第一、二次的总分为6a -4×(a+4.8)=2a -19.2 第六次的得分为3×(a -3.2)-(2a -19.2)=所以,前五次的总分为6a -(a +9.6)=5a -9.6,平均分为a -1.92 于是,前五次的平均分比六次的平均分低了1.92分4、f (13)=40 次数 01234567891011 12 13 …… f 40 20 10 ^5 16 8 4 2 1 4 2 142……从第六次开始,每三次一个周期,4→2→1循环,所以,第2013次的结果是45、这个三位数加1就能被2和5同时整除,所以个位数字是9, 这个数被3整除余1,所以最大的三位数为9796、分类计数:一个三角形构成,19个 四个三角形构成,10个, 九个三角形构成,3个, 总共19+10+3=32(个)7、(鸡兔同笼)两个大人的家庭可以节约20元,两个大人一个小孩的家庭可以节约10元, 假设9个全是两个大人的家庭,则共可以节约20×9=180(元)所以两个大人一个小孩的家庭有(180-120)÷(20-10)=6(个) 所以共有游客3×2+6×3=24(人)8、8(124)232EFC EFO FOC AFO FOB AOB S S S S S S ∆∆∆∆∆∆=+=+==⨯-÷=(平方厘米)9、这个数除以21余2,这样的数可以排列如下:2、23、44、65、86、……另外除以5余1,所以最小的数为86.10、先将另三个人排好队共3×2×1=6(种) 然后小美和欧欧插空,共有4×3=12(种) 所以一共有6×12=72(种)11、(牛吃草问题)骑车人的速度为(1100×5-1500×3)÷(5-3)=500(米/分) 开始时的距离为(1100-500)×5=(1500-500)×3=3000(米) 所以快车的速度为500+3000÷2=2000(米/分)12、设长方形的长为a ,宽为b ,图中六个长方形的周长和为24+26+28+34+32+30=174 所以6a +4b=174长方形的周长为2a +2b=87-a要使周长最小,则要求a 最大,所以要求b 最小。
2013第十三届中环杯四年级决赛试题

第十三届“中环杯”小学生思维能力训练活动四年级决赛题一、填空题(每小题5分,共50分):1、计算:999999÷185185×20=( )。
2、从1开始做乘法:1×2×3…,当乘到( )时,乘积的最后100个数字第一次全部是0。
3、如图所示网格中,要从A到B,方向只能向右或向上,不能经过C以及D,有( )条不同的路径。
4、一个介于500-800之间的三位自然数,正好等于它各位数字和的36倍,则这个自然数是( )。
5、如图所示,有A、B、C、D、E、F共6家商店位于某一条街的两边,商店A位于街上的阴影部分,其他商店的位置关系如下:a、A店的右边是书店;b、书店的对面是花店;c、花店的旁边是面包店;d、E店在D店的对面;e、酒店在E店的旁边;f、E店和文具店在街道的同一侧。
那么,A店是( )店。
6、123123…123÷13的余数是( )。
(2013个123)7、李老师要在下午3时出门去探望朋友。
他估计时间快到了,一看家里的时钟,发现时钟早在中午12时10分就已经停了。
他给钟换好电池没有拨针就离开家了(换电池时间不计)。
到朋友家时,得知当时时间离3时还差10分。
晚上11时,李老师从朋友家出来,回到家看见家中的时钟才9时。
如果李老师来回路上用时相同,他家的钟停了( )小时( )分钟。
8、某商场在春节有促销抽奖活动,规则如下:在暗箱内有四种颜色的小球各若干个,购物每满100元可以摸球一次。
如果消费者能凑齐同样颜色的小球两个就可以参加一次抽奖,若参加抽奖5次都没有中奖则可获得安慰奖一份。
如果消费者想百分之百获奖,至少需要在该商场购买( )元的商品。
9、两个正方形如图放置,图中的每个三角形都是等腰直角三角形。
若其中较小正方形的边长为12厘米,那么较大正方形的面积是( )平方厘米。
10、一支队伍以每分钟100米的速度行进。
此时接到上级命令,要改变目的地,传令员骑摩托车以30千米/时的速度从队伍前端到队伍尾端传达命令后又立即回到队伍前端,共用时3分钟。
【最新2018】中环杯决赛试题-优秀word范文 (4页)

本文部分内容来自网络整理,本司不为其真实性负责,如有异议或侵权请及时联系,本司将立即删除!== 本文为word格式,下载后可方便编辑和修改! ==中环杯决赛试题篇一:201X年第十三届中环杯决赛五年级试题和答案解析篇二:第十四届中环杯小学三年级决赛试题第十四届“中环杯”小学生思维能力训练活动三年级决赛一、填空题:(每小题5分,共50分,请将答案填写在题中横线处)1. 计算:201X-37×13-39×21=______2. 定义:a⊙b=a×b+(a-b),则(3⊙2)⊙4=_____3. 王老师有45颗糖,他决定每天都吃掉一些。
由于这些糖很好吃,所以从第二天开始,他每天吃的糖的数量都是比前一天多3颗,5天正好吃完所有的糖,那么,王老师第二天吃了_____颗糖。
4. 如图,每个小正方形的边长都是4厘米,则阴影部分的面积为______平方厘米。
5. 甲、乙两人比赛射箭,每一局,胜利的一方得7分,输掉的一方减2分,平局则两人各得2分。
比赛10局后,两人的分数之和为43分。
那么,比赛中有_____局平局。
6. 如图,这是一个城市街道的分布图,从A点走到B点的最短路径有P条,从C点走到B点的最短路径有Q条,则P-2Q+201X=______7. 甲、乙、丙三人做游戏,甲心里想一个两位数,然后将这个两位数乘以100,乙心里想一个数,然后将这个一位数乘以10,丙心里想一个一位数,然后将这个数乘以7。
最后,将三个人的乘积全部加起来,得到的结果是2024。
那么,甲、乙、丙原先心里所想的数之和为________8. 将27个数字排成一排,这27个数字里有3个数字1,3个数字2,??3个数字9。
要求第一个1与第二个1之间有一个数字,第二个1与第三个1之间有1个数字;第一个2与第二个2之间有2个数字,第二个2个与第三个2之间有2个数字;??;第一个9与第二个9之间有9个数字,第二个9与第三个9之间有9个数字。
十三届五年级中环杯决赛答案

第十三届“中环杯”中小学生思维能力训练活动 五年级决赛答案
一、填空题: 1. 答: 25502400
1 3 1 3 1 2 3 2 3 2 99 3 99 3 99 1 3 1 3 1 1 2 3 2 3 2 1 99 3 99 3 99 1 99
13225, 24336 ,满足我们的要求。
3/6
第十三届“中环杯”中小学生思维能力训练活动五年级决赛答案
2. 答: 486 设对一个 2 k 的表格进行染色,有 N k 种染色方法。假设 2 k 表格的最后 一 列
的颜色从上到下依次 R、G,则对于 2 k 1 的表格,所增加的一列可以有 3 种染色 方法,如下图。从而得到递推式: Nk 1 3Nk 。利用乘法原理我们得 N1 3 2 ,所 以 N5 2 35 486
用相似模型我们知道
4/6
第十三届“中环杯”中小学生思维能力训练活动五年级决赛答案
知道 AE 、 BF 与 GC 交于同一点,这个点就是点 H ,所以点 H 在线段 GC 上。 20 16 cm 。过点 I 作 KJ AB ,则利用相似 如图 5,我们推出 GH GC CH 4 9 9 16 KI GI GH 16 9 5 c m从 而 推 出 模型我们有 , 而 K I I J K J A D , IJ IB AB 5 45 80 1 1 16 80 640 2 KI cm ,所以 SGHI GH KI cm 61 2 2 9 61 549
R 2T 1 20 X 2T R X 19 。 由于这里一共出现了 10 个字母, 代表了 10 个 F 1 S
2013第十三届中环杯三年级决赛详解

第十三届“中环杯”小学生思维能力训练活动三年级决赛一、填空题(5’×10=50’)1.计算:12345+23451+34512+45123+51234=(166665)。
速算巧算:原式=(1+2+3+4+5)×11111=1666652.水果店原来有156箱苹果和84箱橘子。
苹果和桔子各卖出相等的箱数后,剩下的苹果箱数比橘子箱数多2倍。
苹果和桔子各卖出(48)箱。
和差倍:156-84=72,72÷2=364,84-36=483.在一次学科测试中,小芳的语文、数学、英语、科学4门学科的平均分是88分,前2门的平均分是93分,后3门的平均分为87分,小芳的英语测试成绩是(95)分。
(本题英语成绩无法确定,疑为求数学的成绩)平均数:93×2=186,87×3=261,88×4=352,186+261-352=954.星期天,小军帮助妈妈做一些家务。
各项家务花的时间为:叠被子3分钟,洗碗8分钟,用洗衣机洗衣服30分钟,晾衣服5分钟,拖地板10分钟,削土豆皮12分钟。
经过合理安排,小军至少要用(38)分钟才能完成这些家务。
统筹规划:洗衣机一边洗衣服,小军一边完成其他任务,3+8+5+10+12=385.图中共有16个方格,要把A、B、C、D四个不同的棋子放在四个不同的方格里,并使每行,每列只能出现一个棋子。
共有(576)种不同的放法。
棋盘问题:4!×4!=576或16×9×4×1=5766.如图,正方体的每个角上有一个小圆圈。
请你把2至9这8个数分别填入小圆圈内,使正方体6个面每一面上的4个数之和都相等。
数阵图:2+3+...+9=44,44÷2=22,22=2+3+8+9=2+4+7+9=2+5+7+8=2+5+6+9,结果如图7.如图是某地区所有街道的平面图。
甲、乙两人同时分别从A、B出发,以相同的速度行进。
