三角形重心向量性质的引申及应用

合集下载

三角形外心内心重心垂心与向量性质

三角形的“四心”之青柳念文创作所谓三角形的“四心”是指三角形的重心、垂心、外心及心坎.当三角形是正三角形时，四心重合为一点，统称为三角形的中心.一、三角形的外心定义：三角形三条中垂线的交点叫外心，即外接圆圆心.ABC ∆的重心一般用字母O 暗示.性质：1.外心到三顶点等距，即OC OB OA ==.2.外心与三角形边的中点的连线垂直于三角形的这一边，即AB OF AC OE BC OD ⊥⊥⊥,,.3.向量性质：若点O 为ABC ∆所在的平面内一点，知足AC OA OC CB OC OB BA OB OA ⋅+=⋅+=⋅+)()()(，则点O为ABC ∆的外心.二、三角形的心坎定义：三角形三条角平分线的交点叫做三角形的心坎，即内切圆圆心.ABC ∆的心坎一般用字母I 暗示，它具有如下性质：性质：1.心坎到三角形三边等距，且顶点与心坎的连线平分顶角.2.三角形的面积＝⨯21三角形的周长⨯内切圆的半径． 3.向量性质：设()+∞∈,0λ，则向量||||(AC AB AP +=λ，则动点P的轨迹过ABC ∆的心坎.三、三角形的垂心定义：三角形三条高的交点叫重心.ABC ∆的重心一般用字母H 暗示.性质：1.顶点与垂心连线必垂直对边，即AB CH AC BH BC AH ⊥⊥⊥,,.2.向量性质：结论1：若点O 为ABC ∆所在的平面内一点，知足OA OC OC OB OB OA ⋅=⋅=⋅，则点O 为ABC ∆的垂心.结论2：若点O 为△ABC 所在的平面内一点，知足222222AB OC CA OB BC OA +=+=+，则点O 为ABC ∆的垂心.四、三角形的“重心”：定义：三角形三条中线的交点叫重心.ABC ∆的重心一般用字母G 暗示.性质：G 的连线必平分对边.2.重心定理：三角形重心与顶点的间隔等于它与对边中点的间隔的2倍.即GF GC GE GB GD GA 2,2,2===3.重心的坐标是三顶点坐标的平均值．即3,3CB A GC B A G y y y y x x x x ++=++=.4.向量性质：（1）0=++GC GB GA ；（2）)(31PC PB PA PG ++=.。

三角形重心的向量特征及应用

三角形重心的向量特征及应用
三角形重心，又称重心点，是指在平面内三条边确定的三角形中，一条共线虚
线所过之处。

它是由三角形顶点所确定的重心和三角形两条中线所确定的重心所组合而成。

在三角形中，重心总是位于各边的垂直平分线的交点，也就是三角形的原点。

三角形重心具有一定的向量特征，可以用来表征和求解三角形中不同点的距离。

若设三角形的三顶点分别是A(x1,y1)、B(x2,y2)、C(x3,y3)，则计算其重心的公
式为(x1+x2+x3)/3, (y1+y2+y3)/3，这些新生成的点就是重心G(x, y），在三角
形形成之前，它可以用来表示把三角形本身连接构成的三角形内某点到其重心距离的向量。

三角形重心的应用，在计算机图形学领域广泛研究"重心法"，重心法是根据三
角形重心分配各顶点的权重，以近似三角形的曲线和表面。

重心法可以提高三角形在屏幕中的精度，提高图片的清晰度和质量。

另外，在结构力学中，重心法也用于求解实体块的杆件，单元，复杂平面或几何体的平衡结构力学；在生物领域中也用来推导复杂的系统和模型与外部输入的相互作用。

总之，三角形重心具有一定的向量特征，在计算机图形学、结构力学和生物领
域有重要应用意义，但它也是一个内涵非常深奥的概念，它可以用来分析研究一些大自然无法量化的事物。

三角形“四心”问题与向量的关系

三角形“四心”问题与向量的关系一、三角形的重心与向量重心是三角形三条中线的交点，它到三角形顶点的距离与它到该顶点的对边中点的距离之比为2∶1.在向量表达形式中，设点G是△ABC所在平面内的一点，则当点G是△ABC 的重心时，有+ +=0或=（++）（其中P为平面内的任意一点）；若+ += 0，则点G 是△ABC的重心；设λ∈[0，+∞），则λ（+）是BC边上的中线AD 上的任意向量，其所在直线必过重心.例1 已知O是△ABC所在平面内的一点，若+ += 0，则点O是△ABC的A.外心B.内心C.重心D.垂心解若+ +=0，则+ =-.以，为邻边作平行四边形OAC1B.设OC1与AB交于点D ，可知D为线段AB的中点，由+ =，可得=-，即C，O，D，C1四点共线.同理，设AO与BC交于点E，BO与AC交于点F，可知AE，BF也是△ABC的中线.所以，点O 是△ABC的重心.选C.例2 已知O是平面内的一个定点，A，B，C是平面内不共线的三个点，动点P满足=+λ?（+），λ∈[0，+∞），动点P的轨迹一定通过△ABC的A.重心B.垂心C.外心D.内心解由已知有=λ（+）.由正弦定理可知||sin B=||sin C，则=（+）.设边BC的中点为D，则由平行四边形法则，可知点P在边BC的中线AD所在的射线上，所以动点P 的轨迹一定通过△ABC的重心.选A.二、三角形的垂心与向量垂心是三角形三条高的交点，它与顶点的连线垂直于该顶点的对边.在向量表达形式中，若H是△ABC的垂心，则?=?=?或2+2=2+2=2+2；若?=?=?，则H是△ABC的垂心；设λ∈（0，+∞），则向量λ（+）垂直于边BC，该向量所在的直线通过△ABC的垂心.例3 已知O是△ABC所在平面内的一点，?=?=?，则点O是△ABC的A.外心B.内心C.重心D.垂心解由?=?，得?-?=0，即?（-）=0，可得?=0，所以⊥.同理可证⊥，⊥，所以点O是△ABC的垂心.选D.例4 已知O是平面内的一个定点，A，B，C是平面内不共线的三个点，动点P满足=+λ（+），λ∈（0，+∞），则动点P 的轨迹一定通过△ABC的A.重心B.垂心C.外心D.内心解由已知得=λ（+），则?=λ（+）=λ?（+）=0，可知⊥，所以动点P的轨迹通过△ABC的垂心.选B.三、三角形的内心与向量内心是三角形三条内角平分线的交点，也是三角形内切圆的圆心，它到三角形三边的距离相等.在向量表达形式中，若点O是△ABC的内心，则有||?+||?+||?=0；若||?+||?+||?= 0，则点O是△ABC的内心；设λ∈（0，+∞），则向量λ（+）所在的直线必过三角形的内心.例5 已知O是平面内的一个定点，A，B，C是平面内不共线的三个点，动点P满足=+λ?（+），λ∈（0，+∞），则动点P 的轨迹一定通过△ABC的A.外心B.内心C.重心D.垂心解由已知得= λ（+），是方向上的单位向量，是方向上的单位向量.根据平行四边形法则，可知以和为邻边构成的平行四边形是菱形，点P在∠BAC的角平分线上，故动点P 的轨迹通过△ABC的内心.选B.四、三角形的外心与向量外心是三角形三条边的中垂线的交点，也是三角形外接圆的圆心，它到三角形三个顶点的距离相等.在向量表达形式中，若点O是△ABC的外心，则（+）?=（+）?=（+）?=0（或||=||=||）；若||=||= ||，则点O是△ABC的外心.例6 已知O是平面内的一个定点，若A，B，C是平面内不共线的三个点，动点P满足=+λ（+），λ∈（0，+∞），则动点P的轨迹一定通过△ABC的A.重心B.垂心C.外心D.内心解设线段BC的中点为D，则=.由已知有=λ（+）.由?=λ（+）=λ?（+）=0，可知DP⊥BC，所以点P在线段BC的垂直平分线上，动点P的轨迹通过△ABC的外心.选C.五、三角形的“四心”与向量的综合例7 设H，G，O分别是△ABC的垂心、重心、外心，求证：H，G，O三点共线.证明如右图，圆O为△ABC的外接圆.作圆O的直径BD，连接DA，DC，有=-，DA⊥AB，DC⊥BC，AH⊥BC，CH⊥AB，则CH∥DA，AH∥DC，可知AHCD是平行四边形.=+=+=+-=++，故=++.由点G是△ABC的重心，可知=（++）.于是可得=，所以H，G，O三点共线.（责任编校？筑冯琪）。

三角形重心的向量形式及推论的巧妙应用

三角形重心的向量形式及推论的巧妙应用
三角形重心是一种重要的几何概念，它是三角形内部的一个特殊点，
它的位置可以用向量形式表示。

三角形重心的向量形式及推论的巧妙
应用，可以用来解决许多几何问题，下面我们就来看看它的应用。

首先，三角形重心的向量形式可以用来求解三角形的重心坐标。

假设
三角形的三个顶点分别为A，B，C，则三角形重心的向量形式为：
G=(1/3)A+(1/3)B+(1/3)C。

这样，我们就可以根据三角形的三个顶点
的坐标，求出三角形重心的坐标。

其次，三角形重心的向量形式可以用来求解三角形的外接圆半径。

假
设三角形的三个顶点分别为A，B，C，则三角形外接圆的半径为：
r=|AB|+|BC|+|CA|/3。

这样，我们就可以根据三角形的三个顶点的坐标，求出三角形外接圆的半径。

最后，三角形重心的向量形式可以用来求解三角形的面积。

假设三角
形的三个顶点分别为A，B，C，则三角形的面积为：
S=|AB|*|BC|*|CA|/4。

这样，我们就可以根据三角形的三个顶点的坐标，求出三角形的面积。

以上就是三角形重心的向量形式及推论的巧妙应用，它可以用来解决
许多几何问题，如求解三角形的重心坐标、外接圆半径和面积等。

三角形重心向量性质的引申及应用

三角形重心向量性质的引申及应用新化县第三中学肖雪晖平面向量是高中数学实验教材中新增的一章内容．加入向量，一些传统的中学数学内容和问题就有了新的内涵．在数学教学中引导学生积极探索向量在中学数学中各方面的应用，不仅可深人了解数学教材中新增内容和传统内容的内部联系，构建合理的数学知识结构，而且有利于拓展学生的想像力，激发创新活力，显现出向量作为一个工具在数学中的重要性．下面就向量与三角形的重心关系加以引申和应用．三角形重心向量形式的充要条件：设O 为ABC 所在平面上一点，O 为ABC 的重心⇔0OA OB OC ++=证明：先证必要性：如图1以,OB OC为邻边作平行四边形OBDC,则OD OB OC =+ .又0OA OB OC ++= ，则OB OC OA +=- ，所以,OA OD -=O 为AD 的中点，且A 、O 、D 共线.又E 为OD 的中点,因此，O 是中线AE 的三等分点，且23OA AE =即O 为ABC 的重心.再证充分性:设BO 、OC 与AC 、AB 分别交于F 、G 点，则由三角形的中线公式可得，0AE BF CG ++=又O 为ABC 的重心，得222,,333AO AE BO BF CO CG ===所以0OA OB OC ++=引申1若O为ABC 内任一点，则有...0OAB OBC OAC S OC S OA S OB ++=证明：如图2,设111213,,,OA OA OB OB OC OC λλλ===且O 为ABC 的重心，则1230OA OB OC λλλ++=且AOB BOC AOC S S S == ,记为S,那么，12111sin 12.1sin 2OAB OA OB AOBS SOA OB AOB λλ⋅∠==⋅∠ 即12.AOB SS λλ=同理可得23OBc SS λλ=，13.OAC SS λλ=所以123::::.OBC OAC OAB S S S λλλ= 则...0OAB OBC OAC S OC S OA S OB ++=引申2 如图3,已知点G 是ABC 的重心，过G 作直线与AB 、AC 两边分别交于M 、N两点，且11,,3AM xAB AN y AC x y==+= 则证明：点G 是ABC 的重心，知0GA GB GC ++=,得()()0AG AB AG AC AG -+-+-= 有1()3AG AB AC =+又M 、N 、G 三点共线（A 不在直线AM 上）,于是存在,λμ，使得)AG AM AN λμ=+ (且1λμ+=),有AG xAB yAC λμ=+ 1()3AB AC =+得113x y λμλμ+=⎧⎪⎨==⎪⎩于是得113x y += 运用引申1、引申2可以解决许多数学问题，使解题过程简单。

三角形重心性质的向量表示及其推广

三角形重心的性质的向量表示与推广及其应用吴家华（四川省遂宁中学校 629000）摘要本文给出了三角形重心性质的一个向量表示并进行了推广，同时介绍了它们的简单应用.关键词三角形、重心、向量、推广我们知道，三角形的三条中线相交于一点，这点叫做三角形的重心，重心到顶点的距离与到对边中点的距离的比为1:2，即重心到顶点的距离等于该中线长的三分之二. 重心的这一性质如果我们用向量来表示的话，则有下列结论：定理1 设G 为ABC ∆的重心，则)(31AC AB AG +=；反之也成立. 证明：设BC 的中点为D ，则)(21AC AB AD +=. ∵G 为ABC ∆的重心，∴AD AG 32=. ∴)(31)(213232AC AB AC AB AD AG +=+⋅==.故)(31AC AB AG +=.反之，若)(31AC AB AG +=，则AC AB AG +=3，即0)()(=-+-+AC AG AB AG AG ，0=++CG BG AG ，∴0=++GC GB GA ,故G 为ABC ∆的重心.定理1 得证.笔者在解题研究中，尝试把重心G 改为ABC ∆所在平面内的任意一点，发现定理1可以推广为下列一般形式：定理 2 设分别过ABC ∆的两个顶点C B ,的直线相交于一点P ，且分别交对边所在直线于点M N ,. 若AB AM λ=，AC AN μ=，则AC AB AP λμλμλμμλ--+--=1)1(1)1(.证明：如图1所示，设MC t MP =，NB s NP =，则Mp NBCAACt AM t AM AC t AM MC t AM MP AM AP +-=-+=+=+=)1()(AC t AB t +-=)1(λ.ABs AN s AN AB s AN NB s AN NP AN AP +-=-+=+=+=)1()(AB s AC s +-=)1(μ.∵AB 与AC 不共线，∴⎩⎨⎧=-=-t s s t )1()1(μλ⎪⎪⎩⎪⎪⎨⎧--=--=⇒λμμλλμλμ1)1(1)1(s t . 故AC AB AP λμλμλμμλ--+--=1)1(1)1(.定理2得证.显然，定理2的结论是建立在ABC ∆的基础上的，那么，我们在应用定理2解决问题时就需要一个三角形作依托，也就是说，我们解决问题的关键在于这个三角形的选择. 因此，我们不妨把定理中的这个ABC ∆叫做基底三角形（注意，顶点C B A ,,按逆时针顺序），简称为“基三角”.笔者在教学和解题实践中发现，上述三角形重心性质的向量表示及其推广在解决平面向量和平面几何问题中具有较广泛的应用.下面举例说明之.例1.如图2所示，在ABC ∆中，E D ,分别为AC AB ,的中点，CD 与BE 交于点F ，设a AB =，b AC =，b n a m AF +=，若向量),(n m s =，则=||s （）.A 32 .B 32 .C 65 .D 34图2解：由已知可知，F 为ABC ∆的重心，则由定理1可得：b a b a AF 3131)(31+=+=.∵b n a m AF +=，且a ，b 不共线， ∴31==n m ，则)31,31(=s . ∴32)31()31(||22=+=s ,故选B . 例2.P 是ABC ∆内一点，)(31AC AB AP +=，则ABC ∆的面积与ABP ∆的面积的比值为（）.A 2 .B 3 .C 23.D 6 解：∵)(31AC AB AP +=，∴由定理1知，P 是ABC ∆的重心. ∴31=∆∆ABC ABP S S ,即ABC ∆的面积与ABP ∆的面积的比值为3. 故选B .例3.如图3所示，在OAB ∆中，a OA =，b OB =，N M ,分别是边OB OA ,上的点，且a OM 31=，b ON 21=.设AN 与BM 交于点P ，用向量a ，b 表示OP .图3解：取OAB ∆为基底三角形，因为N M ,分别是边OB OA ,上的点，且a OM 31=，b ON 21=.∴31=λ，21=μ,则由定理2，得：b a b a OP 52511)1(1)1(+=--+--=λμλμλμμλ，即b a OP 5251+=. 例4.如图4所示，在OAB ∆中，a OA =，b OB =，设点M 分AB 所成的比为1:2，点N 分OA 所成的比为1:3，而OM 和BN 交于点P ，试用a 和b 表示OP .解：取ABO ∆为基底三角形，连接AP ，因为点M 分AB 所成的比为1:2，点N 分OA所成的比为1:3，∴AB AM 32=，AO AN 41=，则32=λ，41=μ. 由定理2得：AO AB AO AB AP 101531)1(1)1(+=--+--=λμλμλμμλ.图4∴OA OA OB OA AO AB OA AP OA OP 101)(5310153--+=++=+= b a OB OA 5310353103+=+=，即b a OP 53103+=.例5.如图5所示，在ABC ∆中，点M 是BC 的中点，点N 在边AC 上，且NC AN 2=，AM 与BN 相交于点P ，求PM AP :的值.图5解：取CAB ∆为基底三角形，连接PC ，则由已知得：CA CN 31=，CB CM 21=， ∴31=λ，21=μ. 由定理2得：CB CA CB CA CP 52511)1(1)1(+=--+--=λμλμλμμλ,∴)(5251AC AB AC AC AP -+-=-,即AB AC AP 5252+=.∵点M 是BC 的中点，∴)(21AC AB AM +=. ∴AM AP 54=，即1:4:=PM AP .∴1:4:=PM AP . 例6.（2014年武汉高三调研）如图6所示，在ABC ∆中，AC AN 31=，P 是BN 上的一点，若AC AB m AP 112+=，则实数m 的值为（）.A 119 .B 115 .C 113 .D 112解：取CAB ∆为基底三角形，延长AP 交BC 于点M ，连接PC . ∵AC AN 31=，∴CA CN 32=，即32=λ. 设CB CM μ=，则由定理2，得：CB CA CB CA CP μμμμλμλμλμμλ2323)1(21)1(1)1(-+--=--+--=.则CB CA CA CP AP μμμ23231-+--=-=.又∵CB m CA m CA CA CB m AC AB m AP ++-=--=+=)112(112)(112，且CA ， CB 不共线，∴⎪⎪⎩⎪⎪⎨⎧=-+=-m m μμμ23112231⎪⎪⎩⎪⎪⎨⎧==⇒11575m μ.故应选.BPMNCBA。

三角形重心、垂心、内心、外心的向量性质及简单应用

2019 年第 3 期 (下)
中学数学研究
41
三角形重心、垂心、内心、外心的向量性质及简单应用
广东省珠海市斗门区第一中学 (519100) 陈水松
一、三角形四心的表述与性质
(一) 重心——三角形三条边上的中线的交点叫做三角
形的重心. 重心将中线长度分成 2: 1 的两部分. 1. −O→A + −O−→B + −O−→C = −→0 ⇔O 是 △ABC 的重心.
AC BC −→ + −−→
.
|AC| |BC|
|−B−B+−−→ →CCb| −B)−→C, 所
= 以
4.
−−→ PO
=
−→ aP A
−−→ + bP B + a+b+c
−−→ cP C
⇔
O
为
△ABC
的内心,
P 为平面上任意点.
(二) 垂心——三角形三条高线的交点叫做三角形的垂
证明
因为
O
为
△ABC
证法 1 设 O(x, y), A(x1, y1), B(x2, y2), C(x3, y3),
−→ −−→ −−→ OA+OB+OC
=
−→0
⇔

x=
x1 + x2 + x3
(x1 − x) + (x2 − x) + (x3 − x) = 0 (y1 − y) + (y2 − y) + (y3 − y) = 0
=
−→0 ,
所以
−→ AO
=
2−O−→D,
所以
A、O、D
三点共线,

三角形四心的向量性质及应用（详细答案版）

三角形“四心”的向量性质及其应用三角形“四心”的概念介绍(1)重心—三条中线的交点：重心将中线长度分成2：1；(2)外心—三边中垂线的交点(外接圆的圆心)：外心到三角形各顶点的距离相等；(3)垂心—三条高线的交点：高线与对应边垂直；(4)内心—三条内角平分线的交点(内切圆的圆心)：角平分线上的任意点到角两边的距离相等．工具：O 为ABC △内一点，则有：0+⋅+⋅∆∆∆OC S OB S OA S O O CA O BC 证明：作：OA S OA OCB ⋅=∆'，OB S OB OCA ⋅=∆'，S OC OAB =∆'不难得知：AOB COA BOC OC B S S OC OC OB OB S S ∆∆∆∆⋅=⋅=''''即BO C AO B CO A O C B S S S S ∆∆∆∆⋅⋅=''；同理==∆∆''''O B A O A C S S ''O C B BO C AO B CO A S S S S ∆∆∆∆=⋅⋅ 从而：O 为'''C B A ∆的重心，则+'OA +'OB 0'=OC ，得：0=⋅+⋅+⋅∆∆∆OC S OB S OA S O AB O CA O BC .一、三角形的重心的向量表示及应用知识：G 是ABC △的重心⇔)(31AC AB AG +=⇔0=++GC GB GA ⇔)(31OC OB OA OG ++= (O 为该平面上任意一点)变式：已知D E F ，，分别为ABC △的边BC AC AB ，，的中点．则0=++CF BE AD ．二、三角形的外心的向量表示及应用知识：O 是ABC △的外心⇔222||||||OC OB OA OC OB OA ==⇔== 02sin 2sin 2sin =⋅+⋅+⋅⇔OC C OB B OA A略证：C B A S S S O AB O CA O BC 2sin :2sin :2sin ::=∆∆∆，得：02sin 2sin 2sin =⋅+⋅+⋅OC C OB B OA A ;常用结论：O 是ABC △的外心⇒.2|| ;2||22AC AO AC AB AO AB =⋅=⋅ 三、三角形的垂心的向量表示及应用知识：H 是ABC △的垂心⇔HA HC HC HB HB HA ⋅=⋅=⋅⇔222222||||||||||||AB HC CA HB BC HA +=+=+0tan tan tan =⋅+⋅+⋅⇔HC C HB B HA A略证：C B A S S S H AB H CA H BC tan :tan :tan ::=∆∆∆，得：0tan tan tan =⋅+⋅+⋅HC C HB B HA A ；扩展：若O 是ABC △的外心，点H 满足：OC OB OA OH ++=，则H 是ABC △的垂心．证明：如图：BE 为直径，H 为垂心，O 为外心，D 为BC 中点；'有：为平行四边形AHCE EA CH AB EA AB CH EC AH BC EC BC AH ⇒⎪⎪⎭⎪⎪⎬⎫⇒⎭⎬⎫⊥⊥⇒⎭⎬⎫⊥⊥////进而得到：,//EC AH 且EC AH =，即：EC AH =；又易知：OC OB OD EC +==2；故：OA OH OC OB AH -=+=，即：OC OB OA OH ++=又：OG OC OB OA ⋅=++3（G 为重心），故：OG OH ⋅=3；故：得到欧拉线：ABC △的外心O ，重心G ，垂心H 三点共线(欧拉线)，且GH OG 21=．证毕．四、三角形的内心的向量表示及应用知识：I 是ABC △的内心⇔⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=⎭⎫⎝⎛-⋅=⎭⎫⎝⎛-⋅=⎭⎫⎝⎛-⋅0||||0||||0||||CB CB CA CA CI BC BC BA BA BI AC AC AB AB AI ⇔⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=⎭⎫⎝⎛+⋅=⎭⎫⎝⎛+⋅=⎭⎫⎝⎛+⋅0||||0||||0||||CA CA BC BC CI BA BA CB CB BI AC AC BA BA AI 0=⋅+⋅+⋅⇔IC c IB b IA a c b a OCc OB b OA a OI ++⋅+⋅+⋅=⇔cb a ACc AB b AI ++⋅+⋅=⇔ 0sin sin sin =⋅+⋅+⋅⇔IC C IB B IA A 注：式子中|||,||,|AB c CA b BC a ===，O 为任一点．略证：C B A c b a S S S IAB ICA IBC sin :sin :sin ::::==∆∆∆，得之．五．欧拉线：ABC △的外心O ，重心G ，垂心H 三点共线(欧拉线)，且GH OG 21=．（前已证）测试题一．选择题1．O 是ABC ∆所在平面上一定点，动点P 满足)(AC AB OA OP ++=λ，[)+∞∈,0λ ，则点P 的轨迹一定通过ABC ∆的( )A ．外心B ．内心C ．重心D ．垂心解析：点P 的轨迹为BC 边的中线（射线），选C2．(03全国理4)O 是ABC ∆所在平面上一定点，动点P 满足AC AB OA OP ++=λ，[)+∞∈,0λ ，则点P 的轨迹一定通过ABC ∆的( )A ．外心B ．内心C ．重心D ．垂心解析：AC AB OA OP ++=λ⇔AC AB AP +=λAC AB +必平分BAC ∠，理由如下：ADACABACACABAB=+==1111,1==，故四边形11DCAB为菱形，对角线AD平分一组对角，ADACAB=+必定平分11ACB∠，即BAC∠，从而ACABAP+=λ也平分BAC∠.故知点P的轨迹为A∠的内角平分线（射线），选 B3．O是ABC∆所在平面上一定点，动点P满足ACABOAOP++=λ，R∈λ，则点P的轨迹一定通过ABC∆的( )A．外心B．内心C．重心D．垂心解析：ACABOAOP++=λ⇔ACABAP+=λ由BCACBCABBCACBCABBCAP+=+=⋅λλ得：0|)|||(=+-=⋅BCBCBCAPλ，得BCAP⊥点P的轨迹为BC边的高线所在直线. 选D4．O是ABC∆所在平面上一定点，动点P满足ACABOAOP+=λ，[)+∞∈,0λ，则点P的轨迹一定通过ABC∆的( )A．外心B．内心C．重心D．垂心解析：由于CACCbBcBAB sin||sinsinsin||=⋅=⋅=，知点P的轨迹为BC边的中线（射线）,选C5．O是ABC∆所在平面上一定点，动点P满足2cos cosOB OC AB ACOPAB B AC Cλ⎛⎫+ ⎪=++⎪⎝⎭，R∈λ，则点P的轨迹一定通过ABC△的( )．A．外心B．内心C．重心D．垂心解析：0||||=+-=+=⋅+BCBCBCACBCABBCACAB知点P的轨迹为BC边的中垂线, 选A6．O是ABC∆所在平面上一定点，动点P满足])21()1()1[(31OCOBOAOPλλλ++-+-=，*R∈λ，则点P的轨迹一定通过ABC△的( )．A．内心B．垂心C．重心D．AB边的中点解析：])21()1()1[(31OCOBOAOPλλλ++-+-=OCOD3)21(3)22(λλ++-=（D为AB边的中点）知CDP,,三点共线（因1321322=++-λλ），故知点P 的轨迹为AB 边的中线所在直线，但是0≠λ，故除去重心. 选D 7．已知O 是ABC ∆的重心，动点P 满足)22121(31OC OB OA OP ++=,则点P 一定为ABC △的( ) A ．AB 边中线的中点 B ．AB 边中线的三等分点(非重心)C ．重心D ．AB 边的中点解析：)22121(31OC OB OA OP ++=OC OD 3231+=（D 为AB 边的中点）进而有：PC DP 2=，故为AB 边中线的三等分点(非重心), 选B8．在ABC △中，动点P 满足：CP AB CB CA ⋅-=222，则P 点轨迹一定通过△ABC 的( )Ａ．外心Ｂ．内心 C ．重心 D ．垂心解析：CP AB CB CA ⋅-=222⇔02))((222=⋅-+-=⋅--CP AB CA CB CA CB CP AB CA CB 进而有：02=⋅PD AB （D 为AB 边的中点），故知点P 的轨迹为AB 边的中垂线, 选A9．已知ABC ∆三个顶点C B A 、、及平面内一点P ，满足0=++PC PB PA ，若实数λ满足：AP AC AB λ=+，则λ的值为( )A ．2B ．23C ．3D ．6 解析：P 为重心，得)(31AC AB AP +=，故AP AC AB ⋅=+3,选C10．设点P 是ABC ∆内一点，用ABC S ∆表示ABC ∆的面积，令ABC PBC S S ∆∆=1λ，ABCPCA S S∆∆=2λ，ABC PAB S S ∆∆=3λ．定义),,()(321λλλ=P f ，若)61,31,21()(),31,31,31()(==Q f G f 则( )A ．点Q 在ABG ∆内B ．点Q 在BCG ∆内C ．点Q 在CAG ∆内D ．以上皆不对解析：G 为重心，画图得知, 选A11．若ABC ∆的外接圆的圆心为O ，半径为1，0=++OC OB OA ，则=⋅OB OA ( )A ．21 B ．0 C ．1 D ．21- 解析：由OC OB OA -=+，平方得知, 选D12．O 是平面上一定点，C B A 、、是平面上不共线的三个点，若222OB BC OA =+222AB OC CA +=+，则O 是ABC ∆的( )A ．外心B ．内心C ．重心D ．垂心解析：由2222CA OB BC OA +=+⇔2222BC CA OB OA -=-BA BC CA OB OA BA BC CA BC CA OB OA OB OA ⋅-=+⋅⇔+-=+-⇔)()())(())(( 0)2()(=⋅=-++⋅⇔OC BA CA BC OB OA BA ，得AB OC ⊥；同理得：AC OB ⊥,BC OA ⊥，故为垂心, 选D 13．(06陕西)已知非零向量AB 与AC 满足0||||=⋅⎭⎫⎝⎛+BC AC AC AB AB 21||||=AC AC AB AB , 则ABC ∆为( ) A ．三边均不相等的三角形 B ．直角三角形 C ．等腰非等边三角形 D ．等边三角形解析：21||||=AC AC AB AB 0||||=⋅⎭⎫⎝⎛+BC AC AC AB AB ：表明A ∠的内平分线也垂直于BC （三线合一），知ABC ∆等腰；21||||=AC AC AB AB ：得到︒=∠60A ；两者结合得到ABC ∆为等边三角形. 选D 14．已知ABC ∆三个顶点C B A 、、，若CA BC CB AB AC AB AB ⋅+⋅+⋅=2，则ABC ∆为( )A ．等腰三角形B ．等腰直角三角形C ．直角三角形D ．既非等腰又非直角三角形解析：CA BC CB AB AC AB AB ⋅+⋅+⋅=2CA BC AB CA BC CB AC AB ⋅+=⋅++⋅=2)( 得到：0=⋅CA BC ，得：︒=∠90C ,选C 二．填空题15．ABC ∆的外接圆的圆心为O ，两条边上的高的交点为H ，)(OC OB OA m OH ++=，则实数m = 1 ．解析：直接用结论16．ABC ∆中，7,3,1===BC AC AB ，O 为重心，则=⋅AC AO27．解析：)9(31)(31)(312+⋅=+⋅=+=⋅AC AB AC AC AB AC AC AB AC AO 利用：CB AC AB =-，两边平方得.23=⋅AC AB 故27)923(31=+=⋅AC AO17．点O 在ABC ∆内部且满足032=++OC OB OA ，则:ABC S ∆=∆AOC S 3 ．解析：法1：利用工具结论易知：AOB COA BOC S S S ∆∆∆=::3:2:1，得:ABC S ∆=∆AOC S 32:6= 法2：0422232=+=+++=++OD OE OC OB OC OA OC OB OA （E 为AC 的中点，D 为BC 的中点）易得：D O E ,,三点共线，且OD EO 2=，从而得到：ABC ADC AOC S S S ∆∆∆==3132. 法3：作：OA OA ='，OB OB 2'=，OC OC 3'=则+'OA +'OB 0'=OC ，则O 为'''C B A ∆的重心，则：''''''O B A O A C O C B S S S ∆∆∆==.设为S又⎪⎩⎪⎨⎧======∆∆∆∆∆∆SS SS S S S S S AOB OB A COA OA C BOC OC B 236'''''' 从而得：331:13:)236(:==++=∆∆S S S S S S COA ABC ． 18．点O 在ABC ∆内部且满足AC AB AO 5152+=，则:ABC S ∆=∆AOB S 5 ．解析：法1：AC AB AO 5152+=，用O 拆开得：022=+⋅+⋅OC OB OA ， 'A 'B 'C O)(A BC利用工具结论易知：AO B CO A BO C S S S ∆∆∆=::1:2:2，则:ABC S ∆51:5==∆AO B S 法2：AC AD AC AB AO 51545152+=+=，（D 为AB 边的中点），得到：C O D ,,共线，且OD CO 4=，则:ABC S ∆5:==∆OD CD S AO B . 法3：同上题中法3，此处略.19．已知ABC ∆中，6,5===BC AC AB ，I 为ABC ∆的内心，且BC AB AI μλ+=，则=+μλ1615. 解析：法1：由BC AB BC AB AB AC AB c b a AC c AB b AI ⋅+⋅=+⋅+⋅=++⋅+⋅=++⋅+⋅=165161016)(5555655法2：如图，线长易知，角平分线分线段成比例，得：3:5:=ID AI ，故)21(8585BC AB AD AI ⋅+⋅=⋅=AB +⋅=1658520．已知ABC ∆中，1,1,2-=⋅==AC AB AC AB ，O 为ABC ∆的外心，且BC y AB x AO +=，则=+y x 27．解析：法1：由BC y AB x AO +=AC y AB y x +-=)(，由AC AB y AB y x ABBC y AB y x AB AO AB ⋅+-=⇒+-⋅=⋅22)(2))((，得：y y x --=)(42；同理22)(2))((AC y AC AB y x ACBC y AB y x AC AO AC +⋅-=⇒+-⋅=⋅，得：y y x +--=)(21；易得：34,613==y x ，得27=+y x . 法2：以},{AC AB 为基底，表示：CO BO AO ,,，利用222CO BO AO ==，得之BC y AB x AO +=AC y AB y x +-=)(，y y x y y x AO )(2)(4222--+-=； AC y AB y x AB AO BO +--=-=)1(，y y x y y x BO )1(2)1(4222---+--=； AC y AB y x AC AO CO )1()(-+-=-=，)1)((2)1()(4222----+-=y y x y y x CO ；由22BO AO =0254=--⇒⇒y x 移项做差；由22CO AO =0142=+-⇒⇒y x 移项做差；联立方程解得：34,613==y x ，得27=+y x .BCA MNG21．已知O 为锐角ABC ∆的外心，︒=∠30A ，若AO m B C AC C B AB 2sin cos sin cos =⋅+⋅，则=m 21．解析：由AO m AB B CAC C B AB AB 2)sin cos sin cos (⋅=⋅+⋅⋅ 得：22||sin cos cos ||||sin cos ||AB m B CA AC ABC B AB =⋅⋅⋅+⋅得：C m C A B mc BCA b c CB c sin cos cos cos sin cos cos sin cos 22⋅=+⇒=⋅⋅⋅+⋅得到：C A C A C A C A B C m sin sin cos cos )cos(cos cos cos sin =++-=+=⋅ 得：.2130sin sin =︒==A m 22．在ABC∆中，1,==⊥AD BC AB AD ，则⋅AD AC解析：.33)(2===⋅=⋅+=⋅AD AD AD BC AD BC AB AD AC 三．解答题23．如图，已知点G 是ABC ∆的重心，过G 作直线与AC AB ,两边分别交于N M ,两点，且AM xAB = ，AN yAC = ，求证：113x y+=．解：由N G M ,,三点共线，得：AN t AM t AG ⋅+⋅-=)1(AC ty AB x t ⋅+⋅-=)1(--------①又G 是ABC ∆的重心得：AC AB AG ⋅+⋅=3131 ---------② 由①②得：⎪⎪⎩⎪⎪⎨⎧==-3131)1(ty x t ，消去t 得：113x y +=.24．设O 在ABC ∆的内部，若有正实数321,,λλλ满足：0321=⋅+⋅+⋅OC OB OA λλλ，求证：AO B CO A BO C S S S ∆∆∆=::::321λλλ．证明：作：OA OA ⋅=1'λ，OB OB ⋅=2'λ，OC OC ⋅=3'λ 则+'OA +'OB 0'=OC ，则O 为'''C B A ∆的重心，则：''''''O B A O A C O C B S S S ∆∆∆==.设为S又⎪⎩⎪⎨⎧=⋅==⋅==⋅=∆∆∆∆∆∆SS SS S S S S S AOB OB A COA OA C BOC OC B 2!''13''32''λλλλλλ 从而得：AOB COA BOC S S S SSS∆∆∆==::::::211332321λλλλλλλλλ25．已知向量1OP ，2OP ，3OP 满足条件1OP +2OP +3OP =0，|1OP |=|2OP |=|3OP |=1，求证：321P P P ∆为正三角形．证明：由1OP +2OP +3OP =0⇒1OP +2OP =3OP -平方得：1212112121-=⋅⇒=⋅++OP OP OP OP'A 'B 'C OABC从而得：3||21====P P同理可得：3||||1332==P P P P ，即321P P P ∆为正三角形． 26．在ABC ∆中，︒===60,5,2A AC AB ，求从顶点B A ,出发的两条中线BE AD ,的夹角的余弦值．解：设b AB a AC ==,，则,560cos 25,4,2522=︒⨯⨯=⋅==b a b a且b a BE b a AD -=+=21),(21；则,3)8525(41)2(41)21()(2122=--=-⋅-=-⋅+=⋅b b a a b a b a BE AD2394102521|)(|21||=++==+=b a AD22116202521|)2(|21||=+-==-=b a BE 故：.919149142212393||||,cos ==⋅=>=<BE AD BEAD BE AD27．已知H 是ABC △的垂心，且||||BC AH =，试求∠A 的度数．解：设ABC △的外接圆半径为R ，点O 是ABC △的外心。

三角形重心的性质及应用

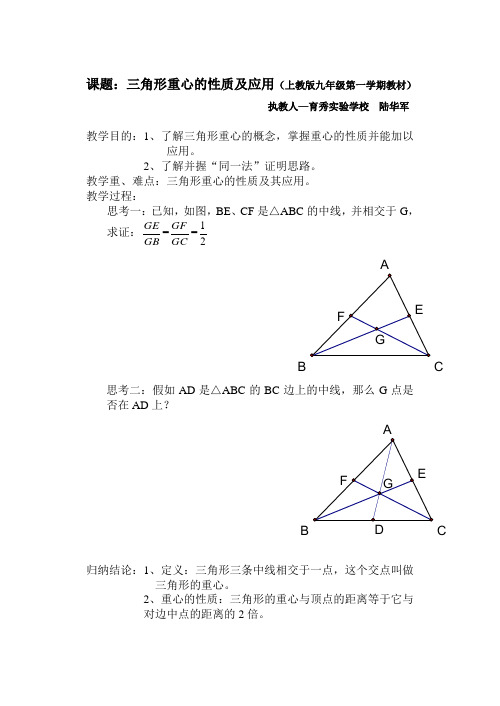
课题：三角形重心的性质及应用（上教版九年级第一学期教材）执教人—育秀实验学校陆华军教学目的：1、了解三角形重心的概念，掌握重心的性质并能加以应用。

2、了解并握“同一法”证明思路。

教学重、难点：三角形重心的性质及其应用。

教学过程：思考一：已知，如图，BE 、CF 是△ABC 的中线，并相交于G ，求证：GB GE =GC GF =21BC思考二：假如AD 是△ABC 的BC 边上的中线，那么G 点是否在AD 上？DB C归纳结论：1、定义：三角形三条中线相交于一点，这个交点叫做三角形的重心。

2、重心的性质：三角形的重心与顶点的距离等于它与对边中点的距离的2倍。

学生练习：1、已知，△ABC中，∠C=900，G是三角形的重心，，AB=8，求：①GC的长；②过点G的直线MN∥AB，交AC于M，BC于N，求MN的长。

B 2、已知，△ABC中，G是三角形的重心，AG⊥GC，AG=3，GC=4，求BG的长。

B C教学小结：由学生归纳总结作业：练习册：A册说课：本堂课的教学内容是三角形重心的概念及其性质的应用，知识难度较高，特别是三角形的三条中线相交于一点的证明需要通过“同一法”进行证明，这种方法对于学生来讲是陌生的。

因此，在课堂教学过程中，我尽量采用学生能够解决的就让学生自己去解决，学生困难的，教师加以引导，帮助学生完成学习任务。

在练习配备方面，书上没有现成的例题，我挑选了两个练习题，主要目的是让学生会利用重心的定义和性质去解决数学问题，并能从中体会出利用重心性质解决问题时的常规添线方法。

当然，在学生练习过程中，允许学生在独立完成问题的基础上，开展交流、探讨活动，教师进行巡回辅导，帮助学困生解决问题。

三角形的五心一定理重心定理：三角形的三条中线交于一点，这点到顶点的离是它到对边中点距离的2倍。

该点叫做三角形的重心。

外心定理：三角形的三边的垂直平分线交于一点。

该点叫做三角形的外心。

垂心定理：三角形的三条高交于一点。

三角形外心内心重心垂心与向量性质

三角形的“四心”时间：2021.03.02创作：欧阳数所谓三角形的“四心”是指三角形的重心、垂心、外心及内心。

当三角形是正三角形时，四心重合为一点，统称为三角形的中心。

一、三角形的外心定义：三角形三条中垂线的交点叫外心，即外接圆圆心。

ABC ∆的重心一般用字母O 表示。

性质：1.外心到三顶点等距，即OC OB OA ==。

2.外心与三角形边的中点的连线垂直于三角形的这一边，即AB OF AC OE BC OD ⊥⊥⊥,,.3.向量性质：若点O 为ABC ∆所在的平面内一点，满足⋅+=⋅+=⋅+)()()(，则点O 为ABC ∆的外心。

二、三角形的内心定义：三角形三条角平分线的交点叫做三角形的内心，即内切圆圆心。

ABC ∆的内心一般用字母I 表示，它具有如下性质：性质：1.内心到三角形三边等距，且顶点与内心的连线平分顶角。

2.三角形的面积＝⨯21三角形的周长⨯内切圆的半径．3.向量性质：设()+∞∈,0λ，则向量||||(AC AB AP =λ，则动点P 的轨迹过ABC ∆的内心。

三、三角形的垂心定义：三角形三条高的交点叫重心。

ABC ∆的重心一般用字母H 表示。

性质：1.顶点与垂心连线必垂直对边，即AB CH AC BH BC AH ⊥⊥⊥,,。

2.向量性质：结论1：若点O 为ABC ∆所在的平面内一点，满足OA OC OC OB OB OA ⋅=⋅=⋅，则点O 为ABC ∆的垂心。

结论2：若点O 为△ABC 所在的平面内一点，满足222222AB OC CA OB BC OA +=+=+，则点O 为ABC ∆的垂心。

四、三角形的“重心”：定义：三角形三条中线的交点叫重心。

ABC ∆的重心一般用字母G 表示。

性质：1.顶点与重心G 的连线必平分对边。

2.重心定理：三角形重心与顶点的距离等于它与对边中点的距离的2倍。

即GF GC GE GB GD GA 2,2,2===3.重心的坐标是三顶点坐标的平均值．即3,3C B AG C B A G y y y y x x x x ++=++=. 4.向量性质：（1）=++；（2）)(31PC PB PA PG ++=。

三角形 “心”的向量关系

三角形 “心”的向量关系我们都知道，在三角形中，因为有三边和三角，故有很多的心。

其中作为学生应掌握的四个心：重心，内心，外心，垂心。

不仅要理解其定义、性质，还需了解和分析其向量的表示形式。

由于向量是一种研究几何图形的另一种工具，所以我们有必要对它们进行整理和归纳，让同行借鉴。

一．各心的定义。

1．重心：三角形三条边的中线的交点。

其性质一是连接重心和顶点，延长后必交于对应边的中点。

其性质二是重心把中线长分成2：1。

2．垂心：三角形三边的高线的交点。

其性质为垂心与顶点的连线必与对应的边垂直。

3．外心：三角形三边的中垂线的交点，即三角形的外接圆的圆心。

其性质是外心到三顶点等距离。

4．内心：三角形三内角平分线的交点，即三角形的内切圆的圆心。

其性质是内心到三边等距离。

二．各心的向量表示。

在三角形ABC 中，点O 为平面内一点，若满足：1．0=++OC OB OA ，则点O 为三角形的重心。

分析：由OB OC OA +=-，以OC OB ,为邻边作一平行四边形OBEC ，点D 为BC 中点，如图，由向量的平行四边形法则，有OB OC OE +=，交BC 于D ，从而有OA AO OD OE -===2故O 为重心。

AB CODE2==，则点O 为三角形的外心。

3．OA OC OC OB OB OA ⋅=⋅=⋅，+=+=+，则点O 为三角形的垂心。

分析：由OA OC OC OB OB OA ⋅=⋅=⋅有三个等式，其中一个如OC OB OB OA ⋅=⋅，则有0)(=-OC OA OB ，有0=⋅CA OB ，故AC OB ⊥。

同理可证，点O 为三角形的垂心。

A B C OD而在三角形ABC 中，记OA a =，OB b =，OC c =，则由2222BO AC CO AB +=+2222)()(b c a c b a +-=+-，展开为c a b a ⋅=⋅22，则0)(=⋅-b c a 故OB AC ⊥ ，同理可证OA BC ⊥，从而点O 为三角形的垂心。

三角形的重心知识点详解2024人教版

三角形的重心知识点详解2024人教版三角形的重心是几何学中的一个重要概念，它不仅在理论上有着丰富的性质和应用，而且在实际生活中也有广泛的应用。

本文将详细介绍三角形重心的定义、性质、计算方法及其应用，帮助读者全面理解这一重要知识点。

一、三角形重心的定义三角形的重心是指三角形三条中线的交点。

中线是从一个顶点到对边中点的线段。

重心具有以下几个重要特点：1. 重心到顶点的距离与重心到对边中点的距离之比为2:1。

这意味着重心将每条中线分成两部分，其中靠近顶点的部分是靠近对边中点部分的两倍。

2. 重心和三角形三个顶点组成的三个三角形面积相等。

这表明重心将三角形分成了三个面积相等的小三角形。

3. 重心到三角形三个顶点距离的平方和最小。

这意味着重心是三角形内到三个顶点距离的平方和最小的点。

二、三角形重心的性质三角形重心具有许多重要的性质，这些性质在几何学中有着广泛的应用。

以下是一些主要性质：1. 重心到顶点的距离与重心到对边中点的距离之比为2:1。

这一性质可以通过中线定理证明。

2. 重心和三角形三个顶点组成的三个三角形面积相等。

这一性质可以通过面积公式证明。

3. 重心到三角形三个顶点距离的平方和最小。

这一性质可以通过向量法或解析几何的方法证明。

4. 重心是三角形内到三边距离之积最大的点。

这一性质可以通过均值不等式证明。

5. 在平面直角坐标系中，重心的坐标是顶点坐标的算术平均。

这一性质可以通过坐标几何的方法证明。

三、三角形重心的计算方法计算三角形重心的方法有很多种，以下是几种常见的方法：1. 坐标法：在平面直角坐标系中，设三角形的三个顶点坐标分别为((x_1, y_1))、((x_2, y_2))和((x_3, y_3))，则重心的坐标为：这一公式表明重心的坐标是三个顶点坐标的算术平均。

2. 向量法：设三角形的三个顶点分别为(mathbf{A})、(mathbf{B})和(mathbf{C})，则重心(mathbf{G})的向量表示为：这一公式表明重心的向量是三个顶点向量的算术平均。

三角形重心、外心、垂心、内心的向量表示及其性质

三角形“四心”向量形式的充要条件应用1．O 是ABC ∆的重心⇔0OC OB OA =++;若O 是ABC ∆的重心，则AB C AOB AOC B OC S 31S S S ∆∆∆∆===故=++;1()3PG PA PB PC =++⇔G 为ABC ∆的重心.2．O 是ABC ∆的垂心⇔OA OC OC OB OB OA ⋅=⋅=⋅;若O 是ABC ∆(非直角三角形)的垂心，则C tan B tan A tan S S S AOB AOC BOC ：：：：=∆∆∆ 故0OC C tan OB B tan OA A tan =++3．O 是ABC ∆的外心⇔|OC ||OB ||OA |==(或222OC OB OA ==)若O 是ABC ∆的外心则C 2sin :B 2sin :A 2sin AOB sin AOC sin BOC sin S S S AOB AOC BOC =∠∠∠=∆∆∆：：：：故0OC C 2sin OB B 2sin OA A 2sin =++ 4．O 是内心ABC ∆的充要条件是(OC (OB (OA =⋅=⋅=-⋅引进单位向量，使条件变得更简洁。

如果记CA ,BC ,AB 的单位向量为321e ,e ,e ，则刚才O 是ABC ∆内心的充要条件可以写成 0)e e ()e e ()e e (322131=+⋅=+⋅=+⋅ ，O 是ABC ∆内心的充要条件也可以是c b a =++ 。

若O 是ABC ∆的内心，则c b a S S S AOB AOC BOC ：：：：=∆∆∆故 0OC C sin OB B sin OA A sin 0OC c OB b OA a =++=++或;||||||0AB PC BC PA CA PB P ++=⇔是ABC ∆的内心;向量()(0)||||AC AB AB AC λλ+≠所在直线过ABC ∆的内心(是BAC ∠的角平分线所在直线)；例1．O 是平面上的一定点，A,B,C 是平面上不共线的三个点，动点P 满足OA OP ++=λ，[)+∞∈,0λ则P 点的轨迹一定通过ABC ∆的（）（A ）外心（B ）内心（C ）重心（D ）垂心解析：因为是向量AB 的单位向量设AB 与AC 方向上的单位向量分别为21e e 和，又AP OA OP =-，则原式可化为)(21e e AP +=λ，由菱形的基本性质知AP 平分BAC ∠，那么在ABC ∆中，AP 平分BAC ∠，则知选B.(二)将平面向量与三角形垂心结合考查“垂心定理”例2． H 是△ABC 所在平面内任一点，⋅=⋅=⋅⇔点H 是△ABC 的垂心. 由AC HB AC HB HA HC HB HC HB HB HA ⊥⇔=⋅⇔=-⋅⇔⋅=⋅00)(,同理AB HC ⊥，⊥.故H 是△ABC 的垂心. （反之亦然（证略））例3.(湖南)P 是△ABC 所在平面上一点，若⋅=⋅=⋅，则P 是△ABC 的（D ）A ．外心B ．内心C ．重心D ．垂心解析:由0=⋅-⋅⋅=⋅得.即0,0)(=⋅=-⋅CA PB PC PA PB 即则AB PC BC PA CA PB ⊥⊥⊥,,同理所以P 为ABC ∆的垂心. 故选D. (三)将平面向量与三角形重心结合考查“重心定理”例4． G 是△ABC 所在平面内一点，GC GB GA ++=0⇔点G 是△ABC 的重心.证明作图如右，图中GE GC GB =+连结BE 和CE ，则CE=GB ，BE=GC ⇔BGCE 为平行四边形⇒D 是BC 的中点，AD 为BC 边上的中线.将=+代入++=0，得+=0⇒2-=-=，故G 是△ABC 的重心.（反之亦然（证略））例5． P 是△ABC 所在平面内任一点.G 是△ABC 的重心⇔)(31PC PB PA PG ++=. 证明 +=+=+=⇒)()(3PC PB PA CG BG AG PG +++++= ∵G 是△ABC 的重心 ∴GC GB GA ++=0⇒CG BG AG ++=0，即PC PB PA PG ++=3 由此可得)(31++=.（反之亦然（证略））例6 若O 为ABC ∆内一点，0OA OB OC ++= ，则O 是ABC ∆ 的（） A ．内心 B ．外心 C ．垂心 D ．重心解析：由0OA OB OC ++=得OB OC OA +=-，如图以OB 、OC 为相邻两边构作平行四边形，则OB OC OD +=，由平行四边形性质知12OE OD =，2OA OE =，同理可证其它两边上的这个性质，所以是重心，选D 。

(完整版)三角形外心内心重心垂心与向量性质

三角形的“四心"所谓三角形的“四心”是指三角形的重心、垂心、外心及内心.当三角形是正三角形时,四心重合为一点，统称为三角形的中心.一、三角形的外心定义:三角形三条中垂线的交点叫外心，即外接圆圆心。

ABC ∆的重心一般用字母O 表示。

性质:1.外心到三顶点等距，即OC OB OA ==.2.外心与三角形边的中点的连线垂直于三角形的这一边，即AB OF AC OE BC OD ⊥⊥⊥,,。

3。

向量性质：若点O 为ABC ∆所在的平面内一点,满足AC OA OC CB OC OB BA OB OA ⋅+=⋅+=⋅+)()()(，则点O 为ABC ∆的外心。

二、三角形的内心定义：三角形三条角平分线的交点叫做三角形的内心，即内切圆圆心。

ABC ∆的内心一般用字母I 表示,它具有如下性质：性质：1。

内心到三角形三边等距，且顶点与内心的连线平分顶角。

2.三角形的面积＝⨯21三角形的周长⨯内切圆的半径． 3。

向量性质:设()+∞∈,0λ，则向量||||(AC AC AB AB AP =λ，则动点P 的轨迹过ABC ∆的内心。

三、三角形的垂心定义：三角形三条高的交点叫重心。

ABC ∆的重心一般用字母H 表示。

性质：1.顶点与垂心连线必垂直对边，即AB CH AC BH BC AH ⊥⊥⊥,,。

2。

向量性质：结论1：若点O 为ABC ∆所在的平面内一点,满足OA OC OC OB OB OA ⋅=⋅=⋅，则点O 为ABC ∆的垂心.结论2：若点O 为△ABC 所在的平面内一点，满足222222AB OC CA OB BC OA +=+=+, 则点O 为ABC ∆的垂心. 四、三角形的“重心"：定义：三角形三条中线的交点叫重心。

ABC ∆的重心一般用字母G 表示。

性质：1.顶点与重心G 的连线必平分对边。

2.重心定理：三角形重心与顶点的距离等于它与对边中点的距离的2倍.即GF GC GE GB GD GA 2,2,2===3.重心的坐标是三顶点坐标的平均值．即3,3C B AG C B A G y y y y x x x x ++=++=。

三角形重心、外心、垂心、内心的向量表示及其性质

向量的重心、垂心、内心、外心、旁心三角形重心、内心、垂心、外心的概念及简单的三角形形状判断方法。

重心：ABC ∆中、每条边上所对应的中线的交点；垂心：ABC ∆中、每条边上所对应的垂线上的交点；内心：ABC ∆中、每个角的角平分线的交点（内切圆的圆心）；外心：ABC ∆中、每条边上所对应的中垂线的交点（外接圆的圆心）。

一、重心1、O 是ABC ∆的重心⇔0=++OC OB OA若O 是ABC ∆的重心，则ABC AOB AOC BOC ∆=∆=∆=∆31故=++,)(31PC PB PA PG ++=⇔G 为ABC ∆的重心.2、 P 是△ABC 所在平面内任一点.G 是△ABC 的重心⇔)(31++=.证明：+=+=+=⇒)()(3PC PB PA CG BG AG PG +++++= ∵G 是△ABC 的重心∴0=++GC GB GA ⇒0=++CG BG AG ，即PC PB PA PG ++=3由此可得)(31++=.（反之亦然（证略））3、已知O 是平面上一定点，A B C ，，是平面上不共线的三个点，动点P 满足()OP OA AB AC λ=++u u u r u u u r u u u r u u u r，(0)λ∈+∞，，则P 的轨迹一定通过ABC △的重心.例1 若O 为ABC ∆内一点，0OA OB OC ++=u u u r u u u r u u u r r，则O 是ABC ∆ 的（）A ．内心B ．外心C ．垂心D ．重心二、垂心1、O 是ABC ∆的垂心⇔•=•=•若O 是ABC ∆(非直角三角形)的垂心，则故tan tan tan =++C B A2、H 是面内任一点，⋅=⋅=⋅⇔点H 是△ABC 的垂心. 由⊥⇔=⋅⇔=-⋅⇔⋅=⋅00)(, 同理⊥，⊥.故H 是ABC ∆的垂心. （反之亦然（证略））3、P 是ABC △所在平面上一点，若PA PC PC PB PB PA ⋅=⋅=⋅，则P 是ABC △的垂心．由PA PB PB PC ⋅=⋅u u u r u u u r u u u r u u u r ，得()0PB PA PC ⋅-=u u u r u u u r u u u r ，即0PB CA ⋅=u u u r u u u r ，所以PB CA u u u r u u u r⊥．同理可证PC AB u u u r u u u r ⊥，PA BC u u u r u u u r ⊥．∴P 是ABC △的垂心．如图1.4、已知O 是平面上一定点，A B C ，，是平面上不共线的三个点，动点P 满足cos cos AB AC OP OA AB B AC C λ⎛⎫ ⎪=++ ⎪⎝⎭u u u r u u u r u u u r u u u r u u u r u u u r，(0)λ∈+∞，，则动点P 的轨迹一定通过ABC △的垂心．例2 P 是△ABC 所在平面上一点，若⋅=⋅=⋅，则P 是△ABC 的（） A ．外心B ．内心C ．重心D ．垂心三、内心1、O 是ABC ∆的内心的充要条件是=⎫⎛•=⎫⎛•=⎫⎛•图1 图⑷引进单位向量，使条件变得更简洁。

三角形重心的向量公式推导

三角形重心的向量公式推导三角形是几何学中最简单的图形之一，同时也是最基础的图形之一。

在三角形的研究中，重心是一个非常重要的概念。

重心是三角形内部所有点到三边距离之积的和与三角形面积之比的交点，是三角形的重要特征之一。

本文将以向量的角度来探讨三角形重心的向量公式推导。

一、向量的基础概念向量是一个有大小和方向的量，通常用箭头表示。

向量的大小称为向量的模，用 ||a|| 表示，方向用箭头表示。

向量 a 和向量 b 相等，当且仅当它们的模相等且方向相同。

向量可以进行加法、减法、数乘等运算，其中向量加法满足交换律和结合律，即 a+b=b+a，(a+b)+c=a+(b+c)。

二、三角形重心的定义三角形重心是三角形内部所有点到三边距离之积的和与三角形面积之比的交点。

设三角形三个顶点分别为 A、B、C，三角形重心为G，AG、BG、CG 分别为三角形三边的中线，AG、BG、CG 交于 G 点，如图所示。

![image.png](attachment:image.png)三角形重心的坐标为 G(x,y)，则有：x = (xA + xB + xC) / 3y = (yA + yB + yC) / 3三角形重心的坐标可以通过三角形三个顶点坐标的平均值得到。

在向量的角度来看，三角形重心也可以通过向量加权平均得到。

三、向量加权平均向量加权平均是将多个向量按照一定的权重进行加权平均，得到一个新的向量。

设有 n 个向量 a1、a2、...、an，对应的权重为 w1、w2、...、wn，则向量加权平均为：b = (w1a1 + w2a2 + ... + wn an) / (w1 + w2 + ... + wn)其中，w1、w2、...、wn 是权重，它们的和为 1。

向量加权平均可以看作是向量的一种加权平均。

四、三角形重心的向量公式在三角形中，三边的中线分别为向量 a、b、c，则有：a = (B+C) / 2b = (C+A) / 2c = (A+B) / 2三角形重心可以用向量加权平均得到，即：G = (w1a + w2b + w3c) / (w1 + w2 + w3)其中，w1、w2、w3 是三边中线的长度，即：w1 = BCw2 = ACw3 = AB代入上式得：G = (BC(B+C) + AC(C+A) + AB(A+B)) / 3(AB+BC+AC)将向量 a、b、c 代入得：G = (BC(B+C) + AC(C+A) + AB(A+B)) / 6S其中，S 为三角形面积。

三角形重心向量结论推导

三角形重心向量结论推导
三角形是初中数学中常见的一个几何图形，它具有丰富的性质和定理。

其中，三角形重心向量是一个重要的概念，在数学物理学中应用广泛。

本文将介绍三角形重心向量的定义及其推导过程。

首先，我们来定义三角形的重心向量：
定义：设三角形ABC的重心为G，向量AG、BG、CG分别为向量a、向量b、向量c，则三角形ABC的重心向量为：
G = 1/3(G + G + G)
接下来，我们来推导重心向量的公式。

假设三角形ABC的顶点坐标分别为A （x1，y1），B （x2，y2），C （x3，y3）。

那么，向量AG的坐标为（X1,Y1）-（Xg,Yg），向量BG的坐标为（X2,Y2）-（Xg,Yg），向量CG的坐标为（X3,Y3）-（Xg，Yg）。

其中，重心G的坐标为：
Xg = (x1 + x2 + x3) / 3，Yg = (y1 + y2 + y3) / 3
现在，我们来计算重心向量：
= [0, 0]
由推导可知，三角形的重心向量是一个位于原点的向量。

这表明重心向量的大小和方向不受三角形形状和大小的影响，只与三角形的顶点坐标有关。

因此，我们可以在使用三角形重心向量时利用这个特性来进行计算，从而简化问题。

最后，需要注意的是，在实际应用中，我们也可以利用向量之间的线性运算（加法、减法、数乘等）来计算三角形重心向量，并利用重心向量来推导出一些相关的结论和定理。

总的来说，三角形重心向量是一个非常重要的概念，在数学、物理、机械等领域有着广泛的应用。

通过本文的推导，希望能够让读者对三角形重心向量有更深入的认识和理解。