概率练习1
概率练习(一)(附答案)

11.1 概率 (一)[基础练习]1、有100张卡片(从1号到100号),从中任取1张,取到的卡号是7的倍数的概率为( )A 、507 B 、1007 C 、487 D 、203 2、袋中有红、黄、白色球各一个,每次任取一个,有放回地抽取3次,则下列事 件中概率是98的是( ) A 、颜色全同 B 、颜色不全同 C 、颜色全不同 D 、颜色无红色3、甲射击命中目标的概率是21,乙命中目标的概率是31,丙命中目标的概率是41,现在三人同时射击目标,则目标被击中的概率为( )A 、43B 、32C 、54D 、107 4、在4次独立重复试验中,随机事件A 恰好发生1次的概率不大于其恰好发生两次的概率,则事件A 在一次试验中发生的概率P 的取值范围是( )A 、)1,6.0[B 、]6.0,0(C 、]4.0,0(D 、)1,4.0[ 5、5个同学任意站成一排,甲、乙两人恰好站在两端的概率是( )A 、81B 、91C 、101D 、111 6、某班有学生36人,按血型分类为:A 型12人,B 型10人,AB 型8人,O型6人,如果从这个班随机抽出2名学生,则这2名学生血型相同的概率是 7、2个篮球运动员在罚球时投球的命中率分别为0.7和0.6,每人投篮3次,则2人都恰好进2球的概率是(保留两位有效数字)8、有一道竞赛题,A 生解出它的概率为21,B 生解出它的概率为31,C 生解出它的概率为41,则A 、B 、C 三人独立解此题只有1人解出的概率为 [典型例题][例1]甲、乙两人参加普法知识问答,共有10个不同的题目,其中选择题6个、判断题4个,甲、乙两人依次各抽一题(1)甲抽到选择题、乙抽到判断题的概率是多少?(2)甲、乙两人至少有一人抽到选择题的概率是多少?解:甲、乙两人依次抽一题的结果有19110C C 个 (1)甲抽到选择题、乙抽到判断题的结果有1416C C 个, 所求概率154)(191101416==C C C C A P (2)甲、乙两人至少有一人抽到选择题的结果有131419110C C C C -个, 所求概率1513)(19110131419110=-=C C C C C C B P [例2]学校文艺队每个队员唱歌、跳舞至少会一门,已知会唱歌的有5人,会跳舞的有7人,现从中选3人,且至少要有一位既会唱歌又会跳舞的概率是2116,问该队有多少人? 解:设该队既会唱歌又会跳舞的有x 人,从而只会唱歌或只会跳舞的有)212(x -人,记“至少要有一位既会唱歌又会跳舞”的事件为A ,则事件A 的对立事件A 是“只会唱歌或只会跳舞”2116)(1)(,)(3123212=-==--A P A P C C A P xx 又 21161)10)(11)(12()210)(21)(212(-=------∴x x x x x x 解得912,3=-∴=x x ,故该队共有9人[例3]在资料室中存放着书籍和杂志,任一读者借书的概率为0.2,而借杂志的概率为0.8,设每人只借一本,现有五位读者依次借阅,计算:(1)5人中有2人借杂志的概率(2)5人中至多有2人借杂志的概率解:记“一位读者借杂志”为事件A ,则“此人借书”为A ,5位读者各借一次可看作n 次独立重复事件,因此:(1)5人中有2人借杂志的概率0512.0)2.0()8.0(3225==C P(2)5人中至多有2人借杂志,包括三种情况:5人都不借杂志,5人中恰有1人借杂志,5人中恰有2人借杂志,因此所求概率05216.0)2.0()8.0()2.0()8.0()2.0()8.0(322541155005=++=C C C P[例4]进入世界排名前8名的乒乓球女子单打选手中有4名中国人抽签平分为甲、乙两组进行比赛,求4名中国选手不都分在同一组的概率。
一年级概率练习题

一年级概率练习题
一年级数学练习题:概率
1. 小红有 4 个红苹果和 6 个绿苹果,她从中随机选择一个苹果。
请问小红选择到红苹果的概率是多少?
2. 在一个有 6 个红色球和 4 个蓝色球的袋子里,小明要从中无放回地抽取两个球。
请问他抽到两个红色球的概率是多少?
3. 一只骰子上有 6 个面,分别标有数字 1,2,3,4,5,6。
小刚将骰子抛掷一次,请问小刚得到偶数的概率是多少?
4. 小李有一个装有 10 个糖果的袋子,其中 4 个是巧克力味的,6 个是水果味的。
小李从袋子中随机取出一个糖果,请问他取到巧克力味糖果的概率是多少?
5. 在一副扑克牌中,红桃和方块是红色的,梅花和黑桃是黑色的。
请问从扑克牌中随机抽取一张牌,抽到红色牌的概率是多少?
6. 一个转盘分为三个区域:红色区域占总面积的 40%,蓝色区域占总面积的 30%,绿色区域占总面积的 30%。
请问转动转盘一次,停留在红色区域的概率是多少?
7. 从数字 1 到 10 中随机选择一个数字。
请问选到的数字是 7 的概率是多少?
8. 在一个有 10 个球的袋子中,有 3 个红球,2 个蓝球,5 个黄球。
小明从袋子中有放回地抽取三次球,请问他连续三次抽到红球的概率是多少?
9. 甲、乙、丙三个人依次抛掷一枚硬币,硬币正面朝上的概率是50%。
请问他们三个人都抛到正面朝上的概率是多少?
10. 今天是周末,小明有 5 本故事书和 2 本游戏书可以选择阅读。
请问他今天选择阅读故事书的概率是多少?
注:以上习题皆为一年级学生的难度水平,旨在提高学生对概率的理解和计算能力。
六年级上册概率练习题

六年级上册概率练习题1. 某班级有40个学生,其中有20个男生和20个女生。
请计算以下概率:- 从这个班级中随机选取一个学生,这个学生是男生的概率是多少?- 从这个班级中随机选取两个学生,这两个学生都是男生的概率是多少?- 从这个班级中随机选取两个学生,至少一个是男生的概率是多少?2. 某餐厅有7个服务员,其中5个会说英语,2个不会说英语。
请计算以下概率:- 从这些服务员中随机选取一个,这个服务员不会说英语的概率是多少?- 从这些服务员中随机选取两个,这两个服务员都不会说英语的概率是多少?- 从这些服务员中随机选取两个,至少一个会说英语的概率是多少?3. 某班级有30个学生,其中10个喜欢阅读书籍,20个不喜欢阅读书籍。
请计算以下概率:- 从这个班级中随机选取一个学生,这个学生喜欢阅读书籍的概率是多少?- 从这个班级中随机选取两个学生,这两个学生都不喜欢阅读书籍的概率是多少?- 从这个班级中随机选取两个学生,至少一个喜欢阅读书籍的概率是多少?4. 某班级有25个学生,其中15个会打篮球,10个不会打篮球。
请计算以下概率:- 从这个班级中随机选取一个学生,这个学生会打篮球的概率是多少?- 从这个班级中随机选取两个学生,这两个学生都会打篮球的概率是多少?- 从这个班级中随机选取两个学生,至少一个会打篮球的概率是多少?5. 某班级有40个学生,其中25个喜欢音乐,15个不喜欢音乐。
请计算以下概率:- 从这个班级中随机选取一个学生,这个学生喜欢音乐的概率是多少?- 从这个班级中随机选取两个学生,这两个学生都不喜欢音乐的概率是多少?- 从这个班级中随机选取两个学生,至少一个喜欢音乐的概率是多少?以上是六年级上册的概率练习题,希望能帮助到你。
概率论与数理统计:概率论练习题1及答案

5 / 8概率论练习题1(本大题共 6 小题,每小题 3 分,共 18 分)1、若当事件A ,B 同时发生时,事件C 必发生,则下列选项正确的是( ) A .()()P C P AB =; B .()()P C P AB ≤; C .()()P C P AB ≥; D .以上答案都不对.2、设随机变量()~X E λ,则下列选项正确的是( )A .X 的密度函数为(),00,0x e x f x x λ-⎧>=⎨≤⎩;B .X 的密度函数为(),00,0x e x f x x λλ-⎧>=⎨≤⎩;C .X 的分布函数为(),00,0x e x F x x λλ-⎧>=⎨≤⎩;D .X 的分布函数为()1,00,0x e x F x x λλ-⎧->=⎨≤⎩.3、设相互独立的连续型随机变量1X ,2X 的概率密度函数分别()1f x ,()2f x ,分布函数分别为()1F x ,()2F x ,则下列选项正确的是( ) A .()()12f x f x +必为某一随机变量的概率密度函数; B .()()12f x f x ⋅必为某一随机变量的概率密度函数; C .()()12F x F x +必为某一随机变量的分布函数; D .()()12F x F x ⋅必为某一随机变量的分布函数.4、设()~,X B n p ,()2~,Y N μσ,则下列选项一定正确的是( ) A .()E X Y np μ+=+; B .()E XY np μ=⋅; C .()()21D X Y np p σ+=-+; D .()()21D XY np p σ=-⋅.5、设随机变量X 与Y 相互独立,且都服从()1,0.2B ,则下列选项正确的是( )6 / 8A .()1P X Y ==;B .()1P X Y ≤=;C .()1P X Y ≥=;D .以上答案都不对. 6、设12,,,,n X X X 为独立的随机变量序列,且都服从参数为()0λλ>的指数分布,当n 充分大时,下列选项正确的是( )A .21nii Xn nλλ=-∑近似服从()0,1N ; Bni X nλ-∑近似服从()0,1N ;C .21ni i X λλ=-∑近似服从()0,1N ; D .1ni i X nnλ=-∑近似服从()0,1N .二、填空题(本大题共 6 小题,每小题 3 分,共 18 分)1、设事件A ,B ,C 相互独立,且()()()P A P B P C ==,()1927P A B C =,则()P A =.2、若()14P A =,()13P B A =,()12P A B =,则()P A B =.3、设()2~10,X N σ,且()10200.3P X <<=,则()010P X <<=.4、设随机变量X 与Y 相互独立,且()~100,0.3X B ,()~4Y P ,则()D X Y -=.5、设平面区域(){},01D x y x y =≤≤≤,二维随机变量(),X Y 在区域D 上服从均匀分布,则(),X Y 的联合分布密度函数为.6、若随机变量X 的分布律为()()2,0,1,2,k P X k ae k -+===,则常数a =.三、解答题(本大题共 6 小题,共 64 分)5 / 81、设盒一装有1支红色笔和2支黑色笔,盒二装有2支红色笔和1支黑色笔,盒三装有3支红色笔和3支黑色笔.现掷一枚匀质骰子,若掷出1点,则从盒一中任取一支笔,若掷出6点,则从盒三中任取一支笔,否则均从盒二中任取一支笔.求取出黑色笔的概率.(10分)2、一盒装有6只灯管,其中有2只次品,4只合格品,随机地抽取一只测试,测试后不放回,直到2只次品都被找出,求所需测试次数X 的概率分布及均值.(10分)3、设连续型随机变量X 的分布密度函数为(),13;0,ax b x f x +<<⎧=⎨⎩其他.,且{}{}23212P X P X <<=-<<,求常数a 和b 的值.(10分)6 / 84、设某工程队完成某项工程所需时间X (天)服从()100,25N .工程队若在100天内完工,可获奖金10万元;若在100~115天内完工,可获奖金3万元;若超过115天完工,则罚款5万元.求该工程队在完成工程时所获奖金的均值(要求用标准正态分布的分布函数值表示).(10分)5、设二维随机变量(),X Y 的概率密度函数为()8,01;,0,xy x y f x y <<<⎧=⎨⎩其他,求关于X 和Y 的边缘分布密度函数()X f x 和()Y f y ,并判别X 与Y 是否相互独立.(10分)5 / 86、设()~,X U a b ,且()0E X =,()13D X =.试确定X 的概率密度函数(6分)7、设随机变量X 服从标准正态分布,求2Y X =的概率密度函数()Y f y .(8分)6 / 8概率论练习题1参考答案一、单项选择题(本大题 6 小题,每小题 3 分,共 18 分) 1、C ; 2、B ; 3、D ; 4、A ; 5、D ; 6、B . 二、填空题(本大题 6 小题,每小题 3 分,共 18 分)1、13; 2、13; 3、0.3; 4、25; 5、()()2,,;,0,x y D f x y ∈⎧⎪=⎨⎪⎩其他.; 6、23e e ---.三、解答题(本大题 6 小题,共 64 分)1、解 设A 表示“取出黑色笔”,iB 表示“从盒i 中取笔”,1,2,3i =.……..2分则()()1316P B P B ==,()246P B =,()123P A B =,()213P A B =,()312P A B =,…………7分故由全概率公式,有()()()31124111563636212iii P A P B P A B ===⋅+⋅+⋅=∑.……………….10分2、解 由题意可知,X 的所有可能取值为2,3,4,5,6,…………….…….2 且{}1215P X ==,{}2315P X ==,{}145P X ==, {}4515P X ==,{}163P X ==,……..7分 所以 ()121411423456151551533E X =⨯+⨯+⨯+⨯+⨯=.……………………10分 3、解 由密度函数的性质()1f x dx +∞-∞=⎰,可得()31421ax b dx a b +=+=⎰,………..3分又由 {}{}23212P X P X <<=-<<,可得()()32212ax b dx ax b dx +=+⎰⎰,即02ab +=,…..7分联立方程,解得11,36a b ==-.………………………………………….10分4、解 方法1 由题设知工程队完成工程所需天数()~100,25X N .设所获奖金为Y 万元,Y 的可能取值为10,3,-5,Y 取各值的概率为()100100{10}{100}(100)00.55P Y P X F -⎛⎫==≤==Φ=Φ= ⎪⎝⎭, ()115100100100{3}{100115}(115)(100)30.555P Y P X F F --⎛⎫⎛⎫==<≤=-=Φ-Φ=Φ- ⎪ ⎪⎝⎭⎝⎭, 115100{5}{115}1(115)11(3)5P Y P X F -⎛⎫=-=>=-=-Φ=-Φ ⎪⎝⎭,…………….8分Y 因此 ()()()()100330.5513E Y =⨯Φ+Φ---Φ⎡⎤⎡⎤⎣⎦⎣⎦()()()100.5330.551383 1.5=⨯+Φ---Φ=Φ-⎡⎤⎡⎤⎣⎦⎣⎦.…………10分方法2 由题设知工程队完成工程所需天数()~100,25X N , 所获奖金10,100;3,100115;5,115.X Y X X ≤⎧⎪=<≤⎨⎪->⎩…………………………………………….2分5 / 8而()100100{10}{100}(100)00.55P Y P X F -⎛⎫==≤==Φ=Φ= ⎪⎝⎭, ()115100100100{3}{100115}(115)(100)30.555P Y P X F F --⎛⎫⎛⎫==<≤=-=Φ-Φ=Φ- ⎪ ⎪⎝⎭⎝⎭, 115100{5}{115}1(115)11(3)5P Y P X F -⎛⎫=-=>=-=-Φ=-Φ ⎪⎝⎭,…….8分因此 ()()()()100330.5513E Y =⨯Φ+Φ---Φ⎡⎤⎡⎤⎣⎦⎣⎦()()()100.5330.551383 1.5=⨯+Φ---Φ=Φ-⎡⎤⎡⎤⎣⎦⎣⎦.…………10分5、解 关于X 的边缘分布密度函数()Xf x :当0x ≤或1x ≥时,(,)0f x y =,所以()(),00Xf x f x y dy dy +∞+∞-∞-∞===⎰⎰,当01x <<时,()()()1212,8441Xxxf x f x y dy xydy xy x x +∞-∞====-⎰⎰,所以,()()241,01;0,X x x x f x ⎧-<<⎪=⎨⎪⎩其他. ………………………….4分关于Y 的边缘分布密度函数()Yf y :当0y ≤或1y ≥时,(,)0f x y =,所以()(),00Yf y f x y dx dx +∞+∞-∞-∞===⎰⎰,当01y <<时,()()230,844yyYf y f x y dx xydx yx y +∞-∞====⎰⎰,所以()34,01;0,Yy y f y ⎧<<⎪=⎨⎪⎩其他..……………………………………………8分于是()()()()32161,01,01;,0,X Y xy x x y f x f y f x y ⎧-<<<<⎪=≠⎨⎪⎩其他,所以X 与Y 不相互独立.……………………………………………10分 6、解 因为()~,X U a b ,所以()2a bE X +=,()()212b a D X -=,于是有()241,2123b a a b -+==,解得 1,3a b =-=,………….…..4分故X 的概率密度函数为()1,13;40,x f x ⎧-<<⎪=⎨⎪⎩其他..………………….6分7、22(0,1),(),.x X N x x ϕ-=-∞<<∞Y 的分布函数为2()()()Y F y P Y y P X y =≤=≤ ……………………2分 当0y ≤时,()()0Y F y P Y y =≤=,从而()0.Y f y = ……………………4分当0y>时,2()(){(YF y P X y P X=≤=≤≤=Φ-Φ…6分从而2()()(((Y Yyf y F yϕϕϕϕ-'''==Φ-Φ==+=7分所以20()0,0-⎧>=≤⎩yYyf yy……………………………………………8分6 / 8。
【数学(人教版)】初三 概率(1) 练习题
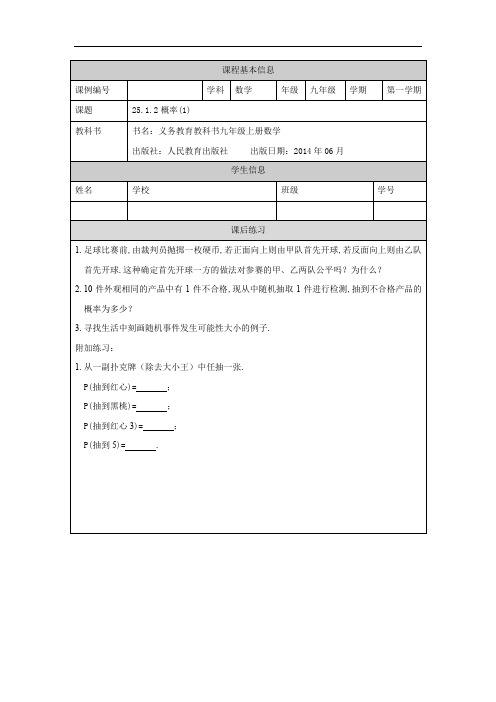
3.寻找生活中刻画随机事件发生可能性大小的例子.
附加练习:
1.从一副扑克牌(除去大小王)中任抽一张.
P(抽到红心)=;
P(抽到黑桃)=;
P(抽到红心3)=;
P(抽到5)=.
课程基本信息
课例编号
学科
数学
年级
九年级
学期
第一学期
课题
25.1.2概率(1)
教科书
书名:义务教育教科书九年级上册数学
出版社:人民教育出版社 出版日期:2014年06月
学生信息
姓名
学校
班级
ห้องสมุดไป่ตู้学号
课后练习
1.足球比赛前,由裁判员抛掷一枚硬币,若正面向上则由甲队首先开球,若反面向上则由乙队首先开球.这种确定首先开球一方的做法对参赛的甲、乙两队公平吗?为什么?
概率问题精练一

1、一个标准的五角星(如图)由10个点连接而成,从这10个点随机选取3个点,则这三个点在同一条直线上的概率为多少,这三个点能构成三角形的概率为多少?如果选取4个点,则这四个点恰好构成平行四边形的概率为多少?2、从立方体的八个顶点中选3个顶点,你能算出:⑴它们能构成多少个三角形?⑵随机取3个顶点,这3个点构成正三角形的可能性有多少?3、一枚硬币连续抛掷3次,求至少有两次正面向上的概率..4、小红的箱子中有4副手套,完全相同,但左、右手不能互换,有一副是姑姑送的,两副是奶奶送的,还有一副是自己买的,她从中任拿一副,恰好是姑姑送的那副的概率是多少?5、如果每个人抽完都放回,任意一个人如果抽中,则后边的人不再抽取,那么每个人抽中的概率为多少?6、神奇的三门游戏:同学们看过电视台举办的猜隐藏在门后面的汽车的游戏吗?游戏是这样的,参赛者会看见三扇关闭了的门,其中一扇的后面有一辆汽车,选中后面有车的那扇门就可以赢得该汽车,而另外两扇门后面则各藏有一只山羊。
当参赛者选定了一扇门,但未去开启它的时候,节目主持人开启剩下两扇门的其中一扇,露出其中一只山羊。
主持人其后会问参赛者要不要换另一扇仍然关上的门。
7、如图所示,将球放在顶部,让它们从顶部沿轨道落下,球落到底部的从左至右的概率依次是_______.81644168、一张圆桌旁有四个座位,A、B、C、D四人随机坐到四个座位上,求A与B不相邻而坐的概率.9、甲、乙两个学生各从09这10个数字中随机挑选了两个数字(可能相同),求:⑴这两个数字的差不超过2的概率,⑵两个数字的差不超过6的概率.10、某小学六年级有6个班,每个班各有40名学生,现要在六年级的6个班中随机抽取2个班,参加电视台的现场娱乐活动,活动中有1次抽奖活动,将抽取4名幸运观众,那么六年级学生小宝成为幸运观众的概率为多少?.11、小明爬楼梯掷骰子来确定自己下一步所跨台阶步数,如果点数小于3,那么跨1个台阶,如果不小于3,那么跨出2个台阶,那么小明走完四步时恰好跨出6个台阶的概率为多少?12、甲、乙、丙3人投篮,投进的概率分别是13,25,12.⑴现三人各投篮一次,求3人都没投进的概率.⑵现在3人各投篮一次,求至少有两人投进的概率.13、一批零件中有9个合格品和3个废品,安装机器时,从这批零件中随机选取一个,如果每次取出的废品不放回去,分别求在取得第一件合格品以前已取出X件废品数的概率,0X ,1,2,3.14、已知10件产品中有3件次品,为了保证使3件次品全部检查出来的概率超过0.6,则抽出来检验的产品最少有件.1、【详解】10个点中任意取3个的情况为3101098120 321C⨯⨯==⨯⨯种,其中涉及到5条直线,每条直线上各有4个点,其中任意3点都共线,所以取这3点不能够成三角形,这样的概率是34511206C⨯=,所以3点构成三角形的概率为15166-=.10个点中取4个点的情形为41010987210 4321C⨯⨯⨯==⨯⨯⨯种,10个点中平行四边形有2种(如上右图实线所示),每种各5个,共10个,所以构成平行四边形的概率为10121021=.2、【详解】⑴这8个顶点任意3点都不在一条直线上,所以从8个顶点中任取3个顶点都能构成三角形,所以应该有3856C=个.⑵如下图所示,只有三角形的3条边分别是正方体各个面上的对角线时,才是正三角形,这样的三角形共有8个。
概率课外练习题1

第一章 概率论的基本概念 课外练习题一、 填空题1. 已知事件A B 、相互独立,且()0.3P A =,()0.6P B =,则__()P A B = , ()P A B ∪= ; 2. 已知()0.3P A =,()0.15P AB =,则条件概率()P B A = ;3. 随机事件,,A B C 两两相互独立,且ABC =Φ,1()()()2P A P B P C ==<,9()16P A B C ∪∪=,则()P A = ; 4. 已知()0.2P AB =,()0.4P A B −=,则()P A = ,(|)P B A = ;5. 设()0.6,()0.5P A P B ==,则()P AB 的最大值为 ,此时事件A 与B 的关系为 ; 6. 已知()04P A =.,()05P B =.,()05P AB =.,()P B A B =∪ ;7. 三人独立地破译密码,他们能单独译出的概率分别为111,,345,则此密码被译出的概率是 ;8. 掷两颗骰子,已知两颗点数之和是7,则其中有一颗为一点的概率是 ; 9.有5条线段,它们的长度分别为1、3、5、7、9,从中任取三条,则这三条线段能构成三角形的概率为 ;10. 一个盒子里有3个红球,5个白球,从中任取两个,则恰好为1红球1白球的概率为 ,球的颜色相同的概率为 .二、 判断题 1. 设A B 、为两个事件,则()()()P A B P A P B −=−;2. 事件A 与B 相互独立,则()()+()P A B P A P B =∪;3. 设A B 、为两个事件,则A B AB B =∪∪;4. 设()0.7P A =,()0.8P B =,()0.8P B A =,则事件A 与B 一定相互独立;5. 若事件A 与B 相互独立,则A 与B 也相互独立;6. 设A B 、为两事件,若()0>A P 且()()B P A B P =,则事件A 与B 相互独立;7. 若1)()(=+B P A P ,则A B 、是互逆的;8. 事件A 发生必然导致事件B 发生,则B A ⊂;9. 必然事件概率为1,反之概率为1的事件一定是必然事件;10. 事件A B 、互斥,则,A B 相互独立 .三、 计算题1. 一个盒子里有10件产品,其中有2件次品,从中任取2件,求(1)取到的两件产品都是正品的概率;(2)至少取到一件正品的概率;(3)已知取到的产品中有一件是正品,求另一件也是正品的概率.2. 将4个球随机放入标号为1、2、3、4的四个杯子中去,求(1)1号杯子空的概率;(2)2号杯子不空的概率;(3)1号杯子空且2号杯子不空的概率.3. 某工厂由甲、乙、丙三台机器生产同一型号的产品,它们的产量各占30%,35%,35%,废品率分别为5%,4%,3%,产品混在一起.(1)从该厂的产品中任取一件,求它是废品的概率;(2)若取出的产品是废品,求它是由甲机器生产的概率.4. 一个机床有1/3的时间加工零件A,其余时间加工零件B.已知加工零件A 时停机的概率是0.3,加工零件B 时停机的概率是0.4.(1)求该机床停机的概率;(2)若该机床已停机,求它是在加工零件A 时发生停机的概率.5. 设三个箱子中,第一个有4个黑球和3个白球,第二个箱子中有3个黑球和3个白球,第三个箱子中有3个黑球和5个白球,从这三个箱子中随机取一箱,再从该箱子中取任意抽取1球.求(1)抽到的球是白球的概率(2)若已知抽到的是白球,求该球恰好是来自第三箱的概率.四、 证明题1. 设事件,A B 相互独立,且0()()1P A P B 、<< 证明:(|)(|)1P A B P A B +=.2. 设1)(0<<B P ,求证:事件A 与B 相互独立的充要条件是)|()|(B A P B A P =.3. 已知事件A、B、C 相互独立,求证:事件A∪B 与C 也相互独立.。
概率初步精选题

1.同时抛掷两枚质地均匀的骰子,骰子的六个面分别刻有1到6的点数,朝上的面的点数中,一个点数能被另一个点数整除的概率是 A.718 B.34 C.1118 D.23362.在一张边长为4cm 的正方形纸上做扎针随机试验,纸上有一个半径为1cm 的圆形阴影区域,则针头扎在阴影区域内的概率为( ) A.116 B. 14 C. 16π D. 4π3.一只小狗在如图的方砖上走来走去,最终停在阴影方砖上的概率是( )A .154 B.31 C.51 D.1524.在6件产品中,有2件次品,任取两件都是次品的概率是( ) A 、51 B 、61 C 、101D 、151 5.在拼图游戏中,从图中的四张纸片中,任取两张纸片,能拼成“小房子”(如图所示)的概率等于( )A .1B .12C .13D .236.为了估计湖里有多少条鱼,有如下方案:从湖里捕上100条做上标记,然后放回湖里,经过一段时间,第二次再捕上200条,若其中有标记的鱼有32条,那么估计湖里大约有 条鱼.二、填空题7.有红、白、蓝三种颜色的小球各一个,它们除颜色外没有其它任何区别。
现将3个小球放入编号为①、②、③的三个盒子里,规定每个盒子里放一个,且只能放一个小球。
(1)请用树状图或其它适当的形式列举出3个小球放入盒子的所有可能情况; (2)求红球恰好被放入②号盒子的概率。
一、填空题1.小华买了一套科普读物,有上、中、下三册,要整齐地摆放在一层书架上,其中恰好摆成“上、中、下”顺序的概率是________________.2.某学校的初一(1)班,有男生20人,女生23人.其中男生有18人住宿,女生有20人住宿.现随机抽一名学生,则:①抽到一名男生的概率是________________;②抽到一名住宿男生的概率是________________g ;③抽到一名走读女生的概率是________________.3.小明和爸爸进行射击比赛,他们每人都射击10次.小明击中靶心的概率为0.6,则他击不中靶心的次数为________________________;爸爸击中靶心8次,则他击不中靶心的概率为___________________. 二、选择题4.随机掷一枚均匀的硬币两次,两次正面都朝上的概率是 A.41 B.21 C.43D.1 5.下列事件中是必然事件的是 A.打开电视机,正在播广告B.从一个只装有白球的缸里摸出一个球,摸出的球是白球C.从一定高度落下的图钉,落地后钉尖朝上D.我走出校门,看到的第一辆汽车的牌照的末位数字是偶数 6.下列说法正确的是A.可能性很小的事件在一次试验中一定不会发生B.可能性很小的事件在一次试验中一定发生C.可能性很小的事件在一次试验中有可能发生D.不可能事件在一次试验中也可能发生7.冰柜里有四种饮料:5瓶特种可乐、12瓶普通可乐、9瓶橘子水、6瓶啤酒,其中特种可乐和普通可乐是含有咖啡因的饮料,那么从冰柜里随机取一瓶饮料,该饮料含有咖啡因的概率是 A.325 B.83 C.3215 D.3217三、解答题8.(2010四川遂宁中考)将分别标有数学2,3,5的三张质地,大小完全一样的卡片背面朝上放在桌面上,(1)随机抽取一张,求抽到奇数的概率;(2)随机抽取一张作为个位上的数字(不放回),再抽取一张作为十位上的数字,能组成哪些两位数?并求出抽取到的两位数恰好是35的概率. 提示:概率=所有事件发生的可能性该事件发生的可能性.9.如图9-19,某电脑公司现有A ,B ,C 三种型号的甲品牌电脑和D ,E 两种型号的乙品牌电脑.希望中学要从甲、乙两种品牌电脑中各选购一种型号的电脑. (1)写出所有选购方案(利用树状图或列表方法表示);(2)如果(1)中各种选购方案被选中的可能性相同,那么A 型号电脑被选中的概率是多少? (3)现知希望中学用10万元购买甲、乙两种品牌电脑共36台(价格如图所示),其中甲品牌电脑为A 型号电脑,求购买的A 型号电脑有多少台?中考压轴题专线训练11、(2008广州)(14分)如图10,扇形OAB 的半径OA=3,圆心角∠AOB=90°,点C 是»AB 上异于A 、B 的动点,过点C 作CD ⊥OA 于点D ,作CE ⊥OB 于点E ,连结DE ,点G 、H 在线段DE 上,且DG=GH=HE(1)求证:四边形OGCH 是平行四边形(2)当点C 在»AB 上运动时,在CD 、CG 、DG 中,是否存在长度不变的线段?若存在,请求出该线段的长度 (3)求证:223CD CH 是定值2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150.求证:△PBC 是正三角形.3.(本小题满分14分)如图12,边长为1的正方形ABCD 被两条与边平行的线段EF 、GH 分割为四个小矩形,EF 与GH 交于点P 。
概率论与数理统计第二版练习1

概率论与数理统计练习题系 专业 班 姓名 学号第一章 随机事件及其概率(一)一.选择题1.对掷一粒骰子的试验,在概率论中将“出现奇数点”称为 [ C ] (A )不可能事件 (B )必然事件 (C )随机事件 (D )样本事件 2.下面各组事件中,互为对立事件的有 [ B ] (A )1A ={抽到的三个产品全是合格品} 2A ={抽到的三个产品全是废品}(B )1B ={抽到的三个产品全是合格品} 2B ={抽到的三个产品中至少有一个废品} (C )1C ={抽到的三个产品中合格品不少于2个} 2C ={抽到的三个产品中废品不多于2个} (D )1D ={抽到的三个产品中有2个合格品} 2D ={抽到的三个产品中有2个废品} 3.下列事件与事件A B -不等价的是 [ C ] (A )A AB - (B )()A B B ⋃- (C )A B (D )A B 4.甲、乙两人进行射击,A 、B 分别表示甲、乙射中目标,则A B ⋃表示 [ C ] (A )二人都没射中 (B )二人都射中 (C )二人没有都射着 (D )至少一个射中5.以A 表示事件“甲种产品畅销,乙种产品滞销”,则其对应事件A 为. [ D ] (A )“甲种产品滞销,乙种产品畅销”; (B )“甲、乙两种产品均畅销”; (C )“甲种产品滞销”; (D )“甲种产品滞销或乙种产品畅销6.设{|},{|02},{|13}x x A x x B x x Ω=-∞<<+∞=≤<=≤<,则AB 表示 [ A ] (A ){|01}x x ≤< (B ){|01}x x <<(C ){|12}x x ≤< (D ){|0}{|1}x x x x -∞<<⋃≤<+∞7.在事件A ,B ,C 中,A 和B 至少有一个发生而C 不发生的事件可表示为 [ A ] (A )C A C B ; (B )C AB ; (C )C AB C B A BC A ; (D )A B C .8.假设随机事件A,B 满足P(AB)=0,则 [ D ] (A )A,B 互为对立事件 (B)A,B 互不相容(C )AB 一定为不可能事件 (D )AB 不一定为不可能事件 二、填空题1.若事件A ,B 满足AB φ=,则称A 与B 互不相容 。
概率统计习题课1

大卫: 大卫:思索者
例1:设A,B是相互独立的事件,P(A∪B)=0.6,P(A)=0.4, 是相互独立的事件,P(A∪B)=0.6,P(A)=0.4, 求P(B). P(B).
P( A ∪ B ) = P( A) + P ( B ) P( AB )
P( A ∪ B) = P( A) + P( B) P( A) P( B)
∫
bHale Waihona Puke af ( x)dx = ∫ cos xdx = sin b sin a
a
b
练习5 下面那个函数不可作为随机变量X的分布函数? 练习5:下面那个函数不可作为随机变量X的分布函数?( )
0 x < 0 2 x ( A) F ( x) = 0 ≤ x <1 2 1 x ≥ 1
ln(1 + x) (C ) F ( x) = 1 + x 0
X 1 ~ b ( 20, 0.01) .
P{ X 1 ≥ 2} = 1 P{ X < 2} = 1 P{ X = 0} P{ X = 1} = 0.0169
80台设备不能得到及时维护 P"80台设备不能得到及时维护" 80台设备不能得到及时维护" = P( A ∪ A ∪ A ∪
1 2 3
(1 P( A) ) P( B) = P( A ∪ B) P( A)
P ( A ∪ B ) P ( A) 1 P( B) = = 1 P ( A) 3
概率第一章练习题

第一章 随机事件与概率练习题1.设 A 、B 、C 为三个事件,用 A 、B 、C 的运算关系表示下列各事件:(1)仅 A 发生;(2) A 与C 都发生,而 B 不发生; (3)所有三个事件都不发生;(4)至少有一个事件发生;(5)至多有两个事件发生; (6)至少有两个事件发生;(7)恰有两个事件发生; (8)恰有一个事件发生分析:利用事件的运算关系及性质来描述事件.解:(1) A BC ;(2) A BC ;(3) A BC 或 AB C ;(4) A BC 或 ABC ABC ABC ABC ABC ABC ABC ;(5) A BC 或ABC ABC ABC ABC ABC ABC ABC ;(6) A BAC BC 或 A BC ABC ABC ABC ;(7) A BC ABC ABC ;(8) A BC ABC ABC .随机事件的关系和运算叫对偶律1.某射手向一目标射击两次,A i 表示事件“第i 次射击命中目标”,i =1,2,B 表示事件“仅第一次射击命中目标”,则B =( )A .A 1A 2B .21A AC .21A AD .21A A2.设A ,B ,C 为随机事件,则事件“A,B ,C 都不发生”可表示为( )A . B.BC C .ABC D.3.设A 、B 、C 为三事件,则事件=C B A ( )A.A C B A B C.( A B )C D.( A B )C4设A 、B 为任意两个事件,则有( )A.(A ∪B )-B=AB.(A-B)∪B=AC.(A ∪B)-B ⊂AD.(A-B)∪B ⊂A5. 设A 、B 为随机事件,且B A ⊂,则B A ⋃等于( )A.AB.BC.ABD.B A ⋃2.古典概型1.从标号为1,2, (101)101个灯泡中任取一个,则取得标号为偶数的灯泡的概率为( )A .10150 B .10151 C .10050 D .10051 2.一批产品共10件,其中有2件次品,从这批产品中任取3件,则取出的3件中恰有一件次品的概率为( ) A .601 B .457 C .51 D .157 3.同时抛掷3枚均匀的硬币,则恰好三枚均为正面朝上的概率为( )恰好有两枚正面朝上的概率为( )设袋内有5个红球、3个白球和2个黑球,从袋中任取3个球,则恰好取到1个红球、1个白球和1个黑球的概率为_________.5. 一个盒子中有6颗黑棋子、9颗白棋子,从中任取两颗,则这两颗棋子是不同色的概率为____________.6. 从0,1,2,3,4五个数中任意取三个数,则这三个数中不含0的概率为___________。
概率统计练习1

概率论与数理统计练习(一)一、填空题1. A 、B 、C 是三个随机事件,且A 与B 相互独立,A 与C 互不相容。
已知P( A ) = 0.2,P( B ) = 0.6,P( B | C ) = 0.5,P( BC ) = 0.4。
请计算以下事件的概率:P(A )= , P( AB ) = , P( AC ) = ,P( C ) = ,P( A+B ) = , P( C | B ) = 。
2. 假设有某种彩票叫“10选2”,每周一期。
其规则是从1到10的10个自然数中不重复地任意选2个数组成一注,每注1元。
如果所选的2个数与本期出奖的结果(也是从1到10中不重复选出的2个自然数)完全相同,则中奖,奖额为40元。
则购买一注彩票能中奖的概率是 。
引进随机变量X ,如果买1注彩票中奖了则令X 等于1,否则令X 等于0,那么X 服从 分布,X 的数学期望等于 。
3. 已知某对夫妇有三个小孩,但不知道他们的具体性别。
设他们有Y 个儿子,如果生男孩的概率为0.5,则Y 服从 分布。
这对夫妇恰好有一个儿子的概率是 。
他们的孩子的男女性别比例最可能是 。
4. 假设东莞市公安机关每天接到的110报警电话次数可以用泊松(Poisson)分布)100(π来描述。
则东莞市公安机关在某一天没有接到一个110报警电话的概率为 。
东莞市公安机关平均每天接到的110报警电话次数为 次。
5. 指数分布又称为寿命分布,经常用来描述电子器件的寿命。
设某款电器的寿命(单位:小时)的密度函数为⎩⎨⎧>=-其它 ,00 ,001.0)(001.0t e t f t 则这种电器没有用到500小时就坏掉的概率为 ,这种电器的平均寿命为 小时。
6. 根据世界卫生组织的数据,全球新生婴儿的平均身长为50厘米,身长的标准差估计为2.5厘米。
设新生婴儿的身长服从正态分布,则全球范围内大约有 %新生婴儿身长超过53厘米,有 %新生婴儿身长不足48厘米,身长在49厘米到51厘米之间的新生婴儿大约占 %。
概率统计练习题1

概率统计练习题一、填空题1.设离散型随机变量X 的分布律:C. 2.设随机变量X,rni 互独立,D(X) = 4,D(y)= b 则D{3X-2Y) = (3•设随机变量X ~ N(1 J)./(X)和F(x)分别为X 的密度函数和分布函数, 则有()班级学号 姓名 序号FCv)为X 的分布函数,则F(l ・5)=( A. 10B. 32C. 14D. 40D. 1A ・P(X <0) = P(X>0) = 0・5B. /(X)= /(-X)J ・€(YO,S)C. P(X<1) = P (X >1) = 05D. F(-x) = I-F(x).xe(-co,co)4•设二维随机变量(X”)的联合概率密度为心=严八 0<5<y<2,则£x=(其他5B. 一5 C.— 18 D.5.若且Xf 相互独立,/ = 12…"则E (为XJ = ((-1B. D.以上都不对二、填空题2•某商店搞抽奖活动•顾客需过三关,第i 关从装有i+1个白球和一个黑球的 袋子中抽取一只,抽到黑球即过关•连过三关者可拿到一等奖•则顾客能拿到 -等奖的概率 __ .,.p (B|A) = 1, P (A|B) =》则P(AUB)= ______________ . 3.某高速公路一天的事故数X 服从参数/t = 3的泊松分布,则一天没有发生事故的概率2.已知且P(A} = -4 B. 03•(结果以e 的形式表示)4.设随机变量X 服从(0,2)的均匀分布,则随机变量Y = X"在(0,4)内的概率密度为/r(y)= 5•设随机变量X 的方差D(X)H O,且Y = aX+bSa>0).则X 和F 的相关系数 PXY =三、解答题0 < A- < 11<%<2 其他试求(1) )X 的分布函数FM, (2) P{Xe(0.5,15)}2•有屮乙两个袋子,甲袋中有两个白球,一个红球;乙袋中有两个红球,一个0球.这 六个球手感上不可区别.今从屮袋中任取一球放入乙袋,搅匀后再从乙袋中任取一球,(1) 问此球是红球的概率(2) 若从乙袋中取到一个红球,则从屮袋放入乙袋的是口球的概率是多少2•已知随机变量X 的概率密度为/(»•) = < X 2-X3.设顾客在某银行的窗口等待服务的时间X (以分计)服从指数分布,其概率密度为匸严X >0 0, 其他某顾客在窗口等待服务,若超过10分钟,他就离开,他一个月要到银行5次,以Y 表示一个月内他未等到服务而离开窗口的次数,(1)求顾客在窗口未等到服务而离开的概率卩(2)求P{Y>\}(结果以e的形式表示)4•设二维随机变量(X, Y)的概率密度/(圮y)= <试求⑴常数人(2)p(y < 1).人£・(2卅y), X > 0, >' > 00, 其他5•箱子中装有10件产品,其中2件是次品,每次从箱子中任取一件产品,共取2次,每次取后不放回,定义随机变量X,Y 如下:0,若第一次取出正品,Y = “ 1,若第一次取出次品,试写出随机变量(X'Y)的联合分布律、边缘分布律,并问X 'j Y 是否相互独立6.设某城市成年男子的身高X 〜N(17O,62)(单位:厘米)(1) 问应如何设计公共汽车车门的高度,使成年男子与车门顶碰头的机会小于(2) 若车门设计高度为282厘果,求W 个成年男子中没有与车门顶碰头的概率 d 若第二次取出正品, 1,若第二次取出次品, x=<(已知4>(2・33) =0.9901,①(2) = 0.9772〉7•某保险公司多年的统计资料表明,在索赔户中被盗索赔户占20%,以X表示在随意抽査的100个索赔户中因被盗向保险公司索赔的户数。
用列举法求概率练习1-完整版PPT

3 (3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
4 (4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
5 (5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
6 (6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
用列举法求概率
1、回顾例1,如果小王在游戏开始时踩中的第一个格上 出现了标号1,则下一步踩在哪一区域比较安全?
用列举法求概率
2、袋子中装有红、绿各一个小球,除颜色外无其他差 别,随机摸出1个小球后话回,再随机摸出一个,求下 列事件的概率: (1)第一次摸到红球,第二次摸到绿球; (2)两次都摸到相同颜色的小球; (3)两次摸底到的球中有一个绿球和一个红球。
P( )= 14 第二次取出的数字能够整除第一次取出的数字
7
36 18
用列举法求概率
4.经过某十字路口的汽车,它可能继续直行,也可能向左转 或向右转,如果这三种可能性大小相同,当有三辆汽车经 过这个十字路口时,求下列事件的概率
(1)三辆车全部继续直行; (2)两辆车向右转,一辆车向左转; (3)至少有两辆车向左转
用列举法求概率
3、在6张卡片上分别写有1~6的整数,随机地抽取一 张后放回,再随机地抽取一张,那么第二次取出的数 字能够整除第一次取出的数字的概率是多少?
用列举法求概率
解: 列出所有可能的结果:
一二 1 2 3 4 5 6
1 (1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
概率练习题含答案

第一章 随机事件及其概率 练习: 1. 判断正误(1)必然事件在一次试验中一定发生,小概率事件在一次试验中一定不发生。
(B ) (2)事件的对立与互不相容是等价的。
(B ) (3)若()0,P A = 则A =∅。
(B )(4)()0.4,()0.5,()0.2P A P B P AB ===若则。
(B )(5)A,B,C 三个事件至少发生两个可表示为AB BC AC ⋃⋃(A ) (6)考察有两个孩子的家庭孩子的性别,{()Ω=两个男孩(,两个女孩),(一个男孩,}一个女孩),则P {}1=3两个女孩。
(B ) (7)若P(A)P(B)≤,则⊂A B 。
(B )(8)n 个事件若满足,,()()()i j i j i j P A A P A P A ∀=,则n 个事件相互独立。
(B )(9)只有当A B ⊂时,有P(B-A)=P(B)-P(A)。
(A )2. 选择题(1)设A, B 两事件满足P(AB)=0,则CA. A 与B 互斥B. AB 是不可能事件C. AB 未必是不可能事件D. P(A)=0 或 P(B)=0 (2)设A, B 为两事件,则P(A-B)等于(C )A. P(A)-P(B)B. P(A)-P(B)+P(AB)C. P(A)-P(AB)D. P(A)+P(B)-P(AB)(3)以A 表示事件“甲种产品畅销,乙种产品滞销”,则其对立事件A 为(D) A. “甲种产品滞销,乙种产品畅销”B. “甲乙两种产品均畅销”C. “甲种产品滞销”D. “甲种产品滞销或乙种产品畅销”(4)若A, B 为两随机事件,且B A ⊂,则下列式子正确的是(A ) A. P(A ∪B)=P(A) B. P(AB)=P(A)C. P(B|A)=P(B)D. P(B-A)=P(B)-P(A) (5)设(),(),()P A B a P A b P B c ⋃===,则()P AB 等于(B )A.()a c c + B . 1a c +-C. a b c +-D. (1)b c -(6)假设事件A 和B 满足P(B|A)=1, 则(B)A. A 是必然事件 B . (|)0P B A = C. A B ⊃ D. A B ⊂ (7)设0<P(A)<1,0<P(B)<1, (|)(|)1P A B P A B += 则(D )A. 事件A, B 互不相容B. 事件A 和B 互相对立C. 事件A, B 互不独立 D . 事件A, B 互相独立8.,,.,,.D ,,.,,.,,1419.(),(),(),(),()37514131433.,.,.,.,37351535105A B A AB A B B AB A B C AB A B D AB A B P B A P B A P AB P A P B A B C φφφφ≠=≠====对于任意两个事件必有(C )若则一定独立;若则一定独立;若则有可能独立;若则一定不独立;已知则的值分别为:(D)三解答题1.(),(),(),(),(),(),().P A p P B q P AB r P A B P AB P A B P AB ===设求下列事件的概率:解:由德摩根律有____()()1()1;P A B P AB P AB r ⋃==-=-()()()();P AB P B AB P B P AB q r =-=-=-()()()()(1)()1;P A B P A P B P AB p q q r r p ⋃=+-=-+--=+-________()()1[()()()]1().P AB P A B P A P B P AB p q r =⋃=-+-=-+-2.甲乙两人独立地对同一目标射击一次,命中率分别是0.6和0.5,现已知目标被命中,求它是甲射击命中的概率。
高二理数《概率统计1》

高二理科数学《概率》练习11.已知射手甲射击一次,命中9环(含9环)以上的概率为0.56,命中8环的概率为0.22,命中7环的概率为0.12.(1)求甲射击一次,命中不足8环的概率;(2)求甲射击一次,至少命中7环的概率.2.已知射手甲射击一次,击中目标的概率是23.(1)求甲射击5次,恰有3次击中目标的概率;(2)假设甲连续2次未击中...目标,则中止其射击,求甲恰好射击5次后,被中止射击的概率.3.某地区试行高考考试改革:在高三学年中举行5次统一测试,学生如果通过其中2次测试即可获得足够学分升上大学继续学习,不用参加其余的测试,而每个学生最多也只能参加5次测试.假设某学生每次通过测试的概率都是31,每次测试时间间隔恰当,每次测试通过与否互相独立. (1)求该学生考上大学的概率.(2)如果考上大学或参加完5次测试就结束,记该生参加测试的次数为ξ,求ξ的分布列4.某射手进行射击训练,假设每次射击击中目标的概率为34,且各次射击的结果互不影响. (1)求射手在3次射击中,3次都击中目标的概率(用数字作答); (2)求射手在3次射击中,恰有两次连续击中目标的概率(用数字作答); (3)求射手第3次击中目标时,恰好射击了4次的概率(用数字作答).5.一个盒子装有六张卡片,上面分别写着如下六个定义域为R的函数:23123456f(x)=x,f(x)=x,f(x)=x,f(x)=sinx,f(x)=cosx,f(x)=2.(1)现从盒子中任取两张卡片,将卡片上的函数相加得一个新函数,求所得函数是奇函数的概率;(2)现从盒子中进行逐一抽取卡片,且每次取出后均不放回,若取到一张记有偶函数的卡片则停止抽取,否则继续进行,求抽取次数ξ的分布列6.甲、乙、丙三人分别独立的进行某项技能测试,已知甲能通过测试的概率是25,甲、乙、丙三人都能通过测试的概率是320,甲、乙、丙三人都不能通过测试的概率是340,且乙通过测试的概率比丙大.(Ⅰ)求乙、丙两人各自通过测试的概率分别是多少;(Ⅱ)求测试结束后通过的人数ξ的数学期望Eξ.0.01频率组距7.某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[)50,40,[)60,50…[]100,90后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:(Ⅰ)求第四小组的频率,并补全这个频率分布直方图; (Ⅱ)估计这次考试的及格率(60分及以上为及格)和 平均分;(Ⅲ) 从成绩是70分以上(包括70分)的学生中选两人, 求他们在同一分数段的概率.8.将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落.小球在 下落的过程中,将3次遇到黑色障碍物,最后落入A 袋或B 袋中.已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是12.(Ⅰ)求小球落入A 袋中的概率()P A ;(Ⅱ)在容器入口处依次放入4个小球,记ξ为落入A 袋中的小球个数,试求3ξ=的概率和ξ的数学期望E ξ.高二理科数学《概率》练习1答案1.解:记“甲射击一次,命中7环以下”为事件A ,“甲射击一次,命中7环”为事件B ,由于在一次射击中,A 与B 不可能同时发生,故A 与B 是互斥事件, (1)“甲射击一次,命中不足8环”的事件为A B +,由互斥事件的概率加法公式,()()()0.120.10.22P A B P A P B +=+=+=. 答:甲射击一次,命中不足8环的概率是0.22.…………………………………6分 (2)方法1:记“甲射击一次,命中8环”为事件C ,“甲射击一次,命中9环(含9环)以上”为事件D ,则“甲射击一次,至少命中7环”的事件为A C D ++, ∴()()()()0.120.220.560.9P A C D P A P C P D ++=++=++=.答:甲射击一次,至少命中7环的概率为0.9.…………………………………12分 2.解:(1)设“甲射击5次,恰有3次击中目标”为事件A ,则()32352180C 33243P A ⎛⎫⎛⎫=⋅= ⎪⎪⎝⎭⎝⎭.答:甲射击5次,恰有3次击中目标的概率为24380.………………………………6分 (2)方法1:设“甲恰好射击5次后,被中止射击”为事件C ,由于甲恰好射击5次后被中止射击,所以必然是最后两次未击中目标,第三次击中目标,第一次与第二次至少有一次击中目标,则()2221222212116C C 33333243P C ⎡⎤⎛⎫⎛⎫=+⋅⋅⋅=⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦.答:甲恰好射击5次后,被中止射击的概率为16243.……………………………12分 方法2:设“甲恰好射击5次后,被中止射击”为事件C ,由于甲恰好射击5次后被中止射击,所以必然是最后两次未击中目标,第三次击中目标,第一次与第二次至少有一次击中目标,则()2222121161C 333243P C ⎡⎤⎛⎫⎛⎫=-⋅⋅=⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦. 答:甲恰好射击5次后,被中止射击的概率为16243.……………………………12分 3.(1)记“该生考上大学”的事件为事件A ,其对立事件为A ,则5415)32()32)(31()(+=C A P2分 243131])32()32)(31([1)(5415=+⋅-=∴C A P 4分 答:该生考上大学的概率为2431315分 (2)参加测试次数ξ的可能取值为2,3,4,5,6分,91)31()2(2===ξP274313231)3(12=⋅⋅⋅==C P ξ 27431)32(31)4(213=⋅⋅⋅==C P ξ 8148)32()32(31)5(4314=+⋅⋅==C P ξ 10分故ξ的分布列为:4.解: (1)记事件“射手在3次射击中,3次都击中目标”为事件A , 3327()()464P A ==;………………………………………4分 (2)记事件“射手在3次射击中,恰有两次连续击中目标”为事件B , 2319()2()4432P B =⋅⋅=;………………………………………8分 (3)记事件“射手第3次击中目标时,恰好射击了4次”为事件C , 31381()3()44256P C =⋅⋅=………………………………………12分 5. 解:(1)记事件A 为“任取两张卡片,将卡片上的函数相加得到的函数是奇函数”,由题意知.51)(2623==C C A P ………………………………………………………………4分(2)ξ可取1,2,3,4.103)2(,21)1(151316131613=⋅=====C C C C P C C P ξξ,201)4(,203)3(1313141115121613141315121613=⋅⋅⋅===⋅⋅==C C C C C C C C P C C C C C C P ξξ; …………8分 故ξ的分布列为6.解(Ⅰ)设乙、丙两人各自通过测试的概率分别是x 、y 依题意得:23,52033(1)(1),540xy x y ⎧=⎪⎪⎨⎪--=⎪⎩ 即3,41.2x y ⎧=⎪⎪⎨⎪=⎪⎩ 或 1,23.4x y ⎧=⎪⎪⎨⎪=⎪⎩(舍去)┅┅┅┅┅┅┅4分 所以乙、丙两人各自通过测试的概率分别是34、12. ┅┅┅┅┅┅┅6分 (Ⅱ)因为3(0)40P ξ== 3(3)20P ξ==2312312317(1)(1)(1)(1)(1)(1)(1)54254254220P ξ==--+--+--=7.(Ⅰ)因为各组的频率和等于1,故第四组的频率:41(0.0250.01520.010.005)100.03f =-+*++*=……2分直方图如右所示……………………………….4分(Ⅱ)依题意,60及以上的分数所在的第三、四、五、六组, 频率和为 (0.0150.030.0250.005)100.75+++*=所以,抽样学生成绩的合格率是75%......................................6分 利用组中值估算抽样学生的平均分123456455565758595f f f f f f ⋅+⋅+⋅+⋅+⋅+⋅………………….8分=450.1550.15650.15750.3850.25950.05⨯+⨯+⨯+⨯+⨯+⨯ =71估计这次考试的平均分是71分………………………………………….9分(Ⅲ)[70,80),[80,90) ,[90,100]”的人数是18,15,3。
小学一年级概率练习题

小学一年级概率练习题1.在一个盒子里有10个红球和5个蓝球,小明随机从盒子中抽取一个球。
求小明抽到红球的概率。
2.在一组彩色贝壳中,有4个红色贝壳和6个绿色贝壳。
小华随机抓取一个贝壳,并立即放回。
然后,小华再次抓取一个贝壳。
求小华第一次抓到红色贝壳,第二次抓到绿色贝壳的概率。
3.在一个宝箱里,有8个金币和2个银币。
小李从宝箱里抓取一枚硬币。
如果小李抓到金币,他将获得1元奖励;如果他抓到银币,则没有奖励。
小李连续抓取3次硬币。
求小李三次都抓到金币的概率。
4.有一张扑克牌,从中随机抽取一张牌,求抽到红桃的概率。
5.一枚硬币被投掷3次。
求至少出现一次正面的概率。
6.在一个带有数字1到6的骰子上,求掷出一个偶数的概率。
7.在一个罐子里有5个苹果和3个橘子。
小明随机从罐子中抓取2个水果。
求小明抓到两个苹果的概率。
8.一袋子里有5个红球和4个蓝球。
小华从袋子里抽取2个球,不放回。
求小华第一次抽到红球,第二次抽到蓝球的概率。
9.小李有一组重复的卡片,其中有3张卡片上写着"动物",4张卡片上写着"水果",和5张卡片上写着"蔬菜"。
小李从中随机抽取两张卡片。
求小李两张卡片上都写着"水果"的概率。
10.一组火柴棍中,有8根红色火柴棍和12根蓝色火柴棍。
小明随机抽取一根火柴棍。
如果他抽到红色火柴棍,他将获得1元奖励;如果他抽到蓝色火柴棍,则没有奖励。
小明连续抽取3根火柴棍。
求小明三次都抽到红色火柴棍的概率。
请根据以上题目,计算出每个问题的概率,并列出计算步骤。
概率统计练习题1

22. 不同的两个小麦品种的种子混杂在一起,已知第一个品种的种子发芽率为 90%,第二 个品种的种子发芽率为 96%,并且已知第一个品种的种子比第二个品种的种子多一倍,求: (1)从中任取一粒种子,它能发芽的概率; (2)如果取到的一粒种子能发芽,那么它是第一个品种的概率是多少?
概率统计练习题
第1章
1. 一口袋装有 10 只球,其中 6 只是红球,4 只是白球,今随机地从中同时取出 2 只球,试 求取到二只球颜色相同的概率。
2. 一口袋装有 10 只球,其中 6 只是红球,4 只是白球,今随机地从中同时取出 2 只球,试 求:(1)2 只都是红球的概率;(2)一只是红球一只是白球的概率。
23. 某保险公司把被保险人分成三类:“好的”,“一般的”与“差的”,统计资料表明,对于 上述三种人而言,在一年内出问题的概率依次为 0.05,0.15,和 0.30,如果“好的”被保险 人占总的保险人数的 20%,“一般的”占 50%,“差的”占 30%,试问在固定的一年中出问 题的人在总保险人数中占多大的比例?如某人在这一年内未出问题,他是属于“好的”的概 率为多少?
3. 在 8 件产品中有 5 件是一级品和 3 件是二级品,现从中任取 2 件,求取得的 2 件中只有 一件是一级品的概率. 如果:(1)2 件产品是无放回的逐次抽取;(2)2 件产品是有放回的 逐次抽取。
4. 将 15 名新生平均分配到三个班级中去,新生中有三名是优秀生,问每一个班级各分配到 一名优秀生的概率是多少?
P( AC) 1 ,求 A,B,C 至少有一个发生的概率。 7
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
概率统计练习1
一、填空:
1、 设,,A B C 是某随机试验样本空间的一个划分,且()0.5,()0.7P A P B ==,则()P C = ,
()P AB = 。
2、已知()0.7,()0.3,P B P AB ==则()P A B = 。
3、事件A 与B 互斥,且()0P B >,则()P A B = 。
4、若事件A 与B 相互独立,且()0.4,()0,7P A P A B == ,则()P B = 。
5、任意写出一个两位数,它能被2或3整除的概率为 。
6、假设一批产品中一、二、三等品各占60%、30%、10%,从中任取一件结果不是三等品,则取到一等品的概率
是 。
7、袋中有50个乒乓球,其中20个黄色球,30个白色球,两人不放回地依次随机从袋中各取一球,则第二个人
取到黄色球的概率为 。
8、同时抛掷两枚硬币,记:A “甲出现反面、乙出现正面”,则A 表示 。
9、在区间[0,1]中随机取两个数,两数之和小于
65
的概率为 。
10、一种零件的加工由两道工序组成,废品率分别为,p q ,则该零件的成品率为 。
二、选择:
1、若事件A 与B 满足 ()0,()0P A P B >>,则一定有()P A B = ( )
a. ()()P A P B +
b. ()()()()P A P B P A P B +-
c. 1()()P A P B -
d. ()()()P A P B P AB +-
2、若事件A 与B 相互独立,且满足 ()0,()0P A P B >>,则一定有()P A B = ( )
a. ()()P A P B +
b. 1()()P A P B +
c. 1()()P A P B -
d. 1()P AB -
3、若事件A 与B 互相对立,则下列各式中( )不成立
a. ()1P A B =
b. ()1P A B =
c. ()0P AB =
d. ()0P B A =
4、每次试验失败的概率为,(01)p p <<,则在三次重复试验中至少成功一次的概率为( )
a. 3(1)p -
b. 3(1)p -
c. 31p -
d. 2
3(1)p p -
三、设两个相互独立的事件A 与B 都不发生的概率为
19
,“A 发生B 不发生”与“B 发生A 不发生”的概率相等,求()P A 。
四、玻璃杯成箱出售,每箱20只,假设各箱含0,1,2只残次品的概率分别为0.8,0.1,0.1,一顾客欲购一箱玻璃
杯,购买时售货员随机取一箱,顾客开箱随机查看四只,若无残次品则买下该箱,否则退回。
求:
1、顾客买下该箱的概率;
2、在顾客买下的一箱中,确实没有残次品的概率。
五、甲乙丙三人按顺序轮流抛掷硬币,直到某人掷出正面为止,先掷出正面者获胜,求各人获胜的概率。
六、设()(),()0,()0P A B P A B P A P B =>>,证明:A 与B 相互独立。
