七桥问题和一笔画
七桥问题与一笔画的通解

七桥问题与一笔画的通解(论文拟稿)在柯尼斯堡的一个公园里,有七座桥将一条河上的两座岛和两岸相连接。
当时有人提出了这么一个问题:如何一次性不重复不遗漏走完七座桥。
后来,数学家欧拉将它变成了一个一笔画问题(如图)。
从欧拉的简化图来看,似乎我们无论如何,也不能一笔画完图形。
但是,这是为什么呢?在这个图中,有ABCD 4个点,有五条线汇聚到A点,三条线汇聚到B,C,D 点,我们可以把这种有奇数条线(3条及以上)汇聚的点称为奇点,作为对应,把有偶数条线(4条及以上)汇聚的点称为偶点。
那么,我们不难发现,在任意封闭图形中,奇点的个数一定是偶数。
因为一条线定连接两个点(或重合),若存在奇数个奇点,则此图形定不符合封闭图形定义。
从一个奇点来看,若要一笔画成,则此奇点定是起笔点或停笔点。
起笔点,停笔点只有两个,所以说,奇点为两个或没有奇点的封闭图形可以一笔画。
回来看七桥问题,图中有四个奇点,以任意两个作为起笔点和落笔点,则还有两个奇点无法连接。
故七桥问题无解。
从上面总结出以下结论:■⒈凡是由偶点组成的连通图,一定可以一笔画成。
画时可以把任一偶点为起点,最后一定能以这个点为终点画完此图。
■⒉凡是只有两个奇点的连通图(其余都为偶点),一定可以一笔画成。
画时必须把一个奇点为起点,另一个奇点为终点。
■⒊其他情况的图都不能一笔画出。
(奇点数除以二便可算出此图需几笔画成。
)我们可以把得到的结论推广到所有一笔画解法存在问题,如汉字“田”,我们观察到,它有四个奇点,故不可以一笔画。
而汉字“日”,只有两个奇点,则可以一笔画。
早在1736年,欧拉在交给彼得堡科学院的《哥尼斯堡7座桥》的论文报告中,就阐述了这种方法,也为后来的数学新分支--拓扑学的建立奠定了基础。
从这里我们可以看出,伟大的创造一开始可能并不像我们想象的那么高深莫测,仔细观察生活,我们也会有了不起的发现。
哥尼斯堡七桥问题与一笔画课件

在18世纪,人们开始对图论进行 研究,探索图的结构和性质,其 中哥尼斯堡七桥问题成为了图论 研究的重要问题之一。
哥尼斯堡七桥问题的起源
哥尼斯堡七桥问题起源于18世纪初,当时有一位名叫欧拉的 人,他是一位数学家和工程师,对图论进行了深入研究。
欧拉在研究哥尼斯堡的桥梁和河流时,提出了一个问题:是 否存在一条路径,能够遍历哥尼斯堡的所有桥梁,每座桥只 过一次?这就是著名的哥尼斯堡七桥问题。
哥尼斯堡七桥问题对一笔画问题的影响
哥尼斯堡七桥问题的解决推动了数学领域的发展,它证明了不存在一条遍历七座 桥的路径,每座桥只过一次,最后回到开始的地方。
这个问题的解决对于一笔画问题的研究具有重要意义,它揭示了一笔画问题的复 杂性和多样性,也促使数学家们深入研究一笔画问题的性质和规律。
一笔画问题在哥尼斯堡七桥问题中的应用
哥尼斯堡七桥问题是一笔画问题的经典案例,它探讨的是从哥尼斯堡的一个地方开 始,能否遍历城市的七座桥,每座桥只过一次,最后回到开始的地方。
一笔画问题则是一个更广泛的几何问题,研究的是在一个连通图上,是否存在一条 路径能够遍历所有的边,每条边只过一次。
哥尼斯堡七桥问题实际上是几何图形的一笔画问题,它为后续一笔画问题的研究提 供了基础。
哥尼斯堡七桥问题的历史意义
哥尼斯堡七桥问题的解决标志着图论 的诞生,成为图论发展史上的一个里 程碑。
该问题的解决为后续的图论研究提供 了基础和指导,推动了数学和图论的 发展。
02 一笔画问题概述
一笔画问题的定义
一笔画问题,也称为欧拉路径问题,是图论中的一个经典 问题。它主要探讨的是在一个给定的图形中,是否存在一 条路径,使得这条路径能够遍历图形的每一条边且只遍历 一次。
地图导航
七桥问题与一笔画

( C点 ) , 如图l 1 . 如 果 要 选 择 最
二
D
个偶 点 : A、 B、 D、 F, 2 个奇点 : C、 , 可 以 一
笔 画成 . 图7 中有2 个 偶点 : 4、 C, 2 个奇 点 :
B、 D, 可 以 一 笔 画 成 .图 8 中有 1 个偶 点 : D。 4 个奇点 : A、 、 C、 D, 不 能 一 笔 画 成 .再
找 几 个 图形 试 一 试 , 你 能 发 现什 么 规 律 吗 ?
【 规律 】
① 可 以 一 笔 画 成 的 图形 . 与 偶 点 个 数
无关 , 与奇点个 数有关 . 也 就是说 , 凡 是 图
短 的线 路 , 谁 先 回到 邮 局 ?
c
形 中没 有 奇 点 的 ( 奇 点 个数 为0 ) , 可 选 任 一
个点做起点 . 且 一 笔 画后 可 以 回到 出 发 点 .
7 2
E F
图 1 1
T 1 n t e 慧 l l i g 散 e n 掌 t m a t h e m a t i c s
条线都只能画一次而不能重复. 图5 一图 8 四个 图 形 中 。 你 能 找 出图5 一
图8 的 每 个 图形 中 奇 点 和 偶 点 的 个 数 吗 ? 请 你 试 一 试 其 中 哪些 可 以一 笔 画 出 ?
E
超
店
图 5
图6
7
图 8
【 分析 】 图5 中有6 个偶 点 : A、 B、 c、 D、
看几 个一 笔 画 的问题 .
先 让 我 们 来 了解 三 个 新 概 念 .
七桥问题和一笔画

七桥问题和一笔画18世纪时,欧洲有一个风景秀丽的小城哥尼斯堡,那里有七座桥。
如图1所示:河中的小岛A与河的左岸B、右岸C各有两座桥相连结,河中两支流间的陆地D与A、B、C各有一座桥相连结。
当时哥尼斯堡的居民中流传着一道难题:一个人怎样才能一次走遍七座桥,每座桥只走过一次,最后回到出发点?大家都试图找出问题的答案,但是谁也解决不了这个问题。
图 1 图 2七桥问题引起了著名数学家欧拉(17071783)的关注。
他把具体七桥布局化归为图2所示的简单图形,于是,七桥问题就变成一个一笔画问题:怎样才能从A、B、C、D中的某一点出发,一笔画出这个简单图形(即笔不离开纸,而且a、b、c、d、e、f、g各条线只画一次不准重复),并且最后返回起点?欧拉经过研究得出的结论是:图2是不能一笔画出的图形。
这就是说,七桥问题是无解的。
这个结论是如何产生呢?请看下面的分析。
如果我们从某点出发,一笔画出了某个图形,到某一点终止,那么除起点和终点外,画笔每经过一个点一次,总有画进该点的一条线和画出该点的一条线,因此就有两条线与该点相连结。
如果画笔经过一个n次,那么就有2n条线与该点相连结。
因此,这个图形中除起点与终点外的各点,都与偶数条线相连。
如果起点和终点重合,那么这个点也与偶数条线相连;如果起点和终点是不同的两个点,那么这两个点部是与奇数条线相连的点。
综上所述,一笔画出的图形中的各点或者都是与偶数条线相连的点,或者其中只有两个点与奇数条线相连。
图2中的A点与5条线相连结,B、C、D各点各与3条线相连结,图中有4个与奇数条线相连的点,所以不论是否要求起点与终点重合,都不能一笔画出这个图形。
1736年,欧拉在圣彼得堡科学院作了一次学术报告。
在报告中,他证明了上述结论。
后来他又给出了鉴别任一图形能否一笔画出的准则,即欧拉定理。
为了介绍这个定理,我们先来看下面的预备知识:由有限条线组成的图形叫做网络,其中每条线都要求有两个不同的端点。
哥尼斯堡七桥问题与一笔画精品PPT课件

著名的哥尼斯堡大学,傍倚于两条支流的河旁, 使这一秀色怡人的区域,又增添了几分庄重的韵味! 有七座桥横跨普累格河及其支流,其中五座把河岸 和河心岛连接起来。这一别致的桥群,古往今来, 吸引了众多的游人来此散步。
这在人类智慧所未及的领域,是很常见的事!
拿起栓有15个圆环的绳子,任选一个桥的支柱作为起点,沿桥依次套圈,看看 是否可以让除起点之外的13个桥柱上都有一个圈。(起点的柱子上有两个圈)。 结论是,不可能实现完成该任务。
❖ 欧拉
欧拉(L.Euler,1707.4.151783.9.18)著名的数学家。生于 瑞士的巴塞尔,卒于彼得堡。大 部分时间在俄国和德国度过。他 早年在数学天才贝努里赏识下开 始学习数学, 17岁获得硕士学位, 毕业后研究数学,是数学史上最高 产的作家。在世发表论文700多篇, 去世后还留下100多篇待发表。其 论著几乎涉及所有数学分支。
课后作业
请你观察生活,设计一个运 用“一笔画”的数学知识来解 决的实际问题。并与同伴交流。
写在最后
经常不断地学习,你就什么都知道。你知道得越多,你就越有力量 Study Constantly, And You Will Know Everything. The More
You Know, The More Powerful You Will Be
②若奇点个数为2,可选其中一个奇点做起点, 而终点一定是另一个奇点,即一笔画后不可以 回到出发点。
③凡是图形中有2个以上奇点的,不能完成一 笔画。
用你发现的规律,说一说七桥问题的答案?
由于七桥问题中的四个点都是奇点,因此可 以判断它是无法一笔画出来的 ,也就是说 根本不存在能不重复走遍七座桥的路线!
七桥问题与一笔画

七桥问题与一笔画18世纪时,风景秀丽的欧洲小城哥尼期堡中有一条河,河的中间有两个小岛,河两岸与两岛之间共建有七座桥(图1)当时小城的居民中流传着一道难题:一个人怎样才能不重复地走过所有的七座桥,再回到出发点?这就是数学史上著名的“七桥问题”,为了解决这个问题,我们首先学习一下“一笔画”吧。
把一个图形用笔描绘一遍,笔不能离开图面,已经描过的地方不可以重复,这个图形叫做一笔画。
如图2,由A点出发先走向B点,从B点先描出圆,回到B点后,再描全矩形,这就是一个一笔画。
但图3就不是一个一笔画。
图的顶点可分为两类,奇点和偶点从某点出发的边的条数是奇数时,这样的点叫做奇点(如图3中A、B、C、D);从某点出发的边的条数是偶数时,这样的点叫偶点(如图2中A、B)由例3我们知道并非所有的图形均可一笔画出,通过研究发现有以下三条规律。
1.凡是仅由偶点组成的图形,一定可以一笔画出,画时可以任意偶点为起点,最后仍回到这点。
2.凡是只有两个奇顶点和任意个偶顶点组成的图形,也可以一笔画出,画时必须以一个奇顶点为起点,而以另一个奇顶点为终点。
3.如果图形中的奇顶点多于两个,那么这个图就不可能一笔画出。
掌握这些结论后,我们就可以顺利的解决七桥问题,首先把被河流隔开的四块区域缩写为A、B、C、D四个点,这样七桥问题就变成了四个点间由七条线相连所成的图(图4)。
因为本图有四个奇点(A、B、C、D),所以一个人不可能不重复地走过所有的七座桥而再回到出发点,这就是著名数学家欧拉研究后得出的结论。
欧拉用他的智慧,把七桥问题变成了一个与位置关系有关的问题,这也为许多现实生活中的七桥问题找到解决的途径。
下面我们来看看它的重要运用。
例1,图5中的线段代表林中小路,在B点A、B两处各有一人,他们约定以相同的速度同时从各自所在的位置出发,走遍林中的每一条小路,最后到达C点,在哪个点出发的人最先到达C点。
分析:从A点出发的人先到。
原因是图中只有A、C两个奇点,由规律可知:从A出发的人可以不重复地走完每一条小路后终止在奇点C;B是偶点,从B点出发不可能不重复地走完每一条小路,他要到达C点,必须在某段小路上重复走一次,从B点出发的人到达C的行程比从A点出发的人更长。
哥尼斯堡七桥问题与一笔画通用课件

问题的意义
01
哥尼斯堡七桥问题推动了图论的 发展,成为图论和几何图形研究 的重要基础。
02
问题揭示了图论中节点和边的概 念,以及它们之间的关系和限制 条件,为后续的图论研究提供了 重要的启示。
02
一笔画问题概述
一笔画的基本概念
一笔画
一笔画是指从一个给定的点开始 ,沿着某些路径(通常是线段) 前进,最后回到起始点,路径在 任何地方都不交叉或重复。
际应用价值。
THANKS。
05
哥尼斯堡七桥问题的解决方案
欧拉解决哥尼斯堡七桥问题的方法
欧拉通过数学分析,证明了哥尼斯堡七桥问题没有一笔画的 可能性,即不存在一条路径能够遍历七座桥而不重复经过任 何一座桥。
欧拉的方法基于图论的基本原理,通过分析图中的奇点(起 点和终点)和偶点(中间的交点),证明了七桥问题没有一 笔画的可能性。
地图染色
地图染色问题是一笔画问题的一个变种,它要求将地图上 的国家或地区按照一定的规则进行染色,使得相邻的国家 或地区颜色不同。
物流配送
在物流配送中,一笔画问题可以用于解决最优配送路线问 题,即如何规划一条或多条路线,使得所有客户都被访问 且只被访问一次,同时总距离最短。
一笔画问题的未来发展
算法优化
现代技术的应用
随着计算机技术的发展,现代数学软件和算法可以模拟和验证图论中的问题,为 解决复杂问题提供了更高效的方法。
现代技术可以用于分析和处理大规模的图数据,例如社交网络、交通网络等,这 些网络结构与哥尼斯堡七桥问题类似,可以通过计算机模拟和算法找到最优解或 近似解。
对其他类似问题的启示
哥尼斯堡七桥问题的解决为图论和其他相关领域的研究提 供了基础和启示,推动了数学和科学的发展。
哥尼斯堡七桥问题与一笔画

年 前 的 一 个 著 名 问 题 —— 哥 尼 斯 堡 七 桥 问
题. 十八世纪 , 东普鲁 士哥尼斯堡城( 今 俄 罗 斯加 里 宁格 勒 ) 有一 条 河 叫普莱 格 尔河 , 它 有 两个 支流 , 在 城 市 的 中心汇 成大 河 , 中间是 岛 区, 河 上 有 7座桥 , 将 河 中的两 个 岛和河 岸 连
图 l
图 2
图 3
如 果 你 画 出来 了 ,那 么 请你 再 看 图 2能 不能一 笔 画 出来?
一
这个问题看起来似乎并不难 ,但人们始
虽然你动了脑筋 ,但我相信你肯定不能 终 没 有 能找 到 答 案 . 最后 , 问题 被 提 到 了大 数
笔 画 出图 2 1这 就是 一笔 画 问题 , 它 是一 种 学 家 欧拉 那 里 .欧 拉 以 深邃 的洞 察力 很 快 证
是奇 点 , 共有 四个 , 所 以这个 图肯定 不 能 一笔 画成. 欧拉对“ 七桥问题” 的 研 究 是 图论 研 究
在 图 中添 上一 条线 段 , 使它 能一 笔画 成 .
的开始 ,同时也为拓扑学的研究提供 了一个
初级 例 子 .
【 例题 赏析 】 图 中添加 最 少 的线段 ,将 其 改成 一 笔 画 的 图
参考路 线 : 4 - 1 _ 2 - 5 — 8 一 - 9 - 6 - 1 0 - 1 1 - 7 - 4 — 3 .
点为终点; ( 4 ) 奇点个数超过两个的图形 , 一定
不能 一笔 画 出 .
现在 对 照七 桥 问题 的 图 ,所有 的顶 点都
一笔画与七桥问题
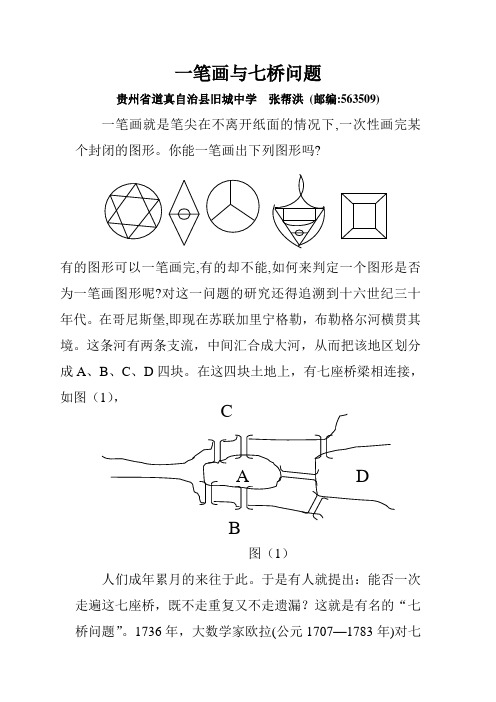
一笔画与七桥问题贵州省道真自治县旧城中学 张帮洪 (邮编:563509)一笔画就是笔尖在不离开纸面的情况下,一次性画完某个封闭的图形。
你能一笔画出下列图形吗?有的图形可以一笔画完,有的却不能,如何来判定一个图形是否为一笔画图形呢?对这一问题的研究还得追溯到十六世纪三十年代。
在哥尼斯堡,即现在苏联加里宁格勒,布勒格尔河横贯其境。
这条河有两条支流,中间汇合成大河,从而把该地区划分成A 、B 、C 、D 四块。
在这四块土地上,有七座桥梁相连接,如图(图(1) 人们成年累月的来往于此。
于是有人就提出:能否一次走遍这七座桥,既不走重复又不走遗漏?这就是有名的“七桥问题”。
1736年,大数学家欧拉(公元1707—1783年)对七桥问题着手研究,并在彼德堡科学院作了一次有趣的报告。
把这一问题归结为如图(2)所示的一笔画问题,并得出一次性走完七桥是不可能的结论。
原因在于A、B、C、D四个点都分出 D了奇数条叉道,奇数条叉道的点不 B可能是一笔画中的“过路点”(即不是图(2)起点,已不是终点),。
因为“过路点”必须是偶数条叉道的交点,因此A、B、C、D四点必为起点或终点,但一笔画图形中只能有一个起点和一个终点(终点和起点可能为合在一起),故七桥问题得以解决。
最后欧拉给了一笔画问题的判定方法:如果把线图中偶数条线的交叉点叫偶点,把奇数条线的交叉点叫奇点,那么,(1)线图中奇点个数不多于2个,这个图就是一笔画图形,否则就不是一笔画图形。
(2)若没有奇点,则始点与终点重合,若有两个奇点,则始点与终点不重合,还必须从一个奇点画起,另一个奇点必须是终点。
(3)奇点数目总是成双出现的。
一笔画问题与七桥问题的解决,为解决最短邮路和规划问题提供了理论依据,为拓朴学的研究奠定了基础。
因此欧拉对哥尼斯堡七桥问题的研究,成了拓朴学研究的先驱。
七桥问题和一笔画

③但凡图形中有2个以上奇点旳,不能完毕一 笔画。
用你发觉旳规律,说一说七桥问题旳答案?
因为七桥问题中旳四个点都是奇点,所以能 够判断它是无法一笔画出来旳 ,也就是说 根本不存在能不反复走遍七座桥旳路线!
● 点A、B体现岛 点C。D体现岸
▎线体现桥
问题分析
问题旳答案怎样呢?让我们先来了解三个新概念。
①有奇数条边相连旳点叫奇点。如:
●
●
●
②有偶数条边相连旳点叫偶点。如:
●
●
●
③一笔画指:1、下笔后笔尖不能离开纸。 2、每条线都只能画一次而不能反复。
活动探究
下图形中。请找出每个图旳奇点个数,偶点个数。试一试哪些能够一笔画出,请填表,从中 你能发觉什么规律?
课堂练习
1、 一辆洒水车要给某城市旳街道洒水,街道地图如下:你能否设计一条洒水车洒水旳路 线,使洒水车不反复地走过全部旳街道,再回到出发点?
小广场
超市 菜市场
文具店 电器城
服装城
课堂练习
2、 下图是一种公园旳平面图,能不能使游 人走遍每一条路不反复?入口和出口又应设 在哪儿?
E ●
●G F ● D●
这就是数学史上著名旳七桥问题,你乐意试一试吗?
问题情景
18世纪时风景秀丽旳小城哥尼斯堡中有一 条河,河旳中间有两个小岛,河旳两岸与两 岛之间共建有七座桥(如图),当初小城旳 居民中流传着一道难题:一种人怎样才干不 反复地走过全部七座桥,再回到出发点?
问题分析
数学家欧拉懂得了七桥问题他用四个点A、B、 C、D分别体现小岛和岸,用七条线段体现七 座桥(如图)于是问题就成为怎样“一笔画”出 图中旳图形?
七桥问题与一笔画

那里风景优美,游人众多.在这美丽的地方, 人们议论着一个有趣的问题:一个游人怎样 才能不重复地一次走遍七座桥,最后又回到 出发点呢?
直到1836年,瑞士著名的数学家欧拉才证明了这个 问题的不可能性。
课后作业
请你观察生活,设计一个运 用“一笔画”的数学知识来解 决的实际问题。并与同伴交流。
●B
图⑴
A●
图⑵ 图⑶
●A
B●
●C
E●
●D
A
●●
图⑷
图1
活动探究 下列图形中。请找出每个图的奇点个数,偶点个数。试一试哪 些可以一笔画出,请填表,从中你能发现什么规律?
奇点个数 偶点个数 能否一笔画
●B
图⑴
2
0
能
A●
●A
图⑵
B●
●C
2
3
能
E●
●D
A
●●
图⑶
0
1
能
图⑷
图1
0
5
能
奇点个数 偶点个数 能否一笔画
①有奇数条边相连的点叫奇点。如:
●
●
●
②有偶数条边相连的点叫偶点。如:
●●●源自③一笔画指:1、下笔后笔尖不能离开纸。 2、每条线都只能画一次而不能重复。 不能遗漏。
活动探究 下列图形中。请找出每个图的奇点个数,偶点个数。试一试哪 些可以一笔画出,请填表,从中你能发现什么规律?
奇点个数 偶点个数 能否一笔画
用你发现的规律,说一说七桥问题的答案?
由于七桥问题中的四个点都是奇点,因此可 以判断它是无法一笔画出来的 ,也就是说 根本不存在能不重复走遍七座桥的路线!
【精品】一笔画(七桥问题)
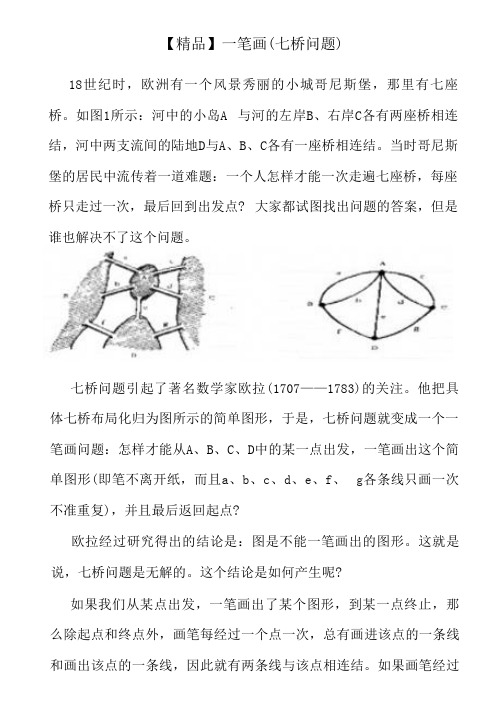
【精品】一笔画(七桥问题)18世纪时,欧洲有一个风景秀丽的小城哥尼斯堡,那里有七座桥。
如图1所示:河中的小岛A 与河的左岸B、右岸C各有两座桥相连结,河中两支流间的陆地D与A、B、C各有一座桥相连结。
当时哥尼斯堡的居民中流传着一道难题:一个人怎样才能一次走遍七座桥,每座桥只走过一次,最后回到出发点? 大家都试图找出问题的答案,但是谁也解决不了这个问题。
七桥问题引起了著名数学家欧拉(1707——1783)的关注。
他把具体七桥布局化归为图所示的简单图形,于是,七桥问题就变成一个一笔画问题:怎样才能从A、B、C、D中的某一点出发,一笔画出这个简单图形(即笔不离开纸,而且a、b、c、d、e、f、g各条线只画一次不准重复),并且最后返回起点?欧拉经过研究得出的结论是:图是不能一笔画出的图形。
这就是说,七桥问题是无解的。
这个结论是如何产生呢?如果我们从某点出发,一笔画出了某个图形,到某一点终止,那么除起点和终点外,画笔每经过一个点一次,总有画进该点的一条线和画出该点的一条线,因此就有两条线与该点相连结。
如果画笔经过一个n次,那么就有2n条线与该点相连结。
因此,这个图形中除起点与终点外的各点,都与偶数条线相连。
如果起点和终点重合,那么这个点也与偶数条线相连:如果起点和终点是不同的两个点,那么这两个点部是与奇数条线相连的点。
综上所述,一笔画出的图形中的各点或者都是与偶数条线相连的点,或者其中只有两个点与奇数条线相连。
图2中的A点与5条线相连结,B、C、D各点各与3条线相连结,图中有4个与奇数条线相连的点,所以不论是否要求起点与终点重合,都不能一笔画出这个图形。
欧拉定理:如果一个图是连通的并且奇顶点的个数等于0或2,那么它可以一笔画出;否则它不可以一笔画出。
一笔画:■1.凡是由偶点组成的连通图,一定可以一笔画成。
画时可以把任一偶点为起点,最后一定能以这个点为终点画完此图。
■2.凡是只有两个奇点的连通图(其余都为偶点),一定可以一笔画成。
小升初数学专项题第七讲 一笔画与七桥问题_通用版

小升初数学专项题第七讲一笔画与七桥问题_通用版第七讲一笔画与七桥问题【知识梳理】1.一笔画是指能够一笔画成的图形。
2.把和一条、三条、五条等奇数条线相连的点叫做奇点,把和两条、四条、六条等偶数条线相连的点叫做偶点,这样图形中要么是奇点,要么是偶点。
3.有2个奇点或0个奇点(全部是偶点)连通图能够一笔画成,否则不能一笔画成。
4.七桥问题可以转化成一笔画问题解决。
【典例精讲1】一笔画就是笔不离纸,笔画不重复,一笔画出一个图形.你能用一笔画出下列图形吗?思路分析:能够一笔画成的图形,首先必须要相连,结果不相连就一定不能一笔画成,能否一笔画成,关键在于判别奇点、偶点的个数:只有偶点,可以一笔画,并且可以以任意一点作为起点;只有两个奇点,可以一笔画,但必须以这两个奇点分别作为起点和终点;奇点超过两个,则不能一笔画。
解答:观察图形可知(1)第一个图形全是偶点,所以能一笔画出;(2)第二个图形是2个奇点,剩下的都是偶点,所以能一笔画出。
小结:解决这类问题首先要看是不是连通图,其次看奇点或偶点的个数,由偶点组成的,或只有两个奇点的连通图才能一笔画成。
【举一反三】1、下面这些图形,哪个能一笔画?哪个不能一笔画?2.“九点连线”是一道著名的数学题,你能用一笔画4条连续的直线段,把图中所有的9个点都连起来吗?请你在下图画出来。
【典例精讲2】在一个城市中有七座桥和四个区域:能不能一次走遍所有的七座桥,而每座桥只准经过一次?思路分析:用“1、2、3、4、5、6、7”表示七座桥,它们连接着A、B、C、D 四个区域(如图所示),这样一来,七座桥的问题,就转变为一个一笔画问题,即能不能一笔从头到尾不重复地画出这个图形.解答:图中有4个奇点和一个偶点,奇点个数不是2个,因为C、D、E都是奇数点。
【答案】::(1)不能不重复地走一次穿过每扇门。
(2)当关闭C和D之间的门;或关闭D和E之间的门;或关闭E通向过道的门时,可一次通过.(用A、B、C、D、E五个点表示五个房间,F点表示过道,用线把两个点连起来,于是走的路线就简化成一笔画问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 七桥问题引起了著名数学家欧拉 (1707—1783)的关注。他把具体七桥 布局化归为图所示的简单图形,于是, 七桥问题就变成一个一笔画问题:怎样 才能从A、B、C、D中的某一点出发,一 笔画出这个简单图形
• 奇偶点。
• 下列图形中,请找出每个图的奇点个数, 偶点个数。试一试哪些可以一笔画出, 从中你能发现什么规律?
七桥问题和一笔画
七桥问题
• • • • • 18世纪时,欧洲有一个风 景秀丽的小城哥尼斯堡, 那里有七座桥。如图所示: 河中的小岛A与河的左岸B、 右岸C各有两座桥相连结,河中两支流间 的陆地D与A、B、C各有一座桥相连结。 当时哥尼斯堡的居民中流传着一道难题: 一个人怎样才能一次走遍七座桥,每座 桥只走过一次,最后回到出发点?
• ■⒈凡是由偶点组成的连通图,一定可 以一笔画成。画时可以把任一偶点为起 点,最后一定能以这个点为终点画完此 图。 ■⒉凡是只有两个奇点的连通图(其余 都为偶点),一定可以一笔画成。画时 必须把一个奇点为起点,另一个奇点终 点。 ■⒊其他情况的图都不能一笔画出。(奇 点数除以二便可算出此图需几笔画成。) •
