计算分析题期末复习讲解1
税收筹划复习提纲重点

《税收筹划》期末复习提纲复习重点:1、计算分析题重点掌握:(1)第2章第3节增值税纳税筹划的基本方法(2)第4章个人所得税的税收筹划(3)第6章典型案例分析2、简答题点掌握:(1)第1章总论-税收筹划的目标;-税收筹划的基本技术;-税收筹划的概念及特点;(2)第2章-增值税税收筹划的范畴;-增值税税收筹划主要围绕哪些税收政策进行;(3)第3章-企业所得税的筹划技巧;(4)第4章-个人所得税有关纳税人税收筹划的途径;-个人所得税的筹划方法;-个人所得税的优惠政策;(5)第5章-企业重组的类型;-企业重组分立过程中的税收筹划技巧;简答题(1)第1章总论-税收筹划的目标;-税收筹划的基本技术;-税收筹划的概念及特点;答:税收筹划的目标:(1)减轻纳税主体的税收负担;(2)争取延期纳税,占有资金的时间价值;(3)争取涉税过程中的零风险;(4)降低税收筹划成本,提高纳税主体的经济效益。
税收筹划的基本技术:减免税技术、分割技术、扣除技术、税率差异技术、抵免技术、退税技术、延期纳税技术、会计政策选择技术税收筹划的概念:纳税行为发生之前,在不违反法律、法规的前提下,通过对纳税主体的经营活动或投资行为等涉税事项做出事先安排,以达到少缴税和递延缴纳目标的一系列谋划活动。
(2)第2章-增值税税收筹划的范畴;-增值税税收筹划主要围绕哪些税收政策进行;答:增值税税收筹划范畴:纳税人身份税收筹划,利用优惠政策税收筹划,利用销项税额和进项税额延缓纳税,销售已用固定资产税收筹划,混合销售税收筹划,兼营行为税收筹划,几种特殊销售税收筹划增值税税收筹划主要围绕哪些税收政策进行(一)一般纳税人和小规模纳税人的征税规定;(二)混合销售行为的征税规定;(三)兼营行为的征税规定;(四)几种特殊销售方式的征税规定;(五)纳税人销售已使用过的固定资产的征税规定;(六)有关销项税额确定和进项税额抵扣的税收规定;(七)有关增值税优惠政策的税收规定。
南平市顺昌县2024-2025学年六年级数学第一学期期末复习检测试题含解析

南平市顺昌县2024-2025学年六年级数学第一学期期末复习检测试题注意事项1.考生要认真填写考场号和座位序号。
2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。
第一部分必须用2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。
3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。
一、仔细填空。
(每小题2分,共20分)1.有一批课外书,按照5∶4分给甲乙两个班同学。
甲班得到125本,乙班得到________本。
2.6300立方厘米=(_______)立方分米0.25立方米=(_______)立方分米2时=(______)分10升=(________)毫升53.一个正方形面积是10平方厘米,从这个正方形上剪下一个最大的圆,这个圆的面积是(____)平方厘米.4.设和都是自然数,且满足,求的值_______________5.把2m长的钢筋平均截成7段,每段长(________)m,其中两段占全长的(________)。
6.3080平方米=(___________)平方分米=(__________)平方千米;3时15分=(__________)时。
7.在3.014,3.01,π,314%,3.104中,最大的数是(____),最小的数是(____)。
8.________的40%是100千克。
9.a÷b=5,(a,b都是非零的自然数),a和b的最大公因数是,最小公倍数是.10.商场内一件羊毛衫原价600元,现价480元,是打(________)折销售;另一件羊毛衫现价344元,原价(________)元。
二、准确判断。
(对的画“√ ”,错的画“×”。
每小题2分,共12分)11.小聪的口袋里,有1个黄球,3个绿球,5个红球.摸出红球的可能性最大.(_____)12.是分母为12的最简真分数,则自然数a的取值只有2个._____13.不为零的自然数,至少有一个约数.(____)14.-10°要比-20°低。
期末复习专题一数的认识与运算计算篇-2022-2023学年四年级数学下册典型例题(原卷版)

20222023学年四年级数学下册典型例题系列之期末复习专题一:数的认识与运算—计算篇(原卷版)编者的话:《20222023学年四年级数学下册典型例题系列》是基于教材知识点和常年考点考题总结与编辑而成的,该系列主要包含典型例题、专项练习、分层试卷三大部分。
典型例题部分是按照单元顺序进行编辑,主要分为计算和应用两大部分,其优点在于考题典型,考点丰富,变式多样。
专项练习部分是从常考题和期末真题中选取对应练习,其优点在于选题经典,题型多样,题量适中。
分层试卷部分是根据试题难度和掌握水平,主要分为基础卷、提高卷、拓展卷三大部分,其优点在于考点广泛,分层明显,适应性广。
本专题是期末复习专题一:数的认识与运算—计算篇。
本部分内容包括多位数的认识,乘法计算以及运算律和计算器的使用等,包括期末常考典型例题,涵盖较广,部分内容和题型较复杂,建议作为期末复习核心内容进行讲解,一共划分为五大篇目,欢迎使用。
【篇目一】认识多位数。
【知识总览】一、多位数的认识。
1.整数数位顺序表。
2.表示物体个数的1,2,3,4,5,6,7,8,……都是自然数,一个物体也没有,用0表示,0也是自然数;所有的自然数都是整数,最小的自然数是0,没有最大的自然数,自然数的个数是无限的。
3.个(一)、十、百、千、万……亿、十亿、百亿、千亿都是计数单位。
4.用数字表示数的时候,这些计数单位要按照一定的顺序排列起来,它们所占的位置叫做数位。
5.每相邻的两个计数单位之间的进率都是十,这种计数方法叫做十进制计数法。
6.我国的计数习惯是从右起每个数位为一级,即个位、十位、百位、千位是个级;万位、十万位,百万位、千万位是万级;亿位、十亿位、百亿位、千亿位是亿级………,其中个级的数表示的是多少个“一”,万级的数表示多少个“万”,亿级的数表示多少个“亿”。
二、大数的读法和写法。
1.读数时,先分级,从高位读起,先读亿级,再读万级,最后读个级;2.读亿级或万级的数按照个级的读法读,再在后面加上一个“亿”字或“万”字;3.每一级末尾0都不读,数中间有一个0或连续有几个0,都只读一个零。
税收筹划复习提纲重点

《税收筹划》期末复习提纲复习重点:1、计算分析题重点掌握:(1)第2章第3节增值税纳税筹划的基本方法(2)第4章个人所得税的税收筹划(3)第6章典型案例分析2、简答题重点掌握:(1)第1章总论-税收筹划的目标;-税收筹划的基本技术;-税收筹划的概念及特点;(2)第2章-增值税税收筹划的范畴;-增值税税收筹划主要围绕哪些税收政策进行;(3)第3章-企业所得税的筹划技巧;(4)第4章-个人所得税有关纳税人税收筹划的途径;-个人所得税的筹划方法;-个人所得税的优惠政策;(5)第5章-企业重组的类型;-企业重组分立过程中的税收筹划技巧;简答题(1)第1章总论-税收筹划的目标;-税收筹划的基本技术;-税收筹划的概念及特点;答:税收筹划的目标:(1)减轻纳税主体的税收负担;(2)争取延期纳税,占有资金的时间价值;(3)争取涉税过程中的零风险;(4)降低税收筹划成本,提高纳税主体的经济效益。
税收筹划的基本技术:减免税技术、分割技术、扣除技术、税率差异技术、抵免技术、退税技术、延期纳税技术、会计政策选择技术税收筹划的概念:纳税行为发生之前,在不违反法律、法规的前提下,通过对纳税主体的经营活动或投资行为等涉税事项做出事先安排,以达到少缴税和递延缴纳目标的一系列谋划活动。
特点:合法性、预期性、风险性、目的性、收益性(2)第2章-增值税税收筹划的范畴;-增值税税收筹划主要围绕哪些税收政策进行;答:增值税税收筹划范畴:纳税人身份税收筹划,利用优惠政策税收筹划,利用销项税额和进项税额延缓纳税,销售已用固定资产税收筹划,混合销售税收筹划,兼营行为税收筹划,几种特殊销售税收筹划增值税税收筹划主要围绕哪些税收政策进行(一)一般纳税人和小规模纳税人的征税规定;(二)混合销售行为的征税规定;(三)兼营行为的征税规定;(四)几种特殊销售方式的征税规定;(五)纳税人销售已使用过的固定资产的征税规定;(六)有关销项税额确定和进项税额抵扣的税收规定;(七)有关增值税优惠政策的税收规定。
沪教版5年级数学上-第19讲-期末复习(一)

学员姓名:学科教师:年级:辅导科目:授课日期时间主题期末复习(一)教学内容1.小数的混合运算及平均数的应用;2.列方程解应用题.(此环节设计时间在20—25分钟)易错题整理一、填空题1、三个连续自然数的和是60,这三个数是()、()和()。
2、一个三位小数四舍五入后是2.56,这个小数最大可能是(),最小可能是()。
3、0.15小时=()分 138分=()小时 13.05t=( )kg5678dm2=( ) m2 3.3m=( )cm 2250ml=( )l4、一个数小数点向右移动2位后,比原数大1237.5,这个数是()。
5、把一个小数的小数点向左移动一位,比原数减少了3.96。
原来的小数是()。
6、一个数乘以大于1的数,积比这个数();一个数乘以小于1的数,积比这个数()。
一个数除以大于1的数,商比这个数();一个数除以小于1的数(0除外),商比这个数()。
7、计算1.68÷0.15,当商是11时,余数是()。
8、一个长方形木框,拉成一个平行四边形,()不变,()变小。
一个平行四边形木框,拉成一个长方形,面积(),周长()。
9、等底等高的三角形是等底等高的平行四边形的面积的()。
一个三角形和一个平行四边形的面积相等,高也相等,那么三角形的底是平行四边形的底的(),如果三角形的底是10cm,那么平行四边形的底是()。
10、由四根木条钉成的一个底是18cm,高是11cm的平行四边形,把它拉成长方形后,面积增加了36cm²,长方形的宽是()cm。
11、如果一个三角形的底和高都扩大10倍,那么它的面积扩大()倍。
12、一个三角形与一个平行四边形等底,平行四边形的高是三角形的3倍,则平行四边形的面积是三角形的()倍。
二、判断题。
1、等底等高的两个三角形面积一定相同。
()2、等底等高的两个三角形形状一定相同。
()3、两个面积相等的三角形一定能拼成一个平行四边形。
()教法指导:先由学生做,同学之间互相批改,错误率高的题目由老师细致讲解,错误率低的题目可以让做对的学生向做错的学生讲解,老师做补充,做得都对的题目可以随机让学生讲解给大家听。
第一学期五年级数学第19讲-期末复习(一)沪教版(含答案)
第19讲—期末复习(一)学员姓名:学科教师:年级:辅导科目:授课日期时间主题第19讲—期末复习(一)1.复习小数的混合运算及平均数的应用;学习目标2.复习巩固列方程解应用题.教学内容(一)上次课课后巩固作业处理,建议让学生互批互改,个别错题可以让学生进行分享,针对共性的错题教师讲解为主。
(二)上次预习思考内容讨论分享本学期前两章易错题整理一、填空题1、三个连续自然数的和是60,这三个数是()、()和()。
2、一个三位小数四舍五入后是2.56,这个小数最大可能是(),最小可能是()。
3、0.15小时=()分 138分=()小时 13.05t=( )kg5678dm2=( ) m2 3.3m=( )cm 2250ml=( )l4、一个数小数点向右移动2位后,比原数大1237.5,这个数是()。
5、把一个小数的小数点向左移动一位,比原数减少了 3.96。
原来的小数是()。
6、一个数乘以大于1的数,积比这个数();一个数乘以小于1的数,积比这个数()。
一个数除以大于1的数,商比这个数();一个数除以小于1的数(0除外),商比这个数()。
7、计算 1.68÷0.15,当商是11时,余数是()。
8、一个长方形木框,拉成一个平行四边形,()不变,()变小。
一个平行四边形木框,拉成一个长方形,面积(),周长()。
9、等底等高的三角形是等底等高的平行四边形的面积的()。
一个三角形和一个平行四边形的面积相等,高也相等,那么三角形的底是平行四边形的底的(),如果三角形的底是10cm,那么平行四边形的底是()。
10、由四根木条钉成的一个底是18cm,高是11cm的平行四边形,把它拉成长方形后,面积增加了36cm2,长方形的宽是()cm。
11、如果一个三角形的底和高都扩大10倍,那么它的面积扩大()倍。
12、一个三角形与一个平行四边形等底,平行四边形的高是三角形的3倍,则平行四边形的面积是三角形的()倍。
二、判断题。
数学分析期末考试题1、2(第二份有答案)复习过程

第三学期数学分析考试题一、判断题(每小题2分,共20分)1.开域是非空连通开集,闭域是非空连通闭集. ()2.当二元函数的重极限与两个累次极限都存在时,三者必相等. ()3.连续函数的全增量等于偏增量之和. ()4.f(x, y)』xy在原点不可微. ()5•若f xy(x,y)与f yx(x, y)都存在,则f xy(x,y) f yx(x, y) •()6. ysinxy dy 在(0,1)内不一致收敛. ()1x(1 y )7•平面图形都是可求面积的. ()8•学过的各种积分都可以以一种统一的形式来定义( )9.第二型曲面积分也有与之相对应的“积分中值定理”()10.二重积分定义中分割T的细度|T不能用max' i} 来代替. ()、填空题(每小题3分,共15分)1•设z e xy sin(x y),则其全微分dz _____________________________ .32•设f (x, y,z) xy yz,则f 在点P o(2, 1,1)处的梯度grad(P o) ___________________23•设L 为沿抛物线y 2x,从0(0,0)到B(1,2)的一段,贝U L xdy ydx ___________ 4•边长为a密度为b的立方体关于其任一棱的转动惯量等于___________________ .5•曲面3x2y2z227在点(3,1,1 )处的法线方程为___________________________ .三、计算题(每小题5分,共20分)1.求极限lim (x2y2)xy.(x,y) (0,0)v'2.设z z(x, y)是由方程x y z e z所确定的隐函数,求Z xy3.设A [0,1] [0,1],求1A (1ydxdy2 2 \ 3. 2 . x y )4.计算抛物线(x y)2ax (a 0)与x轴所围的面积.2 2 2y的物体V由曲面2z x y与z 2所围成,求该物体关于z轴的转动惯量.五、(10分)求第二类曲面积分x2dydzS程.其中S是球面(x a)2(y b)2 2 2(z c) R并取外侧为正向.六、(第1小题8分, 第2小题7分, 共15分).1.求曲线z26, z 在点(1, 1 , 2) 处的切线方程和法平面方2•证明: "dx 2、2,七、(10分)应用积分号下的积分法,求积分b1 1 xcos(ln —)一0x I) axdx (b a 0). ln x四、(10 分)密度(x, y,z) , x2y2dzdx z2dxdy第三学期数学分析参考答案及评分标准一、判断题(每小题2分,共20分)1. 开域是非空连通开集,闭域是非空连通闭集.( )2. 当二元函数的重极限与两个累次极限都存在时,三者必相等. (V )3. 连续函数的全增量等于偏增量之和. ( )4. f(x, y) ,/|xy 在原点不可微.(V ) 5•若 f xy (X,y)与 f yx (x, y)都存在,则 f xy (x,y) f yx (x, y).() 6.ysinxydy 在(0,1)内不一致收敛. (V )1x(1 y 2)7•平面图形都是可求面积的.( )8•学过的各种积分都可以以一种统一的形式来定义 ( V ) 9.第二型曲面积分也有与之相对应的“积分中值定理” ()10.二重积分定义中分割T 的细度T 不能用max{ ,}来代替.(V )1 i n二、填空题(每小题 3分,共15分) 1•设z e xy sin(x y),则其全微分dze xy [y sin(x y) cos(x y)]dx e xy [xsin(x y) cos(x y)]dy .232•设 f (x, y,z) xy yz ,则 f 在点 P o (2, 1,1)处的梯度 grad(P o )(1,-3,-3).23•设 L 为沿抛物线 y 2x .从 0(0,0)到 B(1,2)的一段,贝U L xdy ydx 24•边长为a 密度为b 的立方体关于其任一棱的转动惯量等于-a 5b . 3三、计算题(每小题 5分,共20 分)1.求极限爲%。
八年级物理下学期期末复习计算专题 (1)

八年级物理下学期期末复习计算专题1.随着共享单车在全国各大城市迅速铺开,“共享经济”的概念迅速普及,“共享汽车”也随之悄然进入了人们的视野。
如图所示是某品牌“共享汽车”,其总质量 1.2t,该车在行驶过程中受到的阻力为车重的0.1倍,g取10N/kg,求:(1)汽车所受的重力;(2)该车以54km/h的速度匀速行驶30min,求通过的路程;(3)汽车在行驶过程中受到的阻力。
2.电动汽车是正在大力推广的新型交通工具,它具有节能、环保的特点,如图,是一辆停放在水平地面上的电动汽车,质量为1.6×103kg,每个轮胎和地面的接触面积为2×10﹣2m2,g取10N/kg,求:(1)车对地面的压力;(2)车对地面的压强。
3.在水平地面上,有一质量为5kg的容器内装有35kg的水,如图所示,水面到水底的深度为1.2m,容器的底面积为0.02m2,求:(1)容器底面所受到水的压强和压力;(2)地面受到的压力和压强。
(g=10N/kg)4.图甲是修建造码头时用刚缆绳拉着实心长方体A沿竖直方向以0.3m/s的速度匀速下降的情景。
图乙是A下降到水底之前钢缆绳对A的拉力F随时间t变化的图象(取水的密度为ρ=1.0×103kg/m3,g取10N/kg).求:(1)长方体A的高度。
(2)长方体A浸没在水中后受到的浮力。
(3)长方体A的密度。
5.如图所示,将边长为5cm的实心正方体木块轻轻地放入装满水的溢水杯中,木块静止时,从杯中溢出水的质量为0.1kg(g取10N/kg).求:(1)木块受到的浮力;(2)木块的密度;(3)木块下底面受到水的压强。
6.用弹簧测力计悬挂一实心物块,物块下表面与水面刚好接触,如图甲所示。
从此处匀速下放物块,直至浸没于水中并继续匀速下放(物块未与水底接触)。
物块下放过程中,弹簧测力计示数F与物块下表面浸入水的深度h的关系如图乙。
g取10N/kg,水的密度是1.0×103kg/m3.求:(1)物块受到的重力;(2)物块完全浸没在水中受到的浮力;(3)物块的密度。
2013计算机算法设计与分析期终考试复习题(1)

方向,为每个解过的子问题建立了备忘录以备需要时查看,同样也可避
免相同子问题的重复求解。
6.递归的二分查找算法在divide阶段所花的时间是 O(1) ,conquer阶 段所花的时间是 T(n/2) ,算法的时间复杂度是 O( log n) 。
7.Prim算法利用贪心 策略求解 最小生成树问题,其时间复杂度是 O(n2) 。
参考解答:不相同。目标函数:获得最大利润。最优量度:最大利润/ 重量比。
19 采用回溯法求解的问题,其解如何表示?有什么规定? 参考解答:问题的解可以表示为n元组:(x1,x2,……xn),xi∈Si, Si 为有穷集合,xi∈Si, (x1,x2,……xn)具备完备性,即(x1,x2,…… xn)是合理的,则(x1,x2,……xi)(i<n)一定合理。
12、一个算法的优劣可以用(时间复杂度)与(空间复杂度)与来衡
量。
13、回溯法在问题的解空间中,按(深度优先方式)从根结点出发搜索
解空间树。
14、直接或间接地调用自身的算法称为(递归算法)。
15、 记号在算法复杂性的表示法中表示(渐进确界或紧致界)。
16、在分治法中,使子问题规模大致相等的做法是出自一种(平衡
8.背包问题可用 贪心法 , 回溯法 等策略求解。 9.用动态规划算法计算矩阵连乘问题的最优值所花的时间是 O(n3) ,
子问题空间大小是 O(n2) 。
10.图的m着色问题可用 回溯 法求解,其解空间树中叶子结点个数是 mn ,解空间树中每个内结点的孩子数是 m 。
11.单源最短路径问题可用贪心法 、 分支限界 等策略求解。
12345678
21436587
34127856
43218765
56781234
《基础会计》计算分析题35题第1...

《基础会计》计算分析题35题第1题P71公司2010年1 月末结账前的损益账户余额如下:要求:根据上述账户余额,编制当月利润表。
利润表编制单位:汇丰公司 20XX年1月单位:元要求:根据上述资账户发生额,编制利润表。
(1) 484000 (2)8000 (3) 100000 (4) 100000 (5)75580第2题P53—54大华公司2010年10月的余额试算平衡表如下:补充资料:1、长期待摊费用中将于半年内摊销的是3000元。
2、长期借款期末余额中将于一年内到期归还的长期借款数为50000元。
3、应收账款各明细账余额如下:应收账款——A公司贷方5000——B公司借方余额41400应付账款——C公司贷方余额 39500——D公司借方余额 8100预收账款——E公司贷方余额7200—— F公司借方余额 3000要求:根据上述资料,计算华天公司20210年10月31日资产负债表中下列项目的期末数。
(1)货币资金(2)应收账款(3)预付账款(4)存货(5)应付账款答案:(1)66600 (2)43900 (3)8100 (4)67000 (5)39500(拓展:1、长期借款2、一年内到期的非流动负债 3、长期待摊费用 4、一年内到期的非流动资产 5、固定资产 6、预付账款)第3题(补充1)某企业2010年8月发生的经济业务及登记的总分类账和明细账如下。
要求:根据资料和总分类账的明细分类账的勾稽关系,将总分类和明细分类中空缺的数字填上。
(1)4日,向A企业购入甲材料1000公斤,单价17元,价款17000元,购入乙材料2500公斤,单价9元,价款22500元。
货物已验收入库,款项39500元尚未支付。
(不考虑增值税,不同)(2)8日,向B企业购入甲材料2000公斤,单价17元,价款34000元,货物已验收入库,款项尚未支付。
(3)13日,生产车间为生产产品领用材料,其中领用甲材料1400公斤,单价17元,价值23800元;领用乙材料3000公斤,单价9元,价值27000元。
统计学计算题例题及计算分析
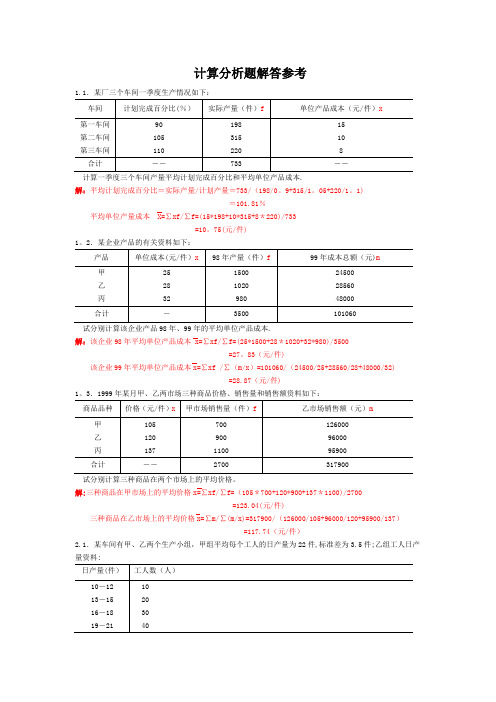
计算分析题解答参考1.1.某厂三个车间一季度生产情况如下:计算一季度三个车间产量平均计划完成百分比和平均单位产品成本.解:平均计划完成百分比=实际产量/计划产量=733/(198/0。
9+315/1。
05+220/1。
1) =101.81%平均单位产量成本 X=∑xf/∑f=(15*198+10*315+8*220)/733 =10。
75(元/件) 1。
2.某企业产品的有关资料如下:试分别计算该企业产品98年、99年的平均单位产品成本.解:该企业98年平均单位产品成本 x=∑xf/∑f=(25*1500+28*1020+32*980)/3500 =27。
83(元/件)该企业99年平均单位产品成本x=∑xf /∑(m/x )=101060/(24500/25+28560/28+48000/32) =28.87(元/件)1。
3.1999年某月甲、乙两市场三种商品价格、销售量和销售额资料如下: 试分别计算三种商品在两个市场上的平均价格。
解:三种商品在甲市场上的平均价格x=∑xf/∑f=(105*700+120*900+137*1100)/2700 =123.04(元/件)三种商品在乙市场上的平均价格x=∑m/∑(m/x)=317900/(126000/105+96000/120+95900/137) =117.74(元/件)2.1.某车间有甲、乙两个生产小组,甲组平均每个工人的日产量为22件,标准差为3.5件;乙组工人日产量资料:试比较甲、乙两生产小组中的哪个组的日产量更有代表性? 解:∵X 甲=22件 σ甲=3。
5件∴V 甲=σ甲/ X 甲=3.5/22=15。
91% 列表计算乙组的数据资料如下:∵x 乙=∑xf/∑f=(11*10+14*20+17*30+20*40)/100 =17(件)σ乙=√[∑(x-x)2f]/∑f =√900/100 =3(件) ∴V 乙=σ乙/ x 乙=3/17=17。
高级财务管理期末复习资料

高级财务管理期末复习资料篇一:一、风险与收益一、选择题1.甲公司面临A、B两个投资项目,它们的预期收益率相等,但A项目的标准差小于B项目的标准差。
对A、B两个项目可以做出的判断为( D )。
A.A项目实际取得的收益会高于其预期收益B.B项目实际取得的收益会低于其预期收益C.A项目取得更高收益和出现更大亏损的可能性均大于B项目D.A项目取得更高收益和出现更大亏损的可能性均小于B项目2.一般来说,无法通过多样化投资予以分散的风险是( A )。
A.系统风险B.非系统风险C.总风险D.公司特有风险3.某投资组合中包含A、B、C三种证券,其中20%的资金投入A,预期收益率为18%,50%的资金投入B,预期收益率为15%,30%的资金投入C,预期收益率为8%,则该投资组合预期收益率为( C )。
A.9.5%B.10.8%C.13.5%D.15.2%4.当两种证券完全正相关时,它们的相关系数是( B)。
A.0B.1C.-1 D.不确定5.根据风险分散理论,如果投资组合中两种证券之间完全负相关,则( B )。
A.该组合的风险收益为零B.该组合的非系统风险可完全抵消C.该组合的投资收益大于其中任一证券的收益D.该组合只承担公司特有风险,不承担市场风险6.如果投资组合由30种资产组成,则构成组合总体方差和协方差的项目个数分别为(C )。
A.30和30B.900和30C.30和870D.930和307.有效集以外的投资组合与有效边界上的组合相比,不包括(D )。
A.相同的标准差和较低的预期收益率B.相同的预期收益率和较高的标准差C.较低的预期收益率和较高的标准差D.较低的标准差和较高的预期收益率8.已知某风险组合的预期收益率和标准差分别为12%和15%,无风险收益率为6%,假设某投资者可以按无风险利率取得资金,将其自有资金800万元和借入资金200万元均投资于风险组合,则该投资者投资的预期收益率和标准差分别为( A)。
人教版七年级数学上册第一章-有理数-解答题复习(一)解析版

第1章有理数解答题复习(一)1.计算:﹣5×2+3÷﹣(﹣1).2.有个填写运算符号的游戏:在“1□2□6□9”中的每个□内,填入+,﹣,×,÷中的某一个(可重复使用),然后计算结果.(1)计算:1+2﹣6﹣9;(2)若1÷2×6□9=﹣6,请推算□内的符号;(3)在“1□2□6﹣9”的□内填入符号后,使计算所得数最小,直接写出这个最小数.】3.计算:(﹣2)3+×8.4.计算:(﹣6)2×(﹣).5.计算:23×(1﹣)×.6.计算:(﹣2)2×(1﹣).!7.观察下列两个等式:2﹣=2×+1,5﹣=5×+1,给出定义如下我们称使等式a﹣b=ab+1成立的一对有理数“a,b”为共生有理数对”,记为(a,b)(1)通过计算判断数对“﹣2,1,“4,”是不是“共生有理数对”;(2)若(6,a)是“共生有理数对”,求a的值;(3)若(m,n)是“共生有理数对”,则“﹣n,﹣m”“共生有理数对”(填“是”或“不是”),并说明理由;(4)如果(m,n)是“共生有理数对”(其中n≠1),直接用含n的代数式表示m.[8.在一条不完整的数轴上从左到右有点A,B,D,C,其中AB=2,BD=3,DC=1,如图所示,设点A,B,D,C所对应数的和是p.(1)①若以B为原点.写出点A,D,C所对应的数,并计算p的值;②若以D为原点,p又是多少(2)若原点O在图中数轴上点C的右边,且CO=x,p=﹣71,求x.9.如图,在一条不完整的数轴上从左到右有点A,B.将线段AB沿数轴向右移动,移动后的线段记为A′B′,按要求完成下列各小题(1)若点A为数轴原点,点B表示的数是4,当点A′恰好是AB的中点时,数轴上点B′表示的数为.·(2)设点A表示的数为m,点A′表示的数为n,当原点在线段A′B之间时,化简回|m|+|n|+|m ﹣n|.10.阅读材料题:求两个正整数的最大公约数是常见的数学问题,中国古代数学专著《九章算术》中便记载了求两个正整数最大公约数的一种方法﹣﹣更相减损术,术曰:“可半者半之,不可半者,副置分母、子之数,以少成多,更相减损,求其等也.以等数约之”,意思是说,要求两个正整数的最大公约数,先用较大的数减去较小的数,得到差,然后用减数与差中的较大数减去较小数,以此类推,当减数与差相等时,此时的差(或减数)即为这两个正整数的最大公约数.例如:求91与56的最大公约数解:91﹣56=3556﹣35=2135﹣21=14…21﹣14=714﹣7=7所以,91与56的最大公约数是7请用以上方法解决下列问题:(1)求108与45的最大公约数;(2)求三个数78、104、143的最大公约数.11.计算2×(﹣5)+22﹣3÷.·12.已知,数轴上三个点A、O、B.点O是原点,固定不动,点A和B可以移动,点A表示的数为a,点B表示的数为b.(1)若AB移动到如图所示位置,计算a+b的值.(2)在图的情况下,B点不动,点A向左移动3个单位长,写出A点对应的数a,并计算b﹣|a|.(3)在图的情况下,点A不动,点B向右移动个单位长,此时b比a大多少请列式计算.13.如图,已知A,B两点在数轴上,点A表示的数为﹣10,OB=3OA,点M以每秒3个单位长度的速度从点A向右运动.点N以每秒2个单位长度的速度从点O向右运动(点M、点N同时出发)(1)数轴上点B对应的数是.!(2)经过几秒,点M、点N分别到原点O的距离相等14.计算:﹣14﹣×[2﹣(﹣3)2].15.观察下列各式的计算过程:①1+8=32;②1+8+16=52;③1+8+16+24=72;④1+8+16+24+32=92.(1)第6个算式为;(2)用含n的代数式表示第n个等式,并验证其正确性.|16.计算:(﹣2)3×8×()3+8÷.17.计算:(1)(﹣2)3÷+3×|1﹣(﹣2)2|(2)﹣12﹣(﹣)÷×[﹣2+(﹣3)2].!18.计算6÷(﹣)时,李明同学的计算过程如下,原式=6÷(﹣)+6÷=﹣12+18=6.请你判断李明的计算过程是否正确,若不正确,请你写出正确的计算过程,另用正确方法计算()÷(﹣)+36÷()的值.19.计算:已知|x|=,|y|=,且x<y<0,求6÷(x﹣y)的值.20.(﹣1)4﹣{﹣[()2+×(﹣1)]÷(﹣2)2}.^第1章有理数解答题复习(一)参考答案与试题解析1.【分析】直接利用有理数的混合运算法则计算得出答案.【解答】解:原式=﹣10+9+1=0.【点评】此题主要考查了有理数的混合运算,正确掌握相关运算法则是解题关键.2.【分析】(1)根据有理数的加减法可以解答本题;\(2)根据题目中式子的结果,可以得到□内的符号;(3)先写出结果,然后说明理由即可.【解答】解:(1)1+2﹣6﹣9=3﹣6﹣9=﹣3﹣9=﹣12;(2)∵1÷2×6□9=﹣6,∴1××6□9=﹣6,"∴3□9=﹣6,∴□内的符号是“﹣”;(3)这个最小数是﹣20,理由:∵在“1□2□6﹣9”的□内填入符号后,使计算所得数最小,∴1□2□6的结果是负数即可,∴1□2□6的最小值是1﹣2×6=﹣11,∴1□2□6﹣9的最小值是﹣11﹣9=﹣20,∴这个最小数是﹣20."【点评】本题考查有理数的混合运算,解答本题得关键是明确有理数混合运算的计算方法.3.【分析】先求(﹣2)3=﹣8,再求×8=4,即可求解;【解答】解:(﹣2)3+×8=﹣8+4=﹣4;【点评】本题考查有理数的计算;熟练掌握幂的运算是解题的关键.4.【分析】原式先计算乘方运算,再利用乘法分配律计算即可求出值.【解答】解:原式=36×(﹣)=18﹣12=6.【点评】此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.5.【分析】原式先计算括号中的减法运算,再计算乘方运算,最后算乘法运算即可得到结果.;【解答】解:原式=8××=3.【点评】此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.6.【分析】直接利用有理数乘方运算法则化简,进而去括号求出答案.【解答】解:(﹣2)2×(1﹣)=4×(1﹣)=4×=1.【点评】此题主要考查了有理数的混合运算,正确掌握运算法则是解题关键.!7.【分析】(1)根据“共生有理数对”的定义即可判断;(2)根据“共生有理数对”的定义,构建方程即可解决问题;(3)根据“共生有理数对”的定义即可判断;(4)根据“共生有理数对”的定义即可解决问题.【解答】解:(1)﹣2﹣1=﹣3,﹣2×1+1=1,∴﹣2﹣1≠﹣2×1+1,∴(﹣2,1)不是“共生有理数对”;∵4﹣=,,,∴(4,)是共生有理数对;(2)由题意得:6﹣a=6a+1,解得a=;(3)是.理由:﹣n﹣(﹣m)=﹣n+m,)﹣n•(﹣m)+1=mn+1,∵(m,n)是“共生有理数对”,∴m﹣n=mn+1,∴﹣n+m=mn+1,∴(﹣n,﹣m)是“共生有理数对”;故答案为:是;(4)∵(m,n)是“共生有理数对”,!∴m﹣n=mn+1,即mn﹣m=﹣(n+1),∴(n﹣1)m=﹣(n+1),∴.【点评】本题考查有理数的混合运算、“共生有理数对”的定义,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考常考题型.8.【分析】(1)①根据以B为原点,则A,D,C所对应的数分别为:﹣2,3,4,进而得到p的值;②以D为原点,A,D,C所对应的数分别为:﹣5,﹣3,1,进而得到p的值;(2)用x的代数式分别表示A,D,C所对应的数,根据题意列方程解答即可.【解答】解:(1)①点A,D,C所对应的数分别为:﹣2,3,4;【p=﹣2+3+4=5;②若以D为原点,P=﹣3﹣5+1=﹣7;(2)由题意,A,B,C,D表示的数分别为:﹣6﹣x,﹣4﹣x,﹣1﹣x,﹣x,﹣6﹣x﹣4﹣x﹣1﹣x﹣x=﹣71,﹣4x=﹣60,x=15.`【点评】本题主要考查了两点间的距离以及数轴的运用,解题时注意:连接两点间的线段的长度叫两点间的距离.9.【分析】(1)根据题意可知A′表示的数为2,根据AB的长度即可求解;(2)根据绝对值的定义,分情况讨论解答即可.【解答】解:(1)∵点B表示的数是4,当点A′恰好是AB的中点时,∴点A′表示的数为2,∴数轴上点B′表示的数为2+4=6.故答案为:6;%(2)由题意知点A′在点A右侧,即m<n,则m﹣n<0.又原点在线段A'B之间,则点A'在原点的左侧,即m<0,n<0,|m|+|n|+|m﹣n|=﹣m﹣n﹣m+n=﹣2m.【点评】本题考查数轴,有理数的加法等知识,解决此类题目时,能理解题意表示出各点表示的数是关键.10.【分析】模仿例题求解即可解决问题.【解答】解:(1)∵108﹣45=63…63﹣45=1845﹣18=2727﹣18=918﹣9=9∴108与45的最大公约数是9.(2)∵104﹣78=26,78﹣26=52,52﹣26=26,{∴104与78的最大公约数是26.∵143﹣104=39,104﹣39=65,65﹣39=26,39﹣26=13,26﹣13=13,∴143与104最大公约数是13.∴78、104、143的最大公约数是13.|【点评】本题考查有理数的除法,有理数的减法等知识,解题的关键是理解题意,学会模仿例题解决问题.11.【分析】原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果.【解答】解:原式=﹣10+4﹣3×2=﹣10+4﹣6=﹣16+4=﹣12.【点评】此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.12.【分析】(1)由图可知,点A表示的数a,点B表示的数b,即可求得a+b的值.((2)由B点不动,点A向左移动3个单位长,可得数a,再根据绝对值求得即可.(3)点A不动,点B向右移动个单位长,可知数b,再列式计算解得.【解答】解:(1)由图可知:a=﹣10,b=2,∴a+b=﹣8故a+b的值为﹣8.(2)由B点不动,点A向左移动3个单位长,可得a=﹣13,b=2∴b﹣|a|=b+a=2﹣13=﹣11)故a的值为﹣13,b﹣|a|的值为﹣11.(3)∵点A不动,点B向右移动个单位长∴a=﹣10 b=∴b﹣a=﹣(﹣10)=故b比a大.【点评】本题考查了数轴、绝对值,当a是负有理数时,a的绝对值是它的相反数﹣a.13.【分析】(1)根据OB=3OA,结合点B的位置即可得出点B对应的数;(2)设经过x秒,点M、点N分别到原点O的距离相等,找出点M、N对应的数,再分点M、点N在点O两侧和点M、点N重合两种情况考虑,根据M、N的关系列出关于x的一元一次方程,解之即可得出结论..【解答】(1)∵OB=3OA=30,∴B对应的数是30.故答案为:30.(2)设经过x秒,点M、点N分别到原点O的距离相等,此时点M对应的数为3x﹣10,点N对应的数为2x.①点M、点N在点O两侧,则10﹣3x=2x,解得x=2;¥②点M、点N重合,则,3x﹣10=2x,解得x=10.所以经过2秒或10秒,点M、点N分别到原点O的距离相等.【点评】本题考查了数轴,根据点与点之间的位置关系找出方程是解题的关键.14.【分析】按照有理数混合运算的顺序,先乘方后乘除最后算加减,有括号的先算括号里面的.【解答】解:原式=﹣1﹣×(2﹣9)=﹣1﹣×(﹣7)!=﹣1+=.【点评】此题要注意正确掌握运算顺序以及符号的处理.15.【分析】(1)由已知等式知第6个算式为1+8+16+24+32+40+48=132.(2)根据已知等式的规律得出1+8+16+24+…+8n=(2n+1)2,再利用等式的运算顺序和运算法则计算可得.【解答】解:(1)根据题意,第6个算式为1+8+16+24+32+40+48=132,故答案为:1+8+16+24+32+40+48=132.#(2)1+8+16+24+…+8n=(2n+1)2,左边=1+8×(1+2+3+…+n)=1+8×=1+4n(n+1)=1+4n2+4n=(2n+1)2=右边,∴1+8+16+24+…+8n=(2n+1)2.【点评】本题主要考查有理数的混合运算与数字的变化规律,解题的关键是根据已知等式得出1+8+16+24+…+8n=(2n+1)2的规律及整式的运算法则.16.【分析】原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果.【解答】解:原式=﹣8×8×+8×8=﹣8+64=56.【点评】此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.17.【分析】(1)原式先计算乘方及绝对值运算,再计算乘除运算,最后算加减运算即可得到结果;(2)原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果.【解答】解:(1)原式=﹣8×+3×3=﹣10+9=﹣1;(2)原式=﹣1+×3×7=﹣1+=.【点评】此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.18.【分析】李明的计算过程不正确,应先计算括号中的加法运算,再计算除法运算.【解答】解:不正确,正确计算过程为:6÷(﹣)=6÷(﹣)=﹣36;原式=(﹣+)×(﹣36)+36÷=﹣18+6﹣4+36×=﹣16+81=65.【点评】此题考查了有理数的混合运算,有理数混合运算注意运算顺序.19.【分析】直接利用绝对值的性质结合有理数混合运算法则计算得出答案.【解答】解:∵|x|=,|y|=,且x<y<0,∴x=﹣,y=﹣,∴6÷(x﹣y)=6÷(﹣+)=﹣36.【点评】此题主要考查了绝对值的性质和有理数混合运算,正确得出x,y的值是解题关键.20.【分析】原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果.【解答】解:原式=1﹣+(﹣)÷4=+﹣=.【点评】此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.。
液压计算题复习(1)
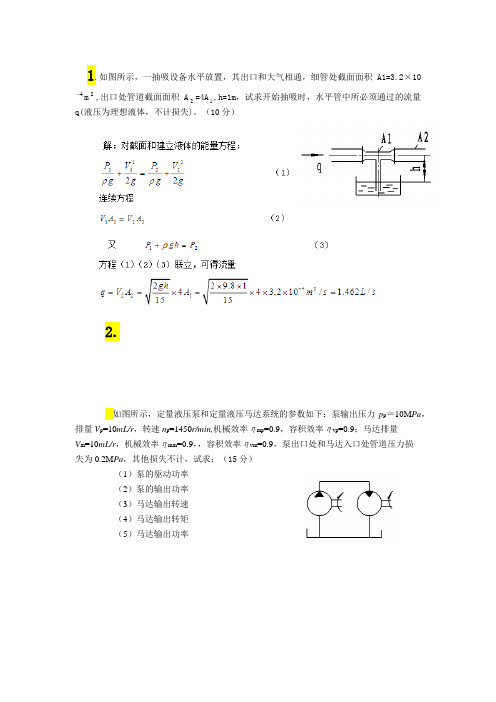
1.如图所示,一抽吸设备水平放置,其出口和大气相通,细管处截面面积A1=3.2×104 m2,出口处管道截面面积A2=4A1,h=1m,试求开始抽吸时,水平管中所必须通过的流量q(液压为理想液体,不计损失)。
(10分)2.如图所示,定量液压泵和定量液压马达系统的参数如下:泵输出压力p p=10M Pa,排量V p=10mL/r,转速n p=1450r/min,机械效率ηmp=0.9,容积效率ηvp=0.9;马达排量V m=10mL/r,机械效率ηmm=0.9,,容积效率ηvm=0.9,泵出口处和马达入口处管道压力损失为0.2M Pa,其他损失不计,试求:(15分)(1)泵的驱动功率(2)泵的输出功率(3)马达输出转速(4)马达输出转矩(5)马达输出功率3、4、 将流量16/min q L =的液压泵安装在油面以下,已知油液的运动粘度20.11/cm s ν=,油液的密度3900/kg m ρ=,弯头处的局部阻力系数ξ=0.2,其他尺寸如图所示,求液压泵入口处的绝对压力。
(17分)解:由已知条件求得吸油管内的流速υ及雷诺数 Re3224441610/0.85/(2)3.140.02600.020.8515452320(3)0.1110e ecx q m s m s d d R R υπυν--⨯⨯===⨯⨯⨯===〈=⨯分分 液流为层流。
(2分)以液压泵的吸油口中心线为基准,对油箱液面和靠近泵的吸入口的截面列实际流体的伯努利方程(油箱液面处的流速 10υ=,压力1a p p =)2211122212222(2)22(1)2a p p h h hggp gh p p αυαυγγρυρ++=++++=++分分式中p ———液流压力损失,包括沿程压力损失1p和局部压力损失2p而1443242222222128(1)128900.0111021610/3.140.02601345/(1)(1)29000.850.2/265/(1)Lp q d N m N m p N m N m μπρυξ--=⨯⨯⨯⨯⨯=⨯⨯==⨯=⨯=分分分分所以,泵的吸入口的压力为2125252()(1)1.013109009.810.7(134565)/1.0610/(2)a p p gh p p N m N m ρ=+-+⎡⎤=⨯+⨯⨯-+⎣⎦=⨯分分5、6、7、。
管理会计典型计算题试卷教案

管理会计计算分析题重点(参考)一、利用高低点法进行混合成本的分解1、某家电生产企业2009年下半年各月的修理费用与相关产量的历史资料如下:要求:用高低点法对修理费用进行分析,以便企业进行费用控制.高点(6800,15800);低点(4400,11000)b=(15800—11000)/(6800-4400)=4800/2400=2元/台将 b=2元/台代入高点或低点,a=15800-6800×2=2200元或a=11000—4400×2=2200元成本模型为y=2200+2x从案例解析可得,修理费用中固定部分为2200元,变动部分为2x。
2、某企业A产品2009年1、2季度各月的维修费与维修工时的历史资料如下:要求:(1)采用高低点法对维修费进行成本性态分析并建立成本模型。
(2)假如7月份预计发生维修工时2300小时,预计7月份的维修费是多少。
(1)高点(2000,3000);低点(1200,2200)b=(3000-2200)/(2000—1200)=800/800=1元/小时将 b=1元/件代入高点或低点,a=3000—2000×1=1000元或a=2200—1200×1=1000元成本模型为y=1000+x从案例解析可得,维修费用中固定部分为1000元,变动部分为x。
(2)7月份的维修费用y=1000+x=1000+2300=3300(元)3、某家电企业专业生产空调,该企业近6个月的产销量及成本水平如下:要求:如果7月份预计产销量为350台,采用高低点法预测7月份的总成本和单位成本(保留整数).高点(360,148000);低点(200,100000)b=(148000-100000)/(360—200)=48000/160=300元/台将 b=300元/台代入高点或低点,a=148000-360×300=40000元或a=100000-200×300=40000元成本模型为y=40000+300x从案例解析可得,制造费用中固定部分为40000元,变动部分为300x。
计算机算法设计与分析期末考试复习题

1、二分搜索算法是利用(A分治策略)实现的算法。
2、下列不是动态规划算法基本步骤的是(A找出最优解的性质)。
3、最大效益优先是(A分支界限法)的一搜索方式。
4、在下列算法中有时找不到问题解的是(B拉斯维加斯算法)。
5. 回溯法解旅行售货员问题时的解空间树是(A子集树)。
6.下列算法中通常以自底向上的方式求解最优解的是(B动态规划法)。
7、衡量一个算法好坏的标准是(C 时间复杂度低)。
8、以下不可以使用分治法求解的是(D 0/1背包问题)。
9. 实现循环赛日程表利用的算法是(A分治策略)。
10、下列随机算法中运行时有时候成功有时候失败的是(C 拉斯维加斯算法)11.下面不是分支界限法搜索方式的是(D深度优先)。
12.下列算法中通常以深度优先方式系统搜索问题解的是(D回溯法)。
13.备忘录方法是那种算法的变形。
(B动态规划法)14.哈弗曼编码的贪心算法所需的计算时间为(BO(nlogn))。
15.分支限界法解最大团问题时,活结点表的组织形式是(B最大堆)。
16.最长公共子序列算法利用的算法是(B动态规划法)。
17.实现棋盘覆盖算法利用的算法是(A分治法)。
18.下面是贪心算法的基本要素的是(C贪心选择性质)。
19.回溯法的效率不依赖于下列哪些因素(D确定解空间的时间)20.下面哪种函数是回溯法中为避免无效搜索采取的策略(B剪枝函数)21、下面关于NP问题说法正确的是(BP类问题包含在NP类问题中)22、蒙特卡罗算法是(B概率算法)的一种。
23.下列哪一种算法不是随机化算法(C动态规划算法)24. (D最优子结构性质)是贪心算法与动态规划算法的共同点。
25. 矩阵连乘问题的算法可由(B动态规划算法)设计实现。
26. 分支限界法解旅行售货员问题时,活结点表的组织形式是(A最小堆)。
27、Strassen矩阵乘法是利用(A分治策略)实现的算法。
29、使用分治法求解不需要满足的条件是(A子问题必须是一样的)。
人教版七年级数学上册第一章 有理数 解答题复习(一)解析版

第1章有理数解答题复习(一)1.计算:﹣5×2+3÷﹣(﹣1).2.有个填写运算符号的游戏:在“1□2□6□9”中的每个□内,填入+,﹣,×,÷中的某一个(可重复使用),然后计算结果.(1)计算:1+2﹣6﹣9;(2)若1÷2×6□9=﹣6,请推算□内的符号;(3)在“1□2□6﹣9”的□内填入符号后,使计算所得数最小,直接写出这个最小数.3.计算:(﹣2)3+×8.4.计算:(﹣6)2×(﹣).5.计算:23×(1﹣)×0.5.6.计算:(﹣2)2×(1﹣).7.观察下列两个等式:2﹣=2×+1,5﹣=5×+1,给出定义如下我们称使等式a﹣b=ab+1成立的一对有理数“a,b”为共生有理数对”,记为(a,b)(1)通过计算判断数对“﹣2,1,“4,”是不是“共生有理数对”;(2)若(6,a)是“共生有理数对”,求a的值;(3)若(m,n)是“共生有理数对”,则“﹣n,﹣m”“共生有理数对”(填“是”或“不是”),并说明理由;(4)如果(m,n)是“共生有理数对”(其中n≠1),直接用含n的代数式表示m.8.在一条不完整的数轴上从左到右有点A,B,D,C,其中AB=2,BD=3,DC=1,如图所示,设点A,B,D,C所对应数的和是p.(1)①若以B为原点.写出点A,D,C所对应的数,并计算p的值;②若以D为原点,p又是多少?(2)若原点O在图中数轴上点C的右边,且CO=x,p=﹣71,求x.9.如图,在一条不完整的数轴上从左到右有点A,B.将线段AB沿数轴向右移动,移动后的线段记为A′B′,按要求完成下列各小题(1)若点A为数轴原点,点B表示的数是4,当点A′恰好是AB的中点时,数轴上点B′表示的数为.(2)设点A表示的数为m,点A′表示的数为n,当原点在线段A′B之间时,化简回|m|+|n|+|m ﹣n|.10.阅读材料题:求两个正整数的最大公约数是常见的数学问题,中国古代数学专著《九章算术》中便记载了求两个正整数最大公约数的一种方法﹣﹣更相减损术,术曰:“可半者半之,不可半者,副置分母、子之数,以少成多,更相减损,求其等也.以等数约之”,意思是说,要求两个正整数的最大公约数,先用较大的数减去较小的数,得到差,然后用减数与差中的较大数减去较小数,以此类推,当减数与差相等时,此时的差(或减数)即为这两个正整数的最大公约数.例如:求91与56的最大公约数解:91﹣56=3556﹣35=2135﹣21=1421﹣14=714﹣7=7所以,91与56的最大公约数是7请用以上方法解决下列问题:(1)求108与45的最大公约数;(2)求三个数78、104、143的最大公约数.11.计算2×(﹣5)+22﹣3÷.12.已知,数轴上三个点A、O、B.点O是原点,固定不动,点A和B可以移动,点A表示的数为a,点B表示的数为b.(1)若AB移动到如图所示位置,计算a+b的值.(2)在图的情况下,B点不动,点A向左移动3个单位长,写出A点对应的数a,并计算b﹣|a|.(3)在图的情况下,点A不动,点B向右移动15.3个单位长,此时b比a大多少?请列式计算.13.如图,已知A,B两点在数轴上,点A表示的数为﹣10,OB=3OA,点M以每秒3个单位长度的速度从点A向右运动.点N以每秒2个单位长度的速度从点O向右运动(点M、点N同时出发)(1)数轴上点B对应的数是.(2)经过几秒,点M、点N分别到原点O的距离相等?14.计算:﹣14﹣×[2﹣(﹣3)2].15.观察下列各式的计算过程:①1+8=32;②1+8+16=52;③1+8+16+24=72;④1+8+16+24+32=92.(1)第6个算式为;(2)用含n的代数式表示第n个等式,并验证其正确性.16.计算:(﹣2)3×8×()3+8÷.17.计算:(1)(﹣2)3÷+3×|1﹣(﹣2)2|(2)﹣12﹣(﹣)÷×[﹣2+(﹣3)2].18.计算6÷(﹣)时,李明同学的计算过程如下,原式=6÷(﹣)+6÷=﹣12+18=6.请你判断李明的计算过程是否正确,若不正确,请你写出正确的计算过程,另用正确方法计算()÷(﹣)+36÷()的值.19.计算:已知|x|=,|y|=,且x<y<0,求6÷(x﹣y)的值.20.(﹣1)4﹣{﹣[()2+0.4×(﹣1)]÷(﹣2)2}.第1章有理数解答题复习(一)参考答案与试题解析1.【分析】直接利用有理数的混合运算法则计算得出答案.【解答】解:原式=﹣10+9+1=0.【点评】此题主要考查了有理数的混合运算,正确掌握相关运算法则是解题关键.2.【分析】(1)根据有理数的加减法可以解答本题;(2)根据题目中式子的结果,可以得到□内的符号;(3)先写出结果,然后说明理由即可.【解答】解:(1)1+2﹣6﹣9=3﹣6﹣9=﹣3﹣9=﹣12;(2)∵1÷2×6□9=﹣6,∴1××6□9=﹣6,∴3□9=﹣6,∴□内的符号是“﹣”;(3)这个最小数是﹣20,理由:∵在“1□2□6﹣9”的□内填入符号后,使计算所得数最小,∴1□2□6的结果是负数即可,∴1□2□6的最小值是1﹣2×6=﹣11,∴1□2□6﹣9的最小值是﹣11﹣9=﹣20,∴这个最小数是﹣20.【点评】本题考查有理数的混合运算,解答本题得关键是明确有理数混合运算的计算方法.3.【分析】先求(﹣2)3=﹣8,再求×8=4,即可求解;【解答】解:(﹣2)3+×8=﹣8+4=﹣4;【点评】本题考查有理数的计算;熟练掌握幂的运算是解题的关键.4.【分析】原式先计算乘方运算,再利用乘法分配律计算即可求出值.【解答】解:原式=36×(﹣)=18﹣12=6.【点评】此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.5.【分析】原式先计算括号中的减法运算,再计算乘方运算,最后算乘法运算即可得到结果.【解答】解:原式=8××=3.【点评】此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.6.【分析】直接利用有理数乘方运算法则化简,进而去括号求出答案.【解答】解:(﹣2)2×(1﹣)=4×(1﹣)=4×=1.【点评】此题主要考查了有理数的混合运算,正确掌握运算法则是解题关键.7.【分析】(1)根据“共生有理数对”的定义即可判断;(2)根据“共生有理数对”的定义,构建方程即可解决问题;(3)根据“共生有理数对”的定义即可判断;(4)根据“共生有理数对”的定义即可解决问题.【解答】解:(1)﹣2﹣1=﹣3,﹣2×1+1=1,∴﹣2﹣1≠﹣2×1+1,∴(﹣2,1)不是“共生有理数对”;∵4﹣=,,∴(4,)是共生有理数对;(2)由题意得:6﹣a=6a+1,解得a=;(3)是.理由:﹣n﹣(﹣m)=﹣n+m,﹣n•(﹣m)+1=mn+1,∵(m,n)是“共生有理数对”,∴m﹣n=mn+1,∴﹣n+m=mn+1,∴(﹣n,﹣m)是“共生有理数对”;故答案为:是;(4)∵(m,n)是“共生有理数对”,∴m﹣n=mn+1,即mn﹣m=﹣(n+1),∴(n﹣1)m=﹣(n+1),∴.【点评】本题考查有理数的混合运算、“共生有理数对”的定义,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考常考题型.8.【分析】(1)①根据以B为原点,则A,D,C所对应的数分别为:﹣2,3,4,进而得到p的值;②以D为原点,A,D,C所对应的数分别为:﹣5,﹣3,1,进而得到p的值;(2)用x的代数式分别表示A,D,C所对应的数,根据题意列方程解答即可.【解答】解:(1)①点A,D,C所对应的数分别为:﹣2,3,4;p=﹣2+3+4=5;②若以D为原点,P=﹣3﹣5+1=﹣7;(2)由题意,A,B,C,D表示的数分别为:﹣6﹣x,﹣4﹣x,﹣1﹣x,﹣x,﹣6﹣x﹣4﹣x﹣1﹣x﹣x=﹣71,﹣4x=﹣60,x=15.【点评】本题主要考查了两点间的距离以及数轴的运用,解题时注意:连接两点间的线段的长度叫两点间的距离.9.【分析】(1)根据题意可知A′表示的数为2,根据AB的长度即可求解;(2)根据绝对值的定义,分情况讨论解答即可.【解答】解:(1)∵点B表示的数是4,当点A′恰好是AB的中点时,∴点A′表示的数为2,∴数轴上点B′表示的数为2+4=6.故答案为:6;(2)由题意知点A′在点A右侧,即m<n,则m﹣n<0.又原点在线段A'B之间,则点A'在原点的左侧,即m<0,n<0,|m|+|n|+|m﹣n|=﹣m﹣n﹣m+n=﹣2m.【点评】本题考查数轴,有理数的加法等知识,解决此类题目时,能理解题意表示出各点表示的数是关键.10.【分析】模仿例题求解即可解决问题.【解答】解:(1)∵108﹣45=6363﹣45=1845﹣18=2727﹣18=918﹣9=9∴108与45的最大公约数是9.(2)∵104﹣78=26,78﹣26=52,52﹣26=26,∴104与78的最大公约数是26.∵143﹣104=39,104﹣39=65,65﹣39=26,39﹣26=13,26﹣13=13,∴143与104最大公约数是13.∴78、104、143的最大公约数是13.【点评】本题考查有理数的除法,有理数的减法等知识,解题的关键是理解题意,学会模仿例题解决问题.11.【分析】原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果.【解答】解:原式=﹣10+4﹣3×2=﹣10+4﹣6=﹣16+4=﹣12.【点评】此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.12.【分析】(1)由图可知,点A表示的数a,点B表示的数b,即可求得a+b的值.(2)由B点不动,点A向左移动3个单位长,可得数a,再根据绝对值求得即可.(3)点A不动,点B向右移动15.3个单位长,可知数b,再列式计算解得.【解答】解:(1)由图可知:a=﹣10,b=2,∴a+b=﹣8故a+b的值为﹣8.(2)由B点不动,点A向左移动3个单位长,可得a=﹣13,b=2∴b﹣|a|=b+a=2﹣13=﹣11故a的值为﹣13,b﹣|a|的值为﹣11.(3)∵点A不动,点B向右移动15.3个单位长∴a=﹣10 b=17.3∴b﹣a=17.3﹣(﹣10)=27.3故b比a大27.3.【点评】本题考查了数轴、绝对值,当a是负有理数时,a的绝对值是它的相反数﹣a.13.【分析】(1)根据OB=3OA,结合点B的位置即可得出点B对应的数;(2)设经过x秒,点M、点N分别到原点O的距离相等,找出点M、N对应的数,再分点M、点N在点O两侧和点M、点N重合两种情况考虑,根据M、N的关系列出关于x的一元一次方程,解之即可得出结论.【解答】(1)∵OB=3OA=30,∴B对应的数是30.故答案为:30.(2)设经过x秒,点M、点N分别到原点O的距离相等,此时点M对应的数为3x﹣10,点N对应的数为2x.①点M、点N在点O两侧,则10﹣3x=2x,解得x=2;②点M、点N重合,则,3x﹣10=2x,解得x=10.所以经过2秒或10秒,点M、点N分别到原点O的距离相等.【点评】本题考查了数轴,根据点与点之间的位置关系找出方程是解题的关键.14.【分析】按照有理数混合运算的顺序,先乘方后乘除最后算加减,有括号的先算括号里面的.【解答】解:原式=﹣1﹣×(2﹣9)=﹣1﹣×(﹣7)=﹣1+=.【点评】此题要注意正确掌握运算顺序以及符号的处理.15.【分析】(1)由已知等式知第6个算式为1+8+16+24+32+40+48=132.(2)根据已知等式的规律得出1+8+16+24+…+8n=(2n+1)2,再利用等式的运算顺序和运算法则计算可得.【解答】解:(1)根据题意,第6个算式为1+8+16+24+32+40+48=132,故答案为:1+8+16+24+32+40+48=132.(2)1+8+16+24+…+8n=(2n+1)2,左边=1+8×(1+2+3+…+n)=1+8×=1+4n(n+1)=1+4n2+4n=(2n+1)2=右边,∴1+8+16+24+…+8n=(2n+1)2.【点评】本题主要考查有理数的混合运算与数字的变化规律,解题的关键是根据已知等式得出1+8+16+24+…+8n=(2n+1)2的规律及整式的运算法则.16.【分析】原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果.【解答】解:原式=﹣8×8×+8×8=﹣8+64=56.【点评】此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.17.【分析】(1)原式先计算乘方及绝对值运算,再计算乘除运算,最后算加减运算即可得到结果;(2)原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果.【解答】解:(1)原式=﹣8×+3×3=﹣10+9=﹣1;(2)原式=﹣1+×3×7=﹣1+3.5=2.5.【点评】此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.18.【分析】李明的计算过程不正确,应先计算括号中的加法运算,再计算除法运算.【解答】解:不正确,正确计算过程为:6÷(﹣)=6÷(﹣)=﹣36;人教版七年级数学上册第一章有理数解答题复习(一)解析版原式=(﹣+)×(﹣36)+36÷=﹣18+6﹣4+36×=﹣16+81=65.【点评】此题考查了有理数的混合运算,有理数混合运算注意运算顺序.19.【分析】直接利用绝对值的性质结合有理数混合运算法则计算得出答案.【解答】解:∵|x|=,|y|=,且x <y<0,∴x=﹣,y=﹣,∴6÷(x﹣y)=6÷(﹣+)=﹣36.【点评】此题主要考查了绝对值的性质和有理数混合运算,正确得出x,y的值是解题关键.20.【分析】原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果.【解答】解:原式=1﹣+(﹣)÷4=+﹣=.【点评】此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.- 11 - / 11。
四年级数学上册期末复习试卷计算题训练50题和答案解析(1)

人教四年级数学上册专项计算题、竖式计算试卷1.直接写得数。
24×5=8×15=26×30=308÷61≈96÷32=80÷5=492×99≈180÷30=899÷31≈520÷5=793×32≈4800÷60=2.直接写出得数。
0÷123=4500÷50=98⨯31≈240⨯3÷80=160⨯5=538÷60≈899÷31≈400⨯50=3.直接写出得数。
83-17=5×900=25×4=150×8=459÷9=560÷80=46×5=840÷20=2400÷30=420÷7×6=621÷90≈350÷71≈4.笔算下面各题。
(最后一题验算)÷=÷=7721940756⨯=506225.笔算下面各题。
(带※的要验算)405×36=※857÷23=181×52=6.竖式计算。
(带★的要验算)502÷76=306⨯24=★966÷23=7.请用竖式计算下面各题,带*请验算。
506×24=184×37=270×36=*854÷64=369÷72=980÷60=8.用竖式计算,带△的要验算。
96÷32=390÷60=△675÷25=780÷30=△207×40=△840÷24=9.列竖式计算。
(带△的要验算)350×32=△82×237=218÷37=△502÷69=670÷30=69×98=10.用竖式计算下面各题,③④题需要验算。
管理会计计算分析题
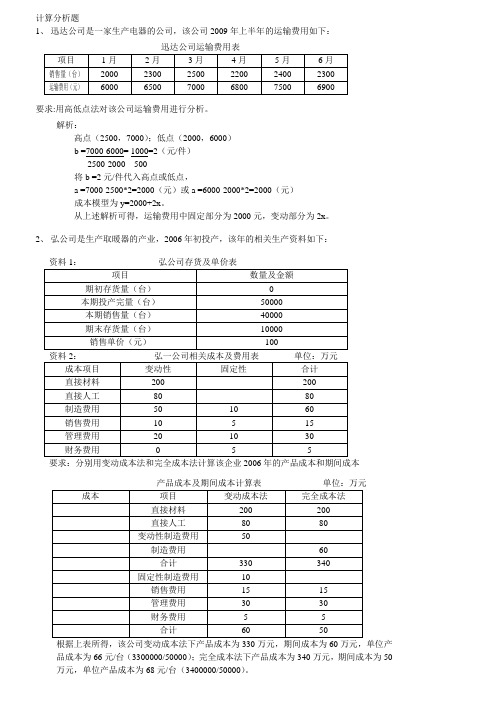
计算分析题12、弘公司是生产取暖器的产业,2006年初投产,该年的相关生产资料如下:3、ABC公司只生产一种产品,已知该产品的单位变动成本为10元,销售单价为20元,固定成本总额为60000元。
该产品的产销量为25000件。
计算该产品的贡献毛益、贡献毛益率及变动成本率、保本销售量入保本销售额。
解析:单位贡献毛益=20-10=10(元)贡献毛益总额=10*25000=250000(元)贡献毛益率=10/20*100%=50%,或=250000/500000*100%=50%变动成本率=10/20*100%=50%,或=250000/500000*100%=50%保本销售量=60000/(20-10)=6000(件)保本销售额=20*6000=120000(元)4、ABC公司在计划期间内同时生产销售甲、乙、丙、丁四种产品,假定产销平衡,固定成本国43040元。
相关的产量、销售单价和成本资料如下表:要求:用加权平均法计算公司的综合贡献毛益率、综合保本销售额以及各种产品的保本销售额。
解析:甲产品贡献边际率=(900-800)/900*100%=11.11%;乙产品贡献边际率=(2000-1600)/2000*100%=20%丙产品贡献边际率=(1000-700)/1000*100%=30%;丁产品贡献边际率=(3000-2000)/3000*100%=33.33%5、要求:1)应用算术平均法预测2009年1月份的销售量;2)应用加权平均法预测2009年1月份的销售量;3)应用指数平滑法预测2009年1月份的销售量(设平滑系数α=0.6,2008年7朋份销售量预测值为940件)解析:1)算术平均法:2009年1月份的销售量=6300/6=1050(件)2)加权平均法:2009年1月份的销售量=900*0.1+1000*0.1+1000*0.15+1100*0.15+1100*0.2+1200*0.3=1085(件)3)指数平滑法:2008年8月预测值=0.6*900+0.4*940=916(件)2008年9月预测值=0.6*1000+0.4*916=966.4(件)2008年10月预测值=0.6*1000+0.4*967.4=986.56(件)2008年11月预测值=0.6*1100+0.4*986.56=1054.624(件)2008年12月预测值=0.6*1100+0.4*1054.624=1081.8496(件)2009年1月预测值=0.6*1200+0.4*1081.8496=1152.73984(件)6要求:利用高低点预测法预测2009年7月份当产品产量为38件时的总成本.解析:高点(40,122);低点(30,100)b =(122-100)/(40-30)=2.2a =122-2.2*40=34总成本模型为=y =34+2.2x已知2009年7月份产品质量预计为38件时,则:y =34+2.2*38=117.6(万元)7要求:请分别利用贡献毛益分析法和差量分析法帮助企业进行产品品种选择决策。
药物分析计算题总结1

(一)杂质限量计算题4道1.检查*药物中的砷盐,取标准砷溶液2ml 〔每1ml 相当于1μg 的As 〕制备标准砷斑,砷盐的限量为0.0001%,应取供试品的量为多少? 答:g 0.2%0001.0%100102g/m l 1%1006=⨯⨯⨯=⨯=-ml L CV S μ 供试品应取2.0g2.取葡萄糖4.0g ,加水30ml 溶解后,加醋酸盐缓冲溶液〔pH3.5〕2.6ml ,依法检查重金属〔中国药典〕,含重金属不得超过百万分之五,问应取标准铅溶液多少ml ?〔每1ml 相当于Pb10μg/ml 〕 答:ml C LS V 2%10010ml /g 10g 0.4105%1006-6=⨯⨯⨯⨯=⨯=-μ 标准铅溶液应取2.0ml.3.肾上腺素中肾上腺酮的检查:称取肾上腺素0.250g ,置于25mL 量瓶中,加0.05mol/L 盐酸液至刻度,量取5mL 置另一25mL 量瓶中,用0.05mol/L 盐酸液稀释至刻度,用此液照分光光度法,在310nm 处测定吸收度,不得大于0.05,问肾上腺素的限量是多少?〔以百分表示,肾上腺素 %1cm 1E =453〕答:%055.0%100g250.0ml 5ml 25ml 25100145305.0=⨯⨯⨯⨯==S CV L 肾上腺酮的限量为0.055%4. Ch.P.〔2010〕泼尼松龙中有关物质的检查:取本品,加三氯甲烷-甲醇〔9∶1〕溶解并稀释制成每1 ml 中约含3 mg 的溶液,作为供试品溶液;精细量取2 ml ,置100 ml 量瓶中,用三氯甲烷-甲醇〔9∶1〕稀释至刻度,摇匀,作为对照溶液。
照薄层色谱法〔附录V B 〕试验,吸取上述两种溶液各5 μl ,分别点于同一硅胶G 薄层板上,以二氯甲烷-乙醚-甲醇-水〔77∶12∶6∶0.4〕为展开剂,展开,晾干,在105 ℃枯燥10分钟,放冷,喷以碱性四氮唑蓝试液,立即检视。
供试品溶液如显杂质斑点,不得多于3个,其颜色与对照溶液的主斑点比拟,不得更深。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
金融统计分析计算分析题期末复习2013年4月3日同学们:大家好!为了帮助大家更好的理解掌握金融统计分析的计算分析题,我就典型的计算分析题的重点与难点问题进行讲解。
1根据连续两年的货币当局资产负债表,分析中央银行货币政策的特点。
解题分析:•根据基期和报告期的货币当局的资产负债表的数据计算每一项的增长量及其增量的结构。
•从货币当局负债方储备货币分析基础货币变动的特点。
•分析货币当局资产操作的特点,指出货币当局资产操作与基础货币变动的关系,给出结论。
2、从分析表中可看出,1994年货币当局的基础货币(储备货币)比1993年增加了4071亿元。
在增加的4071亿元中•发行货币减少了71.8亿元,占全部增量的–1.76%(71.8/4071);•对金融机构负债增加1927.2亿元,占全部增量的47.3%(1927.2/4071);•非金融机构存款增加2215亿元,占全部增量的54.52%(2215/4071)。
3、1994年,中央银行总资产增加3913亿元。
中央银行主要通过其中的两项资产操作放出基础货币:一是大量增加外汇资产。
增加外汇资产的含义是货币当局买进外汇,放出人民币。
1994年货币当局外汇资产增加2832亿元,占全部资产总量的72%。
二是增加对存款货币银行的债权,即增加货币当局对存款货币银行的贷款,促进存款货币银行扩张信用。
1994年货币当局对存款货币银行的债权增加了841.5亿元,占全部资产总量的21.5%2、已知1994年中央银行总资产比1993年增加3913亿元。
其中,94年与93年相比,货币当局外汇资产增加2832亿元,货币当局对国际金融机构的资产增加70亿元,货币当局对政府的债权增加了105亿元,贷币当局对存款货币银行的债权增加了841.5亿元,货币当局对非货币金融机构愤权增加了18亿元,货币当局对非金融部门债权增加了46亿元.要求:计算影响94年中央银行总资产变动的各个因素的影响百分比.分析其中的主要影响因素.并说明这些主要因素的影响对于货币供给的影响含义。
解:•(1)影响94年中央银行总资产变动的各个因素的影响百分比分别是:•货币当局外汇资产增加的影响百分比=2832亿元/3913亿元=72.4%•货币当局对国际金融机构的资产增加的影响百分比=70亿元/3913亿元=1.8%•货币当局对政府的债权增加的影响百分比=105亿元/3913亿元=2.7%•货币当局对存款货币银行的债权增加的影响百分比=841.5亿元/3913亿元=21.5%•货币当岗对非货币金融机构债权增加的影响百分比=18亿元/3913亿元=60.5%•货币当局对非金融部门债权增加的影响百分比46亿元/3913亿元=1.2%(2)从影响百分比看,货币当局外汇资产增加的影响最大,其次是货币当局对存款货币银行的债权增加的影响。
•货币当局外汇资产增加的影响最大主要表现在,中央银行通过大量增加外汇资产的操作放出基础货币。
增加外汇资产的含义是货币当局买进外汇,放出人民币.其次是货币当局对存款货币银行的债权增加的影响主要表现在,中央银行通过增加对存款货币银行的债权,即增加货币当局对存款货币银行的贷教,促进存款货币银行扩张信用。
根据它分析基础货币的结构特点并对该国两年的货币供应量能力进行比较分析。
解:发行货币和金融机构在中央银行的存款是构成基础货币的主要部分,非金融机构在中央银行的存款在基础货币中的比重较小;A、B两年的基础货币总量未变,而且发行货币在基础货币中的比重也没有变化;不同的是B年相对于A年,金融机构在中央银行的存款比重下降而非金融机构在中央银行的比重相应地上升,因此该国家在货币乘数不变的条件下B 年的货币供应量相对于A年是收缩了。
4、 已知1998年基础货币为13146亿元,货币供应量为34880亿元,法定存款准备金率为13%,1999年基础货币为14850亿元,货币供应量为33620亿元,(1)计算1998年和1999年的货币乘数;(2)简述货币乘数作用并对其影响因素进行理论说明;(3)结合计算结果和有关数据请作出基本分析解: 1998年:货币乘数=货币供应量/基础货币 =34880/13146=2.651999年:货币乘数=货币供应量/基础货币 =41250/14850=2.8货币乘数是基础货币和货币供应量之间存在的倍数关系。
它在货币供应量增长和紧缩时,分别起扩大和衰减作用。
理论上认为,货币乘数主要受四个因素的影响,即现金比率、法定存款准备率、超额准备率和非金融机构在中央银行的存款与中央银行全部存款的比率。
其中,法定存款准备率、超额准备率和非金融机构在中央银行的存款与中央银行全部存款的比率与货币乘数的影响是反方向的。
现金比率对货币乘数的影响方向不是完全确定的。
分析99年比98年货币乘数增大的原因主要是基础货币增加,通过货币乘数的作用调节货币供应量5、利用因素分析法分析各个因素对净资本利润率的影响大小和影响方向。
预备知识 因素分析法总指标与从属指标之间的关系:净资本利润率=销售净利润×总资本周转率×权益乘数影响率•销售净利润影响率=(报告期销售净利润率—基期销售净利润率)×基期总资本周转率×基期权益乘数•总资本周转率影响率=报告期销售净利润率(报告期总资本周转率—基期总资本周转率)×基期权益乘数•权益乘数影响率=报告期销售净利润率×报告期总资本周转率×(报告期权益乘数—基期权益乘数)解:净资本利润率影响率=报告期净资本收益率-基期净资本收益率=销售净利润影响率+总资本周转率影响率+权益乘数影响率+净资本利润率影响率000001000111c b a c b a c b a c b a -=-001011c b a c b a -+011111c b a c b a -+净资本利润率影响率=a1b1c1-a0b0c0=43.44%-33.41%=10.03%其中:•总资本周转率影响率=(b1-b0)×a1c0=(1.13-0.80)×18.83×2.37=14.73%•权益乘数影响率=(c1-c0)×a1b1=(2.06-2.37)×18.83×1.13=-6.60%•销售净利润影响率=(a1-a0)×b0c0=(18.83%-17.62%)×0.80×2.37=2.29%综合以上分析,该公司净资本周转率,2000年比1999年提高10.03个百分点。
其中销售净利润的提高,使净资本利润率提高了2.29个百分点;由于总资本周转率的提高,使净资本利润率提高了14.73个百分点;而由于权益乘数的下降,使净资本利润率降低了6.60个百分点。
6、用两只股票的收益序列和市场平均收益序列数据,得到如下两个回归方程:第一只:r=0.021+1.4rm第二只:r=0.024+0.9rm并且有E(rm)=0.018,=0.0016。
第一只股票的收益序列方差0.0041,第二只股票的收益序列方差0.0036。
试分析这两只股票的收益和风险状况。
分析:总风险的分解:市场模型•分析收益利用回归方程计算期望收益率•分析风险分析两只股票的总风险分析两只股票的系统风险分析两只股票的系统风险占比解:第一只股票的期望收益为:E(r1)=0.021+1.4E(rm)=0.0462•第二只股票的期望收益为:E(r1 )= 0.04+0.9E(rm)=0.0402风险分析:1、总风险第一只股票的收益序列方差大于第二只股票收益序列方差(0.0041>0.0036),即第一只股票的总风险较大。
2、系统风险从两只股票的β系数可以发现,第一只股票的系统风险要高于第二只股票β1>β2(1.4>0.9)。
3、系统风险占比第一只股票系统风险为:1.4×1.4×0.0016=0.0031占该股票全部风险的76.5%(0.0031/0.0041×100%)第二只股票系统风险为:0.9×0.9×0.0016=0.0013占该股票总风险的36.11%(0.0013/0.0036×100%)7、利用两只股票的收益序列和市场平均收益序列数据,得到如下两个回归方程:第一只:r=0.030+1.5rm 第二只:r=0.034+1.1rm 并且有E(rm)=0.020,=0.0025。
第一只股票的收益序列方差为0.0081,第二只股票的收益序列方差为0.0072。
试分析这两只股票的收益和风险状况解:•第一只股票的期望收益为:E(r1)=0.030+1.5E(rm)=0.030+1.5×0.020=0.06•第二只股票的期望收益为:E(r2)= 0.034+1.1E(rm)=0.034+1.1×0.020=0.056•由于第一只股票的期望收益高,所以投资于第一只股票的收益要大于第二只股票。
相应地,第一只股票的收益序列方差大于第二只股票(0.0081>0.0072),即第一只股票的总风险较大。
从两只股票的β系数可以发现,第一只股票的系统风险要高于第二只股票,β1>β2(1.5>1.1)。
第一只股票有1.5×1.5×0.0025=0.005625,占该股票全部风险的69.44%(0.005625/0.0081×100%),而第二只股票有1.1×1.1×0.0025=0.003025,仅占总风险的42.01%(0.003025/0.0072×100%)。
8、有5种债券A、B、C、D、E,面值均为1000元,期限都是3年。
其中,债券A以单利每年付息一次,年利率为8%;债券B以复利每年付息一次,年利率为4%;债券C以单利每年付息2次,每次利率为4%;债券D以复利每年付息两次,每次利率为2%.债券E以到期单利付息,年利率为8%;假定投资者认为未来3年的年折算率为r = 8%,要求:(1)计算债券A 、B 、C、 D 、E的投资价值;(2)比较分析5种债券的投资价值。
分析思路:•债券的投资价值是:投资者预期所获货币收入的现值,即投资者未来所获得预期收入按某一适当折算率折算的现值。
•注意:预期收入与折算率的期限要一致。
解:债券A的投资价值:(n=3)=206.1678+793.8322=1000债券B的投资价值:(n=3)=107.0467+793.8322=900.8789债券C的投资价值: (n=6)=210.2121+793.8322=1004.0443债券D的投资价值:(n=6)=904.0906债券E的投资价值:(n=6)=984.312比较:因此5种债券的投资价值由高向低依次为C、A 、E、D 、B 9、计算基金的单位资产净值,分析基金管理人的经营水平。
