微波技术答案(一二章)
微波(第一章第二节和第三节)(12-13-2)

波型
Eo 波
c
波型
c
波型
c
2.613a
波型
c
H11 3.413a H21 2.057a
H01 1.640a H31 1.496a
H41 1.182a H12 1.179a H22 0.937a
H02 0.896a
E01
E31 0.985a
E11 1.640a E21 1.223a
E02 1.138a
返 回 上一页 下一页
微波技术与天线
2、导行波波型的分类 导行波的波型是指能够单独在导波系统中存在的 电磁场结构形式,也叫传输模式。 (1)横电磁波(TEM波) 此传输模式没有电磁场的纵向分量,即Ez=0, Hz=0, 且kc=0。 kc称为截止波数。 TEM波存在于多导体传输系统中。 (2)横电波(TE波)或磁波(H波) 此模式没有电场的纵向分量,即Ez=0,Hz≠0,所 有场分量可由Hz求出。
返 回
上一页
下一页
微波技术与天线
② Eo 波 01 Eo 波 的 特 点 是 : 0, 场 沿 方 向 不 变 化 , m 01
场分布具有轴对称性; 磁场只有 分量,故只存在纵向管 H 壁电流;
Ez在轴线附近最强。
Eo 波 可 用 做 天 线 馈 线 系 中 旋 转 接 头 的 工 作 统 01 波 型 , 还 可 用 于 微 波和 电 子 加 速 器 中 。 管
ZTM 1 ( c )2
ZTEM 120 r r
返 回 上一页 下一页
微波技术与天线
(5)传输功率 导波沿无耗规则导行系统+z方向传输的平均功率
为
1 * P0 Re S ( E H ) d s 2 * 1 Re S ( Et H t ) a z d s 2 2 2 Z 1 S Et d s 2 S H t d s 2Z
微波技术习题解答(部分)
率的波,而是一个含有多种频率的波。这些多种频率成分构成一个“波群”
又称为波的包络,其传播速度称为群速,用 vg 表示,即 vg v 1 c 2
第三章 微波传输线
TEM波:相速
vp
1 v
相波长
p
2
v f
群速 vg vp v
即导波系统中TEM波的相速等于电磁波在介质中的传播速度,而相波长 等于电磁波在介质中的波长(工作波长)
插入衰减 A
A
1 S21 2
A%11 A%12 A%21 A%22 2 4
对于可逆二端口网络,则有
A
1 S21 2
1 S12 2
第四章 微波网络基础
插入相移 argT arg S21
对于可逆网络,有 S21 S12 T ,故
T T e j S12 e j12 S21 e j21
何不同?
答案:截止波长:对于TEM波,传播常数 为虚数;对于TE波和TM波,对 于一定的 kc 和 、 ,随着频率的变化,传播长数 可能为虚数,也可能为实
数,还可以等于零。当 0 时,系统处于传输与截止状态之间的临界状态,此 时对应的波长为截止波长。
当 c 时,导波系统中传输该种波型。 当 c 时,导波系统中不能传输该种波型。
第三章 微波传输线
3-3 什么是相速、相波长和群速?对于TE波、TM波和TEM波,它们的相速 相波长和群速有何不同?
答案: 相速 vp 是指导波系统中传输的电磁波的等相位面沿轴向移动的速
度,公式表示为
vp
相波长 p
是等相位面在一个周期T内移动的距离,有
p
2
欲使电磁波传输信号,必须对波进行调制,调制后的波不再是单一频
T S21 0.98e j 0.98
微波技术与天线习题答案

《微波技术与天线》习题答案章节 微波传输线理路1.1设一特性阻抗为Ω50的均匀传输线终端接负载Ω=1001R ,求负载反射系数1Γ,在离负载λ2.0,λ25.0及λ5.0处的输入阻抗及反射系数分别为多少? 解:31)()(01011=+-=ΓZ Z Z Zπβλ8.02131)2.0(j z j e e --=Γ=Γ31)5.0(=Γλ (二分之一波长重复性)31)25.0(-=ΓλΩ-∠=++= 79.2343.29tan tan )2.0(10010ljZ Z ljZ Z Z Z in ββλΩ==25100/50)25.0(2λin Z (四分之一波长阻抗变换性) Ω=100)5.0(λin Z (二分之一波长重复性)1.2求内外导体直径分别为0.25cm 和0.75cm 的空气同轴线的特性阻抗;若在两导体间填充介电常数25.2=r ε的介质,求其特性阻抗及MHz f 300=时的波长。
解:同轴线的特性阻抗abZ r ln 600ε= 则空气同轴线Ω==9.65ln 600abZ 当25.2=r ε时,Ω==9.43ln600abZ rε 当MHz f 300=时的波长:m f c rp 67.0==ελ1.3题设特性阻抗为0Z 的无耗传输线的驻波比ρ,第一个电压波节点离负载的距离为1min l ,试证明此时的终端负载应为1min 1min 01tan tan 1l j l j Z Z βρβρ--⨯=证明:1min 1min 010)(1min 101min 010in tan l tan j 1/tan tan 1min 1min l j Z Z Z Z l j Z Z l j Z Z Z Z l in l βρβρρββ--⨯=∴=++⨯=由两式相等推导出:对于无耗传输线而言:)(1.4传输线上的波长为:m fr2cg ==ελ因而,传输线的实际长度为:m l g5.04==λ终端反射系数为: 961.0514901011≈-=+-=ΓZ R Z R输入反射系数为: 961.0514921==Γ=Γ-lj in eβ 根据传输线的4λ的阻抗变换性,输入端的阻抗为:Ω==2500120R ZZ in1.5试证明无耗传输线上任意相距λ/4的两点处的阻抗的乘积等于传输线特性阻抗的平方。
电磁场与微波技术第一二三章课后习题及部分答案

第 1 章 习 题1、 求函数()D Cz By Ax u +++=1的等值面方程。
解:根据等值面的定义:标量场中场值相同的空间点组成的曲面称为标量场的等值面,其方程为)( ),,(为常数c c z y x u =。
设常数E ,则,()E D Cz By Ax =+++1, 即:()1=+++D Cz By Ax E针对不同的常数E (不为0),对应不同的等值面。
2、 已知标量场xy u =,求场中与直线042=-+y x 相切的等值线方程。
解:根据等值线的定义可知:要求解标量场与直线相切的等值线方程,即是求解两个方程存在单解的条件,由直线方程可得:42+-=y x ,代入标量场C xy =,得到: 0422=+-C y y ,满足唯一解的条件:02416=⨯⨯-=∆C ,得到:2=C ,因此,满足条件的等值线方程为:2=xy3、 求矢量场z zy y y x xxy A ˆˆˆ222++=的矢量线方程。
解:由矢量线的微分方程:zy x A dz A dy A dx ==本题中,2xy A x =,y x A y 2=,2zy A z =, 则矢量线为:222zy dzy x dy xy dx ==,由此得到三个联立方程:x dy y dx =,z dz x dx =,zy dz x dy =2,解之,得到: 22y x =,z c x 1=,222x c y =,整理, y x ±=,z c x 1=,x c y 3±=它们代表一簇经过坐标原点的直线。
4、 求标量场z y z x u 2322+=在点M (2,0,-1)处沿z z y xy xx t ˆ3ˆˆ242+-=方向的方向导数。
解:由标量场方向导数的定义式:直角坐标系下,标量场u 在可微点M 处沿l 方向的方向导数为γβαcos cos cos zu y u x u l u ∂∂+∂∂+∂∂=∂∂α、β、γ分别是l 方向的方向角,即l 方向与z y xˆˆˆ、、的夹角。
廖承恩《微波技术基础》习题解答(最全的版本)

1 1 =| ΓL | e jφ L = e − j π = − 3 3
sc oc Z0 = Zin (d)Zin (d) = j50×(−j50 ) =50 Ω
课
后
=
kh da
答 案
3 j 2 = 25∠ 2.2°
w.
网
j100 −75e j30° ZL = −j25 j30° 75e − (−j25 )
由于行波状态下沿线电压和电流振幅不变,因而 V0+=Vin=450V 而 I0+=V0+/Z0=1A 所以 AB 段的电压、电流、阻抗表达式为
kh da
课 后
V0+ − j β z e Z0
(图) 解:首先在 BC 段,由于 Z0=Z01=600Ω,ZL=400Ω 且因为 d=λ/4 所以在 BB’处向右看去,Zin=Z012/ZL=6002/400=900Ω 又由于 BB’处有一处负载 R=900Ω,所以对 AB 段的传输线来说 终端负载为 ZL’=Zin//R=450Ω 所以对 AB 段的等效电路为
Zin(d) − jZ0tgβ d Z0 − jZin(d)tgβ d
w.
εr
ln
网
当在空气中时
ε0 =1
b 60 0.75 = ln = 45.5Ω a 2.1 0.25
= 0.69m
co m
(1)
且
sc oc Z0 = Zin (d)Zin (d) sc Zin (d) = jZ0tgβ d
sc Zin (d) jtgβ d = oc Zin (d)
ZL = Z0
2 — 12 画出图 2— 1 所示电路沿线电压、电流和阻抗的振幅分布图,
所以 ΓL =
微波试题及答案

微波试题及答案在现代社会中,微波技术已经广泛应用于通信、雷达、天文学等领域。
掌握微波知识对于从事相关行业的人士来说至关重要。
本篇文章将介绍一些微波试题及其答案,帮助读者深入了解微波技术。
试题一:什么是微波?答案:微波是电磁波的一种,具有较短的波长和高频率特点,通常波长在1毫米至1米之间。
微波具有很强的穿透力和方向性,被广泛应用于通信、雷达、医疗等领域。
试题二:什么是微波导?答案:微波导是一种用于传输微波信号的特殊波导结构。
微波导常见的形式有矩形波导、圆柱波导等,其内部壁面具有优良的导波性能,能够有效地传输微波信号。
试题三:微波的功率和频率有何关系?答案:微波的功率和频率之间呈正比关系。
功率越大,频率也相应增加。
这是因为微波的功率与电磁波的幅度相关,而频率则与波的周期有关。
试题四:什么是微波障碍物?答案:微波障碍物是指在微波传输过程中会对信号产生干扰或反射的物体。
微波障碍物可能导致信号衰减、多径效应等问题,影响信号的传输质量。
试题五:微波天线的作用是什么?答案:微波天线是用于接收和发射微波信号的装置。
它能够将电磁波能量转换成电流或电流转换成电磁波能量,并将其传输到空间中进行无线通信或能量传输。
试题六:什么是微波功率放大器?答案:微波功率放大器是一种用于增加微波信号功率的装置。
它通过引入恒定的电源电压来驱动微波管或半导体器件,实现对微波信号电压的放大。
试题七:什么是微波衰减器?答案:微波衰减器是一种用于降低微波信号功率的装置。
它通过引入衰减材料或实现信号的反向传播等方式,对微波信号进行衰减,用于调节微波信号的强度。
试题八:什么是微波干扰?答案:微波干扰是指在微波传输过程中,由于不同信号的干涉或其他外界干扰因素而导致的信号失真或中断现象。
微波干扰可能影响通信、雷达等应用的正常运行。
试题九:如何解决微波干扰问题?答案:解决微波干扰问题可以采取多种方法。
例如,可以提高微波系统的抗干扰能力,使用合适的隔离器或拐角衰减器,合理安排微波设备的布局等,从而减少微波干扰。
《微波技术与天线》习题答案

第一章1-1解: f=9375MHz, / 3.2,/ 3.1251c f cm l λλ===> , 此传输线为长线。
1-2解: f=150kHz, 4/2000,/0.5101c f m l λλ-===⨯<< ,此传输线为短线。
1-3答: 当频率很高,传输线的长度与所传电磁波的波长相当时,低频时忽略的各种现象与效应,通过沿导体线分布在每一点的损耗电阻,电感,电容和漏电导表现出来,影响传输线上每一点的电磁波传播,故称其为分布参数。
用1111,,,R L C G 表示,分别称其为传输线单位长度的分布电阻,分布电感,分布电容和分布电导。
1-4 解: 特性阻抗050Z ====Ωf=50Hz X 1=ωL 1=2π×50×16.65×10-9Ω/cm=5.23×10-6Ω/cmB 1=ωC 1=2π×50×0.666×10×10-12=2.09×10-9S/cm 1-5 解: ∵ ()22j z j z i r Uz U e U e ββ''-'=+()()2201j z j z i r I z U e U e Z ββ''-'=- 将 2223320,2,42i r U V U V z πβλπλ'===⋅= 代入33223420220218j j z U eej j j Vππλ-'==+=-+=-()3412020.11200z I j j j A λ'==--=- ()()()34,18cos 2j te z uz t R U z e t V ωλπω'=⎛⎫''⎡⎤==- ⎪⎣⎦⎝⎭ ()()()34,0.11cos 2j te z i z t R I z e t A ωλπω'=⎛⎫''⎡⎤==- ⎪⎣⎦⎝⎭ 1-6 解: ∵Z L=Z 0∴()()220j z i r U z U e U β''==()()()212321100j j z z Uz e U z e πβ''-''==()()()()611100,100cos 6jU z e V u z t t V ππω'=⎛⎫=+ ⎪⎝⎭1-7 解: 210.20.2130j L e ccmfπρρλ-Γ=-=-==Γ+==由 011L L L Z Z +Γ=-Γ 得 0110.2100150110.2L LL Z Z -Γ+===Ω+Γ- 由 ()()()22max0.20.2j z j z L z e e z πββ-'-''Γ=Γ==Γ= 得 max1max120,7.54z z cm λπβ''-===1-8 解: (a) ()(),1inin Z z z ''=∞Γ=(b) ()()0100,0in in Z z Z z ''==ΩΓ=(c) ()()00012200,3in in in in Z Z Z z Z z Z Z -''==ΩΓ==+(d) ()()02200,1/3inin Z z Z z ''==ΩΓ=1-9 解: 1 1.21.510.8ρ+Γ===-Γmax 0min 75,33Z Z Z Z ρρ==Ω==Ω1-10 解: min2min124z z cm λ''=-=min1120.2,0.514L z ρππβρλ-'Γ===⨯=+ min1min120.2j z z L e β'-'Γ=-=Γ∴ 2420.20.2j jLeeππ⨯-Γ=-=1-11 解: 短路线输入阻抗 0in Z jZ tg l β= 开路线输入阻抗 0in Z jZ ctg l β=-a) 00252063inZ jZ tgjZ tgj πλπλ=⨯=Ω b) 002252033in Z jZ tg jZ tg j πλπλ=⨯=-Ωc) 0173.23inZ jZ ctgj π=-=-Ωd) 02173.23in Z jZ ctg j π=-=Ω1-12 解: 29.7502050100740.6215010013oj L L L Z Z j j e Z Z j -++Γ=Γ====++1-13 解: 表1-41-17 解: 1350.7j Le Γ=1-18 解: minmax0.6U K U == min143.2o z β'= 用公式求 min1min100min1min111L j tg z K jtg z Z Z Z jtg z jKtg z ρββρββ''--==''-- 0.643.25042.8522.810.643.2oojtg j j tg -==-Ω-⨯ 用圆图求 ()42.522.5LZ j =-Ω短路分支线的接入位置 d=0.016λ时()0.516B =-最短分支线长度为 l=0.174λ()0.516B =-1-19 解: 302.6 1.4,0.3,0.30.16100LL lZ j Y j λ=-===+由圆图求得 0.360.48in Z j =+ 1824in Z j =+Ω1.01 1.31in Y j =- ()0.020.026in Y j S =-1-20 解: 12LY j =+ 0.5jB j =()()()()0.150.6 1.460.150.60.960.20.320.380.2 1.311.54in in in in Y j Y jB j Y j Z j λλλλ=-+=-=+=-∴ 6577inZ j =-Ω 1-21 解: 11 2.5 2.50.20.2L L Y j j Z ===+- 并联支节输入导纳 min 2.5B ctg l β=-=- min 0.061l λ=此时 1/2.5LZ '= 500/2.5200LZ '==Ω(纯电阻)变换段特性阻抗 0316Z '==Ω 1-22 解: 1/0.851.34308.66o o Larctg ϕ=-=-= 由 max120L z ϕβ'=-= 得 max10.43z λ'= 由 min12Lz ϕβπ''=-=- 得 min10.1804L z ϕπλλπ+'== 1-23 解: 原电路的等效电路为由 1inZ j '+= 得 1inZ j '=-向负载方向等效(沿等Γ图)0.25电长度得 1inin Z Z ''='则 ininY Z '''=由inin in Y Y j Z ''''''=+= 得 12in inY Z j j ''''=-=-由负载方向等效0.125电长度(沿等Γ图)得12LY j =+ 0.20.4L Z j =-1-24 答: 对导行传输模式的求解还可采用横向分量的辅助标位函数法。
廖承恩《微波技术基础》习题解答(最全的版本)

(2) (3)
(4)
sc oc 当 Z in (d ) = j100Ω , Z in (d ) = − j 25Ω , Z in (d ) = 75∠30°Ω 时
1562 . 5 +1875 × 75 ×
3 + 62 . 5 j 2
sc oc 2-6 在长度为 d 的无耗线上测得 Z in (d ) = j50Ω , Z in (d ) = − j 50Ω ,接 实
第二三四六七章习题解答 第二章习题解答
2-1 某双导线的直径为 2mm,间距为 10cm,周围介质为空气,求 其特性阻抗。某同轴线的外导体内直径为 23mm,内导体外直径为 10mm, ,求其特性阻抗;若在内外导体之间填充εr 为 2.25 的 介 质 , 求其特性阻抗。
解:双导线:因为直径为 d=2mm=2×10-3m 间距为 D=10cm=10-1m 所以特性阻抗为
ZL = Z0
2 — 12 画出图 2— 1 所示电路沿线电压、电流和阻抗的振幅分布图,
所以 ΓL =
Z L '− Z 02 450 − 450 = =0 Z L '+ Z 02 450 + 450
电磁场与微波技术(第2版)黄玉兰-习题答案

第一章1.3证:4 1 (一6) (-6)A A和B相互垂直B =0A和B相互平行1.11(1)Ax Ay Az [A= divA二—x y z=2x 2x2y 72x2y2z2(2)由高斯散度定理有0 3 0.5 0.5 0.5 2 2 2 2丛d「dz dy (2x+ 2x 72x y z )dz - 0.5 -0.5 0.51.18(1)因为闭合路径在xoy平面内,故有:T 2 2 2A = (e x x e y x e z y z)(e x dx e y dy) = xdx x dy・dl = 8(2)因为S在XOY面内,A• ds 二(e x2yz e z2x)(e x dxdy)二2xdxdyC A • ds)二8s所以,定理成立。
1.21(1) 由梯度公式、 1 方向: ---- (4e 10e^ e z )V117(2)最小值为0,与梯度垂直1.26证明可汉可u = 0T A = 0书上 p10 1.25存“ uu = e x ——ue y—y"u | ez — l (2,1,3):z方向导数最大值为 a io? 「7帝第二章2.1p =q 4 3 a 3V e wr sinJ―3qwrs in°• V e2.3用圆柱坐标系进行求解场点坐标为P(O,O,z). 线电荷元\dl 可以视为点电荷,其到场点的距离矢量 H T「-L第=e^z _ eaL e£z - e 晶 得 Er,rJz 2 + a 2所以P 点的电场强度为R=ErT2二 E 二o2 2(z a I ea=excos e£z - ea[a3))4 ; oeys in eaLdoP a -7 l3E = e z(z 2a 2)22 0z 2a 2(1)r 兰b 时 -4 4sr 2E(r)Eq= 0(b 2b 23r 2)4 r 2dr = 4 (一 -3Eq5y) 57)Q^ds= 丄(b 2r 3 0 (E(r)」(也心3由高斯定理有即4 r 2E(r)=33I)71E0ds= 4 _s一 2Eq = (b 2r o'由高斯定理有 r 2E(r) )4 r2dr 15 b 5E(r)=47h2b 515r 2QE^ds^ q■ :b2l ;?b2「e“2 J,同理: Eab e(市2 o r22a e r 2)r2丿⑵对于r1<b 且在空腔外,E=Eb-Ea□ Eb^s=r: r121 :r1「e M而Ea 2 ;。
微波技术基础期末试题与答案(一)
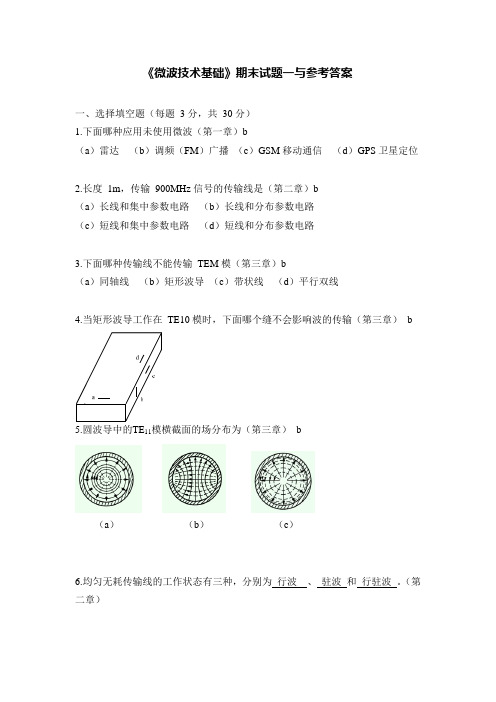
《微波技术基础》期末试题一与参考答案一、选择填空题(每题 3 分,共30 分)1.下面哪种应用未使用微波(第一章)b(a)雷达(b)调频(FM)广播(c)GSM 移动通信(d)GPS 卫星定位2.长度1m,传输900MHz 信号的传输线是(第二章)b(a)长线和集中参数电路(b)长线和分布参数电路(c)短线和集中参数电路(d)短线和分布参数电路3.下面哪种传输线不能传输TEM 模(第三章)b(a)同轴线(b)矩形波导(c)带状线(d)平行双线4.当矩形波导工作在TE10 模时,下面哪个缝不会影响波的传输(第三章)b5.圆波导中的TE11模横截面的场分布为(第三章)b(a)(b)(c)6.均匀无耗传输线的工作状态有三种,分别为行波、驻波和行驻波。
(第二章)Z L 0L 7.耦合微带线中奇模激励的对称面是 电 壁,偶模激励的对称面是 磁 壁。
(第三章)8.表征微波网络的主要工作参量有阻抗参量、 导纳 参量、 传输 参量、散射参量和 转移参量。
9.衰减器有吸收衰减器、 截止衰减器和 极化衰减器三种。
10.微波谐振器基本参量有 谐振波长 、 固有品质因数 和等效电导衰减器三种。
二、传输线理论工作状态(7 分)(第二章)在特性阻抗Z 0=200Ω的传输线上,测得电压驻波比ρ=2,终端为电压波节点,传输线上电压最大值 U max =10V ,求终端反射系数、负载阻抗和负载上消耗的功率。
解: Γ = ρ -1 = 12ρ +1 3由于终端为电压波节点,因此Γ =- 123由Γ =Z L - Z 0= - 12+ Z 3 可得,Z L =100Ω 负载吸收功率为P 2Z 0 ρ三、Smith 圆图(10 分)(第二章)已知传输线特性阻抗Z 0=75Ω,负载阻抗Z L =75+j100Ω,工作频率为 900MHz ,线长l =0.1m ,试用Smith 圆图求距负载最近的电压波腹点与负载的距离和传输线的输入阻抗Z 0Z L解:由工作频率为900 MHz,可得λ=1 m 3而线长为l=0.3λ1.计算归一化负载阻抗ZL=ZLZ= 1+j1.33在阻抗圆图上找到 A 点。
微波遥感智慧树知到答案章节测试2023年长安大学

第一章测试1.世界上第一颗雷达卫星Seasat是哪一年发射成功的 ( )。
A:1972B:1982C:1978D:1957答案:C2.中国高分3号雷达卫星空间分辨率最高可以达到 ( )。
A:2米B:5米C:3米D:1米答案:D3.发展和设计合成孔径雷达SAR系统,从分辨率指标上提高了雷达成像的()。
A:方位向分辨率B:辐射分辨率C:距离向分辨率D:光谱分辨率答案:A4.ERS-1雷达卫星采用的是()波段A:CB:LC:XD:P答案:A5.Radarsat-1雷达卫星方位向分辨率最高可以达到()A:1米B:10米C:3米D:2米答案:B第二章测试1.蝙蝠在洞穴中飞来飞去时,它利用超声脉冲导航非常有效,这种超声脉冲是持续1 ms或不到1 ms的短促发射,且每秒重复发射几次.假定蝙蝠的超声脉冲发射频率为39 000 Hz,在一次正朝着表面平直的墙壁飞扑的期间,则下列判断正确的是( )A:蝙蝠接收到从墙壁反射回来的超声脉冲频率大于墙壁接收的频率B:墙壁接收到的超声脉冲频率等于39000 HzC:蝙蝠接收到从墙壁反射回来的超声脉冲频率等于39000 HzD:蝙蝠接收到从墙壁反射回来的超声脉冲频率等于墙壁接收的频率答案:A2.关于电磁波,下列说法中正确的是()A:均匀变化的电场产生均匀变化的磁场,均匀变化的磁场产生均匀变化的电场B:电场不一定能产生磁场,磁场也不一定能产生电场C:电磁波在真空中的传播速度与电磁波的频率有关D:稳定的电场产生稳定的磁场,稳定的磁场产生稳定的电场答案:B3.电磁波天线是利用电磁波哪种特性制成的()A:相干性B:绕射C:衍射D:叠加答案:A4.电磁波进入两个介质表面时()A:只会产生反射波B:只会产生折射波和散射波C:只会产生散射波D:会产生反射波、折射波和散射波答案:D5.电磁波散射的能量与()有关A:地面反射率B:分界面相对于入射波长的粗糙程度C:分界面的几何尺寸D:地面温度答案:A第三章测试1.下列说法不正确的是()。
微波技术课后习题答案-第二章习题参考答案11
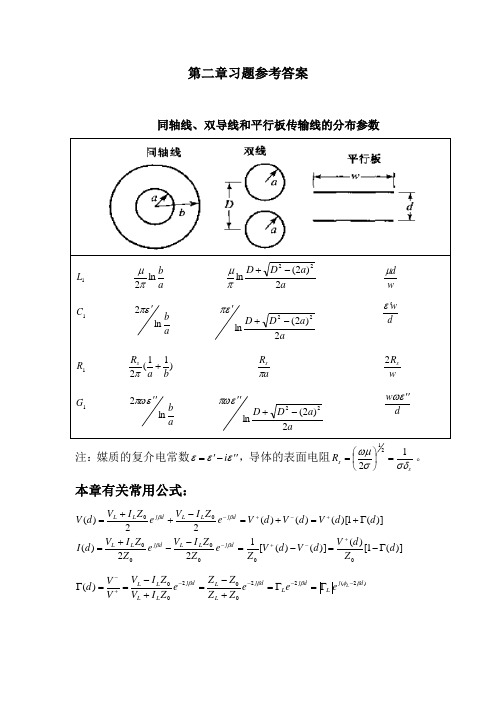
第二章习题参考答案同轴线、双导线和平行板传输线的分布参数注:媒质的复介电常数εεε''-'=i ,导体的表面电阻ss R σδσωμ1221=⎪⎭⎫⎝⎛=。
本章有关常用公式:)](1[)()]()([122)()](1)[()()(22)(00000000d Z d V d V d V Z e Z Z I V e Z Z I V d I d d V d V d V e Z I V e Z I V d V d j L L d j L L dj L L d j L L Γ-=-=--+=Γ+=+=-++=+-+-+-+-ββββ )2(2200200)(d j L d j L dj L L d j L L L L L e e e Z Z Z Z e Z I V Z I V VV d βφβββ----+-Γ=Γ=+-=+-==ΓL Lj L j L L L L L e e Z Z Z Z Z Z Z Z φφΓ=+-=+-=Γ0000dtg jZ Z dtg jZ Z Z d Z L L in ββ++=000)()(1)(1)()()(0d d Z d I d V d Z in Γ-Γ+==LL VV VSWR Γ-Γ+==11minmax2.1无耗或者低耗线的特性阻抗为110C L Z = 平行双导线的特性阻抗:aDa a D D a a D D Z r r rln 11202)2(ln 11202)2(ln 112222000εεεμεπ≈-+=-+=已知平行双导线的直径mm a 22=,间距cm D 10=,周围介质为空气(1=r ε),所以特性阻抗)(6.5521100ln 120ln11200Ω==≈a D Z rε 同轴线的特性阻抗:ab a b Z r rln 60ln 121000εεμεπ==已知同轴线外导体的内直径2mm b 23=,内导体的外直径2mm a 10=,中间填充空气(1=r ε):特性阻抗)(50210223ln 60ln 600Ω===abZ r ε中间填充介质(25.2=r ε):特性阻抗)(3.33210223ln 25.260ln 600Ω===a b Z r ε2.2对于无耗传输线线有相位常数μεωωβ===k C L 11,所以可求出相速度v k C L v p =====μεωβω1111,等于电磁波的传播速度。
电磁场微波技术与天线(盛振华版)第二章答案

天线的极化方式分为线极化、圆极化和椭圆极化三种。线极化是指电场矢量或磁场矢量与 地面平行,圆极化是指电场矢量或磁场矢量在垂直于传播方向上的投影为圆,椭圆极化则 是介于两者之间。
天线的主要参数
工作频率
天线的工作频率决定了其应用范围和性能。不同频率的电磁波具有不 同的传播特性和应用场景。
增益
天线的增益表示其在特定方向上对信号的放大能力。增益越高,天线 的定向性和抗干扰能力越强。
电磁场微波技术与天线(盛振华版) 第二章答案
目录
• 电磁场与微波技术的基本概念 • 天线的种类与工作原理 • 电磁场与天线的关系 • 天线的设计与优化 • 实际天线案例分析
01 电磁场与微波技术的基本 概念
电磁场与电磁波
电磁场与电磁波的形成
电磁波的分类
电磁场是由变化的电场和磁场相互激 发而形成的,而电磁波则是在空间传 播的电磁场。
根据频率的不同,电磁波可分为无线 电波、微波、红外线、可见光、紫外 线、X射线和伽马射线等。
电磁波的波动特性
电磁波具有波动性,表现为振荡的电 场和磁场在空间中传播,具有波长、 频率等参数。
微波技术的基本特点
01
02
03
微波的频率范围
微波的频率范围通常在 300MHz到300GHz之间, 是无线电波中较高频段的 组成部分。
探测和定位。
利用微波传输信号,实 现全球定位系统(GPS)
等导航定位服务。
微波可用于加热物体和 治疗某些疾病,如肿瘤
等。
02 天线的种类与工作原理
天线的分类
按工作频段分类
分为超长波天线、长波天线、 中波天线、短波天线、超短波
天线、微波天线等。
按方向性分类
射频微波电路作业1-7(答案版)(DOC)

第一章射频/微波工程介绍1.简述常用无线电的频段划分和射频的定义。
射频/微波处于普通无线电波与红外线之间,是频率最高的无线电波,它的频带宽度比所有普通无线电波波段总和大1000倍以上2.简述P,L,S,C,X,Ku,K,Ka波段的频段划分方法。
3.简述射频/微波的四种基本特性和相比普通无线电的优点。
四个基本特性:1、似光性;2、穿透性3、非电离性4、信息性优点:(1)(2) 分辨率高。
连续波多普勒雷达的频偏大,成像更清晰,(3) 尺(4)(5)(6) 频谱宽。
频谱不拥挤,不易拥堵,军用设备更可靠。
4. 简述射频铁三角的具体内涵。
由于频率、 阻抗和功率是贯穿射频/微波工程的三大核心指标,故将其称为射频铁三角。
频率功率阻抗振荡器、压控振荡器、频率合成器、分频器、变频器、倍频 器、混频器、滤波器等频率计数器/功率计、频谱分析仪标量/矢量网络分析仪阻抗测量仪、网络分析仪阻抗变换、阻抗匹配、天线等衰减器、功分器、耦合器、 放大器、开关等5. 给出几种分贝的定义:dB, dBm ,dBc ,dBc/Hz ,10 dBm+10 dB=?10dBm+10dB=20dBm第二章 传输线理论1. 解释何为“集肤效应”?集总参数元件的射频特性与低频相比有何特点?在交流状态下,由于交流电流会产生磁场,根据法拉第电磁感应定律,此磁场又会产生电场,与此电场联系的感生电流密度的方向将会与原始电流相反。
这种效应在导线的中心部位(即r=0位置)最强,造成了在r=0附近的电阻显著增加,因而电流将趋向于在导线外表面附近流动,这种现象将随着频率的升高而加剧,这就是通常所说的“集肤效应”。
电阻:在低频率下阻抗即等于电阻R,而随着频率的升高达到 10MHz 以上,电容Ca 的影响开始占优,导致总阻抗降低;当频率达到20GHz 左右时,出现了并联谐振点; 越过谐振点后,引线电感的影响开始表现出来,阻抗又加大并逐渐表现为开路或有限阻抗值。
电容:理想状态下,极板间介质中没有电流。
《微波技术与天线》习题集规范标准答案

《微波技术与天线》习题答案章节 微波传输线理路1.1设一特性阻抗为Ω50的均匀传输线终端接负载Ω=1001R ,求负载反射系数1Γ,在离负载λ2.0,λ25.0及λ5.0处的输入阻抗及反射系数分别为多少?解:1)()(01011=+-=ΓZ Z Z Zπβλ8.02131)2.0(j z j e e --=Γ=Γ31)5.0(=Γλ (二分之一波长重复性)31)25.0(-=ΓλΩ-∠=++=ο79.2343.29tan tan )2.0(10010ljZ Z ljZ Z Z Z in ββλΩ==25100/50)25.0(2λin Z (四分之一波长阻抗变换性)Ω=100)5.0(λin Z (二分之一波长重复性)1.2求内外导体直径分别为0.25cm 和0.75cm 的空气同轴线的特性阻抗;若在两导体间填充介电常数25.2=r ε的介质,求其特性阻抗及MHz f 300=时的波长。
解:同轴线的特性阻抗abZ rln600ε= 则空气同轴线Ω==9.65ln 600abZ 当25.2=r ε时,Ω==9.43ln600abZ rε 当MHz f 300=时的波长:m f c rp 67.0==ελ1.3题设特性阻抗为0Z 的无耗传输线的驻波比ρ,第一个电压波节点离负载的距离为1m in l ,试证明此时的终端负载应为1min 1min 01tan tan 1l j l j Z Z βρβρ--⨯=证明:1min 1min 010)(1min 101min 010in tan l tan j 1/tan tan 1min 1min l j Z Z Z Z l j Z Z l j Z Z Z Z l in l βρβρρββ--⨯=∴=++⨯=由两式相等推导出:对于无耗传输线而言:)(Θ1.4传输线上的波长为:m fr2cg ==ελ因而,传输线的实际长度为:m l g5.04==λ终端反射系数为: 961.0514901011≈-=+-=ΓZ R Z R输入反射系数为: 961.0514921==Γ=Γ-lj in eβ 根据传输线的4λ的阻抗变换性,输入端的阻抗为:Ω==2500120R ZZ in1.5试证明无耗传输线上任意相距λ/4的两点处的阻抗的乘积等于传输线特性阻抗的平方。
微波技术基础简答题整理

对于电场线,总是垂直于理想管壁,平行于理想管壁的分量为 对于磁场线,总是平行于理想管壁,垂直于理想管壁的分量为 ( P82)
0 或不存在; 0 或不存在。
2-10. 矩形波导的功率容量与哪些因素有关? 矩形波导的功率容量与波导横截面的尺寸、模式(或波形) 导中填充介质的击穿强度等因素有关。 (P90)
工作波长 λ,即电磁波在无界媒介中传输时的波长, λ与波导的形状与尺寸无关。 截止波数为传播常数 γ等于 0 时的波数,此时对应的频率称为截止频率,对应的 波长则称为截止波长。它们由波导横截面形状、尺寸,及一定波形等因素决定。 波长只有小于截止波长, 该模式才能在波导中以行波形式传输, 当波长大于截止 波长时,为迅衰场。
2-2. 试从多个方向定性说明为什么空心金属波导中不能传输 TEM模式。※
如果空心金属波导内存在 TEM 波,则要求磁场应完全在波导横截面内,而且是 闭合曲线。 由麦克斯韦第一方程, 闭合曲线上磁场的积分应等于与曲线相交链的 电流。由于空心金属波导中不存在沿波导轴向(即传播方向)的传到电流,所以 要求存在轴向位移电流,这就要求在轴向有电场存在,这与 TEM 波的定义相矛 盾,所以空心金属波导内不能传播 TEM 波。
按损耗特性分类: ( 1)分米波或米波传输线(双导线、同轴线) ( 2)厘米波或分米波传输线(空心金属波导管、带状线、微带线) ( 3)毫米波或亚毫米波传输线(空心金属波导管、介质波导、介质镜像线、微 带线) ( 4)光频波段传输线(介质光波导、光纤)
1-3. 什么是传输线的特性阻抗,它和哪些因素有关?阻抗匹配的物理实质是什 么?
4-5. 微波谐振器的两个主要功能是 储能 和选频 。
4-6. 无耗传输线谐振器串联谐振的条件是 Zin =0,并联谐振的条件是 Zin =∞。
微波技术基础课后答案 李秀萍版

0.22
0.013 j0.004
42.5 - j19
(c) YL
(d) Zin
(e) 0.201 (f) 0.451 4.4 4.5 4.6 略,同 4.3 如果传输线长度为 1.5,重做习题 4.3 略,同 4.3 短路线 (1) (2) (3) (4) (5) 如果 ZL (20 j100) ,重做习题 4.3。
400
L 1 =
第四章
4.1 (1) Zin
60 j35 , Yin 0.0125 j 0.0075
(2) Z L (3)
30 j18.5
o
0 0.27e j 26
0.454
,
0.35 0.27e j 82
o
,
1.9
] 13.99 cos(8t 30.4o ) ] 7.6 cos(2t 48.9o )
j 2t
2.5 电路的稳态电压为: 32cos(t ) 2.6 (1)
10
2 .5
(2) 10 (3) 10 (4) 10 2.7 (1) 10
5
7 .5
0.7
(2) 10 (3) 10 (1)
o
o
(1) A(t ) Re[ Ae
j 6t
] 2 5 cos(6t 3.43o )
(2) B(t ) Re[ Be (3) C (t ) Re[Ce 2.4 (1) 40cos(100t ) (2) 4000sin(100t ) (3)
1 sin(100t ) 1000
j 8t
3.19
1 V0 Z in Z 0 P 2 Z 0 Z in Z 0 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
题 解第 一 章1-1 微波是频率很高,波长很短的一种无线电波。
微波波段的频率范围为8103⨯Hz~12103⨯Hz ,对应的波长范围为1m~0.1mm 。
关于波段的划分可分为粗分和细分两种。
粗分为米波波段、分米波波段、厘米波波段、毫米波波段、亚毫米波段等。
细分为Ka K Ku X C S L UHF 、、、、、、、…等波段,详见表1-1-2。
1-2 简单地说,微波具有下列特点。
(1) 频率极高,振荡周期极短,必须考虑系统中的电子惯性、高频趋肤效应、辐射效应及延时效应;(2) 波长极短,“反射”是微波领域中最重要的物理现象之一,因此,匹配问题是微波系统中的一个突出问题。
同时,微波波长与实验设备的尺寸可以比拟,因而必须考虑传输系统的分布参数效应;(3) 微波可穿透电离层,成为“宇宙窗口”;(4) 量子特性显现出来,可用来研究物质的精细结构。
1-3 在国防工业方面:雷达、电子对抗、导航、通信、导弹控制、热核反应控制等都直接需要应用微波技术。
在工农业方面,广泛应用微波技术进行加热和测量。
在科学研究方面,微波技术的应用也很广泛。
例如,利用微波直线加速器对原子结构的研究,利用微波质谱仪对分子精细结构进行研究,机载微波折射仪和微波辐射计对大气参数进行测量等等。
第 二 章2-1 解 ∵01011Z Z Z Z +-=Γ ∴)(82.811Ω=Z2-2 解图(a )的输入阻抗021Z Z ab =; 图(b )的输入阻抗0Z Z ab =;图(c )的输入阻抗0Z Z ab =;图(d )的输入阻抗052Z Z ab =; 其等效电路自绘。
2-3 解 ∵01011Z Z Z Z +-=Γ ∵e j j 4121)1(21π=+=Γ 2-4 解(1) ∵e j Z Z Z Z 40101122π=+-=Γ ∴83.511ρ11=Γ-Γ+= (2) ∵π2 =l β∴e e j l -j l 4π) β2(11022=Γ=Γϕ 2-5 解 ∵ljZ Z l jZ Z Z Z tg βtg β10010++= ∴)(39.673.8Ω+=j Z in)(24.6009.2201Ω+=j Z)(1005003Ω+=j Z2-6 证明∵)(00ββe e l j l j U U Γ+=-+ )(00ββ0e e l j l j Z U I Γ-=-+ 而I Z E I Z E U g 0-=-=∴e U E l j 0β2-+= 故2EU =+2-7 证明lZ j l j Z l jZ Z l jZ Z Z in tg β1tg βtg βtg β111001++=++= 而 ρ11min =Z ,对应线长为1min l 故 1min 11min 1tg β1tg βρ1l Z j l j Z ++= 整理得 1min 1min 1tg βρρtgβ1l j l j Z --=2-8 解 ∵38.001011=+-=ΓZ Z Z Z而给定的1Z 是感性复阻抗,故第一个出现的是电压腹点,即λ/4线应接在此处。
∴ρ50ρ001==Z Z ∵23.211ρ11=Γ-Γ+=∴)(7.7401Ω=Z︒-=Γ=7.68tg φ1-10.29(m)λφ/4π1max ==d若在电压波节处接4/λ线则m)(04.14λ1max 1min =+'='d d ∴)(334ρ001Ω==Z Z 2-9 解图(a )0=Γc ;31-=Γb ;31=Γa 。
图(b )51-=Γd ;31=Γc ;31-=Γe ;0=Γb ;0=Γa 。
图(c )0=Γc ;0=Γd ;31-=Γb ;31-=Γa 。
图(d )1-=Γc ;0=Γd ;0=Γb ;0=Γa 。
2-10 解 00101=+-=ΓZ R Z R c )(5.372//121Ω===R R R Z b 3100-=+-=ΓZ Z Z Z b b b 31) β2(=Γ=Γ-e l r j b a ϕ )(150Ω=a Z因为0Z Z a >所以a 处是电压波腹点,电流波节点。
)A (94min =+==a i a R R E I I )V (3200min max ===a a Z I U U 又因为0Z Z b <,所以b 处是电压波节点,电流波腹点。
)A (98max ==I I b )V (3100min==U U b 由于2R 的分流作用,故)A (9421==b bc b I I 。
因为01Z R =,所以bc 段载行波 )V (3100=c U )A (94=c I 题解2-10图2-11 解 设负载端的反射系数为 1Γ,传输线上的驻波比为ρ,输入阻抗为in Z则 e j Z Z Z Z 60101154.0π=+-=Γ 54.01=Γ 35.311ρ11=Γ-Γ+= )(4.54604.384tg βtg β10010Ω-=++=j ljZ Z l jZ Z Z Z in 2-12 解 310101=+-=ΓZ Z Z Z d dc 段呈行驻波状态 021Z Z c =3100-=+-=ΓZ Z Z Z c c c bc 段呈行驻波状态2bd ρ=0=Γebe 段呈行波状态 032//Z Z Z Z b b b ='''= 2.0-=Γbab 段呈行驻波状态 0023/2Z Z Z Z b a == 因为c a Z Z >所以a 点为电压腹点、电流节点。
根据输入端等效电路可求得: )A (152min =+==a g m a R R E I I )V (60max ===a a a I Z U U由于be 段为行波,所以b e U U =5.1 - 11b b ab ρ=ΓΓ+=)V (405.1/60/ρmax min ====ab b U U U)A (51min max ===I ρI I ab b)V (40==e b U U)A (1521==Z U I e e)V (2040==bd e ρU)V (4020==d d ρU)A (067.0302040=⨯=d I )A (14.0=e I2-13 解(1)分析工作状态de 段 终端开路,1=Γe ,0=de K ,∞=de ρ,e 和d 为电压腹点、电流节点,距e 点4/λ处为电压节点、电流腹点,线上载驻波。
cd 段 设de 段的输入阻抗为∞='dZ ,则cd 段的等效负载)(225//22Ω=='=Z Z Z Z d d 01Z >,故线上载行驻波,且d 点为电压腹点、电流节点,c 点为电压节点、电流腹点。
31=Γd ,5.0=cd K ,2=cd ρ。
bc 段 0201)(100/Z Z Z Z d c =Ω==,故线上载行波。
0=Γc ,1=bc K ,1=bc ρ。
bf 段 01Z Z =,线上载行波,0=Γf ,1=bf K ,1=bf ρ。
bg 段 g 端短路,线上载驻波,1-=Γg ,0=bg K ,∞=bg ρ。
g 点为电压节点、电流腹点,b 点为点压腹点,电流节点。
ab 段 b 处总阻抗b Z 为三个阻抗的并联:0Z Z b=',0Z Z b ='',∞='''b Z ,故)(50210Ω==Z Z b ,线上载行驻波,b 处为电压节点、电流腹点,a 处为电压腹点、电流节点。
31=Γb ,5.0=ab K ,2=ab ρ。
(2) 求U 、I 沿线分布)(20020Ω==ba Z Z Z )A (61min =+==∴a g g ab a Z Z U I I )V (3100max =⋅==a a ab a Z I U U bf b bc b ab ab ab b I I ρI I I +==⋅==)A (31min max )V (350/max min ===ab ab ab b ρU U U)A (61='=b b bc b Z U I)A (61=''=b b bf b Z U I)V (350==b f U U )V (350max ===b bg bg b U U U)A (0min ==bg bg b I I)A (61/0max max ===Z U I I bg bg gmax )A (61cd bc b bc c I I I === min )V (350cd b bc c U U U === )A (121/max min ===cd cg cd cd g ρI I I )V (3100min max ===cd cd cd cd d ρU U Ude e de de d I I I ===0min e cd d de de dU U U U ====)V (3100max)A (31/0max max ==Z U I de de 0min =de U 将上述各值标绘出来,如图所示题解2-13图 沿线U 、I 分布(3) 负载吸收功率 )W (39.1211==f f I U P )W (24.1)1(2122≈Γ-⋅=d cd d cd d I U P 2-14 解(1)为使ab 段处于行波状态,需使b 处的等效阻抗0Z Z b =,因为d d '处可视为短路,4/2λl =故 )(1002///011Ω===∞=Z R R Z d再经4/1λl =折合到b 处的阻抗,为)(4002/020Ω==='Z Z Z Z d b又经4/3λl =折合到b 处的阻抗,为220/R Z Z b =''0/Z Z Z Z b bb ='''= )(1002/02Ω==Z R(2) 分析工作状态。
求ρab 段呈行波状态,1=ab ρ,cd 段呈驻波状态,∞=cd ρ,d 端为电压节点0min =U ,电流腹点max I ,c 端为电压腹点max "c U ,电流节点0min ='cI , bc 段为行驻波,310101=+-=ΓZ R Z R c ,2=bc ρ, c 端为电压节点min c U ',电流腹点max c I ', b 端为电压腹点max b U ,电流节点min bI ', be 段为行驻波,31=Γe ,2=be ρ, e 端为电压节点min e U ,电流腹点max e I ,b 端为电压腹点max bU '',电流节点min b I ''。
(3) 求U 、I① 输入端等效阻抗为)(2000Ω==Z Z in)A (2.0=+=ing m a Z R E I ,)V (40=⋅=in a a Z I U ② 因为b 点的两段分支完全相同故有 min min )A (1.021b a b I I I '==='' )V (40max max ==''='a b b U U U)A (2.0min max ='='b bc c I ρI max max min )V (20cbc b c U ρU U ''=='=')A (2.0min max =''=bc b e ρI I )V (20max min =''=beb c ρU U)A (1.00max max =''==Z U I I c d 0=d U 按上述所求各值绘出沿线U 、I 分布曲线如图所示。
